Решение составных уравнений 3-4 классы. Карточки

 

 

 

 

Иванова Светлана Романовна

учитель МОБУ СОШ №7 г. Якутска

Республики Саха (Якутия)

 

 

Решение

составных уравнений

3-4 классы

 

                                      

 

 

 

 

 

 

 

 

 

1 карточка                                                       Х + 65 = 165 + 2 43 + Х = 500 : 10 Х — 25 = 100 х 2 320 — Х = 45 х 2 Х х 5 = 280 — 250 35 : Х = 78 — 73 60 х Х = 36 + 84 Х : 4 = 20 х 2	2 карточка   42 + Х = 749 — 26 Х + 100 = 500 х 2 Х — 2 = 4050 — 43 624 — Х = 238 + 300 Х х 2 = 430 + 30 25 : Х = 15 : 3 Х : 10 = ( 42 + 48 ) — 83 42 х Х = 36 + 48
3 карточка   Х + 20000 = 500 х  8 65 + Х = 140 : 2 48 — Х = 140 : 2 — 65 Х — 30 = 650 + 10 Х : 5 = 36 + 14 Х х 30 = 280 + 320 400 : Х = 4 х 2 32 х Х = 25 + 7	4 карточка   Х + 43 = 4 х 2 + 50 86 + Х = 40 х 2 + 50 Х — 25 = 40 + 3 х 20 100 — Х = 42 : 7 х 5 Х х 5 = 20 : 4 + 10 600 : Х = 4 — 1 х 2 40 х Х = 50 х 2 + 20 Х : 4 = 700 — 65 х 10

 

 

 

 

 

5 карточка                                                Х + 150 = 40 х 2 + 36 х 2 41 + Х = 35 х 2 х 2 Х — 25 = 500 — 40 х 10 920 — Х = 801 — 1 х 1 Х х 7 = 5 + 150 : 5 30 х Х = 200 + 2 х 5                  Х : 3 = 27 : 9 х 5 42 : Х = 90 — ( 50 + 34 )	6 карточка   39 + Х = 42 х 2 + 5 Х + 32 = ( 25 + 65 ) х 2 Х — 95 = 66 + 21 + 13 79 — Х = 33 х 2 + 4 х 1 Х : 5 = ( 62 — 22) : 5 33 х Х = ( 23 — 3 ) х 5 — 1 84 : Х = (65 — 60 ) + 37 Х : 100 = ( 45 + 5 ) х 4
7 карточка                                          Х + 4 = 60 х 2 : 4 92 + Х = ( 400 + 2 ) х 2 Х — 35 = ( 765 — 65 ) х 2 98 — Х = 44 х 2 + 2 Х х 3 = 43 + 8 х 4 36 х Х = 64 : 8 х 9 Х : 50 = ( 35 + 15 ) х 4 1800 : Х = 36 : 4 х 60 + 60	8 карточка   15 + Х = 7256 + 2 х 4 Х + 49 = 25 х 4 х 2 + 50 Х — 720 = 49 : 7 х 9 657 — Х = 250 : 5 х 4 Х х 23 = 150 : 3 + 19 75 х Х = 30 х 6 — 30 Х : 50 = 2 х 9 + 2 630 : Х = 36 х 2 — 2

 

 

 

 

9 карточка                                            Х + 64 = 36 : 9 + 21 136 + Х = 50 х 2 х 3 Х — 925 = 600 : 2 + 700 2000 — Х = ( 1000 — 2 ) х 2 Х х 8 = 820 — 45 х 4 70 х Х = 131 + 36 : 4 500 : Х = 25 : 5 х 10 Х : 25 = 42 х 2 — 68	10 карточка   Х + 29 = 990 + 60 х 2 35 + Х = ( 2 + 5 ) х 52 Х — 728 = 2 х 24 х 10 523 — Х = 21 : 3 х 10 Х х 90 = 75 х 2 + 30 60 х Х = 3 х 6 х 10 Х : 5 = 400 : 8 + 5 360 : Х = 85 х 2 + 10
11 карточка                                         Х + 409 = 65 х 3 + 700 260 + Х = 700 + 6 х 5           Х — 612 = 420 : 6 х 9 2694 — Х = 40 х 4 + 2 Х х 30 = ( 502 + 28 ) х 3 45 х Х = 20 х 5 — 10              Х : 200 = 680 — 40 х 2 560 : Х = ( 40 + 30 ) : 10	12 карточка   Х + 500 = 600 х 2 + 300 406 + Х = 925 — 5 х 5 Х — 39 = 1800 : 2 + 33 786 — Х = 32 х 5 : 2 Х х 100 = 59 х 3 х 1000 810 : Х=1000- ( 60 х 3+10 ) 60 х Х = ( 30 х 2 ) х 10 Х : 3 = 59 х 4 : 2

 

 

 

 

13 карточка                                        Х + 429 = 65 х 2 х 5 728 + Х = 500 х 2 + 15 Х — 39 = 360 : 4 + 1 450 — Х = 720 : 8 + 60 Х х 7 = ( 618 + 2 ) + 10 3 х Х = 42 х 3 х 5 Х : 7 = 58 х 9 + 28 650 : Х = 81 : 9 + 1	14 карточка   62 : Х + 38 = 40 73 + (50 : Х + 2) = 100 (100 — Х : 4 ) — 30 = 54 400 — (5 х Х + 125) = 205 ( 40 х Х + 140) х 5 = 2500 5 х ( 69 — 120 : Х) = 45 (150 : Х + 50) : 5 = 73 — 53 150 : (45 : Х + 35) = 27 : 9
15  карточка                                        (720 : Х — 2) + 40 = 128 (4 х Х + 20) + 720 = 900        (Х х 5 + 25 ) — 415 = 60 900 — (4 х Х — 60) = 360        ( 42 : Х — 7 ) х 30 = 420 2 х ( 36 — 52 : Х ) = 20 ( 40 х Х — 40 ) : 4 = 30 480 : (Х : 4 + 1) = 64 : 8	16 карточка   ( 60 : Х + 5 ) + 25 = 50 800 + ( 420 : Х — 10 ) = 1000 ( 400 : Х + 5 ) — 5 = 200 1000 — ( 4500 : Х + 80 ) = 420 (54 : Х + 30 ) х 2 = 72 8 х ( 36 + 4 х Х ) = 480 (6 х Х + 12 ) : 6 = 50 350 : (20 х Х — 15) = 70

 

 

17 карточка                                          420 + (4 х Х + 360) = 940 350 + (600 — 5 х Х) = 450 (4 + Х х 9) — 36 = 40 660 — (8 х Х + 20) = 480 (4 х Х + 2) х 6 = 180 9 х (4 х Х + 10) =810 (150:Х-50):5=73-53              81:(42-3хХ)=66-7х9	18 карточка   (Х : 20 + 40) — 70 = 30 64 + ( Х : 4 + 6) = 100 (64 : Х + 138) — 50 = 90 925 — (80 : Х — 15) = 900 (95 — 45 : Х) х 9 = 810 6 х (20 : Х — 15) = 30 (3 х Х — 30) : 2 = 68 — 8 720:(Хх4-46)=150х3-90

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответы:

 

 1.          102;   7;   225;   230;   6;   7;   2;   160.

 2.         681;   900;   4009;   86;   230;   5;   700;   2.

 3.         2000;   5;   43;   690;   250;   20;   50;   1.

 4.          15;   44;   125;   70;   3;   300;   3;   200.

 5.         2;   99;   125;   120;   5;   7;   45;   7.

 6.         50;   148;   195;   9;   40;   3;   2;   20000.

 7.         26;   712;   1435;   8;   25;   2;  10000; 6.

 8.         7249;   201;   782;   457;   3;   2;   1000;   9.

 9.         89;   164;   1925;   4;   80;   2;   10;   400.

 10.       1081;   329;   1208;   453;   2;   3;   275;   2.

 11.       486;   470;   1242;   2532;   53;   2;   120000;   80.

 12.       1000;   494;   972;   706;   1770;   1;   10;   354.

 13.       221;   287;  130;   300;   90;   210;   3850;   65.

 14.       31;   2;   64;   14;   9;   2;   3;   3.

 15.       8;   40;   90;   150;   2;   2;   4;   236.

 16.       3;   2;   2;   9;   9;   6;   48;   1.

 17.       40;   100;   8;   20;   7;   20;   1;   5.

 18.       1200;   120;   32;   2;   9;   1;   50;    12.

 

 

 

Решение составных уравнений,4 класс

 

1 карточка                                                       Х + 65 = 165 + 2 43 + Х = 500 : 10 Х — 25 = 100 х 2 320 — Х = 45 х 2 Х х 5 = 280 — 250 35 : Х = 78 — 73 60 х Х = 36 + 84 Х : 4 = 20 х 2	2 карточка   42 + Х = 749 — 26 Х + 100 = 500 х 2 Х — 2 = 4050 — 43 624 — Х = 238 + 300 Х х 2 = 430 + 30 25 : Х = 15 : 3 Х : 10 = ( 42 + 48 ) — 83 42 х Х = 36 + 48
3 карточка   Х + 20000 = 500 х  8 65 + Х = 140 : 2 48 — Х = 140 : 2 — 65 Х — 30 = 650 + 10 Х : 5 = 36 + 14 Х х 30 = 280 + 320 400 : Х = 4 х 2 32 х Х = 25 + 7	4 карточка   Х + 43 = 4 х 2 + 50 86 + Х = 40 х 2 + 50 Х — 25 = 40 + 3 х 20 100 — Х = 42 : 7 х 5 Х х 5 = 20 : 4 + 10 600 : Х = 4 — 1 х 2 40 х Х = 50 х 2 + 20 Х : 4 = 700 — 65 х 10

 

 

 

 

 

5 карточка                                                Х + 150 = 40 х 2 + 36 х 2 41 + Х = 35 х 2 х 2 Х — 25 = 500 — 40 х 10 920 — Х = 801 — 1 х 1 Х х 7 = 5 + 150 : 5 30 х Х = 200 + 2 х 5                  Х : 3 = 27 : 9 х 5 42 : Х = 90 — ( 50 + 34 )	6 карточка   39 + Х = 42 х 2 + 5 Х + 32 = ( 25 + 65 ) х 2 Х — 95 = 66 + 21 + 13 79 — Х = 33 х 2 + 4 х 1 Х : 5 = ( 62 — 22) : 5 33 х Х = ( 23 — 3 ) х 5 — 1 84 : Х = (65 — 60 ) + 37 Х : 100 = ( 45 + 5 ) х 4
7 карточка                                          Х + 4 = 60 х 2 : 4 92 + Х = ( 400 + 2 ) х 2 Х — 35 = ( 765 — 65 ) х 2 98 — Х = 44 х 2 + 2 Х х 3 = 43 + 8 х 4 36 х Х = 64 : 8 х 9 Х : 50 = ( 35 + 15 ) х 4 1800 : Х = 36 : 4 х 60 + 60	8 карточка   15 + Х = 7256 + 2 х 4 Х + 49 = 25 х 4 х 2 + 50 Х — 720 = 49 : 7 х 9 657 — Х = 250 : 5 х 4 Х х 23 = 150 : 3 + 19 75 х Х = 30 х 6 — 30 Х : 50 = 2 х 9 + 2 630 : Х = 36 х 2 — 2

 

 

 

 

9 карточка                                            Х + 64 = 36 : 9 + 21 136 + Х = 50 х 2 х 3 Х — 925 = 600 : 2 + 700 2000 — Х = ( 1000 — 2 ) х 2 Х х 8 = 820 — 45 х 4 70 х Х = 131 + 36 : 4 500 : Х = 25 : 5 х 10 Х : 25 = 42 х 2 — 68	10 карточка   Х + 29 = 990 + 60 х 2 35 + Х = ( 2 + 5 ) х 52 Х — 728 = 2 х 24 х 10 523 — Х = 21 : 3 х 10 Х х 90 = 75 х 2 + 30 60 х Х = 3 х 6 х 10 Х : 5 = 400 : 8 + 5 360 : Х = 85 х 2 + 10
11 карточка                                         Х + 409 = 65 х 3 + 700 260 + Х = 700 + 6 х 5           Х — 612 = 420 : 6 х 9 2694 — Х = 40 х 4 + 2 Х х 30 = ( 502 + 28 ) х 3 45 х Х = 20 х 5 — 10              Х : 200 = 680 — 40 х 2 560 : Х = ( 40 + 30 ) : 10	12 карточка   Х + 500 = 600 х 2 + 300 406 + Х = 925 — 5 х 5 Х — 39 = 1800 : 2 + 33 786 — Х = 32 х 5 : 2 Х х 100 = 59 х 3 х 1000 810 : Х=1000- ( 60 х 3+10 ) 60 х Х = ( 30 х 2 ) х 10 Х : 3 = 59 х 4 : 2

 

 

 

 

13 карточка                                        Х + 429 = 65 х 2 х 5 728 + Х = 500 х 2 + 15 Х — 39 = 360 : 4 + 1 450 — Х = 720 : 8 + 60 Х х 7 = ( 618 + 2 ) + 10 3 х Х = 42 х 3 х 5 Х : 7 = 58 х 9 + 28 650 : Х = 81 : 9 + 1	14 карточка   62 : Х + 38 = 40 73 + (50 : Х + 2) = 100 (100 — Х : 4 ) — 30 = 54 400 — (5 х Х + 125) = 205 ( 40 х Х + 140) х 5 = 2500 5 х ( 69 — 120 : Х) = 45 (150 : Х + 50) : 5 = 73 — 53 150 : (45 : Х + 35) = 27 : 9
15  карточка                                        (720 : Х — 2) + 40 = 128 (4 х Х + 20) + 720 = 900        (Х х 5 + 25 ) — 415 = 60 900 — (4 х Х — 60) = 360        ( 42 : Х — 7 ) х 30 = 420 2 х ( 36 — 52 : Х ) = 20 ( 40 х Х — 40 ) : 4 = 30 480 : (Х : 4 + 1) = 64 : 8	16 карточка   ( 60 : Х + 5 ) + 25 = 50 800 + ( 420 : Х — 10 ) = 1000 ( 400 : Х + 5 ) — 5 = 200 1000 — ( 4500 : Х + 80 ) = 420 (54 : Х + 30 ) х 2 = 72 8 х ( 36 + 4 х Х ) = 480 (6 х Х + 12 ) : 6 = 50 350 : (20 х Х — 15) = 70

 

 

17 карточка                                          420 + (4 х Х + 360) = 940 350 + (600 — 5 х Х) = 450 (4 + Х х 9) — 36 = 40 660 — (8 х Х + 20) = 480 (4 х Х + 2) х 6 = 180 9 х (4 х Х + 10) =810 (150:Х-50):5=73-53              81:(42-3хХ)=66-7х9	18 карточка   (Х : 20 + 40) — 70 = 30 64 + ( Х : 4 + 6) = 100 (64 : Х + 138) — 50 = 90 925 — (80 : Х — 15) = 900 (95 — 45 : Х) х 9 = 810 6 х (20 : Х — 15) = 30 (3 х Х — 30) : 2 = 68 — 8 720:(Хх4-46)=150х3-90

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответы:

 

 1.          102;   7;   225;   230;   6;   7;   2;   160.

 2.         681;   900;   4009;   86;   230;   5;   700;   2.

 3.         2000;   5;   43;   690;   250;   20;   50;   1.

 4.          15;   44;   125;   70;   3;   300;   3;   200.

 5.         2;   99;   125;   120;   5;   7;   45;   7.

 6.         50;   148;   195;   9;   40;   3;   2;   20000.

 7.         26;   712;   1435;   8;   25;   2;  10000; 6.

 8.         7249;   201;   782;   457;   3;   2;   1000;   9.

 9.         89;   164;   1925;   4;   80;   2;   10;   400.

 10.       1081;   329;   1208;   453;   2;   3;   275;   2.

 11.       486;   470;   1242;   2532;   53;   2;   120000;   80.

 12.       1000;   494;   972;   706;   1770;   1;   10;   354.

 13.       221;   287;  130;   300;   90;   210;   3850;   65.

 14.       31;   2;   64;   14;   9;   2;   3;   3.

 15.       8;   40;   90;   150;   2;   2;   4;   236.

 16.       3;   2;   2;   9;   9;   6;   48;   1.

 17.       40;   100;   8;   20;   7;   20;   1;   5.

 18.       1200;   120;   32;   2;   9;   1;   50;    12.

 

 

 

Формулы сокращенного умножения

У нас есть сумма (разница) двух чисел и нам необходимо избавиться от скобок, используя формулы для сокращенного умножения:

(x + y)² = x² + 2xy + y²
(x — y)² = x² — 2xy + y²

Пример: если x = 10, y = 5a
(10 + 5a)² = 10² + 2.10.5a + (5a)² = 100 + 100a + 25a²
(10 — 4)² = 10² — 2.10.4 + 4² = 100 — 80 + 16 = 36
Конечно, если мы имеем следующую ситуацию:
25 + 20a + 4a² = 5² + 2.2.5 + (2a)² = (5 + 2a)²

(x + y)³ = x³ + 3x²y + 3xy² + y³
(x — y)³ = x³ — 3x²y + 3xy² — y³

Пример: (1 + a²)³ = 1³ + 3. 1².a² + 3.1.(a²)² + (a²)³ = 1 + 3a² + 3a⁴ + a⁶

(x + y + z)² = x² + y² + z² + 2xy + 2xz + 2yz
(x — y — z)² = x² + y² + z² — 2xy — 2xz + 2yz

---

x² — y² = (x — y)(x + y)

x² + y² = (x + y)² — 2xy
или
x² + y² = (x — y)² + 2xy

Пример: 9a² — 25b² = (3a)² — (5b)² = (3a — 5b)(3a + 5b)

x³ — y³ = (x — y)(x² + xy + y²)
x³ + y³ = (x + y)(x² — xy + y²)

Если n есть натуральное число

xⁿ — yⁿ = (x — y)(x^n-1 + x^n-2y +…+ y^n-2x + y^n-1)

Если n есть чётное (n = 2k)

xⁿ + yⁿ = (x + y)(x^n-1 — x^n-2y +. 2 + 20$

---

3) Решите уравнение: x² — 25 = 0
Решение: x² — 25 = (x — 5)(x + 5)
=> чтобы решить это уравнение мы должны решить 2 следующих выражения:
x — 5 = 0 или x + 5 = 0 и поэтому уравнение имеет два решения: x = 5 и x = -5

Больше

Тест — формулы сокращенного умножения

Действия с многочленами — задачи с решениями

Разложиние на множители — задачи с решениями

Формулы сокращенного умножения в математическом форуме

ГДЗ по Математике 6 класс Дорофеев, Шарыгин. Решебник

ГДЗ по математике для 6 класса Дорофеева – это сборник готовых домашних заданий по задачам и примерам из учебника по арифметике, составленного известными российскими авторами – Г.В. Дорофеевым, И.Ф. Шарыгиным, С.Б. Суворовым и др. Он используется в большинстве общеобразовательных школ России.

Структура ГДЗ по учебнику математики шестого класса от Дорофеева

Во шестом классе школьники углубленно изучают арифметику. Эти знания помогут им постигнуть алгебру и геометрию в старших классах, а также физику, геометрию, химию. Шестиклассники изучают многоугольники и многогранники, обыкновенные и десятичные дроби, проценты и отношения, уравнения с одной переменной, а также множества и комбинаторика.

ГДЗ по математике 6 класса Дорофеева, составленные на основе учебника 2016-2019 гг. в его 4-м издании, включают в себя примеры и задачи на такие темы:

• дроби и проценты;
• прямые на плоскости и в пространстве;
• десятичные дроби;
• действия с десятичными дробями;
• окружность и прямая;
• отношения и проценты;
• центральная и осевая симметрия;
• выражения, формулы, уравнения;
• целые числа
• множества и комбинаторика;
• рациональные числа;
• многоугольники и многогранники.

Изучение перечисленных тем помогает в постижении алгебры и геометрии в старшей школе. Однако для этого важно не просто зазубрить правила и списать в тетрадь готовые домашние задания. Стоит понять теоремы на научиться применять их в решении примеров, задач и уравнений.

Готовые домашние задания для 6 класса на сайте ГДЗ Путина помогают не только ученикам средних школ, но и их родителям. Они могут проверить домашнюю работу своих детей и отказаться от услуг репетитора.

Онлайн-решения от ГДЗ Путина по математике 6 класса к Дорофееву

В интернете немало сайтов с готовыми домашними заданиями по арифметике. При этом ресурс ГДЗ от Путина имеет немало преимуществ для шестиклассников и родителей:

• наличие нескольких вариантов решения примеров и задач;
• ответы по самым свежим изданиям учебников российских школ;
• оформление готовых домашних заданий по требованиям Минобразования РФ;
• круглосуточный доступ со смартфона, планшета, компьютера.

Приведенные факторы делают ГДЗ по математике 6 класса к учебнику Дорофеева удобными и практичными в использовании. Ответы на задачки, примеры и уравнения в нескольких вариантах упростят постижение арифметики шестиклассниками.

Готовые домашние задания включают в себя детальные алгоритмы выполнения примеров и уравнений, что помогает легко разобраться со сложными темами дома без посещения дополнительных занятий.

4- (20) = 0

Пошаговое решение:

Шаг 1:

 
 Попытка разложить на множители как разность квадратов: 
 
 1,1 Факторинг: x  4 -20 
 
 Теория: разница двух полные квадраты, A  2  — B  2  можно разложить на (A + B) • (AB) 
 
 Доказательство: (A + B) • (AB) = 
 A  2  — AB + BA — B  2  = 
 A  2  — AB + AB — B  2  = 
 A  2  — B  2  
 
 Примечание: AB = BA — коммутативное свойство умножения.
 
 Примечание: — AB + AB равно нулю и поэтому исключается из выражения. 
 
 Проверка: 20 не квадрат !! 
 
 Решение: биномиальное число не может быть разложено как разность двух полных квадратов. 
 
 
 Калькулятор полиномиальных корней: 
 
 1. 2 Найдите корни (нули): F (x) = x  4 -20 
 Калькулятор полиномиальных корней — это набор методов, направленных на поиск значений x, для которых F (x) = 0 
 
 Rational Roots Test — один из вышеупомянутых инструментов.Он мог бы найти только рациональные корни, то есть числа x, которые можно выразить как частное двух целых чисел 
 
 Теорема рационального корня утверждает, что если полином обнуляется для рационального числа P / Q, то P является множителем конечной константы и Q является коэффициентом ведущего коэффициента 
 
 В этом случае ведущий коэффициент равен 1, а конечная константа — -20. 
 
 Фактор (ы): 
 
 ведущего коэффициента: 1 
 замыкающей константы: 1, 2, 4, 5, 10, 20 
 
 Давайте проверим…. 
 
 
 
 
 
 
 P 
 
 
 
 Q 
 
 
 
 P / Q 
 
 
 
 F (P / Q) 
 
 
 
 Делитель 
 
 
 
 
 
-1 
 
 
 
 1 
 
 
 
 -1,00 
 
 
 
 -19,00 
 
 
 
 
 
 
 
 
-2 
 
 
 
 1 
 
 
 
 -2,00 
 
 
 
-4. 00 
 
 
 
 
 
 
 
 
-4 
 
 
 
 1 
 
 
 
-4,00 
 
 
 
 236,00 
 
 
 
 
 
 
 
 
-5 
 
 
 
 1 
 
 
 
 -5,00 
 
 
 
 605,00 
 
 
 
 
 
 
 
 
-10 
 
 
 
 1 
 
 
 
 -10.00 
 
 
 
 9980.00 
 
 
 
 
 
 
 
 
-20 
 
 
 
 1 
 
 
 
 -20,00 
 
 
 
 159980.00 
 
 
 
 
 
 
 
 
 1 
 
 
 
 
 
 
 
 1,00 
 
 
 
-19,00 
 
 
 
 
 
 
 
 
 2 
 
 
 
 1 
 
 
 
 2.00 
 
 
 
-4,00 
 
 
 
 
 
 
 
 
 4 
 
 
 
 1 
 
 
 
 4,00 
 
 
 
 236,00 
 
 
 
 
 
 
 
 
 5 
 
 
 
 1 
 
 
 
 5,00 
 
 
 
 605,00 
 
 
 
 
 
 
 
 
 10 
 
 
 
 1 
 
 
 
 10. 00 
 
 
 
 9980.00 
 
 
 
 
 
 
 
 
 20 
 
 
 
 1 
 
 
 
 20.00 
 
 
 
 159980.00 
 
 
 
 
 
 
 
 
 Полиномиальные корни 9 не найдены в конце шага 1:   
 x  4 -20 = 0
 
 Шаг 2: 
 
 Решение уравнения с одной переменной: 
 
 2.1 Решите: x  4 -20 = 0 
 
 Добавьте 20 к обеим частям уравнения: 
 x  4  = 20 
 x = ∜ 20 
 
 Уравнение имеет два действительных решения 
 Эти решения равны x = ± ∜ 20 = ± 2,1147 
 
 
 Были найдены два решения: 
 x = ± ∜20 = ± 2,1147 
 Решить x / 4 = -20 Tiger Algebra Solver 
 
 Переставить: 
 
 Переставить уравнение, вычтя то, что находится справа от знак равенства с обеих сторон уравнения: 
 
 x / 4 — (- 20) = 0 
 
 Пошаговое решение: 
 
 Шаг 1: 
  
 x
 Упростить -
            4
 
 Уравнение в конце шага 1: 
 x
  - - -20 = 0
  4
 
 Шаг 2: 
 Переписывание целого как эквивалентной дроби: 
 2. 1 Вычитание целого из дроби
 Перепишем целое как дробь, используя 4 в знаменателе:
-20-20 • 4
    -20 = ——— = ———————
            1 4
 
 Эквивалентная дробь: Полученная таким образом дробь выглядит иначе, но имеет то же значение, что и целое
 Общий знаменатель: Эквивалентная дробь и другая дробь, участвующие в вычислении, имеют один и тот же знаменатель
  
 Сложение дробей, имеющих общий знаменатель: 
  
 
 2.2 Сложение двух эквивалентных дробей 
 Сложите две эквивалентные дроби, которые теперь имеют общий знаменатель 
 
 Объедините числители вместе, сложите сумму или разность над общим знаменателем, затем уменьшите до наименьшего числа, если возможно: 
 
 x - (-20 • 4) х + 80
 знак равно
       4 4
 
 Уравнение в конце шага 2: 
 x + 80
  —————— = 0
    4
 
 Шаг 3: 
 
 Когда дробь равна нулю: 
  
 3.1 Когда дробь равна нулю ... 
 Если дробь равна нулю, ее числитель, часть, которая находится над чертой дроби, должна быть равна нулю.
 Теперь, чтобы избавиться от знаменателя, Тигр умножает обе части уравнения на знаменатель.
 Вот как:
 x + 80
  ———— • 4 = 0 • 4
   4
 
 Теперь, с левой стороны, 4 отменяет знаменатель, в то время как с правой стороны ноль, умноженный на что-либо, по-прежнему равно нулю.
 Уравнение теперь принимает форму: 
 x + 80 = 0
 
 Решение уравнения с одной переменной: 
 
 3.2 Решите: x + 80 = 0
 Вычтите 80 из обеих частей уравнения: 
 x = -80 
 Было найдено одно решение: 
 x = -80
 Решите линейные и квадратные уравнения с помощью пошаговой математики Решение проблем 
 Решение уравнений — центральная тема алгебры. В этой главе мы изучим некоторые методы решения уравнений с одной переменной. Для этого мы будем использовать навыки, полученные при работе с числами и символами алгебры, а также операции с целыми числами, десятичными и дробями, которые вы изучили в арифметике.
 УСЛОВНЫЕ И ЭКВИВАЛЕНТНЫЕ УРАВНЕНИЯ 
 ЗАДАЧИ 
 По завершении этого раздела вы сможете:
 Классифицируйте уравнение как условное или тождественное.
 Решите простые уравнения мысленно.
 Определите, эквивалентны ли определенные уравнения.
  Уравнение — это выражение в символах, что два числовых выражения равны. 
 Уравнения можно разделить на два основных типа:
 1.Тождество   истинно для всех значений буквальных и арифметических чисел в нем.
  Пример 1  5 x 4 = 20 — это идентичность.
  Пример 2  2 + 3 = 5 — это тождество.
  Пример 3  2x + 3x = 5x — это тождество, поскольку любое значение, замененное на x, даст равенство.
 2. Условное уравнение   верно только для определенных значений буквальных чисел в нем.
  Пример 4  x + 3 = 9 верно, только если буквальное число x = 6.
  Пример 5  3x — 4 = 11 верно, только если x = 5.
 Буквенные числа в уравнении иногда называют  переменными .
 Поиск значений, которые делают условное уравнение истинным, является одной из основных целей этого текста.
 Решение   или  корень  уравнения — это значение переменной или переменных, которые делают уравнение истинным.
 Говорят, что решение или корень для  удовлетворяет уравнению .
  Решение уравнения  означает нахождение решения или корня.
 Многие уравнения можно решить мысленно. Способность мысленно решать уравнение будет зависеть от умения манипулировать числами в арифметике. Чем лучше вы знаете факты умножения и сложения, тем лучше вы будете в умении решать уравнения.
  Пример 6  Решить относительно x: x + 3 = 7
 Решение
 Чтобы получить истинное утверждение, нам нужно значение x, которое при добавлении к 3 даст 7.Наши знания арифметики показывают, что 4 — это необходимое значение. Следовательно, решение уравнения x = 4.
 Какое число, добавленное к 3, равно 7?
  Пример 7  Решить относительно x: x — 5 = 3
 Решение
 Из какого числа вычитаем 5, чтобы получить 3? И снова наш опыт с арифметикой говорит нам, что 8 — 5 = 3. Следовательно, решение x = 8.
  Пример 8  Решить относительно x: 3x = 15
 Решение
 Какое число нужно умножить на 3, чтобы получить 15? Наш ответ — x = 5.
 Решение
 На какое число разделим 2, чтобы получить 7? Наш ответ — 14.
  Пример 10  Решить относительно x: 2x — 1 = 5
 Решение
 Мы бы вычли 1 из 6, чтобы получить 5. Таким образом, 2x = 6. Тогда
х = 3.
 Независимо от того, как решается уравнение, решение всегда следует проверять на правильность.
  Пример 11  Студент решил уравнение 5x — 3 = 4x + 2 и нашел ответ x = 6.Было это правильно или неправильно?
 Решение
 Удовлетворяет ли x = 6 уравнению 5x — 3 = 4x + 2? Чтобы проверить, мы подставляем 6 вместо x в уравнение, чтобы увидеть, получим ли мы истинное утверждение.
 Это неверное утверждение, поэтому ответ x = 6 неверен.
 Другой студент решил то же уравнение и нашел x = 5.
 Это верное утверждение, поэтому x = 5 верно.
 Многие студенты думают, что, когда они нашли решение уравнения, проблема решена. Не так!  Последним шагом всегда должна быть проверка решения.
 Не все уравнения можно решить мысленно. Теперь мы хотим представить идею, которая является шагом к упорядоченному процессу решения уравнений.
 Является ли x = 3 решением x — 1 = 2? 
 Является ли x = 3 решением 2x + I = 7? 
 Что можно сказать об уравнениях x — 1 = 2 и 2x + 1 = 7?
 Два уравнения  эквивалентны , если они имеют одно и то же решение или решения
  Пример 12  3x = 6 и 2x + 1 = 5 эквивалентны, потому что в обоих случаях x = 2 является решением.
 Методы решения уравнений включают процессы преобразования уравнения в эквивалентное уравнение. Если сложное уравнение, такое как 2x — 4 + 3x = 7x + 2 — 4x, можно заменить на простое уравнение x = 3, а уравнение x = 3 эквивалентно исходному уравнению, то мы решили уравнение.
 Два вопроса теперь становятся очень важными.
 Эквивалентны ли два уравнения?
 Как мы можем заменить одно уравнение другим уравнением, которое ему эквивалентно?
 Ответ на первый вопрос находится по принципу подстановки.
  Пример 13  Являются ли 5x + 2 = 6x — 1 и x = 3 эквивалентными уравнениями?
 Решение
 Ответ на второй вопрос включает методы решения уравнений, которые будут обсуждаться в следующих нескольких разделах.
 Чтобы правильно использовать принцип подстановки, мы должны подставить цифру 3 вместо x везде, где x появляется в уравнении.
 ПОДРАЗДЕЛЕНИЕ ПРАВИЛО 
 ЗАДАЧИ 
 По завершении этого раздела вы сможете:
 Используйте правило деления для решения уравнений.
 Решите несколько основных прикладных задач, решение которых связано с использованием правила деления.
 Как упоминалось ранее, мы хотим представить упорядоченную процедуру решения уравнений. Эта процедура будет включать четыре основных операции, первая из которых представлена ​​в этом разделе.
  Если каждый член уравнения равен  делению  на одно и то же ненулевое число, результирующее уравнение будет  эквивалентно  исходному уравнению. 
 Чтобы подготовиться к использованию правила деления для решения уравнений, мы должны обратить внимание на следующий процесс:
 (Мы обычно пишем 1x как x с пониманием коэффициента 1.)
  Пример 1  Решить относительно x: 3x = 10
 Решение
 Наша цель — получить x = некоторое число. Правило деления позволяет нам разделить каждый член 3x = 10 на одно и то же число, и наша цель найти значение x будет означать, что мы делим на 3. Это дало бы нам коэффициент 1 для x.
 Проверить: 3x = 10 и x = эти эквивалентные уравнения?
 Подставляем вместо x в первое уравнение, получая
 Уравнения эквивалентны, поэтому решение правильное.
  Пример 2  Решить относительно x: 5x = 20
 Решение
 Обратите внимание, что правило деления не позволяет нам делить на ноль. Поскольку деление на ноль недопустимо в математике, такие выражения, как
 бессмысленны.
  Пример 3  Решить относительно x: 8x = 4
 Решение
 Ошибки иногда допускаются в очень простых ситуациях.Не обращайте внимания на эту проблему и придите к x = 2! 
 Обратите внимание, что правило деления позволяет нам разделить каждый член уравнения на любое ненулевое число, и полученное уравнение эквивалентно исходному уравнению. 
 Следовательно, мы можем разделить каждую часть уравнения на 5 и получить, что эквивалентно исходному уравнению. 
 Однако деление на 5 не помогает найти решение. На какое число нужно разделить, чтобы найти решение?
  Пример 4  Решите относительно x: 0.5x = 6
 Решение
  Пример 6  Формула для определения длины окружности (C) окружности: C = 2πr, где π представляет радиус окружности и составляет приблизительно 3,14. Найдите радиус круга, если измеренная длина окружности равна 40,72 см. Дайте правильный ответ с точностью до двух знаков после запятой.
 Решение
 Чтобы решить задачу, связанную с формулой, сначала воспользуемся принципом подстановки.
 Окружность означает «расстояние вокруг».»Это периметр круга. 
 Радиус — это расстояние от центра до круга.
 ПРАВИЛО ВЫЧИСЛЕНИЯ 
 ЗАДАЧИ 
 По завершении этого раздела вы сможете использовать правило вычитания для решения уравнений.
 В этом разделе будет обсуждаться второй шаг к упорядоченной процедуре решения уравнений. Вы будете использовать свои знания одинаковых терминов из главы 1, а также методы из раздела  ПРАВИЛО ПОДРАЗДЕЛЕНИЯ .Обратите внимание, как новые идеи в алгебре основываются на предыдущих знаниях.
  Если та же величина равна , вычитая  из обеих частей уравнения, полученное уравнение будет , эквивалентным  исходному уравнению. 
  Пример 1  Решите относительно x, если x + 7 = 12.
 Решение
 Хотя это уравнение легко решить в уме, мы хотим проиллюстрировать правило вычитания. Мы должны думать так:
 «Я хочу решить относительно x, поэтому мне нужно, чтобы x был сам по себе на одной стороне уравнения.Но у меня x + 7. Так что, если я вычту 7 из x + 7, у меня будет только x с левой стороны ». (Помните, что величина, вычтенная из самой себя, дает ноль.) Но если мы вычтем 7 из одной стороны от числа. уравнение, правило требует, чтобы мы вычли 7 из другой стороны. Итак, мы действуем следующим образом:
 Обратите внимание, что x + 0 можно записать просто как x, поскольку ноль, добавленный к любому количеству, равен самому количеству.
  Пример 2  Решить относительно x: 5x = 4x + 3
 Решение
 Здесь и должно развиваться наше мышление.«Я хочу получить все неизвестные величины с одной стороны уравнения и все арифметические числа с другой, поэтому у меня есть уравнение в форме x = некоторое число. Таким образом, мне нужно вычесть Ax из обеих сторон».
 Наша цель — получить x = некоторое число. 
 Помните, что проверка вашего решения — важный шаг в решении уравнений.
  Пример 3  Решить относительно x: 3x + 6 = 2x + 11
 Здесь у нас более сложная задача.Сначала вычтите 6 с обеих сторон.
 Теперь мы должны исключить 2x с правой стороны, вычтя 2x с обеих сторон.
 Теперь мы рассмотрим решение, которое требует использования как правила вычитания, так и правила деления.
 Обратите внимание, что вместо первого вычитания 6 мы могли бы сначала вычесть 2x с обеих сторон, получив 
 3x — 2x + 6 = 2x — 2x + 11 
 x + 6 = 11. 
 Затем, вычитая 6 из обеих сторон, мы имеем 
 х + 6-6 = 11-6 
 х = 5.
 Имейте в виду, что наша цель — x = некоторое число.
  Пример 4  Решите относительно x: 3x + 2 = 17
 Решение
 Сначала мы используем правило вычитания, чтобы вычесть 2 из обеих сторон, получая
 Затем мы используем правило деления, чтобы получить
  Пример 5  Решите относительно x: 7x + 1 = 5x + 9
 Решение
 Сначала воспользуемся правилом вычитания.
 Тогда правило деления дает нам
  Пример 6  Периметр (P) прямоугольника находится по формуле P = 2l + 2w, где l обозначает длину, а w обозначает ширину. Если периметр прямоугольника 54 см, а длина 15 см, какова ширина?
 Решение
 Периметр — это расстояние вокруг. Вы понимаете, почему формула P = 2l + 2w?
 ДОПОЛНИТЕЛЬНОЕ ПРАВИЛО 
 ЗАДАЧИ 
 По завершении этого раздела вы сможете использовать правило сложения для решения уравнений.
 Теперь мы переходим к следующей операции в нашей цели разработки упорядоченной процедуры решения уравнений.Еще раз, мы будем полагаться на предыдущие знания.
  Если та же величина равна , к обеим сторонам уравнения прибавляется , полученное уравнение будет равно , эквивалентному  к исходному уравнению. 
  Пример 1  Решите относительно x, если x — 7 = 2.
 Решение
 Как всегда, решая уравнение, мы хотим прийти к форме «x = некоторое число». Мы замечаем, что 7 было вычтено из x, поэтому, чтобы получить только x в левой части уравнения, мы прибавляем 7 к обеим частям.
 Не забывайте всегда проверять свое решение.
  Пример 2  Решить относительно x: 2x — 3 = 6
 Решение
 Помня о нашей цели получить только x, мы замечаем, что, поскольку 3 было вычтено из 2x, мы добавляем 3 к обеим частям уравнения.
 Теперь мы должны использовать правило деления.
 Почему мы добавляем 3 к обеим сторонам? 
 Обратите внимание, что в примере простое использование правила сложения не решает проблему.
  Пример 3  Решить относительно x: 3x — 4 = 11
 Решение
 Сначала воспользуемся правилом сложения.
 Затем, используя правило деления, получаем
 Здесь мы снова должны были использовать как правило сложения, так и правило деления для решения уравнения.
  Пример 4  Решите относительно x: 5x = 14 — 2x
 Решение
 Здесь наша цель получить только x с одной стороны предполагает, что мы удалим 2x справа, поэтому мы добавляем 2x к обеим сторонам уравнения.
 Далее мы применим правило деления.
 Здесь мы снова должны были использовать как правило сложения, так и правило деления для решения уравнения. 
 Обратите внимание, что мы проверяем, всегда подставляя решение в исходное уравнение.
  Пример 5  Решите относительно x: 3x — 2 = 8 — 2x
 Решение
 Здесь наша задача более сложная. Мы должны подумать об удалении числа 2 из левой части уравнения, а также lx из правой части, чтобы получить только x с одной стороны.Сначала мы можем сделать что-то из этого. Если мы выберем сначала прибавить 2x к обеим сторонам, мы получим
 Теперь прибавляем 2 к обеим сторонам.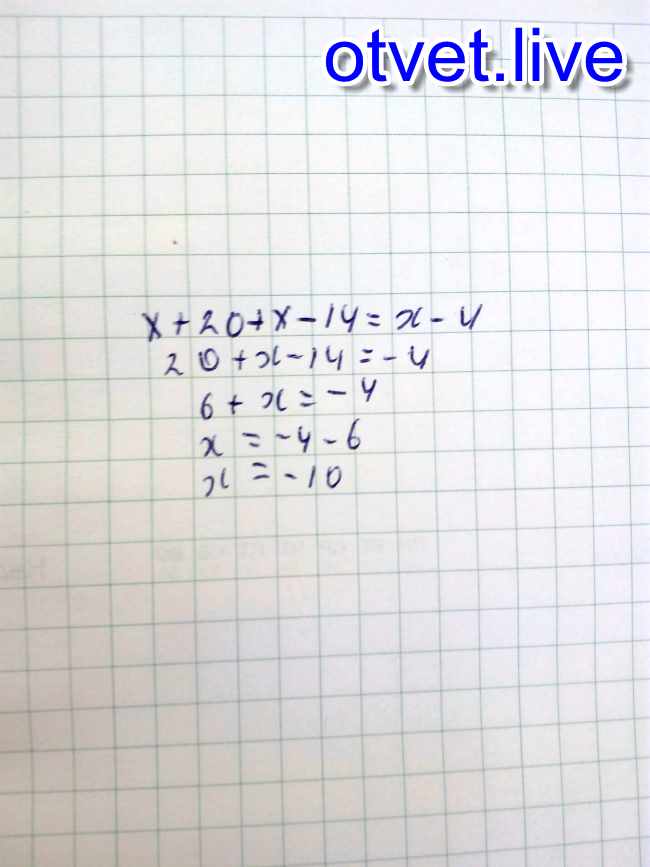
 Наконец, правило деления дает
 Можем ли мы сначала добавить 2 к обеим сторонам? Попробуй!
 ПРАВИЛО УМНОЖЕНИЯ 
 ЗАДАЧИ 
 По завершении этого раздела вы сможете:
 Используйте правило умножения для решения уравнений.
 Решите пропорции.
 Решите основные прикладные задачи, используя правило умножения.
 Теперь мы подошли к последней из четырех основных операций при разработке нашей процедуры решения уравнений. Мы также введем соотношение и пропорции и воспользуемся правилом умножения для определения пропорций.
  Если каждый член уравнения равен , умноженному на  на такое же ненулевое число, результирующее уравнение будет  эквивалентно  исходному уравнению.
 В элементарной арифметике одни из самых сложных операций с дробями. Правило умножения позволяет нам избежать этих операций при решении уравнения, содержащего дроби, путем нахождения эквивалентного уравнения, содержащего только целые числа.
 Помните, что когда мы умножаем целое число на дробь, мы используем правило
 Теперь мы готовы решить уравнение, содержащее дроби.
 Обратите внимание, что в каждом случае только числитель дроби умножается на целое число.
  Пример 4 
 Решение
 Имейте в виду, что мы хотим получить только x на одной стороне уравнения. Мы также хотели бы получить уравнение в целых числах, которое эквивалентно данному уравнению. Чтобы исключить дробь в уравнении, нам нужно умножить на число, которое делится на знаменатель 3. Таким образом, мы используем правило умножения и умножаем каждый член уравнения на 3.
 Теперь у нас есть эквивалентное уравнение, которое содержит только целые числа.Используя правило деления, получаем
 Чтобы исключить дробь, нам нужно умножить ее на число, которое делится на знаменатель. 
 В этом примере нам нужно умножить на число, которое делится на 3. 
 Мы могли бы умножить обе стороны на 6, 9, 12 и так далее, но уравнение проще и легче работать, если мы используем наименьшее несколько.
  Пример 5 
 Решение
 Посмотрите, получите ли вы такое же решение, умножив каждую часть исходного уравнения на 16.
 Всегда проверяйте исходное уравнение.
  Пример 6 
 Решение
 Здесь наша задача такая же, но немного сложнее. Нам нужно исключить две фракции. Мы должны умножить каждый член уравнения на число, которое делится как на 3, так и на 5. Лучше всего использовать наименьшее из таких чисел, которое, как вы помните, — это наименьшее общее кратное . Поэтому мы умножим на 15.
 В арифметике вы могли использовать наименьшее общее кратное как «наименьший общий знаменатель». «
  Пример 7 
 Решение
 Наименьшее общее кратное для 8 и 2 равно 8, поэтому мы умножаем каждый член уравнения на 8.
 Теперь воспользуемся правилом вычитания.
 Наконец, правило деления дает нам
 Перед умножением замените смешанные числа на неправильные дроби. В этом примере измените. 
 Помните, что  каждый член  нужно умножить на 8.
 Обратите внимание, что в этом примере мы использовали три правила для поиска решения.
 Решение простых уравнений путем умножения обеих частей на одно и то же число часто встречается при изучении соотношения и пропорции.
 Соотношение   — это частное двух чисел.
 Отношение числа x к числу y можно записать как x: y или. В общем, дробная форма более значима и полезна. Таким образом, мы запишем отношение 3 к 4 как.
 Соотношение   — это утверждение, что два соотношения равны.
  Пример 8 
 Решение
 Нам нужно найти такое значение x, чтобы отношение x к 15 было равно отношению 2 к 5.
 Умножая каждую часть уравнения на 15, получаем
 Почему мы умножаем обе части на 15? 
 Проверьте это решение в исходном уравнении.
  Пример 9  Какое число x имеет такое же отношение к 3, как 6 к 9?
 Решение
 Чтобы найти x, сначала запишем пропорцию:
 Затем мы умножаем каждую часть уравнения на 9.
 Скажите себе: «2 равно 5, как x равно 10». 
 Проверить!
  Пример 11  Отношение количества женщин к количеству мужчин в математическом классе составляет 7: 8. Если в классе 24 мужчины, сколько женщин в классе?
 Решение
  Пример 12  Два сына должны были разделить наследство в соотношении 3: 5. Если сын, получивший большую часть, получил 20 000 долларов, какова была общая сумма наследства?
 Решение
 Теперь мы добавляем 20 000 долларов США + 12 000 долларов США, чтобы получить общую сумму в 32 000 долларов США.
 Проверить! 
 Опять же, будьте осторожны при настройке пропорций. В соотношении 3/5 доля 5 является большей. Следовательно, поскольку 20 000 долларов — это большая часть, она также должна быть указана в знаменателе.
  Пример 13  Если юридические требования к вместимости комнаты требуют 3 кубических метров воздушного пространства на человека, сколько людей могут законно занимать комнату шириной 6 метров, длиной 8 метров и высотой 3 метра?
 Решение
 Итак, вместимость юридической комнаты составит 48 человек.
 Это означает, что «1 человек составляет 3 кубических метра, а x человек — 144 кубических метра». 
 Проверить решение.
 ОБЪЕДИНЕНИЕ ПРАВИЛ ДЛЯ РЕШЕНИЯ УРАВНЕНИЙ 
 ЗАДАЧИ 
 По завершении этого раздела вы сможете:
 Используйте комбинации различных правил для решения более сложных уравнений.
 Применяйте упорядоченные шаги, описанные в этом разделе, для систематического решения уравнений.
 Многие упражнения в предыдущих разделах требовали использования более чем одного правила в процессе решения.Фактически, вполне возможно, что одна проблема может включать в себя все правила
.
 Не существует обязательного процесса решения уравнений, включающего более одного правила, но опыт показал, что следующий порядок дает более плавную и безошибочную процедуру.
  Первые  Исключите дроби, если они есть, умножив каждый член уравнения на наименьшее общее кратное всех знаменателей дробей в уравнении. 
  Второй  Упростите, комбинируя одинаковые члены с каждой стороны уравнения.
  Третий  Сложите или вычтите необходимые количества, чтобы получить неизвестное количество с одной стороны и числа арифметических с другой стороны. 
  Четвертый  Разделить на коэффициент неизвестной величины. 
  Пятый  Проверьте свой ответ.
 Помните, коэффициент — это число, умноженное на букву. (То есть в выражении 5x коэффициент равен 5.)
 Еще раз убедитесь, что каждый термин
умножить на 3.
 Решение
 Умножение каждого члена на 15 дает
 Вы можете оставить свой ответ в виде неправильной дроби вместо смешанного числа. Любая форма верна, но неправильная форма дроби будет более полезной при проверке вашего решения.
 Обратите внимание, что в этом уравнении есть четыре члена.
  Пример 3  Цена продажи (S) определенного товара составляла 30 долларов.00. Если наценка (M) составляла одну пятую от стоимости (C), найдите стоимость товара. Используйте формулу C + M = S.
 Решение
 Поскольку маржа составляла одну пятую от стоимости, мы можем написать
 РЕЗЮМЕ 
 Ключевые слова 
 Уравнение   — это выражение в символах, что два числовых выражения равны.
 Идентификатор   верен для всех значений буквальных и арифметических чисел в нем.
 Условное уравнение   верно только для определенных значений буквальных чисел в нем.
 Решение   или  корень  уравнения — это значение переменной, которая делает уравнение истинным.
 Два уравнения  эквивалентны , если они имеют один и тот же набор решений.
 Отношение   — это  частное  двух чисел.
 Пропорция   — это утверждение, что два соотношения равны.
 Процедуры 
 Если каждый член уравнения разделить на одно и то же ненулевое число, полученное уравнение эквивалентно исходному уравнению.
 Если из обеих частей уравнения вычесть одну и ту же величину, полученное уравнение эквивалентно исходному уравнению.
 Если к обеим сторонам уравнения добавляется одна и та же величина, полученное уравнение эквивалентно исходному уравнению.
 Если каждая сторона уравнения умножается на одно и то же ненулевое число, полученное уравнение эквивалентно исходному уравнению.
 Чтобы решить уравнение, выполните следующие действия: 
  Шаг 1  Исключите дроби, умножив каждый член на наименьшее общее кратное всех знаменателей в уравнении.
  Шаг 2  Объедините одинаковые члены с каждой стороны уравнения. 
  Шаг 3  Сложите или вычтите члены, чтобы получить неизвестную величину с одной стороны и арифметические числа с другой. 
  Шаг 4  Разделите каждый член на коэффициент неизвестной величины. 
  Шаг 5  Проверьте свой ответ. 
 Решение квадратных уравнений: выбор метода 
 Purplemath 
 Когда вы решаете квадратные уравнения в своем домашнем задании, вы часто можете получить «подсказку» относительно лучшего метода, основанного на теме и заголовке раздела. Например, если вы работаете над домашним заданием в разделе «Решение с помощью факторинга», то вы знаете, что должны решать с помощью факторинга. Но в обзоре главы и на тесте вы не знаете, из какого раздела вашего учебника была взята та или иная квадратичная диаграмма. Какой метод лучше использовать?
 Вы можете использовать квадратичную формулу для всего, но формула может занять много времени.
 Например:
 MathHelp.com 
 Решить (
 x  + 1) ( x  — 3) = 0.
 Чтобы решить это квадратное уравнение, я мог бы перемножить выражение в левой части, упростить поиск коэффициентов, вставить эти значения коэффициентов в квадратную формулу и перейти к ответу.
 Но зачем мне это? Я имею в виду, ради бога, это факторинг, и они уже учли его и установили для меня равным нулю. Хотя квадратичная формула определенно дала бы мне правильный ответ, зачем с ней возиться?
 Вместо этого я сразу решу два фактора, которые они мне дали:
 ( x  + 1) ( x  — 3) = 0
  x  + 1 = 0,  x  — 3 = 0
  x  = –1,  x  = 3
 Это было быстро! И мой ответ:
 Кстати, строгого порядка решений нет. Да, я обычно помещаю свои решения в числовом порядке, поэтому в приведенном выше случае отрицательный ответ предшествовал положительному. Но если ваш инструктор ничего не сказал (и я был бы удивлен, если бы это было так), приведенный выше ответ был бы столь же правильным, если бы он был написан как « x  = 3, –1».
 Квадратичное выражение в левой части знака «равно» не учитывается.
 (Как я очень быстро это узнал? Для факторизации должны быть целые множители  ac  = (1) (- 4) = –4, что в сумме дает  b  = 1.Я вижу, что их нет.)
 Эта квадратичная величина не была предоставлена ​​мне в «(переменная часть)  2  равно (некоторое число)», поэтому решение путем извлечения квадратных корней невозможно.
 Я мог бы решить это уравнение, заполнив квадрат, но это утомительно и чревато ошибками. Я мог бы попытаться решить, построив график, но лучшее, что я смогу сделать, это получить десятичное приближение из моего «программного обеспечения» (то есть моего графического калькулятора).
 Чтобы получить точный и быстрый ответ, я воспользуюсь квадратичной формулой:
 Поскольку в инструкциях ничего не говорится о десятичных приближениях, я оставлю свой ответ в форме квадратного корня:
 Решить 
 x   2  — 3  x  — 4 = 0.
 Это уравнение не настроено для меня как готовое к извлечению квадратного корня, и я никогда не буду использовать завершение квадрата, если они специально не скажут мне об этом. Однако, прежде чем применять квадратичную формулу, я сначала быстро проверю, можно ли факторизовать выражение в левой части этого уравнения.
 Существуют ли целые множители  ac  = (1) (- 4) = –4, которые в сумме дают –3? Да: –4 и +1. Итак, эта квадратичная величина факторизуема, и я уже нашел числа, которые можно использовать для ее разложения (поскольку ведущий коэффициент равен 1):
  x   2  — 3  x  — 4 = 0
 ( x  + 1) ( x  — 4) = 0
  x  + 1 = 0,  x  — 4 = 0
  x  = –1,  x  = 4
 И я закончил, просто так быстро.Мой ответ:
 Квадратичное выражение в левой части этого уравнения содержит всего два члена, и ни один из них не вычитается, поэтому я не буду использовать простые методы разложения на множители. Но я замечаю, что это разница квадратов, и я знаю, что могу множить разницу квадратов.
  x   2  — 4 = 0
 ( x  + 2) ( x  — 2) = 0
  x  + 2 = 0,  x  — 2 = 0
  x  = –2,  x  = 2
 Тогда мой ответ:
 Примечание: я мог бы переместить 4 в правую часть уравнения, а затем извлечь квадратный корень из любой стороны  x   2  = 4. Этот метод дал бы мне тот же ответ, что и приведенный выше факторинг. Если не указано иное, вы должны использовать тот метод, который вам больше нравится.
 Решить 6 
 x   2  + 11  x  — 35 = 0.
 Ик.
 Квадратичное выражение в левой части этого уравнения  может быть множителем , но похоже, что поиск факторизации, если таковая имеется, будет неприятным объемом работы.Сейчас я чувствую себя немного бездумным и ленивым, поэтому я воспользуюсь квадратной формулой. Во время работы мне нужно не забыть поставить ± перед радикалом и поставить черту дроби под всем числителем, представляющим собой целую часть « b   2  ± (корень квадратный)»:
 Значения решения представляют собой дроби без радикалов, что означает, что квадратичное  могло быть разложено на множители . Но теперь у меня есть ответ, поэтому меня больше не волнует факторизация.
 Это квадратное выражение состоит из двух членов и ничего не вычитает, так что либо это разница квадратов (которую я могу разложить на множители), либо ее можно отформатировать как «(переменная часть)  2  равно (число)», чтобы я мог квадратный корень с обеих сторон. Поскольку 48 не является квадратом, я не могу применить формулу разности квадратов. Вместо этого мне придется извлекать квадратный корень из обеих частей:
 Итак, мой точный ответ:
 Примечание: если вам специально не сказано предоставлять десятичное приближение для решений, которые включают радикалы, вы должны предположить, что они хотят, чтобы вы дали «точную» форму ответа; то есть они хотят видеть эти квадратные корни.
 В этом квадратичном выражении есть два члена, которые легко множить на множители:
  x   2 -7 9 1380 x  = 0
  x  ( x -7) = 0
  x  = 0,  x  — 7 = 0
  x  = 0,  x  = 7
 Мой ответ:
 Найдите решения квадратичного уравнения, представленного в таблице ниже: 
  x  -значение
 –1
 0
 1
 2
 3
 4
 5
 6
  y  -значение
 16
 9
 4
 1
 0
 1
 4
 9
 Прежде чем я паникую, я думаю об одном методе «решения», который не включает в себя фактическое квадратное уравнение: решение с помощью построения графиков.
 Когда они хотят, чтобы я решил квадратное уравнение   с помощью построения графиков, они на самом деле просят меня найти точки пересечения  x  соответствующей квадратичной функции  . И под словом «найти» они подразумевают «с красивой картинки». Но дело в том, что они хотят, чтобы я отметил связь между ними и предоставил затем значения  x , когда  y  = 0.
 Я могу сделать это по картинке или по Т-образной диаграмме значений.В данном случае вместо графика мне дали таблицу. Есть две точки, у которых одна из координат равна нулю; а именно (0, 9) и (3, 0). Что из этого я хочу? Тот, у которого  y  = 0, это вторая из двух точек. И мое решение — соответствующее значение  x .
 Скорее всего, вы не увидите много, а может быть, и каких-либо других упражнений этого последнего типа.
 Кстати, если вам интересно, почему было только одно решение этой квадратичной, это потому, что (предполагаемое и лежащее в основе) уравнение было ( x  — 3)  2  = 0. Итак, одно решение было «повторено».
 При решении квадратных уравнений в целом сначала перенесите все на одну сторону от знака «равно» (что уже было сделано в приведенных выше примерах). Затем сначала проверьте, есть ли очевидное факторинг или очевидное извлечение квадратного корня, которое вы можете сделать. Если нет, то обычно лучше прибегать к квадратной формуле. Но не используйте квадратичную формулу для всего; хотя он всегда даст вам ответ — в конечном итоге — это не всегда самый быстрый метод.А скорость может иметь большое значение в тестах на время.
 URL: https://www.purplemath.com/modules/solvquad6.htm
 Решайте уравнения с переменными и константами с обеих сторон — Элементарная алгебра 
  Решение линейных уравнений и неравенств 
 Цели обучения 
 К концу этого раздела вы сможете:
 Решите уравнение с константами с обеих сторон
 Решите уравнение с переменными с обеих сторон
 Решите уравнение с переменными и константами с обеих сторон
 Перед тем, как начать, пройдите тест на готовность.
 Упростите: 
 Если вы пропустили эту проблему, просмотрите (рисунок).
 Решайте уравнения с константами с обеих сторон 
 Во всех уравнениях, которые мы решили до сих пор, все переменные члены находились только на одной стороне уравнения, а константы — на другой. Это происходит не все время, поэтому теперь мы научимся решать уравнения, в которых переменные члены, или постоянные члены, или и то, и другое находятся по обе стороны уравнения.
 Наша стратегия будет заключаться в том, чтобы выбрать одну сторону уравнения как «переменную сторону», а другую сторону уравнения как «постоянную сторону».Затем мы будем использовать свойства равенства вычитания и сложения, чтобы собрать все переменные члены вместе на одной стороне уравнения и постоянные члены вместе на другой стороне.
 Сделав это, мы преобразуем уравнение, которое начиналось с переменных и констант с обеих сторон, в форму. Мы уже знаем, как решать уравнения этой формы, используя свойства равенства или деления или умножения.
 Решить:
 Решение
 В этом уравнении переменная находится только в левой части.Левую часть имеет смысл называть «переменной» стороной. Следовательно, правая сторона будет «постоянной» стороной. Мы напишем метки над уравнением, чтобы помочь нам запомнить, что куда идет.
 Так как левая сторона — это «» или переменная сторона, восьмерка неуместна. Мы должны «отменить» добавление 8, вычтя 8, и, чтобы сохранить равенство, мы должны вычесть 8 из обеих частей.
 Решить:
 Решить:
 Решить:
 Решение
 Обратите внимание, что переменная находится только в левой части уравнения, поэтому мы будем называть эту сторону стороной «переменная», а правая часть — стороной «константы».Так как левая сторона — «переменная», цифра 9 здесь неуместна. Он вычитается из числа, поэтому, чтобы «отменить» вычитание, прибавьте 9 к обеим сторонам. Помните: что бы вы ни делали слева, вы должны делать справа.
 Решить:
 Решить:
 Решение уравнений с переменными с обеих сторон 
 Что, если в обеих частях уравнения есть переменные? Для таких уравнений начните, как мы делали выше — выберите сторону «переменной» и «константу», а затем используйте свойства равенства и вычитания и сложения, чтобы собрать все переменные с одной стороны и все константы с другой стороны.
 Решить:
 Решение
 Здесь переменная находится с обеих сторон, но константы появляются только с правой стороны, поэтому давайте сделаем правую сторону «постоянной». Тогда левая сторона будет «переменной» стороной.
 Решить:
 Решить:
 Решить:
 Решение
 Единственная константа слева, а с обеих сторон. Оставим константу слева, а переменные справа.
 Решить:
 Решить:
 Решить:
 Решение
 Единственная константа находится справа, поэтому пусть левая сторона будет стороной «переменной».
 Решить:
 Решить:
 Решайте уравнения с переменными и константами с обеих сторон 
 В следующем примере будут переменные и константы в обеих частях уравнения.Для решения этого уравнения может потребоваться несколько шагов, поэтому нам нужна четкая и организованная стратегия.
 Как решать уравнения с переменными и константами с обеих сторон
 Решить:
 Решить:
 Решить:
 Мы перечислим шаги ниже, чтобы вы могли легко их выполнить. Но мы назовем это «Начальной стратегией», потому что позже в этой главе мы добавим несколько шагов.
 Начальная стратегия решения уравнений с переменными и константами по обе стороны уравнения.
 Выберите, какая сторона будет «переменной» стороной — другая сторона будет «постоянной» стороной.
 Соберите переменные члены в «переменную» сторону уравнения, используя свойство равенства сложения или вычитания.
 Соберите все константы с другой стороны уравнения, используя свойство равенства сложения или вычитания.
 Сделайте коэффициент переменной равным 1, используя свойство равенства умножения или деления.
 Проверьте решение, подставив его в исходное уравнение.
 На шаге 1 полезный подход состоит в том, чтобы сделать сторону «переменной» стороной, имеющей переменную с большим коэффициентом. Обычно это упрощает арифметику.
 Решить:
 Решение
 На первом этапе выберите сторону переменной, сравнивая коэффициенты переменных на каждой стороне.
 Решить:
 Решить:
 Решить:
 Решение
 На первом этапе выберите сторону переменной, сравнивая коэффициенты переменных на каждой стороне.
 Так как правая часть должна быть «переменной», а левая — «постоянной».
 Решить:
 Решить:
 В последнем примере мы могли бы сделать левую часть «переменной» стороной, но это привело бы к отрицательному коэффициенту на члене переменной. (Попробуйте!) Хотя мы можем работать с негативом, при работе с позитивом вероятность ошибок меньше. Описанная выше стратегия помогает избежать негатива!
 Чтобы решить уравнение с дробями, мы просто следуем шагам нашей стратегии, чтобы получить решение!
 Решить:
 Решение
 Так как, сделайте левую часть «переменной» стороной, а правую часть «постоянной» стороной.
 Решить:
 Решить:
 Мы будем использовать ту же стратегию, чтобы найти решение уравнения с десятичными знаками.
 Решить:
 Решение
 Так как, сделайте левую часть «переменной» стороной, а правую часть «постоянной» стороной.
 Решить:
 Решить:
 Ключевые понятия 
  Начальная стратегия решения уравнения с переменными и константами на обеих сторонах уравнения 
 Выберите, какая сторона будет «переменной» стороной — другая сторона будет «постоянной» стороной.
 Соберите переменные члены в «переменную» сторону уравнения, используя свойство равенства сложения или вычитания.
 Соберите все константы с другой стороны уравнения, используя свойство равенства сложения или вычитания.
 Сделайте коэффициент переменной равным 1, используя свойство равенства умножения или деления.
 Проверьте решение, подставив его в исходное уравнение.
 Практика ведет к совершенству 
  Решение уравнений с константами с обеих сторон 
 В следующих упражнениях решите следующие уравнения с константами с обеих сторон.
  Решение уравнений с переменными с обеих сторон 
 В следующих упражнениях решите следующие уравнения с переменными с обеих сторон.
  Решение уравнений с переменными и константами с обеих сторон 
 В следующих упражнениях решите следующие уравнения с переменными и константами с обеих сторон.
 Повседневная математика 
  Билеты на концерт  На школьный концерт общая стоимость проданных билетов составила 1506 евро. Студенческие билеты продаются за 6 фунтов стерлингов, а взрослые билеты — за 9 фунтов стерлингов. Количество проданных билетов для взрослых было в 5 раз меньше, чем количество студенческих билетов. Найдите количество проданных студенческих билетов,  s , решив уравнение.
  Изготовление забора  У Джовани есть 150 футов ограды, чтобы сделать прямоугольный сад на заднем дворе. Он хочет, чтобы длина была на 15 футов больше ширины. Найдите ширину  w , решив уравнение.
 Письменные упражнения 
 Решите уравнение, объясняющее все этапы вашего решения, как в примерах в этом разделе.
 Решите уравнение, объясняющее все этапы вашего решения, как в примерах в этом разделе.
 Обоснования могут быть разными.
 Почему при решении уравнения с переменными на обеих сторонах обычно лучше выбрать сторону с большим коэффициентом в качестве «переменной» стороны?
 Это решение уравнения? Откуда вы знаете?
 Да. Обоснования будут разными.
 Самопроверка 
 ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
 ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения?
 Решение уравнений — методы и примеры 
 Понимание того, как решать уравнения, — один из самых фундаментальных навыков, которым может овладеть каждый студент, изучающий алгебру. Решения для большинства алгебраических выражений ищутся, применяя этот навык. Таким образом, учащиеся должны лучше понимать, как проводить операцию.
 В этой статье  узнает, как решить уравнение , выполнив четыре основных математических операции:  сложение , вычитание  ,  умножение  и  деление .
 Уравнение обычно состоит из двух выражений, разделенных знаком, обозначающим их взаимосвязь. Выражения в уравнении могут быть связаны знаком равенства (=), меньше (<), больше (>) или сочетанием этих знаков.
 Как решать уравнения? 
 Решение алгебраического уравнения — это обычно процедура манипулирования уравнением. Переменная остается на одной стороне, а все остальное — на другой стороне уравнения.
 Проще говоря, решить уравнение — значит изолировать его, сделав его коэффициент равным 1.Что бы вы ни делали с одной стороной уравнения, сделайте то же самое с противоположной стороной уравнения.
 Решите уравнения, добавив 
 Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.
  
   Пример 1  
 Решите: –7 — x = 9
  Решение 
 –7 — x = 9
 Добавьте 7 к обеим сторонам уравнения. 
 7 — x + 7 = 9 + 7 
 — x = 16
 Умножить обе стороны на –1 
 x = –16
  
   Пример 2  
 Решить 4 = x — 3
  Решение 
 Здесь переменная находится справа в уравнении. Добавьте 3 к обеим сторонам уравнения
 4+ 3 = x — 3 + 3
 7 = x
 Проверьте решение, подставив ответ в исходное уравнение.
 4 = x — 3
 4 = 7 — 3
 Следовательно, x = 7 — правильный ответ.
 Решение уравнений путем вычитания 
 Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.
  
   Пример 3  
 Решите относительно x in x + 10 = 16
  Решение 
 x + 10 = 16
 Вычтите 7 из обеих частей уравнения.
 x + 10-10 = 16-10
 x = 6
   Пример 4  
 Решите линейное уравнение 15 = 26 — y
  Решение 
 15 = 26 — y
 Вычесть 26 с обеих сторон уравнения 
 15-26 = 26-26 -y 
-11 = -y
 Умножить обе части на –1
 y = 11
 Решение уравнений с переменными с обеих сторон, добавив 
 Давайте см. несколько примеров ниже, чтобы понять эту концепцию.
   Пример 4  
 Рассмотрим уравнение 4x –12 = -x + 8.
 Так как уравнение имеет две стороны, вам необходимо выполнить одну и ту же операцию с обеими сторонами.
 Добавьте переменную x к обеим частям уравнения
 ⟹ 4x –12 + x = -x + 8 + x.
 Упростите
 Упростите уравнение, собрав одинаковые члены с обеих сторон уравнения.
 5x — 12 = 8.
 Теперь уравнение имеет только одну переменную с одной стороны.
 Добавьте константу 12 к обеим частям уравнения.
 Константа, прикрепленная к переменной, добавляется с обеих сторон.
 ⟹ 5x — 12 +12 = 8 + 12
 Упростить
 Упростите уравнение, объединив похожие члены. И 12.
 ⟹ 5x = 20
 Теперь разделим на коэффициент.
 Деление обеих частей на коэффициент означает простое деление всего на число, присвоенное переменной.
 Решение этого уравнения, следовательно,
 x = 4.
 Проверьте свое решение
 Проверьте правильность решения, подставив ответ в исходное уравнение.
 4x –12 = -x + 8
 ⟹ 4 (4) –12 = -4 + 8
 4 = 4
 Следовательно, решение верное.
  
   Пример 5  
 Решить -12x -5-9 + 4x = 8x — 13x + 15-8
  Решение 
 Упростить, объединив похожие термины
-8 = -5x +7
 Добавьте 5x с обеих сторон.
 -8x + 5x -14 = -5x + 5x + 7
 -3w -14 = 7
 Теперь прибавьте 14 к обеим сторонам уравнения.
 — 3x — 14 + 14 = 7 + 14
 -3x = 21
 Разделите обе части уравнения на -3
 -3x / -3 = 21/3
 x = 7.
 Решение уравнений с переменными с обеих сторон путем вычитания 
 Давайте посмотрим на несколько примеров ниже, чтобы понять эту концепцию.
  
   Пример 6  
 Решите уравнение 12x + 3 = 4x + 15
  Решение 
 Вычтите 4x из каждой части уравнения.
 12x-4x + 3 = 4x — 4x + 15
 6x + 3 = 15
 Вычтем константу 3 с обеих сторон.
 6x + 3-3 = 15-3
 6x = 12
 Разделить на 6;
 6x / 6 = 12/6
 x = 2
   Пример 7  
 Решите уравнение 2x — 10 = 4x + 30.
  Решение 
 Вычтем 2x из обеих частей уравнения .
 2x -2x -10 = 4x — 2x + 23
-10 = 2x + 30
 Вычтем обе части уравнения на константу 30.
-10-30 = 2x + 30-30
-40 = 2x
 Теперь разделите на 2
 -40/2 = 2x / 2
-20 = x
 Решение линейных уравнений с умножением 
 Линейные уравнения решаются умножением, если при написании уравнения используется деление. Как только вы заметите, что переменная делится, вы можете использовать умножение для решения уравнений.
  
   Пример 7  
 Решите x / 4 = 8
  Решение 
 Умножьте обе части уравнения на знаменатель дроби,
 4 (x / 4) = 8 x 4
 x = 32
   Пример 8  
 Решите -x / 5 = 9
  Решение 
 Умножьте обе стороны на 5.
 5 (-x / 5) = 9 x 5
 -x = 45
 Умножьте обе стороны на -1, чтобы коэффициент переменной был положительным.
 x = — 45
 Решение линейных уравнений с делением 
 Для решения линейных уравнений с делением обе части уравнения делятся на коэффициент переменной. Давайте посмотрим на приведенные ниже примеры.
   Пример 9  
 Решите 2x = 4
  Решение 
 Чтобы решить это уравнение, разделите обе части на коэффициент переменной.
 2x / 2 = 4/2
 x = 2
  
   Пример 10  
 Решите уравнение −2x = −8
  Решение 
 Разделите уравнение на обе части 2.
 −2x / 2 = −8/2
 −x = — 4
 Умножая обе части на -1, получаем;
 x = 4
 Как решать алгебраические уравнения, используя свойство распределенности? 
 Решение уравнений с использованием свойства распределения влечет за собой умножение числа на выражение в круглых скобках. Затем подобные термины объединяются, а затем выделяется переменная.
   Пример 11  
 Решите 2x — 2 (3x — 2) = 2 (x –2) + 20
  Решение 
 2x — 2 (3x — 2) = 2 (x –2) + 20
 Используйте свойство распределения для удаления скобок 
 2x — 6x + 4 = 2x — 4 + 20 
 — 4x + 4 = 2x + 16
 Сложить или вычесть с обеих сторон
 –4x + 4 — 4 –2x = 2x + 16 — 4 –2x 
 –6x = 12 
 x = –2
 Проверьте ответ, подставив решение в уравнение.
 2x — 2 (3x — 2) = 2 (x –2) + 20
 (2 * –2) — 2 ((3 * –2) –2) = 2 (–2 –2) + 20 
 12 = 12
  
   Пример 12  
 Решите относительно x в уравнении -3x — 32 = -2 (5 — 4x)
  Решение 
 Примените свойство распределения для удаления скобок .
 –3x ​​- 32 = — 10 + 8x
 Если сложить обе части уравнения на 3x, получится
 -3x + 3x — 32 = — 10 + 8x + 3x
 = — 10 + 11x = -32
 Сложите обе части уравнения на 10.
 — 10 + 10 + 11x = -32 + 10
 11x = -2
 Разделите все уравнение на 11.
 11x / 11 = -22/11
 x = -2
 Как решать уравнения с дробями? 
 Не паникуйте, когда вы видите дроби в алгебраическом уравнении. Если вы знаете все правила сложения, вычитания, умножения и деления, это легкий кусок пирога для вас.
 Чтобы решить уравнения с дробями, вам необходимо преобразовать их в уравнение без дробей.
 Этот метод также называется « очистка фракций ».
  При решении уравнений с дробями выполняются следующие шаги: 
 Определите наименьшее общее кратное знаменателей (ЖКД) всех дробей в уравнении и умножьте на все дроби в уравнении.
 Изолировать переменную.
 Упростите обе части уравнения, применяя простые алгебраические операции.
 Примените свойство деления или умножения, чтобы коэффициент переменной был равен 1.
   Пример 13  
 Решить (3x + 4) / 5 = (2x — 3) / 3
  Решение 
 На ЖК-дисплее 5 и 3 будет 15, поэтому умножьте оба 
 (3x + 4) / 5 = (2x — 3) / 3
 {(3x + 4) / 5} 15 = {(2x — 3) / 3} 15
 9x +12 = 10x -15
 Изолировать переменную;
 9x -10x = -15-12
 -x = -25
 x = 25
  
   Пример 14  
 Решить относительно x 3 / 2x + 6/4 = 10/3
  Решение 
 ЖК-дисплей 2x, 4 и 3 равен 12x
 Умножьте каждую дробь в уравнении на ЖК-дисплей.
 (3 / 2x) 12x + (6/4) 12x = (10/3) 12x
 => 18 + 18x = 40x
 Изолировать переменную
 22x = 18
 x = 18/22
 Упростить
 x = 9/11
  
   Пример 15  
 Решить относительно x (2 + 2x) / 4 = (1 + 2x) / 8
  Решение 
 LCD = 8
 Умножьте каждую дробь на ЖК-дисплей,
 => 4 + 4x = 1 + 2x
 Изолировать x;
 2x = -3
 x = -1.5
 Предыдущий урок | Главная страница | Следующий урок 
 Соотношения и пропорции и их решение (Алгебра 1, Как решать линейные уравнения) — Mathplanet 
 Давайте поговорим о пропорциях и пропорциях. Когда мы говорим о скорости автомобиля или самолета, мы измеряем ее в милях в час. Это называется ставкой и является разновидностью соотношения. Отношение — это способ сравнения двух величин с использованием деления в милях в час, где мы сравниваем мили и часы.
 Отношение можно записать тремя разными способами, и все они читаются как «отношение x к y»
 $$ x \: to \: y $$
 $$ x: y $$
 $$ \ frac {x} {y} $$
 С другой стороны, пропорция — это уравнение, которое говорит, что два отношения эквивалентны. Например, если один пакет смеси файлов cookie приводит к созданию 20 файлов cookie, это было бы то же самое, что сказать, что два пакета приведут к созданию 40 файлов cookie.
 $$ \ frac {20} {1} = \ frac {40} {2} $$
 Пропорция читается как «x относится к y, как z относится к w»
 $$ \ frac {x} {y} = \ frac {z} {w} \: где \: y, w \ neq 0 $$
 Если одно число в пропорции неизвестно, вы можете найти это число, решив пропорцию.
  Пример 
 Вы знаете, что для приготовления 20 блинов нужно использовать 2 яйца. Сколько яиц нужно для приготовления 100 блинов?
  Яйца 
  блины 
  Небольшое количество 
 2
 20
  Крупная сумма 
 х
 100
 $$ \ frac {яйца} {блины} = \ frac {яйца} {блины} \: \: или \: \: \ frac {блины} {яйца} = \ frac {блины} {яйца} $ $
 Если мы напишем неизвестное число в номинаторе, то мы сможем решить это, как любое другое уравнение
 $$ \ frac {x} {100} = \ frac {2} {20} $$
 Умножаем обе стороны на 100
 $$ {\ color {green} {100 \, \ cdot}} \, \ frac {x} {100} = {\ color {green} {100 \, \ cdot}} \, \ frac {2} { 20} $$
 $$ x = \ frac {200} {20} $$
 $$ x = 10 $$
 Если в знаменателе стоит неизвестное число, мы можем использовать другой метод, включающий перекрестное произведение. Перекрестное произведение — это произведение числителя одного из соотношений и знаменателя второго отношения. Произведения пропорции всегда равны
.
 Если мы снова воспользуемся примером с смесью печенья, использованной выше
 $$ \ frac {{\ color {green} {20}}} {{\ color {blue} {1}}} = \ frac {{\ color {blue} {40}}} {{\ color {зеленый } {2}}} $$
 $$ {\ color {blue} {1}} \ cdot {\ color {blue} {40}} = {\ color {green} {2}} \ cdot {\ color {green} {20}} = 40
 $
 Говорят, что в пропорции, если
 $$ \ frac {x} {y} = \ frac {z} {w} \: где \: y, w \ neq 0 $$
 $$ xw = yz $$
 Если вы посмотрите на карту, она всегда говорит вам в одном из углов, что 1 дюйм карты соответствует гораздо большему расстоянию в реальности.Это называется масштабированием. Мы часто используем масштабирование для изображения различных объектов. Масштабирование подразумевает воссоздание модели объекта и разделение его пропорций, но с разным размером. Можно увеличить (увеличить) или уменьшить (уменьшить).