График функции с модулем и дробью
График функции с модулем и дробью — ещё одна группа заданий номера 23 ОГЭ по математике.
Подобно функциям с переменной в знаменателе, графики таких функций могут содержать выколотую точку. Как и при построении графиков функций с модулем, рассматриваем два варианта раскрытия модуля.
1) Построить график функции
и определите, при каких значениях k прямая y=kx не имеет с графиком общих точек.
Решение:
Так как x²=|х|², формулу, задающую функцию, перепишем в виде
В знаменателе общий множитель |х| вынесем за скобки
Найдём область определения функции.
|х|(|х|-1)≠0
|х|≠0; |х|-1≠0
x≠0; |х|≠1
x≠0, x≠±1.
D(y):x∈(-∞;-1)∪(-1;0)∪(0;1)∪(1;∞).
Сократив дробь на (|х|-1), получаем
При x>0 |х|=x,
— функция обратной пропорциональности. График — гипербола. Для построения гиперболы возьмём несколько точек (включая выколотую x=1):
При x<0 |х|=-x,
— функция обратной пропорциональности.
Прямая y=kx не имеет с графиком общих точек, если она проходит через выколотые точки либо совпадает с осью Ox, то есть при k=±1 и k=0:
Ответ: -1; 0; 1.
2)Постройте график функции
и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
Решение:
В числителе вынесем за скобки общий множитель 0,25x:
Ищем область определения функции.
x+2≠0
x≠-2.
D(y):x∈(-∞;-2)∪(-2;∞).
Сокращаем дробь на (x+2):
Получили функцию, содержащую переменную под знаком модуля (при условии x≠-2).
При x=0, y=0,25·0·|0|=0.
При x>0 |х|=x, y=0,25·x·|x|= y=0,25·x·x=0,25x².
y=0,25x² или
— квадратичная функция. График — парабола, полученная из параболы y=x² сжатием к оси Ox в 4 раза.
При x<0 |х|=-x, y=0,25·x·|x|= y=0,25·x·(-x)=-0,25x².
— квадратичная функция. График — парабола, полученная из параболы y=-x² сжатием к оси абсцисс в 4 раза.
График — парабола, полученная из параболы y=-x² сжатием к оси абсцисс в 4 раза.
Прямая y=m не имеет с графиком ни одной общей точки, если она проходит через выколотую точку, то есть при m=-1:
Ответ: -1.
3) Построить график функции
и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Решение:
Найдём область определения функции: x≠0.
D(y):x∈(-∞;0)∪(0;∞).
Если
то есть при x∈[-4;0)∪[4;∞), то
y=x/4 -функция прямой пропорциональности. График — прямая, проходящая через начало координат.
Для построения прямой достаточно взять одну точку, например, при x=4 y=4/4=1. Вторая точка — точка O — на графике выколотая, так как x≠0. Для более точного построения прямой лучше взять ещё одну точку: при x=-4 y=-4/4=-1.
Если
то есть при x∈(-∞;-4)∪(0;4), то
y=4/x — функция обратной пропорциональности. График — гипербола.
График — гипербола.
Для построения гиперболы возьмём несколько точек из промежутков (-∞;-4)∪(0;4) (-4 и 4 также лучше взять для уточнения построения графика).
Прямая y=m имеет с графиком ровно одну общую точку при m=1 и m=-1:
Ответ: -1; 1.
Построение графиков функций, содержащих знак модуля
Цель урока: получение более широких знаний о модуле числа, различных способах решения уравнений, содержащих знак абсолютной величины.
Задачи урока: использование различных методов исследования: теоретический и практический (решение задач), а так же исследовательский, расширение познавательного интереса к изучению алгебры, углубление знаний по теории модуля и решение задач, выходящих за пределы школьных учебников.
Оборудование: мультимедийное
оборудование, компьютер, классная доска,
планшет, творческие тетради, копировальная
бумага.
Ход урока.
1. Организационный момент.
2. Вступительное слово учителя.
Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это многозначное слово, которое имеет множество значений и применяется не только в математике, но и в архитектуре, физике, технике, программировании и других точных науках.
В архитектуре — это исходная единица измерения, устанавливаемая для данного архитектурного сооружения и служащая для выражения кратных соотношений его составных элементов.
В технике — это термин, применяемый в различных областях техники, не имеющий универсального значения и служащий для обозначения различных коэффициентов и величин, например модуль зацепления, модуль упругости и т.п.
Модуль объемного сжатия (в физике) —
отношение нормального напряжения в
материале к относительному удлинению.
3. Повторение
Чтобы глубоко изучать данную тему, нужно вспомнить простейшие определения, которые нам будут необходимы. Вопросы:
- Что называется уравнением? (Уравнение – это равенство, содержащее переменные.)
- Что называется уравнением с модулем? (Уравнение с модулем – это уравнение, содержащее переменную под знаком абсолютной величины (под знаком модуля). Привести пример уравнения с модулем, используя планшет.)
- Что значит решить уравнение? (Решить уравнение – это значит, найти все его корни, или доказать, что корней нет. Привести пример уравнения, используя планшет).
- Используя планшет, изобразить график функции y=x, y=-x, y=x+2, y=2x.
В математике модуль имеет несколько
значений, но сегодня мы поработаем с одним
из них.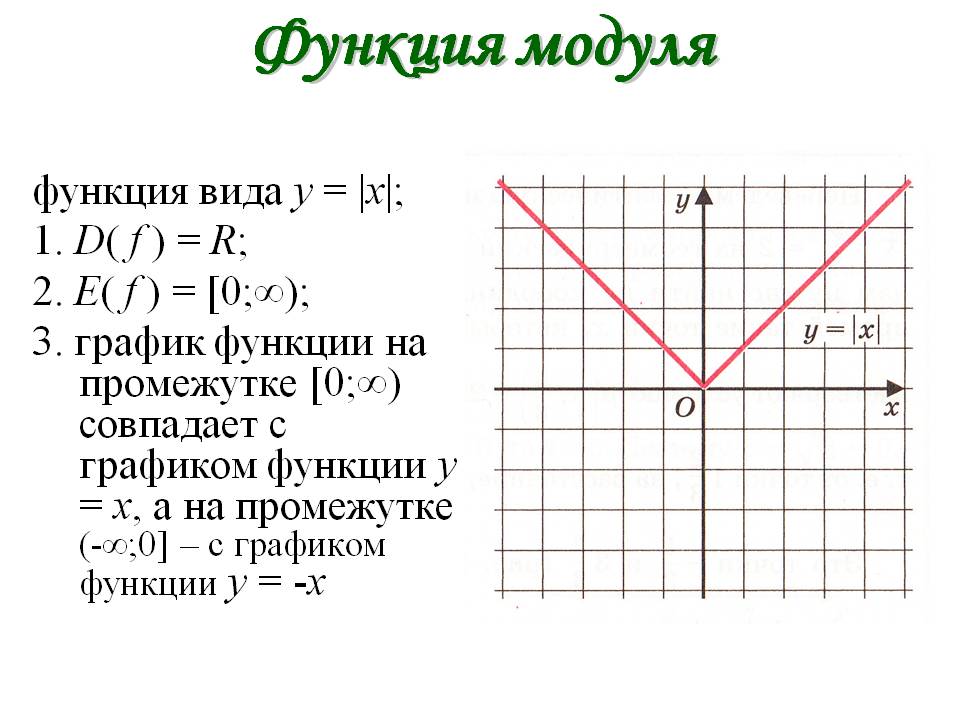
Модуль — абсолютная величина числа, равная расстоянию от начала отсчета до точки на числовой прямой. Любое число можно изобразить точкой на координатной прямой. Расстояние этой точкой от начала отсчёта на этой прямой равно положительному числу или нулю, если точка совпадает с началом отсчёта числовой прямой. Вопросы:
1. Что называется модулем данного числа? (Расстояние точки, изображающей данное число на числовой прямой от начала этой прямой, называется модулем данного числа.)
2. Как обозначается модуль? (Модуль некоторого числа а обозначается |а| .)
Геометрический смысл модуля удобно использовать при решении некоторых уравнений.
Работа у доски.
Решим уравнение |х-6| = 9. Если число 6
мы изобразим точкой А (рисунок 1), то по
определению модуля следует, что точка х
стоит от точки А на 9 единиц.
х = 6-9 = -3.
Следовательно, данное уравнение имеет два решения: х = 15 и х = -3.
Объяснение нового материала.
Теоремы, доказательства, следствия.
При решении уравнений, содержащих несколько выражений со знаком модуля, удобнее пользоваться алгебраическим определением модуля.
Определение. Модуль числа а или абсолютная величина числа а равна а, если а больше или равно нулю и равна -а, если а меньше нуля:
Из определения следует, что для любого действительного числа а, |а|≥0.
4. Объяснение нового материала.
Теорема 1. Абсолютная величина действительного числа а≠0

Доказательство:
1. Если число а положительно, то -а отрицательно, т. е. -а < 0 < а. Отсюда следует, что -а < а. Например, число 7 положительно, тогда -7 — отрицательно и -7< 0 < 7 отсюда -7 < 7. В этом случае |а| = а, т. е. |а| совпадает с большим из двух чисел а и — а.
2. Если а отрицательно, тогда -а положительно и а < — а, т. е. большим числом является -а. По определению, в этом случае, |а| = -а — снова, равно большему из двух чисел -а и а.
Следствие 1. Из теоремы следует, что |-а| = |а|.
В самом деле, как |-а|, так и | а| равны большему из чисел -а и а, а значит, равны между собой
Следствие 2. Для любого
действительного числа а справедливы
неравенства а≤|а|, -а≤|а|.
Умножая второе равенство -а≤|а|, на -1 (при этом знак неравенства изменится на противоположный), мы получим следующие неравенства: а≤|а|, а≥-|а|, справедливые для любого действительного числа а. Объединяя последние два неравенства в одно, получаем:
-|а|≤а≤|а|.
Работа у доски.
Решим уравнение |2х-12|+|6х+48|=160. Найдем корни (нули) каждого выражения, содержащего знак модуля: 2х-12=0, х=6; 6х+48=0, х= -8.
Найденные значения
Решение этого уравнения рассматривается в каждом промежутке отдельно.
В промежутке х<-8 оба выражения,
стоящие под знаком модуля, отрицательны.
Поэтому в этом промежутке при записи
уравнения без знаков модуля знаки этих
выражений меняем на противоположные. Получим уравнение –(2х-12) –(6х+48)=160.
откуда х=-24,5. Это значение принадлежит
рассматриваемому промежутку. Значит, оно
является решением данного уравнения.
Получим уравнение –(2х-12) –(6х+48)=160.
откуда х=-24,5. Это значение принадлежит
рассматриваемому промежутку. Значит, оно
является решением данного уравнения.
Во втором промежутке —8≤х<6 первое выражение отрицательно, а второе положительно. Следовательно, в этом промежутке уравнение запишется так:
-(2х-12)-(6х+48)=160. Откуда х=25 не принадлежит к промежутку.
В третьем промежутке х≥6 оба выражения положительны. Следовательно, в этом промежутке уравнение запишется так:
(2х-12)+(6х+48)=160. Откуда х=15.8. Значит, решением данного уравнения будут значения х =-24,5 и х=15,8
Для построения графиков функций,
содержащих выражения под знаком модуля, как
и при решении уравнений, сначала находят
корни выражений, стоящих под знаком модуля.
Эти корни разбивают числовую прямую на
промежутки. График строят в каждом
промежутке отдельно.
График строят в каждом
промежутке отдельно.
В простейшем случае, когда только одно выражение стоит под знаком модуля и нет слагаемых без знака модуля, можно построить график функции, опустив знак модуля, и затем часть графика, расположенную в области отрицательных значений у, отобразить симметрично относительно оси Ох. Это вытекает из определения модуля числа.
Функция у= |х|.
Рассмотрим график функции у=|х|, где |х| означает абсолютную величину, или модуль, числа х.
Построим её график, пользуясь
определением абсолютной величины. При
положительных х имеем |х|=х, т. Е.
этот график совпадает с графиком у=х и
является лучом, проходящим через начало
координат под углом 45° к оси абсцисс. При х<0
имеем |х|=-х, значит, для
отрицательных х график у=|х| совпадает
с биссектрисой второго координатного угла.
Впрочем, вторую половину графика (для отрицательных значений х) легко получить из первой, если заметить, что функция у=|х| четная, так как |-a|=|a|. Значит, график этой функции симметричен относительно оси Оу, и вторую половину графика можно получит, отразив относительно оси ординат часть, начерченную для положительных значений (рисунок 3).
Рассмотрим функция у=-|х|.
График функции у=-|х| получается симметричным отображением графика
у= |х| относительно оси х (рисунок 4).
Функции у=|х|+2, у=|х|-2
Этот график легко построить
непосредственно. Однако мы его получим из
графика у=|х|. Составим таблицу значений
функций у=|х|+2 и сравним её с такой же
таблицей, составленной для у=|х|, выписав
эти таблицы рядом. Ясно, что из каждой точки
первого графика у=|х| можно получить
точку второго графика у=|х|+2, увеличив |х|
на единицу. Значит, чтобы получить точки
второго графика, надо каждую точку первого
сдвинуть на 2 вверх, т.е. второй график
получается из первого сдвигом вверх на 2.
Значит, чтобы получить точки
второго графика, надо каждую точку первого
сдвинуть на 2 вверх, т.е. второй график
получается из первого сдвигом вверх на 2.
Сравним этот график с графиком у=|х|. Если х=а, у=|а| — точка первого графика, то точка х=а, у=|а|-1 будет лежать на втором графике. Поэтому каждая точка (|а|, |а|-1) второго графика может быть получена точки (а, |а|) первого графика сдвигом вниз на 2 единицы, и весь график получается, если у=|х| сдвинуть вниз на 2 единицы (рисунок 5).
Функции у=|х+2|, у=|х+2|
График этой функции мы тоже можем
получить из графика у=|х|. Напишем опять
рядом две таблицы: для у=|х| и для у=|х+2|.
Если сравнивать значения этих функций при
одинаковых х, то окажется, что для
некоторых х ордината первого графика
больше, чем для второго, а для некоторых
наоборот.
Однако, если внимательно посмотреть на правые столбцы этих двух таблиц, связь между таблицами можно установить. Именно вторая функция принимает те же самые значения, что и первая, только принимает их на две единицы раньше, при меньших значениях. Значит, из каждой точки первого графика у=|х| получается точка второго графика у=|х|+2, сдвинутая на 2 влево; например из точки (-2, 2) получается точка с координатами (-3, 2). Поэтому и весь график у=|х|+2, получится, если сдвинуть график у=|х| на 2 влево вдоль оси абсцисс (рисунок 6).
Функция у=а|х|
График функции у=а|х| получается растяжением графика у=|х| вдоль оси у в а раз при а>1 и сжатием вдоль этой оси в 1/а раз при 0<а<1 (рисунок 7).
Функция у=||х-2|-3|
- Строим график функции у=|х|.
- Строим график функции у=|х-2|.

- Строим график функции у=|х-2|-3.
- Применяем к графику у=|х-2|-3 операцию «модуль» (рисунок 8).
Функции у=|2х-4|+|6+3х|. Находим корни каждого выражения, стоявшего под знаком модуля: 2х – 4 = 0; 6 + 3х = 0, х = -2. В результате ось Ох разбиваем на три промежутка. В каждом промежутке выражение, стоящее перед знаком модуля, имеет определенный знак. Опускаем знаки модуля, берём выражение в каждом промежутке с соответствующим знаком:
- х<-2, у = -(2х-4)-(6+3х)=-5х-2;
- –2≤ х < 2, у= —( 2х-4)+(6+3х)=х+10;
- х≥ 2, у = 2х-4+6+3х = 5х+2
Получим в каждом промежутке выражение
функции без знака модуля. Строим график
функции в промежутке. При правильном
построении в области определения график
должен представлять непрерывную линию (рисунок
9).
5. Итог урока.
Использую копировальную бумагу по вариантам построить график функции: у=|х-4|+2 (у=|х+4|-2).
6. Домашнее задание.
В творческой тетради составить функции, содержащие знак модуля, и построить их графики.
Литература.
- Детская энциклопедия. М., «Педагогика», 1990.
- Глейзер Г. И. История математики в школе. М. «Просвещение», 1982.
- Дынкин Е.Б., Молчанова С.А. Математические задачи. М., «Наука», 1993.
- Петраков И.С. Математические кружки в 8-10 классах. М., «Просвещение», 1987.
- Талочкин П.Б. Неравенства и уравнения. М., «Просвещение», 1989.
- Башмаков М.И. Уравнения и неравенства. Издательство Московского университета, 1974.
Приложение
Модули. Равносильные преобразования (схемы) | Партизанская математика
Когда ученики начинают изучать методы решения задач с модулями, то рано или поздно они встречаются с так называемыми схемами. Для неподготовленного ученика они выглядят очень страшно, и кажется, что простому смертному их в принципе не понять. Зная мощь этого метода, но не понимая происхождения этих формул, некоторые школьники от отчаяния пытаются их зазубрить.
Для неподготовленного ученика они выглядят очень страшно, и кажется, что простому смертному их в принципе не понять. Зная мощь этого метода, но не понимая происхождения этих формул, некоторые школьники от отчаяния пытаются их зазубрить.
Просто беспорядочное нагромождение букв. И это ещё без схем для уравнений!
Однако, такой подход очень вреден.
В данной статье мы попробуем на простых примерах показать, что схемы (они же равносильные преобразования) — это довольно простая вещь, если попытаться разобраться с ними, начиная с азов. Тема с модулями для этого как нельзя кстати, ведь именно в ней нам впервые предстоит так плотно поработать со схемами.
Чтобы понять указанные ниже выкладки желательно предварительно знать, что такое совокупность и система, чем они отличаются и в целом что такое множество решений.
Начнём с самых простых заданий и постепенно перейдём к более общим конструкциям в виде схем.
Схема 1
Итак, давайте решим вот такое элементарное уравнение:
Корни его очевидны. Однако, чтобы лучше прочувствовать решение, переформулируем его так: модуль каких чисел равен 5? Или даже лучше так: чему равно число, модуль которого равен 5?
Очевидно, что это 5 и -5.
Теперь слегка усложним задачу. Решим уравнение:
Тоже переформулируем его так: чему равно выражение 2x-1, если его модуль равен 5? Очевидно, что оно равно -5 или 5. В итоге у нас уравнение распадается на два независимых случая, которые будут давать отдельные решения: 2x-1=5 и 2x-1=-5.
Так как каждый такой случай независим и вносит свой вклад в решение, то мы эти два уравнения объединяем в совокупность.
Такой переход от уравнения к некой равносильной системе или совокупности и называется схемой.
В общем виде она может быть записана в следующем виде. Возьмём некоторое положительное число а. Тогда
Возьмём некоторое положительное число а. Тогда
Это первая, самая простая схема. Очевидно, что при а=0 мы приравниваем к нулю подмодульное выражение, а при отрицательном а у нас просто нет корней (модуль всегда неотрицательное число).
Когда вы работаете со схемами, удобно писать функции не в виде f(x) и g(x), а ограничиться сокращенной записью f и g. Очевидно, что это функции от x, поэтому громоздкие скобки можно убирать. В итоге некоторые схемы будут выглядеть гораздо приятнее.
Например, наша первая схема будет выглядеть вот так:
Схема 2
Теперь усложним задачу и сделаем так, чтобы справа у нас было не число, а какая-то функция.
Пусть, например, мы решаем вот такое уравнение:
Если бы мы знали, что справа стоит положительное число, никаких проблем бы не было. Мы просто бы расписали решение по схеме выше. Но у нас справа функция, которая теоретически может принимать и отрицательные значения. А такие значения справа запрещены, так как это приравнено к модулю, который неотрицателен. Так давайте оставим только разрешенные значения для этой функции. То есть 2x-1 может быть равна 3x или -3x, но с одновременным условием, что правая часть 3x неотрицательна.
Но у нас справа функция, которая теоретически может принимать и отрицательные значения. А такие значения справа запрещены, так как это приравнено к модулю, который неотрицателен. Так давайте оставим только разрешенные значения для этой функции. То есть 2x-1 может быть равна 3x или -3x, но с одновременным условием, что правая часть 3x неотрицательна.
В виде схемы это может быть записано так:
Таким образом для общего уравнения |f(x)|=g(x) мы получаем следующую схему:
Схема 3
Далее рассмотрим равенство |а|=|b|.
По сути нас здесь спрашивают следующее: каковы условия на а и b, чтобы у них были одинаковые модули? Первый ответ очевиден: они должны быть равны, то есть а=b. Немного подумав, мы получим и второй ответ: это могут быть противоположные числа, то есть а=-b
В более общем случае, уже для функций, мы получаем вот такую схему:
Схема 4
Теперь обратимся к более сложным схемам — для неравенств с модулями.
Сразу оговоримся, что для удобства мы будем использовать только строгие неравенства. Для нестрогих неравенств схемы будут такими же, только уже с заменой строгих знаков на нестрогие.
Итак, рассмотрим вот такое простое неравенство:
Переформулируем эту задачу так: какие числа по модулю меньше 7?
Ученики часто ошибаются, думая, что подходят любые числа меньшие 7. Это не верно. Например, число -100 является контрпримером (оно меньше 7, но по модулю больше 7).
Слегка подумав, можно прийти к ответу “x находится между минус семёркой и семёркой”. Это удобно записать в виде двойного неравенства: -7<x<7.
Для наглядности можно изобразить решение на координатной прямой:
Двойное неравенство и чертёж удобны для понимания, но для решения сложных неравенств они не подойдут, поэтому нам нужно расписать это неравенство в виде схемы.
Чтобы убедиться в этом, что она работает, нужно нарисовать две координатные оси и соответственно два решения. Так как у нас неравенства объединены в систему, нас интересуют общие точки. То есть указываем пересечение этих множеств.
Из подобных рассуждений можно получить и схему в общем виде. Для некоторого а>0 получаем:
А как быть, если в правой части неравенства вместо фиксированного положительного числа а будет стоять некоторая функция?
На самом деле в таком случае схема сохранит свой вид:
Объяснение корректности замены в схеме числа а на функцию g(х) довольно громоздко, поэтому оставим это на самостоятельное обдумывание. В реальных задачах обычно достаточно запомнить естественную конструкцию
а потом при необходимости приходить к системе.
Схема 4
Теперь рассмотрим неравенство
Ни в коем случае нельзя просто поменять знаки в схеме для |x|<7 и на этом успокоиться! Мы должны снова аккуратно заново её вывести.
Переформулируем задание: найти все такие числа, которые по модулю больше 7. Очевидно, что это или числа, которые просто больше 7, или числа, которые меньше -7.
Данный факт можно записать как следующую совокупность:
Она даёт нам две независимые (!) порции решений.
Обобщая рассуждения для неравенства |f(x)|>g(x) получаем следующие равносильные преобразования.
Как видите, схема всё-таки отличается от предыдущего случая для неравенства |f(x)|<g(x). Однако, так же, как и в предыдущем варианте, корректно переходить от фиксированного числа слева к функции без изменения схемы.
В заключении обсудим то, как запоминать (а точнее, вспоминать) эти схемы. Небольшой секрет: преподаватели чаще всего эти схемы не помнят и для конкретной задачи в реальной ситуации просто быстро выводят нужное преобразование.
Поэтому ученики, которые пытаются вспомнить их, размышляя “ой, я не помню: если знак “меньше”, то там совокупность или система?” идут по ошибочной и опасной дороге. Это не математика. Ваша задача научиться понимать, что стоит за всеми этими схемами и уметь почти мгновенно их выводить. Если вы осознали все выкладки, которые рассмотрены выше, вывод формул займёт 3-5 секунд.
Это не математика. Ваша задача научиться понимать, что стоит за всеми этими схемами и уметь почти мгновенно их выводить. Если вы осознали все выкладки, которые рассмотрены выше, вывод формул займёт 3-5 секунд.
Когда появится понимание, как построены эти схемы, в некоторых случаях даже не будет необходимости их полностью выписывать.
Например, для задачи |2x-1|<7 можно просто расписать решение в виде двойного неравенства:
То есть иногда хватает и простых рассуждений. Однако, в случае функции в правой части неравенства, таких рассуждений будет недостаточно.
Основы и решение x MOD A = B и A MOD x = B (при A ≥ 0 и B ≥ 0)
Приятно снова с вами пообщаться. Прежде чем мы вернемся к совершенству программирования HP Prime, давайте совершим небольшое путешествие в страну алгебры.
Функция модуля
Определение:
X MOD Y = R, где
R = остаток(X/Y) = frac(X/Y) * Y
Практический способ получить модуль – это получить остаток (другими словами, то, что осталось) деления X/Y.
Например:
13 MOD 5 = 3
Делим 13 на 5, получаем частное от 2 и остаток от 3.
Свойства:
Пусть A и B — целые числа.
A MOD A = 0. Это легко обосновать, поскольку целое число, деленное само на себя, не имеет остатка.
Если B > A, A > 0 и B > 0, то A MOD B = A. При делении любого целого числа на большее целое в остатке будет исходное целое число.
Пример: 11 MOD 12 = 11. При делении 11/12 в частном получается 0, а в остатке 11.
Обычный способ представления функции модуля — это работа с часами и календарями (MOD 12).
x MOD A = B, A ≥ 0 и B ≥ 0
Общее решение: x = B + A*n, где n — любое целое число
Пример:
x MOD 4 = 2.
Просто x = 2 является решением, так как 2/4 оставляет частное 0 и остаток 2.
Заметьте, что x = 6 также работает. 6/4 имеет частное 1 и остаток 2.
Отсюда решение: x = 2 + 4 * n
A MOD x = B, A ≥ 0 и B ≥ 0
Способ найти возможную решения состоит в том, чтобы построить таблицу, используя старый добрый метод проб и ошибок. Остановитесь, когда мы доберемся до A MOD A. (См. раздел «Свойства» выше). Это может стать очень длинным, когда A становится большим. В торговле вы можете легко увидеть решения A MOD x = B (если решения существуют).
Остановитесь, когда мы доберемся до A MOD A. (См. раздел «Свойства» выше). Это может стать очень длинным, когда A становится большим. В торговле вы можете легко увидеть решения A MOD x = B (если решения существуют).
Пример 1: 11 МОД x = 3
11 МОД 1 = 0
11 МОД 2 = 1
11 МОД 3 = 2
11 МОД 4 = 3
11 МОД 5 = 1 0 7
5 11 11 MOD 7 = 4
11 MOD 8 = 3
11 MOD 9 = 2
11 MOD 10 = 1
11 MOD 11 = 0
Отсюда мы находим, что решения равны x = 4 и x = 8.Очень удачный случай.
Пример 2: 13 MOD x = 8
13 MOD 1 = 0
13 MOD 2 = 1
13 MOD 3 = 1
13 MOD 4 = 1
13 MOD 5 = 3
13 MOD 6 = 1 193037 7 = 6
13 МОД 8 = 5
13 МОД 9 = 4
13 МОД 10 = 3
13 МОД 11 = 2
13 МОД 12 = 1
13 МОД 13 = 0
Черт возьми! Нет решения задачи 13 MOD x = 8. Иногда такое случается.
Надеюсь, это будет полезно. Спасибо за ваши комментарии и вопросы. Честно говоря, я не могу отблагодарить вас достаточно. Хорошего дня!
Хорошего дня!
Эдди
Этот блог является собственностью Эдварда Шора. 2013
FAQ: Результаты функции mod(x,y)
Примечание. Этот FAQ основан на вопросе и ответах, появившихся на Статалист.Почему функция mod(x,y) иногда дает загадочные результаты? Почему
mod(0.3,0.1) не равен 0?| Заголовок | Результаты функции mod(x,y) | |
| Автор | Николас Дж.Кокс, Даремский университет, Великобритания Томас Дж. Стейхен |
Мод ( х , у ) функция (см. [FN] functions ) эквивалентна x − y *
этаж(х/у) . Здесь floor() возвращает
наибольшее целое число, не превышающее своего аргумента, так что floor(2) = 2, этаж(2.3) = 2, этаж(-2) = -2, и этаж(-2,3) = -3.Другими словами, это остаток на
деление х на у. Очевидно, что 0,3 кратно 0,1 и что
результат должен быть 0, но учитывая
Очевидно, что 0,3 кратно 0,1 и что
результат должен быть 0, но учитывая
. дисплей мод(0.3,0.1)
Стата показывает 0,1.
Это ошибка? Не совсем, но результат вряд ли будет таким, как вы хочу. Это возникает из-за того, что int(0.3/0.1) = 2 для машинной точности и а не 3, как ожидается из обычной арифметики. Следовательно, 0,1 отображается как остаток или модуль.
Поясним подробнее. Такие числа, как 0,3 и 0,1, нельзя считать
точные бинарные эквиваленты; см. [U] 13.12 Точность и проблемы
там . Чтобы показать это, мы будем использовать %21.18f в качестве формата отображения, который
позволяет нам видеть базовые значения почти с той же точностью, что и Stata.
(Stata также предоставляет специальный формат %21x, который показывает точное значение
в специальном шестнадцатеричном формате, который вы, возможно, захотите изучить. Этот формат
был впервые доступен в конце производственного цикла Stata 6. 0. См. также [У] 12.2 Числа и [U] 12.5.1 Числовые форматы .)
0. См. также [У] 12.2 Числа и [U] 12.5.1 Числовые форматы .)
. ди %21.18f .3
0,299999999999999990
. ди %21.18f .1
0,1000000000000000010
Здесь мы используем практически каждый бит, чтобы получить ближайшее машинное десятичное число. приближение мы можем к истинным десятичным дробям 0,3 и 0,1. Ясно, что ни число представлено точно в машине.
Если мы сравним
.ди %21.18f .3/.1
2,999999999999999600
с участием
. ди %21.18f 3
3.0000000000000000000
также ясно, что в машинном десятичном виде 3 не равно 0,3/0,1. Этот
происходит потому, что 3 можно представить точно, а 0,3/0,1 — это всего лишь
немного меньше из-за приближений, необходимых для представления 0,3 и 0,1.
Ясно, что целая часть 0,3/0,1 = 2,9999999999999999600 равна 2, причем
следствие того, что mod(0.3,0.1) отображается как 0. 1 (точнее, это
равно 0,0999999999999999978 в машинном десятичном виде, но отображение Stata по умолчанию
формат округляет его до 0,1).
1 (точнее, это
равно 0,0999999999999999978 в машинном десятичном виде, но отображение Stata по умолчанию
формат округляет его до 0,1).
Пользователи могут получить лучшие результаты, используя float() и round() , но возможно, лучший совет — предостерегающий: безопаснее не пытаться добиться точности работать с небольшими дробными аргументами для mod() . Вы можете быть лучше рекомендуется работать над эквивалентной задачей, используя целые числа.
Если вам нужна дополнительная информация, введите точность поиска в Stata, чтобы определять различные ресурсы.Сообщения в блоге Уильяма Гулда особенно рекомендуется.
Оператор по модулю Python и деление пола
В дополнение к обычным операторам сложения, вычитания, умножения и деления стандартная библиотека Python включает некоторые арифметические операторы, с которыми вы, возможно, менее знакомы. В этом посте я расскажу об операторах деления по модулю ( % ) и делении на пол ( // ), а также о некоторых распространенных ловушках, связанных с ними.
Что делают деление по модулю и полу?
Модуль
Оператор по модулю используется для выполнения евклидова деления. Вы почти наверняка узнали о евклидовом делении в школе, даже если не знали, как оно называется.
При выполнении евклидова деления вы начинаете с делимого (число, которое вы хотите разделить) и делителя (число, на которое вы хотите разделить делимое). Допустим, 10 и 3 .
В так называемом «стандартном делении» результатом 10/3 будет 3.333 повторяющийся или 3 и третий. В евклидовом делении нас не интересуют числа после запятой. Нам важен целочисленный результат деления (в данном случае 3 ), который называется частным . Сумма, оставшаяся после деления, называется остатком , который в данном случае равен 1 .
Чтобы дать вам еще один пример, 11 / 3 дает нам частное 3 и остаток 2 .
В Python оператор по модулю просто возвращает остаток:
>>> 10 % 3
1
>>> 11 % 3
2
Деление по этажам
Деление по этажам также используется для выполнения евклидова деления, но, в отличие от оператора по модулю, деление по этажам дает частное , а не остаток.
Рассмотрим пару примеров:
>>> 10 // 3
3
>>> 9 // 2
4
Мы можем создать небольшую функцию для вывода полного результата евклидова деления, например:
def euclidean_division(x, y):
частное = х // у
остаток = х % у
print(f"{частное} остаток {остаток}")
euclidean_division(10, 3) # 3 остаток 1
euclidean_division(11, 3) # 3 остаток 2
Однако есть проблема.Что происходит, когда мы вызываем нашу функцию с отрицательными числами?
>>> евклидов_дивизион (10, -3)
-4 остаток -2
Это выглядит неправильно. -3 умножить на -4 равно 12 , что больше, чем 10 . В результате мы должны были получить
В результате мы должны были получить -3 остаток 1 . Итак, что происходит?
Это вина деления пола
Картина, которую я нарисовал для вас ранее о евклидовом делении, не совсем точна.Для положительных целых чисел деление по полу и по модулю работает точно так же, как евклидово деление, но все становится сложнее, когда дело доходит до отрицательных чисел.
Это связано с округлением. Если мы посмотрим на документацию Python по арифметическим операторам, мы найдем подсказку о том, что происходит:
[T]результат [полного деления] — это результат математического деления с применением к результату функции «пол».
Итак, давайте посмотрим на документацию по функции floor .
Возвращает нижний предел x, наибольшее целое число, меньшее или равное x.
И вот в чем проблема. -4 считается менее повторяющимся, чем -3,333 . Это левее на числовой прямой. Это означает, что деление этажа всегда будет округляться от нуля для отрицательных чисел и до нуля для положительных чисел.
Это означает, что деление этажа всегда будет округляться от нуля для отрицательных чисел и до нуля для положительных чисел.
>>> 10 // 3
3 # 3,333 раунда в ноль
>>> 10 // -3
-4 # -3,333 раунда от нуля
>>> 9 // 2
4 # 4.5 раундов до нуля
>>> 9 // -2
-5 # -4,5 раунда до нуля
Так в чем проблема с модулем?
Мы выяснили, почему мы получаем неожиданные результаты от деления на пол и отрицательных чисел, но наш остаток также оказался не таким, как мы ожидали. Так почему же?
Оказывается, деление по модулю и деление на пол являются тесно связанными операторами, о которых вы могли прочитать, если немного заглянули в документацию. Модульное и напольное деление связаны следующим тождеством: x = (x // y) * y + (x % y) .
Это означает, что результат деления этажа напрямую влияет на результат операции по модулю. Мы можем изменить вышеприведенное так: (x % y) = x - (x // y) * y .
Давайте попробуем один из наших предыдущих примеров, 10 % -3 :
10 % -3 = 10 - (-3) * (10 // -3)
10 % -3 = 10 - (-3) * (-4) # Помните, здесь деление пола округляется от нуля
10 % -3 = 10 - 12
10 % -3 = -2
И мы получаем тот же результат, что и раньше: 10 % -3 = -2 .
Несколько заключительных замечаний
В этом заключительном разделе я просто хочу упомянуть еще несколько интересных вещей о делении по модулю и полу. Однако, прежде чем я углублюсь в это, я думаю, важно отметить, что реализация деления по полу и по модулю в Python не является ошибкой. Однако я считаю важным понимать, когда и как такие реализации отличаются от нашего интуитивного понимания, потому что тогда мы сможем использовать эту реализацию как инструмент, и она перестанет быть источником, возможно, неприятных ошибок.
Преобразование типов
Одна из интересных особенностей деления на пол в Python заключается в том, что оно не обязательно производит число с плавающей запятой. Фактически, во всех наших примерах результатом было целое число. Это полностью отличается от стандартного деления в Python, которое всегда дает число с плавающей запятой.
Оператор по модулю работает так же, возвращая целое число, если оба операнда были целыми числами.
Если любой из операндов является числом с плавающей запятой, деление по модулю и по нижнему краю даст число с плавающей запятой.
Использование чисел с плавающей запятой
Хотя все примеры в этом посте были целыми числами, вполне возможно использовать числа с плавающей запятой для любого операнда, и они работают точно так же, они просто дают число с плавающей запятой.
Пример из документации: 3,14 % 0,7 , что даст 0,34 .
Комплексные числа
Комплексные числа — это числа с действительной и мнимой частями. Здесь их стоит отметить только потому, что ни модульное деление, ни деление на пол не могут принимать комплексное число в качестве операнда.Попытка использовать комплексное число для деления на пол или операций по модулю вызовет ошибку TypeError .
Резюме
- Для положительных чисел деление по полу и по модулю работает как евклидово деление, получая частное и остаток соответственно.
- Для отрицательных чисел обе операции приведут к несколько неожиданным результатам.
- Полное деление всегда округляется от нуля для отрицательных чисел, поэтому
-3,5будет округляться до-4, но к нулю для положительных чисел, поэтому3.округляется до 5
5 3. - Деление по полу и модуль связаны следующим тождеством:
x = (x // y) * y + (x % y), поэтому модуль также дает неожиданные результаты для отрицательных чисел, а не только для деления на пол. .
Я надеюсь, что вы узнали что-то новое, и если вы хотите еще больше улучшить свои навыки Python, ознакомьтесь с нашим полным курсом Python.
мод (функции MATLAB)
мод (функции MATLAB)| Справочник по функциям MATLAB |
Модуль после деления
Синтаксис
Описание
M = mod(X,Y) , если Y ~= 0 , возвращает X - n.*Y , где n = пол(X./Y) . Если Y не является целым числом и частное X. находится в пределах ошибки округления целого числа, то 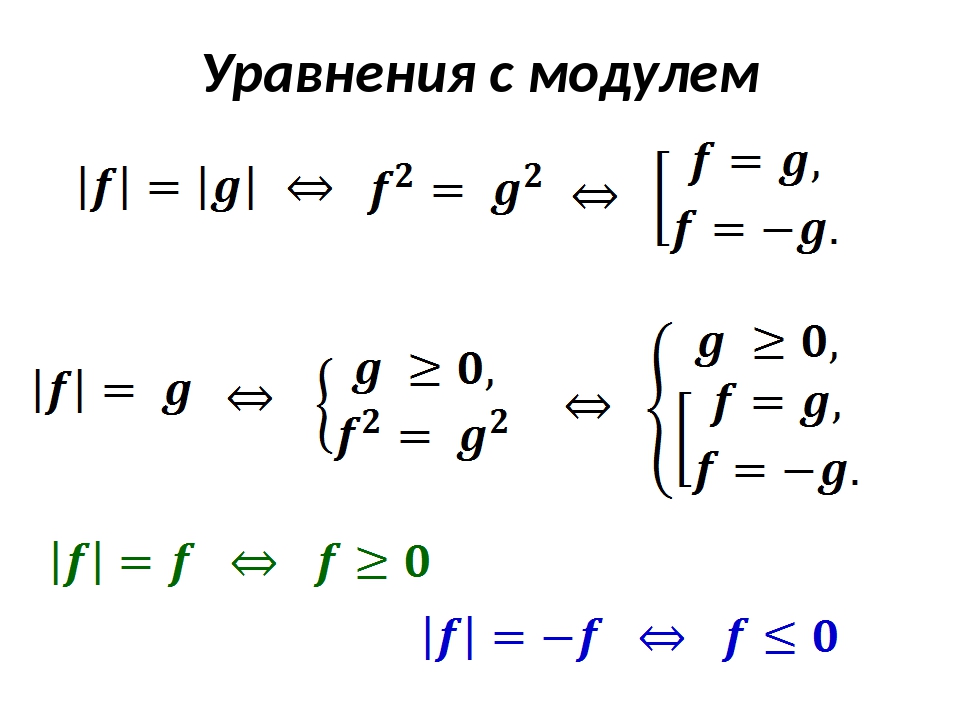 /Y
/Y n является этим целым числом. Входные данные X и Y должны быть действительными массивами одинакового размера или вещественными скалярами.
По соглашению верно следующее:
-
мод(Х,0)этоХ -
мод(Х,Х)есть0 -
mod(X,Y)дляX~=YиY~=0имеет тот же знак, что иY.
Примечания
rem(X,Y) для X~=Y и Y~=0 имеет тот же знак, что и X .
mod(X,Y) и rem(X,Y) равны, если X и Y имеют одинаковый знак, но отличаются на Y , если X и Y имеют разные знаки .
Функция mod полезна для отношений конгруэнтности: x и y конгруэнтны (mod m) тогда и только тогда, когда mod(x,m) == mod(y,m) .
Примеры
мод(13,5) ответ = 3 мод([1:5],3) ответ = 1 2 0 1 2 мод (магия (3), 3) ответ = 2 1 0 0 2 1 1 0 2
См. также
рем
| mmfileinfo | еще |
© 1994-2005 The 9000, Inc.
Honda S660 Modulo X может похвастаться более спортивным стилем и незначительными улучшениями производительности
Honda представила S660 почти три года назад, и компания поднимает планку, представив новый S660 Modulo X.
Разработанный для любителей вождения, S660 Modulo X предлагает ряд модификаций стиля и производительности.
Начиная с экстерьера, модель оснащена агрессивным передним бампером с увеличенными воздухозаборниками и светодиодными дневными ходовыми огнями. Спортивный стиль продолжается и сзади: у родстера черные зеркала заднего вида, уникальный задний бампер и активный спойлер с откидной крышкой. Завершают внешние особенности мягкий верх бордового красного цвета и 15-/16-дюймовые алюминиевые колеса со скрытой черной отделкой.
Особый стиль продолжается и в салоне: водители найдут сиденья с двухцветной обивкой из кожи и замши Lux, а также кожаное рулевое колесо в тон. Дизайнеры также установили кожаный ручной тормоз, бордово-красные акценты на приборной панели и двухцветные коврики с алюминиевым значком Modulo X. Даже переключатель передач уникален для этой модели, поскольку варианты с ручным управлением имеют титановую ручку переключения передач, а автомобили с вариатором оснащены двухцветным кожаным переключателем.
Что касается технических характеристик, то инженеры оснастили автомобиль специально настроенной подвеской с пятью ступенями регулировки демпфирования. Honda говорит, что это позволяет водителям испытать «полноценное спортивное вождение».
Honda говорит, что это позволяет водителям испытать «полноценное спортивное вождение».
Помимо модернизированной подвески, S660 имеет перфорированные роторы и «спортивные» тормозные колодки.
Honda мало рассказала о двигателе, поэтому автомобиль, вероятно, оснащен трехцилиндровым двигателем с турбонаддувом объемом 660 куб. см, который развивает 63 л.с. (64 л.
Honda S660 Modulo X будет выпущена в следующем месяце, а цена начинается с 2 850 120 иен (26 100 долларов США), включая налоги.
ФОТОГАЛЕРЕЯ
Ещефото…
Honda S660 Modulo X представлен в Японии как более спортивная версия микро-родстера
Honda S660 должна быть самым желанным кей-каром прямо сейчас, и эта новая специальная версия Modulo X заставляет нас еще больше завидовать японским покупателям, поскольку они единственные, кто может получить от нее удовольствие.
Modulo X — более спортивная версия стандартного S660, и это очевидно, если взглянуть на более агрессивные бамперы, активный задний спойлер, черные зеркала и легкосплавные диски (доступны 15- или 16-дюймовые размеры). Основные моменты также включают мягкий верх бордового красного цвета и светодиодные ДХО.
Основные моменты также включают мягкий верх бордового красного цвета и светодиодные ДХО.
Интерьер также получил спортивный вид: двухцветная кожа и сиденья Lux Suede сочетаются с кожаным рулевым колесом и акцентами на приборной панели. Ручка переключения передач также уникальна для S660 Modulo X и доступна в двух вариантах: титан для вариантов с ручным управлением и двухцветная кожа для моделей с вариатором. Автомобиль также оснащен кожаным ручным тормозом и двухцветными ковриками.
Мы знаем, что вы ждете производительности, и S660 вас не разочарует, поскольку он оснащен специально настроенной подвеской с пятью ступенями регулировки демпфирования — довольно сложная вещь для кей-кара, не так ли?
Добавьте к этому роторы с перфорацией и модернизированные тормозные колодки, и S660 Modulo X должен предложить более острое вождение.Тем не менее, Honda не предоставляет информацию о двигателе, и это, вероятно, означает, что в этом отделе не было внесено никаких изменений.
Тем не менее, стандартный 0,66-литровый трехцилиндровый двигатель с турбонаддувом мощностью 64 л.с. (63 л.с.) и крутящим моментом 104 Нм (76 фунт-фут) должен быть достаточно мощным для автомобиля весом около 850 кг (1870 фунтов). Естественно, S660 Modulo X лучше всего сочетается с шестиступенчатой механической коробкой передач.
Цены на Honda S660 Modulo X начинаются от 2 850 120 японских иен, что составляет примерно 26 000 долларов США по текущему обменному курсу.
Отсылки к истории: Honda через Carscoops
ПОДРОБНЕЕ: Хонда S660 с тюнингом Liberty Walk выглядит как суперкар категории kei
Введение в теорию чисел
Раздел 5.2 Введение в теорию чисел
Мы использовали натуральные числа для решения задач. Это был правильный набор чисел для работы в дискретной математике, потому что мы всегда имели дело с целым рядом вещей.Натуральные числа были инструментом. Давайте на минутку осмотрим этот инструмент. Какие математические открытия мы можем сделать относительно самих натуральных чисел?
Давайте на минутку осмотрим этот инструмент. Какие математические открытия мы можем сделать относительно самих натуральных чисел?
Это главный вопрос теории чисел: огромного, древнего, сложного и, главное, прекрасного раздела математики. Исторически теория чисел была известна как королева математики и во многом была ветвью чистой математики , изучаемой сама по себе, а не как средство для понимания приложений реального мира.Однако это изменилось в последние годы, когда были обнаружены приложения теории чисел. Вероятно, наиболее известным примером этого является криптография RSA, один из методов, используемых для шифрования данных в Интернете. Это возможно благодаря теории чисел.
Какие вопросы относятся к области теории чисел? Вот мотивирующий пример. Напомним, в нашем исследовании индукции мы спросили:
Какая сумма почтовых расходов может быть точно произведена с использованием только 5-центовых и 8-центовых марок?
Мы смогли доказать, что можно заработать любую сумму больше 27 центов. Вам может быть интересно, что произойдет, если мы изменим номинал марок. Что, если бы вместо этого у нас были марки номиналом 4 и 9 центов? Будет ли существовать некоторая сумма, после которой все суммы будут возможны? Ну, опять же, мы могли бы заменить две марки по 4 цента на марку по 9 центов или три марки по 9 центов на семь марок по 4 цента. В каждом случае мы можем создать еще один цент почтовых расходов. Использование этого в качестве индуктивного случая позволило бы нам доказать, что может быть произведена любая сумма почтовых расходов, превышающая 23 цента.
Вам может быть интересно, что произойдет, если мы изменим номинал марок. Что, если бы вместо этого у нас были марки номиналом 4 и 9 центов? Будет ли существовать некоторая сумма, после которой все суммы будут возможны? Ну, опять же, мы могли бы заменить две марки по 4 цента на марку по 9 центов или три марки по 9 центов на семь марок по 4 цента. В каждом случае мы можем создать еще один цент почтовых расходов. Использование этого в качестве индуктивного случая позволило бы нам доказать, что может быть произведена любая сумма почтовых расходов, превышающая 23 цента.
Что, если бы у нас были марки по 2 и 4 цента.Здесь он выглядит менее перспективным. Если мы возьмем некоторое количество марок по 2 цента и некоторое количество марок по 4 цента, что мы можем сказать об их сумме? Может ли это когда-нибудь быть странным? Не похоже.
Почему работают 5 и 8, 4 и 9 работают, а 2 и 4 не работают? Что не так с этими цифрами? Если бы я дал вам пару цифр, вы бы сразу сказали, будут они работать или нет? Мы ответим на эти и другие вопросы, предварительно изучив некоторые более простые свойства самих чисел.
Подраздел Делимость
Натуральные числа легко складывать и умножать. Если мы расширим наше внимание на все целые числа, то вычитание также будет легким (нам нужны отрицательные числа, чтобы мы могли вычесть любое число из любого другого числа, даже большее из меньшего). Разделение — это первая операция, которая представляет собой вызов. Если бы мы хотели расширить наш набор чисел, чтобы было возможно любое деление (возможно, исключая деление на 0), нам нужно было бы взглянуть на рациональные числа (набор всех чисел, которые можно записать в виде дробей).Это было бы слишком далеко, поэтому мы откажемся от этого варианта.
На самом деле хорошо, что не каждое число можно разделить на другие числа. Это помогает нам понять структуру натуральных чисел и открывает двери для многих интересных вопросов и приложений.
Если заданы числа \(a\) и \(b\text{,}\), возможно, что \(a \div b\) дает целое число. В этом случае мы говорим, что \(b\) делит \(a\text{,}\) в символах, мы пишем \(b \mid a\text{. }\) Если это верно, то \(b\) является делителем или множителем \(a\text{,}\) и \(a\) кратно \(b\text{.}\) In Другими словами, если \(b \mid a\text{,}\), то \(a = bk\) для некоторого целого числа \(k\) (это означает, что \(a\) является некоторым кратным \(b\ )).
}\) Если это верно, то \(b\) является делителем или множителем \(a\text{,}\) и \(a\) кратно \(b\text{.}\) In Другими словами, если \(b \mid a\text{,}\), то \(a = bk\) для некоторого целого числа \(k\) (это означает, что \(a\) является некоторым кратным \(b\ )).
Отношение делимости.
Для заданных целых чисел \(m\) и \(n\text{,}\) мы говорим «\(m\) делит \(n\)» и пишем
\begin{уравнение*} м \ середина п \end{уравнение*}
при условии, что \(n \div m\) является целым числом. Таким образом, следующие утверждения означают одно и то же:
- \(\displaystyle m \mid n\)
- \(n = mk\) для некоторого целого числа \(k\)
- \(m\) является множителем (или делителем) \(n\)
- \(n\) кратно \(m\text{.}\)
Обратите внимание, что \(m \mid n\) является оператором. Это либо правда, либо ложь. С другой стороны, \(n \div m\) или \(n/m\) — это некоторое число. Если мы хотим утверждать, что \(n/m\) не является целым числом, поэтому \(m\) не делится на \(n\text{,}\), то мы можем написать \(m \nmid n\text{ . }\)
}\)
Пример 5.2.1.
Решите, является ли каждое из приведенных ниже утверждений верным или ложным.
- \(\displaystyle 4 \середина 20\)
- \(\displaystyle 20\середина 4\)
- \(\displaystyle 0 \середина 5\)
- \(\displaystyle 5 \mid 0\)
- \(\displaystyle 7\середина 7\)
- \(\displaystyle 1 \середина 37\)
- \(\displaystyle -3 \середина 12\)
- \(\displaystyle 8\середина 12\)
- \(\displaystyle 1642\середина 136299\)
Верно.4 «входит» в 20 пять раз без остатка. Другими словами, \(20 \div 4 = 5\text{,}\) целое число. Мы могли бы также обосновать это, сказав, что \(20\) кратно 4: \(20 = 4\cdot 5\text{.}\)
Ложь. Хотя 20 кратно 4, неверно, что \(4\) кратно 20.
Ложь. \(5 \div 0\) даже не определено, не говоря уже о целом числе.
Верно. На самом деле \(x \mid 0\) верно для всех \(x\text{.}\) Это потому, что 0 кратно каждому числу: \(0 = x\cdot 0\text{.
 }\)
}\)Верно. На самом деле, \(x \mid x\) верно для всех \(x\text{.}\)
Верно. 1 делит каждое число (кроме 0).
Верно. Отрицательные числа прекрасно подходят для отношения делимости. Здесь \(12 = -3 \cdot 4\text{.}\) Также верно, что \(3 \mid -12\) и что \(-3 \mid -12\text{.}\)
Ложь. И 8, и 12 делятся на 4, но это не означает, что \(12\) делится на \(8\text{.}\)
Ложь.Смотри ниже.
Этот последний пример поднимает вопрос: как можно решить, является ли \(m \mid n\text{?}\) Конечно, если бы у вас был надежный калькулятор, вы могли бы запросить у него значение \(n \div m \text{.}\) Если он выдает что-либо, кроме целого числа, вы знаете, что \(m \nmid n\text{.}\) Это немного похоже на мошенничество: у нас нет деления, поэтому мы должны действительно использовать деление для проверки делимости?
Хотя мы и не умеем делить, мы знаем, как умножать.Мы могли бы попробовать умножать \(m\) на все большие и большие числа, пока не приблизимся к \(n\text{. }\) Насколько близко? Ну, мы хотим быть уверены, что если мы умножим \(m\) на следующее большее целое число, мы превысим \(n\text{.}\)
}\) Насколько близко? Ну, мы хотим быть уверены, что если мы умножим \(m\) на следующее большее целое число, мы превысим \(n\text{.}\)
Например, давайте попробуем решить, следует ли \(1642 \mid 136299\text{.}\) начать поиск кратных 1642:
\begin{уравнение*} 1642 \cdot 2 = 3284 \qquad 1642 \cdot 3 = 4926 \qquad 1642\cdot 4 = 6568 \qquad \cdots\text{.} \end{уравнение*}
Все они значительно меньше 136299.Я полагаю, мы можем немного забежать вперед:
\begin{уравнение*} 1642 \cdot 50 = 82100 \qquad 1642 \cdot 80 = 131360 \qquad 1642 \cdot 85 = 139570\text{.} \end{уравнение*}
Ах, так что нам нужно искать где-то между 80 и 85. Попробуйте 83:
\begin{уравнение*} 1642 \cdot 83 = 136286\текст{.} \end{уравнение*}
Это лучшее, что мы можем сделать? Как далеко мы от желаемого 136299? Если мы вычтем, мы получим \(136299 — 136286 = 13\text{.}\) Итак, мы знаем, что не можем увеличить число до 84, это будет слишком много.Другими словами, мы обнаружили, что
\begin{уравнение*}
136299 = 83 \cdot 1642 + 13\текст{.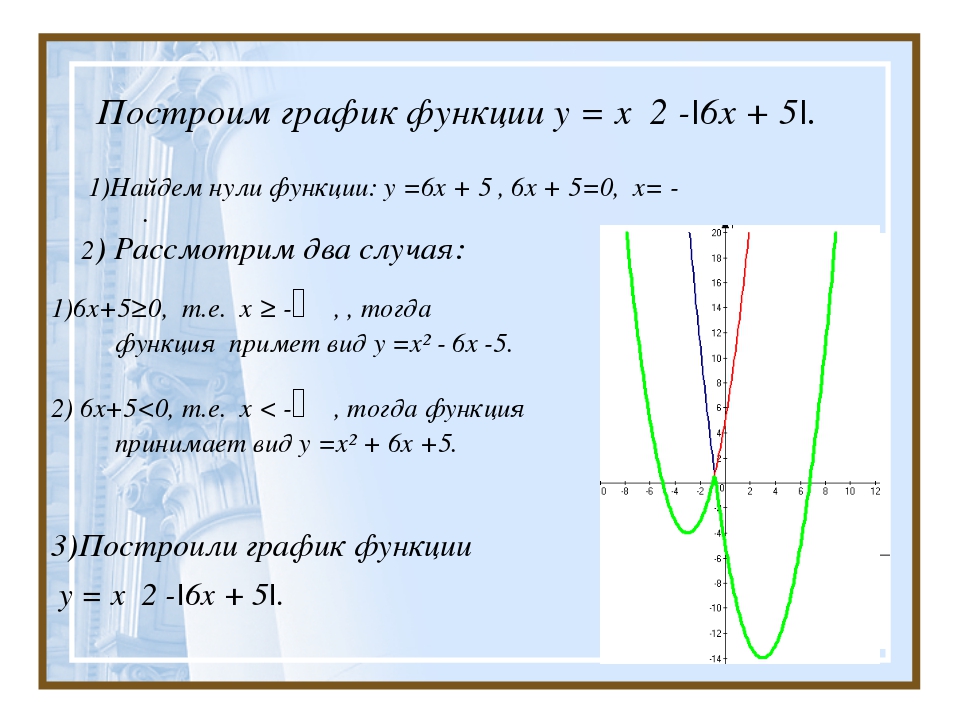 }
\end{уравнение*}
}
\end{уравнение*}
Поскольку \(13 \lt 1642\text{,}\) теперь мы можем с уверенностью сказать, что \(1642 \nmid 136299\text{.}\)
Оказывается, описанный выше процесс можно повторить для любой пары чисел. Мы всегда можем записать число \(a\) как некоторое кратное числу \(b\) плюс некоторый остаток. Мы знаем это, потому что знаем о делении с остатком из начальной школы.Это просто способ сказать это с помощью умножения. Из-за процедурного характера, который можно использовать для нахождения остатка, этот факт обычно называют алгоритмом деления :
.Алгоритм деления.
Для любых двух целых чисел \(a\) и \(b\text{,}\) всегда можно найти целое число \(q\), такое что
\begin{уравнение*} а = qb + г \end{уравнение*}
, где \(r\) — целое число, удовлетворяющее \(0 \le r \lt |b|\)
Идея состоит в том, что мы всегда можем взять достаточно большое число, кратное \(b\), так что остаток \( г\) как можно меньше.Мы допускаем возможность \(r = 0\text{,}\), и в этом случае мы имеем \(b \mid a\text{. }\)
}\)
Классы остатка подраздела
Алгоритм деления говорит нам, что есть только \(b\) возможных остатков при делении на \(b\text{.}\) Если мы зафиксируем этот делитель, мы сможем сгруппировать целые числа по остатку. Каждая группа называется остаточным классом по модулю \(b\) (или иногда остаточным классом ).
Пример 5.2.2.
Описать остальные классы по модулю \(5\text{.}\)
РешениеМы хотим классифицировать числа по тому, какой будет их остаток при делении на \(5\text{.}\) Из алгоритма деления мы знаем, что будет ровно 5 классов остатка, потому что есть только 5 вариантов того, что \( r\) может быть (\(0 \le r \lt 5\)).
Сначала рассмотрим \(r = 0\text{.}\) Здесь мы ищем все числа, делящиеся на \(5\), поскольку \(a = 5q+0\text{.}\) Другими словами, кратны 5. Получаем бесконечное множество
\begin{уравнение*} \{\ldots, -15, -10, -5, 0, 5, 10, 15, 20, \ldots\}\text{.} \end{уравнение*}
Обратите внимание, что мы также включаем отрицательные целые числа.
Теперь рассмотрим \(r = 1\text{.}\) Какие целые числа при делении на 5 дают в остатке 1? Ну, конечно, 1 подходит, как и 6 и 11. Минусы? Здесь мы должны быть осторожны: \(-6\) НЕ имеет остатка 1. Мы можем написать \(-6 = -2\cdot 5 + 4\) или \(-6 = -1 \cdot 5 — 1\text {,}\), но только один из них является «правильным» экземпляром алгоритма деления: \(r = 4\), так как нам нужно, чтобы \(r\) было неотрицательным. Таким образом, чтобы получить \(r = 1\text{,}\), мы должны иметь \(-4\text{,}\) или \(-9\text{,}\) и т. д.Таким образом мы получаем остаток класса
\begin{уравнение*} \{\ldots, -14, -9, -4, 1, 6, 11, 16, 21, \ldots\}\text{.} \end{уравнение*}
Осталось еще три. Остальные классы для \(2\text{,}\) \(3\text{,}\) и \(4\) соответственно
\begin{уравнение*} \{\ldots, -13, -8, -3, 2, 7, 12, 17, 22,\ldots\} \end{уравнение*}
\begin{уравнение*} \{\ldots, -12, -7, -2, 3, 8, 13, 18, 23, \ldots\} \end{уравнение*}
\begin{уравнение*}
\{\ldots, -11, -6, -1, 4, 9, 14, 19, 24, \ldots\}\text{.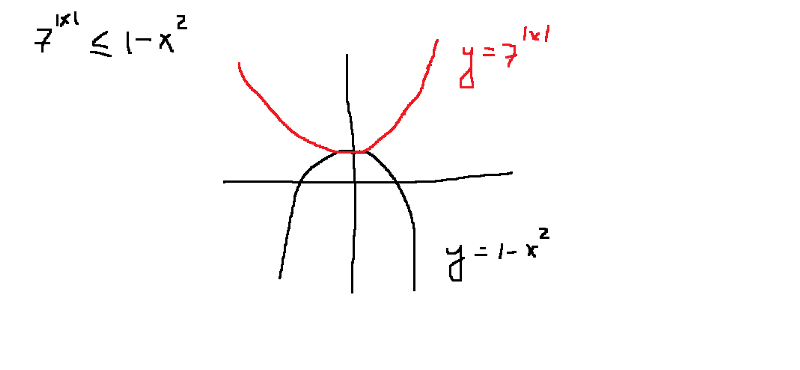 }
\end{уравнение*}
}
\end{уравнение*}
Обратите внимание, что в приведенном выше примере каждое целое число находится ровно в одном классе остатка. Технический способ сказать это состоит в том, что остаточные классы по модулю \(b\) образуют разделов целых чисел. 1 Самый важный факт о разбиениях заключается в том, что можно определить отношение эквивалентности из разбиения: это отношение между парами чисел, которое действует во всех важных отношениях подобно отношению «равно». 2
Можно разработать математическую теорию разбиений, доказать утверждения обо всех разбиениях в целом, а затем применить эти наблюдения к нашему случаю.
Опять же, существует математическая теория отношений эквивалентности, которая применима во многих других случаях, чем тот, который мы здесь рассматриваем.
Если оставить в стороне весь забавный технический язык, идея очень проста. Если два числа принадлежат к одному и тому же классу остатка, то в некотором смысле они одинаковы. То есть это одни и те же с точностью до деления на \(b\) . В случае, когда \(b = 5\) выше, числа \(8\) и \(23\text{,}\) хотя и не являются одним и тем же числом, но при делении на 5 одинаковы, потому что оба есть остаток \(3\text{.}\)
То есть это одни и те же с точностью до деления на \(b\) . В случае, когда \(b = 5\) выше, числа \(8\) и \(23\text{,}\) хотя и не являются одним и тем же числом, но при делении на 5 одинаковы, потому что оба есть остаток \(3\text{.}\)
Имеет значение, какой делитель: \(8\) и \(23\) совпадают до деления на \(5\text{,}\), но не до деления на \(7\text{,} \) так как \(8\) имеет остаток от 1 при делении на 7, а 23 имеет остаток от 2.
Имея все это в виду, давайте введем некоторые обозначения.Мы хотим сказать, что \(8\) и 23 в основном одинаковы, хотя и не равны. Было бы неправильно говорить \(8 = 23\text{.}\) Вместо этого мы пишем \(8 \equiv 23\text{.}\) Но это не всегда верно. Это работает, если мы думаем о делении на 5, поэтому нам нужно как-то это обозначить. На самом деле мы напишем это:
\begin{уравнение*} 8 \экв 23 \pmod{5} \end{уравнение*}
, который читается как «8 сравнимо с 23 по модулю 5» (или просто «по модулю 5»). Конечно, тогда мы могли бы заметить, что
\begin{уравнение*}
8 \не\эквивалент 23 \pmod{7}\text{. }
\end{уравнение*}
}
\end{уравнение*}
Сравнение по модулю \(n\).
Мы говорим, что \(a\) сравнимо с \(b\) по модулю \(n\) , и пишем
\begin{уравнение*} а \ экв б \ pmod {n} \end{уравнение*}
при условии, что \(a\) и \(b\) имеют одинаковый остаток при делении на \(n\text{.}\) Другими словами, при условии, что \(a\) и \(b\) принадлежат одному и тому же класс остатка по модулю \(n\text{.}\)
Во многих книгах конгруэнтность по модулю \(n\) определяется несколько иначе. Говорят, что \(a \equiv b \pmod{n}\) тогда и только тогда, когда \(n \mid a-b\text{.}\) Другими словами, два числа конгруэнтны по модулю \(n\text{,}\), если их разность кратна \(n\text{.}\). Итак, какое определение является правильным? Оказывается, это не имеет значения: они эквивалентны.
Чтобы понять почему, рассмотрим два числа \(a\) и \(b\), которые конгруэнтны по модулю \(n\text{.}\). Тогда \(a\) и \(b\) имеют одинаковый остаток, когда разделить на \(n\text{.}\) У нас есть
\begin{уравнение*}
a = q_1 n + r \qquad\qquad b = q_2 n + r\text{. }
\end{уравнение*}
}
\end{уравнение*}
Здесь два \(r\) действительно одинаковы.Рассмотрим, что мы получим, если возьмем разность \(a\) и \(b\text{:}\)
\begin{уравнение*} a-b = q_1n + r — (q_2n + r) = q_1n — q_2 n = (q_1-q_2)n\text{.} \end{уравнение*}
Итак, \(a-b\) кратно \(n\text{,}\) или, что то же самое, \(n \mid a-b\text{.}\)
С другой стороны, если мы сначала предположим, что \(n \mid ab\text{,}\), поэтому \(ab = kn\text{,}\), то рассмотрим, что произойдет, если мы разделим каждый член на \(n \text{.}\) Деление \(a\) на \(n\) оставит некоторый остаток, как и деление \(b\) на \(n\text{.}\) Однако при делении \(kn\) на \(n\) останется 0 остатка. Таким образом, остатки в левой части должны сокращаться. То есть остатки должны быть одинаковыми.
Таким образом имеем:
Конгруэнтность и делимость.
Для любых целых чисел \(a\text{,}\) \(b\text{,}\) и \(n\text{,}\) мы имеем
\begin{уравнение*}
a \equiv b \pmod{n} \qquad \text{ тогда и только тогда, когда } \qquad n \mid a-b\text{. }
\end{уравнение*}
}
\end{уравнение*}
Также будет полезно переключаться между сравнениями и регулярными уравнениями.Вышеприведенный факт помогает в этом. Мы знаем, что \(a \equiv b \pmod{n}\) тогда и только тогда, когда \(n \mid ab\text{,}\) тогда и только тогда, когда \(ab = kn\) для некоторого целого числа \(k \text{.}\) Переставляя это уравнение, мы получаем \(a = b + kn\text{.}\) Другими словами, если \(a\) и \(b\) конгруэнтны по модулю \(n\ text{,}\), то \(a\) является \(b\) больше, чем некоторое число, кратное \(n\text{.}\). Это согласуется с нашим более ранним наблюдением, что все числа в конкретном остаточном классе являются такая же сумма больше, чем кратно \(n\text{.}\)
Конгруэнтность и равенство.
Для любых целых чисел \(a\text{,}\) \(b\text{,}\) и \(n\text{,}\) мы имеем
\begin{уравнение*} a \equiv b \pmod{n} \qquad \text{ тогда и только тогда, когда } \qquad a = b + kn \mbox{ для некоторого целого числа } k \text{.} \end{уравнение*}
Подраздел Свойства конгруэнтности
Ранее мы говорили, что конгруэнтность по модулю \(n\) ведет себя во многих важных отношениях так же, как и равенство. В частности, мы могли бы доказать, что конгруэнтность по модулю \(n\) является отношением эквивалентности , что потребовало бы проверки следующих трех фактов:
В частности, мы могли бы доказать, что конгруэнтность по модулю \(n\) является отношением эквивалентности , что потребовало бы проверки следующих трех фактов:
Конгруэнтность по модулю \(n\) является отношением эквивалентности.
Для любых целых чисел \(a\text{,}\) \(b\text{,}\) и \(c\text{,}\) и любого положительного целого числа \(n\text{,}\) следующее удержание:
- \(a \equiv a \pmod{n}\text{.}\)
Если \(a \equiv b \pmod{n}\), то \(b \equiv a \pmod{n}\text{.}\)
Если \(a \equiv b \pmod{n}\) и \(b \equiv c \pmod{n}\text{,}\), то \(a \equiv c \pmod{n}\text{ .}\)
Другими словами, конгруэнция по модулю \(n\) рефлексивна, симметрична и транзитивна, как и отношение эквивалентности.
Вы должны уделить минутку, чтобы убедиться, что каждое из приведенных выше свойств на самом деле соответствует конгруэнтности. Попробуйте объяснить каждое из них, используя определение остатка и делимости.
Теперь рассмотрим, как конгруэнтность ведет себя при выполнении основных арифметических операций. Мы уже знаем, что если вычесть два конгруэнтных числа, результат будет равен 0 (будет кратен \(n\)). Что, если мы добавим что-то, сравнимое с 1, с чем-то, сравнимым с 2? Получим ли мы что-то, сравнимое с 3?
Сравнение и арифметика.
Предположим, что \(a \equiv b \pmod{n}\) и \(c \equiv d \pmod{n}\text{.}\) Тогда верно следующее:
- \(a+c \equiv b+d \pmod{n}\text{.}\)
- \(a-c \equiv b-d \pmod{n}\text{.}\)
- \(ac \equiv bd \pmod{n}\text{.}\)
Вышеприведенные факты могут быть написаны немного странно, но идея проста. Если у нас есть истинное соответствие и мы добавляем одно и то же к обеим сторонам, результат все равно будет истинным соответствием. Это звучит так, как будто мы говорим:
Если \(a \equiv b \pmod{n}\), то \(a+c \equiv b+c \pmod{n}\text{.}\)
Конечно, это тоже верно, это частный случай, когда \(c = d\text{. }\) Но то, что мы имеем, работает в более общем случае. Думайте о конгруэнтности как о «в основном равном». Если у нас есть два числа, которые в основном равны, и мы добавляем в основном одно и то же к обеим частям, результат будет в основном равен.
}\) Но то, что мы имеем, работает в более общем случае. Думайте о конгруэнтности как о «в основном равном». Если у нас есть два числа, которые в основном равны, и мы добавляем в основном одно и то же к обеим частям, результат будет в основном равен.
Это кажется разумным. Это правда? Докажем первый факт:
Доказательство.
Предположим, \(a \equiv b \pmod{n}\) и \(c \equiv d \pmod{n}\text{.}\) Это означает \(a = b + kn\) и \(c = d + jn\) для целых чисел \(k\) и \(j\text{.}\) Добавьте эти уравнения:
\begin{уравнение*} a+c = b+d + kn + jn\text{.} \end{уравнение*}
Но \(kn + jn = (k+j)n\text{,}\), что просто кратно \(n\text{.}\), поэтому \(a+c = b+d + (j +k)n\text{,}\) или, другими словами, \(a+c \equiv b+d \pmod{n}\)
Аналогично доказываются два других факта.
Одним из важных следствий этих фактов о сравнениях является то, что мы можем заменить любое число в сравнении любым другим числом, с которым оно сравнимо.Вот несколько примеров, чтобы увидеть, как (и почему) это работает:
Пример 5.
 2.3.
2.3.Найдите остаток от деления \(3491\) на \(9\text{.}\)
РешениеМожно было бы разделить в большую сторону, но есть и другой способ. Мы хотим найти \(x\) такой, что \(x \equiv 3491 \pmod{9}\text{.}\) Теперь \(3491 = 3000 + 400 + 90 + 1\text{.}\) Конечно \(90 \equiv 0 \pmod 9\text{,}\), поэтому мы можем заменить 90 в сумме на 0. Почему это нормально? На самом деле мы вычитаем «одно и то же» с обеих сторон:
.\begin{уравнение*} \begin{align}x \amp \equiv 3000 + 400 + 90 + 1 \pmod 9 \\ — ~~ 0 \ампер\экв 90 \pmod 9 \\ х \амп\экв 3000 + 400 + 0 + 1\pmod 9.\end{выровнено} \end{уравнение*}
Далее обратите внимание, что \(400 = 4 \cdot 100\text{,}\) и \(100 \эквив 1 \pmod 9\) (начиная с \(9 \mid 99\)). Таким образом, мы фактически можем заменить 400 просто 4. Опять же, мы апеллируем к нашему утверждению, что мы можем заменить конгруэнтные элементы, но на самом деле мы апеллируем к свойству 3 арифметики конгруэнтности: мы знаем \(100 \экв 1 \pmod{9}\text{,}\) поэтому, если мы умножим обе части на \(4\text{,}\), мы получим \(400 \equiv 4 \pmod 9\text{. }\)
}\)
Точно так же мы можем заменить 3000 на 3, поскольку \(1000 = 1 + 999 \эквив 1 \pmod 9\text{.}\) Таким образом, наша исходная конгруэнтность становится равной
.\begin{уравнение*} х \экв 3 + 4 + 0 + 1 \pmod 9 \end{уравнение*}
\begin{уравнение*} х \ экв 8 \ pmod 9 \ текст {.} \end{уравнение*}
Следовательно, \(3491\) при делении на 9 дает в остатке 8.
Приведенный выше пример должен убедить вас в том, что известный тест на делимость числа 9 верен: сумма цифр числа делится на 9 тогда и только тогда, когда исходное число делится на 9. На самом деле, теперь мы знаем нечто большее. : любое число конгруэнтно сумме своих цифр по модулю 9.p \pmod n\text{.}\) Это просто применение свойства 3 несколько раз.
До сих пор мы видели, как складывать, вычитать и умножать с помощью сравнений. Что насчет деления? Есть причина, по которой мы ждали, чтобы обсудить это. Оказывается, мы не можем просто разделить. Другими словами, даже если \(ad \equiv bd \pmod n\text{,}\) мы не знаем, что \(a \equiv b \pmod n\text{. }\) Рассмотрим, например:
}\) Рассмотрим, например:
\begin{уравнение*} 18 \экв 42 \pmod 8\текст{.} \end{уравнение*}
Это правда.Теперь \(18\) и \(42\) делятся на 6. Однако
\begin{уравнение*} 3 \не\эквивалент 7 \pmod 8\текст{.} \end{уравнение*}
Хотя это и не работает, обратите внимание, что \(3 \equiv 7 \pmod 4\text{.}\) Мы не можем разделить \(8\) на 6, но мы можем разделить 8 на наибольший общий делитель \( 8\) и \(6\text{.}\) Это всегда будет происходить?
Предположим, что \(ad \equiv bd \pmod n\text{.}\) Другими словами, мы имеем \(ad = bd + kn\) для некоторого целого числа \(k\text{.}\) Конечно \( ad\) делится на \(d\text{,}\), как и \(bd\text{.}\) Таким образом, \(kn\) также должно делиться на \(d\text{.}\) Теперь, если \(n\) и \(d\) не имеют общих делителей (кроме 1), то мы должны есть \(d \mid k\text{.}\) Но вообще, если мы попытаемся разделить \(kn\) на \(d\text{,}\), мы не знаем, что получим целое число кратно \(n\text{.}\) Некоторые из \(n\) также могут быть разделены. Чтобы быть в безопасности, давайте разделим столько \(n\), сколько сможем. Возьмите наибольший множитель как \(d\), так и \(n\text{,}\) и сократите его из \(n\text{.}\). Остальные множители \(d\) придут из \(k\text{,}\) без проблем.
Чтобы быть в безопасности, давайте разделим столько \(n\), сколько сможем. Возьмите наибольший множитель как \(d\), так и \(n\text{,}\) и сократите его из \(n\text{.}\). Остальные множители \(d\) придут из \(k\text{,}\) без проблем.
Мы будем называть наибольший делитель как \(d\), так и \(n\) \(\gcd(d,n)\text{,}\) для наибольшего общего делителя . В нашем примере выше \(\gcd(6,8) = 2\), так как наибольший делитель, общий для 6 и 8, равен 2.
Конгруэнтность и деление.
Предположим, \(ad \equiv bd \pmod n\text{.}\) Тогда \(a \equiv b \pmod{\frac{n}{\gcd(d,n)}}\text{.}\)
Если \(d\) и \(n\) не имеют общих делителей, то \(\gcd(d,n) = 1\text{,}\) поэтому \(a \equiv b \pmod n\text{. }\)
Пример 5.2.5.
Упростите следующие сравнения с помощью деления: (a) \(24 \equiv 39 \pmod 5\) и (b) \(24 \equiv 39 \pmod{15}\text{.}\)
Решение(a) И \(24\), и \(39\) делятся на \(3\text{,}\), а \(3\) и \(5\) не имеют общих делителей, поэтому мы получаем
\begin{уравнение*}
8 \экв 13 \pmod 5\текст{. }
\end{уравнение*}
}
\end{уравнение*}
(b) Опять же, мы можем разделить на 3. Однако, делая это вслепую, мы получаем \(8 \equiv 13 \pmod{15}\), что уже неверно. Вместо этого мы также должны разделить модуль 15 на наибольший общий делитель \(3\) и \(15\text{,}\), который равен \(3\text{.}\) Снова получаем
\begin{уравнение*} 8 \экв 13 \pmod 5\текст{.} \end{уравнение*}
Подраздел Решение сравнений
Теперь, когда у нас есть некоторые алгебраические правила для управления отношениями конгруэнтности, мы можем попытаться найти неизвестное в конгруэнтности. Например, существует ли значение \(x\), которое удовлетворяет
\begin{уравнение*} 3x + 2 \экв 4 \pmod{5}\text{,} \end{уравнение*}
и если да, то что это?
В этом примере, поскольку модуль мал, мы могли бы просто попробовать все возможные значения для \(x\text{.}\) На самом деле нужно рассмотреть только 5, так как любое целое число, удовлетворяющее конгруэнтности, может быть заменено любым другим целым числом, сравнимым по модулю 5. Здесь, когда \(x = 4\), мы получаем \(3x + 2 = 14\), которое действительно сравнимо с 4 по модулю 5. Это означает, что \(x = 9\) и \(x = 14\) и \(x = 19\) и т. д. также будут решением, потому что, как мы Как мы видели выше, замена любого числа в конгруэнтности конгруэнтным числом не меняет истинности конгруэнтности.
Здесь, когда \(x = 4\), мы получаем \(3x + 2 = 14\), которое действительно сравнимо с 4 по модулю 5. Это означает, что \(x = 9\) и \(x = 14\) и \(x = 19\) и т. д. также будут решением, потому что, как мы Как мы видели выше, замена любого числа в конгруэнтности конгруэнтным числом не меняет истинности конгруэнтности.
Итак, в этом примере просто вычислите \(3x + 2\) для значений \(x \in \{0,1,2,3,4\}\text{.}\) Это дает 2, 5, 8, 11 и 14 соответственно, для которых только 14 сравнимо с 4.
Давайте также посмотрим, как вы могли бы решить это, используя наши правила алгебры сравнений. Такой подход был бы намного проще, чем тактика проб и ошибок, если бы модуль был больше. Во-первых, мы знаем, что можем вычесть 2 из обеих частей:
\begin{уравнение*} 3x \экв 2 \pmod{5}\текст{.} \end{уравнение*}
Затем, чтобы разделить обе стороны на 3, мы сначала добавляем 0 к обеим сторонам. Конечно, в правой части мы хотим, чтобы 0 равнялся 10 (да, \(10\) действительно равно 0, поскольку они конгруэнтны по модулю 5). Это дает
Это дает
\begin{уравнение*} 3x \эквив 12 \pmod{5}\текст{.} \end{уравнение*}
Теперь разделите обе части на 3. Поскольку \(\gcd(3,5) = 1\text{,}\) нам не нужно менять модуль:
\begin{уравнение*} х \ эквив 4 \ pmod {5} \ text {.} \end{уравнение*}
Обратите внимание, что это на самом деле дает общее решение : не только \(x = 4\text{,}\), но и \(x\) может быть любым числом, сравнимым с 4. Мы можем оставить это так. , или напишите «\(x = 4 + 5k\) для любого целого числа \(k\text{.}\)”
Пример 5.2.6.
Решите следующие сравнения для \(x\text{.}\)
- \(7x \экв 12 \pmod{13}\текст{.}\)
- \(84x — 38 \экв 79 \pmod{15}\text{.}\)
- \(20x \экв 23 \pmod{14}\text{.}\)
Все, что нам нужно сделать, это разделить обе части на 7. Мы многократно прибавляем 13 к правой части, пока не получим число, кратное 7 (добавление 13 равносильно добавлению 0, так что это допустимо). Получаем \(25\text{,}\) \(38\text{,}\) \(51\text{,}\) \(64\text{,}\) \(77\) — понял .
 Итак имеем:
Итак имеем:\begin{уравнение*} \begin{align}7x \amp\equiv 12 \pmod{13} \\ 7x \amp \equiv 77 \pmod{13} \\ х \amp \equiv 11 \pmod{13}. \end{выровнено} \end{уравнение*}
Здесь, поскольку у нас есть числа, превышающие модуль, мы можем уменьшить их до применения какой-либо алгебры. Имеем \(84 \equiv 9\text{,}\) \(38 \equiv 8\) и \(79 \equiv 4\text{.}\) Таким образом,
\begin{уравнение*} \begin{align}84x — 38 \amp\equiv 79 \pmod{15} \\ 9x — 8 \ампер\экв 4 \pmod{15} \\ 9x \amp \equiv 12 \pmod{15} \\ 9x \amp \equiv 72 \pmod{15}.\end{выровнено} \end{уравнение*}
Мы получили 72, добавив \(0 \equiv 60 \pmod{15}\) к обеим частям сравнения. Теперь разделите обе части на 9. Однако, поскольку \(\gcd(9, 15) = 3\text{,}\), мы также должны разделить модуль на 3:
\begin{уравнение*} х \ эквив 8 \ pmod 5 \ текст {.} \end{уравнение*}
Таким образом, решения — это те значения, которые конгруэнтны 8 или, что то же самое, 3 по модулю 5. Это означает, что в некотором смысле существует 3 решения по модулю 15: 3, 8 и 13.
 Мы можем записать решение:
Мы можем записать решение:\begin{уравнение*} х \экв 3 \pmod{15}; ~~ x \экв 8 \pmod{15}; ~~x \equiv 13 \pmod{15}\text{.} \end{уравнение*}
Сначала уменьшите по модулю 14:
\begin{уравнение*} 20x \экв 23 \pmod{14} \end{уравнение*}
\begin{уравнение*} 6x \эквив 9 \pmod{14}\текст{.} \end{уравнение*}
Теперь мы можем разделить обе части на 3 или попытаться увеличить 9 на кратное 14, чтобы получить кратное 6. Если мы разделим на 3, мы получим
.\begin{уравнение*} 2x \эквив 3 \pmod{14}\текст{.} \end{уравнение*}
Теперь попробуйте сложить числа, кратные 14, к 3, в надежде получить число, которое можно разделить на 2.Так не пойдет! Каждый раз, когда мы прибавляем 14 к правой части, результат все равно будет нечетным. Мы никогда не получим четное число, поэтому мы никогда не сможем разделить на 2. Таким образом, у сравнения нет решений.
Последнее сравнение выше иллюстрирует то, как сравнения могут не иметь решений. Мы могли бы увидеть это сразу на самом деле. Посмотрите на исходное соответствие:
Мы могли бы увидеть это сразу на самом деле. Посмотрите на исходное соответствие:
\begin{уравнение*} 20x \экв 23 \pmod{14}\текст{.} \end{уравнение*}
Если мы запишем это как уравнение, мы получим
\begin{уравнение*} 20x = 23 + 14k\текст{,} \end{уравнение*}
или эквивалентно \(20x — 14k = 23\text{.}\) Легко видеть, что решения этого уравнения в целых числах не будет. Левая часть всегда будет четной, а правая – нечетной. Аналогичная проблема возникла бы, если бы правая часть делилась на 90 386 любого числа 90 387, которого не делила бы левая часть.
Итак, в целом, учитывая соответствие
\begin{уравнение*} топор \ эквив б \ pmod {n} \ text {,} \end{уравнение*}
если \(a\) и \(n\) делятся на число, на которое не делится \(b\), то решений не будет.На самом деле нам действительно нужно проверить только один делитель \(a\) и \(n\text{:}\) наибольшего общего делителя. Таким образом, более компактный способ сказать это:
Сравнений без решений.

Если \(\gcd(a,n) \nmid b\text{,}\), то \(ax \equiv b \pmod{n}\) не имеет решений.
Подраздел Решение линейных диофантовых уравнений
Дискретная математика имеет дело с целым числом вещей. Поэтому, когда мы хотим решить уравнения, мы обычно ищем целых решений.2\text{.}\) Целочисленные решения этого уравнения называются пифагорейскими тройками . В общем, решение диофантовых уравнений сложно (фактически не существует доказуемого общего алгоритма для определения того, имеет ли диофантово уравнение решение, результат, известный как теорема Матиясевича). Мы ограничим наше внимание линейными диофантовыми уравнениями, с которыми значительно легче работать.
Диофантовы уравнения.
Уравнение с двумя или более переменными называется Диофантовым уравнением , если интерес представляют только целые числа. линейное диофантово уравнение принимает вид \(a_1x_1 + a_2x_x + \cdots + a_nx_n = b\) для констант \(a_1,\ldots,
а_н, б\текст{. }\)
}\)
Решение диофантова уравнения — это решение уравнения, состоящее только из целых чисел.
У нас есть инструменты, необходимые для решения линейных диофантовых уравнений. Рассмотрим в качестве основного примера уравнение
\begin{уравнение*} 51x + 87y = 123\text{.} \end{уравнение*}
Общая стратегия состоит в том, чтобы преобразовать уравнение в сравнение, а затем решить это сравнение. 4 Давайте рассмотрим этот конкретный пример, чтобы увидеть, как это может работать.
Конечно, это не единственный способ продолжить. Более распространенным методом было бы применение алгоритма Евклида . Наш способ может быть немного быстрее и представлен здесь в первую очередь для разнообразия.
Во-первых, проверьте, нет ли решений, потому что делитель \(51\) и \(87\) не является делителем \(123\text{.}\) Действительно, нам просто нужно проверить, \( \gcd(51, 87) \mid 123\text{.}\) Этот наибольший общий делитель равен 3, и да \(3 \mid 123\text{. }\) В этот момент мы могли бы также вынести этот наибольший общий делитель. Поэтому вместо этого мы решим:
}\) В этот момент мы могли бы также вынести этот наибольший общий делитель. Поэтому вместо этого мы решим:
\begin{уравнение*} 17x + 29y = 41\text{.} \end{уравнение*}
Теперь заметьте, что если будут решения, то для этих значений \(x\) и \(y\text{,}\) две части уравнения должны иметь одинаковый остаток, независимо от того, на что делим. В частности, если мы разделим обе части на 17, мы должны получить тот же остаток.Таким образом, мы можем смело писать
\begin{уравнение*} 17x + 29y \экв 41 \pmod{17}\text{.} \end{уравнение*}
Мы выбираем 17, потому что \(17x\) будет иметь остаток 0. Это позволит нам свести конгруэнтность только к одной переменной. Мы могли бы также перейти к конгруэнтности по модулю 29, хотя обычно есть веская причина выбрать меньший вариант, так как это позволит нам уменьшить другой коэффициент. В нашем случае мы уменьшаем сравнение следующим образом:
\begin{уравнение*}
\begin{align}17x + 29y \amp\equiv 41 \pmod{17} \\
0x + 12y \amp \equiv 7 \pmod{17} \\
12 лет \amp \equiv 24 \pmod{17} \\
y \amp \equiv 2 \pmod{17}. \end{выровнено}
\end{уравнение*}
\end{выровнено}
\end{уравнение*}
Теперь мы знаем, что \(y = 2 + 17k\) будет работать для любого целого числа \(k\text{.}\). Если мы не ошиблись, мы сможем подключить это обратно к нашему исходное диофантово уравнение для нахождения \(x\text{:}\)
\begin{уравнение*} \begin{align}17x + 29(2 + 17k) \amp = 41\\ 17x \amp = -17 — 29\cdot 17k\\ х \амп = -1-29k. \end{выровнено} \end{уравнение*}
Теперь мы нашли все решения диофантова уравнения. Для каждого \(k\text{,}\) \(x = -1-29k\) и \(y = 2 + 17k\) будет удовлетворяться уравнению.Мы могли бы проверить это для нескольких случаев. Если \(k = 0\text{,}\), то решение равно \((-1,2)\text{,}\) и да, \(-17 + 2\cdot 29 = 41\text{.} \) Если \(k = 3\text{,}\), то решение равно \((-88, 53)\text{.}\) Если \(k = -2\text{,}\), мы получаем \ ((57, -32)\текст{.}\)
Подводя итог этому процессу, чтобы решить \(ax + by = c\text{,}\) мы,
Разделите обе части уравнения на \(\gcd(a,b)\) (если при этом правая часть не остается целой, решений нет).
 Предположим, что \(ax + by = c\) уже приведено таким образом.
Предположим, что \(ax + by = c\) уже приведено таким образом.Выберите меньшее из \(a\) и \(b\) (здесь предположим, что это \(b\)) и преобразуйте в сравнение по модулю \(b\text{:}\)
\begin{уравнение*} ax + by \equiv c \pmod{b}\text{.} \end{уравнение*}
Это приведет к совпадению с одной переменной, \(x\text{:}\)
\begin{уравнение*} топор \equiv c \pmod{b}\text{.} \end{уравнение*}
Решите сравнение, как мы это делали в предыдущем разделе. Запишите решение в виде уравнения, например,
.\begin{уравнение*} х = п + кб\текст{.} \end{уравнение*}
Подставьте это в исходное диофантово уравнение и найдите \(y\text{.}\)
Если мы хотим знать решения в определенном диапазоне (например, \(0 \le x, y \le 20\)), выбирайте разные значения \(k\), пока не получите все требуемые решения.
Вот еще пример:
Пример 5.2.7.
Как можно заработать 6,37 доллара, используя только 5-центовые и 8-центовые марки? Какое наименьшее и наибольшее количество марок вы могли бы использовать?
Решение Во-первых, нам нужно диофантово уравнение. Мы будем работать в цифрах центов. Пусть \(x\) будет количеством \(5\)-центовых марок, а \(y\) будет количеством 8-центовых марок. У нас есть:
Мы будем работать в цифрах центов. Пусть \(x\) будет количеством \(5\)-центовых марок, а \(y\) будет количеством 8-центовых марок. У нас есть:
\begin{уравнение*} 5x + 8y = 637\текст{.} \end{уравнение*}
Преобразовать в сравнение и решить:
\begin{уравнение*} \begin{align}8y \amp\equiv 637 \pmod{5}\\ 3y \amp \equiv 2 \pmod 5\\ 3y \amp \equiv 12 \pmod 5\\ y \amp \equiv 4 \pmod 5. \end{выровнено} \end{уравнение*}
Таким образом, \(y = 4 + 5k\text{.}\) Тогда \(5x + 8(4+5k) = 637\text{,}\) так что \(x = 121 — 8k\text{.}\)
Здесь говорится, что один из способов заработать 6,37 доллара — взять 121 5-центовую марку и 4 8-центовые марки. Чтобы найти наименьшее и наибольшее количество штампов, попробуйте разные значения \(k\text{.}\)
.| \(к\) | \((х,у)\) | Марки |
| -1 | (129, -1) | невозможно |
| 0 | (121, 4) | 125 |
| 1 | (113, 9) | 122 |
| 2 | (105, 13) | 119 |
| \(\вдоц\) | \(\вдоц\) | \(\вдоц\) |
Это неудивительно. Наличие наибольшего количества марок означает, что у нас есть как можно больше 5-центовых марок, а для получения наименьшего количества марок потребуется иметь наименьшее количество 5-центовых марок. Чтобы минимизировать количество 5-центовых марок, мы хотим выбрать \(k\) так, чтобы \(121-8k\) было как можно меньше (но все же положительно). Когда \(k = 15\text{,}\) мы имеем \(x = 1\) и \(y = 79\text{.}\)
Наличие наибольшего количества марок означает, что у нас есть как можно больше 5-центовых марок, а для получения наименьшего количества марок потребуется иметь наименьшее количество 5-центовых марок. Чтобы минимизировать количество 5-центовых марок, мы хотим выбрать \(k\) так, чтобы \(121-8k\) было как можно меньше (но все же положительно). Когда \(k = 15\text{,}\) мы имеем \(x = 1\) и \(y = 79\text{.}\)
Таким образом, чтобы заработать 6,37 доллара, вы можете использовать всего 80 марок (1 марка по 5 центов и 79 марок по 8 центов) или целых 125 марок (121 марка по 5 центов и 4 марки по 8 центов).
Используя этот метод, если вы можете решать линейные сравнения с одной переменной, вы можете решать линейные диофантовы уравнения с двумя переменными. Однако бывают случаи, когда решение линейной конгруэнтности требует много работы. Например, предположим, что вам нужно решить
\begin{уравнение*} 13x \экв 6 \pmod{51}\текст{.} \end{уравнение*}
Вы могли бы продолжать прибавлять 51 к правой части, пока не получите число, кратное 13: вы получите 57, 108, 159, 210, 261, 312, и 312 — первое из них, которое делится на 13. Это работает, но на самом деле слишком много работы. Вместо этого мы могли бы преобразовать обратно в диофантово уравнение:
Это работает, но на самом деле слишком много работы. Вместо этого мы могли бы преобразовать обратно в диофантово уравнение:
\begin{уравнение*} 13x = 6 + 51k\text{.} \end{уравнение*}
Теперь решите это , как в этом разделе. Запишите это как сравнение по модулю 13:
\begin{уравнение*} \begin{align}0 \amp \equiv 6 + 51k \pmod{13}\\ -12k \amp \equiv 6 \pmod{13}\\ 2k \amp \equiv -1 \pmod{13}\\ 2k \amp \equiv 12 \pmod{13}\\ k \amp \equiv 6 \pmod{13}. \end{выровнено} \end{уравнение*}
, так что \(k = 6 + 13j\text{.}\) Теперь вернитесь и вычислите \(x\text{:}\)
\begin{уравнение*} \begin{align}13x \amp = 6 + 51(6+13j)\\ х \амп = 24 + 51j. \end{выровнено} \end{уравнение*}
Конечно, вы можете переключаться между сравнениями и диофантовыми уравнениями сколько угодно раз. Если бы вы использовали эту технику только , вы, по сути, воспроизвели бы алгоритм Евклида, более стандартный способ решения диофантовых уравнений.
Упражнения Упражнения
1.
Предположим, что \(a\text{,}\) \(b\text{,}\) и \(c\) являются целыми числами. Докажите, что если \(a \mid b\text{,}\), то \(a \mid bc\text{.}\)
РешениеДоказательство.
Предположим, что \(a \mid b\text{.}\) Тогда \(b\) кратно \(a\text{,}\) или, другими словами, \(b = ak\) для некоторого \ (k\text{.}\) Но тогда \(bc = akc\text{,}\) и поскольку \(kc\) является целым числом, это говорит о том, что \(bc\) кратно \(a\text {.}\) Другими словами, \(a \mid bc\text{.}\)
2.
Предположим, что \(a\text{,}\) \(b\text{,}\) и \(c\) являются целыми числами.Докажите, что если \(a \mid b\) и \(a \mid c\), то \(a \mid b+c\) и \(a \mid b-c\text{.}\)
3.
Выписать оставшиеся классы для \(n = 4\text{.}\)
Решение\(\{\ldots, -8, -4, 0, 4, 8, 12, \ldots\}\text{,}\) \(\{\ldots, -7, -3, 1, 5, 9, 13, \ldots\}\text{,}\)
\(\{\ldots, -6, -2, 2, 6, 10, 14, \ldots\}\text{,}\) и \(\{\ldots, -5, -1, 3, 7 , 11, 15, \ldots\}\text{. }\)
}\)
4.
Какое наибольшее \(n\) такое, что \(16\) и \(25\) принадлежат одному и тому же остаточному классу по модулю \(n\text{?}\) Выпишите остаточный класс, которому они оба принадлежат, и приведите пример числа больше 100 в этом классе.
5.
Пусть \(a\text{,}\) \(b\text{,}\) \(c\text{,}\) и \(n\) — целые числа. Докажите, что если \(a \equiv b \pmod{n}\) и \(c \equiv d \pmod{n}\text{,}\), то \(ac \equiv bd \pmod{n}\text{ .}\)
РешениеДоказательство.
Предположим, что \(a \equiv b \pmod n\) и \(c \equiv d \pmod n\text{.}\) Это означает \(a = b + kn\) и \(c = d + jn\ ) для некоторых целых чисел \(k\) и \(j\text{.}\) Рассмотрим \(ac\text{.}\) Имеем:
\begin{уравнение*} a-c = b+kn — (d+jn) = b-d + (k-j)n\text{.2 \эквив 2 \pmod 4\текст{.}\) Решение
Для всех из них просто подставьте все целые числа от 0 до модуля, чтобы увидеть, какие из них работают.
Нет решений.
- \(x = 2\text{,}\) \(x = 5\text{,}\) \(x = 8\text{.
 }\)
}\) Нет решений.
9.
Определите, какие из следующих сравнений имеют решения, и найдите любые решения (от 0 до модуля) методом проб и ошибок.
- \(4x \equiv 5 \pmod 7\text{.2 \эквив 2 \pmod 7\текст{.}\)
10.
Решите следующее сравнение \(5x + 8 \equiv 11 \pmod{22}\text{.}\) То есть опишите общее решение.
Решение\(x = 5+22k\) для \(k \in \Z\text{.}\)
11.
Решите сравнение: \(6x \equiv 4 \pmod{10}\text{.}\)
12.
Решите сравнение: \(4x \equiv 24 \pmod{30}\text{.}\)
Решение\(x = 6 + 15k\) для \(k \in \Z\text{.}\)
13.
Решите сравнение: \(341x \equiv 2941 \pmod{9}\text{.}\)
ПодсказкаСначала уменьшите каждое число по модулю 9, что можно сделать, сложив цифры чисел.
14.
Я думаю о числе. Если вы умножите мое число на 7, прибавите 5 и разделите результат на 11, у вас останется остаток 2. Какой остаток вы получите, если разделите мое исходное число на 11?
Решение Мы должны решить \(7x + 5 \equiv 2 \pmod{11}\text{. }\) Это дает \(x \equiv 9 \pmod{11}\text{.}\) В общем, \( x = 9 + 11k\text{,}\), но при делении любого такого \(x\) на 11 в остатке будет 9.
}\) Это дает \(x \equiv 9 \pmod{11}\text{.}\) В общем, \( x = 9 + 11k\text{,}\), но при делении любого такого \(x\) на 11 в остатке будет 9.
15.
Решите следующее линейное диофантово уравнение, используя модульную арифметику (опишите общие решения).
\begin{уравнение*} 6x + 10y = 32\text{.} \end{уравнение*}
РешениеРазделить на 2: \(3x + 5y = 16\text{.}\) Преобразовать в сравнение по модулю 3: \(5y \equiv 16 \pmod 3\text{,}\), которое сводится к \( 2y \equiv 1 \pmod 3\text{.}\) Итак, \(y \equiv 2 \pmod 3\) или \(y = 2 + 3k\text{.}\) Вставьте это обратно в \(3x + 5y = 16\) и найдите \(x\text{,}\), чтобы получить \(x = 2-5k\text{.}\) Таким образом, общее решение: \(x = 2-5k\) и \(y = 2+3k\) для \(k \in \Z\text{.}\)
16.
Решите следующее линейное диофантово уравнение, используя модульную арифметику (опишите общие решения).
\begin{уравнение*} 17x + 8y = 31\text{.} \end{уравнение*}
17.
Решите следующее линейное диофантово уравнение, используя модульную арифметику (опишите общие решения).
\begin{уравнение*} 35x + 47y = 1\текст{.} \end{уравнение*}
18.
У вас есть 13 унций. бутылка и 20 унций. бутылка, с помощью которой вы хотите измерить ровно 2 унции. Однако у вас ограниченный запас воды. Если какая-либо вода попадает в любую из бутылок, а затем выливается, она исчезает навсегда. С каким наименьшим количеством воды вы можете начать и при этом выполнить задание?
ПодсказкаРешите диофантово уравнение \(13x + 20 y = 2\) (почему?). Затем рассмотрим, какое значение \(k\) (параметр в решении) является оптимальным.
.

 5
5  }\)
}\) Итак имеем:
Итак имеем: Мы можем записать решение:
Мы можем записать решение: Предположим, что \(ax + by = c\) уже приведено таким образом.
Предположим, что \(ax + by = c\) уже приведено таким образом. }\)
}\)