6 класс Математика. Решение задач с помощью кругов Эйлера | Презентация к уроку по математике (6 класс):
Конспект урока
6 класс
Предмет: Математика
Тема: Решение задач с помощью кругов Эйлера
Здравствуйте, ребята! Сегодня на занятии мы с вами познакомимся с новым для вас методом решения логических задач — кругами Эйлера. Мы научимся решать некоторые из тех задач, которые входят в группу конкурсных и олимпиадных. Целью нашего урока: является познакомиться с решением простейших логических задач методом кругов.
Разминка
Устно:
- Кирпич весит 3кги ещё полкирпича. Сколько весит кирпич?
- Два спортсмена на соревновании пробежали по стадиону 8 кругов. Сколько кругов пробежал каждый?
- Назовите два числа, разность которых равна их сумме.
- Сколько будет: два плюс пять умножить на три?
Изучение нового материала
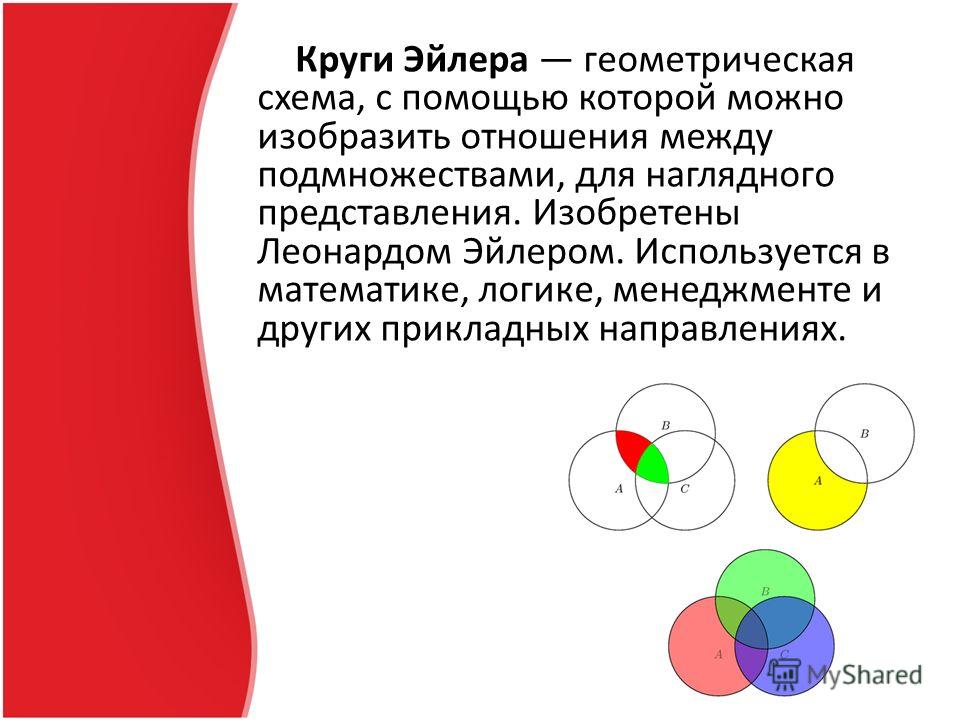
В математике рисунки в виде кругов, изображающих множества, используются очень давно.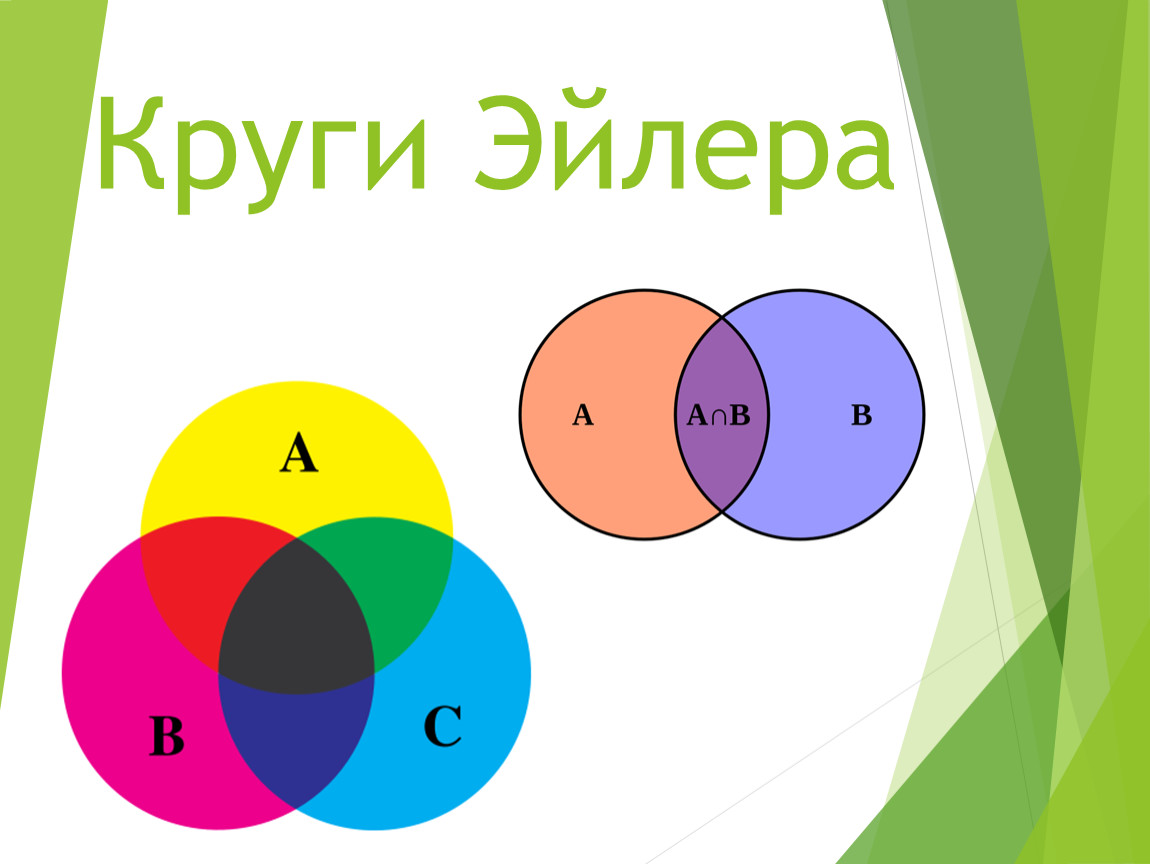 Одним из первых, кто пользовался этим методом, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц (1646-1716). В его черновых набросках были обнаружены рисунки с такими кругами. Затем этот метод довольно основательно развил и Леонард Эйлер. Он долгие годы работал в Петербургской Академии наук.
Одним из первых, кто пользовался этим методом, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц (1646-1716). В его черновых набросках были обнаружены рисунки с такими кругами. Затем этот метод довольно основательно развил и Леонард Эйлер. Он долгие годы работал в Петербургской Академии наук.
Для наглядной геометрической иллюстрации понятий и соотношений между ними используется диаграммы Эйлера-Венна (круги Эйлера). Если имеются какие-либо понятия А, В, С и т.д., то объем каждого понятия (множество) можно представить в виде круга, а отношения между этими объектами (множествами) — в виде пересекающихся кругов.
Перед решением задачи ответьте сначала на следующие вопросы:
- О скольких множествах идет речь в данной задаче?
- Какие из перечисленных в задаче данных относятся к разным множествам одновременно?
Задачи разобрать и записать в тетрадь с правильным оформлением: дано, рисунок (круги Эйлера), решение, ответ.
Задача 1. Домашние любимцы. У всех моих подруг есть домашние питомцы. Шестеро из них любят и держат кошек, а пятеро — собак. И только у двоих есть и те и другие. Угадайте, сколько у меня подруг?
Домашние любимцы. У всех моих подруг есть домашние питомцы. Шестеро из них любят и держат кошек, а пятеро — собак. И только у двоих есть и те и другие. Угадайте, сколько у меня подруг?
Решение: Изобразим два круга, так как у нас два вида питомцев. В одном будем фиксировать владелиц кошек, в другом — собак. Поскольку у некоторых подруг есть и те, и другие животные, то круги нарисуем так, чтобы у них была общая часть. В этой общей части ставим цифру 2 так как кошки и собаки есть у двоих. В оставшейся части «кошачьего» круга ставим цифру 4 (6 — 2 = 4). В свободной части «собачьего» круга ставим цифру 3 (5 — 2 = 3). А теперь рисунок сам подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг.
Ответ. 9 подруг.
Задача 2. Библиотеки. В классе 30 учеников. Все они являются читателями школьной и районной библиотек. Из них 20 ребят берут книги в школьной библиотеке, 15 — в районной. Сколько учеников не являются читателями школьной библиотеки?
Решение: Пусть круг Ш изображает читателей только школьной библиотеки, круг Р — только районной. Тогда ШР — изображение читателей и районной, и школьной библиотек одновременно. Из рисунка следует, что число учеников, не являющихся читателями школьной библиотеки, равно:
Тогда ШР — изображение читателей и районной, и школьной библиотек одновременно. Из рисунка следует, что число учеников, не являющихся читателями школьной библиотеки, равно:
(не Шк.биб) = Р — ШР.
Всего 30 учеников,
Ш = 20 человек,
Р = 15 человек.
Тогда значение ШР может быть найдено так (см. рисунок): ШР = (Ш + Р) — 30 = (20 + 15) — 30 = 5, т.е. 5 учеников являются читателями школьной и районной библиотек одновременно.
Тогда (не Шк.биб) = Р — ШР= 15 — 5= 10.
Ответ: 10 учеников не являются читателями школьной библиотеки.
Задача 3. Любимые мультфильмы. Среди школьников пятого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: «Белоснежка и семь гномов», «Винни Пух», «Микки Маус». Всего в классе 28 человек. «Белоснежку и семь гномов» выбрали 16 учеников, среди которых трое назвали еще «Микки Маус», шестеро — «Винни Пух», а один написал все три мультфильма. Мультфильм «Микки Маус» назвали 9 ребят, среди которых пятеро выбрали по два мультфильма. Сколько человек выбрали мультфильм «Винни Пух»?
Сколько человек выбрали мультфильм «Винни Пух»?
Решение: В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Только «Белоснежку» выбрали 16-6-3-1=6 человек. Только «Микки-Маус» выбрали 9-3-2-1=3 человека.
Только «Винни-Пух» выбрали 28-(6+3+3+2+6+1)=7 человек. Тогда, учитывая, что некоторые выбрали по несколько мультфильмов, получаем, что «Винни-Пух» выбрали 7+6+1+2=16 человек.
Задачи на оценку:
Задача 1. Спортивный класс. В классе 35 учеников. 24 из них играют в футбол, 18 — в волейбол, 12 — в баскетбол. 10 учеников одновременно играют в футбол и волейбол, 8 — в футбол и баскетбол, а 5 — в волейбол и баскетбол. Сколько учеников играют и в футбол, и в волейбол, и в баскетбол одновременно?
Задача 2. Из 40 учащихся нашего класса 32 любят молоко, 21 – лимонад, а 15 – и молоко, и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?
Задача 3. 12 моих одноклассников любят читать детективы , 18 – фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?
Сколько учеников в нашем классе?
Домашнее задание:
Задача 1. Хобби. Из 24 учеников 5 класса музыкальную школу посещают 10 человек, художественную школу — 8 человек, спортивную школу — 12 человек, музыкальную и художественную школу- 3, художественную и спортивную школу — 2, музыкальную и спортивную школу — 2, все три школы посещает 1 человек. Сколько учеников посещают только одну школу? Сколько учащихся ни в чем себя не развивают?
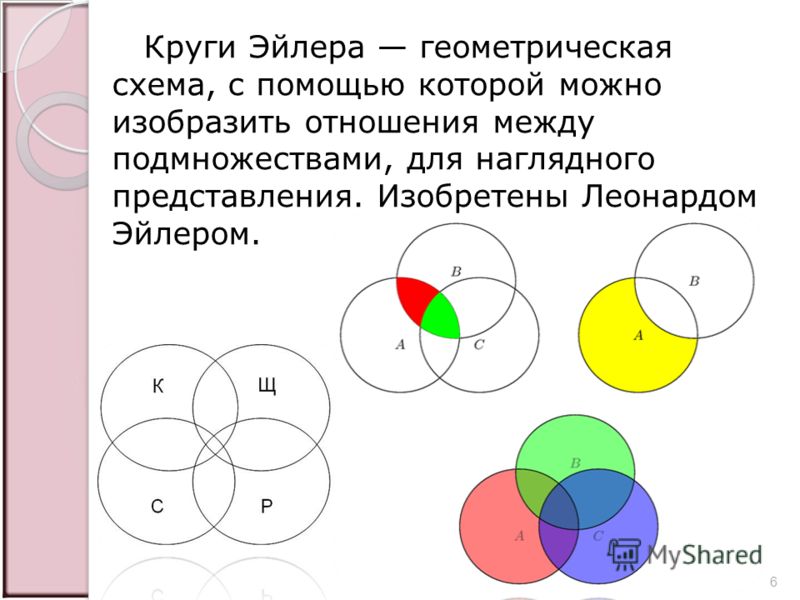
Круги Эйлера в информатике
Сегодня разберём задачи на круги Эйлера в информатике.
Леонард Эйлер — швейцарский, немецкий и российский математик и механик, сыгравший огромную роль в развитии этих наук.
Задача (Простая)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Пушкин | 3500 |
| Лермонтов | 2000 |
| Пушкин | Лермонтов | 4500 |
Какое количество страниц (в тысячах) будет найдено по запросу Пушкин & Лермонтов? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
Видим, что по запросу «Пушкин» в поисковике нашлось 3500 страниц. По запросу «Лермонтов» — 2000 страниц.
Запрос «Пушкин | Лермонтов» обозначает, что поисковик выдаст страницы, где есть слова про «Пушкина», и страницы, где есть слова про «Лермонтова», а так же могут быть страницы, где написано и про «Пушкина», и про «Лермонтова» одновременно.
Если сложить страницы, в которых написано про «Пушкина» и про «Лермонтова» получается 3500 + 2000 = 5500 страниц. Но почему же при запросе «Пушкин | Лермонтов» получается меньше страниц, всего 4500 ?
Этот факт обозначает то, что когда мы подсчитывали страницы про «Пушкина» (3500 страниц), мы подсчитали и те страницы, где было написано и про «Пушкина», и про «Лермонтова» одновременно.
Тоже самое и для количества страниц, где написано про «Лермонтова» (2000 страниц). В этом числе находятся и те, в которых одновременно упоминается и про «Пушкина», и про «Лермонтова».
В вопросе спрашивается, сколько страниц будет по запросу «Пушкин & Лермонтов«. Это обозначает, что как раз нужно найти количество страниц, где будет одновременно написано и про «Пушкина», и про «Лермонтова».
Это обозначает, что как раз нужно найти количество страниц, где будет одновременно написано и про «Пушкина», и про «Лермонтова».
Отсюда получается:
Пушкин & Лермонтов = (3500 + 2000) — 4500 = 5500 — 4500 = 1000 страниц.
Это и будет ответ!
Теперь решим эту задачу с помощью Кругов Эйлера!
У нас всего есть две сущности: «Пушкин» и «Лермонтов». Поэтому рисуем два пересекающихся круга, желательно разными цветами.
Объединение двух кругов в общую фигуру (показано фиолетовым цветом), показывает операцию «Пушкин | Лермонтов». Эта операция всегда стремится увеличить площадь, объединить площади других фигур!
Обратите внимание, что круги пересекаются, из-за этого сумма площадей двух кругов по отдельности (3500 + 2000 = 5500) больше чем у фигуры, которая характеризует логическую операцию «ИЛИ» «Пушкин | Лермонтов» (4500).
Нужно найти площадь фигуры Пушкин & Лермонтов, которая закрашена золотистым цветом. Данная логическая операция «И» стремится уменьшить площадь. Она обозначает общую площадь других фигур.
Данная логическая операция «И» стремится уменьшить площадь. Она обозначает общую площадь других фигур.
Найдём сначала заштрихованную часть синего круга. Она равна: площадь фиолетовой фигуры (4500) минус площадь красного круга (3500).
Теперь легко найти площадь золотистой фигуры. Для этого нужно от площади синего круга вычесть площадь заштрихованной части. Получается:
Пушкин & Лермонтов (Количество страниц) = 2000 — 1000 = 1000
Получается, что по запросу Пушкин & Лермонтов будет найдено 1000 страниц.
Ответ: 1000
Рассмотрим ещё одну не сложную разминочную задачу.
Задача (Разминочная)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Кокос | Ананас | 3400 |
| Кокос & Ананас | 900 |
| Кокос | 2100 |
Какое количество страниц (в тысячах) будет найдено по запросу Ананас?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
Найдём заштрихованную часть красного круга.
Весь красный круг 2100. Золотистая область равна 900. Заштрихованная часть равна 2100 — 900 = 1200.
После того, как нашли заштрихованную часть (такой полумесяц), можно найти уже площадь синего круга. Для этого нужно от площади фиолетовой фигуры отнять площадь заштрихованной части!
Ананас (Количество страниц) = 3400 — 1200 = 2200
Ответ: 2200
Разберём классическую задачу из информатики по кругам Эйлера.
Задача (Классическая)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| (Космос & Звезда) | (Космос & Планета) | 1100 |
| Космос & Планета | 600 |
| Космос & Планета & Звезда | 50 |
Какое количество страниц (в тыс. ) будет найдено по запросу Космос & Звезда?
) будет найдено по запросу Космос & Звезда?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
В этой задаче у нас три сущности: Космос, Планета, Звезда. Поэтому рисуем три круга Эйлера, которые пересекаются между собой.
Могут ли круги не пересекаться ? Могут! Если мы докажем, что площади по отдельности двух кругов в сумме дают площадь фигуры, которая получается при применении операции логического «ИЛИ».
Теперь отметим на нашем рисунке запрос (Космос & Звезда) | (Космос & Планета).
Сначала отменим для себя то, что находится в скобках. Первое Космос & Звезда
Теперь отметим вторую скобку Космос & Планета.
В выражении (Космос & Звезда) | (Космос & Планета) две скобки соединяет знак логического «ИЛИ». Значит, эти две области нужно объединить! Область (Космос & Звезда) | (Космос & Планета) отмечена фиолетовым цветом!
Отметим Космос & Планета ещё раз, т. к. для этого выражения известно количество страниц.
к. для этого выражения известно количество страниц.
Площадь фигуры для выражения Космос & Планета & Звезда будет очень маленькая. Это общая часть для всех трёх кругов. Отметим её оранжевым цветом! Каждая точка этой фигуры должна одновременно быть в трёх кругах!
Найти нужно Космос & Звезда. Отменим на рисунке чёрным цветом ту область, которую нужно найти. Мы эту область уже отмечали салатовым цветом.
Теперь у нас есть все компоненты, чтобы решить эту задачу.
Найдём заштрихованную область.
Вся область Космос & Планета равна 600. А заштрихованная часть равна: область Космос & Планета (600) минус оранжевая область (50).
Количество страниц в заштрихованной части = 600 — 50 = 550
Тогда черная область легко находится: фиолетовая область (1100) минус заштрихованная область (550).
Количество страниц (при запросе Космос & Звезда) = 1100 — 550 = 550
Ответ: 550
Закрепляем материал по задачам на Круги Эйлера.
Задача (На закрепление)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Море & Солнце | 290 |
| Море & Пляж | 355 |
| Море & (Пляж | Солнце) | 465 |
Какое количество страниц (в тысячах) будет найдено по запросу Море & Пляж & Солнце? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
В задаче используются три сущности: Море, Пляж, Солнце. Поэтому нарисуем три пересекающихся круга Эйлера.
Отметим все области для которых нам даны количество страниц.
В начале отметим Море & (Пляж | Солнце). Для начало нарисуем область, которая в скобках (Пляж | Солнце)
Теперь нужно очертить общую часть фиолетовой области и зелёного круга и получится Море & (Пляж | Солнце). Отметим оранжевым цветом.
Теперь отметим Море & Пляж.
Теперь отметим Море & Солнце.
Найти нужно ту область, которая получается в результате выделения общей части для всех трёх кругов! Обозначим её чёрным цветом!
Найдём заштрихованную область!
Количество страниц (в заштрихованной области) =
= Количество страниц (В оранжевой области) — Море & Солнце =
= 465 — 290 = 175
Чтобы найти искомую чёрную область, нужно из Море & Пляж (355) вычесть заштрихованную область (175).
Количество страниц (Море & Пляж & Солнце) =
=
= 355 — 175 = 180
Ответ: 180
Решим ещё одну тренировочную задачу из информатики на Круги Эйлера.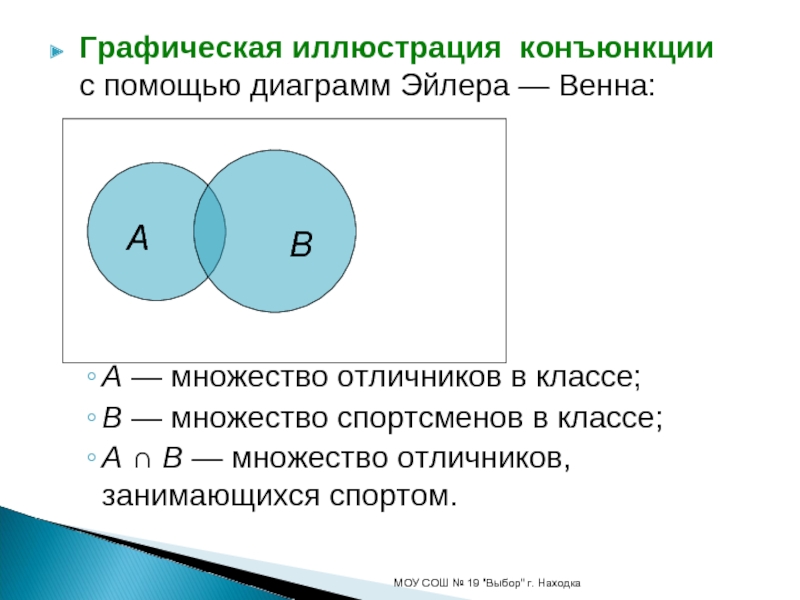
Задача (с 4 сущностями)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Англия & (Уэльс & Шотландия | Ирландия) | 450 |
| Англия & Уэльс & Шотландия | 213 |
| Англия & Уэльс & Шотландия & Ирландия | 87 |
Какое количество страниц (в тысячах) будет найдено по запросу
Англия & Ирландия?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
Нужно нарисовать 4 пересекающихся круга. Сначала нарисуем три круга, как обычно, оставив немного места для четвёртого круга.
Сначала нарисуем три круга, как обычно, оставив немного места для четвёртого круга.
Четвёртый круг для Ирландии нужно нарисовать так, чтобы он проходил через область (Англия & Уэльс & Шотландия). Это нам подсказывает сама таблица, где есть количество страниц для Англия & Уэльс & Шотландия, а так же для Англия & Уэльс & Шотландия & Ирландия.
Нужно отметить на рисунке Англия & (Уэльс & Шотландия | Ирландия). Это будем делать, как всегда поэтапно.
Область Уэльс & Шотландия выглядит так:
Добавим к этой области Ирландию через логическое «ИЛИ». Получается область (Уэльс & Шотландия | Ирландия). Произошло объединение серой области и жёлтого круга!
Теперь нужно сделать операцию логического «И» получившийся области с «Англией». Тогда область Англия & (Уэльс & Шотландия | Ирландия) примет вид:
Т.е. это общее между предыдущем серым контуром и красным кругом!
Отметим Англия & Уэльс & Шотландия — это общая территория трёх кругов: Красного, Синего и Зелёного. Отмечено оранжевым цветом.
Отмечено оранжевым цветом.
Отметим Англия & Уэльс & Шотландия & Ирландия — это общая территория четырёх кругов. Область получается ещё меньше. Если взять точку в этой области, то мы будем находится сразу в четырёх кругах одновременно. Отмечено фиолетовым цветом.
Отметим то, что нужно найти Англия & Ирландия чёрным цветом.
Искомую чёрную область легко найти, если из серой области вычесть кусочек, окрашенный в бирюзовый цвет!
Найдём, сколько страниц приходится на бирюзовый кусочек:
Количество страниц (для бирюзового кусочка) =
= Англия & Уэльс & Шотландия (213) — Англия & Уэльс & Шотландия & Ирландия (87) =
= 213 — 87 = 126
Найдём искомую чёрную область.
Количество станиц (для чёрной области) =
= Англия & (Уэльс & Шотландия | Ирландия) (450) — Количество (для бирюзового кусочка) =
450 — 126 = 324
Это и будет ответ!
Ответ: 324.

Разберём задачу из реального экзамена по информатике, которая была в 2019 году в Москве! (Сейчас в 2021 задачи не встречаются на Круги Эйлера)
Задача (ЕГЭ по информатике, 2019, Москва)
В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:
| Запрос | Найдено страниц (в тысячах) |
| Суфле | 450 |
| Корзина | 200 |
| Эклер | 490 |
| Суфле & Корзина | 70 |
| Суфле & Эклер | 160 |
| Корзина & Эклер | 0 |
Сколько страниц (в тысячах) будет найдено по запросу
Суфле | Корзина | Эклер
Решение:
Видим, что у нас три поисковых разных слова, поэтому будет три разных круга Эйлера!
Так же видим, что логическое «И» между словами Корзина и Эклер даёт 0 страниц. Это значит, что эти круги не пересекаются! Так же круги бы не пересекались, если бы операция логического «ИЛИ» совпадала бы с суммой этих кругов.
Это значит, что эти круги не пересекаются! Так же круги бы не пересекались, если бы операция логического «ИЛИ» совпадала бы с суммой этих кругов.
Видим, что Суфле имеет с двумя кругами пересечения, а Корзина и Эклер не пересекаются.
Отметим всё, что нам дано в условии.
Жёлтым цветом отмечено Суфле | Корзина | Эклер . Объединение всех трёх кругов. Это то, что нужно найти.
Искомая жёлтая фигура складывается из заштрихованных областей и красного круга! Площадь красного круга мы знаем. Нужно найти площади заштрихованных частей.
Левая заштрихованная область находится просто:
Количество страниц (лев. заштрих. область) =
= Эклер (490) — Суфле & Эклер (160) = 330
Так же найдём площадь правой заштрихованной области:
Количество страниц (прав. заштрих. область) =
= Корзина (200) — Суфле & Корзина (70) = 130
Теперь можно найти искомую жёлтую область
Количество страниц (Суфле | Корзина | Эклер) == Красный круг (450) + лев.
 заштрих. область (310) + прав. заштрих. область (130) =
заштрих. область (310) + прав. заштрих. область (130) = = 450 + 330 + 130 = 910
Задача решена, можно писать ответ.
Ответ: 910
Разберём ещё одну задачу из реального ЕГЭ уже 2020 года
Задача (ЕГЭ по информатике, 2020, Москва)
В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:
| Запрос | Найдено страниц (в тысячах) |
| Аврора | 50 |
| Крейсер | 45 |
| Заря | 23 |
| Аврора & Заря | 9 |
| Заря & Крейсер | 0 |
| Заря | Крейсер | Аврора | 93 |
Сколько страниц (в тысячах) будет найдено по запросу
Аврора & Крейсер
Решение:
Количество страниц при запросе Заря & Крейсер равно нулю.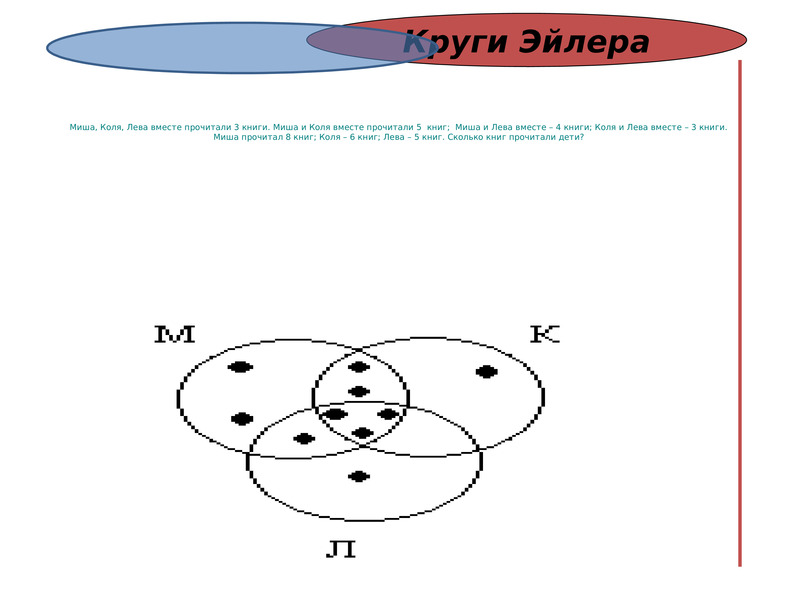 Значит, эти два круга не будут пересекаться.
Значит, эти два круга не будут пересекаться.
Нарисуем все данные на рисунке.
Нужно найти для начала заштрихованную правую часть.
Количество страниц (для двух заштрих. частей) =
З | К | А (93) — Красный круг (50) = 43
Левую заштрихованную область легко найти.
Количество страниц (для левой заштрих. части) =
Синий круг (23) — А & З (9) = 14
Тогда для правой заштрихованной области получается:
Колич. страниц (для правой заштрих. части) =
Колич. страниц (для двух заштрих. частей) (43) — Колич. страниц (для лев. заштрих. части) (14) =
= 43 — 14 = 29
Тогда искомую область легко найти:
Колич. страниц (А & K) =
Зелёный круг (45) — Колич. страниц (для правой заштрих. части) (29) =
45 — 29 = 16
Ответ: 16
На этом всё! Надеюсь, вы теперь будете с удовольствием решать задачи по информатике с помощью Кругов Эйлера.
круги Эйлера — Основы логики и логические основы компьютера
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.Какое количество страниц (в тысячах) будет найдено по запросу Крейсер & Линкор?Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
При помощи кругов Эйлера изобразим условия задачи. При этом цифры 1, 2 и 3 используем, чтобы обозначить полученные в итоге области.
Опираясь на условия задачи, составим уравнения:
Чтобы найти Крейсер & Линкор (обозначенный на чертеже как область 2), подставим уравнение (2) в уравнение (1) и выясним, что:
4800 + 3 = 7000, откуда получаем 3 = 2200.
Теперь этот результат мы можем подставить в уравнение (3) и выяснить, что:
2 + 2200 = 4500, откуда 2 = 2300.
Ответ: 2300 — количество страниц, найденных по запросу Крейсер & Линкор.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
Решение
Для решения задачи отобразим множества Тортов и Пирогов в виде кругов Эйлера.
Обозначим каждый сектор отдельной буквой (А, Б, В).
Из условия задачи следует:
Торты │Пироги = А+Б+В = 12000
Торты & Пироги = Б = 6500
Пироги = Б+В = 7700
Чтобы найти количество Тортов (Торты = А+Б), надо найти сектор А, для этого из общего множества (Торты│Пироги) отнимем множество Пироги.
Торты│Пироги – Пироги = А+Б+В-(Б+В) = А = 1200 – 7700 = 4300
Сектор А равен 4300, следовательно
Торты = А+Б = 4300+6500 = 10800
Задача 3
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| Запрос | Найдено страниц (в тысячах) |
| Пироженое & Выпечка | 5100 |
| Пироженое | 9700 |
| Пироженое | Выпечка | 14200 |
Какое количество страниц (в тысячах) будет найдено по запросуВыпечка?
Для решения задачи отобразим множестваПироженых и Выпечек в виде кругов Эйлера.
Обозначим каждый сектор отдельной буквой (А, Б, В).
Из условия задачи следует:
Пироженое & Выпечка = Б = 5100
Пироженое = А+Б = 9700
Пироженое │ Выпечка = А+Б+В = 14200
Чтобы найти количество Выпечки (Выпечка = Б+В), надо найти секторВ, для этого из общего множества (Пироженое │ Выпечка ) отнимем множество Пироженое.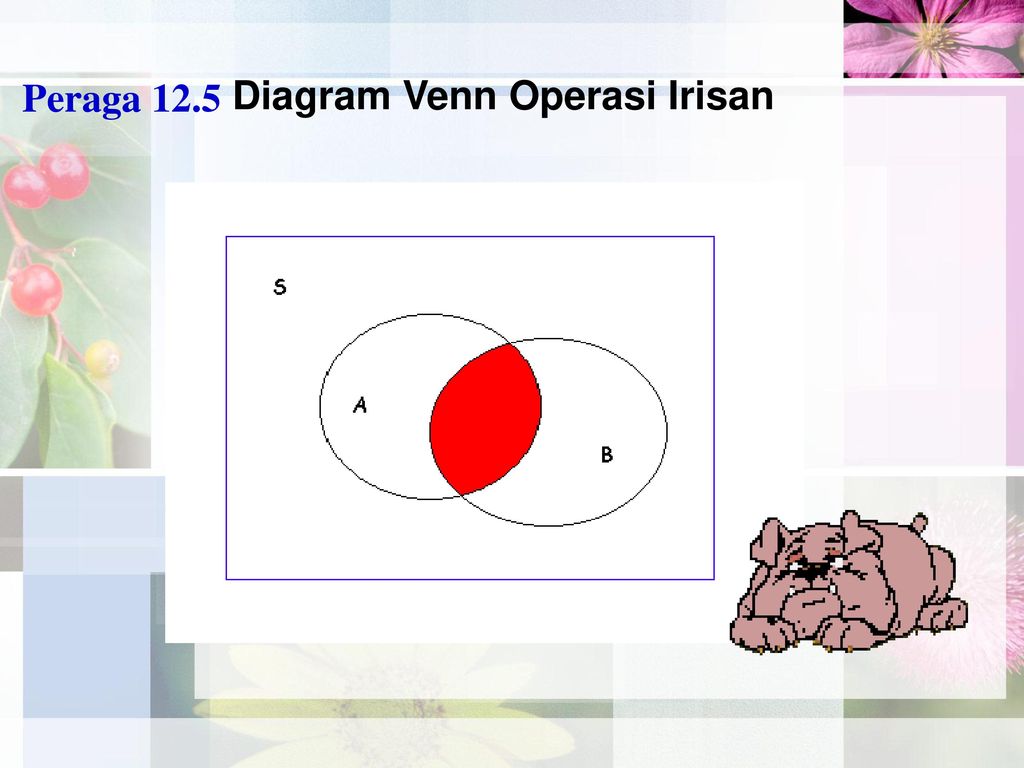
Сектор В равен 4500, следовательно Выпечка = Б + В = 4500+5100 =9600
Задача 4В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | спаниели | (терьеры & овчарки) |
| 2 | спаниели | овчарки |
| 3 | спаниели | терьеры | овчарки |
| 4 | терьеры & овчарки |
Решение
Представим множества овчарок, терьеров и спаниелей в виде кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).
Преобразим условие задачи в виде суммы секторов:
спаниели │(терьеры & овчарки) = Г + Б
спаниели│овчарки = Г + Б + В
спаниели│терьеры│овчарки = А + Б + В + Г
терьеры & овчарки = Б
Из сумм секторов мы видим какой запрос выдал больше количества страниц.
Расположим номера запросов в порядке убывания количества страниц: 3 2 1 4
Задача 5
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | барокко | классицизм | ампир |
| 2 | барокко | (классицизм & ампир) |
| 3 | классицизм & ампир |
| 4 | барокко | классицизм |
Решение
Представим множества классицизм, ампир и классицизм в виде кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).
Преобразим условие задачи в виде суммы секторов:
барокко│ классицизм │ампир = А + Б + В + Гбарокко │(классицизм & ампир) = Г + Б
классицизм & ампир = Б
барокко│ классицизм = Г + Б + А
Из сумм секторов мы видим какой запрос выдал больше количества страниц.
Расположим номера запросов в порядке возрастания количества страниц: 3 2 4 1
Задача 6
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | канарейки | щеглы | содержание |
| 2 | канарейки & содержание |
| 3 | канарейки & щеглы & содержание |
| 4 | разведение & содержание & канарейки & щеглы |
Решение
Для решения задачи представим запросы в виде кругов Эйлера.
K — канарейки,
Щ – щеглы,
С – содержание,
Р – разведение.
Далее будем закрашивать красным цветом сектора согласно запросам, наибольший по величине сектор даст большее количество страниц на запрос.
| канарейки | терьеры | содержание | канарейки & содержание | канарейки & щеглы & содержание | разведение & содержание & канарейки & щеглы |
Самая большая область закрашенных секторов у первого запроса, затем у второго, затем у третьего, а у четвертого запроса самый маленький.
В порядке возрастания по количеству страниц запросы будут представлены в следующем порядке: 4 3 2 1
Обратите внимание что в первом запросе закрашенные сектора кругов Эйлера содержат в себе закрашенные сектора второго запроса, а закрашенные сектора второго запроса содержат закрашенные сектора третьего запроса, закрашенные сектора третьего запроса содержат закрашенный сектор четвертого запроса.
Только при таких условиях мы можем быть уверены, что правильно решили задачу.
Задача 7 (ЕГЭ 2013)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Фрегат | Эсминец | 3400 |
| Фрегат & Эсминец | 900 |
| Фрегат | 2100 |
Какое количество страниц (в тысячах) будет найдено по запросу Эсминец?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Ответ: 2200
Решение: Запрос «Фрегат» обозначим символом «Ф», «Эсминец» — символом «Э».
Э=(Ф|Э)-Ф+(Ф&Э)=3400-2100+900=2200.
Разбор задачи B12 (демо ЕГЭ 2012)
Время выполнения-2 мин, уровень сложности-повышенныйВ языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Шахматы | Теннис | 7770 |
| Теннис | 5500 |
| Шахматы & Теннис | 1000 |
Какое количество страниц (в тысячах) будет найдено по запросу Шахматы?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Ответ: 3270
Решение: Изобразим запросы в виде диаграмм Эйлера-Венна.Запрос «Шахматы» обозначим символом «Ш», «Теннис» — символом «Т».
Ш=(Ш|Т)-Т+(Ш&Т)=7770-5500+1000=3270.
Задачи для самостоятельного решения
Задача 1
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | принтеры & сканеры & продажа |
| 2 | принтеры & продажа |
| 3 | принтеры | продажа |
| 4 | принтеры | сканеры | продажа |
Задача 2
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | физкультура |
| 2 | физкультура & подтягивания & отжимания |
| 3 | физкультура & подтягивания |
| 4 | физкультура | фитнесс |
Круги Эйлера — ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ ПО ИНФОРМАТИКЕ ДЛЯ 5-6 КЛАССОВ — Каталог статей
1.В классе 25 учащихся. Из них 5 человек не умеют играть ни в шашки, ни в шахматы. 18 учащихся умеют играть в шашки, 20 — в шахматы. Сколько учащихся класса играют и в шашки, и в шахматы?2. Каждый из 35 пятиклассников является читателем по
крайней мере одной из двух библиотек: школьной и районной. Из них 25 учащихся
берут книги в школьной библиотеке, 20 — в районной. Сколько из пятиклассников:
Из них 25 учащихся
берут книги в школьной библиотеке, 20 — в районной. Сколько из пятиклассников:
а) не являются читателями школьной библиотеки;
б) не являются читателями районной библиотеки;
в) являются читателями только школьной библиотеки;
г) являются читателями только районной библиотеки;
д) являются читателями обеих библиотек?
3. В одном множестве 40 элементов, а в другом 30. Сколько элементов может быть в их:
а) пересечении;
б) объединении?
4. Каждый ученик в классе изучает либо английский, либо французский язык, либо оба этих языка. Английский язык изучают 25 человек, французский — 27 человек, а тот и другой —18 человек. Сколько всего учеников в классе?
5. На листе бумаги начертили круг площадью 78 см2 и квадрат площадью 55 см2. Площадь пересечения круга и квадрата равна
30 см2.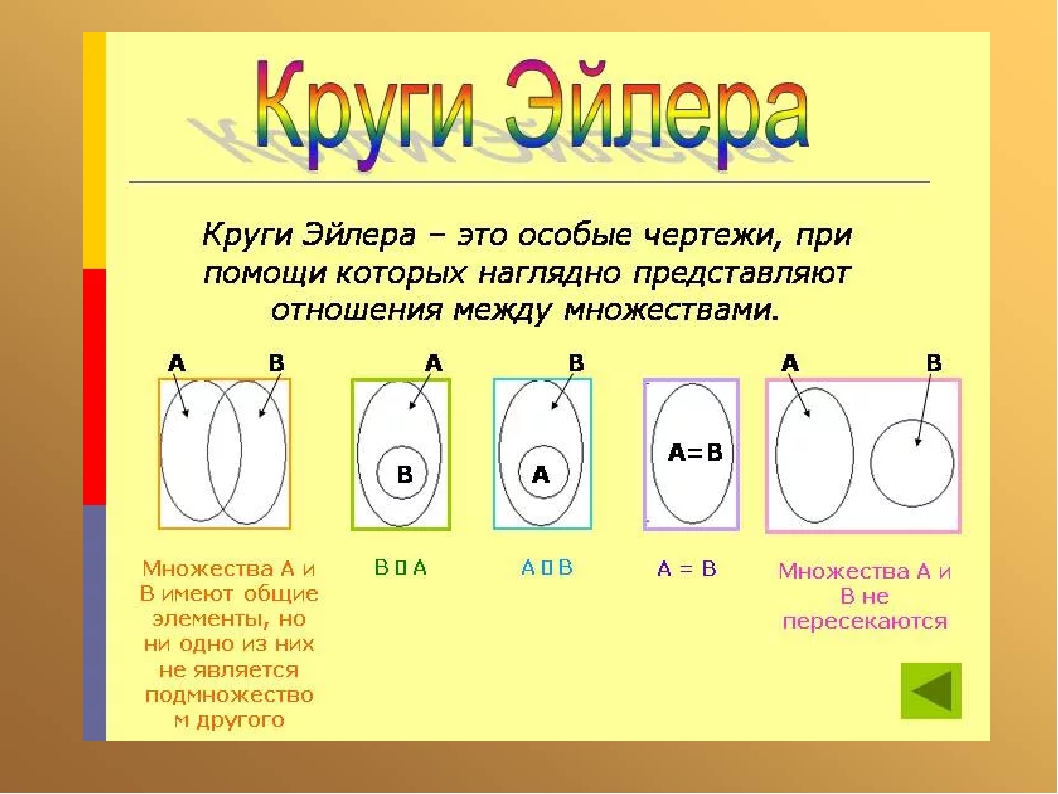 Не занятая кругом и квадратом часть листа имеет площадь 150
см2. Найдите площадь листа.
Не занятая кругом и квадратом часть листа имеет площадь 150
см2. Найдите площадь листа.
6. В бригаде полеводов 25 человек. Среди них 20 человек моложе 30 лет и 15 человек старше 20 лет. Может ли так быть?
7. В детском саду 52 ребенка. Каждый из них любит либо пирожное, либо мороженое, либо и то, и другое. Половина детей любит пирожное, а 20 человек — пирожное и мороженое. Сколько детей любит мороженое?
8. Сколько в классе учащихся, если известно, что лыжным спортом увлекаются 28 человек, отличников в классе — 12, причем отличников-спортсменов, увлекающихся лыжами, — 10?
9. 37 школьников из ученической производственной бригады изъявили желание летом работать на уборке зерновых. Каждый из них имеет права для работы на тракторе или на комбайне, а некоторые могут работать и на тракторе, и на комбайне. Сколько школьников могут работать и на тракторе, и на комбайне, если известно, что трактором хорошо овладели 23 человека, а комбайном — 31 человек?
В ученической
производственной бригаде 86 старшеклассников. 8 из них не умеют работать ни на
тракторе, ни на комбайне. 54 ученика хорошо овладели трактором, 62 — комбайном.
Сколько человек из этой бригады могут работать и на тракторе, и на комбайне?
8 из них не умеют работать ни на
тракторе, ни на комбайне. 54 ученика хорошо овладели трактором, 62 — комбайном.
Сколько человек из этой бригады могут работать и на тракторе, и на комбайне?
В классе 35 учеников, каждый из которых любит футбол, волейбол или баскетбол, а некоторые — два или даже три из этих видов спорта. 24 ученика любят футбол, 18 — волейбол, 12 — баскетбол. При этом 10 учеников одновременно любят футбол и волейбол, 8 — футбол и баскетбол, а 5 — волейбол и баскетбол. Сколько учеников этого класса любят все три вида спорта?
В классе 36 учеников. Многие из них посещают кружки: физический (14 человек), математический (18 человек), химический (10 человек). Кроме того, известно, что 2 человека посещают все три кружка; из тех, кто посещает два кружка, 8 человек занимаются в математическом и физическом кружках, 5 — в математическом и химическом, 3 — в физическом и химическом. Сколько человек не посещают никаких кружков?
10. Сто шестиклассников нашей школы участвовали в опросе, в ходе которого
выяснялось, какие компьютерные игры им нравятся больше: симуляторы, квесты или
стратегии. В результате 20 опрошенных назвали симуляторы, 28 — квесты, 12 —
стратегии. Выяснилось, что 13 школьников отдают одинаковое предпочтение
симуляторам и квестам, 6 учеников — симуляторам и стратегиям, 4 ученика —
квестам и стратегиям, а 9 ребят совершенно равнодушны к названным компьютерным
играм. Некоторые из школьников ответили, что одинаково увлекаются и симуляторами,
и квестами, и стратегиями. Сколько таких ребят?
Сто шестиклассников нашей школы участвовали в опросе, в ходе которого
выяснялось, какие компьютерные игры им нравятся больше: симуляторы, квесты или
стратегии. В результате 20 опрошенных назвали симуляторы, 28 — квесты, 12 —
стратегии. Выяснилось, что 13 школьников отдают одинаковое предпочтение
симуляторам и квестам, 6 учеников — симуляторам и стратегиям, 4 ученика —
квестам и стратегиям, а 9 ребят совершенно равнодушны к названным компьютерным
играм. Некоторые из школьников ответили, что одинаково увлекаются и симуляторами,
и квестами, и стратегиями. Сколько таких ребят?
Конспект занятия «Решение логических задач с помощью кругов Эйлера» 6 класс
Тема: Решение логических задач с помощью кругов Эйлера.
Цели: 1. Рассмотрим новый тип задач;
2. Круги Эйлера, историческая справка;
3. Повторим операции над множествами;
4. Исследовать задачи по теме: «на какой вопрос можно
ответить по этим данным?»
5. Показать практическое применение, решить проблему:
Показать практическое применение, решить проблему:
«Возможно или нет?».
Ход занятия.
1. Решить задачу: «Из 52 школьников 23 собирают значки, 35 собирают марки, а
16 и значки, и марки. Остальные не увлекаются коллекцио-
нированием. Сколько школьников не увлекаются коллекцио-
нированием?».
а) Можно ли решить задачу традиционными способами?
б) Эта задача на операции над множествами.
в) Историческая справка. На экране фотография Леонарда Эйлера. Учитель
кратко излагает его биографию .
г) Повторение операций над множествами: а) АUВ; б) А∩В; в) АכВ; г)А\D.
д) Изобразим множества из задачи. (На доске учащиеся рисуют два круга,
имеющих общую часть. На них записывают данные.)
е) решаем задачу. Какие различные выражения можно составить для решения
задачи?
1) 52-23-(35-16)
2) 52-35-(23-16) 10 учеников
3) 52-(23-16)-(35-16)
2. Изобразить на кругах Эйлера ситуацию, придумать вопросы и
Изобразить на кругах Эйлера ситуацию, придумать вопросы и
ответить
на них.
а) В понедельник в магазине 12 человек купили только телефоны, 4 человека
только автоответчики, а 5 человек – телефон с автоответчиком.
1) Сколько купили телефон?
2) Сколько купили автоответчик?
3) Сколько было покупателей?
б) все 10 человек, которые во вторник купили телефон, купили и
Урок 6 — Информатика 7 класс г Рогачева
Операции над множествами.
Теоретическая часть
Для множеств, как и для высказываний, определены свои операции.
Два множества А и В равны (А=В), если они состоят из одних и тех же элементов.Например, если А={1,2,3,4}, B={3,1,4,2} то А=В.
Пересечение множеств характеризуется логической связкой И и обозначается значком ∩
Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В.
Объединением (суммой) множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств.
Например, если А={1,2,4}, B={3,4,5,6}, то А ∪ B = {1,2,3,4,5,6}
Например, если А={1,2,3,4}, B={3,4,5}, то А\В = {1,2}. Разность А\В читаются следующим образом: «а без бэ».
Видео Операции над множествами
Практическая работа
Задание 1. Даны множества A={a, e, f, j, k}, B={f, i, j, l, y}, С={j, k, l, y}, D={i, j, s, t, u, y, z}.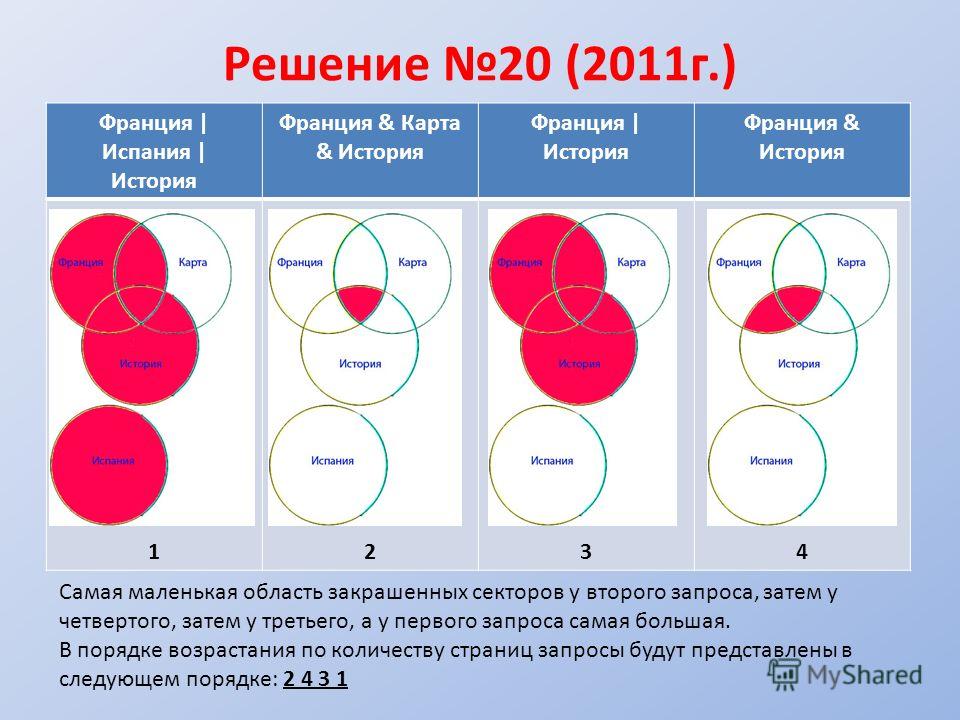 Найдите:
Найдите:
- А ∪ В
- А ∩ В
- C ∩ B
- A ∪ D
- (A ∩ C) ∪ (B ∩ C)
Для каждого задания постройте круги Эйлера.
Задание 2. Даны множества:
Множество обитателей моря: А = {кит, акула, дельфин, медуза, краб}.
Множество млекопитающих: В = {корова, собака, кит, кошка, дельфин}.
Найдите и постройте круги Эйлера для этих множеств:
- А ∪ В
- А ∩ В
Определите истинность высказываний:
а) Кит — обитатель моря или кит — млекопитающее.
б) Дельфин — обитатель моря и дельфин — млекопитающее.
в) Краб — обитатель моря и краб — млекопитающее.
г) Кошка — обитатель моря или кошка — млекопитающее
Электронная рабочая тетрадь
Проверка знаний
Использование метода кругов Эйлера (диаграмм Эйлера–Венна) при решении задач в курсе информатики и ИКТ
1. Введение
В курсе Информатики и ИКТ основной и старшей
школы рассматриваются такие важные темы как
“Основы логики” и “Поиск информации в
Интернет”. При решении определенного типа задач
удобно использовать круги Эйлера (диаграммы
Эйлера-Венна).
При решении определенного типа задач
удобно использовать круги Эйлера (диаграммы
Эйлера-Венна).
Математическая справка. Диаграммы Эйлера-Венна используются прежде всего в теории множеств как схематичное изображение всех возможных пересечений нескольких множеств. В общем случае они изображают все 2n комбинаций n свойств. Например, при n=3 диаграмма Эйлера-Венна обычно изображается в виде трех кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.
2. Представление логических связок в поисковых запросах
При изучении темы “Поиск информации в
Интернет” рассматриваются примеры поисковых
запросов с использованием логических связок,
аналогичным по смыслу союзам “и”, “или”
русского языка. Смысл логических связок
становится более понятным, если
проиллюстрировать их с помощью графической
схемы – кругов Эйлера (диаграмм Эйлера-Венна).
| Логическая связка | Пример запроса | Пояснение | Круги Эйлера |
| & — “И” | Париж & университет | Будут отобраны все страницы, где упоминаются оба слова: Париж и университет | Рис.1 |
| | — “ИЛИ” | Париж | университет | Будут отобраны все страницы, где упоминаются слова Париж и/или университет | Рис.2 |
3. Связь логических операций с теорией множеств
С помощью диаграмм Эйлера-Венна можно наглядно
представить связь логических операций с теорией
множеств. Для демонстрации можно
воспользоваться слайдами в Приложение
1.
Для демонстрации можно
воспользоваться слайдами в Приложение
1.
Логические операции задаются своими таблицами истинности. В Приложении 2 подробно рассматриваются графические иллюстрации логических операций вместе с их таблицами истинности. Поясним принцип построения диаграммы в общем случае. На диаграмме – область круга с именем А отображает истинность высказывания А (в теории множеств круг А – обозначение всех элементов, входящих в данное множество). Соответственно, область вне круга отображает значение “ложь” соответствующего высказывания. Что бы понять какая область диаграммы будет отображением логической операции нужно заштриховать только те области, в которых значения логической операции на наборах A и B равны “истина”.
Например, значение импликации равно “истина”
в трех случаях (00, 01 и 11). Заштрихуем
последовательно: 1) область вне двух
пересекающихся кругов, которая соответствует
значениям А=0, В=0; 2) область, относящуюся только к
кругу В (полумесяц), которая соответствует
значениям А=0, В=1; 3) область, относящуюся и к кругу
А и к кругу В (пересечение) – соответствует
значениям А=1, В=1. Объединение этих трех областей
и будет графическим представлением логической
операции импликации.
Объединение этих трех областей
и будет графическим представлением логической
операции импликации.
4. Использование кругов Эйлера при доказательстве логических равенств (законов)
Для того, чтобы доказать логические равенства можно применить метод диаграмм Эйлера-Венна. Докажем следующее равенство ¬(АvВ) = ¬А&¬В (закон де Моргана).
Для наглядного представления левой части равенства выполним последовательно: заштрихуем оба круга (применим дизъюнкцию) серым цветом, затем для отображения инверсии заштрихуем область за пределами кругов черным цветом:
Рис.3 Рис.4
Для визуального представления правой части равенства выполним последовательно: заштрихуем область для отображения инверсии (¬А) серым цветом и аналогично область ¬В также серым цветом; затем для отображения конъюнкции нужно взять пересечение этих серых областей (результат наложения представлен черным цветом):
Рис. 5 Рис.6 Рис.7
5 Рис.6 Рис.7
Видим, что области для отображения левой и правой части равны. Что и требовалось доказать.
5. Задачи в формате ГИА и ЕГЭ по теме: “Поиск информации в Интернет”
Задача №18 из демо-версии ГИА 2013.
В таблице приведены запросы к поисковому серверу. Для каждого запроса указан его код – соответствующая буква от А до Г. Расположите коды запросов слева направо в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.
| Код | Запрос |
| А | (Муха & Денежка) | Самовар |
| Б | Муха & Денежка & Базар & Самовар |
| В | Муха | Денежка | Самовар |
| Г | Муха & Денежка & Самовар |
Решение:
Для каждого запроса построим диаграмму Эйлера-Венна:
| Запрос А Рис. |
Запрос Б Рис. 9 |
Запрос В Рис. 10 |
Запрос Г Рис. 11 |
Ответ: ВАГБ.
Задача В12 из демо-версии ЕГЭ-2013.
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысяч) |
| Фрегат | Эсминец | 3400 |
| Фрегат & Эсминец | 900 |
| Фрегат | 2100 |
Какое количество страниц (в тысячах) будет найдено по запросу Эсминец?
Считается, что все запросы выполнялись
практически одновременно, так что набор страниц,
содержащих все искомые слова, не изменялся за
время выполнения запросов.
Решение:
Пусть
Ф – количество страниц (в тысячах) по запросу Фрегат;
Э – количество страниц (в тысячах) по запросу Эсминец;
Х – количество страниц (в тысячах) по запросу, в котором упоминается Фрегат и не упоминается Эсминец;
У – количество страниц (в тысячах) по запросу, в котором упоминается Эсминец и не упоминается Фрегат.
Построим диаграммы Эйлера-Венна для каждого запроса:
| Запрос | Диаграмма Эйлера-Венна | Количество страниц |
| Фрегат | Эсминец | Рис.12 | 3400 |
| Фрегат & Эсминец | Рис. 13 13 |
900 |
| Фрегат | Рис.14 | 2100 |
| Эсминец | Рис.15 | ? |
Согласно диаграммам имеем:
- Х+900+У = Ф+У = 2100+У = 3400. Отсюда находим У = 3400-2100 = 1300.
- Э = 900+У = 900+1300= 2200.
Ответ: 2200.
6. Решение логических содержательных задач методом диаграмм Эйлера-Венна
Задача 1.
В классе 36 человек. Ученики этого класса
посещают математический, физический и
химический кружки, причем математический кружок
посещают 18 человек, физический — 14 человек,
химический — 10. Кроме того, известно, что 2
человека посещают все три кружка, 8 человек — и
математический и физический, 5 и математический и
химический, 3 — и физический и химический.
Кроме того, известно, что 2
человека посещают все три кружка, 8 человек — и
математический и физический, 5 и математический и
химический, 3 — и физический и химический.
Сколько учеников класса не посещают никаких кружков?
Решение:
Для решения данной задачи очень удобным и наглядным является использование кругов Эйлера.
Самый большой круг – множество всех учеников класса. Внутри круга три пересекающихся множества: членов математического (М), физического (Ф), химического (Х) кружков.
Пусть МФХ – множество ребят, каждый из которых посещает все три кружка. МФ¬Х – множество ребят, каждый из которых посещает математический и физический кружки и не посещает химический. ¬М¬ФХ — множество ребят, каждый из которых посещает химический кружок и не посещает физический и математический кружки.
Аналогично введем множества: ¬МФХ, М¬ФХ,
М¬Ф¬Х, ¬МФ¬Х, ¬М¬Ф¬Х.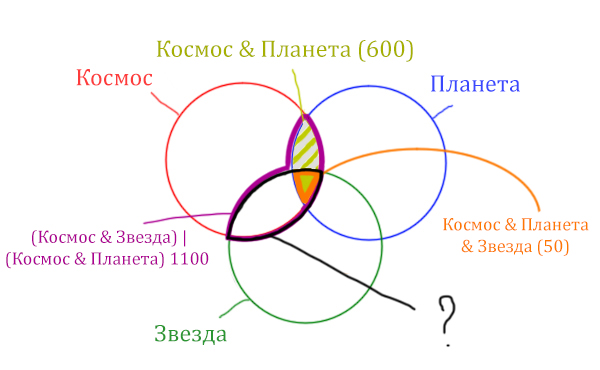
Известно, что все три кружка посещают 2 человека, следовательно, в область МФХ впишем число 2. Т.к. 8 человек посещают и математический и физический кружки и среди них уже есть 2 человека, посещающих все три кружка, то в область МФ¬Х впишем 6 человек (8-2). Аналогично определим количество учащихся в остальных множествах:
| Круги Эйлера с названиями
непересекающихся множеств: Рис. 16 |
Круги Эйлера с количественной
информацией: Рис. 17 Например, количество человек, которые посещают физический кружок 2+6+1+5=14 |
Просуммируем количество человек по всем областям: 7+6+3+2+4+1+5=28. Следовательно, 28 человек из класса посещают кружки.
Значит, 36-28 = 8 учеников не посещают кружки.
Ответ: 8.
Задача 2.
После зимних каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников класса двое не были ни в кино. ни в театре, ни в цирке. В кино побывало 25 человек, в театре — 11, в цирке 17 человек; и в кино, и в театре — 6; и в кино и в цирке — 10; и в театре и в цирке — 4.
Сколько человек побывало и в кино, и в театре, и в цирке?
Решение:
Пусть х – количество ребят, которые побывали и в кино, и в театре, и в цирке.
Тогда можно построить следующую диаграмму и посчитать количество ребят в каждой области:
Рис.18. |
В кино и театре побывало 6 чел., значит,
только в кино и театре (6-х) чел. Аналогично,
только в кино и цирке (10-х) чел. Только в театре и цирке (4-х) чел. В кино побывало 25 чел., значит, из них только в кино были 25 — (10-х) – (6-х) – х = (9+х). Аналогично, только в театре были (1+х) чел. Только в цирке были (3+х) чел. Не были в театре, кино и цирке – 2 чел. Значит, 36-2=34 чел. побывали на мероприятиях. С другой стороны можем просуммировать количество человек, которые были в театре, кино и цирке: (9+х)+(1+х)+(3+х)+(10-х)+(6-х)+(4-х)+х = 34 33+х = 34. Отсюда следует, что только один человек побывал на всех трех мероприятиях. |
Ответ: 1.
Таким образом, круги Эйлера (диаграммы Эйлера-Венна) находят практическое применение при решении задач в формате ЕГЭ и ГИА и при решении содержательных логических задач.
Литература
- В.
 Ю. Лыскова, Е.А. Ракитина. Логика в информатике.
М.: Информатика и Образование, 2006. 155 с.
Ю. Лыскова, Е.А. Ракитина. Логика в информатике.
М.: Информатика и Образование, 2006. 155 с. - Л.Л. Босова. Арифметические и логические основы ЭВМ. М.: Информатика и образование, 2000. 207 с.
- Л.Л. Босова, А.Ю. Босова. Учебник. Информатика и ИКТ для 8 класса: БИНОМ. Лаборатория знаний, 2012. 220 с.
- Л.Л. Босова, А.Ю. Босова. Учебник. Информатика и ИКТ для 9 класса: БИНОМ. Лаборатория знаний, 2012. 244 с.
- Сайт ФИПИ: http://www.fipi.ru/
Диаграммы Эйлера и Венна: они не только для развлечения
(источник) К тому времени, когда вы дочитаете этот пост в блоге, вы должны быть в третьей группе. Диаграммы Венна и Эйлера (произносится как «масленка») невероятно популярны в Интернете как забавные диаграммы. Они предлагают простой способ изобразить концепции теории множеств. Итак, в чем разница между ними? Почему они смешные? Полезны ли они для реальных данных? Оба типа диаграмм используются для отображения концепций теории множеств:
Union — комбинация двух наборов. В диаграммах Венна и Эйлера.
В диаграммах Венна и Эйлера. Intersection — Входит в оба из двух наборов. В диаграммах Венна и Эйлера.
Разница — Все, кроме пересечения двух наборов. В диаграммах Венна и Эйлера.
Относительное дополнение — В одном наборе, а не в другом. В диаграммах Венна и Эйлера.
Абсолютное дополнение — Все, чего нет в другом наборе. Только в диаграммах Эйлера.
Подмножество — Набор, полностью содержащийся в другом наборе.Только в диаграммах Эйлера.
Disjoint — Два набора без общих элементов. Только в диаграммах Эйлера. Все диаграммы Венна являются диаграммами Эйлера, но не все диаграммы Эйлера являются диаграммами Венна. Диаграммы Эйлера имеют только те комбинации пересечений, которые действительно существуют в реальном мире. Диаграммы Венна представляют все гипотетически возможные логические отношения между категориями. Диаграммы Венна по определению должны отображать все возможные комбинации пересечений, что создает некоторые интересные проблемы с компоновкой.
 Когда есть три круга, отображается каждое пересечение, но как только вы переходите к четырем категориям, круги перестают работать. Эллипсы могут работать до пяти категорий, но помимо пяти необходимо использовать странные формы, чтобы вплетаться и выходить из всех комбинаций пересечений. Пять уже довольно сложно читать, но как только эти странные формы вступают в игру, чтение диаграмм становится почти невозможным, а текстовые описания отношений часто легче понять. Это подводит нас к тому, почему так много забавных диаграмм.Диаграмма Венна позвоночных и беспозвоночных, которую мы показали вам ранее, предполагает, что некоторые животные могут одновременно иметь позвоночник и не иметь позвоночника. Хотя это может быть и не смешно, любой, кто учился в шестом классе естественных наук, может сказать вам, что это довольно глупо. При более интересном предмете указание на несуществующие отношения может быть довольно забавным. Некоторые диаграммы достигают юмора, помещая что-то в категорию, к которой это не относится или к которой вы обычно не ожидаете.
Когда есть три круга, отображается каждое пересечение, но как только вы переходите к четырем категориям, круги перестают работать. Эллипсы могут работать до пяти категорий, но помимо пяти необходимо использовать странные формы, чтобы вплетаться и выходить из всех комбинаций пересечений. Пять уже довольно сложно читать, но как только эти странные формы вступают в игру, чтение диаграмм становится почти невозможным, а текстовые описания отношений часто легче понять. Это подводит нас к тому, почему так много забавных диаграмм.Диаграмма Венна позвоночных и беспозвоночных, которую мы показали вам ранее, предполагает, что некоторые животные могут одновременно иметь позвоночник и не иметь позвоночника. Хотя это может быть и не смешно, любой, кто учился в шестом классе естественных наук, может сказать вам, что это довольно глупо. При более интересном предмете указание на несуществующие отношения может быть довольно забавным. Некоторые диаграммы достигают юмора, помещая что-то в категорию, к которой это не относится или к которой вы обычно не ожидаете. Креативная маркировка (как на диаграмме Эйлера ниже) тоже всегда помогает.Мы знаем, что диаграммы Эйлера могут быть забавными, но могут ли они быть полезными? Некоторые диаграммы включают количественную информацию, используя площадь каждой части диаграммы. Хорошим примером этого является Глобальная карта социальных сетей , 2011 г., , составленная Global Web Index. Сами по себе диаграммы Эйлера, подобные этой, дают вам довольно хорошее общее представление о задействованных значениях. Считать их точное количество было бы немного сложно, но для получения общего обзора они хороши. На этом конкретном графике эти диаграммы Эйлера используются как малые кратные, что позволяет сравнивать регионы.Почему в инфографике нет более серьезных диаграмм Эйлера / Венна? Они хорошо демонстрируют совпадение категорий. Они выглядят «круто» — многие дизайнеры считают это важным. Они разумно демонстрируют количество. Они демонстрируют сложные и интересные отношения в простой для понимания манере.
Креативная маркировка (как на диаграмме Эйлера ниже) тоже всегда помогает.Мы знаем, что диаграммы Эйлера могут быть забавными, но могут ли они быть полезными? Некоторые диаграммы включают количественную информацию, используя площадь каждой части диаграммы. Хорошим примером этого является Глобальная карта социальных сетей , 2011 г., , составленная Global Web Index. Сами по себе диаграммы Эйлера, подобные этой, дают вам довольно хорошее общее представление о задействованных значениях. Считать их точное количество было бы немного сложно, но для получения общего обзора они хороши. На этом конкретном графике эти диаграммы Эйлера используются как малые кратные, что позволяет сравнивать регионы.Почему в инфографике нет более серьезных диаграмм Эйлера / Венна? Они хорошо демонстрируют совпадение категорий. Они выглядят «круто» — многие дизайнеры считают это важным. Они разумно демонстрируют количество. Они демонстрируют сложные и интересные отношения в простой для понимания манере. Если вы дизайнер и хотите получить интересные диаграммы, внимательно изучите свои данные. Возможно, вы сможете использовать диаграмму Эйлера или Венна. Дрю Скау — кандидат компьютерных наук, студент-визуализатор UNCC, со степенью бакалавра архитектуры.
Если вы дизайнер и хотите получить интересные диаграммы, внимательно изучите свои данные. Возможно, вы сможете использовать диаграмму Эйлера или Венна. Дрю Скау — кандидат компьютерных наук, студент-визуализатор UNCC, со степенью бакалавра архитектуры.AlphaMC — Euler 2021 (начальная школа)
AlphaMC 2021 будет предлагаться онлайн с 24 апреля по 1 мая . Регистрация уже открыта.
- AlphaMC — Эйлер 2021
- Архив
Alpha Math Contest — Конкурс по математике Эйлера для учащихся начальной школы (3-5 классы). Окно конкурса 24 апреля — 1 мая. Будет предложено онлайн частным лицам и центрам тестирования (школам, математическим кружкам, учебным центрам).Лучшие участники и центры тестирования получат награды.
(*) Тест может быть трудным для большинства учеников 3-х или младших классов, но им разрешено участвовать в конкурсе.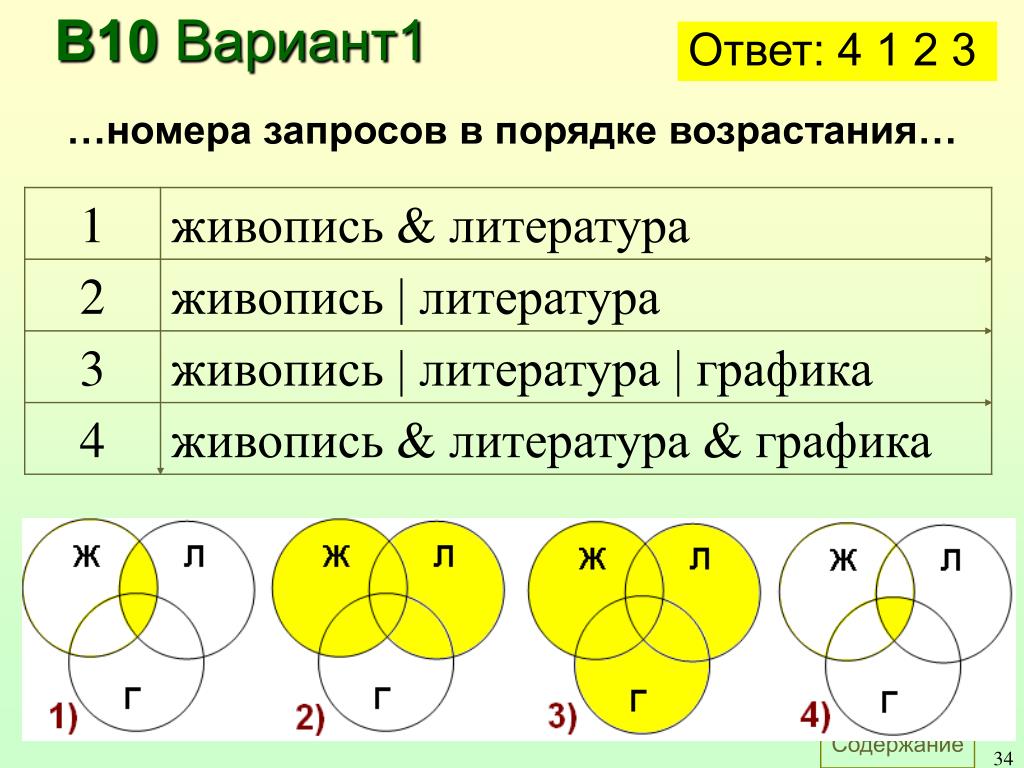 Пожалуйста, проверьте следующий раздел и предыдущие проблемы.
Пожалуйста, проверьте следующий раздел и предыдущие проблемы.
2021 Проблемы и решения
Результаты
Награды испытательного центра
| Награда | Рейтинг | Центр тестирования | Оценка |
|---|---|---|---|
| Золото | 1 | PATh3AI Learning | 1140 |
| Золото | 2 | Начальная школа Харкера | 1100 |
| Серебро | 3 | Искусство физики | 1030 |
| Серебро | 4 | Аргонавт Начальная школа | 999 |
| Серебро | 5 | T H Rogers Math Club | 982 |
| Серебро | 6 | Общественный дом Средний | 908 |
| Бронза | 7 | Санта-Барбара Математический эллипс | 851 |
| Бронза | 8 | Региональная академия ученых Метролина | 810 |
| Бронза | 9 | Лейк-Норман Устав | 575 |
| Бронза | 10 | СДЕЛАТЬ математический круг | 564 |
| Бронза | 11 | Архимедова Академия | 555 |
| Бронза | 12 | Центр обучения христианской праведности | 530 |
Индивидуальные награды
золото, серебро, бронза
| Награда | Рейтинг | Имя студента | Центр тестирования |
|---|---|---|---|
| Золото | 1 | Advika Asthana | — |
| Золото | 1 | Елена Б | Санта-Барбара Математический эллипс |
| Золото | 1 | Sophia Fan | PATh3AI Learning |
| Золото | 4 | Кейси Ф | — |
| Золото | 4 | Dylan W | — |
| Золото | 4 | Franklin Z | Искусство физического воспитания |
| Золото | 4 | Джеффри Ван | Harker Lower School |
| Золото | 4 | Марк Распопов | — |
| Золото | 4 | Юэньчжин Шао | Аргонавт Начальная школа |
| Золото | 10 | Camea C | — |
| Золото | 10 | Кристофер Сакалийски | — |
| Золото | 10 | Hanyu Zhang | PATh3AI Learning |
| Золото | 10 | Laura W | — |
| Золото | 10 | Леон L | — |
| Золото | 10 | Lucas Li | Lake Norman Charter |
| Золото | 10 | Манас A | T H Rogers Math Club |
| Золото | 10 | Маркель Зенг | PATh3AI Learning |
| Золото | 18 | Александр Ши | — |
| Золото | 19 | Александр Б | — |
| Золото | 19 | Эндрю Цзян | Общественный дом Средний |
| Золото | 19 | Шарлин Ли | Начальная школа Харкера |
| Золото | 19 | Эмма Лю | PATh3AI Learning |
| Золото | 19 | Гарри Ван | Общественный дом Средний |
| Золото | 19 | Джереми Чжан | Harker Lower School |
| Золото | 19 | Лорен Ванг | — |
| Золото | 19 | Натан Чен | — |
| Золото | 27 | Джошуа Ван | — |
| Золото | 27 | Thaman Venigalla | — |
| Награда | Рейтинг | Имя студента | Центр тестирования |
|---|---|---|---|
| Серебро | 29 | Аарон L | — |
| Серебро | 29 | Анна Чен | СДЕЛАТЬ математический круг |
| Серебро | 29 | Hongkang Zhao | Harker Lower School |
| Серебро | 29 | Michael T | PATh3AI Learning |
| Серебро | 29 | Оливер Шен | Начальная школа Харкера |
| Серебро | 29 | Paixiao Seeluangsawat | — |
| Серебро | 29 | Timothy W | Искусство физического воспитания |
| Серебро | 36 | Wenda C | Искусство физики |
| Серебро | 37 | Sophia Zhang | Harker Lower School |
| Серебро | 38 | Элвин S | — |
| Серебро | 39 | Эндрю Лю | — |
| Серебро | 39 | Кэтрин Ли | — |
| Серебро | 39 | Yuenjen Li | Argonaut Elementary |
| Серебро | 42 | Alwin Jing | Manhattan ACE |
| Серебро | 42 | Avelyn Jing | Harker Lower School |
| Серебро | 42 | Даниэль Ван | — |
| Серебро | 42 | Дерек Ху | — |
| Серебро | 42 | Keerthi R | T H Rogers Math Club |
| Серебро | 42 | Рори Ху | — |
| Серебро | 42 | Саймон Ян | — |
| Серебро | 49 | Bryant H | Искусство физического воспитания |
| Серебро | 50 | Аттикус L | — |
| Серебро | 51 | Арджун Виджайкумар | Аргонавт Элементарный |
| Серебро | 52 | Ryan Z | T H Rogers Math Club |
| Серебро | 53 | Brandon Wu | Argonaut Elementary |
| Серебро | 54 | Hansita M | T H Rogers Math Club |
| Серебро | 54 | Кэтрин Y | СДЕЛАТЬ математический круг |
| Серебро | 54 | Макс X | PATh3AI Learning |
| Серебро | 57 | Адриан К | — |
| Серебро | 57 | Чаунси Гао | Общественный дом Средний |
| Серебро | 57 | Прапти Венкатараман | Аргонавт Начальная школа |
| Серебро | 57 | Тимоти Y | Искусство физического воспитания |
| Серебро | 61 | Matthew Z | T H Rogers Math Club |
| Серебро | 62 | Майкл Ван | — |
| Серебро | 62 | Mohan L | Искусство физического воспитания |
| Серебро | 64 | Эльвин Чжао | — |
| Серебро | 65 | Olivia H | Metrolina Regional Scholars Academy |
| Серебро | 66 | Адам L | — |
| Серебро | 66 | Клэр С | Региональная академия ученых Метролина |
| Серебро | 66 | Lilian Z | Искусство физического воспитания |
| Серебро | 69 | Deepac Ganesan | — |
| Серебро | 70 | Авиши Гупта | — |
| Серебро | 70 | Аяна Гупта | — |
| Серебро | 70 | Джихан Ли | — |
| Серебро | 70 | Seungyoo K | Santa Barbara Math Ellipse |
| Серебро | 74 | Эдвард H | — |
| Серебро | 74 | Шон Х | PATh3AI Learning |
| Серебро | 76 | Эдвард Фу | — |
| Серебро | 76 | Haoran X | T H Rogers Math Club |
| Серебро | 78 | Абхинав Шринивас | — |
| Серебро | 79 | Джордж Парет | — |
| Серебро | 79 | Исаак Сю | СДЕЛАТЬ математический круг |
| Серебро | 79 | Yiming Sun | PATh3AI Learning |
| Серебро | 82 | Ричард Ли | Начальная школа Харкера |
| Серебро | 83 | Белинда Чжу | — |
| Серебро | 84 | Джейсон К | PATh3AI Learning |
| Серебро | 85 | Daniel D | Metrolina Regional Scholars Academy |
| Серебро | 85 | Кароль Ду | — |
| Награда | Рейтинг | Имя студента | Центр тестирования |
|---|---|---|---|
| Бронза | 87 | Милан Наир | — |
| Бронза | 88 | Miranda L | Santa Barbara Math Ellipse |
| Бронза | 89 | Акшата Арункумар | — |
| Бронза | 90 | Ави Батра | — |
| Бронза | 91 | Arden Kan | Harker Lower School |
| Бронза | 91 | Huixin Shi | PATh3AI Learning |
| Бронза | 93 | Никаш Баер | — |
| Бронза | 93 | Randy Hui | Harker Lower School |
| Бронза | 95 | Иона H | Санта-Барбара Математический эллипс |
| Бронза | 96 | Jerry G | PATh3AI Learning |
| Бронза | 96 | Lekang J | T H Rogers Math Club |
| Бронза | 96 | Софи Хан | Аргонавт Элементарно |
| Бронза | 99 | Люк Син | PATh3AI Learning |
| Бронза | 100 | Langxing Chen | Harker Lower School |
| Бронза | 100 | Ронан Боумик | — |
| Бронза | 102 | Элвин Шен | Средний дом общины |
| Бронза | 102 | Ашват V | Региональная академия ученых Метролина |
| Бронза | 102 | Тереза Чен | PATh3AI Learning |
| Бронза | 105 | Аарон Дж. | PATh3AI Learning |
| Бронза | 105 | Calvin X | Региональная академия ученых Метролина |
| Бронза | 105 | Greta W | T H Rogers Math Club |
| Бронза | 105 | Закари Янг | — |
| Бронза | 109 | Сай Нирмит I | — |
| Бронза | 109 | Shravya I | T H Rogers Math Club |
| Бронза | 111 | Moxi Zhu | Harker Lower School |
| Бронза | 112 | Srijan M | T H Rogers Math Club |
| Бронза | 113 | Christopher Wu | Argonaut Elementary |
| Бронза | 113 | Джейден Y | PATh3AI Learning |
| Бронза | 115 | Anchen Wan | Argonaut Elementary |
| Бронза | 115 | Benjamin Jauregui | АРХИМЕДОВАЯ АКАДЕМИЯ |
| Бронза | 115 | Matthew D | — |
| Бронза | 115 | Мехмет Гельги | — |
| Бронза | 115 | Свара Радж | Дом общины Средний |
| Бронза | 120 | Джошуа Линь | Harker Lower School |
| Бронза | 120 | Тадаши Фудзимура | Начальная школа Харкера |
| Бронза | 122 | Hema V | T H Rogers Math Club |
| Бронза | 122 | Винсент D | PATh3AI Learning |
| Бронза | 124 | Шри Дханви Пули | — |
| Бронза | 125 | София Вэй | Аргонавт Элементарно |
| Бронза | 126 | Виваан Джоши | Общественный дом Средний |
| Бронза | 127 | Adam Y | T H Rogers Math Club |
| Бронза | 127 | Avika G | Coral Academy of Science Las Vegas |
| Бронза | 127 | Джульетта Монтойя | АРХИМЕДОВАЯ АКАДЕМИЯ |
| Бронза | 127 | Rohan C | Региональная академия ученых Метролина |
| Бронза | 131 | Лайя Радж | Дом общины Средний |
| Бронза | 131 | Майкл Л. | Коралловая академия наук Лас-Вегас |
| Бронза | 133 | Рэйчел Ши | Центр обучения христианской праведности |
| Бронза | 134 | Seetha V | T H Rogers Math Club |
| Бронза | 135 | Аня А | Региональная академия ученых Метролина |
| Бронза | 135 | Шашанк Ачют | Дом общины Средний |
| Бронза | 135 | Тиффани Юань | PATh3AI Learning |
| Бронза | 138 | Albert C | PATh3AI Learning |
| Бронза | 138 | Хна Рамани | — |
| Бронза | 140 | Thomas G | — |
| Бронза | 141 | Аадил Нишар Ахмед | Общественный дом Средний |
| Бронза | 141 | Айян А | T H Rogers Math Club |
| Бронза | 141 | Итан Ян | Общественный дом Средний |
| Бронза | 144 | Деврай Бора | Аргонавт Начальная школа |
| Бронза | 145 | Аарон Лунг | Центр обучения христианской праведности |
| Бронза | 145 | Arihant Nanda | — |
| Бронза | 145 | Арджун Р | Региональная академия ученых Метролина |
| Бронза | 145 | Даниэль Ху | — |
| Бронза | 145 | Джессика Ли | Harker Lower School |
| Бронза | 145 | Сахисну A | T H Rogers Math Club |
| Бронза | 145 | Тейлор A | T H Rogers Math Club |
| Бронза | 145 | Taylor Zipse | Общественный дом Средний |
| Бронза | 153 | Harish A | T H Rogers Math Club |
| Бронза | 154 | Даниэль Чжан | Центр обучения христианской праведности |
| Бронза | 154 | Джанни Б | Санта-Барбара Математический эллипс |
| Бронза | 154 | Джозеф Пьедра | Общественный дом Средний |
| Бронза | 154 | Джотин Самаямантри | — |
| Бронза | 154 | Лео Зоу | Harker Lower School |
| Бронза | 154 | Olivier W | Начальная школа Тихоокеанского региона |
| Бронза | 160 | Сет Рамани | — |
| бронза | 161 | Sanjeeva Manimuthu | — |
| Бронза | 162 | Манасви Пауль | — |
| Бронза | 162 | Стивен Чжан | — |
| Бронза | 164 | Джуд К | Валентин-Хиллз Клуб элементарной математики |
| Бронза | 164 | Saachi S | Региональная академия ученых Метролина |
| Бронза | 166 | Аника К | Региональная академия ученых Метролина |
| Бронза | 166 | Иван Т | — |
| Бронза | 166 | Travenshia O | Metrolina Regional Scholars Academy |
| Бронза | 169 | Adhvik P | Региональная академия ученых Метролина |
| Бронза | 170 | Ивана Тахим | АРХИМЕДОВАЯ АКАДЕМИЯ |
| Бронза | 171 | Аарон С.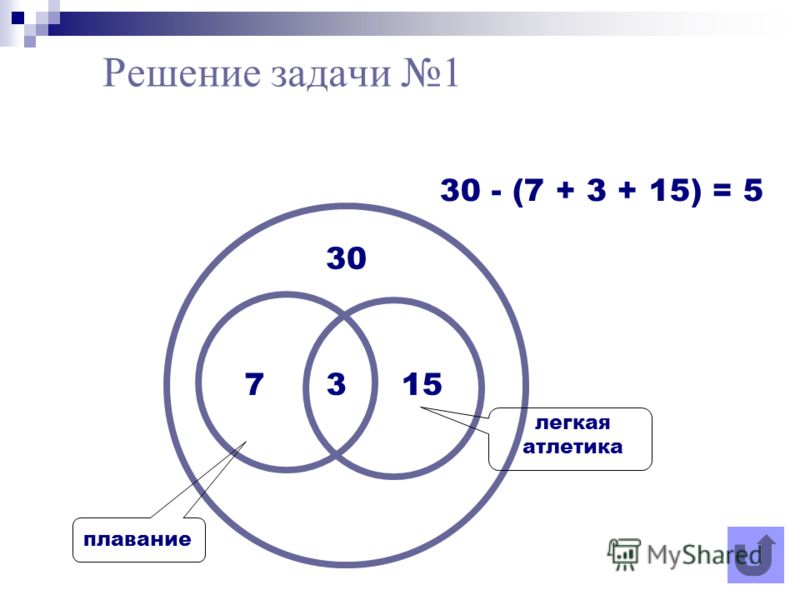 | Начальная школа Тихоокеанского региона |
| Бронза | 172 | Адитан G | Региональная академия ученых Метролина |
Проблема, сложность и темы
Темы включают, но не ограничиваются,
- Алгебра (Порядок операций, дроби, задачи со словами)
- Подсчет (наборы и т. Д.)
- Геометрия (углы, длина, площадь и т. Д.)
- Теория чисел (простые числа, множители, gcd, lcm и т. Д.)
Пожалуйста, ознакомьтесь с задачами AlphaMC 2020 Euler, чтобы получить лучшее представление.
Правила
Для прохождения теста требуется взрослый наблюдающий (учитель, родитель и т. Д.).
Разрешены только карандаши, точилки для карандашей и ластики. Калькуляторы не разрешены.
Даты
| 15 января | Начало индивидуальной регистрации |
| 15 января | Начало подачи заявок в испытательный центр |
| 1 марта | Начало регистрации студентов в центрах тестирования |
| 1 апреля | Участники получают свои онлайн-счета (LMS) |
10 апреля | Срок регистрации |
| 12-23 апреля | Доступен образец теста |
24 апреля — 1 мая | Окно конкурса |
| 2 мая | Проблемы и решения будут опубликованы в Интернете |
| 15 мая | Отчеты и сертификаты участников будут доступны онлайн |
| 15 мая | Результаты будут опубликованы в Интернете |
Регистрация
Все зарегистрированные участники смогут бесплатно пройти онлайн-курс AlphaMC. Пожалуйста, проверьте страницу курса для получения дополнительной информации.
Пожалуйста, проверьте страницу курса для получения дополнительной информации.
Физические лица
Учащиеся должны проконсультироваться со своими школами, прежде чем регистрироваться в качестве физических лиц на конкурсе.
Комиссия: 15 $
Реестр (для физических лиц)
Испытательные центры
Комиссия: Бесплатно
Школы, математические кружки, учебные центры могут предложить конкурс бесплатно в 2021 году. Чтобы провести Alpha Math Contest в вашем регионе, подайте заявку по ссылке ниже. Если ваша заявка будет одобрена, вы получите форму для регистрации студентов.
Подать заявку (для тестовых центров)
Если у вас есть какие-либо вопросы, отправьте электронное письмо по адресу [email protected].
Информация об испытаниях
Это будет индивидуальный тест с 25 вопросами с несколькими вариантами ответов. Возможны однозначные числа (0, 1, 2,…, 9). Ограничение по времени — 40 минут.
Студенты получат 10 баллов за каждый правильный ответ, 1 балл за каждый оставшийся без ответа вопрос и 0 баллов за каждый неправильный ответ.
Онлайн-формат (только)
Тест будет проходить онлайн через систему управления обучением AlphaStar (LMS).
Каждый участник получит онлайн-аккаунт и перед началом конкурса пройдет образец теста онлайн.
Если вы хотите увидеть, как работает LMS сейчас, вы можете зарегистрироваться на бесплатный демонстрационный курс математики.
Награды
Победители будут отмечены на этой странице. Чтобы увидеть победителей прошлых лет, загляните в архив.
Индивидуальные награды
Индивидуальные награды будут основаны на индивидуальных оценках. Участники с одинаковыми оценками получат одинаковую награду (без тай-брейка).
- Золотой сертификат участника: Лучшие 10% всех участников
- Серебряный сертификат участника: Следующие 20% всех участников
- Бронзовый сертификат участника: Следующие 30% всех участников
Награды испытательного центра
Оценка каждого испытательного центра будет рассчитана как сумма оценок пяти лучших участников. Центры тестирования с одинаковыми баллами получат одинаковую награду (без тай-брейка).
Центры тестирования с одинаковыми баллами получат одинаковую награду (без тай-брейка).
- Золотой сертификат испытательного центра: Лучшие 10% всех испытательных центров
- Silver Test Center Сертификат: Следующие 20% всех центров тестирования
- Бронзовый испытательный центр Сертификат: Следующие 30% всех испытательных центров
| Загадка Ферма и тройки Пифагора | ||||||||||||||||||||||||||||||||||||||||||||||
Теорема Пифагора утверждает, что для прямоугольного треугольника с катетами a и b и гипотенузой
c, Числа, соответствующие этому шаблону, называются пифагоровыми тройками. На диаграмме ниже показаны некоторые из этих троек Пифагора. Изучите паттерн в диаграмму, чтобы найти следующие два набора троек. | ||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||
| Будет ли какая-либо из троек удовлетворять Великой теореме Ферма — a 3 + b 3 = c 3 ? А как насчет a 4 + b 4 = c 4 ? Следующие формулы можно использовать для генерации чисел, удовлетворяющих
Теорема Пифагора. Вот пример: пусть x = 7 и y = 6.
Совет: чтобы получить числа a, b и c, у которых нет общих делителей, убедитесь, что ваши числа x и y не имеют общих делителей, например 5 и 6 или 5 и 8, но не 5 и 10. | ||||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Шарлин Эванс | ||||||||||||||||||||||||||||||||||||||||||||||
Ссылка: Коллинз, Уильям и др. Математика: приложения и связи, Курс 3.Гленко / Макгроу Хилл. Огайо. 1998 г. | ||||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | ||||||||||||||||||||||||||||||||||||||||||||||
| Волшебный круг | ||||||||||||||||||||||||||||||||||||||||||||||
Материалы
Предложите учащимся решить три задачи, которые имеют значение только для диаметра. дано. | ||||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Дэвидом Лейбом | ||||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | ||||||||||||||||||||||||||||||||||||||||||||||
| Пентаграммы природы | ||||||||||||||||||||||||||||||||||||||||||||||
Цель: Учащиеся смогут использовать алгебраические понятия при изучении природы. Цель: Учащиеся будут использовать геометрию и концепцию соотношений и применять их для измерения предметов, встречающихся в природе. Материалы: Пятилепестковые цветы, Яблоки, Доллары, Морская звезда. Фокус: Покажите фильм: Дональд Дак в стране математики (его можно получить через Library Media Services, 259 долларов США) Процедура:
Оценка: Попросите учащихся рассказать, что они обнаружили с помощью различных использованных материалов. Они нашли золотые треугольники? Что помогло? Что нужно исправить? | ||||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Дженнифер Гарретсон | ||||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущее | ||||||||||||||||||||||||||||||||||||||||||||||
| Деятельность полосы Мебиуса | ||||||||||||||||||||||||||||||||||||||||||||||
Для этого задания вам понадобится по пять полосок бумаги на каждого учащегося.
 | ||||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Стивом Бикслером | ||||||||||||||||||||||||||||||||||||||||||||||
Рекомендации: Этот проект разработан: [email protected] | ||||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | ||||||||||||||||||||||||||||||||||||||||||||||
| Теорема Пифагора с танграммами | ||||||||||||||||||||||||||||||||||||||||||||||
Цель: Использование танграмм для введения теоремы Пифагора. Цель: Студенты будут использовать танграммы как введение в пифагорейский язык. Теорема. Материалы: Набор Tangram (квадрат 4 x 4 дюйма), бумага, карандаш. Чтобы у каждого учащегося было достаточно деталей для некоторых из этих заданий, вы может позволить студентам работать в парах или предоставить каждому студенту более один набор танграммов. Знакомство с Пифагором Шаг 1 Шаг 2 Шаг 3 Шаг 4 Шаг 5 Шаг 6 (Вот! Ваши ученики только что открыли теорему Пифагора !!!) Это прекрасная возможность поделиться со своими учениками историей Пифагор и как он разработал эту теорему. | ||||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Анжелой Церадски | ||||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | ||||||||||||||||||||||||||||||||||||||||||||||
| Формула Эйлера Активность | ||||||||||||||||||||||||||||||||||||||||||||||
Название урока: Формула Эйлера, зубочистки и мармеладки. Предметная область: Геометрия, преалгебра Уровень оценки: Восьмой Описание или заявление о результатах: Обнаружив информацию о плоских сетях и трехмерных объектах, учащиеся смогут продемонстрировать, как удовлетворить формулу Эйлера. Целей:
Для оценки понимания учащимся представленного материала будут даны устные вопросы и ответы, а также тест с карандашом и бумагой из десяти вопросов. | ||||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Яном Свенсоном | ||||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущее | ||||||||||||||||||||||||||||||||||||||||||||||
| Площадь поверхности и объем | ||||||||||||||||||||||||||||||||||||||||||||||
Это упражнение должно научить ученика вычислять объем и площадь поверхности цилиндра.Эту деятельность можно легко связать с историей, обсуждая, как древние могли измерять объем или даже длину до того, как существовала стандартизированная система измерения. Процедура:
| ||||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Линдси Истридж | ||||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Назад | ||||||||||||||||||||||||||||||||||||||||||||||
| Магические круги Создание усеченного тетраэдра. | ||||||||||||||||||||||||||||||||||||||||||||||
Я приобрел это занятие во время семинара за 259 долларов США в Уичито, штат Канзас, который назывался «Математика в понедельник вечером».Я учил этому классу от третьего класса до колледжа. Это упражнение помогает развивать, укреплять и даже может использоваться для пополнения словарного запаса по математике. Это задание можно выполнить с разными уровнями обучения, просто изменив словарный запас, чтобы он соответствовал уровню навыков, с которым вы работаете. Это отличное упражнение на слушание / мелкую моторику. (Ключевые слова указаны в скобках.) Материалы: один бумажный круг диаметром 7 дюймов, карандаш и линейка. Посмотрите на форму, которую вы держите.Опишите это. Это ( круг, ). Посмотрите на внешний край вашего круга. Как называется расстояние по внешней стороне круга? ( Окружность ) Сложите круг прямо пополам и хорошо согните его. Раскройте круг, полученная складка — это ( диаметр ) круга. Держите кружок на концах складки. Снова сложите круг пополам, но на этот раз совместите конечные точки складки. Раскройте свой круг, это тоже диаметр? Откуда вы знаете? Линии ( пересекаются с )? Да. Есть ли что-то особенное в том, как эти линии пересекаются? Они образуют четыре угла 90 o (или прямых). Этот особый тип перекрестка называется ( перпендикуляр ). Поместите точку, не больше ширины карандаша, в точке соединения складок. Это называется ( центр ) круга. Карандашом нарисуйте одну из линий от центра к краю круга. Эта линия от центра называется (радиус ). Загните один из внешних изогнутых краев круга, пока он не коснется точки в середине. Хорошо согните. Раскройте складку и посмотрите на только что сделанную складку. Это диаметр? Это радиус? Почему или почему нет? Эта линия называется ( аккорд ). Посмотрите на изогнутую часть круга между точками, где эта линия касается внешней стороны круга. Это называется ( дуга ). Можете ли вы найти другие дуги на своем круге? Возьмите противоположную сторону вашего круга и сложите его так, чтобы изогнутая часть касалась центра, а нижняя часть образовывала идеальную точку. Ваш круг будет похож на мороженое ( рожок ). Хорошо согните. Загните верхнюю часть рожка мороженого вниз, пока изогнутая часть не коснется центра круга.Верхние углы должны образовывать идеальные точки, хорошо сгибаться. Теперь опишите свою форму. ( Треугольник ) Вы замечаете что-нибудь особенное в этом треугольнике? Посмотрите на все ( углов ), они такие же, как и все стороны одинаковые. Этот треугольник называется ( равносторонний и / или острый ). Вы также можете использовать ( равносторонний ). Сложите новый треугольник пополам, совместив две точки.Хорошо мнется. Новое прекращение делит треугольник пополам, эта линия называется высотой или высотой ). Можете ли вы что-нибудь выяснить об этом треугольнике? Это ( прямоугольный треугольник ). Раскройте прямоугольный треугольник до равностороннего треугольника. Возьмите верхний угол большого треугольника и сложите его. Сгибая по складке высоты, вы можете совместить верхнюю точку до нижней линии сгиба.Внутри вы увидите три треугольника поменьше. Переверните бумагу, чтобы не было видно складок. Как называется эта форма? Поскольку он имеет четыре стороны, его можно классифицировать как ( четырехугольник ). Поскольку у этого четырехугольника две стороны ( параллельны ) и две противоположные, он также называется ( трапеция ). Переверните его, чтобы теперь были видны все складки.Сложите один из внешних треугольников так, чтобы он лежал прямо поверх центрального треугольника. Переверните его и опишите форму, которую вы сейчас видите. Это не воздушный змей, в небе летают воздушные змеи. Это не бриллиант, я ношу бриллианты на пальцах. В математике эта форма называется ( ромб ). Снова переверните фигуру и снова сложите последний внешний треугольник на центральный. У вас должен получиться равносторонний треугольник меньшего размера. Раскройте все три маленьких треугольника.Соедините три свободные точки вместе, чтобы у вас получилась пирамида ( ). На этом этапе вы можете обсудить ( граней ) ( ребер ) ( точек ) ( вершин ) ( основание ) и тот факт, что это ( треугольная пирамида ), а не квадратная пирамида, как в Египте. Откройте пирамиду до большого равностороннего треугольника. Согните одну из точек так, чтобы она касалась точки посередине. Какую форму вы воссоздали? Трапеция хоть и не традиционной формы, но все же может быть идентифицирована как трапеция. Сложите еще одну точку так, чтобы она касалась точки посередине. Какая у вас форма? ( Пентагон ) Несмотря на то, что это не та традиционная форма, к которой вы привыкли, у него все еще есть пять сторон, поэтому он по-прежнему классифицируется как пятиугольник. Теперь сложите последнюю точку. Какая она сейчас форма? ( Hexagon ) Обсудите ( плоскость ) фигурки. Переверните на другую сторону и вставьте один из углов в лоскут на противоположной стороне треугольника. Возможно, вам придется попробовать несколько. Выберите тот, который вам больше всего подходит. Сдвиньте последний угол под / внутрь других. Вы создали ( усеченный тетраэдр )! Для любой формы во время этого упражнения вы можете попросить учащихся вычислить площадь поверхности, объем, периметр и / или площадь. | ||||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Анжелой Церадски | ||||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | ||||||||||||||||||||||||||||||||||||||||||||||
| Эксперимент с водяным шлангом. | ||||||||||||||||||||||||||||||||||||||||||||||
Это задание можно выполнить за один урок. Чтобы ответить на вопросы и сделать выводы, может потребоваться еще один урок, в зависимости от продолжительности вашего урока. Прекрасно подходит для весны, когда у школьников и учителей весенняя лихорадка.Его цель — найти оптимальный угол для достижения наибольшего расстояния. В зависимости от того, какой класс вы преподаете, это задание можно изменить. История: Простой транспортир — старинный прибор. Создан первый комплексный транспортир для определения положения лодки на навигационных картах. Названный трехрычажным транспортиром или указателем станции, он был изобретен в 1801 году Джозефом Худдартом, капитаном ВМС США. Центральный рычаг неподвижен, а два внешних поворотных, их можно установить под любым углом по отношению к центральному рычагу. Материалы:
Присоедините садовый шланг к водопроводному крану и отрегулируйте поток воды, чтобы он находился под постоянным давлением. Начните с угла 0 градусов к земле, измерьте и запишите расстояние, которое поток проходит в горизонтальном направлении по земле.Повторите эти действия для углов 20 o , 30 o , 45 o , 70 o и 75 o . Вопросы и выводы:
URL: http://inventors.about.com/science/inventors/libr…/blmeasurement.htm?terms=protractor+histor 14.06.00 20:30 | ||||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Эми Траутман | ||||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущий | ||||||||||||||||||||||||||||||||||||||||||||||
| Расчет числа Пи. | ||||||||||||||||||||||||||||||||||||||||||||||
Примерно 4000 лет назад люди впервые начали понимать пи. Считалось, что его стоимость была около трех. Сегодня мы используем лучшее приближение числа Пи. Это 3,14. Пи — иррациональное число. Это означает, что он не повторяется в шаблоне. Пи определяется как отношение длины окружности к диаметру той же окружности. А теперь небольшое упражнение, которое поможет вам определить число Пи. Материалы:
Сначала на листе бумаги сделайте 4 столбца с надписью: объект, диаметр, окружность и соотношение.(См. Пример ниже.) Оберните веревку вокруг объекта. Это измеряет окружность объекта. Измерьте шнур с помощью измерительной линейки. Запишите значение в столбец с надписью «длина окружности». Затем измерьте расстояние прямо поперек объекта. Поместите это значение в столбец, обозначенный как диаметр. Теперь возьмите длину окружности, разделенную на диаметр. Поместите это в столбец с надписью «Соотношение». Это близко к пи? Убедитесь, что вы приняли соотношение до трех или четырех десятичных знаков.
| ||||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Джереми Траутманом | ||||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущий | ||||||||||||||||||||||||||||||||||||||||||||||
| Активность тесселяции. | ||||||||||||||||||||||||||||||||||||||||||||||
Класс: 5 или 6 Время: 20-30 минут уроков Необходимые материалы: Смесь многоугольников, таких как геоблоки, бумага, карандаш и цветные карандаши. Урок 1 Focus: Поместите различные фигуры наверху. Обсудите в классе сходства и различия форм.Сообщите учащимся, что фигуры представляют собой многоугольники (фигура на плоскости). Расскажите о концепции мозаики и о том, как не должно быть разрывов или перекрытий. Продемонстрируйте концепцию наверху с помощью квадрата. Задание: Попросите учащихся предсказать, какие фигуры будут мозаичными, а какие — нет. Составьте диаграмму, показывающую результаты прогнозов учащихся. Дайте каждому столу (или студенту, если возможно) набор фигур. Попросите учащихся индивидуально определить, будет ли фигура мозаикой. Заключение: Обсудите в классе, какая форма плитки на самом деле, а какая нет. Сравните открытия с предсказаниями на картах. Завершение: Попросите учащихся определить многоугольник и то, что они узнали о нем, в короткой дневной записи. Урок 2 В фокусе: Просмотрите концепции многоугольника и мозаики. Расскажите о термине тесселяция и о том, как он соотносится с уроком 1.Обсудите концепции скольжения, вращения (поворота) и отражения (переворачивания) и продемонстрируйте их на потолке. Задание: Попросите учащихся выбрать две или более фигур. Попросите учащихся раскрасить каждую форму в один цвет. Попросите учащихся обвести фигуры черным маркером, если это слайд. Обведите фигуру синим маркером, если это вращение. Отражение следует обвести красным маркером. Заключение: Попросите учащихся поднять руки, когда они закончили.Инструктор проверит результаты. Замыкание: Обсудите, какие различные фигуры объединяют в мозаику результаты построения диаграмм. Разрешите учащимся записывать свои выводы. Урок 3 Фокус: Просмотрите предыдущие уроки. Обсудите, как студенты будут применять свои знания техники мозаики для поиска концепции в искусстве. Активность: Предоставьте несколько произведений разных художников, в том числе несколько произведений М.К. Эшер. Попросите учащихся изучить различные произведения искусства, чтобы выяснить, использует ли художник технику мозаики. Заключение: Попросите учащихся обсудить, что они нашли в этих фрагментах. Выдвиньте гипотезу, почему художники использовали или не использовали технику тесселяции. Закрытие: Попросите учащихся записать свои выводы в своих дневниках. | ||||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено CiCi Naifeh | ||||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | ||||||||||||||||||||||||||||||||||||||||||||||
| Площадь и объем геометрических фигур. | ||||||||||||||||||||||||||||||||||||||||||||||
Площадь геометрических фигур Цель: Дать студенту возможность попрактиковаться в вычислении площади различных геометрических фигур. Необходимые материалы: Использованные журналы, ножницы, линейки, клей, плотная бумага и калькуляторы Процедура:
Чтобы подчеркнуть процесс решения проблемы (решить проблему с помощью метода, о котором вы уже знаете), дайте учащимся упрощенную картинку, взятую из книжек-раскрасок, и попросите их оценить площадь изображения. Используя описанный выше метод, учащиеся должны разделить изображение по формам и вычислить площадь каждой формы, а затем суммировать формы областей, чтобы оценить площадь изображения. Практическое применение: Если кто-то собирается красить комнату, необходимо определить общую площадь всех стен, чтобы купить нужное количество краски. Объем геометрических фигур Цель: Дать учащимся возможность визуально понимать трехмерные геометрические формы и практиковаться в вычислении объема. Необходимые материалы: Домашние ингредиенты для детской игры, плита, кастрюля, ложка, линейки и калькуляторы. Процедура:
| ||||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Джуди Ласатер | ||||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | ||||||||||||||||||||||||||||||||||||||||||||||
| Какой формы ваша земля? | ||||||||||||||||||||||||||||||||||||||||||||||
Целей:
Материалы: Для каждого учащегося или группы: один лист миллиметровой бумаги, приклеенный или наклеенный на гофрированный картон или жесткий пенопласт; замкнутая петля из бечевки длиной 20 сантиметров; примерно шесть прямых булавок или канцелярских кнопок на учащегося или группу; карандаш и бумага для записей. Историческая справка: Согласно римской мифологии Дидона была дочерью царя Тира. Ее брат Пигмалион убил ее мужа, и она сбежала, опасаясь за свою безопасность. Дидона пересекла Средиземное море со всем своим богатством и некоторыми товарищами и высадилась в североафриканском королевстве Ливия. Здесь она искала землю в качестве убежища для своей группы. Король согласился дать ей столько земли, сколько она сможет покрыть шкурой быка. Теперь Дидона кое-что знала о геометрии и хотела как можно больше земли.Она разрезала шкуру быка на тонкие полоски, а затем соединила их в одну длинную прядь. Как вы думаете, какую форму она заключила? Состав: Учащиеся могут выполнять это задание индивидуально или в группах. Возможные групповые роли для четырех участников: два ученика должны создавать формы, один — для вычисления площадей, а один — для записи форм, размеров и площадей. Каждой группе понадобится один набор материалов, как описано выше: миллиметровая бумага на доске, канцелярские кнопки и веревка. Задание: Учащиеся должны использовать веревку и канцелярские кнопки, чтобы разложить плоские фигуры на сетке.Студентам необходимо будет рассчитать площадь каждой фигуры, которую они создают, поэтому выбранные формы будут зависеть от базовых знаний учащихся. Предлагаемые фигуры: квадрат, прямоугольники, треугольники и круг. Напомните учащимся, что они могут образовывать более одного прямоугольника и более одного треугольника. Студенты должны рассчитать площади для каждой сформированной фигуры и решить, какую форму, по их мнению, следует выбрать Дидоне. Примечание: , если это используется как упражнение для представления областей плоских фигур, учащиеся могут находить области, считая квадраты.В качестве дополнительного задания учащиеся должны использовать формулы площади. Следующая таблица или аналогичная может быть предоставлена для ведения учета:
Вопросы для обсуждения:
В конце концов Дидона отмерила форму полукруга, соединив одну точку на берегу с другой. Таким образом, вода составляла одно из ее требований, и у нее было дополнительное преимущество — выход к морю. Ей нужно было только использовать шкуру, чтобы оградить землю, поэтому область, которую она отметила, была как можно больше и желательна. Король Ливии сдержал свое слово и отдал ей землю.Зарекомендовала себя умная Дидона, будущая королева Карфагена. Попросите учащихся развязать петли из веревок и использовать их 20-сантиметровые нити, чтобы сформировать полукруги по краям сетки. Вычислите площадь полученного таким образом полукруга, чтобы понять, насколько умен Дидона. Связанная активность: Следующий трюк может стать забавным введением в занятие. Принесите в класс лист бумаги размером с лист бумаги для принтера.Спросите своих учеников: «Как вы думаете, я могу вырезать отверстие в этом листе бумаги и протолкнуть его (впишите имя какого-нибудь ученика в классе)»? Когда ученики выражают свой скептицизм, прорежьте в бумаге большое отверстие, просуньте руку в отверстие и мягко толкните выбранного ученика. Затем достаньте новый лист бумаги с очень маленьким отверстием. Спросите, как вы думаете, я смогу провести (того же ученика) через лист бумаги с этим отверстием? Общая реакция будет такой, что вы, вероятно, не сможете, хотя некоторые студенты будут искать другой трюк. Чтобы показать им, что вы можете делать то, что вы сказали, возьмите лист бумаги с таким же маленьким отверстием и прорезями, как показано на схеме ниже. Вы можете использовать уже имеющийся у вас лист и вырезать прорези, пока они ждут, но это займет много времени. Откройте прорези, чтобы образовалась одна огромная бумажная петля, и наденьте ее прямо на голову учеников. Вы сделали это! | ||||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Лори Кисс | ||||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | ||||||||||||||||||||||||||||||||||||||||||||||
| Геометрический текстильный дизайн. | ||||||||||||||||||||||||||||||||||||||||||||||
Иногда у студентов возникают проблемы с соотнесением математики с реальным миром; Следовательно, эта деятельность в области геометрического текстильного дизайна будет акцентировать внимание на геометрических формах и узорах в сочетании с художественным дизайном, компьютерными приложениями и возможностями карьерного роста. Цель: Для каждого ученика разработать свой собственный геометрический квадрат из текстиля, который будет превращен в лоскутное одеяло. Необходимые материалы: Тканевые квадраты геометрической формы (5 дюймов х 5 дюймов), шаблонная бумага, цветные карандаши, белые тканевые квадраты (5 дюймов х 5 дюймов), обрезки картона, малярная лента и краска для ткани. Процедура:
| ||||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Джуди Ласатер | ||||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущий | ||||||||||||||||||||||||||||||||||||||||||||||
| Изготовление многогранников. | ||||||||||||||||||||||||||||||||||||||||||||||
Многогранник — это геометрическая фигура, которая является трехмерной версией плоского многоугольника (двумерного). Всего пять правильных многогранников. Это тетраэдр (4 грани), шестигранник или куб (6 граней), октаэдр (8 граней), додекаэдр (12 граней) и икосаэдр (20 граней).Ниже представлены выкройки двух многогранников, которые можно воспроизвести и трансформировать в трехмерные фигуры. Щелкните на фигурах, чтобы открыть окно с фигурой в нем для облегчения печати. | ||||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Сьюзан Истман | ||||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | ||||||||||||||||||||||||||||||||||||||||||||||
Определение диаграммы Венна
Что такое диаграмма Венна?
Диаграмма Венна — это иллюстрация, в которой круги используются для отображения взаимосвязей между вещами или конечными группами вещей.Перекрывающиеся круги имеют общие черты, в то время как круги, которые не перекрываются, не имеют этих черт.
Диаграммы Венна помогают визуально представить сходства и различия между двумя концепциями. Их давно признали за их полезность в качестве учебных пособий. С середины 20-го века диаграммы Венна использовались как часть вводной программы обучения логике и в образовательных планах начального уровня по всему миру.
Ключевые выводы
- Диаграмма Венна использует круги, которые перекрываются или не перекрываются, чтобы показать общие черты и различия между вещами или группами вещей.
- Вещи, которые имеют общие черты, отображаются в виде перекрывающихся кругов, в то время как отдельные элементы выделяются отдельно.
- Диаграммы Венна теперь используются в качестве иллюстраций в бизнесе и во многих академических областях.
Понимание диаграммы Венна
Английский логик Джон Венн популяризировал диаграмму в 1880-х годах. Он назвал их кругами Эйлера в честь швейцарского математика Леонарда Эйлера, создавшего аналогичные диаграммы в 1700-х годах.
Термин диаграмма Венна не появлялся до 1918 года, когда Кларенс Льюис, американский академический философ и возможный основатель концептуального прагматизма, в своей книге «Обзор символической логики» назвал круговое изображение диаграммой Венна.»
Диаграммы Венна используются с середины 20 века в классах от уровня начальной школы до вводной логики.
Венн изучал и преподавал логику и теорию вероятностей в Кембриджском университете, где он разработал свой метод использования диаграмм для иллюстрации раздела математики, известного как теория множеств.
Венн опубликовал прецедентную работу «Логика случая», в которой объяснил частотную теорию вероятности. В нем он утверждал, что вероятность, вопреки распространенному предположению, должна быть установлена на основе регулярности, с которой что-то предсказывается.
В другой книге, Symbolic Logic, Venn основаны и развиты теории алгебры математика Джорджа Буля. Эта работа помогла ему разработать диаграмму Венна.
Приложения для диаграмм Венна
Диаграммы Венна используются для отображения того, как элементы соотносятся друг с другом на фоне общего фона, юниверса, набора данных или среды. Диаграмму Венна можно использовать, например, для сравнения двух компаний в одной отрасли, иллюстрируя продукты, предлагаемые обеими компаниями (где круги перекрываются), и продукты, которые являются эксклюзивными для каждой компании (внешние круги).
Диаграммы Венна на базовом уровне представляют собой простые графические представления отношений, существующих между двумя наборами вещей. Однако они могут быть намного сложнее. Тем не менее, упрощенная цель диаграммы Венна для иллюстрации концепций и групп привела к их популярному использованию во многих областях, включая статистику, лингвистику, логику, образование, информатику и бизнес.
Примеры диаграмм Венна
Можно нарисовать диаграмму Венна, чтобы проиллюстрировать фрукты красного или оранжевого цвета.Ниже мы видим, что есть оранжевые фрукты (круг B), такие как хурма и мандарины, а яблоки и вишня (круг A) имеют красный цвет. Перец и помидоры бывают красного и оранжевого цветов, что представлено областью перекрытия двух кругов.
Изображение Джули Банг © Investopedia 2020Вы также можете нарисовать диаграмму Венна, чтобы решить, какую из двух машин купить. На диаграмме Венна показаны особенности, присущие каждому автомобилю, а также особенности обоих автомобилей.
Ниже мы видим, что Car A — это седан, который работает на бензине и имеет скорость 20 миль на галлон, а Car B — гибрид, который получает 40 миль на галлон за пробег и является хэтчбеком.
Изображение Джули Банг © Investopedia 2020Заштрихованная область, где два круга перекрываются, показывает общие черты обоих автомобилей, в том числе радио, четыре двери, возможность Bluetooth и подушки безопасности.
Диаграмма Венна графически отображает сходства и различия между двумя автомобилями, чтобы помочь решить, какой из них купить.
Часто задаваемые вопросы о диаграмме Венна
Что такое диаграмма Венна в математике?
Диаграмма Венна в математике используется в теории логики и теории множеств, чтобы показать различные наборы или данные и их отношения друг с другом.
Как прочитать диаграмму Венна?
Диаграмму Венна можно прочитать, наблюдая за всеми кругами, составляющими всю диаграмму. Каждый круг — это отдельный элемент или набор данных. Части кругов, которые перекрываются, указывают на области, которые являются общими для различных элементов, тогда как части, которые не перекрываются, указывают на уникальные черты элемента или набора данных, представленных кругом.
Почему они называются диаграммами Венна?
Они называются диаграммами Венна, потому что диаграмма была разработана английским логиком Джоном Венном.
Как называется середина диаграммы Венна?
Середина диаграммы Венна, где перекрываются два или более набора, называется пересечением.
Идентификация Эйлера: «Самое красивое уравнение»
Тождество Эйлера — это равенство, обнаруженное в математике, которое сравнивают с сонетом Шекспира и описывают как «самое красивое уравнение».«Это частный случай фундаментального уравнения сложной арифметики, называемого формулой Эйлера, который покойный великий физик Ричард Фейнман назвал в своих лекциях« нашей жемчужиной »и« самой замечательной формулой в математике ».
В интервью BBC , Профессор Дэвид Перси из Института математики и ее приложений сказал, что «Идентичность Эйлера» была «настоящей классикой, и вы не можете ничего лучше этого… На нее просто взглянуть, но она невероятно глубокая, она включает в себя пять наиболее важных математических констант.
Идентичность Эйлера записывается просто как: e iπ + 1 = 0
Пять констант:
- Число 0.
- Число 1.
- Число π , иррациональное число (с бесконечными цифрами), которое представляет собой отношение длины окружности к ее диаметру. Это примерно 3,14159…
- Число e , тоже иррациональное число. Это основа натуральных логарифмов, которая естественным образом возникает в результате изучения сложных процентов и исчисления.Число e пронизывает математику, появляясь, казалось бы, из ниоткуда в огромном количестве важных уравнений. Это примерно 2,71828….
- Число i , определенное как квадратный корень из отрицательной единицы: √ (-1). Самое фундаментальное из мнимых чисел, названное так потому, что на самом деле никакое число не может быть умножено само на себя, чтобы получить отрицательное число (и, следовательно, отрицательные числа не имеют реальных квадратных корней). Но в математике есть много ситуаций, когда нужно извлечь квадратный корень из отрицательного числа.Таким образом, буква и используется как своего рода подставка для обозначения мест, где это было сделано.
Продуктивный математик
Леонард Эйлер был математиком 18-го века, родившимся в Швейцарии, и разработал множество концепций, которые являются неотъемлемой частью современной математики. Большую часть своей карьеры он провел в Санкт-Петербурге, Россия. По данным Военно-морской академии США (USNA), он был одним из самых плодовитых математиков всех времен, опубликовавшим 886 статей и книг. Большая часть его работ пришлась на последние два десятилетия его жизни, когда он был полностью слеп.Работы было так много, что Петербургская Академия продолжала посмертно публиковать его работы более 30 лет.
Важный вклад Эйлера включает формулу Эйлера и теорему Эйлера, которые могут означать разные вещи в зависимости от контекста. Согласно USNA, в механике существуют «углы Эйлера (для определения ориентации твердого тела), теорема Эйлера (о том, что каждое вращение имеет ось), уравнения Эйлера для движения жидкостей и уравнение Эйлера-Лагранжа (которое исходит из вариационного исчисления).»
Умножение комплексных чисел
Идентичность Эйлера естественным образом проистекает из взаимодействия комплексных чисел, которые представляют собой числа, состоящие из двух частей: действительного числа и мнимого числа; например, 4 + 3 i . Комплексные числа появляются во множестве такие приложения, как волновая механика (исследование в рамках квантовой механики) и разработка схем, использующих переменный ток (обычная практика в электротехнике). Кроме того, комплексные числа (и их родственники, гиперкомплексные числа) обладают свойством, которое делает их особенно полезно для изучения компьютерной графики, робототехники, навигации, динамики полета и орбитальной механики: их умножение заставляет их вращаться.Это свойство поможет нам понять причину тождества Эйлера.
В приведенном ниже примере пять комплексных чисел нанесены на комплексную плоскость и вместе образуют «форму дома». Комплексная плоскость похожа на числовую прямую, за исключением того, что она двумерна. Горизонтальное направление представляет действительные числа, а вертикальная ось представляет собой мнимые числа. Каждое комплексное число в форме дома умножается на комплексное число 4 + 3 i и переносится на график (зеленая стрелка).[Связано: что такое комплексные числа?]
Как видно, умножение на 4 + 3 i приводит к тому, что форма дома расширяется на (увеличивается по площади и удаляется от начала координат 0 + 0 i на столько же) и , вращающийся (наклоняется на некоторый угол). Чтобы показать, что это именно эффект умножения на 4 + 3i, также показан эффект пятикратного увеличения дома и поворота на 36,9 градусов (красная стрелка). Производится точно такой же эффект.
Тот же эффект получается при умножении вершин фигуры на 4 + 3i, повороте фигуры на 36,9 градуса и расширении ее в пять раз. (Изображение предоставлено Робертом Дж. Кулманом)Различные степени расширения и вращения могут производить эффект умножения на любое число на комплексной плоскости.
Полярная форма комплексных чисел
Величина вращения и расширения определяется свойствами, присущими числу 4 + 3 i, , которое, как показано на рисунке ниже, находится в пяти единицах от начала координат ( r = 5) и составляет угол 36.9 градусов по горизонтальной оси ( φ = 36,9 °). Эти измерения используются в так называемой полярной форме комплексного числа ( относительно iφ ) в отличие от нормальной прямоугольной формы ( a + bi ).
Число 4 + 3i находится на расстоянии пяти единиц от начала координат и образует угол 36,9 градуса с горизонтальной осью. (Изображение предоставлено Робертом Дж. Кулманом)Полярная форма требует, чтобы φ было измерено в радианах .Один радиан (1 рад ) составляет приблизительно 57,3 градуса; это мера угла, образующегося при наложении радиуса круга на его длину. Мера π радиан охватывает половину окружности; мера 2 π радиан охватывает полный круг.
Угловая мера в один радиан образуется, когда радиус окружности наматывается на его окружность. Полукруг равен π радиан, а полный круг равен 2π радиан. (Изображение предоставлено Робертом Дж.Coolman)Угловая мера для 4 + 3 i составляет 0,644 радиана (36,9 ° = 0,644 рад ), что означает, что полярная форма 4 + 3 i равна 5 e i 0,644 . Меры для r и φ также могут быть определены для каждой из точек формы дома, и еще один способ достижения эффекта расширения / вращения при умножении на 4 + 3 i состоит в умножении каждого r на пять и прибавьте 36,9 градуса (или 0,644 рад ) к каждому φ .Из этой демонстрации мы видим, что когда комплексные числа умножаются, расстояния умножаются, а углы складываются. Это происходит из-за свойства, присущего показателям степени, которое можно показать алгебраически.
Использование полярной формы комплексных чисел, чтобы показать, почему расстояния умножаются, а углы складываются. (Изображение предоставлено Робертом Дж. Кулманом)С установленной полярной формой комплексных чисел, вопрос идентичности Эйлера является просто частным случаем a + bi для a = -1 и b = 0 .Следовательно, для полярной формы относительно iφ , это составляет r = 1 и φ = π (поскольку π рад = 180 °).
Идентификация Эйлера — это частный случай a + bi для a = -1 и b = 0 и reiφ для r = 1 и φ = π. (Изображение предоставлено Робертом Дж. Кулманом)Получение полярной формы
Хотя тождество Эйлера следует из полярной формы комплексных чисел, невозможно получить полярную форму (в частности, спонтанное появление числа e ) без исчисление.
Общий случай комплексного числа в прямоугольной (a + bi) и полярной (reiφ) форме. (Изображение предоставлено Робертом Дж. Кулманом)Начнем с прямоугольной формы комплексного числа:
a + bi
Из диаграммы и тригонометрии мы можем сделать следующие замены:
( r · cos φ ) + ( r · sin φ ) i
Отсюда мы можем вывести r :
r · (cos φ + i · sin φ )
Иногда «cos φ + i · sin φ » обозначается как cis φ , что является сокращением от « c osine плюс i maginary s ine.”
r · cis φ
Функция cis φ оказывается равной e iφ . Это то, что невозможно показать без исчисления. Два вывода показаны ниже:
Два вывода для cisφ = eiφ. Оба используют какую-то форму исчисления. (Изображение предоставлено Робертом Дж. Кулманом)Таким образом, уравнение r · цис φ записано в стандартной полярной форме r · e iφ .
Дополнительные ресурсы
Измерение углов
Измерение угловПонятие угла
Понятие угла — одно из важнейших понятий в геометрии. Понятия равенства, суммы и разности углов важны и используются во всей геометрии, но предмет тригонометрии основан на измерении углов.Есть две обычно используемые единицы измерения углов.Более знакомая единица измерения — это градусы. Круг делится на 360 равных градусов, так что прямой угол равен 90 °. Пока мы будем рассматривать только углы от 0 ° до 360 °, но позже, в разделе о тригонометрических функциях, мы будем рассматривать углы больше 360 ° и отрицательные углы. Градусы можно разделить на минуты и секунды, но это деление не так универсально, как раньше. Каждый градус делится на 60 равных частей, называемых минут. Итак, семь с половиной градусов можно назвать 7 градусами и 30 минутами, записанными как 7 ° 30 ‘. Каждая минута далее делится на 60 равных частей, называемых секунд, и, например, 2 градуса 5 минут 30 секунд записывается как 2 ° 5 ’30 «. Деление градусов на минуты и угловые секунды аналогично делению на часы в минуты и секунды. |
Части градуса теперь обычно обозначаются десятичной дробью. Например, семь с половиной градусов теперь обычно пишут 7.5 & град.
Когда один угол нарисован на плоскости xy для анализа, мы нарисуем его в стандартной позиции с вершиной в начале координат (0,0), одна сторона угла вдоль x ось, а другая сторона выше оси x .
Радианы
Другое распространенное измерение углов — радианы. Для этого измерения рассмотрим единичный круг (круг радиуса 1), центр которого является вершиной рассматриваемого угла.Затем угол отсекает дугу окружности, и длина этой дуги является мерой угла в радианах. Легко переходить между градусами и радианами. Окружность всего круга равна 2 π , следовательно, 360 ° равняется 2 π радиан. Следовательно, 1 ° равно π /180 радиана также 1 радиан равен 180/ π градусБольшинство калькуляторов можно настроить на использование углов, измеряемых в градусах или радианах.Убедитесь, что вы знаете, в каком режиме работает ваш калькулятор. |
Краткая заметка по истории радианов
Хотя слово «радиан» было придумано Томасом Мьюиром и / или Джеймсом Томпсоном около 1870 года, математики долгое время измеряли углы таким способом. Например, Леонард Эйлер (1707–1783) в его Элементах алгебры явно сказал, что углы измеряются длиной дуги, отрезанной в единичной окружности.Это было необходимо, чтобы дать его знаменитую формулу, включающую комплексные числа, которая связывает функции знака и косинуса с экспоненциальной функцией. e iθ = cos θ + i sin θгде θ — это то, что позже было названо измерением угла в радианах. К сожалению, объяснение этой формулы выходит далеко за рамки этих заметок. Но для получения дополнительной информации о комплексных числах см. Мой Краткий курс комплексных чисел.
Радианы и длина дуги
Альтернативное определение радианов иногда дается в виде отношения. Вместо того, чтобы брать единичную окружность с центром в вершине угла θ , возьмите любую окружность с центром в вершине угла. Тогда радианная мера угла — это отношение длины вытянутой дуги к радиусу r окружности. Например, если длина дуги равна 3, а радиус круга равен 2, тогда радианная мера равна 1.5.Причина, по которой это определение работает, заключается в том, что длина вытянутой дуги пропорциональна радиусу круга. В частности, определение в терминах отношения дает ту же цифру, что и приведенная выше с использованием единичного круга. Однако это альтернативное определение более полезно, поскольку вы можете использовать его для соотнесения длин дуг с углами. Длина дуги равна радиусу r , умноженному на угол θ , где угол измеряется в радианах.
Например, дуга θ = 0,3 радиана в окружности радиуса r = 4 имеет длину 0,3 умноженную на 4, то есть 1,2.
Радианы и площадь сектора
Сектор круга — это часть круга, ограниченная двумя радиусами и дугой окружности, соединяющей их концы. Площадь этого сектора легко вычислить по радиусу r окружности и углу θ между радиусами, если он измеряется в радианах.Так как площадь всего круга равна πr 2 , а сектор относится ко всей окружности, так как угол θ равен 2 π , поэтомуУглы общие
Ниже приведена таблица общих углов для измерения в градусах и радианах. Обратите внимание, что измерение в радианах дано в единицах π . Его, конечно, можно было бы указать в десятичной дроби, но радианы часто появляются с коэффициентом π .| Уголок | Градусов | Радианы |
|---|---|---|
| 90 ° | π /2 | |
| 60 ° | π /3 | |
| 45 ° | π /4 | |
| 30 ° | π /6 |
Упражнения
Эдвин С.Кроули написал книгу Тысяча упражнений в плоской и сферической тригонометрии, Университет Пенсильвании, Филадельфия, 1914. Задачи этого короткого курса взяты из этого текста (но не все 1000 из них!). пять знаков точности, поэтому студентам пришлось потрудиться, чтобы решить их, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении. Студенты должны были уметь пользоваться таблицей синус-косинусов, таблицей касательных, таблицей логарифмов, таблицей log-sin-cos и таблицей log-tan.Теперь мы можем пользоваться калькуляторами! Это означает, что вы можете сосредоточиться на концепциях, а не на трудоемких вычислениях.Кроули использовал не десятичные дроби для дробей градуса, а минуты и секунды.
Каждый комплекс упражнений включает в себя, во-первых, формулировку упражнений, во-вторых, некоторые подсказки для решения упражнений, а в-третьих, ответы на упражнения.
1. Выразите следующие углы в радианах.
(а). 12 градусов, 28 минут, то есть 12 ° 28 ‘.
(б). 36 ° 12 ‘.
2. Сократите следующие числа радианов до градусов, минут и секунд.
(а). 0,47623.
(б). 0,25412.
3. Учитывая угол a и радиус r, найдите длину продолжающейся дуги.
(а). a = 0 ° 17 ’48 дюймов, r = 6,2935.
(б). a = 121 ° 6 ’18 дюймов, r = 0,2163.
4. Учитывая длину дуги l и радиус r, найти угол, стянутый в центре.
(а). l = 0,16296, r = 12,587.
(б). l = 1,3672, r = 1,2978.
5. Зная длину дуги l и угол a , который она проходит в центре, найти радиус.
(а). a = 0 ° 44 ’30 дюймов, l = 0,032592.
(б). a = 60 ° 21 ‘6 дюймов, l = 0,4572.
6. Найдите длину с точностью до дюйма дуги окружности 11 градусов 48,3 минуты, если радиус составляет 3200 футов.
7. Кривая железной дороги образует дугу окружности 9 градусов 36,7 минут, радиус до центральной линии пути составляет 2100 футов. Если калибр 5 футов, найдите разницу в длине двух рельсов с точностью до полудюйма.
9. На сколько можно изменить широту, идя на север на одну милю, если предположить, что Земля представляет собой сферу радиусом 3956 миль?
10. Вычислите длину в футах одной угловой минуты на большом круге Земли. Какова длина дуги в одну секунду?
14. На окружности радиусом 5,782 метра длина дуги составляет 1,742 метра. Какой угол он образует в центре?
23. Воздушный шар, известный как 50 футов в диаметре, сужается к глазу под углом 8 1/2 минут.Как далеко это?
Подсказки
1. Чтобы преобразовать градусы в радианы, сначала преобразуйте количество градусов, минут и секунд в десятичную форму. Разделите количество минут на 60 и прибавьте к количеству градусов. Так, например, 12 ° 28 ‘равно 12 + 28/60, что равно 12,467 °. Затем умножьте на π и разделите на 180, чтобы получить угол в радианах.
2. И наоборот, чтобы преобразовать радианы в градусы, разделите на π и умножьте на 180.Таким образом, 0,47623 разделить на π и умножить на 180 дает 27,286 °. Вы можете преобразовать доли градуса в минуты и секунды следующим образом. Умножьте дробь на 60, чтобы получить количество минут. Здесь 0,286 умножить на 60 равно 17,16, поэтому угол можно записать как 27 ° 17,16 ‘. Затем возьмите любую оставшуюся долю минуты и снова умножьте на 60, чтобы получить количество секунд. Здесь 0,16 умножить на 60 равно примерно 10, поэтому угол также можно записать как 27 ° 17 ’10 «.
3. Чтобы найти длину дуги, сначала преобразуйте угол в радианы. Для 3 (a) 0 ° 17’48 «составляет 0,0051778 радиана. Затем умножьте его на радиус, чтобы найти длину дуги.
4. Чтобы найти угол, разделите его на радиус. Это дает вам угол в радианах. Их можно преобразовать в градусы, чтобы получить ответы Кроули.
5. Как упоминалось выше, радиан умноженный на радиус = длина дуги, поэтому, используя буквы для этой задачи, ar = l, , но a необходимо сначала преобразовать из градусного измерения в радиан .Итак, чтобы найти радиус r, сначала преобразует угол a в радианы, а затем разделит его на длину l дуги.
6. Длина дуги равна радиусу, умноженному на угол в радианах.
7. Помогает нарисовать фигуру. Радиус внешнего рельса равен 2102,5, а радиус внутреннего рельса — 2097,5.
9. У вас получился круг радиусом 3956 миль и дуга этого круга длиной 1 милю.Какой угол в градусах? (Средний радиус Земли был известен довольно точно в 1914 году. Посмотрим, сможете ли вы узнать, каким, по мнению Эратосфена, был радиус Земли, еще в III веке до н. Э.)
10. Угловая минута равна 1/60 градуса. Преобразовать в радианы. Радиус — 3956. Какова длина дуги?
14. Поскольку длина дуги равна радиусу, умноженному на угол в радианах, отсюда следует, что угол в радианах равен длине дуги, деленной на радиус.Радианы легко преобразовать в градусы.
23. Представьте, что диаметр воздушного шара является частью дуги окружности с вами в центре. (Это не совсем часть дуги, но довольно близко). Длина дуги составляет 50 футов. Вы знаете угол, так каков радиус этого круга?
ответы
1. (а). 0,2176. (б). 0,6318.2. (а). 27 ° 17 ’10 «. (B). 14,56 ° = 14 ° 33,6′ = 14 ° 33’36».
3. (а). 0,03259 (б). 2,1137 умножить на 0,2163 равно 0,4572.
4. (а). 0,16296 / 12,587 = 0,012947 радиан = 0 ° 44 ’30 дюймов.
(б). 1,3672 / 1,2978 = 1,0535
радианы = 60,360 ° = 60 ° 21,6 ‘= 60 ° 21’ 35 «.
5. (а). л / год = 0,032592 / 0,01294 = 2,518.
(б). л / год = 0,4572 / 1,0533 = 0,4340.
6. ra = (3200 ‘) (0.20604) = 659,31 ‘= 659’ 4 дюйма.
7. Угол a = 0,16776 радиана. Разница в длине составляет 2102,5 a — 1997,5 a , что составляет 5 a. Таким образом, ответ составляет 0,84 фута, что с точностью до дюйма составляет 10 дюймов.
9. Угол = 1/3956 = 0,0002528 радиан = 0,01448 ° = 0,8690 ‘= 52,14 дюйма.
10. Одна минута = 0,0002909 радиан. 1.15075 миль = 6076 футов.Следовательно, одна секунда будет соответствовать 101,3 фута.
14. a = л / об = 1,742 / 5,782 = 0,3013 радиан = 17,26 ° = 17 ° 16 ‘.
23. Угол a равен 8,5 ‘, что составляет 0,00247 радиана. Таким образом, радиус равен r = л / год = 50 / 0,00247 = 20222 ‘= 3,83 мили, почти четыре мили.
Насчет цифр точности.
Кроули старается давать свои ответы примерно с той же точностью, что и данные в вопросах.Это важно, особенно сейчас, когда у нас есть калькуляторы. Например, в задаче 1 точка отсчета равна 12 ° 28 ‘, что соответствует примерно четырем знакам точности, поэтому ответ 0,2176 также должен быть дан только с точностью до четырех знаков. (Обратите внимание, что ведущие нули не учитываются при вычислении цифр точности.) Ответ 0,21758438 предполагает восемь цифр точности, и это может ввести в заблуждение, поскольку данная информация не была такой точной.Другой пример см. В задаче 3 (a). Данные 0 ° 17’48 «и 6.2935 с точностью до 4 и 5 знаков соответственно. Следовательно, ответ должен быть дан только с точностью до 4 цифр, поскольку ответ не может быть более точным, чем наименее точные данные. Таким образом, ответ, который может дать калькулятор, а именно 0,032586547, следует округлить до четырех цифр (не включая ведущие нули) до 0,03259.
Хотя окончательные ответы должны быть выражены с соответствующим числом цифр точности, вы все равно должны сохранять все цифры для промежуточных вычислений.
(PDF) Компьютерное представление диаграмм Венна и Эйлера
Компьютерное представление диаграмм Венна и Эйлера 6
Международная конференция по достижениям в области ИКТ для развивающихся регионов, 1-2 сентября 2016 г. ICTer2016
Диаграммы 1 и 2 содержат два набора и оставшиеся диаграммы
содержит 3 комплекта. Рисунки для диаграммы 1 были собраны из
сценариев ответов школьников, а остальные
были получены от студентов университетов.На диаграммах 5 и 6 было меньше
ответов из-за более высокой сложности вопроса.
Все ошибки синтаксического анализа связаны с неоднозначностью текста меток
, а некоторые текстовые метки расположены слишком далеко от стрелок
, которые должны быть метками стрелок. На рис. 10 показана диаграмма Венна
с неоднозначными метками набора. Метка
«Cricket» может быть распознана как метка набора универсального набора
или метка набора, представленная первым эллипсом, поскольку она близка к
ближайшему концу строки и границе прямоугольника.Метка набора
«Футбол» может быть или не быть меткой набора для набора
, представленного вторым эллипсом, но она находится слишком далеко от конца строки
. Чтобы устранить эти неоднозначности текстовых меток, необходим более высокий уровень анализа
.
V. ВЫВОДЫ
G. Будущая работа
Можно определить количество возможных дальнейших расширений
применительно к внедренной системе.
В этом исследовании наборы могут быть составлены из нескольких фигур, таких как
прямоугольников, кругов и эллипсов.Этот метод может быть расширен для применения к множествам, нарисованным с помощью любого типа кривых Jordan
. В некоторых представлениях Венна и Эйлера одна метка набора
может иметь более одной кривой Жордана. Этот метод
может быть расширен для обращения к этим представлениям.
Подходы машинного обучения могут использоваться для улучшения классификации и кластеризации меток
. В настоящее время методы машинного обучения
не используются, так как у нас нет значительно большой базы данных векторных изображений
.
Этот метод может быть легко расширен на другие векторные форматы изображений
, поскольку уже разработаны методы преобразования пиксельных изображений формата
в векторный формат. Кроме того, этот метод
может быть расширен для анализа распечатанных изображений.
H. Заключительные замечания
Понимание диаграмм — сложная проблема в области компьютерных исследований
. Структурированные диаграммы
могут быть обработаны с использованием онтологии предметной области, но понимание неструктурированных чертежей
является очень сложной проблемой.В частности,
, имеющий дело с диаграммами, нарисованными человеком, затруднен из-за проблем неоднозначности
и человеческих ошибок.
В этом исследовании мы успешно установили
необходимых методов для интерпретации диаграмм Венна и Эйлера
, представленных в векторном формате SVG, и представили общий формат
для представления диаграммы Венна и Эйлера. Мы полагаем, что
, что решения, которые мы внедрили, помогут разработать
систем, связанных с пониманием изображений, таких как автоматические системы оценки
и системы баз данных изображений.
ПОДТВЕРЖДЕНИЕ
Это исследование финансируется исследовательским грантом Сената Моратувы (SRC) Университета
в 2015 году и исследовательским грантом DL4D 2016
.
СПРАВОЧНАЯ ИНФОРМАЦИЯ
[1]. Р. П. Футрелле, И. Какадиарис, Дж. Александер, К. М. Карриеро, Н.
Николакис и Дж. М. Футрелле, «Понимание диаграмм в технических документах
», IEEE Computer, 1992, Vol. 25 (7), pp. 75-
78.
[2].Р. П. Футрелле и Н. Николакис, «Эффективный анализ сложных диаграмм
с использованием анализа на основе ограничений», в «Анализ документов
и распознавание», в материалах Третьей международной конференции
по IEEE, 1995, Vol. 2. С. 782-790.
[3]. Р. Футрелл, «Неоднозначность в теории визуального языка и ее роль в анализе диаграмм
», в Proceedings 1999 IEEE Symposium on
Visual Languages, 1999.
[4].В. Хуанг, К. Тан и В. К. Леоу (2005, август).
«Связывание текста и графики для научной диаграммы
понимания», Анализ и распознавание документов, в
Труды восьмой международной конференции по IEEE,
2005, стр. 580-584.
[5]. В. Хуанг, К. Тан, «Система для понимания визуализированной инфографики
и ее приложений», в материалах симпозиума
ACM 2007 г. по проектированию документов — DocEng ’07, 2007.
[6]. К. Целонис, Дж. Сарджент и М. М. Вуд, «Соответствие диаграммы
для совместной оценки человека и компьютера», в Proceedings
9-й конференции CAA, 2005.
[7]. Р. Ф. Ганстон и Р. Т. Уайт (1986). «Оценка понимания
с помощью диаграмм Венна», Science Education,
Vol 70 (2), pp. 151-158, 1986.
[8]. А. Цинцифас, «Структура компьютерной оценки
курсовой работы на основе диаграмм», в компьютерных науках и
информационных технологиях, 2002.
[9]. Н. Смит, П. Томас и К. Во, «Интерпретация неточных
диаграмм», Диаграммное представление и вывод.
Springer Berlin Heidelberg, 2004. 239-241.
[10]. П. Томас, К. Во и Н. Смит, «Эксперименты по автоматической маркировке
ER-диаграмм», Бюллетень ACM SIGCSE,
Том 37 (3), стр. 158-162, 2005.
[ 11]. П. Томас, К. Во и Н. Смит, «Обобщенные диаграммы
инструментов с автоматической маркировкой», Инновации в обучении и
обучения в области информационных и компьютерных наук, том 10 (1), стр.
22-34, 2011.
[12]. П. Томас, К. Во и Н. Смит, «Использование шаблонов в
автоматической разметке ER-диаграмм», Бюллетень ACM SIGCSE.
Том. 38 (3), 2006.
[13]. Дж. Амбикеш и М. Шепперд, «Проблема меток в E-
, оценка диаграмм», Журнал образовательных ресурсов в
Computing (JERIC), том 8 (4), стр. 12, 2009.
[ 14]. К. Во, П. Томас и Н. Смит, «На пути к автоматизированной оценке диаграмм сущность-взаимосвязь
», Второй семинар
Сети поддержки обучения и преподавания —
Информация и информатика (TLAD) 2004 г.
[15]. Б. Блай и К. А. Хиггинс, «Формирующая компьютерная оценка
в областях, основанных на диаграммах». Бюллетень ACM SIGCSE,
Том 38 (3), стр. 98-102, 2006
[16]. М. Андерсон и Р. Маккартни, «Обработка диаграмм:
Вычисления с диаграммами», «Искусственный интеллект», том 145 (1),
стр. 181-226, 2003.
[17]. Э. Фоксли, К. Хиггинс, Т. Хегази, П. Симеонидис и А.
Цинцифас. «Система coursemaster cba: улучшения по сравнению с
ceilidh», в The Computer-Assisted Assessment Conference,
2001.
[18]. Ф. Батмаз и К. Дж. Хинде, «Инструмент для рисования диаграмм для полуавтоматической оценки концептуальных диаграмм баз данных
», в
Proceedings of the 10th CAA Conference, 2006.
[19]. Г. Хоггарт и М. Локьер, «Автоматизированная система оценки учащихся с диаграммой
», Бюллетень ACM SIGCSE, Vol. 30 (3), 1998.
[20]. П. А. Роджерс, «Обзор диаграмм Эйлера», Journal of Visual
Languages & Computing, том 25 (3), стр.134-155, 2014.
[21]. (2014) Векторная графика [Онлайн]. Доступно:
https://en.wikipedia.org/wiki/Vector_graphics
. 8
8
 Ю. Лыскова, Е.А. Ракитина. Логика в информатике.
М.: Информатика и Образование, 2006. 155 с.
Ю. Лыскова, Е.А. Ракитина. Логика в информатике.
М.: Информатика и Образование, 2006. 155 с. Убедитесь, что x> y и что один из них нечетный, а другой
даже.
Убедитесь, что x> y и что один из них нечетный, а другой
даже.


 Каждый
полоса должна быть примерно 3 х 14 дюймов. Каждому ученику также понадобится
около двух футов ленты, подойдет либо прозрачная лента, либо лента для изготовления ленты),
ножницы и ручка или карандаш.
Каждый
полоса должна быть примерно 3 х 14 дюймов. Каждому ученику также понадобится
около двух футов ленты, подойдет либо прозрачная лента, либо лента для изготовления ленты),
ножницы и ручка или карандаш. Если отрезать 1/3 пути, что будет
случаться? Сделай это. Примечание: к этому времени многие студенты откажутся от
отгадывать часть деятельности или высказывать абсурдные мнения.
Если отрезать 1/3 пути, что будет
случаться? Сделай это. Примечание: к этому времени многие студенты откажутся от
отгадывать часть деятельности или высказывать абсурдные мнения.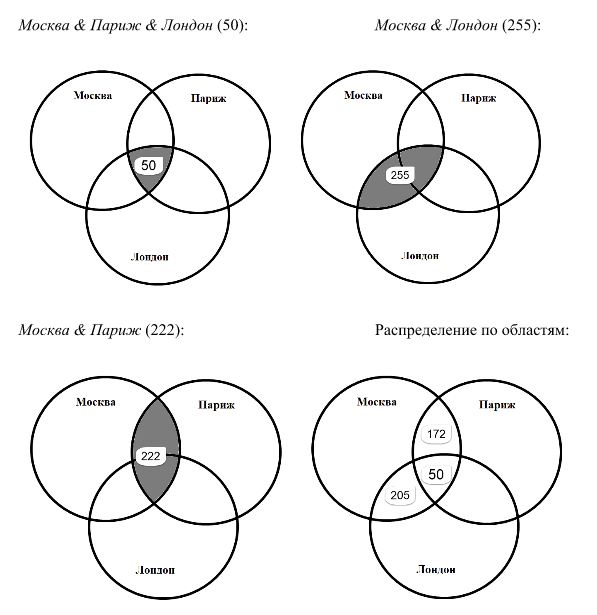 Обозначьте самую длинную сторону треугольника буквой C (гипотенуза) и обозначьте
две другие стороны «А» и «В». Обсудите угол 90 o и два острых угла
и отношения между сторонами. ( c > a ; c > b ; a + b > c )
Обозначьте самую длинную сторону треугольника буквой C (гипотенуза) и обозначьте
две другие стороны «А» и «В». Обсудите угол 90 o и два острых угла
и отношения между сторонами. ( c > a ; c > b ; a + b > c ) Определите, сколько
треугольники потребуются для сторон «А» и «В» (два больших треугольника или пять
из меньших частей.) и для стороны «C». (Все семь частей танграма.)
Определите, сколько
треугольники потребуются для сторон «А» и «В» (два больших треугольника или пять
из меньших частей.) и для стороны «C». (Все семь частей танграма.)
 Какие структуры вы можете придумать, которые почти кричат вам Геометрия? Бейсбольные бриллианты? Баскетбольная площадка? Мост «Золотые ворота? Как насчет центра EPCOT во Флориде?
Какие структуры вы можете придумать, которые почти кричат вам Геометрия? Бейсбольные бриллианты? Баскетбольная площадка? Мост «Золотые ворота? Как насчет центра EPCOT во Флориде?