Тренажёр по информатике и икт (6 класс) на тему: Круги Эйлера. Задачи
Круги Эйлера. Задачи для самостоятельного решения
Задача №1:
Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским – 28, французским – 42. Английским и немецким одновременно владеют 8 человек, английским и французским -10 , немецким и французским – 5, всеми тремя языками – 3.
Сколько туристов не владеют ни одним языком?
Ответ: 20 человек.
Задача №2
В ясельной группе 11 деток любят манную кашу, 13 – гречневую и 7 малышей – перловую. Четверо любят и манную, и гречневую, 3 – манную и перловую, 6- гречневую и перловую, а двое с удовольствием «уплетают» все три вида каши. Сколько детей в этой группе, если в ней нет ни одного ребёнка, вовсе не любящего кашу?
Ответ: 20 человек
Задача №3
В одной семье было много детей. 7 из них любили капусту, 6 – морковь, 5 – горох, 4 – капусту и морковь, 3 – капусту и горох, 2 – морковь и горох, 1 – и капусту, и морковь, и горох. Сколько детей было в семье?
Ответ: 10
Задача №4
В группе 29 студентов. Среди них 14 любителей классической музыки, 15-джаза, 14 – народной музыки. Классическую музыку и джаз слушают 6 студентов, народную музыку и джаз – 7, классику и народную – 9. Пятеро студентов слушают всякую музыку, а остальные не любят никакой музыки. Сколько их?
Ответ:3
Задача №5
Учащиеся 5 и 6 классов отправились на экскурсию. Мальчиков было 16, учащихся 6 класса – 24, пятиклассниц столько, сколько мальчиков из 6 класса. Сколько всего детей побывали на экскурсии?
Ответ: 40
Задача №6
На полу комнаты площадью 24 м² лежат три ковра. Площадь одного из них -10 м², другого – 8 м², третьего – 6 м². Каждые два ковра перекрываются по площади 3 м², а площадь участка пола, покрытого всеми тремя коврами, составляет 1 м². Найдите площадь участка пола:
а)покрытого первым и вторым коврами, но не покрытого третьим ковром;
б)покрытого только первым ковром;
в)не покрытого коврами.
Ответ:10, 5,8
Задача №7
Из 100 приехавших туристов 75 знали немецкий язык и 83 знали французский. 10 человек не знали ни немецкого, ни французского. Сколько туристов знали оба эти языка?
Ответ: 68
Задача №8
Часть жителей нашего дома выписывают только газету «Комсомольская правда», часть – только газету «Известия», а часть – и ту, и другую газету. Сколько процентов жителей дома выписывают обе газеты, если на газету «Комсомольская правда» из них подписаны 85%, а на «Известия» – 75%?
Ответ: 60%
nsportal.ru
«Отношения объектов и их множеств. Круги Эйлера. Практическая работа в Paint №3.»
Конспект урока по «Информатике и ИКТ»
Класс: 6
Урок: №3
Тема: Отношения объектов и их множеств. Круги Эйлера. Практическая работа в Paint №3.
Цель:
Обобщение и систематизация знаний об измерении информации;
Контроль ЗУН;
Формирование представления об отношениях между объектами и их множествами;
Формирование навыков работы с кругами Эйлера.
Оборудование, наглядные пособия: интерактивная доска, мультимедиа презентация, ПК, карточки с заданиями.
Тип урока: комбинированный
Методы: словесный, наглядно- демонстрационный
План урока
Организационный момент (2 мин)
Повторение и закрепление (7 мин)
Самостоятельная работа (4мин)
Новый материал ( 20 мин)
Домашнее задание ( 2 мин)
Практическая работа на пк (15 мин)
Ход урока
1.Организационный момент.
Проверить готовность учащихся к уроку, определить отсутствующих.
Попреветствовать учеников.
Повторение и закрепление материала прошлого урока.
Опрос учащихся с места по основным определениям раздела:
Файл – это информация, хранящаяся в долговременной памяти как единое целое и обозначенная именем.
Имя любого файла состоит из двух частей, разделенных точкой: собственно имени файла и расширения.
Документ – файл, содержащий данные (рисунки, тексты).
Файлы-документы создаются и обрабатываются с помощью прикладных программ (приложений).
Файл характеризуется свойствами:
Рассмотрим, какие бывают типы файлов:
Исполняемые
-
Текстовые
Графические
звуковые

Папка – группа файлов, объединенных по некоторому принципу, имеющая имя.
Файловая система – это совокупность условий и правил, определяющих способ организации файлов на носителях информации.
Бит — единица измерения количества информации, равная одному разряду в двоичной системе счисления.

Операционная система — комплекс взаимосвязанных программ, предназначенных для управления ресурсами компьютера и организации взаимодействия с пользователем.
Задача 1.
Укажите правильный ответ. 512 бит – это:


256 байт
50 байт
Решение:
1 байт = 8 бит
Переведем 512 бит в байты, для этого нужно
512 : 8 = 64 байт
Ответ: 64 байт
Задача 2
1Кбайт – это … Выберите правильный ответ:
1000 байт
8 бит
1024 бит
1024 байт
Ответ: 1024 байт
Задача 3
81 920 бит – это:
80 Кбайт
10 Кбайт
8 Кбайт
1 Мбайт
Решение:
Переведем биты в байты, для этого, имеющееся количество информации разделим на 8:
81 920 : 8 = 10 240 (байт)
Теперь переведем байты в Кбайты:
10240 :1024 = 10 (Кбайт)
Ответ: 10 Кбайт
Самостоятельная работа (4мин)
Самостоятельная работа №2
Вариант1
Наименьшая единица измерения информации – это
Байт
Символ
Бит
Мегабайт
(укажите правильный ответ)
Запишите несколько действий, которые можно совершать с объектом операционной системы Файл.
Сколько байт в слове бит?
Самостоятельная работа №2
Вариант 2
Сколько бит содержится в одном байте?
(укажите правильный ответ)
Запишите несколько действий, которые можно совершать с объектом операционной системы Папка.
Сколько бит в слове байт?
Новый материал ( 20 мин)

Слайд 1
Человек может рассказать не только о признаках объекта, но и об отношения, в которых этот объект находится с другими объектами.
Отношение – это взаимная связь, в которой находятся какие-либо объекты.
Слайд 3-5
Рассмотрение примеров отношений между объектами:
Родители присматривают за ребенком;
Корабль плывет по морю;
Вершина слева находится дальше.
Слайд 6
Обобщение примеров:
Присматривают, плывет, дальше – и есть отношения между объектами.

Слайд 7
Все отношения условно можно разделить на три группы:
Отношения, связывающие два объекта
Отношения, связывающие один объект с множеством объектов;
Отношения, связывающие два множества объектов.

Слайд 8
Рассмотрим пример отношения между двумя объектами:
Колизей находится в Риме.

Слайд 9
Рассмотрим пример отношения, связывающего один объект с множеством объектов. Гепард является хищником

Слайд 10
Рассмотрим пример отношения, связывающего два множества объектов.
Черешни и персики –это плоды.
Слайд 11
Отношения между объектами можно изобразить графически:
Пример 1.
Пусть про населенные пункты А, Б, В, Г, Д, Е известно, что некоторые из них соединены дорогами, как показано на слайде.
Рисунок на слайде называется схемой отношений.
Пример 2: приходится сыном.

Слайд 12
Учащиеся пытаются привести примеры отношений трех изученных видов.
Слайд 13
Графически множества удобно представлять с помощью кругов Эйлера.
Круги Эйлера— геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления отношения между множествами объектов.
Если множества А и В имеют общие элементы, то говорят, что эти множества пересекаются. (Пример: множество электронных писем и множество писем на русском языке)
Если множества не имеют общих элементов, то говорят, что они не пересекаются. (множество компьютерных устройств ввода информации и множество компьютерных устройств вывода информации)
Если каждый элемент множества В является элементом множества А, и наоборот, каждый элемент множества А является элементом множества В, то говорят, что множества А и В равны. (множество равносторонних прямоуголиников и множество квадратов)
Если каждый элемент множества В является элементом множества А, то говорят, что В – подмножество А. (множество учеников и множество шестиклассников)
Решим задачу
№4
Определите отношения между понятиями и изобразите эти отношения в виде кругов Эйлера. Понятия:
Решение: игрушка – конструктор – заводная игрушка – заводной автомобиль.
Домашнее задание ( 2 мин)
Просмотреть и выучить записи в тетради:
Укажите правильный ответ. 512 бит – это:
 Кбайт
Кбайт
256 байт
50 байт
Решение:
1 байт = 8 бит
Переведем 512 бит в байты, для этого нужно
512 : 8 = 64 байт
Ответ: 64 байт
1Кбайт – это … Выберите правильный ответ:
1000 байт
8 бит
1024 бит
1024 байт
Ответ: 1024 байт
81 920 бит – это:
80 Кбайт
10 Кбайт
8 Кбайт
1 Мбайт
Решение:
Переведем биты в байты, для этого, имеющееся количество информации разделим на 8:
81 920 : 8 = 10 240 (байт)
Теперь переведем байты в Кбайты:
10240 :1024 = 10 (Кбайт)
Ответ: 10 Кбайт
Отношение – это взаимная связь, в которой находятся какие-либо объекты.

Круги Эйлера— геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления отношения между множествами объектов.

Если множества А и В имеют общие элементы, то говорят, что эти множества пересекаются.
Если множества не имеют общих элементов, то говорят, что они не пересекаются.
Если каждый элемент множества В является элементом множества А, и наоборот, каждый элемент множества А является элементом множества В, то говорят, что множества А и В
Если каждый элемент множества В является элементом множества А, то говорят, что В – подмножество А.
№4. Определите отношения между понятиями и изобразите эти отношения в виде кругов Эйлера. Понятия:

Определите отношения между понятиями и изобразите эти отношения в виде кругов Эйлера.
№1. Понятия: птица, воробей, перелетная птица, ласточка, аист.
№2. Понятия: космическая система, Земля, Марс, Солнце, Солнечная система.
Повторить единицы измерения информации
4. Практическая работа на пк
Практическая работа №3 в графическом редакторе Paint.
Тема: Графическое представление множеств и отношений между ними с помощью кругов Эйлера и схемы отношений при помощи инструментов графического редактора Paint.
Задание 1
Определите отношения между понятиями и изобразите эти отношения в виде кругов Эйлера. Понятия: горячий чай, чай, чай с лимоном.

Задание 2

Задание 3 (дополнительное)
Нарисуйте зимний пейзаж.
Изобразите каждый элемент по отдельности и соберите в единый сюжет.

15
multiurok.ru
Конспект урока «Круги Эйлера», 6 класс
Тема: Решение задач с помощью кругов Эйлера.
Цели:
Обучающая – познакомить учащихся со способом решения логических задач с помощью кругов Эйлера — Венна
Развивающая – способствовать развитию логического мышления, памяти, самостоятельности и инициативы при выполнении групповых и индивидуальных заданий.
Воспитывающая – способствовать формированию информационной культуры учащихся, ответственности в групповой и индивидуальной работе.
Ход урока:
1) Орг. момент.
— Какие геометрические фигуры вы знаете?
— Как вы думаете, как мы их будем сегодня использовать при решении задач?
— Такое применение геометрических фигур, в основном кругов, при решении логических задач ввел Леонардо Эйлер. Тема нашего сегодняшнего урока «Решение задач с помощью кругов Эйлера»
2) Сообщение исторического материала: сообщение делает учащийся из 6 класса.
 Одним из первых, кто использовал для решения задач круги, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц (1646 – 1716). В его черновых набросках были обнаружены рисунки с кругами. Затем этот метод основательно развил швейцарский математик Леонард Эйлер (1707 – 1783).
Одним из первых, кто использовал для решения задач круги, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц (1646 – 1716). В его черновых набросках были обнаружены рисунки с кругами. Затем этот метод основательно развил швейцарский математик Леонард Эйлер (1707 – 1783).
Леонард Эйлер, крупнейший математик XVIII века, родился в Швейцарии. В 1727г. по приглашению Петербургской академии наук он приехал в Россию. Эйлер попал в круг выдающихся математиков, получил большие возможности для создания и издания своих трудов. Он работал с увлечением и вскоре стал, по единодушному признанию современников, первым математиком мира.
Научное наследие Эйлера поражает своим объемом и разносторонностью. В списке его трудов более 800 названий. Полное собрание сочинений ученого занимает 72 тома.
Леонард Эйлер
(1707 – 1783)
Последние 17 лет жизни Эйлера были омрачены почти полной потерей зрения. Но он продолжал творить так же интенсивно, как в молодые годы. Только теперь он уже диктовал ученикам, которые проводили за него громоздкие вычисления.
С1761 по 1768 год им были написаны знаменитые «Письма к немецкой принцессе», где Эйлер как раз и рассказывал о своем методе, об изображении множеств в виде кругов. Именно поэтому рисунки в виде кругов, обычно называют «кругами Эйлера». Эйлер отмечал, что изображение множеств в виде кругов «очень подходит для того, чтобы облегчить наши рассуждения». Понятно, что слово «круг» здесь весьма условно, множества могут изображаться на плоскости в виде произвольных фигур.
После Эйлера этот же метод разрабатывал чешский математик Бернард Больцано (1781 – 1848). Только в отличие от Эйлера он рисовал не круговые, а прямоугольные схемы. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шредер (1841 – 1902). Этот метод широко используется в его книге «Алгебра логика». Но наибольшего расцвета графические методы достигли в сочинениях английского логика Джона Венна (1843 – 1923). С наибольшей полнотой этот метод изложен им в книге «Символическая логика», изданной в Лондоне в 1881 году. В честь Венна вместо кругов Эйлера соответствующие рисунки называют иногда диаграммами Венна; в некоторых книгах их называют также диаграммами (или кругами) Эйлера – Венна.
3) Пример решения задач:
Задача 1. Все мои друзья занимаются каким-нибудь видом спорта. 16 из них увлекаются футболом, а 12 — баскетболом. И только двое увлекаются и тем и другим видом спорта. Угадайте, сколько у меня друзей?
Решение: Обратимся к кругам Эйлера:
Изобразим два множества (можно вводить обозначения их не только кругами), так как два вида спорта. В одном я буду фиксировать друзей, которые увлекаются футболом, а в другом — баскетболом. Поскольку некоторые из моих друзей увлекаются и тем и другим видом спорта, то квадраты нарисую так, чтобы у них была общая часть (пересечение). В этой общей части ставим цифру 2. В оставшейся части «футболистов» круга ставим цифру 14 (16 − 2= 14). В свободной части «баскетболистов» круга ставим цифру10 (12 − 2 = 10). А теперь рисунок сам подсказывает, что всего у меня 14 + 2 + 10 = 26 друзей.
Ответ: 26 друзей.
Задача 2. Любимые мультфильмыСреди школьников шестого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны», «Волк и теленок». Всего в классе 38 человек. «Белоснежку и семь гномов» выбрали 21 ученик, среди которых трое назвали еще «Волк и теленок», шестеро – «Губка Боб Квадратные Штаны», а один написал все три мультфильма. Мультфильм «Волк и теленок» назвали 13 ребят, среди которых пятеро выбрали сразу два мультфильма. Сколько человек выбрали мультфильм «Губка Боб Квадратные Штаны»?
РешениеВ этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Получаем такой чертеж:

Учитывая условие, что среди ребят, которые назвали мультфильм «Волк и теленок» пятеро выбрали сразу два мультфильма, получаем:

21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».
13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».
Получаем:
 38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны».
38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны».
Делаем вывод, что «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек.
Ответ. 17 человек выбрали мультфильм «Губка Боб Квадратные Штаны».
На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон?
Решение Учитывая условия задачи, чертеж будет таков:  Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона, то 11 – 4 – 2 = 5 – книг прочитал только Гарри. Следовательно,
Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона, то 11 – 4 – 2 = 5 – книг прочитал только Гарри. Следовательно,
26 – 7 – 2 – 5 – 4 = 8 – книг прочитал только Рон.
Ответ. 8 книг прочитал только Рон.
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке? Сколько ребят заняты только спортом?
РешениеИзобразим множества следующим образом:

70 – (6 + 8 + 10 + 3 + 13 + 6 + 5) = 19 – ребят не поют, не увлекаются спортом, не занимаются в драмкружке. Только спортом заняты 5 человек.
Ответ. 5 человек заняты только спортом.
Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?
Решение 
Всеми тремя спортивными снарядами владеют три человека, значит, в общей части кругов вписываем число 3. На скейтборде и на роликах умеют кататься 10 человек, а 3 из них катаются еще и на сноуборде. Следовательно, кататься только на скейтборде и на роликах умеют 10-3=7 ребят. Аналогично получаем, что только на скейтборде и на сноуборде умеют кататься 8-3=5 ребят, а только на сноуборде и на роликах 5-3=2 человека. Внесем эти данные в соответствующие части. Определим теперь, сколько человек умеют кататься только на одном спортивном снаряде. Кататься на сноуборде умеют 30 человек, но 5+3+2=10 из них владеют и другими снарядами, следовательно, только на сноуборде умеют кататься 20 ребят. Аналогично получаем, что только на скейтборде умеют кататься 13 ребят, а только на роликах – 30 ребят. По условию задачи всего 100 ребят. 20+13+30+5+7+2+3=80 – ребят умеют кататься хотя бы на одном спортивном снаряде. Следовательно, 20 человек не умеют кататься ни на одном спортивном снаряде.
Ответ. 20 человек не умеют кататься ни на одном спортивном снаряде.
3 группа: «троечники»
В классе учатся 40 человек. Из них по русскому языку имеют «тройки» 19 человек, по математике – 17 человек и по истории – 22 человека. Только по одному предмету имеют «тройки»: по русскому языку – 4 человека, по математике – 4 человека, по истории – 11 человек. Семь учеников имеют «тройки» и по математике и по истории, а 5 учеников – «тройки» по всем предметам. Сколько человек учится без «троек»? Сколько человек имеют «тройки» по двум из трех предметов?
Р ешение. Нарисуем круги Эйлера. Внутри большего круга, изображающего всех учеников класса, поместим три меньших круга М, Р, И, означающих соответственно математика, русский язык и история.
ешение. Нарисуем круги Эйлера. Внутри большего круга, изображающего всех учеников класса, поместим три меньших круга М, Р, И, означающих соответственно математика, русский язык и история.
Дальнейшие расчеты не представляют большого труда. Так как число ребят, имеющих «тройки» по математике и истории, равно 7, то число учеников, имеющих только две «тройки» — по математике и по истории, равно 7-5=2. Тогда 17-4-5-2=6 учеников имеют две «тройки» — по математике и по русскому языку, а 22-5-2-11=4 ученика только две «тройки» — по истории и по русскому языку. В этом случае без «тройки» учится 40-22-4-6-4=4 ученика. А имеют «тройки» по двум предметам из трех 6+2+4=12 человек.
4 группа: Любители физики
И з 100 семиклассников, выполнивших практическое задание по физике, 75 сделали модели, а 65 эскиз фонтана, а 10 человек ни чего не сделали. Сколько учеников сделали модель и эскиз?
з 100 семиклассников, выполнивших практическое задание по физике, 75 сделали модели, а 65 эскиз фонтана, а 10 человек ни чего не сделали. Сколько учеников сделали модель и эскиз?
Решение: В большом круге, изображающем 100 семиклассников, поместим 2 меньших круга, изображающих учеников, выполнивших модель и эскиз фонтана. Мы видим, что 90 учеников (100-10)выполнили хотя бы одну часть задания; 15 учеников (90-75) сделали только эскиз фонтана, 75-15=50 – учеников сделали эскиз и фонтан.
Ответ: 50 учеников.
4) Итог урока.
— Чем был для вас полезен сегодняшний урок?
5) Домашнее задание: В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, ителевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? |
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? |
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? |
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? |
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? |
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? |
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? |
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? |
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? |
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? |
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? |
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке? Сколько ребят заняты только спортом?
2 группа: ЭкстримИз 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?
3 группа: «троечники»
В классе учатся 40 человек. Из них по русскому языку имеют «тройки» 19 человек, по математике – 17 человек и по истории – 22 человека. Только по одному предмету имеют «тройки»: по русскому языку – 4 человека, по математике – 4 человека, по истории – 11 человек. Семь учеников имеют «тройки» и по математике и по истории, а 5 учеников – «тройки» по всем предметам. Сколько человек учится без «троек»? Сколько человек имеют «тройки» по двум из трех предметов?
4 группа: Любители физики
Из 100 семиклассников, выполнивших практическое задание по физике, 75 сделали модели, а 65 эскиз фонтана, а 10 человек ни чего не сделали. Сколько учеников сделали модель и эскиз?
multiurok.ru
Решение занимательных задач: круги Эйлера. 6-й класс
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Задачи занятия:
Образовательные:
- рассмотреть решение логических задач с помощью кругов Эйлера.
Развивающие:
- развитие логического мышления;
- развитие поисковой, творческой, познавательной деятельности;
- развитие познавательного интереса к предмету;
Воспитывающие:
- формирование эстетического наслаждения от выполненной работы;
- формирование навыков само- и взаимоконтроля.
Оборудование:
- набор задач каждому ученику;
- компьютер, проектор;
- презентация.
Ход занятия:
Слайд 1.
Ребята, сегодня мы продолжим учится решать занимательные задачи и познакомимся с новым способом решения таких задач.
Слайд 2.
(Текст задачи лежит у каждого учащегося на парте.)
Подробный разбор решения задачи № 1. (Используются слайды 2–4.)
Слайд 3.
Слайд 4.
Слайд 5. (Содержит историческую справку.)
Слайд 6.
Задача № 2: (У доски решает сильный ученик.)
Слайд 7.
Задача № 3. (У доски решает сильный ученик.)
Слайд 8.
Задача № 4. (Задачу у доски решает ученик, вызванный по желанию.)
Слайд 9.
Задача № 5. (Задачу у доски решает ученик, вызванный по желанию.)
Слайд №10:
Задача № 6. (Задачу у доски решает ученик, вызванный по желанию.)
Слайд 11.
Задача № 7. (Задачу у доски решает ученик, вызванный по желанию.)
Слайд 12.
Задача № 8. (Задача для самостоятельного решения с последующей проверкой.)
Слайд 13.
Задача № 9. (Задача для самостоятельного решения с последующей проверкой.)
Слайд 14.
Задача № 10. (Задача для самостоятельного решения с последующей проверкой.)
Слайд 15.
Задача № 11. (Задача для самостоятельного решения с последующей проверкой.)
Слайд 16.
Домашнее задание: найти или придумать самим задачу, которая решалась бы с помощью кругов Эйлера. Оформить её решение на альбомном листе.
urok.1sept.ru
Презентация к уроку (6 класс) по теме: Круги Эйлера
Слайд 1
Круги Эйлера Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа №1 г.Суздаля»Слайд 2
Задача №1: Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским – 28, французским – 42. Английским и немецким одновременно владеют 8 человек, английским и французским -10 , немецким и французским – 5, всеми тремя языками – 3. Сколько туристов не владеют ни одним языком? Решение: Выразим условие задачи графически. Обозначим кругом тех, кто знает английский, другим кругом – тех, кто знает французский, и третьим кругом – тех, кто знают немецкий. французский немецкий английский
Слайд 3
Всеми тремя языками владеют три туриста, значит, в общей части кругов вписываем число 3. 3 Английским и французским языками владеют 10 человек, а 3 из них владеют ещё и немецким. Значит, английским и французским владеют 10-3=7 человек. немецкий французский английский В общую часть английского и французского кругов вписываем цифру 7 . 7 Английским и немецким языками владеют 8 человек, а 3 из них владеют ещё и французским. Значит, английским и немецким владеют 8-3=5 человек. В общую часть английского и немецкого кругов вписываем число 5. 5
Слайд 4
немецкий французский английский 3 7 5 Известно, что немецким языком владеют 30 человек, но 5+3+2=10 из них владеют и другими языками, значит, только немецкий знают 20 человек. Английский язык знают 28 человек, но 5+3+7=15 человек владеют и другими языками, значит, только английский знают 13 человек. Французский язык знают 42 человека, но 2+3+7=12 человек владеют и другими языками, значит, только французский знают 30 человек. Немецким и французским языками владеют 5 человек, а 3 из них владеют ещё и английским. Значит, немецким и французским владеют 5-3=2 человека. В общую часть немецкого и французского кругов вписываем цифру 2. 2 20 13 30 По условию задачи всего 100 туристов. 20+30+13 +5+2+3+7=80 туристов знают хотя бы один язык, следовательно, 20 человек не владеют ни одним языком. Ответ: 20 человек.
Слайд 5
Рисунки , подобные тем, что мы рисовали при решении этой задачи, называются «кругами Эйлера». Один из величайших математиков Петербургской академии Леонард Эйлер написал более 850 научных работ. В одной из них и появились эти круги. Эйлер писал тогда, что «они очень подходят для того, чтобы облегчить наши размышления». Наряду с кругами в подобных задачах применяют прямоугольники и другие фигуры.
Слайд 6
Задача №2: В ясельной группе 11 деток любят манную кашу, 13 – гречневую и 7 малышей – перловую. Четверо любят и манную, и гречневую, 3 – манную и перловую, 6- гречневую и перловую, а двое с удовольствием «уплетают» все три вида каши. Сколько детей в этой группе, если в ней нет ни одного ребёнка, вовсе не любящего кашу? Решение: манная перловая гречневая 11 7 13 4 3 6 2 1 4 2 6 0 5 Ответ: 6+1+2+2+0+4+5=20 ребят
Слайд 7
В одной семье было много детей. 7 из них любили капусту, 6 – морковь, 5 – горох, 4 – капусту и морковь, 3 – капусту и горох, 2 – морковь и горох, 1 – и капусту, и морковь, и горох. Сколько детей было в семье? Задача №3: Решение: капуста морковь горох 7 6 5 4 3 2 1 3 2 1 1 1 1 Ответ: 10 человек.
Слайд 8
Задача №4: В группе 29 студентов. Среди них 14 любителей классической музыки, 15-джаза, 14 – народной музыки. Классическую музыку и джаз слушают 6 студентов, народную музыку и джаз – 7, классику и народную – 9. Пятеро студентов слушают всякую музыку, а остальные не любят никакой музыки. Сколько их? Решение: классическая музыка джаз народная музыка 14 15 14 6 7 9 5 1 4 2 7 4 3 Ответ: 29-7-2-1-5-3-4-4=3(человека) – не любят никакую музыку.
Слайд 9
Задача №5: Учащиеся 5 и 6 классов отправились на экскурсию. Мальчиков было 16, учащихся 6 класса – 24, пятиклассниц столько, сколько мальчиков из 6 класса. Сколько всего детей побывали на экскурсии? мальчики 5 класс девочки 6 класс мальчики 6 класс девочки 5 класс 16 24 Ответ: 40 человек. Решение:
Слайд 10
Задача №6: На полу комнаты площадью 24 м² лежат три ковра. Площадь одного из них -10 м², другого – 8 м², третьего – 6 м². Каждые два ковра перекрываются по площади 3 м², а площадь участка пола, покрытого всеми тремя коврами, составляет 1 м². Найдите площадь участка пола: а)покрытого первым и вторым коврами, но не покрытого третьим ковром; б)покрытого только первым ковром; в)не покрытого коврами. Решение: 1 2 3 10 8 6 3 3 3 1 5 3 2 2 2 1 Ответ: а) 10м²; б)5 м²; в) 24-10-5-1=8 м²
Слайд 11
1. Из 100 приехавших туристов 75 знали немецкий язык и 83 знали французский. 10 человек не знали ни немецкого, ни французского. Сколько туристов знали оба эти языка? Задача №7 Решение: немецкий французский 75 83 х 100-10=90 Получим уравнение: 75+83-х=90 158-х=90 х=68 Ответ: 68 человек знали оба языка
Слайд 12
Задача для самостоятельного решения: 1. Из 40 опрошенных человек 32 любят молоко, 21 – лимонад, а 15 – и молоко, и лимонад. Сколько человек не любят ни молоко, ни лимонад? Ответ: 2 человека
Слайд 13
2. В воскресенье 19 учеников нашего класса побывали в планетарии, 10 – в цирке и 6 – в музее. Планетарий и цирк посетили 5 учеников; планетарий и музей – трое, в цирке и музее был один человек. Сколько учеников в нашем классе, если никто не успел посетить все три места, а трое вообще никуда не ходили? Ответ: 20 человек Задача для самостоятельного решения:
Слайд 14
3. В детском лагере отдыхало 70 ребят. Из них 20 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов, а 3 спортсмена посещают и драмкружок, и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты спортом? Ответ: 10 ребят, 11 спортсменов. Задача для самостоятельного решения:
Слайд 15
Задача для самостоятельного решения: 4. Из сотрудников фирмы 16 побывали во Франции, 10 – в Италии, 6 – в Англии. В Англии и Италии – пятеро, в Англии и Франции – 6, во всех трёх странах – 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работает 19 человек, и каждый их них побывал хотя бы в одной из названных стран? Ответ: 7 сотрудников
Слайд 16
До новых встреч с занимательными задачами
nsportal.ru
Урок математики «Круги Эйлера» в 6 классе.
Круги Эйлера.
Цели: — научить новому способу решения логических задач;
— развивать понятие множества, пересечения и объединения
множеств; умения анализировать, сравнивать, делать выводы;
— формировать культуру речи, умение высказывать свою точку
зрения и умение слушать других; интерес к предмету, научное
мировоззрение.
Тип урока Изучение нового материала
Форма Объяснение с активным привлечением учащихся. Фронтальная
форма организации учебной деятельности.
Метод Объяснительно-иллюстративный с элементами проблемного
обучения + творческая деятельность учащихся.
Структура 1.Постановка цели.
2.Актуализация.
3. Подготовка к изучению нового.
4.Изучение нового.
5. Закрепление.
6.Промежуточный контроль.
7. Домашнее задание.
8. Итоги урока.
Организационный момент. Постановка цели.
Сегодня, мы попробуем связать диаграммы Венна , логические задачи и научные результаты великого ученого, нашего соотечественника, жившего в 18 веке, Леонарда Эйлера. Это имя вам уже знакомо: это формула, связывающая число вершин, граней и ребёр многогранника, это и умножение отрицательных чисел, это и теория простых чисел и. В будущем вас ждёт ещё много открытий. Мы же с вами сегодня научимся решать задачи с помощью кругов Эйлера.
Актуализация знаний и умений.
В математике, когда какие-нибудь объекты собираются вместе, говорят одно и то же слово – множество. А предметы или живые существа, входящие во множество называют элементами этого множества.
Например: 6 б- множество учеников, а Катя, Серёжа, Маша…- его элементы.
Назовите элементы множества семья.
Элементами какого множества являются Жигули, Камаз, Мерседес?
Чтобы лучше представить себе множество, используют специальный рисунок, который называется…диаграмма Венна. Это замкнутая линия, внутри которой элементы множества, а снаружи – не элементы множества.
Часть множества – это подмножества.
Множество ЛЕС, а подмножества — хвойный и лиственный.
Общую часть множеств называют пересечением. Как показывают пересечение с помощью диаграмм Венна?
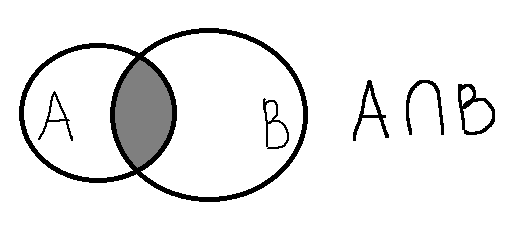
А если общей части у множеств нет?
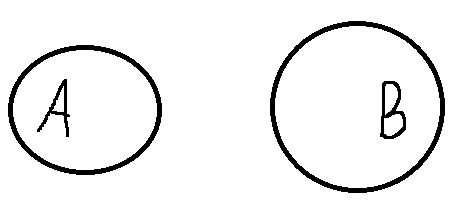
Множества называются непересекающимися.
Объединение множеств – множество всех элементов, принадлежащим данным множествам(к элементам 1-го множества добавляются элементы 2-го множества). Как показывают объединение с помощью диаграмм Венна?
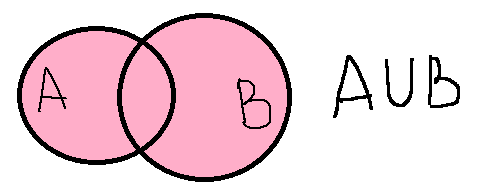
Подготовка к восприятию нового способа действия.
1) Все мои подруги выращивают в своих квартирах какие-нибудь растения. Шестеро из них разводят кактусы, а пятеро – фиалки. И только у двоих есть и кактусы и фиалки. Угадайте, сколько у меня подруг?
Можно, конечно, «угадать» в процессе замысловатых рассуждений, можно – посредством вот таких действий:
6 + 5 = 11.
11 – 2 = 9.
Восприятие нового материала.
Но как грамотно обосновать их? Как ответить на вопрос, что получилось в результате первого действия?
Леонард Эйлер придумал очень красивый способ решения таких задач.
Вот он. Изобразим два круга, так как у нас два вида цветов. В одном будем фиксировать владелиц кактусов, в другом – фиалок. Поскольку у некоторых подруг есть и те, и другие цветы, то круги нарисуем так, чтобы у них была общая часть. В этой общей части ставим цифру 2 (т.к. кактусы и фиалки у двоих). В оставшейся части «кактусового» круга ставим цифру 4 (всего кактусы – у шестерых, а у двух мы уже учли). В свободной части «фиалкового» круга ставим цифру 3 (5 – 2 = 3). А теперь сам рисунок подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг.
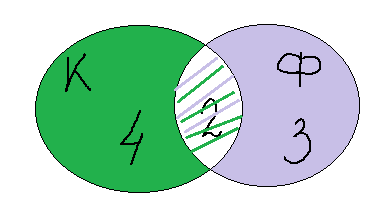
Осмысление нового материала.
2) В классе 15 мальчиков. 10 из них занимаются футболом и 9 баскетболом. Сколько мальчиков занимается и тем и другим?
Изобразим условие с помощью кругов Эйлера. Это поможет нам в рассуждениях. В чем отличие этой задачи от предыдущей? Нет общего количества, но есть ВСЁ количество.
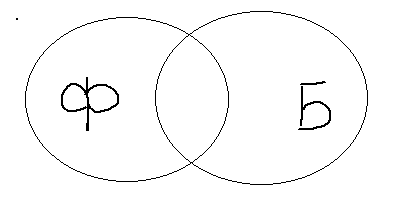
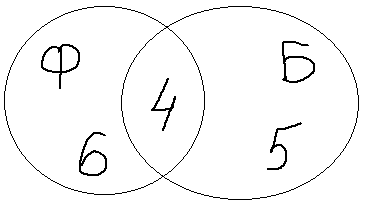
Итак, только баскетболом занимается 15-10=5 мальчиков.
Только футболом занимается 15-9=6 мальчиков.
В двух секциях 15-(5+6)=4 человека.
3) Рассмотрите круги Эйлера:
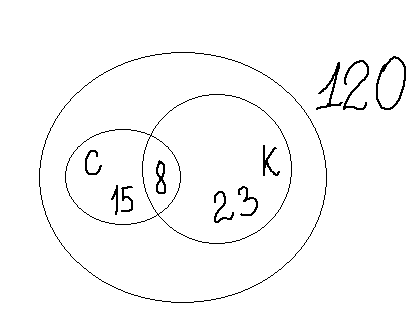
В доме 120 жильцов, у некоторых их них есть собаки и кошки.
С – жильцы с собаками.
К – жильцы с кошками.
Сколько жильцов имеют собак?
Сколько жильцов имеет кошек?
Сколько жильцов не имеет ни кошек, ни собак?
А какой вопрос по задаче я не задала?
Закрепление
4) А совсем недавно мы с ребятами ходили в поход. Прибыв на место, мы обнаружили, что 12 человек привезли с собой бутерброды с колбасой, 5 – с сыром и 9 – с маслом. Трое сделали бутерброды двух видов: и с колбасой, и с маслом, а я захватила с собой из дома бутерброды с маслом и бутерброды с сыром, но не оказалось ни одного отдыхающего, который привез бы бутерброды с колбасой и бутерброды с сыром. Сколько человек было в нашей компании?
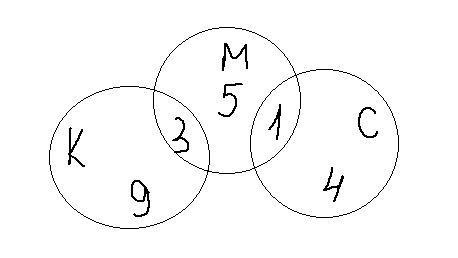 или
или 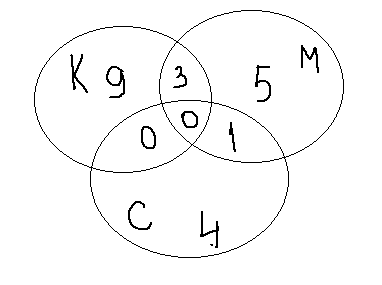
5) В одном классе 25 учеников. Из них 7 любят груши, 11 – черешню. Двое любят груши и черешню; 6 – груши и яблоки; 5 – яблоки и черешню. Но есть в классе два ученика, которые любят всё и четверо таких, что не любят фруктов вообще. Сколько учеников этого класса любят яблоки?
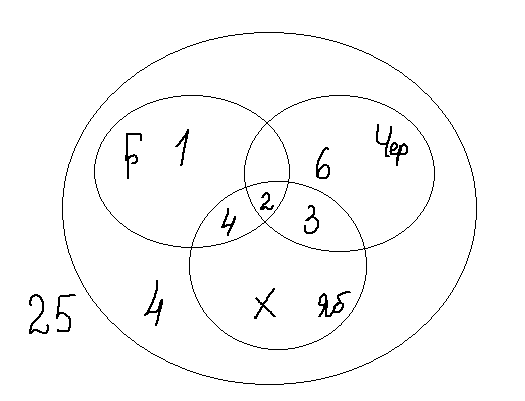
1 + 4 + 2 + 6 + 3 + 4 + х = 25
20 + х = 25
Х = 5 человек любят только яблоки.
4 + 2 +3 + 5 =14 учеников любят яблоки.
Проверочная работа. (по карточкам).
Из 40 учащихся нашего класса 32 любят молоко, 21 – лимонад, а 15 – и молоко, и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?
12 моих одноклассников любят читать детективы , 18 – фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?
По окончании работы провести взаимоконтроль.
Итоги урока. Сегодня мы с вами познакомились с кругами Эйлера, научились их строить и при помощи них решать логические задачи. Сегодня вы научились новому приему решения логических задач. Надеюсь, на последующих уроках математики вам пригодится, то что вы узнали на уроке.
Домашнее задание на карточках
1. В воскресенье 19 учеников нашего класса побывали в театре, 10 – в цирке, 6 – на стадионе. Театр и цирк посетили 5 учеников, театр и стадион – 3, а цирк и стадион – 1. Сколько учеников в нашем классе, если никто не успел посетить все три места, а 3 ученика не посетили ни одного места?
2. Из 100 человек 85 знают английский, 80 испанский, 75 немецкий. Все владеют, по крайней мере, одним иностранным языком. Среди них нет таких, которые знают два иностранных языка, но есть владеющие тремя языками. Сколько человек из этих 100 знают три языка?
infourok.ru
«Отношения объектов и их множеств. Круги Эйлера. Практическая работа в Paint №3.»
Конспект урока по «Информатике и ИКТ»
Класс: 6
Урок: №3
Тема: Отношения объектов и их множеств. Круги Эйлера. Практическая работа в Paint №3.
Цель:
Обобщение и систематизация знаний об измерении информации;
Контроль ЗУН;
Формирование представления об отношениях между объектами и их множествами;
Формирование навыков работы с кругами Эйлера.
Оборудование, наглядные пособия: интерактивная доска, мультимедиа презентация, ПК, карточки с заданиями.
Тип урока: комбинированный
Методы: словесный, наглядно- демонстрационный
План урока
Организационный момент (2 мин)
Повторение и закрепление (7 мин)
Самостоятельная работа (4мин)
Новый материал ( 20 мин)
Домашнее задание ( 2 мин)
Практическая работа на пк (15 мин)
Ход урока
1.Организационный момент.
Проверить готовность учащихся к уроку, определить отсутствующих.
Попреветствовать учеников.
Повторение и закрепление материала прошлого урока.
Опрос учащихся с места по основным определениям раздела:
Файл – это информация, хранящаяся в долговременной памяти как единое целое и обозначенная именем.
Имя любого файла состоит из двух частей, разделенных точкой: собственно имени файла и расширения.
Документ – файл, содержащий данные (рисунки, тексты).
Файлы-документы создаются и обрабатываются с помощью прикладных программ (приложений).
Файл характеризуется свойствами:
Рассмотрим, какие бывают типы файлов:
Исполняемые
Текстовые
Графические
звуковые

Папка – группа файлов, объединенных по некоторому принципу, имеющая имя.
Файловая система – это совокупность условий и правил, определяющих способ организации файлов на носителях информации.
Бит — единица измерения количества информации, равная одному разряду в двоичной системе счисления.

Операционная система — комплекс взаимосвязанных программ, предназначенных для управления ресурсами компьютера и организации взаимодействия с пользователем.
Задача 1.
Укажите правильный ответ. 512 бит – это:
 Кбайт
Кбайт
256 байт
50 байт
Решение:
1 байт = 8 бит
Переведем 512 бит в байты, для этого нужно
512 : 8 = 64 байт
Ответ: 64 байт
Задача 2
1Кбайт – это … Выберите правильный ответ:
1000 байт
8 бит
1024 бит
1024 байт
Ответ: 1024 байт
Задача 3
81 920 бит – это:
80 Кбайт
10 Кбайт
8 Кбайт
1 Мбайт
Решение:
Переведем биты в байты, для этого, имеющееся количество информации разделим на 8:
81 920 : 8 = 10 240 (байт)
Теперь переведем байты в Кбайты:
10240 :1024 = 10 (Кбайт)
Ответ: 10 Кбайт
Самостоятельная работа (4мин)
Самостоятельная работа №2
Вариант1
Наименьшая единица измерения информации – это
Байт
Символ
Бит
Мегабайт
(укажите правильный ответ)
Запишите несколько действий, которые можно совершать с объектом операционной системы Файл.
Сколько байт в слове бит?
Самостоятельная работа №2
Вариант 2
Сколько бит содержится в одном байте?
(укажите правильный ответ)
Запишите несколько действий, которые можно совершать с объектом операционной системы Папка.
Сколько бит в слове байт?
Новый материал ( 20 мин)

Слайд 1
Человек может рассказать не только о признаках объекта, но и об отношения, в которых этот объект находится с другими объектами.
Отношение – это взаимная связь, в которой находятся какие-либо объекты.
Слайд 3-5
Рассмотрение примеров отношений между объектами:
Родители присматривают за ребенком;
Корабль плывет по морю;
Вершина слева находится дальше.
Слайд 6
Обобщение примеров:
Присматривают, плывет, дальше – и есть отношения между объектами.

Слайд 7
Все отношения условно можно разделить на три группы:
Отношения, связывающие два объекта
Отношения, связывающие один объект с множеством объектов;
Отношения, связывающие два множества объектов.

Слайд 8
Рассмотрим пример отношения между двумя объектами:
Колизей находится в Риме.

Слайд 9
Рассмотрим пример отношения, связывающего один объект с множеством объектов. Гепард является хищником

Слайд 10
Рассмотрим пример отношения, связывающего два множества объектов.
Черешни и персики –это плоды.
Слайд 11
Отношения между объектами можно изобразить графически:
Пример 1.
Пусть про населенные пункты А, Б, В, Г, Д, Е известно, что некоторые из них соединены дорогами, как показано на слайде.
Рисунок на слайде называется схемой отношений.
Пример 2: приходится сыном.

Слайд 12
Учащиеся пытаются привести примеры отношений трех изученных видов.
Слайд 13
Графически множества удобно представлять с помощью кругов Эйлера.
Круги Эйлера— геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления отношения между множествами объектов.
Если множества А и В имеют общие элементы, то говорят, что эти множества пересекаются. (Пример: множество электронных писем и множество писем на русском языке)
Если множества не имеют общих элементов, то говорят, что они не пересекаются. (множество компьютерных устройств ввода информации и множество компьютерных устройств вывода информации)
Если каждый элемент множества В является элементом множества А, и наоборот, каждый элемент множества А является элементом множества В, то говорят, что множества А и В равны. (множество равносторонних прямоуголиников и множество квадратов)
Если каждый элемент множества В является элементом множества А, то говорят, что В – подмножество А. (множество учеников и множество шестиклассников)
Решим задачу
№4
Определите отношения между понятиями и изобразите эти отношения в виде кругов Эйлера. Понятия:
Решение: игрушка – конструктор – заводная игрушка – заводной автомобиль.
Домашнее задание ( 2 мин)
Просмотреть и выучить записи в тетради:
Укажите правильный ответ. 512 бит – это:
 Кбайт
Кбайт
256 байт
50 байт
Решение:
1 байт = 8 бит
Переведем 512 бит в байты, для этого нужно
512 : 8 = 64 байт
Ответ: 64 байт
1Кбайт – это … Выберите правильный ответ:
1000 байт
8 бит
1024 бит
1024 байт
Ответ: 1024 байт
81 920 бит – это:
80 Кбайт
10 Кбайт
8 Кбайт
1 Мбайт
Решение:
Переведем биты в байты, для этого, имеющееся количество информации разделим на 8:
81 920 : 8 = 10 240 (байт)
Теперь переведем байты в Кбайты:
10240 :1024 = 10 (Кбайт)
Ответ: 10 Кбайт
Отношение – это взаимная связь, в которой находятся какие-либо объекты.

Круги Эйлера— геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления отношения между множествами объектов.

Если множества А и В имеют общие элементы, то говорят, что эти множества пересекаются.
Если множества не имеют общих элементов, то говорят, что они не пересекаются.
Если каждый элемент множества В является элементом множества А, и наоборот, каждый элемент множества А является элементом множества В, то говорят, что множества А и В равны.
Если каждый элемент множества В является элементом множества А, то говорят, что В – подмножество А.
№4. Определите отношения между понятиями и изобразите эти отношения в виде кругов Эйлера. Понятия:

Определите отношения между понятиями и изобразите эти отношения в виде кругов Эйлера.
№1. Понятия: птица, воробей, перелетная птица, ласточка, аист.
№2. Понятия: космическая система, Земля, Марс, Солнце, Солнечная система.
Повторить единицы измерения информации
4. Практическая работа на пк
Практическая работа №3 в графическом редакторе Paint.
Тема: Графическое представление множеств и отношений между ними с помощью кругов Эйлера и схемы отношений при помощи инструментов графического редактора Paint.
Задание 1
Определите отношения между понятиями и изобразите эти отношения в виде кругов Эйлера. Понятия: горячий чай, чай, чай с лимоном.

Задание 2

Задание 3 (дополнительное)
Нарисуйте зимний пейзаж.
Изобразите каждый элемент по отдельности и соберите в единый сюжет.

15
multiurok.ru




