1.6. Метод интегрирования по частям в определенном интеграле
Здесь новизны еще меньше. Всё, что справедливо для неопределенного интеграла, в полной мере справедливы и для определенного интеграла. Плюсом идёт то, что в формуле интегрирования по частям добавляются пределы интегрирования:
Формулу Ньютона-Лейбница здесь нужно применить дважды: для произведения и после того, как мы возьмём интеграл . Ну и, конечно, подынтегральные функции должна быть непрерывны на , ибо на «нет» и интеграла нет.
Пример я подобрал не самый простой, но очень и очень познавательный:
Пример 8
Вычислить определенный интеграл
Сразу начинаем решение и сразу прерываем его «звёздочкой». Этот тип интеграла не встречался ранее, он тоже берётся по частям. Используем стандартную схему интегрирования по частям:
Интеграл от квадрата тангенса я разбирал в 1-й части курса
Далее открываем решение и на первом шаге
(1) расписываем правую часть формулы :
(2) Для произведения применяем формулу Ньютона-Лейбница. Для оставшегося интеграла используем свойство линейности, разделяя его на два интеграла. Не путаемся в знаках!
(3) Берем два оставшихся интеграла. Интеграл также разобран ранее, однако, не поленюсь:
(4) Применяем формулу Ньютона-Лейбница для двух найденных первообразных.
Далее ответ доводится «до ума». Повторюсь, будьте ПРЕДЕЛЬНО ВНИМАТЕЛЬНЫ при подстановках и заключительных вычислениях. Здесь допускают ошибки чаще всего.
Если честно, я недолюбливаю формулу и, по возможности, … обхожусь вообще без нее! Рассмотрим второй способ решения, который, с моей точки зрения, более рационален:
На первом этапе находим неопределенный интеграл:Интегрируем по частям:
Первообразная функция найдена. …Кстати, все ли поняли, почему в определённом интеграле не имеет смысла приплюсовывать константу ?
…Кстати, все ли поняли, почему в определённом интеграле не имеет смысла приплюсовывать константу ?
В чём преимущество такого похода? Не нужно «таскать за собой» пределы интегрирования, действительно, замучаться можно десяток раз записывать мелкие значки пределов интегрирования.
На втором этапе проводим проверку (обычно на черновике).
Тоже логично. Ведь если неправильно найден неопределённый интеграл, то… правильно! И это лучше выяснить немедленно, дифференцируем ответ:
– получена исходная подынтегральная функция, значит, первообразная найдена верно.
И третий этап – применение формулы Ньютона-Лейбница:
Здесь тоже есть существенная выгода! – это гораздо меньший риск запутаться в подстановках и вычислениях, т.к.
Рассмотренный алгоритм решения
можно применить для любого определенного интеграла!
И нужно, если интеграл трудный. Так, если «чайник» решит разобранный интеграл по формуле (1-м способом), то 99% где-нибудь допустит ошибку.
Уважаемый студент, распечатай и наклей рядом с формулой Ньютона-Лейбница:
1) Сначала находим неопределенный интеграл (первообразную функцию). Если не получилось, повышаем свои навыки интегрирования.
2) Проверяем найденную первообразную дифференцированием. Здесь, кстати, может статься, позабылись производные – и тогда самое время подтянуть свои навыки!
3) Используем формулу Ньютона-Лейбница. Все вычисления проводим ПРЕДЕЛЬНО ВНИМАТЕЛЬНО – тут самое слабое звено задания. Царь тут!
И на холодную закуску интеграл для самостоятельного решения.
Пример 9
Вычислить определенный интеграл
1. xdx.
\]
xdx.
\]
Интегрирование по частям. Первая часть.
В этой теме мы подробно поговорим вычислении неопределённых интегралов с помощью так называемой «формулы интегрирования по частям». Нам понадобится таблица неопределенных интегралов и таблица производных. В первой части будут разобраны стандартные примеры, которые большей частью встречаются в типовых расчётах и контрольных работах. Более сложные примеры разобраны во второй части.
Постановка задачи в стандартном случае следующая. Допустим, под интегралом у нас расположены две функции разной природы: многочлен и тригонометрическая функция, многочлен и логарифм, многочлен и обратная тригонометрическая функция и так далее. В этой ситуации выгодно отделить одну функцию от другой. Грубо говоря, имеет смысл разбить подынтегральное выражение на части, – и разобраться с каждой частью по отдельности. Отсюда и название: «интегрирование по частям». Применение этого метода основано на следующей теореме:
Пусть функции $u(x)$ и $v(x)$ дифференцируемы на некотором промежутке, и на этом промежутке существует интеграл $\int v \; du$. Тогда на этом же промежутке существует и интеграл $\int u \; dv$, при этом верно следущее равенство:
$$ \begin{equation} \int u \; dv=u\cdot v-\int v\; du \end{equation} $$Формулу (1) и называют «формулой интегрирования по частям». Иногда, применяя вышеуказанную теорему, говорят о использовании «метода интегрирования по частям». Нам будет важна суть этого метода, которую и рассмотрим на примерах. Существует несколько стандартных случаев, в которых явно применима формула (1). Именно эти случаи и станут темой данной страницы. Пусть $P_n(x)$ – многочлен n-й степени. Введём два правила:
Правило №1
Для интегралов вида $\int P_n(x) \ln x \;dx$, $\int P_n(x) \arcsin x \;dx$, $\int P_n(x) \arccos x \;dx$, $\int P_n(x)\arctg x \;dx$, $\int P_n(x) \arcctg x \;dx$ принимаем $dv=P_n(x)dx$. 2+14x-5)$. Т.е. запись $\ln x$ нужно воспринимать как своего рода обобщение.
2+14x-5)$. Т.е. запись $\ln x$ нужно воспринимать как своего рода обобщение.
Ещё один момент. Бывает, что формулу интегрирования по частям приходится применять несколько раз. Об этом поговорим подробнее в примерах №4 и №5. Теперь перейдём непосредственно к решению типичных задач. Решение задач, уровень которых чуть выше стандартных, разбирается во второй части.
Пример №1
Найти $\int (3x+4) \cos (2x-1) \; dx$.
Решение
Под интегралом расположен многочлен $3x+4$ и тригонометрическая функция $\cos (2x-1)$. Это классический случай для применения формулы (1), поэтому возьмём заданный интеграл по частям. Формула (1) требует, чтобы интеграл $\int (3x+4) \cos (2x-1) \; dx$ был представлен в форме $\int u \; dv$. Нам нужно выбрать выражения для $u$ и для $dv$. Можно в качестве $u$ принять $3x+4$, тогда $dv=\cos (2x-1)dx$. Можно взять $u=\cos (2x-1)$, тогда $dv=(3x+4)dx$. Чтобы сделать правильный выбор обратимся к правилу №2. Заданный интеграл $\int (3x+4) \cos (2x-1) \; dx$ подпадает под вид $\int P_n(x) \cos x \;dx$ (многочлен $P_n(x)$ в нашем интеграле имеет вид $3x+4$). Согласно правилу №2 нужно выбрать $u=P_n(x)$, т.е. в нашем случае $u=3x+4$. Так как $u=3x+4$, то $dv=\cos(2x-1)dx$.
Однако недостаточно просто выбрать $u$ и $dv$. Нам еще понадобятся значения $du$ и $v$. Так как $u=3x+4$, то:
$$ du=d(3x+4)=(3x+4)’dx=3dx.$$Теперь разберёмся с функцией $v$. Так как $dv=\cos(2x-1)dx$, то согласно определению неопределённого интеграла имеем: $ v=\int \cos(2x-1)\; dx$. Чтобы найти нужный интеграл применим внесение под знак дифференциала:
$$ v=\int \cos(2x-1)\; dx=\frac{1}{2}\cdot \int \cos(2x-1)d(2x-1)=\frac{1}{2}\cdot \sin(2x-1)+C=\frac{\sin(2x-1)}{2}+C. $$Однако нам нужно не всё бесконечное множество функций $v$, которое описывает формула $\frac{\sin(2x-1)}{2}+C$. Нам нужна какая-то одна функция из этого множества. Чтобы получить искомую функцию нужно вместо $C$ подставить какое-либо число. Проще всего, разумеется, подставить $C=0$, получив при этом $v=\frac{\sin(2x-1)}{2}$.
Проще всего, разумеется, подставить $C=0$, получив при этом $v=\frac{\sin(2x-1)}{2}$.
Итак, соберём всё вышеизложенное воедино. Мы имеем: $u=3x+4$, $du=3dx$, $dv=\cos(2x-1)dx$, $v=\frac{\sin(2x-1)}{2}$. Подставляя всё это в правую часть формулы (1) будем иметь:
$$ \int (3x+4) \cos (2x-1) \; dx=(3x+4)\cdot\frac{\sin(2x-1)}{2}-\int \frac{\sin(2x-1)}{2}\cdot 3dx. $$Осталось, по сути, только найти $\int\frac{\sin(2x-1)}{2}\cdot 3dx$. Вынося константу (т.е. $\frac{3}{2}$) за знак интеграла и применяя метод внесения под знак дифференциала, получим:
Итак,
$$\int (3x+4) \cos (2x-1) \; dx=\frac{(3x+4)\cdot\sin(2x-1)}{2}+\frac{3}{4}\cdot \cos (2x-1)+C.$$В сокращенном виде процесс решения записывают так:
$$ \int (3x+4) \cos (2x-1) \; dx=\left | \begin{aligned} & u=3x+4; \; du=3xdx.\\ & dv=\cos(2x-1)dx; \; v=\frac{\sin(2x-1)}{2}. \end{aligned} \right |=\\ =(3x+4)\cdot\frac{\sin(2x-1)}{2}-\int \frac{\sin(2x-1)}{2}\cdot 3dx= \frac{(3x+4)\cdot\sin(2x-1)}{2}-\frac{3}{2}\int \sin(2x-1) \;dx=\\ =\frac{(3x+4)\cdot\sin(2x-1)}{2}-\frac{3}{4}\cdot (-\cos (2x-1))+C= \frac{(3x+4)\cdot\sin(2x-1)}{2}+\frac{3}{4}\cdot \cos (2x-1)+C. $$ Неопределённый интеграл по частям найден, осталось лишь записать ответ.Ответ: $\int (3x+4) \cos (2x-1) \; dx=\frac{(3x+4)\cdot\sin(2x-1)}{2}+\frac{3}{4}\cdot \cos (2x-1)+C$.
Полагаю, здесь не обойдётся без вопроса, поэтому попробую сформулировать его и дать ответ.
Вопрос
Почему мы приняли именно $u=3x+4$ и $dv=\cos(2x-1)dx$? Да, интеграл был решён. Но, может быть, если бы мы взяли $u=\cos (2x-1)$ и $dv=(3x+4)dx$ интеграл тоже был бы найден!
Ответ
Нет, если принять $u=\cos (2x-1)$ и $dv=(3x+4)dx$, то ничего хорошего с этого не выйдет, – интеграл не упростится. 2\cdot\cos(3x+1)}{3} +\frac{2x\sin(3x+1)}{9}-\frac{43\cos(3x+1)}{27}+C$.
2\cdot\cos(3x+1)}{3} +\frac{2x\sin(3x+1)}{9}-\frac{43\cos(3x+1)}{27}+C$.
Применение метода интегрирования по частям в несколько нестандартных случаях, не подпадающих под действие правил №1 и №2, будет дано во второй части.
Интегрирование по частям
Метод интегрирования по частям используется тогда, когда нужно упростить имеющийся неопределенный интеграл или свести его к табличному значению. Чаще всего он применяется в случае наличия показательных, логарифмических, прямых и обратных тригонометрических формул и их сочетаний в подынтегральном выражении.
Основная формула, необходимая для использования этого метода, выглядит так:
∫f(x)dx=∫u(x)d(v(x))=u(x)v(x)-∫v(x)d(u(x))
Она означает, что нам нужно сначала представить выражение под интегралом в качестве произведения функции u(x) и дифференциала функции v(x). После этого мы вычисляем значение функции v(x) каким-либо методом (чаще всего применяется метод непосредственного интегрирования), а полученные выражения подставляем в указанную формулу, сводя исходный интеграл к разности u(x)v(x)-∫v(x)d(u(x)). Полученный в итоге интеграл также можно взять, используя любой метод интегрирования.
Рассмотрим задачу, в которой нужно найти множество первообразных функции логарифма.
Пример 1Вычислите неопределенный интеграл ∫ln(x)dx.
Решение
Используем метод интегрирования по частям. Для этого берем ln(x) как функцию u(x), а остаток подынтегрального выражения – как d(v(x)). В итоге получаем, что ln(x)dx=u(x)d(v(x)), где u(x)=ln(x), d(v(x))=dx.
Дифференциалом функции u(x) является d(u(x))-u'(x)dx=dxx, а функция v(x) может быть представлена как v(x)=∫d(v(x))=∫dx=x
Важно: константа C при вычислении функции v(x) будет считаться равной 0.
Подставим то, что у нас получилось, в формулу интегрирования по частям:
∫ln(x)dx=u(x)v(x)-∫v(x)d(u(x))==ln(x)·x-∫x·dxx=ln(x)·x-∫dx=ln(x)·x-x+C1==x(ln(x)-1)+C
где C=-C1
Ответ: ∫ln(x)dx=x(ln(x)-1)+C.
Наиболее сложным в применении данного метода является выбор, какую именно часть исходного выражения под интегралом взять в качестве u(x), а какую – d(v(x)).
Разберем несколько стандартных случаев.
Если у нас в условии стоят интегралы вида ∫Pn(x)·eaxdx, ∫Pn(x)·sin(ax)dx либо ∫Pn(x)·cos(ax)dx, где a является коэффициентом, а Pn(x) – многочленом степени n, то в качестве функции u(x) нужно взять именно Pn(x).
Пример 2Найдите множество первообразных функции f(x)=(x+1)·sin(2x).
Решение
Мы можем взять по частям неопределенный интеграл ∫(x+1)·sin(2x)dx. Берем x+1 в качестве u(x) и sin(2x)dx в качестве d(v(x)), то есть d(u(x)) = d(x+1) = dx.
Используя непосредственное интегрирование, получим:
v(x)=∫sin(2x)dx=-12cos(2x)
Подставляем в формулу интегрирования по частям:
∫(x+1)·sin(2x)dx=u(x)v(x)-∫v(x)d(u(x))==(x+1)·-12cos(2x)-∫-12cos(2x)dx==-12(x+1)·cos(2x)+12∫cos(2x)·d(x)==-12(x+1)·cos(2x)+14sin(2x)+C
Ответ: ∫(x+1)·sin(2x)dx=-12(x+1)·cos(2x)+14sin(2x)+C.
Пример 3Вычислите неопределенный интеграл ∫(x2+2x)exdx.
Решение
Берем многочлен второго порядка x2+2x в качестве u(x) и d(v(x))-exdx.
∫x2+2xexdx=u(x)=x2+2x, d(v(x))=exdxd(u(x))=(2x+2)dx, v(x)=∫exdx=ex==u(x)v(x)-∫v(x)d(u(x))=(x2+2x)ex-∫(2x+2)exdx
К тому, что у нас получилось, надо опять применить метод интегрирования по частям:
∫(2x+2)exdx=(x2+2x)ex-∫2x+2exdx==u(x)=(2x+2), d(v(x))=exdxd(u(x))=2dx, v(x)=∫exdx=ex==(x2+2x)ex-(2x+2)ex-∫v(x)d(u(x))==(x2+2x)ex-(2x+2)ex-∫2exdx==(x2+2x-2x-2)ex+2∫exdx=(x2-2)ex+2ex+C=x2ex+C
Ответ: ∫(x2+2x)exdx=x2ex+C.
Пример 4Вычислите интеграл ∫x3cos13xdx.
Решение
Согласно методу интегрирования по частям, берем u(x)=x3 и d(v(x))=cos13xdx.
В таком случае d(u(x))=3x2dx и v(x)=∫cos13xdx=3sin13x.
Теперь подставим полученные выражения в формулу:
∫x3cos13xdx=u(x)v(x)-∫v(x)d(u))==x33sin13x-∫3x23sin13xdx==3x3sin13x-9∫x2sin13xdx
У нас получился неопределенный интеграл, который опять же нужно взять по частям:
∫x3cos13xdx=3x3sin13x-9∫x2sin13xdx==u(x)=x2, d(v(x))=sin13xdxd(u(x))=2xdx, v(x)=∫sin13xdx=-3cos13x==3x3sin13x-9-3x2cos13x-∫-3cos13x·2xdx==3x3sin13x+27×2·cos13x-54∫xcos13xdx
Выполняем частичное интегрирование еще раз:
∫x3cos13xdx=3x3sin13x+27×2·cos13x-54∫xcos13xdx==u(x)=x, d(v(x))=cos13xdxd(u(x))=dx, v(x)=∫cos13xdx=3sin13x==3x3sin13x+27x2cos13x-543xsin13x-∫3sin13xdx==3×3-162xsin13x+27x2cos13x+162∫sin13xdx==(3×3-162x)sin13x+27x2cos13x-486cos13x+C==(3×3-162x)sin13x+(27×2-486)cos13x+C
Ответ: ∫x3cos13xdx=(3×3-162x)sin13x+(27×2-486)cos13x+C.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеЕсли же у нас в условии стоят интегралы вида ∫Pn(x)·ln(ax)dx, ∫Pn(x)·arcsin(ax)dx,∫Pn(x)·arccos(ax)dx, ∫Pn(x)·arctg(ax)dx, ∫Pn(x)·arcctg(ax)dx
то нам следует брать в качестве u(x) функции arctg(ax), arcctg(x), ln(ax), arcsin(ax), arcos(ax).
Пример 5Вычислите множество первообразных функции (x+1)ln(2x).
Решение
Принимаем ln(2x) в качестве u(x), а (x+1)dx – в качестве d(v(x)). Получаем:
d(u(x))=(ln(2x))’dx=12x(2x)’dx=dxxv(x)=∫(x+1)dx=x22+x
Подставим эти выражения в формулу:
∫(x+1)ln(2x)dx=u(x)v(x)-∫v(x)d(u(x))==x22+xln2x-∫x22+xdxx==x22+xln(2x)-∫x2+1dx=x22+xln2x-12∫xdx-∫dx==x22+xln(2x)-x24-x+C
Ответ: ∫(x+1)ln(2x)dx=x22+xln(2x)-x24-x+C.
Пример 6Вычислите неопределенный интеграл ∫x·arcsin(2x)dx.
Решение
Решаем, какую часть взять за u(x), а какую – за d(v(x)). Согласно правилу, приведенному выше, в качестве первой функции нужно взять arcsin(2x), а d(v(x)) = xdx. Получим:
d(u(x))=(arcsin(2x)’dx=2x’dx1-(2x)2=2dx1-(2x)2, v(x)=∫xdx=x22
Подставляем значения в формулу:
∫x·arcsin(2x)dx=u(x)v(x)-∫v(x)d(u(x))==x22arcsin(2x)-∫x22-2dx1-(2x)2=x22arcsin(2x)-∫x2dx1-4×2
В итоге мы пришли к следующему равенству:
∫x·arcsin(2x)dx=x22arcsin(2x)-∫x2dx1-4×2
Теперь вычислим получившийся в итоге интеграл ∫x2dx1-4×2:
∫x2dx1-4×2=∫x2dx414-x2=12∫x2dx14-x2=-12∫-x2dx14-x2==-12∫14-x2-1414-x2dx=-1214-x2dx+18∫dx14-x2==-12∫14-x2dx+18arcsin(2x)
Здесь можно применить метод интегрирования по частям и получить:
∫x2dx1-4×2=-12∫14-x2dx+18arcsin(2x)==u(x)=14-x2, d(v(x))=dxd(u(x))=14-x2’dx214-x2=-xdx14-x2, v(x)=∫dx=x==-12u(x)v(x)-∫v(x)d(u(x))+18arcsin(2x)==-12×14-x2-∫-x2dx14-x2+18arcsin(2x)==-12×14-x2-12∫x2dx14-x2+18arcsin(2x)==-12×14-x2-∫x2dx1-4×2+18arcsin(2x)
Теперь наше равенство выглядит так:
∫x2dx1-4×2=-12×14-x2-∫x2dx1-4×2+18arcsin(2x)
Мы видим, что интеграл справа аналогичен тому, что получился слева. Переносим его в другую часть и получаем:
Переносим его в другую часть и получаем:
2∫x2dx1-4×2=-12×14-x2+18arcsin(2x)+C1⇒x2dx1-4×2=-14×14-x2+116arcsin(2x)+C2x2dx1-4×2=-18×14-x2+116arcsin(2x)+C2
где C2=C12
Вернемся к исходным переменным:
∫x·arcsin(2x)dx=x22arcsin(2x)-∫x2dx1-4×2==x22arcsin(2x)—18×1-4×2+116arcsin(2x)+C2==12×2-18arcsin(2x)+18×1-4×2+C
где С=-С2
Ответ: ∫x·arcsin(2x)dx=12×2-18arcsin(2x)+18×1-4×2+C.
Если же у нас в задаче стоит интеграл вида ∫ea·x·sin(bx)dx либо ∫ea·x·cos(bx)dx, то в качестве u(x) может быть выбрана любая функция.
Пример 7Вычислите неопределенный интеграл ∫ex·sin(2x)dx.
Решение
∫exsin(2x)dx=u(x)=sin(2x), d(v(x))=exdxd(u(x))=2cos(2x)dx, v(x)=∫exdx=ex==u(x)v(x)-∫v(x)d(u(x))=sin(2x)ex-∫ex·2cos2xdx==sin(2x)ex-2∫excos(2x)dx=u(x)=cos(2x), d(v(x))=exdxd(u(x))=-2sin(2x)dx, v(x)=∫exdx=ex==sin(2x)ex-2cos(2x)ex-∫(ex(-2sin(2x)dx))==sin(2x)ex=2cos(2x)ex-4∫exsin(2x)dx
В итоге у нас получится:
∫exsin(2x)dx=sin(2x)ex-2cos(2x)ex-4∫exsin(2x)dx
Мы видим одинаковые интегралы слева и справа, значит, можем привести подобные слагаемые:
5∫exsin(2x)dx=sin(2x)ex-2cos(2x)ex⇒∫exsin(2x)dx=15sin(2x)ex-25cos(2x)ex+C
Ответ: ∫exsin(2x)dx=15sin(2x)ex-25cos(2x)ex+C
Этот способ решения является стандартным, и справа нередко получается интеграл, который идентичен исходному.
Мы рассмотрели наиболее типовые задачи, в которых можно точно определить, какую часть выражения взять за d(v(x)), а какую за u(x). В остальных случаях это приходится определять самостоятельно.
Также советуем вам ознакомиться с материалом, посвященным основным методам интегрирования.
Интегрирование по частям с примерами решения
Содержание:
- Приведем примеры использования метода интегрирования по частям
- Пример 1:
- Пример 2:
- Интегрирование по частям примеры с решением
- Примеры с решением
- Пример 3:
- Пример 4:
- Пример 5:
- Пример 6:
- Пример 7:
- Пример 8:
- Интегрирование по частям в неопределенном интеграле
- Пример 9:
- Пример 10:
- Пример 11:
Пусть и две различные функции переменной . Формула для производной произведения дает
Формула для производной произведения дает
Равенство (1) позволяет утверждать, что
В справедливости (2) убеждаемся, находя производную от левой и правой частей этого равенства — при этом мы приходим к верному равенству (1). Перепишем (2) так:
или, что то же самое,
В чем смысл формулы (3). К сожалению, не существует правила, выражающего интеграл от произведения двух функций через интегралы от каждого из сомножителей. Однако если для произведения двух функций известен интеграл от одного из сомножителей:
то интеграл удается выразить через интеграл, в который входит производная Учитывая (4), перепишем (3) в виде
Так как то последний интеграл в (5) есть иногда он бывает проще исходного интеграла
или сводится к известному интегралу. В частности, если степенная функция или многочлен, то тоже степенная функция (многочлен), причем степень на единицу ниже степени
Формула (3), или (5), называется формулой интегрирования по частям. Из нее вытекает и аналогичное соотношение для определенных интегралов:
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Приведем примеры использования метода интегрирования по частям
Пример 1:Найти
Положим тогда
По формуле (3) имеем
Пример 2:Найти
Положим тогда
Пользуясь формулой (3), получаем
откуда, учитывая результаты первого примера, имеем
Для нахождения где многочлен степени приходится раз выполнять интегрирование по частям. При этом в ответе получится выражение вида где многочлен степени Зная это, можно не выполнять раз интегрирование по частям, а прямо находить коэффициенты многочлена
Возможно вам будут полезны данные страницы:
Интегрирование по частям примеры с решением
Теорема Если функции непрерывно дифференцируемы в некотором промежутке то справедлива формула
По условию теоремы подынтегральные функции в (1. 19) непрерывны. Поэтому в силу утверждения 1.1 они имеют первообразные и существуют входящие в (1.19) неопределенные интегралы. Опуская обозначение аргумента по правилу вычисления дифференциала от произведения дифференцируемых функций [II] запишем
19) непрерывны. Поэтому в силу утверждения 1.1 они имеют первообразные и существуют входящие в (1.19) неопределенные интегралы. Опуская обозначение аргумента по правилу вычисления дифференциала от произведения дифференцируемых функций [II] запишем
Отсюда, используя линейность неопределенного интеграла, получаем
В соответствии со свойством 2° (см. 1.3) имеем
Относя произвольную постоянную к неопределенному интегралу из (1.20) и (1.21) получаем (1.19).
Использование формулы (1.19) целесообразно в том случае, когда представление подынтегрального выражения в виде
приводящее к задаче определения функции и интеграла упрощает вычисление исходного интеграла. Уместно дать некоторые рекомендации по процедуре применения (1.19), называемой интегрированием по частям.
| В исчислении и, в более общем смысле, в математическом анализе, интегрирование по частям или частичное интегрирование — это процесс, который находит интеграл от произведения функций в терминах интеграла от произведения их производной и антипроизводной. |
Примеры с решением
Используя формулу (1.19) интегрирования по частям, вычислим
Пример 3:Следуя высказанным рекомендациям, в первом неопределенном интеграле обозначим и запишем
Пример 4:Во втором неопределенном интеграле подведем сомножитель под знак дифференциала:
Для вычисления полученного интеграла в числителе его подынтегрального выражения добавим и вычтем единицу:
В итоге получим
Пример 5:Третий неопределенный интеграл вычислим, подведя под знак дифференциала многочлен:
Пример 6:В четвертом неопределенном интеграле примем
Нетрудно проверить, что выбор сочетания или после применения (1.19) приведет лишь к усложнению подынтегрального выражения.
По аналогии с последним примером при интегрировании по частям функции произойдет понижение степени под знаком интеграла, если в качестве выбрать
Если раз последовательно провести интегрирование по частям, то можно найти искомый неопределенный интеграл Но можно поступить проще. Представив последнее выражение в виде рекуррентного соотношения получим
или
В некоторых случаях интегрированием по частям (иногда — повторным) можно получить в правой части цепочки равенств выражение, содержащее исходный неопределенный интеграл т.е. прийти к уравнению с неопределенным интегралом в качестве неизвестного.
Пример 7:Интегрированием по частям вычисляем
Используя табличный интеграл 15, приходим к равенству
Отсюда, учитывая, что равенство, в обеих частях которого стоят интегралы, верно с точностью до произвольной постоянной, получаем
Пример 8:Найдем неопределенные интегралы
В данном случае в качестве можно выбрать как показательную, так и тригонометрическую функции. Используя первый вариант и интегрируя по частям
приходим к интегралу который тоже возьмем по частям:
Подставляя это выражение в предыдущее, получаем
Интегрирование по частям в неопределенном интеграле
Метод вычисления интегралов, называемый интегрированием по частям, основан на правиле дифференцирования произведения.
Пусть функции, дифференцируемые на некотором промежутке Тогда, как известно, дифференциал произведения этих функций вычисляется по формуле
Взяв неопределенный интеграл от обеих частей этого равенства, получим:
Так как
а
то получаем:
откуда
Поскольку уже содержит произвольную постоянную, в правой части полученного равенства С можно опустить и записать равенство в виде
Полученная формула называется формулой интегрирования по частям.
При выводе формулы (1) мы предположили, что функции дифференцируемы. Этой формулой обычно пользуются в тех случаях, когда подынтегральное выражение проще, чем подынтегральное выражение
Заметим, что одно и то же подынтегральное выражение можно различными способами записать в виде Например,
и т. д. Поэтому иногда приходится испытывать различные формы такой записи, прежде чем метод приведет к успеху. Обычно стараются подынтегральное выражение разбить на части так, чтобы вид был не сложнее, чем вид В частности, полезно иметь в виду, что для таких функций, как производные имеют вид более простой, чем сами функции. Поэтому в большинстве случаев эти функции удобно принимать за
Пример 9:Вычислим
Решение:
Положим Тогда
Используя формулу (1), получаем:
Замечание. При нахождении не пишут промежуточную произвольную постоянную так как она не оказывает влияния на окончательный результат.
Пример 10:Вычислим
Решение:
Положим Тогда
Используя формулу (1), получим:
Чтобы вычислить полученный в правой части равенства (2) интеграл, приходится снова использовать метод интегрирования по частям. Получим (см. пример 1):
Возвращаясь к исходному интегралу и воспользовавшись промежуточным равенством (2), окончательно получаем:
Интегрирование по частям в определенном интеграле. Для определенного интеграла формула интегрирования по частям принимает следующий вид:
В самом деле, если
то по формуле интегрирования по частям для неопределенного интеграла имеем:
Поэтому
и
значит
а это и есть формула (4).
Пример 11:Вычислим
Решение:
Положим
Воспользовавшись формулой (4), получим:
Методы интегрирования в математике: Непосредственное интегрирование, Метод подстановки
Непосредственное интегрирование
Непосредственное интегрирование основано на свойстве 4 неопределенного интеграла Если функции f1(x), … fn(x) имеют первообразные в некотором промежутке, то функция f(x) = f1(x)+f2(x)+f3(x)+…+-fn(x) также имеет первообразную в том же промежутке, причем
т. е. неопределенный интеграл от суммы некоторого числа функций равен такой же сумме неопределенных интегралов от слагаемых.
е. неопределенный интеграл от суммы некоторого числа функций равен такой же сумме неопределенных интегралов от слагаемых.Примеры задач, решаемых с помощью непосредственного интегрирования, рассматриваются на следующем видео
Метод подстановки
Интегрирование производимое введением новой переменной (или метод подстановки) основано на формуле
где x = ф(t) — дифференцируемая функция переменой t.Задачи, решаемые с помощью метода подстановки, рассматриваются на следующем видео
Метод интегрирования по частям
Если u = u (х), v = v (х) — дифференцируемые функции от х, то из формулы для дифференциала произведения двух функций d(uv) = udv+vdu получается формула интегрирования по частям
Эта формула применяется в случае, когда подынтегральная функция представляет собой произведение алгебраической и трансцендентной функций. В качестве и обычно выбирается функция, которая упрощается дифференцированием, в качестве dv — оставшаяся часть подынтегрального выражения, содержащая dx, из которой можно определить v путем интегрирования.
В качестве и обычно выбирается функция, которая упрощается дифференцированием, в качестве dv — оставшаяся часть подынтегрального выражения, содержащая dx, из которой можно определить v путем интегрирования.Для сведения данного интеграла к одной из формул простейших интегралов формулу нужно применить несколько раз. Иногда искомый интеграл определяется из алгебраического уравнения, получающегося с помощью интегрирования по частям.
Смотрите задачи, решаемые методом интегрирования по частям, на следующем видео
3.1 Интеграция по частям — Calculus Volume 2
Цели обучения
- 3.1.1 Определите, когда следует использовать интеграцию по частям.
- 3.1.2 Используйте формулу интегрирования по частям для решения задач интегрирования.
- 3.1.3 Используйте формулу интегрирования по частям для определенных интегралов.
К настоящему времени у нас есть довольно тщательная процедура вычисления многих основных интегралов. Однако, хотя мы можем интегрировать ∫xsin (x2) dx∫xsin (x2) dx с помощью подстановки u = x2, u = x2, нечто столь же простое, как ∫xsinxdx∫xsinxdx, бросает нам вызов.Многие студенты хотят знать, существует ли правило продукта для интеграции. Нет, но есть метод, основанный на правиле произведения для дифференциации, который позволяет нам заменять один интеграл на другой. Мы называем эту технику интеграцией по частям.
Мы называем эту технику интеграцией по частям.
Формула интеграции по частям
Если, h (x) = f (x) g (x), h (x) = f (x) g (x), то, используя правило произведения, мы получаем h ′ (x) = f ′ (x ) g (x) + g ′ (x) f (x). h ′ (x) = f ′ (x) g (x) + g ′ (x) f (x). Хотя сначала это может показаться контрпродуктивным, давайте теперь проинтегрируем обе части этого уравнения: ∫h ′ (x) dx = ∫ (g (x) f ′ (x) + f (x) g ′ (x)) dx.∫h ′ (x) dx = ∫ (g (x) f ′ (x) + f (x) g ′ (x)) dx.
Это дает нам
h (x) = f (x) g (x) = ∫g (x) f ′ (x) dx + ∫f (x) g ′ (x) dx.h (x) = f (x) g (x) = ∫g (x) f ′ (x) dx + ∫f (x) g ′ (x) dx.Теперь решаем относительно ∫f (x) g ′ (x) dx: ∫f (x) g ′ (x) dx:
∫f (x) g ′ (x) dx = f (x) g (x) −∫g (x) f ′ (x) dx.f (x) g ′ (x) dx = f (x) g (x) −g (x) f ′ (x) dx.Сделав замены u = f (x) u = f (x) и v = g (x), v = g (x), которые, в свою очередь, сделают du = f ′ (x) dxdu = f ′ (x) dx и dv = g ′ (x) dx, dv = g ′ (x) dx, имеем более компактную форму
∫udv = uv − ∫vdu.∫udv = uv − ∫vdu.Теорема 3.1
Интегрирование по частям
Пусть u = f (x) u = f (x) и v = g (x) v = g (x) — функции с непрерывными производными.Тогда формула интегрирования по частям для интеграла, включающего эти две функции, имеет следующий вид:
∫udv = uv − ∫vdu.∫udv = uv − ∫vdu.3,1
Преимущество использования формулы интегрирования по частям заключается в том, что мы можем использовать ее для замены одного интеграла на другой, возможно, более простой интеграл. Следующий пример иллюстрирует его использование.
Пример 3.1
Использование интеграции по частям
Используйте интегрирование по частям с u = xu = x и dv = sinxdxdv = sinxdx для вычисления ∫xsinxdx.∫xsinxdx.
Решение
Выбирая u = x, u = x, получаем du = 1dx.du = 1dx. Поскольку dv = sinxdx, dv = sinxdx, получаем v = ∫sinxdx = −cosx. v = ∫sinxdx = −cosx. Эти значения удобно отслеживать следующим образом:
v = ∫sinxdx = −cosx. Эти значения удобно отслеживать следующим образом:
Применение формулы интегрирования по частям дает
∫xsinxdx = (x) (- cosx) −∫ (−cosx) (1dx) Заменить. = — xcosx + ∫cosxdxSimplify. = — xcosx + sinx + C.Использовать∫cosxdx = sinx + C.∫xsinxdx = (x) ( −cosx) −∫ (−cosx) (1dx) Заменить.= −xcosx + ∫cosxdxSimplify. = — xcosx + sinx + C. Используйте cosxdx = sinx + C.Анализ
На данный момент, вероятно, есть несколько вопросов, которые нуждаются в пояснении. Прежде всего, вам может быть любопытно, что бы произошло, если бы мы выбрали u = sinxu = sinx и dv = x.dv = x. Если бы мы сделали это, то получили бы du = cosxdxdu = cosxdx и v = 12×2.v = 12×2. Таким образом, после применения интегрирования по частям имеем ∫ xsinxdx = 12x2sinx − ∫ 12x2cosxdx.∫ xsinxdx = 12x2sinx − ∫ 12x2cosxdx. К сожалению, с новым интегралом мы не в лучшем положении, чем раньше.Важно помнить, что когда мы применяем интеграцию по частям, нам может потребоваться попробовать несколько вариантов для uu и dvdv, прежде чем найти подходящий вариант.
Во-вторых, вы можете задаться вопросом, почему, когда мы находим v = ∫ sinxdx = −cosx, v = ∫ sinxdx = −cosx, мы не используем v = −cosx + K.v = −cosx + K. Чтобы увидеть, что это не имеет значения, мы можем переработать задачу, используя v = −cosx + K: v = −cosx + K:
∫xsinxdx = (x) (- cosx + K) −∫ (−cosx + K) (1dx) = — xcosx + Kx + ∫cosxdx − ∫Kdx = −xcosx + Kx + sinx − Kx + C = −xcosx + sinx + C.∫xsinxdx = (x) (- cosx + K) −∫ (−cosx + K) (1dx) = — xcosx + Kx + ∫cosxdx − ∫Kdx = −xcosx + Kx + sinx − Kx + C = −xcosx + sinx + C.Как видите, в конечном решении это не имеет значения.
Наконец, мы можем проверить правильность нашей первообразной, дифференцируя −xcosx + sinx + C: −xcosx + sinx + C:
ddx (−xcosx + sinx + C) = (- 1) cosx + (- x) (- sinx) + cosx = xsinx. ddx (−xcosx + sinx + C) = (- 1) cosx + (- x) (- sinx ) + cosx = xsinx.
Следовательно, первообразная проверяется.
КПП 3.1
Вычислите ∫ xe2xdx∫ xe2xdx, используя формулу интегрирования по частям с u = xu = x и dv = e2xdx.dv = e2xdx.
Естественный вопрос, который можно задать здесь: как мы узнаем, как выбрать uu и dv? Dv? Иногда это результат проб и ошибок; однако аббревиатура LIATE часто помогает избавиться от некоторых догадок в нашем выборе. Этот акроним означает L огарифмических функций, I nverse тригонометрических функций, A алгебраических функций, T ригонометрических функций и E xponential функций. Эта мнемоника помогает определить правильный выбор для u.u.
Тип функции в интеграле, который появляется первым в списке, должен быть нашим первым выбором u.u. Например, если интеграл содержит логарифмическую функцию и алгебраическую функцию, мы должны выбрать uu в качестве логарифмической функции, потому что L стоит перед A в LIATE. Интеграл в примере 3.1 имеет тригонометрическую функцию (sinx) (sinx) и алгебраическую функцию (x). (X). Поскольку A стоит перед T в LIATE, мы выбрали uu в качестве алгебраической функции. Когда мы выбрали u, u, dvdv выбирается как оставшаяся часть интегрируемой функции вместе с dx.dx.
Почему работает эта мнемоника? Помните, что все, что мы выберем в качестве DVD, должно быть чем-то, что мы можем интегрировать. Поскольку у нас нет формул интегрирования, позволяющих интегрировать простые логарифмические функции и обратные тригонометрические функции, имеет смысл не выбирать их в качестве значений для dv.dv. Следовательно, они должны быть во главе списка как варианты выбора для u.u. Таким образом, мы помещаем LI в начало мнемоники. (Мы могли бы так же легко начать с IL, поскольку эти два типа функций не будут появляться вместе в задаче интеграции по частям.) Экспоненциальные и тригонометрические функции находятся в конце нашего списка, потому что они довольно легко интегрируются и являются хорошим выбором для dv. dv. Таким образом, у нас есть TE в конце нашей мнемоники. (Мы могли бы так же легко использовать ET в конце, поскольку, когда эти типы функций появляются вместе, обычно не имеет значения, какая из них — uu, а какая — dv.) Dv.) Алгебраические функции, как правило, легко интегрировать и и различать, и они входят в середину мнемоники.
dv. Таким образом, у нас есть TE в конце нашей мнемоники. (Мы могли бы так же легко использовать ET в конце, поскольку, когда эти типы функций появляются вместе, обычно не имеет значения, какая из них — uu, а какая — dv.) Dv.) Алгебраические функции, как правило, легко интегрировать и и различать, и они входят в середину мнемоники.
Пример 3.2
Использование интеграции по частям
Оценить ∫lnxx3dx.∫lnxx3dx.
Решение
Начнем с переписывания интеграла:
∫lnxx3dx = ∫ x − 3lnxdx.∫lnxx3dx = ∫ x − 3lnxdx.Поскольку этот интеграл содержит алгебраическую функцию x − 3x − 3 и логарифмическую функцию lnx, lnx, выбираем u = lnx, u = lnx, поскольку L стоит перед A в LIATE. После того, как мы выбрали u = lnx, u = lnx, мы должны выбрать dv = x − 3dx.dv = x − 3dx.
Далее, поскольку u = lnx, u = lnx, имеем du = 1xdx.du = 1xdx.Кроме того, v = ∫ x − 3dx = −12x − 2. v = ∫ x − 3dx = −12x − 2. Подводя итоги,
u = lnxdv = x − 3dxdu = 1xdxv = ∫ x − 3dx = −12x − 2. u = lnxdv = x − 3dxdu = 1xdxv = ∫ x − 3dx = −12x − 2.Подстановка в формулу интегрирования по частям (уравнение 3.1) дает
∫lnxx3dx = ∫ x − 3lnxdx = (lnx) (- 12x − 2) −∫ (−12x − 2) (1xdx) = — 12x − 2lnx + ∫ 12x − 3dxSimplify. = — 12x − 2lnx − 14x − 2 + CIntegrate. = — 12x2lnx − 14×2 + C.Перепишите с целыми положительными числами. Lnxx3dx = ∫ x − 3lnxdx = (lnx) (- 12x − 2) −∫ (−12x − 2) (1xdx) = — 12x− 2lnx + ∫ 12x − 3dxSimplify. = — 12x − 2lnx − 14x − 2 + CIntegrate. = — 12x2lnx − 14×2 + C.Перепишите положительными целыми числами.КПП 3.2
Оценить ∫ xlnxdx.∫ xlnxdx.
В некоторых случаях, как в следующих двух примерах, может потребоваться применить интеграцию по частям более одного раза.
Пример 3.3
Применение интеграции по частям более одного раза
Оценить ∫ x2e3xdx.∫ x2e3xdx.
Решение
Используя LIATE, выберите u = x2u = x2 и dv = e3xdx. dv = e3xdx. Таким образом, du = 2xdxdu = 2xdx и v = ∫e3xdx = (13) e3x.v = ∫e3xdx = (13) e3x. Следовательно,
dv = e3xdx. Таким образом, du = 2xdxdu = 2xdx и v = ∫e3xdx = (13) e3x.v = ∫e3xdx = (13) e3x. Следовательно,
Подстановка в уравнение 3.1 дает
∫x2e3xdx = 13x2e3x − ∫23xe3xdx.∫x2e3xdx = 13x2e3x − ∫23xe3xdx.Мы по-прежнему не можем интегрировать ∫23xe3xdx∫23xe3xdx напрямую, но теперь интеграл имеет меньшую мощность на x.x. Мы можем оценить этот новый интеграл, снова используя интегрирование по частям. Для этого выберите u = xu = x и dv = 23e3xdx.dv = 23e3xdx. Таким образом, du = dxdu = dx и v = ∫ (23) e3xdx = (29) e3x.v = ∫ (23) e3xdx = (29) e3x.Теперь у нас
u = xdv = 23e3xdxdu = dxv = ∫23e3xdx = 29e3x.u = xdv = 23e3xdxdu = dxv = ∫23e3xdx = 29e3x.Подставляя обратно в предыдущее уравнение, получаем
∫ x2e3xdx = 13x2e3x− (29xe3x − ∫ 29e3xdx) .∫ x2e3xdx = 13x2e3x− (29xe3x − ∫ 29e3xdx).После вычисления последнего интеграла и упрощения получаем
∫x2e3xdx = 13x2e3x − 29xe3x + 227e3x + C.∫x2e3xdx = 13x2e3x − 29xe3x + 227e3x + C.Пример 3.4
Применение интеграции по частям, когда LIATE не работает
Оценить ∫ t3et2dt.∫ t3et2dt.
Решение
Если мы используем строгую интерпретацию мнемоники LIATE для выбора u, u, мы получим u = t3u = t3 и dv = et2dt.dv = et2dt. К сожалению, этот выбор не сработает, потому что мы не можем оценить ∫ et2dt. et2dt. Однако, поскольку мы можем вычислить ∫ tet2dx, ∫ tet2dx, мы можем попробовать выбрать u = t2u = t2 и dv = tet2dt.dv = tet2dt. С этим выбором у нас есть
u = t2dv = tet2dtdu = 2tdtv = ∫ tet2dt = 12et2.u = t2dv = tet2dtdu = 2tdtv = ∫ tet2dt = 12et2.Таким образом, получаем
∫t3et2dt = 12t2et2 − ∫12et22tdt = 12t2et2−12et2 + C.∫t3et2dt = 12t2et2 − ∫12et22tdt = 12t2et2−12et2 + C.Пример 3.5
Применение интеграции по частям более одного раза
Вычислить ∫ sin (lnx) dx. sin (lnx) dx.
sin (lnx) dx.
Решение
Похоже, что этот интеграл имеет только одну функцию, а именно sin (lnx) sin (lnx), однако мы всегда можем использовать постоянную функцию 1 в качестве другой функции. В этом примере выберем u = sin (lnx) u = sin (lnx) и dv = 1dx.dv = 1dx. (Решение использовать u = sin (lnx) u = sin (lnx) легко. Мы не можем выбрать dv = sin (lnx) dxdv = sin (lnx) dx, потому что, если бы мы могли его интегрировать, мы не были бы используя интегрирование по частям в первую очередь!) Следовательно, du = (1 / x) cos (lnx) dxdu = (1 / x) cos (lnx) dx и v = ∫ 1dx = x.v = ∫ 1dx = х. После применения интегрирования по частям к интегралу и упрощения получаем
Sin (lnx) dx = xsin (lnx) −∫ cos (lnx) dx.∫ sin (lnx) dx = xsin (lnx) −∫ cos (lnx) dx.К сожалению, этот процесс оставляет нам новый интеграл, очень похожий на исходный. Однако давайте посмотрим, что произойдет, когда мы снова применим интеграцию по частям. На этот раз выберем u = cos (lnx) u = cos (lnx) и dv = 1dx, dv = 1dx, делая du = — (1 / x) sin (lnx) dxdu = — (1 / x) sin (lnx) dx и v = ∫ 1dx = xv = ∫ 1dx = x. Подставляя, получаем
∫ sin (lnx) dx = xsin (lnx) — (xcos (lnx) —∫ −sin (lnx) dx).∫ sin (lnx) dx = xsin (lnx) — (xcos (lnx) —∫ −sin (lnx) dx).После упрощения получаем
∫ sin (lnx) dx = xsin (lnx) −xcos (lnx) −∫ sin (lnx) dx.∫ sin (lnx) dx = xsin (lnx) −xcos (lnx) −∫ sin (lnx) dx.Последний интеграл теперь такой же, как оригинал. Может показаться, что мы просто пошли по кругу, но теперь мы действительно можем вычислить интеграл. Чтобы увидеть, как это сделать более наглядно, подставьте I = ∫ sin (lnx) dx.I = ∫ sin (lnx) dx. Таким образом, уравнение принимает вид
I = xsin (lnx) −xcos (lnx) −I.I = xsin (lnx) −xcos (lnx) −I.Сначала добавьте II к обеим частям уравнения, чтобы получить
2I = xsin (lnx) −xcos (lnx). 2I = xsin (lnx) −xcos (lnx).Далее разделите на 2:
I = 12xsin (lnx) −12xcos (lnx). I = 12xsin (lnx) −12xcos (lnx).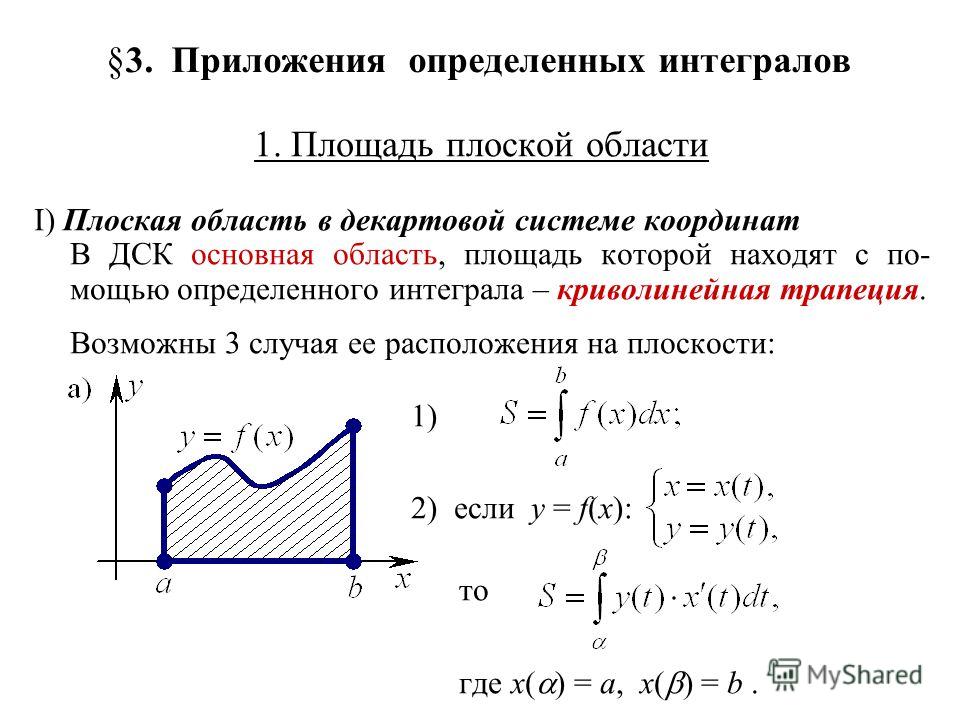
Подставляя снова I = ∫ sin (lnx) dxI = ∫ sin (lnx) dx, получаем
∫ sin (lnx) dx = 12xsin (lnx) −12xcos (lnx). Sin (lnx) dx = 12xsin (lnx) −12xcos (lnx).Отсюда мы видим, что (1/2) xsin (lnx) — (1/2) xcos (lnx) (1/2) xsin (lnx) — (1/2) xcos (lnx) является первообразной sin ( lnx) dx.sin (lnx) dx. Для наиболее общего первообразного добавьте + C: + C:
∫ sin (lnx) dx = 12xsin (lnx) −12xcos (lnx) + C.∫ sin (lnx) dx = 12xsin (lnx) −12xcos (lnx) + C.Анализ
Если этот метод сначала покажется немного странным, мы можем проверить ответ дифференцированием:
ddx (12xsin (lnx) −12xcos (lnx)) = 12 (sin (lnx)) + cos (lnx) · 1x · 12x− (12cos (lnx) −sin (lnx) · 1x · 12x) = sin (lnx) .ddx (12xsin (lnx) −12xcos (lnx)) = 12 (sin (lnx)) + cos (lnx) · 1x · 12x− (12cos (lnx) −sin (lnx) · 1x · 12x) = sin (lnx ).КПП 3.3
Оценить ∫ x2sinxdx. x2sinxdx.
Интеграция по частям для определенных интегралов
Теперь, когда мы успешно использовали интегрирование по частям для вычисления неопределенных интегралов, мы обратим наше внимание на определенные интегралы.Методика интегрирования на самом деле такая же, только мы добавляем шаг для вычисления интеграла на верхнем и нижнем пределе интегрирования.
Теорема 3.2
Интегрирование по частям для определенных интегралов
Пусть u = f (x) u = f (x) и v = g (x) v = g (x) — функции с непрерывными производными на [a, b] . [а, б]. Тогда
Abudv = uv | ab − ∫abvdu.∫abudv = uv | ab − abvdu.3,2
Пример 3.6
Определение района
Найдите площадь области, ограниченную сверху графиком y = tan − 1xy = tan − 1x и ниже осью xx на интервале [0,1].[0,1].
Решение
Эта область показана на Рисунке 3.2. Чтобы найти область, мы должны вычислить ∫01tan − 1xdx.∫01tan − 1xdx.
Рис. 3.2 Чтобы найти площадь заштрихованной области, мы должны использовать интегрирование по частям.
Для этого интеграла возьмем u = tan − 1xu = tan − 1x и dv = dx, dv = dx, в результате чего du = 1×2 + 1dxdu = 1×2 + 1dx и v = x.v = x. После применения формулы интегрирования по частям (уравнение 3.2) получаем
Площадь = xtan − 1x | 01 − ∫01xx2 + 1dx. Площадь = xtan − 1x | 01 − ∫01xx2 + 1dx.Используйте замену u -для получения
∫01xx2 + 1dx = 12ln | x2 + 1 | 01.∫01xx2 + 1dx = 12ln | x2 + 1 | 01.Таким образом,
Площадь = xtan − 1x | 01−12ln | x2 + 1 || 01 = π4−12ln2. Площадь = xtan − 1x | 01−12ln | x2 + 1 || 01 = π4−12ln2.На этом этапе было бы неплохо провести «проверку реальности» на разумность нашего решения. Поскольку π4−12ln2≈0,4388, π4−12ln2≈0,4388, а из рисунка 3.2 мы ожидаем, что наша площадь будет немного меньше 0,5, это решение кажется разумным.
Пример 3,7
В поисках объема революции
Найдите объем твердого тела, полученный вращением области, ограниченной графиком f (x) = e − x, f (x) = e − x, осью x , осью y и линия x = 1x = 1 относительно оси y .
Решение
Лучшим вариантом решения этой проблемы является использование метода оболочки. Начните с рисования области, которую нужно повернуть, вместе с типичным прямоугольником (см. Следующий график).
Рис. 3.3 Мы можем использовать метод оболочки, чтобы найти объем вращения.
Чтобы найти объем с помощью оболочек, мы должны вычислить 2π∫01xe − xdx.2π∫01xe − xdx. Для этого положим u = xu = x и dv = e − x.dv = e − x. Эти выборы приводят к du = dxdu = dx и v = ∫ e − x = −e − x. V = ∫ e − x = −e − x.Подставляя в уравнение 3.2, получаем
Объем = 2π∫01xe − xdx = 2π (−xe − x | 01 + ∫01e − xdx) Использовать интегрирование по частям. = — 2πxe − x | 01−2πe − x | 01Оценка∫01e − xdx = −e − x | 01. = 2π − 4πe. Вычислить и упростить. Объем = 2π∫01xe − xdx = 2π (−xe − x | 01 + ∫01e − xdx) Использовать интегрирование по частям. = — 2πxe − x | 01−2πe − x | 01 Вычислить 01e − xdx = −e − x | 01. = 2π − 4πe. Вычислить и упростить.Анализ
Опять же, неплохо проверить разумность нашего решения. Мы видим, что твердое тело имеет объем немного меньше, чем у цилиндра с радиусом 11, и высоту 1 / e1 / e, добавленную к объему конуса с радиусом основания 11 и высотой 1−1e.1−1д. Следовательно, твердое тело должно иметь объем чуть меньше
. π (1) 21e + (π3) (1) 2 (1−1e) = 2π3e + π3≈1,8177.π (1) 21e + (π3) (1) 2 (1−1e) = 2π3e + π3≈1,8177.Поскольку 2π − 4πe≈1,6603,2π − 4πe≈1,6603, мы видим, что наш расчетный объем является разумным.
КПП 3,4
Вычислить ∫0π / 2xcosxdx.∫0π / 2xcosxdx.
Раздел 3.1 Упражнения
При использовании техники интегрирования по частям вы должны тщательно выбирать, какое выражение будет u. Для каждой из следующих проблем используйте рекомендации в этом разделе, чтобы выбрать u. Не , а не оценивают интегралы.
4.∫x2arctanxdx∫x2arctanxdx
5.∫e3xsin (2x) dx∫e3xsin (2x) dx
Найдите интеграл с помощью простейшего метода. Не все проблемы требуют интеграции по частям.
7.∫lnxdx∫lnxdx ( Подсказка: ∫lnxdx∫lnxdx эквивалентно ∫1 · ln (x) dx.) ∫1 · ln (x) dx.)
9.∫tan − 1xdx∫tan − 1xdx
11.∫xsin (2x) dx∫xsin (2x) dx
17.∫ln (2x + 1) dx∫ln (2x + 1) dx
23.∫sin (ln (2x)) dx∫sin (ln (2x)) dx
24.∫cos (lnx) dx∫cos (lnx) dx
28.∫sin − 1xdx∫sin − 1xdx
29.∫cos − 1 (2x) dx∫cos − 1 (2x) dx
30.∫xarctanxdx∫xarctanxdx
35.∫xсек − 1xdx∫xsec − 1xdx
Вычислить определенные интегралы. Используйте графическую утилиту, чтобы подтвердить свои ответы.
39.∫01xe − 2xdx∫01xe − 2xdx (Выразите ответ в точной форме.)
40.∫01exdx (letu = x) ∫01exdx (letu = x)
41.∫1eln (x2) dx∫1eln (x2) dx
42.∫0πxcosxdx∫0πxcosxdx
43.∫ − ππxsinxdx∫ − ππxsinxdx (Выразите ответ в точной форме.)
44.∫03ln (x2 + 1) dx∫03ln (x2 + 1) dx (Выразите ответ в точной форме.)
45.∫0π / 2x2sinxdx∫0π / 2x2sinxdx (Выразите ответ в точной форме.)
46.∫01x5xdx∫01x5xdx (Ответ выражается пятью значащими цифрами.)
47.Вычислить ∫cosxln (sinx) dx∫cosxln (sinx) dx
Выведите следующие формулы, используя технику интегрирования по частям.Предположим, что n — положительное целое число. Эти формулы называются формулами приведения , потому что показатель степени в члене x был уменьшен на единицу в каждом случае. Второй интеграл проще исходного.
48.∫xnexdx = xnex − n∫xn − 1exdx∫xnexdx = xnex − n∫xn − 1exdx
49.∫xncosxdx = xnsinx − n∫xn − 1sinxdx∫xncosxdx = xnsinx − n∫xn − 1sinxdx
50.∫xnsinxdx = ______ ∫xnsinxdx = ______
51.Интегрируйте ∫2x2x − 3dx∫2x2x − 3dx двумя способами:
- Используя части, пусть dv = 2x − 3dxdv = 2x − 3dx
- Замена, принимающая u = 2x − 3u = 2x − 3
Укажите, будете ли вы использовать интегрирование по частям для оценки интеграла.Если да, укажите u и dv . Если нет, опишите технику, использованную для выполнения интеграции, не выполняя на самом деле проблемы.
55.∫xex2−3dx∫xex2−3dx
57.∫x2sin (3×3 + 2) dx∫x2sin (3×3 + 2) dx
Нарисуйте область, ограниченную сверху кривой, осью x и x = 1, x = 1, и найдите площадь области. Предоставьте точную форму или круглые ответы на указанное количество мест.
58.y = 2xe − xy = 2xe − x (Примерный ответ с точностью до четырех знаков после запятой.)
59.y = e − xsin (πx) y = e − xsin (πx) (Примерный ответ с точностью до пяти знаков после запятой.)
Найдите объем, образованный вращением области, ограниченной заданными кривыми, вокруг заданной линии. Выражайте ответы в точной форме или приблизительно с указанным количеством десятичных знаков.
60.y = sinx, y = 0, x = 2π, x = 3πy = sinx, y = 0, x = 2π, x = 3π вокруг оси y (Выразите ответ в точной форме.)
61.y = e − xy = e − x y = 0, x = −1x = 0; y = 0, x = −1x = 0; about x = 1x = 1 (Выразите ответ в точной форме.)
62.Частица, движущаяся по прямой, имеет скорость v (t) = t2e − tv (t) = t2e − t после t сек. Как далеко он проходит за первые 2 секунды? (Предположим, что единицы измерения выражены в футах, и выразите ответ в точной форме.)
63.Найдите площадь под графиком y = sec3xy = sec3x от x = 0tox = 1.x = 0tox = 1. (Ответ округлите до двух значащих цифр.)
64.Найдите область между y = (x − 2) exy = (x − 2) ex и осью x- от x = 2x = 2 до x = 5.x = 5. (Выразите ответ в точной форме.)
65.Найдите площадь области, ограниченной кривой y = xcosxy = xcosx и осью x для
11π2≤x≤13π2,11π2≤x≤13π2. (Выразите ответ в точной форме.)
66.Найдите объем твердого тела, образованного вращением области, ограниченной кривой y = lnx, y = lnx, осью x и вертикальной линией x = e2x = e2 вокруг оси x . (Выразите ответ в точной форме.)
67.Найдите объем твердого тела, полученный путем вращения области, ограниченной кривой y = 4cosxy = 4cosx и осью x , π2≤x≤3π2, π2≤x≤3π2, относительно оси x .(Выразите ответ в точной форме.)
68.Найдите объем твердого тела, образованный вращением области в первом квадранте, ограниченной y = exy = ex и осью x , от x = 0x = 0 до x = ln (7), x = ln (7) ), около оси y- . (Выразите ответ в точной форме.)
Свойства определенных интегралов
Интегрирует: \ (f \), \ (g \), \ (u \), \ (v \)
Первообразные: \ (F \), \ (G \)
Независимые переменные: \ (x \), \ (t \)
Пределы интегрирования: \ (a \), \ (b \), \ (c \), \ (d \)
Подынтервалы интегрирования: \ (\ Delta {x_i} \)
Произвольная точка подынтервала: \ ({\ xi_i} \)
Натуральные числа: \ (n \), \ (i \)
Площадь криволинейной трапеции: \ (S \)
- Пусть вещественная функция \ (f \ left (x \ right) \) определена и ограничена на интервале \ (\ left [{a, b} \ right] \).{\, \ prime} \ left (x \ right) = g \ left (x \ right). \)
Интеграция по частям | Открытые учебники для Гонконга
На рисунке 5.4 показан метод, называемый интеграция по частям. Если интеграл проще, чем интеграл, то мы можем вычислить более простой, а затем Простая геометрия определяет ту, которую мы хотели. Идентифицируя большой прямоугольник, окружающий обе заштрихованные области, и маленький белый прямоугольник в левом нижнем углу, мы имеем
В случае неопределенного интеграла у нас есть аналогичное соотношение, выведенное из правила произведения:
Интегрируя обе части, получаем следующее соотношение.
Интеграция по частям
Рисунок 5.4 Интеграция по частям
Поскольку определенный интеграл всегда можно получить, вычислив неопределенный интеграл на его верхнем и нижнем пределе, обычно используется эта форма. Интегралы обычно не упаковываются в виде это делает очевидным, что вы должны использовать интеграцию по частям.Уравнение для интегрирования по частям говорит нам о том, что если мы можем разделить подынтегральную функцию на два фактора, один из которых ( ) мы знаем, как интегрировать, у нас есть возможность изменить интеграл в новую форму, в которой этот фактор становится его интегралом, а другой фактор становится его производной. Если мы выберем правильный способ разбиения подынтегральной функции на части, результат может быть упрощением.
Пример
Оценивать
Есть две очевидные возможности для разделения подынтегральной функции на множители:
или же
Первый — тот, который позволяет нам прогрессировать.Если, то , а если, то интеграция дает.
Из двух возможностей, которые мы рассматривали, и причина, по которой эта помогла, заключалась в том, что дифференцирование давало, что было проще, и интегрирование давало, что было не сложнее, чем раньше. Вторая возможность сделала бы ситуацию скорее хуже, чем лучше, потому что интеграция дала бы, что было бы сложнее, чем меньше.
Пример
Оценить
Это немного сложно, потому что оно явно не написано как продукт, и тем не менее мы можем атаковать его, используя интеграцию по частям.Пусть и
Пример
Оценить
Интеграция по частям позволяет нам разделить подынтегральную функцию на два фактора, интегрировать один, дифференцировать другой, а затем выполнить это интеграл. Интеграция или дифференциация ничего не делают. Интегрирование увеличивает показатель степени, что усложняет задачу, в то время как дифференцирование сбивает показатель степени вниз на шаг, что упрощает вид. Пусть и, так что и.Тогда у нас есть
Хотя мы не сразу узнав, как вычислить этот новый интеграл, мы можем подвергнуть его тому же типу интегрирования по частям, теперь с помощью и. После второго интегрирования по частям имеем:
Интеграция по частям
Интеграция по частямОдна из очень частых ошибок, которые обычно делают студенты:
Чтобы убедиться, что это неправильная формула, возьмите f ( x ) = x и г ( x ) = 1.Поэтому может возникнуть вопрос, что делать в этом случае. А частичный ответ дает то, что называется интеграцией Запчасти . Чтобы понять эту технику, вспомните формулу
что подразумевает
Следовательно, если один из двух интегралов
и его легко оценить, мы можем использовать его, чтобы получить
другой. Это основная идея интеграции по частям.
Приведем практические шаги, как выполнять эту технику: где вы определяете две функции f ( x ) и g ( x ).Обратите внимание, что
если вам дана только одна функция, установите вторую как
постоянная функция g ( x ) = 1. Затем вам нужно сделать одну производную ( f ( x )) и одну интеграцию
(из г ( x )), чтобы получить Обратите внимание, что на этом этапе у вас есть выбор, различать ли f ( x ) или g ( x ).Позже мы обсудим это более подробно.
Первая проблема, с которой можно столкнуться при работе с этой техникой
— выбор, с которым мы столкнулись на шаге 2.
Нет общего правила, которому нужно следовать. Это действительно вопрос опыта. Но
советуем не тратить время на размышления о лучшем выборе, просто
идите по любому выбору и сделайте расчеты.Чтобы ценить
был ли ваш выбор лучшим, переходите к шагу 3: если
новый интеграл (вы будете обрабатывать) легче исходного,
тогда ваш выбор был удачным, в противном случае вернитесь к шагу 2 и
сделать переключатель. После многих интегралов вы начнете
есть чувство правильного выбора.
В приведенном выше обсуждении мы только рассматриваются неопределенные интегралы. Для определенного интеграла , у нас есть два пути:
- 1
- Вычислить неопределенный интеграл
который дает
- 2
- Используйте шаги выше, описывающие интеграцию по частям
непосредственно на заданном определенном интеграле.Вот как это происходит:
- (i)
- Запишите данный определенный интеграл
где вы определяете две функции f ( x ) и g ( x ).
- (ii)
- Представьте промежуточные функции u ( x ) и v ( x ) как:
Затем вам нужно сделать одну производную ( f ( x )) и одну интеграцию (из г ( x )), чтобы получить
- (iii)
- Используйте формулу
- (iv)
- Позаботьтесь о новом интеграле.
Следующие примеры иллюстрируют наиболее частые случаи в
который потребуется для использования интеграции по частям:
[Исчисление] [Геометрия] [Алгебра] [Тригонометрия] [Дифференциальные уравнения] [Комплексные переменные] [Матричная алгебра] Домашняя страница S.O.S MATHematics
Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.
Автор: Мохамед Амин ХамсиАвторские права 1999-2021 MathMedics, LLC.Все права защищены.
Свяжитесь с нами
Math Medics, LLC. — П.О. Box 12395 — El Paso TX 79913 — США
пользователей онлайн за последний час
Интеграция по частям дважды
Когда мы впервые узнаем, как интегрировать, в примерах, которые мы видим, используются простые многочлены или отдельные функции, подобные этим:
Интегралы продуктов
Что, если нам нужно найти интеграл произведения двух функций, как в следующем примере?
Пример 1
Вот где нам понадобится важный и полезный метод в исчислении, известный как интегрирование по частям .(Вы можете увидеть полное объяснение, начиная с основных принципов и с дополнительными примерами здесь: Интеграция по частям).
Чтобы найти этот интеграл, мы выбираем « u » так, чтобы его производная была проще, чем u . В этом случае мы выберем u = x и поступим следующим образом:
| u = x | dv = sin x dx |
| du = dx | v = −cos x |
Применяем формулу интегрирования по частям и находим интеграл:
Приведение в порядок дает:
Теперь последний интеграл несложен, и мы можем написать окончательный ответ:
Примечание 1: Константа интегрирования ( C ) появляется после того, как мы сделаем окончательное интегрирование.
Примечание 2: Выбор u и dv может вызвать некоторый стресс, но если вы будете следовать правилу LIATE, это будет проще. Для u выберите то, что стоит наверху в следующем списке, и выберите dv как самое низкое в этом списке.
L — функции логарифмирования
I — Обратные тригонометрические функции
A — Алгебраические функции (простые полиномиальные члены)
T — тригонометрические функции
E — Экспоненциальные функции
Интеграция по частям — дважды
Теперь давайте посмотрим на двуствольный корпус.То есть мы не получаем ответа за один раунд интегрирования по частям, скорее нам нужно выполнить интеграцию по частям два раза.
Пример 2:
В этом примере мы выбираем u = x 2 , так как это сведется к более простому выражению для дифференцирования (и оно выше в списке LIATE), где e x не будет.
| u = x 2 | dv = e x dx |
| du = 2 x dx | v = e x |
Теперь для интеграции по частям:
Мы изменим это так, чтобы получить следующее, которое я называю уравнением [1]:
На этот раз мы не можем сразу сделать окончательный интеграл, поэтому нам нужно снова выполнить интегрирование по частям.Выбирая « u » так, чтобы его производная была проще, чем u снова, мы имеем:
| u = x | dv = e x dx |
| du = dx | v = e x |
Обратите внимание, , что u и v здесь имеют разные значения от u и v в начале примера 2.Это может быть ловушкой, если вы не будете писать внимательно!
Теперь продолжаем интеграцию по частям на:
Последний интеграл прост, и мы получаем следующее, которое я называю уравнением [2]:
Но мы еще не закончили вопрос — мы должны помнить, что находим этот интеграл:
Это был наш ответ на первую интеграцию по частям:
Подставив ответ [2] в уравнение, мы получим:
Убирая это, получаем окончательный ответ:
Обратите внимание на место, где в нашем ответе появляется константа «+ C » — это после того, как было выполнено интегрирование.(Некоторые студенты зацикливаются на этом шаге или добавляют «+ C » перед тем, как это будет уместно, а некоторые вообще забывают добавить его!) Я использовал индекс 1 для первой константы, поскольку это не то же самое значение как окончательное C .
Интегрирование по частям дважды — с решением
Мы также сталкиваемся с интеграцией по частям, где на самом деле нам нужно найти интеграл, который мы находим. Вот пример.
Пример 3:
В этом примере не так ясно, что мы должны выбрать для « u », поскольку дифференцирование e x не дает нам более простого выражения, как и дифференцирование sin x .Мы выбираем «самый простой» вариант следующим образом (хотя e x находится ниже тригонометрических функций в таблице LIATE):
| u = e x | dv = sin x dx |
| du = e x dx | v = −cos x |
Примените формулу интегрирования по частям:
Мы получаем следующее, которое я назову уравнением [3]:
Теперь последний интеграл:
Еще раз, нам нужно решить, какую функцию использовать для и , и остановиться на той, которая дает простейшую производную:
| u = e x | dv = cos x dx |
| du = e x dx | v = sin x |
Повторное применение интеграции по частям:
Получаем уравнение [4]:
Погодите — у нас есть окончательный интеграл, такой же, как и в начале! Если бы мы продолжали идти, мы бы ходили кругами и никогда не финишировали.
Итак, нам нужно проделать следующий «фокус». Мы подставляем наш ответ для второго интегрирования по частям (уравнение [4]) в наш ответ первого интегрирования по частям (уравнение [3].
Снятие скоб:
Теперь это уравнение имеет следующий вид:
p = — q + r — p
Чтобы решить это для p , мы просто добавляем p к обеим сторонам:
2 p = −q + r
Затем разделите обе стороны на 2:
p = (- q + r ) / 2
Итак, сделаем то же самое с нашим интегральным уравнением, числом [5].
Добавляю в обе стороны:
Если разделить обе стороны на 2, получим:
Итак, мы решили уравнение [5] для, что дало нам желаемый результат.
(Обратите внимание, что я использовал «+ K » для первой появившейся константы. Мой последний « C » имеет значение K /2, но обычно нам нужно заботиться только о конечной константе.)
См. 31 комментарий ниже.
Интегралы— Calcworkshop
Что такое интегралы? Как их найти? Изучите все приемы и правила интеграции (т.е., антипроизводные).
1 час 18 мин 6 Примеры
- Что такое антидифференциация и интеграция?
- Для чего используется интеграция?
- Обзор интеграции с использованием сумм Римана и трапецеидальных приближений
- Обозначения и шаги для нахождения сумм Римана
- 6 примеров левой и правой суммы Римана, средней точки и трапецеидальных приближений
1 час 14 мин 9 Примеры
- Сигма-нотация и примеры №1-3: Найдите сумму
- Предел конечной суммы и примеры №4-5: Запишите определенный интеграл как предел
- Обозначение суммирования и пример №6: Оценка с использованием предела конечных сумм
- Пример № 7: Оценка с использованием предела конечных сумм
- Пример № 8: Оценка с использованием предела конечных сумм
- Пример № 9: Оценка с использованием предела конечных сумм
48 мин 14 Примеры
- Введение в основные правила интеграции
- Примеры неопределенных интегралов (9 примеров)
- Примеры определенных интегралов (5 примеров)
49 мин 14 Примеры
- Правила интегрирования для экспоненциальных, логарифмических и тригонометрических функций (9 примеров)
- Правила интегрирования для обратных триггерных функций (дуговых функций) и тождеств полууглов (5 примеров)
40 мин 7 Примеры
- Свойства интеграции (4 примера)
- Основная теорема исчисления № 1 и Основная теорема исчисления № 2 (3 примера)
54 мин 11 Примеры
- Обзор и обозначения для U-замещения
- 11 примеров использования U-подстановки
18 мин 3 Примеры
- Обзор среднего значения (теорема о среднем значении для интегралов)
- Три примера среднего значения
66 мин 6 Примеры
- Обучение написанию определенных интегралов с учетом начальных условий (5 примеров)
- Использование определенных интегралов для нахождения функций скорости и положения
- Обсуждая расстояние vs.Общее расстояние
- Пример использования производных и интегральных методов
38 мин 7 Примеры
- Обзор правила Симпсона
- Пример №1 с использованием правила Симпсона с заданным интегралом
- Пример № 2 с использованием правила Симпсона с таблицей значений
- Пример № 3a Аппроксимация площади под кривой с помощью левой суммы Римана
- Пример # 3b Аппроксимация площади под кривой с использованием правой суммы Римана
- Пример № 3c Аппроксимация площади под кривой с использованием правила средней точки
- Пример # 3d Аппроксимация площади под кривой с использованием правила трапеции
- Пример № 3e Аппроксимация площади под кривой с использованием правил Симпсона
1 час 31 мин 11 Примеры
- Контрольный список методов интеграции (6 примеров)
- Обзор декомпозиции частичных дробей и почему мы используем этот метод интеграции
- Пример использования частичных дробей с учетом линейных коэффициентов
- Пример использования частичных дробей с учетом линейных коэффициентов и определенного интеграла
- Пример использования частичных дробей с учетом повторяющихся множителей
- Пример использования частичных дробей с учетом нелинейных коэффициентов
- Пример использования дробных дробей, где сначала нужно использовать длинное деление
45 мин 6 Примеры
- Обзор интеграции по частям и правилам / стратегиям
- Пример интегрирования по частям для неопределенного интеграла
- Пример интеграции по частям, также использующим U-замену
- Пример интегрирования по частям для определенного интеграла
- Пример использования интеграции по частям дважды
- Пример двукратного использования интегрирования по частям и решения интегрального уравнения
- Пример использования табличного метода для интеграции по частям
1 час 1 мин 7 Примеры
- Обзор интеграции триггеров из предыдущих уроков
- Пример интеграции sec (x)
- Обзор расширенных методов тригонометрической интеграции
- Пример №1 Интегрирование при нечетном синусе
- Пример № 2 Интегрирование при нечетном косинусе
- Пример # 3 Интегрирование при нечетной тангенсе
- Пример # 4 Интегрирование при четном секансе
- Пример # 5 Интегрирование tan (x) в нечетную степень
- Пример # 6 Интегрирование csc (x) в нечетную степень
54 мин 4 Примеры
- Обзор важных тригонометрических идентичностей
- Обзор трех типов методов тригонометрической замены
- Пример 1 неопределенный интеграл для подстановки триггера
- Пример 2: Определенный интеграл для подстановки триггеров
- Пример 3 неопределенный интеграл для подстановки триггера
- Пример 4 неопределенный интеграл для тригонометрической замены, также использующий u-замену
26 мин 5 Примеры
- Обзор неправильных интегралов
- Примеры неправильных интегралов типа 1 (3 примера)
- Примеры неправильных интегралов типа 2 (2 примера)
4 часа 10 минут 37 Примеры
- 37 сложных практических задач
- Отлично подходит для проверки ваших знаний
- Идеально подходит для подготовки к экзамену в классе
Интегральное против первичного | математика — это развлечение
У большинства людей неправильное представление о взаимосвязи между «интеграцией» и «принятием первообразных»; они склонны произносить эти слова как синонимы, но есть небольшая разница.