задачи с решениями :: SYL.ru
В математике существует множество принципов. Некоторые из них достаточно просты и понятны даже новичку, а некоторые требуют определенных объяснений и доказательств. Однако все они весьма эффективны, и их легко можно применять на практике. Одним из них является принцип Дирихле (известный также как принцип голубей/кроликов). Это достаточно простое утверждение, способное помочь в решении многих математических задач.

История
Данный принцип был сформулирован почетным немецким математиком Иоганном Дирихле еще в 1834 году. Сегодня его применяют в комбинаторике, а также в математической физике. В переводе с оригинального немецкого он звучит как «принцип ящиков». Свои исследования ученый проводил с кроликами и контейнерами. Он продемонстрировал, что если поместить, допустим, 5 кроликов в 7 контейнеров, то, по крайней мере, в одном контейнере будет находиться 5/7 от одного животного. Однако кролика нельзя разделить на части, следовательно, хотя бы одна клетка будет пустовать (5/7 равно 0 целых). Точно так же и в обратную сторону, если кроликов 7, а ящиков 5, то хотя бы в одном из них — 2 кролика (7/5 равно 2 целых). Отталкиваясь от этого утверждения, математику удалось сформулировать принцип, который обеспечивает успешное решение задач по математике уже многие годы.
Современная формулировка и доказательство
На сегодняшний день существует несколько разных формулировок данного принципа. Самая понятная и простая подразумевает, что нельзя посадить 8 кроликов в 3 клетки так, чтобы в каждой было не больше 2. Более научная и сложная формулировка, объясняющая принцип Дирихле, гласит: если в k ячеек находится k+1 зайцев, то, по крайней мере, в 1 ячейке будет располагаться больше одного зайца. А если в k ячеек находится k-1 зайцев, то по крайней мере в 1 ячейке будет располагаться меньше одного зайца. Доказательство этого утверждения совсем простое, так сказать, от противного. Если предположить, что в каждой ячейке располагается зайцев меньше, чем k-1/k, тогда в k ячеек зайцев меньше чем k*k-1/k = k-1, а это противоречит первоначальным условиям.
В действительности такой простой и понятный принцип значительно облегчает решение задач по математике и доказательства многих трудоемких теорем. Просто необходимо учитывать, что зайцев и ячейки можно легко заменить на математические предметы и объекты (цифры, точки, отрезки, фигуры и т. д.).
Еще одна формулировка
Иногда задачи на принцип Дирихле — не такие простые и очевидные, как с животными в ящиках. Необходимо переносить этот принцип на математические множества, чтобы отыскать какие-либо решения. В таком случае можно опираться на другую, более сложную формулировку.
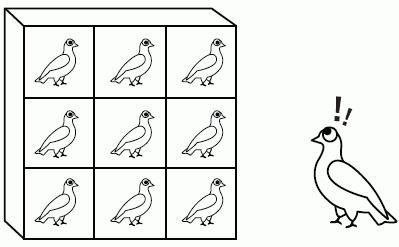
Если отобразить множество S, содержащее d+1 элементов, в множество R с совокупностью d элементов, то два элемента из множества S будут иметь одинаковый образ.
Хотя современные ФГОС по математике предъявляют к ученикам творческие требования и предлагают нестандартные варианты, решение через утверждение Дирихле не всегда такое простое и понятное. Иногда очень трудно определить, какую величину считать животным, а какую – клеткой, и каким образом факт наличия двух животных в одной клетке поможет решению задачи. Да и если удастся в этом разобраться, все равно нельзя определить, в какой именно клетке будет находиться объект. То есть можно просто доказать существование такой ячейки, но нельзя конкретизировать ее.
Пример № 1. Геометрия
Современные примеры решения задач демонстрируют, что животными и клетками могут выступать совершенное различные математические предметы.
Задача
Прямая k проходит через плоскость треугольника ABC, однако не пересекает ни одну его вершину. Необходимо доказать, что она не может пересекать три его стороны.
Решение
Представим, как прямая k разбивает треугольник на две плоскости, назовем их s1 и s2. Будем считать, что s1 и s2 открытые, то есть не содержащие прямую k. Ну а сейчас — самое время применить принцип Дирихле. Задачи с решениями могут продемонстрировать, что под кроликами и ячейками в современных условиях подразумеваются разнообразные объекты. Так, вместо зайцев мы подставим вершины треугольника, а вместо ячеек – полуплоскости. Поскольку проведенная прямая k не пересекает ни одну из вершин, то каждая из них находится в той или иной плоскости. Но поскольку вершины в треугольнике три, а плоскости у нас всего две (s1 и s2), то одна из них будет содержать две вершины. Предположим, что это вершины A и B, и находятся они в полуплоскости s2 (то есть лежат по одну сторону от k). В таком случае отрезок АВ не пересекает прямую k. То есть в треугольнике есть сторона, которую прямая k не пересекает.
Альтернативное решение
В данной задаче мы предположили, что в одной плоскости находятся точки А и В, однако принцип Дирихле не указывает конкретную ячейку, поэтому точно так же мы могли указать, что в одной плоскости разместились вершины С и В, или А и С. Для данной задачи совсем не важно, какую сторону треугольника не пересекает прямая k. Поэтому указанный принцип идеально подходит для ее решения.
Пример № 2. Геометрия
Задача
В середине равностороннего треугольника АВС (у которого АВ = ВС = АС = 1) разместилось 5 точек. Необходимо доказать, что две из них располагаются на расстоянии меньше 0,5.
Решение
Если провести в правильном треугольнике АВС средние линии, они разделят его на 4 маленьких правильных треугольника со сторонами ½ = 0,5. Предположим, что эти треугольники – ячейки, а точки внутри них – кролики. Получается, у нас есть 5 кроликов и 4 ячейки, следовательно, в одной из них будет находиться как минимум два кролика. Учитывая то, что точки не являются вершинами (так как они располагаются внутри треугольника АВС, а не на одной из его сторон), они будут размещаться внутри маленьких фигур. Следовательно, расстояние между ними будет меньше, чем 0,5 (поскольку величина отрезка внутри треугольника никогда не превышает величины его самой большой стороны).
Пример № 3. Комбинаторика
В других областях также можно удачно применять принцип Дирихле: комбинаторика и математическая физика уже давно опираются на него при решении задач.
Задача
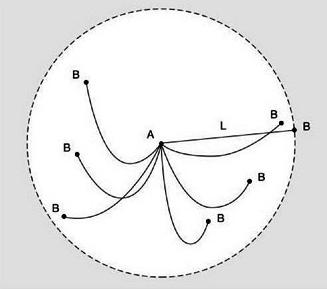
Допустим, вокруг округлённого стола стоят на равном расстоянии друг от друга m флажков разных стран, а за столом сидят m представителей от каждой страны, причем каждый из них расположился рядом с чужим флажком. Нужно доказать, что при определенном вращении стола хотя бы двое из представителей окажутся возле своих флажков.
Решение
Получается, что существует m-1 способов развернуть стол так, чтобы изменилось взаиморасположение представителей и флажков (если исключить начальное размещение стола), но при этом остается m представителей.
Применим к решению утверждение Дирихле и обозначим, что представители выступают кроликами, а определенные положения стола при вращении – ячейками. При этом нужно провести аналогию между расположением представителя рядом с соответствующем флажком и заполненными ячейками. То есть положительный результат (1 представитель размешается возле своего флажка) равносилен результату «кролик оказывается в клетке». Мы понимаем, что у нас на одну ячейку меньше, чем нужно (m-1), а значит, в одной из них окажется как минимум 2 кролика. При этом не исключены ситуации, что какая-то клетка будет пустой (ни один представитель не совпал с флажком), а в какой-то клетке окажется два, три или даже больше кроликов (два, три и больше представителей совпадут с флажками). Таким образом, при одном определенном вращении как минимум два представителя очутятся возле своих флажков (как минимум два кролика попадут в одну ячейку).
Приступая к решению такой задачи, важно понимать, что начальное положение – это тоже ячейка, но по условию задачи она заведомо пустует, поэтому мы уменьшаем общее количество на 1 (m-1).
Пример № 4. Теория чисел
Принцип Дирихле в теории чисел также имеет огромное значение.
Задача
Предположим, на листике тетради в клетку ученик произвольно в узлах клеточек проставил 5 точек. Необходимо доказать, что как минимум один отрезок с вершинами в этих точках пройдет через узел клеточки.
Решение
Для начала нужно изобразить на листе тетради систему координат, основа которой расположится в одном из узлов. Оси системы координат будут совпадать с линиями сетки, а за единичный отрезок принята сторона клеточки. Получается, что все 5 отмеченных точек будут находиться в системе, а их координаты будут только целым числом (четным или нечетным). Таким образом, мы получим 4 варианта координат: (четный; четный), (нечетный; четный), (четный; нечетный) и (нечетный; нечетный). А значит, 2 из 5 точек будут соответствовать одному варианту. Если посмотреть на ситуацию с позиции Дирихле, то необходимо обозначить точки как зайцев, а варианты координат — как ячейки. Мы получаем 5 зайцев и 4 клетки, соответственно, в одной из них будет минимум 2 животных. Допустим, это точки Р и А, с координатами (x4, y3) и (x5, y6). Середина отрезка, соединяющего эти две вершины, будет иметь координаты ((x4+x5) / 2), ((y3+y6) / 2)), которые будут целыми числами в условиях соответствующей четности x4 и x5, y3 и y6. Получается, что середина отрезка расположилась в узле клетки.
Пример № 5
Достаточно много задач разной сложности можно решить через принцип Дирихле. Задачи с решениями разнообразных математических и логических вопросов достаточно часто опираются на этот принцип.
Задача
На прямой дороге вырыты маленькие поперечные канавки. Расстояние между всеми канавками одинаковое и равно оно Ö2 м. Необходимо доказать, что, независимо от ширины канавок, человек, шагающий по дороге с интервалом 1 м, однажды попадет ногой в одну из них.
Решение
Для того чтобы облегчить решение, необходимо вообразить, что дорогу можно «намотать» на окружность длиной в Ö2 метров. Получается, что все канавки сольются в 2 противоположных, а шаги человека будут отображаться в форме дуги, равной 1 м. Нам необходимо последовательно отметить все шаги, пока один из них не окажется в дуге, обозначающей канавку, независимо от того, какая будет длина k дуги (ширина канавки). Конечно, очевидно, что если бы человек шагал на расстояние, равное меньше, чем k, то он рано или поздно наступил бы в канаву. Ведь у человека никак не получится переступить расстояние k, если длина его шага меньше, чем k. А значит, нам необходимо найти два следа, расстояние между которыми не будет превышать величину k. Для этого уместно будет воспользоваться принципом Дирихле. Мы мысленно разделим всю окружность на дуги размером меньше k и будем считать их ячейками. Допустим, их окажется n штук. Предположим, что число шагов будет больше чем число дуг (n + m), хотя никакие два шага не будут совпадать из-за иррациональности числа Ö2, тогда по принципу Дирихле, по крайней мере, в одной из ячеек разместится больше одного шага. А поскольку длина дуги составляет меньше k, то и расстояние между шагами будет меньше. Таким образом, мы обнаружили необходимые для доказательства шаги.
Обобщение принципа
Материалы по математике, кроме стандартных (простых и не очень) формулировок, содержат также одну обобщенную, которая используется для выявления более двух объектов, похожих друг на друга. Она утверждает, что если dm + 1 кроликов поместить в d ячеек, то как минимум m + 1 кролик окажется в одной ячейке.
Пример № 6. Обобщение
Задача
Прямоугольник с площадью 5 х 6 клеток (30 клеток), закрашенных только 19. Можно ли обнаружить квадрат площадью 2 х 2 клетки, в котором минимум три будут закрашены?
Решение
Нашу фигуру необходимо разделить на 6 блоков по 5 клеток. Исходя из утверждения Дирихле, в одной из них будет закрашено не менее 4 клеточек (19/6 = 4). Тогда в одном из квадратов площадью 4 клеточки, расположенном в одном из блоков, будет закрашено минимум 3 клетки.
Пример № 7
Класс, в котором 25 человек. Из любых случайно выбранных 3 учеников двое будут друзьями. Необходимо доказать, что в классе находится школьник, у которого больше 11 приятелей.
Два решения вопроса

Для начала возьмем двух школьников, которые не дружат с друг другом (поскольку если бы все они дружили между собой, то в каждой тройке было бы три друга и каждый ученик дружил бы с 24 другими). Оставшиеся 23 одноклассника будут дружить с одним из нашей двойки, поскольку в противном случае нашлась бы тройка, где нет друзей (а это противоречит изначальному условию задачи). Получается, что один из двух школьников будет дружить как минимум с 12 учениками. В данном случае ученики – это кролики, а условия «друзья они или нет» – это ячейки. Мы имеем 23 животных и только 2 клетки. Соответственно, в одной из них как минимум 23/2 = 11,5, т. е. 12 кроликов. То есть один из 2 выбранных нами учеников будет дружить как минимум с 12 своими одноклассниками (или даже больше). Конечно же, существуют и другие методы решения задачи, однако данный — один из самых понятных и удобных.
www.syl.ru
Принцип ящиков Дирихле — это… Что такое Принцип ящиков Дирихле?
- Принцип ящиков Дирихле
-

9 клеток вмещают 7 голубей, значит, хотя бы 9-7=2 клетки свободны
При́нцип Дирихле́ — утверждение, сформулированное немецким математиком Дирихле. Принцип устанавливает связь между объектами («кроликами») и контейнерами («клетками») при выполнении определённых условий.
Формулировки
Предположим, m кроликов рассажены в n клетках. Наиболее распространена следующая формулировка этого принципа:
Предположим, некоторое число кроликов рассажены в клетках. Если число кроликов больше, чем число клеток, то хотя бы в одной из клеток будет больше одного кролика.
Наиболее общая формулировка звучит так:
Предположим,
Возможны также несколько формулировок для частных случаев:
Если число клеток больше, чем число кроликов, то как минимум одна клетка пуста.
Пусть задана функция
 и мощность множества A больше мощности B, то есть | A | > n | B | , где
и мощность множества A больше мощности B, то есть | A | > n | B | , где  . Тогда некоторое своё значение функция f примет по крайней мере n + 1 раз.
. Тогда некоторое своё значение функция f примет по крайней мере n + 1 раз.Примечания
Принцип Дирихле известен также как принцип голубей и ящиков, когда объектами являются голуби, а контейнерами — ящики. Это название распространено в английском и некоторых других языках.
Wikimedia Foundation. 2010.
- Принцип эквивалентности Эйнштейна
- Принципал
Смотреть что такое «Принцип ящиков Дирихле» в других словарях:
Принцип Дирихле (комбинаторика) — У этого термина существуют и другие значения, см. Принцип Дирихле. 9 клеток содержат 7 голубей, по принципу Дирихле хотя бы одна клетка содержит не больше 7/9 голубя (т.е ноль) … Википедия
ДИРИХЛЕ ТЕОРЕМА — 1) Д. т. в теории диофантовых приближений: для любого действительного числа а и натурального Qсуществуют целые о и q, удовлетворяющие условию Дирихле принцип ящиков позволяет доказать и более общую теорему: для любых действительных чисел a1 … Математическая энциклопедия
Дирихле принцип — (по имени П. Г. Л. Дирихле) 1) принцип ящиков предложение, утверждающее, что в случае m > n при отнесении каждого из m предметов к одному из n классов хотя бы в один класс попадёт не менее двух предметов. Это чрезвычайно простое… … Большая советская энциклопедия
ДИРИХЛЕ ПРИНЦИП — ящиков утверждение, согласно к рому в любой совокупности из пмножеств, содержащих в общей сложности более пэлементов, есть хотя бы одно множество, содержащее не менее двух элементов. Наиболее популярная форма Д. п.: если в п ящиках лежит n+1… … Математическая энциклопедия
Дирихле принцип — 9 клеток вмещают 7 голубей, значит, хотя бы 9 7=2 клетки свободны Принцип Дирихле утверждение, сформулированное немецким математиком Дирихле. Принцип устанавливает связь между объектами («кроликами») и контейнерами («клетками») при выполнении… … Википедия
Принцип дирихле — 9 клеток вмещают 7 голубей, значит, хотя бы 9 7=2 клетки свободны Принцип Дирихле утверждение, сформулированное немецким математиком Дирихле. Принцип устанавливает связь между объектами («кроликами») и контейнерами («клетками») при выполнении… … Википедия
Китайская теорема об остатках — Несколько связанных утверждений известны под именем китайской теоремы об остатках. Эта теорема в её арифметической формулировке была описана в трактате китайского математика Сунь Цзы «Сунь Цзы Суань Цзин» (кит. упр. 孙子算经, пиньинь: sunzi suanjing) … Википедия
Шварц, Карл Герман Амандус — В Википедии есть статьи о других людях с такой фамилией, см. Шварц. Карл Герман Амандус Шварц нем. Karl Hermann Amandus Schwarz … Википедия
Карл Герман Амандус Шварц — Karl Hermann Amandus Schwarz математик Дата рождения: 25 января 1843 Место рождения: Силезия Дата смерти: 30 ноября 1921 Место смерти … Википедия
Шварц, Герман Амандус — Карл Герман Амандус Шварц Karl Hermann Amandus Schwarz математик Дата рождения: 25 января 1843 Место рождения: Силезия Дата смерти: 30 ноября 1921 Место смерти … Википедия
dic.academic.ru
ДИРИХЛЕ ПРИНЦИП — это… Что такое ДИРИХЛЕ ПРИНЦИП?
— метод решения краевых задач для эллиптич. уравнений с частными производными сведением их к вариационным задачам отыскания минимумов нек-рых функционалов в определенных классах функций. В узком смысле Д. п. означает решение 1-й краевой задачи
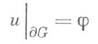 (1)
(1)
в области Gс границей дG для уравнения Лапласа
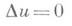 (2)
(2)
сведением ее к отысканию минимума Дирихле интеграла
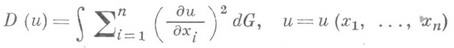
в классе функций, удовлетворяющих условию
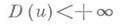 (3)
(3)
и условию (1) (см. Дирихле вариационная задача). Д. п. возник и получил широкое распространение в нач. 19 в. Он применялся как с чисто теоретическими целями для доказательства существования и единственности решений краевых задач, так и при решении практически важных задач. Наиболее четкая и полная формулировка Д. п. для класса функций непрерывных вместе со своими частными производными, по-видимому, была дана в лекциях П. Дирихле (P. Dirichlet), опубликованных в 1876 одним из его учеников. Доказательства, данные Дирихле, были неполны, в частности, у него даже не ставился вопрос о необходимости доказательства существования минимума рассматриваемого функционала в классе допустимых функций, т. е. функций, удовлетворяющих условиям (1) и (3). В конце 60-х гг. 19 в. Д. п. был подвергнут критике К. Вейерштрассом (К. Weierstrass), показавшим на примере, что дифференциальная краевая задача (1), (2) при некрой граничной непрерывной функции j может иметь решение, а соответствующая вариационная задача — нет, за счет того, что в этом случае интеграл Дирихле для решения задачи (1), (2) обращается в бесконечность. Обосновать Д. п. в предположении, что существует хоть одна допустимая функция, удалось лишь Д. Гильберту (D. Hilbert) на рубеже 19 и 20 вв. Дальнейшее существенное развитие Д. п. содержится в работах С. Л. Соболева, показавшего, что всякая функция, определенная на «-мерной области и имеющая в ней обобщенные частные производные достаточно высокого порядка, принадлежащие пространству
 принимает на всяком достаточно гладком m-мерном многообразии,
принимает на всяком достаточно гладком m-мерном многообразии,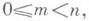 естественные устойчивые граничные значения. Это позволило С. Л. Соболеву сформулировать и обосновать Д. п. для полигармонпч. уравнения, причем и в случае, когда граница области состояла из многообразий различной размерности.
естественные устойчивые граничные значения. Это позволило С. Л. Соболеву сформулировать и обосновать Д. п. для полигармонпч. уравнения, причем и в случае, когда граница области состояла из многообразий различной размерности. Возникновение Д. п. явилось существенным этапом в развитии теории краевых задач уравнений с частными производными, так как оно означало создание принципиально новой точки зрения на эту теорию. Д. п. и его всевозможные модификации, основанные, в конце концов, на сведении рассматриваемой задачи к той или иной вариационной задаче, получили широкое распространение как в различных разделах самой математики, так и в ее приложениях. Это связано с тем, что этот метод позволяет как доказывать общие теоремы о решениях уравнений, так и получать их конкретные решения в виде пределов так наз. минимизирующих последовательностей (т. е. последовательностей допустимых функций, значения минимизирующего функционала на к-рых стремятся к его минимуму), при этом численные методы, основанные на построении минимизирующих последовательностей, удобны для отыскания приближенных решений на ЭВМ.
Л. Д. Кудрявцев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
dic.academic.ru
Принцип Дирихле (комбинаторика) — это… Что такое Принцип Дирихле (комбинаторика)?
 9 клеток содержат 7 голубей, по принципу Дирихле хотя бы одна клетка содержит не больше 7/9 голубя (т.е ноль)
9 клеток содержат 7 голубей, по принципу Дирихле хотя бы одна клетка содержит не больше 7/9 голубя (т.е ноль)  9 клеток содержат 10 голубей, по принципу Дирихле хотя бы в одной клетке находятся более одного голубя
9 клеток содержат 10 голубей, по принципу Дирихле хотя бы в одной клетке находятся более одного голубяВ комбинаторике при́нцип Дирихле́ (нем. Schubfachprinzip, «принцип ящиков») — утверждение, сформулированное немецким математиком Дирихле в 1834 году, устанавливающее связь между объектами («кроликами») и контейнерами («клетками») при выполнении определённых условий. В английском и некоторых других языках утверждение известно как «принцип голубей и ящиков» (англ. Pigeonhole principle), когда объектами являются голуби, а контейнерами — ящики.
Принцип Дирихле применяется, в частности, в теории диофантовых приближений при анализе систем линейных неравенств.
Формулировки
- Наиболее распространена следующая формулировка этого принципа:
Если кролики рассажены в клетки, причём число кроликов больше числа клеток, то хотя бы в одной из клеток находится более одного кролика.
- Более общая формулировка звучит так:
Если m кроликов рассажены в n клеток, то хотя бы в одной клетке находится не менее кроликов, а также хотя бы в одной клетке находится не более кроликов.
- Возможны также несколько формулировок для частных случаев:
Если число клеток больше, чем число кроликов, то как минимум одна клетка пуста.
Обобщение
Существует обобщение данного принципа на случай бесконечных множеств: не существует инъекции более мощного множества в менее мощное.
Литература
dik.academic.ru
Статья по математике «Принцип Дирихле»
Занятие математического кружка в VII классе «Принцип Дирихле».
Многие вещи нам непонятны не потому,
что наши понятия слабы; но потому, что сии
вещи не входят в круг наших понятий.
К. Прутков
Аннотация. В статье представлена разработка занятия математического кружка по теме «Принцип Дирихле» в 7 классе, рассчитанная на 2 часа. В данной статье рассматриваются различные формулировки принципа Дирихле, а также приводятся конкретные примеры применения данного принципа при решении задач разного типа.
Ключевые слова: концепция математического образования, дополнительное математическое образование (ДМО), математический кружок, принцип Дирихле, математические доказательства
Согласно Концепции математического образования значительную роль играет воспитательная составляющая деятельности школы. В круг ее основных задач входит привлечение учащихся в различные мероприятия, направленные на всестороннее развитие творческих и индивидуальных способностей каждого обучающегося, а также на максимальное удовлетворение их потребностей. В настоящее время, как известно, творческий процесс заслуживает самого пристального внимания, поскольку общество нуждается в массовом совершенствовании уже известного, в отказе от устойчивых и привычных, но пришедших в противоречие с имеющимися потребностями и возможностями форм. А это в свою очередь означает возрастание роли внеурочной деятельности. Опытная работа П. М. Горева и его собственная практика обучения школьников математике в ДМО показала, что одной из важных форм организации работы в ДМО являются занятия математического кружка [3].
Вопросы, рассматриваемые на занятиях кружка, выходят за пределы объема обязательных знаний, но вместе с тем они плотно примыкают и тесно взаимосвязаны с основными вопросами программного материала. В этой статье предлагается разработка внеклассного занятия по математике в VII классе «Принцип Дирихле».
Цель занятия: Познакомить учащихся с новым математическим методом решения задач, не рассматриваемом в курсе изучения математики, показать на конкретных примерах применение принципа Дирихле при решении задач.
Вступительная беседа. Из всех областей знаний, известных человечеству, математика является наиболее точной и правильной. И главное ее отличие от других наук – наличие неопровержимых доказательств, являющихся эталоном бесспорности. Порог убедительности математических доказательств значительно выше, чем у других наук.
Давайте, вспомним, что же такое доказательство? (Ответы учеников). Доказательство – это такое рассуждение, которое убеждает нас настолько, что мы готовы убеждать других, используя тоже рассуждение [9]. Математические доказательства бывают прямые и косвенные. Используя прямое доказательство, нам нужно доказать существование объекта с заданными свойствами. Рассмотрим пример прямого доказательства: чтобы доказать, что неравенство имеет решение, нам нужно найти множество всех значений переменной, при которых оно верно. Но также существуют и косвенные доказательства – это, когда обоснование того, что объект существует, происходит без прямого указания на сам объект. Примером косвенного доказательства является логический метод рассуждения — «от противного». Мы рассмотрим одну из форм этого метода – принцип Дирихле.
Принцип назван в честь немецкого математика Питера Густава Дирихле (1805-1895), который успешно применял его к доказательству арифметических утверждений.
В связи со сложившейся традицией принцип Дирихле объясняют на примере «зайцев и клеток». Если мы хотим применить данный принцип при решении конкретной задачи, то в этом случае необходимо разобраться, что мы будем принимать – за «клетки», а что – за «зайцев» [1]. Это обычно является самым трудным на этапе доказательства. В английском и некоторых других языках утверждение известно как “принцип голубей и ящиков” (англ. Pigeonhole principle), когда объектами являются голуби, а контейнерами — ящики.
В шутливой форме этот принцип гласит: «Нельзя посадить семерых зайцев в три клетки, чтобы в каждой клетке находилось не более двух зайцев» [8].
Наиболее распространенная формулировка принципа Дирихле состоит в следующем: «Если в n клеток посадить n+1 зайцев, то найдется хотя бы одна клетка, в которой находятся не менее чем 2 зайца».
Обобщенный принцип Дирихле: «Если в n клеток посадить kn+1 зайцев, то найдется хотя бы одна клетка, в которой находятся не менее чем k+1 заяц».
Рассмотрим примеры различных задач, решаемых с помощью этого принципа.
Задачи для обсуждения на уроке.
Применение принципа Дирихле при решении логических задач.
Но, спросите вы, разве о зайцах идет речь в задачах?
Задача 1.
В городе 15 школ. В них обучается 6015 школьников. В концертном зале городского Дворца культуры 400 мест. Докажите, что найдется школа, ученики которой не поместятся в этом зале.
Решение.
Предположим, что в каждой школе не более 400 учеников. Значит, в 15 школах будет 15*400= 6000 учеников. Но, по условию, в школах обучается 6015 человек. Значит, найдется школа, в которой больше 400 учеников. Поэтому ученики этой школы не поместятся в зале, в котором 400 мест.
Задача 2.
В хвойном лесу растет миллион елей. На каждой ели — не более 600000 иголок. Доказать, что существуют хотя бы две ели с одинаковым числом иголок.
Решение.
Перед нами миллион «зайцев» — елей и, увы, всего лишь 600001 клетка с номерами от 0 до 600000. Каждый «заяц» — ель, сажается нами в клетку с номером, равным количеству иголок на этой ели. Так как «зайцев» гораздо больше, чем клеток, то в какой-то клетке сидит по крайней мере два «зайца» — если бы в каждой сидело не более одного, то всего «зайцев» — елей было бы не более 600001. Но ведь, если два «зайца» — ели, сидят в одной клетке, то количество иголок у них одинаково [2].
Обратите внимание на то, что формулировки этих задач носят тот же налет расплывчатости вывода, что и сам принцип Дирихле. Часто именно такие вопросы решаются с помощью этого принципа.
Применение принципа Дирихле при решении задач на размещения.
Задача 3.
Можно ли вывезти из завода 50 деталей, массы которых соответственно равны 370, 372, 372, …, 468 кг на семи трехтонках?
Решение.
Если бы это удалось осуществить, то на какую-нибудь трехтонку нагрузили бы 8 камней, поскольку 7 ∙ 7 + 1 = 50, потому по принципу Дирихле даже при равномерном распределении по 7 деталей на каждую трехтонку получим в избытке 1 деталь. Но даже 8 легких деталей составляют в сумме S = 370 + 372 + 374 + … + 384 = 3016 кг> 3т. Нельзя.
Отметим, что общая масса всех деталей, как не трудно подсчитать, составляет 20950 кг, а на семь трехтонок можно нагрузить одновременно 21т. Поэтому складывается впечатление, что ответ на вопрос задачи должен быть положительным. Однако это было бы возможно, если бы мы раздробили детали.
Несмотря на совершенную очевидность этого принципа, его применение является весьма эффективным методом решения задач, дающим во многих случаях наиболее простое и изящное решение. С помощью принципа Дирихле обычно доказывается существование некоторого объекта, не указывая, вообще говоря, алгоритм его нахождения и построения. Приводимые ниже задачи показывают, что природа «зайцев» и «клеток» в различных задачах может сильно отличаться друг от друга.
Применение принципа Дирихле при решении геометрических задач.
Рассмотрим геометрические задачи, которые опираются на дискретный принцип Дирихле.
Задача 4.
Внутри равностороннего треугольника со стороной 2см бросили 5 горошин. Доказать, что найдутся две горошины, расстояние между которыми меньше 1см.
Решение.
Разделим треугольник на 4 равных треугольника как показано на рисунке (рис.1). Стороны новых треугольников будут равны 1см.
Поскольку бросают 5 горошин, то в один из полученных треугольников попадет хотя бы 2 горошины, расстояние между которыми будет меньше стороны треугольника, то есть меньше 1см.
Задача 5.
Доказать, что если прямая l, расположенная в плоскости треугольника АВС, не проходит ни через одну из его вершин, то она не может пересечь все три стороны треугольника [1].
Решение.
Полуплоскости, на которые прямая l разбивает плоскость треугольника АВС, обозначим за g1 и g2, эти полуплоскости будем считать открытыми (то есть не содержащими точек прямой l). Вершины рассматриваемого треугольника (точки А, В, С) будут «зайцами», а полуплоскости g1 и g2 будут «клетками». Каждый «заяц» попадает в какую- нибудь «клетку» (ведь прямая l не проходит ни через одну из точек А, В, С). Так как «зайцев» три, а «клеток» только две, то найдутся два зайца, попавшие в одну «клетку»; иначе говоря, найдутся такие две вершины треугольника АВС, которые лежат в одной полуплоскости (рис.2). 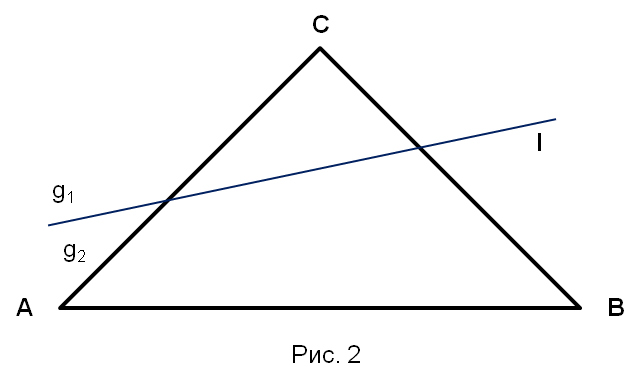
Пусть, скажем, точки А и В находятся в одной полуплоскости, то есть лежат по одну сторону от прямой l. Тогда отрезок АВ не пересекается с l. Итак, в треугольнике АВС нашлась сторона, которая не пересекается с прямой l.
Современные примеры решения задач демонстрируют, что животными и клетками могут выступать совершенное различные математические предметы.
Применение принципа Дирихле при решении задач на раскраски.
Задача 6.
Плоскость раскрашена в два цвета. Докажите, что найдутся две точки одного цвета на расстоянии 1 метр друг от друга [5].
Решение.
Рассмотрим вершины равностороннего треугольника со стороной 1 м. Если две точки разного цвета, то третья обязательно либо первого, либо второго, значит, мы нашли две точки одного цвета.
Задача 7.
Каждая грань куба раскрашена в чёрный или белый цвет. Доказать, что найдутся одинаково раскрашенные грани, имеющие общее ребро [6].
Решение.
Рассмотрим любую вершину куба. В ней пересекаются три грани. Примем за «клетки» цвета, а за зайцев грани, пересекающиеся в одной вершине (их три). Поэтому согласно принципу Дирихле найдутся два «зайца» в одной «клетке», а это и означает, что найдутся две грани имеющие общее ребро (так как они имеют общую точку) и окрашенные одинаково.
Применение принципа Дирихле в теории чисел.
Рассмотрим примеры, когда при решении задач на делимость чисел используют принцип Дирихле.
Задача 8.
Докажите, что среди чисел, состоящих из цифр 3, найдется число, делящееся на 17 [5].
Решение.
Рассмотрим 17 чисел с разным количеством цифр: 3, 33, 333, 3333, … Предположим, что ни одно из них не делится на 17. При этом могут получаться 16 различных остатков: 1, 2, 3, … 16. Значит, среди наших чисел есть два числа с одинаковым остатком при делении на 17. Разность этих чисел делится на 17, и это число вида 333 … 000… (сначала несколько троек, потом нули). Заметим, что 10 взаимно просто с 17, значит, если с конца убрать нули, то получившееся число тоже будет делиться на 17. Но оно состоит из цифр 3. Значит, мы нашли искомое число.
Достаточно много задач разной сложности можно решить через принцип Дирихле. Задачи с решениями разнообразных математических и логических вопросов достаточно часто опираются на этот принцип.
Задачи для самостоятельного решения (в классе или дома).
В мешке лежат шарики двух цветов: чёрного и белого. Какое наименьшее число шариков нужно достать из мешка не глядя, чтобы среди них оказались ровно два шарика одного цвета? [7]
В магазин привезли 25 ящиков с тремя разными сортами яблок (в каждом ящике яблоки только одного сорта). Докажите, что среди них есть по крайней мере 9 ящиков с яблоками одного и того же сорта.
На собеседование пришли 65 школьников. Им предложили 3 контрольные работы. За каждую контрольную ставилась одна из оценок: 2, 3, 4 или 5. Верно ли, что найдутся два школьника, получившие одинаковые оценки на всех контрольных? [4]
Несколько дуг окружности покрасили в синий цвет. Сумма длин окрашенных дуг меньше длины окружности. Докажите, что существует диаметр, оба конца которого не окрашены [7].
Докажите, что равносторонний треугольник нельзя покрыть двумя меньшими равносторонними треугольниками [7].
Кот Базилио пообещал Буратино открыть великую тайну, если он составит чудесный квадрат 6× 6 из чисел +1, −1, 0 так, чтобы все суммы по строкам, по столбцам и по большим диагоналям были различны. Помогите Буратино [4].
Докажите, что среди любых пятнадцати натуральных чисел есть два числа, разность которых делится на 14 [5].
Вывод:
Принцип Дирихле является весьма эффективным методом решения задач. Но для его применения на первых этапах изучения темы надо при решении каждой конкретной задачи научиться определять, какой объект считать зайцем, а какой — клеткой, при этом следить за тем, чтобы зайцев всегда было больше, чем клеток; а затем научиться пользоваться фактом наличия в одной клетке двух зайцев, и делать необходимые выводы.
Ссылки на источники.
Андреев А. А., Горелов Г. Н., Люлев А. И., Савин А. Н. Принцип Дирихле. Учебное издание.Серия А: Математика. Вып. 1. — Самара: Пифагор, 1997. — 21 с., ил.
Генкин С.А., Итенберг И.В., Фомин Д.В. Ленинградские математические кружки. – Киров: АСА, 1994.
Горев П. М. Система внеклассной работы по математике в средней школе № 21 города Кирова / П. М. Горев // Российские регионы: проблемы, суждения, поиск путей развития: тезисы IV межрегиональной научно-практической конференции. – Киров: ВСЭИ, 2001. – С. 174.
Канель-Белов А. Я., Ковальджи А. К. Как решают нестандартные задачи / Под ред. В. О.Бугаенко.|4-е изд., стереотип.|М.: МЦНМО,2008.| 96 c.
Коннова Е.Г. Математика. Поступаем в вуз по результатам олимпиад. 5 – 8 класс. Часть 1. /издание 4-е/ Под редакцией Ф.Ф.Лысенко. – Ростов-на-Дону: Легион; Легион –М, 2010. – 112 с. – (Готовимся к олимпиаде).
Летчиков А.В. Принцип Дирихле. Задачи с указаниями и решениями: Учебное пособие. Ижевск: Изд – во Удм. ун-та, 1992. 108с.
Севрюков П. Ф. Школа решения олимпиадных задач по математике. — М. : Илекса; Ставрополь: Сервисшкола, 2012. — 176 с.
Спивак А.В. Математический праздник. – М.: Бюро Квантум, 2004. – 288 с. – ( Библиотечка «Квант». Вып. 88)
Успенский В. А. Простейшие примеры математических доказательств.— М.: Изд-во МЦНМО, 2009.—56 с.
infourok.ru
Методическая разработка (5 класс) на тему: Принцип Дирихле
Принцип Дирихле
Цели занятия:
- Образовательная цель: познакомить учащихся с принципом Дирихле и типами задач, решаемых этим методом
- Развивающая цель: через решение задач с помощью метода Дирихле развивать умение анализировать, синтезировать, обобщать
- Воспитательная цель: посредством организации занятия воспитывать усидчивость, настойчивость в достижении цели, интерес к математике.
План занятия:
- Вступительная беседа
- Объяснение нового материала
- Закрепление
- Итог занятия
- Малая олимпиада
- Домашнее задание
Вступительная беседа.
Что отличает урок математики от других уроков? Книгу по математике от книг по какому-то другому предмету? Большое количество вычислений? Формул? Но они есть и в других учебниках: в естествознании, физике, химии, астрономмии. Наличие доказательств – вот что прежде всего отличает математику от других областей знания. Конечно, доказательства встречаются и в других сферах человеческой деятельности, например, в юриспруденции. Однако математические доказательства убедительнее тех, которые можно слышать в суде. Математичекие доказательства признаются эталоном бесспорности.
Что же такое доказательство в математике? Доказательство – это такое рассуждение, которое убеждает нас настолько, что мы готовы убеждать других, используя то же рассуждение. В математике большое значение имеют так называемые доказательства существования. Самый простой способ доказатьсуществование объекта с заданными свойствами – это указать его и, разумеется, убедиться, что он обладает нужными свойствами. Например, чтобы убедиться, что уравнение имеет решение, достаточно привести какое-либо его решение. Такие доказательства называются прямыми. Но бывают и косвенные доказательства, когда обоснование того, что объект существует, происходит без прямого указания на сам объект.
Объяснение нового материала.
Рассмотрим пример. В классе 34 ученика. Докажите, что среди них обязательно найдутся по крайней мере два ученика, у которых фамиля начинается с одной буквы.
Доказательство простое. В русском языке алфавит содержит 33 буквы. Предположим, что нет таких учеников, у которых бы фамилия начиналась с одной буквы. Тогда учеников должно быть не более 33, а их 34.
Логический прием, который был использован прирешении этой задачи, называется принципом Дирихле. Дирихле Петер Август Лежен (1805-1859) – немецкий математик, иностранный член Петербургской Академии наук, член многих академий. Дирихле –автор многих достижений в области математики, одна из его заслуг – принцип доказательства, названный его именем.
Существует несколько формулировок этого принципа. Самая популярная следующая: «Если в п клетках сидят т зайцев, причем т>п, то хотя бы в одной клетке сидят, по крайней мере, два зайца»
Например, если 4 кролика разместить в 3 клетках, то найдется хотя бы одна клетка, в которой будет не менее 2 кроликов (сделать рисунок). Предположим, что не существует клетки, где сидят два кролика. Тогда в трех клетках окажется не более 3 кроликов (сделать рисунок), а их 4 – противоречие.
Запишем принцип Дирихле: если по N разложить предметы,число которых M больше N, то найдется ящик, в котором будет находится больше одного предмета.
На первый взгляд непонятно, почему это совершенно очевидное предложение, тем не менее, является мощным математическим методом решения задач, причем, самых разнообразных. Дело в том, что в каждой конкретной задаче нелегко понять, что же здесь выступает в роли «предметов», а что – в роли «ящиков».
Вернемся к первой задаче. Что в ней предметы? (ученики, M=34). Что в ней ящики? (количество букв в алфавите, N =33). M>N, то по принципу Дирихле хотя бы на одну букву будет приходится две фамилии.
Вернемся ко второй задаче. Что в ней предметы? (кролики, M= 4). Что в ней ящики? (клетки, N=3).M>N, то по принципу Дирихле хотя бы в одной клетке окажется два кролика.
Закрепление
1тип «Сколько нужно взять?..»
1.В мешке лежат шарики двух разных цветов.Какое наименьшее число шариков нужновынуть из мешка, чтобы среди ни обязательно оказались два шарика одного цвета?
Решение:
Здесь роль предметов играют шарики (М=?), роль ящиков — цвета (N=2).Чтобы M>N, т.е. в одном ящике оказалось два предмета, их должно быть больше двух, т.е. М=3
2.В коробке лежат карандаши: 7 красных и 5 синих. В темноте берут карандаши. Сколько карандашей надо взять, чтобы среди них было не менее 2 красных и не менее 3 синих?
Решение: Если предположить, что сначала будут попадаться только красные карандаши, то для того, чтобы было 3 синих, нужно взять 7(красные)+3(N)=10. Это «худший» варианнт развития событий, т.к. красных карандашей больше.
3.В мешке лежат 10 черных и 10 белых шаров. Они тщательно перемешены и неразлечимы на ощупь. Какое наименьшеее количество шаров нужно вынуть из мешка, чтобы среди них наверняка оказались два шара 1) одного цвета, 2)разного цвета, 3) белого цвета.
Решение:1)Если предположить, что предметы – шарики, которые нужно взять (М=?), а количество ящиков — цвета N=2, то по принципу Дирихле М=3
2)если предположить, что сначала будут попадаться шары только одного цвета, то N=10,следовательно, М=11
3)если предположить, что все время будут попадаться шары черного цвета, то М=12.
2тип «Докажите, что найдутся двое…»
4.При каком наименьшем количестве учеников школы среди них обязательно найдутся двое, у которых день и месяц рождения совпадают?
Решение: Дней в году N=365 или 366,то принципу Дирихле М= 366 или 367.
5.В лесу растет миллион елок. Известно, что на каждой из них не более 600 000 иголок. Докажите, что в лесу найдутся хотя бы две елки с одинаковым числом иголок.
Решение: Если предположить, что у всех елок разное количество иголок, то таких елок 600 000 (это ящики, N= 600 000), а по условию елок 1000 000=М, то М>N,по принципу Дирихле найдутся хотя бы две елки «в одном ящике», т.те с одинаковым количеством иголок.
6.В городе Санкт-Петербурге живет более 4млн. человек. Докажите, что у каких-то двух из них одинаковое количество волос на голове, если известно, что у любого человека на голове не более миллиона волос.
Решение: Если предположить, что у всех людей разное количество волос, то таких людей N=1000 000 (ящики), а по условию людей М=4 000 000. М>N, то по принципу Дирихле найдутся хотя бы два человека в одинаковым количеством волос.
3 тип. Обобщенный принцип Дирихле: если по N ящикам разложить предметы, число которых М больше, чем N (где к – натуральное число), то найдется ящик, в котором находятся более к предметов.
7.В магазин привезли 25 ящиков с яблоками трех сортов, причем в каждом ящике лежали яблоки какого-то одного сорта. Можно ли найти 9 ящиков с яблоками одного сорта?
Решение. 25:3=8 (ост.1). 25=8*3+1. к=3, N=8, M>N, то принципу Дирихле найдутся хотя бы один ящик, в котором находятся более, чем к=3 предметов, т.е. 4 предмета.
8.На площадке 20 собак восьми разных пород. Докажите, что среди них есть не менее трех собак одной породы.
Решение: 20:8=2(ост. 4), 20=8*2+4. к=2,N=8, М>N, то по принципу Дирихле найдутся хотя бы три собаки одной породы.
9.В классе 27 учеников. Найдется ли месяц, в котором отмечают свои дни рождения не меньше, чем три ученика этого класса?
Решение: В году 12 месяцев. 27:12=2(ост.3), 27=12*2+3. к=2,N=12,M>N, то по принципу Дирихле найдутся хотя бы три ученика, у которых дни рождения в одном месяце.
Итог урока.
Таким образом, применяя данный метод,необходимо:
1)Определить, что удобно взадаче принять за «предметы», а что за «ящики».
2)получит «ящики».Чаще всего, их должнобыть больше,чем предметов.
3)выбрать для решения требуемую формулировку принципа Дирихле.
Малая олимпиада.
1. В ящике лежат носки четырех цветов. Какое наименьшеее количество носков надо вытащить, чтобы из них можно было составить хотя бы одну пару?
Решение: N=4 (это количество цветов), То М=5.
2.В темной кладовой лежат ботинки одного размера: 10 пар черных и 10 пар коричневых. Найдите наименьшее число ботинок, которое нужно взять из кладовой,чтобы среди них оказалась хотя бы одна пара (левый и правый) одного цвета. В темноте нельзя определить не только цвет ботинок, но и левой от правого.
Решение: Если предположить (худший вариант), что подряд попадаются ботинки на одну ногу (20), а затем ботинок на другую ногу, то20+1=21, среди них будут ботинки на одну ногу.
3.В школе учится 1200 учеников. Найдется ли день, в который отмечают свои дни рождения не меньше, чем 4 ученика данной школы?
Решение: 1200:366 =3(ост. 102),к = 3, N=366-количество дней в високосном году, M>N, то по обощенному принципу Дирихле найдутся хотя бы 4>к ученика, у которых дни рождения в один день.
4.В классе 26 учеников, из них более половины мальчики. Докажите, что какие-то 2 мальчика сидят за одним столом (в классе 13 столов).
Решение: Мальчиков более половины, т.е. более 13, М>13, то М :13=1(остатка есть), М=13*1+ ост, к=1, N=13 – количество столов , то по обощенному принципу Дирихле хотя бы 2 мальчика сидят за одним столом.
Домашнее задание.
1.На дискотеку в студенческое общежитие, в котором 42 комнаты, пришли 36 гостей. Докажите, что найдется комната, в которую не пришел ни один гость.
Решение. Обозначив комнаты как предметы (М), а гостей как ящики (N), получим М>N, то по принципу Дирихле найдутся хотя бы две комнаты, в которые должен был прийти один и тот же гость, т.е.пустые комнаты.
2.В классе 37 учеников. Докажите, что среди них найдутся 4 ученика, отмечающие свой день рождения в одном месяце.
Решение: 37:12=3(ост. 1),37=12*3+1. к=3, N=12-количество месяцев в году. M>N, то по обощенному принципу Дирихле найдется болеек, т.е.более 3,значит,4 ученика с днем рождения в одном месяце.
3. В доме живут 5 кошек. У них 16 котят. Докажите, что хотя бы у одной кошки не менее четырех котят.
Решение. 16:5=3(ост.1), 16=5*3+1. к=3, N=5. M>N, то по обощенному принципу Дирихле найдется хотя бы две кошки, у которых более 3, т.е. не менее 4 котят.
4.В ящике 25 белых шаров, 25 черных, 20 синих и 10 красных. На ощупь шары неотличимы друг от друга. Шары вынимают из ящика в темноте. Какое наименьшее количество шаров нужно вынуть, чтобы среди них обязательно оказалось: 1)10 шаров одного цвета; 2) 10 белых шаров?
Решение: 1)в худшем случае это будут 9 белых шаров+9 черных шаров+9 синих+9 красных=36 шаров. В любом случае, следующий шар будет иметь цвет, который станет 10. М=37.
2)В худшем случае это будут 25 черных + 20 синих + 10 красных + 10 белых шаров =65 шаров.
Задания для решения на занятии
1.В мешке лежат шарики двух разных цветов. Какое наименьшее число шариков нужновынуть из мешка, чтобы среди ни обязательно оказались два шарика одного цвета?
2.В коробке лежат карандаши: 7 красных и 5 синих. В темноте берут карандаши. Сколько карандашей надо взять, чтобы среди них было не менее 2 красных и не менее 3 синих?
3.В мешке лежат 10 черных и 10 белых шаров. Они тщательно перемешены и неразлечимы на ощупь. Какое наименьшеее количество шаров нужно вынуть из мешка, чтобы среди них наверняка оказались два шара 1) одного цвета, 2)разного цвета, 3) белого цвета.
4.При каком наименьшем количестве учеников школы среди них обязательно найдутся двое, у которых день и месяц рождения совпадают?
5.В лесу растет миллион елок. Известно, что на каждой из них не более 600 000 иголок. Докажите, что в лесу найдутся хотя бы две елки с одинаковым числом иголок.
6.В городе Санкт-Петербурге живет более 4млн. человек. Докажите, что у каких-то двух из них одинаковое количество волос на голове, если известно, что у любого человека на голове не более миллиона волос.
7.В магазин привезли 25 ящиков с яблоками трех сортов, причем в каждом ящике лежали яблоки какого-то одного сорта. Можно ли найти 9 ящиков с яблоками одного сорта?
8.На площадке 20 собак восьми разных пород. Докажите, что среди них есть не менее трех собак одной породы.
9.В классе 27 учеников. Найдется ли месяц, в котором отмечают свои дни рождения не меньше, чем три ученика этого класса?
Малая олимпиада.
1. В ящике лежат носки четырех цветов. Какое наименьшеее количество носков надо вытащить, чтобы из них можно было составить хотя бы одну пару?
2.В темной кладовой лежат ботинки одного размера: 10 пар черных и 10 пар коричневых. Найдите наименьшее число ботинок, которое нужно взять из кладовой,чтобы среди них оказалась хотя бы одна пара (левый и правый) одного цвета. В темноте нельзя определить не только цвет ботинок, но и левой от правого.
3.В школе учится 1200 учеников. Найдется ли день, в который отмечают свои дни рождения не меньше, чем 4 ученика данной школы?
4.В классе 26 учеников, из них более половины мальчики. Докажите, что какие-то 2 мальчика сидят за одним столом (в классе 13 столов).
nsportal.ru
Принцип Дирихле | Социальная сеть работников образования
li{counter-increment:lst-ctn-kix_list_7-0}#doc9861706 .lst-kix_list_9-0>li{counter-increment:lst-ctn-kix_list_9-0}#doc9861706 ul.lst-kix_list_9-6{list-style-type:none}#doc9861706 .lst-kix_list_11-0>li{counter-increment:lst-ctn-kix_list_11-0}#doc9861706 ul.lst-kix_list_1-3{list-style-type:none}#doc9861706 ul.lst-kix_list_1-4{list-style-type:none}#doc9861706 ul.lst-kix_list_1-1{list-style-type:none}#doc9861706 ul.lst-kix_list_1-2{list-style-type:none}#doc9861706 ul.lst-kix_list_1-7{list-style-type:none}#doc9861706 ol.lst-kix_list_11-8.start{counter-reset:lst-ctn-kix_list_11-8 0}#doc9861706 ul.lst-kix_list_1-8{list-style-type:none}#doc9861706 ul.lst-kix_list_1-5{list-style-type:none}#doc9861706 ul.lst-kix_list_1-6{list-style-type:none}#doc9861706 ol.lst-kix_list_11-2.start{counter-reset:lst-ctn-kix_list_11-2 0}#doc9861706 .lst-kix_list_5-0>li:before{content:»\0025cf «}#doc9861706 ol.lst-kix_list_6-0{list-style-type:none}#doc9861706 .lst-kix_list_5-3>li:before{content:» «}#doc9861706 .lst-kix_list_5-2>li:before{content:» «}#doc9861706 .lst-kix_list_5-1>li:before{content:» «}#doc9861706 .lst-kix_list_5-7>li:before{content:» «}#doc9861706 ul.lst-kix_list_8-4{list-style-type:none}#doc9861706 ul.lst-kix_list_8-5{list-style-type:none}#doc9861706 .lst-kix_list_5-6>li:before{content:» «}#doc9861706 .lst-kix_list_5-8>li:before{content:» «}#doc9861706 ul.lst-kix_list_8-2{list-style-type:none}#doc9861706 ul.lst-kix_list_8-3{list-style-type:none}#doc9861706 ul.lst-kix_list_8-8{list-style-type:none}#doc9861706 ul.lst-kix_list_8-6{list-style-type:none}#doc9861706 ul.lst-kix_list_8-7{list-style-type:none}#doc9861706 .lst-kix_list_5-4>li:before{content:» «}#doc9861706 .lst-kix_list_5-5>li:before{content:» «}#doc9861706 ul.lst-kix_list_8-1{list-style-type:none}#doc9861706 .lst-kix_list_6-1>li:before{content:» «}#doc9861706 .lst-kix_list_6-3>li:before{content:» «}#doc9861706 .lst-kix_list_6-0>li:before{content:»» counter(lst-ctn-kix_list_6-0,decimal) «. «}#doc9861706 .lst-kix_list_6-4>li:before{content:» «}#doc9861706 .lst-kix_list_6-2>li:before{content:» «}#doc9861706 .lst-kix_list_6-8>li:before{content:» «}#doc9861706 ol.lst-kix_list_11-7.start{counter-reset:lst-ctn-kix_list_11-7 0}#doc9861706 .lst-kix_list_6-5>li:before{content:» «}#doc9861706 .lst-kix_list_6-7>li:before{content:» «}#doc9861706 .lst-kix_list_6-6>li:before{content:» «}#doc9861706 .lst-kix_list_2-7>li:before{content:» «}#doc9861706 .lst-kix_list_7-4>li:before{content:» «}#doc9861706 .lst-kix_list_7-6>li:before{content:» «}#doc9861706 .lst-kix_list_2-5>li:before{content:» «}#doc9861706 .lst-kix_list_7-2>li:before{content:» «}#doc9861706 ul.lst-kix_list_3-7{list-style-type:none}#doc9861706 ul.lst-kix_list_3-8{list-style-type:none}#doc9861706 .lst-kix_list_10-1>li:before{content:» «}#doc9861706 ul.lst-kix_list_3-1{list-style-type:none}#doc9861706 ul.lst-kix_list_3-2{list-style-type:none}#doc9861706 .lst-kix_list_7-8>li:before{content:» «}#doc9861706 ul.lst-kix_list_3-0{list-style-type:none}#doc9861706 ul.lst-kix_list_3-5{list-style-type:none}#doc9861706 ol.lst-kix_list_9-0{list-style-type:none}#doc9861706 ul.lst-kix_list_3-6{list-style-type:none}#doc9861706 ul.lst-kix_list_3-3{list-style-type:none}#doc9861706 ul.lst-kix_list_3-4{list-style-type:none}#doc9861706 .lst-kix_list_10-7>li:before{content:» «}#doc9861706 .lst-kix_list_10-5>li:before{content:» «}#doc9861706 .lst-kix_list_10-3>li:before{content:» «}#doc9861706 .lst-kix_list_4-1>li:before{content:» «}#doc9861706 .lst-kix_list_11-7>li{counter-increment:lst-ctn-kix_list_11-7}#doc9861706 .lst-kix_list_9-2>li:before{content:» «}#doc9861706 .lst-kix_list_4-3>li:before{content:» «}#doc9861706 .lst-kix_list_4-5>li:before{content:» «}#doc9861706 .lst-kix_list_9-0>li:before{content:»» counter(lst-ctn-kix_list_9-0,decimal) «. «}#doc9861706 .lst-kix_list_9-6>li:before{content:» «}#doc9861706 .lst-kix_list_11-2>li{counter-increment:lst-ctn-kix_list_11-2}#doc9861706 .lst-kix_list_9-4>li:before{content:» «}#doc9861706 .lst-kix_list_11-3>li:before{content:»» counter(lst-ctn-kix_list_11-3,decimal) «. «}#doc9861706 ol.lst-kix_list_10-0{list-style-type:none}#doc9861706 ul.lst-kix_list_2-8{list-style-type:none}#doc9861706 .lst-kix_list_11-5>li:before{content:»» counter(lst-ctn-kix_list_11-5,lower-roman) «. «}#doc9861706 ul.lst-kix_list_2-2{list-style-type:none}#doc9861706 ul.lst-kix_list_2-3{list-style-type:none}#doc9861706 ul.lst-kix_list_2-0{list-style-type:none}#doc9861706 ul.lst-kix_list_2-1{list-style-type:none}#doc9861706 ol.lst-kix_list_8-0{list-style-type:none}#doc9861706 .lst-kix_list_9-8>li:before{content:» «}#doc9861706 ul.lst-kix_list_2-6{list-style-type:none}#doc9861706 .lst-kix_list_1-1>li:before{content:» «}#doc9861706 ul.lst-kix_list_2-7{list-style-type:none}#doc9861706 .lst-kix_list_11-7>li:before{content:»» counter(lst-ctn-kix_list_11-7,lower-latin) «. «}#doc9861706 ul.lst-kix_list_2-4{list-style-type:none}#doc9861706 ul.lst-kix_list_2-5{list-style-type:none}#doc9861706 .lst-kix_list_1-3>li:before{content:» «}#doc9861706 ul.lst-kix_list_10-8{list-style-type:none}#doc9861706 ul.lst-kix_list_10-7{list-style-type:none}#doc9861706 .lst-kix_list_1-7>li:before{content:» «}#doc9861706 ul.lst-kix_list_10-6{list-style-type:none}#doc9861706 ul.lst-kix_list_10-5{list-style-type:none}#doc9861706 ul.lst-kix_list_10-4{list-style-type:none}#doc9861706 ul.lst-kix_list_10-3{list-style-type:none}#doc9861706 .lst-kix_list_1-5>li:before{content:» «}#doc9861706 ul.lst-kix_list_10-2{list-style-type:none}#doc9861706 ul.lst-kix_list_10-1{list-style-type:none}#doc9861706 .lst-kix_list_2-1>li:before{content:» «}#doc9861706 ol.lst-kix_list_6-0.start{counter-reset:lst-ctn-kix_list_6-0 0}#doc9861706 .lst-kix_list_2-3>li:before{content:» «}#doc9861706 .lst-kix_list_11-8>li{counter-increment:lst-ctn-kix_list_11-8}#doc9861706 ol.lst-kix_list_11-6{list-style-type:none}#doc9861706 ol.lst-kix_list_11-7{list-style-type:none}#doc9861706 ol.lst-kix_list_11-8{list-style-type:none}#doc9861706 ol.lst-kix_list_11-2{list-style-type:none}#doc9861706 ol.lst-kix_list_11-3{list-style-type:none}#doc9861706 .lst-kix_list_3-0>li:before{content:»\0025cf «}#doc9861706 ol.lst-kix_list_11-4{list-style-type:none}#doc9861706 ol.lst-kix_list_11-5{list-style-type:none}#doc9861706 ul.lst-kix_list_5-7{list-style-type:none}#doc9861706 ul.lst-kix_list_5-8{list-style-type:none}#doc9861706 .lst-kix_list_3-1>li:before{content:» «}#doc9861706 .lst-kix_list_3-2>li:before{content:» «}#doc9861706 ul.lst-kix_list_5-5{list-style-type:none}#doc9861706 ol.lst-kix_list_11-0{list-style-type:none}#doc9861706 ul.lst-kix_list_5-6{list-style-type:none}#doc9861706 ol.lst-kix_list_11-1{list-style-type:none}#doc9861706 .lst-kix_list_8-1>li:before{content:» «}#doc9861706 .lst-kix_list_8-2>li:before{content:» «}#doc9861706 .lst-kix_list_6-0>li{counter-increment:lst-ctn-kix_list_6-0}#doc9861706 .lst-kix_list_8-0>li{counter-increment:lst-ctn-kix_list_8-0}#doc9861706 .lst-kix_list_3-5>li:before{content:» «}#doc9861706 ul.lst-kix_list_5-0{list-style-type:none}#doc9861706 .lst-kix_list_10-0>li{counter-increment:lst-ctn-kix_list_10-0}#doc9861706 .lst-kix_list_3-4>li:before{content:» «}#doc9861706 ul.lst-kix_list_5-3{list-style-type:none}#doc9861706 .lst-kix_list_3-3>li:before{content:» «}#doc9861706 ul.lst-kix_list_5-4{list-style-type:none}#doc9861706 ul.lst-kix_list_5-1{list-style-type:none}#doc9861706 .lst-kix_list_8-0>li:before{content:»» counter(lst-ctn-kix_list_8-0,decimal) «. «}#doc9861706 ul.lst-kix_list_5-2{list-style-type:none}#doc9861706 .lst-kix_list_8-7>li:before{content:» «}#doc9861706 ol.lst-kix_list_11-5.start{counter-reset:lst-ctn-kix_list_11-5 0}#doc9861706 .lst-kix_list_3-8>li:before{content:» «}#doc9861706 .lst-kix_list_8-5>li:before{content:» «}#doc9861706 .lst-kix_list_11-1>li{counter-increment:lst-ctn-kix_list_11-1}#doc9861706 .lst-kix_list_8-6>li:before{content:» «}#doc9861706 .lst-kix_list_8-3>li:before{content:» «}#doc9861706 .lst-kix_list_3-6>li:before{content:» «}#doc9861706 .lst-kix_list_3-7>li:before{content:» «}#doc9861706 .lst-kix_list_8-4>li:before{content:» «}#doc9861706 .lst-kix_list_11-2>li:before{content:»» counter(lst-ctn-kix_list_11-2,lower-roman) «. «}#doc9861706 .lst-kix_list_11-1>li:before{content:»» counter(lst-ctn-kix_list_11-1,lower-latin) «. «}#doc9861706 .lst-kix_list_11-0>li:before{content:»» counter(lst-ctn-kix_list_11-0,decimal) «. «}#doc9861706 .lst-kix_list_8-8>li:before{content:» «}#doc9861706 ol.lst-kix_list_11-6.start{counter-reset:lst-ctn-kix_list_11-6 0}#doc9861706 .lst-kix_list_4-8>li:before{content:» «}#doc9861706 .lst-kix_list_4-7>li:before{content:» «}#doc9861706 ul.lst-kix_list_4-8{list-style-type:none}#doc9861706 ul.lst-kix_list_4-6{list-style-type:none}#doc9861706 ul.lst-kix_list_4-7{list-style-type:none}#doc9861706 ul.lst-kix_list_4-0{list-style-type:none}#doc9861706 ul.lst-kix_list_4-1{list-style-type:none}#doc9861706 ul.lst-kix_list_4-4{list-style-type:none}#doc9861706 ul.lst-kix_list_4-5{list-style-type:none}#doc9861706 ul.lst-kix_list_4-2{list-style-type:none}#doc9861706 ul.lst-kix_list_4-3{list-style-type:none}#doc9861706 .lst-kix_list_11-3>li{counter-increment:lst-ctn-kix_list_11-3}#doc9861706 ol.lst-kix_list_11-0.start{counter-reset:lst-ctn-kix_list_11-0 0}#doc9861706 ol.lst-kix_list_8-0.start{counter-reset:lst-ctn-kix_list_8-0 0}#doc9861706 .lst-kix_list_7-0>li:before{content:»» counter(lst-ctn-kix_list_7-0,decimal) «. «}#doc9861706 .lst-kix_list_2-6>li:before{content:» «}#doc9861706 .lst-kix_list_2-4>li:before{content:» «}#doc9861706 .lst-kix_list_2-8>li:before{content:» «}#doc9861706 .lst-kix_list_7-1>li:before{content:» «}#doc9861706 .lst-kix_list_7-5>li:before{content:» «}#doc9861706 .lst-kix_list_7-3>li:before{content:» «}#doc9861706 ol.lst-kix_list_11-1.start{counter-reset:lst-ctn-kix_list_11-1 0}#doc9861706 ul.lst-kix_list_7-5{list-style-type:none}#doc9861706 .lst-kix_list_10-0>li:before{content:»» counter(lst-ctn-kix_list_10-0,decimal) «. «}#doc9861706 ul.lst-kix_list_7-6{list-style-type:none}#doc9861706 ul.lst-kix_list_7-3{list-style-type:none}#doc9861706 ul.lst-kix_list_7-4{list-style-type:none}#doc9861706 ul.lst-kix_list_7-7{list-style-type:none}#doc9861706 ul.lst-kix_list_7-8{list-style-type:none}#doc9861706 .lst-kix_list_11-6>li{counter-increment:lst-ctn-kix_list_11-6}#doc9861706 ul.lst-kix_list_7-1{list-style-type:none}#doc9861706 ul.lst-kix_list_7-2{list-style-type:none}#doc9861706 .lst-kix_list_7-7>li:before{content:» «}#doc9861706 ol.lst-kix_list_10-0.start{counter-reset:lst-ctn-kix_list_10-0 0}#doc9861706 .lst-kix_list_11-4>li{counter-increment:lst-ctn-kix_list_11-4}#doc9861706 .lst-kix_list_10-4>li:before{content:» «}#doc9861706 .lst-kix_list_10-8>li:before{content:» «}#doc9861706 .lst-kix_list_4-0>li:before{content:»\0025cf «}#doc9861706 .lst-kix_list_10-2>li:before{content:» «}#doc9861706 .lst-kix_list_4-4>li:before{content:» «}#doc9861706 .lst-kix_list_4-2>li:before{content:» «}#doc9861706 .lst-kix_list_4-6>li:before{content:» «}#doc9861706 .lst-kix_list_9-3>li:before{content:» «}#doc9861706 ol.lst-kix_list_7-0.start{counter-reset:lst-ctn-kix_list_7-0 0}#doc9861706 .lst-kix_list_10-6>li:before{content:» «}#doc9861706 .lst-kix_list_9-1>li:before{content:» «}#doc9861706 .lst-kix_list_9-7>li:before{content:» «}#doc9861706 .lst-kix_list_11-4>li:before{content:»» counter(lst-ctn-kix_list_11-4,lower-latin) «. «}#doc9861706 .lst-kix_list_9-5>li:before{content:» «}#doc9861706 ul.lst-kix_list_6-6{list-style-type:none}#doc9861706 ul.lst-kix_list_6-7{list-style-type:none}#doc9861706 ul.lst-kix_list_6-4{list-style-type:none}#doc9861706 ul.lst-kix_list_6-5{list-style-type:none}#doc9861706 ul.lst-kix_list_6-8{list-style-type:none}#doc9861706 .lst-kix_list_11-6>li:before{content:»» counter(lst-ctn-kix_list_11-6,decimal) «. «}#doc9861706 .lst-kix_list_1-0>li:before{content:»\0025cf «}#doc9861706 ul.lst-kix_list_6-2{list-style-type:none}#doc9861706 .lst-kix_list_11-8>li:before{content:»» counter(lst-ctn-kix_list_11-8,lower-roman) «. «}#doc9861706 ul.lst-kix_list_6-3{list-style-type:none}#doc9861706 ol.lst-kix_list_11-3.start{counter-reset:lst-ctn-kix_list_11-3 0}#doc9861706 .lst-kix_list_1-2>li:before{content:» «}#doc9861706 ul.lst-kix_list_6-1{list-style-type:none}#doc9861706 .lst-kix_list_1-4>li:before{content:» «}#doc9861706 .lst-kix_list_1-6>li:before{content:» «}#doc9861706 .lst-kix_list_2-0>li:before{content:»\0025cf «}#doc9861706 .lst-kix_list_11-5>li{counter-increment:lst-ctn-kix_list_11-5}#doc9861706 ol.lst-kix_list_11-4.start{counter-reset:lst-ctn-kix_list_11-4 0}#doc9861706 .lst-kix_list_1-8>li:before{content:» «}#doc9861706 .lst-kix_list_2-2>li:before{content:» «}#doc9861706 ol{margin:0;padding:0}#doc9861706 table td,table th{padding:0}#doc9861706 .c13{border-right-style:solid;padding:0pt 5.4pt 0pt 5.4pt;border-bottom-color:#000000;border-top-width:0pt;border-right-width:0pt;border-left-color:#000000;vertical-align:middle;border-right-color:#000000;border-left-width:0pt;border-top-style:solid;border-left-style:solid;border-bottom-width:0pt;width:48pt;border-top-color:#000000;border-bottom-style:solid}#doc9861706 .c12{border-right-style:solid;padding:0pt 5.4pt 0pt 5.4pt;border-bottom-color:#000000;border-top-width:0pt;border-right-width:0pt;border-left-color:#000000;vertical-align:top;border-right-color:#000000;border-left-width:0pt;border-top-style:solid;border-left-style:solid;border-bottom-width:0pt;width:389.8pt;border-top-color:#000000;border-bottom-style:solid}#doc9861706 .c16{border-right-style:solid;padding:0pt 5.4pt 0pt 5.4pt;border-bottom-color:#000000;border-top-width:0pt;border-right-width:0pt;border-left-color:#000000;vertical-align:top;border-right-color:#000000;border-left-width:0pt;border-top-style:solid;border-left-style:solid;border-bottom-width:0pt;width:26.7pt;border-top-color:#000000;border-bottom-style:solid}#doc9861706 .c24{padding-top:5pt;padding-bottom:5pt;line-height:1.5;orphans:2;widows:2;text-align:justify}#doc9861706 .c1{vertical-align:baseline;font-size:12pt;font-family:»Times New Roman»;font-weight:normal;text-decoration:underline}#doc9861706 .c21{vertical-align:baseline;font-size:12pt;font-family:»Arial»;color:#ffffff;font-weight:bold}#doc9861706 .c0{vertical-align:baseline;font-size:12pt;font-family:»Times New Roman»;font-style:italic;font-weight:bold}#doc9861706 .c3{padding-top:0pt;padding-bottom:0pt;line-height:1.5;text-align:center;height:11pt}#doc9861706 .c18{vertical-align:baseline;font-size:12pt;font-family:»Times New Roman»;font-weight:bold}#doc9861706 .c15{vertical-align:baseline;font-size:10pt;font-family:»Times New Roman»;font-weight:normal}#doc9861706 .c22{margin-left:-5.4pt;border-spacing:0;border-collapse:collapse;margin-right:auto}#doc9861706 .c2{padding-top:0pt;padding-bottom:0pt;line-height:1.5;text-align:justify}#doc9861706 .c27{padding-top:0pt;padding-bottom:0pt;line-height:1.0;margin-right:18pt}#doc9861706 .c5{vertical-align:baseline;font-size:12pt;font-family:»Times New Roman»;font-weight:normal}#doc9861706 .c30{background-color:#ffffff;max-width:453.7pt;padding:56.7pt 56.7pt 85pt 85pt}#doc9861706 .c8{padding-top:0pt;padding-bottom:0pt;line-height:1.5}#doc9861706 .c26{padding-top:36pt;padding-bottom:0pt;line-height:1.0}#doc9861706 .c29{padding-top:0pt;padding-bottom:0pt;line-height:1.15}#doc9861706 .c6{color:#000000;text-decoration:none;font-style:normal}#doc9861706 .c14{margin-left:36pt;padding-left:0pt}#doc9861706 .c19{padding:0;margin:0}#doc9861706 .c25{color:#000000}#doc9861706 .c9{font-style:normal}#doc9861706 .c7{height:0pt}#doc9861706 .c4{height:11pt}#doc9861706 .c17{text-align:center}#doc9861706 .c28{font-style:italic}#doc9861706 .c23{color:#ffffff}#doc9861706 .c20{text-indent:36pt}#doc9861706 .c11{text-align:left}#doc9861706 .c10{text-align:right}#doc9861706 .title{padding-top:24pt;color:#000000;font-weight:bold;font-size:36pt;padding-bottom:6pt;font-family:»Arial»;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc9861706 .subtitle{padding-top:18pt;color:#666666;font-size:24pt;padding-bottom:4pt;font-family:»Georgia»;line-height:1.15;page-break-after:avoid;font-style:italic;orphans:2;widows:2;text-align:left}#doc9861706 li{color:#000000;font-size:11pt;font-family:»Arial»}#doc9861706 p{margin:0;color:#000000;font-size:11pt;font-family:»Arial»}#doc9861706 h2{padding-top:24pt;color:#000000;font-weight:bold;font-size:24pt;padding-bottom:6pt;font-family:»Arial»;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc9861706 h3{padding-top:18pt;color:#000000;font-weight:bold;font-size:18pt;padding-bottom:4pt;font-family:»Arial»;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc9861706 h4{padding-top:14pt;color:#000000;font-weight:bold;font-size:14pt;padding-bottom:4pt;font-family:»Arial»;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc9861706 h5{padding-top:12pt;color:#000000;font-weight:bold;font-size:12pt;padding-bottom:2pt;font-family:»Arial»;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc9861706 h5{padding-top:11pt;color:#000000;font-weight:bold;font-size:11pt;padding-bottom:2pt;font-family:»Arial»;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc9861706 h6{padding-top:10pt;color:#000000;font-weight:bold;font-size:10pt;padding-bottom:2pt;font-family:»Arial»;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc9861706 ]]>I городской научно-практический марафон «Шажок в науку»
I этап
СЕКЦИЯ МАТЕМАТИКИ
Принцип Дирихле.
Выполнена учеником 6 класса
Муниципального образовательного учреждения
«Основная общеобразовательная школа №223»
г.Заречного
Лившицом Григорием
Научный руководитель –
учитель математики
Жилякова Т.Н.
2009 год
Оглавление:
Стр.
Введение. | 3 | |
1 | Принцип Дирихле. | |
1.1 | История принципа Дирихле. | 4 |
1.2 | Формулировки принципа Дирихле. | 4 |
2. | Применение принципа Дирихле и способа доказательства от противного. | 5 |
3. | Заключение. | 6 |
Список использованной литературы. | 7 | |
Приложение. |
Введение.
Многие вещи нам непонятны не потому,
что наши понятия слабы; но потому, что сии
вещи не входят в круг наших понятий.
Козьма Прутков
Математика – один из главных школьных предметов. Умение решать задачи, особенно олимпиадные, всегда являлось одним из показателей математической одаренности ученика. Что же такое олимпиадные задачи? Существует такая трактовка: олимпиадные задачи – это задачи, при решении которых используются специальные методы, как правило, не рассматриваемые в школе на уроке. Значит, решение таких задач способствует развитию не только интеллектуальных способностей учащихся, но развивает их творческие способности и познавательный интерес. В данной работе подробно изучается принцип Дирихле, который позволяет находить верное решение в нестандартной ситуации.
Интерес к данному принципу возник при решении следующей задачи:
В классе 30 учеников. В диктанте Вова сделал 13 ошибок, а остальные — меньше. Докажите, что по крайней мере 3 ученика сделали одно и то же число ошибок.
Итак, тема данной работы: Принцип Дирихле.
Объект исследования – сам принцип Дирихле и его формулировки.
Предмет исследования – задачи, решаемые с использованием принципа.
Целью исследования было изучение принципа Дирихле и класса задач, решаемых этим способом.
Поэтому данная работа является обобщением возможностей применения на практике различных формулировок принципа.
Задачи исследования:
- Изучить различные формулировки принципа Дирихле.
- Подобрать и решить ряд задач на применение этого принципа и его возможных формулировок.
- Создать буклет с набором задач по данной тематике.
1. Принцип Дирихле.
1.1. История возникновения принципа Дирихле
Один математик сказал, что Дирихле по частоте упоминания школьниками всегда обеспечено одно из самых высших мест. Кто же такой Петер Густав Лежен Дирихле? Это великий немецкий математик, который изучал арифметику, математический анализ, механику и математическую физику. Он, разумеется, и не подозревал, что его именем назовут столь простой и важный принцип, хотя часто использовал подобные рассуждения при доказательстве своих теорем.
1.2.Формулировки принципа Дирихле.
В несерьезной форме принцип Дирихле гласит: «Нельзя посадить 7 кроликов в 3 клетки, чтобы в каждой было не больше 2 кроликов».
Существует несколько формулировок данного принципа.
1. «Если в n клетках сидит m зайцев, причем m >n, то хотя бы в одной клетке сидят, по крайней мере, два зайца».
Доказывается данный принцип Дирихле методом доказательства от противного:
Пусть не найдется такой клетки, в которой сидят два зайца, тогда количество зайцев m должно быть меньше или равно количеству клеток n, что приводит нас к противоречию.
2. «Пусть в n клетках сидят m зайцев, причем n > m. Тогда найдется хотя бы одна пустая клетка».
Доказательство:
Пусть нет ни одной пустой клетки. Тогда количество зайцев m должно совпадать с количеством клеток n (если в каждой клетке хотя бы по одному зайцу) или быть больше, что противоречит условию.
3. «Если m зайцев сидят в n клетках, то найдется клетка, в которой не менее m/n зайцев».
Не надо бояться дробного числа зайцев – если получается, что в ящике не меньше 7/3 зайцев, значит, их больше двух.
Доказательство:
Допустим, что в каждой клетке число зайцев меньше, чем m/n.. Тогда в n клетках вместе зайцев меньше, чем n • (m/n) = m. Противоречие!
4. «Если в n клетках сидят m зайцев и m > kn + 1 , то в какой-то из клеток сидят, по крайней мере, k + 1 заяц» (обобщенный принцип)
Доказательство:
Пусть не найдется такой клетки, то есть в каждой из n клеток сидят по k зайцев, тогда зайцев должно быть k•n, а по условию зайцев как минимум на одного больше. Пришли к противоречию с условием. Значит, есть клетка, в которой сидят k + 1 заяц.
Некоторые задачи на применение данного принципа также можно решить, используя метод доказательства от противного, но не все.
На первый взгляд, непонятно, почему это совершенно очевидное предложение, тем не менее, является мощным математическим методом решения задач, причем самых разнообразных. Всё дело оказывается в том, что в каждой конкретной задаче нелегко понять, что же здесь выступает в роли «зайцев», а что — в роли «клеток». И почему надо, чтобы «зайцев» было больше, чем «клеток». Выбор «зайцев» и «клеток» часто неочевиден. Далеко не всегда по формулировке задачи можно определить, что следует применить принцип Дирихле.
Таким образом, применяя данный метод, надо:
1) определить, что удобно в задаче принять за «клетки», а что за «зайцев»;
2) получить «клетки». Чаще всего «клеток» меньше (больше), чем «зайцев» на одну;
3) выбрать для решения требуемую формулировку принципа Дирихле.
2. Применение принципа Дирихле
Попробуем решить задачи с применением этого метода.
1. В классе 35 учеников. Можно ли утверждать, что среди них найдутся хотя бы два ученика, фамилии которых начинаются с одной буквы.
«ЗАЙЦЫ» — 35 учеников
«КЛЕТКИ»- Буквы русского алфавита. Исключая Ъ,Ь,Ы, таких букв 30.
Задача свелась к тому, чтобы рассадить 35 зайцев в 30 клеток. Количество зайцев больше количества клеток. Используя принцип Дирихле (формулировка 1), можно сделать вывод, что найдутся хотя бы 2 ученика, фамилии которых начинаются с одной буквы.
Или от противного: Пусть каждый ученик начальной буквой своей фамилии имеют различные буквы алфавита. Так как учеников 35, то и букв в алфавите должно быть не меньше. А мы точно знаем, что их 33. поэтому такая ситуация невозможна. Значит, будут существовать хотя бы два ученика, чьи фамилии начинаются с одной буквы.
2. На дискотеку в студенческое общежитие, в котором 42 комнаты, пришли 36 гостей. Докажите, что найдется комната, в которую не пришел ни один гость.
«ЗАЙЦЫ» — 36 гостей
«КЛЕТКИ»- 42 комнаты.
Теперь необходимо рассадить 36 «зайцев» в 42 «клетки». Так как «зайцев» меньше, чем «клеток», то, используя принцип Дирихле (формулировка 2), можно сделать вывод, что найдется хотя бы одна пустая комната. На самом деле их как минимум 42-36=6.
Или от противного: Пусть в каждую комнату пришел гость, тогда гостей в общежитии должно быть как минимум 42, что противоречит условию. Значит, найдется комната, в которую не пришел ни один гость.
3. В классе 40 учеников. Докажите, что среди них найдутся 4 ученика, отмечающие день рождения в одном месяце.
«ЗАЙЦЫ» — 40 учеников
«КЛЕТКИ»- 12 месяцев
Нам нужно рассадить 40 «зайцев» в 12 «клеток». Используя принцип Дирихле (формулировка 3), можем сделать вывод, что найдется «клетка», в которой сидят не менее 40/12=3 1/3 «зайцев», то есть как минимум 4 «зайца». Значит, можно утверждать, что найдутся 4 ученика, отмечающие день рождения в одном месяце.
Или от противного: Пусть нет 4 учеников, отмечающих день рождения в одном месяце. Тогда их должно быть 3, получается, что в классе должно быть не больше 12*3=36 учеников, что противоречит условию задачи.
4. В магазин привезли 26 ящиков с яблоками трех сортов, причем в каждом ящике лежали яблоки одного сорта. Найдутся ли 9 ящиков одного сорта?
«ЗАЙЦЫ» — 26 ящиков
«КЛЕТКИ»- 3 сорта
Осталось рассадить 26 «зайцев» в 3 «клетки». Так как 26> 3·8+1, то, используя принцип Дирихле (формулировка 4), можем утверждать, что в какой – то из «клеток» сидят 8+1=9 «зайцев». Значит, найдутся 9 ящиков одного сорта.
От противного: Пусть ящиков одного сорта будет не больше 9, то есть 8. Тогда должно быть всего не более 8*3=24 ящиков яблок. Что противоречит условию.
Вернемся к задаче: В классе 30 учеников. В диктанте Вова сделал 13 ошибок, а остальные — меньше. Докажите, что по крайней мере 3 ученика сделали одно и то же число ошибок.
Количество ошибок может быть записано числами от 0 до 12, то есть 13 различных вариантов, их и примем за «КЛЕТКИ». Учеников, кроме Вовы, 29 – их примем за «ЗАЙЦЕВ». Осталось рассадить 29 «зайцев» в 13 «клеток». Так как 29> 13*2+1, то, согласно обобщенному принципу Дирихле, существует «клетка», в которой сидят по крайней мере 2+1=3 «зайца». Таким образом, можно утверждать, что в классе есть 3 человека, сделавших одинаковое количество ошибок.
3. Заключение.
При выполнении этой работы был исследован класс задач на применение принципа Дирихле и различных его формулировок. В ходе работы задачи были решены 2 способами: принципом Дирихле и способом доказательства от противного, то есть мы познакомились с двумя способами решения олимпиадных задач. А также был создан буклет с основными видами задач. (см.Приложение)
Литература:
1. Готовимся к олимпиадам по математике: учеб. метод. пособие/
А.В.Фарков. — М.: Издательство «Экзамен»,2007.
2. Математический праздник. –М.:Бюро Квантум, 2004.(Библиотечка «Квант», вып.88)
3.Популярная комбинаторика /Н.Я.Виленкин – М.:Издательство «Наука», 1975.
4. Андреев А.A., Савин А.Н., Саушкин М.Н. «Принцип Дирихле» (сайт Путеводитель В МИРЕ НАУКИ для школьников http: ermine.narod.ru).
1. 16 учеников сидят за круглым столом, причем больше половины из них девушки. Докажите, что какие-то 2 девушки сидят напротив друг друга.
Образуем 8 пар, в каждую пару включим учеников, сидящих друг против друга.
Тогда «ЗАЙЦЫ» — девушки
«КЛЕТКИ»- 8 пар
Так как девушек больше половины, то есть восьми, то найдется «клетка» (пара), в которой будут находиться 2 девушки (формулировка1 принципа Дирихле).
nsportal.ru

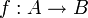 и мощность множества A больше мощности B, то есть | A | > n | B | , где
и мощность множества A больше мощности B, то есть | A | > n | B | , где 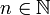 . Тогда некоторое своё значение функция f примет по крайней мере n + 1 раз.
. Тогда некоторое своё значение функция f примет по крайней мере n + 1 раз.