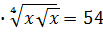Иррациональные уравнения и системы — Математика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Некоторые рекомендации к решению иррациональных уравнений и систем
К оглавлению…
Существуют два равноценных метода решения иррациональных уравнений с квадратными корнями:
- Метод равносильных переходов (с учетом ОДЗ). При этом для правильной записи области допустимых значений, в общем случае необходимо потребовать неотрицательности всех подкоренных выражений, а также выражений, которым равны корни квадратные (если таковые можно алгебраически выразить из уравнения).
- Метод перехода к уравнению-следствию (без учета ОДЗ). В этом методе обязательно требуется проверка корней подстановкой.
Честно говоря, в иррациональных уравнениях порой так сложно правильно записать ОДЗ, что даже если Вы будете пробовать это сделать, то корни всё равно лучше проверять подстановкой, особенно если корни представляют из себя целые числа.
Обратите внимание на очень частую ошибку – если Вы решаете уравнение типа:
То при записи ОДЗ необходимо требовать неотрицательность правой части, то есть накладывать условие:
Причем необходимо понимать, что данное условие нужно дополнительно добавлять в ОДЗ даже если к подобному уравнению Вы пришли уже после нескольких преобразований (возведений в квадрат), а не только в случае, когда уравнение изначально выглядело соответствующим образом.
В иррациональных уравнения особо актуально становится следующее замечание: для того чтобы произведение нескольких множителей было равно нолю, необходимо, чтобы хотя бы один их них равнялся нолю, а остальные существовали. Когда множителями являются корни, а не просто скобки как в рациональных уравнениях, то они часто могут и не существовать. Так возникают ошибки.
Если в иррациональном уравнении много корней, то крайне желательно перед возведением этого уравнения в квадрат перенести корни справа налево или наоборот так, чтобы с каждой из сторон получилась именно сумма корней, то есть заведомо положительное выражение. Если же, по каким-то причинам, Вы решили возводить в квадрат разность корней (т.е. выражение чей знак неизвестен), то будьте готовы получить несколько посторонних корней. В этом случае обязательно нужно проверить все корни подстановкой, потому что правильно записать ОДЗ уже скорее всего не получится.
Если в иррациональном уравнении имеется корень в корне, то необходимо будет несколько раз возводить это уравнение в квадрат, при этом главное понимать, что в соответствии с изложенными выше условиями, при каждом таком возведении могут получаться всё новые и новые условия для ОДЗ. В таких уравнениях при возможности лучше проверять корни подстановкой.
При решении иррациональных уравнений часто удобно использовать замену. При этом главное помнить, что после введения замены в некоторое уравнение это уравнение должно:
- во-первых, стать проще;
- во-вторых, больше не содержать первоначальной переменной.
Кроме того, важно не забывать выполнять обратную замену, т.е. после нахождения значений для новой переменной (для замены), записывать вместо замены то, чему она равна через первоначальную переменную, приравнивать это выражение к найденным значениям для замены и опять решать уравнения.
При решении систем иррациональных уравнений с двумя неизвестными зачастую достаточно действовать по стандартной схеме. А именно, выразить одну из переменных из одного из уравнений и подставить данное выражение вместо соответствующей переменной в другое уравнение. После чего получится некоторое иррациональное уравнение с одной неизвестной, которое затем следует решить с учетом всех правил решения иррациональных уравнений. Значение первой переменной затем нужно найти используя её выражение через уже найденную переменную.
При решении систем иррациональных уравнений с большим количеством переменных также зачастую достаточно использовать метод подстановки. Также при решении систем иррациональных уравнений часто помогает метод замены переменных. При этом нужно понимать, что после введения замены переменных в систему:
- во-первых, она опять-таки должна упроститься;
- во-вторых, новых переменных должно быть столько же сколько и старых;
- в-третьих, система больше не должна содержать старых переменных;
- в-четвёртых, нужно не забыть выполнить обратную замену.
Основные свойства степеней
К оглавлению…
При решении иррациональных уравнений необходимо помнить много свойств степеней и корней. Перечислим ниже основные из них. У математических степеней есть несколько важных свойств:



Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень. Ну а основное свойство отрицательной степени записывается следующим образом:

Основные свойства математических корней
К оглавлению…
Математический корень можно представить в виде обычной степени, а затем пользоваться всеми свойствами степеней приведёнными выше. Для представления математического корня в виде степени используют следующую формулу:

Тем не менее можно отдельно выписать ряд свойств математических корней, которые основываются на свойствах степеней описанных выше:
Для арифметических корней выполняется следующее свойство (которое одновременно можно считать определением корня):
Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство (из под корня нечетной степени можно выносить знак «минус»):
Так как значение корня четной степени может быть только неотрицательным, то для таких корней имеется следующее важное свойство:
Итак всегда нужно помнить, что под корнем четной степени может стоять только неотрицательное выражение, и сам корень тоже есть неотрицательное выражение. Кроме того, нужно отметить, что если используется запись со значком математического корня, то показатель степени этого корня может быть только целым числом, причем это число должно быть больше либо равно двум:
Основные свойства квадратного корня
К оглавлению…
Квадратным корнем называется математический корень второй степени:
Квадратный корень можно извлечь только из неотрицательного числа. При этом значение квадратного корня также всегда неотрицательно:

Для квадратного корня существует два важных свойства, которые важно очень хорошо запомнить и не путать:
Если под корнем стоит несколько множителей, то корень можно извлекать из каждого из них по-отдельности. При этом важно понимать, что каждый из этих множителей по-отдельности (а не только их произведение) должны быть неотрицательными:
Обратите внимание на другой случай использования последнего свойства. Если под корнем квадратным имеется произведение двух отрицательных величин (т.е. по итогу величина положительная, а значит корень существует), то этот корень раскладывается на множители следующим образом:
educon.by
Методы решения иррациональных уравнений
Основные понятия
Опеределение 1. Уравнение f(x) = g(x) называется иррациональным, если функции f(x) и g(x) – алгебраические и по крайней мере одна из них иррациональна относительно x (т.е. содержит переменную x в подкоренном выражении).
Основным техническим приемом, который используется при решении иррациональных уравнений, является возведение обеих частей уравнения в одну и туже степень. Если рассматривать уравнения над полем действительных чисел, то это преобразование регулируется следующими теоремами.
Теорема 1. Уравнение.
Эквивалентно уравнению
Теорема 2. Уравнение.
Эквивалентно смешанной системе:
Пример 1. Решить уравнение
Возведем обе части уравнения в четвертую степень:
Корень x=2 удовлетворяет этому неравенству.
Проверка:
Ответ: 2.
Иррациональные уравнения, если неизвестное находится в подкоренном выражении корня четной степени, имеют, как правило, ограниченную область допустимых значений (ОДЗ). ОДЗ иррационального уравнения определяется условием: Подкоренное выражение корня четной степени должно быть неотрицательным.
Метод уединения радикала
Суть этого метода состоит в следующем. Радикал (корень) оставляют в одной части уравнения, а остальные члены уравнения переносят в другую часть. После этого обе части уравнения возводят в степень, показатель которой равен показателю уединенного радикала. Если уравнение содержит несколько радикалов, то процедура уединения производится над одним из них, после чего повторяется вплоть до полного избавления уравнения от корней.
Пример 2. Решить уравнение
Найдем ОДЗ.
, ,
Решим уравнение.
,
Очевидно, что оба корня входят в ОДЗ, но x=13 не удовлетворяет неравенству x < 8, а следовательно, этот корень посторонний.
Проверка:
Ответ: 5.
Метод замены переменной
Суть метода замены переменной (метод этот универсален и применяется отнюдь не только к иррациональным уравнениям) состоит в том, что некоторое выражение заменяется новой переменной, в результате чего получаем более простое уравнение. Решим это уравнение, выполняем обратную замену и получаем уравнение либо объединение уравнений (в зависимости от количества корней уравнения с новой переменной).
1) Уравнение вида
При решении уравнений этого типа напрашивается замена:
Пример 3. Решить уравнение.
Так как
Уравнение примет вид:
Сделаем замену:
Получим:
Очевидно, что так как:
Противоречит смыслу замены уравнение:
Не может иметь решений, подставим:
Проверка:
Ответ: 64.
Метод приведения иррационального уравнения к системе уравнений
Суть этого метода состоит в том, что два иррациональных выражения обозначаются двумя различными переменными, в результате чего мы получаем систему двух уравнений с двумя неизвестными (в принципе, возможна и замена, приводящая к системе с большим количеством неизвестных).
Пример 4. Решить уравнение.
Сделаем замену:
Поскольку левые части обоих равенств одинаковы, мы вправе приравнять их правые части:
Второе уравнение системы получим, выполнив замену в уравнении:
Решим систему:
Решим уравнение:
Система имеет два решения:
Выполним обратную замену:
Таким образом,
Решение для a и b должны были получиться одинаковыми.
Сделаем проверку, хотя ОДЗ уравнения – множество всех действительных чисел, а в процессе решения мы не прибегали к преобразованиям, которые могли бы привести к появлению посторонних корней.
Ответ:
Список литературы
- Бесчетнов В.М. Математика: Курс лекций для учащихся 7-11 классов: в 2-х т.: Т.1. – М.: Демиург, 1994. – 288 с.
- Гайшут О.Г., Литвиненко Г.М. Алгебра. Решение задач и упражнений. – Киев: “Магистра – S№”, 1997. – 256 с.
- Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер: Пособие для школьников и абитуриентов. – М.: Илекса, Хариков: Гимназия, 1998. – 320 с.
- Олехник С.Н., Потапов М.К., Пасиченко П.И. Уравнения и неравенства. Нестандартные методы решения. – М.: Издательство Фактория, 1997. – 217 с.
- Черкасов О.Ю., Якушев А.Г. Математика: интенсивный курс подготовки к экзамену. – М.: Рольф, 1997. – 384 с.
urok.1sept.ru
Методическая разработка по алгебре на тему: Решение сложных иррациональных уравнений и систем, содержащих иррациональные уравнения. Профильный уровень. 11 класс
Болявина Наталья Сергеевна
Учитель математики
ГБОУ СОШ № 756 г. Москвы
Разработка урока по алгебре и началам анализа в 11 классе
(профильный уровень)
Тема: «Решение сложных иррациональных уравнений и систем, содержащих иррациональные уравнения».
Цель урока: формирование умений и навыков решения сложных иррациональных уравнений и систем, содержащих иррациональные уравнения.
Ход урока.
- Организационный момент (1 минута).
- Проверка домашнего задания (3 минуты).
Цель: актуализация знаний. Ответы и решение сложного уравнения выписаны на доске.
Обозначим
Ответ:
- Решение задач (15 минут).
Рассмотреть условия равенства нулю произведения двух сомножителей.
Пример 1. Решить уравнение .
Решение.
Разложим на множители.
Найдём область определения выражения
.
Ответ: 1;2;3.
Пример 2. Решить уравнение графическим способом.
Решение.
Иногда при решении иррационального уравнения полезно использовать графики. Построим в одной системе координат графики функций и
Графики пересекаются в точке .
Ответ: 6.
Пример 3. Решить систему уравнений
Решение.
Замена: , .
Решим второе уравнение.
Вернёмся к замене.
— нет решений.
Ответ: .
Пример 4. Решить систему уравнений.
Решение.
Применим метод умножения.
Подставив значение 4 вместо y во второе уравнение исходной системы, получим иррациональное уравнение с одной переменной:
Значение -5 не удовлетворяет уравнению (*), значение 5 – удовлетворяет. Получили x=5, y=4. Проверка подстановкой найденных значений в исходную систему убеждает нас в том, что пара (5;4) – решение заданной системы.
Ответ: (5;4).
IV. Самостоятельная работа обучающего характера (12 минут).
Вариант I. а) ; б) ; в) | Вариант II. а) ; б) ; в) | Вариант II. а) ; б) ; в) . |
Решение самостоятельной работы (ВариантII).
а)
Ответ:
б)
Проверка:
не является корнем уравнения, т.к. выражение не имеет смысла.
Ответ: 7.
в)
Обозначим
не удовлетворяет условию
Вернемся к обозначениям:
Ответ: (1;4).
- Анализ результатов самостоятельной работы (10 минут).
Проверка правильности решений на доске. Анализ типичных ошибок, допущенных учащимися.
- Итог урока. Выставление оценок за самостоятельную работу (2 минуты).
- Домашнее задание. Инструктаж по домашнему заданию (2 минуты).
Решить систему уравнений.
а)
б)
Решить уравнение:
.
Список использованных источников информации:
- Виленкин Н.Я., Сурвилло Г.С. и др. Алгебра. 9 класс. С углубленным изучением математики: учебник. – 7-е изд. — М.: Просвещение, 2006. — 368 с.
- Колмогоров А.Н. и др. Алгебра и начала математического анализа. 10-11 классы: учебник. – 17-е изд. — М.: Просвещение, 2008. — 384 с.
- Мордкович А.Г. и др. Алгебра и начала математического анализа. 11 класс. Профильный уровень: учебник. – 3-е изд., стер. — М.: Мнемозина, 2009. — 264 с.
- Мордкович А. Г. Алгебра. Углубленное изучение. 9 касс: учебник. – 2-е изд., стер. – М.: Мнемозина, 2006. – 296 с.
nsportal.ru
Методы решений иррациональных уравнений
Актуализация знаний.
1 способ. Введение новой переменной
Метод замены переменной или метод подстановки очень часто используется при решении иррациональных уравнений и неравенств. Он позволяет значительно упростить решение, разбить его на самостоятельные этапы. Решить уравнение. 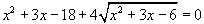 .
.
Решение.

Проверка:
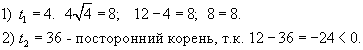
Выполняем обратную подстановку
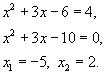
Ответ: -5; 2.
2 способ. Исследование ОДЗ.
Решить уравнение. 
Решение. Замечаем, что ОДЗ уравнения состоит из одной точки х=1. Проверкой убеждаемся, что х=1 – решение уравнения.
Ответ: 1.
3 способ. Умножение обеих частей уравнения на сопряженный множитель.
Решить уравнение 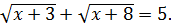
Решение. Умножим обе части уравнения на 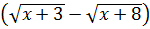 .
.
Получим,  .
.
Имеем, 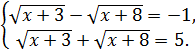
Отсюда, 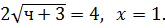
Проверкой убеждаемся, что х = 1 является корнем данного уравнения.
Ответ: 1.
4 способ. Сведение уравнения к системе рациональных уравнений с помощью введения переменной.
Решить уравнение 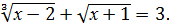
Решение. Положим 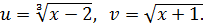 Тогда u+v=3. Так как u3=x-2, v2=x+1, то v2 – u3 =3. Итак, в новых переменных имеем
Тогда u+v=3. Так как u3=x-2, v2=x+1, то v2 – u3 =3. Итак, в новых переменных имеем
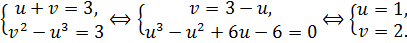
Значит, х=3.
Ответ: 3.
5 способ. Выделение полного квадрата
Решить уравнение 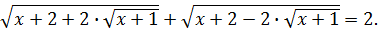
Решение. Заметим, что
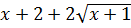 =
= 2,
2,
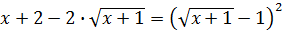 .
.
Следовательно, имеем уравнение

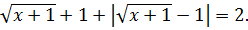
Данное уравнение равносильно совокупности двух систем:
 или
или 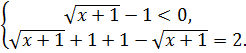
Решением первой системы будет х=0, решением второй системы – все числа, удовлетворяющие неравенству 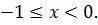
Ответ: [- 1: 0].
6 способ. Использование ограниченности выражений, входящих в уравнение
Решить уравнение 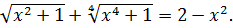
Решение.
Так как 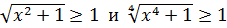 для
для 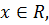 то левая часть уравнения не меньше двух для
то левая часть уравнения не меньше двух для 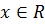 , а правая часть
, а правая часть 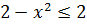 для
для 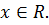 Поэтому уравнение может иметь корнями только те значения х, при которых
Поэтому уравнение может иметь корнями только те значения х, при которых 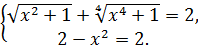
Решая второе уравнение системы, найдем х=0. Это значение удовлетворяет и первому уравнению системы. Итак, х=0 – корень уравнения.
Ответ: 0.
7 способ: Использование свойств монотонности функций.
Решить уравнение 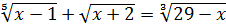 .
.
Р
y


 ешение. Если функция u(x) монотонная, то уравнение и(х) = А либо не имеет решений, либо имеет единственное решение. Отсюда следует, что уравнение и(х) = v(x), где и(х) — возрастающая, a v(x) – убывающая функции, либо не имеет решений, либо имеет единственное решение.
ешение. Если функция u(x) монотонная, то уравнение и(х) = А либо не имеет решений, либо имеет единственное решение. Отсюда следует, что уравнение и(х) = v(x), где и(х) — возрастающая, a v(x) – убывающая функции, либо не имеет решений, либо имеет единственное решение.у
v(x)
v(x)

u(x)

u(x)

x
x
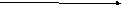
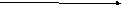
Функции 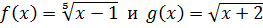 , их сумма возрастающая функция на области определения уравнения. Функция
, их сумма возрастающая функция на области определения уравнения. Функция  убывает на ОДЗ уравнения. Подбором находим, что х=2 и оно единственно.
убывает на ОДЗ уравнения. Подбором находим, что х=2 и оно единственно.
Ответ: 2.
8 способ. Использование векторов.
Решить уравнение 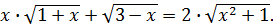
Решение. ОДЗ: 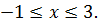 Пусть вектор
Пусть вектор 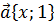 ,
, 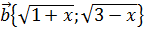 . Скалярное произведение векторов
. Скалярное произведение векторов  — есть левая часть. Найдем произведение их длин
— есть левая часть. Найдем произведение их длин
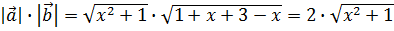 . Это есть правая часть. Получили
. Это есть правая часть. Получили 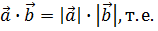 векторы
векторы  — коллинеарны.
— коллинеарны.
Отсюда 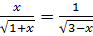 .
.
Возведем обе части в квадрат. Решив уравнение, получим х = 1 и  .
.
Ответ: х = 1 и  .
.
Работа в группах
Класс делится на группы. С первой решаем вместе типичные уравнения у доски. Вторая, третья и четвертая группы выбирают себе серию уравнений по уровню сложности. При необходимости учитель отвечает на вопросы учащихся.
Первая группа:
- Вторая группа:
Третья группа:
Письменная самостоятельная работа с последующей проверкой
Ответ: -5, -6, -8, -9.

Ответ: 1; 2; 10

Ответ: 1.

Ответ: 2

Ответ:

 -25
-25
Ответ: 6561.
Итог урока
Какие методы использовали при решении уравнений?
Какой из методов вам понравился больше всего и почему?
Рефлексия
Выбери из предложенных рисунков тот, который соответствует твоему настроению после пройденного урока и отметь его.



Домашнее задание
x=2
infourok.ru
Решение иррациональных уравнений


Маршрут урока:
истории
иррациональных
чисел
3. Основные
приемы решения
иррациональных
уравнений.
2 . Понятие
иррационального
уравнения
4 . Методы
решения
иррациональных
уравнений.
6 . Примеры
для самостоятельного
решения.
5. Примеры
решения
уравнений
различными
методами .

Иррациональными называются уравнения, в которых переменная содержится под знаком корня (радикала) или под знаком операции возведения в дробную степень.
Примеры иррациональных уравнений:

Основная идея при решении уравнений данного типа – это освобождение их от иррациональности .
Ее можно достичь путем совместного возведения обеих частей в нужную степень.

Либо путем извлечения корня из соответствующей степени выражения.

При возведении обеих частей уравнения в нечетную степень (3,5,7,..) выполняется
равносильное
преобразование уравнения, поэтому посторонние решения не появляются!

Пример решения уравнения:
Ответ: 0; 1.

Возведение обеих частей уравнения в одну и ту же
четную степень является неравносильным преобразованием уравнений, поэтому в решении могут появляться посторонние корни.

Для отсеивания посторонних корней необходимо выполнять проверку или находить ОДЗ .
Рассмотрим примеры решения подобных уравнений:

Возведем обе части уравнения в квадрат:

Выполним проверку:
Ответ: 2.

Найдем ОДЗ:
х
5

Аналогично рассмотренному примеру возведем обе части уравнения в квадрат и решим уравнение:



Также при решении иррациональных уравнений
необходимо учитывать не равносильность преобразований корня четной степени вида:

При разбиении подкоренного выражения возможна потеря корней из-за сужения ОДЗ.

При слиянии корней возможно получение посторонних корней из-за расширения исходного ОДЗ .
Посторонние корни, которые появляются при слиянии корней из-за расширения ОДЗ отбрасывают при их проверке подстановкой в исходное уравнение.

Алгоритм решения
иррациональных уравнений основными методами :
- Найти ОДЗ или после нахождения корней уравнения выполнить проверку.
- Возвести в одну и ту же степень обе части уравнения.
- Решить полученное уравнение.
- Записать ответ.

Методы решения иррациональных уравнений:
- Уединение корня в одной из частей уравнения, а потом возведение обеих частей уравнения в одну и ту же степень.
- Введение новой переменной и решение полученного уравнения любым из известных методов.
- Умножение на сопряженное выражение.
- Метод применения свойств функции.
- Уравнения приводимые к уравнениям с модулями.
6. Искусственные приемы решения иррациональных уравнений.

Уединение корня в одной из частей уравнения, а потом возведение обеих частей уравнения в одну и ту же степень.
Решить уравнение:
Преобразуем уравнение, оставив корень в правой части равенства:
Найдем ОДЗ:
х
1

Возведем обе части в квадрат и приравняем уравнение к нулю.
Ответ: 0.

Введение новой переменной и решение полученного уравнения любым из известных методов.
Решить уравнение:
тогда уравнение принимает вид:
Возведем обе части уравнения дважды в квадрат и преобразуем его:

Возвращаясь к исходной переменной получаем уравнение:
Ответ: -1; 2.

Умножение на сопряженное выражение.
Решить уравнение:

Итак, левая часть уравнения равна 6х , значит наше уравнение принимает вид:
то есть оно имеет решения, если:
при этом
или
замечаем, что

Для упрощения решения, сложим полученное и исходное уравнения, в итоге получаем уравнение следствие:
Решаем его методом возведения в квадрат обеих частей уравнения и получаем:
Выполнив проверку, поочередно подставляя, найденные значения
в заданное уравнение , убеждаемся, что ему
удовлетворяет только значение
Ответ: 4.

Метод применения свойств функции.
№ 1. Решить уравнение:
Для решения воспользуемся свойствами монотонности функции : сумма двух возрастающих функций является возрастающей функцией и всякая монотонная функция каждое свое значение принимает лишь при одном значении аргумента .
(При решении данного уравнения основными методами необходимо будет дважды обе части уравнения возводить во вторую степень.)
Значит, данное уравнение, если имеет корень, то только один . Подбором легко найти, что х=5.
Ответ: 5.

Метод применения свойств функции.
№ 2. Решить уравнение:
(Попытка решить данное уравнение основными методами к успеху не приведет.)
Найдем ОДЗ данного уравнения:

Значит, данное уравнение, имеет корни только из данного промежутка. Проверяя целые значения (1,2,3) , находим, что х=2.
Докажем, что уравнение не имеет других корней.
Ответ: 2.

Уравнения приводимые к уравнениям с модулями.
Решить уравнение:
Каждое подкоренное выражение можно свернуть, как квадрат двучлена:
уравнение принимает вид:
При
откуда

При
уравнение принимает вид:
откуда
уравнение принимает вид:
При
и не имеет корней.
уравнение принимает вид:
При
откуда
Ответ: -6; 5.

Искусственные приемы решения иррациональных уравнений.
Решить уравнение:
Уединение корня и возведение обеих частей уравнения в квадрат привело бы к громоздкому уравнению. Но, если внимательно посмотреть, то можно заметить, что уравнение легко сводится к квадратному, если его обе части умножить на 2. Получаем:

Введем новую переменную, пусть
Получаем квадратное уравнение
Его корни:
Значит, исходное уравнение равносильно совокупности:

Второе уравнение корней не имеет, а из первого следует, что корни уравнения равны:
Так как совокупность уравнений равносильна начальному уравнению, причем уравнение два корней не имеет, то найденные корни можно проверить подстановкой в первое уравнение совокупности.
Эта подстановка показывает, что оба значения х являются корнями этого уравнения, а значит и заданного уравнения.
Ответ: -2; 3,5.

Примеры для самостоятельного решения дома :

Если натуральные числа возникли в процессе счета, а рациональные — из потребности оперировать частями целого, то вещественные числа предназначены для измерения непрерывных величин. Расширение запаса рассматриваемых чисел привело к множеству вещественных чисел, которое помимо чисел рациональных включает также другие элементы, называемые иррациональными числами.


Первоначально термины “рациональный” и “иррациональный” относились не к числам, а к соизмеримым и соответственно не соизмеримым величинам, которые пифагорейцы называли выразимыми и невыразимыми.
Несоизмеримые величины, были названы еще в древности иррациональными.

Гиппас из Метапонта
(ок. 500 гг. до н. э.)
Он показал, что если гипотенуза равнобедренного прямоугольного треугольника содержит целое число единичных отрезков, то это число должно быть одновременно и четным, и нечетным.
Первое доказательство существования иррациональных чисел приписывается Гиппасу, пифагорейцу, который нашёл это доказательство, изучая длины сторон пентаграммы. Гиппас обосновал, что не существует единой единицы длины.
32

Существует легенда, что Гиппас совершил открытие, находясь в морском походе, и был выброшен за борт другими пифагорейцами «за создание элемента вселенной, который отрицает доктрину, что все сущности во вселенной могут быть сведены к целым числам и их отношениям».
Открытие Гиппаса поставило перед пифагорейской математикой серьёзную проблему, разрушив лежавшее в основе всей теории предположение, что числа и геометрические объекты едины и неразделимы.

Математики Индии, Ближнего и Среднего Востока, развивая алгебру, тригонометрию и астрономию, не могли обойтись без иррациональных величин, которые, однако, длительное время не признавали за числа.

В современных учебных руководствах основа определения иррационального числа опирается на идеи ал-Каши, Стевина и Декарта об измерении отрезков и о неограниченном приближении к искомому числу с помощью бесконечных десятичных дробей. Однако обоснованием свойств действительных чисел и полная теория их была разработана лишь в XIX в.
Джамшид ибн Мас‘уд ибн Махмуд Гияс ад-Дин ал-Каши
Рене Декарта
Симон Стевин


Современный знак корня произошел от обозначения, примяемого немецкими математиками XV-XVI вв.:
Скорее всего, в последствии от таких обозначений как раз и образовался знак V , близкий по записи к знакомому школьникам современному знаку, но без верхней черты.

Автором этого знака был преподаватель математики из Вены, уроженец Чехии Криштоф Рудольф. Эти знаком пользовались А.Жирар, С.Стевин
V (2) или V (3).
В 1626г. нидерландский математик А. Жирар видоизменил знак корня Рудольфа и ввел совсем близкое к современному обозначение

Такая форма записи начала вытеснять прежний знак R . Однако некоторое время знак корня писали разрывая верхнюю черту, а именно так:
И только в 1637 году Рене Декарт соединил горизонтальную черту с галочкой, применив новое обозначение в своей книге «геометрия».
32

Блиц опрос.
- Какие уравнения называются иррациональными?
2. Какой метод является основным при решении иррациональных уравнений?
3. Всегда ли необходимо выполнять проверку или находить ОДЗ?
4. Какие еще методы решения иррациональных уравнений вы запомнили?

Используемые источники:
1. http://www.gov.uz/ru/helpinfo/science/245
2. http://ru.wikipedia.org/wiki/Заглавная_страница
3. А.Г. Мордкович, П.В. Семенов «Алгебра и начала анализа 11 класс», профильный уровень, часть 1; Москва; «Мнемозина»; 2007 г.
4. Ю. Н. Макарычев «Алгебра 9«, дополнительные главы к школьному учебнику, учебное пособие для учащихся школ с углубленным изучением математики; Москва; Просвещение; 1997 г.
5. http://www.ankolpakov.ru/2011/03/04/o-znake-kvadratnogo-kornya/
videouroki.net
Методы решения иррациональных уравнений
Методы решений иррациональных уравнений
1. Решить уравнение
Решение. Построим графики функций y = 3x – 2.
2. Сколько решений имеет уравнение
Решение.
2 – x2 = (x – 1)2, 2 – x2 = x2 – 2x + 1, 2x2 – 2x – 1 = 0.
D = 4 + 2·4 = 12;
2 – x2 і 0.
2 – x2 = (–x(x + 1))2, 2 – x2 = x2 + 2x – 1, 2x2 + 2x – 1 = 0;
Графический способ решения:
Ответ: 2 корня.
3. Решить уравнение
ОДЗ: 3 – x >= 0, x <= 3; x – 1 >= 0, x >= 1.
Решение. Подбором находим, что уравнение имеет корень x = 2. Так как в области определения уравнения (то есть на отрезке [1; 3]) функция возрастает, а функция убывает, то других корней уравнение не имеет. Итак, x = 2 — единственный корень уравнения.
4. Решить уравнение
Решение. Замечаем, что x1 = 1 — корень уравнения (2). Но, как и в примере 3, утверждать, что это единственный корень уравнения, мы пока не можем, поскольку и функция и функция возрастают в области определения уравнения (2), то есть на луче Если в примере 3 нам удалось преобразовать уравнение к такому виду, что одна часть представляла собой убывающую, а другая — возрастающую функцию, то здесь нам этого не удается. Поступим по-другому.
Найдем производные функции и Вычислим их в точке x = 1 (в точке пересечения графиков этих функций). Имеем: Далее, Так как то графики функций y1(x), y2(x) имеют общую касательную в точке (1; 1). Но поскольку функция y1(x) выпукла вниз, а функция y2(x) выпукла вверх, то их графики расположены по разные стороны от общей касательной, а поэтому уравнение y1(x) = y2(x) имеет только один корень. Итак, x = 1 — единственный корень уравнения (2).
Ответ: 1.
Векторный метод
5. Решить уравнение векторным методом.
Решение.
Так как то то есть и а следовательно,
Ответ:
6. Решить систему иррациональных уравнений используя теорему Виета и метод подстановки.
Решение. a >= 0, b >= 0.
По теореме Виета a = 5, b = 3.
a + b = 5, a·b = 15; x + 2 = 25, y – 2 = 3; x = 23, y = 5.
Ответ: (23; 5), (11; 27).
7. Сколько решений в зависимости от значения параметра a имеет уравнение
Решение. Построим графики функций y = ax. Графиком функции является окружность R = 1. Найдем точки пересечения функции с осью Ox, решая уравнение y = 0: 4x – x2 – 3 = 0, x2 – 4x – 3 = 0. По теореме Виета x1 = 1, x2 = 3.
Ответ: если a < 0 или a > 1 — нет решений; если a = 1 — одно решение; если 0 <= a < 1 — два решения.
Методы решений иррациональных неравенств
Неравенство вида кроме общего метода можно решать графическим методом. Иногда удается решить неравенство практически устно, если прикинуть эскиз графиков его правой и левой частей. Тогда окажется, что неравенства вида могут быть решены с помощью единственного уравнения. При таком способе необходимо только найти точки пересечения графиков функций, стоящих справа и слева в неравенстве.
1. Решить неравенство
Решение. Построим графики функций y = x + 1, Посмотрим, где первый график выше второго. Для нахождения решения остается решить уравнение D = 9; x1 = –2, x2 = 1.
Графики удобно использовать, если, например, необходимо найти количество решений в задачах с параметром или без него.
Ответ: x [–3; 1).
2. Указать количество целых чисел, входящих в решение неравенства
Решение. Построим графики функций y = 2x + 5. Посмотрим, где первый график выше второго. Видно, что решением является отрезок [–5; x0]. Для нахождения решения остается только найти x0, то есть решить уравнение Теперь можно получить решение исходного неравенства: В это отрезок входит шесть целых чисел от –5 до 0.
Ответ: 6.
3. Решить неравенство
Решение. ОДЗ: | x + 6 | = x + 6, | x – 2 | = 2 – x. Исходное неравенство примет вид
Решим данное неравенство методом интервалов, определив, при каких значениях x обращаются в нуль числитель и знаменатель дроби.
1. 1 – x = x2 + 2x + 1, x2 + 2x = 0, x = 0, x = –3;
2. 9x + 45 = x2 – 10x + 25, x2 – 19x – 20 = 0, x1 = 20, x2 = –1;
x [–5; 1], 0 [–5; 1], 20 [–5; 1].
Ответ: [–3; –1] c [0; 1].
urok.1sept.ru
Иррациональные уравнения и неравенства
Иррациональные уравнения
Рассмотрим теперь понятие рационального неравенства.
Определение 1
Уравнение, в котором неизвестная величина находится под радикалами или в дробных степенях будем называть иррациональным.
Здесь надо всегда помнить о том, что не под любым корнем может быть отрицательное число. В связи с этим здесь будет появляться понятие области определения уравнения (ООУ). Оно заключается в том, что под корнями с четными степенями не может быть отрицательных величин.
Решение классических иррациональных уравнений заключается в следующем: Вначале мы находим ООУ, с помощью простейших преобразований приводим уравнение к виду $\sqrt[n]{P(x)}=\sqrt[n]{Q(x)}$. Возводим в $n$-ю степень и находим корни получившегося уравнения. Выкидываем корни, не попадающие в ООУ.
Пример решения иррационального уравнения
Пример 1
Решить
$\sqrt[5]{x^2-4x+4}-\sqrt[5]{x-2}=2$
Решение.
Применяя формулу квадрата суммы, получим:
$\sqrt[5]{(x-2)^2}-\sqrt[5]{x-2}-2=0$
Так как степень корня нечетна, то нам здесь не требуется нахождения ООУ.
Сделаем замену $\sqrt[5]{x-2}=t$, получим
$t^2-t+2=0$
Это уравнение имеет своими корнями числа $-1$ и $-2$.
Получим два уравнения:
$\sqrt[5]{x-2}=-1$ и $\sqrt[5]{x-2}=-2$
$x-2=-1$ и $x-2=-32$
$x=1$ и $x=-30$
Ответ: $1$ и $-30$.
Иррациональные неравенства
Рассмотрим теперь понятие иррационального неравенства.
Определение 2
Неравенство, которое имеет вид $\sqrt[n]{P(x)}>(≥)\sqrt[n]{Q(x)}$ будем называть иррациональным неравенством.
Чаще всего неравенства решаются методом промежутков (интервалов). В основе этого метода лежит следующее рассуждение.
Пусть нам дана функция $f(x)=\frac{(x-n)(x-m)}{(x-l)(x-k)}$, причем $n
$x∈(-∞,n)$: Используя неравенство (1) будем получать:
$(x-n)
Четыре минуса, в общем, нам дадут плюсовое значение, то есть $f(x)>0$.
$x∈(n,m)$:
Используя неравенство (1) будем получать:
$(x-n)>0,(x-m)
Три минуса, в общем, нам дадут минусовое значение, то есть $f(x)
$x∈(m,l)$:
Используя неравенство (1) будем получать:
$(x-n)>0,(x-m)>0,(x-l)0$.
$x∈(l,k)$:
Используя неравенство (1) будем получать:
$(x-n)>0,(x-m)>0,(x-l)>0,(x-k)
Один минус дает нам минусовое значение, то есть $f(x)
$x∈(k,+∞)$:
Используя неравенство (1) будем получать:
$(x-n)>0,(x-m)>0,(x-l)>0,(x-k)>0$.
Все плюсы нам дадут плюсовое значение, то есть $f(x)>0$
Это рассуждение можно иллюстрировать на числовой прямой (рис. 1).
Эта иллюстрация называется кривой знаков и используется для решения рациональных и других неравенств $q(x)>(≥)0$ методом промежутков.
Замечание 1
На самом деле знаки на такой кривой не всегда чередуются. К примеру такое может быть при наличии в уравнение квадратного множителя.
Суммируя, получим:
Метод промежутков (интервалов)
- Вначале необходимо найти все корни уравнения $q(x)=0$ и значения, в которых область определения имеет разрыв.
- И всех полученных в пункте $1$ числовых значений составляем кривую знаков для данного уравнения.
- Записываем ответ из кривой знаков, с учетом знака неравенства.
Пример решения иррационального неравенства методом промежутков
Пример 2
Решить
$\sqrt[4]{z-1}≤\sqrt[8]{z+5}$
Решение.
Найдем ООУ:
$z-1 ≥0$ и $z+5 ≥0$
$z ≥1$ и $z ≥-5$
ООУ: $[1,∞)$.
Решим для начала следующее уравнение и найдем точки разрыва ее области определения:
$\sqrt[4]{z-1}-\sqrt[8]{z+5}=0$
$\sqrt[4]{z-1}=\sqrt[8]{z+5}$
$z^2-2z+1=z+5$
$z^2-3z-4=0$
Корни: $z=-1$ и $z=4$
Изобразим все полученные точки и ООУ на числовой прямой и построим кривую знаков:
Так как у нас знак неравенства «меньше или равно», то нам нужно выбрать промежуток со знаком минус.
Ответ: $[1,4]$.
spravochnick.ru

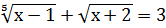
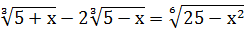
 -25
-25