Извлечение корня из большого числа

   Извлечение корня из большого числа. Дорогие друзья! В этой статье мы с вами разберём как извлекать корень из большого числа без калькулятора. Это необходимо не только для решения некоторых типов задач ЕГЭ (есть такие — на движение), но и для общего математического развития этот аналитический приём знать желательно.

Казалось бы, всё просто: разложи на множители, да извлекай. Проблемы нет. Например число 291600 при разложении даст произведение:

Вычисляем:

Есть одно НО! Способ хорош если легко определяются делители 2, 3, 4 и так далее. А что делать если число, из которого мы извлекаем корень является произведением простых чисел? Например 152881 является произведением чисел 17, 17, 23, 23.  Попробуй-ка сходу найди эти делители.

Суть рассматриваемого нами метода —  это чистый анализ. Корень при наработанном навыке находится быстро. Если навык не отработан, а просто понят подход, то немного медленнее, но всё же определяется.

Извлечём корень из 190969.

Сначала определим — между какими числами (кратными ста) лежит наш результат.

Очевидно, что результат корня из данного числа лежит в пределах от 400 до 500, так как    

400²=160000   и   500²=250000

Действительно:

Далее смотрим, где «стоит» это число: 

посредине, ближе к 160 000 или к 250 000?

Число 190969 находится примерно посредине, но все же  ближе к 160000. Можно сделать вывод, что результат нашего корня будет меньше 450. Проверим:

Действительно, он меньше 450, так как  190 969 < 202 500.

Теперь проверим число 440:

Значит наш результат меньше 440, так как 190 969 < 193 600.

Проверяем число 430:

Мы установили, что результат данного корня лежит в пределах от 430 до 440.

Далее используются свойства произведений чисел. Известно, что:

Произведение чисел имеющих на конце 1 или 9 дают число с 1 в конце. Например, 21 на 21 равно 441.

Произведение чисел имеющих на конце 2 или 8 дают число с 4 в конце. Например, 18 на 18 равно 324.

Произведение чисел имеющих на конце 5 дают число с 5 в конце. Например, 25 на 25 равно 625.

Произведение чисел имеющих на конце 4 или 6 дают число с 6 в конце. Например 26 на 26 равно 676.

Произведение чисел имеющих на конце 3 или 7 дают число с 9 в конце. Например, 17 на 17 равно 289.

Так как число 190969 заканчивается цифрой 9, то это произведение либо числа 433, либо 437.

*Только они при возведении в квадрат могут дать 9 в конце.

Проверяем:

Значит результат корня будет равен 437.

То есть, мы как бы «нащупали» верный ответ.

Как видите, максимум что потребуется это осуществить 5 действий столбиком. Возможно, вы сразу попадёте в точку, или сделаете всего три действия. Всё зависит о того, как точно вы сделаете начальную оценку числа.

Извлеките самостоятельно корень  из  148996

Такой дискриминант получается в задаче:

Теплоход проходит по течению реки до пункта назначения 336 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 5 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается через 48 часов после отплытия из него. Ответ дайте в км/ч.

Посмотреть решение

Результат корня находится между числами 300  и  400:

300²=90000       400²=160000

Действительно, 90000<148996<160000.

Суть дальнейших рассуждений сводится к тому, чтобы определить, как число 148996 расположено (отстоит) относительно этих чисел.

Вычислим разности 148996 — 90000=58996  и 160000 — 148996=11004.

Получается, что 148996 близко (на много ближе) к 160000. Поэтому, результат корня однозначно будет больше 350 и даже 360.

Далее  пробуем возводить в квадрат, например число 370. Как бы «щупаем» результат:

Можем сделать вывод, что наш результат больше 370. Далее ясно: так как 148996 оканчивается цифрой 6, то это означает, что в квадрат надо возводить число, оканчивающееся либо на 4, либо на 6. *Только эти числа при возведении в квадрат дают в конце 6.

Проверяем числа 374, 376, 384, 386, 394 …

Ответ: 386

Объективно говоря, вероятность того, что  вам попадёт подобная задача, очень мала. Но пусть этот приём  в вашем арсенале будет. Впереди вас ждёт много полезного, не пропустите!

Есть ещё метод по извлечению корня из большого числа, называют его алгоритмом Евклида. Его достоинство состоит в том, что можно извлекать корень из любого числа с необходимой точностью до десятых, сотых и тд. То есть корни неизвлекаемые в целых числах. *В будущем статья будет обязательно дополнена.

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

matematikalegko.ru

Исследовательская работа по алгебре на тему «Извлечение квадратных корней из больших чисел без калькулятора».

МБОУ «Гимназия «№ 1»

Наименование предмета: Алгебра

Исследовательская работа

Тема: Извлечение квадратных корней из больших чисел без калькулятора

Автор работы: Боронилов Никита

8 «В» класс

Руководитель:

Яновская Светлана Ивановна,

учитель математики

г. Находка

2019 г.

Оглавление

Введение 3-4 Глава 1. История квадратного корня 4 Глава 2. Способ использования таблицы квадратов двузначных чисел 5

Глава 3. Формула Древнего Вавилона 5 Глава 4. Канадский метод 5 Глава 5. Способ разложения на простые множители 6 Глава 6. Метод вычетов нечётного числа 6 Глава 7. Метод подбора угадыванием (метод оценки) 6-7 Глава 8. Метод отбрасывания полного квадрата 7 Глава 9. Извлечение квадратного корня уголком 7-9 Глава 10. Практическая часть. Диаграммы 8-9

(анкетирования среди учащихся 8-11 класса).

Заключение 10 Список литературы 11

Введение

Актуальность исследования. В этом году я изучал тему квадратные корни. Всё хорошо пока под рукой таблица квадратов, но однажды на уроке геометрии при решении задачи надо было извлечь квадратный корень из большого числа, а таблицы квадратов нет. Пришлось число разложить на простые множители. Корень был извлечён, но вопрос существуют ли другие способы для извлечения квадратного корня, остался. Я решил изучить этот вопрос глубже, чем он изложен в школьной программе.

Практическая значимость: данный материал можно использовать в 8, 9, 10, 11 классах на уроках, олимпиадах, ОГЭ и ЕГЭ.

Цель работы: найти и показать те способы извлечения квадратных корней, которыми можно будет воспользоваться, не имея под рукой калькулятора.

Задачи:

1. Изучить литературу по данному вопросу.

2. Рассмотреть особенности каждого найденного способа и его алгоритм.

3. Показать практическое применение полученных знаний и оценить

степень сложности в использовании различных способов и алгоритмов.

Объект исследования: математические символы – квадратные корни.

Предмет исследования: особенности способов извлечения квадратных корней без калькулятора.

Методы исследования:

1. Поиск способов и алгоритмов извлечения квадратных корней из больших чисел без калькулятора.

2. Сравнение найденных способов.

3. Анализ полученных способов.

Все знают, что извлечь квадратный корень из большого числа без калькулятора — это сложная задача. Когда нет под рукой калькулятора, то начинаем методом подбора стараться вспомнить данные из таблицы квадратов целых чисел, но это не всегда помогает. Также на экзаменах ОГЭ и ЕГЭ пользование калькулятором запрещено и нет таблицы квадратов целых чисел, а надо извлечь корень из чисел больше 100 или 1000.

Но изучая информацию по данной теме, я узнал, что извлекать корни из таких чисел возможно и без таблицы и калькулятора, люди научились делать это задолго до изобретения микрокалькулятора. Исследуя эту тему, я нашел несколько способов решения данной проблемы.

Глава 1. История квадратного корня

Термин корень имеет долгую и сложную историю. Извлечение квадратного корня древние греки понимали строго геометрически. При переводе греческое слово «сторона» превратилась в «мула» (основание, корень). Поэтому при переводе с индийского на арабский использовался термин «джизр» (корень растения).

Современное обозначение впервые употребил немецкий математик Кристоф Рудольф, из школы алгебраистов в 1525 году. Черта над подкоренным выражением вначале отсутствовала; её позже ввёл Декарт для иной цели (вместо скобок), и эта черта вскоре слилась со знаком корня.

Арифметическим квадратным корнем из числа a называется неотрицательное число, квадрат которого равен данному числу a.

Теорема о последней цифре квадрата числа

Если числа оканчиваются на цифру от 1 до 9 и когда мы возводим их в квадрат, то на конце полученного числа будут стоять цифры:

…1²=…1 …6²=…6

…2²=…4 …7²=…9

…3²=…9 …8²=…4

…4²=…6 …9²=…1

…5²=…5

Если в конце числа стоят цифры 2,3,7,8, то полный квадратный корень извлечь из него нельзя.

Чтобы возвести в квадрат числа, заканчивающиеся на 5. Алгоритм прост. Число до последней пятерки умножаем на следующее, т.е. это же число плюс единица и к полученному числу справа приписываем 25. Например,

15² = (1∙(1+1))25 = 225

25² = (2∙(2+1))25 = 625

85² = (8∙(8+1))25 = 7225

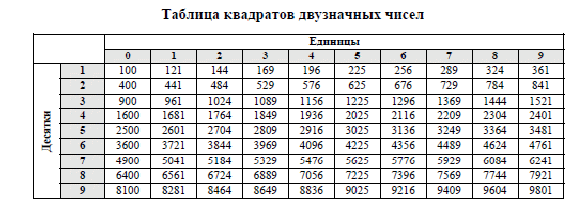
Глава 2. Способ использования таблицы квадратов двузначных чисел.

Быстро, просто, доступно на экзамене. Но сразу понятно, что корни, большие 100 уже этим способом извлечь невозможно. Способ удобен для заданий с маленькими корнями и при наличии таблицы.

Глава 3. Формула Древнего Вавилона.

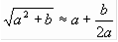
Число x представлено в виде суммы 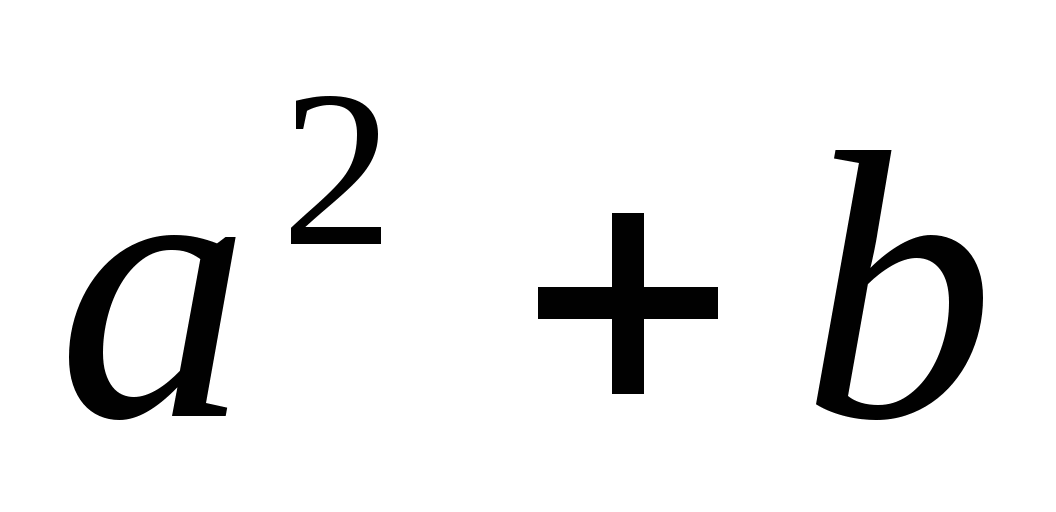, где 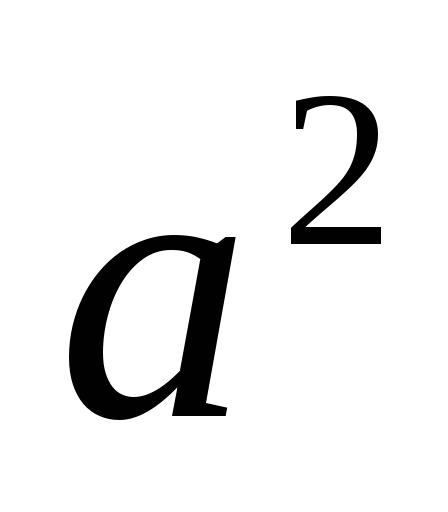ближайший к числу х точный квадрат натурального числа .

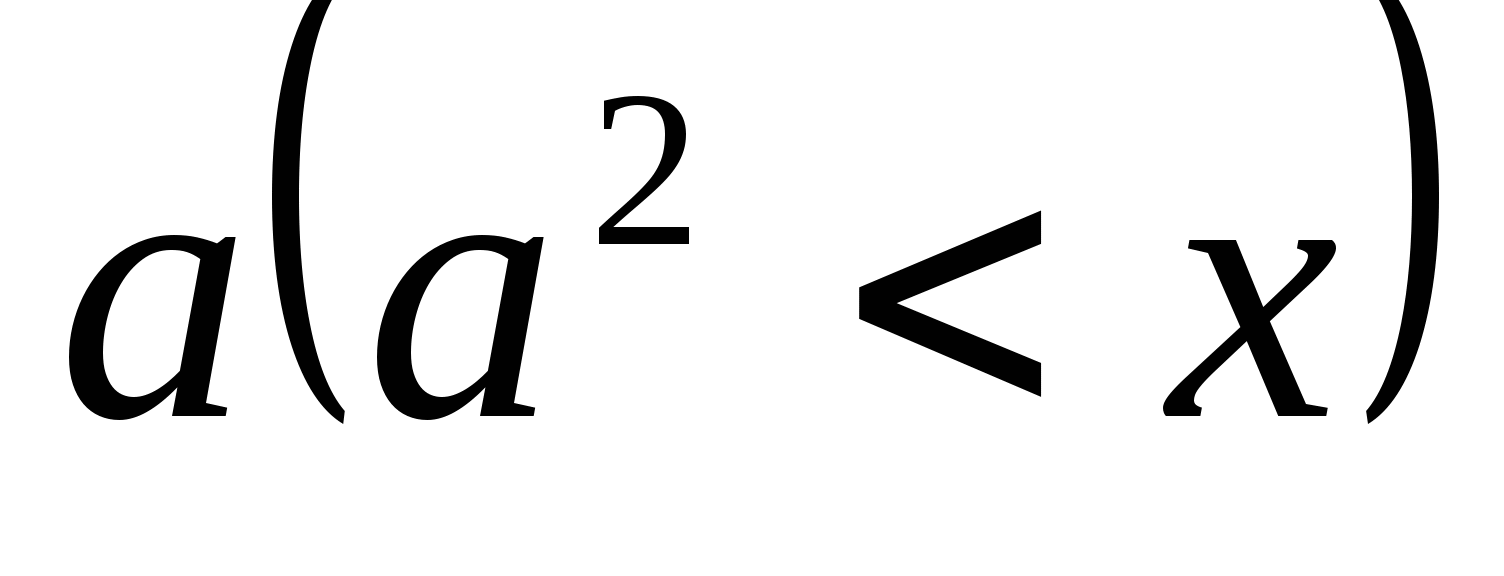Извлечем с помощью этой формулы квадратный корень, например из числа 40:

.

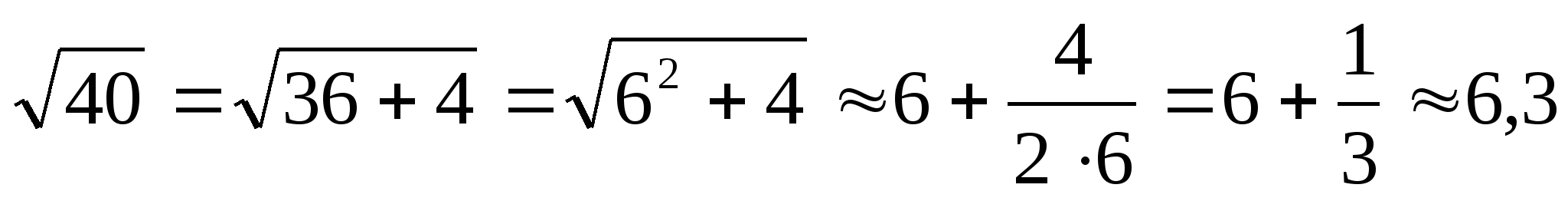Этот способ удобен для нахождения приближённого значения квадратного корня.

Глава 4. Канадский метод.

Этот быстрый метод был открыт молодыми учёными одного из ведущих университетов Канады в 20 веке. Его точность – не более двух – трёх знаков после запятой. Вот их формула: 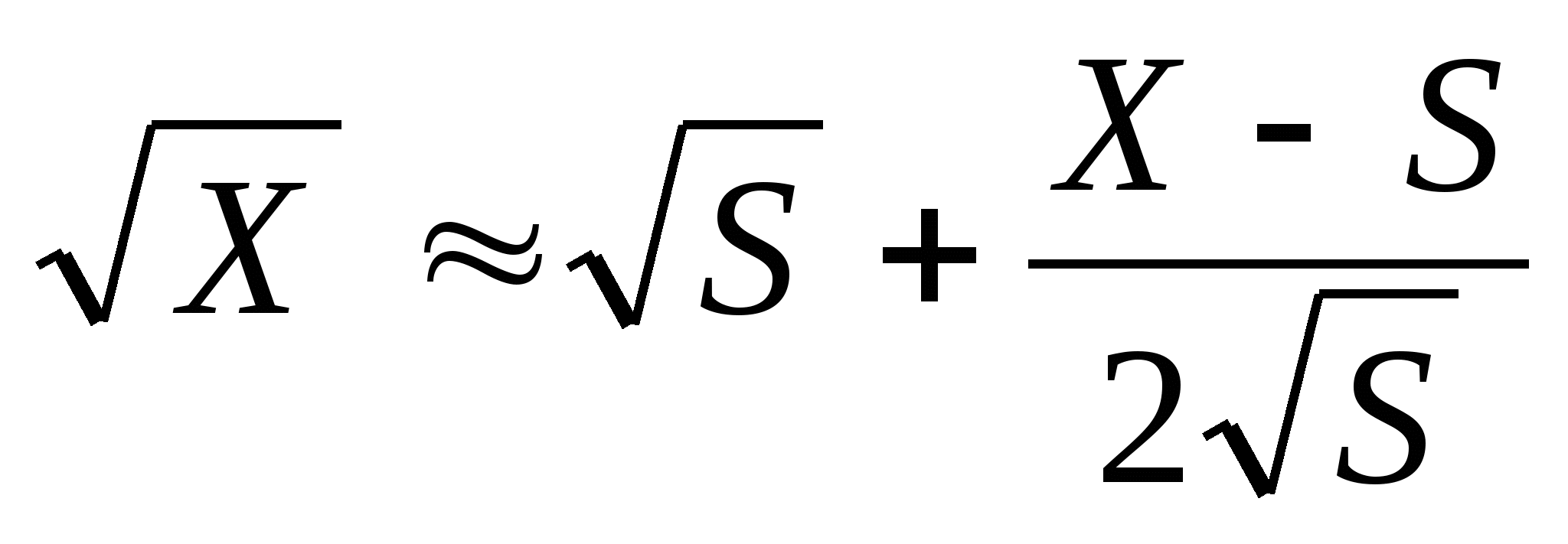, где X — число, из которого необходимо извлечь квадратный корень, а S — число ближайшего точного квадрата.

Давайте попробуем извлечь квадратный корень из 40

.

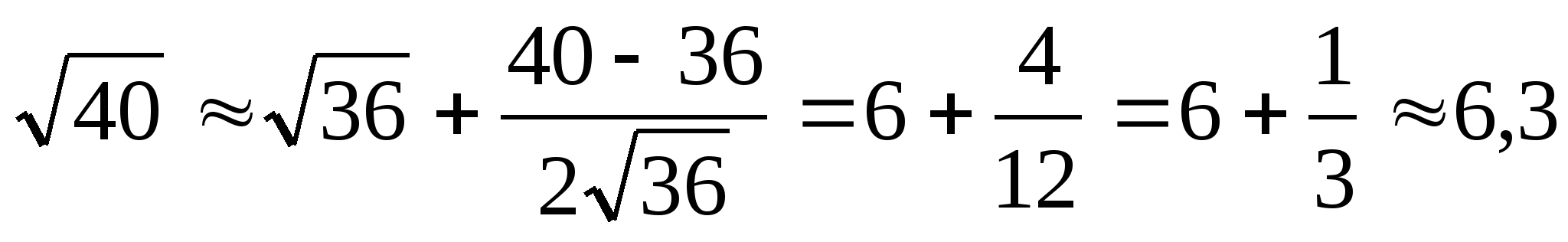
Глава 5. Способ разложения на простые множители

Для извлечения квадратного корня можно разложить число на простые множители и извлечь квадратный корень из произведения.

Таким способом принято пользоваться при решении заданий с корнями

7056

3528

1764

882

441

147

49

7

2

2

2

2

3

3

7

7

.

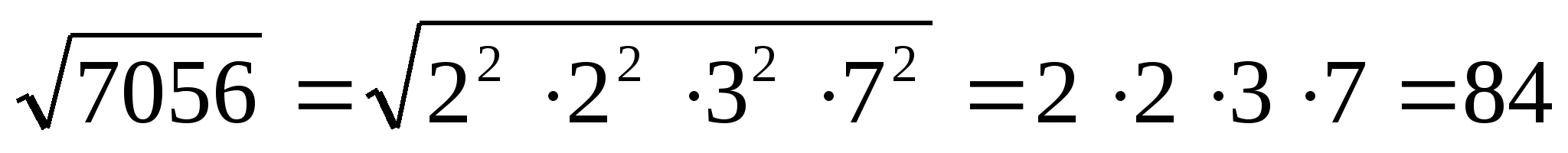Практика показывает, что очень редко предлагаются задания с полным разложением. Чаще мы видим, что корень до конца не извлечь.

Поэтому, этот способ лишь частично решает проблему извлечения без калькулятора.

Глава 6. Метод вычетов нечётного числа.

Суть метода: из подкоренного выражения нужно последовательно вычитать нечетные числа пока разность не станет равной 0 и посчитать количество вычитаний. Например, посчитаем:

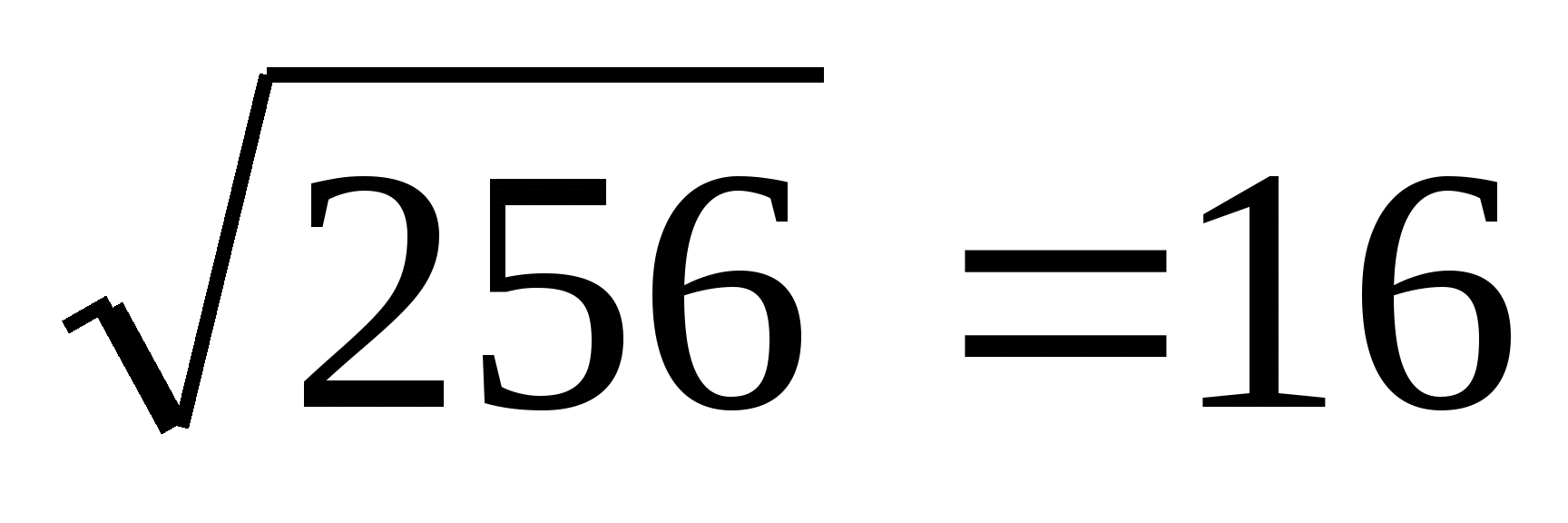
256-1, 255-3, 252-5, 247-7, 240-9, 231-11, 220-13, 207-15, 192-17, 175-19, 156-21, 135-23,

112-25, 87-27, 60-29, 31-31

Общее количество вычитаний равно 16.

Российские ученые называют этот метод извлечения арифметического квадратного корня «методом черепахи» из-за его медлительности.
Недостатком такого способа является то, что если извлекаемый корень не является целым числом, то можно узнать только его целую часть, но не точнее.

Глава 7. Метод подбора угадыванием (метод оценки).

Данный метод эффективно применяется при вычислении квадратных корней из чисел в диапазоне от 100 до 10 000.

Алгоритм извлечения квадратного корня методом оценки.

Рассмотрим пример извлечения квадратного корня из числа 7056.

Шаг №1 — ограничение корней.

6400 < 7056 < 8100,  80² < 7056 < 90², 80 <  < 90.

Шаг №2 – «отсев» лишних чисел. У нас есть 10 чисел — «кандидатов» на корень.

Квадратный корень из 7056 обязательно заканчивается на 4 или на 6, получаем:

80<<90;

=…4 или = …6

Известно, что корень лежит в пределах от 80 до 90, на котором есть только два числа, оканчивающихся на 4 и 6, это числа 84 и 86.

Шаг №3 — финальные вычисления. Итак, у нас осталось 2 числа «кандидата». Чтобы узнать, какое из них является корнем, необходимо взять «золотую середину» — число 85, и возвести его в квадрат 85² = (8∙(8+1))25 = 7225, 7225 > 7056, значит,  = 84.

Глава 8. Метод отбрасывания полного квадрата.

Этот способ применим только для извлечения квадратного корня из точного квадрата, а алгоритм нахождения зависит от величины подкоренного числа. Выделяем из числа квадрат, который оканчивается той же цифрой, что и данное число.

Извлечение корней до числа 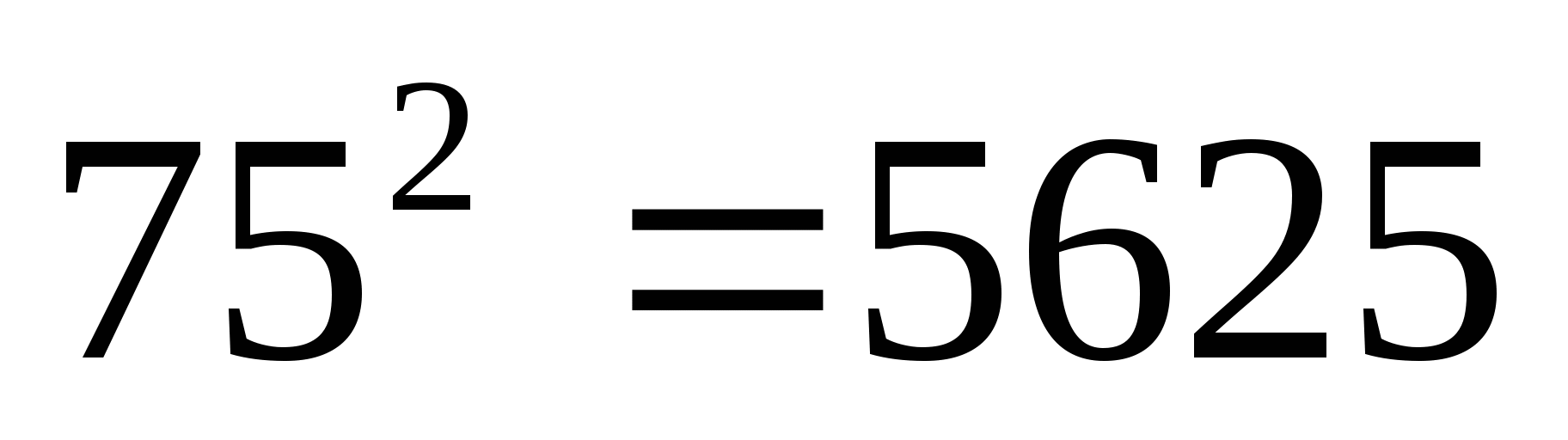. Число 2209 представим в виде суммы, выделив из этого числа квадрат 9, затем выделенный квадрат отбрасываем, к числу сотен первого слагаемого (22) прибавляем всегда 25. Получим ответ 47.

Так можно извлекать только квадратные корни до числа.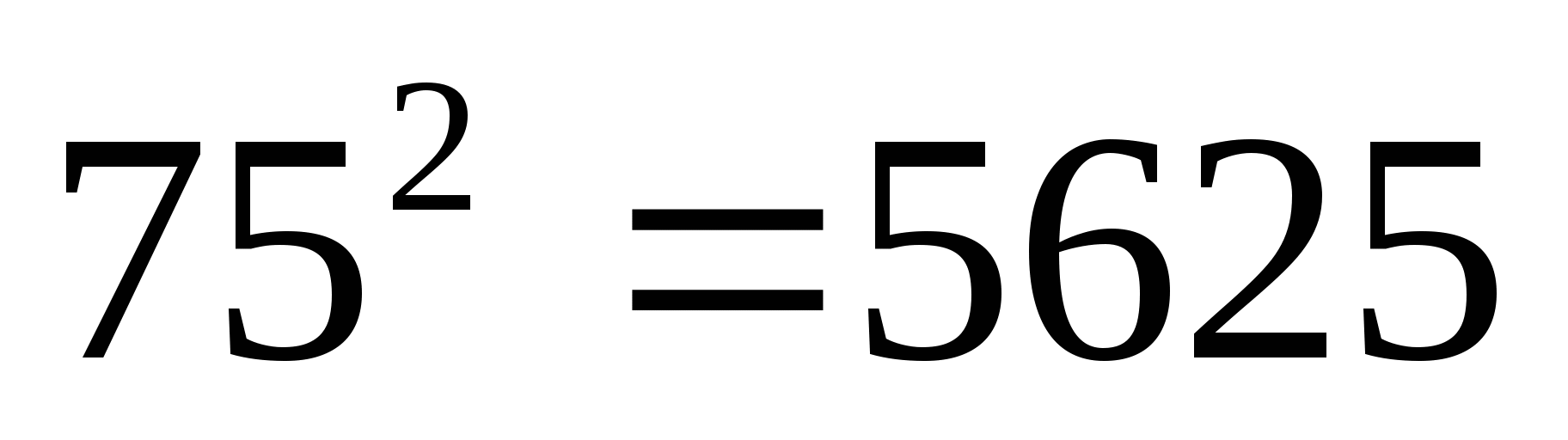

.

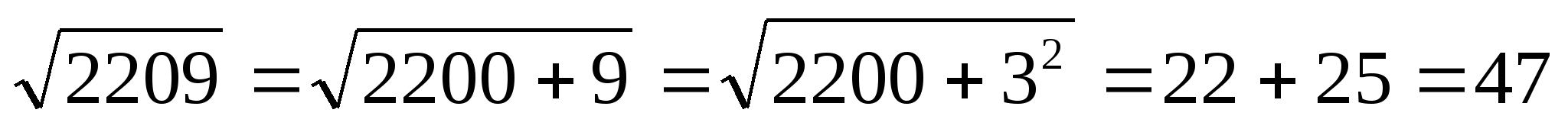Извлечение корней после 75²= 5625, вычисляются следующим образом:

.

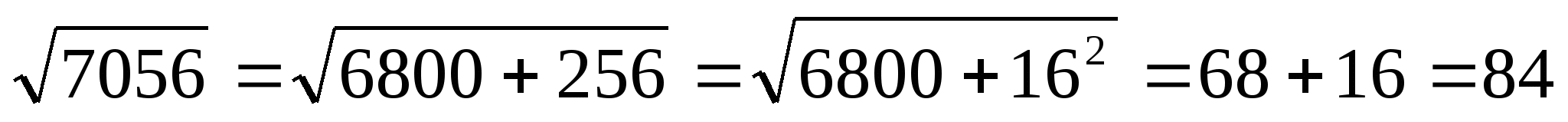Глава 9. Извлечение квадратного корня уголком.

Для извлечения квадратного корня уголком рассмотрим алгоритм:
1-й шаг. Число 7056 разбиваем на грани справа налево, каждая из которых должна содержать две цифры. Получаем две грани: .
2-й шаг. Извлекаем квадратный корень из первой грани 70, получаем 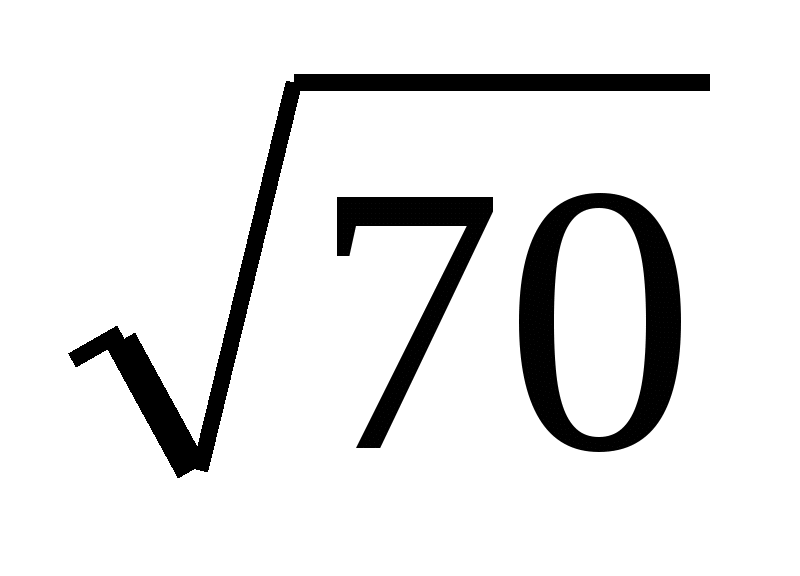≈ 8 с остатком. Цифра 8 –это первая цифра результата.
3-й шаг. Число 8 возводим в квадрат (8² = 64) и число 64 вычитаем из первой грани, получаем 70 — 64=6. Число 6 – первый остаток.
4-й шаг. К остатку 6 приписываем вторую грань 56, получаем число 656.

5-й шаг. Удваиваем первую цифру результата 8 и, записывая слева, получаем-16

К числу 16 нужно приписать такую наибольшую цифру, чтобы произведение числа, которое мы получим, на эту цифру было бы либо равно числу 656, либо меньше. Это цифра 4. Она находится путем подбора: так как 164 ∙ 4 = 656, то цифра 4 – это вторая цифра результата.

6-й шаг. Находим остаток 656 – 656 = 0. Так как остаток равен нулю, то мы получили точное значение корня – 84.

64

= 8 4

64

16 *

*

6 56

16 4

4

6 56

6 56

0

Глава 10. Практическая часть. Диаграммы (анкетирования среди учащихся 8-11 класса).

Получив результаты анкетирования, учащихся я свел все данные в диаграммы. В опросе участвовало 150 учащихся.

Диаграмма № 1 — сложно ли Вам извлекать квадратный корень из числа меньше 100, если нет таблицы квадратов?

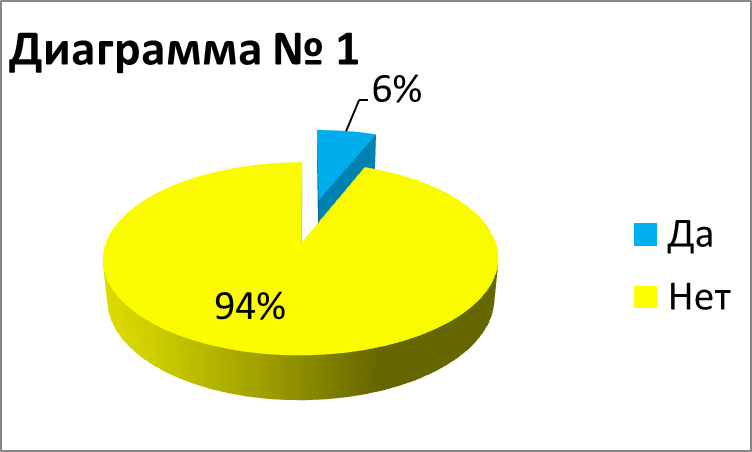
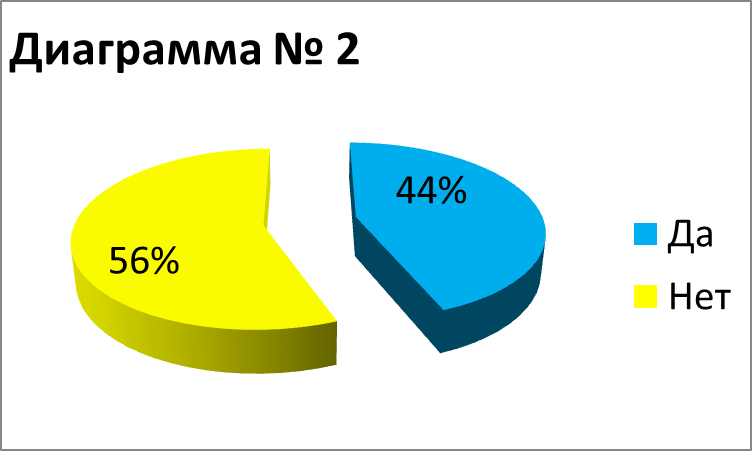
Диаграмма № 2 — сложно ли Вам извлекать квадратный корень из числа больше 100, если нет таблицы квадратов?

Диаграмма № 3 – каким образом Вы извлекаете корень их числа больше 100?

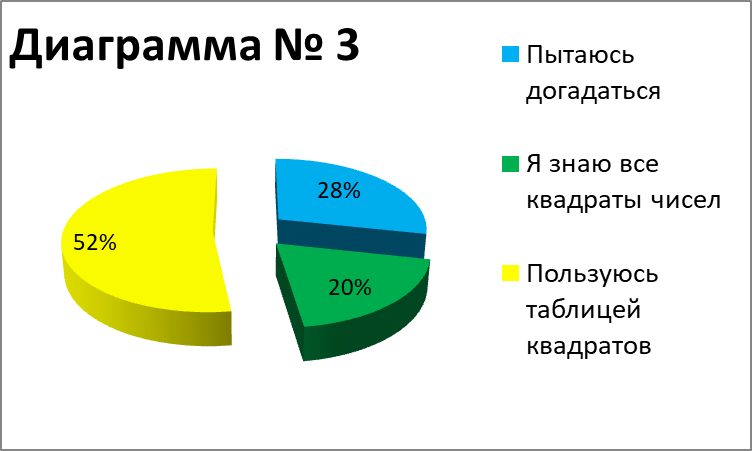
Диаграмма № 4 – интересно Вам было бы знать простые способы извлечение корней?

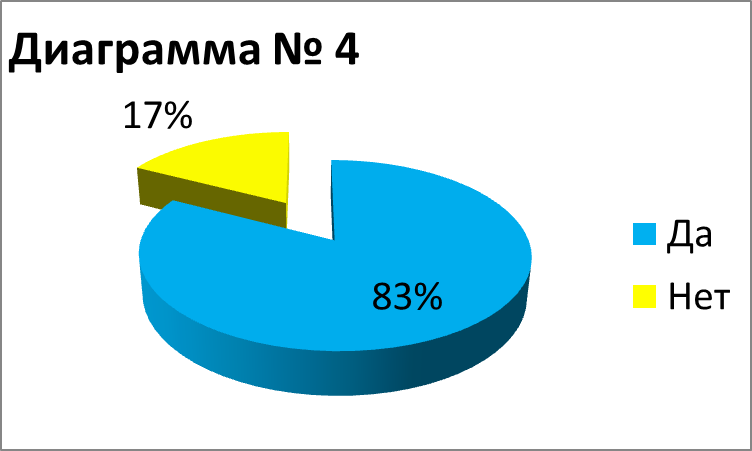
Заключение

В ходе исследования было выявлено, что современной науке известно много способов извлечения квадратного корня, начиная со способа математиков Древнего Вавилона и заканчивая способом степенных рядов сложных степеней из разделов высшей математики. Были изучены и отработаны на практике все найденные способы. Предположение, что существует не менее двух способов извлечения квадратных корней без калькулятора, подтвердилось.

Описанные в работе методы извлечения корней встречаются во многих источниках. Тем не менее, разобраться в них оказалось для меня непростой задачей, что вызвало немалый интерес. Представленные алгоритмы позволят всем, кто заинтересуется данной темой, быстрее овладеть навыками вычисления квадратного корня, их можно использовать при проверке своего решения и не зависеть от наличия в кармане калькулятора. Тем более на экзамене в 9 и 11 классах применение калькулятора не допускается.

Таким образом, цель работы достигнута, задачи выполнены.

Литература и сайты Интернета:

1. И.Н. Сергеев, С.Н. Олехник, С.Б.Гашков «Примени математику». – М.: Наука, 1990

2. Керимов З., «Как найти целый корень?» Научно-популярный физико-математический журнал «Квант» №2, 1980

3. Петраков И.С. «математические кружки в 8-10 классах»; Книга для учителя. – М.: Просвещение,1987

4. Тихонов А.Н., Костомаров Д.П. «Рассказы о прикладной математики». — М.: Наука. Главная редакция физико — математической литературы, 1979

5. Ткачева М.В. Домашняя математика. Книга для учащихся 8 класса учебных заведений. – Москва, Просвещение, 1994г.

6. Жохов В.И., Погодин В.Н. Справочные таблицы по математике. — М.: ООО «Издательство «РОСМЭН-ПРЕСС», 2004.-120 с.

7. http://translate.google.ru/translate

8. http://www.murderousmaths.co.uk/books/sqroot.htm

9. http://ru.wikipedia.ord /wiki /teorema/

infourok.ru

Быстрое извлечение корней без калькулятора

Выбор статьи по меткам03 (1)9 класс (3)10 класс (1)11 класс (2)12 (1)13 (С1) (3)14 ноября (2)14 февраля (1)15 задание ЕГЭ (2)16 задача профиль (1)18 (С5) (2)18 задача ЕГЭ (2)23 марта (1)31 января (1)2016 (2)140319 (1)14032019 (1)C5 (1)RC-цепь (1)А9 (1)Александрова (2)Ампера (2)Архимед (1)Бернулли (1)Бойля-Мариотта (1)В8 (1)В12 (1)В13 (1)В15 (1)ВК (1)ВШЭ (2)ГИА физика задания 5 (1)Герона (1)Герцшпрунга-Рассела (1)Гринвич (1)ДВИ (1)ДПТ (1)Десятичные приставки (1)Дж (1)Диэлектрические проницаемости веществ (1)ЕГЭ 11 (2)ЕГЭ 14 (1)ЕГЭ 15 (2)ЕГЭ 18 (1)ЕГЭ С1 (1)ЕГЭ по математике (25)ЕГЭ по физике (49)ЕГЭ профиль (6)Европа (1)Задача 17 ЕГЭ (6)Задачи на движение (1)Закон Архимеда (2)Законы Ньютона (1)Земля (1)Ио (1)КПД (9)Каллисто (1)Кельвин (1)Кирхгоф (1)Кирхгофа (1)Койпера (1)Колебания (1)Коши (1)Коэффициенты поверхностного натяжения жидкостей (1)Кулона-Амонтона (1)Ломоносов (2)Лоренца (1)Луна (1)МГУ (1)МКТ (7)Максвелл (2)Максвелла (1)Максимальное удаление тела от точки бросания (1)Менделеева-Клапейрона (3)Менелая (3)Метод наложения (2)Метод узловых потенциалов (1)Метод эквивалентных преобразований (1)НОД (1)Нансен (1)НеИСО (1)ОГЭ (11)ОГЭ (ГИА) по математике (27)ОГЭ 3 (ГИА В1) (1)ОГЭ 21 (3)ОГЭ 21 (ГИА С1) (4)ОГЭ 22 (2)ОГЭ 25 (3)ОГЭ 26 (1)ОГЭ 26 (ГИА С6) (1)ОГЭ по физике 5 (1)ОДЗ (12)Обыкновенная дробь (1)Оорта (1)Основные физические константы (1)Отношение объемов (1)Плюк (1)Показатели преломления (1)Показательные неравенства (1)Противо-эдс (1)Работа выхода электронов (1)Радиус кривизны траектории (1)Релятивистское замедление времени (1)Релятивистское изменение массы (1)С1 (1)С1 ЕГЭ (1)С2 (2)С3 (1)С4 (3)С6 (5)СУНЦ МГУ (2)Сиена (1)Синхронная машина (1)Снеллиуса (2)Солнечной системы (1)Солнце (2)СпБ ГУ вступительный (1)Средняя кинетическая энергия молекул (1)Статград физика (3)Таблица Менделеева (1)Текстовые задачи (8)Тьерри Даксу (1)ФИПИ (1)Фазовые переходы (1)Фаренгейт (1)Фобос (1)Френеля (1)Цельсий (1)ЭДС (6)ЭДС индукции (2)Эйлера (1)Электрохимические эквиваленты (1)Эрастофен (1)абсолютная (1)абсолютная влажность (2)абсолютная звездная величина (3)абсолютная температура (1)абсолютный ноль (1)адиабаты (1)аксиомы (1)алгоритм Евклида (2)алгоритм Робертса (1)аморфное (1)амплитуда (3)аналитическое решение (1)анекдоты (1)апериодический переходной процесс (2)аргумент (1)арифметическая прогрессия (5)арифметической прогрессии (1)арки (1)арккосинус (1)арккотангенс (1)арксинус (1)арктангенс (1)архимеда (3)асинхронный (1)атмосферное (2)атмосферном (1)атомная масса (2)афелий (2)база (1)балка (1)банк (1)без калькулятора (1)белого карлика (1)бензин (1)бесконечная периодическая дробь (1)бесконечный предел (1)биквадратные уравнения (1)бипризма (1)биссектриса (3)биссектрисы (2)благоприятный исход (1)блеск (4)блок (2)боковой поверхности (1)большая полуось (1)большем давлении (1)бревно (1)бригада (2)бросили вертикально (1)бросили под углом (3)бросили со скоростью (2)броуновское движение (1)брошенного горизонтально (2)бруски (1)брусок (3)брусок распилили (1)быстрый способ извлечения (1)вариант (3)вариант ЕГЭ (12)вариант ЕГЭ по физике (18)варианты ЕГЭ (6)вариент по физике (1)введение дополнительного угла (1)вектор (5)векторное произведение (2)велосипедисты (1)вероятность (1)вертикальная составляющая (1)вертикально вверх (1)вертикальные углы (1)вес (3)весов (1)вес тела (1)ветви (1)ветвь (2)ветер (1)взаимодействие зарядов (1)видеоразбор (2)видеоразбор варианта (1)видимая звездная величина (2)виртуальный банк (1)виртуальных перемещений (1)витка (1)витков (1)виток (1)вклад (1)влажность (3)влажность воздуха (1)влетает (2)вневписанная окружность (2)внутреннее сопротивление (1)внутреннее сопротивление источника (1)внутреннюю энергию (1)внутренняя энергия (8)вода течет (1)воды (1)возведение в квадрат (1)возвратное уравнение (1)возвратность (1)возвратные уравнения (2)воздушный шар (1)возрастающая (1)возрастет (1)волны (1)вписанная окружность (3)вписанной окружности (1)вписанный угол (4)в правильной пирамиде (1)вращение (1)времени (2)время (24)время в минутах (1)время выполнения (1)время движения (2)время минимально (1)время падения (1)всесибирская олимпиада (1)в стоячей воде (1)встретились (1)встретятся (1)вступительный (1)вступительный экзамен (1)вторая половина пути (1)вторичная (1)вторичная обмотка (1)вторичные изображения (1)второй закон Ньютона (4)выбор двигателя (1)выборка корней (4)выколотая точка (1)выплаты (2)выразить вектор (1)высота (5)высота Солнца (1)высота столба (1)высота столба жидкости (1)высота столбика (1)высоте (3)высоту (1)высоты (3)выталкивающая сила (2)вычисления (2)газ (3)газа (1)газов (1)газовая атмосфера (1)галочка (1)гамма-лучей (1)гармоника (2)гвоздя (1)геометрическая вероятность (1)геометрическая прогрессия (4)геометрические высказывания (1)геометрический смысл (2)геометрическую прогрессию (1)геометрия (7)гигрометр (1)гидродинамика (1)гидростатика (3)гимназия при ВШЭ (1)гипербола (2)гипотенуза (3)гистерезисный двигатель (1)главный период (1)глубина (1)глухозаземленная нейтраль (1)гомотетия (2)гонщик (1)горизонтальная сила (1)горизонтальной спицы (1)горизонтальную силу (1)горка (1)гравитационная постоянная (1)градус (1)грани (2)график (2)графики функций (5)графически (1)графический способ (1)графическое решение (2)груз (2)грузик (2)группа (1)давление (28)давление жидкости (3)давление пара (1)дальность полета (1)двигатель с активным ротором (1)движение под углом (1)движение под углом к горизонту (4)движение по кругу (1)движение по течению (1)движение с постоянной скоростью (2)двойное неравенство (1)двойной фокус (1)двугранный угол при вершине (1)девальвация (1)действительная часть (1)действующее значение (2)деление (1)деление многочленов (2)деление уголком (1)делимость (15)делимость чисел (1)делители (1)делитель (2)делится (3)демонстрационный варант (1)деталей в час (1)диаграмма (1)диаметр (2)диаметру (1)динамика (4)диод (1)диск (1)дискриминант (4)дифракционная решетка (2)дифференцированный платеж (1)диффузия (1)диэлектрик (1)диэлектрическая проницаемость (1)длина (4)длина вектора (1)длина волны (7)длина отрезка (2)длина пружины (1)длина тени (1)длиной волны (2)длину нити (1)длительность разгона (1)длительный режим (1)добротность (1)догнал (1)догоняет (1)докажите (1)долг (1)доля (1)дополнительный угол (1)досок (1)досрочный (2)досрочный вариант (1)дптр (1)дуга (1)единицы продукции (1)единичный источник (1)единичных кубов (1)единственный корень (1)ежесекундно (1)емкость (7)емкость заряженного шара (1)естественная область определения (1)желоб (2)жесткость (6)жеткость (1)живая математика (2)жидкости (1)жидкость (1)завод (1)загадка (2)задание 13 (2)задание 15 (3)задание 23 (1)задания 1-14 ЕГЭ (1)задача 9 (1)задача 13 профиль (1)задача 14 профиль (3)задача 16 (1)задача 16 ЕГЭ (1)задача 16 профиль (3)задача 17 (1)задача 18 (1)задача 26 ОГЭ (2)задача с параметром (6)задачи (1)задачи на доказательство (4)задачи на разрезание (4)задачи на совместную работу (3)задачи про часы (1)задачи с фантазией (1)задерживающее напряжение (1)заземление (1)заказ (1)закон Бернулли (1)закон Гука (1)закон Ома (3)закон Снеллиуса (1)закона сохранения (1)закон движения (1)закон кулона (7)закон сложения классических скоростей (1)закон сохранения импульса (6)закон сохранения энергии (4)законы Кирхгофа (6)законы коммутации (1)законы сохранения (1)закрытым концом (1)замена переменной (2)замкнутая система (2)зануление (1)запаянная (2)заряд (9)заряда (1)заряд конденсатора (1)защитная характеристика (1)звездочка (1)звезды (1)зенит (1)зенитное расстояние (1)зеркало (2)знак неравенства (1)знаменатель (1)знаменатель прогрессии (4)значение выражения (1)идеальный блок (1)идеальный газ (5)извлечение в столбик (1)излом (1)излучение (2)изменение длины (2)изобара (1)изобаричесикй (1)изобарический (2)изобарный (1)изобарный процесс (1)изображение (3)изолированная нейтраль (1)изопроцессы (1)изотерма (2)изотермически (1)изотермический (2)изотермический процесс (1)изотоп (1)изохора (1)изохорический (1)изохорный процесс (1)импульс (9)импульса (1)импульс силы (1)импульс системы (1)импульс системы тел (4)импульс тела (4)импульс частицы (1)инвариантность (1)индуктивно-связанные цепи (1)индуктивное сопротивление (1)индуктивность (1)индукцией (1)индукция (8)интеграл Дюамеля (1)интервал (1)интересное (3)интерференционных полос (1)иррациональность (2)испарение (2)исследование функции (4)источник (1)источник света (1)исход (1)камень (1)камешек (1)капилляр (1)карлик (2)касательная (4)касательного (1)касательные (1)касаются (1)катер (2)катет (3)катушка (4)качаний (2)квадлратичная зависимость (1)квадрант (1)квадрат (3)квадратичная функция (3)квадратное (1)квадратное уравнение (4)квадратную рамку (1)квазар (1)квант (1)квантов (1)кинематика (2)кинематическая связь (1)кинематические связи (1)кинетическая (12)кинетическая энергия (4)кинетической (1)кинетической энергии (1)кинетическую энегрию (1)классический метод (3)классический метод расчета (1)клин (1)ключ (1)кодификатор (1)колебаний (1)колене (1)количество вещества (1)количество теплоты (9)коллектор (1)кольцо (2)комбинаторика (1)комбинированное (1)коммутация (1)комплексное сопротивление (1)комплексное число (1)комплексные числа (1)компонент (1)конвекция (3)конденсатор (10)конденсаторы (1)конденсации (1)конечная скорость (1)конечная температура (1)конечная температура смеси (1)конечный предел (1)консоль (1)контрольная (1)контрольные (1)контур (5)конус (4)концентрация (7)концентрическим (1)координата (5)координаты (3)координаты вектора (2)координаты середины отрезка (1)координаты точки (1)корабля (1)корень (2)корень квадратный (1)корень кубический (1)корни (2)корни иррациональные (1)корни квадратного уравнения (3)корни уравнения (1)корпоративных (1)косинус (2)косинусы (1)котангенс (1)коэффициент (1)коэффициент жесткости (1)коэффициент наклона (3)коэффициент поверхностного натяжения (3)коэффициент подобия (5)коэффициент трансформации (1)коэффициент трения (5)коэффициенты (1)красное смещение (1)красной границы (1)красный (1)кратковременный режим (1)кратные звезды (1)кредит (11)кредитная ставка (4)кредиты (1)криволинейная трапеция (2)кристаллизация (1)критерии оценки (1)круговая частота (1)круговой контур (1)кружок (1)кубическая парабола (1)кулонова сила (1)кульминация (1)кусочная функция (1)левом колене (1)лед (2)лет (1)линейная скорость (2)линейное напряжение (1)линейное уравнение (2)линейный размер (1)линза (2)линзы (2)линии излома (1)линиями поля (1)линия отвеса (1)литров (1)лифт (1)лифта (1)лифте (1)логарифм (10)логарифмические неравенства (3)логарифмические уравнения (1)логарифмическое неравенство (3)логарифмы (1)лунка (1)лучевая (1)льда (1)магнитное поле (2)магнитном поле (2)магнитные цепи (1)максимальная высота (1)максимальная скорость (1)максимум (1)малых колебаний (1)масса (23)масса воздуха (1)массе (1)массивная звезда (1)массовое содержание (1)массой (1)массу (1)математика (4)математический маятник (1)математического маятника (1)маятник (4)мгновенный центр вращения (1)медиана (1)меридиан (1)мертвая вода (1)мертвая петля (1)метод внутреннего проецирования (1)метод замены переменной (4)метод интервалов (3)метод комплексных амплитуд (3)метод контурных токов (1)метод координат (1)метод линий (1)методом внутреннего проецирования (1)метод переброски (1)метод переменных состояния (1)метод подстановки (4)метод рационализации (4)метод решетки (1)метод следов (5)метод сложения (4)метод телескопирования (1)метод узловых напряжений (1)методы расчета цепей (2)методы расчета цепей постоянного тока (1)метод эквивалентного генератора (2)механика (1)механическая характеристика (1)механическое напряжение (1)миля (1)минимальная скорость (1)минимальное (1)минимальной высоты (1)минимальной скоростью (1)минимум (2)мишени (1)мнимая единица (1)мнимая часть (1)многоугольник (1)многочлены (1)мода (2)модули (1)модуль (13)модуль Юнга (1)модуль средней скорости (1)молекулярно-кинетическая теория (2)моль (2)молярная масса (5)момент (7)момент инерции (1)момент инерции двигателя (1)момент нагрузки (1)момент сил (1)монотонная (1)монотонность функции (1)монохроматического (1)мощности силы тяжести (1)мощность (9)мощностью (1)мяч (1)наблюдатель (1)нагревание (1)нагреватель (1)нагревателя (1)нагрели (1)наибольшее (1)наивысшая точка (1)наименьшее (1)наименьшее общее кратное (1)наклон (1)наклонная плоскость (2)налог (1)на подумать (2)направление (1)направление обхода (3)направлении (1)направляющий вектор (1)напряжение (9)напряжение на зажимах (1)напряжение смещения нейтрали (2)напряженность (4)напряженность поля (6)насос (2)насоса (1)насыщенный пар (4)натуральное (7)натуральные (7)натуральных (1)натяжение нити (5)натяжения (1)находился в полете (2)начальная температура (1)начальной скоростью (1)недовозбуждение (1)незамкнутая система (2)нелинейное сопротивление (1)неопределенность типа бесконечность на бесконечность (1)неопределенность типа ноль на ноль (1)непериодическая дробь (1)неравенства (8)неравенство (22)неразрывности струи (1)нерастяжимой (1)нерастяжимой нити (1)нерастянутой резинки (1)несимметричная нагрузка (1)несинусоидальный ток (3)нестандартные задачи (1)нестрогое (1)неупругим (1)нецентральный (1)нечетная функция (2)нечетное (1)нечетность (1)неявнополюсный (1)нити (2)нити паутины (1)нить (2)нить нерастяжима (1)новости (1)нормаль (1)нормальное ускорение (11)нулевой ток (2)обкладками (1)обкладках (1)обкладки (1)область допустимых значений (9)область значений (1)область определения (8)область определения функции (4)оборот (1)обратные тригонометрические функции (1)обратные функции (1)общая хорда (1)общее сопротивление (1)общее сопротивление цепи (1)объем (36)объемный расход (1)объемом (1)объем пара (1)объем параллелепипеда (1)объем пирамиды (1)одинаковые части (1)одновременно (1)одновременно из одной точки (1)окружность (13)окружность описанная (1)олимпиада (2)олимпиады по физике (2)они встретятся (1)операторный метод (4)оптика (1)оптимальный выбор (1)оптимизация (1)оптическая разность хода (1)оптический центр (1)орбитам (1)орбитой (1)оригинал (1)осевое сечение (1)оси (1)основание (2)основание логарифма (2)основания трапеции (1)основное тригонометрическое тождество (1)основное уравнение МКТ (2)основной газовый закон (1)основной период (1)основной уровень (1)основные углы (1)остаток (1)ось (1)отбор корней (5)ответ (1)отданное (1)относительная (1)относительная влажность (3)относительная скорость (1)относительно (2)относительность движениия (1)относительность движения (2)относительность скоростей (1)отношение (5)отношение времен (1)отношение длин (1)отношение площадей (3)отношение скоростей (2)отрезок (1)отсечение невидимых граней (1)очки (1)падает (1)падает луч (1)падает под углом (1)падение (3)падение напряжения (2)падения (1)пар (3)парабола (5)параболы (1)параллакс (5)параллелепепед (2)параллелепипед (3)параллелограмм (4)параллелограмм Виньера (1)параллельно (2)параллельно двум векторам (1)параллельное соединение (3)параллельные прямые (1)параллельными граням (1)параметр (30)параметры (1)парообразование (1)парсек (1)парциальное (1)парциальное давление (1)паскаль (1)первая треть (1)первичная (1)переброски (1)перевозбуждение (1)перегородка (1)перегрузок (1)перелетит (1)переливания (1)переменное магнитное поле (1)переменное основание (2)перемещение (6)перемычка (5)перемычке (1)перемычку (1)переносная скорость (1)пересекает (1)пересечение (1)пересечения (1)переходная проводимость (1)переходное сопротивление (1)переходной процесс (1)переходные процессы (9)перигелий (2)периметр (3)период (15)периодическая дробь (1)период колебаний (2)период малых колебаний (1)период обращения (2)период функции (1)периоды (1)перпендикулярно (1)песок (1)пион (1)пипетка (1)пирамида (7)пирамида шестиугольная (1)пирамиды (2)пирсона (1)плавание (1)плавкие предохранители (1)плавление (1)план (1)планете (1)планеты (3)планиметрия (12)планиметрия профиль (1)пластинами (1)пластинка (1)платеж (8)плечо (2)плоского зеркала (1)плоскопараллельная (1)плоскость (4)плоскость сечения (1)плотности веществ (1)плотность (22)плотность пара (3)плотность сосуда (1)плотность энергии (1)площади (2)площади фигур на клетчатой бумаге (1)площадь (30)площадь круга (1)площадь пластин (1)площадь поверхности (1)площадь под кривой (2)площадь проекции (1)площадь проекции сечения (1)площадь сектора (1)площадь сечения (5)площадь треугольника (1)поверхностная плотность заряда (1)поворот (1)повторно-кратковременный режим (1)погрешность (1)погружено (1)подготовка к контрольным (3)под каким углом (1)подмодульное (1)подмодульных выражений (1)подобен (1)подобие (7)подобия треугольников (1)подобны (1)подпереть (1)под углом (2)под углом к горизонту (3)показателем преломления (1)показательное (1)показатель преломления (4)поле (1)полезной работы (1)полезную мощность (1)полигон частот (1)по линиям сетки (1)полное ускорение (1)половина времени (1)половинный угол (1)положительный знаменатель (1)полония (1)полость (1)полуокружность (1)полупроводник (1)полученное (1)понижение горизонта (1)по окружности (1)по переменному основанию (1)поправка часов (1)по прямой (1)поршень (4)поршня (1)порядок решетки (2)последовательно (1)последовательное соединение (3)последовательность (3)по сторонам клеток (1)посторонние корни (4)постоянная Авогадро (1)постоянная Хаббла (1)постоянная времени (1)постоянная скорость (1)постоянная составляющая (2)постоянный ток (5)построение (2)построение графика функции (1)потенциал (5)потенциал шара (1)потенциальная (13)потенциальная энергия (3)потенциальной (1)потери в стали (2)потеря корней (4)поток (5)по физике (1)правило левой (1)правило моментов (3)правильную пирамиду (1)правильный многоугольник (1)правом колене (1)предел функции (1)преломляющий угол (1)преобразование графиков функций (1)преобразования (3)преподаватели (2)пресс (2)призма (6)призмы (3)признаки подобия (4)признаки равенства треугольников (3)пробн (1)пробник (163)пробник по физике (7)пробниук (1)пробный (1)пробный ЕГЭ (2)пробный ЕГЭ по физике (3)пробный вариант (25)пробный вариант ЕГЭ (17)пробный вариант ЕГЭ по физике (101)пробный вариант по физике (1)провода (1)проводник (1)проводник с током (1)проводящего шара (1)проволока (1)проволоки (1)прогрессия (5)проекции ускорения (2)проекция (6)проекция перемещения (1)проекция скорости (4)проекция ускорения (2)производительность (2)производная (3)промежутка времени (1)промежуток (1)промежуток знакопостоянства (1)пропорциональны (1)проскальзывает (1)проскальзывания (1)противоположное событие (1)противостояние (1)протона (1)прототипы (1)профиль (2)профильный ЕГЭ (1)процент (5)процентная ставка (6)процентное отношение (1)процентное содержание (2)проценты (3)пружин (1)пружина (6)пружинный маятник (1)пружины (1)прямая (6)прямое восхождение (2)прямой (1)прямой АВ (1)прямоугольник (1)пузырек (1)пульсар (1)пуля (1)пути (1)путь (26)пять корней (1)работа (15)работа газа (5)работа тока (1)работу выхода (2)рабочее тело (1)рабочие (1)равнобедренный (1)равновесие (4)равновесия (1)равновесное (1)равнодействующая (1)равномерно (1)равноускоренно (2)равноускоренное (3)равные (1)равные фигуры (1)радиальную ось (1)радикал (1)радиус (11)радиус колеса (1)радиус кривизны (2)радиус описанной сферы (1)радиус темного кольца в отраженном свете (1)разбор (1)разложение на множители (2)размах (1)разности температур (1)разность (2)разность потенциалов (2)разность прогрессии (3)разность хода (1)разрежьте (2)разрезание (5)разрешающая сила (1)разрыв функции (1)рамка (8)рамка с током (1)раскрытие модуля (1)расписание (1)расположение корней квадратного трехчлена (1)распределение частот (1)рассеивающая (1)расстояние (21)расстояние между зарядами (1)расстояние на карте (1)расстояние от точки (1)расстояния (2)раствор (2)растяжение (2)расходуется (1)расцепители (1)расчеты по формулам (1)рационализация (4)рациональные неравенства (1)реактивные элементы (1)реактивный двигатель (1)реакция опоры (4)реакция якоря (1)ребра (1)ребус (2)резервуар (1)резистор (1)рейки (1)рельса (1)рентгеновскую трубку (1)репетитор (1)решебник (1)решение тригонометрических уравнений (1)решение уравнений (2)решение уравнений больших степеней (1)решить в натуральных (1)решить в целых (1)розетка (1)ромб (1)ряд Фурье (1)сарай с покатой крышей (1)сближаются (1)сближения (1)сбрасывают с высоты (1)сверхгигант (2)сверхновая (1)светимость (3)свободно (1)свободного падения (1)свободно падает (2)свойства (2)свойства отрезков (1)свойства степени (1)свойства функции (1)свойства функций (2)свойства чисел (1)свойство биссектрисы (2)свойству биссектрисы (1)сдвинуть (1)сегмент (1)сектор (1)секущая (2)серия решений (1)сертификация (6)сессия (1)сечение (14)сечение наклонной плоскостью (1)сидерический (1)сила (7)сила Архимеда (5)сила Лоренца (4)сила ампера (9)сила взаимодействия (4)сила давления (1)сила на дно (1)сила натяжения (7)сила натяжения нити (4)сила поверхностного натяжения (3)сила реакции опоры (1)сила трения (3)сила тяготения (1)сила тяжести (5)сила упругости (2)силой (2)силу (1)силу натяжения (1)силы трения (2)символический метод (3)симметричная нагрузка (1)симметрия (3)синодический (1)синус (4)синусоида (1)синусоидальный закон (1)синусоидальный ток (5)синусы (1)синхронный компенсатор (1)система (3)система неравенств (7)система отсчета (3)система счисления (1)система уравнений (3)системы уравнений (3)скалярное произведение (3)склонение (1)скольжение (2)скользит (1)скользит равномерно (1)скоросмть (1)скоростей (1)скорости (3)скорости течения (1)скорость (42)скорость реки (1)скорость сближения (3)скорость света (1)скорость теплохода (1)скорость удаления (1)скорость частицы (1)скоростью (1)с лестницы (1)сложение векторов (1)сложная функция (1)смежные углы (1)смекалка (2)смеси (1)смешанное число (1)смещение (2)снаряд (1)собирающая (2)событие (1)соединение звездой (1)соединение треугольником (1)сокращение (1)сокращение дробей (1)соленоид (1)солнечная постоянная (3)солнечная система (1)сообразительность (1)сообщающиеся сосуды (2)соприкосновения (1)сопротивление (13)сопротивления (1)сопряженное (3)составить квадрат (1)составляет с направлением (1)составляющая скорости (2)составляющие (1)составляющие скорости (3)сосуд (1)сосудах (1)сосуде (1)сохранение эне

easy-physic.ru

Приближенные методы извлечения квадратного корня (без использования калькулятора).

Извлечение квадратного корня «вручную»

На примере возьмём число 223729. Для извлечения корня мы должны проделать следующие операции:

А) разбить число справа на лево на разряды по две цифры в разряде, ставя штрихи наверху- 223729→ 22’37’29’. Если бы это было число с нечётным числом цифр, как например, 4765983, то при разбиении к первой цифре слева надо приписать нуль, т.е. 4765983→04’76’59’83’.

Б) Навесить на число радикал и написать знак равенства:

22’37’29’→=… .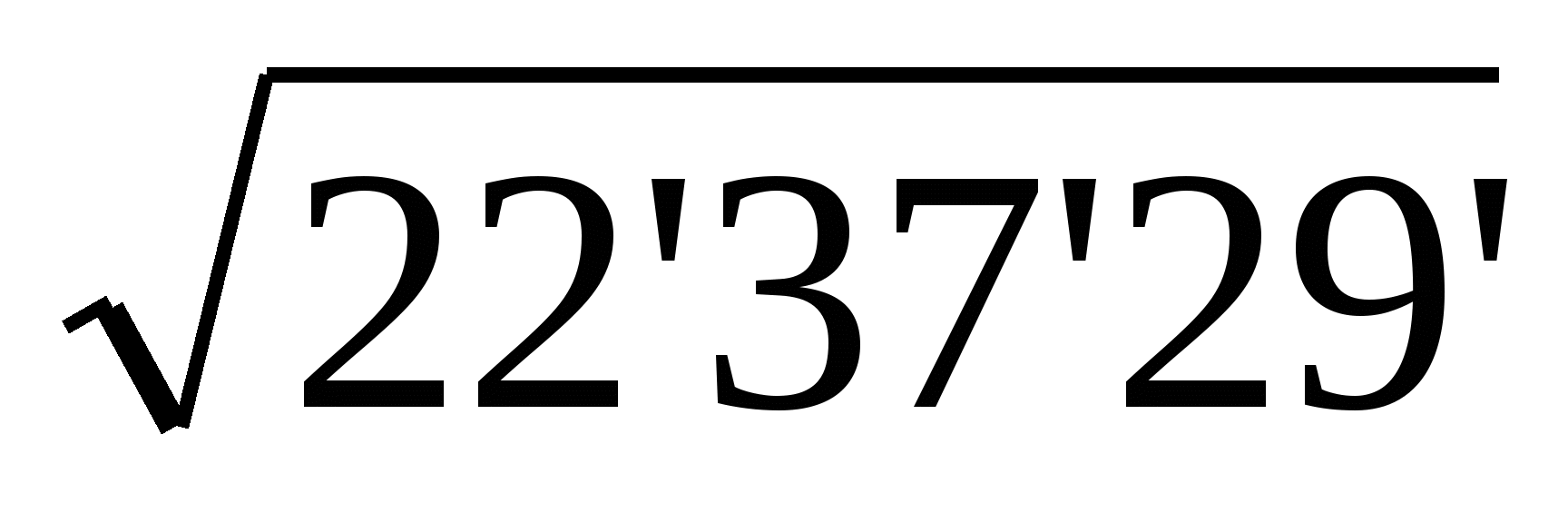

После этого начинаем, собственно, вычислять корень. Это делается шагами, причём на каждом шаге обрабатывается один разряд исходного числа, т.е. две очередных цифры слева направо, и получается одна цифра результата.

Шаг 1 ― извлечение квадратного корня с недостатком из первого разряда:

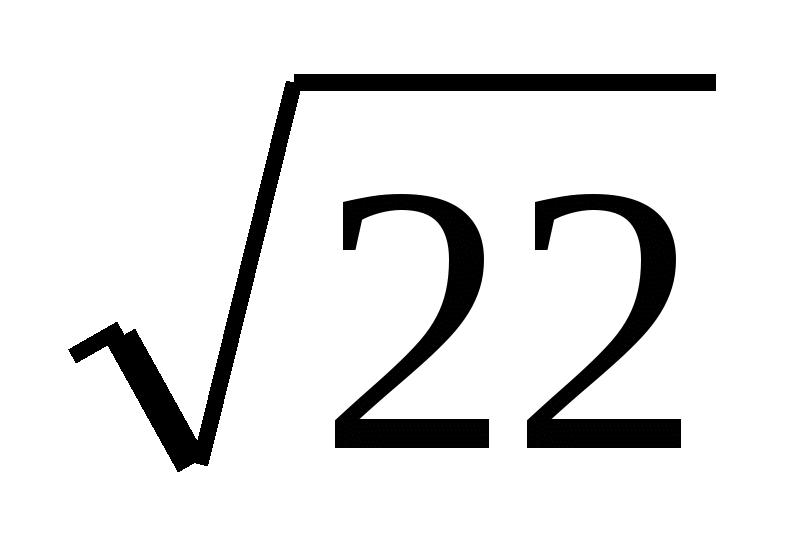= 4… (с недостатком)

Итог шага 1 есть первая цифра искомого числа:

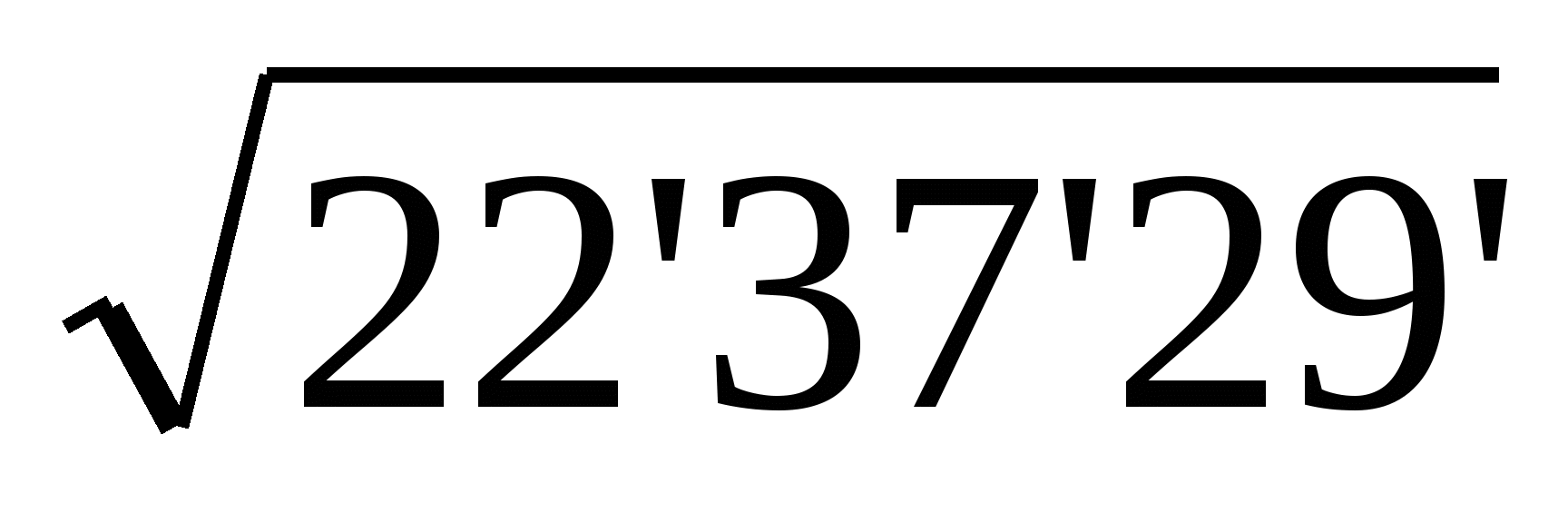= 4…

Шаг 2 ― первую полученную цифру возводим в квадрат, приписываем под первым разрядом и ставим знак минус вот так:

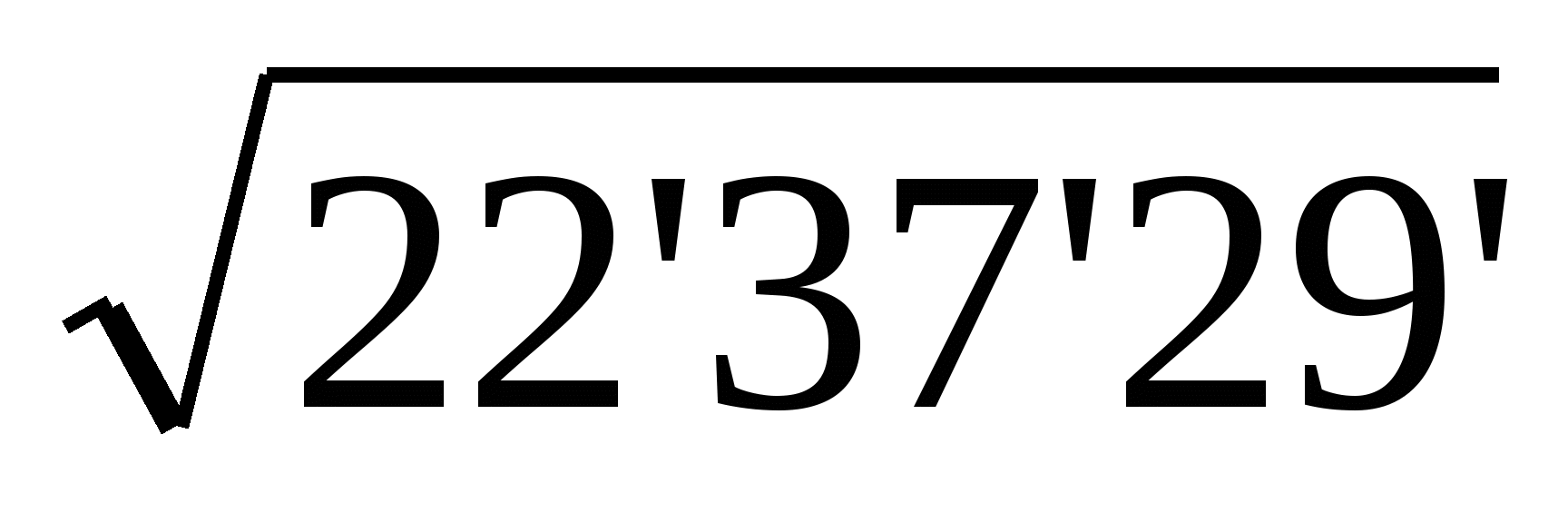= 4…

16

6

И производим вычисление так, как это уже написано.

Шаг 3 ― приписываем справа к результату вычитания две цифры следующего разряда и слева от получившегося числа ставим вертикальную черту вот так:

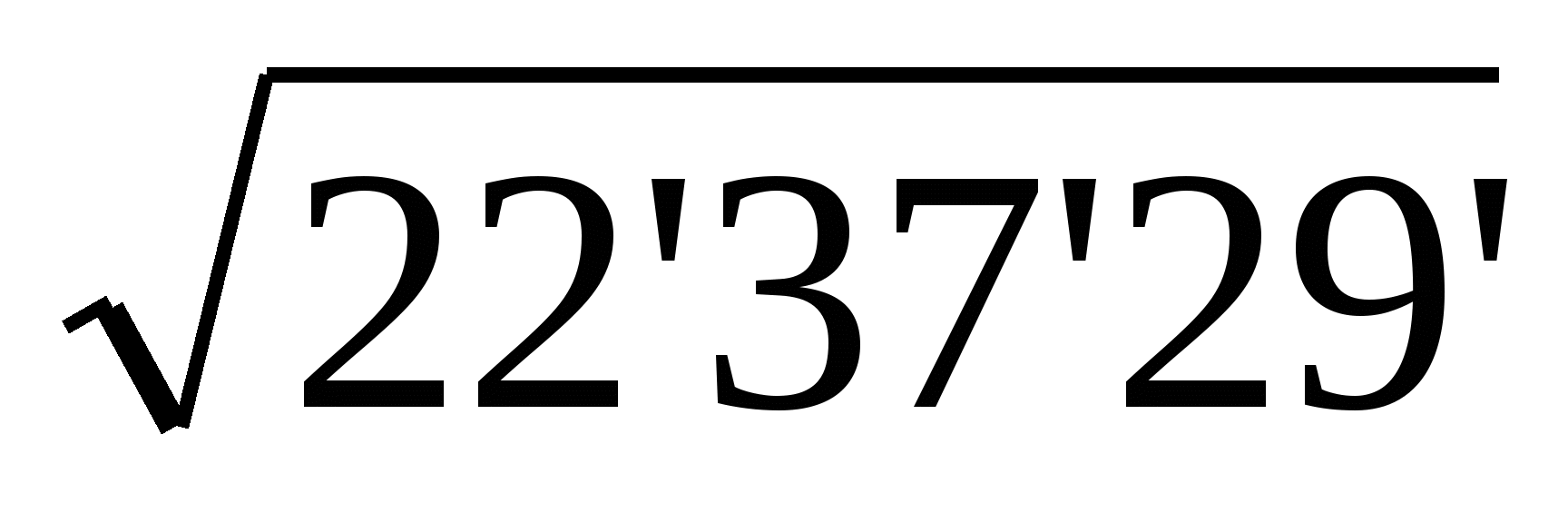
= 4…

16

637

После этого, воспринимая цифры, стоящие после знака =, как обычное число, умножаем его на 2 и приписываем слева от вертикальной черты пропуск, в котором ставим точку и под этой точкой тоже ставим точку:

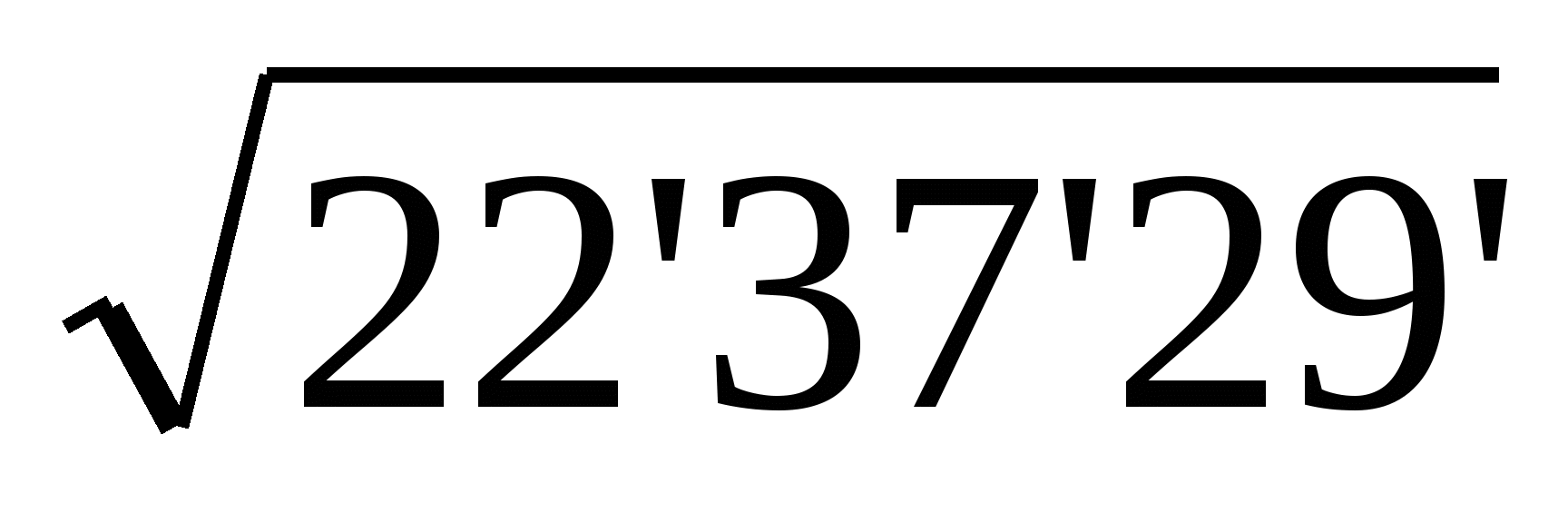
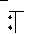= 4…

16

8 637

Поставленная точка обозначает поиск цифры. Эта цифра будет второй в итоговом числе, т.е. встанет после цифры 4. Ищется она по следующему правилу:

Это наибольшая цифра k такая, что число 8k, т.е. число, получающееся из 8 приписыванием цифры k , умноженное на k, не превосходит 637.

В данном случае это цифра 7, т.к. 87∙7=609<637, но 88∙8=704>637. Итак, мы имеем:

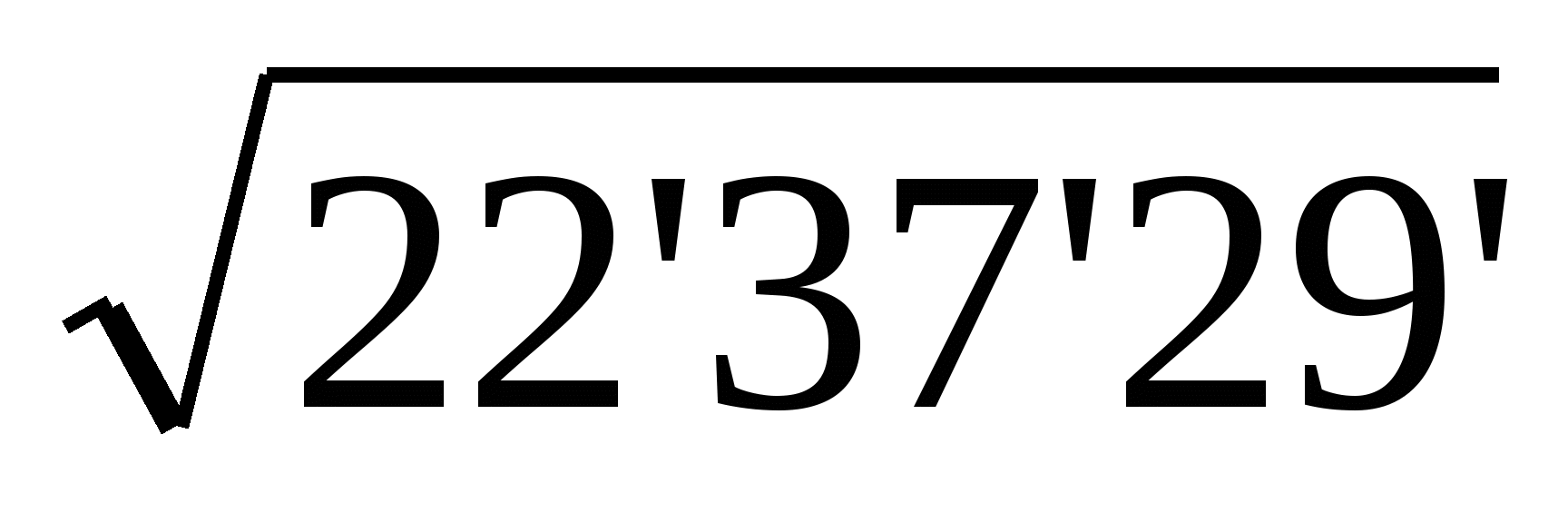= 47..

Шаг 4 ― проведём горизонтальную черту и под ней запишем результат вычитания:

637 – 609 = 28. К числу 28 приписываем последний разряд исходного подкоренного числа и получим число 2829. Слева от него проводим вертикальную черту, умножаем теперь уже 47 на 2 и полученное число 94 приписываем слева от вертикальной черты, оставив место в виде точки для поиска последней цифры. Цифра 3 подходит в точности без остатка, так как 943∙3=2829, значит, это последняя цифра искомого числа, т.е. 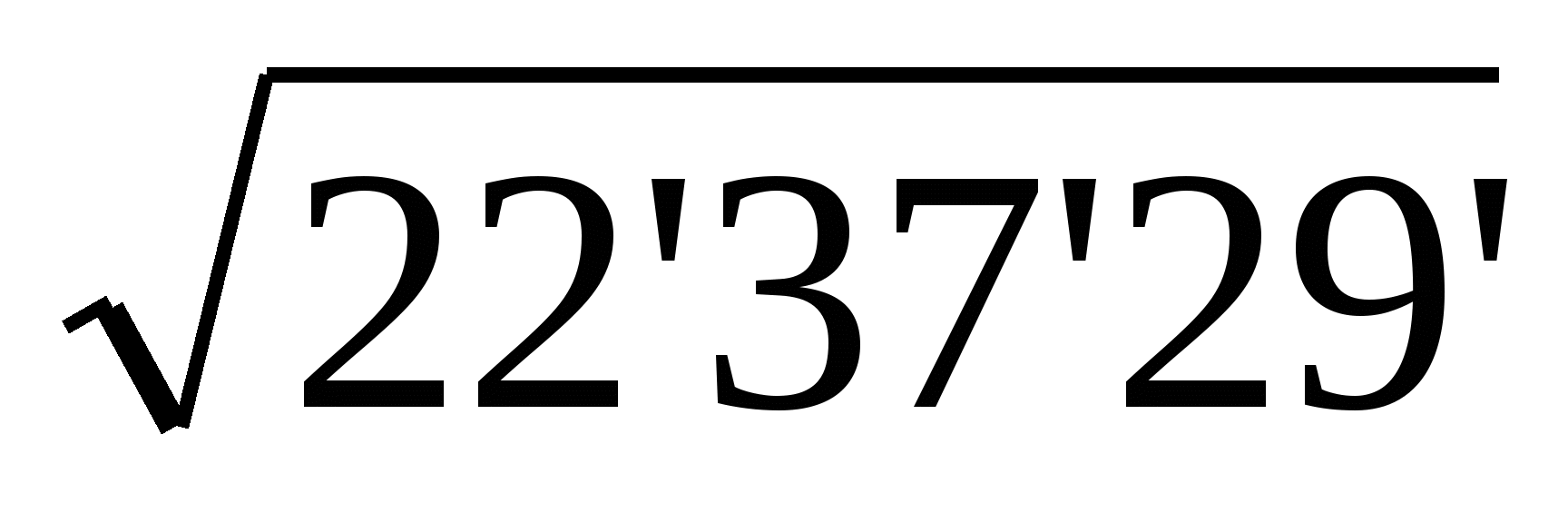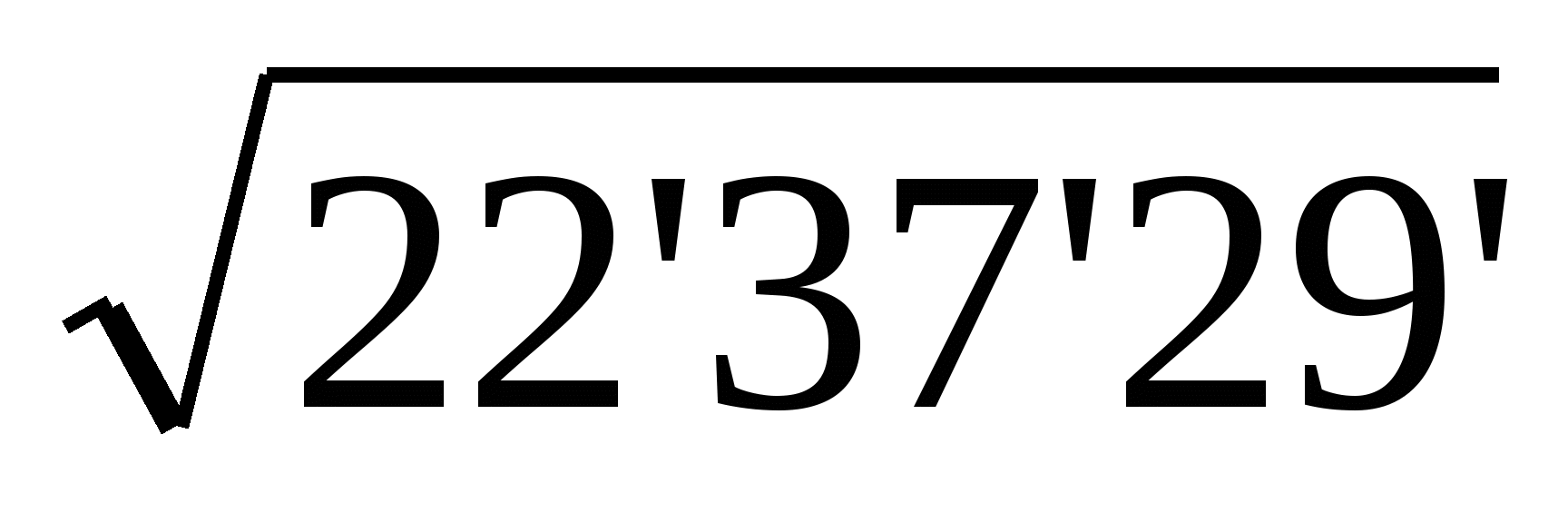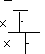= 473.

= 473

16

87 637

7 609

943 2829

3 2829

0

В принципе, если бы остаток получился ненулевой, можно было бы поставить после найденных цифр числа запятую, списать в качестве следующего разряда два десятичных знака числа, или два нуля, если таковые отсутствуют, и продолжать все более и более точно извлекать квадратный корень. Вот например:

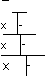
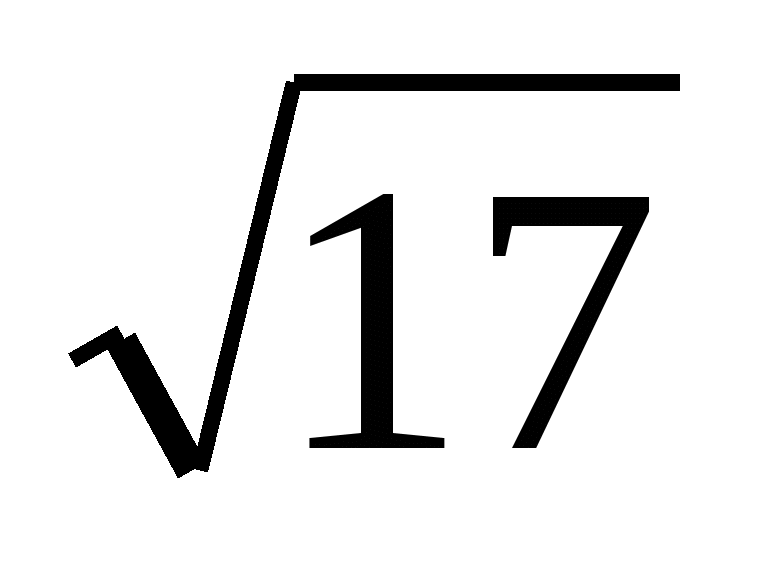= 4,123…

16

81 100

1 81

822 1900

2 1644

8243 25600

3 24729

871…

Приближенные методы извлечения квадратного корня

(без использования калькулятора).

1 метод.

Древние вавилоняне пользовались следующим способом нахождения приближенного значения квадратного корня их числа х. Число х они представляли в виде суммы а²+b, где а²_{ближайший к числу х точный квадрат натурального числа а (а²?х), и пользовались формулой 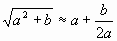. (1)}

Извлечем с помощью формулы (1) корень квадратный, например из числа 28:

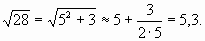
Результат извлечения корня из 28 с помощью калькулятора 5,2915026. Как видим способ вавилонян дает хорошее приближение к точному значению корня.

2 метод.

Исаак Ньютон разработал метод извлечения квадратного корня, который восходил еще к Герону Александрийскому (около 100 г. н.э.). Метод этот (известный как метод Ньютона) заключается в следующем.

Пусть а₁ — первое приближение числа 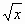(в качестве а₁ можно брать значения квадратного корня из натурального числа — точного квадрата, не превосходящего х) .

Следующее, более точное приближение а₂ числа 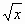найдется по формуле .

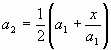Третье, еще более точное приближение 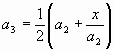и т.д.

(n+1)-е приближение 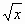найдется по формуле .

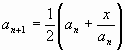Нахождение приближенного значения числа 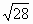методом Ньютона дает следующие результаты: а₁=5; а₂= 5,3; а₃=5,2915.

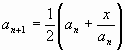— итерационная формула Ньютона для нахождения квадратного корня из числа х (n=2,3,4,…, а_n — n-е приближение .

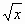Указанный мною способ позволяет извлекать квадратный корень из большого числа с любой точностью, правда с существенным недостатком: громоздкость вычислений.

Список литературы:

1. Пичугин Л.Ф. За страницами учебника алгебры.

2. Ткачева М.В. Домашняя математика.

3. Игнатьев Е. И. В царстве смекалки.

infourok.ru

Квадратный корень без калькулятора (в столбик) (8 класс)

Как извлечь квадратный корень

без калькулятора из любого числа

Пусть дано целое число 2572621. Найдем приближенное значение квадратного корня из этого числа «в столбик». Для этого разобьем цифры по парам, начиная с последней:

Начинаем извлечение корня из первой (справа) пары или, если впереди не пара, а всего одна цифра, то извлекаем корень из нее. Корень из 2приблизительно 1. Одиножды один будет 1 (или 1 в квадрате равен 1). Подпишем единицу под цифрой 2 и найдем разность, она равна 1, снесем сразу две цифры 5 и 7, получится 157. Запишем так:

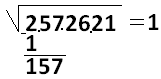
Удвоим единицу (не разность, а первую цифру ответа) 2·1=2 и запишем ответ 2 слева от столбика:

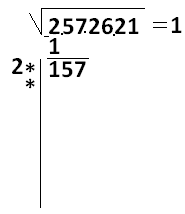
Далее вместо звездочек подберем одну и ту же цифру так, чтобы умножение получилось около 157. Это 6.

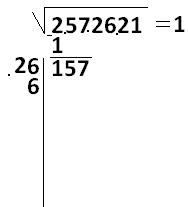
26 · 6 = 156. Разность равна 1.

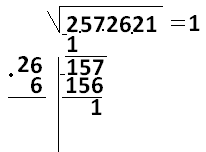
Снесем к разности еще две цифры, получится 126, а числа 26 и 6 (справа) сложим, получится 32.

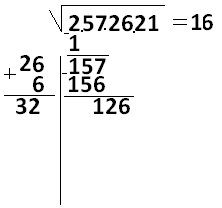
К числу 32 поставим две звездочки:

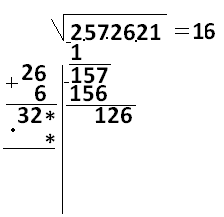
И снова подберем две одинаковые цифры так, чтобы произведение 32* и * было меньше 126. Это 0:

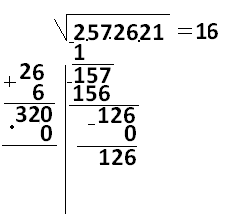
Разность равна 126, снесем две последние цифры, получится 12621, затем 320 и 0 сложим:

Снова вместо звездочек подбираем цифру, она равна 3, умножаем 3203 на 3, получается 9609, разность равна 3012:

Мы закончили целую часть. Ставим запятую, сносим два нуля и продолжаем:

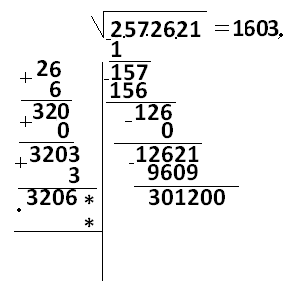
Итак, получилось, что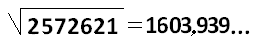

Если число – десятичная дробь, например, 6983,724, то начинаем разбивать на пары от запятой и вправо и влево, добавляя справа нули, если это нужно:

Умножение на 7 дает ответ больший 114700, но он все же ближе к этому числу, чем результат умножения на 6, так как 16706·6=100236, поэтому в данном примере лучше закончить извлечение корня цифрой 7.

Мясникова Татьяна Федоровна

infourok.ru