Проценты / Инструменты для вычислений и измерений / Справочник по математике 5-9 класс

1. Главная
2. Справочники
3. Справочник по математике 5-9 класс
4. Инструменты для вычислений и измерений
5. Проценты

Процентом от некоторой величины называется одна сотая ее часть и обозначают один процент так: 1%.

Чтобы найти процент от некоторой величины, нужно разделить эту величину на 100.

Пример:

1% от 200 т равен 2 т, так как 200 : 100 = 2.

1% от 5 км равен 50 м, т.к. 1 км = 1 000 м, тогда 5 км = 5 000 м, а 5 000 м : 100 = 50 м.

Величина, от которой вычисляются проценты составляет 100 своих сотых долей, т.е. 100 %.

Например, если говорят, что учащийся выполнил 100% домашнего задания, значит, он выполнил все домашнее задание, которое ему было задано.

Пример:

15% = 15 : 100 = 0,15;

60% = 60 : 100 = 0,60 = 0,6;

700% = 700 : 100 = 7;

23,5% = 23,5 : 100 = 0,235.

Обратите внимание: если у числа на конце справа стоит меньше двух нулей, то деление выполняем по правилу деления десятичных дробей на 100, т.е. перемещая запятую влево на две цифры, учитывая то, что у натурального числа запятую мы подразумеваем на конце справа.

Любую десятичную дробь или любое натуральное можно записать в процентах. Для этого нужно десятичную дробь или натуральное число умножить на 100 и к результату приписать знак %.

Пример:

3,5 = 3,5100 = 350%;

0,07 = 0,07100 = 7%;

9 = 9100 = 900%.

Обратите внимание: когда мы умножаем десятичную дробь на 100, то перемещаем запятую вправо на две цифры.

Чтобы найти несколько процентов от числа, нужно это число разделить на 100, а затем, полученный результат, умножить на число, стоящее перед знаком %.

Пример:

1) Найти 15% от числа 800.

800 : 100 = 8 — 1% от числа 800.

815 = 120 — 15% от числа 800.

2) Найти 6% от числа 375.

375 : 100 = 3,75 — 1% от числа 375.

3,756 = 22,50 = 22,5 — 6% от числа 375.

Чтобы найти число по его процентам, нужно разделить число, соответствующее известным процентам от числа, на число стоящее перед знаком % и полученный результат умножить на 100 или можно представить проценты в виде десятичной дроби и разделить значение процентов на эту дробь.

Пример:

Найдите число, если 20% этого числа равны 80?

1 способ:

1) 80 : 20 = 4 — 1% от числа.

2) 4100 = 400.

2 способ:

1) 20% = 0,2

2) 80 : 0,2 = 800 : 2 = 400.

Ответ: 400.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Микрокалькулятор

Скорость

Единицы измерения длины.

Единицы измерения массы

Диаграммы

Графики

Инструменты для вычислений и измерений

Правило встречается в следующих упражнениях:

5 класс

Задание 1609, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 1059, Мерзляк, Полонский, Якир, Учебник

Номер 1070, Мерзляк, Полонский, Якир, Учебник

Номер 1077, Мерзляк, Полонский, Якир, Учебник

Номер 1083, Мерзляк, Полонский, Якир, Учебник

Номер 7, Мерзляк, Полонский, Якир, Учебник

Номер 1097, Мерзляк, Полонский, Якир, Учебник

Номер 1099, Мерзляк, Полонский, Якир, Учебник

Номер 1102, Мерзляк, Полонский, Якир, Учебник

Номер 8, Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 635, Мерзляк, Полонский, Якир, Учебник

Номер 645, Мерзляк, Полонский, Якир, Учебник

Номер 3, Мерзляк, Полонский, Якир, Учебник

Номер 1292, Мерзляк, Полонский, Якир, Учебник

Номер 1332, Мерзляк, Полонский, Якир, Учебник

Задание 505, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 684, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 735, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 807, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1577, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

7 класс

Номер 99, Мерзляк, Полонский, Якир, Учебник

Номер 104, Мерзляк, Полонский, Якир, Учебник

Номер 115, Мерзляк, Полонский, Якир, Учебник

Номер 124, Мерзляк, Полонский, Якир, Учебник

Номер 149, Мерзляк, Полонский, Якир, Учебник

Номер 198, Мерзляк, Полонский, Якир, Учебник

Номер 287, Мерзляк, Полонский, Якир, Учебник

Номер 386, Мерзляк, Полонский, Якир, Учебник

Номер 387, Мерзляк, Полонский, Якир, Учебник

Номер 426, Мерзляк, Полонский, Якир, Учебник

---

© budu5. com, 2021

Пользовательское соглашение

Copyright

Примеры расчета процентов

 

Слово «процент» производная от латинских слов «pro cento», что означает «со ста». Выражение частей целого постоянно в аналогичных долях, исходя из практических соображений, было актуально еще в древности. В настоящем времени задачи связанные с использованием процентов остаются также востребованными, так как сфера их практического приложения весьма значительная.

К примеру, 1% от общей суммы означает 0,01 суммы.

Работа, выполненная полностью, означает 100% выполнение.

Выполнение на 150%, от задуманного, означает выполнение на 1,5 и т.д.

1% = 0,01

27% = 0,27

100% = 1

150% = 1,5

Чтобы узнать процент от заданного числа, к примеру, по вкладу в банке, нужно умножить это число на процент и разделить на 100.

10000 × 5 : 100 = 500 руб.

10000 – сумма вклада в рублях

5 – процентная ставка по вкладам в %

 

Если требуется вычислить число по заданному другому числу в процентах от искомого числа, нужно это число разделить на процент и умножить на 100.

Вес продукта в результате переработки составляет 8% от общего объёма.

Сколько сырья понадобится для изготовления 20кг продукта?

20 : 8 × 100 = 250кг

Чтобы узнать процентное выражение одного числа от другого, необходимо разделить первое число на второе, а затем умножить на

100.

 

Предприятие изготовило за месяц 2000 условных единиц товара. В связи с внедрением новых технологий в следующем месяце было произведено 4000 изделий. Какой процент по отношению к предыдущему месяцу?

4000 : 2000 × 100 = 200%

Что такое проценты и как их считать

Что такое процент?

1 процент — это сколько?

Процент — это сотая доля числа. Обозначается знаком «%». Является способом выразить число как часть целого.

100% 👧 👧 👧 👧 👧 👧 👧 👧 80% 👦 👦 20%  

Предположим, на столе лежит один пирог. Его мы разделим на 100 одинаковых частей.

Один кусочек из ста — это сотая доля пирога, что есть

• в виде обыкновенной дроби: 1 100,
• в виде десятичной дроби: 0,01,
• в процентах: 1% от пирога.

1 : 100 = 1
100 = 0,01 = 1%

25 процентов — это сколько?

25 кусочков — это четверть пирога или 25%.

25 : 100 = 25
100 = 1
4 = 0,25 = 25%

50 процентов — это сколько?

50 кусочков — это половина пирога или 50%.

50 : 100 = 50
100 = 1
2 = 0,5 = 50%

Уменьшить на 50% — значит уменьшить число в 2 раза.

100% чего-либо - 50% чего-либо = 50% чего-либо

100 процентов — это сколько?

Весь пирог — это один пирог или 100%.

100 : 100 = 100
100 = 1 = 100%

Увеличить на 100% — значит увеличить число в 2 раза.

100% чего-либо + 100% чего-либо = 200% чего-либо

150 процентов — это сколько?

Один целый пирог и ещё половина другого — это полтора пирога или 150%.

150 : 100 = 150
100 = 150
100 = 11
2 = 1,5 = 150%

200 процентов — это сколько?

Два пирога — это 200%.

200 : 100 = 200
100 = 2 = 200%

200% от числа — значит увеличить число в 2 раза.

Увеличить на 200% — значит увеличить число в 3 раза.

100% чего-либо + 200% чего-либо = 300% чего-либо

На сколько процентов одно число меньше другого?

Было 1000, стало 300. Разница в процентах?
На сколько процентов уменьшилась выручка, цена, зарплата, объём продаж и другое?
Или планировалось выполнить 1000 единиц, а сделали 300.

100% - 30% = 70%

300 меньше 1000 на 70%
Значение уменьшилось на 70%
План сделан на 30%, он недовыполнен на 70%

На сколько процентов одно число больше другого?

Было 300, стало 1000. Разница в процентах?
На сколько процентов увеличилась выручка, цена, зарплата, объём продаж и другое?
Планировалось выполнить 300 единиц, а сделали 1000.

333,33% - 100% = 233,33%

1000 больше 300 на 233,33%
Значение увеличилось на 233,33%
План сделан на 333,33%, он перевыполнен на 233,33%

Умножение на процентное значение

Умножение целого столбца чисел на процентное значение

Рассмотрим пример таблицы, как на рисунке, в которой нужно умножить несколько чисел на 15 процентов. Даже если в столбце 100 или 1000 ячеек с данными, Excel все равно может обработать его за несколько шагов.

Вот как это сделать:

1. Введите в столбец числа, которые нужно умножить на 15 %.

2. В пустой ячейке введите процент 15 % (или 0,15) и скопируйте это число, нажав CTRL+C.

3. Выберем диапазон ячеек A1:A5 (путем перетаскиванием вниз по столбцу).

4. Щелкните правой кнопкой мыши ячейку, а затем выберите «Специальная вконечная ячейка» (не щелкать стрелку рядом с кнопкой «Специальная вконечная ячейка»).

5. Щелкните «Значения>умножить,а затем нажмите кнопку «ОК».

   В результате все числа умножаются на 15 %.

   
    

Совет: Вы также можете вычитать процентные значения в столбец путем умножения. Чтобы вычесть 15 %, добавьте перед процентным знаком знак «минус» и вычитайте процент из 1 с помощью формулы =1-n%, где n — процент. Чтобы вычесть 15 %, используйте в качестве формулы =1–15%.

Умножение целого столбца чисел на процентное значение

В этом примере мы можем умножить всего несколько чисел на 15 процентов. Даже если в столбце 100 или 1000 ячеек с данными, Excel в Интернете можно обработать его за несколько шагов. Вот что нужно для этого сделать:

1. Введите формулу =A2*$C$2 в ячейку B2. (Не забудьте включить символ $ в формулу перед символами C и 2.)

Символ $ делает ссылку на ячейку C2 абсолютной, то есть при копировании формулы в другую ячейку ссылка всегда будет на ячейку C2. Если вы не использовали символы $ в формуле и перетащили формулу вниз на ячейку B3, Excel в Интернете изменит формулу на =A3*C3, что не будет работать, так как в ячейке C3 нет значения.

1. Перетащите формулу в ячейке B2 вниз в другие ячейки в столбце B.

Совет:  Вы также можете вычитать процентные значения в столбец путем умножения. Чтобы вычесть 15 %, поставьте знак «минус» перед процентным значением и вычтите его из 1 с помощью формулы =1-n%, где n — процентное значение. Таким образом, для вычитания 15 % используйте формулу =1-15%.

Как объяснить детям, что такое проценты / Бери и делай

Тема процентов может показаться сложной не только для детей, но и для взрослых. Ведь даже умение считать их так, как учат в школе, может подвести, если под рукой нет бумаги и ручки, а вам надо быстро получить результат.

«Бери и Делай» рассказывает, как просто и быстро объяснить ребенку, что такое проценты, и как легко решать задачки с ними прямо в уме с помощью нескольких хитростей, о которых не расскажут учителя математики.

Что такое процент

Представим, что у нас есть огромный квадратный торт. Его можно взять и разделить на 100 одинаковых кусочков. Изобразим это схематично, нарисовав на листе в клеточку большой квадрат 10 × 10.

Закрасим 1 клетку, которая символизирует 1 кусочек. Это 1 процент (1 %) от всего торта, так как целый торт представляет собой 100 %.

Таким образом, говоря о процентах, мы представляем себе число в виде целого, разделенного на 100 равных частей. Одна сотая часть этого целого и есть 1 % от числа. Другими словами, разделив любое число на 100, мы получаем 1 % от этого числа.

Используя 100-клеточный квадрат, удобно знакомиться с понятием процентов и тем, какую часть от целого они представляют. Закрасим 10 клеток: это 10 кусков торта, или 10 % от целого торта.

Далее закрасим половину всего квадрата, или 50 клеток. Это 50 кусков торта, или 50 % от целого торта. Аналогичным образом можно изобразить любую процентную часть от целого числа.

✅ Совет: Используйте этот квадрат 10 × 10, чтобы отображать на нем числа в процентах и сравнивать их между собой. С его помощью также будет удобно производить простые действия сложения и вычитания с процентами.

Пример: На картинке выше обозначены 3 красные клетки, соответствующие 3 %, и 9 синих клеток, соответствующие 9 %. Пересчитав все закрашенные клетки или сложив числа, мы получаем 12 %.

Как считать проценты

Выше на картинке изображена элементарная задачка. Справиться с ней легко: если процент — это одна сотая часть числа, то 17 % от числа 100 равняется 17.

Но как быть, если нужно найти процент от иного числа? Например, 17 % от числа 400.

Можно воспользоваться хитростью и представить число 400 как 4 сотни. Тогда 17 % от числа 400 мы рассматриваем как 17 % от каждой сотни, входящей в состав 400. В таком случае достаточно их просто сложить между собой и получить правильный ответ:

17 + 17 + 17 + 17 = 68

Так мы узнали, что 17 % от числа 400 равняется 68. Но подобная хитрость выручит далеко не всегда.

Пример: Нужно вычислить, чему равняется 14 % от 550.

Из определения процента мы помним, что 1 % — это одна сотая от целого числа (разбитого на 100 равных частей). Получается, чтобы найти процент от какого-либо числа, надо это число разделить на 100 и результат деления умножить на количество процентов. Тогда нам нужно сделать 2 действия:

В результате получается, что 14 % от числа 550 составляет 77.

В некоторых задачах ситуация может быть обратной, когда необходимо вычислить, чему равняется 100 %.

Пример: Как найти 100 %, если 65 % составляет 260?

Здесь мы будем двигаться в обратном направлении: сначала узнаем, чему равен 1 %, а затем вычислим, чему равняется 100 %. Получается, нам нужно:

В результате получается, что 100 % равняется 400.

Так можно решать разные задачки с процентами, и чаще всего именно подобным образом принято решать примеры в школе. Но существуют некоторые хитрости и методы, которые значительно упростят этот процесс.

Хитрость № 1: Поменяйте числа и проценты местами

Для любой задачи справедливо правило: X % от Y = Y % от X. Тогда можно поменять числа и проценты местами, если это упростит решение задачи.

Допустим, нужно вычислить 4 % от 75:

Поменяем местами числа и проценты, а затем решим задачу.

Если 4 % от 75 = 75 % от 4,

то посчитаем 75 % от 4 и получим число 3.

Таким образом, 4 % от 75 тоже равняется 3.

Благодаря этой хитрости в некоторых случаях проценты можно вычислять в уме.

Пример: Вам нужно высчитать 18 % от 50. Поменяйте числа местами и вычислите 50 % от 18. Результат — 9. Таким образом, 18 % от 50 тоже равно 9.

Хитрость № 2: Считайте проценты как равные доли

Посмотрите на круговые диаграммы выше: на них проценты представлены в виде частей круга. Например, 50 % занимает половину круга, 25 % только четверть, а 20 % лишь одну пятую.

Получается, чтобы посчитать 50 % от числа, достаточно разделить его на 2, а для того, чтобы вычислить 20 % от числа, нужно разделить его на 5. Далее, следуя этой логике, можно составить следующую таблицу:

Справа от стрелок указано, на какое число необходимо делить число (или делить, а затем умножать) при вычислении конкретного процента от этого числа. Таким образом, не нужно искать значение, к примеру 20 %, а затем умножать его на что-то, рискуя перепутать числа и проценты. Достаточно выполнить одно действие.

Подобным образом можно решать и более сложные задачи. Например, 16 % от 42 можно представить как 10 % + 5 % + 1 %, то есть 4,2 + 2, 1 + 0,42 = 6,72.

Хитрость № 3: Чтобы решить все в одно действие, двигайте знаки

Все просто: сдвинем запятую, отделяющую целую часть числа от дробной, на 1 цифру влево в каждом числе, а затем перемножим эти числа. Например, чтобы вычислить 90 % от 80, умножим 9 на 8 и получим 72. Аналогично, если нужно найти 21 % от 35, умножаем 2,1 на 3,5 и получаем 7,35.

Примеры задач на проценты из реальной жизни

Если в школе требуется решать примеры в тетради, то в быту задачки для детей могут быть достаточно простыми, но направленными на то, чтобы подсказать им, как считать в уме проценты максимально простыми способами.

Например:

• Чтобы вычислить 10 % от 4 кг, достаточно вспомнить, что 10 % — это одна десятая часть сотни, поэтому можно разделить 4 кг на 10. Получится 0,4 кг, или 400 г.
• Чтобы высчитать 5 % от 5 метров, можно представить 5 м как 500 см. Затем разделить 500 на 10 %, получив 50. А уже этот результат разделить пополам, чтобы получить 5 %. Таким образом, получается, что 5 % от 5 м — это 25 см, или 0,25 м.
• Чтобы вычислить 40 % от ₽ 15, достаточно сначала вычислить 10 % от ₽ 15, что составляет ₽ 1,5, а затем умножить на 4. Получается, что 40 % от ₽ 15 равняется ₽ 6.

Освоив такой подход, ребенок уже во взрослой жизни будет гораздо лучше ориентироваться в ситуациях, где умение вычислять проценты может подсказать ему более выгодное предложение.

Задача № 1. В двух онлайн-магазинах продаются две одинаковые модели наушников. В магазине № 1 они стоят € 45, но продавец обещает бесплатную доставку по всему миру. В магазине № 2 цена такая же, но вам готовы предоставить скидку 15 %, правда, за доставку придется отдать € 8. В каком магазине выгоднее купить наушники?

Вспомним, что 15 % — это 10 % + 5 %. Легко посчитать, что 10 % от € 45 — это € 4,5. Тогда 5 % — это € 2,25. Сложим 4,5 и 2, 25 и получим 6,75. Получается, что 15 % от € 45 составляет € 6,75. Значит, в магазине № 2 вы сэкономите € 6,75 при покупке товара, но все равно потратите больше из-за доставки, которая стоит € 8. В таком случае выгоднее покупать товар в магазине № 1.

Задача № 2. На витрине магазина красуются отличные кеды, цена которых — ₽ 2 600. Сегодня распродажа и на весь товар действует дополнительная скидка 25 %. У вас с собой только ₽ 2 000. Хватит ли денег на покупку?

Нам известно, что 25 % — это одна четверть от 100 %. Получается, что надо узнать, чему в рублях равняется 75 %, или три четверти. Для этого цену без скидки разделим на 4 части, а затем умножим на 3:

2600 ÷ 4 = 650

650 × 3 = 1 950

Получается, что цена кед с учетом скидки составляет ₽ 1 950, а значит, вы точно сможете их приобрести.

Задача № 3. Вы пришли в магазин за колбасой. Ее цена — ₽ 376. Вам предлагают купить этот продукт с учетом утренней скидки, которая составляет 11 %, или воспользоваться картой магазина, благодаря которой колбаса обойдется в ₽ 320. Что выгоднее?

Переведем 11 % в деньги. Возьмем цену колбасы и вычислим 1 %, переместив в числе 376 запятую, отделяющую целую часть числа от дробной, на 2 знака влево. Получим, что 1 % равен ₽ 3,76, а 10 %, соответственно, ₽ 37,6. Сложим и получим ₽ 41,36.

Можно было посчитать это иным способом, воспользовавшись хитростью № 3 и просто сдвинув запятую в числах, а затем перемножив их:

1,1 × 37,6 = 41,36

Теперь вычитаем это число из обычной цены колбасы. Получается, что с учетом утренней скидки колбаса будет стоить ₽ 334,64, а значит, покупка будет выгодной, если воспользоваться картой магазина и купить ее за ₽ 320.

Процент, Процентное соотношение

Процент (что означает «на сотню») это сравнение с 100.

Символ процента %. Так, например, 5 процентов записывается как 5%.

Предположим, что в комнате 4 человека.

50% это половина — 2 человека.
25% это четверть — 1 человек.
0% это ничего — 0 человек.
100% это целое — все 4 человека в комнате.
Если в комнату заходят ещё 4 человека, то их колличество становится 200%.

1% это $\frac{1}{100}$
Если всего есть 100 человек, то 1% из них это один человек.

Чтобы выразить математически число X как процент от Y вы делаете следующее:
$X : Y \times 100 = \frac{X}{Y} \times 100$

Пример: Сколько процентов от 160 составляет 80?

Решение:

$\frac{80}{160} \times 100 = 50\%$

Увеличение/Уменьшение процентного соотношения

Когда число увеличивается относительно другого числа, то величина увеличения представляется как:

Увеличение = Новое число — Старое число

Однако, когда число уменьшается относительно другого числа, то эту величину можно представить как:

Уменьшение = Старое число — Новое число

Увеличение или уменьшение числа всегда выражается на основании старого числа.
Поэтому:

%Увеличение = 100 ⋅ (Новое число — Старое число) ÷ Старое число

%Уменьшение = 100 ⋅ (Старое число — Новое число) ÷ Старое число

Например, у Вас было 80 почтовых марок и Вы начали в этом месяце собирать ещё пока общее количество почтовых марок достигло 120. Процентное увеличение числа марок, которые у Вас есть равно

$\frac{120 — 80}{80} \times 100 = 50\%$

Когда у Вас стало 120 марок, Вы и Ваш друг договорились обменять игру «Lego» на несколько из этих марок. Ваш друг взял несколько марок, которые ему понравились, и когда Вы подсчитали оставшиеся марки, то обнаружили, что у Вас осталось 100 марок. Процентное уменьшение числа марок может быть подсчитано как:

$\frac{120 — 100}{120} \times 100 = 16,67\%$

Калькулятор Процентов

Как процентные соотношения помогают в реальной жизни

Есть два способа, как процентные соотношения помогают в решении наших каждодневных проблем:

1. Мы сравниваем две разных величины, когда все величины соотносятся с одной и той же основной величиной равной 100. Чтобы объяснить это, давайте рассмотрим следующий пример:

Пример: Том открыл новую бакалейную лавку. За первый месяц он купил бакалеи за \$650 и продал за \$800, а во втором купил за \$800 и продал за \$1200.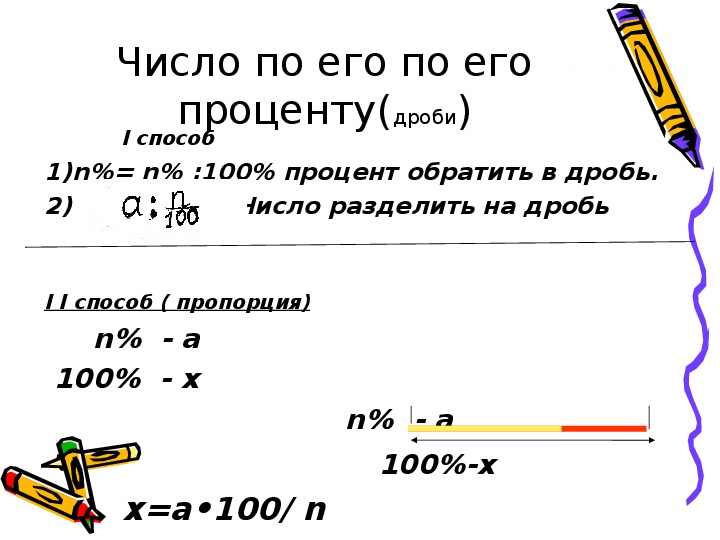 Надо рассчитать делает ли Том больше прибыли или нет.

Решение:

Напрямую из этих чисел мы не можем сказать растёт доход Тома или нет, потому что расходы и выручка каждый месяц разные. Для того, чтобы решить эту задачу, нам нужно соотнести все значения к фиксированной основной величине равной 100. Давайте выразим процентное соотношение его доходов к расходам в первый месяц:

(800 — 650) ÷ 650 ⋅ 100 = 23,08%

Это значит, что если Том тратил \$100, то он делал прибыль в размере 23.08 в первый месяц.

Теперь давайте применим тоже самое ко второму месяцу:

(1200 — 800) ÷ 800 ⋅ 100 = 50%

Так, во втором месяце, если Том тратил \$100, то его доход был \$50(потому что \$100⋅50% = \$100⋅50÷100=\$50). Теперь понятно,что доходы Тома растут.

2. Мы можем определять количество части большей величины, если известно процентное соотношение этой части. Чтобы объяснить это, давайте рассмотрим следующий пример:

Пример: Синди хочет купить 8 метров шланга для своего сада. Она пошла в магазин и обнаружила, что там есть катушка со шлангом длиной 30 метров. Однако, она заметила, что на катушке написано, что 60% уже продано. Она должна узнать хватит ли ей оставшегося шланга.

Решение:

В табличке сказано, что

$\frac{Продано\ длина}{Всего\ длина} \times 100 = 60\%$

$Продано\ длина = \frac{60 \times 30}{100} = 18м$

Поэтому остаток 30 — 18 = 12м, которого вполне достаточно Синди.

Примеры:

1. Райн любит собирать спортивные карточки с его любимыми игроками. У него есть 32 карточки с игроками бейсбола, 25 карточки с футболистами и 47 с баскетболистами. Каково процентное соотношение карточек каждого спорта в его коллекции?

Решение:

Общее количество карточек = 32 + 25 + 47 = 104

Процентное соотношение бейсбольных карточек = 32/104 x 100 = 30,8%

Процентное соотношение футбольных карточек = 25/104 x 100 = 24%

Процентное соотношение баскетбольных карточек = 47/104 x 100 = 45,2%

Обратите внимание, что если сложить все проценты, то получится 100%, что представляет общее количество карточек.

 

2. На уроке был математический тест. Тест состоял из 5 вопросов; за три из них давали по три 3 балла за каждый, а за осташиеся два — по четыре балла. Вам удалось правильно ответить на два вопроса по 3 балла и на один вопрос по 4 балла. Какое процентное соотношение баллов Вы получили за этот тест?

Решение:

Общее количество = 3×3 + 2×4 = 17 баллов

Полученные балы = 2×3 + 4 = 10 баллов

Процентное соотношение полученных баллов = 10/17 x 100 = 58,8%

 

3. Вы купили видео игру за \$40. Потом цены на эти игры подняли на 20%. Какова новая цена видео игры?

Решение:

Увеличение цены равно 40 x 20/100 = \$8

Новая цена равна 40 + 8 = \$48

Урок 65. десятичные дроби и проценты. часть 1 — Математика — 6 класс

Математика

6 класс

Урок № 65

Десятичные дроби и проценты. Часть 1

Перечень рассматриваемых вопросов:

• понятие процента;
• нахождение процента от числа;
• нахождение числа по его процентам;
• нахождение значения процента одной величины от другой.

Тезаурус

Процент – это сотая часть величины.

Вся величина – это сто процентов (100 %).

Обязательная литература:

1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.

Дополнительная литература:

1. Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.

Теоретический материал для самостоятельного изучения

Люди часто используют сотые части величин, например, сотая часть центнера – это килограмм, сотая часть века – год, сотая часть метра – сантиметр и так далее. Для сотой части любой величины придумали специальное название – один процент, и обозначение – 1%.

Так как процент – это сотая часть величины, то для того, чтобы найти один процент от величины, нужно её значение разделить на 100.

Заметим, что 100 процентов величины это 100 сотых величины, то есть 100 процентов величины – это вся величина, или целое.

Чтобы перевести десятичную дробь в проценты, надо её умножить на 100.

0,023 = 0,023 · 100 % = 2,3 %

Чтобы перевести проценты в десятичную дробь, надо разделить число процентов на 100.

49 % = 49 : 100 = 0,49

В начале ученого года вы научились решать простые задачи на проценты с помощью пропорции. Например:

12 % от числа составляют 60. Найдите целое число.

Целое число это 100 %. Запишем данные.

Перед нами прямая пропорциональность, составим пропорцию.

Теперь вы умеете умножать и делить на десятичную дробь, и решать задачи на проценты сможете и другим способом.

Рассмотрим задачи основных типов. Первый тип – это нахождение процентов данного числа.

Задача. Найти 15 процентов от 70 метров.

Решение. 15 процентов – это 15 сотых. То есть нужно найти 0,15 от 70. Помним, что для того, чтобы найти дробь от числа, надо число умножить на эту дробь.

Получим, что 15 процентов от 70 метров это 10,5 метров.

Ответ: 15 % от 70 метров это 10,5 метров.

Второй тип задач – нахождение числа по его процентам.

Задача. Найти число, если 30 процентов этого числа составляют 60.

Решение. Запишем 30 процентов в виде десятичной дроби, это 0,3.

Чтобы найти целое по его части, нужно часть разделить на соответствующую ей дробь.60 разделить на 0,3 десятых получим 200.

30% от числа = 60.

Целое число = ?

60 : 0,3 = 200.

Ответ: целое число это 200.

Третий тип задач. Найти, сколько процентов составляет одна величина от другой.

Задача. Сколько процентов составляет число 6 от 16?

Решение. Чтобы ответить на этот вопрос, нужно сначала выяснить, какую часть составляет число 6 от числа 16. Для этого нужно 6 разделить на 16.

Запишем в виде обыкновенной дроби и сократим её.

И затем умножим на 100 процентов.

Получим 37,5 десятых процентов.

Ответ: число 6 от числа 16 составляет 37,5 %.

Разбор заданий тренировочного модуля

Тип 1. Подстановка элементов в пропуски в тексте.

Впишите верное число.

Решение. Переведём обыкновенную дробь в десятичную.

Теперь переведём десятичную дробь в проценты, умножив её на 100.

0,25 · 100 = 25 %

Тип 2. Подстановка элементов в пропуски в тексте

Впишите пропущенное число.

Закрашено …% площади квадрата.

Решение. Вся площадь квадрата – это 36 клеток. Закрашено 9 клеток. Значит, чтобы найти, сколько процентов закрашено, нужно 9 разделить на 36 и частное умножить на 100 %. Получаем

Ответ: Закрашено 25 % площади квадрата.

Как рассчитать процент, процентное изменение и процентную разницу

1. Руководство по карьере
2. Развитие карьеры
3. Как рассчитать процентное соотношение, процентное изменение и процентную разницу

Редакционная группа Indeed

2 ноября 2021 г.

Знание того, как рассчитать процент от числа является фундаментальной составляющей многих аспектов жизни. Например, вам может потребоваться знать, как рассчитать процент для оплаты автомобиля или определить первоначальный взнос за дом.

Расчет процентов также важен в бизнесе и используется в различных профессиональных целях, например, при расчете налогов или надбавок сотрудников. В этой статье мы исследуем, что такое процент, как рассчитать различные составляющие процента и типы процентов.

Какой процент?

Процент, который также может обозначаться как процент, представляет собой долю от числа 100%. Процент означает «на сотню» и означает часть от общей суммы.

Например, 45% представляет 45 из 100 или 45 процентов от общей суммы.

Процент также может обозначаться как «из 100» или «на каждые 100».

Например, вы можете сказать: «Снег шел 20 дней из каждых 100 дней», или можно сказать: «Снег шел в 20% случаев».

Процент можно записать несколькими способами. Один из способов записать или обозначить процент — это изобразить его в виде десятичной дроби.

Например, 24% можно также записать как.24. Вы можете найти десятичную версию процента, разделив процент на 100. Процент также можно отобразить с помощью знака процента или «%».

Связано: Your Guide to Careers in Finance

Как рассчитать процент

Существует несколько различных способов расчета процента. Следующая формула является стандартной стратегией, используемой для вычисления процента чего-либо:

1. Определите всю или общую сумму того, что вы хотите найти в процентах для

Например, если вы хотите вычислить процент от того, сколько дней за месяц шел дождь, вы должны использовать количество дней в этом месяце как общую сумму.Итак, допустим, мы оцениваем количество дождя в апреле, в котором 30 дней.

2. Разделите число, которое вы хотите определить в процентах, на

Используя приведенный выше пример, предположим, что дождь шел 15 дней из 30 дней в апреле. Вы разделите 15 на 30, что равно 0,5.

3. Умножьте значение из шага два на 100

Продолжая приведенный выше пример, вы должны умножить 0,5 на 100. Это равно 50, что даст вам ответ 50%.Так, в апреле в 50% случаев шел дождь.

Связано: Что такое способности?

Типы процентных проблем

Существует три основных типа процентных проблем, с которыми вы можете столкнуться как в личных, так и в профессиональных условиях. К ним относятся:

1. Нахождение конечного числа

2. Нахождение процентного соотношения

3. Нахождение начального числа

1. Нахождение конечного числа

Ниже приводится пример вопроса, который потребует от вас использовать процентное вычисление, чтобы найти конечное число в задаче: «Что такое 50% от 25?» Для этой проблемы у вас уже есть процент и вся сумма, от которой вы хотите найти процент.

Итак, вы перейдете ко второму шагу, как указано в предыдущем разделе. Однако, поскольку у вас уже есть процентное соотношение, вместо деления вы захотите умножить процент на целое число. Для этого уравнения вы должны умножить 50%, или 0,5, на 25. Это даст вам ответ 12,5. Таким образом, ответ на этот процентный вопрос будет: «12,5 — 50% от 25».

2. Нахождение процентного соотношения

Для задачи с процентным соотношением, в которой вам нужно найти процентное соотношение, можно задать следующий вопрос: «Какой процент от 5 равен 2?» В этом примере вам нужно будет определить в процентах, сколько 2 является частью целого 5.Для этого типа проблемы вы можете просто разделить число, которое вы хотите превратить в процент, на целое. Итак, используя этот пример, вы разделите 2 на 5. Это уравнение даст вам 0,4. Затем вы умножите 0,4 на 100, чтобы получить 40 или 40%. Таким образом, 2 равно 40% от 5.

3. Нахождение начального числа

Процентная задача, которая просит вас найти начальное число, может выглядеть следующим образом: «45% от того, что равно 2?» Обычно это более сложное уравнение, но его легко решить, используя ранее упомянутую формулу.Для этого типа процентной задачи вам нужно разделить целое на заданный процент. Используя пример «45% от 2?», Вы разделите 2 на 45% или 0,45. Это даст вам 4,4, что означает, что 2 составляет 45% от 4,4.

Связано: Узнайте о том, как стать финансовым менеджером

Как рассчитать процентное изменение

Процентное изменение — это математическое значение, которое обозначает степень изменения во времени. Чаще всего он используется в финансах для определения изменения цены ценной бумаги с течением времени.Эту формулу можно применить к любому количеству, которое измеряется с течением времени.

Процентное изменение равно изменению заданного значения. Вы можете рассчитать процентное изменение, разделив все значение на исходное значение, а затем умножив его на 100. Формула расчета процентного изменения следующая:

• Для увеличения цены или процента:
  [(Новая цена — Старая цена) / Старая цена] x 100

• Для снижения цены или процента:
  [(Старая цена — Новая цена) / Старая цена] x 100

Ниже приведен пример увеличения цены / процента. : В прошлом году телевизор стоил 100 долларов, а сейчас стоит 125 долларов.Чтобы определить рост цены, вы должны вычесть старую цену из новой цены: 125 — 100 = 25. Затем вы должны разделить это на старую цену: 25 разделить на 100 равно 0,25. Затем вы умножите это число на 100: 0,25 x 100 = 25, или 25%. Так, цена телевизора за последний год выросла на 25%.

Пример снижения цены / процента: в прошлом году телевизор стоил 100 долларов, а сейчас стоит всего 75 долларов. Чтобы определить снижение цены, вы должны вычесть новую цену из старой: 100 — 75 = 25.Затем вы разделите это число на старую цену: 25 разделенных на 100 равно 0,25. Затем вы умножите это на 100: 0,25 x 100 = 25. или 25%. Это означает, что телевизор стоит на 25% меньше, чем в прошлом году.

Как рассчитать процентную разницу

Вы можете использовать проценты для сравнения двух разных элементов, связанных друг с другом. Например, вы можете определить, сколько стоил продукт в прошлом году по сравнению со стоимостью аналогичного продукта в этом году. Этот расчет даст вам процентную разницу между ценами двух продуктов.

Для расчета процентной разницы используется следующая формула:
| V1 — V2 | / [(V1 + V2) / 2] × 100

В этой формуле V1 равна стоимости одного продукта, а V2 равна стоимости другого товара.

Пример использования этой формулы для определения разницы между стоимостью продукта: продукт стоил 25 долларов в прошлом году, а аналогичный продукт стоит 30 долларов в этом году. Чтобы определить процентную разницу, вы сначала должны вычесть затраты друг из друга: 30-25 = 5.Затем вы должны определить среднее значение этих двух затрат (25 + 30/2 = 27,5). Затем вы разделите 5 на 27,5 = 0,18. Затем вы умножите 0,18 на 100 = 18. Это означает, что стоимость продукта в этом году на 18% больше, чем стоимость продукта в прошлом году.

Калькулятор процентов

Использование калькулятора

Найдите процент или вычислите процент с учетом чисел и значений процентов. Используйте формулы процентов, чтобы вычислить проценты и неизвестные в уравнениях. Добавьте или вычтите процент от числа или решите уравнения.

Как рассчитать проценты

Есть много формул для процентных задач. Вы можете думать о самом простом, как о X / Y = P x 100. Формулы ниже являются математическими вариациями этой формулы.

Давайте рассмотрим три основные процентные проблемы. X и Y — числа, а P — процентное соотношение:

1. Найдите P процентов от X
2. Найдите, какой процент X равен Y
3. Найдите X, если P процентов от него Y

Прочтите, чтобы узнать больше о том, как рассчитывать проценты.

1. Как рассчитать процент от числа. Используйте процентную формулу: P% * X = Y

.

Пример: Что составляет 10% от 150?

• Преобразуйте задачу в уравнение, используя процентную формулу: P% * X = Y
• P равно 10%, X равно 150, поэтому уравнение 10% * 150 = Y
• Преобразуйте 10% в десятичное число, удалив знак процента и разделив на 100: 10/100 = 0,10
• Запасной 0. 10 вместо 10% в уравнении: 10% * 150 = Y становится 0,10 * 150 = Y
• Посчитайте: 0,10 * 150 = 15
• Y = 15
• Итак, 10% от 150 равно 15
• Дважды проверьте свой ответ на исходный вопрос: Что составляет 10% от 150? Умножить 0,10 * 150 = 15

2. Как определить, какой процент от X равен Y. Используйте формулу процента: Y / X = P%

Пример: Какой процент от 60 равен 12?

• Преобразуйте задачу в уравнение, используя процентную формулу: Y / X = P%
• X равно 60, Y равно 12, поэтому уравнение 12/60 = P%
• Посчитайте: 12/60 = 0.20
• Важно! Результат всегда будет в десятичной, а не процентной форме. Вам нужно умножить результат на 100, чтобы получить процент.
• Преобразование 0,20 в процент: 0,20 * 100 = 20%
• Итак, 20% от 60 равно 12.
• Дважды проверьте свой ответ на исходный вопрос: какой процент от 60 составляет 12? 12/60 = 0,20 и умножение на 100, чтобы получить процент, 0,20 * 100 = 20%

3.Как найти X, если P процентов от него Y. Используйте процентную формулу Y / P% = X

Пример: 25 — это 20% от какого числа?

• Преобразуйте задачу в уравнение, используя процентную формулу: Y / P% = X
• Y равно 25, P% равно 20, поэтому уравнение 25/20% = X
• Преобразуйте процент в десятичное число, разделив на 100.
• Преобразование 20% в десятичное: 20/100 = 0,20
• Запасной 0.20 для 20% в уравнении: 25 / 0,20 = X
• Посчитайте: 25 / 0,20 = X
• Х = 125
• Так 25 составляет 20% от 125
• Дважды проверьте свой ответ на исходный вопрос: 25 — это 20% от какого числа? 25 / 0,20 = 125

Помните: как преобразовать проценты в десятичные числа

• Убрать знак процента и разделить на 100
• 15. 6% = 15,6 / 100 = 0,156

Помните: как преобразовать десятичную дробь в проценты

• Умножить на 100 и добавить знак процента
• 0,876 = 0,876 * 100 = 87,6%

---

Процент проблем

Есть девять вариантов трех основных задач, связанных с процентами. Посмотрите, сможете ли вы сопоставить свою проблему с одним из примеров, приведенных ниже. Форматы задач соответствуют полям ввода в калькуляторе выше.Формулы и примеры включены.

Что такое P процентов от X?

• Записывается в виде уравнения: Y = P% * X
• «Что такое» Y, которое мы хотим решить для
• Не забудьте сначала преобразовать процент в десятичное, разделив на 100
• Решение: Решите относительно Y, используя процентную формулу
  Y = P% * X

Пример: Что составляет 10% от 25?

• Записывается по процентной формуле: Д = 10% * 25
• Первое преобразование процента в десятичное число 10/100 = 0. 1
• Y = 0,1 * 25 = 2,5
• Итак, 10% от 25 равно 2,5

Y какой процент от X?

• Записывается в виде уравнения: Y = P%?
х
• «Что» такое P%, которое мы хотим решить для
• Разделите обе части на X, чтобы получить P% с одной стороны уравнения
• Y ÷ X = (P%? X) ÷ X становится Y ÷ X = P%, что совпадает с P% = Y ÷ X
• Решение: Найдите P%, используя процентную формулу
  P% = Y ÷ X

Пример: 12 — это какой процент от 40?

• Записывается по формуле: П% = 12 ÷ 40
• P% = 12 ÷ 40 = 0. 3
• Преобразование десятичной дроби в проценты
• P% = 0,3 × 100 = 30%
• Таким образом, 12 составляет 30% от 40

Y — это P процентов чего?

• Записывается в виде уравнения: Y = P% * X
• Что такое X, которое мы хотим решить для
• Разделите обе части на P%, чтобы получить X на одной стороне уравнения
• Y ÷ P% = (P% × X) ÷ P% становится Y ÷ P% = X, что совпадает с X = Y ÷ P%
• Решение: Решите относительно X, используя процентную формулу
  X = Y ÷ P%

Пример: 9 — это 60% чего?

• Записывается по формуле: X = 9 ÷ 60%
• Преобразовать проценты в десятичные числа
• 60% ÷ 100 = 0. 6
• Х = 9 ÷ 0,6
• Х = 15
• Так 9 составляет 60% от 15

Какой процент X составляет Y?

• Записывается в виде уравнения: P% * X = Y
• «Что» такое P%, которое мы хотим решить для
• Разделите обе части на X, чтобы получить P% с одной стороны уравнения
• (P% * X) ÷ X = Y ÷ X становится P% = Y ÷ X
• Решение: Найдите P%, используя процентную формулу
  P% = Y ÷ X

Пример: Какой процент от 27 равен 6?

• Записывается по формуле: П% = 6 ÷ 27
• 6 ÷ 27 = 0. 2222
• Преобразование десятичной дроби в проценты
• P% = 0,2222 × 100
• P% = 22,22%
• Итак, 22,22% от 27 это 6

P процентов от того, что есть Y?

• Записывается в виде уравнения: P% × X = Y
• Что такое X, которое мы хотим решить для
• Разделите обе части на P%, чтобы получить X на одной стороне уравнения
• (P% × X) ÷ P% = Y ÷ P% становится X = Y ÷ P%
• Решение: Решите относительно X, используя процентную формулу
  X = Y ÷ P%

Пример: 20% от 7?

• Записывается по формуле: Х = 7 ÷ 20%
• Преобразование процентов в десятичные числа
• 20% ÷ 100 = 0. 2
• Х = 7 ÷ 0,2
• Х = 35
• Итак, 20% от 35 равно 7.

P процентов X это что?

• Записывается в виде уравнения: P% * X = Y
• «Что такое» Y, которое мы хотим решить для
• Решение: Решите относительно Y, используя процентную формулу
  Y = P% * X

Пример: 5% из 29 — это что?

• Записывается по формуле: 5% * 29 = Y
• Преобразование процентов в десятичные числа
• 5% ÷ 100 = 0. 05
• Y = 0,05 * 29
• Y = 1,45
• Таким образом, 5% от 29 составляет 1,45

Y из чего P процентов?

• Записывается в виде уравнения: Y / X = P%
• Что такое X, которое мы хотим решить для
• Умножьте обе части на X, чтобы получить X из знаменателя
• (Y / X) * X = P% * X становится Y = P% * X
• Разделите обе части на P% так, чтобы X находился на одной стороне уравнения
• Y ÷ P% = (P% * X) ÷ P% становится Y ÷ P% = X
• Решение: Решите относительно X, используя процентную формулу
  X = Y ÷ P%

Пример: 4 из чего составляет 12%?

• Записывается по формуле: Х = 4 ÷ 12%
• Решить относительно X: X = Y ÷ P%
• Преобразование процентов в десятичные числа
• 12% ÷ 100 = 0. 12
• Х = 4 ÷ 0,12
• Х = 33,3333
• 4 из 33.3333 это 12%

Что из X составляет P процентов?

• Записывается в виде уравнения: Y / X = P%
• «Что такое» Y, которое мы хотим решить для
• Умножьте обе стороны на X, чтобы получить Y на одной стороне уравнения
• (Y ÷ X) * X = P% * X становится Y = P% * X
• Решение: Решите относительно Y, используя процентную формулу
  Y = P% * X

Пример: Какое из 25 составляет 11%?

• Записывается по формуле: Д = 11% * 25
• Преобразование процентов в десятичные числа
• 11% ÷ 100 = 0. 11
• Y = 0,11 * 25
• Y = 2,75
• Таким образом, 2,75 из 25 составляет 11%

Y of X — это какой процент?

• Записывается в виде уравнения: Y / X = P%
• «Что» такое P%, которое мы хотим решить для
• Решение: Найдите P%, используя процентную формулу
  P% = Y / X

Пример: 9 из 13 — это какой процент?

• Записывается по формуле: P% = Y / X
• 9 ÷ 13 = P%
• 9 ÷ 13 = 0. 6923
• Преобразование десятичной дроби в проценты умножением на 100
• 0,6923 * 100 = 69,23%
• 9 ÷ 13 = 69,23%
• Так 9 из 13 это 69.23%

Связанные калькуляторы

Найдите изменение в процентах в виде увеличения или уменьшения, используя Калькулятор процентного изменения.

Преобразование десятичных чисел в процентные с помощью нашего Калькулятор десятичных дробей в проценты.

Преобразование из процентов в десятичные с Процент в десятичный калькулятор.

Если вам нужно конвертировать дроби в проценты, см. Наш Калькулятор дробей в проценты, или наш Калькулятор процентных долей.

Список литературы

Weisstein, Eric W. Percent. Из MathWorld — Интернет-ресурс Wolfram.

Нахождение процентов — Как найти процент

Слово процентов означает одну сотую.

Процент — это дробное число или отношение 100.За числом процентов всегда следует символ процентов (%) . Ниже приведены примеры процентов:

`5%, 10%, 33 1/3% ‘, 67,5%, 100%`

Процент применяется в разных областях. Он обычно используется в бухгалтерском учете и финансах, таких как процентные ставки, прибыль, продажи и налогообложение. В ряде школ и университетов для выражения оценок учащихся использовались проценты. Вероятности, пищевая ценность и загрузка процесс представлены в процентах.

---

Запоминание терминов

Дробь	соотношение между двумя ненулевыми целыми числами.Бывший. 1/2
Коэффициент	отношения между двумя числами. Бывший. 1: 2
Смешанное число	целое число и правильная дробь. Бывший. 1 2/3
Правильная фракция	дробь, числитель которой меньше знаменателя.Бывший. 3/4
Кол-во	число, представляющее сумму или значение
Отличить	идентифицируют различия между двумя или более предметами.

---

Расчет процента

Процент — это результат умножения определенного числа на процент.В большинстве случаев проценты меньше числа, поскольку проценты часть числа или количества. Но бывают случаи, что процент больше числа. Это произойдет, если процент больше 100%.

Короче говоря, процент — это определенный процент от числа.

В большинстве случаев после количества следует фраза «процент от».

Например;

В этом заявлении 50 — это количество, 35 — это процент, а 70% — это процент.

Пример 3:

24

Пояснение:

40 — это процент.

60 — количество.

Процент — это необходимое количество.

Умножение числа на процент;

`60` x` 40% = 60` x `40/100 = 2400/100 = 24`

Следовательно, 40% от 60 равно 24.

Пример 4:

27

Пояснение:

75 — это процент.

36 — количество.

Умножение числа на процент;

`36` x` 75% = 36` x `75/100 = 2700/100 = 27`

Следовательно, 27 составляет 75% от 36.

---

Вычисление процента

При нахождении процента числа разделите процент на количество, а затем умножьте произведение на 100.Поместите символ процента (%) после конечного продукта.

Если процент больше количества, это означает, что процент больше 100%. Процент — это фактор увеличения стоимости количества.

Пример 5:

25%

Пояснение:

18 — это процент.

72 — количество.

Процент спрашивается.

Деление процента на количество;

Умножаем произведение на 100 и ставим знак процента (%) после;

Следовательно, 18 составляет 25% от 72.

Пример 6:

80%

Пояснение:

12 это процент

15 — количество.

Процент спрашивается.

Деление процента на количество;

Умножаем произведение на 100 и ставим знак процента (%) после;

Следовательно, 12 составляет 80% от 15.

Пример 7:

200%

Пояснение:

100 — процент

50 — количество.

Процент спрашивается.

Деление процента на количество;

Умножаем произведение на 100 и ставим знак процента (%) после;

Следовательно, 100 — это 200% от 50.

---

Преобразование процентов в десятичные числа

Для получения процентов необходимо преобразовать процент в десятичную форму, прежде чем умножать его на количество.

Вот шаги по преобразованию процентов в десятичные числа:

1. Пренебрегайте символом процента (%).

2. Переместите десятичную запятую на два разряда влево.

Пример 8:

0,1

Пояснение:

Пропустите символ процента (%) и переместите десятичную запятую на 2 позиции влево.

Следовательно, 10% — это 0,1 в десятичной системе.

Пример 9:

0,0531

Пояснение:

Пропустите символ процента (%) и переместите десятичную запятую на 2 позиции влево.

Следовательно, 0,0531 — это десятичная форма 5,31%.

Пример 10:

4,28

Пояснение:

Пропустите символ процента (%) и переместите десятичную запятую на 2 позиции влево.

Следовательно, 4,28 — это десятичная форма от 428%.

---

Преобразование десятичной дроби в проценты

Преобразовать десятичные дроби в проценты легко: просто переместите десятичную запятую на два разряда вправо, а затем поместите символ процента (%) после.

Пример 11:

60.7%

Пояснение:

Переместите десятичную запятую на 2 разряда вправо и поместите после нее символ процента (%).

Следовательно, 0,607 — это 60,7%.

Пример 12:

120.8%

Пояснение:

Переместите десятичную запятую на 2 разряда вправо и поместите после нее символ процента (%).

Следовательно, 1,208 составляет 120,8%.

---

Преобразование процента в дробь

Иногда более простой способ получить процентное значение — преобразование процента в дробь.Дроби предпочтительнее использовать, чем десятичные, если десятичная дробь имеет много цифр. Это делает умножение более удобным, поскольку для упрощения процента используется только факторизация.

Вот шаги по преобразованию процента в дробь:

1. Пренебрегайте символом процента (%).

2. Разделите процент на 100. Если в числителе есть цифры справа от десятичной точки, перемещайте десятичную точку, пока числитель не станет целым числом.Переместите десятичную точку знаменателя (равную 100) на то же количество десятичных знаков, на которое переместилась десятичная точка числителя.

3. Уменьшите до самых низких сроков.

Пример 13:

`4/25`

Пояснение:

Пропустите символ процента (%) и разделите процент на 100.

Уменьшить до самых низких сроков.

`16/100 = текст (2 x 2 x 2 x 2) / текст (2 x 2 x 5 x 5) = текст (2 x 2) / текст (5 x 5) = 4/25`

Следовательно, 16% в виде дроби составляет «4/25».

Пример 14:

`5/8`

Пояснение:

Пропустите символ процента (%) и разделите процент на 100.

Переместите десятичную точку в числителе и знаменателе на 1 десятичный знак вправо, чтобы числитель стал целым числом.

Уменьшить до самых низких сроков.

`625/1000 = текст (5 x 5 x 5 x 5) / текст (2 x 2 x 2 x 5 x 5 x 5) = 5 / текст (2 x 2 x 2) = 5/8`

Следовательно, 62.5% в долях: «5/8».

Пример 15:

`8 1/25` или` 201/25`

Пояснение:

Пропустите символ процента (%) и разделите процент на 100.

Уменьшить до самых низких сроков.

`804/100 = текст (2 x 2 x 201) / текст (2 x 2 x 5 x 5) = 201 / текст (5 x 5) = 201/25 или 6 1 / 25`

Следовательно, форма дроби для 804% — «8 1/25» или «201/25».

---

Преобразование дроби в проценты

При преобразовании дробей в проценты проще и удобнее сначала преобразовать дробь в десятичную, а затем преобразовать десятичную в проценты.

Вот шаги по преобразованию дробей в проценты:

1. Разделите числитель дроби на знаменатель. Результат в десятичной форме.

2. Умножьте десятичную форму на 100.

3. Поместите символ процента (%) после последней цифры процента.

В случае смешанных номеров;

1. Выполните описанные выше действия только для правильной доли смешанного числа.

2. Умножьте целое число смешанной дроби на 100.

3. Сложите произведение (целое число, умноженное на 100) и десятичную форму правильной дроби.

4. Поместите символ процента (%) после последней цифры процента.

---

Пример 16:

60%

Пояснение:

Разделите числитель на знаменатель.

0,6 5 3,0 0 30 30 0

Умножьте десятичную форму на 100 и поместите символ процента после последней цифры.

Следовательно, «3/5» составляет 60%.

Пример 17:

225%

Пояснение:

Разделите числитель на знаменатель.

`2.25 4 9.00 8 10 8 20 20 0`

Умножьте десятичную форму на 100 и поместите символ процента после последней цифры.

Следовательно, «9/4» составляет 225%.

Пример 18:

112,5%

Пояснение:

Разделите числитель правильной дроби на знаменатель.

`0,125 8 1.000 0 10 8 20 16 40 40 0`

Умножьте десятичную форму на 100.

Умножьте целое число смешанного числа на 100.

Сложите произведение (целое число, умноженное на 100) и десятичную форму правильной дроби.

Следовательно, «1 1/8» составляет 112,5%.

---

Различие процента и процента

Есть некоторые заблуждения относительно использования слов процента и процента.В двух словах есть

процентов относится к определенному числу.

Например;

Бернадетт правильно ответила на 90 процентов вопросов теста.

Она набрала 90% (процентов) в тесте.

процентов — это результат умножения числа на процент. Он обозначает часть и в основном описывается как меньший или более высокий.

Например;

Bernadette получила высокий процент в тесте.

Она получила в тесте процент 90/100.

Как правило, слово «процент» следует после определенного числа, и обычно это целые числа или счетные числа. Он обычно не используется в предложениях, так как всегда заменяется символом процента (%). Слово «процент» стоит перед дробью или после прилагательного (напр.г. высокий, низкий, большой, маленький).

---

Примеры процентов

Пример 1:

процентов

Пояснение:

10 — это конкретное число, поэтому используется процент.

Пример 2:

процентов

Пояснение:

Слово «низкий» используется и, следовательно, используется процентное соотношение.

---

Как рассчитать проценты за 3 простых шага (с примерами)

1. Руководство по карьере
2. Развитие карьеры
3. Как рассчитать проценты за 3 простых шага (с примерами)

Редакционная группа Indeed

22 февраля 2021 г.

Расчет процентов — это простой математический процесс.Иногда, когда необходимо найти соотношение или долю количества как части другого количества, вам нужно будет выразить это в процентах. В этой статье мы покажем вам, что такое проценты, как их вычислить, а также повседневные примеры их использования.

Что такое проценты?

С математической точки зрения проценты — это числа или отношения, выраженные в долях от 100. Обычно они обозначаются как «%» или просто «проценты». В дальнейшем они могут быть представлены как простые дроби или как десятичные дроби.Пример процента — 65% или 65 процентов.

Термин «процент» образован из двух слов «за» и «процент». Cent — это слово латинского и французского происхождения, которое означает «сто», а «процент» означает «за сотню». Например, 90 процентов (или 90%) означает 90 из 100, а 50 процентов (или 50%) означает 50 из 100 или половину целого.

Связанные: 10 лучших навыков для включения в резюме

Как рассчитать проценты

Есть много онлайн-калькуляторов для нахождения процентов, но проценты можно вычислить вручную, выполнив следующие действия:

1. Определите начальный формат число, которое нужно преобразовать в процентное соотношение

2. Выполните математический процесс над числом, которое необходимо преобразовать в процентное соотношение

3. Умножьте результат математического процесса на 100

1.Определите исходный формат числа, которое нужно преобразовать в процент.

Число, которое нужно преобразовать в процент, может быть в десятичном или дробном формате. Хорошим примером десятичного числа является 0,57, которое может быть вычисленным соотношением сравниваемых значений, в то время как пример дроби — 3/20. Исходный формат определит следующий математический процесс, который будет выполняться над числом.

2. Выполните математический процесс над числом, которое нужно преобразовать в проценты.

Если число, которое нужно преобразовать в проценты, является десятичным числом, например 0.57, возможно, вам не нужно будет ничего делать с ним, прежде чем перейти к следующему шагу. Однако, если это дробь вроде 3/20, вы должны сначала разделить числитель (в данном случае 3) на знаменатель (в данном случае 20), чтобы получить десятичное число.

3. Умножьте результат математического процесса на 100

Если вам необходимо преобразовать десятичное число, например 0,57, в процент, вы должны просто умножить его на 100. То есть 0,57 x 100 = 57. Следовательно, 0,57 в процентах = 57% или 57 процентов.Другой пример преобразования десятичной дроби в проценты: 0,03 x 100 = 3% или 3 процента.

Однако, если вам необходимо преобразовать 3/20 в проценты, вы должны разделить 3 на 20 = 0,15. Затем умножьте 0,15 на 100 = 15% или 15 процентов.

Другой пример: если вы хотите преобразовать 5/10 в процент, вы должны разделить 5 на 10 = 0,5. Затем умножьте 0,5 на 100. Следовательно, 0,5 x 100 = 50% или 50 процентов.

Как рассчитать проценты, работая в обратном направлении

Иногда вам потребуется вычислить проценты, работая в обратном направлении.Это также называется обратным процентом и используется, когда указывается процент и окончательное число, а исходное число должно быть вычислено.

Например, если 40% числа равно 500, какое число? Ниже приведены способы вычисления процента, работая в обратном направлении:

1. Найдите процентное соотношение исходного или действительного числа

2. Умножьте окончательное число на 100

3. Разделите результат умножения на процент

1.Найдите процент от исходного или действительного числа

Процент от исходного числа, заданный в математической задаче, составляет 40%.

2. Умножьте окончательное число на 100

Вы должны умножить последнее число, указанное в математической задаче, на 100. Это означает, что 500 x 100 = 50 000.

3. Разделите результат умножения на процентное соотношение

Следующий и последний шаг — разделить результат умножения, выполненного на втором шаге, на процентное число, указанное в вопросе.Это означает, что 50000/40 = 1250. Таким образом, исходное число было 1250.

Связано: Ваш путеводитель по карьере в области финансов

Примеры процентов

Вот несколько примеров процентов и способов их вычисления:

• Преобразуйте десятичное число 3,25 в процент.

• Преобразует десятичное число 0,65 в проценты.

• Преобразует дробь 5/6 в процент.

• Преобразуйте дробь 60/100 в проценты.

• Цена ноутбука снижена на 30% до 120 долларов. Какая была первоначальная цена?

• Найдите цену продажи, если разрешена 20% скидка от указанной цены в 30 долларов.

• Два года назад билет на футбольный матч стоил 20 долларов. В этом году цена увеличена на 60%. Сколько стоит билет в этом году?

Преобразование десятичного числа 3,25 в проценты

Преобразование десятичного числа 3.25 на процент, умножьте его на 100. Таким образом, 3,25 x 100 = 325%

Преобразуйте десятичное число 0,65 в процентное соотношение

Чтобы преобразовать десятичное число 0,65 в процент, умножьте 0,65 на 100. Следовательно, 0,65 x 100 = 65%.

Преобразование дроби 5/6 в проценты

Чтобы преобразовать дробь 5/6 в проценты, вы должны сначала преобразовать 5/6 в десятичную дробь, разделив числитель 5 на знаменатель 6. Это означает, что 5 / 6 = 0,833 с точностью до двух десятичных знаков.Затем умножьте 0,83 на 100 = 83%.

Преобразование дроби 60/100 в проценты

Чтобы преобразовать дробь 60/100 в проценты, вы должны сначала преобразовать 60/100 в десятичную дробь, разделив числитель 60 на знаменатель 100. Это означает, что 60/100 = 0,6. Затем умножьте 0,6 на 100 = 60%.

Цена ноута снижена на 30% до 120 долларов. Какая была первоначальная цена?

Чтобы определить исходную цену, определите процент от исходной цены, вычтя 30% из 100.Затем умножьте окончательную цену на 100. То есть 120 x 100 = 12 000. Наконец, разделите результат на процент, рассчитанный на шаге 1 выше. Это означает, что 12000/70 = 171,43 доллара. Таким образом, первоначальная цена составляет 171,43 доллара США с точностью до двух знаков после запятой.

Найдите цену продажи, если разрешена скидка 20% от указанной цены в 30,00 долларов

Преобразуйте процентное значение в десятичное число = 20/100 = 0,20 и умножьте десятичное число на исходную цену, чтобы получить сумму скидки = 0,20 X 30 долларов = 6 долларов. Цена продажи = полная цена — скидка = 30 $.00 — 6 долларов США = 24 доллара США. Таким образом, цена продажи составляет 24 доллара.

Два года назад билет на футбольный матч стоил 20 долларов.

В этом году цена увеличена на 60%. Сколько стоит билет в этом году?

Возьмите процентное увеличение 60%, разделите его на 100, чтобы определить десятичную форму, и умножьте его на исходную цену = 60% от 20,00 долларов США = 12,00 долларов США. Следовательно, цена билета в этом году = начальная цена + увеличение стоимости билета = 20 долларов + 12 долларов = 32 доллара.00

Проценты — Введение | SkillsYouNeed

Термин «процент» означает «из ста». В математике проценты используются как дроби и десятичные дроби, как способы описания частей целого. Когда вы используете проценты, считается, что целое состоит из ста равных частей. Символ% используется для обозначения числа в процентах, реже может использоваться сокращение «pct».

Вы увидите проценты почти везде: в магазинах, в Интернете, в рекламе и в средствах массовой информации.Умение понимать, что означают проценты, — это ключевой навык, который потенциально сэкономит вам время и деньги, а также сделает вас более трудоспособным.

---

Значение процентов

Процент — это термин из латинского языка, означающий «из ста».

Таким образом, вы можете рассматривать каждое «целое» как разбитое на 100 равных частей, каждая из которых составляет один процент.

В рамке ниже это показано для простой сетки, но это работает одинаково для всего: дети в классе, цены, галька на пляже и т. Д.

Визуализация в процентах

---

В приведенной ниже сетке 100 ячеек.

• Каждая ячейка равна 1% от целого (красная ячейка составляет 1%).
• Две ячейки равны 2% (зеленые ячейки).
• Пять ячеек равны 5% (синие ячейки).
• Двадцать пять ячеек (фиолетовые ячейки) равны 25% от целого или одной четверти (¼).
• Пятьдесят ячеек (желтые ячейки) равны 50% от целого или половины (½).

Сколько там незатененных (белых) ячеек? Каков процент незатененных ячеек?

---

Ответ: Есть два способа решить эту проблему.

1. Подсчитайте белые клетки. Их 17 штук. Таким образом, из 100 ячеек 17% белые.
2. Сложите количество других ячеек и возьмите их из 100. Есть одна красная ячейка, две зеленые, пять синих, 25 фиолетовых и 50 желтых. В сумме получается 83. 100−83 = 17. Опять же, из 100 ячеек 17 белые, или 17%.

Процентное соотношение легко вычислить, когда есть 100 отдельных «вещей», составляющих целое, как в таблице выше.Но что, если их больше или меньше?

Ответ состоит в том, что вы конвертируете отдельных элементов, составляющих целое, в проценты. Например, если бы в сетке было 200 ячеек, каждый процент (1%) составлял бы две ячейки, а каждая ячейка — полпроцента.

Мы используем проценты, чтобы упростить вычисления. Работать с частями от 100 намного проще, чем с третями, двенадцатыми и т. Д., Особенно потому, что довольно много дробей не имеют точного (неповторяющегося) десятичного эквивалента. Важно отметить, что это также значительно упрощает сравнение процентов (которые все имеют общий знаменатель 100), чем между дробями с разными знаменателями. Отчасти поэтому так много стран используют метрическую систему измерения и десятичную валюту.

---

Определение процента

Общее правило для нахождения заданного процента от данного целого:

Определите значение 1%, затем умножьте его на процент, который вам нужно найти.

Проще всего понять это на примере. Предположим, вы хотите купить новый портативный компьютер. Вы проверили местных поставщиков, и одна компания предложила вам скидку 20% от прейскурантной цены в 500 фунтов стерлингов. Сколько будет стоить ноутбук у этого поставщика?

В этом примере вся сумма составляет 500 фунтов стерлингов или стоимость портативного компьютера без учета скидки. Процент, который вам нужно найти, составляет 20% или скидку, предлагаемую поставщиком. Затем вы собираетесь снять это с полной цены, чтобы узнать, сколько вам будет стоить ноутбук.

1. Начнем с определения значения 1%

   Один процент от 500 фунтов стерлингов составляет 500 фунтов стерлингов ÷ 100 = 5 фунтов стерлингов.

2. Умножьте это на процент, который вы ищете

   После того, как вы вычислили значение 1%, вы просто умножаете его на процент, который вы ищете, в данном случае 20%.

   £ 5 × 20 = 100 £.

   Теперь вы знаете, что скидка составляет 100 фунтов стерлингов.

3. Завершите расчет, добавляя или вычитая, если необходимо.

   Цена ноутбука, включая скидку, составляет 500–20% фунтов стерлингов, или 500–100 фунтов стерлингов = 400 фунтов стерлингов фунтов стерлингов.

Легкий способ отработать 1% от любого числа

---

1% — это целое (что бы это ни было), деленное на 100.

Когда мы делим что-то на 100, мы просто перемещаем значения разряда на два столбца вправо (или перемещаем десятичную точку на два разряда влево).

Вы можете узнать больше о числах и разрядах на нашей странице Числа , но вот краткое резюме:

£ 500 состоит из 5 сотен, ноль десятков и ноль единиц.500 фунтов стерлингов также имеют ноль пенсов (центов, если вы работаете в долларах), поэтому их можно записать как 500,00 фунтов стерлингов с нулевыми десятыми или сотыми долями.

Сотни	Десятки	шт.	Путевая точка	Десятые	сотых
5	0	0	.	0	0

Когда мы делим на 100, мы перемещаем наш номер два столбца вправо.500, деленное на 100 = 005, или 5. Начальные нули (нули на «внешнем левом» числе, например, в 005, 02, 00014) не имеют значения, поэтому нам не нужно их записывать.

Вы также можете думать об этом как о перемещении десятичной запятой на два разряда влево.

Сотни	Десятки	шт.	Путевая точка	Десятые	сотых
0	0	5	.	0	0

Это правило применяется ко всем числам, поэтому 327 фунтов стерлингов, разделенные на 100, составляют 3,27 фунтов стерлингов. Это то же самое, что сказать, что 3,27 фунта стерлингов составляют 1% от 327 фунтов стерлингов. 1 фунт стерлингов, разделенный на 100 = 0,01 фунта стерлингов, или один пенс. В фунте сто пенсов (и сто центов в долларе). Таким образом, 1p составляет 1% от 1 фунта стерлингов.

После того, как вы подсчитали 1% от целого, вы можете затем умножить свой ответ на процент, который вы ищете (помощь см. На нашей странице, посвященной умножению на ).

Ментальные математические приемы

---

По мере развития ваших математических навыков вы начнете видеть другие способы прийти к тому же ответу. Приведенный выше пример ноутбука довольно прост, и с практикой вы сможете использовать свои математические навыки, чтобы по-другому подумать об этой проблеме, чтобы облегчить ее. В этом случае вы пытаетесь найти 20%, поэтому вместо того, чтобы найти 1% и затем умножить его на 20, вы можете найти 10%, а затем просто удвоить его. Мы знаем, что 10% — это то же самое, что и 1/10, и мы можем разделить число на 10, переместив десятичный разряд на одну позицию влево (удалив ноль из 500).Следовательно, 10% от 500 фунтов стерлингов составляют 50 фунтов стерлингов, а 20% — 100 фунтов стерлингов.

Полезная ментальная математическая хитрость заключается в том, что проценты обратимы, поэтому 16% от 25 равно 25% от 16. Неизменно одно из этих значений будет намного легче вычислить в нашей голове … попробуйте!

Воспользуйтесь нашим калькулятором процентов , чтобы быстро решить свои проблемы с процентами.

---

---

Работа с процентами

В приведенном выше примере мы рассчитали скидку 20%, а затем вычли ее из целого, чтобы определить, сколько будет стоить новый ноутбук.

Помимо процента, мы также можем добавить процент к числу. Это работает точно так же, но на последнем этапе вы просто добавляете, а не вычитаете.

Например: Джордж повышен в должности и получает повышение заработной платы на 5%. В настоящее время Джордж зарабатывает 24 000 фунтов стерлингов в год, так сколько же он будет зарабатывать после повышения зарплаты?

1. Тренировать 1% от всего

   Целое в этом примере представляет собой текущую зарплату Джорджа, 24 000 фунтов стерлингов.1% от 24 000 фунтов стерлингов составляет 24 000 ÷ 100 = 240 фунтов стерлингов.

2. Умножьте это на процент, который вы ищете

   Джордж получает повышение заработной платы на 5%, поэтому нам нужно знать значение 5%, или 5 раз по 1%.

   £ 240 × 5 = 1200 £.

3. Завершите расчет, добавив к исходной сумме

   Повышение заработной платы Джорджа составляет 1 200 фунтов стерлингов в год. Таким образом, его новая зарплата составит 24 000 фунтов стерлингов + 1 200 фунтов стерлингов = 25 200 фунтов стерлингов.

   Процент более 100%

   ---

   Процент может быть больше 100%. Этот пример один: новая зарплата Джорджа на самом деле составляет 105% от его старой.

   Однако его старая зарплата не на 100% от его новой. Вместо этого он составляет чуть более 95%.

   Когда вы рассчитываете проценты, главное — убедиться, что вы работаете с правильным целым. В данном случае «целое» — это старая зарплата Джорджа.

---

Десятичные и дробные проценты

Один процент — это одна сотая от целого.Следовательно, его можно записать как в виде десятичной дроби, так и в виде дроби.

Чтобы записать процент в виде десятичной дроби, просто разделите его на 100.

Например, 50% становится 0,5, 20% становится 0,2, 1% становится 0,01 и так далее.

Мы можем вычислить проценты, используя эти знания. 50% равно половине, поэтому 50% от 10 равно 5, потому что пять — это половина от 10 (10 ÷ 2). Десятичная дробь 50% равна 0,5. Итак, другой способ найти 50% от 10 — это сказать 10 × 0,5 или 10 половин.

20% от 50 — это то же самое, что сказать 50 × 0.2, что равно 10.

17,5% от 380 = 380 × 0,175, что равно 66,5.

Указанная выше зарплата Джорджа составила 5% от 24 000 фунтов стерлингов. 24000 фунтов стерлингов × 0,05 = 1200 фунтов стерлингов.

Преобразование десятичного числа в процентное — это просто обратный расчет: умножьте десятичное число на 100.

0,5 = 50%
0,875 = 87,5%

Чтобы записать процент в виде дроби, поместите процентное значение над знаменателем 100 и разделите его до наименьшей возможной формы.

50% = 50/100 = 5/10 = ½
20% = 20/100 = 2/10 = 1/5
30% = 30/100 = 3/10

ВНИМАНИЕ!

---

Можно преобразовать дроби в проценты, преобразовав знаменатель (нижнее число дроби) в 100.

Однако преобразовать дроби в проценты труднее, чем проценты в дроби, потому что не каждая дробь имеет точное (единовременное) десятичное число или процент.

Если знаменатель вашей дроби не делит целое число раз на 100, то простого преобразования не будет.Например, 1/3, 1/6 и 1/9 не дают «точных» процентов (это 33,33333%, 16,66666% и 11,11111%).

---

Процентная выработка целого

До сих пор мы рассмотрели основы процентов и то, как добавить или вычесть процент от целого.

Иногда бывает полезно вычислить проценты от целого, когда вам даны соответствующие числа.

Например, предположим, что в организации работают 9 менеджеров, 12 администраторов, 5 бухгалтеров, 3 специалиста по персоналу, 7 уборщиков и 4 работника общественного питания.Какой процент сотрудников каждого типа он нанимает?

1. Начните с проработки всего.

   В этом случае вы не знаете «всю» или общую численность персонала в организации. Поэтому первым шагом является сложение различных типов персонала.

   9 менеджеров + 12 администраторов + 5 бухгалтеров + 3 специалиста по персоналу + 7 уборщиков + 4 работника общественного питания = 40 сотрудников.

2. Определите долю (или долю) персонала в каждой категории.

   Нам известно количество сотрудников в каждой категории, но нам нужно преобразовать это число в дробную часть целого числа, выраженную в десятичной дроби. Расчет, который нам нужно сделать:

   Персонал в категории ÷ Всего (См. Нашу страницу , раздел , чтобы получить помощь по суммам деления или воспользоваться калькулятором)

   В качестве примера можем использовать менеджеров:

   9 менеджеров ÷ 40 = 0,225

   В этом случае может быть полезно, если вместо того, чтобы думать о символе деления «÷» как о значении «делится на», мы можем заменить слова «вне».Мы часто используем это в контексте результатов тестирования, например 8/10 или «8 из 10» правильных ответов. Итак, мы рассчитываем «количество менеджеров из всего штата». Когда мы используем слова для описания вычислений, это может сделать их более понятными.

   
   

3. Преобразование доли целого в проценты

   0,225 — это доля сотрудников, являющихся руководителями, выраженная в десятичном формате. Чтобы преобразовать это число в процент, нам нужно умножить его на 100.Умножение на 100 аналогично делению на сотню, за исключением того, что вы перемещаете числа в другую сторону по шкале значений разряда. Таким образом, 0,225 становится 22,5.

   Другими словами, 22,5% сотрудников организации — менеджеры.

   Затем мы делаем те же два вычисления для каждой другой категории.

• 12 администраторов ÷ 40 = 0,3. 0,3 × 100 = 30%.
• 5 бухгалтеров ÷ 40 = 0,125. 0,125 × 100 = 12,5%.
• 3 специалиста по персоналу ÷ 40 = 0.075. 0,075 × 100 = 7,5%.
• 7 очистителей ÷ 40 = 0,175. 0,175 × 100 = 17,5%.
• 4 работника общепита ÷ 40 = 0,1. 0,1 × 100 = 10%.

СОВЕТ! Убедитесь, что у вас всего 100%

---

Когда вы закончите вычислять свои проценты, рекомендуется сложить их вместе, чтобы убедиться, что они равны 100%. Если нет, проверьте свои расчеты.

Таким образом, мы можем сказать, что организация состоит из:

Роли	Кол-во сотрудников	% персонала
Менеджеры	9	22.5%
Администраторы	12	30%
Бухгалтеры	5	12,5%
Специалисты по персоналу	3	7,5%
Очистители	7	17,5%
Кейтеринг	4	10%
Итого	40	100%

Может быть полезно отобразить процентные данные, представляющие целое, на круговой диаграмме. Вы можете быстро увидеть пропорции категорий персонала в примере.

Подробнее о круговых диаграммах и других типах графиков и диаграмм см. На нашей странице: Графики и диаграммы .

Что нужно запомнить

---

• Проценты — это способ описания частей целого.
• Они немного похожи на десятичные дроби, за исключением того, что целое всегда делится на 100, а не на десятые, сотые, тысячные и т.д. единицы.
• Проценты предназначены для упрощения расчетов.

---

Дополнительные материалы по навыкам, которые вам нужны

---

Пропорция
Часть необходимых навыков Руководство по счету

Эта электронная книга описывает пропорции, когда числа рассматриваются как части других чисел, как части большего целого или по отношению к другим числам. В книге описаны дроби и десятичные дроби, отношения и проценты с рабочими примерами, которые помогут вам развить свои навыки.

Если вы хотите освежить в памяти основы или помочь своим детям в обучении, эта книга для вас.

---

Процент числа с использованием математических вычислений в уме

Научитесь решать процентные задачи в голове! Поскольку 10% — это 1/10, а найти 1/10 любого числа очень легко, мы можем использовать это, чтобы быстро вычислить в уме определенные проценты величин. чтобы найти 20% числа, сначала найдите 10% числа и удвойте это число. И так далее.

Основные концепции и идеи этого урока также объясняются в этом видео:

100% чего-то означает все этого. 1% чего-то означает 1/100 этого.

Чтобы рассчитать процент от количества, мы используйте тот же метод, что и при вычислении дробной части этого количества потому что процентов просто означает сотую часть . Следовательно, проценты — это просто дроби.

Сколько это 1% в 200 кг? Это означает, что это 1/100 от 200 кг? Это просто 2 кг.Просто разделите на 100, чтобы найти сотую часть! Чтобы найти 1% чего-либо (1/100 чего-либо), разделите на 100. Вспомните, как мысленно разделить на 100: просто переместите десятичную запятую на два разряда влево. Например, 1% от 540 — это 5,4. И 1% 8,30 — 0,083.

Чтобы найти 10% некоторого количества, разделите по 10. Почему это работает? 10% составляет 10/100.А 10/100 равно 1/10. Итак, мы просто находим 1/10 Например, из 340 человек 10% — это 34 человека. Точно так же 10% от 2,30 доллара равняется 0,23 доллара. (Делить мысленно на 10 просто переместите десятичную запятую на одну позицию влево.)

1. Найдите 10% этих чисел.

а. 900 _______ г. 160 _______ г. 50 _______

2. Найдите 1% этих чисел.

а. 900 _______ г. 90 560 6 800 _______ г. 550 _______

3. Если 1% от зарплаты Синди составляет 23 доллара, сколько у нее зарплата?

4. Десять процентов от стоимости пул — 430 долларов. Сколько стоит бассейн?

Чтобы найти 2% количества, сначала найдите 1%, а затем удвойте. Например, давайте найдем 2% от 6 долларов США.Поскольку 1% из 6 — 0,06 доллара, затем 2% от 6 — 0,12 доллара.

Вы можете придумать способ найти 20% числа? (Подсказка: начните с поиска 10% от числа.)

7. Заполните таблицу. Использовать ментальная математика.

число / процентов	400	60	78	8	4. 1
1% от числа
2% от числа
10% от числа
20% от числа

8.Заполните это руководство по умственной математике с процентами:

Ментальная математика и процент числа
50% — 1/2. Чтобы найти 50% числа, разделите на ______. 10% равно 1 /. Чтобы найти 10% числа, разделите на ______. 1% составляет 1 /. Чтобы найти 1% от числа, разделите на ______.	50% от 244 _______. 10% из 47 составляет ________. 1% от 530 ________.
Чтобы найти 20%, 30%, 40%, 60%, 70%, 80% или 90% числа, Сначала найдите _________% числа и затем умножьте на 2, 3, 4, 6, 7, 8 или 9.	10% от 120 _______. 30% от 120 _______. 60% от 120 _______.

9. Найдите проценты. Используйте математику в уме.

а. 10% 60 кг ________ 20% от 60 кг ________

б. 10% от 14 $ ________ 30% от 14 $ ________

10. Дэвид платит 20% подоходный налог с его зарплаты в размере 2100 долларов. Сколько долларов стоит налог?

Сколько у него осталось денег после уплаты налога?

12.Определите ошибки, которые сделали эти дети. Затем найдите правильные ответы.

Найдите 90% от 55 долларов. Решение Петра: 10% от 55 долларов это 5,50 доллара Итак, вычтите 100% — 5,50 доллара = 94,50 доллара

Еще несколько уловок в уме:

90% от количества

Сначала найдите 10% количества, а затем вычтите эти 10% из 100%.

25% от количества

25% совпадает с 1/4. Итак, чтобы найти 25% количества, разделите его на 4.

12% от количества

Сначала найдите 10%. Затем найдите 1% и используйте этот 1%. найти 2% от этого. Затем добавьте 10% и 2%.

75% от количества

75% составляет 3/4. Сначала найдите 1/4 количества и умножьте это на 3.

13. Найдите проценты.Используйте математику в уме.

а. 25% из 48 миль _______ 75% от 48 миль ________

14. Найдите проценты от количеств.

а. 50% от 26 дюймов

б. 25% от 40 футов

15. Введите математический метод в уме, чтобы найти 12% от 65 долларов.

10% от 65 долларов составляет ________ долларов.
1% от 65 долларов США составляет _________ долларов США.
2% от 65 долларов составляет _________ долларов.

Теперь сложите, чтобы получить 12% от 54 долларов:
$ _________ + $ _________ = $ ________

18. В своем счете за мобильный телефон Ханна заметила, что 340 текстовых сообщений, которые она отправила в прошлом месяце, 15% были отправлены на более дешевый ночной тариф. Сколько сообщений Ханна отправила на ночь? В течение дня?

20. В картонной коробке 2 литра. тропического сока. Сок состоит из 25% сока манго, 30% ананасового сока и остальное — сок гуавы. Найдите, сколько миллилитров каждого сока ушел в 2-литровую коробку тропического сока.

См. Также

Процент — бесплатное занятие

Как считать проценты — бесплатное занятие

Как считать проценты чисел — бесплатное занятие

Основы процента сдачи — бесплатное занятие

---

Этот урок взят из книги Марии Миллер «Math Mammoth Percent», опубликованной на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер.

---

Как рассчитать процент от числа

Изучите основы вычисления процентов от количества в этом простом уроке! Чтобы найти процентное соотношение любого числа, используйте этот общий принцип ПЕРЕВОДА: замените процент на десятичное число, а слово «из» — на умножение. См. Множество примеров ниже.

Концепции и идеи этого урока также объясняются в этом видео:

Вы узнали, что найти 1% от числа означает найти 1/100 от числа. Это.Точно так же найти 60% числа означает найти 60/100 (или 6/10) его. В этих выражениях слово «из» переводится как умножение: 1% от 90 → 1% × 90 и 60% от 700 долларов → 60% × 700 долларов. Мы также можем записать эти проценты в виде десятичных знаков : 1% от 90 → 0,01 × 90 60% от 700 долларов → 0,6 × 700 долларов. Это дает нам другой способ вычислить процентное отношение числа (или процент некоторого количества):

Чтобы вычислить процент от некоторого числа, измените проценты в десятичную дробь, а слово «из» — в умножение.

Пример 1. Найдите 70% от 80. Следуя ярлыку, запишем это как 0,7 × 80. Помните, что в десятичное умножение, вы умножаете, как если бы не было десятичных знаков, и в ответе будет столько «десятичных цифр» справа от десятичной точки как общее количество десятичных цифр всех множителей. Итак, когда вы умножаете 0,7 × 80, подумайте о умножении 7 × 80 = 560.Поскольку 0,7 имеет одну десятичную цифру, а 80 — нет, В ответе одна десятичная цифра: 56,0 Таким образом, 0,7 × 80 = 56. Вы также можете использовать «здравый смысл», чтобы рассуждать логически: 0,7 × 80 должно быть меньше 80, но больше 1/2 от 80, то есть 40. Поскольку 7 × 8 = 56, вы знаете, что ответ должен быть 56, а не 5,6 или 560.

Пример 2. Найдите 3% от 4000 долларов. Сначала запишите его как 0.03 × 4000 долларов. Затем умножаем 3 × 4000 долларов = 12000 долларов. Наконец, поставьте десятичную точку там, где она дает ответ два. десятичные цифры: 120,00 долларов США.

Пример 3. Найдите 23% из 5 500 км. Запишите выражение как 0,23 × 5 500 км и используйте калькулятор для расчета продукта. Ответ — 1265 км. Этот ответ заставляет смысл, потому что 10% от 5 500 км — 550 км, поэтому 20% — это 1100 км. Таким образом 1265 км как 23% от 5 500 км — разумный ответ.

1. «Перевести» выражения на умножение на десятичную дробь. Рассчитать.

а. 20% от 70 ______ × ______ = ______

б. 90% от 50 ______ × ______ = ______

г. 9% от 3000 ______ × ______ = ______

2. «Перевести» в другую сторону: запишите умножение как выражение «процента от числа».

а. 0,6 × 50 _____% от ______ = ______

б. 0,03 × 400 долл. США _____% от ______ = ______

г. 0,08 × 6 _____% от ______ = ______

3. Используйте калькулятор, чтобы найти проценты от этих количеств.

а. 17% от 4500 долларов

г. 67% от 27 м

4. Используйте в уме математические вычисления, чтобы найти их процентное соотношение. количества.

5. а. Озеро с береговой линией протяженностью 30 км. 6% от этого песочный пляж. Какой процент береговой линии составляет , а не песчаный пляж?

6. Двадцать процентов из 4000 студентов университета имеют стипендия.

а. Что процента учащихся не стипендия?

г. Сколько студентов получают стипендию?

8. Определите ошибки, которые допустила Глэдис. Тогда найдите правильный ответ.

Найдите 80% из 50.

Решение Глэдис:
80 × 50 = 4 000 900 11

9. Найдите выражения с тем же значением, что и 20%. 620 долларов.

0,02 × 620 долл. США	$ 620 ÷ 5
$ 620 ÷ 10 × 2	2 × 62 $
1 5 × 620 долл. США	0.2 × 620 долл. США
20 × 620 долл. США	$ 620 ÷ 4

11. В таблице ниже показано, как Энди использовал время за один день.

а. Подсчитайте время, которое он потратил на каждое занятие.
Округлите минуты до ближайшей минуты.

г. Обозначьте секции на круговой диаграмме значком название каждого вида деятельности.

Использование времени Энди

Активность Процент Минуты Часы / минуты Сон 38% Школа 21% Футбол 10% 144 2 ч 24 мин Играть 11% Питание 9% Работа по дому 9% Гигиена 2% ИТОГО 100% 1440 24 часа

См.