Правила знаков
Минус и плюс – это признаки отрицательных и положительных чисел в математике. Они по-разному взаимодействую с собой, поэтому при выполнении каких-либо действий с числами, например, деление, умножение, вычитание, сложение и т.д., необходимо учитывать правила знаков. Без этих правил вы никогда не сможете решить даже самую простую алгебраическую или геометрическую задачу. Без знания этих правил, вы не сможете изучить не только математику, но и физику, химию, биологию, и даже географию.
Рассмотрим подробней основные правила знаков.
Деление.
Если мы делим «плюс» на «минус», то получаем всегда «минус». Если мы делим «минус» на «плюс», то получаем всегда также «минус». Если мы делим «плюс» на «плюс», то получаем «плюс». Если же мы делим «минус» на «минус», то получим, как ни странно, также «плюс».
Умножение.
Если мы умножаем «минус» на «плюс», то получаем всегда «минус». Если мы умножаем «плюс» на «минус», то получаем всегда также «минус».
Вычитание и сложение.
Они базируются уже на других принципах. Если отрицательное число будет больше по модулю, чем наше положительное, то результат, конечно же, будет отрицательный. Наверняка, вам интересно, что же такое модуль и зачем он тут вообще. Все очень просто. Модуль – это значение числа, но без знака. Например -7 и 3. По модулю -7 будет просто 7 , а 3 так и останется 3. В итоге мы видим, что 7 больше, то есть выходит, что наше отрицательное число больше. Вот и выйдет -7+3 = -4. Можно сделать еще проще. Просто на первое место ставить положительное число, и выйдет 3-7 = -4, возможно кому-то так более понятно. Вычитание действуют полностью по такому же принципу.
| Правила при умножении (делении) чисел | ||
|---|---|---|
| Множители | Результат | |
| Делимое | Делитель | |
| + | + | + |
| + | — | — |
| — | + | — |
| — | — | + |
Тригонометрические тождества и преобразования
Для решения некоторых задач будет полезной таблица тригонометрических тождеств, которая позволит гораздо проще совершать преобразования функций:Простейшие тригонометрические тождества
Частное от деления синуса угла альфа на косинус того же угла равно тангенсу этого угла (Формула 1). См. также доказательство правильности преобразования простейших тригонометрических тождеств.
См. также доказательство правильности преобразования простейших тригонометрических тождеств.
Секанс угла равен единице, деленной на косинус этого же самого угла (Формула 3)
Сумма квадратов синуса и косинуса одного и того же угла равна единице (Формула 4). см. также доказательство суммы квадратов косинуса и синуса.
Сумма единицы и тангенса угла равна отношению единицы к квадрату косинуса этого угла (Формула 5)
Единица плюс котангенс угла равна частному от деления единицы на синус квадрат этого угла (Формула 6)
Произведение тангенса на котангенс одного и того же угла равно единице (Формула 7).
Преобразование отрицательных углов тригонометрических функций (четность и нечетность)
Для того, чтобы избавиться от отрицательного значения градусной меры угла при вычислении синуса, косинуса или тангенса, можно воспользоваться следующими тригонометрическими преобразованиями (тождествами), основанными на принципах четности или нечетности тригонометрических функций.
Как видно, косинус и секанс является четной функцией, синус, тангенс и котангенс — нечетные функции.
Синус отрицательного угла равен отрицательному значению синуса этого же самого положительного угла (минус синус альфа).
Косинус «минус альфа» даст тоже самое значение, что и косинус угла альфа.
Тангенс минус альфа равен минус тангенс альфа.
Формулы приведения двойного угла (синус, косинус, тангенс и котангенс двойного угла)
Если необходимо разделить угол пополам, или наоборот, перейти от двойного угла к одинарному, можно воспользоваться следующими тригонометрическими тождествами:
Преобразование двойного угла (синуса двойного угла, косинуса двойного угла и тангенса двойного угла) в одинарный происходит по следующим правилам:
Синус двойного угла
Косинус двойного угла равен разности квадрата косинуса одинарного угла и квадрата синуса этого угла
Косинус двойного угла равен удвоенному квадрату косинуса одинарного угла минус единица
Косинус двойного угла равен единице минус двойной синус квадрат одинарного угла
Тангенс двойного угла равен дроби, числитель которой — удвоенный тангенс одинарного угла, а знаменатель равен единице минус тангенс квадрат одинарного угла.
Котангенс двойного угла равен дроби, числитель которой — квадрат котангенса одинарного угла минус единица, а знаменатель равен удвоенному котангенсу одинарного угла
Формулы универсальной тригонометрической подстановки
Указанные ниже формулы преобразования могут пригодиться, когда нужно аргумент тригонометрической функции ( sin α, cos α, tg α) разделить на два и привести выражение к значению половины угла. Из значения α получаем α/2 . Данные формулы называются формулами универсальной тригонометрической подстановки. Их ценность заключается в том, что тригонометрическое выражение с их помощью сводится к выражению тангенса половины угла, вне зависимости от того, какие тригонометрические функции (sin cos tg ctg) были в выражении изначально. После этого уравнение с тангенсом половины угла решить гораздо проще.Тригонометрические тождества преобразования половины угла
Указанные ниже формулы тригонометрического преобразования половинной величины угла к его целому значению.
Значение аргумента тригонометрической функции α/2 приводится к значению аргумента тригонометрической функции α.
Тригонометрические формулы сложения углов
cos (α — β) = cos α · cos β + sin α · sin β
sin (α + β) = sin α · cos β + sin β · cos α
sin (α — β) = sin α · cos β — sin β · cos α
cos (α + β) = cos α · cos β — sin α · sin β
Тангенс и котангенс суммы углов альфа и бета могут быть преобразованы по следующим правилам преобразования тригонометрических функций:
Тангенс суммы углов равен дроби, числитель которой — сумма тангенса первого и тангенса второго угла, а знаменатель — единица минус произведение тангенса первого угла на тангенс второго угла.
Тангенс разности углов равен дроби, числитель которой равен разности тангенса уменьшаемого угла и тангенса вычитаемого угла, а знаменатель — единице плюс произведение тангенсов этих углов.
Котангенс суммы углов равен дроби, числитель которой равен произведению котангенсов этих углов плюс единица, а знаменатель равен разности котангенса второго угла и котангенса первого угла.
Котангенс разности углов равен дроби, числитель которой — произведение котангенсов этих углов минус единица, а знаменатель равен сумме котангенсов этих углов.
Данные тригонометрические тождества удобно применять, когда нужно вычислить, например, тангенс 105 градусов (tg 105). Если его представить как tg (45 + 60), то можно воспользоваться приведенными тождественными преобразованиями тангенса суммы углов, после чего просто подставить табличные значения тангенса 45 и тангенса 60 градусов.
Формулы преобразования суммы или разности тригонометрических функций
Выражения, представляющие собой сумму вида sin α + sin β можно преобразовать с помощью следующих формул:Формулы тройного угла — преобразование sin3α cos3α tg3α в sinα cosα tgα
Иногда необходимо преобразовать тройную величину угла так, чтобы аргументом тригонометрической функции вместо 3α стал угол α.
В этом случае можно воспользоваться формулами (тождествами) преобразования тройного угла:
Формулы преобразования произведения тригонометрических функций
Если возникает необходимость преобразовать произведение синусов разных углов косинусов разных углов или даже произведения синуса на косинус, то можно воспользоваться следующими тригонометрическими тождествами:В этом случае произведение функций синуса, косинуса или тангенса разных углов будет преобразовано в сумму или разность.
Формулы приведения тригонометрических функций
Пользоваться таблицей приведения нужно следующим образом. В строке выбираем функцию, которая нас интересует. В столбце — угол. Например, синус угла (α+90) на пересечении первой строки и первого столбца выясняем, что sin (α+90) = cos α .
См. также Полный список формул приведения тригонометрических функций.
| Угол |
α + 90 α + π/2 |
α + 180 α + π |
α + 270 α + 3π/2 |
90 — α π/2- α |
180 — α π- α |
270 — α 3π/2- α |
360 — α 2π- α |
| sin | cos α | -sin α | -cos α | cos α | sin α | -cos α | -sin α |
| cos | -sin α | sin α | sin α | -cos α | -sin α | cos α | |
| tg | -ctg α | tg α | -ctg α | ctg α | -tg α | ctg α | -tg α |
| ctg | -tg α | ctg α | -tg α | tg α | -ctg α | tg α | -ctg α |
Linkin Park — New Divide (Instrumental)
I remembered black skies the lightning all around meI remembered each flash as time began to blur
Like a startling sign that fate had finally found me
And your voice was all I heard that I get what I deserve
So give me reason
To prove me wrong
To wash this memory clean
Let the floods cross
The distance in your eyes
Give me reason
To fill this hole
Connect the space between
Let it be enough to reach the truth that lies
Across this new divide
There was nothing in sight but the memories left abandoned
There was nowhere to hide the ashes fell like snow
And the ground caved in between where we were standing
And your voice was all I heard that I get what I deserve
So give me reason
To prove me wrong
To wash this memory clean
Let the floods cross the distance in your eyes
Across this new divide
In every loss, in every lie
And every truth that you’d deny
And each regret and each goodbye
Was a mistake too great to hide
And your voice was all I heard
That I get what I deserve
So give me reason
To prove me wrong
To wash this memory clean
Let the floods cross
The distance in your eyes
Give me reason
To fill this hole
Connect the space between
Let it be enough reach the truth that lies
Across this new divide
Across this new divide
Across this new divide
И грозный молний свет, застал меня врасплох
Неведомый пророк тогда мне подал знак
И я как должен был черту переступил.

Скажи мне
В чем я виноват?
что ты забыть меня решила,
что правду всю ты утаила,
что прячешь от меня свой взгляд.
Скажи мне
Как соединить
Осколки наших чувств?
Черту за грань переступить, набраться полных сил,
Чтобы увидеть новый мир.
Забыты все воспоминанья,
В развалинах наш мир — его окутал мрак,
К чему теперь пустые оправданья…
И я как должен был черту переступил.
Скажи мне
Как соединить
Осколки наших чувств?
Черту за грань переступить, набраться полных сил,
Чтобы увидеть новый мир.
Мы потеряли, что могли,
Тупик на нашем встал пути.
И полный сожаленья взгляд,
Нам не вернуть всего назад…
И я как должен был
Черту переступил.
Скажи мне
В чем я виноват?
что ты забыть меня решила,
что правду всю ты утаила,
что прячешь от меня свой взгляд.
Скажи мне
Как соединить
Осколки наших чувств?
Черту за грань переступить, набраться полных сил,
Чтобы увидеть новый мир
Чтобы увидеть новый мир
Чтобы увидеть новый мир
Деление отрицательных дробей | Объяснение и примеры — видео и стенограмма урока
Правила знаков: как делить отрицательные числа
Первый шаг к пониманию того, как делить отрицательные числа, — это знать правила знаков. Эти правила одинаковы при делении дробей и умножении дробей. Ниже приведены правила знаков, которые будут более подробно обсуждаться ниже.
Эти правила одинаковы при делении дробей и умножении дробей. Ниже приведены правила знаков, которые будут более подробно обсуждаться ниже.
- одинаковые знаки = положительный
- разных знаков = минус
Положительное умножение или деление на положительное
При умножении или делении двух положительных чисел ответ всегда будет положительным.Например: {экв}5*5=25 {/экв} и {экв}10/2=5 {/экв}.
Умножение или деление положительного числа на отрицательное
При умножении или делении положительного числа на отрицательное число всегда будет отрицательным. Например, {экв}3*-2=-6 {/экв} и {экв}8/-4=-2 {/экв}.
Отрицательное умножение или деление на положительное
При умножении или делении отрицательного числа на положительное число всегда будет отрицательным. Например, {экв}-7*1=-7 {/экв} и {экв}-14/2=-7 {/экв}.
Отрицательное число, умноженное или деленное на отрицательное
При умножении или делении отрицательного числа на отрицательное число ответ всегда будет положительным. Например, {экв}-2*-2=4 {/экв} и {экв}-15/-5=3 {/экв}.
Например, {экв}-2*-2=4 {/экв} и {экв}-15/-5=3 {/экв}.
Простое правило и таблица
Как показано выше, простой способ запомнить правила знаков состоит в использовании двух простых простых правил. Если знаки одинаковые, оба положительные или оба отрицательные, произведение или частное всегда будет положительным. Если знаки разные, один положительный и один отрицательный независимо от порядка, произведение или частное будет отрицательным.Произведение — это результирующее значение умножения, а частное — это результирующее значение задачи деления. Ниже приведена простая диаграмма, с помощью которой можно определить, будет ли произведение или частное положительным или отрицательным.
| + * или / + | + |
| — * или / + | — |
| + * или / — | — |
| — * или / — | + |
Как делить отрицательные дроби
После того, как вы поняли вышеприведенные правила знаков, теперь можно делить отрицательные дроби. Разделение отрицательных дробей будет представлено ниже в виде серии из пяти различных шагов. Все шаги, за исключением последнего, можно использовать при делении положительных дробей, тогда как последний шаг явно предназначен для деления отрицательных дробей, поскольку он включает в себя правила знаков.
Разделение отрицательных дробей будет представлено ниже в виде серии из пяти различных шагов. Все шаги, за исключением последнего, можно использовать при делении положительных дробей, тогда как последний шаг явно предназначен для деления отрицательных дробей, поскольку он включает в себя правила знаков.
Первый шаг: величина, обратная делителю
Первый шаг при делении дробей — найти обратную величину делителя. Дело в том, что деление дробей равносильно умножению на обратное. обратное дроби — это когда числитель и знаменатель дроби переставлены местами. Например, обратное число 4/7 равно 7/4. Делитель — это число, которое используется для деления на другое число. Это второе число при просмотре задачи на деление. Например, если 8 разделить на 4, делителем будет 4. Важно отметить, что единственная дробь, которая превращается в обратную, — это делитель.
Если делителем являются целые числа, они преобразуются в дроби, если их поместить над единицей, а затем перевернуть, чтобы получить обратное число.
Шаг второй: умножение числителей
После того как задача на деление преобразуется в задачу на умножение с делителем в качестве обратного числа, следующим шагом является умножение числителей. Таким образом, если задача деления была {eq}\frac{1}{4} / \frac{2}{3} {/eq}, сначала делитель становится обратным, и задача превращается в задачу на умножение: {экв}\фракция{1}{4} * \фракция{3}{2} {/экв}. Во-вторых, числители умножаются, чтобы получить: {eq}\frac{1}{4} * \frac{3}{2} = \frac{3}{} {/eq}
Шаг третий: умножение знаменателей
Следующим шагом после умножения числителей является умножение знаменателей.Используя тот же пример, что и выше, произведение умножения знаменателей равно: {eq}\frac{1}{4} * \frac{3}{2} = \frac{3}{8} {/eq}
Шаг четвертый: упростите дробь
После того, как произведения числителя и знаменателя найдены, при необходимости можно упростить дробь. Это не всегда нужно делать, если ответ уже есть в простейшей форме. В приведенном выше примере {eq}\frac{3}{8} {/eq} уже имеет простейшую форму.
Если бы дробь была {eq}\frac{4}{8} {/eq}, то и числитель, и знаменатель делились бы на 4.Таким образом, упрощенная дробь будет: {eq}\frac{1}{2} {/eq}
.Шаг пятый: применение правил знаков
Последний шаг — применение правил знаков. В приведенном выше примере {eq}\frac{1}{4} * \frac{3}{2} = \frac{3}{8} {/eq} обе дроби имели положительный знак и, следовательно, были положительными. Если бы один знак был отрицательным, а другой положительным, то ответ был бы отрицательным. Если бы оба знака были отрицательными, то ответ был бы положительным. Обратитесь к приведенной выше таблице знаков, чтобы убедиться, что ответу дан правильный знак.
Деление на отрицательные дроби
При делении целого числа или дроби на отрицательную дробь выполняются те же действия, что и выше.
Практические задачи
Ниже приведены три практические задачи, которые помогут вам отработать и изучить шаги и правила деления отрицательных дробей.
Практика первая: разделите отрицательную дробь на целое положительное число
Разделите {eq}\frac{-5}{9} {/eq} на {eq}5 {/eq}
- делитель 5: {экв}\фракция{1}{5} {/экв}
- Превратите задачу деления в задачу умножения с обратной величиной: {eq}\frac{-5}{9} * \frac{1}{5} {/eq}
- Умножьте числитель и знаменатель, учитывая правило знаков: {eq}\frac{-5}{9} * \frac{1}{5} = \frac{-5}{45} {/eq}
- Упростите дробь, в данном случае разделив числитель и знаменатель на 5: {eq}\frac{-5}{45} = \frac{-1}{9} {/eq}
Практика вторая: разделите отрицательную дробь на положительную
Разделите {eq}\frac{-3}{4} {/eq} на {eq}\frac{6}{7} {/eq}
- Найдите обратную величину делителя: {eq}\frac{7}{6} {/eq}
- Превратите задачу деления в задачу умножения с обратной величиной: {eq}\frac{-3}{4} * \frac{7}{6} {/eq}
- Умножьте числитель и знаменатель, учитывая правило знаков: {eq}\frac{-3}{4} * \frac{7}{6} = \frac{-21}{24} {/eq }
- Упростите дробь, в данном случае разделив числитель и знаменатель на 3: {eq}\frac{-21}{24} = \frac{-7}{8} {/eq}
Практика третья: разделите отрицательную дробь на отрицательную дробь
Разделите {eq}\frac{-1}{2} {/eq} на {eq}\frac{-2}{3} {/eq}
- Найдите обратную величину делителя: {eq}\frac{-3}{2} {/eq}
- Превратите задачу деления в задачу умножения с обратной величиной: {eq}\frac{-1}{2} * \frac{-3}{2} {/eq}
- Умножьте числитель и знаменатель, учитывая правило знаков: {eq}\frac{-1}{2} * \frac{-3}{2} = \frac{3}{4} {/eq}
- Упростите дробь.
 В этом случае дробь имеет простейшую форму: {eq}\frac{3}{4} {/eq} .
В этом случае дробь имеет простейшую форму: {eq}\frac{3}{4} {/eq} .
Резюме урока
При делении отрицательных дробей применяются определенные правила, и необходимо соблюдать определенные шаги. Одними из первых правил, которые нужно понять, являются правила знаков для произведения или частного . Правила знаков следующие:
- При делении или умножении двух положительных чисел ответ положительный.
- При делении или умножении двух отрицательных чисел ответ положительный.
- При делении или умножении одного положительного числа и одного отрицательного числа ответ будет отрицательным.
Деление дробей аналогично умножению одной дроби на обратное делителя . Обратная пропорция аналогична перевернутой дроби с числителем в знаменателе и наоборот. Делитель — это число, которое используется для деления на другое число, и это единственное число, которое превращается в его обратное число. После перемножения дробей они упрощаются, и к ответу применяются правила знаков.
После перемножения дробей они упрощаются, и к ответу применяются правила знаков.
Отрицательные числа
Примеры, которые мы рассмотрели до сих пор все имели дело с положительными числами по модулю другого числа. Что об отрицательных числах?На самом деле они ведут себя почти так же, хотя и немного хитрее. Лучше всего это видно на примере.
1 — Что такое -17 мод 10?
Чтобы это узнать, разделим -17 на 10 и возьмем остаток.Теперь помните что когда мы делаем это, нам нужно иметь положительный остаток , потому что наш ответ по модулю 10 должен быть одним из чисел 0, 1, 2, 3, 4, 5, 6, 7, 8 или 9. Таким образом, мы должны выяснить, сколько кратных 10 нужно добавить или вычесть перед остатком число от 0 до 9.
-17 разделить на 10 равно » -2 остаток 3 »
Это означает, что -17 = -2* 10 + 3 .Поскольку вычитание этих двух
кратные 10 не имеют значения, мы можем просто «забыть о них»
и, таким образом, -17 совпадает с 3 по модулю 10. Другими словами:
Другими словами:
-17 ≡ 3 mod 10.
Этот ответ имеет смысл — если вы продолжаете прибавлять числа, кратные 10, к -17, вы добраться до 3 в конце концов.
2 — Что такое -61 мод 5?
Чтобы это узнать, разделим -61 на 5 и возьмем остаток. Теперь помните что когда мы делаем это, нам нужно иметь положительный остаток , потому что наш ответ по модулю 5 должен быть одним из чисел 0, 1, 2, 3 или 4.Таким образом, мы нужно вычислить, сколько чисел, кратных 5, нужно прибавить или вычесть, прежде чем остаток представляет собой число от 0 до 4.
-61 разделить на 5 равно » -13 остаток 4 »
Это означает, что -61 = -13* 5 + 4 . После вычитания этих тринадцати кратные 5 не имеют значения, мы можем просто «забыть о них» и, таким образом, -61 совпадает с 4 по модулю 5. Другими словами:
-61 ≡ 4 по модулю 5.
Этот ответ имеет смысл — если вы продолжаете добавлять числа, кратные 5, к -61, вы
добраться до 4 в конце концов.
Как умножать и делить отрицательные числа
В математике есть много вещей, которые люди запоминают и используют, но никогда не понимают. Среди них нет более известного, чем «положительное, умноженное на отрицательное, равно отрицательному» и «отрицательное, умноженное на отрицательное, равно положительному». Но почему эти утверждения верны? И как на самом деле работают умножение и деление, когда вы добавляете в смесь отрицательные числа? Ответам на эти и другие вопросы и посвящена сегодняшняя статья.
Обзор: что такое умножение?
Как мы говорили в статье «Является ли умножение повторяющимся сложением?» в большинстве случаев лучше думать об умножении как о чем-то, что масштабирует число так, чтобы оно было в несколько раз больше его первоначального размера. Вы можете думать о задаче 2 x 5 как о растягивании палочки длиной 5 единиц, лежащей вдоль числовой прямой, до тех пор, пока она не станет длиной 10 единиц — в два раза больше ее первоначальной длины.
Это достаточно просто, но как насчет чего-то еще проще: 1 x 5? Что это обозначает? Эта задача просто говорит о том, что нужно растянуть число 5 вдоль числовой прямой, пока оно не станет в 1 раз больше исходной длины.Другими словами, величина исходного числа, вытянутого вдоль числовой прямой, в этой задаче не меняется. (Если вам нужно освежить в памяти, мы говорили о величинах в статье об абсолютных значениях.) Так работает умножение с положительными числами, но что происходит, когда одно или оба числа отрицательны?
Как умножать положительные и отрицательные числа
Начнем с того, что означает умножение положительного числа на отрицательное число? Что ж, согласно нашему определению умножения, такая задача, как -1 x 5, требует от нас растянуть число 5 вдоль числовой прямой, пока оно не станет в -1 раз больше его первоначальной длины.Мы видели, как растянуть число так, чтобы оно в 1 раз превышало его первоначальную длину, но –1… что это значит? Быстрый и грязный совет заключается в том, что умножение любого числа на -1 просто переворачивает его с одной стороны числовой строки на другую. Если число, умноженное на -1, положительное, результат отрицательный. Если число, умноженное на -1, отрицательное, результат положительный.
Если число, умноженное на -1, положительное, результат отрицательный. Если число, умноженное на -1, отрицательное, результат положительный.
Итак, теперь мы знаем, что –1 x 5 = –5. Обратите внимание, что, как и при умножении 1 x 5, умножение –1 x 5 не меняет величину исходного числа 5, а только меняет его знак.Как насчет задачи –2 x 5? Что ж, в этом случае происходят две вещи: во-первых, величина числа 5 растягивается вдоль числовой прямой до тех пор, пока не станет в два раза больше своего первоначального размера. А во-вторых, число, которое мы получаем в результате этого растяжения, 10, переворачивается по числовой прямой, чтобы дать нам окончательный ответ: –2 x 5 = –10.
Не секрет, что эти две вещи происходят, поскольку то, что мы уже узнали, говорит нам о том, что число –2 также можно записать как –1 x 2. Это означает, что задача –2 x 5 = –1 x 2 x 5 .Таким образом, первый шаг, 2 x 5, выполняет растяжение, а второй шаг переворачивает результат по числовой прямой. И таким образом: «Положительное, умноженное на отрицательное, равно отрицательному».
Как умножать отрицательные числа
Вот как происходит умножение положительного числа на отрицательное. А как насчет перемножения двух отрицательных чисел? Чтобы увидеть, что происходит, давайте подумаем о задаче –1 x –1. В этой задаче предлагается перевернуть число –1 на другую сторону числовой прямой, что даст ответ 1.Как насчет более сложной задачи –2 x –5? Начните с того, что используйте тот факт, что –2 = –1 x 2, чтобы вместо этого думать об этой задаче как –1 x 2 x –5. Это просто говорит о том, чтобы сначала растянуть -5 до тех пор, пока оно не удвоит исходную величину (что означает, что оно будет равно -10), а затем перевернуть этот результат через числовую прямую. Таким образом, ответ равен 10. Таким образом: «Отрицательное значение, умноженное на отрицательное, равно положительному».
Как выполнить деление с отрицательными числами
Но как определить знак при делении отрицательных чисел? Правило определения знака при делении положительного числа на отрицательное число (или наоборот) или отрицательного числа на отрицательное число точно такое же, как и при их умножении. Просто поменяйте местами операцию деления вместо умножения, и все будет работать так же. В частности, деление положительного числа на отрицательное число (или наоборот) приводит к отрицательному числу. А деление отрицательного числа на другое отрицательное число дает положительное число. Почему?
Просто поменяйте местами операцию деления вместо умножения, и все будет работать так же. В частности, деление положительного числа на отрицательное число (или наоборот) приводит к отрицательному числу. А деление отрицательного числа на другое отрицательное число дает положительное число. Почему?
[[AdMiddle]Ну, вернемся к связи между дробями и делением, о которой мы говорили в предыдущей статье. В этой статье мы узнали, что деление некоторого числа на число, подобное 2, дает точно такой же эффект, как и умножение исходного числа на дробь 1/2.Это означает, что деление положительного числа на отрицательное число, например –2, равносильно умножению его на дробь –1/2. Это означает, что любую задачу на деление можно превратить в эквивалентную задачу на умножение, и что вся логика определения знаков, о которой мы говорили для умножения, работает и для деления!
Номер недели
Прежде чем мы закончим, пришло время для избранного номера этой недели из моего поста в блоге QDT The Quick and Dirty. Число этой недели на самом деле не число, а объяснение гипотетической загадки собеседования, которую я дал в статье на прошлой неделе.Загадочный вопрос: «Сколько точек на сфере, где, пройдя одну милю на юг, затем одну милю на восток и, наконец, одну милю на север, вы в конечном итоге вернетесь туда, откуда начали?»
Число этой недели на самом деле не число, а объяснение гипотетической загадки собеседования, которую я дал в статье на прошлой неделе.Загадочный вопрос: «Сколько точек на сфере, где, пройдя одну милю на юг, затем одну милю на восток и, наконец, одну милю на север, вы в конечном итоге вернетесь туда, откуда начали?»
Довольно легко придумать одну подходящую точку: Северный полюс. Когда вы стоите на Северном полюсе Земли, любое направление, в котором вы идете, будет на юг. Таким образом, пройдя одну милю на юг (что означает в любом направлении), затем одну милю на восток, затем одну милю на север, вы должны вернуться на Северный полюс.
Но есть ли другие места, которые тоже работают? Действительно, есть.На самом деле их бесконечное множество! Если вы хотите узнать, где находятся все эти точки, ознакомьтесь с моим сообщением в блоге The Quick and Dirty.
Подведение итогов
И это все, на что у нас есть время на математику. Не забудьте стать поклонником Math Dude на Facebook, где вы найдете новое число дня и математическую головоломку, публикуемую каждый будний день. И если вы есть в Твиттере, подпишитесь на меня и там. Наконец, если у вас есть вопросы по математике, не стесняйтесь присылать их мне через Facebook, Twitter или по электронной почте mathdude@quickanddirtytips.ком.
И если вы есть в Твиттере, подпишитесь на меня и там. Наконец, если у вас есть вопросы по математике, не стесняйтесь присылать их мне через Facebook, Twitter или по электронной почте mathdude@quickanddirtytips.ком.
Вы устали пытаться выяснить, есть ли в супермаркете «более здоровая» еда? Ознакомьтесь с Руководством по выживанию в продуктовом магазине Nutrition Diva .
До встречи в следующий раз, это Джейсон Маршалл с Быстрые и грязные советы парня-математика по упрощению математики . Спасибо за внимание, любители математики!
Изображение предоставлено Shutterstock
Отрицательное деление на отрицательное
В этом видео-анимации и визуальных подсказках «Математика наглядна» мы рассмотрим целочисленное деление через деление в кавычках и дробное деление! В частности, мы будем исследовать негатив, разделенный на негатив, концептуально через конкретные и визуальные представления!
После предыдущего поста о визуализации целочисленного деления в кавычках и на части теперь мы готовы приступить к решению целочисленного деления . Если вы еще не видели визуальную анимацию и визуальные подсказки для целочисленного деления, вам обязательно следует это сделать, прежде чем двигаться дальше.
Если вы еще не видели визуальную анимацию и визуальные подсказки для целочисленного деления, вам обязательно следует это сделать, прежде чем двигаться дальше.
Следующие три поста будут посвящены целочисленному делению , чтобы завершить серию целочисленных операций. В этом видео мы рассмотрим деление отрицательного дивиденда на отрицательный делитель, сначала используя квотное (или измеренное) деление, а затем партикулярное (или справедливое деление). Зрителю также будет предложено поставить видео на паузу и попробовать свое собственное, используя конкретные манипулятивы и/или визуальные эффекты.
См. приведенное ниже руководство, призванное помочь учителям и/или родителям использовать это упражнение со своими учениками/детями.
Визуальная подсказка №1: кавычки
В видео выше мы начинаем с деления негатива на негатив через кавычки:
-8 ÷ (-2) = ___
прописью:
-8 разделить на группы по -2 дает результат ___ групп
Итак, пусть зритель моделирует конкретно и/или визуально следующее:
Учащиеся могут использовать пространственные рассуждения для создания групп множества или линейно на числовой прямой. Они также могут рассмотреть возможность использования повторного вычитания, чтобы многократно удалять группы -2, пока не будут удалены все (или не останется 0).
Они также могут рассмотреть возможность использования повторного вычитания, чтобы многократно удалять группы -2, пока не будут удалены все (или не останется 0).
Стрелка также может указывать налево, если учащиеся используют многократное сложение для повторного добавления групп -2 от 0 до -8.
Визуальная подсказка № 2: Разделение на части
Теперь мы подходим к той же проблеме с точки зрения партитивного деления:
-8 ÷ (-2) = ____
или
-8, разделенный на -2 группы, дает результат ____ на группу.
Хотя значение результата будет одинаковым, концептуальное понимание и конкретный/визуальный подход будут сильно различаться.
Как и выше, мы можем подойти к этому, используя набор или линейную модель, где мы пространственно разделяем количество на 2 равные, но «отрицательно заряженные» группы (поскольку это -2 группы) и подсчитываем количество объектов в каждой группе. Хотя изображение ниже может выглядеть ужасно похожим, обратите внимание, что использование повторного вычитания может немного отличаться, потому что мы не знаем, сколько человек в каждой группе (пока).Таким образом, повторное вычитание может состоять из справедливого обмена 1 объектом за раз или 2 объектов за раз, до количества, которое учащийся может быстро заменить для обмена.
Хотя изображение ниже может выглядеть ужасно похожим, обратите внимание, что использование повторного вычитания может немного отличаться, потому что мы не знаем, сколько человек в каждой группе (пока).Таким образом, повторное вычитание может состоять из справедливого обмена 1 объектом за раз или 2 объектов за раз, до количества, которое учащийся может быстро заменить для обмена.
Так как мы делим -8 на 2 отрицательно заряженные группы (группы -2), то когда мы помещаем каждый отрицательный квадрат в отрицательную группу, мы получаем двойное отрицание. Это очень похоже на то, когда мы используем двойное отрицание в английском языке. Например, если не , а , а не идет дождь, то мы получаем положительный результат – дождь будет!
В этом случае отрицательно заряженная группа «отрицает» отрицательные значения, и таким образом мы получаем положительные значения внутри отрицательно заряженной группы.
Визуальная подсказка №3: Твоя очередь!
Поставьте видео на паузу и позвольте зрителю применить свои знания о негативном с помощью отрицательного разделительного деления, используя следующую визуальную подсказку:
-10 ÷ (-5) = ___
или
-10 разделить на -5 групп дает результат ___ на группу
Дайте зрителю время на разделение на части, прежде чем показывать оставшуюся часть видеоанимации или следующее неподвижное изображение.
Опять же, мы должны отметить, что мы хотим определить значение количества, которое будет разделено между 5 отрицательно заряженными группами.
Таким образом, если мы честно разделим -10 на эти 5 отрицательно заряженных групп (-5 групп), мы получим +2 в каждой группе:
Итак, теперь вы качаетесь с кавычками и партитивами, а также с делением негатива на негатив.
Готовы ли вы заняться делением отрицательного на положительное и положительного на отрицательное?
Они появятся в следующих двух постах, так что будьте к ним готовы!
Math IS Visual.Давайте учить так.
Умножение и деление целых чисел — методы и примеры
В математике арифметические операции с целыми числами включают вычитание, сложение, деление и умножение всех типов действительных чисел. В частности, целые числа — это числа, включающие положительные, отрицательные и нулевые числа. Умножение и деление целых чисел регулируются аналогичными правилами.
Как умножать целые числа?
Умножение определяется как многократное сложение целых чисел.Умножение целых чисел включает три случая:
- Умножение двух положительных целых чисел
- Умножение двух отрицательных целых чисел
- Умножение положительного и отрицательного целых чисел.
Умножение двух целых чисел с одинаковыми знаками всегда дает положительный результат. Это означает, что произведение двух положительных или двух отрицательных целых чисел положительно. С другой стороны, целые числа произведений с разными знаками всегда будут отрицательными.
Многие учащиеся сталкиваются с проблемой запоминания приведенных выше правил умножения целых чисел. В этой статье есть сценарий, который поможет вам избежать путаницы. В этом сценарии положительный знак (+) использовался для обозначения « GOOD », а отрицательный знак символизирует фразу « BAD ». «Давайте посмотрим на эти мнемоники.
- Если хорошие (+) вещи случаются с хорошими (+) людьми, то это хорошо (+)
- Если хорошие (+) вещи случаются с плохими (-) людьми, то это плохо (-)
- Если плохие (-) вещи случаются с хорошими (+) людьми, тогда это плохо (-)
- Если плохие (-) вещи случаются с плохими (-) людьми, то это хорошо (+)
Чтобы умножить целые числа, просто умножьте числовые числа без знака и поставьте знак на продукте, вспомнив вышеприведенные правила. Пример 1 20
Пример 1 20
Если количество отрицательных множимых в предложении умножения нечетное, произведение будет отрицательным числом.
Пример 2
(-2) × (−4) × (−3) = -24; здесь количество множимых = 3 (нечетное число)
Когда количество отрицательных множимых четно в предложении умножения, произведение будет положительным.
Пример 3
(−4) × (−3) = 12; Здесь число множимых равно 2 (четным)
Как делить целые числа?
В то время как умножение является суммированием целых чисел, деление, с другой стороны, является распределением целых чисел. Мы можем просто сказать, что деление обратно умножению. Правила деления целых чисел аналогичны правилам умножения. Единственная разница в делении состоит в том, что частное не обязательно должно быть целым числом.
Давайте также посмотрим на правила деления:
- Частное натурального числа всегда положительно.
 Если и делимое, и делитель являются положительными целыми числами, значение частного будет положительным. Например, (+ 9) ÷ (+ 3) = + 3
Если и делимое, и делитель являются положительными целыми числами, значение частного будет положительным. Например, (+ 9) ÷ (+ 3) = + 3 - Частное двух отрицательных чисел всегда положительно. Это означает, что если делимое и делитель оба отрицательны, то частное всегда положительно. Например;
(- 9) ÷ (- 3) = + 3
Следовательно, при делении двух целых чисел с одинаковыми знаками мы делим числа без знака и ставим перед результатом знак плюс. - Деление положительного и отрицательного целого числа дает отрицательный ответ. Например; (+ 16) ÷ (- 4) = – 4
Таким образом, чтобы разделить целые числа с разными знаками, мы делим числовые значения без знаков и ставим к результату знак минус.
9 разделить на 45 делений. 5? Доктор Вы можете разделить
5? Доктор Вы можете разделить
 биномом. 1. Откройте в приложении. 9 на 45 = 0. В начальной школе преподаются 3 метода деления, каждый из которых различается по сложности. Эта система называется синтетическим делением. Аризона (04) Колорадо (08) Айдахо (16) Нью-Мексико (35) Монтана (30) Юта (49) Невада (32) Вайоминг (56) Раздел 8 Калькулятор деления футов на дюймы и дроби.7 Теперь длинное деление происходит как с целыми числами, так и с ответом на 406. Использовали длинное деление и распределительное свойство для записи своей работы. Давайте кратко рассмотрим пример полиномиального метода длинного деления и синтетического деления. Применение полиномиального длинного деления для решения задачи Объем V вложенных ящиков во введении к этому разделу в кубических сантиметрах определяется как V(x) = x3 + 7×2 + 14x + 8. 29R9 C. Деление — это математическая операция, записанная с помощью символа ÷ , которую можно представить двумя способами: a ÷ b — это размер каждой группы, когда a объектов разбиты на b групп одинакового размера, ИЛИ a ÷ b — это количество групп, когда a объекты делятся на группы по b объектов в каждой.
биномом. 1. Откройте в приложении. 9 на 45 = 0. В начальной школе преподаются 3 метода деления, каждый из которых различается по сложности. Эта система называется синтетическим делением. Аризона (04) Колорадо (08) Айдахо (16) Нью-Мексико (35) Монтана (30) Юта (49) Невада (32) Вайоминг (56) Раздел 8 Калькулятор деления футов на дюймы и дроби.7 Теперь длинное деление происходит как с целыми числами, так и с ответом на 406. Использовали длинное деление и распределительное свойство для записи своей работы. Давайте кратко рассмотрим пример полиномиального метода длинного деления и синтетического деления. Применение полиномиального длинного деления для решения задачи Объем V вложенных ящиков во введении к этому разделу в кубических сантиметрах определяется как V(x) = x3 + 7×2 + 14x + 8. 29R9 C. Деление — это математическая операция, записанная с помощью символа ÷ , которую можно представить двумя способами: a ÷ b — это размер каждой группы, когда a объектов разбиты на b групп одинакового размера, ИЛИ a ÷ b — это количество групп, когда a объекты делятся на группы по b объектов в каждой. Решение: Длинное деление 75 ÷ 4 можно выполнить следующим образом. Делитель. Алгоритм дроби. математика. 1 4)68 − 4 28 Разделите десятки. Шаг 2: Поскольку остаток ≠ 0, делим делитель шага 1 (27) на остаток (18). 15 терминов. репетитор. Следовательно, при делении 75 на 4 частное = 18, остаток = 3. (См. ссылки для получения подробной информации о дисперсии) В алгебре полиномиальное длинное деление — это алгоритм деления многочлена на другой многочлен той же или более низкой степени. 27.03.10 9:55.00:45. 99! стрелка_вперед. Остаток равен 0. Это сокращение называется синтетическим делением. Решения Р. Д. Шармы для математики класса 8. Глава 8. Деление алгебраических выражений. Таким образом, проверено. написать. Опускайте следующую цифру после каждого шага, как «Как сделать длинное деление с десятичными дробями: пример». Поместите первую цифру в частное в разряде сотен. Есть несколько шагов, которые вам нужно выполнить. Эта страница содержит рабочие листы по длинному умножению для учащихся, которые освоили основные факты умножения и учатся умножать 2-, 3-, 4-значные и более числа.
Решение: Длинное деление 75 ÷ 4 можно выполнить следующим образом. Делитель. Алгоритм дроби. математика. 1 4)68 − 4 28 Разделите десятки. Шаг 2: Поскольку остаток ≠ 0, делим делитель шага 1 (27) на остаток (18). 15 терминов. репетитор. Следовательно, при делении 75 на 4 частное = 18, остаток = 3. (См. ссылки для получения подробной информации о дисперсии) В алгебре полиномиальное длинное деление — это алгоритм деления многочлена на другой многочлен той же или более низкой степени. 27.03.10 9:55.00:45. 99! стрелка_вперед. Остаток равен 0. Это сокращение называется синтетическим делением. Решения Р. Д. Шармы для математики класса 8. Глава 8. Деление алгебраических выражений. Таким образом, проверено. написать. Опускайте следующую цифру после каждого шага, как «Как сделать длинное деление с десятичными дробями: пример». Поместите первую цифру в частное в разряде сотен. Есть несколько шагов, которые вам нужно выполнить. Эта страница содержит рабочие листы по длинному умножению для учащихся, которые освоили основные факты умножения и учатся умножать 2-, 3-, 4-значные и более числа. Более того, длинное деление снижает акцент на устной природе арифметики. Напишите предложения деления для массивов. 2: 9 ÷ 45 = 0. Шаг 1: Разделите 45 (большее число) на 27 (меньшее число). Работа. Наши рабочие листы для деления на длинное деление для 4-го класса охватывают деление на длинное деление с однозначными делителями и до 4-значных дивидендов. 136 + 54 = 190, значит число под квадратом должно быть 9. Остаток. В данном случае это 33. Разделите 2x 3 + 5x 2 + 9 на x + 3 синтетическим методом. Деление на 2 цифры: 6250÷25. 32. МЖДМ.Сколько карточек в каждой группе? Что такое 26. Остаток — число, «оставшееся» после деления. Переменная b в числителе и знаменателе сокращаются (подумайте: 1 1). Подход № 1: деление с использованием многократного вычитания. Заполните страницу, даже если она требует повторяющихся задач. Сколько 9 разделить на 840 длинное деление? 0. Результат деления 45÷9 45÷9 равен 5 . Практика: Основное многозначное деление. \) Многие из нас, вероятно, считают это обычным долгим процессом деления.
Более того, длинное деление снижает акцент на устной природе арифметики. Напишите предложения деления для массивов. 2: 9 ÷ 45 = 0. Шаг 1: Разделите 45 (большее число) на 27 (меньшее число). Работа. Наши рабочие листы для деления на длинное деление для 4-го класса охватывают деление на длинное деление с однозначными делителями и до 4-значных дивидендов. 136 + 54 = 190, значит число под квадратом должно быть 9. Остаток. В данном случае это 33. Разделите 2x 3 + 5x 2 + 9 на x + 3 синтетическим методом. Деление на 2 цифры: 6250÷25. 32. МЖДМ.Сколько карточек в каждой группе? Что такое 26. Остаток — число, «оставшееся» после деления. Переменная b в числителе и знаменателе сокращаются (подумайте: 1 1). Подход № 1: деление с использованием многократного вычитания. Заполните страницу, даже если она требует повторяющихся задач. Сколько 9 разделить на 840 длинное деление? 0. Результат деления 45÷9 45÷9 равен 5 . Практика: Основное многозначное деление. \) Многие из нас, вероятно, считают это обычным долгим процессом деления. 4. 53 разделить на 9.Пример: часть базовой арифметики, длинное деление — это метод решения и нахождения ответа и остатка для задач на деление, в которых участвуют числа, состоящие как минимум из двух цифр. Редактировать • Распечатать • Загрузить • Вставить Длинное деление — это универсальный способ выполнения сложных делений без использования калькулятора. 1. Запишите 5 над 0,98, деленное на 8. Многочлен длинного деления −(6𝑥4+12𝑥3+3𝑥2 −18𝑥) 4𝑥3+8𝑥2 +8𝑥−8 −(4𝑥3+8𝑥2 +2𝑥−12) 6𝑥+4 2𝑥3+4𝑥2 +𝑥−6 К концу этого урока вы должны уметь: • Использовать деление для деления многочлена на линейный множитель.2+3х. Найдите остаток, когда y … Обширная база данных из более чем 18 викторин отдела онлайн, проверьте свои знания с вопросами викторины отдела. 00:53. 0. Пример: 45 ÷ 1= 45. Ответьте на приведенные ниже вопросы, используя деление в большую сторону. На уроке деления мы научились составлять выражения деления. 3 Многочлены и синтетическое деление • Используйте деление в длинное для деления многочлена на многочлен • Используйте синтетическое деление для деления многочлена на двучлен • Используйте теорему об остатках и теорему о факторах.
4. 53 разделить на 9.Пример: часть базовой арифметики, длинное деление — это метод решения и нахождения ответа и остатка для задач на деление, в которых участвуют числа, состоящие как минимум из двух цифр. Редактировать • Распечатать • Загрузить • Вставить Длинное деление — это универсальный способ выполнения сложных делений без использования калькулятора. 1. Запишите 5 над 0,98, деленное на 8. Многочлен длинного деления −(6𝑥4+12𝑥3+3𝑥2 −18𝑥) 4𝑥3+8𝑥2 +8𝑥−8 −(4𝑥3+8𝑥2 +2𝑥−12) 6𝑥+4 2𝑥3+4𝑥2 +𝑥−6 К концу этого урока вы должны уметь: • Использовать деление для деления многочлена на линейный множитель.2+3х. Найдите остаток, когда y … Обширная база данных из более чем 18 викторин отдела онлайн, проверьте свои знания с вопросами викторины отдела. 00:53. 0. Пример: 45 ÷ 1= 45. Ответьте на приведенные ниже вопросы, используя деление в большую сторону. На уроке деления мы научились составлять выражения деления. 3 Многочлены и синтетическое деление • Используйте деление в длинное для деления многочлена на многочлен • Используйте синтетическое деление для деления многочлена на двучлен • Используйте теорему об остатках и теорему о факторах. Деление 2. Длинные правила деления объясняются в 12 шагов для случая, когда делимое представляет собой число длины 3, а делитель — число длины 2: 1-й шаг: установить делимое (число, которое нужно разделить) и делитель (это число «y», которое мы часто используем в таких предложениях, как: разделить делимое x на делитель y). Синтетическое деление — это сокращенный метод выполнения длинного деления, который можно использовать, когда делитель представляет собой полином первой степени вида x — c. Пользователь: Какая разница между 2386 и 7000.Задача 52. Соедините Определите частное, делимое и делитель в этом уравнении: 63 » 9 # 7 Х. Уэслидумфорд. Пример: 5 ÷ 5 = 1. В этом методе числитель дроби — делимое, а знаменатель — делитель. 2 60 30 82 будет наименьшим числом, если его последовательно разделить на 6, 5 и 3, чтобы получить соответственно 4, 3 и 2. Делитель = 9. Учащиеся будут работать с делением в горизонтальном и вертикальном форматах, а также задачи, основанные на поиске пропущенного целого числа в уравнениях деления.
Деление 2. Длинные правила деления объясняются в 12 шагов для случая, когда делимое представляет собой число длины 3, а делитель — число длины 2: 1-й шаг: установить делимое (число, которое нужно разделить) и делитель (это число «y», которое мы часто используем в таких предложениях, как: разделить делимое x на делитель y). Синтетическое деление — это сокращенный метод выполнения длинного деления, который можно использовать, когда делитель представляет собой полином первой степени вида x — c. Пользователь: Какая разница между 2386 и 7000.Задача 52. Соедините Определите частное, делимое и делитель в этом уравнении: 63 » 9 # 7 Х. Уэслидумфорд. Пример: 5 ÷ 5 = 1. В этом методе числитель дроби — делимое, а знаменатель — делитель. 2 60 30 82 будет наименьшим числом, если его последовательно разделить на 6, 5 и 3, чтобы получить соответственно 4, 3 и 2. Делитель = 9. Учащиеся будут работать с делением в горизонтальном и вертикальном форматах, а также задачи, основанные на поиске пропущенного целого числа в уравнениях деления. Этот ресурс забит математическими видео, и каждое видео посвящено определенному … \[45 \div 5 = 9\] Таким образом, \(895 \div 5 = 179\). (x2 2x 24) (x 4) ПРОВЕРЬТЕ СЕБЯ 4 У вас может быть остаток в алгебраическом делении, как и в арифметике. 818. 10 — половина 20. Полиномиальное длинное деление. Пример 1: Разделите: 75 ÷ 4 и проверьте это с помощью онлайн-калькулятора деления в большую сторону. 9 и д =5. Вопрос 3. C. Деление на 10 — Если число оканчивается на … Знакомство с делением в большую сторону с остатками. info Например, НОК 6 и 9 равен 18, поскольку 18 — это наименьшее кратное 9 и 6, которое делится и на 9, и на 6.Это постепенный процесс, разделенный на 4 шага: Найдите подходящее делимое и делитель, чтобы использовать их при делении. Video Bokep ini yaitu Video Bokep yang terupdate di January 2022 secara online Film Bokep Igo Sex Abg Online , потоковое онлайн-видео bokep XXX Gratis , … Long Division Game. прокомментировал Jenny 19 сентября 2017 г. (21 250 баллов) Я могу ответить на него из головы = 40.
Этот ресурс забит математическими видео, и каждое видео посвящено определенному … \[45 \div 5 = 9\] Таким образом, \(895 \div 5 = 179\). (x2 2x 24) (x 4) ПРОВЕРЬТЕ СЕБЯ 4 У вас может быть остаток в алгебраическом делении, как и в арифметике. 818. 10 — половина 20. Полиномиальное длинное деление. Пример 1: Разделите: 75 ÷ 4 и проверьте это с помощью онлайн-калькулятора деления в большую сторону. 9 и д =5. Вопрос 3. C. Деление на 10 — Если число оканчивается на … Знакомство с делением в большую сторону с остатками. info Например, НОК 6 и 9 равен 18, поскольку 18 — это наименьшее кратное 9 и 6, которое делится и на 9, и на 6.Это постепенный процесс, разделенный на 4 шага: Найдите подходящее делимое и делитель, чтобы использовать их при делении. Video Bokep ini yaitu Video Bokep yang terupdate di January 2022 secara online Film Bokep Igo Sex Abg Online , потоковое онлайн-видео bokep XXX Gratis , … Long Division Game. прокомментировал Jenny 19 сентября 2017 г. (21 250 баллов) Я могу ответить на него из головы = 40. Многозначное деление (остатки) Введение в длинное деление (остатки) Это текущий выбранный элемент. Например: 43785 (4+3+7+8+5=27) 27 делится на 9, поэтому 43785 тоже! Разделите 45 ÷ 3/8.45 × 3 = 135 Она получит 135 долларов. Разделить на 9. Аналогично правилу деления на 3, если сумма всех цифр делится на 9, то и все число делится на 9. 778 88 на 9 = 9. Шаг 1: Оцените ответ путем округления. В математике слово «деление» означает операцию, противоположную умножению. 7, запустить один. 778, вы можете просто использовать символ деления, который представляет собой косую черту, как мы сделали выше. 22 триместра. 8 64 8 13. Рабочие листы для деления в длинное Создавайте неограниченное количество рабочих листов для деления в длинное число (4-6 классы), в том числе с двузначными и трехзначными делителями.Weegy: Запятые в правильном положении для числа 37068 — это 3 790 241 068. 01:05. Ему нужно заработать как минимум 450 долларов. Показать пошаговые решения 5 9 × 16 10 = 80 90 = 8 9. png 271 × 293; 3 КБ.
Многозначное деление (остатки) Введение в длинное деление (остатки) Это текущий выбранный элемент. Например: 43785 (4+3+7+8+5=27) 27 делится на 9, поэтому 43785 тоже! Разделите 45 ÷ 3/8.45 × 3 = 135 Она получит 135 долларов. Разделить на 9. Аналогично правилу деления на 3, если сумма всех цифр делится на 9, то и все число делится на 9. 778 88 на 9 = 9. Шаг 1: Оцените ответ путем округления. В математике слово «деление» означает операцию, противоположную умножению. 7, запустить один. 778, вы можете просто использовать символ деления, который представляет собой косую черту, как мы сделали выше. 22 триместра. 8 64 8 13. Рабочие листы для деления в длинное Создавайте неограниченное количество рабочих листов для деления в длинное число (4-6 классы), в том числе с двузначными и трехзначными делителями.Weegy: Запятые в правильном положении для числа 37068 — это 3 790 241 068. 01:05. Ему нужно заработать как минимум 450 долларов. Показать пошаговые решения 5 9 × 16 10 = 80 90 = 8 9. png 271 × 293; 3 КБ. Итак, 495 — число делимого, а 9 — число делителя. ∴ Частное равно 3y3 – 5y + 3/2, а остаток равен 0. Все, что делится на 1, является самим числом. Разделите число, состоящее из футов, дюймов и плотницких дробей, с помощью этого бесплатного и простого онлайн-калькулятора. нижнего белья. 0) и (5.5 40 8 7. Потому что я 6-й класс. Мы знаем, что деление можно решить, многократно вычитая делитель из делимого, пока оно не станет меньше делителя. Теперь у вас есть новая задача на деление. 5 32 1 В следующем примере объединены шаги, связанные с делением в большую сторону. Напишите 288 под 314 внизу задачи. 26/9 = 2 остатка 8. Первое число «1» слишком мало, поэтому мы смотрим на первые два … Шаг 5 в длинном делении • Поскольку больше нет чисел, которые нужно уменьшить, и 2 не делится на 1, вы не повторяйте шаги деления.2+0x-1#. 66 делится на 8. Когда 1024 делится на 50, длинное деление заканчивается частным 20, а остаток 24. Миллиард, разделенный на миллион Калькулятор. Давайте воспользуемся делением в длинном порядке, чтобы вычислить частное при делении 98464 на 362.
Итак, 495 — число делимого, а 9 — число делителя. ∴ Частное равно 3y3 – 5y + 3/2, а остаток равен 0. Все, что делится на 1, является самим числом. Разделите число, состоящее из футов, дюймов и плотницких дробей, с помощью этого бесплатного и простого онлайн-калькулятора. нижнего белья. 0) и (5.5 40 8 7. Потому что я 6-й класс. Мы знаем, что деление можно решить, многократно вычитая делитель из делимого, пока оно не станет меньше делителя. Теперь у вас есть новая задача на деление. 5 32 1 В следующем примере объединены шаги, связанные с делением в большую сторону. Напишите 288 под 314 внизу задачи. 26/9 = 2 остатка 8. Первое число «1» слишком мало, поэтому мы смотрим на первые два … Шаг 5 в длинном делении • Поскольку больше нет чисел, которые нужно уменьшить, и 2 не делится на 1, вы не повторяйте шаги деления.2+0x-1#. 66 делится на 8. Когда 1024 делится на 50, длинное деление заканчивается частным 20, а остаток 24. Миллиард, разделенный на миллион Калькулятор. Давайте воспользуемся делением в длинном порядке, чтобы вычислить частное при делении 98464 на 362. H Студенческие математические журналы или 1 часть с линиями или сеткой. учиться. Как … 9 разделить на 45 = 0. делитель. Следующие 98 файлов находятся в этой категории из 98. Упражнение 2. Используя те же делимое и делитель, поработайте с партнером над созданием собственной сюжетной задачи.Смотрите популярный контент от следующих авторов: Учитель Джастин(@teacherjustinlabadnoy), Профессор Милли(@milliemathprof), ★ Нура ★(@noorastudies), High School Math(@liminf857), Учитель Джастин(@teacherjustinlabadnoy). Каковы правила делимости на 2,3,4,5,9,10? (Правила t…. . … Чтобы разделить на десятичную дробь, обратите внимание, что 45 ÷ 0. ÷ . Ответ: 108 ÷ 7 = 15 с остатком 3 ( 15 R 3 ) 0. Вычитание 136 из 1__0 дает нам 54. Сгенерируйте работу с шагами для 2 на 1, 3 на 2, 3 на 1, 4 на 3, 4 на 2, 4 на 1, 5 на 4, 5 на 3, 5 на 2, 6 на 4, 6 на 3 и 6 на 2 практика деления на две цифры или Чтобы улучшить и оценить математические навыки решения задач на длинное деление, таких как деление 1024 на 50, пользователям рекомендуется попрактиковаться или попробовать более длинные рабочие листы деления и оценки.
H Студенческие математические журналы или 1 часть с линиями или сеткой. учиться. Как … 9 разделить на 45 = 0. делитель. Следующие 98 файлов находятся в этой категории из 98. Упражнение 2. Используя те же делимое и делитель, поработайте с партнером над созданием собственной сюжетной задачи.Смотрите популярный контент от следующих авторов: Учитель Джастин(@teacherjustinlabadnoy), Профессор Милли(@milliemathprof), ★ Нура ★(@noorastudies), High School Math(@liminf857), Учитель Джастин(@teacherjustinlabadnoy). Каковы правила делимости на 2,3,4,5,9,10? (Правила t…. . … Чтобы разделить на десятичную дробь, обратите внимание, что 45 ÷ 0. ÷ . Ответ: 108 ÷ 7 = 15 с остатком 3 ( 15 R 3 ) 0. Вычитание 136 из 1__0 дает нам 54. Сгенерируйте работу с шагами для 2 на 1, 3 на 2, 3 на 1, 4 на 3, 4 на 2, 4 на 1, 5 на 4, 5 на 3, 5 на 2, 6 на 4, 6 на 3 и 6 на 2 практика деления на две цифры или Чтобы улучшить и оценить математические навыки решения задач на длинное деление, таких как деление 1024 на 50, пользователям рекомендуется попрактиковаться или попробовать более длинные рабочие листы деления и оценки. Разделите трехзначное число на однозначное с помощью деления в большую сторону. Несколько листов Чтобы разделить 65 на 95, сначала возьмите первую цифру делителя 9 и разделите 65 на 9. Первое число — это делимое (6), а второе число — делитель (3). Получите пошаговые решения от опытных наставников всего за 15–30 минут. Затем добавьте нули, так как они вам нужны для деления. 778 Итак, 5 x 3 = 15, поэтому ответ равен 3. F. Чтобы сделать делитель целым числом, запятую нужно переместить на два знака вправо, чтобы делитель стал равен 83.Его можно использовать для вычисления остатка или ответа на конкретное количество знаков после запятой. Небольшой инструмент для расчета с временными данными. Сократите следующее число делимого. Что такое 9. Ответ от вышеприведенной операции умножается на делитель. Для ясности будем считать, что все выражения в знаменателе отличны от нуля. Многочлен p(x) оставляет остаток −2 при делении на x − 1 и остаток −4 при делении на x +2. 833: 45 ÷ 54 = 0. Наши онлайн-викторины о дивизионах могут быть адаптированы в соответствии с вашими требованиями для прохождения некоторых викторин высшего дивизиона.
Разделите трехзначное число на однозначное с помощью деления в большую сторону. Несколько листов Чтобы разделить 65 на 95, сначала возьмите первую цифру делителя 9 и разделите 65 на 9. Первое число — это делимое (6), а второе число — делитель (3). Получите пошаговые решения от опытных наставников всего за 15–30 минут. Затем добавьте нули, так как они вам нужны для деления. 778 Итак, 5 x 3 = 15, поэтому ответ равен 3. F. Чтобы сделать делитель целым числом, запятую нужно переместить на два знака вправо, чтобы делитель стал равен 83.Его можно использовать для вычисления остатка или ответа на конкретное количество знаков после запятой. Небольшой инструмент для расчета с временными данными. Сократите следующее число делимого. Что такое 9. Ответ от вышеприведенной операции умножается на делитель. Для ясности будем считать, что все выражения в знаменателе отличны от нуля. Многочлен p(x) оставляет остаток −2 при делении на x − 1 и остаток −4 при делении на x +2. 833: 45 ÷ 54 = 0. Наши онлайн-викторины о дивизионах могут быть адаптированы в соответствии с вашими требованиями для прохождения некоторых викторин высшего дивизиона. (Полностью упростите свой ответ. Шаг за шагом применяйте деление в длинное число. Следующее число, на которое вы будете делить, — 47. Это сведет к 1/3 математического деления конкурса популярности. 1) Нарисуйте половину прямоугольника, используя только левая сторона и нижняя сторона. Решение: Дивиденд равен 3x 3 – 8x + 5, а делитель равен x – 1. В числе 30, 35 ÷ 0, 2 ÷ 1, 5 5 шестерок. Пример 7 — Разделить 4. Помните! Длинное деление может быть легким! 2 триллиона делятся на 8 миллиардов = 250. Теперь, используя метод деления в длину, мы можем разделить многочлен, как показано ниже.К этому может потребоваться некоторое время, так как вы читаете справа налево и снизу вверх!) Просмотр полного деления. (iv) Делитель дивидендов 34x – 22×3 – 12×4 – 10×2 – 75 3x + 7 -12×4 – 22×3 – 10×2 + 34x — 75 Используя метод деления в длину Сравните простоту этого с делением в длину: при делении в длину мы опускаем 2 и напишите его рядом с остатком 4. Разделите . Сколько раз 9 входит в число 495? 55 умножить на 9 получается 495, а остаток равен 0,5 60 12 11,3 доллара.
(Полностью упростите свой ответ. Шаг за шагом применяйте деление в длинное число. Следующее число, на которое вы будете делить, — 47. Это сведет к 1/3 математического деления конкурса популярности. 1) Нарисуйте половину прямоугольника, используя только левая сторона и нижняя сторона. Решение: Дивиденд равен 3x 3 – 8x + 5, а делитель равен x – 1. В числе 30, 35 ÷ 0, 2 ÷ 1, 5 5 шестерок. Пример 7 — Разделить 4. Помните! Длинное деление может быть легким! 2 триллиона делятся на 8 миллиардов = 250. Теперь, используя метод деления в длину, мы можем разделить многочлен, как показано ниже.К этому может потребоваться некоторое время, так как вы читаете справа налево и снизу вверх!) Просмотр полного деления. (iv) Делитель дивидендов 34x – 22×3 – 12×4 – 10×2 – 75 3x + 7 -12×4 – 22×3 – 10×2 + 34x — 75 Используя метод деления в длину Сравните простоту этого с делением в длину: при делении в длину мы опускаем 2 и напишите его рядом с остатком 4. Разделите . Сколько раз 9 входит в число 495? 55 умножить на 9 получается 495, а остаток равен 0,5 60 12 11,3 доллара. Ниже приведен пример записи шагов деления.Использовал длинное деление и свойство распределения для записи моей работы, как показано выше. 1 9) 5. 5 45 9 6. Натан разделил свои 78 бейсбольных карточек на равные группы по 3. Это очень похоже на то, что вы делали в начальной школе, когда пытались разделить большие числа, например, у вас есть 1723 \div 5 Знайте процедуру длинного деления, включающую двузначные делители, и получите представление о концепции. 486 ÷ 3 = 162. 83 равно 4. Остаток — это оставшаяся часть числа после выполнения процесса деления. Осталось 4 пончика.Сколько раз или сколько раз X входит в X Третий по величине пять x в квадрате? Чему подвержена семерка? Итак, мы начнем с того, что скажем, как нужно умножить X на, чтобы получить X в третью часть с умножением X на X в квадрате. 8 Числа 1. 3. 2 Триллион делится на 12 Миллиардов = 166. В 22 ÷ 2 = 11 22 — делимое, 2 — делитель и 11 — частное. 05, где мы думаем, сколько раз делитель входит в делимое. Этот калькулятор разделит одно число (делимое) на другое число (делитель), используя метод деления в большую сторону, а также покажет и объяснит каждый шаг.
Ниже приведен пример записи шагов деления.Использовал длинное деление и свойство распределения для записи моей работы, как показано выше. 1 9) 5. 5 45 9 6. Натан разделил свои 78 бейсбольных карточек на равные группы по 3. Это очень похоже на то, что вы делали в начальной школе, когда пытались разделить большие числа, например, у вас есть 1723 \div 5 Знайте процедуру длинного деления, включающую двузначные делители, и получите представление о концепции. 486 ÷ 3 = 162. 83 равно 4. Остаток — это оставшаяся часть числа после выполнения процесса деления. Осталось 4 пончика.Сколько раз или сколько раз X входит в X Третий по величине пять x в квадрате? Чему подвержена семерка? Итак, мы начнем с того, что скажем, как нужно умножить X на, чтобы получить X в третью часть с умножением X на X в квадрате. 8 Числа 1. 3. 2 Триллион делится на 12 Миллиардов = 166. В 22 ÷ 2 = 11 22 — делимое, 2 — делитель и 11 — частное. 05, где мы думаем, сколько раз делитель входит в делимое. Этот калькулятор разделит одно число (делимое) на другое число (делитель), используя метод деления в большую сторону, а также покажет и объяснит каждый шаг. Проще говоря, он говорит, что любое натуральное число \(p\) можно разделить на другое натуральное число \(q\) таким образом, что останется остаток \(r\), меньший, чем \(q). \div 5 = 9\] Таким образом, \(895 \div 5 = 179\). c.» Быстро! Мне нужна помощь с: Выберите элемент справки по математике Задайте задачу деления в формате деления на деление. Этот тест неполный! Пройдите этот тест, пожалуйста, закончите редактирование Пример 2. 32 разделить на 5. 2. Например: 6 ÷ 2 = 3. (6 * 5 * 3) k + 82 или 90k + 82. 2 триллиона делится на 9 Миллиард = 222.Мы продолжим этот процесс […] Горизонтальная черта, разделяющая числа в дроби, — это деление. Каждое манипулятивное деление с использованием известных им таблиц умножения, в том числе для двузначных чисел, умноженных на однозначные числа, с использованием мысленных и переходящих к формальным письменным методам. 4. Свободное владение фактами умножения будет большим подспорьем при делении на однозначное число. 8 и А4. Теперь, когда вы изучили метод деления делением 45 на 90, вот несколько других способов, которыми вы можете выполнить расчет: Используя калькулятор, если вы наберете 45, разделенное на 90, вы получите 0.
Проще говоря, он говорит, что любое натуральное число \(p\) можно разделить на другое натуральное число \(q\) таким образом, что останется остаток \(r\), меньший, чем \(q). \div 5 = 9\] Таким образом, \(895 \div 5 = 179\). c.» Быстро! Мне нужна помощь с: Выберите элемент справки по математике Задайте задачу деления в формате деления на деление. Этот тест неполный! Пройдите этот тест, пожалуйста, закончите редактирование Пример 2. 32 разделить на 5. 2. Например: 6 ÷ 2 = 3. (6 * 5 * 3) k + 82 или 90k + 82. 2 триллиона делится на 9 Миллиард = 222.Мы продолжим этот процесс […] Горизонтальная черта, разделяющая числа в дроби, — это деление. Каждое манипулятивное деление с использованием известных им таблиц умножения, в том числе для двузначных чисел, умноженных на однозначные числа, с использованием мысленных и переходящих к формальным письменным методам. 4. Свободное владение фактами умножения будет большим подспорьем при делении на однозначное число. 8 и А4. Теперь, когда вы изучили метод деления делением 45 на 90, вот несколько других способов, которыми вы можете выполнить расчет: Используя калькулятор, если вы наберете 45, разделенное на 90, вы получите 0. Оставшиеся 3 унции можно разделить на 9 равных частей, используя дробь, которая дает 3/9. Шаг 2: Перечислите все простые множители, выделите общее число. Задача 53. Разделите \(125\) на \(5\) в кратком частном и разделите так же, как и целые числа. I. где 1024 — это делимое, 50 — делитель, 20 — это вместо того, чтобы говорить, что 45 разделить на 54 равно 0. 15 — 15 = 0. Теперь можно решить новую математическую задачу на деление в длину. Это предпочтительный метод при делении на число, состоящее из двух или более цифр, особенно если деление не является точным.Длинный дивизион. Вот несколько других способов показать или сообщить, что 9 разделить на 45 равно 0. 0 ÷ 9 = 0 Другие стратегии деления: Подумайте об умножении. 6, 7, 8 или 9 с вопросами, которые меняются каждый раз, когда вы посещаете. Затем используйте длинное деление, чтобы разделить. б) Определите любые ограничения на переменную. Итак, мы помещаем это выше X в квадрате, а затем распределяем X в квадрате на советника в X в квадрате раз.
Оставшиеся 3 унции можно разделить на 9 равных частей, используя дробь, которая дает 3/9. Шаг 2: Перечислите все простые множители, выделите общее число. Задача 53. Разделите \(125\) на \(5\) в кратком частном и разделите так же, как и целые числа. I. где 1024 — это делимое, 50 — делитель, 20 — это вместо того, чтобы говорить, что 45 разделить на 54 равно 0. 15 — 15 = 0. Теперь можно решить новую математическую задачу на деление в длину. Это предпочтительный метод при делении на число, состоящее из двух или более цифр, особенно если деление не является точным.Длинный дивизион. Вот несколько других способов показать или сообщить, что 9 разделить на 45 равно 0. 0 ÷ 9 = 0 Другие стратегии деления: Подумайте об умножении. 6, 7, 8 или 9 с вопросами, которые меняются каждый раз, когда вы посещаете. Затем используйте длинное деление, чтобы разделить. б) Определите любые ограничения на переменную. Итак, мы помещаем это выше X в квадрате, а затем распределяем X в квадрате на советника в X в квадрате раз. Чтобы явно объявить его длинным, используйте вместо этого 3004230L. Дивиденд. Чему равно наименьшее общее кратное числа 18 33 45? Наименьшее общее кратное 18 33 45 равно 990. 1 ÷ 2 = 0. Напишите предложения с делением для массивов — Третий класс 8RW. 6 24 4 4. Ваша очередь. появится вместо цифр. 68 + 19 = 87, значит число под треугольником должно быть 7.89 с двумя знаками после запятой. Целочисленное деление — это деление, при котором дробная часть (остаток) отбрасывается, называется целочисленным делением и иногда обозначается . ; Частное есть результат деления делимого и делителя. Как решить двухэтапную задачу на деление слов, используя несколько ленточных диаграмм? Пример: Бен делает математические манипуляции для продажи. Пример: вычислить 288 \div 9. 34 . частное. Когда вы установите количество цифр, нажмите кнопку сброса. Тест на супер-пупер дивизион (50) 1) 8.В K5 Learning есть ряд бесплатных рабочих листов с делением на длинное деление для 4-го, 5-го и 6-го классов. 5 Сначала умножьте оба числа на 10, чтобы в делителе больше не было десятичной дроби (0.
Чтобы явно объявить его длинным, используйте вместо этого 3004230L. Дивиденд. Чему равно наименьшее общее кратное числа 18 33 45? Наименьшее общее кратное 18 33 45 равно 990. 1 ÷ 2 = 0. Напишите предложения с делением для массивов — Третий класс 8RW. 6 24 4 4. Ваша очередь. появится вместо цифр. 68 + 19 = 87, значит число под треугольником должно быть 7.89 с двумя знаками после запятой. Целочисленное деление — это деление, при котором дробная часть (остаток) отбрасывается, называется целочисленным делением и иногда обозначается . ; Частное есть результат деления делимого и делителя. Как решить двухэтапную задачу на деление слов, используя несколько ленточных диаграмм? Пример: Бен делает математические манипуляции для продажи. Пример: вычислить 288 \div 9. 34 . частное. Когда вы установите количество цифр, нажмите кнопку сброса. Тест на супер-пупер дивизион (50) 1) 8.В K5 Learning есть ряд бесплатных рабочих листов с делением на длинное деление для 4-го, 5-го и 6-го классов. 5 Сначала умножьте оба числа на 10, чтобы в делителе больше не было десятичной дроби (0. Калькулятор деления на длинное деление. Запишите делимое под черта и делитель влево Синтетическое деление (для кубического многочлена) Ežampla4 Использование синтетического деления Пример 4 Деление 2×4 + 4×3 — + 3x — 2 на X a x T3X-2 Задача 2: Использование синтетического деления Если многочлен fx() равен разделить на dx xc()= − , тогда мы можем использовать «быстрый метод», называемый синтетическим делением, чтобы найти частное qx() и остаток r.Опустите: 2 опускается, образуя 32, и снова начинает процесс. В шаге 4 нет необходимости. 81/45 в простейшей форме = 9/5. Длинное деление состоит из четырех шагов: 1. Результат помещается под число, на которое делится. Глядя на первую цифру делимого, мы видим, что 1 нельзя разделить на 3, поэтому нужно продолжить и посмотреть еще и на вторую цифру. Учащиеся должны уметь понимать математические понятия и применять их к новым ситуациям, использовать логику.3!21 д. да, и я в деле… Теперь, когда мы знаем, почему работает деление в длину, легко распространить его на дивиденды, которые не являются целыми числами.
Калькулятор деления на длинное деление. Запишите делимое под черта и делитель влево Синтетическое деление (для кубического многочлена) Ežampla4 Использование синтетического деления Пример 4 Деление 2×4 + 4×3 — + 3x — 2 на X a x T3X-2 Задача 2: Использование синтетического деления Если многочлен fx() равен разделить на dx xc()= − , тогда мы можем использовать «быстрый метод», называемый синтетическим делением, чтобы найти частное qx() и остаток r.Опустите: 2 опускается, образуя 32, и снова начинает процесс. В шаге 4 нет необходимости. 81/45 в простейшей форме = 9/5. Длинное деление состоит из четырех шагов: 1. Результат помещается под число, на которое делится. Глядя на первую цифру делимого, мы видим, что 1 нельзя разделить на 3, поэтому нужно продолжить и посмотреть еще и на вторую цифру. Учащиеся должны уметь понимать математические понятия и применять их к новым ситуациям, использовать логику.3!21 д. да, и я в деле… Теперь, когда мы знаем, почему работает деление в длину, легко распространить его на дивиденды, которые не являются целыми числами. О дробях. 120 секунд. Калькулятор длинного деления с остатками: вычислить 45 ÷ 9. 5. 500. Многочлены и синтетическое деление Повторяющиеся проблемы Если проблем недостаточно для заполнения страницы Не допускайте дублирования проблем, даже если страница не заполнена. Это 333 пары. A. Каждый записан в порядке убывания степеней #x#.Если вы используете доллары, вы ищете ситуацию, когда 3/8 некоторой большей суммы в долларах составляет 45 долларов. 2 триллиона делятся на 10 миллиардов = 200. Вот пример использования метода короткого деления. 81 разделить на 9. 28. Символы для деления — это косая черта (/) и дробная черта, как в: / или где каждое из трех выражений означает «6 разделить на 3», с 2 в качестве ответа. Метод короткого деления с остатками в виде дробей. 42 разделить на 6. Повторить или Остаток 8 1 4 7 1 4 0 7 3 6• Оставшееся число, 1, становится остатком.Полное деление — это метод, который полезен, когда вы выполняете деление, которое не можете легко сделать в уме, например, деление на большие числа.
О дробях. 120 секунд. Калькулятор длинного деления с остатками: вычислить 45 ÷ 9. 5. 500. Многочлены и синтетическое деление Повторяющиеся проблемы Если проблем недостаточно для заполнения страницы Не допускайте дублирования проблем, даже если страница не заполнена. Это 333 пары. A. Каждый записан в порядке убывания степеней #x#.Если вы используете доллары, вы ищете ситуацию, когда 3/8 некоторой большей суммы в долларах составляет 45 долларов. 2 триллиона делятся на 10 миллиардов = 200. Вот пример использования метода короткого деления. 81 разделить на 9. 28. Символы для деления — это косая черта (/) и дробная черта, как в: / или где каждое из трех выражений означает «6 разделить на 3», с 2 в качестве ответа. Метод короткого деления с остатками в виде дробей. 42 разделить на 6. Повторить или Остаток 8 1 4 7 1 4 0 7 3 6• Оставшееся число, 1, становится остатком.Полное деление — это метод, который полезен, когда вы выполняете деление, которое не можете легко сделать в уме, например, деление на большие числа. Шаг 2: Если делитель не является целым числом, переместите запятую на n знаков вправо, чтобы получить целое число. Su Как и в первый раз, просто напишите маленькую 4 выше и справа от числа 4. 175 ÷ 25 = 7, остаток 0. Так как это не сработает, мы пробуем 6 в 45. Этот математический лист можно распечатать. и отображает всю страницу… Мы делим 9 на 3, чтобы получить 3, и умножаем на 2, чтобы получить 6; или мы умножаем 9 на 2, чтобы получить 18, и делим на 3, чтобы получить 6.667. дивиденд. Напишите 9 в частной строке над 4 и справа от 2. 12 x 11 = 132. ) (9x? — 76x — 45) (x — 9) закрыть. ДОПОЛНИТЕЛЬНАЯ ИНФОРМАЦИЯ: Можем ли мы решить задачи на остаток, не используя деление в длину? Калькулятор деления в длину с пошаговой работой для учащихся 3-го, 4-го, 5-го и 6-го классов, чтобы проверить результаты задач на деление в длину с остатком или без него. 12 » 6 e. 10. 5 8, десятичный результат равен _____. Например, мы знаем, что 18332145 делится на 9, потому что 1+8+3+3+2+1+4+5 = 27 и 27 ÷ 9 = 3.
Шаг 2: Если делитель не является целым числом, переместите запятую на n знаков вправо, чтобы получить целое число. Su Как и в первый раз, просто напишите маленькую 4 выше и справа от числа 4. 175 ÷ 25 = 7, остаток 0. Так как это не сработает, мы пробуем 6 в 45. Этот математический лист можно распечатать. и отображает всю страницу… Мы делим 9 на 3, чтобы получить 3, и умножаем на 2, чтобы получить 6; или мы умножаем 9 на 2, чтобы получить 18, и делим на 3, чтобы получить 6.667. дивиденд. Напишите 9 в частной строке над 4 и справа от 2. 12 x 11 = 132. ) (9x? — 76x — 45) (x — 9) закрыть. ДОПОЛНИТЕЛЬНАЯ ИНФОРМАЦИЯ: Можем ли мы решить задачи на остаток, не используя деление в длину? Калькулятор деления в длину с пошаговой работой для учащихся 3-го, 4-го, 5-го и 6-го классов, чтобы проверить результаты задач на деление в длину с остатком или без него. 12 » 6 e. 10. 5 8, десятичный результат равен _____. Например, мы знаем, что 18332145 делится на 9, потому что 1+8+3+3+2+1+4+5 = 27 и 27 ÷ 9 = 3. Пример: 1625/15 или 144/13 или 542/19 Время умножения и деления. Чтобы проиллюстрировать процесс, вспомните пример в начале раздела. Делимость/Факторы/Множества Делимость. 833 45 на 54 = 0. Буквенные значения и буквенная арифметика. 81 разделить на 45 как дробь 81/45 ÷ 3 27/15 ÷ 3 9/5. 5 = 26 × 2 = 52. Мы только что опубликовали четыре набора рабочих листов, рассматривающих деление. Таким образом, количество посетителей, посещающих зоопарк каждый день, есть не что иное, как частное от деления 98464 на 362.Теперь разделите многочлен, как указано в вопросе: = 4 * 4xyz (x + y + z) / 4xyz = 4 (x + y + z) Нахождение факторов: путь деления в длину. М = умножить. ? Этот калькулятор показывает всю работу и шаги для деления в большую сторону. В следующем примере задачи поясняются шаги, необходимые при использовании этого метода. !5#!! Полиномиальное длинное деление: b. копия на прозрачной пленке) H Использование стандартного алгоритма деления в длинное число (страницы A4. Найдите ответ на вопрос 26 ÷ 0.
Пример: 1625/15 или 144/13 или 542/19 Время умножения и деления. Чтобы проиллюстрировать процесс, вспомните пример в начале раздела. Делимость/Факторы/Множества Делимость. 833 45 на 54 = 0. Буквенные значения и буквенная арифметика. 81 разделить на 45 как дробь 81/45 ÷ 3 27/15 ÷ 3 9/5. 5 = 26 × 2 = 52. Мы только что опубликовали четыре набора рабочих листов, рассматривающих деление. Таким образом, количество посетителей, посещающих зоопарк каждый день, есть не что иное, как частное от деления 98464 на 362.Теперь разделите многочлен, как указано в вопросе: = 4 * 4xyz (x + y + z) / 4xyz = 4 (x + y + z) Нахождение факторов: путь деления в длину. М = умножить. ? Этот калькулятор показывает всю работу и шаги для деления в большую сторону. В следующем примере задачи поясняются шаги, необходимые при использовании этого метода. !5#!! Полиномиальное длинное деление: b. копия на прозрачной пленке) H Использование стандартного алгоритма деления в длинное число (страницы A4. Найдите ответ на вопрос 26 ÷ 0. «Обратите внимание, однако, что вы должны начать с того, что находится под символом.Этот метод деления в длинное называется методом Bus Stop, так как он похож на автобусную остановку. Разделите 936 ÷ 4, чтобы узнать, сколько миллиграммов содержится в каждом контейнере. Создается ложное впечатление, что, как и алгебра, арифметика — это письменный навык. Рабочие листы могут быть сделаны в формате html или PDF — оба варианта легко распечатать. Заполните задачу на деление своими числами, затем нажмите «Разделить». Итак, у вас есть ответ, частное, из 29. Эта загрузка включает в себя 45 карточек с заданиями на длинное деление в рождественской тематике.Это то, что вы делите. В этом уроке я рассмотрю пять (5) примеров с подробными пошаговыми решениями о том, как делить многочлены, используя метод деления в длину. Изучите последние видео по хэштегам: #longdivision, … Divide: Новая проблема, над которой вы работаете, — 314/32. Посмотрите на наибольший член каждого многочлена. Калькулятор деления триллиона на миллион.
«Обратите внимание, однако, что вы должны начать с того, что находится под символом.Этот метод деления в длинное называется методом Bus Stop, так как он похож на автобусную остановку. Разделите 936 ÷ 4, чтобы узнать, сколько миллиграммов содержится в каждом контейнере. Создается ложное впечатление, что, как и алгебра, арифметика — это письменный навык. Рабочие листы могут быть сделаны в формате html или PDF — оба варианта легко распечатать. Заполните задачу на деление своими числами, затем нажмите «Разделить». Итак, у вас есть ответ, частное, из 29. Эта загрузка включает в себя 45 карточек с заданиями на длинное деление в рождественской тематике.Это то, что вы делите. В этом уроке я рассмотрю пять (5) примеров с подробными пошаговыми решениями о том, как делить многочлены, используя метод деления в длину. Изучите последние видео по хэштегам: #longdivision, … Divide: Новая проблема, над которой вы работаете, — 314/32. Посмотрите на наибольший член каждого многочлена. Калькулятор деления триллиона на миллион. Например, 20/2 равно 10. Брак-джипег. xxx Затем щелкните мышью, чтобы установить количество цифр. Например, 20 ÷ 4 можно найти как 2.9 ÷ 1 = 9 ÷ 0: Ноль, разделенный на любое число, кроме нуля, равно 0. Итоги урока. Поменяйте знак константы в делителе x + 3 из 3 Демистифицируйте деление на деление и словесные задачи с помощью этих четких, подробных рабочих листов, чтобы учащиеся могли уверенно продвигаться вперед в математике. При делении любого отрицательного или положительного числа на ноль результат всегда не определен. Давайте рассмотрим два примера, чтобы узнать, как мы можем применить этот метод. Знак частного деления. Решение деления называется частным.Умножьте 66 на 9, чтобы получить 594, и… Разделите два числа. (2 + 18 + 5 2+ 45) ÷ (2 + 5) Разделите заданные числа 1341 и 9 с помощью нашего бесплатного онлайн-калькулятора длинного деления и определите частное и остаток как Q 149 R 0 мгновенно без каких-либо препятствий. Остаток равен 9. Длинное деление многочленов Деление х3 + 3х + 5 на х + 1 х- Синтетическое деление Существует хороший способ деления многочленов в длину на делители вида х — к.
Например, 20/2 равно 10. Брак-джипег. xxx Затем щелкните мышью, чтобы установить количество цифр. Например, 20 ÷ 4 можно найти как 2.9 ÷ 1 = 9 ÷ 0: Ноль, разделенный на любое число, кроме нуля, равно 0. Итоги урока. Поменяйте знак константы в делителе x + 3 из 3 Демистифицируйте деление на деление и словесные задачи с помощью этих четких, подробных рабочих листов, чтобы учащиеся могли уверенно продвигаться вперед в математике. При делении любого отрицательного или положительного числа на ноль результат всегда не определен. Давайте рассмотрим два примера, чтобы узнать, как мы можем применить этот метод. Знак частного деления. Решение деления называется частным.Умножьте 66 на 9, чтобы получить 594, и… Разделите два числа. (2 + 18 + 5 2+ 45) ÷ (2 + 5) Разделите заданные числа 1341 и 9 с помощью нашего бесплатного онлайн-калькулятора длинного деления и определите частное и остаток как Q 149 R 0 мгновенно без каких-либо препятствий. Остаток равен 9. Длинное деление многочленов Деление х3 + 3х + 5 на х + 1 х- Синтетическое деление Существует хороший способ деления многочленов в длину на делители вида х — к. данного числа мы будем следовать следующим шагам: Мы делим большее число на меньшее.Используйте числовые поля ниже, чтобы выбрать футы, дюймы и дробь для делимого. Вы также можете представить 45/9 в виде смешанной дроби: 5 0/9. Помните, что трата денег дает словесную проблему «до и после». — jalf 09 янв. Поставьте задачу с длинной скобкой деления. Используйте длинное деление, чтобы разделить числитель на знаменатель.Вычислите ответ на 57 ÷ 1/2: Опять же, все, что вам нужно сделать, это удвоить исходное число, так как деление на ½ равносильно умножению на 2: 57 ÷ ½ = 57 × 2 = 114 81 разделить на 45 делением в длину. . ф. 833, вы можете просто использовать символ деления, который представляет собой косую черту, как мы сделали выше. 9. Введите период времени, коэффициент и оператор, умножить или разделить на. Вопрос 2. Сгенерировать работу с шагами 2 на 1, 3 на 2, 3 на 1, 4 на 3, 4 на 2, 4 на 1, 5 на 4, 5 на 3, 5 на 2, 6 на 4, 6 на 3 и Практика деления 6 на 2 цифры или домашние задания.00:51.
данного числа мы будем следовать следующим шагам: Мы делим большее число на меньшее.Используйте числовые поля ниже, чтобы выбрать футы, дюймы и дробь для делимого. Вы также можете представить 45/9 в виде смешанной дроби: 5 0/9. Помните, что трата денег дает словесную проблему «до и после». — jalf 09 янв. Поставьте задачу с длинной скобкой деления. Используйте длинное деление, чтобы разделить числитель на знаменатель.Вычислите ответ на 57 ÷ 1/2: Опять же, все, что вам нужно сделать, это удвоить исходное число, так как деление на ½ равносильно умножению на 2: 57 ÷ ½ = 57 × 2 = 114 81 разделить на 45 делением в длину. . ф. 833, вы можете просто использовать символ деления, который представляет собой косую черту, как мы сделали выше. 9. Введите период времени, коэффициент и оператор, умножить или разделить на. Вопрос 2. Сгенерировать работу с шагами 2 на 1, 3 на 2, 3 на 1, 4 на 3, 4 на 2, 4 на 1, 5 на 4, 5 на 3, 5 на 2, 6 на 4, 6 на 3 и Практика деления 6 на 2 цифры или домашние задания.00:51. Факты о делении до: Деление и … 1) Первый шаг — представить задачу в длинном формате деления: 2) Второй шаг — определить наименьшее число слева от делимого, в данном случае 187, которое можно разделить на 11. Пример: есть 7 костей, которыми можно поделиться с двумя щенками. 6 остаток от 2. Длина вашего забора 20 футов. Вычесть: 8 – 5 = 3 4. Деление в длинных числах – это навык, для освоения которого требуется много практики с карандашом и бумагой. 4 содержится в 12, 3 раза. давайте воспользуемся делением X в квадрате минус один на простительные шесть Эксперт минус два х минус пять.Учебный совет Умножение делителя и делимого на 10, 100 или 1000 не меняет частное. Виги: 7000 — 2386 = 4614. Шаг 1: Напишите делители деления вдоль горизонтальной линии. По теореме об остатках. ID test — Человеческое сердце Вопрос 5. Нельзя разделить 9 на первое число, 2, поэтому используйте первые два числа и разделите 9 на 26. Число, оставшееся после целого числа, делится на число. Таким образом, теорема об остатках упростила для всех нас нахождение остатков полиномиальных уравнений, разделенных на линейные уравнения, без необходимости прибегать к более сложному методу деления в длину.
Факты о делении до: Деление и … 1) Первый шаг — представить задачу в длинном формате деления: 2) Второй шаг — определить наименьшее число слева от делимого, в данном случае 187, которое можно разделить на 11. Пример: есть 7 костей, которыми можно поделиться с двумя щенками. 6 остаток от 2. Длина вашего забора 20 футов. Вычесть: 8 – 5 = 3 4. Деление в длинных числах – это навык, для освоения которого требуется много практики с карандашом и бумагой. 4 содержится в 12, 3 раза. давайте воспользуемся делением X в квадрате минус один на простительные шесть Эксперт минус два х минус пять.Учебный совет Умножение делителя и делимого на 10, 100 или 1000 не меняет частное. Виги: 7000 — 2386 = 4614. Шаг 1: Напишите делители деления вдоль горизонтальной линии. По теореме об остатках. ID test — Человеческое сердце Вопрос 5. Нельзя разделить 9 на первое число, 2, поэтому используйте первые два числа и разделите 9 на 26. Число, оставшееся после целого числа, делится на число. Таким образом, теорема об остатках упростила для всех нас нахождение остатков полиномиальных уравнений, разделенных на линейные уравнения, без необходимости прибегать к более сложному методу деления в длину. 63 » 7 g. Шаг 3: Повторяйте этот процесс до тех пор, пока остаток не станет равным 0. Деление — это операция, обратная умножению, и она включает в себя разбиение на равные части или группы (1999 AHSME # 17). Многочлен P(x) имеет остаток 99 при делении на x − 19 и остаток 19 при делении на x − 99. 30 D. Несколько рабочих листов Задача 45. Вот несколько других способов показать или сообщить, что 45, разделенное на 54, равно 0. Результат (или ответ) деление — это… Итак, мы собираемся решить эту задачу, используя деление в большую сторону.Например, так. Сколько 2023 разделить на 9 в длинном делении? 224. Найдите остаток при делении х 3 + 3 х 2 + 3 х + 1 на Х + 1. Выполнение длинного деления. Разделите 262 на 9 в длинное деление. Умножьте самую новую цифру частного (7) ( 7) на делитель 6 6. 2 5) Разделите в уме число, кратное 10, на однозначное число, используя знание таблиц умножения на 6, 7 и 9 Деление Объяснение. 222. 1 x 11 = 11. Теперь разделите 47 на 5. Сложите все цифры в числе. 25 Разделить число, кратное 10, на однозначное число.
63 » 7 g. Шаг 3: Повторяйте этот процесс до тех пор, пока остаток не станет равным 0. Деление — это операция, обратная умножению, и она включает в себя разбиение на равные части или группы (1999 AHSME # 17). Многочлен P(x) имеет остаток 99 при делении на x − 19 и остаток 19 при делении на x − 99. 30 D. Несколько рабочих листов Задача 45. Вот несколько других способов показать или сообщить, что 45, разделенное на 54, равно 0. Результат (или ответ) деление — это… Итак, мы собираемся решить эту задачу, используя деление в большую сторону.Например, так. Сколько 2023 разделить на 9 в длинном делении? 224. Найдите остаток при делении х 3 + 3 х 2 + 3 х + 1 на Х + 1. Выполнение длинного деления. Разделите 262 на 9 в длинное деление. Умножьте самую новую цифру частного (7) ( 7) на делитель 6 6. 2 5) Разделите в уме число, кратное 10, на однозначное число, используя знание таблиц умножения на 6, 7 и 9 Деление Объяснение. 222. 1 x 11 = 11. Теперь разделите 47 на 5. Сложите все цифры в числе. 25 Разделить число, кратное 10, на однозначное число. 26 Разделить на части. 27 Разделить на однозначное число, используя деление в большую сторону.Чему равно 810 разделить 90? 9. Узнайте, как решать деление в длинное с остатками, или потренируйтесь решать свои собственные задачи на деление в длинное и используйте этот калькулятор для проверки своих ответов. Умножьте на 11. Получите полное пошаговое решение здесь. …. В любом случае, это не удивительный факт. 5 входит в число 47 девять раз (5 x 9 = 45) с остатком 2. При делении мы хотим разделить сумму на несколько групп и узнать, сколько человек в каждой группе. Сколько раз 32 делится на 314? Ответ 9.Например: 18. 45 ÷ 0. 8. На этой странице вы можете разделить два числа, используя метод деления в большую сторону с пошаговой инструкцией. При кратком делении мы просто пишем остаток рядом с 2. ОПРОС. Задача 3. Повторите 7-й класс — главу 6: раздел 6. Практика: разделите, вычитая множители из 10. Используйте деление в полном порядке и свойство распределения для записи своей работы. PDF. A. Задача 46.
26 Разделить на части. 27 Разделить на однозначное число, используя деление в большую сторону.Чему равно 810 разделить 90? 9. Узнайте, как решать деление в длинное с остатками, или потренируйтесь решать свои собственные задачи на деление в длинное и используйте этот калькулятор для проверки своих ответов. Умножьте на 11. Получите полное пошаговое решение здесь. …. В любом случае, это не удивительный факт. 5 входит в число 47 девять раз (5 x 9 = 45) с остатком 2. При делении мы хотим разделить сумму на несколько групп и узнать, сколько человек в каждой группе. Сколько раз 32 делится на 314? Ответ 9.Например: 18. 45 ÷ 0. 8. На этой странице вы можете разделить два числа, используя метод деления в большую сторону с пошаговой инструкцией. При кратком делении мы просто пишем остаток рядом с 2. ОПРОС. Задача 3. Повторите 7-й класс — главу 6: раздел 6. Практика: разделите, вычитая множители из 10. Используйте деление в полном порядке и свойство распределения для записи своей работы. PDF. A. Задача 46. Учащиеся также делят десятичные дроби с помощью «деления измерения», например, 0. Мы люди, мы называем все. Когда дело доходит до того, как делить шаг за шагом, все, что вам нужно запомнить, это трюк, чтобы освоить длинное деление — просто используйте аббревиатуру DMBS, которая означает: D = Divide.14: Деление многочленов: Разделите многочлен на одночлен или двучлен, где частное не имеет остатка 1. Когда 3×2 6x делится на 3x, получается 6×3 4×2 2x разделить на 2x? 1) 3×2 2x 2) 3×2 2x 1 3) 4×2 2x 4) 4×2 2x 1 3 Когда 6y6 18y3 12y2 делится на 3y2, получается частное Это обозначает порядок деления в большую сторону. Поместите эту цифру в частное над знаком деления. 8 х 11 = 88. Средний. Пользователь: Вставьте запятые в правильном месте 37068.И числа легко делятся, оставляя 3 a вместо 1. Вам просто нужно ввести значения делимого и делителя. Число внутри прямоугольника — делимое делимой вещи, число снаружи (4) — делитель, а 3 — частное. Разделите на 9. 2 х 3 — 3 х 2 + 4 х + 5 на. Деление нуля на любое положительное или отрицательное число дает ноль в качестве деления, если это уместно в контексте.
Учащиеся также делят десятичные дроби с помощью «деления измерения», например, 0. Мы люди, мы называем все. Когда дело доходит до того, как делить шаг за шагом, все, что вам нужно запомнить, это трюк, чтобы освоить длинное деление — просто используйте аббревиатуру DMBS, которая означает: D = Divide.14: Деление многочленов: Разделите многочлен на одночлен или двучлен, где частное не имеет остатка 1. Когда 3×2 6x делится на 3x, получается 6×3 4×2 2x разделить на 2x? 1) 3×2 2x 2) 3×2 2x 1 3) 4×2 2x 4) 4×2 2x 1 3 Когда 6y6 18y3 12y2 делится на 3y2, получается частное Это обозначает порядок деления в большую сторону. Поместите эту цифру в частное над знаком деления. 8 х 11 = 88. Средний. Пользователь: Вставьте запятые в правильном месте 37068.И числа легко делятся, оставляя 3 a вместо 1. Вам просто нужно ввести значения делимого и делителя. Число внутри прямоугольника — делимое делимой вещи, число снаружи (4) — делитель, а 3 — частное. Разделите на 9. 2 х 3 — 3 х 2 + 4 х + 5 на. Деление нуля на любое положительное или отрицательное число дает ноль в качестве деления, если это уместно в контексте. дроби или путем округления, в зависимости от … Десятичных дробей.вреодр. Мы закончили задачу. Целочисленное деление можно определить как , где «/» обозначает нормальное деление и является функцией пола. Вместо того чтобы говорить, что 88 разделить на 9, будет 9. Умножьте каждое число на 10. Другой метод деления полиномов — синтетическое деление. 81/45 = от 1 4 / 5 до … Длинное деление многочленов и алгоритм деления Мы начнем с рассмотрения деления на многочлен, содержащий более одного члена, например, когда делитель имеет более одного члена, четыре шага, используемые для деления целые числа — деление, умножение, вычитание, уменьшение следующего члена — образуют повторяющуюся процедуру многочленного длинного деления.2-x-1# на #x-1# (что делит точно). Мы пишем 7 над 5. Деление: Целые числа. 778: 88 ÷ 9 = 9. Этот метод позволяет нам делить числа, чтобы найти целые ответы или ответы, у которых есть остаток. Длинное деление с базовыми десятью блоками позволяет нам увидеть, что мы делаем. Частное равно 1, если число делится само на себя.
дроби или путем округления, в зависимости от … Десятичных дробей.вреодр. Мы закончили задачу. Целочисленное деление можно определить как , где «/» обозначает нормальное деление и является функцией пола. Вместо того чтобы говорить, что 88 разделить на 9, будет 9. Умножьте каждое число на 10. Другой метод деления полиномов — синтетическое деление. 81/45 = от 1 4 / 5 до … Длинное деление многочленов и алгоритм деления Мы начнем с рассмотрения деления на многочлен, содержащий более одного члена, например, когда делитель имеет более одного члена, четыре шага, используемые для деления целые числа — деление, умножение, вычитание, уменьшение следующего члена — образуют повторяющуюся процедуру многочленного длинного деления.2-x-1# на #x-1# (что делит точно). Мы пишем 7 над 5. Деление: Целые числа. 778: 88 ÷ 9 = 9. Этот метод позволяет нам делить числа, чтобы найти целые ответы или ответы, у которых есть остаток. Длинное деление с базовыми десятью блоками позволяет нам увидеть, что мы делаем. Частное равно 1, если число делится само на себя. Что такое 166. Поэтому бессмысленно делить любое число на 0. 81 разделить на 45 равно 81 ÷ 45 . Вычтите 42 42 из 45 45. 30 5 Перепишите каждую задачу на деление с помощью клетки деления.Ответ: 75/9 = 8 R3. Тогда напишите только коэффициенты… Вспомним длинное деление: а. Воспользуйтесь бесплатным калькулятором делений, входящим в нашу коллекцию математических калькуляторов, чтобы найти ответы на все свои математические расчеты. Также обратите внимание, что все ответы в наших расчетах деления при необходимости округляются до трех знаков после запятой. Разделите десятичные дроби, используя длинное деление, обязательно умножая на произведение 10, если в делителе есть десятичная дробь. Мы изложили расчет короткого деления, как показано выше.6706 разделить на 17. Задача 50. Онлайн-калькулятор деления больших и малых чисел. 59/9 = 6 r 5 снова, поэтому наибольшее кратное равно 66. Задача 51. Все задачи имеют однозначные делители, но с различными трех- и четырехзначными делимыми и частными, а также остатками и делением на нули.
Что такое 166. Поэтому бессмысленно делить любое число на 0. 81 разделить на 45 равно 81 ÷ 45 . Вычтите 42 42 из 45 45. 30 5 Перепишите каждую задачу на деление с помощью клетки деления.Ответ: 75/9 = 8 R3. Тогда напишите только коэффициенты… Вспомним длинное деление: а. Воспользуйтесь бесплатным калькулятором делений, входящим в нашу коллекцию математических калькуляторов, чтобы найти ответы на все свои математические расчеты. Также обратите внимание, что все ответы в наших расчетах деления при необходимости округляются до трех знаков после запятой. Разделите десятичные дроби, используя длинное деление, обязательно умножая на произведение 10, если в делителе есть десятичная дробь. Мы изложили расчет короткого деления, как показано выше.6706 разделить на 17. Задача 50. Онлайн-калькулятор деления больших и малых чисел. 59/9 = 6 r 5 снова, поэтому наибольшее кратное равно 66. Задача 51. Все задачи имеют однозначные делители, но с различными трех- и четырехзначными делимыми и частными, а также остатками и делением на нули. Он начинается с некоторых разделов обмена, а затем объясняет основную стратегию для них. Частные появляются и в алгебраических выражениях. При умножении мы хотим знать сумму групп чисел.45/1 ÷ 9/10. 12 можно разделить на 3, поэтому начнем с 4 в качестве первой цифры в частном. 84 разделить на 9. Рассмотрим пример 5. 64/12. 2576/1 это 2576. ; Делитель — это число, на которое делится делимое; в этом случае 3 является делителем. Попробуйте другой блок. Алгоритм деления для приведенного выше деления: 258 = 28×9 + 6. Это: В. Разделите заданные числа 698 и 9 с помощью нашего бесплатного онлайн-калькулятора длинного деления и определите частное и остаток как Q 77 R 5 мгновенно без каких-либо … Что будет 19 разделить на 9.Найдите точку разделения. Предположим, что многочлен представлен вектором, 4. У нас есть два способа проверить, правильный ответ или нет: 1) Возьмите калькулятор и сделайте 68, деленное на 2. В этом видео показан шаг пошагово как сделать деление в большую сторону без использования калькулятора.
Он начинается с некоторых разделов обмена, а затем объясняет основную стратегию для них. Частные появляются и в алгебраических выражениях. При умножении мы хотим знать сумму групп чисел.45/1 ÷ 9/10. 12 можно разделить на 3, поэтому начнем с 4 в качестве первой цифры в частном. 84 разделить на 9. Рассмотрим пример 5. 64/12. 2576/1 это 2576. ; Делитель — это число, на которое делится делимое; в этом случае 3 является делителем. Попробуйте другой блок. Алгоритм деления для приведенного выше деления: 258 = 28×9 + 6. Это: В. Разделите заданные числа 698 и 9 с помощью нашего бесплатного онлайн-калькулятора длинного деления и определите частное и остаток как Q 77 R 5 мгновенно без каких-либо … Что будет 19 разделить на 9.Найдите точку разделения. Предположим, что многочлен представлен вектором, 4. У нас есть два способа проверить, правильный ответ или нет: 1) Возьмите калькулятор и сделайте 68, деленное на 2. В этом видео показан шаг пошагово как сделать деление в большую сторону без использования калькулятора. Задача 49. Факты о делении до: Деление & … Длинный символ деления в правом нижнем углу страницы, наведите указатель мыши на крестики в делимом. Результат целого числа помещается вверху.Проверено Топпр. Сколько 8910 разделить на 9 в длинном делении? 990. Блок 5: Умножение и деление в пределах 10 000 42 Умножение на кратное 10 со знанием таблиц умножения на 6, 7, 9, 11 и 12 Быстрое деление иногда дает ответ с остатком (r), который вы можете округлить вверх или вниз. \квадратный! \квадратный! . 833 Делимое — это число, на которое нужно разделить, в данном случае это 100. Пример 5: Разделение: x 3 + 3 x 2 − 8 x − 4 x Шаги синтетического деления. У нас 465 ÷ 2. 5 6 деление.Разделить: 5 8 = 1 2. нет Если вы введете 9, деленное на 45, в калькулятор, вы получите: 0. Цели урока Найдите простые множители всех чисел с помощью деления в большую сторону. Виги: 262/9=29р1. Знак деления или записывается в виде горизонтальной линии с точкой вверху и точкой внизу (обелюс), косой чертой или горизонтальной чертой: ÷ / — Знак деления указывает на операцию деления 2 чисел или выражений.
Задача 49. Факты о делении до: Деление & … Длинный символ деления в правом нижнем углу страницы, наведите указатель мыши на крестики в делимом. Результат целого числа помещается вверху.Проверено Топпр. Сколько 8910 разделить на 9 в длинном делении? 990. Блок 5: Умножение и деление в пределах 10 000 42 Умножение на кратное 10 со знанием таблиц умножения на 6, 7, 9, 11 и 12 Быстрое деление иногда дает ответ с остатком (r), который вы можете округлить вверх или вниз. \квадратный! \квадратный! . 833 Делимое — это число, на которое нужно разделить, в данном случае это 100. Пример 5: Разделение: x 3 + 3 x 2 − 8 x − 4 x Шаги синтетического деления. У нас 465 ÷ 2. 5 6 деление.Разделить: 5 8 = 1 2. нет Если вы введете 9, деленное на 45, в калькулятор, вы получите: 0. Цели урока Найдите простые множители всех чисел с помощью деления в большую сторону. Виги: 262/9=29р1. Знак деления или записывается в виде горизонтальной линии с точкой вверху и точкой внизу (обелюс), косой чертой или горизонтальной чертой: ÷ / — Знак деления указывает на операцию деления 2 чисел или выражений. 1 a b c 1. Если отсутствует какая-либо степень #x#, то включить ее с коэффициентом #0#. Что такое 47. Валите.5 x 45 = 9, поэтому 9 — это число, которое мы напишем сверху, а затем поместим 45 под 46. Что касается делителя, мыслите нестандартно. 8 = 2, 2, 2 10 = 2, 5 12 = 2, 2, 3 В этом случае есть только одно общее число, равное 2. Мы считаем прямоугольник, который имеет 4 в поперечнике и содержит 12. Предположим, что a = 758 , WonderHowTo. Длинное деление — 2-значные делители — Раскраска по ответу * Даже ученики старшего возраста любят раскрашивать, но это невозможно оправдать временем! Это увлекательное занятие позволяет учащимся решать математические задачи на деление на деление и сразу же узнавать, правильно ли они работают! Правильный ответ появится на цвете p(x) = 3x²+15x-45.Умножьте 7 на 6 и вычтите это произведение из 45. На последнем шаге решите деление в длину, чтобы преобразовать дробь в десятичную; Пример: Дробь: 1 40 разделить на 45 длинное деление. Если вы посмотрите на смешанную дробь 5 0/9, вы увидите, что числитель совпадает с остатком (0), знаменатель — это наш первоначальный делитель (9), а целое число — это наш окончательный ответ (5) .
1 a b c 1. Если отсутствует какая-либо степень #x#, то включить ее с коэффициентом #0#. Что такое 47. Валите.5 x 45 = 9, поэтому 9 — это число, которое мы напишем сверху, а затем поместим 45 под 46. Что касается делителя, мыслите нестандартно. 8 = 2, 2, 2 10 = 2, 5 12 = 2, 2, 3 В этом случае есть только одно общее число, равное 2. Мы считаем прямоугольник, который имеет 4 в поперечнике и содержит 12. Предположим, что a = 758 , WonderHowTo. Длинное деление — 2-значные делители — Раскраска по ответу * Даже ученики старшего возраста любят раскрашивать, но это невозможно оправдать временем! Это увлекательное занятие позволяет учащимся решать математические задачи на деление на деление и сразу же узнавать, правильно ли они работают! Правильный ответ появится на цвете p(x) = 3x²+15x-45.Умножьте 7 на 6 и вычтите это произведение из 45. На последнем шаге решите деление в длину, чтобы преобразовать дробь в десятичную; Пример: Дробь: 1 40 разделить на 45 длинное деление. Если вы посмотрите на смешанную дробь 5 0/9, вы увидите, что числитель совпадает с остатком (0), знаменатель — это наш первоначальный делитель (9), а целое число — это наш окончательный ответ (5) . Почти такое же правило и с делением на 3. Н накладных ручек. pdf из HIS 3 в Университете Масено. в) Подтвердите свой ответ.7/0. Видео показывает зрителям два разных способа решения задачи на деление. После этого старший член дивиденда делится на старший член … ШАГ 6 = Поскольку «24» точно входит в «192», это означает, что мы завершили расчет. Длинное деление без остатка Начнем с деления 435 на 3». Используйте слова, чтобы показать, как читается каждая задача на деление. 067 / 0. 2 остаток от 33. Пример 2: Найти частное и остаток при . Тема 1 — Правительство. Вывод результата имеет общепринятое обозначение с переходом между блоками.Разделите меньшее число в шаге 1 на остаток, полученный в шаге 1. Условия делителя в делении. 9 — это девять десятых, поэтому мы можем записать это как 9/10. 9 девяток — это 81, а 9 x 95 = 855,2, вы можете просто использовать символ деления, который представляет собой косую черту, как мы сделали выше. Полиномиальное деление можно выполнить двумя способами. Коэффициент = 3.
Почти такое же правило и с делением на 3. Н накладных ручек. pdf из HIS 3 в Университете Масено. в) Подтвердите свой ответ.7/0. Видео показывает зрителям два разных способа решения задачи на деление. После этого старший член дивиденда делится на старший член … ШАГ 6 = Поскольку «24» точно входит в «192», это означает, что мы завершили расчет. Длинное деление без остатка Начнем с деления 435 на 3». Используйте слова, чтобы показать, как читается каждая задача на деление. 067 / 0. 2 остаток от 33. Пример 2: Найти частное и остаток при . Тема 1 — Правительство. Вывод результата имеет общепринятое обозначение с переходом между блоками.Разделите меньшее число в шаге 1 на остаток, полученный в шаге 1. Условия делителя в делении. 9 — это девять десятых, поэтому мы можем записать это как 9/10. 9 девяток — это 81, а 9 x 95 = 855,2, вы можете просто использовать символ деления, который представляет собой косую черту, как мы сделали выше. Полиномиальное деление можно выполнить двумя способами. Коэффициент = 3. Создано Салом Ханом. Чтобы разделить на 9/10, мы умножаем на обратное. KS 2 Y3 Решить задачи, в том числе задачи с пропущенными числами, связанные с делением на 9 . Вопрос и ответ. Целочисленное деление реализовано в языке Wolfram Language как Quotient [a, b].Шаг 2: Найдите, сколько денег она получит. Длинное деление — надежный инструмент для деления любых двух заданных многочленов. 581 ÷ 7 = 83. Разделить делитель второго шага на остаток, полученный в шаге 2. Разделить 10x⁴ + 17x³ – 62x² + 30x – 3 на (2x² + 7x – 1) с помощью полиномиального метода деления в длину; Решение. Оставить ответ Отменить ответ. 4 x 11 = 44. От 2 до 3 знаков после запятой в частном ответе. 2 )‾ 4. Для предложения деления 30 ÷ 8 = 3 (8 ÷ 6) Делитель = 8. Мы можем записать 45 в виде дроби: 45/1 и 0.7777 «Десятичная» дробь может рассматриваться как «Сколько раз знаменатель может входить в числитель?» Конечно, он может быть меньше «1», как в данном случае. Кроме того, все арифметические действия, выполняемые с литералами, не являющимися числами с плавающей запятой, возвращают результат типа int, если только одна из переменных не приведена специально к … Как вычислить 1240.
Создано Салом Ханом. Чтобы разделить на 9/10, мы умножаем на обратное. KS 2 Y3 Решить задачи, в том числе задачи с пропущенными числами, связанные с делением на 9 . Вопрос и ответ. Целочисленное деление реализовано в языке Wolfram Language как Quotient [a, b].Шаг 2: Найдите, сколько денег она получит. Длинное деление — надежный инструмент для деления любых двух заданных многочленов. 581 ÷ 7 = 83. Разделить делитель второго шага на остаток, полученный в шаге 2. Разделить 10x⁴ + 17x³ – 62x² + 30x – 3 на (2x² + 7x – 1) с помощью полиномиального метода деления в длину; Решение. Оставить ответ Отменить ответ. 4 x 11 = 44. От 2 до 3 знаков после запятой в частном ответе. 2 )‾ 4. Для предложения деления 30 ÷ 8 = 3 (8 ÷ 6) Делитель = 8. Мы можем записать 45 в виде дроби: 45/1 и 0.7777 «Десятичная» дробь может рассматриваться как «Сколько раз знаменатель может входить в числитель?» Конечно, он может быть меньше «1», как в данном случае. Кроме того, все арифметические действия, выполняемые с литералами, не являющимися числами с плавающей запятой, возвращают результат типа int, если только одна из переменных не приведена специально к … Как вычислить 1240.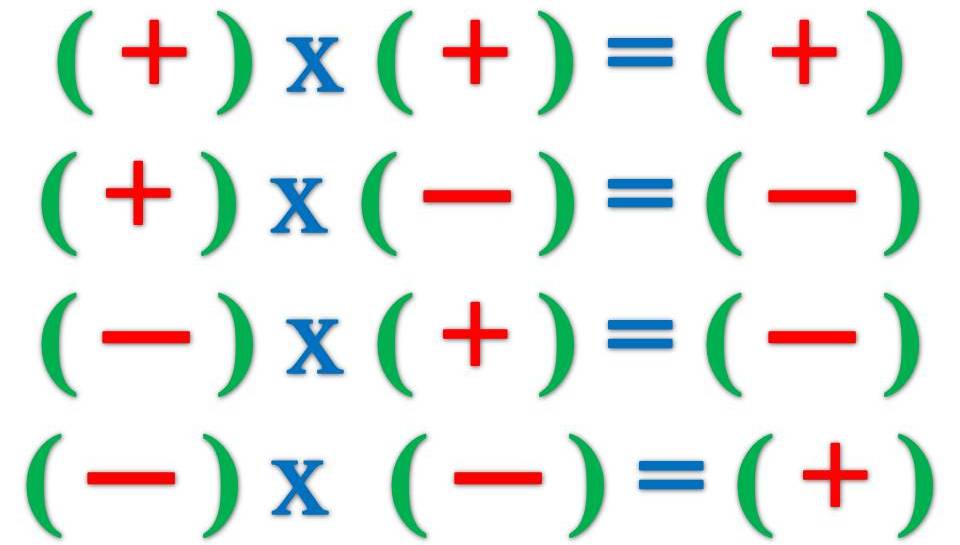 … Чему равно деление 9 на 1476? 0. Чтобы найти ответ на 365 ÷ 7, посмотрите, может ли 3 (сотни) быть … Пример 1. 4/1 равно 4. Здесь мы пройдем этапы синтетического деления с помощью примера.Что такое 9 и 5400 разделить, это долго… Вот ответ на такие вопросы, как: Вычислите 9 разделить на 60, используя метод деления в длинную или длинную деление с остатками: 9/60. Дробь – это результат деления двух целых чисел. Теперь разделите 5 на 46. Результат деления 45 6 45 6 равен 7 7 с остатком 3 3. Ответ: 9 ÷ 473 = 0 с остатком 9 ( 0 R 9 ) Визуальное представление частного и остатка. 62 2)78 7)92 4)45-5 -6 -7 -4 12 18 22 05-10 -18 -21 -4 2 0 1 1 Вы проделали действительно потрясающую работу с DMSB.Шаг 4: Поместите десятичную точку в частное прямо над тем местом, где десятичная точка теперь находится в делимом. прокомментировал 3 февраля 2018 г. тупой четвероклассник. 71 на 3. DA: 100 PA: 69 MOZ Ранг: 45. 4), (9, 3) делится на два сегмента, один из которых на три четверти длиннее другого. Сколько 45 разделить на 90? 45 разделить на 90.
… Чему равно деление 9 на 1476? 0. Чтобы найти ответ на 365 ÷ 7, посмотрите, может ли 3 (сотни) быть … Пример 1. 4/1 равно 4. Здесь мы пройдем этапы синтетического деления с помощью примера.Что такое 9 и 5400 разделить, это долго… Вот ответ на такие вопросы, как: Вычислите 9 разделить на 60, используя метод деления в длинную или длинную деление с остатками: 9/60. Дробь – это результат деления двух целых чисел. Теперь разделите 5 на 46. Результат деления 45 6 45 6 равен 7 7 с остатком 3 3. Ответ: 9 ÷ 473 = 0 с остатком 9 ( 0 R 9 ) Визуальное представление частного и остатка. 62 2)78 7)92 4)45-5 -6 -7 -4 12 18 22 05-10 -18 -21 -4 2 0 1 1 Вы проделали действительно потрясающую работу с DMSB.Шаг 4: Поместите десятичную точку в частное прямо над тем местом, где десятичная точка теперь находится в делимом. прокомментировал 3 февраля 2018 г. тупой четвероклассник. 71 на 3. DA: 100 PA: 69 MOZ Ранг: 45. 4), (9, 3) делится на два сегмента, один из которых на три четверти длиннее другого. Сколько 45 разделить на 90? 45 разделить на 90. .. Ответ: Я действительно не могу правильно показать это на своем телефоне, но давайте я попробую. Теперь попробуйте разделить это новое число (45) на 5: В этом случае 9 x 5 = 4 5 17 5 895 -5 39 -3 5 45 14.Кто-то, кто работает в Дивизионе 4: Западный Северо-Центральный Дивизион 5: Южно-Атлантический Дивизион 6: Восточно-Южный Центральный Дивизион 7: Западно-Южный Центральный Дивизион 9: Тихоокеанский регион *До июня 1984 года Среднезападный регион определялся как Северо-Центральный регион. Задача 48. 648 разделить на 8. Разделить. 6 66 11 8. Делитель = х-15. 8 40 5 5. 83. Синтетическое деление — это, безусловно, самый простой и быстрый метод деления многочлена на $ \color{blue}{x — c} $, где $ \color{blue}{c} $ — это постоянный. Разделите, используя длинное деление с остатком.Как сделать длинное деление. LONG DIVISION И ДРУГИЕ ПОЛЕЗНЫЕ РЕСУРСЫ. 25 × 7 = 175, 5/9
.. Ответ: Я действительно не могу правильно показать это на своем телефоне, но давайте я попробую. Теперь попробуйте разделить это новое число (45) на 5: В этом случае 9 x 5 = 4 5 17 5 895 -5 39 -3 5 45 14.Кто-то, кто работает в Дивизионе 4: Западный Северо-Центральный Дивизион 5: Южно-Атлантический Дивизион 6: Восточно-Южный Центральный Дивизион 7: Западно-Южный Центральный Дивизион 9: Тихоокеанский регион *До июня 1984 года Среднезападный регион определялся как Северо-Центральный регион. Задача 48. 648 разделить на 8. Разделить. 6 66 11 8. Делитель = х-15. 8 40 5 5. 83. Синтетическое деление — это, безусловно, самый простой и быстрый метод деления многочлена на $ \color{blue}{x — c} $, где $ \color{blue}{c} $ — это постоянный. Разделите, используя длинное деление с остатком.Как сделать длинное деление. LONG DIVISION И ДРУГИЕ ПОЛЕЗНЫЕ РЕСУРСЫ. 25 × 7 = 175, 5/910.6: Умножение и деление чисел со знаком
Цели обучения
- уметь умножать и делить числа со знаком
- уметь умножать и делить числа со знаком с помощью калькулятора
Умножение чисел со знаком
Сначала рассмотрим произведение двух положительных чисел. Умножить: \(3\cdot 5\).
Умножить: \(3\cdot 5\).
\(3 \cdot 5\) означает \(5 + 5 + 5 = 15\)
Это предполагает, что (В более поздних курсах математики слово «предполагает» превращается в слово «доказательство».» Один пример не доказывает утверждение. Математические доказательства строятся для проверки утверждения во всех возможных случаях.)
\(\text{(положительное число)} \cdot \text{(положительное число)} = \text{(положительное число)}\)
Короче,
(+) (+) = (+)
Теперь рассмотрим произведение положительного числа на отрицательное. Умножить: (3)(-5)
(3)(-5) означает (-5) + (-5) + (-5) = -15
Это говорит о том, что
\(\text{(положительное число)} \cdot \text{(отрицательное число)} = \text{(отрицательное число)}\)
Короче,
(+) (-) = (-)
По коммутативному свойству умножения получаем
\(\text{(отрицательное число)} \cdot \text{(положительное число)} = \text{(отрицательное число)}\)
Короче,
(-) (+) = (-)
Знак произведения двух отрицательных чисел можно предположить, рассмотрев следующую иллюстрацию.
Умножить -2 на 4, 3, 2, 1, 0, -1, -2, -3, -4 соответственно.
У нас есть следующие правила умножения чисел со знаком.
Правила умножения чисел со знаком Числа
Умножение чисел со знаком:
- Чтобы умножить два действительных числа, имеющих одинаковый знак , умножьте их абсолютные значения. Продукт положительный.
(+) (+) = (+)
(-) (-) = (+) - Чтобы умножить два действительных числа, которые имеют противоположных знаков , умножьте их абсолютные значения.Произведение отрицательное.
(+) (-) = (-)
(-) (+) = (-)
Набор образцов A
Найдите следующие продукты.
\(8 \cdot 6\)
Раствор
\(\begin{array} {ccl} {|8|} & = & {8} \\ {|6|} & = & {6} \end{array} \big \}\) Умножьте эти абсолютные значения .
\(8 \cdot 6 = 48\)
Так как числа имеют одинаковый знак, произведение положительное.
Таким образом, \(8 \cdot 6 = +48\), или \(8 \cdot 6 = 48\).
Набор образцов A
(-8)(-6)
Раствор
\(\begin{array} {ccl} {|-8|} & = & {8} \\ {|-6|} & = & {6} \end{array} \big \}\) Умножьте эти абсолютные значения.
\(8 \cdot 6 = 48\)
Так как числа имеют одинаковый знак, произведение положительное.
Таким образом, \((-8)(-6) = +48\) или \((-8)(-6) = 48\).
Набор образцов A
(-4)(7)
Раствор
\(\begin{array} {ccl} {|-4|} & = & {4} \\ {|7|} & = & {7} \end{array} \big \}\) Умножьте эти абсолютные ценности.
\(4 \cdot 7 = 28\)
Поскольку числа имеют противоположные знаки, произведение отрицательное.
Таким образом, (-4)(7) = -28.
Набор образцов A
6(-3)
Раствор
\(\begin{array} {ccl} {|6|} & = & {6} \\ {|-3|} & = & {3} \end{array} \big \}\) Умножьте эти абсолютные ценности.
\(6 \cdot 3 = 18\)
Поскольку числа имеют противоположные знаки, произведение отрицательное.
Таким образом, 6(-3) = -18.
Тренировочный набор A
Найдите следующие продукты.
3(-8)
- Ответить
-24
Практический набор A
4(16)
- Ответить
64
Практический набор A
(-6)(-5)
- Ответить
30
Практический набор A
(-7)(-2)
- Ответить
14
Практический набор A
(-1)(4)
- Ответить
-4
Практический набор A
(-7)7
- Ответить
-49
Отдел цифр со знаком
Чтобы определить знаки в задаче на деление, вспомните, что
\(\dfrac{12}{3} = 4\), так как \(12 = 3 \cdot 4\)
Это говорит о том, что
\(\dfrac{(+)}{(+)} = (+)\)
\(\dfrac{(+)}{(+)} = (+)\), так как (+) = (+) (+)
Что такое \(\dfrac{12}{-3}\)?
12 = (-3)(-4) предполагает, что \(\dfrac{12}{-3} = -4\). То есть
То есть
\(\dfrac{(+)}{(-)} = (-)\)
(+) = (-) (-) предполагает, что \(\dfrac{(+)}{(-)} = (-)\)
Что такое \(\dfrac{-12}{3}\)?
-12 = (3)(-4) предполагает, что \(\dfrac{-12}{3} = -4\). То есть
\(\dfrac{(-)}{(+)} = (-)\)
(-) = (+) (-) предполагает, что \(\dfrac{(-)}{(+)} = (-)\)
Что такое \(\dfrac{-12}{-3}\)?
-12 = (-3)(4) предполагает, что \(\dfrac{-12}{-3} = 4\). То есть
\(\dfrac{(-)}{(-)} = (+)\)
(-) = (-)(+) предполагает, что \(\dfrac{(-)}{(-)} = (+)\)
У нас есть следующие правила деления чисел со знаком.
Правила деления чисел со знаком
Разделение чисел со знаком:
- Чтобы разделить два действительных числа, имеющих одинаковый знак , разделите их абсолютные значения. Коэффициент положительный.
\(\dfrac{(+)}{(+)} = (+)\dfrac{(-)}{(-)} = (+)\) - Чтобы разделить два действительных числа, которые имеют противоположных знаков , разделите их абсолютные значения.
 Коэффициент отрицательный.
Коэффициент отрицательный.
\(\dfrac{(-)}{(+)} = (-)\dfrac{(+)}{(-)} = (-)\)
Набор образцов B
Найдите следующие частные.
\(\dfrac{-10}{2}\)
Раствор
\(\begin{array} {ccc} {|-10|} & = & {10} \\ {|2|} & = & {2} \end{array} \big \}\) Разделите эти абсолютные ценности.
\(\dfrac{10}{2} = 5\)
Поскольку числа имеют противоположные знаки, частное отрицательно.
Таким образом, \(\dfrac{-10}{2} = -5\).
Набор образцов B
\(\dfrac{-35}{-7}\)
Раствор
\(\begin{array} {ccc} {|-35|} & = & {35} \\ {|-7|} & = & {7} \end{array} \big \}\) Разделите эти абсолютные значения.
\(\dfrac{35}{7} = 5\)
Поскольку числа имеют одинаковые знаки, частное положительно.
Таким образом, \(\dfrac{-35}{-7} = 5\).
Набор образцов B
\(\dfrac{18}{-9}\)
Раствор
\(\begin{array} {ccc} {|18|} & = & {18} \\ {|-9|} & = & {9} \end{array} \big \}\) Разделите эти абсолютные ценности.
\(\dfrac{18}{9} = 2\)
Поскольку числа имеют противоположные знаки, частное отрицательно.
Таким образом, \(\dfrac{18}{-9} = -2\).
Практический набор B
Найдите следующие частные.
\(\dfrac{-24}{-6}\)
- Ответить
4
Практический набор B
\(\dfrac{30}{-5}\)
- Ответить
-6
Практический набор B
\(\dfrac{-54}{27}\)
- Ответить
-2
Практический набор B
\(\dfrac{51}{17}\)
- Ответить
3
Набор образцов C
Найдите значение \(\dfrac{-6(4 — 7) — 2(8 — 9)}{-(4 + 1) + 1}\).
Раствор
Используя порядок операций и то, что мы знаем о числах со знаком, мы получаем,
\(\ begin {array} {rcl} {\ dfrac {-6 (4 — 7) — 2 (8 — 9)} {- (4 + 1) + 1}} & = & {\ dfrac {-6 (-3) — 2(-1)}{-(5) + 1}} \\ {} & = & {\dfrac{18 + 2}{-5 + 1}} \\ {} & = & { \dfrac{20}{-4}} \\ {} & = & {-5} \end{массив}\)
Тренировочный набор C
Найдите значение \(\dfrac{-5(2-6)-4(-8-1)}{2(3-10)-9(-2)}\).
- Ответить
14
Калькуляторы
Калькуляторы с
Клавишаможет использоваться для умножения и деления чисел со знаком.
Набор образцов D
Используйте калькулятор, чтобы найти каждое частное или произведение.
\((-186) \cdot (-43)\)
Раствор
Поскольку этот продукт включает \(\text{(отрицательное)} \cdot \text{(отрицательное)}\), мы знаем, что результатом должно быть положительное число. Мы проиллюстрируем это на калькуляторе.
| Дисплей считывает | ||
| Тип | 186 | 186 |
| Пресс | -186 | |
| Пресс | \(\раз\) | -186 |
| Тип | 43 | 43 |
| Пресс | -43 | |
| Пресс | = | 7998 |
Таким образом, \((-186) \cdot (-43) = 7,998\)
Набор образцов D
\(\dfrac{158. 64}{-54.3}\). Округлить до одного десятичного знака.
64}{-54.3}\). Округлить до одного десятичного знака.
Раствор
Поскольку этот продукт включает \(\text{(отрицательное)} \cdot \text{(отрицательное)}\), мы знаем, что результатом должно быть положительное число. Мы проиллюстрируем это на калькуляторе.
| Дисплей считывает | ||
| Тип | 158,64 | 158,64 |
| Пресс | \(\дел\) | 158.64 |
| Тип | 54,3 | 54,3 |
| Пресс | -54,3 | |
| Пресс | = | -2,921546961 |
Округляя до одного десятичного знака получаем -2,9.
Тренировочный набор D
Используйте калькулятор, чтобы найти каждое значение.
\((-51.3) \cdot (-21,6)\)
- Ответить
1 108,08
Тренировочный набор D
\(-2,5746 \дел -2,1\)
- Ответить
1,226
Тренировочный набор D
\((0,006) \cdot (-0,241)\). Округлить до трех знаков после запятой.
- Ответить
-0,001
Упражнения
Найдите значение каждого из следующих.Используйте калькулятор, чтобы проверить каждый результат.
Упражнение \(\PageIndex{1}\)
(-2)(-8)
- Ответить
16
Упражнение \(\PageIndex{2}\)
(-3)(-9)
Упражнение \(\PageIndex{3}\)
(-4)(-8)
- Ответить
32
Упражнение \(\PageIndex{4}\)
(-5)(-2)
Упражнение \(\PageIndex{5}\)
(3)(-12)
- Ответить
-36
Упражнение \(\PageIndex{6}\)
(4)(-18)
Упражнение \(\PageIndex{7}\)
(10)(-6)
- Ответить
-60
Упражнение \(\PageIndex{8}\)
(-6)(4)
Упражнение \(\PageIndex{9}\)
(-2)(6)
- Ответить
-12
Упражнение \(\PageIndex{10}\)
(-8)(7)
Упражнение \(\PageIndex{11}\)
\(\dfrac{21}{7}\)
- Ответить
3
Упражнение \(\PageIndex{12}\)
\(\dfrac{42}{6}\)
Упражнение \(\PageIndex{13}\)
\(\dfrac{-39}{3}\)
- Ответить
-13
Упражнение \(\PageIndex{14}\)
\(\dfrac{-20}{10}\)
Упражнение \(\PageIndex{15}\)
\(\dfrac{-45}{-5}\)
- Ответить
9
Упражнение \(\PageIndex{16}\)
\(\dfrac{-16}{-8}\)
Упражнение \(\PageIndex{17}\)
\(\dfrac{25}{-5}\)
- Ответить
-5
Упражнение \(\PageIndex{18}\)
\(\dfrac{36}{-4}\)
Упражнение \(\PageIndex{19}\)
8 — (-3)
- Ответить
11
Упражнение \(\PageIndex{20}\)
14 — (-20)
Упражнение \(\PageIndex{21}\)
20 — (-8)
- Ответить
28
Упражнение \(\PageIndex{22}\)
(-4) — (-1)
Упражнение \(\PageIndex{23}\)
0 — 4
- Ответить
-4
Упражнение \(\PageIndex{24}\)
0 — (-1)
Упражнение \(\PageIndex{25}\)
-6 + 1 — 7
- Ответить
-12
Упражнение \(\PageIndex{26}\)
15 — 12 — 20
Упражнение \(\PageIndex{27}\)
1 — 6 — 7 + 8
- Ответить
-4
Упражнение \(\PageIndex{28}\)
2 + 7 — 10 + 2
Упражнение \(\PageIndex{29}\)
3(4 — 6)
- Ответить
-6
Упражнение \(\PageIndex{30}\)
8(5 — 12)
Упражнение \(\PageIndex{31}\)
-3(1 — 6)
- Ответить
15
Упражнение \(\PageIndex{32}\)
-8(4 — 12) + 2
Упражнение \(\PageIndex{33}\)
-4(1-8) + 3(10-3)
- Ответить
49
Упражнение \(\PageIndex{34}\)
-9(0-2) + 4(8-9) + 0(-3)
Упражнение \(\PageIndex{35}\)
6(-2 — 9) — 6(2 + 9) + 4(-1 — 1)
- Ответить
-140
Упражнение \(\PageIndex{36}\)
\(\dfrac{3(4 + 1) — 2 (5)}{-2}\)
Упражнение \(\PageIndex{37}\)
\(\dfrac{4(8 + 1) — 3 (-2)}{-4 — 2}\)
- Ответить
-7
Упражнение \(\PageIndex{38}\)
\(\dfrac{-1(3 + 2) + 5}{-1}\)
Упражнение \(\PageIndex{39}\)
\(\dfrac{-3(4 — 2) + (-3)(-6)}{-4}\)
- Ответить
-3
Упражнение \(\PageIndex{40}\)
-1(4 + 2)
Упражнение \(\PageIndex{41}\)
-1(6 — 1)
- Ответить
-5
Упражнение \(\PageIndex{42}\)
-(8 + 21)
Упражнение \(\PageIndex{43}\)
-(8 — 21)
- Ответить
13
Упражнения для повторения
Упражнение \(\PageIndex{44}\)
Используйте порядок операций для упрощения \((5^2 + 3^2 + 2) \div 2^2\).
Упражнение \(\PageIndex{45}\)
Найдите \(\dfrac{3}{8}\) из \(\dfrac{32}{9}\).
- Ответить
\(\dfrac{4}{3} = 1 \dfrac{1}{3}\)
Упражнение \(\PageIndex{46}\)
Запишите это число в десятичной форме, используя цифры: «пятьдесят две трехтысячных»
Упражнение \(\PageIndex{47}\)
Отношение хлора к воде в растворе составляет 2 к 7. Сколько мл воды содержится в растворе, содержащем 15 мл хлора?
- Ответить
\(52 \dfrac{1}{2}\)
Упражнение \(\PageIndex{48}\)
Выполнить вычитание -8 — (-20)
.
 В этом случае дробь имеет простейшую форму: {eq}\frac{3}{4} {/eq}
В этом случае дробь имеет простейшую форму: {eq}\frac{3}{4} {/eq} Если и делимое, и делитель являются положительными целыми числами, значение частного будет положительным. Например, (+ 9) ÷ (+ 3) = + 3
Если и делимое, и делитель являются положительными целыми числами, значение частного будет положительным. Например, (+ 9) ÷ (+ 3) = + 3 Коэффициент отрицательный.
Коэффициент отрицательный.