Доказательство подобия треугольников
Лемма (О подобных треугольниках) и доказательство
Прямая, параллельная стороне треугольника и пересекающая две другие его стороны, отсекает от данного треугольника ему подобный.
Доказательство. На рисунке 1 в проведена прямая . Докажем, что . Углы равны как соответствующие при параллельных прямых и и секущих и соответственно. Следовательно, углы рассматриваемых треугольников равны. Покажем, что стороны и пропорциональны соответственно сторонам и .
Из теоремы о пропорциональных отрезках следует, что
откуда . Проведем . Аналогично,
Очевидно, что – параллелограмм. Тогда , откуда . Таким образом, было доказано, что
Следовательно, в треугольниках и углы равны и соответствующие стороны пропорциональны. Поэтому, по определению, эти треугольники подобны.
Что и требовалось доказать.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Второй признак подобия треугольников. Видеоурок. Геометрия 8 Класс
Подобными называются такие треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника (см. рис. 1).
Рис. 1. Подобные треугольники
Отношение длин сторон одного треугольника к сходственным сторонам другого называется коэффициентом подобия (
.Первый признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны (см. рис. 2).
Рис. 2. Первый признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум другим сторонам другого треугольника, а углы, заключённые между этими сторонами, равны, то такие треугольники подобны.
; 
; 
; 
(см. рис. 3).Доказать: подобие данных треугольников 
.
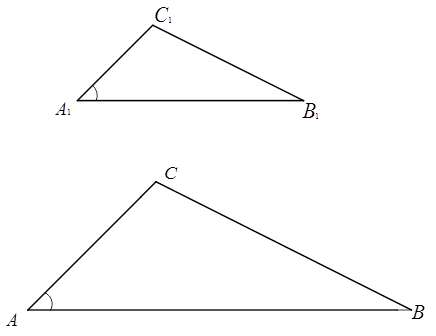
Рис. 3. Иллюстрация к доказательству
Доказательство
Согласно первому признаку подобия треугольников, треугольники подобны, если два угла одного соответственно равны двум углам другого. Поэтому для доказательства того, что 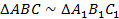, необходимо доказать, что угол 
равен углу 
(угол 
равен углу 
по условию).
Построим треугольник 
, а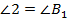 
. Согласно первому признаку подобия треугольников 
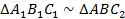(признак подобия по двум углам). 
Рис. 4. Иллюстрация к доказательству
Из подобия этих треугольников следует, что сторона 
как сторона 
относится к стороне 
:
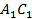Из условия известно, что . Следовательно, 
. Таким образом, 
Получаем, что треугольник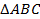и и равны, так как у них равны две стороны и угол между ними ( – общая сторона, и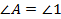 
, поскольку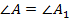
).Отсюда следует, что 
, а так как 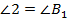, то 
.
У треугольников 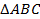и :
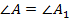
. Согласно первому признаку подобия треугольников эти треугольники подобны: 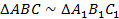. Что и требовалось доказать.По данным рисунка 5 найти длину x, доказать, что 
.
Рис. 5. Иллюстрация к задаче
Решение
1) Рассмотрим два треугольника с общей вершиной 
: 
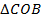, так как они вертикальные.Прилегающие стороны у этих треугольников пропорциональны: 
.
Следовательно, эти треугольники подобны (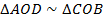
), согласно второму признаку подобия. Коэффициент подобия равен 2. С помощью него определим длину 
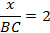
2) Так как 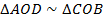, то все углы у них равны. 
– эти углы являются накрест лежащими при пересечении прямых 
и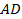 
секущей 
. Таким образом, , что и требовалось доказать.
Ответ: параллельность прямых и 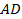доказана; 
.
По данным рисунка найти длину 
, отметить равные углы и доказать, что 
(см. рис. 6).
Рис. 6. Иллюстрация к задаче
Решение
1) 
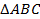является общим для треугольников и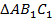 
. К данному углу прилегают сторона 
и сторона 
треугольника 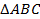, а также сторона 
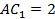и сторона 
треугольника .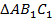
Видно, что 
.
Следовательно, , согласно второму признаку подобия треугольников (общий угол и пропорциональность прилежащих сторон).
2) Коэффициент подобия у этих треугольников равен 3, поэтому можно определить сторону 
: 
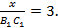
3) Стороны и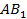 
являются сходствен
interneturok.ru
Подобные треугольники Википедия
Подобные треугольники в евклидовой геометрии — треугольники, углы у которых соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
В данной статье рассматриваются свойства подобных треугольников в евклидовой геометрии. Некоторые утверждения являются неверными для неевклидовых геометрий.
Признаки подобия треугольников[ | ]
Признаки подобия треугольников — геометрические признаки, позволяющие установить, что два треугольника являются подобными, без использования всех элементов.
Первый признак[ | ]
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны. |
то есть: △ABC∼△A1B1C1⇔∠A=∠A1, ∠B=∠B1.{\displaystyle \triangle ABC\sim \triangle A_{1}B_{1}C_{1}\Leftrightarrow \angle A=\angle A_{1},\ \angle B=\angle B_{1}.}
Дано: △ABC{\displaystyle \triangle ABC} и △A1B1C1, ∠A=∠A1, ∠B=∠B1.{\displaystyle \triangle A_{1}B_{1}C_{1},\ \angle A=\angle A_{1},\ \angle B=\angle B_{1}.}
Доказать: △ABC∼△A1B1C1.{\displaystyle \triangle ABC\sim \triangle A_{1}B_{1}C_{1}.}
Доказательство
- Из теоремы о сумме углов треугольника можно получить, что все углы треугольников равны. Распо
ru-wiki.ru
Решение задач на подобие. Подобные треугольники.
Рассмотрим задачи, при решении которых мы будем использовать подобие треугольников. Уделим внимание как базовым задачам, так и задачам посложней. В конце статье вы найдете задачи для самостоятельной работы.
Задача 1.
Через точки М и N, принадлежащие сторонам АВ и ВС треугольника ABC соответственно, проведена прямая МN, параллельная стороне АС. Найдите длину СN, если ВС = 6, МN = 4 и АС = 9. 
Решение: + показать
Задача 2.
Прямая, параллельная основанию треугольника, делит его на треугольник и трапецию, площади которых относятся как 4:5. Периметр образовавшегося треугольника равен 20 см. Найдите периметр данного треугольника.
Решение: + показать
Задача 3.
Через вершину прямого угла прямоугольного треугольника с катетами 6 и 8 см проведен перпендикуляр к гипотенузе. Вычислите площади образовавшихся треугольников.
Решение: + показать
Задача 4.
Из одной точки проведены к кругу две касательные. Длина касательной равна 156, а расстояние между точками касания равно 120. Найдите радиус круга.
Решение: + показать
Задача 5.
В трапеции 
меньшая диагональ 
, равная 6, перпендикулярна основаниям 
и 
. Найдите сумму тупых углов 
и 
.
Решение:+ показать
Задача 6.
Основания трапеции равны a и b. Определите длину отрезка, параллельного основаниям и делящего трапецию на равновеликие части.
Решение: + показать
Задачи для самостоятельной работы
1. Через точки E и F, принадлежащие сторонам АВ и ВС треугольника ABC соответственно, проведена прямая EF, параллельная стороне АС. Найдите длину BС, если EF = 10, AC = 15 и FC = 9. (Ответ: 27).
2. В прямоугольном треугольнике 
проведена высота 
к гипотенузе. 
, 
Найдите катет 
. (Ответ: 20/3).
3. Прямая, параллельная основанию треугольника, отсекает от него треугольник, площадь которого в 8 раз меньше площади оставшейся части. Периметр большего треугольника равен 27. Найдите периметр меньшего треугольника. (Ответ: 9).
4. Основание треугольника 15 см, а боковые стороны 13 и 14 см. Высота разделена в отношении 2:3 (считая от вершины) и через точку деления проведена прямая, параллельная основанию. Найдите площадь образовавшейся при этом трапеции. (Ответ: 70,56 (возможно, вам потребуется формула Герона)).
5. В трапеции с основаниями 
и 
диагонали пересекаются в точке 
. Площадь треугольника 
равна 4, площадь треугольника 
равна 9. Найдите площадь трапеции. (Ответ: 25).
6. Трапеция разделена диагоналями на четыре части. Определить ее площадь, если известны площади ее частей, прилежащих к основаниям 
и 
. (Ответ: 
).
egemaximum.ru
Подобие треугольников Википедия
Подобные треугольники в евклидовой геометрии — треугольники, углы у которых соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
В данной статье рассматриваются свойства подобных треугольников в евклидовой геометрии. Некоторые утверждения являются неверными для неевклидовых геометрий.
Признаки подобия треугольников[ | ]
Признаки подобия треугольников — геометрические признаки, позволяющие установить, что два треугольника являются подобными, без использования всех элементов.
Первый признак[ | ]
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны. |
то есть: △ABC∼△A1B1C1⇔∠A=∠A1, ∠B=∠B1.{\displaystyle \triangle ABC\sim \triangle A_{1}B_{1}C_{1}\Leftrightarrow \angle A=\angle A_{1},\ \angle B=\angle B_{1}.}
Дано: △ABC{\displaystyle \triangle ABC} и △A1B1C1, ∠A=∠A1, ∠B=∠B1.{\displaystyle \triangle A_{1}B_{1}C_{1},\ \angle A=\angle A_{1},\ \angle B=\angle B_{1}.}
Доказать: △ABC∼△A1B1C1.{\displaystyle \triangle ABC\sim \triangle A_{1}B_{1}C_{1}.}
Доказательство
- Из теоремы о сумме углов треугольника можно получить, что все углы треугольников равны. Распо
ru-wiki.ru
math-public:pervyj_priznak_podobiya_treugolnikov [Президентский ФМЛ №239]
Первый признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Доказательство
Первый способ (без использования тригонометрии).
Пусть $\triangle ABC$ и $\triangle A_1B_1C_1$ – два треугольника, у которых $\angle A=\angle A_1,
\angle B=\angle B_1$.
Докажем, что $\triangle ABC\sim\triangle A_1B_1C_1$.
По теореме о сумме углов треугольника $\angle C=180^\circ-\angle A-\angle B=180^\circ-\angle A_1-\angle B_1=\angle C_1$.
Докажем, что стороны треугольника $ABC$ пропорциональны
сходственным сторонам треугольника $A_1B_1C_1$.
Так как $\angle A=\angle A_1$ и $\angle C=\angle C_1$, то
$\dfrac{S_{ABC}}{S_{A_1B_1C_1}}=\dfrac{AB\cdot AC}{A_1B_1\cdot
A_1C_1}$ и $\dfrac{S_{ABC}}{S_{A_1B_1C_1}}=\dfrac{CA\cdot
CB}{C_1A_1\cdot C_1B_1}$.
Из этих равенств следует, что
$\dfrac{AB}{A_1B_1}=\dfrac{BC}{B_1C_1}$.
Аналогично, используя
равенство $\angle A=\angle A_1$, $\angle B=\angle B_1$, получаем, что
$\dfrac{BC}{B_1C_1}=\dfrac{CA}{C_1A_1}$.
Итак, стороны треугольника $ABC$ пропорциональны сторонам треугольника $A_1B_1C_1$.
Второй способ (через тригонометрию).
Пусть $\triangle ABC$ и $\triangle A_1B_1C_1$ – два треугольника, у которых $\angle A=\angle A_1, \angle B=\angle B_1$.
Докажем, что $\triangle ABC\sim\triangle A_1B_1C_1$.
По теореме о сумме углов треугольника $\angle C=180^\circ-\angle A-\angle
B=180^\circ-\angle A_1-\angle B_1=\angle C_1$.
Докажем, что стороны треугольника $ABC$ пропорциональны
сходственным сторонам треугольника $A_1B_1C_1$.
Так как $\angle A=\angle A_1$ и $\angle B=\angle B_1$, то по теореме синусов:
$\dfrac{a}{b}=\dfrac{\sin{A}}{\sin{B}}=\dfrac{\sin{A_1}}{\sin{B_1}}=\dfrac{a_1}{b_1}$,
следовательно $\dfrac{a}{a_1}=\dfrac{b}{b_1}$.
Аналогично можно
получить, что $\dfrac{a}{a_1}=\dfrac{c}{c_1}$.
Следовательно, $\dfrac{a}{a_1}=\dfrac{b}{b_1}=\dfrac{c}{c_1}$.
math-public/pervyj_priznak_podobiya_treugolnikov.txt · Последние изменения: 2016/04/08 18:19 — labreslav
wiki.sch239.net