Объем усеченной пирамиды — формула, пример расчета
Пирамидой называют многогранник, у которого основание представлено произвольным многоугольником, а остальные грани – треугольниками с общей вершиной, которая соответствует вершине пирамиды.
Если в пирамиде провести параллельное основанию сечение, то оно разделить фигуру на две части. Пространство межу нижним основанием и сечением, ограниченное гранями, называется усеченной пирамидой.
Формула объема усеченной пирамиды представляет собой одну треть произведения высоты на сумму площадей верхнего и нижнего основания с их средним пропорциональным:

Рассмотрим пример расчета объема усеченной пирамиды.

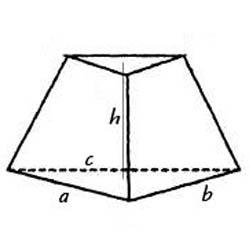
Для расчета объема нам потребуется площадь оснований. Зная длины сторон одного треугольника, мы можем рассчитать площадь по формуле Герона>. Для этого потребуется найти полупериметр:
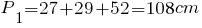
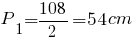
Теперь найдем S2:
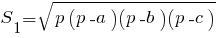
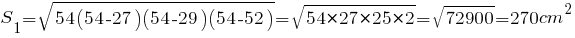
Зная, что пирамида усеченная, делаем вывод, что треугольники, лежащие в основаниях подобны. Коэффициент подобия этих треугольников можно найти из соотношения периметров. Отношение площадей треугольников будет равно квадрату этого коэффициента:
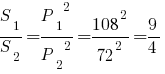

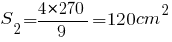
Теперь, когда мы нашли площади оснований усеченной пирамиды, можем легко рассчитать ее объем:

Таким образом, вычислив коэффициент подобия и рассчитав площадь оснований, мы нашли объем заданной усеченной пирамиды.
2mb.ru
Объем пирамиды и конуса. Видеоурок. Геометрия 11 Класс
На этом уроке мы выведем и докажем формулы для нахождения объема пирамиды и конуса, а также формулы для нахождения объема усеченного конуса и усеченной пирамиды.
Легко или сложно вычислять объемы? Пока мы умеем находить лишь объемы параллелепипедов, цилиндров и призм, поэтому задача вычисления объемов кажется довольно легкой. Действительно, и формулы доказывались без труда, и вычисления были не слишком громоздкими. Собственно, формула для нахождения объема прямоугольного параллелепипеда известна еще с начальной школы.
Идея была относительно проста. Мы ввели объем куба, через него нашли объем прямоугольного параллелепипеда, по сути, «разбив» его на кубики, отсюда пришли к призмам, а от них – к цилиндрам. Но в случае пирамиды и конуса «разбить» их на кубики не получится.
Хотя древние греки пробовали. В V веке до н. э. греческим математиком Демокритом было высказано предположение, что объем пирамиды равен трети объема призмы с тем же основанием и той же высотой. Доказать это не смог ни он, ни получивший позднее тот же результат Евклид. Впрочем, данная формула подтверждалась практикой – действительно, мы можем измерить объем любой конкретной пирамиды с любой степенью точности. Например, если взять пирамидку и заполнить ее чем-нибудь (водой, песком), а потом вычислить объем того, чем мы заполняли. Впрочем, ученые и по сей день пытаются разбить призму на три равных пирамиды, что доказало бы формулу.
В наши дни формула давно доказана. И сделано это с помощью интегралов. Помним, что 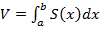 , где
, где  – это площадь сечения фигуры плоскостью, перпендикулярной некоторой оси, которую мы провели.
– это площадь сечения фигуры плоскостью, перпендикулярной некоторой оси, которую мы провели.
С помощью этого метода выведем объем пирамиды. Начнем с объема треугольной пирамиды.
Рассмотрим пирамиду 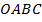 (
(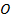 – вершина), обозначим ее объем через
– вершина), обозначим ее объем через 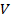 ; площадь ее основания
; площадь ее основания 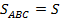 ; ее высота
; ее высота  (см. Рис. 1).
(см. Рис. 1).
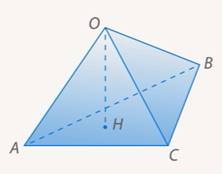
Рис. 1. Пирамида 
Проведем ось 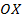 , совпадающую с лучом
, совпадающую с лучом 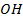 . Рассмотрим произвольную точку
. Рассмотрим произвольную точку 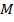 на этой оси внутри пирамиды. Через эту точку проведем сечение
на этой оси внутри пирамиды. Через эту точку проведем сечение  , перпендикулярное нашей оси. Помним, что
, перпендикулярное нашей оси. Помним, что 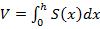
 – площадь сечения
– площадь сечения  (см. Рис. 2). Выразим, чему равно
(см. Рис. 2). Выразим, чему равно  .
.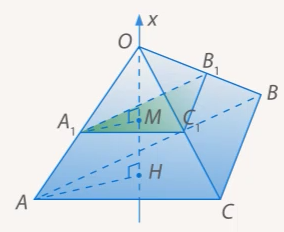
Рис. 2. Проведенные ось 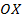 и перпендикулярное оси сечение
и перпендикулярное оси сечение 
Заметим, что 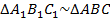 : из того, что плоскости
: из того, что плоскости  и
и 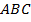 перпендикулярны оси
перпендикулярны оси 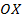 , следует, что плоскости параллельны, а значит,
, следует, что плоскости параллельны, а значит, 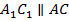
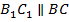 и
и 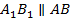 . Тогда получается, что
. Тогда получается, что 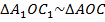 ,
, 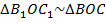 и
и 
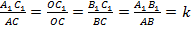 (по третьему признаку подобия) (см. Рис. 3).
(по третьему признаку подобия) (см. Рис. 3).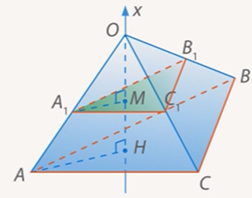
Рис. 3. Подобные треугольники
Найдем, чему равен коэффициент подобия 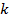 .
.
Рассмотрим 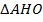 и
и 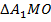
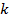 , т. к.
, т. к. 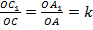 , а значит,
, а значит, 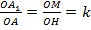 . Из условия
. Из условия 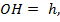 и пусть
и пусть 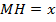 , тогда
, тогда 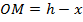
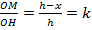 .
.Учитывая, что 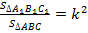 , получаем
, получаем 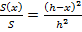 ;
; 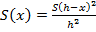 .
.
Окончательно,
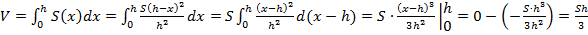
Итак, мы доказали, что объем треугольной пирамиды 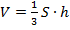
Осталось вывести формулу для произвольной пирамиды. Это делается просто: разбиваем произвольную пирамиду на треугольные (см. Рис. 4).
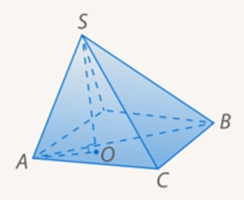
Рис. 4. Разбиение произвольной пирамиды на треугольные
Тогда 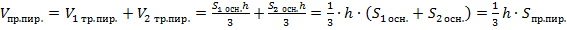
Итак, окончательно, теорема, которую мы доказали: объем пирамиды равен трети произведения площади ее основания и высоты 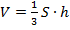
В качестве следствия можно доказать и формулу для вычисления объема усеченной пирамиды (см. Рис. 10): 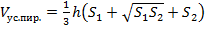 , где
, где 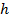 – высота усеченной пирамиды, а
– высота усеченной пирамиды, а 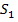 и
и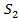 – площади ее оснований.
– площади ее оснований.
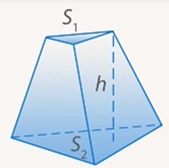
Рис. 10. Усеченная пирамида
Докажем, что 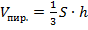 . Как и в первом доказательстве, мы докажем формулу для треугольной пирамиды, а как она обобщается до произвольной, вы уже знаете.
. Как и в первом доказательстве, мы докажем формулу для треугольной пирамиды, а как она обобщается до произвольной, вы уже знаете.
Пусть 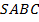 – треугольная пирамида,
– треугольная пирамида, 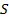 – вершина,
– вершина, 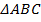 – основание (см. Рис. 5).
– основание (см. Рис. 5).
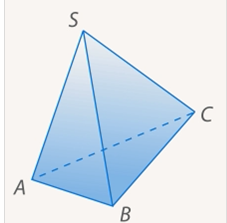
Рис. 5. 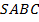 – треугольная пирамида
– треугольная пирамида
Дополним эту пирамиду до призмы с тем же основанием и высотой (см. Рис. 6).
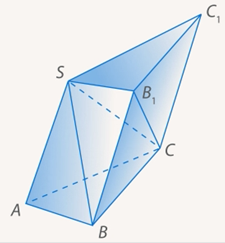
Рис. 6. Призма 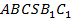
Эта призма составлена из трех пирамид: данной 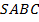 ,
, 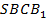 и
и 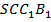 (см. Рис. 7).
(см. Рис. 7).
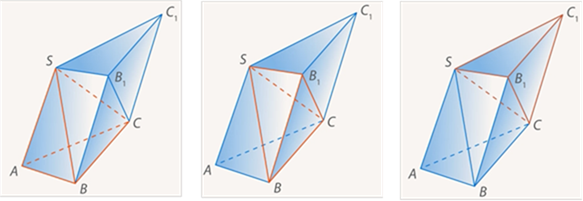
Рис. 7. Призма из трех пирамид
Рассмотрим исходную пирамиду 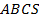 и пирамиду
и пирамиду 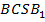 . Заметим, что у них
. Заметим, что у них 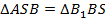 (как треугольники, образовавшиеся при проведении диагонали
(как треугольники, образовавшиеся при проведении диагонали 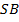 в параллелограмме
в параллелограмме 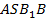 ). Высоты, проведенные из точки
). Высоты, проведенные из точки 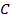 на каждую из этих плоскостей, совпадают
на каждую из этих плоскостей, совпадают 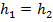 (см. Рис. 8).
(см. Рис. 8).
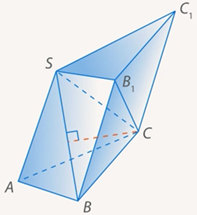
Рис. 8. Высота, проведенная к плоскости 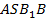
Раз у пирамид 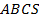 и
и 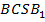 равны высоты и основания, то равны и объемы
равны высоты и основания, то равны и объемы 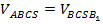 (следует из равенства объемов равновеликих тел).
(следует из равенства объемов равновеликих тел).
Аналогично если рассмотреть пирамиды 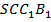 и
и 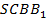 , то
, то 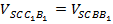 , т. к.
, т. к.
interneturok.ru
| Объем усеченной пирамиды найдем по стандартной формуле. (Формула 1)
Высоту усеченной пирамиды выразим через прямоугольный треугольник, который образован сечением, перпендикулярным углу наклона боковых граней (на рисунке обозначен пересечением зеленой и синих линий). Поскольку сечение имеет форму равнобокой трапеции, то катет этого прямоугольного треугольника равен разности длин оснований пирамиды деленным на два. Второй катет представляет собой высоту пирамиды. Соотношение катетов этого прямоугольного треугольника будет тангенсов угла, который образуют боковые грани и основание. (Формула 2) Поскольку величина угла известна по условию задачи, то мы знаем и значение тангенса этого угла. Поэтому выразим высоту усеченной пирамиды через имеющееся выражение (Формула 3) Подставим получившееся выражение из формулы 3 в формулу объема усеченной пирамиды (Формула 1), получим Формулу 4 Упростим получившееся выражение и получим ответ к задаче — Формула 5 | Об’єм зрізаної піраміди знайдемо за стандартною формулою. (Формула 1)
Висоту усіченої піраміди виразимо через прямокутний трикутник, який утворений перетином, перпендикулярним куту нахилу бічних граней (на рисунку позначений перетинанням зеленої і синіх ліній). Оскільки перетин має форму трапеції, то катет цього прямокутного трикутника дорівнює різниці довжин основ піраміди подiленим на два. Другий катет являє собою висоту піраміди. Співвідношення катетів цього прямокутного трикутника буде тангенсом кута, який утворюють бічні грані і підстава. (Формула 2) Оскільки величина кута відома за умовою задачі, то ми знаємо і значення тангенса цього кута. Тому виразимо висоту усіченої піраміди через тангенс кута (Формула 3) Підставимо отриманий вираз з формули 3 у формулу об’єму усіченої піраміди (Формула 1), отримаємо Формулу 4 Спростимо отримане вираження і отримаємо відповідь до завдання — Формула 5 |
profmeter.com.ua
Объем пирамиды
Теорема. Объём пирамиды равен произведению площади её oснования на треть её высоты.
Сначала докажем эту теорему для пирамиды треугольной, а затем и многоугольной.
1) На основании треугольной пирамиды SABC (черт. 102) построим такую призму SABCDE, у которой высота равна высоте пирамиды, а одно боковое ребро совпадает с ребром SB. Докажем, что объём пирамиды составляет третью часть объёма этой призмы. Отделим от призмы данную пирамиду. Тогда останется четырёхугольная пирамида SADEC (которая для ясности изображена отдельно). Проведём в ней секущую плоскость через вершину S и диагональ основания DC. Получившиеся от этого две треугольные пирамиды имеют общую вершину S и равные основания DEC и DAC, лежащие в одной плоскости; значит, согласно доказанной выше лемме пирамиды эти равновелики. Сравним одну из них, именно SDEC, с данной пирамидой. За основание пирамиды SDEC можно взять \(\Delta\)SDE; тогда вершина её будет в точке С и высота равна высоте данной пирамиды. Так как \(\Delta\)SDE = \(\Delta\)АВС, то согласно той же лемме пирамиды SDEC и SABC равновелики.
Призма ABCDES нами разбита на три равновеликие пирамиды: SABC, SDEC и SDAC. (Такому разбиению, очевидно, можно подвергнуть всякую треугольную призму. Это является одним из важных свойств треугольной призмы.) Таким образом, сумма объёмов трёх пирамид, равновеликих данной, составляет объём призмы; следовательно,
$$ V_{SABC} = \frac{1}{3} V_{SDEABC} = \frac{S_{ABC}\cdot H}{3} = S_{ABC}\frac{H}{3} $$где Н есть высота пирамиды.
2) Через какую-нибудь вершину Е (черт. 103) основания многоугольной пирамиды SABCDE проведём диагонали ЕВ и ЕС.
Затем через ребро SE и каждую из этих диагоналей проведём секущие плоскости. Тогда многоугольная пирамида разобьётся на несколько треугольных, имеющих высоту, общую с данной пирамидой. Обозначив площади оснований треугольных пирамид через b1, b2 , b3 и высоту через Н, будем иметь:
объём SABCDE = 1/3 b1• H + 1/3 b2• H + 1/3 b3• H = (b1 + b2 + b3) • H/3 =
= (площади ABCDE) • H/3.
Следствие. Если V, В и Н означают числа, выражающие в соответствующих единицах объём, площадь основания и высоту какой угодно пирамиды, то
V = 1/3 BH
Теорема. Объём усечённой пирамиды равен сумме объёмов трёх пирамид, имеющих высоту, одинаковую с высотой усечённой пирамиды, а основаниями: одна — нижнее основание данной пирамиды, другая — верхнее основание, а площадь основания третьей пирамиды равна среднему геометрическому площадей верхнего и нижнего оснований.
Пусть площади оснований усечённой пирамиды (черт. 104) будут В и b, высота Н и объём V (усечённая пирамида может быть треугольная или многоугольная — всё равно).
Требуется доказать, что
V = 1/3 BH + 1/3 bH + 1/3 H √Bb = 1/3 H (B + b + √Bb),
где √Bb есть среднее геометрическое между B и b.
Для доказательства на меньшем основании поместим малую пирамиду, дополняющую данную усеченную пирамиду до полной. Тогда объём усечённой пирамиды V мы можем рассматривать как разность двух объёмов — полной пирамиды и верхней дополнительной.
Обозначив, высоту дополнительной пирамиды буквой х, мы найдём, что
V = 1/3 B (Н + х) — 1/3 bх = 1/3( BH + Bх — bх) = 1/3 [ВH + (В — b)х].
Для нахождения высоты х воспользуемся теоремой из раздела, согласно которой мы можем написать уравнение:
$$ \frac{B}{b} = \frac{(H + x)^3}{x^2} $$Для упрощения этого уравнения извлечём из обеих частей его арифметический квадратный корень:
$$ \frac{\sqrt{B}}{\sqrt{b}} = \frac{H + x}{x} $$Из этого уравнения (которое можно рассматривать как пропорцию) получим:
$$ x\sqrt{B} = H\sqrt{b} + x\sqrt{b} $$откуда
$$ (\sqrt{B} — \sqrt{b})x = H\sqrt{b} $$и, следовательно,
$$ x = \frac{H\sqrt{b}}{\sqrt{B} — \sqrt{b}} $$Подставив это выражение в формулу, выведенную нами для объёма V, найдём:
$$ V = \frac{1}{3}\left[BH + \frac{(B-b)H\sqrt{b}}{\sqrt{B} — \sqrt{b}} \right] $$Так как В — b = (√B + √b ) (√B — √b ), то по сокращении дроби на разность √B — √b получим:
$$ V = \frac{1}{3} BH +(\sqrt{B} + \sqrt{b})H\sqrt{b} =\\= \frac{1}{3}(BH+H\sqrt{Bb}+Hb) =\\= \frac{1}{3}H(B+b+\sqrt{Bb}) $$т. е. получим ту формулу, которую требовалось доказать.
razdupli.ru
Объем пирамиды | Мозган калькулятор онлайн
На данной странице калькулятор поможет рассчитать объем пирамиды онлайн. Для расчета задайте площадь, высоту, сторону или количество сторон. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину. Пирамида является частным случаем конуса. Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания.
Пирамида
Формула объема пирамиды через высоту и площадь основания:
S — площадь основания; h — высота пирамиды.Правильная пирамида
Правильная пирамида — пирамида, в основании которой лежит правильный многоугольник, а высота проходит через центр основания.
Формула объема правильной пирамиды через сторону основания, высоту и количество сторон:
a — сторона основания; h — высота пирамиды; n — количество сторон многогранника в основании.Правильная треугольная пирамида
Правильная треугольная пирамида — пирамида, у которой основанием является равносторонний треугольник и грани равные равнобедренные треугольники.
Формула объема правильной треугольной пирамиды через сторону основания и высоту:
a — сторона основания; h — высота пирамиды.Правильная четырехугольная пирамида
Правильная четырехугольная пирамида — пирамида, у которой основанием является квадрат и грани равные равнобедренные треугольники.
Формула объема правильной четырехугольной пирамиды через сторону основания и высоту:
a — сторона основания; h — высота пирамиды.Тетраэдр
Тетраэдр — пирамида, у которой все грани равносторонние треугольники.
Формула объема тетраэдра:
a — ребро тетраэдра.www.mozgan.ru
Материал по математике по теме «Усеченная пирамида»
Усеченная пирамида
Определение . Часть пирамиды, образованная при сечении пирамиды плоскостью, параллельной её основанию, заключенная между секущей плоскостью и основанием, называется усеченной пирамидой.
На рисунке показана пирамида, отбрасывая её часть, лежащую выше секущей плоскости, получаем усеченную пирамиду. Ясно, что малая отбрасываемая пирамида гомотетична большой пирамиде с центром гомотетии в вершине. Коэффициент подобия равен отношению высот: k=h2/h1, или боковых ребер, или других соответствующих линейных размеров обеих пирамид. Мы знаем, что площади подобных фигур относятся, как квадраты линейных размеров; так площади оснований обеих пирамид (т.е. пощади оснований усеченной пирамиды) относятся, как 

Здесь S1 — площадь нижнего основания, а S2 — площадь верхнего основания усеченной пирамиды. В таком же отношении находятся и боковые поверхности пирамид. Сходное правило имеется и для объемов.
Объемы подобных тел относятся, как кубы их линейных размеров; например, объемы пирамид относятся, как произведения их высот на площади оснований, откуда наше правило получается сразу. Оно имеет совершенно общий характер и прямо следует из того, что объем всегда имеет размерность третей степени длины. Пользуясь этим правилом, выведем формулу, выражающую объем усеченной пирамиды через высоту и площади оснований.
Пусть дана усеченная пирамида с высотой h и площадями оснований S1 и S2. Если представить себе, что она продолжена до полной пирамиды, то коэффициент подобия полнорй пирамиды и малой пирамиды легко найти, как корень из отношения S2/S1. Высота усеченной пирамиды выражается как h = h1 — h2 = h1(1 — k). Теперь имеем для объема усеченной пирамиды (через V1 и V2 обозначены объемы полной и малой пирамид)
k2S1=S2, поэтому
Теорема. Объем усеченной пирамиды можно вычислить по формуле:

При нахождении площади боковой поверхности усеченной пирамиды принципы нахождения ПБП обычной пирамиды не теряют актуальности:
Теорема . Если все апофемы усеченной пирамиды равны, то площадь её боковой поверхности можно вычислить по формуле:

Из этой теоремы можно получить подобные:
Теорема. Если все боковые грани усеченной пирамиды наклонены к плоскости основания под одинаковым углом, то площадь её боковой поверхности можно вычислить по формуле:

Теорема. Если пирамида правильная, то площадь её боковой поверхности можно вычислить по формуле:

При нахождении площади поверхности усеченной пирамиды, необладающей ни одним из перечисленных признаков, осуществляется вычисление площадей отдельных граней, а затем производится их суммирование.
Выведем эту формулу. Пусть S — площадь боковой поверхности усеченной пирамиды, обладающей одним из вышеперечисленных признаков, Р1 и Р2 — периметры оснований и а — длина апофемы. Рассуждаем точно так же, как и при выводе формулы для объема. Дополняем пирамиду верхней частью, имеем P2 = kP1, S2=k2S1, где k — коэффициент подобия, P1 и P2 — периметры оснований, а S1 и S2 — лощади боковых поверхностей всей полученной пирамиды и её верхней части соответственно. Для боковой поверхности найдем
(а1 и а2 — апофемы пирамид, а = а1 — а2 = а1(1-k)):

Правильная усеченная пирамида также как и обычная правильная пирамида имеет особенности:
Теорема. В правильной усеченной n-угольной пирамиде все боковые ребра равны между собой.
Теорема. Все боковые грани правильной усеченной n-угольной пирамиды суть равные равнобедренные трапеции (углы при основаниях рабнобедренной трапеции равны), поэтому:
Теорема. В правильной усеченной n-угольной пирамиде все плоские углы при основаниях равны.
Теорема. В правильной усеченной n-угольной пирамиде все двугранные углы при основаниях равны.
Теорема. В правильной усеченной n-угольной пирамиде все двугранные углы при боковых ребрах равны.
videouroki.net
Урок геометрии в 11-м классе: «Объём пирамиды»
Цели и задачи урока:
- вывести формулы: объема пирамиды с использованием основной формулы объема тел и объема усеченной пирамиды.
- систематизировать теоретические знания по теме нахождения объема пирамиды.
- сформировать навык нахождения объема пирамиды, у которой вершина проецируется в центр вписанной или описанной около основания окружности.
- выработать навыки решения типовых задач на применение формул объемов пирамиды и усеченной пирамиды.
Ход урока
I. Объяснение нового материала.
Доказательство теоремы выполняется с помощью мультимедийного проектора
Докажем теорему: объем пирамиды равен одной трети, произведения площади основания на высоту.
Рис. 1
Доказательство:
Сначала докажем теорему для треугольной пирамиды, затем для произвольной.
1. Рассмотрим треугольную пирамиду ОАВС с объемом V, площадью основания S и высотой h . Проведем ось ох (ОМ2— высота), рассмотрим сечение А1В1С1пирамиды плоскостью, перпендикулярной к оси ох и, значит, параллельной плоскости основания. Обозначим через х абсциссу точки М1пересечения этой плоскости с осью ох, а через S{x) — площадь сечения. Выразим S(x) через S, h и х . Заметим, что
В самом деле , следовательно, .
Прямоугольные треугольники , тоже подобны (они имеют общий острый угол с вершиной О).
Применим теперь основную формулу для вычисления объемов тел при a = 0, b = h получаем
Pис. 2
2. Докажем теперь теорему для произвольной пирамиды с высотой h и площадью основания S . Такую пирамиду можно разбить на треугольные пирамиды с общей высотой h. Выразим объем каждой треугольной пирамиды по доказанной нами формуле и сложим эти объемы. Вынося за скобки общий множитель , получим в скобках сумму оснований треугольных пирамид, т.е. площадь S оснований исходной пирамиды.
Таким образом, объем исходной пирамиды равен . Теорема доказана.
II. решить задачи по готовым чертежам .
Задача 1. (рис. 3)
Дано: АВСD – правильная пирамида, АВ =3; AD= . Найти: а)Sосн; б) АО; в) DO г) V.
Задача 2. (рис. 4)
Дано: АВСDF – правильная пирамида, .
Задача 3. (рис. 5)
Дано : АВСDEKF – правильная пирамида,
Найти: а) Sосн; б) V.
Задача 4. (рис. 6)
Найти: V.
Проверка задач выполняется с помощью мультимедийного проектора с подробным анализом поэтапного решения.
Задача 1. (рис. 3)
Решение:
а) (используется формула для вычисления площади правильного треугольника)
АВ = = 3, имеем
б) (формула радиуса описанной окружности через сторону правильного треугольника) .
Задача 2. (рис. 4)
Решение:
1) Рассмотрим следовательно,
– равнобедренный, ОС = FО = 2.
Задача 3. (рис. 5)
Решение:
Задача 4. (рис. 6)
Решение:
III. Проверка вывода формулы для вычисления объема усеченной пирамиды (сообщение ученика у доски выполняется с помощью мультимедийного проектора)
Ответ ученика:
Объем усеченной пирамиды рассматриваем как разность объемов полной пирамиды и той, что отсечена от нее плоскостью, параллельной основанию (рис. 1).
Подставим это выражение для х в первую формулу,
Pабота в форме теста, с проверкой через мультимедийный проектор.
1.В наклонной призме боковое ребро равно 7 см, перпендикулярное сечение — прямоугольный треугольник с катетами: 4 см и 3 см. найдите объем призмы.
а) 10 см3, б) 42 см3, в) 60 см3, г) 30 см3.
2. В правильной шестиугольной пирамиде сторона ее основания 2 см. Объем пирамиды равен 6 см3. Чему равна высота?
3. Объем пирамиды равен 56 см3, площадь основания 14 см2. Чему равна высота?
а) 14 см, б) 12 см, в) 16 см.
4. В правильной треугольной пирамиде высота равна 5 см, стороны основания 3 см. Чему равен объем пирамиды?
5. В правильной четырехугольной пирамиде высота равна 9 см. Сторона основания 4 см. найдите объем пирамиды.
а) 50 см3, б) 48 см3, в) 16 см3.
6. Объем правильной четырехугольной пирамиды равен 27 см3, высота 9 см. найти сторону основания.
а)12 см, б) 9 см, в) 3 см.
7. Объем усеченной пирамиды равен 210 см3, площадь нижнего основания 36 см2, верхнего 9 см2. Найдите высоту пирамиды.
а) 1см, б) 15 см, в) 10см.
8. Равновеликие призма и правильная четырехугольная пирамида имеют равные высоты. Чему равна сторона основания пирамиды, если площадь основания призмы равна S?
Таблица ответов.
| Задача | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Ответ | б | а | б | а | б | в | в | в |
Домашняя работа: 1. Решить задачи №695в, №697, №690
2. Рассмотреть базовые задачи
Задача 1.
Докажите, что если боковые ребра пирамиды равны (или составляют равные углы с плоскостью основания), то вершина пирамиды проецируется в центр окружности, описанной около основания.
Pис. 2
Задача 2.
Докажите, что если двугранные углы при основании пирамиды равны (или равны высоты боковых граней, проведенные из вершины пирамиды), то вершина пирамиды проецируется в центр окружности, вписанной в основание пирамиды.
Pис. 3
urok.1sept.ru