Тождественно равные выражения: определение, примеры

После того, как мы разобрались с понятием тождеств, можно переходить к изучению тождественно равных выражений. Цель данной статьи – объяснить, что это такое, и показать на примерах, какие выражения будут тождественно равными другим.

Тождественно равные выражения: определение

Понятие тождественно равных выражений обычно изучается вместе с самим понятием тождества в рамках школьного курса алгебры. Приведем основное определение, взятое из одного учебника:

Определение 1

Тождественно равными друг другу будут такие выражения, значения которых будут одинаковы при любых возможных значениях переменных, входящих в их состав.

Также тождественно равными считаются такие числовые выражения, которым будут отвечать одни и те же значения.

Это достаточно широкое определение, которое будет верным для всех целых выражений, смысл которых при изменении значений переменных не меняется. Однако позже возникает необходимость уточнения данного определения, поскольку помимо целых существуют и другие виды выражений, которые не будут иметь смысла при определенных переменных. Отсюда возникает понятие допустимости и недопустимости тех или иных значений переменных, а также необходимость определять область допустимых значений. Сформулируем уточненное определение.

Определение 2

Тождественно равные выражения – это те выражения, значения которых равны друг другу при любых допустимых значениях переменных, входящих в их состав. Числовые выражения будут тождественно равными друг другу при условии одинаковых значений.

Фраза «при любых допустимых значениях переменных» указывает на все те значения переменных, при которых оба выражения будут иметь смысл. Это положение мы объясним позже, когда будем приводить примеры тождественно равных выражений.

Можно указать еще и такое определение:

Определение 3

Тождественно равными выражениями называются выражения, расположенные в одном тождестве с левой и правой стороны.

Примеры выражений, тождественно равных друг другу

Используя определения, данные выше, рассмотрим несколько примеров таких выражений.

Для начала возьмем числовые выражения.

Пример 1

Так, 2+4 и 4+2 будут тождественно равными друг другу, поскольку их результаты будут равны (6 и 6).

Пример 2

Точно так же тождественно равны выражения 3 и 30:10, (22)3 и 26(для вычисления значения последнего выражений нужно знать свойства степени). 

Пример 3

А вот выражения 4-2 и 9-1 равными не будут, поскольку их значения разные.

Перейдем к примерам буквенных выражений. Тождественно равными будут a+b

zaochnik.com

Тождества: определение, обозначение, примеры

Начнем разговор о тождествах, дадим определение понятия, введем обозначения, рассмотрим примеры тождеств.

Что представляет собой тождество

Начнем с определения понятия тождества.

Определение 1

Тождество представляет собой равенство, которое верно при любых значениях переменных. Фактически, тождеством является любое числовое равенство.

По мере разбора темы мы можем уточнять и дополнять данное определение. Например, если вспомнить понятия допустимых значений переменных и ОДЗ, то определение тождества можно дать следующим образом.

Определение 2

Тождество – это верное числовое равенство, а также равенство, которое будет верным при всех допустимых значениях переменных, которые входят в его состав.

Про любые значения переменных при определении тождества речь идет в пособиях и учебниках по математике для 7 класса, так как школьная программа для семиклассников предполагает проведение действий исключительно с целыми выражениями (одно- и многочленами). Они имеют смысл при любых значениях переменных, которые входят в их состав.

Программа 8 класса расширяется за счет рассмотрения выражений, которые имеют смысл только для значений переменных из ОДЗ. В связи с этим и определение тождества меняется. Фактически, тождество становится частным случаем равенства, так как не каждое равенство является тождеством.

Знак тождества

Запись равенства предполагает наличие знака равенства «=», от которого справа и слева располагаются некоторые числа или выражения. Знак тождества имеет вид трех параллельных линий «≡». Он также носит название знака тождественного равенства.

Обычно запись тождества ничем не отличается от записи обыкновенного равенства. Знак тождества может быть применен для того, чтобы подчеркнуть, что перед нами не простое равенство, а тождество.

Примеры тождеств

Обратимся к примерам.

Пример 1

Числовые равенства 2≡2 и -3≡-3 это примеры тождеств. Согласно определению, данному выше, любое верное числовое равенство по определению является тождеством, а приведенные равенства верные. Их также можно записать следующим образом 2≡2 и -3≡-3.

  Пример 2

Равенства 2+3=5 и 7−1=2·3 также можно считать тождествами, так как они являются вернными. Здесь также допустима запись 2+3≡5 и 7−1≡2·3

.

Тождества могут содержать не только числа, но также и переменные.

Пример 3

Возьмем равенство 3·(x+1)=3

zaochnik.com

Тождество. Тождественные выражения, преобразования

Тождество – это равенство, обе части которого являются тождественно равными выражениями. Тождества делятся на буквенные и числовые.

Тождественные выражения

Два алгебраических выражения называются тождественными (или тождественно равными), если при любых численных значениях букв они имеют одинаковую численную величину. Таковы, например, выражения:

x(5 + x)   и   5x + x²

Оба представленных выражения, при любом значении x будут равны друг другу, поэтому их можно назвать тождественными или тождественно равными.

Так же тождественными можно назвать и числовые выражения, равные между собой. Например:

20 — 8   и   10 + 2

Буквенные и числовые тождества

Буквенное тождество – это равенство, которое справедливо при любых значениях входящих в него букв. Другими словами, такое равенство, у которого обе части являются тождественно равными выражениями, например:

(a + b)m = am + bm
(a + b)² = a² + 2ab + b²

Числовое тождество – это равенство, содержащее только числа, выраженные цифрами, у которого обе части имеют одинаковую численную величину. Например:

4 + 5 + 2 = 3 + 8
5 · (4 + 6) = 50

Тождественные преобразования выражений

Все алгебраические действия представляют собой преобразование одного алгебраического выражения в другое, тождественное первому.

При вычислении значения выражения, раскрытии скобок, вынесении общего множителя за скобки и в ряде других случаев одни выражения заменяются другими, тождественно равными им. Замену одного выражения другим, тождественно равным ему, называют тождественным преобразованием выражения или просто преобразованием выражения. Все преобразования выражений выполняются на основе свойств действий над числами.

Рассмотрим тождественное преобразование выражения на примере вынесения общего множителя за скобки:

10x — 7x + 3x = (10 — 7 + 3)x = 6x

Выполнение данного преобразования основано на распределительном законе умножения.

naobumium.info

Знак тождества в математике

Тождественность в математике — очень часто используемое понятие. Различают понятия тождественных равенств, тождественных выражений и тождественных преобразований, давайте более подробно разберём, что значит каждое из этих понятий.

Тождественные выражения в математике

Рассмотрим три простых алгебраических выражения:

• $5x + 10$;
• $(x + 2) \cdot 5$
• $\frac{20x + 40}{4}$

Вне зависимости от используемых значений $x$, все три выражения между собой равны.

Для того чтобы доказать это, используем элементарные преобразования, разрешаемые в математике, и получим, что $5x + 10 = 5x + 10 = 5x + 10$, то есть все три выражения равны между собой. При упрощении становится очевидно, что вне зависимости от выбранного $x$ эти выражения всегда будут равны.

Мы подходим непосредственно к определению тождественных выражений:

Определение 1

Выражения называются тождественными друг с другом, если при любых значениях переменных они всегда равны между собой.

Например, можно сказать, что выражение $5x + 10$ тождественно выражениям $(x + 2) \cdot 5$ и $\frac{20x + 40}{4}$.

Стоит также обратить внимание на то, что не всегда выражения тождественны для всех возможных значений переменных, например, выражения $\frac{y^2-4}{y-2}$ и $y+2$ тождественны для любых $y$, кроме $y=2$.

При значении игрека, равному двум, первое из этих двух выражений теряет смысл, так как на нуль делить нельзя, а в знаменателе при этом значении получается нуль.

Данные выражения можно назвать тождественными при всех допустимых значениях переменной $y$, то есть эти выражения тождественны при всех $y$, при которых оба выражения не потеряют свой смысл. Такие выражения называются тождественными на заданном множестве значений.

Понятия «тождество» и «тождественное равенство»

Что же такое тождество в алгебре?

Определение 2

Тождество в математике — это равенство, которое всегда выполняется или, иными словами, является справедливым для всех множеств значений его переменных.

Если два и более тождественных выражения записать непосредственно рядом друг с другом через знак «равно» — то получится тождественное равенство, то есть тождество.

К тожественным равенствам относятся переместительный закон сложения $a+b =b + a$ и сочетательный закон умножения $(ab) \cdot c = a \cdot (bc)$, так как они являются верными вне зависимости от значения переменных $a, b, c$. Формулы для сокращённой записи разности квадратов, квадратов разности и квадратов суммы являются другими примерами тождественных равенств.

Иногда тождествами называются не только выражения, содержащие какие-либо переменные, но и все арифметически верные равенства типа $2+2=4$.

Не любое равенство, содержащее переменные, можно назвать тождеством. Например, равенство $y+5 = 7$ соблюдается только при $y= 2$, при каком-либо другом значении $y$ оно не соблюдается и поэтому тождеством его назвать нельзя.

Знак тождества в математике

Определение 3

Чаще всего тождества записывают через знак «равно» — «$=$», знак «тождественно» — «≡» иногда используют для особого выделения в речи тождественности какого-либо равенства. Обычно знак тождества используется значительно реже, чем знак равенства.

Тождественные преобразования

Очень часто для того чтобы упростить процесс вычисления каких-либо выражений, а также для их сравнения и более удобной подстановки переменных в равенства используют различные математические преобразования. Эти преобразования называются тождественными преобразованиями, так как они не изменяют конечные значения выражений и равенств.

Определение 4

Тождественные преобразования — это преобразования и замены одного выражения другим, тождественным ему, не изменяющие конечное значение выражений и не приводящие к нарушению тождественности равенств.

Любое выражение при любых допустимых значениях переменных, используемых в нём, принимает какое-либо значение. Из этого можно сделать вывод, что применение различных законов, соблюдающихся для арифметических действий приводит к преобразованию исходного выражение в новое, тождественное первоначальному выражению.

Пример 1

Какие выражения тождественны?

1. $(10 + 3)$ и $13 \cdot (1 +5)$.
2. $(x^2 + y^2)$ и $(x – y)(x+y)$.
3. $8$ и $(2 \cdot 3 + 16 – 14)$.
4. $7 + 4$ и $6 + 6$.

Ответ:

Тождественными являются выражения под номером 2 и 3, в случае выражений под номером 2 слева дана сокращённая формула разности квадратов, а справа — развёрнутая. В случае третьего выражения нужно упростить выражение справа:

$(2 \cdot 3 + 16 – 14)= 6 + 16 – 14 = 8$

$8=8$.

spravochnick.ru

что значит «тождественно равно»?

что значит «тождественно равно»?

Если соответственные значения двух выражений, содержащих одни и те же переменные, совпадают при всех допустимых значениях переменных, то выражения называются тождественно равными.

либо тождественно либо равно. еще говорят тождество верно То́ждество (в математике) — равенство, выполняющееся на всём множестве значений входящих в него переменных (равенство, верное при любых значениях переменной),

значит — при любых значениях переменной. знак равно может означать как у уравнении — «при некоторых неизвестных» (потом просят найти эти неизвестные. например, равенство x+x=4 верно только при х, равном двум, это не тождественное равенство. а вот равенство х+х=2х — верно при любом х, это тождественное равенство.

что то мне это напоминает дискретную математику…. это что то типа одно значение или уравнение точно такое, равняется другому))

Функция А, зависящая от каких-то переменных, тождественно равна функции В, зависящей от тех же переменных, если значение А равно значению В при всевозможных значениях переменных. Пример тождественного равенства: x+x=3x-x. Попросту говоря, А и В — одно и то же, но в разном виде. Если соответственные значения двух выражений, содержащих одни и те же переменные, совпадают при всех допустимых значениях переменных, то выражения называются тождественно равными. либо тождественно либо равно. еще говорят тождество верно То́ждество (в математике) — равенство, выполняющееся на всём множестве значений входящих в него переменных (равенство, верное при любых значениях переменной). значит — при любых значениях переменной. знак равно может означать как у уравнении — «при некоторых неизвестных» (потом просят найти эти неизвестные. например, равенство x+x=4 верно только при х, равном двум, это не тождественное равенство. а вот равенство х+х=2х — верно при любом х, это тождественное равенство.!. 🙂

Войдите, чтобы написать ответ

science.ques.ru

Тождества. Видеоурок. Алгебра 7 Класс

Тема: Разложение многочленов на множители

Урок: Тождества

Рассмотрим примеры.

Пример 1:

;

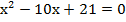Данное уравнение мы решали методом выделения полного квадрата и получили корн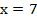и  или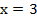

Пример 2:

;

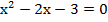Данное уравнение мы также решали методом выделения полного квадрата и получили ответ 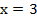 или .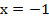

Это означает, что в случае примера 1 только пр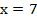и  или 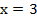 уравнение превращалось в верное числовое равенство, для второго примера только пр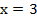и  или 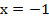 уравнение превращалось в верное числовое равенство.

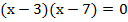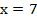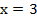 Повторим ход решения примера 1. После преобразований мы получили уравнение , из которого явно видно, что  и  являются решениями данного уравнения.

Уравнение из примера 2 раскладывалось так: 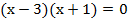 и отсюда тоже явно следует ответ.

Для нас важно то, что приведенные выше выражения справедливы каждое только для своей пары значений переменной и эти значения имеют название корни уравнения.

 Но существуют такие выражения, которые справедливы при любых значениях переменных, которые в них входят. Рассмотрим примеры:

Пример 3:

;

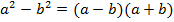Подставив в выражение любые значения 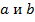, мы получим верное числовое равенство.

Пример 4:

;

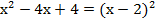Формула квадрата разности утверждает, что данное выражение справедливо при любых значениях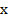

Выражения из примеров 3 и 4 мы будем называть тождествами. Подобных примеров можно привести очень много:

Пример 5:

;

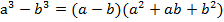Данное выражение также справедливо при любых значениях переменных

В этом и заключается принципиальное отличие уравнения от тождества. Тождество – это такое равенство, которое верно при любых значениях переменных, которые в него входят, уравнение же справедливо только при некоторых значениях переменных.

Уточним, что значит любые значения переменных. Рассмотрим элементарное равенство:

;

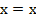какое бы значение 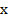 не принимал, равенство будет справедливым.

Разделим обе стороны на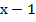

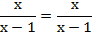
Данное выражение будет справедливо при любых 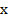, кроме 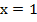, потому что в знаменателе обеих дробей стоит двучлен 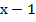, и эти дроби определены, то есть их можно вычислить, только если знаменатель не равен нулю:  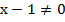, то есть .

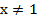Пример 6:

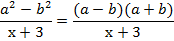
Данное выражение является тождеством, так как оно справедливо во всех случаях кроме тех, когда знаменатель равен нулю. То есть, оно справедливо при всех 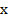, кроме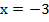

, так как в этом случае дробь не имеет смысла.

Итак, появились значения переменных, при которых даже само выражение не имеет смысла, в связи с этим скорректируем определение тождества: тождество это выражение, обращающееся в верное равенство при всех допустимых значениях переменных, которые в него входят.

Рассмотрим задачи.

Пример 7 – доказать тождество:

;

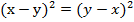Мы уже встречались с подобными примерами, говорили, что .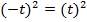

Теперь докажем, что выражение под квадратом можно умножить на минус единицу и получится верное равенство. Для этого в заданном выражении раскроем скобки:

;

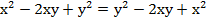
Мы знаем, что от перемены мест слагаемых сумма не меняется, таким образом, тождество доказано.

Но его можно доказать и другим способом:

;

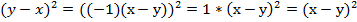Пример 8:

;

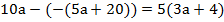Преобразуем левую часть:

;

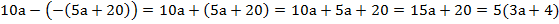После преобразований получаем:

;

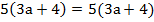Тождество доказано.

Заметим, что тождественные преобразования – это те преобразования, при которых одно выражение заменяется другим, тождественно ему равным.

Пример 9:

;

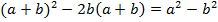Есть два способа решения данной задачи. Первый – это напрямую в левой части раскрыть квадрат, выполнить умножение одночлена на двучлен, привести подобные члены и посмотреть, окажется ли выражение тождеством или нет.

Второй способ – преобразовать левую часть при помощи метода вынесения общего множителя:

;

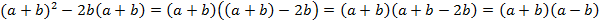Теперь мы видим, что левая часть – это разность квадратов. Преобразует ее:

;

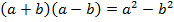Получаем выражение:

;

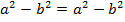Тождество доказано.

Пример 10 – доказать, что если 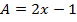, , 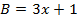, 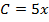то выражения  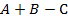 и 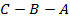 тождественно равны при любых значениях  :

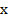Рассмотри два заданных выражения. В первом 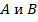 стоят с плюсом, а  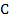с минусом, во втором наоборот  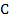стоит с плюсом, а  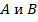стоят с минусом, значит первое выражение равно второму, взятому с противоположным знаком. То есть имеем некоторое выражение :

, , ,

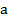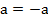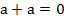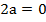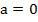
подставим значения A, B и С в заданное выражение:

;

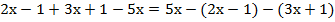Упростим выражение:

;

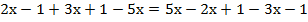Приведем подобные члены:

;

;

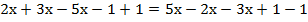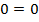Тождество доказано.

Пример 11 – установите, является ли данное равенство тождеством и если да, то укажите допустимые значения переменных:

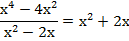
Начнем с определения допустимых значени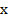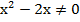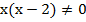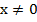й :

, ,  и ;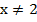

Получили, что все значения 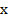, кроме  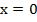и 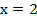 являются допустимыми, так как в этих двух точках знаменатель обращается в ноль и дробь не имеет смысла.

Теперь нужно упростить выражение в левой части. Это алгебраическая дробь и мы знаем, что нужно разложить на множители входящие в нее многочлены и сократить. В числителе применим формулу разности квадратов, а знаменатель оставим:

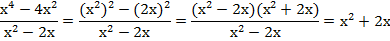
Получаем:

interneturok.ru

равный — это… Что такое тождественно-равный?



тождественно-равный

тождественно-равный

Слитно или раздельно? Орфографический словарь-справочник. — М.: Русский язык. Б. З. Букчина, Л. П. Какалуцкая. 1998.

• тождественно-ложный
• тоже

Смотреть что такое «тождественно-равный» в других словарях:

• тождественно-равный — тожде/ственно ра/вный …   Слитно. Раздельно. Через дефис.

• Полином Жегалкина — Полином Жегалкина  многочлен над кольцом , то есть полином с коэффициентами вида 0 и 1, где в качестве произведения берётся конъюнкция, а в качестве сложения  исключающее или. Полином был предложен в 1927 году… …   Википедия

• Многочлен Жегалкина — Полином Жегалкина  полином над Z2, то есть полином с коэффициентами вида 0 и 1, где в качестве произведения берется конъюнкция, а в качестве сложения исключающее или. Полином был предложен в 1927 году И. И. Жегалкиным в качестве удобного средства …   Википедия

• Фазовые переходы второго рода — фазовые переходы, при которых первые производные термодинамических потенциалов по давлению и температуре изменяются непрерывно, тогда как их вторые производные испытывают скачок. Отсюда следует, в частности, что энергия и объём вещества при… …   Википедия

• Рассуждение — – функционально смысловой тип речи (см.) – (ФСТР), соответствующий форме абстрактного мышления – умозаключению, выполняющий особое коммуникативное задание – придать речи аргументированный характер (прийти логическим путем к новому суждению или… …   Стилистический энциклопедический словарь русского языка

• АЛГЕБРА ЛОГИКИ —         система алгебраич. методов решения логич. задач, а также совокупность задач, решаемых такими методами. А. л. в узком смысле слова алгебраич. (табличное, матричное) построение классич. логики высказываний, в котором рассматриваются… …   Философская энциклопедия

• ИЗОМОРФИЗМ — (от греч. isos – равный, однозначный и morphe – форма) понятие, выражающее тождественность, идентичность форм. В психологии идентичность (теоретическая) между гештальтами в переживании непосредственно созерцаемого и в процессах, совершающихся в… …   Философская энциклопедия

• время — 3.3.4 время tE (time tE): время нагрева начальным пусковым переменным током IА обмотки ротора или статора от температуры, достигаемой в номинальном режиме работы, до допустимой температуры при максимальной температуре окружающей среды. Источник …   Словарь-справочник терминов нормативно-технической документации

• ЭЛЕКТРОДИНАМИКА — классическая, теория (неквантовая) поведения электромагнитного поля, осуществляющего взаимодействие между электрич. зарядами (электромагнитное взаимодействие). Законы классич. макроскопич. Э. сформулированы в Максвелла уравнениях, к рые позволяют …   Физическая энциклопедия

• ТОЖДЕСТВО —         понятие, выражающее предельный случай равенства объектов, когда не только все родовидовые, но и все индивидуальные их свойства совпадают. Совпадение родовидовых свойств (сходство), вообще говоря, не ограничивает числа приравниваемых… …   Философская энциклопедия

dic.academic.ru