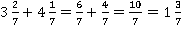Как из целого числа вычесть смешанное
Рассмотрим, как из целого числа вычесть смешанное число (смешанную дробь).
Вычитание из целого числа смешанного аналогично вычитанию дроби из целого числа.
Правило.
Чтобы из целого числа вычесть смешанное, надо:
1) представить целое число в виде смешанной дроби.
Для этого нужно занять единицу у целой части и представить ее в виде дроби, у которой и числитель, и знаменатель равны знаменателю дробной части вычитаемого.
2) выполнить вычитание смешанных чисел.
Для этого нужно из уменьшаемого вычесть вычитаемое: отдельно — целые части, отдельно — дробные.
С помощью букв правило вычитания смешанного числа из целого можно записать так:
Примеры.
Вычесть смешанное число из целого:
Решение:
Светлана МихайловнаОбыкновенные дроби
Сложение и вычитание смешанных чисел (Вольфсон Г.И.). Видеоурок. Математика 5 Класс
На данном уроке вы узнаете правила сложения и вычитания смешанных чисел, научитесь решать различные задачи по теме «Сложение и вычитание смешанных чисел». Сложение и вычитание смешанных чисел основано на свойстве этих чисел. При сложении можно использовать переместительное и сочетательное свойство, а при вычитании чисел можно использовать свойства вычитания числа из суммы и вычитания суммы из числа.
Для начала давайте вспомним, что такое смешанные числа. Смешанное число – число, записанное в таком виде, что у него есть целая часть и дробная часть. Например,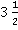 
. Здесь 3 – целая часть, 
Предположим, нам дали такую задачу. Вася пробежал первый из двух кругов дистанции за 1 минуту 40 секунд, а второй круг – за 1 минуту 20 секунд. За какое время Вася пробежал всю дистанцию и насколько быстрее он пробежал второй круг, чем первый?
Решение
Несложно видеть, что мы можем сложить минуты с минутами, секунды – с секундами. Получится 2 мин + 60 секунд, т. е. 3 мин. Но, с другой стороны, 40 секунд – это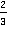 
минуты, а 20 секунд – 
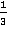. И тогда, по аналогии, чтобы сложить эти смешанные числа, мы можем не переводить их в неправильные дроби, а сразу сложить целые минуты друг с другом, и отдельно – дробные. Это дает 2 минуты и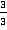 
Можно было все это проделать и так. Заметим, что смешанное число есть сумма своих целой и дробной частей. А дальше воспользуемся переместительным свойством:
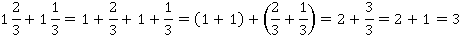
А что с вычитанием? То же самое. Из чисто практических соображений первый круг по минутам одинаков со вторым, а по секундам – на 20 дольше (или на треть минуты). Можно и так:
Думаю, вы уже поняли алгоритм? Из целого вычитаем (к целому прибавляем) целое, из дробного – дробное. Рассмотрим еще несколько примеров.
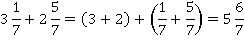
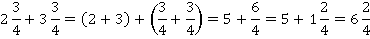
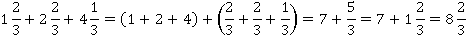
Закрепим эти выкладки правилом. Чтобы сложить два смешанных числа, необходимо:
- сложить их целые части;
- сложить их дробные части;
- если нужно, перевести сумму дробных частей в смешанное число;
- сложить полученные числа.
Перейдем к вычитанию. Рассмотрим несколько примеров, после чего сформулируем общий алгоритм.
Найти ошибки в примерах на сложение
Вычитание смешанных дробей | Математика
Как выполнить вычитание смешанных дробей с одинаковыми знаменателями? Запишем правило и рассмотрим примеры.
Правило.
Чтобы вычесть смешанные дроби, надо отдельно вычесть их целые части, отдельно — дробные.
Если дробная часть уменьшаемого меньше дробной части вычитаемого, сначала надо занять единицу у целой части, представить ее в виде дроби, у которой числитель равен знаменателю, и прибавить эту дробь к дробной части уменьшаемого.
С помощью букв правило вычитания смешанных дробей можно записать так:
Если m<n, то
Примеры.
Выполнить вычитание смешанных дробей:
Решение:
Обычно пишут короче:
Светлана МихайловнаДроби с одинаковыми знаменателями
Конспект урока «Вычитание смешанных чисел»
Муниципальное бюджетное общеобразовательное учреждение «Средняя
общеобразовательная школа №5» г. Биробиджан
Конспект урока по математике в 5 классе
по теме:
Вычитание смешанных чисел
Учитель:
Кошелева Виктория Сергеевна
г. Биробиджан,2016 г.
Тема урока: Вычитание смешанных чисел
Цель урока: сформировать навыки вычитания смешанных чисел с одинаковым знаменателем, способствовать развитию математической речи и оперативной памяти, внимания, логического мышления.
Личностные: способствовать к самооценке на основе критерия успешности учебной деятельности.
Регулятивные: умение определять и формулировать цель на уроке с помощью учителя, проговаривать последовательность действий на уроке, оценивать правильность выполнения действий на уроке, высказывать свое предположение
Познавательные: умение ориентироваться в своей системе знаний, отличать новое от уже изученного, добывать новые знания.
Планируемые образовательные результаты:
Предметные: знать правило вычитания смешанных чисел, уметь безошибочно выполнять вычитание смешанных.
Коммуникативные: уметь оформлять свои мысли в устной форме, слушать и понимать речь других.
Познавательные: добывать новые знания, находить ответы на поставленные вопросы в учебнике, извлекать из математических текстов необходимую информацию.
Тип урока: «открытие» нового знания.
Ход урока
Орг. момент
-Здравствуйте ребята! Прозвенел и смолк звонок, начинается урок. Друг на друга посмотрели и за парты тихо сели. Откройте тетради, запишите в них число и «Классная работа». Сегодня мы продолжим работать с дробями.
2. Актуализация знаний
Какая дробь здесь лишняя? (правильная, несократимая)
Почему дробь осталась?
А какие дроби здесь равные?
Какое задание мы можем сформулировать для данных дробей:
(дробная часть выражена неправильной дробью)
(дробная часть выражена в виде сократимой дроби)
( представить в виде неправильной дроби)
(выделить целую часть)
Мотивационный этап
Рассмотрим с вами две дроби
Какие здания можно сформулировать для данных чисел?
Сравнить дроби
Сложить дроби
На какие группы можно разбить эти выражения?
Найдем разность каждого из выражений.
Как вы думаете, какая у нас сегодня тема урока? А что нам нужно знать для этого? (правило)
— Какие примеры мы с вами еще не решали?
-А как вы думаете, как можно вычесть числа с одинаковыми знаменателями?
Составим алгоритм для вычитания смешанных чисел
Чтобы вычесть смешанные числа, нужно
Вычесть целые части
Вычесть дробные части
При необходимости сократить дробь
Записывают тему урока
Закрепление
Посмотрите на выражения, в тетради записать одни ответы и расположить их в порядке возрастания
Физкультминутка:
Потрудились – отдохнём,
Встанем, глубоко вздохнём.
Руки в стороны, вперёд,
Влево, вправо поворот.
Три наклона, Прямо встань.
Руки вниз и вверх поднять.
всем улыбки подарить.
Домашнее задание.
п. 4.16
№ 991( а,б,в)
992 (а,б,в)
987(а,б)
Где на уроке можно встретиться с вычитанием смешанных чисел?
— Задачи
— Уравнения
Рефлексия
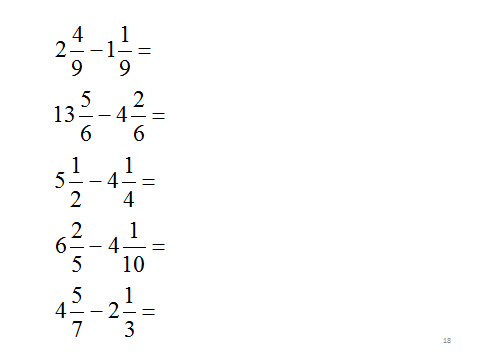
План урока по теме «Сложение и вычитание смешанных чисел»
Тема: Сложение и вычитание смешанных чисел.
Цель:
Познакомить учащихся с алгоритмами сложения и вычитания смешанных чисел путем включения учащихся в практическую деятельность.
Совершенствовать вычислительные навыки, развивать познавательный интерес, внимание, логическое мышление учащихся через игровые моменты.
Воспитывать чувство товарищества и взаимовыручки.
Ход урока.
1. Организационный момент.
Каждый день – всегда, везде,
На занятиях, в игре
Смело четко говорим
И тихонько сидим.
2. Мотивация урока.
Сегодня на уроке мы будем изучать тему «Сложение и вычитание смешанных чисел» и научимся применять новые знания на практике. А урок наш будет необычным – урок-сказка «Цветик-семицветик».
В Математическом царстве, в Арифметическом государстве, в городе Обыкновенная дробь жила-была девочка. Учительница математики дала ей задание: приготовить вопросы и упражнения для урока. Утром девочка отправилась в школу. Идет, по сторонам зевает, вывески читает, ворон считает. Вдруг из-за угла выскочила злая собака, сумку выхватила и убежала.
Села девочка на скамейку и заплакала. Вдруг откуда ни возьмись, Математика – царица наук. И говорит она девочке:
— Не плачь, я тебе помогу. Ты девочка хорошая, хоть и любишь зевать по сторонам. Вот тебе «цветик-семицветик». Он волшебный. Надо только оторвать лепесток и прочитать, что на нем записано.
3. Актуализация опорных знаний. Проверка д/з.
Этот красный лепесток
Начинает наш урок.
Устный счет мы проведем
И рекорды все побьем.
Проверка д/з. Сверка с верными ответами.
Вдруг наш желтый лепесток
Улетает на восток.
К нам с востока возвращается
И работа продолжается.
Фронтальный опрос:
а) Какую дробь называют правильной?
б) Сравните правильную дробь с 1?
в) Какую дробь называют неправильной?
г) Сравните неправильную дробь с 1? 5/6,7/7,2/5,3/10,13/10,18/5
д) Назовите правильные (неправильные) дроби?
е) Как из неправильной дроби выделить целую часть?
ж) Выделите целую часть из неправильных дробей?
з) Как складываются (вычитают) дроби с одинаковыми знаменателями?
Оранжевый лепесток
Продолжает наш урок.
Математический диктант решаем,
Без ошибок отвечаем.
Математический диктант:
Двое учащихся работают на доске, остальные на листах.
1). Из дробей: 7/8, 11/11, 9/4, 16/9, 3/5, 6/13 выберите правильные дроби и неправильные.
2). Сравните выписанные дроби с 1.
3). Выделите в дробях целую часть:
19/8
16/5
25/4
27/11
4). Запишите смешанные числа в виде неправильной дроби:
2 3/7
5 2/3
9 1/12
8 3/7
Поменялись листочками. Сегодня у нас взаимоконтроль, оцените друг друга.
4. Изучение нового материала.
Зеленый цвет весьма приятный,
Лепесточек аккуратный.
Оторвем его мы дружно
И узнаем все, что нужно.
Ребята, а знаете ли вы, как складывают и вычитают смешанные числа?
3 
+ 2 
= (3 + ) + (2 +) = (3 +2) + (+) = 5 + 
= 5
Чтобы смешанные числа сложить
Надо их на части разложить:
3 – это целая часть, прибавим к ней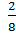
– это дробная часть;
2– это целая часть, прибавим к ней– это дробная часть.
И между суммами поставим знак сложенья.
Чтобы удобно нам было считать
Мы эти числа должны сгруппировать:
Целые части мы сложим отдельно,
И дробные части мы сложим отдельно.
Получили 5– это целая часть,
А– это дробная часть.
Что делать с ними мне скажите
И ответ скорее подскажите. (5 + = 5– получили смешанное число)
Кто может сам сформулировать правило сложения смешанных чисел?
Краткая запись: 3 + 2 = 5
Давайте попробуем выполнить вычитание смешанных чисел (по аналогии):
5– 3 = (5 +) – (3 +)= (5 – 3) + (–) = 2+ = 2
Сформулируйте правило вычитания смешанных чисел.
Краткая запись: 5– 3 = 2.
5. Физминутка
Потрудились — отдохнём,
Встанем, глубоко вздохнём.
Руки в стороны, вперёд,
Влево, вправо поворот.
Три наклона, прямо встать.
Руки вниз и вверх поднять.
Руки плавно опустили,
Всем улыбки подарили.
6. Закрепление нового материала.
Бордовый лепесток мы сорвем,
Ручки в руки мы возьмем.
Смело порешаем
И ответы мы узнаем.
Решить № 748, 750(нечетные), 752(1, 2), 755.
7. Самостоятельная работа.
Серебристый лепесток мы отрываем,
Замок волшебный открываем.
Чтоб в царство знаний нам попасть
Самостоятельно нам надо порешать.
Решить № 752 (3)
8. Итоги урока. Д/з.
— Что такое смешанное число?
— Как сложить смешанные числа?
— Как вычесть смешанные числа?
-Чему мы сегодня научились? ( Складывать и вычитать смешанные числа.)
Это вам поможет справиться с домашним заданием.
Выучить п.26, решить № 749, 750 (2, 4, 6), 756.
Салатовый цветок,
Интересный лепесток.
Его мы отрываем
И кое-что узнаем.
Расшифруйте слова!
1 группа
2 группа
3 группа
4 группа
Ответы:
Смешанных
Чисел
Сложение
Вычитание
(Представитель каждой группы записывает на доске расшифрованное слово).
Изрядно потрудились, собрали вы слова.
Слова же следует теперь соединить,
В какую фразу можно их объединить?
(Сложение и вычитание смешанных чисел).
Вот и закончилась сказка. Добрая волшебница-Математика спасла девочку, а цветик-семицветик помог вам сделать еще один шаг на пути к новым знаниям.
расскажите пожалуйста правило. Как из натурального числа вычесть смешанную дробь?
Разность натурального числа и смешанной дроби представляет собой смешанное число число. Берём натуральное число и вычитаем из него целую часть смешанного числа. Отнимаем ещё единицу. Это будет целая часть искомого смешанного числа. Чтобы получить дробную часть, нужно из знаменателя дробной части данного смешанного числа вычесть числитель — это будет числитель дробной части искомого смешанного числа. Знаменатель равен знаменателю данного смешанного числа. Пример: Вычислить 12 — 4(3/7) 12 — 4 = 8 8 — 1 = 7 Это целая часть искомого смешанного числа 7 — 3 = 4 Это числитель дробной части искомого смешанного числа Знаменатель оставляем прежним. Итак, 12 — 4(3/7) = 7(4/7) Предполагается, что дробная часть данного смешанного числа правильная и несократимая.
Нужно натуральное число записать ввиде дроби. И от дроби отнять смешаное число это делается по специальному правилу.
Не как ххахахахаха гыгыггы
Как вычесть из смешанного числа обыкновенную дробь?
<a href=»/» rel=»nofollow» title=»15907216:##:1OQmRak»>[ссылка заблокирована по решению администрации проекта]</a>
Перевести в неправильную дробь.
переведи смешоное число в неправилную дробь
При вычитании и сложении смешанные числа не переводятся в неправильные дроби. Во-первых, дроби нужно привести к общему знаменателю. Далее, если дробная часть смешанного числа меньше вычитаемой дроби, то из целой части занимается 1 и разбивается на доли. Например: 18 1/4 — 5/6 = 18 3/12 — 10/12 = 17 15/12 — 10/12 = 17 5/12.