Конспект урока «Теорема Фалеса» — геометрия, уроки

Тема: «Теорема Фалеса»

Тип урока: изучение нового материала

Цели:

Образовательные: способствовать закреплению ранее усвоенного теоретического материала; осуществить взаимоконтроль знаний учащихся; сформулировать и доказать теорему Фалеса.

Воспитательные: содействовать в воспитании навыков учебного труда; формировать ответственность за конечный результат; воспитание интерес к предмету.

Развивающие: создать условия для развития логического мышления; выработки умения систематизировать и обобщать.

Ход урока:

1. Организационный момент

Проверить готовность учащихся к уроку.

2. Проверка домашнего задания

Собрать тетради с домашним заданием.

3. Актуализация знаний

1. Какие отрезки называются равными?

2. Какие прямые называются параллельными?

3. Какие углы называются вертикальными, внутренними накрест лежащими?

4. Сформулируйте теорему о свойстве параллельных прямых, пересечённых третьей прямой.

4. Целемотивационный этап

Сегодня на уроке мы с вами познакомимся с новой теоремой, которая носит название «Теорема Фалеса».

Евклид (300г. до н.э.) счёл эту задачу неразрешимой, при этом ранее Фалес (600г. до н.э.) наоборот решил её как частность в своей теореме.

Фалес – купец, политический деятель, астроном, математик, живший в греческом городе Милете, первый доказал ряд геометрических теорем. Эти положения были частично известны еще вавилонянам и египтянам, но в отличие от вавилонской и египетской геометрии, имевшей преимущественно практический характер, греческая геометрия характеризуется стремлением установить, что геометрические факты справедливы в любом случае.

Как философ, Фалес учил, что явления мира не случайны, мир не хаотичен, а закономерен. Он считал, что вода есть начало всего. Из нее возникло все существующее и в нее, в конце концов, опять превращается.

Фалес сделал ряд открытий в области астрономии: установил время равноденствий и солнцестояний, определил продолжительность года, впервые наблюдал Малую медведицу. Особую славу ему принесло предсказание солнечного затмения, происшедшего в 585 г. до н. э. Вот почему он был причислен к группе “семи мудрецов древности”.

Фалес также входил в число знаменитых семи мудрецов, чьи изречения дошли до наших дней.

4. Изучение нового материала

Сформулировать теорему Фалеса.

Теорема (теорема Фалеса). Если на одной стороне угла отложить равные отрезки и через их концы провести параллельные прямые, пересекающие другую сторону угла, то на другой стороне угла отложатся равные отрезки.

Дано: АВ = ВС, АА₁||ВВ₁||СС₁

Доказать: A₁B₁ = B₁C₁.

Доказательство.

1) Проведем AK

A₁C₁, BMA₁C₁, тогда AKBM.

2) ABK=BCM по 2-му признаку (AB=BC по условию, ∠BAK=∠CBM и ∠ABK=∠BCM), значит AK=BM.

3) Т.к. AA₁B₁K и BB₁C₁M — параллелограммы (их противоположные стороны параллельны), то A₁B₁ = AK, B₁C₁ = BM. Значит, A₁B₁ = B₁C₁ ЧТД.

Замечания:

1. Отложенных равных отрезков может быть два, три и более.

2. Теорема Фалеса справедлива не только для сторон угла, но и для произвольных прямых.

Сформулировать теорему, обратную теореме Фалеса.

Теорема (обратная теореме Фалеса). Если на сторонах угла от его вершины отложить равные отрезки, то прямые, проходящие через их концы, будут параллельны.

 

 

 

 

Алгоритм деления отрезка на равные части:

1. Построить отрезок.
2. Построить луч, исходящий из одного из концов отрезка.
3. С помощью циркуля отложить на луче необходимое количество отрезков равной длины.
4. Провести прямую через последнюю точку на луче и другой конец отрезка.
5. Провести прямые, проходящие через оставшиеся точки на луче, параллельные прямой, построенной в предыдущем пункте.
6. Обозначить точки пересечения прямых с отрезком.

Разделить отрезок на три равные части по данному алгоритму на доске.

5. Первичное закрепление изученного материала

Задача на готовом чертеже:

6. Физкультминутка

Разминка шеи, спины и кистей рук.

7. Решение задач

Решаем задачи из учебника:

Устно: № 95, № 96

Письменно: № 98

8.  Домашнее задание: Гл. 1 §7 № 97

9. Подведение итогов. Рефлексия

1. Какова была тема урока?
2. Какую задачу ставили?
3. Каким способом решали поставленную задачу?

• Если вы считаете, что поняли тему урока, то разделите отрезок на 9 равных частей.
• Если вы считаете, что не достаточно усвоили материал, то разделите отрезок на 7 равных частей.
• Если вы считаете, что не поняли тему урока, то разделите отрезок на 3 равные части.

 

 

Алгоритм деления отрезка на равные части:

1. Построить отрезок.
2. Построить луч, исходящий из одного из концов отрезка.
3. С помощью циркуля отложить на луче необходимое количество отрезков равной длины.
4. Провести прямую через последнюю точку на луче и другой конец отрезка.
5. Провести прямые, проходящие через оставшиеся точки на луче, параллельные прямой, построенной в предыдущем пункте.

6. Обозначить точки пересечения прямых с отрезком.

 

 

Алгоритм деления отрезка на равные части:

1. Построить отрезок.
2. Построить луч, исходящий из одного из концов отрезка.
3. С помощью циркуля отложить на луче необходимое количество отрезков равной длины.
4. Провести прямую через последнюю точку на луче и другой конец отрезка.
5. Провести прямые, проходящие через оставшиеся точки на луче, параллельные прямой, построенной в предыдущем пункте.

6. Обозначить точки пересечения прямых с отрезком.

 

 

Алгоритм деления отрезка на равные части:

1. Построить отрезок.
2. Построить луч, исходящий из одного из концов отрезка.
3. С помощью циркуля отложить на луче необходимое количество отрезков равной длины.
4. Провести прямую через последнюю точку на луче и другой конец отрезка.
5. Провести прямые, проходящие через оставшиеся точки на луче, параллельные прямой, построенной в предыдущем пункте.

6. Обозначить точки пересечения прямых с отрезком.

 

 

Алгоритм деления отрезка на равные части:

1. Построить отрезок.
2. Построить луч, исходящий из одного из концов отрезка.
3. С помощью циркуля отложить на луче необходимое количество отрезков равной длины.
4. Провести прямую через последнюю точку на луче и другой конец отрезка.
5. Провести прямые, проходящие через оставшиеся точки на луче, параллельные прямой, построенной в предыдущем пункте.

6. Обозначить точки пересечения прямых с отрезком.

 

 

mega-talant.com

Урок геометрии в 8 классе:»Теорема Фалеса»

Интегрированный урок (математика + информатика)

по теме: «Теорема Фалеса»

Цели урока:

Образовательная: доказать теорему Фалеса, научить применять её при решении задач по математике и информатике.

Развивающая: развивать у учащихся познавательный интерес к учебным дисциплинам, умение применять свои знания на практике.

Воспитательная: воспитывать внимание, аккуратность, расширять кругозор учеников.

Оборудование и материалы:

Компьютер, экран, проектор.
Проектная работа “Теорема Фалеса”.
Программа “Живая геометрия”.
Плакат с рисунками 1,2,3.

Задачи учителей:

Показать практическое применение теоретических знаний учащихся при решении задач по геометрии и информатике.

Выявить глубокие связи между математикой и информатикой.

Ход урока:

Урок начинает учитель математики. Приветствие и вступительное слово о целях урока.

Фронтальный опрос учащихся:

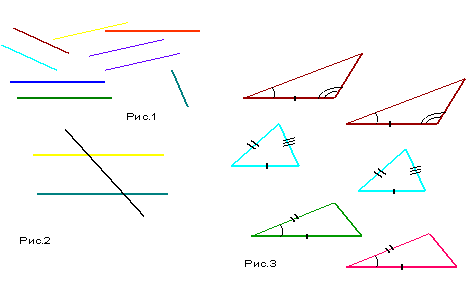
1. Какие отрезки называются равными?

2. Какие прямые называются параллельными? На рис. 1 покажите параллельные прямые.

3. Какие углы называются вертикальными, внутренними накрест лежащими? Покажите их на рис.2

4. Сформулируйте теорему о свойстве параллельных прямых, пересечённых третьей прямой.

5. Сформулируйте признаки равенства треугольников. По каким признакам равны треугольники на рис 3?

Объяснение нового материала

Учитель математики объясняет новую тему с помощью просмотра проектной работы “Теорема Фалеса”.

(Приложение 1)

Сегодня мы докажем теорему, носящую имя древнегреческого учёного Фалеса, который жил в 624-547г.г. до н.э.

 

Великий учёный Фалес Милетский основал одну из прекраснейших наук — геометрию. Известно, что Фалес Милетский имел титул одного из семи мудрецов Греции, что он был поистине первым философом, первым математиком, астрономом и вообще первым по всем наукам в Греции. Короче: он был то же для Греции, что Ломоносов для России.

Карьеру он начинал как купец и ещё в молодости попал в Египет. В Египте Фалес застрял на много лет, изучая науки в Фивах и Мемфисе. Считается, что геометрию и астрономию в Грецию привёз он.

Фалес — математик. Он измерил по тени высоту пирамиды; установил, что окружность диаметром делится пополам, что углы при основании равнобедренного треугольника равны. Ему же принадлежит теорема, что вписанный угол, опирающийся на диаметр окружности- прямой.

Фалес доказал теорему: “Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне”.

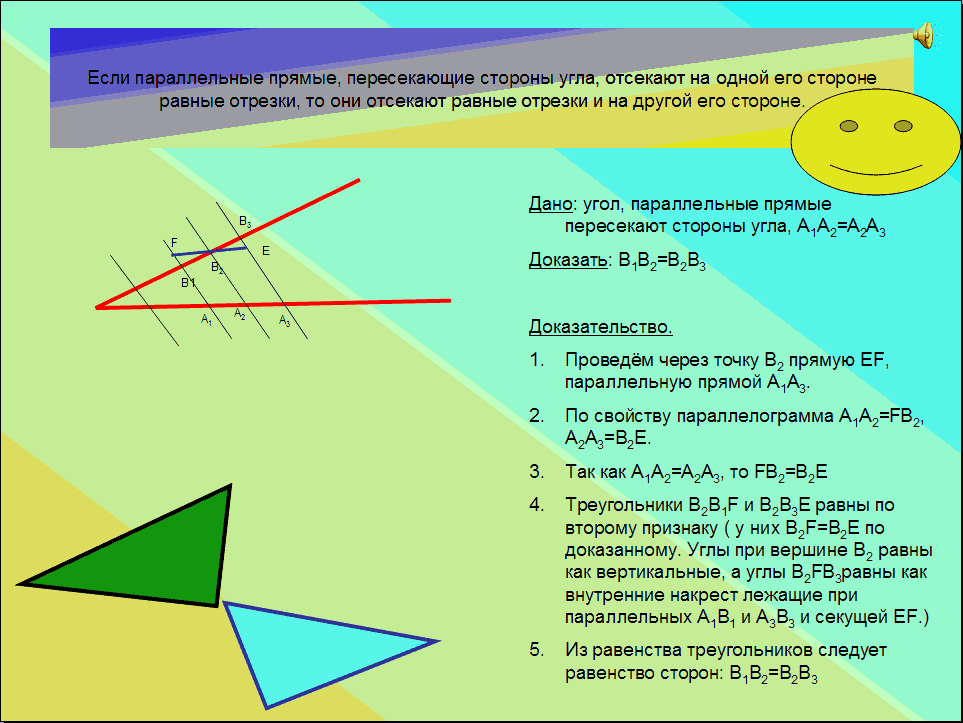
При активном участии учащихся разбирается доказательство теоремы с последовательным показом на экране каждого этапа построения чертежа и доказательства теоремы.

Из условия теоремы Фалеса делается вывод, что вместо сторон угла можно взять любые две прямые.

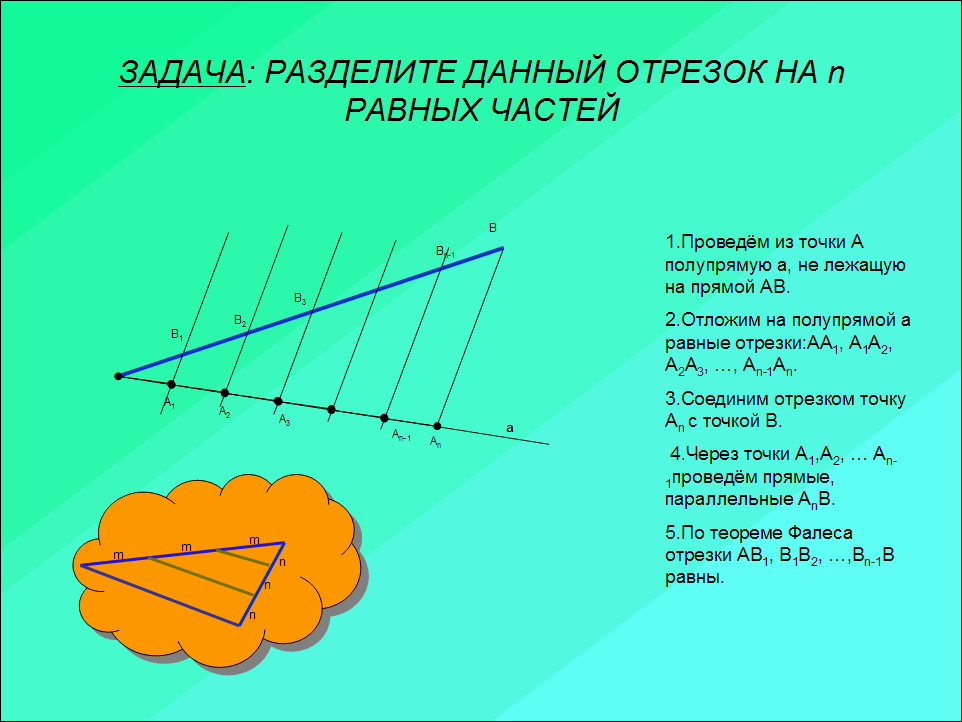
Затем ученики выполняют в тетрадях практическую задачу на деление отрезка длиной в 7см. на 6 равных частей.

Греческие ученые открыли множество геометрических свойств и создали стройную систему геометрических знаний. В ее основу они положили простейшие геометрические свойства, подсказанные опытом. Остальные свойства выводились из простейших с помощью рассуждений.

Все этапы решения задачи учащиеся видят на экране. Это способствует зрительному запоминанию алгоритма решения данной задачи.

Показ проектной работы сопровождается музыкой- игрой на гитаре, что создаёт спокойную рабочую обстановку.

Вторую часть урока ведёт учитель информатики. С помощью программы “Живая геометрия” ученики вместе с учителем на компьютерах делят отрезок на три равные части.

Выполнение практического задания

Разделить данный отрезок на 3-равные части на компьютере с помощью программы “Живая геометрия”.

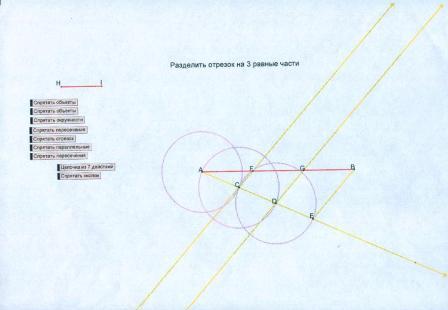
Используемые ИНСТРУМЕНТЫ “Живой геометрии”:

• стрелка;

• линейка (отрезок, луч).

Используемые КОМАНДЫ “Живой геометрии”:

• построения;

• правка;

Порядок работы:

1 .Построим данный отрезок АВ.

2.Проведем из т. А полупрямую а, не лежащую на прямой АВ.

3.Отложим на полупрямой а 3 равных отрезка.

Для этого используем команду ПОСТРОЕНИЯ— “окружность по центру и радиусу”; зададим произвольный радиус СО и построим на полупрямой а 3 окружности.

Они отсекают на полупрямой а равные отрезки АЕ=ЕР=РО.

4.Соединим точки В и О.

5. Проведем через точки Е и Р прямые, параллельные прямой ВО.

6. Они пересекают отрезок АВ в точках Н и I , которые делят отрезок АВ на 3 равные части; т.к. по теореме Фалеса:

Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Домашнее задание.

Задача: Разделить отрезок длиной 5 см. на 7 равных частей. Выучить теорему Фалеса.

Подведение итогов урока.

Приложение

infourok.ru

Теорема Фалеса — это… Что такое Теорема Фалеса?

Эта теорема о параллельных прямых. Об угле, опирающемся на диаметр, см. другую теорему.

Теорема Фалеса — одна из теорем планиметрии.

Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.

В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также неважно, где находятся отрезки на секущих.

Доказательство в случае секущих  

Доказательство в случае параллельных прямых  

Проведем прямую BC. Углы ABC и BCD равны как внутренние накрест лежащие при параллельных прямых AB и CD и секущей BC, а углы ACB и CBD равны как внутренние накрест лежащие при параллельных прямых AC и BD и секущей BC. Тогда по первому признаку равенства треугольников треугольники ABC и DCB равны. Отсюда следует, что AC = BD и AB = CD. ■

Также существует обобщённая теорема Фалеса:

Параллельные прямые отсекают на секущих пропорциональные отрезки:

Теорема Фалеса является частным случаем обобщённой теоремы Фалеса, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.

Обратная теорема

Если в теореме Фалеса равные отрезки начинаются от вершины (часто в школьной литературе используется такая формулировка), то обратная теорема также окажется верной. Для пересекающихся секущих она формулируется так:

Если прямые, пересекающие стороны угла, отсекают на одной и на другой стороне угла равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны.

В обратной теореме Фалеса важно, что равные отрезки начинаются от вершины

Таким образом (см. рис.) из того, что следует, что прямые .

Если секущие параллельны, то необходимо требовать равенство отрезков на обеих секущих между собой, иначе данное утверждение становится неверным (контрпример — трапеция, пересекаемая линией, проходящей через середины оснований).

Вариации и обобщения

Следующее утверждение, двойственно к лемме Соллертинского:

В случае теоремы Фалеса коникой будет бесконечно удалённая точка, соответствующая направлению параллельных прямых.

Это утверждение, в свою очередь, является предельным случаем следующего утверждения:

Пусть  — проективное преобразование коники. Тогда огибающей множества прямых будет коника (возможно, вырожденная).

Теорема Фалеса в культуре

Аргентинская музыкальная группа Les Luthiers (исп.) представила песню, посвящённую теореме. В видеоклипе для этой песни^[1] приводится доказательство для прямой теоремы для пропорциональных отрезков.

Интересные факты

• Теорема Фалеса до сих пор используется в морской навигации в качестве правила о том, что столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется курс судов друг на друга.
• Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла.

Литература

• Атанасян С.Л. Геометрия 7-9. — Изд. 3-е. — М.: Просвещение, 1992.

Примечания

3dic.academic.ru

«Применение теоремы Фалеса для решения практических задач» ( 8 класс)

Пояснительная записка.

Урок геометрии в 8 классе по теме: «Применение теоремы Фалеса для решения практических задач» является 4 уроком в теме «Параллелограмм и трапеция», рассчитанной на 6 часов. Урок практического применения полученных знаний.

Программа общеобразовательных учреждений Геометрия 7-9 классы составитель Т.А.Бурмистрова, 68 часов за год , 2 часа в неделю. Автор учебника — Л.С.Атанасян.

Характеристика класса.

Репродуктивный;

Проблемный;

Частично-поисковый;

Исследовательский

Предпочитают проблемный и поисковый методы обучения.

6. Отношение к различным формам учебной деятельности, в том числе и нестандартных

Принимают различные формы обучения, предпочтение отдают групповой работе, либо соревнование в командах.

Этапы урока.

Домашнее задание:

— выучить теорему Фалеса;

— разделить отрезок на 9 равных частей.

3.Подготовка учащихся к усвоению актуализация опорных знаний.

5

Объяснительно-иллюстративный.

Проверка домашнего задания. Задача, решённая дома встречается при доказательстве теоремы Фалеса, как элемент доказательства.

4.Мотивация учебной деятельности.

5

Проблемная ситуация.

Целеполагание.

Учащимся предлагается разделить отрезок на 5 равных частей. Учащиеся предлагают свои решения, с помощью учителя идёт проверка версий на их состоятельность.

Встаёт проблема деления отрезка на равные части.

5.Изучение нового материала.

10

Использование презентации.

Фронтальная форма работы.

При участии учащихся разбирается доказательство теоремы. Здесь участвует, как элемент доказательства домашняя задача, поэтому один из учащихся выходит к доске и проводит доказательство части теоремы.

6.Применение теории при решении задач.

6

Анализ, сравнение. Воспроизведение.

Использование презентации.

Целеполагание.

Вопрос учителя: Каким образом можно применить теорему, чтобы разделить отрезок на равные части? Если ученик выдвигает устно правильное решение, то учитель показывает с помощью проектора слайды пошагового выполнения действий.

Вопрос учителя: Чьё имя носит эта теорема? Формулируется тема урока.

7.Первичное закрепление нового материала.

7

Письменная работа в тетрадях.

Задание учащимся: Выполнить деление отрезка на 5 равных частей. Учащиеся выполняют построения, потом самостоятельно составляют алгоритм деления отрезка на равные части. Обсуждаем. После обсуждения в справочную тетрадь записываем алгоритм.

8.Первичная проверка усвоения знаний.

9

Работа в группах.

Задания в группах: Разделить ленту (тесьму, верёвку, шнур, деревянную рейку (для мальчиков)) на 3 равные части.

Отчёт групп о проделанной работе.

9.Подведение итогов урока. Рефлексия.

2

Анализ. Беседа

Продолжить предложения:
— На уроке я узнал…
— На уроке научился…

Урок, конспект которого я предлагаю – это урок практического применения полученных знаний. Целями данного урока являлись: развивать у учащихся умение выделять главное, применять раннее полученные знания, сравнивать, анализировать; формирование осознанного отношения к жизненным ситуациям, понимания собственной значимости, аккуратности, умения работать в группе; доказать теорему Фалеса; применить теорему Фалеса при решении задач.

Урок построен на принципах развивающего обучения, что позволило активно задействовать творческую и исследовательскую деятельность.

Особенностями урока является:

1. Интенсивная самостоятельная деятельность учащихся, связанная с эмоциональным переживанием, которая сопровождается эффектом неожиданности задания; помощью и поощрением со стороны учителя.

2. Создание педагогических ситуаций общения на уроке, позволяющих каждому ученику проявлять инициативу, самостоятельность.

3. Создание обстановки для естественного самовыражения ученика.

Всё это позволило учащимся активно включиться в работу с самого начала урока. Успешность и активность работы была достигнута за счет системы заданий, поступающих мелкими порциями. Домашняя задача, разобранная у доски в начале урока, дала возможность учащимся самостоятельно доказать один из этапов доказательства теоремы Фалеса, что создало ситуацию успеха для «слабых» учеников. Наибольший интерес вызвала групповая работа, позволившая практически применить полученные знания. С поставленным заданием учащиеся успешно справились, а значит, цели урока были достигнуты.

Сценарий урока.

Тема урока: «Применение теоремы Фалеса для решения практических задач».

8 класс.

Цели урока:

Развивающая: развивать у учащихся ключевые компетенции — умение выделять главное, применять раннее полученные знания, сравнивать, анализировать;

Воспитывающая: продолжить формирование мировоззрения обучающихся, осознанного отношения к жизненным ситуациям, понимания собственной значимости, аккуратности, умения работать в группе;

Образовательная: сформировать предметные компетенции, доказать теорему Фалеса; применить теорему Фалеса при решении задач.

Ход урока.

1. Организационный момент.

2. Запись домашнего задания: — выучить доказательствотеоремы Фалеса;

— разделить отрезок на 9 равных частей.

3. Проверка домашнего задания.

На доске заготовлен рисунок. Один учащийся выходит к доске и проводит доказательство.

4. Мотивация.

На доске заготовлен отрезок. Учитель формулирует задание:

-разделите отрезок на 4 равные части;

-разделите отрезок на 5 равных частей.

Ясно, что встаёт проблема деления отрезка на равные части. С этой проблемой столкнулись учёные не сейчас, не в этом столетии, а на много веков раннее. И чтобы нам сегодня справиться с возникшей задачей докажем одну из важнейших теорем геометрии.

5. Изучение нового материала, доказательство теоремы.

Теорема: Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.

При участии учащихся разбирается доказательство теоремы. Здесь участвует, как элемент доказательства домашняя задача.

а)

6. Применение теоремы для деления отрезка на равные части.

Вопрос учителя: Как с помощью этой теоремы можно разделить отрезок на равные части?

Учащиеся высказывают своё мнение. Если произносятся верные действия, то с помощью проектора учитель показывает этапы деления отрезка на равные части.

Итак, решение проблемы есть, отрезок разделён на равные части, но кто же был «автором» этой теоремы, чьё имя носит теорема. Здесь учитель обращается к теме урока: «Теорема Фалеса». Фалес — древнегреческий учёный, живший в 624-547г.г. до н.э.

Сопутствующий слайд проектора:

7. Работа в тетрадях.

Задание: Разделите отрезок на 5 равных частей с помощью циркуля и линейки.

Учащиеся выполняют работу, при этом учитель снова показывает слайды по делению отрезка на равные части. Учитель имеет возможность помочь учащимся, которым сложно справиться с заданием.

При участии учащихся записываем в тетрадь алгоритм деления отрезка на равные части.

Алгоритм:

1.Провести луч из конца отрезка.

2.На луче с помощью циркуля отметить равные отрезки.

3.Конец последнего отрезка соединить со свободным концом данного отрезка.

4.Через концы равных отрезков провести прямые параллельные, полученной прямой, до

пересечения с отрезком.

5.Отрезок разделился на равные части.

8. Практическое применение теоремы Фалеса.

Класс делится на группы по 4-5 человек.

Задание для группы: Разделите верёвку (деревянный брусок, ленту, тесьму, шнур) на 5 равных частей.

9. Подведение итогов урока. Рефлексия.
   Продолжить предложения:
   — На уроке я узнал…
   — На уроке научился…

infourok.ru

Теорема Фалеса — это… Что такое Теорема Фалеса?

Эта теорема о параллельных прямых. Об угле, опирающемся на диаметр, см. другую теорему.

Теорема Фалеса — одна из теорем планиметрии.

Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.

В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также неважно, где находятся отрезки на секущих.

Доказательство в случае секущих  

Доказательство в случае параллельных прямых  

Проведем прямую BC. Углы ABC и BCD равны как внутренние накрест лежащие при параллельных прямых AB и CD и секущей BC, а углы ACB и CBD равны как внутренние накрест лежащие при параллельных прямых AC и BD и секущей BC. Тогда по первому признаку равенства треугольников треугольники ABC и DCB равны. Отсюда следует, что AC = BD и AB = CD. ■

Также существует обобщённая теорема Фалеса:

Параллельные прямые отсекают на секущих пропорциональные отрезки:

Теорема Фалеса является частным случаем обобщённой теоремы Фалеса, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.

Обратная теорема

Если в теореме Фалеса равные отрезки начинаются от вершины (часто в школьной литературе используется такая формулировка), то обратная теорема также окажется верной. Для пересекающихся секущих она формулируется так:

Если прямые, пересекающие стороны угла, отсекают на одной и на другой стороне угла равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны.

В обратной теореме Фалеса важно, что равные отрезки начинаются от вершины

Таким образом (см. рис.) из того, что следует, что прямые .

Если секущие параллельны, то необходимо требовать равенство отрезков на обеих секущих между собой, иначе данное утверждение становится неверным (контрпример — трапеция, пересекаемая линией, проходящей через середины оснований).

Вариации и обобщения

Следующее утверждение, двойственно к лемме Соллертинского:

В случае теоремы Фалеса коникой будет бесконечно удалённая точка, соответствующая направлению параллельных прямых.

Это утверждение, в свою очередь, является предельным случаем следующего утверждения:

Пусть  — проективное преобразование коники. Тогда огибающей множества прямых будет коника (возможно, вырожденная).

Теорема Фалеса в культуре

Аргентинская музыкальная группа Les Luthiers (исп.) представила песню, посвящённую теореме. В видеоклипе для этой песни^[1] приводится доказательство для прямой теоремы для пропорциональных отрезков.

Интересные факты

• Теорема Фалеса до сих пор используется в морской навигации в качестве правила о том, что столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется курс судов друг на друга.
• Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла.

Литература

• Атанасян С.Л. Геометрия 7-9. — Изд. 3-е. — М.: Просвещение, 1992.

Примечания

biograf.academic.ru

Теорема Фалеса — это… Что такое Теорема Фалеса?

Эта теорема о параллельных прямых. Об угле, опирающемся на диаметр, см. другую теорему.

Теорема Фалеса — одна из теорем планиметрии.

Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.

В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также неважно, где находятся отрезки на секущих.

Доказательство в случае секущих  

Доказательство в случае параллельных прямых  

Проведем прямую BC. Углы ABC и BCD равны как внутренние накрест лежащие при параллельных прямых AB и CD и секущей BC, а углы ACB и CBD равны как внутренние накрест лежащие при параллельных прямых AC и BD и секущей BC. Тогда по первому признаку равенства треугольников треугольники ABC и DCB равны. Отсюда следует, что AC = BD и AB = CD. ■

Также существует обобщённая теорема Фалеса:

Параллельные прямые отсекают на секущих пропорциональные отрезки:

Теорема Фалеса является частным случаем обобщённой теоремы Фалеса, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.

Обратная теорема

Если в теореме Фалеса равные отрезки начинаются от вершины (часто в школьной литературе используется такая формулировка), то обратная теорема также окажется верной. Для пересекающихся секущих она формулируется так:

Если прямые, пересекающие стороны угла, отсекают на одной и на другой стороне угла равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны.

В обратной теореме Фалеса важно, что равные отрезки начинаются от вершины

Таким образом (см. рис.) из того, что следует, что прямые .

Если секущие параллельны, то необходимо требовать равенство отрезков на обеих секущих между собой, иначе данное утверждение становится неверным (контрпример — трапеция, пересекаемая линией, проходящей через середины оснований).

Вариации и обобщения

Следующее утверждение, двойственно к лемме Соллертинского:

В случае теоремы Фалеса коникой будет бесконечно удалённая точка, соответствующая направлению параллельных прямых.

Это утверждение, в свою очередь, является предельным случаем следующего утверждения:

Пусть  — проективное преобразование коники. Тогда огибающей множества прямых будет коника (возможно, вырожденная).

Теорема Фалеса в культуре

Аргентинская музыкальная группа Les Luthiers (исп.) представила песню, посвящённую теореме. В видеоклипе для этой песни^[1] приводится доказательство для прямой теоремы для пропорциональных отрезков.

Интересные факты

• Теорема Фалеса до сих пор используется в морской навигации в качестве правила о том, что столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется курс судов друг на друга.
• Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла.

Литература

• Атанасян С.Л. Геометрия 7-9. — Изд. 3-е. — М.: Просвещение, 1992.

Примечания

dik.academic.ru