Как избавиться от дроби в уравнении. Как решать уравнения с дробями
До сих пор мы решали только уравнения целые относительно неизвестного, то есть уравнения, в которых знаменатели (если таковые имелись) не содержали неизвестное.
Часто приходится решать уравнения, содержащие неизвестное в знаменателях: такие уравнения называются дробными.
Чтобы решить это уравнение, умножим обе его части на то есть на многочлен, содержащий неизвестное. Будет ли новое уравнение равносильно данному? Чтобы ответить на вопрос, решим это уравнение.
Умножив обе части его на , получим:
Решив это уравнение первой степени, найдём:
Итак, уравнение (2) имеет единственный корень
Подставив его в уравнение (1), получим:
Значит, является корнем и уравнения (1).
Других корней уравнение (1) не имеет. В нашем примере это видно, например, из того, что в уравнении (1)
Как неизвестный делитель должен быть равен делимому 1, разделённому на частное 2, то есть
Итак, уравнения (1) и (2) имеют единственный корень Значит, они равносильны.
2. Решим теперь такое уравнение:
Простейший общий знаменатель: ; умножим на него все члены уравнения:
После сокращения получим:
Раскроем скобки:
Приведя подобные члены, будем иметь:
Решив это уравнение, найдём:
Подставив в уравнение (1), получим:
В левой части получили выражения, не имеющие смысла.
Значит, корнем уравнения (1) не является. Отсюда следует, что уравнения (1) и неравносильны.
Говорят в этом случае, что уравнение (1) приобрело посторонний корень.
Сравним решение уравнения (1) с решением уравнений, рассмотренных нами раньше (см. § 51). При решении этого уравнения нам пришлось выполнить две такие операции, которые раньше не встречались: во-первых, мы умножили обе части уравнения на выражение, содержащее неизвестное (общий знаменатель), и, во-вторых, мы сокращали алгебраические дроби на множители, содержащие неизвестное.
Сравнивая уравнение (1) с уравнением (2), мы видим, что не все значения х, допустимые для уравнения (2), являются допустимыми для уравнения (1).
Именно числа 1 и 3 не являются допустимыми значениями неизвестного для уравнения (1), а в результате преобразования они стали допустимыми для уравнения (2). Одно из этих чисел оказалось решением уравнения (2), но, разумеется, решением уравнения (1) .оно быть не может. Уравнение (1) решений не имеет.
Этот пример показывает, что при умножении обеих частей уравнения на множитель, содержащий неизвестное, и при сокращении алгебраических дробей может получиться уравнение, неравносильное данному, а именно: могут появиться посторонние корни.
Отсюда делаем такой вывод. При решении уравнения, содержащего неизвестное в знаменателе, полученные корни надо проверять подстановкой в первоначальное уравне
www.yuriste.ru
Как решать дробные уравнения. Уравнения с дробями правила решения
Уравнение — это равенство, содержащее букву, значение которой надо найти.
В уравнениях неизвестное обычно обозначается строчной латинской буквой. Чаще всего используют буквы « x » [икс] и « y » [игрек].
Решив уравнение, всегда после ответа записываем проверку.
Информация для родителей
Уважаемые родители, обращаем ваше внимание на то, что в начальной школе и в 5 классе дети НЕ знают тему «Отрицательные числа».
Поэтому они должны решать уравнения, используя только свойства сложения, вычитания, умножения и деления. Методы решения уравнений для 5 класса приведены ниже.
Не пытайтесь объяснить решение уравнений через перенос чисел и букв из одной части уравнения в другую с изменением знака.
Освежить знания по понятиям, связанным со сложением, вычитанием, умножением и делением вы можете в уроке «Законы арифметики».
Решение уравнений на сложение и вычитание
Как найти неизвестное
слагаемое
Как найти неизвестное
уменьшаемое
Как найти неизвестное
вычитаемое
Чтобы найти неизвестное слагаемое, надо от суммы отнять известное слагаемое.
Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Чтобы найти неизвестное вычитаемое, надо от уменьшаемого отнять разность.
x + 9 = 15
x = 15 − 9
x = 6
Проверка
x − 14 = 2
x = 14 + 2
x = 16
Проверка
16 − 2 = 14
14 = 14
5 − x = 3
x = 5 − 3
x = 2
Проверка
Решение уравнений на умножение и деление
Как найти неизвестный
множитель
Как найти неизвестное
делимое
Как найти неизвестный
делитель
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Чтобы найти неизвестное делимое, надо частное умножить на делитель.
Чтобы найти неизвестный делитель, надо делимое разделить на частное.
y · 4 = 12
y = 12: 4
y = 3
Проверка
y: 7 = 2
y = 2 · 7
y = 14
Проверка
8: y = 4
y = 8: 4
y = 2
Проверка
Уравнение — это равенство, содержащее букву, знамение которой нужно найти. Решение уравнения — это тот набор значений букв, при котором уравнение превращается в верное равенство:
Напомним, что для решения уравнении надо слагаемые с неизвестным перенести в одну часть равенства, а числовые слагаемые в другую, привести подобные и получить такое равенство:
Из последнего равенства определим неизвестное по правилу: «один из множителей равен частному, деленному на второй множитель».
ismcomp.ru
Дробные выражения. Видеоурок. Математика 6 Класс
Что же такое дробь? Например, дробь
– это деление числа 7 на число 12, записанное с помощью дробной черты.
Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением.
Примеры дробных выражений:
Дробь также является дробным выражением.
У дробного выражения существуют эквивалентные, равные ему, выражения. Выбрать из всех эквивалентных выражений самое простое – значит упростить дробное выражение.
Пример
Упростить дробное выражение:
Решение
Выполним вычитание в числители и сложение в знаменателе:
Разделим числитель и знаменатель на 17:
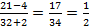
Ответ: 
.
Упростите дробное выражение:
Решение
В числителе и знаменателе – смешанные дроби. Чтобы разделить одну смешанную дробь на другую, нужно обе записать как неправильные.
Получившееся дробное выражение эквивалентно произведению дробных выражений:
Сократим знаменатель первой дроби и числитель второй дроби на 3:
Ответ: 
.
Сложите дробные выражения:
Решение
1 способ
Приведем эти дробные выражения к одному знаменателю, для этого умножим числитель и знаменатель первой дроби на 2:
Чтобы избавиться от десятичной дроби в знаменателе, умножим числитель и знаменатель на 10:
Сократим числитель и знаменатель на 7:
2 способ
Можно сразу избавиться от десятичных дробей в знаменателях, для этого умножим числитель и знаменатель каждой дроби на 10:
Далее приводим два дробных выражения к общему знаменателю:
Сократим числитель и знаменатель на 7:
Ответ: 
.
Упростите дробное выражение:
Решение
Преобразуем числитель и знаменатель в обыкновенные дроби:
Запишем получившееся выражение с помощью знака деления:
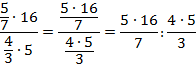
Чтобы разделить на дробь, нужно умножить на перевернутую дробь:
Числитель первой дроби и знаменатель второй можно сократить на 5 и на 4:
Ответ: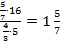 
.
Упростите дробное выражение:
1. 
Решение
Преобразуем числитель и знаменатель в обыкновенные дроби:
Запишем это дробное выражение с помощью знака деления, а далее заменим знак деления на знак умножения и перевернем вторую дробь:
Сократим числитель первой дроби и знаменатель второй на 3 и 7, а числитель второй дроби и знаменатель первой – на 5:
Сократим числитель и знаменатель на 2:
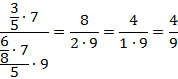
2) 
Решение
Преобразуем числитель первого дробного выражения и знаменатель второго:
Распишем данные дробные выражения с помощью знака деления:
Заменим знаки деления на знаки умножения и перевернем соответствующие дроби:
Первое дробное выражение сократим на 9:
Приведем дробные выражения к общему знаменателю, для этого числитель и знаменатель первого выражения умножим на 3, а числитель и знаменатель второго выражения умножим на 7:
Вычислим числители обеих дробей и сложим эти дроби:
Сократим полученную дробь на 2:
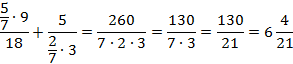
Ответ: 1. 
; 2. 
.
Преобразование «многоэтажных» дробей
Существует очень простой алгоритм, который позволяет за одно действие разобрать «многоэтажную» дробь и получить обычную «двухэтажную».
Необходимо после знака равно начертить дробную черту и для каждого элемента из «многоэтажной» дроби найти его место в новой дроби. Для этого нужно рассмотреть каждое число в исходной дроби.
Если число находилось в исходной дроби нечетное число раз в знаменателе, то в новой дроби оно окажется в знаменателе; если число находилось в исходной дроби четное число раз в знаменателе или не находилось в знаменателе вообще, то в новой дроби оно окажется в числителе.
Рассмотрим примеры.
Упростите дробные выражения.
1. 
Рассмотрим каждое число данного дробного выражения:
Число 5 (в данном выражении две пятерки, их рассматриваем отдельно) находится в числителе дроби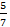 
и в числителе всего исходного дробного выражения. То есть не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;
число 7 находится в знаменателе дроби 
и в числителе всего исходного дробного выражения. То есть находится в знаменателе нечетное число раз, следовательно, в новой дроби это число окажется в знаменателе;
число 16 находится в числителе всего исходного дробного выражения. То есть не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;
число 4 находится в числителе дроби 
и в знаменателе всего исходного дробного выражения. То есть находится в знаменателе нечетное число раз, следовательно, в новой дроби это число окажется в знаменателе;
число 3 находится в знаменателе дроби и в знаменателе всего исходного дробного выражения. То есть находится в знаменателе четное число раз, следовательно, в новой дроби это число окажется в числителе;
число 5 находится в знаменателе всего дробного выражения. То есть находится в знаменателе нечетное число раз, следовательно, в новой дроби это число окажется в знаменателе.
Запишем полученное дробное выражение:
Сократим числитель и знаменатель на 5 и на 4:
2.
Рассмотрим каждое число данного дробного выражения:
Число 3 не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;
число 5 находится в знаменателе дроби 
, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе;
число 7 не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;
число 6 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе;
число 8 находится в знаменателе дроби 
и в знаменателе всего дробного выражения, то есть четное количество раз, следовательно, в новой дроби это число окажется в числителе;
число 7 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе;
число 5 находится в знаменателе всего дробного выражения и в знаменателе выражения 
, то есть четное количество раз, следовательно, в новой дроби это число окажется в числителе;
число 9 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе.
Запишем полученное дробное выражение:
Сократим числитель и знаменатель на 5, 7, 2 и 3:
3.
Рассмотрим числа в каждом дробном выражении:
а) выражение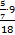 
Число 5 не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;
число 7 находится в знаменателе дроби , то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе;
число 9 не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;
число 18 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе.
б) выражение 
Число 5 не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;
число 2 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе;
число 7 находится в знаменателе дроби 
и в знаменателе всего дробного выражения, то есть четное количество раз, следовательно, в новой дроби это число окажется в числителе;
число 3 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе.
Запишем полученные дробные выражения:
Сократим числитель и знаменатель первого выражения на 9:
Приведем дробные выражения к общему знаменателю, для этого числитель и знаменатель первого выражения умножим на 3, а числитель и знаменатель второго выражения умножим на 7:
Вычислим числители обеих дробей и сложим эти дроби:
Сократим полученную дробь на 2:
Ответ: 1. 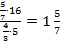; 2. ; 3. .
Чтобы найти значение выражения с переменными, необходимо подставить в это выражение значения этих переменных. Но предварительно имеет смысл упростить выражение, если это возможно.
Найти значение выражения.
1. 
, при 
; 
Решение
Упростим данное выражение. Приведем слагаемые к общему знаменателю, для этого умножим числитель и знаменатель второй дроби на 2:
Подставим в полученное выражение значение переменных:
2. 
, при 
; 
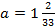Решение
Упростим данное выражение. Приведем слагаемые к общему знаменателю, для этого умножим числитель и знаменатель второй дроби на 2:
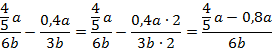
Так как 
, то:
Мы получили ответ, даже не подставив значения переменных.
Ответ: 
. 1; 2. 0.
Список литературы
1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. – М.: Мнемозина, 2012.
2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. – Гимназия. 2006.
3. Депман И.Я., Виленкин Н.Я. За страницами учебн
interneturok.ru
Как избавиться от знаменателя дроби в уравнении. Как решить рациональное уравнение
Дробные уравнения. ОДЗ.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Продолжаем осваивать уравнения. Мы уже в курсе, как работать с линейными уравнениями и квадратными. Остался последний вид – дробные уравнения . Или их ещё называют гораздо солиднее – дробные рациональные уравнения . Это одно и то же.
Дробные уравнения.
Как ясно из названия, в этих уравнениях обязательно присутствуют дроби. Но не просто дроби, а дроби, у которых есть неизвестное в знаменателе . Хотя бы в одном. Например:
Напомню, если в знаменателях только числа , это линейные уравнения.
Как решать дробные уравнения ? Прежде всего – избавиться от дробей! После этого уравнение, чаще всего, превращается в линейное или квадратное. А дальше мы знаем, что делать… В некоторых случаях оно может превратиться в тождество, типа 5=5 или неверное выражение, типа 7=2. Но это редко случается. Ниже я про это упомяну.
Но как избавиться от дробей!? Очень просто. Применяя всё те же тождественные преобразования.
Нам надо умножить всё уравнение на одно и то же выражение. Так, чтобы все знаменатели посокращались! Всё сразу станет проще. Поясняю на примере. Пусть нам требуется решить уравнение:
Как учили в младших классах? Переносим все в одну сторону, приводим к общему знаменателю и т.д. Забудьте, как страшный сон! Так нужно делать, когда вы складываете или вычитаете дробные выражения. Или работаете с неравенствами. А в уравнениях мы сразу умножаем обе части на выражение, которое даст нам возможность сократить все знаменатели (т.е., в сущности, на общий знаменатель). И какое же это выражение?
В левой части для сокращения знаменателя требуется умножение на х+2 . А в правой требуется умножение на 2. Значит, уравнение надо умножать на 2(х+2) . Умножаем:
Это обычное умножение дробей, но распишу подробно:
Обратите внимание, я пока не раскрываю скобку (х + 2) ! Так, целиком, её и пишу:
В левой части сокращается целиком (х+2) , а в правой 2. Что и требовалось! После сокращения получаем линейное уравнение:
А это уравнение уже решит всякий! х = 2 .
Решим ещё один пример, чуть посложнее:
Если вспомнить, что 3 = 3/1, а 2х = 2х/ 1, можно записать:
И опять избавляемся от того, что нам не очень нравится – от дробей.
Видим, что для сокращения знаменателя с иксом, надо умножить дробь на (х – 2) . А единицы нам не помеха. Ну и умножаем. Всю левую часть и всю правую часть:
Опять скобки (х – 2) я не раскрываю. Работаю со скобкой в целом, как будто это одно число! Так надо делать всегда, иначе ничего не сократится.
С чувством глубокого удовлетворения сокращаем (х – 2) и получаем уравнение безо всяких дробей, в линеечку!
А вот теперь уже раскрываем скобки:
Приводим подобные, переносим всё в левую часть и получаем:
Но до того мы другие задачи научимся решать. На проценты. Те ещё грабли, между прочим!
Если Вам нравится этот сайт…
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. В 5 классе школьники по математике изучают довольно много новых тем, одной из которых будет дробные уравнения. Для многих это довольно сложная тема, в которой родители должны помочь разобраться своим детям, а если родители забыли математику, то они всегда могут воспользоваться онлайн программами, решающими уравнения. Так на примере вы сможете быстро понять алгоритм решения уравнений с дробями и помочь своему ребенку.
Ниже для наглядности мы решим несложное дробное линейное уравнение следующего вида:
\[\frac{x-2}{3} — \frac{3x}{2}=5\]
Чтобы решить данного рода уравнения необходимо определить НОЗ и умножить на него левую и правую часть уравнения:
\[\frac {x-2}{3} — \frac{3x}{2}=5\]
Благодаря этому мы получим простое линейное уравнение, поскольку общий знаменатель, а также знаменатель каждого дробного члена сократится:
Сделаем перенос членов с неизвестной в левую сторону:
Выполним деление левой и правой части на -7:
Из полученного результата можно выделить целую часть, что и будет конечным результатом решения данного дробного уравнения:
Где можно решить уравнение с дробями онлайн?
Решить уравнение вы можете на нашем сайте https://сайт. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
Продолжаем разговор про решение уравнений . В этой статье мы подробно остановимся на рациональных уравнениях и принципах решения рациональных уравнений с одной переменной. Сначала р
hookahday.ru
Как решать уравнения с дробями
При решении уравнений с дробями нужно придерживаться очень простого алгоритма:
- Лучше всего найти наименьший общий знаменатель (НОЗ) или просто общий знаменатель.
- Умножить на него все члены.
- Сократить.
После выполнения этих действий мы получим обычное уравнение, которое уже не будет содержать дроби. Далее уравнение решается, но в конце решения необходимо выяснить, не будет ли найденный корень превращать знаменатель в ноль.
Если знаменатель дробей уравнения содержит только числа, то такие уравнения называются линейными.
Пример.
Решим простое уравнение .
Решение.
В левой части уравнения оставим слагаемое с неизвестным, все остальное перенесем в правую часть уравнения:
Умножим обе части уравнения на знаменатель 13:
Ответ. .
Рассмотрим уравнение, в котором знаменатель содержит неизвестное. Такие уравнения называют дробными или дробно-рациональными.
При решении уравнений такого типа также избавляются от дробей, после чего практически всегда они превращаются в линейное или квадратное уравнение.
Необходимо учитывать следующее:
- если при решении получают значение переменной, которое обращает знаменатель в 0, то такое значение не может быть корнем;
- недопустимо умножать или делить уравнение на выражение, которое равно 0.Пример.
Решим дробное уравнение .Решение.
Знаменатель может обратиться в нуль при — не может быть корнем.
В левой части уравнения оставим слагаемые с неизвестным, остальные перенесем в правую часть уравнения:Избавимся от знаменателя с помощью умножения обеих частей уравнения на знаменатель х:
Осталось решить уравнение:
Ответ. .
ru.solverbook.com
Ответы@Mail.Ru: Как избавляются от знаменателя?
На фото изображение практически наразличимо. Если речь идет об избавлении от знаменателя в уравнении, нужно все числители дробей обеих частей уравнения умножить на произведение знаменателей всех дробей и сократить знаменатели.
правую часть разделить на знаменатель
домнажай все части на этот знаменатель
Если вы хотите от него избавиться, надо его кому-нибудь заказать…
тоесть все знаменатели приведи к одному и умнож все числители на него
Домножьте числитель на этот знаменатель. Они и сократятся.
touch.otvet.mail.ru