6 способов найти площадь трапеции

1. Как найти площадь трапеции через основания и высоту

Посчитайте сумму оснований трапеции.

Умножьте результат на высоту и поделите на два.

Иллюстрация: Лайфхакер

• S – искомая площадь трапеции.
• a и b – основания трапеции (её параллельные стороны).
• h – высота трапеции.

2. Как вычислить площадь трапеции через высоту и среднюю линию

Просто умножьте высоту трапеции на среднюю линию.

Иллюстрация: Лайфхакер

• S – искомая площадь трапеции.
• m – средняя линия трапеции (отрезок, соединяющий середины боковых сторон).
• h – высота трапеции.

3. Как найти площадь трапеции через диагонали и угол между ними

Умножьте одну диагональ на другую, а затем — на синус любого угла между ними.

Поделите результат на два.

Иллюстрация: Лайфхакер

• S – искомая площадь трапеции.
• x и y – диагонали трапеции.
• α – любой угол между диагоналями.

4. Как найти площадь трапеции через четыре стороны

Отнимите от большего основания меньшее.

Найдите квадрат полученного числа.

Прибавьте к результату квадрат одной боковой стороны и отнимите квадрат второй.

Поделите полученное число на удвоенную разность оснований.

Найдите квадрат результата и отнимите его от квадрата боковой стороны.

Найдите корень из полученного числа.

Умножьте результат на половину от суммы оснований.

Иллюстрация: Лайфхакер

• S – искомая площадь трапеции.
• a, b – основания трапеции.
• c, d – боковые стороны.

5. Как вычислить площадь равнобедренной трапеции через четыре стороны

Отнимите от большего основания трапеции меньшее и поделите результат на два.

Найдите квадрат полученного числа и отнимите его от квадрата боковой стороны.

Найдите корень из результата.

Умножьте полученное число на сумму оснований и поделите на два.

Иллюстрация: Лайфхакер

• S — искомая площадь трапеции.
• a, b — основания трапеции.
• c, d — боковые стороны (напомним, в равнобедренной трапеции они равны).

6. Как найти площадь равнобедренной трапеции через радиус вписанной окружности и угол

Найдите квадрат радиуса и умножьте его на четыре.

Поделите результат на синус известного угла.

Иллюстрация: Лайфхакер

• r — радиус вписанной окружности.
• α — любой угол трапеции.

Читайте также 📐✏️🎓

Площадь трапеции — онлайн калькулятор

Чтобы найти площадь трапеции воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Через длины оснований и высоту

Чему равна площадь трапеции если известны основания a и b, а также высота h?

Формула

S = ½ ⋅ (a + b) ⋅ h

Пример

Если у трапеции основание a = 3 см, основание b = 6 см, а высота h = 4 см, то её площадь:

S = ½ ⋅ (3 + 6) ⋅ 4 = 36 / 2 = 18 см²

Через среднюю линию и высоту

Чему равна площадь трапеции если известны средняя линия m и высота h?

Формула

S = m ⋅ h

Пример

Если у трапеции средняя линия m = 6 см, а высота h = 4 см, то её площадь:

S = 6 ⋅ 4 = 24 см²

Через длины сторон и оснований

Чему равна площадь трапеции если известны основания a и b, а также стороны c и d?

Формула

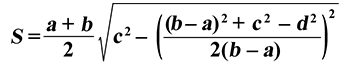
Пример

Если у трапеции основание a = 2 см, основание b = 6 см, сторона c = 4 см, а сторона d = 7 см, то её площадь:

S ≈ 13.555 см²

Через диагонали и угол между ними

Чему равна площадь трапеции если известны диагонали d₁ и d₂ и угол между ними α?

Формула

S = ½ ⋅ d₁ ⋅ d₂ ⋅ sin(α)

Пример

Если у трапеции одна диагональ d₁ = 5 см, другая диагональ d₂ = 7 см, а угол между ними ∠α = 30°, то её площадь:

S = ½ ⋅ 5 ⋅ 7 ⋅ sin (30) = 17.5 ⋅ 0.5= 8.75 см²

Площадь равнобедренной трапеции

Через среднюю линию, боковую сторону и угол при основании

Чему равна площадь равнобедренной трапеции если средняя линия m, боковая сторона с, a угол при основании α?

Формула

S = m ⋅ c ⋅ sin(α)

Пример

Если у равнобедренной трапеции средняя линия m = 6 см, сторона c = 4 см, а угол при основании ∠α = 30°, то её площадь:

S = 6 ⋅ 4 ⋅ sin (30) = 24 ⋅ 0.5 = 12 см²

Через радиус вписанной окружности

Чему равна площадь равнобедренной трапеции если радиус вписанной окружности r, a угол при основании

α?

Формула

S = ^4⋅r² ⁄ _sin(α)

Пример

Если у равнобедренной трапеции радиус вписанной окружности r = 5 см, а угол при основании ∠α = 30°, то её площадь:

S = 4 ⋅ 5² / sin (30) = 100 / 0.5 = 200 см²

См. также

Площадь трапеции (формула) и как ее найти для любой трапеции на рисунке

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В этой статье мы расскажем, как посчитать площадь трапеции. Эту тему подробно изучают в школе в 8-м классе.

Но в классической программе учителя дают далеко не все формулы, с помощью которых можно вычислить нужное значение. И ограничиваются, как правило, одной или двумя.

Мы же дадим максимально развернутый ответ на этот вопрос. Ведь трапеция – это весьма примечательная и сложная фигура в геометрии. А соответственно, и формулы для вычисления ее площади отличаются определенной сложностью и громоздкостью.

Тут нет банальных «перемножить длины сторон», как у площади прямоугольника. Все гораздо мудреней.

Что такое трапеция

Но для начала будет нелишним напомнить, что из себя представляет трапеция.

Трапеция – это геометрическая фигура, которая является четырехугольником, и у которой две противоположные стороны параллельны.

Последнее утверждение очень важное. ТОЛЬКО ДВЕ противоположные стороны параллельны у трапеции. Ведь если бы обе пары лежали на параллельных прямых, то это был бы уже параллелограмм.

Вот так выглядит трапеция:

А вот так параллелограмм:

Кстати, именно по этому принципу древний математик Евклид и разделил все четырехугольники на две большие категории.

Именно он впервые описал разные геометрические фигуры, в том числе трапеции и параллелограммы. И все свои соображения подробно изложил в книге «Начала», которая датируется 300 годом до нашей эры.

Что такое площадь

Раз уж мы решили вычислять эту величину, напомним, что она обозначает.

Площадь – это численное значение геометрической фигуры, нарисованной в двухмерном (плоском) пространстве. А проще говоря, это пространство, которое ограничено границами фигуры, и находится как бы внутри нее.

В нашем случае площадь трапеции – это область, закрашенная синим цветом:

Кстати, в древности вместо термина «площадь» говорили «квадратура». Считалось, что любую фигуру можно разбить на равные квадраты со стороной «один». Частично это понятие докатилось и до наших дней.

Ведь именно в «квадратных метрах» мы измеряем площадь комнаты/квартиры/дачи/офиса. И в «квадратных километрах» частенько озвучивают площадь какой-то территории. Например, когда в телевизионных новостях говорят о масштабах лесных пожаров или наводнений.

Главная формула для вычисления площади трапеции

Та формула, которую изучают в школе, основана на вычислении площади трапеции по длине ее оснований и высоте.

Основания трапеции – это стороны, которые лежат на параллельных прямых. Другая пара сторон называется боковыми.

Высота – это отрезок, проведенный из вершины любого угла к противоположному основанию под углом 90 градусов.

То есть мы имеем вот такие исходные данные:

Здесь «a» и «b» являются основаниями трапеции, а «h» — высотой.

И тогда формула для вычисления площади трапеции выглядит вот так:

Например, если длины сторон и высота равны:

1. a = 7 см
2. b = 3 см
3. h = 5 см

то площадь такой трапеции будет равна:

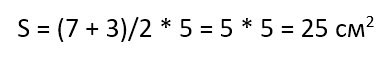
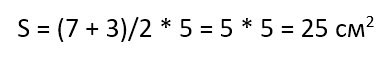
Опять же заметьте, если стороны и высота у трапеции обозначались в сантиметрах, то площадь будет измеряться в квадратных сантиметрах (то самое понятие «квадратуры», о котором мы писали выше).

То же самое – миллиметры/квадратные миллиметры, метры/квадратные метры, километры/квадратные километры и так далее.

Доказательство теоремы о площади трапеции

Любая формула в геометрии требует доказательства. И в нашем случае, формулы вычисления площади трапеции также доказывают во время уроков.

Возьмем для примера трапецию:

В ней AD и BC – основания, BH – высота. Нам надо доказать, что:

Доказательство строится на том, что если провести диагональ BD, то она разделит нашу трапецию на два треугольника. Это будут треугольники ABD и BCD.

И чтобы получить площадь нашей трапеции, нужно посчитать отдельно площади этих треугольников и сложить их.

А как вычислять площадь треугольника, мы уже знаем (или должны знать, согласно школьному курсу). Надо перемножить длину его основания и высоту и поделить на два.

У треугольника ABD высота – это BH. А у треугольника BCD в силу его выпуклости нам пришлось продлить зрительно основание BC, чтобы получить высоту Dh2.

И получается:

Но в случае с трапецией высоты равны, то есть BH = Dh2. И тогда формулу площади для второго треугольника можно заменить на:

И наконец, с учетом всего вышесказанного начинаем вычислять площадь нашей трапеции. Она равна:

Как часто говориться на уроках геометрии – что и требовалось доказать!

Извиняемся за столь подробное описание доказательства. Но, во-первых, это требуется в рамках школьной программы. А во-вторых, всегда ведь интересно докопаться до самой сути и понять, как и почему именно так что-то устроено.

Как еще можно найти площадь трапеции (другие формулы)

На этот раз мы уже не будем приводить подробные доказательства каждой из формул. Иначе это займет слишком много времени и места. Просто поверьте, все они правильные и по ним можно вычислить площадь трапеции.

По высоте и средней линии

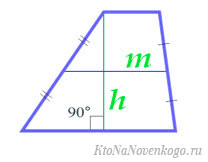
Средняя линия – это та, которая делит боковые стороны трапеции на две равные части. Формула площади выглядит совсем просто:

По четырем сторонам

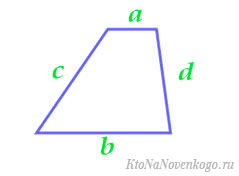
Тут формула гораздо сложнее:

Площадь трапеции через диагонали

По основанию и углам при нем

Формулы площади для равнобедренной трапеции

Равнобедренная трапеция – та, у которой боковые стороны равны. А соответственно, они еще и соприкасаются с основаниями под одинаковыми углами.

Это частный случай, и для него верны все перечисленные формулы. Но с учетом равенства сторон и углов формулы заметно упрощаются.

По четырем сторонам

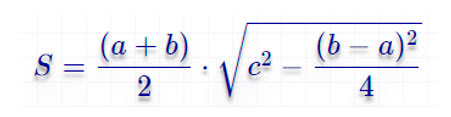
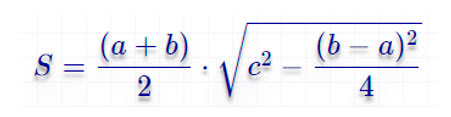
По малому основанию, боковой стороне и углу у большого основания

По большому основанию, углу при нем и боковой стороне

По основаниям и углам

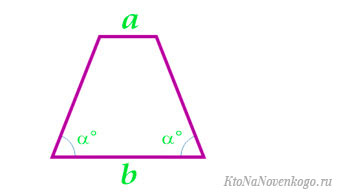
Как видите, формулы громоздкие и весьма сложные сами по себе. Без калькулятора здесь точно не обойтись. С другой стороны, они крайне редко применяются. И служат скорее дополнительными средствами.

Вот и все, что мы хотели рассказать о том, как вычислять площадь трапеции.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Использую для заработка

Рубрика: ЧАстые ВОпросы

формула с основаниями, без высоты

Трапеция – это геометрическая фигура; четырехугольник, имеющий 2 параллельные и 2 непараллельные стороны.

Формулы вычисления площади

По длине оснований и высоте

Площадь трапеции (S) равняется половине суммы ее оснований, умноженной на высоту, проведенную к ним.

Через длины всех сторон (Формула Герона)

Для вычисления площади трапеции необходимо знать длины всех ее сторон:

p – полупериметр трапеции, считается по формуле:

Через диагонали и угол между ними

Площадь трапеции равна половине произведения диагоналей и синуса угла между ними. Вычисляется по одной из двух формул ниже:

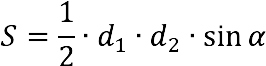
Примеры задач

Задание 1
Найдите площадь трапеции, если ее основания равны 4 и 7 см, а высота – 4 см.

Решение:
Используем первую формулу, рассмотренную выше: S = 1/2 * (4 см + 7 см) * 4 см = 22 см².

Задание 2
Найдите площадь трапеции, если ее основания равны 6 и 12 см, а боковые стороны – 8 и 10 см.

Решение:
Т.к. нам известны длины всех сторон, применим формулу Герона: S = (6+12) / |6-12| * √(18-6)(18-12)(18-6-8)(18-6-10) = 18 / 6 * √576 = 72 см².

Площадь правильного шестиугольника | Мозган калькулятор онлайн

На данной странице калькулятор поможет рассчитать площадь правильного шестиугольника онлайн. Для расчета задайте длину стороны или радиус окружности.

Шестиугольник — многоугольник у которого все стороны равны, а все внутренние углы равны 120°.

Через сторону

---

---

Формула для нахождения площади правильного шестиугольника через сторону:

a — сторона шестиугольника.

---

Через радиус описанной окружности

---

---

Формула для нахождения площади правильного шестиугольника через радиус описанной окружности:

r — радиус описанной окружности.

---

Через радиус вписанной окружности

---

---

Формула для нахождения площади правильного шестиугольника через радиус вписанной окружности:

r — радиус вписанной окружности.

Площадь трапеции. Определение, формула и калькулятор

Площадь трапеции. Определение, формула и калькулятор — Открытый справочник по математике Количество квадратных единиц, необходимое для полного заполнения трапеция.
Формула: Средняя ширина × высота

Попробуйте это Перетащите оранжевые точки, чтобы переместить и изменить размер трапеции. Как размер трапеции изменяется, пересчитывается площадь.

Формула площади

Площадь трапеции — это средняя ширина, умноженная на высоту, или формула: где
b1, b2 — длины каждого основания
h — высота (высота)

Напомним, что основания — это две параллельные стороны трапеции.Высота (или высота) трапеции — это перпендикулярное расстояние между двумя базами.

В приведенном выше апплете нажмите «заморозить размеры». Когда вы перетаскиваете любую вершину, вы увидите, что трапеция перерисовывается, сохраняя неизменными высоту и основания. Обратите внимание, как область в отображаемой формуле не меняется. Площадь зависит только от высоты и длины основания, поэтому, как видите, существует множество трапеций с заданным набором размеров, которые имеют одинаковую площадь.

Вывод формулы

См. Как получить формулу площади трапеции.

Калькулятор

Используйте калькулятор выше, чтобы рассчитать высоту, базовую длину и площадь трапеции.

Введите любые три значения, и будет вычислено недостающее. Например: введите высоту и две базовые длины и нажмите «Рассчитать». Площадь будет рассчитана.

Точно так же, если вы введете площадь и две длины основания, будет рассчитана высота, необходимая для получения этой площади.

Определение высоты по площади

Как найти высоту (высоту) трапеции, задайте две базы и площадь.Приведенная выше основная формула площади имеет четыре переменных (площадь, два основания и высота). Если мы знаем какие-то три, мы всегда можем найти четвертый. Так, например, если мы знаем площадь и две базы, мы можем найти высоту, просто изменив основную формулу: Где a — это площадь, а b1, b2 — две базы.

Поиск базы в районе

Как найти основание трапеции, укажите одно из оснований, высоту и площадь. Приведенная выше основная формула площади имеет четыре переменных (площадь, два основания и высота).Если мы знаем какие-то три, мы всегда можем найти четвертый. Так, например, если мы знаем площадь, одно основание и высоту, мы можем найти недостающее основание, просто изменив основную формулу: Где a — площадь, b — известное основание, а h — высота (высота).

Если известно медианное значение

Напомним, что медиана (м) трапеции — отрезок, соединяющий середины непараллельных сторон. Напомним также, что длина медианы — это среднее значение двух параллельных сторон.См. Медиана трапеции

Где м — это медиана, а ч — высота (высота).

Площадь как сложная форма

Другой способ найти площадь трапеции — рассматривать ее как несколько более простых форм, а затем добавлять или вычитать их площади, чтобы найти результат. Для Например, трапецию можно рассматривать как меньший прямоугольник плюс два прямоугольных треугольника: Дополнительные сведения об этой общей технике см. В разделе «Область неправильных многоугольников».

Координатная геометрия

В координатной геометрии, если вы знаете координаты четырех вершин, вы можете рассчитать различные его свойства, в том числе площадь и периметр.Подробнее об этом см. Площадь и периметр трапеции (координатная геометрия).

Что попробовать

1. На рисунке выше нажмите «скрыть детали»
2. Перетащите оранжевые точки на вершинах, чтобы образовалась трапеция произвольного размера.
3. Рассчитайте площадь по формуле
4. Теперь попробуйте оценить площадь трапеции, просто глядя на
   квадрата внутри нее.
5. Когда вы закончите, нажмите «Показать подробности», чтобы увидеть, насколько близко вы подошли.

Другие полигоны

Общие

Типы многоугольника

Площадь различных типов полигонов

Периметр различных типов полигонов

Углы, связанные с многоугольниками

Именованные полигоны

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

.

Как найти площадь трапеции (формула и видео) // Tutors.com

Содержание

1. Что такое трапеция?
2. Как найти площадь трапеции
3. Площадь трапеции, формула

Площадь трапеции Примеры

Трапеция — это четырехугольник, у которого одна пара параллельных сторон . Итак, этот четырехсторонний многоугольник представляет собой плоскую фигуру и замкнутую фигуру. Он состоит из четырех отрезков и четырех внутренних углов.Параллельные стороны — это две базы трапеции ; две другие стороны — его ноги.

Обычно у трапеции более длинная параллельная сторона — основание , — горизонтально. Перпендикулярная линия от основания к другой параллельной стороне даст вам высоту трапеции или высоту .

Что такое средний по математике?

В математике среднее значение представляет собой сумму группы чисел, деленную на количество элементов в группе.

Итак, если у вас есть три человека, которые держат книги, вы можете найти среднее количество книг, которые они держат, вот так: Мартин держит 5 книг, Мак держит 3 книги, а Мария держит 4 книги. Вместе 12 книг держат 3 человека. Итак, 12 книг ÷ 3 человека = в среднем по 4 книги каждая.

Чтобы найти площадь трапеции, вы найдете среднюю длину двух оснований.

Как найти площадь трапеции

Чтобы найти площадь любой трапеции, начните с обозначения ее основания и высоты.На нашей трапеции обозначьте более длинное основание a и более короткое основание b. Обозначьте линию, перпендикулярную двум основаниям, h для высоты или высоты трапеции.

Обратите внимание, что мы не пометили ноги. Нам не нужно ничего знать о длине ног или углах вершин, чтобы найти площадь.

Площадь трапеции, формула

Формула площади трапеции — это среднее значение оснований, умноженное на высоту. В формуле длинное и короткое основание — это a и b, а высота — h:

Умножение на 12 аналогично делению на 2.Мы берем половину суммы длины двух оснований (их среднее значение), а затем умножаем это на высоту или высоту, чтобы найти площадь в квадратных единицах.

Уравнение площади трапеции

Трапеция LMNO имеет параллельные основания LM и NO. Линейный сегмент LM имеет длину 7 см, а линейный сегмент NO — 13 см. Мы обозначим более длинную сторону NO как a, а короткую сторону LM как b. Высота h 5 см.

Сначала давайте подставим эти числа в нашу формулу:

площадь = 13 см + 7 см2 × 5 см

Далее складываем 13 плюс 7 и получаем:

площадь = 20 см2 × 5 см

Потом делим на два и получаем:

площадь = 10 см × 5 см

Наконец, умножаем и получаем ответ:

площадь = 50 c

.

Как найти площадь трапеции

Овладейте семью столпами успеха в школе

Повысьте успеваемость и снизьте уровень стресса

Common Core Standard 7.G.6

Площадь трапеции с диагоналями

Видеоответы эти вопросы

Зачем использовать формулу 1 / 2h (b1 + b2), чтобы найти площадь трапеции?

Какова площадь трапеции с высотой 10 единиц и сторонами 12 и 16 единиц

Какова площадь трапеции со сторонами 4,5 и 9 единиц?

Чтобы решить этот треугольник, вам нужно найти высоту трапеции.

Найдите площадь трапеции ABCD с диагоналями 6 и 8 единиц.

Используйте формулу d1 * d2 / 2

6 * 8/2 = 48/2 = 24 единицы в квадрате

Внимание! Площадь трапеции можно определить по диагоналям, но диагонали должны пересекаться и образуют перпендикулярные линии.

Это создает четыре прямых угла, и вы можете использовать формулу:

Площадь трапеции

Шаг 2. Чтобы найти длину длинной ноги (которая будет равна высоте трапеции), примените правила

треугольника 30 60 90 , поэтому длинная часть (высота) равна короткой части x √3

• короткий отрезок равен 1/2 гипотенузы
  

• Гипотенуза всегда противоположна прямому углу, поэтому равна 4 единицам
  

• Короткий отрезок равен 1/2 x 4 = 2 единицы
  

• Длинный отрезок равен короткая ножка √3,
  

• Вставьте короткую ножку 2√3 = высота
  

Найдите площадь трапеции с основаниями 5 и 9 и длина ножки — 4 единицы.Угол составляет 60 °.

Шаг 1 . Пожалуйста, не делайте ошибку, используя длину стороны как свой рост.

Высота этой трапеции образует треугольник 30 60 90. Высота становится длинной ногой треугольника 30 60 90.

Шаг 3. Подставьте высоту в формулу площади трапеции 1 / 2h (b1 + b2)

Шаг 4. ½ * 2√3 (14) = ½ 28√3

Шаг 5. 14√3 = квадрат единиц равен площади трапеции

Найдите площадь трапеции высотой 10 единиц, основанием 12 единиц и основанием 16 единиц.

Шаг 1 . Вставьте 12 и 16 для b1 и b2 и 10 для высоты.

½ 10 (12 + 16)

Шаг 2. ½ (10 * 28)

Шаг 3. ½ (280) = 140 единиц

Трапеция — это четырехсторонний многоугольник с одна пара параллельных сторон.Площадь — это количество квадратных единиц, находящихся внутри трапеции. Площадь — это двумерная мера, поэтому она всегда возведена в квадрат. Высота трапеции перпендикулярна двум параллельным основаниям. Одна из распространенных ошибок при вычислении площади трапеции — это использование длины стороны как высоты. Опять же, высота измеряется как линия, перпендикулярная двум параллельным основаниям.

Площадь трапеции можно найти по формуле 1 / 2h (b1 + b2)

Формула для площади трапеции равна 1 / 2h (b1 + b2)

h = высота, b1 = основание, b2 = основание

.

Как найти площадь трапеции?

Прежде чем перейти к вопросу «как найти площадь трапеции», давайте сначала разберемся, что такое трапеция и площадь трапеции. Трапеция — это фигура с четырьмя сторонами, поэтому это четырехугольник, потому что четырехугольники — это фигуры с четырьмя сторонами. Однако две стороны трапеции параллельны, а две другие — нет. Его параллельные стороны называются основанием трапеции, а две другие — ножками или боковыми сторонами.Итак, трапеция — это четырехугольная фигура с одной парой параллельных сторон. Расстояние между двумя основаниями трапеции — высота.

Выражение «трапеция» употребляется в английском языке с 1570 года, от греческого «trapezion» и от позднелатинского trapezium, что дословно означает «столик». В книге Евклида «Элементы» Маринус Прокл сначала описал «трапецию» при написании комментария.

На веб-сайте, который считается одним из лучших, предлагающих студентам услуги по редактированию диссертаций, а также помощь в написании курсовых, рефератов, диссертаций, дипломов и т. Д., вы найдете много информации о том, как найти площадь трапеции и измерить ее.

Особые случаи

• Правая трапеция. Он имеет два смежных прямых угла. Эти виды трапеций применяются в правиле трапеций для определения площадей под кривой.
• Острая трапеция. Он имеет два смежных острых угла на более длинной базовой кромке. Это также равнобедренная трапеция, если ее стороны имеют одинаковую длину, а углы в основании одинаковой меры.Имеет рефлекторную симметрию.
• Тупая трапеция. Он имеет по одному тупому и по одному острому углу на каждом основании. Тупая трапеция, имеющая две пары параллельных сторон, представляет собой параллелограмм, который имеет центральную двукратную симметрию вращения.

Существуют споры о том, следует ли считать параллелограммы с двумя парами параллельных сторон трапециями. Некоторые люди определяют трапецию как четырехугольник с одной парой параллельных сторон (исключительное определение), что исключает параллелограммы.Другие, однако, определяют трапецию как четырехугольник, по крайней мере, с одной парой сторон, которые параллельны (включающее определение), что делает четырехугольники особым видом трапеции. Последнее определение согласуется с его приложениями в высшей математике. Первое определение сделало бы такие понятия, как трапецеидальная аппроксимация определенного интеграла, некорректными.

Согласно включенному определению все параллелограммы (прямоугольники, ромбы и квадраты) являются трапециями.Прямоугольники имеют зеркальную симметрию на средних краях. Ромбы обладают рефлекторной симметрией в вершинах. Квадраты обладают зеркальной симметрией как в вершинах, так и в середине.

Четырехугольник Саккери очень похож на трапецию в гиперболической плоскости с двумя смежными прямыми углами, однако в евклидовой плоскости это прямоугольник. В гиперболической плоскости четырехугольник Ламберта имеет три прямых угла.

Тангенциальная трапеция — это трапеция с вписанной окружностью.

Если четырехугольник выпуклый, следующие свойства взаимны, и каждое предполагает, что четырехугольник является трапецией:

• Он имеет два смежных угла, которые являются дополнительными, т.е.е. они складываются в 180 градусов.
• Угол между диагональю и стороной равен углу между той же диагональю и противоположной стороной.
• Диагонали делят друг друга в одинаковом соотношении.
• Диагонали делят четырехугольник на четыре треугольника, одна противоположная пара которых похожа.
• Диагонали разделяют четырехугольник на четыре треугольника, одна из противоположных пар имеет равные площади.
• Произведение площадей двух треугольников, образованных одной диагональю, равно произведению двух треугольников, образованных другой диагональю.
• Площади T и S некоторых двух противоположных треугольников из четырех треугольников, образованных одной диагональю, удовлетворяют уравнению: √K = √S + √T, где K — площадь четырехугольника.
• Середины двух противоположных сторон и пересечение двух диагоналей коллинеарны.
• sin A sin C = sin B sin D.
• Сумма косинусов двух соседних углов равна 0, как и косинусы двух других углов.
• Сумма котангенсов двух соседних углов равна 0, как котангенсов двух других соседних углов.
• Один бимедиан разрезает четырехугольник на два четырехугольника с равной площадью.
• Удвоенная длина бимедиана, соединяющего середины двух противоположных сторон, равна сумме длин других сторон.

Если при написании рефлексивного эссе вам необходимо измерить площадь трапеции, вот простое объяснение того, как это сделать:

• Чтобы понять, как найти площадь трапеции, измерьте длину двух оснований.Назовем их сторонами a и b. Например, сторона

.