Как складывать корни с разными показателями. Правила вычитания корней
Квадратным корнем из числа X называется число A , которое в процессе умножения самого на себя (A * A ) может дать число X .
Т.е. A * A = A 2 = X , и √X = A .
Над квадратными корнями (√x ), как и над другими числами, можно выполнять такие арифметические операции, как вычитание и сложение. Для вычитания и сложения корней их нужно соединить посредством знаков, соответствующих этим действиям (например √x — √y ).
А потом привести корни к их простейшей форме — если между ними окажутся подобные, необходимо сделать приведение. Оно заключается в том, что берутся коэффициенты подобных членов со знаками соответствующих членов, далее заключаются в скобки и выводится общий корень за скобками множителя. Коэффициент, который мы получили, упрощается по обычным правилам.
Шаг 1. Извлечение квадратных корней
Во-первых, для сложения квадратных корней сначала нужно эти корни извлечь.
Все, пример решен. Но так просто бывает далеко не всегда.
Шаг 2. Вынесение множителя числа из-под корня
Если полных квадратов нет под знаком корня, можно попробовать вынести множитель числа из-под знака корня. Для примера возьмём выражение √24 + √54 .
Раскладываем числа на множители:
24 = 2 * 2 * 2 * 3 ,
54 = 2 * 3 * 3 * 3 .
В числе 24 мы имеем множитель 4 , его можно вынести из-под знака квадратного корня. В числе 54 мы имеем множитель 9 .
Получаем равенство:
√24 + √54 = √(4 * 6) + √(9 * 6) = 2 * √6 + 3 * √6 = 5 * √6 .

Шаг 3. Сокращение знаменателя
Рассмотрим следующую ситуацию: сумма двух квадратных корней — это знаменатель дроби, например, A / (√a + √b) .
Теперь перед нами стоит задача «избавиться от иррациональности в знаменателе».
Воспользуемся следующим способом: умножаем числитель и знаменатель дроби на выражение √a — √b .
Формулу сокращённого умножения мы теперь получаем в знаменателе:
(√a + √b) * (√a — √b) = a — b .
Аналогично, если в знаменателе имеется разность корней: √a — √b , числитель и знаменатель дроби умножаем на выражение √a + √b .
Возьмём для примера дробь:
4 / (√3 + √5) = 4 * (√3 — √5) / ((√3 + √5) * (√3 — √5)) = 4 * (√3 — √5) / (-2) = 2 * (√5 — √3) .
Пример сложного сокращения знаменателя
Теперь будем рассматривать достаточно сложный пример избавления от иррациональности в знаменателе.
Для примера берём дробь: 12 / (√2 + √3 + √5) .
Нужно взять её числитель и знаменатель и перемножить на выражение √2 + √3 — √5 .
Получаем:
12 / (√2 + √3 + √5) = 12 * (√2 + √3 — √5) / (2 * √6) = 2 * √3 + 3 * √2 — √30.
Шаг 4. Вычисление приблизительного значения на калькуляторе
Если вам требуется только приблизительное значение, это можно сделать на калькуляторе путём подсчёта значения квадратных корней. Отдельно для каждого числа вычисляется значение и записывается с необходимой точностью, которая определяется количеством знаков после запятой. Далее совершаются все требуемые операции, как с обычными числами.
Пример вычисления приблизительного значения
Необходимо вычислить приблизительное значение данного выражения √7 + √5 .
В итоге получаем:
√7 + √5 ≈ 2,65 + 2,24 = 4,89 .
Обратите внимание: ни при каких условиях не следует производить сложение квадратных корней, как простых чисел, это совершенно недопустимо. То есть, если сложить квадратный корень из пяти и из трёх, у нас не может получиться квадратный корень из восьми.
Полезный совет: если вы решили разложить число на множители, для того, чтобы вывести квадрат из-под знака корня, вам необходимо сделать обратную проверку, то есть перемножить все множители, которые получились в результате вычислений, и в конечном результате этого математического расчёта должно получиться число, которое нам было задано первоначально. 2=400\\
\hline \end{array}\]
2=400\\
\hline \end{array}\]
Факт 3.
Какие действия можно выполнять с квадратными корнями?
\(\bullet\) Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть \[\sqrt a\pm\sqrt b\ne \sqrt{a\pm b}\]
Таким образом, если вам нужно вычислить, например, \(\sqrt{25}+\sqrt{49}\)
, то первоначально вы должны найти значения \(\sqrt{25}\)
и \(\sqrt{49}\)
, а затем их сложить. Следовательно, \[\sqrt{25}+\sqrt{49}=5+7=12\]
Пример: \(\sqrt{32}\cdot \sqrt 2=\sqrt{32\cdot 2}=\sqrt{64}=8\) ; \(\sqrt{768}:\sqrt3=\sqrt{768:3}=\sqrt{256}=16\) ; \(\sqrt{(-25)\cdot (-64)}=\sqrt{25\cdot 64}=\sqrt{25}\cdot \sqrt{64}= 5\cdot 8=40\) .
 \(\bullet\)
Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
\(\bullet\)
Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.Рассмотрим пример. Найдем \(\sqrt{44100}\) . Так как \(44100:100=441\) , то \(44100=100\cdot 441\) . По признаку делимости число \(441\) делится на \(9\) (так как сумма его цифр равна 9 и делится на 9), следовательно, \(441:9=49\) , то есть \(441=9\cdot 49\) .
Таким образом, мы получили: \[\sqrt{44100}=\sqrt{9\cdot 49\cdot 100}= \sqrt9\cdot \sqrt{49}\cdot \sqrt{100}=3\cdot 7\cdot 10=210\] Рассмотрим еще один пример: \[\sqrt{\dfrac{32\cdot 294}{27}}= \sqrt{\dfrac{16\cdot 2\cdot 3\cdot 49\cdot 2}{9\cdot 3}}= \sqrt{ \dfrac{16\cdot4\cdot49}{9}}=\dfrac{\sqrt{16}\cdot \sqrt4 \cdot \sqrt{49}}{\sqrt9}=\dfrac{4\cdot 2\cdot 7}3=\dfrac{56}3\]
\(\bullet\) Покажем, как вносить числа под знак квадратного корня на примере выражения \(5\sqrt2\) (сокращенная запись от выражения \(5\cdot \sqrt2\) ). Так как \(5=\sqrt{25}\) , то \ Заметим также, что, например,
2) \(5\sqrt3-\sqrt3=4\sqrt3\)
3) \(\sqrt a+\sqrt a=2\sqrt a\) .
 2\)
, поэтому \(\sqrt{16}=4\)
. А вот извлечь корень из числа \(3\)
, то есть найти \(\sqrt3\)
, нельзя, потому что нет такого числа, которое в квадрате даст \(3\)
.
2\)
, поэтому \(\sqrt{16}=4\)
. А вот извлечь корень из числа \(3\)
, то есть найти \(\sqrt3\)
, нельзя, потому что нет такого числа, которое в квадрате даст \(3\)
.Такие числа (или выражения с такими числами) являются иррациональными. Например, числа \(\sqrt3, \ 1+\sqrt2, \ \sqrt{15}\) и т.п. являются иррациональными.
Также иррациональными являются числа \(\pi\) (число “пи”, приблизительно равное \(3,14\) ), \(e\) (это число называют числом Эйлера, приблизительно оно равно \(2,7\) ) и т.д.
\(\bullet\) Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел. Обозначается это множество буквой \(\mathbb{R}\) .
Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.
Факт 5.
\(\bullet\)
Модуль вещественного числа \(a\)
– это неотрицательное число \(|a|\)
, равное расстоянию от точки \(a\)
до \(0\)
на вещественной прямой. 2\\
&2>2,25 \end{aligned}\]
Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и \(\sqrt 2-1Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
2\\
&2>2,25 \end{aligned}\]
Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и \(\sqrt 2-1Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
Возводить обе части уравнения/неравенства в квадрат можно ТОЛЬКО ТОГДА, когда обе части неотрицательные. Например, в неравенстве из предыдущего примера возводить обе части в квадрат можно, в неравенстве \(-3
\(\bullet\)
Следует запомнить, что \[\begin{aligned}
&\sqrt 2\approx 1,4\\
&\sqrt 3\approx 1,7 \end{aligned}\]
Знание приблизительного значения данных чисел поможет вам при сравнении чисел!
\(\bullet\)
Для того, чтобы извлечь корень (если он извлекается) из какого-то большого числа, которого нет в таблице квадратов, нужно сначала определить, между какими “сотнями” оно находится, затем – между какими “десятками”, а потом уже определить последнюю цифру этого числа.
Следовательно, \(\sqrt{28224}=168\) . Вуаля!
Для того чтобы достойно решить ЕГЭ по математике, прежде всего необходимо изучить теоретический материал, который знакомит с многочисленными теоремами, формулами, алгоритмами и т. д. На первый взгляд может показаться, что это довольно просто. Однако найти источник, в котором теория для ЕГЭ по математике изложена легко и понятно для учащихся с любым уровнем подготовки, — на деле задача довольно сложная. Школьные учебники невозможно всегда держать под рукой. А найти основные формулы для ЕГЭ по математике бывает непросто даже в Интернете.
Почему так важно изучать теорию по математике не только для тех, кто сдает ЕГЭ?
- Потому что это расширяет кругозор
. Изучение теоретического материала по математике полезно для всех, кто желает получить ответы на широкий круг вопросов, связанных с познанием окружающего мира. Все в природе упорядоченно и имеет четкую логику. Именно это и отражается в науке, через которую возможно понять мир.

- Потому что это развивает интеллект . Изучая справочные материалы для ЕГЭ по математике, а также решая разнообразные задачи, человек учится логически мыслить и рассуждать, грамотно и четко формулировать мысли. У него вырабатывается способность анализировать, обобщать, делать выводы.
Предлагаем вам лично оценить все преимущества нашего подхода к систематизации и изложению учебных материалов.
Тема про квадратные корни является обязательной в школьной программе курса математики. Без них не обойтись при решении квадратных уравнений. А позже появляется необходимость не только извлекать корни, но и выполнять с ними другие действия. Среди них достаточно сложные: возведение в степень, умножение и деление. Но есть и достаточно простые: вычитание и сложение корней. Кстати, они только на первый взгляд кажутся такими. Выполнить их без ошибок не всегда оказывается просто для того, кто только начинает с ними знакомиться.
Что такое математический корень?
Это действие возникло в противовес возведению в степень. Математика предполагает наличие двух противоположных операций. На сложение существует вычитание. Умножению противостоит деление. Обратное действие степени — это извлечение соответствующего корня.
Математика предполагает наличие двух противоположных операций. На сложение существует вычитание. Умножению противостоит деление. Обратное действие степени — это извлечение соответствующего корня.
Если в степени стоит двойка, то и корень будет квадратным. Он является самым распространенным в школьной математике. У него даже нет указания, что он квадратный, то есть возле него не приписывается цифра 2. Математическая запись этого оператора (радикала) представлена на рисунке.
Из описанного действия плавно вытекает его определение. Чтобы извлечь квадратный корень из некоторого числа, нужно выяснить, какое даст при умножении на себя подкоренное выражение. Это число и будет квадратным корнем. Если записать это математически, то получится следующее: х*х=х 2 =у, значит √у=х.
Какие действия с ними можно выполнять?
По своей сути корень — это дробная степень, у которой в числителе стоит единица. А знаменатель может быть любым. Например, у квадратного корня он равен двум. Поэтому все действия, которые можно выполнить со степенями, будут справедливы и для корней.
И требования к этим действиям у них одинаковые. Если умножение, деление и возведение в степень не встречают затруднений у учеников, то сложение корней, как и их вычитание, иногда приводит в замешательство. А все потому что хочется выполнить эти операции без оглядки на знак корня. И здесь начинаются ошибки.
По каким правилам выполняется их сложение и вычитание?
Сначала нужно запомнить два категорических «нельзя»:
- нельзя выполнять сложение и вычитание корней, как у простых чисел, то есть невозможно записать подкоренные выражения суммы под один знак и выполнять с ними математические операции;
- нельзя складывать и вычитать корни с разными показателями, например квадратный и кубический.
Наглядный пример первого запрета: √6 + √10 ≠ √16, но √(6 + 10) = √16 .
Во втором случае лучше ограничиться упрощением самих корней. А в ответе оставить их сумму.
Теперь к правилам
- Найти и сгруппировать подобные корни. То есть те, у которых не только стоят одинаковые числа под радикалом, но и они сами с одним показателем.

- Выполнить сложение корней, объединенных в одну группу первым действием. Оно легко осуществимо, потому что нужно только сложить значения, которые стоят перед радикалами.
- Извлечь корни в тех слагаемых, в которых подкоренное выражение образует целый квадрат. Другими словами, не оставлять ничего под знаком радикала.
- Упростить подкоренные выражения. Для этого нужно разложить их на простые множители и посмотреть, не дадут ли они квадрата какого-либо числа. Понятно, что это справедливо, если речь идет о квадратном корне. Когда показатель степени три или четыре, то и простые множители должны давать куб или четвертую степень числа.
- Вынести из-под знака радикала множитель, который дает целую степень.
- Посмотреть, не появилось ли опять подобных слагаемых. Если да, то снова выполнить второе действие.
В ситуации, когда задача не требует точного значения корня, его можно вычислить на калькуляторе. Бесконечную десятичную дробь, которая высветится в его окошке, округлить. Чаще всего это делают до сотых. А потом выполнять все операции для десятичных дробей.
Чаще всего это делают до сотых. А потом выполнять все операции для десятичных дробей.
Это вся информация о том, как выполняется сложение корней. Примеры, расположенные ниже, проиллюстрируют вышесказанное.
Первое задание
Вычислить значение выражений:
а) √2 + 3√32 + ½ √128 — 6√18;
б) √75 — √147 + √48 — 1/5 √300;
в) √275 — 10√11 + 2√99 + √396.
а) Если следовать приведенному выше алгоритму, то видно, что для первых двух действий в этом примере ничего нет. Зато можно упростить некоторые подкоренные выражения.
Например, 32 разложить на два множителя 2 и 16; 18 будет равно произведению 9 и 2; 128 — это 2 на 64. Учитывая это, выражение будет записано так:
√2 + 3√(2 * 16) + ½ √(2 * 64) — 6 √(2 * 9).
Теперь нужно вынести из-под знака радикала те множители, которые дают квадрат числа. Это 16=4 2 , 9=3 2 , 64=8 2 . Выражение примет вид:
√2 + 3 * 4√2 + ½ * 8 √2 — 6 * 3√2.
Нужно немного упростить запись. Для этого производится умножение коэффициентов перед знаками корня:
√2 + 12√2 + 4 √2 — 12√2.
В этом выражении все слагаемые оказались подобными. Поэтому их нужно просто сложить. В ответе получится: 5√2.
б) Подобно предыдущему примеру, сложение корней начинается с их упрощения. Подкоренные выражения 75, 147, 48 и 300 будут представлены такими парами: 5 и 25, 3 и 49, 3 и 16, 3 и 100. В каждой из них имеется число, которое можно вынести из-под знака корня:
5√5 — 7√3 + 4√3 — 1/5 * 10√3.
После упрощения получается ответ: 5√5 — 5√3. Его можно оставить в таком виде, но лучше вынести общий множитель 5 за скобку: 5 (√5 — √3).
в) И снова разложение на множители: 275 = 11 * 25, 99 = 11 * 9, 396 = 11 * 36. После вынесения множителей из-под знака корня имеем:
5√11 — 10√11 + 2 * 3√11 + 6√11. После приведения подобных слагаемых получим результат: 7√11.
Пример с дробными выражениями
√(45/4) — √20 — 5√(1/18) — 1/6 √245 + √(49/2).
На множители нужно будет разложить такие числа: 45 = 5 * 9, 20 = 4 * 5, 18 = 2 * 9, 245 = 5 * 49. Аналогично уже рассмотренным, нужно вынести множители из-под знака корня и упростить выражение:
Аналогично уже рассмотренным, нужно вынести множители из-под знака корня и упростить выражение:
3/2 √5 — 2√5 — 5/ 3 √(½) — 7/6 √5 + 7 √(½) = (3/2 — 2 — 7/6) √5 — (5/3 — 7) √(½) = — 5/3 √5 + 16/3 √(½).
Это выражение требует того, чтобы избавиться от иррациональности в знаменателе. Для этого нужно умножить на √2/√2 второе слагаемое:
5/3 √5 + 16/3 √(½) * √2/√2 = — 5/3 √5 + 8/3 √2.
Для полноты действий нужно выделить целую часть у множителей перед корнями. У первого она равна 1, у второго — 2.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.

- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения. 2 = x, ?x = a. Как и над всякими числами, над квадратными корнями дозволено исполнять арифметические операции сложения и вычитания.
2 = x, ?x = a. Как и над всякими числами, над квадратными корнями дозволено исполнять арифметические операции сложения и вычитания.
Инструкция
1. Во-первых, при сложении квадратных корней испробуйте извлечь эти корни. Это будет допустимо, если числа под знаком корня являются полными квадратами. Скажем, пускай задано выражение?4 + ?9. Первое число 4 – это квадрат числа 2. Второе число 9 – это квадрат числа 3. Таким образом получается, что: ?4 + ?9 = 2 + 3 = 5.
2. Если под знаком корня нет полных квадратов, то испробуйте перенести из под знака корня множитель числа. Скажем, пускай дано выражение?24 + ?54. Разложите числа на множители: 24 = 2 * 2 * 2 * 3, 54 = 2 * 3 * 3 * 3. В числе 24 имеется множитель 4, тот, что дозволено перенести из под знака квадратного корня. В числе 54 – множитель 9. Таким образом, получается что: ?24 + ?54 = ?(4 * 6) + ?(9 * 6) = 2 * ?6 + 3 * ?6 = 5 * ?6. В данном примере в итоге выноса множителя из под знака корня получилось упростить заданное выражение.
3. Пускай сумма 2-х квадратных корней является знаменателем дроби, скажем, A / (?a + ?b). И пускай перед вами стоит задача «избавиться от иррациональности в знаменателе». Тогда дозволено воспользоваться дальнейшим методом. Умножьте числитель и знаменатель дроби на выражение?a – ?b. Таким образом в знаменателе получится формула сокращенного умножения: (?a + ?b) * (?a – ?b) = a – b. По аналогии, если в знаменателе дана разность корней: ?a – ?b, то числитель и знаменатель дроби нужно умножить на выражение?a + ?b. Для примера, пускай дана дробь 4 / (?3 + ?5) = 4 * (?3 – ?5) / ((?3 + ?5) * (?3 – ?5)) = 4 * (?3 – ?5) / (-2) = 2 * (?5 – ?3).
4. Разглядите больше непростой пример избавления от иррациональности в знаменателе. Пускай дана дробь 12 / (?2 + ?3 + ?5). Нужно умножить числитель и знаменатель дроби на выражение?2 + ?3 – ?5:12 / (?2 + ?3 + ?5) = 12 * (?2 + ?3 – ?5) / ((?2 + ?3 + ?5) * (?2 + ?3 – ?5)) = 12 * (?2 + ?3 – ?5) / (2 * ?6) = ?6 * (?2 + ?3 – ?5) = 2 * ?3 + 3 * ?2 – ?30.
5. И наконец, если вам нужно только примерное значение, то дозволено посчитать значения квадратных корней на калькуляторе. Вычислите значения отдельно для всего числа и запишите с нужной точностью (скажем, два знака позже запятой). А после этого совершите требуемые арифметические операции, как с обыкновенными числами. Скажем, пускай нужно узнать примерное значение выражения?7 + ?5 ? 2,65 + 2,24 = 4,89.
Видео по теме
Обратите внимание!
Квадратные корни ни в коем случае невозможно складывать как примитивные числа, т.е. ?3 + ?2 ? ?5!!!
Полезный совет
Если вы раскладываете число на множители, дабы перенести квадрат из под знака корня, то совершите обратную проверку – перемножьте все получившиеся множители и получите изначальное число.
Сложение и вычитание квадратных корней примеры. Как складывать квадратные корни
Содержимое:
Складывать и вычитать квадратные корни можно только при условии, что у них одинаковое подкоренное выражение, то есть вы можете сложить или вычесть 2√3 и 4√3, но не 2√3 и 2√5. Вы можете упростить подкоренное выражение, чтобы привести их к корням с одинаковыми подкоренными выражениями (а затем сложить или вычесть их).
Вы можете упростить подкоренное выражение, чтобы привести их к корням с одинаковыми подкоренными выражениями (а затем сложить или вычесть их).
Шаги
Часть 1 Постигаем основы
- 1 (выражение под знаком корня). Для этого разложите подкоренное число на два множителя, один из которых является квадратным числом (число, из которого можно извлечь целый корень, например, 25 или 9). После этого извлеките корень из квадратного числа и запишите найденное значение перед знаком корня (под знаком корня останется второй множитель). Например, 6√50 — 2√8 + 5√12. Числа, стоящее перед знаком корня, являются множителями соответствующих корней, а числа под знаком корня – это подкоренные числа (выражения). Вот как решать данную задачу:
- 6√50 = 6√(25 x 2) = (6 x 5)√2 = 30√2. Здесь вы раскладываете 50 на множители 25 и 2; затем из 25 извлекаете корень, равный 5, и 5 выносите из-под корня. Затем 5 умножаете на 6 (множитель у корня) и получаете 30√2.
- 2√8 = 2√(4 x 2) = (2 x 2)√2 = 4√2.
 Здесь вы раскладываете 8 на множители 4 и 2; затем из 4 извлекаете корень, равный 2, и 2 выносите из-под корня. Затем 2 умножаете на 2 (множитель у корня) и получаете 4√2.
Здесь вы раскладываете 8 на множители 4 и 2; затем из 4 извлекаете корень, равный 2, и 2 выносите из-под корня. Затем 2 умножаете на 2 (множитель у корня) и получаете 4√2. - 5√12 = 5√(4 x 3) = (5 x 2)√3 = 10√3. Здесь вы раскладываете 12 на множители 4 и 3; затем из 4 извлекаете корень, равный 2, и 2 выносите из-под корня. Затем 2 умножаете на 5 (множитель у корня) и получаете 10√3.
- 2 Подчеркните корни, подкоренные выражения которых одинаковы. В нашем примере упрощенное выражение имеет вид: 30√2 — 4√2 + 10√3. В нем вы должны подчеркнуть первый и второй члены (30√2 и 4√2 ), так как у них одинаковое подкоренное число 2. Только такие корни вы можете складывать и вычитать.
- 3 Если вам дано выражение с большим количеством членов, многие из которых имеют одинаковые подкоренные выражения, используйте одинарное, двойное, тройное подчеркивание для обозначения таких членов, чтобы облегчить решение этого выражения.
- 4
У корней, подкоренные выражения которых одинаковы, сложите или вычтите множители, стоящие перед знаком корня, а подкоренное выражение оставьте прежним (не складывайте и не вычитайте подкоренные числа!
).
 Идея в том, чтобы показать, сколько всего корней с определенным подкоренным выражением содержится в данном выражении.
Идея в том, чтобы показать, сколько всего корней с определенным подкоренным выражением содержится в данном выражении.- 30√2 — 4√2 + 10√3 =
- (30 — 4)√2 + 10√3 =
- 26√2 + 10√3
Часть 2 Практикуемся на примерах
- 1 Пример 1: √(45) + 4√5.
- Упростите √(45). Разложите 45 на множители: √(45) = √(9 x 5).
- Вынесите 3 из-под корня (√9 = 3): √(45) = 3√5.
- Теперь сложите множители у корней: 3√5 + 4√5 = 7√5
- 2 Пример 2: 6√(40) — 3√(10) + √5.
- Упростите 6√(40). Разложите 40 на множители: 6√(40) = 6√(4 x 10).
- Вынесите 2 из-под корня (√4 = 2): 6√(40) = 6√(4 x 10) = (6 x 2)√10.
- Перемножьте множители перед корнем и получите 12√10.
- Теперь выражение можно записать в виде 12√10 — 3√(10) + √5. Так как у первых двух членов одинаковые подкоренные числа, вы можете вычесть второй член из первого, а первый оставить без изменений.
- Вы получите: (12-3)√10 + √5 = 9√10 + √5.

- 3 Пример 3. 9√5 -2√3 — 4√5. Здесь ни одно из подкоренных выражений нельзя разложить на множители, поэтому упростить это выражение не получится. Вы можете вычесть третий член из первого (так как у них одинаковые подкоренные числа), а второй член оставить без изменений. Вы получите: (9-4)√5 -2√3 = 5√5 — 2√3.
- 4 Пример 4. √9 + √4 — 3√2.
- √9 = √(3 х 3) = 3.
- √4 = √(2 х 2) = 2.
- Теперь вы можете просто сложить 3 + 2, чтобы получить 5.
- Окончательный ответ: 5 — 3√2.
- 5 Пример 5. Решите выражение, содержащее корни и дроби. Вы можете складывать и вычислять только те дроби, у которых общий (одинаковый) знаменатель. Дано выражение (√2)/4 + (√2)/2.
- Найдите наименьший общий знаменатель этих дробей. Это число, которое делится нацело на каждый знаменатель. В нашем примере на 4 и на 2 делится число 4.
- Теперь вторую дробь умножьте на 2/2 (чтобы привести ее к общему знаменателю; первая дробь уже приведена к нему): (√2)/2 х 2/2 = (2√2)/4.

- Сложите числители дробей, а знаменатель оставьте прежним: (√2)/4 + (2√2)/4 = (3√2)/4 .
- Перед суммированием или вычитанием корней обязательно упростите (если возможно) подкоренные выражения.
Предупреждения
- Никогда не суммируйте и не вычитайте корни с разными подкоренными выражениями.
- Никогда не суммируйте и не вычитайте целое число и корень, например, 3 + (2x) 1/2 .
- Примечание: «х» в одной второй степени и квадратный корень из «х» – это одно и то же (то есть x 1/2 = √х).
Формулы корней. Свойства квадратных корней.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать. 2 = x, √x = a. Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания.
2 = x, √x = a. Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания.
Инструкция
- Во-первых, при сложении квадратных корней попробуйте извлечь эти корни. Это будет возможно, если числа под знаком корня являются полными квадратами. Например, пусть задано выражение √4 + √9. Первое число 4 – это квадрат числа 2. Второе число 9 – это квадрат числа 3. Таким образом получается, что: √4 + √9 = 2 + 3 = 5.
- Если под знаком корня нет полных квадратов, то попробуйте вынести из под знака корня множитель числа. Например, пусть дано выражение √24 + √54. Разложите числа на множители: 24 = 2 * 2 * 2 * 3, 54 = 2 * 3 * 3 * 3. В числе 24 имеется множитель 4, который можно вынести из под знака квадратного корня. В числе 54 — множитель 9. Таким образом, получается что: √24 + √54 = √(4 * 6) + √(9 * 6) = 2 * √6 + 3 * √6 = 5 * √6. В данном примере в результате выноса множителя из под знака корня получилось упростить заданное выражение.

- Пусть сумма двух квадратных корней является знаменателем дроби, например, A / (√a + √b). И пусть перед вами стоит задача «избавиться от иррациональности в знаменателе». Тогда можно воспользоваться следующим способом. Умножьте числитель и знаменатель дроби на выражение √a — √b. Таким образом в знаменателе получится формула сокращенного умножения: (√a + √b) * (√a — √b) = a – b. По аналогии, если в знаменателе дана разность корней: √a — √b, то числитель и знаменатель дроби необходимо умножить на выражение √a + √b. Для примера, пусть дана дробь 4 / (√3 + √5) = 4 * (√3 — √5) / ((√3 + √5) * (√3 — √5)) = 4 * (√3 — √5) / (-2) = 2 * (√5 — √3).
- Рассмотрите более сложный пример избавления от иррациональности в знаменателе. Пусть дана дробь 12 / (√2 + √3 + √5). Необходимо умножить числитель и знаменатель дроби на выражение √2 + √3 — √5:
12 / (√2 + √3 + √5) = 12 * (√2 + √3 — √5) / ((√2 + √3 + √5) * (√2 + √3 — √5)) = 12 * (√2 + √3 — √5) / (2 * √6) = √6 * (√2 + √3 — √5) = 2 * √3 + 3 * √2 — √30.
- И наконец, если вам необходимо только приблизительное значение, то можно посчитать значения квадратных корней на калькуляторе. Вычислите значения отдельно для каждого числа и запишите с необходимой точностью (например, два знака после запятой). А затем совершите требуемые арифметические операции, как с обычными числами. Например, пусть необходимо узнать приблизительное значение выражения √7 + √5 ≈ 2,65 + 2,24 = 4,89.
Свойства квадратных корней
До сих пор мы осуществляли над числами пять арифметических операций: сложение, вычитание, умножение , деление и возведение в степень, причем при вычислениях активно использовали различные свойства этих операций, например а + b = b + а, аn-bn = (аb)n и т. д.
В этой главе введена новая операция — извлечение квадратного корня из неотрицательного числа. Чтобы успешно ее использовать, нужно познакомиться со свойствами этой операции, что мы и сделаем в настоящем параграфе.
Доказательство. Введем следующие обозначения:https://pandia. ru/text/78/290/images/image005_28.jpg» alt=»Равенство»Задание»> Имеются только свойства, касающиеся умножения и деления квадратных корней. Будьте внимательны и осторожны, не принимайте желаемое за действительное.
ru/text/78/290/images/image005_28.jpg» alt=»Равенство»Задание»> Имеются только свойства, касающиеся умножения и деления квадратных корней. Будьте внимательны и осторожны, не принимайте желаемое за действительное.
Завершая параграф, отметим еще одно достаточно простое и в то же время важное свойство:
если a > 0 и n — натуральное число , то
Преобразование выражений, содержащих операцию извлечения квадратного корня
До сих пор мы с вами выполняли преобразования толькорациональных выражений , используя для этого правила действий над многочленами и алгебраическими дробями, формулы сокращенного умножения и т. д. В этой главе мы ввели новую операцию — операцию извлечения квадратного корня; мы установили, что
где, напомним, a, b — неотрицательные числа.
Используя эти формулы , можно выполнять различные преобразования выражений, содержащих операцию извлечения квадратного корня. Рассмотрим несколько примеров, причем во всех примерах будем предполагать, что переменные принимают только неотрицательные значения.
Пример 3. Внести множитель под знак квадратного корня:
Пример 6 . Упростить выражение Решение. Выполним последовательные преобразования:
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Можно ли отнимать корни.
 Как складывать и вычитать квадратные корни
Как складывать и вычитать квадратные корниВ наше время современных электронных вычислительных машин вычисление корня из числа не представляется сложной задачей. Например, √2704=52, это вам подсчитает любой калькулятор. К счастью, калькулятор есть не только в Windows, но и в обычном, даже самом простеньком, телефоне. Правда если вдруг (с малой долей вероятности, вычисление которой, между прочим, включает в себя сложение корней) вы окажитесь без доступных средств, то, увы, придется рассчитывать только на свои мозги.
Тренировка ума никогда не помещает. Особенно для тех, кто не так часто работает с цифрами, а уж тем более с корнями. Сложение и вычитание корней — хорошая разминка для скучающего ума. А еще я покажу поэтапно сложение корней. Примеры выражений могут быть следующие.
Уравнение, которое нужно упростить:
√2+3√48-4×√27+√128
Это иррациональное выражение. Для того чтобы его упростить нужно привести все подкоренные выражения к общему виду. Делаем поэтапно:
Первое число упростить уже нельзя. 2×2)
2×2)
Переписываем выражение с упрощенными слагаемыми:
√2+12×√3-12×√3+8×√2
Теперь складываем числа одним и тем же подкоренным выражением. Нельзя складывать или вычитать выражения с разными подкоренными выражениями. Сложение корней требует соблюдение этого правила.
Ответ получаем следующий:
√2+12√3-12√3+8√2=9√2
√2=1×√2 — надеюсь, то, что в алгебре принято опускать подобные элементы, не станет для вас новостью.
Выражения могут быть представлены не только квадратным корнем, но так же и с кубическим или корнем n-ной степени.
Сложение и вычитание корней с разными показателями степени, но с равнозначным подкоренным выражением, происходит следующим образом:
Если мы имеем выражение вида √a+∛b+∜b, то мы можем упростить это выражение так:
∛b+∜b=12×√b4 +12×√b3
12√b4 +12×√b3=12×√b4 + b3
Мы привели два подобных члена к общему показателю корня. Здесь использовалось свойство корней, которое гласит: если число степени подкоренного выражения и число показателя корня умножить на одно и то же число, то его вычисление останется неизменным.
На заметку: показатели степени складываются только при умножении.
Рассмотрим пример, когда в выражении присутствуют дроби.
5√8-4×√(1/4)+√72-4×√2
Будем решать по этапам:
5√8=5*2√2 — мы выносим из-под корня извлекаемую часть.
4√(1/4)=-4 √1/(√4)= — 4 *1/2= — 2
Если в тело корня представлено дробью, то часто этой дроби не измениться, если извлечь квадратный корень из делимого и делителя. В итоге мы получили описанное выше равенство.
√72-4√2=√(36×2)- 4√2=2√2
10√2+2√2-2=12√2-2
Вот и получился ответ.
Главное помнить, что из отрицательных чисел не извлекается корень с четным показателем степени. Если четной степени подкоренное выражение является отрицательным, то выражение является нерешаемым.
Сложение корней возможно только при совпадении подкоренных выражений, так как они являются подобными слагаемыми. То же самое относиться и к разности.
Сложение корней с разными числовыми показателями степени производиться посредством приведения к общей корневой степени обоих слагаемых. Это закон действует так же как приведение к общему знаменателю при сложении или вычитании дробей.
Это закон действует так же как приведение к общему знаменателю при сложении или вычитании дробей.
Если в подкоренном выражении имеется число, возведенное в степень, то это выражение можно упростить при условии, что между показателем корня и степени существует общий знаменатель.
В математике корни могут быть квадратными, кубическими или иметь любой другой показатель (степень), который пишется слева над знаком корня. Выражение, стоящее под знаком корня, называется подкоренным выражением. Сложение корней похоже на сложение членов алгебраического выражения, то есть требует определения подобных корней.
Шаги
Часть 1 из 2: Определение корнейОбозначение корней. Выражение под знаком корня () означает, что из этого выражения необходимо извлечь корень определенной степени.
- Корень обозначают знаком.
- Показатель (степень) корня пишется слева над знаком корня. Например, кубический корень из 27 записывается так: (27)
- Если показатель (степень) корня отсутствует, то показатель считается равным 2, то есть это квадратный корень (или корень второй степени).

- Число, записанное перед знаком корня, называется множителем (то есть это число умножается на корень), например 5 (2)
- Если множителя перед корнем нет, то он равен 1 (напомним, что любое число, умноженное на 1, равняется самому себе).
- Если вы впервые работаете с корнями, сделайте соответствующие пометки над множителем и показателем корня, чтобы не запутаться и лучше понять их назначение.
Запомните, какие корни можно складывать, а какие нельзя. Так же, как нельзя складывать разные члены выражения, например, 2а + 2b 4ab, вы не можете складывать разные корни.

Определите и сгруппируйте подобные корни. Подобные корни – корни, у которых одинаковые показатели и одинаковые подкоренные выражения. Например, рассмотрим выражение:
2 (3) + (81) + 2 (50) + (32) + 6 (3)
- Во-первых, перепишите выражение так, чтобы корни с одинаковым показателем располагались последовательно.
2 (3) + 2 (50) + (32) + 6 (3) + (81) - Затем перепишите выражение так, чтобы корни с одинаковым показателем и с одинаковым подкоренным выражением располагались последовательно.
2 (50) + (32) + 2 (3) + 6 (3) + (81)
Упростите корни. Для этого разложите (где возможно) подкоренные выражения на два множителя, один из которых вынесите из-под корня. В этом случае вынесенное число и множитель корня перемножаются.
 Таким образом, вы получите упрощенное выражение: 10 (2) + 4 (2) + 2 (3) + 6 (3) + (81)
Таким образом, вы получите упрощенное выражение: 10 (2) + 4 (2) + 2 (3) + 6 (3) + (81)Сложите множители подобных корней. В нашем примере есть подобные квадратные корни из 2 (их можно сложить) и подобные квадратные корни из 3 (их тоже можно сложить). У кубического корня из 3 подобных корней нет.
- Не существует общепринятых правил порядка записи корней в выражении. Потому вы можете записывать корни в порядке возрастания их показателей и в порядке возрастания подкоренных выражений.
Внимание, только СЕГОДНЯ!
Все интересное
Число, которое находится под знаком корня, часто мешает решению уравнения, с ним неудобно работать. Даже если оно возведено в степень, дробно или не может быть представлено в виде целого числа в определенной степени, можно попытаться вывести его из…
Даже если оно возведено в степень, дробно или не может быть представлено в виде целого числа в определенной степени, можно попытаться вывести его из…
Корнем из числа x называется такое число, которое при возведении в степень корня будет равно x. Множителем называется умножаемое число. То есть, в выражении вида x*ª-&radic-y нужно внести x под корень. Инструкция 1Определите степень…
Если подкоренное выражение содержит набор математических действий с переменными, то иногда в результате его упрощения есть возможность получить относительно простое значение, часть которого можно вынести из под корня. Бывает полезно такое упрощение…
Арифметические действия с корнями различной степени могут значительно упростить расчеты в физике и технике и сделать их более точными. При умножении и делении удобнее не извлекать корень из каждого сомножителя или делимого и делителя, а сначала…
Квадратным корнем из числа x называют число a, которое при умножении само на себя дает число x: a * a = a^2 = x, x = a. Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания. Инструкция …
Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания. Инструкция …
Корень в математике может иметь два значения: это арифметическое действие и каждое из решений уравнения, алгебраического, параметрического, дифференциального или любого другого. Инструкция 1Корень n-ной степени из числа a — это такое число, что…
При выполнении различных арифметических действий с корнями часто бывает необходимо умение преобразовывать подкоренные выражения. Для упрощения расчетов может понадобиться вынести множитель за знак радикала или внести под него. Это действие можно…
Корнем называют значок, обозначающий математическую операцию нахождения такого числа, возведение которого в указанную перед знаком корня степень должно дать число, указанное под этим самым знаком. Часто для решения задач, в которых присутствуют…
Знаком корня в математических науках называется условное обозначение для корней. Число, находящееся под знаком корня, называется подкоренным выражением. n = a. Корни нечетной степени существуют для отрицательных и положительных чисел, а корни четной степени — только для положительных.…
n = a. Корни нечетной степени существуют для отрицательных и положительных чисел, а корни четной степени — только для положительных.…
Квадратным корнем из числа X называется число A , которое в процессе умножения самого на себя (A * A ) может дать число X .
Т.е. A * A = A 2 = X , и √X = A .
Над квадратными корнями (√x ), как и над другими числами, можно выполнять такие арифметические операции, как вычитание и сложение. Для вычитания и сложения корней их нужно соединить посредством знаков, соответствующих этим действиям (например √x — √y ).
А потом привести корни к их простейшей форме — если между ними окажутся подобные, необходимо сделать приведение. Оно заключается в том, что берутся коэффициенты подобных членов со знаками соответствующих членов, далее заключаются в скобки и выводится общий корень за скобками множителя. Коэффициент, который мы получили, упрощается по обычным правилам.
Шаг 1.
 Извлечение квадратных корней
Извлечение квадратных корнейВо-первых, для сложения квадратных корней сначала нужно эти корни извлечь. Это можно будет сделать в том случае, если числа под знаком корня будут полными квадратами. Для примера возьмем заданное выражение √4 + √9 . Первое число 4 является квадратом числа 2 . Второе число 9 является квадратом числа 3 . Таким образом, можно получить следующее равенство: √4 + √9 = 2 + 3 = 5 .
Все, пример решен. Но так просто бывает далеко не всегда.
Шаг 2. Вынесение множителя числа из-под корня
Если полных квадратов нет под знаком корня, можно попробовать вынести множитель числа из-под знака корня. Для примера возьмём выражение √24 + √54 .
Раскладываем числа на множители:
24 = 2 * 2 * 2 * 3 ,
54 = 2 * 3 * 3 * 3 .
В числе 24 мы имеем множитель 4 , его можно вынести из-под знака квадратного корня. В числе 54 мы имеем множитель 9 .
Получаем равенство:
√24 + √54 = √(4 * 6) + √(9 * 6) = 2 * √6 + 3 * √6 = 5 * √6 .
Рассматривая данный пример, мы получаем вынос множителя из-под знака корня, тем самым упрощая заданное выражение.
Шаг 3. Сокращение знаменателя
Рассмотрим следующую ситуацию: сумма двух квадратных корней — это знаменатель дроби, например, A / (√a + √b) .
Теперь перед нами стоит задача «избавиться от иррациональности в знаменателе».
Воспользуемся следующим способом: умножаем числитель и знаменатель дроби на выражение √a — √b .
Формулу сокращённого умножения мы теперь получаем в знаменателе:
(√a + √b) * (√a — √b) = a — b .
Аналогично, если в знаменателе имеется разность корней: √a — √b , числитель и знаменатель дроби умножаем на выражение √a + √b .
Возьмём для примера дробь:
4 / (√3 + √5) = 4 * (√3 — √5) / ((√3 + √5) * (√3 — √5)) = 4 * (√3 — √5) / (-2) = 2 * (√5 — √3) .
Пример сложного сокращения знаменателя
Теперь будем рассматривать достаточно сложный пример избавления от иррациональности в знаменателе.
Для примера берём дробь: 12 / (√2 + √3 + √5) .
Нужно взять её числитель и знаменатель и перемножить на выражение √2 + √3 — √5 .
Получаем:
12 / (√2 + √3 + √5) = 12 * (√2 + √3 — √5) / (2 * √6) = 2 * √3 + 3 * √2 — √30.
Шаг 4. Вычисление приблизительного значения на калькуляторе
Если вам требуется только приблизительное значение, это можно сделать на калькуляторе путём подсчёта значения квадратных корней. Отдельно для каждого числа вычисляется значение и записывается с необходимой точностью, которая определяется количеством знаков после запятой. Далее совершаются все требуемые операции, как с обычными числами.
Пример вычисления приблизительного значения
Необходимо вычислить приблизительное значение данного выражения √7 + √5 .
В итоге получаем:
√7 + √5 ≈ 2,65 + 2,24 = 4,89 .
Обратите внимание: ни при каких условиях не следует производить сложение квадратных корней, как простых чисел, это совершенно недопустимо. То есть, если сложить квадратный корень из пяти и из трёх, у нас не может получиться квадратный корень из восьми.
То есть, если сложить квадратный корень из пяти и из трёх, у нас не может получиться квадратный корень из восьми.
Полезный совет: если вы решили разложить число на множители, для того, чтобы вывести квадрат из-под знака корня, вам необходимо сделать обратную проверку, то есть перемножить все множители, которые получились в результате вычислений, и в конечном результате этого математического расчёта должно получиться число, которое нам было задано первоначально.
Извлечение квадрантного корня из числа не единственная операция, которую можно производить с этим математическим явлением. Так же как и обычные числа, квадратные корни складывают и вычитают.
Yandex.RTB R-A-339285-1
Правила сложения и вычитания квадратных корней
Определение 1Такие действия, как сложение и вычитание квадратного корня, возможны только при условии одинакового подкоренного выражения.
Пример 1
Можно сложить или вычесть выражения 2 3 и 6 3 , но не 5 6 и 9 4 . Если есть возможность упростить выражение и привести его к корням с одинаковым подкоренным числом, то упрощайте, а потом складывайте или вычитайте.
Если есть возможность упростить выражение и привести его к корням с одинаковым подкоренным числом, то упрощайте, а потом складывайте или вычитайте.
Действия с корнями: основы
Пример 26 50 — 2 8 + 5 12
Алгоритм действия:
- Упростить подкоренное выражение . Для этого необходимо разложить подкоренное выражение на 2 множителя, один из которых, — квадратное число (число, из которого извлекается целый квадратный корень, например, 25 или 9).
- Затем нужно извлечь корень из квадратного числа и записать полученное значение перед знаком корня. Обращаем ваше внимание, что второй множитель заносится под знак корня.
- После процесса упрощения необходимо подчеркнуть корни с одинаковыми подкоренными выражениями — только их можно складывать и вычитать.
- У корней с одинаковыми подкоренными выражениями необходимо сложить или вычесть множители, которые стоят перед знаком корня. Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!
Совет 1
Если у вас пример с большим количеством одинаковых подкоренных выражений, то подчеркивайте такие выражения одинарными, двойными и тройными линиями, чтобы облегчить процесс вычисления.
Пример 3
Давайте попробуем решить данный пример:
6 50 = 6 (25 × 2) = (6 × 5) 2 = 30 2 . Для начала необходимо разложить 50 на 2 множителя 25 и 2, затем извлечь корень из 25, который равен 5, а 5 вынести из-под корня. После этого нужно умножить 5 на 6 (множитель у корня) и получить 30 2 .
2 8 = 2 (4 × 2) = (2 × 2) 2 = 4 2 . Сперва необходимо разложить 8 на 2 множителя: 4 и 2. Затем из 4 извлечь корень, который равен 2, а 2 вынести из-под корня. После этого нужно умножить 2 на 2 (множитель у корня) и получить 4 2 .
5 12 = 5 (4 × 3) = (5 × 2) 3 = 10 3 . Сперва необходимо разложить 12 на 2 множителя: 4 и 3. Затем извлечь из 4 корень, который равен 2, и вынести его из-под корня. После этого нужно умножить 2 на 5 (множитель у корня) и получить 10 3 .
Результат упрощения: 30 2 — 4 2 + 10 3
30 2 — 4 2 + 10 3 = (30 — 4) 2 + 10 3 = 26 2 + 10 3 .
В итоге мы увидели, сколько одинаковых подкоренных выражений содержится в данном примере. А сейчас попрактикуемся на других примерах.
А сейчас попрактикуемся на других примерах.
Пример 4
- Упрощаем (45) . Раскладываем 45 на множители: (45) = (9 × 5) ;
- Выносим 3 из-под корня (9 = 3) : 45 = 3 5 ;
- Складываем множители у корней: 3 5 + 4 5 = 7 5 .
Пример 5
6 40 — 3 10 + 5:
- Упрощаем 6 40 . Раскладываем 40 на множители: 6 40 = 6 (4 × 10) ;
- Выносим 2 из-под корня (4 = 2) : 6 40 = 6 (4 × 10) = (6 × 2) 10 ;
- Перемножаем множители, которые стоят перед корнем: 12 10 ;
- Записываем выражение в упрощенном виде: 12 10 — 3 10 + 5 ;
- Поскольку у первых двух членов одинаковые подкоренные числа, мы можем их вычесть: (12 — 3) 10 = 9 10 + 5 .
Пример 6
Как мы видим, упростить подкоренные числа не представляется возможным, поэтому ищем в примере члены с одинаковыми подкоренными числами, проводим математические действия (складываем, вычитаем и т.д.) и записываем результат:
(9 — 4) 5 — 2 3 = 5 5 — 2 3 .
Советы:
- Перед тем, как складывать или вычитать, необходимо обязательно упростить (если это возможно) подкоренные выражения.

- Складывать и вычитать корни с разными подкоренными выражениями строго воспрещается.
- Не следует суммировать или вычитать целое число или корень: 3 + (2 x) 1 / 2 .
- При выполнении действий с дробями, необходимо найти число, которое делится нацело на каждый знаменатель, потом привести дроби к общему знаменателю, затем сложить числители, а знаменатели оставить без изменений.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Свойства квадратных корней
До сих пор мы осуществляли над числами пять арифметических операций: сложение, вычитание, умножение , деление и возведение в степень, причем при вычислениях активно использовали различные свойства этих операций, например а + b = b + а, аn-bn = (аb)n и т. д.
В этой главе введена новая операция — извлечение квадратного корня из неотрицательного числа. Чтобы успешно ее использовать, нужно познакомиться со свойствами этой операции, что мы и сделаем в настоящем параграфе.
Доказательство. Введем следующие обозначения:https://pandia.ru/text/78/290/images/image005_28.jpg» alt=»Равенство»Задание»> Имеются только свойства, касающиеся умножения и деления квадратных корней. Будьте внимательны и осторожны, не принимайте желаемое за действительное.
Завершая параграф, отметим еще одно достаточно простое и в то же время важное свойство:
если a > 0 и n — натуральное число , то
Преобразование выражений, содержащих операцию извлечения квадратного корня
До сих пор мы с вами выполняли преобразования толькорациональных выражений , используя для этого правила действий над многочленами и алгебраическими дробями, формулы сокращенного умножения и т. д. В этой главе мы ввели новую операцию — операцию извлечения квадратного корня; мы установили, что
где, напомним, a, b — неотрицательные числа.
Используя эти формулы , можно выполнять различные преобразования выражений, содержащих операцию извлечения квадратного корня. Рассмотрим несколько примеров, причем во всех примерах будем предполагать, что переменные принимают только неотрицательные значения.
Рассмотрим несколько примеров, причем во всех примерах будем предполагать, что переменные принимают только неотрицательные значения.
Пример 3. Внести множитель под знак квадратного корня:
Пример 6 . Упростить выражение Решение. Выполним последовательные преобразования:
Как складывать корни разных степеней. Какие трудности ждут тех, кто взялся выполнять сложение корней? Действие с корнями: сложение и вычитание
Содержимое:
Складывать и вычитать квадратные корни можно только при условии, что у них одинаковое подкоренное выражение, то есть вы можете сложить или вычесть 2√3 и 4√3, но не 2√3 и 2√5. Вы можете упростить подкоренное выражение, чтобы привести их к корням с одинаковыми подкоренными выражениями (а затем сложить или вычесть их).
Шаги
Часть 1 Постигаем основы
- 1 (выражение под знаком корня). Для этого разложите подкоренное число на два множителя, один из которых является квадратным числом (число, из которого можно извлечь целый корень, например, 25 или 9).
 После этого извлеките корень из квадратного числа и запишите найденное значение перед знаком корня (под знаком корня останется второй множитель). Например, 6√50 — 2√8 + 5√12. Числа, стоящее перед знаком корня, являются множителями соответствующих корней, а числа под знаком корня – это подкоренные числа (выражения). Вот как решать данную задачу:
После этого извлеките корень из квадратного числа и запишите найденное значение перед знаком корня (под знаком корня останется второй множитель). Например, 6√50 — 2√8 + 5√12. Числа, стоящее перед знаком корня, являются множителями соответствующих корней, а числа под знаком корня – это подкоренные числа (выражения). Вот как решать данную задачу:- 6√50 = 6√(25 x 2) = (6 x 5)√2 = 30√2. Здесь вы раскладываете 50 на множители 25 и 2; затем из 25 извлекаете корень, равный 5, и 5 выносите из-под корня. Затем 5 умножаете на 6 (множитель у корня) и получаете 30√2.
- 2√8 = 2√(4 x 2) = (2 x 2)√2 = 4√2. Здесь вы раскладываете 8 на множители 4 и 2; затем из 4 извлекаете корень, равный 2, и 2 выносите из-под корня. Затем 2 умножаете на 2 (множитель у корня) и получаете 4√2.
- 5√12 = 5√(4 x 3) = (5 x 2)√3 = 10√3. Здесь вы раскладываете 12 на множители 4 и 3; затем из 4 извлекаете корень, равный 2, и 2 выносите из-под корня. Затем 2 умножаете на 5 (множитель у корня) и получаете 10√3.

- 2 Подчеркните корни, подкоренные выражения которых одинаковы. В нашем примере упрощенное выражение имеет вид: 30√2 — 4√2 + 10√3. В нем вы должны подчеркнуть первый и второй члены (30√2 и 4√2 ), так как у них одинаковое подкоренное число 2. Только такие корни вы можете складывать и вычитать.
- 3 Если вам дано выражение с большим количеством членов, многие из которых имеют одинаковые подкоренные выражения, используйте одинарное, двойное, тройное подчеркивание для обозначения таких членов, чтобы облегчить решение этого выражения.
- 4
У корней, подкоренные выражения которых одинаковы, сложите или вычтите множители, стоящие перед знаком корня, а подкоренное выражение оставьте прежним (не складывайте и не вычитайте подкоренные числа!
). Идея в том, чтобы показать, сколько всего корней с определенным подкоренным выражением содержится в данном выражении.
- 30√2 — 4√2 + 10√3 =
- (30 — 4)√2 + 10√3 =
- 26√2 + 10√3
Часть 2 Практикуемся на примерах
- 1 Пример 1: √(45) + 4√5.

- Упростите √(45). Разложите 45 на множители: √(45) = √(9 x 5).
- Вынесите 3 из-под корня (√9 = 3): √(45) = 3√5.
- Теперь сложите множители у корней: 3√5 + 4√5 = 7√5
- 2 Пример 2: 6√(40) — 3√(10) + √5.
- Упростите 6√(40). Разложите 40 на множители: 6√(40) = 6√(4 x 10).
- Вынесите 2 из-под корня (√4 = 2): 6√(40) = 6√(4 x 10) = (6 x 2)√10.
- Перемножьте множители перед корнем и получите 12√10.
- Теперь выражение можно записать в виде 12√10 — 3√(10) + √5. Так как у первых двух членов одинаковые подкоренные числа, вы можете вычесть второй член из первого, а первый оставить без изменений.
- Вы получите: (12-3)√10 + √5 = 9√10 + √5.
- 3 Пример 3. 9√5 -2√3 — 4√5. Здесь ни одно из подкоренных выражений нельзя разложить на множители, поэтому упростить это выражение не получится. Вы можете вычесть третий член из первого (так как у них одинаковые подкоренные числа), а второй член оставить без изменений.
 Вы получите: (9-4)√5 -2√3 = 5√5 — 2√3.
Вы получите: (9-4)√5 -2√3 = 5√5 — 2√3. - 4 Пример 4. √9 + √4 — 3√2.
- √9 = √(3 х 3) = 3.
- √4 = √(2 х 2) = 2.
- Теперь вы можете просто сложить 3 + 2, чтобы получить 5.
- Окончательный ответ: 5 — 3√2.
- 5 Пример 5. Решите выражение, содержащее корни и дроби. Вы можете складывать и вычислять только те дроби, у которых общий (одинаковый) знаменатель. Дано выражение (√2)/4 + (√2)/2.
- Найдите наименьший общий знаменатель этих дробей. Это число, которое делится нацело на каждый знаменатель. В нашем примере на 4 и на 2 делится число 4.
- Теперь вторую дробь умножьте на 2/2 (чтобы привести ее к общему знаменателю; первая дробь уже приведена к нему): (√2)/2 х 2/2 = (2√2)/4.
- Сложите числители дробей, а знаменатель оставьте прежним: (√2)/4 + (2√2)/4 = (3√2)/4 .
- Перед суммированием или вычитанием корней обязательно упростите (если возможно) подкоренные выражения.
Предупреждения
- Никогда не суммируйте и не вычитайте корни с разными подкоренными выражениями.
 2 = x, √x = a. Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания.
2 = x, √x = a. Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания.Инструкция
- Во-первых, при сложении квадратных корней попробуйте извлечь эти корни. Это будет возможно, если числа под знаком корня являются полными квадратами. Например, пусть задано выражение √4 + √9. Первое число 4 – это квадрат числа 2. Второе число 9 – это квадрат числа 3. Таким образом получается, что: √4 + √9 = 2 + 3 = 5.
- Если под знаком корня нет полных квадратов, то попробуйте вынести из под знака корня множитель числа. Например, пусть дано выражение √24 + √54. Разложите числа на множители: 24 = 2 * 2 * 2 * 3, 54 = 2 * 3 * 3 * 3. В числе 24 имеется множитель 4, который можно вынести из под знака квадратного корня. В числе 54 — множитель 9. Таким образом, получается что: √24 + √54 = √(4 * 6) + √(9 * 6) = 2 * √6 + 3 * √6 = 5 * √6. В данном примере в результате выноса множителя из под знака корня получилось упростить заданное выражение.

- Пусть сумма двух квадратных корней является знаменателем дроби, например, A / (√a + √b). И пусть перед вами стоит задача «избавиться от иррациональности в знаменателе». Тогда можно воспользоваться следующим способом. Умножьте числитель и знаменатель дроби на выражение √a — √b. Таким образом в знаменателе получится формула сокращенного умножения: (√a + √b) * (√a — √b) = a – b. По аналогии, если в знаменателе дана разность корней: √a — √b, то числитель и знаменатель дроби необходимо умножить на выражение √a + √b. Для примера, пусть дана дробь 4 / (√3 + √5) = 4 * (√3 — √5) / ((√3 + √5) * (√3 — √5)) = 4 * (√3 — √5) / (-2) = 2 * (√5 — √3).
- Рассмотрите более сложный пример избавления от иррациональности в знаменателе. Пусть дана дробь 12 / (√2 + √3 + √5). Необходимо умножить числитель и знаменатель дроби на выражение √2 + √3 — √5:
12 / (√2 + √3 + √5) = 12 * (√2 + √3 — √5) / ((√2 + √3 + √5) * (√2 + √3 — √5)) = 12 * (√2 + √3 — √5) / (2 * √6) = √6 * (√2 + √3 — √5) = 2 * √3 + 3 * √2 — √30.
- И наконец, если вам необходимо только приблизительное значение, то можно посчитать значения квадратных корней на калькуляторе. Вычислите значения отдельно для каждого числа и запишите с необходимой точностью (например, два знака после запятой). А затем совершите требуемые арифметические операции, как с обычными числами. Например, пусть необходимо узнать приблизительное значение выражения √7 + √5 ≈ 2,65 + 2,24 = 4,89.
Содержимое:
В математике корни могут быть квадратными, кубическими или иметь любой другой показатель (степень), который пишется слева над знаком корня. Выражение, стоящее под знаком корня, называется подкоренным выражением. Сложение корней похоже на сложение членов алгебраического выражения, то есть требует определения подобных корней.
Шаги
Часть 1 Определение корней
- 1 Обозначение корней. Выражение под знаком корня (√) означает, что из этого выражения необходимо извлечь корень определенной степени.
- Корень обозначают знаком √.

- Показатель (степень) корня пишется слева над знаком корня. Например, кубический корень из 27 записывается так: 3 √(27)
- Если показатель (степень) корня отсутствует, то показатель считается равным 2, то есть это квадратный корень (или корень второй степени).
- Число, записанное перед знаком корня, называется множителем (то есть это число умножается на корень), например 5√(2)
- Если множителя перед корнем нет, то он равен 1 (напомним, что любое число, умноженное на 1, равняется самому себе).
- Если вы впервые работаете с корнями, сделайте соответствующие пометки над множителем и показателем корня, чтобы не запутаться и лучше понять их назначение.
- Корень обозначают знаком √.
- 2 Запомните, какие корни можно складывать, а какие нельзя. Также, как нельзя складывать разные члены выражения, например, 2а + 2b ≠ 4ab, вы не можете складывать разные корни.
- Нельзя складывать корни с разными подкоренными выражениями, например, √(2) + √(3) ≠ √(5). Но вы можете сложить числа, стоящие под одним корнем, например, √(2 + 3) = √(5) (квадратный корень из 2 примерно равен 1,414, квадратный корень из 3 примерно равен 1,732, а квадратный корень из 5 примерно равен 2,236).

- Нельзя складывать корни с одинаковыми подкоренными выражениями, но разными показателями, например, √(64) + 3 √(64) (эта сумма не равна 5 √(64), так как квадратный корень из 64 равен 8, кубический корень из 64 равен 4, 8 + 4 = 12, что гораздо больше, чем корень пятой степени из 64, который примерно равен 2,297).
- Нельзя складывать корни с разными подкоренными выражениями, например, √(2) + √(3) ≠ √(5). Но вы можете сложить числа, стоящие под одним корнем, например, √(2 + 3) = √(5) (квадратный корень из 2 примерно равен 1,414, квадратный корень из 3 примерно равен 1,732, а квадратный корень из 5 примерно равен 2,236).
Часть 2 Упрощение и сложение корней
- 1 Определите и сгруппируйте подобные корни. Подобные корни – корни, у которых одинаковые показатели и одинаковые подкоренные выражения. Например, рассмотрим выражение:
2√(3) + 3 √(81) + 2√(50) + √(32) + 6√(3)- Во-первых, перепишите выражение так, чтобы корни с одинаковым показателем располагались последовательно.
2√(3) + 2√(50) + √(32) + 6√(3) + 3 √(81) - Затем перепишите выражение так, чтобы корни с одинаковым показателем и с одинаковым подкоренным выражением располагались последовательно.
2√(50) + √(32) + 2√(3) + 6√(3) + 3 √(81)
- Во-первых, перепишите выражение так, чтобы корни с одинаковым показателем располагались последовательно.
- 2 Упростите корни.
 Для этого разложите (где возможно) подкоренные выражения на два множителя, один из которых вынесите из-под корня. В этом случае вынесенное число и множитель корня перемножаются.
Для этого разложите (где возможно) подкоренные выражения на два множителя, один из которых вынесите из-под корня. В этом случае вынесенное число и множитель корня перемножаются.- В приведенном выше примере разложите число 50 на 2*25, а число 32 – на 2*16. Из 25 и 16 можно извлечь квадратные корни (соответственно 5 и 4) и вынести 5 и 4 из-под корня, соответственно умножив их на множители 2 и 1. Таким образом, вы получите упрощенное выражение: 10√(2) + 4√(2) + 2√(3) + 6√(3) + 3 √(81)
- Число 81 можно разложить на множители 3*27, а из числа 27 можно извлечь кубический корень, равный 3. Это число 3 можно вынести из-под корня. Таким образом, вы получите еще более упрощенное выражение: 10√(2) + 4√(2) + 2√(3)+ 6√(3) + 3 3 √(3)
- 3 Сложите множители подобных корней. В нашем примере есть подобные квадратные корни из 2 (их можно сложить) и подобные квадратные корни из 3 (их тоже можно сложить). У кубического корня из 3 подобных корней нет.
- 10√(2) + 4√(2) = 14√(2).

- 2√(3)+ 6√(3) = 8√(3).
- Окончательное упрощенное выражение: 14√(2) + 8√(3) + 3 3 √(3)
- 10√(2) + 4√(2) = 14√(2).
- Не существует общепринятых правил порядка записи корней в выражении. Потому вы можете записывать корни в порядке возрастания их показателей и в порядке возрастания подкоренных выражений.
Квадратным корнем из числа X называется число A , которое в процессе умножения самого на себя (A * A ) может дать число X .
Т.е. A * A = A 2 = X , и √X = A .Над квадратными корнями (√x ), как и над другими числами, можно выполнять такие арифметические операции, как вычитание и сложение. Для вычитания и сложения корней их нужно соединить посредством знаков, соответствующих этим действиям (например √x — √y ).
А потом привести корни к их простейшей форме — если между ними окажутся подобные, необходимо сделать приведение. Оно заключается в том, что берутся коэффициенты подобных членов со знаками соответствующих членов, далее заключаются в скобки и выводится общий корень за скобками множителя. Коэффициент, который мы получили, упрощается по обычным правилам.
Коэффициент, который мы получили, упрощается по обычным правилам.Шаг 1. Извлечение квадратных корней
Во-первых, для сложения квадратных корней сначала нужно эти корни извлечь. Это можно будет сделать в том случае, если числа под знаком корня будут полными квадратами. Для примера возьмем заданное выражение √4 + √9 . Первое число 4 является квадратом числа 2 . Второе число 9 является квадратом числа 3 . Таким образом, можно получить следующее равенство: √4 + √9 = 2 + 3 = 5 .
Все, пример решен. Но так просто бывает далеко не всегда.Шаг 2. Вынесение множителя числа из-под корня
Если полных квадратов нет под знаком корня, можно попробовать вынести множитель числа из-под знака корня. Для примера возьмём выражение √24 + √54 .
Раскладываем числа на множители:
24 = 2 * 2 * 2 * 3 ,
54 = 2 * 3 * 3 * 3 .В числе 24 мы имеем множитель 4 , его можно вынести из-под знака квадратного корня.
 В числе 54 мы имеем множитель 9 .
В числе 54 мы имеем множитель 9 .Получаем равенство:
√24 + √54 = √(4 * 6) + √(9 * 6) = 2 * √6 + 3 * √6 = 5 * √6 .Рассматривая данный пример, мы получаем вынос множителя из-под знака корня, тем самым упрощая заданное выражение.
Шаг 3. Сокращение знаменателя
Рассмотрим следующую ситуацию: сумма двух квадратных корней — это знаменатель дроби, например, A / (√a + √b) .
Теперь перед нами стоит задача «избавиться от иррациональности в знаменателе».
Воспользуемся следующим способом: умножаем числитель и знаменатель дроби на выражение √a — √b .Формулу сокращённого умножения мы теперь получаем в знаменателе:
(√a + √b) * (√a — √b) = a — b .Аналогично, если в знаменателе имеется разность корней: √a — √b , числитель и знаменатель дроби умножаем на выражение √a + √b .
Возьмём для примера дробь:
4 / (√3 + √5) = 4 * (√3 — √5) / ((√3 + √5) * (√3 — √5)) = 4 * (√3 — √5) / (-2) = 2 * (√5 — √3) .
Пример сложного сокращения знаменателя
Теперь будем рассматривать достаточно сложный пример избавления от иррациональности в знаменателе.
Для примера берём дробь: 12 / (√2 + √3 + √5) .
Нужно взять её числитель и знаменатель и перемножить на выражение √2 + √3 — √5 .Получаем:
12 / (√2 + √3 + √5) = 12 * (√2 + √3 — √5) / (2 * √6) = 2 * √3 + 3 * √2 — √30.
Шаг 4. Вычисление приблизительного значения на калькуляторе
Если вам требуется только приблизительное значение, это можно сделать на калькуляторе путём подсчёта значения квадратных корней. Отдельно для каждого числа вычисляется значение и записывается с необходимой точностью, которая определяется количеством знаков после запятой. Далее совершаются все требуемые операции, как с обычными числами.
Пример вычисления приблизительного значения
Необходимо вычислить приблизительное значение данного выражения √7 + √5 .
В итоге получаем:
√7 + √5 ≈ 2,65 + 2,24 = 4,89 .

Обратите внимание: ни при каких условиях не следует производить сложение квадратных корней, как простых чисел, это совершенно недопустимо. То есть, если сложить квадратный корень из пяти и из трёх, у нас не может получиться квадратный корень из восьми.
Полезный совет: если вы решили разложить число на множители, для того, чтобы вывести квадрат из-под знака корня, вам необходимо сделать обратную проверку, то есть перемножить все множители, которые получились в результате вычислений, и в конечном результате этого математического расчёта должно получиться число, которое нам было задано первоначально.
Извлечение квадрантного корня из числа не единственная операция, которую можно производить с этим математическим явлением. Так же как и обычные числа, квадратные корни складывают и вычитают.
Yandex.RTB R-A-339285-1
Правила сложения и вычитания квадратных корней
Определение 1Такие действия, как сложение и вычитание квадратного корня, возможны только при условии одинакового подкоренного выражения.

Пример 1
Можно сложить или вычесть выражения 2 3 и 6 3 , но не 5 6 и 9 4 . Если есть возможность упростить выражение и привести его к корням с одинаковым подкоренным числом, то упрощайте, а потом складывайте или вычитайте.
Действия с корнями: основы
Пример 26 50 — 2 8 + 5 12
Алгоритм действия:
- Упростить подкоренное выражение . Для этого необходимо разложить подкоренное выражение на 2 множителя, один из которых, — квадратное число (число, из которого извлекается целый квадратный корень, например, 25 или 9).
- Затем нужно извлечь корень из квадратного числа и записать полученное значение перед знаком корня. Обращаем ваше внимание, что второй множитель заносится под знак корня.
- После процесса упрощения необходимо подчеркнуть корни с одинаковыми подкоренными выражениями — только их можно складывать и вычитать.
- У корней с одинаковыми подкоренными выражениями необходимо сложить или вычесть множители, которые стоят перед знаком корня.
 Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!
Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!
Совет 1
Если у вас пример с большим количеством одинаковых подкоренных выражений, то подчеркивайте такие выражения одинарными, двойными и тройными линиями, чтобы облегчить процесс вычисления.
Пример 3
Давайте попробуем решить данный пример:
6 50 = 6 (25 × 2) = (6 × 5) 2 = 30 2 . Для начала необходимо разложить 50 на 2 множителя 25 и 2, затем извлечь корень из 25, который равен 5, а 5 вынести из-под корня. После этого нужно умножить 5 на 6 (множитель у корня) и получить 30 2 .
2 8 = 2 (4 × 2) = (2 × 2) 2 = 4 2 . Сперва необходимо разложить 8 на 2 множителя: 4 и 2. Затем из 4 извлечь корень, который равен 2, а 2 вынести из-под корня. После этого нужно умножить 2 на 2 (множитель у корня) и получить 4 2 .
5 12 = 5 (4 × 3) = (5 × 2) 3 = 10 3 . Сперва необходимо разложить 12 на 2 множителя: 4 и 3. Затем извлечь из 4 корень, который равен 2, и вынести его из-под корня.
 После этого нужно умножить 2 на 5 (множитель у корня) и получить 10 3 .
После этого нужно умножить 2 на 5 (множитель у корня) и получить 10 3 .Результат упрощения: 30 2 — 4 2 + 10 3
30 2 — 4 2 + 10 3 = (30 — 4) 2 + 10 3 = 26 2 + 10 3 .
В итоге мы увидели, сколько одинаковых подкоренных выражений содержится в данном примере. А сейчас попрактикуемся на других примерах.
Пример 4
- Упрощаем (45) . Раскладываем 45 на множители: (45) = (9 × 5) ;
- Выносим 3 из-под корня (9 = 3) : 45 = 3 5 ;
- Складываем множители у корней: 3 5 + 4 5 = 7 5 .
Пример 5
6 40 — 3 10 + 5:
- Упрощаем 6 40 . Раскладываем 40 на множители: 6 40 = 6 (4 × 10) ;
- Выносим 2 из-под корня (4 = 2) : 6 40 = 6 (4 × 10) = (6 × 2) 10 ;
- Перемножаем множители, которые стоят перед корнем: 12 10 ;
- Записываем выражение в упрощенном виде: 12 10 — 3 10 + 5 ;
- Поскольку у первых двух членов одинаковые подкоренные числа, мы можем их вычесть: (12 — 3) 10 = 9 10 + 5 .
Пример 6
Как мы видим, упростить подкоренные числа не представляется возможным, поэтому ищем в примере члены с одинаковыми подкоренными числами, проводим математические действия (складываем, вычитаем и т.
 д.) и записываем результат:
д.) и записываем результат:(9 — 4) 5 — 2 3 = 5 5 — 2 3 .
Советы:
- Перед тем, как складывать или вычитать, необходимо обязательно упростить (если это возможно) подкоренные выражения.
- Складывать и вычитать корни с разными подкоренными выражениями строго воспрещается.
- Не следует суммировать или вычитать целое число или корень: 3 + (2 x) 1 / 2 .
- При выполнении действий с дробями, необходимо найти число, которое делится нацело на каждый знаменатель, потом привести дроби к общему знаменателю, затем сложить числители, а знаменатели оставить без изменений.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Добавление корней. Умножение корней: основные правила
Квадратным корнем из числа X называется число A , которое в процессе умножения самого на себя (A * A ) может дать число X .
Т.е. A * A = A 2 = X , и √X = A .Над квадратными корнями (√x ), как и над другими числами, можно выполнять такие арифметические операции, как вычитание и сложение.
 Для вычитания и сложения корней их нужно соединить посредством знаков, соответствующих этим действиям (например √x — √y ).
Для вычитания и сложения корней их нужно соединить посредством знаков, соответствующих этим действиям (например √x — √y ).
А потом привести корни к их простейшей форме — если между ними окажутся подобные, необходимо сделать приведение. Оно заключается в том, что берутся коэффициенты подобных членов со знаками соответствующих членов, далее заключаются в скобки и выводится общий корень за скобками множителя. Коэффициент, который мы получили, упрощается по обычным правилам.Шаг 1. Извлечение квадратных корней
Во-первых, для сложения квадратных корней сначала нужно эти корни извлечь. Это можно будет сделать в том случае, если числа под знаком корня будут полными квадратами. Для примера возьмем заданное выражение √4 + √9 . Первое число 4 является квадратом числа 2 . Второе число 9 является квадратом числа 3 . Таким образом, можно получить следующее равенство: √4 + √9 = 2 + 3 = 5 .
Все, пример решен. Но так просто бывает далеко не всегда.
Шаг 2. Вынесение множителя числа из-под корня
Если полных квадратов нет под знаком корня, можно попробовать вынести множитель числа из-под знака корня. Для примера возьмём выражение √24 + √54 .
Раскладываем числа на множители:
24 = 2 * 2 * 2 * 3 ,
54 = 2 * 3 * 3 * 3 .В числе 24 мы имеем множитель 4 , его можно вынести из-под знака квадратного корня. В числе 54 мы имеем множитель 9 .
Получаем равенство:
√24 + √54 = √(4 * 6) + √(9 * 6) = 2 * √6 + 3 * √6 = 5 * √6 .Рассматривая данный пример, мы получаем вынос множителя из-под знака корня, тем самым упрощая заданное выражение.
Шаг 3. Сокращение знаменателя
Рассмотрим следующую ситуацию: сумма двух квадратных корней — это знаменатель дроби, например, A / (√a + √b) .
Теперь перед нами стоит задача «избавиться от иррациональности в знаменателе».
Воспользуемся следующим способом: умножаем числитель и знаменатель дроби на выражение √a — √b .
Формулу сокращённого умножения мы теперь получаем в знаменателе:
(√a + √b) * (√a — √b) = a — b .Аналогично, если в знаменателе имеется разность корней: √a — √b , числитель и знаменатель дроби умножаем на выражение √a + √b .
Возьмём для примера дробь:
4 / (√3 + √5) = 4 * (√3 — √5) / ((√3 + √5) * (√3 — √5)) = 4 * (√3 — √5) / (-2) = 2 * (√5 — √3) .Пример сложного сокращения знаменателя
Теперь будем рассматривать достаточно сложный пример избавления от иррациональности в знаменателе.
Для примера берём дробь: 12 / (√2 + √3 + √5) .
Нужно взять её числитель и знаменатель и перемножить на выражение √2 + √3 — √5 .Получаем:
12 / (√2 + √3 + √5) = 12 * (√2 + √3 — √5) / (2 * √6) = 2 * √3 + 3 * √2 — √30.
Шаг 4. Вычисление приблизительного значения на калькуляторе
Если вам требуется только приблизительное значение, это можно сделать на калькуляторе путём подсчёта значения квадратных корней.
 Отдельно для каждого числа вычисляется значение и записывается с необходимой точностью, которая определяется количеством знаков после запятой. Далее совершаются все требуемые операции, как с обычными числами.
Отдельно для каждого числа вычисляется значение и записывается с необходимой точностью, которая определяется количеством знаков после запятой. Далее совершаются все требуемые операции, как с обычными числами.Пример вычисления приблизительного значения
Необходимо вычислить приблизительное значение данного выражения √7 + √5 .
В итоге получаем:
√7 + √5 ≈ 2,65 + 2,24 = 4,89 .
Обратите внимание: ни при каких условиях не следует производить сложение квадратных корней, как простых чисел, это совершенно недопустимо. То есть, если сложить квадратный корень из пяти и из трёх, у нас не может получиться квадратный корень из восьми.
Полезный совет: если вы решили разложить число на множители, для того, чтобы вывести квадрат из-под знака корня, вам необходимо сделать обратную проверку, то есть перемножить все множители, которые получились в результате вычислений, и в конечном результате этого математического расчёта должно получиться число, которое нам было задано первоначально.

В наше время современных электронных вычислительных машин вычисление корня из числа не представляется сложной задачей. Например, √2704=52, это вам подсчитает любой калькулятор. К счастью, калькулятор есть не только в Windows, но и в обычном, даже самом простеньком, телефоне. Правда если вдруг (с малой долей вероятности, вычисление которой, между прочим, включает в себя сложение корней) вы окажитесь без доступных средств, то, увы, придется рассчитывать только на свои мозги.
Тренировка ума никогда не помещает. Особенно для тех, кто не так часто работает с цифрами, а уж тем более с корнями. Сложение и вычитание корней — хорошая разминка для скучающего ума. А еще я покажу поэтапно сложение корней. Примеры выражений могут быть следующие.
Уравнение, которое нужно упростить:
√2+3√48-4×√27+√128
Это иррациональное выражение. Для того чтобы его упростить нужно привести все подкоренные выражения к общему виду. Делаем поэтапно:
Первое число упростить уже нельзя.
 2×2)
2×2)Переписываем выражение с упрощенными слагаемыми:
√2+12×√3-12×√3+8×√2
Теперь складываем числа одним и тем же подкоренным выражением. Нельзя складывать или вычитать выражения с разными подкоренными выражениями. Сложение корней требует соблюдение этого правила.
Ответ получаем следующий:
√2+12√3-12√3+8√2=9√2
√2=1×√2 — надеюсь, то, что в алгебре принято опускать подобные элементы, не станет для вас новостью.
Выражения могут быть представлены не только квадратным корнем, но так же и с кубическим или корнем n-ной степени.
Сложение и вычитание корней с разными показателями степени, но с равнозначным подкоренным выражением, происходит следующим образом:
Если мы имеем выражение вида √a+∛b+∜b, то мы можем упростить это выражение так:
∛b+∜b=12×√b4 +12×√b3
12√b4 +12×√b3=12×√b4 + b3
Мы привели два подобных члена к общему показателю корня. Здесь использовалось свойство корней, которое гласит: если число степени подкоренного выражения и число показателя корня умножить на одно и то же число, то его вычисление останется неизменным.

На заметку: показатели степени складываются только при умножении.
Рассмотрим пример, когда в выражении присутствуют дроби.
5√8-4×√(1/4)+√72-4×√2
Будем решать по этапам:
5√8=5*2√2 — мы выносим из-под корня извлекаемую часть.
4√(1/4)=-4 √1/(√4)= — 4 *1/2= — 2
Если в тело корня представлено дробью, то часто этой дроби не измениться, если извлечь квадратный корень из делимого и делителя. В итоге мы получили описанное выше равенство.
√72-4√2=√(36×2)- 4√2=2√2
10√2+2√2-2=12√2-2
Вот и получился ответ.
Главное помнить, что из отрицательных чисел не извлекается корень с четным показателем степени. Если четной степени подкоренное выражение является отрицательным, то выражение является нерешаемым.
Сложение корней возможно только при совпадении подкоренных выражений, так как они являются подобными слагаемыми. То же самое относиться и к разности.
Сложение корней с разными числовыми показателями степени производиться посредством приведения к общей корневой степени обоих слагаемых.
 Это закон действует так же как приведение к общему знаменателю при сложении или вычитании дробей.
Это закон действует так же как приведение к общему знаменателю при сложении или вычитании дробей.Если в подкоренном выражении имеется число, возведенное в степень, то это выражение можно упростить при условии, что между показателем корня и степени существует общий знаменатель.
Формулы корней. Свойства квадратных корней.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать.
Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх.
 Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…
Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…Начнём с самой простой. Вот она:
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Содержимое:
Складывать и вычитать квадратные корни можно только при условии, что у них одинаковое подкоренное выражение, то есть вы можете сложить или вычесть 2√3 и 4√3, но не 2√3 и 2√5. Вы можете упростить подкоренное выражение, чтобы привести их к корням с одинаковыми подкоренными выражениями (а затем сложить или вычесть их).
Шаги
Часть 1 Постигаем основы
- 1 (выражение под знаком корня). Для этого разложите подкоренное число на два множителя, один из которых является квадратным числом (число, из которого можно извлечь целый корень, например, 25 или 9).
 После этого извлеките корень из квадратного числа и запишите найденное значение перед знаком корня (под знаком корня останется второй множитель). Например, 6√50 — 2√8 + 5√12. Числа, стоящее перед знаком корня, являются множителями соответствующих корней, а числа под знаком корня – это подкоренные числа (выражения). Вот как решать данную задачу:
После этого извлеките корень из квадратного числа и запишите найденное значение перед знаком корня (под знаком корня останется второй множитель). Например, 6√50 — 2√8 + 5√12. Числа, стоящее перед знаком корня, являются множителями соответствующих корней, а числа под знаком корня – это подкоренные числа (выражения). Вот как решать данную задачу:- 6√50 = 6√(25 x 2) = (6 x 5)√2 = 30√2. Здесь вы раскладываете 50 на множители 25 и 2; затем из 25 извлекаете корень, равный 5, и 5 выносите из-под корня. Затем 5 умножаете на 6 (множитель у корня) и получаете 30√2.
- 2√8 = 2√(4 x 2) = (2 x 2)√2 = 4√2. Здесь вы раскладываете 8 на множители 4 и 2; затем из 4 извлекаете корень, равный 2, и 2 выносите из-под корня. Затем 2 умножаете на 2 (множитель у корня) и получаете 4√2.
- 5√12 = 5√(4 x 3) = (5 x 2)√3 = 10√3. Здесь вы раскладываете 12 на множители 4 и 3; затем из 4 извлекаете корень, равный 2, и 2 выносите из-под корня. Затем 2 умножаете на 5 (множитель у корня) и получаете 10√3.

- 2 Подчеркните корни, подкоренные выражения которых одинаковы. В нашем примере упрощенное выражение имеет вид: 30√2 — 4√2 + 10√3. В нем вы должны подчеркнуть первый и второй члены (30√2 и 4√2 ), так как у них одинаковое подкоренное число 2. Только такие корни вы можете складывать и вычитать.
- 3 Если вам дано выражение с большим количеством членов, многие из которых имеют одинаковые подкоренные выражения, используйте одинарное, двойное, тройное подчеркивание для обозначения таких членов, чтобы облегчить решение этого выражения.
- 4
У корней, подкоренные выражения которых одинаковы, сложите или вычтите множители, стоящие перед знаком корня, а подкоренное выражение оставьте прежним (не складывайте и не вычитайте подкоренные числа!
). Идея в том, чтобы показать, сколько всего корней с определенным подкоренным выражением содержится в данном выражении.
- 30√2 — 4√2 + 10√3 =
- (30 — 4)√2 + 10√3 =
- 26√2 + 10√3
Часть 2 Практикуемся на примерах
- 1 Пример 1: √(45) + 4√5.

- Упростите √(45). Разложите 45 на множители: √(45) = √(9 x 5).
- Вынесите 3 из-под корня (√9 = 3): √(45) = 3√5.
- Теперь сложите множители у корней: 3√5 + 4√5 = 7√5
- 2 Пример 2: 6√(40) — 3√(10) + √5.
- Упростите 6√(40). Разложите 40 на множители: 6√(40) = 6√(4 x 10).
- Вынесите 2 из-под корня (√4 = 2): 6√(40) = 6√(4 x 10) = (6 x 2)√10.
- Перемножьте множители перед корнем и получите 12√10.
- Теперь выражение можно записать в виде 12√10 — 3√(10) + √5. Так как у первых двух членов одинаковые подкоренные числа, вы можете вычесть второй член из первого, а первый оставить без изменений.
- Вы получите: (12-3)√10 + √5 = 9√10 + √5.
- 3 Пример 3. 9√5 -2√3 — 4√5. Здесь ни одно из подкоренных выражений нельзя разложить на множители, поэтому упростить это выражение не получится. Вы можете вычесть третий член из первого (так как у них одинаковые подкоренные числа), а второй член оставить без изменений.
 Вы получите: (9-4)√5 -2√3 = 5√5 — 2√3.
Вы получите: (9-4)√5 -2√3 = 5√5 — 2√3. - 4 Пример 4. √9 + √4 — 3√2.
- √9 = √(3 х 3) = 3.
- √4 = √(2 х 2) = 2.
- Теперь вы можете просто сложить 3 + 2, чтобы получить 5.
- Окончательный ответ: 5 — 3√2.
- 5 Пример 5. Решите выражение, содержащее корни и дроби. Вы можете складывать и вычислять только те дроби, у которых общий (одинаковый) знаменатель. Дано выражение (√2)/4 + (√2)/2.
- Найдите наименьший общий знаменатель этих дробей. Это число, которое делится нацело на каждый знаменатель. В нашем примере на 4 и на 2 делится число 4.
- Теперь вторую дробь умножьте на 2/2 (чтобы привести ее к общему знаменателю; первая дробь уже приведена к нему): (√2)/2 х 2/2 = (2√2)/4.
- Сложите числители дробей, а знаменатель оставьте прежним: (√2)/4 + (2√2)/4 = (3√2)/4 .
- Перед суммированием или вычитанием корней обязательно упростите (если возможно) подкоренные выражения.
Предупреждения
- Никогда не суммируйте и не вычитайте корни с разными подкоренными выражениями.

- Никогда не суммируйте и не вычитайте целое число и корень, например, 3 + (2x) 1/2 .
- Примечание: «х» в одной второй степени и квадратный корень из «х» – это одно и то же (то есть x 1/2 = √х).
Содержимое:
В математике корни могут быть квадратными, кубическими или иметь любой другой показатель (степень), который пишется слева над знаком корня. Выражение, стоящее под знаком корня, называется подкоренным выражением. Сложение корней похоже на сложение членов алгебраического выражения, то есть требует определения подобных корней.
Шаги
Часть 1 Определение корней
- 1 Обозначение корней. Выражение под знаком корня (√) означает, что из этого выражения необходимо извлечь корень определенной степени.
- Корень обозначают знаком √.
- Показатель (степень) корня пишется слева над знаком корня. Например, кубический корень из 27 записывается так: 3 √(27)
- Если показатель (степень) корня отсутствует, то показатель считается равным 2, то есть это квадратный корень (или корень второй степени).

- Число, записанное перед знаком корня, называется множителем (то есть это число умножается на корень), например 5√(2)
- Если множителя перед корнем нет, то он равен 1 (напомним, что любое число, умноженное на 1, равняется самому себе).
- Если вы впервые работаете с корнями, сделайте соответствующие пометки над множителем и показателем корня, чтобы не запутаться и лучше понять их назначение.
- 2 Запомните, какие корни можно складывать, а какие нельзя. Также, как нельзя складывать разные члены выражения, например, 2а + 2b ≠ 4ab, вы не можете складывать разные корни.
- Нельзя складывать корни с разными подкоренными выражениями, например, √(2) + √(3) ≠ √(5). Но вы можете сложить числа, стоящие под одним корнем, например, √(2 + 3) = √(5) (квадратный корень из 2 примерно равен 1,414, квадратный корень из 3 примерно равен 1,732, а квадратный корень из 5 примерно равен 2,236).
- Нельзя складывать корни с одинаковыми подкоренными выражениями, но разными показателями, например, √(64) + 3 √(64) (эта сумма не равна 5 √(64), так как квадратный корень из 64 равен 8, кубический корень из 64 равен 4, 8 + 4 = 12, что гораздо больше, чем корень пятой степени из 64, который примерно равен 2,297).

Часть 2 Упрощение и сложение корней
- 1 Определите и сгруппируйте подобные корни. Подобные корни – корни, у которых одинаковые показатели и одинаковые подкоренные выражения. Например, рассмотрим выражение:
2√(3) + 3 √(81) + 2√(50) + √(32) + 6√(3)- Во-первых, перепишите выражение так, чтобы корни с одинаковым показателем располагались последовательно.
2√(3) + 2√(50) + √(32) + 6√(3) + 3 √(81) - Затем перепишите выражение так, чтобы корни с одинаковым показателем и с одинаковым подкоренным выражением располагались последовательно.
2√(50) + √(32) + 2√(3) + 6√(3) + 3 √(81)
- Во-первых, перепишите выражение так, чтобы корни с одинаковым показателем располагались последовательно.
- 2 Упростите корни. Для этого разложите (где возможно) подкоренные выражения на два множителя, один из которых вынесите из-под корня. В этом случае вынесенное число и множитель корня перемножаются.
- В приведенном выше примере разложите число 50 на 2*25, а число 32 – на 2*16. Из 25 и 16 можно извлечь квадратные корни (соответственно 5 и 4) и вынести 5 и 4 из-под корня, соответственно умножив их на множители 2 и 1.
 Таким образом, вы получите упрощенное выражение: 10√(2) + 4√(2) + 2√(3) + 6√(3) + 3 √(81)
Таким образом, вы получите упрощенное выражение: 10√(2) + 4√(2) + 2√(3) + 6√(3) + 3 √(81) - Число 81 можно разложить на множители 3*27, а из числа 27 можно извлечь кубический корень, равный 3. Это число 3 можно вынести из-под корня. Таким образом, вы получите еще более упрощенное выражение: 10√(2) + 4√(2) + 2√(3)+ 6√(3) + 3 3 √(3)
- В приведенном выше примере разложите число 50 на 2*25, а число 32 – на 2*16. Из 25 и 16 можно извлечь квадратные корни (соответственно 5 и 4) и вынести 5 и 4 из-под корня, соответственно умножив их на множители 2 и 1.
- 3 Сложите множители подобных корней. В нашем примере есть подобные квадратные корни из 2 (их можно сложить) и подобные квадратные корни из 3 (их тоже можно сложить). У кубического корня из 3 подобных корней нет.
- 10√(2) + 4√(2) = 14√(2).
- 2√(3)+ 6√(3) = 8√(3).
- Окончательное упрощенное выражение: 14√(2) + 8√(3) + 3 3 √(3)
- Не существует общепринятых правил порядка записи корней в выражении. Потому вы можете записывать корни в порядке возрастания их показателей и в порядке возрастания подкоренных выражений.
Разность квадратов под корнем как решать.
 2 = x, √x = a. Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания.
2 = x, √x = a. Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания.Инструкция
- Во-первых, при сложении квадратных корней попробуйте извлечь эти корни. Это будет возможно, если числа под знаком корня являются полными квадратами. Например, пусть задано выражение √4 + √9. Первое число 4 – это квадрат числа 2. Второе число 9 – это квадрат числа 3. Таким образом получается, что: √4 + √9 = 2 + 3 = 5.
- Если под знаком корня нет полных квадратов, то попробуйте вынести из под знака корня множитель числа. Например, пусть дано выражение √24 + √54. Разложите числа на множители: 24 = 2 * 2 * 2 * 3, 54 = 2 * 3 * 3 * 3. В числе 24 имеется множитель 4, который можно вынести из под знака квадратного корня. В числе 54 — множитель 9. Таким образом, получается что: √24 + √54 = √(4 * 6) + √(9 * 6) = 2 * √6 + 3 * √6 = 5 * √6. В данном примере в результате выноса множителя из под знака корня получилось упростить заданное выражение.

- Пусть сумма двух квадратных корней является знаменателем дроби, например, A / (√a + √b). И пусть перед вами стоит задача «избавиться от иррациональности в знаменателе». Тогда можно воспользоваться следующим способом. Умножьте числитель и знаменатель дроби на выражение √a — √b. Таким образом в знаменателе получится формула сокращенного умножения: (√a + √b) * (√a — √b) = a – b. По аналогии, если в знаменателе дана разность корней: √a — √b, то числитель и знаменатель дроби необходимо умножить на выражение √a + √b. Для примера, пусть дана дробь 4 / (√3 + √5) = 4 * (√3 — √5) / ((√3 + √5) * (√3 — √5)) = 4 * (√3 — √5) / (-2) = 2 * (√5 — √3).
- Рассмотрите более сложный пример избавления от иррациональности в знаменателе. Пусть дана дробь 12 / (√2 + √3 + √5). Необходимо умножить числитель и знаменатель дроби на выражение √2 + √3 — √5:
12 / (√2 + √3 + √5) = 12 * (√2 + √3 — √5) / ((√2 + √3 + √5) * (√2 + √3 — √5)) = 12 * (√2 + √3 — √5) / (2 * √6) = √6 * (√2 + √3 — √5) = 2 * √3 + 3 * √2 — √30.
- И наконец, если вам необходимо только приблизительное значение, то можно посчитать значения квадратных корней на калькуляторе. Вычислите значения отдельно для каждого числа и запишите с необходимой точностью (например, два знака после запятой). А затем совершите требуемые арифметические операции, как с обычными числами. Например, пусть необходимо узнать приблизительное значение выражения √7 + √5 ≈ 2,65 + 2,24 = 4,89.
Свойства квадратных корней
До сих пор мы осуществляли над числами пять арифметических операций: сложение, вычитание, умножение , деление и возведение в степень, причем при вычислениях активно использовали различные свойства этих операций, например а + b = b + а, аn-bn = (аb)n и т. д.
В этой главе введена новая операция — извлечение квадратного корня из неотрицательного числа. Чтобы успешно ее использовать, нужно познакомиться со свойствами этой операции, что мы и сделаем в настоящем параграфе.
Доказательство. Введем следующие обозначения:https://pandia.
 ru/text/78/290/images/image005_28.jpg» alt=»Равенство»Задание»
ru/text/78/290/images/image005_28.jpg» alt=»Равенство»Задание»
И для тех, кто «очень даже…»)В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать.
Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…
Начнём с самой простой. Вот она:
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.

Корень из числа проще всего вычесть с помощью калькулятора. Но, если у вас нет калькулятора, тогда надо знать алгоритм вычисления квадратного корня. Дело в том, что под корнем сидит число в квадрате. Например, 4 в квадрате — это 16. То есть корень квадратный из 16 будет равен четырем. Так же 5 в квадрате — это 25. Поэтому корень из 25 будет 5. И так далее.
Если число небольшое, то его можно легко вычесть устно, к примеру, корень из 25 будет равен 5, а корень из 144-12. Также на калькуляторе можно посчитать, есть специальный значок корня, нужно вбить число и нажать на значок.
Поможет также таблица квадратных корней:
Есть еще способы, которые более сложные, однако очень эффективные:
Корень из какого либо числа можно вычесть с помощью калькулятора, тем более они есть в каждом телефоне на сегодняшний день.
Можно попробовать примерно прикинуть как может получится данное число, умножив одно число само на себя.
Вычислить корень квадратный из числа не сложно, особенно, если есть специальная таблица.
 Всем хорошо известная таблица еще с уроков алгебры. Такая операция называется извлечение квадратного корня из числа quot;aquot;, другими словами решение уравнения. Почти все калькуляторы, в смартфонах имеют функцию определения квадратного корня.
Всем хорошо известная таблица еще с уроков алгебры. Такая операция называется извлечение квадратного корня из числа quot;aquot;, другими словами решение уравнения. Почти все калькуляторы, в смартфонах имеют функцию определения квадратного корня.Результатом извлечения квадратного корня из известного числа будет другое число, которое, при возведении во вторую степень (квадрат), даст то самое число, которое нам известно. Рассмотрим одно из описаний расчтов, которое представляется кратким и понятным:
Вот видео по теме:
Вычеслить корень квадратный из числа можно несколькими способами.
Самым популярным способом — является использование специальной таблицы кореня (смотрите ниже).
Также на каждом калькуляторе есть функция при помощи которой можно узнать корень.
Или при помощи специальной формулы.
Извлечь квадратный корень из числа можно несколькими способами. Один из них — самый быстрый, с помощью калькулятора.

Но если нет калькулятора, то можно это сделать вручную.
Результат получится точным.
Принцип практически такой же как деление столбиком:
Попробуем без калькулятора найти значение квадратного корняот числа, к примеру, 190969.
Таким образом, вс предельно просто. В вычислениях главное придерживаться определнных простых правил и логически размышлять.
Для этого нужна таблица квадратов
Вот например, корень из 100 = 10, из 20 = 400 из 43 = 1849
Сейчас практически все калькуляторы, в том числе и на смартфонах умеют высчитывать квадратный корень из числа. НО если калькулятора у вас нет, то можно найти корень из числа несколькими простыми способами:
Разложение на простые множители
Разложите подкоренное число на множители, являющиеся квадратными числами. В зависимости от подкоренного числа, вы получите приблизительный или точный ответ.
 Квадратные числа числа, из которых можно извлечь целый квадратный корень. Множители числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как 25 = 5, 36 = 6, 49 = 7. Квадратные множители это множители, являющиеся квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.
Квадратные числа числа, из которых можно извлечь целый квадратный корень. Множители числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как 25 = 5, 36 = 6, 49 = 7. Квадратные множители это множители, являющиеся квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.Например, вычислите квадратный корень из 400 (вручную). Сначала попытайтесь разложить 400 на квадратные множители. 400 кратно 100, то есть делится на 25 это квадратное число. Разделив 400 на 25, вы получите 16, которое также является квадратным числом. Таким образом, 400 можно разложить на квадратные множители 25 и 16, то есть 25 х 16 = 400.
Запишите это как: 400 = (25 х 16).
Квадратные корень из произведения некоторых членов равен произведению квадратных корней из каждого члена, то есть (а х b) = a x b . Воспользовавшись этим правилом, извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.

В нашем примере извлеките корень из 25 и из 16.
Если подкоренное число не раскладывается на два квадратных множителя (а это происходит в большинстве случаев), вы не сможете найти точный ответ в виде целого числа. Но вы можете упростить задачу, разложив подкоренное число на квадратный множитель и обыкновенный множитель (число, из которого целый квадратный корень извлечь нельзя). Затем вы извлечете квадратный корень из квадратного множителя и будете извлекать корень из обыкновенного множителя.
Например, вычислите квадратный корень из числа 147. Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:
Теперь вы можете оценить значение корня (найти приблизительное значение), сравнив его со значениями корней квадратных чисел, находящихся ближе всего (с обеих сторон на числовой прямой) к подкоренному числу. Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня.

Вернемся к нашему примеру. Подкоренное число 3. Ближайшими к нему квадратными числами будут числа 1 (1 = 1) и 4 (4 = 2). Таким образом, значение 3 расположено между 1 и 2. Та как значение 3, вероятно, ближе к 2, чем к 1, то наша оценка: 3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.
Этот метод также работает с большими числами. Например, рассмотрим 35. Подкоренное число 35. Ближайшими к нему квадратными числами будут числа 25 (25 = 5) и 36 (36 = 6). Таким образом, значение 35 расположено между 5 и 6. Та как значение 35 намного ближе к 6, чем к 5 (потому что 35 всего на 1 меньше 36), то можно заявить, что 35 немного меньше 6. Проверка на калькуляторе дает нам ответ 5,92 — мы были правы.
Еще один способ разложите подкоренное число на простые множители. Простые множители числа, которые делятся только на 1 и самих себя.
 Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.
Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.Например, вычислите квадратный корень из 45. Раскладываем подкоренное число на простые множители: 45 = 9 х 5, а 9 = 3 х 3. Таким образом, 45 = (3 х 3 х 5). 3 можно вынести за знак корня: 45 = 35. Теперь можно оценить 5.
Рассмотрим другой пример: 88.
= (2 х 4 х 11)
= (2 х 2 х 2 х 11). Вы получили три множителя 2; возьмите пару из них и вынесите за знак корня.
2(2 х 11) = 22 х 11. Теперь можно оценить 2 и 11 и найти приблизительный ответ.
Может быть полезным будет еще это обучающее видео:
Чтобы извлечь корень из числа следует воспользоваться калькулятором, либо если нет подходящего, советую зайти вот на этот сайт и решить задачу с помощью онлайн калькулятора, который за секунды выдаст правильное значение.
Содержимое:
В математике корни могут быть квадратными, кубическими или иметь любой другой показатель (степень), который пишется слева над знаком корня.
 Выражение, стоящее под знаком корня, называется подкоренным выражением. Сложение корней похоже на сложение членов алгебраического выражения, то есть требует определения подобных корней.
Выражение, стоящее под знаком корня, называется подкоренным выражением. Сложение корней похоже на сложение членов алгебраического выражения, то есть требует определения подобных корней.Шаги
Часть 1 Определение корней
- 1 Обозначение корней. Выражение под знаком корня (√) означает, что из этого выражения необходимо извлечь корень определенной степени.
- Корень обозначают знаком √.
- Показатель (степень) корня пишется слева над знаком корня. Например, кубический корень из 27 записывается так: 3 √(27)
- Если показатель (степень) корня отсутствует, то показатель считается равным 2, то есть это квадратный корень (или корень второй степени).
- Число, записанное перед знаком корня, называется множителем (то есть это число умножается на корень), например 5√(2)
- Если множителя перед корнем нет, то он равен 1 (напомним, что любое число, умноженное на 1, равняется самому себе).
- Если вы впервые работаете с корнями, сделайте соответствующие пометки над множителем и показателем корня, чтобы не запутаться и лучше понять их назначение.

- 2 Запомните, какие корни можно складывать, а какие нельзя. Также, как нельзя складывать разные члены выражения, например, 2а + 2b ≠ 4ab, вы не можете складывать разные корни.
- Нельзя складывать корни с разными подкоренными выражениями, например, √(2) + √(3) ≠ √(5). Но вы можете сложить числа, стоящие под одним корнем, например, √(2 + 3) = √(5) (квадратный корень из 2 примерно равен 1,414, квадратный корень из 3 примерно равен 1,732, а квадратный корень из 5 примерно равен 2,236).
- Нельзя складывать корни с одинаковыми подкоренными выражениями, но разными показателями, например, √(64) + 3 √(64) (эта сумма не равна 5 √(64), так как квадратный корень из 64 равен 8, кубический корень из 64 равен 4, 8 + 4 = 12, что гораздо больше, чем корень пятой степени из 64, который примерно равен 2,297).
Часть 2 Упрощение и сложение корней
- 1 Определите и сгруппируйте подобные корни. Подобные корни – корни, у которых одинаковые показатели и одинаковые подкоренные выражения.
 Например, рассмотрим выражение:
Например, рассмотрим выражение:
2√(3) + 3 √(81) + 2√(50) + √(32) + 6√(3)- Во-первых, перепишите выражение так, чтобы корни с одинаковым показателем располагались последовательно.
2√(3) + 2√(50) + √(32) + 6√(3) + 3 √(81) - Затем перепишите выражение так, чтобы корни с одинаковым показателем и с одинаковым подкоренным выражением располагались последовательно.
2√(50) + √(32) + 2√(3) + 6√(3) + 3 √(81)
- Во-первых, перепишите выражение так, чтобы корни с одинаковым показателем располагались последовательно.
- 2 Упростите корни. Для этого разложите (где возможно) подкоренные выражения на два множителя, один из которых вынесите из-под корня. В этом случае вынесенное число и множитель корня перемножаются.
- В приведенном выше примере разложите число 50 на 2*25, а число 32 – на 2*16. Из 25 и 16 можно извлечь квадратные корни (соответственно 5 и 4) и вынести 5 и 4 из-под корня, соответственно умножив их на множители 2 и 1. Таким образом, вы получите упрощенное выражение: 10√(2) + 4√(2) + 2√(3) + 6√(3) + 3 √(81)
- Число 81 можно разложить на множители 3*27, а из числа 27 можно извлечь кубический корень, равный 3.
 Это число 3 можно вынести из-под корня. Таким образом, вы получите еще более упрощенное выражение: 10√(2) + 4√(2) + 2√(3)+ 6√(3) + 3 3 √(3)
Это число 3 можно вынести из-под корня. Таким образом, вы получите еще более упрощенное выражение: 10√(2) + 4√(2) + 2√(3)+ 6√(3) + 3 3 √(3)
- 3 Сложите множители подобных корней. В нашем примере есть подобные квадратные корни из 2 (их можно сложить) и подобные квадратные корни из 3 (их тоже можно сложить). У кубического корня из 3 подобных корней нет.
- 10√(2) + 4√(2) = 14√(2).
- 2√(3)+ 6√(3) = 8√(3).
- Окончательное упрощенное выражение: 14√(2) + 8√(3) + 3 3 √(3)
- Не существует общепринятых правил порядка записи корней в выражении. Потому вы можете записывать корни в порядке возрастания их показателей и в порядке возрастания подкоренных выражений.
Сложение и вычитание квадратных корней — Элементарная алгебра
Цели обучения
К концу этого раздела вы сможете:
- Сложение и вычитание как квадратный корень
- Сложение и вычитание квадратных корней, требующих упрощения
Прежде чем начать, пройдите этот тест на готовность.

- Добавить: ⓐ ⓑ .
Если вы пропустили эту проблему, просмотрите (рисунок). - Упростить: .
Если вы пропустили эту проблему, просмотрите (рисунок).
Мы знаем, что должны соблюдать порядок операций для упрощения выражений с квадратными корнями. Радикал — это группирующий символ, поэтому сначала мы работаем внутри радикала. Упрощаем таким образом:
Итак, если нам нужно добавить , мы не должны объединять их в один радикал.
Пытаться складывать квадратные корни с разными подкоренными, все равно что пытаться складывать разные члены.
Сложение квадратных корней с одним и тем же основанием аналогично сложению одинаковых членов.Мы называем квадратные корни теми же подкоренными, что и квадратные корни, чтобы напомнить нам, что они работают так же, как и термины.
Как квадратные корни
Квадратные корни с одинаковыми подкоренными называются квадратными корнями.
Мы складываем и вычитаем, как квадратные корни, так же, как складываем и вычитаем одинаковые члены.
 Мы знаем, что это. Аналогично складываем и получается
Мы знаем, что это. Аналогично складываем и получаетсяСкладывать и вычитать как квадратный корень
Подумайте о добавлении похожих терминов с переменными, как в следующих нескольких примерах.Когда у вас есть подкоренные числа, вы просто добавляете или вычитаете коэффициенты. Когда подкоренные не похожи, вы не можете комбинировать термины.
Упрощение: .
Решение
Упрощение: .
Упрощение: .
Упрощение: .
Решение
Упрощение: .
Упрощение: .
Упрощение: .
Решение
Упрощение: .
Упрощение: .
Упрощение: .
Решение
Упрощение: .
Упрощение: .
Упрощение: .
Решение
Упрощение: .

Упрощение: .
Упрощение: .
Решение
Упрощение: .
Упрощение: .
Когда радикалы содержат более одной переменной, если все переменные и их показатели одинаковы, радикалы подобны.
Упрощение: .
Решение
Упрощение: .
Упрощение: .
Сложение и вычитание квадратных корней, требующих упрощения
Помните, что мы всегда упрощаем квадратные корни, удаляя наибольший множитель идеального квадрата.Иногда, когда нам нужно сложить или вычесть квадратные корни, у которых, кажется, нет одинаковых радикалов, мы находим похожие радикалы после упрощения квадратных корней.
Упрощение: .
Решение
Упрощение: .
Упрощение: .
Упрощение: .
Решение
Упрощение: .

Упрощение: .
Точно так же, как мы используем ассоциативное свойство умножения для упрощения и получения , мы можем упростить и получить .Мы будем использовать ассоциативное свойство, чтобы сделать это в следующем примере.
Упрощение: .
Решение
Упрощение: .
Упрощение: .
Упрощение: .
Решение
Упрощение: .
Упрощение: .
Упрощение: .
Решение
Упрощение: .
Упрощение: .
В следующем примере мы удалим из квадратных корней постоянные и переменные множители.
Упрощение: .
Решение
Упрощение: .
Упрощение: .
Упрощение: .
Решение
Упрощение: .

Упрощение: .
Упрощение: .
Решение
Упрощение: .
Упрощение: .
Ключевые понятия
- Чтобы сложить или вычесть одинаковые квадратные корни, сложите или вычтите коэффициенты и сохраните одинаковый квадратный корень.
- Иногда, когда нам нужно сложить или вычесть квадратные корни, которые, как кажется, не имеют одинаковых радикалов, мы находим похожие радикалы после упрощения квадратных корней.
Практика делает совершенным
Сложение и вычитание как квадратный корень
В следующих упражнениях упрощайте.
Сложение и вычитание квадратных корней, требующих упрощения
В следующих упражнениях упрощайте.

Смешанная практика
Математика на каждый день
Художник-декоратор решил использовать квадратную плитку в качестве акцентной полосы в дизайне новой душевой, но она хочет повернуть плитку так, чтобы она выглядела как ромб.
 Она возьмет 9 больших плиток со стороной 8 дюймов и 8 маленьких плиток со стороной 2 дюйма. . Определим ширину акцентной полосы, упростив выражение . (Округлить до десятых долей дюйма.)
Она возьмет 9 больших плиток со стороной 8 дюймов и 8 маленьких плиток со стороной 2 дюйма. . Определим ширину акцентной полосы, упростив выражение . (Округлить до десятых долей дюйма.)Сьюзи хочет использовать квадратную плитку на границе спа-салона, который она устанавливает на заднем дворе. Она будет использовать большие плитки площадью 12 квадратных дюймов, средние плитки площадью 8 квадратных дюймов и маленькие плитки площадью 4 квадратных дюйма.Для одного участка границы потребуется 4 большие плитки, 8 средних плиток и 10 маленьких плиток, чтобы покрыть ширину стены. Упростите выражение для определения ширины стены.
Письменные упражнения
Объясните разницу между подобными радикалами и непохожими радикалами. Убедитесь, что ваш ответ имеет смысл для радикалов, содержащих как числа, так и переменные.
Объясните процесс определения сходства или несовпадения двух радикалов. Убедитесь, что ваш ответ имеет смысл для радикалов, содержащих как числа, так и переменные.

Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство выполнения целей этого раздела.
ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения?
Глоссарий
- как квадратный корень
- Квадратные корни с одинаковыми подкоренными называются квадратными корнями.
Как добавить пользователя и предоставить права root в Ubuntu 16.04
Ubuntu 16.04 LTS предоставляет вам возможность добавить пользователя для любого, кто планирует получить доступ к вашему серверу. Создание пользователя — это базовая настройка, но важная и критическая для безопасности вашего сервера. В этом руководстве мы создадим пользователя и предоставим административный доступ, известный как root, вашему доверенному пользователю.
Предпечатная проверка
- Нам потребуется открыть терминал и войти в систему как пользователь root.

- Мы будем работать как пользователь root на Linux Ubuntu 16.04 Сервер LTS
Создание пользователя с правами root
Создайте имя пользователя для вашего нового пользователя, в моем примере мой новый пользователь — Том:
Затем вам будет предложено ввести пароль для этого пользователя. Мы рекомендуем использовать надежный пароль, поскольку вредоносные боты запрограммированы на угадывание простых паролей. Если вам нужен безопасный пароль, этот сторонний генератор паролей может помочь с его созданием.
~# adduser tom Добавление пользователя `tom'... Добавление новой группы `tom' (1002) ... Добавление нового пользователя "том" (1002) с группой "том"... Создание домашнего каталога `/home/tom'... Копирование файлов из `/etc/skel'... Введите новый пароль UNIX: Повторно введите новый пароль UNIX: passwd: пароль успешно обновленПримечание
Имена пользователей должны быть в нижнем регистре и не содержать специальных символов.
 Если вы получили сообщение об ошибке ниже, измените имя пользователя.
Если вы получили сообщение об ошибке ниже, измените имя пользователя. ~# adduser Том adduser: введите имя пользователя, соответствующее регулярному выражению, настроенному с помощью переменной конфигурации NAME_REGEX[_SYSTEM].Используйте параметр --force-badname, чтобы ослабить эту проверку или перенастроить NAME_REGEX.Затем появится текстовое приглашение с просьбой ввести информацию о вашем новом пользователе. Ввод этой информации является субъективным и не является обязательным. При необходимости эту информацию можно пропустить, нажав Enter в каждом поле. Мы предлагаем добавить столько информации, сколько необходимо для отслеживания использования.
Введите новое значение или нажмите ENTER для значения по умолчанию. Полное имя []: Номер комнаты []: Рабочий телефон []: Домашний телефон []: Другое []:Наконец, система попросит вас проверить точность информации.Введите Y , чтобы перейти к следующему шагу.

Шаг 2: Предоставление привилегий rootИнформация верна? [Да/нет]Назначение root-доступа пользователю означает предоставление ему самых высоких привилегий в нашей системе, поэтому рекомендуется соблюдать осторожность. Как только наш пользователь Том добавлен, он может вносить изменения во всю систему в целом, поэтому очень важно разрешить этот доступ только тем пользователям, которым он нужен. После этого Том сможет выполнять команды, используя параметр sudo, который обычно зарезервирован для пользователя root.
Шаг 3: Проверка нового пользователяКак пользователь root, вы можете переключиться на нового пользователя с помощью команды su — и затем проверить, есть ли у вашего нового пользователя привилегии root.
Если пользователю правильно предоставлен root-доступ, команда ниже отобразит to в списке.
Вот оно! Мы добавили пользователя, а затем предоставили этому пользователю привилегии root на сервере Ubuntu 16.
 04 LTS.
04 LTS.Начните сегодня!
Хотите узнать больше о настройке нового сервера Ubuntu? Позвоните нам по номеру 800.580.4985, или откройте чат или билет с нами, чтобы поговорить с одним из наших опытных консультантов по решениям или хостингу, чтобы узнать, как вы можете воспользоваться этими методами прямо сейчас!
Как изменить пароль root в Ubuntu Linux
Пользователь root (или суперпользователь) — это специальная учетная запись пользователя, которая присутствует во всех Linux и Unix-подобных системах. Он имеет полный доступ к каждой команде и любому ресурсу в системе без каких-либо ограничений.
Если вы переходите на Ubuntu из другого дистрибутива Linux, вам может быть интересно, какой пароль root по умолчанию или как изменить пароль root.По умолчанию в Ubuntu учетная запись пользователя root отключена из соображений безопасности.
В этом руководстве объясняется, как временно изменить учетную запись пользователя root и как установить пароль root в системах Ubuntu.

Временное переключение на root #
Пользователям Ubuntu рекомендуется выполнять задачи системного администрирования, предоставляя привилегии sudo обычным пользователям. Sudo позволяет авторизованным пользователям запускать программы от имени другого пользователя, обычно пользователя root.
Первый пользователь, созданный программой установки Ubuntu, уже является членом группы sudo.Скорее всего, пользователь, под которым вы вошли в систему, уже имеет административные привилегии.
Чтобы временно повысить привилегии пользователя root, выполните команду с префиксом
sudo:имя-команды sudoПри первом использовании sudo в сеансе вам будет предложено ввести пароль пользователя.
Чтобы временно переключиться на учетную запись root в текущем сеансе входа, вы можете использовать команду
sudo suили введите командуsudo -iи введите пароль пользователя:sudo su -Запустите команду
whoami, чтобы убедиться, что пользователь изменен:
97 97whoamiИзменение пароля root #
Пользователь root отключен, но это не означает, что учетная запись root удалена.
 Вход в систему с правами root невозможен, так как для учетной записи root не установлен пароль.
Вход в систему с правами root невозможен, так как для учетной записи root не установлен пароль.Если по какой-то причине вам необходимо включить учетную запись root , все, что вам нужно сделать, это установить пароль для пользователя root. В Ubuntu вы можете установить или изменить пароль учетной записи пользователя с паролем
Чтобы изменить пароль пользователя root в Ubuntu, выполните следующую команду от имени пользователя sudo. :
sudo passwd rootВам будет предложено ввести и подтвердить новый пароль root.
При установке пароля убедитесь, что вы используете уникальный и надежный пароль. Наличие надежного пароля является наиболее важным аспектом безопасности вашей учетной записи. Часто надежный пароль содержит не менее 16 символов, по крайней мере одну заглавную букву, одну строчную букву, одну цифру и один специальный символ.
Пароль не отображается на экране при вводе.
Введите новый пароль UNIX: Повторно введите новый пароль UNIX: passwd: пароль успешно обновленВот и все! Пароль root изменен.

Теперь вы можете войти в свою систему Ubuntu как root, используя новый пароль.
Заключение #
По умолчанию в Ubuntu для учетной записи root пароль не установлен. Рекомендуемый подход — использовать команду
sudoдля запуска команд с привилегиями уровня root.Чтобы иметь возможность напрямую войти в систему как root, вам необходимо установить пароль root.
Если у вас есть какие-либо вопросы или пожелания, не стесняйтесь оставлять комментарии.
Как стать root в Linux
Обновлено: 27.02.2019, автор: Computer Hope
В каждой системе Linux учетная запись root — это специальный пользователь с правами администратора.Вход в систему как root (или выполнение команд с привилегиями root) необходим для многих задач. Если вам нужно выполнять задачи от имени пользователя root, убедитесь, что вы полностью понимаете выполняемые команды и их последствия. Одна неосторожная или неправильно сформированная команда, запущенная от имени пользователя root, может сделать всю операционную систему непригодной для использования.
 Проведите исследование и всегда перепроверяйте каждую команду, прежде чем нажимать Введите .
Проведите исследование и всегда перепроверяйте каждую команду, прежде чем нажимать Введите .Вход в систему как пользователь root
Учетная запись root аналогична любой другой учетной записи тем, что у нее есть имя пользователя («root») и пароль.Если вы знаете пароль root, вы можете использовать его для входа в учетную запись root из командной строки.
Существует специальная команда с именем su (для «суперпользователя» или «сменить пользователя»), которая позволяет временно выполнять команды от имени корневой учетной записи. В командной строке введите:
и
Введите пароль после запроса пароля. В случае успеха вы переключаетесь на пользователя root и можете запускать команды с полными системными привилегиями.
Будьте осторожны при входе в систему как пользователь root.Легко забыть, что в настоящее время вы являетесь пользователем root, и вы можете непреднамеренно запустить команду, думая, что вы всего лишь простой смертный.
 Один из способов напомнить себе, являетесь ли вы root или нет, — это проверить командную строку. Во многих системах командная строка заканчивается знаком доллара (« $ »), если вы вошли в систему как обычный пользователь, и знаком фунта (« # »), если вы являетесь пользователем root.
Один из способов напомнить себе, являетесь ли вы root или нет, — это проверить командную строку. Во многих системах командная строка заканчивается знаком доллара (« $ »), если вы вошли в систему как обычный пользователь, и знаком фунта (« # »), если вы являетесь пользователем root.Или вы можете использовать команду whoami для определения используемой учетной записи.
По завершении административных задач вы можете выполнить команду exit или logout , чтобы вернуться к своей стандартной учетной записи пользователя.
При входе в систему как пользователь root часто полезно использовать одиночный дефис после команды su , например:
вс -
Эта команда имитирует полный вход в систему root. Он выполняет все сценарии инициализации оболочки пользователя root и устанавливает все переменные среды, как если бы пользователь root вошел в новую сессию оболочки. В зависимости от того, какую задачу вам нужно выполнить и как настроен root, эта форма команды su может быть для вас оптимальной.

Запуск команд от имени root без пароля root
Возможно и часто предпочтительнее запускать команды от имени root без входа в учетную запись root с помощью команды sudo , что означает «superuser do.» Если вы добавляете к команде префикс sudo , вам будет предложено ввести пароль (а не пароль root), и ваше имя будет проверено в специальном файле с именем sudoers . Если ваша учетная запись указана там, ваша команда выполняется с правами root привилегии
Использование sudo затрудняет забывание того, что вы являетесь пользователем root, поскольку вы не вошли в систему с учетной записью root и никогда не забудете выйти из системы. Кроме того, ввод sudo каждый раз, когда вы запускаете потенциально разрушительную команду, напоминает вам о необходимости быть особенно осторожным и перепроверять себя.
Если вам нужно добавить пользователя в список sudoers, используйте команду visudo , для запуска которой требуются привилегии суперпользователя и которая позволяет безопасно редактировать конфиденциальный файл sudoers.

4 способа отключить корневую учетную запись в Linux
Учетная запись root является конечной учетной записью в Linux и других Unix-подобных операционных системах. Эта учетная запись имеет доступ ко всем командам и файлам в системе с полными правами на чтение, запись и выполнение. Он используется для выполнения любых задач в системе; для создания/обновления/доступа/удаления учетных записей других пользователей, установки/удаления/обновления программных пакетов и многого другого.
Поскольку пользователь root обладает абсолютными полномочиями, любые действия, которые он/она выполняет, имеют решающее значение для системы. В связи с этим любые ошибки пользователя root могут иметь серьезные последствия для нормальной работы системы. Кроме того, эта учетная запись также может быть использована ненадлежащим или ненадлежащим образом либо случайно, либо злонамеренно, либо из-за надуманного незнания политик.
Поэтому рекомендуется отключить root-доступ на вашем Linux-сервере, вместо этого создать учетную запись администратора, которая должна быть настроена для получения привилегий root-пользователя с помощью команды sudo для выполнения критических задач на сервере.

В этой статье мы расскажем о четырех способах отключения входа в систему с учетной записью root в Linux.
Внимание : Прежде чем заблокировать доступ к учетной записи root , убедитесь, что вы создали учетную запись администратора, способную использовать команду sudo для получения привилегий пользователя root, с помощью команды useradd и задайте этой учетной записи пользователя надежный пароль. Флаг
-mозначает создание домашнего каталога пользователя, а-cпозволяет указать комментарий:# useradd -m -c "Пользователь-администратор" admin # пароль администратора
Затем добавьте этого пользователя в соответствующую группу системных администраторов с помощью команды usermod, где переключатель
-aозначает добавление учетной записи пользователя, а-Gуказывает группу, в которую нужно добавить пользователя (wheel или sudo в зависимости от вашего Linux раздача):# usermod -aG Wheel admin #CentOS/RHEL # usermod -aG sudo admin #Debian/Ubuntu
После того, как вы создали пользователя с правами администратора, переключитесь на эту учетную запись, чтобы заблокировать root-доступ.

#су админ
1. Изменить оболочку пользователя root
Самый простой способ отключить вход пользователя root — изменить его оболочку с
/bin/bashили/bin/bash(или любую другую оболочку, которая разрешает вход пользователя) на/sbin/nologin, в / etc/passwd , который вы можете открыть для редактирования с помощью любого из ваших любимых редакторов командной строки, как показано ниже.$ sudo vim /etc/passwd
Изменить строку:
корень: х: 0: 0: корень: / корень: / bin / bash к корень:x:0:0:корень:/корень: /sbin/nologin
Изменить корневую пользовательскую оболочкуСохраните файл и закройте его.
С этого момента, когда пользователь root входит в систему, он/она будет получать сообщение « Эта учетная запись в настоящее время недоступна. ” Это сообщение по умолчанию, но вы можете изменить его и установить собственное сообщение в файле /etc/nologin.
 txt .
txt .Этот метод эффективен только с программами, которым требуется оболочка для входа пользователя, в противном случае клиенты sudo , ftp и email могут получить доступ к учетной записи root.
2. Отключите вход root через консольное устройство (TTY)
Второй метод использует модуль PAM с именем pam_securetty , который разрешает root-доступ только в том случае, если пользователь входит в систему с « безопасного» TTY , как определено в списке /etc/securetty .
Приведенный выше файл позволяет указать, на каких устройствах TTY пользователю root разрешен вход в систему. Очистка этого файла предотвращает вход в систему root на любых устройствах, подключенных к компьютерной системе.
Чтобы создать пустой файл, запустите.
$ sudo mv /etc/securetty /etc/securetty.orig $ sudo touch /etc/securetty $ sudo chmod 600 /etc/securetty
Этот метод имеет некоторые ограничения, он влияет только на такие программы, как вход в систему, диспетчеры отображения (например, gdm , kdm и xdm ) и другие сетевые службы, запускающие TTY.
 Такие программы, как su, sudo, ssh и другие связанные инструменты openssh, будут иметь доступ к учетной записи root.
Такие программы, как su, sudo, ssh и другие связанные инструменты openssh, будут иметь доступ к учетной записи root.3. Отключить корневой вход SSH
Самый распространенный способ доступа к удаленным серверам или VPS — через SSH, и чтобы заблокировать вход пользователя root под ним, вам необходимо отредактировать файл /etc/ssh/sshd_config .
$ sudo vim /etc/ssh/sshd_config
Затем раскомментируйте (если она закомментирована) директиву PermitRootLogin и установите для нее значение
Отключить root-вход в SShno, как показано на скриншоте.. Когда вы закончите, сохраните и закройте файл. Затем перезапустите службу sshd , чтобы применить последние изменения в конфигурациях.
$ sudo systemctl перезапустить sshd ИЛИ $ sudo service sshd перезапустить
Как вы, возможно, уже знаете, этот метод влияет только на набор инструментов openssh, такие программы, как ssh, scp, sftp, будут заблокированы от доступа к учетной записи root.

4. Ограничить корневой доступ к службам через PAM
Подключаемые модули аутентификации (сокращенно PAM ) — это централизованный, подключаемый, модульный и гибкий метод аутентификации в системах Linux.PAM с помощью модуля /lib/security/pam_listfile.so обеспечивает большую гибкость в ограничении привилегий определенных учетных записей.
Приведенный выше модуль можно использовать для ссылки на список пользователей, которым не разрешено входить в систему через некоторые целевые службы, такие как вход в систему, ssh и любые программы, поддерживающие PAM.
В этом случае мы хотим отключить доступ пользователя root к системе, ограничив доступ к службам входа и sshd. Сначала откройте и отредактируйте файл целевой службы в каталоге /etc/pam.d/, как показано.
$ sudo vim /etc/pam.d/логин ИЛИ sudo vim /etc/pam.d/sshd
Затем добавьте приведенную ниже конфигурацию в оба файла.

требуется авторизация pam_listfile.so \ onerr=успех элемент=пользовательское чувство=запретить файл=/etc/ssh/deniedusersКогда вы закончите, сохраните и закройте каждый файл. Затем создайте простой файл /etc/ssh/deniedusers , который должен содержать по одному элементу в строке и не доступен для чтения всем.
Добавьте в него имя root, затем сохраните и закройте его.
$ sudo vim /etc/ssh/deniedusers
Также установите для этого необходимые разрешения.
$ sudo chmod 600 /etc/ssh/deniedusers
Этот метод влияет только на программы и службы, поддерживающие PAM. Вы можете заблокировать корневой доступ к системе через ftp и почтовые клиенты и многое другое.
Для получения дополнительной информации обратитесь к соответствующим справочным страницам.
$ мужчина pam_securetty $ человек sshd_config $ мужчина пэм
Вот и все! В этой статье мы объяснили четыре способа отключения входа (или учетной записи) пользователя root в Linux.
 Если у вас есть какие-либо комментарии, предложения или вопросы, не стесняйтесь обращаться к нам через форму обратной связи ниже.
Если у вас есть какие-либо комментарии, предложения или вопросы, не стесняйтесь обращаться к нам через форму обратной связи ниже.Если вы цените то, что мы делаем здесь, в TecMint, вам следует подумать:
TecMint — это самый быстрорастущий и пользующийся наибольшим доверием сайт сообщества, где можно найти любые статьи, руководства и книги по Linux в Интернете. Миллионы людей посещают TecMint! искать или просматривать тысячи опубликованных статей, доступных всем БЕСПЛАТНО.
Если вам нравится то, что вы читаете, пожалуйста, купите нам кофе (или 2) в знак признательности.
Мы благодарны за вашу бесконечную поддержку.
Учетные данные корневого пользователя учетной записи AWS и учетные данные пользователя IAM
В AWS существует два разных типа пользователей. Вы либо владелец аккаунта (пользователь root) или вы являетесь пользователем AWS Identity and Access Management (IAM). Пользователь root создается, когда AWS учетная запись создается, а пользователи IAM создаются пользователем root или администратором IAM.
 для счета. У всех пользователей AWS есть учетные данные безопасности.
для счета. У всех пользователей AWS есть учетные данные безопасности.Учетные данные пользователя root
Учетные данные владельца учетной записи разрешают полный доступ ко всем ресурсам учетной записи. Вы не можете использовать политики IAM для явно запретить пользователю root доступ к ресурсам. Вы можете использовать только политику управления сервисами AWS Organizations. (SCP) для ограничения разрешений пользователя root. В связи с этим мы рекомендуем вы создаете пользователя IAM с правами администратора для выполнения повседневных задач AWS и заблокируйте ключи доступа для пользователя root.
Существуют определенные задачи, выполнение которых ограничено пользователем root учетной записи AWS. Например, только пользователь root может закрыть вашу учетную запись. Если вам нужно выполнить задачу, для которой требуется пользователь root, войдите в Консоль управления AWS, используя адрес электронной почты и пароль пользователя root.
 Для большего
информацию см. в разделе Задачи, требующие учетных данных пользователя root.
Для большего
информацию см. в разделе Задачи, требующие учетных данных пользователя root.Учетные данные IAM
С помощью IAM вы можете безопасно контролировать доступ к сервисам и ресурсам AWS для пользователей в вашей учетной записи AWS.Например, если вам требуются права администратора, вы можете создать пользователя IAM, предоставить этому пользователю полный доступ, а затем используйте эти учетные данные для взаимодействия с AWS. Если вам нужно изменить или отозвать свои разрешения, вы можете удалить или изменить политики, связанные с этим пользователь ИАМ.
Если у вас есть несколько пользователей, которым требуется доступ к вашей учетной записи AWS, вы можете создать уникальные учетные данные для каждого пользователя и определить, кто имеет доступ к каким ресурсам.Вам не нужно поделиться учетными данными. Например, вы можете создать пользователей IAM с доступом только для чтения к ресурсов в своей учетной записи AWS и распространять эти учетные данные среди пользователей.

Задачи, требующие учетных данных пользователя root
Мы рекомендуем вам используйте пользователя IAM с соответствующими разрешениями для выполнения задач и доступа к ресурсам AWS. Однако вы можете выполнять задачи, перечисленные ниже, только если вы входите в систему как привилегированный пользователь учетной записи.
Задачи
Измените настройки своей учетной записи.Сюда входят имя учетной записи, адрес электронной почты, пароль пользователя root и ключи доступа пользователя root. Другие настройки учетной записи, такие как контактная информация, предпочтительная валюта платежа и регионы, не требуют учетных данных пользователя root.
Восстановить пользователя IAM разрешения. Если единственный администратор IAM случайно аннулирует разрешений, вы можете войти в систему как пользователь root, чтобы редактировать политики и восстанавливать их.
 разрешения.
разрешения.Активируйте доступ IAM к консоли Billing and Cost Management.
Просмотр определенных налоговых счетов. Пользователь IAM с разрешением aws-portal:ViewBilling может просматривать и загружать счета-фактуры с AWS Europe, но не AWS Inc или Amazon Internet Services Pvt. ООО (АИСПЛ).
Закройте свою учетную запись AWS.
Изменить план поддержки AWS или отменить поддержку AWS план.Дополнительные сведения см. в разделе IAM для поддержки AWS.
Зарегистрируйтесь как продавец в на рынке зарезервированных инстансов.
Настройка корзину Amazon S3, чтобы включить MFA (многофакторную аутентификацию) Удалить.
Изменить или удалить политику корзины Amazon S3, которая включает недопустимый идентификатор VPC или конечную точку VPC.
 Я БЫ.
Я БЫ.Подпишитесь на GovCloud.
Поиск и устранение неисправностей
Если вы не можете выполнить ни одну из этих задач, используя свои учетные данные пользователя root, ваш учетная запись может быть членом организации в организациях AWS. Если ваша организационная администратор использовал политику управления службами (SCP) для ограничения разрешений вашей учетной записи, ваши права пользователя root могут быть затронуты. Дополнительные сведения см. в разделе Политики управления службами в Руководство пользователя организаций AWS .{2}=\влево (-3 \вправо)\cdot \влево (-3 \вправо)=9$$
3 и -3 считаются квадратными корнями из 9.
Все положительные действительные числа имеют два квадратных корня, один положительный квадратный корень и один отрицательный квадратный корень. Положительный квадратный корень иногда называют главным квадратным корнем.
 {2}=a\cdot a=\left (-a \right)\cdot \left (-a \right)$$
{2}=a\cdot a=\left (-a \right)\cdot \left (-a \right)$$Квадратный корень записывается с подкоренным символом √, а число или выражение внутри подкоренного символа, обозначенное ниже a, называется подкоренным.
$$\sqrt{a}$$
Чтобы указать, что нам нужен как положительный, так и отрицательный квадратный корень из подкоренного числа, мы помещаем символ ± (читается как плюс минус) перед корнем.
$$\pm \sqrt{9}=\pm 3$$
Ноль имеет один квадратный корень, равный 0.
$$\sqrt{0}=0$$
Отрицательные числа не имеют действительных квадратных корней, так как квадрат либо положителен, либо равен 0.
Если квадратный корень из целого числа является другим целым числом, то квадрат называется полным квадратом.Например, 25 — это полный квадрат, начиная с
.$$\pm \sqrt{25}= \pm 5$$
Если подкоренное число не является полным квадратом, т.е. квадратный корень не является целым числом, вам необходимо аппроксимировать квадратный корень
$$\pm \sqrt{3}= \pm 1.




 Здесь вы раскладываете 8 на множители 4 и 2; затем из 4 извлекаете корень, равный 2, и 2 выносите из-под корня. Затем 2 умножаете на 2 (множитель у корня) и получаете 4√2.
Здесь вы раскладываете 8 на множители 4 и 2; затем из 4 извлекаете корень, равный 2, и 2 выносите из-под корня. Затем 2 умножаете на 2 (множитель у корня) и получаете 4√2. Идея в том, чтобы показать, сколько всего корней с определенным подкоренным выражением содержится в данном выражении.
Идея в том, чтобы показать, сколько всего корней с определенным подкоренным выражением содержится в данном выражении.



 д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

 После этого извлеките корень из квадратного числа и запишите найденное значение перед знаком корня (под знаком корня останется второй множитель). Например, 6√50 — 2√8 + 5√12. Числа, стоящее перед знаком корня, являются множителями соответствующих корней, а числа под знаком корня – это подкоренные числа (выражения). Вот как решать данную задачу:
После этого извлеките корень из квадратного числа и запишите найденное значение перед знаком корня (под знаком корня останется второй множитель). Например, 6√50 — 2√8 + 5√12. Числа, стоящее перед знаком корня, являются множителями соответствующих корней, а числа под знаком корня – это подкоренные числа (выражения). Вот как решать данную задачу:

 Вы получите: (9-4)√5 -2√3 = 5√5 — 2√3.
Вы получите: (9-4)√5 -2√3 = 5√5 — 2√3. 2 = x, √x = a. Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания.
2 = x, √x = a. Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания.



 Для этого разложите (где возможно) подкоренные выражения на два множителя, один из которых вынесите из-под корня. В этом случае вынесенное число и множитель корня перемножаются.
Для этого разложите (где возможно) подкоренные выражения на два множителя, один из которых вынесите из-под корня. В этом случае вынесенное число и множитель корня перемножаются.
 Коэффициент, который мы получили, упрощается по обычным правилам.
Коэффициент, который мы получили, упрощается по обычным правилам. В числе 54 мы имеем множитель 9 .
В числе 54 мы имеем множитель 9 .


 Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!
Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!  После этого нужно умножить 2 на 5 (множитель у корня) и получить 10 3 .
После этого нужно умножить 2 на 5 (множитель у корня) и получить 10 3 . д.) и записываем результат:
д.) и записываем результат: Для вычитания и сложения корней их нужно соединить посредством знаков, соответствующих этим действиям (например √x — √y ).
Для вычитания и сложения корней их нужно соединить посредством знаков, соответствующих этим действиям (например √x — √y ). 

 Отдельно для каждого числа вычисляется значение и записывается с необходимой точностью, которая определяется количеством знаков после запятой. Далее совершаются все требуемые операции, как с обычными числами.
Отдельно для каждого числа вычисляется значение и записывается с необходимой точностью, которая определяется количеством знаков после запятой. Далее совершаются все требуемые операции, как с обычными числами.
 2×2)
2×2)
 Это закон действует так же как приведение к общему знаменателю при сложении или вычитании дробей.
Это закон действует так же как приведение к общему знаменателю при сложении или вычитании дробей. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…
Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да… После этого извлеките корень из квадратного числа и запишите найденное значение перед знаком корня (под знаком корня останется второй множитель). Например, 6√50 — 2√8 + 5√12. Числа, стоящее перед знаком корня, являются множителями соответствующих корней, а числа под знаком корня – это подкоренные числа (выражения). Вот как решать данную задачу:
После этого извлеките корень из квадратного числа и запишите найденное значение перед знаком корня (под знаком корня останется второй множитель). Например, 6√50 — 2√8 + 5√12. Числа, стоящее перед знаком корня, являются множителями соответствующих корней, а числа под знаком корня – это подкоренные числа (выражения). Вот как решать данную задачу:

 Вы получите: (9-4)√5 -2√3 = 5√5 — 2√3.
Вы получите: (9-4)√5 -2√3 = 5√5 — 2√3.


 Таким образом, вы получите упрощенное выражение: 10√(2) + 4√(2) + 2√(3) + 6√(3) + 3 √(81)
Таким образом, вы получите упрощенное выражение: 10√(2) + 4√(2) + 2√(3) + 6√(3) + 3 √(81) 2 = x, √x = a. Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания.
2 = x, √x = a. Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания.

 ru/text/78/290/images/image005_28.jpg» alt=»Равенство»Задание»
ru/text/78/290/images/image005_28.jpg» alt=»Равенство»Задание»
 Всем хорошо известная таблица еще с уроков алгебры. Такая операция называется извлечение квадратного корня из числа quot;aquot;, другими словами решение уравнения. Почти все калькуляторы, в смартфонах имеют функцию определения квадратного корня.
Всем хорошо известная таблица еще с уроков алгебры. Такая операция называется извлечение квадратного корня из числа quot;aquot;, другими словами решение уравнения. Почти все калькуляторы, в смартфонах имеют функцию определения квадратного корня.
 Квадратные числа числа, из которых можно извлечь целый квадратный корень. Множители числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как 25 = 5, 36 = 6, 49 = 7. Квадратные множители это множители, являющиеся квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.
Квадратные числа числа, из которых можно извлечь целый квадратный корень. Множители числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как 25 = 5, 36 = 6, 49 = 7. Квадратные множители это множители, являющиеся квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.

 Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.
Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня. Выражение, стоящее под знаком корня, называется подкоренным выражением. Сложение корней похоже на сложение членов алгебраического выражения, то есть требует определения подобных корней.
Выражение, стоящее под знаком корня, называется подкоренным выражением. Сложение корней похоже на сложение членов алгебраического выражения, то есть требует определения подобных корней.
 Например, рассмотрим выражение:
Например, рассмотрим выражение: Это число 3 можно вынести из-под корня. Таким образом, вы получите еще более упрощенное выражение: 10√(2) + 4√(2) + 2√(3)+ 6√(3) + 3 3 √(3)
Это число 3 можно вынести из-под корня. Таким образом, вы получите еще более упрощенное выражение: 10√(2) + 4√(2) + 2√(3)+ 6√(3) + 3 3 √(3)
 Мы знаем, что это. Аналогично складываем и получается
Мы знаем, что это. Аналогично складываем и получается



 Она возьмет 9 больших плиток со стороной 8 дюймов и 8 маленьких плиток со стороной 2 дюйма. . Определим ширину акцентной полосы, упростив выражение . (Округлить до десятых долей дюйма.)
Она возьмет 9 больших плиток со стороной 8 дюймов и 8 маленьких плиток со стороной 2 дюйма. . Определим ширину акцентной полосы, упростив выражение . (Округлить до десятых долей дюйма.)

 Если вы получили сообщение об ошибке ниже, измените имя пользователя.
Если вы получили сообщение об ошибке ниже, измените имя пользователя. 
 04 LTS.
04 LTS.
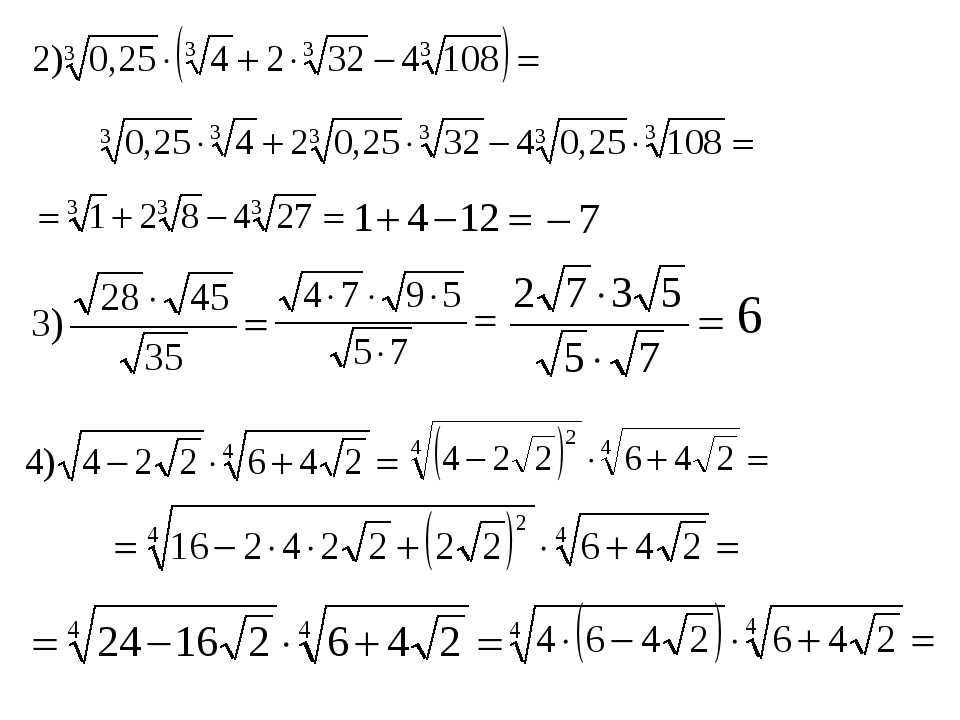 Вход в систему с правами root невозможен, так как для учетной записи root не установлен пароль.
Вход в систему с правами root невозможен, так как для учетной записи root не установлен пароль.
 Проведите исследование и всегда перепроверяйте каждую команду, прежде чем нажимать Введите .
Проведите исследование и всегда перепроверяйте каждую команду, прежде чем нажимать Введите . Один из способов напомнить себе, являетесь ли вы root или нет, — это проверить командную строку. Во многих системах командная строка заканчивается знаком доллара (« $ »), если вы вошли в систему как обычный пользователь, и знаком фунта (« # »), если вы являетесь пользователем root.
Один из способов напомнить себе, являетесь ли вы root или нет, — это проверить командную строку. Во многих системах командная строка заканчивается знаком доллара (« $ »), если вы вошли в систему как обычный пользователь, и знаком фунта (« # »), если вы являетесь пользователем root.



 txt .
txt . Такие программы, как su, sudo, ssh и другие связанные инструменты openssh, будут иметь доступ к учетной записи root.
Такие программы, как su, sudo, ssh и другие связанные инструменты openssh, будут иметь доступ к учетной записи root.

 Если у вас есть какие-либо комментарии, предложения или вопросы, не стесняйтесь обращаться к нам через форму обратной связи ниже.
Если у вас есть какие-либо комментарии, предложения или вопросы, не стесняйтесь обращаться к нам через форму обратной связи ниже. для счета. У всех пользователей AWS есть учетные данные безопасности.
для счета. У всех пользователей AWS есть учетные данные безопасности. Для большего
информацию см. в разделе Задачи, требующие учетных данных пользователя root.
Для большего
информацию см. в разделе Задачи, требующие учетных данных пользователя root.
 разрешения.
разрешения. Я БЫ.
Я БЫ. {2}=a\cdot a=\left (-a \right)\cdot \left (-a \right)$$
{2}=a\cdot a=\left (-a \right)\cdot \left (-a \right)$$