11.4.9.6. Формула представления любого числа в виде логарифма.
Автор Татьяна Андрющенко На чтение 2 мин. Просмотров 2.8k. Опубликовано
p=logaap Любое число можно представить в виде логарифма по любому основанию.
Под знаком логарифма могут находиться только положительные числа, причем, основание логарифма не равно единице.
Примеры.
I. Представить число 2 в виде логарифма по основанию: 1) 3; 2) 5; 3) 10.
Решение.
1) 2=log33²=log39;
2) 2=log55²=log525;
3) 2=lg10²=lg100.
II. Представить в виде десятичного логарифма числа: 1) -1; 2) -2; 3) -3.
Решение.
1) -1=lg10—1=lg0,1;
2) -2=lg10-2=lg0,01;
3) -3=lg10-3=lg0,001.
Решить уравнение:
1) lg (x-9)+lg (2x-1)=2.
Решение.
lg ((x-9)(2x-1))=lg102; представили сумму логарифмов в виде логарифма произведения и число 2 в правой части равенства записали в виде десятичного логарифма (логарифма с основанием 10).
lg (2x2-18x-x+9)=lg100; упростили выражения под знаками логарифмов.
2x2-19x+9=100; получили после потенцирования.
2x2-19x-91=0. Получили квадратное уравнение вида: ax2+bx+c=0.
a=2, b=-19, c=-91. Решим квадратное уравнение по общей формуле.
D=b2-4ac=(-19)2-4∙2∙(-91)=361+728=1089=332>0; два действительных корня:
Проверка. Значение х=-3,5 не удовлетворяет условию существования логарифма.
Значение х=-3,5 не удовлетворяет условию существования логарифма.
Проверяем данное равенство при х=13.
lg (13-9)+lg (2∙13-1)=2;
lg4+lg25=2;
lg (4∙25)=2;
lg100=2;
2=2.
Ответ: 13.
2) log3(x+1)+log3(x+3)=1.
Решение.
Сумму логарифмов заменим логарифмом произведения, единицу в правой части представим в виде логарифма с основанием 3:
log ((x+1)(x+3))=log33;
log (x2+x+3x+3)=log33. Потенцируем:
x2+4x+3=3;
x2+4x=0;
x (x+4)=0;
x=0 или x+4=0, отсюда x=-4.
Анализируем результаты:
х=-4 не подойдет, так как при этом значении под знаком логарифма окажутся отрицательные числа, что недопустимо.
Проверим значение х=0.
Проверка.
log3(0+1)+log
log31+log33=1;
0+1=1;
1=1.
Ответ: 0.
Преобразование выражений с использованием свойств логарифмов: примеры, решения
Если у нас есть выражение, содержащее логарифмы, то мы можем преобразовать его с учетом свойств этих логарифмов. В этом материале мы рассмотрим основные правила, по которым осуществляется данное преобразование.
В этом материале мы рассмотрим основные правила, по которым осуществляется данное преобразование.
В первом пункте приведем основные свойства логарифмов, представив их в виде списка. Далее рассмотрим характерные примеры преобразований с использованием этих свойств. Отдельно остановимся на числовых выражениях и на выражениях с переменными, а также посмотрим, как преобразовывать примеры с использованием модуля.
Свойства логарифмов
Чтобы преобразовывать выражения с логарифмами, обычно используют выражение, называемое основным логарифмическим тождеством: alogab=b, a>0, a≠1, b>0. Также нужно помнить следующие свойства:
Определение 1- loga1=0 при любом a>0, a≠1.
- logaa=1, если a>0, a≠1.
- logaa=1logaa=1 при любом a>0, a≠1.
- logaa=1, если a>0, a≠1.
- logaap=p, при этом a>0, a≠1 и p может быть любым действительным числом.
- loga(x·y)=logax+logay, a>0, a≠1, x>0, y>0. В обобщенном виде это свойство можно представить как loga(x1·x2·…·xn)=logax1+logax2+…+logaxn, a>0, a≠1, x1>0, x2>0, …, xn>0
- ) logaxy=logax-logay.

- logaxy=logax-logay , при этом a>0, a≠1, x>0, y>0.
- logaxy=logax-logay , a>0, a≠1, x>0, y>0.
- logabp=p·logab, при этом a>0, a≠1, b>0, а p может быть любым действительным числом.
- это свойство является следствием предыдущего: logabn=1n·logab , a>0, a≠1, n может быть любым натуральным числом больше 1, b>0.
- logab=logcblogca , при этом a>0, a≠1, b>0, c>0, c≠1.
- свойство, также являющееся следствием: logab=1logba , где a>0, a≠1, b>0, b≠1.
- logaqbp=pq·logab , a>0, a≠1, b>0, p и q могут быть любыми действительными числами, q≠0
- logaqbp=pq , a>0, a≠1, p и q – любые действительные числа, q≠0.
- logaq ap=pq, blogac=clogab , при этом a>0, a≠1, b>0, c>0.
Преобразовывая выражения, мы можем использовать данные равенства как справа налево, так и наоборот. Учить их все наизусть нет необходимости, достаточно знать основные свойства логарифмов и несколько других свойств, например, что bn=b1n , если b≥0. Из них можно вывести остальные свойства. Само решение, правда, при этом будет несколько длиннее. Например, если мы не знаем следствия logaqbp=pq·logab и используем только основные свойства логарифмов, нам нужно будет выполнить несколько последовательных преобразований:
Из них можно вывести остальные свойства. Само решение, правда, при этом будет несколько длиннее. Например, если мы не знаем следствия logaqbp=pq·logab и используем только основные свойства логарифмов, нам нужно будет выполнить несколько последовательных преобразований:
logaq bp=logabploga aq=p·logabq=pq·logab
То же относится и к последнему свойству из списка, выраженному формулой blogac=Clogac=clogab : оно тоже может быть выведено из основных свойств. Нужно учитывать, что если у нас есть степень положительного числа с логарифмом в показателе, то мы всегда можем поменять число под логарифмом и основание степени местами. В принципе, на практике такие задачи встречаются не слишком часто, но мы их все же разберем.
Как преобразовать числовое выражение с логарифмом
После того, как мы вспомнили основные свойства логарифмов, покажем, как использовать их при решении задач. Начнем с того, как преобразовывать числовые выражения, потому что такие вычисления считаются более простыми. Возьмем сперва примитивные примеры, с помощью которых легко проиллюстрировать выбор нужного свойства логарифма, а потом будем наращивать сложность задач. В конце разберем задания, в которых нужно использовать сразу несколько свойств.
Возьмем сперва примитивные примеры, с помощью которых легко проиллюстрировать выбор нужного свойства логарифма, а потом будем наращивать сложность задач. В конце разберем задания, в которых нужно использовать сразу несколько свойств.
Как выбрать свойство логарифма для преобразования
Список свойств, приведенный в первом пункте, довольно большой, и очевидно, что нужно хорошо в нем ориентироваться, чтобы получить нужный результат. Обычно выбор делается по итогам сравнения исходного логарифма/выражения с левыми и правыми частями формул, выражающих свойства. В том случае, когда одна из частей формулы похожа на исходный логарифм или выражение, мы берем именно это свойство и выполняем преобразование с его помощью. Покажем на примерах, как именно это делается.
Для начала преобразуем выражение, используя определение логарифма, выраженное формулой alogab=b, a>0, a≠1, b>0.
Пример 1Условие: преобразуйте и вычислите значение следующих выражений: 1) 5log54 ; 2) 10lg(1+2·π), 3) 2+3log2+3 ln15 ; 4) 2log2(−7); 5) (-5)log-5 e3
Решение
В первом примере прослеживается формула alogab.
Во втором случае a будет равно 10, b – 1+2·π. Необходимое условие выполнено, значит, мы можем записать это в виде равенства: 10lg(1+2·π) =1+2·π.
В третьем выражении у нас есть степень вида alogab, причем a=2+3 и b=ln15. Запишем: 2+3log2+3 ln15=ln15 . Хотя равенство также соответствует формуле alogab, где a равно 2, а b=-7, мы не можем воспользоваться ею для преобразования. Из-за наличия отрицательного числа под знаком логарифма выражение лишается смысла. Кроме того, -7 не соответствует условию b>0, что еще раз подтверждает, что данную формулу мы взять не можем. Следовательно, вычислить значение исходного выражения нельзя, и запись 2log2(−7) =−7 будет ошибочна.
То же самое относится и к четвертому примеру. Мы не можем записать, что -5log-5·e3=e3 , поскольку такое выражение смысла не имеет.
Ответ:1) 5log54=4; 2) 10lg(1+2·π)=1+2·π; 3) 2+3log2+3ln 15=ln 15 ; 4 и 5 — не имеют смысла.
Довольно часто в задачах встречается такой вид преобразования, когда некоторое положительно число представляют в виде степени другого числа, также положительного и не равного 1, имеющего в показателе логарифм. Основной такого преобразования также является основное определение логарифма alogab=b, a>0, a≠1, b>0, но в перевернутом виде, т.е. прочитанное справа налево, например, 3=eln3 или 5=5log55.
Далее возьмем примеры с другими свойствами логарифмов.
Пример 2Условие: вычислите, если возможно: 1) log−21, 2) log11,3) log01, 4) log71, 5) ln1, 6) lg 1,7) log3,751, 8) log5·π71.
Решение
В первых трех примерах мы видим не имеющие смысла выражения log−21, log11, log01. Основанием логарифма не может быть число меньше 1, в т.ч. 0 и отрицательные значения, т.к. для них логарифм не определен. Значит, значение этих выражений вычислить нельзя.
В других случаях логарифмы имеют подходящие основания: 7, e, 10, 3,75 и 5·π7, а под знаками логарифма везде 1. Зная соответствующее свойство логарифма (loga1=0 при любом a>0, a≠1., мы можем сделать вывод, что значения этих выражений равны 0.
Зная соответствующее свойство логарифма (loga1=0 при любом a>0, a≠1., мы можем сделать вывод, что значения этих выражений равны 0.
Ответ: 1, 2, 3 смысла не имеют; 4) log71=0, 5) ln1=0, 6) lg1=0, 7) log3,751=0, 8) log5·e71=0.
Пример 3Условие: вычислите значения: 1) log1313 , 2) ln e, 3) lg 10,4) log5·π3−2(5·π3−2), 5) log−3(−3), 6) log11.
Решение
Нам потребуется свойство логарифма, выраженное формулой logaa=1 при a>0, a≠1. Исходные логарифмы схожи между собой в том, что их основания и числа под знаком логарифма являются одинаковыми. Казалось бы, можно сразу сделать вывод, что значения всех выражений будут равны единице, однако посмотрим внимательнее. В заданиях 1, 2, 3, 4 действительно ответом будет 1, а вот в 5 и 6 исходные выражения смысла не имеют.
Ответ: 1) log13=13=1, 2) ln e=1, 3) lg10=1, 4) log5·π3−2(5·π3−2)=1; 5,6 не имеют смысла.
Пример 4Условие: вычислите: 1) log3311, 2) log1+22(1+22)723 , 3) logπ5(π5)-2 , 4) log−10(−10)6.
Решение
Видим, что под логарифмами находятся некоторые степени основания, значит, нам нужно использовать соответствующее свойство logaap=p, где a>0, a≠1 и p будет любым действительным числом. С учетом этого можно записать следующее:
- log3311=11
- log1+22(1+2·2)723=723
- logπ5(π5)-2=-2
- для этого примера мы не можем написать такое же равенство, как и в предыдущем примере, поскольку log−10(−10)6=6 не имеет смысла.
Ответ: 1) log3311=11, 2) log1+22(1+2·2)723=723 , 3) logπ5(π5)-2=-2 , 4) не имеет смысла.
Пример 5Условие: даны выражения log2,64·127, ln2+1π и lg((−5)·(−12)). Нужно представить их как суммы или разности логарифмов по тому же основанию.
Решение
Смотрим, что находится под знаком логарифма. Там произведение, значит, берем свойство логарифма произведения: loga(x·y) = logax+logay, a>0, a≠1, x>0, y>0. В исходных примерах основания и числа в произведениях положительны, т. е. условие данного свойства соблюдено. Применим его для первого выражения:
е. условие данного свойства соблюдено. Применим его для первого выражения:
log2,64·127=log2,6 4+log2,6127
Чтобы вычислить значение второго выражения, нам нужно свойство логарифма частного: logaxy=logax-logay, a>0, a≠1, x>0, y>0. Здесь в основании стоит положительное число e, также у нас есть положительный числитель 2+1 и знаменатель π, т.е. условия свойства соблюдены. Применяем свойство и записываем, что ln2+1π=ln2+1-ln π .
Разберем третий пример. Начнем с того, что выражение lg((−5)·(−12)) будет иметь смысл, однако формула логарифма произведения для него не подойдет, поскольку оба числа -5 и -12 отрицательны. Значит, преобразование lg((−5) ·(−12))=lg(−5)+lg(−12) не подходит. Какое же свойство тогда использовать?
Проведем предварительное преобразование, чтобы избавиться от отрицательных чисел. Далее мы подробно поговорим, когда нужно выполнять такое действие, а пока ограничимся записью самого решения, которое и так понятно: lg((−5) ·(−12))=lg(5·12)=lg5+lg12.
Ответ: 1) log2,64·127=log2,64+log2,6127 , 2) ln2+1π=ln2+1-ln π , 3) lg((−5)·(−12))=lg5+lg12.
Пример 6Условие: упростите выражения log30,25+log316+log30,5 и ln23-ln13 .
Решение
Здесь мы тоже можем использовать свойства логарифма частного и произведения по аналогии с предыдущим примером, только нам потребуется их обратная запись. Преобразуем сумму логарифмов в логарифм произведения, а разность логарифмов в логарифм частного. В итоге у нас получается в первом примере log30,25+log316+log30,5=log3(0,25·16·0,5)=log32, а во втором ln23-ln13=ln23:13=ln 2.
Ответ: 1) log30,25+log316+log30,5=log3(0,25·16·0,5)=log32, 2) ln23-ln13=ln 2 .
Пример 7Условие: есть выражения log0,7511, log3-1(3-2+5·673)5+1 и log3(−5)6. Нужно избавиться от степени в выражении под знаком логарифма.
Решение
Очевидно, что у нас здесь есть выражения вида logabp. Берем свойство, которое выражается формулой вида
Берем свойство, которое выражается формулой вида
logabp=p·logab, где a>0, a≠1, b>0, p — любое действительное число. Поскольку условия a>0, a≠1, b>0 выполнены, то мы можем преобразовать logabpв произведение p·logab.
- в случае с первым выражением a равно 7, b – пяти и p– 11. Тогда log0,7511=11·log0,75.
- тут a=3-1, b=3-2+5·673, p=5+1 . Нужные условия выполнены, значит, мы можем записать, что:
log3-1(3-2+5·673)5+1==5+1·log3-1(3-2+5·673) - у нас есть выражение той же структуры: logabp, a=3, b=−5, p=6, однако одно из условий не выполняется, а именно b у нас меньше 0. Значит, эту формулу мы применить не можем, и нам будет нужно предварительно преобразовать выражение под знаком логарифма. Решение будет таким: log3(−5)6=log356=6·log35.
Ответ: 1) log0,7511=11·log0,75, 2) log3-1(3-2+5·673)5+1==5+1·log3-1(3-2+5·673) 3) log3(−5)6=6·log35.
Применение формулы в обратном порядке в виде p·logab=logabp требуется довольно часто. При таком преобразовании важно соблюсти все те же условия для числовых значений переменных. Например, 3·ln 5=ln 53 и lg 2·log23=log23lg2.
При таком преобразовании важно соблюсти все те же условия для числовых значений переменных. Например, 3·ln 5=ln 53 и lg 2·log23=log23lg2.
Условие: согласно таблице логарифмов, lg2≈0,3010 и lg5≈0,6990. Вычислите, сколько будет log25. Здесь же: запишите ln 11ln 3 в виде логарифма, основание которого равно 3.
Решение
Воспользуемся формулой перехода к новому основанию и представим исходный логарифм как отношение десятичных логарифмов с известными нам значениями.
log25=lg 5lg 2
Вычисляем и находим ответ: lg 5lg 2≈0,69900,3010≈2,3223 .
Во втором примере также будет достаточно формулы перехода к новому основанию, только в обратном порядке, т.е. logcblogca=logab .
Считаем: ln 11ln 3=log311
Ответ: 1) log25≈2,3223, 2) ln 11ln 3=log311 .
Мы разобрали множество примеров, где для осуществления преобразования достаточно применить одну формулу свойства логарифма или его определение. Теперь мы можем перейти к более сложным задачам, в которых нужно последовательно применять несколько свойств, а также делать дополнительные преобразования. Однако перед этим запишем еще один важный пример использования следствий из основных свойств логарифмов.
Теперь мы можем перейти к более сложным задачам, в которых нужно последовательно применять несколько свойств, а также делать дополнительные преобразования. Однако перед этим запишем еще один важный пример использования следствий из основных свойств логарифмов.
Условие: 1) дан логарифм ln1+π7 . Необходимо избавиться от корня под знаком логарифма; 2) выполните преобразование дроби 1log25 в логарифм с основанием 4; 3) преобразуйте логарифм loge2345 так, чтобы избавиться от степени в основании; 4) вычислите, сколько будет log2-13216 ; 5) осуществите замену 2,3log73 на степень с основанием 3.
Решение
- Вспоминаем следствие из свойства логарифма степени, которое выражается формулой logabn=1n·logab .В первом случае можем сразу же подсчитать: ln1+π7=17·ln(1+π) .
- во втором случае нам понадобится формула logab=1logba , примененная в обратном порядке. Получим 1log25=log52.
- здесь нам потребуется свойство logaqbp=pq·logab .
 Применяем его и получаем loge2345=452·ln 3=25·ln 3.
Применяем его и получаем loge2345=452·ln 3=25·ln 3. - в этом случае нам нужно будет следствие, выраженное формулой logaqap=pq: log(2)-13216=16-13=-12
- используем формулу свойства blogac=clogab и вычисляем ответ:
2,3log7·3=3log72,3
Ответ: 1) ln1+π7=17·ln(1+π) ; 2) 1log25=log52 ; 3) loge2345=25·ln 3; 4) log(2)-13216=-12 . 5) 2,3log7·3=3log72,3 .
Задачи с применением нескольких свойств логарифмов
В действительности чаще встречаются более сложные задания, чем те, что мы разобрали в предыдущем параграфе. В них приходится выполнять преобразования в несколько шагов, применяя последовательно одно свойство за другим. Кроме того, они зачастую включают в себя необходимость раскрывать скобки, приводить подобные слагаемые, сокращать обыкновенные дроби и др. Это не так сложно, как кажется, главное – соблюдать правильную последовательность действий.
Пример 10Условие: вычислите, сколько будет (log315−log35) ·7log75.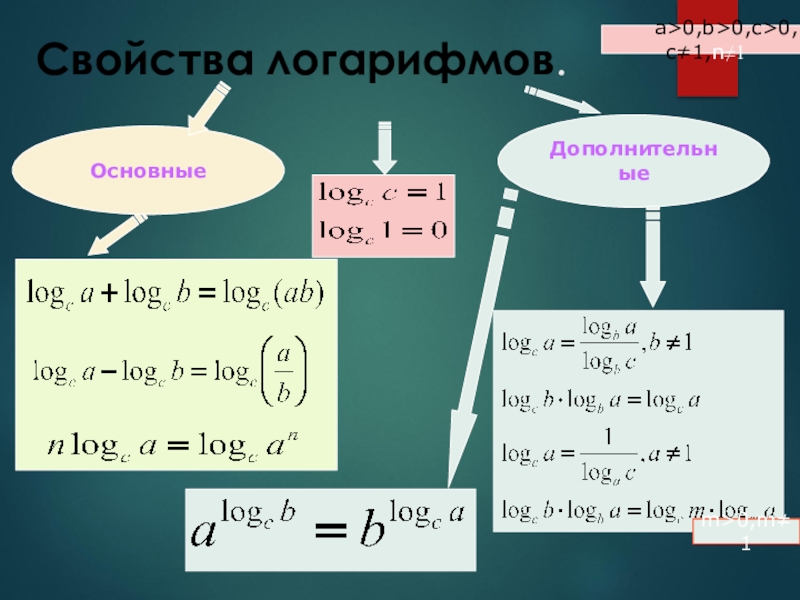
Решение
Мы можем заменить выражение в скобках логарифмом log3(15:5), используя свойство частного. Вычисляем его значение и получаем log3(15:5) =log33=1.
Согласно основному определению логарифма, значением 7log75 будет 5. Подставим в исходное выражение получившиеся результаты и найдем, что (log315−log35) ·7log75=1·5=5.
Вот все решение без комментариев:
(log315−log35)·7log75=log3 (15:5)·5==log33·5=1·5=5
Ответ: (log315−log35) ·7log75=5.
Пример 11Условие: вычислите, чему равен log3log223−1.
Решение
Начнем с преобразования логарифма, который, в свою очередь, сам находится под знаком логарифма. Используем для этого формулу логарифма степени log223=3. Получим, что log3log223=log33, а дальше log33=1. Следовательно, log3log223−1=1−1=0.
Ответ: log3log223−1=0.
Пример 12Условие: выполните упрощение выражения 3ln 5ln 3log52 .
Решение
Берем формулу перехода к новому основанию. С ее помощью можно представить отношение логарифмов ln 5ln 3 как log35. У нас получилось 3log35log52 . Теперь применяем формулу основного определения логарифма 3log35=5 и получаем, что 3log35log52 . Нам осталось лишь вычислить значение этого выражения. Оно будет равно 2.
Ответ: 3ln 5ln 3log52=2 .
Перейдем к дальнейшему пункту обсуждения логарифмических преобразований. У нас есть выражения log334, 52+log53, lg 0,01. Они не напоминают нам ни об одной известной нам формуле свойства, но их все же можно изменить этим способом, если выполнить предварительные преобразования: 52+log53=52·5log53=25·3=75, log334=log31234=412=8 и lg 0,01=lg 10−2=−2. Разберем подробнее, как именно это делается.
Предварительное преобразование перед применением основных свойств логарифмов
На практике мы часто можем встретить логарифмы, которые внешне не похожи ни на одну часть формулы свойства. Однако при этом преобразование требует применения именно этих формул. Это возможно, если перед этим привести их к соответствующему виду. Это процесс называется тождественным преобразованием.
Однако при этом преобразование требует применения именно этих формул. Это возможно, если перед этим привести их к соответствующему виду. Это процесс называется тождественным преобразованием.
В роли таких действий могут выступать почти любые преобразования выражений, в том числе раскрытие скобок, вынесение за скобки множителей, применение формул тригонометрии и т.д. Это очевидно, поскольку выражения под знаком логарифма могут содержать практически все, что угодно: модули, скобки, дроби, степени и др. Поэтому нужно уметь выполнять разные виды преобразований, чтобы успешно решать такие задачи.
Данная статья не имеет целью осветить все возможные случаи преобразований, поскольку их очень много. Мы выбрали только четыре, которые наиболее распространены.
Определение 2- Довольно часто приходится получать степени под знаком и в основании, чтобы потом использовать формулу логарифма степени и последствия данного свойства. Мы выполняем такое преобразование, если в видим в условии логарифмы следующего вида: ln2532332 , log381.

- Также нужно уметь выполнять преобразование, связанное со свойствами степени. Оно нужно нам для последующего использования формулы, которая отвечает определению логарифма. Мы применяем его, когда у нас есть выражения, подобные 2log223, 32·log35, 71+log74, 25(log35)-3 и др.
- Обязательно нужно преобразовывать выражения с десятичными дробями под знаком логарифма или в его основании. Иногда после этого мы обнаруживаем, что основание под знаком степени и основание логарифма будут равны, как, например, здесь: log15(0,2)7
- Также нужно знать правила преобразования выражений, где под знаком логарифма стоит отрицательное число. Мы расскажем, что нужно делать, если в условии стоят выражения вроде lg(−3)−4, log6((−9)·(−4)) и др.
Разберем подробно каждый вид преобразования.
Как выделить степень в основании логарифма и под его знаком
Сразу возьмем конкретный пример. У нас есть выражение log1981 , структура которого не подсказывает нам ни одного возможного свойства логарифмов, которое можно было бы использовать. Значит, нам надо начать с преобразования самого выражения или сразу с вычисления его значения. Как же это сделать? Обратите внимание на числа 81 и 19. Их легко представить в виде степени с основанием 3 : 81=34 и 19=3−2. Значит, все выражение можно переписать как log3-234 , а здесь уже видна возможность использования свойства logaqbp=pq·logab . Таким образом, log1981=log3-2=4-2=-2 .
Значит, нам надо начать с преобразования самого выражения или сразу с вычисления его значения. Как же это сделать? Обратите внимание на числа 81 и 19. Их легко представить в виде степени с основанием 3 : 81=34 и 19=3−2. Значит, все выражение можно переписать как log3-234 , а здесь уже видна возможность использования свойства logaqbp=pq·logab . Таким образом, log1981=log3-2=4-2=-2 .
Этот пример иллюстрирует нам следующую мысль: если есть возможность, нужно выделить степень в основании и под знаком логарифма, чтобы впоследствии применить свойство логарифма степени. Ниже мы приведем некоторые советы, как именно выделять степени в таких примерах.
В некоторых случаях число можно преобразовать в целую степень, как в примере выше. В задачах то и дело встречаются степени чисел 2 и 3, которые легко узнать с первого взгляда: 243=35, 81=34, 8=23, 64=26 и др. Для решения примеров полезно иметь таблицу степеней натуральных чисел в пределах 10, чтобы сразу видеть возможности преобразования выражений.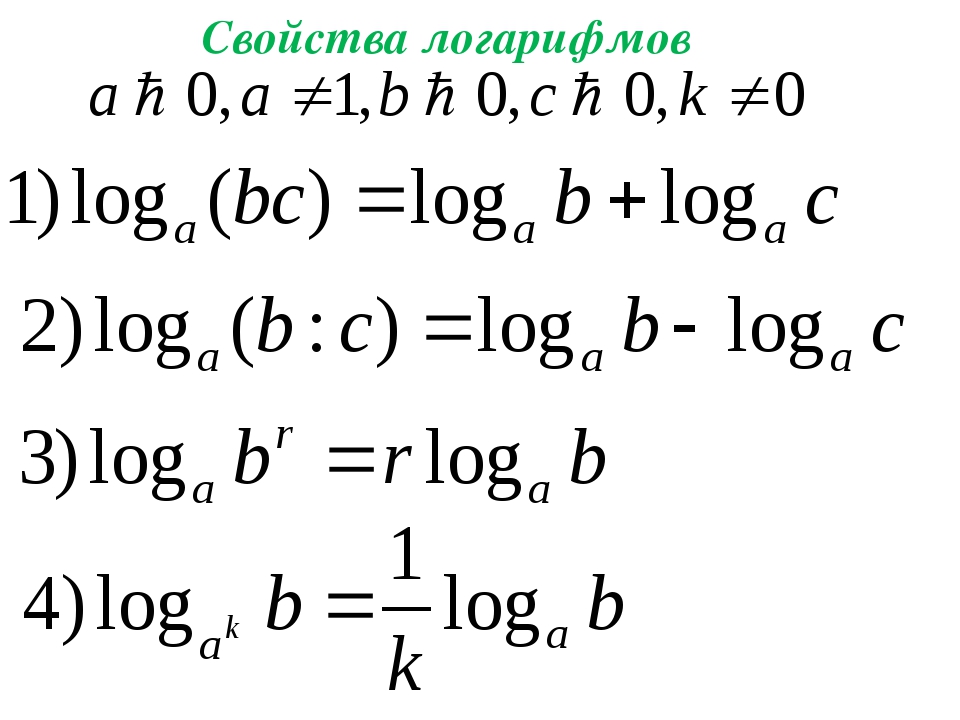 Также легко работать с выражениями, включающими целые степени 10, 100 и др.
Также легко работать с выражениями, включающими целые степени 10, 100 и др.
Условие: вычислите или упростите выражения log6216, log3431243, log0,0000010,001.
Решение
- В первом случае мы сразу видим, что 216 можно представить в виде 63. Значит, log6216=log663=3.
- у нас есть числа 343 и 1243. Обратимся к таблице степеней и увидим, что их можно представить в виде 73 и 3−4. Выполняем дальнейшие преобразования и получаем:
log3431243=log733-4==-43·log73=-113·log73 - Поскольку 0,000001=10−6 и 0,001=10−3, тогда log0,0000010,001=log10−610−3= -3-6=12
Ответ: 1) log6216=3, 2) log3431243=-113·log73 ; 3) log0,0000010,001=12.
Если исходного числа нет в таблице степеней, то мы можем разложить его на простые множители.
Пример 14Условие: упростите выражение log3648·log23.
Решение
Выполняем разложение 648 на простые множители.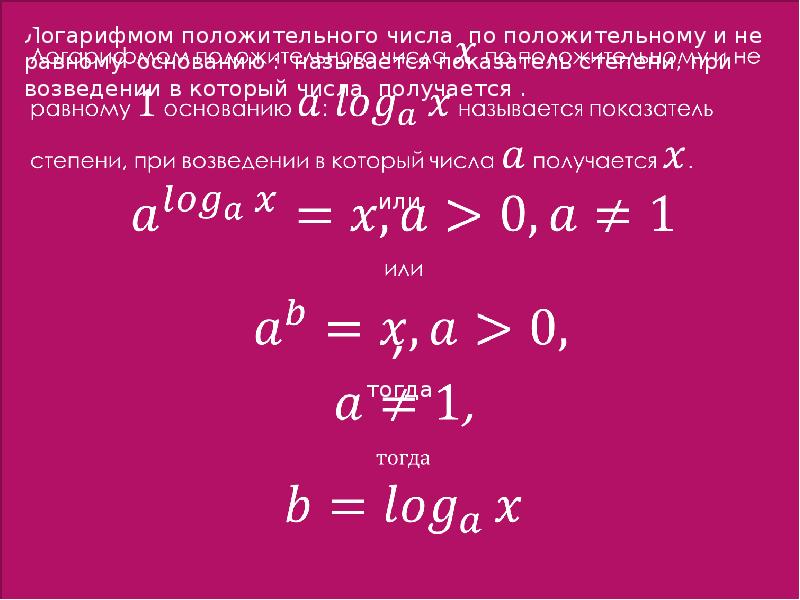
64832416281931222333
Значит, это число можно представить в виде 648=23·34. Следовательно, log3648·log23=log3(23·34)·log23
Теперь мы можем преобразовать исходный логарифм произведения в сумму, а потом воспользоваться формулой логарифма степени.
log3(23·34)·log23=(log323+log334)·log23= =(3·log32+4)·log23.
Упрощаем выражение через раскрытие скобок:
(3·log32+4)·log23=3·log32·log23+4·log23.
В полученном выражении log32·log23 является произведением взаимно обратных чисел, которое равно 1. Следовательно, формулируем ответ как 3·log32·log23+4·log23=3·1+4·log23=3+4·log23.
Ответ: log3648·log23=3+4·log23.
Зачастую под логарифмом записываются выражения, представляющие собой отношения или произведения корней: 323·3-2, 2·2273 и т.д. Они также приводятся к виду степени: сначала мы выполняем переход от корня к степени, используя соответствующие свойства. С помощью таких преобразований мы можем получить выражение, удобное для применения формулы логарифма степени.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 15Условие: найдите значение выражений log52·5-0.5·5-153454 и log372919.
Решение
В первом случае у нас есть произведение степеней, имеющих одинаковые основания. Используя нужное свойство, получим: 52·5−0,5·5−1=52−0,5−1=50,5. Для преобразования дроби сначала выполним переход от корня к степени, затем используем свойство отношения степеней с одинаковыми основаниями:
53454=5344=534-4=5-314
Полученное выражение подставим в исходный логарифм, применив формулу logaqaq=pq, и получим ответ:
log52·5-0.5·5-153454=log50.55-314=-3140.5==-13412=-132=-612
Во втором случае представим число 729 как 36 , а 19 как 3−2. Исходный логарифм приобретет вид log3363-2. Используя свойство корня из степени, преобразуем основание логарифма и получим:
336=333=31-3=3-2
Заканчиваем преобразование: log3363-2=log3-23-2=1 .
Ответ: 1) log52·5-0.5·5-153454=-612 ; 2) log372919=1
Преобразования, которые нужно сделать, чтобы получить под знаком логарифма нужную степень, могут значительно отличаться от примера к примеру.
Пример 16Условие: вычислите значения log13-1132·3+1-5 и log2·cos1(1+cos2)3 .
Решение
Первое, что нам нужно сделать, – это избавиться от иррациональности в знаменателе первой дроби, лежащей в основании логарифма:
13-1=3+13-1·3+1=3+132-12=3+12
Мы получили результат, схожий с дробью под знаком логарифма. Применим к нему свойства степеней и получим:
132·3+1-5=3+1532=3+1525=3+125
В результате преобразований у нас получился логарифм степени основания log3+123+135 . Значение данного выражения будет равно 5.
Чтобы преобразовать второе выражение, надо воспользоваться тригонометрическими формулами, а конкретно формулой понижения степени cos2a=1+cos2a2 :
log2·cos1(1+cos2)3=log2·cos1(2·cos21)3
Преобразуем второй логарифм, записав его как степень 2·cos2112 или же 2·cos123=2·cos16. Оба выражения будут иметь одно и то же значение, равное шести.
Оба выражения будут иметь одно и то же значение, равное шести.
Ответ: 1) log13-1132·3+1-5=5 ; 2) log2·cos1(1+cos2)3=6 .
Как применять свойства степени при преобразовании выражений с логарифмами
Ранее мы уже использовали свойства степеней, чтобы преобразовать выражения под знаком логарифма и его основание. Посмотрим, в каких еще характерных случаях потребуется такая подготовка.
Для начала возьмем задачи на применение свойства степеней с одинаковыми основаниями ap·aq=ap+q. Чаще всего его применяют в обратном порядке, т.е. справа налево.
Пример 17Условие: вычислите значения 3−2+log37 и 0,72−log0,70,1.
Решение
В первом примере нужно представить исходную степень как произведение двух степеней, т.е. 3−2+log37=3−2·3log37. Теперь найдем, чему равен первый множитель. Возведем его в степень, потом вычислим значение второго множителя, используя определение логарифма, и подсчитаем их произведение:
3−2·3log37= (19) ·7=79
Во втором примере нам надо подготовить выражение к преобразованию, выполнив переход к произведению степеней: 0,72−log0,70,1=0,72·0,7−log0,70,1. После этого нам нужно представить показатель −log0,70,1 в виде llog0,7(0,1)−1=log0,710. Теперь все, что нам осталось, – это закончить вычисления:
После этого нам нужно представить показатель −log0,70,1 в виде llog0,7(0,1)−1=log0,710. Теперь все, что нам осталось, – это закончить вычисления:
0,72·0,7−log0,70,1=0,49·0,7log0,710=0,49·10=4,9
Ответ: 1) 3−2+log37=79; 2) 0,72−log0,70,1=4,9.
Также для предварительных преобразований нужно обязательно знать свойство степени в степени, которое выражается формулой (ap)q=ap·q, например, если у нас есть выражение (eln2)3, то мы можем заключить, что значение части в скобках будет равно 2. Значит, (eln2)3=23=8. А если в условии указано (e3)ln2 или (e3)ln2, то мы сначала приводим их к виду (eln2)3:
e3·ln2=eln2·3=(eln2)3 и (e3)ln2=e3·ln2=eln2·3=(eln2)3.
Посмотрим пример решения такой задачи.
Пример 18Условие: выполните упрощение выражений 2log223−3log23 и 5(log85) −1.
Решение
Отметим, что выражения 2log223и 2log223 не являются равными друг другу. Мы можем представить 2log223 как 2log23·log23. Используя свойство степени, представим его как (2log23)log23, что будет тождественно равным 3log23. В итоге мы имеем, что 2log223−3log23=3log23−3log23=0.
Используя свойство степени, представим его как (2log23)log23, что будет тождественно равным 3log23. В итоге мы имеем, что 2log223−3log23=3log23−3log23=0.
Вот запись всего решения:
2log223−3log23=2log23·log23−3log23==(2log23)log23−3log23=3log23−3log23=0
Перейдем ко второму примеру. Запись 25(log85)-1 не будет равна (25log85)−1. Мы можем представить степень (log85)−1 как дробь 1log85 . Ее нужно преобразовать, используя следствие свойства перехода к новому основанию по формуле logab=1logba, чтобы получить log58.
Так, 25(log85)-1=25log58. Поскольку 25 – это 52, имеем 5log58= (52)log58. То, что у нас получилось, представляем в виде (5log58). Нам осталось только вычислить значение: (5log58)2=82=64.
Ответ: 1) 2log223−3log23=0, 2) 25(log85)−1=64.
Также встречаются примеры, где предварительная подготовка к использованию свойств логарифмов заключается в применении и свойства умножения степеней с одинаковыми основаниями, и свойства степени в степени. Например,
Например,
4−0,5+2·log43=4−0,5·42·log43==12·(4log43)2=12·32=12·9=4,5
Преобразование логарифмов с десятичными дробями
Применить свойства логарифмов можно и тогда, когда под знаком логарифма у нас стоит десятичная дробь. Что можно сделать с выражением log0,4253? Отметим, что 25 и 0,4 равны между собой 0,4=410=25, то есть это разные формы записи для одного и то же числа.
В целом можно сказать, что в случае наличия десятичной дроби под знаком логарифма необходимо выполнить переход к обыкновенной дроби. Это поможет увидеть возможности использования свойств логарифмов.
Разберем подобную задачу.
Пример 19Условие: вычислите значение выражения log0,46,25.
Решение
Начнем с перехода от десятичных дробей к обыкновенным.
log0,46,25=log410625100=log25254
Теперь видно, что мы можем преобразовать 254 в виде (25)−2 и воспользоваться формулой логарифма степени. Вычисляем значение:
log25254=log2525-2=-2
Ответ: -2.
Преобразование выражений с отрицательными числами под знаком логарифма
Еще один случай, который мы хотели бы рассмотреть – это преобразование выражений, в которых под знаком логарифма стоит отрицательное число, например, log3-93-27 или log3((−2)·(−5)).
Мы не можем сразу воспользоваться формулами свойств логарифмов в том виде, в каком приводили их в последнем пункте, например, сразу перейти от log3((−2)·(−5)) к log3(−2)+log3(−5), применить свойство логарифма степени к log2(−2)6 или логарифма частного к log3-93-27 , поскольку отрицательные числа не могут находиться под знаком логарифма и в его основании.
Что это значит на практике? Вернемся к нашему примеру log3((−2)·(−5)). Структура выражения соответствует формуле loga(x·y), где a равно 3, x-3 и y-5. Поскольку условия a>0, a≠1, x>0, y>0 не выполнены, формулу loga(x·y)=logax+logay мы применить не можем, и равенство log3((−2)·(−5)) =log3(−2) +log3(−5) записать нельзя. Преобразования вида log3-93-27=log3-93-log3(-27) также будут неправильными.
Это не значит, что выражения с отрицательными числами не могут быть преобразованы с использованием свойств логарифмов. Это допускается при условии предварительных преобразований, позволяющих избавиться от минуса. Они базируются на хорошо известных нам правилах работы с числами, меньшими 0.
Вернемся опять к нашему примеру. Согласно правилам умножения, (−2)·(−5) =2·5, значит, log3((−2)·(−5))=log3(2·5). К выражению в таком виде мы уже можем применить формулу log3(2·5) =log32+log35. А вот для примера log2(−2)6 нужно будет выполнить следующие действия:
(−2)6= ((−1)·2)6=(−1)6·26=1·26=26
Значит, log2(−2)6=log226=6.
Пример 20Условие: найдите значение выражения log2-163-2-23.
Решение
Сначала заключим, что данное выражение имеет смысл. Воспользоваться сразу свойством логарифма частного у нас нет возможности из-за отрицательных чисел под знаком логарифма, поэтому выполним преобразования.
Определив корень нечетной степени из отрицательного числа, выполним переход от -163-2-23 к -163-2-23 . Согласно правилам деления, получим -163-2-23=1632-23 . Теперь нам нужно получившуюся дробь представить в виде степени числа 2 и найти значение получившегося логарифма.
1632-23=2432-23=2432-23=243—23=22log2-163-2-23=log222=2
Ответ: log2-163-2-23=2 .
Некоторые свойства, например, логарифма частного, степени с четным показателем и произведения, можно распространить и на отрицательные числа с помощью модулей. Как это делается, мы покажем далее. Так, поскольку свойство логарифма произведения выглядит как loga(x·y)=loga|x|+loga|y|, где a>0, a≠1, x≠0, y≠0, то после преобразования мы получим log3((−2)·(−5)) =log3|−2|+log3|−5|=log32+log35.
Как преобразовать логарифмическое выражение с переменными
В предыдущих параграфах мы разобрали, как работать с числовыми выражениями, содержащими логарифмы. Однако если требуется решить логарифмическое неравенство или уравнение, нам понадобится умение работать с теми случаями, когда под знаком логарифма содержится выражение с переменными. В целом при этом мы руководствуемся теми же принципами, что и с числовыми выражениями, но тут следует отдельно пояснить некоторые нюансы, незнание которых ведет к ошибкам.
Особенности преобразований выражений с переменными
Основная трудность состоит в том, что при работе с такими выражениями числа, расположенные под знаком логарифма и в его основании, должны соответствовать особым условиям, а в случае определенных переменных из области допустимых значений эти условия могут оказаться невыполненными. Приведем один наглядный пример.
У нас есть логарифмическое выражение log2(x+1)4. При преобразовании нужно обязательно учитывать область допустимых значений, поэтому первым шагом должно стать ее нахождение. Здесь она определена неравенством (x+1)4>0, значение которого является числовым множеством (−∞, −1) ∪ (−1, +∞). Решить его можно с помощью метода интервалов.
Исходное выражение соответствует формуле logABp, где A равно 2, B – x+1, а p – четырем.
Мы видим, что заданное выражение соответствует виду logABp, где A=2, B=x+1 и p=4. Такие выражения преобразовываются по свойству логарифма степени logabp=p·logab. Можно ли поступить так с этим выражением? Вычислим значение исходного логарифма и выражения, которое получилось после преобразования, например, при x=−2. В итоге: log2(−2+1)4=log21=0, а 4·log2(−2+1) =4·log2(−1) –выражение, не имеющее смысла. Значит, мы ошиблись.
Причина ошибки в том, что мы взяли формулу logabp=p·logab, но это допустимо лишь при условии a>0, a≠1, b>0, p — любое действительное число. Иными словами, проделанное нами преобразование возможно, если x+1>0, что аналогично x>−1 (для A и p – условия выполнены). Однако в нашем случае ОДЗ переменной x для исходного выражения состоит не только из промежутка x>−1, но и из промежутка x <−1. Но для x <−1 мы не имели права осуществлять преобразование по выбранной формуле.
Почему надо учитывать область допустимых значений
Продолжая работу с выражением log2(x+1)4, проанализируем, как изменится область значений, когда мы выполним переход к виду 4·log2(x+1). Ранее мы уже определили эту область как множество (−∞, −1) ∪ (−1, +∞). Теперь вычислим, какова будет область допустимых значений для 4·log2(x+1). Она определяется условием x+1>0, а ему, в свою очередь, будет отвечать множество (−1, +∞). Мы видим, что область допустимых значений сузилась, а это может привести к различным ошибочным последствиям, поэтому таких преобразований следует избегать.
Важно следить, как меняется область значений во время каждого преобразования. Если на каком-либо этапе происходит ее сужение, это повод тщательно проверить все вычисления и определить, правомерно ли использования данного преобразования.
Чаще всего при решении задач приходится иметь дело с выражениями, область допустимых значений которых не ограничивает применение свойств логарифмов в прямом и обратном порядке, но не следует относиться так ко всем примерам. Нужно всегда проверять, что происходит с областью допустимых значений, и своевременно отслеживать возможные ошибки.
Запишем, в ходе каких преобразований чаще всего происходит непреднамеренное сужение области значений:
Определение 3- когда мы переходим от логарифма произведения к сумме, например, ln(x·(x+3)) =lnx+ln(x+3) сузит нужную область.
- Когда мы переходим от логарифма частного к разности. Пример такого преобразования – замена log2xsin x на log2x−log2sinx .
- Когда мы выносим четный показатель степени, используя формулу логарифма степени logabp=p·logab и формулу logabp=pq·logab . Примеры таких преобразований – logx3(x-8)2=23·logx(x-8) , ln(x+3)−4=−4·ln(x+3).
Иногда в результате преобразования область допустимых значений может не сужаться, а расширяться, например, при переходе от 4·log2(x+1) к log2(x+1)4. В этом случае область расширяется от (−1, +∞) до (−∞, −1) ∪ (−1, +∞). Такие преобразования имеют место, если оставаться в рамках ОДЗ для исходного выражения. Так, преобразование 4·log2(x+1) =log2(x+1)4 имеет место на области значений переменной x для исходного выражения 4·log2(x+1), то есть, при x+1>0, что аналогично (−1, +∞).
Теперь, когда мы обговорили тонкости, на которые нужно обращать внимание при преобразовании выражений с переменными с использованием свойств логарифмов, остается разобраться, как правильно эти преобразования проводить.
Правила проведения преобразований
Мы говорили ранее, что чаще всего область допустимых значений позволяет нам применять свойства логарифмов в привычных формулировках.
Пример 21Условие: упростите 3·lg(x+2)7−lg(x+2) −5·lg(x+2)4.
Решение
На первый взгляд данное выражение нужно преобразовать, используя логарифм степени, то есть сначала вынести нужную степень в виде коэффициента и потом привести подобные слагаемые. Давайте разберемся, правомерно ли применение выбранного свойства в этом случае.
Чтобы перейти от lg(x+2)7 к 7·lg(x+2) и от lg(x+2)4к 4·lg(x+2), нам нужно, чтобы x+2>0. Выясним, будет ли соблюдено данное условие. Для этого нам нужно определить область допустимых значений переменной x. Ее можно выразить с помощью системы неравенств (x+2)7>0,x+2>0,(x+2)4>0 , которая будет равносильной условию x+2>0 (если нужно, повторите материал о решении систем неравенств). Следовательно, мы можем взять формулу логарифма степени. Считаем:
3·lg(x+2)7−lg(x+2)−5·lg(x+2)4==3·7·lg(x+2)−lg(x+2)−5·4·lg(x+2)==21·lg(x+2)−lg(x+2)−20·lg(x+2)==(21−1−20)·lg(x+2)=0
Область допустимых значений позволяет нам использовать и другой вариант вычисления, например, такой:
3·lg(x+2)7-lg(x+2)-5·lg(x+2)4==lg((x+2)7)3-lg(x+2)-lg((x+2)4)5==lg(x+2)21-lg(x+2)-lg(x+2)20==lg(x+2)21(x+2)·(x+2)20=lg1=0
Ответ: 3·lg(x+2)7−lg(x+2) −5·lg(x+2)4=0.
А как быть в случае, если в области допустимых значений нужные условия не будут выполняться? Возьмем соответствующий пример и разберем его.
Пример 22Условие: выполнить упрощение выражения lg(x+2)4−lg(x+2)2.
Решение
Здесь свободно использовать свойство логарифма степени мы не можем. Область допустимых значений x можно представить в виде объединения промежутков x>−2 и x<−2. Если x>−2, то применяем нужное свойство и действуем по аналогии с тем, как мы решали задачу выше: lg(x+2)4−lg(x+2)2=4·lg(x+2) −2·lg(x+2) =2·lg(x+2). Однако в области значений есть и промежуток x+2<0, и в случае с ним подобное преобразование будет некорректным. Как же нам быть тогда?
Применим знаки модуля. Вспомним определение данного понятия и представим x+2 при x+2<0 как −|x+2|. В таком случае мы можем выполнить переход от lg(x+2)4−lg(x+2)2 к lg(−|x+2|)4−lg(−|x+2|)2, и далее к lg|x+2|4−lg|x+2|2 .То, что у нас получилось в итоге, может быть преобразовано с использованием свойства логарифма степени, ведь |x+2|>0 при любом x.
Модуль нам больше не нужен, значит, избавляемся от него. С учетом того, что мы преобразовывали при |x+2|<0, имеем 2·lg|x+2|=2·lg(−(x+2)). Это и будет ответом на поставленный вопрос.
Ответ: lg(x+2)4-lg(x+2)2=2·lg(x+2), x+2>02·lg(-(x+2)), x+2<0 . Можно записать ответ компактнее, используя знаки модуля: lg(x+2)4-lg(x+2)2=2·lgx+2 .
Возьмем еще один пример, чтобы закрепить навыки работы с модулями.
Пример 23Условие: представьте выражение lnx-1·x-2x-3 как сумму и разность логарифмов линейных двучленов x−1, x−2 и x−3.
Решение
Вычисляем область допустимых значений данного выражения:
x-1·x-2x-2>0,(1, 2)∪3, +∞
Поскольку значения x−1, x−2 и x−3 будут положительны на промежутке от трех до плюс бесконечности, то мы можем использовать формулы свойств логарифма суммы и разности:
lnx-1·x-2x-3==ln(x-1)+ln(x-2)-ln(x-3)
А на интервале от одного до двух значение x−1 будет положительным, а x−2 и x−3 – отрицательными. Значит, отрицательные значения нам нужно заключить в знаки модуля. У нас получится, что:
lnx-1·x-2x-3=lnx-1·-x-2-x-3==ln(x-1)·x-2x-3
После этого можно спокойно применять формулу логарифма произведений и частного, поскольку на интервале от одного до двух значения всех трех выражений x−1, |x−2| и |x−3| будут положительными. В итоге имеем:
lnx-1·x-2x-3=ln(x-1)+lnx-2-lnx-3==lnx-1+ln(-(x-2))-ln(-(x-3))
Теперь объединяем получившиеся результаты.
Ответ: lnx-1·x-2x-3=lnx-1+ln(-(x-2))-ln(-(x-3))
С помощью таких рассуждений и свойств логарифмов отношения, произведения и степени можно вывести несколько результатов, полезных на практике и удобных в использовании:
Определение 4- сумма логарифмов loga|X|+loga|Y|, a>0, a≠1 может быть использована вместо логарифма произведения loga(X·Y).
- Разность логарифмов loga|X|−loga|Y|, где a>0, a≠1, X и Y являются произвольными выражениями, может быть использована вместо логарифма частного.
- Выражение p·loga|B|, где a>0, a≠1, p является четным числом, а B – произвольным выражением, может быть использована вместо логарифма B в четной степени p.
Условие: выполните упрощение выражения 13·log8((x+4)·(x-2))-log8x+413x-2 .
Решение
На первый взгляд, мы должны взять формулы логарифмов разности, суммы и степени. Давайте посмотрим, насколько правомерно их использование в данном случае. Для начала вычислим область допустимых значений:
(x+4)·(x-2)>0,(x+4)13x-2>0-∞, -4∪2, +∞
У нас получилось, что значения выражений x+4, x−2 и (x+4)13 в данной области могут быть как положительными, так и отрицательными. Значит, нам нужно использовать модули.
13·log8((x+4)·(x-2))-log8(x+4)13x-2==13·log8x+4+13·log8x-2—log8x+413-log8x-2==13·log8x+4+13·log8x-2—log8(x+14)13+log8x-2==13·log8x+4-log8(x+4)13+14·log8x-2
Зная свойства модуля, перепишем x+413 в виде x+413 . Значит, что:
13·log8x+4-log8(x+4)13+14·log8x-2==13·log8x+4-log8x+413+14·log8x-2
Теперь мы можем свободно применить формулу логарифма степени и выполнить приведение подобных слагаемых:
13·log8x+4-log8x+413+14·log8x-2==13·log8x+4-13·log8x+4+14·log8x-2==14·log8x-2
Возможны и другие преобразования, которые дают тот же результат:
13·log8((x+4)·(x-2))-log8x+413x-2==log8((x+4)·(x-2))13-log8x+413x-2==log8((x+4)13·(x-2))13-log8x+413x-2==log8(x+4)13·(x-2)13x+413x-2=log8(x-2)14
Поскольку на области допустимых значений x−2 может быть и положительным, и отрицательным, необходимо заключить это выражение под знак модуля во время вынесения четного показателя степени. У нас получится, что log8(x-2)14=14·log8x-2
А что было бы, если бы мы не стали использовать модуль, а сразу начали применять свойства логарифмов? У нас получился бы результат 14·log8(x−2), который был бы верен при x∈ (2, +∞), однако ошибочен на всей остальной области допустимых значений.
Ответ: 13·log8((x+4)·(x-2))-log8x+413x-2=14·log8x-2 .
Преобразование выражений с использованием свойств логарифмов: примеры, решения
Если у нас есть выражение, содержащее логарифмы, то мы можем преобразовать его с учетом свойств этих логарифмов. В этом материале мы рассмотрим основные правила, по которым осуществляется данное преобразование.
В первом пункте приведем основные свойства логарифмов, представив их в виде списка. Далее рассмотрим характерные примеры преобразований с использованием этих свойств. Отдельно остановимся на числовых выражениях и на выражениях с переменными, а также посмотрим, как преобразовывать примеры с использованием модуля.
Свойства логарифмов
Чтобы преобразовывать выражения с логарифмами, обычно используют выражение, называемое основным логарифмическим тождеством: alogab=b, a>0, a≠1, b>0. Также нужно помнить следующие свойства:
Определение 1- loga1=0 при любом a>0, a≠1.
- logaa=1, если a>0, a≠1.
- logaa=1logaa=1 при любом a>0, a≠1.
- logaa=1, если a>0, a≠1.
- logaap=p, при этом a>0, a≠1 и p может быть любым действительным числом.
- loga(x·y)=logax+logay, a>0, a≠1, x>0, y>0. В обобщенном виде это свойство можно представить как loga(x1·x2·…·xn)=logax1+logax2+…+logaxn, a>0, a≠1, x1>0, x2>0, …, xn>0
- ) logaxy=logax-logay.
- logaxy=logax-logay , при этом a>0, a≠1, x>0, y>0.
- logaxy=logax-logay , a>0, a≠1, x>0, y>0.
- logabp=p·logab, при этом a>0, a≠1, b>0, а p может быть любым действительным числом.
- это свойство является следствием предыдущего: logabn=1n·logab , a>0, a≠1, n может быть любым натуральным числом больше 1, b>0.
- logab=logcblogca , при этом a>0, a≠1, b>0, c>0, c≠1.
- свойство, также являющееся следствием: logab=1logba , где a>0, a≠1, b>0, b≠1.
- logaqbp=pq·logab , a>0, a≠1, b>0, p и q могут быть любыми действительными числами, q≠0
- logaqbp=pq , a>0, a≠1, p и q – любые действительные числа, q≠0.
- logaq ap=pq, blogac=clogab , при этом a>0, a≠1, b>0, c>0.
Преобразовывая выражения, мы можем использовать данные равенства как справа налево, так и наоборот. Учить их все наизусть нет необходимости, достаточно знать основные свойства логарифмов и несколько других свойств, например, что bn=b1n , если b≥0. Из них можно вывести остальные свойства. Само решение, правда, при этом будет несколько длиннее. Например, если мы не знаем следствия logaqbp=pq·logab и используем только основные свойства логарифмов, нам нужно будет выполнить несколько последовательных преобразований:
logaq bp=logabploga aq=p·logabq=pq·logab
То же относится и к последнему свойству из списка, выраженному формулой blogac=Clogac=clogab : оно тоже может быть выведено из основных свойств. Нужно учитывать, что если у нас есть степень положительного числа с логарифмом в показателе, то мы всегда можем поменять число под логарифмом и основание степени местами. В принципе, на практике такие задачи встречаются не слишком часто, но мы их все же разберем.
Как преобразовать числовое выражение с логарифмом
После того, как мы вспомнили основные свойства логарифмов, покажем, как использовать их при решении задач. Начнем с того, как преобразовывать числовые выражения, потому что такие вычисления считаются более простыми. Возьмем сперва примитивные примеры, с помощью которых легко проиллюстрировать выбор нужного свойства логарифма, а потом будем наращивать сложность задач. В конце разберем задания, в которых нужно использовать сразу несколько свойств.
Как выбрать свойство логарифма для преобразования
Список свойств, приведенный в первом пункте, довольно большой, и очевидно, что нужно хорошо в нем ориентироваться, чтобы получить нужный результат. Обычно выбор делается по итогам сравнения исходного логарифма/выражения с левыми и правыми частями формул, выражающих свойства. В том случае, когда одна из частей формулы похожа на исходный логарифм или выражение, мы берем именно это свойство и выполняем преобразование с его помощью. Покажем на примерах, как именно это делается.
Для начала преобразуем выражение, используя определение логарифма, выраженное формулой alogab=b, a>0, a≠1, b>0.
Пример 1Условие: преобразуйте и вычислите значение следующих выражений: 1) 5log54 ; 2) 10lg(1+2·π), 3) 2+3log2+3 ln15 ; 4) 2log2(−7); 5) (-5)log-5 e3
Решение
В первом примере прослеживается формула alogab. У нас есть a=5, b=4, что соответствует необходимому условию a>0, a≠1, b>0. Используем нужное равенство alogab=b и получим 5log54=4.
Во втором случае a будет равно 10, b – 1+2·π. Необходимое условие выполнено, значит, мы можем записать это в виде равенства: 10lg(1+2·π) =1+2·π.
В третьем выражении у нас есть степень вида alogab, причем a=2+3 и b=ln15. Запишем: 2+3log2+3 ln15=ln15 . Хотя равенство также соответствует формуле alogab, где a равно 2, а b=-7, мы не можем воспользоваться ею для преобразования. Из-за наличия отрицательного числа под знаком логарифма выражение лишается смысла. Кроме того, -7 не соответствует условию b>0, что еще раз подтверждает, что данную формулу мы взять не можем. Следовательно, вычислить значение исходного выражения нельзя, и запись 2log2(−7) =−7 будет ошибочна.
То же самое относится и к четвертому примеру. Мы не можем записать, что -5log-5·e3=e3 , поскольку такое выражение смысла не имеет.
Ответ:1) 5log54=4; 2) 10lg(1+2·π)=1+2·π; 3) 2+3log2+3ln 15=ln 15 ; 4 и 5 — не имеют смысла.
Довольно часто в задачах встречается такой вид преобразования, когда некоторое положительно число представляют в виде степени другого числа, также положительного и не равного 1, имеющего в показателе логарифм. Основной такого преобразования также является основное определение логарифма alogab=b, a>0, a≠1, b>0, но в перевернутом виде, т.е. прочитанное справа налево, например, 3=eln3 или 5=5log55.
Далее возьмем примеры с другими свойствами логарифмов.
Пример 2Условие: вычислите, если возможно: 1) log−21, 2) log11,3) log01, 4) log71, 5) ln1, 6) lg 1,7) log3,751, 8) log5·π71.
Решение
В первых трех примерах мы видим не имеющие смысла выражения log−21, log11, log01. Основанием логарифма не может быть число меньше 1, в т.ч. 0 и отрицательные значения, т.к. для них логарифм не определен. Значит, значение этих выражений вычислить нельзя.
В других случаях логарифмы имеют подходящие основания: 7, e, 10, 3,75 и 5·π7, а под знаками логарифма везде 1. Зная соответствующее свойство логарифма (loga1=0 при любом a>0, a≠1., мы можем сделать вывод, что значения этих выражений равны 0.
Ответ: 1, 2, 3 смысла не имеют; 4) log71=0, 5) ln1=0, 6) lg1=0, 7) log3,751=0, 8) log5·e71=0.
Пример 3Условие: вычислите значения: 1) log1313 , 2) ln e, 3) lg 10,4) log5·π3−2(5·π3−2), 5) log−3(−3), 6) log11.
Решение
Нам потребуется свойство логарифма, выраженное формулой logaa=1 при a>0, a≠1. Исходные логарифмы схожи между собой в том, что их основания и числа под знаком логарифма являются одинаковыми. Казалось бы, можно сразу сделать вывод, что значения всех выражений будут равны единице, однако посмотрим внимательнее. В заданиях 1, 2, 3, 4 действительно ответом будет 1, а вот в 5 и 6 исходные выражения смысла не имеют.
Ответ: 1) log13=13=1, 2) ln e=1, 3) lg10=1, 4) log5·π3−2(5·π3−2)=1; 5,6 не имеют смысла.
Пример 4Условие: вычислите: 1) log3311, 2) log1+22(1+22)723 , 3) logπ5(π5)-2 , 4) log−10(−10)6.
Решение
Видим, что под логарифмами находятся некоторые степени основания, значит, нам нужно использовать соответствующее свойство logaap=p, где a>0, a≠1 и p будет любым действительным числом. С учетом этого можно записать следующее:
- log3311=11
- log1+22(1+2·2)723=723
- logπ5(π5)-2=-2
- для этого примера мы не можем написать такое же равенство, как и в предыдущем примере, поскольку log−10(−10)6=6 не имеет смысла.
Ответ: 1) log3311=11, 2) log1+22(1+2·2)723=723 , 3) logπ5(π5)-2=-2 , 4) не имеет смысла.
Пример 5Условие: даны выражения log2,64·127, ln2+1π и lg((−5)·(−12)). Нужно представить их как суммы или разности логарифмов по тому же основанию.
Решение
Смотрим, что находится под знаком логарифма. Там произведение, значит, берем свойство логарифма произведения: loga(x·y) = logax+logay, a>0, a≠1, x>0, y>0. В исходных примерах основания и числа в произведениях положительны, т.е. условие данного свойства соблюдено. Применим его для первого выражения:
log2,64·127=log2,6 4+log2,6127
Чтобы вычислить значение второго выражения, нам нужно свойство логарифма частного: logaxy=logax-logay, a>0, a≠1, x>0, y>0. Здесь в основании стоит положительное число e, также у нас есть положительный числитель 2+1 и знаменатель π, т.е. условия свойства соблюдены. Применяем свойство и записываем, что ln2+1π=ln2+1-ln π .
Разберем третий пример. Начнем с того, что выражение lg((−5)·(−12)) будет иметь смысл, однако формула логарифма произведения для него не подойдет, поскольку оба числа -5 и -12 отрицательны. Значит, преобразование lg((−5) ·(−12))=lg(−5)+lg(−12) не подходит. Какое же свойство тогда использовать?
Проведем предварительное преобразование, чтобы избавиться от отрицательных чисел. Далее мы подробно поговорим, когда нужно выполнять такое действие, а пока ограничимся записью самого решения, которое и так понятно: lg((−5) ·(−12))=lg(5·12)=lg5+lg12.
Ответ: 1) log2,64·127=log2,64+log2,6127 , 2) ln2+1π=ln2+1-ln π , 3) lg((−5)·(−12))=lg5+lg12.
Пример 6Условие: упростите выражения log30,25+log316+log30,5 и ln23-ln13 .
Решение
Здесь мы тоже можем использовать свойства логарифма частного и произведения по аналогии с предыдущим примером, только нам потребуется их обратная запись. Преобразуем сумму логарифмов в логарифм произведения, а разность логарифмов в логарифм частного. В итоге у нас получается в первом примере log30,25+log316+log30,5=log3(0,25·16·0,5)=log32, а во втором ln23-ln13=ln23:13=ln 2.
Ответ: 1) log30,25+log316+log30,5=log3(0,25·16·0,5)=log32, 2) ln23-ln13=ln 2 .
Пример 7Условие: есть выражения log0,7511, log3-1(3-2+5·673)5+1 и log3(−5)6. Нужно избавиться от степени в выражении под знаком логарифма.
Решение
Очевидно, что у нас здесь есть выражения вида logabp. Берем свойство, которое выражается формулой вида
logabp=p·logab, где a>0, a≠1, b>0, p — любое действительное число. Поскольку условия a>0, a≠1, b>0 выполнены, то мы можем преобразовать logabpв произведение p·logab.
- в случае с первым выражением a равно 7, b – пяти и p– 11. Тогда log0,7511=11·log0,75.
- тут a=3-1, b=3-2+5·673, p=5+1 . Нужные условия выполнены, значит, мы можем записать, что:
log3-1(3-2+5·673)5+1==5+1·log3-1(3-2+5·673) - у нас есть выражение той же структуры: logabp, a=3, b=−5, p=6, однако одно из условий не выполняется, а именно b у нас меньше 0. Значит, эту формулу мы применить не можем, и нам будет нужно предварительно преобразовать выражение под знаком логарифма. Решение будет таким: log3(−5)6=log356=6·log35.
Ответ: 1) log0,7511=11·log0,75, 2) log3-1(3-2+5·673)5+1==5+1·log3-1(3-2+5·673) 3) log3(−5)6=6·log35.
Применение формулы в обратном порядке в виде p·logab=logabp требуется довольно часто. При таком преобразовании важно соблюсти все те же условия для числовых значений переменных. Например, 3·ln 5=ln 53 и lg 2·log23=log23lg2.
Пример 8Условие: согласно таблице логарифмов, lg2≈0,3010 и lg5≈0,6990. Вычислите, сколько будет log25. Здесь же: запишите ln 11ln 3 в виде логарифма, основание которого равно 3.
Решение
Воспользуемся формулой перехода к новому основанию и представим исходный логарифм как отношение десятичных логарифмов с известными нам значениями.
log25=lg 5lg 2
Вычисляем и находим ответ: lg 5lg 2≈0,69900,3010≈2,3223 .
Во втором примере также будет достаточно формулы перехода к новому основанию, только в обратном порядке, т.е. logcblogca=logab .
Считаем: ln 11ln 3=log311
Ответ: 1) log25≈2,3223, 2) ln 11ln 3=log311 .
Мы разобрали множество примеров, где для осуществления преобразования достаточно применить одну формулу свойства логарифма или его определение. Теперь мы можем перейти к более сложным задачам, в которых нужно последовательно применять несколько свойств, а также делать дополнительные преобразования. Однако перед этим запишем еще один важный пример использования следствий из основных свойств логарифмов.
Пример 9Условие: 1) дан логарифм ln1+π7 . Необходимо избавиться от корня под знаком логарифма; 2) выполните преобразование дроби 1log25 в логарифм с основанием 4; 3) преобразуйте логарифм loge2345 так, чтобы избавиться от степени в основании; 4) вычислите, сколько будет log2-13216 ; 5) осуществите замену 2,3log73 на степень с основанием 3.
Решение
- Вспоминаем следствие из свойства логарифма степени, которое выражается формулой logabn=1n·logab .В первом случае можем сразу же подсчитать: ln1+π7=17·ln(1+π) .
- во втором случае нам понадобится формула logab=1logba , примененная в обратном порядке. Получим 1log25=log52.
- здесь нам потребуется свойство logaqbp=pq·logab . Применяем его и получаем loge2345=452·ln 3=25·ln 3.
- в этом случае нам нужно будет следствие, выраженное формулой logaqap=pq: log(2)-13216=16-13=-12
- используем формулу свойства blogac=clogab и вычисляем ответ:
2,3log7·3=3log72,3
Ответ: 1) ln1+π7=17·ln(1+π) ; 2) 1log25=log52 ; 3) loge2345=25·ln 3; 4) log(2)-13216=-12 . 5) 2,3log7·3=3log72,3 .
Задачи с применением нескольких свойств логарифмов
В действительности чаще встречаются более сложные задания, чем те, что мы разобрали в предыдущем параграфе. В них приходится выполнять преобразования в несколько шагов, применяя последовательно одно свойство за другим. Кроме того, они зачастую включают в себя необходимость раскрывать скобки, приводить подобные слагаемые, сокращать обыкновенные дроби и др. Это не так сложно, как кажется, главное – соблюдать правильную последовательность действий.
Пример 10Условие: вычислите, сколько будет (log315−log35) ·7log75.
Решение
Мы можем заменить выражение в скобках логарифмом log3(15:5), используя свойство частного. Вычисляем его значение и получаем log3(15:5) =log33=1.
Согласно основному определению логарифма, значением 7log75 будет 5. Подставим в исходное выражение получившиеся результаты и найдем, что (log315−log35) ·7log75=1·5=5.
Вот все решение без комментариев:
(log315−log35)·7log75=log3 (15:5)·5==log33·5=1·5=5
Ответ: (log315−log35) ·7log75=5.
Пример 11Условие: вычислите, чему равен log3log223−1.
Решение
Начнем с преобразования логарифма, который, в свою очередь, сам находится под знаком логарифма. Используем для этого формулу логарифма степени log223=3. Получим, что log3log223=log33, а дальше log33=1. Следовательно, log3log223−1=1−1=0.
Ответ: log3log223−1=0.
Пример 12Условие: выполните упрощение выражения 3ln 5ln 3log52 .
Решение
Берем формулу перехода к новому основанию. С ее помощью можно представить отношение логарифмов ln 5ln 3 как log35. У нас получилось 3log35log52 . Теперь применяем формулу основного определения логарифма 3log35=5 и получаем, что 3log35log52 . Нам осталось лишь вычислить значение этого выражения. Оно будет равно 2.
Ответ: 3ln 5ln 3log52=2 .
Перейдем к дальнейшему пункту обсуждения логарифмических преобразований. У нас есть выражения log334, 52+log53, lg 0,01. Они не напоминают нам ни об одной известной нам формуле свойства, но их все же можно изменить этим способом, если выполнить предварительные преобразования: 52+log53=52·5log53=25·3=75, log334=log31234=412=8 и lg 0,01=lg 10−2=−2. Разберем подробнее, как именно это делается.
Предварительное преобразование перед применением основных свойств логарифмов
На практике мы часто можем встретить логарифмы, которые внешне не похожи ни на одну часть формулы свойства. Однако при этом преобразование требует применения именно этих формул. Это возможно, если перед этим привести их к соответствующему виду. Это процесс называется тождественным преобразованием.
В роли таких действий могут выступать почти любые преобразования выражений, в том числе раскрытие скобок, вынесение за скобки множителей, применение формул тригонометрии и т.д. Это очевидно, поскольку выражения под знаком логарифма могут содержать практически все, что угодно: модули, скобки, дроби, степени и др. Поэтому нужно уметь выполнять разные виды преобразований, чтобы успешно решать такие задачи.
Данная статья не имеет целью осветить все возможные случаи преобразований, поскольку их очень много. Мы выбрали только четыре, которые наиболее распространены.
Определение 2- Довольно часто приходится получать степени под знаком и в основании, чтобы потом использовать формулу логарифма степени и последствия данного свойства. Мы выполняем такое преобразование, если в видим в условии логарифмы следующего вида: ln2532332 , log381.
- Также нужно уметь выполнять преобразование, связанное со свойствами степени. Оно нужно нам для последующего использования формулы, которая отвечает определению логарифма. Мы применяем его, когда у нас есть выражения, подобные 2log223, 32·log35, 71+log74, 25(log35)-3 и др.
- Обязательно нужно преобразовывать выражения с десятичными дробями под знаком логарифма или в его основании. Иногда после этого мы обнаруживаем, что основание под знаком степени и основание логарифма будут равны, как, например, здесь: log15(0,2)7
- Также нужно знать правила преобразования выражений, где под знаком логарифма стоит отрицательное число. Мы расскажем, что нужно делать, если в условии стоят выражения вроде lg(−3)−4, log6((−9)·(−4)) и др.
Разберем подробно каждый вид преобразования.
Как выделить степень в основании логарифма и под его знаком
Сразу возьмем конкретный пример. У нас есть выражение log1981 , структура которого не подсказывает нам ни одного возможного свойства логарифмов, которое можно было бы использовать. Значит, нам надо начать с преобразования самого выражения или сразу с вычисления его значения. Как же это сделать? Обратите внимание на числа 81 и 19. Их легко представить в виде степени с основанием 3 : 81=34 и 19=3−2. Значит, все выражение можно переписать как log3-234 , а здесь уже видна возможность использования свойства logaqbp=pq·logab . Таким образом, log1981=log3-2=4-2=-2 .
Этот пример иллюстрирует нам следующую мысль: если есть возможность, нужно выделить степень в основании и под знаком логарифма, чтобы впоследствии применить свойство логарифма степени. Ниже мы приведем некоторые советы, как именно выделять степени в таких примерах.
В некоторых случаях число можно преобразовать в целую степень, как в примере выше. В задачах то и дело встречаются степени чисел 2 и 3, которые легко узнать с первого взгляда: 243=35, 81=34, 8=23, 64=26 и др. Для решения примеров полезно иметь таблицу степеней натуральных чисел в пределах 10, чтобы сразу видеть возможности преобразования выражений. Также легко работать с выражениями, включающими целые степени 10, 100 и др.
Пример 13Условие: вычислите или упростите выражения log6216, log3431243, log0,0000010,001.
Решение
- В первом случае мы сразу видим, что 216 можно представить в виде 63. Значит, log6216=log663=3.
- у нас есть числа 343 и 1243. Обратимся к таблице степеней и увидим, что их можно представить в виде 73 и 3−4. Выполняем дальнейшие преобразования и получаем:
log3431243=log733-4==-43·log73=-113·log73 - Поскольку 0,000001=10−6 и 0,001=10−3, тогда log0,0000010,001=log10−610−3= -3-6=12
Ответ: 1) log6216=3, 2) log3431243=-113·log73 ; 3) log0,0000010,001=12.
Если исходного числа нет в таблице степеней, то мы можем разложить его на простые множители.
Пример 14Условие: упростите выражение log3648·log23.
Решение
Выполняем разложение 648 на простые множители.
64832416281931222333
Значит, это число можно представить в виде 648=23·34. Следовательно, log3648·log23=log3(23·34)·log23
Теперь мы можем преобразовать исходный логарифм произведения в сумму, а потом воспользоваться формулой логарифма степени.
log3(23·34)·log23=(log323+log334)·log23= =(3·log32+4)·log23.
Упрощаем выражение через раскрытие скобок:
(3·log32+4)·log23=3·log32·log23+4·log23.
В полученном выражении log32·log23 является произведением взаимно обратных чисел, которое равно 1. Следовательно, формулируем ответ как 3·log32·log23+4·log23=3·1+4·log23=3+4·log23.
Ответ: log3648·log23=3+4·log23.
Зачастую под логарифмом записываются выражения, представляющие собой отношения или произведения корней: 323·3-2, 2·2273 и т.д. Они также приводятся к виду степени: сначала мы выполняем переход от корня к степени, используя соответствующие свойства. С помощью таких преобразований мы можем получить выражение, удобное для применения формулы логарифма степени.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 15Условие: найдите значение выражений log52·5-0.5·5-153454 и log372919.
Решение
В первом случае у нас есть произведение степеней, имеющих одинаковые основания. Используя нужное свойство, получим: 52·5−0,5·5−1=52−0,5−1=50,5. Для преобразования дроби сначала выполним переход от корня к степени, затем используем свойство отношения степеней с одинаковыми основаниями:
53454=5344=534-4=5-314
Полученное выражение подставим в исходный логарифм, применив формулу logaqaq=pq, и получим ответ:
log52·5-0.5·5-153454=log50.55-314=-3140.5==-13412=-132=-612
Во втором случае представим число 729 как 36 , а 19 как 3−2. Исходный логарифм приобретет вид log3363-2. Используя свойство корня из степени, преобразуем основание логарифма и получим:
336=333=31-3=3-2
Заканчиваем преобразование: log3363-2=log3-23-2=1 .
Ответ: 1) log52·5-0.5·5-153454=-612 ; 2) log372919=1
Преобразования, которые нужно сделать, чтобы получить под знаком логарифма нужную степень, могут значительно отличаться от примера к примеру.
Пример 16Условие: вычислите значения log13-1132·3+1-5 и log2·cos1(1+cos2)3 .
Решение
Первое, что нам нужно сделать, – это избавиться от иррациональности в знаменателе первой дроби, лежащей в основании логарифма:
13-1=3+13-1·3+1=3+132-12=3+12
Мы получили результат, схожий с дробью под знаком логарифма. Применим к нему свойства степеней и получим:
132·3+1-5=3+1532=3+1525=3+125
В результате преобразований у нас получился логарифм степени основания log3+123+135 . Значение данного выражения будет равно 5.
Чтобы преобразовать второе выражение, надо воспользоваться тригонометрическими формулами, а конкретно формулой понижения степени cos2a=1+cos2a2 :
log2·cos1(1+cos2)3=log2·cos1(2·cos21)3
Преобразуем второй логарифм, записав его как степень 2·cos2112 или же 2·cos123=2·cos16. Оба выражения будут иметь одно и то же значение, равное шести.
Ответ: 1) log13-1132·3+1-5=5 ; 2) log2·cos1(1+cos2)3=6 .
Как применять свойства степени при преобразовании выражений с логарифмами
Ранее мы уже использовали свойства степеней, чтобы преобразовать выражения под знаком логарифма и его основание. Посмотрим, в каких еще характерных случаях потребуется такая подготовка.
Для начала возьмем задачи на применение свойства степеней с одинаковыми основаниями ap·aq=ap+q. Чаще всего его применяют в обратном порядке, т.е. справа налево.
Пример 17Условие: вычислите значения 3−2+log37 и 0,72−log0,70,1.
Решение
В первом примере нужно представить исходную степень как произведение двух степеней, т.е. 3−2+log37=3−2·3log37. Теперь найдем, чему равен первый множитель. Возведем его в степень, потом вычислим значение второго множителя, используя определение логарифма, и подсчитаем их произведение:
3−2·3log37= (19) ·7=79
Во втором примере нам надо подготовить выражение к преобразованию, выполнив переход к произведению степеней: 0,72−log0,70,1=0,72·0,7−log0,70,1. После этого нам нужно представить показатель −log0,70,1 в виде llog0,7(0,1)−1=log0,710. Теперь все, что нам осталось, – это закончить вычисления:
0,72·0,7−log0,70,1=0,49·0,7log0,710=0,49·10=4,9
Ответ: 1) 3−2+log37=79; 2) 0,72−log0,70,1=4,9.
Также для предварительных преобразований нужно обязательно знать свойство степени в степени, которое выражается формулой (ap)q=ap·q, например, если у нас есть выражение (eln2)3, то мы можем заключить, что значение части в скобках будет равно 2. Значит, (eln2)3=23=8. А если в условии указано (e3)ln2 или (e3)ln2, то мы сначала приводим их к виду (eln2)3:
e3·ln2=eln2·3=(eln2)3 и (e3)ln2=e3·ln2=eln2·3=(eln2)3.
Посмотрим пример решения такой задачи.
Пример 18Условие: выполните упрощение выражений 2log223−3log23 и 5(log85) −1.
Решение
Отметим, что выражения 2log223и 2log223 не являются равными друг другу. Мы можем представить 2log223 как 2log23·log23. Используя свойство степени, представим его как (2log23)log23, что будет тождественно равным 3log23. В итоге мы имеем, что 2log223−3log23=3log23−3log23=0.
Вот запись всего решения:
2log223−3log23=2log23·log23−3log23==(2log23)log23−3log23=3log23−3log23=0
Перейдем ко второму примеру. Запись 25(log85)-1 не будет равна (25log85)−1. Мы можем представить степень (log85)−1 как дробь 1log85 . Ее нужно преобразовать, используя следствие свойства перехода к новому основанию по формуле logab=1logba, чтобы получить log58.
Так, 25(log85)-1=25log58. Поскольку 25 – это 52, имеем 5log58= (52)log58. То, что у нас получилось, представляем в виде (5log58). Нам осталось только вычислить значение: (5log58)2=82=64.
Ответ: 1) 2log223−3log23=0, 2) 25(log85)−1=64.
Также встречаются примеры, где предварительная подготовка к использованию свойств логарифмов заключается в применении и свойства умножения степеней с одинаковыми основаниями, и свойства степени в степени. Например,
4−0,5+2·log43=4−0,5·42·log43==12·(4log43)2=12·32=12·9=4,5
Преобразование логарифмов с десятичными дробями
Применить свойства логарифмов можно и тогда, когда под знаком логарифма у нас стоит десятичная дробь. Что можно сделать с выражением log0,4253? Отметим, что 25 и 0,4 равны между собой 0,4=410=25, то есть это разные формы записи для одного и то же числа.
В целом можно сказать, что в случае наличия десятичной дроби под знаком логарифма необходимо выполнить переход к обыкновенной дроби. Это поможет увидеть возможности использования свойств логарифмов.
Разберем подобную задачу.
Пример 19Условие: вычислите значение выражения log0,46,25.
Решение
Начнем с перехода от десятичных дробей к обыкновенным.
log0,46,25=log410625100=log25254
Теперь видно, что мы можем преобразовать 254 в виде (25)−2 и воспользоваться формулой логарифма степени. Вычисляем значение:
log25254=log2525-2=-2
Ответ: -2.
Преобразование выражений с отрицательными числами под знаком логарифма
Еще один случай, который мы хотели бы рассмотреть – это преобразование выражений, в которых под знаком логарифма стоит отрицательное число, например, log3-93-27 или log3((−2)·(−5)).
Мы не можем сразу воспользоваться формулами свойств логарифмов в том виде, в каком приводили их в последнем пункте, например, сразу перейти от log3((−2)·(−5)) к log3(−2)+log3(−5), применить свойство логарифма степени к log2(−2)6 или логарифма частного к log3-93-27 , поскольку отрицательные числа не могут находиться под знаком логарифма и в его основании.
Что это значит на практике? Вернемся к нашему примеру log3((−2)·(−5)). Структура выражения соответствует формуле loga(x·y), где a равно 3, x-3 и y-5. Поскольку условия a>0, a≠1, x>0, y>0 не выполнены, формулу loga(x·y)=logax+logay мы применить не можем, и равенство log3((−2)·(−5)) =log3(−2) +log3(−5) записать нельзя. Преобразования вида log3-93-27=log3-93-log3(-27) также будут неправильными.
Это не значит, что выражения с отрицательными числами не могут быть преобразованы с использованием свойств логарифмов. Это допускается при условии предварительных преобразований, позволяющих избавиться от минуса. Они базируются на хорошо известных нам правилах работы с числами, меньшими 0.
Вернемся опять к нашему примеру. Согласно правилам умножения, (−2)·(−5) =2·5, значит, log3((−2)·(−5))=log3(2·5). К выражению в таком виде мы уже можем применить формулу log3(2·5) =log32+log35. А вот для примера log2(−2)6 нужно будет выполнить следующие действия:
(−2)6= ((−1)·2)6=(−1)6·26=1·26=26
Значит, log2(−2)6=log226=6.
Пример 20Условие: найдите значение выражения log2-163-2-23.
Решение
Сначала заключим, что данное выражение имеет смысл. Воспользоваться сразу свойством логарифма частного у нас нет возможности из-за отрицательных чисел под знаком логарифма, поэтому выполним преобразования.
Определив корень нечетной степени из отрицательного числа, выполним переход от -163-2-23 к -163-2-23 . Согласно правилам деления, получим -163-2-23=1632-23 . Теперь нам нужно получившуюся дробь представить в виде степени числа 2 и найти значение получившегося логарифма.
1632-23=2432-23=2432-23=243—23=22log2-163-2-23=log222=2
Ответ: log2-163-2-23=2 .
Некоторые свойства, например, логарифма частного, степени с четным показателем и произведения, можно распространить и на отрицательные числа с помощью модулей. Как это делается, мы покажем далее. Так, поскольку свойство логарифма произведения выглядит как loga(x·y)=loga|x|+loga|y|, где a>0, a≠1, x≠0, y≠0, то после преобразования мы получим log3((−2)·(−5)) =log3|−2|+log3|−5|=log32+log35.
Как преобразовать логарифмическое выражение с переменными
В предыдущих параграфах мы разобрали, как работать с числовыми выражениями, содержащими логарифмы. Однако если требуется решить логарифмическое неравенство или уравнение, нам понадобится умение работать с теми случаями, когда под знаком логарифма содержится выражение с переменными. В целом при этом мы руководствуемся теми же принципами, что и с числовыми выражениями, но тут следует отдельно пояснить некоторые нюансы, незнание которых ведет к ошибкам.
Особенности преобразований выражений с переменными
Основная трудность состоит в том, что при работе с такими выражениями числа, расположенные под знаком логарифма и в его основании, должны соответствовать особым условиям, а в случае определенных переменных из области допустимых значений эти условия могут оказаться невыполненными. Приведем один наглядный пример.
У нас есть логарифмическое выражение log2(x+1)4. При преобразовании нужно обязательно учитывать область допустимых значений, поэтому первым шагом должно стать ее нахождение. Здесь она определена неравенством (x+1)4>0, значение которого является числовым множеством (−∞, −1) ∪ (−1, +∞). Решить его можно с помощью метода интервалов.
Исходное выражение соответствует формуле logABp, где A равно 2, B – x+1, а p – четырем.
Мы видим, что заданное выражение соответствует виду logABp, где A=2, B=x+1 и p=4. Такие выражения преобразовываются по свойству логарифма степени logabp=p·logab. Можно ли поступить так с этим выражением? Вычислим значение исходного логарифма и выражения, которое получилось после преобразования, например, при x=−2. В итоге: log2(−2+1)4=log21=0, а 4·log2(−2+1) =4·log2(−1) –выражение, не имеющее смысла. Значит, мы ошиблись.
Причина ошибки в том, что мы взяли формулу logabp=p·logab, но это допустимо лишь при условии a>0, a≠1, b>0, p — любое действительное число. Иными словами, проделанное нами преобразование возможно, если x+1>0, что аналогично x>−1 (для A и p – условия выполнены). Однако в нашем случае ОДЗ переменной x для исходного выражения состоит не только из промежутка x>−1, но и из промежутка x <−1. Но для x <−1 мы не имели права осуществлять преобразование по выбранной формуле.
Почему надо учитывать область допустимых значений
Продолжая работу с выражением log2(x+1)4, проанализируем, как изменится область значений, когда мы выполним переход к виду 4·log2(x+1). Ранее мы уже определили эту область как множество (−∞, −1) ∪ (−1, +∞). Теперь вычислим, какова будет область допустимых значений для 4·log2(x+1). Она определяется условием x+1>0, а ему, в свою очередь, будет отвечать множество (−1, +∞). Мы видим, что область допустимых значений сузилась, а это может привести к различным ошибочным последствиям, поэтому таких преобразований следует избегать.
Важно следить, как меняется область значений во время каждого преобразования. Если на каком-либо этапе происходит ее сужение, это повод тщательно проверить все вычисления и определить, правомерно ли использования данного преобразования.
Чаще всего при решении задач приходится иметь дело с выражениями, область допустимых значений которых не ограничивает применение свойств логарифмов в прямом и обратном порядке, но не следует относиться так ко всем примерам. Нужно всегда проверять, что происходит с областью допустимых значений, и своевременно отслеживать возможные ошибки.
Запишем, в ходе каких преобразований чаще всего происходит непреднамеренное сужение области значений:
Определение 3- когда мы переходим от логарифма произведения к сумме, например, ln(x·(x+3)) =lnx+ln(x+3) сузит нужную область.
- Когда мы переходим от логарифма частного к разности. Пример такого преобразования – замена log2xsin x на log2x−log2sinx .
- Когда мы выносим четный показатель степени, используя формулу логарифма степени logabp=p·logab и формулу logabp=pq·logab . Примеры таких преобразований – logx3(x-8)2=23·logx(x-8) , ln(x+3)−4=−4·ln(x+3).
Иногда в результате преобразования область допустимых значений может не сужаться, а расширяться, например, при переходе от 4·log2(x+1) к log2(x+1)4. В этом случае область расширяется от (−1, +∞) до (−∞, −1) ∪ (−1, +∞). Такие преобразования имеют место, если оставаться в рамках ОДЗ для исходного выражения. Так, преобразование 4·log2(x+1) =log2(x+1)4 имеет место на области значений переменной x для исходного выражения 4·log2(x+1), то есть, при x+1>0, что аналогично (−1, +∞).
Теперь, когда мы обговорили тонкости, на которые нужно обращать внимание при преобразовании выражений с переменными с использованием свойств логарифмов, остается разобраться, как правильно эти преобразования проводить.
Правила проведения преобразований
Мы говорили ранее, что чаще всего область допустимых значений позволяет нам применять свойства логарифмов в привычных формулировках.
Пример 21Условие: упростите 3·lg(x+2)7−lg(x+2) −5·lg(x+2)4.
Решение
На первый взгляд данное выражение нужно преобразовать, используя логарифм степени, то есть сначала вынести нужную степень в виде коэффициента и потом привести подобные слагаемые. Давайте разберемся, правомерно ли применение выбранного свойства в этом случае.
Чтобы перейти от lg(x+2)7 к 7·lg(x+2) и от lg(x+2)4к 4·lg(x+2), нам нужно, чтобы x+2>0. Выясним, будет ли соблюдено данное условие. Для этого нам нужно определить область допустимых значений переменной x. Ее можно выразить с помощью системы неравенств (x+2)7>0,x+2>0,(x+2)4>0 , которая будет равносильной условию x+2>0 (если нужно, повторите материал о решении систем неравенств). Следовательно, мы можем взять формулу логарифма степени. Считаем:
3·lg(x+2)7−lg(x+2)−5·lg(x+2)4==3·7·lg(x+2)−lg(x+2)−5·4·lg(x+2)==21·lg(x+2)−lg(x+2)−20·lg(x+2)==(21−1−20)·lg(x+2)=0
Область допустимых значений позволяет нам использовать и другой вариант вычисления, например, такой:
3·lg(x+2)7-lg(x+2)-5·lg(x+2)4==lg((x+2)7)3-lg(x+2)-lg((x+2)4)5==lg(x+2)21-lg(x+2)-lg(x+2)20==lg(x+2)21(x+2)·(x+2)20=lg1=0
Ответ: 3·lg(x+2)7−lg(x+2) −5·lg(x+2)4=0.
А как быть в случае, если в области допустимых значений нужные условия не будут выполняться? Возьмем соответствующий пример и разберем его.
Пример 22Условие: выполнить упрощение выражения lg(x+2)4−lg(x+2)2.
Решение
Здесь свободно использовать свойство логарифма степени мы не можем. Область допустимых значений x можно представить в виде объединения промежутков x>−2 и x<−2. Если x>−2, то применяем нужное свойство и действуем по аналогии с тем, как мы решали задачу выше: lg(x+2)4−lg(x+2)2=4·lg(x+2) −2·lg(x+2) =2·lg(x+2). Однако в области значений есть и промежуток x+2<0, и в случае с ним подобное преобразование будет некорректным. Как же нам быть тогда?
Применим знаки модуля. Вспомним определение данного понятия и представим x+2 при x+2<0 как −|x+2|. В таком случае мы можем выполнить переход от lg(x+2)4−lg(x+2)2 к lg(−|x+2|)4−lg(−|x+2|)2, и далее к lg|x+2|4−lg|x+2|2 .То, что у нас получилось в итоге, может быть преобразовано с использованием свойства логарифма степени, ведь |x+2|>0 при любом x.
Модуль нам больше не нужен, значит, избавляемся от него. С учетом того, что мы преобразовывали при |x+2|<0, имеем 2·lg|x+2|=2·lg(−(x+2)). Это и будет ответом на поставленный вопрос.
Ответ: lg(x+2)4-lg(x+2)2=2·lg(x+2), x+2>02·lg(-(x+2)), x+2<0 . Можно записать ответ компактнее, используя знаки модуля: lg(x+2)4-lg(x+2)2=2·lgx+2 .
Возьмем еще один пример, чтобы закрепить навыки работы с модулями.
Пример 23Условие: представьте выражение lnx-1·x-2x-3 как сумму и разность логарифмов линейных двучленов x−1, x−2 и x−3.
Решение
Вычисляем область допустимых значений данного выражения:
x-1·x-2x-2>0,(1, 2)∪3, +∞
Поскольку значения x−1, x−2 и x−3 будут положительны на промежутке от трех до плюс бесконечности, то мы можем использовать формулы свойств логарифма суммы и разности:
lnx-1·x-2x-3==ln(x-1)+ln(x-2)-ln(x-3)
А на интервале от одного до двух значение x−1 будет положительным, а x−2 и x−3 – отрицательными. Значит, отрицательные значения нам нужно заключить в знаки модуля. У нас получится, что:
lnx-1·x-2x-3=lnx-1·-x-2-x-3==ln(x-1)·x-2x-3
После этого можно спокойно применять формулу логарифма произведений и частного, поскольку на интервале от одного до двух значения всех трех выражений x−1, |x−2| и |x−3| будут положительными. В итоге имеем:
lnx-1·x-2x-3=ln(x-1)+lnx-2-lnx-3==lnx-1+ln(-(x-2))-ln(-(x-3))
Теперь объединяем получившиеся результаты.
Ответ: lnx-1·x-2x-3=lnx-1+ln(-(x-2))-ln(-(x-3))
С помощью таких рассуждений и свойств логарифмов отношения, произведения и степени можно вывести несколько результатов, полезных на практике и удобных в использовании:
Определение 4- сумма логарифмов loga|X|+loga|Y|, a>0, a≠1 может быть использована вместо логарифма произведения loga(X·Y).
- Разность логарифмов loga|X|−loga|Y|, где a>0, a≠1, X и Y являются произвольными выражениями, может быть использована вместо логарифма частного.
- Выражение p·loga|B|, где a>0, a≠1, p является четным числом, а B – произвольным выражением, может быть использована вместо логарифма B в четной степени p.
Условие: выполните упрощение выражения 13·log8((x+4)·(x-2))-log8x+413x-2 .
Решение
На первый взгляд, мы должны взять формулы логарифмов разности, суммы и степени. Давайте посмотрим, насколько правомерно их использование в данном случае. Для начала вычислим область допустимых значений:
(x+4)·(x-2)>0,(x+4)13x-2>0-∞, -4∪2, +∞
У нас получилось, что значения выражений x+4, x−2 и (x+4)13 в данной области могут быть как положительными, так и отрицательными. Значит, нам нужно использовать модули.
13·log8((x+4)·(x-2))-log8(x+4)13x-2==13·log8x+4+13·log8x-2—log8x+413-log8x-2==13·log8x+4+13·log8x-2—log8(x+14)13+log8x-2==13·log8x+4-log8(x+4)13+14·log8x-2
Зная свойства модуля, перепишем x+413 в виде x+413 . Значит, что:
13·log8x+4-log8(x+4)13+14·log8x-2==13·log8x+4-log8x+413+14·log8x-2
Теперь мы можем свободно применить формулу логарифма степени и выполнить приведение подобных слагаемых:
13·log8x+4-log8x+413+14·log8x-2==13·log8x+4-13·log8x+4+14·log8x-2==14·log8x-2
Возможны и другие преобразования, которые дают тот же результат:
13·log8((x+4)·(x-2))-log8x+413x-2==log8((x+4)·(x-2))13-log8x+413x-2==log8((x+4)13·(x-2))13-log8x+413x-2==log8(x+4)13·(x-2)13x+413x-2=log8(x-2)14
Поскольку на области допустимых значений x−2 может быть и положительным, и отрицательным, необходимо заключить это выражение под знак модуля во время вынесения четного показателя степени. У нас получится, что log8(x-2)14=14·log8x-2
А что было бы, если бы мы не стали использовать модуль, а сразу начали применять свойства логарифмов? У нас получился бы результат 14·log8(x−2), который был бы верен при x∈ (2, +∞), однако ошибочен на всей остальной области допустимых значений.
Ответ: 13·log8((x+4)·(x-2))-log8x+413x-2=14·log8x-2 .{\frac{1}{2}}}=\sqrt{4}=2\)), а вот \( \displaystyle {{\log }_{-4}}2\) не существует.
Поэтому и отрицательные основания проще выбросить, чем возиться с ними.
Ну а поскольку основание a у нас бывает только положительное, то в какую бы степень мы его ни возводили, всегда получим число строго положительное.
Значит, аргумент должен быть положительным.
Например, \( \displaystyle {{\log }_{2}}\left( -4 \right)\) не существует, так как \( 2\) ни в какой степени не будет отрицательным числом (и даже нулем, поэтому \( \displaystyle {{\log }_{2}}0\) тоже не существует).
В задачах с логарифмами первым делом нужно записать ОДЗ.
Приведу пример:
Решим уравнение \( \displaystyle {{\log }_{x}}\left( x+2 \right)=2\).
Вспомним определение: логарифм \( \displaystyle {{\log }_{x}}\left( x+2 \right)\) – это степень, в которую надо возвести основание \( x\), чтобы получить аргумент \( \displaystyle \left( x+2 \right)\).
И по условию, эта степень равна \( 2\): \( \displaystyle {{x}^{2}}=x+2\).{2}}-x-2=0\).
Решим его с помощью теоремы Виета: сумма корней равна \( 1\), а произведение \( -2\). Легко подобрать, это числа \( 2\) и \( -1\).
Но если сразу взять и записать оба этих числа в ответе, можно получить 0 баллов за задачу на ЕГЭ.
Почему?
Давайте подумаем, что будет, если подставить эти корни в начальное уравнение?
\( \displaystyle x=2\text{: }{{\log }_{2}}\left( 2+2 \right)={{\log }_{2}}4=2\) – верно.
\( \displaystyle x=-1\text{: }{{\log }_{-1}}\left( -1+2 \right)=2\) – это явно неверно, так как основание не может быть отрицательным, то есть корень \( x=-1\) – «сторонний».
Чтобы избежать таких неприятных подвохов, нужно записать ОДЗ еще до начала решения уравнения:
\( \displaystyle \left\{ \begin{array}{l}x>0\\x\ne 1\\x+2>0\end{array} \right.\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}x>0\\x\ne 1.\end{array} \right.\)
Тогда, получив корни \( x=2\) и \( x=-1\), сразу отбросим корень \( -1\), и напишем правильный ответ.
Пример 1 (попробуй решить самостоятельно)
Найдите корень уравнения \( \displaystyle {{\log }_{x+1}}\left( 2x+5 \right)=2\). Если корней несколько, в ответе укажите меньший из них.
Решение:
\( \displaystyle {{\log }_{x+1}}\left( 2x+5 \right)=2\).
В первую очередь напишем ОДЗ:
\( \displaystyle \left\{ \begin{array}{l}x+1>0\\x+1\ne 1\\2x+5>0\end{array} \right.\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}x>-1\\x\ne 0\\x>-\frac{5}{2}\end{array} \right.\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}x>-1\\x\ne 0.\end{array} \right.\)
Теперь вспоминаем, что такое логарифм: в какую степень нужно возвести основание \( \displaystyle x+1\), чтобы получить аргумент \( \displaystyle 2x+5\)?
Хотите читать учебник без ограничений? Зарегистрируйтесь:
Во вторую. То есть:
\( \displaystyle {{\left( x+1 \right)}^{2}}=2x+5\text{ }\Leftrightarrow \text{ }{{x}^{2}}+2x+1=2x+5\text{ }\Leftrightarrow \text{ }{{x}^{2}}-4=0\text{ }\Leftrightarrow \text{ }\left[ \begin{array}{l}x=2\\x=-2.{2 n}}{n}+\ldots, |x| \lt 1$
Читать дальше: десятичный логарифм.
Таблица и формула для перехода от натуральных логарифмов к десятичным Если Вам известен натуральный логарифм какого-то числа Х (равный ln(X)), то десятичный логарифм этого числа (равный lg(X)) будет равен, согласно основным свойствам логарифмов : lg(X)=lg(e)*ln(X)=M*ln(X), т.е. десятичный логарифм числа, равен натуральному логарифму этого числа умноженному на число М=lg(e). Для быстрых оценок приводим табличку: Таблица для перехода от натуральных логарифмов к десятичным (таблица умножения на «число М» (у англосаксов это «число A») = lg е = 0,4342945…)
|
Действия с логарифмами. Набиваем руку!
В данном уроке мы будем учиться работать с логарифмом на уже весьма и весьма приличном уровне. Поэтому для успешного решения примеров этого урока рекомендую погулять по ссылкам:
Что такое логарифм?
Действия с логарифмами. Постигаем азы!
Почитайте, пока не поздно.) Почитали? Всё понятно! Отлично! Тогда движемся дальше.)
Теперь настал черёд завязывания более крепкой дружбы с логарифмами и, соответственно, решения серьёзных (в том числе сложных и нестандартных) примеров.
Чтобы не скакать из темы в тему, прежде всего я ещё разочек выпишу все основные свойства и формулы логарифмов. Вот они:
Это основной набор формул, необходимых для успешной работы с логарифмами практически на любом уровне сложности. Иногда в школе (и в некоторых продвинутых учебниках) дают больше формул, но в целом приведённого перечня для решения большей части примеров оказывается вполне достаточно. Эти формулы надо помнить! Но, ещё раз повторяю, не просто помнить, а уметь применять! Причём в обоих направлениях — как слева направо, так и справа налево. Вроде бы это всё и так понятно и очевидно, но… дальше всё поймёте.) Как надо помнить формулы, я вам вряд ли смогу подсказать, а вот как уметь применять — подробно расскажу и покажу в этом уроке.
Итак, продолжаем наши игры!
Все формулы. Все степени. Много дробей! Двоюродные и троюродные братья.
Ну что ж, теперь приступаем к работе со всеми формулами (кроме последней формулы перехода к новому основанию). Используем все свойства степеней и активно включаем в работу степени с отрицательными и дробными показателями. Поди сообрази, что, например,
0,04 = 5-2.
Или
Это уже не родные, а двоюродные и троюродные братья по степени получаются…)
Посему, если есть пробелы в степенях, то для начала милости прошу сюда:
Что такое степень. Свойства степеней.
Ну, а для тех, кто со степенями давно на «ты» — продолжаем.)
Пример 1
За что зацепиться? Хорошо, если сразу догадались, а если нет? Если нет, значит, перечитываем первый практический совет прошлого урока — переходим к обыкновенным дробям!
У нас в одну кучу намешаны десятичная дробь и смешанное число. Вот и перейдём к единообразию — к обычным дробям. А там, глядишь, и забрезжит свет в конце тоннеля…
Пишем:
Так, уже кое-чего проясняется: 49 с семёркой родня, а 100 — с десяткой:
49 = 72
100 = 102
Стало быть, по свойствам степеней можно записать:
Ну, вот и спасительный лучик света! Выносим двойку за логарифм и получаем:
Уже всё стало выглядеть гораздо симпатичнее. Всё бы ничего, только основание 7/10 и аргумент 10/7 у нас записаны кверху ногами. Что делать? Да свойства степеней вспомнить! На этот раз — с отрицательным показателем:
И снова выносим показатель степени (минус единицу) за знак логарифма, переворачиваем аргумент и получаем:
Ответ: -2
Готово дело.) Теперь пробуем самостоятельно:
Ответ: -1
А теперь вовлекаем в наш увлекательный процесс корни. То есть, не что иное, как… степени с дробными показателями. Да-да!
Пример 2
Надеюсь, вы не забыли, что lg — это просто логарифм по основанию 10? Или десятичный логарифм? Пример достаточно простой, без заморочек. Надо всего лишь вспомнить, что корень кубический из 7000 — это 70001/3. С семёркой — аналогично. А дальше по формуле разности логарифмов да по формуле деления степеней. Получим:
Ответ: 1
Вот так вот. Здесь мы снова перешли к обычным дробям. Но не от десятичных дробей или смешанных чисел, а от корней. В этом безобидном примере вполне можно было бы и без дробей обойтись, работать напрямую с корнями, но в более сложных примерах корни могут вконец запутать. Как, например, вот в таком примерчике:
Пример 3
С чего начать? И тройка есть, и девятка. Правда, три в квадрате — это и будет девятка… Но в примере ещё и корни разных степеней смешались в кучу — квадратный и кубический! Ужас… Но паниковать и сдаваться рано. Перейдём-ка от корней к степеням с дробными показателями! Распишем девятку как 32. А там, того гляди, всё и наладится.)
Верные мысли! Итак, по свойствам степеней для основания и для аргумента мы можем записать:
Вот всё и прояснилось.) Оба числа — и основание, и аргумент — оказались… родственниками! По тройке.) Только совсем уж дальними. Даже не троюродными, а десятиюродными братьями: основание — это три в степени 3/2, а аргумент — та же тройка, но в степени 7/3… Тем не менее факт остаётся фактом — родство по степени (хоть и очень дальнее) установлено. Вот и все формулы и свойства заработали! Выносим наши дробные показатели из за знак логарифма и аккуратно считаем:
Вот так. Здесь уже, конечно, немножко повозиться со степенями пришлось. А что делать… Так что не стесняемся переходить от корней к дробям! И всё получится. Обязательно.)
Вот вам и очередные практические советы:
При наличии дробей в примере, переходим от дробей к степеням с отрицательными показателями.
При наличии корней переходим от корней к степеням с дробными показателями.
Что ж, пришла пора разгрызть и какой-нибудь особо крепкий орешек. Как, например, вот такой примерчик:
Пример 4
Вычислить:
Опять же, с чего начинать? Если имеете хоть малейшее представление — флаг вам в руки. Вперёд и с песнями, как говорится.) Если понятия не имеете — подключаем зелёные практические советы и размышляем синим цветом. Примерно так:
«Ух, наворотили… Кошмар! Напролом явно не решается, надо сначала как-то преобразовывать пример. Но — как? Будем вспоминать практические советы.
1. Если в одном примере смешались в кучу разные типы дробей, то переходим к обыкновенным дробям.
Где здесь дроби? Дробей не видно. Ладно, этот пункт пока пропустим. Что там у нас ещё есть? Вот это:
2. Степени популярных чисел надо знать. В лицо! При наличии в примере разных чисел пытаемся найти «братьев по степени».
Так, кое-какая зацепочка уже появилась… 121 — это 11 в квадрате. Ещё можно расписать 125 как 5 в кубе и 9 как 3 в квадрате, но 5 и 3 — никакие не братья и не сёстры по степени. Пригодится или нет — пока непонятно, но к сведению примем. Поехали дальше.)
3. Любую степень можно записать множителем перед логарифмом. И наоборот — любой числовой коэффициент можно спрятать внутрь логарифма. Если он мешает, конечно.
Коэффициентов в нашем примере нет, логарифмы и так чистые. Отметаем этот совет. Что у нас там ещё припасено?
4. Всегда прикидываем, нельзя исходное выражение преобразовать под какую-нибудь готовую формулу?
Вот и прикидываем: на что похож внешний вид нашего примера? Ну же? Ну, конечно! На самую первую формулу — основное логарифмическое тождество! Единственная формула, где логарифм тусуется в показателе степени.
С ним мы пока что ни разу не работали. Что ж, поработаем! Попробуем преобразовать наш пример под эту формулу: других вариантов как-то выкрутиться у нас просто нет!
Но в формуле в показателе стоит один логарифм! А у нас — сумма. Что нам мешает сложить логарифмы по соответствующей формуле суммы? Основания мешают! Они… они — разные! Ну-ка, может, ещё не все практические советы у нас использованы? Вспоминаем:
5. При наличии дробей в примере, переходим от дробей к степеням с отрицательными показателями. При наличии корней переходим от корней к степеням с дробными показателями.
Так, ну дробей в нашем примере нету, это видно. А вот корень в основании — преобразуем. Вот так:
А во втором логарифме в основании тоже стоит 11, только в квадрате… Уже кое-какие проблески! Выпишу-ка я показатель отдельно, дабы не запутаться… С учётом наших размышлений.)
Уже лучше. Теперь выносим показатели степеней из оснований перед логарифмами (не забыть бы перевернуть…):
Великолепно! Основания логарифмов выровнялись! Только вот новая беда… Коэффициенты появились… Хотелось бы сложить логарифмы, ан нет, не канает… Так стоп! Чего же я туплю-то! Можно же их по другой формуле спрятать вовнутрь!
Ну вот. Уже идеально для формулы сложения! Только внутри логарифмов что-то несусветное стало твориться. Не беда, перейдём к маленьким числам: зря, что ли, мы 125 и 9 в виде степеней пятёрки и тройки расписывали?
Пока всё чин-чинарём. Теперь, по правилам действий со степенями, можно записать:
Вот, практически, и всё. Досчитываем наш показатель по формуле сложения логарифмов:
Пример становится всё лучше и лучше! Возвращаемся к нашему исходному примеру, вставляем в него наш преобразованный показатель и получаем ответ!
Йес!!! Ничего себе, примерчик, однако ж…»
Ответ: 75
Вот такой пример. Запутанный, да, я не спорю. И зачем я так детально его разобрал? С практическими советами, мыслями… Мог бы и в пару строк уложиться… Дело в том, что разбор одного конкретного примера — занятие бесполезное. Не попадётся он. А вот разъяснить на конкретном примере, как именно надо выкручиваться в любом (да-да, любом!) задании — совсем другое дело!
Главное в этом разборе — подход. Мы применяем весь наш арсенал инструментов к конкретному примеру. Пробуем поочерёдно все инструменты, как ключики к замку. Что-то срабатывает, а что-то нет. Это не страшно и не смертельно. Не подошло — пробуем что-то другое! Что-то обязательно подойдёт! Сложные и запутанные задания именно так и решаются. И никак иначе.)
Конечно, с опытом всё будет делаться гораздо короче и какие-то шаги будут в уме делаться и вообще пропускаться. За ненадобностью. Тут практика рулит. Тренироваться и решать надо. Используя изложенный здесь подход. И тогда всё получится. Обязательно!
Формула перехода к новому основанию. Немного приколов… И немного формул сокращённого умножения.
Поднимаемся ещё на ступень повыше. Запускаем теперь в дело самую последнюю формулу из нашего списка — это формула перехода к новому основанию. Вот она:
В чём суть этой формулы, когда она применяется и как именно она работает? Объясняю по пунктам.
Формула эта применяется, когда основания логарифмов — разные. Но не просто разные, а ещё и не родственные по степени! Которые друг в друга через простую степень не превращаются. Скажем, 2 и 3. Или 5 и 7. Заметьте, что нам уже встречались разные основания у логарифмов в одном и том же примере, но там или всё и так славненько срасталось, или переход был через степени. Например, если основания логарифмов 1/125 и 25, то можно догадаться, что это родня! По пятёрке. Ибо 1/125 = 5-3, а 25 = 52. Не так очевидно, конечно, но и мы уже всё-таки на серьёзном уровне с вами. А дальше дело техники: выносим показатели за логарифмы и — вперёд.
Но если основания не родственные, а без выравнивания оснований в примере никак, то выход только один — работать по этой формуле.
Запомнить её очень легко. По шагам:
1) Слева пишем логарифм, основание которого нам не нравится. Справа рисуем черту дроби.
2) В числитель пишем логарифм числа b, но уже по новому основанию k. Какому именно основанию? А какому угодно! В том-то весь и фокус! Естественно, тому, которое нам удобнее. Кроме единицы, разумеется.)
3) В знаменатель пишем логарифм старого основания a по тому же новому основанию k.
Обратите внимание на саму структуру формулы: слева в основании буквы k вообще нет! В этом-то и вся фишка! Это означает, что новому логарифму мы можем выбрать какое угодно основание. Обычно выбирают то, которое нам удобно в конкретном примере. Если, скажем, в примере куча логарифмов по основанию 3 и затесался один по основанию 7, то его и менять будем. На тройку.
А в знаменатель пишем логарифм старого основания. Так уже математика требует. В результате логарифм со старым основанием исчезает из примера. Вот и всё. Вот и вся суть формулы перехода. Ну что, посмотрим на формулу перехода в действии?
Пример 5
Вычислить:
Что тут можно увидеть? Ну, во-первых, разные основания. Причём не родственные: из четвёрки пятёрку простым возведением в степень никак не получить. Во-вторых, наблюдаем произведение логарифмов. Такой формулы в наших свойствах нету. Не путаем с логарифмом произведения! Или с суммой логарифмов… Что же делать? Первым делом перейдём к одному основанию. Что-то же делать всё равно надо! К какому основанию пойдём? Ну, ясное дело, что не к 30 или 1,234. У нас на выбор два варианта — либо к четвёрке, либо к пятёрке. В данном примере абсолютно без разницы, к чему переходить. Давайте к четвёрке пойдём: всё-таки число поменьше.) Итак, первый логарифм не трогаем (у него и так основание четыре), а вот второй логарифм превращаем по формуле перехода в дробь:
Всё. Логарифм по основанию 5 из примера благополучно исчез, и в основаниях остались только четвёрки. Вставляем полученную дробь в наш пример, упрощаем и считаем:
Ответ: 2
Вот так. Откуда же я узнал, что надо переходить к другому основанию? Ведь я мог и что-то ещё замутить. Скажем, log516 расписать как
log516 = log524 = 4log52
и дальше как-то ещё выкручиваться. Да. Можно. Но с богатым опытом приходит уже так называемое математическое чутьё на формулы и преобразования.) Когда в уме наперёд уже умеешь просчитывать, к чему может привести тот или иной манёвр и не идёшь по заведомо негодному пути.
Вот вам очередной практический совет на данную тему.
Если перед вами сложное логарифмическое выражение, в котором основания логарифмов разные, то первым делом пробуем сделать их одинаковыми. Или через степени или по формуле перехода. Очень часто этот манёвр срабатывает проясняет дальнейшую ситуацию.
А теперь рассмотрим один фокус на формулу перехода, который частенько любят проделывать составители примеров. По-другому эту фишку даже и не назовёшь. Настолько элементарна, а в тупик может поставить даже отличника!
Пример 6
Вычислить:
Основания уже одинаковые, но формулы деления логарифмов не существует, да… Можно, конечно, сообразить, что 125 = 53 и старым добрым способом, но что делать, если внутри логарифмов сидит что-нибудь более навороченное? Вот и впадают в ступор…
Здесь же достаточно всего лишь разглядеть формулу перехода к новому основанию. Вернее, не просто формулу, а её правую часть! И, если запустить эту формулу справа налево, то сразу получим:
И все дела! Да-да! Это ответ.)
Ответ: 3
Частенько эту фишку применяют с какими-нибудь совершенно дикими основаниями. На испуг берут, типа.) Как, например, вот такое задание:
Пример 7
Вычислить:
В основании число «пи», как тут не испугаться… Однако, если догадаться, что наша ужасная дробь — всего лишь правая часть формулы перехода к новому основанию и сработать справа налево, то получим всего-навсего:
Вот и всё. И нету больше никакого «пи».) А уж сложить парочку логарифмов с одинаковыми основаниями — пустяшное дело. Не пример, а одно удовольствие:
log1236 + log124 = log12144 = 2
Ответ: 2
Вот такой вот приёмчик. Теперь, надеюсь, не растеряетесь, в случае чего.)
Рассмотрим ещё одну распространённую фишку с формулой перехода. Вернее, её частный случай.
Что произойдёт, если за новое основание мы возьмём аргумент логарифма? Давайте посмотрим!
Во как! Оказывается, если поменять местами a и b, то наш новый логарифм станет всего лишь обратным к старому! Весьма и весьма полезная формулка. Имеет смысл запомнить.) Решим примерчик и на эту тему:
Пример 8
Вычислить:
Что делать будем? Скобки раскрывать? Можно, конечно, но пример явно намекает на более элегантное преобразование. Перейдём в логарифме по основанию 40 к основанию 2. Двойка чем-то привлекательнее, чем сорок, не находите?) Поскольку в аргументе логарифма стоит также двойка, то при переходе к основанию 2 достаточно просто перевернуть этот логарифм. И все дела.)
Получим:
И что дальше? Куда пристегнуть тройку? А дальше новый фокус! Дело всё в том, что мы не можем напрямую сложить логарифм и число. Но зато логарифмы между собой — запросто! Как выкрутимся? А сделаем-ка из тройки… логарифм! Да-да! Для этого сначала выберем ему основание. Вариантов выбора много, но я предлагаю выбрать 2. Думаю, возражений не будет?)
А дальше пишем вот такое простое равенство:
3 = log223
Всё легко и просто: тройка уходит показателем в степень нашего выбранного основания. Сама цепочка превращений выглядит вот так:
По этапам:
1) Вместо тройки пишем степень с выбранным основанием 2 и показателем, равным этой самой тройке.
2) Берём логарифм от этой степени по тому же самому основанию 2.
3) Всё!
Конечно, можно было бы и сразу тройку на логарифм заменить, благо здесь числа совсем простые, но лучше запомнить эту простую цепочку. А то придётся где-нибудь, к примеру, превращать в логарифм по основанию 11 число 1/7… А по цепочке всё совсем элементарно:
Просекли фишку? Тогда возвращаемся к нашим баранам и дорешиваем:
Ответ: 1
Да… Кто бы мог подумать.)
Конечно, в числовых выражениях этот приёмчик с превращением числа в логарифм достаточно экзотичен. Но вот в логарифмических уравнениях и неравенствах он применяется на полную катушку! Имейте его в виду.)
Заметьте, что обычно мы стараемся поступать наоборот — упрощать всякие ужасы типа дробей, корней, синусов да логарифмов. Доводить их, по возможности, до конечного числа. А тут — наоборот, из числа делаем логарифм. Что хотим, то и творим! Так что математика — на самом деле весьма и весьма творческая наука! Во многом даже искусство.)
Запоминаем:
При необходимости любое число можно превратить в логарифм по любому основанию (кроме единицы, конечно).
Осталось разобраться с совсем уж хардкорными примерами. Где и так пробуешь и сяк, но не упрощается он никак! На такие примеры есть своё особое секретное оружие.) Срабатывает безотказно. Если уметь грамотно им пользоваться, конечно. Как вам такой примерчик!
Пример 9
Вычислить:
За что зацепиться? Все основания уже одинаковые (семёрка), но это особо не спасает. Кстати, обращаю ваше внимание на весьма и весьма частый косяк. В числителе стоят квадраты логарифмов. Именно самих логарифмов, а не их аргументов! Это означает, что вынести двойки из логарифмов наружу мы не имеем права! Не там двойки стоят… Стало быть, уже привычных нам логарифмических формул, готовых к употреблению, нету. Что же делать?
Спокойно! Без паники! Никто и никогда не может гарантировать, что сразу влёт всё решится.) К сожалению…
Чтобы расправиться с этим злым примером, забудем на минутку про логарифмы и плавненько переместимся в седьмой класс. Формулы сокращённого умножения не забыли, надеюсь? А теперь внимательно присматриваемся к нашему примеру. Что ещё, кроме логарифмов, в нём можно увидеть? Разность… Разность ква… Ну, конечно! Разность квадратов! Такая родная и до боли знакомая формула:
a2–b2 = (a—b)(a+b)
Правда, в применении к логарифмам. Ну и что из этого? Ведь в формуле под буковками a и b может скрываться всё что угодно — и логарифмы, и синусы, и степени — любые выражения! Формула всё равно сработает!
Итак, заменяем наш числитель на произведение скобок по формуле разности квадратов:
Вот и всё встало на свои места! И все формулы заработали! Решать пример стало одно удовольствие.)
В первых скобках (разность) получается:
Во вторых скобках (сумма) будет:
Вставляем в пример наши промежуточные результаты, сокращаем и получаем:
Ответ: 1
Простенько и со вкусом.) Здесь-то всё ясно. Но в тревожной боевой обстановке ЕГЭ подобный пример может и в ступор вогнать. Дело всё в том, что большинство учеников подсознательно пытаются решить пример в том формате, в котором он задан. Например, если задан пример на логарифмы, то мы с головой погружены в логарифмы и варимся только в них, а вынырнуть на поверхность да оглядеться вокруг — не можем. С тригонометрией аналогично — решаем пример только в рамках тригонометрии. И, в случае чего, не можем напрячься и выскочить из этих жёстких рамок… А надо уметь! Хотя бы иногда.)
Посему очередной по счёту практический совет:
Замороченные примеры проверяем на алгебру седьмого класса — разложение на множители, формулы сокращённого умножения и т.п.
Ещё из той же оперы для самостоятельного решения:
lg24 + lg16·lg25 + lg225 =
Ответ: 4
Ну что, поздравляю! Вот мы и набрались достаточного количества знаний для уверенной работы с логарифмами практически на любом уровне сложности! Дальше путь только один — решать примеры! Как можно больше.) И особо рекомендую не пренебрегать зелёными советами. Они не зря даются в материале.) Их надо помнить и им надо следовать.) И тогда не логарифмы будут командовать вами, а вы — логарифмами.)
До встречи!
Формула смены базы | Purplemath
Purplemath
Есть еще одно «правило» журнала, но это больше формула, чем правило.
Возможно, вы заметили, что в вашем калькуляторе есть ключи только для вычисления значений для общего (то есть с основанием 10) журнала и естественного (то есть с основанием e ) журнала. Ключей к другим базам нет.Некоторые студенты пытаются обойти это, «оценивая» что-то вроде «log 3 (6)» с помощью следующих нажатий клавиш:
[ LOG ] [ 3 ] [ (] [ 6 ] [) ]
Конечно, тогда они получают неправильный ответ, потому что вышеупомянутое на самом деле (обычно) вычисляет значение «log 10 (3) × 6».Это не то, что было задумано.
MathHelp.com
Чтобы оценить журнал с нестандартной базой, вы должны использовать формулу изменения базы:
Формула смены базы:
Практически это правило говорит о том, что вы можете оценить журнал с нестандартной базой, преобразовав его в долю формы «(стандартный журнал аргумента), разделенный на (журнал с той же стандартной базой нестандартной базы) ».Я держу это прямо, глядя на положение вещей. В исходном журнале аргумент находится «над» базой (поскольку база имеет нижний индекс), поэтому я оставляю все так, когда разделяю их:
Вот простой пример применения этой формулы:
Журнал оценок
3 (6). Округлите ответ до трех десятичных знаков.
Аргумент — 6, основание — 3.Я подключу их к формуле смены базы, используя натуральный логарифм в качестве журнала новой базы:
Тогда ответ, округленный до трех десятичных знаков, будет:
.Я получил бы тот же окончательный ответ, если бы использовал общий журнал вместо натурального журнала, хотя числитель и знаменатель промежуточной дроби были бы другими, чем то, что я показал выше:
Как видите, не имеет значения, какой стандартный журнал вы используете, если вы используете одну и ту же базу для числителя и знаменателя.
Хотя я показал значения числителя и знаменателя в приведенных выше расчетах, на самом деле лучше всего выполнять вычисления полностью на вашем калькуляторе. Вам не нужно беспокоиться о написании этого промежуточного шага.
На самом деле, чтобы свести к минимуму ошибки округления, лучше попытаться выполнить все шаги деления и вычисления в вашем калькуляторе за один раз. В приведенном выше вычислении вместо того, чтобы записывать первые восемь или около того десятичных знаков в значениях ln (6) и ln (3) и затем делить их, вы просто выполняете «ln (6) ÷ ln (3)» в своем калькулятор.
Вы можете получить несколько простых (но довольно бесполезных) упражнений по этой теме. Не завидуйте им; это простые пункты, пока вы держите в голове формулу смены основы. Например:
Преобразуйте журнал
3 (6) в выражение с логарифмами с основанием 5.
Я не могу придумать какой-либо конкретной причины, по которой журнал base-5 может быть полезен, поэтому я думаю, что единственный смысл этих проблем — дать вам возможность попрактиковаться в использовании смены базы.Отлично; Я подключу-н-пыхтю:
Преобразуйте ln (4) в выражение, записанное в виде общего журнала.
Зачем мне это делать («в реальной жизни»), если я уже могу вычислить натуральный логарифм в моем калькуляторе? Я бы не стал; это упражнение предназначено только для практики (и простых моментов).
Я поделюсь с формулой замены базы:
Так как получение фактического десятичного значения не является целью в упражнениях подобного рода (главное — преобразование с использованием изменения базы), просто оставьте ответ в виде логарифмической дроби.
Хотя приведенные выше упражнения были довольно бессмысленными, использование формулы изменения базы может быть очень удобно для поиска точек графика при построении графиков нестандартных журналов, особенно когда предполагается, что вы используете графический калькулятор.
Используйте вашу графическую утилиту для построения графика
y = log 2 ( x ).
Если бы я работал вручную, я бы использовал определение журналов, чтобы отметить, что:
- так как 2 -2 = ¼, то лог 2 (¼) = -2
- , поскольку 2 –1 = ½, затем журнал 2 (½) = –1
- , поскольку 2 0 = 1, тогда журнал 2 (1) = 0
- , поскольку 2 1 = 2, тогда журнал 2 (2) = 1
- , поскольку 2 2 = 4, тогда журнал 2 (4) = 2
- , поскольку 2 3 = 8, затем журнал 2 (8) = 3
- , поскольку 2 4 = 16, затем журнал 2 (16) = 4
А потом рисовал бы свой график от руки.
(Почему я выбрал именно эти значения x ? Потому что что-то меньшее было бы слишком маленьким, чтобы рисовать вручную, а что-то большее привело бы к смехотворно широкому графику. Я выбрал значения, которые соответствуют моим потребностям.)
Но в этом случае я должен строить график с помощью своего графического калькулятора. Как я могу это сделать? (Или что, если бы я просто хотел использовать функцию «ТАБЛИЦА» моего графического калькулятора, чтобы найти несколько хороших аккуратных точек графика?) У меня нет кнопки «log-base-two».Однако я могу ввести данную функцию в свой калькулятор, используя формулу изменения базы, чтобы преобразовать исходную функцию в то, что указано в терминах базы, которую мой калькулятор может понять. Подбрасывая монетку, выбираю натуральный логарифм:
(Я мог бы также использовать общий журнал. В этом случае функция была бы « y 1 = log ( x ) / log (2)».)
В моем графическом калькуляторе после настройки окна просмотра для отображения полезных частей плоскости график будет выглядеть примерно так:
Между прочим, вы можете проверить, содержит ли график ожидаемые «аккуратные» точки (то есть точки, которые я бы вычислил вручную, как показано выше), чтобы убедиться, что изображение отображает правильный график:
URL: https: // www.purplemath.com/modules/logrules5.htm
Преобразование между логарифмической и экспоненциальной формой
Результаты обучения
- Преобразование из логарифмической в экспоненциальную форму.
- Преобразование экспоненты в логарифмическую форму.
Чтобы анализировать магнитуду землетрясений или сравнивать магнитуды двух разных землетрясений, нам необходимо иметь возможность преобразовывать логарифмическую и экспоненциальную форму.{y} [/ latex] тоже функция. Как и в случае со всеми обратными функциями, мы просто меняем местами x и y и решаем относительно y , чтобы найти обратную функцию. Чтобы представить y как функцию x , мы используем логарифмическую функцию вида [latex] y = {\ mathrm {log}} _ {b} \ left (x \ right) [/ latex]. Основание b логарифм числа — это показатель степени, на который мы должны возвести b , чтобы получить это число.
Мы читаем логарифмическое выражение как: «Логарифм с основанием b из x равен y » или, упрощенно, «логарифм с основанием b из x равен y .{y} = x, \ text {} b> 0, b \ ne 1 [/ латекс]
Обратите внимание, что основание b всегда положительно.
Поскольку логарифм — это функция, его наиболее правильно записать как [latex] {\ mathrm {log}} _ {b} \ left (x \ right) [/ latex], используя круглые скобки для обозначения оценки функции, как в случае с [латекс] е \ влево (х \ вправо) [/ латекс]. Однако, когда входные данные представляют собой одну переменную или число, круглые скобки обычно опускаются, а выражение без скобок записывается как [latex] {\ mathrm {log}} _ {b} x [/ latex].{y} = x [/ latex], где
- мы читаем [latex] {\ mathrm {log}} _ {b} \ left (x \ right) [/ latex] как «логарифм с основанием b из x » или «логарифм с основанием . b из x ».
- логарифм y — это показатель степени, до которого нужно возвести b , чтобы получить x .
- , если основание [латекс] b [/ латекс] не указано, основание логарифма принимается равным [латекс] 10 [/ латекс].
Кроме того, поскольку логарифмическая и экспоненциальная функции переключают значения x и y , область и диапазон экспоненциальной функции меняются местами для логарифмической функции.Следовательно,
- область определения функции логарифма с основанием [latex] b \ text {is} \ left (0, \ infty \ right) [/ latex].
- диапазон функции логарифма с основанием [латекс] b \ text {is} \ left (- \ infty, \ infty \ right) [/ latex].
Вопросы и ответы
Можем ли мы взять логарифм отрицательного числа?
Нет. Поскольку основание экспоненциальной функции всегда положительно, никакая степень этого основания не может быть отрицательной. Мы никогда не сможем логарифмировать отрицательное число.Кроме того, мы не можем логарифмировать ноль. В комплексном режиме калькуляторы могут выводить логарифм отрицательного числа, но логарифм отрицательного числа не является действительным числом.
Практическое руководство. Для данного уравнения в логарифмической форме [латекс] {\ mathrm {log}} _ {b} \ left (x \ right) = y [/ latex] преобразовать его в экспоненциальную форму
- Изучите уравнение [латекс] y = {\ mathrm {log}} _ {b} x [/ latex] и определите b , y и x .
- Перепишите [latex] {\ mathrm {log}} _ {b} x = y [/ latex] как [latex] {b} ^ {y} = x [/ latex]. {- 4} = \ frac {1} {10,000} [/ латекс]
Сначала определите значения b , y и x .{-1} = \ frac {1} {2} [/ latex] равно [latex] {\ text {log}} _ {2} \ left (\ frac {1} {2} \ right) = — 1 [/ латекс]
Внесите свой вклад!
У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.
Улучшить эту страницуПодробнее
Как преобразовать Ln в журнал 10
Обновлено 4 декабря 2020 г.
Автор Oxana Fox
Логарифм числа — это степень, в которую необходимо возвести основание, чтобы получить это число; например, логарифм 25 с основанием 5 равен 2, поскольку 5 2 равно 25.«Ln» обозначает натуральный логарифм, в основе которого лежит постоянная Эйлера, приблизительно 2,71828. Натуральные логарифмы используются не только в математике, но и в естественных науках. «Общий» логарифм имеет основу 10 и обозначается как «журнал». Следующая формула позволяет получить натуральный логарифм, используя десятичный логарифм:
\ ln (\ text {number}) = \ frac {\ log (\ text {number})} {\ log (2.71828)}
TL; DR (слишком долго; не читал)
Чтобы преобразовать число из натурального в общий журнал, используйте уравнение ln ( x ) = log ( x ) ÷ журнал (2.71828).
Проверка значения числа
Перед тем, как вычислить логарифм числа, проверьте его значение. Логарифмы определены только для чисел больше нуля, т.е. положительных и ненулевых. Однако результатом логарифма может быть любое действительное число — отрицательное, положительное или нулевое.
Вычислить общий журнал
Введите число, которое вы хотите логарифмировать на своем калькуляторе. Нажмите кнопку «журнал», чтобы вычислить общий журнал числа.Например, чтобы найти общий журнал 24, введите «24» на вашем калькуляторе и нажмите клавишу «log». Общий логарифм 24 равен 3,17805.
Вычислить общий журнал e
Введите на калькуляторе константу «e» (2,71828) и нажмите кнопку «log» для вычисления журнала 10 :
\ log_ {10} (2,71828) = 0,43429
Преобразовать натуральный журнал в общий журнал
Разделите общий журнал числа на общий журнал e, 0.43429, чтобы найти натуральный логарифм через общий журнал. В этом примере:
\ ln (24) = \ frac {1.3802} {0.43429} = 3,17805
Логарифмы
Логарифмы
Автор (ы)
Дэвид М. ЛейнПредварительные требования
РаспределенияЦели обучения
- Вычислить журналы с использованием различных баз
- Выполнение основных арифметических операций с использованием журналов
- Укажите взаимосвязь между бревнами и пропорциональным изменением
Преобразование журнала уменьшает положительный перекос.Это может быть полезно как для того, чтобы сделать данные более интерпретируемыми, так и для того, чтобы соответствовать предположениям выводимой статистики.
Основы логарифмов (журналов)
Бревна в некотором смысле противоположны экспонентам. Рассмотрим следующее простое выражение:
10 2 = 100
Здесь можно сказать, что основание 10 возведено во вторую степень. Вот пример журнала:
Лог 10 (100) = 2
Это можно читать так: 10 из 100 в логарифме равняется 2.В результате получается степень, до которой необходимо возвести основание 10, чтобы оно сравнялось со значением (100). Аналогично
Лог 10 (1000) = 3
, поскольку 10 необходимо возвести в третью степень, чтобы получить 1000.
Во всех этих примерах использовалась база 10, но можно было использовать любую базу. Существует основание, которое приводит к «натуральным логарифмам» и называется е и равно примерно 2,718. Объяснение того, что в этом «естественного», выходит за рамки этой книги.Натуральные логарифмы могут быть обозначены как: Ln (x) или log e (x).
Изменение основания журнала изменяет результат на мультипликативную константу. Чтобы преобразовать журнал 10 в натуральный логарифм, умножьте его на 2,303. Аналогично, чтобы преобразовать в обратном направлении, вы разделите на 2,303.
Взятие антилогарифма числа отменяет операцию взятия журнала. Следовательно, поскольку Log 10 (1000) = 3, антилогарифм 10 из 3 равен 10 3 = 1000.Взятие антилогарифма числа просто увеличивает основание рассматриваемого логарифма до этого числа.
Журналы и пропорциональное изменение
Ряд чисел, которые увеличиваются пропорционально, будут увеличиваться на равные величины при преобразовании в журналы. Например, числа в первом столбце таблицы 1 увеличиваются в 1,5 раза, так что каждая строка в 1,5 раза выше, чем предыдущая. Преобразованные числа Log 10 увеличиваются с равным шагом 0.176.
Таблица 1. Пропорциональные исходные изменения равны в единицах логарифма.| Необработанный | Журнал |
|---|---|
4,0 | 0.602 0.778 0.954 1.130 |
В качестве другого примера, если один ученик увеличил свой результат со 100 до 200, а второй ученик увеличил свой результат со 150 до 300, процентное изменение (100%) будет одинаковым для обоих учеников.Разница в журналах также такая же, как показано ниже.
Журнал 10 (100) = 2.000
Журнал 10 (200) = 2,301
Разница: 0,301
Журнал 10 (150) = 2,176
Журнал 10 (300) = 2,477
Разница: 0,301
Арифметические операции
Правила для журналов продуктов и коэффициентов приведены ниже.
Журнал (AB) = Журнал (A) + Журнал (B)
Журнал (A / B) = Журнал (A) — Журнал (B)
Например,
Журнал 10 (10 x 100) = Журнал 10 (10) + Журнал 10 (100) = 1 + 2 = 3.
Аналогично,
Журнал 10 (100/10) = Журнал 10 (100) — Журнал 10 (10) = 2 — 1 = 1.
Пожалуйста, ответьте на вопросы:
Калькулятор логарифмов
Что такое логарифм?
Напомним, экспоненциальные функции очень интересны как модели для описания природных процессов, физических величин, а также экономических и социальных проблем.{f (x)} $. Эта функция, обратная экспоненциальной функции, называется \ underline {логарифмической функцией} для основания $ a $.
Пьер-Симон Лаплас назвал логарифмы: «замечательная уловка, которая, сокращая до нескольких дней труд многих месяцев, удваивает срок службы астронома и избавляет его от ошибок и отвращения, которые неотделимы от долгих вычислений ».
| Log b x | |||
|---|---|---|---|
| Log 10 2 | 0.301 | ||
| Лог 2 2 | 1 | ||
| Лог 2 10 | 3,3219 | ||
| Лог 2 5 | 2,3219 | ||
| Лог 2 100 | 6,6439 | ||
| Лог 2 6 | 2,585 | ||
| Лог 2 1000 | 9.9658 | 0 1000 | 9.9658 |
| Лог 2 32 | 5 | ||
| Лог 2 7 | 2,8074 | ||
| Лог 10 20 | 1,301 | 05 1075 905 | |
| Журнал 10 4 | 0.6021 | ||
| Журнал 10 100 | 2 | ||
| Журнал 10 5 | 0,699 | ||
| Журнал139 | |||
| Лог 10 6 | 0,7782 | ||
| Лог 10 2 | 0,301 | ||
| Лог 10 1 | Лог 10 1 | Лог 0 | 05 |
| лн (2) | 0,6931 | ||
| лн (0) | -∞ | ||
| лн (3) | 1,0986 | ||
| лн (20) 905 905 10) | 2.3026 | ||
| лн (1) | 0 | ||
| лн (д) | 1 |
Изменение базовой формулы или правила
Я обсуждал большинство правил журнала в отдельном уроке. Однако я намеренно оставил одну, чтобы обсудить это здесь подробно. Правило журнала называется Формула изменения базы .
Если вас интересует, почему работает замена формулы, щелкните следующую ссылку, чтобы увидеть доказательство: Доказательства свойств логарифма.
Логарифм с основанием 10 известен как десятичный логарифм , а логарифм с основанием e известен как натуральный логарифм .
Число \ large {\ color {red} {e}}
Примечание: Число e — математическая константа, имеющая числовое значение e \ приблизительно 2,71828. Это иррациональное число, потому что его нельзя выразить как отношение двух целых чисел или дробь. Более того, число e является основанием натурального логарифма.
Таким образом, десятичный и натуральный логарифмы используют стандартное основание : 10 и e, соответственно.
- десятичный логарифм
- записывается как \ large {\ color {red} \ log x = {\ log _ {10}} x}
- натуральный логарифм
- записывается как \ large {\ color {blue} \ ln x = {\ log _e} x}
Прежде чем мы продолжим, я хотел бы указать на некоторые нюансы и тонкости, касающиеся математических выражений обычного и натурального логарифмов.
Кнопки LOG и LN графического калькулятора
Большинство графических калькуляторов имеют функции или клавиши, которые непосредственно вычисляют логарифмы чисел по основанию 10 и основанию е. Таким образом, вы увидите только две кнопки: LOG для десятичного логарифма и LN для натурального логарифма.
Очевидно, что проблема возникает, когда мы хотим вычислить логарифм числа, используя нестандартные основания, такие как 2, 3, 7, 0,5 и 0,25.
В приведенных выше логарифмах используется НЕСТАНДАРТНОЕ основание, поскольку они не являются ни \ large {\ color {green} 10}, ни числом \ large {\ color {green} e}.
Как начать вводить числа на графическом калькуляторе? Как я упоминал ранее, большинство калькуляторов ограничены вычислением логарифмов только с основанием 10 и основанием e.
Именно здесь на помощь приходит гоночная модель Formula со сменой базы. Он может преобразовывать логарифм с нестандартным основанием как отношение двух логарифмических операций, которые используют стандартное основание 10 или константу e.
Что такое формула изменения базы ?
Формула изменения базы — это инструкция о том, как переписать или преобразовать данное логарифмическое выражение в виде отношения или доли двух логарифмических операций с использованием любой допустимой базы.
Это означает, что если у нас есть логарифм с использованием определенного основания, то мы можем превратить его в эквивалентное отношение или долю двух логарифмических операций, чтобы мы могли выбрать любое основание, которое захотим. Мы можем буквально выбрать любую базу, если она положительна, но не равна \ color {red} 1.
Но если мы хотим вычислить или узнать значение логарифма, мы должны выбрать основание-10 или основание-е, поскольку большинство калькуляторов имеют эти функциональные клавиши. Ключ log [log] вычисляет общий логарифм (с основанием 10), а ключ ln [ln] вычисляет натуральный (с основанием e) логарифм.
Давайте разберем, как формула преобразовала исходный логарифм в эквивалентное выражение как отношение двух операций журнала.
- Аргумент исходного логарифма становится аргументом логарифма числителя.
- Основание исходного логарифма становится аргументом логарифма знаменателя.
- Логарифмы в числителе и знаменателе имеют одинаковое основание. Значение base \ large \ color {green} c — это любая основа, которую мы выбрали.
Примеры формулы замены базы
Первые два примера (Пример №1 и №2) являются идеальными учебными задачами, потому что аргумент и основание логарифма могут быть выражены как степени общего числа (положительного числа, не равного 1), которое служит новая база при применении правила изменения базы.
Пример 1: Вычислить \ large {\ log {} _48}.
Первое, что я понял, это то, что и аргумент, и его основание могут быть выражены как степень двойки.k}} \ right) = k \ cdot {\ log _b} \ left (x \ right)}
- \ large {\ color {red} {\ log _b} b = 1}
Вот полное решение.
Пример 2: Оценить \ large {\ log {} _ {\ large {{1 \ over {27}}}} \ left (9 \ right)}.
Вы можете подумать, что с вопросом возникла проблема, потому что логарифм основан на дроби. Помните, что основание логарифма должно быть положительным, но не может равняться 1. Таким образом, основание \ large {1 \ over {27}} совершенно нормально.Очевидно, что это положительное число, и оно не равно 1.
.Дробь \ large {1 \ over {27}} может быть переписана в степень 3. Здесь пригодится отрицательное правило экспоненты.
Правило отрицательной экспоненты позволяет нам инвертировать дробь (обратная), но мы должны переключить знак экспоненты. 2}.k}} \ right) = k \ cdot {\ log _b} \ left (x \ right)}
- \ large {\ color {red} {\ log _b} b = 1}
Ниже представлено полное решение.
Пример 3: Вычислить значение \ large {\ log {} _ {\ large {5}} \ left ({12} \ right)}. Округлите ответ до ближайшей тысячной.
Это уже не «хорошая» проблема, потому что аргумент и основание логарифма не могут быть выражены как степени общего числа. Другими словами, не существует сценария, в котором мы могли бы выразить 5 и 12 как экспоненциальные числа с одинаковым основанием.
Чтобы решить эту проблему, мы можем использовать правило изменения базы, чтобы переписать исходный логарифм как отношение двух логарифмов основания по нашему выбору. У нас есть два варианта: использовать base-10 или base-e. Неважно, какой из них мы выберем, потому что ответ будет одинаковым. Для этой задачи воспользуемся основанием 10.
Не забудьте округлить свой ответ до трех десятичных знаков, потому что нас просят округлить его до ближайшей тысячной.
Наш калькулятор должен подтвердить, что наш ответ правильный.
Пример 4: Вычислить значение \ large {\ log {} _ {\ large {7}} \ left ({9} \ right)}. Округлите ответ до ближайшей сотой.
В предыдущем примере мы использовали десятичное основание для вычисления логарифма. На этот раз мы будем использовать натуральное число \ color {red} e в качестве основы выбора при применении формулы замены базы.
Обратите внимание, что нам не нужно записывать натуральный логарифм как \ large {{{\ log} _e} \ left (x \ right)}. Мы можем пропустить этот шаг и сразу записать его как \ large {\ ln \ left (x \ right)}.Я добавил это как один из шагов ниже для ясности и акцента.
Давайте продолжим и применим правило смены базы, чтобы преобразовать \ large {\ log {} _7 \ left (9 \ right)} как отношение или долю двух операций натурального логарифма.
Кроме того, не забудьте округлить ответ до двух десятичных знаков, поскольку задача требует, чтобы окончательный ответ выражался с точностью до сотых.
Ваш калькулятор должен выдать результат, аналогичный приведенному ниже.
Пример 5: Изменить \ large {\ log {} _ {\ large {6}} \ left ({0.1} \ right)} как частное двух натуральных логарифмов. Вычислите его значение и округлите до ближайшей десятой.
Эта задача требует, чтобы мы изменили данный логарифм как частное от натуральных логарифмов. Это означает, что у нас нет другого выбора, кроме как использовать натуральное число \ large \ color {red} e в качестве основы, когда мы применяем формулу замены базы. Не забывайте также, что нам велят округлить наш ответ до ближайшей десятой (одного десятичного знака).
Вот наше решение:
Наш калькулятор согласен с нашим ответом.
Пример 6: Измените \ color {blue} \ large {\ log \ left (7 \ right)} как частное от натурального логарифма. Затем вычислите его значение. Округлите ответ до ближайшей десятитысячной.
Я допускаю, что, хотя мы можем напрямую решить значение \ color {red} \ log \ left (7 \ right) с помощью калькулятора, поскольку он имеет ключ LOG , эта проблема требует, чтобы мы пошли по длинному пути. Не потому, что это бесполезное занятие нашего времени, но, что более важно, это возможность для нас применить наше твердое понимание формулы смены основы.
Помните, что когда вы видите операцию журнала без базы, предполагается, что она имеет базу 10. Поэтому наш самый первый шаг — переписать \ log \ left (7 \ right) как {\ log _ {10}} \ left (7 \ right), чтобы было намного легче увидеть, с какими числами мы имеем дело на этапе смены базы.
Это прекрасное чувство, когда калькулятор выводит значение, подтверждающее наш ответ.
Пример 7: Измените \ color {blue} \ large \ ln \ left ({13} \ right) как отношение в единицах десятичного логарифма.Затем рассчитайте его стоимость. Округлите ответ до ближайшей десятитысячной.
Как и в примере №6, нет необходимости применять формулу изменения базы, потому что мы можем вычислить ее напрямую с помощью калькулятора. Однако цель этой проблемы — продемонстрировать наше глубокое понимание десятичных и натуральных логарифмов и того, как правильно обращаться с формулой.
Итак, давайте преобразуем \ large \ ln \ left ({13} \ right) в LOG форму , где основание — \ large \ color {blue} e, таким образом, \ large {\ log _ {\ large {e} }} \ left ({13} \ right).Теперь мы используем формулу замены основания, чтобы выразить это как отношение двух десятичных логарифмов. Помните, что в десятичном логарифме используется основание 10.
Да! Калькулятор согласен с нашим ответом.
Это закон, тоже законы логарифмов
Его закон, так и законы логарифмовАвторские права 20022021 Стэн Браун
Резюме: У вас проблемы с запоминанием законов логарифмов? Делать вы знаете, почему вы можете изменить log (x) + log (y) на другую форму, но не журнал (x + y)? Эта страница поможет вам разобраться в законах логарифмы.
См. Также: Все законы логарифмов текут прямо из законов экспонентов . Если ты чувствуешь себя немного неустойчивый с законами экспонент, просмотрите их перед тем, как продолжить.
Логарифм? Что такое логарифм?
Логарифм — это просто показатель степени.
Чтобы быть конкретным, логарифм числа x по основанию b это просто показатель степени, который вы положили на b , чтобы получить результат равно x .Например, поскольку 5 = 25, мы знаем, что 2 ( степень) — это логарифм 25 с основанием 5. Символически, журнал 5 (25) = 2.
В более общем смысле, если x = b y , то мы скажем, что y — это логарифм x с основанием b или логарифм по основанию b x . В символах y = log b ( x ), часто пишется без скобок, y = журнал b x .Каждое экспоненциальное уравнение можно переписать в виде логарифмического уравнения: и наоборот, просто поменяв местами x и y этим способом.
Вы нечасто видите это слово, но можете также говорят, что x — это антилогарифм от y до база б . Логарифм — это показатель степени, а антилогарифм — результат возведения основания в этот показатель.
Еще один способ взглянуть на это: журнал b x функция определяется как обратная b x функция.Эти два утверждения выражают это обратное соотношение, показывающее, как экспоненциальное уравнение эквивалентно логарифмическому уравнению:
x = b y такой же как y = журнал b x
В любом уравнении x — антилогарифм и y — логарифм, по основанию b .
Пример 1: 1000 = 10 3 совпадает с 3 = журнал 10 1000.Логарифм равен 3, а антилогарифм равен 1000.
Пример 2: журнал 3 81 =? та же как 3 ? = 81. Неизвестный ? — логарифм, а 81 — антилогарифм.
Нельзя сказать слишком часто: логарифм — это не что иное, как показатель степени. Вы можете написать приведенное выше определение компактно, и показать журнал как экспоненту, подставив второе уравнение в первое, чтобы исключить y :
Прочтите это как логарифм x по основанию b — это экспонента, которую вы положили на b , чтобы получить в результате x .
Откуда взялись бревна?
Раньше карманные калькуляторы несколько десятилетий назад, но в студенческие годы это возраст динозавровответ было просто. Вам нужны журналы для вычисления большинства мощностей и корней с честным точность; даже умножение и деление большинства чисел было проще с журналами. В каждой приличной книге по алгебре были страницы и страницы журнальных таблиц на спина.
Изобретение бревен в начале 1600-х годов послужило толчком для научных революция. Тогда ученые, особенно астрономы, тратили огромные суммы чисел на бумаге.Сокращая время, которое они тратили на арифметические, логарифмы эффективно давали им более продуктивную жизнь. Логарифмическая линейка, когда-то почти мультяшный товарный знак ученого, был не чем иным, как устройством, созданным для выполнения различных вычислений быстро, используя логарифмы. См. Eli Maors e: The Story of a Number для получения дополнительной информации. это.
Сегодня журналы больше не используются в рутинной обработке чисел. Но все же есть веские причины для их изучения.
Почему мы заботимся?
Почему мы вообще используем логарифмы? Я мог бы написать целую статью о них может быть когда-нибудь.Но сейчас. …
- Узнать количество платежей на заем или время для получения инвестиционная цель.
- Для моделирования многих природных процессов, особенно в живых системах. Мы воспринимаем громкость звука как логарифм реального звука. интенсивность, а дБ (децибелы) — логарифмическая шкала. Звездные величины равны измеряется в логарифмической шкале.
- Для измерения pH или кислотности химического раствора. PH — это отрицательный логарифм концентрации свободных ионы водорода.
- Для измерения силы землетрясений по шкале Рихтера.
- Для анализа экспоненциальных процессов. Поскольку функция журнала является обратной экспоненциальной функции, мы часто анализируем экспоненциальную кривую с помощью логарифмы. Нанесение набора измеренных точек на бревенчатую или полуборочную бумагу может легко выявить такие отношения. Применения включают охлаждение мертвого тела, рост бактерий, и распад радиоактивных изотопов. Распространение эпидемии среди населения часто следует за измененным логарифмическая кривая называется логистической.
- Для решения некоторых форм задач с площадью в исчислении. (Площадь под кривой 1/ x , между x = 1 и x = A , равна ln A .)
- Также в расчетах дифференциация сложного продукта становится намного проще, если вы сначала возьмете логарифм.
(Исторически основная причина преподавания журналы в начальной школе было для упрощения вычислений, потому что журнал умножения понижает его до прибавления, а журнал мощности выражение понижает его до умножения.Конечно, с повсеместной доступностью персональных вычислительных устройств, сложность вычислений больше не вызывает беспокойства, но в журналах все еще есть многие приложения сами по себе.)
Основные факты
Из определения бревна как инверсии экспоненциально, можно сразу получить некоторые основные факты. Например, если вы построите график y = 10 x (или экспоненту с любым другим положительным основанием), вы увидеть, что его диапазон положительный реал; поэтому область y = log x (по любому основанию) — положительные числа.В другом слова, вы не можете взять журнал 0 или журнал отрицательного числа.
(На самом деле, если вы хотите выйти за рамки реалов, вы можете взять журнал отрицательного числа. Этой технике обучают на многих курсах тригонометрии.)
Логарифм из 1, логарифм равняется 1
| Вы знаете, что значение нулевой степени равно 1: b 0 = 1. Измените это на логарифмическую форму с определением журналов, и вы получите | |
| log b 1 = 0 для любого основания b | |
| Точно так же вы знаете, что первая степень любого числа — это именно это число: b 1 = b .Опять же, переведите это в логарифмическую форму, и вы получите | |
| log b b = 1 для любой базы b | |
Пример 3: ln 1 = 0
Пример 4: журнал 5 5 = 1
Записать как обратное
Журнал — это показатель степени, потому что функция журнала — это обратная экспоненциальной функции. Обратная функция отменяет действие исходной функции.(Я не большой поклонник использования термина отмена в математике, но это вписываются в эту ситуацию.)
| Это означает, что если вы возьмете логарифм экспоненты (конечно, с той же базой), вы вернетесь туда, откуда начали: | |
| log b b x = x для любой базы b | |
| Этот факт позволяет вычислять многие логарифмы без калькулятора. | |
Пример 5: журнал 5 125 = журнал 5 (5) = 3
Пример 6: журнал 10 10 3,16 = 3,16
Пример 7: ln e — k t /2 = — k t /2
Whats ln?
В качестве основания логарифмов подходит любое положительное число, но две базы используются больше, чем любые другие:
| основание из логарифмов | символ | имя |
|---|---|---|
| 10 | журнал (если основание не показано) | десятичный логарифм |
| e | пер. | натуральный логарифм, произносится как ell-enn или lahn |
| Натуральные бревна — это бревна, которые подчиняются тем же правилам, что и любой другой логарифм.Просто помните: | |
| ln x означает журнал e x | |
Почему base e? Что такого особенного в е? Большинство объяснений требует некоторого исчисления, например, что e x — единственная функция, которая является самостоятельным целым и его собственная производная, или что e имеет это красивое определение в условия факториалов:
е = 1/0! + 1/1! + 1/2! + 1/3! + …
В числовом выражении e около 2.7182818284. Его иррациональное (десятичное расширение никогда не заканчивается и никогда не повторяется), и на самом деле, как и π, его трансцендентный (ни одно полиномиальное уравнение с целыми коэффициентами не имеет π или e как корень.)
e (например, π) встречается во всевозможных маловероятные места, такие как вычисления сложных процентов. Для объяснения потребовалась бы книга, и к счастью, — это книга, Эли Маорс e: История одного Номер . Он также занимается историей логарифмов, и книга стоит взять из вашей библиотеки.
Объединение журналов с одной базой
Через минуту посмотрите на различные комбинации. Но сначала ты может захотеть узнать общий принцип: журналов сокращают количество операций на один уровень. Бревна превращают умножение в сложение, деление на вычитание, показатель степени на умножение и радикальное разделение. Теперь давайте разберемся, почему, и рассмотрим несколько примеров.
Умножение чисел, складывание их логарифмов
Умножение двух выражений соответствует сложению их логарифмов.Можем ли мы понять это?
| По компактному определению | ||
| x = b log b x и y = b log b y | 09 и x 91 и y , | |
|---|---|---|
| x y = b log b x b log b y | ||
| x y = b log b x + log b y | ||
| Теперь примените компактное определение 3 | = 9057:||
| b log b ( x y ) = x y | ||
| Объедините это с предыдущим уравнением, чтобы получить | ||
| b журнал b ( x y ) = b журнал b x + журнал b 9057 у нас есть две степени одной базы.Если степени равны, то и показатели степени также должны быть равны. Следовательно, | ||
| log b ( x y ) = log b x + log b y | ||
Так что же в итоге? Умножая два числа и беря log — это то же самое, что брать их логи и добавлять.
Пример 8: журнал 8 ( x ) + журнал 8 ( x ) совпадает с журнал 8 ( x x ) или просто журнал 8 ( x ).(Как вы увидите в следующем разделе, это может быть далее упрощено до 3log 8 x .)
Пример 9: журнал 10 (20) + журнал 10 (50) = журнал 10 (2050) = журнал 10 (1000) = 3.
Показатель степени, умножить логарифм
Продолжая нашу тему логарифмов, снижая уровень операций, если у вас есть степень y числа и взять log, результат будет y раз больше log числа.Вот почему, начиная с x y :
| Начнем с компактного определения логарифма: | ||
| x = b log b x | ||
| и поднимите обе стороны до y power: | ||
| x y = ( b log b x ) y | ||
| Степень эквивалентна простому умножению на степень.Упростите правую часть: | ||
| x y = b ( y log b x ) | ||
| Перепишите левую часть, используя компактное определение | log: | |
|---|---|---|
| b log b ( x y ) = x y | ||
| (шрифт может быть трудно читаемым: То есть x в степени y слева и справа.) и объедините последние два уравнения: | ||
| b log b ( x y ) = b ( y log b x ) 9058 | степени 91 равны и основания равны, экспоненты должны быть равны:||
| журнал b ( x y ) = y журнал b x | ||
Пример 10: ln (2 6 ) = 6 ln 2 (где ln означает log e , естественное логарифм).
Пример 11: log 5 (5 x ) равно , а не равно 2 журнала 5 (5 x ). Будьте внимательны с порядком действий! 5 x равно 5 ( x ), а не (5 x ). log 5 (5 x ) необходимо сначала разложить как бревно товара: журнал 5 5 + журнал 5 ( x ). Тогда второй член может использовать правило мощности, журнал 5 ( x ) = 2 журнала 5 x .Первый член всего 1. Подводя итоги, журнал 5 (5 x ) = 1 + 2 журнала 5 x .
Возведение чисел в любую степень
Уловка для вычисления таких выражений, как 6,7 4,4 , заключается в использовать правило экспоненты и определение логарифма как обратного:
х = 6,7 4,4
журнал x = 4,4 (журнал 6,7) = около 3,634729132
x = 10 3,63472 … = около 4312,5
Здесь нет ничего особенного в журналах base-10.В расчет с таким же успехом может быть
х = 6,7 4,4
ln x = 4,4 (ln 6,7) = примерно 8,369 273116
x = e 8,36927 … = около 4312,5
Это будет работать для любого положительного основания и любого реального показателя степени, поэтому например
х = π π
журнал x = π (журнал π) = примерно 1,561842388
x = 10 1,5618 … = около 36,46215961
Вы можете комбинировать это с умножение чисел = добавление правила логарифма к оцените возможности, которые слишком велики для вашего калькулятора.Например, что такое 671 217 ?
х = 671 217
журнал x = 217 (журнал 671) = около 613,3987869
Теперь разделите целую и дробную части логарифм.
журнал x = около 0,3987869 + 613
х = 10 0,3987869 + 613
х = 10 0,3987869 10 613
x = около 2,505 10 613
Для таких примеров вам действительно нужно использовать base-10 журналы.
Если основание отрицательное или показатель сложный, см. Силы и корни комплексного числа.
Разделите числа, вычтите их логарифмы
Так как деление противоположно умножению, а вычитание противоположность сложения, неудивительно, что деление двух выражения соответствует вычитанию их журналов. Пока мы могли пойти вернемся к компактному определению, его вероятно, проще использовать два предыдущих свойства.
| Начнем с того, что 1/ y = y −1 (см. Определение отрицательных показателей): | |
| x / y = x (1/ y ) = x y −1 | |
| и возьмите лог с обеих сторон: | |
| log b ( x / y ) = log b ( x y −1 ) | |
| Правая часть — лог продукта , которая становится суммой журналов: | |
| log b ( x / y ) = log b x + log b ( y −1 ) | |
| журнал b ( x / y ) = журнал b x — журнал b y | |
Словами, если разделить и взять журнал , это то же самое, что и вычитая отдельные журналы.
Пример 12: 67515 = 45, поэтому журнал 10 675 — журнал 10 15 = log 10 45. (Попробуйте на своем калькуляторе!)
Пример 13: журнал ( x y ) — журнал ( x y ) = журнал ( x y / x y ) = журнал ( x / y ) = журнал ( x ) — журнал ( y ).
Замена базы
Теперь у вас есть все необходимое для изменения логарифмов с единицы база к другому.Посмотрите еще раз на компакт уравнение, определяющее журнал в базе b :
| Чтобы изменить журнал с базы b на другую базу (назовите ее a ), вы хотите найти журнал a ( x ). Поскольку у вас уже есть x на одной стороне приведенного выше уравнения, кажется, что хорошее начало — взять основание — , журнал для обеих сторон: | |
| log a ( b log b x ) = log a x | |
| Но левая часть этого уравнения — это всего лишь логарифм. власти.Вы помните, что журнал ( x y ) — это просто журнал ( x ), умноженный на y . Таким образом, уравнение упрощается до | |
| (журнал a b ) (журнал b x ) = журнал a x | |
Обратите внимание, что это журнал 10 a 9 9 постоянный. Этот означает, что журналы всех чисел в данной базе a пропорционально логам таких же номеров в другой базе b , а константа пропорциональности log a b равна журнал одной базы в другой базе.Если вы похожи на меня, у вас могут быть проблемы с запоминанием умножать или делить. Если да, просто выведите уравнение, как видите, занимает всего два шага.
| В некоторых учебниках формула замены базы представлена в виде дроби. Чтобы получить дробь из приведенного выше уравнения, просто разделите на коэффициент пропорциональности log a b : | |
| журнал b x = (журнал a x ) / (журнал a b ) | |
Пример 14: журнал 4 16 = (журнал 16) / (журнал 4).(Вы можете проверить это на своем калькуляторе, так как вы знать журнал 4 16 должно быть равно 2.)
Пример 15: Большинство калькуляторов не могут построить график y = log 3 x напрямую. Но вы можете изменить базу на e и легко построить график y = (ln x ) (ln 3). (Вы могли одинаково хорошо используйте базу 10.)
| Интересный переулок ведет из приведенной выше формулы. Замените x везде на a , это допустимо, поскольку формула верна для всех положительных значений a , b и x .Получаете | |
| log b a = (log a a ) / (log a b ) | |
| Но log a = a (см. Журнал 1 выше), поэтому формула принимает вид | |
| log b a = 1 / (log a b ) | |
Пример 16: журнал 10 e = 1 / (ln 10).(Вы можете проверить это на своем калькуляторе.)
Пример 17: журнал 125 5 = 1 / (журнал 5 125). В этом легко убедиться: 5 3 = 125, а 5 — кубический корень из 125. Следовательно, log 125 5 = 1/3 и log 5 125 = 3, и 1/3 действительно равно 1/3.
Сводка
Законы логарифмов были разбросаны по этому длинному
страницу, поэтому было бы полезно собрать их в одном месте. Делать
это еще более полезно,
Ради бога, не пытайтесь запомнить эту таблицу! Просто используйте это, чтобы по мере необходимости пробуждайте память. Еще лучше, поскольку журнал является экспонентой, используйте законы экспонентов, чтобы повторно получить любую собственность логарифмов, которые вы могли забыть. Таким образом, вы действительно получите владение этим материалом, и вы будете чувствовать себя уверенно операции.
| экспоненты | логарифмы |
|---|---|
| (Все законы применяются для любых положительных значений a , b , x и y .) | |
| x = b y такой же как y = журнал b x | |
| b 0 = 1 | журнал b 1 = 0 |
| b 1 = b | журнал b b = 1 |
| b (лог b x ) = x | журнал b b x = x |
| b x b y | лог b ( x y ) = лог b x + лог b y |
| b 90/ y = b x — y | журнал b ( x / y ) = журнал b x — журнал b y |
| ( b y = b x y | журнал b ( x y ) = y журнал b x |
| (журнал a b ) (журнал b x ) = журнал a x | |
| журнал b 9 = a x ) / (лог a b ) | |
| лог b a = 1 / (лог a b ) | |
Не проявляйте творчества! Большинство вариантов вышеизложенного недействительны.
Пример 18: журнал (5+ x ) не то же самое, что журнал 5 + журнал x . Как вы знаете, журнал 5 + журнал x = журнал (5 x ), а не журнал (5+ x ). Внимательно посмотрите на приведенную выше таблицу, и вы увидите что вы ничего не можете сделать, чтобы разделить журнал ( x + y ) или журнал ( x — y ).
Пример 19: (журнал x ) / (log y ) не то же самое, что log ( x / y ).В Фактически, когда вы делите два журнала на одну базу, вы обратная работа по формуле замены базы. Хотя это не часто полезно, (журнал x ) / (журнал y ) = журнал y x . Только не пишите журнал ( x / y )!
Пример 20: (журнал 5) (журнал x ) не является то же, что и журнал (5 x ). Вы знаете, что журнал (5 x ) журнал 5 + журнал x . На самом деле ты мало что можешь делать с произведением двух бревен, когда они имеют одинаковую основу.(Вы можете переписать продукт как журнал ( x журнал 5 ), но это вряд ли попроще.)
См. Также: Объединение операций (распределительные законы)
Заключение
Ну вот и все: законы логарифмов демистифицировано! Общее правило заключается в том, что журналы просто отбрасывают операцию. на один уровень вниз: показатели становятся множителями, деления становятся вычитания и так далее. Если вы когда-нибудь не уверены в операции, например как сменить базу, работа это с помощью определения журнала и применяя законы экспонент, и вы не ошибетесь.
Что нового
- 28 мая 2021 г. : Добавил ссылку на мою новую страницу звездных величин и удалили утверждение, которое мы воспринимаем интенсивность света логарифмически, поскольку недавние исследования поставили под сомнение на том.
- 7 декабря 2020 г. :
- 20/23 октября 2020 г. : преобразованная страница из HTM 4.

 Применяем его и получаем loge2345=452·ln 3=25·ln 3.
Применяем его и получаем loge2345=452·ln 3=25·ln 3.