Углы параллелограмма сколько градусов. Как найти острый угол параллелограмма
Параллелограммом называется четырехугольник, у которго противоположные стороны параллельны, т.е. лежат на параллельных прямых
Свойства параллелограмма:
Теорема 22. Противоположные стороны параллелограма равны.
Доказательство. В параллелограмме АВСD проведем диагональ АС. Треугольники АСD и АСВ равны, как имеющие общую сторону АС и две пары равных углов. прилежащих к ней: ∠
САВ=∠
АСD, ∠
АСВ=∠
DAC (как накрест лежащие углы при параллельных прямых AD и ВС). Значит, АВ=CD и ВС=AD, как соответственные стороны равных треугольников, ч.т.д. Из равенства этих треугольников также следует равенство соответственных углов треугольников:
Теорема 23. Противоположные углы параллелограмма равны: ∠
А=∠
С и ∠
В=∠
D.
Равенство первой пары идет из равенства треугольников АВD и CBD, а второй — АВС и ACD.
Теорема 24. Соседние углы параллелограмма, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов.
Это так, потому что они являются внутренними односторонними углами.
Теорема 25. Диагонали параллелограмма делят друг друга в точке их пересечения пополам.
Доказательство. Рассмотрим треугольники ВОС и АОD. По первому свойству AD=ВС ∠ ОАD=∠ ОСВ и ∠ ОDА=∠ ОВС как накрест лежащие при параллельных прямых AD и ВС. Поэтому треугольники ВОС и АОD равны по стороне и прилежащим к ней углам. Значит, ВО=ОD и АО=ОС, как соответственные стороны равных треугольников, ч.т.д.
Признаки параллелограмма
Теорема 26. Если противоположные стороны четырехугольника попарно равны, то он является параллелограммом.
Доказательство. Пусть у четырехугольника АВСD стороны AD и ВС, АВ и CD соответственно равны (рис2). Проведем диагональ АС. Треугольникик АВС и ACD равны по трем сторонам. Тогда углы ВАС и DСА равны и, следовательно, АВ параллельна CD. Параллельность сторон ВС и AD следует из равенства углов CAD и АСВ.

Пусть ∠ А=∠ С и ∠ В=∠ D. Т.к. ∠ А+∠ В+∠ С+∠ D=360 о, то ∠ А+∠ В=180 о и стороны AD и ВС параллельны (по признаку параллельности прямых). Также докажем и параллельность сторон АВ и CD и заключим, что АВСD является параллелограммом по определению.
Теорема 28. Если соседние углы четырехугольника, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов, то он является параллелограммом.
Если внутренние односторонные углы в сумме составляют 180 градусов, то прямые праллельны. Значит АВ парал CD и ВС парал AD. Четырехугольник оказывается параллелограммом по определению.
Теорема 29. Если диагонали четырехугольника взаимно делятся в точке пересечения пополам, то четырехугольник — параллелограмм.
Доказательство. Если АО=ОС, ВО=ОD, то треугольники АOD и ВОС равны, как имеющие равны углы (вертикальные) при вершине О, заключенные между парами равных сторон. Из равенства треугольников заключаем, что AD и ВС равны. Также равны стороны АВ и CD, и четырехугольник оказывается параллелограммом по признаку 1.

Теорема 30. Если четырехугольник имеет пару равных, параллельных между собой сторон, то он является параллелограммом.
Пусть в четырехугольнике АВСD стороны АВ и CD параллельны и равны. Проведем диагонали АС и ВD. Из параллельности этих прямых следует равенство накрест лежащих углов АВО=СDО и ВАО=ОСD. Треугольники АВО и CDО равны по стороне и прилежащим к ней углам. Поэтому АО=ОС, ВО=ОD, т.е. диагонали точкой пересечения делятся пополам и четырехугольник оказывается параллелограммом по признаку 4.
В геометрии рассматривают частные случаи параллелограмма.
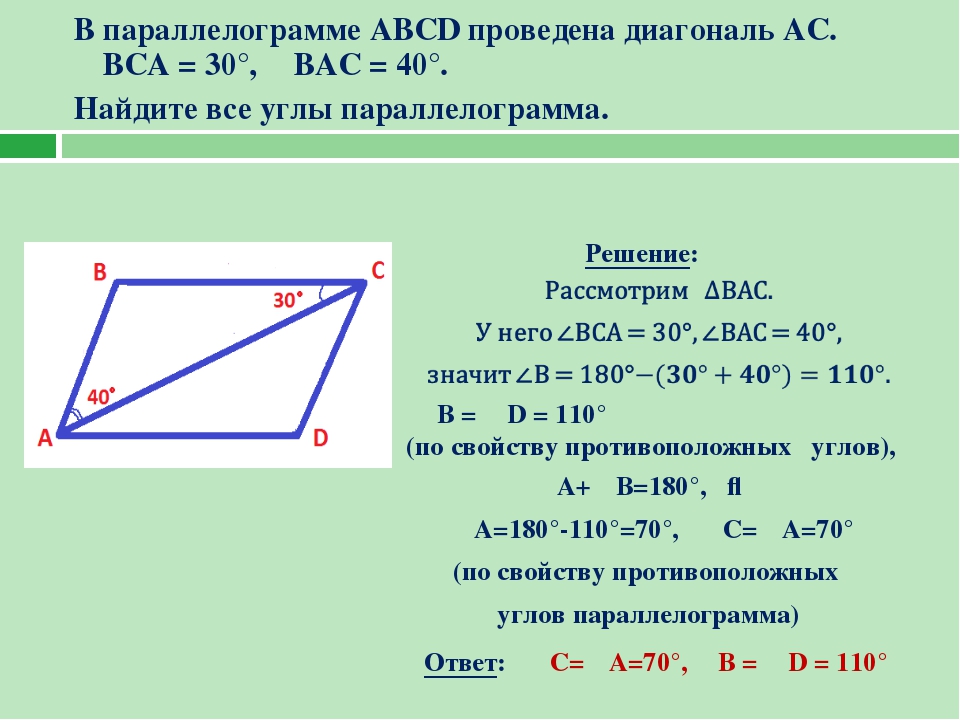
Задача 1 . Один из углов параллелограмма равен 65°. Найти остальные углы параллелограмма.
∠C =∠A = 65° как противоположные углы параллелограмма.
∠А +∠В = 180° как углы, прилежащие к одной стороне параллелограмма.
∠В = 180° — ∠А = 180° — 65° = 115°.
∠D =∠B = 115° как противолежащие углы параллелограмма.
Ответ: ∠А =∠С = 65°; ∠В =∠D = 115°.
Задача 2. Сумма двух углов параллелограмма равна 220°. Найти углы параллелограмма.
Найти углы параллелограмма.
Так как у параллелограмма имеется 2 равных острых угла и 2 равных тупых угла, то нам дана сумма двух тупых углов, т.е. ∠В +∠D = 220°. Тогда ∠В =∠D = 220°: 2 = 110°.
∠А +∠В = 180° как углы, прилежащие к одной стороне параллелограмма, поэтому ∠А = 180° — ∠В = 180° — 110° = 70°. Тогда ∠C =∠A = 70°.
Ответ: ∠А =∠С = 70°; ∠В =∠D = 110°.
Задача 3. Один из углов параллелограмма в 3 раза больше другого. Найти углы параллелограмма.
Пусть ∠А =х. Тогда ∠В = 3х. Зная, что сумма углов параллелограмма, прилежащих к одной его стороне равна 180°, составим уравнение.
х = 180 : 4;
Получаем: ∠А =х = 45°, а ∠В = 3х = 3 ∙ 45° = 135°.
Противолежащие углы параллелограмма равны, следовательно,
∠А =∠С = 45°; ∠В =∠D = 135°.
Ответ: ∠А =∠С = 45°; ∠В =∠D = 135°.
Задача 4. Докажите, что если у четырехугольника две стороны параллельны и равны, то этот четырехугольник – параллелограмм.
Доказательство.
Проведем диагональ BD и рассмотрим Δ ADB и Δ CBD.
AD = BC по условию. Сторона BD – общая. ∠1 = ∠2 как внутренние накрест лежащие при параллельных (по условию) прямых AD и BC и секущей BD. Следовательно, Δ ADB = Δ CBD по двум сторонам и углу между ними (1-й признак равенства треугольников). В равных треугольниках соответственные углы равны, значит, ∠3 =∠4. А эти углы являются внутренними накрест лежащими при прямых AB и CD и секущей BD. Отсюда следует параллельность прямых AB и CD. Таким образом, в данном четырехугольнике ABCD противолежащие стороны попарно параллельны, следовательно, по определению ABCD – параллелограмм, что и требовалось доказать.
Задача 5. Две стороны параллелограмма относятся как 2 : 5, а периметр равен 3,5 м. Найти стороны параллелограмма.
∙ (AB + AD).
Обозначим одну часть через х. тогда AB = 2x, AD = 5x метров. Зная, что периметр параллелограмма равен 3,5 м, составим уравнение:
2 ∙ (2x + 5x) = 3,5;
2 ∙ 7x = 3,5;
x = 3,5 : 14;
Одна часть составляет 0,25 м. Тогда AB = 2 ∙ 0,25 = 0,5 м; AD = 5 ∙ 0,25 = 1,25 м.
Тогда AB = 2 ∙ 0,25 = 0,5 м; AD = 5 ∙ 0,25 = 1,25 м.
Проверка.
Периметр параллелограмма P ABCD = 2 ∙ (AB + AD) = 2 ∙ (0,25 + 1,25) = 2 ∙ 1,75 = 3,5 (м).
Так как противоположные стороны параллелограмма равны, то CD = AB = 0,25 м; BC = AD = 1,25 м.
Ответ: CD = AB = 0,25 м; BC = AD = 1,25 м.
Параллелограммом называется такой четырехугольник, в котором противоположные стороны попарно параллельны.
Параллелограмм обладает всеми свойствами четырехугольников, но кроме этого имеет и свои отличительные особенности. Зная их, мы можем с легкостью находить как стороны, так и углы параллелограмма.
Свойства параллелограмма
- Сумма углов в любом параллелограмме, как и в любом четырехугольнике, равна 360°.
- Средние линии параллелограмма и его диагонали пересекаются в одной точке и делятся ею пополам. Эту точку принято называть центром симметрии параллелограмма.
- Противоположные стороны у параллелограмма всегда равны.

- Также у этой фигуры всегда равны противоположные углы.
- Сумма углов, которые прилегают к любой из сторон параллелограмма, всегда составляет 180°.
- Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон. Это выражается формулой:
- d 1 2 + d 2 2 = 2 (a 2 +b 2), где d 1 и d 2 — диагонали, a и b — смежные стороны.
- Косинус тупого угла всегда меньше нуля.
Как найти углы заданного параллелограмма, применяя эти свойства на практике? И какие еще формулы могут нам в этом помочь? Рассмотрим конкретные задания, в которых требуют: найдите величины углов параллелограмма.
Нахождение углов параллелограмма
Случай 1. Известна мера тупого угла, требуется найти острый угол.
Пример: В параллелограмме ABCD угол A равен 120°. Найдите меру остальных углов.
Решение: Пользуясь свойством № 5, мы можем найти меру угла B, смежного с тем углом, который дан в задании. Он будет равен:
А теперь, пользуясь свойством №4, мы определяем, что два оставшихся угла C и D противоположны тем углам, которые мы уже нашли. Угол C противоположен углу A, угол D — углу B. А следовательно они попарно им равны.
Угол C противоположен углу A, угол D — углу B. А следовательно они попарно им равны.
- Ответ: B = 60°, C = 120°, D=60°
Случай 2. Известны длины сторон и диагонали
В таком случае нам необходимо воспользоваться теоремой косинусов.
Мы можем сначала по формуле вычислить косинус нужного нам угла, а потом по специальной таблице найти, чему равен сам угол.
Для острого угла формула такая:
- cosa = (А² + В² — d²) / (2 * А * В), где
- а — это искомый острый угол,
- А и В — стороны параллелограмма,
- d — меньшая диагональ
Для тупого угла формула немного меняется:
- cosß = (А² + В² — D²) / (2 * А * В), где
- ß — это тупой угол,
- А и В — стороны,
- D — большая диагональ
Пример: необходимо найти острый угол параллелограмма, стороны которого равны 6 см и 3 см, а меньшая диагональ равна 5.2 см
Подставляем значения в формулу для нахождения острого угла:
- cosa = (6 2 + 3 2 — 5.
 2 2) / (2 * 6 * 3) = (36 + 9 — 27.04) / (2 * 18) = 17.96/36 ~ 18/36 ~1/2
2 2) / (2 * 6 * 3) = (36 + 9 — 27.04) / (2 * 18) = 17.96/36 ~ 18/36 ~1/2 - cosa = 1/2. По таблице выясняем, что искомый угол равен 60°.
Параллелограммом называют четырехугольник противолежащие стороны которого попарно параллельны. Также параллелограмм владеет такими свойствами, как противоположные стороны равны, противоположные углы равны, сумма всех углов равна 360 градусов.
Вам понадобится
- Знания по геометрии.
Инструкция
1. Представим дан один из углов параллелограмма и равен A. Обнаружим значения остальных 3. По свойству параллелограмма противоположные углы равны. Значит угол, лежащий наоборот данного равен данному и его значение равно А.
2. Обнаружим оставшиеся два угла. Потому что сумма всех углов в параллелограмме равна 360 градусов, а противоположные углы между собой равны, то получается, что угол, принадлежащий одной стороне с данным, равен (360 — 2А)/2. Ну либо позже реформирования получим 180 — А.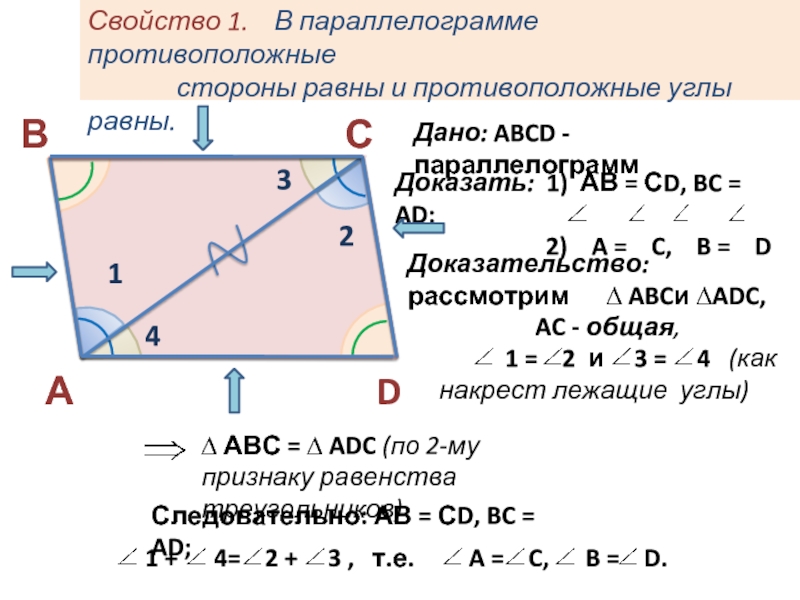
Обратите внимание!
Значение одного угла не может превышать 180 градусов. Полученные значения углов дозволено легко проверить. Для этого сложите их и, если сумма равна 360, все посчитано правильно.
Полезный совет
Прямоугольник и ромб являются частным случаем параллелограмма, следственно все свойства и способы вычисления углов применимы и к ним.
Параллелограмм представляет собой четырехугольник, у которого противоположные стороны попарно параллельны. Это определение уже достаточно, так как остальные свойства параллелограмма следуют из него и доказываются в виде теорем.
Основными свойствами параллелограмма являются:
- параллелограмм — это выпуклый четырехугольник;
- у параллелограмма противоположные стороны попарно равны;
- у параллелограмма противоположные углы попарно равны;
- диагонали параллелограмма точкой пересечения делятся пополам.

Параллелограмм — выпуклый четырехугольник
Докажем сначала теорему о том, что параллелограмм является выпуклым четырехугольником . Многоугольник является выпуклым тогда, когда какая бы его сторона не была продлена до прямой, все остальные стороны многоугольника окажутся по одну сторону от этой прямой.
Пусть дан параллелограмм ABCD, у которого AB противоположная сторона для CD, а BC — противоположная для AD. Тогда из определения параллелограмма следует, что AB || CD, BC || AD.
У параллельных отрезков нет общих точек, они не пересекаются. Это значит, что CD лежит по одну сторону от AB. Поскольку отрезок BC соединяет точку B отрезка AB с точкой C отрезка CD, а отрезок AD соединяет другие точки AB и CD, то отрезки BC и AD также лежат по ту же сторону от прямой AB, где лежит CD. Таким образом, все три стороны — CD, BC, AD — лежат по одну сторону от AB.
Аналогично доказывается, что по отношению к другим сторонам параллелограмма три остальные стороны лежат с одной стороны.
Противоположные стороны и углы равны
Одним из свойств параллелограмма является то, что в параллелограмме противоположные стороны и противоположные углы попарно равны . Например, если дан параллелограмм ABCD, то у него AB = CD, AD = BC, ∠A = ∠C, ∠B = ∠D. Доказывается эта теорема следующим образом.
Параллелограмм является четырехугольником. Значит, у него две диагонали. Так как параллелограмм — это выпуклый четырехугольник, то любая из них делит его на два треугольника. Рассмотрим в параллелограмме ABCD треугольники ABC и ADC, полученные в результате проведения диагонали AC.
У этих треугольников одна сторона общая — AC. Угол BCA равен углу CAD, как вертикальные при параллельных BC и AD. Углы BAC и ACD также равны как вертикальные при параллельных AB и CD. Следовательно, ∆ABC = ∆ADC по двум углам и стороне между ними.
В этих треугольниках стороне AB соответствует сторона CD, а стороне BC соответствует AD. Следовательно, AB = CD и BC = AD.
Углу B соответствует угол D, т. е. ∠B = ∠D. Угол A параллелограмма представляет собой сумму двух углов — ∠BAC и ∠CAD. Угол же C равен состоит из ∠BCA и ∠ACD. Так как пары углов равны друг другу, то ∠A = ∠C.
е. ∠B = ∠D. Угол A параллелограмма представляет собой сумму двух углов — ∠BAC и ∠CAD. Угол же C равен состоит из ∠BCA и ∠ACD. Так как пары углов равны друг другу, то ∠A = ∠C.
Таким образом, доказано, что в параллелограмме противоположные стороны и углы равны.
Диагонали делятся пополам
Так как параллелограмм — это выпуклый четырехугольник, то у него две две диагонали, и они пересекаются. Пусть дан параллелограмм ABCD, его диагонали AC и BD пересекаются в точке E. Рассмотрим образованные ими треугольники ABE и CDE.
У этих треугольников стороны AB и CD равны как противоположные стороны параллелограмма. Угол ABE равен углу CDE как накрест лежащие при параллельных прямых AB и CD. По этой же причине ∠BAE = ∠DCE. Значит, ∆ABE = ∆CDE по двум углам и стороне между ними.
Также можно заметить, что углы AEB и CED вертикальные, а следовательно, тоже равны друг другу.
Так как треугольники ABE и CDE равны друг другу, то равны и все их соответствующие элементы.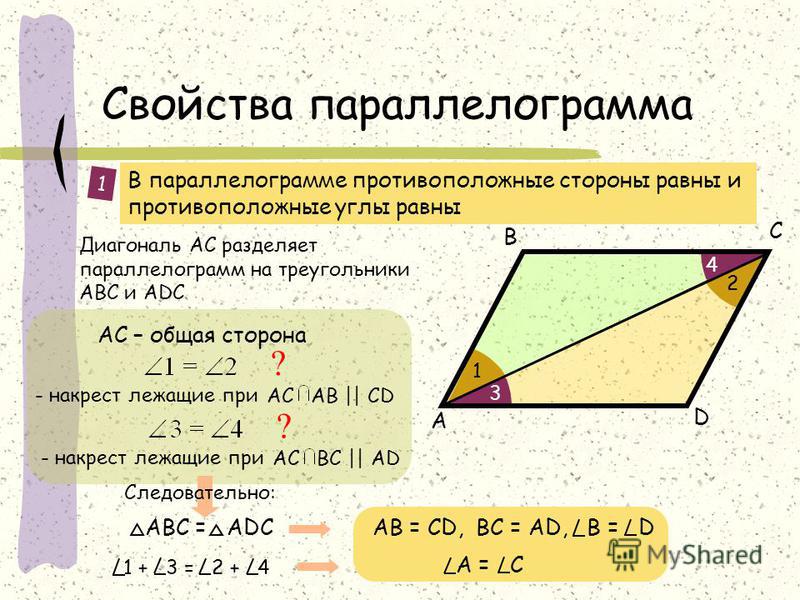 Стороне AE первого треугольника соответствует сторона CE второго, значит, AE = CE. Аналогично BE = DE. Каждая пара равных отрезков составляет диагональ параллелограмма. Таким образом доказано, что диагонали параллелограмма делятся точкой пересечения пополам .
Стороне AE первого треугольника соответствует сторона CE второго, значит, AE = CE. Аналогично BE = DE. Каждая пара равных отрезков составляет диагональ параллелограмма. Таким образом доказано, что диагонали параллелограмма делятся точкой пересечения пополам .
Как найти синус угла параллелограмма если известны. Площадь параллелограмма
Тогда (Так как в прямоугольном треугольнике катет, который лежит против угла в 30 о, равен половине гипотенузы).
Но СD = АВ. Тогда АВ: НD = 2: 1.
3.
4.
Ответ: АВ: НD = 2: 1,
Задача 4.
Одна из диагоналей параллелограмма длиною 4√6, составляет с основанием угол 60 о, а вторая диагональ составляет с тем же основанием угол 45 о. Найти вторую диагональ.
Решение.
1. АО = 2√6.
2. К треугольнику АОD применим теорему синусов.
АО/sin D = OD/sin А.
2√6/sin 45 о = OD/sin 60 о.
ОD = (2√6sin 60 о) / sin 45 о = (2√6 · √3/2) / (√2/2) = 2√18/√2 = 6.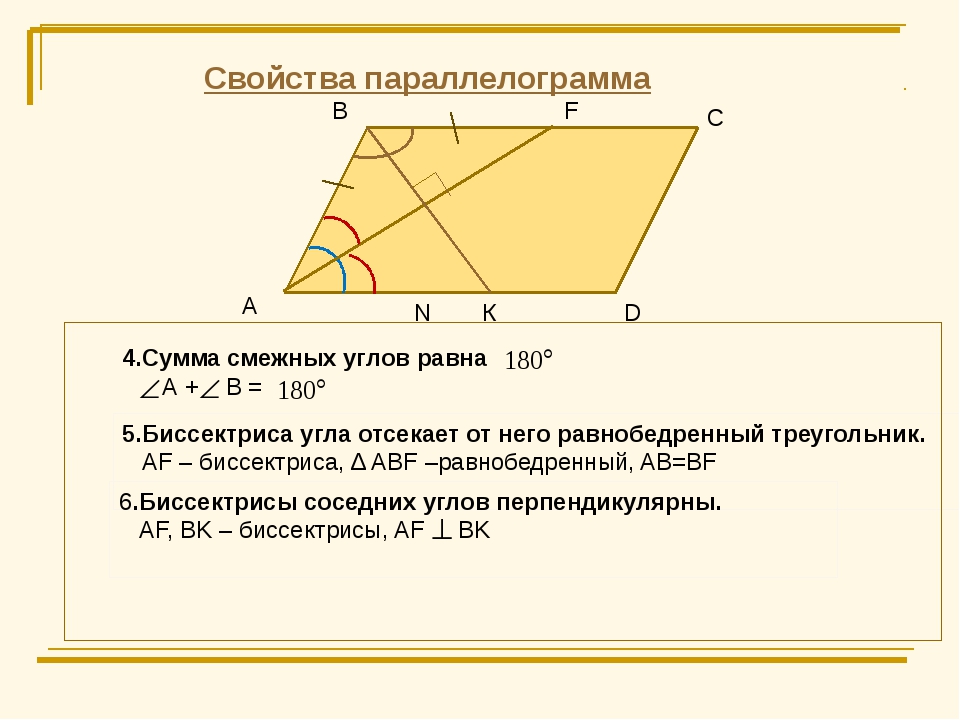
Ответ: 12.
Задача 5.
У параллелограмма со сторонами 5√2 и 7√2 меньший угол между диагоналями равен меньшему углу параллелограмма. Найдите сумму длин диагоналей.
Решение.
Пусть d 1 , d 2 – диагонали параллелограмма, а угол между диагоналями и меньший угол параллелограмма равен ф.
1. Посчитаем двумя разными
способами его площадь.
S ABCD = AB · AD · sin A = 5√2 · 7√2 · sin ф,
S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin ф.
Получим равенство 5√2 · 7√2 · sin ф = 1/2d 1 d 2 sin ф или
2 · 5√2 · 7√2 = d 1 d 2 ;
2. Используя соотношение между сторонами и диагоналями параллелограмма запишем равенство
(АВ 2 + АD 2) · 2 = АС 2 + ВD 2 .
((5√2) 2 + (7√2) 2) · 2 = d 1 2 + d 2 2 .
d 1 2 + d 2 2 = 296.
3. Составим систему:
{d 1 2 + d 2 2 = 296,
{d 1 + d 2 = 140.
Умножим второе уравнение системы на 2 и сложим с первым.
Получим (d 1 + d 2) 2 = 576. Отсюда Id 1 + d 2 I = 24.
Отсюда Id 1 + d 2 I = 24.
Так как d 1 , d 2 – длины диагоналей параллелограмма, то d 1 + d 2 = 24.
Ответ: 24.
Задача 6.
Стороны параллелограмма 4 и 6. Острый угол между диагоналями равен 45 о. Найдите площадь параллелограмма.
Решение.
1. Из треугольника АОВ, используя теорему косинусов, запишем соотношение между стороной параллелограмма и диагоналями.
АВ 2 = АО 2 + ВО 2 2 · АО · ВО · cos АОВ.
4 2 = (d 1 /2) 2 + (d 2 /2) 2 – 2 · (d 1 /2) · (d 2 /2)cos 45 о;
d 1 2 /4 + d 2 2 /4 – 2 · (d 1 /2) · (d 2 /2)√2/2 = 16.
d 1 2 + d 2 2 – d 1 · d 2 √2 = 64.
2. Аналогично запишем соотношение для треугольника АОD.
Учтем, что
Получим уравнение d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
3. Имеем систему
{d 1 2 + d 2 2 – d 1 · d 2 √2 = 64,
{d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
Вычитая из второго уравнения первое, получим 2d 1 · d 2 √2 = 80 или
d 1 · d 2 = 80/(2√2) = 20√2
4. S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin α = 1/2 · 20√2 · √2/2 = 10.
S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin α = 1/2 · 20√2 · √2/2 = 10.
Примечание: В этой и в предыдущей задаче нет надобности, решать полностью систему, предвидя то, что в данной задаче для вычисления площади нам нужно произведение диагоналей.
Ответ: 10.
Задача 7.
Площадь параллелограмма равна 96, а его стороны равны 8 и 15. Найдите квадрат меньшей диагонали.
Решение.
1. S ABCD = AВ · АD · sin ВAD. Сделаем подстановку в формулу.
Получим 96 = 8 · 15 · sin ВAD. Отсюда sin ВAD = 4 / 5 .
2. Найдём cos ВАD. sin 2 ВAD + cos 2 ВАD = 1.
(4 / 5) 2 + cos 2 ВАD = 1. cos 2 ВАD = 9 / 25 .
По условию задачи мы находим длину меньшей диагонали. Диагональ ВD будет меньшей, если угол ВАD острый. Тогда cos ВАD = 3 / 5.
3. Из треугольника АВD по теореме косинусов найдём квадрат диагонали ВD.
ВD 2 = АВ 2 + АD 2 – 2 · АВ · ВD · cos ВАD.
ВD 2 = 8 2 + 15 2 – 2 · 8 · 15 · 3 / 5 = 145.
Ответ: 145.
Остались вопросы? Не знаете, как решить геометрическую задачу?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Вывод формулы площади параллелограмма сводится к построению прямоугольника, равного данному параллелограмму по площади. Примем одну сторону параллелограмма за основание, а перпендикуляр, проведенный из любой точки противолежащей стороны на прямую, содержащую основание будем называть высотой параллелограмма. Тогда площадь параллелограмма будет равна произведению его основания на высоту.
Теорема. Площадь параллелограмма равна произведению его основания на высоту.
Доказательство . Рассмотрим параллелограмм с площадью. Примем сторонуза основание и проведем высотыи(рисунок 2.3.1). Требуется доказать, что.
Рисунок 2.3.1
Докажем
сначала, что площадь прямоугольника
также равна.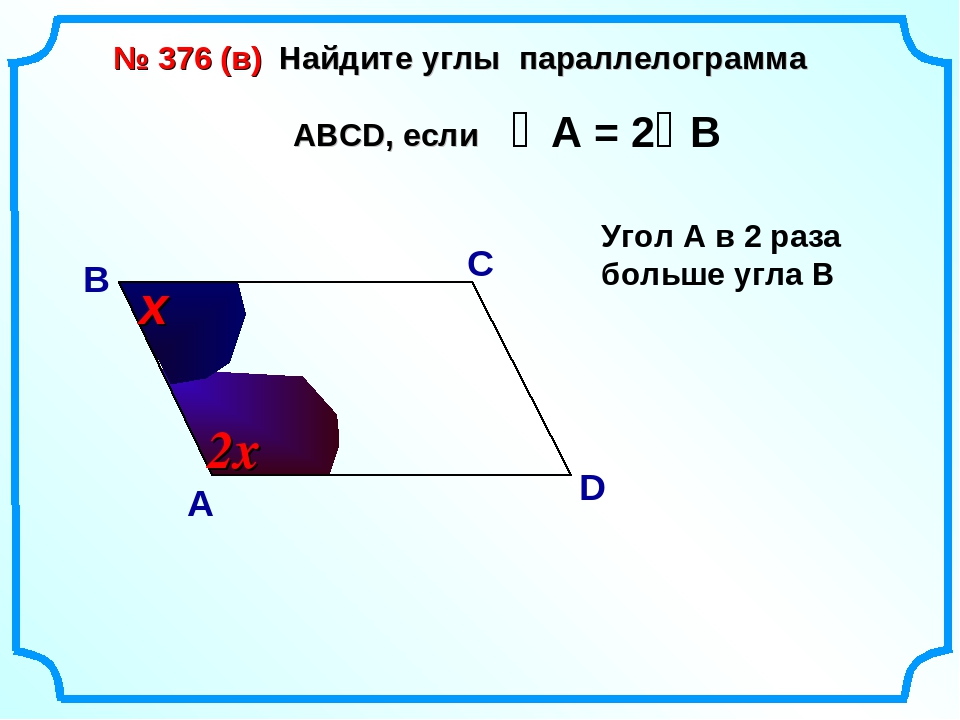 Трапециясоставлена из параллелограммаи треугольника.
С другой стороны, она составлена из
прямоугольника НВСК и треугольника.
Но прямоугольные треугольникии
равны
по гипотенузе и острому углу (их
гипотенузыиравны как противоположные стороны
параллелограмма, а углы 1 и 2 равны как
соответственные углы при пересечении
параллельных прямыхисекущей),
поэтому их площади равны. Следовательно,
площади параллелограммаи прямоугольникатакже равны, то есть площадь прямоугольникаравна.
По теореме о площади прямоугольника,
но так как,
то.
Трапециясоставлена из параллелограммаи треугольника.
С другой стороны, она составлена из
прямоугольника НВСК и треугольника.
Но прямоугольные треугольникии
равны
по гипотенузе и острому углу (их
гипотенузыиравны как противоположные стороны
параллелограмма, а углы 1 и 2 равны как
соответственные углы при пересечении
параллельных прямыхисекущей),
поэтому их площади равны. Следовательно,
площади параллелограммаи прямоугольникатакже равны, то есть площадь прямоугольникаравна.
По теореме о площади прямоугольника,
но так как,
то.
Теорема доказана.
Пример 2.3.1.
В ромб со стороной и острым углом вписана окружность. Определить площадь четырёхугольника, вершинами которого являются точки касания окружности со сторонами ромба.
Решение:
Радиус
вписанной в ромб
окружности (рисунок 2.3.2),
поскольку
Четырёхугольникявляется прямоугольником, так как его
углы опираются на диаметр окружности.
Его площадь,
где(катет, лежащий против угла),.
Рисунок
2. 3.2
3.2
Итак,
Ответ:
Пример 2.3.2.
Дан ромб , диагонали которого равны 3 см и 4 см. Из вершины тупого угла проведены высотыиВычислить площадь четырёхугольника
Решение:
Площадь ромба (рисунок 2.3.3).
Итак,
Ответ:
Пример 2.3.3.
Площадь четырёхугольника равна Найти площадь параллелограмма, стороны которого равны и параллельны диагоналям четырёхугольника.
Решение:
Так как и(рисунок 2.3.4), то– параллелограмм и, значит,.
Рисунок 2.3.4
Аналогично получаем откуда следует, что.
Ответ: .
2.4 Площадь треугольника
Существует несколько формул для вычисления площади треугольника. Рассмотрим те, что изучаются в школе.
Первая формула вытекает из формулы площади параллелограмма и предлагается учащимся в виде теоремы.
Теорема. Площадь треугольника равна половине
произведения его основания на высоту .
Доказательство. Пусть – площадь треугольника. Примем сторонуза основание треугольника и проведем высоту. Докажем что:
Рисунок 2.4.1
Достроим треугольник до параллелограмматак, как показано на рисунке. Треугольникииравны по трем сторонам (– их общая сторона,икак противоположные стороны параллелограма), поэтому их площади равны. Следовательно, площадь S треугольника АВС равна половине площади параллелограмма, т.е.
Теорема доказана.
Важно обратить внимание учащихся на два следствия, вытекающих из данной теоремы. А именно:
площадь прямоугольного треугольника равна половине произведения его катетов.
если высоты двух треугольников равны, то их площади относятся как основания.
Эти два следствия играют важную роль в решении разного рода задач. С опорой на данную доказывается еще одна теорема, имеющая широкое применение при решении задач.
Теорема. Если
угол одного треугольника равен углу
другого треугольника, то их площади
относятся как произведения сторон,
заключающих равные углы.
Доказательство . Пусть и– площади треугольникови, у которых углыиравны.
Рисунок 2.4.2
Докажем, что: .
Наложим треугольник . на треугольниктак, чтобы вершинасовместилась с вершиной, а стороныиналожились соответственно на лучии.
Рисунок 2.4.3
Треугольники иимеют общую высоту, поэтому,. Треугольникиитакже имеют общую высоту –, поэтому,. Перемножая полученные равенства, получим.
Теорема доказана.
Вторая формула. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними. Существует несколько способов доказательства этой формулы, и я воспользуюсь одним из них.
Доказательство. Из геометрии известна теорема о том, что площадь треугольника равна половине произведения основания на высоту, опущенную на это основание:
В случае остроугольного треугольника . В случае тупого угла. Ho, а поэтому. Итак, в обоих случаях. Подставив вместов геометрической формуле площади треугольника, получим тригонометрическую формулу площади треугольника:
Теорема
доказана.
Третья формула для площади треугольника – формула Герона , названа так в честь древнегреческого ученого Герона Александрийского, жившего в первом веке нашей эры. Эта формула позволяет находить площадь треугольника, зная его стороны. Она удобна тем, что позволяет не делать никаких дополнительных построений и не измерять углов. Ее вывод основывается на второй из рассмотренных нами формул площади треугольника и теореме косинусов: и .
Прежде чем перейти к реализации этого плана, заметим, что
Точно так же имеем:
Теперь выразим косинус через и:
Так как любой угол в треугольнике больше и меньше, то. Значит,.
Теперь отдельно преобразуем каждый из сомножителей в подкоренном выражении. Имеем:
Подставляя это выражение в формулу для площади, получаем:
Тема
«Площадь треугольника» имеет большое
значение в школьном курсе математики.
Треугольник – простейшая из геометрических
фигур. Он является «структурным элементом»
школьной геометрии. Подавляющее
большинство геометрических задач
сводятся к решению треугольников. Не
исключение и задача о нахождении площади
правильного и произвольного
n-угольника.
Подавляющее
большинство геометрических задач
сводятся к решению треугольников. Не
исключение и задача о нахождении площади
правильного и произвольного
n-угольника.
Пример 2.4.1.
Чему равна площадь равнобедренного треугольника, если его основание , а боковая сторона?
Решение :
–равнобедренный,
Рисунок 2.4.4
Проведём по свойству равнобедренного треугольника – медиана и высота. Тогда
В по теореме Пифагора:
Находим площадь треугольника:
Ответ:
Пример 2.4.2.
В прямоугольном треугольнике биссектриса острого угла делит противоположный катет на отрезки длиной 4 и 5 см. Определить площадь треугольника.
Решение:
Пусть (рисунок 2.4.5). Тогдаи(посколькуBD – биссектриса). Отсюда имеем , то есть. Значит,
Рисунок 2.4.5
Ответ:
Пример 2.4.3.
Найти
площадь равнобедренного треугольника,
если его основание равно
,
а длина высоты, проведённой к основанию,
равна длине отрезка, соединяющего
середины основания и боковой стороны.
Решение:
По условию, – средняя линия (рисунок 2.4.6). Так какВимеем:
или
,
откудаСледовательно,
Формула для площади параллелограмма
Площадь параллелограмма равна произведению его стороны на высоту, опущенную на эту сторону.
Доказательство
Если параллелограмм — прямоугольник, то равенство выполнено по теореме о площади прямоугольника. Далее считаем, что углы параллелограмма не прямые.
Пусть в параллелограмме $ABCD$ угол $\angle BAD$ острый и $AD > AB$. Иначе переименуем вершины. Тогда высота $BH$ из вершины $B$ на прямую $AD$ падает на сторону $AD$, так как катет $AH$ короче гипотенузы $AB$, а $AB
Сравним площадь параллелограмма $ABCD$ и площадь прямоугольника $HBCK$. Площадь параллелограмма больше на площадь $\triangle ABH$, но меньше на на площадь $\triangle DCK$. Так как эти треугольники равны, то и их площади равны. Значит, площадь параллелограмма равна площади прямоугольника со сторонами длиной в сторону и высоту параллелограмма.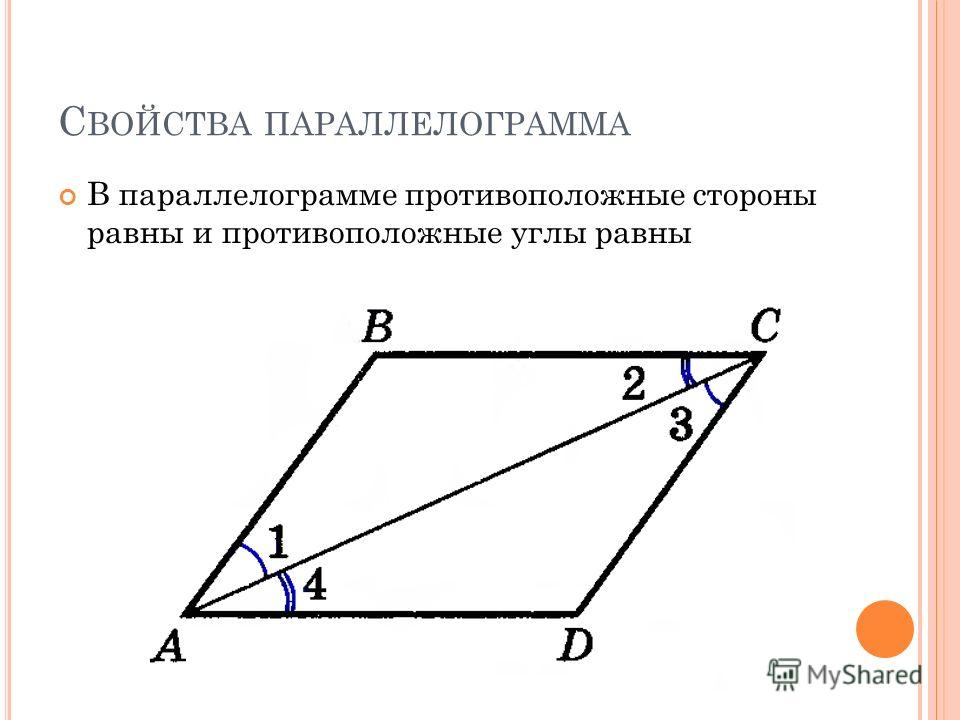 \circ — \angle AOD$. Значит, синусы углов при пересечении диагоналей равны $\sin \alpha$.
\circ — \angle AOD$. Значит, синусы углов при пересечении диагоналей равны $\sin \alpha$.
$S_{ABCD}=S_{\triangle AOB} + S_{\triangle BOC} + S_{\triangle COD} + S_{\triangle AOD}$
по аксиоме измерения площади. Применяем формулу площади треугольника $S_{ABC} = \dfrac{1}{2} \cdot AB \cdot BC \sin \angle ABC$ для этих треугольников и углов при пересечении диагоналей. Стороны каждого равны половинам диагоналей, синусы также равны. Следовательно, площади всех четырёх треугольников равны $S = \dfrac{1}{2} \cdot \dfrac{AC}{2} \cdot \dfrac{BD}{2} \cdot \sin \alpha = \dfrac{AC \cdot BD}{8} \sin \alpha$. Суммируя всё вышесказанное, получаем
$S_{ABCD} = 4S = 4 \cdot \dfrac{AC \cdot BD}{8} \sin \alpha = \dfrac{AC \cdot BD \cdot \sin \alpha}{2}$
Прежде чем узнать, как найти площадь параллелограмма, нам необходимо вспомнить, что такое параллелограмм и что называется его высотой. Параллелограмм – четырехугольник, противолежащие стороны которого попарно параллельны (лежат на параллельных прямых).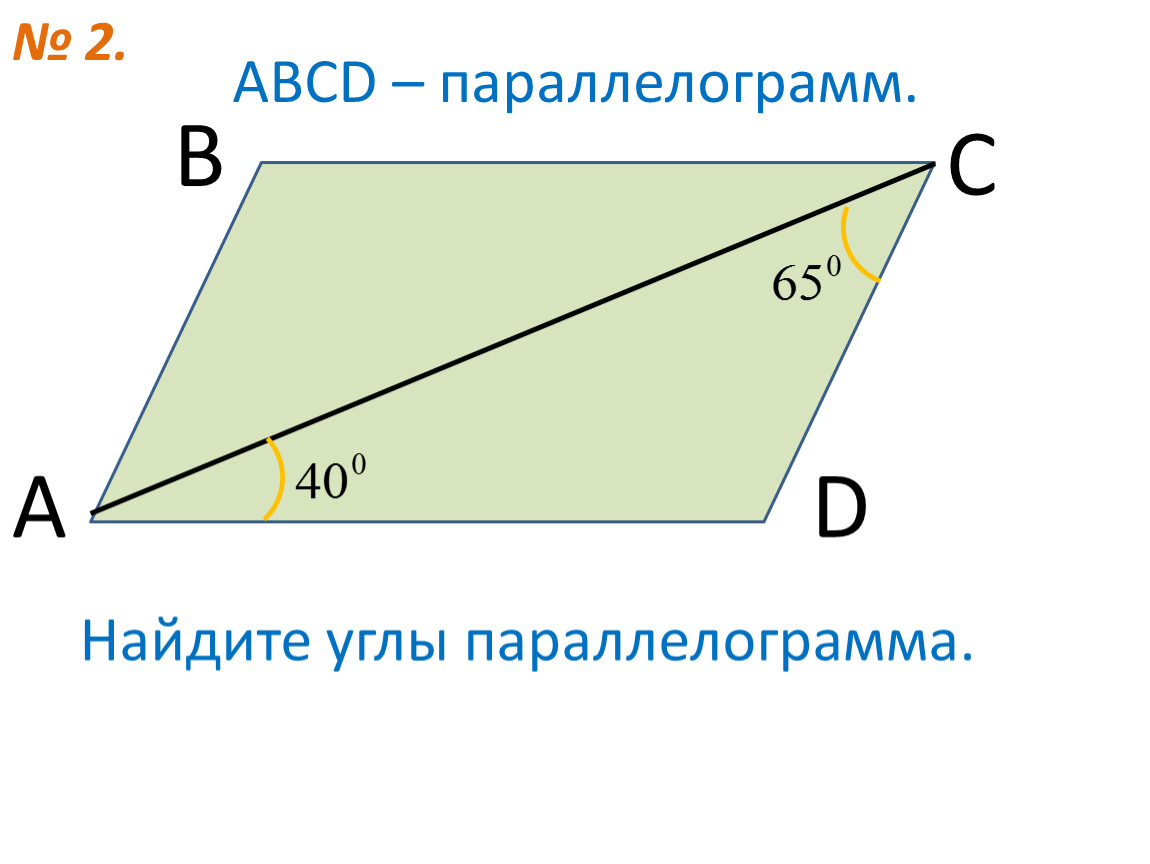 Перпендикуляр, проведенный из произвольной точки противоположной стороны к прямой, содержащей эту сторону называется высотой параллелограмма.
Перпендикуляр, проведенный из произвольной точки противоположной стороны к прямой, содержащей эту сторону называется высотой параллелограмма.
Квадрат, прямоугольник и ромб – это частные случаи параллелограмма.
Площадь параллелограмма обозначается как (S).
Формулы нахождения площади параллелограмма
S=a*h , где а – это основание, h – это высота, которая проведена к основанию.
S=a*b*sinα , где a и b – это основания, а α — угол между основаниями а и b.
S =p*r , где р – это полупериметр, r – это радиус окружности, которая вписана в параллелограмм.
Площадь параллелограмма, который образован векторами a и b равна модулю произведения заданных векторов, а именно:
Рассмотрим пример №1: Дан параллелограмм, сторона которого равна 7 см, а высота 3 см. Как найти площадь параллелограмма, формула для решения нам необходима.
Таким образом, S= 7×3. S=21. Ответ: 21 см 2 .
Рассмотрим пример №2: Даны основания 6 и 7 см, а также дан угол между основаниями 60 градусов. Как найти площадь параллелограмма? Формула, используемая для решения:
Как найти площадь параллелограмма? Формула, используемая для решения:
Таким образом, сначала найдем синус угла. Синус 60 = 0,5, соответственно S = 6*7*0,5=21 Ответ: 21 см 2 .
Надеюсь, что эти примеры Вам помогут при решении задач. И помните, главное – это знание формул и внимательность
Как найти стороны параллелограмма
Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
1. Формулы длины сторон через диагонали и угол между ними.
a, b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α, β — углы между диагоналями
Формулы сторон параллелограмма через диагонали и угол между ними (по теореме косинусов), (a, b):
Формулы сторон параллелограмма через диагонали и сторону, (a, b):
Формулы сторон параллелограмма , (a, b):
2. Формулы длины сторон параллелограмма через высоту.
Формулы длины сторон параллелограмма через высоту.
a, b — стороны параллелограмма
Hb — высота на сторону b
Ha — высота на сторону a
α, β — углы параллелограмма
Формулы сторон параллелограмма через высоту, (a, b):
3. Дополнительные, интересные формулы параллелограмма:
a, b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α — острый угол между диагоналями
Формула суммы квадратов диагоналей:
Формула разности квадратов сторон:
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Вариант 1 1. 2.Найти стороны параллелограмма, если одна сторона больше другой в 2 раза, а периметр его 36см. 3.В параллелограмме АВСД периметр равен 60см. ∠С=30°, а перпендикуляр к прямой СД равен 7см. Найти углы и стороны параллелограмма. | Вариант 2 1.Найти углы параллелограмма, если один угол больше другого в 2 раза. 2.Найти стороны параллелограмма, если одна сторона больше другой на 7 см, а периметр его 66см. 3.В параллелограмме АВСД периметр равен 78см. ∠С=30°, а перпендикуляр к прямой СД равен 10см. Найти углы и стороны параллелограмма. |
Вариант 3 1.Найти углы параллелограмма, если один угол меньше другого на 16°. 2.Найти стороны параллелограмма, если одна сторона больше другой в 3 раза, а периметр его 40см. 3.В параллелограмме АВСД периметр
равен 48см. | Вариант 4 1.Найти углы параллелограмма, если один угол больше другого в 3 раза. 2.Найти стороны параллелограмма, если одна сторона больше другой на 4см, а периметр его 36см. 3.В параллелограмме АВСД периметр равен 52см. ∠С=30°, а перпендикуляр к прямой СД равен 8см. Найти углы и стороны параллелограмма. |
Вариант 5 1.Найти углы параллелограмма, если один угол больше другого на 34°. 2.Найти стороны параллелограмма, если одна сторона больше другой в 5 раз, а периметр его 144см. 3.В параллелограмме АВСД периметр равен 120см. ∠С=30°, а перпендикуляр к прямой СД равен 14см. Найти углы и стороны параллелограмма. | Вариант 6 1.Найти углы параллелограмма, если один угол больше другого в 9раз. 2. 3.В параллелограмме АВСД периметр равен 34см. ∠С=30°, а перпендикуляр к прямой СД равен 3см. Найти углы и стороны параллелограмма. |
Вариант 7 1.Найти углы параллелограмма, если один угол больше другого на 24°. 2.Найти стороны параллелограмма, если одна сторона больше другой в 4 раза, а периметр его 140см. 3.В параллелограмме АВСД периметр равен 80см. ∠ С=30°, а перпендикуляр к прямой СД равен 8см. Найти углы и стороны параллелограмма. | Вариант 8 1.Найти углы параллелограмма, если один угол больше другого в 17 раз. 2.Найти стороны параллелограмма, если одна сторона больше другой на 2см, а периметр его 68см. 3.В параллелограмме АВСД периметр
равен 18см. ∠С=30°, а перпендикуляр к прямой СД равен 4см. Найти углы
и стороны параллелограмма. |
В параллелограмме углы при основании равны. Параллелограмм
Параллелограммом называется четырехугольник, у которого противоположные стороны параллельны, т. е. лежат на параллельных прямых (рис.1).
Теорема 1. О свойстве сторон и углов параллелограмма. В параллелограмме противоположные стороны равны, противоположные углы равны и сумма углов, прилежащих к одной стороне параллелограмма, равна 180°.
Доказательство. В данном параллелограмме ABCD проведем диагональ АС и получим два треугольника ABC и ADC (рис.2).
Эти треугольники равны, так как ∠ 1 = ∠ 4, ∠ 2 = ∠ 3 (накрест лежащие углы при параллельных прямых), а сторона АС общая. Из равенства Δ ABC = Δ ADC следует, что АВ = CD, ВС = AD, ∠ B = ∠ D. Сумма углов, прилежащих к одной стороне, например углов А и D, равна 180° как односторонних при параллельных прямых. Теорема доказана.
Замечание. Равенство противоположных сторон параллелограмма означает, что отрезки параллельных, отсекаемых параллельными, равны.
Следствие 1. Если две прямые параллельны, то все точки одной прямой находятся на одном и том же расстоянии от другой прямой.
Доказательство. В самом деле, пусть а || b (рис.3).
Проведем из каких-нибудь двух точек В и С прямой b перпендикуляры ВА и CD к прямой а. Так как АВ || CD, то фигура ABCD — параллелограмм, и следовательно, АВ = CD.
Расстоянием между двумя параллельными прямыми называется расстояние от произвольной точки одной из прямых до другой прямой.
По доказанному оно равно длине перпендикуляра, проведенного из какой-нибудь точки одной из параллельных прямых к другой прямой.
Пример 1. Периметр параллелограмма равен 122 см. Одна из его сторон больше другой на 25 см. Найти стороны параллелограмма.
Решение. По теореме 1 противоположные стороны параллелограмма равны. Обозначим одну сторону параллелограмма через х, другую через у. Тогда по условию
$$\left\{\begin{matrix}
2x + 2y = 122
\\x — y = 25
\end{matrix}\right.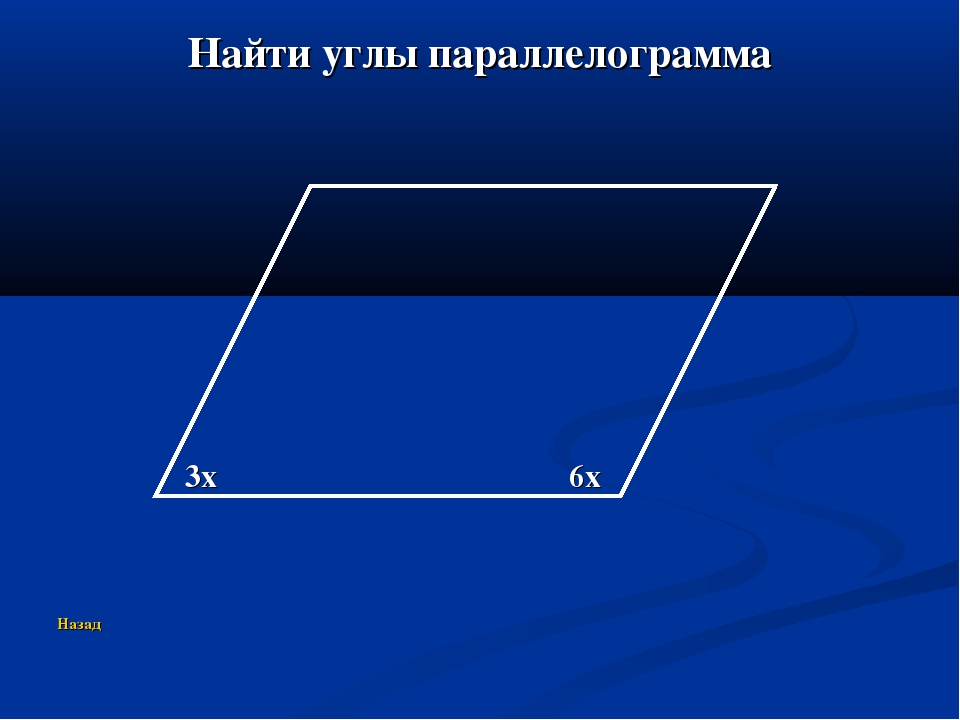 $$
Решая эту систему, получим х = 43, у = 18. Таким образом, стороны параллелограмма равны 18, 43, 18 и 43 см.
$$
Решая эту систему, получим х = 43, у = 18. Таким образом, стороны параллелограмма равны 18, 43, 18 и 43 см.
Пример 2.
Решение. Пусть условию задачи отвечает рисунок 4.
Обозначим АВ через х, а ВС через у. По условию периметр параллелограмма равен 10 см, т. е. 2(x + у) = 10, или х + у = 5. Периметр треугольника ABD равен 8 см. А так как АВ + AD = х + у = 5 то BD = 8 — 5 = 3 . Итак, BD = 3 см.
Пример 3. Найти углы параллелограмма, зная, что один из них больше другого на 50°.
Решение. Пусть условию задачи отвечает рисунок 5.
Обозначим градусную меру угла А через х. Тогда градусная мера угла D равна х + 50°.
Углы BAD и ADC внутренние односторонние при параллельных прямых АВ и DC и секущей AD. Тогда сумма этих названных углов составит 180°, т. е.
х + х + 50° = 180°, или х = 65°. Таким образом, ∠ A = ∠ C = 65°, a ∠ B = ∠ D = 115°.
Пример 4. Стороны параллелограмма равны 4,5 дм и 1,2 дм. Из вершины острого угла проведена биссектриса. На какие части делит она большую сторону параллелограмма?
Из вершины острого угла проведена биссектриса. На какие части делит она большую сторону параллелограмма?
Решение. Пусть условию задачи отвечает рисунок 6.
АЕ — биссектриса острого угла параллелограмма. Следовательно, ∠ 1 = ∠ 2.
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.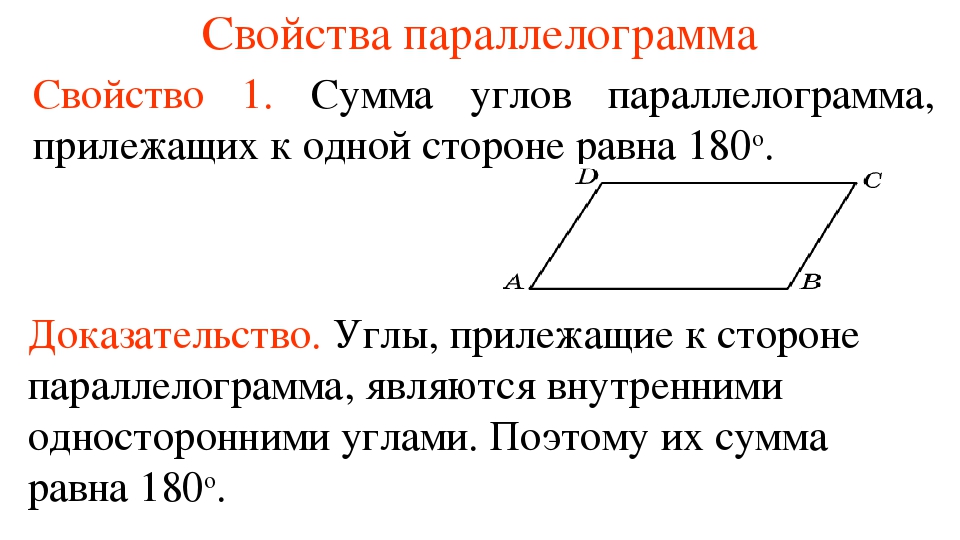
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Задача 1 . Один из углов параллелограмма равен 65°. Найти остальные углы параллелограмма.
∠C =∠A = 65° как противоположные углы параллелограмма.
∠А +∠В = 180° как углы, прилежащие к одной стороне параллелограмма.
∠В = 180° — ∠А = 180° — 65° = 115°.
∠D =∠B = 115° как противолежащие углы параллелограмма.
Ответ: ∠А =∠С = 65°; ∠В =∠D = 115°.
Задача 2. Сумма двух углов параллелограмма равна 220°. Найти углы параллелограмма.
Сумма двух углов параллелограмма равна 220°. Найти углы параллелограмма.
Так как у параллелограмма имеется 2 равных острых угла и 2 равных тупых угла, то нам дана сумма двух тупых углов, т.е. ∠В +∠D = 220°. Тогда ∠В =∠D = 220°: 2 = 110°.
∠А +∠В = 180° как углы, прилежащие к одной стороне параллелограмма, поэтому ∠А = 180° — ∠В = 180° — 110° = 70°. Тогда ∠C =∠A = 70°.
Ответ: ∠А =∠С = 70°; ∠В =∠D = 110°.
Задача 3. Один из углов параллелограмма в 3 раза больше другого. Найти углы параллелограмма.
Пусть ∠А =х. Тогда ∠В = 3х. Зная, что сумма углов параллелограмма, прилежащих к одной его стороне равна 180°, составим уравнение.
х = 180 : 4;
Получаем: ∠А =х = 45°, а ∠В = 3х = 3 ∙ 45° = 135°.
Противолежащие углы параллелограмма равны, следовательно,
∠А =∠С = 45°; ∠В =∠D = 135°.
Ответ: ∠А =∠С = 45°; ∠В =∠D = 135°.
Задача 4. Докажите, что если у четырехугольника две стороны параллельны и равны, то этот четырехугольник – параллелограмм.
Доказательство.
Проведем диагональ BD и рассмотрим Δ ADB и Δ CBD.
AD = BC по условию. Сторона BD – общая. ∠1 = ∠2 как внутренние накрест лежащие при параллельных (по условию) прямых AD и BC и секущей BD. Следовательно, Δ ADB = Δ CBD по двум сторонам и углу между ними (1-й признак равенства треугольников). В равных треугольниках соответственные углы равны, значит, ∠3 =∠4. А эти углы являются внутренними накрест лежащими при прямых AB и CD и секущей BD. Отсюда следует параллельность прямых AB и CD. Таким образом, в данном четырехугольнике ABCD противолежащие стороны попарно параллельны, следовательно, по определению ABCD – параллелограмм, что и требовалось доказать.
Задача 5. Две стороны параллелограмма относятся как 2 : 5, а периметр равен 3,5 м. Найти стороны параллелограмма.
∙ (AB + AD).
Обозначим одну часть через х. тогда AB = 2x, AD = 5x метров. Зная, что периметр параллелограмма равен 3,5 м, составим уравнение:
2 ∙ (2x + 5x) = 3,5;
2 ∙ 7x = 3,5;
x = 3,5 : 14;
Одна часть составляет 0,25 м. Тогда AB = 2 ∙ 0,25 = 0,5 м; AD = 5 ∙ 0,25 = 1,25 м.
Тогда AB = 2 ∙ 0,25 = 0,5 м; AD = 5 ∙ 0,25 = 1,25 м.
Проверка.
Периметр параллелограмма P ABCD = 2 ∙ (AB + AD) = 2 ∙ (0,25 + 1,25) = 2 ∙ 1,75 = 3,5 (м).
Так как противоположные стороны параллелограмма равны, то CD = AB = 0,25 м; BC = AD = 1,25 м.
Ответ: CD = AB = 0,25 м; BC = AD = 1,25 м.
Параллелограммом называется четырехугольник, у которго противоположные стороны параллельны, т.е. лежат на параллельных прямых
Свойства параллелограмма:
Теорема 22. Противоположные стороны параллелограма равны.
Доказательство. В параллелограмме АВСD проведем диагональ АС. Треугольники АСD и АСВ равны, как имеющие общую сторону АС и две пары равных углов. прилежащих к ней: ∠
САВ=∠
АСD, ∠
АСВ=∠
DAC (как накрест лежащие углы при параллельных прямых AD и ВС). Значит, АВ=CD и ВС=AD, как соответственные стороны равных треугольников, ч.т.д. Из равенства этих треугольников также следует равенство соответственных углов треугольников:
Теорема 23.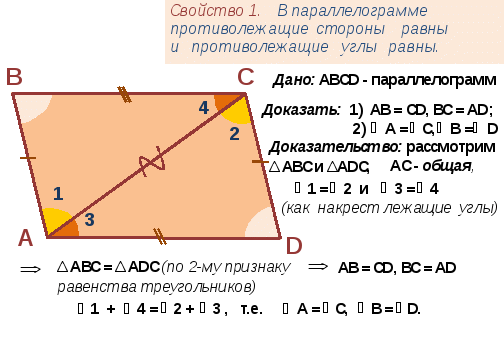 Противоположные углы параллелограмма равны: ∠
А=∠
С и ∠
В=∠
D.
Противоположные углы параллелограмма равны: ∠
А=∠
С и ∠
В=∠
D.
Равенство первой пары идет из равенства треугольников АВD и CBD, а второй — АВС и ACD.
Теорема 24. Соседние углы параллелограмма, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов.
Это так, потому что они являются внутренними односторонними углами.
Теорема 25. Диагонали параллелограмма делят друг друга в точке их пересечения пополам.
Доказательство. Рассмотрим треугольники ВОС и АОD. По первому свойству AD=ВС ∠
ОАD=∠
ОСВ и ∠
ОDА=∠
ОВС как накрест лежащие при параллельных прямых AD и ВС. Поэтому треугольники ВОС и АОD равны по стороне и прилежащим к ней углам. Значит, ВО=ОD и АО=ОС, как соответственные стороны равных треугольников, ч.т.д.
Признаки параллелограмма
Теорема 26. Если противоположные стороны четырехугольника попарно равны, то он является параллелограммом.
Доказательство. Пусть у четырехугольника АВСD стороны AD и ВС, АВ и CD соответственно равны (рис2).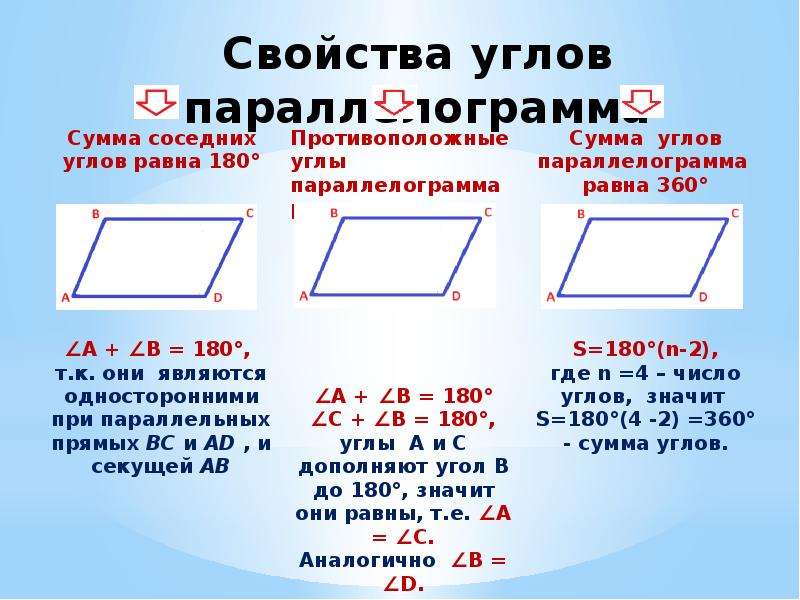 Проведем диагональ АС. Треугольникик АВС и ACD равны по трем сторонам. Тогда углы ВАС и DСА равны и, следовательно, АВ параллельна CD. Параллельность сторон ВС и AD следует из равенства углов CAD и АСВ.
Проведем диагональ АС. Треугольникик АВС и ACD равны по трем сторонам. Тогда углы ВАС и DСА равны и, следовательно, АВ параллельна CD. Параллельность сторон ВС и AD следует из равенства углов CAD и АСВ.
Теорема 27. Если противоположные углы четырехугольника попарно равны, то он является параллелограммом.
Пусть ∠
А=∠
С и ∠
В=∠
D. Т.к. ∠
А+∠
В+∠
С+∠
D=360 о, то ∠
А+∠
В=180 о и стороны AD и ВС параллельны (по признаку параллельности прямых). Также докажем и параллельность сторон АВ и CD и заключим, что АВСD является параллелограммом по определению.
Теорема 28. Если соседние углы четырехугольника, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов, то он является параллелограммом.
Если внутренние односторонные углы в сумме составляют 180 градусов, то прямые праллельны. Значит АВ парал CD и ВС парал AD. Четырехугольник оказывается параллелограммом по определению.
Теорема 29. Если диагонали четырехугольника взаимно делятся в точке пересечения пополам, то четырехугольник — параллелограмм.
Доказательство. Если АО=ОС, ВО=ОD, то треугольники АOD и ВОС равны, как имеющие равны углы (вертикальные) при вершине О, заключенные между парами равных сторон. Из равенства треугольников заключаем, что AD и ВС равны. Также равны стороны АВ и CD, и четырехугольник оказывается параллелограммом по признаку 1.
Теорема 30. Если четырехугольник имеет пару равных, параллельных между собой сторон, то он является параллелограммом.
Пусть в четырехугольнике АВСD стороны АВ и CD параллельны и равны. Проведем диагонали АС и ВD. Из параллельности этих прямых следует равенство накрест лежащих углов АВО=СDО и ВАО=ОСD. Треугольники АВО и CDО равны по стороне и прилежащим к ней углам. Поэтому АО=ОС, ВО=ОD, т.е. диагонали точкой пересечения делятся пополам и четырехугольник оказывается параллелограммом по признаку 4.
В геометрии рассматривают частные случаи параллелограмма.
|
Обозначения в формулах эквивалентны обозначениям на рисунках, а именно: а — стороны, параллелограмма, параллельные друг другу b — боковые стороны параллелограмма h — высота параллелограмма d — диагональ параллелограмма S — площадь параллелограмма α — острый угол при основании параллелограмма Высота параллелограмма равна соотношению площади к основанию (Формула 1) Высота параллелограмма равна произведению боковой стороны на синус угла при основании (Формула 2) Соотношение оснований параллелограмма равно обратно пропорциональному соотношению высот, опущенных на соответствующие стороны (Формула 3) Высоты параллелограмма, опущенные из одной вершины, образуют угол, равный углу параллелограмма при соседней вершине (Рисунок 2) Высота параллелограмма равна, корню из разности квадрата боковой стороны и квадрата длины отрезка, образующего прямоугольный треугольник, другими сторонами которого являются боковая сторона и высота (Формула 4) Высота параллелограмма равна корню из разности квадрата диагонали, из которой опущена высота и квадрата длины отрезка между точкой, из которой проведена диагональ и точкой пересечения высоты и основания (Формула 5) | Позначення у формулах еквівалентні позначенням на малюнках, а саме:
а — сторони, паралелограма, паралельні один одному b — бічні сторони паралелограма h — висота паралелограма d — дiагональ паралелограма S — площа паралелограма α — гострий кут при основі паралелограма Висота паралелограма дорівнює співвідношенню площі до підстави (Формула 1) Висота паралелограма дорівнює твору бічної сторони на синус кута при його основі (Формула 2) Співвідношення підстав паралелограма дорівнює обернено пропорційному співвідношенню висот, опущених на відповідні сторони (Формула 3) Висоти паралелограма, опущені з однієї вершини, утворюють кут, рівний куту паралелограма при сусідній вершині (Малюнок 2) Висота паралелограма рівна, корню з різниці квадрата бічної сторони і квадрата довжини відрізка, створюючого прямокутний трикутник, іншими сторонами якого є бічна сторона і висота (Формула 4) Висота паралелограма дорівнює корню з різниці квадрата діагоналі, з якої опущена висота і квадрата довжини відрізка між точкою, з якої проведена діагональ і точкою пересічення висоти і основання (Формула 5) |
Периметр параллелограмма
Параллелограмм это геометрическая фигура имеющая четыре параллельные стороны, противоположных друг другу. В школьной программе все задания по решению параллелограмма, направлены на нахождение высоты, площади, диагонали и периметра. О них и пойдет речь.
В школьной программе все задания по решению параллелограмма, направлены на нахождение высоты, площади, диагонали и периметра. О них и пойдет речь.
Параллелограмм обладает свойствами, такими как:
В параллелограмме и углы и стороны, которые противоположны между собой одинаковы: АВ = CD, BC =AD. Так же как углы АВС = ADC и ВАD = BCD.
Диагонали проведенные из углов параллелограмма в месте пересечения разделятся на две одинаковые части. АО = ОС, ОВ = OD.
Сумма двух углов, одной стороны всегда 180 градусов.
углы: А + В = 1800, В + С = 1800, С + D =1800, A + D = 1800 .
Любая диагональ разделяет параллелограмм на две одинаковые фигуры (треугольник) как по площади так и по размеру.
Зачастую встречается такое интересное свойство как, сума диагоналей в квадрате одинакова с суммой сторон в квадрате.
АС2 + BD2 = (AB2 + BC2). AC2 + BD2 = 2 * (AB2 + BC2)
У параллелограмма есть несколько основных признаков.

— Четырехугольная фигура с противоположными сторонами параллельными друг другу и есть параллелограмм.
— Четырехугольная фигура имеющая одинаковые противоположные стороны, есть параллелограмм.
— Четырехугольная фигура имеющая одинаковые параллельные и противоположные стороны, есть параллелограмм.
— Когда встречающиеся диагонали четырехугольной фигуры в месте пересечения разделяются на равные части. Данная фигура является параллелограммом.
— Четырехугольная фигура в которой противоположные углы одинаковы называется параллелограммом.
Периметр параллелограмма находится по формуле
Р = 2 (а+b)
что означает что периметр равняется двойной сумме сторон.
Биссектриса параллелограмма
Из школьной программы помню определение которое засело в памяти на всю жизнь — Биссектриса это крыса, что ходит по углам и делит угол пополам. Если же говорить научным языком, то:
Биссектрисы углов находящихся на одной стороне встречаются в точке пересечения под углом в 90 градусов.
Так же они могут совпадать и быть параллельны друг другу.
Так же в параллелограмме можно найти высоту, она обозначается в виде отрезка исходящего из угла к основанию, следовательно, от каждого угла их можно провести две.
Площадь параллелограмма это произведение стороны и высоты приведенную к ней. Находится по формуле.
S = a * ha = b * hb
Есть еще один способ вычисления, но им не так часто пользуются в расчетах. Она звучит как площадь параллелограмма это произведение рядом лежащих сторон умноженный на синус угла находящегося между ними.
S = a * b * sin(?) = a * b * sin(?)
Все приведенные в данной статье формулы помогут Вам в решении различных задач по нахождению величин параллелограмма, это не сложно но очень интересно.
Заметка: если Вы находитесь в поиске персонала. Империя кадров поможет вам в этом вопросе. Просто перейдите по ссылке персонал временный (http://www. imperia.ru/client/temp_staff/) и узнайте подробнее.
imperia.ru/client/temp_staff/) и узнайте подробнее.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
углов параллелограмма — теоремы, доказательства, свойства
В параллелограмме четыре внутренних угла, а сумма внутренних углов параллелограмма всегда равна 360°. Противолежащие углы параллелограмма равны, а смежные углы параллелограмма попарно смежны. Познакомимся подробнее со свойствами углов параллелограмма.
Свойства углов параллелограмма
Параллелограмм – это четырехугольник с равными и параллельными противоположными сторонами.Есть некоторые особые свойства параллелограмма, которые отличают его от других четырехугольников. Обратите внимание на следующий параллелограмм, чтобы соотнести его свойства, указанные ниже:
- Противоположные углы параллелограмма конгруэнтны (равны). Здесь ∠А = ∠С; ∠Д = ∠В.
- Сумма всех углов параллелограмма равна 360°.
 Здесь ∠A + ∠B + ∠C + ∠D = 360°.
Здесь ∠A + ∠B + ∠C + ∠D = 360°. - Все соответствующие последовательные углы являются дополнительными. Здесь ∠A + ∠B = 180°; ∠В + ∠С = 180°; ∠С + ∠D = 180°; ∠D + ∠А = 180°
Теоремы, относящиеся к углам параллелограмма
Теоремы, относящиеся к углам параллелограмма, помогают решать задачи, связанные с параллелограммом.Ниже приведены две важные теоремы:
- Противоположные углы параллелограмма равны.
- Смежные углы параллелограмма являются дополнительными.
Давайте подробно узнаем об этих двух специальных теоремах параллелограмма.
Противоположные углы параллелограмма равны
Теорема: В параллелограмме противоположные углы равны.
Дано: ABCD — параллелограмм с четырьмя углами ∠A, ∠B, ∠C, ∠D соответственно.
К Докажите: ∠A =∠C и ∠B=∠D
Доказательство: В параллелограмме ABCD диагональ AC делит параллелограмм на два треугольника. О сравнении треугольников ABC и ADC. Здесь у нас есть:
О сравнении треугольников ABC и ADC. Здесь у нас есть:
AC = AC (общие стороны)
∠1 = ∠4 (чередующиеся внутренние углы)
∠2 = ∠3 (чередующиеся внутренние углы)
Таким образом, два треугольника конгруэнтны, △ABC ≅ △ADC
.
Это дает ∠B = ∠D по CPCT (соответствующие части конгруэнтных треугольников).
Точно так же мы можем показать, что ∠A = ∠C.
Отсюда доказано, что противоположные углы в любом параллелограмме равны.
Обратная теорема гласит, что если противоположные углы четырехугольника равны, то это параллелограмм. Докажем то же самое.
Дано: ∠A =∠C и ∠B=∠D в четырехугольнике ABCD.
Доказать: ABCD — параллелограмм.
Доказательство:
Сумма всех четырех углов этого четырехугольника равна 360°.
= [∠A + ∠B + ∠C + ∠D = 360º]
= 2(∠A + ∠B) = 360º (Мы можем заменить ∠C на ∠A и ∠D на ∠B, так как известно, что ∠A =∠C и ∠B =∠D)
= ∠А + ∠В = 180º. Это показывает, что соседние углы являются дополнительными. Следовательно, это означает, что AD || ДО Н.Э. Аналогично можно показать, что AB || КОМПАКТ ДИСК.
Это показывает, что соседние углы являются дополнительными. Следовательно, это означает, что AD || ДО Н.Э. Аналогично можно показать, что AB || КОМПАКТ ДИСК.
Следовательно, АД || до н.э. и АВ || КОМПАКТ ДИСК.
Следовательно, ABCD — параллелограмм.
Смежные углы параллелограмма являются дополнительными
Последовательные углы параллелограмма являются дополнительными.Докажем это свойство, учитывая следующий факт и используя тот же рисунок.
Дано: ABCD — параллелограмм с четырьмя углами ∠A, ∠B, ∠C, ∠D соответственно.
Чтобы доказать: ∠A + ∠B = 180°, ∠C + ∠D = 180°.
Доказательство: Если AD считается секущей и AB || КОМПАКТ ДИСК.
По свойству секущей мы знаем, что внутренние углы, лежащие по одну сторону от секущей, являются дополнительными.
Следовательно, ∠A + ∠D = 180°.
Аналогично,
∠В + ∠С = 180°
∠С + ∠D = 180°
∠А + ∠В = 180°
Следовательно, сумма соответствующих двух смежных углов параллелограмма равна 180°.
Таким образом, доказано, что смежные углы параллелограмма являются дополнительными.
Похожие статьи об углах параллелограмма
Ознакомьтесь с приведенными ниже интересными статьями, посвященными углам параллелограмма.
Часто задаваемые вопросы об углах параллелограмма
Углы параллелограмма в сумме составляют 360°?
Да, все внутренние углы параллелограмма в сумме составляют 360°.Например, в параллелограмме ABCD ∠A + ∠B + ∠C + ∠D = 360°. Согласно свойству суммы углов многоугольников, сумма внутренних углов в многоугольнике может быть рассчитана с помощью количества треугольников, которые могут быть сформированы внутри него. В данном случае параллелограмм состоит из 2-х треугольников, значит, сумма внутренних углов равна 360°. Это также можно рассчитать по формуле S = (n — 2) × 180 °, где «n» представляет количество сторон в многоугольнике. Здесь «n» = 4. Следовательно, сумма внутренних углов параллелограмма = S = (4 — 2) × 180 ° = (4 — 2) × 180 ° = 2 × 180 ° = 360 °.
Какая связь между смежными углами параллелограмма?
Смежные углы параллелограмма также известны как последовательные углы, и они всегда являются дополнительными (180°).
Как связаны противоположные углы параллелограмма?
Противоположные углы параллелограмма всегда равны, а смежные углы параллелограмма всегда смежны.
Как найти недостающие углы параллелограмма?
Мы можем легко найти недостающие углы параллелограмма с помощью трех специальных свойств:
- Противоположные углы параллелограмма равны.
- Последовательные углы параллелограмма являются дополнительными.
- Сумма всех углов параллелограмма равна 360°.
Что такое внутренние углы параллелограмма?
Углы, образуемые внутри параллелограмма и образуемые каждой парой смежных сторон, являются его внутренними углами. Сумма внутренних углов параллелограмма равна 360°, а любые два соседних (последовательных) угла параллелограмма являются дополнительными.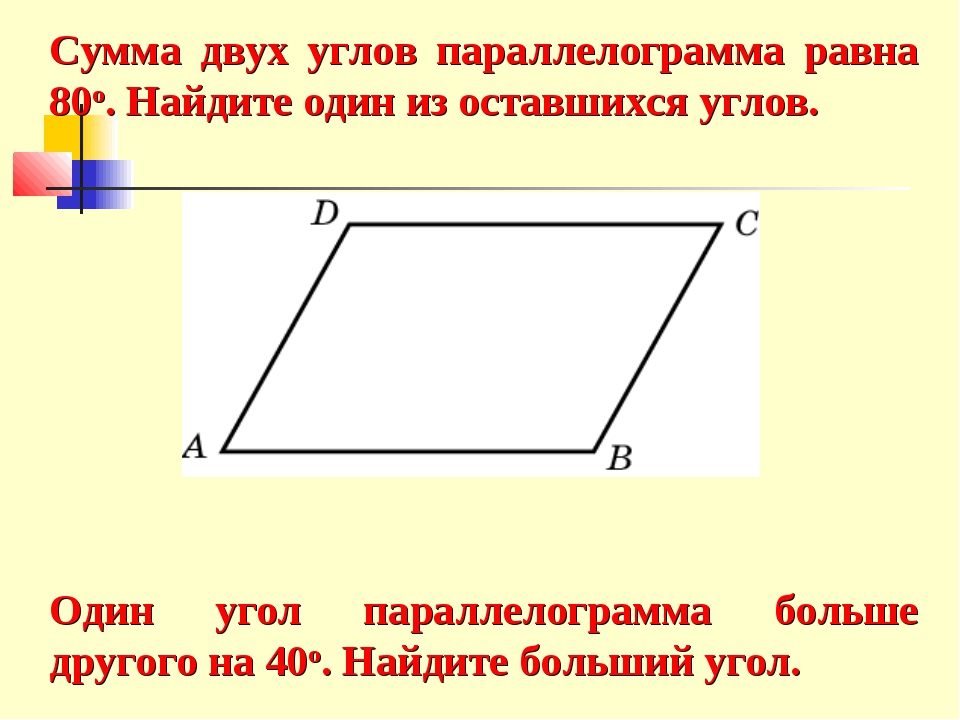
Все ли углы параллелограмма равны?
Нет, не все углы параллелограмма равны. Существуют две основные теоремы, касающиеся углов параллелограмма, которые утверждают, что противоположные углы параллелограмма равны, а последовательные (смежные) углы являются дополнительными.
Чему равна сумма внутренних углов параллелограмма?
Сумма внутренних углов параллелограмма всегда равна 360°. Согласно свойству суммы углов многоугольников, сумма внутренних углов многоугольника может быть найдена по формуле S = (n — 2) × 180 °, где «n» показывает количество сторон в многоугольнике.В этом случае ‘n’ = 4. Следовательно, сумма внутренних углов параллелограмма = S = (4 — 2) × 180 ° = (4 — 2) × 180 ° = 2 × 180 ° = 360 °.
Углы параллелограмма равны 90 градусов?
В некоторых параллелограммах, таких как прямоугольники и квадраты, все углы равны 90°. Однако углы других параллелограммов не обязательно могут быть равны 90°.
Конгруэнтны ли противоположные углы параллелограмма?
Да, противоположные углы параллелограмма равны. Однако смежные углы параллелограмма всегда являются дополнительными.
Однако смежные углы параллелограмма всегда являются дополнительными.
Конгруэнтны ли последовательные углы параллелограмма?
Нет, последовательные (прилежащие) углы параллелограмма не равны, они дополнительные.
Являются ли противоположные углы параллелограмма дополнительными?
Нет, согласно теоремам, основанным на углах параллелограмма, противолежащие углы не являются дополнительными, они равны.
Как найти недостающие углы в параллелограммах | Геометрия
Как найти недостающие углы в параллелограмме
Шаг 1: Определите недостающие углы параллелограмма на диаграмме.
Шаг 2: Для каждого угла нужно найти
- проверьте, указан ли на схеме противоположный угол. Два противоположных угла параллелограмма равны.
- проверьте, указан ли на схеме последовательный угол. Два последовательных угла параллелограмма являются дополнительными.
Как найти недостающие углы в параллелограммах Словарь
Параллелограмм: Параллелограмм – это четырехугольник с двумя парами параллельных сторон.
- Внутренние углы параллелограмма: Противолежащие углы равны, а смежные углы смежны.
- Стороны параллелограмма: Противоположные стороны параллельны и равны.
Последовательные углы: Когда две прямые пересекаются линией, называемой поперечной линией, два угла, лежащие по одну сторону от линии пересечения и находящиеся внутри двух прямых, называются последовательными углами.
Дополнительные углы: Два угла являются дополнительными, если сумма их углов составляет 180 градусов.
Давайте потренируемся находить недостающие углы в параллелограмме на следующих двух примерах.
Как найти недостающие углы в параллелограмме Пример 1
Найдите недостающие измерения угла {eq}\angle B {/eq} и {eq}\угол C {/eq} в показанном параллелограмме.
Шаг 1: Определите, какие внутренние углы параллелограмма на диаграмме нам нужно найти.
Нам нужно найти {eq}\угол B {/eq} и {eq}\угол C {/eq} параллелограмма ABCD.
Шаг 2: Для каждого угла нужно найти
- проверьте, указан ли на схеме противоположный угол. Два противоположных угла параллелограмма равны.
- проверьте, указан ли на схеме последовательный угол. Два последовательных угла параллелограмма являются дополнительными, то есть в сумме дают 180 градусов. Повторите это для всех недостающих углов.
Для обоих {экв}\угол B {/eq} и {eq}\угол C {/eq} даны противоположные углы.{\ круг} } {/экв}
Как найти недостающие углы в параллелограмме Пример 2
Найдите недостающие измерения угла {eq}\angle B {/eq}, {eq}\угол C {/eq} и {eq}\угол D {/eq} в показанном параллелограмме.
Шаг 1: Определите, какие внутренние углы параллелограмма на диаграмме нам нужно найти.
Нам нужно найти {eq}\угол B {/eq}, {eq}\угол C {/eq} и {eq}\угол D {/экв}.
Шаг 2: Для каждого угла нужно найти
- проверьте, указан ли на схеме противоположный угол.
 {\circ} {/экв}.{\ круг} } {/экв} Получите доступ к тысячам практических вопросов и пояснений!
{\circ} {/экв}.{\ круг} } {/экв} Получите доступ к тысячам практических вопросов и пояснений!Недостающие углы в четырехугольниках
Возможно, вы уже знаете, что все углы прямоугольника равны девяноста градусам.Отсюда видно, что 4(90°) = 360°. Другими словами, в четырехугольнике всего 360°.
Мы можем использовать этот факт для определения недостающего угла в любом четырехугольнике или четырехугольнике.Вот несколько примеров.
Пример 1 :
Нам даны три угла, и нам нужно определить размер четвертого.
Шаг 1: Сложите величины известных углов.
98° + 44° + 73° = 215°
Шаг 2: Вычтите сумму из 360°, чтобы определить, что осталось для четвертого угла.
360° — 215° = 145°
Мера неизвестного угла равна 145°.
Пример 2:
Здесь у нас есть параллелограмм.Самое замечательное в параллелограммах то, что два последовательных угла должны быть дополнительными.
 Поэтому нам не нужно использовать другие углы на рисунке.
Поэтому нам не нужно использовать другие углы на рисунке.Напомним, что сумма дополнительных углов равна 180°.
Шаг 1: Вычесть известный угол из 180°.
180° — 51° = 129°
Недостающий угол равен 129°.
Шаг 2: Давайте проверим нашу работу. Противоположные углы в параллелограмме равны. Таким образом, будет два угла, равных 51°, и два угла, равных 129°.
51° + 51° + 129° + 129° = 360°
Здесь мы видим, что если недостающий угол равен 129°, то сумма всех четырех углов будет 360°.
Пример 3:
Здесь у нас есть трапеция. Квадраты в углу говорят нам, что эти углы прямые, и они равны 90°.
Шаг 1: : Сложите величины известных углов.
90° + 90° + 146° = 326°
Шаг 2: : Вычтите сумму из 360°.
360° — 326° = 34°
Угол w равен 34°.
Рассмотрим
Четырехугольники имеют 360°. Используйте это вместе с другой информацией о фигуре, чтобы определить величину недостающего угла.
 Если у вас есть прямоугольник или квадрат, каждый из углов равен 90°. Если у вас есть параллелограмм или ромб, противоположные углы равны, а следующие друг за другом углы являются дополнительными. Для других типов четырехугольников вам может понадобиться сложить заданные углы, а затем вычесть из 360°.
Если у вас есть прямоугольник или квадрат, каждый из углов равен 90°. Если у вас есть параллелограмм или ромб, противоположные углы равны, а следующие друг за другом углы являются дополнительными. Для других типов четырехугольников вам может понадобиться сложить заданные углы, а затем вычесть из 360°.Видео-вопрос: нахождение меры угла в параллелограмме, зная меры трех других углов
Стенограмма видео
𝐴𝐵𝐶𝐷 — параллелограмм в мера угла 𝐵𝐸𝐶 равна 79 градусам, а мера угла 𝐸𝐶𝐵 равняется 56 градусам. Определить меру угла 𝐸𝐴𝐷.
Потому что нам сказали, что 𝐴𝐵𝐶𝐷 параллелограмм, это означает, что мы можем сказать, что прямая 𝐷𝐶 параллельна прямой 𝐴𝐵 и прямая 𝐴𝐷 параллельна прямой 𝐵𝐶.Нам даны два угла измерения 𝐵𝐸𝐶 и 𝐸𝐶𝐵, и нас просят найти этот угол 𝐸𝐴𝐷. Чтобы отработать этот угол измерения, нам нужно запомнить некоторые свойства углов в параллелограммы.

Во-первых, мы можем помнить, что противоположные углы равны, и мы могли бы также помнить, что сумма двух смежных углы составляют 180 градусов. В этом параллелограмме угол противоположный 𝐴 будет угол 𝐶.Однако мы не знаем этой суммы угол 𝐷𝐶𝐵. Мы знаем только, что 𝐸𝐶𝐵 равно 56. градусов. Если мы посмотрим на наше второе свойство, если бы мы нашли измерение угла 𝐵, то это помогло бы нам вычислить 𝐴. Итак, как мы можем найти измерение угла 𝐵?
Помимо участия в параллелограмм, этот угол при 𝐵 также является частью треугольника. Мы знаем, что углы в треугольник в сумме дает 180 градусов.Таким образом, этот угол 𝐶𝐵𝐸 равен 180 градусов вычесть 79 градусов вычесть 56 градусов. 180 вычесть 79 дает нам 101 градусов, и вычитание 56 из этого дает нам 45 градусов. Помните, что это не наша ответ, так как нам еще нужно отработать угол 𝐸𝐴𝐷.
 Используя то свойство, что сумма
два смежных угла составляют 180 градусов, тогда мы вычисляем 180 вычитаем 45 градусов,
давая нам наш ответ 135 градусов.
Используя то свойство, что сумма
два смежных угла составляют 180 градусов, тогда мы вычисляем 180 вычитаем 45 градусов,
давая нам наш ответ 135 градусов.Параллелограммы и трапеции — Бесплатная помощь по математике
Параллелограмм – это четырехугольник, у которого обе пары противоположных сторон параллельны.Между мерами последовательных углов, противоположных углов и противоположных сторон параллелограмма существуют особые отношения. Квадрат — самый простой параллелограмм, потому что он имеет 2 набора параллельных сторон. Естественно, все его углы и стороны совпадают по длине или размеру.
Факты о параллелограмме
(1) Градусная мера четырех углов параллелограмма в сумме составляет 360 градусов. Помните, что все четырехугольники (четырехсторонние фигуры) имеют углы, сумма которых составляет 360 градусов.Вот образец:
Тогда: a + b + c + d = 360 градусов
(2) Градусная мера любых двух последовательных углов в сумме составляет 180 градусов.
 В параллелограмме ABCD:
В параллелограмме ABCD:угол а + угол b = 180 градусов
угол b + угол c = 180 градусов
угол c + угол d = 180 градусов
угол a + угол d = 180 градусов(3) Противоположные углы имеют одинаковую меру в градусах.
В параллелограмме ABCD:
угол а = угол с
угол b = угол dСтороны параллелограмма
В параллелограмме ABCD:
(1) Противоположные стороны параллельны:
сторона AD || сторона ВС
сторона АВ || боковой CDПРИМЕЧАНИЕ. Символ || значит параллельно.
(2) Противоположные стороны имеют одинаковую длину:
сторона AD = сторона BC
сторона AB = сторона CDДиагонали параллелограмма
Диагонали параллелограмма делят параллелограмм на два расположенных рядом треугольника. Как показано на рисунке ниже, диагональ AC образует равные чередующиеся внутренние углы с каждой парой параллельных сторон. Мы также можем видеть, что на картинке ниже есть два треугольника.
 Треугольник 1 конгруэнтен треугольнику 2 по методу ASA (угол-сторона-угол).
Треугольник 1 конгруэнтен треугольнику 2 по методу ASA (угол-сторона-угол).Откуда взялись два треугольника? Они были образованы диагональю AC.
Должен также отметить, что диагонали параллелограмма делят друг друга пополам, как показано на рисунке ниже.
АЕ = ЕС
Германия = ЕВ
где Е — середина ОБЕИХ диагоналей.Пример:
В параллелограмме WXYZ угол X = 4a — 40, а угол Z = 2a — 8. Найдите величину угла W?
Решение:
(1) Найдите значение a.
Поскольку углы X и Z являются противоположными углами параллелограмма WXYZ, они имеют одинаковую меру. Приравниваем члены и находим а.
4а — 40 = 2а — 8
4а — 2а = 40 — 8
2а = 32
а = 32/2
а = 16(2) Так как а = 16, мы теперь найдем меру угла X, подставив 16 вместо а в 4а — 40.
угол Х = 4а — 40
угол Х = 4(16) — 40
угол Х = 64 — 40
угол Х = 24(3) Мы также знаем, что последовательные углы параллелограмма являются дополнительными (в сумме они дают 180 градусов), поэтому этот факт используется для нахождения меры угла W.

угол W = 180 — угол X
угол Ш = 180 — 24
угол W = 156Урок, проведенный мистером Фелизом
Площадь параллелограмма – объяснение и примеры
Как следует из названия, параллелограмм представляет собой четырехугольник, образованный двумя парами параллельных прямых . Он отличается от прямоугольника мерой углов при углах. У параллелограмма противоположные стороны равны по длине и противоположные углы равны по размеру, а у прямоугольника все углы равны 90 градусов.
В этой статье вы узнаете, как вычислить площадь параллелограмма, используя формулу площади параллелограмма.
Чтобы узнать, чем его площадь отличается от площади других четырехугольников и многоугольников, посетите предыдущие статьи.
Как найти площадь параллелограмма?
Площадь параллелограмма – это пространство, ограниченное двумя парами параллельных прямых. Прямоугольник и параллелограмм имеют схожие свойства, поэтому площадь параллелограмма равна площади прямоугольника.

Площадь параллелограмма Формула
Рассмотрим параллелограмм ABCD , показанный ниже. Площадь параллелограмма – это пространство, ограниченное сторонами AD, DC, CB, и AB.
Площадь состояний формулы параллелограмма;
Площадь параллелограмма = основание х высота
A = (b * h) кв. единицы
Где b = основание параллелограмма и,
h = высота или высота параллелограмма.
Высота или высота – это перпендикулярная линия (обычно пунктирная) от вершины параллелограмма к любому из оснований.
Пример 1
Вычислите площадь параллелограмма, основание которого равно 10 сантиметрам, а высота 8 сантиметрам.
Раствор
A = (b * h) кв. единицы.
A = (10 * 8)
A = 80 см
Раствор
A = (b * h) кв. единицы.
= (24 * 13) квадратных дюймов.
= 312 квадратных дюймов.

Пример 3
Если основание параллелограмма в 4 раза больше высоты, а площадь равна 676 см², найдите основание и высоту параллелограмма.
Решение
Пусть высота параллелограмма = x
и основание = 4x
Но площадь параллелограмма = b * h
676 см² = (4x * x) кв.
676 = 4x 2
Разделив обе части на 4, получим
169 = x 2
. .
Основание = 4 * 13 = 52 см
Высота = 13 см.
Следовательно, основание и высота параллелограмма равны 52 см и 13 см соответственно.
Помимо формулы площади параллелограмма, существуют и другие формулы для вычисления площади параллелограмма.
Давайте посмотрим.
Как найти площадь параллелограмма без высоты?
Если высота параллелограмма нам неизвестна, мы можем использовать понятие тригонометрии, чтобы найти его площадь.
Площадь = абсинус (α) = абсинус (β)
Где a и b — длины параллельных сторон, а β или α — угол между сторонами параллелограмма.

Пример 4
Найдите площадь параллелограмма, если две его параллельные стороны равны 80 см и 40 см, а угол между ними равен 56 градусов.
Решение
Пусть a = 80 см и b = 40 см.
Угол между a и b = 56 градусов.
Площадь = абсинус (α)
Замена.
A = 80 × 40 синусов (56)
A = 3200 синусов 56
A = 2652,9 кв.см.
Пример 5
Вычислите углы между двумя сторонами параллелограмма, если длины его сторон равны 5 м и 9 м, а площадь параллелограмма равна 42,8 м 2 .
Раствор
площадь параллелограммы = ab синус (α)
42,8 м 2 = 9 * 5 синус (α)
42,8 = 45 синус (α)
Разделите обе стороны к 45.
0,95111 = SIN (α)
α = Sine -1 0,9523-1 0,95111
α = 72 °
, но β + α = 180 °
β = 180 ° С 72 °
= 108 °
Следовательно, углы между двумя параллельными сторонами параллелограмма равны; 108° и 72°.

Пример 6
Вычислите высоту параллелограмма, параллельные стороны которого равны 30 см и 40 см, а угол между этими двумя сторонами равен 36 градусам.Примите основание параллелограмма равным 40 см.
Решение
Площадь = ab синус (α) = bh
30 * 40 синус (36) = 40 * h
1200 синус (36) = 40 * h.
Обе стороны делим на 40.
h = (1200/40) синус 36
= 30 синус 36
h = 17,63 см
Итак, высота параллелограмма 17,63 см.
Как найти площадь параллелограмма по диагоналям?
Предположим, что d 1 и d 2 являются диагоналями параллелограмма ABCD, тогда площадь параллелограмма определяется как β) = ½ × d 1 × d 2 синус (α)
Где β или α — угол пересечения диагоналей d 1 и d 2 .
Пример 7
Вычислите площадь параллелограмма, диагонали которого равны 18 см и 15 см, а угол пересечения диагоналей равен 43°.

Раствор
Пусть d 1 = 18 см и d 2 = 15 см.
β = 43°.
A = ½ × D 1 × D 2 × D 2 синус (β)
= ½ × 18 × 15 синус (43 °)
= 135Sine 43 °
= 92,07 см 2
площадь параллелограмма 92.07 см 2 .
Площадь параллелограмма по сторонам и углам Калькулятор
- Назначение
- Викторина по геометрии.
- Комментарий/Запрос
- Не могли бы вы указать, как вы получили решение?
[1] 2020/03/23 18:52 Младше 20 лет / Высшая школа/ Университет/ Аспирант / Немного /
- Цель использования
- Вычислить площадь параллелограмма, необходимую для построения фрактильного узора для художественного проекта по дереву.

[2] 14/07/2019 14:58 40-летний уровень / Самозанятые люди / Полезные /
- пошаговый процесс, показывающий пользователям, как перейти от цифр к ответам.
[3] 2019/04/18 02:24 Младше 20 лет / Старшая школа/ Университет/ Аспирант / Немного /
- Цель использования
- решение задачи по математике, дал мне ответ, но нет шагов для его решения
[4] 2018/12/05 16:45 Младше 20 лет / Другое / Немного /
[5] 22.11.2018 03:22 Младше 20 лет / Начальная школа / Ученик средней школы / Очень /
- Цель использования
- Для выполнения домашнего задания по математике
- Комментарий/запрос
- все сработало хорошо
- Цель использования
- Программа
[6] 12/04/2018 04:28 Младше 20 лет / Высшая школа/ Университет/ Аспирант / Очень /
- Цель использования
- ответить на мои неизвестные вопросы
- Комментарий/запрос
- Я не вижу, как он это делает
Вы добавляете кнопку ниже как минимум для студентов, которые хотят учиться
[18/0 20 18 12:09 Младше 20 лет / Высшая школа/ Университет/ Аспирант / Совсем нет /
- Цель использования
- Из карты сайта, которая представляла собой идеальный параллелограмм, проверьте квадратные футы (и площадь в акрах).
- Комментарий/Запрос
- Для нематематиков основные единицы измерения и синтаксис символов всегда неприятны. Было бы здорово иметь ввод угла либо в десятичном виде, либо в градусах-минутах-секундах (несложно преобразовать, но требует дополнительных шагов). Также было бы неплохо иметь формулу Excel. В Excel функция Sin требует ввода в радианах, поэтому side1 * side2 * sin( pi() / 180 )
[8] 13.
 06.2017 01:13 60 лет и старше / Самозанятые / Очень /
06.2017 01:13 60 лет и старше / Самозанятые / Очень /- Цель использования
- Повторение математики
- Комментарий/запрос
- как вы получили площадь с заданными сторонами и углами? Каков был метод?
- из Кейсана
- Площадь параллелограмма = основание * высота = a*(b*sinθ)
[9] 2017/03/26 10:00 Младше 20 лет / Средняя школа/ Университет/ Аспирант / Полезное /
- Назначение
- Узнать площадь параллелограмма по сторонам и углам
- Комментарий/Запрос
- Это очень просто и быстро.

[10] 2015/10/10 02:45 30-летний уровень / Учитель / Исследователь / Очень /

 2 2) / (2 * 6 * 3) = (36 + 9 — 27.04) / (2 * 18) = 17.96/36 ~ 18/36 ~1/2
2 2) / (2 * 6 * 3) = (36 + 9 — 27.04) / (2 * 18) = 17.96/36 ~ 18/36 ~1/2
 Найти углы параллелограмма, если
один угол больше другого на 10°.
Найти углы параллелограмма, если
один угол больше другого на 10°. ∠С=30°, а перпендикуляр к прямой СД равен 5 см. Найти
углы и стороны параллелограмма.
∠С=30°, а перпендикуляр к прямой СД равен 5 см. Найти
углы и стороны параллелограмма. Найти стороны параллелограмма, если
одна сторона больше другой на 9см, а периметр его 66см.
Найти стороны параллелограмма, если
одна сторона больше другой на 9см, а периметр его 66см.
 Здесь ∠A + ∠B + ∠C + ∠D = 360°.
Здесь ∠A + ∠B + ∠C + ∠D = 360°. {\circ} {/экв}.{\ круг} } {/экв} Получите доступ к тысячам практических вопросов и пояснений!
{\circ} {/экв}.{\ круг} } {/экв} Получите доступ к тысячам практических вопросов и пояснений!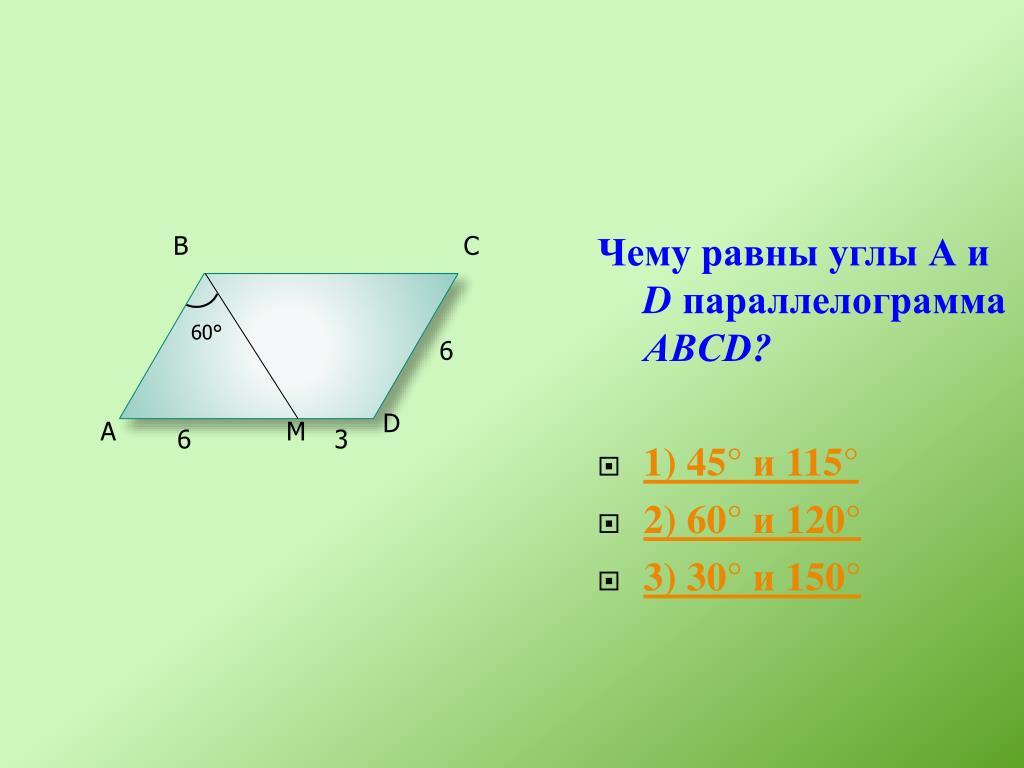 Поэтому нам не нужно использовать другие углы на рисунке.
Поэтому нам не нужно использовать другие углы на рисунке. Если у вас есть прямоугольник или квадрат, каждый из углов равен 90°. Если у вас есть параллелограмм или ромб, противоположные углы равны, а следующие друг за другом углы являются дополнительными. Для других типов четырехугольников вам может понадобиться сложить заданные углы, а затем вычесть из 360°.
Если у вас есть прямоугольник или квадрат, каждый из углов равен 90°. Если у вас есть параллелограмм или ромб, противоположные углы равны, а следующие друг за другом углы являются дополнительными. Для других типов четырехугольников вам может понадобиться сложить заданные углы, а затем вычесть из 360°.
 Используя то свойство, что сумма
два смежных угла составляют 180 градусов, тогда мы вычисляем 180 вычитаем 45 градусов,
давая нам наш ответ 135 градусов.
Используя то свойство, что сумма
два смежных угла составляют 180 градусов, тогда мы вычисляем 180 вычитаем 45 градусов,
давая нам наш ответ 135 градусов. В параллелограмме ABCD:
В параллелограмме ABCD: Треугольник 1 конгруэнтен треугольнику 2 по методу ASA (угол-сторона-угол).
Треугольник 1 конгруэнтен треугольнику 2 по методу ASA (угол-сторона-угол).




 06.2017 01:13 60 лет и старше / Самозанятые / Очень /
06.2017 01:13 60 лет и старше / Самозанятые / Очень /