примеры и решения, формулы и теоремы
Длина вектора — основные формулы
Длину вектора a→ будем обозначать a→. Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.
Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат Oxy. Пусть в ней задан некоторый вектор a→ с координатами ax;ay. Введем формулу для нахождения длины (модуля) вектора a→ через координаты ax и ay.
От начала координат отложим вектор OA→=a→. Определим соответственные проекции точки A на координатные оси как Ax и Ay . Теперь рассмотрим прямоугольник OAxAAy с диагональю OA.
Из теоремы Пифагора следует равенство OA2=OAx2+OAy2, откуда OA=OAx2+OAy2. Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что OAx2=ax2 и OAy2=ay2, а по построению длина OA равна длине вектора OA→, значит, OA→=OAx2+OAy2.
Отсюда получается, что формула для нахождения длины вектора a→=ax;ay имеет соответствующий вид: a→=ax2+ay2.
Если вектор a→ дан в виде разложения по координатным векторам a→=ax·i→+ay·j→, то вычислить его длину можно по той же формуле a→=ax2+ay2, в данном случае коэффициенты ax и ay выступают в роли координат вектора a→ в заданной системе координат.
Пример 1Вычислить длину вектора a→=7;e, заданного в прямоугольной системе координат.
Решение
Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатамa→=ax2+ay2: a→=72+e2=49+e
Ответ: a→=49+e.
Формула для нахождения длины вектора a→=ax;ay;az по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)
В данном случае OA2=OAx2+OAy2+OAz2 (так как ОА – диагональ прямоугольного параллелепипеда), отсюда OA=OAx2+OAy2+OAz2. Из определения координат вектора можем записать следующие равенства OAx=ax; OAy=ay; OAz=az; , а длина ОА равна длине вектора, которую мы ищем, следовательно, OA→=OAx2+OAy2+OAz2.
Отсюда следует, что длина вектора a→=ax;ay;az равна a→=ax2+ay2+az2.
Пример 2Вычислить длину вектора a→=4·i→-3·j→+5·k→, где i→,j→,k→ — орты прямоугольной системы координат.
Решение
Дано разложение вектора a→=4·i→-3·j→+5·k→, его координаты равны a→=4,-3,5. Используя выше выведенную формулу получим a→=ax2+ay2+az2=42+(-3)2+52=52.
Ответ:a→=52.
Слишком сложно?
Не парься, мы поможем разобраться и подарим скидку 10% на любую работу
Опиши заданиеДлина вектора через координаты точек его начала и конца
Итак, даны точки с заданными координатами A(ax;ay) и B(bx;by), отсюда вектор AB→ имеет координаты (bx-ax; by-ay)значит, его длина может быть определена по формуле: AB→=(bx-ax)2+(by-ay)2
А если даны точки с заданными координатами A(ax;ay;az) и B(bx;by;bz) в трехмерном пространстве, то длину вектора AB→ можно вычислить по формуле
AB→=(bx-ax)2+(by-ay)2+(bz-az)2
Пример 3Найти длину вектора AB→, если в прямоугольной системе координат A1, 3, B-3, 1.
Решение
Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим AB→=(bx-ax)2+(by-ay)2: AB→=(-3-1)2+(1-3)2=20-23.
Второй вариант решения подразумевает под собой применение данных формул по очереди: AB→=(-3-1; 1-3)=(-4; 1-3); AB→=(-4)2+(1-3)2=20-23.-
Ответ: AB→=20-23.
Пример 4Определить, при каких значениях длина вектора AB→ равна 30, еслиA(0, 1, 2); B(5, 2, λ2) .
Решение
Для начала распишем длину вектора AB→ по формуле: AB→=(bx-ax)2+(by-ay)2+(bz-az)2=(5-0)2+(2-1)2+(λ2-2)2=26+(λ2-2)2
Затем полученное выражение приравняем к 30, отсюда найдем искомые λ:
26+(λ2-2)2=3026+(λ2-2)2=30(λ2-2)2=4λ2-2=2 или λ2-2=-2 λ1=-2, λ2=2, λ3=0.
Ответ: λ1=-2, λ2=2, λ3=0.
Нахождение длины вектора по теореме косинусов
Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.
Пусть заданы длины двух векторов AB→, AC→ и угол между ними (или косинус угла), а требуется найти длину вектора BC→ или CB→. В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ABC, вычислить длину стороны BC, которая и равна искомой длине вектора.
Рассмотрим такой случай на следующем примере.
Пример 5Длины векторов AB→ и AC→ равны 3 и 7 соответственно, а угол между ними равен π3. Вычислить длину вектора BC→.
Решение
Длина вектора BC→ в данном случае равна длине стороны BC треугольника △ABC. Длины сторон AB и AC треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов:BC2=AB2+AC2-2·AB·AC·cos∠(AB,→AC→)=32+72-2·3·7·cosπ3=37 ⇒BC=37 Таким образом, BC→=37.
Ответ:BC→=37.
Итак, для нахождения длины вектора по координатам существуют следующие формулы a→=ax2+ay2 или a→=ax2+ay2+az2, по координатам точек начала и конца вектора AB→=(bx-ax)2+(by-ay)2 или AB→=(bx-ax)2+(by-ay)2+(bz-az)2, в некоторых случаях следует использовать теорему косинусов.
Как найти длину вектора по координатам точек. Нахождение длины вектора, примеры и решения. Вычисление длины вектора по его координатам
На оси абсцисс и ординат называются координатами вектора . Координаты вектора общепринято указывать в виде (х, у) , а сам вектор как: =(х, у).
Формула определения координат вектора для двухмерных задач.
В случае двухмерной задачи вектор с известными координатами точек A(х 1 ;у 1) и B(x 2 ; y 2 ) можно вычислить:
= (x 2 — x 1 ; y 2 — y 1).
Формула определения координат вектора для пространственных задач.
В случае пространственной задачи вектор с известными координатами точек A(х 1 ;у 1 ; z 1 ) и B(x 2 ; y 2 ; z 2 ) можно вычислить применив формулу:
= (

Координаты дают всеобъемлющую характеристику вектора, поскольку по координатам есть возможность построить и сам вектор. Зная координаты, легко вычислить и длину вектора . (Свойство 3, приведенное ниже).
Свойства координат вектора.
1. Любые равные векторы в единой системе координат имеют равные координаты .
2. Координаты коллинеарных векторов пропорциональны. При условии, что ни один из векторов не равен нулю.
3. Квадрат длины любого вектора равен сумме квадратов его координат .
4.При операции умножения вектора на действительное число каждая его координата умножается на это число.
5. При операции сложения векторов вычисляем сумму соответствующие координаты векторов .
6. Скалярное произведение двух векторов равняется сумме произведений их соответствующих координат.
Нахождение координат вектора довольно часто встречаемое условие многих задач в математике.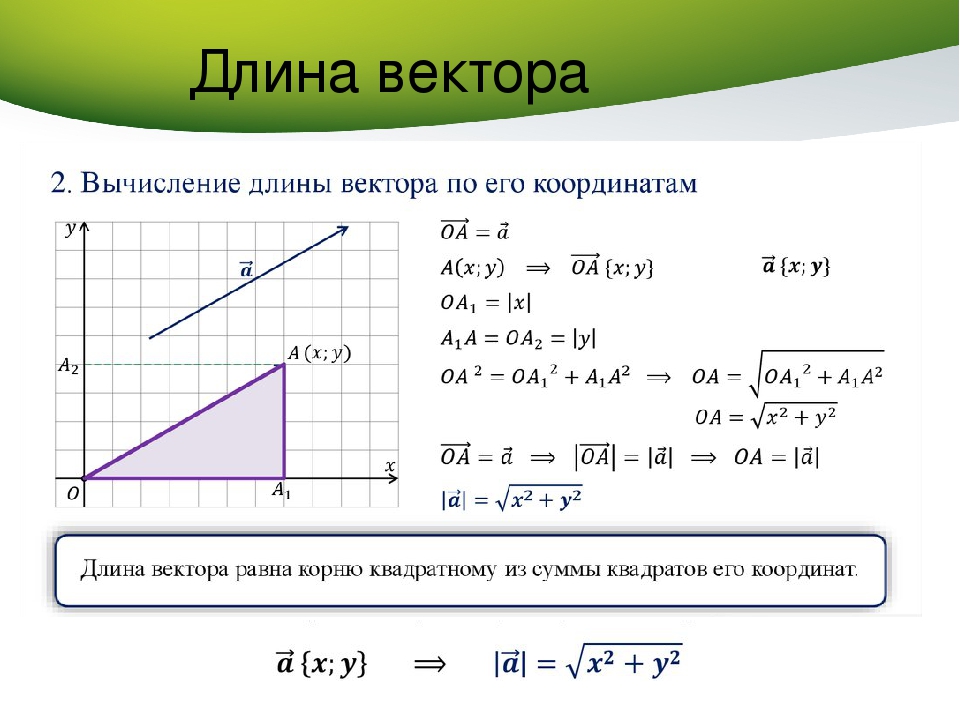 Умение находить координаты вектора поможет вам в других, более сложных задачах со схожей тематикой. В данной статье мы рассмотрим формулу нахождения координат вектора и несколько задач.
Умение находить координаты вектора поможет вам в других, более сложных задачах со схожей тематикой. В данной статье мы рассмотрим формулу нахождения координат вектора и несколько задач.
Нахождение координат вектора в плоскости
Что такое плоскость? Плоскостью считается двухмерное пространство, пространство с двумя измерениями (измерение x и измерение y). К примеру, бумага – плоскость. Поверхность стола – плоскость. Какая-нибудь необъемная фигура (квадрат, треугольник, трапеция) тоже является плоскостью. Таким образом, если в условии задачи нужно найти координаты вектора, который лежит на плоскости, сразу вспоминаем про x и y. Найти координаты такого вектора можно следующим образом: Координаты AB вектора = (xB – xA; yB – xA). Из формулы видно, что от координат конечной точки нужно отнять координаты начальной точки.
Пример:
- Вектор CD имеет начальные (5; 6) и конечные (7; 8) координаты.
- Найти координаты самого вектора.
- Используя вышеупомянутую формулу, получим следующее выражение: CD = (7-5; 8-6) = (2; 2).

- Таким образом, координаты CD вектора = (2; 2).
- Соответственно, x координата равна двум, y координата – тоже двум.
Нахождение координат вектора в пространстве
Что такое пространство? Пространство это уже трехмерное измерение, где даны 3 координаты: x, y, z. В случае, если нужно найти вектор, который лежит в пространстве, формула практически не меняется. Добавляется только одна координата. Для нахождения вектора нужно от координат конца отнять координаты начала. AB = (xB – xA; yB – yA; zB – zA)
Пример:
- Вектор DF имеет начальные (2; 3; 1) и конечные (1; 5; 2).
- Применяя вышеупомянутую формулу, получим: Координаты вектора DF = (1-2; 5-3; 2-1) = (-1; 2; 1).
- Помните, значение координат может быть и отрицательным, в этом нет никакой проблемы.
Как найти координаты вектора онлайн?
Если по каким-то причинам вам не хочется находить координаты самостоятельно, можно воспользоваться онлайн калькулятором . Для начала, выберите размерность вектора. Размерность вектора отвечает за его измерения. Размерность 3 означает, что вектор находится в пространстве, размерность 2 – что на плоскости. Далее вставьте координаты точек в соответствующие поля и программа определит вам координаты самого вектора. Все очень просто.
Для начала, выберите размерность вектора. Размерность вектора отвечает за его измерения. Размерность 3 означает, что вектор находится в пространстве, размерность 2 – что на плоскости. Далее вставьте координаты точек в соответствующие поля и программа определит вам координаты самого вектора. Все очень просто.
Нажав на кнопку, страница автоматически прокрутится вниз и выдаст вам правильный ответ вместе с этапами решения.
Рекомендовано хорошо изучить данную тему, потому что понятие вектора встречается не только в математике, но и в физике. Студенты факультета Информационных Технологий тоже изучают тему векторов, но на более сложном уровне.
 Площадь параллелограмма.
Площадь параллелограмма.



 Матрицы и действия над ними. Ранг матрицы.
Матрицы и действия над ними. Ранг матрицы.
Вектором называется направленный отрезок. Длиной или модулем вектора называется длина соответствующего направленного отрезка.
Модуль вектора a обозначается . Векторa называется единичным, если . Векторы называются коллинеарными, если они параллельны одной прямой. Векторы называются компланарными, если они параллельны одной плоскости.
2. Умножение вектора на число. Свойства операции.
Умножение вектора на число, даёт противоположно направленный вектор в длиной враз больше. Умножение вектора на число в координатной форме производится умножением всех координат на это число:
Исходя из определения получается выражение для модуля вектора, умноженного на число:
Аналогично как и числами, операции сложение вектора с самим с собой можно записать через умножение на число:
А вычитание векторов можно переписать через сложение и умножение:
Исходя из того, что умножение на не меняет длины вектора, а меняет только направление и учитывая определение вектора, получаем:
3. Сложение векторов, вычитание векторов.
Сложение векторов, вычитание векторов.
В координатном представлении вектор суммы получается суммированием соответствующих координат слагаемых:
Для геометрического построения вектора суммы используют различные правила (методы), однако они все дают одинаковый результат. Использование того или иного правила обосновывается решаемой задачей.
Правило треугольника
Правило треугольника наиболее естественно следует из понимания вектора как переноса. Ясно, что результат последовательного применения двух переносов инекоторой точки будет тем же, что применение сразу одного переноса, соответствующего этому правилу. Для сложения двух векторовипо правилутреугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.
Это правило прямо и естественно обобщается для сложения любого количества векторов, переходя в правило ломаной :
Правило многоугольника
Начало
второго вектора совмещается с концом
первого, начало третьего — с концом
второго и так далее, сумма же
векторов
есть вектор, с началом, совпадающим с
началом первого, и концом, совпадающим
с концом-го
(то есть изображается направленным
отрезком, замыкающим ломаную). Так же
называется правилом ломаной.
Так же
называется правилом ломаной.
Правило параллелограмма
Для сложения двух векторов ипо правилупараллелограмма оба эти векторы переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала. (Легко видеть, что эта диагональ совпадает с третьей стороной треугольника при использовании правила треугольника).
Правило параллелограмма особенно удобно, когда есть потребность изобразить вектор суммы сразу же приложенным к той же точке, к которой приложены оба слагаемых — то есть изобразить все три вектора имеющими общее начало.
Модуль суммы векторов
Модуль суммы двух векторов можно вычислить, использую теорему косинусов :
Где — косинус угла между векторамии.
Если
векторы изображены в соответствии с
правилом треугольника и берется угол
по рисунку — между сторонами
треугольника — что не совпадает с
обычным определением угла между
векторами, а значит и с углом в приведенной
формуле, то последний член приобретает
знак минус, что соответствует теореме
косинусов в ее прямой формулировке.
Для суммы произвольного количества векторов применима аналогичная формула, в которой членов с косинусом больше: по одному такому члену существует для каждой пары векторов из суммируемого набора. Например, для трех векторов формула выглядит так:
Вычитание векторов
Два вектора и вектор их разности
Для получения разности в координатной форме надо вычесть соответствующие координаты векторов:
Для получения вектора разности начала векторов соединяются и началом векторабудет конец, а концом — конец. Если записать, используя точки векторов, то.
Модуль разности векторов
Три вектора , как и при сложении, образуют треугольник, и выражение для модуля разности получается аналогичным:
где — косинус угла между векторамии
Отличие
от формулы модуля суммы в знаке перед
косинусом, при этом надо хорошо следить,
какой именно угол берется (вариант
формулы модуля суммы с углом между
сторонами треугольника при суммировании
по правилу треугольника по виду не
отличается от данной формулы для модуля
разности, но надо иметь в виду, что для
тут берутся разные углы: в случае суммы
берётся угол, когда вектор
переносится
к концу вектора,
когда же ищется модель разности, берётся
угол между векторами, приложенными к
одной точке; выражение для модуля суммы
с использованием того же угла, что в
данном выражении для модуля разности,
отличается знаком перед косинусом).
Длину вектора a → будем обозначать a → . Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.
Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат O x y . Пусть в ней задан некоторый вектор a → с координатами a x ; a y . Введем формулу для нахождения длины (модуля) вектора a → через координаты a x и a y .
От начала координат отложим вектор O A → = a → . Определим соответственные проекции точки A на координатные оси как A x и A y . Теперь рассмотрим прямоугольник O A x A A y с диагональю O A .
Из теоремы Пифагора следует равенство O A 2 = O A x 2 + O A y 2 , откуда O A = O A x 2 + O A y 2 . Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что O A x 2 = a x 2 и O A y 2 = a y 2 , а по построению длина O A равна длине вектора O A → , значит, O A → = O A x 2 + O A y 2 .
Отсюда получается, что формула для нахождения длины вектора a → = a x ; a y имеет соответствующий вид: a → = a x 2 + a y 2 .
Если вектор a → дан в виде разложения по координатным векторам a → = a x · i → + a y · j → , то вычислить его длину можно по той же формуле a → = a x 2 + a y 2 , в данном случае коэффициенты a x и a y выступают в роли координат вектора a → в заданной системе координат.
Пример 1
Вычислить длину вектора a → = 7 ; e , заданного в прямоугольной системе координат.
Решение
Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатам a → = a x 2 + a y 2: a → = 7 2 + e 2 = 49 + e
Ответ: a → = 49 + e .
Формула для нахождения длины вектора a → = a x ; a y ; a z по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)
В данном случае O A 2 = O A x 2 + O A y 2 + O A z 2 (так как ОА – диагональ прямоугольного параллелепипеда), отсюда O A = O A x 2 + O A y 2 + O A z 2 . Из определения координат вектора можем записать следующие равенства O A x = a x ; O A y = a y ; O A z = a z ; , а длина ОА равна длине вектора, которую мы ищем, следовательно, O A → = O A x 2 + O A y 2 + O A z 2 .
Отсюда следует, что длина вектора a → = a x ; a y ; a z равна a → = a x 2 + a y 2 + a z 2 .
Пример 2
Вычислить длину вектора a → = 4 · i → — 3 · j → + 5 · k → , где i → , j → , k → — орты прямоугольной системы координат.
Решение
Дано разложение вектора a → = 4 · i → — 3 · j → + 5 · k → , его координаты равны a → = 4 , — 3 , 5 . Используя выше выведенную формулу получим a → = a x 2 + a y 2 + a z 2 = 4 2 + (- 3) 2 + 5 2 = 5 2 .
Ответ: a → = 5 2 .
Длина вектора через координаты точек его начала и конца
Выше были выведены формулы, позволяющие находить длины вектора по его координатам. Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.
Итак, даны точки с заданными координатами A (a x ; a y) и B (b x ; b y) , отсюда вектор A B → имеет координаты (b x — a x ; b y — a y) значит, его длина может быть определена по формуле: A B → = (b x — a x) 2 + (b y — a y) 2
А если даны точки с заданными координатами A (a x ; a y ; a z) и B (b x ; b y ; b z) в трехмерном пространстве, то длину вектора A B → можно вычислить по формуле
A B → = (b x — a x) 2 + (b y — a y) 2 + (b z — a z) 2
Пример 3
Найти длину вектора A B → , если в прямоугольной системе координат A 1 , 3 , B — 3 , 1 .
Решение
Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим A B → = (b x — a x) 2 + (b y — a y) 2: A B → = (- 3 — 1) 2 + (1 — 3) 2 = 20 — 2 3 .
Второй вариант решения подразумевает под собой применение данных формул по очереди: A B → = (- 3 — 1 ; 1 — 3) = (- 4 ; 1 — 3) ; A B → = (- 4) 2 + (1 — 3) 2 = 20 — 2 3 . —
Ответ: A B → = 20 — 2 3 .
Пример 4
Определить, при каких значениях длина вектора A B → равна 30 , если A (0 , 1 , 2) ; B (5 , 2 , λ 2) .
Решение
Для начала распишем длину вектора A B → по формуле: A B → = (b x — a x) 2 + (b y — a y) 2 + (b z — a z) 2 = (5 — 0) 2 + (2 — 1) 2 + (λ 2 — 2) 2 = 26 + (λ 2 — 2) 2
Затем полученное выражение приравняем к 30 , отсюда найдем искомые λ:
26 + (λ 2 — 2) 2 = 30 26 + (λ 2 — 2) 2 = 30 (λ 2 — 2) 2 = 4 λ 2 — 2 = 2 и л и λ 2 — 2 = — 2 λ 1 = — 2 , λ 2 = 2 , λ 3 = 0 .
Ответ: λ 1 = — 2 , λ 2 = 2 , λ 3 = 0 .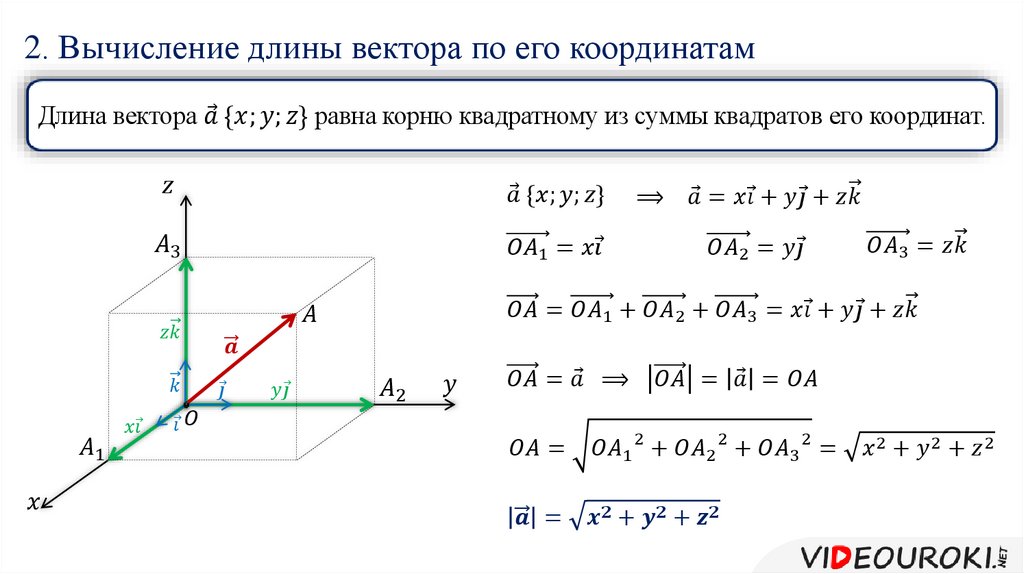
Нахождение длины вектора по теореме косинусов
Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.
Пусть заданы длины двух векторов A B → , A C → и угол между ними (или косинус угла), а требуется найти длину вектора B C → или C B → . В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ A B C , вычислить длину стороны B C , которая и равна искомой длине вектора.
Рассмотрим такой случай на следующем примере.
Пример 5
Длины векторов A B → и A C → равны 3 и 7 соответственно, а угол между ними равен π 3 . Вычислить длину вектора B C → .
Решение
Длина вектора B C → в данном случае равна длине стороны B C треугольника △ A B C . Длины сторон A B и A C треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов: B C 2 = A B 2 + A C 2 — 2 · A B · A C · cos ∠ (A B , → A C →) = 3 2 + 7 2 — 2 · 3 · 7 · cos π 3 = 37 ⇒ B C = 37 Таким образом, B C → = 37 .
Ответ: B C → = 37 .
Итак, для нахождения длины вектора по координатам существуют следующие формулы a → = a x 2 + a y 2 или a → = a x 2 + a y 2 + a z 2 , по координатам точек начала и конца вектора A B → = (b x — a x) 2 + (b y — a y) 2 или A B → = (b x — a x) 2 + (b y — a y) 2 + (b z — a z) 2 , в некоторых случаях следует использовать теорему косинусов.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Oxy
О А ОА .
, откуда ОА .
Таким образом, .
Рассмотрим пример.
Пример.
Решение.
:
Ответ:
Oxyz в пространстве.
А ОА будет диагональю.
В этом случае (так как ОА ОА .
Таким образом, длина вектора .
Пример.
Вычислите длину вектора
Решение.
, следовательно,
Ответ:
Прямая на плоскости
Общее уравнение
Ax + By + C ( > 0).
Вектор = (А; В) — нормальный вектор прямой.
В векторном виде: + С = 0 , где — радиус-вектор произвольной точки на прямой (рис. 4.11).
Частные случаи:
1) By + C = 0 — прямая параллельна оси Ox ;
2) Ax + C = 0 — прямая параллельна оси Oy ;
3) Ax + By = 0 — прямая проходит через начало координат;
4) y = 0 — ось Ox ;
5) x = 0 — ось Oy .
Уравнение прямой в отрезках
где a, b — величины отрезков, отсекаемых прямой на осях координат.
Нормальное уравнение прямой (рис. 4.11)
где — угол, образуемый нормально к прямой и осью Ox ; p — расстояние от начала координат до прямой.
Приведение общего уравнения прямой к нормальному виду:
Здесь — нормируемый множитель прямой; знак выбирается противоположным знаку C , если и произвольно, если C = 0 .
Нахождение длины вектора по координатам.
Длину вектора будем обозначать . Из-за такого обозначения длину вектора часто называют модулем вектора.
Начнем с нахождения длины вектора на плоскости по координатам.
Введем на плоскости прямоугольную декартову систему координат Oxy . Пусть в ней задан вектор и он имеет координаты . Получим формулу, позволяющую находить длину вектора через координаты и .
Отложим от начала координат (от точки О ) вектор . Обозначим проекции точки А на координатные оси как и соответственно и рассмотрим прямоугольник с диагональю ОА .
В силу теоремы Пифагора справедливо равенство , откуда . Из определения координат вектора в прямоугольной системе координатмы можем утверждать, что и , а по построению длина ОА равна длине вектора , следовательно, .
Таким образом, формула для нахождения длины вектора по его координатам на плоскости имеет вид .
Если вектор представлен в виде разложения по координатным векторам , то его длина вычисляется по этой же формуле , так как в этом случае коэффициенты и являются координатами вектора в заданной системе координат.
Рассмотрим пример.
Пример.
Найдите длину вектора , заданного в декартовой системе координат.
Решение.
Сразу применяем формулу для нахождения длины вектора по координатам :
Ответ:
Теперь получим формулу для нахождения длины вектора по его координатам в прямоугольной системе координат Oxyz в пространстве.
Отложим от начала координат вектор и обозначим проекции точки А на координатные оси как и . Тогда мы можем построить на сторонах и прямоугольный параллелепипед, в котором ОА будет диагональю.
В этом случае (так как ОА – диагональ прямоугольного параллелепипеда), откуда . Определение координат вектора позволяет нам записать равенства , а длина ОА равна искомой длине вектора, следовательно, .
Таким образом, длина вектора в пространстве равна корню квадратному из суммы квадратов его координат , то есть, находится по формуле .
Пример.
Вычислите длину вектора , где — орты прямоугольной системы координат.
Решение.
Нам дано разложение вектора по координатным векторам вида , следовательно, . Тогда по формуле нахождения длины вектора по координатам имеем .
Нахождение длины вектора через координаты начала и. Вектор. Координаты вектора
На оси абсцисс и ординат называются координатами вектора . Координаты вектора общепринято указывать в виде (х, у) , а сам вектор как: =(х, у).
Формула определения координат вектора для двухмерных задач.
В случае двухмерной задачи вектор с известными координатами точек A(х 1 ;у 1) и B(x 2 ; y 2 ) можно вычислить:
= (x 2 — x 1 ; y 2 — y 1).
Формула определения координат вектора для пространственных задач.
В случае пространственной задачи вектор с известными координатами точек A(х 1 ;у 1 ; z 1 ) и B(x 2 ; y 2 ; z 2 ) можно вычислить применив формулу:
= (x 2 — x 1 ; y 2 — y 1 ; z 2 — z 1 ).
Координаты дают всеобъемлющую характеристику вектора, поскольку по координатам есть возможность построить и сам вектор. Зная координаты, легко вычислить и длину вектора . (Свойство 3, приведенное ниже).
Свойства координат вектора.
1. Любые равные векторы в единой системе координат имеют равные координаты .
2. Координаты коллинеарных векторов пропорциональны. При условии, что ни один из векторов не равен нулю.
3. Квадрат длины любого вектора равен сумме квадратов его координат .
4.При операции умножения вектора на действительное число каждая его координата умножается на это число.
5. При операции сложения векторов вычисляем сумму соответствующие координаты векторов .
6. Скалярное произведение двух векторов равняется сумме произведений их соответствующих координат.
Векторы. Действия с векторами. В этой статье мы поговорим о том, что такое вектор, как находить его длину, и как умножать вектор на число, а также как находить сумму, разность и скалярное произведение двух векторов.
Как обычно, немного самой необходимой теории.
Вектор — это направленный отрезок, то есть такой отрезок, у которого есть начало и конец:
Здесь точка А — начало вектора, а точка В — его конец.
У вектора есть два параметра: его длина и направление.
Длина вектора — это длина отрезка, соединяющего начало и конец вектора. Длина вектора обозначается
Два вектора называются равными , если они имеют одинаковую длину и сонаправлены.
Два вектора называются сонаправленными , если они лежат на параллельных прямых и направлены в одну сторону: вектора и сонаправлены:
Два вектора называются противоположно направленными, если они лежат на параллельных прямых и направлены в противоположные стороны: вектора и , а также и направлены в противоположные стороны:
Вектора, лежащие на параллельных прямых называются коллинеарными : вектора , и — коллинеарны.
Произведением вектора на число называется вектор, сонаправленный вектору , если title=»k>0″>, и направленный в противоположную сторону, если , и длина которого равна длине вектора , умноженной на :
Чтобы сложить два вектора
и , нужно начало вектора соединить с концом вектора . Вектор суммы соединяет начало вектора с концом вектора :
Вектор суммы соединяет начало вектора с концом вектора :
Это правило сложения векторов называется правилом треугольника .
Чтобы сложить два вектора по правилу параллелограмма , нужно отложить вектора от одной точки и достроить до параллелограмма. Вектор суммы соединяет точку начала векторов с противоположным углом параллелограмма:
Разность двух векторов определяется через сумму: разностью векторов и называется такой вектор , который в сумме с вектором даст вектор :
Отсюда вытекает правило нахождения разности двух векторов : чтобы из вектора вычесть вектор , нужно отложить эти вектора от одной точки. Вектор разности соединяет конец вектора с концом вектора (то есть конец вычитаемого с концом уменьшаемого):
Чтобы найти угол между вектором и вектором , нужно отложить эти вектора от одной точки. Угол, образованный лучами, на которых лежат вектора, называется углом между векторами:
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:
Предлагаю вам решить задачи из Открытого банка заданий для , а затем сверить све решение с ВИДЕОУРОКАМИ:
1
. Задание 4 (№ 27709)
Задание 4 (№ 27709)
Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину разности векторов и .
2 . Задание 4 (№ 27710)
Две стороны прямоугольника ABCD равны 6 и 8. Найдите скалярное произведение векторов и . (чертеж из предыдущей задачи).
3 . Задание 4 (№ 27711)
Две стороны прямоугольника ABCD O . Найдите длину суммы векторов и .
4 . Задание 4 (№ 27712)
Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке O . Найдите длину разности векторов и . (чертеж из предыдущей задачи).
5 . Задание 4 (№ 27713)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора .
6 . Задание 4 (№ 27714)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора + .
7 .Задание 4 (№ 27715)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора — .(чертеж из предыдущей задачи).
8 .Задание 4 (№ 27716)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора — .
Найдите длину вектора — .
9 . Задание 4 (№ 27717)
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора + .
10 . Задание 4 (№ 27718)
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора — .(чертеж из предыдущей задачи).
11 .Задание 4 (№ 27719)
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите скалярное произведение векторов и .(чертеж из предыдущей задачи).
12 . Задание 4 (№ 27720)
ABC равны Найдите длину вектора +.
13 . Задание 4 (№ 27721)
Стороны правильного треугольника ABC равны 3. Найдите длину вектора -.(чертеж из предыдущей задачи).
14 . Задание 4 (№ 27722)
Стороны правильного треугольника ABC равны 3. Найдите скалярное произведение векторов и . (чертеж из предыдущей задачи).
Вероятно, Ваш браузер не поддерживается. Чтобы использовать тренажёр «Час ЕГЭ», попробуйте скачать
Firefox
Oxy
О А ОА .
, откуда ОА .
Таким образом, .
Рассмотрим пример.
Пример.
Решение.
:
Ответ:
Oxyz в пространстве.
А ОА будет диагональю.
В этом случае (так как ОА ОА .
Таким образом, длина вектора .
Пример.
Вычислите длину вектора
Решение.
, следовательно,
Ответ:
Прямая на плоскости
Общее уравнение
Ax + By + C ( > 0).
Вектор = (А; В) — нормальный вектор прямой.
В векторном виде: + С = 0 , где — радиус-вектор произвольной точки на прямой (рис. 4.11).
Частные случаи:
1) By + C = 0 — прямая параллельна оси Ox ;
2) Ax + C = 0 — прямая параллельна оси Oy ;
3) Ax + By = 0 — прямая проходит через начало координат;
4) y = 0 — ось Ox ;
5) x = 0 — ось Oy .
Уравнение прямой в отрезках
где a, b — величины отрезков, отсекаемых прямой на осях координат.
Нормальное уравнение прямой (рис. 4.11)
где — угол, образуемый нормально к прямой и осью Ox ; p — расстояние от начала координат до прямой.
Приведение общего уравнения прямой к нормальному виду:
Здесь — нормируемый множитель прямой; знак выбирается противоположным знаку C , если и произвольно, если C = 0 .
Нахождение длины вектора по координатам.
Длину вектора будем обозначать . Из-за такого обозначения длину вектора часто называют модулем вектора.
Начнем с нахождения длины вектора на плоскости по координатам.
Введем на плоскости прямоугольную декартову систему координат Oxy . Пусть в ней задан вектор и он имеет координаты . Получим формулу, позволяющую находить длину вектора через координаты и .
Отложим от начала координат (от точки О ) вектор . Обозначим проекции точки А на координатные оси как и соответственно и рассмотрим прямоугольник с диагональю ОА .
Обозначим проекции точки А на координатные оси как и соответственно и рассмотрим прямоугольник с диагональю ОА .
В силу теоремы Пифагора справедливо равенство , откуда . Из определения координат вектора в прямоугольной системе координатмы можем утверждать, что и , а по построению длина ОА равна длине вектора , следовательно, .
Таким образом, формула для нахождения длины вектора по его координатам на плоскости имеет вид .
Если вектор представлен в виде разложения по координатным векторам , то его длина вычисляется по этой же формуле , так как в этом случае коэффициенты и являются координатами вектора в заданной системе координат.
Рассмотрим пример.
Пример.
Найдите длину вектора , заданного в декартовой системе координат.
Решение.
Сразу применяем формулу для нахождения длины вектора по координатам :
Ответ:
Теперь получим формулу для нахождения длины вектора по его координатам в прямоугольной системе координат Oxyz в пространстве.
Отложим от начала координат вектор и обозначим проекции точки А на координатные оси как и . Тогда мы можем построить на сторонах и прямоугольный параллелепипед, в котором ОА будет диагональю.
В этом случае (так как ОА – диагональ прямоугольного параллелепипеда), откуда . Определение координат вектора позволяет нам записать равенства , а длина ОА равна искомой длине вектора, следовательно, .
Таким образом, длина вектора в пространстве равна корню квадратному из суммы квадратов его координат , то есть, находится по формуле .
Пример.
Вычислите длину вектора , где — орты прямоугольной системы координат.
Решение.
Нам дано разложение вектора по координатным векторам вида , следовательно, . Тогда по формуле нахождения длины вектора по координатам имеем .
Прежде всего надо разобрать само понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок . Введем следующее определение.
Введем следующее определение.
Определение 1
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.
Определение 2
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).
Одной маленькой буквой: $\overline{a}$ (рис. 1).
Введем теперь, непосредственно, понятие длин вектора.
Определение 3
Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|\overline{a}|$
Понятие длины вектора связано, к примеру, с таким понятием, как равенство двух векторов.
Определение 4
Два вектора будем называть равными, если они удовлетворяют двух условиям:
1. Они сонаправлены;
1. Их длины равны (рис. 2).
Они сонаправлены;
1. Их длины равны (рис. 2).
Для того, чтобы определять векторы вводят систему координат и определяют координаты для вектора во введенной системе. Как мы знаем, любой вектор можно разложить в виде $\overline{c}=m\overline{i}+n\overline{j}$, где $m$ и $n$ – действительные числа, а $\overline{i}$ и $\overline{j}$ — единичные векторы на оси $Ox$ и $Oy$, соответственно.
Определение 5
Коэффициенты разложения вектора $\overline{c}=m\overline{i}+n\overline{j}$ будем называть координатами этого вектора во введенной системе координат. Математически:
$\overline{c}={m,n}$
Как найти длину вектора?
Для того, чтобы вывести формулу для вычисления длины произвольного вектора по данным его координатам рассмотрим следующую задачу:
Пример 1
Дано: вектор $\overline{α}$, имеющий координаты ${x,y}$. Найти: длину этого вектора.
Введем на плоскости декартову систему координат $xOy$. От начал введенной системы координат отложим $\overline{OA}=\overline{a}$. 2}$.
2}$.
Вывод: Чтобы найти длину вектора, у которого задан его координаты, необходимо найти корень из квадрата суммы этих координат.
Пример задач
Пример 2
Найдите расстояние между точками $X$ и $Y$, которые имеют следующие координаты: $(-1,5)$ и $(7,3)$, соответственно.
Любые две точки можно легко связать с понятием вектора. Рассмотрим, к примеру, вектор $\overline{XY}$. Как мы уже знаем, координаты такого вектора можно найти, вычтя из координат конечной точки ($Y$) соответствующие координаты начальной точки ($X$). Получим, что
Сумма векторов. Длина вектора. Дорогие друзья, в составе типов задний экзамена присутствует группа задач с векторами. Задания довольно широкого спектра (важно знать теоретические основы). Большинство решается устно. Вопросы связаны с нахождением длины вектора, суммы (разности) векторов, скалярного произведения. Так же много заданий, при решении которых необходимо осуществить действия с координатами векторов.
Теория касающаяся темы векторов несложная, и её необходимо хорошо усвоить. В этой статье разберём задачи связанные с нахождением длины вектора, также суммы (разности) векторов. Некоторые теоретические моменты:
В этой статье разберём задачи связанные с нахождением длины вектора, также суммы (разности) векторов. Некоторые теоретические моменты:
Понятие вектора
Вектор — это направленный отрезок.
Все векторы, имеющие одинаковое направление и равные по длине являются равными.
*Все представленные выше четыре вектора равны!
То есть, если мы будем при помощи параллельного переноса перемещать данный нам вектор, то всегда получим вектор равный исходному. Таким образом, равных векторов может быть бесчисленное множество.
Обозначение векторов
Вектор может быть обозначен латинскими заглавными буквами, например:
При данной форме записи сначала записывается буква обозначающая начало вектора, затем буква обозначающая конец вектора.
Ещё вектор обозначается одной буквой латинского алфавита (прописной):
Возможно также обозначение без стрелок:
Суммой двух векторов АВ и ВС будет являться вектор АС .
Записывается как АВ +ВС =АС .
Это правило называется – правилом треугольника .
То есть, если мы имеем два вектора – назовём их условно (1) и (2), и конец вектора (1) совпадает с началом вектора (2), то суммой этих векторов будет вектор, начало которого совпадает с началом вектора (1), а конец совпадает с концом вектора (2).
Вывод: если мы имеем на плоскости два вектора, то всегда сможем найти их сумму. При помощи параллельного переноса можно переместить любой из данных векторов и соединить его начало с концом другого. Например:
Перенесём вектор b , или по-другому – построим равный ему:
Как находится сумма нескольких векторов? По тому же принципу:
* * *
Правило параллелограмма
Это правило является следствием изложенного выше.
Для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах.
Построим вектор равный вектору b так, чтобы его начало совпадало с концом вектора a , и мы можем построить вектор, который будет являться их суммой:
Ещё немного важной информации, необходимой для решения задач.
Вектор, равный по длине исходному, но противоположно направленный, обозначается также но имеет противоположный знак:
Эта информация крайне полезна для решения задач, в которых стоит вопрос о нахождении разности векторов. Как видите, разность векторов это та же сумма в изменнёном виде.
Пусть даны два вектора, найдём их разность:
Мы построили вектор противоположный вектору b, и нашли разность.
Координаты вектора
Чтобы найти координаты вектора, нужно из координат конца вычесть соответствующие координаты начала:
То есть, координаты вектора представляют собой пару чисел.
Если
И координаты векторов имеют вид:
То c 1 = a 1 + b 1 c 2 = a 2 + b 2
Если
То c 1 = a 1 – b 1 c 2 = a 2 – b 2
Модуль вектора
Модулем вектора называется его длина, определяется по формуле:
Формула для определения длины вектора, если известны координаты его начала и конца:
Рассмотрим задачи:
Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке О. Найдите длину разности векторов АО
и ВО
.
Диагонали пересекаются в точке О. Найдите длину разности векторов АО
и ВО
.
Найдём вектор, который будет являться результатом АО –ВО:
АО –ВО =АО +(–ВО )=АВ
То есть разность векторов АО и ВО будет являться вектор АВ. А его длина равна восьми.
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора АВ +AD .
Найдём вектор, который будет являться суммой векторов AD и AB BC равен вектору AD . Значит AB +AD =AB +BC =AC
AC это длина диагонали ромба АС , она равна 16.Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора АО +ВО .
Найдём вектор, который будет являться суммой векторов АО и ВО ВО равен вектору OD, з начит
AD это длина стороны ромба. Задача сводится к нахождению гипотенузы в прямоугольном треугольнике AOD. Вычислим катеты:По теореме Пифагора:
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора АО
–ВО
.
Найдём вектор, который будет являться результатом АО –ВО :
АВ это длина стороны ромба. Задача сводится к нахождению гипотенузы АВ в прямоугольном треугольнике AOB. вычислим катеты:По теореме Пифагора:
Стороны правильного треугольника ABC равны 3.
Найдите длину вектора АВ –АС .
Найдём результат разности векторов:
СВ равна трём, так как в условии сказано, что треугольник равносторонний и его стороны равны 3.27663. Найдите длину вектора а (6;8).
27664. Найдите квадрат длины вектора АВ .
Найти длину вектора известны координаты точек. Нахождение длины вектора по координатам
Найдем длину вектора по его координатам (в прямоугольной системе координат), по координатам точек начала и конца вектора и по теореме косинусов (задано 2 вектора и угол между ними).
Вектор – это направленный отрезок прямой.
Длина этого отрезка определяет числовое значение вектора и называется
длиной вектора или модулем вектора.
1. Вычисление длины вектора по его координатам
Если даны координаты вектора в плоской (двухмерной) прямоугольной системе координат, т.е. известны a x и a y , то длину вектора можно найти по формуле
В случае вектора в пространстве добавляется третья координата
В MS EXCEL выражение =КОРЕНЬ(СУММКВ(B8:B9)) позволяет вычислить модуль вектора (предполагается, что координаторы вектора введены в ячейки B8:B9 , см. файл примера ).
Функция СУММКВ() возвращает сумму квадратов аргументов, т.е. в данном случае эквивалентна формуле =B8*B8+B9*B9 .
В файле примера также вычислена длина вектора в пространстве.
Альтернативной формулой является выражение =КОРЕНЬ(СУММПРОИЗВ(B8:B9;B8:B9)) .
2. Нахождение длины вектора через координаты точек
Если вектор задан через координаты точек его начала и конца, то формула будет другой =КОРЕНЬ(СУММКВРАЗН(C28:C29;B28:B29))
В формуле предполагается, что координаты точек начала и конца введены в диапазоны C28:C29 и B28:B29 соответственно.
Функция СУММКВРАЗН() в озвращает сумму квадратов разностей соответствующих значений в двух массивах.
По сути, в формуле сначала вычисляются координаты вектора (разности соответствующих координат точек), затем вычисляется сумма их квадратов.
3. Нахождение длины вектора по теореме косинусов
Если требуется найти длину вектора по теореме косинусов, то обычно заданы 2 вектора (их модули и угол между ними).
Найдем длину вектора с используя формулу =КОРЕНЬ(СУММКВ(B43:C43)-2*B43*C43*COS(B45))
В ячейках B43:B43 содержатся длины векторов а и b, а в ячейке В45 — угол между ними в радианах (в долях числа ПИ() ).
Если угол задан в градусах, то формула будет немного отличаться =КОРЕНЬ(B43*B43+C43*C43-2*B43*C43*COS(B46*ПИ()/180))
Примечание : для наглядности в ячейке со значением угла в градусах можно применить , см. например, статью
Прежде всего надо разобрать само понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок . Введем следующее определение.
Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок . Введем следующее определение.
Определение 1
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.
Определение 2
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).
Одной маленькой буквой: $\overline{a}$ (рис. 1).
Введем теперь, непосредственно, понятие длин вектора.
Определение 3
Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|\overline{a}|$
Понятие длины вектора связано, к примеру, с таким понятием, как равенство двух векторов.
Определение 4
Два вектора будем называть равными, если они удовлетворяют двух условиям: 1. Они сонаправлены; 1. Их длины равны (рис. 2).
Для того, чтобы определять векторы вводят систему координат и определяют координаты для вектора во введенной системе. Как мы знаем, любой вектор можно разложить в виде $\overline{c}=m\overline{i}+n\overline{j}$, где $m$ и $n$ – действительные числа, а $\overline{i}$ и $\overline{j}$ — единичные векторы на оси $Ox$ и $Oy$, соответственно.
Определение 5
Коэффициенты разложения вектора $\overline{c}=m\overline{i}+n\overline{j}$ будем называть координатами этого вектора во введенной системе координат. Математически:
$\overline{c}={m,n}$
Как найти длину вектора?
Для того, чтобы вывести формулу для вычисления длины произвольного вектора по данным его координатам рассмотрим следующую задачу:
Пример 1
Дано: вектор $\overline{α}$, имеющий координаты ${x,y}$. Найти: длину этого вектора.
Введем на плоскости декартову систему координат $xOy$. 2}$.
2}$.
Вывод: Чтобы найти длину вектора, у которого задан его координаты, необходимо найти корень из квадрата суммы этих координат.
Пример задач
Пример 2
Найдите расстояние между точками $X$ и $Y$, которые имеют следующие координаты: $(-1,5)$ и $(7,3)$, соответственно.
Любые две точки можно легко связать с понятием вектора. Рассмотрим, к примеру, вектор $\overline{XY}$. Как мы уже знаем, координаты такого вектора можно найти, вычтя из координат конечной точки ($Y$) соответствующие координаты начальной точки ($X$). Получим, что
Прежде всего надо разобрать само понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок . Введем следующее определение.
Определение 1
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.
Направление указывается от его начала к концу отрезка.
Определение 2
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).
Одной маленькой буквой: $\overline{a}$ (рис. 1).
Введем теперь, непосредственно, понятие длин вектора.
Определение 3
Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|\overline{a}|$
Понятие длины вектора связано, к примеру, с таким понятием, как равенство двух векторов.
Определение 4
Два вектора будем называть равными, если они удовлетворяют двух условиям: 1. Они сонаправлены; 1. Их длины равны (рис. 2).
Для того, чтобы определять векторы вводят систему координат и определяют координаты для вектора во введенной системе. Как мы знаем, любой вектор можно разложить в виде $\overline{c}=m\overline{i}+n\overline{j}$, где $m$ и $n$ – действительные числа, а $\overline{i}$ и $\overline{j}$ — единичные векторы на оси $Ox$ и $Oy$, соответственно.
Определение 5
Коэффициенты разложения вектора $\overline{c}=m\overline{i}+n\overline{j}$ будем называть координатами этого вектора во введенной системе координат. Математически:
$\overline{c}={m,n}$
Как найти длину вектора?
Для того, чтобы вывести формулу для вычисления длины произвольного вектора по данным его координатам рассмотрим следующую задачу:
Пример 1
Дано: вектор $\overline{α}$, имеющий координаты ${x,y}$. Найти: длину этого вектора.
Введем на плоскости декартову систему координат $xOy$. От начал введенной системы координат отложим $\overline{OA}=\overline{a}$. Построим проекции $OA_1$ и $OA_2$ построенного вектора на оси $Ox$ и $Oy$, соответственно (рис. 3).
Построенный нами вектор $\overline{OA}$ будет радиус вектором для точки $A$, следовательно, она будет иметь координаты ${x,y}$, значит
$=x$, $[ OA_2]=y$
Теперь мы легко можем найти искомую длину с помощью теоремы Пифагора, получим
$|\overline{α}|^2=^2+^2$
$|\overline{α}|^2=x^2+y^2$
$|\overline{α}|=\sqrt{x^2+y^2}$
Ответ: $\sqrt{x^2+y^2}$.
Вывод: Чтобы найти длину вектора, у которого задан его координаты, необходимо найти корень из квадрата суммы этих координат.
Пример задач
Пример 2
Найдите расстояние между точками $X$ и $Y$, которые имеют следующие координаты: $(-1,5)$ и $(7,3)$, соответственно.
Любые две точки можно легко связать с понятием вектора. Рассмотрим, к примеру, вектор $\overline{XY}$. Как мы уже знаем, координаты такого вектора можно найти, вычтя из координат конечной точки ($Y$) соответствующие координаты начальной точки ($X$). Получим, что
Стандартное определение: «Вектор — это направленный отрезок». Обычно этим и ограничиваются знания выпускника о векторах. Кому нужны какие-то «направленные отрезки»?
А в самом деле, что такое векторы и зачем они?
Прогноз погоды. «Ветер северо-западный, скорость 18
метров в секунду». Согласитесь, имеет значение и направление ветра (откуда он дует), и модуль (то есть абсолютная величина) его скорости.
Величины, не имеющие направления, называются скалярными. Масса, работа, электрический заряд никуда не направлены. Они характеризуются лишь числовым значением — «сколько килограмм» или «сколько джоулей».
Масса, работа, электрический заряд никуда не направлены. Они характеризуются лишь числовым значением — «сколько килограмм» или «сколько джоулей».
Физические величины, имеющие не только абсолютное значение, но и направление, называются векторными.
Скорость, сила, ускорение — векторы. Для них важно «сколько» и важно «куда». Например, ускорение свободного падения направлено к поверхности Земли, а величина его равна 9,8 м/с 2 . Импульс, напряженность электрического поля, индукция магнитного поля — тоже векторные величины.
Вы помните, что физические величины обозначают буквами, латинскими или греческими. Стрелочка над буквой показывает, что величина является векторной:
Вот другой пример.
Автомобиль движется из A
в B
. Конечный результат — его перемещение из точки A
в точку B
, то есть перемещение на вектор .
Теперь понятно, почему вектор — это направленный отрезок. Обратите внимание, конец вектора — там, где стрелочка. Длиной вектора называется длина этого отрезка. Обозначается: или
Обозначается: или
До сих пор мы работали со скалярными величинами, по правилам арифметики и элементарной алгебры. Векторы — новое понятие. Это другой класс математических объектов. Для них свои правила.
Когда-то мы и о числах ничего не знали. Знакомство с ними началось в младших классах. Оказалось, что числа можно сравнивать друг с другом, складывать, вычитать, умножать и делить. Мы узнали, что есть число единица и число ноль.
Теперь мы знакомимся с векторами.
Понятия «больше» и «меньше» для векторов не существует — ведь направления их могут быть разными. Сравнивать можно только длины векторов.
А вот понятие равенства для векторов есть.
Равными называются векторы, имеющие одинаковые длины и одинаковое направление. Это значит, что вектор можно перенести параллельно себе в любую точку плоскости.
Единичным называется вектор, длина которого равна 1
. Нулевым — вектор, длина которого равна нулю, то есть его начало совпадает с концом.
Удобнее всего работать с векторами в прямоугольной системе координат — той самой, в которой рисуем графики функций. Каждой точке в системе координат соответствуют два числа — ее координаты по x
и y
, абсцисса и ордината.
Каждой точке в системе координат соответствуют два числа — ее координаты по x
и y
, абсцисса и ордината.
Вектор также задается двумя координатами:
Здесь в скобках записаны координаты вектора — по x
и по y
.
Находятся они просто: координата конца вектора минус координата его начала.
Если координаты вектора заданы, его длина находится по формуле
Сложение векторов
Для сложения векторов есть два способа.
1 . Правило параллелограмма. Чтобы сложить векторы и , помещаем начала обоих в одну точку. Достраиваем до параллелограмма и из той же точки проводим диагональ параллелограмма. Это и будет сумма векторов и .
Помните басню про лебедя, рака и щуку? Они очень старались, но так и не сдвинули воз с места. Ведь векторная сумма сил, приложенных ими к возу, была равна нулю.
2
. Второй способ сложения векторов — правило треугольника. Возьмем те же векторы и . К концу первого вектора пристроим начало второго. Теперь соединим начало первого и конец второго. Это и есть сумма векторов и .
Это и есть сумма векторов и .
По тому же правилу можно сложить и несколько векторов. Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.
Представьте, что вы идете из пункта А в пункт В , из В в С , из С в D , затем в Е и в F . Конечный результат этих действий — перемещение из А в F .
При сложении векторов и получаем:
Вычитание векторов
Вектор направлен противоположно вектору . Длины векторов и равны.
Теперь понятно, что такое вычитание векторов. Разность векторов и — это сумма вектора и вектора .
Умножение вектора на число
При умножении вектора на число k получается вектор, длина которого в k раз отличается от длины . Он сонаправлен с вектором , если k больше нуля, и направлен противоположно , если k меньше нуля.
Скалярное произведение векторов
Векторы можно умножать не только на числа, но и друг на друга.
Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними.
Обратите внимание — перемножили два вектора, а получился скаляр, то есть число. Например, в физике механическая работа равна скалярному произведению двух векторов — силы и перемещения:
Если векторы перпендикулярны, их скалярное произведение равно нулю.
А вот так скалярное произведение выражается через координаты векторов и :
Из формулы для скалярного произведения можно найти угол между векторами:
Эта формула особенно удобна в стереометрии. Например, в задаче 14 Профильного ЕГЭ по математике нужно найти угол между скрещивающимися прямыми или между прямой и плоскостью. Часто задача 14 решается в несколько раз быстрее, чем классическим.
В школьной программе по математике изучают только скалярное произведение векторов.
Оказывается, кроме скалярного, есть еще и векторное произведение, когда в результате умножения двух векторов получается вектор. Кто сдает ЕГЭ по физике , знает, что такое сила Лоренца и сила Ампера. В формулы для нахождения этих сил входят именно векторные произведения.
Векторы — полезнейший математический инструмент. В этом вы убедитесь на первом курсе.
Как найти длину вектора с помощью координат
Как найти?
Формула длины вектора на плоскости:
Формула длины вектора в пространстве:
Если даны координаты точек начала и конца вектора $ A(a_x; a_y) $ и $ B(b_x; b_y) $, то найти длину можно по формулам:
Примеры решений
| Пример 1 |
| Найти длину вектора по его координатам $ overline = (4;-3) $ |
| Решение |
| Ответ |
| Длина вектора $|overline| = 5 $ |
| Пример 2 |
| Найти длину вектора по координатам $ overline=(4;2;4) $ |
| Решение |
| Ответ |
| Длина вектора $|overline|=6 $ |
| Пример 3 |
| Найти длину вектора, если известны координаты его начала и конца. $ A=(2;1), B=(-1;3) $ |
| Решение |
| Ответ |
| $|overline|=sqrt <13>$ |
В статье мы ответили на вопрос:»Как найти длину вектора?» с помощью формул. А также рассмотрели практические примеры решения задач на плоскости и в пространстве. Следует заметить, что существуют аналогичные формулы для пространств больше, чем трёхмерные.
Понятие длины вектора
Для того, чтобы разобраться с понятием длины вектора, прежде всего надо разобрать само понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок. Введем следующее определение.
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу – его концом. Направление указывается от его начала к концу отрезка.
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $overline$ – (где $A$ его начало, а $B$ – его конец).
Одной маленькой буквой: $overline$ (рис. 1).
Введем теперь, непосредственно, понятие длин вектора.
Попробуй обратиться за помощью к преподавателям
Понятие длины вектора связано, к примеру, с таким понятием, как равенство двух векторов.
Два вектора будем называть равными, если они удовлетворяют двух условиям: 1. Они сонаправлены; 1. Их длины равны (рис. 2).
Для того, чтобы определять векторы вводят систему координат и определяют координаты для вектора во введенной системе. Как мы знаем, любой вектор можно разложить в виде $overline=moverline+noverline$, где $m$ и $n$ – действительные числа, а $overline$ и $overline$ – единичные векторы на оси $Ox$ и $Oy$, соответственно.
Коэффициенты разложения вектора $overline=moverline+noverline$ будем называть координатами этого вектора во введенной системе координат. Математически:
Задай вопрос специалистам и получи
ответ уже через 15 минут!
Как найти длину вектора?
Для того, чтобы вывести формулу для вычисления длины произвольного вектора по данным его координатам рассмотрим следующую задачу:
Дано: вектор $overline<α>$, имеющий координаты $$. Найти: длину этого вектора.
Введем на плоскости декартову систему координат $xOy$. От начал введенной системы координат отложим $overline=overline$. Построим проекции $OA_1$ и $OA_2$ построенного вектора на оси $Ox$ и $Oy$, соответственно (рис. 3).
От начал введенной системы координат отложим $overline=overline$. Построим проекции $OA_1$ и $OA_2$ построенного вектора на оси $Ox$ и $Oy$, соответственно (рис. 3).
Построенный нами вектор $overline$ будет радиус вектором для точки $A$, следовательно, она будет иметь координаты $$, значит
Теперь мы легко можем найти искомую длину с помощью теоремы Пифагора, получим
Вывод: Чтобы найти длину вектора, у которого задан его координаты, необходимо найти корень из квадрата суммы этих координат.
Пример задач
Найдите расстояние между точками $X$ и $Y$, которые имеют следующие координаты: $(-1,5)$ и $(7,3)$, соответственно.
Любые две точки можно легко связать с понятием вектора. Рассмотрим, к примеру, вектор $overline$. Как мы уже знаем, координаты такого вектора можно найти, вычтя из координат конечной точки ($Y$) соответствующие координаты начальной точки ($X$). Получим, что
Теперь, найдя длину этого вектора по формуле, выведенной выше, мы и получим искомую длину. Получим:
Получим:
Из этой задачи можно вывести формулу для вычисления такого расстояния. Пусть две точки имеют координаты $<(x’,y’)>$ и $<(x”,y”)>$. Тогда длину между такими точками можно найти по следующей формуле:
Пусть нам дан треугольник своими координатами вершин $(5,-9)$, $(12,-2)$ и $(4,0)$. Найдем его периметр.
Найдем для начала длины всех его сторон по формуле из замечания к задаче 2.
Первая сторона равняется:
Вторая сторона равняется:
Третья сторона равняется:
Так и не нашли ответ
на свой вопрос?
Просто напиши с чем тебе
нужна помощь
Длина вектора – основные формулы
Длину вектора a → будем обозначать a → . Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.
Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат O x y . Пусть в ней задан некоторый вектор a → с координатами a x ; a y . Введем формулу для нахождения длины (модуля) вектора a → через координаты a x и a y .
Введем формулу для нахождения длины (модуля) вектора a → через координаты a x и a y .
От начала координат отложим вектор O A → = a → . Определим соответственные проекции точки A на координатные оси как A x и A y . Теперь рассмотрим прямоугольник O A x A A y с диагональю O A .
Из теоремы Пифагора следует равенство O A 2 = O A x 2 + O A y 2 , откуда O A = O A x 2 + O A y 2 . Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что O A x 2 = a x 2 и O A y 2 = a y 2 , а по построению длина O A равна длине вектора O A → , значит, O A → = O A x 2 + O A y 2 .
Отсюда получается, что формула для нахождения длины вектора a → = a x ; a y имеет соответствующий вид: a → = a x 2 + a y 2 .
Если вектор a → дан в виде разложения по координатным векторам a → = a x · i → + a y · j → , то вычислить его длину можно по той же формуле a → = a x 2 + a y 2 , в данном случае коэффициенты a x и a y выступают в роли координат вектора a → в заданной системе координат.
Вычислить длину вектора a → = 7 ; e , заданного в прямоугольной системе координат.
Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатам a → = a x 2 + a y 2 : a → = 7 2 + e 2 = 49 + e
Формула для нахождения длины вектора a → = a x ; a y ; a z по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)
В данном случае O A 2 = O A x 2 + O A y 2 + O A z 2 (так как ОА – диагональ прямоугольного параллелепипеда), отсюда O A = O A x 2 + O A y 2 + O A z 2 . Из определения координат вектора можем записать следующие равенства O A x = a x ; O A y = a y ; O A z = a z ; , а длина ОА равна длине вектора, которую мы ищем, следовательно, O A → = O A x 2 + O A y 2 + O A z 2 .
Отсюда следует, что длина вектора a → = a x ; a y ; a z равна a → = a x 2 + a y 2 + a z 2 .
Вычислить длину вектора a → = 4 · i → – 3 · j → + 5 · k → , где i → , j → , k → – орты прямоугольной системы координат.
Дано разложение вектора a → = 4 · i → – 3 · j → + 5 · k → , его координаты равны a → = 4 , – 3 , 5 . Используя выше выведенную формулу получим a → = a x 2 + a y 2 + a z 2 = 4 2 + ( – 3 ) 2 + 5 2 = 5 2 .
Длина вектора через координаты точек его начала и конца
Выше были выведены формулы, позволяющие находить длины вектора по его координатам. Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.
Итак, даны точки с заданными координатами A ( a x ; a y ) и B ( b x ; b y ) , отсюда вектор A B → имеет координаты ( b x – a x ; b y – a y ) значит, его длина может быть определена по формуле: A B → = ( b x – a x ) 2 + ( b y – a y ) 2
А если даны точки с заданными координатами A ( a x ; a y ; a z ) и B ( b x ; b y ; b z ) в трехмерном пространстве, то длину вектора A B → можно вычислить по формуле
A B → = ( b x – a x ) 2 + ( b y – a y ) 2 + ( b z – a z ) 2
Найти длину вектора A B → , если в прямоугольной системе координат A 1 , 3 , B – 3 , 1 .
Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим A B → = ( b x – a x ) 2 + ( b y – a y ) 2 : A B → = ( – 3 – 1 ) 2 + ( 1 – 3 ) 2 = 20 – 2 3 .
Второй вариант решения подразумевает под собой применение данных формул по очереди: A B → = ( – 3 – 1 ; 1 – 3 ) = ( – 4 ; 1 – 3 ) ; A B → = ( – 4 ) 2 + ( 1 – 3 ) 2 = 20 – 2 3 . –
Ответ: A B → = 20 – 2 3 .
Определить, при каких значениях длина вектора A B → равна 30 , если A ( 0 , 1 , 2 ) ; B ( 5 , 2 , λ 2 ) .
Для начала распишем длину вектора A B → по формуле: A B → = ( b x – a x ) 2 + ( b y – a y ) 2 + ( b z – a z ) 2 = ( 5 – 0 ) 2 + ( 2 – 1 ) 2 + ( λ 2 – 2 ) 2 = 26 + ( λ 2 – 2 ) 2
Затем полученное выражение приравняем к 30 , отсюда найдем искомые λ :
26 + ( λ 2 – 2 ) 2 = 30 26 + ( λ 2 – 2 ) 2 = 30 ( λ 2 – 2 ) 2 = 4 λ 2 – 2 = 2 и л и λ 2 – 2 = – 2 λ 1 = – 2 , λ 2 = 2 , λ 3 = 0 .
Ответ: λ 1 = – 2 , λ 2 = 2 , λ 3 = 0 .
Нахождение длины вектора по теореме косинусов
Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.
Пусть заданы длины двух векторов A B → , A C → и угол между ними (или косинус угла), а требуется найти длину вектора B C → или C B → . В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ A B C , вычислить длину стороны B C , которая и равна искомой длине вектора.
Рассмотрим такой случай на следующем примере.
Длины векторов A B → и A C → равны 3 и 7 соответственно, а угол между ними равен π 3 . Вычислить длину вектора B C → .
Длина вектора B C → в данном случае равна длине стороны B C треугольника △ A B C . Длины сторон A B и A C треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов: B C 2 = A B 2 + A C 2 – 2 · A B · A C · cos ∠ ( A B , → A C → ) = 3 2 + 7 2 – 2 · 3 · 7 · cos π 3 = 37 ⇒ B C = 37 Таким образом, B C → = 37 .
Итак, для нахождения длины вектора по координатам существуют следующие формулы a → = a x 2 + a y 2 или a → = a x 2 + a y 2 + a z 2 , по координатам точек начала и конца вектора A B → = ( b x – a x ) 2 + ( b y – a y ) 2 или A B → = ( b x – a x ) 2 + ( b y – a y ) 2 + ( b z – a z ) 2 , в некоторых случаях следует использовать теорему косинусов.
Как определить длину вектора
Вектор характеризуется не только абсолютной длиной, но и направлением. Поэтому для того, чтобы «закрепить» его в пространстве используются различные системы координат. Именно зная координаты вектора можно определить его длину с помощью специальных математических формул.Вам понадобитсяЕсли вектор находится на плоскости, то его начало и конец имеют координаты (x1;y1), (x2;y2). Чтобы найти его длину произведите следующие математические операции:: 1. Найдите координаты , для чего из координат конца вектора, отнимаем координаты начала x=x2-x1, y=y2-y1.2. Возведите каждую из координат в квадрат и найдите их сумму x²+y². 3. Из числа, полученного при выполнении п.2, извлеките корень квадратный.Это и будет длина вектора, расположенного на плоскости.
3. Из числа, полученного при выполнении п.2, извлеките корень квадратный.Это и будет длина вектора, расположенного на плоскости.
В том случае если вектор располагается в пространстве, он имеет три координаты x, y и z, которые вычисляются по тем же правилам, что и для вектора, расположенного на плоскости. Найдите его длину, сложив квадраты всех трех координат, и извлеките из результата сложения корень квадратный.
Если известна одна из координат вектора и угол между ним и осью ОХ (если известен угол между осью OY и вектором то, чтобы найти искомый угол, отнимите его от 90º), найдите длину из соотношений, которые характеризуют полярные координаты: 1. длина вектора равна отношению координаты x к косинусу данного угла; 2. длина вектора равна отношения координаты y к синусу данного угла.
Чтобы найти длину вектора, который представляет собой сумму двух векторов, найдите его координаты, сложив соответствующие координаты, а затем найдите длину вектора, координаты которого известны.
Если же координаты векторов неизвестны, а известны только длины, перенесите один из векторов так, чтобы он начинался в той точке, где заканчивается второй. Измерьте угол между ними. Затем от суммы квадратов длин векторов отнимите их удвоенное произведение, умноженное на косинус угла между ними. Из полученного числа извлеките корень квадратный. Это и будет длина вектора, который является суммой двух векторов. Постройте его, соединив начало второго вектора с концом первого.
Связь между координатами вектора и координатами его начала и конца 9 класс онлайн-подготовка на Ростелеком Лицей |
Тема 27.
Связь между координатами вектора и координатами его начала и конца.
Ты уже знаком с понятием координат вектора. Ими называют коэффициенты разложения данного вектора по единичным координатным векторам i⃗ и j⃗.
Сегодня мы ответим на вопрос «Как связаны координаты вектора с координатами его начала и конца?».
Но для начала вернёмся к координатам точки в прямоугольной системе координат.
Напомним, что для их определения нужно опустить перпендикуляры из данной точки к осям.
Точки пересечения данных прямых с осями обозначим как M1 и M2.
Абсциссой точки М является число x, которое является длиной отрезка OM1. А ординатой — число y, которое является длиной отрезка OM2.
M(x; y) x = OM1, y = OM2
Мы вспомнили, как определять координаты точек, а теперь вернёмся к общему случаю и, уже рассмотренной, точке M.
Проведём вектор из точки O к точке M. Запомни, вектор OM⃗ называют радиус-вектором точки M.
Сейчас докажем следующее утверждение: координаты точки M равны соответствующим координатам её радиус-вектора.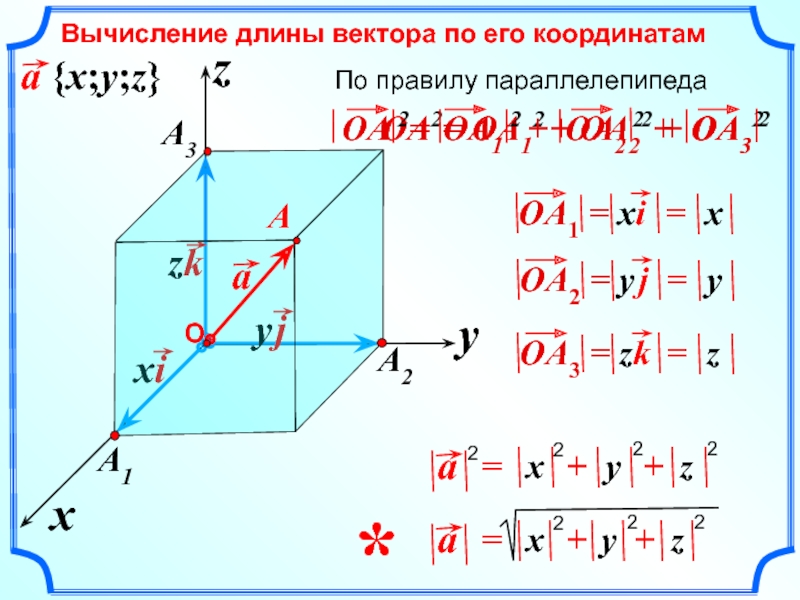
Доказать: M(x;y)=OM⃗x;y
Понятно, что вектор OM⃗=ОM1⃗+ОM2⃗ по правилу параллелограмма.
Теперь необходимо доказать, что вектор
OM1⃗=xi⃗, а вектор OM2⃗=yj⃗
Тем самым мы докажем, что вектор OM⃗x;y.
Если x > 0, то x = OM1, а векторы OM1⃗ и i⃗ сонаправлены, поэтому
OM1⃗=OM1∙i⃗=xi⃗
Если x x = OM1, а векторы OM1⃗ и i⃗ противоположно направлены. Поэтому OM1⃗=-OM1∙i⃗=xi⃗.
Наконец, если x = 0
OM1⃗=0⃗ и равенство OM1=xi⃗ в этом случае так же справедливо. Таким образом, в любом случае ОM1⃗=xi⃗. Аналогично доказывается, что ОM2⃗=yj⃗.
Следовательно,OM⃗=ОM1⃗+ОM2⃗=xi⃗+yj⃗
Отсюда следует, что координаты радиус-вектора OM равны (x; y), то есть равны соответствующим координатам точки M.
Пользуясь доказанным утверждением, выразим координаты вектора AB⃗ через координаты его начала A и конца B. Пусть точка A имеет координаты x1;y1, а точка B – координаты x2;y2.
Вектор AB⃗ равен разности векторов OB⃗ и OA⃗, поэтому его координаты равны разностям соответствующих координат векторов OB⃗ и OA⃗. Но OB⃗ и OA⃗ – радиус-векторы точек B и A, и, значит, OB⃗ имеет координаты x2;y2, а OA⃗ имеет координаты x1;y1. Следовательно, вектор AB⃗ имеет координаты x2-x1;y2-y1.
Таким образом, каждая координата вектора равна разности соответствующих координат его конца и начала.
Введение системы координат дает возможность изучать геометрические фигуры и их свойства с помощью уравнений и неравенств и, таким образом, использовать в геометрии методы алгебры. Такой подход к изучению свойств геометрических фигур называется методом координат.
Рассмотрим три вспомогательные задачи:
-
Как найти координаты середины отрезка.

Пусть в системе координат Oxy точка A имеет координаты x1;y1, а точка B – координаты x2;y2. Выразим координаты x;y середины C отрезка AB через координаты его концов. Так как точка C – середина отрезка AB, то
OC⃗=12OA⃗+OB⃗.
x=x1+x22; y=y1+y22
Таким образом, каждая координата середины отрезка равна полусумме соответствующих координат его концов.
-
Вычисление длины вектора по его координатам.
Пусть вектор a⃗x;y, тогда длина вектора вычисляется по формуле:
a⃗=x2+y2
-
Вычисление расстояния между двумя точками. Пусть точка M1 имеет координаты (x1; y1), точка M2 – координаты (x2; y2).
 Выразим расстояние d между точками M1 и M2 через их координаты.
Выразим расстояние d между точками M1 и M2 через их координаты.
Рассмотрим вектор M1M2⃗. Его координаты равны x2-x1;y2-y1. Следовательно, длина этого вектора может быть найдена по формуле:
M1M2⃗=x2-x12+y2-y12
Пример:
-
Найти длину вектора a⃗-3;4
a⃗=x2+y2=-32+42=25=5
Ответ: 5
-
Найти расстояние между точкой A(2; 7) и точкой B(-2; 7)
d=-2-22+7-72=16=4
Ответ: 4
Величина и направление векторов
Величина вектора
Величина вектора
п
Q
→
это расстояние между начальной точкой
п
и конечная точка
Q
. В символах величина
п
Q
→
записывается как
|
п
Q
→
|
.
Если заданы координаты начальной и конечной точек вектора, Формула расстояния можно использовать для определения его величины.
| п Q → | знак равно ( Икс 2 — Икс 1 ) 2 + ( у 2 — у 1 ) 2
Пример 1:
Найдите величину вектора
п
Q
→
чья начальная точка
п
Я сидел
(
1
,
1
)
и конечная точка находится в
Q
Я сидел
(
5
,
3
)
.
Решение:
Используйте формулу расстояния.
Подставьте значения Икс 1 , у 1 , Икс 2 , и у 2 .
|
п
Q
→
|
знак равно
(
5
—
1
)
2
+
(
3
—
1
)
2
знак равно
4
2
+
2
2
знак равно
16
+
4
знак равно
20
≈
4. 5
5
Величина п Q → около 4.5 .
Направление вектора
Направление вектора — это мера угла, который он образует с горизонтальная линия .
Для определения направления вектора можно использовать одну из следующих формул:
загар θ знак равно у Икс , где Икс горизонтальное изменение и у это вертикальное изменение
или
загар
θ
знак равно
у
2
—
у
1
Икс
2
—
Икс
1
, где
(
Икс
1
,
у
1
)
начальная точка и
(
Икс
2
,
у
2
)
это конечная точка.
Пример 2:
Найдите направление вектора п Q → чья начальная точка п Я сидел ( 2 , 3 ) и конечная точка находится в Q Я сидел ( 5 , 8 ) .
Приведены координаты начальной и конечной точек.Подставьте их в формулу загар θ знак равно у 2 — у 1 Икс 2 — Икс 1 .
загар θ знак равно 8 — 3 5 — 2 знак равно 5 3
Найдите обратный загар и воспользуйтесь калькулятором.
θ знак равно загар — 1 ( 5 3 ) ≈ 59 °
Вектор п Q → имеет направление около 59 ° .
Вектор положения— объяснение и примеры
Мы можем использовать вектор положения , чтобы сообщить нам местоположение одного объекта относительно другого.В частности, вектор позиция:
«вектор А, который указывает местоположение или положение заданной точки относительно произвольной точки отсчета, такие как происхождение.»
В этом разделе мы обсудим следующие аспекты векторов положения:
- Что такое вектор положения?
- Как найти вектор положения
Что такое вектор положения?
Часто векторы, которые начинаются в начале координат и заканчиваются в любой произвольной точке, называются векторами положения. Они используются для определения положения точки относительно начала координат.
Они используются для определения положения точки относительно начала координат.
Направление вектора положения от исходной точки к заданной точке. В c \ декартовой системе координат, если точка O — начало координат, а Q — некоторая точка (x1, y1), тогда вектор положения, направленный из точки O в точку Q, представлен как OQ . В трехмерном пространстве, если O = (0,0,0) и Q = (x1, y1, z1), то вектор положения r точки Q представлен следующим образом:
r = x1i + y1j + z1k
Предположим, у нас есть два вектора A и B с векторами положения a = (2,4) и b = (3, 5) соответственно.Затем мы можем записать координаты векторов A, и B как:
A = (2,4), B = (3, 5)
Как найти вектор положения
Перед мы определяем вектор положения точки, сначала нам нужно определить координаты этой точки. Предположим, у нас есть две точки, M и N, где M = (x1, y1) и N = (x2, y2). Затем мы хотим найти вектор положения из точки M в точку N, который является вектором MN .Чтобы определить этот вектор положения, мы просто вычтем соответствующие компоненты M из N :
Предположим, у нас есть две точки, M и N, где M = (x1, y1) и N = (x2, y2). Затем мы хотим найти вектор положения из точки M в точку N, который является вектором MN .Чтобы определить этот вектор положения, мы просто вычтем соответствующие компоненты M из N :
MN = (x2-x1, y2-y1)
Формула вектора положения
Используя информацию выше, мы можем обобщить формулу, которая определит вектор положения между двумя точками, если бы мы знали положение точек в плоскости xy.
Например, рассмотрим точку P, которая имеет координаты (xk, yk) в плоскости xy, и другую точку Q, которая имеет координаты (xk + 1, yk + 1).Формула для определения вектора положения от P до Q:
PQ = ((xk + 1) -xk, (yk + 1) -yk)
Помните, что вектор положения PQ относится к вектору, который начинается в точке P и заканчивается в точке Q. Аналогично, если мы хотим найти вектор положения из точки Q в точку P, мы можем написать:
QP = (xk — (xk + 1), yk — (yk + 1))
Примеры
В этом разделе мы обсудим некоторые примеры задач вектора положения и их пошаговые решения. Это поможет глубже понять векторы позиций.
Это поможет глубже понять векторы позиций.
Пример 1
Учитывая две точки A = (-4, 6) и B = (5, 12), определите вектор положения AB. Затем , вычисляют величину вектора AB .
Решение
Учитывая две точки в системе координат xy, мы можем использовать следующую формулу, чтобы найти вектор положения AB :
AB = (x2-x1, y2-y1)
Где , x1, y1 представляют координаты точки A, а x2, y2 представляют координаты точки B.Таким образом, просто подставив значения точек A и B в приведенное выше уравнение, мы можем найти вектор положения AB :
AB = (5 — (- 4), 12-6)
AB = ((5+ 4), 12-6)
AB = (9, 6)
Таким образом, вектор положения AB эквивалентен вектору, который начинается в начале координат и направлен в точку на 9 единиц, чтобы вправо по оси x и на 6 единиц вверх по оси y. 2
2
| AB | = √81 + 36
| AB | = √117
| AB | = 3√13
Пример 2
Учитывая две точки A = (-4, 6) и B = (5, 12), определите вектор положения BA. Затем вычислите величину вектора BA и опишите взаимосвязь между вектором положения AB и вектором положения BA .
Решение
Учитывая две точки в системе координат xy, мы можем использовать следующую формулу, чтобы найти вектор положения BA :
BA = (x1-x2, y1-y2)
Где , x1, y1 представляют координаты точки A, а x2, y2 представляют координаты точки B.Обратите внимание, что вектор положения BA представляет собой вектор, направленный от точки B к точке A. Он отличается от вектора положения AB, , который направлен от A к B. Таким образом, просто помещая значения точек A и B в приведенном выше уравнении мы можем найти вектор положения BA:
BA = (-4-5), 6-12)
BA = (-9, -6)
Таким образом, вектор положения BA эквивалентен вектору, который начинается в начале координат и направлен в точку на 9 единиц влево по оси x и на 6 единиц вниз по оси y. 2
2
| BA | = √81 + 36
| BA | = √117
| BA | = 3√13
Напомним, что в первом примере мы нашли вектор положения AB, для тех же точек, а в этом примере мы определили вектор положения BA. Два вектора положения имеют одинаковую величину. Поскольку они имеют противоположные направления, отношения между ними следующие:
BA = -1 * (9, 6)
BA = -1 * AB
BA = — AB
Таким образом, два вектора положения параллельны друг другу и противоположны друг другу.То есть они являются отрицаниями друг друга.
Пример 3
Учитывая, что вектор положения точки, S1, равен OS1 = (2, 3), и что вектор S1S2 = (-3, 6), определить вектор положения точки точка S2, OS2 .
Решение
Сначала мы строим вектор OS1 с его начальной точкой в начале координат (0,0) и его конечной точкой в точке (2,3). Мы также строим вектор OS2, , который начинается в начале координат и заканчивается в точке S2.Обозначим неизвестное положение S2 произвольными координатными точками (x, y). Поскольку мы знаем вектор положения S1S2 и знаем, что он дает взаимосвязь между точками S1 и S2, мы также можем нарисовать S1S2. Это направленный вектор, начальная точка которого находится в S1 и направлен на три единицы влево и на шесть единиц вверх. Из изображения ниже видно, что у нас есть треугольник 0S1S2. Таким образом, теперь мы можем использовать закон треугольника (или правило «голова к хвосту») сложения векторов для определения координат точки S2 следующим образом:
Мы также строим вектор OS2, , который начинается в начале координат и заканчивается в точке S2.Обозначим неизвестное положение S2 произвольными координатными точками (x, y). Поскольку мы знаем вектор положения S1S2 и знаем, что он дает взаимосвязь между точками S1 и S2, мы также можем нарисовать S1S2. Это направленный вектор, начальная точка которого находится в S1 и направлен на три единицы влево и на шесть единиц вверх. Из изображения ниже видно, что у нас есть треугольник 0S1S2. Таким образом, теперь мы можем использовать закон треугольника (или правило «голова к хвосту») сложения векторов для определения координат точки S2 следующим образом:
S1S2 = OS1 + OS2
OS2 = S1S2 — OS1
Подставляя данные значения в это уравнение, мы получаем:
OS2 = (-3, 6) — (2, 3)
OS2 = (-3, 6) + ( -2, -3)
OS2 = (-3-2, 6-3)
OS2 = (-5, 3)
Таким образом, OS2 = (- 5, 3) является вектор положения для точки S2.
Пример 4
Учитывая две точки M = (4, m) и Q = (-n, -3), определите вектор положения QM.
Решение
Учитывая две точки в системе координат xy, мы можем использовать следующую формулу для определения вектора положения Q :
QM = (-n-4, -3-m) .
Так как нам неизвестны координаты QM или значения n и m, мы не можем дальше упрощать уравнение.2
| R | = √100 + 25 + 9
| R | = √100 + 25 + 9
| R | = √134
Пример 6
Учитывая точки c = 5i + 6j + 3k и d = 2i + 5j — 2k в ортогональной системе, определите вектор положения между этими двумя точками, CD.
Решение
Учитывая две точки, мы можем использовать следующую формулу для определения вектора положения CD :
CD = (2-5, 5-5, -2-3)
CD = (-3, 0, -5)
CD = -3i + 0j -5k
Практические вопросы
- Пусть u = (-1, 4) и v = (2 , 5).
 Определите вектор положения, представленный UV .
Определите вектор положения, представленный UV . - Пусть u = (-1, 4) и v = (2, 5). Определите вектор положения, представленный VU .
- Пусть v = (3, 5) и VM = (-6, 3). Найдите вектор положения точки m.
- Дано b = (3,2,5), определите его вектор положения, R. Затем найдите длину вектора
- Пусть вектор AB начинается с a = (1, 2) и заканчивается на Ь = (2, 3). Определите его вектор положения и его длину.
- Пусть вектор OB начинается с o = (0,0) и заканчивается на b = (-2, 6). Определите его вектор положения.
Ответы
- UV = (3,1). Направление UV на 3 единицы вправо по оси x и на 1 единицу вверх.
- VU = (-3, -1). Направление VU составляет 3 единицы влево по оси x и 1 единицу вниз. Два вектора UV и VU противоположны по направлению.

- Вектор положения точки m может быть задан следующим образом: OM = (-9, -2)
- R = 3i + 2j + 5k — вектор положения, и его длина составляет | R | = √38
- Вектор положения равен AB = (1,1), а его длина равна | AB | = √2
- Вектор положения — OB = (-2,6), а его длина равна | OB | = √40
Предыдущий урок | Главная страница | Следующий урок
2.1 Векторы на плоскости — Исчисление Том 3
Задачи обучения
- 2.1.1 Опишите плоский вектор, используя правильные обозначения.
- 2.1.2 Выполнение основных векторных операций (скалярное умножение, сложение, вычитание).
- 2.1.3 Выразите вектор в виде компонентов.
- 2.1.4 Объясните формулу величины вектора.
- 2.1.5 Выразите вектор через единичные векторы.

- 2.1.6 Приведите два примера векторных величин.
При описании движения самолета в полете важно передать две части информации: направление, в котором летит самолет, и скорость самолета.При измерении силы, такой как тяга двигателей самолета, важно описать не только силу этой силы, но и направление, в котором она действует. Некоторые величины, такие как или сила, определяются как размером (также называемым величиной , величина ) и направлением. Величина, имеющая величину и направление, называется вектором. В этом тексте мы обозначаем векторы жирным шрифтом, например v .
Определение
Вектор — это величина, которая имеет как величину, так и направление.
Векторное представление
Вектор на плоскости представлен направленным отрезком линии (стрелкой). Конечные точки отрезка называются начальной и конечной точкой вектора. Стрелка от начальной точки к конечной указывает направление вектора. Длина отрезка представляет его величину. Мы используем обозначение ‖v‖‖v‖ для обозначения модуля вектора v.v. Вектор с одинаковой начальной и конечной точкой называется нулевым вектором и обозначается 0.0. Нулевой вектор — единственный вектор без направления, и по соглашению можно считать, что он имеет любое направление, удобное для рассматриваемой задачи.
Стрелка от начальной точки к конечной указывает направление вектора. Длина отрезка представляет его величину. Мы используем обозначение ‖v‖‖v‖ для обозначения модуля вектора v.v. Вектор с одинаковой начальной и конечной точкой называется нулевым вектором и обозначается 0.0. Нулевой вектор — единственный вектор без направления, и по соглашению можно считать, что он имеет любое направление, удобное для рассматриваемой задачи.
Векторы с одинаковой величиной и направлением называются эквивалентными векторами. Мы рассматриваем эквивалентные векторы как равные, даже если они имеют разные начальные точки. Таким образом, если vv и ww эквивалентны, мы пишем
Определение
Векторы называются эквивалентными векторами, если они имеют одинаковую величину и направление.
Стрелки на рисунке 2.2 (б) эквивалентны. Каждая стрелка имеет одинаковую длину и направление. Тесно родственное понятие — идея параллельных векторов. Два вектора называются параллельными, если они имеют одинаковое или противоположное направление. Мы рассмотрим эту идею более подробно позже в этой главе. Вектор определяется его величиной и направлением, независимо от того, где находится его начальная точка.
Мы рассмотрим эту идею более подробно позже в этой главе. Вектор определяется его величиной и направлением, независимо от того, где находится его начальная точка.
Использование полужирных строчных букв для именования векторов — обычное представление в печати, но есть альтернативные обозначения. Например, при написании имени вектора от руки легче нарисовать стрелку над переменной, чем имитировать жирный шрифт: v → .v →. Когда вектор имеет начальную точку PP и конечную точку Q, Q, обозначение PQ → PQ → полезно, поскольку оно указывает направление и местоположение вектора.
Пример 2.1
Наброски векторов
Нарисуйте вектор на плоскости от начальной точки P (1,1) P (1,1) до конечной точки Q (8,5).Q (8,5).
Решение
См. Рисунок 2. 3. Поскольку вектор идет из точки PP в точку Q, Q, мы назовем его PQ → .PQ →.
3. Поскольку вектор идет из точки PP в точку Q, Q, мы назовем его PQ → .PQ →.
Контрольно-пропускной пункт 2.1
Нарисуйте вектор ST → ST →, где SS — точка (3, −1) (3, −1), а TT — точка (−2,3). (- 2,3).
Объединение векторов
Vectors имеет множество реальных приложений, включая ситуации, связанные с силой или скоростью.Например, рассмотрим силы, действующие на лодку, пересекающую реку. Двигатель лодки создает силу в одном направлении, а течение реки создает силу в другом направлении. Обе силы — векторы. Мы должны принимать во внимание как величину, так и направление каждой силы, если мы хотим знать, куда пойдет лодка.
Второй пример с векторами — квотербек, бросающий футбольный мяч. Квотербек не бросает мяч параллельно земле; вместо этого он целится в воздух.Скорость его броска может быть представлена вектором. Если мы знаем, с какой силой он бросает мяч (величина — в данном случае скорость) и угол (направление), мы можем сказать, как далеко мяч пройдет по полю.
Если мы знаем, с какой силой он бросает мяч (величина — в данном случае скорость) и угол (направление), мы можем сказать, как далеко мяч пройдет по полю.
Действительное число в математике и физике часто называют скаляром. В отличие от векторов, считается, что скаляры имеют только величину, но не направление. Умножение вектора на скаляр изменяет величину вектора. Это называется скалярным умножением. Обратите внимание, что изменение величины вектора не означает изменения его направления.Например, ветер, дующий с севера на юг, может увеличивать или уменьшать скорость, сохраняя направление с севера на юг.
Определение
Произведение kvkv вектора v и скаляра k представляет собой вектор с величиной | k || k | умноженное на величину v, v, и с направлением, которое совпадает с направлением vv, если k> 0, k> 0, и противоположным направлению vv, если k <0.k <0. Это называется скалярным умножением. Если k = 0k = 0 или v = 0, v = 0, то kv = 0.kv = 0.
Если k = 0k = 0 или v = 0, v = 0, то kv = 0.kv = 0.
Как и следовало ожидать, если k = −1, k = −1, мы обозначим произведение kvkv как
kv = (- 1) v = −v.kv = (- 1) v = −v.Обратите внимание, что −v − v имеет ту же величину, что и v, v, но имеет противоположное направление (рисунок 2.4).
Рисунок 2.4 (a) Исходный вектор v имеет длину n единиц. (б) Длина 2v2v равна 2n2n единицам. (c) Длина v / 2v / 2 равна n / 2n / 2 единиц. (d) Векторы vv и −v − v имеют одинаковую длину, но противоположные направления. Другая операция, которую мы можем выполнить с векторами, — это сложение их вместе при сложении векторов, но поскольку каждый вектор может иметь собственное направление, процесс отличается от сложения двух чисел.Наиболее распространенный графический метод сложения двух векторов — поместить начальную точку второго вектора в конечную точку первого, как показано на рисунке 2.5 (a). Чтобы понять, почему это имеет смысл, предположим, например, что оба вектора представляют смещение. Если объект движется сначала из начальной точки в конечную точку вектора v, v, а затем из начальной точки в конечную точку вектора w, w, общее смещение будет таким же, как если бы объект совершил всего одно движение из от начальной точки до конечной точки вектора v + w.v + w. По понятным причинам такой подход называется методом треугольника. Обратите внимание: если бы мы поменяли порядок так, чтобы ww был нашим первым вектором, а v был нашим вторым вектором, мы оказались бы в том же месте. (Снова см. Рисунок 2.5 (a).) Таким образом, v + w = w + v.v + w = w + v.
Если объект движется сначала из начальной точки в конечную точку вектора v, v, а затем из начальной точки в конечную точку вектора w, w, общее смещение будет таким же, как если бы объект совершил всего одно движение из от начальной точки до конечной точки вектора v + w.v + w. По понятным причинам такой подход называется методом треугольника. Обратите внимание: если бы мы поменяли порядок так, чтобы ww был нашим первым вектором, а v был нашим вторым вектором, мы оказались бы в том же месте. (Снова см. Рисунок 2.5 (a).) Таким образом, v + w = w + v.v + w = w + v.
Второй метод сложения векторов называется методом параллелограмма. С помощью этого метода мы размещаем два вектора так, чтобы у них была одна и та же начальная точка, а затем рисуем параллелограмм с векторами в качестве двух смежных сторон, как на рисунке 2.5 (б). Длина диагонали параллелограмма равна сумме. Сравнивая рис. 2.5 (b) и рис. 2.5 (a), мы видим, что при использовании любого метода мы получаем одинаковый ответ. Вектор v + wv + w называется векторной суммой.
Вектор v + wv + w называется векторной суммой.
Определение
Сумма двух векторов vv и ww может быть построена графически, поместив начальную точку ww в конечную точку v.v. Тогда векторная сумма v + w, v + w — это вектор с начальной точкой, которая совпадает с начальной точкой vv и имеет конечную точку, которая совпадает с конечной точкой w.ш. Эта операция известна как сложение векторов.
Рисунок 2.5 (a) При сложении векторов методом треугольника начальная точка ww является конечной точкой v.v. (б) При сложении векторов методом параллелограмма векторы vv и ww имеют одинаковую начальную точку.Здесь также уместно обсудить векторное вычитание. Определим v − wv − w как v + (- w) = v + (- 1) w.v + (- w) = v + (- 1) w. Вектор v − wv − w называется векторной разностью. Графически вектор v − wv − w изображается путем рисования вектора от конечной точки ww до конечной точки vv (рисунок 2.6).
Рисунок 2.6 (a) Разность векторов v − wv − w изображается путем проведения вектора от конечной точки ww к конечной точке v. v. (b) Вектор v − wv − w эквивалентен вектору v + (- w) .v + (- w).
v. (b) Вектор v − wv − w эквивалентен вектору v + (- w) .v + (- w).На рис. 2.5 (a) начальная точка v + wv + w является начальной точкой v.v. Конечная точка v + wv + w является конечной точкой w.w. Эти три вектора образуют стороны треугольника. Отсюда следует, что длина любой одной стороны меньше суммы длин остальных сторон.Итак, у нас
‖V + w‖≤‖v‖ + ‖w‖.‖v + w‖≤‖v‖ + ‖w‖.Это более широко известно как неравенство треугольника. Однако есть один случай, когда результирующий вектор u + vu + v имеет ту же величину, что и сумма величин uu и v.v. Это происходит только тогда, когда uu и vv имеют одинаковое направление.
Пример 2.2
Объединение векторов
Для векторов vv и ww, показанных на рисунке 2.7, нарисуйте векторы
.- 3w3w
- v + wv + w
- 2v − w2v − w
Фигура 2.7 Векторы vv и ww лежат в одной плоскости.
Решение
- Вектор 3w3w имеет то же направление, что и w; w; он в три раза длиннее, чем w.
 w.
w.
Вектор 3w3w имеет то же направление, что и ww, и в три раза длиннее. - Используйте любой метод сложения, чтобы найти v + w.v + w.
Рис. 2.8 Чтобы найти v + w, v + w, выровняйте векторы в их начальных точках или поместите начальную точку одного вектора в конечную точку другого. (a) Вектор v + wv + w — это диагональ параллелограмма со сторонами vv и ww. (b) Вектор v + wv + w — это третья сторона треугольника, образованного ww, помещенным в конечную точку v.Версия - Чтобы найти 2v − w, 2v − w, мы можем сначала переписать выражение как 2v + (- w) .2v + (- w). Затем мы можем нарисовать вектор −w, −w, а затем добавить его к вектору 2v.2v.
Рисунок 2.9. Чтобы найти 2v − w, 2v − w, просто добавьте 2v + (- w) .2v + (- w).
КПП 2.2
Используя векторы vv и ww из примера 2.2, нарисуйте вектор 2w − v.2w − v.
Компоненты вектора
Работать с векторами на плоскости проще, когда мы работаем в системе координат. Когда начальные и конечные точки векторов задаются в декартовых координатах, вычисления становятся простыми.
Когда начальные и конечные точки векторов задаются в декартовых координатах, вычисления становятся простыми.
Пример 2.3
Сравнение векторов
Эквивалентны ли векторы vv и ww?
- vv имеет начальную точку (3,2) (3,2) и конечную точку (7,2) (7,2)
ww имеет начальную точку (1, −4) (1, −4) и конечную точку ( 1,0) (1,0) - vv имеет начальную точку (0,0) (0,0) и конечную точку (1,1) (1,1)
ww имеет начальную точку (−2,2) (- 2,2) и конечную точку (- 1,3) (- 1,3)
Решение
- Каждый вектор имеет длину 44 единицы, но ориентирован в разных направлениях.Таким образом, vv и ww не эквивалентны (рис. 2.10).
Рисунок 2.10 Эти векторы не эквивалентны.
- Из рисунка 2.11 и с использованием некоторой геометрии ясно, что эти векторы имеют одинаковую длину и одинаковое направление, поэтому vv и ww эквивалентны.
Рисунок 2.
 11 Эти векторы эквивалентны.
11 Эти векторы эквивалентны.
КПП 2.3
Какие из следующих векторов эквивалентны?
Мы видели, как построить вектор, когда нам даны начальная и конечная точки.Однако, поскольку вектор можно разместить в любом месте на плоскости, может быть проще выполнять вычисления с вектором, когда его начальная точка совпадает с началом координат. Мы называем вектор с его начальной точкой в начале координат вектором стандартной позиции. Поскольку известно, что начальная точка любого вектора в стандартном положении находится в (0,0), (0,0), мы можем описать вектор, глядя на координаты его конечной точки. Таким образом, если вектор v имеет свою начальную точку в начале координат и конечную точку в (x, y), (x, y), мы запишем вектор в компонентной форме как
Когда вектор записывается в форме компонентов, подобной этой, скаляры x и y называются компонентами v. Версия
Версия
Определение
Вектор с начальной точкой (0,0) (0,0) и конечной точкой (x, y) (x, y) может быть записан в компонентной форме как
Скаляры xx и yy называются компонентами v.v.
Напомним, что векторы именуются строчными буквами жирным шрифтом или путем рисования стрелки над их именем. Мы также узнали, что мы можем назвать вектор по форме его компонента, с координатами его конечной точки в угловых скобках. Однако при написании компонентной формы вектора важно различать 〈x, y〉 〈x, y〉 и (x, y).(х, у). Первая упорядоченная пара использует угловые скобки для описания вектора, тогда как вторая использует круглые скобки для описания точки на плоскости. Начальная точка 〈x, y〉 〈x, y〉 — это (0,0); (0,0); конечная точка 〈x, y〉 〈x, y〉 — это (x, y). (x, y).
Когда у нас есть вектор, который еще не находится в стандартной позиции, мы можем определить его компонентную форму одним из двух способов. Мы можем использовать геометрический подход, при котором мы рисуем вектор в координатной плоскости, а затем рисуем эквивалентный вектор стандартного положения. В качестве альтернативы, мы можем найти его алгебраически, используя координаты начальной и конечной точек. Чтобы найти его алгебраически, мы вычитаем координату x начальной точки из координаты x конечной точки, чтобы получить компонент x , и мы вычитаем координату y начальной точки из y — координата конечной точки, чтобы получить компонент y .
В качестве альтернативы, мы можем найти его алгебраически, используя координаты начальной и конечной точек. Чтобы найти его алгебраически, мы вычитаем координату x начальной точки из координаты x конечной точки, чтобы получить компонент x , и мы вычитаем координату y начальной точки из y — координата конечной точки, чтобы получить компонент y .
Правило: Составная форма вектора
Пусть v вектор с начальной точкой (xi, yi) (xi, yi) и конечной точкой (xt, yt).(xt, yt). Тогда мы можем выразить v в компонентной форме как v = 〈xt − xi, yt − yi〉 .v = 〈xt − xi, yt − yi〉.
Пример 2.4
Выражение векторов в форме компонентов
Выразите вектор vv с начальной точкой (−3,4) (- 3,4) и конечной точкой (1,2) (1,2) в компонентной форме.
Решение
- Геометрический
- Нарисуйте вектор в координатной плоскости (рисунок 2.12).
- Конечная точка находится на 4 единицы правее и на 2 единицы ниже начальной точки.
- Найдите точку, которая на 4 единицы правее и на 2 единицы ниже исходной точки.
- В стандартном положении этот вектор имеет начальную точку (0,0) (0,0) и конечную точку (4, −2) 🙁 4, −2):
v = 〈4, −2〉. v = 〈4, −2〉.Рисунок 2.12 Эти векторы эквивалентны.
- Алгебраические
В первом решении мы использовали набросок вектора, чтобы увидеть, что конечная точка находится на 4 единицы вправо. Мы можем сделать это алгебраически, найдя разность координат x :
xt − xi = 1 — (- 3) = 4.xt − xi = 1 — (- 3) = 4.
Точно так же разность координат y показывает длину вектора по вертикали.
yt − yi = 2−4 = −2. yt − yi = 2−4 = −2.
yt − yi = 2−4 = −2.
Итак, в компонентном виде
v = 〈xt − xi, yt − yi〉 = 〈1 — (- 3), 2−4〉 = 〈4, −2〉. v = 〈xt − xi, yt − yi〉 = 〈1 — (- 3 ), 2−4〉 = 〈4, −2〉.
КПП 2.4
Вектор ww имеет начальную точку (−4, −5) (- 4, −5) и конечную точку (−1,2). (- 1,2). Выразите ww в виде компонентов.
Чтобы найти величину вектора, мы вычисляем расстояние между его начальной и конечной точкой.Величина вектора v = 〈x, y〉 v = 〈x, y〉 обозначается ‖v‖, ‖v‖ или | v |, | v | и может быть вычислена по формуле
‖V‖ = x2 + y2.‖v‖ = x2 + y2.Обратите внимание, что, поскольку этот вектор записан в форме компонентов, он эквивалентен вектору в стандартной позиции с его начальной точкой в начале координат и конечной точкой (x, y). (X, y). Таким образом, достаточно вычислить величину вектора в стандартном положении. Используя формулу расстояния для вычисления расстояния между начальной точкой (0,0) (0,0) и конечной точкой (x, y), (x, y), мы имеем
‖V‖ = (x − 0) 2+ (y − 0) 2 = x2 + y2. ‖V‖ = (x − 0) 2+ (y − 0) 2 = x2 + y2.
‖V‖ = (x − 0) 2+ (y − 0) 2 = x2 + y2.На основании этой формулы ясно, что для любого вектора v, v, ‖v‖≥0, ‖v‖≥0 и ‖v‖ = 0‖v‖ = 0 тогда и только тогда, когда v = 0. v = 0.
Величину вектора можно также вычислить с помощью теоремы Пифагора, как показано на следующем рисунке.
Рисунок 2.13. Если вы используете компоненты вектора для определения прямоугольного треугольника, величина вектора равна длине гипотенузы треугольника.
Мы определили скалярное умножение и сложение векторов геометрически.Выражение векторов в форме компонентов позволяет нам выполнять те же операции алгебраически.
Определение
Пусть v = 〈x1, y1〉 v = 〈x1, y1〉 и w = 〈x2, y2〉 w = 〈x2, y2〉 — векторы, и пусть kk — скаляр.
Скалярное умножение: kv = 〈kx1, ky1〉 kv = 〈kx1, ky1〉
Сложение векторов: v + w = 〈x1, y1〉 + 〈x2, y2〉 = 〈x1 + x2, y1 + y2〉 v + w = 〈x1, y1〉 + 〈x2, y2〉 = 〈x1 + х2, у1 + у2〉
Пример 2. 5
5
Выполнение операций в форме компонента
Пусть vv — вектор с начальной точкой (2,5) (2,5) и конечной точкой (8,13), (8,13), и пусть w = 〈- 2,4〉.w = 〈- 2,4〉.
- Выразите vv в виде компонентов и найдите ‖v‖.‖v‖. Затем с помощью алгебры найдите
- в + ш, в + ш,
- 3В, 3В и
- v − 2w.v − 2w.
Решение
- Чтобы поместить начальную точку vv в начало координат, мы должны переместить вектор на 22 единицы влево и на 55 единиц вниз (рис. 2.15). Используя алгебраический метод, мы можем выразить vv как v = 〈8−2,13−5〉 = 〈6,8〉: v = 〈8−2,13−5〉 = 〈6,8〉:
‖V‖ = 62 + 82 = 36 + 64 = 100 = 10. v‖ = 62 + 82 = 36 + 64 = 100 = 10.
Рисунок 2.14 В компонентной форме v = 〈6,8〉 .v = 〈6,8〉. - Чтобы найти v + w, v + w, добавьте компоненты x и компоненты y по отдельности:
v + w = 〈6,8〉 + 〈- 2,4〉 = 〈4,12〉. v + w = 〈6,8〉 + 〈- 2,4〉 = 〈4,12〉.
v + w = 〈6,8〉 + 〈- 2,4〉 = 〈4,12〉. - Чтобы найти 3v, 3v, умножьте vv на скаляр k = 3: k = 3:
3v = 3 · 〈6,8〉 = 〈3 · 6,3 · 8〉 = 〈18,24〉. 3v = 3 · 〈6,8〉 = 〈3 · 6,3 · 8〉 = 〈18,24 〉. - Чтобы найти v − 2w, v − 2w, найдите −2w − 2w и добавьте его к v: v:
v − 2w = 〈6,8〉 −2 · 〈−2,4〉 = 〈6,8〉 + 〈4, −8〉 = 〈10,0〉. v − 2w = 〈6,8〉 −2 · 〈−2,4〉 = 〈6,8〉 + 〈4, −8〉 = 〈10,0〉.
КПП 2.5
Пусть a = 〈7,1〉 a = 〈7,1〉 и пусть bb — вектор с начальной точкой (3,2) (3,2) и конечной точкой (−1, −1). (- 1, −1).
- Найдите a‖.‖a‖.
- Express bb в компонентной форме.
- Найдите 3a − 4b.3a − 4b.
Теперь, когда мы установили основные правила векторной арифметики, мы можем сформулировать свойства векторных операций. Мы докажем два из этих свойств. Остальные можно доказать аналогичным образом.
Теорема 2.1
Свойства векторных операций
Пусть u, v, и wu, v иw — векторы на плоскости. Пусть r, sr и s — скаляры.
Пусть r, sr и s — скаляры.
Доказательство коммутативности собственности
Пусть u = 〈x1, y1〉 u = 〈x1, y1〉 и v = 〈x2, y2〉 .v = 〈x2, y2〉. Примените свойство коммутативности для действительных чисел:
u + v = 〈x1 + x2, y1 + y2〉 = 〈x2 + x1, y2 + y1〉 = v + u. u + v = 〈x1 + x2, y1 + y2〉 = 〈x2 + x1, y2 + y1 〉 = V + u.
u + v = 〈x1 + x2, y1 + y2〉 = 〈x2 + x1, y2 + y1 〉 = V + u.□
Доказательство распределительной собственности
Примените распределительное свойство для вещественных чисел:
r (u + v) = r · 〈x1 + x2, y1 + y2〉 = 〈r (x1 + x2), r (y1 + y2)〉 = 〈rx1 + rx2, ry1 + ry2〉 = 〈rx1, ry1〉 + 〈Rx2, ry2〉 = ru + rv.r (u + v) = r · 〈x1 + x2, y1 + y2〉 = 〈r (x1 + x2), r (y1 + y2)〉 = 〈rx1 + rx2 , ry1 + ry2〉 = 〈rx1, ry1〉 + 〈rx2, ry2〉 = ru + rv.□
КПП 2.6
Докажите аддитивное обратное свойство.
Мы нашли компоненты вектора по его начальной и конечной точкам. В некоторых случаях у нас может быть только величина и направление вектора, а не точки.Для этих векторов мы можем определить горизонтальные и вертикальные компоненты с помощью тригонометрии (рис. 2.15).
Рис. 2.15. Компоненты вектора образуют катеты прямоугольного треугольника с вектором в качестве гипотенузы.
Рассмотрим угол θθ, образованный вектором v и положительной осью x . Из треугольника видно, что компоненты вектора vv суть 〈‖v‖cosθ, ‖v‖sinθ〉. 〈‖V‖cosθ, ‖v‖sinθ〉. Следовательно, учитывая угол и величину вектора, мы можем использовать косинус и синус угла, чтобы найти компоненты вектора.
Из треугольника видно, что компоненты вектора vv суть 〈‖v‖cosθ, ‖v‖sinθ〉. 〈‖V‖cosθ, ‖v‖sinθ〉. Следовательно, учитывая угол и величину вектора, мы можем использовать косинус и синус угла, чтобы найти компоненты вектора.
Пример 2.6
Нахождение компонентной формы вектора с помощью тригонометрии
Найдите форму составляющей вектора с величиной 4, который образует угол -45 ° -45 ° с осью x .
Решение
Пусть xx и yy представляют компоненты вектора (рисунок 2.16). Тогда x = 4cos (−45 °) = 22x = 4cos (−45 °) = 22 и y = 4sin (−45 °) = — 22.y = 4sin (−45 °) = — 22. Компонентная форма вектора 〈22, −22〉. 〈22, −22〉.
Рис. 2.16. Используйте тригонометрические отношения, x = ‖v‖cosθx = ‖v‖cosθ и y = ‖v‖sinθ, y = ‖v‖sinθ, чтобы определить компоненты вектора.КПП 2.7
Найдите компонентную форму вектора vv с величиной 1010, которая образует угол 120 ° 120 ° с положительной осью x .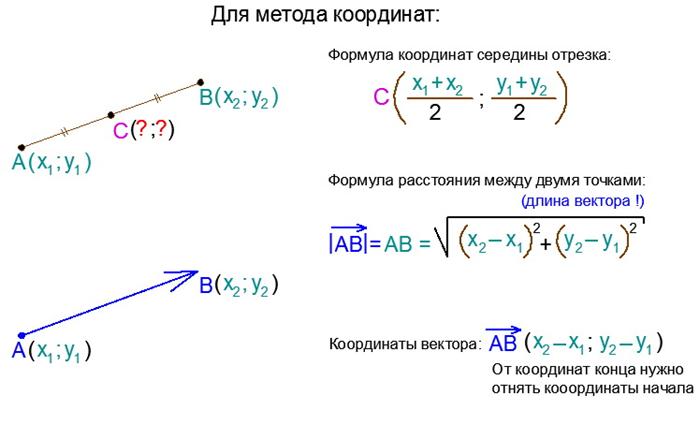
Единичные векторы
Единичный вектор — это вектор с величиной 1,1. Для любого ненулевого вектора v, v мы можем использовать скалярное умножение, чтобы найти единичный вектор uu, который имеет то же направление, что и v.v. Для этого умножаем вектор на величину, обратную его величине:
Напомним, что при определении скалярного умножения мы отметили, что ‖kv‖ = | k | · ‖v‖.‖Kv‖ = | k | · ‖v‖. Если u = 1‖v‖v, u = 1‖v‖v, то ‖u‖ = 1‖v‖ (‖v‖) = 1.‖u‖ = 1‖v‖ (‖v‖) = 1. Мы говорим, что uu — это единичный вектор в направлении vv (рисунок 2.17). Процесс использования скалярного умножения для нахождения единичного вектора с заданным направлением называется нормализацией.
Рис. 2.17. Вектор vv и связанный с ним единичный вектор u = 1‖v‖v.u = 1‖v‖v. В этом случае v‖> 1.‖v‖> 1.Пример 2.7
Нахождение единичного вектора
Пусть v = 〈1,2〉 .v = 〈1,2〉.
- Найдите единичный вектор с тем же направлением, что и v.
 Версия
Версия - Найдите вектор ww с тем же направлением, что и vv, такой, что ‖w‖ = 7.‖w‖ = 7.
Решение
- Сначала найдите величину v, v, затем разделите компоненты vv на величину:
V‖ = 12 + 22 = 1 + 4 = 5‖v‖ = 12 + 22 = 1 + 4 = 5
u = 1‖v‖v = 15 〈1,2〉 = 〈15,25〉. u = 1‖v‖v = 15 〈1,2〉 = 〈15,25〉. - Вектор uu находится в том же направлении, что и vv, и u‖ = 1.‖u‖ = 1. Используйте скалярное умножение, чтобы увеличить длину uu без изменения направления:
w = 7u = 7 〈15,25〉 = 〈75,145〉.w = 7u = 7 〈15,25〉 = 〈75,145〉.
КПП 2.8
Пусть v = 〈9,2〉 .v = 〈9,2〉. Найдите вектор с величиной 55 в направлении, противоположном v.v.
Мы видели, насколько удобно может быть запись вектора в компонентной форме. Однако иногда удобнее записать вектор как сумму горизонтального вектора и вертикального вектора. Чтобы упростить эту задачу, давайте посмотрим на стандартные единичные векторы. Стандартные единичные векторы — это векторы i = 〈1,0〉 i = 〈1,0〉 и j = 〈0,1〉 j = 〈0,1〉 (рисунок 2.18).
Стандартные единичные векторы — это векторы i = 〈1,0〉 i = 〈1,0〉 и j = 〈0,1〉 j = 〈0,1〉 (рисунок 2.18).
Применяя свойства векторов, можно выразить любой вектор через ii и jj в том, что мы называем линейной комбинацией :
v = 〈x, y〉 = 〈x, 0〉 + 〈0, y〉 = x 〈1,0〉 + y 〈0,1〉 = xi + yj. v = 〈x, y〉 = 〈x, 0 〉 + 〈0, y〉 = x 〈1,0〉 + y 〈0,1〉 = xi + yj.Таким образом, vv — это сумма горизонтального вектора с величиной x, x и вертикального вектора с величиной y, y, как показано на следующем рисунке.
Рис. 2.19. Вектор vv представляет собой сумму xixi и yj.yj.Пример 2.8
Использование стандартных единичных векторов
- Выразите вектор w = 〈3, −4〉 w = 〈3, −4〉 через стандартные единичные векторы.
- Вектор uu — это единичный вектор, который образует угол 60 ° 60 ° с положительной осью x . Используйте стандартные единичные векторы для описания u.
 u.
u.
Решение
- Преобразование вектора ww в вектор с нулевой компонентой y и вектор с нулевой компонентой x :
w = 〈3, −4〉 = 3i − 4j.w = 〈3, −4〉 = 3i − 4j. - Поскольку uu является единичным вектором, конечная точка лежит на единичной окружности, когда вектор помещается в стандартное положение (рисунок 2.20).
u = 〈cos60 °, sin60 °〉 = 〈12,32〉 = 12i + 32j.u = 〈cos60 °, sin60 °〉 = 〈12,32〉 = 12i + 32j.
Рисунок 2.20. Конечная точка uu лежит на единичной окружности (cosθ, sinθ). (Cosθ, sinθ).
КПП 2.9
Пусть a = 〈16, −11〉 a = 〈16, −11〉 и пусть bb будет единичным вектором, который образует угол 225 ° 225 ° с положительной осью x .Выразите aa и bb через стандартные единичные векторы.
Приложения векторов
Поскольку векторы имеют как направление, так и величину, они являются ценными инструментами для решения проблем, связанных с такими приложениями, как движение и сила. Вспомните пример с лодкой и пример защитника, которые мы описали ранее. Здесь мы подробно рассмотрим два других примера.
Вспомните пример с лодкой и пример защитника, которые мы описали ранее. Здесь мы подробно рассмотрим два других примера.
Пример 2.9
Нахождение результирующей силы
Машина Джейн застряла в грязи. Лиза и Джед едут на грузовике, чтобы помочь вытащить ее.Они прикрепляют один конец буксирного ремня к передней части автомобиля, а другой конец к сцепному устройству грузовика, и грузовик начинает тянуть. Тем временем Джейн и Джед садятся за машину и толкаются. Грузовик создает на автомобиль горизонтальную силу в 300-300 фунтов. Джейн и Джед толкаются под небольшим углом вверх и создают на машине силу в 150–150 фунтов. Эти силы могут быть представлены векторами, как показано на рисунке 2.21. Угол между этими векторами составляет 15 ° 0,15 °. Найдите результирующую силу (векторную сумму) и укажите ее величину с точностью до десятых долей фунта и угол направления от положительной оси x .
Рисунок 2.21 Две силы, действующие на автомобиль в разных направлениях.
Решение
Чтобы найти эффект объединения двух сил, сложите их репрезентативные векторы. Во-первых, выразите каждый вектор в форме компонентов или в терминах стандартных единичных векторов. Для этого проще всего выровнять один из векторов с положительной осью x . Таким образом, горизонтальный вектор имеет начальную точку (0,0) (0,0) и конечную точку (300,0). (300,0).Он может быть выражен как 〈300,0〉 〈300,0〉 или 300i.300i.
Второй вектор имеет величину 150150 и составляет угол 15 ° 15 ° с первым, поэтому мы можем выразить его как 〈150cos (15 °), 150sin (15 °)〉, 〈150cos (15 °), 150sin (15 °). °)〉, или 150cos (15 °) i + 150sin (15 °) j.150cos (15 °) i + 150sin (15 °) j. Тогда сумма векторов или результирующий вектор будет r = 〈300,0〉 + 〈150cos (15 °), 150sin (15 °)〉, r = 〈300,0〉 + 〈150cos (15 °), 150sin (15 °)〉, и имеем
‖R‖ = (300 + 150cos (15 °)) 2+ (150sin (15 °)) 2≈446.6. R‖ = (300 + 150cos (15 °)) 2+ (150sin (15 °)) 2≈ 446. 6.
6.Угол θθ, образованный rr и положительной осью x , имеет tanθ = 150sin15 ° (300 + 150cos15 °) ≈0.09, tanθ = 150sin15 ° (300 + 150cos15 °) ≈0.09, поэтому θ≈tan − 1 (0,09 ) ≈5 °, θ≈tan − 1 (0,09) ≈5 °, что означает, что результирующая сила rr имеет угол 5 ° 5 ° над горизонтальной осью.
Пример 2.10
Нахождение результирующей скорости
Самолет летит прямо на запад со скоростью 425425 миль в час. Ветер дует с северо-востока, скорость 4040 миль в час. Какая путевая скорость у самолета? Какой пеленг у самолета?
Решение
Начнем с наброска описанной ситуации (рисунок 2.22).
Рис. 2.22. Сначала самолет летит строго на запад. Ветер северо-восточный, поэтому дует юго-западный. Угол между курсом самолета и ветром составляет 45 ° 0,45 °. (Рисунок не в масштабе.) Создайте эскиз так, чтобы начальные точки векторов лежали в начале координат. Тогда вектор скорости самолета p = −425i.p = −425i. Вектор, описывающий ветер, составляет угол 225 ° 225 ° с положительной осью x :
Тогда вектор скорости самолета p = −425i.p = −425i. Вектор, описывающий ветер, составляет угол 225 ° 225 ° с положительной осью x :
Когда воздушная скорость и ветер действуют на самолет вместе, мы можем сложить их векторы, чтобы найти результирующую силу:
p + w = −425i + (- 402i − 402j) = (- 425−402) i − 402j.p + w = −425i + (- 402i − 402j) = (- 425−402) i − 402j.Величина результирующего вектора показывает влияние ветра на путевую скорость самолета:
‖P + w‖ = (- 425−402) 2 + (- 402) 2≈454,17 миль / ч‖p + w‖ = (- 425−402) 2 + (- 402) 2≈454,17 миль / чВ результате ветра самолет движется со скоростью около 454454 миль / ч относительно земли.
Чтобы определить пеленг самолета, мы хотим найти направление вектора p + w: p + w:
tanθ = −402 (−425−402) ≈0,06θ≈3,57 ° .tanθ = −402 (−425−402) ≈0,06θ≈3,57 °.
Общее направление плоскости 3,57 ° 3,57 ° к югу от запада.
Контрольно-пропускной пункт 2.10
Самолет летит прямо на север со скоростью 550550 миль в час. Ветер дует с северо-запада, скорость 5050 миль / ч. Какая путевая скорость у самолета?
Раздел 2.1. Упражнения
Для следующих упражнений рассмотрите точки P (−1,3), P (−1,3), Q (1,5), Q (1,5) и R (−3,7 ).R (-3,7). Определите требуемые векторы и выразите каждый из них a. в виде компонентов и b. используя стандартные единичные векторы.
6.PQ → −PR → PQ → −PR →
7.2PQ → −2PR → 2PQ → −2PR →
8.2PQ → + 12PR → 2PQ → + 12PR →
9.Единичный вектор в направлении PQ → PQ →
10.Единичный вектор в направлении PR → PR →
11.Вектор vv имеет начальную точку (−1, −3) (- 1, −3) и конечную точку (2,1). (2,1). Найдите единичный вектор в направлении v.v. Выразите ответ в виде компонентов.
12. Вектор vv имеет начальную точку (−2,5) (- 2,5) и конечную точку (3, −1).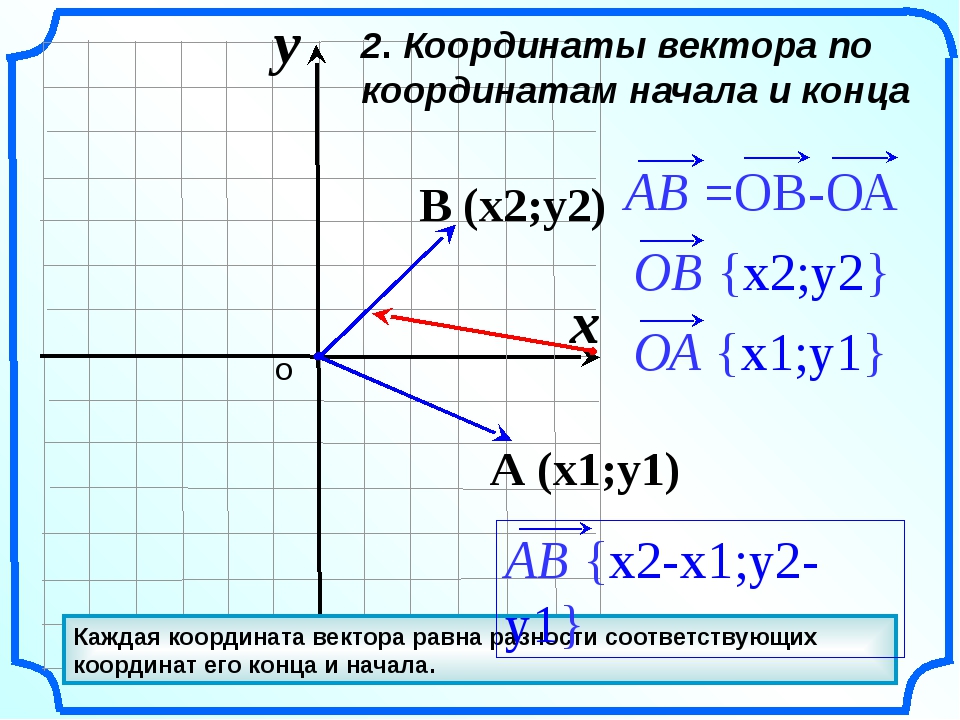 (3, −1). Найдите единичный вектор в направлении v.v. Выразите ответ в виде компонентов.
(3, −1). Найдите единичный вектор в направлении v.v. Выразите ответ в виде компонентов.
Вектор vv имеет начальную точку P (1,0) P (1,0) и конечную точку QQ, которая находится на оси y и выше начальной точки. Найдите такие координаты конечной точки QQ, чтобы величина вектора vv была 5,5.
14.Вектор vv имеет начальную точку P (1,1) P (1,1) и конечную точку QQ, которая находится на оси x и слева от начальной точки.Найдите такие координаты конечной точки QQ, чтобы величина вектора vv была 10,10.
Для следующих упражнений используйте указанные векторы aa и b.b.
- Определите векторную сумму a + ba + b и выразите ее как в форме компонентов, так и с использованием стандартных единичных векторов.
- Найдите разность векторов a − ba − b и выразите ее как в компонентной форме, так и с использованием стандартных единичных векторов.
- Убедитесь, что векторы a, a, b, b и a + b, a + b и, соответственно, a, a, b, b и a − ba − b удовлетворяют неравенству треугольника.

- Определите векторы 2a, 2a, −b, −b и 2a − b. 2a − b. Выразите векторы как в форме компонентов, так и с использованием стандартных единичных векторов.
a = 2i + j, a = 2i + j, b = i + 3jb = i + 3j
16.a = 2i, a = 2i, b = −2i + 2jb = −2i + 2j
17.Пусть aa будет вектором стандартного положения с конечной точкой (−2, −4). (- 2, −4). Пусть bb — вектор с начальной точкой (1,2) (1,2) и конечной точкой (−1,4). (- 1,4). Найдите модуль вектора −3a + b − 4i + j. − 3a + b − 4i + j.
18.Пусть aa будет вектором стандартной позиции с конечной точкой в (2,5).(2,5). Пусть bb — вектор с начальной точкой (−1,3) (- 1,3) и конечной точкой (1,0). (1,0). Найдите модуль вектора a − 3b + 14i − 14j.a − 3b + 14i − 14j.
19. Пусть uu и vv — два неэквивалентных вектора, отличных от нуля. Рассмотрим векторы a = 4u + 5va = 4u + 5v и b = u + 2vb = u + 2v, определенные через uu и v.v. Найдите скаляр λλ такой, что векторы a + λba + λb и u − vu − v эквивалентны.
Пусть uu и vv — два неэквивалентных вектора, отличных от нуля. Рассмотрим векторы a = 2u − 4va = 2u − 4v и b = 3u − 7vb = 3u − 7v, определенные через uu и v.v. Найдите скаляры αα и ββ такие, что векторы αa + βbαa + βb и u − vu − v эквивалентны.
21.Рассмотрим вектор a (t) = 〈cost, sint〉 a (t) = 〈cost, sint〉 с компонентами, которые зависят от действительного числа t.t. При изменении числа tt компоненты a (t) a (t) также меняются в зависимости от функций, которые их определяют.
- Запишите векторы a (0) a (0) и a (π) a (π) в компонентной форме.
- Покажите, что величина ‖a (t) ‖‖a (t) ‖ вектора a (t) a (t) остается постоянной для любого действительного числа t.т.
- При изменении tt покажите, что конечная точка вектора a (t) a (t) описывает окружность с центром в начале радиуса 1.1.
Рассмотрим вектор a (x) = 〈x, 1 − x2〉 a (x) = 〈x, 1 − x2〉 с компонентами, зависящими от действительного числа x∈ [−1,1] . x∈ [−1, 1]. Поскольку число xx изменяется на , , компоненты a (x) a (x) также меняются в зависимости от функций, которые их определяют.
x∈ [−1, 1]. Поскольку число xx изменяется на , , компоненты a (x) a (x) также меняются в зависимости от функций, которые их определяют.
- Запишите векторы a (0) a (0) и a (1) a (1) в компонентной форме.
- Покажите, что величина ‖a (x) ‖‖a (x) ‖ вектора a (x) a (x) остается постоянной для любого действительного числа xx
- При изменении xx покажите, что конечная точка вектора a (x) a (x) описывает окружность с центром в начале радиуса 1.1.
Покажите, что векторы a (t) = 〈cost, sint〉 a (t) = 〈cost, sint〉 и a (x) = 〈x, 1 − x2〉 a (x) = 〈x, 1 − x2〉 являются эквивалентно для x = 1x = 1 и t = 2kπ, t = 2kπ, где kk — целое число.
24.Покажите, что векторы a (t) = 〈cost, sint〉 a (t) = 〈cost, sint〉 и a (x) = 〈x, 1 − x2〉 a (x) = 〈x, 1 − x2〉 являются напротив, если x = rx = r и t = π + 2kπ, t = π + 2kπ, где kk — целое число.
Для следующих упражнений найдите вектор vv с заданной величиной и в том же направлении, что и вектор u. u.
u.
‖v‖ = 7, u = 〈3,4〉 ‖v‖ = 7, u = 〈3,4〉
26.‖v‖ = 3, u = 〈- 2,5〉 ‖v‖ = 3, u = 〈- 2,5〉
27.‖v‖ = 7, u = 〈3, −5〉 ‖v‖ = 7, u = 〈3, −5〉
28.‖v‖ = 10, u = 〈2, −1〉 ‖v‖ = 10, u = 〈2, −1〉
Для следующих упражнений найдите компонентную форму вектора u, u, учитывая его величину и угол, который вектор образует с положительной осью x . По возможности дайте точные ответы.
29.‖u‖ = 2, ‖u‖ = 2, θ = 30 ° θ = 30 °
30.‖u‖ = 6, ‖u‖ = 6, θ = 60 ° θ = 60 °
31.‖u‖ = 5, u‖ = 5, θ = π2θ = π2
32.‖u‖ = 8, u‖ = 8, θ = πθ = π
33.‖u‖ = 10, ‖u‖ = 10, θ = 5π6θ = 5π6
34.u‖ = 50, ‖u‖ = 50, θ = 3π4θ = 3π4
Для следующих упражнений задается вектор uu. Найдите угол θ∈ [0,2π) θ∈ [0,2π), который вектор uu образует с положительным направлением оси x против часовой стрелки.
37. Пусть a = 〈a1, a2〉, a = 〈a1, a2〉, b = 〈b1, b2〉, b = 〈b1, b2〉 и c = 〈c1, c2〉 c = 〈c1, c2〉 три ненулевых вектора. Если a1b2 − a2b1 ≠ 0, a1b2 − a2b1 ≠ 0, то покажите, что существуют два скаляра αα и β, β, такие что c = αa + βb.c = αa + βb.
Если a1b2 − a2b1 ≠ 0, a1b2 − a2b1 ≠ 0, то покажите, что существуют два скаляра αα и β, β, такие что c = αa + βb.c = αa + βb.
Рассмотрим векторы a = 〈2, −4〉, a = 〈2, −4〉, b = 〈- 1,2〉, b = 〈- 1,2〉 и c = 0 Определим скаляры αα и ββ такие, что c = αa + βb.c = αa + βb.
39.Пусть P (x0, f (x0)) P (x0, f (x0)) будет фиксированной точкой на графике дифференциальной функции ff с областью определения, которая является набором действительных чисел.
- Определите действительное число z0z0 так, чтобы точка Q (x0 + 1, z0) Q (x0 + 1, z0) находилась на прямой, касательной к графику ff в точке P.P.
- Определите единичный вектор uu с начальной точкой PP и конечной точкой Q.Q.
Рассмотрим функцию f (x) = x4, f (x) = x4, где x∈ℝ.x∈ℝ.
- Определите действительное число z0z0 так, чтобы точка Q (2, z0) Q (2, z0) s находилась на прямой, касательной к графику ff в точке P (1,1) .
 P (1,1).
P (1,1). - Определите единичный вектор uu с начальной точкой PP и конечной точкой Q.Q.
Рассмотрим две функции ff и gg, определенные на одном и том же наборе действительных чисел D.D. Пусть a = 〈x, f (x)〉 a = 〈x, f (x)〉 и b = 〈x, g (x)〉 b = 〈x, g (x)〉 два вектора, описывающие графики функции, где x∈D.x∈D. Покажите, что если графики функций ff и gg не пересекаются, то векторы aa и bb не эквивалентны.
42.Найдите x∈ℝx∈ℝ такое, что векторы a = 〈x, sinx〉 a = 〈x, sinx〉 и b = 〈x, cosx〉 b = 〈x, cosx〉 эквивалентны.
43.Вычислите координаты точки DD так, чтобы ABCDABCD был параллелограммом с A (1,1), A (1,1), B (2,4), B (2,4) и C (7,4). .С (7,4).
44.Рассмотрим точки A (2,1), A (2,1), B (10,6), B (10,6), C (13,4), C (13,4) и D (16 , −2) .D (16, −2). Определить компонентную форму вектора AD →.AD →.
45. Скорость объекта — это величина связанного с ним вектора скорости. Футбольный мяч, брошенный квотербеком, имеет начальную скорость 7070 миль в час и угол возвышения 30 ° 0,30 °. Определите вектор скорости в милях в час и выразите его в виде компонентов. (Округляем до двух десятичных знаков.)
Определите вектор скорости в милях в час и выразите его в виде компонентов. (Округляем до двух десятичных знаков.)
Бейсболист бросает бейсбольный мяч под углом 30 ° 30 ° к горизонтали. Если начальная скорость мяча составляет 100–100 миль в час, найдите горизонтальную и вертикальную составляющие вектора начальной скорости бейсбольного мяча.(Округляем до двух десятичных знаков.)
47.Пуля выстреливается с начальной скоростью 15001500 фут / сек под углом 60 ° 60 ° к горизонтали. Найдите горизонтальную и вертикальную составляющие вектора скорости пули. (Округляем до двух десятичных знаков.)
48.[T] Спринтер весом 65 кг прилагает усилие 798798 Н под углом 19 ° 19 ° к земле на стартовой колодке в момент начала забега. Найдите горизонтальную составляющую силы. (Округлить до двух десятичных знаков.)
49. [T] На один и тот же объект действуют две силы, горизонтальная сила 4545 фунтов и еще одна 5252 фунтов. Угол между этими силами составляет 25 ° 0,25 °. Найдите величину и угол направления от положительной оси x результирующей силы, действующей на объект. (Округляем до двух десятичных знаков.)
Угол между этими силами составляет 25 ° 0,25 °. Найдите величину и угол направления от положительной оси x результирующей силы, действующей на объект. (Округляем до двух десятичных знаков.)
[T] На один и тот же объект действуют две силы, вертикальная сила 2626 фунтов и еще одна 4545 фунтов. Угол между этими силами составляет 55 ° 0,55 °.Найдите величину и угол направления от положительной оси x результирующей силы, действующей на объект. (Округляем до двух десятичных знаков.)
51. [T] На объект действуют три силы. Две из этих сил имеют величины 5858 Н и 2727 Н и составляют углы 53 ° 53 ° и 152 °, 152 °, соответственно, с положительной осью x . Найдите величину и угол направления от положительной оси x третьей силы так, чтобы результирующая сила, действующая на объект, была равна нулю. (Округляем до двух десятичных знаков.)
(Округляем до двух десятичных знаков.)
Три силы с величинами 8080 фунтов, 120120 фунтов и 6060 фунтов действуют на объект под углами 45 °, 45 °, 60 ° 60 ° и 30 °, 30 °, соответственно, с положительной осью x . Найдите величину и угол направления от положительной оси x результирующей силы. (Округляем до двух десятичных знаков.)
53.[T] Самолет летит в направлении 43 ° 43 ° к востоку от севера (также сокращенно N43E) N43E) со скоростью 550550 миль в час.Ветер со скоростью 2525 миль / ч дует с юго-запада в пеленге N15E.N15E. Какая путевая скорость и новое направление полета самолета?
54.[T] Лодка движется по воде со скоростью 3030 миль в час в направлении N20EN20E (то есть 20 ° 20 ° к востоку от севера). Сильное течение движется со скоростью 1515 миль в час в направлении N45E.N45E. Какая новая скорость и направление движения лодки?
55.
[T] Груз весом 50 фунтов подвешивается на тросе таким образом, чтобы две части троса образовывали углы 40 ° 40 ° и 53 °, 53 ° соответственно с горизонтом.Найдите величины сил натяжения T1T1 и T2T2 в кабелях, если результирующая сила, действующая на объект, равна нулю. (Округляем до двух десятичных знаков.)
56.[T] Груз весом 62 фунта свешивается на веревке, которая образует углы 29 ° 29 ° и 61 °, 61 ° соответственно с горизонтом. Найдите величины сил натяжения T1T1 и T2T2 в кабелях, если результирующая сила, действующая на объект, равна нулю. (Округляем до двух десятичных знаков.)
57. [T] Лодка весом 1500 фунтов припаркована на пандусе, который составляет угол 30 ° 30 ° с горизонтом.Вектор веса лодки направлен вниз и представляет собой сумму двух векторов: горизонтального вектора v1v1, параллельного пандусу, и вертикального вектора v2v2, перпендикулярного наклонной поверхности.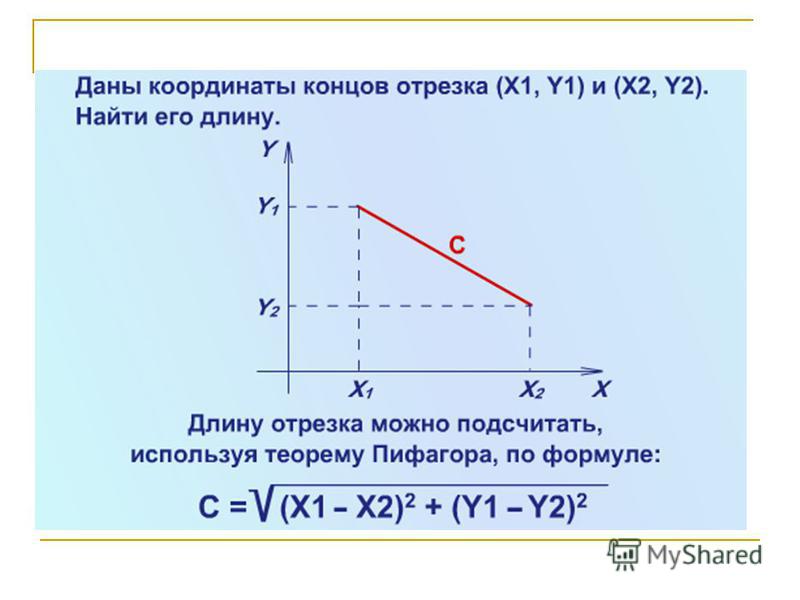 Величины векторов v1v1 и v2v2 представляют собой соответственно горизонтальную и вертикальную составляющие вектора веса лодки. Найдите величины v1v1 и v2.v2. (Округлить до ближайшего целого.)
Величины векторов v1v1 и v2v2 представляют собой соответственно горизонтальную и вертикальную составляющие вектора веса лодки. Найдите величины v1v1 и v2.v2. (Округлить до ближайшего целого.)
[T] Ящик весом 85 фунтов находится в покое на склоне 26 ° 26 °. Определите величину силы, параллельной наклону, необходимой для предотвращения скольжения коробки.(Округлить до ближайшего целого.)
59.Растяжка поддерживает столб высотой 7575 футов. Один конец провода прикрепляют к верху столба, а другой конец прикрепляют к земле на расстоянии 5050 футов от основания столба. Определите горизонтальную и вертикальную составляющие силы натяжения в тросе, если ее величина составляет 5050 фунтов (округлите до ближайшего целого числа).
60. Растяжка телефонного столба имеет угол подъема 35 ° 35 ° по отношению к земле. Сила натяжения троса составляет 120–120 фунтов.Найдите горизонтальную и вертикальную составляющие силы натяжения. (Округлить до ближайшего целого.)
(Округлить до ближайшего целого.)
Векторов
Мы рисовали точки в Rn как точки на линии, плоскости, пространстве и т. Д. Мы также можем нарисовать их как стрелок . Поскольку мы имеем в виду две геометрические интерпретации, теперь мы обсудим взаимосвязь между двумя точками зрения.
Точки и векторы
Опять же, точка в Rn рисуется как точка.
Вектор — это точка в Rn, нарисованная в виде стрелки.
Разница чисто психологическая: точек и вектора — это просто списки чисел .
Когда мы думаем о точке в Rn как о векторе, мы обычно пишем ее вертикально, как матрицу с одним столбцом:
v = E13F.
Мы также запишем 0 для нулевого вектора.
Зачем нужно различать точки и векторы? Вектор не обязательно должен начинаться в начале координат: он может располагаться где угодно ! Другими словами, стрелка определяется ее длиной и направлением, а не местоположением.Например, все эти стрелки представляют вектор E12F.
Если не указано иное, мы будем считать, что все векторы начинаются в начале координат.
Векторы имеют смысл в реальном мире: многие физические величины, такие как скорость, представлены как векторы. Но имеет смысл думать о скорости автомобиля как о приближении к машине.
Здесь мы узнаем, как складывать векторы вместе и как умножать векторы на числа, как алгебраически, так и геометрически.
Сложение векторов и скалярное умножение
- Мы можем сложить два вектора:
CabcD + CxyzD = Ca + xb + yc + zD.
- Мы можем умножить или масштабировать вектор на действительное число c:
cCxyzD = Cc · xc · yc · zD.
Мы называем c скаляром , чтобы отличить его от вектора. Если v — вектор, а c — скаляр, то cv называется скалярным числом , кратным v.
Сложение и скалярное умножение работают одинаково для векторов длины n.
Закон параллелограмма для сложения векторов
Геометрически сумма двух векторов v, w получается следующим образом: поместите хвост w в начало v. Тогда v + w — это вектор, хвост которого является хвостом v, а голова — головой w. В обоих случаях получается параллелограмм. Например,
Тогда v + w — это вектор, хвост которого является хвостом v, а голова — головой w. В обоих случаях получается параллелограмм. Например,
E13F + E42F = E55F.
Почему? Ширина v + w равна сумме ширин, а также высот.
vwwvv + w5 = 1 + 4 = 4 + 15 = 2 + 3 = 3 + 2Вычитание вектора
Геометрически разность двух векторов v, w получается следующим образом: поместите хвосты v и w в одну и ту же точку.Тогда v − w — это вектор от вершины w к вершине v. Например,
E14F-E42F = E-32F.
Почему? Если вы добавите v − w к w, вы получите v.
.Скалярное умножение
Скалярное кратное вектора v имеет то же (или противоположное) направление, но разную длину. Например, 2v — это вектор в направлении v, но в два раза длиннее, а -12v — вектор в направлении, противоположном v, но вдвое короче. Обратите внимание, что набор всех скалярных кратных (ненулевого) вектора v представляет собой строку .
Somemultiplesofv.v2v − 12v0vAllmultiplesofv.
Мы можем складывать и масштабировать векторы в одном уравнении.
Определение
Пусть c1, c2, …, ck — скаляры, и пусть v1, v2, …, vk — векторы в Rn. Вектор в Rn
c1v1 + c2v2 + ··· + ckvk
называется линейной комбинацией векторов v1, v2, …, vk с весами или коэффициентами c1, c2, …, ck.
Геометрически линейная комбинация получается растяжением / сжатием векторов v1, v2 ,…, vk согласно коэффициентам, а затем сложить их вместе по закону параллелограмма.
Рисунок 17 Линейные комбинации двух векторов в R2: перемещайте ползунки, чтобы изменить коэффициенты v1 и v2. Обратите внимание, что любой вектор на плоскости может быть получен как линейная комбинация v1, v2 с подходящими коэффициентами.Пример (линейные комбинации одного вектора)
Линейная комбинация одного вектора v = A12B — это просто скалярное кратное v. Поэтому некоторые примеры включают
v = E12F, 32v = E3 / 23F, −12v = E − 1 / 2−1F ,. ..
..Набор всех линейных комбинаций — это строки от до v . (Если v = 0, в этом случае любое скалярное кратное v снова равно 0.)
Пример (линейные комбинации коллинеарных векторов)
Набор всех линейных комбинаций векторов
v1 = E22F и v2 = E − 1−1F
— это строка , , содержащая оба вектора.
Разница между этим и предыдущим примером в том, что оба вектора лежат на одной линии. Следовательно, любые скалярные числа, кратные v1, v2, лежат на этой прямой, как и их сумма.
Решения для домашнего задания
Решения для домашнего задания| Hmwk, Ch 2 | Домашнее задание Страница назначения | PHY 1350-х Домашняя страница | Hmwk, Ch 4 |Домашнее задание
Ch 3, Векторы
Кан 3; 2, 20, 37, 44, 50, 51, 57, 61
Вопросы 3, 5, 6, 7, 8
Дополнительные проблемы из четвертого издания Serway
(4 изд) 3. 1 Точка находится в полярной системе координат
по координатам r = 2,50 м и
= 35,0 o .
1 Точка находится в полярной системе координат
по координатам r = 2,50 м и
= 35,0 o .
Найдите декартовы координаты этой точки, считая, что два системы координат имеют одинаковое начало.
Концептуальные вопросы
Q3.3 Значения двух векторов A и B равны A = 5 ед. и B = 2 шт. Найдите наибольшее и наименьшее значения возможно для результирующего вектора R = A + B.
Если векторы A и B указывают на то же направление, величина R составляет 7 единиц.
Если векторы A и B указывают на напротив направление, величина R составляет 3 единицы.
Q3.5 Если компонента вектора A вдоль направления вектора B равен нулю, что вы можете сделать об этих двух векторах.
Два вектора перпендикуляр (также может быть
сказали, что они ортогональны ).
Q3.6 Может ли величина вектора иметь отрицательную величину? ценность?
Нет, величина всегда равна положительному или нулю.
Q3.7 Какие из следующих векторов, а какие? нет:
усилие -> вектор
температура -> скаляр
объем -> скаляр
рейтинг телешоу -> скаляр
высота -> вектор (колодец имел бы отрицательную высоту)
скорость -> вектор
возраст -> скаляр
3 кв.8 При каких обстоятельствах ненулевой вектор, лежащий в в плоскости xy всегда есть компоненты, равные по величина?
Если вектор лежит вдоль линии 45 o в первой или
В третьем квадранте два компонента будут в точности равны. Если
вектор лежит по линии 45 o во втором или четвертом
квадранты двух компонентов будут равны по величине.
Задачи из текущего (5-го) издания Serway и Байхнер.
3,2 Две точки в плоскости xy имеют декартовы координаты (2,00, — 4,00) м и (- 3,00, 3,00) м.
Определить
(а) расстояние между этими точками и
Мы можем найти расстояние между двумя точками от Теорема Пифагора,расстояние = d = КОРЕНЬ [(x) 2 + (у) 2 ]d = КОРЕНЬ [(- 3,00 — 2,00) 2 + (3.00 — (- 4,00)) 2 ] м
d = КОРЕНЬ [(- 5) 2 + (7,00) 2 ] м
d = SQRT [25,00 + 49,00] м
d = SQRT [74,00] м
d = 8,60 м
(б) их полярные координаты
P 1 = (2,00, — 4,00) мP 1 расстояние от начала координат или его радиус r 1 , это
r 1 = КОРЕНЬ [(2.00) 2 + (- 4,00) 2 ] m = SQRT [4 + 16] m = SQRT [20] м
r 1 = 4,47 м
коричневый [ 1 ] = opp / adj = y 1 / х 1 = (- 4) / 2 = — 2
1 = — 63,4 o
Декартовы координаты (r,) для точки P 1 , это
П 1 = (4.47 м, — 63,4 o )Теперь то же самое для точки P 2 ,
P 2 = (- 3,00, 3,00) мP 2 расстояние от начала координат или его радиус r 2 , это
r 2 = КОРЕНЬ [(- 3.00) 2 + ( 3.00) 2 ] m = SQRT [9 + 9] m = SQRT [18] мr 2 = 4,24 м
коричневый [ 2 ] = opp / adj = y 2 / х 2 = 3 / (- 3) = — 1
2 = 135 o
Декартовы координаты (r,) для пункта P 2 , это
П 2 = (4.24 м, 135 o )
ВНИМАНИЕ! Всегда соблюдайте осторожность с обратной тангенсой функция (и все другие обратные триггерные функции). Когда ты говоришь ваш калькулятор, который вы хотите получить арктангенс от (- 1) it вероятно скажет вам, что угол составляет — 45 o . An угол — 45 o действительно имеет тангенс — 1. A точка, расположенная в (+ 3, — 3), расположена под углом — 45 o (измерено от оси x).Но наша точка зрения, P 2 , находится по адресу (- 3, + 3). Итак, из диаграммы мы Делаем вывод, что он расположен под углом 135 o .
3.20 Найдите горизонтальную и вертикальную составляющие 100-метровой перемещение супергероя, который летит с вершины высокого здания по пути, показанному на рисунке P3.19.
x = r cos = (100 м) cos 30 o = (100 м) (0,866)x = 86,6 м
г = г грех = — (100 м) sin 30 o = — (100 м) (0.
500)
y = — 50,0 м
(x, y) = (86,6 м, — 50,0 м)
3,37 Вид вертолета на рис. P3.37 показывает двух человек. натягивает упрямого мула.
Найдите
(a) единственная сила, эквивалентная двум силам показано, и
(b) сила, которую третье лицо должно было бы применить к мула, чтобы равнодействующая сила была равна нулю.
Нам нужно получить результат R, R = F 1 + F 2После хорошей диаграммы большинство задач сложения векторов начинаются с нахождение компонентов векторов.
F 1x = F 1 cos 60 o = (120 Н) (0,50) = 60 НF 1y = F 1 sin 60 o = (120 N) ( 0,866) = 104 Н
F 1 = 60 N i + 104 N j
F 2x = — F 2 cos 75 o = — (80 Н) (0,260) = — 20,8 Н
F 2y = F 2 sin 75 o = (80 N) ( 0.
966) = 77,3 N
F 2 = — 20,8 N i + 77,3 N J
R = F 1 + F 2
R = ( 60 N i + 104 N j) + ( 20,8 N i + 77.3 N j)
R = ( 60 — 20,8 ) N i + ( 104 + 77.3 ) N j
R = 39.2 N i + 181,3 N J
Как и раньше, теперь нам нужно найти величину результирующего и его направление,
R = SQRT [R x 2 + R и 2 ]R = SQRT [39,2 2 + 181,3 2 ] NR = 186,5 Н
Обратите внимание на диаграмму, что теперь мы измеряем угол от положительной оси абсцисс; следовательно,
загар = OPP / adj = R R / R x = 181.= 78 o3 / 39,2 = 4,65
3,44 Инструкции по поиску кладов, включая следующий:
Идти 75 шагов на 240 o ,
поверните на 135 o и пройдите 125 шагов,
, затем совершите 100 шагов со скоростью 160 o .
Определите результирующее смещение от начальной точки.
Каждая часть этих направлений представляет собой смещение векторA: Пройдите 75 шагов при 240 oA x = A cos = (75 шагов) cos 240 o = (75 шагов) (- 0.5) = — 37,5 шагаA y = грех = (75 шагов) sin 240 o = (75 шагов) (- 0,866) = — 64,95 шага
То есть
A = — 37,5 i — 64,95 jB: поверните на 135 o и пройдите 125 шагов
B x = B cos = (125 шагов) cos 135 o = (125 шагов) (- 0.707) = — 88,39 шага
B y = B sin = (125 шагов) sin 135 o = (125 шагов) (0,707) = 88,39 шага
То есть
B = — 88..39 i + 88,39 jC: ход 100 шагов при 160 o
C x = C cos = (100 шагов) cos 160 o = (100 шагов) (- 0.940) = — 93,97 шагаC y = C sin = (100 шагов) sin 160 o = (100 шагов) (0,342) = 34,20 шага
То есть
C = — 93,97 i + 34,2 jТеперь мы складываем эти векторы смещения, чтобы найти результат, R
R = A + B + CПомните, что векторная запись или векторное сложение действительно элегантное сокращение для два скаляра уравнения
R x = A x + B x + С xи
R y = A y + B y + C yИспользуя числовые значения для них, мы имеем
R x = A x + B x + C xR x = (- 37.
50 — 88,39 — 93,97) шагов
R x = — 219,86 шага
и
R y = A y + B y + C yR y = (- 64,95 + 88,39 + 34,20) шагов
R y = 57,64 шага
Итак, мы ожидаем, что клад будет находиться по адресу
.(X, Y) = ( R x , R y ) = (- 219.86, 57,64) шаговИли мы можем найти это смещение в полярных координатах,
R = SQRT [X 2 + Y 2 ] = SQRT [(- 219,86) 2 + (57,64) 2 ] шаговR = 227,29 шага
загар = opp / adj = Y / X = 57 / (- 220) = — 0,26
= 165,5 o
Таким образом, мы можем сформулировать этот результат как
R = (R, ) = (227.3 шага, 165,5 o )
3,50 Самолет, вылетающий из аэропорта А, летит в 300 км на восток, затем 350 км 30,0 o к западу от севера, а затем 150 км к северу до Прибытие в аэропорт Б. В этот день без ветра.
(a) На следующий день другой самолет летит прямо из пункта А в пункт Б. по прямой. В каком направлении пилот должен двигаться в этом прямой полет?
(b) Как далеко поедет пилот по этой прямой рейс?
Мы можем описать каждый отрезок пути этого самолета как вектор:Самолет пролетает 300 км на восток, затем 350 км 30.0 o к западу от севера
, а затем 150 км к северу
Теперь мы можем сложить этих векторов, чтобы получить результат R,
Чтобы выполнить это сложение векторов, мы можем записать векторы A, B, и C в виде компонентов.
A = 300 км i + 0 jПомни, на этот раз нам даны, и мы найдем, углы, измеренные от Северный (или у). Будьте осторожны при использовании триггерных функций.
B = — (350 км) sin 30 o i + (350 км) cos 30 o j
B = — (350 км) (0,500) i + (350 км) (0,866) дж
B = — 175 км i + 303 км j
C = 0 i + 150 км j
R = A + B + C
R = ( 300 км i + 0 j) + ( — 175 км i + 303 км j) + ( 0 i + 150 км к)
R = ( 300 — 175 + 0 ) км i + ( 0 + 303 + 150 ) км j
R = 125 км i + 453 км j
Теперь мы хотим записать этот результат в полярных координатах.
R = SQRT [R x 2 + R и 2 ]координаты, определение его длины и направления.
R = SQRT [125 2 + 453 2 ] км
R = 470 км
загар = opp / adj = RR x / R Y = 125/453 = 0,276
= 15 или
R = (470 км, 15 o )
3.51 Три вектора ориентированы, как показано на рисунке P3.51, где | A | = A = 20,0 шт., | B | = B = 40,0 единиц, и | C | = c = 30,0 шт.
Найдите (а) компоненты x и y результирующего вектора (выраженного в обозначении единичного вектора) и (б) величина и направление результирующий вектор (т.е. в полярных координатах)
Сначала разложите три вектора на их x- и
y-компоненты.
| x = 0 B x = B cos 45 o B x = (40) (0.707) B x = 28,28 Cx = C cos 45 o Сх = (30) (0,707) Сх = 21,21 R x = A x + B x + C x R x = 0 + 28,28 + 21,21 Rx = 49,49 | А y = 20.0 B y = B sin 45 o B y = (40) (0,707) B и = 28,28 Cy = — C sin 45 o Cy = — (30) (0,707) Cy = — 21,21 Ry = Ay + By + Cy Ry = 20. Ry = 27,07 |
R = SQRT [R x 2 + R и 2 ]
R = КОРЕНЬ [(49,49) 2 + (27,07) 2 ]
R = 56,4
загар = опп / прил = рэндов и рэндов / рэндов x
загар = 27,07 / 49,49 = 0,547
= 28,7 или
3,57 Человек, идущий на прогулку, следует по тропе, показанной на Рисунок P3.57. Общий маршрут состоит из четырех прямых маршрутов. В конец прогулки, каково результирующее перемещение человека измеряется от начальной точки?
[ Помните: «Смещение» — это вектор , поэтому Ответ — звездной величины и направление . ]
Мы также можем обозначить векторы D 1 1 , D 2 , D 3 и D 4 :
| D 1 = 100 м, 0 o | D 1x = 100 м | D 1г = 0 |
| D 2 = 300 м, 90 o CW | D 2x = 0 | D 2л = — 300 м |
| D 3 = 150 м, 150 o CW | D 3x = (150 м) cos 150 o D 3x = — (150 м) cos 30 o D 3x = — (150 м) (0. D 3x = — 130 м | D 3 года = (150 м) sin 150 o D 3 года = — (150 м) sin 30 o D 3x = — (150 м) (0,500) D 3x = — 75 м |
| D 4 = 200 м, 240 o CW | D 4x = (200 м) cos 240 o D 4x = — (200 м) cos 60 o D 4x = — (200 м) (0.500) D 4x = — 100 м | D 4y = (200 м) sin 240 o D 4y = — (200 м) sin 60 o D 4y = — (200 м) (0,866) D 4л = — 173,2 м |
| R = D 1 + Д 2 + Д 3 + Д 4 | R x = (100 + 0 — 130 — 100) м R x = — 130 м | R y = (0-300-75 + 173. 2) м 2) мR y = — 201,8 |
R = SQRT [R x 2 + R и 2 ]
R = SQRT [(130) 2 + (201,8) 2 ] м
R = 240 м
загар = R y / R x = — 201,8 / (- 130) = 1,55
По моему калькулятору это означает
знак равно 57,2 илиЭто правильно?
Это зависит от обстоятельств. Будьте осторожны! Угол (или направление) равен, действительно, 57.2 o , как показано на схеме. Обычно мы рассматриваем углы против часовой стрелки как положительный , поэтому запишем это как
знак равно — 57,2 oНикогда вслепую запишите ответ. Всегда будь уверен вы поймете , что это значит. Это очень важно!
3,61 Прямоугольный параллелепипед имеет размеры a, b и
c, как на рисунке P3.61.
(a) Получите векторное выражение диагонали лица Р 1 .Какова величина этого вектора?
(b) Получите векторное выражение для вектора диагонали тела Р 2 .
Обратите внимание, что R 1 , c k , и R 2 составьте прямоугольный треугольник и докажите, что величина R 2 — SQRT ( 2 + b 2 + c 2 ).
————————
R 1 — гипотенуза прямоугольного треугольника в xy plane — или диагональ прямоугольника в плоскости xy.В стороны — это a (по x) и b (по y). Следовательно,
R 1 = SQRT (a 2 + b 2 ) R 2 — гипотенуза прямоугольного треугольника в
плоскость, содержащая R 1 и c k (или ось z)
— или диагональ прямоугольника в этой плоскости. Стороны
R 1 (по R 1 ) и c (по оси z). Следовательно,
Следовательно,
Решения дополнительных проблем от четвертого Serway выпуск
(4 изд) 3.2 Точка расположена в полярной системе координат по координаты r = 2,50 м и = 35,0 o .
Найдите декартовы координаты этой точки, считая, что два системы координат имеют одинаковое начало.
x = r cos = (2,50 м) cos 35 o = (2,50 м) (0,819)c) Дуг Дэвис, 2001 г .x = 2,05 м
г = г грех = (2,50 м) sin 35 o = (2,50 м) (0,574)
y = 1,43 м
(х, у) = (2.05 м, 1,43 м)
| Hmwk, Ch 2 | Домашнее задание Страница назначения | PHY Домашняя страница 1350-х | Hmwk, глава 4 |
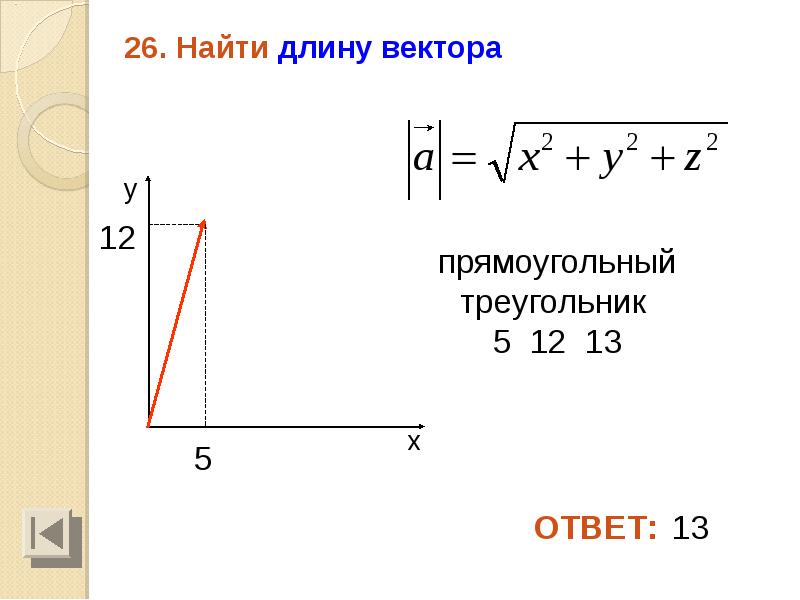 ; все права защищены
; все права защищены3D векторов | Superprof
Мы живем в трехмерном мире, что означает, что у нас есть 3 оси в качестве ориентира. Эти оси — ось x, ось y и ось z. Векторное знание применимо в реальной жизни, что в конечном итоге означает, что применяются все векторные законы, но в предыдущих источниках мы были привязаны к 2-мерному, изменяет ли 3-мерный мир все законы? Абсолютно! но разве это изменение слишком велико? Нет, все, что вам нужно сделать, это добавить третье измерение (ось z) ко всем этим законам.Трехмерный вектор — это отрезок прямой в трехмерном пространстве, идущий от точки A (хвост) до точки B (голова).
Каждый вектор имеет величину (или длину) и направление. Помните, что основы не изменятся, потому что мы просто добавляем здесь еще одно измерение. Это не означает, что то, что вы изучали раньше, будет полностью изменено, всего несколько изменений в формуле, но концепция останется той же. Если вы хорошо понимаете предыдущие законы, то понимание законов в трехмерном пространстве не будет для вас проблемой.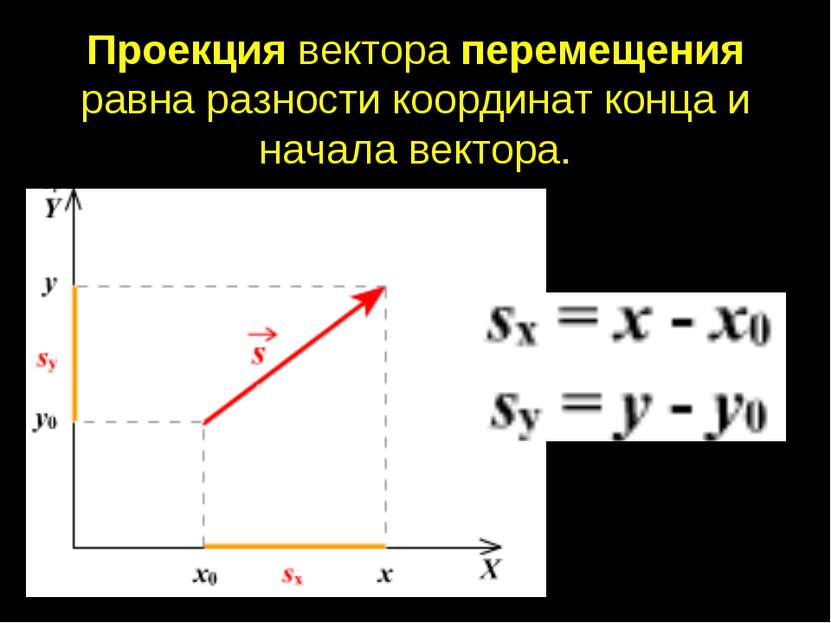
Компоненты трехмерного вектора
Когда мы работаем в трехмерном пространстве, мы всегда рассматриваем все три базы координат, которые являются осью x, осью y и осью z. Например, у нас есть две точки в трехмерном пространстве, и это точка A и точка B. Координаты точек A и B будут записаны (в трехмерном пространстве) следующим образом:
и. Ваш учитель также попросил вас найти вектор, но как вы это сделаете в трехмерном пространстве? Такая же голова без хвоста? Да точно так же! Вам нужно вычесть координату головы из координаты хвоста.Вычислите компоненты векторов, которые можно нарисовать в треугольнике с вершинами
и.Не забывайте, что вектор состоит из двух вещей: одна — это направление, а другая — величина. Если вы измените направление, это означает, что все координаты вектора также будут перевернуты:
Величина или длина вектора
Величина является ключевым элементом вектора, а вектор без величины — просто направление без силы.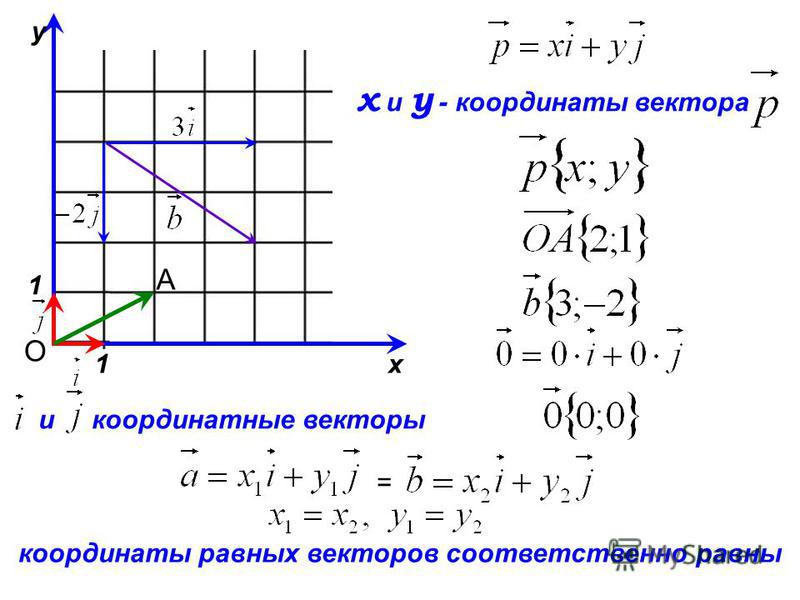 Величина вектора равна длине отрезка линии, который его определяет. Величина вектора всегда представлена положительным числом, и только нулевой вектор имеет величину ноль .
Величина вектора равна длине отрезка линии, который его определяет. Величина вектора всегда представлена положительным числом, и только нулевой вектор имеет величину ноль .
Расчет величины для определения ее компонентов
Возможно, вы знакомы с формулой величины, которая равна
, но с третьим новым измерением все будет немного иначе. Чтобы найти величину трехмерного вектора, вам нужно просуммировать все возведенные в квадрат компоненты различных осей, а затем извлечь квадратный корень из ответа.Ниже приведен решенный вопрос для уточнения.
Учитывая векторы
и, найдите величины и ·Расчет модуля, зная координаты точек
Чтобы вычислить величину, мы воспользуемся формулой расстояния, но с небольшим изменением. Возможно, вы раньше сталкивались с проблемами двух измерений, поэтому в то время вы использовали только компоненты x и y, но теперь все изменилось. На этот раз вы будете использовать три компонента, но не волнуйтесь, если вы хорошо понимаете формулу расстояния, это будет для вас кусок пирога. Например, у вас есть две точки A и B. Координаты точки A равны
На этот раз вы будете использовать три компонента, но не волнуйтесь, если вы хорошо понимаете формулу расстояния, это будет для вас кусок пирога. Например, у вас есть две точки A и B. Координаты точки A равны
Первый шаг — вычесть компонент хвоста из компонента головы, как вы делали это раньше. Найдите разницу для всех компонентов, а затем возьмите квадрат всех этих ответов. Сложите все эти квадраты ответов, а затем извлеките квадратный корень из полученного ответа, и это будет ваша величина из двух разных векторов, или вы можете использовать приведенную ниже формулу и просто подставить значения и найти ответ всего за один шаг.
Расстояние между двумя точками
Формула для расстояния между двумя точками такая же, как и для определения величины двух векторов.
ПРИМЕР
Найдите расстояние между точками
и.Единичный вектор
Векторы бывают самых разных форм и размеров, но как мы описываем эти векторы? С помощью единичного вектора. Определение единичного вектора довольно просто, это вектор с величиной
Определение единичного вектора довольно просто, это вектор с величиной
К Б или не к Б? Процедура python, представленная в листинге 1, в первую очередь зависит от использования векторной точки
продукт, чтобы определить, является ли самый короткий
расстояние Ввод координат начало (1, 0, 2) конец (4.5, 0, 0.5) Балл: пнт (2, 0, 0.5) Рисунок 2 Координаты Y линии и точки равны нулю, и поэтому оба лежат в плоскости XZ. Шаг 1Преобразуйте линию и точку в векторы. Координаты вектор, представляющий точку, относительно начала линия. line_vec = вектор (начало, конец) # (3,5; 0; -1,5)
pnt_vec = вектор (начало, pnt) # (1, 0, -1,5) Шаг 2Масштабируйте оба вектора по длине линии. line_len = длина (line_vec) # 3. Шаг 3Вычислите скалярное произведение масштабированных векторов. Значение соответствует на расстояние, показанное черным цветом, вдоль единичного вектора до перпендикулярно, показано зеленым. t = точка (line_unitvec, pnt_vec_scaled) # 0,397 Шаг 4Установите ‘t’ в диапазоне от 0 до 1.Масштабируйте вектор линии на ‘t’, чтобы найти ближайшее местоположение, показанное на зеленый, чтобы конец точечного вектора. Рассчитайте расстояние от ближайшего местоположение до конца вектора точки. , если t 1.0:
t = 1.0
ближайшее = масштаб (line_vec, t) # (1,388, 0,0, -0,595)
dist = distance (ближайший, pnt_vec) # 0.985 Шаг 5 Переведите «ближайшую» точку относительно начала линии. |

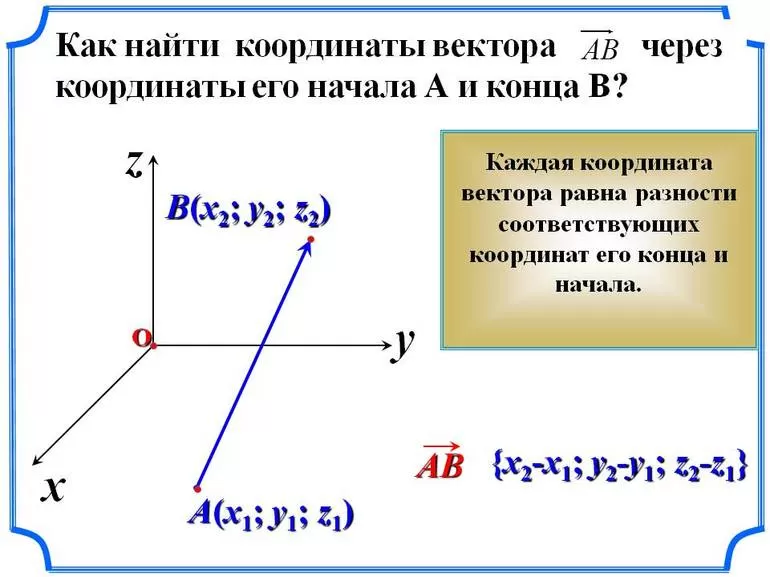 Сложение векторов, вычитание векторов.
Сложение векторов, вычитание векторов.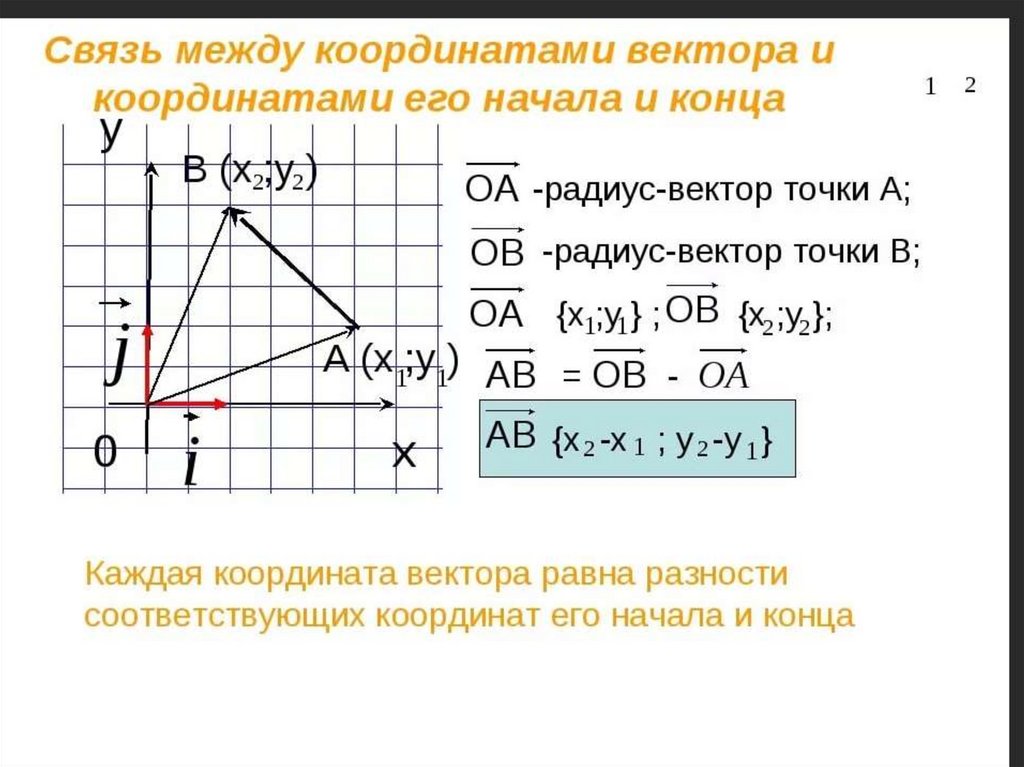
 А именно $ a_x=4, a_y=2, a_z=4 $. Для нахождения длины вектора используем вторую формулу. Подставляем неизвестные в неё:
А именно $ a_x=4, a_y=2, a_z=4 $. Для нахождения длины вектора используем вторую формулу. Подставляем неизвестные в неё:
 Выразим расстояние d между точками M1 и M2 через их координаты.
Выразим расстояние d между точками M1 и M2 через их координаты.
 Определите вектор положения, представленный UV .
Определите вектор положения, представленный UV .

 w.
w.  11 Эти векторы эквивалентны.
11 Эти векторы эквивалентны. yt − yi = 2−4 = −2.
yt − yi = 2−4 = −2.  5
5 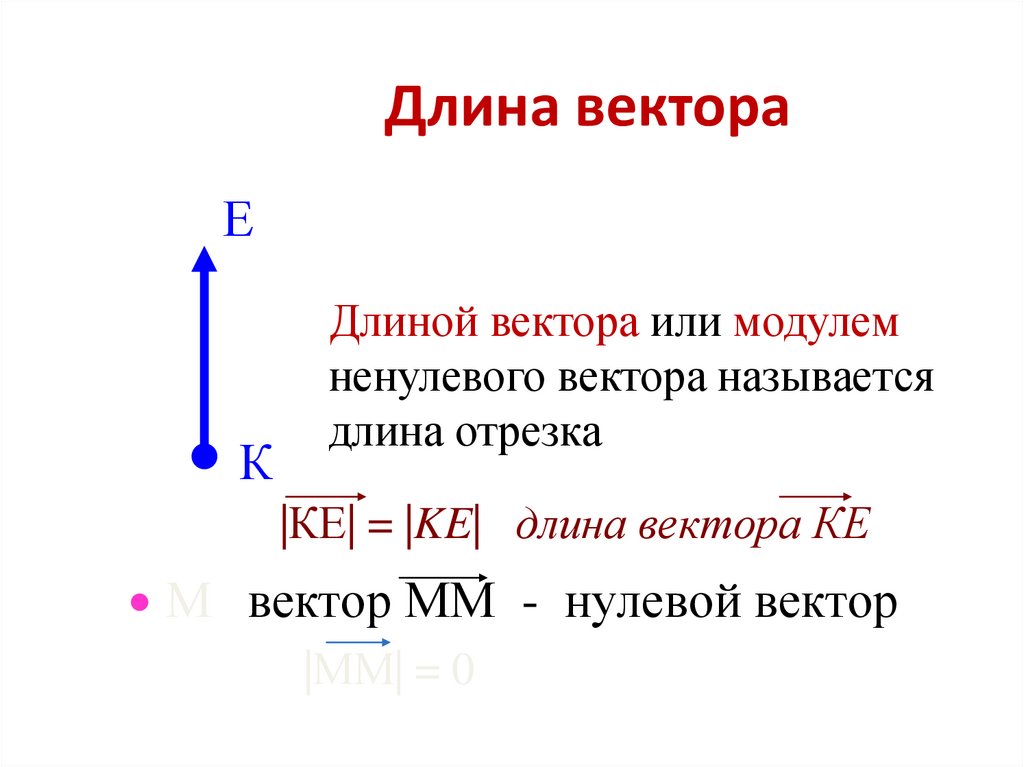 v + w = 〈6,8〉 + 〈- 2,4〉 = 〈4,12〉.
v + w = 〈6,8〉 + 〈- 2,4〉 = 〈4,12〉. Версия
Версия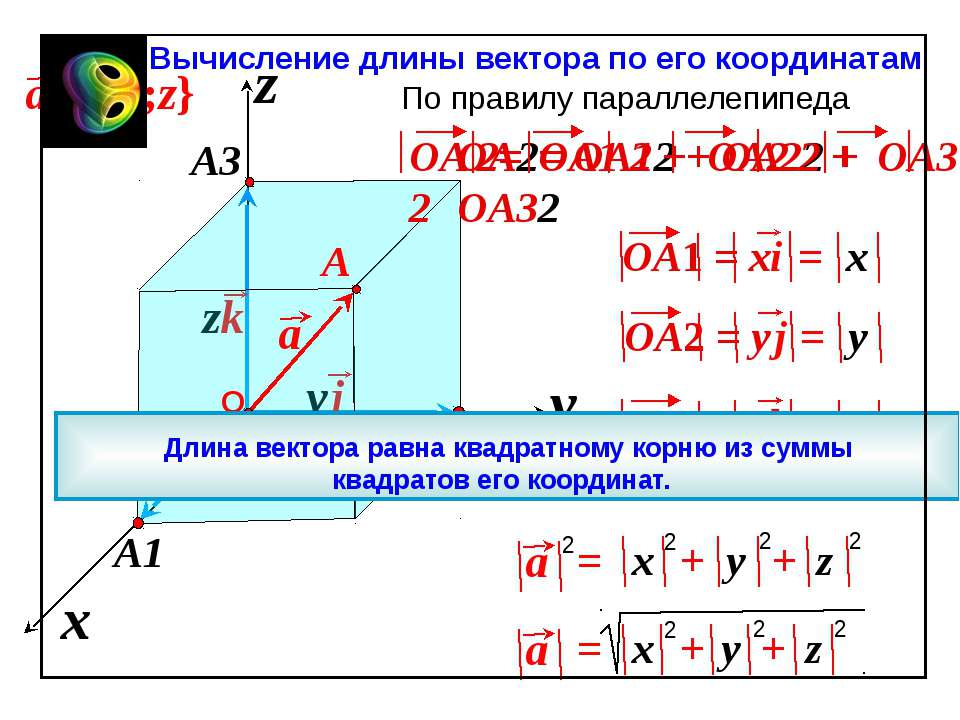 u.
u.
 P (1,1).
P (1,1). 00) 2 + (-
4,00) 2 ] m = SQRT [4 + 16] m = SQRT
[20] м
00) 2 + (-
4,00) 2 ] m = SQRT [4 + 16] m = SQRT
[20] м 24 м, 135 o )
24 м, 135 o ) 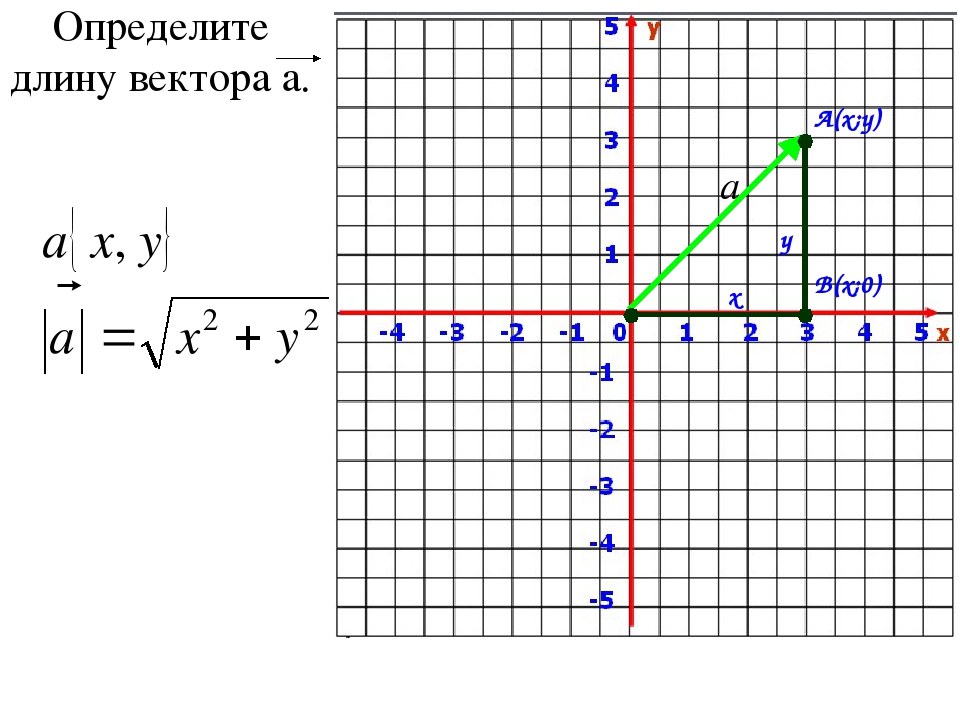 500)
500) 966) = 77,3 N
966) = 77,3 N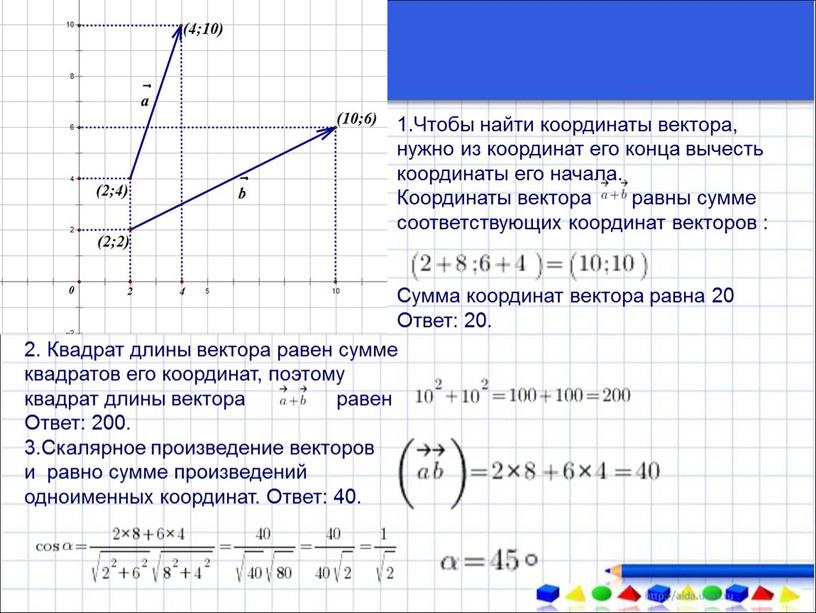 3 / 39,2 = 4,65
3 / 39,2 = 4,65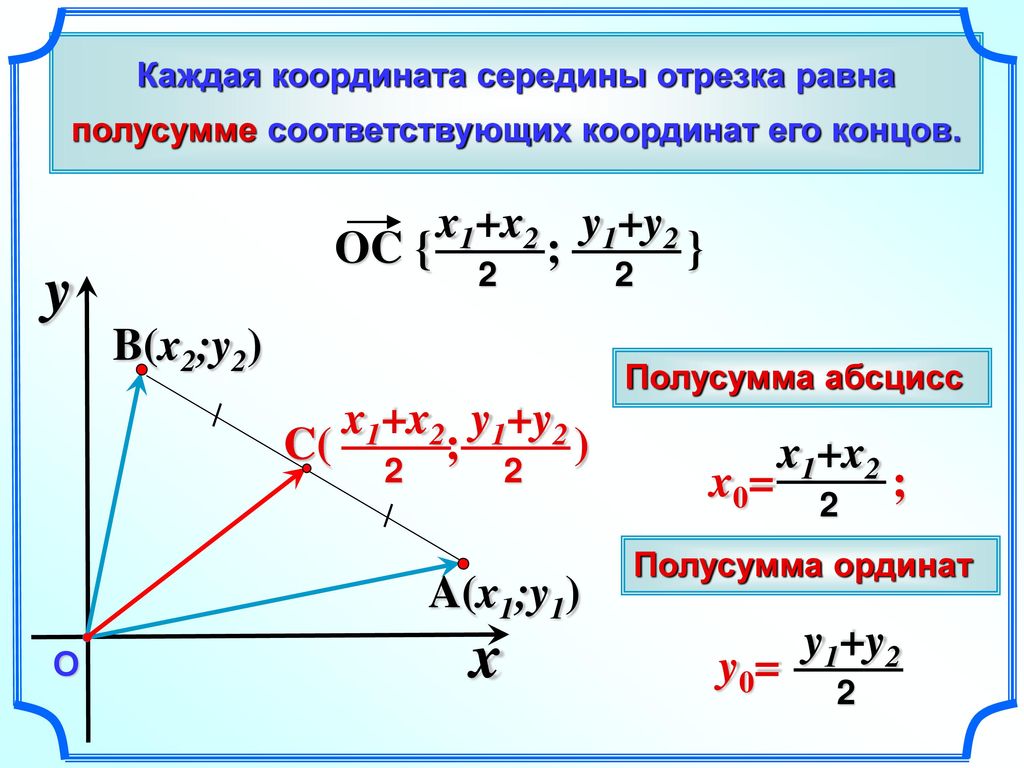 707) =
— 88,39 шага
707) =
— 88,39 шага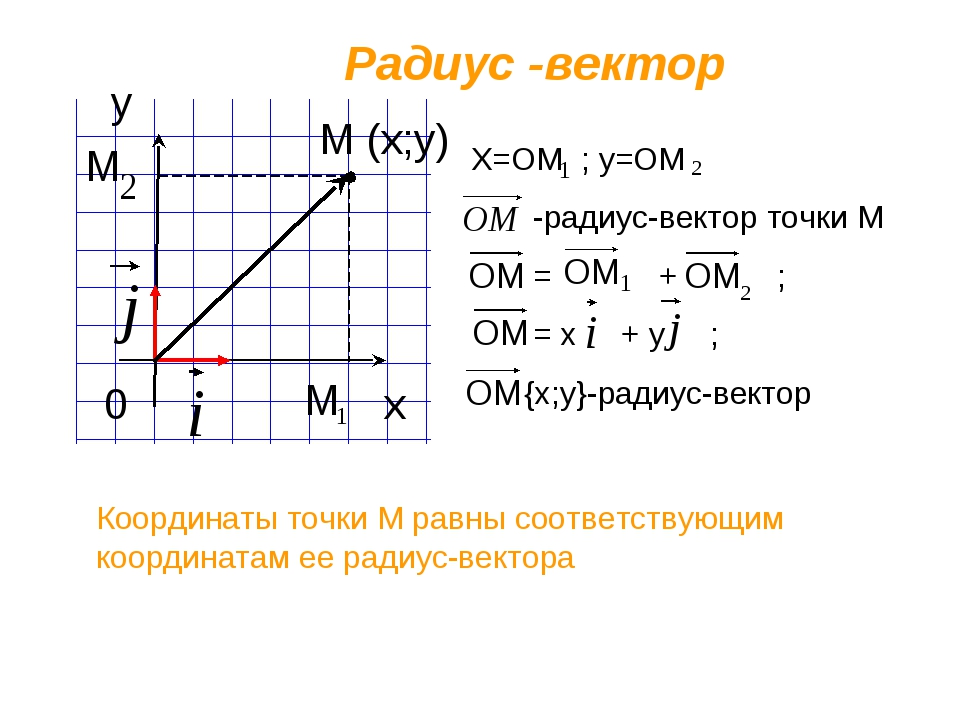 50 — 88,39 — 93,97) шагов
50 — 88,39 — 93,97) шагов 3 шага, 165,5 o )
3 шага, 165,5 o ) Помни, на этот раз нам даны, и мы найдем, углы, измеренные от
Северный (или у). Будьте осторожны при использовании триггерных функций.
Помни, на этот раз нам даны, и мы найдем, углы, измеренные от
Северный (или у). Будьте осторожны при использовании триггерных функций. координаты, определение его длины и направления.
координаты, определение его длины и направления. 0 + 28,28 — 21,21
0 + 28,28 — 21,21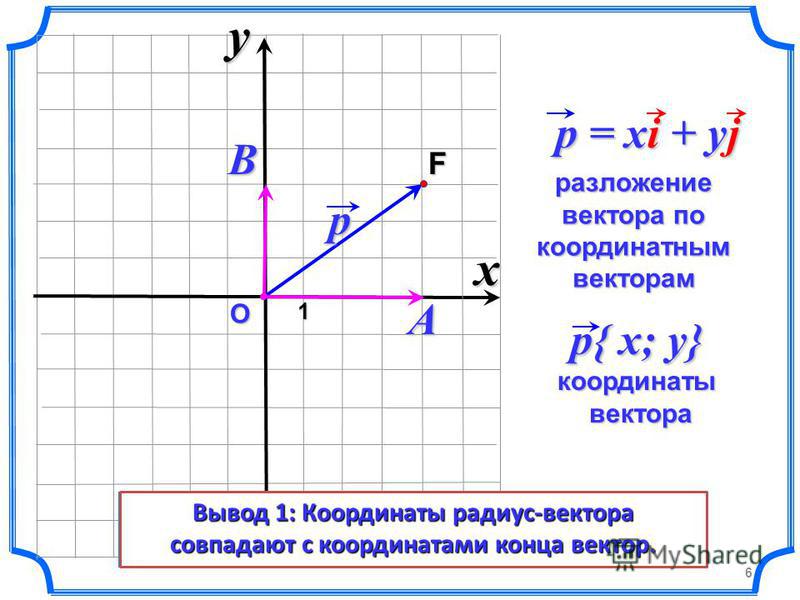 866)
866) Процедура
Процедура  808
line_unitvec = unit (line_vec) # (0,919, 0,0, -0,394)
pnt_vec_scaled = масштаб (pnt_vec, 1.0 / line_len) # (0,263, 0,0, -0,393)
808
line_unitvec = unit (line_vec) # (0,919, 0,0, -0,394)
pnt_vec_scaled = масштаб (pnt_vec, 1.0 / line_len) # (0,263, 0,0, -0,393) 