Как вычислить длину отрезка по координатам точек. Нахождение координат середины отрезка: примеры, решения
Определить длину отрезка возможно разными способами. Для того чтобы узнать, как найти длину отрезка, достаточно иметь в наличии линейку или знать специальные формулы для расчета.
Длина отрезка с помощью линейки
Для этого прикладываем к построенному на плоскости отрезку линейку с миллиметровыми делениями, причем начальную точку необходимо совместить с нулем шкалы линейки. Затем следует отметить на данной шкале расположение конечной точки данного отрезка. Полученное количество целых делений шкалы и будет являться длиной отрезка, выраженной в см. и мм.
Метод координат на плоскости
Если известны координаты отрезка (х1;у1) и (х2;у2), то следует рассчитать его длину следующим образом. Из координат на плоскости второй точки следует вычесть координаты первой точки. В итоге должно получиться два числа. Каждое из таких чисел необходимо возвести в квадрат, а потом найти сумму этих квадратов.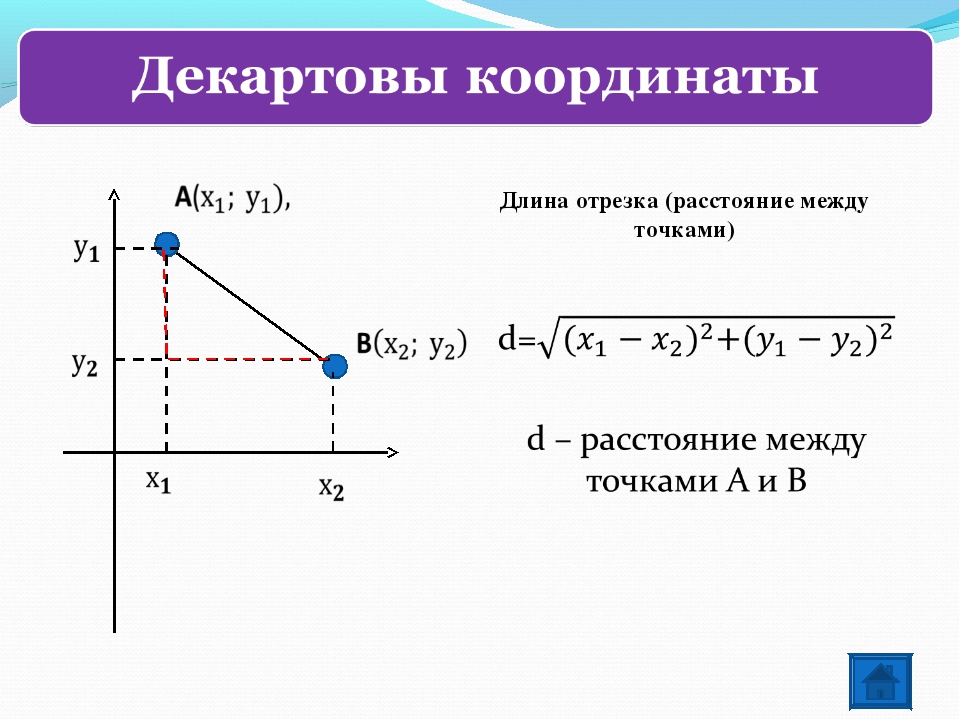 Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками. Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.
Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками. Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.
Рассмотрим пример, как найти длину отрезка по координатам. Есть координаты двух точек (-1;2) и (4;7). При нахождении разности координат точек получаем следующие значения: х = 5, у =5. Полученные числа и будут являться координатами отрезка. Затем каждое число возводим в квадрат и находим сумму результатов, она равна 50. Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.
Метод координат в пространстве
Для этого необходимо рассмотреть, как найти длину вектора. Именно он и будет являться отрезком в евклидовом пространстве. Находится он почти таким же образом, как длина отрезка на плоскости. Построение вектора происходит в разных плоскостях . Как найти длину вектора?
- Найдите координаты вектора, для этого из координат его конечной точки нужно вычесть координаты его начальной точки.

- После этого нужно возвести каждую координату вектора в квадрат.
- Затем складываем квадраты координат.
- Чтобы найти длину вектора, нужно извлечь квадратный корень из суммы квадратов координат.
Рассмотрим алгоритм вычисления на примере. Необходимо найти координаты вектора АВ. Точки А и В имеют следующие координаты: А (1;6;3) и В (3;-1;7). Начало вектора лежит в точке А, конец расположен в точке В. Таким образом, чтобы найти его координаты, необходимо вычесть координаты точки А из координат точки В: (3 — 1; -1 — 6;7 — 3) = (2;-7;4).
Теперь возводим каждую координату в квадрат и складываем их: 4+49+16=69. И наконец, извлекает квадратный корень из данного числа. Его трудно извлечь, поэтому результат записываем таким образом: длина вектора равна корню из 69.
Если же вам не важно самому высчитывать длину отрезков и векторов, а нужен просто результат, то вы можете воспользоваться онлайн-калькулятором, например, этим .
Теперь, изучив данные способы и рассмотрев представленные примеры, вы без проблем сможете найти длину отрезка в любой задаче.
Существуют три основных системы координат, используемых в геометрии, теоретической механике, других разделах физики: декартова, полярная и сферическая. В этих системах координат вся точка имеет три координаты. Зная координаты 2-х точек, дозволено определить расстояние между этими двумя точками.
Вам понадобится
- Декартовы, полярные и сферические координаты концов отрезка
Инструкция
1. Разглядите для начала прямоугольную декартову систему координат. Расположение точки в пространстве в этой системе координат определяется координатами x,y и z. Из начала координат к точке проводится радиус-вектор. Проекции этого радиус-вектора на координатные оси и будут координатами этой точки.Пускай у вас сейчас есть две точки с координатами x1,y1,z1 и x2,y2 и z2 соответственно. Обозначьте за r1 и r2, соответственно, радиус-векторы первой и 2-й точки. Видимо, что расстояние между этими двумя точками будет равно модулю вектора r = r1-r2, где (r1-r2) – векторная разность. 2))
2))
Видео по теме
Длина, как уже отмечалось, обозначается знаком модуля.
Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле
Если даны две точки пространства и , то длину отрезка можно вычислить по формуле
Примечание: Формулы останутся корректными, если переставить местами соответствующие координаты: и , но более стандартен первый вариант
Пример 3
Решение: по соответствующей формуле:
Ответ:
Для наглядности выполню чертёж
Отрезок – это не вектор , и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.
Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:
Во-первых, в ответе ставим размерность: «единицы».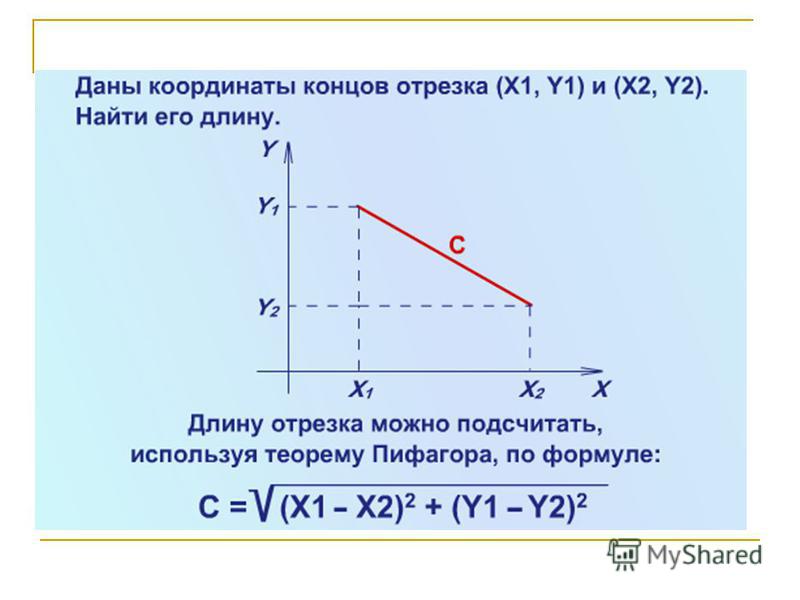 В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:
Обратите внимание на важный технический приём – вынесение множителя из-под корня . В результате вычислений у нас получился результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: . Конечно, оставить ответ в виде не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.
Вот другие распространенные случаи:
Нередко под корнем получается достаточно большое число, например . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: . Да, разделилось нацело, таким образом: . А может быть, число ещё раз удастся разделить на 4? . Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
Готово.
Вывод: если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.
В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.
Давайте заодно повторим возведение корней в квадрат и другие степени:
Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.
Задание для самостоятельного решения с отрезком в пространстве:
Пример 4
Даны точки и . Найти длину отрезка .
Решение и ответ в конце урока.
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Yandex.RTB R-A-339285-1 Определение 1
Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .
Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .
Определение 2
Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .
Определение 3
Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B
Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B .
Поскольку точка C является серединой отрезка А В, верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.
| А С | = | С В | ⇔ x C — x A = x B — x C
Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — (x B — x C)
Из первого равенства выведем формулу для координаты точки C: x C = x A + x B 2 (полусумма координат концов отрезка).
Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A (x A) и B (x B):
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .
Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y).
Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y . И тогда, опираясь на полученную ранее формулу, получим:
x C = x A + x B 2 и y C = y A + y B 2
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов A (x A , y A) и B (x B , y B) определяются как :
(x A + x B 2 , y A + y B 2)
Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A (x A , y A , z A) и B (x B , y B , z B) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .
Необходимо определить координаты точки C , являющейся серединой отрезка A B .
A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.
Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z
Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:
x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A (x A , y A) и B (x B , x B) . Точка C – середина отрезка A B .
Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т.е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2
Следовательно, точка C имеет координаты:
x A + x B 2 , y A + y B 2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C (x A + x B 2 , y A + y B 2 , z A + z B 2)
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Рассмотрим характерные примеры.
Пример 1
Исходные данные: на плоскости – точки с заданными координатами А (- 7 , 3) и В (2 , 4) . Необходимо найти координаты середины отрезка А В.
Решение
Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .
x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2
Ответ : координаты середины отрезка А В — 5 2 , 7 2 .
Пример 2
Исходные данные: известны координаты треугольника А В С: А (- 1 , 0) , В (3 , 2) , С (9 , — 8) . Необходимо найти длину медианы А М.
Решение
- По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M:
x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (- 8) 2 = — 3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М:
A M = (6 — (- 1)) 2 + (- 3 — 0) 2 = 58
Ответ: 58
Пример 3
Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · (- 4) — 0 = — 8
Ответ: координаты точки А (7 , 3 , — 8) .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Существует целая группа заданий (входящих в экзаменационные типы задач), связанная с координатной плоскостью. Это задачи начиная с самых элементарных, которые решаются устно (определение ординаты или абсциссы заданной точки, либо точки симметричной заданной и другие), заканчивая задачами в которых требуется качественное знание, понимание и хорошие навыки (задачи связанные с угловым коэффициентом прямой).
Это задачи начиная с самых элементарных, которые решаются устно (определение ординаты или абсциссы заданной точки, либо точки симметричной заданной и другие), заканчивая задачами в которых требуется качественное знание, понимание и хорошие навыки (задачи связанные с угловым коэффициентом прямой).
Постепенно мы с вами рассмотрим все их. В этой статье начнём с элементарных. Это простые задачи на определение: абсциссы и ординаты точки, длинны отрезка, середины отрезка, синуса или косинуса угла наклона прямой. Большинству эти задания будут не интересны. Но изложить их считаю необходимым.
Дело в том, что не все учатся в школе. Очень многие сдают ЕГЭ спустя 3-4 и более лет после её окончания и что такое абсцисса и ордината помнят смутно. Будем разбирать и другие задачи, связанные с координатной плоскостью, не пропустите, подпишитесь, на обновление блога. Теперь н емного теории.
Построим на координатной плоскости точку А с координатами х= 6, y=3.
Говорят, что абсцисса точки А равна шести, ордината точки А равна трём.
Если выразиться просто, то ось ох это ось абсцисс, ось оу это ость ординат.
То есть, абсцисса это точка на оси ох в которую проецируется точка заданная на координатной плоскости; ордината это точка на оси оу в которую проецируется оговоренная точка.
Длина отрезка на координатной плоскости
Формула для определения длины отрезка, если известны координаты его концов:
Как вы видите, длина отрезка — это длина гипотенузы в прямоугольными треугольнике с катетами равными
Х В – Х А и У В – У А
* * *
Середина отрезка. Её Координаты.
Формула для нахождения координат середины отрезка:
Уравнение прямой проходящей через две данные точки
Формула уравнения прямой походящей через две данные точки имеет вид:
где (х 1 ;у 1 ) и (х 2 ;у 2 ) координаты заданных точек.
Подставив значения координат в формулу, она приводится к виду:
y = kx + b , где k — это угловой коэффициент прямой
Эта информация нам понадобиться при решении другой группы задач связанных с координатной плоскостью. Статья об этом будет, не пропустите!
Статья об этом будет, не пропустите!
Что ещё можно добавить?
Угол наклона прямой (или отрезка) это угол между осью оХ и этой прямой, лежит в пределах от 0 до 180 градусов.
Рассмотрим задачи.
Из точки (6;8) опущен перпендикуляр на ось ординат. Найдите ординату основания перпендикуляра.
Основание перпендикуляра опущенного на ось ординат будет иметь координаты (0;8). Ордината равна восьми.
Ответ: 8
Найдите расстояние от точки A с координатами (6;8) до оси ординат.
Расстояние от точки А до оси ординат равно абсциссе точки А.
Ответ: 6.
A (6;8) относительно оси Ox .
Точка симметричная точке А относительно оси оХ имеет координаты (6;– 8).
Ордината равна минус восьми.
Ответ: – 8
Найдите ординату точки, симметричной точке A (6;8) относительно начала координат.
Точка симметричная точке А относительно начала координат имеет координаты (– 6;– 8).
Её ордината равна – 8.
Ответ: –8
Найдите абсциссу середины отрезка, соединяющего точки O (0;0) и A (6;8).
Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (0;0) и (6;8).
Вычисляем по формуле:
Получили (3;4). Абсцисса равна трём.
Ответ: 3
*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку. Середину отрезка несложно будет определить по клеткам.
Найдите абсциссу середины отрезка, соединяющего точки A (6;8) и B (–2;2).
Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (–2;2) и (6;8).
Вычисляем по формуле:
Получили (2;5). Абсцисса равна двум.
Ответ: 2
*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку.
Найдите длину отрезка, соединяющего точки (0;0) и (6;8).
Длина отрезка при данных координатах его концов вычисляется по формуле:
в нашем случае имеем О(0;0) и А(6;8). Значит,
*Порядок координат при вычитании не имеет значения. Можно из абсциссы и ординаты точки О вычесть абсциссу и ординату точки А:
Ответ:10
Найдите косинус угла наклона отрезка, соединяющего точки O (0;0) и A (6;8), с осью абсцисс.
Угол наклона отрезка – это угол между этим отрезком и осью оХ.
Из точки А опустим перпендикуляр на ось оХ:
То есть, угол наклона отрезка это угол ВОА в прямоугольном треугольнике АВО.
Косинусом острого угла в прямоугольном треугольнике является
отношение прилежащего катета к гипотенузе
Необходимо найти гипотенузу ОА.
По теореме Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Таким образом, косинус угла наклона равен 0,6
Ответ: 0,6
Из точки (6;8) опущен перпендикуляр на ось абсцисс. Найдите абсциссу основания перпендикуляра.
Через точку (6;8) проведена прямая, параллельная оси абсцисс. Найдите ординату ее точки пересечения с осью оУ .
Найдите расстояние от точки A с координатами (6;8) до оси абсцисс.
Найдите расстояние от точки A с координатами (6;8) до начала координат.
Математический портал. Высшая математика. Математический анализ.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Зная координаты точек $M_1(x_1, y_1, z_1)$ и $M_2(x_2, y_2, z_2)$ и отношение $\lambda,$ в котором точка $M$ делит направленный отрезок $\overline{M_1M_2},$ найдем координаты точки $M.$
Пусть $O -$ начало координат. Обозначим $\overline{OM_1}=r_1,$ $\overline{OM_2}=r_2,$ $\overline{OM}=r. $ Так как, $$\overline{M_1M}=r-r_1, \overline{MM_2}=r_2-r,$$ то $r-r_1=\lambda(r_2-r),$ откуда (так как $\lambda\neq -1$) $$r=\frac{r_1+\lambda r_2}{1+\lambda}.$$ Полученная форма и дает решение задачи в векторной форме. Переходя в этой формуле к координатам, получим $$x=\frac{x_1+\lambda x_2}{1+\lambda}, y=\frac{y_1+\lambda y_2}{1+\lambda}, z=\frac{z_1+\lambda z_2}{1+\lambda}.$$
$ Так как, $$\overline{M_1M}=r-r_1, \overline{MM_2}=r_2-r,$$ то $r-r_1=\lambda(r_2-r),$ откуда (так как $\lambda\neq -1$) $$r=\frac{r_1+\lambda r_2}{1+\lambda}.$$ Полученная форма и дает решение задачи в векторной форме. Переходя в этой формуле к координатам, получим $$x=\frac{x_1+\lambda x_2}{1+\lambda}, y=\frac{y_1+\lambda y_2}{1+\lambda}, z=\frac{z_1+\lambda z_2}{1+\lambda}.$$
Примеры.
2.57. Отрезок с концами в точках $A(3, -2)$ и $B(6, 4)$ разделен на три равные части. Найти координаты точек деления.
Решение.
Пусть $C(x_C, y_C)$ и $D(x_D, y_D) -$ точки, которые делят отрезок $AB$ на три равные части. Тогда $$\lambda_1=\frac{AC}{CB}=\frac{1}{2};$$ $$x_C=\frac{x_A+\lambda_1x_B}{1+\lambda_1}=\frac{3+\frac{1}{2}\cdot 6}{1+\frac{1}{2}}=4;$$
$$y_C=\frac{y_A+\lambda_1y_B}{1+\lambda_1}=\frac{-2+\frac{1}{2}\cdot 4}{1+\frac{1}{2}}=0.$$
Далее находим координаты точки $D:$
$$\lambda_2=\frac{AD}{DB}=\frac{2}{1}=2;$$ $$x_D=\frac{x_A+\lambda_2x_B}{1+\lambda_2}=\frac{3+2\cdot 6}{1+2}=5;$$
$$y_D=\frac{y_A+\lambda_2y_B}{1+\lambda_2}=\frac{-2+2\cdot 4}{1+2}=2. $$
$$
Ответ: $(4, 0)$ и $(5, 2).$
2.58.Определить координаты концов отрезка, который точками $C(2, 0, 2)$ и $D(5, -2, 0)$ разделен на три равные части.
Решение.
Пусть $A(x_A, y_A, z_A)$ и $B(x_B, y_B, z_B) -$ концы заданного отрезка.
Выпишем формулы для нахождения координат точки $C$ и подставим известные координаты:
$$\lambda_1=\frac{AC}{CB}=\frac{1}{2};$$ $$x_C=\frac{x_A+\lambda_1x_B}{1+\lambda_1}\Rightarrow 2=\frac{x_A+\frac{1}{2}\cdot x_B}{1+\frac{1}{2}}=2\frac{x_A+\frac{1}{2}\cdot x_B}{3}\Rightarrow $$ $$\Rightarrow 3=x_A+\frac{1}{2}\cdot x_B;$$
$$y_C=\frac{y_A+\lambda_1y_B}{1+\lambda_1}\Rightarrow 0=\frac{y_A+\frac{1}{2}\cdot y_B}{1+\frac{1}{2}}\Rightarrow 0=y_A+\frac{1}{2}\cdot y_B;$$
$$z_C=\frac{z_A+\lambda_1z_B}{1+\lambda_1}\Rightarrow 2=\frac{z_A+\frac{1}{2}\cdot z_B}{1+\frac{1}{2}}=2\frac{z_A+\frac{1}{2}\cdot z_B}{3}\Rightarrow$$ $$\Rightarrow 3=z_A+\frac{1}{2}\cdot z_B. $$
$$
Аналогичные равенства запишем для точки $D:$
$$\lambda_2=\frac{AD}{DB}=\frac{2}{1}=2;$$ $$x_D=\frac{x_A+\lambda_2x_B}{1+\lambda_2}\Rightarrow 5=\frac{x_A+2\cdot x_B}{1+2}=\frac{x_A+2\cdot x_B}{3}\Rightarrow $$ $$\Rightarrow 15=x_A+2\cdot x_B;$$
$$y_D=\frac{y_A+\lambda_2y_B}{1+\lambda_2}\Rightarrow -2=\frac{y_A+2\cdot y_B}{1+2}\Rightarrow -6=y_A+2\cdot y_B;$$
$$z_D=\frac{z_A+\lambda_2z_B}{1+\lambda_2}\Rightarrow 0=\frac{z_A+2\cdot z_B}{1+2}\Rightarrow 0=z_A+2\cdot z_B.$$
Далее запишем полученные уравнения относительно $x_A, x_B;$ $y_A, y_B$ и $z_A, z_B$ попарно в виде систем и решим их:
$$\left\{\begin{array}{lcl}x_A+\frac{1}{2}x_B=3\\x_A+2x_B=15\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}x_A=3-0,5x_B\\3-0,5x_B+2x_B=15\end{array}\right.\Rightarrow$$ $$\Rightarrow\left\{\begin{array}{lcl}x_A=3-0,5\cdot8=-1\\x_B=\frac{12}{1,5}=8\end{array}\right.$$
$$\left\{\begin{array}{lcl}y_A+\frac{1}{2}y_B=0\\y_A+2y_B=-6\end{array}\right. \Rightarrow\left\{\begin{array}{lcl}y_B=-2y_A\\y_A-4y_A=-6\end{array}\right.\Rightarrow$$ $$\Rightarrow\left\{\begin{array}{lcl}y_B=-4\\y_A=2\end{array}\right.$$
\Rightarrow\left\{\begin{array}{lcl}y_B=-2y_A\\y_A-4y_A=-6\end{array}\right.\Rightarrow$$ $$\Rightarrow\left\{\begin{array}{lcl}y_B=-4\\y_A=2\end{array}\right.$$
$$\left\{\begin{array}{lcl}z_A+\frac{1}{2}z_B=3\\z_A+2z_B=0\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}-2z_B+0,5z_B=3\\z_A=-2z_B\end{array}\right.\Rightarrow$$ $$\Rightarrow\left\{\begin{array}{lcl}z_B=-2\\z_A=4\end{array}\right.$$
Таким образом, получили координаты концов отрезка $A(-1, 2, 4)$ и $B(8, -4, -2).$
Ответ: $A(-1, 2, 4),$ $B(8, -4, -2).$
формула, как по координатам его концов, блок схема
Что такое середина отрезка
Отрезок — это геометрическая фигура, представляющая собой ограниченный с двух сторон участок прямой.
Пусть точки A и B не совпадают. Если провести через них прямую, то образуется отрезок AB или BA, который ограничен точками A и B. Данные точки являются концами отрезка.
Длина отрезка — это расстояние между двумя точками, ограничивающими данный отрезок. Длина отрезка AB обозначается как модуль данной геометрической фигуры, то есть |AB|.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Серединой отрезка является такая точка C, принадлежащая отрезку AB, которая расположена в центре данного отрезка, то есть |AC|=|CB|.
Правила нахождения координат середины отрезка, формулы
Середина отрезка на координатной прямой
Предположим, что несовпадающие точки A и B лежат на координатной прямая Ох. Известно, что A и B соответствуют действительные числа xA и xB, а точка С делит AB пополам. Определите координату xC, соответствующую С.
Так как C — это середина AB, то справедливо следующее равенство:
\(\left|AC\right|=\left|CB\right|\)
Вычислим расстояние между A и C, а также между C и B. Для этого определим модуль разницы их координат. На математическом языке это будет иметь вид:
Для этого определим модуль разницы их координат. На математическом языке это будет иметь вид:
\(\left|AC\right|=\left|CB\right|\Leftrightarrow\left|x_C-x_A\right|=\left|x_B-x_C\right|\)
Опустим знак модуля и получим справедливость двух выражений:
\(x_C-x_A=x_B-x_C\)
\(x_C-x_A=-\left(x_B-x_C\right)\)
Исходя из первого равенства, получим формулу нахождения xC, согласно которой координата точки С равна половине суммы координат A и B:
\(x_C=\frac{x_A+x_B}2\)
Следствием второго равенства будет следующее утверждение:
\(x_A=x_B\)
Это противоречит заданным условиям, следовательно, формула определения координат середины отрезка выглядит так:
\(x_C=\frac{x_A+x_B}2\)
Середина отрезка на плоскости
В декартовой системе координат Oxy расположены две точки A(xA,yA) и B(xB,yB), которые не совпадают между собой. Точка C является центром AB. Необходимо произвести вычисление координат xC и yC, соответствующих С.
Необходимо произвести вычисление координат xC и yC, соответствующих С.
Пусть произвольные точки А и В лежат на одной координатной прямой, а также не принадлежат прямым, располагающимся перпендикулярно к оси абсцисс или ординат. Опустим от заданных точек A, B, C перпендикуляры на ось x на ось y. Полученные точки пересечения с осями координат Ax, Ay; Bx, By; Cx, Cy — это проекции исходных точек.
По построению прямые AAx, BBx, CCx относительно друг друга находятся параллельно. Прямые AAy, BBy, CCy не пересекаются, то есть являются параллельными. Согласно равенству AB=BC, далее применим теорему Фалеса и получим:
\(A_xC_x=C_xB_x\)
\(A_yC_y=C_yB_y\)
Это значит, что Cx и Cy являются серединами отрезков AxBx и AyBy соответственно. Теперь воспользуемся формулой определения координат середины отрезка на координатной прямой и получим:
Теперь воспользуемся формулой определения координат середины отрезка на координатной прямой и получим:
\(x_C=\frac{x_A+x_B}2\)
\(y_C=\frac{y_A+y_B}2\)
Данные формулы подходят для вычисления координат середины отрезка в случае его расположения на осях абсцисс и ординат, а также при перпендикулярности одной из них. Следовательно, координаты центра отрезка AB, находящегося в плоскости и ограниченного точками A(xA,yA) и B(xB,yB), вычисляются следующим образом:
\(\left(\frac{x_A+x_B}2,\frac{y_A+y_B}2\right)\)
Середина отрезка в пространстве
Допустим, что в трехмерной системе координат Oxyz любые две точки с соответствующими им координатами A(xA, yA, zA) и B(xB, yB, zB). C(xC, yC, zC) — это центр АВ. Задание заключается в том, чтобы определить xC, yC, zC.
Проведем от исходных точек перпендикуляры к прямым Ox, Oy и Oz. Образовавшиеся точки пересечения с координатными осями — Ax, Ay, Az; Bx, By, Bz; Cx, Cy, Cz — проекции точек A, B, C на них.
Воспользуемся теоремой Фалеса:
\(\left|A_xC_x\right|=\left|C_xB_x\right|\)
\(\left|A_yC_y\right|=\left|C_yB_y\right|\)
\(\left|A_zC_z\right|=\left|C_zB_z\right|\)
Исходя из полученных равенств следует, что Cx, Cy, Cz — делят AxBx, AyBy, AzBz пополам, то есть являются серединами перечисленных отрезков. Значит, для определения координат центра AB с концами A(xA,yA,zA) и B(xB,yB,zB) используем формулу:
\(\left(\frac{x_A+x_B}2,\frac{y_A+y_B}2,\;\frac{z_A+z_B}2\right)\)
Метод с использованием координат радиус-векторов концов отрезка
Трактовка векторов в алгебре позволяет составить формулу для расчета координат середины отрезка.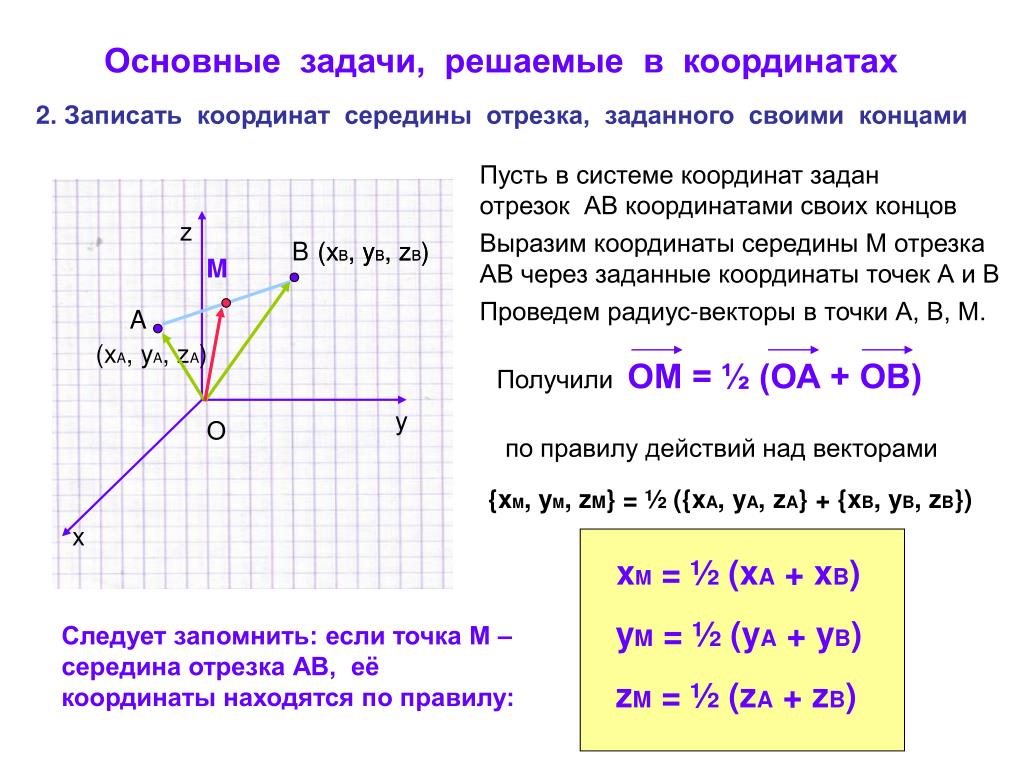
Дано: прямоугольная система координат Oxy, в которой лежат произвольные точки A(xA,yA) и B(xB,yB), а также C, делящая пополам отрезок, ограниченный A и B.
По определению действий над вектором в геометрии:
\((1)\;\overrightarrow{OC}=\frac12\times\left(\overrightarrow{OA}+\overrightarrow{OB}\right)\)
В рассматриваемой ситуации в точке C пересекаются диагонали параллелограмма с основаниями: \(\overrightarrow{OA},\;\overrightarrow{OB} \).
Это значит, что С — это центр диагоналей.
Поскольку координаты радиус вектора совпадают с координатами точки, имеем: \(\overrightarrow{OA}=\left(x_A,\;y_A\right),\;\overrightarrow{OB}=\left(x_B,\;y_B\right) \).
Произведем подстановку в формулу (1):
\(\overrightarrow{OC}=\frac12\times\left(\overrightarrow{OA}+\overrightarrow{OB}\right)=\left(\frac{x_A+x_B}2,\;\frac{y_A+y_B}2\right) \).
Получили формулу определения координат середины отрезка, находящегося в декартовой системе координат:
\(\left(\frac{x_A+x_B}2,\;\frac{y_A+y_B}2\right)\)
По аналогично схеме можно вывести формулу для расчета координат центра отрезка, лежащего в пространстве:
\(\left(\frac{x_A+x_B}2,\frac{y_A+y_B}2,\;\frac{z_A+z_B}2\right)\)
Примеры решения задач
Задача № 1Дано: в декартовой системе координат имеются точки M(5,4) и N(1,−2). 2}=\sqrt{56,25+30,25}=\sqrt{86,5}
\).
2}=\sqrt{56,25+30,25}=\sqrt{86,5}
\).
Ответ: √86,5.
Как найти длину зная координаты точек. Нахождение координат середины отрезка: примеры, решения
Отрезком называют часть прямой линии, состоящей из всех точек этой линии, которые расположены между данными двумя точками — их называют концами отрезка.
Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.
Итак, в системе координат начертим отрезок с заданными координатами его концов (x1; y1) и (x2; y2) . На оси X и Y из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.
Вычислим длину данных проекций. Итак, на ось Y длина проекции равна y2-y1 , а на ось Х длина проекции равна x2-x1 . Применим теорему Пифагора: |AB|² = (y2 — y1)² + (x2 — x1)² . В данном случае |AB| является длиной отрезка.
Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3) и (2;5) . Применяя теорему Пифагора, получаем: |AB|² = (2 — 1)² + (5 — 3)² = 1 + 4 = 5 . А это значит, что длина нашего отрезка равна 5:1/2 .
Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.
Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник.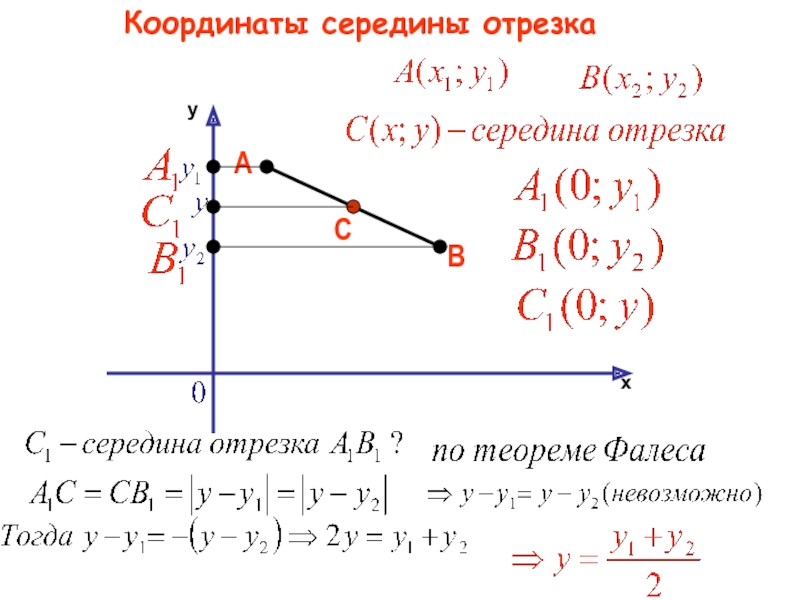 Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.
Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.
Найдем длины проекций (X и Y) исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1 .
Рассчитаем длину отрезка А , для этого найдем квадратный корень:
A = √(X²+Y²) = √ ((X2-X1)²+(Y2-Y1)²) .
Если наш отрезок расположен между точками, координаты которых 2;4 и 4;1 , то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61 .
Длина, как уже отмечалось, обозначается знаком модуля.
Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле
Если даны две точки пространства и , то длину отрезка можно вычислить по формуле
Примечание: Формулы останутся корректными, если переставить местами соответствующие координаты: и , но более стандартен первый вариант
Пример 3
Решение: по соответствующей формуле:
Ответ:
Для наглядности выполню чертёж
Отрезок – это не вектор , и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.
Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.
Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:
Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:
Обратите внимание на важный технический приём – вынесение множителя из-под корня . В результате вычислений у нас получился результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: . Конечно, оставить ответ в виде не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.
Вот другие распространенные случаи:
Нередко под корнем получается достаточно большое число, например . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: . Да, разделилось нацело, таким образом: . А может быть, число ещё раз удастся разделить на 4? . Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
Готово.
Вывод: если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.
В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.
Давайте заодно повторим возведение корней в квадрат и другие степени:
Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.
Задание для самостоятельного решения с отрезком в пространстве:
Пример 4
Даны точки и . Найти длину отрезка .
Решение и ответ в конце урока.
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Yandex.RTB R-A-339285-1 Определение 1
Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .
Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .
Определение 2
Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .
Определение 3
Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B
Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа x A и x B . Точка C – середина отрезка A B: необходимо определить координату x C .
Поскольку точка C является серединой отрезка А В, верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.
| А С | = | С В | ⇔ x C — x A = x B — x C
Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — (x B — x C)
Из первого равенства выведем формулу для координаты точки C: x C = x A + x B 2 (полусумма координат концов отрезка).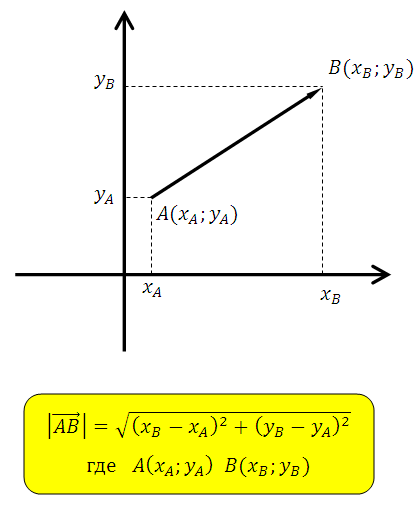
Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A (x A) и B (x B):
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y).
Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y . И тогда, опираясь на полученную ранее формулу, получим:
И тогда, опираясь на полученную ранее формулу, получим:
x C = x A + x B 2 и y C = y A + y B 2
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов A (x A , y A) и B (x B , y B) определяются как :
(x A + x B 2 , y A + y B 2)
Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A (x A , y A , z A) и B (x B , y B , z B) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .
A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.
Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z
Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:
Тогда, для определения координат середины отрезка в пространстве верны формулы:
x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A (x A , y A) и B (x B , x B) . Точка C – середина отрезка A B .
Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т.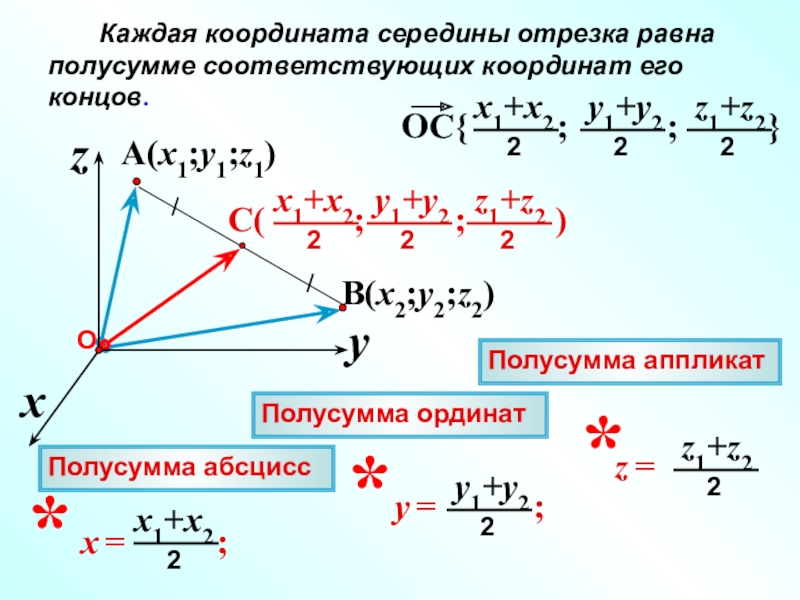 е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2
Следовательно, точка C имеет координаты:
x A + x B 2 , y A + y B 2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C (x A + x B 2 , y A + y B 2 , z A + z B 2)
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Рассмотрим характерные примеры.
Пример 1
Исходные данные: на плоскости – точки с заданными координатами А (- 7 , 3) и В (2 , 4) . Необходимо найти координаты середины отрезка А В.
Решение
Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .
x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2
Ответ : координаты середины отрезка А В — 5 2 , 7 2 .
Пример 2
Исходные данные: известны координаты треугольника А В С: А (- 1 , 0) , В (3 , 2) , С (9 , — 8) . Необходимо найти длину медианы А М.
Решение
- По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M:
x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (- 8) 2 = — 3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М:
A M = (6 — (- 1)) 2 + (- 3 — 0) 2 = 58
Ответ: 58
Пример 3
Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · (- 4) — 0 = — 8
Ответ: координаты точки А (7 , 3 , — 8) .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Существуют три основных системы координат, используемых в геометрии, теоретической механике, других разделах физики: декартова, полярная и сферическая. В этих системах координат вся точка имеет три координаты. Зная координаты 2-х точек, дозволено определить расстояние между этими двумя точками.
В этих системах координат вся точка имеет три координаты. Зная координаты 2-х точек, дозволено определить расстояние между этими двумя точками.
Вам понадобится
- Декартовы, полярные и сферические координаты концов отрезка
Инструкция
1. Разглядите для начала прямоугольную декартову систему координат. Расположение точки в пространстве в этой системе координат определяется координатами x,y и z. Из начала координат к точке проводится радиус-вектор. Проекции этого радиус-вектора на координатные оси и будут координатами этой точки.Пускай у вас сейчас есть две точки с координатами x1,y1,z1 и x2,y2 и z2 соответственно. Обозначьте за r1 и r2, соответственно, радиус-векторы первой и 2-й точки. Видимо, что расстояние между этими двумя точками будет равно модулю вектора r = r1-r2, где (r1-r2) – векторная разность.Координаты вектора r, видимо, будут следующими: x1-x2, y1-y2, z1-z2. Тогда модуль вектора r либо расстояние между двумя точками будет равно: r = sqrt(((x1-x2)^2)+((y1-y2)^2)+((z1-z2)^2)). 2))
2))
Видео по теме
Определить длину отрезка возможно разными способами. Для того чтобы узнать, как найти длину отрезка, достаточно иметь в наличии линейку или знать специальные формулы для расчета.
Длина отрезка с помощью линейки
Для этого прикладываем к построенному на плоскости отрезку линейку с миллиметровыми делениями, причем начальную точку необходимо совместить с нулем шкалы линейки. Затем следует отметить на данной шкале расположение конечной точки данного отрезка. Полученное количество целых делений шкалы и будет являться длиной отрезка, выраженной в см. и мм.
Метод координат на плоскости
Если известны координаты отрезка (х1;у1) и (х2;у2), то следует рассчитать его длину следующим образом. Из координат на плоскости второй точки следует вычесть координаты первой точки. В итоге должно получиться два числа. Каждое из таких чисел необходимо возвести в квадрат, а потом найти сумму этих квадратов. Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками. Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.
Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.
Рассмотрим пример, как найти длину отрезка по координатам. Есть координаты двух точек (-1;2) и (4;7). При нахождении разности координат точек получаем следующие значения: х = 5, у =5. Полученные числа и будут являться координатами отрезка. Затем каждое число возводим в квадрат и находим сумму результатов, она равна 50. Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.
Метод координат в пространстве
Для этого необходимо рассмотреть, как найти длину вектора. Именно он и будет являться отрезком в евклидовом пространстве. Находится он почти таким же образом, как длина отрезка на плоскости. Построение вектора происходит в разных плоскостях . Как найти длину вектора?
- Найдите координаты вектора, для этого из координат его конечной точки нужно вычесть координаты его начальной точки.
- После этого нужно возвести каждую координату вектора в квадрат.

- Затем складываем квадраты координат.
- Чтобы найти длину вектора, нужно извлечь квадратный корень из суммы квадратов координат.
Рассмотрим алгоритм вычисления на примере. Необходимо найти координаты вектора АВ. Точки А и В имеют следующие координаты: А (1;6;3) и В (3;-1;7). Начало вектора лежит в точке А, конец расположен в точке В. Таким образом, чтобы найти его координаты, необходимо вычесть координаты точки А из координат точки В: (3 — 1; -1 — 6;7 — 3) = (2;-7;4).
Теперь возводим каждую координату в квадрат и складываем их: 4+49+16=69. И наконец, извлекает квадратный корень из данного числа. Его трудно извлечь, поэтому результат записываем таким образом: длина вектора равна корню из 69.
Если же вам не важно самому высчитывать длину отрезков и векторов, а нужен просто результат, то вы можете воспользоваться онлайн-калькулятором, например, этим .
Теперь, изучив данные способы и рассмотрев представленные примеры, вы без проблем сможете найти длину отрезка в любой задаче.
Как найти длину отрезка если известны координаты
Длина, как уже отмечалось, обозначается знаком модуля.
Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле
Если даны две точки пространства и , то длину отрезка можно вычислить по формуле
Примечание: Формулы останутся корректными, если переставить местами соответствующие координаты: и , но более стандартен первый вариант
Пример 3
Решение: по соответствующей формуле:
Ответ:
Для наглядности выполню чертёж
Отрезок – это не вектор , и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.
Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:
Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:
Обратите внимание на важный технический приём – вынесение множителя из-под корня . В результате вычислений у нас получился результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: . Конечно, оставить ответ в виде не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.
Вот другие распространенные случаи:
Нередко под корнем получается достаточно большое число, например . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: . Да, разделилось нацело, таким образом: . А может быть, число ещё раз удастся разделить на 4? . Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
Готово.
Вывод: если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.
В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.
Давайте заодно повторим возведение корней в квадрат и другие степени:
Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.
Задание для самостоятельного решения с отрезком в пространстве:
Пример 4
Даны точки и . Найти длину отрезка .
Решение и ответ в конце урока.
Инструкция
Если координаты крайних точек отрезка даны в двухмерной координат, то проведя через эти точки линии, перпендикулярные осям координат, вы получите прямоугольный треугольник. Его гипотенузой будет исходный отрезок, а катеты образуют отрезки, длина которых равна гипотенузы на каждую из координатных осей. Из теоремы Пифагора, определяющей длины гипотенузы как сумму квадратов длин катетов, можно сделать , что для нахождения длины исходного отрезка достаточно найти длины двух его проекций на координатные оси.
Его гипотенузой будет исходный отрезок, а катеты образуют отрезки, длина которых равна гипотенузы на каждую из координатных осей. Из теоремы Пифагора, определяющей длины гипотенузы как сумму квадратов длин катетов, можно сделать , что для нахождения длины исходного отрезка достаточно найти длины двух его проекций на координатные оси.
Найдите длины (X и Y) проекций исходного отрезка на каждую ось системы координат. В двухмерной системе из крайних точек представлена парой числовых значений (X1;Y1 и X2;Y2). Длины проекций вычисляются нахождением разницы координат этих точек по каждой оси: X = X2-X1, Y = Y2-Y1. Возможно, что одно или оба полученных значения будут , но в данном случае это не никакой роли.
Рассчитайте длину исходного отрезка (A), найдя квадратный корень из квадратов рассчитанных на предыдущем шаге длин проекций на оси координат: A = √(X²+Y²) = √ ((X2-X1)²+(Y2-Y1)²). Например, если отрезок проведен между точками с координатами 2;4 и 4;1, то длина его будет равна √((4-2)²+(1-4)²) = √13 ≈ 3,61.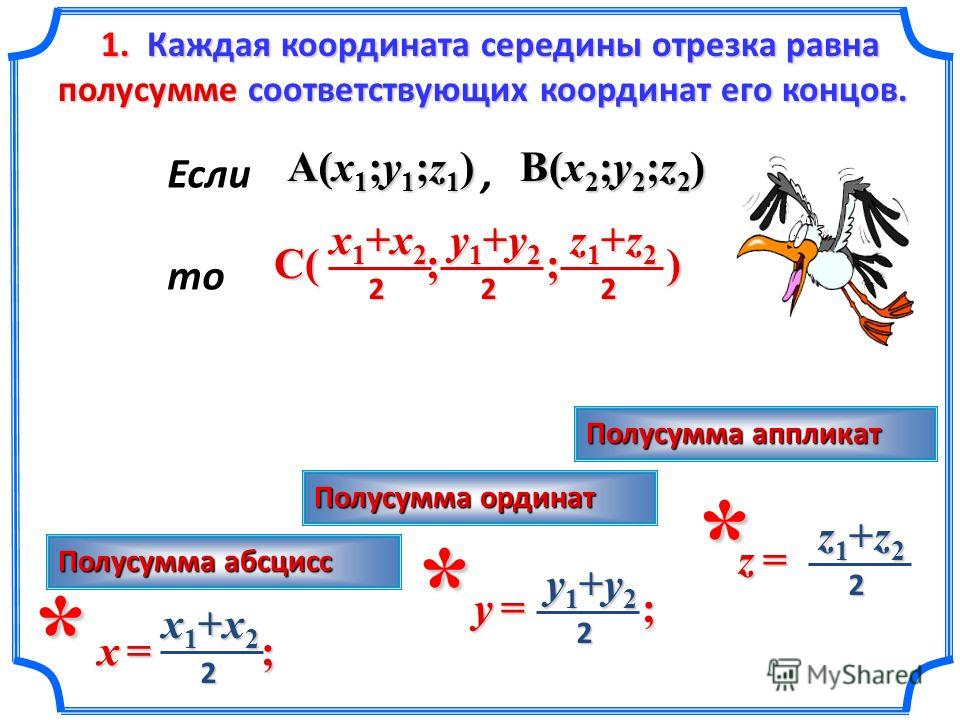 1/2.
1/2.
Видео по теме
Источники:
- Длина отрезка
- что такое длина отрезка
Иногда в повседневной деятельности может возникнуть необходимость найти середину отрезка прямой линии. Скажем, если предстоит сделать выкройку, эскиз изделия или просто распилить на две равные части деревянный брусок. На помощь приходит геометрия и немного житейской смекалки.
Вам понадобится
- Циркуль, линейка; булавка, карандаш, нить
Инструкция
Воспользуйтесь обычными инструментами, предназначенными для длины. Это самый простой способ отыскать середину отрезка. Измерьте линейкой или длину отрезка, разделите полученное пополам и отмерьте от одного из концов отрезка полученный результат. Вы получите точку, соответствующую середине отрезка.
Установите расстояние между ножками циркуля так, чтобы оно было равным длине отрезка или же большим, чем половина отрезка. Затем поставьте иглу циркуля в один из концов отрезка и проведите так, чтобы она пересекала отрезок.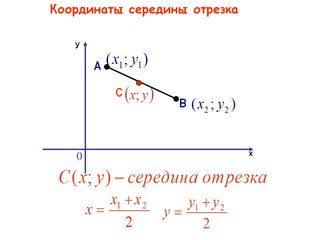 Переставьте иглу в другой конец отрезка и, не меняя размах ножек циркуля, проведите вторую полуокружность точно таким же образом.
Переставьте иглу в другой конец отрезка и, не меняя размах ножек циркуля, проведите вторую полуокружность точно таким же образом.
Если под рукой не оказалось циркуля или длина отрезка существенно превышает допустимый размах его ножек, можно воспользоваться простым приспособлением из подручных . Изготовить его можно из обычной булавки, нитки и карандаша. Привяжите концы нитки к булавке и карандашу, при этом длина нитки должна немного превышать длину отрезка. Таким импровизированным заменителем циркуля остается проделать шаги, описанные выше.
Видео по теме
Полезный совет
Достаточно точно найти середину доски или бруска вы можете, использовав обычную нитку или шнур. Для этого отрежьте нить так, чтобы она соответствовала длине доски или бруска. Остается сложить нить точно пополам и разрезать на две равные части. Приложите один конец полученной мерки к концу измеряемого предмета, а второй конец будет соответствовать его середине.
Существуют три основных системы координат, используемых в геометрии, теоретической механике, других разделах физики: декартова, полярная и сферическая. В этих системах координат каждая точка имеет три координаты. Зная координаты двух точек, можно определить расстояние между этими двумя точками.
В этих системах координат каждая точка имеет три координаты. Зная координаты двух точек, можно определить расстояние между этими двумя точками.
Вам понадобится
- Декартовы, полярные и сферические координаты концов отрезка
Инструкция
Рассмотрите для начала прямоугольную декартову координат. Положение точки в пространстве в этой координат определяется координатами x,y и z. Из начала координат к точке проводится радиус- . Проекции этого радиус-вектора на координатные оси и будут координатами этой точки.
Пусть у вас теперь есть две точки с координатами x1,y1,z1 и x2,y2 и z2 соответственно. Обозначьте за r1 и r2, соответственно, радиус-векторы первой и точки. Очевидно, что расстояние между этими точками будет модулю вектора r = r1-r2, где (r1-r2) — векторная разность.
Координаты вектора r, очевидно, будут следующими: x1-x2, y1-y2, z1-z2. Тогда вектора r или расстояние между двумя точками будет равно: r = sqrt(((x1-x2)^2)+((y1-y2)^2)+((z1-z2)^2)). 2))
2))
Видео по теме
Отрезок прямой определяется двумя крайними точками и состоит из множества точек, лежащих на проходящей через крайние точки прямой линии. Если отрезок помещен в какую-либо систему координат, то, найдя средние точки его проекций на каждую из осей, можно узнать координаты середины отрезка . По сути, операция сводится к нахождению среднего арифметического значения пар чисел для каждой из координатных осей.
Инструкция
Делите пополам сумму начальной и конечной координат крайних точек отрезка вдоль каждой оси, чтобы средней точки вдоль этой оси. Например, пусть отрезок помещен в трехмерную систему координат XYZ и известны координаты его крайних точек A(Xa,Ya,Za) и C(Xc,Yc,Zc). Тогда координаты его средней точки E(Xe,Ye,Ze) можно по формулам Xe=(Xa+Xc)/2, Ye=(Ya+Yc)/2, Ze=(Za+Zc)/2.
Используйте любой из калькуляторов, если вычислить средние значения координат крайних точек отрезка в уме не представляется возможным. Если под рукой нет такого гаджета, то используйте программный из состава ОС Windows. Его можно запустить, если, щелкнув кнопку «Пуск» раскрыть меню системы. В меню надо перейти в раздел «Стандартные», затем в подраздел «Служебные», а потом в секции «Все » выбрать пункт «Калькулятор». Можно обойтись без главного меню, если нажать сочетание клавиш WIN + R, ввести команду calc, а затем нажать клавишу Enter.
Если под рукой нет такого гаджета, то используйте программный из состава ОС Windows. Его можно запустить, если, щелкнув кнопку «Пуск» раскрыть меню системы. В меню надо перейти в раздел «Стандартные», затем в подраздел «Служебные», а потом в секции «Все » выбрать пункт «Калькулятор». Можно обойтись без главного меню, если нажать сочетание клавиш WIN + R, ввести команду calc, а затем нажать клавишу Enter.
Суммируйте попарно начальные и конечные координаты крайних точек отрезка вдоль каждой оси и делите результат на два. Интерфейс программного калькулятора имитирует обычный калькулятор, а вводить числовые значения и символы математических операций можно как щелкая кнопки курсором мыши на экране, так и нажимая клавиши на клавиатуре. Никаких сложностей с этими вычислениями возникнуть не .
Записывайте математические операции в текстовом виде и вводите их в поле поискового запроса на главной странице сайта Google, если -либо не можете использовать калькулятор, но имеете доступ в интернет. Этот поисковик имеет встроенный многофункциональный калькулятор, пользоваться которым намного проще, чем любым другим. Здесь нет интерфейса с кнопками — вводить все данные надо в текстовом виде в единственное поле. Например, если известны координаты крайних точек отрезка в трехмерной системе координат A(51,34 17,2 13,02) и A(-11,82 7,46 33,5), то координаты средней точки отрезка C((51,34-11,82)/2 (17,2+7,46)/2 (13,02+33,5)/2). Вводя в поле поискового запроса (51,34-11,82)/2, затем (17,2+7,46)/2 и (13,02+33,5)/2, можно с помощью Google получить координаты С(19,76 12,33 23,26).
Этот поисковик имеет встроенный многофункциональный калькулятор, пользоваться которым намного проще, чем любым другим. Здесь нет интерфейса с кнопками — вводить все данные надо в текстовом виде в единственное поле. Например, если известны координаты крайних точек отрезка в трехмерной системе координат A(51,34 17,2 13,02) и A(-11,82 7,46 33,5), то координаты средней точки отрезка C((51,34-11,82)/2 (17,2+7,46)/2 (13,02+33,5)/2). Вводя в поле поискового запроса (51,34-11,82)/2, затем (17,2+7,46)/2 и (13,02+33,5)/2, можно с помощью Google получить координаты С(19,76 12,33 23,26).
Определить длину отрезка возможно разными способами. Для того чтобы узнать, как найти длину отрезка, достаточно иметь в наличии линейку или знать специальные формулы для расчета.
Длина отрезка с помощью линейки
Для этого прикладываем к построенному на плоскости отрезку линейку с миллиметровыми делениями, причем начальную точку необходимо совместить с нулем шкалы линейки. Затем следует отметить на данной шкале расположение конечной точки данного отрезка. Полученное количество целых делений шкалы и будет являться длиной отрезка, выраженной в см. и мм.
Затем следует отметить на данной шкале расположение конечной точки данного отрезка. Полученное количество целых делений шкалы и будет являться длиной отрезка, выраженной в см. и мм.
Метод координат на плоскости
Если известны координаты отрезка (х1-у1) и (х2-у2), то следует рассчитать его длину следующим образом. Из координат на плоскости второй точки следует вычесть координаты первой точки. В итоге должно получиться два числа. Каждое из таких чисел необходимо возвести в квадрат, а потом найти сумму этих квадратов. Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками. Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.
Рассмотрим пример, как найти длину отрезка по координатам. Есть координаты двух точек (-1-2) и (4-7). При нахождении разности координат точек получаем следующие значения: х = 5, у =5. Полученные числа и будут являться координатами отрезка. Затем каждое число возводим в квадрат и находим сумму результатов, она равна 50. Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.
Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.
Метод координат в пространстве
Для этого необходимо рассмотреть, как найти длину вектора. Именно он и будет являться отрезком в евклидовом пространстве. Находится он почти таким же образом, как длина отрезка на плоскости. Построение вектора происходит в разных плоскостях . Как найти длину вектора?
- Найдите координаты вектора, для этого из координат его конечной точки нужно вычесть координаты его начальной точки.
- После этого нужно возвести каждую координату вектора в квадрат.
- Затем складываем квадраты координат.
- Чтобы найти длину вектора, нужно извлечь квадратный корень из суммы квадратов координат.
Рассмотрим алгоритм вычисления на примере. Необходимо найти координаты вектора АВ. Точки А и В имеют следующие координаты: А (1-6-3) и В (3—1-7). Начало вектора лежит в точке А, конец расположен в точке В. Таким образом, чтобы найти его координаты, необходимо вычесть координаты точки А из координат точки В: (3 — 1- -1 — 6-7 — 3) = (2—7-4).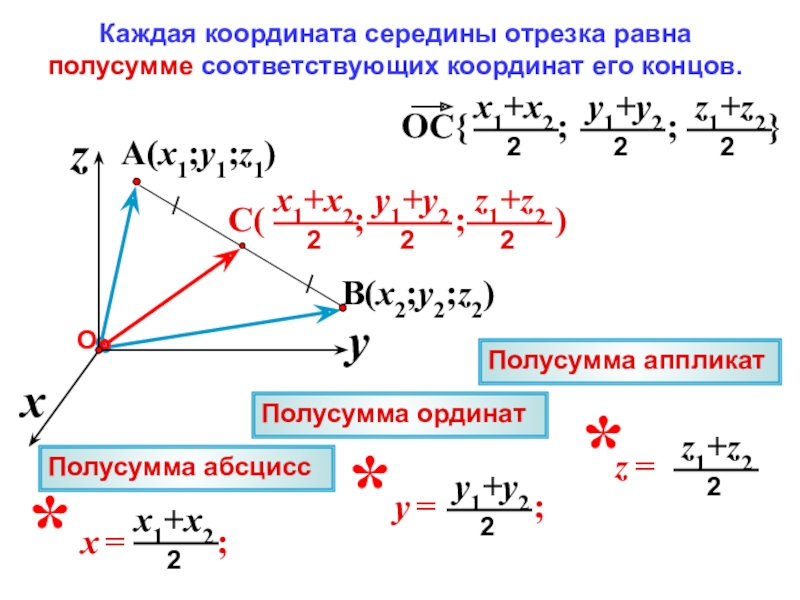
Теперь возводим каждую координату в квадрат и складываем их: 4+49+16=69. И наконец, извлекает квадратный корень из данного числа. Его трудно извлечь, поэтому результат записываем таким образом: длина вектора равна корню из 69.
Если же вам не важно самому высчитывать длину отрезков и векторов, а нужен просто результат, то вы можете воспользоваться онлайн-калькулятором, например, этим .
Теперь, изучив данные способы и рассмотрев представленные примеры, вы без проблем сможете найти длину отрезка в любой задаче.
Существует целая группа заданий (входящих в экзаменационные типы задач), связанная с координатной плоскостью. Это задачи начиная с самых элементарных, которые решаются устно (определение ординаты или абсциссы заданной точки, либо точки симметричной заданной и другие), заканчивая задачами в которых требуется качественное знание, понимание и хорошие навыки (задачи связанные с угловым коэффициентом прямой).
Постепенно мы с вами рассмотрим все их. В этой статье начнём с элементарных. Это простые задачи на определение: абсциссы и ординаты точки, длинны отрезка, середины отрезка, синуса или косинуса угла наклона прямой.
Большинству эти задания будут не интересны. Но изложить их считаю необходимым.
Это простые задачи на определение: абсциссы и ординаты точки, длинны отрезка, середины отрезка, синуса или косинуса угла наклона прямой.
Большинству эти задания будут не интересны. Но изложить их считаю необходимым.
Дело в том, что не все учатся в школе. Очень многие сдают ЕГЭ спустя 3-4 и более лет после её окончания и что такое абсцисса и ордината помнят смутно. Будем разбирать и другие задачи, связанные с координатной плоскостью, не пропустите, подпишитесь, на обновление блога. Теперь н емного теории.
Построим на координатной плоскости точку А с координатами х= 6, y=3.
Говорят, что абсцисса точки А равна шести, ордината точки А равна трём.
Если выразиться просто, то ось ох это ось абсцисс, ось оу это ость ординат.
То есть, абсцисса это точка на оси ох в которую проецируется точка заданная на координатной плоскости; ордината это точка на оси оу в которую проецируется оговоренная точка.
Длина отрезка на координатной плоскости
Формула для определения длины отрезка, если известны координаты его концов:
Как вы видите, длина отрезка — это длина гипотенузы в прямоугольными треугольнике с катетами равными
Х В – Х А и У В – У А
* * *
Середина отрезка. Её Координаты.
Её Координаты.
Формула для нахождения координат середины отрезка:
Уравнение прямой проходящей через две данные точки
Формула уравнения прямой походящей через две данные точки имеет вид:
где (х 1 ;у 1 ) и (х 2 ;у 2 ) координаты заданных точек.
Подставив значения координат в формулу, она приводится к виду:
y = kx + b , где k — это угловой коэффициент прямой
Эта информация нам понадобиться при решении другой группы задач связанных с координатной плоскостью. Статья об этом будет, не пропустите!
Что ещё можно добавить?
Угол наклона прямой (или отрезка) это угол между осью оХ и этой прямой, лежит в пределах от 0 до 180 градусов.
Рассмотрим задачи.
Из точки (6;8) опущен перпендикуляр на ось ординат. Найдите ординату основания перпендикуляра.
Основание перпендикуляра опущенного на ось ординат будет иметь координаты (0;8). Ордината равна восьми.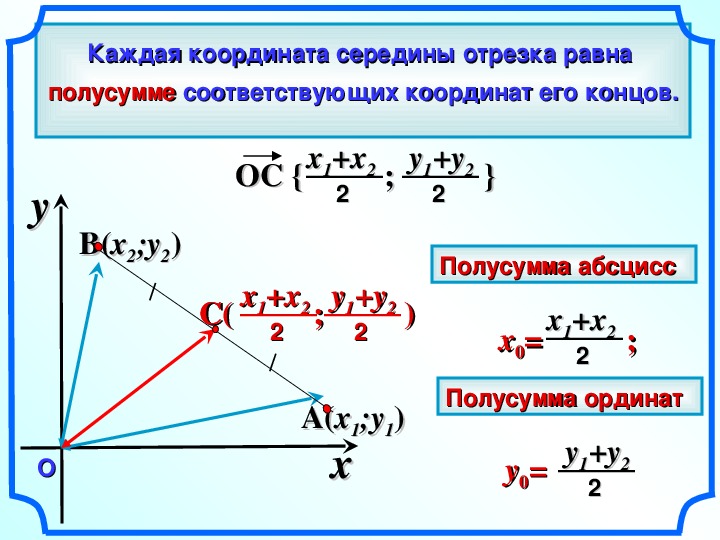
Ответ: 8
Найдите расстояние от точки A с координатами (6;8) до оси ординат.
Расстояние от точки А до оси ординат равно абсциссе точки А.
Ответ: 6.
A (6;8) относительно оси Ox .
Точка симметричная точке А относительно оси оХ имеет координаты (6;– 8).
Ордината равна минус восьми.
Ответ: – 8
Найдите ординату точки, симметричной точке A (6;8) относительно начала координат.
Точка симметричная точке А относительно начала координат имеет координаты (– 6;– 8).
Её ордината равна – 8.
Ответ: –8
Найдите абсциссу середины отрезка, соединяющего точки O (0;0) и A (6;8).
Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (0;0) и (6;8).
Вычисляем по формуле:
Получили (3;4). Абсцисса равна трём.
Ответ: 3
*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку. Середину отрезка несложно будет определить по клеткам.
Середину отрезка несложно будет определить по клеткам.
Найдите абсциссу середины отрезка, соединяющего точки A (6;8) и B (–2;2).
Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (–2;2) и (6;8).
Вычисляем по формуле:
Получили (2;5). Абсцисса равна двум.
Ответ: 2
*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку.
Найдите длину отрезка, соединяющего точки (0;0) и (6;8).
Длина отрезка при данных координатах его концов вычисляется по формуле:
в нашем случае имеем О(0;0) и А(6;8). Значит,
*Порядок координат при вычитании не имеет значения. Можно из абсциссы и ординаты точки О вычесть абсциссу и ординату точки А:
Ответ:10
Найдите косинус угла наклона отрезка, соединяющего точки O (0;0) и A (6;8), с осью абсцисс.
Угол наклона отрезка – это угол между этим отрезком и осью оХ.
Из точки А опустим перпендикуляр на ось оХ:
То есть, угол наклона отрезка это угол ВОА в прямоугольном треугольнике АВО.
Косинусом острого угла в прямоугольном треугольнике является
отношение прилежащего катета к гипотенузе
Необходимо найти гипотенузу ОА.
По теореме Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Таким образом, косинус угла наклона равен 0,6
Ответ: 0,6
Из точки (6;8) опущен перпендикуляр на ось абсцисс. Найдите абсциссу основания перпендикуляра.
Через точку (6;8) проведена прямая, параллельная оси абсцисс. Найдите ординату ее точки пересечения с осью оУ .
Найдите расстояние от точки A с координатами (6;8) до оси абсцисс.
Найдите расстояние от точки A с координатами (6;8) до начала координат.
Определить длину отрезка возможно разными способами. Для того чтобы узнать, как найти длину отрезка, достаточно иметь в наличии линейку или знать специальные формулы для расчета.
Длина отрезка с помощью линейки
Для этого прикладываем к построенному на плоскости отрезку линейку с миллиметровыми делениями, причем начальную точку необходимо совместить с нулем шкалы линейки. Затем следует отметить на данной шкале расположение конечной точки данного отрезка. Полученное количество целых делений шкалы и будет являться длиной отрезка, выраженной в см. и мм.
Метод координат на плоскости
Если известны координаты отрезка (х1;у1) и (х2;у2), то следует рассчитать его длину следующим образом. Из координат на плоскости второй точки следует вычесть координаты первой точки. В итоге должно получиться два числа. Каждое из таких чисел необходимо возвести в квадрат, а потом найти сумму этих квадратов. Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками. Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.
Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.
Рассмотрим пример, как найти длину отрезка по координатам. Есть координаты двух точек (-1;2) и (4;7). При нахождении разности координат точек получаем следующие значения: х = 5, у =5. Полученные числа и будут являться координатами отрезка. Затем каждое число возводим в квадрат и находим сумму результатов, она равна 50. Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.
Метод координат в пространстве
Для этого необходимо рассмотреть, как найти длину вектора. Именно он и будет являться отрезком в евклидовом пространстве. Находится он почти таким же образом, как длина отрезка на плоскости. Построение вектора происходит в разных плоскостях . Как найти длину вектора?
- Найдите координаты вектора, для этого из координат его конечной точки нужно вычесть координаты его начальной точки.
- После этого нужно возвести каждую координату вектора в квадрат.

- Затем складываем квадраты координат.
- Чтобы найти длину вектора, нужно извлечь квадратный корень из суммы квадратов координат.
Рассмотрим алгоритм вычисления на примере. Необходимо найти координаты вектора АВ. Точки А и В имеют следующие координаты: А (1;6;3) и В (3;-1;7). Начало вектора лежит в точке А, конец расположен в точке В. Таким образом, чтобы найти его координаты, необходимо вычесть координаты точки А из координат точки В: (3 — 1; -1 — 6;7 — 3) = (2;-7;4).
Теперь возводим каждую координату в квадрат и складываем их: 4+49+16=69. И наконец, извлекает квадратный корень из данного числа. Его трудно извлечь, поэтому результат записываем таким образом: длина вектора равна корню из 69.
Если же вам не важно самому высчитывать длину отрезков и векторов, а нужен просто результат, то вы можете воспользоваться онлайн-калькулятором, например, этим .
Теперь, изучив данные способы и рассмотрев представленные примеры, вы без проблем сможете найти длину отрезка в любой задаче.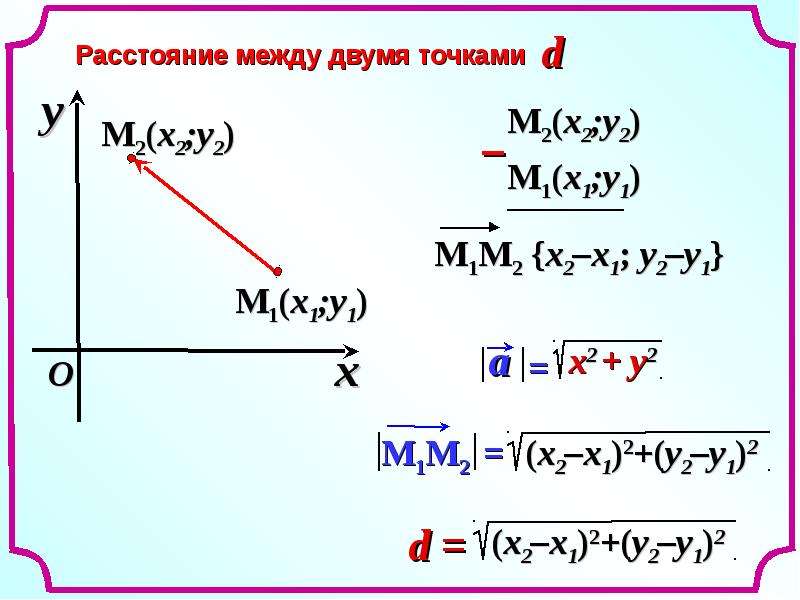
| 726 | Даны точки A(1; -2; -3), B(2; -3; 0), C(3; 1; -9), D(-1; 1; -12). Вычислить расстояние между 1). А и С, 2). B и D, 3). C и D. | |
| 727 | Вычислить расстояния от начала координат О до точек A(4; -2; -4), B(-4; 12; 6), C(12; -4; 3), D(12; 16; -15). | |
| 728 | Доказать, что треугольник с вершинами A(3; -1; 2), B(0; -2; 2), C(-3; 2; 1) равнобедренный. | |
| 729 | Доказать, что
треугольник с вершинами A1(3; -1;
6), A2(-1; 7; -2), A3(1; -3; 2) прямоугольный. | |
| 730 | Определить, есть ли тупой угол среди внутренних углов треугольника с вершинами M1(4; -1; 4), M2(0; 7; -4), M3(3; 1; -2). | |
| 731 | Доказать, что внутренние углы треугольника M(3; -2; 5), N(-2; 1; -3), P(5; 1; -1) острые. | |
| 732 | На ось абсцисс найти точку, расстояние от которой до точки А(-3; 4; 8) равно 12. | |
| 733 | На оси ординат найти точку, равноудаленную отточек А(1; -3; 7) и В(5; 7; -5). | |
| 734 | Найти центр C и
радиус R шаровой поверхности, которая проходит
через точку P(4; -1; -1) и касается всех трех
координатных плоскостей. | |
| 735 | Даны вершины M1(3; 2; -5), M2(1; -4; 3), M3(-3; 0; 1) треугольника. Найти середины его сторон. | |
| 736 | Даны вершины A(2; -1; 4). B(3; 2; -6), C(-5; 0; 2) треугольника. Вычислить длину его медианы, проведенной из вершины А. | |
| 737 | Центр масс однородного стержня находится в точке С(1; -1; 5), один из его концов есть точка A(-2; -1; 7). Определить координаты другого конца стержня. | |
| 738 | Даны две вершины A(2;
-3; -5), B(-1; 3; 2) параллелограмма ABCD и точка
пересечения его диагоналей E(4; -1; 7).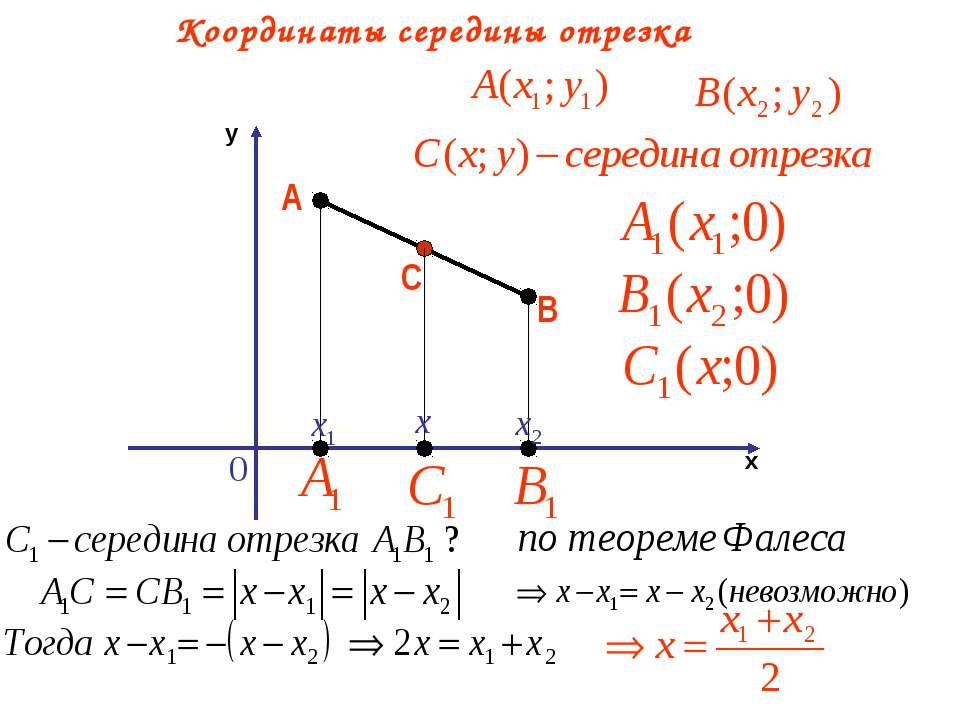 Определить
две другие вершины этого параллелограмма. Определить
две другие вершины этого параллелограмма. | |
| 739 | Даны три вершины A(3; -4; 7), B(-5; 3; -2), C(1; 2; -3) параллелограмма ABCD. Найти его четвертую вершину D, противоположную B. | |
| 740 | Даны три вершины A(3; -1; 2), B(1; 2; -4), C(-1; 1; 2) параллелограмма ABCD. Найти его четвертую вершину D. | |
| 741 | Отрезок прямой, ограниченный точками A(-1; 8; 3), B(9; -7; -2), разделен точками C, D, E. F на пять равных частей. Найти координаты этих точек. | |
| 742 | Определить координаты концов отрезка, который точками C(2; 0; 2), D(5; -2; 0) разделен на три равные части | |
| 743 | Даны вершины
треугольника A(1; 1; -1), B(2; -1; 3), C(-4; 7; 5). Вычислить
длину биссектрисы его внутреннего угла при
вершине B. Вычислить
длину биссектрисы его внутреннего угла при
вершине B. | |
| 744 | Даны вершины треугольника A(1; -1; -3), B(2; 1; -2), C(-5; 2; -6). Вычислить длину биссектрисы его внутреннего угла при вершине А. | |
| 745 | В вершинах тетраэдра A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3), D(x4, y4, z4) сосредоточены равные массы. Найти координаты центра масс этой системы. | |
| 746 | В вершинах
тетраэдра A1(x1, y1, z1),
A2(x, y2, z2), A3(x3, y3,
z3), A4(x4, y4, z4) сосредоточены массы m1, m2,
m3, m4. Найти координаты
центра масс этой системы. Найти координаты
центра масс этой системы. | |
| 747 | Прямая проходит через две точки M1(-1; 6; 6) и M2(3; -6; -2). Найти точки ее пересечения с координатными плоскостями. |
Что значит найти длину отрезка
Длина, как уже отмечалось, обозначается знаком модуля.
Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле
Если даны две точки пространства и , то длину отрезка можно вычислить по формуле
Примечание: Формулы останутся корректными, если переставить местами соответствующие координаты: и , но более стандартен первый вариант
Пример 3
Решение: по соответствующей формуле:
Ответ:
Для наглядности выполню чертёж
Отрезок – это не вектор , и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.
Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.
Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:
Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:
Обратите внимание на важный технический приём – вынесение множителя из-под корня . В результате вычислений у нас получился результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: . Конечно, оставить ответ в виде не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.
Вот другие распространенные случаи:
Нередко под корнем получается достаточно большое число, например . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: . Да, разделилось нацело, таким образом: . А может быть, число ещё раз удастся разделить на 4? . Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
Готово.
Вывод: если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.
В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.
Давайте заодно повторим возведение корней в квадрат и другие степени:
Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.
Задание для самостоятельного решения с отрезком в пространстве:
Пример 4
Даны точки и . Найти длину отрезка .
Решение и ответ в конце урока.
Определить длину отрезка возможно разными способами. Для того чтобы узнать, как найти длину отрезка, достаточно иметь в наличии линейку или знать специальные формулы для расчета.
Длина отрезка с помощью линейки
Для этого прикладываем к построенному на плоскости отрезку линейку с миллиметровыми делениями, причем начальную точку необходимо совместить с нулем шкалы линейки. Затем следует отметить на данной шкале расположение конечной точки данного отрезка. Полученное количество целых делений шкалы и будет являться длиной отрезка, выраженной в см. и мм.
Метод координат на плоскости
Если известны координаты отрезка (х1-у1) и (х2-у2), то следует рассчитать его длину следующим образом. Из координат на плоскости второй точки следует вычесть координаты первой точки. В итоге должно получиться два числа. Каждое из таких чисел необходимо возвести в квадрат, а потом найти сумму этих квадратов. Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками. Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.
Каждое из таких чисел необходимо возвести в квадрат, а потом найти сумму этих квадратов. Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками. Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.
Рассмотрим пример, как найти длину отрезка по координатам. Есть координаты двух точек (-1-2) и (4-7). При нахождении разности координат точек получаем следующие значения: х = 5, у =5. Полученные числа и будут являться координатами отрезка. Затем каждое число возводим в квадрат и находим сумму результатов, она равна 50. Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.
Метод координат в пространстве
Для этого необходимо рассмотреть, как найти длину вектора. Именно он и будет являться отрезком в евклидовом пространстве. Находится он почти таким же образом, как длина отрезка на плоскости. Построение вектора происходит в разных плоскостях . Как найти длину вектора?
- Найдите координаты вектора, для этого из координат его конечной точки нужно вычесть координаты его начальной точки.

- После этого нужно возвести каждую координату вектора в квадрат.
- Затем складываем квадраты координат.
- Чтобы найти длину вектора, нужно извлечь квадратный корень из суммы квадратов координат.
Рассмотрим алгоритм вычисления на примере. Необходимо найти координаты вектора АВ. Точки А и В имеют следующие координаты: А (1-6-3) и В (3—1-7). Начало вектора лежит в точке А, конец расположен в точке В. Таким образом, чтобы найти его координаты, необходимо вычесть координаты точки А из координат точки В: (3 — 1- -1 — 6-7 — 3) = (2—7-4).
Теперь возводим каждую координату в квадрат и складываем их: 4+49+16=69. И наконец, извлекает квадратный корень из данного числа. Его трудно извлечь, поэтому результат записываем таким образом: длина вектора равна корню из 69.
Если же вам не важно самому высчитывать длину отрезков и векторов, а нужен просто результат, то вы можете воспользоваться онлайн-калькулятором, например, этим .
Теперь, изучив данные способы и рассмотрев представленные примеры, вы без проблем сможете найти длину отрезка в любой задаче.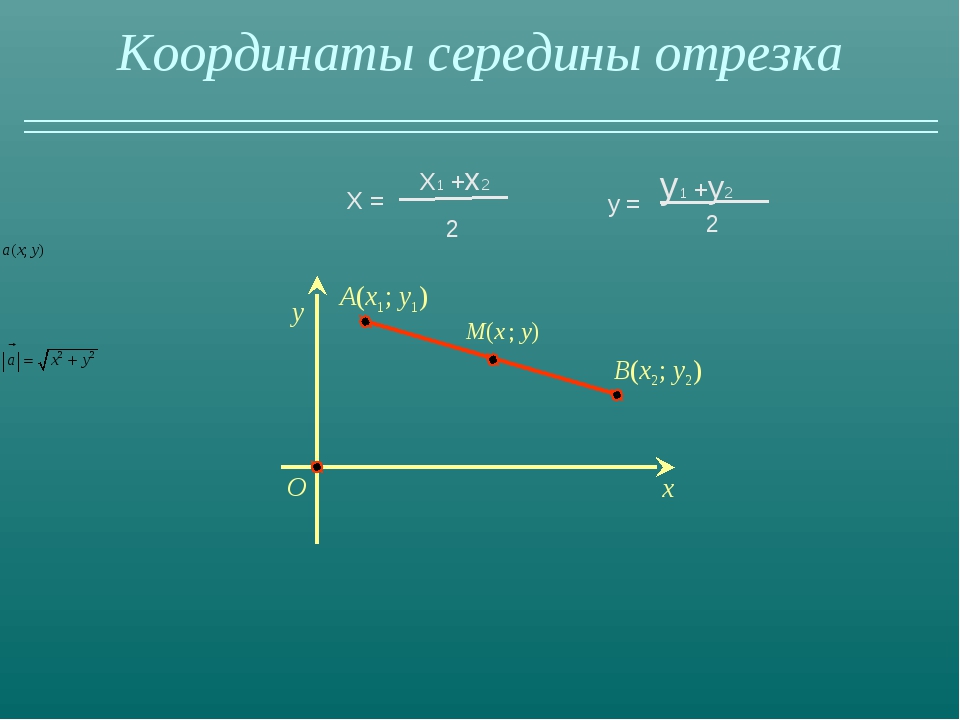
Отрезком называют часть прямой линии, состоящей из всех точек этой линии, которые расположены между данными двумя точками — их называют концами отрезка.
Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.
Итак, в системе координат начертим отрезок с заданными координатами его концов (x1; y1) и (x2; y2) . На оси X и Y из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.
Вычислим длину данных проекций. Итак, на ось Y длина проекции равна y2-y1 , а на ось Х длина проекции равна x2-x1 . Применим теорему Пифагора: |AB|² = (y2 — y1)² + (x2 — x1)² . В данном случае |AB| является длиной отрезка.
Применим теорему Пифагора: |AB|² = (y2 — y1)² + (x2 — x1)² . В данном случае |AB| является длиной отрезка.
Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3) и (2;5) . Применяя теорему Пифагора, получаем: |AB|² = (2 — 1)² + (5 — 3)² = 1 + 4 = 5 . А это значит, что длина нашего отрезка равна 5:1/2 .
Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.
Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник. Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.
Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.
Найдем длины проекций (X и Y) исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1 .
Рассчитаем длину отрезка А , для этого найдем квадратный корень:
A = √(X²+Y²) = √ ((X2-X1)²+(Y2-Y1)²) .
Если наш отрезок расположен между точками, координаты которых 2;4 и 4;1 , то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61 .
Существует целая группа заданий (входящих в экзаменационные типы задач), связанная с координатной плоскостью. Это задачи начиная с самых элементарных, которые решаются устно (определение ординаты или абсциссы заданной точки, либо точки симметричной заданной и другие), заканчивая задачами в которых требуется качественное знание, понимание и хорошие навыки (задачи связанные с угловым коэффициентом прямой).
Постепенно мы с вами рассмотрим все их. В этой статье начнём с элементарных. Это простые задачи на определение: абсциссы и ординаты точки, длинны отрезка, середины отрезка, синуса или косинуса угла наклона прямой. Большинству эти задания будут не интересны. Но изложить их считаю необходимым.
Дело в том, что не все учатся в школе. Очень многие сдают ЕГЭ спустя 3-4 и более лет после её окончания и что такое абсцисса и ордината помнят смутно. Будем разбирать и другие задачи, связанные с координатной плоскостью, не пропустите, подпишитесь, на обновление блога. Теперь н емного теории.
Построим на координатной плоскости точку А с координатами х= 6, y=3.
Говорят, что абсцисса точки А равна шести, ордината точки А равна трём.
Если выразиться просто, то ось ох это ось абсцисс, ось оу это ость ординат.
То есть, абсцисса это точка на оси ох в которую проецируется точка заданная на координатной плоскости; ордината это точка на оси оу в которую проецируется оговоренная точка.
Длина отрезка на координатной плоскости
Формула для определения длины отрезка, если известны координаты его концов:
Как вы видите, длина отрезка — это длина гипотенузы в прямоугольными треугольнике с катетами равными
Х В – Х А и У В – У А
* * *
Середина отрезка. Её Координаты.
Формула для нахождения координат середины отрезка:
Уравнение прямой проходящей через две данные точки
Формула уравнения прямой походящей через две данные точки имеет вид:
где (х 1 ;у 1 ) и (х 2 ;у 2 ) координаты заданных точек.
Подставив значения координат в формулу, она приводится к виду:
y = kx + b , где k — это угловой коэффициент прямой
Эта информация нам понадобиться при решении другой группы задач связанных с координатной плоскостью. Статья об этом будет, не пропустите!
Что ещё можно добавить?
Угол наклона прямой (или отрезка) это угол между осью оХ и этой прямой, лежит в пределах от 0 до 180 градусов.
Рассмотрим задачи.
Из точки (6;8) опущен перпендикуляр на ось ординат. Найдите ординату основания перпендикуляра.
Основание перпендикуляра опущенного на ось ординат будет иметь координаты (0;8). Ордината равна восьми.
Ответ: 8
Найдите расстояние от точки A с координатами (6;8) до оси ординат.
Расстояние от точки А до оси ординат равно абсциссе точки А.
Ответ: 6.
A (6;8) относительно оси Ox .
Точка симметричная точке А относительно оси оХ имеет координаты (6;– 8).
Ордината равна минус восьми.
Ответ: – 8
Найдите ординату точки, симметричной точке A (6;8) относительно начала координат.
Точка симметричная точке А относительно начала координат имеет координаты (– 6;– 8).
Её ордината равна – 8.
Ответ: –8
Найдите абсциссу середины отрезка, соединяющего точки O (0;0) и A (6;8).
Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (0;0) и (6;8).
Координаты концов нашего отрезка (0;0) и (6;8).
Вычисляем по формуле:
Получили (3;4). Абсцисса равна трём.
Ответ: 3
*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку. Середину отрезка несложно будет определить по клеткам.
Найдите абсциссу середины отрезка, соединяющего точки A (6;8) и B (–2;2).
Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (–2;2) и (6;8).
Вычисляем по формуле:
Получили (2;5). Абсцисса равна двум.
Ответ: 2
*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку.
Найдите длину отрезка, соединяющего точки (0;0) и (6;8).
Длина отрезка при данных координатах его концов вычисляется по формуле:
в нашем случае имеем О(0;0) и А(6;8). Значит,
Значит,
*Порядок координат при вычитании не имеет значения. Можно из абсциссы и ординаты точки О вычесть абсциссу и ординату точки А:
Ответ:10
Найдите косинус угла наклона отрезка, соединяющего точки O (0;0) и A (6;8), с осью абсцисс.
Угол наклона отрезка – это угол между этим отрезком и осью оХ.
Из точки А опустим перпендикуляр на ось оХ:
То есть, угол наклона отрезка это угол ВОА в прямоугольном треугольнике АВО.
Косинусом острого угла в прямоугольном треугольнике является
отношение прилежащего катета к гипотенузе
Необходимо найти гипотенузу ОА.
По теореме Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Таким образом, косинус угла наклона равен 0,6
Ответ: 0,6
Из точки (6;8) опущен перпендикуляр на ось абсцисс. Найдите абсциссу основания перпендикуляра.
Через точку (6;8) проведена прямая, параллельная оси абсцисс. Найдите ординату ее точки пересечения с осью оУ .
Найдите расстояние от точки A с координатами (6;8) до оси абсцисс.
Найдите расстояние от точки A с координатами (6;8) до начала координат.
Инструкция
Если координаты крайних точек отрезка даны в двухмерной координат, то проведя через эти точки линии, перпендикулярные осям координат, вы получите прямоугольный треугольник. Его гипотенузой будет исходный отрезок, а катеты образуют отрезки, длина которых равна гипотенузы на каждую из координатных осей. Из теоремы Пифагора, определяющей длины гипотенузы как сумму квадратов длин катетов, можно сделать , что для нахождения длины исходного отрезка достаточно найти длины двух его проекций на координатные оси.
Найдите длины (X и Y) проекций исходного отрезка на каждую ось системы координат. В двухмерной системе из крайних точек представлена парой числовых значений (X1;Y1 и X2;Y2). Длины проекций вычисляются нахождением разницы координат этих точек по каждой оси: X = X2-X1, Y = Y2-Y1. Возможно, что одно или оба полученных значения будут , но в данном случае это не никакой роли.
Длины проекций вычисляются нахождением разницы координат этих точек по каждой оси: X = X2-X1, Y = Y2-Y1. Возможно, что одно или оба полученных значения будут , но в данном случае это не никакой роли.
Рассчитайте длину исходного отрезка (A), найдя квадратный корень из квадратов рассчитанных на предыдущем шаге длин проекций на оси координат: A = √(X²+Y²) = √ ((X2-X1)²+(Y2-Y1)²). Например, если отрезок проведен между точками с координатами 2;4 и 4;1, то длина его будет равна √((4-2)²+(1-4)²) = √13 ≈ 3,61.
Если координаты точек, ограничивающих отрезок, даны в трехмерной системе координат (X1;Y1;Z1 и X2;Y2;Z2), то длины (A) этого отрезка будет аналогична полученной на предыдущем шаге. В этом случае надо найти квадратный корень из суммы квадратов проекций на три координатные оси: A = √((X2-X1)²+(Y2-Y1)²+(Z2-Z1)²). Например, если отрезок проведен между точками , с координатами 2;4;1 и 4;1;3, то длина его будет равна √((4-2)²+(1-4)²+(3-1)²) = √17 ≈ 4,12. 1/2.
1/2.
Видео по теме
Источники:
- Длина отрезка
- что такое длина отрезка
Иногда в повседневной деятельности может возникнуть необходимость найти середину отрезка прямой линии. Скажем, если предстоит сделать выкройку, эскиз изделия или просто распилить на две равные части деревянный брусок. На помощь приходит геометрия и немного житейской смекалки.
Вам понадобится
- Циркуль, линейка; булавка, карандаш, нить
Инструкция
Воспользуйтесь обычными инструментами, предназначенными для длины. Это самый простой способ отыскать середину отрезка. Измерьте линейкой или длину отрезка, разделите полученное пополам и отмерьте от одного из концов отрезка полученный результат. Вы получите точку, соответствующую середине отрезка.
Установите расстояние между ножками циркуля так, чтобы оно было равным длине отрезка или же большим, чем половина отрезка. Затем поставьте иглу циркуля в один из концов отрезка и проведите так, чтобы она пересекала отрезок. Переставьте иглу в другой конец отрезка и, не меняя размах ножек циркуля, проведите вторую полуокружность точно таким же образом.
Переставьте иглу в другой конец отрезка и, не меняя размах ножек циркуля, проведите вторую полуокружность точно таким же образом.
Если под рукой не оказалось циркуля или длина отрезка существенно превышает допустимый размах его ножек, можно воспользоваться простым приспособлением из подручных . Изготовить его можно из обычной булавки, нитки и карандаша. Привяжите концы нитки к булавке и карандашу, при этом длина нитки должна немного превышать длину отрезка. Таким импровизированным заменителем циркуля остается проделать шаги, описанные выше.
Видео по теме
Полезный совет
Достаточно точно найти середину доски или бруска вы можете, использовав обычную нитку или шнур. Для этого отрежьте нить так, чтобы она соответствовала длине доски или бруска. Остается сложить нить точно пополам и разрезать на две равные части. Приложите один конец полученной мерки к концу измеряемого предмета, а второй конец будет соответствовать его середине.
Существуют три основных системы координат, используемых в геометрии, теоретической механике, других разделах физики: декартова, полярная и сферическая. В этих системах координат каждая точка имеет три координаты. Зная координаты двух точек, можно определить расстояние между этими двумя точками.
В этих системах координат каждая точка имеет три координаты. Зная координаты двух точек, можно определить расстояние между этими двумя точками.
Вам понадобится
- Декартовы, полярные и сферические координаты концов отрезка
Инструкция
Рассмотрите для начала прямоугольную декартову координат. Положение точки в пространстве в этой координат определяется координатами x,y и z. Из начала координат к точке проводится радиус- . Проекции этого радиус-вектора на координатные оси и будут координатами этой точки.
Пусть у вас теперь есть две точки с координатами x1,y1,z1 и x2,y2 и z2 соответственно. Обозначьте за r1 и r2, соответственно, радиус-векторы первой и точки. Очевидно, что расстояние между этими точками будет модулю вектора r = r1-r2, где (r1-r2) — векторная разность.
Координаты вектора r, очевидно, будут следующими: x1-x2, y1-y2, z1-z2. Тогда вектора r или расстояние между двумя точками будет равно: r = sqrt(((x1-x2)^2)+((y1-y2)^2)+((z1-z2)^2)). 2))
2))
Видео по теме
Отрезок прямой определяется двумя крайними точками и состоит из множества точек, лежащих на проходящей через крайние точки прямой линии. Если отрезок помещен в какую-либо систему координат, то, найдя средние точки его проекций на каждую из осей, можно узнать координаты середины отрезка . По сути, операция сводится к нахождению среднего арифметического значения пар чисел для каждой из координатных осей.
Инструкция
Делите пополам сумму начальной и конечной координат крайних точек отрезка вдоль каждой оси, чтобы средней точки вдоль этой оси. Например, пусть отрезок помещен в трехмерную систему координат XYZ и известны координаты его крайних точек A(Xa,Ya,Za) и C(Xc,Yc,Zc). Тогда координаты его средней точки E(Xe,Ye,Ze) можно по формулам Xe=(Xa+Xc)/2, Ye=(Ya+Yc)/2, Ze=(Za+Zc)/2.
Используйте любой из калькуляторов, если вычислить средние значения координат крайних точек отрезка в уме не представляется возможным.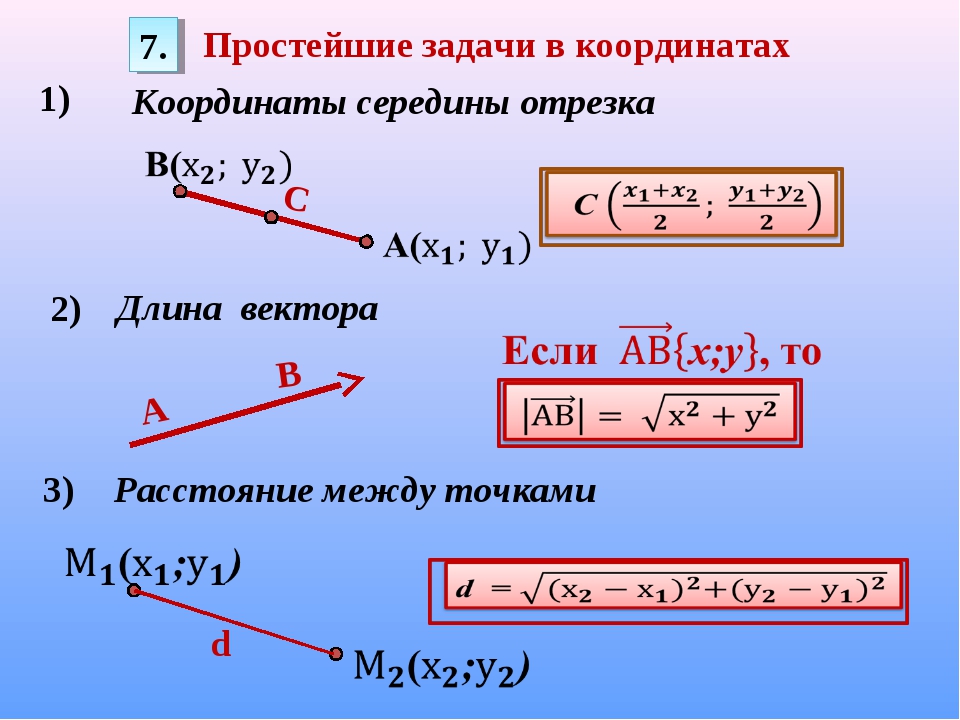 Если под рукой нет такого гаджета, то используйте программный из состава ОС Windows. Его можно запустить, если, щелкнув кнопку «Пуск» раскрыть меню системы. В меню надо перейти в раздел «Стандартные», затем в подраздел «Служебные», а потом в секции «Все » выбрать пункт «Калькулятор». Можно обойтись без главного меню, если нажать сочетание клавиш WIN + R, ввести команду calc, а затем нажать клавишу Enter.
Если под рукой нет такого гаджета, то используйте программный из состава ОС Windows. Его можно запустить, если, щелкнув кнопку «Пуск» раскрыть меню системы. В меню надо перейти в раздел «Стандартные», затем в подраздел «Служебные», а потом в секции «Все » выбрать пункт «Калькулятор». Можно обойтись без главного меню, если нажать сочетание клавиш WIN + R, ввести команду calc, а затем нажать клавишу Enter.
Суммируйте попарно начальные и конечные координаты крайних точек отрезка вдоль каждой оси и делите результат на два. Интерфейс программного калькулятора имитирует обычный калькулятор, а вводить числовые значения и символы математических операций можно как щелкая кнопки курсором мыши на экране, так и нажимая клавиши на клавиатуре. Никаких сложностей с этими вычислениями возникнуть не .
Записывайте математические операции в текстовом виде и вводите их в поле поискового запроса на главной странице сайта Google, если -либо не можете использовать калькулятор, но имеете доступ в интернет. Этот поисковик имеет встроенный многофункциональный калькулятор, пользоваться которым намного проще, чем любым другим. Здесь нет интерфейса с кнопками — вводить все данные надо в текстовом виде в единственное поле. Например, если известны координаты крайних точек отрезка в трехмерной системе координат A(51,34 17,2 13,02) и A(-11,82 7,46 33,5), то координаты средней точки отрезка C((51,34-11,82)/2 (17,2+7,46)/2 (13,02+33,5)/2). Вводя в поле поискового запроса (51,34-11,82)/2, затем (17,2+7,46)/2 и (13,02+33,5)/2, можно с помощью Google получить координаты С(19,76 12,33 23,26).
Этот поисковик имеет встроенный многофункциональный калькулятор, пользоваться которым намного проще, чем любым другим. Здесь нет интерфейса с кнопками — вводить все данные надо в текстовом виде в единственное поле. Например, если известны координаты крайних точек отрезка в трехмерной системе координат A(51,34 17,2 13,02) и A(-11,82 7,46 33,5), то координаты средней точки отрезка C((51,34-11,82)/2 (17,2+7,46)/2 (13,02+33,5)/2). Вводя в поле поискового запроса (51,34-11,82)/2, затем (17,2+7,46)/2 и (13,02+33,5)/2, можно с помощью Google получить координаты С(19,76 12,33 23,26).
Калькулятор средней точки — Найдите середину отрезка
Используйте этот калькулятор для определения координат средней точки (M) отрезка, определяемого двумя его конечными точками (A, B). Найдите середину отрезка АВ.
Быстрая навигация:
- Что такое середина?
- Формула средних точек
- Середины в геометрии
- Приложения в физике
В геометрии середина — это точка на отрезке прямой линии, которая делит ее на две равные половины, поэтому ее иногда называют средней точкой . Отрезок однозначно определяется двумя точками (скажем, A и B) и имеет единственную точку (скажем, M), которая находится посередине. Более технический способ описания средней точки M состоит в том, чтобы сказать, что она делит пополам отрезок AB.
Отрезок однозначно определяется двумя точками (скажем, A и B) и имеет единственную точку (скажем, M), которая находится посередине. Более технический способ описания средней точки M состоит в том, чтобы сказать, что она делит пополам отрезок AB.
В двумерной декартовой координатной плоскости каждая точка имеет две координаты — по одной на каждой оси. Простая визуализация середины прямой линии AB и соответствующих координат показана ниже:
Точка M делит длину AB на две равные части.Используя калькулятор средней точки, можно найти координаты средней точки, зная координаты конечных точек. В качестве альтернативы, если координаты одной конечной точки и средней точки известны, то можно определить и координаты другой точки. См. наш калькулятор конечной точки.
Формула средней точкиУравнение для нахождения координат середины прямой линии AB , определяемой точками A и B :
где ( x A , y A ) — координаты точки A, ( x B , y B , y B ) — координаты 2, x 9 B 902 точки A , x A ) — это координаты M — середины AB, как показано на рисунке выше.
Как видно из формулы, координата x середины M отрезка AB является средним арифметическим координат x двух концов отрезка. Точно так же координата y средней точки является средним значением координат y конечных точек. Формулу достаточно легко применить даже без помощи калькулятора, но использование калькулятора формулы средней точки, безусловно, упрощает эту задачу.
Средние точки в геометрии
Пример использования уравнения средней точки проще всего привести в геометрии.Если заданы (или измерены линейкой) координаты двух конечных точек, можно определить среднюю точку. Пример задачи:
Какова середина отрезка AB , если координаты первой конечной точки (A) равны (2,6), а второй (B) равны (4, 18)?
Чтобы ответить, что такое середина AB, просто замените значения в формуле, чтобы найти координаты середины. В данном случае это (2 + 4)/2 = 3 и (6 + 18)/2 = 12. Итак, (x M , y M ) = (3, 12) — середина отрезка, определенного по А и Б.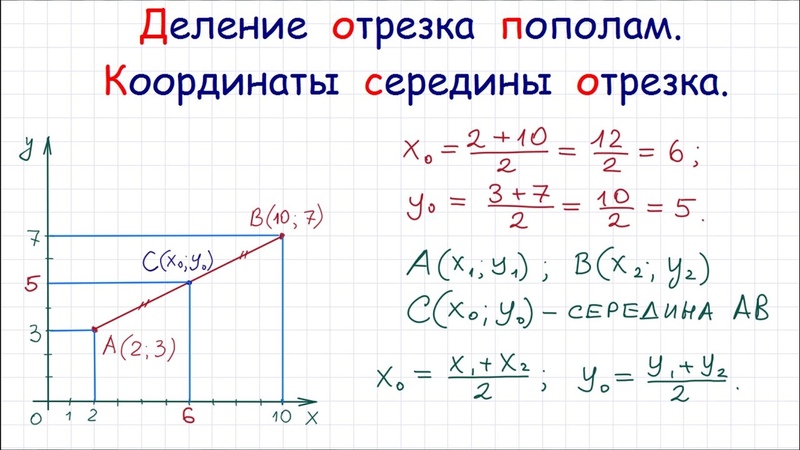
В физике расчет средней точки имеет несколько важных применений. Например, центр масс данного объекта является его центром тяжести. Чтобы сбалансировать этот объект, необходимо обеспечить поддержку в средней точке, чтобы противодействовать силе тяжести таким образом, чтобы ни один из концов не начал опускаться. Поиск конечной точки имеет очевидную пользу.
В задачах, связанных с транспортировкой или перемещением объектов по прямой через двумерное пространство, вычисление формулы средней точки может быть полезно для определения того, в какой точке или когда транспортное средство находится на полпути к месту назначения.Очевидно, что объекты редко имеют возможность двигаться по прямой на большие расстояния, поэтому такие приложения в основном предназначены для учебных целей.
Конечная точка: определение и формула — видео и расшифровка урока
Формула середины
На каждом отрезке есть точка, которая находится посередине между конечными точками. Эта точка называется серединой и лежит на отрезке на равном расстоянии от каждой из конечных точек. Проще говоря, середина лежит в середине отрезка.На графике показан отрезок прямой и его середина.
Эта точка называется серединой и лежит на отрезке на равном расстоянии от каждой из конечных точек. Проще говоря, середина лежит в середине отрезка.На графике показан отрезок прямой и его середина.
Средняя точка M имеет координаты (5, 3) и находится посередине между A и B . В общем, когда у нас есть конечные точки отрезка ( x1 , y1 ) и ( x2 , y2 ), мы можем найти координаты средней точки, найдя среднее значение каждой из координат. Координата x средней точки находится путем сложения двух координат x, x1 и x2 , и деления их на 2.Точно так же координата y средней точки находится путем сложения двух координат y, y1 и y2 , и деления на 2. Это дает нам формулу средней точки.
На нашем графике отрезка AB с серединой M конечные точки обозначены как (2, 2) и (8, 4), поэтому мы имеем x1 = 2, x2 = 8, y1 = 2 и y2 = 4. Подставляем эти значения в формулу средней точки, чтобы получить:
Подставляем эти значения в формулу средней точки, чтобы получить:
M = ((2 + 8) / 2, (2 + 4) / 2) = (10 / 2, 6 / 2) = (5, 3)
Таким образом, наша средняя точка равна (5, 3), как показано на графике.
Формула конечной точки
Когда нам даны одна конечная точка и середина отрезка, мы можем определить другую конечную точку, используя формулу конечной точки. Формула конечной точки получена из формулы средней точки.
Если середина отрезка равна ( м1 , м2 ), а конечные точки — ( x1, y1 ) и ( x2, y2 ), то формула середины равна :
M1 = ( x1 + x2 + x2 ) / 2
м2 = ( y1 + y2 ) / 2
Решение каждого из них для x2 и y2 :
x2 = 2( м1 ) — x1
Y2 = 2 (м2 = 2 (м2 ) — y1
( x2 , y2 ) = (2 ( м1 ) — x1 , 2 ( м2 ) — y1 )
Мы видим, что если нам даны одна конечная точка и середина отрезка, то мы можем использовать формулу конечной точки, чтобы найти другую конечную точку. Давайте снова посмотрим на наш пример графика.
Давайте снова посмотрим на наш пример графика.
Предположим, нам дана конечная точка A с координатами (2, 2) и середина M с координатами (5, 3), и мы хотим найти другую конечную точку нашей линии. сегмент.
x1 = 2 x1 = 2
y1 = 2
м1 = 5 м1 = 5
м2 = 3
Мы подключаем эти значения в нашу формулу конечной точки, чтобы получить следующее:
( x2 , y2 ) = (2*5 — 2, 2*3 — 2) = (10 — 2, 6 — 2) = (8, 4)
Таким образом, наша другая конечная точка (8, 4), как показано на график.
Примеры
Давайте рассмотрим пару примеров задач, используя то, что мы только что узнали.
1) На графике укажите любые отрезки, лучи, конечные и средние точки.
У нас есть отрезки AB , AC и BC . Есть луч, который начинается в точке D . Все точки могут быть конечными точками, поскольку A и B являются конечными точками отрезка AB , C является конечной точкой отрезка AC , а D является конечной точкой луча.Точка B является средней точкой отрезка AC .
Есть луч, который начинается в точке D . Все точки могут быть конечными точками, поскольку A и B являются конечными точками отрезка AB , C является конечной точкой отрезка AC , а D является конечной точкой луча.Точка B является средней точкой отрезка AC .
2) Если отрезок имеет одну конечную точку (1, 5) и среднюю точку (-2, 7), найдите другую конечную точку.
Мы видим, что
x1 = 1 x1 = 1
y1 = 5
м1 = -2 м1 = -2
м2 = 7
Подключение этих значений в формулу конечной точки
( x2 , y2 ) = (2 м1 — x1 , 2 м2 — y1 ) = (2*-2 — 1, 2*7 — 5) = (-5, 9)
Таким образом , наша другая конечная точка (-5, 9).
Резюме урока
Сегмент линии — это именно то, на что похоже название — сегмент линии. Луч — это линия, которая начинается в точке и бесконечно продолжается в одном направлении.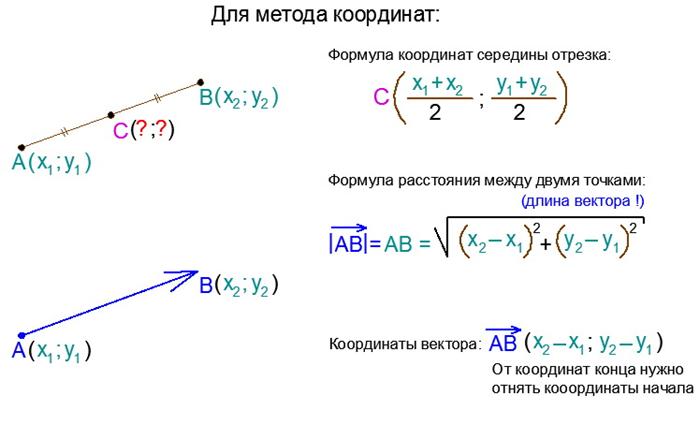 Конечные точки — это точки на любом конце сегмента прямой или на одном конце луча. Середина отрезка — это точка, которая находится посередине между конечными точками.
Конечные точки — это точки на любом конце сегмента прямой или на одном конце луча. Середина отрезка — это точка, которая находится посередине между конечными точками.
Формула для определения середины отрезка:
( м1 , м2 ) = (( x1 + x2 ) / 2, ( y1 65 +
) )
Формула для определения конечной точки, когда известна середина:
( x2 , y2 ) = (2( м1 ) — x1 , 2( 0 0 м2 ) 9000 )
Результаты обучения
Это видео должно помочь вам:
- Объяснить, что такое отрезок
- Определение конечной точки луча или сегмента линии
- Продемонстрируйте, как использовать формулу средней точки
- Понимание того, как использовать формулу конечной точки
Калькулятор средней точки
Использование калькулятора
Середина отрезка — это точка, которая находится посередине между двумя точками. Средняя точка находится на одинаковом расстоянии от каждой конечной точки.
Средняя точка находится на одинаковом расстоянии от каждой конечной точки.
Используйте этот калькулятор, чтобы вычислить среднюю точку, расстояние между двумя точками или найти конечную точку, зная среднюю и другую конечные точки.
Решения для расчета средней и конечной точек
Введите две точки, используя числа, дроби, смешанные числа или десятичные дроби. Калькулятор средней точки показывает работу, которую нужно найти:
- Середина между двумя заданными точками
- Конечная точка задана одной конечной точкой и средней точкой
- Расстояние между двумя конечными точками
Калькулятор также предоставляет ссылку на Калькулятор уклона, который решит и продемонстрирует работу по нахождению уклона, уравнениям линии и точкам пересечения x и y для заданных двух точек.
Как рассчитать среднюю точку
Вы можете найти середину отрезка по двум конечным точкам (x 1 , y 1 ) и (x 2 , y 2 ). Добавьте каждую координату x и разделите на 2, чтобы найти x средней точки. Добавьте каждую координату y и разделите на 2, чтобы найти y средней точки.
Добавьте каждую координату x и разделите на 2, чтобы найти x средней точки. Добавьте каждую координату y и разделите на 2, чтобы найти y средней точки.
Рассчитайте среднюю точку (x M , y M ), используя формулу средней точки:
\((x_{M}, y_{M}) = \left(\dfrac {x_{1} + x_{2}} {2}, \dfrac {y_{1} + y_{2}} {2 }\справа) \)
Важно отметить, что середина — это средняя точка на линии. сегмент .Истинная линия в геометрии бесконечно длинна в обоих направлениях. Но отрезок прямой имеет 2 конечные точки, поэтому можно вычислить среднюю точку. Луч имеет один конец и бесконечно длинный в другом направлении.
Пример: найти середину
Предположим, вы знаете две точки на отрезке прямой, и их координаты равны (6, 3) и (12, 7). Найдите середину по формуле средней точки.
\((x_{M}, y_{M}) = \left(\dfrac {x_{1} + x_{2}} {2}, \dfrac {y_{1} + y_{2}} {2 }\справа) \)
- Сначала добавьте координаты x и разделите на 2.
 Это дает вам x-координату средней точки, x M
Это дает вам x-координату средней точки, x M - Во-вторых, добавьте координаты y и разделите на 2. Это даст вам координату y средней точки, y M
- Возьмите каждый результат, чтобы получить среднюю точку.2} \)
Формула расстояния между точками получена из теоремы Пифагора, определяющей длину гипотенузы. Смотрите наши Калькулятор теоремы Пифагора для более подробного изучения.
Пример.
 2} \)
2} \) - Найдите квадрат каждого члена
- Добавить результаты
- Найдите квадратный корень, и вы нашли расстояние между двумя точками
\( х_{М} = \dfrac {х_{1} + х_{2}} {2} \)
\(x_{M} = \dfrac {6 + 12} {2} \)
\(x_{M} = \dfrac {18} {2} \)
\( х_{М} = {9} \)
\(у_{М} = \dfrac {у_{1} + у_{2}} {2} \)
\(y_{M} = \dfrac {3 + 7} {2} \)
\(y_{M} = \dfrac {10} {2} \)
\(у_{М} = {5} \)
\(d = \sqrt {36 + 64} \)
\(d = \sqrt {100} \)
\(d = 10\)
Подобно этому калькулятору средней точки, наш Калькулятор двухмерного расстояния.Расстояние между 2 точками в 3 измерениях с координатами (x, y, z) см. 3-х мерный калькулятор расстояний.
Как рассчитать конечную точку
Если вы знаете конечную точку и среднюю точку отрезка, вы можете вычислить отсутствующую конечную точку. Начните с формулы средней точки сверху и определите координаты неизвестной конечной точки.
- Сначала возьмем формулу средней точки:
- И разбить его, чтобы у вас были отдельные уравнения для координат x и y средней точки
- Переставьте каждое уравнение так, чтобы вы решали x 2 и y 2
\( x_{2} = 2x_{M} — x_{1} \)
\(у_{2} = 2у_{М} — у_{1} \)
- Поскольку вы знаете середину, вставьте ее координаты вместо x M и y M в каждом уравнении
- Вставьте координаты вашей известной конечной точки в значения для x 1 и г 1
- Наконец, решите каждое уравнение, чтобы найти x 2 и y 2 , которые будут координатами вашей отсутствующей конечной точки
\((x_{M}, y_{M}) = \left(\dfrac {x_{1} + x_{2}} {2}, \dfrac {y_{1} + y_{2}} {2 }\справа) \)
\( х_{М} = \dfrac {х_{1} + х_{2}} {2} \)
\(у_{М} = \dfrac {у_{1} + у_{2}} {2} \)
Пример: найти конечную точку
Используя шаги, описанные выше, давайте найдем конечную точку отрезка, где мы знаем, что одна конечная точка равна (6, -4), а средняя точка — (1, 7). Конечная точка – это (x 1 , y 1 ) координат. Середина – это (x M , y M ) координат.
Конечная точка – это (x 1 , y 1 ) координат. Середина – это (x M , y M ) координат.
- Сначала возьмем формулу средней точки:
- И переставьте уравнения так, чтобы вы решали x2 и y2
- Вставьте координаты вашей средней точки (1, 7) вместо x M и y M в каждом уравнении
- Вставьте координаты вашей известной конечной точки (6, -4) в значения для x 1 и у 1
- Решите каждое уравнение, чтобы найти x 2 и y 2 .

- Ваша отсутствующая конечная точка (x 2 , y 2 ) равно (-4, 18)
\((x_{M}, y_{M}) = \left(\dfrac {x_{1} + x_{2}} {2}, \dfrac {y_{1} + y_{2}} {2 }\справа) \)
\( х_{2} = 2х_{М} — х_{1} \)
\(у_{2} = 2у_{М} — у_{1} \)
\( х_{2} = 2(1) — х_{1} \)
\(у_{2} = 2(7) — у_{1} \)
\( х_{2} = 2(1) — 6 \)
\(у_{2} = 2(7) — (-4) \)
\( х_{2} = 2 — 6 \)
\(х_{2} = -4 \)
\( у_{2} = 14 + 4 \)
\( у_{2} = 18 \)
— как найти среднюю точку? Примеры, формулы
Середина относится к точке, которая находится в середине линии, соединяющей две точки.Две опорные точки являются конечными точками линии, а средняя точка лежит между двумя точками. Середина делит линию, соединяющую эти две точки, на две равные половины. Кроме того, если провести линию, делящую пополам линию, соединяющую эти две точки, линия проходит через середину.
Формула средней точки используется для нахождения средней точки между двумя точками, координаты которых нам известны. Формула средней точки также используется для нахождения координат конечной точки, если известны координаты другой конечной точки и средней точки. В координатной плоскости, если провести линию, соединяющую две точки (4, 2) и (8, 6), то координаты середины линии, соединяющей эти две точки, равны ({4 + 8}/2, {2 + 6}/2) = (12/2, 8/2) = (6, 4). Давайте узнаем больше о формуле средней точки и различных методах нахождения середины линии.
В координатной плоскости, если провести линию, соединяющую две точки (4, 2) и (8, 6), то координаты середины линии, соединяющей эти две точки, равны ({4 + 8}/2, {2 + 6}/2) = (12/2, 8/2) = (6, 4). Давайте узнаем больше о формуле средней точки и различных методах нахождения середины линии.
Что такое средняя точка?
Средняя точка — это точка, лежащая между двумя точками и находящаяся посередине линии, соединяющей эти две точки. Для двух точек, если провести линию, соединяющую две точки, то средней точкой будет точка в середине линии, равноудаленная от двух точек.Для любых двух точек, скажем, A и C, середина — это точка B, расположенная посередине между точками A и C. Следовательно, чтобы вычислить середину, мы можем просто измерить длину отрезка и разделить ее на 2.
Обратите внимание, что точка B равноудалена от A и C. Середина существует только для отрезка прямой. Линия или луч не могут иметь середины, потому что линия неопределенна в обоих направлениях, а луч имеет только один конец и поэтому может быть продолжен.
Формула средней точки
Формула средней точки определена для точек на осях координат.Пусть (x\(_1\), y\(_1\)) и (x\(_2\), y\(_2\)) — концы отрезка. Средняя точка равна половине суммы x-координат двух точек и половине суммы y-координат двух точек. Формула средней точки для вычисления середины отрезка, соединяющего эти точки, может быть представлена как
.Формула средней точки в математике:
Учитывая две точки A (x\(_1\), y\(_1\)) и B (x\(_2\), y\(_2\)), середина между A и B определяется как,
М(х\(_3\), у\(_3\)) = [(х\(_1\) + х\(_2\))/2, (у\(_1\) + у\(_2\) ))/2)]
, где M — середина между A и B, а (x\(_3\), y\(_3\)) — ее координаты.
Давайте посмотрим на этот пример и найдем середины двух точек на одномерной оси. Предположим, у нас есть две точки, 5 и 9, на числовой прямой. Середина будет рассчитана как: (5 + 9)/2 = 14/2 = 7. Итак, 7 — это середина 5 и 9.
Получение формулы средней точки
Рассмотрим отрезок с концами (x\(_1\), y\(_1\)) и (x\(_2\), y\(_2\)). Для любого линейного отрезка средняя точка находится посередине между двумя его конечными точками.Выражение для координаты x средней точки равно (x\(_1\) + x\(_2\))/2, что является средним значением координат x. Точно так же выражение для координаты y равно (y\(_1\) + y\(_2\))/2, что является средним значением координат y.
Для любого линейного отрезка средняя точка находится посередине между двумя его конечными точками.Выражение для координаты x средней точки равно (x\(_1\) + x\(_2\))/2, что является средним значением координат x. Точно так же выражение для координаты y равно (y\(_1\) + y\(_2\))/2, что является средним значением координат y.
Таким образом, формула для средней точки: [(x\(_1\) + x\(_2\))/2, (y\(_1\) + y\(_2\))/2)]
Давайте рассмотрим пример, чтобы увидеть применение формулы средней точки.
Пример: Используя формулу средней точки, найдите среднюю точку между точками X(5, 3) и Y(7, 8).
Решение: Пусть M будет средней точкой между X и Y.
М = ((5 + 7)/2, (3 + 8)/2) = (6, 11/2)
Ответ: Координаты середины между X и Y равны (6, 11/2).
Как найти середину?
Далее, на основе точек и значений их координат используются следующие два метода для нахождения середины линии, соединяющей две точки.
Метод 1: Если отрезок прямой вертикальный или горизонтальный, то, разделив длину на 2 и считая это значение от любой из конечных точек, мы получим середину отрезка прямой.Посмотрите на рисунок, показанный ниже. Координаты точек A и B равны (-3, 2) и (1, 2) соответственно. Длина горизонтальной линии \(\overline{AB}\) равна 4 единицам. Половина этой длины составляет 2 единицы. Перемещение на 2 единицы из точки (-3, 2) даст (-1, 2). Итак, (-1, 2) — это середина \(\overline{AB}\).
Метод 2: Другой способ найти среднюю точку — использовать формулу средней точки . Координаты точек A и B равны (-3, -3) и (1, 4) соответственно.Используя формулу средней точки, мы имеем: ({-3 + 1}/2, {-3 + 4}/2) = (-2/2, 1/2) = (-1,1/2).
Метод 3: Один из способов найти середину прямой, заданной на плоскости, — это построение. Мы можем использовать конструкцию циркуля и линейки, чтобы сначала построить линзу, используя дуги окружности одинакового (и достаточно большого) радиуса с центрами в двух конечных точках, а затем соединив вершины линзы (две точки, где дуги пересекаются). Точка пересечения линии, соединяющей бугры и отрезок, является серединой отрезка.
Точка пересечения линии, соединяющей бугры и отрезок, является серединой отрезка.
Вот пример поиска координат конечной точки по средней точке и координатам другой конечной точки.
Пример: Середина R между точками P и Q имеет координаты (4, 6). Если координаты Q равны (8, 10), то каковы координаты точки P? Решите его, используя формулу средней точки.
Решение:
Пусть координата x точки P равна m, а координата y точки P равна n.
Р = (м, н)
Q = (8, 10)
R = (4, 6)
Используя формулу средней точки,
R = ((m + 8)/2, (n + 10)/2) = (4, 6)
Решение для m,
(м + 8)/2 = 4
м + 8 = 8
м = 0
Решение для n,
(n + 10)/2 = 6
п + 10 = 12
п = 2
Следовательно, координаты P равны (0, 2).
Важные примечания по средней точке:
Следующие точки являются важными свойствами средних точек.
- Середина делит отрезок в равном соотношении, то есть 1:1.

- Середина делит отрезок на две равные части.
- Биссектриса отрезка пересекает его середину.
Формулы, относящиеся к средней точке
Формула средней точки включает вычисления отдельно для x-координаты точек и y-координаты точек.Кроме того, вычисления точек между двумя заданными точками также включают в себя аналогичные вычисления координаты x и координаты y заданных точек. Следующие две формулы тесно связаны с формулой средней точки.
- Центроид формулы треугольника
- Формула раздела
Точка пересечения медиан треугольника называется центром тяжести треугольника. Медиана — это линия, соединяющая вершину с серединой противоположной стороны треугольника.Центроид делит медиану треугольника в отношении 2:1. Для треугольника с вершинами (x\(_1\), y\(_1\)), (x\(_2\), y\(_2\)), (x\(_3\), y\(_3\) )) формула для нахождения координат центра тяжести треугольника выглядит следующим образом.
Формула сечения полезна для нахождения координат любой точки, которая находится на линии, соединяющей две точки. Далее, отношение, в котором точка разделила линию, соединяющую две заданные точки, необходимо, чтобы узнать координаты точки.Точка может располагаться между точками или в любом месте за точками, но на одной линии. Формула сечения для нахождения координат точки, которая делит прямую, соединяющую точки (x\(_1\), y\(_1\)) и (x\(_2\), y\(_2\)) в отношении m:n выглядит следующим образом. Знак плюс используется в формуле для нахождения координат точки, которая делит точки внутри, а знак минус используется, если точка делится снаружи.
☛ Темы, связанные с средней точкой:
Ознакомьтесь с еще несколькими интересными статьями, содержащими дополнительные концептуальные идеи, связанные с Формулой средней точки.
Часто задаваемые вопросы о Midpoint Formula
Что такое формула средней точки в координатной геометрии?
Формула средней точки в координатной геометрии определяется как формула для нахождения центральной точки прямой линии с использованием координат ее концов. Формула средней точки используется для нахождения половины пути, то есть точки, которая делит прямую на две равные части.
Формула средней точки используется для нахождения половины пути, то есть точки, которая делит прямую на две равные части.
Что означает середина?
Средняя точка определяется как точка, которая находится в середине линии, соединяющей две точки.Это точка, которая равноудалена от обеих конечных точек и, таким образом, делит отрезок пополам.
Как использовать формулу средней точки?
Формула средней точки очень проста, когда дело доходит до ее применения.
- Шаг 1: Определите сегмент линии или две конечные точки.
- Шаг 2: Найдите их координаты.
- Шаг 3: Сложите координаты x обеих конечных точек и разделите на 2.
- Шаг 4: Сложите координаты Y обеих конечных точек и разделите на 2.
- Шаг 5: Запишите значения, полученные на шагах 3 и 4, при упоминании координат любой точки.
☛ Также проверьте: Вы можете попробовать этот калькулятор средней точки, чтобы проверить результат, полученный для средней точки отрезка линии — Калькулятор средней точки
Что такое формула средней точки в словах?
Для середины линии, соединяющей две точки, координаты которых заданы, формула середины точки словами может быть описана как половина суммы x-координат двух точек и половина суммы y-координат две точки.
Почему важна формула средней точки?
Формула средней точкиимеет различные применения в реальной жизни, например, для целей строительства и т. Д. Она имеет важное значение в геометрии, например,
.- Нахождение координат центра тяжести треугольника.
- Нахождение медианы треугольника.
- Нахождение середины отрезка.
Может ли середина быть дробью?
Да, значение средней точки также может быть дробным.Это в основном зависит от числового значения двух точек. Средняя точка представляет собой сумму числового значения двух точек, деленную на 2. Для таких точек, как -4 и 5 на числовой прямой, средняя точка равна +1/2.
Как рассчитать среднюю точку?
Середину можно найти по формуле {(x\(_1\) + x\(_2\))/2, (y\(_1\) + y\(_2\))/2}. Здесь (x\(_1\), y\(_1\)) и (x\(_2\), y\(_2\)) — координаты двух точек, а середина — точка, лежащая на равном расстоянии между эти две точки.
Может ли середина быть нулем?
Средняя точка может быть нулевой. Это зависит от значения двух точек. Для двух точек на числовой прямой в точках со значениями -4 и 4 середина равна 0. А для двух точек, таких как (-2, 5) и (2, -5), середина равна (0 , 0).
Это зависит от значения двух точек. Для двух точек на числовой прямой в точках со значениями -4 и 4 середина равна 0. А для двух точек, таких как (-2, 5) и (2, -5), середина равна (0 , 0).
Что такое середина линии?
Середина линии — это точка, равноудаленная от концов линии и в середине линии. Если конечными точками линии являются (x\(_1\), y\(_1\) и (x\(_2\), y\(_2\)), то формула для средней точки линии будет { (х\(_1\) + х\(_2\))/2, (у\(_1\) + у\(_2\))/2}.
Что такое середина кривой?
Середина кривой — это середина наибольшей хорды, которую можно провести для кривой. Середина окружности — это середина ее наибольшей хорды, которая является диаметром окружности.
Что такое середина треугольника?
Середина треугольника является центром тяжести треугольника. Центроид – это точка пересечения медиан треугольника. Центр тяжести любого объекта треугольной формы находится в его центре тяжести.
Что такое середина круга?
Середина окружности — это центр окружности. Наибольшая хорда окружности — это диаметр, а середина диаметра окружности — середина окружности. Середина окружности равноудалена от каждой точки окружности.
Наибольшая хорда окружности — это диаметр, а середина диаметра окружности — середина окружности. Середина окружности равноудалена от каждой точки окружности.
Формула средней точки – объяснение и примеры
Формула средней точки — это метод нахождения точного центра отрезка.
Поскольку отрезок по определению конечен, он имеет две конечные точки.Следовательно, другой способ думать о формуле средней точки — думать о ней как о способе найти точку точно между двумя другими точками.
Формула средней точки требует от нас нанесения точек и досконального знания дробей.
В этом разделе мы рассмотрим:
- Что такое формула средней точки?
- Как найти середину прямой
Что такое формула средней точки?
с учетом двух очков (X 1 , Y 1 ) и (x 2 , Y 2 ), формула средней точки ( + x 2 ) / 2 , (у 1 + у 2 ) / 2 ).
Если мы пытаемся найти центр отрезка, точки (x 1 , y 1 ) и (x 2 , y 2 ) являются конечными точками отрезка.
Обратите внимание, что вывод формулы средней точки не является числом. Это набор координат (x, y). То есть формула средней точки дает нам координаты точки, которая находится точно между двумя заданными точками. Это точная середина отрезка, соединяющего две точки.
Расстояние от любой точки до середины равно половине расстояния между двумя начальными точками.
Как найти середину прямой
Сначала выберите точку (x 1 , y 1 ) и точку (x 2 , y 2 ). Не имеет большого значения, что есть что, но в некоторых случаях нам может потребоваться определить координаты двух точек по графику.
Тогда мы можем подключить значения x 1 , Y 1 , x 2 , а также Y 2 в формулу ( + x 2 ) / 2 , (у 1 + у 2 ) / 2 ).
Помните изучение средних и средних значений? Чтобы найти среднее или среднее двух чисел, мы складываем два числа вместе и делим на два. Это именно то, что мы делаем в формуле!
Следовательно, мы можем думать о формуле средней точки как о нахождении точки, являющейся средним значением x-членов и y-терминов.
Примеры
В этом разделе мы рассмотрим несколько примеров использования формулы средней точки и их пошаговые решения.
Пример 1
Рассмотрим отрезок, который начинается в начале координат и заканчивается в точке (0, 4).Какова середина этой линии?
Пример 1 Решение
Легко видеть, что эта линия имеет длину 4 единицы и ее середина равна (2, 0). Это позволяет легко проиллюстрировать, как работает формула средней точки.
Во-первых, обозначим начало координат (0, 0) как (x 1 , y 1 ) и точку (4, 0) как (x 2 , y 2 ). Затем мы можем подключить их к формуле средней точки:
(6 (x 1 + x 2 ) / 2 , (Y 1 + Y 2 ) / 2 ).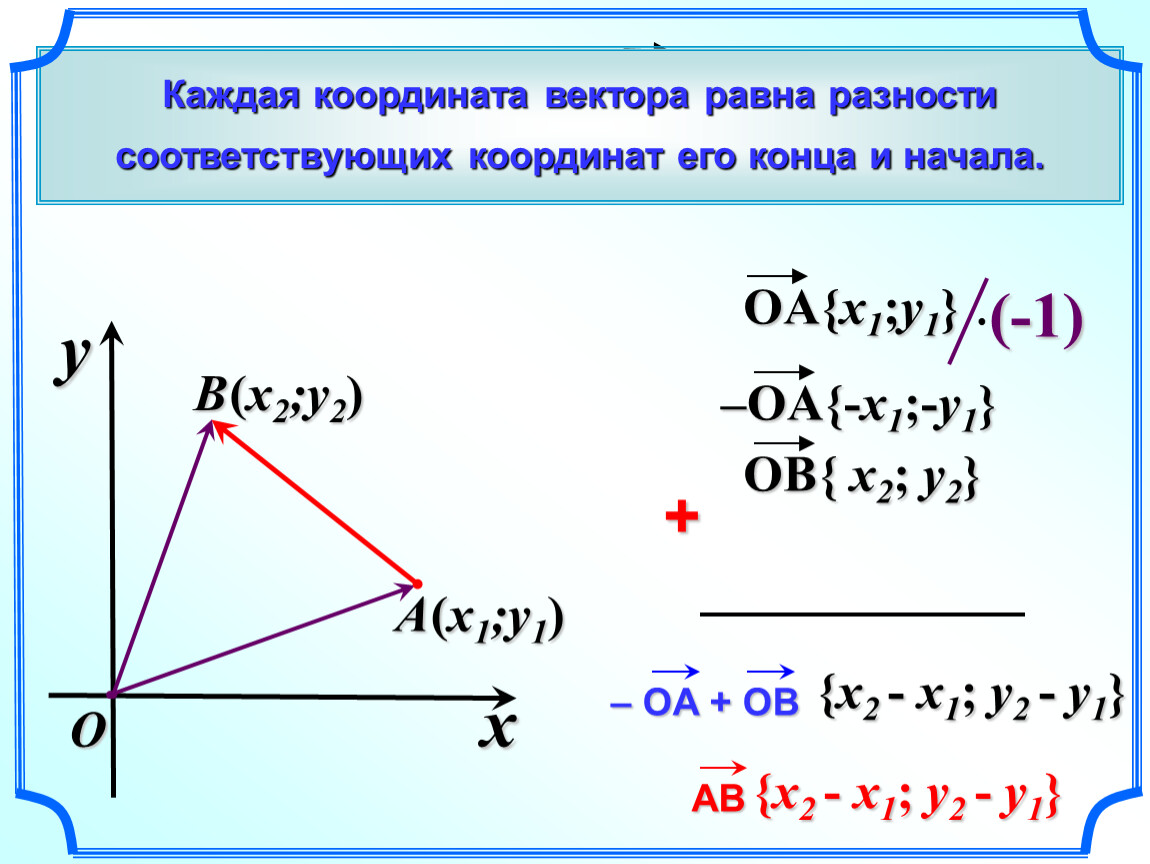
( ( 4+0 ) / 2 , ( 0+0 ) / 2 ).
( 4 / 2 , 0)
(2, 0).
Это соответствует нашей интуиции. В конце концов, середина 0 и 4 равна 2.
Пример 2
Рассмотрим отрезок, который начинается в (0, 2) и заканчивается в (0, 4). Какова середина этого отрезка?
Пример 2 Решение
Опять же, мы можем видеть, что это отрезок длиной 2 единицы.Его середина находится на расстоянии одной единицы от каждой конечной точки (0, 3). Это еще раз позволяет легко продемонстрировать, как работает формула средней точки.
Пусть (0, 2) будет (x 1 , y 1 ) и (0, 4) будет (x 2 , y 2 ). Затем, подставив значения в формулу средней точки, мы получим:
( (0+0) / 2 , (4+2) / 2 )
(0, 6
1 / 2 )(0, 3).
Следовательно, середина равна (0, 3), и, как и прежде, это соответствует нашей интуиции.
Пример 3
Найдите середину отрезка, который проходит от (-9, -3) до (18, 2).
Пример 3 Решение
Не так сразу очевидно, где находится середина этой линии. Но мы все еще можем назначить одну точку (скажем, (-9, -3) как (x 1 , y 1 )) и другую точку как (x 2 , y 2 ). Затем мы можем подставить значения в полуночную формулу:
( (-9+18) / 2 , (-3+2) / 2 )
( 9
1 / 2 , -1 / 2 ).В этом случае мы можем просто оставить два числа как дроби для нашего ответа. Ниже представлены все три точки.
Пример 4
На приведенном ниже графике показан отрезок k. Что является серединой отрезка?
Пример 4 Решение
Прежде чем мы сможем определить середину этого отрезка, нам нужно найти координаты его концов. Конечная точка во втором квадранте находится на четыре единицы левее начала координат и на одну единицу выше него. Конечная точка в четвертом квадранте находится на три единицы правее начала координат и на три единицы ниже его. Это означает, что конечные точки равны (-4, 1) и (3, -3) соответственно. Пусть они также будут (x 1 , y 1 ) и (x 2 , y 2 ) соответственно.
Конечная точка в четвертом квадранте находится на три единицы правее начала координат и на три единицы ниже его. Это означает, что конечные точки равны (-4, 1) и (3, -3) соответственно. Пусть они также будут (x 1 , y 1 ) и (x 2 , y 2 ) соответственно.
Подставив эти значения в формулу средней точки, мы получим:
( (-4+3) / 2 , (3+1) / 2 )
( 1
6 — 1
6 / 2 , -2 / 2 )( -1 / 2 , -1 ).
Следовательно, точный центр этого отрезка является точкой ( -1 / 2 , -1).
Пример 5
Ученый находит на острове два гнезда для вымирающей птицы. Одно гнездо находится в 1,2 милях к северу и в 1,4 милях к востоку от исследовательского центра ученого. Второе гнездо находится в 2,1 милях к югу и в 0,4 милях к востоку от объекта. Ученый хочет установить одну камеру в месте, максимально близком к обоим гнездам, в надежде заснять птиц. Куда ей поставить эту камеру?
Куда ей поставить эту камеру?
Пример 5 Решение
Точка, которая минимизирует расстояние до каждого гнезда, является средней точкой между координатами двух гнезд.
Пусть север и восток будут положительными направлениями. Поскольку первое гнездо находится в 1,2 мили к северу и в 1,4 мили к востоку, мы можем нанести его координаты на (1.4, 1.2). Точно так же координаты второго гнезда находятся в (0,4, -2,1).
Если координаты первого гнезда (x 1 , y 1 ) и координаты второго гнезда (x 2 , y 2 ), то середина:
( (1.4 + 0,4) / 2 , (1.2-2.1) / 2 )
( 1.8 / 2 , -0, / 2 )
(0,9, -0,9 / 2 )
То есть ученый должен установить свою камеру по координатам (0,9, -0,9 / 2 ). Поскольку -0,9 / 2 равно -0,45, камера должна находиться в точке в 0,45 мили к северу от объекта и в 0,9 мили к востоку от него.
Пример 6
Середина отрезка равна (9, 4).Одна из конечных точек отрезка (-8, -2). Какова другая конечная точка этого отрезка?
Пример 6 Решение
Мы можем подставить известные нам значения в формулу средней точки и работать в обратном порядке. Мы знаем, что середина (9, 4) и одна конечная точка (-8, -2). Пусть это будет (x 1 , y 1 ). Тогда имеем:
(-8+x 2 )/2=9 и (-2+y 2 )/2=4.
Теперь мы можем умножить обе части обоих уравнений на 2, что даст нам:
-8+x 2 =18 и -2+y 2 =8.
Наконец, добавление 8 к обеим частям уравнения слева и 2 к обеим частям уравнения справа дает нам x 2 = 26 и y 2 = 10.
Следовательно, другая конечная точка (26, 10).
Формула средней точки — ChiliMath
Прежде чем мы действительно углубимся и узнаем, как применять или использовать формулу средней точки для решения проблем, давайте на мгновение остановимся и получим практическое понимание этого. Думайте о средней точке как о «половине» или средней точке отрезка прямой.Эта так называемая центральная точка делит отрезок прямой на две равные или конгруэнтные части.
Думайте о средней точке как о «половине» или средней точке отрезка прямой.Эта так называемая центральная точка делит отрезок прямой на две равные или конгруэнтные части.
ПРИМЕЧАНИЕ : Середина отрезка линии AC, обозначенная символом \overline {AC}, расположена в точке B. Это означает, что отрезок линии AB обозначается как \overline {AB} , а отрезок линии BC обозначается также как \ overline {BC} , имеют равную меру. Следовательно, \overline {AB} = \overline {BC} .
В двух словах, формула для нахождения середины двух заданных точек выглядит следующим образом.
Формула средней точки
Средняя точка
2 м из сегмента линии с конечными точками A ( x 1 , Y 1 ) и B ( x 2 , y 2 ) рассчитывается следующим образом:
Наблюдения:
а) Координата x средней точки представляет собой среднее значение x значений из заданных точек.
b) Координата y средней точки представляет собой среднее значение y -значений из заданных точек.
Примеры использования формулы средней точки
Давайте рассмотрим пять (5) различных примеров, чтобы увидеть формулу средней точки в действии!
Пример 1: Найдите середину отрезка, соединенного конечными точками (–3, 3) и (5, 3) .
Когда вы наносите точки на оси xy и соединяете их с помощью линейки, отрезок линии, очевидно, горизонтален, поскольку координаты y точек равны.При этом легко аппроксимировать или угадать среднюю точку даже без формулы средней точки. Вы можете сделать это, посчитав одинаковое количество единиц с обеих сторон конечных точек, пока они не достигнут центра.
Тем не менее, давайте вычислим это, используя формулу, чтобы найти среднюю точку.
Пусть (–3, 3) будет первой точкой, поэтому x 1 = –3 и y 1 = 3. Таким же образом, если (5,3) – вторая точка, тогда x 2 = 5 и у 2 = 3.Подставьте эти значения в формулу и упростите, чтобы получить среднее значение.
Таким же образом, если (5,3) – вторая точка, тогда x 2 = 5 и у 2 = 3.Подставьте эти значения в формулу и упростите, чтобы получить среднее значение.
Здесь представлены точки, нанесенные на декартовой плоскости, вместе с рассчитанным значением средней точки.
Пример 2: Найдите центральную точку отрезка, соединенного конечными точками (1, 5) и (1, –1) , используя формулу средней точки.
Этот конкретный отрезок явно вертикальный, потому что две точки имеют одинаковые координаты x. Более того, нанесение точек на ось XY подтверждает правильность случая.Как и в нашем предыдущем примере, середину этого вертикального отрезка можно легко аппроксимировать, посчитав одинаковое количество единиц с обеих сторон от конечных точек.
В любом случае, давайте решим это с помощью формулы.
Вот как это выглядит на графике.
Пример 3: Найдите середину отрезка, соединенного конечными точками (–4, 5) и (2, –3) .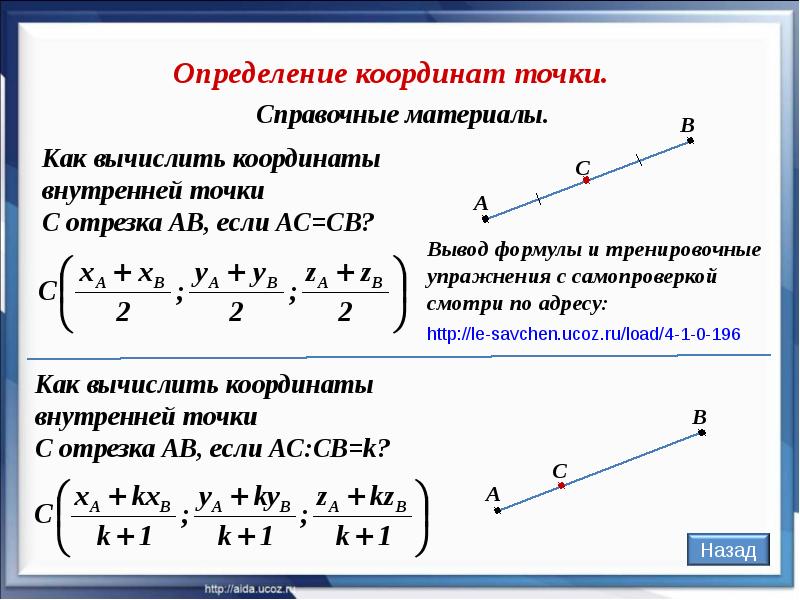
Обратите внимание, что при построении сегмента линии, созданного заданными конечными точками, результирующий сегмент линии не является ни горизонтальным, ни вертикальным, в отличие от последних двух примеров.Вместо этого вы получите сегмент диагональной линии. На этот раз сложнее угадать или приблизиться к средней точке. Однако при использовании формулы это не должно быть проблемой.
Мы можем позволить ( x 1 , y 1 ) = (- 4, 5) и ( x 2 , y 2 ) = (2, -3).
Теперь подставьте и оцените значения в формуле средней точки.
Вот график.
Пример 4: Найдите пропущенное значение h в точках (5, 7) и (1, h ) , если его середина находится в ) (9, 0 24) (3, 0 24) .
Поскольку средняя точка фактически задана нам, начните с установки формулы, равной числовому значению средней точки. Просто так…
Просто так…
мы позволяем ( x 1 , y 1 ) = (5, 7) и ( x 2 , y 2 ) = (1, h ). Затем подставьте эти значения в формулу.
Если вы заметили, две точки равны, если их соответствующие координаты совпадают. То есть значения x равны, и значения y также равны.
Обратите внимание, оба значения x равны 3. Отлично!
Но мы хотим сделать то же самое с координатами и , установив их равными друг другу. Таким образом, мы создали простое уравнение, которое можно решить для недостающего значения ч .
Пример 5: Найдите центр окружности, диаметр которой имеет конечные точки (–1, –5) и (5, –1) .
Если подумать, центр круга — это всего лишь середина диаметра.Эта задача просто сводится к нахождению середины отрезка с концами (−1,−5) и (5,−1).
Я уверен, что вы уже знаете, как это сделать. Просто предостережение: будьте очень осторожны при сложении или вычитании чисел с одинаковыми или разными знаками. Именно здесь случаются глупые ошибки, потому что учащиеся склонны «расслабляться» при выполнении основных арифметических операций. Так что не будь.
Вот график круга с указанием его диаметра и центра.
Практика с рабочими листами
Вас также может заинтересовать:
Формула расстояния
Основы координатной геометрии — Формула сечения
На этом уроке мы установим формулу для нахождения координат точки, которая делит отрезок, соединяющий две заданные точки в заданном отношении.Формула известна как формула раздела . Начнем!
Рассмотрим две точки P(x 1 , y 1 ) и Q(x 2 , y 2 ) . Нам нужно найти координаты точки R , которая делит PQ в отношении m : n , то есть PR / RQ = m / n .
Учитывая соотношение, точка R может либо лежать между P и Q , либо вне отрезка PQ .Взгляни.
(Обратите внимание, что на приведенном выше рисунке м и n не обозначают длины PR и QR . Они просто указывают соотношение.)
Давайте рассмотрим эти случаи один за другим.
Случай I – R лежит между P и QСначала я проиллюстрирую уродливый (но действенный) метод вычисления координат R , используя то, что мы уже знаем — формулу расстояния. Как я упоминал ранее, существует (в общем) несколько методов решения задачи координатной геометрии.Это один из таких случаев. Идея состоит в том, чтобы развить ваш уровень мышления и дать вам представление о том, какие методы хороши, а какие нет.
Вот как можно подумать: «Поскольку есть два неизвестных x и y (т. е. координаты R ), мне нужно найти два уравнения, или два геометрических условия, которые я преобразую в ( разрешимых) уравнений, используя известные мне формулы».
е. координаты R ), мне нужно найти два уравнения, или два геометрических условия, которые я преобразую в ( разрешимых) уравнений, используя известные мне формулы».
Хм.. одно условие уже задано, PR/RQ = m/n , или n.2}\)
Я остановлюсь здесь. Возможно, вы поняли, почему это не лучший метод. На самом деле, как мы увидим позже, методы, использующие формулу расстояния, обычно становятся довольно сложными и трудными для решения.
Итак, какова наша альтернатива? Немного геометрии — давайте сделаем некоторые построения.
Я нарисовал RA и QB параллельно оси Y , а PA и RB параллельно оси X .Тогда треугольники RPA и QRB подобны по АА-подобию.
Чем это поможет? Нам дано PR/QR , что с помощью подобия равно RA/QB и PA/RB .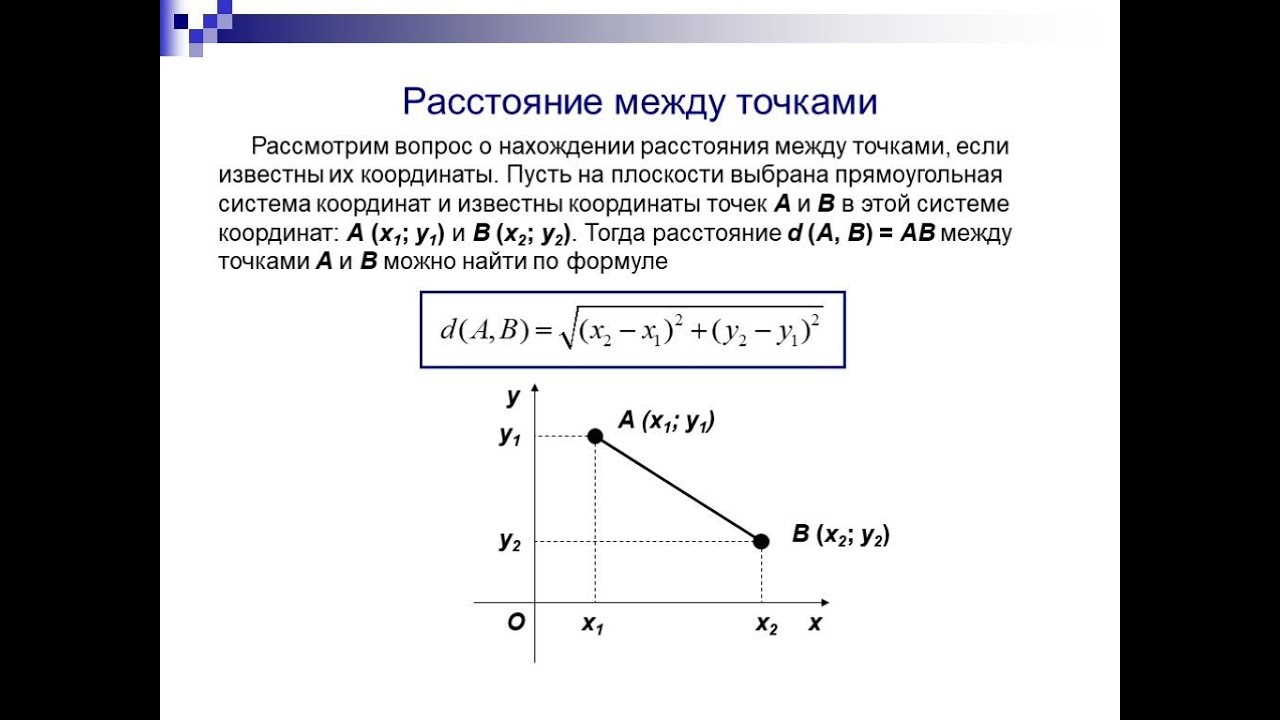 Позвольте мне написать это лучше:
Позвольте мне написать это лучше:
\(\frac{PR}{QR} = \frac{RA}{QB} = \frac{PA}{RB} = \frac{m}{n}\)
Итак, PA = x – x 1 и RB = x 2 – x (я объяснял это в предыдущем уроке.)
Следовательно, мы можем написать
\(\frac{PA}{RB}=\frac{x-x_1}{x_2-x}=\frac{m}{n}\)
Решив вышесказанное для x , мы получим
х = \(\frac{mx_2+nx_1}{m+n}\)
А как насчет и ?
На рисунке выше RA = y – y 1 и QB = y 2 – y .
Теперь мы можем использовать тот же процесс, чтобы получить
.y = \(\frac{my_2+ny_1}{m+n}\)
И так мы имеем координаты точки R , которая делит PQ в отношении m : n .
Когда R лежит между P и Q , мы говорим, что R делит PQ в отношении m : n внутри . Вот симуляция, которая показывает две точки A и B , а также точку C , разделяющую соединяющий их отрезок в некотором отношении.
Вот симуляция, которая показывает две точки A и B , а также точку C , разделяющую соединяющий их отрезок в некотором отношении.
Попробуйте изменить значения м и n и посмотрите координаты C . Вы получаете те же координаты, используя формулу сечения?
Давайте посмотрим, что произойдет, когда R окажется за пределами PQ .
Корпус II – R лежит снаружи PQПриведенное условие такое же, т.е. PR/RQ = m/n , но цифра будет немного другая.
В этом случае говорят, что R делит PQ внешне в отношении m : n .
Я не собираюсь выводить это. Пожалуйста, попробуйте сделать это сами. Метод тот же, что и в первом случае – найти подобные треугольники, выразить данное отношение через х 1 , х 2 , y 1 и 305
3 4
3
4 2 .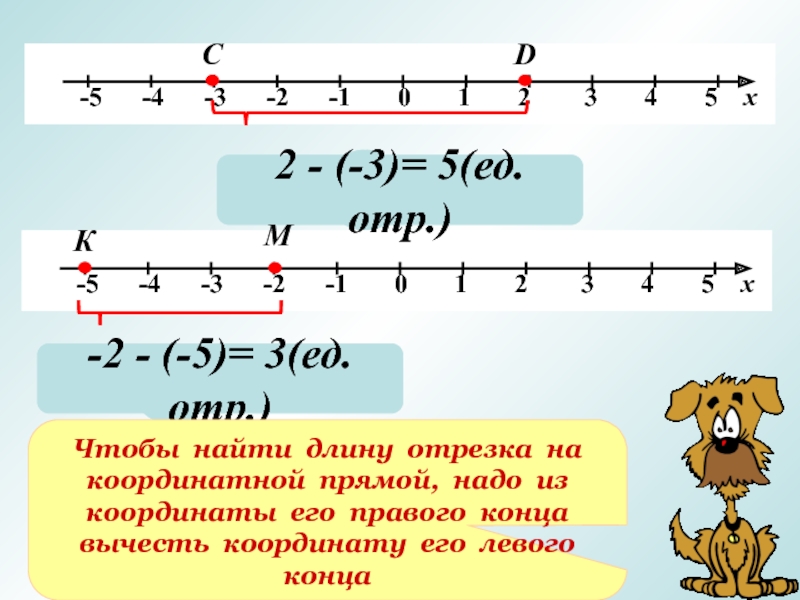
Если вы все сделаете правильно, вы должны получить
х = \( \frac{mx_2-nx_1}{mn}\)
y = \( \frac{my_2-ny_1}{mn}\)
Краткое содержание урока
- Координаты точки, разделяющегося сегментом линии присоединение (x 1 , Y 1 ) и (x 2 , Y 2 ) В соотношении м: N Внутренний на \(\left ( \frac{mx_2+nx_1}{m+n}, \frac{my_2+ny_1}{m+n} \right) \)
- Координаты точки, разделяющей отрезок, соединяющий (x 1 , y 1 ) и (x 2 , y 2 ) , задаются внешним образом 24 м : \(\left (\frac{mx_2-nx_1}{mn}, \frac{my_2+ny_1}{m+n} \right) \)
Вот и все.Увидимся на следующем уроке с некоторыми примерами и применениями формулы сечения!
.





 Это дает вам x-координату средней точки, x M
Это дает вам x-координату средней точки, x M 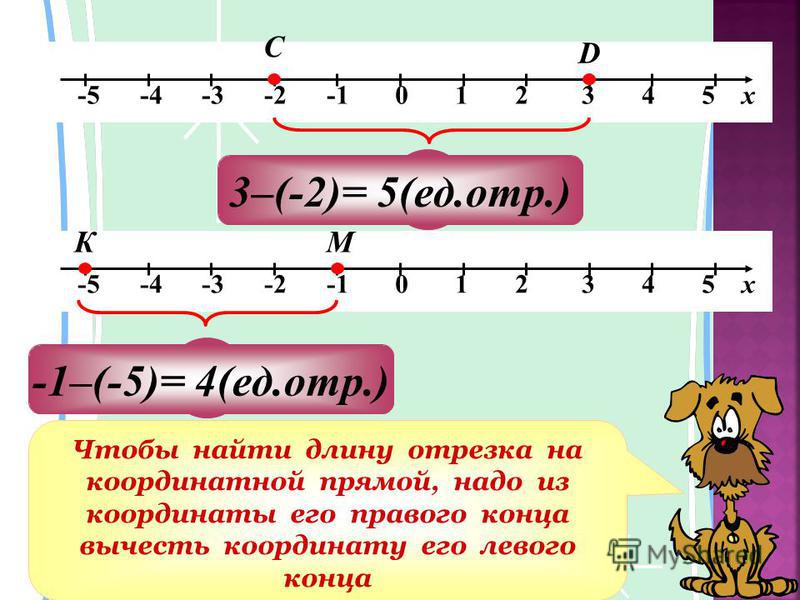 2} \)
2} \)
