2.3. Численный и линейный масштабы карты

Численный масштаб — это масштаб карты, выраженный дробью, числитель которой единица, а знаменатель — число, показывающее, во сколько раз уменьшены на карте линейные размеры всех объектов. Чем меньше знаменатель, тем крупнее масштаб карты. Так, например, масштаб 1:25 000 показывает, что все линейные размеры элементов и объектов местности при изображении на карте уменьшены в 25 000 раз.

Расстояние на местности в метрах и километрах, соответствующее 1 см на карте, называется величиной масштаба (см. табл. 5). Она указывается на карте под численным масштабом.

При пользовании численным масштабом расстояние, измеренное на карте в сантиметрах, умножают на знаменатель численного масштаба в метрах. Например, на карте масштаба 1:50 000 расстояние между двумя объектами равно 4,7 см; на местности оно будет 4,7×500=2350 м. Если расстояние, измеренное на местности, необходимо отложить на карте, то его надо разделить на знаменатель численного масштаба. Например, на местности расстояние между двумя объектами составляет 1525 м; на карте масштаба 1:50 000 оно будет 1525:500-3,05 см .

Линейный масштаб представляет собой графическое выражение численного масштаба. На шкале линейного масштаба оцифрованы отрезки, соответствующие расстояниям на местности в метрах и километрах. Это облегчает процесс измерения расстояний, так как не требуется производить вычисления.

Измерения по линейному масштабу выполняют с помощью циркуля — измерителя. Длинные прямые линии и извилистые линии на карте измеряют по частям.

Точность измерения длины прямолинейных отрезков на карте с помощью циркуля — измерителя не превышает 0,1 мм. Эта величина называется предельной графической точностью масштаба карты. Графическая ошибка измерения длины отрезка на карте зависит от деформации бумаги и условий измерения. Обычно она колеблется в пределах 0,5- 1мм.

Ошибки в определении расстояний по топографическим картам различных масштабов приведены в табл. 7.

Таблица 7

Масштаб карты	Предельная графическая ошибка, м	Средняя ошибка, м
1:25 000	2,5	12-25
1:50 000	5	25-50
1:100 000	10	50-100
1:200 000	20	100-200
1:500 000	50	250-500
1:1000 000	100	500-1000

2.4. Географические координаты на карте

Внутренними рамками топографических карт являются отрезки параллелей и меридианов. Их широта и долгота подписана на углах каждого листа карты. На картах 1:25 000 — 1:200 000 стороны рамок разделены на отрезки, равные 1′. Эти отрезки оттенены через один и разделены точками (кроме карты масштаба 1:200 000) на части по 10».

На каждом листе карты 1:50 000 и 1:100 000 показаны, кроме того, пересечение средних меридиана и параллели с оцифровкой в градусах и минутах, а по внутренней рамке — выходы минутных делений штрихами длиной 2-3 мм это позволяет при необходимости прочерчивать параллели и меридианы на карте, склеенной из нескольких листов.

При составлении карт 1:500 000 и 1:1 000 000 на них наносят картографическую сетку параллелей и меридианов. Параллели проводят соответственно через 20 и 40′, а меридианы — через 30′ и 1 °. На линиях параллелей и меридианов каждого листа карты этих масштабов подписывают широту и долготу, наносят штрихи соответственно через 5 и 10′, что позволяет легко определять географические координаты точек на отдельном листе и на склейке карты.

Географические координаты точки определяют от ближайших к ней параллели и меридиана, широта и долгота которых известна. Точность определения географических координат по картам 1:25 000 — 1:200 000 составляет около 2 и 10» соответственно (рис. 10).

Рис. 10. Определение географических координат точек по карте (точка А) и нанесение на карту точек по географическим координатам (точка Б)

studfile.net

Найти численный масштаб по именному масштабу:

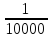– численный масштаб

В 1 см 5000 см – именной

а) в 1 см — 500 м — 1 : 50 000

б) в 1 см — 10 км — 1 : 1 000 000

в) в 1 см — 250 км — 1 : 25 000 000

2. Найти точность масштаба:

Точность масштаба — это отрезок горизонтального проложения линии, соответствующий 0,1 мм на плане. Значение 0,1 мм для определения точности масштаба принято из-за того, что это минимальный отрезок, который человек может различить невооруженным глазом. Например, для масштаба 1:10 000 точность масштаба будет равна 1 м. В этом масштабе 1 см на плане соответствует 10 000 см (100 м) на местности, 1 мм — 1 000 см (10 м), 0,1 мм — 100 см (1 м).

точностью масштаба t, она определяется по формуле: t = 0,1 × М.

3. Вычислить расстояние на местности по расстоянию на карте и ее масштабу:

4. Определить номер шестиградусной зоны по географическим координатам:

Например: x=5876354,86м

y=7564806,51м

в Y: 7 – номер зоны, 5 – сдвиг на 500 км

5. Определить положение точки в шестиградусной зоне по прямоугольным координатам:

6. Определить номенклатуру листа карты по номенклатуре смежного листа:

Масштаб карты	Масштаб исходного листа	Исходный лист делится на	Протяжение по широте (по вертикали) и долготе (по горизонтали	Пример номенклатуры для последнего листа
Топокарты 1:1000000 1:500000 1:200000 1:100000 1:50000 1:25000 1:10000 1:5000 1:2000	— 1:1000000 1:1000000 1:1000000 1:100000 1:50000 1:25000 1:100000 1:5000	— 2×2 6×6 12×12 2×2 2×2 2×2 16×16 3×3	4°х6° 2°x6° 40’x1° 20’x30’ 10’x15’ 5’x7.5’ 2.5’x3.75’ 1.25’x1.875’ 25’’x37.5’’	N-37 N-37-Г N-37-XXXVI N-37-144 N-37-144-Г N-37-144-Г-2 N-37-144-Г-2-4 N-37-144-(256) N-37-144-(256-И)
Планы 1:5000 1:2000 1:1000 1:500	— 1:5000 1:2000 1:2000	— 2×2 2х2 4×4	40×40см 50×50см 50х50см 50×50см	6 6-Г 6-Г-IV 6-Г-16

Пример разграфки листа миллионной карты на карты масштаба 1:500 000 (синие), 1:200 000 (зелёные) и 1:100 000 (жёлтые)

Пример разграфки листа стотысячной карты на карты масштаба 1:50 000 (синие) и 1:25 000 (зеленые)

7. Нарисовать горизонтали по 4-м опорным точкам:

8. Определить уклон дороги по масштабу, заложению и высоте сечения рельефа:

i=h/d*ρ”=h₀/d*m

d-расстояние

m-знаменатель масштаба

9. Определить число горизонталей между опорными точками с заданной высотой сечения рельефа:

10. Найти высоту горизонтали по ближайшей к ней точке:

Абсолютную высоту какой-либо точки местности, отметка которой на карте не подписана, определяют по отметке ближайшей к ней горизонтали. Поэтому необходимо уметь определять отметки горизонталей, используя отметки других горизонталей и характерных точек местности, подписанных на карте.

Например, отметку горизонтали а (рис.3) можно определить по отметке высоты 197,4 и высоте сечения рельефа 10 м.

Рис.3 Определение отметки горизонтали по отметке точки.

Отметка горизонтали а равна 190 м. Зная отметку горизонтали а, можно легко определить отметки всех других горизонталей. Так, горизонталь b будет иметь отметку 160 м, так как она расположена ниже горизонтали а на величину, равную трем высотам сечения рельефа (30 м). В случае когда точка расположена между горизонталями, находят высоту ближайшей к ней горизонтали и к полученной высоте прибавляют превышение данной точки над горизонталью, определенное на глаз. Например, мельница, обозначение которой находится между горизонталями (рис.3), имеет абсолютную высоту 162 м.

11. Вычислить площадь участка по числу квадратов палетки и масштабу карты:

12. Вычислить цену деления планиметра по размеру обводимого квадрата, отсчетам и масштабу карты:

N₁ — отсчет первый

N₂ — отсчет второй

a – сторона квадрата (мм, см)

m – знаменатель масштаба карты

цена деления: ȵ = S/(N₂-N₁)=a²m²/(N₂-N₁)

13. Вычислить дирекционный угол по румбу или значению румба и знакам приращения координат:

r=arctg

14. Вычислить дирекционный угол по истинному азимуту и сближению меридиан:

α= γ-А_н

γ – сближение меридиан

А_н – истинный азимут

15. Вычислить истинный азимут по магнитному азимуту и склонению магнитной стрелки:

А_н=А_м+δ

А_н – истинный азимут

А_м – магнитный азимут

δ – склонение магнитной стрелки

16. Вычислить коллимационную ошибку теодолита по отсчетам по горизонтальному кругу:

С=

17. Обработать отсчеты по горизонтальному кругу при измерении углов способами приемов и круговых приемов:

а) Способ приемов (если один угол): по часовой стрелке

	КЛ	КП
А	228°41′	48°42’
В	17°27’	197°29’

N=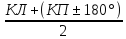 — средний отсчет N(_A)=228°41,5′ N(_B) =17°28’

Β=N(_B) – N(_A). Если искомый угол получается отрицательным, то прибавляем 360°.

б) Способ круговых приемов (более двух углов, но не более 5)

	КЛ	КП	N
A	(1) 0°4’	(1)180°6’	0°5’
B	(2)107°37’	(2)287°39’	107°38’
C	(3)251°3’	(3)71°6’	251°4.5’
A	(4)0°6’	(4)180°7’	0°6.5’
	∆ +2’	∆ +1’

и после этого — значения углов относительно первого (начального) направления.

18. Найти угол наклона и место нуля по отсчетам по вертикальному кругу:

— место нуля

ν = КЛ-МО=МО-КП=(КЛ-КП)/2 – угол наклона

19. Вычислить угол наклона по зенитному расстоянию:

ν = 90° — Z

Z – зенитное расстояние — угол между вертикальным направлением и направлением линии местности.

20. Вычислить расстояние по отсчетам по дальномерным нитям теодолита:

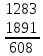D=60,8м

21. Вычислить поправку в измеренное расстояние по результатам компарирования рулетки:

Например, на 20м отрезке рулетка показала 20,015

D=200м

_∆d=0,015м

_∆D=_∆d*n=-0,15, где n – число уложенных лент.

При длине ленты больше номинальной – поправка положительная, при длине меньше номинальной – отрицательная.

22. Вычислить горизонтальное проложение по наклонной длине и превышению:

d=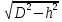

23. Вычислить недоступное расстояние по базису и измеренным от него горизонтальным углам:

d=

24. Вычислить результаты поверки главного условия нивелира по отсчетам по рейке:

I ст	а1	b1
II ст	а2	b2

h₁ = a₁-b₁ — превышение

h₂=a₂-b₂

Х=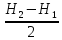

studfile.net

Что такое масштаб и как его найти

Масшта́б (нем. Maßstab, букв. «мерная палка»: Maß «мера», Stab «палка») — в общем случае отношение двух линейных размеров. Во многих областях практического применения масштабом называют отношение размера изображения к размеру изображаемого объекта. Понятие наиболее распространено в геодезии, картографии и проектировании — отношение натуральной величины объекта к величине его изображения. Человек не в состоянии изобразить большие объекты, например дом, в натуральную величину, поэтому при изображении большого объекта в рисунке, чертеже, макете и т. п. человек уменьшает величину объекта в несколько раз: в два, пять, десять, сто, тысячу и так далее. Число, показывающее, во сколько раз уменьшен изображенный объект, есть масштаб. Масштаб применяется и при изображении микромира. Человек не может изобразить живую клетку, которую рассматривает в микроскоп, в натуральную величину и поэтому увеличивает величину ее изображения в несколько тысяч раз. Число, показывающее, во сколько раз произведено увеличение или уменьшение реального явления при его изображении, определено как масштаб. Масштаб показывает, во сколько раз каждая линия, нанесенная на карту или чертёж, меньше или больше её действительных размеров. Есть три вида масштаба: численный, именованный, графический. Масштабы на картах и планах могут быть представлены численно или графически. Численный масштаб записывают в виде дроби, в числителе которой стоит единица, а в знаменателе — степень уменьшения проекции. Например, масштаб 1:5 000 показывает, что 1 см на плане соответствует 5 000 см (50 м) на местности. Более крупным является тот масштаб, у которого знаменатель меньше. Например, масштаб 1:1 000 крупнее, чем масштаб 1:25 000. Именованный масштаб показывает какое расстояние на местности соответствует 1 см на плане. Записывается, например: «В 1 сантиметре 100 километров», или «1 см = 100 км». Графические масштабы подразделяются на линейные и поперечные. Линейный масштаб — это графический масштаб в виде масштабной линейки, разделённой на равные части. Поперечный масштаб — это графический масштаб в виде номограммы, построение которой основано на пропорциональности отрезков параллельных прямых, пересекающих стороны угла. Поперечный масштаб применяют для более точных измерений длин линий на планах. Поперечным масштабом пользуются следующим образом: откладывают на нижней линии поперечного масштаба замер длины таким образом, чтобы один конец (правый) был на целом делении ОМ, а левый заходил за 0. Если левая ножка попадает между десятыми делениями левого отрезка (от 0), то поднимаем обе ножки измерителя вверх, пока левая ножка не попадёт на пересечение к-либо трансвенсали и какой-либо горизонтальной линии. При этом правая ножка измерителя должна находиться на этой же горизонтальной линии. Наименьшая ЦД=0,2 мм, а точность 0,1. Точность масштаба — это отрезок горизонтального проложения линии, соответствующий 0,1 мм на плане. Значение 0,1 мм для определения точности масштаба принято из-за того, что это минимальный отрезок, который человек может различить невооруженным глазом. Например, для масштаба 1:10 000 точность масштаба будет равна 1 м. В этом масштабе 1 см на плане соответствует 10 000 см (100 м) на местности, 1 мм — 1 000 см (10 м), 0,1 мм — 100 см (1 м).

touch.otvet.mail.ru