Школьный туризм
Масштаб карты
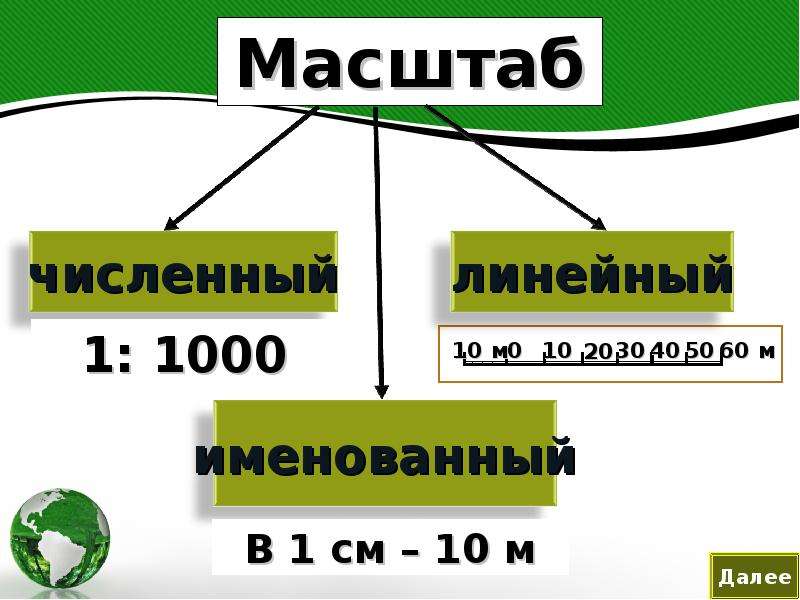
Масштабом называют соотношение настоящих размеров объекта к изображению, модели объекта. Географический масштаб помогает определить, во сколько раз на карте уменьшили все реальные размеры — площадь территории, отдельных объектов, длину рек, дорог и т.д.
В древности масштаба не знали, потому объекты располагали на карте на произвольном расстоянии друг от друга. Пользуясь такой картой, человек не мог определить, будет он добираться до нужного места 2 дня, 2 недели или 2 месяца. Первым
картографом, применившим в составлении карты масштаб, был Анаксимандр Милетский — древнегреческий учёный (VI – V вв. до н. э.),
придумавший термин «закон» и предложивший первую формулировку закона сохранения материи. В зависимости от масштаба карты условно
разделяют на:
— мелкомасштабные (обзорные) — менее 1:1 000 000;
— среднемасштабные (обзорно-топографические) — от 1:200 000 до 1:1 000 000;
— крупномасштабные (топографические) — от 1:10 000 до 1:100 000.
Масштабы до 1:5 000 используют преимущественно в составлении топографического плана. Вид масштаба: масштабы графические, численные, именованные В легендах географических карт используют графический (он же — линейный) и численный масштаб, редко прибегают к именованному.
Масштаб численный
Для его записи применяют дроби, в которых числители — это 1 см (если не оговорено иного), а знаменатели — числа, показывающие, в какое количество раз уменьшен показатель. К примеру, масштаб 1:25 000 демонстрирует, что 1 см карты соответствует 25 000 см (250 м) местности. Чем меньше знаменатель, тем крупнее масштаб: 1:1000 крупнее, чем 1:5 000, т.к. в первом случае в 1 см карты «умещается» 10 м, а во втором — 50 м. Карты с крупным масштабом подробнее, содержательнее, но использовать их можно для небольших участков местности.
Линейный(графический)
Масштаб Линейный, или графический масштаб, особенно удобен и даёт возможность узнавать расстояния, размеры без
расчётов и переводов длин из масштабных в реальные.
Именованный масштаб
Именованный масштаб отличается от прочих тем, что в нём словами прописано, сколько в 1 см содержится метров или километров.
Например: в 1 см — 250 м; в 1 см — 5 км. Где искать масштаб на карте? Чтобы узнать масштаб географической карты, нужно посмотреть
углы карты или её легенду. Легендой называют список обозначений с их разъяснением. Очень часто на картах приводятся все 3 вида
масштабов, чтобы каждый человек смог разобраться, во сколько раз реальные расстояния уменьшены на карте. Стандарты численных
масштабов В Российской Федерации приняты следующие стандарты численного масштаба:
-1:25 000;
-1:50 000;
-1:100 000;
-1:200 000;
-1:300 000;
-1:500 000;
-1:1 000 000;
Существуют также карты с масштабом 1:2 000, 1:5 000.
 Их используют для специальных задач, т.к. столь крупные масштабы — область применения топографических планов.
Их используют для специальных задач, т.к. столь крупные масштабы — область применения топографических планов.Параметры точности масштаба
Точность масштаба на чертеже ограничена расстоянием в 0,01 см. Количество метров, соответствующее этому показателю на местности, и
называется определением «графическая точность».
Чтобы узнать этот показатель, нужно воспользоваться градусной сеткой и провести некоторые вычисления. Лучше всего использовать
численный масштаб. Берем его знаменатель и делим на 10 000, поскольку 1 см плана содержит 10 тысяч отрезков по 0,01 см. Полученное
число и будет соответствовать размеру точности.
Например, если карта имеет масштаб 1:25 000, его точность на местности будет составлять 2,5 метра, а для схемы 1:100 000 – 10 метров
и так далее.
Способ определения масштаба
В начале статьи мы уже описывали, как можно определить масштаб изображения с помощью километровой сетки и линейки. Но есть и другие
способы установить степень уменьшения и масштабирование на конкретном плане местности.
Номенклатура карты: чтобы воспользоваться данным способом, нужно внимательно рассмотреть реквизиты карты. Фактически, номенклатура –
это буквенно-числовое название листа. У каждого масштабного ряда есть свое обозначение. Например, М-35 соответствует масштабу
1:1000000, а М-35-18-А-6-1 – 1:10000. Конечно, для определения данным способом нужно наизусть знать номенклатурные обозначения.
Известные расстояния: в данном случае на карте нужно найти изображения километровых столбов, которые обычно устанавливают на шоссе.
Прямо на карте нужно измерить расстояние между ними. В данном случае количество сантиметров на карте будет соответствовать одному
километру на местности.

Как определить масштаб карты
Определить степень уменьшения объектов на карте можно путем простых вычислений На картах с масштабом 1:2000000 обычно указывается расстояние между определенными населенными пунктами в километрах. В данном случае, для определения масштаба нужно измерить расстояние на карте линейкой. Потом расстояние, указанное в километрах, следует разделить на полученное число в сантиметрах. В результате у вас получится число, которое будет соответствовать количеству километров в одном сантиметре.
Правила оформления
Если топографическая карта местности была изготовлена правильно, на ней должен обязательно быть указан масштаб. Исключение могут быть
только самодельные карты или планы местности, нарисованные вручную. Во всех остальных случаях масштаб должен быть оформлен согласно
ГОСТу.
Если карта была составлена правильно, находить даже уменьшенные объекты не составит труда, ведь все измерения точно соответствуют
расположению на местности.
Порядок определения масштаба на готовом чертеже
Масштаб нужно не только для того, чтобы определить расстояние на карте. Он также используется при составлении чертежей . Важно правильно выбрать масштаб для чертежа детали. Например, небольшие или сборные элементы лучше выполнять в натуральную величину, то есть в масштабе 1:1. Но иногда, для удобства чтения объект, нарисованный на бумаге, уменьшают или увеличивают. Узнать масштаб чертежа несложно, так как он определяется примерно так же, как и географический. В первую очередь нужно внимательно изучить чертеж. Согласно ГОСТу, масштаб должен быть указан в правом нижнем углу. При этом в машиностроении и приборостроении обычно используют увеличение, а на строительных чертежах – уменьшение.
Масштаб на чертеже
Информация о размерах нарисованной детали относительно реальной обычно указывают в правом нижнем углу чертежа
Если по каким-то причинам вы не можете найти масштаб на готовом чертеже невозможно, можно попытаться определить его. Если под рукой
есть деталь, можно просто измерить ее штангенциркулем. Также можно определить масштаб по габаритным размерам детали, указанным на
чертежах.
Если под рукой
есть деталь, можно просто измерить ее штангенциркулем. Также можно определить масштаб по габаритным размерам детали, указанным на
чертежах.
Как измерять линейный масштаб. Что такое масштаб? Масштаб фотографий, масштаб карт
Масштаб – степень уменьшения горизонтальных проложений линий местности при их изображении на плане и карте. М вычисляют как отношение длины линии на чертеже, плане, карте к длине горизонтального проложения этой линии на местности.
Горизонтальное проложение – ортогональная проекция линии с физической поверхности Земли на горизонтальную плоскость. Виды Масштаба:
а) численный;
Численный масштаб записывают в виде дроби, в числителе которой стоит единица, а в знаменателе — степень уменьшения проекции. Например, масштаб 1:5 000 показывает, что 1 см на плане соответствует 5 000 см (50 м) на местности.
Более
крупным является тот масштаб, у которого
знаменатель меньше. Например, масштаб
1:1 000
крупнее, чем масштаб 1:25 000.
б) именованный;
вид масштаба, словесное указание того, какое расстояние на местности соответствует 1 см на карте, плане, снимке.
в) линейный;
Линейный масштаб— это графический масштаб в виде масштабной линейки, разделённой на равные части.
г) поперечный
масштаб — график (обычно на металлической пластинке) для измерения и откладывания расстояний на карте с предельной графической точностью (0,1 мм).
Расстояние на местности, соответствующее наименьшему делению линейного масштаба карты. Расстояние на местности, соответствующее 0,1 мм в масштабе карты, называется предельной точностью масштаба .
Виды карт: Оперативные (1:10 6 ,500к,200к) тактические (1:100к,50к,25к,10к). Типы: Мелко-(1,2), средне-(3,4), крупномасштабные(5,6,7)
Виды карт | Масштаб карты | Типы карт | Порядок образования листа карты | Схема образования листа карты | Размер листа карты | Пример номенклатуры |
Оперативные | Мелкомасштабные | деление земного эллипсоида параллелями, меридианами | ||||
деление листа миллионной карты на 4 части | ||||||
Среднемасштабные | деление листа миллионной карты на 36 частей | |||||
Тактические | деление листа миллионной карты на 144 части | |||||
Крупномасштабные | деление
листа карты
М. | |||||
деление листа карты М. 1:50 000 на 4 части | ||||||
деление листа карты М. 1:25 000 на 4 части | 2″ 30″ × 3″ 45″ |
4.Понятия о плане и карте. Условные знаки.
План местности — простейшая разновидность географической карты; чертёж небольшого участка местности в крупном масштабе. Планы применяются туристами, коммунальными и аварийными службами, в сельском хозяйстве и в других местах, где нужно ориентироваться на местности и изучать участки
Карта —
Географической картой называется
уменьшенное в определенном масштабе
изображение на плоскости земной
поверхности в определенной картографической
проекции. Это изображение обычно
условное, так же это может быть чертеж
земной поверхности или объекта, в
уменьшенном или обобщенном виде.
Это изображение обычно
условное, так же это может быть чертеж
земной поверхности или объекта, в
уменьшенном или обобщенном виде.
В отличие от плана карта имеет более мелкий масштаб. Так на плане он крупнее, чем 1: 5000. Изображения земной поверхности с более мелким масштабом можно считать картами.
Масштаб влияет на изображаемую площадь. Чем крупнее масштаб, тем меньшую площадь можно изобразить. Соответственно на планах изображается небольшая территория, а на картах можно изобразить любую площадь, в том числе и весь земной шар.
На планы обычно стараются нанести все детали изображаемой местности, а на карту только наиболее существенные объекты. Причем карты бывают разного типа, и соответственно важные объекты для каждого типа карты свои.
На планы не наносят параллели и меридианы, в то время как на картах их обозначают всегда.
Условные знаки служат для того, чтобы на карте показать тот или иной объект (очень простым языком)
Картографические
условные знаки — система символических
графических обозначений (знаков),
применяемая для изображения на картах
различных объектов и явлений, их
качественных и количественных
характеристик. Условные знаки иногда
также называют «легенда карты».
Условные знаки иногда
также называют «легенда карты».
Например: Леса (вырубленный, горелый и др), колодцы, пещеры, ямы, болота, мосты, скалы, пещеры, ключи, жд дороги, овраги и тд.
ВОТ ВАМ КАК ПРИМЕР
Масштаб — это отношение 2-х линейных размеров, которое используется при создании чертежей и моделей и позволяет показывать крупные объекты в уменьшенном виде, а мелкие в укрупненном. Иными словами, это отношение длины отрезка на карте к истинной длине на местности. Разные практические ситуации могут потребовать от вас знания о том, как найти масштаб.
Когда появляется необходимость в определении масштаба? В основном это происходит в следующих ситуациях:
- при использовании карты;
- при выполнении чертежа;
- при изготовлении моделей различных объектов.
Виды масштаба
Под численным масштабом следует понимать масштаб, выраженный дробью. Ее числитель — единица, а знаменателем является число, показывающее, во сколько раз изображение меньше реального объекта.
Линейный масштаб — это мерная линейка, которую вы можете увидеть на картах. Этот отрезок поделен на равные части, подписанные значениями соразмерных им расстояний на реальной местности. Удобен линейный масштаб тем, что обеспечивает возможность измерять и строить расстояния на планах и картах.
Именованный масштаб представляет собой словесное описание того, какое расстояние в реальности соответствует одному сантиметру на карте. К примеру, в одном километре 100000 сантиметров. При этом численный масштаб выглядел бы следующим образом: 1:100000.
Как найти масштаб карты?
Возьмите, к примеру, школьный атлас и взгляните на любую его страницу. В нижней части вы можете увидеть линейку, на которой указано, какое расстояние на реальной местности соответствует одному сантиметру на вашей карте.
Масштаб в атласах обычно указывается в сантиметрах, которые нужно будет перевести в километры. К примеру, увидев надпись 1:9 500 000, вы поймете, что 95 километрам реальной местности соответствует всего-навсего 1 см карты.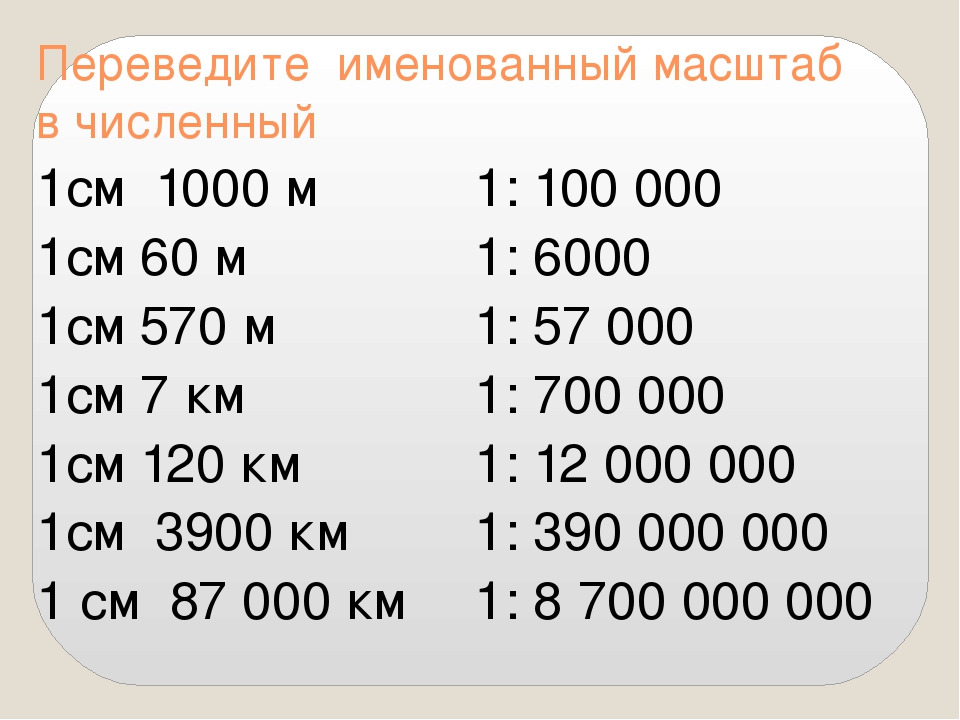
Если, вы к примеру знаете, что расстояние между вашим городом и соседним — 40 км, то можно просто измерить линейкой промежуток между ними на карте и определить соотношение. Итак, если путем измерения вы получили расстояние 2 см, то получите масштаб 2:40=2:4000000=1:2000000. Как видите, находить масштаб совсем несложно.
Другие случаи использования масштаба
При изготовлении моделей самолетов, танков, кораблей, автомобилей и других объектов используются определенные стандарты масштабирования. К примеру, это может быть масштаб 1:24, 1:48, 1:144. При этом изготовленные модели должны быть меньше своих прототипов именно в указанное число раз.
Масштабирование может понадобиться, к примеру, при увеличении какого-либо рисунка. При этом изображение разделяется на клетки определенного размера, к примеру, 0.5 см. Лист бумаги надо будет тоже расчертить на клетки, но уже увеличенные в необходимое число раз (примеру, длины их сторон могут составлять полтора сантиметра, если рисунок нужно увеличить в 3 раза). Нанеся контуры исходного рисунка на расчерченный лист, можно будет получить изображение, очень близкое к оригиналу.
Нанеся контуры исходного рисунка на расчерченный лист, можно будет получить изображение, очень близкое к оригиналу.
Инструкция
Внимательно рассмотрите карту и найдите километровую сетку, которая должна быть на ней проставлена. Стороны квадратов сетки соответствуют определенному количеству , узнать это количество вы можете по подписям на выходах линии стеки у края рамки карты. К примеру, расстояние между двумя соседними линиями сетки равно 1 км. Измерьте это расстояние линейкой. Допустим, вы получили 2 см. Таким образом, масштаб карты: в 1 см 500 м или 1:50000.
Второй способ определения масштаб а – по номенклатуре карты. Внимательно рассмотрите реквизиты карты. Номенклатура представляет собой буквенно-числовое листа карты. Любой масштаб ный ряд имеет свое конкретное , по которому специалист легко определит масштаб карты. Например, номенклатурное обозначение М-35 масштаб 1:1000000; М-35-XI обозначает масштаб 1:200000; М-35-18-А-6-1 – масштаб 1:10000 и т. д. Разумеется, для определения масштаб а таким способом необходимо иметь представление о номенклатурных обозначениях и определенный опыт обращения с топографическими картами.
д. Разумеется, для определения масштаб а таким способом необходимо иметь представление о номенклатурных обозначениях и определенный опыт обращения с топографическими картами.
Третий способ определения масштаб а карты – по известным расстояниям. Найдите изображения километровых столбов на шоссейных дорогах. Измерьте по расстояние от одного столба до другого. Вы сразу узнаете масштаб карты (число сантиметров карты будет соответствовать одному километру местности).
На картах масштаб а 1:200000 на дорогах обозначены расстояния между населенными пунктами в . В таком случае измерьте по карте при помощи линейки расстояние в сантиметрах от одного населенного пункта до другого, а подписанное количество километров разделите на расстояние, выраженное в сантиметрах. Таким образом, вы получили величину масштаб а карты, то есть число километров в .
Если вы находитесь на местности, которая изображена на карте, определите ее масштаб по измеренным расстояниям.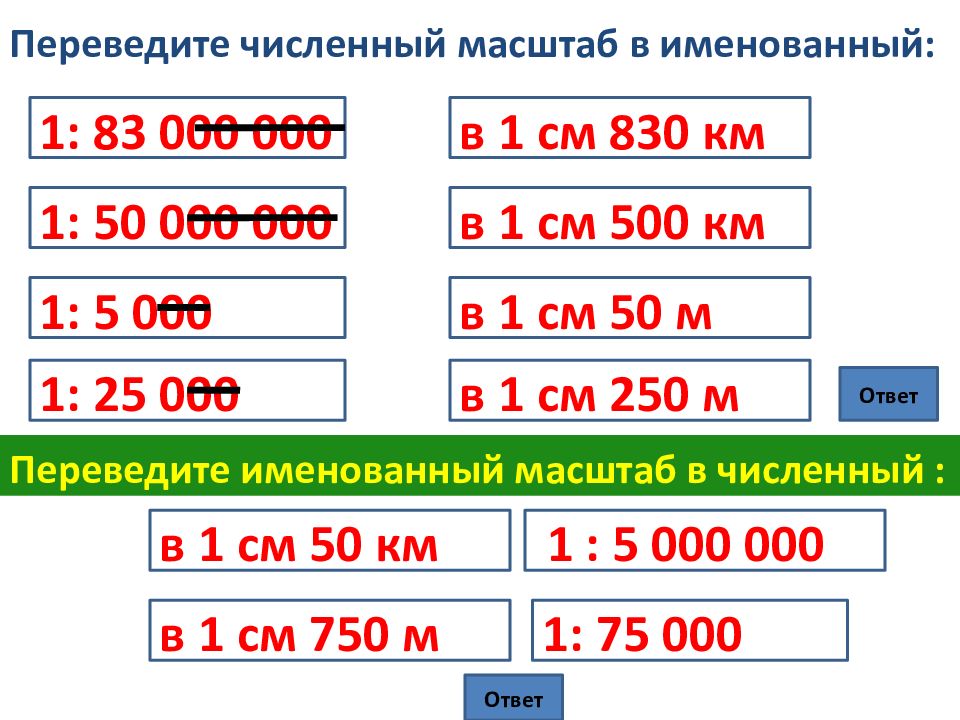 Для этого измерьте расстояние между нанесенными на карту объектами.
Для этого измерьте расстояние между нанесенными на карту объектами.
Используйте также знание длины дуги меридиана. Одна минута по равна примерно 2 км, а более точно – 1,85 км. На боковой стороне рамки карты даны подписи градусов и минут, каждая минута шашечкой. Если, допустим, длина одной минуты равна 3,7 см, то масштаб карты будет 1:50000 (один сантиметр на карте равен 0,5 км на местности).
Источники:
- Как определить масштаб
- Точность масштаба Длины линий на местности, соответствующие
Изображение крупных обьектов можно получить на бумажном или любом другом носителе только в уменьшенном виде. Это, в первую очередь, касается различных карт местности. Масштабом карты называется отношение длины линии, нанесенной между двумя точками на плане или карте к тому же расстоянию на местности. Знать масштаб необходимо для того, чтобы измерять расстояния по карте.
Инструкция
Обычно, любой карты или указан в ее легенде – сопровождающем пояснительном тексте. Масштаб может быть изображен в виде шкалы или текста, в котором указывается, сколько метров или километров на местности равен 1 см расстояния, отложенного по данной . Масштаб 1: 50000 , что 1 см, отложенный на данной карте, равен 500 метрам или 0,5 км в натуре. Чем крупнее масштаб, тем меньшее число указывается в его числителе. Топографические карты масштаба 1:10000 и крупнее относятся к сведениям, гриф «секретно».
Масштаб может быть изображен в виде шкалы или текста, в котором указывается, сколько метров или километров на местности равен 1 см расстояния, отложенного по данной . Масштаб 1: 50000 , что 1 см, отложенный на данной карте, равен 500 метрам или 0,5 км в натуре. Чем крупнее масштаб, тем меньшее число указывается в его числителе. Топографические карты масштаба 1:10000 и крупнее относятся к сведениям, гриф «секретно».
Если по какой-то причине масштаб карты не указан, отсутствует зарамочное или легенда, то определить его можно с помощью геоинформационных картографических серверов GoogleEarth или YandexMap, включив их в режиме «Гибрид», который позволяет одновременно со спутниковой фотографической основой видеть оцифрованное изображение местности – , границы городов, отдельно стоящие здания.
Определите географическое положение изображенной на ней местности. Выберите на ней две характерные точки, которые можно будет легко идентифицировать по спутниковому снимку данной местности. Обычно, удобно использовать для этого перекрестки магистралей или усовершенствованных шоссе, автодорог.
Обычно, удобно использовать для этого перекрестки магистралей или усовершенствованных шоссе, автодорог.
Найдите эти две точки по спутниковому снимку местности. Инструментом «Линейка» измерьте расстояние между ними. При активации инструмента появляется табличка, где автоматически будет высвечиваться расстояние между двумя указанными вами точками на космическом спутниковом снимке. Задайте удобные для вас единицы измерения – метры, километры.
Разделите полученное по спутниковым снимкам расстояние на количество сантиметров, измеренных по карте. Вы получите значение масштаба данной карты .
Видео по теме
Масштаб показывает, во сколько раз карта уменьшает реальную местность, которая на ней изображена. Только зная эту величину, можно откладывать на карте или схеме местности реальные расстояния. Узнать масштаб можно по маркировке на карте. Если таковой не имеется, рассчитайте его по линиям параллелей.
Вам понадобится
- — различные карты;
- — линейка;
- — калькулятор.

Инструкция
Если на плане или нанесена номенклатура листа, то по специальной таблице определите масштаб карты. Например, если на листе карты есть М-35-А, то ее масштаб составляет 1:500000. Это значит, что 1 см , на местности составляет 500000 см или 5 км.
Если маркировки нет, обратите внимание на километровую сетку, которая наносится на любую топографическую карту. Сторона квадрата такой сетки соответствует фиксированному количеству . Измерьте линейкой сторону этого квадрата в см и найдите отношение расстояния на карте к реальному. Это и будет масштаб. Например, если стека на карте 4 км, а расстояние между линиями составляет 2 см, то масштаб будет равен 2:4 км=2:400000 см=1:200000 см.
Если более крупного с параллелями, то определите его с помощью этой сетки. Для этого измерьте расстояние между двумя нанесенными рядом параллелями в сантиметрах. На этих рядом стоящих параллелях от большего числового значения вычтите меньшее. Поскольку один параллели соответствует 111 км, непосредственно на местности, умножьте полученную разницу на это число, а также число 100000 для того, чтобы это расстояние в сантиметры.
Найдите отношение измеренного линейкой расстояния к результату вычислений. Получите масштаб карты. Например, если параллели идут 0?, 10?, 20? и т.д. найдите разницу двух близлежащих линий. Она составит 10. Затем, умножьте это число на 111 и 100000. Получите 10 111 100000=111000000. Если расстояние измеренное линейкой равно 4,5 см, получите масштаб 4,5:111000000 см?1:25000000 см. Это значит, что одном карты умещается 250 км местности.
Измеряйте масштаб по реальным расстояниям. Для этого известное расстояние отложите на карте, и соотнесите с реальным. Например, если расстояние между двумя составляет 400 км, а на карте оно равно 8 см, найдите соотношение 8:400 км=8:40000000=1:5000000. Это и есть масштаб карты.
Топографические планы и карты, составленные на их основе, являются точными изображениями земной поверхности, спроектированными на плоскость. Масштаб – отношение размера любого топографического объекта на карте к его реальному размеру на местности, позволяет производить по ней линейные и площадные измерения.
Перед тем как начать рассматривать стандартные масштабы чертежей, следует понять, что именно представляет собой данное понятие. Итак, подобное значение является в общем случае соотношением двух линейных размеров. Однако более широко известно такое толкование данного определения, как отношение размера чертежа к габаритам реального объекта. Следовательно, можно совершенно справедливо предположить, что вышеописанный термин нашел широкое применение в картографии, геодезии и, конечно же, проектировании.
Зачем это необходимо?
Как уже говорилось ранее, реальные объекты могут иметь как достаточно значительные размеры, так и очень маленькие. Однако человек не может зарисовать все в натуральную величину, поскольку для отображения на листе бумаги потребуется полотно колоссальных габаритов, а, в свою очередь, для воссоздания мелких элементов (как, например, в часовом механизме) потребовалась бы высокая степень детализации. В результате человек приспособился изображать необходимые объекты, которые в определенное количество раз уменьшены (либо увеличены) для простоты восприятия и так называемой «читабельности» рисунка.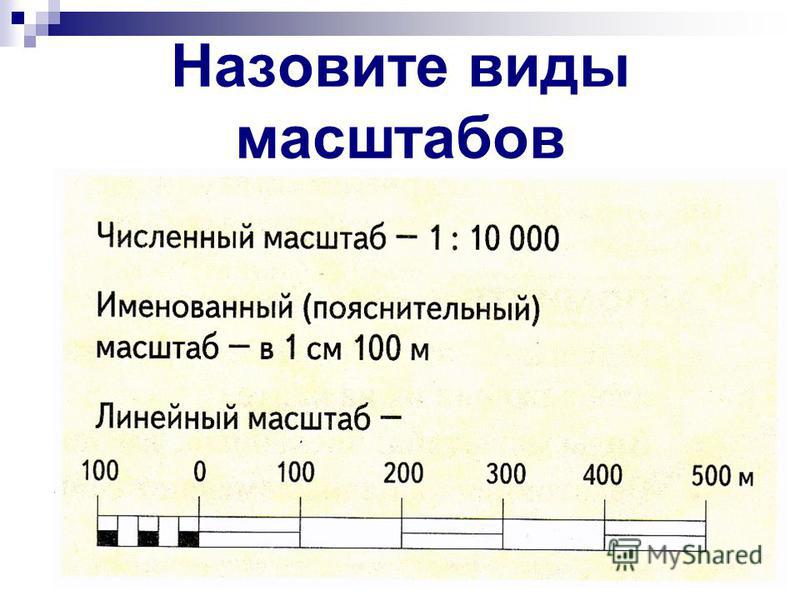 В настоящее время действуют определенные стандарты, к примеру, ГОСТ «Масштабы чертежей», которые описывают все требования, предъявляемые к виду и наполнению соответствующих изображений.
В настоящее время действуют определенные стандарты, к примеру, ГОСТ «Масштабы чертежей», которые описывают все требования, предъявляемые к виду и наполнению соответствующих изображений.
Крупные объекты
Как уже говорилось ранее, для отображения зданий и иных крупногабаритных предметов необходимо использовать масштабы чертежей так называемого уменьшения. Они стандартизированы, а значит, произвольная выборка не подойдет. Наиболее часто встречаются следующие величины: 1: 2; 2,5; 4; 5; 10; 15; 20; 25; 40; 50; 75; 100; 200; 400; 500; 800; 1000. Рассмотрим, что означает запись подобного вида. Итак, реальный (иными словами, натуральный) габарит какого-либо объекта выражается в виде надписи 1: 1. Следовательно, при уменьшении масштабы чертежей сначала описывают исходный размер (1), а затем число, которое показывает, во сколько раз чертеж уменьшен по отношению к реальным габаритам. В строительстве, помимо вышеперечисленных стандартных записей, могут также использоваться указатели 1: 2000; 5000; 10 000; 20 000; 25 000; 50 000.
Мелкие детали
В том случае, если на рисунке необходимо изобразить небольшие предметы, то традиционно используются масштабы чертежей увеличения. В данном случае нет такого большого разнообразия значений, однако стандартом оговорены наиболее часто используемые величины. Итак, типовой ряд выглядит следующим образом: 2; 2,5; 4; 5; 10; 20; 40; 50; 100: 1. Расшифровка подобных надписей читается так: сначала число, указывающее во сколько раз изображение на чертеже увеличено сравнительно с исходным объектом. Второй цифрой, стоящей после двоеточия, отображается реальный (он же — натуральный или настоящий) размер рассматриваемого объекта (принимается равным 1).
Заключение
В данной статье были рассмотрены масштабы чертежей и их стандартные ряды. Следует также отметить, что на самих планах, проектах и изображениях величина масштаба указывается в специально отведенной графе в рамке, иначе называемой штампом.
Обычно на каждой карте изображен линейный или численный масштаб. Но как быть, если по той или иной причине масштаб отсутствует? Опытный специалист по внешнему виду может сразу назвать масштаб рассматриваемой карты. Если же вы этого сделать не можете, то следует прибегнуть к следующим способам.
Но как быть, если по той или иной причине масштаб отсутствует? Опытный специалист по внешнему виду может сразу назвать масштаб рассматриваемой карты. Если же вы этого сделать не можете, то следует прибегнуть к следующим способам.
По километровой сетке. На всех топографических картах печатается километровая сетка. Стороны квадратов сетки соответствуют определенному количеству километров. Это легко узнать по подписям на выходах линий сетки у рамки карты. Допустим, что расстояние между двумя соседними линиями сетки равно 1 км. Измеряем это расстояние линейкой; у нас получается 2 см. Значит, масштаб карты в 1см 500 м (1000:2) или 1:50 000.
По номенклатуре листа. Номенклатура — это буквенно-числовое название листа карты. Каждый масштабный ряд имеет свое обозначение, по которому нетрудно определить масштаб карты. Например:
масштаб 1 | ||
масштаб 1 | ||
масштаб 1 | ||
масштаб 1 | ||
масштаб 1 | ||
масштаб 1 | ||
М-35- 18-А-6-1; | масштаб 1 |
По известным расстояниям. ме-сте измерить расстояние от одного столба до другого, и мы сразу узнаем масштаб карты (число сантиметров карты, соответствующее одному километру местности).
ме-сте измерить расстояние от одного столба до другого, и мы сразу узнаем масштаб карты (число сантиметров карты, соответствующее одному километру местности).
На других картах, например, масштаба 1: 200 000, на дорогах поставлены расстояния в километрах между населенными пунктами. В этом случае надо измерить по карте линейкой расстояние в сантиметрах от одного населенного пункта до другого и подписанное количество километров разделить на расстояние в сантиметрах. Полученное число будет означать величину масштаба карты (число километров в одном сантиметре).
По измеренным расстояниям. В том случае, если мы находимся на местности, которая изображена на карте, масштаб ее можно определить непосредственным измерением расстояния между предметами, нанесенными на карту (а на карте дажедетские городкиотмечают).
По длине дуги меридиана. Чтобы пользоваться этим способом, нужно твердо помнить, что одна минута по меридиану равна примерно 2 км (точнее 1,85). Подписи градусов и минут всегда даются на боковых сторонах рамки карты и, кроме того, каждая минута выделена шашечкой.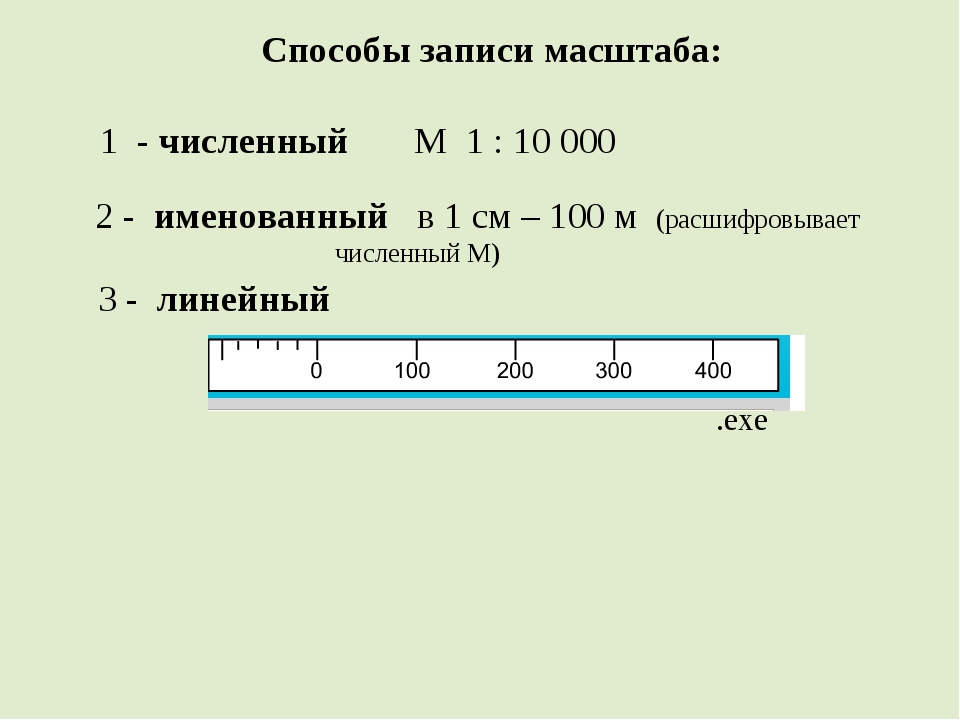 На рис. 24 длина одной минуты равна 3,7 см. Значит, масштаб карты будет 1: 50 000, т. е. один см на карте соответствует 0,5 км на местности. Для уяснения сущности масштаба решим несколько задач.
На рис. 24 длина одной минуты равна 3,7 см. Значит, масштаб карты будет 1: 50 000, т. е. один см на карте соответствует 0,5 км на местности. Для уяснения сущности масштаба решим несколько задач.
Задача 1. Масштаб карты 1: 50 000. На какое число надо разделить знаменатель дроби, чтобы узнать длину линии местности, соответствующей 1 см карты?
Обычно расстояния на местности даются в метрах, а метр, как известно, содержит 100 см. Значит, знаменатель надо делить на 100 (50 000: 100 = 500 м).
Для решения таких задач полезно запомнить правило: если в знаменателе масштаба зачеркнуть два последних нуля, то оставшееся число покажет, сколько метров местности содержится в 1 см на карте.
Задача 2. Какая карта крупнее, если масштаб одной 1: 50 000, а другой 1: 100 000 и во сколько?
Как уже нам известно, масштаб выражается в виде дроби, числитель которой равен единице, а знаменатель число, показывающее, во сколько раз все линии на карте меньше соответствующих линий на местности. А дробь при одинаковом числителе будет больше та, у которой меньше знаменатель. Значит, карта масштаба 1: 50 000 будет крупнее карты масштаба 1: 100 000 ровно в два раза.
А дробь при одинаковом числителе будет больше та, у которой меньше знаменатель. Значит, карта масштаба 1: 50 000 будет крупнее карты масштаба 1: 100 000 ровно в два раза.
А если вам встретится такое выражение: «Масштаб карты более 1 км в 1 см», что же это будет за карта? Крупнее или мельче, чем карта масштаба 1: 100 000, у которой 1 см точно соответствует 1 км? Оказывается, мельче, потому что величина 1 км помещается в знаменателе, а чем больше знаменатель, тем мельче масштаб карты.
Рекомендуем также
Найти именованный масштаб для численных 1 100. Масштаб карты
Что же такое масштаб? Масштаб — в общем случае отношение двух линейных размеров. В областях практического применения масштабом называют отношение размера изображения к размеру изображаемого объекта.
То есть, на картах, планах, аэро- или космических снимках это отношение длины отрезка к его действительной длине на местности. Принято, на картах принимать за единицу измерения — 1 сантиметр, а на местности измерять расстояние в метрах.
Виды указания масштабов
Существует три вида указания масштаба:
- численный;
- именованный;
- линейный.
Численный масштаб (самый распространенный и удобный) — масштаб дробного вида, где числитель — единица, а знаменатель — число, показывающее во сколько раз уменьшено данное изображение територии (пример: 1:100 000; 1:15 000). Обе цифры указаны в сантиметрах, что делает невозможным ошибку в переводе, конвертации одних единиц измерения в другие. Но на практике использование такого масштаба не является удобным. Поэтому, при роботе непосредственно на местности, численный масштаб чаще всего переводят в именованный.
Именованный (или словесный) масштаб — словесное указание того, какое расстояние на местности соответствует 1 сантиметру на карте (пример: в 1 см 5 км или 1 см = 500 метров). Такой вид масштаба понятен человеческому уму, но будет сложно производить расчеты и очень легко сделать ошибку.
Существует так же и третий вид указания масштаба. Это линейный масштаб.
Это линейный масштаб.
Линейный масштаб — вспомогательная мерная линейка на картах для быстрого измерения расстояний, без расчетов.
Масштаб карт всегда одинаков во всех ее точках.
Стандартные масштабы
В России приняты стандартные численные масштабы:
1:1 000 000
1:500 000
1:200 000
1:100 000
1:50 000
1:25 000
1:10 000.
*Для специальных целей создают также топографические карты в масштабах 1:5 000 и 1:2 000.
Перевод численного масштаба в именованный
Так как длины линий на местности принято измерять в метрах, а на картах и планах — в сантиметрах, то масштабы удобней всего выражать в словесной форме, например:
в одном сантиметре 100 метров. Это соответствует численному масштабу 1:10 000. Поскольку 1 метр равняется 100 сантиметрам, то число метров на местности, содержащееся в 1 см на карте, легко определяется путем деления знаменателя численного масштаба на 100. Или на 100 000 — для перевода в км.
То есть, численный масштаб 1:30 000 означает, что в 1 см на карте 300 метров (30 000/100).
Масштаб можно написать цифрами или словами, или изобразить графически.
- Численный.
- Именованный.
- Графический.
- Линейный.
- Поперечный.
Численный масштаб
Численный масштаб подписывают цифрами внизу плана или карты. Например, масштаб «1: 1000» означает, что на плане все расстояния уменьшены в 1000 раз. 1 см на плане соответствует 1000 см на местности, или, по-скольку 1000 см =10 м, 1 см на плане соответствует 10 м на мест-ности.
Именованный масштаб
Именованный масштаб плана или карты обозначают словами. Например может быть написано «в 1 см — 10 м».
Линейный масштаб
Удобнее всего пользоваться масштабом, изображённым в виде отрезка прямой линии, разделённой на равные части, обычно сантиметры (рис. 15). Такой масштаб называется линейным , он также показывается внизу карты или плана. Обратите внимание , что при вычерчивании линейного масштаба нуль ставят, отступая на 1 см от левого конца отрезка, а первый сантиметр делят на пять частей (по 2 мм).
Обратите внимание , что при вычерчивании линейного масштаба нуль ставят, отступая на 1 см от левого конца отрезка, а первый сантиметр делят на пять частей (по 2 мм).
Возле каждого сантимет-ра подписано, какому расстоянию это соответствует на плане. Один сантиметр разделен на части, возле которых написано, како-му расстоянию на карте они соответствуют. Циркулем-измерите-лем или линейкой измеряют длину какого-либо отрезка на плане и, прикладывая этот отрезок к линейному масштабу, определяют его длину на местности.
Зная масштаб, можно определять расстояния между географи-ческими объектами, измерять сами объекты.
Если расстояние от дороги до реки на плане с масштабом 1: 1000 («в 1 см — 10 м») равно 3 см, значит, на местности оно равно 30 м. Материал с сайта
Предположим, от одного объекта до другого 780 м. По-казать в натуральную величину это расстояние на бумаге невоз-можно, поэтому придётся вычертить его в масштабе. Например, если все расстояния будут изображены в 10 000 раз меньшими, чем в дей-ствительности, т. е. 1 см на бумаге будет соответствовать 10 тыс. см (или 100 м) на местности. Тогда в масштабе расстоя-ние в нашем примере от одного объекта до другого будет равно 7 см и 8 мм.
е. 1 см на бумаге будет соответствовать 10 тыс. см (или 100 м) на местности. Тогда в масштабе расстоя-ние в нашем примере от одного объекта до другого будет равно 7 см и 8 мм.
Картинки (фото, рисунки)
На этой странице материал по темам:
Масштабом называют степень уменьшения линий при перенесении их на план или карту.
Численный масштаб – это правильная дробь, числитель которой единица, а знаменатель – число (М), показывающее степень уменьшения линий.
Например, численный масштаб или 1:2000 показывает, что все линии на местности уменьшены в М = 2000 раз или 1 см на плане или карте соответствует 2000 см в действительности, или в одном сантиметре содержится 20 м.
Линейный масштаб – это график, при помощи которого определяются расстояния между точками на карте или плане.
Построение линейного масштаба включает проведение на бумаге прямой линии, деление ее на равные отрезки по 2 или 1 см, и деление первого отрезка на более мелкие деления, например по 2 или 1 мм (рис. 52).
52).
Рис. 52. Линейный масштаб
На рис. 52 видно, что один сантиметр на карте масштаба 1:10000 – это 100 м на местности. В двух сантиметрах будет содержаться 200 м. Двухсантиметровый отрезок разделен на 20 частей, следовательно, 1 мм на карте будет соответствовать 10 м на местности. Отложенное расстояние на линейном масштабе составляет 590 м.
Поперечный масштаб – это график, посредством которого определяются расстояния на плане или карте с принятой точностью 0,2 мм. Такой график представлен на рис. 53.
Рис.53. Нормальный поперечный масштаб
На этом графике отрезок аb есть наименьшее деление поперечного масштаба. Основание А поперечного масштаба составляет 2 см и может быть разделено на m равных частей. Высота Н этого масштаба равна 2,5 см и включает в общем случае n равных частей.
Отрезок , а отрезок .
Из соотношения получим .
Для нормального поперечного масштаба m = n =10, тогда
ab = 0,2 мм.
Точность поперечного масштаба t – это расстояние на местности, соответствующее точности графических построений 0,2 мм:
где М – знаменатель численного масштаба.
Например, точность поперечного масштаба 1:25000 составит
или t = 5 м.
Пример1 . Определить длину измеренного расстояния se в масштабах 1:5000 и 1:25000.
В масштабе 1:5000 2 см это 100 м в действительности, а в масштабе 1:25000 – 500 м. Так как основание масштаба разделено на 10 равных частей, то одной ее десятой (отрезок cd ) соответствует расстояние 10 м в масштабе 1:5000, а в масштабе 1:25000 – 50 м. Высота масштаба Н разделена на 10 равных частей, поэтому в отрезке аb содержится 1 м при пользовании масштабом 1:5000 и 5 м при масштабе 1:25000.
Для того чтобы измерить расстояния между точками на карте необходимо иглами циркуля коснуться к точкам и полученный раствор циркуля приложить к поперечному масштабу таким образом, чтобы одна игла находилась на пересечении наклонной и горизонтальной линий масштаба (точка s ), а другая – на горизонтальной и вертикальной линий (точка e ). Измеряемый отрезок se состоит из трех частей so , or и re . Этим частям соответствуют расстояния на местности в масштабе 1:5000 40 + 6 + 4 = 446 м, а в масштабе 1:25000 – 200 + 30 + 2000 = 2230 м.
Измеряемый отрезок se состоит из трех частей so , or и re . Этим частям соответствуют расстояния на местности в масштабе 1:5000 40 + 6 + 4 = 446 м, а в масштабе 1:25000 – 200 + 30 + 2000 = 2230 м.
Пример 2 . Определить на карте масштаба 1:25000 расстояние между точкой в квадрате 6507 «Отметка 214,3» и точкой в квадрате 6508 «Отметка 197,1» (см. рис. 2).
В результате измерения на настоящей карте, а не на ее схематичном изображении, получен результат: 1480 м.
Масштаб 1: 100 000
1 мм на карте — 100 м (0,1 км) на местности
1 см на карте — 1000 м (1 км) на местности
10 см на карте — 10000 м (10 км) на местности
Масштаб 1:10000
1 мм на карте — 10 м (0,01 км) на местности
1 см на карте — 100 м (0,1 км) на местности
10 см на карте — 1000м (1 км) на местности
Масштаб 1:5000
1 мм на карте — 5 м (0,005 км) на местности
1 см на карте — 50 м (0,05 км) на местности
10 см на карте — 500 м (0,5 км) на местности
Масштаб 1:2000
1 мм на карте — 2 м (0,002 км) на местности
1 см на карте — 20 м (0,02 км) на местности
10 см на карте — 200 м (0,2 км) на местности
Масштаб 1:1000
1 мм на карте — 100 см (1 м) на местности
1 см на карте — 1000см (10 м) на местности
10 см на карте — 100 м на местности
Масштаб 1:500
1 мм на карте — 50 см (0,5 метра) на местности
1 см на карте — 5 м на местности
10 см на карте — 50 м на местности
Масштаб 1:200
1 мм на карте — 0,2 м (20 см) на местности
1 см на карте — 2 м (200 см) на местности
10 см на карте — 20 м (0,2 км) на местности
Масштаб 1:100
1 мм на карте — 0,1 м (10 см) на местности
1 см на карте — 1 м (100 см) на местности
10 см на карте — 10м (0,01 км) на местности
Переведите численный масштаб карты в именованный:
Решение:
Для более легкого перевода численного масштаба в именованный нужно посчитать, на сколько нулей кончается число в знаменателе.
Например, в масштабе 1: 500 000 в знаменателе после цифры 5 находится пять нулей.
Если после цифры в знаменателе пять и более нулей, то, закрыв (пальцем, авторучкой или просто зачеркнув) пять нулей, получим число километров на местности, соответствующее 1 сантиметру на карте.
Пример для масштаба 1: 500 000
В знаменателе после цифры — пять нулей. Закрыв их, получим для именованного масштаба: в 1 см на карте 5 километров на местности.
Если после цифры в знаменателе менее пяти нулей, то, закрыв два нуля, получим число метров на местности, соответствующее 1 сантиметру на карте.
Если, например, в знаменателе масштаба 1: 10 000 закроем два нуля, получим:
в 1 см — 100 м.
Ответы :
в 1 см — 2 км;
в 1 см — 100 км;
в 1 см — 250 м.
Используйте линейку, накладывайте на карты для облегчения измерения расстояний.
Переведите именованный масштаб в численный:
в 1 см — 500 м
в 1 см — 10 км
в 1 см — 250 км
Решение:
Для более легкого перевода именованного масштаба в численный нужно перевести расстояние на местности, указанное в именованном масштабе, в сантиметры.
Если расстояние на местности выражено в метрах, тогда чтобы получить знаменатель численного масштаба, нужно приписать два нуля, если в километрах, то пять нулей.
Например, для именованного масштаба в 1 см — 100 м расстояние на местности выражено в метрах, поэтому для численного масштаба приписываем два нуля и получаем: 1: 10 000.
Для масштаба в 1 см — 5 км приписываем к пятерке пять нулей и получаем: 1: 500 000.
Ответы :
Карты в зависимости от масштабов условно подразделяют на следующие типы:
топографические планы — 1:400 — 1:5 000;
крупномасштабные топографические карты — 1:10 000 — 1:100 000;
среднемасштабные топографические карты — от 1:200 000 — 1:1 000 000;
мелкомасштабные топографические карты — менее 1:1 000 000.
Карты масштабов:
называются крупномасштабными.
Сказка про карту в масштабе 1:1
Жил-был Капризный Король. Однажды он объехал своё королевство и увидел, как велика и прекрасна его земля. Он увидел извилистые реки, огромные озёра, высокие горы и чудесные города. Он возгордился своими владениями и захотел, чтобы весь мир узнал о них. И вот, Капризный Король приказал картографам создать карту королевства. Картографы трудились целый год и, наконец, преподнесли Королю замечательную карту, на которой были обозначены все горные гряды, крупные города и большие озёра и реки.
Он увидел извилистые реки, огромные озёра, высокие горы и чудесные города. Он возгордился своими владениями и захотел, чтобы весь мир узнал о них. И вот, Капризный Король приказал картографам создать карту королевства. Картографы трудились целый год и, наконец, преподнесли Королю замечательную карту, на которой были обозначены все горные гряды, крупные города и большие озёра и реки.
Однако Капризный Король остался недоволен. Он хотел видеть на карте не только очертания горных цепей, но и изображение каждой горной вершины. Не только крупные города, но и мелкие, и селения. Он хотел видеть небольшие речки, впадающие в реки.
Картографы вновь принялись за работу, трудились много лет и нарисовали другую карту, размером в два раза больше предыдущей. Но теперь Король пожелал, чтобы на карте были видны перевалы между горными вершинами, маленькие озерца в лесах, ручейки, крестьянские домики на окраине селений. Картографы рисовали все новые и новые карты.
Капризный Король умер, так и не дождавшись окончания работы. Наследники один за другим вступали на трон и умирали в свою очередь, а карта все составлялась и составлялась. Каждый король нанимал новых картографов для составления карты королевства, но всякий раз оставался недовольным плодами труда, находя карту недостаточно подробной.
Наследники один за другим вступали на трон и умирали в свою очередь, а карта все составлялась и составлялась. Каждый король нанимал новых картографов для составления карты королевства, но всякий раз оставался недовольным плодами труда, находя карту недостаточно подробной.
Наконец картографы нарисовали Невероятную карту!!! Карта изображала всё королевство в мельчайших подробностях — и была точно такого же размера, как само королевство. Теперь уже никто не мог найти различия между картой и королевством.
Где же собирались хранить Капризные Короли свою замечательную карту? Ларца для такой карты не хватит. Понадобится огромное помещение вроде ангара, и в нем карта будет лежать во много слоев. Только нужна ли такая карта? Ведь карта в натуральную величину может быть с успехом заменена самой местностью..))))
Масштаб карты виды масштаба цель
Масштаб карты. Виды масштаба
Цель:
— Сформировать у учащихся понятие о масштабе и его видах
— Научить учащихся пользоваться масштабом, переводить из численного в именованный и обратно
Оборудование:
Карты различных масштабов
Карточки – лото
Карточки для закрепления изученного
Ход урока
I Организационный момент
II Поверка знаний по изученному материалу
Задания на знание определений
— Что называется планом местности?
— Что такое карта?
— Как делятся карты по охвату территории, содержанию, масштабу?
— Что такое условные знаки?
— Назовите виды условных знаков
2. Задание на знание условных
знаков
Задание на знание условных
знаков
А) Учитель показывает карточки с условными обозначениями, а учащиеся записывают описание знака в тетрадях (оценочная работа)
Б) Игра «Лото»
Играют двое или один ученик (лучше двое, чтобы работу можно было сразу оценить). Игрокам выдается одна большая карточка и шесть маленьких. Большая карточка расчерчена на шесть полей, на каждом поле – условный знак, а на шести маленьких карточках – словесное описание условных обозначений. Необходимо найти соответствие. Работу можно организовать и наоборот: на большой карточке – словесное описание, на маленьких – условные обозначения. Например,
В) Топографический диктант (оценочная работа)
Необходимо заменить слова условными топографическими знаками.
От деревянного моста мы пошли по шоссе через луг. Слева виднелось болото, справа кустарник. Вскоре мы вошли в лиственный лес, пересекли овраг и подошли к озеру
III Изучение нового материала
Учитель предлагает детям выполнить
невыполнимое проблемное задание –
начертить в тетрадях план пришкольного
участка в натуральную величину.
— Почему не можете начертить план? (Он большой, а тетрадь маленькая)
— Что нужно сделать, чтобы выполнить задание? (Уменьшить план или увеличить тетрадь)
— Посмотрите на карты (Учитель показывает карты разных масштабов). Что можете сказать о реках, озерах, морях, городах? (Они уменьшены. На одних картах – сильнее, на других меньше)
— Но как выразить уменьшение?
Прочитайте в учебнике (§2, стр 11, «Масштаб»). Учащиеся читают и отвечают, что уменьшение выражают дробью, которая показывает, во сколько раз расстояние на карте умешено по сравнению с реальным расстоянием на местности. Это дробное число называют масштабом (определение учащиеся записывают в тетрадь)
Затем учитель предлагает заполнить схему «Виды масштабов» (используя текст учебника)
По окончании самостоятельной работы учеников учитель сам объясняет виды масштаба.
Масштаб (нем mab-мера, stab – палка) – отношение длины отрезка на
карте или плане к его действительной
длине на местности.
Масштаб может быть выражен дробью, где числитель равен единице, а знаменатель – число, показывающее во сколько раз уменьшено изображение, — это численный масштаб.
Например:
1:50 – 1 см на карте соответствует 50 см на местности;
1:100 – 1 см на карте соответствует 100 см на местности;
1:1000 – 1 см на карте соответствует 1000 см на местности;
1:100000000 – 1 см на карте соответствует 100000000 см на местности;
Задание.
Начертите в тетрадях квадрат со сторонами 100 см в масштабе 1:50 (квадрат со стороной 2 см)
Кроме численного есть именованный масштаб. Он показывает, какое расстояние на местности соответствует одному сантиметру на карте или плане. Например, в1 см – 1м
Задание
Начертите в этом масштабе (в 1 см – 1 м) квадрат со сторонами 3 (квадрат со стороной 3 см)
— А что делать, если именованный
масштаб не указан, а имеется численный,
например, 1:1000000 см. Что нужно сделать?
(В правой части перевести сантиметры в
метры и , если требуется в километры. т.е. в 1см 10 км
т.е. в 1см 10 км
— Используя масштабы карт в учебнике (§2, стр 11), переведите численный масштаб в именованный. Например:
1:15000000 ( в 1 см 150 км)
1:3000000 ( в 1 см 30 км)
1:1950000 ( в 1 см 19,5 км)
Третий вид масштаба – линейный. Он показан в виде вспомогательной мерной линейки (§2, стр 11), наносимой на картах для удобства измерения расстояний. Линейный масштаб обычно не заменяет численный и именной, а приводится наряду с ними. Первый сантиметр слева делится на равные мелкие участки.
IV Закрепление
Выполнить задания (тетрадь – тренажер, стр 11 «Считаем и сравниваем»)
Определите, во сколько раз уменьшено расстояние на планах, построенных в масштабе:
А) 1:50 Б) 1:100 В) 1:5000
Какой из этих масштабов мелкий?
Определите численный масштаб плана местности, если расстояние в 4 км показано на нем отрезком длиной 8 см.
Рассчитайте, отрезком какой длины (в см) может быть выражено расстояние в 50м при масштабе плана 1:2500
Переведите численные масштабы в именованные:
А) 1:10000 б) 1:250000 в) 1:500000
V Игра «Путешествие в страну Масштабию»
Групповая работа. Число групп –
четное. Учащиеся передвигаются по
этапам. Результаты записываются в
тетради.
Число групп –
четное. Учащиеся передвигаются по
этапам. Результаты записываются в
тетради.
Первый этап.
Перевести именованный масштаб в численный
В 1 см – 10 м в 1см – 200 м
В 1 см – 50 км в 1см – 750 км
Второй этап
Перевести численный масштаб в именованный
1:10000 1:30000
1:750000 1:100000
Третий этап
Измерить расстояние на карте и вычислить расстояние на местности (на топографической карте)
Четвертый этап
Определите масштаб плана, если дорога длиной 5 км на нем имеет длину 20 см
Пятый этап
Учащиеся прошли на север 5000 м. начертите маршрут движения с помощью масштаба в 1 см – 1 км.
По окончании работы группы
обмениваются тетрадями и вместе с
учителем определяют правильные ответы.
После проверки дается устная оценка
работ. Тем, кто допустил ошибки,
предлагается с особой тщательностью
подойти к выполнению домашнего задания.
Тем, кто допустил ошибки,
предлагается с особой тщательностью
подойти к выполнению домашнего задания.
Домашнее задание: §2, стр 11, записи
Урок географии в 5 классе по теме «Масштаб»
Класс: 5 Предмет: география .
Тема: Масштаб. Виды масштаба.
Цель урока: Формирование знаний о масштабе и его видах
Ведущие понятия урока: масштаб, именованный масштаб, численный масштаб, линейный масштаб.
Ожидаемые результаты:
1. Репродуктивный уровень: конкретизировать и углубить понятия масштаб. Знать виды масштаба и способы их записи.
2.Конструктивный уровень: определять расстояния с помощью масштаба, решать практические задачи по переводу масштабов из численного в именованный и обратно.
3.Творческий уровень: решать проблемные вопросы и задачи, развивать навыки работы в группе, навыки работы с текстом, схемами, таблицами.
Методы обучения: частично- поисковый, проблемный
Тип урока: комбинированный.
Вид урока: урок усвоения нового материала
Формы работы: индивидуальная, групповая, фронтальная
Ход урока.
1 этап. Организационный момент.
Учитель приветствует детей. Проверяет готовность к уроку. Сегодня на уроке географии мы будем использовать математические знания. А так как математика любит точность, давайте будем ей соответствовать и проверим принадлежности, необходимые для урока (учитель называет учебные принадлежности: учебник, тетрадь, ручка, карандаш, линейка, ластик).
2 этап. Проверка домашнего задания (1 у доски пишет на обороте)
(СЛАЙД 1)
Проверка
(СЛАЙД 2)
3 этап. Изучение нового материала
Проблемное задание: для изображения поверхности Земли картографам предстояло решить математическую задачу: уменьшить изображение и решить, какие показать при этом объекты на географической карте.
-Посмотрите на географические карты. (СЛАЙД 3)
—Что можете сказать о морях, реках? (уменьшены, на одной карте сильнее, на другой меньше)
—Как выразить уменьшение? (Тема урока, цель) (СЛАЙД 4)
— Чем можно измерить размеры предметов, расстояние на местности? (Линейкой, рулеткой, мерной лентой, шагами).
-Какие единицы длины вы знаете?
-Как соотносятся единицы длины? Продолжите цепочку:
а)1мм;1см;… (1дм;1м;1км)
б)1км=1000м=… (10 000 дм = 100 000 см =1 000 000 мм)
-Сможете ли вы начертить план стола ? Почему? (Прямоугольник такого размера не уместится на странице)
-Чтобы начертить большой предмет на листе бумаги, нужно уменьшить его размеры в одинаковое количество раз.
Демонстрация глобуса.
Учитель.
-что такое глобус?
-назовите черты сходства и различия планеты Земля и ее модели – глобуса
(Все объекты даны без искажений; земля показана в уменьшенном виде; на глобусе показаны только самые важные географические объекты).
— главное отличие: изображение на глобусе уменьшены в десятки миллионов раз.
Учитель:
-как определить во сколько раз изображение Земли уменьшено?
Если ученики затрудняются в ответе, учитель обращает их внимание цифры, подписанные в южной части Тихого океана. Что это за цифры? Правильно, масштаб.
-вспомните, что называется масштабом в математике?
-запишите масштаб глобуса (1: 60 000 000) Прочитайте масштаб (1 к шестидесяти миллионам).
-формулируйте, что называется масштабом в географии? (откройте учебник стр. 34) Что называется, что показывает? (СЛАЙД 5)
Масштаб — это число, которое показывает, во сколько раз расстояния на местности уменьшены при изображении их на плане. (Запись в тетрадь)
-Как записывают масштаб?
Работа с текстом учебника стр. 34-35. Проверка (СЛАЙД 6)
Учитель знакомит учащихся, как записываются виды масштаба, используя учебник на странице 34-35 (ЗАПИСЬ В ТЕТРАДИ) .
-численный масштаб записывается цифрами (1: 10 000)
-чтобы по длине линии на плане или карте удобно было узнавать расстояния на местности, у численного масштаба пишут пояснение: в 1 см — 10 км,
в 1 см — 100 м, в 1 см — 10 м и т. д. То есть сантиметры переводят в метры и километры. Такой масштаб называют именованным.
-линейный масштаб позволяет измерять расстояния на плане и карте, не прибегая к вычислениям. Он представляет собой прямую линию, разделенную на равные части. У каждого деления линии подписывают соответствующие ему расстояния на местности. Для измерения расстояний используется циркуль.
Расскажите по таблице (СЛАЙД 7) – самост. работа в тетрадь пишут
Виды масштаба
Как изображается
Что показывает
Для чего используется
Именованный
Словами и числами
Во сколько раз уменьшается расстояние на карте
Для краткой записи
Численный
Дробью
Величину масштаба
Для определения величины масштаба
Линейный
Делениями на линии
Соответствующие делениям расстояния на местности
Для измерения расстояний циркулем.
-а теперь применим теоретические знания на практике. Выполним несколько заданий
СЛАЙД 8 разобрать
Переведите численный масштаб в именованный и наоборот
(СЛАЙД 9)
Какой из масштабов крупнее? (СЛАЙД 10)
После выполнения заданий ответы проверяются.
Задачи.
На плане дорога длиной 500м изображена линией в 5 см. Определите масштаб.
Туристы прошли на север 5000м. Начертить маршрут движения в масштабе в 1см – 1 км.
4 этап. Первичное закрепление знаний и способов действий.
1.Что называется масштабом?
2. Какие виды масштабов вы узнали?
5 этап. Оценочная деятельность
6этап. Рефлексия.
Продолжите фразу:
— Сегодня на уроке …
— Теперь я знаю …
— Мы работали с …
— Мне на уроке …
Учитель
-на этом уроке мы познакомились только с одной областью применения масштаба. На самом деле вам придется еще не раз применить знания масштаба и на других предметах (математика, технология, рисование и др.), а также в практической деятельности в будущем.
На самом деле вам придется еще не раз применить знания масштаба и на других предметах (математика, технология, рисование и др.), а также в практической деятельности в будущем.
7 этап. Постановка домашнего задания.
Стр.34-35, выучить в тетради, цветные карандаши.
Карточка – инструкция (1 группа)
Практическая работа: «Определить по атласу (карта полушарий) с помощью масштаба расстояние от г. Москвы до Северного полюса».
Выбрать способ определения расстояния на глобусе. Объяснить свой выбор.
Прописать последовательность ваших действий в тетради.
Представить отчет о проделанной работе.
Карточка – инструкция (2 группа)
Практическая работа: «Определить по атласу (карта полушарий) с помощью масштаба расстояние от г. Москвы до Южного полюса».
1. Выбрать способ определения расстояния на глобусе. Объяснить свой выбор.
Объяснить свой выбор.
2. Прописать последовательность ваших действий в тетради.
3. Представить отчет о проделанной работе.
Карточка – инструкция (3 группа)
Практическая работа: «Определить по атласу (карта полушарий) с помощью масштаба расстояние от г. Москвы до экватора».
1. Выбрать способ определения расстояния на глобусе. Объяснить свой выбор.
2. Прописать последовательность ваших действий в тетради.
3. Представить отчет о проделанной работе.
Масштаб — География — справочник
МАСШТАБ
Расстояние на местности измеряют рулеткой или специальными приборами. При изображении местности на листе бумаги приходится расстояние уменьшать. Для этого надо выбрать масштаб. Масштаб — это дробь, у которой в числителе единица, а знаменатель — число, указывающее, во сколько раз расстояние на плане или карте меньше, чем сама местность. С помощью масштаба по карте легко прочитать, во сколько раз уменьшено картографическое изображение, сколько сантиметров на местности содержится в одном сантиметре плана или карты. Это важнейшая характеристика карты или плана, так как от нее зависит полнота и подробность изображения местности, она дает возможность выполнить измерения по карте или плану, определить общий размер изображаемой территории.
С помощью масштаба по карте легко прочитать, во сколько раз уменьшено картографическое изображение, сколько сантиметров на местности содержится в одном сантиметре плана или карты. Это важнейшая характеристика карты или плана, так как от нее зависит полнота и подробность изображения местности, она дает возможность выполнить измерения по карте или плану, определить общий размер изображаемой территории.
Существует несколько видов записи масштаба:
— численный масштаб 1:1 000
— именованный масштаб (в 1 см — 10 м) . Расстояние на местности, соответствующее 1 см плана или карты, называется величиной масштаба. В данном случае величина масштаба — 10 м.
— линейный масштаб. Это прямая линия, разделен ная на равные части (обычно сантиметры) . У каждого деления линии подписывают соответствующее ему расстояние на местности. С помощью линейного масштаба можно определить не только размеры объектов, но и расстояние между ними. В данной работе используют циркуль-измеритель. На любой карте, как правило, можно увидеть все три вида записи масштаба в углу карты или на ее легенде.
В данной работе используют циркуль-измеритель. На любой карте, как правило, можно увидеть все три вида записи масштаба в углу карты или на ее легенде.
Все географические карты по своему масштабу подразделяются на крупномасштабные, среднемасштабные и мелкомасштабные. К крупномасштабным относятся карты масштабов от 1:10 000 до 1:200 000 включительно. К среднемасштабным — от 1:200 000 до 1:1 000 000 включительно. К мелкомасштабным — менее 1:1 000 000.
Наиболее подробно географические объекты и их очертания изображаются на крупномасштабных картах. При уменьшении масштаба карты подробности приходится исключать и обобщать (генерализовать) . Отдельные объекты заменяются их собирательными значениями. Отбор и обобщение становятся очевидными при сравнении разномасштабных карт населенного пункта. В масштабе 1:10 000 он дается в виде отдельных строений. На такой карте четко прослеживаются улицы, различные объекты. В масштабе же 1:1 000 000 этот населенный пункт изображен в виде условного знака. В зависимости от назначения необходимы и те, и другие карты.
В зависимости от назначения необходимы и те, и другие карты.
Точными и подробными являются топографические карты и планы, составляемые в масштабах 1:1 000 000 (в 1 см — 10 км) и крупнее.
Масштабы и единицы измерения карты
Масштаб и единицы измерения карты Лаборатория наук о ЗемлеКАРТА МАСШТАБЫ И ЕДИНИЦЫ
Этот раздаточный материал был разработан, чтобы помочь вам понять взаимосвязь между
различные масштабы карты, единицы карты, расстояние и площадь. Вы должны понять
логика того, как они используются и как они должны выглядеть на реальном
топографические карты. На предстоящем лабораторном экзамене вы также должны быть в состоянии
конвертировать один тип масштаба карты в другой и вычислять разницу в размерах
(коэффициент масштаба, коэффициент площади) между разными картами.
A. Обзор распространенных типов масштабов карт
Все масштабы карты являются выражением числового соотношения между
КАРТА и ЗЕМЛЯ, которая представлена. Единица MAP всегда упоминается
первый.
Единица MAP всегда упоминается
первый.
1. Вербальная шкала : Вербальная шкала — это просто предложение, в котором говорится что «1 единица карты = X наземных единиц». Из соображений удобства обычно используется смесь единиц, например
1 дюйм = 1 миля
Однако НЕТ требований, согласно которым блоки должны быть разные! Выражение «1 дюйм = 63 360 дюймов» по-прежнему
словесная шкала.Сочетание картографических и наземных единиц составляет словесную шкалу.
сложно сравнивать разные карты — сначала нужно конвертировать
представительной фракции (см. ниже).
2. Представительная фракция (R.F.) : An R.F. шкала представляет собой отношение или дробь, выражающая математическую связь между КАРТА и ЗЕМЛЯ, такие как 1 : 24 000
, что означает «1 единица карты эквивалентна 24 000 единиц земли». Поскольку Р.Ф. не содержит единиц измерения (дюймы, сантиметры и т. ), это значит
что Р.Ф. масштабы можно сравнивать между различными картами. Преобразование
РФ масштабировать до словесной шкалы очень легко; просто выберите ОДИН блок и
примените его к ОБЕ карты и номера земли. Приведенный выше пример можно записать
в словесной шкале как «1 дюйм = 24 000 дюймов» или «1 метр = 24 000
метров», и т. д. (Примечание: ВЫ НЕ МОЖЕТЕ СМЕШИВАТЬ ЕДИНИЦЫ в РФ! Это приведет к
изменить числовое соотношение РФ)
), это значит
что Р.Ф. масштабы можно сравнивать между различными картами. Преобразование
РФ масштабировать до словесной шкалы очень легко; просто выберите ОДИН блок и
примените его к ОБЕ карты и номера земли. Приведенный выше пример можно записать
в словесной шкале как «1 дюйм = 24 000 дюймов» или «1 метр = 24 000
метров», и т. д. (Примечание: ВЫ НЕ МОЖЕТЕ СМЕШИВАТЬ ЕДИНИЦЫ в РФ! Это приведет к
изменить числовое соотношение РФ)
3. Графическая шкала : Графическая шкала представляет собой гистограмму или «линейка», нарисованная внизу топографической карты.Это масштаб которые вы должны использовать, когда вас просят измерить расстояния на карте. Быть Осторожно : Обратите внимание, что нулевая метка не расположена в левом конце графический масштаб. Для вашего удобства графическая шкала расширяется до слева от нулевой отметки для обозначения долей единиц, например 1/10 миля. Вы можете измерять расстояния, отмечая 2 конечные точки на края листа бумаги и совместите край бумаги с графическая шкала (убедитесь, что одна из ваших отметок стоит на нуле).

B. ПРЕОБРАЗОВАНИЕ ВЕРБАЛЬНОЙ ШКАЛЫ В R.F.
При преобразовании словесной шкалы в RF стратегия заключается в преобразовании от смешанных единиц (вербальная шкала) до одной единицы (Р.Ф.). Это основное различие между этими двумя типами масштабов карты.
Пример:
Если ваша словесная шкала «1 дюйм = 1 миля» как это выражается как РФ?
Решение:
1. Решите, какую ОДНУ единицу преобразовать в : Стать RF, и карта, и наземные юниты (теперь 2 разных типа) должны быть такой же. У вас есть 2 варианта на выбор: вы можете конвертировать мили в дюймы или дюймов в мили. Обычно легче преобразовать от большей к меньшей единице («сколько дюймов в миле?» проще, чем «сколько миль в дюйме?»). Итак, мы будем тогда преобразовать «1 милю земли» в «количество X дюймов».
2. Удалить ненужную единицу путем умножения : Одно из основных правил алгебры состоит в том, что любое число или единица, разделенная на
сам по себе равен 1. Если вы начали с миль и хотите избавиться от миль
и в конечном итоге с дюймами, как вы это делаете?
Если вы начали с миль и хотите избавиться от миль
и в конечном итоге с дюймами, как вы это делаете?
Сначала избавьтесь от «миль» на , умножив его на дробь, содержащую
«миль» в знаменателе и эквивалентное количество меньших единиц
в числителе. Вы можете не знать, сколько дюймов в миле,
но вы должны знать, что в миле 5280 футов.Это получит
избавится от миль, но оставит вас с «ногами», которые все равно не те
единица измерения карты (дюймы). Чтобы получить дюймы, избавьтесь от «футов», умножив
дробью, которая содержит «футы» в знаменателе и эквивалент
количество дюймов в числителе:
1 миля X | (5280 футов) (1 миля) | X (12 дюймов) (1 фут) | = 63 360 дюймов |
Теперь, когда исходная единица земли «1 миля» была преобразована в 63 630
дюймов, и карта, и наземные единицы теперь одного типа, а R. Ф.
записывается простым удалением единиц и заменой двоеточия на
знак равенства:
Ф.
записывается простым удалением единиц и заменой двоеточия на
знак равенства:
1 дюйм = 63 360 дюймов
1 : 63 360
Нет «правильного» или «неправильного» способа умножения — вы должны решить как настроить дроби так, чтобы единицы, которые вам не нужны, отменялись, и единица, которую вы хотите, оказывается вашим ответом.
C. ПРЕОБРАЗОВАНИЕ ВЧ ПО ВЕРБАЛЬНОЙ ШКАЛЕ
Преобразование R.Ф. в словесной шкале обычно гораздо легче, чем в обеспечить регресс. По определению, R.F. означает, что и карта, и земля единицы одинаковы, , поэтому вы можете выбрать любую ОДНУ единицу: 1 : 24 000 может быть «1 см = 24 000 см» или «1 дюйм = 24 000», так долго поскольку вы не используете два разных устройства. Помните, НЕТ ТРЕБОВАНИЕ, что словесная шкала должна использовать разные единицы измерения!
Д. СРАВНЕНИЕ МАСШТАБОВ И ПЛОЩАДЕЙ НА РАЗНЫХ КАРТАХ
Одним из основных преимуществ использования радиоприемника R. F. (Представительная фракция)
Масштаб заключается в том, что он позволяет напрямую сравнивать размеры объектов между
разные карты. Поскольку Р.Ф. исключает использование конкретных единиц (таких как
как дюймы, футы, мили и т. д.), нет необходимости в сложных преобразованиях.
F. (Представительная фракция)
Масштаб заключается в том, что он позволяет напрямую сравнивать размеры объектов между
разные карты. Поскольку Р.Ф. исключает использование конкретных единиц (таких как
как дюймы, футы, мили и т. д.), нет необходимости в сложных преобразованиях.
Сравнение РФ. Масштабы между разными картами
Просто разделите больший масштаб карты на меньший, чтобы получить МАСШТАБ
ФАКТОР:
КОЭФФИЦИЕНТ МАСШТАБА = | р.F. карты A = Р.Ф. карты B | 1:50 000 1:10 000 | = 5 |
Связь между масштабом и площадью
Карта масштаб измеряет расстояние , которая является одномерной
Блок. Площадь представляет собой двумерную величину, рассчитанную путем измерения
«Длина Х Ширина». Обратите внимание, что при изменении масштаба карты определенным
числовой фактор, площадь изменяется на квадрат этого числа. В прочем
слов, если масштаб в 2 раза больше, площадь становится в 4 раза больше;
если масштаб в 5 раз больше, площадь становится 25 раз больше:
В прочем
слов, если масштаб в 2 раза больше, площадь становится в 4 раза больше;
если масштаб в 5 раз больше, площадь становится 25 раз больше:
| Карта А | Карта Б | ||||||||||||||||||||||||||
Площадь = (500 футов по горизонтали) X (500 футов по вертикали)
На приведенной выше карте показана территория площадью 500 футов X 500 футов = 250 000 квадратных футов.  | Площадь = (100 футов по горизонтали) X (100 футов по вертикали)
|
Обратите внимание, что хотя обе карты имеют одинаковый размер, карта A охватывает 500 единиц. расстояния против только 100 единиц для карты B. Но, Карта A (500×500 = 250 000 кв. футов) покрывает 25 РАЗ ПЛОЩАДИ карты B (100×100 = 10 000 кв. футов/).
Таким образом, соотношение между МАСШТАБНЫМ ФАКТОРОМ и ПЛОЩАДЬЮ:
КОЭФФИЦИЕНТ ПЛОЩАДИ = (МАСШТАБНЫЙ КОЭФФИЦИЕНТ) 2
Copyright © 1996, Уильям К.
 Тонг.
Тонг.Чертежи в масштабе
Карта не может быть того же размера, что и область, которую она представляет. Так что измерения уменьшены до , чтобы сделать карту такого размера, который может быть удобно использовать такие пользователи, как автомобилисты, велосипедисты и бушволкеры.Чертеж здания (или моста) в масштабе имеет то же самое. форму реального здания (или моста), которое оно представляет, но отличается размер. Строители используют чертежи в масштабе для создания зданий и мостов. Соотношение используется в масштабных чертежах карт и зданий. То есть:
Аналогично имеем:
Масштаб обычно выражается одним из двух способов:
- в единицах от 1 см до 1 км
- без явного упоминания единиц, как в 1 : 100 000.
Примечание:
Масштаб 1 : 100 000 означает, что реальное расстояние в 100 000 раз больше
длина 1 ед. по карте или чертежу.
по карте или чертежу.
Пример 14
Запишите масштаб от 1 см до 1 м в форме отношения.
Решение:
Пример 15
Упрощение масштаба 5 мм : 1 м.
Решение:
Пример 16
Упрощение масштаба 5 см : 2 км.
Решение:
Расчет фактического расстояния с использованием шкалы
Если масштаб 1 : x , то умножьте расстояние карты на x , чтобы рассчитать фактическое расстояние.
Пример 17
На конкретной карте показан масштаб 1 : 5000.Что на самом деле расстояние, если расстояние карты составляет 8 см?
Решение:
Расстояние карты = 8 см
Пусть фактическое расстояние будет a см.
Альтернативный способ:
Расстояние карты = 8 см
Расчет масштабированного расстояния с использованием фактического расстояния
Если масштаб 1 : x , то разделите фактическое расстояние на x , чтобы рассчитать расстояние по карте.
Пример 18
На одной карте показан масштаб 1 см : 5 км. Что бы карта расстояние (в см) быть, если фактическое расстояние составляет 14 км?
Решение:
Итак, расстояние карты составляет 2,8 см.
Альтернативный способ:
Итак, расстояние карты составляет 2,8 см.
Основные термины
чертеж в масштабе, карта, в масштабе вниз, масштаб чертежа, карта шкала
Шкалы измерений и типы данных
В статистическом анализе важно знать о различных шкалах измерения, а именно:
- ИНТЕРВАЛ
Шкала с фиксированным и определенным интервалом e. г. температура или время.
г. температура или время. - НОМЕР
Шкала для упорядочивания наблюдений от низкого к высокому с любыми связями, связанными с отсутствием чувствительности измерения, например, балл из анкеты. - НОМИНАЛ при заказе
Шкала для группировки по категориям с порядком напр. легкой, средней или тяжелой степени. Это может быть трудно отделить от порядкового номера. - НОМИНАЛ без заказа
Шкала для группировки по уникальным категориям e.г. цвет глаз. - ДИХОТОМИЧЕСКИЙ
То же, что и для номинального, но только две категории мужской женский.
В дополнение к классификации шкал измерений для описания типов данных используются другие родственные термины:
- КАТЕГОРИЧЕСКАЯ и ЧИСЛОВАЯ (количественная или качественная)
Данные, представляющие категории, такие как дихотомические (две категории) и номинальные (более двух категорий) наблюдения, в совокупности называются категориальными (качественными). Данные, которые подсчитываются или измеряются численно определенным методом, называются числовыми (количественными).
Данные, которые подсчитываются или измеряются численно определенным методом, называются числовыми (количественными). - ДИСКРЕТНЫЙ и ПОРЯДОЧНЫЙ КАТЕГОРИЧЕСКИЙ
Дискретные данные получаются из наблюдений, которые могут принимать только определенные числовые значения, обычно подсчеты, такие как количество детей или количество пациентов, посещающих клинику за год. Упорядоченные категориальные данные иногда обрабатываются как дискретные данные, это неправильно. Например, используя классификацию социального класса Генерального регистратора, было бы неправильно говорить, что класс I в пять раз превышает социально-экономический статус класса V, поскольку между этими категориями нет строгой числовой зависимости.Из этого следует, что средний социальный класс является бессмысленной статистикой. Таким образом, упорядоченные категориальные данные не следует рассматривать как дискретные данные для статистического анализа. Дискретные данные можно рассматривать как упорядоченные категориальные данные в статистическом анализе, но при этом теряется некоторая информация.
- НЕПРЕРЫВНЫЙ
Непрерывные данные — это числовые данные, которые теоретически могут быть измерены в бесконечно малых единицах. Например, кровяное давление обычно измеряется с точностью до 2 мм рт. ст., но оно может быть измерено с гораздо большим разрешением разницы.Шкала интервальных измерений предназначена для непрерывных данных. Иногда непрерывным данным при определенных пороговых значениях присваиваются дискретные значения, например, возраст последнего дня рождения является дискретным значением, но сам возраст является непрерывной величиной; в этих ситуациях разумно рассматривать дискретные значения как непрерывные. Помните, что информация теряется, когда непрерывные данные записываются только в диапазонах (упорядоченных категориях), а статистический анализ непрерывных данных является более мощным, чем анализ категорийных данных. - ПРОЦЕНТЫ и ОТНОШЕНИЯ
Проценты или отношения обобщают две части информации, а именно составляющие их значения числителя и знаменателя. Простые соотношения (от 0 до 1, т. е. знаменатель — это максимально возможное значение, которое может принимать числитель) можно рассматривать как непрерывные данные. Более сложные для анализа данные возникают, когда отношение представляет собой изменение, и значение может быть отрицательным. Отношения наблюдений по сравнению с эталонными значениями, т.е.г. рост по отношению к среднему значению референтной популяции для данного пола и возраста трудно обрабатывать, поскольку значения могут падать в обе стороны от 1 (100%).
Простые соотношения (от 0 до 1, т. е. знаменатель — это максимально возможное значение, которое может принимать числитель) можно рассматривать как непрерывные данные. Более сложные для анализа данные возникают, когда отношение представляет собой изменение, и значение может быть отрицательным. Отношения наблюдений по сравнению с эталонными значениями, т.е.г. рост по отношению к среднему значению референтной популяции для данного пола и возраста трудно обрабатывать, поскольку значения могут падать в обе стороны от 1 (100%).
Многие статистические методы подходят только для данных определенных шкал измерений. При выборе статистического метода важно понимать, как были измерены данные для анализа. Лучшей стадией исследования для обдумывания шкал измерений является стадия проектирования, на которой статистические ограничения, накладываемые определенными шкалами измерений, могут повлиять на ваш выбор наблюдений и методов измерения.
Обратите внимание, что преобразование данных изменяет их шкалу измерения.
См. также:
Нормальные баллы
Стандартизация
Рейтинг
Преобразование единиц измерения
Что такое рейтинговая шкала опроса? + [Типы и примеры вопросов]
При проведении систематического исследования исследователю может потребоваться, чтобы респонденты оценили его или ее знания или степень удовлетворенности конкретным продуктом или услугой.Чтобы сделать это объективно, ему или ей может понадобиться включить в анкету или опросник различные типы рейтинговых шкал.
С помощью оценочной шкалы исследователь может легко количественно оценить знания и мнения респондентов в виде определенных значений, которые могут быть числовыми или иными. Рейтинговая шкала обычно используется в количественных и качественных методах наблюдения для оценки различных мнений о предмете исследования.
Рейтинговая шкала — это распространенный метод сбора данных, который используется для сбора сравнительной информации о конкретном предмете исследования.В частности, рейтинговая шкала представляет собой тип вопроса с несколькими вариантами ответов и позволяет респондентам опроса присвоить ценность продукту или услуге.
Этот метод сбора данных позволяет респондентам опроса измерить свои чувства, восприятие, интересы и предпочтения. Существуют различные типы рейтинговых шкал, в том числе числовые шкалы, шкалы сердечного ритма и шкалы Лайкерта, и каждая из этих шкал имеет определенные особенности, которые отличают одну от другой.
Типы оценочных шкал Цифровая шкала — это тип оценочной шкалы, который требует, чтобы респондент предоставил свой отзыв в виде числовых значений.Этот тип рейтинговой шкалы приравнивает варианты ответов сравнительного опроса к упорядоченному набору числовых значений, чтобы респонденты могли количественно выразить свое мнение.
Этот тип рейтинговой шкалы позволяет исследователю рассматривать ответы на опрос как количественную символизацию. Числовая рейтинговая шкала обычно используется для количественной оценки качественных данных, таких как боль, чувства, удовлетворенность продуктом, вероятность рекомендации, лояльность клиентов и тому подобное.
Обычно исследователь помечает конечные точки числовой рейтинговой шкалы с точки зрения измеряемого значения так, чтобы оба конца представляли крайние значения этого значения.Примеры числовых рейтинговых шкал включают в себя одиночные простые вопросы и вероятность рекомендовать вопросы.
Образцы числовой шкалы оценок- Насколько вероятно, что вы порекомендуете наш продукт или услугу? (1 = очень маловероятно; 5 = очень вероятно)
- Насколько простым или трудным вы считаете этот тест? (1 = очень сложно; 7 = очень просто)
Шкала Лайкерта — это тип оценочной шкалы, которая позволяет респондентам указать, насколько они согласны или не согласны с утверждением или утверждением. Он используется для измерения психологического настроя или отношения респондента к определенному предмету.
Он используется для измерения психологического настроя или отношения респондента к определенному предмету.
Шкала Лайкерта обычно имеет форму 5-балльной или 7-балльной рейтинговой системы, которая позволяет объективно оценить мнения, восприятие и поведение респондентов. Он также включает умеренный или нейтральный рейтинг, учитывающий мнения, которых нет ни здесь, ни там.
Этот тип рейтинговой шкалы является безразмерным по своей природе, и его также можно использовать для измерения согласованности, частоты, качества, вероятности и важности.Он был разработан в 1932 году социальным психологом Ренсисом Лайкертом и является полезным инструментом для исследования рынка.
Шкала Гутмана, шкала Богардуса и шкала Терстона также являются распространенными вариантами шкалы Лайкерта.
Вопрос Образцы шкалы ЛайкертаНасколько вы удовлетворены нашим продуктом?
- Очень доволен
- Удовлетворен
- Нейтрально
- Не удовлетворен
- Очень недоволен
Мне было трудно ориентироваться на сайте.
- Категорически не согласен
- Не согласен
- Ни согласен, ни не согласен
- Согласен
- Полностью согласен
. Шкала радиочастот позволяет исследователю узнать, как часто респондент выполняет то или иное действие.
Этот тип рейтинговой шкалы можно использовать для измерения частоты действия с точки зрения определенного количества раз, например, ежемесячно, еженедельно или ежегодно.Это также может быть с точки зрения общих временных рамок, таких как редко, всегда, редко и т.п. Это также известно как вербальная шкала частот.
При создании шкалы частот важно соответствующим образом расположить значения частот.
Вопрос Образцы частотной шкалы- Как часто вы используете наш продукт?
- Ежедневно
- Еженедельно
- Ежемесячно
- Ежегодно
- Перед использованием продукта я прочитал инструкции.
- Никогда
- Редко
- Иногда
- Всегда
Этот тип рейтинговой шкалы обычно используется для сравнения конкретных качеств или характеристик продукта, бренда или услуги.
Шкала парного сравнения позволяет респонденту сообщить о своих предпочтениях и является отличным способом сбора отзывов покупателей об упаковке продукта.Картинки и видео также могут быть представлены в парной шкале сравнения.
Образцы вопросов шкалы парного сравнения- Какой пакет вы предпочитаете?
- Lite
- Business
- Какой веб-сайт вам подходит?
- Ориентированная на пользователя
- Ориентированная на бизнес
Сравнительная шкала — это тип рейтинговой шкалы, который используется для измерения предпочтений респондентов в отношении популярных внешних ориентиров, таких как известные поставщики услуг.Ее также называют шкалой сравнительной интенсивности.
Этот тип оценочной шкалы позволяет респонденту оценить свои предпочтения с точки зрения различных атрибутов конкретного предмета. Это неметрическая шкала, которая позволяет респондентам одновременно оценивать 2 пункта, используя ряд параметров.
Как следующее влияет на ваше решение о покупке?
- Цена
- Особенности
- Торговая марка
- Популярность
Шкала с несколькими флажками — это тип рейтинговой шкалы, в которой перечислены различные положительные и отрицательные атрибуты, описывающие восприятие респондентом продукта, услуги или опыта.Респондентам опроса разрешается выбирать различные варианты, отражающие их отношение к рассматриваемому вопросу.
Шкала с несколькими флажками часто используется для оценки отношения к бренду, пользовательского опыта или для определения качества продукта. Положительные и отрицательные параметры обычно перечислены спорадически, то есть в рандомизированном порядке представления.
Пример шкалы с несколькими флажкамиКакой из следующих вариантов лучше всего описывает ваш опыт?
- Exciting
- Professional
- Простые в использовании
- сложно
- сложно
- недоступный
- isdisfying
звездная шкала рейтинга — это тип рейтинга, позволяющей респонденту зарегистрировать его или ее удовлетворение или неудовлетворение с продуктом или услугой в зависимости от количества звезд. Он использует ранжированные атрибуты, которые представлены звездочками на шкале вместо флажков, цифр или переключателей.
Он использует ранжированные атрибуты, которые представлены звездочками на шкале вместо флажков, цифр или переключателей.
В звездной рейтинговой шкале каждая звездочка представляет собой числовое значение, что несколько похоже на числовую рейтинговую шкалу. Этот тип рейтинговой шкалы обычно используется организациями для обзоров фильмов, опросов удовлетворенности клиентов и анкет.
Образцы для звездной рейтинговой шкалы- Как бы вы оценили качество наших услуг?
- Как бы вы оценили сценарий фильма?
Шкала выбора изображения — это разновидность рейтинговой шкалы, которая обычно используется в вопросах выбора изображения.Это позволяет респондентам оставить отзыв о визуальном качестве продукта, услуги или предмета, например рекламы или логотипа.
Шкала выбора изображений также называется визуальной или графической оценочной шкалой и часто используется для медицинских обследований. Это наиболее подходит для исследовательских контекстов, в которых респондент может не владеть целевым языком.
Шкала сердечного ритма — это разновидность шкалы оценки, в которой используются ранжированные параметры, представленные в виде сердечек, а не флажков, переключателей или цифр.Как и в звездной рейтинговой шкале, сердечки здесь представляют числовое значение для каждого атрибута на шкале.
Шкала сердцебиения используется для измерения уровня удовлетворенности респондента продуктом или услугой и является распространенным средством объективного сбора отзывов клиентов. Шкала оценки сердечных сокращений является распространенным типом графической шкалы оценки.
Образцы вопросов для шкалы сердечного ритма
- Как бы вы оценили качество наших услуг?
- Как бы вы оценили это событие?
Создавайте опросы по рейтинговой шкале с помощью Formplus
Шкала смайликов — это разновидность рейтинговой шкалы, в которой смайлики используются для представления эмоций в диапазоне от отрицательных до нейтральных и положительных.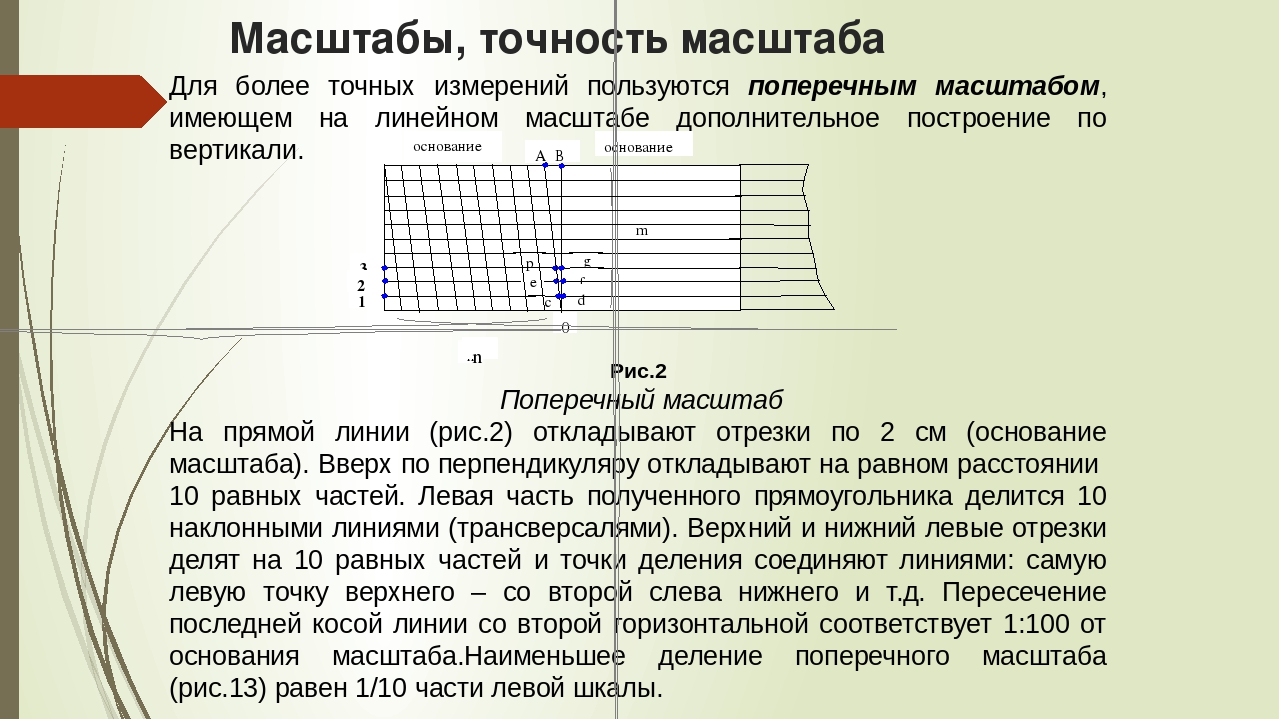 Это 5-балльная оценочная шкала, которая быстро передает эмоции респондента и используется для сбора качественных данных.
Это 5-балльная оценочная шкала, которая быстро передает эмоции респондента и используется для сбора качественных данных.
Он позволяет респонденту сообщить свои отзывы, мнения и опыт с точки зрения удовлетворенности или неудовлетворенности продуктом или услугой. Эту шкалу также можно использовать для определения привлекательности элемента, и это тип шкалы визуальной оценки.
Вопрос Образец шкалы со смайликамиНасколько вы удовлетворены нашей службой доставки?
- Очень доволен
- несколько доволен
- Нейтральный
- Нейтральный
- Очень недоволен
- Очень недоволен
- Очень недоволен
PROPPPLUS позволяет собирать различные информации от респондентов того, как вам нравится, используя наши динамические онлайн-формы.Вы можете добавить различные типы рейтинговых шкал в форму онлайн-опроса в конструкторе форм Formplus, просто перетащив поля рейтинга в форму.
Вот пошаговое руководство по созданию рейтинговой шкалы в форме опроса с помощью Formplus. Мы покажем, как создать 2 типа рейтинговых шкал: шкалу Лайкерта и звездную рейтинговую шкалу: форма.Чтобы получить доступ к конструктору Formplus, вам необходимо создать учетную запись на Formplus.
После этого войдите в свою учетную запись и нажмите «Создать форму», чтобы начать.
- Нажмите на опцию «Рейтинги» в разделе «Входные данные» конструктора форм. Это откроет раскрывающееся меню с доступными параметрами рейтинговой шкалы в конструкторе форм.
- Нажмите на опцию оценки «Звезда», чтобы добавить ее в форму. Вы также можете перетащить это поле в онлайн-форму опроса.Звездный рейтинг будет автоматически добавлен в вашу форму.
- Если вы хотите добавить в форму шкалу Лайкерта, нажмите на опцию оценки «шкала» в раскрывающемся меню.
- Затем щелкните значок редактирования рядом с полем формы, чтобы изменить шкалу оценок в соответствии с вопросом опроса.
 Вы можете изменить поле, чтобы оно было доступно только для чтения или скрыто.
Вы можете изменить поле, чтобы оно было доступно только для чтения или скрыто. - Нажмите «Сохранить»
- Форма предварительного просмотра.
Рейтинговая шкала является полезным инструментом для количественного и качественного наблюдения и сбора данных.Существуют различные типы рейтинговых шкал, и каждая из них может быть адаптирована для качественного или количественного наблюдения.
Если вы хотите получить обратную связь с числовым значением, вы можете использовать числовую шкалу оценок. С другой стороны, если вы хотите собрать данные, касающиеся опыта пользователя с продуктом или услугой, вы можете использовать шкалу рейтинга смайликов.
- Рейтинговая шкала помогает упростить сбор и анализ данных в исследованиях.
- При количественном наблюдении рейтинговая шкала может использоваться для сравнительного анализа данных, особенно когда это связано с исследованием рынка.

- Его легко администрировать, и он снижает вероятность систематической ошибки в опросе и исключения ответов из опроса. Это потому, что это легко понять, и респондентам не нужно тратить много времени, пытаясь расшифровать суть опроса?
- Использование рейтинговой шкалы для сбора данных поможет вам сэкономить время; особенно при создании онлайн-опроса с использованием платформ сбора данных, таких как Formplus.
- Рейтинговая шкала также является удобным методом выборки мнений.
- На нее распространяются ограничения данных.Рейтинговая шкала не позволяет собирать конкретные данные об опыте респондента. Хотя она может выявить общее отношение респондента к продукту или услуге, она не собирает никакой информации о причине такого поведения
- Рейтинговая шкала направлена на исследование в сравнительном, а не в индивидуальном порядке. Следовательно, хотя он может рассказать вам о чувствах и восприятиях респондента, он не позволит вам узнать причину этого восприятия.

- Рейтинговая шкала имеет ограниченную надежность.Это означает, что на него нельзя полностью полагаться в исследованиях; особенно в качественных исследованиях.
- Также возможны существенные изменения.
- Благодаря простоте использования рейтинговая шкала может быть легко истолкована неверно; особенно когда процессом анализа данных занимается не профессионал.
- Это неэффективный инструмент управления бизнесом.
При выборе рейтинговой шкалы важно учитывать процесс исследования и общую цель систематического исследования.Это связано с тем, что некоторые рейтинговые шкалы лучше подходят для определенных типов исследований, чем другие, например, числовая рейтинговая шкала лучше подходит для количественных исследований.
Существуют различные типы оценочных шкал, включая шкалу Лайкерта, радиочастотную шкалу и шкалу сердечного ритма. Вы можете легко создать эти различные шкалы в конструкторе Formplus, щелкнув или перетащив нужные поля рейтинговой шкалы в форму.
Создайте анкеты рейтинговой шкалы на Formplus
Шкалы измерения / Уровень измерения
Четыре шкалы измерения
Посмотрите видео с обзором четырех шкал измерения.
Видео не видно? Кликните сюда.
Данные можно классифицировать по одной из четырех шкал: номинальной, порядковой, интервальной или относительной. Каждый уровень измерения имеет некоторые важные свойства, которые полезно знать. Например, только шкала отношений имеет значащие нули.
Каждый уровень измерения имеет некоторые важные свойства, которые полезно знать. Например, только шкала отношений имеет значащие нули.
На круговой диаграмме отображаются группы номинальных переменных (т. е. категории).
1. Номинальная шкала. Номинальные переменные (также называемые категориальными переменными) могут быть помещены в категории. Они не имеют числового значения , поэтому их нельзя складывать, вычитать, делить или умножать. У них тоже нет порядка; если кажется, что они имеют порядок, то у вас, вероятно, вместо этого есть порядковые переменные.Порядковая шкала классифицирует по рангу.
2. Порядковая шкала. Порядковая шкала содержит вещи, которые можно расположить по порядку. Например, от самого горячего к самому холодному, от легкого к самому тяжелому, от самого богатого к самому бедному. По сути, если вы можете ранжировать данные по 1-му, 2-му, 3-му месту (и так далее), то у вас есть данные в порядковой шкале.
3. Интервальная шкала. Интервальная шкала имеет упорядоченные числа со значащими делениями. Температура находится на интервальной шкале: разница в 10 градусов между 90 и 100 означает то же самое, что и 10 градусов между 150 и 160. Сравните это с рейтингом средней школы (который является порядковым), где разница между 1-м и 2-м может быть 0,01. и между 10 и 11 .5. Если у вас есть значимые деления, у вас есть что-то на шкале интервалов.
Вес измеряется на весах пропорций.
4. Шкала соотношений. Шкала отношений точно такая же, как и шкала интервалов, с одним важным отличием: ноль имеет смысл. Например, высота, равная нулю, имеет смысл (это означает, что вы не существуете). Сравните это с нулевой температурой, которая, пока существует, ничего особенного не значит (хотя, надо признать, по шкале Цельсия это точка замерзания воды).Каталожные номера
Агрести А. (1990) Категориальный анализ данных. Джон Уайли и сыновья, Нью-Йорк.
Додж, Ю. (2008). Краткая энциклопедия статистики. Спрингер.
Эверитт, Британская Колумбия; Скрондал, А. (2010), Кембриджский статистический словарь, издательство Кембриджского университета.
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице Facebook .
Логарифмический или линейный? Различные интуитивные представления о шкале чисел в культурах коренных народов Запада и Амазонки
Abstract
Отображение чисел в пространстве имеет фундаментальное значение для измерения и математики. Является ли это картографирование культурным изобретением или универсальной интуицией, разделяемой всеми людьми, независимо от культуры и образования? Мы исследовали отображения числового пространства у мундуруку, коренной амазонской группы с ограниченным числовым лексиконом и практически без формального образования. Во всех возрастных группах мундуруку сопоставляли символические и несимволические числа с логарифмической шкалой, в то время как взрослые западные люди использовали линейное сопоставление с маленькими или символическими числами и логарифмическое сопоставление, когда числа представлялись несимволически в условиях, препятствующих счету. Таким образом, отображение чисел в пространство есть всеобщее созерцание, и это исходное созерцание числа логарифмично. Концепция линейной числовой прямой кажется культурным изобретением, которое не может развиваться без формального образования.
Во всех возрастных группах мундуруку сопоставляли символические и несимволические числа с логарифмической шкалой, в то время как взрослые западные люди использовали линейное сопоставление с маленькими или символическими числами и логарифмическое сопоставление, когда числа представлялись несимволически в условиях, препятствующих счету. Таким образом, отображение чисел в пространство есть всеобщее созерцание, и это исходное созерцание числа логарифмично. Концепция линейной числовой прямой кажется культурным изобретением, которое не может развиваться без формального образования.
Ключевые слова: Подросток, Взрослый, Антропология, Культура, Бразилия, Ребенок, Культурная эволюция, Образовательный статус, Женщины, Люди, Индейцы, Южноамериканцы, Интуиция, Мужчины, Математика, Средний возраст
Что же такое математика, если она не является уникальной, строгой, логической структурой? Это ряд великих интуиций, тщательно просеянных и организованных с помощью логики, которую люди хотят и могут применить в любое время
— Моррис Клайн, Математика: потеря уверенности (стр.
312)
Отображение чисел в пространстве играет существенную роль в математике, от измерения и геометрии до изучения иррациональных чисел, декартовых координат, линии действительных чисел и комплексной плоскости (1, 2). Как человеческий разум получает доступ к таким абстрактным математическим понятиям? Конструктивистские теории рассматривают математику как набор культурных изобретений, которые постепенно совершенствуются в истории математики и медленно усваиваются в детстве и юности (3).Однако ментальное построение математики может иметь более глубокие основания. Математические объекты могут найти свое окончательное происхождение в базовых интуитивных представлениях о пространстве, времени и числе, которые были интернализированы в течение миллионов лет эволюции в структурированной среде и которые возникают в начале онтогенеза, независимо от образования (2, 4). Здесь мы представляем доказательства, которые примиряют эти две точки зрения: наши результаты показывают, что все люди разделяют интуицию о том, что числа отображаются в пространстве, но культурно-специфический опыт изменяет форму этого отображения.
Предыдущие исследования в области психологии и нейровизуализации подтверждают мнение о том, что чувство числа присутствует у людей и многих других видов в раннем возрасте и с воспроизводимым субстратом в двусторонней внутритеменной борозде (5–8). Эта область удивительно близка или даже перекрывается с областями, участвующими в кодировании пространственных измерений, таких как размер, местоположение и направление взгляда (9–11). Следовательно, на этом уровне могут происходить взаимодействия между числовыми и пространственными кодами в теменной коре.Действительно, у взрослых людей простое представление арабской цифры автоматически вызывает пространственное смещение как в моторных реакциях, так и в ориентации внимания (11–13). У пациентов с поражением головного мозга наблюдаются соответствующие нарушения в сравнении и разделении пополам отрезков и чисел (14), а некоторые люди даже сообщают о ярком опыте видения чисел в фиксированных местах на идиосинкразической пространственно непрерывной «числовой форме» (15, 16).
Недавние эксперименты зафиксировали заметный сдвиг в представлениях детей о том, как числа отображаются в пространстве (17–19).Когда детей просят указать правильное место для произносимого числового слова на отрезке линии, помеченном 0 слева и 100 справа, даже детсадовцы понимают задачу и ведут себя неслучайно, систематически помещая меньшие числа слева и большие числа справа. Однако они распределяют числа неравномерно и вместо этого отводят больше места небольшим числам, применяя сжатое логарифмическое отображение. Например, они могут поместить число 10 в середине сегмента 0–100. Эта компрессионная реакция хорошо согласуется с исследованиями на животных и младенцах, которые демонстрируют, что численное восприятие подчиняется закону Вебера, вездесущему психофизическому закону, согласно которому все большие величины представляются с пропорционально большей неточностью, совместимой с логарифмическим внутренним представлением с фиксированным шумом (7, 20, 21). .Переход от логарифмического к линейному отображению происходит позже в развитии, между 1-м -м и 4-м -м классом, в зависимости от опыта и диапазона тестируемых чисел (17–19).
Однако все эти наблюдения были сделаны на западных субъектах, которые в раннем возрасте имели доступ к математическому образованию и культуре. До формального школьного обучения западные дети могут усвоить понятие числовой линии из арабских цифр, которые можно увидеть на лифтах, линейках, книгах и т. д. Таким образом, существующие исследования не раскрывают, какие аспекты отображения числового пространства составляют основную интуицию, которая будет продолжать существовать. при отсутствии структурированного математического языка и образования.В частности, мы не знаем, будет ли переход от логарифмического к линейному происходить спонтанно в процессе созревания мозга или же для этого потребуется знакомство с критически важным учебным материалом или культурно-специфическими устройствами, такими как линейки или графики.
Чтобы решить эти проблемы, мы собрали данные психологических экспериментов в мундуруку, коренной культуре амазонок с ограниченным доступом к образованию (22, 23). Предыдущие исследования установили, что, хотя их словарный запас числовых слов ограничен, и у них практически нет доступа к линейкам, измерительным приборам, графикам или картам, мундуруку используют сложные понятия как числа, так и пространства, хотя и в приблизительной и невербальной манере. 22, 23).Поэтому мы спросили, считают ли они эти две области связанными систематическим отображением, и если да, то какую форму принимает это отображение числового пространства.
В общей сложности 33 взрослых и детей мундуруку были индивидуально протестированы в числово-пространственном задании ()(24). В каждом испытании на экране компьютера отображался отрезок линии с одной точкой слева и десятью точками справа (или в отдельном блоке 10 и 100 точек соответственно). Затем в случайном порядке предъявлялись другие числа в различных формах (наборы точек, последовательности тонов, произносимые слова мундуруку, произносимые португальские слова).Для каждого числа участник указывал на место на экране, и этот ответ записывался щелчком мыши без обратной связи. Было представлено только два тренировочных испытания с наборами точек, количество которых соответствовало концам шкалы (например, один и десять). Участникам сказали, что эти два стимула принадлежат их соответствующим концам, но другие стимулы могут быть размещены в любом месте. Поскольку в обучении не использовались промежуточные числа, результаты всех последующих испытаний служили для выявления того, будут ли участники спонтанно использовать систематическое картирование, и если да, то будет ли их картирование компрессионным или линейным.
Задача сопоставления чисел с числами 1–10. Горизонтальный сегмент, помеченный набором из одной точки слева и набором из 10 точек справа, постоянно присутствовал на экране. Числа представлялись визуально в виде набора точек или на слух в виде последовательностей тонов (см. 24), цифр мундуруку или португальских цифр. Для числительных мундуруку дан грубый перевод на арабские цифры (например, «pũg põgbi xex xep bodi» ≈ «одна горсть (и) две сбоку» ≈ 7; «xex xep põgbi» ≈ «две горсти» ≈ 10).Для каждого стимула участники указывали на место на линии, и экспериментатор щелкал по нему компьютерной мышью, в результате чего появлялась небольшая полоса.
Скупые ответы мундуруку показали, что они поняли задачу. Хотя некоторые участники, как правило, использовали только конечные точки шкалы (см. 24), большинство использовали континуум полного ответа и применяли последовательную стратегию сопоставления последовательных чисел с последовательными местоположениями (см. 24). Существовала значительная положительная корреляция между номером стимула и средним местоположением ответа, независимо от модальности, в которой были представлены числа.Задача была легкой, когда стимулы представляли собой наборы точек, похожие на эталонные метки, расположенные на концах (цифры 1–10, r 2 = 92,6%, 8 df; цифры 10–100, r 2 = 91,9%, 8 дф). Однако мундуруку продолжали использовать систематическое отображение числового пространства с необученными стимулами, которые разделяли с эталонными метками только абстрактное понятие числа: последовательности тонов 1–10 (r 2 = 92,5%, 8 df), разговорный мундуруку. числовые слова (r 2 =91,8, 6.df) и португальские числовые слова (r 2 =91.1%, 8 d.f), хотя небольшая доля случайных ответов имела тенденцию к небольшому сглаживанию кривых. Обратите внимание, что стимулы мундуруку включали сложные выражения, которые очень редко произносятся, такие как «pũg põgbi ebadipdip bodi» [примерный перевод: «одна горсть (и) четыре на боку»]. Результаты показывают, что мундуруку частично понимают количество, к которому относятся эти выражения.
Среднее расположение чисел на горизонтальном отрезке, отдельно для участников Мундуруку (левая колонка) и для американских участников (правая колонка).Данные являются средними +/- стандартная ошибка среднего. Графики успеваемости в разбивке по возрастным группам и уровню образования доступны в качестве дополнительного материала (24).
Однако важно отметить, что линейная регрессия не обеспечила наилучшую модель ответов участников. Скорее, для всех модальностей представления кривые были отрицательно ускорены. Процедура множественной регрессии оценивала вклад логарифмического регрессора сверх линейного регрессора. Эффект логарифмического сжатия был значительным для всех модальностей стимула, хотя он был незначительным только для португальских слов (односторонний p = 0.04; см. уровни значимости и веса регрессии на ). Дополнительный анализ позволил нам исключить интерпретации с точки зрения линейного ответа с разным наклоном для малых и больших чисел, ошибки параллакса, предвзятости экспериментатора или бимодального ответа (см. 24). Мундуруку, кажется, придерживаются интуитивных представлений о числах как о логарифмической шкале, где середина интервала от 1 до 10 равна 3 или 4, а не 5 или 6. эксперимент включал несимволические визуальные и слуховые числа.Таким образом, было важно проверить, линейно или логарифмически оценивались эти новые стимулы у образованных западных испытуемых. Как показано на рисунке, взрослые американцы линейно оценили все числа, представленные в английском и испанском языках, а также наборы из 1–10 точек, которые можно было легко сосчитать. Однако они показали значительный логарифмический компонент с наборами из 10–100 точек и последовательностями тонов. Когда две группы участников сравнивали напрямую, мундуруку показали большую нелинейность сжатия, чем американские испытуемые, только с наборами из 1–10 точек (p = 0.003) и числительными на родном языке (р=0,033). Этот вывод согласуется с предыдущими данными, свидетельствующими о том, что западные испытуемые оценивают большое число приблизительно и сжато (25, 26). Их суждения линейны только тогда, когда числа представлены в символической форме или в виде небольших наборов, количество которых можно точно оценить.
Население мундуруку неоднородно, и некоторые из наших участников, особенно дети, получили небольшое образование. Чтобы изучить влияние этой переменной, мы рассчитали для каждого участника индекс нелинейности в отображении числового пространства: вес логарифмического регрессора в множественной регрессии данных на линейных и логарифмических регрессорах.Для этого анализа мы объединили испытания с точками 1–10 и числовыми словами, но исключили те с точками 10–100 и тонами, для которых западные испытуемые показали некоторую нелинейность. Индекс подтвердил очень значительную нелинейность у участников Mundurucu (t = 6,20, 34 df, p <10 -6 ). У американских участников производительность не отклонялась от линейности (p = 0,08) и заметно отличалась от таковой у мундуруку (Welch t = 4,37, 48,6 df, p <0,0001). Важно отметить, что нелинейность мундуруку оставалась значительной даже при ограничении анализа взрослыми (t = 4.34, 23 df, p = 0,0002), говорящим на одном языке (t = 5,36, 29 df, p <10 –5 ), или необразованным участникам (t = 2,60, 7 df, p = 0,035; см. рисунки S7– S10 для графического изображения производительности подгрупп) (24). Т-тесты, линейный и ранговый регрессионный анализ не показали влияния пола, возраста, образования или двуязычия. Наблюдалась только тенденция к уменьшению нелинейности в зависимости от возраста (тау Кендалла = -0,23, р = 0,055). Хотя это наблюдение предполагает, что пожилые мундуруку могут развиваться в сторону большего понимания линейной числовой линии, следует отметить, что у западных детей отображение становится линейным в диапазоне 10–100 к 1-му -му или 2-му -му классу. (17–19), в то время как в наших данных даже самые старые взрослые мундуруку (возраст> 40 лет) продолжали демонстрировать весьма значительную нелинейность в диапазоне 1–10 (1 = 3.36, 11 г. д., р=0,006).
Наконец, мы проанализировали особый случай португальских числительных. Хотя общая успеваемость была логарифмической, деление по уровню образования показало, что логарифмический ответ имел место для участников с 1–2 годами образования (t = 3,15, 16 df, p = 0,006; рисунок S9), но не для тех, у кого вообще не было образования или с дополнительным образованием. У необразованных участников работа с португальскими числительными была сильно вариабельной и слабо коррелировала с числом (r 2 = 39.0, р=0,053; рисунок S8), предполагая, что многие из этих испытуемых просто не знали значения португальских числительных. С другой стороны, для наиболее образованной группы результаты были строго линейными (r 2 = 94,5%, p<10 -5 ; рисунок S10). Исключая участников без образования, мы обнаружили, что более высокий уровень образования значительно изменил ответы на португальский язык с логарифмических на линейные (t = 2,48, 16,6 df, p = 0,024), но оставил без изменений ответы на цифры и узоры точек мундуруку (p> 0,024).5), что дает значительное взаимодействие (p = 0,008). Поразительно, но в более образованной группе результаты значительно различались в зависимости от записи чисел (t = 3,12, 9 d.f., p = 0,012), поскольку они были линейными для португальских цифр, но логарифмическими для цифр мундуруку и точечных узоров 1–10.
В целом, эти результаты раскрывают как универсальные, так и зависящие от культуры грани чувства числа. После минимального периода обучения даже представители отдаленной культуры с ограниченным словарным запасом и образованием легко понимают, что число может быть отображено в пространственной шкале.Однако точная форма этого отображения резко меняется с логарифмической на линейную, в зависимости от возраста, в котором люди проходят тестирование, полученного ими образования и формата, в котором представлены числа.
В свете поведения взрослых амазонок становится ясно, что умственная революция в числовом ряду западных детей не является результатом простого процесса созревания: логарифмическое мышление сохраняется у мундуруку и во взрослом возрасте даже для очень малых чисел в диапазоне 1. –10, независимо от того, представлены ли они в виде точек, тонов или произнесенных слов мундуруку.Каковы источники этого универсального логарифмического отображения? Исследования мозговых механизмов восприятия числа выявили сжатый числовой код, при котором отдельные нейроны в теменной и префронтальной коре демонстрируют кривую настройки Гаусса на логарифмической оси числа (27). Как впервые заметил Густав Фехнер, такая постоянная неточность в логарифмическом масштабе может объяснить закон Вебера — тот факт, что большие числа требуют пропорционально большей разницы, чтобы оставаться одинаково различимыми.Действительно, недавняя модель предполагает, что свойства настройки числовых нейронов могут объяснить многие детали элементарной ментальной арифметики у людей и животных (21). Как правило, логарифмическая шкала обеспечивает компактное нейронное представление величин в несколько порядков с фиксированной относительной точностью.
Пока неизвестно, какой критический образовательный или культурный опыт превращает это исходное представление в линейную шкалу.Когда у отдаленного населения наблюдаются культурные различия в концептуальной репрезентации, часто ссылаются на гипотезу Уорфа (28), согласно которой язык определяет организацию мышления. В данном случае, однако, объяснение Уорфа не работает, поскольку ни лингвистическая компетентность per se (присутствует у всех мундуруку), ни числовой словарный запас и вербальный счет (присутствующие у большинства мундуруку, включая некоторых говорящих на одном языке и маленьких детей, см. 24) достаточно, чтобы вызвать логарифмический сдвиг (17–19).Умозрительно, двумя факторами, лежащими в основе сдвига, могут быть опыт измерения, посредством которого фиксированная числовая единица применяется к различным пространственным положениям, и опыт сложения и вычитания, в конечном итоге дающий интуитивное представление о том, что все последовательные числа разделены одним и тем же интервалом +1. Наиболее образованные мундуруку в конечном итоге понимают, что линейное масштабирование, которое позволяет измерять и сохранять неизменность по сравнению с сложением и вычитанием, является центральным элементом португальской системы числовых слов. В то же время они по-прежнему не распространяют этот принцип на числовые слова мундуруку, где перцептивное сходство между количествами по-прежнему рассматривается как наиболее важное свойство чисел.Система числовых слов мундуруку может быть культурным приемом, который не делает упор на измерение или неизменность путем сложения / вычитания как определяющую черту числа, в отличие от западных цифр.
Одновременное присутствие линейных и сжатых мысленных представлений чисел, вероятно, не уникально для мундуруку. У американских детей логарифмическое отображение не исчезает сразу, а исчезает сначала для небольших чисел, а гораздо позже для больших чисел от 1 до 1000 (до 4-го -го или 6-го -го класса у некоторых детей) (17–19). .На самом деле логарифмическое представление может дремать у всех нас для очень больших чисел или всякий раз, когда мы аппроксимируем числа (29), включая цены (30). Таким образом, логарифмические и линейные шкалы могут быть глубоко укоренены во всей нашей умственной деятельности (31).
Как считать предметы с помощью счетных весов
Ресурс
Использование счетных весов для подсчета мелких деталей может сэкономить много времени. В этом руководстве мы дадим вам пошаговые инструкции по подсчету предметов с помощью счетных весов.
Если вы не знаете массу образца
Счетные весы «подсчитывают» путем взвешивания образцов и деления общего веса на индивидуальный вес. Если вы уже знаете вес штуки, вы можете просто ввести его в весы и начать считать. Вот как узнать вес, если у вас его нет:
- Поместите контейнер на платформу весов
- Тарирование контейнера с помощью кнопки тарирования
- Поместите гирю образца в тарированный контейнер.Вы можете разместить один образец или несколько, если знаете точное количество.
- После взвешивания образца используйте цифровую клавиатуру для ввода количества взвешенных штук.
- После ввода количества штук нажмите клавишу SMPL. Это сохранит введенное вами количество штук, и при необходимости весы рассчитают вес отдельных штук.
- 3 дисплея помечены.У вас есть вес, который представляет собой общий вес на весах (минус все, что вы тарировали). Единичный вес – это индивидуальный вес каждого предмета. Количество штук – это количество штук на весах.
- Теперь вы можете положить предметы на весы, они их посчитают и дадут вам общий вес. Вес единицы может измениться, поскольку весы уточняют точный вес образца.
Тарирование контейнера
Введите количество взвешенных штук
Нажмите клавишу SMPL, чтобы сохранить количество взвешенных штук
Если вы уже знаете удельный вес, вместо шагов 3-5 вам следует сделать следующее:
- Введите вес с цифровой клавиатуры.
- После того, как вы ввели вес, нажмите клавишу «U.Wt». Это сохранит введенный вами вес в качестве веса единицы, и это число будет использоваться для подсчета остальных частей.
 1:100 000 на 4 части
1:100 000 на 4 части
 г. температура или время.
г. температура или время. Данные, которые подсчитываются или измеряются численно определенным методом, называются числовыми (количественными).
Данные, которые подсчитываются или измеряются численно определенным методом, называются числовыми (количественными).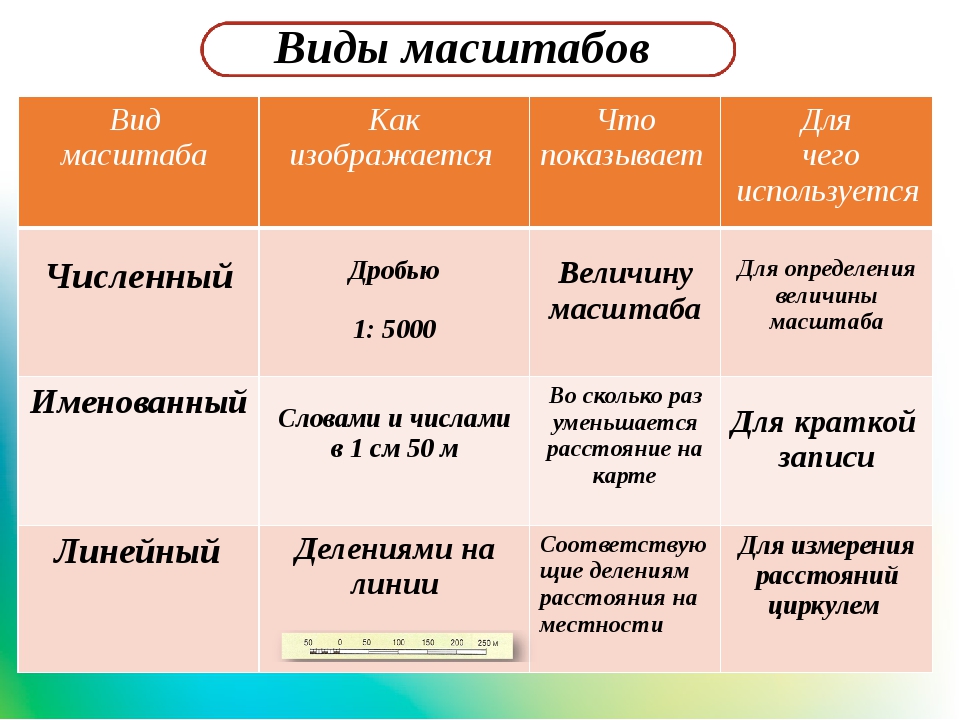
 Простые соотношения (от 0 до 1, т. е. знаменатель — это максимально возможное значение, которое может принимать числитель) можно рассматривать как непрерывные данные. Более сложные для анализа данные возникают, когда отношение представляет собой изменение, и значение может быть отрицательным. Отношения наблюдений по сравнению с эталонными значениями, т.е.г. рост по отношению к среднему значению референтной популяции для данного пола и возраста трудно обрабатывать, поскольку значения могут падать в обе стороны от 1 (100%).
Простые соотношения (от 0 до 1, т. е. знаменатель — это максимально возможное значение, которое может принимать числитель) можно рассматривать как непрерывные данные. Более сложные для анализа данные возникают, когда отношение представляет собой изменение, и значение может быть отрицательным. Отношения наблюдений по сравнению с эталонными значениями, т.е.г. рост по отношению к среднему значению референтной популяции для данного пола и возраста трудно обрабатывать, поскольку значения могут падать в обе стороны от 1 (100%). Вы можете изменить поле, чтобы оно было доступно только для чтения или скрыто.
Вы можете изменить поле, чтобы оно было доступно только для чтения или скрыто.

 312)
312)