Радиус описанной окружности трапеции | Треугольники
Как найти радиус описанной окружности для трапеции?
В зависимости от данных условия, сделать это можно разными способами. Готовой формулы радиуса описанной около трапеции окружности нет.
I. Радиус описанной около трапеции окружности как радиус окружности, описанной около треугольника, вершины которого — вершины трапеции
Описанная около трапеции окружность проходит через все её вершины, следовательно, является описанной для любого из треугольников, вершины которых являются вершинами трапеции.
В общем случае радиус описанной около треугольника окружности может быть найден по одной из формул
где a — сторона треугольника, α — противолежащий ей угол;
либо по формуле
где a, b, c — стороны, S — площадь треугольника.
Для трапеции ABCD радиус может быть найден, например, как радиус окружности, описанной около треугольника ABD:
или
где синус угла A можно найти из прямоугольного треугольника ABF:
III. Радиус описанной около трапеции окружности как расстояние до точки пересечения серединных перпендикуляров
Радиус описанной около трапеции окружности как расстояние до точки пересечения серединных перпендикуляров
Радиус описанной окружности — точка пересечения серединных перпендикуляров с сторонам трапеции. (Можно рассуждать иначе: в равнобедренном треугольнике AOD (AO=OD=R) высота ON является также медианой. Для треугольника BOC — аналогично).
Если известна высота трапеции KN=h, основания AD=a, BC=b, можно обозначить ON=x.
Если центр окружности лежит внутри трапеции, OK=h-x, из прямоугольных треугольников ANO и BKO можно выразить
и приравнять правые части
Решив это уравнения относительно x, можно найти R.
IV. Если диагональ трапеции перпендикулярна боковой стороне, центр описанной окружности лежит на середине большего основания и радиус равен половине большего основания.
точка O — середина AD
Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной окружности лежит вне трапеции, за большим основанием.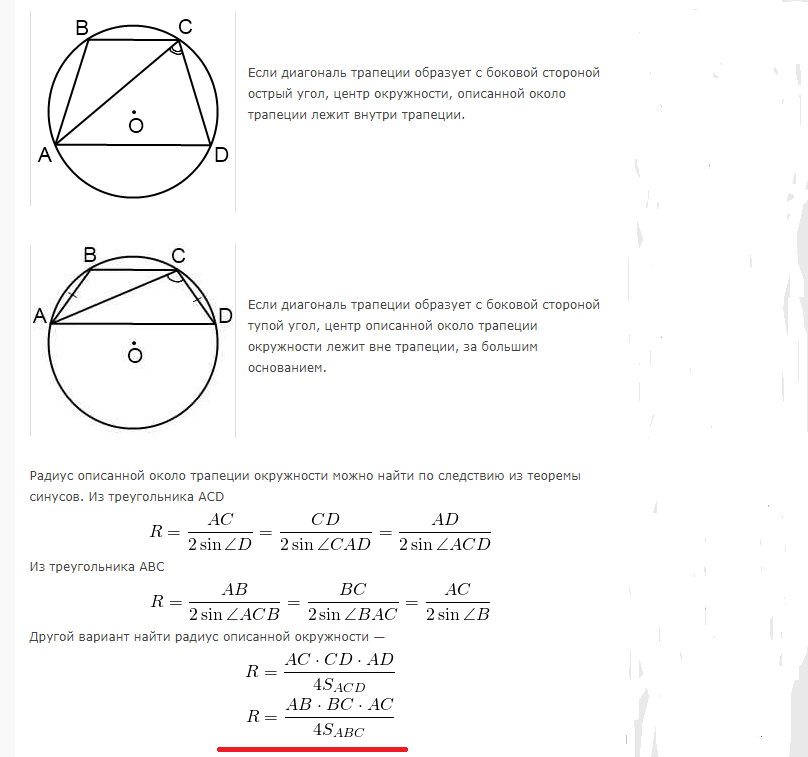
I вариант нахождения радиуса для этого случая не изменяется.
Во II случае OK=h+x, соответственно, изменяется уравнение для нахождения x и R.
Позже рассмотрим конкретные задачи нахождения радиуса описанной около трапеции окружности.
Свойства трапеции, описанной около окружности: формулы и теоремы
Трапеция — это геометрическая фигура с четырмя углами. При построении трапеции важно учитывать, что две противоположные стороны параллельны, а две другие, наоборот, не параллельны относительно друг друга. Это слово пришло в современность из Древней Греции и звучало как «трапедзион», что означало «столик», «обеденный столик».
Эта статья рассказывает о свойствах трапеции, описанной около окружности. Также мы рассмотрим виды и элементы этой фигуры.
Элементы, виды и признаки геометрической фигуры трапеция
Параллельные стороны в этой фигуре называют основаниями, а те, что не параллельны — боковыми сторонами.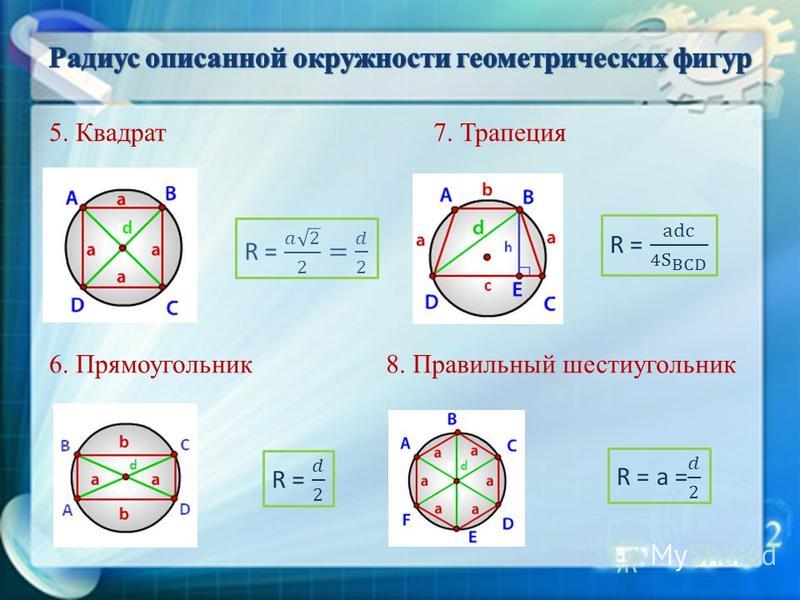 При условии, что боковые стороны одинаковой длины, трапеция считается равнобедренной. Трапеция, боковые стороны которой лежат перпендикулярно основанию под углом в 90°, называется прямоугольной.
При условии, что боковые стороны одинаковой длины, трапеция считается равнобедренной. Трапеция, боковые стороны которой лежат перпендикулярно основанию под углом в 90°, называется прямоугольной.
У этой, казалось бы, незамысловатой фигуры имеется немалое количество свойств, ей присущих, подчеркивающих ее признаки:
- Если провести среднюю линию по боковым сторонам, то она будет параллельна основаниям. Этот отрезок будет равен 1/2 разности оснований.
- При построении биссектрисы из любого угла трапеции образуется равносторонний треугольник.
- Из свойств трапеции, описанной около окружности, известно, что сумма параллельных боковых сторон должна быть равна сумме оснований.
- При построении диагональных отрезков, где одна из сторон является основанием трапеции, полученные треугольники будут подобны.
- При построении диагональных отрезков, где одна из сторон является боковой, полученные треугольники будут иметь равную площадь.
- Если продолжить боковые линии и построить отрезок из центра основания, то образованный угол будет равен 90°.
 Отрезок, соединяющий основания, будет равен 1/2 их разности.
Отрезок, соединяющий основания, будет равен 1/2 их разности.
Свойства трапеции, описанной около окружности
Заключить окружность в трапецию возможно лишь при одном условии. Данное условие заключается в том, что сумма боковых сторон должна быть ровна сумме оснований. Например, при построении трапеции AFDM применимо AF + DM = FD + AM. Только в таком случае в трапецию можно заключить круг.
Итак, подробнее о свойствах трапеции, описанной около окружности:
- Если в трапецию заключена окружность, то для того, чтобы найти длину ее линии, пересекающей фигуру пополам, необходимо найти 1/2 от суммы длин боковых сторон.
- При построении трапеции, описанной около окружности, образованная гипотенуза тождественна радиусу круга, а высота трапеции по совместительству является и диаметром круга.
- Еще одним свойством равнобедренной трапеции, описанной около окружности, является то, что ее боковая сторона сразу видна от центра окружности под углом 90°.
Еще немного о свойствах трапеции, заключенной в окружность
Только равнобедренная трапеция может быть вписана в окружность. Это значит, что нужно соблюсти условия, при которых построенная трапеция AFDM будет отвечать следующим требованиям: AF + DM = FD + MA.
Теорема Птолемея гласит, что в трапеции, заключенной в окружность, произведение диагоналей тождественно и равно сумме умноженных противоположных сторон. Это значит, что при построении окружности, описанной около трапеции AFDM, применимо: AD × FM = AF × DM + FD × AM.
На школьных экзаменах довольно часто встречаются задачи, требующие решения задач с трапецией. Большое количество теорем необходимо запоминать, но если выучить сразу не получиться — не беда. Лучше всего периодически прибегать к подсказке в учебниках, чтобы эти знания сами собой, без особого труда уложились в голове.
Как найти радиус описанной вокруг трапеции окружности. Материал по геометрии на тему «трапеция и ее свойства»
Добрый вечер! Ох уж эти описанные, или вписанные окружности, геометрические фигуры. Так сложно запутаться. что да когда.
Так сложно запутаться. что да когда.
Давайте попробуем разобраться для начала с формулировкой. Нам дана окружность описанная около . Иными словами — данная трапеция вписана в окружность.
Давайте вспомним, что описать окружность мы можем только вокруг . А равнобедренная трапеция в свою очередь — это трапеция, у которой боковые стороны равны.
Давайте попробуем решить задачку. Нам известно, что основания равнобедренной трапеции ADCB равны 6 (DC) и 4 (AB). А радиус описанной окружности равен 4. Нужно найдите высоту трапеции FK.
FK — высота трапеции. её нам нужно найти, но перед этим вспомним, что точка О — это центр окружности. А ОС, ОD, OA, OB — известные радиусы .
В OFC нам известна гипотенуза, которая является радиусом окружности, а катет FC = половине основания DC = 3 см (так как DF = FC).
Теперь по найдём OF:
А в прямоугольном треугольнике OKB нам тоже известна гипотенуза, так как это радиус окружности. А KB равняется половине AB; KB = 2 см.
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции .
Данный отрезок параллелен основаниям трапеции .
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными .
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.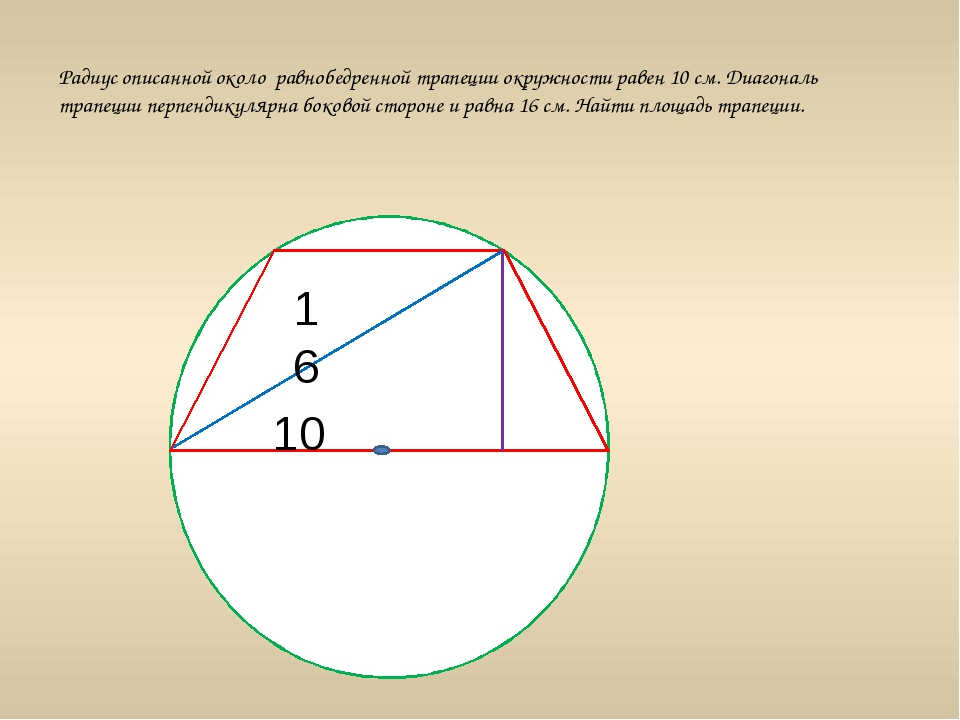
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований .
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции
(BC/AD).KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка , проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
Формулы для нахождения диагоналей трапеции
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1.
2 . Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
3 . Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту
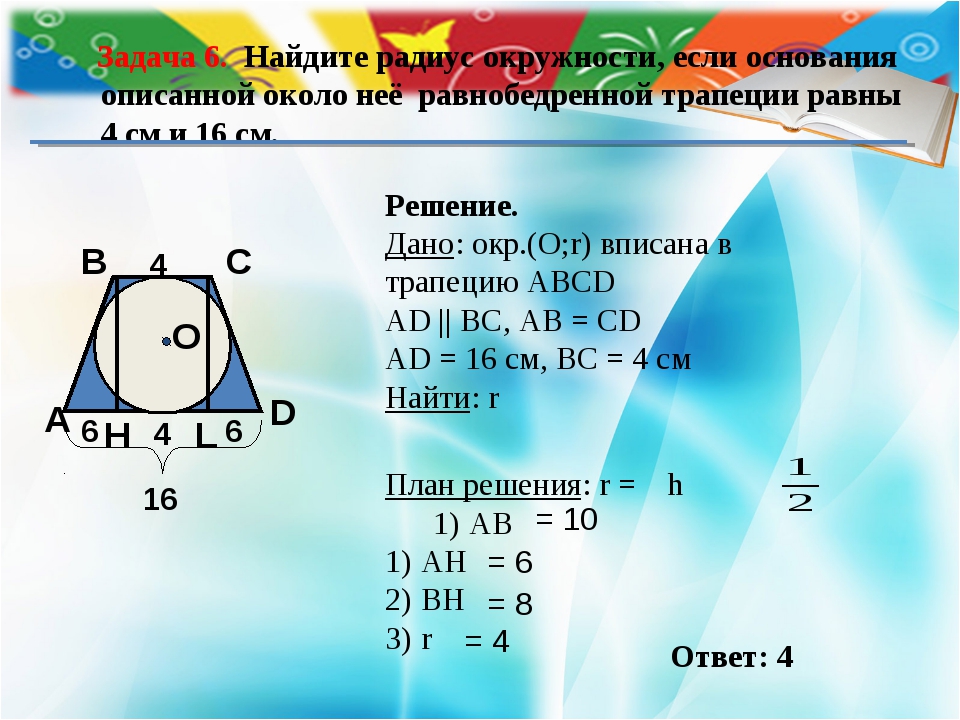
Задача .
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.
Решение .
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Ответ : 16 см
Задача
.
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.
Решение
.
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2
Учтем, что a = 16 — b , тогда в первом уравнении
h 2 + (24 — 16 + b) 2 = 425
h 2 = 425 — (8 + b) 2
Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 — (8 + b) 2 + (24 — b) 2 = 169
-(64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Откуда
h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5
Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2
Ответ : площадь трапеции равна 80 см 2 .
В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.
В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.
Свойства диагоналей трапеции
Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.
- Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 .
- Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k 2 . - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
- Еще одно свойство трапеции включает в себя построение диагоналей.
 Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т. - Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ .
- А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b) .
Свойства средней линии трапеции
Среднюю линию проведите в трапеции параллельно ее основаниям.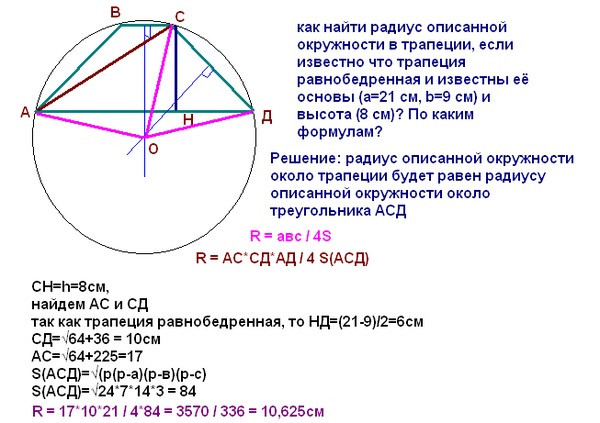
- Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2 .
- Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Свойства углов трапеции
- Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180 0: α + β = 180 0 и γ + δ = 180 0 .
- Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2 .

- Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.
Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.
- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
- Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.
- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.

- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2 .
- Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
- На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .
Свойства трапеции, вписанной в окружность
Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.
Так и поймете быстрее, и запомните лучше.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
- Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
- Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ .
- Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника.
 Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников. - Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S АМЕ .
Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2 .
- У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ .
- Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.

- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab .
- И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, прилежащая к прямому углу, равны.
 Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу. - Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.
Что и требовалось доказать.
Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной :
- Для начала проведем прямую МХ – МХ || КЕ.
 Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.
МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.
Задача для повторения
Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150 0 с меньшим основанием. Требуется найти площадь трапеции.
Решение: Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.
Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180 0 . Поэтому КАН = 30 0 (на основании свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30 0 . Поэтому КН = ½АВ = 4 см.
Поэтому КН = ½АВ = 4 см.
Площадь трапеции находим по формуле: S АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см 2 .
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.
Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.
Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Трапеция — это геометрическая фигура с четырмя углами.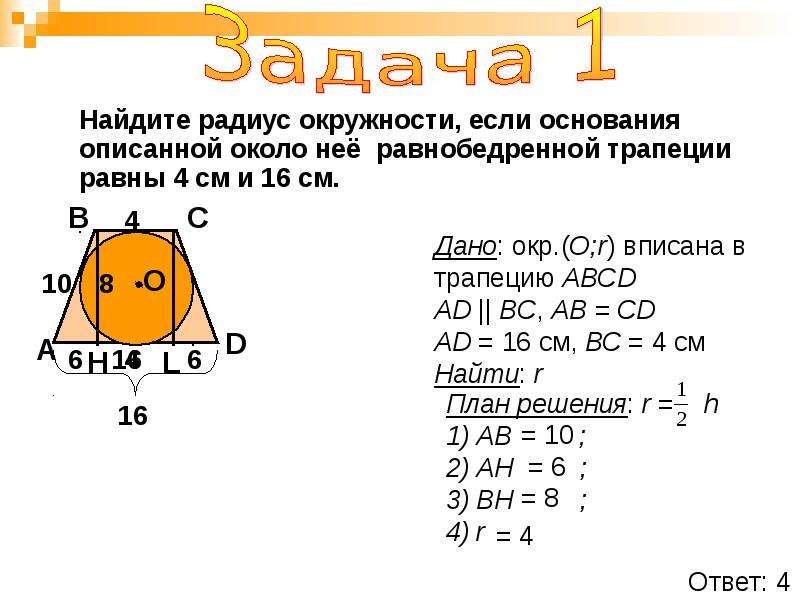 При построении трапеции важно учитывать, что две противоположные стороны параллельны, а две другие, наоборот, не параллельны относительно друг друга. Это слово пришло в современность из Древней Греции и звучало как «трапедзион», что означало «столик», «обеденный столик».
При построении трапеции важно учитывать, что две противоположные стороны параллельны, а две другие, наоборот, не параллельны относительно друг друга. Это слово пришло в современность из Древней Греции и звучало как «трапедзион», что означало «столик», «обеденный столик».
Эта статья рассказывает о свойствах трапеции, описанной около окружности. Также мы рассмотрим виды и элементы этой фигуры.
Элементы, виды и признаки геометрической фигуры трапеция
Параллельные стороны в этой фигуре называют основаниями, а те, что не параллельны — боковыми сторонами. При условии, что боковые стороны одинаковой длины, трапеция считается равнобедренной. Трапеция, боковые стороны которой лежат перпендикулярно основанию под углом в 90°, называется прямоугольной.
У этой, казалось бы, незамысловатой фигуры имеется немалое количество свойств, ей присущих, подчеркивающих ее признаки:
- Если провести среднюю линию по боковым сторонам, то она будет параллельна основаниям. Этот отрезок будет равен 1/2 разности оснований.

- При построении биссектрисы из любого угла трапеции образуется равносторонний треугольник.
- Из свойств трапеции, описанной около окружности, известно, что сумма параллельных боковых сторон должна быть равна сумме оснований.
- При построении диагональных отрезков, где одна из сторон является основанием трапеции, полученные треугольники будут подобны.
- При построении диагональных отрезков, где одна из сторон является боковой, полученные треугольники будут иметь равную площадь.
- Если продолжить боковые линии и построить отрезок из центра основания, то образованный угол будет равен 90°. Отрезок, соединяющий основания, будет равен 1/2 их разности.
Свойства трапеции, описанной около окружности
Заключить окружность в трапецию возможно лишь при одном условии. Данное условие заключается в том, что сумма боковых сторон должна быть ровна сумме оснований. Например, при построении трапеции AFDM применимо AF + DM = FD + AM. Только в таком случае в трапецию можно заключить круг.
Итак, подробнее о свойствах трапеции, описанной около окружности:
- Если в трапецию заключена окружность, то для того, чтобы найти длину ее линии, пересекающей фигуру пополам, необходимо найти 1/2 от суммы длин боковых сторон.
- При построении трапеции, описанной около окружности, образованная гипотенуза тождественна радиусу круга, а высота трапеции по совместительству является и диаметром круга.
- Еще одним свойством равнобедренной трапеции, описанной около окружности, является то, что ее боковая сторона сразу видна от центра окружности под углом 90°.
Еще немного о свойствах трапеции, заключенной в окружность
Только равнобедренная трапеция может быть вписана в окружность. Это значит, что нужно соблюсти условия, при которых построенная трапеция AFDM будет отвечать следующим требованиям: AF + DM = FD + MA.
Теорема Птолемея гласит, что в трапеции, заключенной в окружность, произведение диагоналей тождественно и равно сумме умноженных противоположных сторон. \circ\)
.
\circ\)
.
2) Т.к. \(AD\parallel BC\)
и \(BD\)
– секущая, то \(\angle DBC=\angle
BDA\)
как накрест лежащие.
Также \(\angle BOC=\angle AOD\)
как вертикальные.
Следовательно, по двум углам \(\triangle BOC \sim \triangle AOD\)
.
Докажем, что \(S_{\triangle AOB}=S_{\triangle COD}\) . Пусть \(h\) – высота трапеции. Тогда \(S_{\triangle ABD}=\frac12\cdot h\cdot AD=S_{\triangle ACD}\) . Тогда: \
Определение
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство*
1) Докажем параллельность.
Проведем через точку \(M\) прямую \(MN»\parallel AD\) (\(N»\in CD\) ). Тогда по теореме Фалеса (т.к. \(MN»\parallel AD\parallel BC, AM=MB\) ) точка \(N»\) — середина отрезка \(CD\) . Значит, точки \(N\) и \(N»\) совпадут.
2) Докажем формулу.
Проведем \(BB»\perp AD, CC»\perp AD\)
. Пусть \(BB»\cap MN=M», CC»\cap
MN=N»\)
.
Пусть \(BB»\cap MN=M», CC»\cap
MN=N»\)
.
Тогда по теореме Фалеса \(M»\) и \(N»\) — середины отрезков \(BB»\) и \(CC»\) соответственно. Значит, \(MM»\) – средняя линия \(\triangle ABB»\) , \(NN»\) — средняя линия \(\triangle DCC»\) . Поэтому: \
Т.к. \(MN\parallel AD\parallel BC\) и \(BB», CC»\perp AD\) , то \(B»M»N»C»\) и \(BM»N»C\) – прямоугольники. По теореме Фалеса из \(MN\parallel AD\) и \(AM=MB\) следует, что \(B»M»=M»B\) . Значит, \(B»M»N»C»\) и \(BM»N»C\) – равные прямоугольники, следовательно, \(M»N»=B»C»=BC\) .
Таким образом:
\ \[=\dfrac12 \left(AB»+B»C»+BC+C»D\right)=\dfrac12\left(AD+BC\right)\]
Теорема: свойство произвольной трапеции
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем, что точки \(P\)
, \(N\)
и \(M\)
лежат на одной прямой.
Проведем прямую \(PN\) (\(P\) – точка пересечения продолжений боковых сторон, \(N\) – середина \(BC\) ). Пусть она пересечет сторону \(AD\) в точке \(M\) . Докажем, что \(M\) – середина \(AD\) .
Рассмотрим \(\triangle BPN\) и \(\triangle APM\) . Они подобны по двум углам (\(\angle APM\) – общий, \(\angle PAM=\angle PBN\) как соответственные при \(AD\parallel BC\) и \(AB\) секущей). Значит: \[\dfrac{BN}{AM}=\dfrac{PN}{PM}\]
Рассмотрим \(\triangle CPN\) и \(\triangle DPM\) . Они подобны по двум углам (\(\angle DPM\) – общий, \(\angle PDM=\angle PCN\) как соответственные при \(AD\parallel BC\) и \(CD\) секущей). Значит: \[\dfrac{CN}{DM}=\dfrac{PN}{PM}\]
Отсюда \(\dfrac{BN}{AM}=\dfrac{CN}{DM}\) . Но \(BN=NC\) , следовательно, \(AM=DM\) .
2) Докажем, что точки \(N, O, M\) лежат на одной прямой.
Пусть \(N\)
– середина \(BC\)
, \(O\)
– точка пересечения диагоналей. Проведем прямую \(NO\)
, она пересечет сторону \(AD\)
в точке \(M\)
. Докажем, что \(M\)
– середина \(AD\)
.
Докажем, что \(M\)
– середина \(AD\)
.
\(\triangle BNO\sim \triangle DMO\) по двум углам (\(\angle OBN=\angle ODM\) как накрест лежащие при \(BC\parallel AD\) и \(BD\) секущей; \(\angle BON=\angle DOM\) как вертикальные). Значит: \[\dfrac{BN}{MD}=\dfrac{ON}{OM}\]
Аналогично \(\triangle CON\sim \triangle AOM\) . Значит: \[\dfrac{CN}{MA}=\dfrac{ON}{OM}\]
Отсюда \(\dfrac{BN}{MD}=\dfrac{CN}{MA}\) . Но \(BN=CN\) , следовательно, \(AM=MD\) .
\[{\Large{\text{Равнобедренная трапеция}}}\]
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
1) Рассмотрим равнобедренную трапецию \(ABCD\)
.
Из вершин \(B\) и \(C\) опустим на сторону \(AD\) перпендикуляры \(BM\) и \(CN\) соответственно. Так как \(BM\perp AD\) и \(CN\perp AD\) , то \(BM\parallel CN\) ; \(AD\parallel BC\) , тогда \(MBCN\) – параллелограмм, следовательно, \(BM = CN\) .
Рассмотрим прямоугольные треугольники \(ABM\) и \(CDN\) . Так как у них равны гипотенузы и катет \(BM\) равен катету \(CN\) , то эти треугольники равны, следовательно, \(\angle DAB = \angle CDA\) .
2)
Т.к. \(AB=CD, \angle A=\angle D, AD\) – общая, то по первому признаку . Следовательно, \(AC=BD\) .
3) Т.к. \(\triangle ABD=\triangle ACD\) , то \(\angle BDA=\angle CAD\) . Следовательно, треугольник \(\triangle AOD\) – равнобедренный. Аналогично доказывается, что и \(\triangle BOC\) – равнобедренный.
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
Рассмотрим трапецию \(ABCD\) , такую что \(\angle A = \angle D\) .
Достроим трапецию до треугольника \(AED\) как показано на рисунке. Так как \(\angle 1 = \angle 2\) , то треугольник \(AED\) равнобедренный и \(AE = ED\) . Углы \(1\) и \(3\) равны как соответственные при параллельных прямых \(AD\) и \(BC\) и секущей \(AB\) . Аналогично равны углы \(2\) и \(4\) , но \(\angle 1 = \angle 2\) , тогда \(\angle 3 = \angle 1 = \angle 2 = \angle 4\) , следовательно, треугольник \(BEC\) тоже равнобедренный и \(BE = EC\) .
В итоге \(AB = AE — BE = DE — CE = CD\) , то есть \(AB = CD\) , что и требовалось доказать.
2) Пусть \(AC=BD\) . Т.к. \(\triangle AOD\sim \triangle BOC\) , то обозначим их коэффициент подобия за \(k\) . Тогда если \(BO=x\) , то \(OD=kx\) . Аналогично \(CO=y \Rightarrow AO=ky\) .
Т.к. \(AC=BD\)
, то \(x+kx=y+ky \Rightarrow x=y\)
. Значит \(\triangle AOD\)
– равнобедренный и \(\angle OAD=\angle ODA\)
.
Таким образом, по первому признаку \(\triangle ABD=\triangle ACD\) (\(AC=BD, \angle OAD=\angle ODA, AD\) – общая). Значит, \(AB=CD\) , чтд.
Задачи В8 ЕГЭ по математике. Многоугольник и окружность
Задача 1. Периметр треугольника равен а радиус вписанной окружности равен Найдите площадь этого треугольника.
Решение: + показать
Задача 2. Площадь треугольника равна а радиус вписанной окружности равен Найдите периметр этого треугольника.
Решение: + показать
Задача 3. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна
Решение: + показать
Задача 4. Сторона правильного треугольника равна . Найдите радиус окружности, вписанной в этот треугольник.
Решение: + показать
Задача 5. Радиус окружности, вписанной в правильный треугольник, равен Найдите сторону этого треугольника.
Решение: + показать
Задача 6.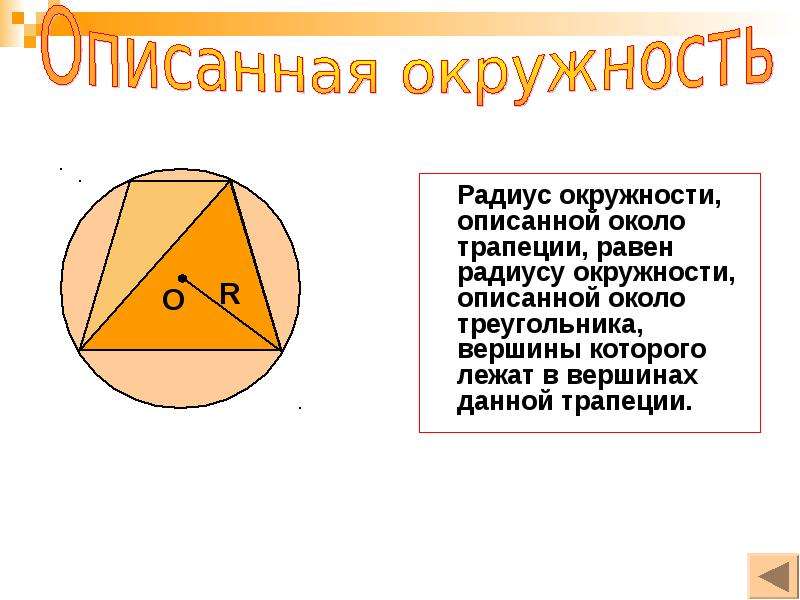 Около окружности, радиус которой равен описан многоугольник, периметр которого равен Найдите его площадь.
Около окружности, радиус которой равен описан многоугольник, периметр которого равен Найдите его площадь.
Решение: + показать
Задача 7. В четырехугольник вписана окружность, Найдите периметр четырехугольника.
Решение: + показать
Раз в выпуклый четырехугольник вписана окружность, то
Тогда .
Ответ:
Задача 8. Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как Найдите большую сторону этого четырехугольника, если известно, что его периметр равен
Решение: + показать
Задача 9. Сторона ромба равна острый угол равен ˚. Найдите радиус вписанной окружности этого ромба.
Решение: + показать
Задача 10. Найдите высоту трапеции, в которую вписана окружность радиуса
Решение: + показать
Высота трапеции – есть диаметр вписанной окружности в трапецию:
Ответ:
Задача 11. Боковые стороны трапеции, описанной около окружности, равны и Найдите среднюю линию трапеции.
Боковые стороны трапеции, описанной около окружности, равны и Найдите среднюю линию трапеции.
Решение: + показать
Задача 12. Периметр прямоугольной трапеции, описанной около окружности, равен ее большая боковая сторона равна Найдите радиус окружности.
Решение: + показать
Задача 13. Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен .
Решение: + показать
Шестиугольник составлен из правильных равных треугольников.
Рассмотрим правильный треугольник :
В нем
– медиана и высота;
Ответ:
Задача 14. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной
Решение: + показать
Задача 15. Катеты равнобедренного прямоугольного треугольника равны Найдите радиус окружности, вписанной в этот треугольник.
Решение: + показать
Обозначим временно катеты за Тогда гипотенуза есть
Тогда
Итак,
Ответ:
Задача 16. В треугольнике стороны угол равен °. Найдите радиус вписанной окружности.
Решение: + показать
Воспользуемся формулой:
Ответ:
Задача 17. Боковые стороны равнобедренного треугольника равны основание равно Найдите радиус вписанной окружности.
Решение: + показать
Задача 18. Боковые стороны равнобедренного треугольника равны основание равно Найдите радиус вписанной окружности.
Решение: + показать
Воспользуемся формулой Герона:
,
где – полупериметр, – стороны треугольника.
Поскольку
то
Наконец,
Ответ:
Задача 19. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны и считая от вершины, противолежащей основанию. Найдите периметр треугольника.
Найдите периметр треугольника.
Решение: + показать
Задача 20. К окружности, вписанной в треугольник проведены три касательные. Периметры отсеченных треугольников равны Найдите периметр данного треугольника.
Решение: + показать
Вы можете пройти тест по теме «Окружность и многоугольник»
Окружность около трапеции. Запоминаем и применяем свойства трапеции
Описанная окружность и трапеция. Здравствуйте! Для вас ещё одна публикация, в которой рассмотрим задачи с трапециями. Задания входят в состав экзамена по математике. Здесь они объединены в группу, дана не просто одна трапеция, а комбинация тел – трапеция и окружность. Большинство из таких задачек решаются устно. Но есть и такие на которые нужно обратить особое внимание, например, задача 27926.
Какую теорию необходимо помнить? Это:
Задачи с трапециями, которые имеются на блоге можно посмотреть здесь .
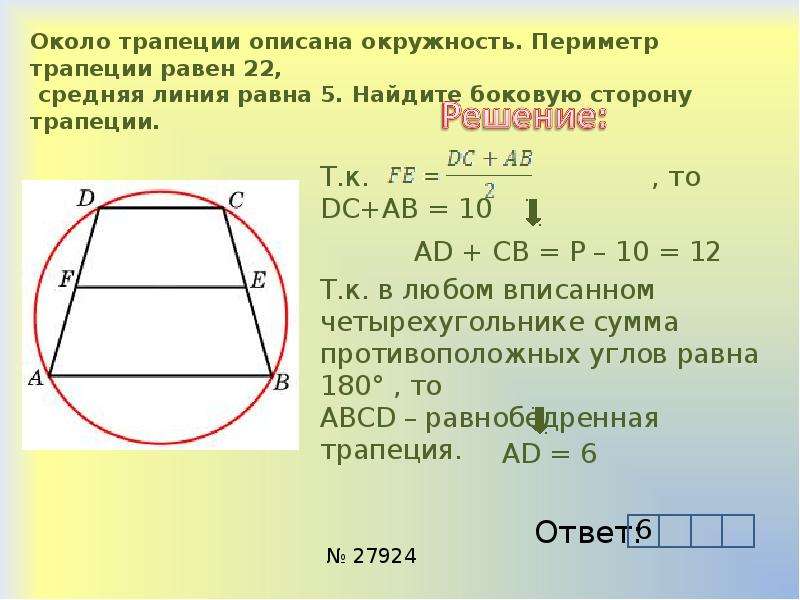
27924. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.
Отметим, что описать окружность можно только около равнобедренной трапеции. Нам дана средняя линия, значит можем определить сумму оснований, то есть:
Значит сумма боковых сторон будет равна 22–10=12 (периметр минус основания). Так как боковые стороны равнобедренной трапеции равны, то одна сторона будет равна шести.
27925. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60 0 , большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
Если вы решали задачи с окружностью и вписанным в неё шестиугольником, то сразу озвучите ответ – радиус равен 6. Почему?
Посмотрите: равнобедренная трапеция с углом при основании равным 60 0 и равными сторонами AD, DC и CB, представляет собой половину правильного шестиугольника:
В таком шестиугольнике отрезок соединяющий противоположные вершины проходит через центр окружности. *Центр шестиугольника и центр окружности совпадают, подробнее
*Центр шестиугольника и центр окружности совпадают, подробнее
То есть большее основание этой трапеции совпадает с диаметром описанной окружности. Таким образом радиус равен шести.
*Конечно, можно рассмотреть равенство треугольников ADO, DOС и OCB. Доказать что они равносторонние. Далее сделать вывод о том, что угол AOB равен 180 0 и точка О равноудалена от вершин A, D, C и B, а и значит АО=ОВ=12/2=6.
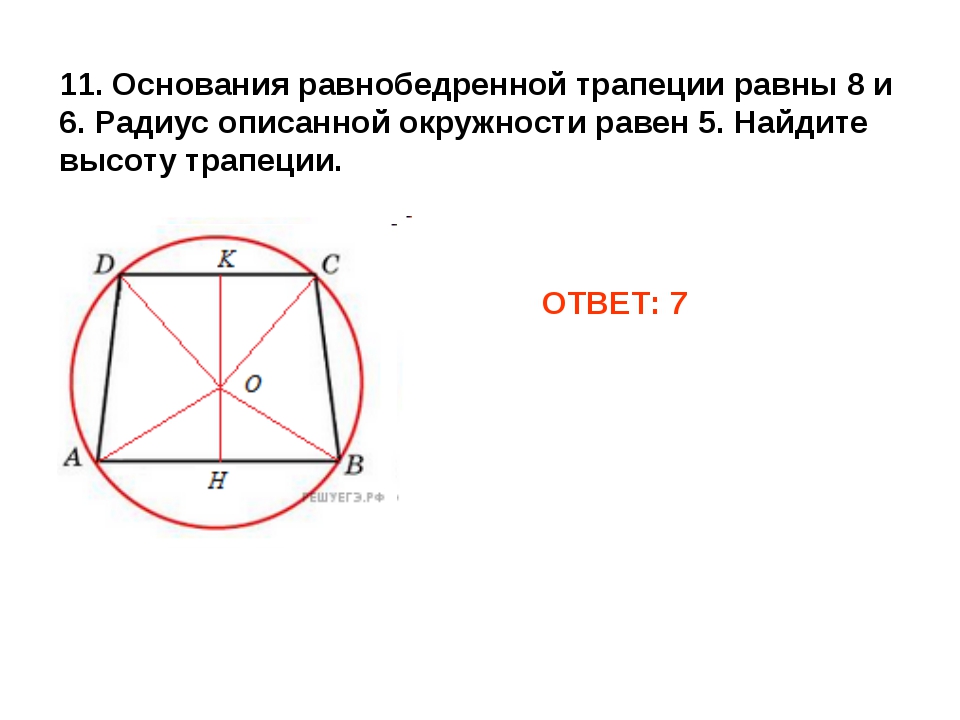
27926. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.
Отметим, что центр описанной окружности лежит на оси симметрии, при чём если построить высоту трапеции проходящую через этот центр, то она при пересечении с основаниями разделит их пополам. Покажем это на эскизе, также соединим центр с вершинами:
Отрезок EF является высотой трапеции, его нам нужно найти.
В прямоугольном треугольнике OFC нам известна гипотенуза (это радиус окружности), FC=3 (так как DF=FC). По теореме Пифагора можем вычислить OF:
В прямоугольном треугольнике OEB нам известна гипотенуза (это радиус окружности), EB=4 (так как AE=EB). По теореме Пифагора можем вычислить OE:
По теореме Пифагора можем вычислить OE:
Таким образом EF=FO+OE=4+3=7.
Теперь важный нюанс!
В этой задаче на рисунке чётко показано, что основания лежат по разные стороны от центра окружности, поэтому задача решается именно так.
А если бы в условии не было дано эскиза?
Тогда у задачи было бы два ответа. Почему? Посмотрите внимательно – в любую окружность можно вписать две трапеции с заданными основаниями:
*То есть при данных основаниях трапеции и радиусе окружности существует две трапеции.
И решение будет «второго варианта» будет следующим.
По теореме Пифагора вычисляем OF:
Также вычислим OE:
Таким образом EF=FO–OE=4–3=1.
Конечно, в задаче с кратким ответом на ЕГЭ двух ответов быть не может, и подобная задача без эскиза дана не будет. Поэтому обратите особое внимание на эскиз! А именно: как расположены основания трапеции. А вот в заданиях с развёрнутым ответом такая в прошлые годы присутствовала (немного с усложнённым условием). Тот, кто рассматривал только один вариант расположения трапеции теряли балл на этом задании.
Тот, кто рассматривал только один вариант расположения трапеции теряли балл на этом задании.
27937. Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.
Здесь сразу следует вспомнить свойство четырёхугольника описанного около окружности:
Суммы противоположных сторон любого четырёхугольника описанного около окружности равны.
Трапеция — это геометрическая фигура с четырмя углами. При построении трапеции важно учитывать, что две противоположные стороны параллельны, а две другие, наоборот, не параллельны относительно друг друга. Это слово пришло в современность из Древней Греции и звучало как «трапедзион», что означало «столик», «обеденный столик».
Эта статья рассказывает о свойствах трапеции, описанной около окружности. Также мы рассмотрим виды и элементы этой фигуры.
Элементы, виды и признаки геометрической фигуры трапеция
Параллельные стороны в этой фигуре называют основаниями, а те, что не параллельны — боковыми сторонами. При условии, что боковые стороны одинаковой длины, трапеция считается равнобедренной. Трапеция, боковые стороны которой лежат перпендикулярно основанию под углом в 90°, называется прямоугольной.
При условии, что боковые стороны одинаковой длины, трапеция считается равнобедренной. Трапеция, боковые стороны которой лежат перпендикулярно основанию под углом в 90°, называется прямоугольной.
У этой, казалось бы, незамысловатой фигуры имеется немалое количество свойств, ей присущих, подчеркивающих ее признаки:
- Если провести среднюю линию по боковым сторонам, то она будет параллельна основаниям. Этот отрезок будет равен 1/2 разности оснований.
- При построении биссектрисы из любого угла трапеции образуется равносторонний треугольник.
- Из свойств трапеции, описанной около окружности, известно, что сумма параллельных боковых сторон должна быть равна сумме оснований.
- При построении диагональных отрезков, где одна из сторон является основанием трапеции, полученные треугольники будут подобны.
- При построении диагональных отрезков, где одна из сторон является боковой, полученные треугольники будут иметь равную площадь.
- Если продолжить боковые линии и построить отрезок из центра основания, то образованный угол будет равен 90°.
 Отрезок, соединяющий основания, будет равен 1/2 их разности.
Отрезок, соединяющий основания, будет равен 1/2 их разности.
Свойства трапеции, описанной около окружности
Заключить окружность в трапецию возможно лишь при одном условии. Данное условие заключается в том, что сумма боковых сторон должна быть ровна сумме оснований. Например, при построении трапеции AFDM применимо AF + DM = FD + AM. Только в таком случае в трапецию можно заключить круг.
Итак, подробнее о свойствах трапеции, описанной около окружности:
- Если в трапецию заключена окружность, то для того, чтобы найти длину ее линии, пересекающей фигуру пополам, необходимо найти 1/2 от суммы длин боковых сторон.
- При построении трапеции, описанной около окружности, образованная гипотенуза тождественна радиусу круга, а высота трапеции по совместительству является и диаметром круга.
- Еще одним свойством равнобедренной трапеции, описанной около окружности, является то, что ее боковая сторона сразу видна от центра окружности под углом 90°.
Еще немного о свойствах трапеции, заключенной в окружность
Только равнобедренная трапеция может быть вписана в окружность. Это значит, что нужно соблюсти условия, при которых построенная трапеция AFDM будет отвечать следующим требованиям: AF + DM = FD + MA.
Теорема Птолемея гласит, что в трапеции, заключенной в окружность, произведение диагоналей тождественно и равно сумме умноженных противоположных сторон. Это значит, что при построении окружности, описанной около трапеции AFDM, применимо: AD × FM = AF × DM + FD × AM.
На школьных экзаменах довольно часто встречаются задачи, требующие решения задач с трапецией. Большое количество теорем необходимо запоминать, но если выучить сразу не получиться — не беда. Лучше всего периодически прибегать к подсказке в учебниках, чтобы эти знания сами собой, без особого труда уложились в голове.
Проектная работа « Интересные свойства трапеции » Выполнили: ученицы 10 класса Кудзаева Эллина Баззаева Диана МКОУ СОШ с.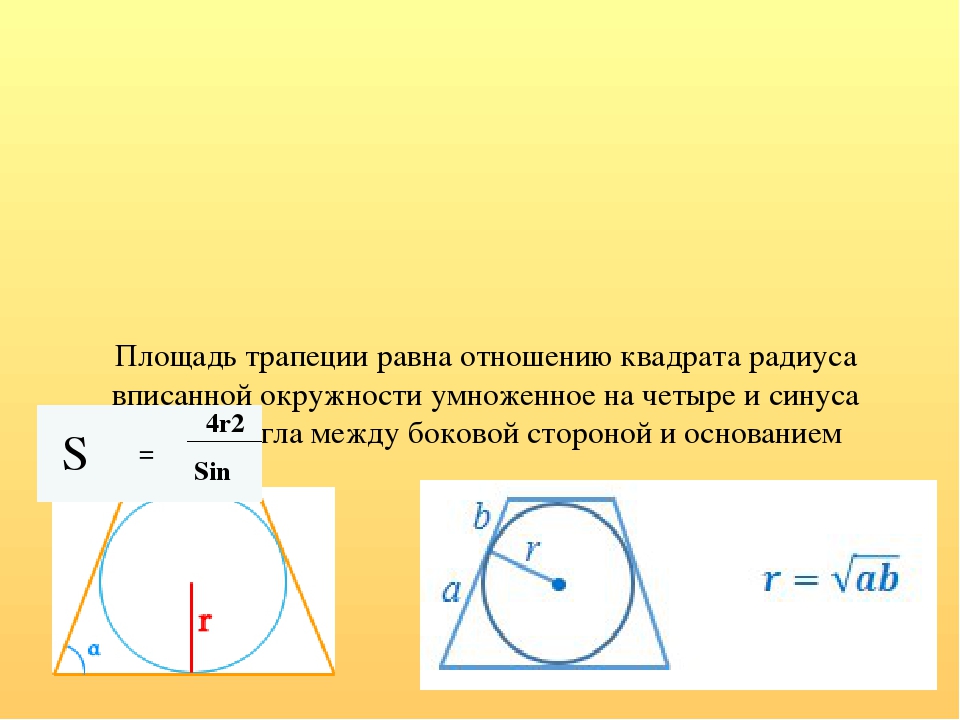 Н.Батако Руководитель: Гагиева А.О. 20.11.2015 года
Н.Батако Руководитель: Гагиева А.О. 20.11.2015 года
Цель работы: Рассмотреть свойства трапеции, которые в школьном курсе геометрии не изучаются, но при решении геометрических задач ЕГЭ из развернутой части С 4 бывает необходимо знать и уметь применять именно эти свойства.
Свойства трапеции: Если трапеция разделена прямой, параллельной ее основаниям, равным a и в, на две равновеликие трапеции. Тогда отрезок к этой прямой, заключенный между боковыми сторонами, равен a В к
Свойство отрезка, проходящего через точку пересечения диагоналей трапеции. Отрезок, параллельный основаниям, проходящий через точку пересечения диагоналей равен: а в с
Свойства трапеции: Отрезок прямой, параллельной основаниям трапеции, заключенный внутри трапеции, разбивается ее диагоналями на три части. Тогда отрезки, прилегающие к боковым сторонам, равны между собой. МР=ОК Р М О К
Свойства равнобедренной трапеции: Если в трапецию можно вписать окружность, то радиус окружности есть среднее пропорциональное отрезков, на которые точка касания делит боковую сторону. О С В А Д. Е О
О С В А Д. Е О
Свойства равнобедренной трапеции: Если центр описанной окружности лежит на основании трапеции, то её диагональ перпендикулярна боковой стороне О А В С Д
Свойства равнобедренной трапеции: В равнобедренную трапецию можно вписать окружность, если боковая сторона равна её средней линии. С В А Д h
1)Если в условии задачи сказано, что в прямоугольную трапецию вписана окружность, можно использовать следующие свойства: 1. Сумма оснований трапеции равна сумме боковых сторон. 2. Расстояния от вершины трапеции до точек касания вписанной окружности равны. 3. Высота прямоугольной трапеции равна ее меньшей боковой стороне и равна диаметру вписанной окружности. 4. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции. 5. Если точка касания делит боковую сторону на отрезки m и n , то радиус вписанной окружности равен
Свойства прямоугольной трапеции, в которую вписана окружность: 1) Четырехугольник, образованный центром вписанной окружности, точками касания и вершиной трапеции — квадрат, сторона которого равна радиусу. (AMOE и BKOM — квадраты со стороной r). 2) Если в прямоугольную трапецию вписана окружность, то площадь трапеции равна произведению ее оснований: S=AD*BC
(AMOE и BKOM — квадраты со стороной r). 2) Если в прямоугольную трапецию вписана окружность, то площадь трапеции равна произведению ее оснований: S=AD*BC
Доказательство: Площадь трапеции равна произведению полусуммы ее оснований на высоту: Обозначим CF=m , FD=n . Поскольку расстояния от вершин до точек касания равны, высота трапеции равна двум радиусам вписанной окружности, а
I. Биссектрисы углов при боковой стороне трапеции пересекаются под углом 90º . 1)∠ABC+∠BAD=180º(как внутренние односторонние при AD∥BC и секущей AB). 2) ∠ABK+∠KAB=(∠ABC+∠BAD):2=90º(так как биссектрисы делят углы пополам). 3) Так как сумма углов треугольника равна 180º, в треугольнике ABK имеем: ∠ABK+∠KAB+∠AKB=180º, отсюда ∠AKB=180-90=90º. Вывод: Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом. Это утверждение применяется при решении задач на трапецию, в которую вписана окружность.
I I .Точка пересечения биссектрис трапеции, прилежащих к боковой стороне, лежит на средней линии трапеции. Пусть биссектриса угла ABC пересекает сторону AD в точке S. Тогда треугольник ABS — равнобедренный с основанием BS Значит, его биссектриса AK является также медианой, то есть точка K — середина BS. Если M и N — середины боковых сторон трапеции, то MN — средняя линия трапеции и MN∥AD. Так как M и K — середины AB и BS, то MK — средняя линия треугольника ABS и MK∥AS. Поскольку через точку M можно провести лишь одну прямую, параллельную данной, точка K лежит на средней линии трапеции.
Пусть биссектриса угла ABC пересекает сторону AD в точке S. Тогда треугольник ABS — равнобедренный с основанием BS Значит, его биссектриса AK является также медианой, то есть точка K — середина BS. Если M и N — середины боковых сторон трапеции, то MN — средняя линия трапеции и MN∥AD. Так как M и K — середины AB и BS, то MK — средняя линия треугольника ABS и MK∥AS. Поскольку через точку M можно провести лишь одну прямую, параллельную данной, точка K лежит на средней линии трапеции.
III. Точка пересечения биссектрис острых углов при основании трапеции принадлежит другому основанию. В этом случае треугольники ABK и DCK — равнобедренные с основаниями AK и DK соответственно. Таким образом, BC=BK+KC=AB+CD. Вывод: Если биссектрисы острых углов трапеции пересекаются в точке, принадлежащей меньшему основанию, то меньшее основание равно сумме боковых сторон трапеции. У равнобедренной трапеции в этом случае меньшее основание в два раза больше боковой стороны.
I V. Точка пересечения биссектрис тупых углов при основании трапеции принадлежит другому основанию. В этом случае треугольники ABF и DCF — равнобедренные с основаниями BF и CF соответственно. Отсюда AD=AF+FD=AB+CD. Вывод: Если биссектрисы тупых углов трапеции пересекаются в точке, принадлежащей большему основанию, то большее основание равно сумме боковых сторон трапеции. У равнобедренной трапеции в этом случае большее основание в два раза больше боковой стороны.
В этом случае треугольники ABF и DCF — равнобедренные с основаниями BF и CF соответственно. Отсюда AD=AF+FD=AB+CD. Вывод: Если биссектрисы тупых углов трапеции пересекаются в точке, принадлежащей большему основанию, то большее основание равно сумме боковых сторон трапеции. У равнобедренной трапеции в этом случае большее основание в два раза больше боковой стороны.
Если равнобедеренную трапецию со сторонами а,в,с, d можно вписать и около неё можно описать окружности, то площадь трапеции равна
\[{\Large{\text{Произвольная трапеция}}}\]
Определения
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами.
Высота трапеции – это перпендикуляр, опущенный из любой точки одного основания к другому основанию.
Теоремы: свойства трапеции
1) Сумма углов при боковой стороне равна \(180^\circ\)
. \circ\)
.
\circ\)
.
2) Т.к. \(AD\parallel BC\)
и \(BD\)
– секущая, то \(\angle DBC=\angle
BDA\)
как накрест лежащие.
Также \(\angle BOC=\angle AOD\)
как вертикальные.
Следовательно, по двум углам \(\triangle BOC \sim \triangle AOD\)
.
Докажем, что \(S_{\triangle AOB}=S_{\triangle COD}\) . Пусть \(h\) – высота трапеции. Тогда \(S_{\triangle ABD}=\frac12\cdot h\cdot AD=S_{\triangle ACD}\) . Тогда: \
Определение
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство*
1) Докажем параллельность.
Проведем через точку \(M\) прямую \(MN»\parallel AD\) (\(N»\in CD\) ). Тогда по теореме Фалеса (т.к. \(MN»\parallel AD\parallel BC, AM=MB\) ) точка \(N»\) — середина отрезка \(CD\) . Значит, точки \(N\) и \(N»\) совпадут.
2) Докажем формулу.
Проведем \(BB»\perp AD, CC»\perp AD\)
. Пусть \(BB»\cap MN=M», CC»\cap
MN=N»\)
.
Пусть \(BB»\cap MN=M», CC»\cap
MN=N»\)
.
Тогда по теореме Фалеса \(M»\) и \(N»\) — середины отрезков \(BB»\) и \(CC»\) соответственно. Значит, \(MM»\) – средняя линия \(\triangle ABB»\) , \(NN»\) — средняя линия \(\triangle DCC»\) . Поэтому: \
Т.к. \(MN\parallel AD\parallel BC\) и \(BB», CC»\perp AD\) , то \(B»M»N»C»\) и \(BM»N»C\) – прямоугольники. По теореме Фалеса из \(MN\parallel AD\) и \(AM=MB\) следует, что \(B»M»=M»B\) . Значит, \(B»M»N»C»\) и \(BM»N»C\) – равные прямоугольники, следовательно, \(M»N»=B»C»=BC\) .
Таким образом:
\ \[=\dfrac12 \left(AB»+B»C»+BC+C»D\right)=\dfrac12\left(AD+BC\right)\]
Теорема: свойство произвольной трапеции
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем, что точки \(P\)
, \(N\)
и \(M\)
лежат на одной прямой.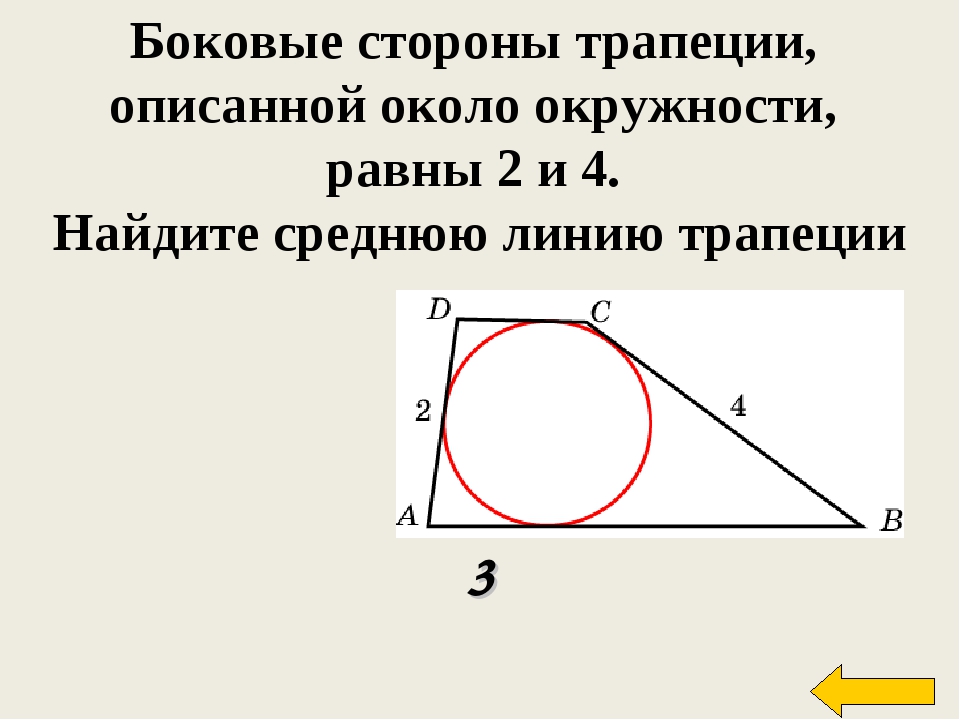
Проведем прямую \(PN\) (\(P\) – точка пересечения продолжений боковых сторон, \(N\) – середина \(BC\) ). Пусть она пересечет сторону \(AD\) в точке \(M\) . Докажем, что \(M\) – середина \(AD\) .
Рассмотрим \(\triangle BPN\) и \(\triangle APM\) . Они подобны по двум углам (\(\angle APM\) – общий, \(\angle PAM=\angle PBN\) как соответственные при \(AD\parallel BC\) и \(AB\) секущей). Значит: \[\dfrac{BN}{AM}=\dfrac{PN}{PM}\]
Рассмотрим \(\triangle CPN\) и \(\triangle DPM\) . Они подобны по двум углам (\(\angle DPM\) – общий, \(\angle PDM=\angle PCN\) как соответственные при \(AD\parallel BC\) и \(CD\) секущей). Значит: \[\dfrac{CN}{DM}=\dfrac{PN}{PM}\]
Отсюда \(\dfrac{BN}{AM}=\dfrac{CN}{DM}\) . Но \(BN=NC\) , следовательно, \(AM=DM\) .
2) Докажем, что точки \(N, O, M\) лежат на одной прямой.
Пусть \(N\)
– середина \(BC\)
, \(O\)
– точка пересечения диагоналей. Проведем прямую \(NO\)
, она пересечет сторону \(AD\)
в точке \(M\)
. Докажем, что \(M\)
– середина \(AD\)
.
Докажем, что \(M\)
– середина \(AD\)
.
\(\triangle BNO\sim \triangle DMO\) по двум углам (\(\angle OBN=\angle ODM\) как накрест лежащие при \(BC\parallel AD\) и \(BD\) секущей; \(\angle BON=\angle DOM\) как вертикальные). Значит: \[\dfrac{BN}{MD}=\dfrac{ON}{OM}\]
Аналогично \(\triangle CON\sim \triangle AOM\) . Значит: \[\dfrac{CN}{MA}=\dfrac{ON}{OM}\]
Отсюда \(\dfrac{BN}{MD}=\dfrac{CN}{MA}\) . Но \(BN=CN\) , следовательно, \(AM=MD\) .
\[{\Large{\text{Равнобедренная трапеция}}}\]
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
1) Рассмотрим равнобедренную трапецию \(ABCD\)
.
Из вершин \(B\) и \(C\) опустим на сторону \(AD\) перпендикуляры \(BM\) и \(CN\) соответственно. Так как \(BM\perp AD\) и \(CN\perp AD\) , то \(BM\parallel CN\) ; \(AD\parallel BC\) , тогда \(MBCN\) – параллелограмм, следовательно, \(BM = CN\) .
Рассмотрим прямоугольные треугольники \(ABM\) и \(CDN\) . Так как у них равны гипотенузы и катет \(BM\) равен катету \(CN\) , то эти треугольники равны, следовательно, \(\angle DAB = \angle CDA\) .
2)
Т.к. \(AB=CD, \angle A=\angle D, AD\) – общая, то по первому признаку . Следовательно, \(AC=BD\) .
3) Т.к. \(\triangle ABD=\triangle ACD\) , то \(\angle BDA=\angle CAD\) . Следовательно, треугольник \(\triangle AOD\) – равнобедренный. Аналогично доказывается, что и \(\triangle BOC\) – равнобедренный.
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
Рассмотрим трапецию \(ABCD\) , такую что \(\angle A = \angle D\) .
Достроим трапецию до треугольника \(AED\) как показано на рисунке. Так как \(\angle 1 = \angle 2\) , то треугольник \(AED\) равнобедренный и \(AE = ED\) . Углы \(1\) и \(3\) равны как соответственные при параллельных прямых \(AD\) и \(BC\) и секущей \(AB\) . Аналогично равны углы \(2\) и \(4\) , но \(\angle 1 = \angle 2\) , тогда \(\angle 3 = \angle 1 = \angle 2 = \angle 4\) , следовательно, треугольник \(BEC\) тоже равнобедренный и \(BE = EC\) .
В итоге \(AB = AE — BE = DE — CE = CD\) , то есть \(AB = CD\) , что и требовалось доказать.
2) Пусть \(AC=BD\) . Т.к. \(\triangle AOD\sim \triangle BOC\) , то обозначим их коэффициент подобия за \(k\) . Тогда если \(BO=x\) , то \(OD=kx\) . Аналогично \(CO=y \Rightarrow AO=ky\) .
Т.к. \(AC=BD\)
, то \(x+kx=y+ky \Rightarrow x=y\)
. Значит \(\triangle AOD\)
– равнобедренный и \(\angle OAD=\angle ODA\)
.
Таким образом, по первому признаку \(\triangle ABD=\triangle ACD\) (\(AC=BD, \angle OAD=\angle ODA, AD\) – общая). Значит, \(AB=CD\) , чтд.
Трапеция — это частный случай четырехугольника, у которого одна пара сторон является параллельной. Термин «трапеция» произошел от греческого слова τράπεζα, означающего «стол», «столик». В этой статье мы рассмотрим виды трапеции и её свойства. Кроме того, разберемся, как рассчитывать отдельные элементы этой Например, диагональ равнобокой трапеции, среднюю линию, площадь и др. Материал изложен в стиле элементарной популярной геометрии, т. е. в легкодоступной форме.
Общие сведения
Для начала давайте разберемся, что такое четырехугольник. Данная фигура является частным случаем многоугольника, содержащего четыре стороны и четыре вершины. Две вершины четырехугольника, которые не являются соседними, называются противоположными. То же можно сказать и о двух несмежных сторонах. Основные виды четырехугольников — это параллелограмм, прямоугольник, ромб, квадрат, трапеция и дельтоид.
Итак, вернемся к трапециям. Как мы уже говорили, у этой фигуры две стороны являются параллельными. Их называют основаниями. Две другие (непараллельные) — боковые стороны. В материалах экзаменов и различных контрольных работ очень часто можно встретить задачи, связанные с трапециями, решение которых зачастую требует от учащегося знаний, не предусмотренных программой. Школьный курс геометрии знакомит учеников со свойствами углов и диагоналей, а также средней линии равнобедренной трапеции. Но ведь, помимо этого, упомянутая геометрическая фигура имеет и другие особенности. Но о них чуть позже…
Виды трапеции
Существует много видов данной фигуры. Однако чаще всего принято рассматривать два из них — равнобедренную и прямоугольную.
1. Прямоугольная трапеция — это фигура, у которой одна из боковых сторон перпендикулярна основаниям. У нее два угла всегда равны девяноста градусам.
2. Равнобедренная трапеция — это геометрическая фигура, у которой боковые стороны равны между собой. А значит, и углы у оснований также попарно равны.
А значит, и углы у оснований также попарно равны.
Главные принципы методики изучения свойств трапеции
К основному принципу можно отнести использование так называемого задачного подхода. По сути, нет необходимости для ввода в теоретический курс геометрии новых свойств этой фигуры. Их можно открывать и формулировать в процессе решения различных задач (лучше системных). При этом очень важно, чтобы преподаватель знал, какие задания необходимо поставить перед школьниками в тот или иной момент учебного процесса. Более того, каждое свойство трапеции может быть представлено в виде ключевой задачи в системе задач.
Вторым принципом является так называемая спиральная организация изучения «замечательных» свойств трапеции. Это подразумевает возврат в процессе обучения к отдельным признакам данной геометрической фигуры. Таким образом, учащимся легче их запоминать. Например, свойство четырех точек. Его можно доказывать как при изучении подобия, так и впоследствии с помощью векторов. А равновеликость треугольников, прилегающих к боковым сторонам фигуры, можно доказывать, применяя не только свойства треугольников с равными высотами, проведенными к сторонам, которые лежат на одной прямой, но и с помощью формулы S= 1/2(ab*sinα). Кроме того, можно отработать на вписанной трапеции или прямоугольный треугольник на описанной трапеции и т. д.
А равновеликость треугольников, прилегающих к боковым сторонам фигуры, можно доказывать, применяя не только свойства треугольников с равными высотами, проведенными к сторонам, которые лежат на одной прямой, но и с помощью формулы S= 1/2(ab*sinα). Кроме того, можно отработать на вписанной трапеции или прямоугольный треугольник на описанной трапеции и т. д.
Применение «внепрограммных» особенностей геометрической фигуры в содержании школьного курса — это задачная технология их преподавания. Постоянное обращение к изучаемым свойствам при прохождении других тем позволяет учащимся глубже познавать трапецию и обеспечивает успешность решения поставленных задач. Итак, приступим к изучению этой замечательной фигуры.
Элементы и свойства равнобедренной трапеции
Как мы уже отмечали, у данной геометрической фигуры боковые стороны равны. Еще она известна как правильная трапеция. А чем же она так примечательна и почему получила такое название? К особенностям данной фигуры относится то, у нее равны не только боковые стороны и углы у оснований, но и диагонали.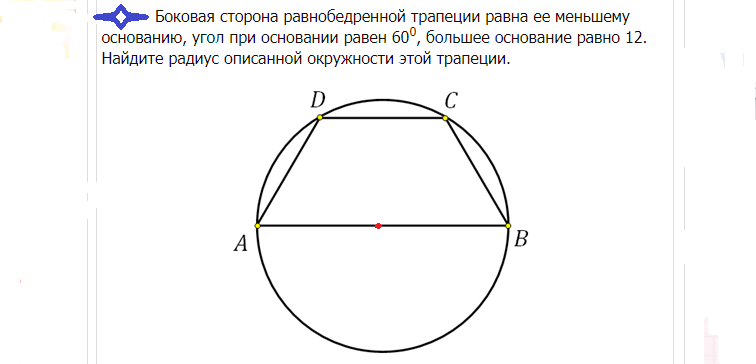 Кроме того, сумма углов равнобедренной трапеции равна 360 градусам. Но и это еще не все! Из всех известных трапеций только вокруг равнобедренной можно описать окружность. Это связано с тем, что сумма противоположных углов у этой фигуры равна 180 градусам, а только при таком условии можно описать окружность вокруг четырехугольника. Следующим свойством рассматриваемой геометрической фигуры является то, что расстояние от вершины основания до проекции противолежащей вершины на прямую, которая содержит это основание, будет равно средней линии.
Кроме того, сумма углов равнобедренной трапеции равна 360 градусам. Но и это еще не все! Из всех известных трапеций только вокруг равнобедренной можно описать окружность. Это связано с тем, что сумма противоположных углов у этой фигуры равна 180 градусам, а только при таком условии можно описать окружность вокруг четырехугольника. Следующим свойством рассматриваемой геометрической фигуры является то, что расстояние от вершины основания до проекции противолежащей вершины на прямую, которая содержит это основание, будет равно средней линии.
А теперь давайте разберемся, как найти углы равнобедренной трапеции. Рассмотрим вариант решения этой задачи при условии, что известны размеры сторон фигуры.
Решение
Обычно четырехугольник принято обозначать литерами А, Б, С, Д, где БС и АД — это основания. В равнобедренной трапеции боковые стороны равны. Будем считать, что их размер равен Х, а размеры оснований равны Y и Z (меньшего и большего соответственно). Для проведения вычисления необходимо из угла В провести высоту Н. В результате получился прямоугольный треугольник АБН, где АБ — гипотенуза, а БН и АН — катеты. Вычисляем размер катета АН: от большего основания отнимаем меньшее, и результат делим на 2. Запишем в виде формулы: (Z-Y)/2 = F. Теперь для вычисления острого угла треугольника воспользуемся функцией cos. Получаем следующую запись: cos(β) = Х/F. Теперь вычисляем угол: β=arcos (Х/F). Далее, зная один угол, мы можем определить и второй, для этого производим элементарное арифметическое действие: 180 — β. Все углы определены.
В результате получился прямоугольный треугольник АБН, где АБ — гипотенуза, а БН и АН — катеты. Вычисляем размер катета АН: от большего основания отнимаем меньшее, и результат делим на 2. Запишем в виде формулы: (Z-Y)/2 = F. Теперь для вычисления острого угла треугольника воспользуемся функцией cos. Получаем следующую запись: cos(β) = Х/F. Теперь вычисляем угол: β=arcos (Х/F). Далее, зная один угол, мы можем определить и второй, для этого производим элементарное арифметическое действие: 180 — β. Все углы определены.
Существует и второе решение данной задачи. В начале опускаем из угла В высоту Н. Вычисляем значение катета БН. Нам известно, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Получаем: БН = √(Х2- F2). Далее используем тригонометрическую функцию tg. В результате имеем: β = arctg (БН/ F). Острый угол найден. Далее определяем аналогично первому способу.
Свойство диагоналей равнобедренной трапеции
Сначала запишем четыре правила. Если диагонали в равнобедренной трапеции перпендикулярны, то:
Если диагонали в равнобедренной трапеции перпендикулярны, то:
Высота фигуры будет равна сумме оснований, деленной на два;
Ее высота и средняя линия равны;
Центр окружности является точкой, в которой пересекаются ;
Если боковая сторона делится точкой касания на отрезки Н и М, тогда равен квадратному корню произведения этих отрезков;
Четырехугольник, который образовался точками касания, вершиной трапеции и центром вписанной окружности — это квадрат, у которого сторона равна радиусу;
Площадь фигуры равна произведению оснований и произведению полусуммы оснований на ее высоту.
Подобные трапеции
Данная тема весьма удобна для изучения свойств этой Например, диагонали разбивают трапецию на четыре треугольника, причем прилежащие к основаниям являются подобными, а к боковым сторонам — равновеликими. Это утверждение можно назвать свойством треугольников, на которые разбита трапеция ее диагоналями. Первая часть этого утверждения доказывается через признак подобия по двум углам. Для доказательства второй части лучше воспользоваться способом, приведенным ниже.
Для доказательства второй части лучше воспользоваться способом, приведенным ниже.
Доказательство теоремы
Принимаем, что фигура АБСД (АД и БС — основы трапеции) разбивается диагоналями ВД и АС. Точка их пересечения — О. Получаем четыре треугольника: АОС — у нижнего основания, БОС — у верхнего основания, АБО и СОД у боковых сторон. Треугольники СОД и БОС имеют общую высоту в том случае, если отрезки БО и ОД являются их основаниями. Получаем, что разность их площадей (П) равна разности этих отрезков: ПБОС/ПСОД = БО/ОД = К. Следовательно, ПСОД = ПБОС/К. Аналогично, треугольники БОС и АОБ имеют общую высоту. Принимаем за их основания отрезки СО и ОА. Получаем ПБОС/ПАОБ = СО/ОА = К и ПАОБ = ПБОС/К. Из этого следует, что ПСОД = ПАОБ.
Для закрепления материала учащимся рекомендуется найти связь между площадями полученных треугольников, на которые разбита трапеция ее диагоналями, решив следующую задачу. Известно, что у треугольников БОС и АОД площади равны, необходимо найти площадь трапеции. Так как ПСОД = ПАОБ, значит, ПАБСД = ПБОС+ПАОД+2*ПСОД. Из подобия треугольников БОС и АОД следует, что БО/ОД = √(ПБОС/ПАОД). Следовательно, ПБОС/ПСОД = БО/ОД = √(ПБОС/ПАОД). Получаем ПСОД = √(ПБОС*ПАОД). Тогда ПАБСД = ПБОС+ПАОД+2*√(ПБОС*ПАОД) = (√ПБОС+√ПАОД)2.
Так как ПСОД = ПАОБ, значит, ПАБСД = ПБОС+ПАОД+2*ПСОД. Из подобия треугольников БОС и АОД следует, что БО/ОД = √(ПБОС/ПАОД). Следовательно, ПБОС/ПСОД = БО/ОД = √(ПБОС/ПАОД). Получаем ПСОД = √(ПБОС*ПАОД). Тогда ПАБСД = ПБОС+ПАОД+2*√(ПБОС*ПАОД) = (√ПБОС+√ПАОД)2.
Свойства подобия
Продолжая развивать эту тему, можно доказывать и другие интересные особенности трапеций. Так, с помощью подобия можно доказать свойство отрезка, который проходит через точку, образованную пересечением диагоналей этой геометрической фигуры, параллельно основаниям. Для этого решим следующую задачу: необходимо найти длину отрезка РК, который проходит через точку О. Из подобия треугольников АОД и БОС следует, что АО/ОС=АД/БС. Из подобия треугольников АОР и АСБ следует, что АО/АС=РО/БС=АД/(БС+АД). Отсюда получаем, что РО=БС*АД/(БС+АД). Аналогично из подобия треугольников ДОК и ДБС следует, что ОК=БС*АД/(БС+АД). Отсюда получаем, что РО=ОК и РК=2*БС*АД/(БС+АД). Отрезок, проходящий через точку пересечения диагоналей, параллельный основаниям и соединяющий две боковые стороны, делится точкой пересечения пополам. Его длина — это среднее гармоническое оснований фигуры.
Его длина — это среднее гармоническое оснований фигуры.
Рассмотрим следующее качество трапеции, которое называют свойством четырех точек. Точки пересечения диагоналей (О), пересечения продолжения боковых сторон (Е), а также середины оснований (Т и Ж) всегда лежат на одной линии. Это легко доказывается методом подобия. Полученные треугольники БЕС и АЕД подобны, и в каждом из них медианы ЕТ и ЕЖ делят угол при вершине Е на равные части. Следовательно, точки Е, Т и Ж лежат на одной прямой. Точно так же на одной прямой располагаются точки Т, О, и Ж. Все это следует из подобия треугольников БОС и АОД. Отсюда делаем вывод, что все четыре точки — Е, Т, О и Ж — будут лежать на одной прямой.
Используя подобные трапеции, можно предложить учащимся найти длину отрезка (ЛФ), который разбивает фигуру на две подобные. Данный отрезок должен быть параллелен основаниям. Так как полученные трапеции АЛФД и ЛБСФ подобны, то БС/ЛФ=ЛФ/АД. Отсюда следует, что ЛФ=√(БС*АД). Получаем, что отрезок, разбивающий трапецию на две подобные, имеет длину, равную среднему геометрическому длин оснований фигуры.
Рассмотрим следующее свойство подобия. В его основе лежит отрезок, который делит трапецию на две равновеликие фигуры. Принимаем, что трапеция АБСД разделена отрезком ЕН на две подобные. Из вершины Б опущена высота, которая разбивается отрезком ЕН на две части — В1 и В2. Получаем: ПАБСД/2 = (БС+ЕН)*В1/2 = (АД+ЕН)*В2/2 и ПАБСД = (БС+АД)*(В1+В2)/2. Далее составляем систему, первое уравнение которой (БС+ЕН)*В1 = (АД+ЕН)*В2 и второе (БС+ЕН)*В1 = (БС+АД)*(В1+В2)/2. Отсюда следует, что В2/ В1 = (БС+ЕН)/(АД+ЕН) и БС+ЕН = ((БС+АД)/2)*(1+В2/ В1). Получаем, что длина отрезка, делящего трапецию на две равновеликие, равна среднему квадратичному длин оснований: √((БС2+АД2)/2).
Выводы подобия
Таким образом, мы доказали, что:
1. Отрезок, соединяющий у трапеции середины боковых сторон, параллелен АД и БС и равен среднему арифметическому БС и АД (длина основания трапеции).
2. Черта, проходящая через точку О пересечения диагоналей параллельно АД и БС, будет равна среднему гармоническому чисел АД и БС (2*БС*АД/(БС+АД)).
3. Отрезок, разбивающий трапецию на подобные, имеет длину среднего геометрического оснований БС и АД.
4. Элемент, делящий фигуру на две равновеликие, имеет длину среднего квадратичного чисел АД и БС.
Для закрепления материала и осознания связи между рассмотренными отрезками учащемуся необходимо построить их для конкретной трапеции. Он без труда сможет отобразить среднюю линию и отрезок, который проходит через точку О — пересечение диагоналей фигуры — параллельно основаниям. А вот где будут находиться третий и четвертый? Этот ответ приведет учащегося к открытию искомой связи между средними величинами.
Отрезок, соединяющий середины диагоналей трапеции
Рассмотрим следующее свойство этой фигуры. Принимаем, что отрезок МН параллелен основаниям и делит диагонали пополам. Точки пересечения назовем Ш и Щ. Данный отрезок будет равен полуразности оснований. Разберем это более детально. МШ — средняя линия треугольника АБС, она равна БС/2. МЩ — средняя линия треугольника АБД, она равна АД/2. Тогда получаем, что ШЩ = МЩ-МШ, следовательно, ШЩ = АД/2-БС/2 = (АД+ВС)/2.
Тогда получаем, что ШЩ = МЩ-МШ, следовательно, ШЩ = АД/2-БС/2 = (АД+ВС)/2.
Центр тяжести
Давайте рассмотрим, каким образом определяется этот элемент для данной геометрической фигуры. Для этого необходимо продлить основания в противоположные стороны. Что это значит? Нужно к верхнему основанию прибавить нижнее — в любую из сторон, например, вправо. А нижнее продлеваем на длину верхнего влево. Далее соединяем их диагональю. Точка пересечения этого отрезка со средней линией фигуры и есть центр тяжести трапеции.
Вписанные и описанные трапеции
Давайте перечислим особенности таких фигур:
1. Трапеция может быть вписана в окружность тольков том случае, если она равнобедренная.
2. Около окружности можно описать трапецию, при условии, что сумма длин их оснований равна сумме длин боковых сторон.
Следствия вписанной окружности:
1. Высота описанной трапеции всегда равна двум радиусам.
2. Боковая сторона описанной трапеции наблюдается из центра окружности под прямым углом.
Первое следствие очевидно, а для доказательства второго требуется установить, что угол СОД является прямым, что, по сути, также не составит большого труда. Зато знание данного свойства позволит при решении задач применять прямоугольный треугольник.
Теперь конкретизируем эти следствия для равнобедренной трапеции, которая вписана в окружность. Получаем, что высота является средним геометрическим оснований фигуры: Н=2R=√(БС*АД). Отрабатывая основной прием решения задач для трапеций (принцип проведения двух высот), учащийся должен решить следующее задание. Принимаем, что БТ — высота равнобедренной фигуры АБСД. Необходимо найти отрезки АТ и ТД. Применяя формулу, описанную выше, это будет сделать не сложно.
Теперь давайте разберемся, как определить радиус окружности, используя площадь описанной трапеции. Опускаем из вершины Б высоту на основание АД. Так как окружность вписана в трапецию, то БС+АД = 2АБ или АБ = (БС+АД)/2. Из треугольника АБН находим sinα = БН/АБ = 2*БН/(БС+АД). ПАБСД = (БС+АД)*БН/2, БН=2R. Получаем ПАБСД = (БС+АД)*R, отсюда следует, что R = ПАБСД/(БС+АД).
ПАБСД = (БС+АД)*БН/2, БН=2R. Получаем ПАБСД = (БС+АД)*R, отсюда следует, что R = ПАБСД/(БС+АД).
Все формулы средней линии трапеции
Теперь пора перейти к последнему элементу данной геометрической фигуры. Разберемся, чему равна средняя линия трапеции (М):
1. Через основания: М = (А+Б)/2.
2. Через высоту, основание и углы:
М = А-Н*(ctgα+ctgβ)/2;
М = Б+Н*(ctgα+ctgβ)/2.
3. Через высоту, диагонали и угол между ними. К примеру, Д1 и Д2 — диагонали трапеции; α , β — углы между ними:
М = Д1*Д2*sinα/2Н = Д1*Д2*sinβ/2Н.
4. Через площадь и высоту: М = П/Н.
Правильная трапеция свойства. Свойства трапеции, описанной около окружности: формулы и теоремы
— (греч. trapezion). 1) в геометрии четырехугольник, у которого две стороны параллельны, а две нет. 2) фигура, приспособленная для гимнастических упражнений. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТРАПЕЦИЯ… … Словарь иностранных слов русского языка
Трапеция — Трапеция. ТРАПЕЦИЯ (от греческого trapezion, буквально столик), выпуклый четырехугольник, в котором две стороны параллельны (основания трапеции). Площадь трапеции равна произведению полусуммы оснований (средней линии) на высоту. … Иллюстрированный энциклопедический словарь
ТРАПЕЦИЯ (от греческого trapezion, буквально столик), выпуклый четырехугольник, в котором две стороны параллельны (основания трапеции). Площадь трапеции равна произведению полусуммы оснований (средней линии) на высоту. … Иллюстрированный энциклопедический словарь
Четырехугольник, снаряд, перекладина Словарь русских синонимов. трапеция сущ., кол во синонимов: 3 перекладина (21) … Словарь синонимов
— (от греческого trapezion, буквально столик), выпуклый четырехугольник, в котором две стороны параллельны (основания трапеции). Площадь трапеции равна произведению полусуммы оснований (средней линии) на высоту … Современная энциклопедия
— (от греч. trapezion букв. столик), четырехугольник, в котором две противоположные стороны, называемые основаниями трапеции, параллельны (на рисунке АD и ВС), а другие две непараллельны. Расстояние между основаниями называют высотой трапеции (на… … Большой Энциклопедический словарь
ТРАПЕЦИЯ, четырехугольная плоская фигура, в которой две противоположные стороны параллельны. Площадь трапеции равна полусумме параллельных сторон, умноженной на длину перпендикуляра между ними … Научно-технический энциклопедический словарь
Площадь трапеции равна полусумме параллельных сторон, умноженной на длину перпендикуляра между ними … Научно-технический энциклопедический словарь
ТРАПЕЦИЯ, трапеции, жен. (от греч. trapeza стол). 1. Четырехугольник с двумя параллельными и двумя непараллельными сторонами (мат.). 2. Гимнастический снаряд, состоящий из перекладины, подвешенной на двух веревках (спорт.). Акробатические… … Толковый словарь Ушакова
ТРАПЕЦИЯ, и, жен. 1. Четырёхугольник с двумя параллельными и двумя непараллельными сторонами. Основания трапеции (её параллельные стороны). 2. Цирковой или гимнастический снаряд перекладина, подвешенная на двух тросах. Толковый словарь Ожегова. С … Толковый словарь Ожегова
Жен., геом. четвероугольник с неравными сторонами, из коих две опостенны (паралельны). Трапецоид, подобный четвероугольник, у которого все стороны идут врознь. Трапецоэдр, тело, ограненное трапециями. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
— (Trapeze), США, 1956, 105 мин. Мелодрама. Начинающий акробат Тино Орсини поступает в цирковую труппу, где работает Майк Риббл, известный в прошлом воздушный гимнаст. Когда то Майк выступал вместе с отцом Тино. Молодой Орсини хочет, чтобы Майк… … Энциклопедия кино
Мелодрама. Начинающий акробат Тино Орсини поступает в цирковую труппу, где работает Майк Риббл, известный в прошлом воздушный гимнаст. Когда то Майк выступал вместе с отцом Тино. Молодой Орсини хочет, чтобы Майк… … Энциклопедия кино
Четырехугольник, две стороны которого параллельны, а дведругие стороны не параллельны. Расстояние между параллельными сторонаминаз. высотою Т. Если параллельные стороны и высота содержат а, b и hметров, то площадь Т. содержит квадратных метров … Энциклопедия Брокгауза и Ефрона
Описанная окружность и трапеция. Здравствуйте! Для вас ещё одна публикация, в которой рассмотрим задачи с трапециями. Задания входят в состав экзамена по математике. Здесь они объединены в группу, дана не просто одна трапеция, а комбинация тел – трапеция и окружность. Большинство из таких задачек решаются устно. Но есть и такие на которые нужно обратить особое внимание, например, задача 27926.
Какую теорию необходимо помнить? Это:
Задачи с трапециями, которые имеются на блоге можно посмотреть здесь .
27924. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.
Отметим, что описать окружность можно только около равнобедренной трапеции. Нам дана средняя линия, значит можем определить сумму оснований, то есть:
Значит сумма боковых сторон будет равна 22–10=12 (периметр минус основания). Так как боковые стороны равнобедренной трапеции равны, то одна сторона будет равна шести.
27925. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60 0 , большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
Если вы решали задачи с окружностью и вписанным в неё шестиугольником, то сразу озвучите ответ – радиус равен 6. Почему?
Посмотрите: равнобедренная трапеция с углом при основании равным 60 0 и равными сторонами AD, DC и CB, представляет собой половину правильного шестиугольника:
В таком шестиугольнике отрезок соединяющий противоположные вершины проходит через центр окружности. *Центр шестиугольника и центр окружности совпадают, подробнее
*Центр шестиугольника и центр окружности совпадают, подробнее
То есть большее основание этой трапеции совпадает с диаметром описанной окружности. Таким образом радиус равен шести.
*Конечно, можно рассмотреть равенство треугольников ADO, DOС и OCB. Доказать что они равносторонние. Далее сделать вывод о том, что угол AOB равен 180 0 и точка О равноудалена от вершин A, D, C и B, а и значит АО=ОВ=12/2=6.
27926. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.
Отметим, что центр описанной окружности лежит на оси симметрии, при чём если построить высоту трапеции проходящую через этот центр, то она при пересечении с основаниями разделит их пополам. Покажем это на эскизе, также соединим центр с вершинами:
Отрезок EF является высотой трапеции, его нам нужно найти.
В прямоугольном треугольнике OFC нам известна гипотенуза (это радиус окружности), FC=3 (так как DF=FC). По теореме Пифагора можем вычислить OF:
В прямоугольном треугольнике OEB нам известна гипотенуза (это радиус окружности), EB=4 (так как AE=EB). По теореме Пифагора можем вычислить OE:
По теореме Пифагора можем вычислить OE:
Таким образом EF=FO+OE=4+3=7.
Теперь важный нюанс!
В этой задаче на рисунке чётко показано, что основания лежат по разные стороны от центра окружности, поэтому задача решается именно так.
А если бы в условии не было дано эскиза?
Тогда у задачи было бы два ответа. Почему? Посмотрите внимательно – в любую окружность можно вписать две трапеции с заданными основаниями:
*То есть при данных основаниях трапеции и радиусе окружности существует две трапеции.
И решение будет «второго варианта» будет следующим.
По теореме Пифагора вычисляем OF:
Также вычислим OE:
Таким образом EF=FO–OE=4–3=1.
Конечно, в задаче с кратким ответом на ЕГЭ двух ответов быть не может, и подобная задача без эскиза дана не будет. Поэтому обратите особое внимание на эскиз! А именно: как расположены основания трапеции. А вот в заданиях с развёрнутым ответом такая в прошлые годы присутствовала (немного с усложнённым условием). Тот, кто рассматривал только один вариант расположения трапеции теряли балл на этом задании.
Тот, кто рассматривал только один вариант расположения трапеции теряли балл на этом задании.
27937. Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.
Здесь сразу следует вспомнить свойство четырёхугольника описанного около окружности:
Суммы противоположных сторон любого четырёхугольника описанного около окружности равны.
В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.
И две не параллельны – это боковые стороны.
В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.
Свойства диагоналей трапеции
Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.
- Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 .
- Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.

Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k 2 . - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
- Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т. - Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ).
 Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ .
Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ . - А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b) .
Свойства средней линии трапеции
Среднюю линию проведите в трапеции параллельно ее основаниям.
- Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2 .
- Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Свойства углов трапеции
- Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180 0: α + β = 180 0 и γ + δ = 180 0 .
- Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2 .
- Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.
Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.
- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.

- Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.
- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2 .
- Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
- На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка.
 Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .
Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .
Свойства трапеции, вписанной в окружность
Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
- Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.

- Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ .
- Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
- Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S АМЕ .
Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2 .
- У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ .
- Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab .
- И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.

Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
- Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию.
 Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.
Что и требовалось доказать.
Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной :
- Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.
МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.
Задача для повторения
Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150 0 с меньшим основанием.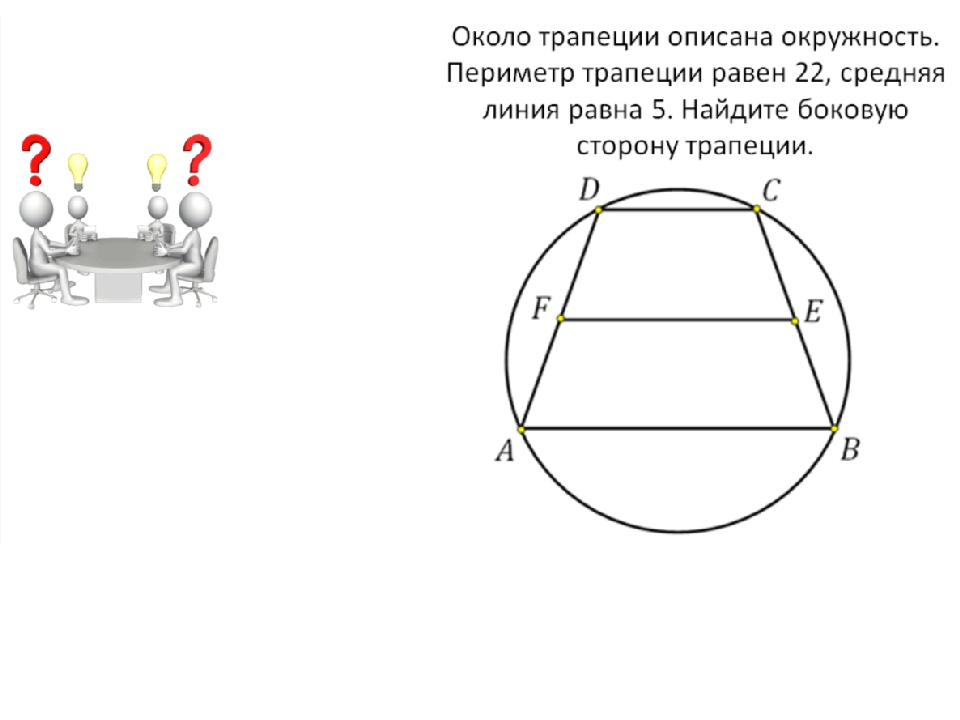 Требуется найти площадь трапеции.
Требуется найти площадь трапеции.
Решение: Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.
Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180 0 . Поэтому КАН = 30 0 (на основании свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30 0 . Поэтому КН = ½АВ = 4 см.
Площадь трапеции находим по формуле: S АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см 2 .
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.
Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.
Но вы сами убедились, что разница огромна.
Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Трапеция — это геометрическая фигура с четырмя углами. При построении трапеции важно учитывать, что две противоположные стороны параллельны, а две другие, наоборот, не параллельны относительно друг друга. Это слово пришло в современность из Древней Греции и звучало как «трапедзион», что означало «столик», «обеденный столик».
Эта статья рассказывает о свойствах трапеции, описанной около окружности. Также мы рассмотрим виды и элементы этой фигуры.
Элементы, виды и признаки геометрической фигуры трапеция
Параллельные стороны в этой фигуре называют основаниями, а те, что не параллельны — боковыми сторонами.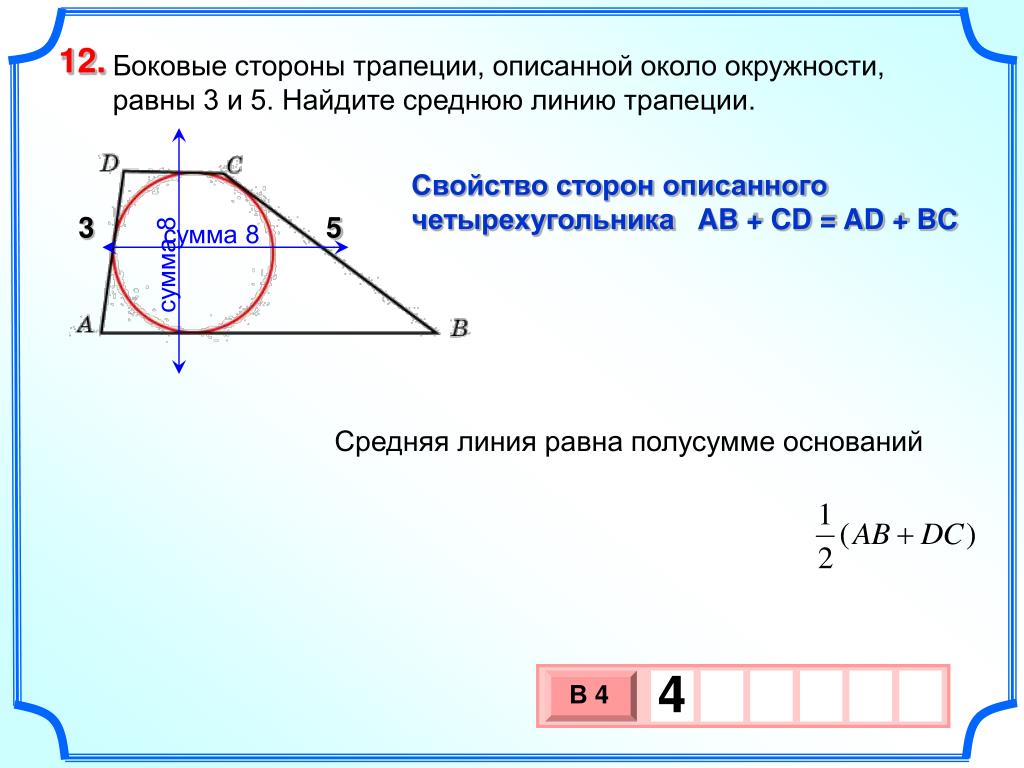 При условии, что боковые стороны одинаковой длины, трапеция считается равнобедренной. Трапеция, боковые стороны которой лежат перпендикулярно основанию под углом в 90°, называется прямоугольной.
При условии, что боковые стороны одинаковой длины, трапеция считается равнобедренной. Трапеция, боковые стороны которой лежат перпендикулярно основанию под углом в 90°, называется прямоугольной.
У этой, казалось бы, незамысловатой фигуры имеется немалое количество свойств, ей присущих, подчеркивающих ее признаки:
- Если провести среднюю линию по боковым сторонам, то она будет параллельна основаниям. Этот отрезок будет равен 1/2 разности оснований.
- При построении биссектрисы из любого угла трапеции образуется равносторонний треугольник.
- Из свойств трапеции, описанной около окружности, известно, что сумма параллельных боковых сторон должна быть равна сумме оснований.
- При построении диагональных отрезков, где одна из сторон является основанием трапеции, полученные треугольники будут подобны.
- При построении диагональных отрезков, где одна из сторон является боковой, полученные треугольники будут иметь равную площадь.
- Если продолжить боковые линии и построить отрезок из центра основания, то образованный угол будет равен 90°.
 Отрезок, соединяющий основания, будет равен 1/2 их разности.
Отрезок, соединяющий основания, будет равен 1/2 их разности.
Свойства трапеции, описанной около окружности
Заключить окружность в трапецию возможно лишь при одном условии. Данное условие заключается в том, что сумма боковых сторон должна быть ровна сумме оснований. Например, при построении трапеции AFDM применимо AF + DM = FD + AM. Только в таком случае в трапецию можно заключить круг.
Итак, подробнее о свойствах трапеции, описанной около окружности:
- Если в трапецию заключена окружность, то для того, чтобы найти длину ее линии, пересекающей фигуру пополам, необходимо найти 1/2 от суммы длин боковых сторон.
- При построении трапеции, описанной около окружности, образованная гипотенуза тождественна радиусу круга, а высота трапеции по совместительству является и диаметром круга.
- Еще одним свойством равнобедренной трапеции, описанной около окружности, является то, что ее боковая сторона сразу видна от центра окружности под углом 90°.
Еще немного о свойствах трапеции, заключенной в окружность
Только равнобедренная трапеция может быть вписана в окружность. Это значит, что нужно соблюсти условия, при которых построенная трапеция AFDM будет отвечать следующим требованиям: AF + DM = FD + MA.
Теорема Птолемея гласит, что в трапеции, заключенной в окружность, произведение диагоналей тождественно и равно сумме умноженных противоположных сторон. Это значит, что при построении окружности, описанной около трапеции AFDM, применимо: AD × FM = AF × DM + FD × AM.
На школьных экзаменах довольно часто встречаются задачи, требующие решения задач с трапецией. Большое количество теорем необходимо запоминать, но если выучить сразу не получиться — не беда. Лучше всего периодически прибегать к подсказке в учебниках, чтобы эти знания сами собой, без особого труда уложились в голове.
Проектная работа « Интересные свойства трапеции » Выполнили: ученицы 10 класса Кудзаева Эллина Баззаева Диана МКОУ СОШ с. Н.Батако Руководитель: Гагиева А.О. 20.11.2015 года
Н.Батако Руководитель: Гагиева А.О. 20.11.2015 года
Цель работы: Рассмотреть свойства трапеции, которые в школьном курсе геометрии не изучаются, но при решении геометрических задач ЕГЭ из развернутой части С 4 бывает необходимо знать и уметь применять именно эти свойства.
Свойства трапеции: Если трапеция разделена прямой, параллельной ее основаниям, равным a и в, на две равновеликие трапеции. Тогда отрезок к этой прямой, заключенный между боковыми сторонами, равен a В к
Свойство отрезка, проходящего через точку пересечения диагоналей трапеции. Отрезок, параллельный основаниям, проходящий через точку пересечения диагоналей равен: а в с
Свойства трапеции: Отрезок прямой, параллельной основаниям трапеции, заключенный внутри трапеции, разбивается ее диагоналями на три части. Тогда отрезки, прилегающие к боковым сторонам, равны между собой. МР=ОК Р М О К
Свойства равнобедренной трапеции: Если в трапецию можно вписать окружность, то радиус окружности есть среднее пропорциональное отрезков, на которые точка касания делит боковую сторону. О С В А Д. Е О
О С В А Д. Е О
Свойства равнобедренной трапеции: Если центр описанной окружности лежит на основании трапеции, то её диагональ перпендикулярна боковой стороне О А В С Д
Свойства равнобедренной трапеции: В равнобедренную трапецию можно вписать окружность, если боковая сторона равна её средней линии. С В А Д h
1)Если в условии задачи сказано, что в прямоугольную трапецию вписана окружность, можно использовать следующие свойства: 1. Сумма оснований трапеции равна сумме боковых сторон. 2. Расстояния от вершины трапеции до точек касания вписанной окружности равны. 3. Высота прямоугольной трапеции равна ее меньшей боковой стороне и равна диаметру вписанной окружности. 4. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции. 5. Если точка касания делит боковую сторону на отрезки m и n , то радиус вписанной окружности равен
Свойства прямоугольной трапеции, в которую вписана окружность: 1) Четырехугольник, образованный центром вписанной окружности, точками касания и вершиной трапеции — квадрат, сторона которого равна радиусу. (AMOE и BKOM — квадраты со стороной r). 2) Если в прямоугольную трапецию вписана окружность, то площадь трапеции равна произведению ее оснований: S=AD*BC
(AMOE и BKOM — квадраты со стороной r). 2) Если в прямоугольную трапецию вписана окружность, то площадь трапеции равна произведению ее оснований: S=AD*BC
Доказательство: Площадь трапеции равна произведению полусуммы ее оснований на высоту: Обозначим CF=m , FD=n . Поскольку расстояния от вершин до точек касания равны, высота трапеции равна двум радиусам вписанной окружности, а
I. Биссектрисы углов при боковой стороне трапеции пересекаются под углом 90º . 1)∠ABC+∠BAD=180º(как внутренние односторонние при AD∥BC и секущей AB). 2) ∠ABK+∠KAB=(∠ABC+∠BAD):2=90º(так как биссектрисы делят углы пополам). 3) Так как сумма углов треугольника равна 180º, в треугольнике ABK имеем: ∠ABK+∠KAB+∠AKB=180º, отсюда ∠AKB=180-90=90º. Вывод: Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом. Это утверждение применяется при решении задач на трапецию, в которую вписана окружность.
I I .Точка пересечения биссектрис трапеции, прилежащих к боковой стороне, лежит на средней линии трапеции. Пусть биссектриса угла ABC пересекает сторону AD в точке S. Тогда треугольник ABS — равнобедренный с основанием BS Значит, его биссектриса AK является также медианой, то есть точка K — середина BS. Если M и N — середины боковых сторон трапеции, то MN — средняя линия трапеции и MN∥AD. Так как M и K — середины AB и BS, то MK — средняя линия треугольника ABS и MK∥AS. Поскольку через точку M можно провести лишь одну прямую, параллельную данной, точка K лежит на средней линии трапеции.
Пусть биссектриса угла ABC пересекает сторону AD в точке S. Тогда треугольник ABS — равнобедренный с основанием BS Значит, его биссектриса AK является также медианой, то есть точка K — середина BS. Если M и N — середины боковых сторон трапеции, то MN — средняя линия трапеции и MN∥AD. Так как M и K — середины AB и BS, то MK — средняя линия треугольника ABS и MK∥AS. Поскольку через точку M можно провести лишь одну прямую, параллельную данной, точка K лежит на средней линии трапеции.
III. Точка пересечения биссектрис острых углов при основании трапеции принадлежит другому основанию. В этом случае треугольники ABK и DCK — равнобедренные с основаниями AK и DK соответственно. Таким образом, BC=BK+KC=AB+CD. Вывод: Если биссектрисы острых углов трапеции пересекаются в точке, принадлежащей меньшему основанию, то меньшее основание равно сумме боковых сторон трапеции. У равнобедренной трапеции в этом случае меньшее основание в два раза больше боковой стороны.
I V. Точка пересечения биссектрис тупых углов при основании трапеции принадлежит другому основанию. В этом случае треугольники ABF и DCF — равнобедренные с основаниями BF и CF соответственно. Отсюда AD=AF+FD=AB+CD. Вывод: Если биссектрисы тупых углов трапеции пересекаются в точке, принадлежащей большему основанию, то большее основание равно сумме боковых сторон трапеции. У равнобедренной трапеции в этом случае большее основание в два раза больше боковой стороны.
В этом случае треугольники ABF и DCF — равнобедренные с основаниями BF и CF соответственно. Отсюда AD=AF+FD=AB+CD. Вывод: Если биссектрисы тупых углов трапеции пересекаются в точке, принадлежащей большему основанию, то большее основание равно сумме боковых сторон трапеции. У равнобедренной трапеции в этом случае большее основание в два раза больше боковой стороны.
Если равнобедеренную трапецию со сторонами а,в,с, d можно вписать и около неё можно описать окружности, то площадь трапеции равна
1 1 Около окружности — Документ
1.Около окружности, радиус которой равен , описан правильный шестиугольник. Найдите радиус окружности, описанной около этого шестиугольника.
1.1 Около окружности, радиус которой равен , описан правильный шестиугольник. Найдите радиус окружности, описанной около этого шестиугольника.
1.2
Около окружности, радиус которой равен ,
описан правильный шестиугольник. Найдите
радиус окружности, описанной около
этого шестиугольника.
1.3 Около окружности, радиус которой равен , описан правильный шестиугольник. Найдите радиус окружности, описанной около этого шестиугольника.
1.4 Около окружности, радиус которой равен , описан правильный шестиугольник. Найдите радиус окружности, описанной около этого шестиугольника.
2.Около окружности, радиус которой равен , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.
2.1 Около окружности, радиус которой равен , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.
2.2 Около окружности, радиус которой равен , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.
2.3 Около окружности, радиус которой равен , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.
2.4 Около окружности, радиус которой равен , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.
3.К
окружности, вписанной в треугольник ABC, проведены три касательные.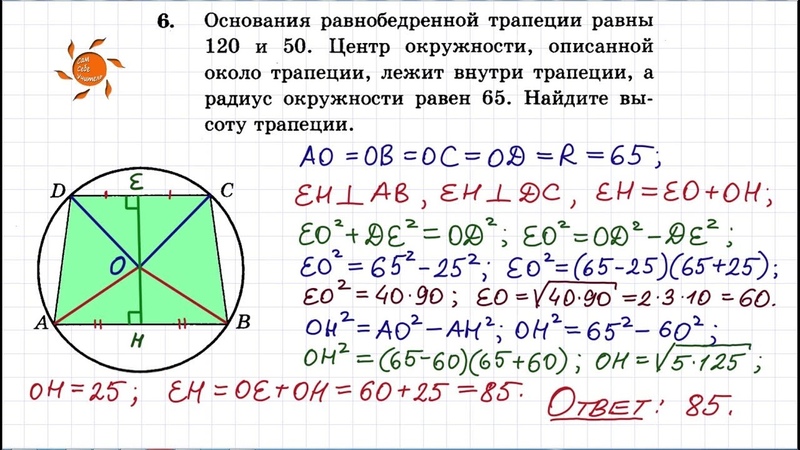 Периметры отсеченных треугольников
равны 10, 23, 34. Найдите периметр данного
треугольника.
Периметры отсеченных треугольников
равны 10, 23, 34. Найдите периметр данного
треугольника.
3.1 К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 8, 28, 67. Найдите периметр данного треугольника.
3.2 К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 8, 28, 67. Найдите периметр данного треугольника.
3.3 К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 8, 29, 53. Найдите периметр данного треугольника.
3.4 К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 10, 19, 85. Найдите периметр данного треугольника.
4.Три
стороны описанного около окружности
четырехугольника относятся (в
последовательном порядке) как
.
Найдите большую сторону этого
четырехугольника, если известно, что
его периметр равен 48.
4.1 Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 60.
4.2 Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 20.
4.3 Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 150.
4.4 Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 48.
5.В четырехугольник ABCD вписана окружность, , и . Найдите четвертую сторону четырехугольника.
5.1
В четырехугольник ABCD вписана окружность,
,
и
. Найдите четвертую сторону четырехугольника.
Найдите четвертую сторону четырехугольника.
5.2 В четырехугольник ABCD вписана окружность, , и . Найдите четвертую сторону четырехугольника
5.3 В четырехугольник ABCD вписана окружность, , и . Найдите четвертую сторону четырехугольника.
5.4 В четырехугольник ABCD вписана окружность, , и . Найдите четвертую сторону четырехугольника.
6.Периметр четырехугольника, описанного около окружности, равен 56, две его стороны равны 15 и 21. Найдите большую из оставшихся сторон.
6.1 Периметр четырехугольника, описанного около окружности, равен 48, две его стороны равны 14 и 20. Найдите большую из оставшихся сторон.
6 2 Периметр четырехугольника, описанного около окружности, равен 56, две его стороны равны 5 и 23. Найдите большую из оставшихся сторон.
6.3 Периметр четырехугольника, описанного около окружности, равен 26, две его стороны равны 4 и 5. Найдите большую из оставшихся сторон.
6.4
Периметр четырехугольника, описанного
около окружности, равен 48, две его стороны
равны 15 и 21. Найдите большую из оставшихся
сторон.
Найдите большую из оставшихся
сторон.
7. В четырехугольник ABCD вписана окружность, , . Найдите периметр четырехугольника.
7.1 В четырехугольник ABCD вписана окружность, , . Найдите периметр четырехугольника.
7.2 В четырехугольник ABCD вписана окружность, , . Найдите периметр четырехугольника.
7.3 В четырехугольник ABCD вписана окружность, , . Найдите периметр четырехугольника.
7.4 В четырехугольник ABCD вписана окружность, , . Найдите периметр четырехугольника.
8. Периметр прямоугольной трапеции, описанной около окружности, равен 100, ее большая боковая сторона равна 37. Найдите радиус окружности.
8.1 Периметр прямоугольной трапеции, описанной около окружности, равен 100, ее большая боковая сторона равна 36. Найдите радиус окружности.
8.2
Периметр прямоугольной трапеции,
описанной около окружности, равен 100,
ее большая боковая сторона равна 44.
Найдите радиус окружности.
8.3 Периметр прямоугольной трапеции, описанной около окружности, равен 100, ее большая боковая сторона равна 27. Найдите радиус окружности.
8.4 Периметр прямоугольной трапеции, описанной около окружности, равен 100, ее большая боковая сторона равна 48. Найдите радиус окружности.
9. Около окружности описана трапеция, периметр которой равен 88. Найдите ее среднюю линию.
9.1 Около окружности описана трапеция, периметр которой равен 100. Найдите ее среднюю линию.
9.2 Около окружности описана трапеция, периметр которой равен 188. Найдите ее среднюю линию.
9.3 Около окружности описана трапеция, периметр которой равен 24. Найдите ее среднюю линию.
9.4 Около окружности описана трапеция, периметр которой равен 152. Найдите ее среднюю линию.
10. Боковые стороны трапеции, описанной около окружности, равны 28 и 4. Найдите среднюю линию трапеции.
10.1
Боковые стороны трапеции, описанной
около окружности, равны 5 и 1. Найдите
среднюю линию трапеции.
Найдите
среднюю линию трапеции.
10.2 Боковые стороны трапеции, описанной около окружности, равны 27 и 4. Найдите среднюю линию трапеции.
10.3 Боковые стороны трапеции, описанной около окружности, равны 8 и 1. Найдите среднюю линию трапеции.
10.4 Боковые стороны трапеции, описанной около окружности, равны 13 и 1. Найдите среднюю линию трапеции.
11. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 18 и 2, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
11.1 Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 6 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
11.2
Окружность, вписанная в равнобедренный
треугольник, делит в точке касания одну
из боковых сторон на два отрезка, длины
которых равны 18 и 3, считая от вершины,
противолежащей основанию. Найдите
периметр треугольника.
Найдите
периметр треугольника.
11.3 Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 8 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
11.4 Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 26 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
12. Боковые стороны равнобедренного треугольника равны 109, основание равно 182. Найдите радиус вписанной окружности.
12.1 Боковые стороны равнобедренного треугольника равны 596, основание равно 408. Найдите радиус вписанной окружности.
12.2 Боковые стороны равнобедренного треугольника равны 404, основание равно 792. Найдите радиус вписанной окружности.
12.3
Боковые стороны равнобедренного
треугольника равны 409, основание равно
782. Найдите радиус вписанной окружности.
12.4 Боковые стороны равнобедренного треугольника равны 401, основание равно 798. Найдите радиус вписанной окружности.
13. В треугольнике ABC , , угол C равен . Найдите радиус вписанной окружности.
13.1 В треугольнике ABC , , угол C равен . Найдите радиус вписанной окружности.
13.2 В треугольнике ABC , , угол C равен . Найдите радиус вписанной окружности.
13.3 В треугольнике ABC , , угол C равен . Найдите радиус вписанной окружности.
13.4 В треугольнике ABC , , угол C равен . Найдите радиус вписанной окружности.
14. Катеты равнобедренного прямоугольного треугольника равны . Найдите радиус окружности, вписанной в этот треугольник.
14.1 Катеты равнобедренного прямоугольного треугольника равны . Найдите радиус окружности, вписанной в этот треугольник.
14.2
Катеты равнобедренного прямоугольного
треугольника равны
. Найдите радиус окружности, вписанной
в этот треугольник.
Найдите радиус окружности, вписанной
в этот треугольник.
14.3 Катеты равнобедренного прямоугольного треугольника равны . Найдите радиус окружности, вписанной в этот треугольник.
14.4 Катеты равнобедренного прямоугольного треугольника равны . Найдите радиус окружности, вписанной в этот треугольник.
15. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 17. Найдите гипотенузу c этого треугольника. В ответе укажите .
15.1 Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 20. Найдите гипотенузу c этого треугольника. В ответе укажите .
15.2 Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 23. Найдите гипотенузу c этого треугольника. В ответе укажите .
15.3 Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 42. Найдите гипотенузу c этого треугольника. В ответе укажите .
15.4
Радиус окружности, вписанной в
равнобедренный прямоугольный треугольник,
равен 22. Найдите гипотенузу c этого
треугольника. В ответе укажите
.
Найдите гипотенузу c этого
треугольника. В ответе укажите
.
16. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен . Найдите n.
16.1 Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен . Найдите n.
16.2 Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен . Найдите n.
16.3 Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен . Найдите n.
16.4
Угол между стороной правильного n-угольника, вписанного в окружность,
и радиусом этой окружности, проведенным
в одну из вершин стороны, равен
. Найдите n.
Найдите n.
17. Периметр правильного шестиугольника равен 144. Найдите диаметр описанной окружности.
17.1 Периметр правильного шестиугольника равен 180. Найдите диаметр описанной окружности.
17.2 Периметр правильного шестиугольника равен 222. Найдите диаметр описанной окружности.
17.3 Периметр правильного шестиугольника равен 18. Найдите диаметр описанной окружности.
17.4 Периметр правильного шестиугольника равен 276. Найдите диаметр описанной окружности.
18.Углы A, B и C четырехугольника ABCD относятся как . Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.
18.1
Углы A, B и C четырехугольника ABCD относятся как
.
Найдите угол D, если около данного
четырехугольника можно описать
окружность. Ответ дайте в градусах.
18.2 Углы A, B и C четырехугольника ABCD относятся как . Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.
18.3 Углы A, B и C четырехугольника ABCD относятся как . Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.
18.4 Углы A, B и C четырехугольника ABCD относятся как . Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.
Как рисовать круги с подпиской и подпиской
Рисование описанной окружности
Чтобы нарисовать круг, вам нужно знать две вещи. Вам нужно знать, где поставить центр, и вам нужно знать, какой длины должен быть радиус. Когда у вас есть эти два, вы можете настроить компас, установить центральную точку и нарисовать круг. Давайте сначала рассмотрим, как это сделать, когда вы хотите, чтобы ваш круг проходил за пределами объекта (ограниченного).
Во-первых, можно ли? Вот уловка.Вы можете описать круг вокруг многоугольника (там, где он касается всех углов), только если перпендикулярные биссектрисы , линии, проведенные под углом 90 ° от точного центра каждой стороны, пересекаются в одной точке. В противном случае ни один из нарисованных вами кругов не будет описан правильно. Если это так, то теперь у вас есть центр нашего круга. Давай попробуем.
Нарисуйте неправильный четырехугольник, как показано на рисунке ABCD.Если вы хотите убедиться, что сможете описать круг вокруг него, сначала нарисуйте круг, а затем нарисуйте четырехугольник внутри круга, так чтобы все углы касались внешнего края круга. Таким образом, вы знаете, что это сработает для упражнения.
Хорошо, пора вспомнить эту практику геометрии. Помните, как построить серединный перпендикуляр?
Помните, как построить серединный перпендикуляр?
- Установите компас на длину, немного превышающую половину длины стороны многоугольника, которую вы пытаетесь разделить пополам, и установите точку компаса на одном конце стороны.
- Сделайте небольшую легкую дугу с обеих сторон линии.
- Установите точку циркуля на другом конце стороны и снова сделайте две отметки.
- Места пересечения дуг являются центральными точками. Соедините эти точки, и вы получите серединный перпендикуляр.
Хорошо, самая сложная часть сделана. Радиус вашего круга будет расстоянием от вашего центра до любого угла четырехугольника.Установите радиус, поместите точку циркуля в центр и нарисуйте круг вокруг четырехугольника. Если у вас есть подходящий многоугольник, это будет работать каждый раз. Также обратите внимание, что, поскольку все биссектрисы будут пересекаться только в одной точке, вам фактически нужно сделать только две из них, а затем использовать точку, в которой они пересекаются! Однако рисование всех серединных перпендикуляров позволит вам узнать, есть ли у вас подходящий многоугольник. Помните, что все треугольники и правильные (все стороны одинаковой длины) многоугольники можно описать окружностью.
Помните, что все треугольники и правильные (все стороны одинаковой длины) многоугольники можно описать окружностью.
Создание круга
Создание круга внутри многоугольника аналогично, но теперь вы собираетесь использовать биссектрисы угла (линия, разделяющая угол на два равных меньших угла). Например, взгляните на показанный треугольник ABC.
Первое, что вам нужно сделать, это провести биссектрису угла как минимум от двух углов к центру.Место встречи двух биссектрис будет центром круга.
Хорошо, вернемся к великой практике геометрии. Помните, как делить угол пополам?
Помните, как делить угол пополам?
- Установите компас на некотором расстоянии короче, чем обе стороны от вашего угла.
- Сделайте отметки с каждой стороны. Места, где отметки пересекают углы, будут вашими ориентирами для вашего компаса.
- Установите компас в одну из двух точек пересечения и нарисуйте дугу примерно в центре угла.Потом то же самое с другого пункта пропуска. Место пересечения двух дуг находится в центре угла.
- Проведите линию от угла до точки пересечения дуги. Это ваш биссектриса угла!
После того, как вы установите биссектрисы (вам понадобится как минимум две). теперь у вас есть центр вашего круга, прямо там, где они пересекаются. Пришло время нарисовать круг.Установите компас на кратчайшее расстояние между отмеченным центром и одной из сторон. Поместите точку циркуля в центр и нарисуйте круг. Если вы сделали свою работу правильно, теперь у вас есть начертанный круг!
Если вы сделали свою работу правильно, теперь у вас есть начертанный круг!
Резюме урока
Описанная окружность построена вокруг внешней стороны многоугольника, касаясь каждого угла. Вписанный круг находится внутри, образуя касательную (линия, которая просто касается края круга) с каждой стороны.Постройте две биссектрисы (линия, которая встречается под прямым углом и пересекает точный центр), чтобы найти центр описанной окружности, или построить две биссектрисы угла (линия, разделяющая угол на равные половины), чтобы найти центр вписанной окружности. Любой треугольник или правильный многоугольник (равные длины сторон) можно описать или вписать в круг. Некоторые неправильные многоугольники также можно описать, если все серединные перпендикуляры пересекаются. С практикой это может стать довольно легко!
Раздел 4.
 5 Обсуждение
5 ОбсуждениеТекст представляет собой интуитивно понятный и неформальный подход к темам окружности и площади круга. Определений избегают, потому что, по сути, формальное определение требует использования пределов. Начнем с предложения Евклида о том, что
« площади любых двух кругов друг относительно друга равны квадратам их диаметров »
Это очень согласуется с теоремой 4.14 и ее следствиями.Соотношение площадей одинаковых многоугольных фигур пропорционально квадрату отношения соответствующих линейных мер. Если рассматривать круг как предельный случай n-стороннего многоугольника, то расширение до кругов является разумным.
Уравнение предложения Евклида:
Это означает, что отношение площади любого круга к квадрату его диаметра является константой:
Предполагается, что в наборе задач 4 должно быть рассмотрено доказательство. 6 НЕТ ПРОБЛЕМ НАБОР 4.6 !!! На данный момент мы можем обозначить эту константу
6 НЕТ ПРОБЛЕМ НАБОР 4.6 !!! На данный момент мы можем обозначить эту константу
С другой стороны, также известно, что окружности двух окружностей связаны друг с другом как соответствующие диаметры
и, следовательно, мы можем написать
Это означает, что отношение длины окружности к ее диаметру является константой, и мы пишем
Конечно, константы k и k ‘ равны, и значение константы равно.
Правдоподобный аргумент в пользу вывода формулы площади круга из формулы его длины.
Суть этого аргумента в том, что если мы выразим площадь n-стороннего правильного многоугольника, по мере того, как n становится больше, площадь многоугольника приближается к площади круга. Мы можем получить формулу для площади многоугольника с точки зрения его периметра, посмотрев на сектор вписанного n-угольника следующим образом:
Мы можем получить формулу для площади многоугольника с точки зрения его периметра, посмотрев на сектор вписанного n-угольника следующим образом:
Оценка Архимеда
Стратегия, приписываемая Архимеду для оценки стоимости суммируется путем изучения описанного n-угольника вокруг единичной окружности и вписанного n-угольника в единичную окружность.По мере увеличения количества сторон области двух полигонов становятся все ближе и ближе друг к другу. Поэтому мы можем использовать разницу двух областей в пределе, чтобы приблизить .
Задача Бена Смита о трапеции
Проблема от Бена Смита была отправлена по электронной почте. Некоторые из вас предложили решение, и здесь есть ссылки на файлы GSP.
Проблема:
Дана равнобедренная трапеция с известными длинами a и b, рисунок трапеции с диагоналями и средним арифметическим.
Итак, среднее значение разделено на 3 части диагоналями, образующими несколько одинаковых треугольников. Вопрос просит найти длину меньшего среднего участка среднего арифметического. Однако проблема не дает никаких значений по высоте. Есть ли у этой проблемы решение?
Есть ли решение этой проблемы? Почему Бен задал этот вопрос? Казалось, он распознал ключевые геометрические идеи.
Одним из элементов решения, если он существует, было бы показать, что результат не зависит от высоты трапеции.
Файл GSP с моим решением
Файл GSP с решением Виктора
Файл GSP с решением Allyson
Файл GSP с решением Джеки
Все мы представили по сути одно и то же решение. Есть ли альтернативные решения? Мы не использовали «несколько похожих треугольников», о которых говорил Бен Смит. Диагонали трапеции пересекаются в точке, соответствующей гармоническому среднему.
Можно ли использовать подобные треугольники или что-то вроде гармонических и арифметических средств?
Рассмотрим эту альтернативу.
Создайте CX параллельно DA. XB = b — а
AXCD — параллелограмм с G в качестве середины диагонали AC
.XD — это диагональ AXCD, поэтому G — это середина XD
.H — это середина DB.
Следовательно, по теореме о среднем сегменте треугольника.
Задача тригонометрии представлена в классе
Два предложения:
1.Используйте возвышенный треугольник, чтобы получить значения для sin 18 и cos 36
.См. Файл GSP для решения Кэти Рэдфорд
Другие решения см. В файле GSP
2. Используйте тригонометрическое уравнение
Окружность / секанс / касательная задача
Если P — точка на секущей AB вне окружности, а PT — касательная к окружности, такая что PT = AB.
Поместите C внутри круга так, чтобы PC = PT.При необходимости см. Файл GSP.
Проблема с использованием прямоугольного треугольника 3-4-5
Задача о пяти круглых дисках
Пять единиц дисков размещены с центрами в вершинах правильного пятиугольника и все проходят через центр пятиугольника.
Каков радиус самой большой круглой области, которую могли бы покрыть диски? OA =?
Примечание: Диски имеют радиус 1, а их центры находятся в вершинах пятиугольника.Таким образом, этот пятиугольник вписан в круг с единичным радиусом.
Пересечения дисков образуют больший правильный пятиугольник, и задача определяет радиус описывающей окружности большего пятиугольника.
Набор задач 4.
5
Формула, как найти радиус описанной окружности треугольника. Как найти радиус круга: в помощь школьникам
Видно, что каждая сторона треугольника , перпендикуляр, проведенный из его середины, и отрезки, соединяющие точку пересечения перпендикуляров с вершинами, образуют два равных прямоугольных треугольника … Отрезки MA, MB, MC являются равный.
Вам дан треугольник. Найдите середину каждой стороны — возьмите линейку и измерьте стороны.Полученные размеры разделите пополам. Отложите сверху на каждую половину своего размера. Отметьте результаты точками.
От каждой точки проложите перпендикуляр в сторону. Точка пересечения этих перпендикуляров будет центром описанной окружности. Чтобы найти центр круга, достаточно двух перпендикуляров. Третий создан для самотестирования.
Обратите внимание — в треугольнике, где все углы острые, пересечения находятся внутри треугольника … В прямоугольном треугольнике — лежит на гипотенузе. Б — вне его. Причем перпендикуляр к стороне, противоположной тупому углу, идет не к центру треугольника , а наружу.
Б — вне его. Причем перпендикуляр к стороне, противоположной тупому углу, идет не к центру треугольника , а наружу.
примечание
Существует теорема синусов, которая устанавливает связь между сторонами треугольника, его углами и радиусами описанной окружности. Эта зависимость выражается формулой: a / sina = b / sinb = c / sinc = 2R, где a, b, c — стороны треугольника; sina, sinb, sinc — синусы углов, противоположных этим сторонам; R — радиус круга, который можно описать вокруг треугольника.
Источники:
- как описать окружность четырехугольника
По определению, описываемая окружность должна проходить через все вершины углов указанного многоугольника. В этом случае совершенно не важно, что это за многоугольник — треугольник, квадрат, прямоугольник, трапеция или что-то еще. Также не имеет значения, является ли это правильным или неправильным многоугольником. Нужно только учитывать, что есть многоугольники, вокруг которых окружность не описывается.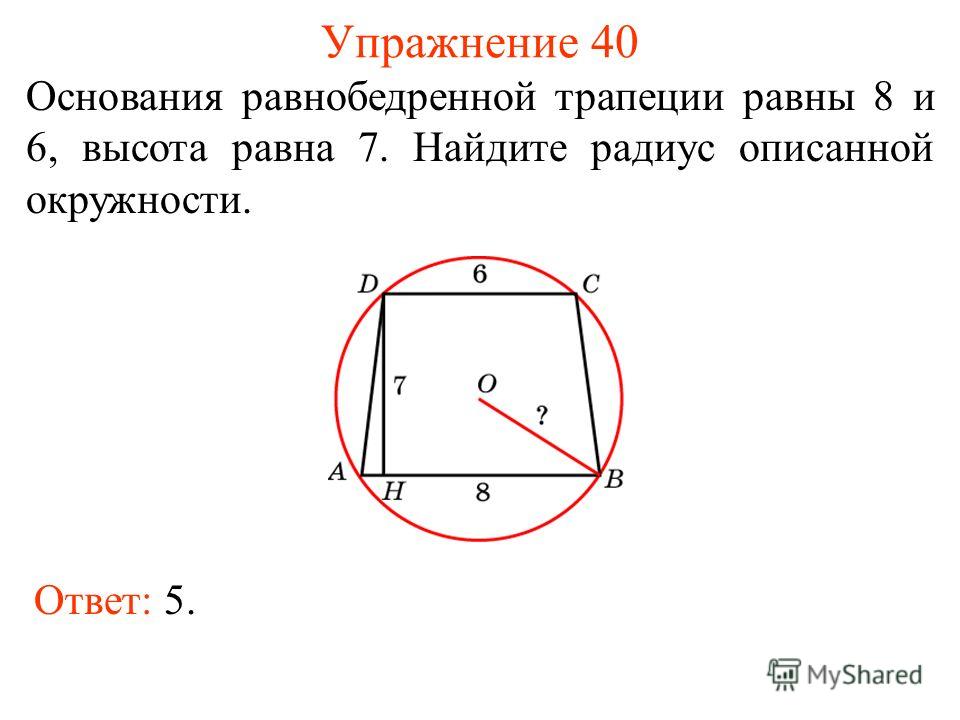 Всегда можно описать круг вокруг треугольника. Что касается четырехугольников, то круг можно описать вокруг квадрата, прямоугольника или равнобедренной трапеции.
Всегда можно описать круг вокруг треугольника. Что касается четырехугольников, то круг можно описать вокруг квадрата, прямоугольника или равнобедренной трапеции.
Вам понадобится
- Предустановленный многоугольник
- Линейка
- Гон
- Карандаш
- Компас
- Транспортир
- Таблицы синусов и косинусов
- Математические концепции и формулы
- Теорема Пифагора
- Теорема S Теорема косинусов
- Признаки подобия треугольников
Инструкции
Построить многоугольник с заданными параметрами и можно ли вокруг него описать круг … Если вам дан четырехугольник, посчитайте суммы его противоположных углов. Каждый из них должен быть равен 180 °.
Чтобы описать окружность , нужно вычислить ее радиус. Помните, где находится центр круга в разных многоугольниках. В треугольнике он находится на пересечении всех высот этого треугольника.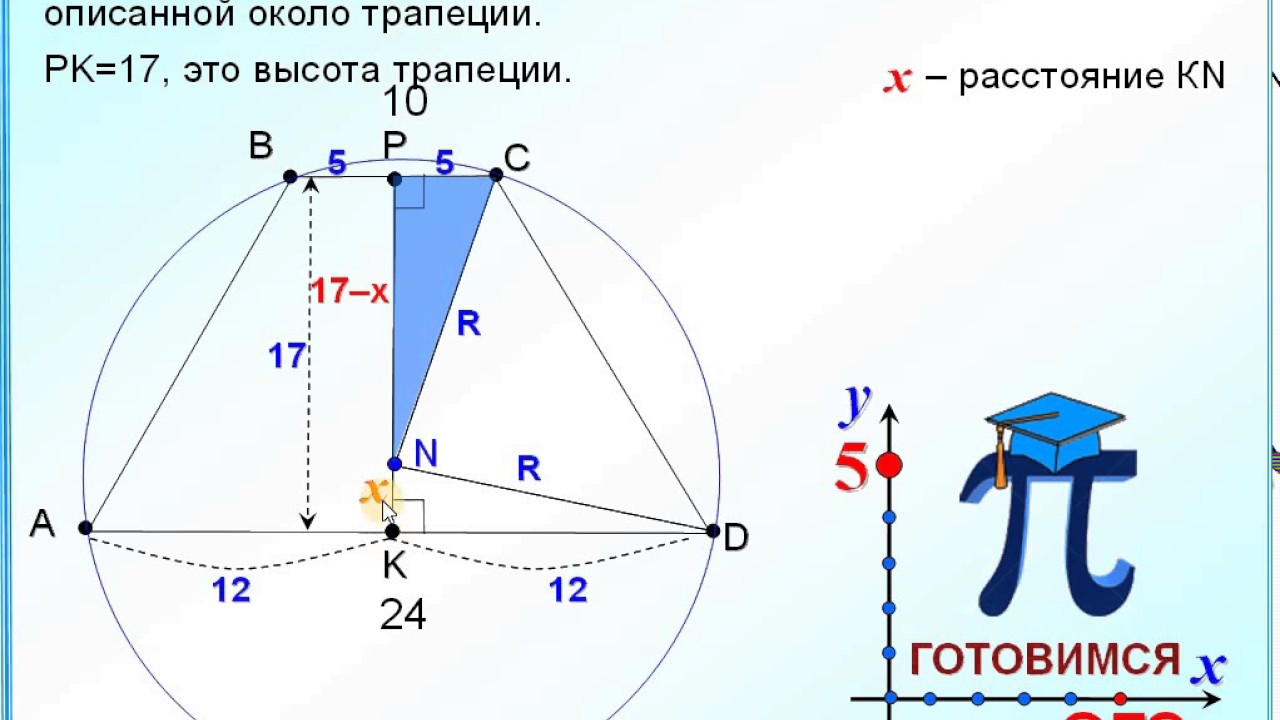 В квадрате и прямоугольниках — в точке пересечения диагоналей, для трапеции — в точке пересечения оси симметрии с линией, соединяющей середины сторон, а для любого другого выпуклого многоугольника — в точке пересечения пересечение середины перпендикуляра сторонам.
В квадрате и прямоугольниках — в точке пересечения диагоналей, для трапеции — в точке пересечения оси симметрии с линией, соединяющей середины сторон, а для любого другого выпуклого многоугольника — в точке пересечения пересечение середины перпендикуляра сторонам.
Вычислите диаметр круга, описанного вокруг квадрата и прямоугольника, используя теорему Пифагора. Он будет равен квадратному корню из суммы квадратов сторон прямоугольника. Для квадрата со всеми равными сторонами диагональ равна квадратному корню из двойного квадрата стороны. Разделив диаметр на 2, вы получите радиус.
Вычислите радиус описанной окружности треугольника. Поскольку параметры треугольника указаны в условиях, рассчитываем радиус по формуле R = a / (2 sinA), где a — одна из сторон треугольника ,? это противоположный ему угол.Вместо этой стороны можно взять сторону и противоположный ей угол.
Вычислить радиус окружности трапеции. R = a * d * c / 4 v (p * (pa) * (pd) * (pc)) В этой формуле a и b известны из условий основания трапеции, h — высота, d — диагональ, p = 1/2 * (a + d + c). Рассчитайте недостающие значения. Высоту можно вычислить по теореме синусов или косинусов, длины сторон трапеции и углы указаны в условиях.Зная высоту и учитывая сходство треугольников, рассчитайте диагональ. После этого остается рассчитать радиус по приведенной выше формуле.
Рассчитайте недостающие значения. Высоту можно вычислить по теореме синусов или косинусов, длины сторон трапеции и углы указаны в условиях.Зная высоту и учитывая сходство треугольников, рассчитайте диагональ. После этого остается рассчитать радиус по приведенной выше формуле.
Видео по теме
Полезный совет
Чтобы вычислить радиус окружности, описанной вокруг другого многоугольника, выполните ряд дополнительных построений. Получите более простые формы, параметры которых вы знаете.
Прямоугольником называется треугольник, угол при одной из вершин которого равен 90 °.Сторона, противоположная этому углу, называется гипотенузой, а стороны, противоположные двум острым углам треугольника, называются катетами. Если длина гипотенузы и величина одного из острых углов известны, то этих данных достаточно, чтобы построить треугольник как минимум двумя способами.
Определение 2
Многоугольник, удовлетворяющий условию определения 1, называется описанным вокруг окружности.
Рисунок 1. Вписанный круг
Теорема 1 (о круге, вписанном в треугольник)
Теорема 1
В любой треугольник можно вписать круг, причем только один.
Доказательство.
Рассмотрим треугольник $ ABC $. Нарисуем на нем биссектрисы, которые пересекаются в точке $ O $, и проведем от нее перпендикуляры к сторонам треугольника (рис. 2)
Рис. 2. Иллюстрация теоремы 1
Существование: начертите круг с центром в точке $ O $ и радиусе $ OK. \ $ Поскольку точка $ O $ лежит на трех биссектрисах, она равноудалена от сторон треугольника $ ABC $. То есть $ OM = OK = OL $. Следовательно, построенная окружность также проходит через точки $ M \ и \ L $.Поскольку $ OM, OK \ и \ OL $ перпендикуляры сторонам треугольника, то по теореме о касательной к окружности построенная окружность касается всех трех сторон треугольника. Следовательно, в силу произвольности треугольника в любой треугольник можно вписать круг.
Единственность: Предположим, что в треугольник $ ABC $ можно вписать еще одну окружность с центром в точке $ O «$. Его центр равноудалён от сторон треугольника и, следовательно, совпадает с точкой $ O $. и имеет радиус равный длине $ OK $ Но тогда этот круг совпадет с первым.
Его центр равноудалён от сторон треугольника и, следовательно, совпадает с точкой $ O $. и имеет радиус равный длине $ OK $ Но тогда этот круг совпадет с первым.
Теорема доказана.
Следствие 1: Центр окружности, вписанной в треугольник, лежит в точке пересечения его биссектрис.
Вот еще несколько фактов, связанных с концепцией вписанного круга:
Не каждый четырехугольник можно вписать в круг.
В любом описанном четырехугольнике суммы противоположных сторон равны.
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
Определение 3
Если все вершины многоугольника лежат на окружности, то окружность называется описанной вокруг многоугольника (рис. 3).
Определение 4
Многоугольник, удовлетворяющий условию определения 2, называется вписанным в круг.
Рис. 3. Описанная окружность
Теорема 2 (на окружности, описанной вокруг треугольника)
Теорема 2
Вокруг любого треугольника можно описать круг, причем только один.
Доказательство.
Рассмотрим треугольник $ ABC $. Нарисуем в нем перпендикуляры, пересекающиеся в точке $ O $, и соединим его с вершинами треугольника (рис. 4)
Рис. 4. Иллюстрация теоремы 2
Существование: построить окружность с центром $ O $ и радиус $ OC $. Точка $ O $ равноудалена от вершин треугольника, то есть $ OA = OB = OC $. Следовательно, построенная окружность проходит через все вершины этого треугольника, а значит, она описана вокруг этого треугольника.
Уникальность: Предположим, что вокруг треугольника $ ABC $ может быть описана еще одна окружность с центром в точке $ O «$. Ее центр равноудален от вершин треугольника и, следовательно, совпадает с точкой $ O $ и имеет радиус, равный длине $ OC. $ Но тогда этот круг совпадет с первым.
Теорема доказана.
Следствие 1: Центр окружности, описанной вокруг треугольника, совпадает с точкой пересечения его срединных перпендикуляров. 0 $, то вокруг него можно описать круг.
0 $, то вокруг него можно описать круг.
Пример задачи на понятиях вписанной и описанной окружности
Пример 1
В равнобедренном треугольнике основание 8 см, боковая сторона 5 см. Найдите радиус вписанной окружности.
Решение.
Рассмотрим треугольник $ ABC $. По следствию 1 мы знаем, что центр вписанной окружности лежит на пересечении биссектрис. Нарисуем биссектрисы $ AK $ и $ BM $, которые пересекаются в точке $ O $.2 + 1 \] \ \ \
Ответ: $ \ frac (4) (3) $.
Вам понадобится
- Треугольник с заданными параметрами
- Компас
- Линейка
- Гон
- Таблица синусов и косинусов
- Математические концепции
- Определение высоты треугольника
- Формулы синуса и косинуса
- Формула для площадь треугольника
Инструкции
Нарисуйте треугольник с нужными параметрами.Треугольник бывает либо с трех сторон, либо с двух сторон и угла между ними, либо со стороны и двух прилегающих к нему углов. Обозначьте вершины треугольника как A, B и C, углы как α, β и γ, а стороны, противоположные вершинам, как a, b и c.
Обозначьте вершины треугольника как A, B и C, углы как α, β и γ, а стороны, противоположные вершинам, как a, b и c.
Проведите до всех сторон треугольника и найдите точку их пересечения. Обозначьте высоту буквой h с индексами, соответствующими сторонам. Найдите точку их пересечения и обозначьте ее О. Это будет центр круга.Таким образом, радиусами этого круга будут отрезки OA, OB и OS.
Найдите радиус по двум формулам. Во-первых, вам нужно сначала рассчитать. Он равен всем сторонам треугольника синусом любого из углов, деленным на 2.
В этом случае радиус описанной окружности рассчитывается по формуле
Для другой стороны длина одной стороны и синуса противоположного угла достаточно.
Вычислите радиус и обведите треугольник.
Полезный совет
Запомните, какова высота треугольника. Это перпендикуляр, проведенный от угла к противоположной стороне.
Площадь треугольника также может быть представлена как произведение квадрата одной из сторон на синусы двух смежных углов, деленное на удвоенный синус суммы этих углов.
S = a2 * sinβ * sinγ / 2sinγ
Источники:
- таблица с радиусами описанной окружности
- Радиус описанной окружности около равносторонней
Считается, что он описан вокруг многоугольника, если он касается всех его вершин.Примечательно, что центр таких окружностей совпадает с точкой пересечения перпендикуляров, проведенных из середин сторон многоугольника. Радиус описанных окружностей полностью зависит от многоугольника, вокруг которого описывается.
Вам понадобится
- Знать стороны многоугольника, его площадь / периметр.
Инструкции
примечание
Окружность может быть описана вокруг многоугольника, только если она правильная, т.е.е. все его стороны равны и все углы равны.
Тезис о том, что центр окружности, описанной вокруг многоугольника, является пересечением его перпендикуляров, справедлив для всех правильных многоугольников.
Источники:
- как найти радиус многоугольника
Если можно построить описанную окружность для многоугольника, то площадь этого многоугольника меньше, чем площадь описанной окружности, но больше, чем площадь вписанной окружности. 1/2.
1/2.
Для многоугольника не всегда можно узнать соотношение вписанных радиусов и длин его сторон. Чаще всего они ограничиваются построением таких кругов вокруг многоугольника, а затем физическим радиусом кругов с использованием измерительных приборов или векторного пространства.
Чтобы построить описанную окружность выпуклого многоугольника, строятся биссектрисы двух его углов; центр описанной окружности лежит на их пересечении. Радиус — это расстояние от точки пересечения биссектрис до вершины любого угла многоугольника.Центр вписывается в точку пересечения перпендикуляров, построенных внутри многоугольника из центров сторон (эти перпендикуляры срединные). Достаточно построить два таких перпендикуляра. Радиус вписанной окружности равен расстоянию от точки пересечения срединных перпендикуляров до стороны многоугольника.
Видео по теме
note
Невозможно вписать круг и описать круг вокруг него в произвольно заданном многоугольнике.
Полезный совет
Круг можно вписать в четырехугольник, если a + c = b + d, где a, b, c, d — стороны четырехугольника по порядку.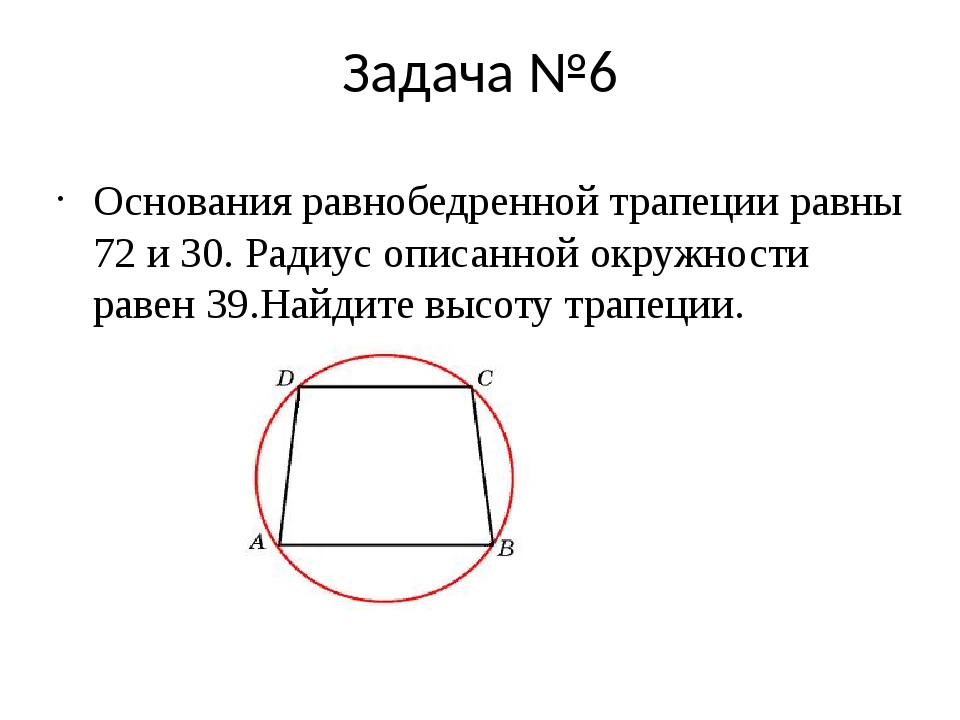 Круг можно описать вокруг четырехугольника, если его противоположные углы в сумме составляют 180 градусов;
Круг можно описать вокруг четырехугольника, если его противоположные углы в сумме составляют 180 градусов;
Для треугольника такие окружности существуют всегда.
Определение площади треугольника — одна из самых распространенных задач школьной планиметрии. Знания трех сторон треугольника достаточно, чтобы определить площадь любого треугольника.В частных случаях и равносторонних треугольниках достаточно знать длины двух и одной стороны соответственно.
Вам понадобится
- длин сторон треугольников, формула Герона, теорема косинусов
Инструкции
Формула Герона для вычисления площади треугольника выглядит следующим образом: S = sqrt (p (p-a) (p-b) (p-c)). Если раскрасить полупериметр p, получим: S = sqrt (((a + b + c) / 2) ((b + ca) / 2) ((a + cb) / 2) ((a + bc) / 2)) = (sqrt ((a + b + c) (a + bc) (a + cb) (b + ca))) / 4.2). Подставив синус в формулу для площади и записав ее, вы можете получить формулу для площади треугольника ABC.
Видео по теме
Три точки, которые однозначно определяют треугольник в декартовой системе координат, являются его вершинами. Зная их положение относительно каждой из осей координат, можно вычислить любые параметры этой плоской фигуры, в том числе ограниченную ее периметром квадрат … Это можно сделать несколькими способами.
Инструкции
Используйте формулу Герона для вычисления площади треугольник … Он использует размеры трех сторон фигуры, поэтому начните расчет с. Длина каждой стороны должна быть равна корню из суммы квадратов длин ее проекций на оси координат. Если обозначить координаты A (X₁, Y₁, Z₁), B (X₂, Y₂, Z₂) и C (X₃, Y₃, Z₃), длины их сторон можно выразить как: AB = √ ((X₁-X₂ ) ² + (Y₁ -Y₂) ² + (Z₁-Z₂) ²), BC = √ ((X₂-X₃) ² + (Y₂-Y₃) ² + (Z₂-Z₃) ²), AC = √ ((X₁ -X₃) ² + (Y₁-Y₃) ² + (Z₁-Z₃) ²).
Для упрощения расчетов введите вспомогательную переменную — полупериметр (P). Поскольку это половина суммы длин всех сторон: P = ½ * (AB + BC + AC) = ½ * (√ ((X₁-X₂) ² + (Y₁-Y₂) ² + (Z₁-Z₂) ² ) + √ ((X₂-X₃) ² + (Y₂-Y₃) ² + (Z₂-Z₃) ²) + √ ((X₁-X₃) ² + (Y₁-Y₃) ² + (Z₁-Z₃) ²).
Вычислить квадрат (S) по формуле Герона — извлечь корень из произведения полупериметра на разницу между ним и длиной каждой стороны. В общем, это можно записать следующим образом: S = √ ( P * (P-AB) * (P-BC) * (P-AC)) = √ (P * (P-√ ((X₁-X₂) ² + (Y₁-Y₂) ² + (Z₁-Z₂) ² )) * (P-√ ((X₂-X₃) ² + (Y₂-Y₃) ² + (Z₂-Z₃) ²)) * (P-√ ((X₁ -X₃) ² + (Y₁-Y₃) ² + (Z₁-Z₃) ²)).
Для практических расчетов удобно использовать специализированные калькуляторы. Это скрипты, размещенные на серверах некоторых сайтов, которые сделают все необходимые вычисления на основе координат, введенных вами в соответствующей форме. Единственная такая услуга — она не дает пояснений и обоснований для каждого шага расчетов. Поэтому, если вас интересует только конечный результат, а не общие расчеты, перейдите, например, на страницу http: // planetcalc.ru / 218 /.
В поля формы введите каждую координату каждой из вершин треугольника — они здесь как Ax, Ay, Az и т. Д. Если треугольник задан двумерными координатами, укажите в полях ноль — Az, Bz и Cz. В поле «Точность вычисления» установите необходимое количество десятичных разрядов, щелкнув мышью «плюс» или «минус». Необязательно нажимать оранжевую кнопку «Рассчитать», расположенную под формой, расчеты будут производиться без нее. Ответ вы найдете рядом с надписью «Area Triangle » — она находится сразу под оранжевой кнопкой.
В поле «Точность вычисления» установите необходимое количество десятичных разрядов, щелкнув мышью «плюс» или «минус». Необязательно нажимать оранжевую кнопку «Рассчитать», расположенную под формой, расчеты будут производиться без нее. Ответ вы найдете рядом с надписью «Area Triangle » — она находится сразу под оранжевой кнопкой.
Источники:
- найти площадь треугольника с вершинами в точках
Иногда выпуклый многоугольник можно нарисовать так, чтобы вершины всех углов лежали на нем. Такой круг по отношению к многоугольнику следует называть описанным. Ее Центр не обязательно должен находиться внутри периметра вписанной фигуры, но, используя свойства описанных окружностей , найти эту точку обычно не очень сложно.
Вам понадобится
- Линейка, карандаш, транспортир или угольник, циркуль.
Инструкции
Если многоугольник, вокруг которого вы хотите описать круг, нарисован на бумаге, найти Центр и круг достаточно с помощью линейки, карандаша и транспортира или квадрата. Измерьте длину любой из сторон фигуры, определите ее середину и поставьте в этом месте рисунка вспомогательную точку. Используя квадрат или транспортир, нарисуйте отрезок линии, перпендикулярный этой стороне внутри многоугольника, пока он не пересечется с противоположной стороной.
Измерьте длину любой из сторон фигуры, определите ее середину и поставьте в этом месте рисунка вспомогательную точку. Используя квадрат или транспортир, нарисуйте отрезок линии, перпендикулярный этой стороне внутри многоугольника, пока он не пересечется с противоположной стороной.
Сделайте то же самое для любой другой стороны многоугольника. Пересечение двух построенных отрезков и будет искомой точкой. Это следует из основного свойства описываемых окружностей — ее Центр в выпуклом многоугольнике с любой стороны всегда лежит в точке пересечения средних перпендикуляров, проведенных к этим
.Очень часто при решении геометрических задач приходится выполнять действия со вспомогательными фигурами. Например, найдите радиус вписанной или описанной окружности и т. Д.Эта статья покажет вам, как найти радиус круга вокруг треугольника. Или, другими словами, радиус круга, в который вписан треугольник.
Как найти радиус круга вокруг треугольника — общая формула
Общая формула выглядит следующим образом: R = abc / 4√p (p — a) (p — b) (p — c), где R — радиус описанной окружности, p — периметр треугольника, деленный на 2 (полупериметр). a, b, c — стороны треугольника.
a, b, c — стороны треугольника.
Найдите радиус описанной окружности треугольника, если a = 3, b = 6, c = 7.
Таким образом, по приведенной выше формуле вычисляем полупериметр:
p = (a + b + c) / 2 = 3 + 6 + 7 = 16. => 16/2 = 8.
Подставляем значения в формулу и получаем:
R = 3 × 6 × 7 / 4√8 (8–3) (8–6) (8–7) = 126 / 4√ (8 × 5 × 2 × 1) = 126 / 4√80 = 126/16 √5.
Ответ: R = 126 / 16√5
Как найти радиус круга вокруг равностороннего треугольника
Чтобы найти радиус окружности, описанной вокруг равностороннего треугольника, есть довольно простая формула: R = a / √3, где a — размер его стороны.
Пример: сторона равностороннего треугольника равна 5. Найдите радиус описанной окружности.
Поскольку все стороны равностороннего треугольника равны, для решения задачи вам просто нужно записать его значение в формулу. Получаем: R = 5 / √3.
Ответ: R = 5 / √3.
Как найти радиус окружности прямоугольного треугольника
Формула выглядит так: R = 1/2 × √ (a² + b²) = c / 2, где a и b — катеты, а c — гипотенуза. Если сложить квадраты катетов прямоугольного треугольника, мы получим квадрат гипотенузы. Как видно из формулы, это выражение находится под корнем. Вычисляя корень из квадрата гипотенузы, получаем саму длину. Умножение полученного выражения на 1/2 в конечном итоге приводит к выражению 1/2 × c = c / 2.
Если сложить квадраты катетов прямоугольного треугольника, мы получим квадрат гипотенузы. Как видно из формулы, это выражение находится под корнем. Вычисляя корень из квадрата гипотенузы, получаем саму длину. Умножение полученного выражения на 1/2 в конечном итоге приводит к выражению 1/2 × c = c / 2.
Пример: вычислить радиус описанной окружности, если стороны треугольника равны 3 и 4. Подставьте значения в формулу.Получаем: R = 1/2 × √ (3² + 4²) = 1/2 × √25 = 1/2 × 5 = 2,5.
В этом выражении 5 — длина гипотенузы.
Ответ: R = 2,5.
Как найти радиус окружности равнобедренного треугольника
Формула выглядит так: R = a² / √ (4a² — b²), где a — длина бедра треугольника, а b — длина основания.
Пример: вычислить радиус круга, если его бедро = 7, а основание = 8.
Решение: подставьте эти значения в формулу и получите: R = 7² / √ (4 × 7² — 8²).
R = 49 / √ (196 — 64) = 49 / √132. Ответ можно записать так.
Ответ: R = 49 / √132
Интернет-ресурсы для расчета радиуса окружности
Можно очень легко запутаться во всех этих формулах. Поэтому при необходимости вы можете воспользоваться онлайн-калькуляторами, которые помогут вам в решении задач найти радиус. Принцип работы таких мини-программ очень прост. Подставьте значение стороны в соответствующее поле и получите готовый ответ.Вы можете выбрать несколько вариантов округления ответа: до десятичных, сотых, тысячных и т. Д.
Тема «Вписанные и описанные окружности в треугольниках» — одна из самых сложных тем в курсе геометрии. На уроках ей уделяется очень мало времени.
Геометрические задачи данной темы включены во вторую часть экзаменационной работы ЕГЭ по курсу средней школы. Успешное выполнение этих задач требует твердого знания основных геометрических фактов и некоторого опыта решения геометрических задач.
В каждом треугольнике есть только одна описанная окружность. Это круг, на котором лежат все три вершины треугольника с заданными параметрами. Нахождение его радиуса может понадобиться не только на уроке геометрии. С этим постоянно сталкиваются дизайнеры, закройщики, слесари и представители многих других профессий. Чтобы найти его радиус, необходимо знать параметры треугольника и его свойства. Центр описанной окружности находится на пересечении серединных перпендикуляров треугольника.
Нахождение его радиуса может понадобиться не только на уроке геометрии. С этим постоянно сталкиваются дизайнеры, закройщики, слесари и представители многих других профессий. Чтобы найти его радиус, необходимо знать параметры треугольника и его свойства. Центр описанной окружности находится на пересечении серединных перпендикуляров треугольника.
Предлагаю вашему вниманию все формулы для нахождения радиуса описанной окружности, а не только треугольника. Можно просмотреть формулы для вписанного круга.
а, б. с — стороны треугольника,
α — противоположный угол a,
S — площадь треугольника ,
п — полупериметр.
Затем, чтобы найти радиус ( R ) описанной окружности, используйте формулы:
В свою очередь, площадь треугольника можно рассчитать по одной из следующих формул:
А вот еще несколько формул.
1. Радиус описанной окружности около правильного треугольника. Если — сторона треугольника , то
Если — сторона треугольника , то
2. Радиус описанной окружности около равнобедренного треугольника. Пусть будет a, b — стороны треугольника, тогда
Решатель проблем с геометрией — трапеция
Они дают трекам, что некоторые проблемы могут быть решены автоматически, числовые значения не имеют значения в различных примерах.
Трасса 1
Равнобедренная трапеция имеет высоту 20 м, большее основание 80 м, меньшее основание 50 м. Рассчитайте периметр и площадь трапеции.
Колея 2
Равнобедренная трапеция имеет наклонную сторону 20 см; имеет основание большее 80 см, имеет меньшее основание 50 см. Рассчитайте периметр.
Колея 3
Прямоугольная трапеция имеет высоту 40 м, основание большее 80 м, меньшее основание 50 м.Рассчитайте периметр и площадь трапеции.
Колея 4
Равнобедренная трапеция с основанием больше 80 см, имеет меньшее основание 50 см, имеет площадь 1300 см. Рассчитайте высоту трапеции.
Рассчитайте высоту трапеции.
Колея 5
Прямоугольник в форме трапеции имеет площадь 1500 см; имеет высоту 30 см. Вычисляет сумму двух оснований.
Колея 6
Равнобедренная трапеция имеет площадь 1500 см; имеет высоту 30 см.Вычисляет сумму двух оснований.
Колея 7
Равнобедренная трапеция имеет периметр 150 см; имеет основание больше 50 см; имеет меньшую базу 30 см. Рассчитайте длину скошенной стороны.
Направляющая 8
Равнобедренная трапеция имеет периметр 150 см, меньшее основание 30 см, наклонную сторону 35 см. Рассчитайте длину более длинного основания.
Направляющая 9
Равнобедренная трапеция имеет периметр 150 см, основание больше 50 см, наклонную сторону 35 см.Рассчитайте длину более короткого основания.
Колея 10
Прямоугольная трапеция имеет основание больше 50 см, имеет меньшее основание 30 см; имеет наклонную сторону 35 см. Рассчитайте периметр и площадь.
Рассчитайте периметр и площадь.
Колея 11
Прямоугольник трапеции имеет периметр 180 см; имеет основание больше 60 см, имеет наклонную сторону 50 см; имеет высоту 40 см. Рассчитайте длину более короткого основания.
Колея 12
Прямоугольник трапеции имеет периметр 180 см; имеет меньшую базу 30 см; имеет косую сторону 50 см; имеет высоту 40 см.Рассчитайте длину более длинного основания.
Колея 13
Прямоугольник трапеции имеет периметр 180 см; имеет меньшую базу 30 см; имеет высоту 40 см; имеет базу больше 60 см. Рассчитайте длину скошенной стороны.
Колея 14
Прямоугольник трапеции имеет периметр 180 см; имеет меньшую базу 30 см; имеет косую сторону 50 см; имеет базу больше 60 см. Рассчитывает длину высоты.
Колея 15
Равнобедренная трапеция имеет основание больше 20 см, наклонную сторону 5 см; имеет высоту 4 см. Рассчитайте меньшую базу.
Рассчитайте меньшую базу.
Колея 16
Равнобедренная трапеция имеет меньшее основание 14 см; имеет скошенную сторону 5 см; имеет высоту 4 см. Вычисляет большую базу.
Колея 17
Равнобедренная трапеция имеет основание больше 20 см, наклонную сторону 5 см; имеет выступ скошенной стороны на большее основание 3 см. Рассчитайте периметр.
Колея 18
Равнобедренный треугольник имеет меньшее основание 14 см; имеет наклонную сторону 5 см. Имеет экранирование наклонной стороны на большем основании 3 см.Рассчитайте периметр.
Трасса 19
Равнобедренная трапеция имеет площадь 2400 см, высоту 40 см, основы составляют треть от другой. Определите периметр.
Дорожка 20
Трапеция образована квадратом и треугольником. Учитывая, что площадь треугольника составляет 6 см, а разница между основаниями трапеции составляет 4 см, рассчитайте площадь трапеции.
Колея 21
Равнобедренная трапеция имеет наклонную сторону 20 см; имеет основание большее 90 см, имеет меньшее основание, равное 2/3 большего основания.Рассчитайте периметр.
Колея 22
Прямоугольная трапеция эквивалентна 1/4 квадрата с периметром 160 см. Учитывая, что высота трапеции составляет 20 см и 6 см, рассчитайте площадь прямоугольника, размеры которого совпадают с размерами оснований трапеции.
Направляющая 23
Прямоугольник в форме трапеции, описанный по кругу, длина скошенной стороны составляет 40 см, а высота равна 3/5 наклонной стороны.Рассчитайте периметр и площадь трапеции.
Дорожка 24
Площадь трапециевидного прямоугольника составляет 2250 см. Зная, что разница размеров проекции наклонной стороны на большее основание и высоты составляет 15 см, а их соотношение составляет 3/4, рассчитайте периметр трапеции.
Трасса 25
Периметр равнобедренной трапеции 250 см, высота 30 см, меньшее основание на 4/7 больше, чем косая сторона. Вычислите площадь трапеции.
Вычислите площадь трапеции.
Колея 26
Большая база прямоугольной формы трапеции со скошенной стороной под углом 45; зная, что основания 25 см и 15 см, вычисляет площадь трапеции.
Трасса 27
Равнобедренная трапеция ABCD образована тремя равнобедренными равнобедренными треугольниками, периметр каждого из которых равен 170 см, а наклонная сторона равна 6/5 основания. Рассчитайте периметр трапеции.
Дорожка 28
Равнобедренная трапеция ABCD имеет площадь 900 см. Основание AB является двойным, его высота составляет 20 см. Определите площадь треугольника ACD
Track 29
В равнобедренной трапеции площадь составляет 1032 см, а два основания имеют размер 61 см и 25 см соответственно. Вычислите меру высоты и периметра.
Колея 30
В прямоугольной трапеции с наклонной стороной образует большое основание под широким углом 30. Две базы размером 50 см и 30 см соответственно определяют периметр и площадь трапеции.
Две базы размером 50 см и 30 см соответственно определяют периметр и площадь трапеции.
Track 31
В равнобедренной трапеции сумма и разница размеров двух оснований составляет соответственно 74 см и 14 см. Вычисляет площадь и периметр трапеции, зная, что наклонная сторона равна 25 см.
Колея 32
Периметр равнобедренной трапеции 176 см. Зная, что меньшее основание составляет 4/3 наклонной стороны, а большее основание составляет 19/10 меньшего основания, вычисляется площадь трапеции.
Трасса 33
Каждая из наклонных сторон равнобедренной трапеции составляет треть меньшего основания. Зная, что периметр равен 230 см, а наибольшее основание — 105 см, вычисляется размер меньшего основания и площадь трапеции.
Колея 34
В прямоугольной трапеции нижняя диагональ перпендикулярна наклонной стороне. Зная, что эта диагональная линия и наклонная сторона 24 см и 18 см соответственно, найдите периметр и площадь трапеции.
Колея 35
В прямоугольной трапеции с наклонной стороной образует большое основание под широким углом 30. Рассчитайте периметр трапеции, зная, что высота 11,56 см, а площадь 462,42 см.
Направляющая 36
В трапеции главное основание и вспомогательное основание имеют длину 55 см и 30 см, а периметр — 140 см. Определяет длину наклонных сторон, зная, что одна составляет 6/5 другой.
Колея 37
Разница между основаниями равнобедренной трапеции составляет 30 см, меньшее основание — 5/8 большего основания, периметр — 180 см.Рассчитывает размер наклонных сторон.
Track 38
Из равнобедренной трапеции вы знаете, что: а) высота составляет 20 см. б) разница между двумя базами 30 см. в) основание больше 80 см. Рассчитайте периметр и площадь трапеции.
Колея 39
Периметр трапеции, имеющей высоту 34,60 см, составляет 203,49 см. Вычислите площадь трапеции, зная, что наклонные стороны образуют с большим основанием острые углы шириной 45 и 60.
Вычислите площадь трапеции, зная, что наклонные стороны образуют с большим основанием острые углы шириной 45 и 60.
Track 40
Площадь трапециевидного прямоугольника составляет 1080 квадратных сантиметров, а высота — 24 см. Вычислите размеры двух оснований, зная, что периметр равен 140 см.
Колея 41
Периметр равнобедренной трапеции составляет 152 см, а длина скошенной стороны — 26 см. Вычислите высоту и площадь трапеции, зная, что меньшее основание имеет длину 40 см.
Направляющая 42
В прямоугольной трапеции основное основание, меньшее основание и высота составляют соответственно 60 см в длину, 50 см и 24 см.Вычисляет площадь и периметр трапеции.
Track 43
Вычислите площадь трапеции, у которой большее основание составляет 8/5 меньшего основания, что, в свою очередь, равно высоте, составляющей 50 см.
Колея 44
Сумма оснований трапеции 80 см, основание 5/3 другого, высота 2/3 вспомогательного основания. Вычислите размер каждой диагонали ромба, эквивалентного трапеции, зная, что одна диагональ равна 25/16 другой.
Вычислите размер каждой диагонали ромба, эквивалентного трапеции, зная, что одна диагональ равна 25/16 другой.
Дорожка 45
Трапеция образована квадратом со стороной 48 см и двумя треугольниками, катет которых совпадает с одной из двух противоположных сторон квадрата. Гипотенуза двух треугольников составляет 60 см и 50 см соответственно. Рассчитайте периметр и площадь трапеции.
Колея 46
Разносторонняя трапеция имеет периметр 180 см; вычисляет все стороны, зная, что AB = 8/5 DC, DC — AB = 30 см, AD = 2/5 DC.
Track 47
У равнобедренной трапеции ABCD основание CD составляет 15/22 большего основания, наклонные стороны превышают 7 см 3/5 меньшего основания, периметр составляет 124 см. Какой район?
Направляющая 48
Увеличенное основание, высота и наклонная сторона прямоугольника до трапеции соответственно размером 80 см, 48 см и 50 см. Рассчитайте периметр и площадь трапеции.
Колея 49
Окружность имеет радиус 50 см; две параллельные хорды AB и CD расположены на противоположных частях относительно центра и имеют размер соответственно 96 см и 28 см.Вычисляет площадь и периметр трапеции, в основе которой лежат две хорды.
Колея 50
Равнобедренная трапеция имеет высоту 20 м, основание больше 80 м, меньшее основание 50 м. Вычислите радиус окружности, описанной трапецией.
Трасса 51
Трапеция имеет основания для диаметра окружности длиной 50 см и параллельной ей веревкой длиной 30 см. Рассчитайте периметр и площадь трапеции.
Дорожка 52
В круге с радиусом 50 см сделайте две параллельные хорды, расположенные на противоположных сторонах относительно центра и на расстоянии 14 см и 48 см от него соответственно. Вычисляет площадь и периметр трапеции, у которой есть основания для двух струн.
Колея 53
Прямоугольник и равнобедренная трапеция равны по высоте, периметр прямоугольника 140 см, разница размеров прямоугольника между ними 30 см, наклонная сторона трапеции 25 см. Вычислить:
Вычислить:
размер оснований прямоугольника;
протяженность оснований трапеции;
площадь трапеции и прямоугольника;
периметр трапеции.
Направляющая 54
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого. Вычислите площадь круга, радиус которого соответствует наклонной стороне, зная, что площадь трапеции составляет 1320 см.
Направляющая 55
Равнобедренная трапеция имеет высоту 24 см и основание соответственно 28 и 8 см.Вычислите периметр, площадь и две диагонали.
Направляющая 56
Прямоугольная трапеция имеет высоту 24 см и основания соответственно 18 и 10 см. Вычислите периметр, площадь и две диагонали.
Колея 57
Прямоугольная трапеция, сумма оснований 110 см, высота 24 см. Рассчитывает площадь.
Колея 58
Равнобедренная трапеция, сумма оснований 110 см, высота 24 см. Рассчитывает площадь.
Рассчитывает площадь.
Колея 59
Равнобедренная трапеция имеет площадь 336 см, сумма оснований 28 см. Рассчитайте высоту.
Дорожка 60
Прямоугольник трапеции имеет площадь 336 см, сумма оснований 28 см. Рассчитайте высоту.
Колея 61
Равнобедренная трапеция имеет большее основание 50 см, меньшее основание 30 см. Рассчитайте высоту, зная, что наклонная сторона равна 26 см.
Колея 62
Равнобедренная трапеция имеет большее основание 72 см, меньшее основание 8 см. Вычислите радиус круга, вписанного в трапецию, зная, что высота равна 24 см.
Колея 63
Равнобедренная трапеция имеет большее основание 72 см, меньшее основание 8 см. Рассчитайте диаметр круга, вписанного в трапецию, зная, что высота 24 см.
Колея 64
Прямоугольная трапеция имеет большее основание 48 см, меньшее основание 16 см. Вычислите радиус круга, вписанного в трапецию, зная, что высота равна 24 см.
Вычислите радиус круга, вписанного в трапецию, зная, что высота равна 24 см.
Колея 65
Прямоугольная трапеция имеет большее основание 48 см, меньшее основание 16 см. Рассчитайте диаметр круга, вписанного в трапецию, зная, что высота 24 см.
Колея 66
Равнобедренная трапеция имеет большее основание 80 см, меньшее основание 50 см. Рассчитайте диаметр круга на трапеции, зная, что высота равна 48.75 дюймов.
Колея 67
Равнобедренная трапеция имеет большее основание 80 см, меньшее основание 50 см. Вычислите длину круга, окружающего трапецию, зная, что высота составляет 48,75 дюйма.
Колея 68
Равнобедренная трапеция имеет большее основание 80 см, меньшее основание 50 см. Вычислите площадь описанной круговой трапеции, зная, что высота составляет 48,75 дюйма.
Колея 69
Равнобедренная трапеция имеет большее основание 80 см, меньшее основание 50 см.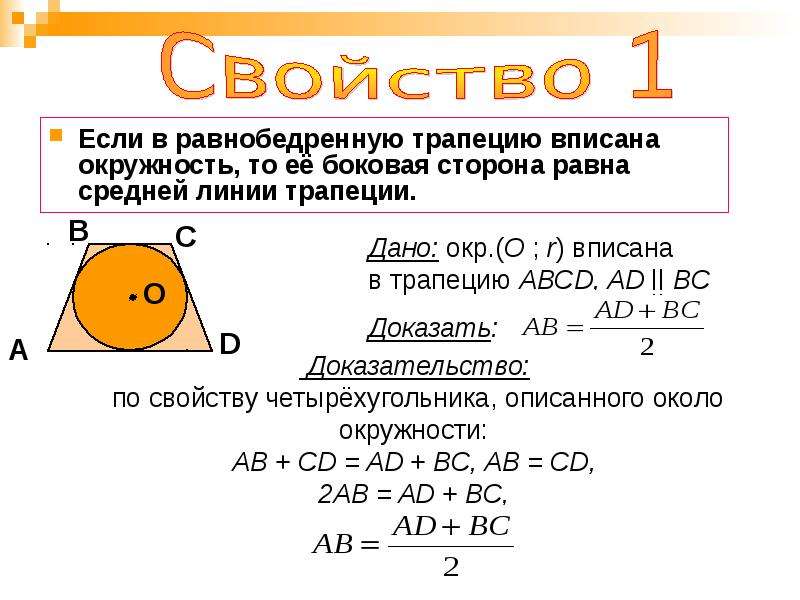 Вычислите:
Вычислите:
площадь круга, описанного трапецией, зная, что высота составляет 48,75 дюйма;
расстояние от центра хорды AB;
расстояние каната от центра CD;
длина дуги АВ;
длина дуги CD;
центральный угол АОБ;
центральный угол COD;
площадь кругового сектора AOB; площадь кругового сектора наложенным платежом.
Направляющая 70
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого.Вычислите площадь круга, радиус которого соответствует большему основанию, зная, что площадь трапеции составляет 1320 см.
Направляющая 71
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого. Вычислите площадь круга, радиус которого соответствует диагонали, зная, что площадь трапеции составляет 1320 см.
Направляющая 72
Прямоугольная трапеция имеет высоту 24 см и основание соответственно 60 и 50 см. Вычислите радиус окружности, соответствующей трапеции.
Вычислите радиус окружности, соответствующей трапеции.
Направляющая 73
Прямоугольник в форме трапеции имеет площадь 1320 см и основания соответственно 60 см и 50 см. Вычислите площадь круга, радиус которого соответствует высоте трапеции.
Колея 74
Прямоугольник в форме трапеции имеет площадь 1320 см и основания соответственно 60 и 50 см. Вычислите площадь круга, диаметр которого соответствует диагонали трапеции.
Направляющая 75
Прямоугольник трапеции имеет периметр 160 см, меньшее основание 50 см, высоту 24 см и наклонную сторону 26 см. Вычислите площадь круга, диаметр которого соответствует основанию трапеции.
Дорожка 76
Прямоугольник трапеции имеет большое основание 60 см, меньшее основание 50 см, высоту 24 см. Вычислите площадь окружности, имеющей изопериметрическую длину окружности трапеции.
Направляющая 77
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого. Вычислите площадь круга, радиус которого соответствует меньшему основанию, зная, что площадь трапеции составляет 1320 см.
Вычислите площадь круга, радиус которого соответствует меньшему основанию, зная, что площадь трапеции составляет 1320 см.
Колея 78
Равнобедренная трапеция имеет высоту 24 см, а основания составляют одну из 5/7 другой. Вычислите площадь круга, радиус которого соответствует меньшему основанию, зная, что площадь трапеции составляет 1440 см.
Направляющая 79
Равнобедренная трапеция имеет высоту 24 см, а основания составляют одну из 5/7 другой.Вычислите площадь круга, радиус которого соответствует большему основанию, зная, что площадь трапеции составляет 1440 см.
Направляющая 80
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого. Вычислите площадь круга, радиус которого соответствует малой диагонали, зная, что площадь трапеции составляет 1320 см.
Трасса 81
Равнобедренная трапеция имеет высоту 10 см и основания, которые являются одним из 7/17 другого. Вычислите площадь круга, радиус которого равен диагонали, зная, что площадь трапеции составляет 240 см.
Вычислите площадь круга, радиус которого равен диагонали, зная, что площадь трапеции составляет 240 см.
Дорожка 82
Равнобедренная трапеция имеет высоту 24 см и основание соответственно 60 и 50 см. Вычислите радиус окружности, соответствующей трапеции.
Трасса 83
Равнобедренная трапеция имеет площадь 1320 см и основания соответственно 60 и 50 см. Вычислите площадь круга, радиус которого соответствует высоте трапеции.
Направляющая 84
Прямоугольник в форме трапеции имеет площадь 360 см и основания соответственно 10 см и 20 см. Вычислите площадь круга, диаметр которого меньше диагонали трапеции.
Track 85
Равнобедренная трапеция имеет площадь 240 см и основания соответственно 34 см и 14 см. Вычислите площадь круга, диаметр которого соответствует диагонали трапеции.
Track 86
Равнобедренная трапеция имеет периметр 186 см, меньшее основание 50 см, высоту 24 см и наклонную сторону 26 см. Вычислите площадь круга, диаметр которого соответствует основанию трапеции.
Вычислите площадь круга, диаметр которого соответствует основанию трапеции.
Трасса 87
Равнобедренная трапеция имеет большое основание 70 см, малое основание 50 см, высоту 24 см. Вычислите площадь окружности, имеющей изопериметрическую длину окружности трапеции.
Track 88
Рассчитайте площадь и периметр разносторонней трапеции, зная, что большее основание составляет 80 см, а меньшее основание — 50 см, а наклонные стороны имеют длину соответственно 30 см и 20 см.
Направляющая 89
Равнобедренная трапеция имеет меньшее основание 8,4 см и выступ скошенной стороны на большем основании 10,8 см. Зная, что диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Направляющая 90
Прямоугольная трапеция имеет меньшее основание 19,2 см и выступ скошенной стороны на большем основании 10,8 см. Зная, что нижняя диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Направляющая 91
Прямоугольник в форме трапеции имеет наклонную сторону 18 см и проекцию наклонной стороны на большее основание 10,8 см. Зная, что нижняя диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Колея 92
Равнобедренная трапеция имеет наклонную сторону 18 см и выступание наклонной стороны на большее основание 10,8 см. Зная, что диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Колея 93
Равнобедренная трапеция имеет основание 30 см и выступ скошенной стороны на большее основание 10,8 см. Зная, что диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Направляющая 94
Прямоугольная трапеция имеет основание 30 см и выступ скошенной стороны на большее основание 10,8 см. Зная, что нижняя диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.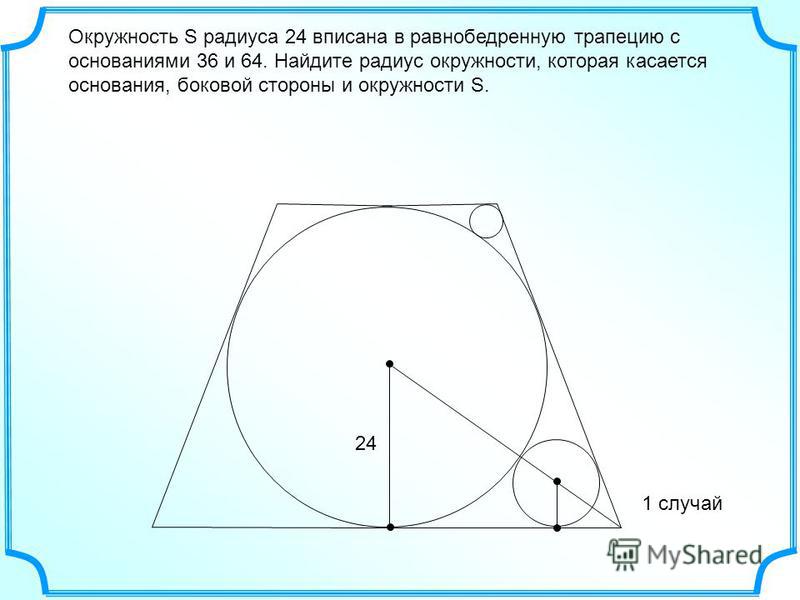
Направляющая 95
Прямоугольная трапеция имеет основание 30 см и наклонную сторону 18 см. Зная, что нижняя диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Колея 96
Равнобедренная трапеция имеет основание 30 см и наклонную сторону 18 см. Зная, что диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Колея 97
Периметр равнобедренной трапеции составляет 204 см, а каждая наклонная сторона — 30 см.Вычислите площадь и протяженность оснований, зная, что большее — это 5/3 второстепенного.
Колея 98
Основание большей формы равнобедренной трапеции с косой стороной под углом 45; зная, что основания 35 см и 15 см, вычисляет площадь и периметр трапеции.
***********
Правильный многоугольник, описанный в круг Калькулятор
- Цель использования
- Для определения открытого диаметра раздвижной кольцевой конструкции с 8-ю петлями.

[1] 2021/05/06 21:39 Уровень 30 лет / Средняя школа / Университет / аспирант / Очень /
- Цель использования
- Определение длины сторон многоугольной рамки вокруг круглого прохода
[2] 2021/01/08 23:00 Уровень 40 лет / Средняя школа / Университет / аспирант / Очень /
- Цель использования
- Расчет скругленного корня для зазора между зубьями шестерни
[3] 2020/04/19 04:16 60 лет и старше / Пенсионер / Очень /
- Цель использования
- определение наименьшего размера поворотной платформы для поддержки 36 путей на модели железной дороги в масштабе HO
[4] 2019 / 08/10 13:45 Уровень 50 лет / Инженер / Очень /
- Цель использования
- Планирование игровых элементов центральной игровой станции
[5] 2019/04 / 05 12:52 Уровень 60 лет и старше / Пенсионер / Очень /
- Назначение 914 96
- Хотелось бы, чтобы вы могли войти в периметр, и он дал вам радиус
[6] 2019/02/19 20:14 Уровень 20 лет / Средняя школа / ВУЗ / Аспирант / Немного /
- Цель использования
- Используется для создания Пентагона для рабочего места электроинструмента с максимально большими сторонами.
 Спасибо за калькулятор и приложенные усилия.
Спасибо за калькулятор и приложенные усилия.
[7] 2018/06/09 12:47 Уровень 60 лет и старше / Пенсионеры / Очень /
- Цель использования
- Строительство деревянного каркаса. Не хотел тратить время на расчеты сам.
[8] 2018/03/20 15:04 Уровень 60 и старше / Инженер / Полезно /
- Комментарий / Запрос
- Площадь правильного многоугольника, описанного вокруг окружности
[9] 2018/03/20 11:37 Моложе 20 лет / Средняя школа / Университет / аспирант / — /
- Цель использования
- Вырезание циферблата
[10] 2017/09/13 11:17 Уровень 50 лет / Другое / Очень /
Циклические четырехугольники — определение, свойства, теорема
Циклические четырехугольники (в евклидовой геометрии) — это замкнутые четырехугольники, все вершины которых лежат на одной окружности.Этот круг называется описанной окружностью или описанной окружности, или описанной окружностью , а вершины совпадают с окружностью .
Центр окружности называется центром описанной окружности , а ее радиус известен как радиус описанной окружности .
ОпределениеЧетырехугольник, описанный в окружности, называется вписанным четырехугольником, то есть все четыре вершины четырехугольника лежат на окружности окружности.2} {2 (ad + bc)} \)
\ (sin A = \ frac {2 \ sqrt {(s-a) (s-b) (s-c) (s-d)}} {ad + bc} \)
\ (tan \ frac {A} {2} = \ sqrt {\ frac {(s-b) (s-c)} {(s-a) (s-d)}} \)
ДиагоналиКак известно, стороны также можно записать как
\ (a \) = AB
\ (b \) = BC
\ (c \) = CD
\ (d \) = DA
и пусть длина диагоналей равна \ (d_1 \) = AC и \ (d_2 \) = BD.
Тогда мы можем выразить диагонали как
\ (d_1 = \ sqrt {\ frac {(ac + bd) (ad + bc)} {ab + cd}} \) и
\ (d_2 = \ sqrt {\ frac {(ac + bd) (ab + cd} {ad + bc}} \)
ПлощадьПлощадь (A) кругового четырехугольника со сторонами \ (a, b, c \ mbox {&} d \), а \ (s \) является полупериметром.Т.е. \ (s = \ frac {1} {2} (a + b + c + d) \)
Следовательно, по формуле Брахмагупты
\ (A = \ sqrt {(s-a) (s-b) (s-c) (s-d)} \)
Следствие формулы Бретшнайдера для общего четырехугольника, поскольку противоположные углы являются дополнительными в циклическом случае.
Если \ (d = 0 \), вписанный четырехугольник становится треугольником, формула сводится к формуле Герона.
Примечание: Узнайте больше о площади четырехугольника.
РадиусПусть \ (R \) будет радиусом, тогда
\ (R = \ frac {1} {4} \ sqrt {\ frac {(ab + cd) (ac + bd) (ad + bc)} {(s — a) (s — b) (s — c ) (s — d)}} \)
Теорема о циклических четырехугольникахСостояние: Сумма любой пары противоположных углов в круговом четырехугольнике являются дополнительными.
Доказательство: Дано, вписанный четырехугольник ABCD в окружность с центром О. {\ circ} \)
Верно и обратное утверждение этой теоремы,
и.е. если противоположные углы данного четырехугольника являются дополнительными, то данный четырехугольник является вписанным.
Отношение сторон к диагоналямПусть PQ, QR, RS и SP — четыре стороны четырехугольника, а \ (d_1 \) & \ (d_2 \) — диагонали.
Если четырехугольник вписан в круг,
, то произведение диагоналей равно сумме произведений двух пар его противоположных сторон.
то есть
Если PQRS — вписанный четырехугольник,
PQ и RS, а также QR и PS — противоположные стороны,
PR (\ (d_2 \)) и QS (\ (d_1 \)) — диагонали.2} {2 (ad + bc)} \)
Здесь a, b, c и d — четыре стороны, & A, B, C и D — четыре угла циклического четырехугольника.
Площадь, \ (A = \ sqrt {(sa) (sb) (sc) (sd)} \)
Здесь \ (s \) — это полу периметр, то есть \ (s = \ frac {a + b + c + d} {2} \)
- \ (d_1 = \ sqrt {\ frac {(ac + bd) (ad + bc)} {ab + cd}} \)
- \ (d_2 = \ sqrt {\ frac {(ac + bd) (ab + cd} {ad + bc}} \)
Здесь \ (d_1 \ mbox {&} d_2 \) — две диагонали четырехугольника.
(Поскольку углы, образуемые дугой в любой точке окружности, равны)
{SP — диаметр} Часто задаваемые вопросы Что такое вписанный четырехугольник?
Циклический четырехугольник (в евклидовой геометрии) — это замкнутый четырехугольник, все вершины которого лежат на одной окружности. Эта окружность называется описанной или описанной окружностью, а ее вершины прилегают друг к другу.
Равны ли противоположные стороны вписанного четырехугольника?Противоположные стороны циклического четырехугольника могут (частный случай i.{\ circ} \)).
Может ли пареллограмма быть циклической?Как известно, все прямоугольники и квадраты являются пареллограммами. Следовательно, прямоугольники и квадраты циклические, за исключением этих двух случаев отдыха пареллограммы не циклические.
Видео с вопросом: вычисление длины стороны правильного ограниченного пятиугольника с учетом радиуса окружности
стенограмма видео
Правильный пятиугольник описан вокруг круга радиусом два сантиметра.Найдите длину одной стороны пятиугольника. Ответьте правильно с точностью до одного десятичного знака.
Вот круг. Во-первых, мы можем добавить центр к этому кругу. И затем у нас есть пять мест, где пятиугольник касается этой окружности. Мы знаем, что расстояние от центра до любой точки внешнего круга — это радиус. А мы знаем, что радиус составляет два сантиметра. Мы замечаем, что вершина пятиугольника — это пересечение двух касательных, что говорит нам о том, что каждая из этих касательных имеет одинаковую длину.Мы также должны помнить, что когда касательная пересекает радиус, пересечение составляет 90 градусов.
На данный момент может показаться, что мы больше ничего не можем добавить. Но мы знаем, что это правильный пятиугольник. А это значит, что мы можем либо запомнить каждый из этих углов, либо знать, как их вычислить. Если вы не помните, каковы внутренние углы правильного многоугольника, вы можете вычислить внутренние углы любого многоугольника по формуле: 𝑠 равно 𝑛 минус два раза на 180 градусов.Где 𝑠 представляет собой сумму внутренних углов, а 𝑛 — количество сторон многоугольника.
У пятиугольника пять сторон. Итак, нам нужно пять минус два раза по 180 градусов. Пять минус два — три. Трижды 180 равно 540. Но помните, что это сумма всех пяти углов. Но поскольку это правильный пятиугольник, все пять углов равны. А это означает, что если мы разделим 540 на пять, мы сможем найти меру каждого из этих углов. 540, разделенное на пять, дает 108. В правильном пятиугольнике все углы составляют 108 градусов.Но это все равно нам не совсем помогает.
Но что произойдет, если мы проведем линию между одной из вершин и центром круга? Эта линия делит эти углы пополам. Вместо 108 каждый из них был бы 54 градуса. На этом этапе, вероятно, будет полезно увеличить масштаб того, о чем мы говорим.
У нас есть радиус в два сантиметра, одна часть пятиугольника и линия, которую мы только что провели от вершины пятиугольника к центру круга. Мы знаем, что радиус и касательная пересекаются под прямым углом, и что этот угол составляет 54 градуса.В любом треугольнике все углы нужно складывать до 180 градусов. Это означает, что 90 градусов плюс 54 градуса плюс некоторый угол должны равняться 180 градусам. Когда мы складываем 90 и 54, мы получаем 144. И если мы вычитаем 144 из 180, мы обнаруживаем, что наш недостающий угол составляет 36 градусов.
Помните, наша цель — найти длину одной стороны этого правильного многоугольника. Поскольку это правильный многоугольник, мы знаем, что все стороны имеют одинаковую длину. А это означает, что если мы найдем длину одной стороны, мы найдем длину всех сторон.Если мы добавим еще один радиус, мы снова увидим, что у нас есть две касательные, которые будут равной длины. А это означает, что если мы можем найти это расстояние, нам нужно умножить его на два, чтобы найти длину одной стороны пятиугольника. А это значит, что нам нужно рассмотреть этот прямоугольный треугольник. И нам нужно найти эту недостающую длину стороны.
Поскольку теперь мы имеем дело с прямоугольными треугольниками, мы можем использовать нашу тригонометрию прямоугольного треугольника. Если мы подумаем о трех тригонометрических отношениях, у нас есть синус, косинус и тангенс.Синус противоположен гипотенузе. Косинус является смежным по гипотенузе. А касательная равна противоположной по соседней. Длина желтой стороны — это гипотенуза, и мы не знаем, какова ее длина. Мы знаем радиус розовой стороны и хотим знать длину другой стороны. Нас не интересует гипотенуза. А это значит, что лучше всего использовать касательную связь.
Если мы начнем с угла в 54 градуса, мы можем сказать, что тангенс 54 градуса равен длине противоположной стороны, два сантиметра.А длина соседней стороны — это наша недостающая сторона 𝑠. Но это не единственный вариант. Мы также могли бы взять тангенс 36 градусов, где противоположная сторона равна длине стороны 𝑠, а длина смежной стороны равна радиусу двух сантиметров. Любой из них будет работать. Но я собираюсь выбрать тангенс 36 градусов, поскольку математика будет немного проще, потому что длина стороны находится в числителе дроби, а не в знаменателе. Таким образом, у нас будет на один шаг меньше, чем при использовании тангенса в 54 градуса.
В этом случае нам просто нужно умножить обе части уравнения на два сантиметра. И у нас получится, что два сантиметра, умноженные на тангенс 36 градусов, равны длине стороны. Когда мы умножаем тангенс 36 градусов на два раза, получаем 1.45308. Если вы этого не понимаете, убедитесь, что на калькуляторе, который вы используете, установлены градусы, а не радианы.
Здесь нам нужно быть осторожными, потому что это продолжение 1.45308 составляет только половину этой стороны пятиугольника. Оба эти расстояния равны 1.45308 продолжающихся сантиметров. И вместе они образуют длину одной стороны этого правильного пятиугольника. Таким образом, длина одной стороны этого пятиугольника равна двум умноженным на два сантиметра тангенсу 36 градусов, или двум умноженным на 1,45308 сантиметрам продолжительности. Когда мы проделаем это умножение, мы получим 2,
.
Мы округляем до первого десятичного знака. Это означает, что нам нужно смотреть вправо, на сотню. Поскольку в разряде сотен стоит ноль, мы округляем до 2.9 сантиметров.
. Отрезок, соединяющий основания, будет равен 1/2 их разности.
Отрезок, соединяющий основания, будет равен 1/2 их разности.
 Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.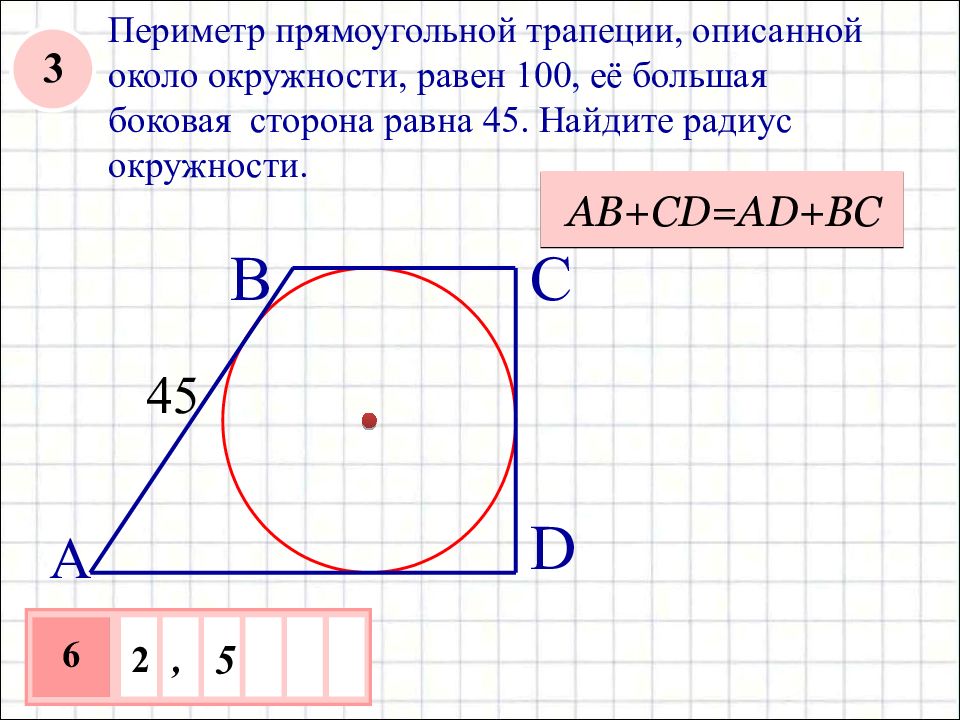

 Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
 Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.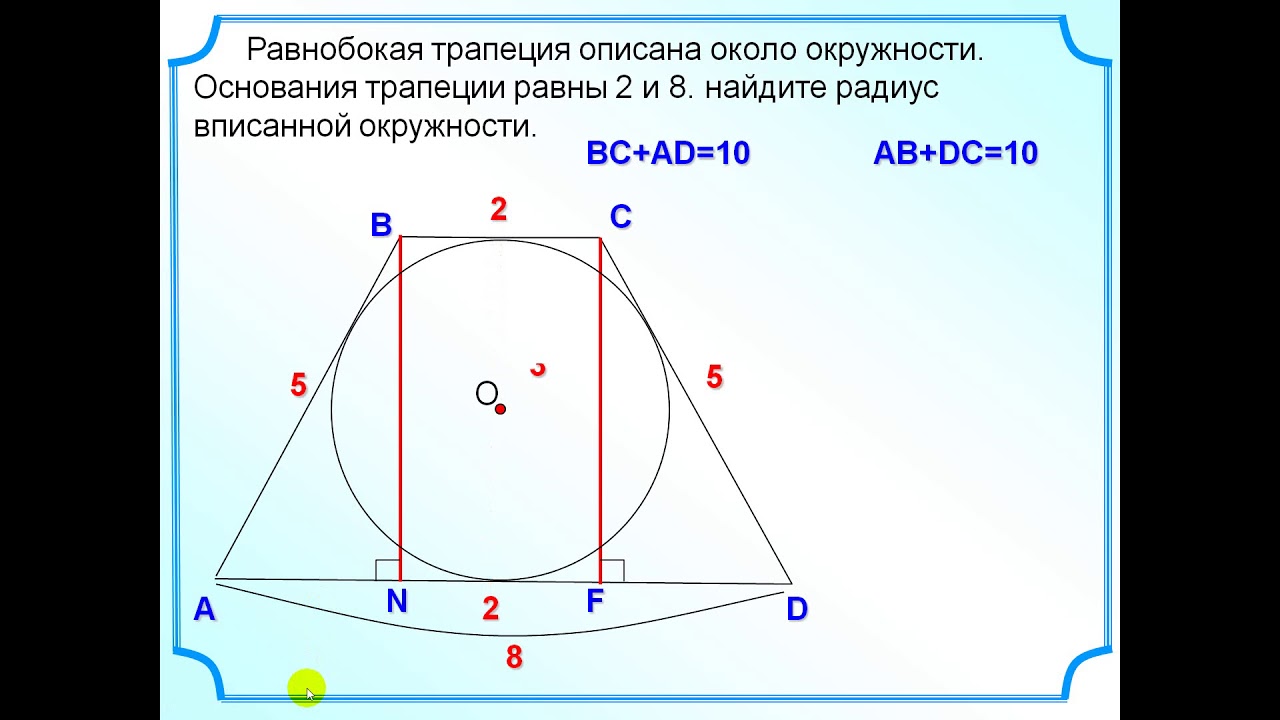 Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
 Отрезок, соединяющий основания, будет равен 1/2 их разности.
Отрезок, соединяющий основания, будет равен 1/2 их разности.

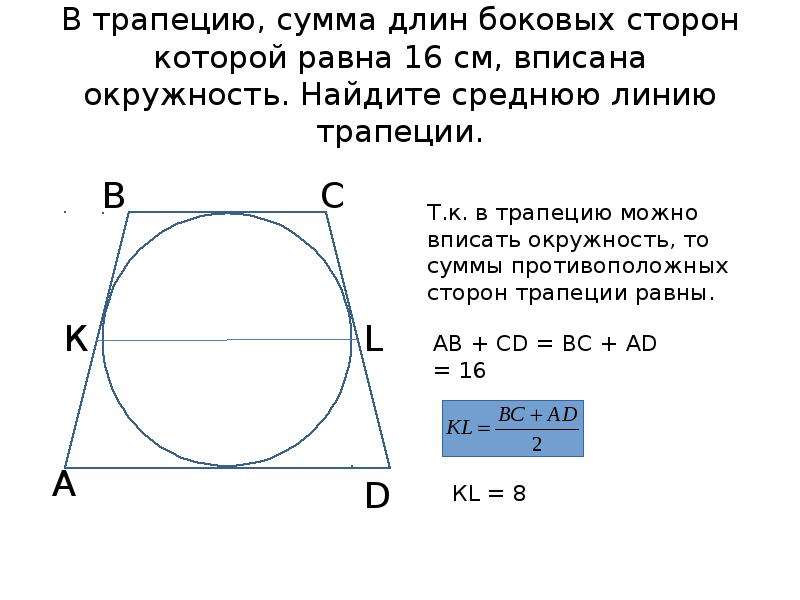 Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ .
Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ .
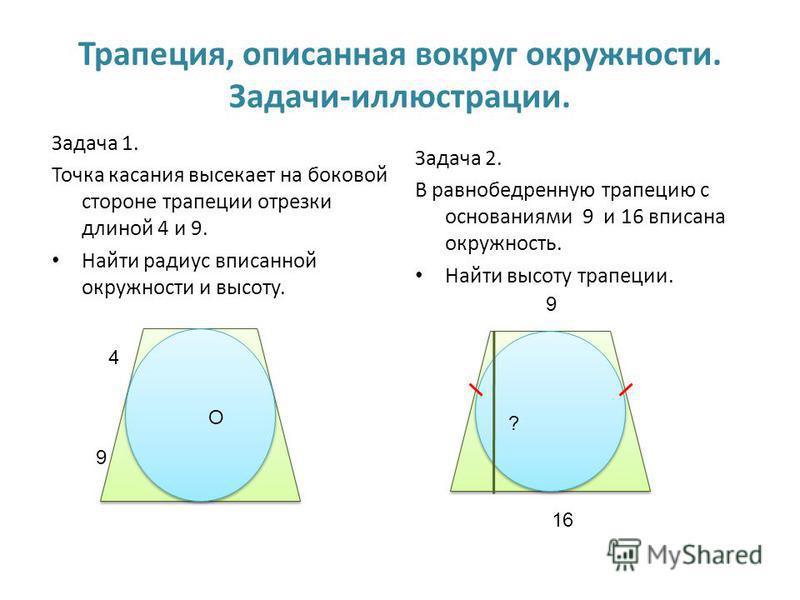 Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .
Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .

 Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК). Отрезок, соединяющий основания, будет равен 1/2 их разности.
Отрезок, соединяющий основания, будет равен 1/2 их разности.
 Итак, среднее значение разделено на 3 части диагоналями, образующими несколько одинаковых треугольников. Вопрос просит найти длину меньшего среднего участка среднего арифметического. Однако проблема не дает никаких значений по высоте. Есть ли у этой проблемы решение?
Итак, среднее значение разделено на 3 части диагоналями, образующими несколько одинаковых треугольников. Вопрос просит найти длину меньшего среднего участка среднего арифметического. Однако проблема не дает никаких значений по высоте. Есть ли у этой проблемы решение? Можно ли использовать подобные треугольники или что-то вроде гармонических и арифметических средств?
Можно ли использовать подобные треугольники или что-то вроде гармонических и арифметических средств? Поместите C внутри круга так, чтобы PC = PT.При необходимости см. Файл GSP.
Поместите C внутри круга так, чтобы PC = PT.При необходимости см. Файл GSP. 5
5
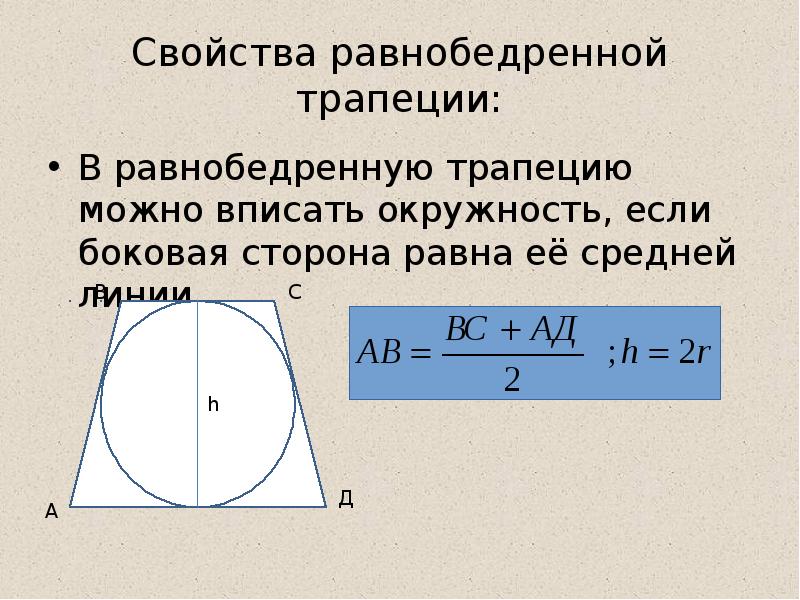 Спасибо за калькулятор и приложенные усилия.
Спасибо за калькулятор и приложенные усилия.