Задачи на движение 4-5 класс: скорость, время и расстояние
Скорость – это физическая величина, показывающая какое расстояние пройдет объект за единицу времени.
Сегодня мы будем решать задачи на:
- движение
- скорость \(v=s/t\)
- время \(t=s/v\)
- расстояние \(s=v*t\)
Расстояние — путь, который нужно преодолеть во время движения.
Время — промежуток действия движения.
Скорость — характеристика движения.
Для решения задач необходимо ввести неизвестную, верно составить и решить уравнение.
Задача 1. Легковая машина прошла расстояние в \(160\) км за два часа. С какой скоростью двигалась машина?
Решение.
\(160/2=80\) км/час
Ответ: \(80.\)
Задача 2. Из города Минск в Смоленск, расстояние между которыми \(346\) км, отправились одновременно велосипедист и автомобилист. Скорость автомобиля \(20\) м/с, а велосипедиста \(20\) км/ч.
Решение.
Мы не можем складывать разные единицы измерения, поэтому надо перевести м/с в км/ч. Как нам перевести км/ч в м/с? В км – 1000 м, в \(1\) ч \(-3600\), в \(1\) км/час\(-1000/3600\) м/c, то есть в \(1\) км/c \(-3600/1000\) м/c. \(20*\frac{3600}{1000}=72\). Итого скорость автомобиля \(72\) км/ч.
Так как автомобилист и велосипедист выехали из одного места и двигаются в одном направлении, расстояние между ними будет нарастать со скоростью:
- 72-20=52(км/ч)
- 52∗2=104 (км) – расстояние между ними через два часа.
Ответ: \(104\) км.
В таких задачах важно понимать:
- если мы умножаем скорость на время, то получаем расстояние;
- если расстояние делим на время, то получаем скорость;
- если расстояние делим на скорость, то получаем время ;
Задача 3. Из А в В тронулись в одно время турист пешком, а второй турист – на велосипеде.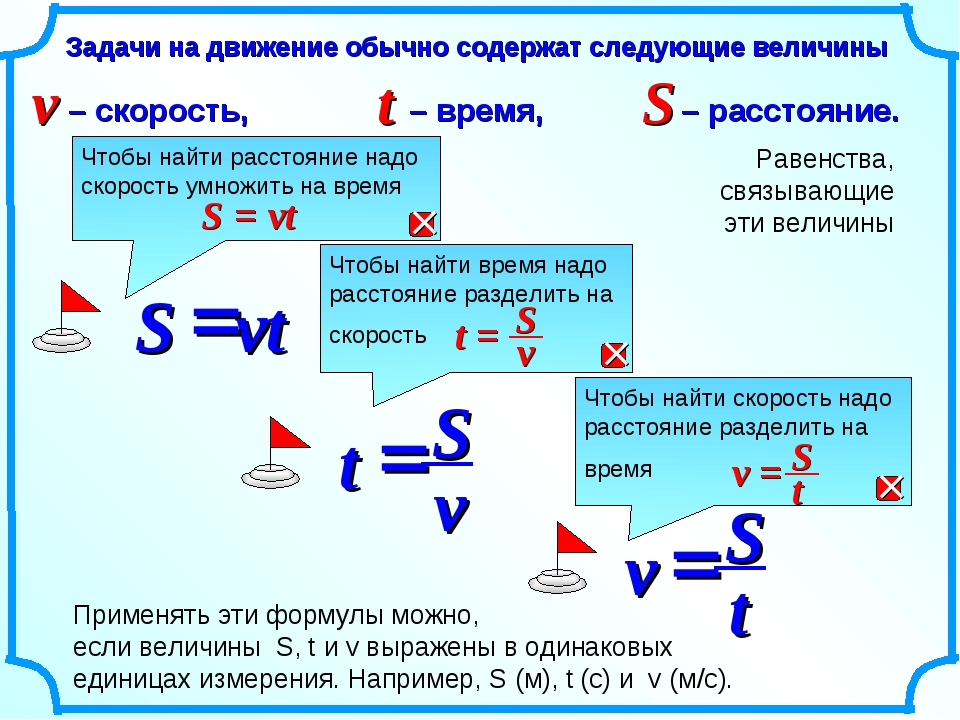 В то же время из В в А выдвинулся мотоцикл, который встретился с велосипедистом через 3 часа, а с пешеходом через 4 часов после своего выезда из В. Найти расстояние от А до В, зная, что скорость пешехода 3 км/ч, а велосипедиста 10 км/ч.
В то же время из В в А выдвинулся мотоцикл, который встретился с велосипедистом через 3 часа, а с пешеходом через 4 часов после своего выезда из В. Найти расстояние от А до В, зная, что скорость пешехода 3 км/ч, а велосипедиста 10 км/ч.
10 * 3 = 30 (км) – мотоциклист от А через 3 часа.
3* 4 = 12 (км) – мотоциклист от А через 4 часов.
30 – 12 = 18 (км/ч) – скорость автомобиля.
10 + 18 = 28 (км/ч) – скорость сближения мотоциклиста и велосипедиста.
28 * 3 = 84 (км) – расстояние от А до В.
Ответ: 84 км.
Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Оставить заявкуРепетитор по математике
Белорусский государственный университетПроведенных занятий:
Форма обучения:
Репетитор 5-9 классов.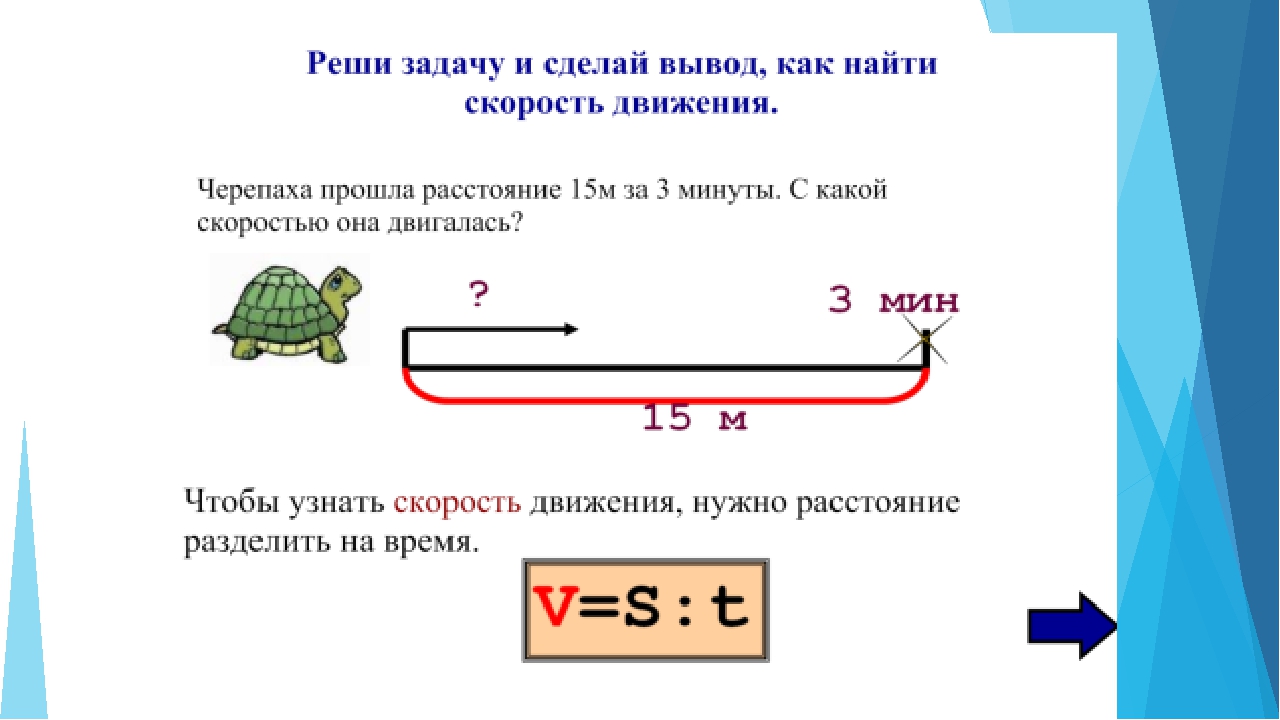 Люблю математику, потому что она логична и красива, она приносит удовольствие и развивает ум, ее нельзя переписать, например, как историю. Хочу, чтобы дети не боялись ее и полюбили, как я. Когда у ребенка начинает получаться, он становится счастливее. Сделать счастливее ваших детей — это моя главная задача!
Люблю математику, потому что она логична и красива, она приносит удовольствие и развивает ум, ее нельзя переписать, например, как историю. Хочу, чтобы дети не боялись ее и полюбили, как я. Когда у ребенка начинает получаться, он становится счастливее. Сделать счастливее ваших детей — это моя главная задача!
Брестский государственный университет им. А.С. Пушкина
А.С. Пушкина
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-10 классов. Люблю математику за то, что она дисциплинирует человека, систематизирует мысли, помогает другим наукам, без неё никуда! Помогу ученикам закрепить знания, которые имеются, восполню «пробелы» и научу новому. Также помогу с домашним заданием. Индивидуальный подход к каждому ученику. Жду Вас на своих занятиях! Оставить заявку
Люблю математику за то, что она дисциплинирует человека, систематизирует мысли, помогает другим наукам, без неё никуда! Помогу ученикам закрепить знания, которые имеются, восполню «пробелы» и научу новому. Также помогу с домашним заданием. Индивидуальный подход к каждому ученику. Жду Вас на своих занятиях! Оставить заявкуСамаркандский государственный университет
Проведенных занятий:
Форма обучения:Дистанционно (Скайп)
Репетитор 5-9 классов. Учитель первой категории. Я люблю математику не только потому, что она находит применение в технике, но и потому, что она красива. Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели. Объясняю доступно, ясно, легко. Учитываю личность, характер ученика. К нахожу индивидуальный подход.
Учитель первой категории. Я люблю математику не только потому, что она находит применение в технике, но и потому, что она красива. Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели. Объясняю доступно, ясно, легко. Учитываю личность, характер ученика. К нахожу индивидуальный подход.
Математика по Skype
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Математика 10 класс
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Похожие статьи
Задачи на движение | YouClever
Допустим, тебе надо проплыть \( \displaystyle10\) км.
Когда ты преодолеешь это расстояние быстрее? Когда ты будешь двигаться по течению или против?
Решим задачку и проверим.
Добавим к нашему пути данные о скорости течения – \( \displaystyle 3\) км/ч и о собственной скорости плота – \( \displaystyle 7\) км/ч. Какое время ты затратишь, двигаясь по течению и против него?
Конечно, ты без труда справился с этой задачей! По течению – \( \displaystyle 1\) час, а против течения аж \( \displaystyle 2,5\) часа!
В этом и есть вся суть задач на движение с течением. Несколько усложним задачу.
Пример №13
Лодка с моторчиком плыла из пункта \( \displaystyle A\) в пункт \( \displaystyle B\) \( \displaystyle 3\) часа, а обратно – \( \displaystyle 2\) часа. Найдите скорость течения, если скорость лодки в стоячей воде – \( \displaystyle 40\) км/ч.
Обозначим расстояние между пунктами, как \( \displaystyle AB\), а скорость течения – как \( \displaystyle x\).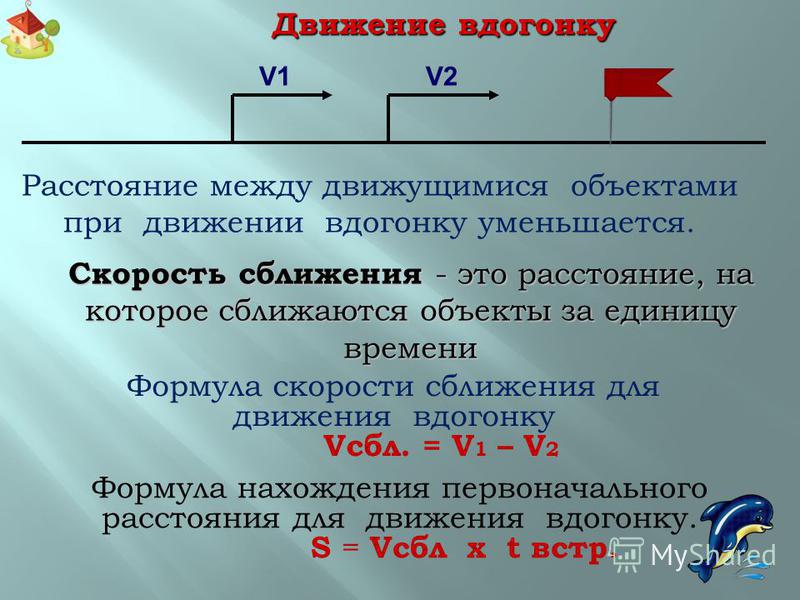
Все данные из условия занесем в таблицу:
| Путь S | Скорость v, км/ч | Время t, часов |
|---|---|---|
| A –> B (против течения) | \( \displaystyle 40-x\) | 3 |
| B –> A (по течению) | \( \displaystyle 40+x\) | 2 |
Мы видим, что лодка проделывает один и тот же путь, соответственно:
\( \displaystyle \left( 40-x \right)\cdot 3\text{ }=\text{ }\left( 40+x \right)\cdot 2\) \( \displaystyle 120-\text{ }\text{ }3x\text{ }=\text{ }80+2x\) \( \displaystyle 40=5x\) \( \displaystyle x=8\)Что мы брали за \( \displaystyle x\)? Скорость течения. Тогда это и будет являться ответом:) Скорость течения равна \( \displaystyle 8\) км/ч.
Пример №14Байдарка в \( \displaystyle 8:00\) вышла из пункта \( \displaystyle A\) в пункт \( \displaystyle B\), расположенный в \( \displaystyle 26\) км от \( \displaystyle A\).
Пробыв в пункте \( \displaystyle B\) \( \displaystyle 1\) час \( \displaystyle 20\) минут, байдарка отправилась назад и вернулась в пункт \( \displaystyle A\) в \( \displaystyle 20:00\).
Определите (в км/ч) собственную скорость байдарки, если известно, что скорость течения реки \( \displaystyle 5\) км/ч.
Итак, приступим. Прочитай задачу несколько раз и сделай рисунок. Думаю, ты без труда сможешь решить это самостоятельно.
Все величины у нас выражены в одном виде? Нет. Время отдыха у нас указано и в часах, и в минутах.
Переведем это в часы:
\( \displaystyle 1\) час \( \displaystyle 20\) минут = \( \displaystyle 1\frac{20}{60}=1\frac{1}{3}\) ч.
Теперь все величины у нас выражены в одном виде. Приступим к заполнению таблицы и поиску того, что мы возьмем за \( \displaystyle x\).
Пусть \( \displaystyle x\) – собственная скорость байдарки. Тогда, скорость байдарки по течению равна \( \displaystyle x+5\), а против течения равна \( \displaystyle x-5\).
Запишем эти данные, а так же путь (он, как ты понимаешь, одинаков) и время, выраженное через путь и скорость, в таблицу:
| Путь S | Скорость v, км/ч | Время t, часов | |
| Против течения | 26 | \( \displaystyle x-5\) | \( \displaystyle \frac{26}{x-5}\) |
| По течению | 26 | \( \displaystyle x+5\) | \( \displaystyle \frac{26}{x+5}\) |
Посчитаем, сколько времени байдарка затратила на свое путешествие:
\( \displaystyle 20.00-8.00\text{ }=\text{ }12\) часов.
Все ли \( \displaystyle 12\) часов она плыла? Перечитываем задачу.
Нет, не все. У нее был отдых \( \displaystyle 1\) час \( \displaystyle 20\) минут, соответственно, из \( \displaystyle 12\) часов мы вычитаем время отдыха, которое, мы уже перевели в часы:
\( \displaystyle 12-1\frac{1}{3}=10\frac{2}{3}\) ч байдарка действительно плыла.
Догадываешься, что мы делаем дальше? Правильно! Приравниваем полученное время к тому времени, которое мы выразили в таблице через путь и скорость. {2}}-25 \right)\)
{2}}-25 \right)\)
Раскроем скобки и приведем подобные слагаемые. Далее решаем получившееся квадратное уравнение.
С этим, я думаю, ты тоже справишься самостоятельно. Какой ответ у тебя получился? У меня \( \displaystyle 8\) км/ч.
Урок 35. задачи на движение — Математика — 5 класс
Математика
5 класс
Урок № 35
Задачи на движение
Перечень вопросов, рассматриваемых в теме:
- Понятия скорости, времени, расстояния.
- Формулы нахождения скорости, времени, расстояния.
- Понятия скорости сближения, скорости удаления.
Глоссарий по теме
Расстояние – это длина от одного пункта до другого.
Большие расстояния, в основном, измеряются в метрах и километрах.
Расстояние обозначается латинской буквой S.
Чтобы найти расстояние, надо скорость умножить на время движения:
S = v ∙ t
Скорость – это расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Скорость обозначается латинской буквой v.
Чтобы найти скорость, нужно расстояние разделить на время движения:
v = S : t
Время – это продолжительность каких-то действий, событий.
Время движения обозначается маленькой латинской буквой t.
Чтобы найти время, нужно расстояние разделить на скорость движения:
t = S : v
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Основная литература
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К., Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
2. Потапов М. К., Шевкин А. В. Математика. Книга для учителя. 5 – 6 классы — М.: Просвещение, 2010
Дополнительная литература
1. Чесноков А. С., Нешков К. И. Дидактические материалы по математике 5 кл. – М.: Академика учебник, 2014
2. Бурмистрова Т. А. Математика. Сборник рабочих программ. 5–6 классы // Составитель Бурмистрова Т. А.
3. Потапов М. К. Математика: дидактические материалы. 6 кл. // Потапов М. К., Шевкин А. В. — М.: Просвещение, 2010
Теоретический материал для самостоятельного изучения
Очень часто нам встречаются задачи на нахождение скорости, времени и расстояния. Что же всё это такое? Сейчас нам предстоит в этом разобраться.
Расстояние – это длина от одного пункта до другого. (Например, расстояние от дома до школы 2 километра). В основном большие расстояния измеряются в метрах и километрах. Общепринятое обозначение расстояния – заглавная латинская буква S.
В основном большие расстояния измеряются в метрах и километрах. Общепринятое обозначение расстояния – заглавная латинская буква S.
Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда. Скорость обозначается маленькой латинской буквой v.
Рассмотрим задачу:
Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 200 метров. Первый школьник добежал за 50 секунд. Второй за 100 секунд. Кто из ребят бежал быстрее?
Решение:
Быстрее бежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. Чтобы найти скорость, нужно расстояние разделить на время движения.
Давайте найдём скорость первого школьника. Для этого разделим 200 метров на время движения первого школьника, то есть на 50 секунд:
200 м : 50 с = 4
Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
У нас расстояние дано в метрах, а время в секундах. Значит, скорость измеряется в метрах в секунду:
200 м : 50 с = 4 (м/с)
Скорость движения первого школьника составляет 4 метра в секунду.
Теперь найдём скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника:
200 м : 100 c = 2 (м/с)
Скорость движения первого школьника – 4 (м/с).
Скорость движения второго школьника – 2 (м/с).
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит, он бежал до спортплощадки быстрее.
Иногда возникает ситуация, когда требуется узнать, за какое время тело преодолеет то или иное расстояние. Время движения обозначается маленькой латинской буквой t.
Рассмотрим задачу:
От дома до спортивной секции 1200 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 600 метров в минуту. За какое время мы доедем до спортивной секции?
Решение:
Если за одну минуту мы будем проезжать 600 метров, то сколько таких минут нам понадобится для преодоления тысячи двухсот метров? Очевидно, что надо разделить 1200 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 600 метров. Тогда мы получим время, за которое мы доедем до спортивной секции:
Тогда мы получим время, за которое мы доедем до спортивной секции:
1200 : 600 = 2 (мин)
Ответ: мы доедем до спортивной секции за 2 минуты.
Скорость, время и расстояние связаны между собой.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:
S = v ∙ t
Рассмотрим задачу:
Мы вышли из дома и направились в магазин. Мы дошли до магазина за 15 минут. Наша скорость была 60 метров в минуту. Какое расстояние мы прошли?
Решение:
Если за одну минуту мы прошли 60 метров, то сколько таких отрезков по шестьдесят метров мы пройдём за 15 минут? Очевидно, что умножив 60 метров на 15 минут, мы определим расстояние от дома до магазина:
v = 60 (м/мин)
t = 15 (минут)
S = v ∙ t = 60 ∙ 15 = 900 (метров)
Ответ: мы прошли 900 метров.
Если известно время и расстояние, то можно найти скорость:
v = S : t
Рассмотрим задачу:
Расстояние от дома до школы 800 метров.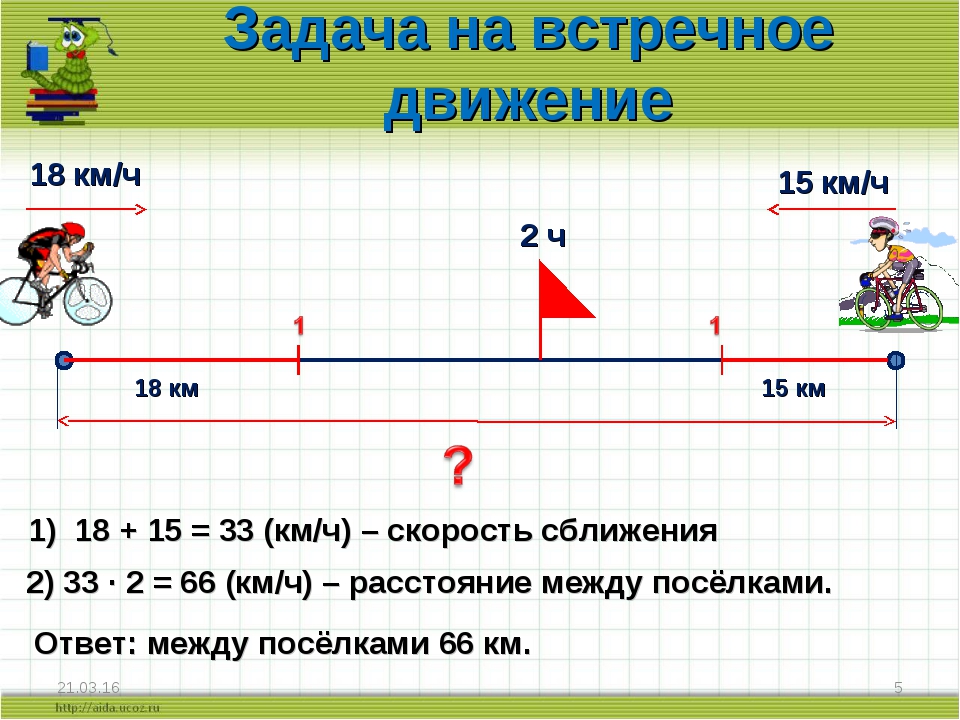 Школьник дошёл до этой школы за 8 минут. Какова была его скорость?
Школьник дошёл до этой школы за 8 минут. Какова была его скорость?
Скорость движения школьника – это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 800 метров, то какое расстояние он преодолевал за одну минуту?
Чтобы ответить на этот вопрос, нужно разделить расстояние на время движения школьника:
S = 800 метров
t = 8 минут
v = S : t = 800 : 8 = 100 (м/мин)
Ответ: скорость школьника была 100 м/мин.
Если известна скорость и расстояние, то можно найти время:
t = S : v
Рассмотрим задачу:
От дома до спортивной секции 600 метров. Мы должны дойти до неё пешком. Наша скорость будет 120 метров в минуту (120 м/мин). За какое время мы дойдём до спортивной секции?
Если за одну минуту мы будем проходить 120 метров, то сколько таких минут со ста двадцатью метрами будет в шестистах метрах?
Чтобы ответить на этот вопрос, нужно 600 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 120. Тогда мы получим время, за которое мы дойдём до спортивной секции:
Тогда мы получим время, за которое мы дойдём до спортивной секции:
S = 600 метров
v = 120 (м/мин)
t = S : v = 600 : 120 = 5 (минут).
Ответ: мы дойдём до спортивной секции за 5 минут.
Итак, все рассмотренные нами формулы мы можем представить в виде треугольника для лучшего запоминания:
Теперь рассмотрим типы задач на движение.
Задачи на сближение.
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причём скорость первого будет 100 метров в минуту, а второго – 105 метров в минуту, то скорость сближения будет составлять 100 плюс 105, то есть 205 метров в минуту. Значит, каждую минуту расстояние между пешеходами будет уменьшаться на 205 метров.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Задача.
Из двух пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 13 км/ч, а скорость второго – 15 км/ч. Через 3 часа они встретились. Определите расстояние между населёнными пунктами.
Скорость первого велосипедиста 13 км/ч, а скорость второго – 15 км/ч. Через 3 часа они встретились. Определите расстояние между населёнными пунктами.
Решение:
- Найдём скорость сближения велосипедистов:
13 км/ч + 15 км/ч = 28 км/ч
- Определим расстояние между населёнными пунктами. Для этого скорость сближения умножим на время движения:
28 ∙ 3 = 84 км
Ответ: расстояние между населёнными пунктами 84 км.
Задачи на скорость удаления.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причём скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4 плюс 6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиваться на 10 километров.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Рассмотрим задачу:
С причала одновременно в противоположных направлениях отправились теплоход и катер. Скорость теплохода составляла 60 км/ч, скорость катера 130 км/ч. Какое расстояние будет между ними через 2 часа?
Решение:
- Определим скорость удаления. Для этого сложим их скорости:
60 + 130 = 190 км/ч.
Получили скорость удаления равную 190 км/ч. Данная скорость показывает, что за час расстояние между теплоходом и катером будет увеличиваться на 190 километров.
- Чтобы узнать какое расстояние будет между ними через два часа, нужно 190 умножить на 2:
190 ∙ 2 = 380 км.
Ответ: через 2 часа расстояние между теплоходом и катером будет составлять 380 километров.
Задачи на движение объектов в одном направлении.
В предыдущих пунктах мы рассматривали задачи, в которых объекты (люди, машины, лодки) двигались либо навстречу друг другу, либо в противоположных направлениях. В первом случае мы находили скорость сближения – в ситуации, когда два объекта двигались навстречу друг другу. Во втором случае мы находили скорость удаления – в ситуации, когда два объекта двигались в противоположных направлениях. Но объекты также могут двигаться в одном направлении, причём с различной скоростью.
В первом случае мы находили скорость сближения – в ситуации, когда два объекта двигались навстречу друг другу. Во втором случае мы находили скорость удаления – в ситуации, когда два объекта двигались в противоположных направлениях. Но объекты также могут двигаться в одном направлении, причём с различной скоростью.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Рассмотрим задачу:
Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 130 км/ч, а скорость автобуса 90 км/ч. Какое расстояние будет между ними через 1 час? Через 3 часа?
Решение:
- Найдём скорость удаления. Для этого из большей скорости вычтем меньшую:
130 км/ч − 90 км/ч = 40 км/ч
- Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 3 часа в три раза больше:
40 ∙ 3 = 120 км
Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через три часа – 120 км.
Рассмотрим ситуацию, в которой объекты начали своё движение из разных пунктов, но в одном направлении.
Задача.
Пусть на одной улице имеется дом, школа и аттракцион. Дом находится на одном конце улицы, аттракцион на другом, школа между ними. От дома до школы 900 метров. Два пешехода отправились в аттракцион в одно и то же время. Причём первый пешеход отправился в аттракцион от дома со скоростью 90 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 85 метров в минуту. Какое расстояние будет между пешеходами через 3 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Решение:
- Определим расстояние, пройденное первым пешеходом за 3 минуты. Он двигался со скоростью 90 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 270 метров:
90 ∙ 3 = 270 метров
- Определим расстояние, пройденное вторым пешеходом за 3 минуты. Он двигался со скоростью 85 метров в минуту.
 За три минуты он пройдёт в три раза больше, то есть 255 метров:
За три минуты он пройдёт в три раза больше, то есть 255 метров:
85 ∙ 3 = 255 метров
- Теперь найдём расстояние между пешеходами. Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (900м) прибавить расстояние, пройденное вторым пешеходом (255м), и из полученного результата вычесть расстояние, пройденное первым пешеходом (270м):
900 + 255 = 1155 м
1155 – 270 = 885 м
Либо из расстояния от дома до школы (900 м) вычесть расстояние, пройденное первым пешеходом (270 м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (255 м):
900 – 270 = 630 м
630 + 255 = 885 м
Таким образом, через три минуты расстояние между пешеходами будет составлять 885 метров.
- Теперь давайте ответим на вопрос: через сколько минут после начала движения первый пешеход догонит второго?
В самом начале пути между пешеходами было расстояние 900 м. Через минуту после начала движения расстояние между ними будет составлять 895 метров, поскольку первый пешеход двигается на 5 метров в минуту быстрее второго:
90 ∙ 1 = 90 м
85 ∙ 1 = 85 м
900 + 85 – 90 = 985 – 90 = 895 м
Через три минуты после начала движения расстояние уменьшится на 15 метров и будет составлять 885 метров.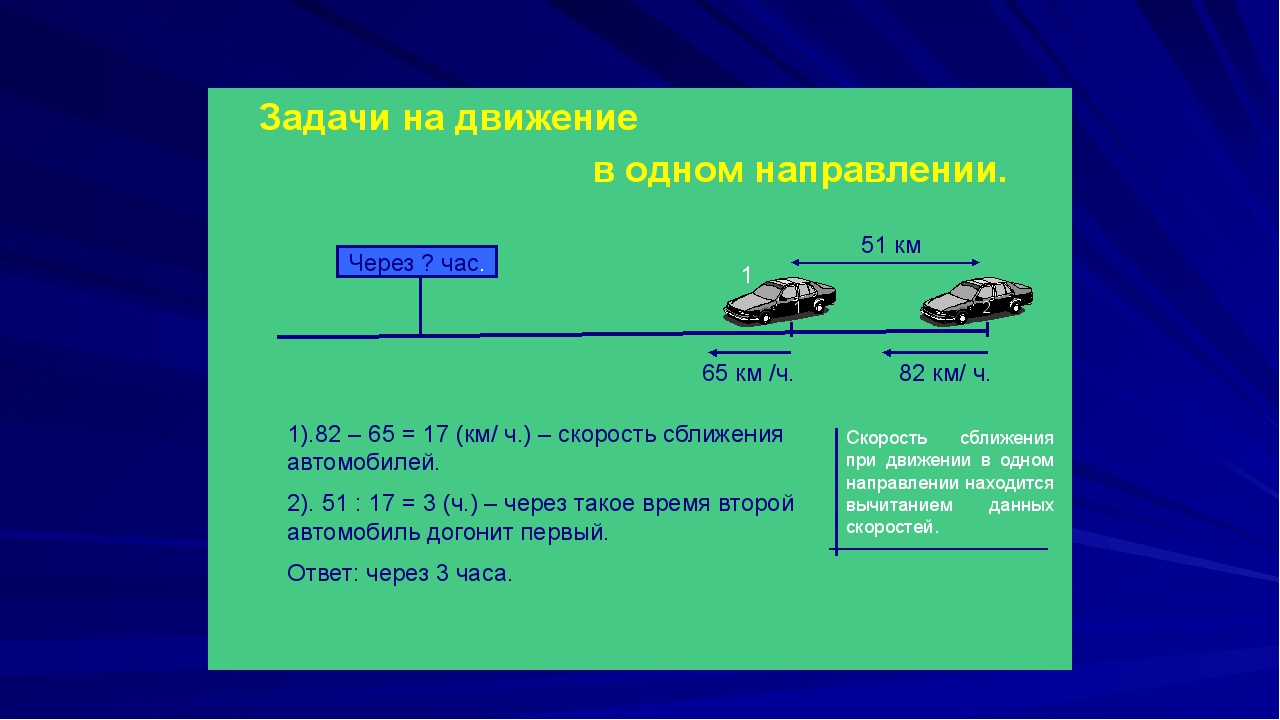 Это был наш ответ на первый вопрос задачи:
Это был наш ответ на первый вопрос задачи:
90 ∙ 3 = 270 м
85 ∙ 3 = 255 м
900 + 255 – 270 = 1155 – 270 = 885 м
Можно сделать вывод, что каждую минуту расстояние между пешеходами будет уменьшаться на 5 метров.
А раз изначальные 900 метров с каждой минутой уменьшаются на одинаковые 5 метров, то мы можем узнать сколько раз 900 метров содержат по 5 метров, тем самым определяя через сколько минут первый пешеход догонит второго:
900 : 5 = 180 минут.
Ответ: через три минуты расстояние между пешеходами будет составлять 885 метров, первый пешеход догонит второго через 180 минут = 3 часа.
Разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Заполните таблицу:
S | v | t | |
1. | 135 км | 9 км/ч | ____ ч |
2. | ____ м | 12 м/с | 4 с |
3. | 132 м | ____ м/мин | 11 мин |
Для заполнения пропусков воспользуемся формулами нахождения скорости, времени, расстояния:
- Надо найти время: t = S : v
135 : 9 = 15 часов.
- Надо найти расстояние: S = v ∙ t
12 ∙ 4 = 48 м.
- Надо найти скорость: v = S : t
132 : 11 = 12 м/мин.
Верный ответ:
S | v | t | |
1. | 135 км | 9 км/ч | 15 часов |
2. | 48 м | 12 м/с | 4 с |
3. | 132 м | 12 м/мин | 11 мин |
№2. Тип задания: единичный / множественный выбор
Выберите верный ответ к задаче:
Из пунктов А и В, расстояние между которыми 300 км, отправились одновременно навстречу друг другу мотоциклист и автомобилист. Скорость автомобиля 60 км/ч, а мотоцикла 30 км/ч. Какое расстояние будет между ними через 3 часа?
Скорость автомобиля 60 км/ч, а мотоцикла 30 км/ч. Какое расстояние будет между ними через 3 часа?
Варианты ответов:
- 70
- 30
- 270
- 240
Эта задача относится к типу задач на сближение, т.е. нам надо:
- сложить скорости мотоциклиста и автомобилиста:
60 + 30 = 90 км/ч – скорость сближения;
- узнать, сколько километров они пройдут за 3 часа вместе. Для этого:
90 ∙ 3 = 270 км;
- из общего расстояния нам осталось вычесть пройденное:
300 – 270 = 30 км
Верный ответ: 2. 30 км.
Текстовые задачи на движение – легко! Алгоритм решения и успех на ЕГЭ
Смотри видео «Текстовые задачи на ЕГЭ по математике».
Почему текстовые задачи относятся к простым?
Во-первых, все такие задачи решаются по единому алгоритму, о котором мы вам расскажем. Во-вторых, многие из них однотипны — это задачи на движение или на работу. Главное — знать к ним подход.
Главное — знать к ним подход.
Внимание! Чтобы научиться решать текстовые задачи, вам понадобится всего три-четыре часа самостоятельной работы, то есть два-три занятия. Всё, что нужно, — это здравый смысл плюс умение решать квадратное уравнение. И даже формулу для дискриминанта мы вам напомним, если вдруг забыли.
Прежде чем перейти к самим задачам — проверьте себя.
Запишите в виде математического выражения:
- на больше
- в пять раз больше
- на меньше, чем
- меньше в раза
- на меньше, чем
- частное от деления на в полтора раза больше
- квадрат суммы и равен
- составляет процентов от
- больше на процентов
Пока не напишете — в ответы не подглядывайте! 🙂
Казалось бы, на первые три вопроса ответит и второклассник. Но почему-то у половины выпускников они вызывают затруднения, не говоря уже о вопросах и . Из года в год мы, репетиторы, наблюдаем парадоксальную картину: ученики одиннадцатого класса долго думают, как записать, что « на больше ». А в школе в этот момент они «проходят» первообразные и интегралы 🙂
А в школе в этот момент они «проходят» первообразные и интегралы 🙂
Итак, правильные ответы:
больше, чем . Разница между ними равна пяти. Значит, чтобы получить большую величину, надо к меньшей прибавить разницу.
больше, чем , в пять раз. Значит, если умножить на , получим .
меньше, чем . Разница между ними равна . Чтобы получить меньшую величину, надо из большей вычесть разницу.
меньше, чем . Значит, если из большей величины вычтем разницу, получим меньшую.
На всякий случай повторим терминологию:
Сумма — результат сложения двух или нескольких слагаемых.
Разность — результат вычитания.
Произведение — результат умножения двух или нескольких множителей.
Частное — результат деления чисел.
Мы помним, что .
Если принять за , то на процентов больше, то есть .
Начнем мы с задач на движение. Они часто встречаются в вариантах ЕГЭ. Здесь всего два правила:
- Все эти задачи решаются по одной-единственной формуле: , то есть расстояние скорость время.
 Из этой формулы можно выразить скорость или время .
Из этой формулы можно выразить скорость или время . - В качестве переменной удобнее всего выбирать скорость. Тогда задача точно решится!
Для начала очень внимательно читаем условие. В нем все уже есть. Помним, что текстовые задачи на самом деле очень просты.
. Из пункта в пункт , расстояние между которыми км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт на часа позже автомобилиста. Ответ дайте в км/ч.
Что здесь лучше всего обозначить за ? Скорость велосипедиста. Тем более, что ее и надо найти в этой задаче. Автомобилист проезжает на километров больше, значит, его скорость равна .
Нарисуем таблицу. В нее сразу можно внести расстояние — и велосипедист, и автомобилист проехали по км. Можно внести скорость — она равна и для велосипедиста и автомобилиста соответственно. Осталось заполнить графу «время».
Его мы найдем по формуле: . Для велосипедиста получим , для автомобилиста .
Эти данные тоже запишем в таблицу.
Вот что получится:
Остается записать, что велосипедист прибыл в конечный пункт на часа позже автомобилиста. Позже — значит, времени он затратил больше. Это значит, что на четыре больше, чем , то есть
Решаем уравнение.
Приведем дроби в левой части к одному знаменателю.
Первую дробь домножим на , вторую — на .
Если вы не знаете, как приводить дроби к общему знаменателю (или — как раскрывать скобки, как решать уравнение…), подойдите с этим конкретным вопросом к вашему учителю математики и попросите объяснить. Бесполезно говорить учительнице: «Я не понимаю математику» — это слишком абстрактно и не располагает к ответу. Учительница может ответить, например, что она вам сочувствует. Или, наоборот, даст какую-либо характеристику вашей личности. И то и другое неконструктивно.
А вот если вы зададите конкретный вопрос: «Как приводить дроби к одному знаменателю» или «Как раскрывать скобки» — вы получите нужный вам конкретный ответ.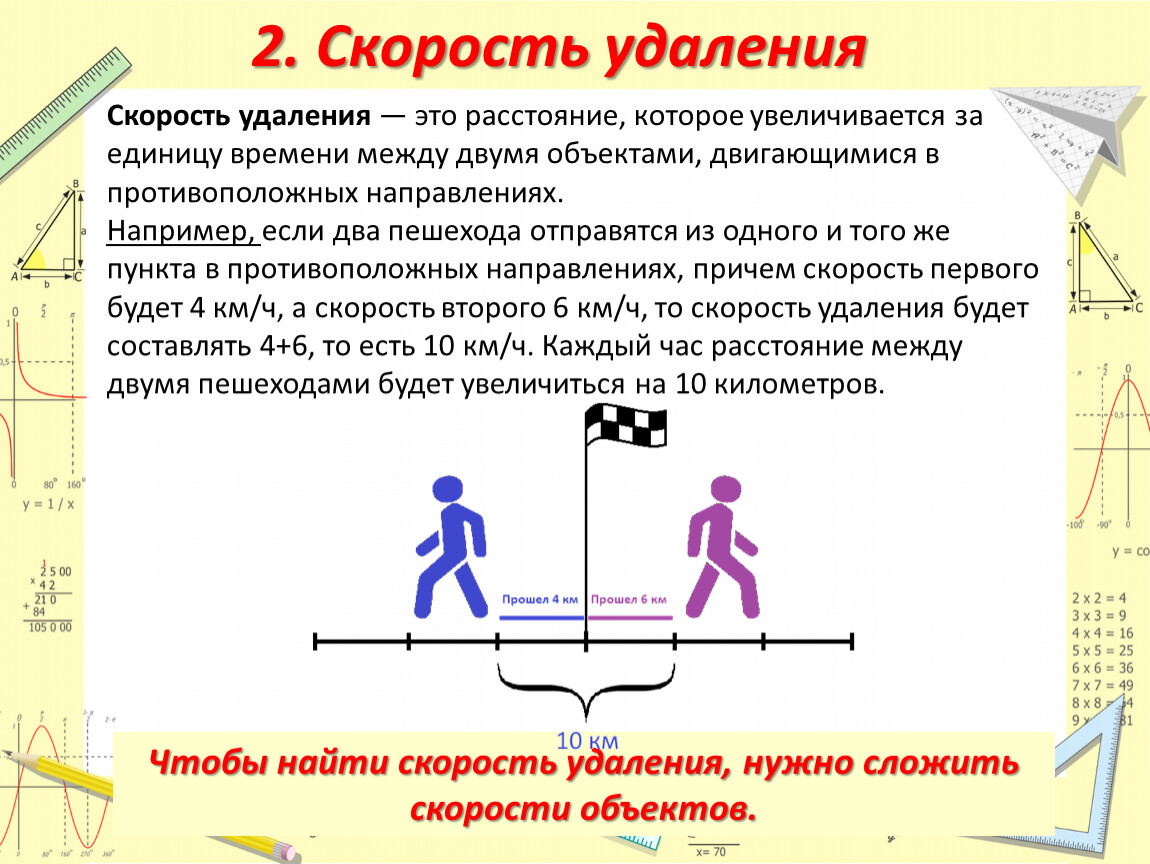 Вам ведь необходимо в этом разобраться! Если педагог занят, договоритесь о времени, когда вы можете с ним (или с ней) встретиться, чтобы получить консультацию. Используйте ресурсы, которые у вас под рукой!
Вам ведь необходимо в этом разобраться! Если педагог занят, договоритесь о времени, когда вы можете с ним (или с ней) встретиться, чтобы получить консультацию. Используйте ресурсы, которые у вас под рукой!
Получим:
Разделим обе части нашего уравнения на . В результате уравнение станет проще. Но почему-то многие учащиеся забывают это делать, и в результате получают сложные уравнения и шестизначные числа в качестве дискриминанта.
Умножим обе части уравнения на . Получим:
Раскроем скобки и перенесем всё в левую часть уравнения:
Мы получили квадратное уравнение. Напомним, что квадратным называется уравнение вида . Решается оно стандартно — сначала находим дискриминант по формуле , затем корни по формуле .
В нашем уравнении , , .
Найдем дискриминант и корни:
, .
Ясно, что не подходит по смыслу задачи — скорость велосипедиста не должна быть отрицательной.
Ответ: .
Следующая задача — тоже про велосипедиста.
2. Велосипедист выехал с постоянной скоростью из города в город , расстояние между которыми равно км. На следующий день он отправился обратно со скоростью на км/ч больше прежней. По дороге он сделал остановку на часа. В результате он затратил на обратный путь столько же времени, сколько на путь из в . Найдите скорость велосипедиста на пути из в . Ответ дайте в км/ч.
Пусть скорость велосипедиста на пути из в равна . Тогда его скорость на обратном пути равна . Расстояние в обеих строчках таблицы пишем одинаковое — километров. Осталось записать время. Поскольку , на путь из в велосипедист затратит время , а на обратный путь время .
На обратном пути велосипедист сделал остановку на часа и в результате затратил столько же времени, сколько на пути из в . Это значит, что на обратном пути он крутил педали на часа меньше.
Значит, на три меньше, чем . Получается уравнение:
Как и в предыдущей задаче, сгруппируем слагаемые:
Точно так же приводим дроби к одному знаменателю:
Разделим обе части уравнения на .
Напомним — если вам непонятны какие-либо действия при решении уравнений, обращайтесь к учительнице! Показывайте конкретную строчку в решении задачи и говорите: «Пожалуйста, объясните, как это делать». Для нее такое объяснение — дело пятнадцати минут, а вы наконец научитесь решать уравнения, что очень важно для сдачи ЕГЭ по математике.
Умножим обе части уравнения на , раскроем скобки и соберем все в левой части.
Находим дискриминант. Он равен .
Найдем корни уравнения:
. Это вполне правдоподобная скорость велосипедиста. А ответ не подходит, так как скорость велосипедиста должна быть положительна.
Ответ: .
Ты нашел то, что искал? Поделись с друзьями!
Следующий тип задач — когда что-нибудь плавает по речке, в которой есть течение. Например, теплоход, катер или моторная лодка. Обычно в условии говорится о собственной скорости плавучей посудины и скорости течения. Собственной скоростью называется скорость в неподвижной воде.
При движении по течению эти скорости складываются. Течение помогает, по течению плыть — быстрее.
Скорость при движении по течению равна сумме собственной скорости судна и скорости течения.
А если двигаться против течения? Течение будет мешать, относить назад. Теперь скорость течения будет вычитаться из собственной скорости судна.
3. Моторная лодка прошла против течения реки км и вернулась в пункт отправления, затратив на обратный путь на часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна км/ч. Ответ дайте в км/ч.
Пусть скорость лодки в неподвижной воде равна .
Тогда скорость движения моторки по течению равна , а скорость, с которой она движется против течения .
Расстояние и в ту, и в другую сторону одинаково и равно км.
Занесем скорость и расстояние в таблицу.
Заполняем графу «время». Мы уже знаем, как это делать. При движении по течению , при движении против течения , причем на два часа больше, чем .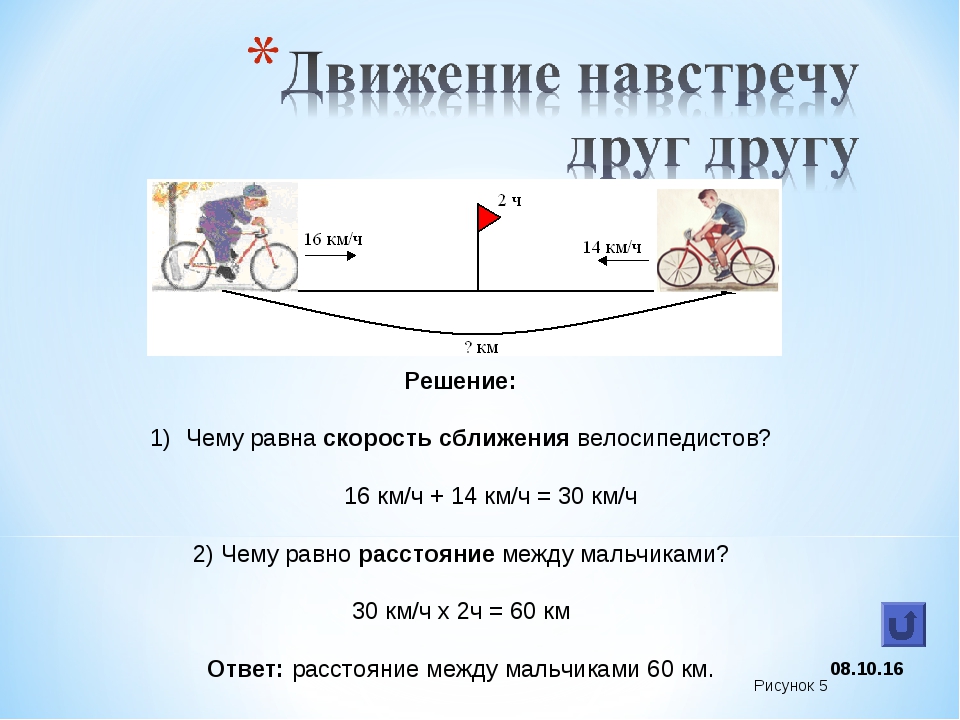
Условие « на два часа больше, чем » можно записать в виде:
Составляем уравнение:
и решаем его.
Приводим дроби в левой части к одному знаменателю
Раскрываем скобки
Делим обе части на , чтобы упростить уравнение
Умножаем обе части уравнения на
Вообще-то это уравнение имеет два корня: и (оба этих числа при возведении в квадрат дают ). Но конечно же, отрицательный ответ не подходит — скорость лодки должна быть положительной.
Ответ: .
4. Теплоход проходит по течению реки до пункта назначения км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна км/ч, стоянка длится часов, а в пункт отправления теплоход возвращается через часов после отплытия из него. Ответ дайте в км/ч.
Снова обозначим за скорость течения. Тогда скорость движения теплохода по течению равна , скорость его движения против течения равна .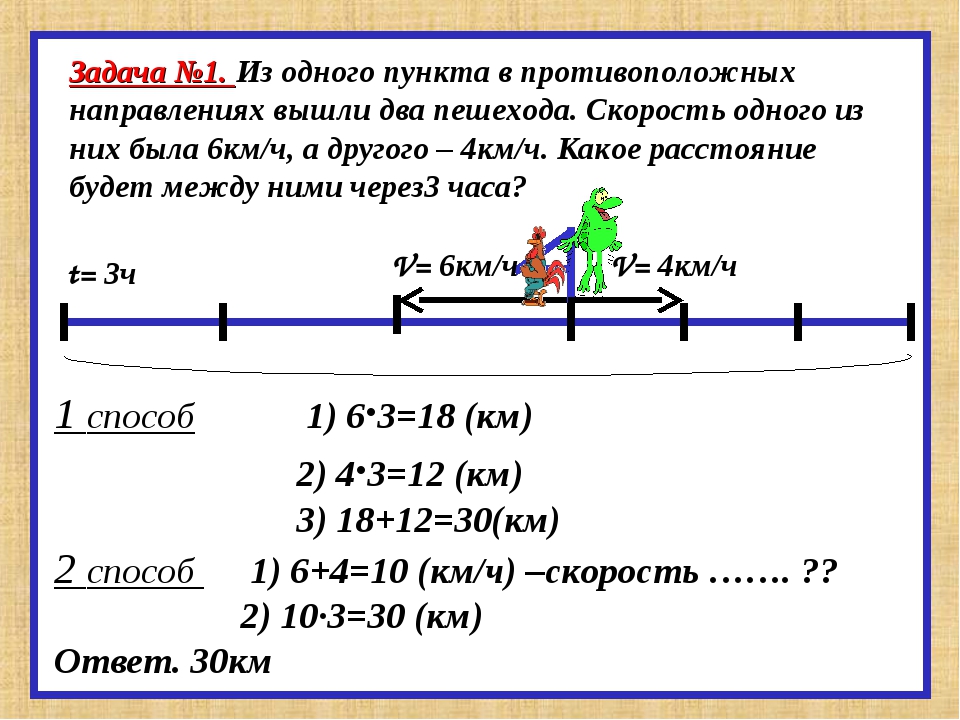 Расстояния — и туда, и обратно — равны км.
Расстояния — и туда, и обратно — равны км.
Теперь графа «время».
Поскольку , время движения теплохода по течению равно , которое теплоход затратил на движение против течения, равно .
В пункт отправления теплоход вернулся через часов после отплытия из него. Стоянка длилась часов, следовательно, часов теплоход плыл — сначала по течению, затем против.
Значит,
Прежде всего разделим обе части уравнения на . Оно станет проще!
Мы не будем подробно останавливаться на технике решения уравнения. Всё уже понятно — приводим дроби в левой части к одному знаменателю, умножаем обе части уравнения на , получаем квадратное уравнение . Поскольку скорость течения положительна, получаем: .
Ответ: .
Наверное, вы уже заметили, насколько похожи все эти задачи. Текстовые задачи хороши еще и тем, что ответ легко проверить с точки зрения здравого смысла. Ясно, что если вы получили скорость течения, равную километров в час — задача решена неверно.
5. Баржа в вышла из пункта в пункт , расположенный в км от . Пробыв в пункте — час минут, баржа отправилась назад и вернулась в пункт в . Определите (в км/час) скорость течения реки, если известно, что собственная скорость баржи равна км/ч.
Пусть скорость течения равна . Тогда по течению баржа плывет со скоростью , а против течения со скоростью .
Сколько времени баржа плыла? Ясно, что надо из вычесть , а затем вычесть время стоянки. Обратите внимание, что час минут придется перевести в часы: час минут часа. Получаем, что суммарное время движения баржи (по течению и против) равно часа.
Возникает вопрос — какой из пунктов, или , расположен выше по течению? А этого мы никогда не узнаем! 🙂 Да и какая разница — ведь в уравнение входит сумма , равная .
Итак,
Решим это уравнение. Число в правой части представим в виде неправильной дроби: .
Приведем дроби в левой части к общему знаменателю, раскроем скобки и упростим уравнение. Получим:
Получим:
Работать с дробными коэффициентами неудобно! Если мы разделим обе части уравнения на и умножим на , оно станет значительно проще:
Поскольку скорость течения положительна, .
Ответ: 2.
Еще один тип текстовых задач в вариантах ЕГЭ по математике — это задачи на работу.
Движение навстречу друг другу | Математика
Задачи на движение навстречу друг другу (встречное движение) — один из трех основных видов задач на движение.
Если два объекта движутся навстречу друг другу, то они сближаются:
Чтобы найти скорость сближения двух объектов, движущихся навстречу друг другу, надо сложить их скорости:
Скорость сближения больше, чем скорость каждого из них.
Скорость, время и расстояние связаны между собой формулой пути:
Рассмотрим некоторые задачи на встречное движение.
Задача 1
Два велосипедиста выехали навстречу друг другу. Скорость одного из низ 12 км/ч, а другого — 10 км/ч. Через 3 часа они встретились. Какое расстояние было между ними в начале пути?
Скорость одного из низ 12 км/ч, а другого — 10 км/ч. Через 3 часа они встретились. Какое расстояние было между ними в начале пути?
Решение:
Условие задач на движение удобно оформлять в виде таблицы:
v, км/ч | t, ч | s, км | |
I велосипедист | 12 | 3 | ? |
II велосипедист | 10 | 3 | ? |
1) 12+10=22 (км/ч) скорость сближения велосипедистов
2) 22∙3=66 (км) было между велосипедистами в начале пути.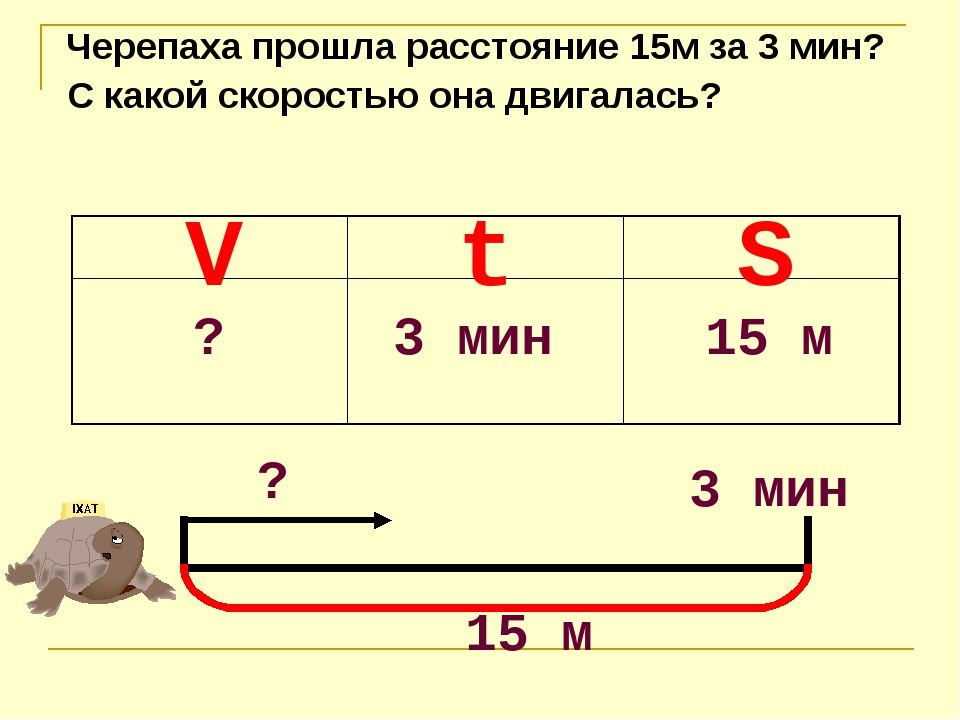
Ответ: 66 км.
Задача 2
Два поезда идут навстречу друг другу. Скорость одного из них 50 км/ч, скорость другого — 60 км/ч. Сейчас между ними 440 км. Через сколько часов они встретятся?
Решение:
v, км/ч | t, ч | s, км | |
I поезд | 60 | ? | ? |
II поезд | 50 | ? | ? |
1) 60+50=110 (км/ч) скорость сближения поездов
2) 440:110=4 (ч) время, через которое поезда встретятся.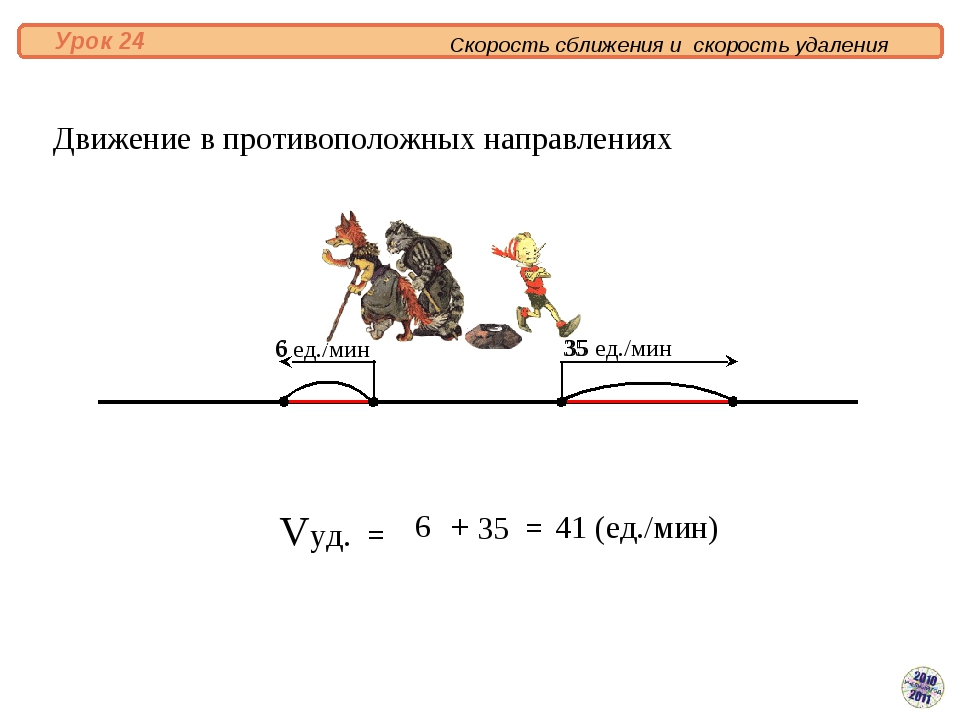
Ответ: через 4 ч.
Задача 3.
Два пешехода находились на расстоянии 20 км друг от друга. Они вышли одновременно навстречу друг другу и встретились через 2 часа. Скорость одного пешехода 6 км/ч. Найти скорость другого пешехода.
v, км/ч | t, ч | s, км | |
I пешеход | 6 | 2 | ? |
II пешеход | ? | 2 | ? |
1) 20:2=10 (км/ч) скорость сближения пешеходов
2) 10-6=4 (км/ч) скорость другого пешехода.
Ответ: 4 км/ч.
Задачи на встречное движение (нахождение времени и скорости)
– Вера, привет. Мне очень нужна твоя помощь.
– Что опять случилось? Наверное, ты не можешь решить задачу по математике?
– Мне просто надо решить аж две задачи и … и что-то я запутался. Помоги мне, пожалуйста.
– Хорошо, я тебе помогу. Только ты внимательно слушай и запоминай. Читай условие первой задачи.
Из двух городов, расстояние между которыми 840 км, выехали одновременно навстречу друг другу Генри на машине и Мари на поезде. Машина Генри двигалась со скоростью 95 км/ч, а поезд, в котором ехала Мари, двигался со скоростью 115 км/ч. Через сколько часов встретятся Мари и Генри?
Ты мне прошлый раз объясняла задачи на встречное движение. Её я научился решать. Но это ведь уже совсем другая задача.
–
Нет, эта задача тоже на встречное движение,
посмотри, в задаче написано «выехали одновременно навстречу друг другу».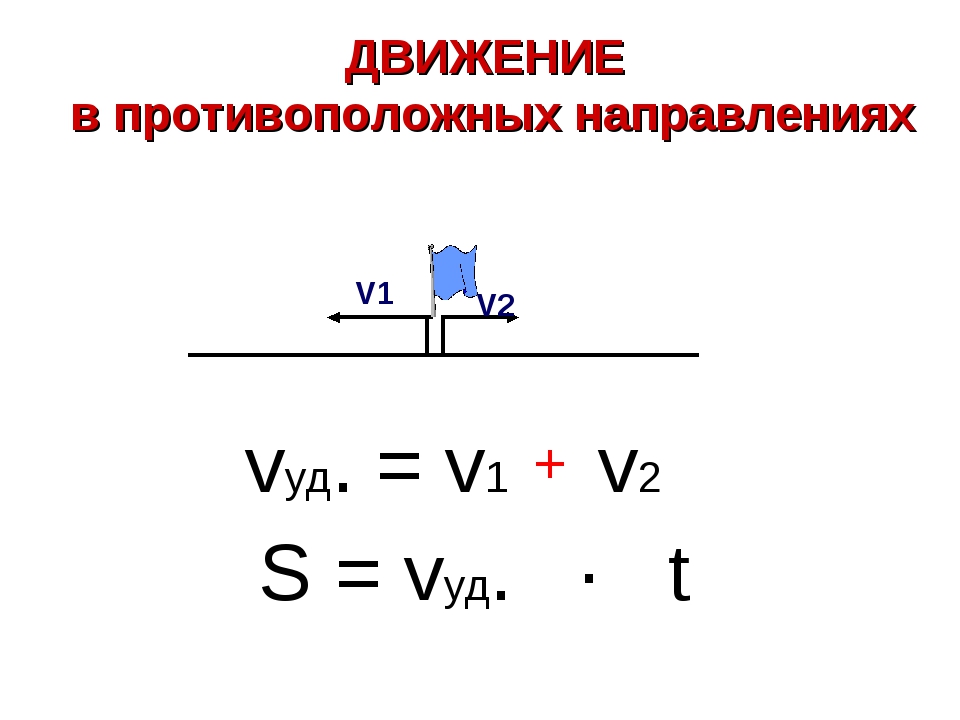
Давай изобразим всё на рисунке.
Итак, обозначим расстояние между двумя городами отрезком.
Город, из которого выехал Генри обозначим буквой А, стрелочкой укажем направление, и укажем его скорость. Второй город обозначим буквой В, так же укажем направление движения и скорость поезда, в котором едет Мари. Теперь мы хорошо видим, что движение у нас встречное. Так же мы знаем, что расстояние между городами 840 км. Надо узнать, через сколько часов встретятся Мари и Генри?
В этой задаче известно расстояние между городами и скорости, с которыми двигались машина и поезд.
Итак, мы знаем, что за каждый час Генри приближался к месту встречи по 95 км, Мари за каждый час приближалась по 115 км.
Мы можем узнать, на сколько они приближались вместе за один час.
Помнишь
ли ты, при разборе таких задач мы говорили о скорости сближения.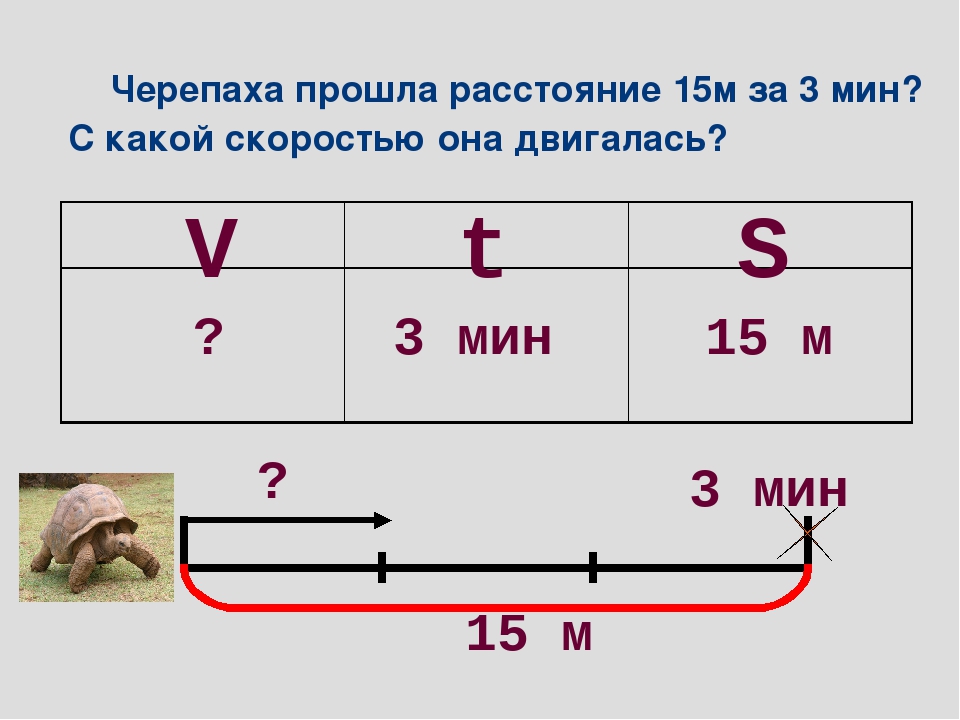 А что такое скорость сближения?
А что такое скорость сближения?
– Это сумма скоростей двух приближающихся друг к другу объектов.
– В этой задаче нам тоже понадобится скорость сближения, ведь расстояние преодолевал не каждый по отдельности. Это расстояние преодолено ими совместно.
Значит и скорость должна быть совместной, т.е. скорость сближения. Находим её:
1) 95 + 115 = 210 км/ч.
Мы нашли скорость сближения поезда и машины.
Дальше они продолжали двигаться до места встречи с той же скоростью сближения.
Мы знаем, расстояние между городами – 720 км, а теперь и скорость сближения – 210 км. Так как найти время?
– Надо расстояние разделить на скорость сближения, и мы узнаем время, через которое встретились Генри и Мари.
Ответ: Генри и Мари встретились через 4 часа.
–
Да–а–а, я думал, что задача на встречное движение бывает только одного вида,
оказывается, я ошибался.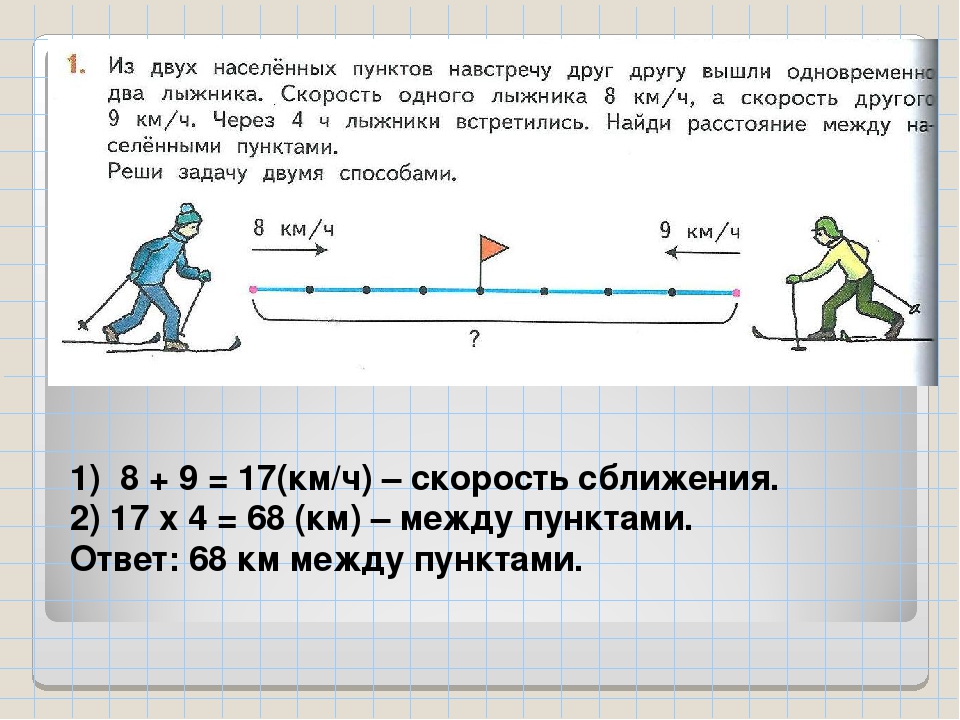
– Нет, Миша, есть ещё один вид задач. Только теперь попробуй решить такую задачу сам.
Из двух мест, расстояние между которыми 95 км, вылетели навстречу друг другу Пчёла и его подруга Скрути. Встретились они через 5 часов. Пчёла летел со скоростью 12 км/ч. С какой скоростью летала Скрути?
– Итак, мы знаем расстояние между местами, время которое они летели и скорость Пчёла. Надо узнать скорость Скрути. Чтобы узнать с какой скоростью летала Скрути, надо знать расстояние, которое она пролетела и время, которое она была в пути. Так ведь в задаче не сказано, какое расстояние пролетела Скрути.
– А ты подумай. Чтобы узнать, какое расстояние пролетела Скрути, надо знать всё расстояние и какую его часть пролетел Пчёла. А остальное – это будет та часть, которую пролетала Скрути. Всё расстояние мы знаем, а вот как найти расстояние, которое пролетел Пчёла?
–
А мы это легко можем найти. Мы ведь знаем его скорость и время, которое он был
в пути. Чтобы узнать расстояние, мы скорость умножаем на время.
Мы ведь знаем его скорость и время, которое он был
в пути. Чтобы узнать расстояние, мы скорость умножаем на время.
1) 12 * 5 = 60 км – пролетел Пчёла.
Скрути пролетала часть от всего пути. Чтобы узнать какое расстояние пролетала Скрути, надо от всего расстояния (95) вычесть расстояние, которое пролетел Пчёла (60 км). Получается 35 км пролетела Скрути.
– Молодец, правильно. А теперь посмотри, мы знаем расстояние, которое пролетела Скрути и время, которое она находилась в пути. И теперь, зная расстояние и время, мы можем узнать скорость Скрути.
– Та-а-ак, мы знаем расстояние, которое пролетела Скрути и время, которое она была в пути. Значит, чтобы узнать её скорость мы должны расстояние разделить на время, т.е.:
3) 35 : 5 = 7 км/ч –скорость движения Скрути.
Ответ: скорость движения Скрути 7 км/ч.
Ура!
У меня получилось! Спасибо тебе большое.
– Я рада, что тебе всё понятно. Надеюсь, что теперь ты без труда сможешь решать задачи на встречное движение. Удачи!
Задачи на движение по окружности с решением
Лень разбираться с решением задач? Добро пожаловать к нам в телеграм, где собрана интересная и полезная информация для учащихся и не только.
Движение по окружности: определение, примеры
Движение по окружности – самый простой случай криволинейного движения.
Примеры движения по окружности:
- грузовик движется по мосту с радиусом кривизны R;
- атлет крутит шар в руке, перед тем как бросить его;
- космическая станция летает по кругу над поверхностью Земли;
- катафот вращается на раскрученном колесе велосипеда.
Приведем ниже кинематические соотношения для поступательного и вращательного движений:
Вопросы на движение по окружности
Вопрос 1. Как направлено центростремительное ускорение?
Как направлено центростремительное ускорение?
Ответ. Центростремительное ускорение направлено по радиус-вектору к центру окружности.
Вопрос 2. Велосипед катится по прямой. Как можно описать движение точки на ободе его колеса? Является ли это движение движением по окружности?
Ответ. Это одновременно поступательное движение и движение по окружности. Траекторией такого движения будет спираль.
Вопрос 3. Как направлено ускорение, если тело движется по окружности неравномерно?
Ответ. В таком случае к центростремительному (или нормальному) ускорению добавляется тангенциальное ускорение, направленное по касательной к окружности. Полное ускорение тела представляет собой векторную сумму тангенциального и нормального ускорений.
Вопрос 4. Что такое линейная и угловая скорость?
Ответ. Линейная скорость – это скорость точки, движущейся поступательно. Она измеряется в метрах в секунду. Угловая скорость – скорость, с которой меняется угол, на который поворачивается радиус-вектор точки при движении по окружности.
Она измеряется в метрах в секунду. Угловая скорость – скорость, с которой меняется угол, на который поворачивается радиус-вектор точки при движении по окружности.
Вопрос 5. При поступательном движении мерой инерции является масса. А что является мерой инерции при вращательном движении?
Ответ. При вращательном движении мерой инерции является момент инерции. Это отдельная обширная тема, задачи на нахождение и использование момента инерции рассмотрены в других статьях по физике.
Задачи на движение по окружности
Как решать задачи на движение по окружности? Так же, как и все остальные! Для начала, вот памятка по решению физических задач и полезный список формул. Кстати! Для всех наших читателей действует скидка 10% на любой вид работы.
Задача №1. Нахождение линейной скорости при движении по окружности
Условие
Тело движется по окружности с ускорением 3 метра на секунду в квадрате по окружности радиусом 40 метров. Какова линейная скорость тела?
Какова линейная скорость тела?
Решение
В данном случае ввиду имеется нормальное ускорение. Поэтому, для решения достаточно вспомнить всего одну формулу:
Ответ: 10,9 м/с.
Задача №2. Нахождение углового ускорения
Условие
Колесо, вращаясь с постоянным ускорением, достигло угловой скорости 20 рад/с через 10 оборотов после начала вращения. Найти угловое ускорение колеса.
Решение
Запишем закон вращения, учитывая, что по условию начальная угловая скорость равна нулю:
Выразим угловое ускорение из первого уравнения, а время – из второго. Затем подставим выраженное время в выражение для ускорения и сократим:
Ответ: 3,2 радиан на секунду в квадрате.
Чтобы перевести угол из радианов в градусы достаточно запомнить соотношение: в одном полном обороте 2пи радиан, или 360 градусов. Следовательно, в одном радиане примерно 57,3 градуса.
Задача №3. Нахождение скорости движения по окружности
Условие
Во сколько раз линейная скорость точки обода колеса радиусом 8 см больше линейной скорости точки, расположенной на 3 см ближе к оси вращения колеса?
Решение
Две точки вращаются на одном колесе, а значит, с одинаковой частотой. Используем соотношения для скорости:
Ответ: скорость точки на ободе больше в 1,6 раза.
Задача №4. Нахождение периода и частоты при движении по окружности
Условие
Маховик равномерно вращается и за время t=1 мин совершает N=2400 оборотов. Какова частота вращения маховика, период обращения и линейная скорость точки, расположенной на расстоянии 10 сантиметров от центра маховика?
Решение
По определению:
Подставим значения, предварительно переведя все величины в систему СИ, и вычислим:
Ответ: 40 Гц; 0,025 с; 25,12 м/с. 2. Нужно найти полное ускорение точки, находящейся на расстоянии 10 см от оси вращения в момент времени t=4c.
2. Нужно найти полное ускорение точки, находящейся на расстоянии 10 см от оси вращения в момент времени t=4c.
Решение
Полное ускорение – векторная сумма нормального и тангенциального ускорений.
Вспоминаем, что скорость и ускорение можно вычислить через производные, зная закон движения:
Подставляем значение t из условия и вычисляем:
Ответ: 1,65 метра в секунду.
Нужна помощь в выполнении заданий? Обращайтесь в профессиональный студенческий сервис в любое время.
Уравнения для скорости, скорости и ускорения
Обновлено 15 декабря 2020 г.
Карен Дж. Блаттлер
Проблемы, связанные с вычислением скорости, скорости и ускорения, обычно возникают в физике. Часто эти задачи требуют расчета относительного движения поездов, самолетов и автомобилей. Эти уравнения также могут применяться к более сложным задачам, таким как скорости звука и света, скорость планетарных объектов и ускорение ракет.
Формула скорости
Скорость означает расстояние, пройденное за определенный период времени.Обычно используемая формула для скорости вычисляет среднюю скорость, а не мгновенную скорость. Расчет средней скорости показывает среднюю скорость всего пути, а мгновенная скорость показывает скорость в любой момент поездки. Спидометр автомобиля показывает мгновенную скорость.
Среднюю скорость можно найти, используя общее пройденное расстояние, обычно обозначаемое как d, разделенное на общее время, необходимое для прохождения этого расстояния, обычно обозначаемое как t. Итак, если автомобилю требуется 3 часа, чтобы преодолеть общее расстояние в 150 миль, средняя скорость равна 150 миль, разделенным на 3 часа, что равняется средней скорости 50 миль в час:
\ frac {150} {3} = 50
Мгновенная скорость — это расчет скорости, который будет обсуждаться в разделе скорости.
Единицы скорости показывают длину или расстояние во времени. Мили в час (мили / час или миль в час), километры в час (км / час или км / ч), футы в секунду (фут / с или фут / сек) и метры в секунду (м / с) — все указывают на скорость.
Формула скорости
Скорость — это векторное значение, означающее, что скорость включает направление. Скорость равна пройденному расстоянию, деленному на время движения (скорость) плюс направление движения. Например, скорость поезда, идущего на 1500 километров к востоку от Сан-Франциско за 12 часов, будет составлять 1500 км, разделенных на 12 часов к востоку, или 125 км / ч к востоку.
Возвращаясь к проблеме скорости автомобиля, представьте, что две машины начинают движение из одной и той же точки и едут с одинаковой средней скоростью 50 миль в час. Если одна машина едет на север, а другая на запад, машины не останутся в одном месте. Скорость машины, идущей на север, будет 50 миль в час на север, а скорость машины, идущей на запад, будет 50 миль в час на запад. Их скорости разные, хотя их скорости одинаковы.
Мгновенная скорость, чтобы быть полностью точной, требует вычисления для оценки, потому что для приближения к «мгновенной» требуется сокращение времени до нуля.Однако можно сделать приближение, используя уравнение: мгновенная скорость (v i ) равна изменению расстояния (Δd), деленному на изменение во времени (Δt), или:
v_i = \ frac {\ Delta d} {\ Delta t}
Установив изменение времени как очень короткий период времени, можно рассчитать почти мгновенную скорость. Греческий символ дельты, треугольник (Δ), означает изменение.
Например, если движущийся поезд прошел 55 км на восток в 5:00 и достиг 65 км на восток в 6:00, изменение расстояния составит 10 км на восток с изменением времени на 1 час.Вставка этих значений в формулу дает:
v_i = \ frac {10} {1} = 10
или 10 км / ч на восток (по общему признанию, медленная скорость для поезда). Мгновенная скорость будет 10 км / ч на восток, по спидометру двигателя — 10 км / ч. Конечно, час не «мгновенный», но он служит для примера.
Вместо этого предположим, что ученый измеряет изменение положения (Δd) объекта на 8 метров за интервал времени (Δt) в 2 секунды. Используя формулу, мгновенная скорость равна 4 метрам в секунду (м / с) на основе расчета:
v_i = \ frac {8} {2} = 4
В качестве векторной величины мгновенная скорость должна включать направление.Однако многие проблемы предполагают, что объект продолжает двигаться в том же направлении в течение этого короткого промежутка времени. Тогда направленность объекта игнорируется, что объясняет, почему это значение часто называют мгновенной скоростью.
Уравнение ускорения
Какая формула ускорения? Исследования показывают два явно разных уравнения. Одна формула из второго закона Ньютона связывает силу, массу и ускорение в уравнении: сила (F) равна массе (м), умноженной на ускорение (а), записывается как F = ma.Другая формула, ускорение (a) равняется изменению скорости (Δv), деленному на изменение во времени (Δt), вычисляет скорость изменения скорости во времени. Эту формулу можно записать:
a = \ frac {\ Delta v} {\ Delta t}
Поскольку скорость включает в себя как скорость, так и направление, изменения ускорения могут быть результатом изменений скорости или направления, либо обоих. В науке единицами измерения ускорения обычно являются метры в секунду в секунду (м / с / с) или метры в секунду в квадрате (м / с 2 ).
Эти два уравнения не противоречат друг другу. Первый показывает соотношение силы, массы и ускорения. Второй рассчитывает ускорение на основе изменения скорости за определенный период времени.
Ученые и инженеры называют увеличение скорости положительным ускорением, а уменьшение скорости — отрицательным ускорением. Однако большинство людей используют термин замедление вместо отрицательного ускорения.
Ускорение свободного падения
Вблизи поверхности Земли ускорение свободного падения является постоянной величиной: a = -9.8 м / с 2 (метров в секунду в секунду или метров в секунду в квадрате). Как предположил Галилей, объекты с разной массой испытывают одинаковое ускорение силы тяжести и будут падать с одинаковой скоростью.
Онлайн-калькуляторы
Вводя данные в онлайн-калькулятор скорости, можно рассчитать ускорение. Онлайн-калькуляторы можно использовать для вычисления уравнения скорости, ускорения и силы. Использование калькулятора ускорения и расстояния требует знания скорости и времени.
2.2 Скорость и скорость — физика
Цели обучения разделу
К концу этого раздела вы сможете делать следующее:
- Рассчитать среднюю скорость объекта
- Связать смещение и среднюю скорость
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим ученикам овладеть следующими стандартами:
- (4) Научные концепции.Учащийся знает и применяет законы движения в различных ситуациях. Ожидается, что студент:
- (B) описывают и анализируют движение в одном измерении, используя уравнения с понятиями расстояния, смещения, скорости, средней скорости, мгновенной скорости и ускорения.
Кроме того, Руководство лаборатории по физике для старших классов рассматривает содержание этого раздела лаборатории под названием «Положение и скорость объекта», а также следующие стандарты:
- (4) Научные концепции.Учащийся знает и применяет законы движения в различных ситуациях. Ожидается, что студент:
- (В) описывать и анализировать движение в одном измерении, используя уравнения с понятиями расстояния, смещения, скорости, средней скорости, мгновенной скорости и ускорения.
Раздел Ключевые термины
| средняя скорость | средняя скорость | мгновенная скорость |
| мгновенная скорость | скорость | скорость |
Поддержка учителя
Поддержка учителя
В этом разделе учащиеся применяют то, что они узнали о расстоянии и смещении, к понятиям скорости и скорости.
[BL] [OL] Прежде чем студенты прочитают раздел, попросите их привести примеры того, как они слышали слово «скорость». Затем спросите их, слышали ли они слово «скорость». Объясните, что эти слова часто используются как синонимы в повседневной жизни, но их научные определения различаются. Скажите студентам, что они узнают об этих различиях по мере чтения раздела.
[AL] Объясните учащимся, что скорость, как и смещение, является векторной величиной. Попросите их поразмышлять о том, чем скорость отличается от скорости.После того, как они поделятся своими идеями, задайте вопросы, которые углубят их мыслительный процесс, например: Почему вы так думаете? Какой пример? Как можно применить эти термины к движению, которое вы видите каждый день?
Скорость
Движение — это не только расстояние и смещение. Такие вопросы, как: «Сколько времени занимает пешая гонка?» и «Какая была скорость бегуна?» невозможно ответить без понимания других концепций. В этом разделе мы рассмотрим время, скорость и скорость, чтобы расширить наше понимание движения.
Описание того, насколько быстро или медленно движется объект, — это его скорость. Скорость — это скорость, с которой объект меняет свое местоположение. Как и расстояние, скорость — это скаляр, потому что у нее есть величина, но не направление. Поскольку скорость — это показатель, она зависит от временного интервала движения. Вы можете рассчитать прошедшее время или изменение времени ΔtΔt движения как разницу между временем окончания и временем начала
Единицей времени в системе СИ является секунда (с), а единицей измерения скорости в системе СИ являются метры в секунду (м / с), но иногда километры в час (км / ч), мили в час (миль / ч) или другие единицы измерения. скорость используются.
Когда вы описываете скорость объекта, вы часто описываете среднее значение за определенный период времени. Средняя скорость, v avg , представляет собой пройденное расстояние, разделенное на время, в течение которого происходит движение.
vavg = distancetimevavg = distancetimeВы, конечно, можете изменить уравнение для решения либо расстояния, либо времени
время = distancevavg.time = distancevavg. distance = vavg × timedistance = vavg × timeПредположим, например, что автомобиль проезжает 150 километров за 3.2 часа. Его средняя скорость за поездку —
. vavg = расстояние-время = 150 км3,2 ч = 47 км / ч. vavg = расстояние-время = 150 км3,2 ч = 47 км / ч.Скорость автомобиля, вероятно, увеличится и уменьшится во много раз за 3,2 часа поездки. Однако его скорость в определенный момент времени — это его мгновенная скорость. Спидометр автомобиля показывает его мгновенную скорость.
Поддержка учителей
Поддержка учителей
[OL] [AL] Предупредите учащихся, что средняя скорость не всегда равна средней начальной и конечной скорости объекта.Например, предположим, что автомобиль проезжает 100 км. Первые 50 км он движется со скоростью 30 км / ч, а вторые 50 км — со скоростью 60 км / ч. Его средняя скорость будет составлять расстояние / (временной интервал) = (100 км) / [(50 км) / (30 км / ч) + (50 км) / (60 км / ч)] = 40 км / ч. Если бы автомобиль на этих скоростях проехал равное время на 30 и 60 км, а не на равные расстояния, его средняя скорость составила бы 45 км / ч.
[BL] [OL] Предупредите учащихся, что термины «скорость», «средняя скорость» и «мгновенная скорость» на обыденном языке часто называют просто скоростью.Подчеркните важность в науке использования правильной терминологии, чтобы избежать путаницы и правильно передавать идеи.
Рис. 2.8 За 30 минут до магазина туда и обратно общее расстояние составляет 6 км. Средняя скорость 12 км / ч. Смещение для обхода туда и обратно равно нулю, потому что не было чистого изменения положения.
Рабочий пример
Расчет средней скорости
Мрамор катится 5,2 м за 1,8 с. Какая была средняя скорость мрамора?
Стратегия
Мы знаем расстояние, которое проходит мрамор, 5.2 м, интервал времени 1,8 с. Мы можем использовать эти значения в уравнении средней скорости.
Решение
vavg = расстояние время = 5,2 м 1,8 с = 2,9 м / с vavg = расстояние время = 5,2 м 1,8 с = 2,9 м / сОбсуждение
Средняя скорость — это скаляр, поэтому мы не включаем направление в ответ. Мы можем проверить разумность ответа, оценив: 5 метров разделить на 2 секунды — это 2,5 м / с. Поскольку 2,5 м / с близко к 2,9 м / с, ответ разумный. Речь идет о скорости быстрой ходьбы, так что это тоже имеет смысл.
Практические задачи
8.Питчер перебрасывает бейсбольный мяч от насыпи питчера к своей тарелке за 0,46 с. Дистанция 18,4 м. Какая была средняя скорость бейсбольного мяча?
- 40 м / с
- -40 м / с
- 0,03 м / с
- 8,5 м / с
Кэсси шла к дому своей подруги со средней скоростью 1,40 м / с. Расстояние между домами 205 м. Как долго она продолжала путешествие?
- 146 с
- 0.01 с
- 2,50 мин.
- 287 с
Скорость
Векторная версия скорости — это скорость. Скорость описывает скорость и направление объекта. Как и в случае со скоростью, полезно описывать либо среднюю скорость за период времени, либо скорость в конкретный момент. Средняя скорость — это смещение, деленное на время, в течение которого смещение происходит.
vavg = время смещения = ΔdΔt = df − d0tf − t0vavg = время смещения = ΔdΔt = df − d0tf − t0Скорость, как и скорость, выражается в единицах СИ в метрах в секунду (м / с), но поскольку это вектор, вы также должны включить направление.Кроме того, переменная v для скорости выделена жирным шрифтом, потому что это вектор, в отличие от переменной v для скорости, которая выделена курсивом, потому что это скалярная величина.
Советы для успеха
Важно помнить, что средняя скорость — это не то же самое, что средняя скорость без направления. Как мы видели в предыдущем разделе со смещением и расстоянием, изменение направления во временном интервале больше влияет на скорость и скорость.
Предположим, что пассажир двигался к задней части самолета со средней скоростью –4 м / с. Мы не можем сказать по средней скорости, остановился ли пассажир на мгновение или отступил, прежде чем он добрался до задней части самолета. Чтобы получить более подробную информацию, мы должны рассмотреть меньшие сегменты поездки за меньшие промежутки времени, такие как те, что показаны на рисунке 2.9. Если вы рассматриваете бесконечно малые интервалы, вы можете определить мгновенную скорость, которая является скоростью в определенный момент времени.Мгновенная скорость и средняя скорость одинаковы, если скорость постоянна.
Рис. 2.9. На диаграмме представлена более подробная запись пассажира самолета, направлявшегося к задней части самолета, показаны более мелкие отрезки его полета.
Ранее вы читали, что пройденное расстояние может отличаться от величины смещения. Точно так же скорость может отличаться от величины скорости. Например, вы едете в магазин и через полчаса возвращаетесь домой.Если одометр вашего автомобиля показывает, что общее пройденное расстояние составило 6 км, то ваша средняя скорость составила 12 км / ч. Однако ваша средняя скорость была равна нулю, потому что ваше смещение в оба конца равно нулю.
Watch Physics
Расчет средней скорости или скорости
В этом видео рассматриваются векторы и скаляры и описывается, как рассчитать среднюю скорость и среднюю скорость, когда вы знаете смещение и изменение во времени. В видео также рассказывается, как преобразовать км / ч в м / с.
Проверка захвата
Что из следующего полностью описывает вектор и скалярную величину и правильно дает пример каждого из них?
- Скалярная величина полностью описывается своей величиной, в то время как вектор нуждается как в величине, так и в направлении, чтобы полностью описать его.Смещение — это пример скалярной величины, а время — пример векторной величины.
- Скалярная величина полностью описывается своей величиной, в то время как вектор нуждается как в величине, так и в направлении, чтобы полностью описать его. Время — это пример скалярной величины, а смещение — пример векторной величины.
- Скалярная величина полностью описывается своей величиной и направлением, в то время как вектору нужна только величина, чтобы полностью описать его.Смещение — это пример скалярной величины, а время — пример векторной величины.
- Скалярная величина полностью описывается своей величиной и направлением, в то время как вектору нужна только величина, чтобы полностью описать его. Время — это пример скалярной величины, а смещение — пример векторной величины.
Teacher Support
Teacher Support
Это видео хорошо подчеркивает разницу между векторами и скалярами.Студент знакомится с идеей использования «s» для обозначения смещения, которое вы можете поощрять, а можете и не поощрять. Прежде чем ученики посмотрят видео, укажите, что преподаватель использует s → s → для смещения вместо d, как в этом тексте. Объясните, что использование маленьких стрелок над переменными является обычным способом обозначения векторов в курсах физики более высокого уровня. Предупредите учащихся, что в этом видео не используются общепринятые сокращения для часа и секунды. Напомните учащимся, что в своей работе они должны использовать сокращения h для часа и s для секунд.
Рабочий пример
Расчет средней скорости
Студент перемещается на 304 м к северу за 180 с. Какая была средняя скорость ученика?
Стратегия
Мы знаем, что смещение составляет 304 м к северу, а время — 180 с. Мы можем использовать формулу для средней скорости, чтобы решить задачу.
Решение
vavg = ΔdΔt = 304 м180 с = 1,7 м / с на север vavg = ΔdΔt = 304 м180 с = 1,7 м / с на север2,1
Обсуждение
Поскольку средняя скорость является векторной величиной, вы должны включить в ответ направление и величину.Обратите внимание, однако, что направление можно не указывать до конца, чтобы не загромождать проблему. Обратите внимание на значащие цифры в задаче. Расстояние 304 м состоит из трех значащих цифр, а временной интервал 180 с — только двух, поэтому частное должно состоять только из двух значащих цифр.
Советы для успеха
Обратите внимание на способ представления скаляров и векторов. В этой книге d обозначает расстояние и перемещение. Точно так же v обозначает скорость, а v обозначает скорость.Переменная, которая не выделена жирным шрифтом, указывает на скалярную величину, а выделенная жирным шрифтом переменная указывает на векторную величину. Иногда векторы представлены маленькими стрелками над переменной.
Поддержка учителя
Поддержка учителя
Используйте эту задачу, чтобы подчеркнуть важность использования правильного количества значащих цифр в вычислениях. Некоторые студенты имеют тенденцию включать много цифр в свои окончательные вычисления. Они ошибочно полагают, что повышают точность своего ответа, записывая многие цифры, указанные на калькуляторе.Обратите внимание, что это приводит к ошибкам в расчетах. В более сложных расчетах эти ошибки могут распространяться и приводить к неправильному окончательному ответу. Вместо этого напомните учащимся всегда использовать одну или две дополнительные цифры в промежуточных вычислениях и округлять окончательный ответ до правильного количества значащих цифр.
Рабочий пример
Решение смещения, когда известны средняя скорость и время
Лейла бегает трусцой со средней скоростью 2.4 м / с на восток. Каково ее смещение через 46 секунд?
Стратегия
Мы знаем, что средняя скорость Лейлы составляет 2,4 м / с на восток, а временной интервал составляет 46 секунд. Мы можем изменить формулу средней скорости, чтобы найти смещение.
Решение
vavg = ΔdΔtΔd = vavgΔt = (2,4 м / с) (46 с) = 1,1 × 102 м на восток vavg = ΔdΔtΔd = vavgΔt = (2,4 м / с) (46 с) = 1,1 × 102 м на восток2,2
Обсуждение
Ответ: примерно в 110 м к востоку, что является разумным смещением для чуть менее минуты бега трусцой.Калькулятор показывает ответ как 110,4 м. Мы решили написать ответ, используя научную нотацию, потому что мы хотели прояснить, что мы использовали только две значащие цифры.
Советы для успеха
Размерный анализ — хороший способ определить, правильно ли вы решили проблему. Запишите расчет, используя только единицы измерения, чтобы убедиться, что они совпадают на противоположных сторонах отметки равенства. В рассмотренном примере у вас
м = (м / с) (с). Поскольку секунды находятся в знаменателе средней скорости и в числителе времени, единица вычитает, оставляя только m и, конечно же, m = m.
Рабочий пример
Решение для времени, когда известны смещение и средняя скорость
Филипп идет по прямой дорожке от своего дома до школы. Сколько времени ему потребуется, чтобы добраться до школы, если он пройдет 428 м на запад со средней скоростью 1,7 м / с на запад?
Стратегия
Мы знаем, что смещение Филиппа составляет 428 м к западу, а его средняя скорость составляет 1,7 м / с к западу. Мы можем рассчитать время, необходимое для поездки, переписав уравнение средней скорости.
Решение
vavg = ΔdΔtΔt = Δdvavg = 428 м 1,7 м / с = 2,5 × 102 svavg = ΔdΔtΔt = Δdvavg = 428 м 1,7 м / с = 2,5 × 102 с2,3
Обсуждение
Здесь нам снова пришлось использовать научную запись, потому что ответ мог состоять только из двух значащих цифр. Поскольку время является скаляром, ответ включает только величину, а не направление.
Практические задачи
10.Дальнобойщик проезжает по прямой трассе 0,25 ч со смещением 16 км к югу.Какова средняя скорость дальнобойщика?
- 4 км / ч север
- 4 км / ч юг
- 64 км / ч север
- 64 км / ч юг
Птица летит со средней скоростью 7,5 м / с на восток от ветки к ветке за 2,4 с. Затем он делает паузу перед полетом со средней скоростью 6,8 м / с на восток в течение 3,5 с к другому ответвлению. Каково полное смещение птицы от начальной точки?
- 42 м запад
- 6 м запад
- 6 м на восток
- 42 м на восток
Virtual Physics
The Walking Man
В этом симуляторе вы наведете курсор на человека и переместите его сначала в одном направлении, а затем в противоположном.Не отключайте вкладку Introduction . Вы можете использовать вкладку Charts после того, как узнаете о графическом движении позже в этой главе. Внимательно следите за знаком чисел в полях положения и скорости. Пока не обращайте внимания на поле ускорения. Посмотрите, сможете ли вы сделать положение человека положительным, а скорость — отрицательным. Затем посмотрите, сможете ли вы сделать обратное.
Проверка захвата
Какая ситуация правильно описывает, когда положение движущегося человека было отрицательным, но его скорость была положительной?
- Человек движется к 0 слева от 0
- Человек движется к 0 справа от 0
- Человек движется от 0 слева от 0
- Мужчина движется от 0 справа от 0
Teacher Support
Teacher Support
Это мощная интерактивная анимация, которую можно использовать для многих уроков.На этом этапе его можно использовать, чтобы показать, что смещение может быть как положительным, так и отрицательным. Он также может показать, что при отрицательном смещении скорость может быть как положительной, так и отрицательной. Позже с его помощью можно будет показать, что скорость и ускорение могут иметь разные знаки. Настоятельно рекомендуется оставить учащихся на вкладке Введение . Вкладку Charts можно использовать после того, как студенты узнают о графическом движении позже в этой главе.
Проверьте свое понимание
12.Два бегуна движутся по одному и тому же прямому пути. Они начинаются в одно и то же время и заканчиваются в одно и то же время, но на полпути у них разные мгновенные скорости. Возможно ли, чтобы они имели одинаковую среднюю скорость за поездку?
- Да, потому что средняя скорость зависит от чистого или полного смещения.
- Да, потому что средняя скорость зависит от общего пройденного расстояния.
- Нет, потому что скорости обоих бегунов должны оставаться одинаковыми на протяжении всего пути.
- Нет, потому что мгновенные скорости бегунов должны оставаться такими же на полпути, но могут быть разными в другом месте.
Если вы разделите общее расстояние, пройденное за поездку на автомобиле (определенное одометром), на время поездки, вычисляете ли вы среднюю скорость или величину средней скорости, и при каких обстоятельствах эти две величины одинаковы? ?
- Средняя скорость. Оба они одинаковы, когда автомобиль движется с постоянной скоростью и меняет направление.
- Средняя скорость. Оба они одинаковы, когда скорость постоянна и автомобиль не меняет своего направления.
- Величина средней скорости. Оба варианта одинаковы, когда автомобиль движется с постоянной скоростью.
- Величина средней скорости. И то, и другое одинаково, когда машина не меняет своего направления.
Может ли средняя скорость быть отрицательной?
- Да, в случаях, когда чистое смещение отрицательное.
- Да, если тело постоянно меняет направление во время движения.
- Нет, средняя скорость описывает только величину, а не направление движения.
- Нет, средняя скорость описывает только величину в положительном направлении движения.
Поддержка учителей
Поддержка учителей
Используйте вопросы «Проверьте свое понимание », чтобы оценить достижение учащимися учебных целей по разделам. Если учащиеся не справляются с какой-либо конкретной целью, «Проверьте свое понимание» поможет определить, кто из них и направит их к соответствующему содержанию.Тестовые задания в TUTOR позволят вам переоценить.
3.4 Движение с постоянным ускорением — University Physics Volume 1
Учебные цели
К концу этого раздела вы сможете:
- Определите, какие уравнения движения следует использовать для решения неизвестных.
- Используйте соответствующие уравнения движения для решения задачи преследования двух тел.
Вы можете догадаться, что чем больше ускорение, скажем, у автомобиля, удаляющегося от знака «Стоп», тем больше смещение автомобиля за данный момент времени.Но мы не разработали конкретное уравнение, которое связывает ускорение и смещение. В этом разделе мы рассмотрим некоторые удобные уравнения кинематических отношений, начиная с определений смещения, скорости и ускорения. Сначала мы исследуем движение одного объекта, называемого движением одного тела. Затем мы исследуем движение двух объектов, называемое задачами преследования двух тел.
Обозначение
Во-первых, сделаем несколько упрощений в обозначениях. Принятие начального времени равным нулю, как если бы время измерялось секундомером, является большим упрощением.Поскольку прошедшее время равно Δt = tf − t0Δt = tf − t0, взятие t0 = 0t0 = 0 означает, что Δt = tfΔt = tf, последнее время на секундомере. Когда начальное время принимается равным нулю, мы используем индекс 0 для обозначения начальных значений положения и скорости. То есть x0x0 — это начальная позиция , а v0v0 — начальная скорость . Мы не ставим индексы на окончательные значения. То есть t — это конечный момент времени , x — конечная позиция , а v — конечная скорость . Это дает более простое выражение для затраченного времени: Δt = tΔt = t.Это также упрощает выражение для смещения x , которое теперь равно Δx = x − x0Δx = x − x0. Кроме того, это упрощает выражение для изменения скорости, которое теперь равно Δv = v − v0Δv = v − v0. Подводя итог, используя упрощенные обозначения, с начальным временем, принятым равным нулю,
Δt = tΔx = x − x0Δv = v − v0, Δt = tΔx = x − x0Δv = v − v0,, где нижний индекс 0 обозначает начальное значение, а отсутствие нижнего индекса означает конечное значение в любом рассматриваемом движении.
Теперь мы делаем важное предположение, что ускорение постоянно .Это предположение позволяет нам избегать использования расчетов для определения мгновенного ускорения. Поскольку ускорение постоянно, среднее и мгновенное ускорения равны, то есть
a– = a = постоянная. a– = a = постоянная.Таким образом, мы можем использовать символ a для ускорения в любое время. Предположение, что ускорение является постоянным, не серьезно ограничивает ситуации, которые мы можем изучить, и не ухудшает точность нашего лечения. Во-первых, ускорение равно постоянным в большом количестве ситуаций.Кроме того, во многих других ситуациях мы можем точно описать движение, приняв постоянное ускорение, равное среднему ускорению для этого движения. Наконец, для движения, во время которого ускорение резко меняется, например, когда автомобиль разгоняется до максимальной скорости, а затем тормозит до остановки, движение можно рассматривать в отдельных частях, каждая из которых имеет собственное постоянное ускорение.
Смещение и положение от скорости
Чтобы получить наши первые два уравнения, мы начнем с определения средней скорости:
Замена упрощенных обозначений для ΔxΔx и ΔtΔt дает
v– = x − x0t.v– = x − x0t.Решение относительно x дает нам
x = x0 + v – t, x = x0 + v – t,3,10
, где средняя скорость
v– = v0 + v2.v– = v0 + v2.3,11
Уравнение v– = v0 + v2v– = v0 + v2 отражает тот факт, что при постоянном ускорении v – v– представляет собой просто среднее значение начальной и конечной скоростей. Рисунок 3.18 графически иллюстрирует эту концепцию. В части (а) рисунка ускорение является постоянным, а скорость увеличивается с постоянной скоростью. Средняя скорость в течение 1-часового интервала от 40 км / ч до 80 км / ч составляет 60 км / ч:
v– = v0 + v2 = 40 км / ч + 80 км / ч3 = 60 км / ч.v– = v0 + v2 = 40 км / ч + 80 км / ч3 = 60 км / ч.В части (b) ускорение не является постоянным. В течение 1-часового интервала скорость ближе к 80 км / ч, чем к 40 км / ч. Таким образом, средняя скорость больше, чем в части (а).
Рисунок 3.18 (a) График зависимости скорости от времени с постоянным ускорением, показывающий начальную и конечную скорости v0andvv0andv. Средняя скорость равна 12 (v0 + v) = 60 км / ч 22 (v0 + v) = 60 км / ч. (б) График зависимости скорости от времени с изменением ускорения со временем. Средняя скорость не равна 12 (v0 + v) 12 (v0 + v), но превышает 60 км / ч.Решение окончательной скорости по ускорению и времени
Мы можем вывести еще одно полезное уравнение, манипулируя определением ускорения:
Подстановка упрощенных обозначений для ΔvΔv и ΔtΔt дает
а = v − v0t (константа). a = v − v0t (константа).Решение для v дает
v = v0 + at (constanta). v = v0 + at (constanta).3,12
Пример 3,7
Расчет конечной скорости
Самолет приземляется с начальной скоростью 70.0 м / с, а затем ускоряется против движения со скоростью 1,50 м / с 2 за 40,0 с. Какова его конечная скорость?Стратегия
Сначала мы идентифицируем известные: v0 = 70 м / с, a = -1,50 м / с2, t = 40sv0 = 70 м / с, a = -1,50 м / с2, t = 40 с.Во-вторых, мы идентифицируем неизвестное; в данном случае это конечная скорость vfvf.
Наконец, мы определяем, какое уравнение использовать. Для этого мы выясняем, какое кинематическое уравнение дает неизвестное в терминах известных. Мы рассчитываем окончательную скорость, используя уравнение 3.12, v = v0 + atv = v0 + at.
Решение
Подставьте известные значения и решите: v = v0 + при = 70,0 м / с + (- 1,50 м / с2) (40,0 с) = 10,0 м / с v = v0 + при = 70,0 м / с + (- 1,50 м / с2) (40,0 с) = 10,0 м / с.Рисунок 3.19 представляет собой эскиз, показывающий векторы ускорения и скорости.
Рис. 3.19. Самолет приземляется с начальной скоростью 70,0 м / с и замедляется до конечной скорости 10,0 м / с, прежде чем направиться к терминалу. Обратите внимание, что ускорение отрицательное, потому что его направление противоположно его скорости, которая положительна.
Значение
Конечная скорость намного меньше начальной скорости, требуемой при замедлении, но все же положительная (см. Рисунок). В реактивных двигателях обратная тяга может поддерживаться достаточно долго, чтобы самолет остановился и начал движение назад, на что указывает отрицательная конечная скорость, но в данном случае это не так.Помимо полезности при решении задач, уравнение v = v0 + atv = v0 + at дает нам представление о взаимосвязях между скоростью, ускорением и временем.Мы видим, например, что
- Конечная скорость зависит от того, насколько велико ускорение и как долго оно длится
- Если ускорение равно нулю, то конечная скорость равна начальной скорости ( v = v 0 ), как и ожидалось (другими словами, скорость постоянна)
- Если a отрицательное, то конечная скорость меньше начальной скорости
Все эти наблюдения соответствуют нашей интуиции. Обратите внимание, что всегда полезно исследовать основные уравнения в свете нашей интуиции и опыта, чтобы убедиться, что они действительно точно описывают природу.
Решение для конечного положения с постоянным ускорением
Мы можем объединить предыдущие уравнения, чтобы найти третье уравнение, которое позволяет нам вычислить окончательное положение объекта, испытывающего постоянное ускорение. Начнем с
Добавление v0v0 к каждой стороне этого уравнения и деление на 2 дает
v0 + v2 = v0 + 12at. v0 + v2 = v0 + 12at.Так как v0 + v2 = v – v0 + v2 = v– для постоянного ускорения, имеем
v– = v0 + 12at.v– = v0 + 12at.Теперь мы подставляем это выражение для v – v– в уравнение для смещения, x = x0 + v – tx = x0 + v – t, что дает
х = х0 + v0t + 12at2 (константа).х = х0 + v0t + 12at2 (константа).3,13
Пример 3.8
Расчет смещения ускоряющегося объекта
Драгстеры могут развивать среднее ускорение 26,0 м / с 2 . Предположим, драгстер ускоряется из состояния покоя с этой скоростью в течение 5,56 с. Рис. 3.20. Как далеко он пролетит за это время?Рис. 3.20. Пилот Top Fuel в армии США Тони «Сержант» Шумахер начинает гонку с контролируемого выгорания. (Источник: подполковник Уильям Термонд. Фото любезно предоставлено США.Армия.)
Стратегия
Сначала нарисуем набросок Рис. 3.21. Нас просят найти смещение, которое составляет x , если мы возьмем x0x0 равным нулю. (Думайте о x0x0 как о стартовой линии гонки. Она может быть где угодно, но мы называем ее нулевой и измеряем все остальные позиции относительно нее.) Мы можем использовать уравнение x = x0 + v0t + 12at2x = x0 + v0t + 12at2 когда мы идентифицируем v0v0, aa и t из постановки задачи.Рис. 3.21. Эскиз разгоняющегося драгстера.
Решение
Во-первых, нам нужно определить известные.Запуск из состояния покоя означает, что v0 = 0v0 = 0, a задается как 26,0 м / с 2 и t задается как 5,56 с.Во-вторых, мы подставляем известные значения в уравнение, чтобы найти неизвестное:
x = x0 + v0t + 12at2.x = x0 + v0t + 12at2.Поскольку начальное положение и скорость равны нулю, это уравнение упрощается до
Подстановка идентифицированных значений на и t дает
x = 12 (26,0 м / с2) (5,56 с) 2 = 402 м. x = 12 (26,0 м / с2) (5,56 с) 2 = 402 м.Значение
Если мы переведем 402 м в мили, мы обнаружим, что пройденное расстояние очень близко к четверти мили, стандартному расстоянию для дрэг-рейсинга. Итак, наш ответ разумный. Это впечатляющий водоизмещение всего за 5,56 с, но первоклассные драгстеры могут преодолеть четверть мили даже за меньшее время. Если бы драгстеру была присвоена начальная скорость, это добавило бы еще один член в уравнение расстояния. Если в уравнении использовать те же ускорение и время, пройденное расстояние будет намного больше.Что еще мы можем узнать, исследуя уравнение x = x0 + v0t + 12at2? X = x0 + v0t + 12at2? Мы видим следующие отношения:
- Смещение зависит от квадрата истекшего времени, когда ускорение не равно нулю. В примере 3.8 драгстер преодолевает только четверть общего расстояния за первую половину прошедшего времени.
- Если ускорение равно нулю, то начальная скорость равна средней скорости (v0 = v -) (v0 = v–), и x = x0 + v0t + 12at2becomesx = x0 + v0t.x = x0 + v0t + 12at2becomesx = x0 + v0t.
Решение окончательной скорости на основе расстояния и ускорения
Четвертое полезное уравнение может быть получено путем другой алгебраической обработки предыдущих уравнений. Если мы решим v = v0 + atv = v0 + at для t , мы получим
Подставляя это и v– = v0 + v2v– = v0 + v2 в x = x0 + v – tx = x0 + v – t, получаем
v2 = v02 + 2a (x − x0) (constanta). v2 = v02 + 2a (x − x0) (constanta).3,14
Пример 3.9
Расчет конечной скорости
Рассчитайте конечную скорость драгстера в Примере 3.8 без использования информации о времени.Стратегия
Уравнение v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) идеально подходит для этой задачи, поскольку оно связывает скорости, ускорение и смещение и не требует информации о времени.Решение
Сначала мы идентифицируем известные значения. Мы знаем, что v 0 = 0, поскольку драгстер запускается из состояния покоя. Мы также знаем, что x — x 0 = 402 м (это был ответ в примере 3.8). Среднее ускорение было равно , а = 26.0 м / с 2 .Во-вторых, мы подставляем известные значения в уравнение v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) и решаем относительно v :
v2 = 0 + 2 (26,0 м / с2) (402 м). v2 = 0 + 2 (26,0 м / с2) (402 м).Таким образом,
v2 = 2,09 × 104 м2 / с2 v = 2,09 × 104 м2 / с2 = 145 м / с. v2 = 2,09 × 104 м2 / с2v = 2,09 × 104 м2 / с2 = 145 м / с.Значение
Скорость 145 м / с составляет около 522 км / ч или около 324 миль / ч, но даже эта головокружительная скорость не достигает рекорда для четверти мили. Также обратите внимание, что квадратный корень имеет два значения; мы взяли положительное значение, чтобы указать скорость в том же направлении, что и ускорение.Изучение уравнения v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) может дать дополнительное понимание общих соотношений между физическими величинами:
- Конечная скорость зависит от величины ускорения и расстояния, на котором оно действует.
- При фиксированном ускорении автомобиль, который едет вдвое быстрее, не просто останавливается на удвоенном расстоянии. Чтобы остановиться, нужно гораздо дальше. (Вот почему у нас есть зоны с пониженной скоростью возле школ.)
Объединение уравнений
В следующих примерах мы продолжаем исследовать одномерное движение, но в ситуациях, требующих немного большего количества алгебраических манипуляций.Примеры также дают представление о методах решения проблем. Следующее примечание предназначено для облегчения поиска необходимых уравнений. Имейте в виду, что эти уравнения не являются независимыми. Во многих ситуациях у нас есть два неизвестных, и нам нужно два уравнения из набора для решения для неизвестных. Для решения данной ситуации нам нужно столько уравнений, сколько неизвестных.
Сводка кинематических уравнений (константа
a ) х = х0 + v0t + 12at2x = x0 + v0t + 12at2 v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0)Прежде чем мы перейдем к примерам, давайте более внимательно рассмотрим некоторые уравнения, чтобы увидеть поведение ускорения при экстремальных значениях.Переставляя уравнение 3.12, получаем
Из этого мы видим, что в течение конечного времени, если разница между начальной и конечной скоростями мала, ускорение невелико, приближаясь к нулю в пределе, когда начальная и конечная скорости равны. Напротив, в пределе t → 0t → 0 при конечной разности начальной и конечной скоростей ускорение становится бесконечным.
Аналогичным образом, переставляя уравнение 3.14, мы можем выразить ускорение в терминах скоростей и смещения:
а = v2-v022 (х-х0).а = v2-v022 (х-х0).Таким образом, при конечной разнице между начальной и конечной скоростями ускорение становится бесконечным, в пределе смещение приближается к нулю. Ускорение приближается к нулю в пределе, разница в начальной и конечной скоростях приближается к нулю для конечного смещения.
Пример 3.10
Как далеко уезжает машина?
На сухом бетоне автомобиль может ускоряться противоположно движению со скоростью 7,00 м / с 2 , тогда как на мокром бетоне он может ускоряться противоположно движению со скоростью всего 5.00 м / с 2 . Найдите расстояния, необходимые для остановки автомобиля, движущегося со скоростью 30,0 м / с (около 110 км / ч) по (а) сухому бетону и (б) мокрому бетону. (c) Повторите оба вычисления и найдите смещение от точки, где водитель видит, что светофор становится красным, принимая во внимание время его реакции 0,500 с, чтобы он нажал ногу на тормоз.Стратегия
Для начала нам нужно нарисовать набросок Рис. 3.22. Чтобы определить, какие уравнения лучше всего использовать, нам нужно перечислить все известные значения и точно определить, что нам нужно решить.Рис. 3.22. Пример эскиза для визуализации ускорения, противоположного движению и тормозному пути автомобиля.
Решение
- Во-первых, нам нужно определить известные и то, что мы хотим решить. Мы знаем, что v 0 = 30,0 м / с, v = 0 и a = -7,00 м / с 2 ( a отрицательно, потому что он находится в направлении, противоположном скорости) . Возьмем x 0 равным нулю. Ищем смещение ΔxΔx, или x — x 0 .
Во-вторых, мы определяем уравнение, которое поможет нам решить проблему. Лучшее уравнение для использования — v2 = v02 + 2a (x − x0). v2 = v02 + 2a (x − x0). Это уравнение лучше всего, потому что оно включает только одно неизвестное, x . Нам известны значения всех других переменных в этом уравнении. (Другие уравнения позволили бы нам решить для x , но они требуют, чтобы мы знали время остановки, t , которое мы не знаем. Мы могли бы использовать их, но это потребовало бы дополнительных вычислений.)
В-третьих, мы изменим уравнение, чтобы найти x : x − x0 = v2 − v022ax − x0 = v2 − v022a и подставляем известные значения: х − 0 = 02− (30.0 м / с) 22 (-7,00 м / с2). X-0 = 02- (30,0 м / с) 22 (-7,00 м / с2). Таким образом, x = 64,3 м на сухом бетоне. x = 64,3 м на сухом бетоне. - Эта часть может быть решена точно так же, как (а). Единственное отличие состоит в том, что ускорение составляет −5,00 м / с 2 . Результат xwet = 90,0 м по мокрому бетону. xwet = 90,0 м по мокрому бетону.
- Когда водитель реагирует, тормозной путь такой же, как в (a) и (b) для сухого и влажного бетона. Итак, чтобы ответить на этот вопрос, нам нужно вычислить, как далеко проехал автомобиль за время реакции, а затем добавить это время ко времени остановки.Разумно предположить, что скорость остается постоянной в течение времени реакции водителя.
Для этого мы снова определяем известные и то, что мы хотим решить. Мы знаем, что v– = 30,0 м / sv– = 30,0 м / с, treaction = 0,500streaction = 0,500s и areaction = 0areaction = 0. Примем x0-реакцию x0-реакцию равной нулю. Ищем xreactionxreaction.
Во-вторых, как и раньше, мы определяем лучшее уравнение для использования. В этом случае x = x0 + v – tx = x0 + v – t работает хорошо, потому что единственное неизвестное значение — x , что мы и хотим найти.
В-третьих, мы подставляем известные для решения уравнения: x = 0 + (30,0 м / с) (0,500 с) = 15,0 м. x = 0 + (30,0 м / с) (0,500 с) = 15,0 м. Это означает, что автомобиль проезжает 15,0 м, в то время как водитель реагирует, в результате чего общее смещение в двух случаях с сухим и мокрым бетоном на 15,0 м больше, чем если бы он реагировал мгновенно.
Наконец, мы добавляем смещение во время реакции к смещению при торможении (рис. 3.23), xbraking + xreaction = xtotal, xbraking + xreaction = xtotal, и найдите (a) равным 64,3 м + 15,0 м = 79.3 м в сухом виде и (b) должно составлять 90,0 м + 15,0 м = 105 м во влажном состоянии.
Рис. 3.23. Расстояние, необходимое для остановки автомобиля, сильно различается в зависимости от дорожных условий и времени реакции водителя. Здесь показаны значения тормозного пути для сухого и мокрого покрытия, рассчитанные в этом примере для автомобиля, движущегося со скоростью 30,0 м / с. Также показаны общие расстояния, пройденные от точки, когда водитель впервые видит, что свет загорается красным, при условии, что время реакции составляет 0,500 с.
Значение
Смещения, обнаруженные в этом примере, кажутся разумными для остановки быстро движущегося автомобиля.Остановка автомобиля на мокром асфальте должна длиться дольше, чем на сухом. Интересно, что время реакции значительно увеличивает смещения, но более важен общий подход к решению проблем. Мы идентифицируем известные и определяемые величины, а затем находим соответствующее уравнение. Если существует более одного неизвестного, нам нужно столько независимых уравнений, сколько неизвестных необходимо решить. Часто есть несколько способов решить проблему. Фактически, различные части этого примера могут быть решены другими методами, но представленные здесь решения являются самыми короткими.Пример 3.11
Время расчета
Предположим, автомобиль въезжает в движение по автостраде на съезде длиной 200 м. Если его начальная скорость равна 10,0 м / с, а он ускоряется со скоростью 2,00 м / с 2 , сколько времени потребуется автомобилю, чтобы преодолеть 200 м по рампе? (Такая информация может быть полезна транспортному инженеру.)Стратегия
Сначала мы рисуем набросок Рис. 3.24. Нам предлагается решить за время т . Как и раньше, мы идентифицируем известные величины, чтобы выбрать удобное физическое соотношение (то есть уравнение с одним неизвестным, t .)Рис. 3.24. Эскиз автомобиля, ускоряющегося на съезде с автострады.
Решение
Опять же, мы определяем известные и то, что мы хотим решить. Мы знаем, что x0 = 0, x0 = 0,v0 = 10 м / с, a = 2,00 м / с2v0 = 10 м / с, a = 2,00 м / с2 и x = 200 м.
Нужно решить для т . Уравнение x = x0 + v0t + 12at2x = x0 + v0t + 12at2 работает лучше всего, потому что единственной неизвестной в уравнении является переменная t , которую нам нужно решить. Из этого понимания мы видим, что когда мы вводим известные значения в уравнение, мы получаем квадратное уравнение.
Нам нужно изменить уравнение, чтобы найти t , затем подставив известные значения в уравнение:
200 м = 0 м + (10,0 м / с) t + 12 (2,00 м / с2) t2. 200 м = 0 м + (10,0 м / с) t + 12 (2,00 м / с2) t2.Затем мы упрощаем уравнение. Единицы измерения отменяются, потому что они есть в каждом члене. Мы можем получить единицы секунд для отмены, взяв t = t s, где t — величина времени, а s — единица измерения. Остается
Затем мы используем формулу корней квадратного уравнения, чтобы найти t ,
t2 + 10t − 200 = 0t = −b ± b2−4ac2a, t2 + 10t − 200 = 0t = −b ± b2−4ac2a,, что дает два решения: t = 10.0 и t = −20,0. Отрицательное значение времени неразумно, так как это будет означать, что событие произошло за 20 секунд до начала движения. Мы можем отказаться от этого решения. Таким образом,
Значение
Всякий раз, когда уравнение содержит неизвестный квадрат, есть два решения. В некоторых проблемах имеют смысл оба решения; в других случаях разумно только одно решение. Ответ 10,0 с кажется разумным для типичной автострады на съезде.Проверьте свое понимание 3.5
Ракета ускоряется со скоростью 20 м / с. 2 во время пуска.Сколько времени нужно, чтобы ракета достигла скорости 400 м / с?
Пример 3.12
Ускорение космического корабля
Космический корабль покинул орбиту Земли и направляется к Луне. Разгоняется со скоростью 20 м / с 2 за 2 мин и преодолевает расстояние в 1000 км. Каковы начальная и конечная скорости космического корабля?Стратегия
Нас просят найти начальную и конечную скорости космического корабля. Глядя на кинематические уравнения, мы видим, что одно уравнение не дает ответа.Мы должны использовать одно кинематическое уравнение для решения одной из скоростей и подставить его в другое кинематическое уравнение, чтобы получить вторую скорость. Таким образом, мы решаем два кинематических уравнения одновременно.Решение
Сначала мы решаем для v0v0, используя x = x0 + v0t + 12at2: x = x0 + v0t + 12at2: x − x0 = v0t + 12at2x − x0 = v0t + 12at21.0 × 106m = v0 (120.0s) +12 (20,0 м / с2) (120,0 с) 21,0 × 106 м = v0 (120,0 с) +12 (20,0 м / с2) (120,0 с) 2v0 = 7133,3 м / с. V0 = 7133,3 м / с.Затем мы подставляем v0v0 в v = v0 + atv = v0 + at, чтобы найти окончательную скорость:
v = v0 + at = 7133.3 м / с + (20,0 м / с2) (120,0 с) = 9533,3 м / с. V = v0 + at = 7133,3 м / с + (20,0 м / с2) (120,0 с) = 9533,3 м / с.Значение
Есть шесть переменных смещения, времени, скорости и ускорения, которые описывают движение в одном измерении. Начальные условия данной задачи могут быть множеством комбинаций этих переменных. Из-за такого разнообразия решения могут быть не такими простыми, как простая подстановка в одно из уравнений. Этот пример показывает, что решения кинематики могут потребовать решения двух одновременных кинематических уравнений.Освоив основы кинематики, мы можем перейти ко многим другим интересным примерам и приложениям. В процессе разработки кинематики мы также увидели общий подход к решению проблем, который дает как правильные ответы, так и понимание физических взаимоотношений. Следующий уровень сложности наших задач кинематики связан с движением двух взаимосвязанных тел, который называется задачами преследования двух тел .
Проблемы с преследованием двух тел
До этого момента мы рассматривали примеры движения с участием одного тела.Даже для задачи с двумя автомобилями и тормозным путем на мокрой и сухой дороге мы разделили эту задачу на две отдельные задачи, чтобы найти ответы. В задаче преследования двух тел движения объектов связаны, то есть искомое неизвестное зависит от движения обоих объектов. Чтобы решить эти проблемы, мы пишем уравнения движения для каждого объекта, а затем решаем их одновременно, чтобы найти неизвестное. Это показано на Рисунке 3.25.
Рис. 3.25 Сценарий преследования с двумя телами, в котором автомобиль 2 имеет постоянную скорость, а автомобиль 1 идет сзади с постоянным ускорением.Автомобиль 1 догонит автомобиль 2 позже.
Время и расстояние, необходимое для того, чтобы автомобиль 1 догнал автомобиль 2, зависит от начального расстояния, на которое автомобиль 1 находится от автомобиля 2, а также от скорости обоих автомобилей и ускорения автомобиля 1. Кинематические уравнения, описывающие движение обоих автомобилей, должны быть решил найти эти неизвестные.
Рассмотрим следующий пример.
Пример 3.13
Гепард ловит газель
Гепард прячется за кустом. Гепард замечает пробегающую мимо газель со скоростью 10 м / с.В момент, когда газель проезжает мимо гепарда, гепард ускоряется из состояния покоя со скоростью 4 м / с 2 , чтобы поймать газель. а) Сколько времени нужно гепарду, чтобы поймать газель? б) Что такое смещение газели и гепарда?Стратегия
Мы используем систему уравнений для постоянного ускорения, чтобы решить эту проблему. Поскольку есть два движущихся объекта, у нас есть отдельные уравнения движения, описывающие каждое животное. Но то, что связывает уравнения, — это общий параметр, который имеет одинаковое значение для каждого животного.Если мы внимательно рассмотрим проблему, становится ясно, что общим параметром для каждого животного является их положение x , позднее t . Поскольку оба они начинают с x0 = 0x0 = 0, их смещения будут такими же в более позднее время t , когда гепард догонит газель. Если мы выберем уравнение движения, которое решает смещение для каждого животного, мы можем затем установить уравнения, равные друг другу, и решить для неизвестного, то есть времени.Решение
- Уравнение для газели: Газель имеет постоянную скорость, которая является ее средней скоростью, поскольку она не ускоряется.Поэтому мы используем уравнение 3.10 с x0 = 0x0 = 0: x = x0 + v – t = v – t. x = x0 + v – t = v – t. Уравнение для гепарда: гепард ускоряется из состояния покоя, поэтому мы используем уравнение 3.13 с x0 = 0x0 = 0 и v0 = 0v0 = 0: x = x0 + v0t + 12at2 = 12at2.x = x0 + v0t + 12at2 = 12at2. Теперь у нас есть уравнение движения для каждого животного с общим параметром, который можно исключить, чтобы найти решение. В этом случае мы решаем для t : x = v – t = 12at2t = 2v – a.x = v – t = 12at2t = 2v – a. Газель имеет постоянную скорость 10 м / с, что составляет ее среднюю скорость.Ускорение гепарда составляет 4 м / с 2 . Оценивая t , время, за которое гепард достигнет газели, имеем t = 2v – a = 2 (10 м / с) 4m / s2 = 5s. t = 2v – a = 2 (10 м / с) 4m / s2 = 5s.
- Чтобы получить смещение, мы используем уравнение движения гепарда или газели, поскольку оба они должны дать одинаковый ответ.
Смещение гепарда: x = 12at2 = 12 (4 м / с2) (5) 2 = 50 м. x = 12at2 = 12 (4 м / с2) (5) 2 = 50 м. Водоизмещение газели: x = v – t = 10 м / с (5) = 50 м. x = v – t = 10 м / с (5) = 50 м.Мы видим, что оба смещения равны, как и ожидалось.
Значение
Важно анализировать движение каждого объекта и использовать соответствующие кинематические уравнения для описания отдельного движения. Также важно иметь хорошую визуальную перспективу задачи преследования двух тел, чтобы увидеть общий параметр, который связывает движение обоих объектов.Проверьте свое понимание 3.6
Велосипед имеет постоянную скорость 10 м / с. Человек начинает с отдыха и начинает бежать, чтобы догнать велосипед через 30 секунд, когда велосипед находится в том же положении, что и человек.Какое ускорение у человека?
Решение задач с равномерным движением — элементарная алгебра
Цели обучения
К концу этого раздела вы сможете:
- Решение приложений с равномерным движением
Решение задач с равномерным движением
При планировании автомобильной поездки часто бывает полезно знать, сколько времени потребуется, чтобы добраться до пункта назначения или как далеко нужно ехать каждый день. Мы бы использовали формулу расстояния, скорости и времени, которую мы уже видели.
В этом разделе мы будем использовать эту формулу в ситуациях, требующих немного больше алгебры для решения, чем те, которые мы видели ранее. Как правило, мы будем сравнивать два сценария, например, когда два автомобиля едут с разной скоростью или в противоположных направлениях. Когда скорость каждого транспортного средства постоянна, мы называем такие приложения задачами равномерного движения .
Наши стратегии решения проблем по-прежнему применимы, но мы добавим их к первому шагу. Первый шаг будет включать рисование диаграммы, которая показывает, что происходит в примере.Рисование диаграммы помогает нам понять, что происходит, и написать соответствующее уравнение. Затем мы составим таблицу для систематизации информации, как мы это делали для денежных приложений.
Шаги перечислены здесь для удобства:
Используйте стратегию решения проблем в приложениях для определения расстояния, скорости и времени.
- Прочтите проблему. Убедитесь, что все слова и идеи понятны.
- Нарисуйте диаграмму, чтобы проиллюстрировать, что это происходит.
- Создайте таблицу для организации информации.
- Обозначьте столбцы скорость, время, расстояние.
- Перечислите два сценария.
- Напишите информацию, которую вы знаете.
- Определите , что мы ищем.
- Имя то, что мы ищем. Выберите переменную, чтобы представить это количество.
- Заполните таблицу.
- Используйте выражения переменных, чтобы представить это количество в каждой строке.
- Умножьте коэффициент на время, чтобы получить расстояние.
- Переведите в уравнение.
- Переформулируйте проблему одним предложением со всей важной информацией.
- Затем переведите предложение в уравнение.
- Решите уравнение, используя хорошие методы алгебры.
- Проверьте ответ в проблеме и убедитесь, что он имеет смысл.
- Ответьте на вопрос полным предложением.
Экспресс и пригородный поезд отправляются из Питтсбурга в Вашингтон, округ Колумбия. Поездка на экспрессе занимает 4 часа, а на местном поезде — 5 часов. Скорость экспресса на 12 миль в час выше скорости местного поезда. Найдите скорость обоих поездов.
Решение
Шаг 1. Прочтите о проблеме. Убедитесь, что все слова и идеи понятны.
- Нарисуйте диаграмму, чтобы проиллюстрировать, что это происходит.Ниже показан набросок того, что происходит в примере.
- Создайте таблицу для организации информации.
- Обозначьте столбцы «Скорость», «Время» и «Расстояние».
- Перечислите два сценария.
- Напишите информацию, которую вы знаете.
Шаг 2. Определите , что мы ищем.
- Нас просят определить скорость обоих поездов.
- Обратите внимание, что в формуле расстояния используется слово «скорость», но чаще используется слово «скорость», когда мы говорим о транспортных средствах на повседневном английском языке.
Шаг 3. Назовите то, что мы ищем. Выберите переменную, чтобы представить это количество.
- Заполните таблицу
- Используйте выражения переменных, чтобы представить это количество в каждой строке.
- Ищем скорость поездов. Пусть r представляет скорость местного поезда. Поскольку скорость экспресса на 12 миль в час выше, мы представляем это как
Введите скорости в таблицу.
Умножьте коэффициент на время, чтобы получить расстояние.
Шаг 4. Переведите в уравнение.
- Переформулируйте проблему одним предложением со всей важной информацией.
- Затем переведите предложение в уравнение.
- Уравнение для моделирования этой ситуации будет получено из соотношения между расстояниями. Посмотрите на схему, которую мы нарисовали выше. Как расстояние, пройденное экспрессом, соотносится с расстоянием, пройденным пригородным поездом?
- Поскольку оба поезда отправляются из Питтсбурга в Вашингтон, Д.C. они проходят одинаковое расстояние. Итак, пишем:
Шаг 5. Решите уравнение, используя хорошую алгебру.
Шаг 6. Проверьте ответ в проблеме и убедитесь, что он имеет смысл.
| экспресс | |
| пригородный поезд |
Шаг 7. Ответьте на вопрос полным предложением.
- Скорость местного поезда составляет 48 миль в час, а скорость экспресса — 60 миль в час.
Уэйн и Деннис любят кататься по велосипедной дорожке от Риверсайд-парка до пляжа. Скорость Денниса на семь миль в час выше скорости Уэйна, поэтому Уэйн добирается до пляжа за 2 часа, а Деннис за 1,5 часа. Найдите скорость обоих байкеров.
Уэйн 21 миль / ч, Деннис 28 миль / ч
Джероми может доехать от своего дома в Кливленде до колледжа в Чикаго за 4,5 часа. Его матери требуется 6 часов, чтобы проделать такую же поездку. Джероми едет на 20 миль в час быстрее, чем его мать.Найдите скорость Джероми и скорость его матери.
Джероми 80 миль / ч, мать 60 миль / ч
В последнем примере (рисунок) у нас было два поезда, идущих на одинаковое расстояние. Диаграмма и диаграмма помогли нам написать решенное уравнение. Посмотрим, как это работает в другом случае.
Кристофер и его родители живут в 115 милях друг от друга. Они встретились в ресторане между их домами, чтобы отпраздновать день рождения его матери. Кристофер ехал 1,5 часа, а его родители ехали 1 час до ресторана.Средняя скорость Кристофера была на 10 миль в час выше, чем средняя скорость его родителей. Какова была средняя скорость Кристофера и его родителей, когда они ехали в ресторан?
Решение
Шаг 1. Прочтите о проблеме. Убедитесь, что все слова и идеи понятны.
- Нарисуйте диаграмму, чтобы проиллюстрировать, что это происходит. Ниже показан набросок происходящего в примере.
- Создайте таблицу для организации информации.
- Обозначьте столбцы скорость, время, расстояние.
- Перечислите два сценария.
- Напишите информацию, которую вы знаете.
Шаг 2. Определите , что мы ищем.
- Нас просят найти средние скорости Кристофера и его родителей.
Шаг 3. Назовите то, что мы ищем. Выберите переменную, чтобы представить это количество.
- Заполните таблицу.
- Используйте выражения переменных, чтобы представить это количество в каждой строке.
- Ищем их средние скорости. Пусть r представляют среднюю скорость родителей. Поскольку скорость Christopher на 10 миль в час выше, мы представляем это как .
Введите скорости в таблицу.
Умножьте коэффициент на время, чтобы получить расстояние.
Шаг 4. Переведите в уравнение.
- Переформулируйте проблему одним предложением со всей важной информацией.
- Затем переведите предложение в уравнение.
- Опять же, нам нужно определить взаимосвязь между расстояниями, чтобы написать уравнение. Посмотрите на диаграмму, которую мы создали выше, и обратите внимание на взаимосвязь между расстоянием, которое прошел Кристофер, и расстоянием, которое прошли его родители.
Расстояние, которое преодолел Кристофер, плюс расстояние, которое прошли его родители, должно составлять 115 миль. Итак, мы пишем:
Шаг 5. Решите уравнение, используя хорошую алгебру.
| Теперь решите это уравнение. | |
| Значит, скорость родителей была 40 миль в час. | |
| Скорость Кристофера. | |
| Скорость Кристофера составляла 50 миль в час. |
Шаг 6. Проверьте ответ в проблеме и убедитесь, что он имеет смысл.
| Кристофер вел | |
| Его родители водили |
| Шаг 7.Ответьте на вопрос полным предложением. | Скорость Кристофера составляла 50 миль в час. Скорость его родителей составляла 40 миль в час. |
Карина едет из своего дома в Анахайме в Беркли в тот же день, когда ее брат едет из Беркли в Анахайм, поэтому они решают встретиться за обедом по дороге в Баттонвиллоу. Расстояние от Анахайма до Беркли составляет 410 миль. Карина добирается до Баттонвиллоу за 3 часа, а ее брат добирается туда за 4 часа.Средняя скорость, которую ехал брат Карины, была на 15 миль в час выше, чем средняя скорость Карины. Найдите среднюю скорость Карины и ее брата.
Карина 50 миль / ч, брат 65 миль / ч
Эшли учится в колледже в Миннеаполисе, в 234 милях от ее дома в Су-Фолс. Она хочет, чтобы родители принесли ей больше зимней одежды, поэтому они решают встретиться в ресторане на дороге между Миннеаполисом и Су-Фолс. Эшли и ее родители ехали 2 часа до ресторана. Средняя скорость Эшли на семь миль в час превышала среднюю скорость ее родителей.Найдите среднюю скорость Эшли и ее родителей.
родители 55 миль в час, Эшли 62 миль в час
Читая следующий пример, подумайте о соотношении пройденных расстояний. Какой из двух предыдущих примеров больше похож на эту ситуацию?
Два водителя грузовика одновременно покидают зону отдыха на межгосударственной автомагистрали. Один грузовик едет на восток, а другой на запад. Грузовик, едущий на запад, движется со скоростью 70 миль в час, а грузовик, едущий на восток, имеет среднюю скорость 60 миль в час.Как долго они будут путешествовать, прежде чем их разделяют 325 миль?
Решение
Шаг 1. Прочтите о проблеме. Убедитесь, что все слова и идеи понятны.
- Нарисуйте диаграмму, чтобы проиллюстрировать, что это происходит.
- Создайте таблицу для организации информации.
Шаг 2. Определите , что мы ищем.
- Нас просят определить количество времени, в течение которого грузовики проедут до расстояния 325 миль.
Шаг 3. Назовите то, что мы ищем. Выберите переменную, чтобы представить это количество.
- Ищем пройденное время. Оба грузовика проедут одинаковое время. Назовем время t . Поскольку их скорости различаются, они будут преодолевать разные расстояния.
- Заполните таблицу.
Шаг 4. Переведите в уравнение.
- Нам нужно найти связь между расстояниями, чтобы написать уравнение.Глядя на диаграмму, каково соотношение между расстоянием, которое проедет каждый из грузовиков?
- Расстояние, пройденное грузовиком на западе, плюс расстояние, пройденное грузовиком на востоке, должно составлять в сумме 325 миль. Итак, пишем:
Шаг 5. Решите уравнение, используя хорошую алгебру.
| Теперь решите это уравнение. |
Так возьмем грузовики 2.5 часов до 325 миль.
Шаг 6. Проверьте ответ в проблеме и убедитесь, что он имеет смысл.
| Грузовик едет на запад | |
| Грузовик едет на восток | *** QuickLaTeX не может составить формулу:
\ begin {array} {ccc} \ text {60 миль в час (2,5 часа)} \ hfill & = \ hfill & \ underset {\ text {________}} {\ text {150 миль}} \ hfill \\ & & \ text {325 миль} \ hfill \ end {array}
*** Сообщение об ошибке:
Не указан $ вставлен.начальный текст: ... нижний предел {\ text {________}} {\ text {150 миль}}
Отсутствует {вставлен.
начальный текст: ... нижний предел {\ text {________}} {\ text {150 миль}}
Отсутствует {вставлен.
начальный текст: ... нижний предел {\ text {________}} {\ text {150 миль}}
Отсутствует {вставлен.
начальный текст: ... нижний предел {\ text {________}} {\ text {150 миль}}
Отсутствует {вставлен.
начальный текст: ... нижний предел {\ text {________}} {\ text {150 миль}}
Отсутствует {вставлен.
начальный текст: ... нижний предел {\ text {________}} {\ text {150 миль}}
Отсутствует {вставлен.начальный текст: ... нижний предел {\ text {________}} {\ text {150 миль}}
Отсутствует {вставлен.
начальный текст: ... нижний предел {\ text {________}} {\ text {150 миль}}
Отсутствует {вставлен.
начальный текст: ... нижний предел {\ text {________}} {\ text {150 миль}}
Не указан $ вставлен.
начальный текст: ... нижний предел {\ text {________}} {\ text {150 миль}}
|
| Шаг 7. Ответьте на вопрос полным предложением. | Примет грузовики 2.5 часов до 325 миль. |
Пьер и Моник одновременно покидают свой дом в Портленде. Пьер едет на север по магистрали со скоростью 75 миль в час, а Моник едет на юг со скоростью 68 миль в час. Как долго они будут разделять 429 миль?
Тхань и Нхат одновременно покидают свой офис в Сакраменто. Тхань едет на север по I-5 со скоростью 72 мили в час. Нхат едет на юг по I-5 со скоростью 76 миль в час.Как долго они будут разделять 330 миль?
Соответствующие единицы в задачах
При использовании формулы скорости расстояния и времени важно убедиться, что единицы измерения совпадают. Например, если скорость указывается в милях в час, время должно быть в часах.
Кэти Мэй идет в школу за 30 минут. Если она катается на велосипеде, это займет у нее 15 минут. Когда она едет на велосипеде, ее скорость на три мили в час выше, чем при ходьбе. Какова ее скорость ходьбы и скорость езды на велосипеде?
Решение
Сначала мы рисуем диаграмму, которая представляет ситуацию, чтобы помочь нам увидеть, что происходит.
Нас просят найти ее скорость ходьбы и езды на велосипеде. Назовем ее скорость ходьбы r . Поскольку ее скорость езды на велосипеде на три мили в час выше, мы назовем эту скорость. Записываем скорости в таблицу.
Скорость выражается в милях в час, поэтому нам нужно также выразить время в часах, чтобы единицы были одинаковыми. Помните, что один час — это 60 минут. Итак:
*** QuickLaTeX не может составить формулу:
\ begin {array} {} \\ \ text {30 минут} \ phantom {\ rule {0.4em} {0ex}} \ frac {30} {60} \ phantom {\ rule {0.4em} {0ex}} \ text {или} \ phantom {\ rule {0.4em} {0ex}} \ frac {1} {2} \ phantom {\ rule {0.4em} {0ex}} \ text {hour} \ hfill \\ \ text {15 минут} \ phantom {\ rule {0.4em} {0ex}} \ frac {15} {60} \ phantom {\ rule {0.4em} {0ex}} \ text {или} \ phantom {\ rule {0.4em} {0ex}} \ frac {1} {4} \ phantom {\ rule {0.4em } {0ex}} \ text {час} \ hfill \ end {массив}
*** Сообщение об ошибке:
В преамбуле выравнивания вставлен пропущенный #.
начальный текст: $ \ begin {array} {}
Не указан $ вставлен.
начальный текст: ... is} \ phantom {\ rule {0.4em} {0ex}} \ frac {30} {60}
Extra}, или забытый $.
начальный текст: ... is} \ phantom {\ rule {0.4em} {0ex}} \ frac {30} {60}
Отсутствует} вставлено.
начальный текст: ... правило {0.4em} {0ex}} \ text {час} \ hfill \\ \ text
Extra}, или забытый $.
начальный текст: ... правило {0.4em} {0ex}} \ text {час} \ hfill \\ \ text
Отсутствует} вставлено.
начальный текст: ... правило {0.4em} {0ex}} \ text {час} \ hfill \\ \ text
Extra}, или забытый $.
начальный текст: ... правило {0.4em} {0ex}} \ text {час} \ hfill \\ \ text
Отсутствует} вставлено.начальный текст: ... правило {0.4em} {0ex}} \ text {час} \ hfill \\ \ text
Extra}, или забытый $.
начальный текст: ... правило {0.4em} {0ex}} \ text {час} \ hfill \\ \ text
Отсутствует} вставлено.
Затем мы умножаем скорость на время, чтобы заполнить столбец расстояния.
Уравнение исходит из того факта, что расстояние от дома Кэти Мэй до ее школы одинаково, независимо от того, идет она пешком или катается на велосипеде.
Итак, мы говорим:
Сьюзи нужно 50 минут, чтобы подняться в гору от стоянки до смотровой башни.Ей требуется 30 минут, чтобы вернуться на парковку. Ее скорость при спуске на 1,2 мили в час выше, чем при подъеме. Узнайте скорости Сюзи на подъеме и спуске.
под гору 1,8 мили в час, под гору 3 мили в час
Ллевину требуется 45 минут, чтобы проехать на лодке вверх по течению от причала до своего любимого места для рыбалки. Ему нужно 30 минут, чтобы спуститься вниз по течению к причалу. Скорость лодки при движении вниз по течению на четыре мили в час выше, чем при движении вверх по течению.Найдите скорость лодки вверх и вниз по течению.
вверх по потоку 8 миль в час, ниже по потоку 12 миль в час
В формуле расстояния, скорости и времени время представляет собой фактическое количество прошедшего времени (в часах, минутах и т. Д.). Если проблема дает нам время начала и окончания как часы, мы должны найти прошедшее время, чтобы использовать формулу.
Гамильтон любит путешествовать в Лас-Вегас, в 255 милях от своего дома в округе Ориндж. В свою последнюю поездку он вышел из дома в 14:00.Первая часть его поездки проходила по загруженным городским автострадам. В 16:00 движение прекратилось, и он смог проехать по пустыне со скоростью в 1,75 раза быстрее, чем когда он ехал по густонаселенному району. Он прибыл в Лас-Вегас в 18:30. Насколько быстро он ехал на каждом этапе поездки?
Решение
Схема поможет нам смоделировать эту поездку.
Затем мы создаем таблицу для организации информации.
Мы знаем, что общее расстояние составляет 255 миль.Ищем скорость на каждом участке пути. Скорость в пустыне в 1,75 раза выше, чем в городе. Если ставить ставку в городе, то в пустыне ставка
Время здесь указано как часы. Гамильтон выехал из дома в 14:30 и вошел в пустыню в 16:30. Таким образом, он провел два часа за рулем перегруженных автострад в городе. Затем он ехал быстрее с 16:00 до 18:30 по пустыне. Так он ехал 2,5 часа по пустыне.
Теперь мы умножаем ставки в раз.
Глядя на диаграмму ниже, мы видим, что сумма пройденного расстояния в городе и пройденного расстояния в пустыне составляет 255 миль.
Круз тренируется, чтобы соревноваться в триатлоне. Он вышел из дома в 6:00 и бежал до 7:30. Затем он ехал на велосипеде до 9:45. Он преодолел в общей сложности 51 милю. Его скорость при езде на велосипеде в 1,6 раза превышала его скорость при беге. Узнайте скорость езды и бега Круза.
на велосипеде 16 миль / ч, бег 10 миль / ч
Фуонг выехал из дома на велосипеде в 10:00.Он ехал по ровной улице до 11:15, затем ехал в гору до 11:45. Он проехал 31 милю. Его скорость на подъеме была в 0,6 раза больше, чем на ровной улице. Найдите его скоростной велосипед, едущий в гору и по ровной улице.
в гору 12 миль / ч, ровная улица 20 миль / ч
Практика ведет к совершенству
Решение приложений с равномерным движением
В следующих упражнениях решите.
Лайла переезжает из Портленда в Сиэтл. Ехать на поезде у нее три часа.Мейсон покидает вокзал в Портленде и едет на вокзал в Сиэтле со всеми ящиками Лайлы в своей машине. Ему нужно 2,4 часа, чтобы добраться до Сиэтла со скоростью 15 миль в час, превышающей скорость поезда. Найдите скорость Мейсона и скорость поезда.
Мейсон 75 миль / ч, поезд 60 миль / ч
Кэти и Шерил идут на сбор средств. Кэти завершает курс за 4,8 часа, а Шерил — за 8 часов. Кэти ходит на две мили в час быстрее, чем Шерил.Найдите скорость Кэти и скорость Шерил.
Два автобуса отправляются из Сакраменто в Сан-Диего. Автобус-экспресс делает поездку за 6,8 часа, а местный автобус — за 10,2 часа. Скорость автобуса-экспресса на 25 миль в час выше, чем скорость местного автобуса. Найдите скорость обоих автобусов.
автобус-экспресс, скорость 75 миль в час, местный 50 миль в час
Коммерческий и частный самолет летят из Денвера в Феникс. Полет коммерческим самолетом занимает 1,1 часа, а частному самолету — 1.8 часов. Скорость коммерческого самолета на 210 миль в час превышает скорость частного самолета. Найдите скорость обоих самолетов.
Саул проехал на своем грузовике 3 часа из Далласа в сторону Канзас-Сити и остановился на стоянке для грузовиков, чтобы пообедать. На стоянке грузовиков он встретил Эрвина, который ехал 4 часа из Канзас-Сити в сторону Далласа. Расстояние между Далласом и Канзас-Сити составляет 542 мили, а скорость Эрвина на восемь миль в час ниже скорости Сола. Найдите скорость двух дальнобойщиков.
Саул 82 миль / ч, Эрвин 74 миль / ч
Чарли и Вайолет встретились за обедом в ресторане между Мемфисом и Новым Орлеаном. Чарли покинул Мемфис и ехал 4,8 часа в сторону Нового Орлеана. Вайолет покинула Новый Орлеан и ехала 2 часа в сторону Мемфиса со скоростью на 10 миль в час быстрее, чем скорость Чарли. Расстояние между Мемфисом и Новым Орлеаном составляет 394 мили. Найдите скорость двух драйверов.
Сестры Хелен и Анна живут в 332 милях друг от друга. На День Благодарения они встретились в доме своей другой сестры, где-то между их домами.Хелен ехала 3,2 часа, а Анна — 2,8 часа. Средняя скорость Хелен была на четыре мили в час быстрее, чем у Анны. Найдите среднюю скорость Хелен и среднюю скорость Анны.
Хелен 60 миль / ч, Энн 56 миль / ч
Итан и Лео начинают кататься на велосипедах на противоположных концах 65-мильной велосипедной дорожки. После того, как Итан проехал 1,5 часа, а Лео — 2 часа, они встречаются на пути. Скорость Итана на шесть миль в час выше скорости Лео. Найдите скорость двух байкеров.
Эльвира и Алетейя живут 3.1 миля друг от друга на той же улице. Они находятся в группе по изучению, которая встречается в кафе между их домами. Эльвире потребовалось полчаса, а Алетейе две трети часа, чтобы дойти до кофейни. Скорость Алетейи на 0,6 мили в час меньше скорости Эльвиры. Найдите скорость ходьбы обеих женщин.
Алетейя 2,4 миль / ч, Эльвира 3 миль / ч
ДаМаркус и Фабиан живут в 23 милях друг от друга и играют в футбол в парке между своими домами. ДаМаркус ехал на велосипеде три четверти часа, а Фабиан ехал на велосипеде полчаса, чтобы добраться до парка.Скорость Фабиана была на шесть миль в час быстрее, чем скорость ДаМаркуса. Найдите скорость обоих футболистов.
Синди и Ричард одновременно покидают общежитие в Чарльстоне. Синди едет на велосипеде на север со скоростью 18 миль в час. Ричард едет на своем велосипеде на юг со скоростью 14 миль в час. Как долго они будут разделять 96 миль?
Мэтт и Крис одновременно покидают дом своего дяди в Фениксе. Мэтт едет на запад по I-60 со скоростью 76 миль в час.Крис едет на восток по I-60 со скоростью 82 мили в час. Сколько часов им понадобится, чтобы разойтись на 632 мили?
Из Биллингса отправляются два автобуса одновременно. Автобус из Сиэтла направляется на запад по I-90 со скоростью 73 мили в час, а автобус из Чикаго направляется на восток со скоростью 79 миль в час. Сколько часов им понадобится, чтобы разойтись на 532 мили?
Две лодки одновременно выходят из одного дока в Каире. Один направляется на север по реке Миссисипи, а другой — на юг.Лодка, идущая на север, движется со скоростью четыре мили в час. Лодка, идущая на юг, идет со скоростью восемь миль в час. Как долго они будут разделять 54 мили?
Лорена идет по дорожке вокруг парка за 30 минут. Если она бегает трусцой, это займет у нее 20 минут. Ее скорость бега на 1,5 мили в час выше, чем скорость ходьбы. Найдите скорость ходьбы и бега Лорены.
ходьба 3 мили в час, бег 4,5 миль в час
Джулиан едет на велосипеде в гору в течение 45 минут, затем разворачивается и едет обратно под гору.Ему требуется 15 минут, чтобы вернуться к тому, с чего он начал. Его скорость на подъеме на 3,2 мили в час ниже, чем на спуске. Узнайте скорость Джулиана на подъеме и спуске.
Кассий ведет лодку вверх по течению 45 минут. Ему нужно 30 минут, чтобы вернуться вниз по течению. Его скорость вверх по течению на три мили в час ниже, чем скорость вниз по течению. Найдите его восходящую и нисходящую скорости.
вверх по течению 6 миль в час, вниз по течению 9 миль в час
Дарлайн добирается до работы за 20 минут в условиях небольшого движения.Ей нужно 36 минут, чтобы вернуться домой в загруженном транспортном потоке. Ее скорость в условиях легкого движения на 24 мили в час выше, чем в условиях интенсивного движения. Найдите ее скорость в условиях легкого и интенсивного движения.
В 1:30 Марлон вышел из дома, чтобы отправиться на пляж, расстояние 7,6 миль. Он катался на скейтборде до 2:15, а затем прошел остаток пути. Он прибыл на пляж в 3:00. Скорость Марлона на скейтборде в 2,5 раза превышает скорость ходьбы. Найдите его скорость при катании на скейтборде и при ходьбе.
скейтбординг 8 миль / ч, ходьба 3,2 миль / ч
Аарон уехал в 9:15, чтобы поехать в свою горную хижину в 108 милях. Он ехал по автостраде до 10:45, а затем поехал по горной дороге. Он прибыл в 11:05. Его скорость на автостраде в три раза превышала его скорость на горной дороге. Найдите скорость Аарона на автостраде и на горной дороге.
Марисоль вылетела из Лос-Анджелеса в 2:30, чтобы поехать в Санта-Барбару, расстояние 95 миль. Движение было интенсивным до 3:20.Остаток пути она проехала в условиях очень слабого движения и прибыла в 4:20. Ее скорость в условиях интенсивного движения была на 40 миль в час ниже, чем в условиях легкого движения. Найдите ее скорость в плотном и легком движении.
интенсивное движение 30 миль / ч, легкое движение 70 миль / ч
Лизетт готовится к марафону. В 7:00 она вышла из дома и бежала до 8:15, потом гуляла до 11:15. Она преодолела в общей сложности 19 миль. Ее скорость бега была на пять миль в час выше, чем скорость ходьбы.Найдите ее скорость бега и ходьбы.
Повседневная математика
Джон покинул свой дом в Ирвине в 8:35, чтобы поехать на собрание в Лос-Анджелес, что в 45 милях от него. Он прибыл на встречу в 9:50. В 15:30 он покинул собрание и поехал домой. Он прибыл домой в 5:18.
- ⓐ Какова была его средняя скорость на пути из Ирвина в Лос-Анджелес?
- ⓑ Какова была его средняя скорость на пути из Лос-Анджелеса в Ирвин?
- ⓒ Сколько всего времени он провел на дороге на встречу и обратно?
- ⓓ Джон проехал 90 миль туда и обратно.Найдите его среднюю скорость. (Округлите до ближайшей десятой.)
ⓐ 36 миль / ч ⓑ 25 миль / ч ⓒ 3,05 часа ⓓ 29,5 миль / ч
Сара хочет приехать на свадьбу подруги в 3:00. Расстояние от дома Сары до свадьбы составляет 95 миль. Основываясь на обычных схемах движения, Сара предсказывает, что первые 15 миль она сможет проехать со скоростью 60 миль в час, следующие 10 миль — со скоростью 30 миль в час, а оставшуюся часть пути — со скоростью 70 миль в час.
- ⓐ Сколько времени потребуется Саре, чтобы проехать первые 15 миль?
- ⓑ Сколько времени потребуется Саре, чтобы проехать следующие 10 миль?
- ⓒ Сколько времени потребуется Саре, чтобы проехать остаток поездки?
- ⓓ В какое время Сара должна покинуть свой дом?
Письменные упражнения
При решении задачи равномерного движения, как вам может помочь составление диаграммы ситуации?
Чем может помочь создание таблицы при решении задачи равномерного движения?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения?
Как решить проблемы равномерного движения — Криста Кинг Математика
Два водителя выезжают из одного и того же места
Пример
Кэсси едет с постоянной скоростью ??? 30 ??? миль / ч по трассе. ??? 4 ??? несколько часов спустя ее подруга Сьюзан начинает с той же точки и едет с постоянной скоростью ??? 60 ??? миль в час и проходит Кэсси.Сколько часов в машине нужно каждой девушке, чтобы оказаться в одном и том же месте на шоссе? И как далеко проехала каждая девушка?
Когда они окажутся в одном и том же месте на шоссе, они оба пройдут одинаковое расстояние. Мы можем признать, что это проблема равномерного движения. Мы можем использовать формулу ??? D = RT ??? где D??? расстояние, пройденное каждым из них, ??? R ??? скорость, с которой они путешествовали, и ??? T ??? время, которое им потребовалось, чтобы добраться туда. Мы можем использовать индексы, чтобы создать модель путешествия каждой женщины.
Кэсси: ??? D_c = R_cT_c ???
Сьюзен: ??? D_s = R_sT_s ???
Проблема говорит нам, что Кэсси путешествовала со скоростью ??? 30 ??? миль в час, скорость поездки Сьюзан составила ??? 60 ??? миль в час, а что потребовалось Сьюзан ??? 4 ??? на то же расстояние меньше, чем Кэсси (потому что она уехала на 4 часа позже).
Давайте установим то, что мы знаем.
Кэсси:
??? D_c = ????
??? R_c = 30 \ \ text {mph} ???
??? T_c = ????
??? D_c = (30 \ \ text {mph}) T_c ???
Сьюзен:
??? D_s = ????
??? R_s = 60 \ \ text {mph} ???
??? T_s = T_c-4 ???
??? D_s = (60 \ \ text {mph}) (T_c-4) ???
Помните, Кэсси и Сьюзен прошли одинаковое расстояние.Поскольку их расстояния равны, можно сказать, что ??? D_c = D_s ??? и получите
??? (30 \ \ text {mph}) T_c = (60 \ \ text {mph}) (T_c-4) ???
??? \ frac {(30 \ \ text {mph}) T_c} {60 \ \ text {mph}} = \ frac {(60 \ \ text {mph}) (T_c-4)} {60 \ \ text {mph}} ???
??? \ frac {1} {2} T_c = T_c-4 ???
??? \ frac {1} {2} T_c-T_c = T_c-T_c-4 ???
??? — \ frac {1} {2} T_c = -4 ???
??? — 2 \ cdot- \ frac {1} {2} T_c = -2 \ cdot-4 ???
??? T_c = 8 ??? часов
Теперь можно сказать, что Кэсси ушла ??? 8 ??? часов, чтобы преодолеть расстояние.Так что понадобилось Сьюзан ??? 4 ??? часов меньше, чем Кэсси, чтобы пройти такое же расстояние.
??? T_s = T_c-4 ???
??? Т_с = 8-4 ???
??? T_s = 4 ??? часов
Теперь, когда у нас есть скорость и время Кэсси и Сьюзен, мы можем проверить, что они прошли одинаковое расстояние.
Кэсси:
??? D_c = R_cT_c ???
??? D_c = 30 (8) ???
??? D_c = 240 ??? миль
Сьюзен:
??? D_s = R_sT_s ???
??? D_s = 60 (4) ???
??? D_s = 240 ??? миль
Время, скорость и скорость | Физика
Цели обучения
К концу этого раздела вы сможете:
- Объясните взаимосвязь между мгновенной скоростью, средней скоростью, мгновенной скоростью, средней скоростью, смещением и временем.
- Вычислить скорость и скорость с учетом начального положения, начального времени, конечного положения и конечного времени.
- Постройте график зависимости скорости от времени с учетом графика положения от времени.
- Расскажите о графике зависимости скорости от времени.
Движение — это не только расстояние и смещение. Такие вопросы, как: «Сколько времени занимает пешая гонка?» и «Какая была скорость бегуна?» невозможно ответить без понимания других концепций. В этом разделе мы добавляем определения времени, скорости и скорости, чтобы расширить наше описание движения.
Как обсуждалось в разделе «Физические величины и единицы», наиболее фундаментальные физические величины определяются тем, как они измеряются. Так обстоит дело со временем. Каждое измерение времени включает в себя измерение изменения некоторой физической величины. Это может быть число на цифровых часах, сердцебиение или положение Солнца на небе. В физике время определяется просто: время — это изменение , или интервал, в течение которого происходит изменение. Невозможно знать, что время прошло, если что-то не изменится.
Время или изменение калибруется путем сравнения со стандартом. Единицей измерения времени в системе СИ является секунда, сокращенно с. Мы можем, например, наблюдать, что некий маятник совершает полный оборот каждые 0,75 с. Затем мы могли бы использовать маятник для измерения времени, считая его колебания или, конечно, подключая маятник к часовому механизму, который регистрирует время на циферблате. Это позволяет нам не только измерить количество времени, но и определить последовательность событий.
Как время связано с движением? Обычно нас интересует время, затраченное на конкретное движение, например, сколько времени требуется пассажиру самолета, чтобы добраться от своего места до задней части самолета.Чтобы найти истекшее время, мы отмечаем время в начале и в конце движения и вычитаем два. Например, лекция может начаться в 11:00 утра. и закончится в 11:50 утра, чтобы прошедшее время составило 50 минут. Истекшее время Δ t — разница между временем окончания и временем начала,
Δ т = т f — т 0 ,
, где Δ t — изменение во времени или прошедшее время, t f — время окончания движения, а t 0 — время начала движения.(Как обычно, символ дельты, Δ, означает изменение количества, которое следует за ним.)
Жизнь проще, если время начала t 0 принять равным нулю, как при использовании секундомера. Если бы мы использовали секундомер, он просто показывал бы ноль в начале лекции и 50 минут в конце. Если t 0 = 0, то Δ t = t f ≡ t .
В этом тексте для простоты
- движение начинается в момент времени, равный нулю ( t 0 = 0)
- символ t используется для истекшего времени, если не указано иное (Δ t = t f ≡ t )
Ваше понятие скорости, вероятно, совпадает с ее научным определением.Вы знаете, что если у вас есть большое смещение за небольшой промежуток времени, у вас есть большая скорость, и эта скорость выражается в единицах расстояния, разделенных на время, таких как мили в час или километры в час.
Средняя скоростьСредняя скорость — это смещение (изменение положения), деленное на время перемещения ,
[латекс] \ bar {v} = \ frac {\ Delta x} {\ Delta t} = \ frac {{x} _ {f} — {x} _ {0}} {{t} _ {f} — {t} _ {0}} [/ latex],
, где [латекс] \ bar {v} [/ latex] — средняя скорость (обозначена полосой над v ), Δ x — изменение положения (или смещения), а x f и x 0 — конечная и начальная позиции в моменты времени t f и t 0 соответственно.Если время пуска t 0 принять равным нулю, то средняя скорость будет просто
.[латекс] \ bar {v} = \ frac {\ Delta x} {t} [/ latex].
Обратите внимание, что это определение указывает, что скорость является вектором, потому что смещение — это вектор . У него есть и величина, и направление. Единица измерения скорости в системе СИ — это метры в секунду или м / с, но широко используются многие другие единицы, такие как км / ч, миль / ч (также обозначаются как мили в час) и см / с. Предположим, например, что пассажиру самолета потребовалось 5 секунд, чтобы переместиться на −4 м (отрицательный знак указывает, что смещение происходит в сторону задней части самолета).Его средняя скорость будет
.[латекс] \ bar {v} = \ frac {\ Delta x} {t} = \ frac {-4 \ text {m}} {5 \ text {s}} = — \ text {0,8 м / с. } [/ латекс]
Знак минус указывает, что средняя скорость также направлена к задней части самолета.
Однако средняя скорость объекта ничего не говорит нам о том, что с ним происходит между начальной и конечной точкой. Например, по средней скорости мы не можем сказать, останавливается ли пассажир самолета на мгновение или отступает назад, прежде чем он уйдет в заднюю часть самолета.Чтобы получить более подробную информацию, мы должны рассмотреть меньшие сегменты поездки за меньшие промежутки времени.
Чем меньше временные интервалы, учитываемые в движении, тем более подробная информация. Когда мы доводим этот процесс до его логического завершения, у нас остается бесконечно малый интервал. В течение такого интервала средняя скорость становится мгновенной скоростью или скоростью в конкретный момент . Например, автомобильный спидометр показывает величину (но не направление) мгновенной скорости автомобиля.(Полиция выдает билеты на основе мгновенной скорости, но при расчете времени, которое потребуется, чтобы добраться из одного места в другое во время поездки, вам необходимо использовать среднюю скорость.) Мгновенная скорость v — это средняя скорость при заданной скорости. конкретный момент времени (или бесконечно малый интервал времени).
Математически, определение мгновенной скорости, v , в точный момент t может включать определение предела, операцию вычисления, выходящую за рамки этого текста.Однако во многих случаях мы можем найти точные значения мгновенной скорости без расчетов.
В повседневном языке большинство людей используют термины «скорость» и «скорость» как синонимы. В физике, однако, они не имеют одинакового значения и представляют собой разные концепции. Одно из основных различий заключается в том, что скорость не имеет направления. Таким образом, скорость является скаляром . Так же, как нам нужно различать мгновенную скорость и среднюю скорость, нам также необходимо различать мгновенную скорость и среднюю скорость.
Мгновенная скорость — величина мгновенной скорости. Например, предположим, что пассажир самолета в один момент времени имел мгновенную скорость -3,0 м / с (минус означает направление к задней части самолета). При этом его мгновенная скорость составляла 3,0 м / с. Или предположим, что однажды во время похода по магазинам ваша мгновенная скорость составляет 40 км / ч на север. Ваша мгновенная скорость в этот момент будет 40 км / ч — такая же величина, но без указания направления.Однако средняя скорость сильно отличается от средней скорости. Средняя скорость — это пройденное расстояние, разделенное на затраченное время.
Мы отметили, что пройденное расстояние может быть больше перемещения. Таким образом, средняя скорость может быть больше средней скорости, которая равна смещению, разделенному на время. Например, если вы едете в магазин и возвращаетесь домой через полчаса, а одометр вашего автомобиля показывает, что общее пройденное расстояние составило 6 км, то ваша средняя скорость составила 12 км / ч. Однако ваша средняя скорость была равна нулю, потому что ваше смещение в оба конца равно нулю.(Смещение — это изменение положения и, таким образом, равно нулю для поездки туда и обратно.) Таким образом, средняя скорость равна , а не просто величине средней скорости.
Другой способ визуализировать движение объекта — использовать график. График положения или скорости как функции времени может быть очень полезным. Например, для этой поездки в магазин графики положения, скорости и зависимости скорости от времени показаны на рисунке 4. (Обратите внимание, что на этих графиках изображена очень упрощенная модель поездки .Мы предполагаем, что скорость постоянна во время поездки, что нереально, учитывая, что мы, вероятно, остановимся в магазине. Но для простоты мы смоделируем его без остановок и изменений скорости. Мы также предполагаем, что маршрут между магазином и домом является совершенно прямой линией.)
Калькулятор скорости| Определение | Формула
Этот калькулятор скорости представляет собой универсальный инструмент, позволяющий оценить скорость объекта. Если вы когда-нибудь задумывались, как найти скорость, здесь вы можете сделать это в тремя разными способами .Первый основан на базовом определении скорости, в котором используется хорошо известное уравнение скорости. Второй метод вычисляет изменение скорости, вызванное ускорением за определенный промежуток времени. Наконец, третья часть калькулятора скорости использует формулу средней скорости, которая может быть полезна, если вам нужно проанализировать поездки с разными скоростями на разные расстояния.
Мы также подготовили краткую, но информативную статью о самой скорости. Продолжайте читать, чтобы узнать, что такое формула скорости и каковы наиболее распространенные единицы скорости.Знаете ли вы, что есть существенная разница между скоростью и скоростью? Мы писали об этом с точки зрения физика в тексте ниже.
Что такое скорость? — определение скорости
Определение скорости гласит, что это скорость изменения положения объекта как функция времени. Это одно из фундаментальных понятий классической механики, рассматривающее движение тел. Если вы хотите записать это правило в виде математической формулы, уравнение скорости будет следующим:
скорость = расстояние / время
Имейте в виду, что эта формула скорости работает только тогда, когда объект имеет постоянную скорость в постоянном направлении или если вы хотите найти среднюю скорость на определенном расстоянии (в отличие от мгновенной скорости).Вы, наверное, заметили, что мы используем слова скорость и скорость как синонимы, но вы не можете делать это каждый раз. Чтобы узнать об этом больше, перейдите в раздел «Скорость против скорости».
Помимо линейной скорости, которой мы посвятили этот калькулятор, существуют также другие типы скорости, такие как вращательная или угловая скорость с соответствующими физическими величинами: кинетическая энергия вращения, угловое ускорение или момент инерции массы. Когда объект имеет только угловую скорость, он не смещается (расстояние равно нулю), и вы не можете использовать формулу средней скорости.
Формула средней скорости и единицы скорости
Формула средней скорости описывает взаимосвязь между длиной вашего маршрута и временем, которое требуется на путешествие. Например, если вы едете на машине на расстояние 70 миль за один час, ваша средняя скорость будет равна 70 милям в час. В предыдущем разделе мы ввели основное уравнение скорости, но, как вы, вероятно, уже поняли, в калькуляторе скорости есть и другие уравнения. Перечислим и систематизируем их ниже:
- Простое уравнение скорости:
скорость = расстояние / время
- Скорость после определенного времени разгона:
конечная скорость = начальная скорость + ускорение * время
- Формула средней скорости — средневзвешенная скорость:
средняя скорость = скорость₁ * время₁ + скорость₂ * время₂ +...
Вам следует использовать формулу средней скорости, если вы можете разделить свой маршрут на несколько сегментов. Например, вы едете на автомобиле со скоростью 25 миль в час за 1 час в городе, а затем достигаете 70 миль в час за 3 часа на шоссе. Какая у вас средняя скорость? С помощью калькулятора скорости вы можете определить, что это будет около 59 миль в час .
Из приведенных выше уравнений вы также можете представить , что такое единицы скорости .Британские имперские единицы: футы в секунду футов в секунду и миль в час миль в час. В метрической системе СИ единицами измерения являются метры в секунду м / с и километры в час км / ч . Помните, что вы всегда можете легко переключаться между ними в нашем инструменте!
Соотношение между расстоянием и временем также необходимо при оценке расхода топлива вашим автомобилем. Чтобы рассчитать, сколько газа будет израсходовано в конкретном путешествии, воспользуйтесь нашим калькулятором газа.
Как рассчитать скорость - скорость в зависимости от скорости
Прежде чем мы объясним, как рассчитать скорость, мы хотели бы отметить, что есть небольшая разница между скоростью и скоростью. Первое определяется разницей между конечным и исходным положением и направлением движения, а второе требует только пройденного расстояния. Другими словами, скорость - это вектор (с величиной и направлением), а скорость - это скаляр (только с величиной).
Пора применить на практике формулу средней скорости.Если объект прошел 500 метров за 3 минуты , для расчета средней скорости необходимо выполнить следующие шаги:
- Измените минуты на секунды (чтобы окончательный результат был в метрах в секунду).
3 минуты = 3 * 60 = 180 секунд, - Разделите расстояние на время:
скорость = 500/180 = 2,77 м / с.
Попробуем другой пример. Вы хотите участвовать в гонке на своей новой машине, которая может изменять скорость с ускорением примерно 6.95 м / с² . Конкурс только начался. Какой будет ваша скорость через 4 секунды ?
- Установите начальную скорость на ноль, вы не двигаетесь в начале гонки.
- Умножьте ускорение на время, чтобы получить изменение скорости:
изменение скорости = 6,95 * 4 = 27,8 м / с. - Поскольку начальная скорость была равна нулю, конечная скорость равна изменению скорости.
- Вы можете преобразовать единицы в
км / ч, умножив результат на 3.6:27,8 * 3,6 ≈ 100 км / ч.
Конечно, вы можете значительно упростить вычисления, используя калькулятор средней скорости. Все, что вам нужно сделать, это ввести расстояние и время. Одним из преимуществ использования этого калькулятора является то, что вам не нужно вручную переводить единицы измерения . Наш инструмент сделает все за вас!
Помните, что вы не можете гонять везде, нормальные дороги и шоссе не созданы для сверхвысоких скоростей! Воспользуйтесь калькулятором ДТП, чтобы узнать, насколько опасными могут быть автомобильные столкновения.Не садитесь за руль после употребления алкоголя и регулярно осматривайте свой автомобиль.
Конечная скорость, космическая скорость и релятивистская скорость
Скорость присутствует во многих аспектах физики, и мы создали для нее множество калькуляторов! Первая скорость - это так называемая конечная скорость, которая представляет собой наивысшую скорость, достижимую для свободно падающего объекта. Конечная скорость возникает в жидкостях (например, в воздухе или воде) и зависит от плотности жидкости. Вы можете узнать больше об этом в нашем калькуляторе свободного падения с воздушным сопротивлением.
Знание того, как вычислить скорость, имеет особое значение в астрофизике, поскольку результаты должны быть очень точными. Если вас интересует мир массивных небесных объектов, таких как солнца или планеты, посетите наш калькулятор космической скорости или калькулятор орбитальной скорости. Там можно многому научиться!
В области высоких энергий есть еще одна важная скорость - релятивистская скорость. Это связано с тем, что ни один объект с ненулевой массой не может достичь скорости света.Почему? Когда он приближается к скорости света, его кинетическая энергия становится недостижимой, очень большой или даже бесконечной. Вы можете проверить это с помощью релятивистского калькулятора кинетической энергии, заполнив поле скоростей скоростью света 299 792 458 м / с или 2,998e8 м / с в экспоненциальной нотации. Более того, это причина других явлений, таких как релятивистское сложение скоростей, замедление времени и сокращение длины. Знаменитая формула Альберта Эйнштейна E = mc2 также основана на концепции релятивистской скорости.
Надеюсь, мы убедили вас, что скорость играет важную роль в повседневной жизни, а не только в науке, и мы надеемся, что вам понравился наш калькулятор скорости. Не стесняйтесь изучить другие наши калькуляторы. Это может быть удивительно, но их гораздо больше, связанных со скоростью, о которых мы не упоминали, исследуйте!
FAQ
Какова скорость полета порожней ласточки?
Ну, это зависит от того, говорите ли вы о европейском или африканском разнообразии.Для европейского типа это примерно 11 м / с, или 24 мили в час . Если вам нужна наша знакомая африканская птица, то, боюсь, вам не повезло, жюри все еще в составе.
Как найти мгновенную скорость?
- Найдите уравнение, описывающее, как расстояние (x) изменяется во времени (t).
- Продифференцируйте формулу по времени.
- Пусть dx / dt = мгновенная скорость.
- Введите желаемое время в дифференцированную формулу.Результат - мгновенная скорость в момент времени t.
Сколько времени нужно, чтобы достичь предельной скорости?
Среднему человеку потребуется примерно 15 секунд, , чтобы достичь 99% предельной скорости, когда его живот будет обращен к Земле. Достичь 100% -ной конечной скорости очень сложно, если не невозможно, поскольку ускорение экспоненциально падает, когда объект приближается к своей конечной скорости. Это время изменится, если человек изменит положение тела.
Может ли скорость быть отрицательной?
Да, скорость может быть отрицательной .Скорость - это направленная скорость, поэтому, если объект движется против направления, определенного как положительное направление, оно будет отрицательным. Два объекта с равными, но противоположными скоростями имеют одинаковую скорость, но просто движутся в противоположных направлениях.
Как найти начальную скорость вращения?
- Определите, какое из смещения (S), конечной скорости (V), ускорения (A) и времени (T) вы должны решить для начальной скорости (U).
- Если у вас есть В, A и T , используйте U = V - AT.
- Если у вас S, V и T , используйте U = 2 (S / T) - V.
- Если у вас S, V и A , используйте U = SQRT (V 2 - 2AS).
- Если у вас S, A и T , используйте U = (S / T) - (AT / 2).
Как определить конечную скорость?
- Определите, какое из смещения (S), начальной скорости (U), ускорения (A) и времени (T) вы должны решить для конечной скорости (V).
- Если у вас U, A и T , используйте V = U + AT.
- Если у вас S, U и T , используйте V = 2 (S / T) - U.
- Если у вас S, A и T , используйте V = (S / T) + (AT / 2).
Что такое космическая скорость?
Скорость выхода составляет минимальная скорость, необходимая объекту, чтобы избежать гравитационного притяжения другого объекта . Наиболее распространенным примером этого является скорость, необходимая космическому кораблю, чтобы покинуть Землю для далеких планет, которая составляет примерно 11,2 км / с.
В чем разница между скоростью и ускорением?
Скорость - это скорость и направление , с которыми движется объект, а ускорение - это то, как скорость этого объекта изменяется на во времени.Единицы измерения скорости - м / с, а для ускорения - м / с 2 .
Что вызывает изменение скорости?
Взаимодействие с другими объектами вызывает изменение скорости . Когда движущийся объект сталкивается с другим объектом на своем пути, он замедляется (если он сталкивается с чем-то меньшим, например, с частицей воздуха) или останавливается (если он ударяется о стену). Если объект выбрасывает за собой материю , он разгоняется, как ракета. Объект также будет ускоряться по направлению к другим объектам за счет силы тяжести .
Как рассчитать космическую скорость?
- Найдите массу объекта в килограммах, M, и его радиус в метрах, R.
- Умножьте M на гравитационную постоянную (6,674 x 10 -11 ), а затем на 2.
- Разделите результат шага 2 на R.
- Увеличьте результат шага 3 на 0,5.
 За три минуты он пройдёт в три раза больше, то есть 255 метров:
За три минуты он пройдёт в три раза больше, то есть 255 метров:
 Из этой формулы можно выразить скорость или время .
Из этой формулы можно выразить скорость или время .