Точки экстремума функции. Как найти? :: SYL.ru

Математический анализ — это довольно-таки занятный раздел математики, с которым сталкиваются абсолютно все ученики выпускных классов и студенты. Тем не менее далеко не каждому нравится матан. Некоторые не могут понять даже элементарных вещей наподобие, казалось бы, стандартного исследования функции. Данная статья призвана исправить подобную оплошность. Хотите поподробнее узнать об анализе функции? Желаете узнать, что такое точки экстремума и как их найти? Тогда данная статья для вас.

Исследование графика функции

Для начала стоит понять, зачем вообще необходимо анализировать график. Существуют простые функции, начертить которые не составит труда. Ярким примером подобной функции может служить парабола. Начертить ее график не составит труда. Все что необходимо, так это с помощью простого преобразования найти числа, при которых функция принимает значение 0. И в принципе это все что знать для того, чтобы начертить график параболы.

Но что делать, если функция, график которой нам нужно начертить, намного сложнее? Поскольку свойства сложных функций довольно-таки неочевидны, необходимо проводить целый анализ. Только после этого можно изобразить функцию графически. Как же это сделать? Ответ на этот вопрос вы сможете найти в данной статье.

План анализа функции

Первое, что необходимо сделать, так это провести поверхностное исследование функции, в ходе которого мы найдем область определения. Итак, начнем по порядку. Область определения — это совокупность тех значений, которыми функция задается. Проще говоря, это те числа, которые можно использовать в функции вместо х. Для того чтобы определить область определения, необходимо просто взглянуть на запись. К примеру, очевидно, что у функции у (х) = х³ + х² — х + 43 область определения — множество действительных чисел. Ну а с функцией наподобие (х² — 2х)/х все немного иначе. Поскольку число в знаменателе не должно равняться 0, то областью определения данной функции будут все действительные числа, помимо нуля.

Далее необходимо найти так называемые нули функции. Это те значения аргумента, при которых вся функция принимает значения ноль. Для этого необходимо приравнять функцию к нулю, подробно ее рассмотреть и совершить некоторые преобразования. Возьмём уже знакомую нам функцию у(х) = (х² — 2х)/х. Из школьного курса мы знаем, что дробь равна 0 тогда, когда числитель равен нулю. Поэтому знаменатель мы отбрасываем и начинаем работать с числителем, приравнивая его к нулю. Получаем х² — 2х = 0 и выносим х за скобочки. Отсюда х (х — 2) = 0. В итоге получаем, что наша функция равна нулю тогда, когда х равняется 0 или же 2.

Точки экстремума на графике функции

Во время исследования графика функции многие сталкиваются с проблемой в виде точек экстремума. И это странно. Ведь экстремумы — это довольно-таки простая тема. Не верите? Убедитесь сами, прочитав данную часть статьи, в которой мы поговорим о точках минимума и максимума.

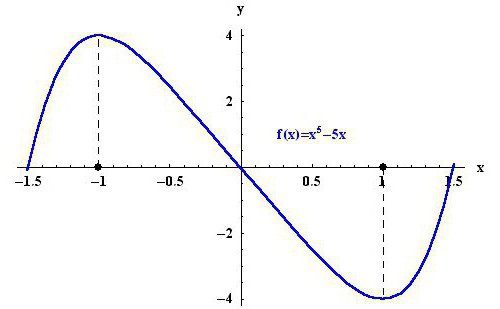
Для начала стоит разобраться в том, что собой представляет экстремум. Экстремум — это предельное значений, которое достигает функция на графике. Отсюда получается, что существует два крайних значения — максимум и минимум. Для наглядности можно посмотреть на картинку, что расположена выше. На исследованной области точка -1 является максимумом функции у (х) = х⁵ — 5х, а точка 1, соответственно, минимумом.

Также не стоит путать между собой понятия. Точки экстремума функции — это те аргументы, при которых заданная функция приобретает крайние значения. В свою очередь, экстремумом называют значение минимумов и максимумов функции. К примеру, вновь рассмотрим рисунок выше. -1 и 1 — это точки экстремума функции, а 4 и -4 — это сами экстремумы.

Нахождение точек экстремума

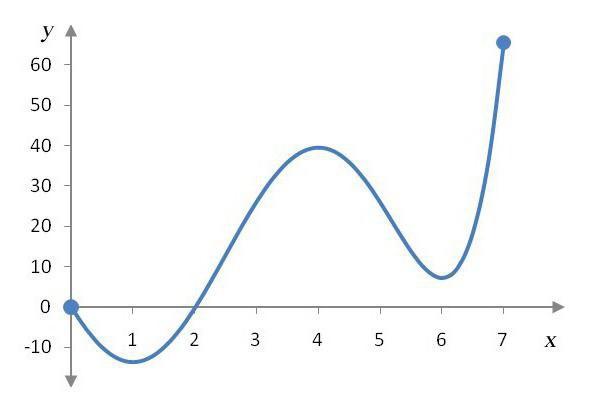
Но как все-таки найти точки экстремума функции? Все довольно-таки просто. Первое, что необходимо сделать — найти производную уравнения. Допустим, мы получили задание: «Найдите точки экстремума функции y (x), x — аргумент. Для наглядности возьмем функцию у (х) = х³ + 2х² + х + 54. Проведем дифференцирование и получим следующее уравнение: 3х² + 4х + 1. В итоге мы получили стандартное квадратное уравнение. Все, что необходимо сделать дальше — приравнять его к нулю и найти корни. Поскольку дискриминант больше нуля (D = 16 — 12 = 4), данное уравнение определяется двумя корнями. Находим их и получаем два значения: 1/3 и -1. Это и будут точки экстремума функции. Однако как все-таки определить, кто есть кто? Какая точка является максимумом, а какая минимумом? Для этого нужно взять соседнюю точку и узнать ее значение. К примеру, возьмем число -2, которое находится слева по координатной прямой от -1. Подставляем это значение в наше уравнение у(-2) = 12 — 8 + 1 = 5. В итоге мы получили положительное число. Это значит, что на промежутке от 1/3 до -1 функция возрастает. Это, в свою очередь, обозначает, что на промежутках от минус бесконечности до 1/3 и от -1 до плюс бесконечности функция убывает. Таким образом, можно сделать вывод, что число 1/3 — точка минимума функции на исследованном промежутке, а -1 — точка максимума.

Сумма точек экстремума функции

Также стоит отметить, что на ЕГЭ требуют не просто найти точки экстремума, Но и провести с ними какую-то операцию (прибавить, умножить и т.д.). Именно по этой причине стоит обратить особое внимание на условия задачи. Ведь из-за невнимательности можно потерять баллы.

www.syl.ru

Экстремумы функции, максимум и минимум

ОПРЕДЕЛЕНИЕ

Экстремумами (максимумами и минимумами) функции называются значения функции в точках максимума и минимума.

Точки экстремума функции

Говорят, что в точке максимум (минимум), если существует такая -окрестность точки — , что для всех из этой окрестности, отличных от выполняется неравенство .

ОПРЕДЕЛЕНИЕ

Точки максимума и минимума называются точками экстремума.

ОПРЕДЕЛЕНИЕ Точки области определения, в которых производная функции равна нулю или не существует, называются критическими точками.

Необходимое условие существования экстремума функции. Пусть функция дифференцируема в промежутке . Если в некоторой точке функция имеет экстремум, то в этой точке производная равна нулю: .

Достаточное условие существования экстремума функции. Если производная функции равна нулю в точке и при переходе через эту точку в сторону возрастания меняет знак с «+» («-») на «-» («+»), то в точке функция имеет максимум (минимум). Если же при переходе через точку производная функции не меняет знак, то в этой точке функция экстремума не имеет.

Для исследования функции на экстремум необходимо:

1. найти критические точки функции;
2. проверить, изменяет ли знак производная функции при переходе через критическую точку;
3. вычислить значения максимума или минимума .

Примеры исследования функции на экстремум

ПРИМЕР 1

Задание	Найти экстремум функции
Решение	Найдем критические точки функции, для этого вычислим производную заданной функции     приравняем её к нулю и найдем корни полученного квадратного уравнения     Получили две критические точки . Обозначим найденные корни на числовой оси и определим знак производной на полученных интервалах. В точке производная меняет знак с «+» на «-», значит в этой точке максимум. Вычислим значение максимума     В точке производная меняет знак с «-» на «+», значит, — точка минимума. Значение минимума соответственно равно
Ответ

ПРИМЕР 2

Задание	Найти экстремум функции
Решение	Область определения функции — вся числовая прямая, за исключением точки , то есть . Вычислим производную заданной функции и найдем критические точки     Приравниваем к нулю производную     Получаем одну критическую точку . Обозначим на числовой оси область определения функции и найденную критическую точку и определим знак производной на полученных интервалах В точке производная меняет знак с «-» на «+», значит, в этой точке минимум. Значение минимума соответственно равно
Ответ

Читайте также:

Монотонность функции

Нули функции

Наибольшее и наименьшее значение функции

Точки перегиба функции

Промежутки выпуклости и вогнутости функции

Исследование функции

ru.solverbook.com

Экстремумы функции.

Точка х₀называетсяточкой максимума(минимума) функцииf(х), если в некоторой окрестности точки х₀выполняется неравенствоf(х) ≤f(х₀) (f(х) ≥f(х₀

)).

Значение функции в этой точке называется соответственно максимумомилиминимумомфункции. Максимум и минимум функции объединяются общим названиемэкстремумафункции.

Экстремум функции в этом смысле часто называют локальным экстремумом, подчеркивая тот факт, что это понятие связано лишь с достаточно малой окрестностью точки х₀. На одном и том же промежутке функция может иметь несколько локальных максимумов и минимумов, которые не обязательно совпадают сглобальным максимумомилиминимумом(т.е. наибольшим или наименьшим значением функции на всем промежутке).

Необходимое условие экстремума. Для того, чтобы функция имела экстремум в точке, необходимо, чтобы ее производная в этой точке равнялась нулю или не существовала.

Для дифференцируемых функций это условие вытекает из теоремы Ферма. Кроме того, оно предусматривает и случай, когда функция имеет экстремум в точке, в которой она не дифференцируема.

Точки, в которых выполнено необходимое условие экстремума, называются критическими(илистационарнымидля дифференцируемой функции). Эти точки должны входить в область определения функции.

Таким образом, если в какой-либо точке имеется экстремум, то эта точка критическая (необходимость условия). Заметим, что обратное утверждение неверно. Критическая точка вовсе не обязательно является точкой экстремума, т.е. сформулированное условие не является достаточным.

Первое достаточное условие экстремума. Если при переходе через некоторую точку производная дифференцируемой функции меняет свой знак с плюса на минус, то это точка максимума функции, а если с минуса на плюс, — то точка минимума.

Доказательство этого условия вытекает из достаточного условия монотонности (при изменении знака производной происходит переход либо от возрастания функции к убыванию, либо от убывания к возрастанию).

Второе достаточное условие экстремума. Если первая производная дважды дифференцируемой функции в некоторой точке равна нулю, а вторая производная в этой точке положительна, то это точка минимума функции; а если вторая производная отрицательна, то это точка максимума.

Доказательство этого условия также основано на достаточном условии монотонности. В самом деле, если вторая производная положительна, то первая производная является возрастающей функцией. Поскольку в рассматриваемой точке она равна нулю, следовательно, при переходе через нее она меняет знак с минуса на плюс, что возвращает нас к первому достаточному условию локального минимума. Аналогично если вторая производная отрицательна, то первая убывает и меняет знак с плюса на минус, что является достаточным условием локального максимума.

Исследование функции на экстремумв соответствии со сформулированными теоремами включает следующие этапы:

1. Найти первую производную функции f`(x).

2. Проверить выполнение необходимого условия экстремума, т.е. найти критические точки функции f(x), в которых производнаяf`(x) = 0 или не существует.

3. Проверить выполнение достаточного условия экстремума, т.е. либо исследовать знак производной слева и справа от каждой критической точки, либо найти вторую производную f«(x) и определить ее знак в каждой критической точке. Сделать вывод о наличии экстремумов функции.

4. Найти экстремумы (экстремальные значения) функции.

Нахождение глобального максимума и минимума функциина некотором промежутке также имеет большое прикладное значение. Решение этой задачи на отрезке основано на теореме Вейерштрасса, в соответствии с которой непрерывная функция принимает на отрезке свои наибольшее и наименьшее значения. Они могут достигаться как в точках экстремума, так и на концах отрезка. Поэтому решение включает следующие этапы:

1. Найти производную функции f`(x).

2. Найти критические точки функции f(x), в которых производнаяf`(x) = 0 или не существует.

3. Найти значения функции в критических точках и на концах отрезка и выбрать из них наибольшее и наименьшее.

studfile.net

Найти экстремумы функции | Онлайн калькулятор

Данный калькулятор предназначен для нахождения экстремумов функции.
Следует различать понятия точек экстремума и экстремумов функции. Точки экстремума – точки максимума и минимума функции, это значения на оси Ox. Точка x₀ является точкой максимума функции y=f(x), если для всех x из ее окрестности выполняется неравенство f(x₀)≥f(x). Точка x₀ является точкой минимума функции y=f(x), если из ее окрестности для всех x выполняется неравенство f(x₀)≤f(x). Значения функции, которые соответствуют точкам экстремума, называются экстремумами функции, это значения на оси Oy.
Для того чтобы найти экстремумы функции можно использовать любой из трех условий экстремума, если функция удовлетворяет эти условиям.
Первым достаточным условием экстремума являются следующие утверждения: если в точке x

0 функция непрерывна, и в ней производная меняет знак с плюса на минус, то точка x₀ является точкой максимума, а если в данной точке производная меняет знак с минуса на плюс, то x₀ – точка минимума.

Вторым признаком экстремума является следующее утверждение: если производная второго порядка от x₀ больше нуля, то x₀ – точка минимума; если меньше нуля, то x₀ – точка максимума. Третье достаточное условие экстремума функции заключается в следующем. Пусть функция y=f(x) имеет производные до n-ого порядка в окрестности точки x0 и производные до n+1-ого порядка в самой точке x₀; пусть f’(x₀)= f’’(x₀)= f’’’(x₀)=…=f⁽ⁿ⁾( x₀)=0 и f⁽ⁿ⁺¹⁾( x₀)≠0. Тогда, если n – нечетное, то x₀ – точка экстремума. Если f⁽ⁿ⁺¹⁾( x₀)>0, то x₀ – точка минимума, а, если f

(n+1)( x₀)0 – точка максимума. Для того чтобы найти экстремумы функции, введите эту функцию в ячейку. Основные примеры ввода функций для данного калькулятора указаны ниже. Для получения полного хода решения нажимаем в ответе Step-by-step.

allcalc.ru

Экстремумы функции (Лекция №9)

Рассмотрим график непрерывной функции y=f(x), изображенной на рисунке.

Значение функции в точке x₁ будет больше значений функции во всех соседних точках как слева, так и справа от x₁. В этом случае говорят, что функция имеет в точке x₁ максимум. В точке x₃ функция, очевидно, также имеет максимум. Если рассмотреть точку x₂, то в ней значение функции меньше всех соседних значений. В этом случае говорят, что функция имеет в точке x₂ минимум. Аналогично для точки

x₄.

Функция y=f(x) в точке x₀ имеет максимум, если значение функции в этой точке больше, чем ее значения во всех точках некоторого интервала, содержащего точку x₀, т.е. если существует такая окрестность точки x₀, что для всех x≠x₀, принадлежащих этой окрестности, имеет место неравенство f(x)<f(x₀).

Функция y=f(x) имеет минимум в точке x₀, если существует такая окрестность точки x₀, что для всех x≠x₀, принадлежащих этой окрестности, имеет место неравенство f(x)>f(x₀.

Точки, в которых функция достигает максимума и минимума, называются точками экстремума, а значения функции в этих точках экстремумами функции.

Обратим внимание на то, что функция, определенная на отрезке, может достигать максимума и минимума только в точках, заключенных внутри рассматриваемого отрезка.

Отмети, что если функция имеет в точке максимум, то это не означает, что в этой точке функция имеет наибольшее значение во всей области определения. На рисунке, рассмотренном выше, функция в точке x₁ имеет максимум, хотя есть точки, в которых значения функции больше, чем в точке x₁. В частности, f(x₁) < f(x₄) т.е. минимум функции больше максимума. Из определения максимума следует только, что это самое большое значение функции в точках, достаточно близкихк точке максимума.

Теорема 1. (Необходимое условие существования экстремума.) Если дифференцируемая функция y=f(x) имеет в точке x= x₀ экстремум, то ее производная в этой точке обращается в нуль.

Доказательство. Пусть для определенности в точке x₀ функция имеет максимум. Тогда при достаточно малых приращениях Δx имеем f(x₀+ Δx)<f(x₀), т.е. Но тогда

Переходя в этих неравенствах к пределу при Δx→ 0 и учитывая, что производная f ‘(x₀) существует, а следовательно предел, стоящий слева, не зависит от того как Δx → 0, получаем: при Δx → 0 – 0 f’(x₀) ≥ 0 а при Δx → 0 + 0 f’(x₀) ≤ 0. Так как f ‘(x₀) определяет число, то эти два неравенства совместны только в том случае, когда f ‘(x₀) = 0.

Доказанная теорема утверждает, что точки максимума и минимума могут находиться только среди тех значений аргумента, при которых производная обращается в нуль.

Мы рассмотрели случай, когда функция во всех точках некоторого отрезка имеет производную. Как же обстоит дело в тех случаях, когда производная не существует? Рассмотрим примеры.

Примеры.

1. y=|x|.

   Функция не имеет производной в точке x=0 (в этой точке график функции не имеет определенной касательной), но в этой точке функция имеет минимум, так как y(0)=0, а при всех x≠ 0y > 0.

2.  

   Функция не имеет производной при x=0, так как обращается в бесконечность приx=0. Но в этой точке функция имеет максимум.

3.  

   Функция не имеет производной при x=0, так как при x→0. В этой точке функция не имеет ни максимума, ни минимума. Действительно, f(x)=0 и при x<0f(x)<0, а при x>0f(x)>0.

   Таким образом, из приведенных примеров и сформулированной теоремы видно, что функция может иметь экстремум лишь в двух случаях: 1) в точках, где производная существует и равна нулю; 2) в точке, где производная не существует.

   Однако, если в некоторой точке x₀ мы знаем, что f ‘(x₀)=0, то отсюда нельзя делать вывод, что в точке x₀ функция имеет экстремум.

   Например. .

   Но точка x=0 не является точкой экстремума, поскольку слева от этой точки значения функции расположены ниже оси Ox, а справа выше.

   Значения аргумента из области определения функции, при которых производная функции обращается в нуль или не существует, называются критическими точками.

   Из всего вышесказанного следует, что точки экстремума функции находятся среди критических точек, и, однако, не всякая критическая точка является точкой экстремума. Поэтому, чтобы найти экстремум функции, нужно найти все критические точки функции, а затем каждую из этих точек исследовать отдельно на максимум и минимум. Для этого служит следующая теорема.

   Теорема 2. (Достаточное условие существования экстремума.) Пусть функция непрерывна на некотором интервале, содержащем критическую точку x₀, и дифференцируема во всех точках этого интервала (кроме, быть может, самой точки x₀). Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то в точке x = x₀ функция имеет максимум. Если же при переходе через x₀ слева направо производная меняет знак с минуса на плюс, то функция имеет в этой точке минимум.

   Таким образом, если

   1. f ‘(x)>0 при x<x₀ и f ‘(x)<0 при x> x₀, то x₀ – точка максимума;
   2. при x<x₀ и f ‘(x)>0 при x> x₀, то x₀ – точка минимума.

   Доказательство. Предположим сначала, что при переходе через x₀ производная меняет знак с плюса на минус, т.е. при всех x, близких к точке x₀f ‘(x)>0 для x< x₀, f ‘(x)<0 для x> x₀. Применим теорему Лагранжа к разности f(x) — f(x₀) = f ‘(c)(x- x₀), где c лежит между x и x₀.

   1. Пусть x < x₀. Тогда c< x₀ и f ‘(c)>0. Поэтомуf ‘(c)(x- x₀)<0и, следовательно,

      f(x) — f(x₀)<0,т.е. f(x)< f(x₀).

   2. Пусть x > x₀. Тогда c> x₀ и f ‘(c)<0. Значитf ‘(c)(x- x₀)<0. Поэтому f(x) — f(x₀)<0,т.е.f(x) < f(x₀).

   Таким образом, для всех значений x достаточно близких к x₀f(x) < f(x₀). А это значит, что в точке x₀ функция имеет максимум.

   Аналогично доказывается вторая часть теоремы о минимуме.

   Проиллюстрируем смысл этой теоремы на рисунке. Пусть f ‘(x₁)=0 и для любых x, достаточно близких к x₁, выполняются неравенства

   f ‘(x)<0 при x< x₁, f ‘(x)>0 при x> x₁.

   Тогда слева от точки x₁ функция возрастает, а справа убывает, следовательно, при x = x₁ функция переходит от возрастания к убыванию, то есть имеет максимум.

   Аналогично можно рассматривать точки x₂ и x₃.

   
   Схематически все вышесказанное можно изобразить на картинке:

   Правило исследования функции y=f(x) на экстремум

   1. Найти область определения функции f(x).
   2. Найти первую производную функции f ‘(x).
   3. Определить критические точки, для этого:
      1. найти действительные корни уравнения f ‘(x)=0;
      2. найти все значения x при которых производная f ‘(x) не существует.
   4. Определить знак производной слева и справа от критической точки. Так как знак производной остается постоянным между двумя критическими точками, то достаточно определить знак производной в какой-либо одной точке слева и в одной точке справа от критической точки.
   5. Вычислить значение функции в точках экстремума.

   Примеры. Исследовать функции на минимум и максимум.

   1. . Область определения функции D(y)=R.

      Найдем производную заданной функции

      Определим критические точки . Производная не существует при х₂= 0. Следовательно, критические точки: 0 и 2/5. Нанесем их на числовую ось и определим знак производной на каждом из полученных промежутков.

   2.  

      Критическая точка функции x =3. Точка x= –1 не входит в область определения функции.

   НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ НА ОТРЕЗКЕ

   Наибольшим значением функции на отрезке называется самое большое из всех ее значений на этом отрезке, а наименьшим – самое маленькое из всех ее значений.

   Рассмотрим функцию y=f(x) непрерывную на отрезке [a, b]. Как известно, такая функция достигает своего наибольшего и наименьшего значений, либо на границе отрезка, либо внутри него. Если наибольшее или наименьшее значение функции достигается во внутренней точке отрезка, то это значение является максимумом или минимумом функции, то есть достигается в критических точках.

   Таким образом, получаем следующее правило нахождения наибольшего и наименьшего значений функции на отрезке[a, b]:

   1. Найти все критические точки функции в интервале (a, b) и вычислить значения функции в этих точках.
   2. Вычислить значения функции на концах отрезка при x = a, x = b.
   3. Из всех полученных значений выбрать наибольшее и наименьшее.

   Примеры.

   1. Найти наибольшее и наименьшее значения функции на отрезке [–2; –0,5].

      Найдем критические точки функции.

      Вычислим значения функции в найденной точке и на концах заданного отрезка.

      Итак,

   2. Найти наибольшее и наименьшее значения функцииy=x-2·ln x на [1; e].

   3. Чему равна наименьшая площадь боковой поверхности прямого кругового конуса объема 3π?

      По теореме Пифагора

      .

      Следовательно, .

      .

      Найдем критические точки функции S: S‘ = 0, т.е.

      Покажем, что при найденном значении h функция S_бок достигает минимума.

      .

   4. Найти радиус основания и высоту цилиндра наибольшего объема, который можно вписать в шар радиусом R.

      Пусть r – радиус основания цилиндра, h – высота.

      Нам нужно максимизировать объем цилиндра .

      Используя условие задачи, найдем связь между r и h. По теореме Пифагора из треугольника ABC следует, что . Отсюда .

      , по смыслу задачи 0≤h≤2R.

      .

      Покажем, что при найденном значении h функция V принимает наибольшее значение.

toehelp.ru

Экстремумы функции

Обратимся  к графику функции у = х³ – 3х². Рассмотрим окрестность точки х = 0, т.е. некоторый интервал, содержащий эту точку. Логично, что существует такая окрестность точки х = 0, что наибольшее значение функция у = х³ – 3х² в этой окрестности принимает в точке х = 0. Например, на интервале (-1; 1) наибольшее значение, равное 0, функция принимает в точке х = 0. Точку х = 0 называют точкой максимума этой функции.

Аналогично, точка х = 2 называется точкой минимума функции х³ – 3х², так как в этой точке значение функции не больше ее значения в иной точке окрестности точки х = 2, например, окрестности (1,5; 2,5).

Таким образом, точкой максимума функции f(х) называется точка х₀, если существует окрестность точки х₀ – такая, что выполняется неравенство f(х) ≤ f(х₀) для всех х из этой окрестности.

Например, точка х₀ = 0 – это точка максимума функции f(х) = 1 – х², так как f(0) = 1 и верно неравенство f(х) ≤ 1 при всех значениях х.

Точкой минимума функции f(х) называется точка х₀, если существует такая окрестность точки х₀, что выполняется неравенство f(х) ≥ f(х₀) для всех х из этой окрестности.

Например, точка х₀ = 2 – это точка минимума функции f(х) = 3 + (х – 2)², так как f(2) = 3 и f(х) ≥ 3 при всех х.

Точками экстремума называются точки минимума и точки максимума.

Обратимся к функции f(х), которая определена в некоторой окрестности точки х₀ и имеет в этой точке производную.

Если х₀ – точка экстремума дифференцируемой функции f(х), то f ‘(х₀) = 0. Это утверждение называют теоремой Ферма.

Теорема Ферма имеет наглядный геометрический смысл: в точке экстремума касательная параллельна оси абсцисс и поэтому ее угловой коэффициент
f ‘(х₀) равен нулю.

Например, функция f(х) = 1 – 3х² имеет в точке х₀ = 0 максимум, ее производная f ‘(х) = -2х, f ‘(0) = 0.

Функция f(х) = (х – 2)² + 3 имеет минимум в точке х₀ = 2, f ‘(х) = 2(х – 2), f ‘(2) = 0.

Отметим, что если f ‘(х₀) = 0, то этого недостаточно, чтобы утверждать, что х₀ – это обязательно точка экстремума функции f(х).

Например, если f(х) = х³, то f ‘(0) = 0. Однако точкой экстремума точка х = 0 не является, так как на всей числовой оси функция х³ возрастает.

Итак, точки экстремума дифференцируемой функции необходимо искать лишь среди корней уравнения
f ‘(х) = 0, но корень этого уравнения не всегда является точкой экстремума.

Стационарными точками называют точки, в которых производная функции равна нулю.

Таким образом, для того, чтобы точка х₀ была точкой экстремума, необходимо, чтобы она была стационарной точкой.

Рассмотрим достаточные условия того, что стационарная точка является точкой экстремума, т.е. условия, при выполнении которых стационарная точка является точкой минимума или максимума функции.

Если производная левее стационарной точки положительна, а правее – отрицательна, т.е. производная меняет знак «+» на знак «–» при переходе через эту точку, то эта стационарная точка – это точка максимума.

Действительно, в данном случае левее стационарной точки функция возрастает, а правее – убывает, т.е. данная точка – это точка максимума.

Если производная меняет знак «–» на знак «+» при переходе через стационарную точку, то эта стационарная точка является точкой минимума.

Если производная знак не меняет при переходе через стационарную точку, т.е. слева и справа от стационарной точки производная положительна или отрицательна, то эта точка не является точкой экстремума.

Рассмотрим одну из задач. Найти точки экстремума функции f(х) = х⁴ – 4х³.

Решение.

1) Найдем производную: f ‘(х) = 4х³ – 12х² = 4х² (х – 3).

2) Найдем стационарные точки: 4х²(х – 3) = 0, х₁ = 0, х₂ = 3.

3) Методом интервалов устанавливаем, что производная f ‘(х) = 4х²(х – 3) положительна при х > 3, отрицательна при х < 0 и при 0 < х < 3.

4) Так как при переходе через точку х₁ = 0 знак производной не меняется, то эта точка не является точкой экстремума.

5) Производная меняет знак «–» на знак «+» при переходе через точку х₂ = 3. Поэтому х₂ = 3 – точка минимума.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Экстремумы функции ℹ️ как найти точку минимума и максимума функции, примеры, как найти условный экстремум на графике производной, алгоритм нахождения

Экстремумы представляют собой точки минимума и максимума на графике функции. Работа с функциями представляет собой один из базовых навыков математики, необходимый для дальнейшего развития знаний. Поэтому перед непосредственно переходом к вычислениям рассмотрим вкратце сами функции.

Что такое функция

Возьмем знаменитую формулу силы тока:

I = ​ Здесь I — собственно сила тока, U — напряжение и R — сопротивление. Налицо зависимость значения силы тока от показателя напряжения. Функция — это общенаучное понятие, выражающее посредством формул зависимость между объектами. Примеры некоторых распространенных формул:

y = x

y = x²

Способом наглядного изображения характера зависимости является график функции. Например, рис.1 и 2. Рис.1. График y=x Рис.2. График y=x² Подставляя вместо  конкретные числа, находим конкретные точки на координатной сетке, через которые проходит график. Отметим, что видов функций великое множество, среди них тригонометрические, логарифмические и так далее. О них подробнее в соответствующих статьях. Также часто вместо y встречается знак ƒ(x), что означает “функция”. Соответственно — можно встретить выражения типа:

ƒ(x) = x

или

y = ƒ(x) = x

Можно сказать, что они синонимичны друг с другом.

Несколько слов о производной

Точки экстремума тесно связаны с производной. Это очень важное понятие как для математики, так и для естественных наук. Поясним, что это, на примере. Представьте себе пешехода, преодолевшего за время t расстояние S(t). Затем представим некое время t₂, прошедшее после момента t. Суммарный путь обозначим S(t + t₂). Тогда S(t₂) = S(t + t₂) – S(t). Если t₂ невелико, то скорость движения пешехода в этот момент примерно равна средней скорости. Тогда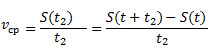 Чем t₂ меньше, тем v(t₂) ближе к v_ср, ⇒ v(t) можно обозначить как предел ​\( \frac{S(t₂)}{t₂} \)​ при стремлении t₂ к нулю. Выразим это формулой: В итоге по указанной формуле через S(x) можно вычислить расстояние, пройденное в x момент времени. Теперь вспомним формулу касательной к графику (подробнее в отдельной статье). Она выглядит так: Сравнив обе формулы, видим, что в обоих случаях применялось нахождение предела отношения приращения функции  и приращения аргумента  при условии, что приращение аргумента стремится к нулю. Обобщив эту информацию, получаем, что для любой ƒ(x) величина является производной функции в точке x₀. Она обозначается как ƒ(x₀). Для работы с производными существуют специальные формулы, подробнее о которых в соответствующей статье.

Важно! Если в x₀ функция имеет производную, она называется дифференцированной.

Экстремальные задачи

Понятие экстремума связано с решением соответствующих задач. На самом деле подобные задачи часто встречаются в нашей жизни. Например: найти наименьшую возможную площадь прямоугольного треугольника, если известна сумма длин его катетов. Это пример задачи на поиск минимума (min). Соответственно, если нужно найти максимальную площадь, мы будем искать максимум (max). Оба этих понятия объединяются термином экстремум. Задачи на поиск экстремумов называются экстремальными. Подобные задания известны еще с Древней Греции, но лишь с XVII в. начали вырабатываться универсальные алгоритмы их решения.

Решение заданий на поиск экстремума

Допустим, что имеется некая функция ƒ(x). Она ограничена определенным интервалом (a, b), который содержит в себе точку x₀. Ее часто называют локальным экстремумом функции ƒ(x). Если найдется интервал (a₀, b₀), который принадлежит (a, b) и также содержащий x₀, что условия ƒ(x) ≥ ƒ(x₀), или ƒ(x) ≤ ƒ(x₀), будет выполняться для всех x из подынтервала (a₀, b₀). Другими словами, в точке функция  достигает своего экстремального (минимального или максимального) значения. Чтобы найти экстремумы функции, необходимо найти производную исследуемой функции. Экстремумами будут точки, при которых производная обратится в 0.

Пример решения

Дано: ƒ(x) = x³ — 3x, соответственно,

ƒ′(x) = 3x² − 3

приравниваем к 0

3x² − 3 = 0

сокращаем

x² − 1 = 0

x² = 1

Получаем ответ: x₁ = 1; x₂ = –1. Эти точки и являются экстремумами.  — min, — max. Изобразим это на графике (рис.3) оригинальной функции ƒ(x) = x³ — 3x Рис.3. Точки экстремума  

Важно! Как видно, после точек экстремума график продолжается. Таким образом, можно заключить, что указанные точки являются экстремумами на отрезке [–1, 1] по оси x. Поэтому указанные точки будут локальными экстремумами.

Но как тогда найти глобальные точки экстремума? Для этого обратимся к задаче из начала текста. Обозначим площадь треугольника как S, сумму длин катетов как a и как x — длину одного из катетов. Получаем формулу:

S(x) = x(a−x)²

x — не может быть отрицательным, поэтому его диапазон [0, a]. Следовательно функция дифференцируема на интервале (0, a). Находим производную

S′(x) = 0,5 − x

решаем как уравнение

0,5 − x = 0

x = 0,5a = ​\( \frac{a}{2} \)​

Эта точка будет локальным максимумом. Далее среди чисел S(0) = 0, S(​\( \frac{a}{2} \)​) = ​​\( \frac{a2}{8} \)​​​, S(a) = 0 максимальной будет S(​\( \frac{a}{2} \))​, следовательно — в точке x = ​\( \frac{a}{2} \)​ функция достигает глобального максимума на отрезке [0, a]. Таким образом заключаем, что при заданной сумме длин катетов наибольшей площадью обладает равнобедренный треугольник. Тема экстремумов функции безусловно сложна, поэтому нет ничего постыдного, если вы что-то не поняли с первого раза. Перечитайте статью несколько раз, “переварите” информацию у себя в голове, и все получится. Для лучшего усвоения материала рекомендуем ознакомиться с видео.

nauka.club