Как найти у равнобедренного треугольника высоту – Высота равнобедренного треугольника | Формулы и расчеты онлайн — Детская игровая комната «Волшебный лес»

Posted on 13.07.202026.12.2019 by alexxlab

Содержание

Как найти неизвестную сторону равнобедренного треугольника

Треугольник, у которого две стороны равны, называется равнобедренным. Равные стороны в таком треугольнике называются боковыми, третья — основанием. Периметр равнобедренного треугольника (Р) будет равен сумме двух одинаковых боковых сторон (а) и основания (b):

Р = 2а + b

Против равных сторон лежат равные углы. Перпендикуляр, опущенный из вершины треугольника к его основанию, называется высотой равнобедренного треугольника. Проведенные к основанию биссектриса, медиана и высота совпадают между собой, делят треугольник на 2 равных прямоугольных треугольника, гипотенузой которых будет боковая сторона (а), а катетами — высота (h) и половина основания равнобедренного треугольника (b/2). По теореме Пифагора квадрат гипотенузы равен сумме квадратов его катетов, в нашем случае квадрат боковой стороны а (как гипотенузы) равен сумме половины основания (b/2), возведенного в квадрат, и высоте h в квадрате:

а² = (b/2)

2+h²

Отсюда, боковая сторона будет равна корню из суммы половины основания в квадрате и высоты, также возведенной в квадрат:

а = √(b/2)²+h²,

где а — боковая сторона, b/2 — половина основания, h — высота.

Если в прямоугольном треугольнике известна гипотенуза (в нашем случае это боковая сторона равнобедренного треугольника — а) и один из катетов (высота h), неизвестный катет находим, воспользовавшись теоремой Пифагора. Заметим, что неизвестный катет является половиной основания равнобедренного треугольника (b/2). Тогда, квадрат катета прямоугольного треугольника равен квадрату гипотенузы минус квадрат другого катета:

(b/2)² = a² — h²

Половина основания треугольника (b/2) равняется корню квадратному из квадрата гипотенузы минус квадрат другого катета:

b/2 = √а² — h²,

где b/2 — половина основания, а — боковая сторона, h — высота.

Умножив полученный результат на 2, находим всю длину основания.

Расчет длины стороны равнобедренного треугольника зная сторону и высоту

infofaq.ru

Высота и сторона «A» равнобедренного треугольника

Так как высота равнобедренного треугольника, опущенная на основание, является одновременно и биссектрисой и медианой, следовательно, она делит основание и угол при вершине на две равные части, образуя прямоугольный треугольник со сторонами a и b/2. Из теоремы Пифагора в таком треугольнике можно найти само основание, а затем рассчитать все остальные возможные данные. (рис.88.2) h^2+(b/2)^2=a^2 b=√(a^2-h^2 )/2

Чтобы вычислить периметр равнобедренного треугольника, надо к двум боковым сторонам прибавить основание или приведенный выше радикал через высоту. P=2a+b=2a+√(a^2-h^2 )/2

Площадь равнобедренного треугольника через высоту и основание по определению вычисляется как половина их произведения. Заменив основание на соответствующее ему выражение, получаем площадь через высоту и боковую сторону равнобедренного треугольника. S=hb/2=(h√(a^2-h^2 ))/4

В равнобедренном треугольнике равны не только боковые стороны, но и углы при основании, а так как в сумме они дают всегда 180 градусов, то любой из углов можно найти, зная другой. Первый угол вычисляется по теореме косинусов, приведенной для равных боковых сторон, а второй можно найти через разность от 180. (рис.88.1) cos⁡α=(b^2+c^2-a^2)/2bc=(b^2+a^2-a^2)/2ba=b^2/2ba=b/2a cos⁡β=(a^2+a^2-b^2)/(2a^2 )=(2a^2-b^2)/(2a^2 ) α=(180°-β)/2 β=180°-2α

Центральные медиана и биссектриса, опущенные на основание совпадают с высотой, а боковые медианы, высоты и биссектрисы можно найти по следующим формулам для равнобедренных треугольников. Чтобы вычислить их через высоту и боковую сторону, нужно заменить основание на эквивалентное ему выражение. (рис. 88.3) m_a=√(2a^2+2b^2-a^2 )/2=√(a^2+2b^2 )/2

Высота, опущенная на боковую сторону, через высоту, опущенную на основание и боковую сторону равнобедренного треугольника. (рис.88.8) h_a=(b√((4a^2-b^2)))/2a=(√(a^2-h^2 ) √((4a^2-a^2+h^2)))/2a=√((a^2-h^2)(3a^2+h^2))/2

Биссектрисы, направленные в боковые стороны, также могут быть выражены через боковую сторону и центральную высоту треугольника . (рис. 88.4) l_a=√(ab(2a+b)(a+b-a) )/(a+b)=√(a(a^2-h^2)(2a+√(a^2-h^2 )) )/(a+√(a^2-h^2 ))

Средняя линия проводится параллельно любой стороне треугольника, соединяя середины боковых в ее отношении сторон. Таким образом, она всегда оказывается равна половине параллельной ей стороны. Вместо неизвестного основания в формулу можно подставить используемый радикал, чтобы найти среднюю линию через высоту и боковую сторону равнобедренного треугольника(рис. 88.5) M_b=b/2=√(a^2-h^2 )/2 M_a=a/2

Радиус окружности, вписанной в равнобедренный треугольник, начинается от точки на пересечении биссектрис и уходит перпендикулярно в любую из сторон. Чтобы его найти через высоту и боковую сторону треугольника, надо заменить основание в формуле на радикал. (рис. 88.6) r=1/2 √(((a^2-h^2)(2a-√(a^2-h^2 )))/(2a+√(a^2-h^2 )))

Радиус окружности, описанной вокруг равнобедренного треугольника, также выводится из общей формулы путем подстановки радикала через высоту и боковую сторону вместо основания. (рис. 88.7) R=a^2/√(3a^2-h^2 )

geleot.ru

Высота и угол «α» равнобедренного треугольника

Высота равнобедренного треугольника, которая лежит под прямым углом к основанию, создает внутри еще два одинаковых прямоугольных треугольника, являясь катетом в каждом из них. Второй катет такого треугольника представляет собой половину основания, так как эта высота является одновременно медианой и биссектрисой, а гипотенузой будет боковая сторона равнобедренного треугольника. Соответственно, зная высоту и угол α при основании, через прямоугольный треугольник можно узнать стороны равнобедренного треугольника. (рис.88.2) a=h/sin⁡α b=2h/tan⁡α

Поскольку сумма всех углов в треугольнике равна 180 градусам, следовательно, угол при вершине будет равен разности 180 градусов и двух углов при основании. β=180°-2α

Периметр равнобедренного треугольника через высоту и угол α равен сумме двух отношений высоты к синусу угла и двух отношений высоты к тангенсу. Площадь, в свою очередь, преобразовывается в квадрат высоты, деленный на тангенс. P=2a+b=2h/sin⁡α +2h/tan⁡α S=hb/2=h^2/tan⁡α

Чтобы найти высоту, опущенную на боковую сторону равнобедренного треугольника (любую, так как они одинаковы), можно воспользоваться готовой формулой через стороны треугольника, заменив их на тригонометрические отношения и упростив выражение. Аналогично вычисляются медианы и биссектрисы через высоту. m_a=√(a^2+2b^2 )/2=√((h/sin⁡α )^2+2(2h/tan⁡α )^2 )/2=(h√(1/cos⁡α +8))/(2 tan⁡α ) h_a=(b√((4a^2-b^2)))/2a=(b√((4(h/sin⁡α )^2-(2h/tan⁡α )^2)))/(2 h/sin⁡α )=b sin^2⁡α l_a=(b√(a(2a+b) ))/(a+b)=(2h/tan⁡α √(h/sin⁡α (2 h/sin⁡α +2h/tan⁡α )))/(h/sin⁡α +2h/tan⁡α )=(2h√(2+2/cos⁡α ))/(tan⁡α+2 sin⁡α )

Чтобы вычислить среднюю линию, необходимо разделить на два ту сторону треугольника, которая ей параллельна. Поскольку ни одна из сторон не известна, то средняя линия, параллельная основанию, равна высоте, деленной на тангенс угла α, а средняя линия, параллельная боковой стороне равна высоте, деленной на два синуса угла α. (рис.88.5) M_b=b/2=h/tan⁡α M_a=a/2=h/(2 sin⁡α )

Чтобы вычислить радиус вписанной в равнобедренный треугольник окружности, нужно подставить вместо сторон a и b в формулу отношения высоты и тангенса или синуса соответственно, а затем упростить выражение (рис.88.6) r=b/2 √((a-2b)/(a+2b))=h/tan⁡α √((h/sin⁡α -2 2h/tan⁡α )/(h/sin⁡α +2 2h/tan⁡α ))=h/tan⁡α √((1-4 cos⁡α)/(1+4 cos⁡α ))

Радиус окружности, описанной вокруг равнобедренного треугольника также зависит от обеих сторон – основания и боковой стороны, поэтому его формула видоизменяется аналогично радиусу вписанной окружности. (рис.88.7) R=a^2/√(4a^2-b^2 )=(h/sin⁡α )^2/√(4(h/sin⁡α )^2-(2h/tan⁡α )^2 )=h/(2 sin^2⁡α )

geleot.ru

Как найти высоту равнобедренного треугольника

Как найти высоту равнобедренного треугольника?
Не забываем, что у равнобедренного треугольника боковые стороны равны между собой, а сторону, к которой будем проводить высоту, принято называть основанием.
Рассмотрим несколько формул, которые позволят рассчитать высоту равнобедренного треугольника.

Формула 1.
Высоту равнобедренного треугольника можно вычислить с помощью теоремы Пифагора:

Формула 2.
Используем формулу Герона:

В этой формуле

, так как у равнобедренного треугольника боковые стороны равны.
Для простоты будем обозначать эти стороны просто .
Подставим значение для p в формулу высоты и получим:

Под корнем получили произведение двух одинаковых выражений, но с разными знаками. Применим к ним формулу сокращенного умножения:

Подставим полученный результат в формулу, выполним упрощение и вынесение из-под знака корня:

Пользуйтесь на здоровье!

ru.solverbook.com

Все формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

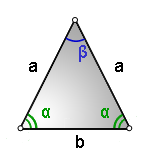
b — сторона (основание)

a — равные стороны

α — углы при основании

β — угол образованный равными сторонами

Формулы длины стороны (основания), (b):

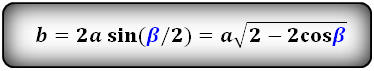
Формулы длины равных сторон , (a):

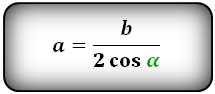
Подробности: Автор: Administrator; Опубликовано: 11 октября 2011; Обновлено: 16 мая 2017

www-formula.ru

Как найти основание равнобедренного треугольника если известны его боковые стороны и высота

высота в равнобедренном треугольнике является и медианой, следовательно она делит треугольник на две равные части. По теореме пифагора (сумма квадратов катетов равна квадрату гипотенузы) находишь сначала катет одного треугольника, а потом второго. складываешь и у тебя получается основание

теорему пифагора вспомни
Ха-ха. Теорему Пифагора не учили еще?
по тереме пифагора. половина основания будет равна квадратному корню из разности квадрата гипотенузы от квадрата высоты. а потом половину эту умножить на 2
по теореме Пифагора. боковая сторона — гипотенуза, половина основания и высота — катеты
Не слушай их! Загляни в учебник геометрики за 6-й класс, примерно.. . Или на обложку тетрадки по арифметике для 6-го класса, в клеточку которая.. . (на заднюю обложку, а не на переднюю, куда ж ты смотришь!!!!).

1. Возводишь длину боковой стороны в квадрат. 2. Отнимаешь от того, что получилось в п. 1 возведенную в квадрат длину высоты. 3.Из того, что получилось в п. 2 находишь корень и умножаешь на два. — это и есть ответ!
Кароче столкнулся с такой же фигнёй, Надо знать тиорему Пифагора. Тобишь 1 действием тебе надо найти КВАДРАТ ПОЛОВИНЫ ОСНОВАНИЯ 2)Половину основание 3)площадь. Изи!

Например бок -17, выс — 15. Теор виета. (17-15)(17+15) = корень 2*32=64=8 половина основания
Люди, вы вкурсе что сейчас в России крупные мировые компании разыгрывают подарки и деньги за ответы на их вопросы? На www.fond2019.ru можете почитать подробнее. Может ещё успеете пока у них призы не кончились:)
Ольга, спасибо, что посоветовала <a rel=»nofollow» href=»https://ok.ru/dk?cmd=logExternal&st.cmd=logExternal&st.link=http://mail.yandex.ru/r?url=http://fond2019.ru/&https://mail.ru &st.name=externalLinkRedirect&st» target=»_blank»>fond2019.ru</a> Выплатили 28 тысяч за 20 минут как ты и написала. Жаль что раньше не знала про такие фонды, на работу бы ходить не пришлось:)

touch.otvet.mail.ru
Площадь равнобедренного треугольника | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Проще всего найти площадь равнобедренного треугольника через высоту и основание. Высота делит такой треугольник пополам,

и используя формулу для нахождения площади прямоугольного треугольника, получаем, что 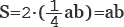, а в нашем случае .
Используя эту же формулу, можем найти площадь равнобедренного треугольника через стороны и основание. Для этого проведем в треугольнике высоту и воспользуемся теоремой Пифагора. Получим выражение . Отсюда , и соответственно . Теперь площадь треугольника вычислить можно будет по формуле , подставив полученное выражение вместо .
Найти площадь равнобедренного треугольника, зная сторону и угол при вершине (между одинаковыми сторонами), можно используя аналогичную формулу для обычного треугольника, в котором известны две стороны: . Подставив вместо второй стороны ту же самую a (так как в равнобедренном треугольнике боковые стороны равны), получим . Если известен угол при основании, то формула будет выглядеть по-другому – .
Зная основание и угол равнобедренного треугольника, нужно найти его высоту, тогда станет возможным рассчитать площадь. Из прямоугольного треугольника, который образует высота: . Тогда площадь будет равна:
geleot.ru