Формула вершины параболы
☰
Обычно формулу координаты x вершины параболы используют, когда имеют дело с квадратичной функцией.
Квадратичная функция имеет вид: y = ax2 + bx + c.
Ее график — это парабола с вершиной, координаты которой определяются по формулам:
Однако формулу координаты y знать и использовать не обязательно. Обычно проще подставить найденное значение x в саму квадратичную функцию и найти оттуда y.
Например, если дана функция y = 2x2 – 4x + 5, то координата x ее вершины будет равна:
x = –(–4 / (2 × 2)) = 1
Координату же y вычислим, подставив найденный x в саму функцию:
y = 2 × 12 – 4 × 1 + 5 = 3
Таким образом, вершина графика функции y = 2x2 – 4x + 5 находится в точке с координатами (1; 3).
В остальном парабола квадратичной функции вида y = ax2 + bx + c такая же как функции вида y = ax
Формулы вершины параболы получаются при преобразовании квадратичной функции к виду y = f(x + l) + m. Делается это методом выделения полного квадрата. Как известно функции вида y = f(x + l) + m отличаются от функций y = f(x) сдвигом из графиков по оси x на –l и по оси y на m. Именно l в преобразованной квадратичной функции оказывается равным –b/2a, а m = (4ac – b2) / 4a. То есть l и m — это координаты x0 и y0 соответственно.
Доказывается это применением метода выделения полного квадрата к квадратному трехчлену общего вида ax2 + bx + c. При этом выполняются следующие преобразования:
- Объединим первые два члена многочлена: y = (ax 2 + bx) + c
Вынесем коэффициент a за скобку, при этом b разделится на a:
Представим, что у нас есть квадрат суммы, в котором x одно из слагаемых, а из выражения в скобках надо получить его полный квадрат суммы. Одночлен (b/a)x умножим на 2 и разделим на 2 одновременно. Также прибавим и вычтем квадрат второго слагаемого квадрата суммы. Получим:
Выделим квадрат суммы:
Умножим на a:
Приведем к общему знаменателю свободные члены:
Поменяем знак:
Таким образом, мы привели функцию y = ax2 + bx + c к виду y = a(x + l)2 + m, что соответствует функции y = f(x + l) + m, где f(x) = ax2. А как строить графики последней известно.
Как найти вершину параболы ℹ️ методы решения квадратичных уравнений, определение координат функции по формуле, примеры вычислений

Общие сведения
Парабола — кривая, состоящая из равноудаленных точек от заданной точки (вершина) и прямой. Последняя называется директрисой. График функции имеет ось симметрии, которая проходит по определенной траектории и зависит от функции кривой (рис. 1). Ее вершина находится в центре координат.
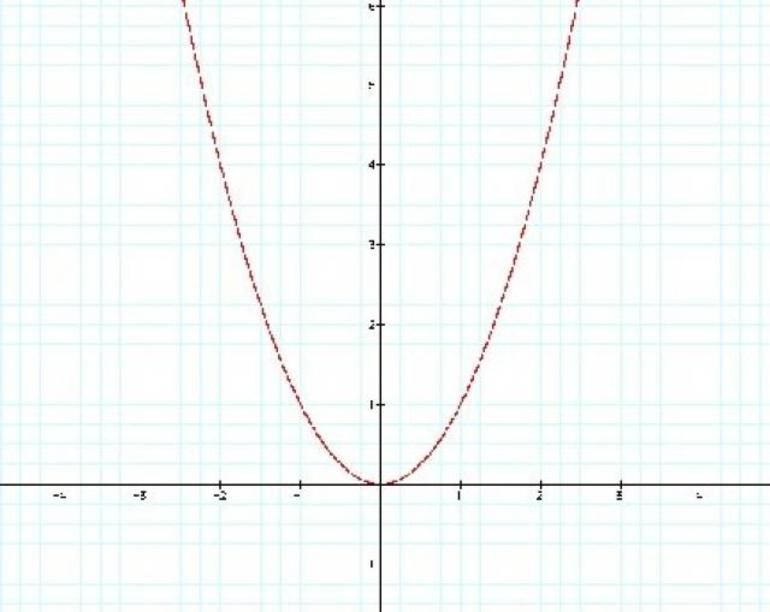
Рисунок 1. График квадратичной функции с вершиной в начале координат.
Однако существуют и другие случаи прохождения кривой. Она может пересекать оси абсцисс или ординат. В некоторых случаях ее ветви направлены вниз. При вращении вокруг оси симметрии получается поверхность, которая используется в различных устройствах. По этому принципу изготовлены фары автомобиля, зеркала в телескопах и т. д. Кроме того, парабола — это квадратичная зависимость переменных друг от друга. Парабола имеет некоторые свойства:

- Парабола — кривая второго порядка.
- Ось симметрии перпендикулярна директрисе и проходит через фокус и вершины.
- Оптическое свойство отражения.
- Отрезок, который соединяет середину любой хорды параболы и точку пересечения касательных прямых, является перпендикуляром относительно директрисы.
- Подобность всех парабол.
- Траектория фокуса, которая катится по произвольной прямой — цепная молния.
Следует отметить, что оптическое свойство — это способность отражать свет от источника. Если пучок лучей, которые являются параллельными ее оси, отражаются в параболе, то они собираются в фокусе кривой. При нахождении источника света в фокусе происходит отражение параллельного пучка лучей относительно ее оси.
Уравнения квадратичной функции
Параболу можно описать несколькими способами. Каждый из них нужно применять в конкретных случаях для удобства вычислений. Существует три формы описания кривой:
- Каноническая.
- Квадратичная.
- Общая.
В первой форме она имеет следующий вид: y 2 = 2px. Если поменять местами оси декартовой системы, то получится следующий вид: x 2 = 2yp. Коэффициент p — фокальный параметр. Он соответствует расстоянию между фокусом и директрисой. Кроме того, его значение всегда больше нуля. Вершина лежит всегда между фокусом и директрисой кривой на расстоянии, равном p/2 (рис. 2).
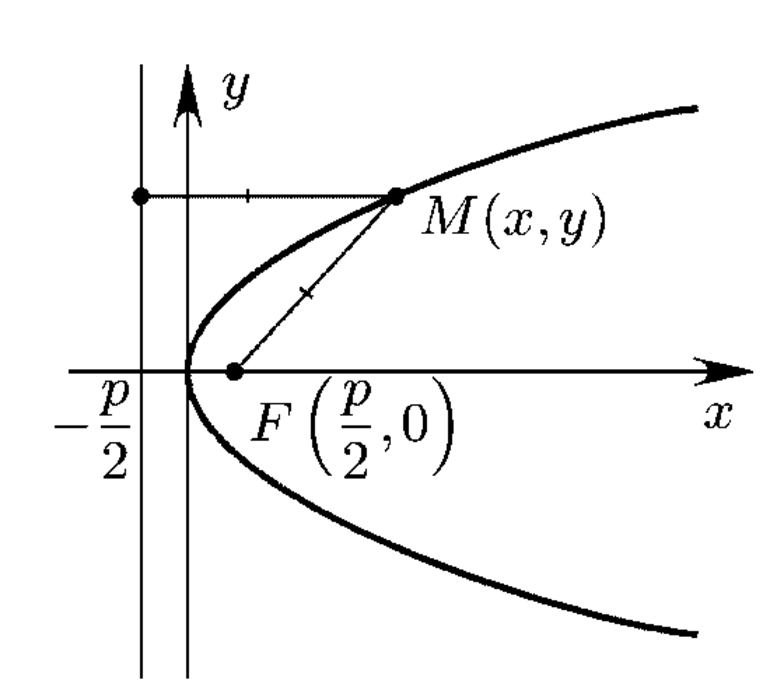
Рисунок 2. Директриса и фокус.
Пусть уравнение директрисы (прямая, которая параллельна оси ОУ) имеет следующий вид: х + p/2 = 0. Координаты фокуса F — (р/2;0). Начало координат делит луч, проходящий из точки F и точки пересечения с директрисой на 2 равных отрезка. Величина FM рассчитывается таким образом: FM = [(x — p/2)^2 + y 2 ]^0.5. Отрезок (луч) из точки М до директрисы равен p/2 + x. Если приравнять оба выражения, то равенство имеет такой вид: p/2 + x = [(x — p/2)^2 + y 2 ]^0.5. При возведении в квадрат и приведении подобных слагаемых, получается искомое уравнение параболы (y 2 = 2px).
Парабола может задаваться квадратичной функцией. Она имеет такой вид: y = ax 2 + bx + c. Следует учитывать, что коэффициент «a» не должен быть равен 0. Если a=1, b = 0 и с = 0, функция принимает такой вид: y = ax 2 . В этом случае формула нахождения вершины параболы выглядит таким образом:

- Абсцисса вершины параболы: xa = -b / 2a.
- Координата «игрек» по оси ординат: yb = — D / 2a.
В последней формуле переменная D является дискриминантом квадратного уравнения искомой функции. Он вычисляется с помощью такого соотношения: D = b 2 — 4ac. При а>0 фокус лежит на оси, и находится над вершиной. Ось симметрии параллельна оси ординат. Кроме того, она проходит через вершину кривой. Расстояние до нее равно ¼ величины «а». Если а<0, то ось ее симметрии параллельна оси абсцисс. Расстояние до фокуса также равно ¼а. Уравнение y = a (x — xa)^2 + ya — функция, определяющая кривую II порядка, как параболу.
Поскольку искомую функцию можно назвать кривой второго порядка, то ее уравнение может быть записано в виде квадратного многочлена в декартовой системе координат. Вид его имеет такой вид: Ax 2 + Bxy + Cy 2 + Dx + Ey + F = 0. Дискриминант равен нулю (при старших членах).
В полярной системе координат с осями p и v уравнение квадратичной функции имеет такой вид: p (1 + cos (v)) = p. Расстояние от фокуса до директрисы обозначается фокальным коэффициентом p. Кроме того, p соответствует удвоенной длине отрезка, проведенного от фокуса до вершины.
Методы нахождения вершины
В математике есть три способа нахождения координат точки вершины кривой: по формуле, выделением полного квадрата и нахождением производной. Следует отметить, что первый способ не подойдет в том случае, когда функция отличается от вида y = ax 2 + bx + c. Первый способ — расчет по формуле вершины параболы квадратичной функции. Координата x0 вычисляется таким образом: x0 = -b / 2a. Для нахождения координаты y0 следует подставить в функцию найденное значение x0.
Когда функция представлена неполным квадратом, нужно прибавить или отнять одинаковое число к двум частям уравнения. Если воспользоваться этим методом, то можно вычислить сразу значения х и у. Алгоритм нахождения вершины для функции у = x 2 + 4x + 2 имеет такой вид:

- Приравнять многочлен к нулю, и перенести свободный член в правую сторону с противоположным знаком: x 2 + 4x = -2.
- Дополнить до полного квадрата. Необходимо вычислить свободный член по такому соотношению: с = (b/2)^2 = (4/2)^2 = 4.
- Записать полный квадрат, отняв и прибавив свободный член: x 2 + 4x + 4 — 4 = -2.
- Выделить квадрат: (x 2 + 2x + 4) — 4 = -2.
- Перенести свободное число в правую сторону с противоположным знаком: (x 2 + 2x + 4) = 4 — 2.
- Уравнение принимает следующий вид: (x + 2)^2 = 2.
- Для того чтобы вычислить x0, нужно решить уравнение (x + 2)^2 = 0. Следовательно, x = -2.
- Ординату точки определить очень просто, поскольку ее значение соответствует числу (нужно брать с противоположным знаком), которое находится в правой части уравнения, т. е. у = -2.
При изображении графика вершину нужно сместить в точку (-2;2). Третий способ позволяет узнать координаты вершины с помощью определения производной. Находить ее следует от заданной функции. Для вычисления координат вершины нужно действовать по следующему алгоритму:
- Найти производную и приравнять ее к нулю: f'(x) = (ax 2 + bx + c)’ = 2ax + b.
- Выразить х: х = -b / (2a).
- Подставить в функцию для вычисления y.
- Записать координаты точки.
Однако эти все три метода относятся к ручному вычислению. Автоматизация действий осуществляется с помощью специализированного программного обеспечения. Для этой цели подойдет онлайн-калькулятор, поддерживающий функцию нахождения точек вершины квадратичной кривой. Программы рекомендуется применять только для проверки решения, поскольку очень важно знать методы нахождения этой точки.
Алгоритм построения
В различных задачах нужно выполнить построение графика функции. В некоторых случаях даются координаты вершины, а в других — их следует искать, используя какой-либо метод. Чтобы построить квадратичную функцию, нужно воспользоваться таким алгоритмом:
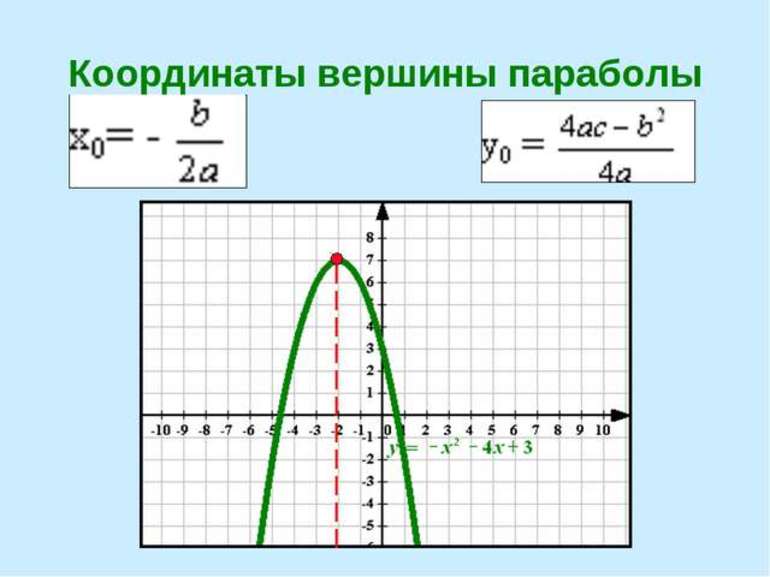
- Если вершина не задана, то нужно найти ее любым из методов.
- Определить точки пересечения с осями декартовой системы координат.
- Построить таблицу зависимости ординаты от абсциссы. Для этой цели нужно выделить минимум 3 значения «х». Вершина должна находиться по центру таблицы.
- Выполнить построение, соединив точки.
Если необходим более точный график, то необходимо брать больше точек. Значения рассчитываются при подстановке значений «х» в функцию. Когда парабола задана функцией y = x 2 + c, нет смысла брать разные значения. Нужно использовать для построения искомой таблицы числа с противоположными знаками. Например, x1 = 2 и x2 = -2.
Специалисты-математики настоятельно рекомендуют не усложнять вычисления. Возможно, в школьных программах и рассматриваются различные случаи. Однако в высших учебных заведениях основной аспект изучения дисциплин с физико-математическим уклоном сводится к оптимизации процесса решения задачи.
Примеры решений
В математике существует определенная классификация заданий на простые и сложные типы. Все они считаются однотипными, но отличаются только объемами вычислений и необходимостью построения графиков. Для решения нужно воспользоваться рекомендуемыми алгоритмами, которые существенно оптимизируют вычисления.
«Корень» трудностей при расчете — отсутствие систематизации вычислений. Не все ими пользуются. В результате простая задача становится очень сложной, поскольку в ней присутствует много ненужных вычислений. Кроме того, как отмечалось выше, рекомендуется «набить руку» на ручных вычислениях, ведь не всегда можно будет воспользоваться программами.
Упрощенная задача
Простым примером задания является следующий: необходимо вычислить координаты вершины точки параболы y = x 2 + 3x — 18. Следует продемонстрировать решение тремя способами. Решение первым методом:
- Координата по оси абсцисс: х0 = -3 / (2 * 1) = -1,5.
- По ординате: (-1,5)^2 + 3 * (-1,5) — 18 — y= 0. Отсюда, y = -20,25.
Следовательно, вершина находится в точке (-1,5;20,25). Второй способ решения данной задачи имеет такой вид:
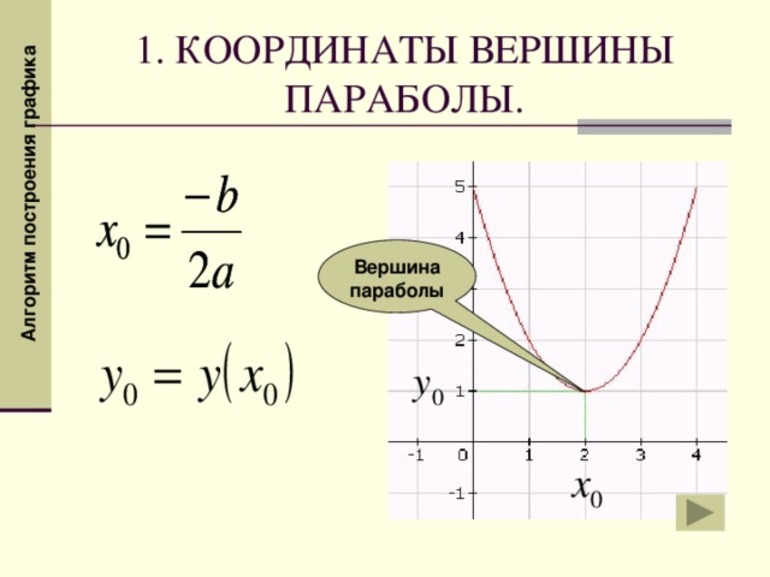
- Составить уравнение и перенести свободный член: x 2 + 3x = 18.
- Вычислить свободный член: с = (b/2)^2 = 2,25.
- Записать выражение: x 2 + 3x + 2,25 — 2,25 = 18.
- Выделить квадрат: (x 2 + 3x + 2,25) = 20,25.
- Определить координаты: (x + 1,5)^2 = 20,25.
- Искомая точка: (-1,5;20,25).
Для решения третьим методом следует найти производную: y’ = (x 2 + 3x — 18)’ = 2x + 3. Затем нужно приравнять ее к нулю: 2х + 3 = 0. Уравнение является простым, а его переменная легко находится: x = -3 / 2 = -1,5. После этого необходимо подставить абсциссу в функцию, приравняв ее к 0: y = 20,25.
Повышенная сложность
Задания повышенной сложности сводятся к вычислению нескольких значений. Кроме того, в некоторых случаях следует построить график параболы y = x 2 — 7x +10. Необходимо выполнить такие действия:
- Пересечение с осями.
- Вычислить экстремум (вершину) всеми методами.
- Выполнить графический эскиз (график).
Точек пересечения по ОУ нет. Они есть по оси абсцисс. Следует приравнять функцию к 0. Нахождение корней выполняется по теореме Виета: x1 = 2 и x2 = 5.
Для нахождения вершины необходимо воспользоваться тремя методами. При решении первым способом находится координата x0 = 7 / (2 * 1) = 3,5. Ордината определяется таким образом: y0 = (3,5)^2 — (7 * 3,5) + 10 = -2,25. Точка экстремума имеет координаты (3,5;-2,25). Находить вершину параболы необходимо по такому алгоритму:
- Записать уравнение, и выполнить перенос свободного члена: x 2 — 7x = -10.
- Найти свободный член: с = (7/2)^2 = 12,25.
- Составить уравнение: x 2 — 7x + 12,25 — 12,25 = -10.
- Выделить квадрат: (x — 3,5)^2 = 2,25.
- Экстремум: (3,5;-2,25).
Для следующего метода нужно найти производную: y’ = (x 2 — 7x +10)’ = 2x — 7. Далее нужно приравнять y’ к нулю: 2x — 7 = 0. Значение по оси абсцисс равно х0 = 3,5, а y0 = -2,25. Далее нужно заполнить таблицу зависимостей ординаты от переменной.
| y | 4 | 0 | -2 | -2,25 | -2 | 0 | 4 |
| x | 1 | 2 | 3 | 3,5 | 4 | 5 | 6 |
Таблица 1. Зависимость y от x.
После заполнения таблицы следует построить график искомой функции (рис. 3). Таблица состоит из следующих элементов: вершины, точек пересечения с осью абсцисс и 4 произвольных значений.

Рисунок 3. График функции.
Математики рекомендуют использовать для построения графика полученные значения при расчетах, поскольку подстановка и вычисление произвольных х существенно снижает скорость вычислений.
Таким образом, нахождение координат вершины параболы является довольно простой задачей, поскольку существует несколько методов. Из них можно выбрать оптимальный, который подходит в конкретной ситуации.
Формула нахождения вершины параболы
Определение 1
Парабола – это геометрическое множество точек, равноудалённых от точки F, не лежащей на параболе, и прямой $d$, не проходящей через точку $F$.
Что значит вершина параболы
Определение 2
Вершина параболы – это точка, ближайшая к директрисе параболы. Она является центром отрезка, ограниченного точкой фокуса параболы $F$ и директрисой $d$.
Производная в вершине квадратичной параболы равна нулю.
Каноническое уравнение параболы $y^2 = 2px$ справедливо для параболы, вершина которой находится в центре осей.
Для того, чтобы определить, принадлежит ли точка графику заданной параболы, необходимо подставить её координаты в формулу $y = ax^2 + bx + c$.
Если равенство выполняется — точка принадлежит графику.
Как найти вершины параболы, задающейся квадратичной функцией
Рисунок 1. Пример уравнения и графика квадратичной параболы
Довольно часто парабола задаётся квадратичной функцией вида $y = ax^2 + bx + c$, вершина такой параболы находится в произвольной точке.
Какой-то единой формулы для нахождения сразу обеих координат вершины параболы нет, но при этом определить координаты вершины параболы по уравнению довольно просто.
Алгоритм для нахождения вершины параболы такой:
- Запишите коэффициенты $a, b, c$ из уравнения. Если коэффициент $a$ при $y$ положительный, то ветви параболы будут смотреть вверх, а если отрицательный, то вниз.
- Найдите абсциссу вершины параболы ($x$ вершины) по формуле $x = — \frac{b}{2a}$, для этого воспользуйтесь коэффициентами $a, b, c$ из уравнения.
- Подставьте найденный $x$ в уравнение параболы и вычислите ординату вершины параболы $y$.
- Запишите полученные координаты x и y вершины параболы в форме точки $(x; y)$.
Пример 1
Рассмотрим уравнение параболы $y = x^2 – 5x + 7$
- Коэффициенты этой параболы $a = 1$, $b = -5$, $c = 7$.
- Для вычисления x вершины параболы подставьте $a = 1$ и $b = -5$ в формулу $x = — \frac{b}{2a}= \frac{5}{2}=2.5$
- Подставьте найденный $x$ в исходное уравнение:
- $y = 2,5^2 – 5 \cdot 2.5 + 7$
- $y = 0,75$
- Координаты вершины этой параболы $(2.5;0.75)$.
Вершина кубической параболы
Чтобы найти вершины (точки локальных минимумов и максимумов) кубической параболы, необходимо найти её производную, приравнять её к нулю и затем вычислить $x$ и $y$.
Если же необходимо найти точку перегиба кубической параболы, необходимо найти вторую производную и также приравнять её к нулю.
Координаты вершины параболы | Алгебра
Как найти координаты вершины параболы? Для этого достаточно запомнить всего одну короткую формулу (она же — корень квадратного уравнения для случая, если дискриминант равен нулю).
I. Абсциссу координаты вершины параболы — графика квадратичной функции y=ax²+bx+c, где a, b, c — числа, причем a≠0, находят по формуле
Для нахождения ординаты достаточно подставить в формулу функции xₒ вместо каждого x:
Можно также найти ординату вершины параболы, воспользовавшись формулой
(минус дискриминант, деленный на 4a).
Примеры.
Найти координаты вершины параболы:
1) y=x²-7x+3;
2) y= -x²+8x+2;
3) y= -3x²-12x-4;
4) y= 0,2x²+x+5.
Решение:
Вершина параболы y=x²-7x+3 — точка (3,5; -9,25).
Вершиной параболы y= -x²+8x+2является точка (4; 18).
(-2; 8) — вершина параболы y= -3x²-12x-4.
Следовательно, (-2,5; 3,75) — вершина параболы y=0,2x²+x+5.
II. Абсциссу вершины параболы можно также найти как среднее арифметическое между нулями функции (в том случае, если функция имеет нули):
Этим способом удобно находить вершину параболы, когда квадратичная функция задана в виде y=a(x-x1)(x-x2).
Пример.
Найдём координаты вершины параболы y=5(x-1)(x+7). Ищем нули функции:
5(x-1)(x+7)=0. Это уравнение типа произведение равно нулю.
x-1=0 или x+7=0
x=1; x=-7.
Точка (-3; -80) — вершина параболы y=5(x-1)(x+7).
III. Если функция задана в виде
то её вершина — точка (xₒ; yₒ). Например, вершиной параболы
является точка (-3; -1).
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | cos((5pi)/12) | |
| 3 | Найти точное значение | arctan(-1) | |
| 4 | Найти точное значение | sin(75) | |
| 5 | Найти точное значение | arcsin(-1) | |
| 6 | Найти точное значение | sin(60 град. ) | |
| 7 | Найти точное значение | sin(pi/3) | |
| 8 | Найти точное значение | arctan(- квадратный корень 3) | |
| 9 | Найти точное значение | cos(pi/3) | |
| 10 | Найти точное значение | sin(0) | |
| 11 | Найти точное значение | cos(pi/12) | |
| 12 | Найти точное значение | sin(30 град. ) | |
| 13 | Найти точное значение | cos(60 град. ) | |
| 14 | Найти точное значение | cos(30 град. ) | |
| 15 | Найти точное значение | sin((2pi)/3) | |
| 16 | Найти точное значение | arcsin(1) | |
| 17 | Найти точное значение | sin(pi/2) | |
| 18 | График | f(x)=x^2 | |
| 19 | Найти точное значение | sin(45 град. ) | |
| 20 | Найти точное значение | sin(15) | |
| 21 | Упростить | квадратный корень x^2 | |
| 22 | Найти точное значение | arccos(-1) | |
| 23 | Найти точное значение | tan(60 град. ) | |
| 24 | Найти точное значение | cos(45 град. ) | |
| 25 | Вычислить | логарифм по основанию 2 от 8 | |
| 26 | Упростить | квадратный корень x^3 | |
| 27 | Найти точное значение | arcsin(-1/2) | |
| 28 | Найти точное значение | cos(45) | |
| 29 | Найти точное значение | tan(30 град. ) | |
| 30 | Найти точное значение | tan(30) | |
| 31 | Найти точное значение | arcsin(1) | |
| 32 | Найти точное значение | arctan( квадратный корень 3) | |
| 33 | Найти точное значение | sin(45) | |
| 34 | Найти точное значение | cos(0) | |
| 35 | Найти точное значение | tan(45 град. ) | |
| 36 | Найти точное значение | arctan(0) | |
| 37 | Преобразовать из радианов в градусы | pi/3 | |
| 38 | График | y=x^2 | |
| 39 | Вычислить | натуральный логарифм 1 | |
| 40 | Вычислить | логарифм по основанию 3 от 81 | |
| 41 | Найти точное значение | cos(15) | |
| 42 | Вычислить | логарифм по основанию 5 от 125 | |
| 43 | Упростить | кубический корень из квадратного корня 64x^6 | |
| 44 | Вычислить | логарифм по основанию 3 от 81 | |
| 45 | Вычислить | логарифм по основанию 2 от 8 | |
| 46 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 47 | Найти точное значение | cos(75) | |
| 48 | Найти точное значение | sin((3pi)/4) | |
| 49 | Упростить | (1/( квадратный корень x+h)-1/( квадратный корень x))/h | |
| 50 | Упростить | кубический корень x^3 | |
| 51 | Найти точное значение | sin((5pi)/12) | |
| 52 | Найти точное значение | arcsin(-1/2) | |
| 53 | Найти точное значение | sin(30) | |
| 54 | Найти точное значение | sin(105) | |
| 55 | Найти точное значение | tan((3pi)/4) | |
| 56 | Упростить | квадратный корень s квадратный корень s^7 | |
| 57 | Упростить | корень четвертой степени x^4y^2z^2 | |
| 58 | Найти точное значение | sin(60) | |
| 59 | Найти точное значение | arccos(-( квадратный корень 2)/2) | |
| 60 | Найти точное значение | tan(0) | |
| 61 | Найти точное значение | sin((3pi)/2) | |
| 62 | Вычислить | логарифм по основанию 4 от 64 | |
| 63 | Упростить | корень шестой степени 64a^6b^7 | |
| 64 | Вычислить | квадратный корень 2 | |
| 65 | Найти точное значение | arccos(1) | |
| 66 | Найти точное значение | arcsin(( квадратный корень 3)/2) | |
| 67 | График | f(x)=2^x | |
| 68 | Найти точное значение | sin((3pi)/4) | |
| 69 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 70 | Вычислить | логарифм по основанию 5 от 25 | |
| 71 | Найти точное значение | tan(pi/2) | |
| 72 | Найти точное значение | cos((7pi)/12) | |
| 73 | Упростить | 1/( кубический корень от x^4) | |
| 74 | Найти точное значение | sin((5pi)/6) | |
| 75 | Преобразовать из градусов в радианы | 150 | |
| 76 | Найти точное значение | tan(pi/2) | |
| 77 | Множитель | x^3-8 | |
| 78 | Упростить | корень пятой степени 1/(x^3) | |
| 79 | Упростить | корень пятой степени 1/(x^3) | |
| 80 | Найти точное значение | sin(135) | |
| 81 | Преобразовать из градусов в радианы | 30 | |
| 82 | Преобразовать из градусов в радианы | 60 | |
| 83 | Найти точное значение | sin(120) | |
| 84 | Найти точное значение | tan((2pi)/3) | |
| 85 | Вычислить | -2^2 | |
| 86 | Найти точное значение | tan(15) | |
| 87 | Найти точное значение | tan((7pi)/6) | |
| 88 | Найти точное значение | arcsin(( квадратный корень 3)/2) | |
| 89 | Найти точное значение | sin(pi/2) | |
| 90 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 91 | Упростить | кубический корень 8x^7y^9z^3 | |
| 92 | Упростить | arccos(( квадратный корень 3)/2) | |
| 93 | Упростить | i^2 | |
| 94 | Вычислить | кубический корень 24 кубический корень 18 | |
| 95 | Упростить | квадратный корень 4x^2 | |
| 96 | Найти точное значение | sin((3pi)/4) | |
| 97 | Найти точное значение | tan((7pi)/6) | |
| 98 | Найти точное значение | tan((3pi)/4) | |
| 99 | Найти точное значение | arccos(-1/2) | |
| 100 | Упростить | корень четвертой степени x^4 |
Определить вид кривой 2-го порядка онлайн · Как пользоваться Контрольная Работа РУ

Приведём примеры кривых второго порядка, для которых можно определить канонический вид онлайн:
Кривая
| Уравнение | Канонический вид | Тип | Измерение |
|---|---|---|---|
| 9x^2+12xy+4y^2-24x-16y+3=0 | x^2=1 | Две параллельные прямые | Кривая |
| x^2-2xy+y^2-10x-6y+25=0 | y^2=4*sqrt(2)*x | Парабола | Линия |
| 5x^2+4xy+y^2-6x-2y+2=0 | x^2/(1/sqrt(2*sqrt(2)+3))^2 + y^2/(1/sqrt(-2*sqrt(2)+3))^2=0 | Вырожденный эллипс | Линия |
| 5*x^2+ 4*x*y+8*y^2+8*x+14*y+5=0 | x^2/(3/4)^2+y^2/(1/2)^2=1 | Эллипс |
Ислледование на определение вида кривой будет выглядеть примерно так:
Имеется два способа: Прямой метод и метод инвариантов:
Дано ур-ние кривой 2-порядка: $$5 x^{2} + 4 x y + 8 x + 8 y^{2} + 14 y + 5 = 0$$ Это уравнение имеет вид: $$a_{11} x^{2} + 2 a_{12} x y + 2 a_{13} x + a_{22} y^{2} + 2 a_{23} y + a_{33} = 0$$ где $$a_{11} = 5$$ $$a_{12} = 2$$ $$a_{13} = 4$$ $$a_{22} = 8$$ $$a_{23} = 7$$ $$a_{33} = 5$$ Вычислим определитель $$\Delta = \left|\begin{matrix}a_{11} & a_{12}\\a_{12} & a_{22}\end{matrix}\right|$$ или, подставляем $$\Delta = \left|\begin{matrix}5 & 2\\2 & 8\end{matrix}\right|$$ $$\Delta = 36$$ Т.к. $$\Delta$$ не равен 0, то находим центр канонической системы координат. Для решаем систему уравнений $$a_{11} x_{0} + a_{12} y_{0} + a_{13} = 0$$ $$a_{12} x_{0} + a_{22} y_{0} + a_{23} = 0$$ подставляем коэффициенты $$5 x_{0} + 2 y_{0} + 4 = 0$$ $$2 x_{0} + 8 y_{0} + 7 = 0$$ тогда $$x_{0} = — \frac{1}{2}$$ $$y_{0} = — \frac{3}{4}$$ Тем самым мы перешли к уравнению в системе координат O’x’y’ $$a’_{33} + a_{11} x’^{2} + 2 a_{12} x’ y’ + a_{22} y’^{2} = 0$$ где $$a’_{33} = a_{13} x_{0} + a_{23} y_{0} + a_{33}$$ или $$a’_{33} = 4 x_{0} + 7 y_{0} + 5$$ $$a’_{33} = — \frac{9}{4}$$ тогда ур-ние превратится в $$5 x’^{2} + 4 x’ y’ + 8 y’^{2} — \frac{9}{4} = 0$$ Делаем поворот системы полученной координат на угол φ $$x’ = \tilde x \cos{\left (\phi \right )} — \tilde y \sin{\left (\phi \right )}$$ $$y’ = \tilde x \sin{\left (\phi \right )} + \tilde y \cos{\left (\phi \right )}$$ φ — определяется из формулы $$\cot{\left (2 \phi \right )} = \frac{a_{11} — a_{22}}{2 a_{12}}$$ подставляем коэффициенты $$\cot{\left (2 \phi \right )} = — \frac{3}{4}$$ тогда $$\phi = — \frac{1}{2} \operatorname{acot}{\left (\frac{3}{4} \right )}$$ $$\sin{\left (2 \phi \right )} = — \frac{4}{5}$$ $$\cos{\left (2 \phi \right )} = \frac{3}{5}$$ $$\cos{\left (\phi \right )} = \sqrt{\frac{1}{2} \cos{\left (2 \phi \right )} + \frac{1}{2}}$$ $$\sin{\left (\phi \right )} = \sqrt{- \cos^{2}{\left (\phi \right )} + 1}$$ $$\cos{\left (\phi \right )} = \frac{2 \sqrt{5}}{5}$$ $$\sin{\left (\phi \right )} = — \frac{\sqrt{5}}{5}$$ подставляем коэффициенты $$x’ = \frac{2 \sqrt{5}}{5} \tilde x + \frac{\tilde y}{5} \sqrt{5}$$ $$y’ = — \frac{\tilde x}{5} \sqrt{5} + \frac{2 \sqrt{5}}{5} \tilde y$$ тогда ур-ние превратится из $$5 x’^{2} + 4 x’ y’ + 8 y’^{2} — \frac{9}{4} = 0$$ в $$8 \left(- \frac{\tilde x}{5} \sqrt{5} + \frac{2 \sqrt{5}}{5} \tilde y\right)^{2} + 4 \left(- \frac{\tilde x}{5} \sqrt{5} + \frac{2 \sqrt{5}}{5} \tilde y\right) \left(\frac{2 \sqrt{5}}{5} \tilde x + \frac{\tilde y}{5} \sqrt{5}\right) + 5 \left(\frac{2 \sqrt{5}}{5} \tilde x + \frac{\tilde y}{5} \sqrt{5}\right)^{2} — \frac{9}{4} = 0$$ упрощаем $$4 \tilde x^{2} + 9 \tilde y^{2} — \frac{9}{4} = 0$$ Данное уравнение является эллипсом $$\frac{\tilde x^{2}}{\left(\frac{3}{4}\right)^{2}} + \frac{\tilde y^{2}}{\left(\frac{1}{2}\right)^{2}} = 1$$ — приведено к каноническому виду.
Центр канонической системы координат в точке O:
(-1/2, -3/4)
Базис канонической системы координат $$\vec e_1 = \left ( \frac{2 \sqrt{5}}{5}, \quad — \frac{\sqrt{5}}{5}\right )$$ $$\vec e_2 = \left ( \frac{\sqrt{5}}{5}, \quad \frac{2 \sqrt{5}}{5}\right )$$
Метод инвариантов
Дано ур-ние линии 2-порядка: $$5 x^{2} + 4 x y + 8 x + 8 y^{2} + 14 y + 5 = 0$$ Это уравнение имеет вид: $$a_{11} x^{2} + 2 a_{12} x y + 2 a_{13} x + a_{22} y^{2} + 2 a_{23} y + a_{33} = 0$$ где $$a_{11} = 5$$ $$a_{12} = 2$$ $$a_{13} = 4$$ $$a_{22} = 8$$ $$a_{23} = 7$$ $$a_{33} = 5$$ Инвариантами данного уравнения при преобразовании координат являются определители: $$I_{1} = a_{11} + a_{22}$$
|a11 a12|
I2 = | |
|a12 a22|
$$I_{3} = \left|\begin{matrix}a_{11} & a_{12} & a_{13}\\a_{12} & a_{22} & a_{23}\\a_{13} & a_{23} & a_{33}\end{matrix}\right|$$ $$I{\left (\lambda \right )} = \left|\begin{matrix}a_{11} — \lambda & a_{12}\\a_{12} & a_{22} — \lambda\end{matrix}\right|$$
|a11 a13| |a22 a23|
K2 = | | + | |
|a13 a33| |a23 a33|
подставляем коэффициенты $$I_{1} = 13$$
|5 2|
I2 = | |
|2 8|
$$I_{3} = \left|\begin{matrix}5 & 2 & 4\\2 & 8 & 7\\4 & 7 & 5\end{matrix}\right|$$ $$I{\left (\lambda \right )} = \left|\begin{matrix}- \lambda + 5 & 2\\2 & — \lambda + 8\end{matrix}\right|$$
|5 4| |8 7|
K2 = | | + | |
|4 5| |7 5|
$$I_{1} = 13$$ $$I_{2} = 36$$ $$I_{3} = -81$$ $$I{\left (\lambda \right )} = \lambda^{2} — 13 \lambda + 36$$ $$K_{2} = 0$$ Т.к. $$I_{2} > 0 \wedge I_{1} I_{3} < 0$$ то по признаку типов линий:
данное уравнение имеет тип : эллипс.
Составляем характеристическое уравнение для нашей линии: $$- I_{1} \lambda + I_{2} + \lambda^{2} = 0$$ или $$\lambda^{2} — 13 \lambda + 36 = 0$$ $$\lambda_{1} = 9$$ $$\lambda_{2} = 4$$ тогда канонический вид уравнения будет $$\tilde x^{2} \lambda_{1} + \tilde y^{2} \lambda_{2} + \frac{I_{3}}{I_{2}} = 0$$ или $$9 \tilde x^{2} + 4 \tilde y^{2} — \frac{9}{4} = 0$$ $$\frac{\tilde x^{2}}{\left(\frac{1}{2}\right)^{2}} + \frac{\tilde y^{2}}{\left(\frac{3}{4}\right)^{2}} = 1$$ — приведено к каноническому виду.