НОД и НОК
Продолжаем изучать деление. В данном уроке мы рассмотрим такие понятия, как НОД и НОК.
НОД — это наибольший общий делитель.
НОК — это наименьшее общее кратное.
Тема довольно скучная, но разобраться в ней нужно обязательно. Не понимая этой темы, не получится эффективно работать с дробями, которые являются настоящей преградой в математике.
Наибольший общий делитель
Определение. Наибольшим общим делителем чисел a и b называется наибольшее число, на которое a и b делятся без остатка.
Чтобы хорошо понять это определение, подставим вместо переменных a и b любые два числа. Например, вместо переменной a подставим число 12, а вместо переменной b — число 9. Теперь попробуем прочитать это определение:
Наибольшим общим делителем чисел 12 и 9 называется наибольшее число, на которое 
Из определения понятно, что речь идёт об общем делителе чисел 12 и 9. Причем делитель является наибольшим из всех существующих делителей. Этот наибольший общий делитель (НОД) нужно найти.
Для нахождения наибольшего общего делителя двух чисел, используется три способа. Первый способ довольно трудоёмкий, но зато позволяет хорошо понять суть темы и прочувствовать весь ее смысл.
Второй и третий способы довольны просты и дают возможность быстро найти НОД. Рассмотрим все три способа. А какой применять на практике — выбирать вам.
Первый способ заключается в поиске всех возможных делителей двух чисел и в выборе наибольшего из них. Рассмотрим этот способ на следующем примере: найти наибольший общий делитель чисел 12 и 9.
Сначала найдём все возможные делители числа 12. Для этого разделим 12 на все делители в диапазоне от 1 до 12. Если делитель позволит разделить 12 без остатка, то мы будем выделять его синим цветом и в скобках делать соответствующее пояснение.
12 : 1 = 12
(12 разделилось на 1 без остатка, значит 1 является делителем числа 12)
12 : 2 = 6
(12 разделилось на 2 без остатка, значит 2 является делителем числа 12)
12 : 3 = 4
(12 разделилось на 3 без остатка, значит 3 является делителем числа 12)
12 : 4 = 3
(12 разделилось на 4 без остатка, значит 4 является делителем числа 12)
12 : 5 = 2 (2 в остатке)
(12 не разделилось на 5 без остатка, значит 5 не является делителем числа 12)
12 : 6 = 2
(12 разделилось на 6 без остатка, значит 6 является делителем числа 12)
12 : 7 = 1 (5 в остатке)
(12 не разделилось на 7 без остатка, значит 7 не является делителем числа 12)
12 : 8 = 1 (4 в остатке)
(12 не разделилось на 8 без остатка, значит 8 не является делителем числа 12)
12 : 9 = 1 (3 в остатке)
(12 не разделилось на 9 без остатка, значит 9 не является делителем числа 12)
12 : 10 = 1 (2 в остатке)
(12 не разделилось на 10 без остатка, значит 10 не является делителем числа 12)
12 : 11 = 1 (1 в остатке)
(12 не разделилось на 11 без остатка, значит 11 не является делителем числа 12)
12 : 12 = 1
(12 разделилось на 12 без остатка, значит 12 является делителем числа 12)
Теперь найдём делители числа 9. Для этого проверим все делители от 1 до 9
Для этого проверим все делители от 1 до 9
9 : 1 = 9
(9 разделилось на 1 без остатка, значит 1 является делителем числа 9)
9 : 2 = 4 (1 в остатке)
(9 не разделилось на 2 без остатка, значит 2 не является делителем числа 9)
9 : 3 = 3
(9 разделилось на 3 без остатка, значит 3 является делителем числа 9)
9 : 4 = 2 (1 в остатке)
(9 не разделилось на 4 без остатка, значит 4 не является делителем числа 9)
9 : 5 = 1 (4 в остатке)
(9 не разделилось на 5 без остатка, значит 5 не является делителем числа 9)
9 : 6 = 1 (3 в остатке)
(9 не разделилось на 6 без остатка, значит 6 не является делителем числа 9)
9 : 7 = 1 (2 в остатке)
(9 не разделилось на 7 без остатка, значит 7 не является делителем числа 9)
9 : 8 = 1 (1 в остатке)
(9 не разделилось на 8 без остатка, значит 8 не является делителем числа 9)
9 : 9 = 1
(9 разделилось на 9 без остатка, значит 9 является делителем числа 9)
Теперь выпишем делители обоих чисел. Числа выделенные синим цветом и являются делителями. Их и выпишем:
Числа выделенные синим цветом и являются делителями. Их и выпишем:
Выписав делители, можно сразу определить какой является наибольшим и общим.
Согласно определению, наибольшим общим делителем чисел 12 и 9, является число, на которое 12 и 9 делятся без остатка. Наибольшим и общим делителем чисел 12 и 9 является число 3
И число 12 и число 9 делятся на 3 без остатка:
12 : 3 = 4
9 : 3 = 3
Значит НОД (12 и 9) = 3
Второй способ нахождения НОД
Теперь рассмотрим второй способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, чтобы разложить оба числа на простые множители и перемножить общие из них.
Пример 1. Найти НОД чисел 24 и 18
Сначала разложим оба числа на простые множители:
Теперь перемножим их общие множители. Чтобы не запутаться, общие множители можно подчеркнуть.
Смотрим на разложение числа 24. Первый его множитель это 2. Ищем такой же множитель в разложении числа 18 и видим, что он там тоже есть.
Снова смотрим на разложение числа 24. Второй его множитель тоже 2. Ищем такой же множитель в разложении числа 18 и видим, что его там второй раз уже нет. Тогда ничего не подчёркиваем.
Следующая двойка в разложении числа 24 также отсутствует в разложении числа 18.
Переходим к последнему множителю в разложении числа 24. Это множитель 3. Ищем такой же множитель в разложении числа 18 и видим, что там он тоже есть. Подчеркиваем обе тройки:
Итак, общими множителями чисел 24 и 18 являются множители 2 и 3. Чтобы получить НОД, эти множители необходимо перемножить:
2 × 3 = 6
Значит НОД (24 и 18) = 6
Третий способ нахождения НОД
Теперь рассмотрим третий способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, что числа подлежащие поиску наибольшего общего делителя раскладывают на простые множители. Затем из разложения первого числа вычеркивают множители, которые не входят в разложение второго числа.
Пример 1. Найти НОД чисел 28 и 16.
В первую очередь, раскладываем числа 28 и 16 на простые множители:
Получили два разложения: и
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит семёрка. Её и вычеркнем из первого разложения:
Теперь перемножаем оставшиеся множители и получаем НОД:
Число 4 является наибольшим общим делителем чисел 28 и 16. Оба этих числа делятся на 4 без остатка:
28 : 4 = 7
16 : 4 = 4
НОД (28 и 16) = 4
Пример 2. Найти НОД чисел 100 и 40
Раскладываем на множители число 100
Раскладываем на множители число 40
Получили два разложения: 2 × 2 × 5 × 5 и 2 × 2 × 2 × 5
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа.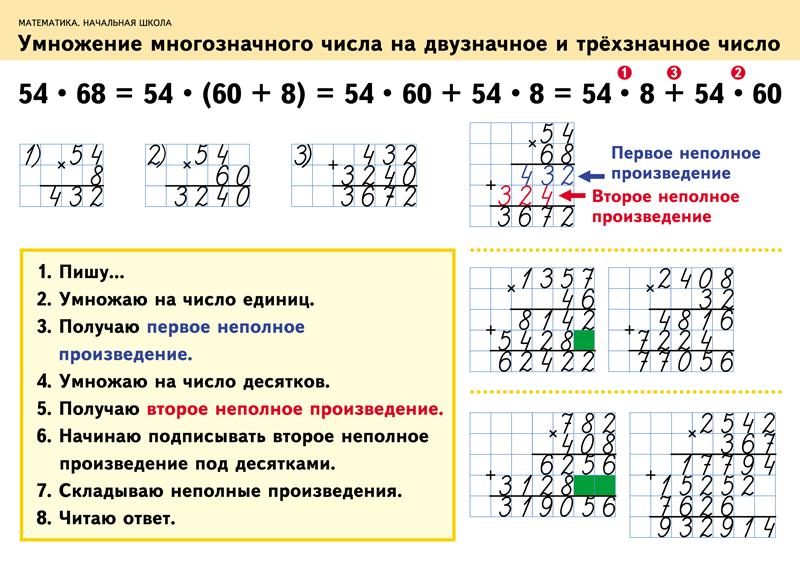 В разложение второго числа не входит одна пятерка (там только одна пятёрка). Её и вычеркнем из первого разложения
В разложение второго числа не входит одна пятерка (там только одна пятёрка). Её и вычеркнем из первого разложения
Перемножим оставшиеся числа:
Получили ответ 20. Значит число 20 является наибольшим общим делителем чисел 100 и 40. Эти два числа делятся на 20 без остатка:
100 : 20 = 5
40 : 20 = 2
НОД (100 и 40) = 20.
Пример 3. Найти НОД чисел 72 и 128
Раскладываем на множители число 72
Раскладываем на множители число 128
Получили два разложения: 2 × 2 × 2 × 3 × 3 и 2 × 2 × 2 × 2 × 2 × 2 × 2.
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входят две тройки (там их вообще нет). Их и вычеркнем из первого разложения:
Перемножим оставшиеся числа:
Получили ответ 8. Значит число 8 является наибольшим общим делителем чисел 72 и 128. Эти два числа делятся на 8 без остатка:
72 : 8 = 9
128 : 8 = 16
НОД (72 и 128) = 8
Нахождение НОД для нескольких чисел
Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.
Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.
Например, найдём НОД для чисел 18, 24 и 36
Разложим на множители число 18
Разложим на множители число 24
Разложим на множители число 36
Получили три разложения:
Теперь найдём и подчеркнём общие множители:
Мы видим, что общие множители для чисел 18, 24 и 36 это множители 2 и 3. Эти множители входят во все три разложения. Перемножив эти множители, мы получим НОД, который ищем:
2 × 3 = 6
Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 18, 24 и 36. Эти три числа делятся на 6 без остатка:
18 : 6 = 3
24 : 6 = 4
36 : 6 = 6
НОД (18, 24 и 36) = 6
Пример 2. Найти НОД для чисел 12, 24, 36 и 42
Разложим на простые множители каждое число. Затем найдём произведение общих простых множителей.
Разложим на множители число 12
Разложим на множители число 24
Разложим на множители число 36
Разложим на множители число 42
Получили четыре разложения:
Теперь найдём и подчеркнём общие множители:
Мы видим, что общие множители для чисел 12, 24, 36, и 42 это множители 2 и 3. Перемножив эти множители, мы получим НОД, который ищем:
2 × 3 = 6
Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 12, 24, 36 и 42. Эти числа делятся на 6 без остатка:
12 : 6 = 2
24 : 6 = 4
36 : 6 = 6
42 : 6 = 7
НОД (12, 24 , 36 и 42) = 6
Наименьшее общее кратное
Из предыдущего урока мы знаем, что если какое-то число без остатка разделилось на другое, его называют кратным этого числа.
Оказывается, кратное может быть общим у нескольких чисел. И сейчас нас будет интересовать кратное двух чисел, причем оно должно быть максимально маленьким.
Определение. Наименьшее общее кратное (НОК) чисел a и b — это наименьшее число, которое кратно a и b. Другими словами, это такое маленькое число, которое делится без остатка на число a и число b.
Определение содержит две переменные a и b. Давайте подставим вместо этих переменных любые два числа. Например, вместо переменной a подставим число 9, а вместо переменной b подставим число 12. Теперь попробуем прочитать определение:
Наименьшее общее кратное (НОК) чисел 9 и 12 — это наименьшее число, которое кратно 9 и 12. Другими словами, это такое маленькое число, которое делится без остатка на число 9 и на число 12.
Из определения понятно, что наименьшее общее кратное это наименьшее число, которое делится без остатка на 9 и на 12. Это наименьшее общее кратное требуется найти.
Для нахождения наименьшего общего кратного (НОК) можно пользоваться тремя способами. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.
Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.
В первую очередь, найдем первые кратные для числа 9. Чтобы найти кратные для 9, нужно эту девятку поочерёдно умножить на числа от 1 до 9. Получаемые ответы будут кратными для числа 9.
Итак, начнём. Кратные будем выделять синим цветом:
Теперь находим кратные для числа 12. Для этого поочерёдно умножим число 12 на все числа 1 до 12:
Теперь выпишем кратные обоих чисел:
Теперь найдём общие кратные обоих чисел. Найдя, сразу подчеркнём их:
Общими кратными для чисел 9 и 12 являются кратные 36 и 72. Наименьшим же из них является 36.
Значит наименьшее общее кратное для чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:
36 : 9 = 4
36 : 12 = 3
НОК (9 и 12) = 36
Второй способ нахождения НОК
Второй способ заключается в том, что числа для которых ищется наименьшее общее кратное раскладываются на простые множители. Затем выписываются множители, входящие в первое разложение, и добавляют недостающие множители из второго разложения. Полученные множители перемножают и получают НОК.
Затем выписываются множители, входящие в первое разложение, и добавляют недостающие множители из второго разложения. Полученные множители перемножают и получают НОК.
Применим данный способ для предыдущей задачи. Найдём НОК для чисел 9 и 12.
Разложим на множители число 9
Разложим на множители число 12
Выпишем первое разложение:
Теперь допишем множители из второго разложения, которых нет в первом разложении. В первом разложении нет двух двоек. Их и допишем:
Теперь перемножаем эти множители:
Получили ответ 36. Значит наименьшее общее кратное чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:
36 : 9 = 4
36 : 12 = 3
НОК (9 и 12) = 36
Говоря простым языком, всё сводится к тому, чтобы организовать новое разложение куда входят оба разложения сразу. Разложением первого числа 9 являлись множители 3 и 3, а разложением второго числа 12 являлись множители 2, 2 и 3.
Наша задача состояла в том, чтобы организовать новое разложение куда входило бы разложение числа 9 и разложение числа 12 одновременно. Для этого мы выписали разложение первого числа и дописали туда множители из второго разложения, которых не было в первом разложении. В результате получили новое разложение 3 × 3 × 2 × 2. Нетрудно увидеть воочию, что в него одновременно входят разложение числа 9 и разложение числа 12
Пример 2. Найти НОК чисел 50 и 180
Разложим на множители число 50
Разложим на множители число 180
Выпишем первое разложение:
Теперь допишем множители из второго разложения, которых нет первом разложении. В первом разложении нет ещё одной двойки и двух троек. Их и допишем:
Теперь перемножаем эти множители:
Получили ответ 900. Значит наименьшее общее кратное чисел 50 и 180 это число 900. Данное число делится на 50 и 180 без остатка:
900 : 50 = 18
900 : 180 = 5
НОК (50 и 180) = 900
Пример 3. Найти НОК чисел 8, 15 и 33
Найти НОК чисел 8, 15 и 33
Разложим на множители число 8
Разложим на множители число 15
Разложим на множители число 33
Выпишем первое разложение:
Теперь допишем множители из второго и третьего разложения, которых нет первом разложении. Допишем множители 3 и 5 из второго разложения, и множитель 11 из третьего разложения:
Теперь перемножаем эти множители:
Получили ответ 1320. Значит наименьшее общее кратное чисел 8, 15 и 33 это число 1320. Данное число делится на 8, 15 и 33 без остатка:
1320 : 8 = 165
1320 : 15 = 88
1320 : 33 = 40
НОК (8, 15 и 33) = 1320
Третий способ нахождения НОК
Есть и третий способ нахождения наименьшего общего кратного. Он работает при условии, что его ищут для двух чисел и при условии, что уже найден наибольший общий делитель этих чисел.
Данный способ разумнее использовать, когда одновременно нужно найти НОД и НОК двух чисел.
К примеру, пусть требуется найти НОД и НОК чисел 24 и 12. Сначала найдем НОД этих чисел:
Теперь для нахождения наименьшего общего кратного чисел 24 и 12, нужно перемножить эти два числа и полученный результат разделить на их наибольший общий делитель.
Итак, перемножим числа 24 и 12
Разделим полученное число 288 на НОД чисел 24 и 12
Получили ответ 24. Значит наименьшее общее кратное чисел 24 и 12 равно 24
НОК (24 и 12) = 24
Пример 2. Найти НОД и НОК чисел 36 и 48
Найдем НОД чисел 36 и 48
Перемножим числа 36 и 48
Разделим 1728 на НОД чисел 36 и 48
Получили 144. Значит наименьшее общее кратное чисел 36 и 48 равно 144
НОК (36 и 48) = 144
Для проверки можно найти НОК обычным вторым способом, которым мы пользовались ранее. Если мы всё сделали правильно, то должны получить 144
Не расстраивайтесь, если сразу не научитесь находить НОД и НОК. Главное понимать, что это такое и как оно работает. А ошибки вполне естественны на первых порах. Как говорят: «На ошибках учимся».
Главное понимать, что это такое и как оно работает. А ошибки вполне естественны на первых порах. Как говорят: «На ошибках учимся».
Задания для самостоятельного решения
Задание 1. Найдите НОД чисел 12 и 16
Решение:
Задание 2. Найдите НОК чисел 12 и 16
Решение:
Задание 3. Найдите НОД чисел 40 и 32
Решение:
Задание 4. Найдите НОК чисел 40 и 32
Решение:
Задание 5. Найдите НОД чисел 54 и 86
Решение:
Задание 6. Найдите НОК чисел 54 и 86
Решение:
Задание 7. Найдите НОД чисел 98 и 35
Решение:
Задание 8. Найдите НОК чисел 98 и 35
Решение:
Задание 9. Найдите НОД чисел 112 и 82
Решение:
Задание 10. Найдите НОК чисел 112 и 82
Решение:
Задание 11. Найдите НОД чисел 24, 48, 64
Решение:
Задание 12. Найдите НОК чисел 24, 48, 64
Решение:
Задание 13. Найдите НОД чисел 18, 48, 96
Найдите НОД чисел 18, 48, 96
Решение:
Задание 14. Найдите НОК чисел 18, 48, 96
Решение:
Задание 15. Найдите НОД чисел 28, 24, 76
Решение:
Задание 16. Найдите НОК чисел 28, 24, 76
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
как научиться работе с цифрами
Этого не должно было случиться, но почему-то произошло: 11 класс остался в далеком прошлом, а вы стали вовсе не художником или рок-звездой, а интернет-маркетологом. И школьная учительница оказалась права: математика еще пригодится, вот увидишь!
Где учиться цифрам с нуля, как не сойти с ума от цифр и почему в школе было так сложно (а сейчас легче не станет).
Почему математика такая страшная
В любой вещи, которую вы не понимаете, мало приятного. Но математику особенно не любят. Или даже боятся ее.
Дело не только в том, что у учительницы по алгебре был слишком грозный вид. Математическая тревожность — явление, которое исследуют ученые. И под тревожностью имеют в виду все ее проявления: панику, дрожь в руках. Непонятно, что появляется раньше: неспособности к математике и, как следствие, страх перед ней или же сам страх не дает научиться вычислениям.
Хорошая новость в том, что математическая тревожность слабо коррелирует с результатами тестов IQ.
Что мы знаем про способности к математике
Наверняка вы говорили о себе: «У меня нет математических способностей». И вообще закончили гуманитарный класс.
Большинство ученых с вами согласятся, но лишь потому, что в принципе не доказано существование врожденных способностей к математике. Исследователи много лет пытаются узнать о наследуемости этого навыка. Пока одним из самых громких за последнее время стала работа ученых из университета Питтсбурга (США). Они доказали, что есть корреляция между способностями к математике у детей и родителей. Но ее причина — не только в генетике, но и в социальных факторах.
Пока одним из самых громких за последнее время стала работа ученых из университета Питтсбурга (США). Они доказали, что есть корреляция между способностями к математике у детей и родителей. Но ее причина — не только в генетике, но и в социальных факторах.
Кроме способностей к математике, существует математическое чувство, и оно наследуется. Это благодаря ему мы определяем самую короткую очередь, не считая количество людей. Ученые из США сравнили, как дети в шесть месяцев и три с половиной года воспринимают цифры и количество предметов. Оказалось, что малыши, которые в раннем возрасте демонстрировали лучшие математические способности, показали лучший результат и спустя три года, причем общий уровень развития не коррелировал с математическими способностями.
Но выдыхать рано (вы наверняка уже решили, что оказались бы в этом эксперименте среди детей с заурядными результатами). Другая группа исследователей проверила, можно ли развить математические способности и научиться работе с цифрами во взрослом возрасте. Оказалось, что можно. Добровольцы решали задачи, а затем половина участников эксперимента тренировали математические навыки, а контрольная группа — нет, как и полагается контрольной группе. После этого все участники снова решили арифметические примеры. Занимавшаяся математикой группа показала результаты гораздо выше, чем контрольная.
Оказалось, что можно. Добровольцы решали задачи, а затем половина участников эксперимента тренировали математические навыки, а контрольная группа — нет, как и полагается контрольной группе. После этого все участники снова решили арифметические примеры. Занимавшаяся математикой группа показала результаты гораздо выше, чем контрольная.
Как выучить математику во взрослом возрасте
Сначала решите, для чего вам нужна математика, какие темы нужно знать и как вы оцените, что цель выполнена. Для повседневной работы в маркетинге вам вряд ли понадобятся линал или понимание задач тысячелетия. Быстрое вычисление, работа с процентами, понимание математических функций.
Полезные курсы по математике
Проект «Математика с нуля»
Текстовые уроки по основным темам.
Интернет-Урок:
(Математика, 1-6 класс)
(Алгебра, 7-11 класс)
Уроки школьной программы по математике в формате видео. Рассчитаны на детей и подростков, но разве это вас остановит?
Stepik.
 Основы статистики
Основы статистики На практике пригодится чаще, чем основы по математике. Если вы не помните из статистики ничего, пройдите курс перед изучением веб-аналитики.
Stepik. Теория вероятностей
Курс по теории вероятностей посвящен базовым вероятностным методам, которые можно использовать в работе и повседневной жизни.
Открытый университет. Теория игр
Теория игр полезна для многих специальностей. Развивает способность к анализу информации, постановке целей и созданию стратегий.
Вводный курс по матанализу
Если вы уже готовы к высшей математике, но плохо помните университетскую программу.
Khana Academy
Курсы разделены темам и по уровням. Дается сразу теория и тренажер, обучение геймифицировано. Уроки только на английском языке.
Книги по изучению математики с нуля
http://www.alleng.ru/
Подборка школьных учебников, если скучаете по ним.
Математика для взрослых.
 Кьяртан Поскитт
Кьяртан ПоскиттНе научит теории, но избавит от ежедневных страданий, когда нужно сделать простые вычисления.
Если вы аналитик и занимаетесь, например, аналитикой в Instagram или других соцсетях удобней всего использовать Popsters.
Итого:
- Многие люди и правда боятся математику. Ученые не понимают: страх из-за незнания или незнание от страха.
- Чувство числа наследуется от родителей. А вот математические способности можно развить.
- Взрослые люди могут с нуля выучить математику. Для этого есть бесплатные курсы и книги.
Узнаем как выучить математику с нуля самостоятельно?
Математика наравне с родным языком является одной из самых главных наук, и не только в школе. Зачастую без нее не обойтись ни в повседневной жизни, ни в карьере. Кроме того, математику необходимо сдавать в выпускных классах. Но как быть, если все упущено? Давайте разберемся, как выучить эту науку самостоятельно, да еще и с нуля, и подготовиться к экзаменам.
Эта статья будет полезна также тому, кто давно окончил школу, но есть желание поступить в колледж или вуз по технической специальности. В этом случае тоже нужно постигать математику с азов или же подтянуть знания в тех темах, которые были не понятны при учебе или попросту забыты.
Предлагаем воспользоваться приведенными ниже инструкциями. Но обращаем внимание: успех полностью зависит от самого учащегося.
Моральная подготовка
Прежде чем приступить к изучению математики, следует морально подготовиться. Особенно это касается тех, кому данный предмет в школе практически не давался. Ведь бывает так, что у человека не математический, а гуманитарный склад ума.
Ниже мы обсудим, что делать, если не получается разобраться в одной из тем. Но в любом случае нужно быть готовым к долгому изучению, ибо быстро выучить математику на самом деле практически невозможно.
Моральная подготовка заключается в том, чтобы:
- Постараться дать себе понять, что при желании можно изучить любую науку.
 Ведь как-то отличники и хорошисты разбираются в дисциплине. Тем более если учитель говорит, что это легкая тема, то стоит поверить.
Ведь как-то отличники и хорошисты разбираются в дисциплине. Тем более если учитель говорит, что это легкая тема, то стоит поверить. - На время отложить развлечения, общение с друзьями и различные мероприятия, которые не столь важны, ради того чтобы подтянуть знания по царице всех наук. Пусть основная часть времени будет посвящена изучению непонятных тем.
- Перед началом занятий дать себе хорошенько отдохнуть. Например, погулять на свежем воздухе в парке, выполнить несколько физических упражнений или неотложных дел. Ибо очень важно, чтобы никакие заботы и просьбы со стороны не отвлекали.
- Настроиться на тренировку памяти с целью запомнить правила и формулы. Они на самом деле не такие сложные, как кажется.
- Понять, что математика по большей части требует от человека логического мышления и смекалки.
- Воспринимать науку не как что-то должное, а как игру в головоломку, в которой нужно пройти конкретные этапы и проверить «запасным вариантом» правильность решения задачи.

- Убедить себя в том, что тренировка на запоминание полезна для мозга.
- Понять, что решение многих задач и примеров, построение фигур и графиков, а также различные геометрические доказательства – это увлекательный процесс, который можно применить на практике.
Пусть подобные рекомендации станут для вас помощниками каждый раз, когда вам захочется оставить изучение сложных тем. Оказывается, не так уж и сложно выучить математику с нуля.
Оценка своих знаний
Очень важно уметь оценить свои знания. Например, вы являетесь учеником 9 класса, или же на данный момент лето, и стоит цель хорошо подучить пропущенные и непонятые ранее темы. В таком случае делаем так: открываем учебник 5-го класса, находим любую сложную задачу и решаем ее. Если ответ правильный, то с легкостью приступаем к задачам за 6-й класс и проверяем себя по ним. Желательно прорешать по паре заданий из каждой темы.
А теперь разберем, как быстро выучить правила математики.
Обязательно найдется такая задача, которую вы затруднитесь решить. Например, тема связана с квадратными уравнениями, но пример дан в виде двух произведений со скобками, которые нужно раскрыть. А вы забыли правила раскрытия скобок, вследствие чего ответ неправильный, проверочное решение не сходится. Стоит в таком случае отметить в отдельном листе-плане, что нужно разобраться, в каком случае ставится знак «+», а в каком «–» при раскрытии скобок. Также следует проработать и остальные темы.
Например, тема связана с квадратными уравнениями, но пример дан в виде двух произведений со скобками, которые нужно раскрыть. А вы забыли правила раскрытия скобок, вследствие чего ответ неправильный, проверочное решение не сходится. Стоит в таком случае отметить в отдельном листе-плане, что нужно разобраться, в каком случае ставится знак «+», а в каком «–» при раскрытии скобок. Также следует проработать и остальные темы.
Немного геометрии
Что касается геометрии, то ее тоже следует начинать изучать сначала, чтобы понять, что такое фигуры, теоремы, как вообще работать в данной дисциплине.
Но как выучить математику за короткий срок, если практически все темы непонятны или незнакомы, и возможно ли это? Вот несколько рекомендаций.
Если многое упущено
Стоит ли говорить о том, что математику с нуля лучше всего разбирать с репетитором или родственником, одноклассником? Самому изучить этот предмет довольно сложно, особенно по сравнению с историей или географией. Но тем не менее, если есть много свободного времени, можно пробовать решать примеры самостоятельно. Возможно, для этого придется детально изучить более простые темы, которые в основном входят в программу 5-го класса.
Но тем не менее, если есть много свободного времени, можно пробовать решать примеры самостоятельно. Возможно, для этого придется детально изучить более простые темы, которые в основном входят в программу 5-го класса.
Теперь составим план наших действий:
- Приобретите учебники и решебники за все классы средней школы. Программа должна соответствовать тому, что вы изучаете в школе.
- Составьте список всех тем, которые имеются.
- Подготовьте чистую тетрадь для решения задач. Не рекомендуется решать примеры на клочках бумаги, пусть все проведенные действия будут перед глазами, даже если они с помарками и ошибками.
- Если у вас сохранились конспекты с пройденными уроками и решенными в классе примерами, обязательно проработайте их. Выпишите в тетрадь задачку, затем закройте конспект, начните решать самостоятельно. Как закончите, сверьтесь, что вы сделали правильно, а что не так.
- Выучите правило и формулы по текущей теме. Помните о том, что математика не «любит» зубрить, она «любит» понимать определение.

Такой подход поможет самостоятельно выучить математику. Как запомнить все и сразу? На самом деле этого делать не нужно.
Лучший способ запомнить
Как было сказано выше, обычное зазубривание не поможет. Нужно разобраться. Допустим, у вас тема связана с нахождением определения объема фигур в геометрии. Эти формулы довольно простые, их легко запомнить. Но чтобы лучше усвоить урок, желательно, следуя формуле, решить задачу. Заодно вы заметите последовательность: что от чего зависит и как выводится. Например, элементарное нахождение площади прямоугольника: умножаем длины двух сторон, не лежащих параллельно. И все, задача решена. Куда сложнее определить площадь круга или объем цилиндра, но если запомнить формулы, то и это не составит труда.
А как выучить математические правила, если они с формулами не связаны? Все довольно просто. Например, то же раскрытие скобок. Нужно лишь запомнить, что «умножение минуса на минус дает плюс, а умножение минуса на плюс (и наоборот) всегда дает минус». И все. В дальнейшем решить даже самые сложные задачи на раскрытие скобок будет получаться на раз-два!
И все. В дальнейшем решить даже самые сложные задачи на раскрытие скобок будет получаться на раз-два!
Успешное освоение
Полученные знания всегда следует закреплять. Вы запомнили формулу дискриминанта или заучили последовательность нахождения неизвестной через построение графиков. Обязательно прорешайте различные примеры на эту тему еще и еще, чтобы отложилось все в памяти.
Учителя, да и репетиторы, рекомендуют время от времени возвращаться к пройденной теме, чтобы проверить себя. Это, на самом деле, отнимет несколько минут. Наверняка вы замечали, что те, кто успевает по математике, способны за 15-20 минут сдать работу, которая рассчитана на полчаса. Что здесь удивительного? Просто тема была освоена достаточно хорошо и не нужно долго ломать голову, вспоминать формулы или пытаться спросить у соседа.
Как выучить математику за 5 минут до контрольной, и возможно ли это? Разумеется, если предыдущие разделы освоены хорошо, а нынешний не изучен по каким-то причинам, то можно пробежаться по правилам и формулам. Но успех будет лишь в том случае, если тема логически продолжает ранее изученные.
Но успех будет лишь в том случае, если тема логически продолжает ранее изученные.
Не дается и все тут
К сожалению, большинство учащихся не могут разобраться в науке ни в классе, ни самостоятельно. Нужно, чтобы тему объяснили отдельно. Зачастую приходится прибегать к помощи репетитора.
Но есть возможность выучить математику с нуля самостоятельно и бесплатно. Естественно, с помощью вездесущего интернета:
- видеоуроки на YouTube,
- ознакомительные курсы на математических сайтах,
- онлайн-репетитор.
Таким образом, можно найти способ без лишних затрат разобраться в теме. Существует множество видеоуроков на отдельно взятые темы, которые легко изучить, посмотрев, как правильно и в какой последовательности решаются задачи. Желательно повторить пройденный урок самостоятельно.
Если тема очень сложная
В математике сложных тем достаточно много, особенно в 9, 10 и 11 классах. Зачастую без помощи знающих людей не обойтись. Поэтому стоит внимательно слушать урок, чтобы не возникло проблем в будущем.
Ведь даже самая сложная тема поддается объяснению и пониманию. Только нужно тренировать в себе усидчивость, терпение и желание учиться. Ведь неспроста это слово означает «учи себя». Многие ученики ближе к выпускным экзаменам спрашивают, как выучить математику, чтобы балл был высокий. Все просто: готовиться следует заранее (прорабатывать все темы и решать предлагающиеся задачи).
Необходимые инструменты для работы
Многие учителя настоятельно требуют, чтобы ученики запоминали таблицу умножения, учились считать в уме и обходились без калькуляторов насколько это возможно. Действительно, существовала же как-то математика без электронно-вычислительной техники? Были счеты, но они только развивали мышление. А современные гаджеты, наоборот, ослабляют мыслительную деятельность и ухудшают запоминание. Поэтому современному школьнику лучше позаботиться заранее о том, как выучить математику, а точнее арифметику, чтобы в будущем было проще решать любые задачи без помощи калькулятора.
Как видите, математика – сложная наука, требующая усидчивости. Быстро выучить ее не удастся. Поэтому желательно изучать внимательно каждую тему начиная с младших классов.
Как изучать математику | Фоксфорд.Медиа
Слово «математика» происходит от греческого «матема» — знание, познание. Математика, как и шахматы — это способ научиться думать логически, рационально. Особенность математики в том, что её методы служат другим наукам. Например, в социологии и психологии данные опросов обрабатываются статистически. В генетике анализируют распределение признаков с помощью сложных моделей расчёта.
Одни называют математику точной наукой, другие — искусством. Каждый даёт определение в силу своего математического опыта и фантазии. Если человек научился складывать целые положительные числа в пределах сотни, то он будет считать математику точной наукой. При этом те, кто знаком с комплексными числами и неевклидовой геометрией, с ним не согласятся.
Определение математики зависит от отношения к ней. Для тех, кому на уроках было сложно и скучно, она сухая и точная. Влюблённые в математику воспринимают её как искусство. Хорошая новость в том, что строить хорошие отношения с математикой никогда не поздно, если ученик хочет в ней разбираться.
Для тех, кому на уроках было сложно и скучно, она сухая и точная. Влюблённые в математику воспринимают её как искусство. Хорошая новость в том, что строить хорошие отношения с математикой никогда не поздно, если ученик хочет в ней разбираться.
Зачем нужна математика и что значит «знать» её
Кое-что из математики используется в повседневной жизни: когда нужно поделить пиццу на 8 равных частей, посчитать стоимость товара со скидкой 20%, выбрать сумку к новым туфлям и брюкам. По мнению математика и педагога Марис Сегинёвой, обычному человеку для жизни достаточно изучить математику в объёме 5—7 класса школьной программы:
«Всё зависит от того, в какой момент в учебнике появляются отрицательные числа. Конечно, можно увидеть на термометре значение минус 10 градусов Цельсия, но вот в США пользуются шкалой Фаренгейта, а вообще кроме погоды в быту эти знания не пригодятся».
Для наглядности — в чём разница между шкалой Цельсия и Фаренгейта
В математике выделяют несколько областей знания, и то, что изучается в большинстве начальных школ правильнее называть арифметикой. Это раздел математики, который изучает числа и действия с ними: сложение, вычитание, умножение и деление целых и дробных чисел.
Это раздел математики, который изучает числа и действия с ними: сложение, вычитание, умножение и деление целых и дробных чисел.
«Если школьник знает математику, у него и с другими предметами будет хорошо. Он научился думать, он научился видеть целое и собирать его из частей. Обратно этот принцип не работает: если ученик успешен в других предметах, нет гарантий, что он поймёт и математику», — Марис Сегинёва.
Редко в начальном курсе математики встречаются задачи на комбинаторику, логику и теорию вероятностей. Поэтому для большинства людей «знать математику» — значит уметь применить расчёты для решения житейских задач: сколько нужно продуктов, чтобы приготовить в два раза больше окрошки; какую сумму нужно сдать на общий подарок имениннику; во сколько выезжать из дома, чтобы приехать к началу спектакля.
Для чего изучают математику в старших классах
По замыслу разработчиков образовательной программы выпускники школы поступают в вузы. В вузах они осваивают профессии для того, чтобы стать практиками или исследователями в различных областях. Специалистам технических и естественнонаучных областей математика полезна, а учёным — необходима.
В вузах они осваивают профессии для того, чтобы стать практиками или исследователями в различных областях. Специалистам технических и естественнонаучных областей математика полезна, а учёным — необходима.
Марис Сегинёва: «Современная наука основана на математических методах. Когда абитуриент думает, что будет заниматься микробиологией, генетикой, психологией, социологией, лингвистикой или экономикой, в конечном счёте ему придётся заниматься и математикой тоже».
Авторы школьных учебников не знают, кто именно из выпускников станет учителем литературы, кто музейным работником, а кто программистом, поэтому на всякий случай все старшеклассники знакомятся с алгеброй и началами математического анализа.
Решать задачи с логарифмами и брать производные будет полезно любому ученику общеобразовательной школы. Будущим инженерам и математикам уроки будут подспорьем, поскольку школьная алгебра — мостик от арифметики к высшей математике, которую изучают в вузе.
Тем, кто выбрал сдавать профильный ЕГЭ по математике, лучше не останавливаться и решать задачи при каждом удобном случае. Будущим историкам, художникам и музыкантам стоит как можно скорее изучить демовариант базового ЕГЭ по математике, чтобы знать, какие темы изучать пристально, а какими можно будет пренебречь.
Будущим историкам, художникам и музыкантам стоит как можно скорее изучить демовариант базового ЕГЭ по математике, чтобы знать, какие темы изучать пристально, а какими можно будет пренебречь.
С чего начать отношения с математикой
Древнеегипетские жрецы умели умножать только на два, и считались очень продвинутыми. А в Средние века математики собирались в городе Пиза на конкурс деления чисел, записанных римскими цифрами. Соревновались, например, кто быстрее правильно поделит число LXXIV пополам.
Сейчас, благодаря десятичной системе счисления и приёмам работы с числами, обычный третьеклассник даст фору средневековым преподавателям. Но когда-то не было большей части того, что сегодня называется математикой.
Отношения с математикой можно начать в любой момент.
- Самый простой способ — найти учителя или курс, который поможет поверить в свои силы и заняться интересными вещами из области математики: олимпиадный кружок для ребят более младшего возраста, онлайн-курс, журнал или заочная математическая школа.

- Полезно смотреть видеоролики популяризаторов математики на русском и английском языке.
- Можно отыскать вдохновение в книгах. Биографии известных учёных, рассказы, написанные математиками и пособия для начинающих.
Список вдохновляющих ресурсов преподавателя математики Марис Сегинёвой
- Ютьюб-каналы Алексея Савватеева и Артура Шарифова, англоязычный канал Numberphile.
- Статья «Плач математика» Пола Локхарта.
- Ученикам младшей и средней школы: произведения «Нолик-мореход», «Три дня в Карликании» В. А. Лёвшина, «Островитянка» , «Научные сказки» Ника Горькавого, «Уроки дедушки Гаврилы, или Развивающие каникулы», пособие «Наглядная геометрия» И. Ф. Шарыгина. А также книга и рабочая тетрадь «Наглядная геометрия» В. А. Смирновой, И. М. Смирновой и И. В. Ященко.
- На сайте Центра непрерывного математического образования можно скачивать задания и брошюры, а также узнавать о математических конкурсах и мероприятиях для школьников.

- Журналы «Лучик», «Квантик» и «Квант».
- Банк задач разного уровня сложности problems.ru для школьников и учителей.
- Заочная математическая школа петербургского образовательного центра: присылают задания каждую неделю и дают комментарии в ответ на решения учеников.
Понять математику может любой. Если ученику трудно освоить какую-то тему или раздел, нужно спуститься на ступеньку ниже. С математикой никогда не стоит торопиться, ею следует заниматься в своём темпе и с удовольствием.
ТОП-46 бесплатных курсов по математике для программистов [2021] с нуля
Автор Кристина Василец На чтение 36 мин Просмотров 10.2к. Обновлено
Для программистов. С абсолютного нуля до университетской программы.
1. «Математика» от Khan Academy
Длительность: свыше 1 000+ уроков.
Сертификат: нет.
Формат обучения: видеоуроки + текстовые материалы + тесты.
Программа обучения: содержит большое количество материала для пользователей с разным уровнем подготовки. Можно начать с изучения школьной программы (сложение, вычитание, а также алгебра и геометрия средней и старшей школы).
Есть уроки для продвинутых пользователей (статистика и вероятность, интегралы, комплексные числа и др.). Каждый раздел дополняется тестами, которые помогут проверить знания и понять что нужно повторить.
Что изучите:
- Необходимые разделы математики для дальнейшего применения в программировании.
Плюсы:
- Обширная учебная программа для студентов с разным уровнем подготовки.
- Субтитры для тех, кто лучше воспринимает информацию в виде текста.
- В каждом уроке есть демонстрация примеров для лучшего усвоения темы.

Минусы:
💰 На правах рекламы. 39 бесплатных курсов по востребованным digital-профессиям от Skillbox 💰
🤩 Освой прибыльные и востребованные интернет-профессии на курсах Skillbox! 🏆
Пройди бесплатные онлайн-курсы по:
2. «Математический анализ. Часть 1» от Stepik
Длительность: 17 уроков.
Сертификат: да.
Формат обучения: видеоуроки + тесты.
Программа обучения: представляет студийную запись лекций университетской программы, посвящена основам математического анализа. Преподаватель знакомит слушателей с последовательностями, непрерывностью, пределами. Прохождение курса рекомендовано студентам технических факультетов.
Какие темы рассматриваются:
- Способы нахождения экстремумов функции.

- Действия с определёнными и неопределёнными интегралами.
- Исследование функции на непрерывность.
- Математические последовательности чисел.
Плюсы:
- Подробное изложение теории.
- Нет сложных терминов.
- Хорошая подборка задач для наработки практики.
Минусы:
- Не обнаружены.
3. «Введение в математическое мышление» от Coursera
Длительность: 9 недель.
Сертификат: выдаётся (платно).
Формат обучения: видеолекции + тесты.
Программа обучения: способствует развитию математического мышления, которое пригодится для решения нестандартных задач в разных сферах. Курс больше подойдёт старшеклассникам, планирующим осваивать специальность, тесно связанную с математикой.
Что изучите:
- Основы теории чисел и реального анализа.

- Основы математической логики.
Плюсы:
- Полезный контент, дающий ценные знания и навыки.
- Сложные моменты объясняются пошагово простым языком.
Минусы:
- Не обнаружены.
4. «Высшая математика. Линейная алгебра и элементы топологии» от Open Education
Длительность: 17 недель.
Сертификат: выдаётся (платно).
Формат обучения: видеолекции + задачи.
Программа обучения: охватывает базовые понятия линейной алгебры и некоторые вопросы по топологии.
Какие темы изучите:
- Линейная алгебра и многочлены.
- Работа с линейными операторами.
- Основы многомерного анализа.
- Матрицы и системы линейных уравнений.
- Что такое квадратичные формы.

- Теорема Брауэра.
- Метрические пространства.
Плюсы:
- Неформальная подача материала с живыми примерами.
- Минимум сложных терминов и определений.
Минусы:
- Не обнаружены.
5. «Линейная алгебра» от Stepik
Длительность: 9 уроков.
Сертификат: да.
Формат обучения: видео + тесты + задачи.
Программа обучения: кратко изложены основы линейной алгебры. Курс является оптимальным вариантом для изучения данной дисциплины всем, кто связан с программированием либо другим направлением в IT.
Чему научитесь:
- Разбираться в базовых понятиях линейной алгебры.
- Решать системы линейных уравнений.
- Вычислять определитель матрицы.
Плюсы:
- Лёгкое изложение информации.

- Нестандартные задачи, требующие усилий.
Минусы:
- Информация представлена поверхностно, и курс больше подходит для закрепления темы, чем для изучения с нуля.
6. «Mathematical Thinking in Computer Science» от Coursera
Длительность: 6 недель.
Сертификат: выдаётся (платно).
Формат обучения: видео + статьи + тесты.
Программа обучения: посвящена знакомству с математическим мышлением и его важностью в различных сферах (наука о данных, компьютерная графика, машинное обучение и др.).
Также преподаватель научит грамотно использовать инструменты дискретной математики в программировании. Изучение материала подразумевает решение задач, для этой цели необходимо базовое знание Python.
Какие темы рассматриваются на курсе:
- Основы дискретной математики.

- Теория доказательства и математическая индукция.
- Математическая логика.
Плюсы:
- Интерактивные задачи для развития практических навыков.
- Есть русскоязычные субтитры.
Минусы:
- Поверхностный обзор многих тем без объяснения сложных моментов.
7. «Высшая математика. Алгебра: введение в теорию групп» от Open Education
Длительность: 13 недель.
Сертификат: выдаётся (платно).
Формат обучения: видеолекции + конспекты + задачи и упражнения. Желающие могут сдать экзамен.
Программа обучения: посвящена базовым понятиям и фактам общей теории групп. Преподаватели расскажут об основных классах групп и базовых теоремах, а также о тенденциях развития теории групп. Программа будет полезна студентам младших курсов, чья будущая специальность связана с информатикой и математикой.
Чему научитесь:
- Владеть основной терминологией.
- Применять полученные знания для доказательства теорем.
- Работать с математической литературой (справочники, энциклопедии).
- Применять методы теории групп на практике.
Плюсы:
- Полезный учебный контент.
- Оптимальное сочетание теории и практики.
- Задачи разного уровня сложности.
- Профессиональный преподавательский состав.
Минусы:
8. «Основы перечислительной комбинаторики» от Stepik
Длительность: 19 уроков.
Сертификат: да.
Формат обучения: видеолекции + тесты + задачи.
Программа обучения: на уроках рассматриваются элементы классической комбинаторики, из них большая часть посвящена базовым методам и подходам, которые применяются для решения комбинаторных задач. Курс пригодится всем, кто планирует углублённое изучение дискретной математики.
Курс пригодится всем, кто планирует углублённое изучение дискретной математики.
Чему научитесь:
- Решать задачи по перечислительной комбинаторике.
Плюсы:
- Учебный контент без воды и лишней информации.
- Лёгкая и увлекательная подача материала, нет сложных терминов.
- Возможность практиковаться на задачах.
Минусы:
- Не обнаружены.
9. «Combinatorics and Probability» от Coursera
Длительность: 6 недель.
Сертификат: выдаётся (платно).
Формат обучения: видеоуроки + текстовые материалы + тесты.
Программа обучения: посвящена знакомству с комбинаторными настройками и основами теории вероятностей. Также подразумевается самостоятельное написание небольшой программы на Python.
Что изучите:
- Случайные переменные.
- Вероятностные интерпретации.
- Основы комбинаторики.
Плюсы:
- Программа на уровне университета.
- Субтитры на русском языке.
Минусы:
- Плохая презентация.
10. «Высшая математика. Математический анализ» от Open Education
Длительность: 13 недель.
Сертификат: выдаётся (платно).
Формат обучения: видеозаписи + задачи.
Программа обучения: охватывает базовые понятия математического анализа. Рекомендуется преимущественно новичкам. Но предоставленный материал может быть полезен и продвинутым пользователям для закрепления или углубления знаний.
Какие темы изучите:
- Предел и его применение.

- Функциональные последовательности и ряды.
- Построение графиков функций.
Плюсы:
- Неформальный стиль изложения материала.
- Отсутствие сложных терминов.
Минусы:
11. «Теоретическая информатика: сложность вычислений» от Stepik
Длительность: 35 уроков.
Сертификат: да.
Формат обучения: видеоуроки + интерактивные задачи + тесты.
Программа обучения: разработана для студентов технических факультетов и начинающих программистов.
Чему научитесь:
- Отгадывать числа, сортировать и находить максимум.
- Решать переборные задачи.
- Использовать метод резолюций.
Плюсы:
- При небольшой продолжительности курс охватывает много тем.

- Много заданий для приобретения опыта.
Минусы:
- Слабое описание математических объектов.
12. «Introduction to Graph Theory» от Coursera
Длительность: 5 недель.
Сертификат: выдаётся (платно).
Формат обучения: видеозаписи + текстовый материал + тесты.
Программа обучения: курс ознакомительный, и его цель — предоставление общих сведений о теории графов. Программа будет интересна всем, кто планирует делать карьеру в IT.
Что изучите:
- Что такое теория графов, в каких сферах она применяется.
Плюсы:
- Достойное введение в теорию графов.
- Не требуется предварительная подготовка.
- Наличие русскоязычных субтитров.
Минусы:
- Слишком простые тесты, не требующие знаний по теме.

- Сложный академический стиль изложения материала.
13. «Курс математического анализа (первый семестр)» от Open Education
Длительность: 15 недель.
Сертификат: выдаётся (платно).
Формат обучения: видеолекции + задачи.
Программа обучения: охватывает идеи современной математики. Он рассчитан преимущественно на студентов младших курсов математических факультетов. Некоторые уроки посвящены интересным фактам об известных учёных, которые сделали важные открытия в области математики. В конце курса все желающие смогут разобраться с основными понятиями математического анализа.
Какие темы изучите:
- Элементы теории множеств.
- Элементы топологии числовой прямой.
- Функциональные последовательности и ряды.
- Дифференциальное исчисление.
- Непрерывные функции и их свойства.

Преимущества:
- Насыщенная учебная программа.
- Последовательное изложение материала.
- Большой выбор задач для отработки полученных знаний и навыков.
Недостатки:
- Не обнаружены.
14. «Основы дискретной математики» от Stepik
Длительность: 2 месяца.
Сертификат: да.
Формат обучения: видеоуроки + конспекты + тесты + интерактивные задачи.
Программа обучения: охватывает базовые понятия комбинаторики, теории графов, дискретной вероятности. Курс будет полезен студентам технических факультетов, а также всем, кому нужна дискретная математика для применения в программировании.
Что изучите:
- Основы комбинаторики.
- Базовые понятия условной и дискретной вероятности.

- Характеристики случайных величин.
- Способы применения теории графов для решения задач.
Плюсы:
- Хорошая структура курса.
- Чёткое объяснение теории.
- Материал раскрывает азы дискретной математики.
Минусы:
- Предоставленного материала недостаточно для решения задач.
- Не хватает реальных примеров для лучшего раскрытия темы.
15. «Number Theory and Cryptography» от Coursera
Длительность: 4 недели.
Сертификат: выдаётся (платно).
Формат обучения: видеолекции + статьи + тесты.
Программа обучения: специально разработана для студентов IT-факультетов, начинающих программистов и старшеклассников, владеющих математикой и синтаксисом Python. На уроках рассматриваются основы теории чисел, отдельные темы посвящаются криптографической системе RSA. Слушатели узнают, как теория чисел применяется для шифрования и дешифрования сообщений, также все желающие смогут пройти криптографический квест.
Слушатели узнают, как теория чисел применяется для шифрования и дешифрования сообщений, также все желающие смогут пройти криптографический квест.
Что изучите:
- Базовые принципы теории чисел и криптографии.
Плюсы:
- Лёгкая подача материала.
- Чёткое объяснение алгоритмов RSA.
- Увлекательный криптографический квест.
- Русскоязычные субтитры.
Минусы:
- Не хватает примеров.
16. «Математический анализ. Теория функций одной переменной» от Open Education
Длительность: 15 недель.
Сертификат: выдаётся (платно).
Формат обучения: видеолекции + тесты.
Программа обучения: классический курс, раскрывающий основы математического анализа. Ключевые темы — теория числовых последовательностей, понятие множества и свойство вещественных чисел.:max_bytes(150000):strip_icc()/GettyImages-157684140-57ed53655f9b586c35e986f9.jpg) Курс будет полезен студентам математических факультетов, учителям математики и преподавателям вузов.
Курс будет полезен студентам математических факультетов, учителям математики и преподавателям вузов.
Чему научитесь:
- Владеть базовыми понятиями математического анализа, и применять их для решения прикладных задач.
Плюсы:
- Самостоятельное планирование графика обучения.
- Последовательное изложение материала.
Минусы:
- Не обнаружены.
17. «Алгоритмы: теория и практика. Методы» от Stepik
Длительность: 47 уроков.
Сертификат: да.
Формат обучения: видеолекции + интерактивные задачи + тесты.
Программа обучения: на уроках рассматриваются основные алгоритмические методы. Кроме теоретической базы будут приведены примеры алгоритмов на языках Python, C++, Java. Желающие смогут реализовать рассмотренные на лекциях алгоритмы (подразумевается автоматическая проверка тестирующей системой). Курс предусмотрен для старшеклассников и студентов первых курсов математических факультетов.
Курс предусмотрен для старшеклассников и студентов первых курсов математических факультетов.
Что узнаете:
- Основы динамического программирования.
- Как использовать жадные алгоритмы.
- Общие практики написания кода.
Плюсы:
- Понятное изложение материала.
- Примеры реализации алгоритмов на языках программирования.
- Разные типы задач для практики и закрепления навыков.
Минусы:
- Для понимания некоторых моментов требуется самостоятельный поиск информации.
18. «Delivery Problem» от Coursera
Длительность: 3 недели.
Сертификат: выдаётся (платно).
Формат обучения: видеолекции + упражнения + статья.
Программа обучения: вводный мини-курс посвящён разработке эффективной программы для решения проблем компаний-доставщиков с помощью приёмов дискретной математики и языка Python.
Учебный план рассчитан преимущественно на продвинутых пользователей, уже изучивших комбинаторику и теорию графов. А данный курс станет стартовой точкой для практики и покажет, в каких сферах могут пригодиться полученные знания.
Чему научитесь:
- Решать поставленные задачи с использованием методов динамического программирования и алгоритмов аппроксимации.
Плюсы:
- Программа больше ориентирована на практику, чем на теорию.
Минусы:
19. «Теория вероятностей» от Stepik
Длительность: 31 урок.
Сертификат: да.
Формат обучения: видеозаписи + тесты.
Программа обучения: даёт теоретическую базу в области теории вероятностей — случайные величины, условная вероятность, дисперсия, вероятностное пространство. Кроме теории будут разобраны реальные примеры и доказаны некоторые теоремы. Слушатели должны владеть базовыми знаниями в области математического анализа и выполнять простые операции с множествами.
Кроме теории будут разобраны реальные примеры и доказаны некоторые теоремы. Слушатели должны владеть базовыми знаниями в области математического анализа и выполнять простые операции с множествами.
Что изучите:
- Классическая версия теории вероятностей.
- Основы комбинаторики.
- Закон больших чисел.
- Математическое ожидание.
- Центральная предельная теорема.
Плюсы:
- Подробная и структурированная теория.
- Материал хорошо дополняет университетскую программу (актуально для студентов).
Минусы:
- Курс ориентирован преимущественно на теорию, не хватает практики.
- Некоторые задачи по уровню сложности не совпадают с изученным материалом.
- Преподаватель игнорирует вопросы учеников в комментариях.
20. «Математическая логика и теория алгоритмов» от «Лекториума»
Длительность: 40 лекций.
Сертификат: да.
Формат обучения: видеолекции + задания. Желающие получить сертификат могут пройти итоговый тест.
Программа обучения: курс для всех, кто хочет вникнуть в основы математической логики. Программа подойдёт студентам инженерно-технических факультетов, а также учащимся старших классов с математическим уклоном, которые интересуются логикой и математикой.
Для прохождения некоторых разделов требуется знание императивного программирования и математического анализа хотя бы на начальном уровне.
Что изучите:
- Что подразумевается под математической логикой.
- Основы теории множеств, операции над множествами.
- Основы пропозициональной логики.
- Языки первого подряда.
- Аксиоматический метод и его применение.
- Теория алгоритмов и математическое доказательство.
Плюсы:
- Нестандартные задачи для проверки и закрепления знаний.

- Можно получить постоянный доступ к материалам.
- Отзывчивая техподдержка.
Минусы:
- Не обнаружены.
Об авторах: Валентин Зюзьков, старший научный сотрудник и автор учебных работ, профессор кафедры «Компьютерные системы в управлении и проектировании» ТУСУР, имеет педагогический стаж 45 лет.
21. «Introduction to Calculus» от Coursera
Длительность: 5 недель.
Сертификат: выдаётся (платно).
Формат обучения: видеозаписи + статьи + тесты.
Программа обучения: поможет понять важность применения математики в науке, технике, торговле. Преподаватель расскажет об истории исчислений, а также даст теоретическую базу в области фундаментальной математики.
Чему научитесь:
- Выполнять операции с уравнениями и функциями.

- Практиковать методы интегрального и дифференциального исчисления.
Плюсы:
- Грамотный лектор с профессиональным подходом к обучению.
- Лекции строго по теме без воды.
- Идеальный баланс между теорией и практикой.
Минусы:
22. «Основы статистики» от Stepik
Длительность: 3 недели.
Сертификат: да.
Формат обучения: видеолекции + тесты.
Программа обучения: универсальный курс, который будет интересен и студентам, и научным сотрудникам всех сфер. Материал отлично подойдёт для освоения математической статистики. Много внимания уделяется математическим идеям, логике, интуиции.
Что изучите:
- Дисперсионный, регрессионный и кластерный анализ.
- Принципы построения регрессионных уравнений.

- Способы расчёта коэффициентов корреляции.
Плюсы:
- Курс полностью раскрывает основы статистики.
- Интересная живая подача материала.
- Небольшая продолжительность видеозаписей.
Минусы:
23. «Криптография I» от Coursera
Длительность: 7 недель.
Сертификат: выдаётся (платно).
Формат обучения: видеоуроки + тесты.
Программа обучения: учеников ждёт знакомство с устройством и принципом внутренней работы криптографических систем, а также правилами использования их в приложениях. Дополнительно на лекциях обсуждаются криптографические атаки и частые ошибки при работе с криптографическими системами.
Какие темы изучите:
- Криптография с открытым ключом.

- Алгоритм с симметричным ключом.
Плюсы:
- Качественная зарубежная программа.
- Наличие субтитров на русском языке.
Минусы:
- Много сложных терминов без объяснения.
24. «Введение в логику» от «Хекслет»
Длительность: 7 занятий.
Сертификат: нет.
Формат обучения: видеокурс.
Программа обучения: охватывает базовые принципы логики, которые должен знать каждый программист. Спикер расскажет о важности математической логики в современном мире, приведёт примеры в виде реальных ситуаций. Также слушателей ждёт знакомство с логическими операциями и способами применения полученных знаний для доказательства теорем.
Спикер расскажет о важности математической логики в современном мире, приведёт примеры в виде реальных ситуаций. Также слушателей ждёт знакомство с логическими операциями и способами применения полученных знаний для доказательства теорем.
Что изучите:
- Базовые понятия классической логики.
- Основные функции в логике.
- Предикаты и кванторы.
- Классические парадоксы логики.
Плюсы:
- Материал доступен без регистрации.
- Нет ограничений по времени.
- Живой стиль изложения на уроках.
Минусы:
- Не обнаружены.
25. «Теория игр» от Coursera
Длительность: 2 месяца.
Сертификат: выдаётся (платно).
Формат обучения: видеозаписи + статьи + тесты.
Программа обучения: специальный курс будет полезен разработчикам игр. Он помогает расширить кругозор и способствует профессиональному развитию. На лекциях рассматриваются базовые принципы стратегического взаимодействия, смешанные, доминирующие и доминируемые стратегии. Также преподаватели расскажут краткую историю теории игр.
Он помогает расширить кругозор и способствует профессиональному развитию. На лекциях рассматриваются базовые принципы стратегического взаимодействия, смешанные, доминирующие и доминируемые стратегии. Также преподаватели расскажут краткую историю теории игр.
Какие темы охватывает курс:
- Основные термины и методы теории игр.
- Байесовские игры.
- Концепция равновесия Байеса-Нэша.
- Игры с неполной информацией.
Плюсы:
- Содержательный курс, дающий базовые знания по теории игр.
- Реальные примеры (классические игры и приложения).
- Креативные задачи для проверки знаний.
Минусы:
26. «Математическая теория программирования» от Андрея Миронова
Длительность: 42 занятия.
Сертификат: нет.
Формат обучения: видеокурс.
Программа обучения: спецкурс для студентов профильных факультетов и практикующих программистов с математическими знаниями. Спикер объясняет связь между математикой и программированием на примере задач.
Какие темы рассматриваются:
- Использование метода Флойда.
- Теория неподвижных точек функциональных программ.
- Теория процессов и основные операции с процессами.
Плюсы:
- Изучение материала без регистрации и ограничений по времени.
- Рекомендация книг с полезным материалом и задачами.
Минусы:
27. «Data Science Math Skills» от Coursera
Длительность: 4 недели.
Сертификат: выдаётся (платно).
Формат обучения: видеоуроки + статьи + тесты.
Программа обучения: вводный курс охватывает математические концепции, тесно связанные с наукой о данных. Слушатели изучат базовые термины алгебры, а также основы теории вероятности. Программа разработана преимущественно для новичков, владеющих только школьным курсом математики.
Какие темы рассматриваются:
- Теория множеств.
- Операции с неравенствами.
- Логарифмы и функция натурального логарифма.
- Основы математики на декартовой плоскости.
- Построение функций на плоскостях X и Y.
Плюсы:
- Субтитры на русском языке.
Минусы:
- Мало полезного материала по теме, многие моменты рассмотрены поверхностно.
28. «Mathematics for Machine Learning: Linear Algebra» от Coursera
Длительность: 5 недель.
Сертификат: выдаётся (платно).
Формат обучения: видеоурокии + статьи + тесты.
Программа обучения: охватывает основы линейной алгебры, её связь с векторами и матрицами. Программа не подразумевает глубокое изучение линейной алгебры. Учебный материал пригодится тем, кто планирует вход в сферу машинного обучения, и нуждается в базовой математической подготовке.
Какие темы изучите:
- Работа с векторами и матрицами.
- Как работает алгоритм Pagerank.
- Применение концепций линейной алгебры в машинном обучении.
Плюсы:
- Можно учиться в комфортном режиме.
- Наличие русскоязычных субтитров.
Минусы:
- Непоследовательная подача информации, а некоторые задания не совпадают с пройденным материалам.

29. «Mathematics for Machine Learning: Multivariate Calculus» от Coursera
Длительность: 6 недель.
Сертификат: выдаётся (платно).
Формат обучения: видеозаписи + конспекты + задания.
Программа обучения: вводный курс в многомерное исчисление для создания методов машинного обучения. Слушатели узнают основные концепции математического анализа. Кроме общей теории на уроках рассматривается создание инструментов для выполнения расчётов.
Какие темы изучите:
- Линейная регрессия и метод векторного исчисления.
- Многопараметрическое исчисление.
Плюсы:
- Удобная структура курса.
- Хорошее качество видео и графики.
- Есть русскоязычные субтитры.
Минусы:
- Поверхностное раскрытие тем.

- В некоторых уроках полностью отсутствуют примеры.
30. «Mathematics for Machine Learning» от Coursera
Длительность: 4 недели.
Сертификат: выдаётся (платно).
Формат обучения: видеолекции + статьи + упражнения + тесты.
Программа обучения: курс среднего уровня охватывает базовую статистику наборов данных и математических концепций, необходимых для разработки алгоритмов машинного обучения. Для решения некоторых упражнений требуется знание линейной алгебры и Python.
Что узнаете:
- Способы реализации математических концепций с помощью реальных данных.
- Принцип работы ортогональных проекций.
Плюсы:
- Есть субтитры на русском языке.
Минусы:
- Сухая теория без реальных примеров.

- Необходим продвинутый уровень Python.
31. «Linear Algebra — Foundations to Frontiers» от edX
Длительность: 15 недель.
Сертификат: да (при доплате 49 долларов).
Формат обучения: видео + упражнения по программированию.
Программа обучения: будет полезна студентам профильных вузов, а также специалистам, чья работа связана с большими объёмами данных. Программа включает стандартные темы, которые изучаются в большинстве современных университетов.
Что узнаете:
- Векторные и матричные операции.
- Способы решения линейных уравнений.
- Характеристики разделенных и специальных матриц.
- Векторные пространства.
Плюсы:
- Материалы из университетской программы в свободном доступе.
- Увлекательная подача информации с визуализацией и интересными заданиями.

Минусы:
- Необходимо знание английского языка.
32. «Pre-University Calculus» от edX
Длительность: 8 недель.
Сертификат: да (при доплате 50 долларов).
Формат обучения: видеолекции + экзамен.
Программа обучения: вводный курс по исчислению для подготовки к полноценному изучению математического анализа в университете. Кроме теории непосредственно по теме есть мотивирующие уроки, посвящённые значимости математики в различных отраслях (наука, техника, передовые технологии).
Чему научитесь:
- Понимать математические термины и концепции.
- Использовать методы интеграции.
- Решать математические задачи.
Плюсы:
- Возможность подготовиться к обучению в университете или на продвинутых курсах без финансовых затрат.

- Качественная подборка материала, полезный контент без воды и ненужной информации.
Минус:
- Необходимо знание английского языка.
33. «Calculus 1A: Differentiation» от edX
Длительность: 13 недель.
Сертификат: да (при условии доплаты 100 долларов).
Формат обучения: видеокурс.
Программа обучения: изучение предоставленного материала поможет открыть для себя производную, научиться её вычислять и применять для решения реальных задач. На уроках рассматриваются математическое обозначение, физический смысл и геометрическая интерпретация производной.
Чему научитесь:
- Вычислять производную функции.
- Делать графики функций.
Плюсы:
- Удобная структура курса.

- Материал даёт качественную теоретическую базу.
Минусы:
- Для прослушивания лекций необходимо знание английского языка.
34. «Calculus 1B: Integration» от edX
Длительность: 15 недель.
Сертификат: да (при доплате 100 долларов).
Формат обучения: видеокурс.
Программа обучения: курс знакомит слушателей с интегралом. Спикер расскажет, что это такое и в каких сферах он важен, как вычислить интеграл, а также как использовать вычисления для решения различных задач.
Что узнаете:
- Геометрическая интерпретация интеграла.
- Связь между интегралом и производной.
- В чём заключается физический смысл интеграла.
- Методы численного и символьного интегрирования функций.
- Способы применения интеграла для решения задач.

Плюсы:
- Обучение в комфортном режиме.
- Качественный учебный контент.
Минусы:
- Нужно знание английского языка.
35. «Introduction to Probability» от edX
Длительность: 10 недель.
Сертификат: да (оплачивается отдельно).
Формат обучения: видеокурс.
Программа обучения: содержит подборку уроков по введению в вероятность. Спикер расскажет, как вероятность и статистика помогают решать сложные проблемы. Теория дополняется различными примерами от медицинского тестирования до составления спортивных прогнозов.
Что узнаете:
- Способы применения условной вероятности для решения нестандартных задач.
Плюсы:
- Прохождение в комфортном темпе.

- Университетская программа.
Минусы:
- Необходимо владение английским языком.
36. «Probability — the Science of Uncertainty and Data» от edX
Длительность: 16 недель.
Сертификат: да (при доплате 300 долларов).
Формат обучения: видеокурс.
Программа обучения: курс охватывает базовые понятия вероятности, необходимые для развития в области науки о данных. Спикер расскажет о дискретных и непрерывных случайных величинах, законах больших чисел, процессах Пуассона.
Какие темы рассматриваются:
- Структура и элементы вероятностных моделей.
- Работа со случайными переменными.
- Принципы вероятностных расчетов.
- Применение законов больших чисел.
Плюсы:
- Международная учебная программа.

- Лёгкая подача материала.
Минусы:
- Необходимо знание английского языка.
37. «Многопараметрическое исчисление» от MIT OpenCourseWare
Длительность: 98 лекций.
Сертификат: нет.
Формат обучения: видеолекции + конспекты лекций + упражнения + финальный экзамен.
Программа обучения: представляет подборку записей лекций Массачусетского института. Подразумевается самостоятельная работа с материалом. Много внимания уделяется интегральному, дифференциальному и векторному исчислению. Рассматриваемые инструменты необходимы специалистам в области математики и программирования.
Что изучите:
- Матрицы и векторы.
- Функции двух переменных.
- Градиентные и направленные производные.
- Множители Лагранжа.
- Ограниченные дифференциалы.

- Двойные и линейные интегралы.
- Тройные интегралы.
- Векторные поля в пространстве.
Плюсы:
- Насыщенная программа с теоретической базой и примерами решения задач.
- Свободный доступ к лекциям без ограничения по времени.
- Можно скачать учебные материалы для личного использования.
Минусы:
- Для прослушивания лекций нужно хорошо знать английский язык.
38. «Discrete Math and Analyzing Social Graphs» от Coursera
Длительность: 6 недель.
Сертификат: выдаётся (платно).
Формат обучения: видеоуроки + презентации + тесты.
Программа обучения: поможет быстро вникнуть в основы дискретной математики. Курс будет полезен всем, кто связан с информатикой и анализом данных. От слушателей требуется знание языка Python на продвинутом уровне.
Какие знания даёт курс:
- Основы комбинаторики.
- Базовая теория вероятностей.
- Основы теории графов.
Плюсы:
- Лаконично составленные лекции.
- Интересные практические задания.
- Русскоязычные субтитры упрощают просмотр уроков.
Минусы:
39. «Calculus and Optimization for Machine Learning» от Coursera
Длительность: 6 недель.
Сертификат: выдаётся (платно).
Формат обучения: видеоматериалы + статьи + тесты.
Программа обучения: подготовлена преимущественно для студентов IT-специальностей. Но лекционный материал может пригодиться для общего развития специалистам из области анализа данных. Для продуктивной работы с учебным материалом необходим хотя бы начальный уровень математической подготовки.
Что изучите:
- Числовые множества и пределы.
- Вычисления дискретного предела.
- Многомерные функции.
- Вычисление производной функции.
Плюсы:
- Качественная программа для получения релевантных знаний в области вычислений.
- Есть русскоязычные субтитры.
Минусы:
- Плохое качество презентаций.
- Сложная подача материала, многие моменты лектор не объясняет.
40. «First Steps in Linear Algebra for Machine Learning» от Coursera
Длительность: 4 недели.
Сертификат: выдаётся (платно).
Формат обучения: видеоуроки + статьи + тесты.
Программа обучения: подразумевает изучение основных концепций линейной алгебры, необходимых в сфере анализа данных и машинного обучения. Подойдёт пользователям, имеющим представление о линейной алгебре и матричном анализе. Для выполнения некоторых упражнений понадобится знание Python. Также материал будет полезен студентам профильных факультетов.
Подойдёт пользователям, имеющим представление о линейной алгебре и матричном анализе. Для выполнения некоторых упражнений понадобится знание Python. Также материал будет полезен студентам профильных факультетов.
Чему научитесь:
- Работать с данными в векторной и матричной форме.
- Решать линейные уравнения.
- Находить и применять основные матричные разложения.
Плюсы:
- Доступное изложение основ линейной алгебры.
- Идеальный баланс теории и практики.
- Много наглядных примеров.
Минусы:
- Некачественная презентация.
41. «Probability, Theory, Statistics and Exploratory Data Analysis» от Coursera
Длительность: 6 недель.
Сертификат: выдаётся (платно).
Формат обучения: видеозаписи + конспекты + тесты.
Программа обучения: включает некоторые концепции теории вероятности и основы статистики. На лекциях рассматриваются разделы, которые необходимы для начала карьеры в Data Science. Обязательно понимание основ комбинаторики и исчислений.
Чему научитесь:
- Работать с вероятностями, анализом и визуализацией данных в Python.
Плюсы:
- Хорошая структура курса и много интересных заданий.
- Интересный стиль изложения материала.
- Подробное разъяснение сложных моментов с примерами.
- Грамотный лектор и профессиональный подход к обучению.
Минусы:
- Не обнаружены.
42. «Matrix Algebra for Engineers» от Coursera
Длительность: 4 недели.
Сертификат: выдаётся (платно).
Формат обучения: видеолекции + статьи + задачи.
Программа обучения: краткий курс по линейной алгебре для инженеров, программистов и других технических специалистов. Основной акцент сделан на матрицы. Подразумевается, что слушатели уже знакомы с исчислением одной переменной. В целом, программа подойдёт всем, кто заинтересован в изучении основ матричной алгебры, и при возникновении сложностей и готов самостоятельно искать недостающую информацию.
Что изучите:
- Основы линейной алгебры и инженерной математики.
- Системы линейных уравнений.
- Матрицы и векторные пространства.
Плюсы:
- Насыщенная программа при короткой продолжительности курса.
- Хорошее изложение и структура лекций.
- Наглядная демонстрация разных видов матричных операций.
- Наличие русскоязычных субтитров.
- Можно скачать материалы для дальнейшего использования.
Минусы:
43.
 «Introduction to Complex Analysis» от Coursera
«Introduction to Complex Analysis» от CourseraДлительность: 2 месяца.
Сертификат: выдаётся (платно).
Формат обучения: видеозаписи + слайды + упражнения.
Программа обучения: вводный курс в комплексный анализ. Сначала преподаватель даст базовые представления о комплексной плоскости и алгебре комплексных чисел.
Позже учащиеся познакомятся с интегрированием и дифференциацией. Несмотря на двухмесячную продолжительность курса, основная часть обучения подразумевает выполнение домашних заданий.
Упражнения не рассчитаны на быстрое выполнение, может потребоваться дополнительный поиск информации.
Также представленный материал можно использовать в качестве дополнения к классическому университетскому учебнику.
Какие темы изучите:
- Комплексные числа и комплексный анализ.
- Конформное отображение.

Плюсы:
- Хорошая теоретическая база для понимания основ комплексного анализа.
- Свободный стиль изложения способствует лёгкому восприятию материала.
- Наличие русскоязычных субтитров.
Минусы:
44. «Essence of Linear Algebra» от 3Blue1Brown
Длительность: 16 занятий.
Сертификат: нет.
Формат обучения: видеокурс.
Программа обучения: даёт представление об основах линейной алгебры.
Что узнаете:
- Что подразумевается под определением «вектор» в контексте линейной алгебры.

- Размеренность, базис, линейная комбинация вектора.
- Линейные преобразования и матрицы.
- Трёхмерные линейные преобразования.
- Обратные матрицы.
- Скалярное произведение и двойственность.
- Геометрическая интерпретация.
- Собственные векторы, значения, базисы.
- Способы вычисления собственных значений.
- Абстрактные векторные пространства.
Плюсы:
- Качественная визуализация для лучшего восприятия материала.
Минусы:
45. «Introduction to Higher Mathematics» от Bill Shillito
Длительность: 19 занятий.
Сертификат: нет.
Формат обучения: видеокурс.
Программа обучения: вводный курс в высшую математику для студентов, программистов, инженеров.
Какие темы изучите:
- Аксиомы и математическое доказательство.
- Основы теории множеств.
- Использование математической индукции.
- Теория чисел.
- Натуральные числа и действительные числа.
- Основы топологии.
- Основы абстрактной алгебры.
Плюсы:
- Отличное качество видео и структура лекций.
- Отсутствие сложных терминов.
Минусы:
- Для прослушивания лекций нужен продвинутый уровень английского языка.
46. «Дискретная математика» от Coursera
Длительность: 11 недель.
Сертификат: выдаётся (платно).
Формат обучения: видеокурс.
Программа обучения: поверхностный курс охватывает базовые концепции дискретной математики, которые являются основой информатики. На уроках рассматриваются множества, функции, графики. Помимо теории подразумевается выполнение заданий для взаимной оценки.
Какие темы изучите:
- Отношения и функции.
- Перечислительная комбинаторика.
- Основы теории графов.
- Сетевой поток и сопоставления.
Плюсы:
- Субтитры на русском языке.
Минусы:
- Отсутствует объяснение сложных терминов.
- Недостаточно реальных примеров.
Зачем нужно учить математику. Как математические знания помогают в жизни
Идея среднего школьного образования заключается в том, чтобы развить детей разносторонне, дать им комплексные знания об окружающем мире, научить мыслить и выражать свою точку зрения. Поэтому в школьную программу включены гуманитарные, точные и естественные дисциплины.
Поэтому в школьную программу включены гуманитарные, точные и естественные дисциплины.
Но у каждого человека свои склонности, и, с удовольствием изучая один предмет, школьник может от души ненавидеть другой, потому что он кажется сложным. Дети часто спрашивают, для чего им нужен тот или иной предмет. Они не видят связи между изучением его в теории и применением в реальной жизни.
Зачем нужна математика и как она может пригодиться в жизни и работе
Математика — это фундаментальная наука, базовые принципы которой используются в большинстве других наук. Оперируя абстрактными понятиями, она дает возможность выстраивать математические модели любых реальных процессов, поэтому может иметь прикладной характер.
Интересно!
Великие умы прошлого считали эту науку основой образования. К примеру, гениальный ученый Ломоносов, как известно, обладавший универсальным умом, считал, что математика приводит в порядок ум, и уже только поэтому ее необходимо изучать. Английский естествоиспытатель Роджер Бэкон говорил, что, не зная математики, не только невозможно изучать другие науки, но даже и собственное невежество обнаружить нельзя.
Английский естествоиспытатель Роджер Бэкон говорил, что, не зная математики, не только невозможно изучать другие науки, но даже и собственное невежество обнаружить нельзя.
Занятия математикой приносят много пользы:
- развивают интеллект, являясь своеобразным тренажером для мозга;
- учат анализировать, обобщать, находить закономерности;
- дают навык логических рассуждений;
- развивают навыки планирования;
- учат принимать решения;
- упорядочивают мышление.
Таким образом, для развития интеллекта и навыка комплексного мышления эта дисциплина просто необходима.
Важно!
Применение математики мы постоянно наблюдаем в повседневной жизни. Все архитектурные конструкции, мебель и бытовые приборы, которые нас окружают, просчитаны математически. Математические модели используются для расчета движения транспорта, работы торговли. Любой человек постоянно занимается планированием с привлечением математических методов: рассчитывает бюджет, планирует путешествия и расписание дня.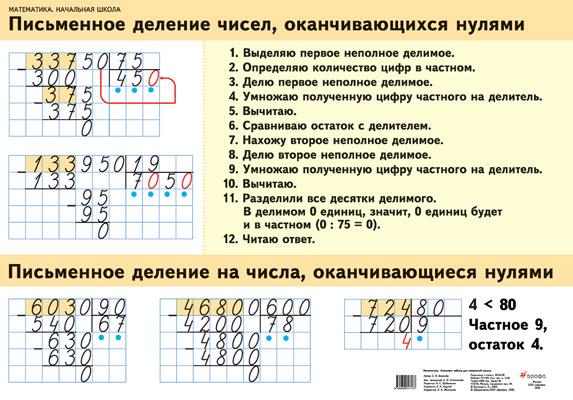 Математика настолько вплетена в нашу жизнь, что мы ее не замечаем.
Математика настолько вплетена в нашу жизнь, что мы ее не замечаем.
Математика лежит и в основе многих профессий:
- математик,
- архитектор,
- экономист,
- программист,
- инженер,
- проектировщик,
- логист.
Важно!
Все эти профессии — базовые, они в любые времена сохраняют актуальность.
Современная тенденция на рынках труда, особенно в развитых странах — замена рутинного человеческого труда роботами. Специальности, для которых нужно учить математику — наукоемкие, а значит, такого специалиста роботом не заменить.
Постоянно появляются новые специальности, основанные на взаимодействии нескольких дисциплин. В СНГ они не всегда доступны для освоения, так как наша образовательная система настроена, скорее, на сохранение академических традиций, чем на гибкость и передовой подход.
Другая ситуация с образованием в Германии. Здесь традиционно много математических профессий, а вузы нацелены, прежде всего, на то, чтобы их студенты получали актуальные, востребованные специальности, которые позволят им быстро трудоустроиться после учебы и успешно строить карьеру.
Вам также может быть интересно:
В немецких вузах доступны такие специальности с математикой, как: экономист-математик, юрист-экономист, экономист-химик, экономист-географ, экологический информатик, физик-экономист, урбанист, статистик и другие.
Какая из них подойдет вам — задача для карьерного ориентирования, которое, кстати, тоже использует математические методы.
Пройдите его, и получите не только ответы на интересующие вас вопросы о профессиональном самоопределении, но и конкретные сведения о том, где и как получить соответствующее образование.
Большой выбор востребованных направлений — не единственная причина, по которой нужно обратить особое внимание на немецкие университеты. Высшее образование в ФРГ бесплатное для всех студентов, включая тех, кто прибыл из-за рубежа, поступление — более простое, чем в СНГ, поскольку не требуются баллы за ЕГЭ, а документы можно подавать в неограниченное количество вузов. Заранее продумайте вместе со специалистом, как подобрать вузы с разным уровнем рейтинга, чтобы не упустить престижный вуз и подстраховаться на случай, если в него не зачислят. Наше время стоит очень дорого, и поступать лучше с первого раза.
Наше время стоит очень дорого, и поступать лучше с первого раза.
Важно!
Полученное в немецком вузе образование обеспечит вам большие перспективы в жизни. Вы сможете устроиться на работу в Германии, а проработав два года, получить вид на жительство.
Советуем изучить: Подбор программ обучения в немецких вузах
Для чего математика нужна гуманитариям
Часто можно услышать: «Я гуманитарий, у меня от этой вашей математики голова кругом!» На самом деле, эту фразу можно перевести так: «У меня ленивый мозг, я хочу заниматься только тем, что легко дается».
Ведь речь не идет о том, чтобы, забыв о своей природе, становиться математиком. Умение просчитывать варианты, пользоваться математическими моделями необходимо любому человеку в быту.
Учить математику необходимо даже тем, кто твердо определился с выбором гуманитарной профессии, ведь она учит размышлять, выстраивать логические цепочки, планировать, а это — ценные навыки в любой профессии.
К примеру, такие гуманитарные профессии, как юрист или филолог, только выигрывают от того, что их представители умеют логически мыслить и рационально излагать результаты своих размышлений. Если вы — гуманитарий, но сильны в математике, вы будете на голову выше конкурентов.
Важно!
Математическое мышление — это навык, который тренируется решением математических задач. Развитие навыков доступно всем, разница лишь в том, что математически одаренный человек разовьет их лучше других.
Учить математику должны и представители творческих направлений. Например, законы гармонии пропорций и цветовых сочетаний просчитаны математически, так же как гармония музыкальных и литературных произведений. Все, кто занимается творчеством профессионально, а не на любительском уровне, знают это.
Как начать учить математику с нуля
Нуль — в данном случае, скорее, фигура речи. Любой из нас учил основы математики еще в дошкольном, а затем и в школьном возрасте. Освоение только школьной программы уже дает хороший базовый уровень.
Освоение только школьной программы уже дает хороший базовый уровень.
Проблемы возникают, когда в знаниях появляется пробел. Математика — наука последовательная. Если есть пробел в основах, дальнейшее ее изучение все больше затрудняется, а учащемуся кажется, что просто он не способен учить математику.
Поэтому изучение математики в рамках школьного курса с привлечением, по необходимости, репетитора — рациональный и эффективный способ.
Для развития математического мышления также подходят интеллектуальные игры, квесты, математические головоломки.
Как выучить математику во взрослом возрасте
В детстве людям часто непонятно, для чего учить математику или какой-либо другой предмет, особенно, если он усваивается не так легко, как хотелось бы. Грамотный учитель, который умеет подать сложную информацию в игровой форме, может привить ребенку любовь к своему предмету и заинтересовать на многие годы. Но что делать, если такой не встретился, учить математику в школе не хотелось, а спустя годы появилось понимание, насколько она необходима?
Интересно!
Человеку свойственна нейропластичность, которая позволяет осваивать новые знания и навыки даже в зрелом возрасте. Научные исследования показывают, что люди старше 30–40 лет, уже имеющие опыт получения образования, демонстрируют более высокую обучаемость, чем выпускники школ. Получить новое образование, например, в Германии — вполне реальная задача, доступная в среднем возрасте. Этот шаг может полностью изменить жизнь.
Научные исследования показывают, что люди старше 30–40 лет, уже имеющие опыт получения образования, демонстрируют более высокую обучаемость, чем выпускники школ. Получить новое образование, например, в Германии — вполне реальная задача, доступная в среднем возрасте. Этот шаг может полностью изменить жизнь.
Имея базу, полученную в школе, взрослый человек может составить план по освоению математики:
- Определитесь, для чего вам нужно учить математику. Нужна теория или прикладной вариант.
- На каком уровне вы должны знать предмет для достижения ваших целей.
- Где и каким образом достигнуть этот уровень.
Для некоторых целей достаточно будет освежить в уме школьный учебник или посмотреть видеолекции, для других — позаниматься на тренажерах, а иногда и поработать с репетитором и поступить на математический факультет.
Профессии, для которых нужно учить математику — востребованные и актуальные всегда. К сожалению, не все школьники осознают важность этой науки, но, даже если школьный курс прошел мимо, нет ничего не возможного для человека, который поставил перед собой цель. Цель получить образование, цель изменить свою жизнь. Учить математику можно и во взрослом возрасте. Это открывает широкие перспективы, например, поступление на бесплатную учебу в один из сотен немецких вузов, в которых огромное количество направлений, связанных с математикой. Сбор и отправка пакета документов в немецкий вуз — занятие, требующее поистине математической точности. Чтобы не ошибиться, доверьтесь помощи специалиста.
Цель получить образование, цель изменить свою жизнь. Учить математику можно и во взрослом возрасте. Это открывает широкие перспективы, например, поступление на бесплатную учебу в один из сотен немецких вузов, в которых огромное количество направлений, связанных с математикой. Сбор и отправка пакета документов в немецкий вуз — занятие, требующее поистине математической точности. Чтобы не ошибиться, доверьтесь помощи специалиста.
Как понять Геометрию? Основы с нуля
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Идеальные объекты
Геометрия — раздел математики, который изучает пространственные структуры и отношения, а также их обобщения.
Основные геометрические объекты: окружность, квадрат, ромб, прямоугольник, равносторонний треугольник, равнобедренный треугольник, правильный многоугольник, эллипс и другие.
Все эти фигуры обладают двумя свойствами:
- симметрия
- равенство или подобие составных частей.
Равенство частей можно заметить у квадрата, ромба или равностороннего треугольника — равенство сторон. Также у них есть одна или несколько линий симметрии.
У шара бесконечное количество осей симметрии и плоскостей симметрии, но отсутствует равенство или подобие составных частей.
Все типы правильных многогранников обладают симметрией, при этом составлены из некоторого количества одинаковых фигур (треугольников, квадратов, пятиугольников).
Из всего этого можно сделать вывод, что отличить правильную геометрическую фигуру от произвольной совсем не сложно. Достаточно выяснить, имеет ли данная фигура оси или плоскости симметрии, а также из каких повторяющихся частей она состоит.
Таким образом, именно по наличию или отсутствию симметрии и равенства или подобия составных частей можно оценивать различные объекты окружающего мира на соответствие правильному геометрическому виду.
Например, возьмем два треугольника. На первый взгляд, они похожи, но у одного из них одна сторона вогнутая, вторая — выпуклая. А у другого наоборот.
Математика занимается идеальными объектами и делает о них некие заключения, которые называют теоремами. Эти треугольники похожи, и о них можно сделать близкое заключение, которое будет описывать свойства обоих.
Например, теорема Пифагора звучит так: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. А затем это свойство можно применять при решении задач и составлении чертежей.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Базовые геометрические объекты
Базовые геометрические фигуры — это точки, отрезки, лучи, прямые, плоскости.
Точка — это идеальный математический объект, у которого нет длины и ширины.
Отрезок — это часть прямой, у которого есть начало и конец.
Смежные отрезки — это отрезки, которые не лежат на одной прямой и имеют один общий конец. На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.
Прямая — это «не кривая». Более точное определение вряд ли можно сформулировать.
Когда мы рисуем прямую на листе бумаги, мы изображаем только ее часть, потому что прямая не имеет начала и конца.
Обозначать прямые принято малыми латинскими буквами (a, b,c), но можно и большими латинскими буквами (АВ, CD, MN). Точки всегда обозначают большими латинскими буквами (А, В, С).
Два варианта расположения точек относительно прямой:
- Точки лежат на данной прямой. Или еще говорят, что прямая проходит через эти точки — на рисунке выше такими точками являются А и В. При решении задач для краткости используют запись A ∈ a (читается так: точка А принадлежит прямой a или точка А лежит на прямой a), аналогично будет и для точки В (B ∈ b).

- Точки не лежат на данной прямой. Говорят так: прямая не проходит через эти точки — на рисунке такими точками являются С и D. При решении задач для краткости используют запись C ∉ a (читается так: точка С не принадлежит прямой a или точка С не лежит на прямой a), аналогично будет и для точки D (D ∉ a).
Важно знать
Через любые две точки можно провести прямую и притом только одну.
Если рассмотреть две прямые, то возможны два варианта их расположения:
- Прямые пересекаются, то есть имеют одну общую точку.
Для записи пересекающихся прямых используют специальный знак — ∩ , то есть a ∩ b (читают: прямая a пересекает прямую b).
- Прямые не пересекаются, то есть не имеют общих точек.
Для записи не пересекающихся прямых используют специальный знак — ,
то есть m n (читают: прямая m не пересекает прямую n).
Луч — это часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.
Луч имеет начало, но не имеет конца.
На рисунке точка О разбивает прямую АВ на две части:
Каждая из этих частей называется лучом, а точка О является началом одного и другого луча.
Назовем получившиеся лучи:
- Луч ОА, точка О — начало луча ОА; конца у луча ОА нет.
- Луч ОВ, точка О — начало луча ОВ; конца у луча ОВ нет.
Лучи ОА и ОВ принадлежат одной прямой АВ. Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.
Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, которые проходят через какие-либо две точки плоскости
Комбинации простейших объектов
Поговорим про комбинации простейших объектов. Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны).
Когда прямые пересекаются, можно ввести понятие отношения между двумя прямыми. Аналогично мы поступали с числами: ввели натуральные числа — количество предметов в множестве. А после этого изучали отношения между этими числами: дроби, возведение в степень.
Аналогично мы поступали с числами: ввели натуральные числа — количество предметов в множестве. А после этого изучали отношения между этими числами: дроби, возведение в степень.
Точно так же мы изучали множества, а после — отношения между множествами, функции.
Две прямые образуют углы. По сути, угол — это отношение между прямыми. Если один из них нулевой, то прямые параллельны. Если нет — прямые пересекаются.
Максимальный угол – это полный оборот, он составляет 360 градусов.
Угол — это часть плоскости, ограниченная двумя лучами, которые выходят из одной точки. Углы измеряются в градусах. Углов бесконечно много, так как от 0° до 360° угол может принимать бесконечное множество значений.
Есть разные виды углов, выделим самые часто встречающиеся:
- Если градусная мера угла меньше 90° — угол острый.
- Если градусная мера угла равна 90° — угол прямой.
- Если градусная мера угла больше 90°, но меньше 180° — угол тупой.

- Если градусная мера угла равна 180° — угол развернутый.
Точка называется вершиной угла, а лучи — сторонами угла.
Два угла называются вертикальными, если их стороны являются дополнительными лучами. Свойство вертикальных углов звучит так: вертикальные углы равны.
Два угла называются смежными, если одна сторона у них общая, а две другие являются дополнительными лучами. Свойство смежных углов: сумма смежных углов равна 180°.
Биссектриса угла — это луч с началом в вершине угла, который делит угол на две равные части.
А теперь посмотрим на взаимное расположение трех прямых.
Первый случай: все три прямые параллельны.
Второй случай: две прямые параллельны, а третья их пересекает.
Третий случай: если провести три прямые на плоскости случайным образом, велика вероятность образования треугольника. Поэтому этой фигуре мы уделяем так много времени в школе на уроках геометрии.
Поэтому этой фигуре мы уделяем так много времени в школе на уроках геометрии.
Треугольник
Треугольник образуют три прямые. Но на треугольник также можно посмотреть, как на фигуру, которая состоит из трех отрезков.
Из треугольников можно получить остальные многоугольники и к треугольникам можно приближать другие фигуры. Например, пятиугольник состоит из трех треугольников.
Треугольник можно использовать для измерения расстояний. А еще треугольник можно рассматривать в отношениях с окружностью, которая тоже является элементарной конструкцией. Читайте про вписанные и описанные углы.
Треугольник можно легко вычислить, то есть найти его площадь по трем элементам:
- две стороны и угол между ними;
- два угла и сторону;
- три стороны.
Свойства треугольников
Раз треугольник можно задать тремя элементами, значит их можно классифицировать. Если два треугольника похожи, значит у них есть общие свойства.
Треугольник можно составить совсем не из любых трех отрезков: они должны удовлетворять важному свойству — неравенству треугольника.
Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет. Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок.
Неравенство треугольника Сумма любых двух сторон треугольника больше его третьей стороны. |
Еще одно свойство верное для всех треугольников: сумма всех углов треугольника составляет половину полного оборота. Или по-другому: сумма углов треугольника — два прямых угла.
Мы знаем, что две геометрические фигуры считают равными, если их можно совместить наложением. Это справедливо и для треугольников. Равные фигуры имеют равные размеры и формы. Значит, если два треугольника равны — элементы одного треугольника соответственно равны элементам другого треугольника.
Равенство треугольников ABC и A1B1C1 обозначается так: ΔABC = ΔA1B1C1.
Есть даже специальные теоремы про равенство треугольников.
Первый признак равенства треугольников звучит так:
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны
ΔABC = ΔA1B1C1, так как AC = A1C1, AB = A1B1 и ∠A = ∠A1 (∠A лежит между сторонами AC и AB, а ∠A1 между A1C1 и A1B1).
Второй признак равенства треугольников
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
ΔABC = ΔA1B1C1, так как AB = A1B1, ∠A = ∠A1, ∠B = ∠B1.
Третий признак равенства треугольников
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
ΔABC = ΔA1B1C1, так как AC = A1C1, AB = A1B1 и BC = B1C1.
Из теоремы следует, что треугольник — жесткая фигура, то есть фигура, которую невозможно деформировать.
Подобные треугольники
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
Треугольники АВС и A1B1C1 будут подобны, если
∠ А = A1, ∠ В = B1, ∠ С = C1,
Число k, которое равно отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.
Подобие треугольников обозначают специальным символом — ∾. На рисунке треугольники АВС и A1B1C1 подобны, это можно записать так: ΔАВС ∾ ΔA1B1C1.
На рисунке треугольники АВС и A1B1C1 подобны, это можно записать так: ΔАВС ∾ ΔA1B1C1.
Теорема о первом признаке подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такое треугольники подобны.
Второй признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны — такие треугольники подобны.
Третий признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Средняя линия треугольника — это отрезок, который соединяет середины двух его сторон. В каждом треугольнике можно провести три средних линии, при пересечении которых получается четыре равных треугольника, подобных исходному с коэффициентом подобия 1/2.
На рисунке изображен треугольник АВС. Отрезки МЕ, МК и КЕ — средние линии данного треугольника, ΔВМЕ = ΔАМК = ΔСЕК = ΔМЕК.
Теорема о средней линии звучит так:
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Важно понимать, что подобие в математике — это то, что в обычной жизни мы называем схожестью. Нарисовали треугольники или прямоугольники и говорим, что они похожи потому, что их стороны пропорциональны.
Пример подобия — карта. Она подобна местности, которую отражает. А масштаб — это и есть коэффициент подобия. С треугольниками или другими фигурами точно также.
Классификация треугольников по их сторонам
Для классификации треугольников можно использовать их типологию.
Один из распространенных типов — прямоугольный треугольник. Если один из углов прямой, то это накладывает определенные свойства на треугольник. Прямоугольный треугольник — это также половина прямоугольника.
Свойства прямоугольного треугольника
- Теорема Пифагора: сумма длин квадратов катетов равна квадрату гипотенузы
- Свойство медианы: медиана, проведенная из вершины с прямым углом, равняется половине гипотенузы.
С прямоугольных треугольников начинается изучение тригонометрии. Можно измерять углы с помощью отношений, использовать понятия синуса, косинуса. Помним, что угол можно задать двумя числами, их отношением.
Если две стороны треугольника равны, то это равнобедренный треугольник — и тогда у него есть ось симметрии. Если нарисовать такой треугольник и сложить лист пополам, то две части треугольника совпадут. Эта особенность дает треугольнику определенные свойства.
Симметричный треугольник, у которого все углы и стороны равны — это равносторонний треугольник. У таких треугольников три оси симметрии. Это значит, что если мы повернем треугольник на 60 градусов, то получим точно такой же треугольник.
Такой треугольник задается одним параметром — длиной стороны. Она полностью определяет все другие значения и размеры в этом треугольнике.
От правильного треугольника может плавно перейти к правильным многоугольникам. У треугольника 3 угла, у четырехугольника — 4, а у пятиугольника — 5 углов. У многоугольника много углов🙃
Четырехугольники
Про четырехугольники мы много говорим на уроках в школе: прямоугольник, квадрат, ромб.
Но говорим о них не в общем случае, как для треугольников (такие вещи, как теорема синусов, косинусов), а можем формулировать только какие-то свойства для определенных видов четырехугольников.
Четырехугольникам лучше уделить побольше времени — у каждого из них есть особые свойства, которые не пригодятся для других фигур. Поэтому каждый четырехугольник лучше внимательно изучить на уроке или почитать в наших материалах:
Окружность
Окружность — это еще один объект, который полезно изучить. Ее легко описать, она задается одним параметром — радиусом. А еще часто встречается в физике и в обычной жизни. Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.
А еще часто встречается в физике и в обычной жизни. Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.
Взаимодействие объектов
Следующий уровень — это взаимодействие всех-всех объектов, о которых мы говорили раньше.
Например, окружность и прямая. Прямая может находиться где-то в стороне от окружности, может ее пересекать, а может касаться, то есть пересекать в одной точке.
Если прямая проходит через центр окружности, то она пересекает окружность в двух точках — концах диаметра, который лежит на на этой прямой.
На рисунке прямая a проходит через центр окружности (точку О) и пересекает ее в двух точках А и В, которые являются концами диаметра АВ данной окружности.
Если прямая a не проходит через центр О окружности радиуса r, то возможны три случая взаимного расположения прямой и окружности — в зависимости от соотношения между радиусом r этой окружности и расстоянием d от центра окружности до прямой a.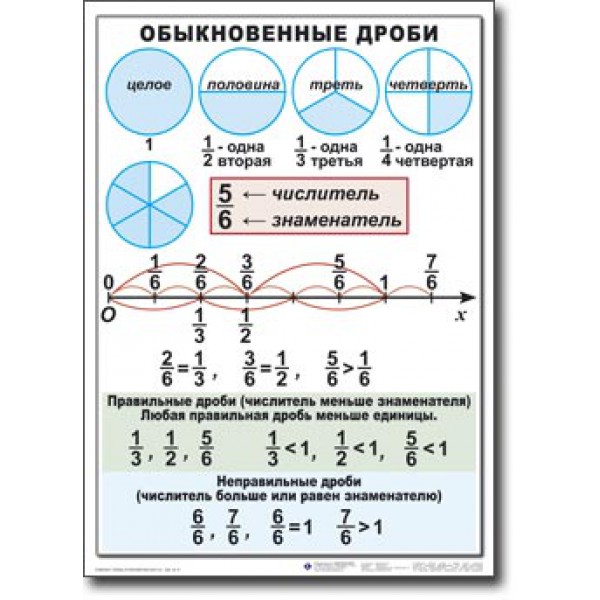 Вот эти случаи:
Вот эти случаи:
- Если расстояние от центра окружности до прямой меньше радиуса окружности (d < r), то прямая и окружность имеют две общие точки. В этом случае прямая называется секущей по отношению к окружности.
- Если расстояние от центра окружности до прямой равно радиусу окружности (d = r), то прямая и окружность имеют только одну общую точку. В этом случае прямая называется касательной по отношению к окружности.
- Если расстояние от центра окружности до прямой больше радиуса окружности (d > r), то прямая и окружность не имеют общих точек.
Окружность вписанная в многоугольник — это окружность, которая касается всех сторон многоугольника. Центр вписанной окружности лежит внутри многоугольника, в который она вписана. Описанный около окружности многоугольник — это многоугольник, в который вписана окружность.
На рисунке четырехугольник АВСD описан около окружности с центром О, а четырехугольник АЕКD не является описанным около этой окружности, так как сторона ЕК не касается окружности.
В любой треугольник можно вписать только одну окружность, и вокруг любого ее можно описать.
Все это верно только для треугольников. Не в любой четырехугольник можно вписать окружность, и не вокруг любого можно описать. Более подробно эту тему можно изучить на уроках математики: признаки, теоремы и правила.
Практическая сторона геометрии
Название «геометрия» переводится с греческого, как «гео» — земля и «метрео» — мерить. Изначально геометрию использовали для разметки земли и других работ с землей. Но, оказалось, что сфера ее влияния безгранична.
Чтобы понять, зачем нам нужны знания по геометрии, просто оглянитесь вокруг: геометрия окружает нас в предметах разных форм. Взять хотя бы круг: его используют в искусстве, строительстве, технике. То же самое и с другими фигурами: чтобы сконструировать автомобиль или айфон, сшить одежду или построить дом — не обойтись без геометрии.
А еще геометрия помогает научиться рассуждать логически, искать связи и противоречия — полезный навык в диджитал-мире, когда информация окружает нас повсюду.
Вот, в каких профессиях пригодится геометрия: архитектор, айтишник, дизайнер, инженер, конструктор, строитель, smm-менеджер, декоратор, летчик, водитель, художник, проектировщик, астроном, спортсмен, музыкант и другие.
Почему изучать геометрию просто: мы видим объемный мир каждый день и регулярно прикасаемся к предметам, строим планы, размышляем и считаем в уме. В геометрии все знания подкреплены научными теориями — это помогает взаимодействовать с пространством по-другому, более осознанно.
Почему изучать геометрию сложно: некоторые правила придется учить наизусть.
Чтобы понять геометрию, двигайтесь от простого к сложному. Многие теоремы могут показаться очевидными. Но эта видимость может быть верной только для одного рисунка. Невозможно нарисовать все ситуации, ведь их их бесконечное множество. Именно поэтому важно доказать истину, чтобы никогда не сомневаться в ней.
Как научить себя математике
Немногие предметы вызывают столько воспоминаний о боли и тревоге, сколько уроки математики. Запутанные символы, сложные процедуры и ужасающие графики и диаграммы.
Запутанные символы, сложные процедуры и ужасающие графики и диаграммы.
Некоторые люди сейчас даже предполагают, что изучение математики может быть травмирующим опытом, что-то пережитое, а не усвоенное.
Жаль, что многие люди переживают болезненную историю с математикой, потому что математика невероятно полезна. Многие из лучших профессий происходят из областей науки, науки и техники, и полагаются на понимание математики.Понимание новостей и мировых событий все чаще становится уроком статистики. Наконец, математика, если ее правильно понимать, позволяет решать многие ваши собственные проблемы.
В этой статье я хотел бы объяснить, как можно научиться любой математике, будь то статистика, алгебра или алгоритмы.
Шаг первый: начните с объяснения
Первый шаг к изучению любой математики — получить предварительное объяснение темы.
Есть много мест, где вы можете получить эту информацию.Вот несколько хороших ресурсов, охватывающих широкий круг тем:
- KhanAcademy — Огромные бесплатные ресурсы видео почти по каждой математической теме
- MIT OCW — Они начинаются на уровне университета, но обрабатывают много сложной математики.

- Coursera — много уроков по математике
Кроме того, есть еще и специализированные ресурсы. Они, как правило, не охватывают все мыслимые темы, но часто более интересны, интуитивно понятны и полезны для тех, кто занимается:
- BetterExplained — отличные статьи, дающие интуитивное понимание исчисления, алгебры, экспонент и т. Д.
- 3Blue1Brown — Отличные видеоролики на YouTube, в которых подробно рассматриваются математические концепции.
- Numberphile — Беседы с математиками на интересные математические темы
Где бы вы ни получили свое объяснение, ваш первый шаг — это посмотреть его один раз, чтобы вы почувствовали, что понимаете основы того, как это работает.
Что делать, если я не понимаю объяснения?
Если вы посмотрите объяснение, но не поняли его, есть две возможные проблемы:
- У вас отсутствуют некоторые предпосылки для понимания этой части математики . Это означает, что вам нужно сделать резервную копию и пройти через это снова.
 Если вам кажется, что это «пошло слишком быстро» или вы не знаете, что делает учитель, вам, возможно, придется вернуться на несколько уроков и выучить их лучше, прежде чем продолжить.
Если вам кажется, что это «пошло слишком быстро» или вы не знаете, что делает учитель, вам, возможно, придется вернуться на несколько уроков и выучить их лучше, прежде чем продолжить. - Вы слишком много пытаетесь охватить, не переходя на тренировку .Хороший образец — просмотреть отрывок объяснения, а затем попробовать его самостоятельно. Если вы только смотрите, но никогда не тренируетесь, это все равно что смотреть видео о лыжах и никогда не кататься на склонах. В конце концов, объяснения потеряют смысл, потому что у вас не будет личного опыта.
Попробуйте следующее: посмотрите объяснение один раз полностью в качестве отправной точки.
Шаг второй: практические задачи
Математика — это не то, что вы смотрите и запоминаете, а то, что вы делаете.
Если вы проводите все свое время за просмотром видео, а затем решаете ряд задач, вам может быть очень трудно применить свои математические знания. Это может привести к ощущению, что вы «плохо разбираетесь в математике», даже если проблема просто в том, что вы используете паршивый метод для ее изучения.
Это может привести к ощущению, что вы «плохо разбираетесь в математике», даже если проблема просто в том, что вы используете паршивый метод для ее изучения.
Вы можете исправить это, приступив к решению проблем как можно скорее. Хорошая проблема должна казаться сложной, но не невозможной. Если вы видите решение и даже не понимаете, как оно было получено, скорее всего, вы действуете слишком быстро — вернитесь и изучите некоторые основы, прежде чем двигаться дальше.
Что делать, если у меня нет проблем, которые нужно решать?
Если у вас нет указанных проблем, вы можете сделать несколько вещей:
- Работа над проблемами выполняется в объяснении, но не глядя на ответ.
- Создавайте собственные проблемы и пытайтесь их решить.
- Попробуйте доказать концепции в классе. Это продвинутая техника, но она необходима для того, чтобы по-настоящему усвоить более сложную математику.
Попробуйте следующее: после просмотра вашего объяснения решите достаточно задач, чтобы чувствовать себя комфортно и понимать процедуру.
Шаг третий: узнайте, почему математика работает
Интуитивное понимание очень важно для математики в отличие от других предметов. Хотя интуиция словарного запаса слов на иностранном языке может помочь, их все же необходимо запомнить. Однако запоминание математики может быть опасным, если заставляет вас изучать ее, не понимая.
Следующий шаг — убедить себя в том, что вы знаете, почему математика работает. Моя любимая техника для этого — техника Фейнмана, которую я демонстрирую здесь:
Техника Фейнмана требует времени, поэтому вам не нужно полностью применять ее к каждому аспекту каждой математической задачи, с которой вы сталкиваетесь.Скорее применяйте его выборочно к наиболее важным концепциям и тем, которые кажутся вам запутанными, несмотря на достаточную практику.
Попробуйте следующее: определите основные концепции математики, которую вы изучаете, и используйте технику Фейнмана, чтобы убедить себя, что вы их понимаете.
Шаг четвертый: поиграйте с математикой
Практика — это хорошо, понимание лучше, но лучше всего играть с математикой.
После того, как вы ответили на несколько заданных вам вопросов и убедились, что понимаете их, естественным продолжением является попытка поиграть с математикой, которую вам предложили.Как все меняется, когда вы пытаетесь изменить числа или применить это к другим задачам?
Например, предположим, что вы совсем недавно научились рассчитывать сложные проценты. Вы можете самостоятельно произвести простой расчет процентов и понять, почему они работают. Как вы могли играть с этой математикой?
- Вы могли видеть, что происходит, когда увеличивается скорость начисления сложных процентов.
- Что бы произошло, если бы процент был отрицательным?
- Вы можете попытаться подсчитать свои собственные сбережения, если бы вложили их по разным ставкам.

- Попробуйте представить, какую часть ипотечного кредита вы платите в виде процентов по сравнению с основной суммой.
Excel — это хороший способ поиграть с математикой, поскольку вы можете вводить формулы напрямую, без необходимости выполнять столько алгебры или повторения вычислений.
Попробуйте следующее: возьмите тему математики, которую вы недавно изучили, и посмотрите, как вы можете изменять переменные, применять их к разным вещам и изменять формулы.
Шаг пятый: применение математики вне класса
В конечном счете, целью изучения математики должно быть ее использование, а не просто сдача теста.Однако для этого вам нужно освободить свое понимание от примеров из учебника и применить его к ситуациям реального мира.
Это сложнее, чем просто решить проблему. Когда вы решите проблему, вы начнете запоминать схему решения. Это часто позволяет решать проблемы, не понимая принципов их работы.
Применение математики к реальной жизни, напротив, требует распознавания ситуации, перевода ее в математику, а затем решения созданной вами проблемы. Это строго сложнее, чем решать проблемы, поэтому, если вы хотите действительно использовать то, что вы узнали, вам нужно попрактиковаться в этом.
Это строго сложнее, чем решать проблемы, поэтому, если вы хотите действительно использовать то, что вы узнали, вам нужно попрактиковаться в этом.
Попробуйте следующее: возьмите тему, которую вы недавно изучали по математике, и попытайтесь найти реальную ситуацию, в которой вы могли бы ее вычислить, используя свои собственные числа или оценки, если они недоступны.
Все это звучит как слишком много работы!
Выполнение всех этих пяти шагов по каждому предмету, который вы изучаете по математике, займет много времени.Это нормально, вам не нужно делать это для каждой мелочи, которую вам нужно выучить.
Считайте это индикатором выполнения. Каждая математическая концепция, которую вы изучаете, может проходить от первого до пятого шагов, углубляя ваши знания и каждый раз повышая полезность математики. Некоторые концепции будут настолько важны, что вы захотите применить их полностью. Другие будут достаточно редки, чтобы просто посмотреть объяснение — это все, что вы можете сэкономить.
В частности, вы должны стараться сосредоточить внимание на наиболее важных концепциях для каждой идеи.Математика имеет тенденцию быть глубокой, поэтому часто на занятиях в течение всего семестра может быть только горстка действительно больших идей, а все остальные идеи являются просто различными проявлениями этой основной концепции.
Большинство курсов по математике первого года обучения, например, все сосредоточены вокруг концепции производной, причем все, что преподается, является просто различными расширениями и приложениями этой основной идеи. Если вы действительно понимаете, что такое производная и как она работает, эти другие части будет намного легче изучить.
Мои 9 шагов к самообучению
Если вы понимаете простой английский и имеете доступ к Интернету, то вы определенно можете изучать математику самостоятельно .
После того, как вы реализуете все, что описано в этом руководстве, вы поймете, что нет никого, кто мог бы научить вас быстрее и лучше, чем вы сами. (Особенно если использовать Anki!)
(Особенно если использовать Anki!)
Просто небольшое предупреждение: хотя я сказал, что может это делать любой, , я на 100% уверен, что не все, сделают это.
Вообще-то, это немного неудобно, особенно если вы делаете это впервые. (Но очень полезно.)
В этом посте вы точно узнаете 9-шаговый подход, который я использовал, чтобы научить себя математике, не полагаясь на кого-то, кто меня научит.
- Образ мышления №1, который многие упускают из виду при самостоятельном изучении математики
- Лучшие ресурсы для самостоятельного изучения математики
- Как вывести свои математические навыки на новый уровень
Давайте начнем.
Сможете ли вы действительно самостоятельно изучить математику? Во-первых, если вы думаете, что вы не «математик» (в любом случае, как выглядит человек-математик), вы можете подумать, что вам понадобится кто-то другой, чтобы научить вас математике в классе.
Но разве это не то же самое, что использование онлайн-инструментов? Главное здесь — просто создать свою собственную структуру, подобную программам, которые вы используете в школе.
Благодаря обилию бесплатной информации, лекций, учебных программ, электронных книг и MOOCS вы, безусловно, можете самостоятельно изучать математику, как если бы вы учились в колледже.
Самое приятное то, что вы делаете это в своем собственном темпе .
Никаких строгих графиков, только самоотдача.
Однако вы должны думать об этом иначе, если хотите пожинать плоды.
То есть осознать, , что умственные усилия, которые вы тратите на отработку математической темы, — это цена, которую вы платите за то, чтобы упростить будущие математические навыки .
Или, точнее, это цена, которую вы платите, чтобы не усложнять обучение для себя в будущем.
Математика — это все о совокупных знаниях.
В отличие от школы, вы будете чувствовать себя как дерьмо, потому что вы не меняете темы относительно времени — теперь вы меняете темы в зависимости от того, насколько быстро вы овладеваете навыком .
Я собираюсь ненадолго прервать вас, чтобы кое-что прояснить: я создал это руководство, чтобы помочь людям, которые чувствуют, что они отстают в своих математических навыках и хотят его пересмотреть, или людям, которые просто хотят изучать математику на своих владеть по какой-то причине.
Каждый пример, который я вам дам, всего лишь пример, который поможет вам понять то, что я пытаюсь донести. Вы все еще должны применить эти шаги в своей ситуации.
Шаг 1. Сначала определите, где вы хотите закончить.
Математика строится сама по себе, поэтому, если вы хотите изучить какой-либо предмет, например, математический анализ, всегда спрашивайте:
Какие предметы являются предпосылками для этого предмета?
В моем собственном исследовании я часто задаю себе вопрос, основанный на «навыках», а не актуальный.
«Какие навыков мне нужно изучить, чтобы стать лучше в этом?»
В конце концов, решение проблем — это навык. Вы не сможете лучше решать проблемы, если у вас нет инструментов; индивидуальное владение необходимыми темами.
Вы не сможете лучше решать проблемы, если у вас нет инструментов; индивидуальное владение необходимыми темами.
Это подводит меня к следующему пункту.
Шаг 2. Определите, с чего начать, очевидно,
Теперь, когда вы определили конечную тему, пора решить, с какой общей темы начать.
Например, исчисление и его приложения станут проще, если у вас есть знания в области аналитической геометрии и тригонометрии.
Но в аналитическую геометрию включены некоторые элементы тригонометрии.
Итак, вы можете начать с тригонометрии.
Однако, если вы не знаете, «что является предпосылкой для чего», я настоятельно рекомендую вам найти учебную программу онлайн.
Вот хороший план для тех, кто изучает математику для науки о данных.
Шаг 3. Найдите программу, чтобы избежать ненужной глубины
Если вы заблудились, зайдите на Google Карты.
Итак, что вы делаете, когда у вас нет дорожной карты или последовательности для изучения математики?
Используйте уже разработанный Syllabus. Они станут дорожной картой к вашему успеху в самообучении.
Они станут дорожной картой к вашему успеху в самообучении.
Как я уже упоминал ранее, их легко найти в Интернете.
Я имею в виду, что всего один поиск в Google даст вам то, что вы ищете.
Или вы можете просто просмотреть ресурсы своего университета и проверить планы по математике.
Шаг 4. Соберите ссылки, руководства по решениям и типы книг «Решенные проблемы»
Обычное обучение математике требует, чтобы вы ходили в школу, посещали занятия, выполняли домашнее задание, а затем ждали его проверки, прежде чем завершить цикл обратной связи.
Я говорю, что это очень неэффективно.
Когда есть руководства по решениям или книги типа «Решенные проблемы», лучше использовать их бок о бок с вашей собственной рутиной решения проблем.
Для этого, мне нравится серия книг «Schaum’s Outlines».
Проблемы довольно сложные, обсуждения краткие и прямо по делу, но вы, безусловно, научитесь решать проблемы ЛЕГКО.
Для ясности, я не говорю, что вам следует искать решения каждый раз, когда вы решаете проблему, но , когда вы застрянете, вы можете легко выйти и фактически быстрее изучить решения.
Этот жесткий цикл обратной связи позволит нам изучать математику БЫСТРО и в нашем СОБСТВЕННОМ темпе.
«Что делать, если я не понимаю материала?»
Либо вы не освоили предварительные условия (или совсем не усвоили), либо используете слишком сложную книгу.
Наконец, здравый смысл подсказывает, что это руководство не является исчерпывающим средством самостоятельного изучения математики. Вы всегда можете проконсультироваться с другими, когда действительно застряли, даже если у вас есть руководство по решению (возможно, в нем есть опечатка или что-то в этом роде).
Шаг 5. Сделайте ставку на глубокое концептуальное обучение
Это вызвано вышеупомянутым вопросом, который заключается в использовании руководств по решениям для изучения математики для создания быстрого цикла обратной связи.
Однако некоторые студенты его неправильно понимают.
Они считают, что когда они могут запомнить, как решается трудная проблема, это хорошо.
Это БОЛЬШАЯ ошибка — запоминать то, чего вы не понимаете.
Соответственно, это тоже БОЛЬШАЯ ошибка — просто понимать что-то, но не практиковать это.
Узнайте, ПОЧЕМУ шаги работают, потому что если вы сделаете это, вы узнаете один раз и решите многие.
Шаг 6. Поместите ссылки на ресурсы в одном месте
Поскольку вы собираетесь в основном заниматься самообучением с использованием цифровых ресурсов, удобно собрать их все в одном месте.
Возможно, сделайте их домашней страницей вашего браузера.
Сделайте ярлык или что-то в этом роде.
Дело в том, что нужно НАСТОЛЬКО упростить вам доступ к своим ресурсам, чтобы у вас не возникало трений, когда вы хотите учиться самостоятельно.
Так легче сформировать учебу, что всегда лучше в долгосрочной перспективе.
Шаг 7. Выделите время ОБЕИМ для изучения и решения проблем
Как я уже упоминал ранее, простого понимания недостаточно.
Вы должны практиковать то, что вы узнали.
Подобно тому, как новичок не может сыграть на пианино сразу после того, как кто-то хороший научит его этому, так и изучение новых вещей в математике не происходит в моменты «ага».
Обучение происходит, когда вы вспоминаете информацию из головы, а не когда пытаетесь что-то туда вложить.
Итак, помимо вашего «увлекательного» времени, выделите время для практики.
Шаг 8. Развивайте глубокую работу
Во время практики важно, чтобы вы не отвлекались.
Работа без внутренних и внешних отвлекающих факторов и сознательная сосредоточенность на текущей задаче, также известная как «Глубокая работа», улучшает взаимодействие нейронов при активации.
Это происходит потому, что оболочка под названием миелин образуется всякий раз, когда вы извлекаете информацию или практикуете навык.
Когда ваше внимание направлено на практику решения проблем, вы эффективно говорите своему мозгу, что ТОЛЬКО те нейроны, которые активируются во время решения проблем, должны быть покрыты миелином.
Однако, когда вы отвлекаетесь, это происходит плохо, и блоки обучения не формируются очень хорошо.
Шаг 9. Избегайте «Практика, практика, практика», делайте это вместо этого
Это, наверное, самый распространенный совет, который дают ученикам, которые спрашивают «как мне улучшить математику?».
Нам не нужно больше времени для практики. Нам просто нужно потренироваться лучше .
Практика, безусловно, жизненно важна, но есть два вида практики: Непродуктивная практика и Продуктивная практика.
Если вы делаете все в течение длительного периода времени, нечасто в течение недели, и просто повторяете одну и ту же задачу несколько раз, пока не «поймете ее», прежде чем переходить к следующей, то это непродуктивная практика.
Производственная практика — разумная практика.
Вот как это сделать. Два ЛЕГКИХ шага.
- Распространяйте свою практику в течение дня и в течение недели.
- Когда вы получите базовое представление о концепции, не отвечайте на несколько проблем одним и тем же решением; ответьте на несколько несвязанных задач. (Чередование)
Делая это, вы экономите ТОННУ времени и энергии на изучении математики.
Один из простых способов сделать это — использовать Anki , но вам придется проявить немного творчества при создании колод и настроек.
Ключ — изучить основы, поэтому я создал бесплатный курс.
Кто сказал, что изучение математики должно быть утомительным и трудоемким?
Ресурсы для самостоятельного изучения математики Пока я работал над этой статьей, я нашел некоторые ресурсы, которые, как мне кажется, наверняка помогут вам в вашем задании по самообучению.
Вот некоторые из лучших, которые я нашел:
Руководство:Как научиться математике, Скотт Янг
Скотт Янг — человек — .
Когда дело доходит до самообучения, он определенно лучший парень.
В конце концов, он закончил четырехлетний курс CS в Массачусетском технологическом институте всего за 12 месяцев, так что я почти уверен, что он знает, о чем говорит.
Уроки: MOOCS: Как узнать больше по высшей математике (БЕСПЛАТНЫЕ ресурсы)Если вы хотите поднять свои знания математики на новый уровень, вот несколько полезных ссылок.
Я не могу научить вас сам, поэтому вот лучшие ресурсы, которые обсуждают эту тему:
математических основ с нуля
Для развлечения на геометрическую тематику попробуйте прочитать Исаака Ньютона о математической определенности и методе Никколо Гвиччардини, когда вы рассматриваете здесь геометрические задачи, поскольку Ньютон утверждал, что геометрический синтез помог ему сделать математические открытия при написании Принципов , выполнив геометрический синтез для доказательства того, что эффекты, которые он наблюдал посредством анализа. .
.
Исаак Ньютон поступил в Тринити-колледж в 1661 году в качестве субсизара, что означало субсидированное обучение в обмен на то, что он работал неоплачиваемым слугой в университетском городке. В то время Кембридж был всего лишь фабрикой дипломов, там редко были какие-либо лекции, и научные сотрудники (аспиранты) выступали в качестве наставников, чтобы пополнить свой доход. Степень бакалавра состояла из того, что один из этих преподавателей давал вам список книг для чтения. Согласно его записной книжке Тринити-колледжа, которая до сих пор хранится в Кембридже, это был большой список для чтения греческих и римских классиков на латыни: Органон и Метафизика Аристотеля, Исагога Порфирия , Платон и рукописи комментариев к Аристотелю, обычно написанные другими товарищи продать старшекурсникам.Это произошло из-за возрождения Аристотеля в средние века, который сформировал логические курсы на следующие несколько столетий. Ньютон мало читал Аристотеля или какую-либо из назначенных ему книг, но позже он утверждал, что прочитал достаточно, чтобы научиться правильно классифицировать проблему, как мыслить логически, а позже, когда он написал Начала , как решать используйте причину, чтобы доказать следствие. Его лекции по алгебре, которые позже стали книгой Arithmetica Universalis , описывали различные «виды», то есть: аристотелевские категории математических объектов, которые можно комбинировать вместе, по сути, он описывал типы.
Его лекции по алгебре, которые позже стали книгой Arithmetica Universalis , описывали различные «виды», то есть: аристотелевские категории математических объектов, которые можно комбинировать вместе, по сути, он описывал типы.
Согласно записным книжкам Ньютона и трудам его близкого друга ДеМуавра, вот как Ньютон изучал математику. Бродя по городской ярмарке в 1663 году, он натыкается на книгу по астрологии и из любопытства покупает копию, поскольку Ньютон всегда увлекался алхимией и другими оккультными темами. В ней есть тригонометрия, которую он не понимает, поэтому он идет на математический факультет Кембриджа, чтобы найти книги по тригонометрии, но обнаруживает, что все там глубоко погружены в работу Декарта. Они дают ему Клавис Евклида и Отреда.Он повторяет попытку Евклида Элементов после того, как перестал читать его раньше, и видит доказательство теоремы Пифагора, которое заставляет его захотеть прочитать остальную часть текста. Записные книжки колледжа Ньютона показывают, что на него повлияли книги II (геометрическая алгебра), V (пропорции), VII (теория чисел) и X (иррациональные числа), и что Евклид научил его писать доказательства, в то время как система логики Аристотеля, которую он изучал, дала ему тщательная мысль, чтобы иметь возможность следить за доказательствами.
Поскольку его кембриджский диплом — это, по сути, шутка, а школа настолько расслаблена, что никого не волнует, что вы делаете, он отказывается от официальной учебной программы, чтобы остальные студенты оставались на математическом факультете.Он следит за книгой Кеплера и Отреда, пишет, что понимает ее, за исключением квадратных и кубических уравнений, однако в своих заметках он делает вывод о том, что алгебру можно использовать для исследования, что он начинает делать, записывая сотни примеров. Он получил степень бакалавра искусств. в 1665 году, несмотря на то, что он никогда не заканчивал ни одну из официальных учебных программ, и предлагается быть избранным младшим товарищем, ищущим магистра, но школа закрыта из-за чумы летом 1665 года.
Рисунок 2: Декартова геометрия по раритетам Van Schooten Он идет домой, на свою семейную ферму, и берет с собой двухтомный латинский перевод книги Декарта «Геометрия» ван Скутена 1659 года с приложениями и комментариями других картезианских математиков-исследователей. Позже Ньютон записывает в своей школьной тетради, как доказательство Хадда для оценки наклона с касательной в приложении научило его, как преобразовать один тип проблемы в другой, чтобы изучать ее по-другому. Эта книга считалась очень сложным текстом и современным анализом 17-го века, в котором используются почти те же обозначения, которые мы используем сегодня. Он прочитал 10 страниц или около того, не смог понять текст и перечитал сначала. Поехал немного дальше, потом снова перестал возвращаться к началу.Он повторяет этот алгоритм все лето и осень, пока, наконец, не дочитает весь текст. Он неправильно понимает технику Декарта в своих интересах, когда он думает, что Декарт намекает, что читатель может выяснить любые свойства кривой, и, пытаясь сделать это, в процессе упражнения развивает его собственный сложный анализ, выходящий далеко за рамки книги или любой другой книги по этому вопросу. время. Именно в этот период он начал работать по 18 часов в сутки, 7 дней в неделю. Он не прекращал эту трудовую этику, пока не умер, даже после того, как стал чрезвычайно богатым и жил в Лондоне с племянницей-подростком, которая писала, что он не будет до четырех утра над чем-то работать.
Позже Ньютон записывает в своей школьной тетради, как доказательство Хадда для оценки наклона с касательной в приложении научило его, как преобразовать один тип проблемы в другой, чтобы изучать ее по-другому. Эта книга считалась очень сложным текстом и современным анализом 17-го века, в котором используются почти те же обозначения, которые мы используем сегодня. Он прочитал 10 страниц или около того, не смог понять текст и перечитал сначала. Поехал немного дальше, потом снова перестал возвращаться к началу.Он повторяет этот алгоритм все лето и осень, пока, наконец, не дочитает весь текст. Он неправильно понимает технику Декарта в своих интересах, когда он думает, что Декарт намекает, что читатель может выяснить любые свойства кривой, и, пытаясь сделать это, в процессе упражнения развивает его собственный сложный анализ, выходящий далеко за рамки книги или любой другой книги по этому вопросу. время. Именно в этот период он начал работать по 18 часов в сутки, 7 дней в неделю. Он не прекращал эту трудовую этику, пока не умер, даже после того, как стал чрезвычайно богатым и жил в Лондоне с племянницей-подростком, которая писала, что он не будет до четырех утра над чем-то работать.
Зимой 1665 года он читает Arithmetica Infinitorum Уоллиса, который представляет собой арифметику бесконечно малых величин, и еще одну очень большую книгу Вите Opera Mathematica . Менее чем за год Ньютон сумел полностью освоить все достижения математики середины 17 века. На этом этапе он открывает обобщенную биномиальную теорему и анализ бесконечных рядов, которые он изобрел, чтобы найти короткие пути к вычислениям.В 1666 году он ненадолго возвращается в Кембридж, прежде чем тот снова закрывается из-за чумы. Из его записей видно, что он закончил свое дифференциальное и интегральное исчисление за эти несколько месяцев в школе.
Описывая свою деятельность во время второго года чумы: «Мне стыдно рассказывать, во сколько мест я переносил эти вычисления, не имея в то время другого дела, потому что тогда я действительно слишком наслаждался этими изобретениями». Он вел записи о вычислении логарифма до 52-й десятичной запятой.Он возвращается в Кембридж в 1667 году и где-то в этот период становится одержимым открытием древнего анализа, используемого в классической геометрии. Книга Паппа 7 содержит комментарий к утерянной группе инструментов и предположений, которые использовали Евклид, Аполлоний, Эратосфен и другие геометры того времени, которые Папп называл «сокровищницей анализа». Эти потерянные Поризмы (следствия) теоретически являются проективной геометрией Ньютона.
Книга Паппа 7 содержит комментарий к утерянной группе инструментов и предположений, которые использовали Евклид, Аполлоний, Эратосфен и другие геометры того времени, которые Папп называл «сокровищницей анализа». Эти потерянные Поризмы (следствия) теоретически являются проективной геометрией Ньютона.
Ньютон в своих лекциях на кафедре Лукаса сказал, что древние никогда не потрудились бы ввести алгебру кривых с геометрией, потому что вы теряете простоту работы с геоэлементами, весь смысл был в том, чтобы избежать утомительных вычислений, просто рисуя линии и круги.Он также утверждает, что такие книги, как Pappus Collectio , намеренно скрывали анализ, поскольку он считался неизящным инструментом и что древний синтез, в котором они выводили следствие из заданной предпосылки (следствия) с использованием визуальных средств, был лучшим методом, поскольку анализ не мог быть обращенным по шагам, подобным геометрическому синтезу. Он пошел еще дальше и заявил, что если вы хотите обнаружить, казалось бы, не связанные друг с другом следствия, вы должны использовать синтез, описывая анализ своего времени как «утомительную груду вероятностей, используемых неумелыми людьми».
В неавторизованной книге Arithmetica Universalis , выпущенной его преемником в Кембридже, который обнаружил в библиотеке лекции Ньютона Лукаса и опубликовал их как есть, Ньютон пишет, как Декарт пытается включить в стандартную геометрию плоскости различные кривые, такие как параболы, больше, чем просто кривые. пустая трата времени, они «портят простоту геометрии». На рисунке 108 он показывает, как он решил бы эту проблему, переосмысливая эллипс, аргументируя это тем, что декартовы методы не понимают смысла делать все с помощью только линейки и циркуля.
Позже он написал в рукописи по геометрии, что механика движения была тем, что породило всю геометрию, и что древние понимали это так же, как и геометрические объекты, создаваемые движением по прямой кромке, кругами с помощью движения компаса или переводом, как в Предложении 4 Книги 1 Евклида Элементы , где одна форма треугольника перемещается для сравнения с другой. Затем он продемонстрировал, что механическое вращение линеек на самом деле является преобразованием плоскости, что формально не было разработано другими математиками в течение следующих 200 лет.
Ньютон изобрел пределы при написании Principia на этапе геометрического синтеза своего анализа инфинтезимальных. Он решил, что ограничения, демонстрируемые как геометрические исчезающие дополнения, «должны быть более гармоничными с геометрией древних в том смысле, что не должно быть необходимости вводить в геометрию бесконечно малые фигуры». Поскольку анализ инфинтезимальных был для него просто эвристическим инструментом, он понизил оценку инфинитезимальных (у которых в любом случае не было устоявшейся теории с доказательствами), чтобы предпочесть свой новый метод предельного доказательства, полученный им из синтеза геометрии, и очень похожий на то, что сегодня все используют в современном исчислении. курсы.
«Сравнивая сегодня тексты Ньютона с комментариями его последователей, удивительно, насколько оригинальное изложение Ньютона более современно, понятнее и богаче идеями, чем перевод комментаторов его геометрических идей на формальный язык исчисления Лейбница.
«-Владимир Арнольд 1990 г.
Изучай математику бесплатно — Mathplanet
Math planet — это онлайн-ресурс, на котором можно бесплатно изучать математику.Пройдите наши курсы математики в старших классах по преалгебре, алгебре 1, алгебре 2 и геометрии. Мы также подготовили практические тесты для SAT и ACT.
Учебный материал ориентирован на математики средней школы США . Однако, поскольку математика одинакова во всем мире, мы приглашаем всех изучать математику вместе с нами бесплатно.
Mattecentrum — шведская некоммерческая членская организация, основанная в 2008 году в Швеции. С тех пор центр оказывает бесплатную помощь по математике всем, кто изучает математику.Целью Mattecentrum является содействие получению равных знаний, а также повышение уровня знаний и интереса к математике и другим предметам, связанным с STEM. Возраст участников колеблется от 6 до 26 лет.
Центр предлагает БЕСПЛАТНЫЕ математические лаборатории в Швеции в школах, библиотеках и других помещениях в 34 городах.
Более 5000 студентов по всей стране ежемесячно получают индивидуальную помощь в учебе от 500 активных волонтеров Mattecentrum. В 2019 году ок. 30 000 студентов приняли участие в наших математических лабораториях, летних лагерях и математическом съезде.
Mattecentrum также предлагает БЕСПЛАТНУЮ онлайн-справку помимо Mathplanet:
- Mathplanet — это онлайн-книга на английском языке по математике с теорией, видеоуроками и упражнениями на счет для школьных курсов математики. В 2019 году у сайта было 8,4 млн уникальных пользователей.
- Matteboken.se — это полный учебник по шведской математике с теорией, видеоуроками и упражнениями на счет. Matteboken.se доступен на шведской и арабской версиях. В 2019 году сайт посетили более 2,9 млн уникальных пользователей.
- Arabiska.matteboken.se содержит те же теоретические упражнения и упражнения по счету, что и выше, но в настоящее время отсутствуют видеоуроки (для чего мы ищем финансирование).
 Материал охватывает начальные классы 3–9 и маты 1, 2 и 3 для старших классов средней школы. В 2019 году на сайте было 413,1 трлн уникальных пользователей.
Материал охватывает начальные классы 3–9 и маты 1, 2 и 3 для старших классов средней школы. В 2019 году на сайте было 413,1 трлн уникальных пользователей. - Pluggakuten.se — это шведский форум, где вы можете задавать вопросы по математике, STEM или другим школьным предметам, чтобы получить помощь или помочь кому-то другому.В 2019 году у сайта было 781,8 трлн уникальных пользователей.
- Formelsamlingen.se содержит все необходимые формулы по математике, физике и химии. На Formelsamlingen.se было оказано 68 452 помощи. В течение 2019 года на сайте было 348,8 трлн уникальных пользователей.
Для получения дополнительной информации о нас посетите mattecentrum.se.
Присоединяйтесь к нам в Facebook @mathplanet, Twitter @mathplanet или Instagram @our_mathplanet.
Чтобы связаться с Mattecentrum, отправьте электронное письмо по адресу: mathplanet @ mattecentrum.se
Поддерживая Mattecentrum, вы помогаете нам повышать уровень знаний и интереса к математике среди детей и молодежи. Нажмите на кнопку пожертвования и поддержите Mattecentrum!
Нажмите на кнопку пожертвования и поддержите Mattecentrum!
Как изучать математику для науки о данных, самостоятельный путь
Вам нужно иметь докторскую степень по математике, чтобы стать специалистом по данным? Точно нет! Это руководство покажет вам, как изучать математику для науки о данных и машинного обучения, не посещая медленные и дорогие курсы.
Количество математических вычислений, которые вы будете выполнять ежедневно как специалист по анализу данных, сильно зависит от вашей должности. Продолжайте читать, чтобы узнать, какие концепции вам нужно будет освоить, чтобы добиться успеха в своих целях.
Для выполнения этого руководства вам потребуются как минимум базовые навыки программирования на Python *. Мы будем изучать математику на практике.
Ознакомьтесь с нашим руководством «Как изучить Python для науки о данных, самостоятельный запуск», чтобы узнать о самом быстром способе освоить Python. Мы рекомендуем выполнить как минимум до Step 2 в этом руководстве.
Мы рекомендуем выполнить как минимум до Step 2 в этом руководстве.
* примечание: другие языки тоже подходят, но примеры будут на Python.
Математика, необходимая для науки о данных
Объем математики, который вам понадобится, зависит от должности. Во-первых, каждому специалисту по данным необходимо знать некоторую статистику и теорию вероятностей. Для этого у нас есть руководство:
А как насчет других видов математики? Что ж, вот где ответ более тонок … это зависит от того, сколько оригинальных исследований в области машинного обучения вы собираетесь проводить.
Позиции для прикладного машинного обучения
На практике, особенно в ролях начального уровня, вы часто будете использовать готовые реализации машинного обучения.На многих языках программирования существуют надежные библиотеки общих библиотек. Не нужно изобретать велосипед.
Даже в этом случае интервьюеры могут протестировать вашу базовую линейную алгебру и многомерное исчисление . Почему они это делают?
Почему они это делают?
Что ж, в какой-то момент вашей команде все еще может понадобиться создавать собственные реализации алгоритмов машинного обучения. Например, вам может потребоваться адаптировать один к своему техническому стеку или расширить его базовую функциональность. Для этого вы должны уметь откатывать алгоритмы машинного обучения и работать с их внутренностями.
Позиции для интенсивного машинного обучения в НИОКР
Для других ролей требуется гораздо больше оригинальных исследований и разработок машинного обучения. Возможно, вам потребуется перевести алгоритмы из научных статей в рабочий код. Или вы можете изучить улучшения, основанные на уникальных задачах вашего бизнеса.
Другими словами, вы будете гораздо чаще реализовывать алгоритмы с нуля.
Для этих должностей, знание как линейной алгебры, так и многомерного исчисления является обязательным.
Лучший способ изучать математику для науки о данных
Самостоятельный способ изучения математики для науки о данных — это учиться, «делая дерьмо». Итак, мы собираемся заняться линейной алгеброй и исчислением, используя их в реальных алгоритмах!
Итак, мы собираемся заняться линейной алгеброй и исчислением, используя их в реальных алгоритмах!
Даже в этом случае вы захотите изучить или проанализировать основную теорию заранее. Вам не нужно читать весь учебник, но сначала вы захотите изучить ключевые понятия.
Вот 3 шага к изучению математики, необходимой для науки о данных и машинного обучения:
- 1
Линейная алгебра для науки о данных
Матричная алгебра и собственные значения.
- 2
Расчет для науки о данных
Производные и градиенты.
- 3
Градиентный спуск с нуля
Реализуйте простую нейронную сеть с нуля.
Шаг 1. Линейная алгебра для науки о данных
Многие концепции машинного обучения связаны с линейной алгеброй. Например, PCA требует собственных значений, а регрессия требует умножения матриц.
Кроме того, большинство приложений машинного обучения работают с многомерными данными (данными с множеством переменных). Этот тип данных лучше всего представлен в виде матриц.
Этот тип данных лучше всего представлен в виде матриц.
Вот несколько лучших бесплатных ресурсов, которые мы нашли для изучения линейной алгебры для науки о данных:
Для ролей с тяжелыми приложениями …
Khan Academy предлагает короткие практические уроки линейной алгебры. Они охватывают самые важные темы.
Для научно-исследовательских и опытно-конструкторских работ …
MIT OpenCourseWare предлагает класс строгой линейной алгебры.Все видео-лекции и материалы курса включены.
И если нужно только просмотреть:
Шаг 2. Исчисление для науки о данных
Calculus важен для нескольких ключевых приложений машинного обучения. Например. вам нужно будет уметь рассчитывать производные и градиенты для оптимизации.
Фактически, одним из наиболее распространенных методов оптимизации является градиентный спуск.
Вот некоторые из лучших ресурсов для изучения исчисления для науки о данных:
Для ролей с тяжелыми приложениями.
 ..
..Khan Academy предлагает короткие практические уроки многомерного исчисления. Они охватывают самые важные концепции.
Для научно-исследовательских и опытно-конструкторских работ …
MIT OpenCourseWare предлагает строгий класс многомерного исчисления. Все видео-лекции и материалы курса включены.
И если нужно только просмотреть:
- Обзор многомерного исчисления (видео) — это быстрый обзор многомерного исчисления в формате решения практических задач.Рекомендуется, если вы уже занимались многомерным исчислением и просто хотите быстро повторить.
Шаг 3. Простая нейронная сеть с нуля
Поздравляем! У вас нет теории. Пришло время по-настоящему весело.
Один из лучших способов изучить математику для науки о данных и машинного обучения — построить простую нейронную сеть с нуля.
Вы будете использовать линейную алгебру для представления сети и исчисления для ее оптимизации. В частности, вы создадите код градиентного спуска с нуля.
В частности, вы создадите код градиентного спуска с нуля.
Пока особо не беспокойтесь о нюансах нейронных сетей. Ничего страшного, если вы просто следуете инструкциям и пишете код. Мы подробно рассмотрим машинное обучение в другом руководстве, так как оно предназначено для целевой математической практики.
Следуйте инструкциям и пересматривайте теорию по мере продвижения. Кроме того, у вас будет классный проект, который вы потом добавите в свое портфолио.
Вот несколько замечательных пошаговых руководств:
- Нейронная сеть на Python, часть 2 — это невероятное руководство, которое проведет вас через простую нейронную сеть от начала до конца.Он содержит полезные иллюстрации, и вы узнаете, как подходит градиентный спуск.
- Нейронные сети для распознавания рукописных цифр — Нам очень нравится этот ресурс! Это бесплатная онлайн-книга, в которой вы познакомитесь с известным применением нейронных сетей. Он очень интуитивно объясняет идеи, и это самый подробный учебник в этом списке.

- Реализация нейронной сети с нуля — более короткое руководство, которое также проведет вас через пошаговые инструкции.
Царапины по каждому предмету: математика
В этой коллекции ресурсов Math + Scratch рассказывается о многих способах, с помощью которых учащиеся развивают математические знания, создавая свои собственные проекты в Scratch.
- Автор оригинала: Мэри Аделаида
- Уровень образования: Начальная школа, Средняя школа, Высшая школа
- Типы контента: Действие, Учебная программа, План урока, Образец проекта, Учебное пособие, Инструмент
- Учебные направления: Математика
- Ключевые слова: математика, скретч-проекты, математическое образование, интеграция учебной программы, скретч по всем предметам
Для многих студентов изучение математики и понимание ее реальных приложений может быть проблемой. Им может наскучить идея изучения формул или их запугать абстрактные проблемы и сложные правила. Вот где может помочь Scratch.
Им может наскучить идея изучения формул или их запугать абстрактные проблемы и сложные правила. Вот где может помочь Scratch.
С самого начала студенты, использующие Scratch, изучают математические концепции, начиная с декартовых координат, которые они должны понимать, чтобы перемещать спрайты по экрану. Чтобы сделать эту идею более явной, учащиеся могут рисовать плоскости координат в Scratch или переделывать один из многих связанных проектов, чтобы добавить свой собственный поворот (например, эта игра с декартовыми координатами — хороший способ попрактиковаться и дала несколько ремиксов).Этот ресурс от Бена Джонсона помогает студентам определять координаты, необходимые для рисования их имен в Scratch, что можно сделать с помощью функции пера. Скретчеры также создали несколько полезных проектов, знакомящих других с координатной плоскостью — вот один пример.
Учащиеся могут углубить свое понимание системы координат, смешивая подобные игры.
В качестве ключевой части координатной плоскости отрицательные числа быстро вступают в игру во время начальных исследований Scratch. Углы / градусы добавляются к смеси по мере того, как учащиеся ищут способы точной настройки движения своих спрайтов, и могут стать основой для творческих игр, таких как эти два примера. И эти темы, хотя и предоставляют много возможностей для изучения, являются лишь началом концепций, которые можно воплотить в жизнь с помощью Scratch.
Углы / градусы добавляются к смеси по мере того, как учащиеся ищут способы точной настройки движения своих спрайтов, и могут стать основой для творческих игр, таких как эти два примера. И эти темы, хотя и предоставляют много возможностей для изучения, являются лишь началом концепций, которые можно воплотить в жизнь с помощью Scratch.
Изучение математики с помощью Scratch не обязательно должно ограничиваться математическими проектами. Короткие задачи можно легко превратить в игры, решение которых может позволить игроку продвинуться в игре или собрать больше валюты.Практически любой тип проекта позволяет студентам практиковать основы, такие как декартовы координаты, поэтому студенты могут выполнять проекты, основанные на личных интересах, при этом привыкая к этим концепциям.
Альваро Молина Аюсо, учитель математики в средней школе в Испании, предлагает ученикам создавать проекты Scratch, демонстрирующие практическое применение идей, изложенных в каждом разделе. Например, его ученики, изучающие проценты, использовали Scratch для изображения сценария, такого как интернет-магазин, который требует расчета скидки на продукт.
Например, его ученики, изучающие проценты, использовали Scratch для изображения сценария, такого как интернет-магазин, который требует расчета скидки на продукт.
Другой способ визуализировать, как работают проценты, особенно для тех, кто совершенно не знаком с этой темой, — использовать команду «масштабировать» с различными процентами и отмечать, как соответственно изменяется размер спрайта. Визуализация изменений формы или объекта путем изменения спрайта также может помочь учащимся узнать о преобразованиях, которые могут программировать спрайты для выполнения перемещений, вращений и отражений. Карен Рэндалл делится несколькими предложениями по проектам, связанным с преобразованиями, геометрией, вероятностью и другими темами в этом ресурсе.Она также описывает здесь образцы геометрических проектов.
Создавая подобный проект Карен Рэндалл, студенты могут изучать фундаментальные концепции геометрии.
Для учителей из США, которые хотят интегрировать Scratch в классы, руководствуясь стандартами Common Core, Келли Воган предлагает серию из трех уроков математики для учеников средней школы. На этих уроках шестиклассники рисуют многоугольники в координатной плоскости, семиклассники изучают масштабные чертежи геометрических фигур, а восьмиклассники создают программы для функциональных машин.
На этих уроках шестиклассники рисуют многоугольники в координатной плоскости, семиклассники изучают масштабные чертежи геометрических фигур, а восьмиклассники создают программы для функциональных машин.
Несколько учителей пришли к выводу, что Scratch может быть хорошей платформой для объединения учеников вне границ их классов. Старшим школьникам может понравиться наставлять своих младших коллег по использованию Scratch, а также они могут создавать игры, которые позволяют младшим школьникам весело проводить время, практикуя решение задач в соответствии с их оценкой. Например, игры, подобные этой, которую поделил Бен Джонсон, могут быть запрограммированы на одну ступень ниже их.
Помимо знакомства с операциями и концепциями, Scratch может помочь учащимся увидеть красоту математики.Многие Скретчеры создали творческие проекты, демонстрируя красочные узоры, фракталы и многое другое. В этой студии есть несколько хороших примеров, как и в этой студии работы 10-классников, которую преподает Мария Беатрис Рапаччини.
Показ студентам примеров проектов, таких как эта студия работы учеников 10-х классов в классе Марии Беатрис Рапаччини, может пробудить любопытство и вдохновить их на решение сложных задач.
Все еще ищете идеи?
- Посмотрите эту презентацию Марка Трантера, включая ряд алгоритмов, которые можно изобразить с помощью Scratch, или этот набор видео, которыми поделился Себ Шмоллер из Citizen Maths.Национальный совет учителей математики опубликовал статью, в которой рассказывается о многочисленных приложениях Scratch, специально разработанных для преподавателей математики.
- На ScratchEd доступно множество дополнительных ресурсов, которые помогут вам интегрировать математику в класс, их можно найти здесь, а также вы можете задавать вопросы другим учителям на дискуссионных форумах. Если у вас есть конкретная тема, которую вы надеетесь направить учащимся в изучении с помощью Scratch, поиск в Scratch связанных ключевых слов, таких как «дроби», может дать полезные примеры проектов.

- Просмотрите образцы математических проектов — включая синус, косинус и касательные волны, а также математического дракона — в этой коллекции Scratch-проектов по учебной программе.
- Для получения дополнительных советов по интеграции Scratch в учебную программу по математике ознакомьтесь с ресурсами в Руководстве по межучебной интеграции Scratch.
И, пожалуйста, поделитесь с онлайн-сообществом найденными или созданными ресурсами!
Как изучать математику
Как изучать математику Лоуренс Нефф Стаут,Математический факультет,
Уэслианский университет штата Иллинойс,
Блумингтон, Иллинойс 61702-2900
В этом эссе описывается ряд стратегий обучения на уровне колледжа. математика.В нем есть разделы, озаглавленные
- Чем отличается математика в колледже?
- Что делать с определением
- Теоремы, предложения, леммы и следствия
- Собираем объект вместе
- Как разобраться в пруфе
- Развивающая техника
- Несколько заключительных предложений
 Н. Домашняя страница Стаута.
Н. Домашняя страница Стаута.Чем математика в колледже отличается от старшей школьная математика?
В старших классах математики большую часть времени вы тратили на изучение алгоритмов. и манипулятивные техники, которые вы должны были применять в определенных четко определенных ситуациях.Это ограничение материала и ожиданий вашей успеваемости, вероятно, привели вас к развитию учебных привычек, которые подходили для школьной математики, но могут быть недостаточными для математика в колледже. Это может быть для вас источником большого разочарования и для ваших инструкторов. Моя цель при написании этого эссе — помочь облегчить это разочарование, описав некоторые учебные стратегии, которые могут помочь вам направить ваши способности и энергию в продуктивном направлении. Первое существенное различие между математикой средней школы и колледжем
математика — это акцент на том, что студент назвал бы теорией —
точное изложение определений и теорем и логических процессов
по которым эти теоремы устанавливаются. Математику этот материал,
вместе с примерами, показывающими, почему выбранные определения являются правильными
и то, как теоремы могут быть применены на практике, составляет суть
математика. Описание курса с использованием термина « строгий » указывает на то, что
что будет уделено особое внимание формулировке определений и
теоремы, и доказательства будут даны для теорем, а не просто
аргументы правдоподобия. Если ваш подход заключается в том, чтобы сразу перейти к проблемам
лишь поверхностно прочитав « теорию », этот аспект математики в колледже
вызовет у вас трудности.
Математику этот материал,
вместе с примерами, показывающими, почему выбранные определения являются правильными
и то, как теоремы могут быть применены на практике, составляет суть
математика. Описание курса с использованием термина « строгий » указывает на то, что
что будет уделено особое внимание формулировке определений и
теоремы, и доказательства будут даны для теорем, а не просто
аргументы правдоподобия. Если ваш подход заключается в том, чтобы сразу перейти к проблемам
лишь поверхностно прочитав « теорию », этот аспект математики в колледже
вызовет у вас трудности.
Второе различие между математикой колледжа и математикой средней школы
входит в подход к технике и прикладным задачам. В старшей школе
вы изучали одну технику за раз — может решить набор задач или подразделение,
например, при решении квадратных уравнений факторизацией или использованием
квадратичной формулы, но она не научит обоих и не попросит вас решить
что было лучшим подходом для конкретных проблем. Конечно, ты
при таком подходе хорошо выучить отдельные техники, но вряд ли вы
чтобы узнать, как решить проблему, для которой вам не говорят, какой метод
использовать или который не совсем похож на другие приложения, которые вы видели. Колледж
математика предложит множество методов, которые могут быть применены для конкретного
тип проблемы — отдельные проблемы могут иметь много возможных подходов,
некоторые из них работают лучше других. Часть задачи по работе с такими
Проблема заключается в выборе подходящей техники. Это требует изучения
привычки, которые развивают рассудительность, а также техническую компетентность.
Колледж
математика предложит множество методов, которые могут быть применены для конкретного
тип проблемы — отдельные проблемы могут иметь много возможных подходов,
некоторые из них работают лучше других. Часть задачи по работе с такими
Проблема заключается в выборе подходящей техники. Это требует изучения
привычки, которые развивают рассудительность, а также техническую компетентность.
Мы рассмотрим проблему изучения математики, рассмотрев
конкретные аспекты индивидуально. Сначала мы рассмотрим определения — сначала
потому что они составляют основу любой части математики и необходимы
для понимания теорем.Затем мы рассмотрим теоремы, леммы, предложения,
и следствия, и как изучить, как предмет сочетается друг с другом. В
Далее идет тема доказательств, как их расшифровать и зачем они нам нужны.
И, наконец, мы обсудим развитие суждения при решении проблем.
К оглавлению
Что делать с определением?
Определение в математике — это точное определение, описывающее и называющее понятие, связывая его с ранее определенными понятиями или такими неопределенными понятия как « число » или « множество ». ‘Необходимы точные определения, чтобы
что мы точно знаем, о чем говорим. К сожалению, для многих
понятий в математике бакалавриата определение довольно сложно
понять, так часто на низких уровнях интуитивное ощущение смысла
срока — это все, что дано или требуется. Это интуитивное ощущение, в то время как
необходимо, недостаточно на уровне колледжа. Это означает, что вы
необходимо усвоить формальную формулировку определений и
их значения. Как ты это делаешь?
‘Необходимы точные определения, чтобы
что мы точно знаем, о чем говорим. К сожалению, для многих
понятий в математике бакалавриата определение довольно сложно
понять, так часто на низких уровнях интуитивное ощущение смысла
срока — это все, что дано или требуется. Это интуитивное ощущение, в то время как
необходимо, недостаточно на уровне колледжа. Это означает, что вы
необходимо усвоить формальную формулировку определений и
их значения. Как ты это делаешь?Шаг 1.Убедитесь, что вы понимаете, что говорится в определении.
Звучит очевидно, но может вызвать некоторые трудности, особенно для определения со сложной логической структурой (например, определение предел функции в точке ее области определения). Определения не хорошее место, чтобы попрактиковаться в скорочтении. В общем, зря нет слова или посторонние символы в устоявшихся определениях и легко упускаемые из виду маленькие слова вроде и, или, если … то для всех и получается ваши ключи к логической структуре определения.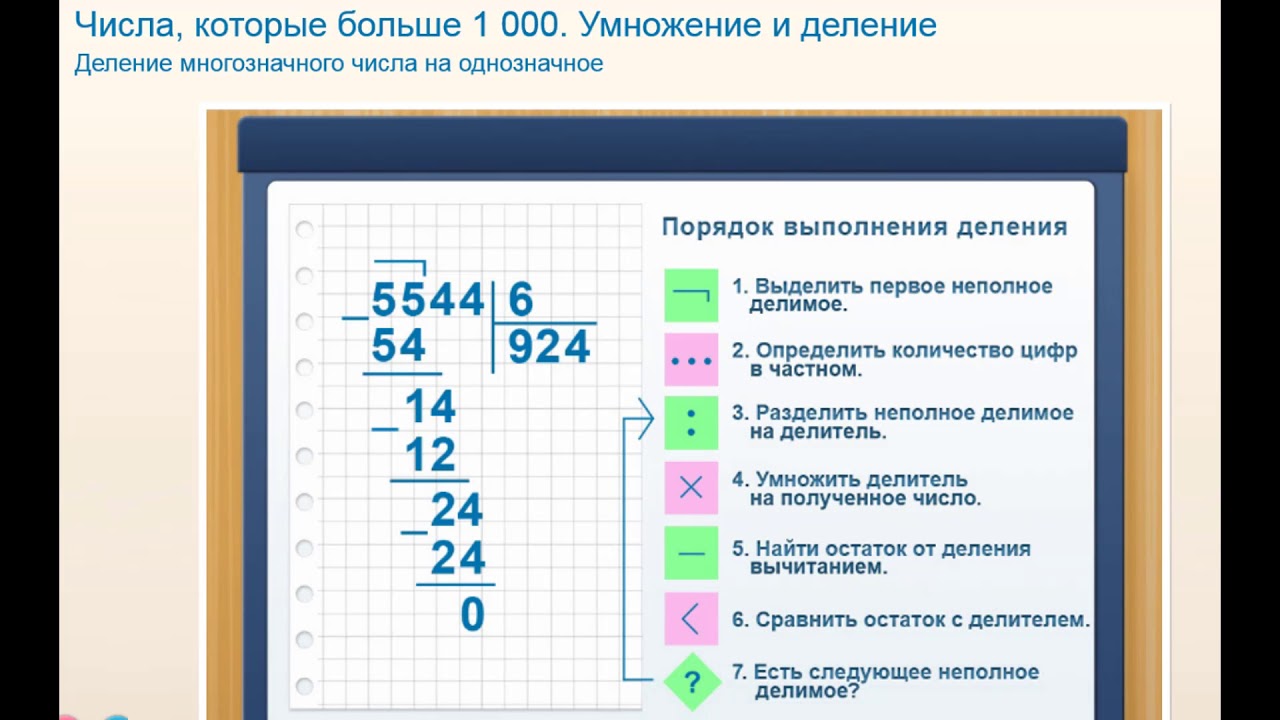
Сначала определите, о каком общем классе вещей идет речь: определение полинома описывает особый вид алгебраических выражение; определение непрерывной функции определяет вид функция; определение основы для векторного пространства указывает вид набора векторов.
Далее расшифруйте логическую структуру определения. Что у тебя есть сделать, чтобы показать, что член вашего общего класса вещей удовлетворяет определение: что вам нужно сделать, чтобы показать, что выражение является многочленом, либо функция непрерывна, либо набор векторов является базисом.
Шаг 2. Определите объем определения с помощью примеров.
К большинству определений прилагаются стандартные примеры. Пока эти полезны, они могут заставить вас ожидать, что все примеры будут выглядеть как стандартный пример. Чтобы понять определение, вы должны придумать собственное примеры: найдите три примера, которые удовлетворяют определению, но которые максимально отличаются друг от друга; найти два примера предметов в общем классе, описываемом определением, которое ему не удовлетворяет. Докажите, что ваши пять примеров делают то, что вы думаете, — такие доказательства
обычно короткие, достаточно внимательно следите за структурой определения и
очень помочь в понимании определения. Эти примеры должны быть
аккуратно написаны, чтобы вы могли к ним обратиться позже. Ваши собственные примеры
будет иметь большее значение для вас, чем моя или книга, когда придет время
для обзора.
Докажите, что ваши пять примеров делают то, что вы думаете, — такие доказательства
обычно короткие, достаточно внимательно следите за структурой определения и
очень помочь в понимании определения. Эти примеры должны быть
аккуратно написаны, чтобы вы могли к ним обратиться позже. Ваши собственные примеры
будет иметь большее значение для вас, чем моя или книга, когда придет время
для обзора.Шаг 3. Запомните точную формулировку определения.
Этот шаг может показаться мелочным, но использование определений требует знаний. именно то, что они говорят.По этой причине вы можете рассчитывать на то, что вас спросят для постановки любого определения на экзамене. Важность точного формулировка должна быть прояснена вашими примерами на шаге 2, и это, безусловно, существенен в доказательстве теорем. Твердое знание определений — это более трети битвы. Время
потраченные на получение таких знаний не тратятся зря.
К оглавлению
Теоремы, предложения, леммы и следствия
Иногда определения полезны сами по себе, но обычно мы необходимо связать их друг с другом и с общими проблемами, прежде чем они смогут заставить работать на нас. В этом роль теории.
В этом роль теории. Относительная важность и предполагаемое использование утверждений, которые
Затем на доказанное намекают имена, которые им даны. Теоремы обычно
важные результаты, которые показывают, как заставить концепции решать проблемы или давать
глубокое понимание работы предмета. Они часто вовлекали
и глубокие доказательства. Предложения дают меньшие результаты, часто относящиеся к разным
определения друг друга или предоставление альтернативных форм определения.
Доказательства предложений обычно менее сложны, чем доказательства теорем.Леммы — это технические результаты, используемые при доказательстве теорем. Часто это
обнаружил, что один и тот же прием используется несколько раз в одном доказательстве или в
доказательство нескольких теорем. Когда это происходит, трюк изолируется в
лемму, так что ее доказательство не придется повторять каждый раз, когда она используется.
Это часто делает доказательства теорем короче и, хочется надеяться, нагляднее.
Следствия являются непосредственными следствиями теорем либо дающих специальные
случаев или подчеркивая интерес и важность теоремы. Если
автор или преподаватель были осторожны (не все авторы и преподаватели
are) с помощью этих ярлыков, они помогут вам понять, что
главное в теме.
Если
автор или преподаватель были осторожны (не все авторы и преподаватели
are) с помощью этих ярлыков, они помогут вам понять, что
главное в теме.
Шаги к пониманию и усвоению теоремы следуют одним и тем же направлениям. как шаги к пониманию определения.
Шаг 1. Убедитесь, что вы понимаете, о чем говорит теорема.
Частично это проблема со словарным запасом. В теоремах используются термины, которые были даны точные значения по определениям. Поэтому вам может потребоваться просмотреть определения понимать слова теоремы. Далее вам необходимо понять логическую структуру теоремы: что
такие гипотезы и каковы выводы? Если у вас есть несколько гипотез,
должны ли они все быть удовлетворены (то есть есть ли у них и между ними) или будет достаточно иметь только некоторые из них ( или между ними)? В большинстве случаев теоремы требуют, чтобы все их гипотезы
быть довольным. Теорема ничего не говорит вам о ситуации, которая
не удовлетворяют гипотезе.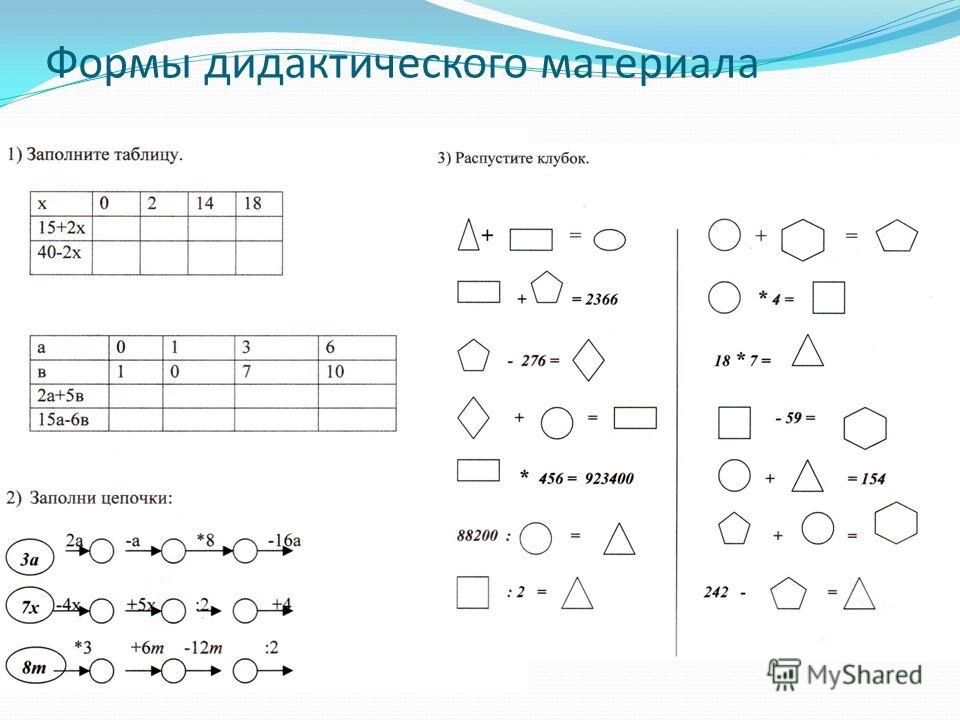 Гипотеза говорит вам, что вы должны показать
чтобы теорема могла быть применена к частному случаю. Выводы
расскажу вам, что говорит вам теорема о каждом случае.
Гипотеза говорит вам, что вы должны показать
чтобы теорема могла быть применена к частному случаю. Выводы
расскажу вам, что говорит вам теорема о каждом случае.
Шаг 2. Определите, как используется теорема.
Это включает в себя поиск примеров проблем, для которых теорема дает методика поиска ответа. Придумывайте свои проблемы и показывайте как теорема в них помогает. Снова записав это, вы укрепите теорема в уме и упростит рассмотрение.Шаг 3. Узнайте, что здесь делают гипотезы.
Это немного сложно и, вероятно, более важно на курсах продвинутого уровня. чем в начальных курсах. Что вы делаете, так это находите примеры (либо свои собственные или чьей-либо другой), чтобы показать, что если отдельные гипотезы опущены, вывод может быть ложным. Например, в исчислении многие теоремы имеют гипотеза о том, что задействованные функции непрерывны; почему теорема потерпят неудачу, если эта гипотеза не будет учтена? Обычно пример делает это яснее, чем рассмотрение того, как гипотеза использовалась в доказательстве будет. Каталог таких примеров может быть очень полезным. См., Например,
книги Контрпримеры в анализе и Контрпримеры в топологии.
Каталог таких примеров может быть очень полезным. См., Например,
книги Контрпримеры в анализе и Контрпримеры в топологии.В некоторых случаях гипотеза включается только потому, что она делает иначе сложное доказательство легко. Это означает, что вы не сможете найти примеры которые показывают, что каждая гипотеза важна.
Шаг 4. Запомните формулировку теоремы.
Если вы собираетесь использовать теорему, вам нужно точно знать, о чем она говорит. Обратите особое внимание на гипотезы.К доказательствам мы вернемся позже, но а пока позвольте мне заметить, что не стоит пытаться запомнить доказательство теоремы. Вам нужно достаточно хорошо понять доказательство того, что вы можете доказать теорему самостоятельно.К оглавлению
Собираем объект вместе
Математика — это не набор разных техник, а скорее образ мышления — единый предмет. Часть задачи изучения математики получает различные определения и теоремы, должным образом относящиеся к каждому разное.Это особенно важно в конце курса, но поможет вам понять содержание и организацию предмета, если вы помните об общей организации по мере продвижения. Есть две техники
Я знаю, что поможет в этом процессе: обратная работа и теорема определения
очертания.
Есть две техники
Я знаю, что поможет в этом процессе: обратная работа и теорема определения
очертания.Шаг 1. Работа в обратном направлении
В общем, очень легко распознать главный результат, когда вы доберетесь до этого. Хороший способ увидеть, как работает объект, — это изучить доказательство основного результата и посмотреть, какие предыдущие результаты были использованы в нем.Затем проследите эти результаты до более ранних результатов, использованных для их подтверждения. В конце концов вы вернетесь к определениям (если нет теорем без доказательства — в исчислении, например, доказательство промежуточного теорема о ценности часто опускается, потому что она требует более глубокого понимания действительных чисел, чем обычно доступно в начале исчисления 1). Эта информация может быть помещена в своего рода генеалогическую таблицу для получения результатов. который поможет вам сразу увидеть, как результаты совпадают.Это помогает иметь описательные имена для ваших теорем и лемм. Такая диаграмма может
выглядят примерно так:
Такая диаграмма может
выглядят примерно так:Теорема о среднем значении Теорема Ролля Кандидат леммы Значение знака производной Определение производной Определение максимума и минимума Существование max и min для непрерывных функций на [a, b] Определение максимума и минимума Определение закрытого интервала Аксиома наименьшей верхней границы Определение непрерывностиС такой дорожной картой через теорию вы сможете сказать, как вы попали туда, где находитесь, если не туда, куда вы направляетесь.
Шаг 2. Составьте набросок теоремы об определении.
После того, как вы вернетесь к определениям для каждого из ваших основных теоремы в разделе, вы должны иметь хорошее представление о том, какие результаты необходимо, прежде чем можно будет доказать другие. Некоторые определения не имеют смысла пока не будут доказаны определенные теоремы (например, размерность векторного пространства: вы не можете дать номеру имя, пока не поймете, что говорите об уникальном число, а для этого нужна теорема). Схема теоремы определения — это
расположение результатов в таком порядке, чтобы каждый результат был представлен
прежде, чем это понадобится в доказательстве.Он должен содержать точные утверждения
всех определений и теорем и набросок доказательства каждой теоремы.
Набросок доказательства покажет, какие предыдущие результаты использовались и как они
были объединены. Обычно опускаются вычисления, упрощающие формы выражений.
и регулярные проверки того, что гипотезы удовлетворяются. Этот план является как
хороший способ начать обзор и полезная вещь, на которую можно сослаться.
Схема теоремы определения — это
расположение результатов в таком порядке, чтобы каждый результат был представлен
прежде, чем это понадобится в доказательстве.Он должен содержать точные утверждения
всех определений и теорем и набросок доказательства каждой теоремы.
Набросок доказательства покажет, какие предыдущие результаты использовались и как они
были объединены. Обычно опускаются вычисления, упрощающие формы выражений.
и регулярные проверки того, что гипотезы удовлетворяются. Этот план является как
хороший способ начать обзор и полезная вещь, на которую можно сослаться. К оглавлению
Как разобраться в доказательстве
Математика на уровне колледжа требует, чтобы студент проработал (или хоть просиди) много доказательств.Я думаю, что это часто непопулярно. потому что тяжело следовать доказательству, трудному труду незнакомого типа. Доказательства в основном отсутствуют или не являются обязательными в математике в старших классах; это ни отсутствующий, ни факультативный в математике колледжа.
Шаг 1. Убедитесь, что вы знаете, о чем говорит теорема.
Если вы перепутаете гипотезы с выводами, вы не узнаете какие предположения могут быть сделаны, и вы не будете знать, к какому выводу вы пришли пытаюсь достичь.Шаг 2. Составьте общий план доказательства.
Это то, что вы сделали бы в наброске теоремы об определении. Посмотри, что за использовались предыдущие результаты, и выясняем, какова основная стратегия доказательства является. На этом проезде опустите детали, иначе вы пропустите направление дороги из-за слишком внимательного изучения кирпичей на тротуаре. Большинство теорем имеют форму импликации: если гипотезы верны,
тогда следует вывод. Самая простая структура для использования доказательства —
принять гипотезы и объединить их, используя предыдущие результаты, чтобы достичь
вывод через цепочку следствий.Некоторые доказательства используют другие стратегии:
контрапозитивный аргумент, сокращение до абсурда, математическая индукция,
возможно, даже лемма Цорна (форма избранной аксиомы). Более сложный
виды доказательств необходимо будет обсудить в классе.
Более сложный
виды доказательств необходимо будет обсудить в классе.
Шаг 3. Заполните все детали.
Как только вы поймете стратегию доказательства, сконцентрируйтесь на его тактике. Практически все изложения доказательств в учебниках математики для бакалавриата (и все экспозиции на более высоких уровнях) упускают многие рутинные шаги.An выражение будет упрощено, не показывая, как именно получить из одного строка к следующей. Заполните эти данные. Теорема будет процитирована и применена. без явной проверки всех своих гипотез. Проверь их. Некоторые части Доказательства будут изложены с подробностями, оставленными читателю. Ставить в этих деталях. Когда вы закончите, вы должны знать, почему следует каждый шаг из того, что было раньше. Возможно, вы не понимаете, как кто-то мог подумать сделайте доказательство таким образом, но вы должны убедиться, что оно правильно.Зачем вообще заморачиваться с доказательствами?
Для математика, специализирующегося на математике, на этот вопрос легко ответить — большая часть математики состоит из доказательств. Математик наслаждается логическим
головоломка, которую необходимо решить, чтобы найти доказательство и получить эстетическое удовлетворение
от элегантности в доказательствах. Студент, желающий получить специальность математика
должен делать это из-за способности расшифровывать и предъявлять доказательства и
удовольствие, получаемое от хорошо сделанных доказательств. У майора также должны быть навыки
в решении проблем и поиске приложений.
Математик наслаждается логическим
головоломка, которую необходимо решить, чтобы найти доказательство и получить эстетическое удовлетворение
от элегантности в доказательствах. Студент, желающий получить специальность математика
должен делать это из-за способности расшифровывать и предъявлять доказательства и
удовольствие, получаемое от хорошо сделанных доказательств. У майора также должны быть навыки
в решении проблем и поиске приложений.Но многие из вас скажут: «Я не математик; Я хочу приложения так что я могу использовать инструменты из математики в моей области » или « Я просто беру этот курс, потому что это требование моей специальности, и мне вроде как понравилось математика в старшей школе ». Зачем вам нужно изучать доказательство?
Приложения, которые встречаются в других сферах, вряд ли будут выглядеть точно
например, приложения из учебников математики, выбранные из-за их привлекательности
для традиционной аудитории (в основном инженеров) и для их представителей
персонаж. Другие приложения работают аналогично, хотя и не совсем так
способ. Это означает, что вам нужно научиться применять концепции в своей
математические курсы к ситуациям, не обсуждаемым в этих курсах. (Здесь нет
способ, которым в курсе можно обсудить все возможные известные приложения: о
Каждые две недели с заявками появляются 500 статей, а это просто
приложения, опубликованные в « математической » литературе!) Для этого
вам нужно как можно лучше понимать математику, которую вы хотите
применять.Безусловно это означает, что вам необходимо знать гипотезы теорем
чтобы вы не применяли их там, где они не работают. Полезно знать
доказательство, чтобы вы могли увидеть, как обойти провалившуюся гипотезу, если
необходимый. Одна из главных ловушек прикладной математики, особенно
как практикуется нематематиками, есть опасность упустить из виду
предположения математической модели. (Математики пытаются применить
математики с большей вероятностью попадут в ловушку создания моделей, которые
не имеют отношения к реальности.
Другие приложения работают аналогично, хотя и не совсем так
способ. Это означает, что вам нужно научиться применять концепции в своей
математические курсы к ситуациям, не обсуждаемым в этих курсах. (Здесь нет
способ, которым в курсе можно обсудить все возможные известные приложения: о
Каждые две недели с заявками появляются 500 статей, а это просто
приложения, опубликованные в « математической » литературе!) Для этого
вам нужно как можно лучше понимать математику, которую вы хотите
применять.Безусловно это означает, что вам необходимо знать гипотезы теорем
чтобы вы не применяли их там, где они не работают. Полезно знать
доказательство, чтобы вы могли увидеть, как обойти провалившуюся гипотезу, если
необходимый. Одна из главных ловушек прикладной математики, особенно
как практикуется нематематиками, есть опасность упустить из виду
предположения математической модели. (Математики пытаются применить
математики с большей вероятностью попадут в ловушку создания моделей, которые
не имеют отношения к реальности. )
)
Многие приложения состоят из распознавания определения математического концепция сформулирована в терминах другой дисциплины — более знакомой вы согласны с определением, тем больше вероятность, что вы сможете распознать замаскированная версия в другом месте. Нюансы определений вынесены наиболее ясно в доказательствах предложений, связывающих определения и указывающих неожиданные эквивалентные варианты, некоторые из которых могут больше походить на ситуацию в дисциплине, отличной от той, которая используется в вашем классе математики.
Аргументы в пользу теории как помощи в применении основываются на очевидной посылке: гораздо легче применить то, что вы досконально понимаете. Это, однако лучший аргумент в пользу внимательности при изучении формулировок теорем чем потратить время на понимание доказательств. Лучшее оправдание для включения доказательства в математические классы более философски:
Доказательство — это окончательное испытание
валидность в математике.
После принятия логических процессов, участвующих в доказательстве, больше нет наблюдение или изменение моды изменит обоснованность математического результат.Ни в одной другой дисциплине нет такого неизменного критерия достоверности.
Основное преимущество образования — это способность мыслить.
ясно и сделать взвешенное суждение. Каждая дисциплина должна учить тело
материала, соответствующие способы мышления при работе с этим материалом,
и средство для определения действительности сделанных выводов. А
учебная программа по химии без лабораторных работ будет серьезно дефицитной, поскольку
эксперимент — это проверка достоверности в науке. Точно так же математика без
Доказательства сильно несовершенны, ведь это не математика.
К оглавлению
Развивающая техника
Примерно от трети до половины любого курса математики посвящены технике — процессу. заставить теоремы работать на вас в конкретных ситуациях, а не в общая установка, в которой они обычно указываются.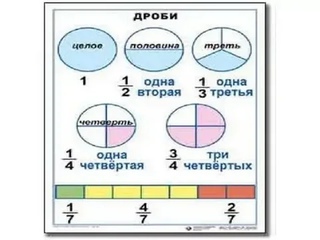 Иногда это справедливо
легко: многие доказательства дают явные конструкции, которым вы следуете для
особый случай. В этих ситуациях единственные проблемы связаны с алгебраическими
и тригонометрические манипуляции и отслеживание того, где вы находитесь в
процесс.В других ситуациях (хороший пример — техника интеграции)
существует множество подходов, которые можно применить к данной проблеме, и несколько
уловки, которые можно использовать, чтобы сделать проблему более разрешимой. Для этих
вам нужно развивать суждение.
Иногда это справедливо
легко: многие доказательства дают явные конструкции, которым вы следуете для
особый случай. В этих ситуациях единственные проблемы связаны с алгебраическими
и тригонометрические манипуляции и отслеживание того, где вы находитесь в
процесс.В других ситуациях (хороший пример — техника интеграции)
существует множество подходов, которые можно применить к данной проблеме, и несколько
уловки, которые можно использовать, чтобы сделать проблему более разрешимой. Для этих
вам нужно развивать суждение.Шаг 1. Прочтите теоремы и примеры.
Некоторые студенты делают весь процесс обучения тому, как решать задачи, более трудно вести себя так, как будто это не имеет никакого отношения к другому материалу в курс. Часто проблемы следуют схеме, которая явно указана в доказательство основной теоремы, которой они следуют.Зная общую закономерность заранее легче, чем пытаться найти его методом проб и ошибок.Шаг 2. Проработайте достаточно задач, чтобы овладеть техникой.
 На этом этапе вы должны проработать достаточно задач, чтобы единственная техника
которые иллюстрируют проблемы, прочно запомнились вам. Поскольку у вас есть окончательная
ответственность за свое образование, вы должны проявить инициативу в работе
достаточно проблем для вашей собственной практики. Это вполне может быть больше проблем
чем назначены для сдачи.
На этом этапе вы должны проработать достаточно задач, чтобы единственная техника
которые иллюстрируют проблемы, прочно запомнились вам. Поскольку у вас есть окончательная
ответственность за свое образование, вы должны проявить инициативу в работе
достаточно проблем для вашей собственной практики. Это вполне может быть больше проблем
чем назначены для сдачи.Шаг 3.Решите несколько задач как можно большим количеством разных способов.
Слишком часто практика, полученная на шаге 2, заставляет ученика думать, что к каждой проблеме есть только один подход. Иногда один подход прост а другой сложен, но часто срабатывают несколько разных атак Одинаково хорошо. Сложные подходы дают студенту практику в решении задачи, требующие более одного шага и более одной техники.Шаг 4. Составьте себе набор случайно выбранных задач.
Одна трудность с изучением множества техник для решения определенного вида проблема в том, что вы должны выяснить, какую технику использовать, прежде чем вы можете приступить к работе над решением. Это усугубляется тенденцией
проблемы должны быть сгруппированы таким образом, чтобы использовать подходящую технику
тот, который непосредственно предшествовал поставленной задаче. Ставим два или три
задачи из каждой из задач, поставленных в главе о технике на 3 по
5 карт, а затем перетасовка карт даст вам набор задач на
которые нужно практиковать, решая, какую технику использовать.
Это усугубляется тенденцией
проблемы должны быть сгруппированы таким образом, чтобы использовать подходящую технику
тот, который непосредственно предшествовал поставленной задаче. Ставим два или три
задачи из каждой из задач, поставленных в главе о технике на 3 по
5 карт, а затем перетасовка карт даст вам набор задач на
которые нужно практиковать, решая, какую технику использовать. К оглавлению
Несколько заключительных предложений
Математическая проза имеет очень низкую степень избыточности, а математика очень накопительная тема.При чтении обращайте пристальное внимание — после того, как вы познакомились, концепция редко повторяется и будет принята позже. Позволять себе достаточно времени, чтобы прочитать книгу, прежде чем приступить к задаче. Немногие ученики пишут достаточно быстро, чтобы делать полные и удобочитаемые заметки на
класс. По этой причине полезно в ближайшее время вернуться к своим заметкам в классе.
после каждого занятия и сделайте полную копию со всеми определениями
и теоремы четко сформулированы. Эта практика также поможет вам определить
части, которую вы не понимаете, так что вы можете спросить о них своего профессора в
своевременная мода.
Эта практика также поможет вам определить
части, которую вы не понимаете, так что вы можете спросить о них своего профессора в
своевременная мода.
Не позволяйте себе отставать. Математика требует точности, привычек
ясной мысли и практики. Подготовка к экзамену не только провалится
для получения желаемого результата на экзамене это также усилит плохой
привычка — пытаться заниматься математикой путем запоминания, а не понимания.
Хороший ночной сон и ясная голова послужат вам лучше, чем в последнюю минуту
запоминание.
К оглавлению

 Ведь как-то отличники и хорошисты разбираются в дисциплине. Тем более если учитель говорит, что это легкая тема, то стоит поверить.
Ведь как-то отличники и хорошисты разбираются в дисциплине. Тем более если учитель говорит, что это легкая тема, то стоит поверить.



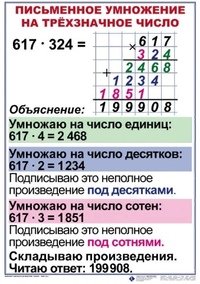
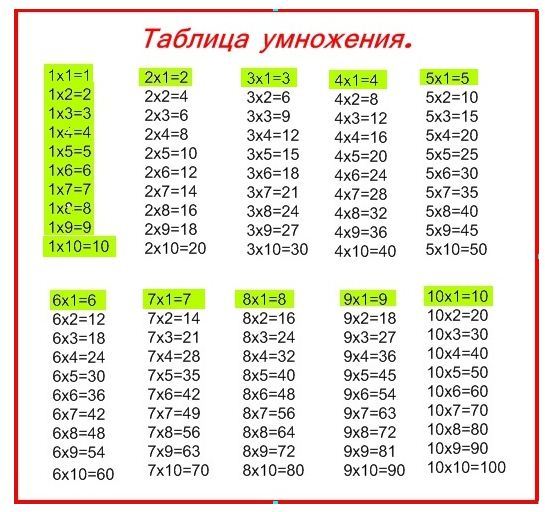









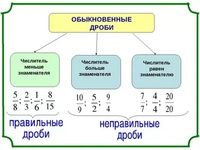



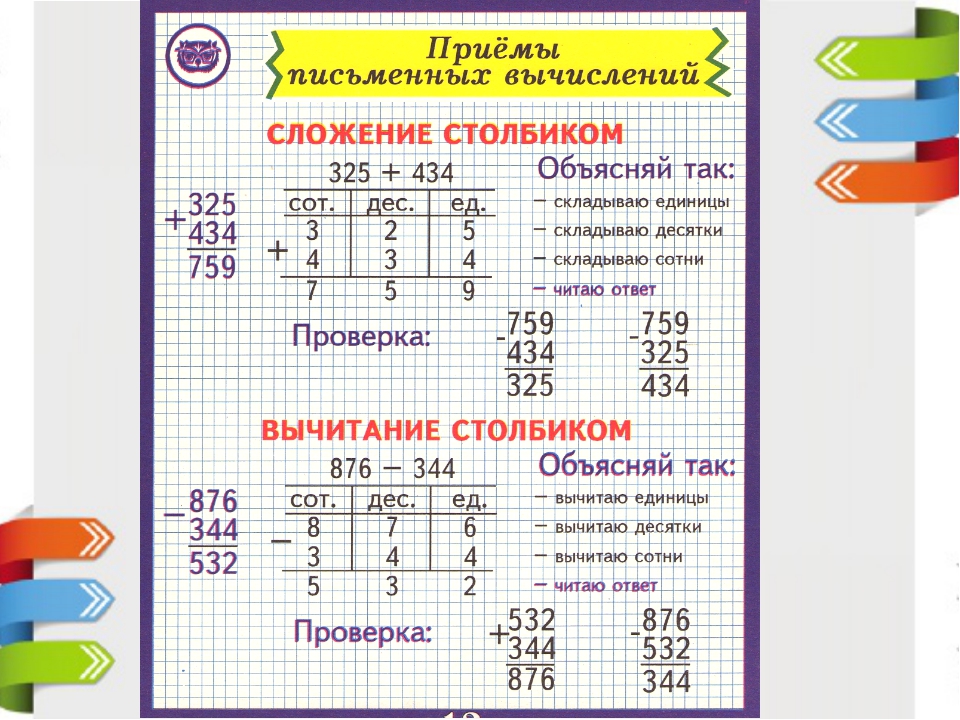














 Если вам кажется, что это «пошло слишком быстро» или вы не знаете, что делает учитель, вам, возможно, придется вернуться на несколько уроков и выучить их лучше, прежде чем продолжить.
Если вам кажется, что это «пошло слишком быстро» или вы не знаете, что делает учитель, вам, возможно, придется вернуться на несколько уроков и выучить их лучше, прежде чем продолжить.
 «-Владимир Арнольд 1990 г.
«-Владимир Арнольд 1990 г. Материал охватывает начальные классы 3–9 и маты 1, 2 и 3 для старших классов средней школы. В 2019 году на сайте было 413,1 трлн уникальных пользователей.
Материал охватывает начальные классы 3–9 и маты 1, 2 и 3 для старших классов средней школы. В 2019 году на сайте было 413,1 трлн уникальных пользователей.
