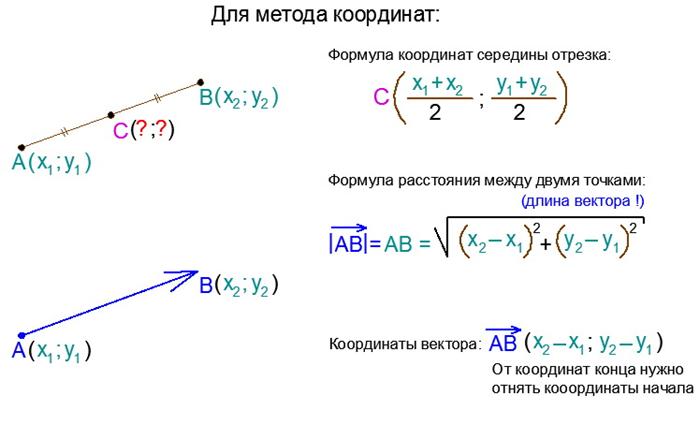
Расстояние между точками на координатной прямой
Расстояние между двумя точками является длиной отрезка, между этими точками. Как найти расстояние между двумя заданными точками?
Для того чтобы найти длину отрезка на координатной прямой надо из координаты ее конца вычесть координату начала по модулю.
Пример . Найдите расстояние между точками:
- \(A(-15)\) и \(B(3)\)
- \(C(3,2)\) и \(D(7,8)\)
- \(E(5)\) и \(K(-17)\)
Для понимания важно знать какая из точек находится правее, а какая левее. Хотя это не важно, так как мы берем расстояние по модулю, то есть отрицательным значение не может быть.
Решение:
\(|AB|=b-a\)
1) \(|AB| = 3-(-15)=|18|=18\)
2) \(|CD| = (3;2)-(7;8)=|(-4;-6)|=(4;6)-\) это означает на рисунке выше по оси x расстояние равно четырем единицам и по оси y 6 единицам длины.
3) \(|EK| = 5-(-17)=|22|=22\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Оставить заявкуРепетитор по математике
Университет штата Аризона
Проведенных занятий:
Дистанционно (Скайп)
Преподаватель 1- 7 классов.
Хотите учить английский интересно и добиваться результатов?Тогда давайте сделаем это вместе! Для каждого ученика я использую совершенно индивидуальный подход учитывая его интересы, цели, способности и возможности. Именно тогда изучение английского будет интересным и даст результат. Я объясняю даже очень сложный материал просто и красочно для детей разных возрастов. Очень люблю общаться с детьми и подростками, отлично понимаю насколько трудно изучать новый язык и поэтому хочу помочь каждому ребенку достичь успехов в освоении английского языка!
Репетитор по математике
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 8-11 классов по обществознанию.
Моя основная задача — помочь школьнику с комфортом подготовиться к сдаче выпускных экзаменов на максимальный для ученика балл. В своей деятельности использую собственные наработки, только современные и актуальные материалы. Мои выпускники являются студентами/выпускниками СПбГУ, ВШЭ, МГИМО, РГПУ им. А.И. Герцена, ВУМО, РАНХиГС, РТА и др.
Репетитор по математике
Крымский федеральный университет имени В.
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике для 5-11 классов.
Помощь в подготовке к ОГЭ и ЕГЭ. Магистр математических наук. В школе к математике относился нейтрально, понимал на среднем уровне, но после школы мне попался замечательный учитель, который смог донести всю красоту и простоту обычными, простыми словами, а не замысловатыми книжными терминами. Ведь книгу можно почитать и без учителя. С тех пор серьезно увлекся математикой и упор делаю именно на прозрачном и понятном объяснении, простыми словами, ведь главное не заумные термины, а понимание сути процесса.
Похожие статьи
Расстояние между двумя точками на поверхности Земли | by shemanovskiy
Представим, что для чего-то понадобилось измерить расстояние между двумя точками на поверхности Земли, например, расстояние между Красной площадью и Эрмитажем.
Конечно, можно попробовать решить задачу в лоб и посчитать евклидово расстояние по формуле:
но этот подход не заработает по той простой причине, что евклидова метрика предназначена для вычисления расстояния на плоскости, а поверхность Земли — это всё-таки фигура, очень близкая к сфере.
Для решения такой задачи нужно обратиться к редко используемым тригонометрическим функциям.
Одна из таких функций, называется синус-верзус, или, по-другому, версинус. Он представляет собой расстояние от центральной точки дуги, измеряемой удвоенным данным углом, до центральной точки хорды, стягивающей дугу. Вычисляется версинус по формуле:
Гаверсинус — это просто половина версинуса, и именно эта функция поможет нам в решении задачи с поиском расстояния:
Для любых двух точек на сфере гаверсинус центрального угла между ними вычисляется по формуле:
В этой формуле:
- d — это центральный угол между двумя точками, лежащими на большом круге
- r — радиус сферы
- φ₁ и φ₂ — широта первой и второй точек в радианах
- λ₁ и λ₂ — долгота первой и второй точек в радианах
Обозначим временно гаверсинус отношения длины к радиусу как переменную h:
Тогда длину d можно вынести за знак равенства:
а для того, чтобы избавиться от дроби, выразим гаверсинус через арксинус:
затем раскроем переменную h:
подставим формулу гаверсинуса и получим формулу вычисления расстояния:
Теперь вернёмся к исходной задаче поиска расстояния между Красной площадью и Эрмитажем.
Для Красной площади Гугл подсказал координаты (55.7539° N, 37.6208° E), а для Эрмитажа — (59.9398° N, 30.3146° E).
Прежде, чем подставлять координаты в формулу, их нужно перевести в радианы.
Для того, чтобы вычислить длину, нужно полученное значение арксинуса умножить на два радиуса сферы. Подсчёты усложняет тот факт, что Земля не является идеальной сферой и её радиус немного варьируется. Воспользуемся усреднённым значением радиуса, которое, в соответствии со стандартом WGS84 приблизительно равно 6371 км:
Произведя умножение, получаем искомое значение, которое приблизительно равно 634.57 км.
Кстати, из-за того, что Земля — не идеальная сфера, погрешность расчётов с использованием этой формулы, составляет около 0,5%.
Как инструменты близости вычисляют расстояние—ArcGIS Pro
Как определяется расстояние
Расстояние между любыми двумя объектами вычисляется как минимальный интервал между ними, т.е., там, где два объекта расположены ближе всего друг к другу.
Эта логика действует во всех инструментах геообработки, которые вычисляют расстояние, включая такие инструменты, как Ближайший объект, Построить таблицу ближайших объектов и Пространственное соединение (с опцией ближайших совпадений).
Измерения расстояний имеют наибольшую точность, если входные данные используют систему координат равнопромежуточной проекции. Хотя вычисление расстояния может быть выполнено независимо от системы координат, результат может оказаться не точным или даже бессмысленным, если данные используют географическую систему координат или система координат задана неправильно.
Более подробно о картографических проекциях и системах координат
Для дальнейшего обсуждения, расстоянием всегда будет считаться минимальный интервал между двумя объектами.
Особые соображения
- Несколько объектов могут оказаться на одинаковом удалении от другого объекта. В таком случае один из равноудаленных объектов будет выбираться в качестве ближайшего случайным образом.
- Если один из объектов содержит другой или находится внутри другого объекта, расстояние между ними равно 0.
- Это означает, что если объект находится внутри полигона, расстояние между ним и окружающим его полигоном равно 0.
- Расстояние между двумя объектами равняется нулю всякий раз, когда у них имеется хотя бы одна общая координата x,y.
- Это означает, что при пересечении, перекрытии или касании двух объектов, расстояние между ними равняется 0.
- Расстояние всегда вычисляется до границы полигонального объекта, не до центра или центроида полигона.
- Как отмечено выше, если объект полностью находится внутри полигона, расстояние между ним и окружающим его полигоном равно 0.
- Расстояние между двумя объектами (любого типа) не меняется в зависимости от направления измерения.
Основные операции для определения расстояния
Вычисление расстояния зависит от типа геометрии объектов, а также от других факторов, таких как система координат.
Однако есть три основных правила, подробнее описанные ниже, которые определяют способ вычисления расстояния.
- Расстояние между двумя точками является прямой линией, соединяющей их.
- Расстояние от точки до линии измеряется либо как перпендикуляр, либо как расстояние до ближайшей вершины.
- Расстояние между полилиниями определяется вершинами сегментов.
Правило 1: расстояние между двумя точками является прямой линией, соединяющей их
На рисунке ниже показано расстояние между двумя точками, вместе с несколькими ключевыми словами и объектами, использующимися инструментами близости.
Ключевые слова в вышеуказанных выносках (IN_FID, NEAR_DIST, NEAR_FID, NEAR_X, NEAR_Y и NEAR_ANGLE) являются полями, добавляемыми к выходным данным инструментами Построить таблицу ближайших объектов и , а также к входному классу объектов при использовании инструмента Ближайший объект.
Расстояние между мультиточками
Для особого случая, когда определяется расстояние между мультиточками, вычисляются расстояния от каждой точки входного мультиточечного объекта до каждой точки ближайшего мультиточечного объекта с помощью Правила 1, минимальное из этих трех расстояний станет расстоянием между мультиточечными объектами.
Кроме того, когда одна из точек мультиточечного объекта находится поверх одной из точек другого мультиточечного объекта, расстояние между ними равняется 0. Это справедливо для всех составных объектов.
Правило 2: расстояние от точки до полилинии измеряется либо как перпендикуляр, либо как расстояние до ближайшей вершины
В ArcGIS линейные объекты называются полилиниями. Эти два термина, линия и полилиния, взаимозаменяемы. Полилиния является упорядоченным набором точек, эти точки называются вершинами. An individual vertice is a vertex. Полилиния может иметь любое количество вершин. Линия, заданная двумя вершинами, называется сегментом. Две вершины, которые задают сегмент линии, называются конечными вершинами.
Сходным образом, полигон является замкнутой областью, заданной одной или несколькими полилиниями.
Кратчайшим расстоянием от точки до сегмента линии является перпендикуляр к ней. Если в пределах конечных вершин сегмента перпендикуляр провести не удается, кратчайшим расстоянием будет расстояние до ближайшей конечной вершины.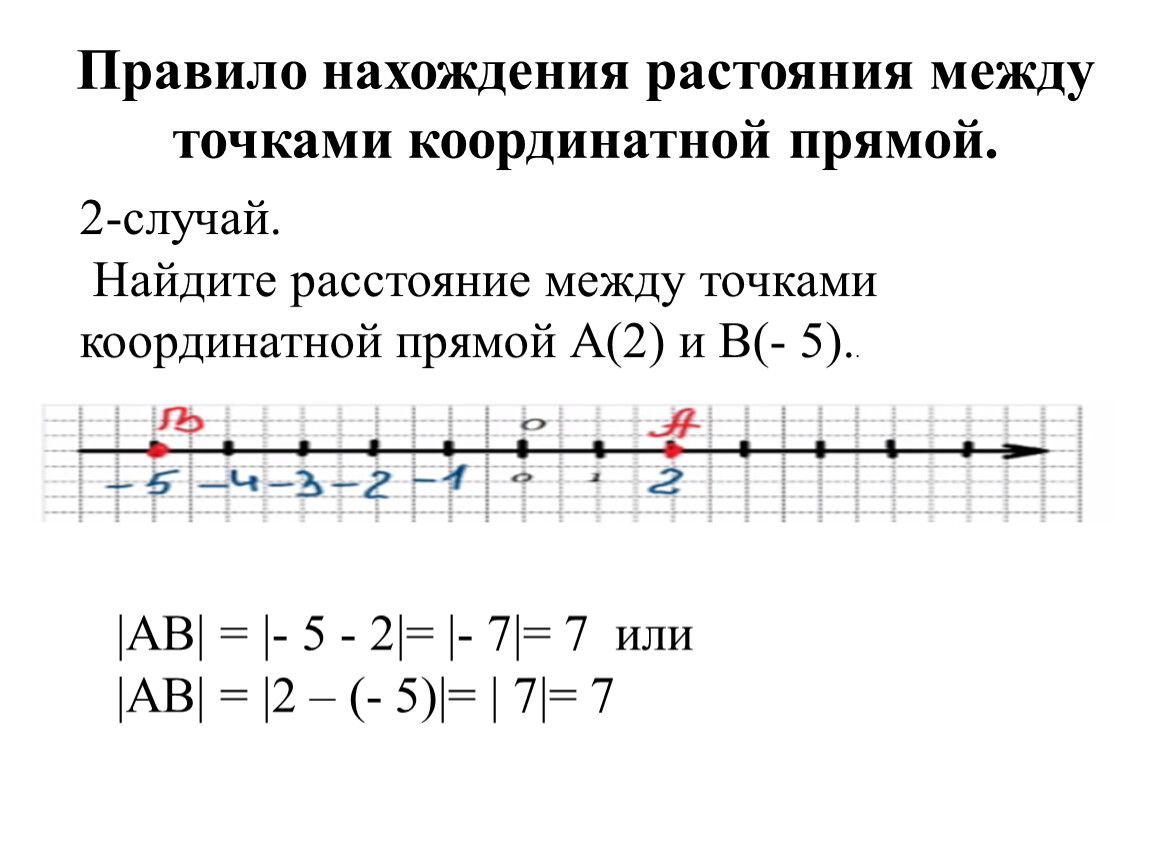
Расстояние от точки до полилинии
Если полилиния содержит только один сегмент, для вычисления расстояния применяется Правило 2.
Если полилиния состоит из нескольких сегментов (чаще всего), сначала определяется ближайший к точке сегмент линии, затем для вычисления расстояния применяется Правило 2.
Расстояние от точки до полигона
Поскольку полигон является замкнутой областью, образованной набором сегментов линий, вычисление расстояния от точки до полигона включает определение ближайшего к точке сегмента, затем применяется Правило 2.
Расстояние будет определяться, только если точка находится вне полигона; иначе, расстояние равно 0.
На рисунке выше, для точек 2 и 3 расстояние равно 0, для точек 1 и 4 – расстояние положительно.
Правило 3: расстояние между полилиниями определяется вершинами сегментов линии
Для двух объектов, не являющихся точками, таких как два сегмента линий:
- Расстояние вычисляется от каждой из конечных вершин входного сегмента до ближайшего сегмента с использованием Правила 2.
- Расстояние вычисляется от каждой из конечных вершин ближайшего сегмента до входного сегмента.
Расстояние от полилинии до полилинии
В простейшем случае, предположим, что оба полилинейных объекта состоят из одного сегмента. На рисунке ниже показан перпендикуляр CX от вершины C до сегмента, заданного вершинами AB. Перпендикуляр от вершины D также вычисляется, но это расстояние больше, чем расстояние CX. Поэтому CX является кратчайшим расстоянием от сегмента CD до сегмента AB.
Обратите внимание, что перпендикуляр от вершины A или B до сегмента CD провести нельзя, поэтому, кратчайшее расстояние вычисляется от вершин A и B до вершины C. В результате, именно AC является кратчайшим расстоянием между сегментами AB и CD.
Из двух вычисленных расстояний (AC и CX), CX является кратчайшим между двумя сегментами, поскольку это минимальное расстояние из всех расстояний между вершинами и сегментом.
Когда обе полилинии состоят из нескольких сегментов, определяются два наиболее близкорасположенных друг к другу сегмента, затем вычисляется расстояние, согласно Правилу 3.
Расстояние от полилинии до полигона
При вычислении расстояния между полилинией и полигоном определяются два наиболее близкорасположенных сегмента: один сегмент полилинии и один сегмент из образующих границу полигона. Расстояние между этими двумя сегментами определяется так же, как описано в Правиле 3.
Краткая информация
На следующем рисунке показано, как измеряется расстояние между объектами различных типов и определяется положение ближайших объектов. Показаны не все возможные комбинации.
Связанные разделы
Отзыв по этому разделу?
Как вычислить расстояние между двумя точками, зная только их географические координаты? | Excel, судоку, артобъекты…
Задача простая. Нужно вычислить расстояние между двумя точками на карте, при этом известны только их географические координаты, то есть широта и долгота.
Для примера вычислим расстояние между Москвой и Питером, но данная методика, конечно же, будет применима и к другим двум точкам местности. В наше время у многих людей есть такие компасы, например при смартфонах, которые показывают не только направление, но и географические координаты.
Итак, задача: вычислить расстояние между двумя городами. Известно только одно – географические координаты, то есть широта и долгота. Посмотрим эти данные в справочнике, ну или в Википедии.
Итак, что нам известно: координаты Москвы:
55,7522 град. с.ш., 37.6156 град. в.д.
Координаты Петербурга:
59,89444 град. с.ш., 30,26417 град. в.д.
Построим с помощью Excel трапецию:
Рисунок 1.Рисунок 1.
Итак, у нас есть трапеция ABCD. На ней точка D – это Москва, точка B – это Петербург. Отрезок AB проходит по меридиану Петербурга, BC – по параллели Петербурга, CD – по меридиану Москвы и AD – по параллели Москвы.
Что нам известно? Во-первых известны все географические координаты каждой из точек:
A: 55,7522, 30,26417;
B: 59,89444, 30,26417;
C: 59,89444, 37,6156;
D: 55,7522, 37,6156.
Вычислить AB и CD достаточно просто. На меридианах в градусе примерно одинаковое число километров. Это расстояние можно взять из справочных данных, и оно составляет примерно 111,1 км в каждом градусе.
Нужная нам разница в градусах – это 59,89444-55,7522, или 4,14224. А это значит, что разница в километрах – это 4,14224*111,1=460,2029 км.
Что же касается оснований трапеции, там тоже все достаточно просто. Экватор – это ноль градусов северной широты, и длина каждого градуса на экваторе около 111,3 км. Поскольку косинус ноля – это единица, то для любой параллели верна следующая формула: длина каждого градуса равна произведению 111,3 на косинус того угла, который числится в градусах северной широты (ну или южной, если это происходит южнее экватора).
Итак, с помощью Excel вычислим нужные нам косинусы:
- cos(55.7522) = 0,562773
- cos(59.89444) = 0,501595
Это значит, что 1 градус в верхнем основании нашей трапеции =111,3*0,501595=55,82749 км, а один градус в нижнем основании трапеции =111,3*0,562773=62,6366 км. Поскольку число градусов одинаково как в верхнем, так и в нижнем основаниях трапеции и составляет 37,6156-30,26417, то есть 7,35143 градуса. Но число километров в верхнем и нижнем основаниях трапеции не одинаковое.
Рассчитаем эти расстояния в километрах. BC=7,35143*55,82749=410,4119 км.
AD=7,35143*62,6366=460,469 км.
Теперь проведем высоту BH в нашей трапеции:
Рисунок 2.Рисунок 2.
В прямоугольном треугольнике ABH нам известно, что гипотенуза равна 460,2029 км, малый катет тоже известен (это половина разницы между длинами оснований трапеции, то есть 0,5*[460,469-410,4119], то есть 0,5*50,05711, или 25,02856 км).
Итак, найдем высоту трапеции ABCD, ее можно вычислить с помощью теоремы Пифагора. Напомню, что мы знаем и длину гипотенузы, и длину наименьшего из катетов.
- Квадрат гипотенузы: 211786,7
- Квадрат известного катета: 626,4
- Разность между этими числами: 211160,2
Корень из этой разности – 459,5218 км. Это и есть наша высота трапеции, то есть BH.
Задача почти решена. Для нахождения расстояния между Москвой и Питером нам нужно вычислить диагональ трапеции, то есть BD. Нарисуем эту линию:
Рисунок 3.Рисунок 3.
Итак, у нас есть треугольник BHD. BH мы только что вычислили (459,5218 км), HD тоже известно (нужно от большего основания трапеции отнять AH. 460,469-25,02856=435,4404).
Два катета известны, нужно найти гипотенузу. По той же теореме Пифагора, и мы увидим, что гипотенуза будет равна 633,0629 км.
Это и есть расстояние от Питера до Москвы.
Проверим наши вычисления, спросив у Яндекса, сколько составляет расстояние от Питера до Москвы.
Рисунок 4.Рисунок 4.
Мы увидим ответ – 634 км. При вычислениях по нашей методике получилось чуть больше, чем 633 км. Это значит, что погрешность при данном виде вычислений достаточна мала. Но если учесть, что крупные города — это не маленькие точки, а большие расстояния с севера на юг и с запада на восток, то можно сказать, что мы вычислили все правильно.
А на этом пока всё, подписывайтесь на мой канал и до новых встреч!
Какое кратчайшее расстояние между двумя двумерными точками на поверхности цилиндра?
В моем исследовательском проекте я столкнулся с непредвиденной проблемой внедрения.
В принципе, я даю две двумерные точки [P1 = (x1, y1) и P2 = (x2, y2)] на листе бумаги (т. Е. 2D-плоскость).
Затем я складываю этот лист бумаги в цилиндр. Например, если самая левая x-координата по оси x равна 0, а самая правая — 999, то после складывания бумаги в цилиндр 0 и 999 находятся рядом друг с другом по оси x (на задней/скрытая сторона цилиндра).
Другими словами, бумага была сложена таким образом, чтобы левый и правый края бумаги касались друг друга.
Теперь мне нужно найти кратчайшее расстояние между P1 и P2, которые теперь расположены на поверхности этого цилиндра (я считаю, что это называется геодезической).
К сожалению, несмотря на часы поиска, я не могу найти ответ, который:
a) Относится к этой же ситуации.
б) Является математически достаточно простым для понимания и реализации в программе.
Один ответ, который я нашел ( http://www.ifsc.usp.br /~gabriel.luchini/comment_1.pdf ) описал эту точную ситуацию, но уравнение было умопомрачительно сложным, включая дифференциацию, интеграцию и тонну эзотерических символов, смысл которых ускользает от меня.
Другой ответ ( https://stackoverflow.com/questions/7981815/projection-of -a-plane-on-a-cylinder ), похоже, описывает, как преобразовать координаты 2D-точки в эквивалентные 3D-координаты на поверхности цилиндра, но я не уверен, что это правильно, и даже если бы это было так, я все еще не знал, как вычислить расстояние между результирующими точками.
Технически я знаю длину «дуги» вдоль «фронта» поверхности цилиндра, между двумя точками — я предполагаю, что он просто такой же, как евклидово расстояние между теми же двумя точками на исходной двумерной плоскости (прежде чем я свернул его в цилиндр). Однако я понятия не имею, как получить другую дугу по «спине» поверхности цилиндра.
Итак, имея в виду, что мои математические навыки плохие, кто-то, пожалуйста, дайте мне простую формулу (без дифференциации и/или интеграции), чтобы найти кратчайшее расстояние между двумя 2D-точками вдоль поверхности цилиндра?
Извините за длинный вопрос и спасибо за ваше время!
Определение расстояний на поверхности Земли Размеры и форма Земли Для решения многих задач навигации и составления карт мелкого масштаба Землю принимают за сферу (шар). Средний радиус Земли R = 6371210 м.
Законы сферической тригонометрии позволяют рассчитывать расстояния между точками, расположенными на сфере. cos(d) = sin(φА)·sin(φB) + cos(φА)·cos(φB)·cos(λА − λB), где φА и φB — широты, λА, λB — долготы данных пунктов, d — расстояние между пунктами, измеряемое в радианах длиной дуги большого круга земного шара. L = d·R, где R = 6371 км — средний радиус земного шара.
Таблица расстояний (с точностью 1 км), рассчитанными по этим формулам,
Для расчета расстояния между пунктами, расположенными в разных полушариях (северное-южное, восточное-западное), знаки (±) у соответствующих параметров (широт или долгот) должны быть разными. Пример: (см. таблицу ниже) d = 1,848988 для вычисления расстояния между Турой и Нью-Йорком (США) применяем формулу: d = 1,308259 Расстояние L = d·R = 8 334,92 км. В таблице расстояния определены с точностью 1 км.
Координаты географических пунктов ЭАО смотрите здесь страница обновлена 25. |
ш.
03.10Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.
LANGUAGE}}
{{$select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}Расстояние между двумя точками — формула, вывод, примеры
Расстояние между двумя точками — это длина отрезка линии, соединяющего две заданные точки.
Расстояние между двумя точками в координатной геометрии можно рассчитать, найдя длину отрезка линии, соединяющего данные координаты. Давайте поймем формулу для нахождения расстояния между двумя точками в двухмерной и трехмерной плоскости.
Какое расстояние между двумя точками?
Расстояние между любыми двумя точками — это длина отрезка линии, соединяющего точки.Есть только одна линия, проходящая через две точки. Итак, расстояние между двумя точками можно рассчитать, найдя длину этого отрезка прямой, соединяющего две точки. Например, если A и B — две точки, и если \ (\ overline {AB} = 10 \) см, это означает, что расстояние между A и B составляет 10 см.
Расстояние между двумя точками — это длина соединяющего их отрезка (но НЕ МОЖЕТ быть длиной соединяющей их кривой). Обратите внимание, что расстояние между двумя точками всегда положительно.
Формула расстояния между двумя точками
Расстояние между двумя точками с использованием заданных координат можно рассчитать, применив формулу расстояния.
Для любой точки, заданной на двумерной плоскости, мы можем применить формулу двумерного расстояния или формулу евклидова расстояния, заданную как
Формула расстояния между двумя точками:
Формула для расстояния \ (d \) между двумя точками с координатами \ ((x_1, y_1) \) и \ ((x_2, y_2 \)):
d = √ [(\ (x_2 \) — \ (x_1 \)) 2 + (\ (y_2 \) — \ (y_1 \)) 2 ]
Это называется формулой расстояния .
Чтобы найти расстояние между двумя точками, заданными на трехмерной плоскости, мы можем применить формулу трехмерного расстояния, заданную как,
d = √ [(\ (x_2 \) — \ (x_1 \)) 2 + (\ (y_2 \) — \ (y_1 \)) 2 + (\ (z_2 \) — \ (z_1 \ )) 2 ]
Давайте узнаем, как вывести эту формулу дальше.
Вывод формулы для расстояния между двумя точками
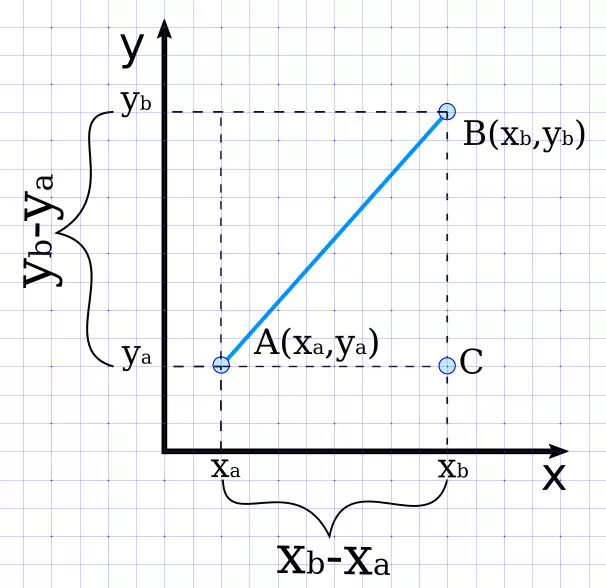
Чтобы вывести формулу для вычисления расстояния между двумя точками на двумерной плоскости, предположим, что есть две точки с координатами, заданными как, A (\ (x_1, y_1 \)) B (\ (x_2, y_2 \))
Далее мы предположим, что отрезок линии, соединяющий A и B, равен \ (\ overline {AB} = d \).
Теперь мы нанесем данные точки на координатную плоскость и соединим их линией.
Затем мы построим прямоугольный треугольник с гипотенузой \ (\ overline {AB} \).
Применение теоремы Пифагора для △ ABC:
AB 2 = AC 2 + BC 2
d 2 = (\ (x_2 \) — \ (x_1 \)) 2 + (\ (y_2 \) — \ (y_1 \)) 2 (Значения с рисунка)
Здесь вертикальное расстояние между заданными точками равно | \ (y_2 \) — \ (y_1 \) |.
Горизонтальное расстояние между заданными точками равно | \ (x_2 \) — \ (x_1 \) |.
d = √ [(\ (x_2 \) — \ (x_1 \)) 2 + (\ (y_2 \) — \ (y_1 \)) 2 ] (извлечение квадратного корня с обеих сторон)
Таким образом, формула расстояния для нахождения расстояния между двумя точками доказана.
Примечание: если две точки A и B находятся на оси x, то есть координаты A и B равны (\ (x_1 \), 0) и (\ (x_2 \), 0) соответственно, тогда расстояние между двумя точками AB = | \ (x_2 \) — \ (x_1 \) |.
Используя аналогичные шаги и концепцию, мы также можем вывести формулу для нахождения расстояния между двумя точками, заданными на трехмерной плоскости.
Как найти расстояние между двумя точками?
Расстояние между двумя точками с использованием заданных координат можно рассчитать с помощью следующих шагов:
- Запишите координаты двух заданных точек на координатной плоскости как A (\ (x_1, y_1 \)) и B (\ (x_2, y_2 \)).
- Мы можем применить формулу расстояния, чтобы найти расстояние между двумя точками, d = √ [(\ (x_2 \) — \ (x_1 \)) 2 + (\ (y_2 \) — \ (y_1 \)) 2 ]
- Выразите данный ответ в единицах.
Примечание: мы можем применить формулу трехмерного расстояния в случае, если две точки заданы на трехмерной плоскости, d = √ [(\ (x_2 \) — \ (x_1 \)) 2 + (\ (y_2 \) — \ (y_1 \)) 2 + (\ (z_2 \) — \ (z_1 \)) 2 ]
Пример: Найдите расстояние между двумя точками с координатами A = (1, 2) и B = (1, 5).
Решение:
Расстояние между двумя точками с использованием координат может быть задано как, d = √ [(\ (x_2 \) — \ (x_1 \)) 2 + (\ (y_2 \) — \ (y_1 \)) 2 ], где (\ (x_1, y_1 \)) и (\ (x_2, y_2 \)) — координаты двух точек.
⇒ d = √ [(1 — 1) 2 + (5 — 2) 2 ]
⇒ d = 3 шт.
Из приведенного выше примера мы также можем заметить, что, когда x-координаты данных точек совпадают, мы можем найти расстояние между двумя точками, найдя разницу между y-координатами.
Расстояние между двумя точками на сложной плоскости
Расстояние между двумя точками на комплексной плоскости или двумя комплексными числами z \ (_ 1 \) = a + ib и z \ (_ 2 \) = c + id в комплексной плоскости — это расстояние между точками (a, b) и (c, d), заданное как,
| z \ (_ 1 \) — z \ (_ 2 \) | = √ [(а — в) 2 + (б — г) 2 ]
Связанные темы:
Важные примечания относительно расстояния между двумя точками:
- Расстояние d между двумя точками с координатами \ ((x_1, y_1) \) и \ ((x_2, y_2 \)): d = √ [(\ (x_2 \) — \ (x_1 \) ) 2 + (\ (y_2 \) — \ (y_1 \)) 2 ]
- Расстояние от точки (a, b) от:
(i) ось x — это | b |.
(ii) ось y — это | a |.
Мы использовали знаки абсолютного значения, потому что расстояние никогда не может быть отрицательным.
Часто задаваемые вопросы о расстоянии между двумя точками
Что означает расстояние между двумя точками?
Расстояние между двумя точками определяется как длина прямой линии, соединяющей эти точки в координатной плоскости. Это расстояние никогда не может быть отрицательным, поэтому мы берем абсолютное значение при нахождении расстояния между двумя заданными точками.
Как рассчитать расстояние между двумя точками на двухмерной плоскости?
Расстояние между любыми двумя точками, заданными на двумерной плоскости, можно рассчитать, используя их координаты. Расстояние между двумя точками A (\ (x_1, y_1 \)) и B (\ (x_2, y_2 \)) можно рассчитать как, d = √ [(\ (x_2 \) — \ (x_1 \)) 2 + (\ (y_2 \) — \ (y_1 \)) 2 ].
Как найти расстояние между двумя точками на 3D-плоскости?
Чтобы вычислить расстояние между двумя точками на трехмерной плоскости, мы можем применить формулу трехмерного расстояния, заданную следующим образом: d = √ [(\ (x_2 \) — \ (x_1 \)) 2 + (\ (y_2 \) — \ (y_1 \)) 2 + (\ (z_2 \) — \ (z_1 \)) 2 ], где ‘d’ — расстояние между двумя точками, а (\ (x_1, y_1, z_1 \)), (\ (x_2, y_2, z_2 \)) — координаты двух точек.
Какое кратчайшее расстояние между двумя точками?
Кратчайшее расстояние между двумя точками можно рассчитать, найдя длину прямой линии, соединяющей обе точки. Мы можем применить формулу расстояния, чтобы найти это расстояние в зависимости от координат, заданных в двух- или трехмерной плоскости.
Как найти расстояние между двумя точками с помощью теоремы Пифагора?
Расстояние между двумя точками на декартовой плоскости можно вычислить, применив теорему Пифагора.Мы можем сформировать прямоугольный треугольник, используя линию, соединяющую данные две точки, в качестве гипотенузы. Здесь перпендикуляр и основание будут прямыми, параллельными осям x и y, с одним концом как одна из заданных точек, а другой конец как их точка пересечения. Используя теорему Пифагора, (гипотенуза) 2 = (основание) 2 + (перпендикуляр) 2 , мы можем найти длину гипотенузы с помощью заданных координат двух точек. Эта длина равна расстоянию между двумя точками.
Какова формула расстояния для определения расстояния между двумя точками в координатной геометрии?
В координатной геометрии формула расстояния между двумя точками задается как, d = √ [(\ (x_2 \) — \ (x_1 \)) 2 + (\ (y_2 \) — \ (y_1 \)) 2 ], где (\ (x_1, y_1 \)), (\ (x_2, y_2 \)) — координаты двух точек. Мы можем применить другую формулу, если данные точки liw в трехмерной плоскости, d = √ [(\ (x_2 \) — \ (x_1 \)) 2 + (\ (y_2 \) — \ (y_1 \)) 2 + (\ (z_2 \) — \ (z_1 \)) 2 ], где ‘d’ — расстояние между двумя точками, а (\ (x_1, y_1, z_1 \)), (\ (x_2, y_2 , z_2 \)) — координаты двух точек.
Как вывести формулу для определения расстояния между двумя точками?
Мы можем применить теорему Пифагора, чтобы получить формулу расстояния между двумя точками. Мы можем принять линию, соединяющую две точки, как гипотенузу прямоугольного треугольника, образованного в декартовой плоскости. Длину гипотенузы можно вычислить с помощью теоремы Пифагора и заданных координат двух точек, чтобы получить формулу расстояния между двумя точками.
Как найти расстояние по вертикали между двумя точками?
Расстояние по вертикали между двумя точками можно найти, вычислив разность y-координат двух точек, т.е.е., расстояние по вертикали между двумя точками, \ (d_y \) = \ (y_2 — y_1 \), где (\ (x_1, y_1 \)), (\ (x_2, y_2 \)) — координаты двух точек .
Как найти евклидово расстояние между двумя точками?
Евклидово расстояние между двумя точками можно рассчитать с помощью следующих шагов:
- Запишите координаты обеих заданных точек как (\ (x_1, y_1 \)) и (\ (x_2, y_2 \)).
- Примените формулу евклидова расстояния, расстояние, d = √ [(\ (x_2 \) — \ (x_1 \)) 2 + (\ (y_2 \) — \ (y_1 \)) 2 ]
- Выразите данный ответ в единицах.
Вычислить расстояние между двумя точками в Python
В этом руководстве мы рассмотрим, как рассчитать расстояние между двумя точками в Python с помощью некоторых примеров.
Есть несколько способов вычислить расстояние между двумя точками в Python.
Вы можете вычислить расстояние напрямую или использовать методы из таких библиотек, как math , scipy , numpy и т. Д.
Евклидово расстояние между двумя точками
Обычно мы имеем в виду евклидово расстояние, когда говорим о расстоянии между двумя точками.Чтобы вычислить евклидово расстояние между точками (x1, y1) и (x2, y2), вы можете использовать формулу:
Например, расстояние между точками (2, 3) и (5, 7) равно 5. Обратите внимание, что приведенная выше формула может быть расширена до n-мерных измерений.
Евклидово расстояние в Python
Теперь, когда мы знаем, как математически вычисляется расстояние между двумя точками, мы можем приступить к его вычислению в Python.
Python имеет ряд библиотек, которые помогают вычислять расстояния между двумя точками, каждая из которых представлена последовательностью координат.Прежде чем мы перейдем к использованию стандартных методов, давайте напрямую вычислим расстояние между точками (x1, y1) и (x2, y2).
# точка а
х1 = 2
y1 = 3
# точка б
х2 = 5
y2 = 7
# расстояние ч / б а и б
расстояние = ((x1 - x2) ** 2 + (y1 - y2) ** 2) ** 0,5
# отобразить результат
print ("Расстояние между точками ({}, {}) и ({}, {}) равно {}". format (x1, y1, x2, y2, distance)) Выход:
Расстояние между точками (2, 3) и (5, 7) составляет 5,0
Как видите, мы получаем расстояние между точками (2, 3) и (5, 7) как 5.Обратите внимание, что приведенная выше формула работает только для точек в двух измерениях.
Давайте теперь напишем обобщенную функцию, которая может обрабатывать точки с любым количеством измерений.
def get_distance (p, q):
"" "
Вернуть евклидово расстояние между точками p и q
предполагая, что оба имеют одинаковое количество измерений
"" "
# сумма квадратов разности координат
s_sq_difference = 0
для p_i, q_i в zip (p, q):
s_sq_difference + = (p_i - q_i) ** 2
# извлекаем квадратный корень из суммы квадратов разности
расстояние = s_sq_difference ** 0.5
расстояние возврата
# проверяем функцию
а = (2, 3, 6)
Ь = (5, 7, 1)
# расстояние ч / б а и б
d = get_distance (a, b)
# отобразить результат
принт (г) Выход:
7.0710678118654755
Как видите, мы использовали функцию для получения расстояния между двумя точками с тремя измерениями в каждой.
Теперь мы можем использовать эту функцию для вычисления расстояний между двумя точками любых размеров.
Обратите внимание, что указанная выше функция может быть дополнительно улучшена путем использования векторизации для вычисления разницы между координатами.
Евклидово расстояние с использованием математической библиотеки
Вы можете использовать функцию math.dist () , чтобы получить евклидово расстояние между двумя точками в Python. Например, давайте использовать его для получения расстояния между двумя трехмерными точками, каждая из которых представлена кортежем.
импорт математики # два балла а = (2, 3, 6) Ь = (5, 7, 1) # расстояние ч / б а и б d = math.dist (a, b) # отобразить результат принт (г)
Выход:
7.
0710678118654755 Получаем то же значение, что и выше.
Евклидово расстояние с использованием библиотеки
numpy Евклидово расстояние эквивалентно норме l2 разницы между двумя точками, которая может быть вычислена в numpy с помощью функции numpy.linalg.norm () .
импортировать numpy как np # два балла a = np.array ((2, 3, 6)) b = np.array ((5, 7, 1)) # расстояние ч / б а и б d = np.linalg.norm (a-b) # отобразить результат принт (г)
Выход:
7.0710678118654755
Получаем тот же результат, что и выше.Обратите внимание, что здесь мы передаем разницу между точками a и b в виде массива numpy в функцию np..
linalg.norm ()
Евклидово расстояние с использованием библиотеки
scipy Библиотека scipy содержит ряд полезных функций научных вычислений в Python. Используйте функцию distance.euclidean () , доступную в scipy.spatial , чтобы вычислить евклидово расстояние между двумя точками в Python.
из scipy.расстояние пространственного импорта # два балла а = (2, 3, 6) Ь = (5, 7, 1) # расстояние ч / б а и б d = расстояние. евклидово (a, b) # отобразить результат принт (г)
Выход:
7.0710678118654755
Получаем тот же результат, что и выше.
Подробнее о функции расстояния см. Ее документацию.
На этом мы подошли к концу этого урока. Примеры кода и результаты, представленные в этом руководстве, были реализованы в Jupyter Notebook с питоном (версия 3.8.3) ядро с версией numpy 1.18.5 и версией pandas 1.0.5
Подпишитесь на нашу рассылку новостей, чтобы получить более информативные руководства и обучающие материалы.
Мы не рассылаем спам, и вы можете отказаться от рассылки в любой момент.
Формула расстояния
Вы знаете, что расстояние А B между двумя точками на плоскости с Декартово координаты А ( Икс 1 , у 1 ) и B ( Икс 2 , у 2 ) дается следующей формулой:
А B знак равно ( Икс 2 — Икс 1 ) 2 + ( у 2 — у 1 ) 2
Формула расстояния на самом деле просто
Теорема Пифагора
в маскировке.
Чтобы рассчитать расстояние А B между точкой А ( Икс 1 , у 1 ) и B ( Икс 2 , у 2 ) сначала нарисуйте прямоугольный треугольник с отрезком А B ¯ как его гипотенуза.
Если длины сторон равны а и б , то по теореме Пифагора
( А B ) 2 знак равно ( А C ) 2 + ( B C ) 2
Решение на расстоянии А B , у нас есть:
А B знак равно ( А C ) 2 + ( B C ) 2
С
А
C
горизонтальное расстояние, это просто разница между
Икс
-координаты:
|
(
Икс
2
—
Икс
1
)
|
.
Так же,
B
C
это вертикальное расстояние
|
(
у
2
—
у
1
)
|
.
Поскольку мы все равно возводим эти расстояния в квадрат (а квадраты всегда неотрицательны), нам не нужно беспокоиться об этих знаках абсолютного значения.
А B знак равно ( Икс 2 — Икс 1 ) 2 + ( у 2 — у 1 ) 2
Пример:
Найдите расстояние между точками А и B на рисунке выше.
В приведенном выше примере мы имеем:
А ( Икс 1 , у 1 ) знак равно ( — 1 , 0 ) , B ( Икс 2 , у 2 ) знак равно ( 2 , 7 )
так
А B знак равно ( 2 — ( — 1 ) ) 2 + ( 7 — 0 ) 2 знак равно 3 2 + 7 2 знак равно 9 + 49 знак равно 58
или примерно
7.
6
единицы.
Формула расстояния | Purplemath
Purplemath
Формула расстояния — это вариант теоремы Пифагора, которую вы использовали еще в геометрии. Вот как мы переходим от одного к другому:
Предположим, вам даны две точки (–2, 1) и (1, 5), и они хотят, чтобы вы выяснили, насколько они далеко друг от друга.Очки выглядят так:
MathHelp.com
Вы можете рисовать линии, образующие прямоугольный треугольник, используя эти точки как два угла:
Легко найти длины горизонтальной и вертикальной сторон прямоугольного треугольника: просто вычтите значения x и значения y :
Затем используйте теорему Пифагора, чтобы найти длину третьей стороны (которая является гипотенузой прямоугольного треугольника):
.
..so:
Этот формат верен всегда. Имея две точки, вы всегда можете построить их, нарисовать прямоугольный треугольник, а затем найти длину гипотенузы. Длина гипотенузы — это расстояние между двумя точками. Поскольку этот формат работает всегда, его можно превратить в формулу:
Формула расстояния: учитывая две точки ( x 1 , y 1 ) и ( x 2 , y 2 ), дается расстояние d между этими точками. по формуле:
Пусть вас не пугают индексы.Они только указывают на то, что есть «первая» точка и «вторая» точка; то есть у вас есть два очка.
Какой из них вы назовете «первым» или «вторым» — решать вам. В любом случае расстояние будет таким же.
Найдите расстояние между точками (–2, –3) и (–4, 4).
Я просто подставляю координаты в формулу расстояния:
Тогда расстояние будет sqrt (53), или около 7.28 с округлением до двух десятичных знаков.
URL: https://www.purplemath.com/modules/distform.htm
Урок по формуле расстояния— Бесплатная справка по математике
Введение
Мы используем так называемую формулу расстояния , чтобы получить расстояние между любыми двумя точками в пространстве.
2} $$
Разрушение
На первый взгляд, эта формула выглядит как беспорядок! Но просто подумайте о компонентах \ (x_ {2} -x_ {1} \) и \ (y_ {2} -y_ {1} \) как о длине в каждом направлении.Используя эти два значения, мы математически строим воображаемый треугольник с двумя катетами, длину которых мы можем вычислить. Позвольте мне показать вам, что я имею в виду визуально:
Мы просто измеряем расстояние вдоль каждой оси, а затем используем теорему Пифагора для вычисления длины гипотенузы, которая представляет собой воображаемую линию непосредственно между двумя нашими точками. Не имеет значения, какая точка равна \ ((x_ {1}, y_ {1}) \), а какая — \ ((x_ {2}, y_ {2}) \). Ключевая идея, которую следует извлечь из этого графика, заключается в том, что вас интересует только изменение на по x и изменение на по y.2} $$
Как мы пришли к этой формуле? Это просто теорема Пифагора, которая позволяет нам найти гипотенузу прямоугольного треугольника.
В нашем случае гипотенуза — это расстояние между двумя точками!
Давайте теперь посмотрим на простой пример:
Пример:
Найдите расстояние между двумя точками (5,5) и (1,2), используя формулу расстояния.
Решение:
Вместо того, чтобы слепо подставлять числа в формулы, нарисуйте график, чтобы знать, что происходит.2} $$ $$ \ text {расстояние} = \ sqrt {16 + 9} $$ $$ \ text {расстояние} = \ sqrt {25} $$ $$ \ text {distance} = 5 $$
Как только мы узнали, что \ (x_ {2} -x_ {1} \) равно 4 и \ (y_ {2} -y_ {1} \) равно 3, мы просто вставили эти числа в формулу расстояния , чтобы решить .
Вам может быть интересно, что произойдет, если перевернуть точки? Помните, что мы имеем дело с расстояниями, которые по своей сути положительны. Расстояние одинаково в любом направлении, от точки 1 до точки 2 или наоборот. Итак, просто используйте положительное расстояние между двумя точками.Если вы посмотрите на формулу, вы заметите, что \ (x_ {2} -x_ {1} \) и \ (y_ {2} -y_ {1} \) возведены в квадрат, что в любом случае автоматически делает их положительными.
2} $$
$$ \ text {distance} = \ sqrt {25 + 121} $$
$$ \ text {расстояние} = \ sqrt {146} $$
$$ \ text {distance} = 12.08 $$
Формула расстояния несложная — вам просто нужно попрактиковаться с графиком, чтобы понимать, что происходит. Вы просто строите треугольник и находите длину гипотенузы. Формула расстояния — это просто теорема Пифагора!
Расширение до трех измерений
А как насчет трехмерного пространства? Как найти расстояние между точками (1,5,0) и (2,0, 8)? Конечно, построить график и измерить расстояние намного сложнее! Формула трехмерного расстояния на самом деле очень проста.2} $$
Если вы зашли так далеко, надеюсь, вы лучше понимаете формулу расстояния. Если это не так, вот еще один урок по формуле расстояния, доступный в Интернете.
Популярные вопросы:
Случайный преобразователь | Онлайн-конвертеры единиц измерения Конвертер длины и расстоянияПреобразователь массыКонвертер объема сухого воздуха и общих измерений при варкеПреобразователь площадиПреобразователь объёма и общего измерения при варкеПреобразователь температурыПреобразователь давления, напряжения, модуля ЮнгаПреобразователь энергии и работыПреобразователь силыПреобразователь силыКонвертер времениЛинейный конвертер скорости и скоростиКонвертер угла Хранение данныхКурсы обмена валютыРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаПреобразователь момента инерцииПреобразователь момента силыКонвертер крутящего моментаПреобразователь удельной энергии, теплоты сгорания (на единицу температуры) Конвертер интерваловКонвертер теплового расширенияКонвертер термического сопротивленияПреобразователь теплопроводности Конвертер удельной теплоемкости ter Конвертер скорости передачиКонвертер уровня звукаКонвертер чувствительности микрофонаКонвертер уровня звукового давления (SPL) Конвертер уровня звукового давления с выбираемым эталонным давлениемКонвертер яркостиКонвертер яркостиКонвертер яркостиКонвертер разрешения цифрового изображенияПреобразователь частоты и длины волныОптическая мощность (диоптрия) в преобразователь фокусного расстоянияПреобразователь оптической мощности (диоптрий) в увеличение (X) Конвертер электрического заряда Конвертер плотности зарядаКонвертер плотности поверхностного зарядаКонвертер объёмной плотности заряда Конвертер электрического токаЛинейный преобразователь плотности токаПреобразователь плотности поверхностного токаПреобразователь напряженности электрического поляПреобразователь электрического потенциала и напряженияПреобразователь электрического сопротивленияПреобразователь электрического сопротивленияПреобразователь электрической проводимостиПреобразователь электрической проводимостиПреобразователь емкостиПреобразователь индуктивностиПреобразователь реактивной мощности переменного токаПреобразователь напряжения магнитного поля в ваттах и дБм Конвертер плотности потока Конвертер мощности поглощенной дозы излучения, Конвертер мощности дозы полного ионизирующего излученияРадиоактивность. Этот онлайн-конвертер единиц измерения позволяет быстро и точно преобразовывать многие единицы измерения из одной системы в другую. Страница преобразования единиц представляет собой решение для инженеров, переводчиков и для всех, чья деятельность требует работы с величинами, измеряемыми в различных единицах. Вы можете использовать этот онлайн-конвертер для преобразования нескольких сотен единиц (включая метрические, британские и американские) в 76 категорий или нескольких тысяч пар, включая ускорение, площадь, электрическую энергию, энергию, силу, длину, свет, массу, массовый расход, плотность, удельный объем, мощность, давление, напряжение, температура, время, крутящий момент, скорость, вязкость, объем и емкость, объемный расход и многое другое. Стандартные преобразователи единицКонвертер длины и расстояния : метр, километр, сантиметр, миллиметр, нанометр, ярд, фут, дюйм, парсек, световой год, астрономическая единица, расстояние до Луны (от Земли до Луны), лига , миля, морская миля (международная), сажень, длина кабеля (международная), точка, пиксель, калибр, планковская длина… Конвертер массы : грамм, килограмм, миллиграмм, тонна (метрическая), фунт, унция, камень (США), камень (Великобритания), карат, зерно, талант (библейский греческий), драхма (библейский греческий), денарий (библейский римский), шекель (библейский иврит), масса Планка, масса протона, атомная единица массы, масса электрона (покой), масса Земли, масса Солнца . Сухой объем и стандартные измерения при приготовлении пищи : литр, бочка сухой (США), пинта сухой (США), квартовый сухой (США), peck (США), peck (Великобритания), bushel (США), bushel (UK), cor (библейский), homer (библейский), ephah (библейский) ), seah (библейский), omer (библейский), cab (библейский), log (библейский), кубометр. Конвертер площади : миллиметр², сантиметр², метр², километр², гектар, акр, дюйм², фут², ярд², миля², сарай, круглый дюйм, поселок, роуд, стержень², окунь², усадьба, шест², сабин, арпент, куэрда, квадратная верста, квадратный аршин, квадратный фут, квадратный сажень, площадь Планка … Конвертер объёма и общепринятых единиц измерения температуры : метр³, километр³, миллиметр³, литр, гектолитр, миллилитр, капля, бочка (масло), бочка (США) ), баррель (Великобритания), галлон (США), галлон (Великобритания), кварта (США), кварта (Великобритания), пинта (США), пинта (Великобритания), баррель (нефть), баррель (США), баррель (Великобритания ), галлон (США), галлон (Великобритания), кварта (США), кварта (Великобритания), пинта (США), пинта (Великобритания), ярд³, фут³, дюйм³, регистровая тонна, 100 кубических футов. Преобразователь температуры : кельвин, градус Цельсия, градус Фаренгейта, градус Ренкина, градус Реомюра, температура Планка. Преобразователь давления, напряжения, модуля Юнга : паскаль, килопаскаль, мегапаскаль, миллипаскаль, микропаскаль, нанопаскаль, атмосферно-техническая, стандартная атмосфера, ksi, psi, ньютон / метр², бар, миллибар, килограмм-сила / метр², грамм- сила / сантиметр², тонна-сила (короткая) / фут², фунт-сила / фут², миллиметр ртутного столба (0 ° C), дюйм ртутного столба (32 ° F), сантиметр водяного столба (4 ° C), фут водяного столба (4 ° C) , метр морской воды… Конвертер энергии и работы : джоуль, килоджоуль, мегаджоуль, миллиджоуль, мегаэлектронвольт, электрон-вольт, эрг, киловатт-час, мегаватт-час, ньютон-метр, килокалория (IT), калория (пищевая), Британские тепловые единицы (IT), мегабтеки (IT), тонна-час (охлаждение), тонна нефтяного эквивалента, баррель нефтяного эквивалента (США), мегатонна, тонна (взрывчатые вещества), килограмм в тротиловом эквиваленте, дин-сантиметр, грамм-сила-сантиметр, килограмм-сила-метр, килопонд-метр, фут-фунт, дюйм-фунт, энергия Планка . Преобразователь мощности : ватт, киловатт, мегаватт, милливатт, лошадиные силы, вольт-ампер, ньютон-метр / секунда, джоуль / секунда, мегаджоуль в секунду, килоджоуль в секунду, миллиджоуль в секунду, джоуль в час, килоджоуль в час, эрг в секунду, британские тепловые единицы (IT) в час, килокалории (IT) в час… Преобразователь силы : ньютон, килоньютон, миллиньютон, дин, джоуль / метр, джоуль / сантиметр, грамм-сила, килограмм-сила, тонна-сила (короткая), кип-сила, килопунт-сила, фунт-сила сила, унция-сила, фунтал, фунт-фут / секунда², pond, sthene, грав-сила, миллиграв-сила … Преобразователь времени : секунда, миллисекунда, наносекунда, пикосекунда, минута, час, день, неделя, месяц, год, декада, век, тысячелетие, планковское время, год (юлианский), год (високосный), год (тропический), год (сидерический), год (григорианский), две недели, встряска… Преобразователь линейной скорости и скорости : метр в секунду, километр в час, километр в секунду, миля в час, фут в секунду, миля в секунду, узел, узел (Великобритания), скорость света в вакууме, космический скорость — первая, космическая скорость — вторая, космическая скорость — третья, скорость Земли, скорость звука в чистой воде, Мах (стандарт СИ), Мах (20 ° C и 1 атм), ярд / секунду . Угол Преобразователь : градус, радиан, град, гон, минута, секунда, знак, мил, оборот, круг, поворот, квадрант, прямой угол, секстант. Конвертер топливной экономичности, расхода топлива и экономии топлива : метр / литр, километр / литр, миля (США) / литр, морская миля / литр, морская миля / галлон (США), километр / галлон (США), литр / 100 км, галлон (США) / миля, галлон (США) / 100 миль, галлон (Великобритания) / миля, галлон (Великобритания) / 100 миль … Конвертер чисел : двоичный, восьмеричный, десятичный, шестнадцатеричный, основание-3, основание-4, основание-5, основание-6, основание-7, основание-9, основание-10, основание-11, основание-12, основание-13, основание-14, основание-15, основание-20, основание-21, основание-22, основание-23, основание-24, основание-28, основание-30, основание-32, основание-34, основание-36… Преобразователь единиц информации и хранения данных : бит, байт, слово, четверное слово, MAPM-слово, блок, килобит (10³ бит), кибибит, кибибайт, килобайт (10³ байтов), мегабайт (10⁶) байтов), гигабайт (10⁹ байтов), терабайт (10¹² байтов), петабайт (10¹⁵ байтов), эксабайт (10¹⁸ байтов), гибкий диск (3,5 ED), гибкий диск (5,25 HD), Zip 250, Jaz 2 ГБ, CD (74 минут), DVD (2 слоя 1 сторона), диск Blu-ray (однослойный), диск Blu-ray (двухслойный) . Курс обмена валют : евро, доллар США, канадский доллар, британский фунт стерлингов, японская иена, швейцарский франк, аргентинское песо, австралийский доллар, бразильский реал, болгарский лев, чилийское песо, китайский юань, чешская крона, датская крона, египетский фунт, венгерский форинт, исландская крона, индийская рупия, индонезийская рупия, новый израильский шекель , Иорданский динар, малайзийский ринггит, мексиканское песо, новозеландский доллар, норвежская крона, пакистанская рупия, филиппинское песо, румынский лей, российский рубль, саудовский риял, сингапурский доллар, Южноафриканский рэнд, южнокорейский вон, шведская крона, новый тайваньский доллар, тайский бат, турецкая лира, украинская гривна… Размеры женской одежды и обуви : женские платья, костюмы и свитера, женская обувь, женские купальные костюмы, размер букв, бюст, дюймы, естественная талия, дюймы, заниженная талия, дюймы, бедра, дюймы, бюст, сантиметры, Натуральная талия, сантиметры, Заниженная талия, сантиметры, Бедра, сантиметры, Длина стопы, мм, Торс, дюймы, США, Канада, Великобритания, Европа, континентальный, Россия, Япония, Франция, Австралия, Мексика, Китай, Корея . Размеры мужской одежды и обуви : мужские рубашки, мужские брюки / брюки, размер мужской обуви, размер букв, шея, дюймы, грудь, дюймы, рукав, дюймы, талия, дюймы, шея, сантиметры, грудь, сантиметры, Рукав, сантиметры, Талия, сантиметры, Длина стопы, мм, Длина стопы, дюймы, США, Канада, Великобритания, Австралия, Европа, континентальный, Япония, Россия, Франция, Италия, Испания, Китай, Корея, Мексика… МеханикаПреобразователь угловой скорости и частоты вращения : радиан / секунда, радиан / день, радиан / час, радиан / минута, градус / день, градус / час, градус / минута, градус / секунда, оборот / день, оборот / час, оборот / минута, оборот / секунда, оборот / год, оборот / месяц, оборот / неделя, градус / год, градус / месяц, градус / неделя, радиан / год, радиан / месяц, радиан / неделя. Преобразователь ускорения : дециметр / секунда², метр / секунда², километр / секунда², гектометр / секунда², декаметр / секунда², сантиметр / секунда², миллиметр / секунда², микрометр / секунда², нанометр / секунда², пикометр / секунда², фемтометр / секунда² , аттометр в секунду², галлон, галилей, миля в секунду², ярд в секунду², фут в секунду², дюйм в секунду², ускорение свободного падения, ускорение свободного падения на Солнце, ускорение свободного падения на Меркурии, ускорение свободного падения на Венере , ускорение свободного падения на Луне, ускорение свободного падения на Марсе, ускорение свободного падения на Юпитере, ускорение свободного падения на Сатурне. Конвертер плотности : килограмм / метр³, килограмм / сантиметр³, грамм / метр³, грамм / сантиметр³, грамм / миллиметр³, миллиграмм / метр³, миллиграмм / сантиметр³, миллиграмм / миллиметр³, экзаграмма / литр, петаграмм / литр, тераграмм / литр, гигаграмм / литр, мегаграмм / литр, килограмм / литр, гектограмм / литр, декаграмм / литр, грамм / литр, дециграмм / литр, сантиграмм / литр, миллиграмм / литр, микрограмм / литр, нанограмм / литр, пикограмм / литр , фемтограмм / литр, аттограмм / литр, фунт / дюйм³ … Конвертер удельного объема : метр³ / килограмм, сантиметр³ / грамм, литр / килограмм, литр / грамм, фут³ / килограмм, фут³ / фунт, галлон (США ) / фунт, галлон (Великобритания) / фунт. Преобразователь момента инерции : килограмм-метр², килограмм-сантиметр², килограмм-миллиметр², грамм-сантиметр², грамм-миллиметр², килограмм-сила-метр-секунда², унция-дюйм², унция-сила-дюйм-секунда², фунт-фут², фунт-сила-фут-секунда, фунт²-дюйм , фунт-сила-дюйм-секунда², ударный фут². Конвертер момента силы : метр ньютон, метр килоньютон, метр миллиньютон, метр микроньютон, метр тонна-сила (короткий), метр тонна-сила (длинный), метр тонна-сила (метрический), метр килограмм-сила, грамм-сила-сантиметр, фунт-сила-фут, фунт-фут, фунт-дюйм. Гидротрансформатор : ньютон-метр, ньютон-сантиметр, ньютон-миллиметр, килоньютон-метр, дин-сантиметр, дин-миллиметр, килограмм-сила-метр, килограмм-сила-сантиметр, килограмм-сила-миллиметр, грамм-сила-метр, грамм- сила-сантиметр, грамм-сила-миллиметр, унция-сила-фут, унция-сила-дюйм, фунт-сила-фут, фунт-сила-дюйм. Термодинамика — тепло Конвертер удельной энергии, теплоты сгорания (на массу) : джоуль / килограмм, килоджоуль / килограмм, калория (IT) / грамм, калория (th) / грамм, британские тепловые единицы (IT) / фунт, БТЕ (th) / фунт, килограмм / джоуль, килограмм / килоджоуль, грамм / калория (IT), грамм / калория (th), фунт / BTU (IT), фунт / Btu (th), фунт / лошадиная сила-час, грамм / лошадиная сила (метрическая) -час, грамм / киловатт-час. Конвертер удельной энергии, теплоты сгорания (на объем) : джоуль / метр³, джоуль / литр, мегаджоуль / метр³, килоджоуль / метр³, килокалория (IT) / метр³, калория (IT) / сантиметр³, терм / фут³, терм / галлон (Великобритания), британские тепловые единицы (IT) на фут³, британские тепловые единицы на фут³, CHU / фут³, метр³ / джоуль, литр / джоуль, галлон (США) / лошадиные силы-час, галлон (США) / лошадиные силы (метрические единицы) )-час. Конвертер теплопроводности : ватт / метр / K, ватт / сантиметр / ° C, киловатт / метр / K, калория (IT) / секунда / сантиметр / ° C, калория (th) / секунда / сантиметр / ° C , килокалория (IT) / час / метр / ° C, килокалория (th) / час / метр / ° C, BTU (IT) дюйм / секунда / фут² / ° F, BTU (th) дюйм / секунда / фут² / ° F , Btu (IT) фут / час / фут² / ° F, Btu (th) фут / час / фут² / ° F, BTU (IT) дюйм / час / фут² / ° F, Btu (th) дюйм / час / фут² / ° F. Конвертер удельной теплоемкости : джоуль / килограмм / K, джоуль / килограмм / ° C, джоуль / грамм / ° C, килоджоуль / килограмм / K, килоджоуль / килограмм / ° C, калория (IT) / грамм / ° C, калория (IT) / грамм / ° F, калория (th) / грамм / ° C, килокалория (IT) / килограмм / ° C, килокалория (th) / килограмм / ° C, килокалория (IT) / килограмм / K , килокалория (th) / килограмм / K, килограмм-сила-метр / килограмм / K, фунт-сила-фут / фунт / ° R, Btu (IT) / фунт / ° F, Btu (th) / фунт / ° F, Btu (IT) / фунт / ° R, Btu (th) / фунт / ° R, Btu (IT) / фунт / ° C, CHU / фунт / ° C. Конвертер плотности теплового потока : ватт / метр², киловатт / метр², ватт / сантиметр², ватт / дюйм², джоуль / секунда / метр², килокалория (IT) / час / метр², килокалория (IT) / час / фут², калория (IT) / минута / сантиметр², калория (IT) / час / сантиметр², калория (th) / минута / сантиметр², калория (th) / час / сантиметр², дина / час / сантиметр, эрг / час / миллиметр², фут-фунт / минута на фут², мощность в лошадиных силах на фут², мощность (метрическая) на фут², BTU (IT) / секунда на фут², BTU (IT) / минута на фут², Btu (IT) / час на фут², BTU (th) / секунда на дюйм² , Btu (th) / секунда / фут², Btu (th) / минута / фут², Btu (th) / час / фут², CHU / час / фут². Преобразователь коэффициента теплопередачи : ватт / метр² / K, ватт / метр² / ° C, джоуль / секунда / метр² / K, килокалория (IT) / час / метр² / ° C, килокалория (IT) / час / фут² / ° C, Btu (IT) / секунда / фут² / ° F, Btu (th) / секунда / фут² / ° F, BTU (IT) / час / фут² / ° F, BTU (th) / час / фут² / ° F, CHU / час / фут² / ° C. Гидравлика — жидкостиКонвертер объемного расхода : метр³ / секунда, метр³ / день, метр³ / час, метр³ / минута, сантиметр³ / день, сантиметр³ / час, сантиметр³ / минуту, сантиметр³ / секунда, литр / день, литр в час, литр в минуту, литр в секунду, миллилитр в день, миллилитр в час, миллилитр в минуту, миллилитр в секунду, галлон (США) в день, галлон (США) в час, галлон (США) в минуту, галлон (США) в секунду, галлон (Великобритания) в день, галлон (Великобритания) в час, галлон (Великобритания) в минуту, галлон (Великобритания) в секунду, килобаррель (США) в день, баррель (США) в день… Конвертер массового расхода : килограмм / секунда, грамм / секунда, грамм / минута, грамм / час, грамм / день, миллиграмм / минута, миллиграмм / час, миллиграмм / день, килограмм / минута, килограмм / час , килограмм / день, экзаграмм / секунда, петаграмма / секунда, тераграмма / секунда, гигаграмма / секунда, мегаграмм / секунда, гектограмм / секунда, декаграмма / секунда, дециграмма / секунда, сантиграмма / секунда, миллиграмм / секунда, микрограмм / секунда, тонна (метрическая) / секунда, тонна (метрическая) / минута, тонна (метрическая) / час, тонна (метрическая) / день . Конвертер молярной скорости потока : моль / секунда, экзамен / секунда, петамоль / секунда, терамоль / секунда, гигамоль / секунда, мегамоль / секунда, киломоль / секунда, гектомоль / секунда, декамоль / секунда, децимоль / секунда, сантимоль / секунда, миллимоль / секунда, микромоль / секунда, наномоль / секунда, пикомоль / секунда, фемтомоль / секунда, аттомоль в секунду, моль в минуту, моль в час, моль в день, миллимоль в минуту, миллимоль в час, миллимоль в день, километр в минуту, километр в час, километр в день. Mass Flux Converter : грамм / секунда / метр², килограмм / час / метр², килограмм / час / фут², килограмм / секунда / метр², грамм / секунда / сантиметр², фунт / час / фут², фунт / секунда / фут². Конвертер молярной концентрации : моль / метр³, моль / литр, моль / сантиметр³, моль / миллиметр³, километр / метр³, километр / литр, километр / сантиметр³, километр / миллиметр³, миллимоль / метр³, миллимоль / литр, миллимоль / сантиметр³, миллимоль / миллиметр³, моль / дециметр³, молярный, миллимолярный, микромолярный, наномолярный, пикомолярный, фемтомолярный, аттомолярный, зептомолярный, йоктомолярный. Массовая концентрация в конвертере раствора : килограмм / литр, грамм / литр, миллиграмм / литр, часть / миллион, гран / галлон (США), гран / галлон (Великобритания), фунт / галлон (США), фунт / галлон (Великобритания), фунт / миллион галлон (США), фунт / миллион галлон (Великобритания), фунт / фут³, килограмм / метр³, грамм / 100 мл. Конвертер динамической (абсолютной) вязкости : паскаль-секунда, килограмм-сила-секунда на метр², ньютон-секунда на метр², миллиньютон-секунда на метр², дин-секунда на сантиметр², равновесие, экзапуаз, петапуаз, терапуаз, гигапуаз, мегапуаз, килопуаз, гектопуаз, декапуаз, деципуаз, сантипуаз, миллипуаз, микропуаз, наноуаз, пикопуаз, фемтопуаз, аттопуаз, фунт-сила-секунда / дюйм², фунт-сила-секунда / фут², фунт-секунда / фут², грамм / сантиметр / секунда… Конвертер кинематической вязкости : метр² / секунда, метр² / час, сантиметр² / секунда, миллиметр² / секунда, фут² / секунда, фут² / час, дюйм² / секунда, стоксы, экзастоки, петастоки, терастоки, гигастоксы, мегастоксы, килостоки, гектостоки, декастоки, децистоки, сантистоки, миллистоки, микростоки, наностоки, пикостоки, фемтостоки, аттостоки. Преобразователь поверхностного натяжения : ньютон на метр, миллиньютон на метр, грамм-сила на сантиметр, дина на сантиметр, эрг / сантиметр², эрг / миллиметр², фунт на дюйм, фунт-сила / дюйм. Акустика — ЗвукПреобразователь чувствительности микрофона : децибел относительно 1 вольт на 1 паскаль, децибел относительно 1 вольта на 1 микропаскаль, децибел относительно 1 вольта на 1 дин на квадратный сантиметр, децибел относительно 1 вольта на 1 микробар, вольт на паскаль, милливольт на паскаль, микровольт на паскаль. Преобразователь уровня звукового давления (SPL) : ньютон на квадратный метр, паскаль, миллипаскаль, микропаскаль, дин / квадратный сантиметр, бар, миллибар, микробар, уровень звукового давления в децибелах. Фотометрия — свет Конвертер яркости : кандела на метр², кандела на сантиметр², кандела на фут², кандела на дюйм², килокандела на метр², стильб, люмен на метр² на стерадиан, люмен на сантиметр на квадратный метр на стерадиан на квадратный метр, люмен на сантиметр на квадратный метр на квадратный дюйм. Конвертер силы света : кандела, свеча (немецкий язык), свеча (Великобритания), десятичная свеча, свеча (пентан), пентановая свеча (мощность 10 свечей), свеча Хефнера, единица измерения яркости, десятичный буж, люмен / стерадиан, свеча (Международный). Конвертер освещенности : люкс, метр-свеча, сантиметр-свеча, фут-свеча, фот, nox, кандела стерадиан на метр², люмен на метр², люмен на сантиметр², люмен на фут², ватт на сантиметр² (при 555 нм) . Преобразователь частоты и длины волны : герц, эксагерц, петагерц, терагерц, гигагерц, мегагерц, килогерц, гектогерц, декагерц, децигерц, сантигерц, длина волны / миллигерц, микрогерц, микрогерц, микрогерц, секунда, миллигерц , длина волны в петаметрах, длина волны в тераметрах, длина волны в гигаметрах, длина волны в мегаметрах, длина волны в километрах, длина волны в гектометрах, длина волны в декаметрах. Конвертер оптической силы (диоптрии) в фокусное расстояние : Оптическая сила (диоптрическая сила или преломляющая сила) линзы или другой оптической системы — это степень, в которой система сходится или рассеивает свет. Он рассчитывается как величина, обратная фокусному расстоянию оптической системы и измеряется в инверсных метрах в СИ или, чаще, в диоптриях (1 диоптрия = м⁻¹) ЭлектротехникаКонвертер электрического заряда : кулон, мегакулон , килокулон, милликулон, микрокулон, нанокулон, пикокулон, абкулон, EMU заряда, статкулон, ESU заряда, франклин, ампер-час, миллиампер-час, ампер-минута, ампер-секунда, фарадей (на основе углерода 12), элементарный обвинение. Преобразователь электрического тока : ампер, килоампер, миллиампер, биот, абампер, ЭДС тока, статампер, ЭДС тока, СГС э.м. единица, CGS e.s. единица, микроампер, наноампер, ток Планка. Линейный преобразователь плотности тока : ампер / метр, ампер / сантиметр, ампер / дюйм, абампер / метр, абампер / сантиметр, абампер / дюйм, эрстед, гильберт / сантиметр, ампер / миллиметр, миллиампер / метр, миллиампер , миллиампер / сантиметр, миллиампер / миллиметр, микроампер / метр, микроампер / дециметр, микроампер / сантиметр, микроампер / миллиметр. Конвертер поверхностной плотности тока : ампер / метр², ампер / сантиметр², ампер / дюйм², ампер / мил², ампер / круговой мил, абампер / сантиметр², ампер / миллиметр², миллиампер / миллиметр², микроампер / миллиметр², миллиампер / миллиметр², миллиампер / миллиметр² миллиампер / сантиметр², микроампер / сантиметр², килоампер / сантиметр², ампер / дециметр², миллиампер / дециметр², микроампер / дециметр², килоампер / дециметр². Преобразователь напряженности электрического поля : вольт на метр, киловольт на метр, киловольт на сантиметр, вольт на сантиметр, милливольт на метр, микровольт на метр, киловольт на дюйм, вольт на дюйм, вольт на мил, абвольт на сантиметр, статвольт / сантиметр, статвольт / дюйм, ньютон / кулон, вольт / микрон. Преобразователь электрического потенциала и напряжения : вольт, милливольт, микровольт, нановольт, пиковольт, киловольт, мегавольт, гигавольт, теравольт, ватт / ампер, абвольт, EMU электрического потенциала, статвольт, ESU электрического потенциала, планковский электрический потенциал. Преобразователь электрического сопротивления : Ом, мегаом, микром, вольт / ампер, обратный сименс, абом, EMU сопротивления, статом, ESU сопротивления, квантованное сопротивление Холла, импеданс Планка, миллиом, кОм. Преобразователь удельного электрического сопротивления : ом-метр, ом-сантиметр, ом-дюйм, микром-сантиметр, микром-дюйм, ом-сантиметр, статом-сантиметр, круговой мил-ом / фут, ом-кв.миллиметр на метр. Преобразователь электрической проводимости : сименс, мегасименс, килосименс, миллисименс, микросименс, ампер / вольт, mho, gemmho, micromho, abmho, statmho, квантованная проводимость Холла. Конвертер электропроводности : сименс / метр, пикосименс / метр, mho / метр, mho / сантиметр, abmho / метр, abmho / сантиметр, статмо / метр, статмо / сантиметр, сименс / сантиметр, миллисименс / метр, миллисименс / сантиметр, микросименс / метр, микросименс / сантиметр, единица электропроводности, коэффициент проводимости, доли на миллион, шкала 700, шкала частей на миллион, шкала 500, частей на миллион, шкала 640, TDS, частей на миллион, шкала 640, TDS, части на миллион, шкала 550, TDS, частей на миллион, шкала 500, TDS, частей на миллион, шкала 700. Преобразователь емкости : фарад, экзафарад, петафарад, терафарад, гигафарад, мегафарад, килофарад, гектофарад, декафарад, децифарад, сентифарад, миллифарад, микрофарад, емкость, нанофарад, аттофарад, ед. , статфарад, ЭСУ емкости. Преобразователь индуктивности : генри, экзагенри, петагенри, терагенри, гигагенри, мегагенри, килогенри, гектогенри, декагенри, децигенри, сантигенри, миллигенри, микрогенри, наногенри, пикогенри, атогенри, атогенри, энтогенри, энтогенри , статенри, ЭСУ индуктивности. Преобразователь реактивной мощности переменного тока : реактивный вольт-ампер, реактивный милливольт-ампер, реактивный киловольт-ампер, реактивный мегавольт-ампер, реактивный гигавольт-ампер. Преобразователь американского калибра проводов : Американский калибр провода (AWG) — это стандартизированная система калибра проводов, используемая в США и Канаде для измерения диаметров цветных электропроводящих проводов, включая медь и алюминий. Магнитостатика, магнетизм и электромагнетизмПреобразователь магнитного потока : Вебер, милливебер, микровебер, вольт-секунда, единичный полюс, мегалин, килолин, линия, максвелл, тесла-метр², тесла-сантиметр², гаусс-сантиметр², квант магнитного потока. Преобразователь плотности магнитного потока : тесла, Вебер / метр², Вебер / сантиметр², Вебер / дюйм², Максвелл / метр², Максвелл / сантиметр², Максвелл / дюйм², Гаусс, линия / сантиметр², линия / дюйм², гамма. Radiation and Radiology Конвертер мощности поглощенной дозы излучения, суммарной мощности дозы ионизирующего излучения : серый цвет в секунду, эксагрей в секунду, петагрей в секунду, тераграрей в секунду, гигагрей в секунду, мегагрей в секунду, килограмм в секунду, гектоград. Радиоактивность. Конвертер радиоактивного распада : беккерель, петабеккерель, терабеккерель, гигабеккерель, мегабеккерель, килобеккерель, миллибеккерель, кюри, килокюри, милликюри, микрокюри, нанокюри, пикокюри, резерфорд, одно / секунда, дезинтеграция. Конвертер облучения : кулон на килограмм, милликулон на килограмм, микрокулон на килограмм, рентген, миллирентген, микрорентген, тканевый рентген, Паркер, респ. Радиация. Конвертер поглощенной дозы : рад, миллирад, джоуль / килограмм, джоуль / грамм, джоуль / сантиграм, джоуль / миллиграмм, серый, эксагрей, петагрей, терагрей, гигагрей, мегагрей, килограмм, гектагрей, декаграй, декаграй, сантигрей, микрогрей, миллиграм , наногрей, пикграй, фемтогрей, аттогрей, зиверт, миллизиверт, микрозиверт . Прочие преобразователиКонвертер метрических префиксов : нет, yotta, zetta, exa, peta, tera, giga, mega, kilo, hecto, deka , деци, санти, милли, микро, нано, пико, фемто, атто, зепто, йокто. Преобразователь передачи данных : бит в секунду, байт в секунду, килобит в секунду (SI по умолчанию), килобайт в секунду (SI по умолчанию), кибибит в секунду, кибибайт в секунду, мегабит в секунду (SI по умолчанию) , мегабайт в секунду (SI по умолчанию), мебибит в секунду, мебибайт в секунду, гигабит в секунду (SI по умолчанию), гигабайт в секунду (SI по умолчанию), гибибит в секунду, гибибит в секунду, терабит в секунду (SI по умолчанию). .), терабайт в секунду (по умолчанию SI), тебибит в секунду, тебибайт в секунду, Ethernet, Ethernet (быстрый), Ethernet (гигабит), OC1, OC3, OC12, OC24, OC48 … Типографика и цифровой Конвертер единиц изображения : твип, метр, сантиметр, миллиметр, символ (X), символ (Y), пиксель (X), пиксель (Y), дюйм, пика (компьютер), пика (принтер), точка (DTP / PostScript) ), point (компьютер), point (принтер), en, cicero, em, Didot point. Конвертер единиц измерения объема пиломатериалов : кубический метр, кубический фут, кубический дюйм, футы для досок, тысяча футов для досок, шнур, шнур (80 фут3), футы для шнура, узел, поддон, поперечина, стяжка переключателя. Калькулятор молярной массы : Молярная масса — это физическое свойство, которое определяется как масса вещества, деленная на его количество в молях. Другими словами, это масса одного моля определенного вещества. Периодическая таблица : Периодическая таблица представляет собой список всех химических элементов, упорядоченных слева направо и сверху вниз по их атомным номерам, электронным конфигурациям и повторяющимся химическим свойствам, расположенным в форме таблицы таким образом, чтобы элементы с аналогичные химические свойства отображаются в вертикальных столбцах, называемых группами.У некоторых групп есть имена, а также номера. Например, все элементы группы 1, кроме водорода, являются щелочными металлами, а элементы группы 18 — благородными газами, которые ранее назывались инертными газами. У вас есть трудности с переводом единицы измерения на другой язык? Помощь доступна! Задайте свой вопрос в TCTerms , и вы получите ответ от опытных технических переводчиков в считанные минуты. |
Преобразователь радиоактивного распада Преобразователь радиационного воздействияРадиация. Конвертер поглощенной дозы Конвертер метрических префиксов Конвертер передачи данных Конвертер единиц типографии и цифрового изображения Конвертер единиц измерения объема древесиныКалькулятор молярной массыПериодическая таблица
..
..
..
..
..
.
..
..
стерадиан, нит, миллинит, ламберт, миллиламберт, фут-ламберт, апостиль, блондель, брил, скот.
..
Чем больше площадь поперечного сечения провода, тем выше его допустимая нагрузка по току.Чем больше номер AWG, также называемый калибром провода, тем меньше физический размер провода. Самый большой размер AWG — 0000 (4/0), а самый маленький — 40. В этой таблице перечислены размеры и сопротивления AWG для медных проводников. Используйте закон Ома для расчета падения напряжения на проводнике.
/ секунда, декаграй / секунда, дециграй / секунда, сантигрей / секунда, миллиграй / секунда, микрогрей / секунда, наногрей / секунда, пикграй / секунда, фемтогрей / секунда, аттогрей / секунда, рад / секунда, джоуль / килограмм / секунда, ватт на килограмм, зиверт в секунду, миллизиверт в год, миллизиверт в час, микрозиверт в час, бэр в секунду, рентген в час…
..
Различные строки таблицы называются периодами, потому что это расположение отражает периодическое повторение сходных химических и физических свойств химических элементов по мере увеличения их атомного номера. Элементы одного периода имеют одинаковое количество электронных оболочек.Формула расстояния | Блестящая вики по математике и науке
Предположим, что A = x1A = x_1A = x1 и B = x2B = x_2B = x2 — две точки, лежащие на прямой действительных чисел. Тогда расстояние между AAA и BBB равно
d (A, B) = ∣x1 − x2∣. d (A, B) = \ lvert x_1 — x_2 \ rvert. d (A, B) = ∣x1 — x2 ∣.
На плоскости мы можем рассматривать ось xxx как одномерную числовую линию, поэтому мы можем вычислить расстояние между любыми двумя точками, лежащими на оси xxx, как абсолютное значение разности их xxx-координат.
2} .d (P1, P2) = (x1 — x2) 2+ (y1 — y2) 2.
Поскольку ∣x1 − x2∣ \ lvert x_1 — x_2 \ rvert∣x1 −x2 ∣ — это расстояние между xxx-координатами двух точек и ∣y1 − y2∣ \ lvert y_1 — y_2 \ rvert∣y1 — y2 ∣ — расстояние между yyy-координатами двух точек, формулу расстояния в плоскости xyxyxy можно представить как длину гипотенузы прямоугольного треугольника с вершинами P1 = (x1, y1) P_1 = ( x_1, y_1) P1 = (x1, y1), P2 = (x2, y2), P_2 = (x_2, y_2), P2 = (x2, y2) и P = (x2, y1) P = (x_2, y_1) P = (x2, y1).Тогда формула расстояния — это просто утверждение теоремы Пифагора.
И в 1D, и в 2D функция расстояния удовлетворяет следующим свойствам:
- d (P, Q) ≥0d (P, Q) \ geq 0d (P, Q) ≥0 для всех точек P, Q P, QP, Q с равенством тогда и только тогда, когда P = QP = QP = Q
- d (P, Q) = d (Q, P) d (P, Q) = d (Q, P) d (P, Q) = d (Q, P) для всех точек P, QP, QP, Q
- d (P, Q) ≤d (P, R) + d (R, Q) d (P, Q) \ leq d (P, R) + d (R, Q) d (P, Q) ≤d (P, R) + d (R, Q) для всех точек P, Q, RP, Q, RP, Q, R.
Каково расстояние между точками (0,5) (0,5) (0,5) и (0,13) (0,13) (0,13)?
Обратите внимание, что обе эти точки лежат на оси yyy, и поэтому расстояние между точками является абсолютной величиной разности yyy-координат, которая составляет ∣5−13∣ = ∣ − 8∣ = 8.□ \ lvert 5-13 \ rvert = \ lvert -8 \ rvert = 8. \ _ \ Square∣5−13∣ = ∣ − 8∣ = 8. □
Чтобы обобщить вышеупомянутую проблему, если две точки P1 = (x1, y1) P_1 = (x_1, y_1) P1 = (x1, y1) и P2 = (x2, y2) P_2 = (x_2, y_2) P2 = (X2, y2) имеют одинаковую координату xxx, т.е. x1 = x2x_1 = x_2x1 = x2, тогда расстояние между двумя точками равно d (P1, P2) = ∣y1 − y2∣ d (P_1 , P_2) = | y_1-y_2 | d (P1, P2) = ∣y1 −y2 ∣, а отрезок P1P2‾ \ overline {P_1P_2} P1 P2 является вертикальным отрезком.
Аналогично, если P1P_1P1 и P2P_2P2 имеют одинаковую yyy-координату (y1 = y2y_1 = y_2y1 = y2), то d (P1, P2) = ∣x1 − x2∣d (P_1, P_2) = | x_1- x_2 | d (P1, P2) = ∣x1 −x2 ∣, а отрезок P1P2‾ \ overline {P_1P_2} P1 P2 — горизонтальный отрезок.
.Найдите площадь прямоугольника в плоскости xyxyxy с вершинами
A = (6, −3), B = (6,7), C = (2,7) и D = (2, −3). A = (6, -3), B = (6, 7), C = (2, 7), \ text {и} D = (2, -3). A = (6, −3), B = (6,7), C = (2,7) и D = (2, −3).
Точки AAA и BBB имеют одинаковую xxx-координату, что означает d (A, B) = ∣7 — (- 3) ∣ = 10d (A, B) = \ lvert 7 — (-3) \ rvert = 10d ( А, В) = ∣7 — (- 3) ∣ = 10. Точки BBB и CCC имеют одинаковую yyy-координату, откуда d (B, C) = ∣6−2∣ = 4d (B, C) = \ lvert 6-2 \ rvert = 4d (B, C) = ∣6− 2∣ = 4.Мы проверяем, что точки CCC и DDD имеют одинаковую xxx-координату, а DDD и AAA имеют одинаковую yyy-координату, что означает, что точки действительно являются вершинами прямоугольника.
Тогда площадь прямоугольника равна [ABCD] = AB⋅BC = 4⋅10 = 40. □ [ABCD] = AB \ cdot BC = 4 \ cdot 10 = 40. \ _ \ square [ABCD] = AB⋅BC = 4⋅10 = 40. □
