Как научиться решать простые и сложные уравнения
Как научиться решать простые и сложные уравнения
Уважаемые родители!
Без базовой математической подготовки невозможна постановка образования современного человека. В школе математика служит опорным предметом для многих смежных дисциплин. В послешкольной жизни реальной необходимостью становится непрерывное образование, что требует базовой общешкольной подготовки, в том числе и математической.
В начальной школе закладываются не только знания по основным темам, но и развивается логическое мышление, воображение и пространственные представления, а также формируется интерес к данному предмету.
Соблюдая принцип преемственности, мы сделаем упор на важнейшую тему, а именно «Взаимосвязь компонентов действий при решении составных уравнений».
С помощью данного урока можно без труда научиться решать усложненные уравнения. На уроке вы подробно познакомитесь с пошаговой инструкцией решения усложненных уравнений.
Многих, родителей ставит в тупик вопрос – как же заставить детей научиться решать простые и сложные уравнения. Если уравнения простые — это еще пол беды, но ведь бывают и сложные – например интегральные. Кстати, для сведения, есть и такие уравнения, над решением которых бьются лучшие умы нашей планеты и за решение которых выдаются очень весомые денежные премии. Например, если вспомнить Перельмана и невостребованную им денежную премию в размере нескольких миллионов.
Однако вернемся для начала к простым математическим уравнениям и повторим виды уравнений и названия компонентов. Небольшая разминка:
_________________________________________________________________________
РАЗМИНКА
Найди лишнее число в каждом столбике:
2) Какого слова не хватает в каждом столбике?
3) Соедините слова из первого столбика со словами из 2 столбика.
«Уравнение» «Равенство»
4) Как вы объясните, что такое «равенство»?
5) А «уравнение»? Это равенство? Что в нем особенного?
слагаемое сумма
уменьшаемое разность
вычитаемое произведение
множитель равенство
делимое
уравнение
Вывод: Уравнение – это равенство с переменной, значение которой надо найти.
_______________________________________________________________________
Предлагаю каждой группе написать на листке фломастером уравнения: (на доску)
1 группе — с неизвестным слагаемым; 2 группе — с неизвестным уменьшаемым; 3 группе – с неизвестным вычитаемым; 4 группе – с неизвестным делителем; 5 группе – с неизвестным делимым; 6 группе – с неизвестным множителем. | 1 группа х + 8 = 15 2 группа х – 8 = 7 3 группа 48 – х = 36 4 группа 540 : х = 9 5 группа х : 15 = 9 6 группа х * 10 = 360 |
Один из группы должен на математическом языке прочитать свое уравнение и прокомментировать их решение, т. е. проговорить выполняемую операцию с известными компонентами действий (алгоритм).
е. проговорить выполняемую операцию с известными компонентами действий (алгоритм).
Вывод: Умеем решать простые уравнения всех видов по алгоритму, читать и записывать буквенные выражения.
_____________________________________________________________________________
Предлагаю решить задачу, в которой появляется новый тип уравнений.
Х + 2кг 5кг и 3 кг | С какой величиной связан рисунок? Составьте и запишите по этому рисунку уравнение: Подберите для полученного уравнения подходящее уравнение: х + а = в а : х = в х : а = в х * а = в х – а = в а – х = в |
Вывод: Познакомились с решением уравнений, в одной из частей которых содержится числовое выражение, значение которого надо найти и получить простое уравнение.
________________________________________________________________________
Рассмотрим еще один вариант уравнения, решение которого сводится к решению цепочки простых уравнений. Вот один из введения составных уравнений.
а + в * с (х – у) : 3 2 * d + (m – n) Являются ли уравнениями записи? Почему? Как называют такие действия? Прочитайте их, называя последнее действие: | Нет. Это не уравнения, т. к. в уравнении должен быть знак «=». Выражения а + в * с — сумма числа а и произведения чисел в и с; (х – у) : 3 — частное разности чисел х и у; 2 * d + (m – n) — сумма удвоенного числа d и разности чисел m и n. |
Предлагаю каждому записать на математическом языке предложение:
Произведение разности чисел х и 4 и числа 3 равно 15.
Запишите на математическом языке предложение: произведение разности чисел х и 4 и числа 3 равно 15 | (х – 4) * 3 = 15 |
ВЫВОД: Возникшая проблемная ситуация мотивирует постановку цели урока: научиться решать уравнения в которых неизвестный компонент является выражением. Такие уравнения являются составными уравнениями.
__________________________________________________________________________
А может нам помогут уже изученные виды уравнений? (алгоритмы)
На какое из известных уравнений похоже наше уравнение? Х * а = в
ОЧЕНЬ ВАЖНЫЙ ВОПРОС: Чем является выражение в левой части – суммой, разностью, произведением или частным?
(х – 4) * 3 = 15 (Произведением)
Почему? (т.к. последнее действие – умножение)
Вывод: Такие уравнения еще не рассматривались. Но можно решить, если на выражение х – 4 наложить карточку (у — игрек), и получится уравнение, которое легко можно решить, используя простой алгоритм нахождения неизвестного компонента.
При решении составных уравнений необходимо на каждом шаге осуществлять выбор действия на автоматизированном уровне, комментируя, называя компоненты действия.
↓
↓
↓
↓
| (у – 5) * 4 = 28 |
Вывод: В классах с разной подготовкой эта работа может быть организована по-разному. В более подготовленных классах даже для первичного закрепления могут быть использованы выражения, в которых не два, а три и более действий, но их решение требует большего числа шагов с каждым шагом упрощая уравнение, до тех пор пока не получится простое уравнение. И каждый раз можно наблюдать, как меняется неизвестный компонент действий.
В более подготовленных классах даже для первичного закрепления могут быть использованы выражения, в которых не два, а три и более действий, но их решение требует большего числа шагов с каждым шагом упрощая уравнение, до тех пор пока не получится простое уравнение. И каждый раз можно наблюдать, как меняется неизвестный компонент действий.
_____________________________________________________________________________
ЗАКЛЮЧЕНИЕ:
Когда речь идёт о чём-нибудь очень простом, понятном, мы часто говорим: «Дело ясно, как дважды два — четыре!».
А ведь прежде чем додуматься до того, что дважды два — четыре, людям пришлось учиться много, много тысяч лет.
Многие правила из школьных учебников арифметики и геометрии были известны древним грекам две с лишним тысячи лет назад.
Всюду, где надо что-то считать, измерять, сравнивать, без математики не обойтись.
А чем дальше, тем больше и точнее нужно было считать. С каждым десятилетием математика становилась всё нужнее людям.
С каждым десятилетием математика становилась всё нужнее людям.
Трудно представить, как жили бы люди, если бы не умели считать, измерять, сравнивать. Этому учит математика.
Сегодня Вы окунулись в школьную жизнь, побывали в роли учеников и я предлагаю Вам, уважаемые родители, оценить свои умения по шкале.
Мои умения | Дата и оценка |
Компоненты действий. | |
Составление уравнения с неизвестным компонентом. | |
Чтение и запись выражений. | |
Находить корень уравнения в простом уравнении. | |
Находить корень уравнения, в одной из частей которых содержится числовое выражение. | |
Находить корень уравнения, в которых неизвестный компонент действия является выражением. |
Курс по алгебре «Как научиться решать уравнения на отлично» (9 класс).
Муниципальное образовательное учреждение
средняя общеобразовательная школа № 82
Дзержинского района г. Волгограда
Программа
по математике
для учащихся девятых классов
«Как развить умение решать уравнения на «отлично»!»
(или
«Возвращаюсь в «вечному вопросу»
алгебры — уравнениям!»)
Выполнила: учитель высшей квалификационной категории, учитель математики МОУ СОШ № 82
Веремеенко Татьяна Васильевна
Волгоград 2016
Пояснительная записка.
Программа курса «Как развить умение решать уравнения на «отлично»!» составлена с учетом особенностей математического образования девятиклассников по теме «Уравнения» и с учетом специфики, особенностей, приоритетов учащихся школы. Данный курс создан под потребности учеников 9 класса школы при изучении математики иметь в запасе набор приемов, позволяющих в стандартной ситуации использовать их быстро и с высокой степенью надежности получить ожидаемый результат. Назначение курса – обобщить изученный ранее материал, иметь возможность взглянуть на задачи «как бы сверху», увидеть повторяемость действий при решении и линейных и квадратичных, и дробно-рациональных, и уравнений с модулем, с параметром, которые могут стать алгебраическим инструментом при решении текстовых задач.
Желание оценить свои возможности и выявить необходимые качества, обеспечивающие такое поведение, желание иметь потребность в результате (тем самым достичь своего успеха) являются мотивами для участия подростков в математических олимпиадах и конкурсах различного уровня.
Цель курса «Как развить умение решать уравнения на «отлично»!» — формирование алгоритмической культуры школьника, умение выводить рассуждения на обобщение. При этом решаются задачи:
Уметь работать с различными источниками информации, находить информацию по данной теме.
Систематизировать и классифицировать задачи, выбирать задачи в соответствии с готовыми критериями (возможно, создавать новые).
Находить аналоги в практической жизни для решения задач с уравнением, составлять математические модели к практическим ситуациям, превращать их в задачи и решать эти проблемы.
Создавать продукты мыследеятельности, определять качество этих продуктов, корректировать качество, подчеркивать положительные характеристики созданных продуктов и их авторов.
Предъявлять свою позицию в решении уравнений на основе того или иного приема в письменной и устной форме, уметь читать и понимать графическую задачу, понимать «красоту уравнения», уметь преобразовывать уравнения грамотно, по правилам.

Определять степень сложности задачи по теме «Как развить умение решать уравнения на «отлично»!» с учетом критериев сложности задачи.
Данный курс имеет необходимое оборудование: большинство родителей имеют высшее образование, связанное с изучением математики и достаточный уровень научно-популярной, учебной, справочной литературы в домашней библиотеке. Каждый ученик имеет дома компьютер, медиа-обеспечение и возможность выхода в Интернет. В связи с этим самостоятельная работа с данными средствами или совместная работа с родителями позволит каждому ученику подобрать необходимый учебный материал по истории математики и задачный материал для его дальнейшего использования в курсе. Этому способствует и достаточный библиотечный фонд и методическое обеспечение кабинета математики.
Создаваемые учащимися продукты деятельности в ходе освоения данного курса позволят его освоить в форме тренингов, семинаров, практических, презентационных работ и др. Повторяемость организационных форм занятий позволит сделать процесс математического образования более адаптационным. Серии «семинар», «лекция», «тренинг»»практикум» позволяют учесть принцип повторяемости (что благоприятно сказывается на развитие учебной ситуации, т.к. делает ее определенной, подчиненной правилам) и принцип введения нового элемента (что является необходимой потребностью учеников подросткового возраста в поиске нового, знакомстве с новым, необычным). Множество занятий в форме тренинга позволит достичь необходимых трудовых и практических навыков школьников, тем самым основную часть трудных для них задач преобразовать в разряд типичных, решаемых известным методом. Лекционная форма работы предусмотрена в каждой серии занятий, причем роль учителя при этом меняется – от чтения лекции к чтению лекции с элементами семинара, семинара-практикума до подготовки лекции силами лучших учеников группы.
Повторяемость организационных форм занятий позволит сделать процесс математического образования более адаптационным. Серии «семинар», «лекция», «тренинг»»практикум» позволяют учесть принцип повторяемости (что благоприятно сказывается на развитие учебной ситуации, т.к. делает ее определенной, подчиненной правилам) и принцип введения нового элемента (что является необходимой потребностью учеников подросткового возраста в поиске нового, знакомстве с новым, необычным). Множество занятий в форме тренинга позволит достичь необходимых трудовых и практических навыков школьников, тем самым основную часть трудных для них задач преобразовать в разряд типичных, решаемых известным методом. Лекционная форма работы предусмотрена в каждой серии занятий, причем роль учителя при этом меняется – от чтения лекции к чтению лекции с элементами семинара, семинара-практикума до подготовки лекции силами лучших учеников группы.
Количество часов, отводимое на освоение той или иной темы, предполагает учёт времени на повторение учебного материала, ознакомление с новым материалом, на проведение занятия в той или иной форме. Коррекция количества часов на изучение отдельных тем предусмотрена: возможно увеличение количества часов на подготовку к празднику успеха и его проведение за счет систематизации учебного материала по теме «Знакомимся с веером приемов решения уравнений (разложением на множители, заменой переменных, графическим методом и др.)», преподнесения всех приемов в виде отдельного блока. Успешное освоение идеи преобразований и скорость техники освоения в ходе тренинга таких преобразований позволит констатировать определенный уровень готовности учащихся к обучению в условиях старшей школы по программам углубленного изучения математики или получения профильного обучения.
Коррекция количества часов на изучение отдельных тем предусмотрена: возможно увеличение количества часов на подготовку к празднику успеха и его проведение за счет систематизации учебного материала по теме «Знакомимся с веером приемов решения уравнений (разложением на множители, заменой переменных, графическим методом и др.)», преподнесения всех приемов в виде отдельного блока. Успешное освоение идеи преобразований и скорость техники освоения в ходе тренинга таких преобразований позволит констатировать определенный уровень готовности учащихся к обучению в условиях старшей школы по программам углубленного изучения математики или получения профильного обучения.
Констатация результатов и промежуточных результатов курса «Как развить умение решать уравнения на «отлично»!» для учащихся 9 класса представлена:
степенью участия школьников в создании учебных материалов по данной теме,
уровнем сложности и многообразия подготовленных материалов,
готовностью к систематизации подобранных задач,
умением выбирать задачи по заданным критериям и создавать новые, аналогичные данным задачам под известные критерии,
умением отделять те типы уравнения, которые под известные критерии не подходят,
умением определять качество и улучшать качество учебных материалов в ходе их использования,
умением определять самого успешного ученика в изучении данной темы,
умением организовать презентацию своего способа решения уравнения, представления нового метода решения задач в аудитории,
умением демонстрировать графическую культуру при решении уравнений,
умением видеть красивые решения уравнений,
умением анализировать олимпиадные задачи и распределять их по степени трудности в ходе совместного обсуждения.

Предполагается, что те задачи, которые будут предложены учащимися и учителем, но не будут рассмотрены в программе курса для учащихся 9 класса «Как развить умение решать уравнения на «отлично»!» станут основой для дальнейшего освоения темы «Уравнения и их приложения» в ходе освоения курса в условиях профильного обучения на старшей ступени.
Учебно-тематический план.
Знакомимся с уравнениями с параметрами2
Знакомство с видами уравнений с параметрами и стандартными приемами их решения.
10.
Пробуем решать простейшие уравнения с параметрами.
2
Отработка алгоритмов решения линейных, квадратичных уравнений с параметрами.
11.
Мы решаем уравнения на «отлично»!
1
Решение олимпиадных задач по теме «Уравнения», знакомство со спецификой решения олимпиадных задач
Содержание программы .
Занятие 1. Вводное занятие.
«История математики: понятие уравнений и их место в науке»,
«Уравнение в практической жизни»
Любознательность математиков. Желание описать события языком математики (составить уравнение). Ф. Виет, Д. Кардано и формулы решения уравнений:
ах2bхс , квадратное уравнение решаем по формулам Виета.
D = b2 – 4ac ;
х3pxq., кубическое уравнение , которое можно решить по формуле Кардано.
X= +
Решить уравнение:
х3 15х 124 0.
Решение. Это уравнение можно решить,разложив левую часть уравнения на множители способом группировки:
x3 – 16x + 31x + 124 = 0$
x (x2-16) + 31(x + 4) = 0;
x (x- 4) (x+ 4) + 31(x + 4) = 0;
(x+ 4) (x2 – 4x + 31) = 0;
x+ 4 = 0; или x2 – 4x + 31= 0;
x = — 4; D = 14 – 124, D меньше 0, нет корней. Ответ: -4
Ответ: -4
Решите старинную задачу.
Вопросил некто некоего учителя: «Сколько имеешь учеников у себя, так как хочу отдать своего сына к тебе в училище». Учитель ответил: «Если ко мне придет учеников еще столько же, сколько имею, и полстолько, и четвертая часть, и твой сын, тогда у меня учеников 100». Сколько было у учителя учеников?
Число десятков двузначного числа составляет две трети числа единиц, а число, написанное теми же цифрами, но в обратном порядке, больше первоначального на 18.
Найти число.
(Решите эту задачу двумя способами).
Занятие 2. Создаем копилку задач, обеспечивающую тему «Уравнения».
1.О.Д.З. уравнения
Задания: найти О.Д.З. уравнений
Тема для дискуссии:
Как распознать посторонние корни при решении уравнения (3)?
Сколько способов и какой из них рациональный?
Равносильные уравнения
Задание: Равносильны ли уравнения?
и
и
и
3. Освобождение от знаменателя.
Освобождение от знаменателя.
Задание. Решить уравнение
1)
2)
3)
4)
5)
Занятия 3-8 . Равносильные преобразования.
Отработаем умение освобождаться от знаменателя.
Работаем с областью определения и равносильностью уравнений
Отрабатываем приемы равносильных преобразований.
Выделяем трудности решения уравнений вида
К(х)· р(х)=0
Знакомимся с веером приемов решения уравнений (разложением на множители, заменой переменных, графическим методом и др)
Демонстрируем умения видеть необходимый способ решения задачи на основе известного приема и умение применять этот прием для получения результата
Уравнение b(x)q(x)p(x)0 равносильно совокупности уравнений
b(x) 0,
q(x) 0,
p(x) 0.
Решить уравнения: 1) (х22х4)(х29)=0
2) (х210х25)(2х7)(х1)=0
2. Освобождение от знака абсолютной величины.
х, х 0,
Определение модуля: х х, х 0.
Освободиться от модуля: 1) b(x) 0 3)b(x) q(x) 0
2) b(x) с 4) b(x) q(x) с
Задания для самостоятельной работы: Решить уравнения:
х2 3
х4 13х
3х2 3х 2 х2 4
Проверьте, что: 1)b(x) q(x) (( b(x) q(x) или b(x) q(x)) и q(x) 0).
q(x) 0
2) b(x) q(x) b2(x) q(x)
Задания для самостоятельной работы.
Решить уравнения:
х26х х,
х26х х26х,
5х1 х,
х25х 9х.

Целые корни уравнения с целыми коэффициентам.
Возьмем уравнение 5х214х30. Предположим, что число m – корень этого уравнения, т.е. 5m214m30. Это равенство можно переписать так: m(5m14)3. Число, записанное слева, делится на m, поэтому и равное ему число 3, также делится на m.
Вывод: если уравнение 5х214х30 имеет целый корень, то он является делители свободного члена. Теперь понятно как этот корень можно отыскать: нужно выписать все делители свободного члена и затем подстановкой проверить, является ли какое-нибудь из этих чисел корнем уравнения.
Этот прием (решения уравнения) носит общий характер. Его можно использовать для нахождения целых корней уравнений более высоких степеней.
Задание: Решить уравнение 183х2184х10.
Пример. Найти целые корни уравнения 2х3х25х20.
Решение.
Делители свободного члена: 1; -1; 2; -2.
Подставим их в уравнение: 213125120,
223225220,
2(1)3(1)25(1)20,
2(2)3(2)25(2)20.
Уравнение имеет два целых корня: 1 и 2.
Задания для самостоятельной работы: Решите уравнения в целых числах.
3х42х230
х53х45х315х24х120
Разложение на множители.
Для разложения многочлена на множители, пользовались специальными приемами – вынесение общего множителя с помощью формул, формулами сокращенного умножения, способом группировки. А теперь еще будем знать, что многочлен можно разложить на множители, один из которых есть разность между переменной и найденным целым корнем.
Научимся делить многочлен на многочлен уголком.
Пример.
_ 2х2х15 х3
2х26х 2х5
5х15
5х15
0
Получим: 2х2х15(х3)(2х5).
Задания для самостоятельной работы. Решить уравнения:
х42х3х20,
х312х29х220,
2х37х290,
5х354х239х100.
3.Замена переменной.
Этот способ позволяет: понизить степень уравнения, свести уравнение к линейному или квадратному уравнениям.
Задания: Решить уравнение
(х3)413(х3)2360
(х1)2(х22х5)0
(х24х1)(х24х4)4
(х27х13)2(х3)( х4)0
(х24х2)5(х2х)100
(х216х2)4(х4х)110
х21х23х3х20
х21х28х8х90
х628х3270
х69х380
(х1)(х2)(х3)х314х2
х(х1)(х2) (х1)(х2)(х3)
Графический способ
Умения: 1. Построение основных графиков:
Построение основных графиков:
уkхb; уaх2; уkх; у aх2bхc; уkх; уb(х).
уa; уb.
2.Чтение графика
С помощью графика можно ответить на вопросы:
Есть ли корни у уравнения?
Сколько корней имеет уравнение?
Найти приближенные значения корней.
Найти знаки корней.
Задания для самостоятельной работы
Есть ли корни у уравнения и если есть, то сколько?
(х1)22/х,
х26х48х0,
х2 х2,
5х х2,
х¼ х0,
х2х2,
5х1х,
х218,
хх23,
х12х2,
х24х4х22,
х34х30.

Занятия 9 – 12.
Собираем и рассматриваем текстовые задачи различного типа, решаемые с помощью уравнений
Решаем текстовые задачи различного типа с помощью уравнений
Решение задач на составление уравнений.
На плоскости отмечено несколько точек, некие три из которых не лежат на одной прямой. Все они попарно соединены отрезками. Сколько всего отмечено точек, если проведено 105 отрезков?
Цена товара была дважды повышена на одно и тоже число процентов. На сколько процентов повышалась цена товара каждый раз, если его первоначальная стоимость 200р., а окончательная 338р.?
Туристический маршрут состоит из двух участков: 9 км подъема и 12км спуска. При подъеме скорость туристов на 3 км/ч меньше, чем при спуске, а их средняя скорость на всем маршруте равна 4,2 км/ч. Чему равна скорость туристов при спуске?
Смешали 10%-ный и 25%-ный растворы соли и получили 3 кг 20%-ого раствора.
 Какое количество каждого раствора взяли?
Какое количество каждого раствора взяли?
Имеется сталь двух сортов с содержанием никеля в 5% и 40%. Сколько нужно взять каждого сорта стали, чтобы получить 140m стали с содержанием никеля в 30%.
Два насоса различной мощности, работая вместе, наполняют бассейн за 4ч. Для заполнения половины бассейна первому насосу требуется времени на 4 ч больше, чем второму для заполнения ¾ бассейна. За какое время может наполнить бассейн каждый насос в отдельности?
От пристани А вниз по течению отправились катер и плот. Катер доплыл до В, повернул обратно и встретил плот через 4 ч. после выхода из А. Сколько времени шел катер от А до В?
Знакомимся с уравнениями с параметрами
Пробуем решать простейшие уравнения с параметрами.
Уравнения с параметрами.
Линейное уравнение.
Уравнение с одной переменной в первой степени сводится к решению уравнения pxq. Сколько решений может иметь это уравнение?
I. p0, х q / p – одно решение.
II. p0 и q 0, х – любое число.
III. p0 и q0, нет решения.
Задания для самостоятельной работы.
При каких значениях а и b уравнение (а – 2)х = b + 1 не имеет корней?
При каких значениях а и b любое число является решением уравнения (а + 3)х = b – 1 ?
(m+1)(n-2)x = (m-1)(n-2). При каких значениях m и n уравнение:
а) не имеет решения?
в) имеет бесконечно много решений?
Решить уравнение: (а2-1)х = а+1.

Решить уравнение: х+1 +а1-2х=1,5.
Найти а, при которых уравнение а-2х+1=х+3 имеет единственное решение.
2. Квадратное уравнение.
Решение квадратного уравнения с параметрами должно выполняться как естественный ход решения, которое опирается на знания формул Виета и формул корней.
Ах2+bx+с = 0.
-b-D -b+D
Формулы корней: х1= ; х1= ; D=b-4ac
2a 2a
Если: D0, два корня
-b
D=0, один корень х=
2a
D0, нет корней
Формулы Виета: х1+х2= -b/2а и х1х2= с/а.
Задания для самостоятельной работы.
Найдите все целые значения p, при которых данное уравнение х2+pх+15=0 имеет целые корни.

Найдите все положительные значения q, при которых уравнение х2+5х+ q=0 имеет целые корни. Найдите несколько целых отрицательных значений q, при которых уравнение имеет целые корни. Можно ли перечислить все такие значения q?
Найдите все целые значения m, при которых квадратный трехчлен можно разложить на линейные двучлены с целыми коэффициентами: с2+ mс+10.
Найдите значение k, при котором разложение на множители трехчлена 2х2 — 5х+ k содержит множитель (2х+3).
При каких значениях с уравнение х2+2х+с=0 не имеет корней? Укажите одно из таких значений с.
При каких значениях с уравнение х2+6х+с=0 имеет два корня? Укажите одно из таких значений с.

При каких значениях k уравнение х2+kх+9=0 имеет корни?
При каких значениях k уравнение 16х2+kх+1=0 не имеет корней?
При каких значениях с уравнение 15х2+ сх+ ¼ =0 имеет два корня?
При каких значениях k уравнение kх2-6х+k=0 имеет два корня?
При каких значениях а уравнение ах2+х-3=0 имеет два корня?
Решите уравнение ах2+(2а2-1)х — 2а=0.
При каких значениях параметра b уравнение bх2-х+b=0 имеет ровно один корень?
Решите уравнение (а+1)х2 — 2х+1- а=0 и определите, при каком а уравнение имеет единственный корень.

Решите уравнение ах2 — (2а+ b)х+2b = 0.
При каком значении параметра а уравнение 25х2 — 20+а = 0 будет иметь равные корни?
Найдите все значения параметра а, при которых корни х1 и х2 уравнения х2 — (а-2)х — (а+3) = 0 удовлетворяет условию х12+х22=9.
Занятие 17
Решение олимпиадных задач по теме «Уравнения», знакомство со спецификой решения олимпиадных задач
Литература для учащихся.
1. Учебник. Математика – 8. Г.В. Дорофеев, «Дрофа», 2012г.
2. Учебник. Математика – 9. Г.В. Дорофеев, «Дрофа», 2012г.
За страницами учебника алгебры. Л.Ф. Пичурин. «Просвещение», 1990г.

Шаг за шагом (математ-р.т.) – 9, И. Шарыгин., М. 1995г.
Дидактический материал 9 кл., алгебра. С.Н. Зеленская.
«Учитель», 2012г.
Литература для учителя.
Уравнения. Моск. универ. М.К. Потапов., 1992г.
Дидактический материал, алгебра – 7, алгебра – 8. С-П, Б.Г. Зив, 2013г.
Дидактический материал, алгебра – 9. В. «Учитель»,
С.Н. Зеленская, 2012г.
За страницами учебника алгебры. Л.Ф. Пичурин.
«Просвещение», 1990г.
514 задач с параметрами. С.А. Тынянкин. Волг. 1991г.
Как научиться решать химические уравнения
Химические уравнения — это реакции, которые происходят при взаимодействии веществ, выраженные при помощи специальных формул. Именно химические уравнения показывают экспериментаторам, какие вещества вступают во взаимодействие (реакцию) и какие получаются в результате такой химической реакции.
Именно химические уравнения показывают экспериментаторам, какие вещества вступают во взаимодействие (реакцию) и какие получаются в результате такой химической реакции.Прежде всего, хотелось бы сказать — для того чтобы решить любое химическое уравнение, важно знать определенные методы, способы и подходы к данному процессу, о чем и пойдет речь ниже.
Для начала важно знать, что в основе составления абсолютно любого химического уравнения лежит закон сохранения массы. А также любое химическое уравнение показывает соотношение количества веществ, которые участвуют в реакции. Зная это, можно приступать к следующим действиям.
Изучите внимательно условие своей задачи. Запишите кратко условие на лист бумаги или в тетрадь. Составьте уравнение химической реакции. Запишите над составленным уравнением все известные и неизвестные величины. Производя такие действия, важно не просто указать цифры, но также поставить соответствующие единицы измерения для чистых веществ без примесей.
Определите изначально содержание чистого вещества при вступлении в реакцию веществ, содержащих примеси.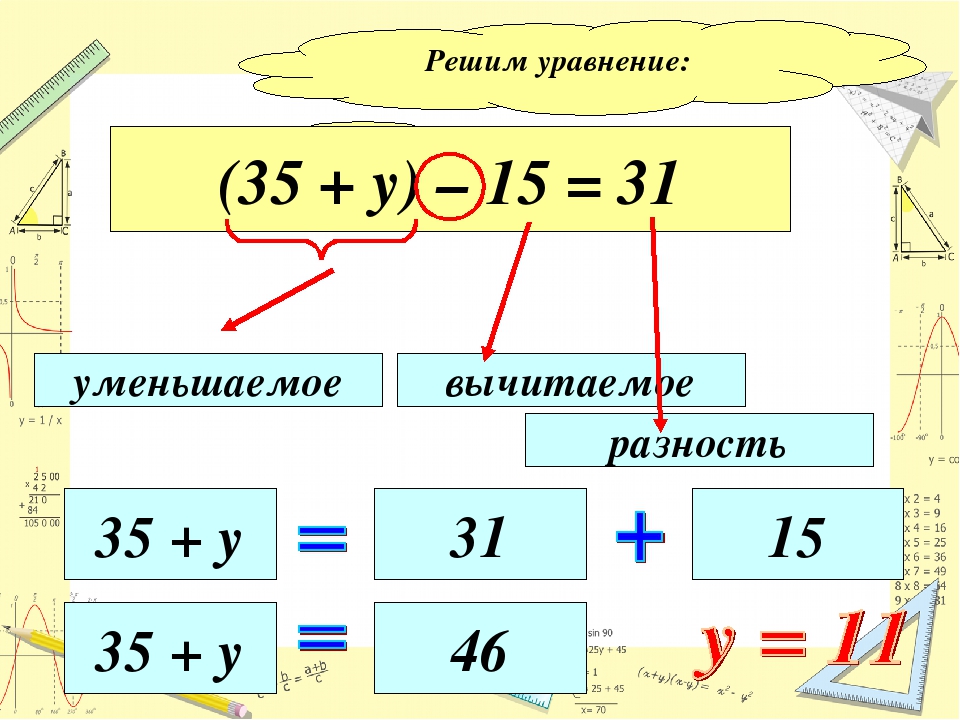
Запишите соответствующие значения величин, найденных по уравнению химической реакции, под формулами веществ с известными и неизвестными. Составьте пропорцию и решите ее. Запишите ответ.
Проделайте подобные действия, взяв другие вещества. Помните, что чем больше времени вы будете уделять на решение химических уравнений, тем легче будет для вас данный процесс.
При изучении и решении химических уравнений следует знать и помнить то, что данные уравнения отличны от других (математических). В химическом уравнении ни в коем случае нельзя менять местами правую и левую части, так как вещества правой части – это продукты реакции, а вещества левой части – названия реагентов. В случае если вами будет произведена перестановка указанных двух частей, в итоге получится химическое уравнение совершенно другой реакции.
Урок математики в 3-м классе «Решение уравнений»
Тип урока: урок введения новых знаний.
Цель: познакомить с уравнениями
нового вида.
Задачи:
- Учить решать уравнения нового вида, которые будут вводиться через текстовую задачу.
- Развивать умение переносить ранее изученные знания на новый материал.
- Развивать интеллектуальные и коммуникативные умения, умения самостоятельно оценивать результат своих действий.
Оборудование:
- мультимедийный проектор, компьютер, презентация.
- Лист самооценки учащихся представлен в Приложение 1
- Тема на плакате. Решение уравнений (закрыта)
- Листики для работы в группах
- (Х + 2 = 5 x 3)
- Учебник «Моя математика» Т.Е.Демидова, С.А.Козлова, А.П.Тонких Часть 2.
- Карточки с домашним заданием ( разноуровневые задания).
Ход урока
I. Организация класса.
Организация класса.
Положительный настрой на работу.
II. Актуализация знаний.
Ребята, вы согласны, что в жизни пригодиться такое умение — как быстро считать?
А знать о пользе разных продуктов?
Вы любите ягоды? Не случайно вас спрашиваю. Вы сейчас потренируетесь в счёте и заодно узнаете о пользе и лечебных свойствах некоторых ягод и фруктов.
1. Математическая разминка + тема здоровья (лечебные свойства ягод, фруктов)
Послушайте задачи и запишите выражения в тетрадях:
а) Семья собрала летом с одного куста 2 кг черноплодной рябины. Сколько всего кг рябины собрала семья с 11 таких кустов?
В плодах черноплодной рябины витамина «Р» в 20 раз больше, чем в яблоках и апельсинах. Витамины — необходимы для растущего организма.
б) Юля разделила поровну 30 мандаринов среди пяти своих подруг. Сколько мандаринов получила каждая из них?
При простуде и кашле — рекомендуется каждое
утро выпивать по стакану мандаринового сока. Эфирное масло мандарина поднимает настроение.
Эфирное масло мандарина поднимает настроение.
в) На зиму заготовили 4 баночки брусники, а клюквы в 6 раз больше. Сколько банок с клюквой заготовили на зиму?
Раны и ожоги, промытые клюквенным соком, моментально заживают. Брусника повышает остроту зрения и рекомендуются пилотам, морякам, водителям, работающим с напряжением зрения и ученикам.
г) Масса арбуза 12 кг, Сколько кг в ? арбуза?
Арбузы прекрасно утоляют жажду и выводят из организма ядовитые вещества.
Проверьте. (Слайд № 2 по щелчку)
- 2 x 11= 22(кг)
- 30 : 5 = 6(м.)
- 4 x 6= 24(б.)
- 12 : 2= 6(кг) ( Самоконтроль. Самопроверка.
Дети выполняют отметку в листе самооценки. Приложение 1.)
Какие знания понадобились для решения задач? (Знания таблицы умножения и деления)
Отлично справились с заданием.
Продолжаем математическую разминку:
2. Игра.
Игра.
На какие 2 группы можно разбить записи? (Слайд № 3 по щелчку)
505 — 5
Х+ 20= 70
Х- 40 =30
808 — 8
150 — Х = 70 (Уравнения и числовые выражения)
Что такое уравнение? (Равенство с неизвестным)
Каждый ряд решает своё уравнение. (1 ряд - первое уравнение -Х+ 20= 70, 2 ряд- второе уравнение Х- 40 =30, 3 ряд -150 — Х = 70)
Проверка решения уравнений по рядам. (Слайд № 4).
Оцените своё решение (Дети делают отметку в листе самооценки. Приложение 1.)
III. Подводящий диалог к формулированию новой темы.
1. Работа с рисунками. Рисунки к задаче № 1 стр.88 (слайд № 5 )
Ребята, перечислите предметы, которые здесь изображены художником? (Весы, рыба, гири).
Что за цифры на гирях. Зачем они? (Указывают массу гирь)
Скажите, в каком положении находятся весы (Весы находятся в равновесии)
Запишем то, что видите на картинке с помощью цифр, математических знаков(слайд № 6 пощелчку)
Что лежит сначала на левой чаше весов? (Рыба)
Какова её масса? (Неизвестна)
Как её можно обозначить?( Давайте обозначим массу рыбы буквой Х)
Что ещё находиться на этой же чаше? (Гиря массой в 2 кг)
Если это вместе на одной чаше весов, какой знак между числами поставим? ( х+2)
(Аналогично с правой чашей весов) Перечисляют и появляется запись: 5 5 5
Весы в равновесии, какой знак поставим между записями ? (Равно)
Интересная запись! Х + 2 = 5 x 3
Давайте это запишем в тетрадь.
А я догадалась, как правую часть проще записать, а вы? (5 x 3 сумма одинаковых слагаемых)
Здорово!
Х + 2 = 5 x 3
Что вы заметили? Что напоминает вам эта запись? (Похоже на уравнение)
А решали такие сложные уравнения?(Нет)
Тогда сформулируйте тему нашего урока. (Решение уравнений)
(тему открываю)
Как думаете, чему мы будем учиться мы на уроке? (Учиться решать новые виды уравнений).
IV. Оздоровительная минутка.
Зрительная гимнастика (слайд № 7). Следят за движением рыбки, затем дельфина.
V. Совместное «открытие» нового знания.
Работа в группах.
Проведём свои наблюдения, исследовательскую работу. Помогайте друг другу.
С чего бы вы начали решение этого уравнения?
Сделайте его проще!(Можно найти произведение 5 и 3. Мы получили уравнение, которое уже умеем решать: Х +2 = 15)
Неизвестно 1 слагаемое. Чтобы его найти,
необходимо из суммы вычесть известное слагаемое.
Чтобы его найти,
необходимо из суммы вычесть известное слагаемое.
Корень — 13 (слайд № 8 по щелчку)
Молодцы! Вы сделали открытие!
Смогли сами справиться с таким сложным заданием.
Сделайте отметку в листе самооценки. Делают отметку в листе самооценки.
(работа в группах)
Если уч-ся не смогут самостоятельно решить данное уравнение, то предложить готовое решение Вити.( № 1 стр. 88 учебника)
Расскажите, как Витя решал это уравнение?
Откуда появляется число 15 в уравнении? (Произведение 5 и 3)
Витя решил уравнение так:
Х + 2 = 5 x 3
Х + 2 = 15
Х = 15 — 2
Х = 13
Ответ 13 килограммов масса камбалы.
Чему же равна масса рыбы?(Масса рыбы — 13 кг)
VI. Первичное закрепление.
Попробуем полученные знания применить на практике
Откройте учебник стр. 88 № 3 (а)
Чтение про себя, вслух.
Костя выполнил 2 рисунка и решил составить к ним уравнения. Какие задачи к ним можно придумать?
(слайды № 9, 10 по щелчку)
Что положили на левую чашу весов? (гири — 2 кг и 15 кг)
Что положили на правую чашу весов? (Гирю 5 кг, арбуз)
Какова масса арбуза? (Какова масса арбуза?)
Что необходимо будет узнать в придуманной вами задаче? (Определить массу арбуза)
Какую задачу можно придумать?
Заслушиваются задачи, составленные учащимися. (Например: На одной чашке весов гиря массой 5 кг и арбуз, а на другой чашке весов гири 5 кг и 15 кг. Какова масса арбуза?)
Если вы решите данное уравнение, Х + 5= 15 + 2 то сможем узнать :
(массу арбуза)
Решите уравнение:
Дети записывают в тетрадях:
Х+5= 17
Х=17- 5
Х= 12
Ответ: 12 кг масса арбуза..)
VII. Повторение и систематизация изученного материала.
Попытайтесь сами решить уравнение
Самостоятельная работа по вариантам (слай № 11)
х +3 = 17 — 2 — 1 вариант
9 — у = 13 — 6 — 2 вариант( Самостоятельно работают).
Проверка самостоятельной работы. (слайд № 12)
VIII. Итог урока. Рефлексия.
Чему учились на уроке? (Учились решать сложные уравнения)
Проанализируйте свою деятельность.
(лист самооценки) Вложите в свои тетради. (Заполненный лист самооценки вкладывают в тетради, тетради сдают).
Как работалось в команде?( Ответы детей)
О пользе каких ягод и фруктов вы узнали?(клюквы, брусники, арбуза, мандаринов, черноплодной рябины)
IX. Домашнее задание. (дифференцированное)
Чтобы научиться решать задачи с уравнениями, вы
потренируйтесь в решении уравнений дома. Здесь и
пригодятся полученные знания новой темы урока.
(Учащимся предлагаются разноуровневые карточки с уравнениями. Дети, оценивая степень усвоения, выбирают себе карточку легче по уровню или труднее)
1 уровень:
Х + 4= 3+3+3+3
3 + Х= 2 x 6
7+ у = 16 — 3
40 — а =30+ 8
*2 уровень
9 + у = 12 x 6
40- а = 30 : 5
88: с = 55 : 5
Х x 10 = 16 x 5
X. Дополнительный материал. (если останется время) Слайд № 13.
Игра.
Найдите уравнения, с которыми вы сегодня познакомились на уроке математики.
Х+5=19
Х+3= 7 x 4
7+Х= 6+6+6
Х+5=13+6
7+Х = 18
Спасибо за урок!
Этап урока Методы и приемы | Хроно-метраж | Содержание урока | Формируемые УУД | |
Деятельность учителя | Деятельность учащихся | |||
I. Психологический настрой | 1 мин | — Здравствуйте, ребята! Меня зовут Анастасия Владиковна. Сегодня я проведу у вас урок математики. Итак, давайте проверим готовность к уроку. У вас на парте должны быть учебник, тетрадь, линейка, карандаш, ручка. Сейчас сядут те, кто готов к уроку и хочет научиться новому. Откройте ваши тетради, отступите 4 клетки вниз и запишите число: сегодня 11 февраля классная работа. | Проверяют готовность к уроку. Настраиваются на работу.
| Р: саморегуляция как способность к мобилизации сил и энергии, к волевому усилию и преодолению препятствий |
II. Актуализация знаний и мотивация
Практический: выполнение упражнений (устный счет) | 4 мин | -Начнем наш урок. — Рассмотрите запись. 8 а 18 х 3 с 15 S 54 п 5 — Что написано? — Какие цифры мы будем писать на минутки чистописания? — Что можно сказать про буквы? -К чему мы стремимся на минутке чистописания? — Запишем строчку чисел и латинских букв в тетрадь, стараясь писать по образцу. — Сравните с образцом. — Подчеркните те цифры и буквы, которые получились неудачно. — Оцените себя: * кто ничего не подчеркнул, тот ставит себе «5» * кто подчеркнул 1 или 2 знака, тот ставит себе «4» * у кого подчеркнуто больше 3 знаков, тот ставит себе «3» -Сейчас будем записывать выражения и находить их значения. А помогут нам числа, которые мы использовали в минутке чистописания. Кто поможет у доски? А все остальные записывают в тетрадь. 18 уменьшить на 3. (18-3=15) 54 увеличить на 3. (54+3=57) 3 увеличить в 8 раза. 15 уменьшить в 3 раза. (15:3=5) — Давайте проверим. Спасибо за помощь. Присаживайся. За работу у доски ты получил. — Давайте вспомним, как называются компоненты при вычитании, сложении , делении, умножении? |
Числа/цифры и буквы.
1, 3,4, 5, 8. Они латинские. писать цифры разборчиво, аккуратно и правильно |
П: построение логической цепи рассуждений |
III. Постановка учебной задачи
Словесный: ответы на вопросы.
Практический: решение выражения. | 5 мин | — Задание усложняется. Кто попробует у доски? — А теперь внимательно меня послушайте. Я задумала число, увеличила его в 3 раза и получила 54. — Посмотрите на минутку чистописания. -Проверим запись у доски. х*3=54 -Посмотрите на записанные нами ранее выражения и скажите, что в них общего? 18-3=15 54+3=57 3*8=24 15:3=5 х*3=54 -Чем отличается последнее равенство от четырех предыдущих? -Как обозначаем неизвестное число? — Как называется это равенство? — Что же такое уравнение? (Уравнение – это равенство, которое содержит неизвестное число) — Что значит решить уравнение? — Посмотрите на минутку чистописания и попробуйте составить с этими числами и буквами уравнения на умножение и деление. (18:у=3, 3*х=15, х:8=5) (сама записываю составленные уравнения) -Как вы думаете, какая тема урока сегодня? —Что нам нужно знать, чтобы решить уравнение? -Ребята, а числа при делении и умножении
связаны между собой? Как они связаны? Объясните связь чисел при умножении,
при делении. -Посмотрите на составленные вами уравнения. Как найдем неизвестное число, зная взаимосвязь чисел? -Значит, кроме умения делить и умножать, кроме знания таблицы умножения, мы что еще сегодня должны применять при решении уравнений на деление и умножение? — Наша цель сегодня на уроке…? |
это равенства
в нем есть неизвестное число
латинской буквой уравнение найти неизвестное число
Решение уравнений
Знать таблицу умножения, уметь делить и умножать Да. Проверкой. Умножение можно проверить делением и наоборот. Знание взаимосвязи чисел при делении и умножении. Научиться решать уравнения на основе взаимосвязи между компонентами | К: высказывание своей точки зрения и попытка ее обосновать, приводя аргументы; принятие правильной точки зрения
П:формулированиетемы урока, уметь
ставить учебную задачу на основе соотнесения того, что уже известно и усвоено
учащимися и того, что еще неизвестно. |
IV. Открытие нового знания Практический: упражнение.
| 8 мин. | — Мы с вами говорили, что на уроке математике мы: решаем примеры, уравнения, задачи. — Уравнения и примеры мы с вами решили, что у нас еще осталось? — Как вы думаете, можем ли мы использовать уравнения для решения задач? — Давайте проверим. — Вернемся к минутки чистописания. (на экране) — Какая буква отличается от других? Почему? — Что обозначают заглавной буквой S в математике? — Прочитайте задачу. Катя и Миша решили в зал купить ковра. Они знают, что площадь зала 36 м², а ширина 3 м. Какой длины должен быть ковер. — О чем задача? — Давайте вспомним формулу площади. — Что такое а, в, S. — Что нам известно? — Что надо найти? — Даю минутку подумать, составить и
записать уравнение. — Давайте все известные данные подставим в формулу площади. Что у нас получилось? а*3=36 3 х а=36 — Какие знания нам пригодятся, чтобы решить уравнения? — Какой компонент нам неизвестен? — Как найти неизвестный множитель? — Решите самостоятельно. (Проверка с экрана) — Чему должна равняться длина ковра? — Итак, какой вывод мы можем сделать? — Оцените уровень самостоятельности решения задачи. Оценка своей работы: *Если вы самостоятельно составили и решили уравнения, то ставите «5». * Если вы не смогли самостоятельно составить уравнения, но решили правильно, то ставите «4» * Если вы не смогли самостоятельно составить уравнения, и допустили одну вычислительную ошибку, то ставите «3» |
Задачи
Да.
S. Площадь.
О ковре. a*b=S. а- длина, в – ширина и S – площадь. S=36м², а ширина 3м. длину ковра.
Уравнение
Взаимосвязь компонентов. Множитель. надо произведение Разделить на известный множитель.
12 м. С помощью уравнения мы можем решать задачи. | П.: осуществляют
сравнение и анализ, классификацию слов по самостоятельно определенным
Р.: осознают и принимают
К.: обмениваются мнениями; умеют слушать друг
Л.: определение границ собственного знания и незнания
|
V. Практический: решение задачи | 5 мин. | А сейчас ребята, мы с вами поработаем с задачей под № 4. — Кто прочитает нам задачу? -О чем говорится в задаче? — Что известно в задачи? -Что нужно найти? -Прочитайте вопрос задачи? -Какой способ краткой записи лучше выбрать? — Кто хочет к доске и запиши таблицу. -Как будут называться столбцы и строки таблицы? -Что такое 19 человек? -Что такое 2 и 3 банки? -Что надо узнать в задаче? — Как можно найти, сколько всего взяли банок? -Каким действиям будем решать? Каким выражением запишем? Составьте выражение.+ Запишите первый способ решения и ответ. (2+3)*19=95(б) Ответ:95 банок консервов взяли всего — А кто догадался, как можно эту задачу решить другим способом? Нужно вычислить, сколько взяли мясных консервов на 19
человек, затем сколько взяли овощных консервов на 19 человек, затем сложить
результаты. — Какими действиями будем решать? Каким выражением запишем? Запишите второй способ решения и ответ. 1)19*2=38(б)-мясные консервы 2)19*3=57(б)-овощные консервы 3) 38+57=95 (б) Ответ: 95 банок взяли Какой способ удобнее? Ребята, а сейчас давайте немного разомнемся. Физминутка Как
живёшь? |
Таблицей. столбцы: кол-во банок на человека;кол-во туристов;общее кол-во банок. строки:мясные консервы ,овощные консервы. Кол-во туристов. Кол-во банок на человека. Сколько всего банок
взяли. Нужно вычислить сколько взяли всего банок на каждого человека , потом умножить кол-во банок на кол-во туристов
Первый/второй. | П: применять базовые знания для решения конкретной проблемы. П: Владеть общими приемами решения задач. Строить логическую цепь рассуждений.
|
VI.Самостоятельная работа с самопроверкой Практический: Самостоятельная работа | 5 мин | — А мы переходим к заданию под № 2 , выполним мы его самостоятельно в тетрадях. — На это задание вам 2 минуты. — А теперь берем другого цвета карандаш, меняемся тетрадью с соседом и проверяем его по образцу. (Чтобы найти неизвестный множитель…(надо произведение разделить на известный множитель) Чтобы найти неизвестное делимое…(надо частное умножить на делитель) Чтобы найти неизвестный делитель…(надо делимое разделить на частное)) Оценка своего соседа: -нет ошибок — зеленым карандашом ставим «+» — 1 ошибка — желтым ставим «+» — 2 ошибки – Красным ставим «+». | Выполняют
самостоятельно задание. | Л: самооценка; адекватное понимание причин успеха П: рефлексия способов и условий действий; контроль и оценка процесса и результатов деятельности.
|
VII.Включение в систему знаний Словесный: ответы на вопросы Практический: выполнение упражнений; решение задач
| 7 мин | — Ребята, открывайте учебник на странице 20 посмотрите на уравнения. Объясните решения уравнений и проверку. 1 уравнение нам объясняет…, 2 …., 3 ….. Молодцы! -Как проверили правильность решения. — Посмотрите на задание под номером 1, что мы должны сделать? — Все работают в тетрадках, а (Коля) выходит к
доске и объясняет нам первое уравнение, обращаю ваше внимание, что вы можете
смотреть на образец решения уравнений, который мы только что, с вам
разобрали. — Что ты сделал, что бы найти неизвестное число? — Ребята, давайте вернемся к № 3, это задание выполняем устно. Обращаю ваше внимание, что выполняем его с полным объяснением.
-Ребята, сейчас откройте ваши дневники и запишите домашнее задание: с. 20 № 5 и 7. |
Объясняют уравнения.
Проверкой. решить уравнения с объяснением
поделил число 54 на 18.
| К: высказывание своей точки зрения и попытка обосновать её, приводя аргументы; принятие правильной точки зрения, готовность изменить свою точку зрения
П: построение речевого высказывания К: участвуют в учебном диалоге. Р: осуществлять самоконтроль за ходом выполнения работы и полученного результата; контроль, коррекция, оценка; волевая саморегуляция в
ситуации затруднения. |
VIII.Рефлексия деятельности Словесный: обобщение учителя и учеников | 5 мин | Наш урок подходит к завершению. Давайте с
вами подведем итоги. Чем мы сегодня занимались? Какую цель мы ставили? Кто и
как достиг ее? Молодцы, я за вас рада! И КРАСНЫЙ – вам ничего не понятно и сегодняшний урок не понравился. Молодцы! Вы сегодня очень хорошо поработали. Спасибо за урок. |
Оценивают свою деятельность на уроке
| Р:выделение
и осознание учащимся того, что уже усвоено и что еще подлежит усвоению,
осознание качества и уровня усвоения. |
Решение задач с помощью уравнений
В решении задач с помощью уравнений, необходимо соблюдать следующее: во-первых, записать условие задачи алгебраическим языком, т.е. таким образом, чтобы получить уравнение; во-вторых, упростить это уравнение до такого вида, в котором неизвестная величина будет стоять с одной стороны, а все известные величины — на противоположной стороне. Способы этого уже были рассмотрены ранее.
Один из основных принципов алгебраических решений, это то, что величина должна присутствовать в уравнении. Это позволит нам записать условия так, как если бы задача уже была решена. После этого, останется лишь решить уравнение и найти общее значение всех известных величин. Так как эти величины равны неизвестной величине на другой стороне уравнения, то величина всех известных значений будет означать, что задача решена.
Задача 1. Человек на вопрос, сколько он заплатил за часы, ответил: «Если умножить цену на 4, и к результату прибавить 70, а из этой суммы вычесть 50, то остаток будет равен 220 долларов». Сколько он заплатил за часы?
Сколько он заплатил за часы?
Чтобы решить эту задачу, мы должны сначала записать условие задачи как алгебраическое выражение, то есть как уравнение.
Пусть цена часов равна $x$
Эта цена была умножена на 4, то есть получаем $4x$
К произведению прибавили 70, то есть $4x + 70$
Из этого вычли 50, то есть $4x + 70 — 50$
Таким образом, мы записали условие задачи с помощью чисел в алгебраической форме, но у нас еще нет уравнения. Однако, согласно последнему условию задачи, все предыдущие действия в итоге привели к результату, который равен $220$.
Поэтому, это уравнение выглядит так: $4x + 70 — 50 = 220$
После проведения операций с уравнением, получаем, что $x = 50$.
То есть, значение $x$ равно 50 долларов, что и есть искомой ценой часов.
Чтобы проверить, что мы получили верное значение искомой величины, мы должны подставить это значение вместо $х$ в уравнение, которое мы записали по условию задачи. Если в результате этой подстановки значения сторон будут равны, мы провели вычисление правильно.
Если в результате этой подстановки значения сторон будут равны, мы провели вычисление правильно.
Уравнение задачи имело вид $4x + 70 — 50 = 220$
Подставляя 50 вместо $x$, получаем $4 \cdot 50 + 70 — 50 = 220$
Отсюда, $220 = 220$.
Задача 2. Если к числу прибавить его половину, а из этого результата вычесть $20$, то получим четверть первоначального числа. Что это за число?
В задачах такого типа, где рассматриваются дроби, надо помнить, что $\left(\frac{1}{3}\right)x$ то же самое, что и $\frac{x}{3}$; отсюда $\left(\frac{2}{5}\right)x = \frac{2x}{5}$.
Обозначим через x искомое число.
Тогда согласно условию $x + \frac{x}{2} — 20 = \frac{x}{4}$
После выполнения операций на уравнением, получим $x = 16$.
Проверка: $16 + \frac{16}{2} — 20 = \frac{16}{4}$.
Задача 3. Отец разделил наследство между своими тремя сыновьями так, что:
Первый сын получил на $\$1000$ меньше, чем половина всего наследства;
Второй сын получил на $\$800$ меньше, чем треть всего наследства;
Третий сын получил на $\$600$ меньше, чем четверть всего наследства;
Какая сумма была всего наследства?
Если обозначить все наследство как x, тогда три сына получили $\frac{x}{2} — 1000, \frac{x}{3} — 800$ и $\frac{x}{4} — 600$.
Так как эти части все вместе представляют все наследство, то их сумма равна $x$.
Тогда мы имеем равенство $\frac{x}{2} — 1000 + \frac{x}{3} — 800 + \frac{x}{4} — 600 = x$.
После выполения операций с членами уравнения, получим, что $x = 28800$
Проверка: $\frac{28800}{2} — 1000 + \frac{28800}{3} — 800 + \frac{28800}{4} — 600 = 28800$.
Чтобы избежать лишнего представления неизвестных величин в уравнении, иногда хорошо заметить, что когда дана сумма или разница двух значений, обе эти величины могут быть выражена одной и той же буквой. Так, если одна из двух величин вычитается из суммы этих величин, очевидно, что остаток буде равен другому вычитаемому. А если разница этих двух величин вычитается из большего, то остаток будет равен меньшему.
Так, если сумма двух чисел равна 20
И если один из них будет представлен через $x$
То другой будет равен $20 — x$.
Задача 4. Разделите 48 на две такие части, что если меньшая разделена на 4, а большая часть на 6, то суммая частных будет равна 9.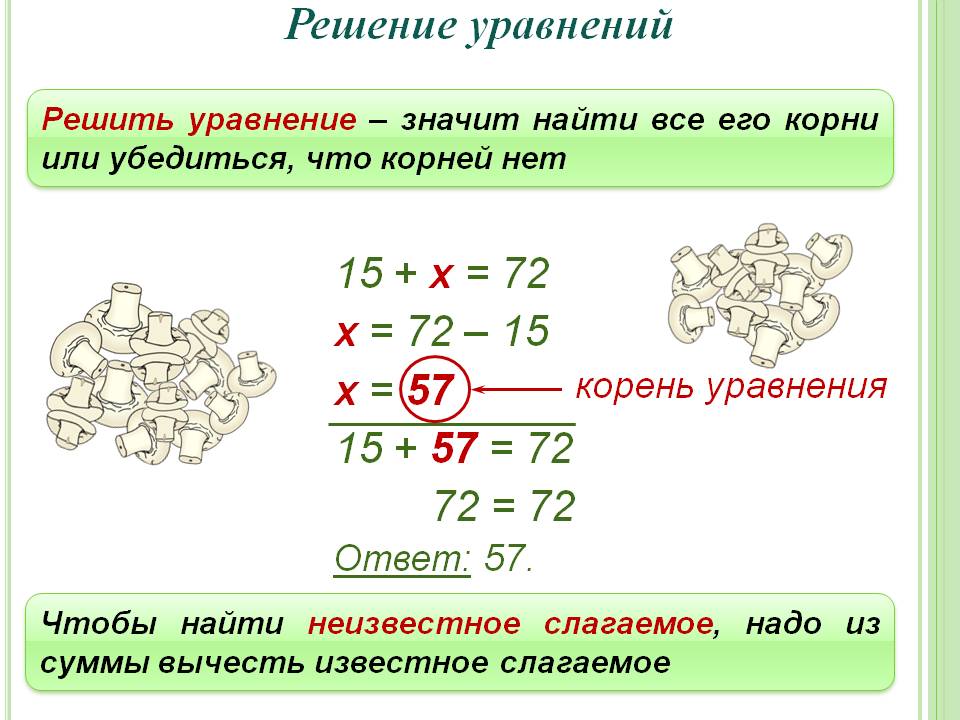
Здесь, если $x$ выразить как меньшую часть, то большая часть будет $48 — x$.
Согласно условию задачи, $\frac{x}{4} + \frac{48 — x}{6} = 9$.
Поэтому, $x = 12$, то есть меншая часть.
И $48 — x = 36 -$ большая часть.
Буквы могут быть использованы для выражения как известных величин в уравнении, так и неизвестных. Определенные значения присваиваются числам, а в конце они слова записываются как числа.
Задача 5. Если к определенному числу прибавить 720 и сумму разделить на 125, то результат будет равен 7392, разделенному на 462. Что это за число?
Обозначим через $x$ искомое число.
a = 720 d = 7392
b = 125 h = 462
Тогда, согласно условию задачи $\frac{x + a}{b} = \frac{d}{h}$
Поэтому $x = \frac{bd — ah}{h}$
Возвращая числа в уравнение, получим $х = \frac{(125.7392) — (720.462)}{462} = 1280$.
Когда решение уравнения дает отрицательный ответ, это показывает, что значение неизвестной величины противоположно значениям, которые по условию вопроса » рассматриваются как положительные.
Задача 6. Торговец получает или теряет при проведении сделки определенную сумму. Во второй сделке он получает 350 долларов, а в третьей теряет $60$. В конце концов, он обнаруживает, что получил 200 долларов за результатами трех сделок. Сколько он получил или потерял в первой сделке?
В этом примере, так как прибыль и убыток противоположны по природе, то они должны иметь противоположные знаки. Если прибыль обозначается с «+», то убыток должен обозначаться с «-«.
Пусть x = искомой сумме.
Тогда, согласно условию $x + 350 — 60 = 200$
и x = -90.
Отрицательный знак перед ответом показывает, что первая сделка прошла с убытком.
Задача 7. Корабль плывет 4 градуса на север, потом 13 на юг. После этого 17 на север, потом 19 на юг и в конце оказывается на 11 градусе южной широты. С какой широты начал плыть корабль?
Пусть $x$ — искомая широта.
Тогда, обозначаем с «+» северное направление, а южное с «-«.
Согласно условию, x + 4 — 13 + 17 — 19 = -11
и x = 0.
Ответ означает, что корабль начал свой путь с экватора, который не имеет широты.
Задача 8. Если определенное число разделить на 12, частное, делимое и делитель, сложенные вместе, дадут 64. Что это за число?
Пусть x — искомое число.
Тогда $\frac{x}{12} + x + 12 = 64$.
Отсюда $x — \frac{624}{13} = 48$.
Задача 9. Недвижимость была разделена между четырьмя детьми так, что,
Первый получил на 200 долларов больше чем $\frac{1}{4}$ всей недвижимости,
Второй получил на 340 долларов больше чем $\frac{16}{5}$ всей недвижимости,
Третий получил на 300 долларов больше чем $\frac{1}{6}$ всей недвижимости,
Четвертый получил на 400 долларов больше чем $\frac{1}{8}$ всей недвижимости.
Какова стоимость недвижимости?
Ответ: 4800 долларов.
Задача 10. Есть два числа, разница которых равна 40 и которые относятся друг к другу как 6 к 5. Что это за числа?
Ответ: 240 и 200.
Задача 11. Если число умножить в три раза, то оно будет относится к 12, как 2 к 9? Что это за число?
Ответ: 8.
Задача 12. Катер и лодка одновременно отправляются в путь по реке. Катер проходит пристань на реке, когда лодка находится ниже пристани на 13 миль. Катер проходит пять миль, а лодка проходит три мили. На каком расстоянии ниже пристани они встретятся? Ответ: $32,5$ мили.
Задача 13. Найдите число, если шестая его часть больше его восьмой части на 20?
Ответ: 480.
Задача 14. Разделите приз в 2000 долларов на две такие части, при которых одна из частей относится к другой как 9 к 7.
Ответ: 1125 и 875.
Задача 15. Найдите сумму денег, для которой третья, четвертая и пятая части, сложенные вместе, дадут 94 доллара?
Ответ: 120 долларов.
Задача 16. Человек провел одну треть жизни в Англии, одну четвертую в Шотландии, а остаток жизни, который равнялся 20-и годам — в США. До какого возраста он дожил? Ответ: $48$ лет.
Задача 17. Найдите число, для которого $frac{1}{4}$ этого числа больше $\frac{1}{5}$ его на 96?
Задача 18. Палка находится вертикально в воде. $\frac{3}{7}$ длины палки находится в воде, а 13 футов — над водой. Какая длина палки?
Палка находится вертикально в воде. $\frac{3}{7}$ длины палки находится в воде, а 13 футов — над водой. Какая длина палки?
Ответ: 35 футов.
Задача 19. Если к числу прибавить 10, то $\frac{3}{5}$ этой суммы будет равняться 66. Что это за число?
Задача 20. Из всех деревьев в саду $\frac{3}{4}$ — яблони, $\frac{1}{10}$ — персики, а оставшиеся деревья — груши, которых на $20$ больше чем $\frac{1}{8}$ всех деревьев. Сколько всего деревьев в саду?
Ответ: 800.
Задача 21. Джентльмен купил несколько галлонов вина за $94$ долларов и после использования 7 галлонов он продал $\frac{1}{4}$ от оставшихся галлонов за 20 долларов. Сколько галлонов у него было вначале?
Ответ: 47.
Задача 22. Если сложить $\frac{1}{3}, \frac{1}{4}, \frac{2}{7}$ числа, то сумма будет равна $73$. Что это за число?
Ответ: 84.
Задача 23. После того, как человек истратил на 100 долларов больше чем $\frac{1}{3}$ его дохода, у него осталось на 35 долларов больше чем $\frac{1}{2}$ его дохода. Чему равнялся его доход?
Чему равнялся его доход?
Задача 24. В составе пороха было:
селитры на 10 фунтов больше чем $\frac{2}{3}$ всего веса пороха,
серы на 4,5 фунта меньше чем $\frac{1}{5}$ всего веса пороха,
древесного угля на 2 фунта меньше чем $\frac{1}{7}$ селитры.
Какой вес пороха? Ответ: 69 фунтов.
Задача 25. Бочка емкостью 146 галлонов была наполнена смесью бренди, вина и воды. Причем, вина было на 15 галлонов больше, чем бренди, а воды столько же, сколько бренди и вина вместе. Чему равнялось количество каждой жидкости?
Задача 26. Четыре человека купили ферму за 4755 долларов, из которых B заплатил в три раза больше, чем А; С заплатил столько же, сколько и B, а D заплатил столько же, сколько C и B. Сколько заплатил каждый из них?
Ответ: 317, 951, 1268, 2219.
Задача 27. Отец разделил небольшую сумму денег между своими четырьмя сыновьями.
Третий сын получил на 9 шиллингов больше, чем четвертый;
Второй сын получил на 12 шиллингов больше, чем третий;
Первый получил на 18 шиллингов больше, чем второй;
А вся сумма денег была на 6 шиллингов больше чем умноженная в 7 раз сумма, которую получил самый младший.
Чему была равна вся сумма?
Ответ: 153.
Задача 28. У фермера было два стада овец, каждое из которых состояло из одной и того же числа животных. Продав из одного стада 39 овец, а с другого стада — $93$ овцы, он посчитал овец и обнаружил, что в одном стаде осталось в два раза больше овец чем в другом. Сколько первоначально овец было в каждом стаде?
Задача 29. Экспресс, двигаясь со скоростью 60 миль в день, был отправлен на 5 дней в путь ранее второго, который двигался со скоростью 75 миль в день. Когда второй экспресс догнал второго? Ответ: $20$ дней.
Задача 30. Возраст А вдвое больше, чем В, возраст B втрое больше чем С, а сумма всех их возрастов равна $140$. Какой возраст каждого из них?
Задача 31. Было куплено два куска ткани одинаковой цены, но разной длины. Стоимость одного куска — 5 долларов, а другого — 6,5. Если удлинить каждый кусок на $10$ м, то эти длины будет относится друг к другу как 5 к 6. Найдите длину каждого куска.
Задача 32. Если к числу прибавить 36 и 52, то первая сумма будет относиться ко второй, как 3 к 4. Что это за число?
Если к числу прибавить 36 и 52, то первая сумма будет относиться ко второй, как 3 к 4. Что это за число?
Задача 33. Джентльмен купил фаэтон, лошадь и упряжь на 360 долларов. Стоимость лошади вдвое больше чем упряжи, а фаэтон стоил вдвое больше, чем упряжь и лошадь вместе. Какова была цена каждой покупки?
Задача 34. Из бочки вина, из которой просочилось $\frac{1}{3}$ часть вина, 21 галлон вина впоследствии было использовано. После этого бочка оказалась наполовину полной. Сколько первоначально было вина в бочке?
Задача 35. У Человек имеет 6 сыновей, каждый из которых на 4 года старше следующего младшего брата, а самый старший в три раза старше, чем самый младший. Каков возраст каждого из них?
Задача 36. Разделите число 49 на две части с условием, что если большую часть увеличить на 6, а от меньшей отнять 11, то они относились бы друг к другу как 9 к 2.
Задача 37. Два числа относятся друг к другу как 2 к 3. Если к каждому из них прибавить 4, то полученные суммы относились бы друг к другу как 5 к 7. Найдите эти два числа.
Найдите эти два числа.
Задача 38. Человек купил две бочки портера, одна из которых была в 3 раза больше, чем другая. Из каждой бочки он отлил по 4 галлона, а затем он обнаружил, что в большей бочке осталось в $4$ раза больше галлонов чем в меньшей бочке. Сколько галлонов было в каждой из бочек?
Задача 39. Разделите число 68 на две такие части, чтобы разница между большей частью и 84 должна быть равна утроенной разнице между меньшей частью и 40.
Задача 40. разделите число 36 на 3 такие части, что $\frac{1}{2}$ первой части, $\frac{1}{3}$ второй и $\frac{1}{4}$ третьей равны между собой.
Задача 41. Генерал после проигранной битвы обнаружил, что у него осталось только половина армии +3600 человек, годных для действий; $\frac{1}{8}$ армии +600 человек было ранено; а остальная часть солдат, которая равнялась $\frac{1}{5}$ от всей армии, были либо убита, либо взята в плен или пропала без вести. Какова была численность армии?
Ответ: 24000.
Для решения многих алгебраических задач, требуется уметь обращаться со степенями и арифметическими корнями. Поэтому необходимо изучить соответствующий раздел до окончания изучения уравнений.
Поэтому необходимо изучить соответствующий раздел до окончания изучения уравнений.
4 совета и рекомендации для обучения школьников решению линейных уравнений
Мои ученики приходят в восьмой класс с довольно хорошими знаниями одно- и двухшаговых уравнений. В этом году с новой программой седьмого класса мои обычные ученики по математике приходят ко мне, никогда не решая уравнение с переменной на каждой стороне. В течение нескольких коротких недель мы рассмотрим двухшаговые уравнения, обсудим уравнения, включающие Распределительное свойство и Объединение одинаковых членов, решим множество уравнений, в каждой из которых есть переменная; в том числе с дробными коэффициентами и специальными решениями, а также изучать текстовые задачи со сценариями, смоделированными линейными уравнениями.
Решение линейных уравнений является чрезвычайно важным навыком для учащихся средних и старших классов. Крайне важно, чтобы студенты понимали что им нужно делать и почему им нужно это делать. В этом посте я хотел бы поделиться некоторыми стратегиями и ресурсами, которые я использую на уроках математики в восьмом классе.
В этом посте я хотел бы поделиться некоторыми стратегиями и ресурсами, которые я использую на уроках математики в восьмом классе.1 – Носки и обувь: понимание «обратного порядка операций»
Всякий раз, когда это возможно, я стараюсь связать то, что мы делаем в классе, с тем, что ученики понимают в своей жизни.На прошлой неделе я сравнил решение уравнений с надеванием носков и обуви. Утром при подготовке к рабочему дню сначала надеваются носки, затем обувь. Но в конце концов сначала снимается обувь, потом носки. То же верно и для уравнений. Рассмотрим уравнение 3x+1=-14. Когда x «подготовился» с использованием порядка операций, он был бы умножен на 3, а затем добавился бы 1. Итак, чтобы отменить операции, начните с удаления 1, а затем 3. Я использовал эту аналогию год за годом, и она доказала свою эффективность для моих студентов.2 — Требовать красивой работы: запретить «Детские символы»
Мне нужны очень четкие доказательства баланса уравнений — даже для одношаговых уравнений. Я хочу, чтобы учащиеся поняли, почему они могут складывать/вычитать/умножать/делить. Очень быстро мы переходим от одношагового обзора к решению уравнений с четырьмя и более шагами. Я обнаружил, что учащиеся, которые ленятся показывать свою работу в начале модуля, склонны спотыкаться, когда им нужно отслеживать гораздо больше шагов, переменных и чисел. Я также видел еще много ошибок с целыми числами и некорректных операций, когда работа сделана нечетко.Всегда есть какие-то стоны и стоны, но я знаю, что через неделю это имеет огромное значение.
Я хочу, чтобы учащиеся поняли, почему они могут складывать/вычитать/умножать/делить. Очень быстро мы переходим от одношагового обзора к решению уравнений с четырьмя и более шагами. Я обнаружил, что учащиеся, которые ленятся показывать свою работу в начале модуля, склонны спотыкаться, когда им нужно отслеживать гораздо больше шагов, переменных и чисел. Я также видел еще много ошибок с целыми числами и некорректных операций, когда работа сделана нечетко.Всегда есть какие-то стоны и стоны, но я знаю, что через неделю это имеет огромное значение.
 Я также не разрешаю использовать традиционный символ «разделить на». Я призываю своих учеников использовать дробную черту, чтобы показать свое деление. На прошлой неделе один студент сказал мне, что ему не нравится дробная черта, потому что тогда он не может сказать, дробь это или деление. Ах! Я привел пару основных примеров, чтобы показать, что они представляют одно и то же. Наконец, я не позволяю ученикам делить на дробь. Я требую умножения на обратное. Я помогаю учащимся вовлечься, демонстрируя, как это на самом деле экономит их время и работу, если они умножают непосредственно в своих организованных шагах.
Я также не разрешаю использовать традиционный символ «разделить на». Я призываю своих учеников использовать дробную черту, чтобы показать свое деление. На прошлой неделе один студент сказал мне, что ему не нравится дробная черта, потому что тогда он не может сказать, дробь это или деление. Ах! Я привел пару основных примеров, чтобы показать, что они представляют одно и то же. Наконец, я не позволяю ученикам делить на дробь. Я требую умножения на обратное. Я помогаю учащимся вовлечься, демонстрируя, как это на самом деле экономит их время и работу, если они умножают непосредственно в своих организованных шагах.3 – Используйте основанный на открытиях подход к особым случаям и стратегиям
Я большой поклонник баланса обучения на основе открытий и традиционной практики. Особые случаи могут быть сложными для понимания. Я отношу «x=0» к особым случаям, потому что его часто путают с отсутствием решения. Чтобы помочь учащимся понять смысл и понять не решение, а все действительные числа, я создал рабочие листы на основе открытий, которые приводят учащихся к большим идеям. Они узнают не только о том, что нужно искать, чтобы идентифицировать особые решения, но и о том, что на самом деле означает наличие особого решения уравнения.
Они узнают не только о том, что нужно искать, чтобы идентифицировать особые решения, но и о том, что на самом деле означает наличие особого решения уравнения.
Я использую аналогичный подход при обучении студентов уравнениям, в которых используются дроби и десятичные дроби. Я создал рабочий лист на основе открытий, который показывает учащимся, как убрать дроби и десятичные дроби из уравнений. Они узнают, как выбрать множитель, на который они должны умножать каждую часть уравнения, и ясно заметят, насколько проще может быть работа с уравнением, если потратить время на очистку дробей или десятичных знаков с самого начала.
4 – Тренируйтесь весело и увлекательно Лучший способ для учащихся освоить решение линейных уравнений — много практиковаться.Но практика не обязательно должна основываться на рабочих листах. Вот некоторые из упражнений, которые я использую, чтобы помочь студентам научиться решать уравнения:
Праздничная тематическая партнерская практика : В первые несколько лет моей преподавательской деятельности были каникулы, и я был так взволнован! Я хотел отметить праздник в своем классе, но так и не смог найти ничего математически осмысленного. Вот почему я решил создать свою линейку партнерских станций на праздничную тематику! Учащиеся путешествуют парами, каждый решает свою задачу.Если они правы, они будут иметь тот же ответ, что и их партнер. Отличная деятельность по самоконтролю. Забавный компонент расшифровки в конце тоже!
Вот почему я решил создать свою линейку партнерских станций на праздничную тематику! Учащиеся путешествуют парами, каждый решает свою задачу.Если они правы, они будут иметь тот же ответ, что и их партнер. Отличная деятельность по самоконтролю. Забавный компонент расшифровки в конце тоже!
·
Практика на доске спереди : Мои восьмиклассники любят писать на моей доске. Я вызываю пятерых студентов на доску одновременно. У всех остальных есть бумага и карандаши, поэтому они продолжают практиковаться, даже если на них не обращают внимания. Я читаю вслух уравнение, которое все решают одновременно. Я меняю учеников, которые сидят у доски, чтобы все поднимались 2-3 раза.
Практическая работа с мини-доской : У меня есть набор мини-досок, которые я использую на своих занятиях. Учащиеся решают уравнение на доске, а затем, когда я даю сигнал, все они держат доски со своей работой и ответом, чтобы я мог быстро получить обратную связь об уровне понимания в классе и указать ученикам, с которыми мне следует связаться. .
.
Карточки с заданиями : Я люблю карточки с заданиями! Моя любимая стратегия использования карточек с заданиями заключалась в том, чтобы оставить их в мусорном ведре в передней части комнаты, а ключ к ответу был вывешен рядом.Каждый учащийся берет одну карточку, проверяет свой ответ и заменяет свою карточку новой, как только ответит правильно. Я делал это индивидуально или в парах.
Scavenger Hunt : Я купил Scavenger hunt типа CSI, чтобы использовать его со своими учениками. Я спрятал «подсказки» в нашей аудитории, и мы отправились на «экскурсию». Учащимся нравилось выходить из обычной классной обстановки, работать в своем собственном темпе и нестандартным способом, а также в процессе находить ответы на загадки.Спасибо 21 st Century Math Projects!
Аманда Никс из Free to Discover живет в Нью-Гэмпшире со своим мужем, малышом и английской шоколадной лабораторией. Ей нравится работать со школьниками-математиками! После пяти лет работы учителем математики в восьмом классе она перешла на неполный рабочий день в качестве специалиста по математике в 5-8 классах. У нее настоящая страсть к обучению математике с использованием веселых интерактивных методов. Она имеет степень магистра математического образования Университета Лесли и считает, что учится на протяжении всей жизни.Она любит делиться своими идеями и стратегиями преподавания математики в блоге Free to Discover. Вы также можете связаться с ней на Pinterest, Facebook и Instagram!
У нее настоящая страсть к обучению математике с использованием веселых интерактивных методов. Она имеет степень магистра математического образования Университета Лесли и считает, что учится на протяжении всей жизни.Она любит делиться своими идеями и стратегиями преподавания математики в блоге Free to Discover. Вы также можете связаться с ней на Pinterest, Facebook и Instagram!
Понимание шагов решения уравнения — видео и расшифровка урока
Начало и конец уравнений
Когда вы впервые начинаете решать математическую задачу, в самом начале вам дают как минимум две истины.
Первое — это исходное(ые) уравнение(я) и/или условия для задачи.Вы можете предположить, что эти условия/уравнения полностью верны, и вы можете смело основывать все, что собираетесь делать, на этом предположении.
Например, возможно, вас попросили найти x в следующем уравнении:
5 x + 7 = 7 x — 3
Что ж, ради решения задачи предположим, что это уравнение так же верно и справедливо, как и закон всемирного тяготения. Хотя некоторые задачи не имеют решения, мы будем считать, что эта имеет.Нашей конечной целью будет другое уравнение, где x = что-то; это наша вторая правда.
Хотя некоторые задачи не имеют решения, мы будем считать, что эта имеет.Нашей конечной целью будет другое уравнение, где x = что-то; это наша вторая правда.
Важно помнить, что знак равенства (=) устанавливает «контракт», где сам знак равенства является судьей. Все, что вы будете делать для решения уравнения, должно поддерживать действие контракта; две стороны знака равенства должны всегда оставаться равными. Если вы нарушите правила, нарушив знак равенства, ваша задача потерпит крах.
Жизнеспособная стратегия
Жизнеспособная стратегия — это подход к решению проблемы, который имеет логический смысл для данного уравнения.Это практичный способ добраться до «конечной зоны» вашей проблемы. Дойти до конца можно несколькими способами, но жизнеспособная стратегия — это та, которая сработает.
Глядя на уравнение в предыдущем разделе, мы можем начать строить нашу стратегию и защищать наш подход, используя логические аргументы.
Начнем с вопросов. Во-первых, что вы уже знаете? В случае указанной выше проблемы вы знаете, что 5 x + 7 = 7 x — 3 и что вам нужно значение для x (в форме ‘x = некоторое число’), которое сделает уравнение верным.
Во-первых, что вы уже знаете? В случае указанной выше проблемы вы знаете, что 5 x + 7 = 7 x — 3 и что вам нужно значение для x (в форме ‘x = некоторое число’), которое сделает уравнение верным.
Какие шаги вы предпримете для получения такого результата? Если мы проанализируем обе части исходного уравнения, мы сможем увидеть конкретные причины, по которым оно не похоже на желаемый результат.
- В обеих частях данного уравнения содержится x членов, но только в левой части искомого ответа.
- В обеих частях уравнения есть числа, но только в правой части желаемого ответа.
- Термины размером x в настоящее время умножаются на числа, отличные от 1, и в ответе, который мы ищем, нет числа (кроме 1), умножаемого на x .
Хорошо, теперь о наших жизнеспособных аргументах , которые являются логическими утверждениями, которые верны и будут поддерживать наш подход к решению проблемы, и позволят нам логически защищать наш подход, если кто-то с ним не согласен. Эти аргументы основаны на правилах, которые дают нам математики, а также на наших собственных логических выводах.
Эти аргументы основаны на правилах, которые дают нам математики, а также на наших собственных логических выводах.
- Мы можем сохранить равенство (сохранить контракт), всегда выполняя одну и ту же операцию с обеих сторон уравнения.
- Если какой-либо термин становится равным 0, он больше не имеет значения и может быть удален.
- Мы хотим, чтобы все элементы размером x находились в левой части уравнения и были упрощены, поэтому мы можем перейти к x .
- Мы хотим, чтобы все числовые термины были расположены справа и были упрощены, чтобы мы могли сказать, чему равно x .
- Чтобы получить ответ, мы можем умножать, делить, складывать или вычитать все, что захотим, при условии, что мы делаем одно и то же с обеими частями уравнения.
Решение для
XИтак, как мы можем получить из
5 x + 7 = 7 x — 3
некоторое число =
x ?
Используя наши убедительные аргументы, мы можем разработать стратегию решения нашей проблемы. Мы применим следующие шаги:
Мы применим следующие шаги:
- Изолируем термины размером x с одной стороны и числовые термины с другой.
- Объединить их в единые термины.
- Удалите любой коэффициент (число, которое умножается на переменную) члена x , чтобы найти значение самого x .
Применяя нашу стратегию, начинаем:
Изолируем термины
Притягиваем 7 x к левой части уравнения.Мы можем сделать это, вычитая x с обеих сторон (аргументы 1, 2, 3 и 5).
5 x — 7 x + 7 = 7 x — 7 x — 3
x — 3 x + 70061 x + 7 = -3Консолидация в один Условий
Потяните 7 к правая часть уравнения. Мы можем сделать это, вычитая 7 с обеих сторон (аргументы 1, 2, 4 и 5).
-2 x + 7 — 7 = -3 — 7
-2 x = -10
Удалите коэффициент
Мы можем удалить коэффициент, разделив обе части на -2 (аргументы 1 , 3, 4 и 5).
-2 х / -2 = -10 / -2
х = 5
Поскольку наше уравнение теперь имеет форму, которую мы искали, наша работа выполнена.
Сводка урока
Давайте уделим несколько минут тому, чтобы повторить то, что мы узнали о понимании шагов решения уравнения.
Жизнеспособная стратегия решения математической задачи — это логичный подход, который действительно работает для получения желаемого результата. Жизнеспособный аргумент для математической задачи — это набор утверждений, основанных на правилах, которые являются верными и логичными и которые обеспечивают поддержку, необходимую нам для разработки нашей стратегии решения проблемы.Если вы используете жизнеспособные стратегии и жизнеспособные аргументы, вы можете решить (и поддержать свое решение) любую математическую задачу, с которой вы столкнетесь!
Этот простой совет для изучения математических уравнений действительно работает
Существует множество различных стратегий для максимизации вашего учебного потенциала, но один из самых простых стимуляторов учебы буквально у вас под рукой.
Австралийские исследователи обнаружили, что школьники лучше решают математические задачи, когда проводят пальцами по практическим примерам, превосходя учеников, которые просто читают вопросы, не прикасаясь к ним.
«Наши результаты имеют ряд последствий как для учителей, так и для студентов», — сказал психолог-педагог Пол Джиннс из Сиднейского университета. «Они показывают, что изучение математики юными учениками может быть существенно улучшено простым добавлением инструкций к элементам математических задач, основанным на следовании пальцами».
Исследователи провели два отдельных исследования с участием 275 школьников в возрасте от 9 до 13 лет и обнаружили, что обведение пальцами геометрических фигур и цифр в ранее неизвестных математических задачах, включающих геометрию, алгебру и арифметику, помогло учащимся решить вопросы. быстро и легко.
Один из экспериментов показал градиент результатов: студенты, которые обводили непосредственно по персонажам, превосходили тех, кто обводил рядом с ними, которые, в свою очередь, превзошли тех, кто вообще не обводил.
Не совсем понятно, почему простое движение пальцем по вопросу во время его чтения облегчит получение ответа, но исследователи считают, что это один из способов облегчить когнитивную нагрузку, связанную с обработкой информации.
Например, физическое касание и отслеживание углов треугольника может привести к тому, что эта информация получит приоритет в вашем мозгу, в то время как регистрация той же информации только визуальными средствами не приведет к такому же эффекту.
Таким образом, физическое действие может уменьшить нагрузку на рабочую память и способность мозга хранить и удерживать сложный материал путем «объединения» информации, считают исследователи.
Хотя результаты исследований новы, сам метод обучения таковым не является. Учащиеся в школах Монтессори уже давно используют тактильный подход к обучению алфавиту с помощью букв наждачной бумаги, предназначенный для того, чтобы помочь детям представить физическую форму отдельных символов, чтобы помочь им легче учиться.
Это исследование подтверждает этот метод, и если будущие исследования смогут подтвердить его выводы, это может стать простым и экономичным способом улучшить результаты обучения в школах.
«На уровне класса учителя могут помочь учащимся освоить новое математическое содержание, давая инструкции по «отслеживанию» важных элементов рабочих примеров, которые уже появляются в учебниках по математике или рабочих листах», — сказал Джиннс. «Этот простой и бесплатный подход к обучению может повысить эффективность обучения математике в различных областях предмета.»
Так может ли кто-нибудь извлечь пользу из выполнения этого во время учебы или домашних заданий? Исследователи не знают наверняка, но вполне возможно, что тот же подход может сработать для старших школьников — и в предметных областях, отличных от тех, которые исследователям так
«Мы с осторожностью уверены, что такие эффекты могут быть применены в классе и к предметам, не связанным с математикой, но явно требуются дополнительные исследования», — сказал Джинн. Прикладная когнитивная психология .
Прикладная когнитивная психология .
1.1: Почему это важно — Решение уравнений и неравенств
Зачем решать линейные уравнения и неравенства?
Возможно, вы удивитесь, узнав, что приложения линейных уравнений встречаются не только в математических классах, но и во многих других местах. Знание того, как их решать, является базовым математическим навыком, используемым почти в каждой академической дисциплине и на многих работах. Одним из фундаментальных принципов решения линейных уравнений является обращение или отмена математических операций, таких как сложение и вычитание.Чтобы увидеть линейное уравнение в действии, давайте рассмотрим уравнение, которое используется судебными экспертами для расчета содержания алкоголя в крови.
Неудивительно, что содержание алкоголя в крови (BAC) — это показатель количества алкоголя в чьей-то крови. Обычно измеряется в граммах и в процентах. Например, BAC 0,30% составляет три десятых от 1% и указывает на то, что на 1000 граммов крови приходится 3 грамма алкоголя, что на самом деле очень много. BAC 0,05% ухудшает мышление и способность концентрироваться.BAC 0,30% может привести к потере сознания, одышке и потере контроля над мочевым пузырем. В большинстве штатов допустимый уровень алкоголя в крови составляет 0,08%.
BAC 0,05% ухудшает мышление и способность концентрироваться.BAC 0,30% может привести к потере сознания, одышке и потере контроля над мочевым пузырем. В большинстве штатов допустимый уровень алкоголя в крови составляет 0,08%.
BAC обычно определяется по результатам алкотестера, анализа мочи или крови. Шведский врач Э. М. П. Видмарк разработал уравнение, которое хорошо подходит для оценки BAC без использования одного из этих тестов. Формула Видмарка широко используется судебно-медицинскими экспертами:
\(\text{B} = -0.015t +\left(\frac{2.84N}{Wg}\right)\)
где
- B = процент BAC
- t = количество часов с момента первой порции
- N = количество «стандартных напитков» (стандартный напиток — это один бокал пива на 12 унций, один бокал вина на 5 унций или один 1.5 унций ликера). N должно быть не менее 1.
- Вт = вес в фунтах
- г = гендерная константа: 0,68 для мужчин и 0,55 для женщин
В следующей таблице прогрессирующие эффекты алкоголя определены для диапазонов содержания алкоголя в крови.
| Прогрессивные эффекты алкоголя | ||||||
|---|---|---|---|---|---|---|
| BAC (% от Vol.) | Поведение | УПРАВЛЕНИЕ | 2 | 0,001-0292 | 0.001-0.029
| |
упражнений, которые сделают отработку многошаговых уравнений потрясающими
Моя история с обучением многошаговым уравнениям не была красивой, но предупреждаю, спойлер, есть счастливый конец. Несколько лет назад я преподавал вместе с относительно новым учителем, и я чувствовал большое давление, чтобы показать ему веревки. Я был новичком в математических стандартах 8-го класса. Все шло хорошо в течение первого учебного месяца, пока мы не дошли до решения многошаговых уравнений. Мы работали целых две недели и учили студентов тому, как нас учили многошаговым уравнениям. Дети взорвали модульный тест. Это было разрушительно. Потом у нас появилась возможность переучить большинство детей, и мы попробовали что-то еще.Это также не удалось. Это был по меньшей мере унизительный опыт.
Несколько лет назад я преподавал вместе с относительно новым учителем, и я чувствовал большое давление, чтобы показать ему веревки. Я был новичком в математических стандартах 8-го класса. Все шло хорошо в течение первого учебного месяца, пока мы не дошли до решения многошаговых уравнений. Мы работали целых две недели и учили студентов тому, как нас учили многошаговым уравнениям. Дети взорвали модульный тест. Это было разрушительно. Потом у нас появилась возможность переучить большинство детей, и мы попробовали что-то еще.Это также не удалось. Это был по меньшей мере унизительный опыт.
Я отступил назад и посмотрел на концепт. Я потратил много времени, пытаясь понять, где дети были сбиты с толку. Для очень многих детей было слишком много вещей, чтобы помнить. Поэтому я придумал способ решения этих уравнений, который называется методом ящиков. Через несколько недель мы снова научили студентов решать многошаговые уравнения, на этот раз с помощью ящиков, но у нас было на это всего два дня.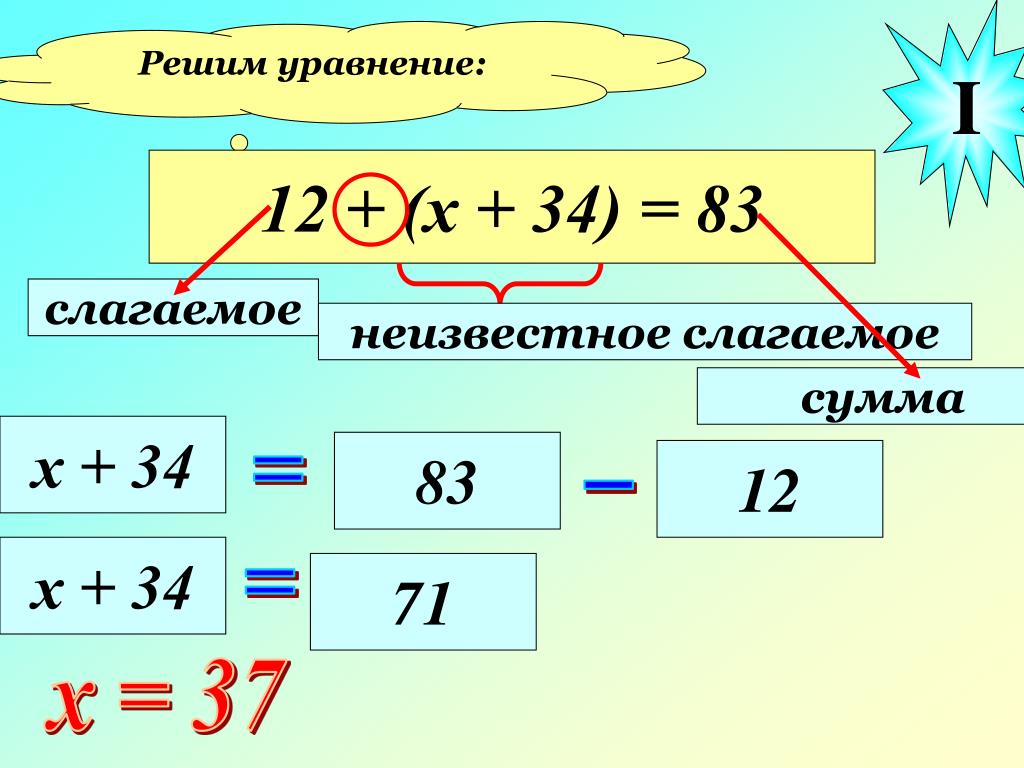 Даже всего за два дня это было явно самое успешное, что мы когда-либо делали.
Даже всего за два дня это было явно самое успешное, что мы когда-либо делали.
Я знал, что в следующем году, когда придет время учить многошаговые уравнения, мы с самого начала будем учить его по методу ящиков. И я был уверен, что у нас все получится. Удивительно, но это оказалось даже более правильным, чем я надеялся. На втором курсе мы начали обучение по этой методике, и подавляющее большинство детей усвоили ее с первого раза. Мы использовали этот метод в течение всего года, и наши ученики стали намного лучше, чем когда-либо прежде. Чтобы увидеть пошаговое руководство по обучению с помощью этого метода, ознакомьтесь с постом «Как преподавать многошаговые уравнения, как босс».
Независимо от того, как вы обучаете учащихся многошаговым уравнениям, как только они узнают, как решать многошаговые уравнения, у них будет много разных способов попрактиковаться. И как бы вы ни решили практиковаться, ученикам нужно много возможностей для отработки этого навыка. Вот подборка некоторых упражнений, которые мне нравится использовать на уроках.
Решение лабиринтов с многошаговыми уравнениями (для печати и в цифровом виде)
Переменные прохода по галерее с обеих сторон
Целевая игра с карточками заданий
Белая доска с рабочими листами
Модель интерактивных весов
Навык многошаговых уравнений под угрозой
Бинго
Ловцы Кути
Шмуп Видео
Иллюстративное задание по математике
Алгебра Meltdown Онлайн-игра
Действия по решению многошаговых уравненийПриведенные ниже упражнения можно использовать в разных частях урока.Некоторые хорошо работают в качестве упреждающих сетов, в то время как другие отлично подходят для практики. Все они интересны, и многие из них поощряют сотрудничество. Некоторые из действий выполняются на компьютере, в то время как другие используют бумагу.
Вот описание каждого действия и несколько советов по их использованию:
В моем классе много лабиринтов. Это отличный способ начать день. Их можно использовать для звонка после вводного урока или в качестве циклического повторения.Эти конкретные лабиринты имеют переменные с обеих сторон. Кроме того, они увеличивают сложность от лабиринта к лабиринту. В уравнениях, которые они решают, есть целые числа и некоторые дроби. Учащимся нравится их выполнять, и они даже не осознают, что выполняют работу.
Это отличный способ начать день. Их можно использовать для звонка после вводного урока или в качестве циклического повторения.Эти конкретные лабиринты имеют переменные с обеих сторон. Кроме того, они увеличивают сложность от лабиринта к лабиринту. В уравнениях, которые они решают, есть целые числа и некоторые дроби. Учащимся нравится их выполнять, и они даже не осознают, что выполняют работу.
Теперь у этих лабиринтов есть и цифровая версия! Эта версия встроена в Google Slides и может быть легко назначена в Google Classroom (или другой LMS). Они просты в использовании и интерактивны для учащихся, а стрелки позволяют отмечать путь с помощью перетаскивания.
Кстати, это отличный шанс зарегистрироваться в БЕСПЛАТНОМ клубе «Лабиринт месяца», если вы еще этого не сделали. Каждый месяц я отправляю членам клуба MotM бесплатный эксклюзивный лабиринт по различным математическим концепциям средней школы прямо на их почтовые ящики (как в цифровой, так и в печатной версии!) Присоединяйтесь сегодня и попробуйте некоторые математические лабиринты в своем классе:
Нажмите здесь, чтобы вступить в клуб «Лабиринт месяца».

Эта прогулка по галерее является бесплатным ресурсом (перейдите по ссылке здесь).Когда вы попадаете на веб-сайт, вам нужно прокрутить вниз, а затем загрузить Gallery Walk. На этом сайте представлено множество других мероприятий. Самое замечательное в этом занятии то, что все готово к работе. 30 задач, включенных в эту галерею, усложняются, и многие из них можно использовать в качестве контрольных задач. Некоторые из задач бросят вызов быстрым финишерам или могут быть полезны в продвинутом классе. Наконец, прогулки по галерее действительно вовлекают детей и помогают им двигаться по классу.
Карточки заданий можно использовать по-разному. Один из способов — использовать их со всем классом и сыграть с ним в игру. Вы можете сделать это с помощью Target Game на доске или Trashketball, используя мусорное ведро. Обе игры требуют, чтобы учащиеся выполнили задачу, а затем вы смоделировали ответ для класса. Затем кто-то получает возможность бросить липкий мяч в цель на доске или бросить скомканную бумагу в мусорное ведро. Им нравится задача целевой части, и весь класс обычно действительно в нее входит.Так просто, но так весело.
Им нравится задача целевой части, и весь класс обычно действительно в нее входит.Так просто, но так весело.
Я использую некоторые карточки с задачами из этого набора карточек с многошаговыми уравнениями в качестве задач для этой игры (она поставляется как в печатной, так и в цифровой версии). Это легко, и тогда у меня есть все задачи, которые мне нужны для игры. Я ставлю баллы всем детям, правильно ответившим на вопрос. Количество очков зависит от того, как поступил тот, кто бросил мяч или пробил. Несмотря на то, что я не придаю большого значения очкам, дети все равно в восторге.
4- Доска с рабочими листамиМне нравится, когда ученики работают на доске. В моем классе есть набор из 6 больших досок, и ученикам нравится на них работать. Они могут быть на стене или ученики могут снять их, чтобы поработать над ними. Перейдите по этой ссылке, чтобы перейти к серии рабочих листов. Вы найдете 15 рабочих листов, которые идут от простого к сложному и работают с десятичными числами и дробями
.
Мы редко просто делаем рабочие листы в моем классе, но мне нравится, что эти задачи готовы к использованию.Например, когда я работаю на доске, у меня есть группа из 2 или 3 человек, которые вместе работают над одной и той же проблемой. Я моделирую математическую беседу, которую хочу, и стараюсь очень хорошо осознавать, как я группирую студентов. Затем учащиеся приступают к совместному решению на белой доске, демонстрируя свои математические рассуждения на доске и обсуждая свою стратегию решения задач со своими одноклассниками. Это упражнение хорошо работает в качестве практического занятия, предвосхищающего набора или действия с губкой.
Иногда нужно, чтобы учащиеся работали с уравнениями конкретным образом.Эта модель баланса от Math Playground помогает вашим детям увидеть, что они делают, решая уравнения. Им понадобится небольшой опыт работы с уравнениями, прежде чем вы назначите эту модель. Одна из интересных частей заключается в том, что для них установлены уравнения, а затем ученики работают с ними на балансе. Это упреждающий набор для меня на 3-й или 4-й день модуля по решению многошаговых уравнений.
Это упреждающий набор для меня на 3-й или 4-й день модуля по решению многошаговых уравнений.
Jeopardy давно существует как способ проверки концепций. Мы играли в Jeopardy, когда я учился в средней школе (и это было в 80-х — ух ты!).Вы можете играть в Jeopardy всем классом, где каждый должен ответить на вопрос. Учащиеся отслеживают свои индивидуальные баллы.
Эта конкретная игра Jeopardy от Jeopardy Labs основана на необходимых навыках для многошаговых уравнений, включая свойство распределения и комбинирование подобных терминов. Это довольно быстрая игра для моих восьмиклассников. Мне нравится использовать подобные игры в качестве упреждающего набора. Мы не доигрываем всю игру, а играем минут 5-7. Это идеальный способ активировать предыдущие знания и вовлечь детей в урок.
Бинго — один из моих любимых способов обсудить любую тему. Обычно мы делаем это в день теста или за день до теста. Это зависит от того, сколько времени займет тест. Вы можете предложить учащимся положить карты бинго в рукав SmartPal или пометить свои листы разными символами. Чтобы решить 30 задач, требуется много времени, и мы обычно не решаем их все. Обычно я тщательно выбираю уравнения, которые, как мне кажется, придадут ученику уверенности и помогут найти основные камни преткновения.Эта игра в бинго включает в себя уравнения с дробями и уравнения с переменными с обеих сторон.
Чтобы решить 30 задач, требуется много времени, и мы обычно не решаем их все. Обычно я тщательно выбираю уравнения, которые, как мне кажется, придадут ученику уверенности и помогут найти основные камни преткновения.Эта игра в бинго включает в себя уравнения с дробями и уравнения с переменными с обеих сторон.
Bingo — отличная циклическая обзорная игра. Редко кто не хочет играть в бинго. Я даю призы победителям. Часто призом является Jolly Rancher, маленький карандаш или ластик. Удивительно, как усердно дети будут работать ради этого маленького поощрения.
Использование ловцов кути, или того, что некоторые люди называют гадалками, — это интересный способ привлечь учащихся. Я считаю, что эти занятия хорошо работают с детьми, которые опасаются темы многошаговых уравнений.Эта тема может быть немного сложной для многих студентов, и когда они решают уравнения с партнером, играя в небольшую игру, они, кажется, теряют бдительность.
У каждого напарника есть кути-кетчер с разными проблемами. Затем каждый партнер работает над другой проблемой. Студенты могут играть один на один и посмотреть, кто даст больше правильных ответов за определенное время.
Затем каждый партнер работает над другой проблемой. Студенты могут играть один на один и посмотреть, кто даст больше правильных ответов за определенное время.
Проблемы в этой конкретной деятельности ловца кути включают дроби и свойство распределения.Я узнал, что учащимся нужны разные ситуации, когда дело доходит до уравнений. В противном случае они просто запоминают какие-то шаги, а потом, после юнит-теста, быстро забывают, что делают.
(дополнение 2020 г. — недавно мы рассказали учителю, что она попросила своих учеников использовать это упражнение на практике, следя за тем, чтобы они были социально дистанцированы, чтобы они «на самом деле не ловили пизды». Так весело!)
В этом дурацком видео от Shmoop показан пример того, почему при решении уравнения необходимо выполнять любую операцию с обеих сторон.В видео использована история о красноносом северном олене Рудольфе. Это видео — отличный выбор для упреждающего набора через пару дней после установки. Кроме того, это может быть использовано в качестве заключительного занятия в конце модуля, чтобы увидеть, что понимают учащиеся.
Мне нравится, когда учащиеся получают возможность делать больше, чем просто решать задачи, когда они действительно применяют то, что изучают. Что ж, это задание от Illustrative Mathematics идеально подходит для этого. Это дает учащимся простой пример того, как мы моделируем математику.Затем он предлагает учащимся решить уравнение математически и символически. Это действительно бросает вызов мышлению учащихся, особенно если математика дается им легко. Что-то подобное действительно может вывести их из зоны комфорта.
Это задание является расширенным ответом и займет у учащихся 15-45 минут. Есть несколько частей, и если у вас меньше времени, они могут использовать часть. Быстрые финишеры могут работать над этим по мере продвижения модуля, когда они заканчивают работу в классе. Ниже начало задания.Нажав на картинку, вы перейдете ко всему заданию.
Algebra Meltdown — это онлайн-игра, которая делает изучение алгебры интересным и конкретным. Студенты должны пройти через ряд уравнений и внутри лаборатории ученого. Задачи становятся все сложнее и сложнее по мере их выполнения и работают до многошаговых уравнений. Некоторым ученикам это поначалу может показаться сложным. Поскольку это игра, это отличный способ напомнить учащимся, что, как и в видеоиграх, можно потерпеть неудачу и попробовать еще раз.Так мы узнаем новое.
Задачи становятся все сложнее и сложнее по мере их выполнения и работают до многошаговых уравнений. Некоторым ученикам это поначалу может показаться сложным. Поскольку это игра, это отличный способ напомнить учащимся, что, как и в видеоиграх, можно потерпеть неудачу и попробовать еще раз.Так мы узнаем новое.
Студенты любят играть в такие игры, и в классе есть таблица лидеров. Вы можете отслеживать лидеров в течение дня или недели. Вы также можете подарить пятерым победителям какой-нибудь небольшой приз — просто невероятно, как далеко может зайти Веселый фермер или милый ластик!
Попробуйте одну вещь… Этот набор идей может показаться большим количеством действий, если вы попытаетесь реализовать их все сразу. Просто попробуйте выполнить одно задание и посмотрите, как оно пойдет в вашем классе.После этого можно попробовать другой. Чем больше стратегий вовлечения вы испробуете, тем легче вам будет найти еще больше способов добавить изюминку в занятия по математике.
Спасибо за прочтение! До скорого.
РодственныеИспользование нейронных сетей для решения сложных математических уравнений
Facebook AI создал первую систему искусственного интеллекта, которая может решать сложные математические уравнения, используя символьные рассуждения.Разработав новый способ представления сложных математических выражений в виде своего рода языка, а затем рассматривая решения как проблему перевода для нейронных сетей последовательностей, мы построили систему, которая превосходит традиционные вычислительные системы при решении задач интеграции и как первого, так и второго порядка. дифференциальные уравнения второго порядка.
Ранее подобные задачи считались недоступными для моделей глубокого обучения, поскольку для решения сложных уравнений требуется точность, а не приближение.Нейронные сети преуспевают в обучении успешному приближению, например, распознавая, что конкретный набор пикселей, вероятно, является изображением собаки или что особенности предложения в одном языке совпадают с чертами в другом. Решение сложных уравнений также требует умения работать с символьными данными, такими как буквы в формуле b — 4ac = 7 . Такие переменные нельзя напрямую складывать, умножать или делить, и, используя только традиционное сопоставление с образцом или статистический анализ, нейронные сети были ограничены чрезвычайно простыми математическими задачами.
Решение сложных уравнений также требует умения работать с символьными данными, такими как буквы в формуле b — 4ac = 7 . Такие переменные нельзя напрямую складывать, умножать или делить, и, используя только традиционное сопоставление с образцом или статистический анализ, нейронные сети были ограничены чрезвычайно простыми математическими задачами.
Наше решение было совершенно новым подходом, который рассматривает сложные уравнения как предложения в языке. Это позволило нам использовать проверенные методы нейронного машинного перевода (NMT), обучающие модели, чтобы по существу преобразовывать проблемы в решения. Реализация этого подхода потребовала разработки метода преобразования существующих математических выражений в синтаксис, подобный языку, а также создания крупномасштабного обучающего набора данных из более чем 100 миллионов парных уравнений и решений.
При представлении тысяч невидимых выражений — уравнений, которые не были частью ее обучающих данных — наша модель работала со значительно большей скоростью и точностью, чем традиционные программы для решения уравнений на основе алгебры, такие как Maple, Mathematica и Matlab. Эта работа не только демонстрирует, что глубокое обучение можно использовать для символического мышления, но также предполагает, что нейронные сети могут решать более широкий спектр задач, в том числе те, которые обычно не связаны с распознаванием образов. Мы делимся подробностями о нашем подходе, а также о методах, которые помогут другим создавать аналогичные обучающие наборы.
Эта работа не только демонстрирует, что глубокое обучение можно использовать для символического мышления, но также предполагает, что нейронные сети могут решать более широкий спектр задач, в том числе те, которые обычно не связаны с распознаванием образов. Мы делимся подробностями о нашем подходе, а также о методах, которые помогут другим создавать аналогичные обучающие наборы.
Новый способ применения NMT
Люди, особенно хорошо разбирающиеся в символической математике, часто полагаются на своего рода интуицию. У них есть представление о том, как должно выглядеть решение данной задачи — например, наблюдение, что если в функции, которую мы хотим проинтегрировать, есть косинус, то в ее интеграле может быть и синус, — а затем выполнить необходимую работу, чтобы Докажите это.Это отличается от прямого вычисления, необходимого для алгебры. Обучив модель обнаруживать закономерности в символьных уравнениях, мы полагали, что нейронная сеть сможет собрать воедино подсказки, которые привели к их решениям, примерно так же, как подход человека к сложным задачам, основанный на интуиции. Поэтому мы начали исследовать символическое рассуждение как задачу NMT, в которой модель может предсказывать возможные решения на основе примеров задач и соответствующих им решений.
Поэтому мы начали исследовать символическое рассуждение как задачу NMT, в которой модель может предсказывать возможные решения на основе примеров задач и соответствующих им решений.
Пример того, как наш подход расширяет существующее уравнение (слева) в дерево выражений, которое может служить входными данными для модели перевода.Для этого уравнения ввод последовательности предварительного порядка в нашу модель будет следующим: (плюс, умножить, 3, мощность, х, 2, минус, косинус, умножить, 2, х, 1).
Чтобы реализовать это приложение с помощью нейронных сетей, нам понадобился новый способ представления математических выражений. Системы NMT обычно представляют собой модели последовательностей (seq2seq), использующие последовательности слов в качестве входных данных и выводящие новые последовательности, что позволяет им переводить полные предложения, а не отдельные слова. Мы использовали двухэтапный подход, чтобы применить этот метод к символьным уравнениям.Во-первых, мы разработали процесс, который эффективно распаковывает уравнения, укладывая их в разветвленную древовидную структуру, которую затем можно развернуть в последовательности, совместимые с моделями seq2seq. Константы и переменные действуют как листья, а операторы (такие как плюс и минус) и функции являются внутренними узлами, соединяющими ветви дерева.
Константы и переменные действуют как листья, а операторы (такие как плюс и минус) и функции являются внутренними узлами, соединяющими ветви дерева.
Хотя это может и не выглядеть как традиционный язык, такая организация выражений обеспечивает аналогичный языку синтаксис для уравнений — числа и переменные являются существительными, а операторы действуют как глаголы.Наш подход позволяет модели NMT научиться согласовывать шаблоны заданной древовидной структуры с ее соответствующим решением (также выраженным в виде дерева), аналогично сопоставлению предложения на одном языке с его подтвержденным переводом. Этот метод позволяет нам использовать мощные готовые модели NMT seq2seq, заменяя последовательности слов последовательностями символов.
Создание нового набора данных для обучения
Хотя синтаксис нашего дерева выражений теоретически позволял модели NMT эффективно преобразовывать сложные математические задачи в решения, для обучения такой модели потребовался бы большой набор примеров. А поскольку в двух классах задач, на которых мы сосредоточились — интегрировании и дифференциальных уравнениях — случайно сгенерированная задача не всегда имеет решение, мы не могли просто собирать уравнения и вводить их в систему. Нам нужно было сгенерировать совершенно новый обучающий набор, состоящий из примеров решенных уравнений, реструктурированных в виде деревьев выражений, читаемых моделью. В результате появились пары «проблема-решение», похожие на корпус предложений, переведенных с одного языка на другой. Наш набор также должен быть значительно больше, чем обучающие данные, использованные в предыдущих исследованиях в этой области, в которых пытались обучать системы на тысячах примеров.Поскольку нейронные сети обычно работают лучше, когда у них больше обучающих данных, мы создали набор с миллионами примеров.
А поскольку в двух классах задач, на которых мы сосредоточились — интегрировании и дифференциальных уравнениях — случайно сгенерированная задача не всегда имеет решение, мы не могли просто собирать уравнения и вводить их в систему. Нам нужно было сгенерировать совершенно новый обучающий набор, состоящий из примеров решенных уравнений, реструктурированных в виде деревьев выражений, читаемых моделью. В результате появились пары «проблема-решение», похожие на корпус предложений, переведенных с одного языка на другой. Наш набор также должен быть значительно больше, чем обучающие данные, использованные в предыдущих исследованиях в этой области, в которых пытались обучать системы на тысячах примеров.Поскольку нейронные сети обычно работают лучше, когда у них больше обучающих данных, мы создали набор с миллионами примеров.
Создание этого набора данных потребовало от нас применения ряда методов очистки и генерации данных. Например, для наших уравнений символьного интегрирования мы перевернули подход к переводу: вместо того, чтобы генерировать проблемы и находить их решения, мы генерировали решения и находили их проблему (их производную), что является гораздо более легкой задачей. Такой подход к созданию проблем из их решений — то, что инженеры иногда называют лазейками — сделал возможным создание миллионов примеров интеграции.Наш результирующий набор данных, вдохновленный переводом, состоит примерно из 100 миллионов парных примеров с подмножествами задач интеграции, а также дифференциальных уравнений первого и второго порядка.
Такой подход к созданию проблем из их решений — то, что инженеры иногда называют лазейками — сделал возможным создание миллионов примеров интеграции.Наш результирующий набор данных, вдохновленный переводом, состоит примерно из 100 миллионов парных примеров с подмножествами задач интеграции, а также дифференциальных уравнений первого и второго порядка.
Мы использовали этот набор данных для обучения модели преобразователя seq2seq с восемью головками внимания и шестью слоями. Преобразователи обычно используются для задач перевода, и наша сеть была построена для прогнозирования решений для различных типов уравнений, таких как определение примитива для заданной функции. Чтобы оценить производительность нашей модели, мы представили ей 5000 невидимых выражений, заставив систему распознавать закономерности в уравнениях, которые не появлялись при ее обучении.Наша модель продемонстрировала точность 99,7% при решении задач интегрирования и точность 94% и 81,2% соответственно для дифференциальных уравнений первого и второго порядка. Эти результаты превзошли результаты всех трех традиционных решателей уравнений, которые мы тестировали. Mathematica достигла следующих лучших результатов с точностью 84% для тех же задач интегрирования и 77,2% и 61,6% для результатов дифференциальных уравнений. Наша модель также вернула большинство прогнозов менее чем за 0.5 секунд, в то время как другим системам требовалось несколько минут, чтобы найти решение, а иногда и вовсе истекало время.
Эти результаты превзошли результаты всех трех традиционных решателей уравнений, которые мы тестировали. Mathematica достигла следующих лучших результатов с точностью 84% для тех же задач интегрирования и 77,2% и 61,6% для результатов дифференциальных уравнений. Наша модель также вернула большинство прогнозов менее чем за 0.5 секунд, в то время как другим системам требовалось несколько минут, чтобы найти решение, а иногда и вовсе истекало время.
Наша модель использовала в качестве входных данных уравнения слева — уравнения, которые не смогли решить ни Mathematica, ни Matlab — и смогла найти правильные решения (показаны справа) менее чем за одну секунду.
Сравнение сгенерированных решений с эталонными решениями позволило нам легко и точно проверить результаты. Но наша модель также способна давать несколько решений для данного уравнения.Это похоже на то, что происходит в машинном переводе, где есть много способов перевести входное предложение.
Что будет дальше с искусственным интеллектом для решения уравнений
В настоящее время наша модель работает с задачами с одной переменной, и мы планируем расширить ее до уравнений с несколькими переменными. Этот подход также может быть применен к другим областям, основанным на математике и логике, таким как физика, что потенциально может привести к созданию программного обеспечения, помогающего ученым в широком диапазоне работы.
Этот подход также может быть применен к другим областям, основанным на математике и логике, таким как физика, что потенциально может привести к созданию программного обеспечения, помогающего ученым в широком диапазоне работы.
Но наша система имеет более широкое значение для изучения и использования нейронных сетей.Обнаружив способ использования глубокого обучения там, где оно ранее считалось невозможным, эта работа предполагает, что другие задачи могут выиграть от ИИ. Будь то дальнейшее применение методов НЛП к областям, которые традиционно не ассоциировались с языками, или еще более открытые исследования распознавания образов в новых или, казалось бы, не связанных задачах, воспринимаемые ограничения нейронных сетей могут быть ограничениями воображения, не технологии.
Линейная алгебра для машинного обучения: решение системы линейных уравнений | by Khuyen Tran
Как алгебра является подчеркнутым механизмом алгоритмов машинного обучения
Начнем с обычного графика в науке о данных: Диаграмма рассеяния
Получена из Chartio График выше представляет корреляцию между диаметром и высотой дерева. Каждая точка является образцом дерева. Наша задача состоит в том, чтобы найти наиболее подходящую линию для предсказания высоты при заданном диаметре.
Каждая точка является образцом дерева. Наша задача состоит в том, чтобы найти наиболее подходящую линию для предсказания высоты при заданном диаметре.
Как мы можем это сделать? Вот тогда и нужна линейная алгебра.
Получено от Edutin AcademyЛинейная регрессия является примером линейных систем уравнений . Линейная алгебра предназначена для работы с линейными системами уравнений. Вместо того, чтобы работать со скалярами, мы начинаем работать с матрицами и векторами .
Линейная алгебра — это ключ к пониманию вычислений и статистики, необходимых для машинного обучения.Если вы сможете понять методы машинного обучения на уровне векторов и матриц, вы улучшите свое понимание того, как и когда они работают . Лучшая линейная алгебра поднимет вашу игру по всем направлениям.
А как лучше понять линейную алгебру? Реализуйте это. Существует 2 метода решения системы линейных уравнений: прямые методы и итерационные методы. В данной статье мы будем использовать прямые методы, в частности метод Гаусса.
Существует 2 метода решения системы линейных уравнений: прямые методы и итерационные методы. В данной статье мы будем использовать прямые методы, в частности метод Гаусса.
Так как чаще всего мы работаем с данными со многими свойствами (или переменными).Мы сделаем нашу систему линейных уравнений более общей, работая с трехмерными данными.
Давайте создадим пример для приведенного выше графика:
, где коэффициенты x_0, x_1 и x_2 и соответствующие значения 8, 4, 5 являются образцами точек на графике. Уравнения можно разбить на матрицы A, x и b
, где A и b — матрицы известных констант, x — вектор неизвестных переменных.
A = np.массив([[2, 1, 5],
[4, 4, -4],
[1, 3, 1]])
b= np.array([8,4,5])
Объедините матрицы A и b, чтобы получить
n = A.shape[0]C=np.
c_[A,b.reshape(-1,1)]
Теперь мы готовы решить наши задачи в 2 шага:
- Применить метод исключения Гаусса, чтобы уменьшить приведенную выше матрицу до треугольной матрицы
, которая может быть представлена уравнением:
2. Применить обратную замену, чтобы получить результат
Начнем с первого шага
Чтобы получить эту матрицу:
идея проста:
- Начнем с опорного значения в первой строке и первом столбце: строка =0, столбец = 0
- Найдите максимум абсолютное значение столбца сводной таблицы.Если все значения в этом столбце равны 0, мы останавливаемся.
- В противном случае мы поменяем местами E_0 и E_1
Затем примените эквивалентные преобразования, чтобы преобразовать все записи ниже опорной точки в 0:
- Найдите отношение между элементом j,i и опорной точкой i,i (т.
 е., 2 /4 = 1/2).
е., 2 /4 = 1/2). - Умножьте все элементы в E0 на 1/2. Вычтите все элементы в строке 1 на 1/2 E0 (т.е. 2-(4*1/2)=2–2 =0)
#строка
для j в диапазоне (i+1, n):c = C[j,i]/C[i,i]
C[j,:] = C[j,:] - c*C[i,:]
После упрощения каждого столбца переходим к следующий столбец справа.
Повторите процедуру:
Опорная точка: строка = 1, столбец = 1. Максимальное абсолютное значение: 2 в строке 2. Затем переставьте E_1 и E_2
Применение эквивалентного преобразования для преобразования всех записей ниже опорной в 0
Собери все вместе
Отлично! Теперь у нас есть система уравнений:
Как только мы доберемся до этой точки, эту систему уравнений невероятно легко решить с помощью обратной подстановки
Из метода исключения Гаусса мы получим треугольную матрицу
Идея состоит в том, чтобы решить приведенную выше систему уравнений с помощью решение снизу вверх. Используйте значение, полученное из последнего уравнения, чтобы найти другие значения.
Используйте значение, полученное из последнего уравнения, чтобы найти другие значения.
Начните со строки 3. Разделите 8 на 8, чтобы получить значение x_3.
X[n-1] = T[n-1,n]/T[n-1,n-1]
Теперь во второй строке имеем:
x_2 можно легко решить с помощью
Повторить с x1
Таким образом, в общем случае обратную подстановку можно представить так:
Удивительно! Мы получаем решение, как мы предсказываем. Чтобы убедиться, что это правильно при работе с большей матрицей, мы можем использовать встроенную в NumPy функцию
>>> np.linalg.solve(A,b)array([1., 1., 1.])
Мы получаем вектор решений, где каждый элемент соответствует x_0, x_1, x_2
Поздравляем, вы продвинулись так далеко! Надеюсь, эта статья поможет вам понять, что такое линейная алгебра и один из механизмов решения системы линейных уравнений.





 Какое количество каждого раствора взяли?
Какое количество каждого раствора взяли?

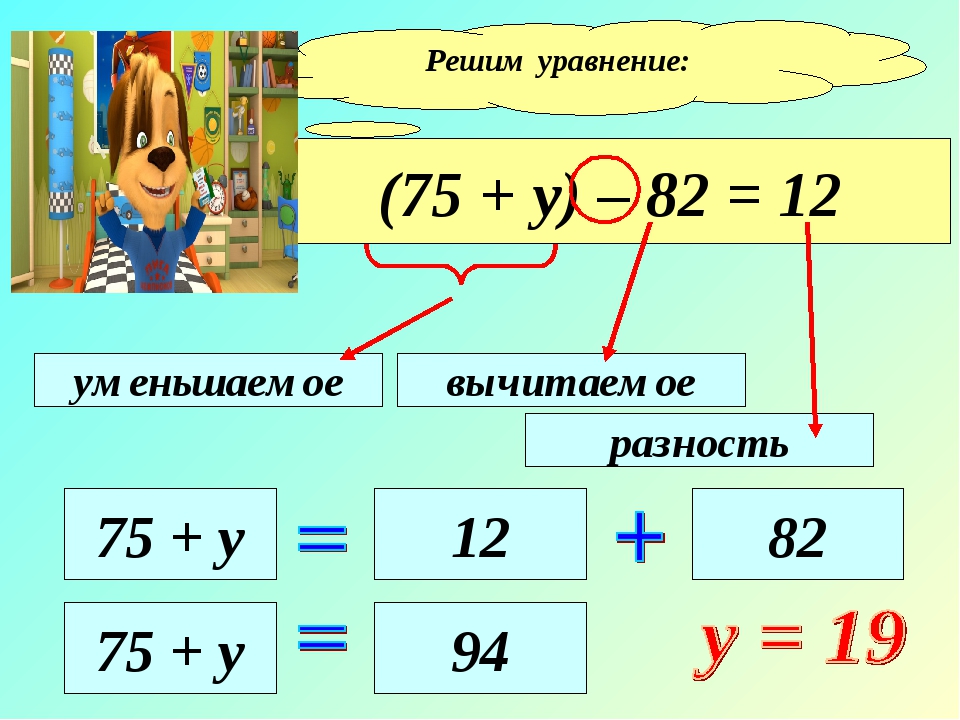


 Этап
самоопределения к деятельности
Этап
самоопределения к деятельности
 (3*8=24)
(3*8=24) Она
вам поможет. Подумайте и запишите выражение.
Она
вам поможет. Подумайте и запишите выражение.


 Она заглавная.
Она заглавная. Первичное
закрепление
Первичное
закрепление





 c_[A,b.reshape(-1,1)]
c_[A,b.reshape(-1,1)]  е., 2 /4 = 1/2).
е., 2 /4 = 1/2).