Сравнение чисел с разными степенями и основаниями: Сравнение степеней с разными показателями степеней и одинаковым основанием — Детская игровая комната «Волшебный лес»

Posted on 29.10.197510.02.2022 by alexxlab

Содержание

Как сравнивать степени | Логарифмы

Как сравнивать степени с одинаковыми основаниями? С одинаковыми показателями? Можно ли сравнить степени, если и основания, и показатели различны?

Как и сравнение логарифмов, сравнение степеней основано на свойстве показательной функции.

Сравнение степеней с одинаковыми основаниями

Если основание степени больше единицы (a>1), показательная функция возрастает, большему значению аргумента соответствует большее значение функции, соответственно, знак неравенства между показателями степеней и между степенями одинаковый.

Если основание степени меньше единицы (0<a<1), функция убывает, большему значению аргумента соответствует меньшее значение функции, знак неравенства между показателями степеней противоположен знаку между степенями.

С помощью схемы сравнение степеней с равными основаниями можно изобразить так:

Примеры.

№1. Сравнить значения выражений:

Решение:

Сравниваем показатели степеней: 1,5<1,9.

Основание a=2/7 меньше единицы, функция убывает, знак неравенства между степенями меняется на противоположный:

Решение:

Сравниваем показатели степеней:

Основание a=5,2 больше единицы, функция возрастает, знак неравенства между степенями не меняется:

№2. Сравнить показатели m и n, если известно, что для степеней выполняется неравенство:

Решение:

Основание a=0,21<1, функция убывает, поэтому знак неравенства между показателя степеней нужно изменить на противоположный: m>n.

Решение:

Основание

функция возрастает, поэтому знак неравенства между показателями степеней не изменяется: m<n.

Сравнение степеней с одинаковыми показателями.

1) Для возрастающих функций ( x>0):

Пример.

Для положительных значений аргумента

например,

Для отрицательных значений аргумента

например,

2) Для убывающих функций:

Пример.

Для положительных значений аргумента

например,

Для отрицательных значений аргумента:

например,

Как сравнивать степени, если и основания, и показатели различны?

Можно попробовать, например, сравнить каждую из степеней с единицей. Любая степень с основанием, большим единицы, при положительных значениях аргумента принимает значения, большие единицы:

при отрицательных — меньшие 1:

Если основание меньше единицы — соответственно,

Пример.

Сравнить

Решение:

В алгебре сравнивать степени чаще всего приходится при решении показательных неравенств.

Как решать показательные неравенства, мы рассмотрим позже.

Действие со степенями с разными основаниями. Свойства степеней: формулировки, доказательства, примеры

После того как определена степень числа , логично поговорить про свойства степени .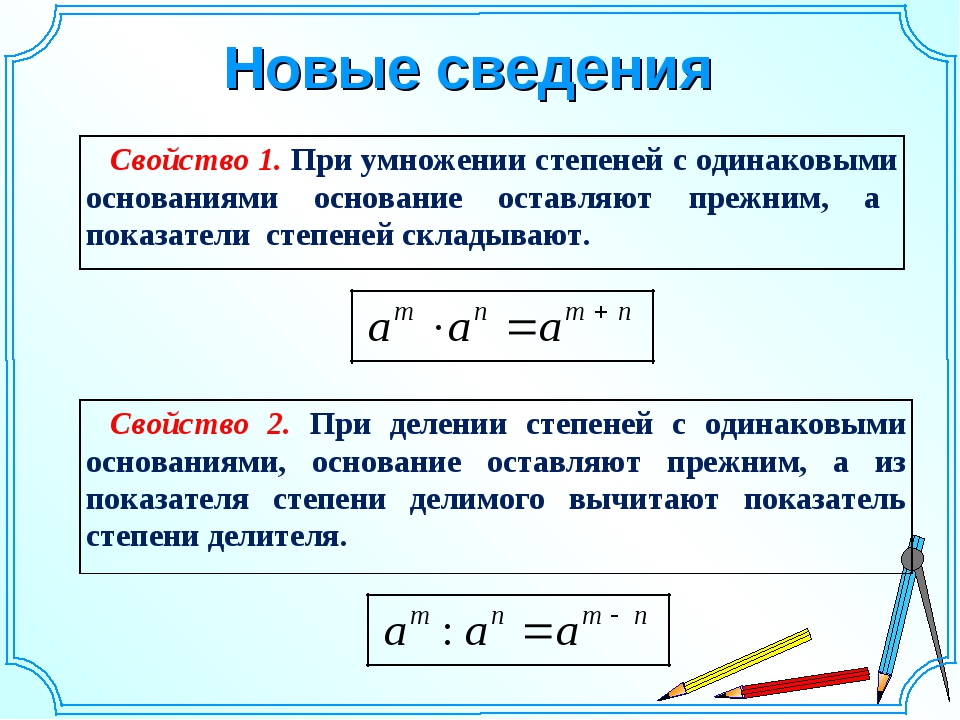 В этой статье мы дадим основные свойства степени числа, при этом затронем все возможные показатели степени. Здесь же мы приведем доказательства всех свойств степени, а также покажем, как применяются эти свойства при решении примеров.

Навигация по странице.

Свойства степеней с натуральными показателями

По определению степени с натуральным показателем степень a n представляет собой произведение n множителей, каждый из которых равен a . Отталкиваясь от этого определения, а также используя свойства умножения действительных чисел

, можно получить и обосновать следующие свойства степени с натуральным показателем :

основное свойство степени a m ·a n =a m+n , его обобщение ;
свойство частного степеней с одинаковыми основаниями a m:a n =a m−n ;
свойство степени произведения (a·b) n =a n ·b n , его расширение ;
свойство частного в натуральной степени (a:b) n =a n:b n ;
возведение степени в степень (a m) n =a m·n , его обобщение (((a n 1) n 2) …) n k =a n 1 ·n 2 ·…·n k ;
сравнение степени с нулем:
- если a>0 , то a n >0 для любого натурального n ;
- если a=0 , то a n =0 ;
- если a0 , если a
если a и b – положительные числа и a
если m и n такие натуральные числа, что m>n , то при 00 справедливо неравенство a m >a n .

Сразу заметим, что все записанные равенства являются

тождественными при соблюдении указанных условий, и их правые и левые части можно поменять местами. Например, основное свойство дроби a m ·a n =a m+n при упрощении выражений часто применяется в виде a m+n =a m ·a n .

Теперь рассмотрим каждое из них подробно.

Начнем со свойства произведения двух степеней с одинаковыми основаниями, которое называют основным свойством степени : для любого действительного числа a и любых натуральных чисел m и n справедливо равенство a m ·a n =a m+n .

Докажем основное свойство степени. По определению степени с натуральным показателем произведение степеней с одинаковыми основаниями вида a m ·a n можно записать как произведение . В силу свойств умножения полученное выражение можно записать как , а это произведение есть степень числа a с натуральным показателем m+n , то есть, a m+n . На этом доказательство завершено.

Приведем пример, подтверждающий основное свойство степени.

Основное свойство степени на базе свойств умножения можно обобщить на произведение трех и большего числа степеней с одинаковыми основаниями и натуральными показателями. Так для любого количества k натуральных чисел n 1 , n 2 , …, n k справедливо равенство a n 1 ·a n 2 ·…·a n k =a n 1 +n 2 +…+n k .

Например, (2,1) 3 ·(2,1) 3 ·(2,1) 4 ·(2,1) 7 = (2,1) 3+3+4+7 =(2,1) 17 .

Можно переходить к следующему свойству степеней с натуральным показателем –

свойству частного степеней с одинаковыми основаниями

Прежде чем привести доказательство этого свойства, обговорим смысл дополнительных условий в формулировке. Условие a≠0 необходимо для того, чтобы избежать деления на нуль, так как 0 n =0 , а при знакомстве с делением мы условились, что на нуль делить нельзя. Условие m>n вводится для того, чтобы мы не выходили за рамки натуральных показателей степени. Действительно, при m>n показатель степени a m−n является натуральным числом, в противном случае он будет либо нулем (что происходит при m−n ), либо отрицательным числом (что происходит при m

Доказательство. Основное свойство дроби позволяет записать равенство a m−n ·a n =a (m−n)+n =a m . Из полученного равенства a m−n ·a n =a m и из следует, что a m−n является частным степеней a m и a n . Этим доказано свойство частного степеней с одинаковыми основаниями.

Приведем пример. Возьмем две степени с одинаковыми основаниями π и натуральными показателями 5 и 2 , рассмотренному свойству степени отвечает равенство π 5:π 2 =π 5−3 =π 3 .

Теперь рассмотрим свойство степени произведения : натуральная степень n произведения двух любых действительных чисел a и b равна произведению степеней a n и b n , то есть, (a·b) n =a n ·b n .

Действительно, по определению степени с натуральным показателем имеем . Последнее произведение на основании свойств умножения можно переписать как , что равно a n ·b n .

Приведем пример: .

Данное свойство распространяется на степень произведения трех и большего количества множителей. То есть, свойство натуральной степени n произведения k множителей записывается как (a 1 ·a 2 ·…·a k) n =a 1 n ·a 2 n ·…·a k n .

Для наглядности покажем это свойство на примере. Для произведения трех множителей в степени 7 имеем .

Следующее свойство представляет собой свойство частного в натуральной степени : частное действительных чисел a и b , b≠0 в натуральной степени n равно частному степеней a n и b n , то есть, (a:b) n =a n:b n .

Доказательство можно провести, используя предыдущее свойство. Так (a:b) n ·b n =((a:b)·b) n =a n , а из равенства (a:b) n ·b n =a n следует, что (a:b) n является частным от деления a n на b n .

Запишем это свойство на примере конкретных чисел: .

Теперь озвучим свойство возведения степени в степень : для любого действительного числа a и любых натуральных чисел m и n степень a m в степени n равна степени числа a с показателем m·n , то есть, (a m) n =a m·n .

Например, (5 2) 3 =5 2·3 =5 6 .

Доказательством свойства степени в степени является следующая цепочка равенств: .

Рассмотренное свойство можно распространить на степень в степени в степени и т.д. Например, для любых натуральных чисел p , q , r и s справедливо равенство . Для большей ясности приведем пример с конкретными числами: (((5,2) 3) 2) 5 =(5,2) 3+2+5 =(5,2) 10 .

Осталось остановиться на свойствах сравнения степеней с натуральным показателем.

Начнем с доказательства свойства сравнения нуля и степени с натуральным показателем.

Для начала обоснуем, что a n >0 при любом a>0 .

Произведение двух положительных чисел является положительным числом, что следует из определения умножения. Этот факт и свойства умножения позволяют утверждать, что результат умножения любого числа положительных чисел также будет положительным числом. А степень числа a с натуральным показателем n по определению является произведением n множителей, каждый из которых равен a . Эти рассуждения позволяют утверждать, что для любого положительного основания a степень a n есть положительное число. В силу доказанного свойства 3 5 >0 , (0,00201) 2 >0 и .

Достаточно очевидно, что для любого натурального n при a=0 степень a n есть нуль. Действительно, 0 n =0·0·…·0=0 . К примеру, 0 3 =0 и 0 762 =0 .

Переходим к отрицательным основаниям степени.

Начнем со случая, когда показатель степени является четным числом, обозначим его как 2·m , где m — натуральное. Тогда . По каждое из произведений вида a·a равно произведению модулей чисел a и a , значит, является положительным числом. Следовательно, положительным будет и произведение и степень a 2·m . Приведем примеры: (−6) 4 >0 , (−2,2) 12 >0 и .

Наконец, когда основание степени a является отрицательным числом, а показатель степени есть нечетное число 2·m−1 , то . Все произведения a·a являются положительными числами, произведение этих положительных чисел также положительно, а его умножение на оставшееся отрицательное число a дает в итоге отрицательное число. В силу этого свойства (−5) 3 .

Переходим к свойству сравнения степеней с одинаковыми натуральными показателями, которое имеет следующую формулировку: из двух степеней с одинаковыми натуральными показателями n меньше та, основание которой меньше, а больше та, основание которой больше. Докажем его.

Неравенство a n свойств неравенств справедливо и доказываемое неравенство вида a n .

Осталось доказать последнее из перечисленных свойств степеней с натуральными показателями. Сформулируем его. Из двух степеней с натуральными показателями и одинаковыми положительными основаниями, меньшими единицы, больше та степень, показатель которой меньше; а из двух степеней с натуральными показателями и одинаковыми основаниями, большими единицы, больше та степень, показатель которой больше. Переходим к доказательству этого свойства.

Докажем, что при m>n и 00 в силу исходного условия m>n , откуда следует, что при 0

Осталось доказать вторую часть свойства. Докажем, что при m>n и a>1 справедливо a m >a n . Разность a m −a n после вынесения a n за скобки принимает вид a n ·(a m−n −1) . Это произведение положительно, так как при a>1 степень a n есть положительное число, и разность a m−n −1 есть положительное число, так как m−n>0 в силу начального условия, и при a>1 степень a m−n больше единицы. Следовательно, a m −a n >0 и a m >a n , что и требовалось доказать. Иллюстрацией этого свойства служит неравенство 3 7 >3 2 .

Свойства степеней с целыми показателями

Так как целые положительные числа есть натуральные числа, то все свойства степеней с целыми положительными показателями в точности совпадают со свойствами степеней с натуральными показателями, перечисленными и доказанными в предыдущем пункте.

Степень с целым отрицательным показателем , а также степень с нулевым показателем мы определяли так, чтобы оставались справедливыми все свойства степеней с натуральными показателями, выражаемые равенствами. Поэтому, все эти свойства справедливы и для нулевых показателей степени, и для отрицательных показателей, при этом, конечно, основания степеней отличны от нуля.

Итак, для любых действительных и отличных от нуля чисел a и b , а также любых целых чисел m и n справедливы следующие свойства степеней с целыми показателями :

a m ·a n =a m+n ;
a m:a n =a m−n ;
(a·b) n =a n ·b n ;
(a:b) n =a n:b n ;
(a m) n =a m·n ;
если n – целое положительное число, a и b – положительные числа, причем ab −n ;
если m и n – целые числа, причем m>n , то при 01 выполняется неравенство a m >a n .

При a=0 степени a m и a n имеют смысл лишь когда и m , и n положительные целые числа, то есть, натуральные числа. Таким образом, только что записанные свойства также справедливы для случаев, когда a=0 , а числа m и n – целые положительные.

Доказать каждое из этих свойств не составляет труда, для этого достаточно использовать определения степени с натуральным и целым показателем, а также свойства действий с действительными числами. Для примера докажем, что свойство степени в степени выполняется как для целых положительных чисел, так и для целых неположительных чисел. Для этого нужно показать, что если p есть нуль или натуральное число и q есть нуль или натуральное число, то справедливы равенства (a p) q =a p·q , (a −p) q =a (−p)·q , (a p) −q =a p·(−q) и (a −p) −q =a (−p)·(−q) . Сделаем это.

Для положительных p и q равенство (a p) q =a p·q доказано в предыдущем пункте. Если p=0 , то имеем (a 0) q =1 q =1 и a 0·q =a 0 =1 , откуда (a 0) q =a 0·q . Аналогично, если q=0 , то (a p) 0 =1 и a p·0 =a 0 =1 , откуда (a p) 0 =a p·0 . Если же и p=0 и q=0 , то (a 0) 0 =1 0 =1 и a 0·0 =a 0 =1 , откуда (a 0) 0 =a 0·0 .

Теперь докажем, что (a −p) q =a (−p)·q . По определению степени с целым отрицательным показателем , тогда . По свойству частного в степени имеем . Так как 1 p =1·1·…·1=1 и , то . Последнее выражение по определению является степенью вида a −(p·q) , которую в силу правил умножения можно записать как a (−p)·q .

Аналогично .

И .

По такому же принципу можно доказать все остальные свойства степени с целым показателем, записанные в виде равенств.

В предпоследнем из записанных свойств стоит остановиться на доказательстве неравенства a −n >b −n , которое справедливо для любого целого отрицательного −n и любых положительных a и b , для которых выполняется условие a. Так как по условию a0 . Произведение a n ·b n тоже положительно как произведение положительных чисел a n и b n . Тогда полученная дробь положительна как частное положительных чисел b n −a n и a n ·b n . Следовательно, откуда a −n >b −n , что и требовалось доказать.

Последнее свойство степеней с целыми показателями доказывается так же, как аналогичное свойство степеней с натуральными показателями.

Свойства степеней с рациональными показателями

Степень с дробным показателем мы определяли, распространяя на нее свойства степени с целым показателем. Иными словами, степени с дробными показателями обладают теми же свойствами, что и степени с целыми показателями. А именно:

Доказательство свойств степеней с дробными показателями базируется на определении степени с дробным показателем, на и на свойствах степени с целым показателем. Приведем доказательства.

По определению степени с дробным показателем и , тогда . Свойства арифметического корня позволяют нам записать следующие равенства . Дальше, используя свойство степени с целым показателем, получаем , откуда по определению степени с дробным показателем имеем , а показатель полученной степени можно преобразовать так: . На этом доказательство завершено.

Абсолютно аналогично доказывается второе свойство степеней с дробными показателями:

По схожим принципам доказываются и остальные равенства:

Переходим к доказательству следующего свойства. Докажем, что для любых положительных a и b , a b p . Запишем рациональное число p как m/n , где m – целое число, а n – натуральное. Условиям p0 в этом случае будут эквивалентны условия m0 соответственно. При m>0 и a

Аналогично, при mb m , откуда , то есть, и a p >b p .

Осталось доказать последнее из перечисленных свойств. Докажем, что для рациональных чисел p и q , p>q при 00 – неравенство a p >a q . Мы всегда можем привести к общему знаменателю рациональные числа p и q , пусть при этом мы получим обыкновенные дроби и , где m 1 и m 2 – целые числа, а n — натуральное. При этом условию p>q будет соответствовать условие m 1 >m 2 , что следует из . Тогда по свойству сравнения степеней с одинаковыми основаниями и натуральными показателями при 01 – неравенство a m 1 >a m 2 . Эти неравенства по свойствам корней можно переписать соответственно как и . А определение степени с рациональным показателем позволяет перейти к неравенствам и соответственно. Отсюда делаем окончательный вывод: при p>q и 00 – неравенство a p >a q .

Свойства степеней с иррациональными показателями

Из того, как определяется степень с иррациональным показателем , можно заключить, что она обладает всеми свойствами степеней с рациональными показателями. Так для любых a>0 , b>0 и иррациональных чисел p и q справедливы следующие свойства степеней с иррациональными показателями :

a p ·a q =a p+q ;
a p:a q =a p−q ;
(a·b) p =a p ·b p ;
(a:b) p =a p:b p ;
(a p) q =a p·q ;
для любых положительных чисел a и b , a0 справедливо неравенство a p b p ;
для иррациональных чисел p и q , p>q при 00 – неравенство a p >a q .

Отсюда можно сделать вывод, что степени с любыми действительными показателями p и q при a>0 обладают этими же свойствами.

Список литературы.

Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. МатематикаЖ учебник для 5 кл. общеобразовательных учреждений.
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 7 кл. общеобразовательных учреждений.
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 8 кл. общеобразовательных учреждений.
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 9 кл. общеобразовательных учреждений.
Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений.
Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы).

I. Произведение n сомножителей, каждый из которых равен а называется n -й степенью числа а и обозначается а n .

Примеры. Записать произведение в виде степени.

1) mmmm; 2) aaabb; 3) 5·5·5·5·ccc; 4) ppkk+pppk-ppkkk.

Решение.

1) mmmm=m 4 , так как, по определению степени, произведение четырех сомножителей, каждый из которых равен m , будет четвертой степенью числа m .

2) aaabb=a 3 b 2 ; 3) 5·5·5·5·ccc=5 4 c 3 ; 4) ppkk+pppk-ppkkk=p 2 k 2 +p 3 k-p 2 k 3 .

II. Действие, посредством которого находится произведение нескольких равных сомножителей, называется возведением в степень. Число, которое возводится в степень, называется основанием степени. Число, которое показывает, в какую степень возводится основание, называется показателем степени. Так, а n – степень, а – основание степени, n – показатель степени. Например:

2 3 — это степень. Число 2 — основание степени, показатель степени равен 3 . Значение степени 2 3 равно 8, так как 2 3 =2·2·2=8.

Примеры. Написать следующие выражения без показателя степени.

5) 4 3 ; 6) a 3 b 2 c 3 ; 7) a 3 -b 3 ; 8) 2a 4 +3b 2 .

Решение.

5) 4 3 = 4·4·4; 6) a 3 b 2 c 3 = aaabbccc; 7) a 3 -b 3 = aaa-bbb; 8) 2a 4 +3b 2 = 2aaaa+3bb.

III. а 0 =1 Любое число (кроме нуля) в нулевой степени равно единице. Например, 25 0 =1.
IV. а 1 =а Любое число в первой степени равно самому себе.

V. a m ∙ a n = a m + n При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.

Примеры. Упростить:

9) a·a 3 ·a 7 ; 10) b 0 +b 2 ·b 3 ; 11) c 2 ·c 0 ·c·c 4 .

Решение.

9) a·a 3 ·a 7 =a 1+3+7 =a 11 ; 10) b 0 +b 2 ·b 3 = 1+b 2+3 =1+b 5 ;

11) c 2 ·c 0 ·c·c 4 = 1·c 2 ·c·c 4 =c 2+1+4 =c 7 .

VI. a m : a n = a m — n При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.

Примеры. Упростить:

12) a 8:a 3 ; 13) m 11:m 4 ; 14) 5 6:5 4 .

12) a 8:a 3 =a 8-3 =a 5 ; 13) m 11:m 4 =m 11-4 =m 7 ; 14) 5 6:5 4 =5 2 =5·5=25.

VII. (a m ) n = a mn При возведении степени в степень основание оставляют прежним, а показатели перемножают.

Примеры. Упростить:

15) (a 3) 4 ; 16) (c 5) 2 .

15) (a 3) 4 =a 3·4 =a 12 ; 16) (c 5) 2 =c 5·2 =c 10 .

Обратите внимание , что, так как от перестановки множителей произведение не меняется, то :

15) (a 3) 4 =(a 4) 3 ; 16) (c 5) 2 =(c 2) 5 .

V I II . (a∙b) n =a n ∙b n При возведении произведения в степень возводят в эту степень каждый из множителей.

Примеры. Упростить:

17) (2a 2) 5 ; 18) 0,2 6 ·5 6 ; 19) 0,25 2 ·40 2 .

Решение.

17) (2a 2) 5 =2 5 ·a 2·5 =32a 10 ; 18) 0,2 6 ·5 6 =(0,2·5) 6 =1 6 =1;

19) 0,25 2 ·40 2 =(0,25·40) 2 =10 2 =100.

IX. При возведении в степень дроби возводят в эту степень и числитель и знаменатель дроби.

Примеры. Упростить:

Решение.

Страница 1 из 1 1

Ранее мы уже говорили о том, что такое степень числа. Она имеет определенные свойства, полезные в решении задач: именно их и все возможные показатели степени мы разберем в этой статье. Также мы наглядно покажем на примерах, как их можно доказать и правильно применить на практике.

Yandex.RTB R-A-339285-1

Вспомним уже сформулированное нами ранее понятие степени с натуральным показателем: это произведение n -ного количества множителей, каждый из которых равен а. Также нам понадобится вспомнить, как правильно умножать действительные числа. Все это поможет нам сформулировать для степени с натуральным показателем следующие свойства:

Определение 1

1. Главное свойство степени: a m · a n = a m + n

Можно обобщить до: a n 1 · a n 2 · … · a n k = a n 1 + n 2 + … + n k .

2. Свойство частного для степеней, имеющих одинаковые основания: a m: a n = a m − n

3. Свойство степени произведения: (a · b) n = a n · b n

Равенство можно расширить до: (a 1 · a 2 · … · a k) n = a 1 n · a 2 n · … · a k n

4. Свойство частного в натуральной степени: (a: b) n = a n: b n

5. Возводим степень в степень: (a m) n = a m · n ,

Можно обобщить до: (((a n 1) n 2) …) n k = a n 1 · n 2 · … · n k

6. Сравниваем степень с нулем:

если a > 0 , то при любом натуральном n, a n будет больше нуля;
при a , равном 0 , a n также будет равна нулю;
при a
при a

7. Равенство a n

8. Неравенство a m > a n будет верным при условии, что m и n – натуральные числа, m больше n и а больше нуля и меньше единицы.

В итоге мы получили несколько равенств; если соблюсти все условия, указанные выше, то они будут тождественными. Для каждого из равенств, например, для основного свойства, можно поменять местами правую и левую часть: a m · a n = a m + n — то же самое, что и a m + n = a m · a n . В таком виде оно часто используется при упрощении выражений.

1. Начнем с основного свойства степени: равенство a m · a n = a m + n будет верным при любых натуральных m и n и действительном a . Как доказать это утверждение?

Основное определение степеней с натуральными показателями позволит нам преобразовать равенство в произведение множителей. Мы получим запись такого вида:

Это можно сократить до (вспомним основные свойства умножения). В итоге мы получили степень числа a с натуральным показателем m + n . Таким образом, a m + n , значит, основное свойство степени доказано.

Разберем конкретный пример, подтверждающий это.

Пример 1

Итак, у нас есть две степени с основанием 2 . Их натуральные показатели — 2 и 3 соответственно. У нас получилось равенство: 2 2 · 2 3 = 2 2 + 3 = 2 5 Вычислим значения, чтобы проверить верность этого равенства.

Выполним необходимые математические действия: 2 2 · 2 3 = (2 · 2) · (2 · 2 · 2) = 4 · 8 = 32 и 2 5 = 2 · 2 · 2 · 2 · 2 = 32

В итоге у нас вышло: 2 2 · 2 3 = 2 5 . Свойство доказано.

В силу свойств умножения мы можем выполнить обобщение свойства, сформулировав его в виде трех и большего числа степеней, у которых показатели являются натуральными числами, а основания одинаковы. Если обозначить количество натуральных чисел n 1 , n 2 и др. буквой k , мы получим верное равенство:

a n 1 · a n 2 · … · a n k = a n 1 + n 2 + … + n k .

Пример 2

2. Далее нам необходимо доказать следующее свойство, которое называется свойством частного и присуще степеням с одинаковыми основаниями: это равенство a m: a n = a m − n , которое справедливо при любых натуральным m и n (причем m больше n)) и любом отличном от нуля действительном a .

Для начала поясним, каков именно смысл условий, которые упомянуты в формулировке. Если мы возьмем a, равное нулю, то в итоге у нас получится деление на нуль, чего делать нельзя (ведь 0 n = 0). Условие, чтобы число m обязательно было больше n , нужно для того, чтобы мы могли удержаться в рамках натуральных показателей степени: вычтя n из m , мы получим натуральное число. Если условие не будет соблюдено, у нас получится отрицательное число или ноль, и опять же мы выйдем за пределы изучения степеней с натуральными показателями.

Теперь мы можем перейти к доказательству. Из ранее изученного вспомним основные свойства дробей и сформулируем равенство так:

a m − n · a n = a (m − n) + n = a m

Из него можно вывести: a m − n · a n = a m

Вспомним про связь деления и умножения. Из него следует, что a m − n – частное степеней a m и a n . Это и есть доказательство второго свойства степени.

Пример 3

Подставим конкретные числа для наглядности в показатели, а основание степени обозначим π : π 5: π 2 = π 5 − 3 = π 3

3. Следующим мы разберем свойство степени произведения: (a · b) n = a n · b n при любых действительных a и b и натуральном n .

Согласно базовому определению степени с натуральным показателем мы можем переформулировать равенство так:

Вспомнив свойства умножения, запишем: . Это значит то же самое, что и a n · b n .

Пример 4

2 3 · — 4 2 5 4 = 2 3 4 · — 4 2 5 4

Если множителей у нас три и больше, то это свойство также распространяется и на этот случай. Введем для числа множителей обозначение k и запишем:

(a 1 · a 2 · … · a k) n = a 1 n · a 2 n · … · a k n

Пример 5

С конкретными числами получим следующее верное равенство: (2 · (- 2 , 3) · a) 7 = 2 7 · (- 2 , 3) 7 · a

4. После этого мы попробуем доказать свойство частного: (a: b) n = a n: b n при любых действительных a и b , если b не равно 0 , а n – натуральное число.

Для доказательства можно использовать предыдущее свойство степени. Если (a: b) n · b n = ((a: b) · b) n = a n , а (a: b) n · b n = a n , то из этого выходит, что (a: b) n есть частное от деления a n на b n .

Пример 6

Подсчитаем пример: 3 1 2: — 0 . 5 3 = 3 1 2 3: (- 0 , 5) 3

Пример 7

Начнем сразу с примера: (5 2) 3 = 5 2 · 3 = 5 6

А теперь сформулируем цепочку равенств, которая докажет нам верность равенства:

Если у нас в примере есть степени степеней, то это свойство справедливо для них также. Если у нас есть любые натуральные числа p , q , r , s , то верно будет:

a p q y s = a p · q · y · s

Пример 8

Добавим конкретики: (((5 , 2) 3) 2) 5 = (5 , 2) 3 + 2 + 5 = (5 , 2) 10

6. Еще одно свойство степеней с натуральным показателем, которое нам нужно доказать, – свойство сравнения.

Для начала сравним степень с нулем. Почему a n > 0 при условии, что а больше 0 ?

Если умножить одно положительное число на другое, то мы получим также положительное число. Зная этот факт, мы можем сказать, что от числа множителей это не зависит – результат умножения любого числа положительных чисел есть число положительное. А что же такое степень, как не результат умножения чисел? Тогда для любой степени a n с положительным основанием и натуральным показателем это будет верно.

Пример 9

3 5 > 0 , (0 , 00201) 2 > 0 и 34 9 13 51 > 0

Также очевидно, что степень с основанием, равным нулю, сама есть ноль. В какую бы степень мы не возводили ноль, он останется им.

Пример 10

0 3 = 0 и 0 762 = 0

Если основание степени – отрицательное число, тот тут доказательство немного сложнее, поскольку важным становится понятие четности/нечетности показателя. Возьмем для начала случай, когда показатель степени четный, и обозначим его 2 · m , где m – натуральное число.

Вспомним, как правильно умножать отрицательные числа: произведение a · a равно произведению модулей, а, следовательно, оно будет положительным числом. Тогда и степень a 2 · m также положительны.

Пример 11

Например, (− 6) 4 > 0 , (− 2 , 2) 12 > 0 и — 2 9 6 > 0

А если показатель степени с отрицательным основанием – нечетное число? Обозначим его 2 · m − 1 .

Тогда

Все произведения a · a , согласно свойствам умножения, положительны, их произведение тоже. Но если мы его умножим на единственное оставшееся число a , то конечный результат будет отрицателен.

Тогда получим: (− 5) 3

Как это доказать?

a n

Пример 12

Например, верны неравенства: 3 7 (0 , 75) 124

8. Нам осталось доказать последнее свойство: если у нас есть две степени, основания которых одинаковы и положительны, а показатели являются натуральными числами, то та из них больше, показатель которой меньше; а из двух степеней с натуральными показателями и одинаковыми основаниями, большими единицы, больше та степень, показатель которой больше.

Докажем эти утверждения.

Для начала нам нужно убедиться, что a m

Вынесем a n за скобки, после чего наша разность примет вид a n · (a m − n − 1) . Ее результат будет отрицателен (поскольку отрицателен результат умножения положительного числа на отрицательное). Ведь согласно начальным условиям, m − n > 0 , тогда a m − n − 1 –отрицательно, а первый множитель положителен, как и любая натуральная степень с положительным основанием.

У нас вышло, что a m − a n

Осталось привести доказательство второй части утверждения, сформулированного выше: a m > a справедливо при m > n и a > 1 . Укажем разность и вынесем a n за скобки: (a m − n − 1) .Степень a n при а, большем единицы, даст положительный результат; а сама разность также окажется положительна в силу изначальных условий, и при a > 1 степень a m − n больше единицы. Выходит, a m − a n > 0 и a m > a n , что нам и требовалось доказать.

Пример 13

Пример с конкретными числами: 3 7 > 3 2

Основные свойства степеней с целыми показателями

Для степеней с целыми положительными показателями свойства будут аналогичны, потому что целые положительные числа являются натуральными, а значит, все равенства, доказанные выше, справедливы и для них. Также они подходят и для случаев, когда показатели отрицательны или равны нулю (при условии, что само основание степени ненулевое).

Таким образом, свойства степеней такие же для любых оснований a и b (при условии, что эти числа действительны и не равны 0) и любых показателей m и n (при условии, что они являются целыми числами). Запишем их кратко в виде формул:

Определение 2

1. a m · a n = a m + n

2. a m: a n = a m − n

3. (a · b) n = a n · b n

4. (a: b) n = a n: b n

5. (a m) n = a m · n

6. a n b − n при условии целого положительного n , положительных a и b , a

7. a m n и 0 1 a m > a n .

Если основание степени равно нулю, то записи a m и a n имеют смысл только лишь в случае натуральных и положительных m и n . В итоге получим, что формулировки выше подходят и для случаев со степенью с нулевым основанием, если соблюдаются все остальные условия.

Доказательства этих свойств в данном случае несложные. Нам потребуется вспомнить, что такое степень с натуральным и целым показателем, а также свойства действий с действительными числами.

Разберем свойство степени в степени и докажем, что оно верно и для целых положительных, и для целых неположительных чисел. Начнем с доказательства равенств (a p) q = a p · q , (a − p) q = a (− p) · q , (a p) − q = a p · (− q) и (a − p) − q = a (− p) · (− q)

Условия: p = 0 или натуральное число; q – аналогично.

Если значения p и q больше 0 , то у нас получится (a p) q = a p · q . Схожее равенство мы уже доказывали раньше. Если p = 0 , то:

(a 0) q = 1 q = 1 a 0 · q = a 0 = 1

Следовательно, (a 0) q = a 0 · q

Для q = 0 все точно так же:

(a p) 0 = 1 a p · 0 = a 0 = 1

Итог: (a p) 0 = a p · 0 .

Если же оба показателя нулевые, то (a 0) 0 = 1 0 = 1 и a 0 · 0 = a 0 = 1 , значит, (a 0) 0 = a 0 · 0 .

Вспомним доказанное выше свойство частного в степени и запишем:

1 a p q = 1 q a p q

Если 1 p = 1 · 1 · … · 1 = 1 и a p q = a p · q , то 1 q a p q = 1 a p · q

Эту запись мы можем преобразовать в силу основных правил умножения в a (− p) · q .

Так же: a p — q = 1 (a p) q = 1 a p · q = a — (p · q) = a p · (- q) .

И (a — p) — q = 1 a p — q = (a p) q = a p · q = a (- p) · (- q)

Остальные свойства степени можно доказать аналогичным образом, преобразовав имеющиеся неравенства. Подробно останавливаться мы на этом не будем, укажем только сложные моменты.

Доказательство предпоследнего свойства: вспомним, a − n > b − n верно для любых целых отрицательных значений nи любых положительных a и b при условии, что a меньше b .

Тогда неравенство можно преобразовать следующим образом:

1 a n > 1 b n

Запишем правую и левую части в виде разности и выполним необходимые преобразования:

1 a n — 1 b n = b n — a n a n · b n

Вспомним, что в условии a меньше b , тогда, согласно определению степени с натуральным показателем: — a n 0 .

a n · b n в итоге дает положительное число, поскольку его множители положительны. В итоге мы имеем дробь b n — a n a n · b n , которая в итоге также дает положительный результат. Отсюда 1 a n > 1 b n откуда a − n > b − n , что нам и нужно было доказать.

Последнее свойство степеней с целыми показателями доказывается аналогично свойству степеней с показателями натуральными.

Основные свойства степеней с рациональными показателями

В предыдущих статьях мы разбирали, что такое степень с рациональным (дробным) показателем. Их свойства такие же, что и у степеней с целыми показателями. Запишем:

Определение 3

1. a m 1 n 1 · a m 2 n 2 = a m 1 n 1 + m 2 n 2 при a > 0 , а если m 1 n 1 > 0 и m 2 n 2 > 0 , то при a ≥ 0 (свойство произведения степеней с одинаковыми основаниями).

2. a m 1 n 1: b m 2 n 2 = a m 1 n 1 — m 2 n 2 , если a > 0 (свойство частного).

3. a · b m n = a m n · b m n при a > 0 и b > 0 , а если m 1 n 1 > 0 и m 2 n 2 > 0 , то при a ≥ 0 и (или) b ≥ 0 (свойство произведения в дробной степени).

4. a: b m n = a m n: b m n при a > 0 и b > 0 , а если m n > 0 , то при a ≥ 0 и b > 0 (свойство частного в дробной степени).

5. a m 1 n 1 m 2 n 2 = a m 1 n 1 · m 2 n 2 при a > 0 , а если m 1 n 1 > 0 и m 2 n 2 > 0 , то при a ≥ 0 (свойство степени в степени).

6. a p 0 ; если p b p (свойство сравнения степеней с равными рациональными показателями).

7. a p q при 0 0 – a p > a q

Для доказательства указанных положений нам понадобится вспомнить, что такое степень с дробным показателем, каковы свойства арифметического корня n -ной степени и каковы свойства степени с целыми показателем. Разберем каждое свойство.

Согласно тому, что из себя представляет степень с дробным показателем, получим:

a m 1 n 1 = a m 1 n 1 и a m 2 n 2 = a m 2 n 2 , следовательно, a m 1 n 1 · a m 2 n 2 = a m 1 n 1 · a m 2 n 2

Свойства корня позволят нам вывести равенства:

a m 1 · m 2 n 1 · n 2 · a m 2 · m 1 n 2 · n 1 = a m 1 · n 2 · a m 2 · n 1 n 1 · n 2

Из этого получаем: a m 1 · n 2 · a m 2 · n 1 n 1 · n 2 = a m 1 · n 2 + m 2 · n 1 n 1 · n 2

Преобразуем:

a m 1 · n 2 · a m 2 · n 1 n 1 · n 2 = a m 1 · n 2 + m 2 · n 1 n 1 · n 2

Показатель степени можно записать в виде:

m 1 · n 2 + m 2 · n 1 n 1 · n 2 = m 1 · n 2 n 1 · n 2 + m 2 · n 1 n 1 · n 2 = m 1 n 1 + m 2 n 2

Это и есть доказательство. Второе свойство доказывается абсолютно так же. Запишем цепочку равенств:

a m 1 n 1: a m 2 n 2 = a m 1 n 1: a m 2 n 2 = a m 1 · n 2: a m 2 · n 1 n 1 · n 2 = = a m 1 · n 2 — m 2 · n 1 n 1 · n 2 = a m 1 · n 2 — m 2 · n 1 n 1 · n 2 = a m 1 · n 2 n 1 · n 2 — m 2 · n 1 n 1 · n 2 = a m 1 n 1 — m 2 n 2

Доказательства остальных равенств:

a · b m n = (a · b) m n = a m · b m n = a m n · b m n = a m n · b m n ; (a: b) m n = (a: b) m n = a m: b m n = = a m n: b m n = a m n: b m n ; a m 1 n 1 m 2 n 2 = a m 1 n 1 m 2 n 2 = a m 1 n 1 m 2 n 2 = = a m 1 m 2 n 1 n 2 = a m 1 · m 2 n 1 n 2 = = a m 1 · m 2 n 2 · n 1 = a m 1 · m 2 n 2 · n 1 = a m 1 n 1 · m 2 n 2

Следующее свойство: докажем, что для любых значений a и b больше 0 , если а меньше b , будет выполняться a p b p

Представим рациональное число p как m n . При этом m –целое число, n –натуральное. Тогда условия p 0 будут распространяться на m 0 . При m > 0 и a

Используем свойство корней и выведем: a m n

Учитывая положительность значений a и b , перепишем неравенство как a m n

Таким же образом при m b m , получаем a m n > b m n значит, a m n > b m n и a p > b p .

Нам осталось привести доказательство последнего свойства. Докажем, что для рациональных чисел p и q , p > q при 0 0 будет верно a p > a q .

Рациональные числа p и q можно привести к общему знаменателю и получить дроби m 1 n и m 2 n

Здесь m 1 и m 2 – целые числа, а n – натуральное. Если p > q , то m 1 > m 2 (учитывая правило сравнения дробей). Тогда при 0 1 – неравенство a 1 m > a 2 m .

Их можно переписать в следующем виде:

a m 1 n a m 2 n

Тогда можно сделать преобразования и получить в итоге:

a m 1 n a m 2 n

Подводим итог: при p > q и 0 0 – a p > a q .

Основные свойства степеней с иррациональными показателями

На такую степень можно распространить все описанные выше свойства, которыми обладает степень с рациональными показателями. Это следует из самого ее определения, которое мы давали в одной из предыдущих статей. Сформулируем кратко эти свойства (условия: a > 0 , b > 0 , показатели p и q – иррациональные числа):

Определение 4

1. a p · a q = a p + q

2. a p: a q = a p − q

3. (a · b) p = a p · b p

4. (a: b) p = a p: b p

5. (a p) q = a p · q

6. a p b p

7. a p 0 , то a p > a q .

Таким образом, все степени, показатели которых p и q являются действительными числами, при условии a > 0 обладают теми же свойствами.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Урок на тему: «Правила умножения и деления степеней с одинаковыми и разными показателями. Примеры»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 7 класса
Пособие к учебнику Ю. n

Add

Новыe решебники

© 2021Copyright. Все права защищены. Правообладатель SIA Ksenokss.
Адрес: 1069, Курземес проспект 106/45, Рига, Латвия.
Тел.: +371 29-851-888 E-mail: [email protected]

Наименьшее общее кратное / Обыкновенные дроби / Справочник по математике 5-9 класс

Главная
Справочники
Справочник по математике 5-9 класс
Обыкновенные дроби
Наименьшее общее кратное

Задача:

Петя строит железную дорогу из частей, длина которых 4 см, а Сережа, из частей длина которых 6 см. Какую наименьшую протяженность дорожного полотна построят мальчики равной длины?

Решение:

Длина дороги, построенной мальчиками, должна делиться нацело на 4 и 6, так как части, из которых строят дорогу Петя и Сережа равны 4 см и 6 см соответственно, то есть длина построенной железной дороги должна быть кратной и 4, и 6.

Числа кратные 4:

4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60…

Числа кратные 6:

6, 12, 18, 24, 30, 36, 42, 48, 54, 60…

То есть общими кратными чисел 4 и 6 являются числа (выделено синим):

12, 24, 36, 48, 60…

Но наименьшим из них является 12. Это число называется наименьшим общим кратным.

То есть наименьшая протяженность дорожного полотна равной длины у Пети и Сережи 12 см.

Наименьшее натуральное число, которое делится нацело на каждое из двух данных натуральных чисел, то есть кратно каждому из них, называют наименьшим общим кратным этих чисел.

Наименьшее общее кратное чисел и обозначают так: НОК(; ), то есть мы можем записать НОК(4; 6) = 12.

Нахождение наименьшего общего кратного:

1 способ:

Найдем НОК(12; 15).

Выбираем наибольшее из двух чисел, в нашем случае это число 15, и записываем числа кратные ему, до тех пор, пока не получим число, которое будет кратно второму числу, в нашем случае числу 12.

Получаем: 15, 30, 45, 60.

Число 60 является наименьшим общим кратным чисел 12 и 15, то есть НОК(12; 15) = 60.

2 способ:

Разложим данные числа на простые множители:

12 = 223 15 = 35.

Далее для выписываем простые множители, которые входят в разложение первого числа, и добавляем множители из разложения второго числа, которых нет в разложении первого, то есть в нашем случае, это множитель 5.

Итак, мы получим 4 множителя 2235, произведение данных множителей равно числу 60, которое является наименьшим общим кратным чисел 12 и 15, то есть мы снова получили НОК(12; 15) = 60.

Таким же образом можно найти НОК трех и более чисел.

Чтобы найти НОК нескольких натуральных чисел, надо:

разложить их на простые множители;
выписать множители, входящие в разложение одного из чисел;
добавить к ним недостающие множители из разложений остальных чисел;
найти произведение получившихся множителей.

Заметим, что если одно из данных чисел делится на все остальные числа, то это число и является наименьшим общим кратным данных чисел.

3 способ:

Найдем НОК(2520; 4620). Для это разложим данные числа на простые множители и запишем разложение в виде произведения степеней:

2 520 = 2³3²5¹7¹ 4 620 = 2²3¹5¹7¹11¹.

Далее используем правило:

Выбрать степени, основания которых встречаются только в одном из разложений.
Из каждой пары степеней с одинаковыми основаниями выбрать степень с бóльшим показателем.
Перемножить выбранные степени. Полученное произведение является искомым наименьшим общим кратным.

В нашем случае:

Встречается только в одном разложении: 11¹.
Степени с бóльшими показателями: 2³, 3², 5¹, 7¹.
Находим произведение данных степеней, то есть искомый наименьшее общее кратное: НОК(2520; 4620) = 2³3²5¹7¹11 = 27 720.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Доли. Обыкновенные дроби

Сравнение дробей

Делители и кратные

Признаки делимости на 10, на 5 и на 2

Четные и нечетные числа

Признаки делимости на 9 и на 3

Простые и составные числа

Разложение на простые множители

Наибольший общий делитель

Деление и дроби

Сложение и вычитание дробей с одинаковыми знаменателями

Смешанное число

Сложение и вычитание смешанных чисел

Основное свойство дроби

Решето Эратосфена

Приведение дробей к общему знаменателю

Сравнение, сложение и вычитание дробей с разными знаменателями

Умножение обыкновенных дробей

Деление обыкновенных дробей

Обыкновенные дроби

Правило встречается в следующих упражнениях:

6 класс

Номер 2, Мерзляк, Полонский, Якир, Учебник

Номер 166, Мерзляк, Полонский, Якир, Учебник

Номер 172, Мерзляк, Полонский, Якир, Учебник

Номер 177, Мерзляк, Полонский, Якир, Учебник

Номер 355, Мерзляк, Полонский, Якир, Учебник

Номер 356, Мерзляк, Полонский, Якир, Учебник

Номер 359, Мерзляк, Полонский, Якир, Учебник

Задание 240, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 305, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1473, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

7 класс

Номер 45, Мерзляк, Полонский, Якир, Учебник

Номер 46, Мерзляк, Полонский, Якир, Учебник

Номер 47, Мерзляк, Полонский, Якир, Учебник

Номер 48, Мерзляк, Полонский, Якир, Учебник

Номер 349, Мерзляк, Полонский, Якир, Учебник

Номер 529, Мерзляк, Полонский, Якир, Учебник

Номер 562, Мерзляк, Полонский, Якир, Учебник

Номер 692, Мерзляк, Полонский, Якир, Учебник

Номер 693, Мерзляк, Полонский, Якир, Учебник

Пользовательское соглашение

Как сравнивать логарифмы с разным основанием

Как сравнивать логарифмы с разным основанием.

При решении показательных и логарифмических неравенств нередко возникает необходимость сравнить логарифмы с разным основанием.

Рассмотрим, как это сделать.

Пример 1. Сравнить и .

Чтобы сравнить эти логарифмы, нужно найти число, которое стоит на числовой прямой между и .

Нетрудно увидеть, что ,

То есть , следовательно,

Чаще ситуация выглядит сложнее.

Пример 2. Сравнить и .

Так как , следовательно, . Аналогично, , следовательно, .

То есть значение обоих логарифмов — дробное число, лежащее в пределах от 1 до 2. Подобрать промежуточное число, которое стоит на числовой прямой между и уже сложнее.

Поступим так. Предположим, в знаменателе промежуточного числа стоит 2. Умножим оба логарифма на 2, то есть сравним числа

Перенесем 2 в показатель степени:

Теперь нетрудно увидеть, что , следовательно, .

Если умножение на 2 не приводит к желаемому результату, нужно попытаться умножить на 3, потом на 4 и т.д.

Пример 3. В некоторых случаях прежде чем сравнивать логарифмы, нужно выполнить определенные преобразования.

Сравнить и

Так как , мы можем преобразовать логарифм с основанием 2:

Итак, мы сравниваем числа и .

Прибавим к обоим числам 2:

Преобразуем:

Теперь нам нужно сравнить числа

Значение обоих логарифмов — дробное число, принадлежащее промежутку .

Предположим, в знаменателе промежуточного числа стоит 2. Умножим оба логарифма на 2, то есть сравним числа

Перенесем 2 в показатель степени:

, следовательно, .

Получили, что , следовательно, .

Репетитор по математике Инна Владимировна Фельдман.

Приемы и методы сравнения логарифмов

Сравнение значений логарифмов или значения логарифма с некоторым числом встречается в школьной практике решения задач не только как самостоятельная задача. Сравнивать логарифмы приходится, например, при решении уравнений и неравенств. Материалы статьи (задачи и их решения) располагаются по принципу “от простого к сложному” и могут быть использованы для подготовки и проведения урока (уроков) по данной теме, а также на факультативных занятиях. Количество рассматриваемых задач на уроке зависит от уровня класса, его профильного направления. В классах с углубленным изучением математики этот материал может быть использован для двухчасового урока-лекции.

1. (Устно.) Какие из функций являются возрастающими, а какие убывающими:

Замечание. Это упражнение является подготовительным.

2. (Устно.) Сравните с нулем:

Замечание. При решении упражнения № 2 можно использовать как свойства логарифмической функции с привлечением графика логарифмической функции, так и следующее полезное свойство:

если положительные числа a и b лежат на числовой прямой правее 1 или левее 1 (то есть a>1 и b>1 или 0<a<1 и 0<b<1), то log_ab > 0 ;
если положительные числа a и b лежат на числовой прямой по разные стороны от 1(то есть 0<a<1<b или 0<b<1<a), то log_ab < 0 [4].

Покажем использование этого свойства при решении № 2(а).

Так как

Так как функция y = log₇t возрастает на R₊, 10 > 7, то log₇10 > log₇7, то есть log₇10 > 1. Таким образом, положительные числа sin3 и log₇10 лежат по разные стороны от 1. Следовательно, log_sin3log₇10 < 0.

3. (Устно.) Найдите ошибку в рассуждениях:

. Функция y = lgt возрастает на R₊, тогда ,

Разделим обе части последнего неравенства на . Получим, что 2 > 3.

Решение.

Положительные числа и 10 (основание логарифма) лежат по разные стороны от 1. Значит, < 0. При делении обеих частей неравенства на число знак неравенства следует изменить на противоположный.

4. (Устно.) Сравните числа:

Замечание. При решении упражнений № 4(a–c) используем свойство монотонности логарифмической функции. При решении № 4(d) используем свойство:

если c > a >1, то при b>1 справедливо неравенство log_ab > log_cb.

Решение 4(d).

Так как 1 < 5 < 7 и 13 > 1, то log₅13 > log₇13.

5. Сравните числа log₂6 и 2.

Решение.

Первый способ (использование монотонности логарифмической функции).

2 = log₂4;

Функция y = log₂t возрастает на R₊, 6 > 4. Значит, log₂6 > log₂4 и log₂5 > 2.

Второй способ (составление разности).

Составим разность .

6. Сравните числа и -1.

Решение.

-1 = ;

Функция y = убывает на R₊_, 3 < 5. Значит, > и > -1.

7. Сравните числа и 3log₈26.

Решение.

Функция y = log₂t возрастает на R₊, 25 < 26. Значит, log₂25 < log₂26 и .

Решение.

Первый способ.

Умножим обе части неравенства на 3:

Функция y = log ₅t возрастает на R₊ , 27 > 25. Значит,

Второй способ.

Составим разность
. Отсюда .

9. Сравните числа log₄26 и log₆17.

Решение.

Оценим логарифмы, учитывая, что функции y = log₄t и y = log₆t возрастающие на R₊:

Решение.

Учитывая, что функции убывающие на R₊, имеем:

. Значит,

Замечание. Предложенный метод сравнения называют методом “вставки” или методом “разделения” (мы нашли число 4, разделяющее данные два числа).

11. Сравните числа log₂3 и log₃5.

Решение.

Заметим, что оба логарифма больше 1, но меньше 2.

Первый способ. Попробуем применить метод “разделения”. Сравним логарифмы с числом .

Второй способ (умножение на натуральное число).

Замечание 1. Суть метода “умножения на натуральное число” в том, что мы ищем натуральное число k, при умножении на которое сравниваемых чисел a и b получают такие числа ka и kb, что между ними находится хотя бы одно целое число.

Замечание 2. Реализация вышеописанного метода бывает весьма трудоемка, если сравниваемые числа очень близки друг к другу.
В этом случае можно попробовать сравнение методом “вычитания единицы”. Покажем его на следующем примере.

12. Сравните числа log₇8 и log₆7.

Решение.

Первый способ (вычитание единицы).

Вычтем из сравниваемых чисел по 1.

В первом неравенстве мы воспользовались тем, что

если c > a > 1, то при b > 1 справедливо неравенство log_ab > log_cb.

Во втором неравенстве – монотонностью функции y = log_ax.

Замечание. Вычитать из сравниваемых чисел можно любое натуральное число n. При этом часто бывает достаточно взять n = 1.

Второй способ (применение неравенства Коши).

13. Сравните числа log₂₄72 и log₁₂18.

Решение.

14. Сравните числа log₂₀80 и log₈₀640.

Решение.

Пусть log₂5 = x . Заметим, что x > 0.

Получаем неравенство .

Найдем множество решений неравенства , удовлетворяющих условию x > 0.

Возведем обе части неравенства в квадрат (при x > 0 обе части неравенства положительны). Имеем 9x² < 9x + 28.

Множеством решений последнего неравенства является промежуток .

Учитывая, что x > 0, получаем: .

Ответ: неравенство верно.

Практикум по решению задач.

1. Сравните числа:

2. Расположите в порядке возрастания числа:

3. Решите неравенство 4⁴ – 2·2⁴⁺¹ – 3 < 0. Является ли число √2 решением данного неравенства? (Ответ: (–∞; log₂3); число √2 является решением данного неравенства. )

Заключение.

Методов сравнения логарифмов много. Цель уроков по данной теме – научить ориентироваться в многообразии методов, выбирать и применять наиболее рациональный способ решения в каждой конкретной ситуации.

В классах с углубленным изучением математики материал по данной теме может быть изложен в форме лекции. Такая форма учебной деятельности предполагает, что материал лекции должен быть тщательно отобран, проработан, выстроен в определенной логической последовательности. Записи, которые делает учитель на доске, должны быть продуманными, математически точными.

Закрепление лекционного материала, отработку навыков по решению задач целесообразно проводить на уроках-практикумах. Цель практикума – не только закрепить и проверить полученные знания, но и пополнить их. Поэтому задания должны содержать задачи разного уровня, от самых простых задач до задач повышенной сложности. Учитель на таких практикумах выступает в роли консультанта.

Литература.

Галицкий М.Л. и др.Углубленное изучение курса алгебры и математического анализа: Метод. рекомендации и дидактические материалы: Пособие для учителя.– М.: Просвещение, 1986.
Зив Б.Г., Гольдич В.А. Дидактические материалы по алгебре и началам анализа для 10 класса. – СПб.: “ЧеРо-на-Неве”, 2003.
Литвиненко В.Н., Мордкович А. Г. Практикум по элементарной математике. Алгебра. Тригонометрия.: Учебное издание. – М.: Просвещение, 1990.
Рязановский А.Р. Алгебра и начала анализа:500 способов и методов решения задач по математике для школьников и поступающих в вузы. – М.: Дрофа, 2001.
Садовничий Ю.В. Математика. Конкурсные задачи по алгебре с решениями. Часть 4. Логарифмические уравнения, неравенства, системы. Учебное пособие.-3-е изд., стер.-М.:Издательский отдел УНЦДО, 2003.
Шарыгин И.Ф., Голубев В.И.Факультативный курс по математике: Решение задач: Учеб. пособие для 11 кл. сред.шк.– М.: Просвещение, 1991.

открытых учебников | Сиявула

Математика

Наука

- Читать онлайн
- Учебники
  - Английский
    - Класс 7А
    - Класс 7Б
    - Класс 7 (объединенные А и В)
  - Африкаанс
    - Граад 7А
    - Граад 7Б
    - Graad 7 (A en B saam)
- Пособия для учителя
- Читать онлайн
- Учебники
  - Английский
    - Класс 8А
    - Класс 8Б
    - Класс 8 (объединенные А и В)
  - Африкаанс
    - Граад 8А
    - Граад 8Б
    - Graad 8 (A en B saam)
- Пособия для учителя
- Читать онлайн
- Учебники
  - Английский
    - Класс 9А
    - Класс 9Б
    - Класс 9 (объединенные А и В)
  - Африкаанс
    - Граад 9А
    - Граад 9Б
    - Graad 9 (A en B saam)
- Пособия для учителя
- Читать онлайн
- Учебники
  - Английский
    - Класс 4А
    - Класс 4Б
    - Класс 4 (объединенные A и B)
  - Африкаанс
    - Граад 4А
    - Граад 4Б
    - Graad 4 (A en B saam)
- Пособия для учителя
- Читать онлайн
- Учебники
  - Английский
    - Класс 5А
    - Класс 5Б
    - Класс 5 (объединенные A и B)
  - Африкаанс
    - Граад 5А
    - Граад 5Б
    - Graad 5 (A en B saam)
- Пособия для учителя
- Читать онлайн
- Учебники
  - Английский
    - Класс 6А
    - Класс 6Б
    - Класс 6 (объединенные A и B)
  - Африкаанс
    - Граад 6А
    - Граад 6Б
    - Graad 6 (A en B saam)
- Пособия для учителя

Лицензирование нашей книги

Эти книги не только бесплатны, но и имеют открытую лицензию! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:

CC-BY-ND (фирменные версии)

Вам разрешается и поощряется свободное копирование этих версий. Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.

Узнайте здесь больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.

CC-BY (версии без торговой марки)

Эти небрендированные версии одного и того же контента доступны для совместного использования, адаптации, преобразования, изменения или дальнейшего развития любым способом, при единственном требовании — отдать должное Сиявуле. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.

Номер | математика 9

К концу этого раздела вы сможете:

SCO 1 Демонстрировать понимание степеней с целочисленными основаниями (исключая основание 0) и целыми показателями степени путем: представления многократного умножения с использованием степеней; использование патернов, чтобы показать, что степень с нулевым показателем степени равна единице; решать проблемы, связанные с полномочиями.
1.1 Продемонстрируйте различия между показателем степени и основанием, построив модели данной степени.
1.2 Объясните, используя многократное умножение, разницу между двумя заданными степенями, в которых показатель степени и основание меняются местами.
1.3 Выразите заданную степень в виде многократного умножения.
1.4 Выразите заданное многократное умножение в степени.
1.5 Объясните роль скобок в степенях, оценив данный набор степеней.
1.6 Продемонстрируйте, используя шаблоны, что aº равно 1 для заданного значения a(a≠0).
1.7 Вычислять степени с целыми основаниями (исключая основание 0) и целыми показателями степени.

SCO 2 Продемонстрировать понимание операций над степенями с целочисленными основаниями (исключая основание 0) и целыми показателями степени.
2.1 Объясните на примерах показательные законы степеней с целыми основаниями (исключая основание 0) и целыми числами показателей степени.
2.2 Вычислите заданное выражение, применяя законы экспоненты.
2.3 Определить сумму двух заданных мощностей и записать процесс.
2.4 Определить разность двух заданных мощностей и записать процесс.
2.5 Определить ошибку(и) в заданном упрощении выражения, включающего степени.

SCO 3 Продемонстрировать понимание рациональных чисел путем сравнения и упорядочивания рациональных чисел и решения задач, связанных с арифметическими операциями над рациональными числами.
3.1 Упорядочить заданный набор рациональных чисел в дробной и десятичной форме, поместив их в числовую строку.
3.2 Определить рациональное число, которое находится между двумя заданными рациональными числами.
3.3 Решите заданную задачу, включающую операции над рациональными числами в дробной или десятичной форме.

SCO 4 Объясните и примените порядок операций, включая показатели, с технологией и без нее.
4.1 Решить заданную задачу, применяя порядок операций без использования техники.
4.2 Решить поставленную задачу, применяя порядок операций с использованием технологии.
4.3 Определить ошибку в применении порядка операций в заданном неверном решении.

SCO 5 Определение точного квадратного корня из положительных рациональных чисел.
5.1 Определить, является ли заданное рациональное число квадратным, и объяснить, почему это происходит.
5.2 Определить квадратный корень из заданного положительного рационального числа, являющегося полным квадратом.
5.3 Определить ошибку, допущенную при данном вычислении квадратного корня.
5.4 Определить положительное рациональное число, зная квадратный корень из этого положительного рационального числа.

SCO 6 Определить приближенный квадратный корень из положительных рациональных чисел
6.1. Оцените квадратный корень из заданного рационального числа, не являющегося полным квадратом, используя корни полных квадратов в качестве эталона.
6.2 Определить приблизительный квадратный корень заданного рационального числа, который не является полным квадратом, с помощью технологии (например, калькулятора, компьютера).
6.3 Объясните, почему квадратный корень из заданного рационального числа, показанный на калькуляторе, может быть приближенным.
6.4 Определить число с квадратным корнем, которое находится между двумя заданными числами.

Показатель степени

Показатель степени числа говорит , сколько раз использовать число при умножении.

В 8 ² «2» говорит о том, что 8 нужно использовать дважды при умножении, поэтому: в степени 2″ или «8 во второй степени», или просто «8 в квадрате»

Показатель степени также называется степенью

Использование показателя степени является сокращением для повторного умножения.

Повторное умножение может быть записано как показатель степени или степени.

Математика — это весело
Письменная информация и интерактивы

Скобки и показатели степени

При отсутствии скобок отрицание НЕ ПРИМЕНЯЕТСЯ при повторном умножении — оно встречается только один раз!

Скобки используются, когда степень имеет отрицательное основание, чтобы показать, что отрицательный знак является частью основания и остается на протяжении всего повторного умножения.

aº всегда равно 1

Проверьте шаблон:

Законы показателей степени

Операции с показателями степени можно эффективно выполнять с законами использования показателей.

Изучение законов экспонентов: используйте его
математические интерактивные средства — изучать Альберта

Изучить законы исполнения показателей: исследовать его
математические интерактивные средства — изучить ALBERTA

Rational Numbers

Rational Number — любое число, которое можно записать в виде дроби (a/b), где b не равно нулю.Иррациональные числа нельзя записать в виде дроби, они не заканчиваются и не повторяются (иррациональные = сумасшедшие!).

Независимо от того, где стоит знак (-), каждая из этих дробей равна -¾ или -0,75.

Сравнение и упорядочивание рациональных чисел

Эталоны числовых линий

Эталон — это стандарт для оценки чего-либо с использованием нескольких чисел. Например, значения ниже 0 и 1 используются в качестве ориентиров для сравнения различных дробей.

Запомните

отрицательное число ВСЕГДА меньше положительного
шагов шагов
0

1. Преобразовать в общий стандарт (фракция или десятичное число)

2. Нижняя строка 40021403. Место на номер

3. Место в порядке на номер

Заказ Rational Numbers
Интерактивная — Khan Academy

Rational Numbers
Игра — SoftSchools

Jeopardy — Сравнение и упорядочивание Rational Numbers
Полноценная игра — работает только на ноутбуках/компьютерах

Порядок операций

BEDMA можно использовать для запоминания порядка выполнения операций.Важно, чтобы уравнения решались по этим правилам.

Скобки группируют символы, чтобы мы могли рассматривать их как один термин.

Экспоненты выполняются перед умножением, поскольку экспоненты представляют повторное умножение.

Умножение и деление выполняются до сложения и вычитания, потому что они повторяются сложением и вычитанием; решать по мере их появления.

Сложение и вычитание выполняются последними в порядке их следования.

0

Порядок изучения операций: Используйте его
Интерактивное — Alberta Education

Порядок эксплуатации
— 4NUMS

квадратных корней рациональных номеров

квадратов и квадратных корней являются обратными операциями — они противоположности, такие как сложение и вычитание, умножение и деление.

Совершенные квадраты — это квадраты целых чисел.

Квадратные и квадратные корни
Письменная информация: Math is Fun

IXL: Perfect Squares
Практика

).

Узнайте больше о степенях, скобках и знаках

В этой статье мы узнаем о важности круглых скобок при выполнении вычислений со знаками (отрицательными) в степенях.

Все мы знаем, что умножение — это сокращенная форма записи повторяющейся суммы. Например, 2 + 2 + 2 + 2 + 2 можно проще записать как 2 x 5.

Таким же образом мы используем степени для выражения умножения числа на себя несколько раз более сокращенным способом.Например, 2 x 2 x 2 можно выразить как 2³.

Прежде всего, давайте быстро рассмотрим элементы силы.

Элементы питания

Степени формируются основанием и показателем степени, как показано на следующем рисунке. Основание – это число, которое умножается несколько раз. Показатель степени — это количество раз, когда умножается основание.

После небольшого обзора элементов силы давайте перейдем к делу.Скобки в отрицательных основных степенях очень важны. Мы должны помнить о них, когда приступаем к операциям. Часто они являются причинами ошибок, которые приводят нас к ошибочным решениям.

Давайте посмотрим на разницу между (-5)² и -5²

Если основание находится в скобках, как в нашем первом случае, показатель степени влияет на все, что находится внутри скобки, то есть на знак и число.

Однако, если основание не указано в скобках, как во втором случае, показатель степени влияет только на непосредственное значение слева, то есть только на число без знака.

Как видите, пара скобок может полностью изменить результат.

Давайте посмотрим еще несколько примеров работы со скобками в полномочиях.

Полномочия: пример 1

Полномочия: Пример 2

Это может показаться запутанным, и требуется немного практики, чтобы привыкнуть к вычислениям, но это несложно, поэтому я призываю вас начать Smartick и практиковать этот предмет среди многих других предметов математики в начальной школе.

Надеюсь, это помогло вам. И не забывайте о важности скобок!

Узнать больше:

Веселье — любимый способ обучения нашего мозга

Дайан Акерман
Smartick — увлекательный способ изучения математики

15 минут веселья в день

Адаптируется к уровню вашего ребенка

Миллионы учеников с 2009 года

Группа создания контента.
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.

Степени и степени

Прежде чем вы начнете работать со степенями и показателями, необходимо дать некоторые основные определения.

Показатель степени является положительным или отрицательным числом или 0, расположенным выше и справа от количества. Он выражает степень, до которой количество должно быть увеличено или уменьшено. В 4 ³ 3 — показатель степени. Он показывает, что 4 нужно использовать как множитель три раза: 4 × 4 × 4 (умножить на себя дважды). 4 ³ читается как четыре в третьей степени (или четыре в кубе ).

2 ⁴ = 2 × 2 × 2 × 2 = 16

3 ² = 3 × 3 = 9

5 ³ = 5 × 5 × 5 = 125

Помните: x ¹ = x и x ⁰ = 1, если x .

Следует отметить два конкретных типа степеней: квадратов и кубов. Чтобы возвести число в квадрат, просто умножьте его само на себя так, как вы находите площадь квадрата (показатель степени равен 2).Например, 6 в квадрате (пишется как 6 ² ) равно 6 × 6, или 36, 36 называется полным квадратом (квадрат целого числа). Ниже приведен неполный список идеальных квадратов:

1 ² = 1

2 ² = 4

3 ² = 9

4 ² = 16

5 ² = 25

6 ² = 36

7 ² = 49

8 ² = 64

9 ² = 81

10 ² = 100

11 ² = 121

12 ² = 144

Чтобы куб число, просто умножьте его дважды само на себя, как вы бы нашли объем куба (показатель степени равен 3). Например, 5 в кубе (записывается как 5 ³ равно 5 × 5 × 5, или 125. 125 называется совершенным кубом (кубом целого числа). Ниже приведен неполный список совершенных кубов.

1 ³ = 1 × 1 × 1 = 1

2 ³ = 2 × 2 × 2 = 8

3 ³ = 3 × 3 × 3 = 27

4 ³ = 4 × 4 × 4 = 64

5 ³ = 5 × 5 × 5 = 125

6 ³ = 6 × 6 × 6 = 216

7 ³ = 7 × 7 × 7 = 343

Чтобы умножить два числа с показателями степени, если основные числа одинаковы, просто сохраните основное число и добавьте показатели степени.

Умножьте следующие числа, оставив ответы с показателями степени.

2 ³ × 2 ⁵

3 ² × 3 ⁵

5 ⁴ × 5 ⁷

Чтобы разделить два числа с показателями степени, если основания чисел одинаковы, просто сохраните основание и вычтите второй показатель степени из первого или показатель степени знаменателя из степени числителя.

Разделите следующее, оставив ответы с показателями степени.

Чтобы умножить или разделить числа с показателями степени, если основания чисел различны, вы должны сначала упростить каждое число с показателем степени, а затем выполнить операцию.

Упростите и выполните указанную операцию.

Для проблем, подобных описанным в примере , возможны некоторые упрощения.

Чтобы складывать или вычитать числа с показателями степени, независимо от того, одинаковы ли основания чисел или разные, вы должны сначала упростить каждое число с показателем степени, а затем выполнить указанную операцию.

Упростите и выполните указанную операцию.

3 ² – 2 ³

5 ² + 3 ³

4 ² + 9 ³

2 ³ – 2 ²

3 ² – 2 ³ = 9 – 8 = 1

5 ² + 3 ³ = 25 + 27 = 52

4 ² + 9 ³ = 16 + 729 = 745

2 ³ – 2 ² = 8 – 4 = 4

Если число с показателем степени возводится в другую степень (4 ² ) ³ , просто сохраните исходное основание и умножьте показатели степени.

Умножьте следующие числа и оставьте ответы с показателями степени.

(6 ³ ) ²

(3 ² ) ⁴

(5 ⁴ ) ³

(6 ³ ) ² = 6 ^{(3 × 2)} = 6 ⁶

(3 ² ) ⁴ = 3 ^{(2 × 4)} = 3 ⁸

(5 ⁴ ) ³ = 5 ^{(4 × 3)} = 5 ¹²

Сравнение чисел, вычисленных по разным основаниям .. .

К точно сравнивать числа, они должны быть вычисленный на такой же основа, с помощью такой же определения .

Если Есть различия в методология, ты должен пересчитывать в числа с помощью такой же методология .

Несравнимый Информация является часто при условии от правительство. Определения являются измененный за разные политический причины. Часто методология используется для вычисление и сравнение является затемненный.Числа являются вычисленный на разные базы из год до год до «вращение» в числа. Сравнение несравненный числа возможно использовал к покажи это в экономика растущий когда это нет, или определенные группы люди нужно больше (или менее) правительство помощь, или там не достаточно (или слишком много) учителя, и Т. Д.

Тем не мение, Там есть просто нет путь к сравнивать числа вычисленный с использованием разные определения как основа для расчет . это абсолютно существенный вычислить цифры на то же основа до сравнение их.

экспоненциальных функций
экспоненциальная функция Примечания, урок 4.1
Экспоненциальные функции
Три разных кейса | Законы экспонентов | Приложения экспоненциальных функций
Проверка концепций
Три разных случая для функции:

Случай 1: а > 1
Что общего у всех этих экспоненциальных функций?

Что изменится, если значение и увеличится?

Случай 2: а = 1
Какое влияние оказывает значение x на график?

Это экспоненциальная функция?

Случай 3: 0 < a < 1
Что общего у всех этих экспоненциальных функций?

Что изменится, если значение и увеличится?

Сравните случаи 1 и 3. Чем отличается от , и какая разница в графике?

Законы Экспоненты

Экспоненциальные функции

Приложения экспоненциальных функций
В телепередаче «Кто хочет стать миллионером?» Выиграл Экспоненциальная формула?

Ниже показаны три сценария.Деньги за настоящие телешоу количество последовательных вопросов, на которые были даны правильные ответы, указано под Рубрика, «Реальное шоу».

В сценарии «Истинно экспоненциальный» каждое значение равно 2,511886432. в степени числа последовательных правильных ответов. Эта база 2,511886432 было рассчитано так, что 1) количество последовательных правильных ответами будет показатель степени, а 2) в 15-й степени ответ будет быть один миллион.

В сценарии «Тот же старт» мы начинаем с приза в 100 долларов, а затем по-настоящему удваивать каждый ответ (что не всегда происходит в реальном телешоу).

Ниже данные сценария в таблице — это сюжет каждого сценария.

Настоящее шоу Действительно экспоненциальный То же начало

1 100 1 2,511886432 1 100

2 200 2 6.309573445 2 200

3 300 3 15.84893192 3 400

4 500 4 39.81071706 4 800

5 1000 5 100 5 1600

6 2000 6 251. 1886432 6 3200

7 4000 7 630,9573445 7 6400

8 8000 8 1584.893192 8 12800

9 16000 9 3981.071706 9 25600

10 32000 10 10000 10 51200

11 64000 11 25118.86432 11 102400

12 125000 12 63095.73445 12 204800

13 250000 13 158489.3192 13 409600

14 500000 14 398107. 1706 14 819200

15 1000000 15 1000000 15 1638400

Сюжет 3 сценария данные из приведенной выше таблицы

Синий: настоящее шоу; Желтый: Действительно экспоненциальный; Фиолетовый: то же начало
На этом графике показаны данные из таблицы выше.Как видно из заголовка выше, синяя кривая представляет собой график фактического показывают выигрыши, желтая кривая использовала сценарий «Истинно экспоненциальный», а фиолетовая кривая показывает, как выглядела бы кривая, если бы шоу действительно началось по $100 и удваивать приз за каждый дополнительный вопрос.

Некоторые заметки из класса

Экспоненциальный Функции @ Фиолетовая математика

Заговор Экспоненциальные функции @ Purple Math

Решение Экспоненциальные уравнения @ Purple Math

Экспоненциальный словесные задачи @ Purple Math

Проверка концепций

#1: Что из следующего растет быстрее всего?
Выбери один у = 2х у = 2 ^ х у = х ^ 2

#2: Экспоненциальные функции подходят:
Выбери один Модели населения Модели распада Модели населения и распада Ни один

#3: Для общей функции Есть ____ случаев, которые необходимо рассмотреть.
Выбери один 1 2 3 4 бесконечное количество

№ 4. Если мы умеем строить графики , как бы мы изменили график, чтобы представить ?
Выбери один Переместить график вниз на два и вправо на 3 Переместить график вниз на два и влево на 3 Инвертировать график и двигаться влево 3 Инвертировать график и двигаться вправо 3

#5 Функция специально для использования в исчислении, потому что….
Выбери один Наклон касательной к кривой в точке (0,1) равен 1. Наклон касательной к кривой в любой точке равен всегда равна его координате y. е — иррациональное число.

отрицательных показателей | Государственный университет Среднего Теннесси

Если a – ненулевое вещественное число, а n и m – целые числа, тогда

a ³ расширяется до a • a • a

a ⁿ • a ^m = a ^{n + m} Правило произведения: при умножении двух чисел с одинаковым основанием сложите показатели степени

a ⁿ / a ^m = a ^{n — m} Правило частного: при делении двух чисел с одним и тем же основанием вычесть показатель степени знаменателя (делителя) от показателя степени числителя (делимого).

( a ⁿ ) ^m = a ^нм Правило степени: при возведении возведенного в степень числа в степень умножьте экспонента, умноженная на мощность.

( x + 2 ) ^{2 ) ( x + a ) и упрощает x}
2 + 2 Ax + AX + ^{2
( x — 2 ) ² расширяется до ( x 9097 a ) ( a ) и упрощает x ² — 2 ax + a ²
При возведении в квадрат двучлена произведение ВСЕГДА будет трехчленом!
сопряженные биномии разница квадратов
( x + a — a ) x
2} — A ²

Положительный показатель означает, что мы умножаемся база.
Пример: 2 ³ = 2 • 2 • 2 = 8

Отрицательный показатель степени означает, что мы делим на основание.
Пример: 2 ^–3 = 1/2 • 1/2 • 1/2 = 1/8

Чтобы изменить знак экспоненты, инвертируйте (переверните) основание.