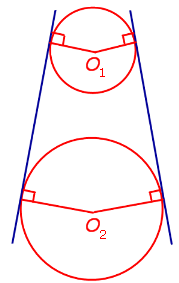
Полуокружность Википедия
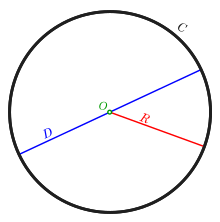 Окружность (C), её центр (O), радиус (R) и диаметр (D)
Окружность (C), её центр (O), радиус (R) и диаметр (D)Окру́жность — замкнутая плоская кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки[1]: эта точка называется центром окружности. Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом; радиусом называется также и длина этого отрезка. Окружность разбивает плоскость на две части[2] — конечную внутреннюю и бесконечную внешнюю. Внутренность окружности называется кругом; граничные точки (то есть саму окружность) в зависимости от подхода, круг может включать или не включать.
 Построение окружности циркулем
Построение окружности циркулемПрактическое построение окружности возможно с помощью циркуля.
Окружность нулевого радиуса (вырожденная окружность) является точкой, далее этот случай исключается из рассмотрения, если не оговорено иное.
Окружность называется единичной, если её радиус равен единице. Единичная окружность является одним из основных объектов тригонометрии.
Далее всюду буква R{\displaystyle R} обозначает радиус окружности.
Хорды, дуги и касательные[ | ]
ru-wiki.ru
Взаимное расположение двух окружностей / Метод координат / Справочник по геометрии 7-9 класс
Исследуем взаимное расположение двух окружностей в зависимости от их радиусов 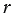 , и расстояния между их центрами . Пусть
, и расстояния между их центрами . Пусть 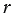
 .
.
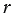 лежит внутри круга радиуса :
лежит внутри круга радиуса :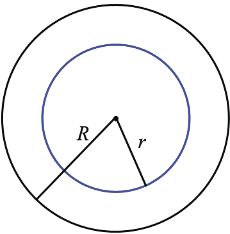
Пусть 0. Введём прямоугольную систему координат 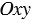 так, чтобы точка совпала с центром окружности радиуса , а точка 1 с координатами
так, чтобы точка совпала с центром окружности радиуса , а точка 1 с координатами 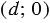 являлась центром второй окружности. Тогда в данной системе координат уравнения первой и второй окружностей имеют вид:
являлась центром второй окружности. Тогда в данной системе координат уравнения первой и второй окружностей имеют вид:
 ,
, 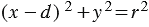 . (1)
. (1)
Если система уравнений (1) имеет решением пару чисел 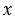
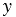 =
= 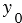 , то точка
, то точка  — общая точка данных окружностей, и обратно: если точка
— общая точка данных окружностей, и обратно: если точка  — общая точка данных окружностей, то пара чисел
— общая точка данных окружностей, то пара чисел 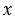 = ,
= , 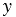 =
= 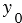 является решением системы уравнений (1):
является решением системы уравнений (1):Пусть система (1) имеет решением пару чисел 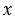 = ,
= , 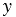
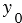 , т.е. справедливы числовые равенства
, т.е. справедливы числовые равенства ,
, 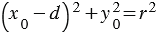 . (2)
. (2)
Вычтем второе равенство из первого, получим равенство 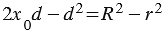 . Выражаем из данного равенства :
. Выражаем из данного равенства :
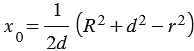 . (3)
. (3)
Так как 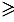
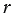 и 0, то 0. В то же время из первого равенства (2) следует, что
и 0, то 0. В то же время из первого равенства (2) следует, что  , т.е. для величин ,
, т.е. для величин , 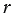
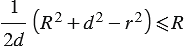 или
или  . Последнее неравенство запишем в виде
. Последнее неравенство запишем в виде  . Следовательно,
. Следовательно,  или
или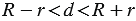 . (4)
. (4)
Отметим, что = , если = — 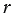 или = +
или = + 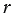 , и
, и 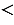 , если
, если 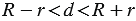 .
.
Итак, если система уравнений (1) имеет решение, то величина удовлетворяет неравенствам (4). Поэтому, если не выполнено какое-то из неравенств (4), то система (1) не имеет решений и данные окружности не имеют общих точек. Так может быть в двух случаях:
1. 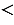 —
— 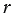 , т.е. +
, т.е. + 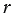
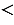 :
:
В этом случае окружность радиуса 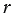 лежит внутри круга радиуса . Говорят также, что одна окружность лежит внутри другой.
лежит внутри круга радиуса . Говорят также, что одна окружность лежит внутри другой.
2. + 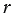 :
:
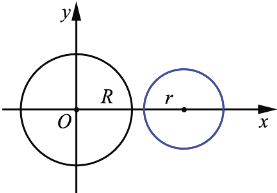
В этом случае говорят, что одна окружность лежит вне другой.
Если неравенства (4) выполнены, то возможны три случая:
3. = — 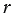 , при этом из того что 0 следует, что
, при этом из того что 0 следует, что 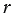 . Выше мы говорили, что =, поэтому из первого из равенств (2) следует, что
. Выше мы говорили, что =, поэтому из первого из равенств (2) следует, что 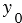 =0. Подставив пару чисел
=0. Подставив пару чисел 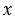 = ,
= , 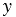 =0 в систему равенств (4), мы получим, что данные числа являются ее решением. Значит, в данном случае окружности имеют ровно одну общую точку:
=0 в систему равенств (4), мы получим, что данные числа являются ее решением. Значит, в данном случае окружности имеют ровно одну общую точку:
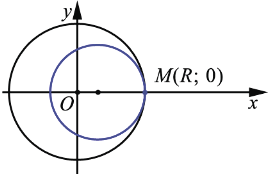
Говорят, что окружности касаются изнутри.
4. = + 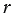 . В данном случае также =, поэтому
. В данном случае также =, поэтому 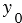 =0. Подставив пару чисел
=0. Подставив пару чисел 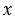 = ,
= , 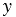 =0 в систему равенств (4), мы получим, что данные числа являются ее решением. В данном случае, как и в случае 3, окружности имеют одну общую точку, но расположены друг относительно друга иначе:
=0 в систему равенств (4), мы получим, что данные числа являются ее решением. В данном случае, как и в случае 3, окружности имеют одну общую точку, но расположены друг относительно друга иначе:
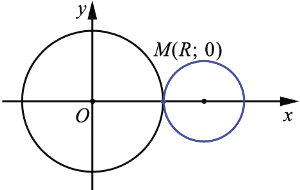
Говорят, что окружности касаются извне.
5. 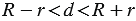 . Выше мы говорили, что число , которое определяется равенством (
. Выше мы говорили, что число , которое определяется равенством (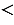 , поэтому из первого равенства (2) получаем два значения
, поэтому из первого равенства (2) получаем два значения 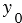 :
: 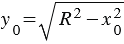 и
и 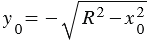 . То есть в данном случае система (1) имеет два решения:
. То есть в данном случае система (1) имеет два решения: 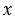 = ,
= , 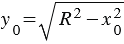 и
и 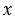 = ,
= , 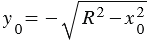 :
:
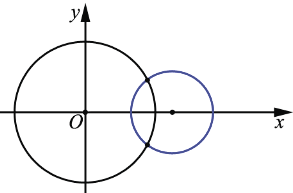
Следовательно, окружности пересекаются в двух точках.
Итак, если расстояние
между центрами двух окружностей отлично от нуля, то возможны пять случаев, описанных выше, взаимного расположения двух окружностей.budu5.com
Взаимное расположение двух окружностей
Прежде чем приступить к изучению нового материала, давайте вспомним,
каким уравнением задается окружность с центром в точке  и
радиусом r.
и
радиусом r.

Также вспомним уравнение окружности, центром которой является начало координат.

Запишем уравнения, которые задают произвольную прямую.
 ;
;
 ;
;
 – угловой коэффициент прямой.
– угловой коэффициент прямой.
Сегодня мы с вами посмотрим, как могут располагаться две окружности.
Сначала перечислим все возможные случаи взаимного расположения. Окружности могут не пересекаться. Центры окружностей могут совпадать, Окружности могут касаться друг друга, окружности могут пересекаться в двух точках.

Сначала рассмотрим случай, когда центры окружностей совпадают. Такие окружности называются концентрическими. Если радиусы окружностей не равны, то такие окружности образуют кольцо. Если радиусы окружностей равны, то окружности совпадают.

Теперь давайте рассмотрим случаи, когда центры окружностей не совпадают. Соединим их прямой d, которую назовем линией центров данной пары окружностей.
В данном случае взаимное расположение окружностей будет зависеть от
соотношения между величиной d и величинами радиусов
окружностей. Для того, чтобы было понятно о какой окружности идет речь, радиус
одной из окружностей обозначим за r, а радиус второй
окружности – за R. И будем считать, что  .
.
Если  ,
то очевидно, что окружности не пересекаются. В этом случае говорят, что одна
окружность лежит вне другой.
,
то очевидно, что окружности не пересекаются. В этом случае говорят, что одна
окружность лежит вне другой.

Если  ,
то тогда одна окружность лежит внутри другой, но они не пересекаются.
,
то тогда одна окружность лежит внутри другой, но они не пересекаются.

Если  ,
тогда малая окружность лежит внутри большой, но имеет с ней одну общую точку на
линии центров. Такой случай называют внутренним касанием, а такие
окружности называют внутренне касающимися.
,
тогда малая окружность лежит внутри большой, но имеет с ней одну общую точку на
линии центров. Такой случай называют внутренним касанием, а такие
окружности называют внутренне касающимися.

Если  ,
то окружности пересекаются в двух точках и называются пересекающимися.
,
то окружности пересекаются в двух точках и называются пересекающимися.

Если  ,
то такие окружности имеют одну общую точку, причем центр одной из них
расположен за пределами второй окружности. Такой вид касания называется внешним
касанием, а такие окружности называются внешне касающимися. Точка касания
внешне касающихся окружностей лежит на линии центров.
,
то такие окружности имеют одну общую точку, причем центр одной из них
расположен за пределами второй окружности. Такой вид касания называется внешним
касанием, а такие окружности называются внешне касающимися. Точка касания
внешне касающихся окружностей лежит на линии центров.

Решим несколько задач.
Задача. Как располагаются окружности, если:
а)  ;
б)
;
б)  ;
в)
;
в)  ;
;
г)  ;
д)
;
д)  .
.
Решение.
а) 
б) 
в) 
г) 
д) 

Рассмотрим еще одну задачу.
Задача. Наименьшее расстояние между точками двух
концентрических окружностей равно  ,
а наибольшее равно
,
а наибольшее равно  .
Найдите радиусы этих окружностей.
.
Найдите радиусы этих окружностей.
Решение.










Ответ:  .
.
Задача. Радиусы двух концентрических окружностей относятся как  .
Найти диаметры этих окружностей, если ширина кольца, образованного ими, равна
.
Найти диаметры этих окружностей, если ширина кольца, образованного ими, равна  см.
см.
Решение.


 (см)
(см)





Ответ:  .
.
Задача. Даны два круга – один внутри другого. Через их центры
проведен в большем круге диаметр, который делится окружностью меньшего круга на
три части, равные  .
Найти расстояние между центрами кругов.
.
Найти расстояние между центрами кругов.
Решение.

 ,
,
 ,
,
 .
.

Найдем радиусы окружностей.



Ответ:  .
.
Подведем итоги урока. Сегодня мы рассмотрели варианты расположения двух окружностей в пространстве в зависимости от соотношения расстояния между центрами окружностей и их радиусами.
videouroki.net
Взаимное расположение окружностей | Треугольники
Выясним, каким может быть взаимное расположение двух окружностей.
Две окружности могут пересекаться, не пересекаться либо касаться друг друга.
I. Пересекающиеся окружности имеют две общие точки.
Расстояние между центрами двух пересекающихся окружностей больше разности, но меньше суммы их радиусов:
II. Не пересекающиеся окружности не имеет общих точек.
Если одна окружность лежит внутри другой, то расстояние между центрами меньше разности их радиусов:
Если одна окружность находится вне другой, расстояние между центрами больше суммы их радиусов:
III. Касающиеся окружности имеют одну общую точку — точку касания.
При внешнем касании расстояние между центрами окружностей равно сумме их радиусов:
При внутреннем касании расстояние между центрами равно разности радиусов:
Концентрические окружности разного радиуса не пересекаются. Расстояние между центрами концентрических окружностей равно нулю: O1O2=0.
www.treugolniki.ru
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости | 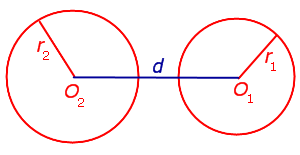 | Взаимное расположение на плоскости двух окружностей радиусов r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей d = O1O2 |
| Каждая из окружностей лежит вне другой | 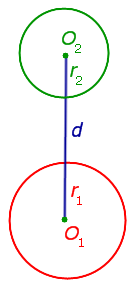 | Расстояние между центрами окружностей больше суммы их радиусов d > r1 + r2 |
| Внешнее касание двух окружностей |  | Расстояние между центрами окружностей равно сумме их радиусов d = r1 + r2 |
| Внутреннее касание двух окружностей |  | Расстояние между центрами окружностей равно разности их радиусов d = r1 – r2 |
| Окружности пересекаются в двух точках | 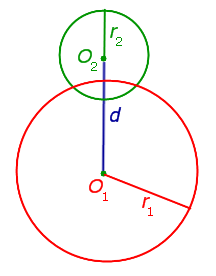 | Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 < d < r1 + r2 |
| Одна из окружностей лежит внутри другой |  | Расстояние между центрами окружностей меньше разности их радиусов d < r1 – r2 |
| Две окружности на плоскости | |
 | Взаимное расположение на плоскости двух окружностей радиусов r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей d = O1O2 |
| Каждая из окружностей лежит вне другой | |
 | Расстояние между центрами окружностей больше суммы их радиусов d > r1 + r2 |
| Внешнее касание двух окружностей | |
 | Расстояние между центрами окружностей равно сумме их радиусов d = r1 + r2 |
| Внутреннее касание двух окружностей | |
 | Расстояние между центрами окружностей равно разности их радиусов d = r1 – r2 |
| Окружности пересекаются в двух точках | |
 | Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 < d < r1 + r2 |
| Одна из окружностей лежит внутри другой | |
 | Расстояние между центрами окружностей меньше разности их радиусов d < r1 – r2 |
| Две окружности на плоскости |
  Взаимное расположение на плоскости двух окружностей радиусов r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей d = O1O2 |
| Каждая из окружностей лежит вне другой |
 Расстояние между центрами окружностей больше суммы их радиусов d > r1 + r2 |
| Внешнее касание двух окружностей |
 Расстояние между центрами окружностей равно сумме их радиусов d = r1 + r2 |
| Внутреннее касание двух окружностей |
 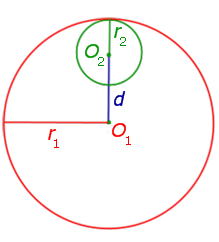 Расстояние между центрами окружностей равно разности их радиусов d = r1 – r2 |
| Окружности пересекаются в двух точках |
 Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 < d < r1 + r2 |
| Одна из окружностей лежит внутри другой |
 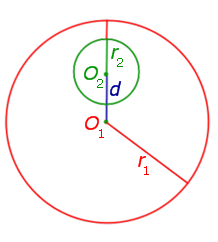 Расстояние между центрами окружностей меньше разности их радиусов d < r1 – r2 |
Общие касательные к двум окружностям
| Фигура | Рисунок | Свойства |
| Внешняя касательная к двум окружностям |  | Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой. |
| Внутренняя касательная к двум окружностям |  | Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой. |
| Внутреннее касание двух окружностей |  | Существует единственная общая внешняя касательная. Других общих касательных нет. |
| Окружности пересекаются в двух точках | 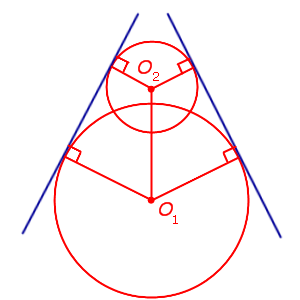 | Существуют две общих внешних касательных. Других общих касательных нет. |
| Внешнее касание двух окружностей |  | Существует единственная общая внутренняя касательная, а также |
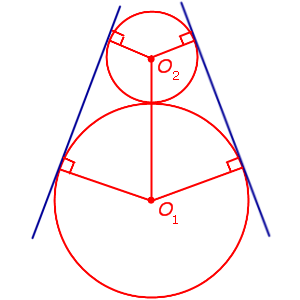 | ||
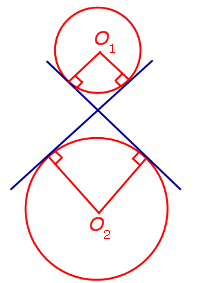
Каждая из окружностей лежит вне другой |
| Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет |
 |
Формулы для длин общих касательных и общей хорды двух окружностей
Доказательства формул для длин общих касательных и общей хорды двух окружностей
Утверждение 1. Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле
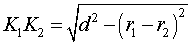
Доказательство. Для того, чтобы найти длину отрезка K1K2, опустим из точки O2 перпендикуляр O2K3 на прямую O1K1 (рис.1).


Рис.1
Поскольку четырёхугольник O2K2K1K3 – прямоугольник, то справедливы равенства
O2K3 = K1K2 , K1K3 = r2 , O1K3 = r1 – r2 .
Воспользовавшись этими равенствами, из прямоугольного треугольника O1O2K3 получаем:

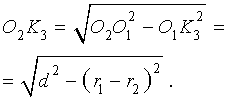
Следовательно,
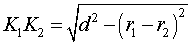
что и требовалось доказать.
Утверждение 2. Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d, то длина общей внутренней касательной к этим окружностям вычисляется по формуле

Доказательство. Для того, чтобы найти длину отрезка K1K2 , опустим из точки O2 перпендикуляр O2K3 на прямую O1K1 (рис.2).
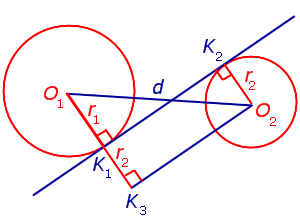
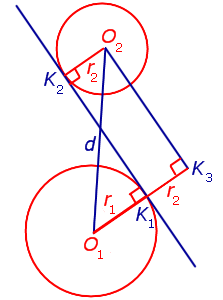
Рис.2
Поскольку четырёхугольник O2K2K1K3 – прямоугольник, то справедливы равенства
O2K3 = K1K3 , K1K3 = r2 , O1K3 = r1 + r2 .
Воспользовавшись этими равенствами, из прямоугольного треугольника O1O2K3 получаем:
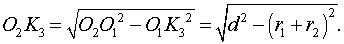

Следовательно,

что и требовалось доказать.
Утверждение 3. Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d, то длина общей хорды AB этих окружностей вычисляется по формуле
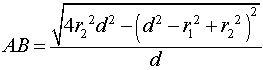
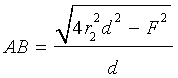
где
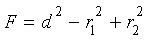
Доказательство. Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3,
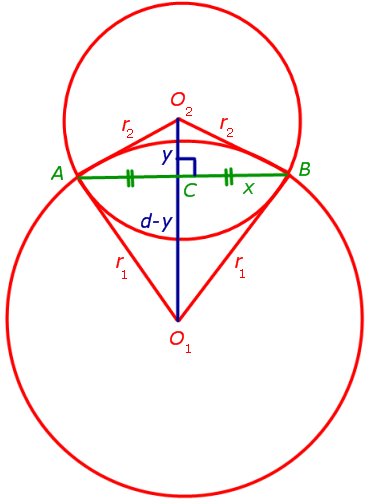
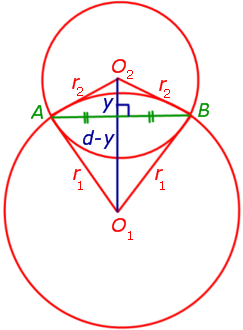
Рис.3
следующие обозначения:
O2C = y, CB = x .
Тогда, воспользовавшись теоремой Пифагора для треугольников O1CB и O2CB, получим
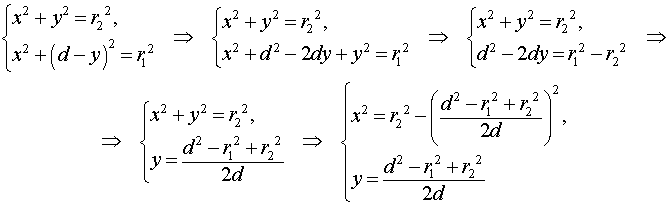
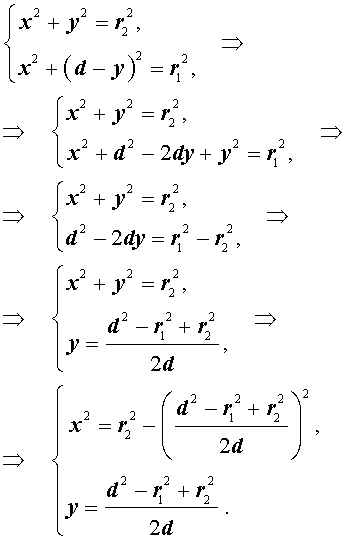
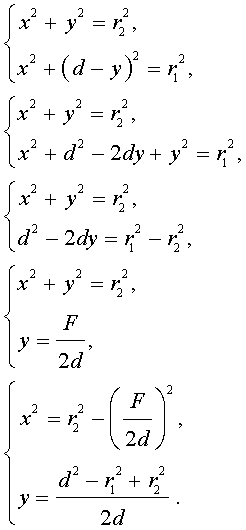
Поэтому
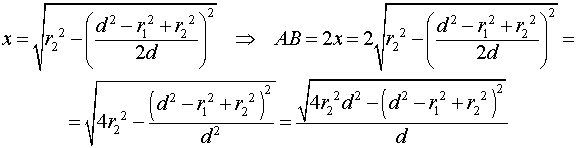

Таким образом, справедлива формула:
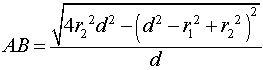
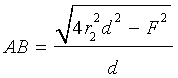
где
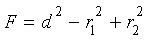
что и требовалось доказать.

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
www.resolventa.ru