Как обозначается подобие: «Как выглядит знак подобия в геометрии?» — Яндекс.Кью — Детская игровая комната «Волшебный лес»

Posted on 20.08.197429.01.2022 by alexxlab

Содержание

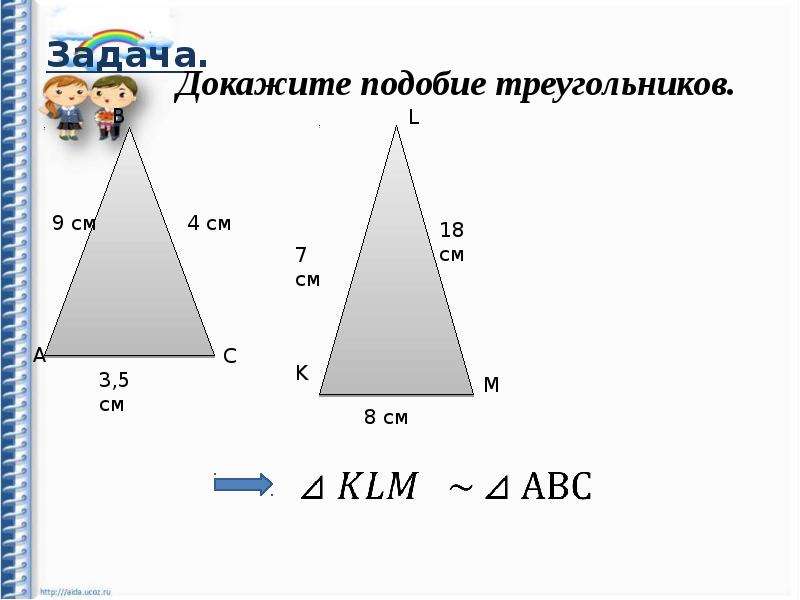
Подобные треугольники. Отношение площадей подобных треугольников 8 класс онлайн-подготовка на Ростелеком Лицей |

Подобные треугольники. Отношение площадей подобных треугольников.

При сравнении двух величин возникает вопрос: во сколько раз одна больше другой?

Например, во сколько раз собака пробежит быстрее некоторое расстояние, чем это же расстояние проползёт жук? Или какую часть всех деревьев парка составляют дубы?

Ответ в таких случаях дается в виде частного двух чисел, которое называют отношением. Отношение показывает, во сколько раз первое число больше второго, или какую часть первое число составляет от второго.

Отношением отрезков АВ и СD называется отношение их длин, т. е. ABCD (или AB:CD).

На рисунке отрезки AB и CD пропорциональны отрезкам A₁B₁ и C₁D₁, если AB:A₁B₁= CD:C₁D₁.

В геометрии фигуры одинаковой формы называют подобными.

Любые два квадрата и любые два круга являются подобными.

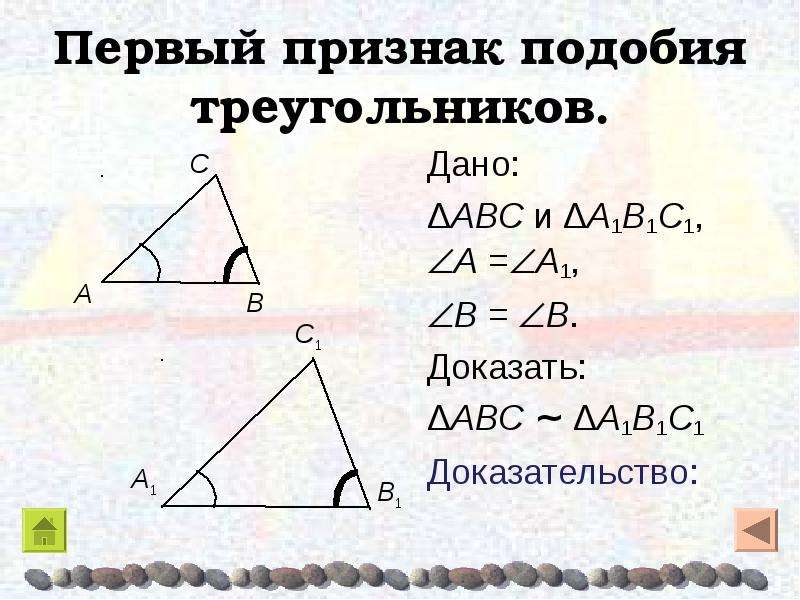
А какие два треугольника называют подобными? Возьмём два треугольника ABC и A₁B₁C₁, у которых угол А равен углу A₁, угол B равен углу B₁, а угол C равен углу C₁.

Тогда стороны AB и A₁B₁, BC и B₁C₁, AC и A₁C₁ называются сходственными. И если эти сходственные стороны пропорциональны, то есть AB:A₁B₁= BC:B₁C₁= AC:A₁C₁, то треугольники ABC и A₁B₁C₁ являются подобными. Подобие треугольников обозначается следующим образом ⊿ABC∼⊿A1B1C1.

Подобными называются треугольники, у которых углы соответственно равны, а сходственные стороны пропорциональны.

Отношение сходственных сторон называют

коэффициентом подобия.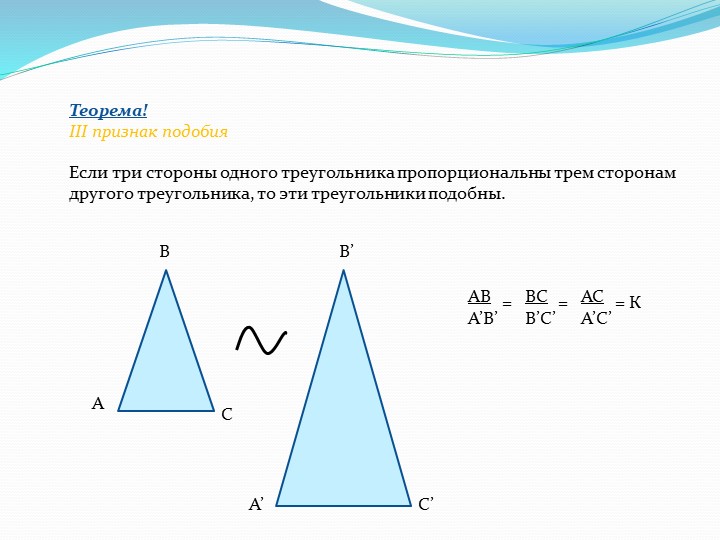

Если стороны треугольника ABC в два раза больше сторон треугольника A₁B₁C₁, то отношение сходственных сторон равно 2, то есть коэффициент подобия равен 2.

Подобие треугольников можно установить, проверив только некоторые из равенств:

AB:A₁B₁= BC:B₁C₁= AC:A₁C₁= 2, то есть k=2.

Теорема. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Дано: ⊿ABC∼⊿A1B1C1, k — коэффициент подобия.

Найти: отношение площадей ABC и A₁B₁C₁

Решение:

Обозначим S_ABC_{= S, S_A₁_B₁_C₁= S₁.}

∠A = ∠A₁

, значит, SS1=AB∙ACA1B1∙A1C1 (площади треугольников, имеющих равный угол, относятся как произведения сторон, содержащих этот угол).

ABA1B1=k

ACA1C1=k

Следовательно, SS1=k2.

Задача. Площади подобных треугольников АВС и А₁В₁С₁ равны соответственно 20 см² и 5 см². Сторона А₁В₁= 2 см. Найдите сходственную ей сторону АВ треугольника АВС.

Выше мы доказали, что отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

SS1=k2, значит, 205=k2, следовательно k=2.

k=ABA1B1=2, значит, AB=2∙A1B1=2∙4=8 см.

Ответ: 8 см.

Определение подобных треугольников / Подобные треугольники / Справочник по геометрии 7-9 класс

Главная
Справочники
Справочник по геометрии 7-9 класс
Подобные треугольники
Определение подобных треугольников

Пусть у АВС и А₁В₁С₁ углы соответственно равны: А =А₁, В =В₁, С =С₁.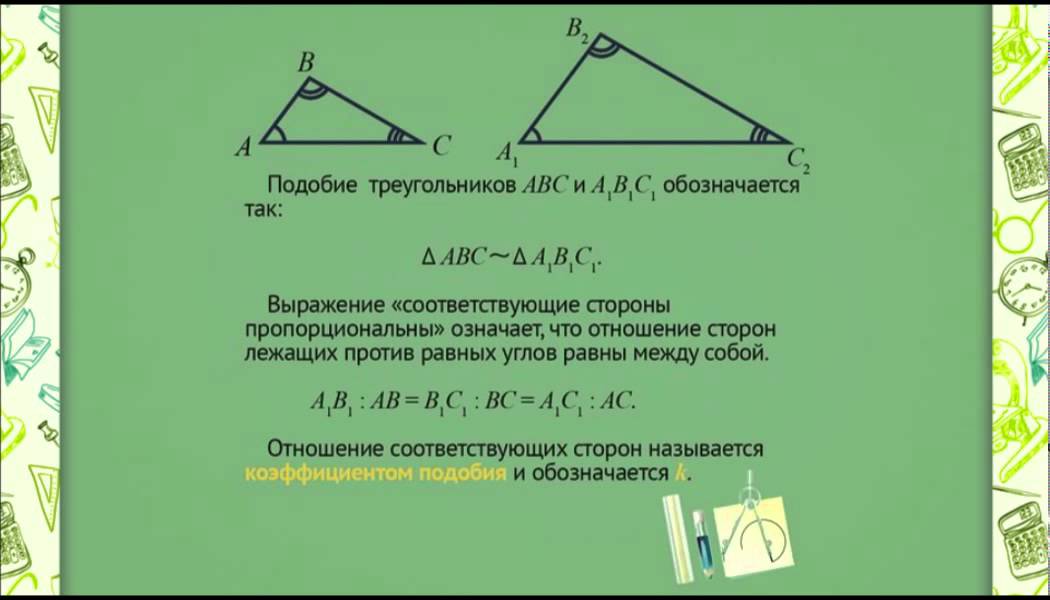 Тогда стороны АВ и А₁В₁, ВС и В₁С₁, СА и С₁А₁называются сходственными (Рис.1).

Определение

Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника .

Треугольники АВС и А₁В₁С₁ будут подобны, если

А =А₁, В =В₁, С =С₁, (1)

. (2)

Число , равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.

Подобие треугольников обозначают специальным символом — . На рисунке 1 треугольники АВС

и А₁В₁С₁ подобны, значит, можно записать:

АВСА₁В₁С₁.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Пропорциональные отрезки

Отношение площадей подобных треугольников

Первый признак подобия треугольников

Второй признак подобия треугольников

Третий признак подобия треугольников

Средняя линия треугольника

Пропорциональные отрезки в прямоугольном треугольнике

Практические приложения подобия треугольников

О подобии произвольных фигур

Синус, косинус и тангенс острого угла прямоугольного треугольника

Значение синуса, косинуса и тангенса для углов 30, 45 и 60

Подобные треугольники

Правило встречается в следующих упражнениях:

7 класс

Задание 543, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 546, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 549, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 559, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 582, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 586, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 856, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 871, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 872, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1117, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Пользовательское соглашение

Презентация по математике «Подобие фигур»

Подобие фигур

Пример из жизни

На рисунке изображен колодец «журавль». Короткое плечо имеет длину 2 метра, а длинное плечо – 4 метра. На сколько метров опустится ведро, когда конец короткого плеча поднимется на 1, 5 метра?

Разделы

Преобразование подобия
Подобные фигуры и их свойства
Признак подобия треугольников по двум углам
Признак подобия треугольников по двум сторонам и углу между ними
Признак подобия треугольников по трем сторонам
Подобие прямоугольных треугольников

Преобразование подобия

Преобразование одной фигуры в другую называется преобразованием подобия , если при этом преобразовании расстояние между точками изменится в одно и то же число раз

Свойства преобразования подобия

Проверь себя

Иллюстрация определения

Задание 1

Задание 2

8см

32 см

Пример преобразования подобия

5 см

Расстояние между соответствующими точками изменилось в 4 раза, значит, фигуры были подвергнуты преобразованию подобия

20 см

Свойства преобразования подобия

Свойство 1:

Преобразование подобия переводит прямые в прямые, полупрямые в полупрямые, отрезки в отрезки;

Свойство 2:

Преобразование подобия сохраняет углы между полупрямыми

Задание 1

Квадрат F1 был подвергнут некоторому преобразованию. В результате была получена фигура F2. Будет ли данное преобразование являться преобразованием подобия? Свой ответ обоснуйте.

F 2

F 1

3 м

2 м

Задание 2

У подобных треугольников АВС и А 1 В 1 С 1 ∠А=30°, АВ=1 м, ВС=2м, В 1 С 1 = 3м. Чему равны

∠ А 1 и сторона А 1 В 1 ?

А 1

В 1

1 м

30°

С 1

Проверь себя

Что такое преобразование подобия?

Какие свойства преобразования подобия ты знаешь?

Что такое коэффициент подобия?

Подобные фигур

Две фигуры называются подобными , если они переводятся друг в друга преобразованием подобия

Свойства подобных фигур

Иллюстрация определения

Проверь себя

Задание 1

Задание 2

5см

15см

6 см

18 см

Подобные фигуры

Расстояние между соответствующими точками изменилось в одно и то же число раз, значит, треугольники были подвергнуты преобразованию подобия, следовательно треугольники подобны:

∆ АВС ∾ ∆А 1 В 1 С 1

число 3 – коэффициент подобия

∾ — знак подобия фигур

А 1

4см

В 1

С 1

12см

Свойства подобных фигур

Если фигура А подобна фигуре В, а фигура В подобна фигуре С, то фигуры А и С подобны;

У подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны.

Пример 1

Пример 2

Пример 1

Квадрат А ∾ квадрату В, а квадрат В ∾ квадрату С

квадрат А ∾ квадрату С

3 см

2 см

5 см

Пример 2

∆ АВС ∾ ∆КМН

∠ А=∠ К, ∠В=∠М, ∠С=∠Н

и АВ:КМ=ВС:МН=АС:КН

Против равных углов лежат пропорциональные стороны

Задание 1

Дано : ∆АРЕ ∾ ∆НРО

Определите:

пары равных соответственных углов;

Составьте:

отношение

соответствующих сторон

6 см

7 см

Задание 2

Дано : ∆АВС ∾ ∆МРН

АВ:МН=2

Найти : х, у, z

8 см

Проверь себя

Какие фигуры называются подобными?

Каким знаком обозначается подобие фигур?

Как записывается подобие треугольников?

Признак подобия треугольников по двум углам( I признак подобия)

Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны

Иллюстрация

Проверь себя

I признака

Задание 1

Задание 3

Задание 2

I признак подобия треугольников

Если ∠А= ∠М и ∠В= ∠Р, то

∆ АВС ∾ ∆ МРН

Задание 1

Докажите подобие треугольников

35°

65°

35°

80°

Задание 2

Докажите подобие треугольников и запишите равенство отношений соответствующих сторон.

Задание 3

Дано: АМРТ — трапеция

МО=4см, ТО=12 см, ТА=24 см

Найти:

длину меньшего основания трапеции

Проверь себя

Какие условия должны выполняться для подобия треугольников по первому признаку?

Будут ли подобны треугольники, если:

∆ АВС: ∠А=65°, ∠В=80°, ∠С=35°

∆ А 1 В 1 С 1: ∠А 1 =35°, ∠В 1 =55°?

Признак подобия треугольников по двум сторонам и углу между ними (II признак подобия)

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны , то треугольники подобны

Иллюстрация

Проверь себя

II признака

Задание 1

Задание 2

Задание 3

II признак подобия треугольников

Если ∠В= ∠В 1 и ВА:В 1 А 1 =ВС:В 1 С 1

В 1

∆ АВС ∾ ∆А 1 В 1 С 1

А 1

С 1

4 см

3,5 см

8 см

7 см

Задание 1

Определите, будут ли треугольники подобны по второму признаку

40°

В 1

40°

А 1

С 1

5 см

10 см

10см

Задание 2

Докажите подобие треугольников по второму признаку и определите коэффициент подобия

40°

В 1

70°

А 1

С 1

Задание 3

АО=2 см, ОС=5см, ЕО=4см, МО=10 см, АС=6 см

Найти: длину МЕ

Проверь себя

Перечисли условия для подобия треугольников по второму признаку.

Дополни условие так, чтобы треугольники были подобны по второму признаку:

∆ АВС: АВ=16 см, СА=20, ∠С=35°

∆ А 1 В 1 С 1: А 1 В 1 =4 см, ∠С 1 =35°, С 1 А 1 = …

Признак подобия треугольников по трем сторонам (III признак подобия)

Если стороны одного треугольника пропорциональны сторонам другого треугольника , то такие треугольники подобны

Иллюстрация III признака

Задание 1

Задание 2

Задание 3

Проверь себя

III признак подобия треугольников

∆ АВС ∾ ∆ А 1 В 1 С 1

А 1

С 1

В 1

Задание 1

Подобны ли два равносторонних треугольника?

10 см

20 см

Задание 2

Подобны ли треугольники АВС и МРК, если:

АВ=1 м, АС=2 м, ВС= 1,5 м и
АВ=1 м, АС=2 м, ВС= 1,5 м и

МР=8м, МК=16 м, РК=12 м;

АВ=1 м, АС=2 м, ВС= 1,25 м и
АВ=1 м, АС=2 м, ВС= 1,25 м и

МР=10м, МК=20 м, РК=13 м;

16 м

Задание 3

Стороны треугольника равны 8 м, 16 м и 2 м. Найдите стороны подобного ему треугольника, периметр которого равен 55 м.

2 м

Р=55 м

8 м

Проверь себя

Сформулируй условие, при котором треугольники будут подобны по III признаку подобия.

Измени условие так, чтобы треугольники были подобны по III признаку:

∆ АВС : АВ=12 см, ВС=15 см, АС=18 см

∆ А 1 В 1 С 1 : А 1 В 1 =24 см, С 1 А 1 =45 см, В 1 С 1 = 30 см

Подобие прямоугольных треугольников

Для подобия прямоугольных треугольников достаточно, чтобы у них было по одному острому углу

Иллюстрация признака подобия

Проверь себя

Задание 1

Задание 2

Задание 3

Подобие прямоугольных треугольников

Если треугольники прямоугольные и

∠ С= ∠С 1

В 1

∆ АВС ∾ ∆ А 1 В 1 С 1

А 1

С 1

Задание 1

Найди пары подобных треугольников и докажи их подобие

Задание 2

В треугольнике МНК известны длины катетов МН=4 см и КН=3 см, а в треугольнике МСО – длина катета СО, равная 9 см. Найдите длину катета МС треугольника МСО.

Задание 3

Дано: АВМН – прямоугольник

АК=8 см, АН= см

Найти: ВН, АВ

Проверь себя

Назовите условие, при котором прямоугольные треугольники подобны.

Будут ли подобны прямоугольные треугольники, если у одного острый угол равен 40°, а у другого – 50 °?

Подобие треугольников. Часть 1

Определение и свойства подобных треугольников

Числа a₁, a₂, a₃, …, a_n называются пропорциональными числам b₁, b₂, b₃, …, b_n, если выполняется равенство: a₁/b₁ = а₂/b₂ = a₃/b₃ = … = a_n/b_n = k, где k – некоторое число, которое называют коэффициентом пропорциональности.

Пример. Числа 6; 7,5 и 15 пропорциональны числам ‑4; 5 и 10. Коэффициентом пропорциональности является число ‑1,5, поскольку

6/-4 = -7,5/5 = 15/-10 = -1,5.

Пропорциональность чисел имеет место быть, если эти числа связаны пропорцией.

Известно, что пропорцию можно составить не менее чем из четырех чисел, поэтому понятие пропорциональности применимо как минимум к четырем числам (одна пара чисел пропорциональна другой паре, или одна тройка чисел пропорциональна другой тройке, и т.д.).

Рассмотрим на рис. 1 два треугольника АВС и А₁В₁С₁ с равными попарно углами: A = A₁, B = B₁, C = C₁.

Стороны, которые противолежат равным парам углов обоих треугольников, называются сходственными. Так, на рис. 1 стороны AB и A₁B₁, AC и A₁C₁, BC и B₁C₁, сходственные, поскольку лежат напротив соответственно равных углов треугольников ABC и A₁B₁C₁.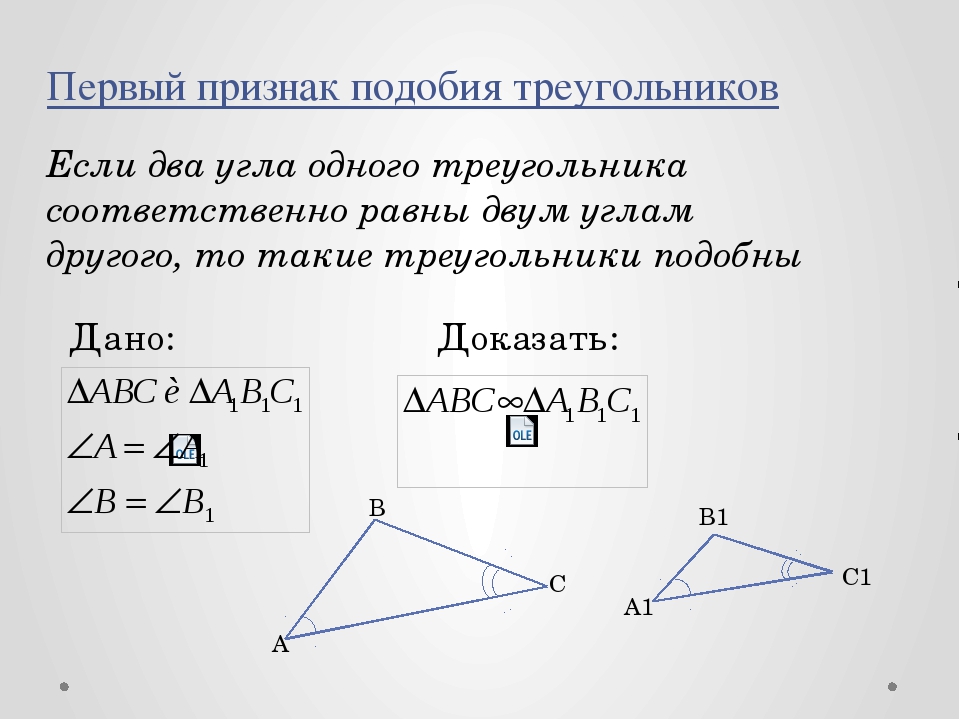

Дадим определение подобных треугольников:

Два треугольника называются подобными, если их углы попарно равны, а сходственные стороны пропорциональны.

Отношение сходственных сторон подобных треугольников называется коэффициентом подобия.

Подобные треугольники обозначаются следующим образом: Δ ABC ~ Δ A₁B₁C₁.

Итак, на рис. 2 имеем: Δ ABC ~ Δ A₁B₁C₁

углы A = A₁, B = B₁, C = C₁ и AB/A₁B₁ = ВC/В₁C₁ = АС/А₁С₁ = k, где k – коэффициент подобия. Из рис. 2 видно, что у подобных треугольников одинаковые пропорции, и отличаются они лишь масштабом.

Замечание 1: Равные треугольники подобны с коэффициентом 1.

Замечание 2: При обозначении подобных треугольников следует упорядочить их вершины таким образом, чтобы углы при них были попарно равны. Например, для треугольников, изображенных на рисунке 2 говорить, что Δ ABC ~ Δ B₁C₁A₁некорректно. Соблюдая правильный порядок вершин, удобно выписывать пропорцию, связывающую сходственные стороны треугольников, не обращаясь к чертежу: в числителе и знаменателе соответствующих отношений должны стоять пары вершин, занимающих одинаковые позиции в обозначении подобных треугольников. К примеру, из записи «Δ ABC ~ Δ KNL» следует, что углы A = K, B = N, C = L, и АВ/KN = BC/NL = AC/KL.

Замечание 3: Те требования, которые перечислены в определении подобных треугольников, являются избыточными. Признаки подобия треугольников, которые содержат меньше требований к подобным треугольникам докажем чуть позже.

Сформулируем свойства подобных треугольников:

Отношение соответственных линейных элементов подобных треугольников равно коэффициенту их подобия. К таким элементам подобных треугольников относятся те, которые измеряются в единицах длины. Это, например, сторона треугольника, периметр, медиана. Угол или площадь к таким элементам не относятся.
Отношение площадей подобных треугольников равно квадрату коэффициента их подобия.

Пусть треугольники ABC и A₁B₁C₁ подобны с коэффициентом k (рис. 2).

Докажем, что S_ABC/S_A1_B1_C1 = k².

Поскольку углы подобных треугольников попарно равны, т.е A = A₁, и по теореме об отношении площадей треугольников, имеющих по равному углу, имеем:

S_ABC/S_A1_B1_C1 = (AB · AC) / (A₁B₁ · A₁C₁) = AB/A₁B₁ · AC/A₁C₁.

В силу подобия треугольников AB/A₁B₁= k и AC/A₁C₁= k,

поэтому S_ABC/S_A1_B1_C1 = AB/A₁B₁ · AC/A₁C₁= k · k = k².

Замечание: Сформулированные выше свойства подобных треугольников справедливы и для произвольных фигур.

Признаки подобия треугольников

Требования, которые предъявляются к подобным треугольникам определением (это равенство углов и пропорциональность сторон) являются избыточными. Устанавливать подобие треугольников можно и по меньшему количеству элементов.

Так, при решении задач чаще всего используется первый признак подобия треугольников, утверждающий, что для подобия двух треугольников достаточно равенства их углов:

Первый признак подобия треугольников (по двум углам): Если два угла одного треугольника соответственно равны двум углам второго треугольника, то эти треугольники подобны (рис. 3).

Пусть даны треугольники Δ ABC, Δ A₁B₁C₁, в которых углы A = A₁, B = B₁. Необходимо доказать, что Δ ABC ~ Δ A₁B₁C₁.

Доказательство.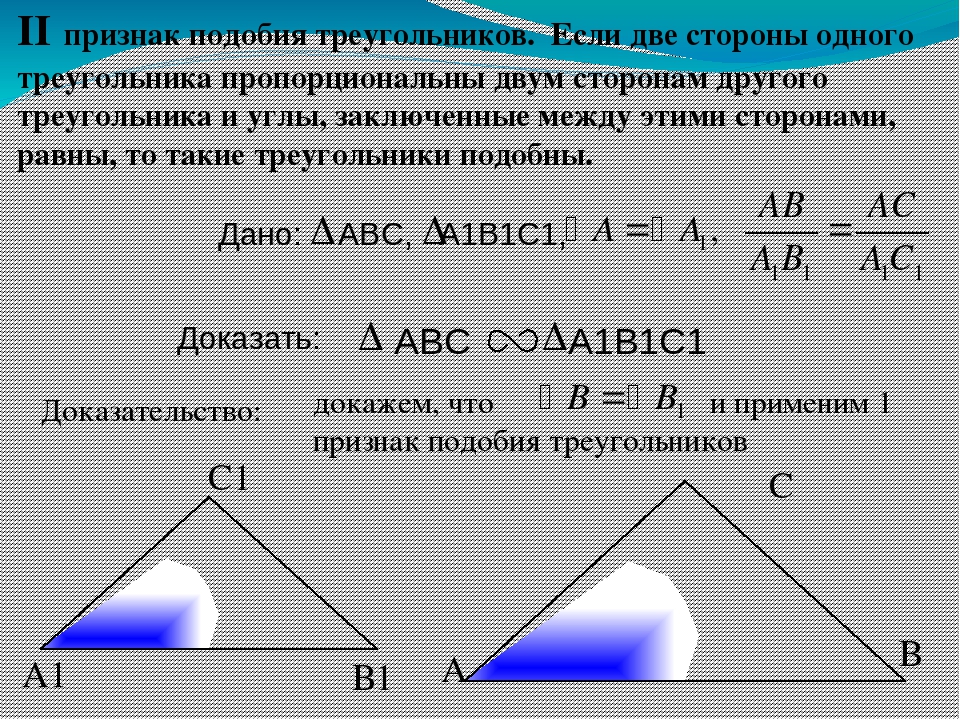

1) По теореме о сумме углов треугольника имеем:

угол C = 180^° (угол A + угол B) = 180° (угол A₁ + угол B₁) = угол C₁.

2) По теореме об отношении площадей треугольников, имеющих по равному углу,

S_ABC/S_A1_B1_C1 = (AB · AC) / (A₁B₁ · A₁C₁) = (AB · ВC) / (A₁B₁ · В₁C₁) = (AС · ВC) / (A₁С₁· В₁C₁).

3) Из равенства (AB · AC) / (A₁B₁ · A₁C₁) = (AB · ВC) / (A₁B₁ · В₁C₁) следует, что AC/A₁C₁ = BС/В₁С₁.

4) Из равенства (AB · ВC) / (A₁B₁ · В₁C₁) = (AС · ВC) / (A₁С₁ · В₁C₁) следует, что AВ/A₁В₁= АС/А₁С₁.

Таким образом, у треугольников ABCи A₁B₁C₁ DA = DA₁, DB = DB₁, DC = DC₁, и AB/A₁B₁ = АС/А₁С₁.

5) AB/A₁B₁ = АС/А₁С₁ = ВC/В₁C₁, то есть сходственные стороны пропорциональны. А значит, Δ ABC ~ Δ A₁B₁C₁ по определению.

Теорема о пропорциональных отрезках. Деление отрезка в заданном отношении

Теорема о пропорциональных отрезках является обобщением теоремы Фалеса.

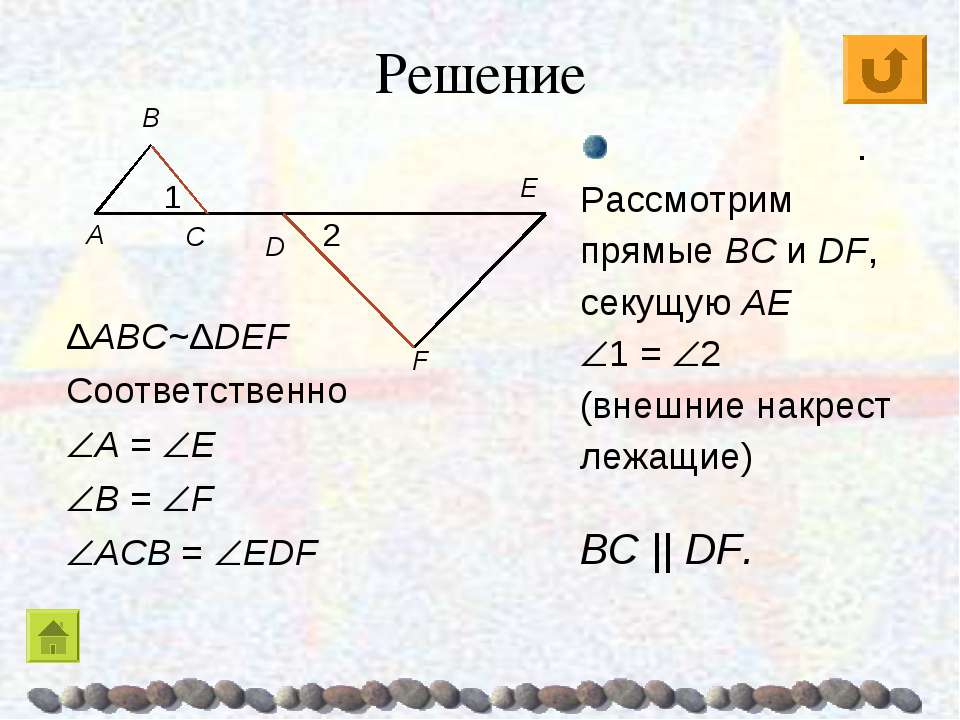
Для использования теоремы Фалеса необходимо, чтобы параллельные прямые, пересекающие две данные прямые, отсекали на одной из них равные отрезки. Обобщенная же теорема Фалеса утверждает, что если параллельные прямые пересекают две данные прямые, то отрезки, отсекаемые ими на одной прямой, пропорциональны отрезкам, отсекаемым на второй прямой.

Теорема о пропорциональных отрезках доказывается аналогично теореме Фалеса (только вместо равенства треугольников здесь используется их подобие).

Теорема о пропорциональных отрезках (обобщенная теорема Фалеса): Параллельные прямые, пересекающие две данные прямые, отсекают на них пропорциональные отрезки.

Свойство медиан треугольника

Первый признак подобия треугольников позволяет доказать свойство медиан треугольника:

Свойство медиан треугольника: Медианы треугольника пересекаются в одной точке, и делятся этой точкой в отношении 2 : 1, считая от вершины (рис. 4).

Точка пересечения медиан называется центроидом треугольника.

Пусть дан Δ ABC, у которого AA₁, BB₁, CC₁ – медианы, кроме того, AA₁∩CC₁ = O. Необходимо доказать, что BB₁∩ CC₁ = O и АО/ОА₁ = ВО/ОВ₁ = СО/ОС₁ = 2.

Доказательство.

1) Проведем среднюю линию A₁C₁. По теореме о средней линии треугольника A₁C₁ || AC, и A₁C₁ = AC/2.

2) Треугольники AOC и A₁OC₁ подобны по двум углам (угол AOC = углу A₁OC₁ как вертикальные, угол OAC = углу OA₁C₁ как внутренние накрест лежащие при A₁C₁|| AC и секущей AA₁), следовательно, по определению подобных треугольников АО/А₁О = ОС/ОС₁ = АС/А₁С₁= 2.

3) Пусть BB₁∩CC₁ = O₁. Аналогично пунктам 1 и 2 можно доказать, что ВО/О₁В₁= СО₁/О₁С = 2. Но поскольку на отрезке СС₁ существует единственная точка О, делящая его в отношении СО : ОС₁ = 2 : 1, то точки О и О₁ совпадают. Значит, все медианы треугольника пересекаются в одной точке, делящей каждую из них в отношении 2 : 1, считая от вершины.

В курсе геометрии в теме «площади многоугольников» доказывается тот факт, что медиана разбивает произвольный треугольник на две равновеликие части. Кроме того, при пересечении трех медиан треугольника образуется шесть равновеликих треугольников.

Остались вопросы? Не знаете, как решать задачи на подобие треугольников?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

Контрольные вопросы по геометрии для повторения теоретического материала

geo.docx

Тема: «Отрезок. Луч. Угол»

1. Объясните, что такое отрезок с концами А и В. Как он обозначается?
2. Какие отрезки называются равными?
3. Объясните, как сравнить два отрезка.
4. Какая точка называется серединой отрезка?
5. Объясните, что такое луч. Как обозначаются лучи? Какие лучи называются дополнительными?
6. Какая фигура называется углом? Объясните, что такое вершины и стороны угла. Как обозначается угол?
7. Какой угол называется развернутым?
8. Какие углы считаются равными?
9. Объясните, как сравнить два угла?
10. Какой луч называется биссектрисой угла?
11. Точка С делит отрезок АВ на два отрезка. Как найти длину отрезка АВ, если известные длины отрезков АС и СВ?
12. Что такое градусная мера?
13. Луч ОС делит угол АОВ на два угла. Как найти градусную меру углов АОВ, если известны градусные меры углов АОС и СОВ?
14. Какой угол называется острым? Прямым? Тупым?
15. Какие углы называются смежными?
16. Докажите, что сумма смежных углов равна 180о.
17. Какие углы называются вертикальными? Докажите, что вертикальные углы равны.
18. Какие углы называются перпендикулярными? Что называется серединным перпендикуляром к отрезку?
19. Объясните, какой отрезок называется перпендикуляром, проведенным из данной точке к данной прямой.
20. Сформулируйте теорему о перпендикуляре, проведенном из данной точки к данной прямой.

Тема: « Треугольники»

1. Какая фигура называется треугольником? Начертите треугольник и покажите его стороны, вершины и углы. Что такое периметр треугольника?
2. Какой угол называется внешним углом треугольника?
3. Какой отрезок называется биссектрисой треугольника?
4. Какой отрезок называется медианой треугольника? Сколько медиан имеет треугольник?
5. Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник?
6. Какой треугольник называется остроугольный? Какой треугольник называется тупоугольным?
7. Какой треугольник называется прямоугольным? Как называются стороны прямоугольного треугольника?
8. Какой треугольник называется равнобедренным? Как называются его стороны?
9. Какой треугольник называется равносторонним?
10. Какие треугольники называются равными?
11. Сформулируйте и докажите первый признак равенства треугольников.
12. Сформулируйте второй признак равенства треугольников.
13. Сформулируйте теорему о сумме двух внутренних углов треугольника.
14. Сформулируйте теорему о соотношении внешнего угла треугольника с его внутренним углом, не смежным с этим внешним.
15. Докажите, что углы при основании равнобедренного треугольника равны.
16. Сформулируйте теорему о биссектрисе равнобедренного треугольника, проведенной к основанию.
17. Сформулируйте третий признак равенства треугольников.

Тема: «Основные геометрические построения»

1. Какая геометрическая фигура называется окружностью? Что называется радиусом окружности?
2. Что такое секущая, хорда окружности? Какая хорда называется диаметром?
3. Объясните, как построить треугольник по трём сторонам?
4. Объясните, как отложить от данного луча угол, равный данному углу.
5. Объясните, как построить биссектрису данного угла.
6. Объясните, как провести серединный перпендикуляр к данному отрезку.
7. Объясните, как разделить данный отрезок пополам.
8. Объясните, как через данную точку провести прямую, перпендикулярную прямую данной прямой.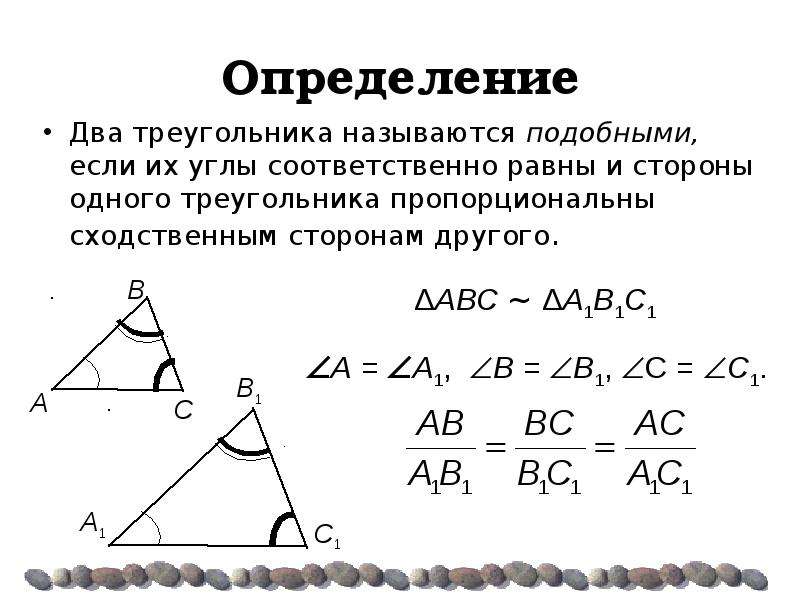

Тема: «Параллельные прямые»

1. Какие прямые называются параллельными?
2. Что такое секущая по отношению к двум прямым?
3. Какие углы называются накрест лежащими?
4. Какие углы называются соответственными?
5. Объясните, какие углы называются односторонними.
6. Сформулируйте признаки параллельности прямых.
7. Каково взаимное расположение двух прямых, перпендикулярных
Одной и той же прямой?
8. Сформулируйте аксиому о параллельных прямых.
9. Можно ли утверждать, что две различные прямые, параллельные
третьей, параллельны между собой?
10. Сформулируйте теорему об углах, образованных двумя параллельными прямыми секущей.

Тема: «Сумма углов треугольника»

1. Докажите теорему о сумме углов треугольника.
2. Чему равна сумма острых углов прямоугольного треугольника?
3. Чему равен каждый острый угол равнобедренного прямоугольного треугольника?
4. Чему равны углы равностороннего треугольника?
5. Какими могут быть углы в любом треугольнике?
6. Докажите, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
7. Докажите, что в треугольнике против большей стороны лежит больший угол. Сформулируйте обратную теорему.
8. Сформулируйте признак равнобедренного треугольника
9. Что такое равенство треугольников?
10. Что называется расстоянием от точки до прямой?
11. Сформулируйте два признака равенства прямоугольных треугольников, непосредственно следующих из первого и второго признаков равенства треугольников.
12. Докажите признак равенства прямоугольных треугольников по гипотенузе и острому углу.
13. Сформулируйте признак равенства прямоугольных треугольных треугольников по гипотенузе и катету.

Тема: «Четырехугольники»

1. Какая фигура называется четырехугольником?
2. Какие вершины четырехугольника называются соседними, какие противолежащими?
3. Что такое диагонали четырехугольника?
4. Какие стороны четырехугольника называются смежными? Какие называются противоположными?
5. Что такое параллелограмм?
6. Сформулируйте и докажите свойство сторон и углов параллелограмма.
7. Что называется расстоянием между параллельными прямыми?
8. Сформулируйте свойства параллелограмма.
9. Сформулируйте признаки параллелограмма.
10. Какой параллелограмм называется прямоугольником?
11. Докажите, что диагонали прямоугольника равны.
12. Сформулируйте признак прямоугольника .
13. Какой параллелограмм называется ромбом? Докажите, что диагонали ромба взаимно перпендикулярны и делят углы пополам.
14. Какой прямоугольник называется квадратом? Сформулируйте основные свойства квадрата.
15. Сформулируйте и докажите теорему Фалеса.
16. Какой отрезок называется средней линией треугольника?
Сформулируйте теорему о средней линии треугольника.
17. Какой четырёхугольник называется трапецией?
18. Как называются стороны трапеции?
19. Какая трапеция называется равнобедренной, какая – прямоугольной?
20. Какой отрезок называется средней линией трапеции?
Сформулируйте теорему о средней линии трапеции.
21. Какие две точки называются симметричными относительно данной точки?
22. Какая фигура называется симметричной относительно данной точки?
23. Какие две точки называются симметричными относительно данной прямой?
24. Какая фигура называется симметричной относительно данной прямой? Приведите примеры фигур, обладающих: а) центральной симметрией; б) осевой симметрией; в) и центральной и осевой симметрией.
25. Что называется отношением двух отрезков? В каком случае отрезки AB и CD пропорциональны отрезкам A1 B1 и C1 D1?

Тема: «Тригонометрические функции острого угла. Теорема Пифагора»

1. Что называется косинусом, синусом и тангенсом острого угла прямоугольного треугольника?
2. Сформулируйте и докажите теорему Пифагора.
3. Приведите основные тригонометрические тождества.
4. Чему равны значения синуса, косинуса и тангенса для углов 30о, 45о, 60о?
5. Как выражается катет прямоугольного треугольника через гипотенузу и острый угол?
6. Как выражается катет прямоугольного треугольника через другой катет и острый угол?
7. В чем состоит решение прямоугольного треугольника?
8. Каковы основные случаи решения прямоугольного треугольника?

Тема: «Прямоугольные координаты»

1. Что называется координатной осью?
2. Что называется координатной точки, лежащей на оси Ох?
3. Объясните, как вводится прямоугольная система координат на плоскости.
4. Приведите формулу для вычисления расстояния между двумя точками по их координатам.
5. Напишите формулы координат середины отрезка.
6. Дайте определение синуса, косинуса и тангенса для любого угла от 0 до 180о.
7. Докажите, что для любого угла α, 00

Тема: «Векторы»

1. Что называется вектором?
2. Что называется абсолютной величиной вектора?
3. Какой вектор называется единичным?
4. Какой вектор называется нулевым?
5. Какие векторы называются коллинеарными?
6. Дайте определение равных векторов.
7. Какие векторы называются противоположными?
8. Какой вектор называется суммой двух векторов ?
9. Какой вектор называется разностью двух векторов?
10. Какой вектор называется произведением данного вектора и данного действительного числа?
11. В чем состоит разложение вектора по осям Оx и Оy?
12. Что называется координатами вектора?
13. Сформулируйте правила нахождения координат суммы и разности вектора, а также произведения вектора на число по заданным координатам векторов.
14. Что такое скалярное произведение двух векторов?
15. Как определяется угол между векторами? Чему равно скалярное произведение двух векторов?

Тема: «Подобие»

1. Какие треугольники называются подобными?
2. Сформулируйте и докажите первый признак подобия треугольников.
3. Сформулируйте второй признак подобия треугольников.
4. Сформулируйте третий признак подобия треугольников.
5. Какие четыре точки называются замечательными точками треугольника?
6. Какие две фигуры называются подобными?
7. Что называется коэффициентом подобия?
8. Что называется гомотетией?
9. Какие фигуры называются гомотетичными?
10. Что такое параллельный перенос?

Тема: «Окружность»

1. Какая прямая называется касательной к окружности?
2. Что значит: окружности касаются в данной точке?
3. Какое касание окружностей называется внутренним, какое – внешним?
4. Что называется плоским углом?
5. Какой угол называется центральным?
6. Какой угол называется вписанным в окружность?
7. Докажите, что вписанный в окружность угол равен половине соответствующего центрального угла.
8. Какая окружность называется вписанной в треугольник?
9. Докажите, что центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.
10. Какая окружность называется описанной около треугольника?
11. Где лежит центр окружности, описанной около треугольника?
Тема: «Решение треугольника».
1. Сформулируйте и докажите теорему синусов.
2. Сформулируйте теорему косинусов.
3. В чём состоит решение треугольников?
4. Каковы основные случаи решения треугольников?

Тема: «Многоугольники. Длина окружности»

1. Что такое ломаная?
2. Что такое многоугольник?
3. Какой многоугольник называется выпуклым?
4. Чему равна сумма углов выпуклого n-угольника?
5. Какой многоугольник называется вписанным в окружность?
6. Какой многоугольник называется описанным около окружности?
7. Какой многоугольник называется правильным?
8. Приведите формулы для радиусов вписанной и описанной окружностей правильного n-угольника.
9. Найдите радиусы вписанной и описанной окружностей для правильного треугольника, четырехугольника (квадрата), шестиугольника.
10. По какой формуле вычисляется длина окружности?
11. По какой формуле вычисляется длина дуги окружности?
12. Что такое радианная мера угла?
13. Чему равны радианные меры развернутого и прямого углов?

Тема: «Площадь плоских фигур»

1. Сформулируйте свойства площади для простых фигур.
2. Докажите теорему о вычислении площади параллелограмма.
3. Докажите теорему о вычислении площади треугольника.
4. Какие вам известны формулы для площади прямоугольного треугольника и ромба?
5. Докажите теорему о площади трапеции.
6. Сформулируйте теорему о площади правильного многоугольника.
7. Чему равна площадь круга?
8. Чему равна площадь сектора?

Преобразование фигур в геометрии с примерами решения

Содержание:

Отображение плоскости на себя, которое сохраняет расстояния между точками, называется движением. Примерами движения являются такие преобразования, как центральная симметрия, осевая симметрия, поворот (вращение), скольжение.

Поворот:

Пусть, заданы точка О и угол

1. Если точка А не совпадает с точкой О, то

2. Если точка А совпадает с точкой О, то точки совпадают.

Пример 1. Угол поворота равен 45°. Точка А совершила поворот вокруг точки О, на угол 45° по часовой стрелке.

Пример 2. Проанализируйте последовательность шагов, при котором совершается поворот треугольника вокруг точки О, на угол 120°. Повторите эти шаги, выполнив построение в тетради.

1. Соедините точку О и точку С отрезком прямой.
2. При помощи транспортира от ОС постройте угол 120° в направлении по часовой стрелке и циркулем отложите отрезок , конгруэнтный отрезку ОС.
3. Потому же правилу соедините точку О с точками А и В. Постройте отрезки конгруэнтные полученным отрезкам OA и ОВ и составляющие с ними угол 120°. Точки являются вершинами нового треугольника. Соедините эти точки.

Примечание. Центральная симметрия является поворотом плоскости относительно центра симметрии на 180°.

Исследуйте и начертите в тетради:

На рисунке показана последовательность шагов, которые выполняются при повороте треугольника с вершинами А( 4;1), В( 3;5),С( 1;3) на угол 90° в направлении по часовой стрелке.

При повороте на угол 90″ в направлении по часовой стрелке координаты вершин изменяются следующим образом.

Отношения, пропорция

Свойства пропорции

Если то,

Пропорциональные отрезки

Практическая работа. Пропорциональные отрезки.

1. Начертите в тетради 3 параллельные прямые.

2. Проведите 3 секущие, которые пересекают эти прямые.

3. Измерьте отрезки АВ, ВС, AC, DE, EF, DF, GH, HI и GI.

4. Запишите и вычислите следующие отношения

5. Можно ли по результатам сказать, что параллельные линии делят секущие на пропорциональные отрезки? Пропорциональные отрезки

Если для отрезков АВ, CD, , C1D1 выполняется , то отрезки АВ и CD пропорциональны отрезкам

Теорема. Параллельные линии, пересекающие стороны угла, отсекают от них пропорциональные отрезки.

Доказательство. Допустим, что параллельные прямые пересекают стороны угла А в точках В и С, . Для простоты, предположим, что существует отрезок длины такой, что он помещается целое число раз как в отрезке АС, так и в отрезке , Разделим отрезок АС на равные отрезки длиной в количестве раз. В этом случае, одной из точек деления будет точка . Через точки деления проведём прямые, параллельные ВС. По теореме Фалеса эти прямые разобьют отрезок АВ на равные отрезки некоторой длины . Получим, что Отсюда Таким образом,

Подобные четырехугольники, подобные треугольники

Подобными называются фигуры одинаковые по форме и у которых соответствующие размеры пропорциональны. Например, все квадраты подобны друг другу, так же как и окружности разных радиусов.

Подобными называются многоугольники, у которых соответствующие углы конгруэнтны, а соответствующие стороны являются пропорциональными отрезками. Например, на рисунке четырёхугольники ABCD и EFGH являются подобными четырёхугольниками. Так как,

У подобных треугольников соответствующие углы конгруэнтны, а соответствующие стороны являются пропорциональными отрезками. Здесь, говоря о соответствующих сторонах, имеются в виду стороны, которые находятся напротив конгруэнтных углов. На рисунке для имеем:

Так как , то являются подобными треугольниками. Подобие обозначается знаком Отношение соответствующих сторон называется коэффициентом подобия и обозначается буквой Коэффициент подобия треугольников на рисунке равен 3.

Периметр подобных многоугольников

Теорема. Отношение периметров двух подобных многоугольников равно отношению соответствующих сторон (или коэффициенту подобия)

Если , то

Запишите доказательство теоремы, приняв коэффициент подобия за . Для этого можно использовать равенство , которое следует, из отношения соответствующих сторон.

Признаки подобия треугольников

Признак подобия УУ (угол угол)

Если два угла одного треугольника конгруэнтны двум углам другого треугольника, то такие треугольники подобны. Этот признак подобия коротко записывается как УУ.

Признак подобия ССС

Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника, то такие треугольники подобны. Этот признак подобия коротко записывается как ССС.

Признак подобия СУС

Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами конгруэнтны, то такие треугольники подобны. Этот признак подобия коротко записывается как СУС.

Подобие прямоугольных треугольников

Высота, проведенная к гипотенузе

Теорема. Высота, проведённая из вершины прямого угла прямоугольного треугольника, делит его на два подобных треугольника, каждый из которых подобен данному треугольнику.

Доказательство данной теоремы проводится на основании признака подобия УУ Для каждого из трёх треугольников нужно определить два конгруэнтных угла.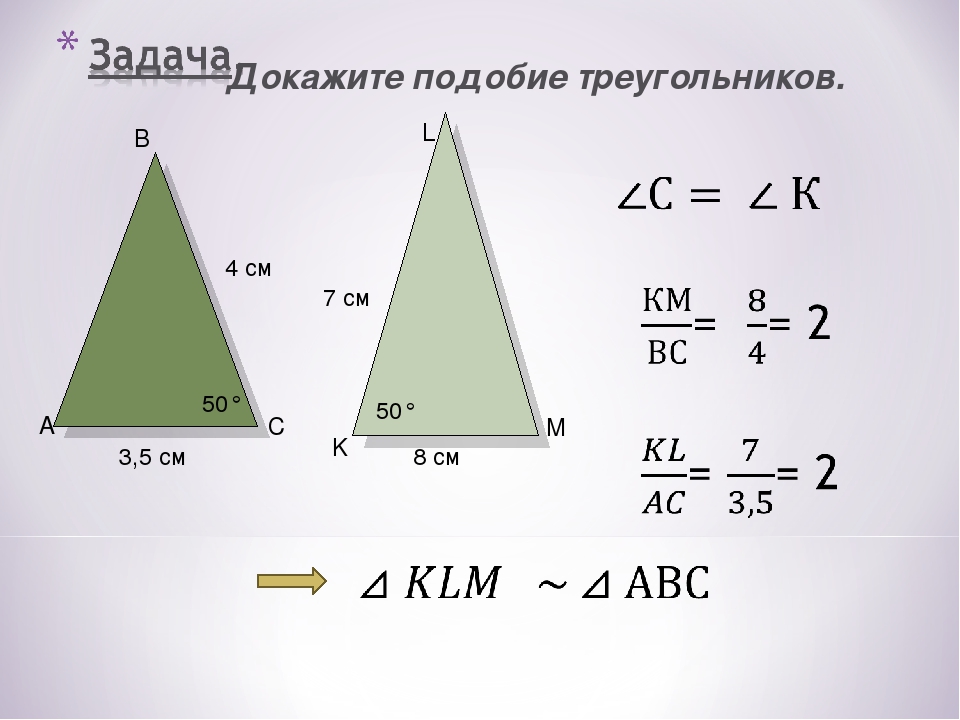

Среднее геометрическое

Среднее геометрическое. Для положительных чисел а и b средним геометрическим называется положительное число , удовлетворяющее равенству

Высота, проведённая из вершины прямого угла на гипотенузу, делит её на два отрезка (на рисунке AD и DB) Здесь отрезки AD и DB являются проекциями катетов АС и ВС на гипотенузу, соответственно.

Следствие 1. Высота прямоугольного треугольника, опущенная из вершины прямого угла есть среднее геометрическое отрезков, на которые она делит гипотенузу.

Следствие 2. Каждый катет прямоугольного треугольника есть среднее геометрическое между гипотенузой и проекцией этого катета на гипотенузу.

Применение подобия треугольников

Пропорциональные отрезки

Теорема. Прямая, пересекающая две стороны треугольника, и параллельная третьей стороне делит стороны на пропорциональные отрезки.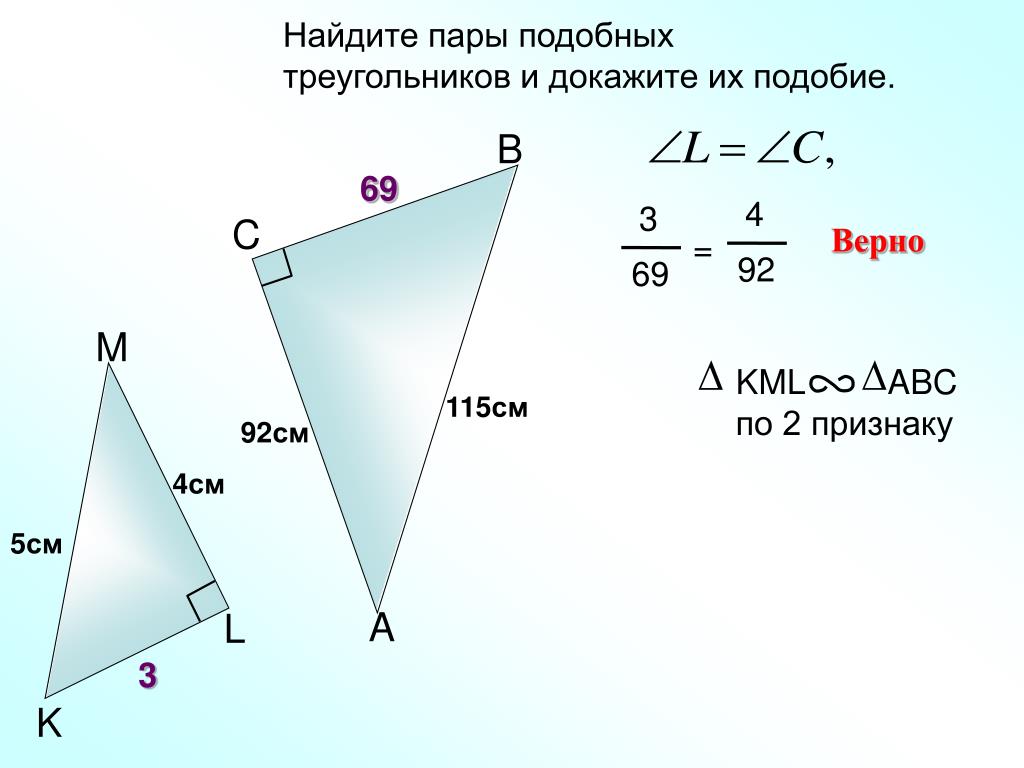

Если

Обратная теорема. Если прямая, пересекающая две стороны треугольника делит их на пропорциональные отрезки, то эта прямая параллельна третьей стороне.

Если , то

Высоты, медианы и биссектрисы подобных треугольников

Теорема 1. Если два треугольника подобны, то отношение длин соответствующих высот равны отношению длин соответствующих сторон.

Теорема 2. Если два треугольника подобны, то отношение длин соответствующих медиан равны отношению длин д соответствующих сторон.

Теорема 3. Если два треугольника подобны, то отношение длин соответствующих биссектрис равны отношению длин соответствующих сторон.

Свойство биссектрисы треугольника

Теорема. Биссектриса треугольника делит противоположную сторону на отрезки пропорциональные двум другим сторонам.

Теорема. Свойство медиан треугольника

Медианы треугольника пересекаются в одной точке и делятся в точке пересечения в отношении 2:1, начиная от вершины.

Точка пересечения медиан называется центром тяжести треугольника.

Доказательство теоремы представлено в виде двухстолбчатой таблицы.

Дано: CD и AE медианы треугольника

Доказать: AO:OE=CO:OD=BO:OF=2:1

Доказательство: соединим точки O и E.

Преобразование подобия, гомотетия

Гомотетия

Преобразование плоскости на себя, при котором расстояние между любыми двумя точками изменяется в одно и то же число раз называется преобразованием подобия. Фигуры называются подобными, если одна фигура переводится в другую преобразованием подобия. Если при преобразовании подобия точки А и В на плоскости соответственно преобразованы в точки Число называется коэффициентом подобия. Преобразование подобия при называется движением. Предположим, что заданы точка О и число . Преобразование плоскости на себя при котором для произвольной точки А плоскости и преобразованной точки выполняется равенство называется гомотетией. Точка О называется центром гомотетии, число — коэффициентом гомотетии, точки А и гомотетичными точками.

Если , то фигура увеличивается относительно изначальной фигуры.

Если , то фигура уменьшается относительно изначальной фигуры.

Если , то фигура конгруэнтна изначальной фигуре.

Площади подобных фигур

Теорема. Отношение площадей подобных фигур равно квадрату коэффициента подобия. Например, если отношение соответствующих сторон двух подобных четырёхугольников равно , то отношение площадей равно

Самостоятельная работа ( с элементами тестирования) по теме «Подобие фигур»

Фамилия __________________ Имя__________________ Класс_______ Число________________

1) Подобными геометрическими фигурами называются фигуры _____________________________ ____________________________________________________________________________________ .

2) Коэффициентом подобия называется __________________________________________________ _________________________________________________________________________________________________________________________________________________________________________ .

3) Коэффициент подобия обозначается буквой ________ .

4) Стороны подобных треугольников, лежащих напротив соответственно _____________________ ________ , называют _____________________________________.

5) Треугольники называются подобными, если ____________________________________________ ____________________________________________________________________________________ .

6) При увеличение треугольника с сохранением его формы, величины углов треугольника _______ __________________________________.

7) Стороны треугольника ABC равны 7 см, 12 см и 14 см. Найдите стороны подобного треугольника с вершинами М, N и К, зная, что большая сторона равна 7 см. (Задачу решаем в тетради, в карточку заносим только ответ).

Фамилия __________________ Имя__________________ Класс_______ Число________________

3) Коэффициент подобия обозначается буквой ________ .

6) При увеличение треугольника с сохранением его формы, величины углов треугольника _______ __________________________________.

Фамилия __________________ Имя__________________ Класс_______ Число________________

3) Коэффициент подобия обозначается буквой ________ .

6) При увеличение треугольника с сохранением его формы, величины углов треугольника _______ __________________________________.

определение сходства по The Free Dictionary

(см. также ЭКВИВАЛЕНТНОСТЬ .)

отколоть старый блок Сын, похожий на своего отца внешне или поведением. Считается, что это выражение придумал Эдмунд Берк (1729–1797), обращаясь к британской палате общин, говоря о Питте Младшем. Однако цитата из OED датирует аналогичную фразу началом 1.7 века.

Разве я не дитя того же Адама… чип того же блока, с ним? (бп.Роберт Сандерсон, Проповеди , 1627)

Отколоть старый блок — это современная форма фразы; Чип старого или того же блока это оригинал. Намек очевиден. Чип имеет те же характеристики, что и блок, из которого он изготовлен. Любая связь с «родословной» забавна, но сомнительна.

подражатель Имитатор; тот, кто копирует чужой стиль или работу. Термин используется с начала века.

Хороший архитектор не был «подражателем»; и не пинал следы. ( Oxford Times , 24 апреля 1931 г.)

Подражатель иногда используется как глагол, означающий «подражать». следовать примеру или руководству другого; имитировать работу предшественника. Подразумевается, что для того, чтобы быть похожим на уважаемого и обожаемого человека, нужно следовать его примеру, то есть следовать образным стопам, которые он прошел на своем пути к успеху.

Вы обязаны идти по стопам своих предшественников в добродетели. ( Жалоба Шотландии , 1549)

Вариант ходить по стопам . Аналогичное выражение, образно относящееся к ногам почитаемого человека, — большой или большая обувь, чтобы заполнить , подразумевая, что потребуются значительные усилия, чтобы соответствовать стандартам, установленным предшественником.

следовать примеру Подражать или подражать; действовать так же, как и его предшественник.Этот термин уходит корнями в карточные игры, такие как бридж или неудача, где правила диктуют, что, если возможно, участник должен следовать их примеру, то есть играть картой той же масти, что и ход.

присоединиться к побеждающей стороне Поддержать конкретного кандидата или дело, обычно когда успех кажется гарантированным и не сопряжено с большим риском; часто лезут на борт подножки . В эпоху политического штурма фургоны возили на парад музыкантов. Теория гласит, что, когда по округе проезжали фургоны с кандидатами, местные политики буквально запрыгивали на борт фаворитов кандидатов, тем самым публично поддерживая их.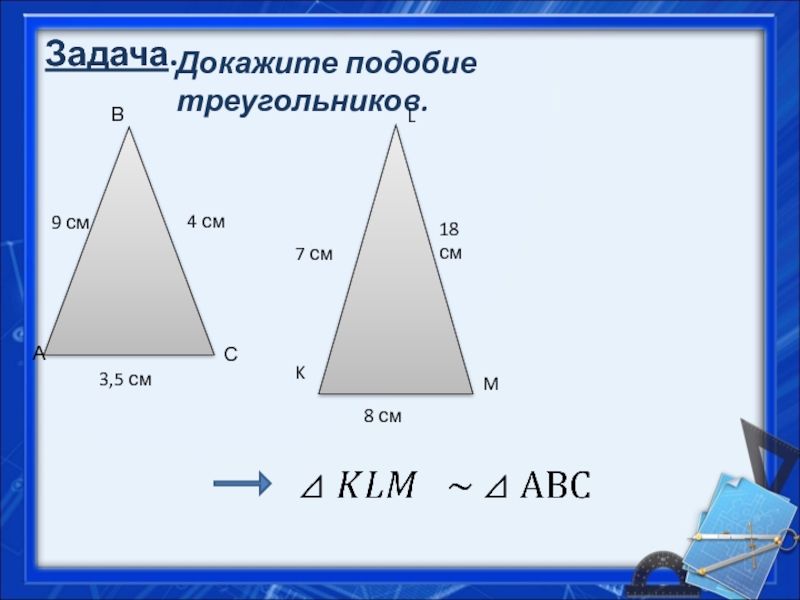 Образное использование термина подножка восходит к началу 1900-х:

Многие из тех демократов… которые бросились на подножку Брайана… теперь будут видны переползающими через задний борт. ( New York Evening Post , 4 сентября 1906 г.)

Хотя чаще всего ассоциируется с политикой, подножка используется и в других контекстах:

Джо Салтис (который недавно присоединился к фаворитам Капоне) и «Дингбат» О’Берта.(Артур Б. Рив, Золотой век преступности , 1931)

человек моей почки Человек, чей характер и нрав похожи на вас самих. В этом выражении почка несет переносное значение природы, темперамента или конституции. Фраза появилась в произведении Шекспира « проказниц Виндзора»:

Подумайте об этом, человек моей почки; … это так же подвержено теплу, как масло. (III, v)

Это образное использование почек иногда относится к роду или типу человека.

Это была большая и довольно разношерстная партия, но все из правой почки. (Бенджамин Дизраэли, Эндимион , 1880)

играть в обезьяну Подражать, копировать чей-то стиль, подделывать. Это выражение намекает на то, как обезьяны имитируют выражения и жесты людей. Он появился в печати к 1500-м годам. Роберт Льюис Стивенсон популяризировал это выражение в своих « воспоминаний и портретов » (1882 г.):

Я играл усердную обезьяну Хэзлитту, Лэмбу, Вордсворту, сэру Томасу Брауну….Нравится вам это или нет, но это способ научиться писать.

звонок См. ПРИТЯЖЕНИЕ .

коса и изображение Точное подобие, изображение или аналог; дубликат, двойник; обломок старого блока. Это выражение подразумевает, что два человека настолько похожи (обычно внешне), что, по крайней мере в переносном смысле, один мог бы быть выплюнут изо рта другого, интересная концепция, особенно в свете недавних прорывов в области генетики и клонирования. .Поскольку более ранним выражением было та самая коса, изображение служит для того, чтобы подчеркнуть внешнее сходство.

Она похожа на бедную леди, которая умерла и ушла, она — выдумка. (Замок Эгертон, Свет Скартни , 1895)

Вариации: точная копия и точная копия .

взять страницу из [чьей-то] книги Следовать чужому примеру, копировать или подражать кому-то другому; также взять лист из [чьей-то] книги .Намек на литературный плагиат, но выражение теперь используется только в положительном смысле.

Очень жаль, что некоторые из наших инструкторов по более важным вопросам… не возьмут листа из той же книги. (Томас Хьюз, Том Браун в Оксфорде , 1861)

просмоленные одной кистью Все имеют одни и те же недостатки; каждый так же виновен, как и следующий. Это выражение происходит от практики маркировки всех овец одного стада общей меткой, сделанной кистью, смоченной в смоле.Некоторые говорят, что метка предназначалась только для идентификации; другие утверждают, что это было сделано для защиты овец от клещей или для лечения язв. Вариант этого выражения — , нарисованный той же кистью . Эти выражения обычно подразумевают, что то, что отличает данную группу людей, — это их общая вина или их сходные негативные характеристики.

Труляля и Труляля Настолько похожи, что неразличимы или неразличимы. Хотя эти имена были популяризированы известной парой в произведении Льюиса Кэрролла « в Зазеркалье » (1871), термины были придуманы в 1725 году Джоном Байромом, который использовал их в сатирической поэме о ссорящихся музыкантах.При этом он явно играл со значением tweedle «издавать пронзительные музыкальные звуки».

Странная должна быть вся эта разница,
Twixt Tweedle-dum и
Tweedle-dee!
( Гендель и Бонончини )

Еще до того, как вымышленные творения Кэрролла были названы таким образом, эти термины использовались фигурально в контекстах, касающихся незначительных разногласий, мелких ссор, придирчивых споров и т. д., например, в следующем приложении:

А … словесная война из-за аферистов тонких доктринальных разногласий и аферистов церковного государственного устройства.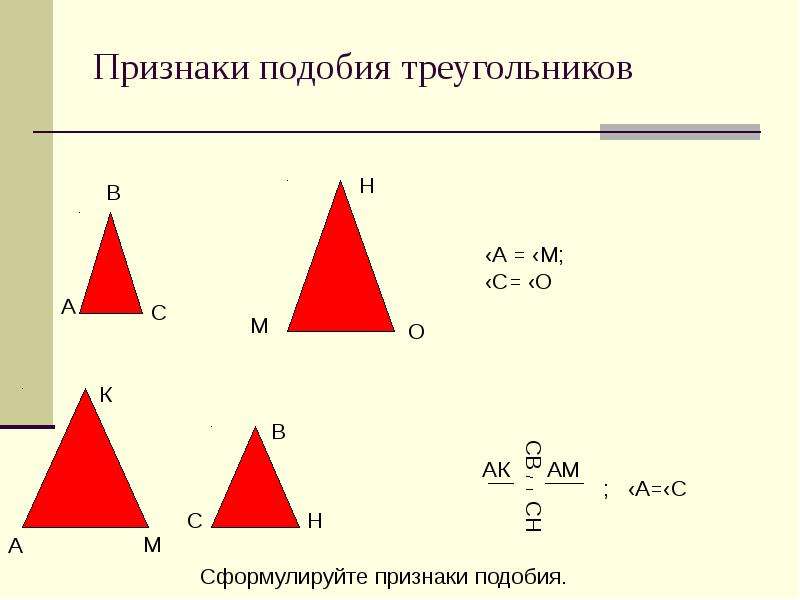 ( Church Endeavour Times , август 1911 г.)

Что такое сходство | Похожие фигуры | Определения | Примеры

Папа: Она права.

Папа: Из-за их формы и расстояния. Этот признак также называют свойством подобия.

В этом мини-уроке вы познакомитесь со свойствами подобия и их ролью в геометрии.

Что вы подразумеваете под сходством?
Когда два или более объектов или фигур кажутся одинаковыми или равными из-за их формы, это свойство называется сходством.
Когда мы увеличиваем или уменьшаем похожие фигуры, они всегда накладываются друг на друга.
Например, два круга (любого радиуса) всегда будут накладываться друг на друга, потому что они похожи:
Таким же образом два квадрата (с любой длиной стороны) всегда будут подобны:
Каковы правила подобия?
Если две линейные фигуры похожи, это означает, что:
Все соответствующие пары углов равны.
Все соответствующие стороны пропорциональны.
Однако из-за его широкого применения мы обсудим подобие треугольников. Мы используем правила, когда у нас нет информации обо всех сторонах и всех углах двух треугольников.
Посмотрим правила подобия треугольников.
Критерий сходства AA
Критерий сходства треугольников АА утверждает, что если три угла одного треугольника соответственно равны трем углам другого, то два треугольника будут подобны.Короче говоря, равноугольные треугольники подобны.
В идеале название этого критерия должно быть критерием AAA (угол-угол-угол), но мы называем его критерием AA, потому что нам нужно, чтобы только две пары углов были равны — третья пара автоматически будет равна свойство суммы углов треугольников.
Рассмотрим следующий рисунок, на котором \(\Delta ABC\) и \(\Delta DEF\) равноугольны, т.е.
\(\угол A\) = \(\угол D\)
\(\угол B\) = \(\угол E\)
\(\угол C\) = \(\угол F\)
Используя критерий АА, мы можем сказать, что эти треугольники подобны.
Критерий подобия SSS
Критерий подобия SSS гласит, что если три стороны одного треугольника соответственно пропорциональны трем сторонам другого, то эти два треугольника подобны.
По существу это означает, что любая такая пара треугольников также будет равноугольной (все соответствующие пары углов равны).
Рассмотрим следующий рисунок, на котором стороны двух треугольников (\(\Delta ABC\) и \(\Delta DEF\)) соответственно пропорциональны:
То есть дано, что:
\[\frac{{AB}}{{DE}} = \frac{{BC}}{{EF}} = \frac{{AC}}{{DF}}\]
Критерий подобия SAS
Критерий подобия SAS гласит, что если две стороны одного треугольника соответственно пропорциональны двум соответствующим сторонам другого и если углы между ними равны, то два треугольника подобны.
Обратите внимание на ударение слова , включающего . Если равный угол является невключенным углом, то два треугольника могут быть не подобны.
Рассмотрим следующую цифру:
Дано, что
\[\begin{align}& \frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} \end{align}\]
\[\угол A = \угол D \]
Критерий SAS говорит нам, что \(\Delta ABC\) ~ \(\Delta DEF\).
В чем разница между сходством и конгруэнтностью?
Когда две фигуры имеют одинаковую форму и размер, они конгруэнтны.Если фигуры имеют одинаковую форму, но разные размеры, они подобны.
Посмотрите на эту пару монет, они конгруэнтны, так как имеют одинаковую форму и равный радиус обеих монет.
Конгруэнтные фигуры равны во всех аспектах, т. е. периметр, длина и площадь конгруэнтных фигур всегда равны.
Основное отличие состоит в том, что все конгруэнтные фигуры подобны, но подобные фигуры не конгруэнтны.
Какое применение подобия?
Некоторые приложения подобия упомянуты ниже.
Подобие широко используется в архитектуре. 2}\)
Решенные примеры

Рассмотрим следующую цифру:
Найдите значение \(\угол E\).
Раствор
Сопоставьте самую длинную сторону с самой длинной стороной и самую короткую сторону с самой короткой стороной и проверьте все три соотношения.
Заметим, что три стороны двух треугольников соответственно пропорциональны:
\[\begin{align}& \left\{ \begin{gathered}\frac{{DE}}{{AB}} = \frac{{4.2}}{6} = 0,7\\ \frac{{DF }}{{AC}} = \frac{{2,8}}{4} = 0,7\\ \frac{{EF}}{{BC}} = \frac{{3,5}}{5} = 0,7 \end{ собрано} \right.\\&\quad\frac{{DE}}{{AB}} = \frac{{DF}}{{AC}} = \frac{{EF}}{{BC}} \end {выравнивание}\]
Таким образом, по критерию подобия SAS \(\Delta ABC \sim \Delta DEF\)
Это означает, что они также равноугольные.0}}
\конец{массив}\]

Рассмотрим два подобных треугольника, \(\Delta ABC\) и \(\Delta DEF\):
\(AP\) и \(DQ\) – медианы в двух треугольниках соответственно. Покажите, что
\[\frac{{AP}}{{BC}} = \frac{{DQ}}{{EF}}\]
Раствор
Так как эти два треугольника подобны, они равноугольные.
Это означает, что
\[\угол B = \угол E\]
Также
\[\begin{align} \frac{{AB}}{{DE}} &= \frac{{BC}}{{EF}}\\ \Rightarrow \quad\frac{{AB}}{{DE }} &= \frac{{BC/2}}{{EF/2}} = \frac{{BP}}{{EQ}} \end{align}\]
Следовательно, по критерию подобия SAS
\[\Delta ABP \sim \Delta DEQ\]
Таким образом, стороны этих двух треугольников будут соответственно пропорциональны, а значит:
\[\begin{align} \frac{{AB}}{{DE}} &= \frac{{AP}}{{DQ}}\\ \Rightarrow \quad\frac{{AP}}{{DQ }} &= \frac{{BC}}{{EF}}\\ \Rightarrow \quad\frac{{AP}}{{BC}} &= \frac{{DQ}}{{EF}} \end {выравнивание}\]
\(\поэтому\) поле утверждения ответа

Сложные вопросы
Рассмотрим треугольник ABC, показанный на следующем рисунке, где RQ = 13 дюймов, QM = 12 дюймов, RM = 5 дюймов см и \(\угол\) QRM = \(\угол\) QPR . Каково отношение периметра \(\Delta\) PMR к периметру треугольника \(\Delta\) QMR?

Интерактивные вопросы
Вот несколько упражнений для практики. Выберите/введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.

Подведем итоги
Мини-урок был посвящен интересному понятию хорды окружности.Мы надеемся, что вам понравилось узнавать о диаметре и хордах теоремы о окружности с вопросами о моделировании и практике. Теперь равные хорды по кругу и неравные хорды по кругу для вас не более сложны.
О Куэмате
Наша команда экспертов по математике в Cuemath стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу «обучение-обучение-обучение» учителя изучают тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любая другая форма отношений, это логическое мышление и разумный подход к обучению, в который мы в Cuemath верим.
Часто задаваемые вопросы
1.Как используется сходство в реальной жизни?
Подобие используется при проектировании, решении задач на высоту и расстояние и т. д.
2. Каковы правила подобия?
Три правила сходства: сходство SSS, сходство SAS и сходство AA или AAA.
3. Является ли SSA теоремой подобия?
Нет, SSA не является теоремой подобия.
4. Что такое заявление о сходстве?
Когда два или более объектов или фигур кажутся одинаковыми или равными из-за их формы, это свойство называется сходством.
5. Что такое теорема подобия SSS?
Критерий подобия SSS утверждает, что если три стороны одного треугольника соответственно пропорциональны трем сторонам другого, то эти два треугольника подобны.
6. Что такое теорема подобия SAS?
Критерий сходства SAS утверждает, что если две стороны одного треугольника соответственно пропорциональны двум соответствующим сторонам другого и если углы между ними равны, то два треугольника подобны.
7. Что такое теорема подобия АА?
Критерий сходства треугольников АА гласит, что если три угла одного треугольника соответственно равны трем углам другого, то два треугольника будут подобны.
Определение для изучающих английский язык из Словаря для учащихся Merriam-Webster
^{сходство
/ˌsɪməˈlerəti/
имя существительное множественное число сходство
множественное число сходство
Ученическое определение ПОДОБИЯ :
качество, делающее одного человека или вещь похожей на другую [считать]
Сомневаюсь, что эти слова связаны кроме сходства в звучании.
Книги имеют сходство идей.
Я вижу в них много сходства с .
— часто + между [не в счет]
Глядя на эти окаменелости, я вижу некоторое сходство с современными птицами.
Я вижу очень мало сходства между вашей ситуацией и его.
Обе женщины имеют двоих детей и любят спорт, но на этом сходство заканчивается. [=они не похожи в остальном]
Похожие рисунки: определение и примеры — видео и стенограмма урока
Подобные полигоны
Многоугольник представляет собой двумерный объект с минимум тремя прямыми сторонами и тремя углами.Некоторые распространенные многоугольники, с которыми мы знакомы, это треугольники, прямоугольники, шестиугольники и восьмиугольники. Два многоугольника могут быть похожими. Например, рассмотрим эти два одинаковых прямоугольника:
Как мы уже говорили, одинаковые фигуры имеют одинаковую форму. Следовательно, когда у нас есть две одинаковые фигуры, одна из них является большей или меньшей копией другой. Из-за этого, когда два многоугольника подобны, их стороны пропорциональны . Пропорциональность означает, что отношения соответствующих сторон подобных многоугольников равны. Например, рассмотрим эти два одинаковых прямоугольника. Обратите внимание, что отношение соответствующих более коротких сторон равно отношению соответствующих более длинных сторон.
Отношение более коротких сторон = 2/6 = 1/3
Отношение более длинных сторон = 3/9 = 1/3
Поскольку 1/3 = 1/3, эти два прямоугольника пропорциональны.
Определение сходства двух многоугольников
Мы можем использовать тот факт, что стороны подобных многоугольников пропорциональны, чтобы определить, подобны ли два многоугольника.Чтобы определить, подобны ли два многоугольника, мы просто устанавливаем отношения соответствующих сторон и смотрим, равны ли они. Если да, то эти два многоугольника подобны. Если нет, то они не похожи.
Например, рассмотрим это изображение. Похожи ли эти два многоугольника?
Чтобы решить, подобны ли эти два многоугольника, мы смотрим на отношения соответствующих сторон. Многоугольник имеет четыре стороны, поэтому мы будем смотреть на отношение каждой из соответствующих сторон.Если все они равны, то многоугольники подобны:
Сторона 1: 4/8 = 1/2
Сторона 2: 1/2
Сторона 3: 5/10 = 1/2
Сторона 4: 6/12 = 1/2
Мы видим, что отношения соответствующих сторон равны. Следовательно, стороны пропорциональны, а два многоугольника подобны.
Использование подобных фигурок
Часто подобные фигурки можно использовать для решения определенных проблем, которые могут возникнуть в окружающем нас мире.Например, предположим, что вы хотите узнать расстояние до пруда. Есть мост, который пересекает пруд, но он наклонен, поэтому он не дает точного расстояния через пруд. Сценарий изображен на этом изображении, и показаны известные нам измерения.
Нам говорят, что треугольник, образованный прудом и мостом, подобен треугольнику, образованному деревом и веревкой, идущей от вершины дерева к земле. Следовательно, мы знаем, что соответствующие стороны этих двух треугольников пропорциональны.Если мы представим неизвестное расстояние через пруд размером x , то мы можем использовать тот факт, что отношения соответствующих сторон равны, чтобы составить это уравнение:
x / 25 = 4 / 20
Теперь мы можем решить для x путем умножения обеих сторон на 25:
x = 25 (4 / 20) = 100 / 20 = 5
Следовательно, это 5 футов поперек пруда, и мы смогли рассчитать это расстояние без намокнуть!
В этих расчетах мы установили х /25 равным отношению 4/20.Мы могли бы использовать другие соответствующие стороны и получить тот же ответ. То есть мы могли бы составить это уравнение:
x / 25 = 6 / 30
Чтобы решить, мы должны умножить обе части на 25.
x = 25 (6 / 30) = 150/ 30 = 5
Как видим, мы получаем тот же ответ. Это связано с тем, что все соответствующие стороны имеют одинаковое отношение в подобных многоугольниках.
Резюме урока
Подобные фигуры — это фигуры, которые имеют одинаковую форму, но могут иметь разные размеры.Многоугольник — это двумерный объект с минимум тремя прямыми сторонами и тремя углами. Эти типы фигур часто появляются в окружающем нас мире.
Подобные фигуры пропорциональны , поэтому, когда два многоугольника подобны, отношения их соответствующих сторон равны. Подобные фигуры могут быть использованы для решения некоторых задач в архитектуре, технике, строительстве и многих других областях. Теперь мы знакомы с подобными фигурами и их свойствами.
Обобщаемое определение химического сходства для прочтения | Journal of Cheminformatics
Отпечатки пальцев
Мы решили оценить производительность 9 различных алгоритмов отпечатков пальцев, которые реализованы в библиотеках Chemistry Development Kit (CDK).Хотя они подпадают под общее определение отпечатков пальцев, некоторые из них являются структурными ключами, а не отпечатками на основе хеширования.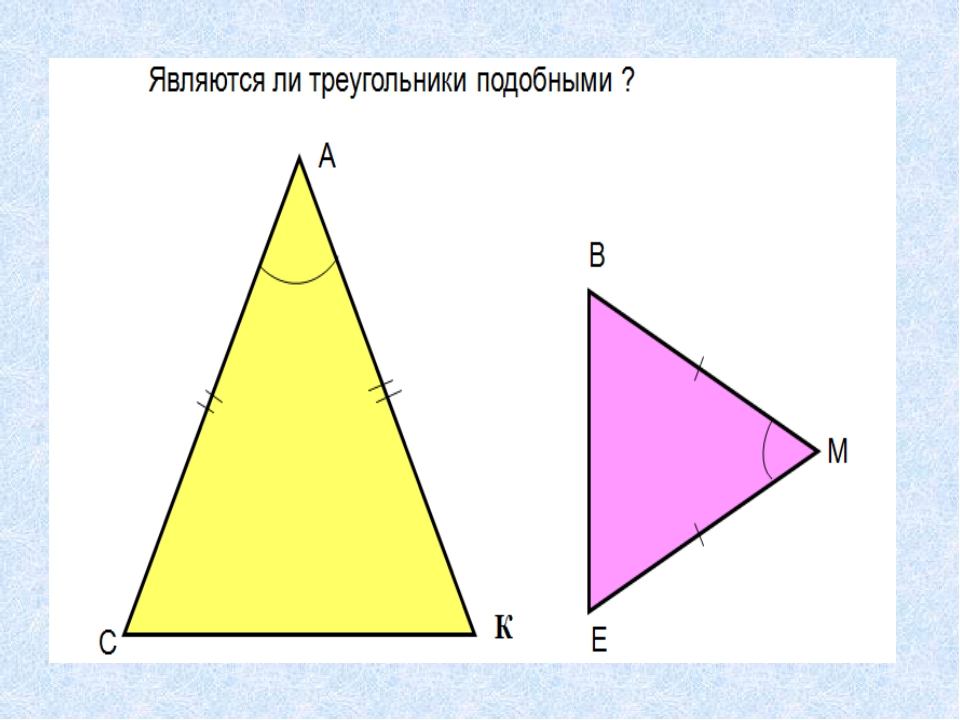 В частности, здесь рассматриваются следующие отпечатки пальцев:
1. Отпечатки пальцев по умолчанию (как определено Daylight [10]),
2. Расширенные отпечатки пальцев (то же, что и по умолчанию, но с дополнительными битами, учитывающими особенности кольца),
3. Отпечатки пальцев только для графика (то же, что и по умолчанию, но без учета ордеров на облигации),
4. Отпечатки пальцев гибридизации (то же, что и по умолчанию, но не выполняют восприятие ароматичности),
5. фрагмента E-State (79-битные отпечатки, описанные Киером и Холлом [16]),
6. отпечатки пальцев Клекота-Рота (набор из 4860 химических субструктур, обогащенных биологической активностью [17]),
7. Ключи MACCS (структурный ключ из набора 166 бит [18]),
8. Отпечатки пальцев Pubchem (структурный ключ из 881 ключа [19]),
9. Отпечатки подструктуры (структурный ключ из 307 бит [20].
Молекулярные дескрипторы на основе структурных ключей
Мы решили создать три структурных ключа на основе молекулярных дескрипторов, связанных с конституциональными проблемами. Гипотеза, которая привела к этим ключам, заключалась в том, чтобы проверить, может ли такая информация успешно сочетаться с использованием отпечатков пальцев, чтобы эти ключи могли заполнить информационный пробел отпечатков пальцев.Поскольку эти ключи состоят из молекулярных дескрипторов, они больше не являются бинарными ключами. Дескрипторы, используемые для этих ключей, были рассчитаны собственным программным модулем JAVA на основе библиотек CDK; для определения дескрипторов за основу была взята коммерческая программа Dragon [21].
Три ключа:
Конституционные дескрипторы (CD): этот ключ состоит из 35 конституционных дескрипторов, как указано в таблице 1
Таблица 1 Дескрипторы в ключе конституционных дескрипторов (CD) Дескрипторы гетероатомов (HD): этот ключ состоит из 11 счетчиков для различных типов гетероатомов, как указано в таблице 2.Эти дескрипторы являются подмножеством конституционных дескрипторов. Мы решили построить ключ с этим подмножеством, чтобы иметь возможность придавать ему разные веса, чтобы отметить особенность, которую он представляет при вычислении химического сходства. Это связано с наблюдением, что часто на общее представление о химическом сходстве сильно влияют небольшие различия в числе и типе гетероатомов, т.) можно считать существенно разными только потому, что они различаются наличием/отсутствием некоторых гетероатомов.
Таблица 2 Дескрипторы в ключе дескрипторов гетероатомов (HD) Функциональные группы (FG): этот ключ состоит из 154 функциональных групп, определенных в Dragon.
Коэффициенты подобия
Мы построили два набора коэффициентов подобия для тестирования соответственно с выбранными отпечатками пальцев (двоичные коэффициенты) и ключами на основе дескрипторов (недвоичные коэффициенты).Выбраны бинарные коэффициенты 44, представленные в таблице 3, взятые из работы Todeschini et al. [14]. Выбраны недвоичные коэффициенты равные 6, приведенные в таблице 4, взятые из работы Холлидея [22]. Все коэффициенты реализованы в собственном программном модуле JAVA.
Таблица 3 Двоичные коэффициенты подобия Таблица 4 Небинарные коэффициенты подобия Индекс подобия
Чтобы объединить отпечаток пальца с ключами на основе дескрипторов, мы разработали общую схему для индекса подобия SI, определяемого следующим образом:
SIA,B=SbFPa,FPbWfp*SnbCDa,CDbWcd*SnbHDa,HDbWhd *SnbFGa,FGbWfg
(1)
где:
A и B — две сравниваемые молекулы;
FP _{A 9072, CD _A, HD _A, HD _A, FG _A, FG _A, FP _B, CD _B, HD _B, HD _B, FG _B — это отделка отпечатков пальцев, конституционные дескрипторы, гетероатом.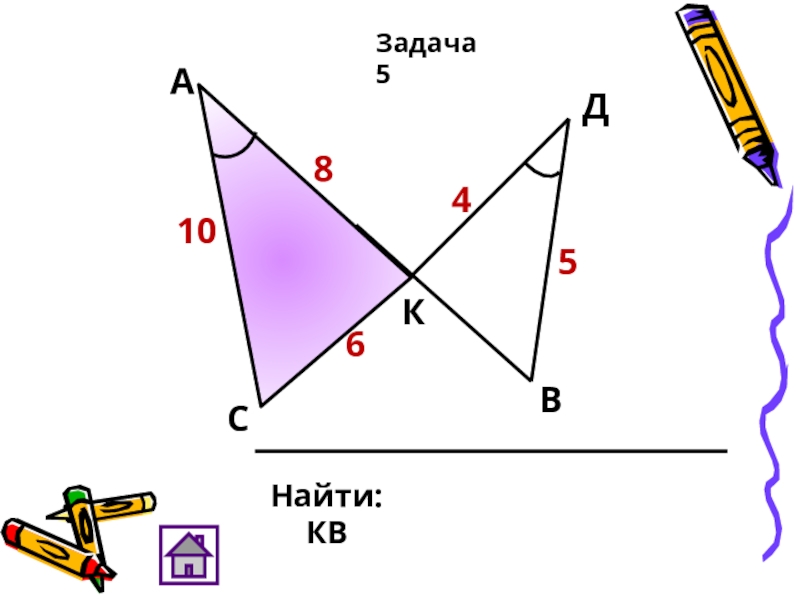 и ключи функциональных групп, как определено ранее, рассчитанные соответственно для двух молекул А и В;}
Sb(X _a ,X _b ) — результат применения бинарного коэффициента подобия к двум отпечаткам пальцев X _a и X _b , где результирующие значения находятся в интервале [0,1 ];
Snb(X _a ,X _b ) — результат применения небинарного коэффициента подобия к двум дескрипторам на основе ключей X _a и X _b , где результирующие значения находятся в интервале [0,1];
W _fp , W _cd , W _hd , W _fg — относительные веса четырех вкладов при условии:
Как видно, предложенный индекс просто учитывает разный вклад сходства (рассчитанный с выбранным коэффициентом), каждый с заданным весом.
Наборы данных и модель сквозного чтения
Мы выбрали два общедоступных набора данных из проекта VEGA. Набор данных фактора биоконцентрации в рыбе (BCF) включает 473 соединения с экспериментальными значениями BCF. Набор данных коэффициента распределения вода/октанол (LogP) состоит из 10 005 соединений с экспериментальными значениями logP.
Выбор проверки индекса подобия для этих двух наборов данных обусловлен целью найти настройку для SI, которая потенциально может дать хорошие результаты для различных типов данных, тем самым реализуя «общую» идею химического сходства.Более подробно, мы сосредоточили наш анализ на конечной точке, относящейся к токсичности (BCF), и на физико-химических свойствах (logP) с несколькими приложениями, кроме того, с заметно разным размером (BCF: 860 молекул; logP 10005 молекул).
В целях тестирования характеристик предлагаемого индекса сходства с различными настройками мы внедрили в собственный модуль JAVA простую модель прогнозирования на основе перекрестного чтения , в которой свойство прогнозируется для данного соединения путем нахождения три наиболее похожих соединения набора данных в соответствии с SI и вычисление среднего их трех экспериментальных значений, взвешенных по их значениям SI.
В нашей процедуре мы рассчитывали прогнозы на основе стратегии «пропуск-один-пропуск» , принятой для перекрестной проверки. Итеративно одна молекула за раз исключалась из набора данных, чтобы ее можно было предсказать с использованием нашего подхода сквозного считывания оставшихся молекул.
Наконец, поскольку описанный выше модельный подход аналогичен регрессионной модели, мы рассчитали значения коэффициента детерминации (R ² ) и среднеквадратической ошибки (RMSE) для всех прогнозов набора данных, и использовал эти значения для количественной оценки качества модели, которая напрямую связана с тем, насколько хороши настройки СИ.
Процесс оценки
Мы применили комбинаторную стратегию для проверки всех возможных комбинаций различных настроек (коэффициент подобия, бинарные отпечатки пальцев, небинарные дескрипторы, схема взвешивания), вычислив для каждой из этих настроек модель сквозного считывания для двух наборы данных и получившиеся R ² и RMSE.
На предварительном этапе мы обработали оба набора данных со всеми комбинациями различных отпечатков пальцев и бинарных коэффициентов подобия, всего около 400 перестановок.На этом уровне мы выбрали лучшие комбинации (на основе R ² и RMSE).
Затем мы провели второй анализ, в котором использовали выбранную пару отпечатков пальцев/коэффициентов и набор комбинаций весов для вкладов SI и небинарных коэффициентов сходства для ключей дескрипторов. Мы выбрали следующие диапазоны весов:
W _fp : от 0,3 до 1,0 с шагом 0,1
W _cd : от 0,0 до 0,4 с шагом 0.05
W _hd : между 0,0 и 1,0, с шагом 0,05
W _fg : между 0,0 и 1,0, с шагом 0,05
при обычных условиях, когда сумма весов равна единице. Пакетный процесс генерировал в общей сложности около 7200 комбинаций весов/коэффициентов.
Три значения сходства
Мы можем сказать, что два объекта похожи, если они похожи друг на друга. Говоря простым языком, предметы одинаковой формы, независимо от того, имеют они одинаковый размер или нет, обычно называют подобными. В математике все по-другому. В этом посте мы собираемся изучить три математических значения сходства.
В математике два объекта подобны, если выполняется любое из следующих трех условий.
1. При уменьшении или увеличении одной фигуры она становится конгруэнтной другой
Первое значение основано на определении конгруэнтности. То есть, когда две фигуры подобны, если одну фигуру увеличить или уменьшить, то они станут конгруэнтными с другой.Это определение лучше проиллюстрировать графически с помощью рисунка или апплета, как показано ниже.

В апплете перетащите ползунок k до тех пор, пока две одинаковые фигуры не наложатся друг на друга.
2. Отношение соответствующих отрезков постоянно и соответствующие углы равны
Второе значение связано с соотношением отрезков и угловых мер. Две фигуры подобны, если отношение длин их соответствующих сторон постоянно или их соответствующие углы равны.Большинство авторов выбирают это значение в качестве определения, потому что его легко использовать в доказательствах. Условия подобия треугольников, а именно SSS, SAS, AA и т. Д., Используют это значение для доказательства того, что два треугольника подобны.
3. Когда их можно поставить в положение сходства
Третье значение связано с позиционными отношениями между фигурами. Если две фигуры можно поставить в положение сходства путем преобразования (переноса, поворота, отражения), то эти две фигуры подобны.Обратите внимание, что когда две фигуры находятся в положении подобия, если их вершины соединены линиями, то эти линии пересекаются в одной точке, называемой точкой подобия . Эту точку также иногда называют точкой подобия или центром подобия. В приведенном выше апплете точка O является точкой сходства, а ABC и A’B’C’ находятся в положении сходства.
Обратите внимание, что каждое из трех приведенных выше значений подобия может стоять отдельно, и каждое из них следует из других.Любое из этих трех значений может быть выбрано в качестве определения подобия. Опять же, большинство книг просто выбрали второе, потому что его можно легко использовать для доказательства сходства двух фигур.
Конгруэнтность и подобие | Определения и примеры
Все конгруэнтные фигуры подобны, но не все подобные фигуры конгруэнтны. Конгруэнтность означает, что два объекта (будь то двухмерные или трехмерные) идентичны по размеру и форме. Все в них — их углы, длины сторон, габаритные размеры — идентичны. Подобные фигурки имеют одинаковую форму и пропорции, но не обязательно одного размера.
Содержание
Конгруэнтность
Попробуй!
Геометрия Попробуйте!
Подобие
Использование конгруэнтности и сходства
Конгруэнтность
Два объекта могут иметь одинаковый размер и форму, но не иметь одинаковой ориентации. Они по-прежнему конгруэнтны, как эти морские звезды:
[вставьте два изображения одной и той же морской звезды {морской звезды}, не защищенные авторскими правами, но поверните одно изображение на 36° так, чтобы его шипы были ориентированы по-разному]
Или вот эти шахматные фигуры.Один рыцарь на высокой полке, другой на низкой полке. Тот факт, что они находятся в разных плоскостях в трех измерениях, не исключает их конгруэнтности. Они по-прежнему конгруэнтны:
[вставить рисунок книжной полки с конями {или пешками или любыми шахматными фигурами} на двух разных полках]
В геометрии конгруэнтных фигур обладают тремя свойствами:
Тот же размер
Та же форма
Соответствующие части конгруэнтны
Эта последняя часть объясняет, почему в доказательствах геометрии мы иногда видим CPCFC, что означает: «Соответствующие части конгруэнтных фигур конгруэнтны.»
Попробуй!
Какие пары фигур ниже равны?
[в массив два на два вставьте два одинаковых изображения морского ежа без авторских прав; два изображения плоских морских ежей, одно меньше другого; два одинаковых изображения рыбы-клоуна; и изображения лобстера и краба]
Морские ежи и рыбы-клоуны конгруэнтны. Песчаные доллары, хотя и одинаковой формы, имеют , а не одинаковый размер. Они подобны. Ракообразные — это два совершенно разных животных, поэтому они не конгруэнтны и не похожи.
Геометрия Попробуйте!
Какие пары фигур ниже равны?
[В массиве два на два: квадрат и прямоугольник; два изображения одинаковых правильных пятиугольников; {второй ряд} два одинаковых равносторонних треугольника, но один повернут на 90°; и два одинаковых круга]
Квадрат и прямоугольник не равны. Пары пятиугольников, треугольников и кругов имеют одинаковый размер и форму. У них есть конгруэнтность. Они конгруэнтны.
Подобие
Подобие означает одинаковую форму и пропорции, но не обязательно одинаковый размер.Углы подобных фигур будут равны, но длины сторон обычно не равны.
Пары конгруэнтных фигур автоматически подобны, но это отношение не работает в обратную сторону. Все конгруэнтные фигуры подобны, но не все подобные фигуры конгруэнтны:
[вставить массив «три на один»: рисование двух одинаковых прямоугольников, один из которых больше другого; два одинаковых круга один больше другого; и два равных квадрата]
Оба прямоугольника имеют одинаковые пропорции. Все круги подобны. Однако ни пара прямоугольников, ни окружностей не являются конгруэнтными. Только квадраты, будучи конгруэнтными, еще и подобны друг другу.
Использование конгруэнтности и подобия
Знание свойств конгруэнтности и подобия позволяет использовать их в доказательствах. Вы можете установить отношения между соответствующими частями двух одинаковых цифр, например:
Здесь отношение ширины к длине одинаковое:
3 см/5 см = 1,5 см/2.5 см
Соотношения соответствующих деталей также одинаковы:
Используя эти отношения и конгруэнтность углов, вы знаете, что формы подобны. Они имеют одинаковую форму и пропорциональны друг другу. Вы можете использовать сходство в более сложных доказательствах:
Здесь отношение ширины к длине одинаковое:
Дано: Правый △PYH и △TON, ST ≅ SH
Докажите: PY/NO = PH/NT
Заявление Причина
∠PYT, ∠TON правильные ∠s (Дано)
СТ ≅ Ш
∠PYT ≅ ∠TON Правые ∠ все ≅
∠STH ≅ ∠SHT Если две стороны △ равны ≅, ∠s напротив
эти стороны также ≅.}