Как обозначить окружность: Окружность и круг — урок. Математика, 5 класс. — Детская игровая комната «Волшебный лес»

Posted on 17.04.197128.12.2021 by alexxlab

Содержание

Радиус окружности — что такое, формула, как найти ⚪

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Возможно тебе интересно узнать — как найти длину окружности?

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных.

Далее рассмотрим девять формул разной степени сложности.

Если известна площадь круга

R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Если известна длина

R = P : 2 * π, где P — длина (периметр круга).

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Если известен диаметр окружности

R = D : 2, где D — диаметр.

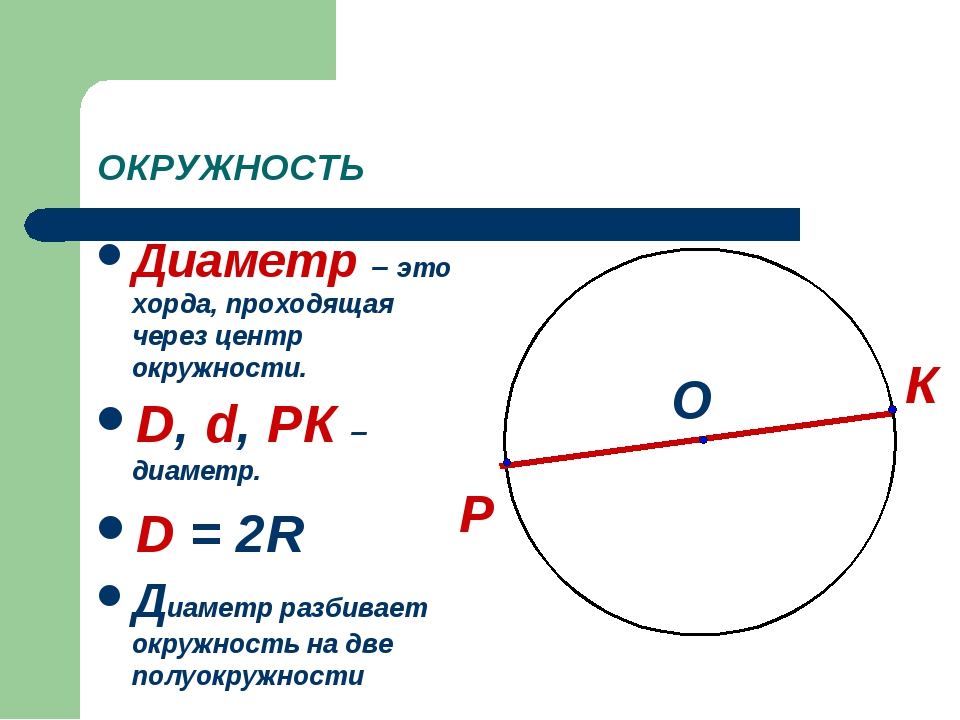
Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

d = √ a² + b², где a, b — стороны вписанного прямоугольника.

Если известна сторона описанного квадрата

R = a : 2, где a — сторона.

Сторона описанного квадрата равна диаметру окружности.

Если известны стороны и площадь вписанного треугольника

R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.

Если известна площадь и полупериметр описанного треугольника

R = S : p, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Если известна площадь сектора и его центральный угол

R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.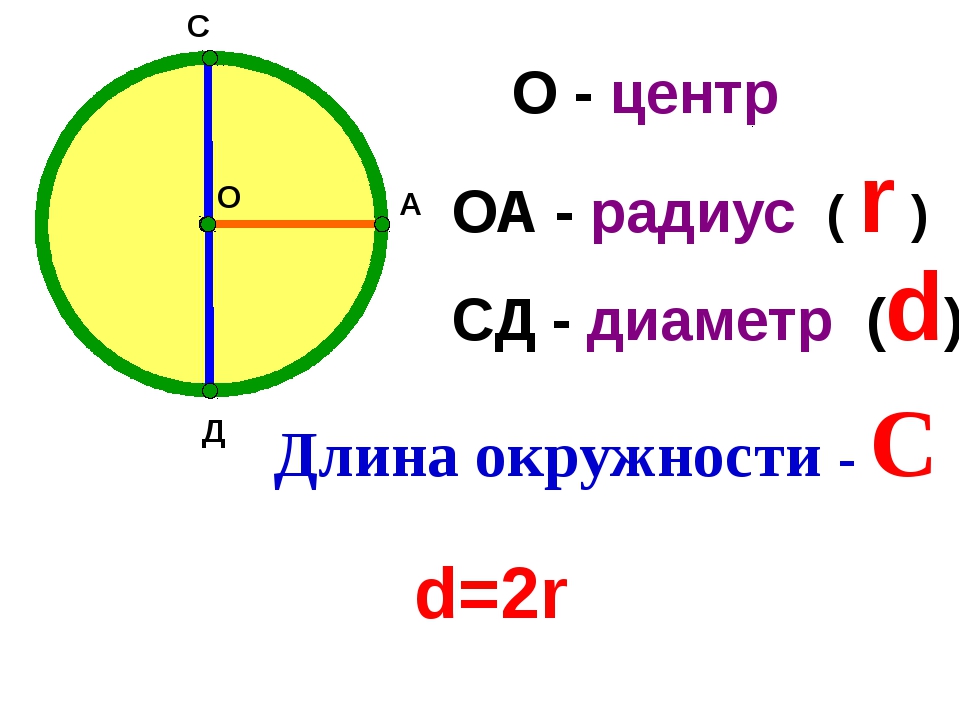

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Урок 33. круг. окружность (центр, радиус, диаметр) — Математика — 3 класс

Математика, 3 класс

Урок №33. Круг. Окружность (центр, радиус, диаметр)

Перечень вопросов, рассматриваемых в теме:

— что такое окружность и круг?

— какие элементы имеет окружность?

— чем отличается круг от окружности?

Глоссарий по теме:

Окружность — это замкнутая кривая, все точки которой одинаково удалены от центра.

Круг – это геометрическая фигура, которая ограничена окружностью.

Радиус- это отрезок, соединяющий центр окружности с любой точкой на окружности.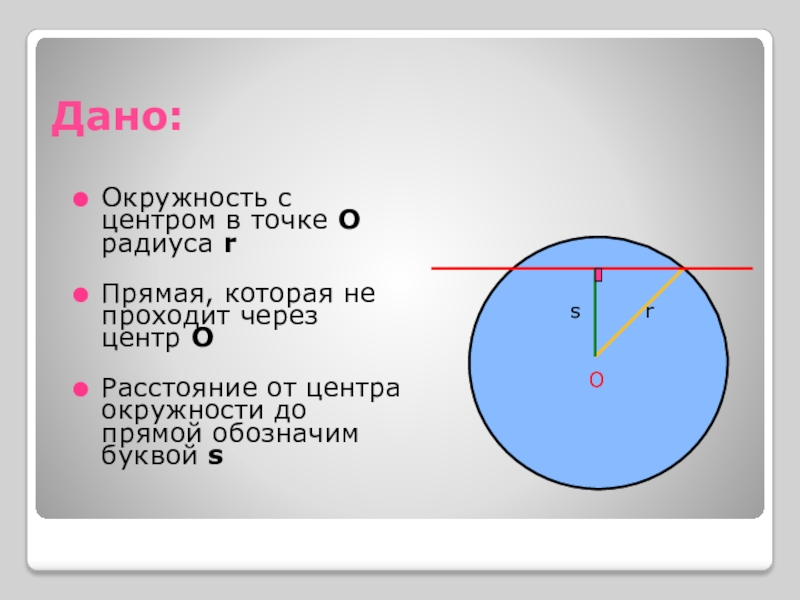

Диаметр – отрезок, который соединяет две точки окружности, проходящий через центр.

Основная и дополнительная литература по теме урока:

1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. с. 94-96.

2. Рудницкая В. Н. Тесты по тматематике:3 класс. М.:Издательство «Экзамен», 2016 с. 48-51.

3. Рудницкая В.Н. Контрольные работы по математике:3 класс. М.: Издательство»Экзамен», 2017, с. 49-54.

4. Рудницкая В. Н. КИМ ВПР. Математика .3 класс. М.: Издательство «Экзамен», 2018, с. 77-79.

Теоретический материал для самостоятельного изучения

С незапамятных времен люди используют в своей жизни круг.

1. Около 3300 года до нашей эры стали применять гончарный круг, делать круглую посуду – тарелки, вазы, кастрюли, горшки, сковородки. У посуды есть окружность (верхний край) и круг (дно).

2. Мы не можем представить свою жизнь без машин: автобус, велосипед, швейная, машинки, самолет, луноход, различные станки, подъемный кран…Они не похожи друг на друга, но присмотримся к ним повнимательнее. Есть у них у всех похожие части – детали, и одна из них – колесо. Сначала колеса были круглые и гладкие, чтобы по земле легко катились, а потом человек придумал много разных колес.

3. Круг и окружность широко применяются в архитектуре и искусстве: круглые арки, своды, купола. Круг – это форма кочевых шатров и поселений. Еще древние греки обнаружили, что с помощью циркуля и линейки можно построить множество фигур, включая шестиугольники, квадраты и другие правильные многоугольники, и создавать волшебные узоры.

4. Необозрима сфера применения круга в математике: тригонометрический круг, круги Эйлера, задачи на построение, круговые диаграммы и т.д. Многие приборы имеют круглую шкалу, в математике таким прибором является транспортир .

5. Картинки с волшебными кругами люди используют в медицинских целях, когда на них смотришь, кажется, что они двигаются. Если смотреть на них несколько минут, то проходит головная боль.

6. Также человек использует круг, как универсальный символ, означающий целостность, непрерывность, первоначальное совершенство. Три концентрических круга символизируют прошлое, настоящее и будущее; три сферы земли: землю, воздух и воду.

Круг в жизни человека имеет очень важную роль, и без использования круглых предметов обойтись невозможно.

Окружность и круг – удивительно гармоничные, совершенные, простые фигуры. Окружность – единственная замкнутая кривая, которая может “скользить сама по себе”, вращаясь вокруг центра, поэтому колеса делают круглыми, а не квадратными или треугольными.

Круг – это колесо. Колесо – это прогресс – движение вперед. Если остановится колесо, то остановится колесо Истории. Остановятся все виды транспорта, остановятся все часы и механизмы, фабрики и заводы.

Круг – символ цикличности, повторяемости. Все движется по кругу.

Круг дает ощущение взаимосвязи с Космосом.

Сама природа выбирает эту удобную и компактную форму как шар и круг.

Сравним две фигуры.

На 1 рисунке видим замкнутую кривую линию, на которой находятся точки К и С на одинаковых расстояниях от точки О. Такая замкнутая кривая называется окружностью. Точка О — центр окружности. Все точки, поставленные на окружности, находятся на одинаковом расстоянии от центра!

Есть специальный инструмент, который позволяет чертить окружности – это циркуль.

На рисунке 2 видим геометрическую фигуру, которая ограничена окружностью. Эта фигура называется круг.

Вывод: окружность — граница круга; круг — часть внутри окружности. В таблице указаны отличительные признаки круга и окружности:

Если соединить любую точку окружности с ее центром, то получится отрезок, который называется радиусом.

Если соединить 2 точки окружности, проходящих через центр, получится отрезок, который называется диаметром.

Диаметр делит круг на две равные части и все диаметры у окружности равной длины.

Задания тренировочного модуля:

1. Длина радиуса составляет 6 см. Чему равен диаметр окружности?

6см; 12 см; 3см.

Правильный ответ: 12см.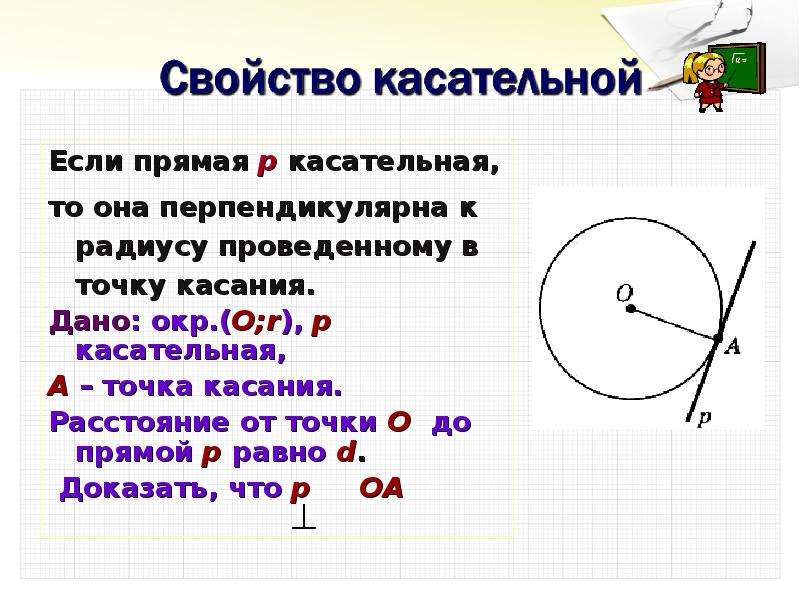

2. Заполните таблицу

радиус	4 см	3 см	7 дм	5 дм
диаметр

Правильный ответ:

радиус	4 см	3 см	7 дм	5 дм
диаметр	8 см	6 см	14 дм	10 дм

Окружность — что это такое

Обновлено 21 июля 2021 Просмотров: 174 183 Автор: Дмитрий Петров

Что такое окружность
Радиус и диаметр
Формула окружности

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.

Есть два геометрических понятия, которые встречаются в абсолютно любой области человеческой деятельности.

Одна из них – прямая, а вторая – окружность. И о ней мы более подробно поговорим в этой статье.

Что такое окружность

Окружность действительно является одной из базовых составляющих не только науки, но и нашей повседневной жизни. Мы едем в транспорте, у которого круглые колеса. Мы едим из тарелок и пьем из кружек, которые также имеют форму окружности.

Да даже все планеты нашей Солнечной системы круглые, и движутся они по окружности.

С самим понятием окружности каждый из нас сталкивается еще в начальной школе. Вот как выглядит определение из учебников математики:

Окружность – это кривая, которая состоит из множества точек, равноудаленных от одной заданной точки.

В данном примере той точкой, от которой равноудалены все остальные, является точка О (см. рисунок выше). И официально она называется центром окружности.

Впервые окружности и все, что с ними связано, были описаны в Древней Греции. В книге «Начала» знаменитого математика Евклида. Этой теме он посвятил всю третью часть своего произведения.

Радиус и диаметр окружности

Чтобы начертить окружность, нужен специальный инструмент. Сделать это от руки не получится. Даже если человек будет максимально аккуратен, все равно линия получится неидеальной. Поэтому не обойтись без циркуля.

Пользоваться им просто. Одна ножка с острым концом устанавливается в центре будущей окружности. А вторая с грифелем чертит вокруг центра ровную окружность. А вот расстояние между ними, которое на данном рисунке обозначено AB, называется радиусом.

Радиус окружности – отрезок, который соединяет центр окружности с любой точкой на ее поверхности.

Обозначается радиус всегда латинской буквой «R» или «r». Количество радиусов для любой окружности бесконечно.

А второе базовое понятие для любой окружности – диаметр.

Диаметр – отрезок, который соединяет две противоположные точки на поверхности окружности, и при этом обязательно проходит через ее центр.

Обозначается диаметр другой латинской буквой – «D» или «d». Как видно из этого рисунка, диаметр равен сумме двух радиусов. И эта формула известна каждому школьнику.

Окружность, у которой радиус равен 1, принято называть единичной. С ней связано очень много понятий в тригонометрии. А вот окружность с нулевым радиусом, является обычной точкой.

Формула окружности

И еще два базовых понятия, которые связаны с окружностью.

Для вычисления длины окружности (что это?) используется формула:

А для вычисления площади круга:

И в данных формулах наибольший интерес представляет буква «π», которая называется числом «пи» (это что?) и является математической постоянной. А равна она 3,14.

Хотя на самом деле количество знаков после запятой бесконечно, но для упрощения принято использовать только до сотых значений. Более подробно о числе «пи» вы можете прочитать в отдельной статье.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.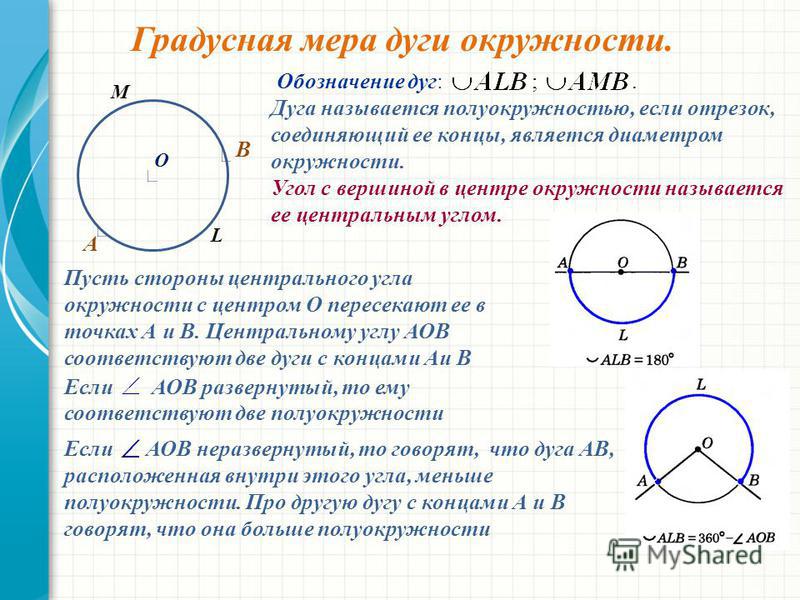 ru

Эта статья относится к рубрикам:

Как обозначать числа с пи на числовой окружности?

Надеюсь, вы уже прочитали про числовую окружность и знаете, почему она называется числовой, где на ней начало координат и в какой стороне положительное направление. Если нет, то бегом читать! Если вы, конечно, собираетесь находить точки на числовой окружности.

Обозначаем числа $2π$, $π$, $\frac{π}{2}$, $-\frac{π}{2}$, $\frac{3π}{2}$

Как вы знаете из прошлой статьи, радиус числовой окружности равен $1$. Значит, длина окружности равняется $2π$ (вычислили по формуле $l=2πR$). С учетом этого отметим $2π$ на числовой окружности. Чтобы отметить это число нужно пройти от $0$ по числовой окружности расстояние равно $2π$ в положительном направлении, а так как длина окружности $2π$, то получается, что мы сделаем полный оборот. То есть, числу $2π$ и $0$ соответствует одна и та же точка. Не переживайте, несколько значений для одной точки — это нормально для числовой окружности.

Теперь обозначим на числовой окружности число $π$. $π$ – это половина от $2π$. Таким образом, чтобы отметить это число и соответствующую ему точку, нужно пройти от $0$ в положительном направлении половину окружности.

Отметим точку $\frac{π}{2}$. $\frac{π}{2}$ – это половина от $π$, следовательно чтобы отметить это число, нужно от $0$ пройти в положительном направлении расстояние равное половине $π$, то есть четверть окружности.

Обозначим на окружности точки $-$$\frac{π}{2}$. Двигаемся на такое же расстояние, как в прошлый раз, но в отрицательном направлении.

Нанесем $-π$. Для этого пройдем расстояние равное половине окружности в отрицательном направлении.

Теперь рассмотрим пример посложнее. Отметим на окружности число $\frac{3π}{2}$. Для этого дробь $\frac{3}{2}$ переведем в смешанный вид $\frac{3}{2}$$=1$$\frac{1}{2}$, т.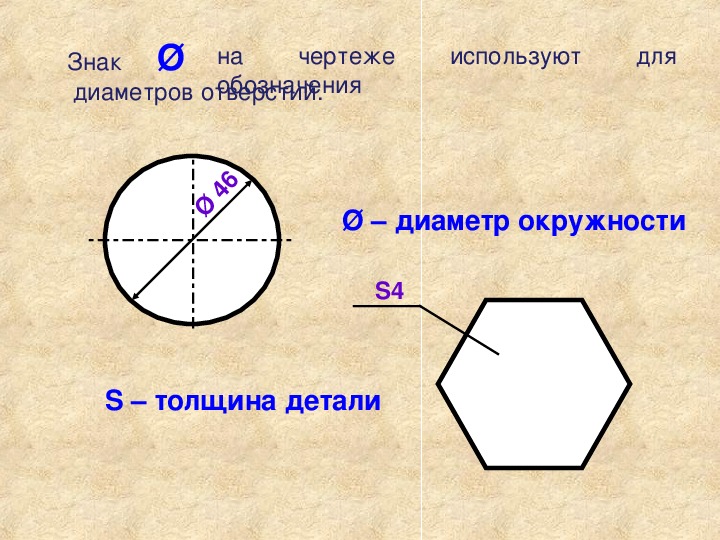 е. $\frac{3π}{2}$$=π+$$\frac{π}{2}$. Значит, нужно от $0$ в положительную сторону пройти расстояние в пол окружности и еще в четверть.

Задание 1. Отметьте на числовой окружности точки $-2π$,$-$$\frac{3π}{2}$.

Обозначаем числа $\frac{π}{4}$, $\frac{π}{3}$, $\frac{π}{6}$

Выше мы нашли значения в точках пересечения числовой окружности с осями $x$ и $y$. Теперь определим положение промежуточных точек. Для начала нанесем точки $\frac{π}{4}$, $\frac{π}{3}$ и $\frac{π}{6}$.
$\frac{π}{4}$ – это половина от $\frac{π}{2}$ (то есть, $\frac{π}{4}$ $=$$\frac{π}{2}$$:2)$ , поэтому расстояние $\frac{π}{4}$ – это половина четверти окружности.

$\frac{π}{4}$ – это треть от $π$ (иначе говоря,$\frac{π}{3}$$=π:3$), поэтому расстояние $\frac{π}{3}$ – это треть от полукруга.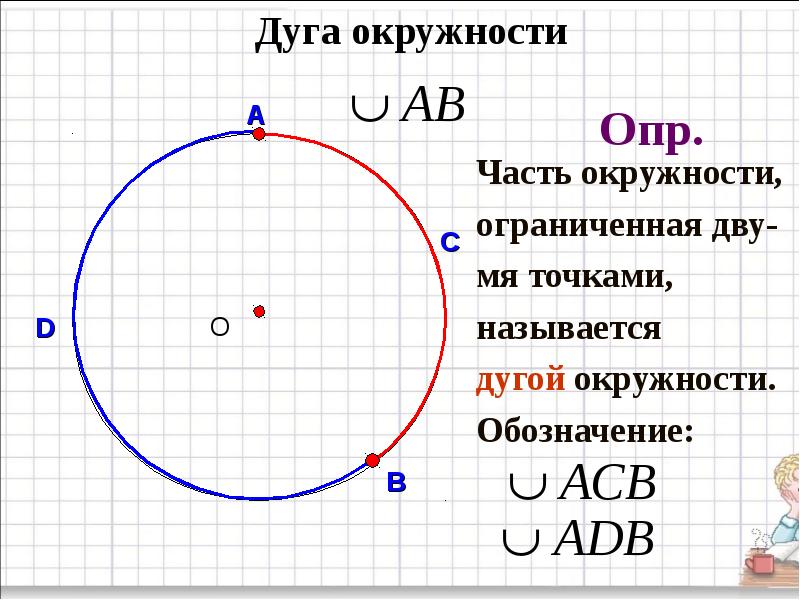

$\frac{π}{6}$ – это половина $\frac{π}{3}$ (ведь $\frac{π}{6}$$=$$\frac{π}{3}$$:2$) поэтому расстояние $\frac{π}{6}$ – это половина от расстояния $\frac{π}{3}$.

Вот так они расположены друг относительно друга:

Замечание: Расположение точек со значением $0$, $\frac{π}{2}$,$π$, $\frac{3π}{2}$, $\frac{π}{4}$, $\frac{π}{3}$, $\frac{π}{6}$ лучше просто запомнить. Без них числовая окружность, как компьютер без монитора, вроде бы и полезная штука, а использовать крайне неудобно.

Разные расстояние на окружности наглядно:

Обозначаем числа $\frac{7π}{6}$, $-\frac{4π}{3}$, $\frac{7π}{4}$

Обозначим на окружности точку $\frac{7π}{6}$, для этого выполним следующие преобразования: $\frac{7π}{6}$$=$$\frac{6π + π}{6}$$=$$\frac{6π}{6}$$+$$\frac{π}{6}$$=π+$$\frac{π}{6}$. Отсюда видно, что от нуля в положительную сторону надо пройти расстояние $π$, а потом еще $\frac{π}{6}$.

Отметим на окружности точку $-$$\frac{4π}{3}$. Преобразовываем: $-$$\frac{4π}{3}$$=-$$\frac{3π}{3}$$-$$\frac{π}{3}$$=-π-$$\frac{π}{3}$. Значит надо от $0$ пройти в отрицательную сторону расстояние $π$ и еще $\frac{π}{3}$.

Нанесем точку $\frac{7π}{4}$, для этого преобразуем $\frac{7π}{4}$$=$$\frac{8π-π}{4}$$=$$\frac{8π}{4}$$-$$\frac{π}{4}$$=2π-$$\frac{π}{4}$. Значит, чтобы поставить точку со значением $\frac{7π}{4}$, надо от точки со значением $2π$ пройти в отрицательную сторону расстояние $\frac{π}{4}$.

Задание 2. Отметьте на числовой окружности точки $-$$\frac{π}{6}$,$-$$\frac{π}{4}$,$-$$\frac{π}{3}$,$\frac{5π}{4}$,$-$$\frac{7π}{6}$,$\frac{11π}{6}$, $\frac{2π}{3}$,$-$$\frac{3π}{4}$.

Обозначаем числа $10π$, $-3π$, $\frac{7π}{2}$ ,$\frac{16π}{3}$, $-\frac{21π}{2}$, $-\frac{29π}{6}$

Запишем $10π$ в виде $5 \cdot 2π$. Вспоминаем, что $2π$ – это расстояние равное длине окружности, поэтому чтобы отметить точку $10π$, нужно от нуля пройти расстояние равное $5$ окружностям. Нетрудно догадаться, что мы окажемся снова в точке $0$, просто сделаем пять оборотов.

Из этого примера можно сделать вывод:

Числам с разницей в $2πn$, где $n∈Z$ (то есть $n$ — любое целое число) соответствует одна и та же точка.

То есть, чтобы поставить число со значением больше $2π$ (или меньше $-2π$), надо выделить из него целое четное количество $π$ ($2π$, $8π$, $-10π$…) и отбросить. Тем самым мы уберем из числа, не влияющие на положение точки «пустые обороты».

Еще один вывод:

Точке, которой соответствует $0$, также соответствуют все четные количества $π$ ($±2π$,$±4π$,$±6π$…).

Теперь нанесем на окружность $-3π$. $-3π=-π-2π$, значит $-3π$ и $–π$ находятся в одном месте на окружности (так как отличаются на «пустой оборот» в $-2π$).

Кстати, там же будут находиться все нечетные $π$.

Точке, которой соответствует $π$, также соответствуют все нечетные количества $π$ ($±π$,$±3π$,$±5π$…).

Сейчас обозначим число $\frac{7π}{2}$. Как обычно, преобразовываем: $\frac{7π}{2}$$=$$\frac{6π}{2}$$+$$\frac{π}{2}$$=3π+$$\frac{π}{2}$$=2π+π+$$\frac{π}{2}$. Два пи – отбрасываем, и получается что, для обозначения числа $\frac{7π}{2}$ нужно от нуля в положительную сторону пройти расстояние равное $π+$$\frac{π}{2}$ (т.е. половину окружности и еще четверть).

Отметим $\frac{16π}{3}$. Вновь преобразования: $\frac{16π}{3}$$=$$\frac{15π + π}{3}$$=$$\frac{15π}{3}$$+$$\frac{π}{3}$$=5π+$$\frac{π}{3}$$=4π+π+$$\frac{π}{3}$. Ясно, что от нуля надо пройти расстояние равное $π+$$\frac{π}{3}$ – и мы найдем место точки $\frac{16π}{3}$.

Нанесем на окружность число $-$$\frac{21π}{2}$.
$-$$\frac{21π}{2}$$= -$$\frac{20π}{2}$$-$$\frac{π}{2}$$=-10π-$$\frac{π}{2}$. Значит, место $-$$\frac{21π}{2}$ совпадает с местом числа $-$$\frac{π}{2}$.

Обозначим $-$$\frac{29π}{6}$.
$-$$\frac{29π}{6}$$=-$$\frac{30π}{6}$$+$$\frac{π}{6}$$=-5π+$$\frac{π}{6}$$=-4π-π+$$\frac{π}{6}$. Для обозначение $-$$\frac{29π}{6}$, на числовой окружности надо от точки со значением $–π$ пройти в положительную сторону $\frac{π}{6}$.

Задание 3. Отметьте на числовой окружности точки $-8π$,$-7π$, $\frac{11π}{4}$,$-$$\frac{7π}{3}$,$\frac{17π}{6}$,$-$$\frac{20π}{3}$,$-$$\frac{11π}{2}$.

Скачать статью

Не удается найти страницу | Autodesk Knowledge Network

(* {{l10n_strings. REQUIRED_FIELD}})

{{l10n_strings.CREATE_NEW_COLLECTION}}*

{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}

{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}
{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings. LANGUAGE}} {{$select.selected.display}}
{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}
{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}
Знак диаметра
В тех случаях, когда требуется указать размер диаметра, используют знак в виде окружности с линией «Ø». Этот символ наносят перед размерным числом.
Примеры использования знака диаметра:
Знаки диаметра на деталях вращения цилиндрической и конической формы

Размеры наносимые при недостатке места
на размерной линии

Обозначение размеров при недостатке места
для стрелок

Диаметр – это длинна отрезка прямой соединяющей поверхности окружности. Отрезок диаметра, в любом случае проходит только через центр окружности. Обозначают его обычно латинской буквой «D» или знаком «Ø». Если радиус окружности умножить на два, суммой будет диаметр. Все объемные тела, имеющие сферическую форму, а также те, хотя бы одно из возможных сечений которых представляет собой круг, обозначаются символами диаметра. Слово «диаметр» произошло от греческого слова «diametros» – поперечник.
Пример обозначения четырёх отверстий
с указанием диаметра

На технических чертежах диаметры обозначаются символом в виде перечеркнутой окружности «Ø». Данный знак, ставится перед размерными числами деталей, которые могут быть как цилиндрическими, так и коническими.

В сечение конус представляет собой прямоугольный треугольник, один из катетов которого параллелен или сосен телу вращения. Его параметры имеют следующими обозначениями: «D» – больший диаметр, «d» – меньший диаметр, «L» – длина. На чертеже диаметры конуса обозначаются цифрами, перед которыми ставятся знаки «Ø» а числовое значение длинны без буквенных обозначений.

К наиболее распространенным деталям с цилиндрическими поверхностями, относятся валы различного назначения. Цилиндрические тела, образованные вращением прямоугольника около одной из его сторон обозначаются диаметром. Гладкие валы имеют некоторые конструктивные особенности, и разделяются на разновидности: прямые, ступенчатые односторонние, ступенчатые двусторонние и тяжелые. К примеру, валы асинхронных двигателей, в которых ротор сопрягается с валом методом запрессовки на наибольший его диаметр, а по обеим сторонам имеются ступени под подшипники, вентиляторы, и шкивы. Двусторонние ступенчатые валы можно встретить так же в различных механизмах там, где требуются, какие либо другие конструктивные особенности. Цилиндрические детали, как правило, имеют общую максимальную длину и наружный диаметр. В зависимости от конкретной конфигурации того или иного изделия в её состав могут входить такие элементы как внутренние и наружные канавки, ступени, выточки и др. с различными диаметрами перед значениями которых ставятся знаки «Ø».
Пример нанесения знака диаметра
на сферической поверхности

К деталям с коническими поверхностями относятся инструментальные переходные втулки, у которых наружная и внутренняя поверхность конические. Такие втулки обеспечивают высокую точность центрирования и быстродействие смены инструмента с достаточной жёсткостью при использовании их на станках. Переходные втулки бывают короткие и длинные.

Конические инструментальные детали данного типа называются «конус Морзе» и делятся на номера. Углы, длины и диаметры переходных втулок можно взять из специальных таблиц. В табличных данных используются буквенные обозначения такие как – «d» меньший диаметр, «D» большой диаметр, «L» длина детали. На чертежах диаметры и длины обозначаются цифровыми значениями, причём перед числами диаметра ставится знак «Ø».
«Конус Морзе» – помимо переходных втулок применяется при изготовлении хвостовиков спиральных свёрл, концевых фрез, приспособлений и оправок. Инструментальные конусы фиксируются за счёт упругой и пластической деформации. Для реализации таких соединений в шпинделях фрезерных и токарных станков, предусмотрены конические отверстия для установки вспомогательного инструмента. Кроме того у токарного станка пиноль задней бабки имеет такое же коническое отверстие.
В технике используются большое количество деталей и их элементов для обозначения, которых используется знак диаметра. Для стандартных размеров диаметров используются параметрический ряд, в который входят стандартные размеры. При разработке технических изделий расчётные диаметры округляются до ближайших их величин. При обозначении на технических чертежах знак диаметра должен сопровождаться обозначением оси штрихпунктирной линией, что указывает на круглое сечение участка детали.

Градусная мера дуги окружности / Окружность / Справочник по геометрии 7-9 класс
Главная

Справочники

Справочник по геометрии 7-9 класс

Окружность

Градусная мера дуги окружности

На рисунке 1 две точки А и В разделяют окружность на две дуги. На каждой дуге отмечают промежуточную точку, например L и М, для того, чтобы различать эти дуги. Обозначают дуги так: АLB и АМВ. Если в задаче ясно, о какой из двух дуг идет речь, то используют обозначение без промежуточной точки: АВ.
Если отрезок, соединяющий концы дуги является диаметром то, такая дуга называется полуокружностью. На рисунке 2 изображена окружность с центром О, концы диаметра АВ разделяют данную окружность на две полуокружности: АКB и АСВ.
Центральный угол — угол с вершиной в центре окружности. Пусть стороны центрального угла окружности с центром О пересекают ее в точках А и В. Центральному углу АОВ соответствуют две дуги с концами А и В.

Измерение дуги окружности
Дугу окружности можно измерять в градусах.
Если дуга АВ окружности с центром О меньше полуокружности (Рис. 3, а) или является полуокружностью (Рис. 2), то ее градусная мера считается равной градусной мере центрального угла АОВ.
Если дуга АВ окружности с центром О больше полуокружности (Рис. 3, б), то ее градусная мера считается равной 360⁰ — АОВ.
Сумма градусных мер двух дуг окружности с общими концами равна 360⁰.
Градусная мера дуги АВ (дуги АLВ), как и сама дуга, обозначается символом АВ ( АLВ). На рисунке 4 градусная мера дуги САВ равна 145⁰. Обычно говорят кратко: «Дуга САВ равна 145⁰» и пишут: САВ = 145⁰. Также на рисунке 4 АDВ = 360⁰ — 115⁰ = 245⁰, СDВ = 360⁰ — 145⁰ = 215⁰, DВ = 180⁰.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Взаимное расположение прямой и окружности
Касательная к окружности
Теорема о вписанном угле
Свойство биссектрисы угла
Свойства серединного перпендикуляра к отрезку
Теорема о пересечении высот треугольника
Вписанная окружность
Описанная окружность
Окружность
Правило встречается в следующих упражнениях:
7 класс
Задание 649, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 660, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 704, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 705, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 11, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 717, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 884, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1109, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 10, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 22, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
© budu5. com, 2021

Пользовательское соглашение

Copyright

Обведите что-нибудь в Word
Редактировать документы Word
Редактировать текст в Word
Редактировать гиперссылку в Word
Водяной знак в Word
Редактировать изображение в Word
Добавить комментарии в Word
Нарисуйте в Word
Закладка в Word
Верхний и нижний колонтитулы в Word
Будьте изобретательны в Word
Дополнительные советы по редактированию слов
Попробовать бесплатно Попробовать бесплатно Попробовать бесплатно
Если вы хотите узнать , как нарисовать круг в слове , тогда процесс очень прост. Чтобы нарисовать круг в слове, функциональность была встроена в программу, и поэтому нет необходимости искать ключевые слова, например, как нарисовать круг в слове. Круг снова можно рассматривать как одну из лучших форм, которые можно добавить в текстовые документы. Это позволяет полностью выделить важную область. Почти каждая версия MS Word поддерживает эту функцию, и она очень удобна, поэтому используется в основном для презентаций.
Как нарисовать круг в Word 2016, 2013, 2010
Как уже упоминалось выше, круг можно безупречно добавить в MS Word, поэтому настоятельно рекомендуется выполнить следующие шаги.Общее управление формами также осуществляется на словах. Это просто означает, что кроме процесса, описанного ниже, вам не нужны дополнительные инструменты для выполнения работы. Шаги указаны ниже.
Откройте пустой документ, который является началом процесса. Он может быть расположен в любом месте вашей системы в зависимости от используемой вами ОС.
Нажмите вкладку «Вставка» в верхней части документа. На вкладке есть несколько параметров, которые вы можете изучить, чтобы узнать больше о документе.
На вкладке «Вставка» есть часть, известная как «Иллюстрации». Нажмите эту вкладку, чтобы открыть раскрывающееся меню, и еще раз нажмите вкладку «Фигуры» в списке.
Теперь щелкните параметр «Линии и соединители», чтобы раскрыть формы. Найдите Круг и затем щелкните по нему, чтобы добавить в документ. Есть несколько форм кружков, которые можно добавить к документу. Перетащите мышью столько, сколько хотите, чтобы круг был. Отпустите кнопку, чтобы добавить кружок в документ.На этом процесс полностью завершен.
Формы в MS Word крайне необходимы профессионалам для разделения данных и обеспечения хорошего внешнего вида презентаций. Управление данными становится простым и понятным. Формы также позволяют пользователям не обращать внимания на неважные моменты. Это экономит время и силы, поэтому для быстрого выполнения работы всегда следует использовать формы. Еще одно важное преимущество фигур состоит в том, что они могут быть связаны с данными.Например, если нарисована таблица, фигуры можно использовать для графического представления.
Wondershare PDFelement — PDF Editor высоко ценится пользователями и поэтому широко используется. Его простота — единственное, что позволяет пользователям познакомиться с программой. Он может помочь вам рисовать круги в документах PDF напрямую, не конвертируя документы PDF в какие-либо другие форматы. Открыв в нем PDF-файл, щелкните вкладку «Комментарий» и выберите инструмент «Круг», чтобы добавить его в PDF-документ.Щелкните правой кнопкой мыши добавленную фигуру и выберите «Свойства». На правой панели измените такие свойства, как «Стиль» и «Толщина». Узнайте больше о том, как добавлять аннотации к PDF здесь.
Советы: преимущества формата PDF
Формат PDF имеет много преимуществ перед Word. Есть несколько моментов, которые гарантируют, что PDF-файл останется поверх Word. Анализ PDF-документа очень прост по сравнению с форматом Word. Настоятельно рекомендуется извлечь журнал аудита, чтобы знать, как и когда был осуществлен доступ к документу.
PDF-файлы очень безопасны по сравнению с Word. В MS Word есть собственный механизм редактирования, поэтому его легко редактировать. PDF, с другой стороны, требует специальных инструментов, чтобы убедиться, что редактирование выполнено.
Читаемость формата PDF очень интерактивна по сравнению с Word. Форматирование Word может искажаться на разных устройствах, в отличие от PDF.
Облачные системы, разработанные Adobe, можно использовать для взаимодействия с файлами PDF из разных мест, что значительно упрощает совместную работу.
Особенности PDFelement:
Открывайте, сохраняйте, печатайте и помечайте PDF-файлы с помощью программы.
Подтвердите подпись документов в цифровом виде.
Используйте OCR для извлечения текста из изображений PDF.
Частичное распознавание текста также может выполняться для определенных пользователем полей PDF.
Защитите файлы PDF паролями с помощью программы.
Скачать бесплатно или Купить PDFelement Сейчас!
Скачать бесплатно или Купить PDFelement Сейчас!
Купить PDFelement Сейчас!
Купить PDFelement Сейчас!
Как построить круг с помощью циркуля — Видео и стенограмма урока
Что такое компас?
Компас — это инструмент, обычно металлический, который можно использовать для рисования окружностей или дуг, а также для измерения расстояний для геометрических построек.У него есть две регулируемые ручки, одна с заостренным металлическим наконечником, а другая — с маленьким прикрепленным карандашом. Некоторые компасы имеют элементы управления для фиксации ширины рукояток и фиксации высоты кончика карандаша и металлического наконечника.
Построение круга
Хорошо, вот шаги для рисования идеального круга:
Найдите и отметьте место, где вы хотите центр вашего круга.
Определите радиус. Это может быть размер или расстояние между другими точками на чертеже.Убедитесь, что вы точно знаете, какой длины должен быть радиус.
Поместите циркуль и грифель близко друг к другу и убедитесь, что они установлены примерно на одинаковую длину. Так будет легче рисовать круг. Затяните ручки карандаша и циркуля.
Расширьте рукоятки компаса до нужного радиуса и затяните петлю вверху (как при блокировке рукояток).
Еще раз измерьте радиус, чтобы убедиться, что стрелки компаса не соскользнули.
Поместите металлический наконечник циркуля на отметку, сделанную вами в центре круга.
Равномерно нажимая на металлический наконечник и карандаш, поверните ручку в верхней части циркуля, перемещая наконечник карандаша по всему кругу. Если круг слишком светлый, сделайте это еще раз, надавив немного сильнее.
Теперь, когда мы знаем, как построить круг с помощью циркуля, давайте рассмотрим пару примеров: сначала построение круга на существующем чертеже, а затем построение круга с заданным размером.
Пример 1
Давайте построим круг с центром в конце линии и краем круга, касающимся другой точки.В этом проекте вы будете использовать расстояние на чертеже, чтобы установить ширину компаса.
Местоположение центра круга отмечено на картинке, так что эту часть легко.
Радиус — это расстояние между двумя отмеченными точками.
Совместите точку компаса и кончик карандаша.
Расширьте стрелки циркуля на расстояние между двумя точками и затяните.
Убедитесь, что стрелки компаса точно совпадают с точками на чертеже.
Поместите металлический наконечник компаса в правильную точку.
Вращайте карандашом по кругу. Если вы все сделаете правильно, круг просто коснется второй точки.
Пример 2
Хорошо, давайте теперь нарисуем круг на основе заданного измерения:
Как мы видим, нам нужно нарисовать три круга, каждый с радиусом 4 см, с отмеченными здесь метками в их центрах.
Для каждого центра, отмеченного в примере, вы нарисуете круг.
С помощью линейки установите расстояние между металлическим острием и кончиком карандаша равным 4 см, затем затяните. Поскольку все три круга имеют одинаковый радиус, вам не придется изменять этот параметр во время упражнения.
Убедитесь, что стрелки циркуля равны точно 4 см.
Для каждого из назначенных кругов поместите металлический наконечник циркуля в центр «x», затем поверните карандаш по кругу. Когда вы закончите, у вас должно получиться три идеальных круга, каждый с радиусом 4 см и центром в одной из точек «x».

Резюме урока
Давайте на мгновение вспомним, что мы узнали о построении круга с помощью циркуля. Круг — это набор точек на плоскости, которые находятся на одинаковом расстоянии от данной точки. Эта точка называется центром круга. Расстояние от центра, которое должно быть одинаковым для всех точек окружности, называется радиусом .Чтобы сделать вещи точными, нам понадобится специальный инструмент, о котором мы в первую очередь узнали на этом уроке: компас.
Компас — это инструмент с двумя руками, который предназначен для рисования окружностей и дуг, а также может использоваться для измерений. Построение круга с помощью компаса выполняется путем определения местоположения центра, установки и фиксации стрелок компаса на правильный радиус, установки металлической точки там, где идет центр, а затем вращения компаса, чтобы сделать отметку круглым карандашом.Теперь с компасом в руке вы должны быть готовы с легкостью строить круги!
Как вырезать большие круги — обязательный совет по шитью!
Большие круги из ткани могут пригодиться для многих вещей, включая формы подушек (вы можете видеть, что я сделал связку), выкройки лоскутных одеял, юбок и скатертей. В этом выпуске «Шитье 201» я покажу вам простой способ вырезать большие круглые круги любого размера.
Во-первых, чтобы избежать путаницы (и убедиться, что вы получили круг нужного размера), давайте договоримся о нескольких словах.Диаметр вашего круга — это то, что вы получите, если измерить всю ширину самой широкой точки. Радиус — это то, что вы получите, если будете измерять от центра (или центра) до края. Радиус всегда равен 1/2 диаметра.
После того, как вы решите, каким должен быть диаметр вашего круга (или формы подушки), определите радиус. Это действительно просто, так как вы просто разделите диаметр пополам. Но я все равно сделал удобную диаграмму. Добавьте 1/2 дюйма к радиусу, если вы делаете подушечки, так как вам понадобится припуск на шов.
Теперь возьмите карандаш или ручку, веревку и линейку (или используйте коврик для резки).
1. Надежно обвяжите конец веревки вокруг ручки или карандаша на расстоянии около дюйма от кончика.
2. Поместите ручку вертикально кончиком на линейку (или измерительную часть коврика для резки). Кончик пера должен «указывать» на желаемое значение радиуса. На картинке выше я использовал радиус 9 1/2 дюймов.
3. Наклоните тетиву вниз до отметки «0» на линейке и сделайте отметку на веревке.Я использовал фломастер, чтобы вы могли видеть мою отметку.
Вы сделали компас своими руками!
4. Сложите ткань пополам. Как видите, я просто сложила конец ткани на четыре части.
5. Одной рукой возьмитесь за веревку в том месте, где вы поставили отметку в центральном углу квадрата.
6. С помощью самодельного циркуля начертите четверть круга. Я провел по своей линии фломастером, чтобы вы могли видеть.
7. Как только ваша четверть круга будет нарисована, прорежьте все слои острыми ножницами.Вот мой список из 7 лучших швейных ножниц (3 пары, без которых вы не сможете шить, и еще 4, которые вам тоже понравятся).
Разверните и
Альт! Большой круг.
Сделайте много больших кругов для всех ваших круговых потребностей.
Чтобы сделать подушку круглой формы, сшейте два круга одинакового размера с припуском на шов 1/2 дюйма. Не забудьте оставить около 4 дюймов для переворачивания и набивки. Когда ваша подушка станет достаточно пухлой, заверните необработанные края и зашейте отверстие.
И на вашем месте я бы сделал много круглых подушек, потому что у меня скоро будет потрясающий рождественский урок, в котором они будут использоваться!
Посмотрите мои круглые тафтинговые подушки здесь и другие интересные вещи, которые можно сшить для вашего дома, ниже:
Поделиться — это забота!
Раскрытие информации: некоторые из моих сообщений содержат партнерские ссылки.Если вы купите что-то по одной из этих ссылок, я могу получить небольшую комиссию, поэтому благодарим вас за поддержку SewCanShe при совершении покупок! Все мнения принадлежат мне, и я предлагаю только те продукты, которые действительно использую. 🙂
Разметка круга
Петра,
У нас есть для вас два ответа: один от Стивена, а второй от Пенни.
Привет, Питер. Я нарисовал круг радиусом 18 м с центром в начале графика и нарисовал дугу длиной 5 м.
Первое, что следует вспомнить, это то, что для любого круга, центр которого находится в начале графика, ВСЕ точки на окружности имеют форму (r cos A, r sin A), где r — радиус, а A — начальный угол. от правой руки и поворачивая против часовой стрелки. Вы увидите, что я пометил это на схеме. Вы знаете, что радиус r равен 18 м, поэтому, если вы можете определить угол A, вы можете просто ввести различные числа от 0 до A, чтобы получить выборку промежуточных точек вдоль интересующего вас участка дуги (я раскрасил он зеленый на схеме).
Чтобы вычислить A, мы думаем о том, какую часть окружности описывает наша дуга. Мы знаем, что радиус круга равен 18 м, поэтому длина его окружности в 2 раза больше: около 113,1 м. А 5 над 113,1 составляет около 0,0442, поэтому мы описываем 4,42% круга. Теперь круг составляет 360 градусов по всему периметру, поэтому 4,42% от 360 градусов составляют 15,92 градуса. Это A.
Теперь вы можете просто вычислить некоторые значения для (x, y), чтобы получить выборку точек данных, которые вы ищете.Просто подсчитайте баллы по формуле:
(18 cos t, 18 sin t), где t — угол между 0 и 15,92 градуса,
Надеюсь, это поможет,
Стивен Ла Рок.
Привет, Питер,
Я повернул диаграмму Сью так, чтобы дуга оказалась наверху, и разделила 15,92 градуса Сью на 2, получив 7,96 градуса, а затем нашла 90 — 7,96 = 82,04 градуса. Таким образом, точка P имеет координаты
.
(18 cos 82.04, 18 sin 82,04) = (2,49, 17,83)
Вот увеличенная дуга над прямой.
Уравнение круга
x ² + y ² = 18 ²
и, следовательно, чтобы найти высоту смещения (h), измерьте t метров от левого конца линии и вычислите
h = Sqrt [18 ² — (-2.49 + т) ²] — 17,83
где Sqrt — квадратный корень. Например, если t = 1 м, то
h = Sqrt [18 ² — (-2,49 + 1) ²] — 17,83
= Sqrt [18 ² — (-1,49) ²] — 17,83 = 17,94 — 17,83 = 0,11 м
Пенни
кругов и использование циркуля
частей круга
Дуга является частью окружности.

Сектор — это часть окружности между двумя радиусами.

Сегмент — это часть окружности, которая находится между хордой и окружностью.

Полукруг — это половина круга.

Компас
Компас — инструмент, используемый для рисования кругов или частей окружности называются дугами.Он состоит из двух шарнирно соединенных между собой подвижных рычагов. где одна рука имеет заостренный конец, а другая держит карандаш.
Обратите внимание, что компас также называется парой циркуля.

Чтобы нарисовать круг (или дугу) с помощью циркуля:
убедитесь, что петля в верхней части компаса затянут так, чтобы не скользило
затяните фиксатор карандаша, чтобы он не соскальзывал
совместите грифель карандаша с иглой циркуля
нажмите на иглу и поверните ручку в верхней части циркуль для рисования круга (или дуги)

Пример 2
С помощью циркуля начертите круг радиусом 4 см.
Решение:
Шаг 1: С помощью линейки установите расстояние от точки компаса до грифель карандаша на 4 см.
Шаг 2: Поместите конец циркуля в центр круга.
Шаг 3: Нарисуйте круг, повернув компас на 360.

Деятельность 10,1
1. С помощью циркуля начертите круг радиусом 5 см.
2. С помощью циркуля начертите круг диаметром 12 см.
3а. С помощью циркуля начертите круг радиусом 4,5 см.
3б. Нарисуйте диаметр круга; и используйте линейку, чтобы измерить длина диаметра.
3с. Напишите уравнение, чтобы представить соотношение между радиусом, r , и диаметром d .
4а. С помощью циркуля начертите круг радиусом 5,5 см.
4б. Нарисуйте диаметр и обозначьте его PQ .
4с. Нарисуйте треугольник PQR , где R находится на полукруге.
4д. С помощью транспортира измерьте размер уголка PRQ .
5а. С помощью циркуля начертите круг радиусом 6,5 см.
5б. Нарисуйте диаметр и обозначьте его PQ .
5с. Нарисуйте треугольник PQR , где R находится на полукруге.
5д. С помощью транспортира измерьте размер уголка PRQ .
6а.С помощью циркуля начертите круг радиусом 7,5 см.
6б. Нарисуйте диаметр и обозначьте его PQ .
6с. Нарисуйте треугольник PQR , где R находится на полукруге.
6д. С помощью транспортира измерьте размер уголка PRQ .
7. Используйте результаты вопросов 4, 5 и 6, чтобы заполнить следующие Выписки:
а. Размер угла на диаметр окружности с вершиной на по кругу
б.Если треугольник нарисован полукругом, используя диаметр как ребро, угол касания изогнутой части треугольника равен

Ключевые термины
круг, центр круга, радиус, периметр, окружность, радиусы, линии круга, секущая, хорда, диаметр, касательная, части круга, дуга, сектор, сегмент, полукруг, циркуль, циркуль
Как нарисовать круг в Photoshop
На протяжении многих лет мне нужно было делать простые иллюстрации для своих сообщений в блоге, но я был в тупике, рисуя простые круги. Поиск руководств о том, как это сделать в PhotoShop, привел меня к запутанным, странным или просто неправильным методам. Однако недавно я хотел нарисовать круг для своего поста на расстоянии до горизонта и решил спросить эксперта: Маленького астронома, который показал мне, как это сделать примерно за 20 секунд. Я записал, что она сказала, и что, черт возьми: если я опубликую это здесь, в блоге, я смогу сослаться на это, и, возможно, это поможет и вам.
Для справки, в настоящее время я использую Photoshop CS3 версии 8 на Mac под управлением OS X 10.4. Я не думаю, что это имеет большое значение. Если да, оставьте комментарий! И, эй, прокомментируйте, если вы тоже знаете другой метод. Чем больше тем лучше.
Итак:
0) Выполните обычные действия — откройте изображение или создайте новое.
1) Щелкните инструмент «Перо» на панели инструментов.
2) На новой панели инструментов, отображаемой вверху, нажмите кнопку с эллипсом внутри.
3) Нарисуйте круг, перетаскивая курсор, удерживая нажатой клавишу Shift (иначе вы получите эллипс). Вы получаете не изображение круга, а так называемый «путь». Потерпи меня здесь. При необходимости отрегулируйте размер. Примечание: место, где вы первоначально щелкаете пером, отмечает центр круга, поэтому вы можете записать координаты (x и y) центра, если вы планируете возиться с кругом позже.
4) Перейти к инструменту «Карандаш». Выберите желаемую толщину (вы также можете сделать это перед рисованием круга). Убедитесь, что вы выбрали нужный цвет!
5) Вернитесь к инструменту «Перо».
Oooooo, Ahhhhhh
6) Щелкните правой кнопкой мыши где-нибудь на изображении. Выберите «Обводка контура». Перечислены варианты. В раскрывающемся меню выберите «Карандаш».
7) Теперь у вас нарисован круг. Но вы все еще увидите пунктирную линию — это путь, который был пройден ранее. Чтобы удалить его, щелкните еще раз правой кнопкой мыши. Нажмите «удалить путь». Это избавляет от первоначального кругового пути и оставляет у вас красивый круг желаемой толщины.
Это может показаться сложным для новичка (вроде меня), но на самом деле это совсем несложно, и вы увидите, что существует множество вариаций (вы можете создать нечеткий круг, взяв кисть вместо карандаша, Например).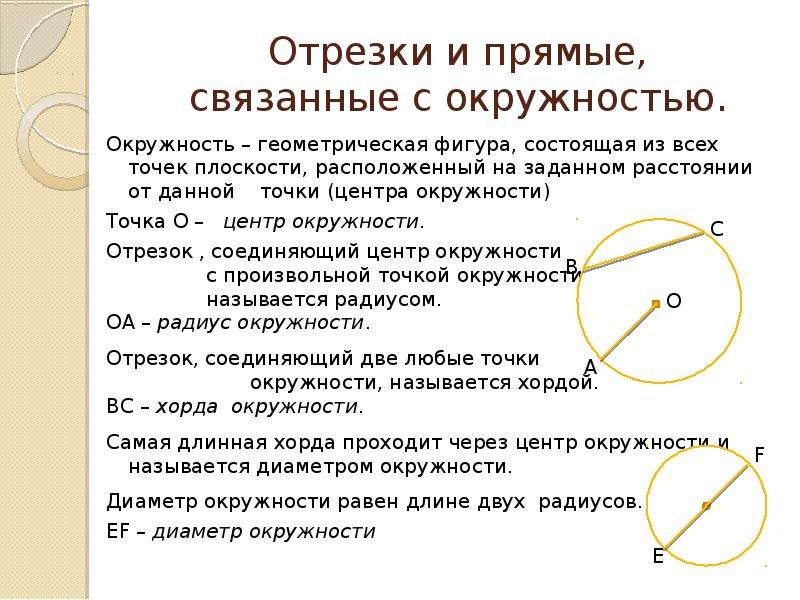
И я рад, потому что теперь я могу делать еще более глупые изображения для своих сообщений. Ура!
Изменить тип метки на экране
Вы можете изменить тип меток, отображаемых в представлении, в соответствии с вашим анализом. Например, вы можете изменить метки с полос на линии. В этой статье описывается, как изменить тип меток, используемых в представлении, и объясняются различные доступные типы меток. Дополнительную информацию о метках см. В разделах «Управление внешним видом меток на карточке« Просмотр »и« Метки ».
Изменить вид метки
Для изменения типа отметки:
Описание каждого типа метки см. В следующих разделах:

Марка автомат
Если в раскрывающемся меню «Маркировка карты» установлено значение «Автоматически», Tableau автоматически выбирает лучший тип метки для просмотра данных.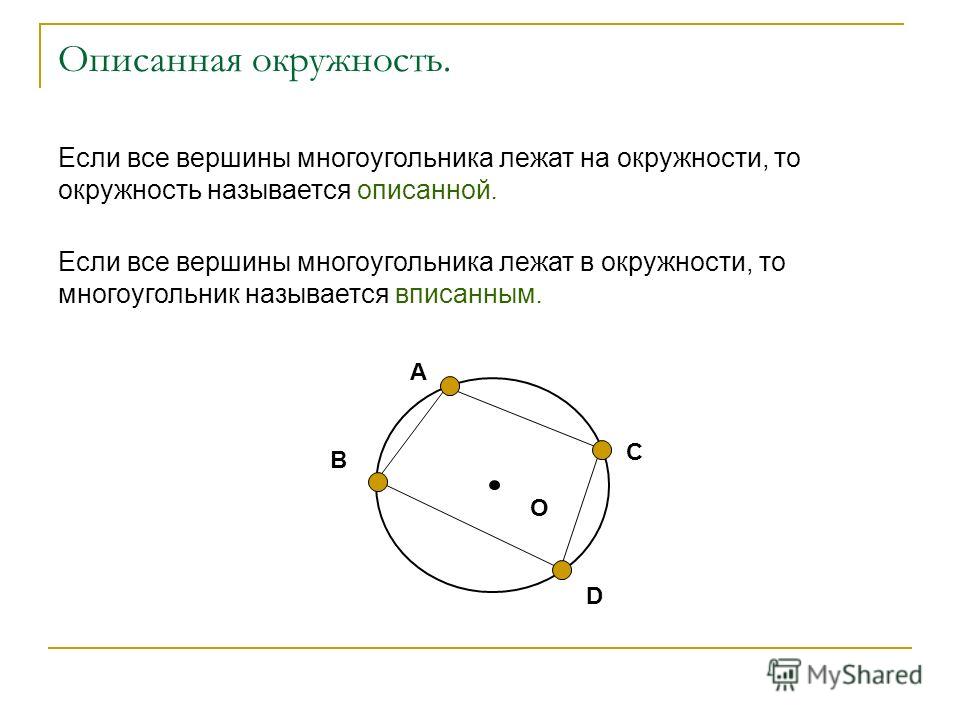 Тип метки, который выбирается автоматически, определяется внутренними полями на полках «Строки» и «Столбцы».Значок в раскрывающемся меню карточки «Отметки» указывает, какой тип отметки был выбран автоматически. Приведенные ниже типы отметок выбираются автоматически для следующих сценариев.
Текст
Тип метки «Текст» выбирается автоматически, если есть размеры в виде внутренних полей на полках «Строки» и «Столбцы».
Форма
Тип метки «Форма» выбирается, если в качестве внутренних полей на полках «Строки» и «Столбцы» есть меры.
Бар
Тип отметки «Полоса» выбирается, когда есть измерение и мера в качестве внутренних полей на полках «Строки» и «Столбцы».
Строка
Тип метки «Линия» выбирается, когда есть поле даты и мера в качестве внутренних полей на полках «Строки» и «Столбцы».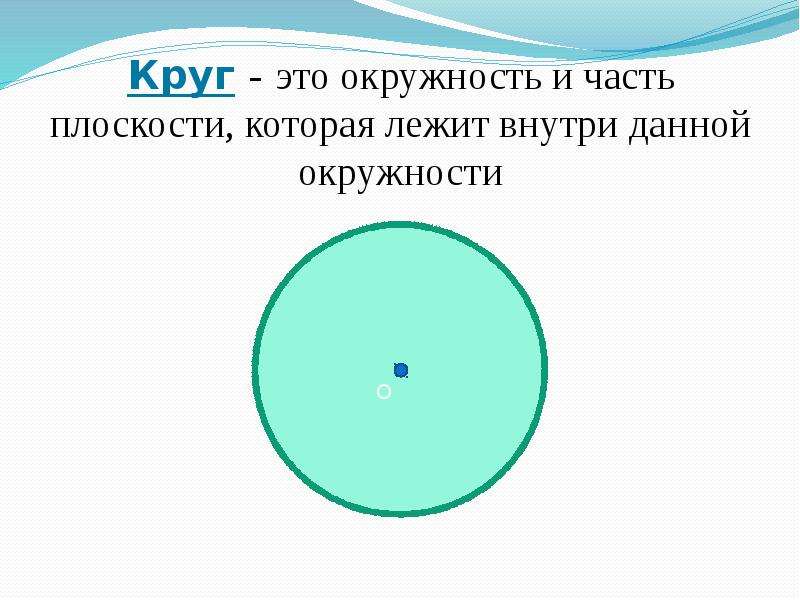
Примечание: Вы можете отменить выбор по умолчанию и использовать любой тип метки что дает представление о ваших данных.Однако вам следует заниматься спортом. соблюдать осторожность при выборе типа метки вручную, поскольку в результате вид может скрыть важную информацию о ваших данных.
Штанга
Тип отметки Bar полезен, когда вы хотите сравнить меры. по категориям или когда вы хотите разбить данные на группы бары. Tableau отображает ваши данные в виде столбцов, когда:
В раскрывающемся меню карточки «Отметки» установлено значение «Автоматически», и вы размещаете измерение и меру в качестве внутренних полей на полках «Строки» и «Столбцы».Если измерение является измерением даты, строка вместо этого используется знак.
Выберите «Панель» в раскрывающемся меню «Маркировка».
Метки складываются автоматически.
Примечание : Для представлений, в которых тип метки — «Полоса» и есть непрерывные (зеленые) поля как в строках, так и в столбцах, Tableau поддерживает дополнительные параметры и значения по умолчанию для изменения размера меток столбцов на оси, где столбцы закреплены.Дополнительные сведения см. В разделе «Изменение размера меток на непрерывной оси» в статье «Изменение размера меток».
Представление данных, показанное ниже, отображает измерение в виде столбцов таблицы и меру в виде строк таблицы. Он также имеет цветовую кодировку по измерению (Категория). Потому что раскрывающееся меню карточки «Отметки» установлен на Автоматически, данные отображаются в виде полосок.
Чтобы попробовать несколько практических упражнений по построению гистограмм, см. Построение гистограммы.
Знак линии
Тип отметки линии полезен, когда вы хотите увидеть тенденции в данных с течением времени ваши данные упорядочены, или интерполяция делает смысл. Таблица отображает данные в виде линий, когда:
В раскрывающемся меню карточки «Отметки» установлено значение «Автоматически», и вы размещаете одну или несколько мер на полке столбцов или полку «Строки», а затем нанесите меры против измерения даты или непрерывного измерения.
Выберите «Линия» в раскрывающемся меню карточки «Отметки».
Примечание : В представлениях, которые используют тип метки линии, вы можете использовать свойство Путь в карточке Метки, чтобы изменить тип метки линии (линейная, ступенчатая или скачкообразная) или для кодирования данные путем соединения меток с использованием определенного порядка рисования. Дополнительные сведения см. В разделе «Свойства пути» в разделе «Управление внешним видом меток на виде
».
Представление данных, показанное ниже, отображает измерение даты как столбцы таблицы и меру как строки таблицы.
По мере увеличения плотности данных тенденции часто легче видеть при использовании линий. Это представление показывает 93 точки данных.
Чтобы попробовать несколько практических упражнений по построению линейных диаграмм, см. Построение линейных диаграмм.
Отметка площади
Тип отметки Area полезен, когда у вас есть представление, где отметки сложены и делают не перекрываются. Для получения дополнительной информации о метках стопки см. Метки стопки. На диаграмме с областями расстояние между каждой линией и следующая строка залита цветом. Этот тип диаграммы не является лучший способ показать конкретные значения вдоль линии, но он может четко показать общие значения, чтобы вы могли понять, как вносит свой вклад в общую тенденцию.Tableau отображает ваши данные использование площадей при:
В раскрывающемся меню «Маркировка» задано значение «Автоматически» и одно или несколько мер. отображается по отношению к измерению даты или непрерывному измерению. Параметр Анализ> Метки стека также должны быть выбраны.
Представление ниже показывает измерение даты на полке столбцов и мера на полке рядов. Каждая строка представляет продажи для категория продукта. Линии уложены так, чтобы они не перекрываются.
Примечание. Вы можете добавлять метки, редактировать цветовые обозначения и выделять области. Кроме того, вы можете включить цветовые эффекты, такие как отметка границы. Для получения дополнительной информации см. Управление внешним видом меток в просмотре.
Квадратная отметка
Тип квадратной метки полезен, когда вы хотите четко увидеть отдельные точки данных.Когда вы выбираете квадрат из раскрывающееся меню карточки «Отметки», на Табло отображаются ваши данные. с помощью квадратов.
Представленный ниже вид отображает несколько размеров на обоих полки рядов и столбцов. По умолчанию данные отображаются в виде текста. Однако, когда вы помещаете меру в Color, Tableau преобразует метки в квадраты и создает тепловую карту. Чтобы попробовать несколько практических упражнений по созданию таблиц выделения, см. Создание таблицы выделения или тепловой карты.
Когда вы добавляете дополнительные уровни детализации, помещая размер в Детализация, Цвет, Форма, Размер или Метка на карточке Метки, квадраты отображаются бок о бок и обертываются, чтобы заполнить ячейку. Если окно слишком мало для отображения всех квадратов, эллипсы указывают на то, что значений больше, чем вы можете увидеть.
Вы также можете использовать квадратную метку для создания карт деревьев. На карте дерева иерархические данные отображаются в виде набора вложенных прямоугольников. Чтобы попробовать практическое упражнение по построению карты дерева, см. Создание карты дерева.
Знак круга
Когда вы выбираете Круг в раскрывающемся меню карты Метки, Tableau отображает ваши данные в виде закрашенных кружков.
Если был установлен тип метки Автоматически, на Табло будет отображаться данные с использованием формы (то есть открытого круга).
Знак формы
Тип метки формы полезен, когда вы хотите четко просматривать отдельные точки данных, а также просматривать связанные с ними категории с этими точками. Tableau отображает ваши данные в форме, когда:
В раскрывающемся меню карточки «Отметки» установлено значение «Автоматически», и вы размещаете одну или несколько мер как в строках, так и в Колонны полки.
Выберите «Форма» в раскрывающемся меню карточки «Метки».
Представление, показанное ниже, отображает данные двух показателей. Так как в раскрывающемся меню карточки «Отметки» установлено значение «Автоматически», данные отображаются в форме.
По умолчанию используется форма открытого круга.Выбирать другую фигуру, щелкните Фигура на карточке Метки. Доступно двадцать уникальных форм:
Чтобы добавить больше данных в представление, вы можете поместить поле в поле «Форма» на карточке «Метки». Табло разделяет отметки в соответствии со значениями в поле. Если поле является размером, каждому члену назначается уникальная форма. Если поле является мерой, эта мера автоматически разбивается на отдельные сегменты, и каждому сегменту назначается уникальная форма.Появится легенда формы. как распределяются формы.
Как показано ниже, размерность режима корабля помещается в поле «Форма» на карточке «Метки» для кодирования каждой метки с информацией о том, как был отправлен заказ.
Для получения подробной информации о том, как построить диаграмму рассеяния, см. Построение диаграммы рассеяния.
Текстовый знак
Тип текстовой метки полезен, когда вы хотите отобразить числа, связанные с одним или несколькими элементами измерения.Этот тип представления часто называют текстовой таблицей, кросс-таблицей или сводной таблицей. Tableau отображает ваши данные в виде текста, когда:
В раскрывающемся меню карточки «Отметки» установлено значение «Автоматически», и вы размещаете одно или несколько измерений в качестве внутренних полей на обоих полки «Ряды» и «Столбцы».
Выберите «Текст» в раскрывающемся меню карточки «Отметки».
Первоначально данные отображаются как Abc .
Для завершения просмотра необходимо поместить поле (обычно меру) в поле «Текст» на карточке «Метки». В представлении ниже показатель продаж, которая суммируется, используется для заполнения таблицы.
Примечание: Чтобы создать кросс-таблицу любого представления данных, выберите Рабочий лист> Дублировать.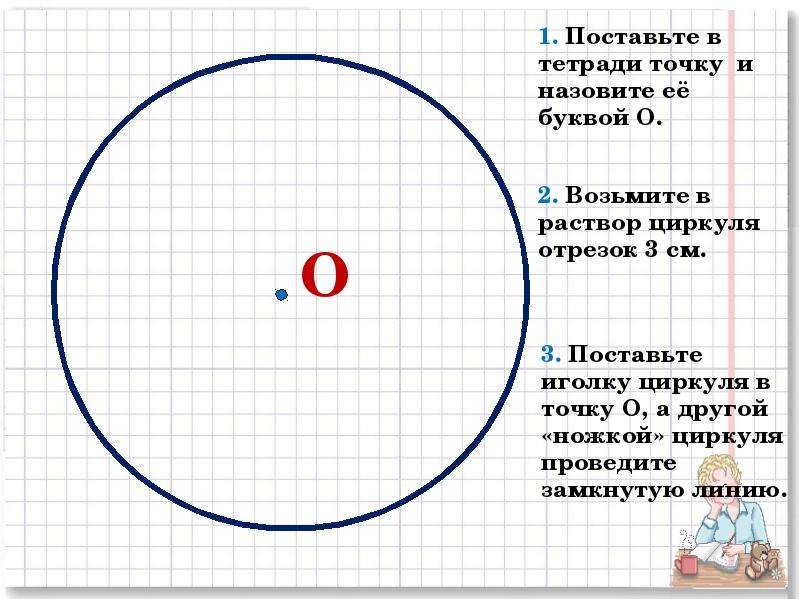 как Crosstab.
Когда вы добавляете дополнительные уровни детализации, помещая размер в Детализация, Цвет, Форма, Размер или Текст на карточке Метки, значения отображаются рядом и обертываются, чтобы заполнить ячейку. Разрешение наложения текста позволяет создавать визуализации облака слов, подобные показанной ниже.
Если окно приложения слишком мало для всех текстовых значений, некоторые из отображаемых текстовых значений будут усечены.
Если окно приложения слишком мало для всех текстовых значений, в ячейке отображается многоточие, указывающее на то, что имеется больше значений, чем может быть отображено. Числовые значения, которые не могут быть отображены, обозначаются знаками решетки (#).
Подробнее о том, как создать текстовую таблицу, см. В разделе Создание текстовой таблицы.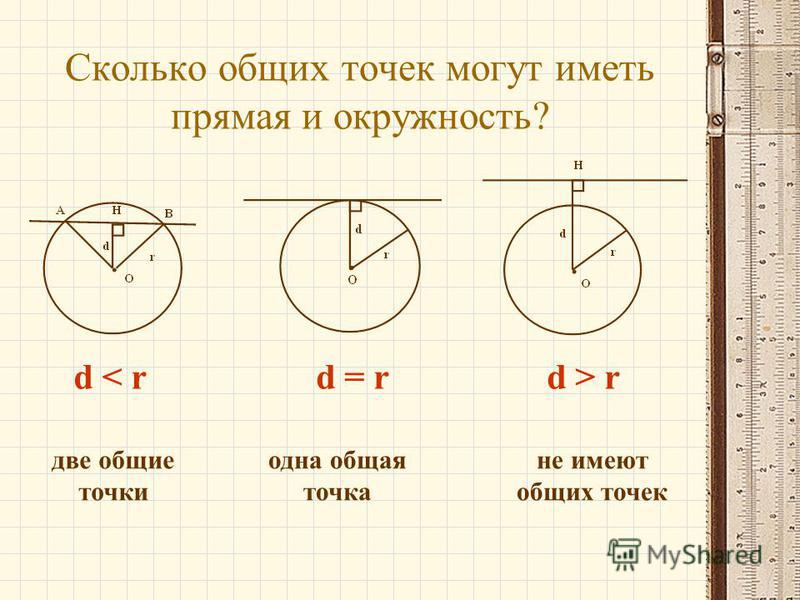
Отметка на карте
Тип метки карты использует геокодирование для заливки многоугольника или линии. с цветом на основе данных.Основное использование отметки на карте Тип предназначен для создания полигональных или линейных карт. Заполняемая область определяется географическим поля, используемые в представлении. Tableau отображает данные с использованием заполненной карты когда:
Географическое измерение находится в деталях на карточке «Метки», а также на полках «Широта» и «Долгота» на полках «Строки» и «Столбцы». Мера или непрерывное измерение добавляется в Цвет на карточке Метки.
Выберите «Карта» в раскрывающемся меню карты «Отметки».
В представлении данных ниже показана карта с географическим измерением штата. о деталях на карточке Знаков. Показатель прибыли указан в цвете. на карточке Метки.
Многоугольник для каждого состояния заполнен цветом на основе прибыль для этого государства. Прибыль в Техасе низкая (фактически отрицательная), а прибыль в Калифорнии высокий.
Вы также можете использовать тип отметки «Карта» при черчении. две меры друг против друга.По умолчанию размещение мер на полках «Строки» и «Столбцы» создается диаграмма рассеяния. Тем не мение, добавление географического измерения позволяет изменить тип отметки для отображения. Каждая отметка становится областью, определенной географическим поле. Например, в представлении ниже показаны продажи по сравнению с прибылью для подборка состояний. Вместо того, чтобы показывать круглую метку с этикеткой для каждого состояния в представлении используется тип метки карты для рисования план каждого государства. Хотя это хорошо работает для узнаваемых областей, это не лучший выбор для областей, которые похожи по форме или трудно распознать.
Дополнительные сведения о построении карт см. В разделах «Приступая к работе с картированием с помощью Tableauand Maps» и «Анализ географических данных в Tableau».
Марка пирога
Вы можете использовать знак пирога, чтобы показать пропорции. Несмотря на то что как правило, этот тип информации может быть лучше показан с помощью сложенных гистограммы, бывают случаи, когда круговые метки могут быть очень эффективными, например, при попытке передать процентное соотношение распределение маркетинговых расходов по штатам, в которых расходуется географически близкие государства очень актуальны.
Tableau никогда не будет использовать знак пирога в качестве автоматического типа метки, но вы можете выбрать «Пирог» в раскрывающемся меню карточки «Отметки».
Когда вы выбираете тип круговой метки, на карточке меток отображается дополнительная цель с именем «Угол». Цель Angle определяет угловую меру дольки пирога. Например, если вы разместите такую меру, как Продажи на Угол на карточке Метки, 360 градусов круговой диаграммы соответствуют общая сумма продаж, и каждый клин делится на значения поле Цвет на карточке Метки.
На представлении ниже показано время, которое потребовалось для отправки продуктов различными корабельные режимы. Данные накладываются на карту и показывают данные по штатам. Мы видим, что доставка стандартным классом занимает больше всего времени в большинстве областей.
Подробные сведения о том, как создавать и использовать круговые диаграммы, см. В разделах Создание круговой диаграммы и Начало работы с картами с помощью Tableau.
Марка стержня Ганта
В раскрывающемся меню «Маркировка» установлено значение «Автоматически» и вы размещаете одно или несколько измерений на полке столбцов или полку Строки, а затем нанесите размеры против постоянного количества.
Вы выбираете шкалу Ганта в раскрывающемся меню карты «Метки».
Отличительной особенностью планок Ганта является то, что длина каждой отметки пропорциональна размеру, указанному на карточке отметок.
Представление ниже отображает размер как функцию непрерывного свидания. Если раскрывающееся меню карточки «Отметки» отображается установлен автоматический, данные будут отображаться с использованием бары.Выбор шкалы Ганта и добавление в дополнительных полях будет отображаться следующий вид.
В частности, при измерении количества дней до отгрузки по размеру на карточке меток приводит к тому, что каждая полоса в представлении быть нарисованным с длиной, которая указывает время доставки Заказ. Кроме того, размещение измерения режима корабля на карте «Цвет» каждая полоса окрашивается в соответствии с режимом корабля.
Подробнее о том, как построить столбчатую диаграмму Ганта, см. В разделе Построение диаграммы Ганта.
Знак многоугольника
Многоугольники — это точки, соединенные линиями, ограничивающими область. Знак многоугольника Тип полезен, когда вы хотите соединить точки для создания областей данных. Tableau отображает данные с помощью многоугольников, когда вы выбираете Polygon из меню «Метки».
Знак многоугольника обычно не используется и часто требует специально сконструированный источник данных.
Представленный ниже вид взят из специально созданных данных. источник, содержащий географические данные и данные о выборах. Он отображает 48 смежных штатов США в зависимости от широты и долготы и закодирует каждый штат по результатам президентских выборов 2000 года цветом.
Если для отметок установлено значение Автоматически, данные будут отображаться в форме. Выбор многоугольника вручную а добавление дополнительных полей к представлению приводит к созданию другого представления.
‘
Каждое состояние рассматривается как многоугольник в источнике данных. Поле PolygonID в целевой области сведений индивидуально для каждого штата США. Ты сможешь удалить состояния из представления, отфильтровав это поле.
Дополнительно можно указать порядок рисования линий которые составляют каждый многоугольник, помещая поле в цель Path. В этом примере мерой PointOrder является используется для рисования каждого состояния.
Отметка плотности (тепловая карта)
Отметку плотности можно использовать для визуализации закономерностей или тенденций в плотных данных с множеством перекрывающихся отметок. Хотя обычно этот тип информации может быть показан с помощью кружка, есть случаи, когда метки плотности могут быть очень эффективными — например, когда в области много точек данных, и вам нужно понимать, где эти метки наиболее сконцентрированы. Метку плотности можно эффективно использовать с картами или диаграммами, в которых используются точечные метки (диаграммы рассеяния, единичные гистограммы, прямоугольные диаграммы по отдельным меткам или точечные карты).
Tableau делает это, группируя перекрывающиеся метки и кодируя их цветом в зависимости от количества меток в группе.
Знаки плотности
используют цвет, чтобы показать относительную интенсивность данных в заданной области диаграммы. Вы можете настроить цвета метки плотности, выбрав Цвет на карточке Метки.Выберите из десяти цветовых палитр плотности или любую из существующих цветовых палитр.
В меню «Цвет» используйте ползунок «Интенсивность», чтобы увеличить или уменьшить яркость меток плотности. Например, увеличение интенсивности или яркости снижает количество точек «максимального нагрева» в ваших данных, поэтому появляется больше.
Низкая интенсивность (50%) Высокая интенсивность (80%)
Представление, показанное ниже, получено из источника данных, который содержит множество географических точек для одного месяца сбора такси на Манхэттене. Он отображает местонахождение и частоту получения такси, причем чаще всего используются более светлые цвета.
Вы можете выбрать «Плотность» в раскрывающемся меню карты «Метки».
Подробнее о том, как построить карту плотности или диаграмму плотности, см. В разделах «Создание тепловых карт, отображающих тенденции или плотности в таблице», и «Построение с метками плотности (тепловая карта)».
.