Решение системы линейных уравнений методом гаусса-жордана

метод Гаусса–Жордана — один из наиболее известных и широко применяемых методов решения систем линейных уравнений. Матричный метод и метод Крамера обладают тем недостатком, что они не дают ответа в том случае, когда detA = 0, а определяют лишь единственное решение при detA неравном 0. Еще одним недостатком является то, что объем математических вычислений в рамках этих методов резко возрастает с ростом числа уравнений. Метод Гаусса практически свободен от этих недостатков.

Алгоритм метода Гаусса

1. На основании системы линейных уравнений составляем расширенную матрицу системы;
2. Приводим матрицу к «треугольному» виду;
3. Определяем ранги основной и расширенной матриц, и на основании этого делаем вывод о совместности системы и количестве допустимых решений;
4. В случае, если система имеет единственное решение производим обратную подстановку и находим его, если система имеет множество решений: выражаем базисные переменные через переменные которые могут принимать произвольные значения;

Комментарий к шагу 2 Метода Гаусса. Треугольной называют матрицу, в которой все элементы расположенные ниже главной диагонали равны нулю.

Для приведения исходной расширенной матрицы к треугольному виду используем следующие два свойства определителей:

Свойство 1. Определитель не изменит свое значение, если ко всем элементам какой-либо строки (столбца) матрицы прибавить соответствующие элементы параллельной строки (столбца), умноженные на произвольное одно и то же число.

Свойство 2. При перестановке двух любых столбцов или строк матрицы ее определитель меняет знак на противоположный, а абсолютная величина определителя остается неизменной.

На основании этих свойств определителей составим алгоритм преобразования матрицы к треугольному виду:

1. Рассматриваем строку i(начиная с первой). Если, элемент a i i равен нулю, меняем местами i-ю и i+1-ю строки матрицы. Знак определителя при этом изменится на противоположный. Если a 1 1 отличен от нуля — переходим к следующему шагу;
2. Для каждой строки j, ниже i-й находим значение коэффициента K j =a j i /a i i ;
3. Пересчитываем элементы всех строк j, расположенных ниже текущей строки i, с использованием соответствующих коэффициентов по формуле: a j k нов. =a j k -K j *a i k ; После чего, возвращаемся к первому шагу алгоритма и рассматриваем следующую строку, пока не доберемся до строки i=n-1, где n — размерность матрицы A
4. В полученной треугольной матрице расчитываем произведение всех элементов главной диагонали Пa i i , которое и будет являтся определителем;

Другими словами, суть метода можно сформулировать следующим образом. Нам необходимо сделать нулевыми все элементы матрицы ниже главной диагонали. Сначала мы получаем нули в первом столбце. Для этого мы последовательно вычитаем первую строку, домноженную на нужное нам число (такое, чтоб при вычитании мы получили ноль в первом элементе строки), из всех ниже лежащих строк. Затем проделываем то же самое для второй строки, чтобы получить нули во втором столбце ниже главной диагонали матрицы. И так далее пока не доберемся до предпоследней строки.

Здесь вы сможете бесплатно решить систему линейных уравнений методом Гаусса онлайн больших размеров в комплексных числах с очень подробным решением. Наш калькулятор умеет решать онлайн как обычную определенную, так и неопределенную систему линейных уравнений методом Гаусса, которая имеет бесконечное множество решений. В этом случае в ответе вы получите зависимость одних переменных через другие, свободные. Также можно проверить систему уравнений на совместность онлайн, используя решение методом Гаусса.

О методе

При решении системы линейных уравнений онлайн методом Гаусса выполняются следующие шаги.

1. Записываем расширенную матрицу.
2. Фактически решение разделяют на прямой и обратный ход метода Гаусса. Прямым ходом метода Гаусса называется приведение матрицы к ступенчатому виду. Обратным ходом метода Гаусса называется приведение матрицы к специальному ступенчатому виду. Но на практике удобнее сразу занулять то, что находится и сверху и снизу рассматриваемого элемента. Наш калькулятор использует именно этот подход.
3. Важно отметить, что при решении методом Гаусса, наличие в матрице хотя бы одной нулевой строки с НЕнулевой правой частью (столбец свободных членов) говорит о несовместности системы. Решение линейной системы в таком случае не существует.

Чтобы лучше всего понять принцип работы алгоритма Гаусса онлайн введите любой пример, выберите «очень подробное решение» и посмотрите его решение онлайн.

Однажды немецкий математик Вильгельм Йордан (мы неверно транскрибируем с немецкого Jordan как Жордан) сел решать очередную систему уравнений. Он любил этим заниматься и в свободное время совершенствовал свои навыки. Но вот настал момент, когда ему наскучили все методы решения и метод Гаусса в том числе…

Предположим, дана система с тремя уравнениями, тремя неизвестными и записана её расширенная матрица . В наиболее распространенном случае получаются стандартные ступеньки , и так каждый день…. Одно и то же – как беспросветный ноябрьский дождь.

На некоторое время развевает тоску другой способ приведения матрицы к ступенчатому виду: , причём он совершенно равноценен и может быть неудобен только по причине субъективного восприятия. Но всё рано или поздно приедается…. И подумал тогда Ж

о рдан – а зачем вообще мучиться с обратным ходом гауссовского алгоритма? Не проще ли сразу получить ответ с помощью дополнительных элементарных преобразований?

…да, такое бывает только по любви =)

Для освоения данного урока «чайникам» придётся пойти путём Жо рдана и прокачать элементарные преобразования хотя бы среднего уровня, прорешав, минимум, 15-20 соответствующих заданий. Поэтому если вы смутно понимаете, о чём идёт разговор и/или у вас возникнет недопонимание чего-либо по ходу занятия, то рекомендую ознакомиться с темой в следующем порядке:

Ну, и совсем замечательно, если отработано понижение порядка определителя .

Как все поняли, метод Гаусса-Жордана представляет собой модификацию метода Гаусса и с реализацией основной, уже озвученной выше идеи, мы встретимся на ближайших экранах. Кроме того, в число немногочисленных примеров данной статьи вошло важнейшее приложение – нахождение обратной матрицы с помощью элементарных преобразований

.

Не мудрствуя лукаво:

Пример 1

Решить систему методом Гаусса-Жордана

Решение : это первое задание урока Метод Гаусса для чайников , где мы 5 раз трансформировали расширенную матрицу системы и привели её к ступенчатому виду:

Теперь вместо обратного хода в игру вступают дополнительные элементарные преобразования. Сначала нам необходимо получить нули на этих местах: ,
а потом ещё один ноль вот здесь: .

Идеальный с точки зрения простоты случай:

(6) Ко второй строке прибавили третью строку. К первой строке прибавили третью строку.

(7) К первой строке прибавили вторую строку, умноженную на –2.

Не могу удержаться от иллюстрации итоговой системы:

Ответ :

Предостерегаю читателей от шапкозакидательского настроения – это был простейший демонстрационный пример. Для метода Гаусса-Жордана характерны свои специфические приёмы и не самые удобные вычисления, поэтому, пожалуйста, настройтесь на серьёзную работу.

Не хочу показаться категоричным или придирчивым, но в подавляющем большинстве источников информации, которые я видел, типовые задачи рассмотрены крайне плохо – нужно обладать семью пядями во лбу и потратить массу времени/нервов на тяжёлое неуклюжее решение с дробями. За годы практики мне удалось отшлифовать, не скажу, что самую лучшую, но рациональную и достаточно лёгкую методику, которая доступна всем, кто владеет арифметическими действиями:

Пример 2

Решить систему линейных уравнений методом Гаусса-Жордана.

Решение : первая часть задания хорошо знакома:

(1) Ко второй строке прибавили первую строку, умноженную на –1. К третьей строке прибавили первую строку, умноженную на 3. К четвертой строке прибавили первую строку, умноженную на –5.

(2) Вторую строку разделили на 2, третью строку разделили на 11, четвёртую строку разделили на 3.

(3) Вторая и третья строки пропорциональны, 3-ю строку удалили. К четвёртой строке прибавили вторую строку, умноженную на –7

(4) Третью строку разделили на 2.

Очевидно, что система имеет бесконечно много решений, и наша задача – привести её расширенную матрицу к виду .

Как действовать дальше? Прежде всего, следует отметить, что мы лишились вкусного элементарного преобразования – перестановки строк. Точнее говоря, переставить-то их можно, но в этом нет смысла (просто выполним лишние действия). И далее целесообразно придерживаться следующего шаблона:

Находим наименьшее общее кратное чисел третьего столбца (1, –1 и 3), т.е. – наименьшее число, которое бы делилось без остатка и на 1, и на –1 и на 3. В данном случае, это, конечно же, «тройка». Теперь

в третьем столбце нам нужно получить одинаковые по модулю числа , и этими соображениями обусловлено 5-е преобразование матрицы:

(5) Первую строку умножаем на –3, вторую строку умножаем на 3. Вообще говоря, первую строку можно было умножить тоже на 3, но это было бы менее удобно для следующего действия. К хорошему привыкаешь быстро:

(6) Ко второй строке прибавили третью строку. К первой строке прибавили третью строку.

(7) Во втором столбце два ненулевых значения (24 и 6) и нам снова нужно получить одинаковые по модулю числа . В данном случае всё сложилось довольно удачно – наименьшее кратное 24, и эффективнее всего умножить вторую строку на –4.

(8) К первой строке прибавили вторую.

(9) Заключительный штрих: первую строку разделили на –3, вторую строку разделили на –24 и третью строку разделили на 3. Это действие выполняется

В ПОСЛЕДНЮЮ ОЧЕРЕДЬ! Никаких преждевременных дробей!

В результате элементарных преобразований получена эквивалентная исходной система:

Элементарно выражаем базисные переменные через свободную:

и записываем:

Ответ : общее решение:

В подобных примерах применение рассмотренного алгоритма чаще всего оправдано, поскольку обратный ход метода Гаусса обычно требует трудоёмких и неприятных вычислений с дробями.

И, разумеется, крайне желательна проверка, которая выполняется по обычной схеме, рассмотренной на уроке Несовместные системы и системы с общим решением .

Для самостоятельного решения:

Пример 3

Найти базисное решение с помощью элементарных преобразований

Такая формулировка задачи предполагает использование метода Гаусса-Жордана, и в образце решения матрица приводится к стандартному виду с базисными переменными . Однако всегда держите на заметке, что в качестве базисных можно выбрать и другие переменные . Так, например, если в первом столбце громоздкие числа, то вполне допустимо привести матрицу к виду (базисные переменные ), или к виду (базисные переменные ), или даже к виду с базисными переменными . Существуют и другие варианты.

Но всё-таки это крайние случаи – не стОит лишний раз шокировать преподавателей своими знаниями, техникой решения и уж тем более не надо выдавать экзотических жордановсих результатов вроде . Впрочем, бывает трудно удержаться от нетипового базиса, когда в исходной матрице, скажем, в 4-м столбце есть два готовых нуля.

Примечание : термин «базис» имеет алгебраический смысл и понятие геометрического базиса здесь не при чём!

Если в расширенной матрице данных размеров вдруг обнаруживается пара линейно зависимых строк, то её следует попытаться привести к привычному виду с базисными переменными . Образец такого решения есть в Примере №7 статьи об однородных системах линейных уравнений , причём там выбран другой базис .

Продолжаем совершенствовать свои навыки на следующей прикладной задаче:

Как найти обратную матрицу методом Гаусса?

Обычно условие формулируют сокращённо, но, по существу, здесь также работает алгоритм Гаусса-Жордана. Более простой метод нахождения обратной матрицы для квадратной матрицы мы давным-давно рассмотрели на соответствующем уроке, и суровой поздней осенью тёртые студенты осваивают мастерский способ решения.

Краткое содержание предстоящих действий таково: сначала следует записать квадратную матрицу в тандеме с единичной матрицей: . Затем с помощью элементарных преобразований необходимо получить единичную матрицу слева, при этом (не вдаваясь в теоретические подробности) справа нарисуется обратная матрица. Схематически решение выглядит следующим образом:

(Понятно, что обратная матрица должна существовать)

Демо-пример 4

Найдём обратную матрицу для матрицы с помощью элементарных преобразований. Для этого запишем её в одной упряжке с единичной матрицей, и понеслась «двойка скакунов»:

(1) Ко второй строке прибавили первую строку, умноженную на –3.

(2) К первой строке прибавили вторую строку.

(3) Вторую строку разделили на –2.

Ответ :

Сверьтесь с ответом первого примера урока Как найти обратную матрицу?

Но то была очередная заманивающая задачка – в действительности решение гораздо более длительно и кропотливо. Как правило, вам будет предложена матрица «три на три»:

Пример 5

Решение : присоединяем единичную матрицу и начинаем выполнять преобразования, придерживаясь алгоритма «обычного» метода Гаусса :

(1) Первую и третью строки поменяли местами. На первый взгляд, перестановка строк кажется нелегальной, но на самом деле переставлять их можно – ведь по итогу слева нам нужно получить единичную матрицу, а справа же «принудительно» получится именно матрица (вне зависимости от того будем ли мы переставлять строки в ходе решения или нет) . Обратите внимание, что здесь вместо перестановки можно организовать «шестёрки» в 1-м столбце (наименьшее общее кратное (НОК) чисел 3, 2 и 1) . Решение через НОК особенно удобно, когда в первом столбце отсутствуют «единицы».

(2) Ко 2-й и 3-й строкам прибавили 1-ю строку, умноженную на –2 и –3 соответственно.

(3) К 3-й строке прибавили 2-ю строку, умноженную на –1

Вторая часть решения проводится по уже известной из предыдущего параграфа схеме: перестановки строк становятся бессмысленными, и мы находим наименьшее общее кратное чисел третьего столбца (1, –5, 4): 20. Существует строгий алгоритм нахождения НОК, но здесь обычно хватает подбора. Ничего страшного, если взять бОльшее число, которое делится и на 1, и на –5, и на 4, например, число 40. Отличие будет в более громоздких вычислениях.

К слову о вычислениях. Для решения задачи совсем не зазорно вооружиться микрокалькулятором – числа здесь фигурируют немалые, и будет очень обидно допустить вычислительную ошибку.

(4) Третью строку умножаем на 5, вторую строку на 4, первую строку на «минус двадцать»:

(5) К 1-й и 2-й строкам прибавили третью строку.

(6) Первую и третью строки разделили на 5, вторую строку умножили на –1.

(7) Наименьшее общее кратное ненулевых чисел второго столбца (–20 и 44) равно 220. Первую строку умножаем на 11, вторую строку – на 5.

(8) К первой строке прибавили вторую строку.

(9) Первую строку умножили на –1, вторую строку разделили «обратно» на 5.

(10) Теперь на главной диагонали левой матрицы целесообразно получить наименьшее общее кратное чисел диагонали (44, 44 и 4). Совершенно понятно, что это число 44. Третью строку умножаем на 11.

(11) Каждую строку делим на 44. Данное действие выполняется в последнюю очередь!

Таким образом, обратная матрица:

Внесение и вынесение -й, в принципе, лишние действия, но того требует протокол оформления задачи.

Ответ :

Проверка выполняется по обычной схеме, рассмотренной на уроке об обратной матрице .

Продвинутые люди могут несколько сократить решение, но должен предупредить, спешка тут чревата ПОВЫШЕННЫМ риском допустить ошибку.

Аналогичное задание для самостоятельного решения:

Пример 6

Найти обратную матрицу методом Гаусса-Жордана.

Примерный образец оформления задачи внизу страницы. И ради того, чтобы вы «не проехали мимо с песнями» я оформил решение в уже упомянутом стиле – исключительно через НОК столбцов без единой перестановки строк и дополнительных искусственных преобразований. По моему мнению, эта схема – если и не самая, то одна из самых надёжных .

Иногда бывает удобно более короткое «модернистское» решение, которое заключается в следующем: на первом шаге всё как обычно: .

На втором шаге накатанным приёмом (через НОК чисел 2-го столбца) организуются сразу два нуля во втором столбце: . Перед данным действием особенно трудно устоять, если во 2-м столбце нарисовались одинаковые по модулю числа, например, те же банальные «единицы».

И, наконец, на третьем шаге точно так же получаем нужные нули в третьем столбце: .

Что касается размерности, то в большинстве случаев приходится разруливать матрицу «три на три». Однако время от времени встречается лайт-версия задачи с матрицей «два на два» и хард… – специально для всех читателей сайт:

Пример 7

Найти обратную матрицу с помощью элементарных преобразований

Это задание из моей собственной физматовской контрольной работы по алгебре, …эх, где мой первый курс =) Пятнадцать лет назад (листочек на удивление ещё не пожелтел) , я уложился в 8 шагов, а сейчас – всего лишь в 6! Матрица, кстати, весьма творческая – на первом же шаге просматривается несколько заманчивых путей решения. Моя поздняя версия внизу страницы.

И заключительный совет – после таких примеров очень полезна гимнастика для глаз и какая-нибудь хорошая музыка для релаксации =)

Желаю успехов!

Решения и ответы:

Пример 3: Решение : запишем расширенную матрицу системы и с помощью элементарных преобразований получим базисное решение:


(1) Первую и вторую строки поменяли местами.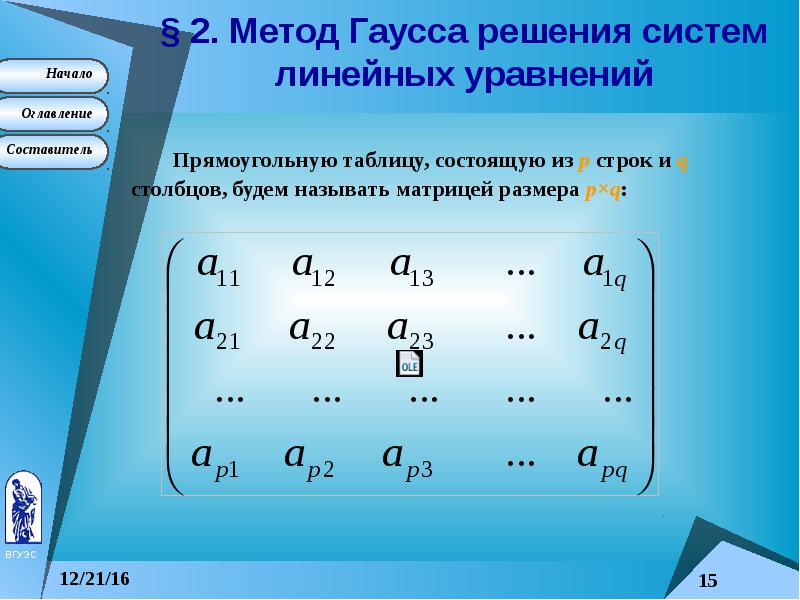
(2) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на 5.
(3) Третью строку разделили на 3.
(4) К третьей строке прибавили вторую строку, умноженную на 2.
(5) Третью строку разделили на 7.
(6) Наименьшее кратное чисел 3-го столбца (–3, 5, 1) равно 15. Первую строку умножили на 5, вторую строку умножили на –3, третью строку умножили на 15.
(7) К первой строке прибавили 3-ю строку. Ко второй строке прибавили 3-ю строку.
(8) Первую строку разделили на 5, вторую строку разделили на –3, третью строку разделили на 15.
(9) Наименьшее кратное ненулевых чисел 2-го столбца (–2 и 1) равно: 2. Вторую строку умножили на 2
(10) К первой строке прибавили вторую строку.
(11) Вторую строку разделили на 2.
Выразим базисные переменные через свободные переменные :

Ответ : общее решение:

Пример 6: Решение : обратную матрицу найдём с помощью элементарных преобразований:


(1) Первую строку умножили на –15, вторую строку умножили на 3, третью строку умножили на 5.
(2) Ко 2-й и 3-й строкам прибавили первую строку.
(3) Первую строку разделили на –15, вторую строку разделили на –3, третью строку разделили на –5.
(4) Вторую строку умножили на 7, третью строку умножили на –9.
(5) К третьей строке прибавили вторую строку.


(6) Вторую строку разделили на 7.
(7) Первую строку умножили на 27, вторую строку умножили на 6, третью строку умножили на –4.
(8) К первой и второй строкам прибавили третью строку.
(9) Третью строку разделили на –4. К первой строке прибавили вторую строку, умноженную на –1.
(10) Вторую строку разделили на 2.
(11) Каждую строку разделили на 27.
В результате:
Ответ :

Пример 7: Решение : найдём обратную матрицу методом Гаусса-Жордана:
(1) К 1-й и 4-й строкам прибавили 3-ю строку.
(2) Первую и четвёртую строки поменяли местами.
(3) Ко 2-й строке прибавили 1-ю строку. К 3-й строке прибавили 1-ю строку, умноженную на 2:


(4) К 3-й строке прибавили 2-ю строку, умноженную на –2. К 4-й строке прибавили 2-ю строку.
(5) К 1-й и 3-й строкам прибавили 4-ю строку, умноженную на –1.
(6) Вторую строку умножили на –1, третью строку разделили на –2.
Ответ :

Березнёва Т. Д.

Тема 7

«СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.

МЕТОД ГАУССА – ЖОРДАНА.»

(Учебная дисциплина “Введение в линейную алгебру и аналитическую геометрию”)

СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.

МЕТОД ГАУССА – ЖОРДАНА.

Основные понятия

Уравнение с n переменными называется линейным , если все переменные (x 1 , x 2 , … x n ) входят в него в степени 1. Общий вид такого уравнения формально записывается следующим образом:

a 1 x 1 + a 2 x 2 + … a j x j + … a n x n = b , (*)

= b .

Величины a j , j = 1,…, n , и b являются известными (заданными). Величиныa j называются коэффициентами при переменных (при неизвестных), а b — свободным членом .

Решением линейного уравнения (*) ,,…,) значений переменных, который при подстановке в уравнение (т.е. при заменеx j на при всехj от 1до n обращает его в тождество. Подчеркнем, что решение уравнения с n переменными всегда есть набор из n чисел и каждый такой набор из n чисел представляет собой одно решение. Очевидно, что если хотя бы один коэффициент при переменных не равен 0, то уравнение (*) имеет решение. В противном случае решение существует только при b = 0, и это все произвольные наборы из n чисел.

Рассмотрим одновременно m уравнений вида (*), т.е. систему m линейных алгебраических уравнений с n переменными . Пусть каждое i — е уравнение, i = 1,2,…,m, задается коэффициентами при переменных a i 1 , a i 2 , …, a in и свободным членом b i , т.е. имеет вид

a i1 x 1 + a i2 x 2 + … + a ij x j + … + a in x n = b i .

Тогда в общем виде система m линейных алгебраических уравнений с n переменными может быть записана в виде:

a 11 x 1 + a 12 x 2 + … + a 1j x j + … + a 1n x n = b 1

a 21 x 1 + a 22 x 2 + … + a 2j x j + … + a 2n x n = b 2

………………………………………………………………………………

a i1 x 1 + a i2 x 2 + … + a ij x j + … + a in x n = b i (1)

…………………………………………………

a m1 x 1 + a m2 x 2 + … + a mj x j + … + a mn x n = b m

или, что то же самое,

= b i , i = 1,…, m .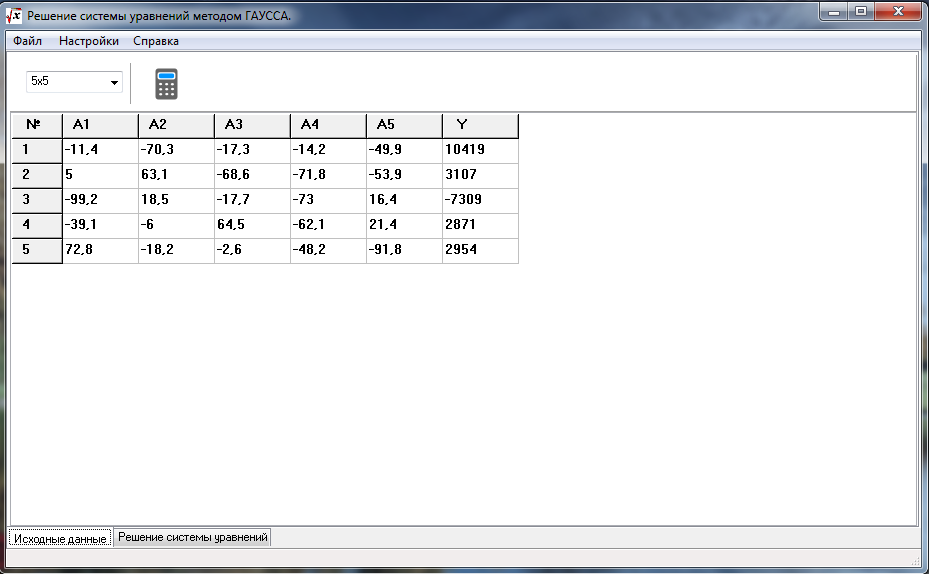

Если все свободные члены равны нулю, то система (1) называется однородной , т.е. имеет вид

= 0, i = 1,…, m, (1 0 )

в противном случае — неоднородной . Система (1 0 ) является частным случает общей системы (1) .

Решением системы уравнений (1) называется упорядоченный набор (,,…,) значений пере­менных, который при подстановке в урав­нения системы (1) (т.е. при заменеx j на , j = 1,…,n) все эти уравнения обращает в тождества, т.е.
=b i при всех i = 1,…,m.

Система уравнений (1) называется совместной, если у нее существует хотя бы одно решение. В противном случае система называется несовместной .

Совокупность всех решений системы уравнений (1) мы будем называть множеством ее решений и обозначать X b (X 0 , если система однородная). Если система несовместна, то X b = .

Основная задача теории систем линейных алгебраических уравнений состоит в том, чтобы выяснить, совместна ли система (1), и, если совместна, то описать множество всех её решений. Существуют методы анализа таких систем, которые позволяют описывать множество всех решений в случае совместных систем или убеждаться в несовместности в противном случае. Одним из таких универсальных методов является метод последовательного полного исключения неизвестных, или метод Гаусса — Жордана , который мы будем подробно изучать.

Прежде, чем переходить к описанию метода Гаусса — Жордана, приведем ряд полезных для дальнейшего определений и утверждений.

Две системы уравнений называются эквивалентными , если они имеют одно и то же множество решений. Другими словами, каждое решение одной системы является решением другой, и наоборот. Все несовместные системы считаются эквивалентными между собой.

Из определений эквивалентности и множества решений систем вида (1) сразу же вытекает справедливость следующих утверждений, которые мы сформулируем в виде теоремы.

Теорема 1. Если в системе (1) имеется уравнение с номером k , 1k m , такое, что a kj = 0 j , то

Справедливость утверждений теоремы становится очевидной, если заметить, что k – е уравнение имеет вид

0 x 1 + 0 x 2 + … + 0 x j + … + 0 x n = b k .

Теорема 2. Если к одному уравнению системы (1) прибавить другое уравнение этой же системы, умноженное на любое число, то получится система уравнений, эквивалентная исходной системе.

Доказательство. Умножим, например, второе уравнение системы (1) на некоторое число и прибавим его к первому уравнению. В результате этого преобразования получим систему (1’), в которой все уравнения, начиная со второго, не изменились, а первое имеет следующий вид

= b 1 + b 2 .

Очевидно, если какой-нибудь набор (,,…,) значений переменных обращает в тождества все уравнения системы (1), то он обращает в тождества и все уравнения системы (1’). Наоборот, решение (x’ 1 ,x’ 2 ,…,x’ j , … ,x’ n) системы (1’) является также решением системы (1), так как система (1) получается из системы (1’) с помощью аналогичного преобразования, когда к первому уравнению системы (1’) прибавляется второе уравнение системы (1’), умноженное на число (-).

Точно также доказывается и следующее утверждение.

Теорема 2’ . Умножение произвольного уравнения системы (1) на любое число, отличное от нуля, переводит систему (1) в эквивалентную ей систему уравнений .

Теоремы 2 и 2’ дают два вида преобразований, которым подвергалась система (1), оставаясь эквивалентной:

а) умножение (или деление) произвольного уравнения системы (1) на любое число, отличное от нуля;

б) прибавление (или вычитание) к одному уравнению другого, умноженного на некоторое число.

Такие преобразования а) и б) называются элементарными преобразованиями системы уравнений (1).

Если к системе уравнений (1) несколько раз применить элементарные преобразования, то полученная в результате система, очевидно, также будет эквивалентна первоначальной.

Систему уравнений (1) можно записать в табличной форме:

Прямоугольная таблица чисел, составленная из коэффициентов a ij при неизвестных системы (1), называется матрицей системы (1) и обозначается A (в ней m строк и n столбцов), столбец свободных членов обозначается b. Прямоугольная таблица, составленная из коэффициентов a ij при неизвестных и из столбца свободных членов b системы (1), называется расширенной матрицей системы (1) и обозначается (в нейm строк и (n+1) столбцов), т.е = (A, b). В i – ой строке матрицы содержатся всеизвестные параметры, характеризующие i — ое уравнение системы (1), i = 1,…, m. В j – м столбце матрицы A содержатся все коэффициенты при неизвестном x j , встречающиеся в системе (1).

Числа a ij называются элементами матрицы А. Элемент a ij находится в i — ой строкеи в j — м столбце матрицы А. Принято говорить, что элементa ij находится на пересечении i — ой строки и j — го столбца матрицы А. Если все элементы строки (столбца) матрицы А (кроме одного) равны нулю, а ненулевой элемент равен единице, то такая строка (столбец) называется единичной (единич­ным).

Элементарным преобразованиям системы (1) соответствуют следующие элементарные преобразования таблицы (2):

а) умножение (или деление) всех элементов произвольной строки таблицы (2) на любое число, отличное от нуля ,

б) прибавление (или вычитание) к одной строке (поэлементно) другой строки, умноженной на некоторое число.

В результате любого элементарного преобразования получается новая таблица , в которой вместо той строки, к которой прибавляли (или умножали на любое число, отличное от нуля), пишется новая строка , а осталь­ные строки (в том числе и та, которую прибавляли) пишутся без из­менения . Новая таблица соответствует системе уравнений, эквивалентной исходной системе .

Применяя элементарные преобразования можно таблицу (2) и соответственно систему (1) упростить так, что решить исходную систему становится просто. На этом и основан предлагаемый метод.

Метод последовательного полного исключения неизвестных

(Метод Гаусса — Жордана)

Метод последовательного полного исключения неизвестных, или метод Гаусса – Жордана , является универсальным методом анализа любых (заранее неизвестно, каких — совместных или несовместных) систем линейных алгебраических уравнений. Он позволяет решать совместные системы или убеждаться в несовместности несовместных систем.

Отметим принципиальное отличие предлагаемого метода решения систем линейных алгебраических уравнений от метода решения, ска­жем, стандартного квадратного уравнения. Оно решается с помощью хорошо известных формул, в которых неизвестные выражаются через коэффициенты уравнения. В случае общих систем линейных алгебраических уравнений мы таких формул не имеем и используем для отыскания решения метод итераций , или итеративный метод , или итерационный метод . Такие методы задают не формулы, а последовательность действий.

Метод Гаусса — Жордана представляет собой последовательную реализацию ряда однотипных больших шагов (или итераций ). Это конкретный итерационный метод — один из многих методов итераций, предложенных для решения систем линейных алгебраических уравнений вида (1). Он состоит из начального этапа, основного этапа и заключительного этапа . Основной этап содержит повторяющиеся итерации – наборы однотипных действий.

Пусть задана конкретная система линейных алгебраических уравнений (1). Это значит, что известны n , m , a ij , b i , i = 1,…, m ; j = 1,…, n . Опишем предлагаемый метод решения этой системы.

Начальный этап включает в себя построение таблицы I (0) вида (2) и выбор в ней ведущего элемента – любого ненулевого коэффициента при переменных из таблицы (2). Столбец и строка, на пересечении которых стоит ведущий элемент, называются ведущими . (Пусть выбран элемент a i 0 j 0 . Тогда i 0 – ая строка ведущая, j 0 — й столбец ведущий.) Переходим к основному этапу. Заметим, что часто ведущий элемент называют разрешающим .

Основной этап состоит из повторяющихся однотипных итераций с номерами k = 1, 2,…. Опишем подробно итерации метода Гаусса — Жордана.

К началу каждой итерации известна некоторая таблица I вида (2), в ней выбран ведущий (разрешающий) элемент и, соответственно, ведущий столбец и ведущая строка. Кроме того, имеется информация о том, какие строки и столбцы уже были ведущими. (Так, например, после начального этапа, т.е. на итерации 1 известны I (0) , ведущий (разрешающий) элемент a i 0 j 0 и i 0 – ая строка ведущая, j 0 — ой столбец ведущий.)

Итерация(с номером k ) состоит из следующих действий.

Преобразование ведущего столбца (т.е. столбца, содержащего ведущий элемент) в единичный с 1 на месте ведущего элемента путем последовательного поэлементного вычитания ведущей строки (т.е. строки, содержащей ведущий элемент), умноженной на некоторые числа, из остальных строк таблицы. Сама ведущая строка преобразуется путем поэлементного деления ее на ведущий элемент.

Выписы­вается новая таблица I (k) , (k — номер итерации), в которой все столбцы, которые были когда-либо ведущими, – единичные .

Проверяется, можно ли в таблице I (k) выбрать новый ведущий (разрешающий) элемент . По определению это любой ненулевой элемент, который стоит на пересечении строки и столбца, которые еще не были ведущими .

Если такой выбор возможен, то столбец и строка, на пересечении которых стоит ведущий (разрешающий) элемент, называются ведущими . Затем итерация повторяется с новой таблицей I (k) , т.е. действия 1 – 3 повторяются с новой таблицей I (k) . При этом строится новая таблица I (k +1) .

Если нельзя выбрать новый ведущий элемент, то переходим к заключительному этапу.

Заключительный этап. Пусть проделано r итераций, получена таблица I (r) , состоящая из матрицы коэффициентов при переменных A (r) и столбца свободных членов b (r) , и в ней нельзя выбрать новый ведущий элемент, т. е. метод остановился . Заметим, что метод обязательн о остановится за конечное число шагов , т.к. r не может быть больше min{m,n}.

Каковы варианты остановки метода? Что значит «нельзя выбрать новый ведущий элемент»? Это значит, что после r – ой итерации в матрице A (r) новой системы, эквивалентной системе (1), либо

а) все строки A (r) были ведущими, т.е. в каждой строке стоит одна и ровно одна единица, которая не стоит больше не в какой другой строке,

б) остались строки в A (r) , состоящие только из нулей.

Рассмотрим эти варианты.

а) В этом случае r = m, m n. Переставив строки и перенумеровав переменные (т.е. переставив столбцы), можно таблицу I (r) представить в виде

Подчеркнем, что в таблице (3) каждая переменная с номером i, не превосходящим r, встречается только в одной строке. Таблица (3) соответствует системе линейных уравнений вида

x 1 +
=b (r) 1 ,

x 2 +
=b (r) 2 ,

………………………, (4)

x r +
=b (r) r ,

в которой каждая переменная с номером i, не превосходящим r , однозначно выражается через переменные x r +1 , … ,x n , коэффициенты матрицы a (r) ij , j = r+1,…,n, и свободный член b (r) i , представленные в таблице (3). На переменные x r +1 , … , x n не накладываются никакие ограничения , т.е. они могут принимать любые значения . Отсюда произвольное решение системы, описываемой таблицей (3), или, что то же самое, произвольное решение системы (4), или, что то же самое, произвольное решение системы (1) имеет вид

x i = b (r) i — a (r) ij x j , i = 1,…,r = m; x j – любое при j = (r+1),…,n. (5)

Тогда множество решений системы (1) можно записать как

X b = {x=(x 1 , … ,x n) : x i = b (r) i — a (r) ij x j при i = 1,…, r = m; x j – любое при j =(r+1),…,n.}.

б) В этом случае r r, (предполагаем, что сделана перестановка строк и столбцов такая же, как в пункте а)) такая, что a (r) kj = 0 при всех j. Тогда, если соответствующий свободный член b (r) k не равен 0, то k — е уравнение не имеет решения, и, следовательно, вся система не имеет решения, т.е. система (1) несовместна .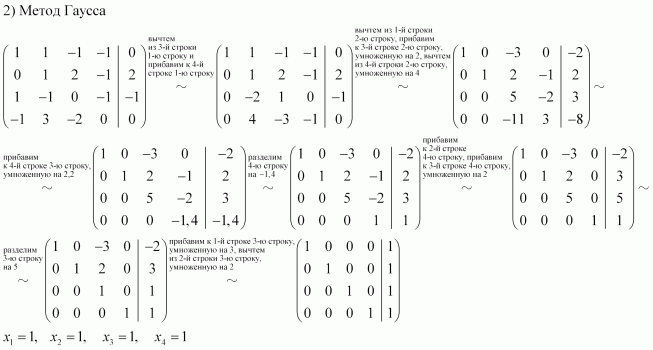

Если же соответствующий b (r) k равен 0, то k — ое уравнение является лишним и его можно отбросить. Отбросив все такие уравнения, получим, что система (1) эквивалентна системе изr уравнений с n переменными, которая через r шагов записывается с помощью таблицы вида (3), в которой все строки были ведущими. Таким образом, мы пришли к рассмотренному выше случаю а) и можем выписать решение вида (5).

Метод Гаусса – Жордана описан полностью. За конечное число итераций система линейных алгебраических уравнений будет решена (если она совместна) или будет очевидно, что она несовместна (если она действительно несовместна).

Переменные, соответствующие ведущим (разрешающим) элементам , или стоящие в ведущих столбцах, принято называть базисными , а ос­тальные переменные —свобод­ными .

Обратим внимание на следующее.

1) Когдамы начинаем решать систему методом Гаусса — Жордана, мы можем не знать, совместна эта система или нет. Метод Гаусса — Жордана за конечное число итераций r даст ответ на этот вопрос. В случае совместной системы на основании последней таблицы выписывается общее решение исход­ной системы. В этом случае число базисных переменных обязательно равно номеру r последней итерации, т.е. числу выполненных итераций. Число r всегда не превосходит min{m,n},гдеm — число уравнений системы,а n — число переменных системы. Если r , то ( n – r) равно числу свободных переменных.

2) При записи общего решения не нужно перенумеровывать переменные, как это делалось для простоты понимания при описании Заключительного этапа. Это сделано для более ясного понимания.

3) При решении системы (1) методом Гаусса — Жордана базисными переменными будут только переменные, соответствующие столбцам, которые на каких-то итерациях выступали в роли ведущих , и наоборот, если на какой-то итерации столбец выступал в качестве ведущего, соответствующая ему переменная обязательно будет в числе базисных.

4) Если общее решение системы (1) содержит хотя бы одну свободную переменную, то эта система имеет бесконечно много част­ных решений, если же свободных переменных нет, то система имеет единственное решение, которое совпадает с общим решением.

5) Ведущие элементы могут быть выбраны на каждой итерации различным способом. Важно только то, что это ненулевые коэффициенты, стоящие на пересечении строки и столбца, которые до этого не были ведущими. Различный выбор ведущих элементов может дать различные записи множества решений. Однако, само множество решений при любой записи одно и то же.

Поясним работу метода на примерах.

Пример I. Решить следующую систему линейных алгебраических уравнений

2 x 1 – 3 x 2 + 3 x 3 + 5 x 4 = -1,

3 x 1 + 4 x 2 — 2 x 3 + 6 x 4 = 2, (6)

5 x 1 – 4 x 2 + 6 x 3 + 10 x 4 = 2

методом последовательного полного исключения неизвестных (методом Гаусса — Жордана).

Начальный этап. Сначала выпишем систему уравнений (6) в более удобной форме — в виде таблицы I (0) .

Каждой системе линейных уравнений поставим в соответствие расширенную матрицу , полученную присоединением к матрице А столбца свободных членов:

Метод Жордана–Гаусса применяется для решения системы m линейных уравнений с n неизвестными вида:

Данный метод заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе уравнений с матрицей определенного вида.

Над строками расширенной матрицы осуществляем следующие элементарные преобразования:

1. перестановка двух строк ;

2. умножение строки на любое число, отличное от нуля ;

3. прибавление к одной строке другой строки, умноженной на некоторое число ;

4. отбрасывание нулевой строки (столбца) .

Пример 2.11. Решить методом Жордана–Гаусса системы линейных уравнений:

а ) Х 1 + Х 2 + 2Х 3 = -1

2Х 1 — Х 2 + 2Х 3 = -4

4Х 1 + Х 2 + 4Х 3 = -2

Решение: Составим расширенную матрицу:

Итерация 1

В качестве направляющего элемента выбираем элемент . Преобразуем первый столбец в единичный. Для этого ко второй и третьей строкам прибавляем первую строку, соответственно умноженную на (-2) и (-4). Получим матрицу:

На этом первая итерация закончена.

Итерация 2

Выбираем направляющий элемент . Так как , то делим вторую строку на -3. Затем умножаем вторую строку соответственно на (-1) и на 3 и складываем соответственно с первой и третьей строками. Получим матрицу

Итерация 3

Выбираем направляющий элемент . Так как , то делим третью строку на (-2). Преобразуем третий столбец в единичный. Для этого умножаем третью строку соответственно на (-4/3) и на (-2/3) и складываем соответственно с первой и второй строками. Получим матрицу

откуда Х 1 = 1, Х 2 = 2, Х 3 = -2.

Закончив решение, на этапе обучения необходимо выполнять проверку, подставив найденные значения в исходную систему, которая при этом должна обратиться в верные равенства.

б ) Х 1 – Х 2 + Х 3 – Х 4 = 4

Х 1 + Х 2 + 2Х 3 +3Х 4 = 8

2Х 1 +4Х 2 + 5Х 3 +10Х 4 = 20

2Х 1 – 4Х 2 + Х 3 – 6Х 4 = 4

Решение: Расширенная матрица имеет вид:

Применяя элементарные преобразования, получим:

Исходная система эквивалентна следующей системе уравнений:

Х 1 – 3Х 2 – 5Х 4 = 0

2Х 2 + Х 3 + 4Х 4 = 4

Последние две строки матрицы A (2) являются линейно зависимыми.

Определение. Строки матрицы e 1 , e 2 ,…, e m называются линейно зависимыми , если существуют такие числа , не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:

где 0 =(0, 0…0). Строки матрицы являются линейно независимыми , когда комбинация этих строк равна нулю тогда и только тогда, когда все коэффициенты равны нулю.

В линейной алгебре очень важно понятие ранга матрицы , т.к. оно играет очень большое значение при решении систем линейных уравнений.

Теорема 2.3 (о ранге матрицы). Ранг матрицы равен максимальному числу её линейно независимых строк или столбцов, через которые линейно выражаются все остальные её строки (столбцы).

Ранг матрицы A (2) равен 2, т.к. в ней максимальное число линейно независимых строк равно 2 (это первые две строки матрицы).

Теорема 2.4 (Кронекера–Капели). Система линейных уравнений совместна и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.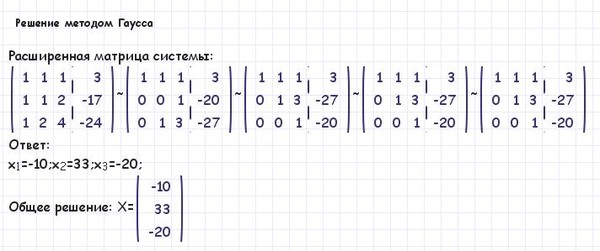

1. Если ранг матрицы совместной системы равен числу переменных, т.е. r = n, то система имеет единственное решение.

2. Если ранг матрицы системы меньше числа переменных, т.е. r

В данном случае система имеет 4 переменных, а её ранг равен 2, следовательно, она имеет бесконечное множество решений.

Определение. Пусть r n , r переменных x 1 , x 2 ,…, x r называются базисными , если определитель матрицы из коэффициентов при них (базисный минор ) отличен от нуля. Остальные n – r переменных называются свободными .

Определение. Решение системы, в котором все n – r свободных переменных равны нулю, называется базисным .

Совместная система m линейных уравнений с n переменными (m ) имеет бесконечное множество решений, среди которых базисных решений конечное число, не превосходящее , где .

В нашем случае , т. е. система имеет не более 6 базисных решений.

Общее решение имеет вид:

Х 1 = 3Х 2 +5Х 4

Х 3 = 4 – 2Х 2 – 4Х 4

Найдем базисные решения. Для этого полагаем Х 2 = 0, Х 4 = 0, тогда Х 1 =0, Х 3 = 4. Базисное решение имеет вид: (0, 0, 4, 0).

Получим другое базисное решение. Для этого в качестве свободных неизвестных примем Х 3 и Х 4 . Выразим неизвестные Х 1 и Х 2 через неизвестные Х 3 и Х 4:

Х 1 = 6 – 3/2Х 2 – Х 4

Х 2 = 2 – 1/2Х 3 – 2Х 4 .

Тогда базисное решение имеет вид: (6, 2, 0, 0).

Пример 2.12. Решить систему:

X 1 + 2X 2 – X 3 = 7

2X 1 – 3X 2 + X 3 = 3

4X 1 + X 2 – X 3 = 16

Решение.Преобразуем расширенную матрицу системы

Итак, уравнение, соответствующее третьей строке последней матрицы, противоречиво – оно привелось к неверному равенству 0 = –1, следовательно, данная система несовместна. Данный вывод можно также получить, если заметить, что ранг матрицы системы равен 2, тогда как ранг расширенной матрицы системы равен 3.

qusivaf онлайн калькулятор решение неоднородной системы линейных алгебраических

онлайн калькулятор решение неоднородной системы линейных алгебраических Решение системы M линейных уравнений с N неизвестными (СЛУ) методом Гаусса — OnLine Калкулятор. Система уравнений (СЛУ) будет решена методом Гаусса, прямо на сайте, с выводом всех промежуточных результатов и комментариями. Общее и базисное решения системы линейных алгебраических уравнений. Итак, система линейных алгебраических уравнений (СЛАУ) называется однородной , если все свободные члены этой системы равны нулю. Сервисы по высшей математике для студентов и преподавателей. Бесплатное решение системы линейных уравнений с выводом всех промежуточных . Данный онлайн калькулятор находит общее решение однородной системы линейных уравнений. Дается подробное решение. Для вычисления . Онлайн-калькулятор предназначен для исследования системы линейных уравнений. единственное решение (используются метод Крамера, метод обратной матрицы. Перейти: Онлайн калькулятор Решение произвольной системы уравнений →. Решение системы линейных уравнений методом Крамера. Это он -лайн сервис в два шага: Ввести количество уравнений в системе. Общее решение неоднородной системы линейных уравнений онлайн. Данный онлайн калькулятор находит общее решение однородной системы линейных уравнений. Решение системы линейных уравнений методом Крамера, онлайн сервис . решения квадратных систем линейных алгебраических уравнений (СЛАУ) . Онлайн Калькуляторы. Любое решение исходной системы есть линейная комбинация решений ФСР. Общее решение неоднородной СЛАУ равно сумме частного решения неоднородной СЛАУ и общего решения соответствующей однородной СЛАУ. Решение системы линейных уравнений метод Крамера (определителей). Решение СЛУ матричный метод (обратной матрицы) Решение и исследование систем линейных уравнений. Решение проводится в онлайн режиме и оформляется в формате Word. Приведение к треугольной. Транспонирование матрицы. Алгебраические дополнения. Системы линейных неоднородных уравнений (количество. Онлайн калькуляторы . Введите данные вашей задачи, и вы получите подробное решение. Линейное неоднородное уравнение второго порядка с постоянными коэффициентами. Обратная матрица (метод алгебраических дополнений). Решение системы линейных уравнений методом Крамера. Взаимосвязь решений неоднородной и соответствующей однородной системы уравнений. Пример 5. Дана система линейных алгебраических уравнений. Требуется: 1) найти общее решение Наш калькулятор умеет решать онлайн как обычную определенную, так и неопределенную систему линейных уравнений методом Гаусса, которая имеет бесконечное множество решений. Используя этот онлайн калькулятор для решения систем линейных уравнений (СЛУ) методом Гаусса, вы сможете очень просто и быстро найти . Онлайн Калькуляторы . Примеры Подробных Решений. Теория. Решение системы линейных алгебраических уравнений (СЛАУ) онлайн. Решение неоднородной системы линейных алгебраических уравнений матричным методом из коллекции онлайн калькуляторов Planetcalc. Решение систем линейных уравнений. Эта страничка поможет решить Системы Линейных Алгебраических Уравнений (СЛАУ) методом Гаусса, матричным методом или методом Крамера, исследовать их на совместность (теорема Кронекера-Капелли), определить количество. Данный онлайн калькулятор находит общее решение однородной системы линейных уравнений. Дается подробное решение. Теоретическую часть нахождения общего решения неоднородной системы линейных уравнений смотрите здесь. Решение системы линейных уравнений методом Крамера, онлайн сервис . решения квадратных систем линейных алгебраических уравнений (СЛАУ) .

Калькулятор не найдет строку сокращенного эшелона формы

ang=»ru»>

Калькулятор не найдет строку сокращенного эшелона формы — Ramac-rc ar bn de en es fr it ja ko ms pt ru tr tw

2021-12-29 02:15

Related Contents

Hot Contents

• Могу ли я заставить vim изменить поведение курсора?
• Did two unquestionably democratic states ever engage in war?
• Как добавить . o в статическую библиотеку с Eclipse?
• помогите понять XPath
• невозможно получить значения списка с веб-сайта
• Как добавить стороннюю библиотеку в приемник событий sharepoint 2010
• Подсчет уникальных событий в качестве показателя по названиям рекламных кампаний Google в качестве параметра в Google Data Studio
• Swift SourceKitService разбился
• Используйте tf.cond для реализации предварительного обучения
• Алгоритм сравнения картинок/форм на уникальность

©2021 Ramac-rc

. . . . . . . . . . . . . . . . . . . . . . . . . . . .

Библиотека — приборы и технологии производства

Приложение калькулятор ГПМ

4 апреля 2016 года

Создание

Приложение «Калькулятор ГПМ» — помогает максимально точно определять давление в системе грузопоршневого манометра с учетом поправок и удобно подбирать массы грузов.

Поверка манометра на ГСКА

3 сентября 2015 года

Приборы для Минобороны

7 октября 2014 года

Создание

По заказу Минобороны России — разработали специальное изделие для поверки шинных манометров.

Разработка производилась с «нуля», аналогов этого прибора не существует. Особые требования предъевлялись к массогабаритным характеристикам, уровню шума и метрологическим характеристикам.

Особенности приборов

7 июля 2014 года

Ускорение свободного падения для 122 городов

24 июня 2014 года

	Город		м/сек²

	Город		м/сек²
	Архангельск		9,8225
	Актобе		9,8100
	Алма-Ата		9,8010
	Арзамас		9,8150
	Астана		9,8110
	Астрахань		9,8075
	Атырау		9,8080
	Ашхабад		9,7985
	Баку		9,8010
	Барнаул		9,8130
	Белгород		9,8105
	Бишкек		9,8010
	Благовещенск		9,8105
	Бобруйск		9,8130
	Брест		9,8120
	Брянск		9,8130
	Великий Новгород		9,8180
	Вильнюс		9,8145
	Виннца		9,8095
	Витебск		9,8150
	Владивосток		9,8045
	Владикавказ		9,8025
	Владимир		9,8160
	Волгоград		9,8095
	Вологда		9,8185
	Воронеж		9,8120
	Гомель		9,8125
	Гродно		9,8140
	Грозный		9,8035
	Днепропетровск		9,8090
	Душанбе		9,7970
	Екатеринбург		9,8160
	Ереван		9,7990
	Житомир		9,8105
	Запорожье		9,8090
	Ивано-Франковск		9,8085
	Ижевск		9,8160
	Йошкар-Ола		9,8165
	Иркутск		9,8110

	Казань		9,8155
	Калининград		9,8150
	Калуга		9,8140
	Каменец-Подольский		9,8090
	Караганда		9,8090
	Каунас		9,8150
	Кемерово		9,8150
	Киев		9,8105
	Киров		9,8180
	Кировоград		9,8090
	Кишинев		9,8080
	Клайпеда		9,8155
	Коканд		9,7990
	Кокшетау		9,8130
	Костанай		9,8130
	Кострома		9,8170
	Краснодар		9,8060
	Красноярск		9,8150
	Курган		9,8150
	Курск		9,8120
	Кызылорда		9,8055
	Луганск		9,8090
	Луцк		9,8110
	Львов		9,8095
	Мары		9,7985
	Махачкала		9,8035
	Минск		9,8140
	Москва		9,8155
	Мурманск		9,8255
	Муром		9,8150
	Нижний Новгород		9,8160
	Николаев		9,8080
	Новокузнецк		9,8130
	Новосибирск		9,8145
	Одесса		9,8075
	Омск		9,8150
	Орел		9,8125
	Оренбург		9,8120
	Пенза		8,8130
	Пермь		9,8175
	Петрозаводск		9,8205
	Петропавловск		9,8150

	Полоцк		9,8150
	Полтава		9,8100
	Псков		9,8175
	Рига		9,8165
	Ровно		9,8110
	Ростов-на-Дону		9,8085
	Рязань		9,8145
	Самара		9,8135
	Санкт-Петербург		9,8195
	Саранск		9,8140
	Саранск		9,8140
	Саратов		9,8120
	Семей		9,8100
	Симферополь		9,8065
	Смоленск		9,8145
	Ставрополь		9,8050
	Сумы		9,8110
	Сыктывкар		9,8205
	Таллин		9,8185
	Тамбов		9,8130
	Тараз		9,8020
	Ташкент		9,8010
	Тбилиси		9,8020
	Тверь		9,8160
	Тернополь		9,8095
	Томск		9,8160
	Тула		9,8140
	Тюмень		9,8170
	Улан-Удэ		9,8105
	Ульяновск		9,8145
	Уфа		9,8145
	Хабаровск		9,8095
	Харьков		9,8100
	Херсон		9,8075
	Чебоксары		9,8160
	Челябинск		9,8145
	Чернигов		9,8125
	Черновцы		9,8085
	Чита		9,8100
	Шяуляй		9,8155
	Якутск		9,8205
	Ярославль		9,8170

Скачать таблицу в ПДФ или ЭКСЕЛЬ.
Точные значения ускорения свободного падения «g» уточняйте в региональном ЦСМ.

Исключение по Гауссу · Учебные материалы для студентов-математиков CEGEP

Обзор

На этой странице мы обсуждаем матрицы в редуцированной строковой форме (RREF), и как использовать строковые операции, чтобы добавить в эту расширенную матрицу SLE форму, используя методы исключения Гаусса или Гаусса-Жордана Ликвидация .

Важно

Базовые и продвинутые цели обучения, перечисленные ниже, предназначены для того, чтобы вы представление о материале, который вам следует изучить в этом разделе.Это в основном предназначен для использования в курсе, использующем подход активного обучения, где студенты должны «читать вперед» перед каждым уроком — но в равной степени можно использовать в более традиционной обстановке курса.

Если ваш учитель не даст вам конкретных инструкций, это до , вы до решите, сколько из перечисленных ресурсов вам нужно прочитать или посмотреть — вы наверное вообще , а не нужно все это перебирать. Вы также можете захотеть посмотрите общие советы и рекомендации по обучению страницу для некоторых рекомендаций о том, как эффективно учиться по учебнику математики и видео.

Основные цели обучения

Это те задачи, которые вы должны уметь выполнять с разумной беглость , когда вы придете на следующую встречу в классе . Важное нововведение словарный запас выделен курсивом .

• Распознавать, находится ли данная матрица в форме эшелона строк, сокращенный эшелон строк форма, или ни то, ни другое.
• Построить решения линейных систем, соответствующие расширенные матрицы которых находятся в форме эшелона строки или формы сокращенного эшелона строки.

Расширенные цели обучения

Помимо выполнения основных задач, вот задачи, которые вы должен уметь выполнять после занятий, с практикой :

• Используйте метод исключения Гаусса, чтобы найти общее решение линейной системы.
• Используйте метод исключения Гаусса-Жордана, чтобы найти общее решение линейной системы.
• Анализировать однородные линейные системы.

Для подготовки к

классу

Уменьшенная форма рядка-эшелон (RREF)

• Посмотрите это короткое видео, которое показывает разницу между рядами форма и сокращенная форма рядов (RREF):

• Посмотрите это видео, в котором объясняется (с несколькими подробными примерами), как узнать количество решений из RREF, и как записать решения в параметрической форме, когда решений бесконечно много:

После класса

Исключение Гаусса и исключение Гаусса-Джордана

• Посмотрите это видео, в котором показан метод исключения Гаусса с «Обратная подстановка» на примере СКВ \ (3 \ times 3 \) (с уникальным решением ):

• Посмотрите это видео, в котором показан метод исключения Гаусса-Джордана на пример \ (3 \ times 3 \) SLE (с уникальным решением ):

• Посмотрите это видео, в котором показан геометрический эффект на плоскостях, когда с использованием метода исключения Гаусса-Жордана на \ (3 \ times 3 \) SLE (с уникальным решением ):

Гаусс-Джордан с бесконечным множеством решений

• Посмотрите это видео, в котором показан метод исключения Гаусса-Джордана на пример \ (2 \ times 3 \) SLE (с бесконечным числом решений ):

• Посмотрите это видео, в котором показан метод исключения Гаусса на пример \ (3 \ times 3 \) SLE (с бесконечным числом решений ) — и который также демонстрирует изящный (и настоятельно рекомендуемый) трюк с использованием row-контрольная сумма для перепроверки ваших вычислений:

• Посмотрите это видео, в котором показан метод исключения Гаусса на пример \ (4 \ times 6 \) SLE (с бесконечным числом решений ) — и который также показывает , как записывать решения в параметрической векторной форме :

Онлайн-калькуляторы RREF

Есть много веб-сайтов, которые предлагают «Калькулятор RREF», некоторые даже показывают пошаговые решения. У большинства из них есть недостаток в том, что они используют только «официальное», прямое применение алгоритма Гаусса-Джордана — что не всегда является самым быстрым или лучшим (что часто создает неприятные дроби чего в противном случае можно было бы избежать гораздо позже).

Следующий веб-сайт, кажется, намного лучше показывает «умный» последовательность операций со строками в большинстве случаев:

https://matrix.reshish.com/gauss-jordanElimination.php

Примечание:

В пошаговых решениях на этом веб-сайте показана операция «добавления кратное число строк другому »в 3 отдельных шага: сначала умножив строки по номеру, затем прибавляя к другой строке — и затем «восстанавливая» исходный ряд.Вы должны , а не написать это на бумаге вот так — это сделано только здесь, чтобы вы могли лучше видеть шаги и расчеты.

Наконец, помните, что вы должны использовать этот (и другие веб-сайты) с умом, чтобы пример, чтобы перепроверить свою работу, или, если вы действительно застряли — не просто используйте это, чтобы получить отметки «бесплатно» на вашем WebWork, иначе вы сильно потеряетесь в экзамен . .. Или, как сказали бы другие:

С большой силой приходит большая ответственность.

---

• «Системы линейных уравнений
• Геометрия линейных систем »

Уравновешивание химических уравнений методом исключения Гаусса

с использованием метода исключения Гаусса

Этот калькулятор использует метод исключения Гаусса для определения стехиометрических коэффициентов химического уравнения.Исключение Гаусса (также известное как сокращение строк) — это численный метод решения системы линейных уравнений. Метод назван в честь немецкого математика Карла Фридриха Гаусса (1777-1855).




Все химические уравнения должны быть сбалансированы. Что значит быть сбалансированным? Это означает, что соблюдается закон сохранения массы. Закон сохранения массы гласит, что в обычной химической реакции материя не создается и не разрушается, то есть химическое уравнение должно иметь одинаковое количество атомов каждого элемента на обеих сторонах уравнения. 2 +)

• Чтобы ввести знак уравнения, вы можете использовать символы «=», «->» или «→».
• Уравнение можно записать строчными буквами. Если элементы в химической формуле правильно написаны с заглавной буквы, преобразователь смарт-кейсов оставит их так, как вы ввели.
• Чтобы указать физические состояния, которые вы можете использовать для твердого тела, (l) для жидкостей, (g) для газов и (aq) для веществ, растворенных в воде.

Примеры химических уравнений

Балансировка окислительно-восстановительных реакций

Две проблемы могут возникнуть при балансировании окислительно-восстановительных реакций математическими методами:

1.Уравновешивание уравнений окислительно-восстановительных реакций путем проверки или математического метода (например, метода исключения Гаусса) может дать результаты, которые будут математически точными, но не химически. Это связано с тем, что уравнения окислительно-восстановительных реакций также должны удовлетворять электронному балансу, то есть количество электронов, высвобождаемых в реакции окисления, должно быть равно количеству электронов, полученных в реакции восстановления.

Метод изменения окислительного числа

2.Уравнения окислительно-восстановительного потенциала часто записываются таким образом, что вода и ее ионы не учитываются. H ₂ O, H ⁺ или OH ^— (в зависимости от среды) могут быть добавлены по мере необходимости, поскольку предполагается, что реакция протекает в воде. В противоположность этому математический метод требует, чтобы все частицы, участвующие в реакции, были явно указаны.

Метод изменения окислительного числа

Форма

Row Echelon Form и уменьшенная форма Row Echelon Form

Содержание (Щелкните, чтобы перейти к этому разделу:

1. Что такое форма эшелона?
2. Форма ступенчатого эшелона
3. Форма ступенчатого редуктора
4. Исключение по Гауссу
5. Ранг матрицы

Посмотрите видео с определениями эшелонов, рядов и пониженных рядов:

Не можете посмотреть видео? Кликните сюда.

Что такое форма эшелона?

Форма

Echelon означает, что матрица находится в одном из двух состояний:

• Рядная форма эшелона.
• Уменьшенная форма эшелона строки.

Это означает, что матрица удовлетворяет следующим трем требованиям:

1. Первое число в строке (называемое ведущим коэффициентом) — 1. Примечание: некоторые авторы не требуют, чтобы ведущий коэффициент был равен 1; это могло быть любое число. Вы можете узнать у своего инструктора, какой версии этого правила они придерживаются).
2. Каждая ведущая единица находится справа от первой.
3. Любые ненулевые строки всегда находятся над строками со всеми нулями.

Следующие примеры представляют собой матрицы в эшелонированной форме:

Следующие примеры представляют собой , а не в эшелонированной форме:

Матрица A не имеет все нулевые строки ниже ненулевых строк.
Матрица B имеет 1 на второй позиции в третьей строке. Для формы эшелона строки он должен быть справа от ведущего коэффициента над ним.Другими словами, он должен быть на четвертой позиции вместо 3.
Matrix C имеет 2 в качестве ведущего коэффициента вместо 1.
Matrix D имеет -1 в качестве ведущего коэффициента вместо 1.

Другой способ думать о матрице в форме эшелона — это то, что матрица подверглась гауссовскому исключению, которое представляет собой серию операций со строками.

Уникальность и формы эшелона

Эшелонированная форма матрицы не уникальна, что означает, что при сокращении строк возможно бесконечное количество ответов.Уменьшенная форма эшелона строки находится на другом конце спектра; уникально , что означает, что сокращение строк в матрице даст один и тот же ответ независимо от того, как вы выполняете одни и те же операции со строками.
Вернуться к началу.

Что такое форма эшелона строк?

Матрица находится в форме эшелона строк, если она соответствует следующим требованиям:

• Первое ненулевое число слева («ведущий коэффициент») всегда находится справа от первого ненулевого числа в строке выше.
• Строки, состоящие из нулей, находятся внизу матрицы.

Форма рядного эшелона. «А» может представлять любое число.

Технически ведущий коэффициент может быть любым числом. Однако в большинстве учебников линейной алгебры утверждается, что ведущим коэффициентом должно быть число 1. Чтобы добавить путаницы, некоторые определения формы эшелона строк утверждают, что должны быть нули как выше , так и на ниже ведущего коэффициента. Поэтому лучше всего следовать определению, данному в учебнике, которому вы следуете (или тому, который дал вам ваш профессор).Если вы не уверены (то есть сейчас воскресенье, у вас должна быть домашняя работа, и вы не можете связаться с профессором), безопаснее всего использовать 1 в качестве ведущего коэффициента в каждой строке.

Если ведущим коэффициентом в каждой строке является ненулевое число только в этом столбце, матрица называется уменьшенной эшелонированной строкой.

Матрица 3 × 5 в сокращенной форме эшелона строк.

Строковые формы эшелона обычно встречаются в линейной алгебре, когда вас иногда просят преобразовать матрицу в эту форму.Форма эшелона строк может помочь вам увидеть, что представляет собой матрица, а также является важным шагом к решению систем линейных уравнений.

Онлайн-калькулятор формы эшелона строк

Этот онлайн-калькулятор преобразует любую матрицу, и предоставляют операции со строками, которые помогут вам от шага к шагу. На следующем изображении (из калькулятора Университета Старого Доминиона показано, как матрица [01, 00, 59] приводится к форме эшелона строк с помощью двух простых операций со строками:

Back to Top.

Что такое форма сокращенного эшелона строк?

Уменьшенная форма эшелона строк — это тип матрицы, используемой для решения систем линейных уравнений. Форма пониженного ряда имеет четыре требования:

• Первое ненулевое число в первой строке (, ведущая запись ) — это число 1.
• Вторая строка также начинается с цифры 1, которая находится правее первой записи в первой строке. В каждом последующем ряду цифра 1 должна быть правее.
• Начальная запись в каждой строке должна быть единственным ненулевым числом в ее столбце.
• Любые ненулевые строки помещаются внизу матрицы.

Матрица 3 × 5 в сокращенной форме эшелона строк.

Преобразование матрицы в форму сокращенного эшелона строк

Любая матрица может быть преобразована в сокращенную форму эшелона строк с помощью метода, называемого исключением по Гауссу. Это особенно полезно для решения систем линейных уравнений. Большинство графических калькуляторов (например, TI-83) имеют функцию rref, которая преобразует матрицу в сокращенную форму эшелона строк.См. Эту статью на веб-сайте Университета штата Колорадо, где приведены инструкции по использованию TI-89 и TI-83 для расчета формы сокращенного эшелона строки.
Этот онлайн-калькулятор на веб-сайте Old Dominion University преобразует вводимую вами матрицу в сокращенную форму эшелона строк.

Для ручного расчета требуется знание элементарных операций со строками, а именно:

1. Поменяйте местами одну строку с другой.
2. Умножьте одну строку на ненулевую константу.
3. Заменить одну строку на: одну строку плюс константу, умноженную на другую строку.

Кроме того, недостаточно просто знать правила, вы должны уметь смотреть на матрицу и принимать логическое решение о том, какое правило вы собираетесь использовать и когда. Вы пытаетесь преобразовать матрицу в сокращенный ряд строк, поэтому вам также необходимо выполнить четыре требования в начале этой статьи. Если вам нужно вручную преобразовать матрицу в сокращенную форму эшелона строк, рекомендуется использовать один из приведенных выше калькуляторов, чтобы проверить свою работу. Фактически, если вы используете онлайн-калькулятор ODU, он даже предоставит вам операции со строками.На изображении ниже показано преобразование калькулятором матрицы [204,923]:

Вернуться к началу.

Что такое метод исключения Гаусса?

Метод исключения Гаусса — это способ найти решение системы линейных уравнений. Основная идея состоит в том, что вы выполняете математическую операцию над строкой и продолжаете, пока не останется только одна переменная. Например, некоторые возможные операции со строками:

• Поменять местами любые два ряда
• Сложите две строки вместе.
• Умножьте одну строку на ненулевую константу (т.е. 1/3, -1, 5)

Вы также можете выполнять более одной строковой операции одновременно. Например, умножьте одну строку на константу, а затем добавьте результат к другой строке.

После этого цель состоит в том, чтобы получить матрицу в сокращенной форме эшелона строк, где ведущий коэффициент, 1, в каждой строке находится справа от ведущего коэффициента в строке над ней. Другими словами, вам нужно получить 1 в верхнем левом углу матрицы. В следующей строке должен быть 0 в позиции 1 и 1 в позиции 2.Это дает вам решение системы линейных уравнений.

Пример исключения по Гауссу

Решите следующую систему линейных уравнений методом исключения Гаусса:

• х + 5у = ​​7
• -2x — 7y = -5

Шаг 1: Преобразуйте уравнение в форму матрицы коэффициентов . Другими словами, просто возьмите коэффициент для чисел и забудьте пока о переменных:

Шаг 2. Превратите числа в нижней строке в положительные, прибавив 2 раза первую строку:

Шаг 3: Умножьте вторую строку на 1/3.Это дает вам второй ведущий 1:

Шаг 4: Умножьте строку 2 на -5, а затем добавьте это к строке 1:

Вот и все!
В первой строке у вас x = -8, а во второй строке y = 3. Обратите внимание, что x и y находятся в тех же положениях, что и при преобразовании уравнения на шаге 1, поэтому все, что вам нужно сделать, это прочтите решение:

Вернуться к началу.

Что такое ранг матрицы?

Ранг матрицы равен количеству линейно независимых строк. Линейно независимая строка — это строка, которая не является комбинацией других строк.

Следующая матрица имеет две линейно независимых строки (1 и 2). Однако, когда в смесь добавляется третья строка, вы можете видеть, что первая строка теперь равна сумме второй и третьей строк. Следовательно, ранг этой конкретной матрицы равен 2, так как имеется только две линейно независимых строки.

Ранг матрицы всегда будет на меньше, чем количества ненулевых строк или количества столбцов в матрице.Если все строки в матрице линейно независимы, матрица имеет ранг , полный ранг строки . Для квадратной матрицы она имеет полный ранг только в том случае, если ее определитель не равен нулю.

Выяснить ранг матрицы, пытаясь определить на глаз, сколько строк или столбцов линейно независимы, может быть практически невозможно. Более простой (и, возможно, очевидный) способ — преобразовать в форму эшелона строк.

Как найти матрицу Рейтинг

Найти ранг матрицы просто, если вы знаете, как найти матрицу эшелона строк. Чтобы найти ранг любой матрицы:

1. Найдите матрицу эшелонов строк.
2. Подсчитать количество ненулевых строк.

Преобразование матрицы в форму эшелона строк.

Вышеупомянутая матрица была преобразована в форму эшелона строк с двумя ненулевыми строками. Следовательно, ранг матрицы равен 2.

Вы также можете найти отличный инструмент для конвертации на сайте Old Dominion University.

Вернуться к началу.

Список литературы

Эверитт, Б.S .; Скрондал, А. (2010), Кембриджский статистический словарь, Cambridge University Press.
Гоник Л. (1993). Мультяшный справочник по статистике. HarperPerennial.
Серл, С. (2017). Матричная алгебра, полезная для статистики (серия Уайли по вероятности и статистике), 2-е издание. Вайли.

————————————————— ————————-

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!

Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .

РЕШЕНИЕ: Для следующей системы уравнений сделайте следующее: i Напишите соответствующую расширенную матрицу ii. Используйте исключение Гаусса (с помощью компьютера или калькулятора), чтобы привести к сокращенной форме rOw-echelon (rref) iii. Запишите систему уравнений, соответствующую t0 приведенному rOw 4x + 8y = 44 2x ~ y = -3 ~ Ax 12y = 36 X 2x + Y + 27 = MI 2x Et3 3x + 2y + 2 = 9 X-2y + 7 = 4 3x — 6y 31 = 12 ~ 2x + 4y

Стенограмма видео

в этой проблеме.У нас есть система уравнений, и мы хотим решить ее, используя сокращенную форму эшелона строк. И если мы остановимся и сначала подумаем об этом концептуально, каждое уравнение представляет собой плоскость. А поскольку у нас всего два уравнения, у нас есть только две плоскости. Итак, если они пересекаются, они пересекаются по линии или находятся в одной плоскости. Так что мы не сможем получить только один ответ. Единая упорядоченная тройка. Для этой задачи мы получим бесконечно много ответов, но, возможно, сможем описать их в виде каких-то отношений.Итак, первое, что мы хотим сделать, это преобразовать наши уравнения в расширенную матрицу. Таким образом, первое уравнение преобразуется в единицу в отрицательную 31, а второе уравнение в отрицательную тройку отрицательную 58 в отрицательную. 29. Нам разрешено использовать наши калькуляторы для решения этой проблемы. Отсюда я ввожу эту матрицу в свой калькулятор, и мой калькулятор находит сформированный для меня сокращенный ряд строк. Итак, у нас есть калькуляторы, и мы хотим перейти в меню «Матрица» и отредактировать выделенную матрицу a, а затем ввести размеры матрицы до четырех и ввести все числа.Как видите, я уже сделал. Как только он у нас есть, мы выходим из матричного меню. Итак, мы возвращаемся к главному экрану, а затем снова в меню Матрицы, к математике и прокручиваем вниз, пока не найдем R R E F, что означает сокращенную форму эшелона строк. Выбираем его, затем возвращаемся в меню матрицы и выбираем матрицу A. Затем нажимаем Enter. И это наша сокращенная форма эшелона строк, поэтому мы запишем ее и интерпретируем из нее наш ответ. Итак, чтобы найти решение системы, мы можем преобразовать каждую строку обратно в уравнение.Итак, первая строка — X минус Z равняется 53. И если мы увидим, что для X, мы получим, что X равно Z плюс 53, а затем для второго уравнения у нас будет, почему минус Z равен отрицательному 26. И если мы увидели это, то почему мы имеем y равно Z минус 26. Итак, у нас действительно бесконечно много решений, и это соотношение между координатами XY и Z для всех решений. Вот и ответ на нашу проблему.

Уменьшение количества строк с помощью калькулятора TI83 или TI84 (rref)

Строка сокращения матрицы может помочь нам найти решение системы уравнений (в случае расширенных матриц), понять свойства набора векторов и многое другое.-1] для входа в матричное меню. Обратите внимание, что на некоторых старых калькуляторах есть кнопка, на которой просто написано [MATRX]. Нажимайте стрелку вправо, пока не попадете в меню ПРАВКА.

Нажмите [ENTER], и теперь вы можете редактировать матрицу A.

Шаг 2: Введите матрицу в калькулятор.

Первая информация, которую вам задают, — это размер матрицы. Эта матрица имеет 3 строки и 3 столбца, поэтому это матрица 3 x 3. Введите эти числа, нажимая [ENTER] после каждого.

Теперь вы можете вводить каждое число, набирая его и нажимая [ENTER].-1], но оставайтесь в меню ИМЕНА.

Теперь нажмите [ENTER], чтобы выбрать матрицу A.

Закройте круглые скобки, нажав [)], а затем [ENTER], чтобы получить уменьшенную матрицу.

(примечание: вам не нужно закрывать круглые скобки, чтобы это работало, но это хорошая привычка — или, может быть, просто не закрывающие круглые скобки сводят меня с ума… один из таких…).

Интересно! Эта матрица оказывается строковым эквивалентом единичной матрицы. Если вы в настоящее время изучаете линейную алгебру, вы знаете, что это полезный факт о матрице. Есть много свойств, которые теперь автоматически верны для нашей матрицы A!

В любом случае, мы закончили. Теперь у нас есть сокращенная по строкам матрица A.

Дроби и десятичные числа

Одна вещь, которая может произойти, когда вы сокращаете строку, — это то, что вы получите беспорядочные десятичные дроби. С помощью одного дополнительного шага вы можете преобразовать их в дроби. Итак, предположим, что мы сократили матрицу и получили следующее:

Перед нажатием любых других кнопок нажмите [MATH], а затем выберите> FRAC, нажав [ENTER].

Теперь нажмите [ENTER], чтобы получить уменьшенную матрицу с дробями вместо десятичных.

Это намного лучше! Вы захотите использовать это для большинства математических задач, поскольку дроби являются точными значениями, а десятичные дроби раньше были приблизительными.

объявление

Дополнительное чтение

Теперь, когда вы привыкли к сокращению строк с помощью калькулятора, вы можете научиться умножать матрицы с помощью TI83 / 84 или находить обратную величину с помощью калькулятора!

Подпишитесь на нашу рассылку новостей!

Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.

Подпишитесь, чтобы время от времени получать электронные письма (раз в пару или три недели) с информацией о новинках!

Связанные

efunda Cool Calculators

Калькулятор преобразования единиц Имея более 800 единиц в нашей базе данных (и она продолжает расти), мы даем определение единиц и размеры в системе СИ в дополнение к преобразованию одной единицы в другие единицы того же семейства.	Калькулятор дробей Инженеры-конструкторы, когда-нибудь задумывались, какое число 32 и ближе всего к десятичной дроби? Этот калькулятор подскажет, где находится ваша десятичная дробь на шкале 1/8, 1/16, 1/32 и 1/64.
Калькулятор калибра Существует очень много систем для измерения проводов и листов . Этот калькулятор позволяет вам переводить данные из шкалы в фактические десятичные числа в различных стандартах и ​​обратно.	Калькулятор уплотнительных колец Этот калькулятор выводит внутренний диаметр уплотнительного кольца и диапазон диаметров поперечного сечения уплотнительного кольца, которые будут соответствовать установленным пользователем ограничениям на диаметры канавки и отверстия и сжатие уплотнительного кольца.
Пружинные калькуляторы Расстроены, читая каталоги пружин, пытаясь выяснить, какая пружина дает вам правильную силу или смещение? Возможно, вам поможет один из этих калькуляторов 8 .Скоро будут добавлены другие калькуляторы!	Твердость прибл. Преобразователь Этот калькулятор объясняет и преобразует часто используемые шкалы твердости, включая шкалы твердости по Бринеллю, Кнупу, Моосу, Роквеллу, Шору и Виккерсу.
Калькулятор балки Включает калькуляторы 11 , которые выводят смещение, вращение, силу, момент и сдвиг для балок с различными граничными условиями при различных нагрузках.	SDOF Вибрация Этот калькулятор возвращает естественные коэффициенты трения, коэффициент демпфирования и решение в замкнутой форме для системы масса-пружина-демпфер с одной степенью свободы.
Число Рейнольдса Этот калькулятор быстро дает вам число Рейнольдса для потока через пластину или потока в трубе.	Расходомер Вентури Этот калькулятор выводит расход через сужение Вентури для заданного перепада давления.
Трение трубы Разочарованы использованием Moody Chart для расчета потерь давления в трубах? Этот калькулятор сделает это за вас и подскажет число Рейнольдса, падение давления и расход для трубы с постоянным поперечным сечением.	Излучение Вы когда-нибудь задумывались, сколько тепла в секунду излучается от вашей (лысой) головы в темное ночное небо, если вы стоите в открытом поле? Вы можете использовать этот калькулятор, чтобы выяснить это!
Пластина с ламинарным потоком Тепловая конвекция за счет принудительного ламинарного обтекания изотермической пластины.	Преобразование напряжения Помните Круг Мора ? Мы предоставляем калькуляторы, которые выполняют математические вычисления по кругу Мора для случаев Плоское напряжение и Плоское напряжение .
Главное напряжение Вам нужно найти главные напряжения и их направления для заданного входного напряженного состояния? Эти калькуляторы выполнят математические вычисления для случая Плоское напряжение и Плоское напряжение .	Упругие постоянные Хорошо, мы все помним, что изотропный материал требует только 2 упругих постоянных для описания его поведения материала. Но какие 2 константы использовать? модуль Юнга , коэффициент Пуассона , модуль упругости или модуль объемной упругости ? Не переживайте — этот калькулятор позволяет конвертировать любые 2 константы во все другие, которые обычно используются.
Критерии отказа Помните, как применять критерии фон Мизеса и максимального сдвига для оценки риска отказа? Как насчет максимального напряжения или теории Мора? Мы рекомендуем вам освежить в памяти основы, но, помимо этого, вот 2 калькулятора для применения критериев отказа к хрупким материалам и пластичным материалам .	Калькуляторы тарелок Включает калькуляторы 11 , которые выводят максимальное смещение и напряжение для обычных пластин с разными граничными условиями при различных нагрузках.
Концентрация напряжений 11 Калькуляторы предназначены для расчета коэффициента концентрации напряжений K для общих элементов, таких как выемки, отверстия, канавки и заплечики.	Изгиб колонны Калькулятор критической нагрузки вычисляет критическую нагрузку, коэффициент граничных условий и эффективную длину колонны; Калькулятор колонн из конструкционной стали разработан специально для колонн из конструкционной стали для расчета допустимого напряжения с учетом заданного коэффициента безопасности.
Композитные материалы 3 Калькуляторы предназначены для помощи в определении механических свойств многослойного композитного материала.Сначала оцениваются эквивалентные материальные постоянные одиночного слоя вдоль основных направлений. Затем строятся матрицы жесткости и податливости такого слоя. Наконец, пластинки «склеиваются» и строятся матрицы жесткости A, B и D ламината.	Стол насыщенного пара Температура и давление насыщенного пара тесно связаны. Когда один из них дан, другой определяется.Этот калькулятор вычисляет плотность, удельный объем, внутреннюю энергию, энтальпию и энтропию насыщенного пара на основе табличных данных с использованием интерполяции.

Исключение по Гауссу — предварительное вычисление | Сократик

ПРИМЕР:

Используйте метод исключения Гаусса для решения следующей системы уравнений.

# x + 2y + 3z = -7 #
# 2x-3y-5z = 9 #
# -6z-8y + z = -22 #

Решение:

Настроить расширенную матрицу формы.

# ((1,2,3, |, -7), (2,3, -5, |, 9), (- 6, -8,1, |, 22)) #

Цель 1. Получите 1 в верхнем левом углу.

Уже сделано.

Цель 2a: Получите ноль под 1 в первом столбце.

Умножьте строку 1 на # -2 #, чтобы получить

# ((- 2, -4, -6, |, 14)) #

Добавьте результат в строку 2 и поместите результат в строку 2.

Обозначим операции как # -2R_2 + R_1 → R_2 #.

# ((1,2,3, |, -7), (2,3, -5, |, 9), (- 6, -8,1, |, 22)) stackrel (-2R_1 + R_2 → R_2) (→) ((1,2,3, |, -7), (0, -7, -11, |, 23), (- 6, -8,1, |, 22)) #

Цель 2b: Получите еще один ноль в первом столбце.

Для этого нам понадобится операция # 6R_1 + R_3 → R_3 #.

# ((1,2,3, |, -7), (0, -7, -11, |, 23), (- 6, -8,1, |, 22)) stackrel (6R_2 + R_3 → R_3) (→) ((1,2,3, |, -7), (0, -7, -11, |, 23), (0,4,19, |, -64)) #

Цель 2c. Получите оставшийся ноль.

Умножьте строку 2 на # -1 / 7 #.

# ((1,2,3, |, -7), (0, -7, -11, |, 23), (0,4,19, |, -64)) stackrel (- (1/7 ) R_2 → R_2) (→) ((1,2,3, |, -7), (0,1,11 / 7, |, -23 / 7), (0,4,19, |, -64 )) #

Теперь используйте операцию # -4R_2 + R_3 → R_3 #.