Коллинеарность векторов, условия коллинеарности векторов.
Условия коллинеарности векторов
Два вектора будут коллинеарны при выполнении любого из этих условий:
Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, чтоa = n · b
Условия коллинеарности векторов 2. Два вектора коллинеарны, если отношения их координат равны.
N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.
N.B. Условие 3 применимо только для трехмерных (пространственных) задач.
Примеры задач на коллинеарность векторов
Примеры задач на коллинеарность векторов на плоскости
Пример 1. Какие из векторов a = {1; 2}, b = {4; 8}, c = {5; 9} коллинеарны?Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:
Значит:
| Вектора a и b коллинеарны т.к. | 1 | = | 2 | . |
| 4 | 8 |
| Вектора a и с не коллинеарны т.к. | 1 | ≠ | 2 | . |
| 5 | 9 |
| Вектора с и b не коллинеарны т.к. | 5 | ≠ | 9 | . |
| 4 | 8 |
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
b = na.
Для этого найдем ненулевой компонент вектора a в данном случае это ay. Если вектора колинеарны то
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение na:
na = {2 · 0; 2 · 3} = {0; 6}Так как b = na, то вектора a и b коллинеарны.
Пример 3. найти значение параметра n при котором вектора a = {3; 2} и b = {9; n} коллинеарны.Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
Значит:
Решим это уравнение:
Ответ: вектора a и b коллинеарны при n = 6.
Примеры задач на коллинеарность векторов в пространстве
Пример 4. Какие из векторов a = {1; 2; 3}, b = {4; 8; 12}, c = {5; 10; 12} коллинеарны?Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:
| ax | = | ay | az | . | |
| bx | by | bz |
Значит:
Вектора a и b коллинеарны т.к. 14 = 28 = 312
Вектора a и с не коллинеарны т.к. 15 = 210 ≠ 312
Вектора с и b не коллинеарны т.к. 54 = 108 ≠ 1212
Пример 5. Доказать что вектора a = {0; 3; 1} и b = {0; 6; 2} коллинеарны.Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
b = na.
Для этого найдем ненулевой компонент вектора a в данном случае это ay. Если вектора колинеарны то
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение na:
na = {2 · 0; 2 · 3; 2 · 1} = {0; 6; 2}Так как b = na, то вектора a и b коллинеарны.
Пример 6. найти значение параметров n и m при которых вектора a = {3; 2; m} и b = {9; n; 12} коллинеарны.Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | = | az | . |
| bx | by | bz |
Значит:
Из этого соотношения получим два уравнения:
Решим эти уравнения:
Ответ: вектора a и b коллинеарны при n = 6 и m = 4.
ru.onlinemschool.com
Коллинеарные векторы и условия коллинеарности
ОПРЕДЕЛЕНИЕУсловия коллинеарности векторов
Два вектора и будут коллинеарны при выполнении любого из следующих условий.
Условие коллинеарности 1. Два вектора и коллинеарны, если существует такое число , что
Условие коллинеарности 2. Два вектора и коллинеарны, если отношения их координат равны:
ЗАМЕЧАНИЕ
Это условие неприменимо, если одна из координат вектора равна нулю.
Условие коллинеарности 3. Два вектора коллинеарны и , если их векторное произведение равно нулевому вектору:
ЗАМЕЧАНИЕ
Это условие применимо только для векторов, заданных в пространстве.
Примеры решения задач с коллинеарными векторами
ПРИМЕР| Задание | Исследовать векторы и на коллинеарность. |
| Решение |
Воспользуемся вторым условием коллинеарности. Для заданных векторов оно запишется в виде:
Поскольку получили неверное равенство, то делаем вывод, что векторы и неколлинеарные. |
| Ответ |
| Задание | При каком значении параметра вектора и коллинеарны? |
| Решение |
Согласно второму условию коллинеарности, рассматриваемые вектора будут коллинеарными, если их координаты будут пропорциональными, то есть
Откуда
|
| Ответ |
ru.solverbook.com
Коллинеарные вектора — это… Что такое Коллинеарные вектора?
Два вектора называются коллинеа́рными, если они лежат на параллельных прямых или на одной прямой. Допусти́м, но не рекомендуется, синоним — «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или противоположно направлены (в последнем случае их иногда называют «антиколлинеарными» или «антипараллельными»).
Обозначения
- Коллинеарные векторы:

- Сонаправленные векторы:

- Противоположно направленные векторы:

Свойства коллинеарности
Пусть
 — векторы пространства
— векторы пространства  . Тогда верны следующие утверждения:
. Тогда верны следующие утверждения:Другие объекты
Выше описанные критерии коллинеарности позволяют определить это понятие для векторов, понимаемых не в геометрическом смысле (а, например, как элементы произвольного линейного пространства).
Иногда коллинеарными называют те точки (или другие объекты), которые лежат на (принадлежат) одной прямой.
См. также
- Коллинеарные векторы:
Wikimedia Foundation. 2010.
- Коллинеарные векторы
- Коллинз, Вильям
Смотреть что такое «Коллинеарные вектора» в других словарях:
Коллинеарные векторы — Два вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой. Допустим, но не рекомендуется, синоним «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или… … Википедия
КОЛЛИНЕАРНЫЕ ВЕКТОРЫ — векторы, лежащие на одной прямой или на параллельных прямых. Для того чтобы два ненулевых вектора были коллинеарны, необходимо и достаточно, чтобы их координаты были пропорциональны. Нулевой вектор коллинеарен всякому вектору. Аналогично,… … Математическая энциклопедия
Коллинеарность — Два коллинеарных противоположно направленных вектора Два ненулевых (не равных 0) вектора называются … Википедия
Вектор — направленный отрезок прямой, или отрезок, один из концов которого называется началом вектора, а другой его концом. Различают: 1) коллинеарные векторы, лежащие на одной прямой или на параллельных прямых; 2) компланарные векторы, лежащие в одной… … Начала современного естествознания
dic.academic.ru
Как найти вектор коллинеарный вектору — энциклопедический справочник и словарь для студента от А до Я
ФОРМУЛА
Для того чтобы вектор \(\ \overline{a}=\left(a_{x} ; a_{y}\right) \) был коллинеарным вектором \(\ \overline{b}=\left(b_{x} ; b_{y}\right) \), необходимо, чтобы его соответствующие координаты были пропорциональны, то есть их координаты удовлетворяли условию
\(\ \frac{a_{x}}{b_{x}}=\frac{a_{y}}{b_{y}} \)
Если векторы задаются в пространстве своими координатами: \(\ \overline{a}=\left(a_{x} ; a_{y} ; a_{z}\right), \overline{b}=\left(b_{x} ; b_{y} ; b_{z}\right) \), тогда условие коллинеарности имеет вид:
\(\ \frac{a_{x}}{b_{x}}=\frac{a_{y}}{b_{y}}=\frac{a_{z}}{b_{z}} \)
КОЛЛИНАРНЫЙ ВЕКТОРНЫЙ ПОДХОД
ПРИМЕР
\(\ \frac{a_{x}}{b_{x}}=\frac{a_{y}}{b_{y}} \)
Подставьте координаты заданных векторов в это равенство и найдите значение \(\ m \):
\(\ \frac{2}{-1}=\frac{-3}{m} \)
В пропорции имеем:
\(\ 2 \cdot m=(-1) \cdot(-3) \Rightarrow 2 \cdot m=3 \Rightarrow m=\frac{3}{2}=1,5 \)
ПРИМЕР
\(\ \frac{4}{2}=\frac{-m}{-3}=\frac{1}{n} \)
А потом по значениям неизвестных параметров \(\ m \quadи\quad n \) определим из равенств
\(\ \frac{m}{3}=2 \Rightarrow m=6 \)
\(\ \frac{1}{n}=2 \Rightarrow n=\frac{1}{2}=0,5 \)
sciterm.ru
Коллинеарность и ортогональность векторов | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Чтобы определить коллинеарность и ортогональность векторов, воспользуемся стандартными действиями с векторами, основанными на использовании тригонометрических функций синуса и косинуса.
Коллинеарные векторы – это векторы, которые расположены параллельно друг к другу, то есть при наложении дают угол в 0 градусов. Поэтому чтобы проверить коллинеарность векторов, нужно доказать что угол между векторами равен 0, а это проще всего сделать через функцию синуса, так как sin0°=0. В аналитической геометрии синус используется для нахождения векторного произведения двух векторов, которое равно произведению длин векторов на синус угла между ними. Поэтому когда между ними нулевой угол, то синус равен нулю, и все векторное произведение становится равно нулю. Из этого можно сделать и обратный вывод: если векторное произведение двух векторов равно нулю, то эти векторы коллинеарны. =[
=[ ×
× ]=|
]=| ||
|| | sinα
| sinα  =0,=> sinα=0,=> α=0.
=0,=> sinα=0,=> α=0.
Ортогональные векторы расположены по отношению друг к другу под углом 90 градусов. Для их определения используем функцию косинуса, которая дает 0 именно при угле в 90 градусов. Косинус в аналитической геометрии встречается в вычислении скалярного произведения векторов, поэтому, когда он равен нулю, то и скалярное произведение векторов становится равным нулю. Это равноценно заявлению о том, что если скалярное произведение векторов равно нулю, то эти векторы – ортогональны.
 =|
=| ||
|| |cosα
|cosα 
 =0,=>cosα=0,=>α=0
=0,=>cosα=0,=>α=0
geleot.ru
Коллинеарность векторов, условия коллинеарности векторов.
Условия коллинеарности векторов
Два вектора будут коллинеарны при выполнении любого из этих условий: Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, чтоa = n · b
Условия коллинеарности векторов 2. Два вектора коллинеарны, если отношения их координат равны.
N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.
N.B. Условие 3 применимо только для трехмерных (пространственных) задач.
Доказательство третего условия коллинеарности
Пусть есть два коллинеарные вектора a = {ax; ay; az} и b = {nax; nay; naz}. Найдем их векторное произведение
| a × b = | i | j | k | = i (aybz — azby) — j (axbz — azbx) + k (axby — aybx) = |
| ax | ay | az | ||
| bx | by | bz |
= i (aynaz — aznay) — j (axnaz — aznax) + k (axnay — aynax) = 0i + 0j + 0k = 0
Примеры задач на коллинеарность векторов на плоскости
Пример 1. Какие из векторов a = {1; 2}, b = {4; 8}, c = {5; 9} коллинеарны?Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:
Значит:
| Вектора a и b коллинеарны т.к. | 1 | = | 2 | . |
| 4 | 8 |
| Вектора a и с не коллинеарны т.к. | 1 | ≠ | 2 | . |
| 5 | 9 |
| Вектора с и b не коллинеарны т.к. | 5 | ≠ | 9 | . |
| 4 | 8 |
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
b = na.
Для этого найдем ненулевой компонент вектора a в данном случае это a y. Если вектора колинеарны то
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение na:
na = {2 · 0; 2 · 3} = {0; 6}Так как b = na, то вектора a и b коллинеарны.
Пример 3. найти значение параметра n при котором вектора a = {3; 2} и b = {9; n} коллинеарны.Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
Значит:
Решим это уравнение:
Ответ: вектора a и b коллинеарны при n = 6.
Примеры задач на коллинеарность векторов в пространстве
Пример 4. Какие из векторов a = {1; 2; 3}, b = {4; 8; 12}, c = {5; 10; 12} коллинеарны?Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:
| ax | = | ay | = | az | . |
| bx | by | bz |
Значит:
| Вектора a и b коллинеарны т.к. | 1 | = | 2 | = | 3 | . |
| 4 | 8 | 12 |
| Вектора a и с не коллинеарны т.к. | 1 | = | 2 | ≠ | 3 | . |
| 5 | 10 | 12 |
| Вектора с и b не коллинеарны т.к. | 5 | = | 10 | ≠ | 12 | . |
| 4 | 8 | 12 |
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
b = na.
Для этого найдем ненулевой компонент вектора a в данном случае это ay. Если вектора колинеарны то
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение na:
na = {2 · 0; 2 · 3; 2 · 1} = {0; 6; 2}Так как b = na, то вектора a и b коллинеарны.
Пример 6. найти значение параметров n и m при которых вектора a = {3; 2; m} и b = {9; n; 12} коллинеарны.Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | = | az | . |
| bx | by | bz |
Значит:
Из этого соотношения получим два уравнения:
Решим эти уравнения:
Ответ: вектора a и b коллинеарны при n = 6 и m = 4.
0oq.ru
Как понять, что векторы коллинеарны?
векторы называються колинеарными если находяться в одной прямой, или в параллельных прямых.)
параллельны и не обязательно равны . могут лежать на одной прямой <img src=»//content.foto.my.mail.ru/mail/babuba/_answers/i-44.jpg» >
паралельны и идут в одном направлении
Векторы коллинеарны, значит они лежат на параллельных прямых, либо на одной прямой.
Если это надо проверить для пары векторов — можно посчитать их векторное произведение. Оно должно быть равно 0. >^.^<
По их координатам. У коллинеарных векторов координаты пропорциональны.
touch.otvet.mail.ru
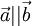
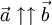
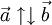
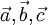 — векторы пространства
— векторы пространства 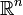 . Тогда верны следующие утверждения:
. Тогда верны следующие утверждения: