Виды уравнений, формулы и примеры

Определение и основные виды уравнений

Например.

Некоторые классы уравнений решаются аналитически (среди алгебраических это линейные, квадратные, кубические уравнения и уравнения четвертой степени), то есть решение записывается в виде формулы. Алгебраические уравнения высших степеней (более, чем четвертая) в общем случае аналитического решения не имеют, хотя некоторые сводятся к уравнениям низших степеней.

В общем случае, если аналитическое решение не существует, применяют численные методы.

Алгебраические уравнения

Алгебраическим уравнением называется уравнение вида

   

где — многочлен переменных , которые называются переменными или неизвестными.

Например.

Степенью алгебраического уравнения называется степень многочлена .

Линейным уравнением от неизвестных называется уравнение вида

   

Например. — линейное уравнение с одной переменной.

Квадратным уравнением (уравнением второй степени)

называется уравнение

   

Здесь — переменная, — старший или первый коэффициент, — второй коэффициент, — свободный коэффициент.

Например.

Квадратное уравнение называется приведенным, если старший коэффициент равен единице.

Например.

Уравнением с параметрами называется математическое равенство, внешний вид и решение которого зависит от значений одного или нескольких параметров.

Например.

Уравнение, содержащее трансцендентные функции, называется трансцендентным.

Например.

Трансцендентная функция — это аналитическая функция, не являющаяся алгебраической. Алгебраической называется элементарная функция, которая в окрестности каждой точки области определения может быть неявно задана с помощью алгебраического уравнения.

Функциональным называется уравнение, которое определяет связь между значением функции (или функций) в одной точке с её значениями в других точках.

Например.

Уравнение, в котором неизвестная функция стоит под знаком производной, называется дифференциальным.

Например.

Интегральным уравнением называется уравнение, в котором неизвестная функция находится под знаком интеграл.

Например.

Решение уравнения — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 июля 2018; проверки требуют 20 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 июля 2018; проверки требуют 20 правок.

В математике, решение уравнения — это задача по нахождению таких значений аргументов (чисел, функций, наборов и т. д.), при которых выполняется равенство (выражения слева и справа от знака равенства становятся эквивалентными). Значения неизвестных переменных, при которых это равенство достигается, называются решениями или

корнями данного уравнения. Решить уравнение означает найти множество всех его решений (корней) или доказать, что корней нет вовсе (либо нет тех, что удовлетворяют заданным условиям).

Например, уравнение x+y=2x−1{\displaystyle x+y=2x-1} решается для неизвестного x{\displaystyle x} с помощью замены x=y+1,{\displaystyle x=y+1,} так как замена переменной x{\displaystyle x} на выражение y+1{\displaystyle y+1} превращает уравнение в тождество: (y+1)+y=2(y+1)−1.{\displaystyle (y+1)+y=2(y+1)-1.} Кроме того, если положить неизвестной переменную y,{\displaystyle y,} тогда уравнение решается с помощью замены y=x−1{\displaystyle y=x-1}. Замена переменной y{\displaystyle y} на выражение x−1{\displaystyle x-1} превращает уравнение в тождество: x+(x−1)=2x−1.{\displaystyle x+(x-1)=2x-1.} Также

УРАВНЕНИЯ | Энциклопедия Кругосвет

Содержание статьи

УРАВНЕНИЯ. Уравнением называется математическое соотношение, выражающее равенство двух алгебраических выражений. Если равенство справедливо для любых допустимых значений входящих в него неизвестных, то оно называется тождеством; например, соотношение вида (

x – 1)² = (x – 1)(x – 1) выполняется при всех значениях переменной x. Для обозначения тождества часто вместо обычного знака равенства = пишут знак є, который читается «тождественно равно». Тождества используются в алгебре при записи разложения многочленов на множители (как в приведенном выше примере). Встречаются они и в тригонометрии в таких соотношениях, как sin²x + cos²x = 1, а в общем случае выражают формальное отношение между двумя на первый взгляд различными математическими выражениями.

Если уравнение, содержащее переменную x, выполняется только при определенных, а не при всех значениях x, как в случае тождества, то может оказаться полезным определить те значения

x, при которых это уравнение справедливо. Такие значения x называются корнями или решениями уравнения. Например, число 5 является корнем уравнения 2x + 7= 17.

Уравнения служат мощным средством решения практических задач. Точный язык математики позволяет просто выразить факты и соотношения, которые, будучи изложенными обычным языком, могут показаться запутанными и сложными. Неизвестные величины, обозначаемые в задаче символами, например x, можно найти, сформулировав задачу на математическом языке в виде уравнений. Методы решения уравнений составляют в основном предмет того раздела математики, который называется теорией уравнений.

ТИПЫ УРАВНЕНИЙ

Алгебраические уравнения.

Уравнения вида f_n = 0, где f_n – многочлен от одной или нескольких переменных, называются алгебраическими уравнениями. Многочленом называется выражение вида

f_n = a₀ xⁱy^j … v^k + a₁ x^ly^m … vⁿ + ј + a_sx^py^q … v^r,

где x, y,…, v – переменные, а i, j,…, r – показатели степеней (целые неотрицательные числа). Многочлен от одной переменной записывается так:

f(x) = a₀xⁿ + a₁xⁿ – 1 +… + a_n – 1x + aⁿ

или, в частном случае, 3x⁴ – x³ + 2x² + 4x – 1. Алгебраическим уравнением с одним неизвестным называется любое уравнение вида f(x) = 0. Если a₀ № 0, то n называется степенью уравнения. Например, 2x

+ 3 = 0 – уравнение первой степени; уравнения первой степени называются линейными, так как график функции y = ax + b имеет вид прямой. Уравнения второй степени называются квадратными, а уравнения третьей степени – кубическими. Аналогичные названия имеют и уравнения более высоких степеней.

Трансцендентные уравнения.

Уравнения, содержащие трансцендентные функции, такие, как логарифмическая, показательная или тригонометрическая функция, называются трансцендентными. Примером могут служить следующие уравнения:

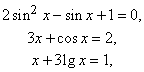
где lg – логарифм по основанию 10.

Дифференциальные уравнения.

Так называются уравнения, содержащие одну или несколько функций и их производные или дифференциалы. Дифференциальные уравнения оказались исключительно ценным средством точной формулировки законов природы. См. также ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.

Интегральные уравнения.

Уравнения, содержащие неизвестную функцию под знаком интеграла, например,

f (s) = тK (s, t) f (t) dt, где f (s) и K(s,t) заданы, а f (t) требуется найти.

Диофантовы уравнения.

Диофантовым уравнением называется алгебраическое уравнение с двумя или более неизвестными с целыми коэффициентами, решение которого ищется в целых или рациональных числах. Например, уравнение 3x – 5y = 1 имеет решение x = 7, y = 4; вообще же его решениями служат целые числа вида x = 7 + 5n, y = 4 + 3n.

РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

Для всех перечисленных выше типов уравнений общих методов решения не существует. И все же во многих случаях, особенно для алгебраических уравнений определенного типа, имеется достаточно полная теория их решения.

Линейные уравнения.

Эти простые уравнения решаются путем их сведения к эквивалентному уравнению, из которого непосредственно видно значение неизвестного. Например, уравнение

x + 2 = 7 можно свести к эквивалентному уравнению x = 5 вычитанием числа 2 из правой и левой частей. Шаги, совершаемые при сведении простого уравнения, например, x + 2 = 7, к эквивалентному, основаны на использовании четырех аксиом.

1. Если равные величины увеличить на одно и то же число, то результаты будут равны.

2. Если из равных величин вычесть одно и то же число, то результаты будут равны.

3. Если равные величины умножить на одно и то же число, то результаты будут равны.

4. Если равные величины разделить на одно и то же число, то результаты будут равны.

Например, чтобы решить уравнение 2x + 5 = 15, мы воспользуемся аксиомой 2 и вычтем число 5 из правой и левой частей, в результате чего получим эквивалентное уравнение 2x = 10. Затем мы воспользуемся аксиомой 4 и разделим обе части полученного уравнения на 2, в результате чего исходное уравнение сведется к виду x = 5, что и является искомым решением.

Квадратные уравнения.

Решения общего квадратного уравнения ax² + bx + c = 0 можно получить с помощью формулы

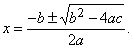
Таким образом, существуют два решения, которые в частном случае могут совпадать.

Другие алгебраические уравнения.

Явные формулы, аналогичные формуле для решения квадратного уравнения, можно выписать только для уравнений третьей и четвертой степеней. Но и эти формулы сложны и далеко не всегда помогают легко находит корни. Что же касается уравнений пятой степени или выше, то для них, как доказал Н.Абель в 1824, нельзя указать общую формулу, которая выражала бы корни уравнения через его коэффициенты при помощи радикалов. В отдельных частных случаях уравнения высших степеней удается легко решить, факторизуя их левую часть, т.е. разлагая ее на множители.

Например, уравнение x³ + 1 = 0 можно записать в факторизованном виде (

x + 1)(x² – x + 1) = 0. Решения мы находим, полагая каждый из множителей равным нулю:

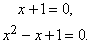
Таким образом, корни равны x = –1, 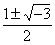, т.е. всего 3 корня.

Если уравнение не факторизуется, то следует воспользоваться приближенными решениями. Основные методы нахождения приближенных решений были разработаны Горнером, Ньютоном и Греффе. Однако во всех случаях существует твердая уверенность в том, что решение существует: алгебраическое уравнение n-й степени имеет ровно n корней.

Системы линейных уравнений.

Два линейных уравнения с двумя неизвестными можно записать в виде

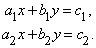
Решение такой системы находится с помощью определителей

Оно имеет смысл, если 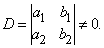Если же D = 0, то возможны два случая. (1) По крайней мере один из определителе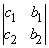й и отличен от нуля. В этом случае решения уравнений не существует; уравнения несовместны. Численный пример такой ситуации – система

(2) Оба определителя равны нулю. В этом случае второе уравнение просто кратно первому и существует бесконечное число решений.

Общая теория рассматривает m линейных уравнений с n переменными:

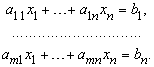
Если m = n и матрица (a_ij) невырожденна, то решение единственно и может быть найдено по правилу Крамера:

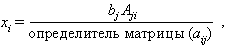
где A_ji – алгебраическое дополнение элемента a_ijв матрице (a_ij). В более общем плане существуют следующие теоремы. Пусть r – ранг матрицы (a_ij), s – ранг окаймленной матрицы (a_ij; b_i), которая получается из a_ij присоединением столбца из чисел b_i. Тогда: (1) если r = s, то существует n – r линейно независимых решений; (2) если r , то уравнения несовместны и решений не существует.

что такое? Определение термина, примеры

В курсе школьной математики, ребенок впервые слышит термин «уравнение». Что такое это, попробуем разобраться вместе. В данной статье рассмотрим виды и способы решения.

Математика. Уравнения

Для начала предлагаем разобраться с самим понятием, что это такое? Как гласят многие учебники математики, уравнение — это некоторые выражения, между которыми стоит обязательно знак равенства. В этих выражениях присутствуют буквы, так называемые переменные, значение которых и необходимо найти.

Что такое переменная? Это атрибут системы, который меняет свое значение. Наглядным примером переменных являются:

• температура воздуха;
• рост ребенка;
• вес и так далее.

В математике они обозначаются буквами, например, х, а, b, с… Обычно задание по математике звучит следующим образом: найдите значение уравнения. Это значит, что необходимо найти значение данных переменных.

Разновидности

Уравнение (что такое, мы разобрали в предыдущем пункте) может быть следующего вида:

• линейные;
• квадратные;
• кубические;
• алгебраические;
• трансцендентные.

Для более подробного знакомства со всеми видами, рассмотрим каждый в отдельности.

Линейное уравнение

Это первый вид, с которым знакомятся школьники. Они решаются довольно-таки быстро и просто. Итак, линейное уравнение, что такое? Это выражение вида: ах=с. Так не особо понятно, поэтому приведем несколько примеров: 2х=26; 5х=40; 1,2х=6.

Разберем примеры уравнений. Для этого нам необходимо все известные данные собрать с одной стороны, а неизвестные в другой: х=26/2; х=40/5; х=6/1,2. Здесь использовались элементарные правила математики: а*с=е, из этого с=е/а; а=е/с. Для того чтобы завершить решение уравнения, выполним одно действие (в нашем случае деление) х=13; х=8; х=5. Это были примеры на умножение, теперь просмотрим на вычитание и сложение: х+3=9; 10х-5=15. Известные данные переносим в одну сторону: х=9-3; х=20/10. Выполняем последнее действие: х=6; х=2.

Также возможны варианты линейных уравнений, где используется более одной переменной: 2х-2у=4. Для того чтобы решить, необходимо к каждой части прибавить 2у, у нас получается 2х-2у+2у=4-2у, как мы заметили, по левую часть знака равенства -2у и +2у сокращаются, при этом у нас остается: 2х=4-2у. Последним шагом делим каждую часть на два, получаем ответ: икс равен два минус игрек.

Задачи с уравнениями встречаются даже на папирусах Ахмеса. Вот одна из задач: число и четвертая его часть дают в сумме 15. Для ее решения мы записываем следующее уравнение: икс плюс одна четвертая икс равняется пятнадцати. Мы видим еще один пример линейного уравнения, по итогу решения, получаем ответ: х=12. Но эту задачу можно решить и другим способом, а именно египетским или, как его называют по-другому, способом предположения. В папирусе используется следующее решение: возьмите четыре и четвертую ее часть, то есть единицу. В сумме они дают пять, теперь пятнадцать необходимо разделить на сумму, мы получаем три, последним действием три умножаем на четыре. Мы получаем ответ: 12. Почему мы в решении пятнадцать делим на пять? Так узнаем, во сколько раз пятнадцать, то есть результат, который нам необходимо получить, меньше пяти. Таким способом решали задачи в средние века, он стал зваться методом ложного положения.

Квадратные уравнения

Кроме рассмотренных ранее примеров, существуют и другие. Какие именно? Квадратное уравнение, что такое? Они имеют вид ax²+bx+c=0. Для их решения необходимо ознакомиться с некоторыми понятиями и правилами.

Во-первых, нужно найти дискриминант по формуле: b²-4ac. Есть три варианта исхода решения:

• дискриминант больше нуля;
• меньше нуля;
• равен нулю.

В первом варианте мы можем получить ответ из двух корней, которые находятся по формуле: -b+-корень из дискриминанта разделенные на удвоенный первый коэфициент, то есть 2а.

Во втором случае корней у уравнения нет. В третьем случае корень находится по формуле: -b/2а.

Рассмотрим пример квадратного уравнения для более подробного знакомства: три икс в квадрате минус четырнадцать икс минус пять равняется нулю. Для начала, как и писалось ранее, ищем дискриминант, в нашем случае он равен 256. Отметим, что полученное число больше нуля, следовательно, мы должны получить ответ состоящих из двух корней. Подставляем полученный дискриминант в формулу нахождения корней. В результате мы имеем: икс равняется пяти и минус одной третьей.

Особые случаи в квадратных уравнениях

Это примеры, в которых некоторые значения равны нулю (а, b или с), а возможно и несколько.

Для примера возьмем следующее уравнение, которое является квадратным: два икс в квадрате равняется нулю, здесь мы видим, что b и с равны нулю. Попробуем его решить, для этого обе части уравнения делим на два, мы имеем: х²=0. В итоге получаем х=0.

Другой случай 16х²-9=0. Здесь только b=0. Решим уравнение, свободный коэфициент переносим в правую часть: 16х²=9, теперь каждую часть делим на шестнадцать: х²= девять шестнадцатых. Так как у нас х в квадрате, то корень из 9/16 может быть как отрицательным, так и положительным. Ответ записываем следующим образом: икс равняется плюс/минус три четвертых.

Возможен и такой вариант ответа, как у уравнения корней вовсе нет. Посмотрим на такой пример: 5х²+80=0, здесь b=0. Для решения свободный член перекидываете в правую сторону, после этих действий получаем: 5х²=-80, теперь каждую часть делим на пять: х²= минус шестнадцать. Если любое число возвести в квадрат, то отрицательное значение мы не получим. По этому наш ответ звучит так: у уравнения корней нет.

Разложение трехчлена

Задание по квадратным уравнениям может звучать и другим образом: разложить квадратный трехчлен на множители. Это возможно осуществить, воспользовавшись следующей формулой: а(х-х₁)(х-х₂). Для этого, как и в другом варианте задания, необходимо найти дискриминант.

Рассмотрим следующий пример: 3х²-14х-5, разложите трехчлен на множетели. Находим дискриминант, пользуясь уже известной нам формулой, он получается равным 256. Сразу отмечаем, что 256 больше нуля, следовательно, уравнение будет иметь два корня. Находим их, как в предыдущем пункте, мы имеем: х= пять и минус одна третья. Воспользуемся формулой для разложения трехчлена на множетели: 3(х-5)(х+1/3). Во второй скобке мы получили знак равно, потому что в формуле стоит знак минуса, а корень тоже отрицательный, пользуясь элементарными знаниями математики, в сумме мы имеем знак плюса. Для упрощения, перемножим первый и третий член уравнения, чтобы избавиться от дроби: (х-5)(х+1).

Уравнения сводящиеся к квадратному

В данном пункте научимся решать более сложные уравнения. Начнем сразу с примера:

(x² – 2x)² – 2(x² – 2x) – 3 = 0. Можем заметить повторяющиеся элементы: (x² – 2x), нам для решения удобно заменить его на другую переменную, а далее решать обычное квадратное уравнение, сразу отмечаем, что в таком задании мы получим четыре корня, это не должно вас пугать. Обозначаем повторение переменной а. Мы получаем: а²-2а-3=0. Наш следующий шаг — это нахождение дискриминанта нового уравнения. Мы получаем 16, находим два корня: минус один и три. Вспоминаем, что мы делали замену, подставляем эти значения, в итоге мы имеем уравнения: x² – 2x=-1; x² – 2x=3. Решаем их в первом ответ: х равен единице, во втором: х равен минусу одному и трем. Записываем ответ следующим образом: плюс/минус один и три. Как правило, ответ записывают в порядке возрастания.

Кубические уравнения

Рассмотрим еще один возможный вариант. Речь пойдет о кубических уравнениях. Они имеют вид: ax ³ + b x ² + cx + d =0. Примеры уравнений мы рассмотрим далее, а для начала немного теории. Они могут иметь три корня, так же существует формула для нахождения дискриминанта для кубического уравнения.

Рассмотрим пример: 3х³+4х²+2х=0. Как его решить? Для этого мы просто выносим х за скобки: х(3х²+4х+2)=0. Все что нам остается сделать — это вычислить корни уравнения в скобках. Дискриминант квадратного уравнения в скобках меньше нуля, исходя из этого, выражение имеет корень: х=0.

Алгебра. Уравнения

Переходим к следующему виду. Сейчас мы кратко рассмотрим алгебраические уравнения. Одно из заданий звучит следующим образом: методом группировки разложить на множетели 3х⁴+2х³+8х²+2х+5. Самым удобным способом будет следующая группировка: (3х⁴+3х²)+(2х³+2х)+(5х²+5). Заметим, что 8х² из первого выражения мы представили в виде суммы 3х² и 5х². Теперь выносим из каждой скобки общий множитель 3х²(х2+1)+2х(х²+1)+5(х²+1). Мы видим, что у нас есть общий множитель: икс в квадрате плюс один, выносим его за скобки: (х²+1)(3х²+2х+5). Дальнейшее разложение невозможно, так как оба уравнения имеют отрицательный дискриминант.

Трансцендентные уравнения

Предлагаем разобраться со следующим типом. Это уравнения, которые содержат трансцендентные функции, а именно логарифмические, тригонометрические или показательные. Примеры: 6sin²x+tgx-1=0, х+5lgx=3 и так далее. Как они решаются вы узнаете из курса тригонометрии.

Функция

Завершающим этапом рассмотрим понятие уравнение функции. В отличии от предыдущих вариантов, данный тип не решается, а по нему строится график. Для этого уравнение стоит хорошо проанализировать, найти все необходимые точки для построения, вычислить точку минимума и максимума.

виды уравнений

Вы искали виды уравнений? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и виды уравнений и способы их решения, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «виды уравнений».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как виды уравнений,виды уравнений и способы их решения,все виды уравнений,все виды уравнений и их решения,уравнения и их виды и. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и виды уравнений. Просто введите задачу в окошко и нажмите «решить» здесь (например, все виды уравнений).

Где можно решить любую задачу по математике, а так же виды уравнений Онлайн?

Решить задачу виды уравнений вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Уравнения

В алгебре рассматриваются два вида равенств – тождества и уравнения.

Тождество – это равенство, которое выполняется при всех (допустимых) значениях входящих в него букв.

Уравнение – это равенство, которое выполняется лишь при некоторых значениях входящих в него букв.

Буквы, входящие в уравнение, могут быть неравноправными: одни могут принимать все свои допустимые значения, которые называют коэффициентами (иногда – параметрами) уравнения, другие, значения которых требуется отыскать, называют неизвестными данного уравнения (как правило, их обозначают последними буквами латинского алфавита x, y, z, u, v, w, или теми же буквами, снабженными индексами.

Уравнения бывают:
Квадратные уравнения
Рациональные уравнения
Уравнения, содержащие переменную под знаком модуля
Иррациональные уравнения
Показательные уравнения
Логарифмические уравнения

Системы уравнений:
Системы рациональных уравнений
Системы нелинейных уравнений
Симметрические системы
Смешанные системы

Посторонние корни, возникшие в процессе преобразований, можно выявить проверкой. Конечно, если все преобразования приводили нас к цепочке равносильных уравнений, то проверка необязательна. Однако этого не всегда можно добиться, легче следить за тем, чтобы каждое уравнение цепочки являлось следствием предыдущего, т.е. чтобы не происходила потеря корней. В этом случае проверка является элементом решения. Следует отметить, что часто легче сделать проверку, чем обосновать то, что в ней нет необходимости. Кроме того, проверка является средством контроля правильности проделанных вычислений. Иногда полезно поступать так: на каждом этапе решения уравнения определять промежутки, в которых могут находиться корни уравнения. Все корни, не принадлежащие этим промежуткам, являются посторонними и должны быть отброшены. Однако остальные корни всё равно необходимо проверить подстановкой в исходное уравнение.

Каждое алгебраическое уравнение всегда имеет хотя бы одно решение, действительное или комплексное.

В аналитической геометрии одно уравнение с двумя неизвестными интерпретируется при помощи кривой на плоскости, координаты всех точек которой удовлетворяют данному Уравнению. Одно Уравнение с тремя неизвестными интерпретируется при помощи поверхности в трёхмерном пространстве. При этой интерпретации решение системы Уравнение совпадает с задачей о разыскании точек пересечения линий, поверхностей и т.д. Уравнение с большим числом неизвестных интерпретируются при помощи многообразий в n-мерных пространствах.

Добро пожаловать!

Уравнения математической физики — дифференциальные уравнения с частными производными, а также некоторые родственные уравнения иных типов (интегральные, интегро-дифференциальные и т.д.), к которым приводит математический анализ физических явлений. Для теории Уравнения математической физики характерна постановка задач в таком виде, как это необходимо при исследовании физического явления. Круг Уравнения математической физики с расширением области применения математического анализа также неуклонно расширяется. При систематизации полученных результатов появляется необходимость включить в теорию Уравнения математической физики уравнения и задачи более общего вида, чем те, которые появляются при анализе конкретных явлений; однако и для таких уравнений и задач характерно то, что их свойства допускают более или менее наглядное физическое истолкование.

Уравнения химические — изображения реакций химических посредством знаков химических, формул химических, чисел и математических знаков. На возможность такого описания химических реакций указал в 1789 А. Лавуазье, основываясь на сохранения массы законе; однако всеобщее применение Уравнения химические получили только в 1-й половине 19 в.

 

АЛГЕБРАИЧЕСКОЕ УРАВНЕНИЕ — это… Что такое АЛГЕБРАИЧЕСКОЕ УРАВНЕНИЕ?

— уравнение вида где 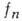— многочлен n -й степени от одного или нескольких переменных 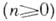. А. у. с одним неизвестным наз. уравнение вида:

Здесь п — целое неотрицательное число,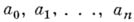 наз. коэффициентами уравнения и являются данными, хназ. неизвестным и является искомым. Коэффициенты А. у. (1) предполагаются не все равными нулю. Если то 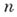наз. степенью уравнения.

Значения неизвестного х, к-рые удовлетворяют уравнению (1), т. е. при подстановке вместо хобращают уравнение в тождество, наз. корнями уравнения (1), а также корнями многочлена

f_n(x) = a₀xⁿ+ a₁x^n-1+…+a_n.(2)

Корни многочлена связаны с его коэффициентами по формулам Виета (см. Виета теорема). Решить уравнение — значит найти все его корни, лежащие в рассматриваемой области значений неизвестного.

Для приложений наиболее важен случай, когда коэффициенты и корни уравнения — числа той или иной природы (напр., рациональные, действительные или комплексные). Рассматривается также и случай, когда коэффициенты и корни — элементы произвольного поля. Если данное число (или элемент поля) с — корень многочлена f_n (х), то согласно Безу теореме f_n (х).делится на х- с без остатка. Деление можно выполнять по Горнера схеме.

Число (или элемент поля) с наз. k-к ратным корнем многочлена f(x)(k — натуральное число), если f(x).делится на ( х- с)^k, но не делится на (x-с)^k+1. Корни кратности 1 наз. простыми корнями многочлена.

Каждый многочлен f(x).степени n>0 с коэффициентами из поля Римеет в поле Рне более пкорней, считая каждый корень столько раз, какова его кратность (и, значит, не более празличных корней).

В алгебраически замкнутом поле каждый многочлен степени пимеет ровно пкорней (считая их кратность). В частности, это справедливо для поля комплексных чисел.

Уравнение (1) степени пс коэффициентами из поля Рназ. неприводимым над полем Р, если многочлен (2) неприводим над этим полем, т. е. не может быть представлен в виде произведения других многочленов над полем Р, степени к-рых меньше п. В противном случае многочлен и соответствующее уравнение наз. приводимыми. Многочлены нулевой степени и сам нуль не причисляются ни к приводимым, ни к неприводимым. Свойство данного многочлена быть приводимым или неприводимым над полем Рзависит от рассматриваемого поля. Так, многочлен х ²-2 неприводим над полем рациональных чисел, т. к. иначе он имел бы рациональные корни, но приводим над полем действительных чисел: х ² —2=(х+ Ц2)( х- Ц2) . Аналогично, многочлен х ² +1 неприводим над полем действительных чисел, но приводим над полем комплексных чисел. Вообще, над полем комплексных чисел неприводимы только многочлены 1-й степени, и всякий многочлен может быть разложен на линейные множители. Над полем действительных чисел неприводимы только многочлены 1-й степени и многочлены 2-й степени, не имеющие действительных корней (и всякий многочлен разлагается в произведение линейных и неприводимых квадратных многочленов). Над полем рациональных чисел существуют неприводимые многочлены любых степеней, таковы, напр., многочлены вида 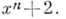Неприводимость многочлена над полем рациональных чисел устанавливается критерием Эйзенштейна: если для многочлена (2) степени 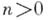с целыми коэффициентами существует простое число р такое, что старший коэффициент 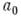не делится на р, все остальные коэффициенты делятся на 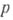, а свободный член 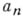не делится на 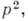то этот многочлен не-нриводим над полем рациональных чисел.

Пусть Р — произвольное поле. Для любого многочлена 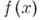степени 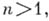неприводимого над полем Р, существует такое расширение поля Р, в к-ром содержится хотя бы один корень многочлена 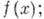более того, существует поле разложения многочлена 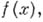т. е. расширение поля Р, в к-ром этот многочлен может быть разложен на линейные множители. Любое поле имеет алгебраически замкнутое расширение.

 

Разрешимость алгебраических уравнений в радикалах. Всякое А. у. степени, не превосходящей 4, решается в радикалах. Решение задач, приводящихся к частным видам уравнении 2-й и 3-й степеней, можно найти еще в древнем Вавилоне (2000 лет до н. э.) (см. Квадратное уравнение, Кубическое уравнение). Первое изложение теории решения квадратных уравнений дано в книге Диофанта «Арифметика» (3 в. н. э.). Решение в радикалах уравнений 3-Й л 4-Й степенен с буквенными коэффициентами было получено итальянскими математиками в 16 в. (см. Кардано формула, Феррари метод). В течение почти 300 лет после этого делались безуспешные попытки решить в радикалах уравнение с буквенными коэффициентами 5-й и более высоких степеней. Наконец, в 1826 Н. Абель (N. Abel) доказал, что такое решение невозможно.

Современная формулировка теоремы Абеля: пусть (1) Ч уравнение степени 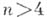с буквенными коэффициентами Ч любое поле и РЧ поле рациональных функций от с коэффициентами из К; тогда корни уравнения (1) (лежащие в нек-ром расширении поля Р) нельзя выразить через коэффициенты этого уравнения при помощи конечного числа действий сложения, вычитания, умножения, деления (имеющих смысл в поле Р) и знаков корня (имеющих смысл в расширении поля Р). Иными словами, общее уравнение степени n>4 неразрешимо в радикалах (см. [3], с. 226).

Теорема Абеля не исключает, однако, того, что каждое А. у. с данными числовыми коэффициентами (или коэффициентами из данного поля) решается в радикалах. Уравнения любой степени пнек-рых частных видов решаются в радикалах (напр., двучленные уравнения). Полное решение вопроса о том, при каких условиях А. у. разрешимо в радикалах, было получено ок. 1830 Э. Галуа (Е. Galois).

Основная теорема Галуа теории о разрешимости А. у. в радикалах формулируется следующим образом: пусть 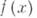Ч многочлен с коэффициентами из поля K, неприводимый над K; тогда: 1) если хотя бы один корень уравнения выражается в радикалах через коэффициенты этого уравнения, причем показатели радикалов не делятся на характеристику ноля K, то группа Галуа этого уравнения над полем Кразрешима; 2) обратно, если группа Галуа уравнения f(x) = Q над полем Кразрешима, причем характеристика поля K или равна нулю, или больше всех порядков композиционных факторов этой группы, то все корни уравнения представляются в радикалах через его коэффициенты, причем все показатели встречающихся радикалов 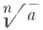Ч простые числа, а соответствующие этим радикалам двучленные уравнения неприводимы над полями, к к-рым эти радикалы присоединяются.

Э. Галуа доказал эту теорему для случая, когда К Ч поле рациональных чисел; при этом все условия на характеристику поля K, содержащиеся в формулировке теоремы, становятся ненужными.

Теорема Абеля является следствием теоремы Галуа, так как группа Галуа уравнения степени пс буквенными коэффициентами над полем Ррациональных функции от коэффициентов уравнения с коэффициентами из любого поля КЧ симметрич. группа 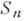и при 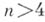неразрешима. Для любого существуют уравнения степени пс рациональными (и даже целыми) коэффициентами, неразрешимые в радикалах. Примером такого уравнения для 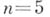может служить уравнение 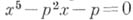, где рЧ простое число. В теории Галуа применяется метод сведения решения данного А. у. к цепочке более простых уравнений, наз. резольвентами данного уравнения.

Разрешимость уравнений в радикалах тесно связана с вопросом о геометрич. построениях с помощью циркуля и линейки, в частности задача о делении окружности на n равных частей (см. Деления круга многочлен, Первообразный корень).

Алгебраические уравнения с одним неизвестным с числовыми коэффициентами. Для отыскания корней А. у. с коэффициентами из поля действительных или комплексных чисел степени выше 2-й, как правило, используются методы приближенных вычислений (напр., Парабол метод). При этом удобно сначала освободиться от кратных корней. Число с является k-кратным корнем многочлена 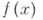тогда и только тогда, когда многочлен и его производные до порядка kЧ1 включительно обращаются в нуль при 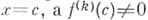. Если разделить 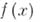на наибольший общий делитель 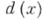этого многочлена и его производной, то получится многочлен, имеющий те же корни, что и многочлен 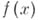, но только первой кратности. Можно даже построить многочлены, имеющие в качестве простых корней все корни многочлена 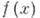одинаковой кратности. Многочлен имеет кратные корни тогда и только тогда, когда его дискриминант равен нулю.

Часто возникают задачи определения границ и числа корней. За верхнюю границу модулей всех корней (как действительных, так и комплексных) А. у. (1) с любыми комплексными коэффициентами можно взять число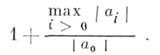

В случае действительных коэффициентов более точную границу обычно дает Ньютона метод. К определению верхней границы положительных корней сводится определение нижней границы положительных, а также верхней и нижней границ отрицательных корней.

Для определения числа действительных корней проще всего применить Декарта теорему. Если известно, что все корни данного многочлена действительны (как, напр., для характеристич. многочлена действительной симметрич. матрицы), то теорема Декарта дает точное число корней. Рассматривая многочлен 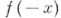, можно с помощью этой же теоремы найти число отрицательных корней 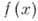. Точное число действительных корней, лежащих на данном интервале (в частности, число всех действительных корней) многочлена с действительными коэффициентами, не имеющего кратных корней, можно найти по Штурма правилу. Теорема Декарта является частным случаем Бюдана Ч Фурье теоремы, дающей оценку сверху числа действительных корней многочлена с действительными коэффициентами, заключенных в нек-ром фиксированном интервале.

Иногда интересуются разысканием корней специального вида, так, напр., критерий Гурвица дает необходимое и достаточное условие для того, чтобы все корни уравнения (с комплексными коэффициентами) имели отрицательные действительные части (см. Рауса Ч Гурвица критерий).

Для многочлена с рациональными коэффициентами существует метод вычисления всех его рациональных корней. Многочлен 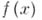с рациональными коэффициентами имеет те же корни, что и многочлен 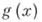с целыми коэффициентами, получающийся из 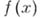умножением на общее кратное всех знаменателей коэффициентов 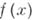Рациональными корнями многочлена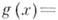 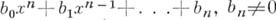с целыми коэффициентами могут быть только те несократимые дроби вида 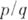, у к-рых рЧ делитель числ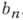а , а 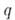Ч делитель числа (и даже только те из этих дробей, для к-рых при любом целом число 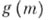делится на ).

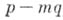Если 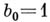, то все рациональные корни многочлена 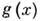(если они у него вообще есть) Ч целые числа, являющиеся делителями свободного члена, и могут быть найдены перебором.

Системы алгебраических уравнений. О системах А. у. 1-й степени см. Линейное уравнение.

Систему двух А. у. любых степеней с двумя неизвестными х и у можно записать в виде:

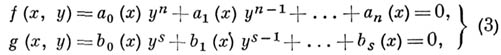
где 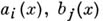Ч многочлены от одного неизвестного х.

Если хпридать нек-рое числовое значение, получится система двух уравнений от одного неизвестного ус постоянными коэффициентами 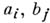. Результантом этой системы будет следующий определитель:

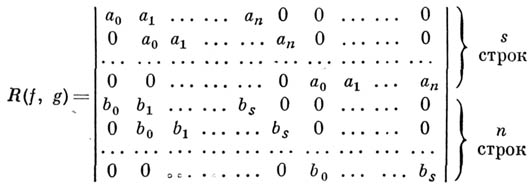
Справедливо утверждение: число 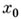тогда и только тогда является корнем результанта 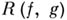, когда или многочлены 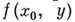и 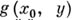имеют общий корень 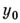, или оба старших коэффициента 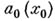и 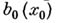равны нулю.

Таким образом, для решения системы (3) надо найти все корни результанта 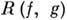, подставить каждый из этих корней в систему (3) и найти общие корни этих двух уравнений с одним неизвестным у. Кроме того, надо найти общие корни двух многочленов 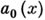и 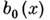и также подставить их в систему (3) и проверить, не имеют ли полученные уравнения с одним неизвестным уобщих корней. Иными словами, решение системы двух А. у. с двумя неизвестными сводится к решению одного уравнения с одним неизвестным и вычислению общих корней двух уравнений с одним неизвестным (общие корни двух или нескольких многочленов с одним неизвестным являются корнями их наибольшего общего делителя).

Аналогично рассмотренному случаю решается система любого числа А. у. с любым числом неизвестных. Эта задача приводит к громоздким вычислениям. Она связана с так наз. исключения теорией.

Лит.:[1] Курош А. Г., Курс высшей алгебры, 10 изд., М., 1971; [2] Сушкевич А. К., Основы высшей алгебры, 4 изд., М. алгебра, пер. с нем., ч. 1Ч2, 2 изд., М.

И. В. Проскуряков.

Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.