График линейного уравнения с двумя переменными: алгоритм построения
Линейное уравнение с двумя переменными — любое уравнение, которое имеет следующий вид: a*x + b*y =с. Здесь x и y есть две переменные, a,b,c – некоторые числа.
Решением линейного уравнения a*x + b*y = с , называется любая пара чисел (x,y) которая удовлетворяет этому уравнению, то есть обращает уравнение с переменными x и y в верное числовое равенство. Линейное уравнение имеет бесконечное множество решений.
Если каждую пару чисел, которые являются решением линейного уравнения с двумя переменными, изобразить на координатной плоскости в виде точек, то все эти точки образуют график линейного уравнения с двумя переменными. Координатами точками будут служить наши значения x и у. При этом значение х будет являться абсциссой, а значение у – ординатой.
График линейного уравнения с двумя переменными
Графиком линейного уравнения с двумя переменными называется множество всевозможных точек координатной плоскости, координаты которых будут являться решениями этого линейного уравнения. Несложно догадаться, что график будет представлять собой прямую линию. Поэтому такие уравнения и называются линейными.
Алгоритм построения
Алгоритм построения графика линейного уравнения с двумя переменным.
1. Начертить координатные оси, подписать их и отметить единичный масштаб.
2. В линейном уравнении положить х = 0, и решить полученное уравнение относительно у. Отметить полученную точку на графике.
3. В линейном уравнении в качестве у взять число 0, и решить полученное уравнение относительно х. Отметить полученную точку на графике
4. При необходимости взять произвольное значение х, и решить полученное уравнение относительно у. Отметить полученную точку на графике.
5. Соединить полученные точки, продолжить график за них. Подписать получившуюся прямую.
Пример: Построить график уравнения 3*x – 2*y =6;
Положим х=0, тогда – 2*y =6; y= -3;
Положим y=0, тогда 3*x = 6; x=2;
Отмечаем полученные точки на графике, проводим через них прямую и подписываем её. Посмотрите на рисунок ниже, график должен получиться именно таким.
Нужна помощь в учебе?
Предыдущая тема: Линейное уравнение с двумя переменными: решение и свойства
Следующая тема:   Системы линейных уравнений с двумя переменными
Все неприличные комментарии будут удаляться.
Графики уравнений. Видеоурок. Алгебра 9 Класс
Тема: Системы уравнений
Урок: Графики уравнений
Мы рассматриваем рациональное уравнение вида 
и системы рациональных уравнений вида 
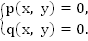
Мы говорили, что каждое уравнение в этой системе имеет свой график, если конечно имеются решения уравнений. Мы рассмотрели несколько графиков различных уравнений.
Сейчас мы систематически рассмотрим каждое из известных нам уравнений, т.е. выполним обзор по графикам уравнений.
1. Линейное уравнение с двумя переменными 
x, y – в первой степени; a,b,c – конкретные числа.
Пример: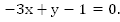
Графиком этого уравнения является прямая линия.
Мы действовали равносильными преобразованиями – y оставили на месте, всё остальное перенесли в другую сторону с противоположными знаками. Исходное и полученное уравнения равносильны, т.е. имеют одно и то же множество решений. График этого уравнения мы умеем строить, и методика его построения такова: находим точки пересечения с координатными осями и по ним строим прямую.
|
X |
0 |
|
|
Y |
1 |
0 |
В данном случае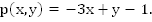 
Зная график уравнения, мы можем многое сказать о решениях исходного уравнения, а именно: если 
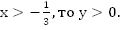
Эта функция возрастает, т.е. с увеличением x увеличивается y. Мы получили два частных решения, а как записать множество всех решений?
Если точка имеет абсциссу x, то ордината этой точки
Значит, решением исходного уравнения является множество пар чисел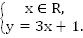 
У нас было уравнение, мы построили график, нашли решения. Множество всех пар – сколько их? Бесчисленное множество.
2. 
Это рациональное уравнение, 
Найдем y, равносильными преобразованиями получаем 
Положим 
и получаем квадратичную функцию, ее график нам известен.
Пример: 
Построить график рационального уравнения.
Графиком является парабола, ветви направлены вверх.
Найдем корни уравнения: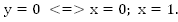
Схематически изобразим график (Рис. 2).
С помощью графика мы получаем всевозможные сведения и о функции, и о решениях рационального уравнения. Мы определили промежутки знакопостоянства, теперь найдем координаты вершины параболы.
У уравнения 
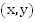, удовлетворяющих уравнению, но все 
А каким может быть x? Любым!Если мы зададим любое x, то получим точку 
Решением исходного уравнения является множество пар 
3. Построить график уравнения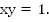 
Необходимо выразить y. Рассмотрим два варианта.
Графиком функции является гипербола, функция не определена при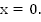 
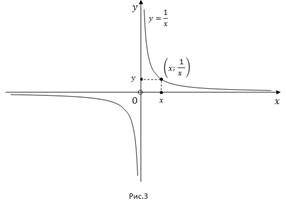
Функция 
убывающая.
Если 
Если мы возьмем точку с абсциссой 
, то ее ордината будет равна 
Решением исходного уравнения является множество пар 
Построенную гиперболу можно сдвигать относительно осей координат.
Например, график функции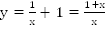 
– тоже гипербола – будет сдвинут на единицу вверх по оси ординат.
4. Уравнение окружности 
Это рациональное уравнение с двумя переменными. Множеством решений являются точки окружности. Центр в точке 
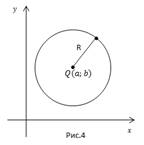
Рассмотрим конкретные примеры.
a.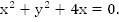 
Приведем уравнение к стандартному виду уравнения окружности, для этого выделим полный квадрат суммы:
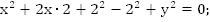
– получили уравнение окружности с центром в 
.
Построим график уравнения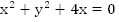 
(Рис. 5).
b. Построить график уравнения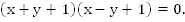 
Вспомним, что произведение равно нулю тогда и только тогда, когда один из сомножителей равен нулю, а второй существует.
График заданного уравнения состоит из совокупности графиков первого и второго уравнений, т.е. двух прямых.
Построим его (Рис. 6).
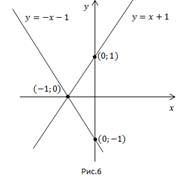
Построим график функции 
Прямая будет проходить через точку (0; -1). Но как она пройдет – будет возрастать или убывать? Определить это нам поможет угловой коэффициент, коэффициент при x, он отрицательный, значит функция убывает. Найдем точку пересечения с осью ox, это точка (-1; 0).
Аналогично строим график второго уравнения. Прямая проходит через точку (0; 1), но возрастает, т.к. угловой коэффициент положителен.
Координаты всех точек двух построенных прямых и являются решением уравнения.
Итак, мы проанализировали графики важнейших рациональных уравнений, они будут использоваться и в графическом методе и в иллюстрации других методов решения систем уравнений.
Список рекомендованной литературы
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
Рекомендованные ссылки на интернет-ресурсы
1. Раздел College.ru по математике (Источник).
2. Интернет-проект «Задачи» (Источник).
3. Образовательный портал «РЕШУ ЕГЭ» (Источник).
Рекомендованное домашнее задание
1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 95-102.
Методическая разработка по алгебре (7 класс) по теме: Методическая разработка для урока алгебры в 7 классе по теме «Построение графика линейного уравнения с двумя переменными»
Методическая разработка
для урока алгебры в 7 классе
по теме «Построение графика линейного уравнения с двумя переменными»
Федотова Е.А., учитель математики
Задание: постройте график линейного уравнения с двумя переменными: 3х-у=7
Алгоритм построения:
1. Выражаем «у» В уравнении у=-7+3х коэффициенты отличны от нуля, поэтому его графиком является прямая. | – у = 7-3х у=-7+3х |
2. Находим координаты двух точек, для удобства строим таблицу. Значения «х» берем произвольно, значение «у» вычисляем по формуле у=-7+3х. | у = -7+30= -7 у = -7+32= -1 ( 0; -7 ), ( 2; -1 ) – пара точек |
3. Отмечаем точки на координатной плоскости | |
4. Проводим через отмеченные точки прямую (тоненьким карандашом!) Эта прямая- график уравнения 3х-у=7 |
Задание 2: постройте график функции с двумя переменными: а) 5х-у=25 б) х-у=1 в) 5х-у=25 г) 7х-7у=14
Презентация к уроку алгебры (7 класс) по теме: Презентация урока по алгебре в 7 классе. «График линейного уравнения с двумя переменными»
Слайд 1
График линейного уравнения с двумя переменнымиСлайд 2
Цель урока: ввести понятие графика уравнения с двумя переменными; повторить построение графика линейной функции по двум точкам; закрепить навыки нахождения одной переменной через другую.
Слайд 3
Устные упражнения а) 3х – у = 14 б) 5у + х² = 16 в) 7ху – 5у = 12 г) 5х + 2у = 16 Ответ: 3х – у = 14 5х + 2у = 16
Слайд 4
Выбрать точку, которая принадлежит графику уравнения 2х + 5у = 12 А(-1; -2), В(2; 1), С(4; -4), D (11; -2). D (11; -2).
Слайд 5
x 8 6 4 2 -2 е ж з и к л м а б в г д у ф х ц ч ш щ й э ю я п р с н о т й (6;4) (-2;-2) (4;4) (-2;-2) (4;6) (-6;4) (0;2) М О Л О Д Е Ц y -8 -6 -4 -2 0 2 4 6 8
Слайд 6
Построение графика функции y= 3 x. Х у Х у Х у — независимая переменная (придумываем) — зависимая переменная (считаем) 0 2 0 6 х у -4 0 2 4 6 8 6 4 2 -2 -4 Построение графика функции y= -2 x. Построение графика функции y= -2 x +3 . 0 2 0 -4 0 2 3 -1
Слайд 7
Каждая пара чисел, являющаяся решением уравнения с переменными х и у, изображается в координатной плоскости точкой, координатами которой служит пара чисел. Все эти точки образуют график уравнения.
Слайд 8
Выясним, что представляет собой график уравнения 3х+2у=6 Выразим переменную у через х у=-1,5х+3 Формулой у=-1,5х+3 задается линейная функция, графиком которой служит прямая. Уравнения 3х+2у=6 и у=-1,5х+3 равносильны, то эта прямая является и графиком уравнения 3х+2у=6
Слайд 9
Построим график функции y= -1,5 x +3 . Х 0 2 у 3 0 х у 3 2 1 -1 -2 Пары точек (0;3) и (2;0) Являются решением данного уравнения 3х+2у=6
Слайд 10
Графиком уравнения с двумя переменными называется множество всех точек координатной плоскости, координаты которых являются решениями этого уравнения
Слайд 11
Если в линейном уравнении коэффициент при х равен нулю, то графиком такого уравнения является прямая y=kx + b – линейная функция . y= 0 x + b , тогда y=b Прямые параллельны оси х х у 6 4 2 -2 -4 у=6 у=4 у=-4
Слайд 12
Если в линейном уравнении коэффициент при у равен нулю, то графиком такого уравнения является прямая y=kx + b – линейная функция . 0 y + kx =b , тогда х =b / k Прямые параллельны оси у у 6 4 2 -2 -4 х=-4 х=4 х=2
Слайд 13
Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.
Слайд 14
Уравнение ax+by=c , в котором оба коэффициента при переменных равны нулю, имеет вид 0 x+ 0 y=c . При с=0 любая пара чисел является решением этого уравнения, а его графиком -вся координатная плоскость. При с ≠0 уравнение не имеет решений и его график не содержит ни одной точки
Слайд 15
Физкультминутка Упражнение 1 «Глядя в небо» Цель этого упражнения — устранение вредных эффектов от неподвижного сидения в течение длительного периода времени и профилактика грыжи межпозвоночных дисков поясничного отдела. Поза: стоя В положении стоя положите руки на бедра. Медленно отклоняйтесь назад, глядя на небо или в потолок. Вернитесь в исходное положение. Повторите 10 раз .
Слайд 16
№ 1048(Б)
Слайд 18
е
Слайд 20
Самостоятельная работа 1 вариант 1. Какие из пар чисел (1;1), (6;5), (9;11) являются решением уравнения 5х – 4у — 1 =0? 2. Постройте график функции 2х + у = 4. 2 вариант 1. Какие из пар чисел (1;1), (1;2), (3;7) являются решением уравнения 7х – 3у — 1 =0? 2. Постройте график функции 5х + у – 4 = 0.
Слайд 21
Самостоятельная работа 1 вариант № 1 (1;1), (9;11) 2 вариант № 1 1. (1;2)
Слайд 22
Х У 2 0 1 в № 2 4
Слайд 23
Х У 1 0 2 в № 2 4
Слайд 24
У меня все отлично У меня все хорошо Возникли трудности
Слайд 25
П.41, №1045, 1048 (а, в,д)
График линейного уравнения с двумя переменными
Цели.
Образовательная:
1. Знать определение графика уравнения с двумя переменными;
2. Знать, что является графиком линейного уравнения с двумя переменными;
3. Уметь строить график линейного уравнения с двумя переменными.
Развивающая: учить анализировать, сравнивать, обобщать определять и объяснять понятия, т.е. умение мыслить.
Воспитательная: развивать нравственные отношения у школьников с окружающим миром (качество честности, трудолюбие).
Оборудование:
рабочая карта;
кроссворд;
карта-таблица;
карточки для дополнительного уровневого задания;
таблица “Уравнения с двумя переменными и их графики”;
таблица “Расположение графиков линейного уравнения с двумя переменными относительно осей координат”.
Ход урока
1. Запись домашней работы: (учитель проговаривает)
п.41, повторить п.п.15-16.
№1046, №1049, для желающих № 1152 — график с параметром.
2. Проверка домашнего задания. (До урока на перемене)
Выразить одну переменную через другую (а, б)
№1034(б), №1140 (а)
На доске “Проверь себя” (До урока на перемене учащиеся проверяют домашнее задание, сверяя с решением на доске.) – решение уравнений, критерии оценок.
(Выразить одну переменную через другую (а, б))
а) 6х — у = 12;
у = 6х — 12.
б) 10х + 7у = 0;
10х = -7у;
х = -0,7у.
№1034(б).
6х + 2у =7;
2у = 7 — 6х;
у = (7 — 6х) / 2;
у = 3,5 – 3х;
Точки: (0; 3,5), (1; 0,5), (2;-2,5).
№1140 (а).
ах – 2у = 1, х=5, у = 7, а = ?
5а — 14 = 1;
5а = 15;
а=3.
Критерий:
Все решено правильно и самостоятельно — “5”;
Все решено правильно, но с помощью — “4”;
Решено с помощью и с ошибкой — “3”.
№ 1140 — оценивается по тем же критериям, только “5” и “4”.
После записи домашней работы предлагаю выставить оценки согласно критериям каждому за свою домашнюю работу (самооценка) в рабочую карту (предварительно подписав карт). Рабочая карта отражена на рисунке 4.
3. Совместная постановка цели урока.
Читаем тему урока на доске.
— Ребята, как вы думаете, что должны знать и чему научиться на этом уроке?
[1. Знать определение графика уравнения с двумя переменными.]
[2. Что является графиком линейного уравнения с двумя переменными.]
[3. Уметь строить график линейного уравнения с двумя переменными.]
А что бы этого достичь, нужно анализировать, сравнивать, объяснять понятия. Работая в классе, необходимо с уважением относиться к окружающим и быть предельно честным.
Для успешной работы повторим теоретический материал, разгадывая кроссворд. Кроссворды находятся в каждой группе (на работу 3 минуты).
Рисунок 1. Кроссворд.
Вопросы к кроссворду:
1. Что является графиком линейной функции?
2. Один из способов задания функции.
3. Пара чисел, изображающаяся в координатной плоскости.
4. Независимая переменная.
5. Множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
6. Зависимость между переменными, при которой каждому значению независимой переменной соответствует единственной значение зависимой переменной.
7. Какими называются уравнения с двумя переменными имеющие одни и те же решения, или не имеющие решений?
Чья группа угадает быстрее, получает жетон. Всего дается три жетона, т.е. первым трем группам.
Для тех, кто закончил работу, на доске задание (устно):
1. Назвать коэффициенты в уравнениях;
2. Выразить у через х из уравнений:
3х – у = 2;
у = 3х — 2.
5х + 2у = 7;
у = 3,5 — 2,5х.
х + 2у = 4;
у = 2 — 0,5х.
2х – у = 11;
у = 2х — 11.
3. Как назвать эти равенства:
х2+у2=20;
ху=12;
|х|+ |у| = 10.
Внимание на доску, проверим кроссворд. (Ответы на кроссворд и критерий оценки работы на доске:)
1. Прямая.
2. Формула.
3. Точка.
4. Аргумент.
5. График.
6. Функция.
7. Равносильными.
Критерий: Быстро и правильно — два “+”, отметить на жетоне номер группы;
Правильно — один “+”.
— Поднимите руку, кто получил два “+”, один “+”. Кто не угадал, повторить определения.
Переходим к проверке (решению) устного упражнения:
1. Проговариваем коэффициенты;
2. Выражаем у через х из уравнений;
3. Называем эти равенства — уравнениями с двумя переменными.
— Что является решением уравнения с двумя переменными? (Пара значений переменных — х и у)
— Сколько решений имеет уравнение с двумя переменными? (Много)
— Как изображается пара значений переменных на координатной плоскости? (Точкой)
— Сколько таких точек можно изобразить? (Много)
— Что является координатами каждой из этих точек? (Абсцисса — значение х, ордината - значение у)
— Что образуют все эти точки на координатной плоскости? (График)
— Так что называется графиком уравнения с двумя переменными? (Множество всех точек координатной плоскости, координаты которых являются решениями этого уравнения)
— Откройте учебник, п.41 и найдите это определение. Прочитаем его. Повторим. А теперь посмотрите на доску. (На доске таблица уравнений с двумя переменными и их графики – рисунок 2).
Рисунок 2. Уравнения с двумя переменными и их графики.
— Что вы видите на таблице? (Уравнения с двумя переменными и их графики).
— Есть ли среди них линейные уравнения с двумя переменными? (Нет)
— Графики этих уравнение вы будите изучать в старших классах. А мы с вами должны узнать, что является графиком линейного уравнения с двумя переменными.
4. Изучение нового материала.
— Открыли тетради, записали тему урока. Дайте определение линейной функции и запишем:
у = kх + b,
где х и у — переменные, k, b - некоторые числа.
— Дайте определение линейного уравнения с двумя переменными и запишем:
ах + bу = с,
где х и у — переменные, а, b, с - некоторые числа.
— Сравните, что общего в этих видах математической записи (входят две переменные х и у, числа).
— Как по-другому называются числа? (Коэффициенты).
— Чем отличаются? (Количеством чисел 2 и 3; в первом — выражена зависимость — функция, во втором — не выражена — уравнение).
— А можно ли в линейном уравнении с двумя переменными выразить зависимость одной переменной от другой? (Да).
— Давайте выразим зависимость переменной у от переменной х в линейном уравнении с двумя переменными:
ах+by = с,
где х и у — переменные, а, b, с - некоторые числа.
— Выражаем в общем виде: bу = с — ах.
— Что сейчас мы должны обязательно оговорить? (Что коэффициент при переменной у не равен нулю):
у = (с – ах) / b, при условии b 0.
у = (с / b) – (а / b)х.
— Запишем в стандартном виде:
у = – (а / b)х + (с / b).
— Таким образом, мы получили вид линейной функции у = kx + b, только по-другому записаны числа.
— Что является графиком линейной функции? (Прямая).
— Что необходимо, что бы построить прямую? (Построить две точки).
— А почему две точки? (Согласно аксиоме).
— Так что же является графиком линейного уравнения с двумя переменными, если коэффициент при у не равен нулю (т.е. b 0)? (Прямая).
— Что является координатами каждой из точек? (Пара значений переменных х и у, которые являются решением данного уравнения).
— Запишем уравнение 2х — у = 3. Коэффициент при переменной у не равен нулю. Запишите одно решение (спрашиваю троих и записываю три решения).
— Как проверить, что каждая пара значений переменных х и у, является решением этого уравнения? (Подставить в уравнение вместо переменных х и у их значения. Если равенство верное, значит, пара чисел является решением).
— Как нашли это решение? (Х — произвольное значение, у — находим).
— Какую фигуру будет изображать пара чисел, являющаяся решением линейного уравнения на координатной плоскости? (Точку).
— Сколько пар решений нужно, чтобы построить график? (Две пары).
— Мы рассмотрели с вами общий случай построения графика линейного уравнения с двумя переменными. Кроме общего случая существуют частные случаи построения графиков, когда хотя бы один из коэффициентов равен нулю.
Постановка проблемного вопроса.
— А что же является графиком линейного уравнения с двумя переменными, если хотя бы один из коэффициентов равен нулю?
— Для ответа на этот вопрос предлагается работа по группам. Возьмите карты-таблицы “Что является графиком уравнения ax + by = с, если хотя бы один из коэффициентов равен нулю?”. Подпишите их. Карта-таблица представлена на рисунке 3.
— Смотрим таблицу. В первом столбце записаны уравнения. Второй столбец вы должны заполнить, записывая коэффициенты линейных уравнений. Потом записываете пары решений для каждого из уравнений. Затем в соответствии с координатной плоскостью строите графики. И в последнем столбце записываете, что является графиком. Таблица заполняется по строкам. (При этой работе вызываю по одному ученику для заполнения карты-таблицы на доске после некоторого времени, когда большинство заполнят).
— Если группа заканчивает работу раньше других, то на доске задание, которое выполняется устно.
По окончании работы заслушиваю двух человек. Обобщаем, что же является графиком линейного уравнения, если хотя бы один из коэффициентов равен нулю? (Прямая).
Рисунок 3. Карта-таблица “Что является графиком уравнения ax + by = с, если хотя бы один из коэффициентов равен нулю?”.
Внимание на доску! (На доске таблица с графиками линейных уравнений).
— Какого случая у нас нет? (а 0, b 0, с = 0). Что является графиком? (Прямая пропорциональность).
— А теперь найдите в тексте учебника п.41 определение графика линейного уравнения с двумя переменными и зачитайте его.
— Повторим, что является графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов не равен нулю? (Прямая).
— А можно ли по виду линейного уравнения с двумя переменными определить, что является графиком данного уравнения? (Можно).
На доске записаны линейные уравнения с двумя переменными:
1) 4х — 3у = 5;
2) -7х = 14;
3) 0х + 0у = 0;
4) 0х = — 6;
5) 2у — 6 = 0;
6) 0у = 10.
— Назвать уравнения, графиком которых является прямая, плоскость, нет графика. (Прямая — 1, 2, 5; плоскость — 3; нет графика — 4, 6).
— И еще раз, что же является графиком линейного уравнения с двумя переменными, если хотя бы один из коэффициентов отличен от нуля.
— А сейчас за работу с картой-таблицей консультант проставит каждому оценки в рабочую карту. Критерий оценки — как для домашнего задания. Поднимите руку, кто справился на “5”, кто на “4”.
5. Закрепление материала.
— Самостоятельная работа на доске (проверка у консультанта, консультант проверяет у группы).
Постройте график уравнения:
а) 2х — у = 6;
б) х + 6у = 0;
в) 1,2х = — 4,8;
г) 1,5у = 6.
Критерий оценки (на доске):
правильно решены все — “5”;
правильно решены 4-5 — “4”;
правильно решены 3 — “3”.
— Поднимите руку, кто справился на “5”, кто на “4”, кто на “3”.
Тому, кто закончит раньше, даются уровневые карточки.
6. Рефлексия.
На рабочей карте (рисунок 4) имеются незаконченные предложения. Пожалуйста, закончите их.
На уроке мне было легко при…
На уроке я испытывал(а) трудности при…
Рисунок 4. Рабочая карта.
Рабочие карты сдать консультанту для итоговой оценки. Консультанты сдадут мне.
Урок окончен! До свидания!
План-конспект урока по алгебре (7 класс) на тему: график линейного уравнения с двумя переменными
График линейного уравнения с двумя переменными» 7 класс
Цель урока: познакомить учащихся с понятием графика линейного уравнения с двумя переменными; научить построению графиков линейного уравнения с двумя переменными;
Тип урока: урок усвоения новых знаний.
Ход урока:
I. Организационный момент
2.Фронтальная проверка д/з.
а) проверка по тетрадям ответов к упражнениям;
б) работа учащегося у доски.
Задание: Выразить из уравнения у через х: х+5у=15; найти пару чисел, являющихся решением уравнения.
3. Актуализация знаний, игра «Микрофон».
-Дайте определение линейного уравнения с двумя переменными?
Ответ. Линейным уравнением с двумя переменными называется уравнения вида ах+ву =с, где х и у – переменные, а, в и с — некоторые числа.
-Какие уравнения являются линейными с двумя переменными?
1) 2х- 3у=5; 2) х+ у = -3; 3) 2х – х у=4; 4) у-1/2х =2.
— Что называется решением линейного уравнения с двумя
переменными?
Ответ. Решением линейного уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.
-Что представляет пара чисел, являющаяся решением уравнения с двумя переменными в системе координат?
Ответ. Точку с координатами х и у.
Молодцы! А теперь продолжим дальше.
3. Объяснение темы урока.
Таких пар чисел линейного уравнения с двумя переменными- множество, и все вместе они образуют график уравнения.
Формулируется определение понятия графика уравнения с двумя переменными.
Графиком уравнения с двумя переменными называется множество точек координатной плоскости, координаты которых являются решением этого уравнения.
Б) Что является графиком данного уравнения: 3х+2у=6?
1. выразим у через х:
2у=6-3х /:2
у= 3 – 1,5х.
-Ребята ,что напоминает вам это уравнение?
У: Задание линейной функции.
-Что является графиком линейной функции, давайте вспомним?
У: Графиком линейной функции является прямая, для построения которой достаточно задать две точки.
— Уравнения 3х+2у=6 и у=3-1,5х –равносильны, поэтому графиком уравнения 3х+2у=6 является прямая.
Вывод: Графиком любого линейного уравнения с переменными х и у, в котором коэффициент при у отличен от нуля, является прямая.
-Если коэффициент при у=0, то графиком будет являться прямая, параллельная оси у. Если оба коэффициента будут равны нулю, то графиком уравнения будет являться вся координатная плоскость.
-Теперь построим в тетрадях график уравнения: 3х-4у=12.
Алгоритм для построения графика линейного уравнения с двумя переменными:
1: Выразить переменную у через переменную х.
2: Найти несколько решений равносильного уравнения (необходимо всего 2 решения).
4: Отметить найденные 2 решения на координатной плоскости.
5: Провести прямую через эти две точки.
4.Закрепление изученного.
Решить №1045, № 1048 а) б).
№ 1049 а) -выполняет 1 вариант, №1049 б) -выполняет 2 вариант.
5.Итог урока. Рефлексия.
6.домашнее задание: п.41, №1046, 1048 в) г).
Конспект урока на тему «Линейное уравнение с двумя переменными и его график»
Линейное уравнение с двумя переменными и его график
Тип урока: Урок изучения нового знания Класс: 7
Содержательная цель: сформировать понятие «график линейного уравнения с двумя переменными»; научить учащихся правильному построению графиков линейных уравнений с двумя переменными.
Деятельностная цель: введение понятия линейного уравнения как математической модели реальной ситуации; формирование умения по виду определять линейное уравнение и его коэффициенты; формирование умения по заданному значению х находить соответствующее значение у, и наоборот; введение алгоритма построения графика линейного уравнения и применение его на практике; составление линейного уравнения, как математической модели задачи.
Предметные: знает содержание понятия «линейное уравнение с двумя переменными», алгоритм нахождения корней линейного уравнения с двумя переменными, приемы составления математической модели реальной ситуации в виде линейного уравнения с двумя переменными, графический и алгебраический способы нахождения точек пересечения двух прямых; умеет решать задачи по алгоритму, создавать алгоритмы деятельности, переводить информацию из одной знаковой ситуации в другую.
Личностные: формирование познавательного интереса к предмету исследования, формирование устойчивой мотивации к изучению и закреплению материала.
Метапредметные:
а) Регулятивные: ставит учебную задачу на основе того, что уже известно и усвоено, и что подлежит усвоению, осознает качество и уровень усвоения.
б) Познавательные: определяет основную и второстепенную информацию, выделяет и формулирует проблему, ориентируясь на разные способы решения задачи.
в) Коммуникативные: использует адекватные языковые средства для отображения своих мыслей и чувств, описывает содержание совершаемых действий с целью ориентировки предметно-практической деятельности, проявляет готовность к обсуждению разных точек зрения и выработке общей (групповой) позиции.
готовность к выполнению норм и требований учителя2.
Актуализация знаний (4-5 мин.)
Повторение, подготовка к изучению нового материала (фронтальная работа).
— Что такое координатная плоскость?
— Определение оси абцисс и ординат.
— Алгоритм построения точки М (а; b) в прямоугольной системе координат хОу
— Что значить решить уравнение?
Отвечают на вопросы учителя.
— Взаимно перпендикулярные координатные прямые с началом отсчета в точке их пересечения.
— Ось абсцисс – горизонтальная координатная прямая (или ось x). Ось ординат – вертикальная координатная прямая (или ось у)
— 1. Построить прямую x=a
2. Построить прямую y=b
3. Найти точку пересечения построенных прямых
— Решить уравнение – значит найти значения переменной, при которых уравнение обращается в верное числовое равенство.
Регулятивные: планировать пути достижения целей; преобразовывать практическую задачу в познавательную; самостоятельно анализировать условия достижения цели на основе ориентиров, выделенных учителем.
Познавательные: устанавливать причинно-следственные связи; строить логическое рассуждение, включающее установление причинно-следственных связей.
Коммуникативные: аргументировать свою точку зрения; владеть устной речью.
3.
Постановка учебной задачи. Мотивация деятельности (4-5 мин.)
— Решите уравнения:
5х=10;
1,5х-3=0;
64+4х=40;
3х+2у=12
— Какое уравнение вызвало затруднение? Почему?
— Итак, тема сегодняшнего урока: «Линейное уравнение с двумя переменными и его график». Вы узнаете, какое уравнение называется линейным уравнением с двумя переменными, что является решением такого уравнения, какие уравнения с двумя переменными называются равносильными, что называется графиком линейного уравнения.
Выходят к доске, решают уравнения.
Последнее уравнение вызывает затруднения, потому что появилась еще одна переменная.
Записывают в тетрадь тему урока.
Личностные: умение вести диалог на основе равноправных отношений и взаимного уважения и принятия.
Регулятивные: преобразовывать практическую задачу в познавательную
Познавательные: проводить наблюдение; строить логическое рассуждение, включающее установление причинно-следственных связей; Коммуникативные: аргументировать свою точку зрения; владеть устной речью.
4.
«Открытие» нового знания (построение проекта выхода из затруднения) (7-8 мин.)
Рассмотрим такую реальную ситуацию. (слайд 3)
Из городов A и B, расстояние между которыми 500 км, навстречу друг другу вышли два поезда, каждый со своей постоянной скоростью. Известно, что первый поезд вышел на 2 ч раньше второго. Через 3 ч после выхода второго поезда они встретились. Чему равны скорости поездов?
Составим математическую модель задачи. Пусть x км/ч — скорость первого поезда, y км/ч — скорость второго поезда. Первый был в пути 5 ч и, значит, прошел путь 5x км. Второй поезд был в пути 3 ч, т.е. прошел путь Зy км. Их встреча произошла в пункте C. На алгебраическом языке ситуацию можно описать так: 5x +3y=500. Эту математическую модель называют линейным уравнением с двумя переменными x, y.
Уравнение вида ax+by+c=0,
где a, b, c — числа, причем a ≠ 0, b ≠ 0, — линейное уравнение с двумя переменными x и y (или с двумя неизвестными x и y).
Вернемся к уравнению 5x + 3y = 500. Замечаем, что если x = 40, y = 100, то 5 • 40 + 3 • 100 = 500 — верное равенство. Значит, ответ на вопрос задачи может быть таким: скорость первого поезда 40 км/ч, скорость второго поезда 100 км/ч. Пару чисел x = 40, y = 100 называют решением уравнения 5x + 3y = 500.
Учитель ставит вопрос о единственности решения линейного уравнения. Для этого предлагается проверить, является ли решениями этого уравнения пары чисел: (64;60), (70;50), (45;80), (80;60).
— Какой вывод можно сделать?
Если на координатной прямой отметить пары чисел, являющиеся решением линейного уравнения, и соединить их, то получится прямая.
Теорема 1. Графиком любого линейного уравнения ax + by + c = 0 является прямая.
Сколько точек необходимо, чтобы провести прямую? Какой вывод можно из этого сделать?
Рисуют чертеж в тетрадях.
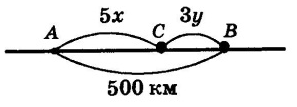
Записывают определение в тетрадь.
Выходят к доске, проверяют, являются ли пары чисел решением уравнения.
Приходят к выводу, что линейное уравнение с двумя переменными имеет бесконечное число решений.
Записывают в тетрадь.
Из курса геометрии знают, что необходимо две точки.
Чтобы нарисовать график линейного уравнения с двумя переменными, нужно найти две пары его решения.
Личностные: готовность и способность к выполнению норм и обязанностей ученика; устойчивый познавательный интерес и становление смыслообразующей функции познавательного мотива. Регулятивные: осуществлять целеполагание, преобразовывать практическую задачу в познавательную; Познавательные: строить логическое рассуждение, включающее установление причинно-следственных связей; создавать модели и схемы для решения задачи; осуществлять логическую операцию перехода от видовых признаков к родовому понятию.
Коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве с одноклассниками; аргументировать свою точку зрения; владеть устной речью.
5.
Первичное закрепление (4-5 мин.)
Класс получает задание:
Построить график уравнения
3x — 2y +6=0.
— Расскажите, как вы это делали.
Решение данного уравнения вы подбирали, угадывали. Угадать что-либо всегда труднее, чем действовать по определенному правилу. Как вы думаете, можно ли применить какое-то правило здесь?
Например, можно дать переменной x конкретное значение, например x = 0 (обычно пишут х1 = 0). Подставив это значение в уравнение 3x — 2у + 6 = 0,
получим: 3 • 0 — 2y + 6 = 0, т.е. -2y + 6 = 0. Из этого уравнения находим: y = 3 (обычно пишут у1 = 3). Значит, если x = 0, то y = 3; пара (0; 3) — решение данного уравнения. Дадим переменной x еще одно конкретное значение, например x = -2 (обычно пишут x2 = -2). Подставив это значение в уравнение 3x — 2y + 6 = 0, получим: 3 • (-2) — 2y + 6 = 0, т. е. — 2y = 0. Из этого уравнения находим y = 0 (обычно пишут y2 = 0). Значит, если x = -2, то y = 0; пара (- 2; 0) — решение данного уравнения.
Давайте запишем алгоритм построения графика ax + by + c = 0.
1. Придать переменной x конкретное значение х = x1; найти из уравнения
ax1 + by + c = 0 соответствующее значение y = y1.
2. Придать переменной x другое значение x = x2 найти из уравнения
ax2 + by + c = 0 соответствующее значение y: y = y2.
3. Построить на координатной плоскости xOy две точки (x1; y1) и (x2; y2).
4. Провести через эти две точки прямую — она и будет графиком уравнения
ax + by + c = 0.
Класс выполняет задание в тетради.
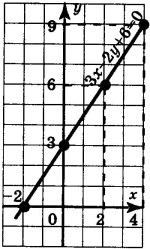
Отвечают, что подбирали наугад пары чисел решения уравнения, отмечали их на графике и соединяли.
Записывают в тетрадь.
Личностные: готовность и способность к выполнению норм и обязанностей ученика; умение вести диалог на основе равноправных отношений и взаимного уважения и принятия; устойчивый познавательный интерес и становление смыслообразующей функции познавательного мотива. Регулятивные: осуществлять целеполагание, преобразовывать практическую задачу в познавательную; самостоятельно анализировать условия достижения цели на основе ориентиров, выделенных учителем; самостоятельно оценивать правильность 5 выполнения действий и вносить необходимые коррективы. Познавательные: строить логическое рассуждение, включающее установление причинно-следственных связей; создавать модели и схемы для решения задачи; осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Коммуникативные: формулировать собственное мнение и аргументировать свою точку зрения; сравнивать разные точки зрения, прежде чем принимать решения и делать выбор; владеть устной речью.
6.
Самостоятельная работа с проверкой по эталону. Самоанализ и самоконтроль (4-5 мин.)
По алгоритму постройте график уравнения 4x+3y-12=0
Каждый учащийся самостоятельно в тетради выполняет построение графиков, после чего кто-то выходит к доске и показывает решение, учитель поправляет.
Личностные: готовность и способность к выполнению норм и обязанностей ученика; устойчивый познавательный интерес и становление смыслообразующей функции познавательного мотива.
Познавательные: строить логическое рассуждение, включающее установление причинно-следственных связей. Коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве с одноклассниками; аргументировать свою точку зрения; владеть устной речью.
7.
Рефлексия деятельности. Итоги урока (7-8 мин.)
Ребята, наш урок подходит к концу. Давайте вспомним, что мы узнали сегодня. У кого есть вопросы по данной теме?
Ученики задают вопросы.
На уроке мы проделали следующую работу:
— познакомились с линейным уравнением с двумя переменными
— научились строить график линейного уравнения с двумя переменными
— учились строить графики функций, используя свойство периодичности
-составлять математическую модель реальной ситуации
Личностные: умение вести диалог на основе равноправных отношений и взаимного уважения и принятия.
Регулятивные: адекватно самостоятельно оценивать правильность выполнения действия и вносить необходимые коррективы в исполнение как в конце действия, так и по ходу его реализации; основам прогнозирования как предвидения будущих событий и развития процесса.
Коммуникативные: отображать в речи (описание, объяснение) содержание совершаемых действий как в форме громкой социализированной речи, так и в форме внутренней речи.
9.
Постановка домашнего задания (1-2 мин)
Личностные: готовность к выполнению норм и требований учителя