Чётность нуля — Википедия

Иллюстрация чётности нуля: 0 объектов поровну разделили между чашами весов, и они находятся в равновесии

Чётность нуля — вопрос, считать ли ноль чётным или нечётным числом. Ноль — чётное число. Однако чётность нуля вызывает сомнения в среде людей, недостаточно знакомых с математикой. Большинство людей задумываются дольше, прежде чем идентифицировать 0 как чётное число, по сравнению с идентификацией обычных чисел вроде 2, 4, 6 или 8. Некоторые студенты, изучающие математику, и даже некоторые преподаватели, ошибочно считают ноль нечётным числом, или чётным и нечётным одновременно, или не относят его ни к одной категории.

По определению, чётное число — такое целое число, которое делится на 2 без остатка. Ноль обладает всеми свойствами, которые присущи чётным числам, например, 0 с обеих сторон граничит с нечетными числами, каждое десятичное целое число имеет такую же чётность, как и последняя цифра этого числа, поэтому, поскольку 10 является чётным, то 0 также будет чётным. Если y{\displaystyle y} является четным числом, тогда y+x{\displaystyle y+x} имеет такую чётность, что имеет x{\displaystyle x}, а x{\displaystyle x} и 0+x{\displaystyle 0+x} всегда имеют одинаковую чётность.

Ноль также соответствует закономерностям, которые образуют другие чётные числа. Правила чётности в арифметике, такие как чётное−чётное=чётное, предполагают, что 0 также должно быть чётным числом. Ноль является аддитивным нейтральным элементом группы чётных чисел, и он является началом, с которого рекурсивно определены другие чётные натуральные числа. Применение такой рекурсии по теории графов к вычислительной геометрии полагается на то, что ноль является чётным. Ноль делится не только на 2, он делится на все степени двойки. В этом смысле, 0 является «наиболее чётным» числом из всех чисел.

Чтобы доказать, что ноль является чётным, можно непосредственно использовать стандартное определение «чётного числа». Число называют чётным, если это число кратно 2. Например, причиной того, что число 10 является чётным, является то, что оно равно 5 × 2. В то же время, ноль также является целым кратным 2, то есть 0 × 2, следовательно ноль является чётным

[1].

Кроме того, можно объяснить, почему ноль является чётным, не применяя формальных определений.

Простые объяснения[править | править код]

Слева изображены группы с 0, 2 и 4 белыми объектами по парам; справа с 1, 3 и 5 объектами, где объект без пары обозначен красным. Область с 0 объектами не содержит красных объектов^[2].

Ноль — это число, а числа используются для счёта. Если существует множество объектов, то числа используют, чтобы описать, сколько их. Ноль — это мера в случае, когда нет ни одного объекта

; в более формальном смысле, это количество объектов в пустом множестве. Используя понятие чётности, создадим группы по паре объектов. Если объекты множества можно разделить и маркировать по парам без остатка, тогда количество объектов чётное. Если существует объект, не вошедший в группы, тогда количество объектов является нечётным. Пустое множество содержит 0 пар объектов и не имеет никакого остатка от такой группировки, поэтому ноль является чётным^[3].

Все эти доводы можно проиллюстрировать, нарисовав объекты по парам. Трудно изобразить нулевые пары или показать отсутствие нечётного остатка, поэтому удобным будет нарисовать другие группы и сравнить их с нулём. Например, в группе из пяти объектов существуют две пары. Кроме того, в ней есть объект, который не относится ни к одной паре — поэтому число 5 является нечётным. В группе из четырёх объектов нет объектов, которые остались, только две пары, поэтому 4 является чётным. В группе только с одним объектом нет пар и есть один остаток, поэтому 1 является нечётным. В группе с нулём объектов нет пар и нет остатка, поэтому 0 является чётным

[4]^[5].

Числа можно изобразить с помощью точек на числовой оси. Если на ней нанести чётные и нечётные числа, их общая закономерность становится очевидной, особенно если добавить и отрицательные числа:

Чётные и нечётные числа чередуются между собой. Нет причины пропустить число ноль^[6].

С помощью операции умножения чётность можно определить более формальным образом, используя арифметические выражения. Для каждого целого числа будет актуальна одна из форм: (2 × N) + 0 или (2 × N) + 1. Первое выражение соответствует чётным числам, а второе нечётным. Например, 1 является нечётным, поскольку 1 = (2 × 0) + 1, а 0 будет чётным, так как 0 = (2 × 0) + 0. Если такие выражения записать в таблицу по порядку, снова получим закономерность как на числовой оси

[7].

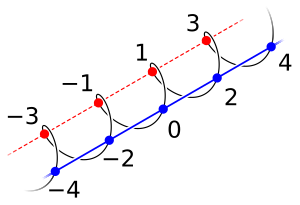Чётные (синие) — подмножество Z 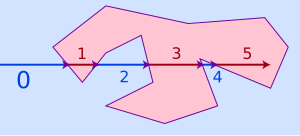Многоугольники с числами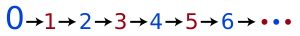

Численные результаты теории обращаются к основной теореме арифметики и алгебраическим свойствам чётных чисел, поэтому вышеупомянутая конвенция имеет далеко идущие последствия. Например, факт, что положительные числа имеют уникальную факторизацию, означает, что для отдельного числа можно определить, имеет ли оно чётное или нечётное количество различных простых множителей. Поскольку 1 не является простым числом, а также не имеет простых множителей, оно является пустым произведением простых чисел; поскольку 0 — чётное число, 1 имеет чётное количество простых множителей. Из этого следует, что функция Мёбиуса принимает значение μ (1) = 1, что необходимо, чтобы она была мультипликативной функцией и работала формула вращения Мёбиуса

[8]^[9].

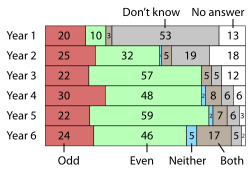Результат опроса школьников 1-6 классов в Великобритании^[10]

Вопрос, является ли ноль чётным числом, поднимался в системе школьного образования Великобритании. Проводились многочисленные опросы мнения школьников по данному вопросу. Выяснилось, что ученики по-разному оценивают чётность нуля: некоторые считают его чётным, некоторые — нечётным, иные полагают, что он является особым числом — и тем и другим одновременно или ни тем ни другим. Причём ученики пятых классов дают правильный ответ чаще, чем ученики шестых классов

[11].

Как показали исследования, даже преподаватели в школах и вузах недостаточно осведомлены о чётности нуля. Так, например, порядка 2/3 преподавателей Университета Южной Флориды ответили «нет» на вопрос «Является ли ноль чётным числом?»^[12].

1. ↑ Penner, 1999, p. 34 Lemma B.2.2, The integer 0 is even and is not odd . Penner uses the mathematical symbol ∃, the existential quantifier, to state the proof: «To see that 0 is even, we must prove that ∃k (0 = 2 k ) and this follows from the equality 0 = 2 ⋅ 0.»
2. ↑ Compare Lichtenberg, 1972, p. 535 Fig. 1
3. ↑ Lichtenberg, 1972, pp. 535—536 «… numbers answer the question How many ? for the set of objects … zero is the number property of the empty set … If the elements of each set are marked off in groups of two … then the number of that set is an even number.»
4. ↑ Lichtenberg, 1972, pp. 535—536 «Zero groups of two stars are circled. No stars are left. Therefore, zero is an even number.»
5. ↑ Dickerson & Pitman, 2012, p. 191
6. ↑ Lichtenberg, 1972, p. 537; compare her Fig. 3. «If the even numbers are identified in some special way … there is no reason at all to omit zero from the pattern.»
7. ↑ Lichtenberg, 1972, pp. 537—538 «At a more advanced level … numbers expressed as (2 × ▢) + 0 are even numbers … zero fits nicely into this pattern.»
8. ↑ Devlin, 1985, pp. 30–33
9. ↑ Dehaene, Bossini & Giraux, 1993, pp. 376–377
10. ↑ Frobisher, 1999, p. 41
11. ↑ Levenson, Tsamir & Tirosh, 2007, pp. 83–95
12. ↑ See data throughout Dehaene, Bossini & Giraux, 1993, and summary by Nuerk, Iversen & Willmes, 2004, p. 837.

• Anderson, Ian (2001), A First Course in Discrete Mathematics, London: Springer, ISBN 1-85233-236-0 
• Anderson, Marlow & Feil, Todd (2005), A First Course in Abstract Algebra: Rings, Groups, And Fields, London: CRC Press, ISBN 1-58488-515-7 
• Andrews, Edna (1990), Markedness Theory: the union of asymmetry and semiosis in language, Durham: Duke University Press, ISBN 0-8223-0959-9 
• Arnold, C. L. (January 1919), «The Number Zero», The Ohio Educational Monthly Т. 68 (1): 21–22, <https://books.google.com/books?id=v3QbAQAAIAAJ&pg=PA21>. Проверено 11 апреля 2010. 
• Arsham, Hossein (January 2002), Zero in Four Dimensions: Historical, Psychological, Cultural, and Logical Perspectives, <http://www.pantaneto.co.uk/issue5/arsham.htm>. Проверено 24 сентября 2007.  Архивная копия от 25 сентября 2007 на Wayback Machine
• Ball, Deborah Loewenberg; Hill, Heather C. & Bass, Hyman (2005), «Knowing Mathematics for Teaching: Who Knows Mathematics Well Enough To Teach Third Grade, and How Can We Decide?»,
  American Educator, <http://deepblue.lib.umich.edu/handle/2027.42/65072>. Проверено 16 сентября 2007. 
• Ball, Deborah Loewenberg; Lewis, Jennifer & Thames, Mark Hoover (2008), «Making mathematics work in school», Journal for Research in Mathematics Education Т. M14: 13–44 and 195–200, <http://www-personal.umich.edu/~dball/articles/BallLewisThames08.pdf>. Проверено 4 марта 2010. 
• Barbeau, Edward Joseph (2003), Polynomials, Springer, ISBN 0-387-40627-1 
• Baroody, Arthur & Coslick, Ronald (1998), Fostering Children’s Mathematical Power: An Investigative Approach to K-8, Lawrence Erlbaum Associates, ISBN 0-8058-3105-3 
• Berlinghoff, William P.; Grant, Kerry E. & Skrien, Dale (2001), A Mathematics Sampler: Topics for the Liberal Arts (5th rev. ed.), Rowman & Littlefield, ISBN 0-7425-0202-3 
• Border, Kim C. (1985), Fixed Point Theorems with Applications to Economics and Game Theory, Cambridge University Press, ISBN 0-521-38808-2 
• Brisman, Andrew (2004), Mensa Guide to Casino Gambling: Winning Ways, Sterling, ISBN 1-4027-1300-2 
• Bunch, Bryan H. (1982), Mathematical Fallacies and Paradoxes, Van Nostrand Reinhold, ISBN 0-442-24905-5 
• Caldwell, Chris K. & Xiong, Yeng (27 December 2012), «What is the Smallest Prime?», Journal of Integer Sequences Т. 15 (9), <http://cs.uwaterloo.ca/journals/JIS/VOL15/Caldwell1/cald5.html> 
• Column 8 readers (10 March 2006a), Column 8 (First ed.), с. 18, Factiva SMHH000020060309e23a00049 
• Column 8 readers (16 March 2006b), Column 8 (First ed.), с. 20, Factiva SMHH000020060315e23g0004z 
• Crumpacker, Bunny (2007), Perfect Figures: The Lore of Numbers and How We Learned to Count, Macmillan, ISBN 0-312-36005-3 
• Cutler, Thomas J. (2008), The Bluejacket’s Manual: United States Navy (Centennial ed.), Naval Institute Press, ISBN 1-55750-221-8 
• Dehaene, Stanislas; Bossini, Serge & Giraux, Pascal (1993), «The mental representation of parity and numerical magnitude», Journal of Experimental Psychology: General Т. 122 (3): 371–396, doi:10.1037/0096-3445.122.3.371, <http://www.unicog.org/publications/Dehaene_ParitySNARCeffect_JEPGeneral1993.pdf>. Проверено 13 сентября 2007.  Архивная копия от 19 июля 2011 на Wayback Machine
• Devlin, Keith (April 1985), «The golden age of mathematics», New Scientist Т. 106 (1452) 
• Diagram Group (1983), The Official World Encyclopedia of Sports and Games, Paddington Press, ISBN 0-448-22202-7 
• Dickerson, David S & Pitman, Damien J (July 2012), Tai-Yih Tso, ed., «Advanced college-level students’ categorization and use of mathematical definitions», Proceedings of the 36th Conference of the International Group for the Psychology of Mathematics Education Т. 2: 187–195, <http://www.diva-portal.org/smash/get/diva2:542328/FULLTEXT01.pdf#page=193> 
•  
• Educational Testing Service (2009), Mathematical Conventions for the Quantitative Reasoning Measure of the GRE® revised General Test, Educational Testing Service, <http://www.ets.org/s/gre/pdf/gre_math_conventions.pdf>. Проверено 6 сентября 2011. 
• Freudenthal, H. (1983), Didactical phenomenology of mathematical structures, Dordrecht, The Netherlands: Reidel 
• Frobisher, Len (1999), Anthony Orton, ed., Primary School Children’s Knowledge of Odd and Even Numbers, London: Cassell, с. 31–48 
• Gouvêa, Fernando Quadros (1997), p-adic numbers: an introduction (2nd ed.), Springer-Verlag, ISBN 3-540-62911-4 
• Gowers, Timothy (2002), Mathematics: A Very Short Introduction, Oxford University Press, ISBN 978-0-19-285361-5 
• Graduate Management Admission Council (September 2005), The Official Guide for GMAT Review (11th ed.), McLean, VA: Graduate Management Admission Council, ISBN 0-9765709-0-4 
• Grimes, Joseph E. (1975), The Thread of Discourse, Walter de Gruyter, ISBN 90-279-3164-X 
• Hartsfield, Nora & Ringel, Gerhard (2003), Pearls in Graph Theory: A Comprehensive Introduction, Mineola: Courier Dover, ISBN 0-486-43232-7 
• Hill, Heather C.; Blunk, Merrie L.; Charalambous, Charalambos Y. & Lewis, Jennifer M. (2008), «Mathematical Knowledge for Teaching and the Mathematical Quality of Instruction: An Exploratory Study», Cognition and Instruction Т. 26 (4): 430–511, DOI 10.1080/07370000802177235 
• Hohmann, George (25 October 2007), Companies let market determine new name, с. P1C, Factiva CGAZ000020071027e3ap0001l 
• Kaplan Staff (2004), Kaplan SAT 2400, 2005 Edition, Simon and Schuster, ISBN 0-7432-6035-X 
• Keith, Annie (2006), Mathematical Argument in a Second Grade Class: Generating and Justifying Generalized Statements about Odd and Even Numbers, IAP, ISBN 1-59311-495-8 
• Krantz, Steven George (2001), Dictionary of algebra, arithmetic, and trigonometry, CRC Press, ISBN 1-58488-052-X 
• Levenson, Esther; Tsamir, Pessia & Tirosh, Dina (2007), «Neither even nor odd: Sixth grade students’ dilemmas regarding the parity of zero», The Journal of Mathematical Behavior Т. 26 (2): 83–95, DOI 10.1016/j.jmathb.2007.05.004 
• Lichtenberg, Betty Plunkett (November 1972), «Zero is an even number», The Arithmetic Teacher Т. 19 (7): 535–538 
• Lorentz, Richard J. (1994), Recursive Algorithms, Intellect Books, ISBN 1-56750-037-4 
• Lovas, William & Pfenning, Frank (22 January 2008), «A Bidirectional Refinement Type System for LF», Electronic Notes in Theoretical Computer Science Т. 196: 113–128, doi:10.1016/j.entcs.2007.09.021, <http://www.sciencedirect.com/science/article/pii/S1571066108000418>. Проверено 16 июня 2012. 
• Lovász, László; Pelikán, József & Vesztergombi, Katalin L. (2003), Discrete Mathematics: Elementary and Beyond, Springer, ISBN 0-387-95585-2 
• Morgan, Frank (5 April 2001), Old Coins, The Mathematical Association of America, <http://www.maa.org/features/mathchat/mathchat_4_5_01.html>. Проверено 22 августа 2009. 
• Nipkow, Tobias; Paulson, Lawrence C. & Wenzel, Markus (2002), Isabelle/Hol: A Proof Assistant for Higher-Order Logic, Springer, ISBN 3-540-43376-7 
• Nuerk, Hans-Christoph; Iversen, Wiebke & Willmes, Klaus (July 2004), «Notational modulation of the SNARC and the MARC (linguistic markedness of response codes) effect», The Quarterly Journal of Experimental Psychology A Т. 57 (5): 835–863, DOI 10.1080/02724980343000512 
• Partee, Barbara Hall (1978), Fundamentals of Mathematics for Linguistics, Dordrecht: D. Reidel, ISBN 90-277-0809-6 
• Penner, Robert C. (1999), Discrete Mathematics: Proof Techniques and Mathematical Structures, River Edje: World Scientific, ISBN 981-02-4088-0 
• Salzmann, H.; Grundhöfer, T.; Hähl, H. & Löwen, R. (2007), The Classical Fields: Structural Features of the Real and Rational Numbers, Cambridge University Press, ISBN 0-521-86516-6 
• Siegel, Robert (19 November 1999), Analysis: Today’s date is signified in abbreviations using only odd numbers. 1-1, 1-9, 1-9-9-9. The next time that happens will be more than a thousand years from now., National Public Radio, <https://www.npr.org/templates/story/story.php?storyId=1066881> 
• Smock, Doug (6 February 2006), The odd bets: Hines Ward vs. Tiger Woods, с. P1B, Factiva CGAZ000020060207e226000bh 
• Snow, Tony (23 February 2001), Bubba’s fools, <http://www.jewishworldreview.com/tony/snow022301.asp>. Проверено 22 августа 2009. 
• Sones, Bill & Sones, Rich (8 May 2002), To hide your age, button your lips, с. C07, <http://www.deseretnews.com/article/912430/To-hide-your-age-button-your-lips.html?pg=all>. Проверено 21 июня 2014. 
• Starr, Ross M. (1997), General Equilibrium Theory: An Introduction, Cambridge University Press, ISBN 0-521-56473-5 
• Steinberg, Neil (30 November 1999), Even year, odd facts (5XS ed.), с. 50, Factiva chi0000020010826dvbu0119h 
• Stewart, Mark Alan (2001), 30 Days to the GMAT CAT, Stamford: Thomson, ISBN 0-7689-0635-0 
• Stingl, Jim (5 April 2006), 01:02:03 04/05/06; We can count on some things in life (Final ed.), с. B1, <http://www.jsonline.com/story/index.aspx?id=413306>. Проверено 21 июня 2014.  Архивная копия от 27 апреля 2006 на Wayback Machine
• Tabachnikova, Olga M. & Smith, Geoff C. (2000), Topics in Group Theory, London: Springer, ISBN 1-85233-235-2 
• The Math Forum participants (2000), A question around zero, Drexel University, <http://mathforum.org/kb/message.jspa?messageID=1178542>. Проверено 25 сентября 2007. 
• Turner, Julian (13 July 1996), Sports Betting – For Lytham Look to the South Pacific, с. 23, Factiva grdn000020011017ds7d00bzg 
• Wilden, Anthony & Hammer, Rhonda (1987), The rules are no game: the strategy of communication, Routledge Kegan & Paul, ISBN 0-7100-9868-5 
• Wise, Stephen (2002), GIS Basics, CRC Press, ISBN 0-415-24651-2 
• Wong, Samuel Shaw Ming (1997), Computational Methods in Physics and Engineering, World Scientific, ISBN 981-02-3043-5 

Четные числа — это… Что такое Четные числа?

Чётность в теории чисел — характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет — нечётным (примеры: 1, 3, 75, −19). Нуль считается чётным числом. ^[1]

Чётное число — целое число, которое делится без остатка на 2:   …−4, −2, 0, 2, 4, 6, 8…

Нечётное число — целое число, которое не делится без остатка на 2:   …−3, −1, 1, 3, 5, 7, 9…

Иными словами, чётные и нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.

Признак чётности

Если в десятичной форме записи числа последняя цифра является чётным числом (0, 2, 4, 6 или 8), то всё число так же является чётным, в противном случае — нечётным.
42, 104, 11110, 9115817342 — чётные числа.
31, 703, 78527, 2356895125 — нечётные числа.

Арифметика

• Сложение и вычитание:
  • Чётное ± Чётное = Чётное
  • Чётное ± Нечётное = Нечётное
  • Нечётное ± Чётное = Нечётное
  • Нечётное ± Нечётное = Чётное
• Умножение:
  • Чётное × Чётное = Чётное
  • Чётное × Нечётное = Чётное
  • Нечётное × Нечётное = Нечётное
• Деление:
  • Чётное / Чётное — однозначно судить о чётности результата невозможно (если результат целое число, то оно может быть как чётным, так и нечётным)
  • Чётное / Нечётное = если результат целое число, то оно Чётное
  • Нечётное / Чётное — результат не может быть целым числом, а соответственно обладать атрибутами чётности
  • Нечётное / Нечётное = если результат целое число, то оно Нечётное

История и культура

Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. Так, в древнекитайской мифологии нечётные числа соответствовали Инь, а чётные — Ян.

В разных странах существуют связанные с количеством даримых цветов традиции, например в США, Европе и некоторых восточных странах считается что чётное количество даримых цветов приносит счастье. В России чётное количество цветов принято приносить лишь на похороны умершим; в случаях когда в букете много цветов, чётность или нечётность их количества уже не играет такой роли.

Примечания

1. ↑ «Чётные числа» в БСЭ.

Wikimedia Foundation. 2010.

Игра с мячом, чтобы объяснить детям чётные и нечётные числа, десятки и числовые ряды

Однажды у меня был очень интересный урок на семинаре для учителей. Группа учителей подобралась отличная — все включенные, заинтересованные, улыбающиеся! Если бы во всех начальных школах были такие учителя, можно было бы с куда большим оптимизмом смотреть на развитие образования в этом городе и в этой стране.

Первый класс. Рассылка

Ценные советы и бесценная поддержка для родителей первоклассников

В самом начале семинара у меня был открытый урок с семилетками — на час примерно. Из шести детей — три Сони. Урок был очень показательный и красноречивый. Дети играли активно, старались, и было очень хорошо видно, какие именно сложности у них возникают почти на ровном месте.

Начали мы с простых вещей, чтобы точно у всех получилось.

Я тебе кидаю мяч и говорю число, а ты мне мяч кидай обратно и говори число на 1 больше.

— Семь?

— Восемь!

— Одиннадцать?

— Двенадцать!

— 19? — 20!

— 39? — 40!

Это всем легко, и в шесть лет тоже, потому что надо просто сказать следующее число — следующее слово в скороговорке.

Теперь я тебе число, а ты мне — число на 2 больше.

Это сложнее, но тоже справляются.

— 14? — 16!

— 11? — 13!

— 9? — 11!

— 16? — 18!

Отлично! А теперь я тебе число, а ты мне — число на один меньше. Уже половине не то чтобы сложно, но требуется время для ответа (пробормотать тихонько ряд числительных до нужной точки).

Я тебе число, а ты мне — число на 2 меньше. Это сложнее, и не все могут. Но некоторые рвутся в бой. Хорошо же!

Я тебе говорю число, а вы мне — число на 10 больше моего. Родители и учителя считают, что я дала очень простое задание. Как бы не так!

— Уууу, — тянут дети. — Это сложно.

— Ну, кто готов попробовать?

— Ну давайте я попробую, — вызывается Соня.

— Четыре.

— Щас! — Соня начинает перебирать пальцами и бормотать. 5, 6, 7, 8, 9, 10, 11, 12, 13, 14. — Ага, будет 14!

Я тем временем выписываю на доске ряд чисел, один десяток под другим, чтобы было удобнее отсчитывать.

1 2 3 4 5 6 7 8 9 10

11 12 13 14 15 16 17 18 19 20

21 22 23 24 25…

Тогда и другие дети решают попробовать, и некоторые даже, кажется, в итоге поняли идею. Ну, не на сто процентов поняли, но хоть немного приблизились к пониманию.

После этого похлопали по коленкам — громко-тихо, громко-тихо, называя числа: один (громко) — два — три (снова громко) — четыре — пять (громко) — шесть… Это всем легко, идею все поняли, отлично.

Тогда давайте нарисуем улицу, и с одной стороны улицы у нас дома 12, 14, 16, а какой следующий дом на той же стороне?

А на другой стороне улицы дома с номерами 11, 13, 15, а потом? Кому-то это уже не настолько очевидно.

А потом мы делили шоколадки — и дети пытались выяснить, почему одни шоколадки можно поровну на двоих поделить, а другие — не получается.

Я предполагала дать и несколько задач более сложных, но вскоре обнаружила, что некоторые дети считают, что 100 — это аж два десятка. То есть, ой, четыре. После этого я решила в такие дебри не лезть.

Некоторые задачи в итоге у нас остались без ответа, мы их «пообсуждали», но до решения с ходу не добрались.

Мне очень нравится идея из книги А. З. Звонкина, что вопросы и задачи куда важнее, чем ответы и разжёвывание решения. Именно этим, по-моему, полезны олимпиады. Правда, взрослым, увы, бывает страшно сложно удержаться и не подсказывать детям.

Фото: iStockphoto (bokan76)

Чётные и нечётные числа | Математика

Чётность в теории чисел

— характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится на два, оно называется чётным (примеры: 2, 28, —8, 40), если нет — нечётным (примеры: 1,3, 75, —19). Ноль считается чётным числом[1].

Чётное число — целое число, которое делится на 2 без остатка:   …−4,−2,0,2,4,6,8,10…

Например 4 это четное число его можно разделить на 2. Это помогает в сложении.

Нечётное число — целое число, которое не делится на 2 без остатка:   …−3,−1,1,3,5,7,9…

Иными словами чётное и нечётное — собственные названия классов вычетов [0] и [1] по модулю 2.

Признак чётности

Если в десятичной форме записи последняя цифра числа делится на два без остатка — число чётное. Если не делится — то нечётное.

Арифметика

Сложение и вычитание

• чётное ± чётное = чётное
• чётное ± нечётное = нечётное
• нечётное ± чётное=нечётное
• нечётное ± нечётное = чётное

Умножение:

• чётное × чётное = чётное
• чётное × нечётное = чётное
• нечётное × нечётное = нечётное

Деление:

• чётное / чётное — может быть любым
• чётное / нечётное = чётное, если целое
• нечётное / чётное — не может быть целым
• нечётное / нечётное = нечётное, если целое

История и культура

Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. Так, в древнекитайской мифологии нечётные числа соответствовали Инь, а чётные — Ян.

В разных странах существуют связанные с количеством даримых цветов традиции, например в США, Европе и некоторых восточных странах считается что чётное количество даримых цветов приносит счастье. В России чётное количество цветов принято приносить лишь на похороны умершим. В случаях когда в букете много цветов чётность или нечётность их количества уже не играет такой роли.

Примечания

1. ↑ См., например, статью «Чётные числа» в большой советской энциклопедии.

ar:أعداد فردية و زوجية bg:Четни и нечетни числа ca:Nombre senar cs:Sudá a lichá čísla da:Lige og ulige tal

el:Άρτιοι και περιττοί αριθμοί

eu:Zenbaki bakoiti

he:מספר זוגי hu:Páros és páratlan számok io:Para e ne-para nombri is:Oddatala

lmo:Nümar díspari lt:Lyginiai ir nelyginiai skaičiai nds:Evene un unevene Tallen nl:Even nn:Oddetal og partal no:Partall pl:Liczby parzyste i nieparzyste

simple:Even number sk:Párne a nepárne čísla sl:Soda in liha števila sr:Парни и непарни бројеви sv:Jämna och udda tal th:จำนวนคู่และจำนวนคี่

ur:جفت عددШаблон:Ш2Шаблон:Ш2Шаблон:Ш2Шаблон:Ш2

Обсуждение:Чётные и нечётные числа — Википедия

Материал из Википедии — свободной энциклопедии

Чётное число — целое число, которое делится на 2:   …−4,−2,0,2,4,6,8…и.т.д
Нечётное число — целое число, которое не делится на 2:   …−3,−1,1,3,5,7,9…

Все числа делятся на 2 (например 3/2=1,5), но чётные делятся без остатка —Ustas 19:37, 16 января 2006 (UTC)

Замечание мне кажется справедливым. С. Л. 19:42, 16 января 2006 (UTC)

• Господа, лажа какая-то. 303/3 = 101 (целое). 303 — нечётное, 3 — нечётное. Критерий-то глюкавый. #!George Shuklin 17:46, 7 апреля 2007 (UTC)

Всё верно, в критерии указано, что если получившееся число окажется целым (101), то оно будет нечётным. Я тоже не сразу понял, что означает запись «если целое». Сейчас попробую сформулировать иначе. — bms 09:10, 22 апреля 2009 (UTC)

«В соответствии с этим определением нуль является чётным числом». Забавно, с каким же: «Чётное число — целое число, которое делится без остатка на 2»?

• Да. — bms 04:41, 9 февраля 2011 (UTC)

Сергей Михайлович,12 апреля 2012 Нуль-вообще не число. Это значок для обозначения пустого разряда, изобретен индийскими математиками в 6-5 веке н.э. в процессе изобретения системы позиционной записи чисел.Если он делится на 2 без остатка, так что ж тут удивительного — какой остаток может быть от нуля? Он и на 3 делится без остатка. На числовой оси нуль не достижим:какое бы сколь угодно малое число вы не назначили, от него до нуля будет бесконечное число чисел, а все потому, что нуль не число. Всё бы это было философией, если бы в статистике это непонимание не приводило к некоторым забавным результатам. А сегодня моя внучка получила 4 за то, что самым маленьким чётным числом назвала 2, а не 0. 92.243.166.245 11:53, 12 апреля 2012 (UTC)

• Сделал приписку по этому поводу. Считаю, целесообразно. Во всяком случае, мы с ребёнком почти час по этому поводу разбирались. —Gorvzavodru 09:54, 21 января 2015 (UTC)
  • АИ выражаю намерение подобрать. После того как убежусь, что правка не будет немедленно откачена непримиримыми. —Gorvzavodru 09:58, 21 января 2015 (UTC)

* Пара состоит из двух элементов.

• Любое число, которое делится на два без остатка, и содержит по меньшей мере одну пару элементов, называется чётным числом.


Ноль разделить на два, результат ноль пар и нулевой остаток.

• Ноль пар — значит ноль не является чётным числом.
• Нулевой остаток – значит ноль не является нечётным числом.

Ноль не является нечётным или чётным числом.
Спасибо. —Gvitalie 06:01, 31 июля 2015 (UTC)

Замечательная идея — дать своё собственное, никем не признанное определение чётного числа, а потом торжественно доказать, что ноль ему не удовлетворяет. В энциклопедии признаются только определения из авторитетных источников, а все прочие считаются оригинальными исследованиями и не принимаются во внимание. Все любительские придумки лучше публиковать в другом месте, мы тут и так не скучаем. Недавно, например, один джентльмен доказывал, что ноль — вообще не число (потому что нет его в реальной природе), другой — что число Пи равно точно трём, а уж доказательствами трисекции угла и великой теоремы Ферма можно всю зиму печку топить. LGB 11:09, 31 июля 2015 (UTC)

Спасибо. —Gvitalie 10:11, 2 августа 2015 (UTC)

в ответ на ошибку выше по тексту,что ноль это не число ,замечу: ..ноль это целое число,о чем указано в статье Википедии «целое число» — Эта реплика добавлена участником 194.9.227.159 (о • в) 12:55, 25 января 2017 (UTC).

Напрасно беспокоитесь, все математики без исключения считают ноль полноценным числом. Упомянутое вами мнение «выше по тексту» есть личное мнение его автора, авторитетное только для него самого. LGB (обс.) 13:30, 25 января 2017 (UTC)

ок. — Эта реплика добавлена с IP 194.9.227.159 (о) 13:14, 26 января 2017 (UTC).

все четные числа от 1 до 1000

обратные нечетным

вам все перечислить?)))))))))

2,4,6 и так далее с ращницей в 2

Начиная с 2 через одно

те которые делятся на два, и на саму себя 2 4 6 8 10 12 14 16 18

вот полный список: 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48 50 52 54 56 58 60 62 64 66 68 70 72 74 76 78 80 82 84 86 88 90 92 94 96 98 100 102 104 106 108 110 112 114 116 118 120 122 124 126 128 130 132 134 136 138 140 142 144 146 148 150 152 154 156 158 160 162 164 166 168 170 172 174 176 178 180 182 184 186 188 190 192 194 196 198 200 202 204 206 208 210 212 214 216 218 220 222 224 226 228 230 232 234 236 238 240 242 244 246 248 250 252 254 256 258 260 262 264 266 268 270 272 274 276 278 280 282 284 286 288 290 292 294 296 298 300 302 304 306 308 310 312 314 316 318 320 322 324 326 328 330 332 334 336 338 340 342 344 346 348 350 352 354 356 358 360 362 364 366 368 370 372 374 376 378 380 382 384 386 388 390 392 394 396 398 400 402 404 406 408 410 412 414 416 418 420 422 424 426 428 430 432 434 436 438 440 442 444 446 448 450 452 454 456 458 460 462 464 466 468 470 472 474 476 478 480 482 484 486 488 490 492 494 496 498 500 502 504 506 508 510 512 514 516 518 520 522 524 526 528 530 532 534 536 538 540 542 544 546 548 550 552 554 556 558 560 562 564 566 568 570 572 574 576 578 580 582 584 586 588 590 592 594 596 598 600 602 604 606 608 610 612 614 616 618 620 622 624 626 628 630 632 634 636 638 640 642 644 646 648 650 652 654 656 658 660 662 664 666 668 670 672 674 676 678 680 682 684 686 688 690 692 694 696 698 700 702 704 706 708 710 712 714 716 718 720 722 724 726 728 730 732 734 736 738 740 742 744 746 748 750 752 754 756 758 760 762 764 766 768 770 772 774 776 778 780 782 784 786 788 790 792 794 796 798 800 802 804 806 808 810 812 814 816 818 820 822 824 826 828 830 832 834 836 838 840 842 844 846 848 850 852 854 856 858 860 862 864 866 868 870 872 874 876 878 880 882 884 886 888 890 892 894 896 898 900 902 904 906 908 910 912 914 916 918 920 922 924 926 928 930 932 934 936 938 940 942 944 946 948 950 952 954 956 958 960 962 964 966 968 970 972 974 976 978 980 982 984 986 988 990 992 994 996 998 1000

будет 500 четный и 500 нечетных

2,4,6 и так далее с ращницей в 2

for Cicle=1 to 1000 do if Frac(Cicle/2)=0 then begin …Ваши действия end;

для печати чётных 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 100, 102, 104, 106, 108, 110, 112, 114, 116, 118, 120, 122, 124, 126, 128, 130, 132, 134, 136, 138, 140, 142, 144, 146, 148, 150, 152, 154, 156, 158, 160, 162, 164, 166, 168, 170, 172, 174, 176, 178, 180, 182, 184, 186, 188, 190, 192, 194, 196, 198, 200, 202, 204, 206, 208, 210, 212, 214, 216, 218, 220, 222, 224, 226, 228 для печати чётных в браузере

2,4,6,8,10,12,14,16,18,20,22,24,26,28,30,32,34,36,38,40,42,44,46,48,50,52,54,56,58,60,62,64,66,68,70,72,74,76,78,80,82,84,86,88,90,92,94,96,98,100,102,104,106,108,110,112,114,116,116,118,120,122,124