Урок 18. сечения многогранников — Геометрия — 11 класс
Геометрия, 11 класс
Урок №18. Сечения многогранников
Перечень вопросов, рассматриваемых в теме:
Решение задач, сводящихся к доказательству, связанному с построением сечения многогранника
Построение сечения многогранников
Решение задач на нахождение площадей сечений многогранников
Площадь
треугольника S=½hа
трапеции S=½h(а+b)
параллелограмма S=hа
Основная литература:
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия. 10–11 классы : учеб.для общеобразоват. организаций : базовый и углубл. уровни – М.: Просвещение, 2014. – 255, сс. 121-126.
Дополнительная литература:
Шарыгин И.Ф. Геометрия. 10–11 кл. : учеб.для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 178-196.
Потоскуев Е.В., Звавич Л.И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-30.
Открытые электронные ресурс:
Образовательный портал “Решу ЕГЭ”. https://mathb-ege.sdamgia.ru/test?theme=177
Теоретический материал для самостоятельного изучения
Сечение — это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.
Определение: две прямые параллельны, если они лежат в одной плоскости и не пересекаются. Если через две прямые нельзя провести одну плоскость, то такие прямые скрещиваются.
Теорема о параллельности трех прямых: если a∥b, b∥c, то и a∥c. Определение: прямая и плоскость параллельны, если они не имеют общих точек. Признак параллельности прямой и плоскости: прямая, не лежащая в плоскости, параллельна этой плоскости, если она параллельна некоторой прямой из этой плоскости.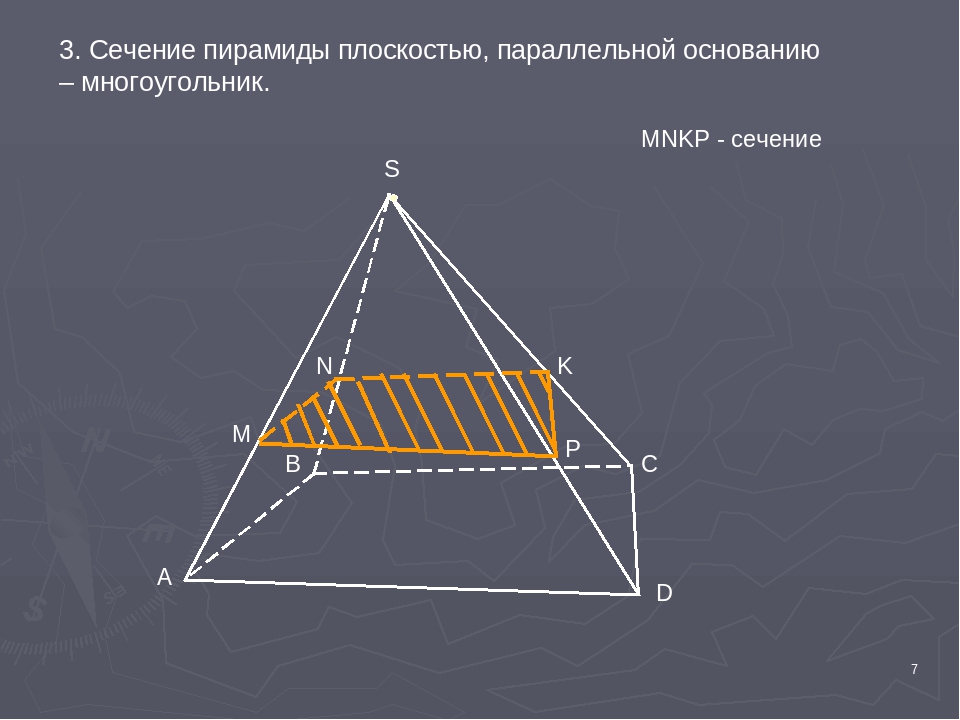
Определение: две плоскости параллельны, если они не имеют общих точек.
Признак параллельности двух плоскостей: если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости параллельны.
Если две плоскости пересекаются, то их линия пересечения — прямая.
Если две параллельные плоскости пересечены третьей, то их линии пересечения параллельны (см. рис.)
Если плоскости α и β пересекаются по прямой a, а плоскости β и γ пересекаются по прямой b, причем a∥b, то плоскости α и γ пересекутся по прямой c∥a∥b.
Следом называется прямая, по которой плоскость сечения пересекает плоскость любой из граней многогранника.
Примеры и разбор решения заданий тренировочного модуля
№1 SABCD – четырехугольная пирамида, в основании которой лежит квадрат ABCD, а две боковые грани SAB и SAD представляют собой прямоугольные треугольники с прямым углом ∠A. Найдите площадь сечения пирамиды плоскостью α, если SA=AB=a.
Решение:
сначала построим сечение по условию задачи.
1)Пусть AC∩BD=O. Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Заметим, что т.к. ∠SAB=∠SAD=90∘⇒SA⊥(ABC). Проведем в плоскости SAC прямую OK∥SC. Т.к. O – середина AC, то по теореме Фалеса K – середина SA. Через точку K в плоскости SAB проведем KM∥SB (следовательно, M – середина AB). Таким образом, плоскость, проходящая через прямые OK и KM, и будет искомой плоскостью. Необходимо найти сечение пирамиды этой плоскостью. Соединив точки O и M, получим прямую MN. Т.к. α∥(SBC),то α пересечет плоскость SCD по прямой NP∥SC (если NP∩SC≠∅, то α∩(SBC)≠∅, что невозможно ввиду их параллельности). Таким образом, KMNP – искомое сечение, причем KP∥AD∥MN⇒ это трапеция.
2)Т.к. все точки K,M,N,P – середины отрезков SA,AB,CD,SD соответственно, то: а) MN=AD=a б) KP=1/2AD=a/2 в) KM=1/2SB=a 2/2 Заметим, что по теореме о трех перпендикулярах SB⊥BC⇒KM⊥MN.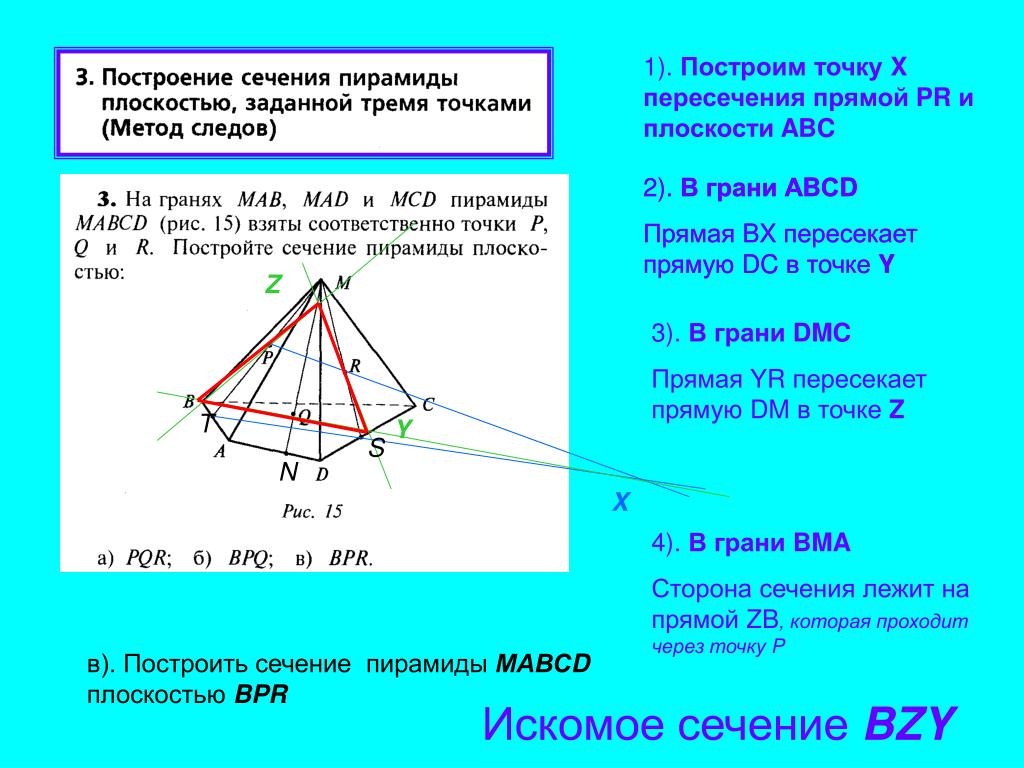
Ответ:3 a2/8
№2 Найди площадь сечения прямой призмы, проходящей через середины ребер, если =120°, АВ=5 см, ВС=3см и наибольшая из площадей боковых граней равна 35см2 .
Решение:
боковая грань прямой призмы является прямоугольником.
Площадь каждой боковой грани равна произведению высоты призмы на сторону основания.
То есть большая боковая грань содержит большую сторону основания.
По условию =120°, – тупой, а поскольку напротив большей стороны лежит больший угол, то большей стороной основания будет сторона АС. Вычислим длину стороны АС по теореме косинусов.
Получим, что длина стороны АС=7см.
Зная большую сторону основания и площадь наибольшей боковой грани призмы, длину высоты призмы вычислить нетрудно.
Получим, что длина высоты призмы равна .
Найдем площадь основания, а оно равно площади сечения, по формуле .
Мы воспользуемся второй формулой. Получим, что площадь основания равна .
Ответ: 15 /4 см2
№3 На ребре AB правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка Q, причём AQ:QB=1:2. Точка P — середина ребра AS.
Найдите площадь сечения DPQ, если площадь сечения DSB равна 6.
Решение:
пусть сторона основания пирамиды равна 3а, а высота пирамиды равна h. Тогда площадь сечения DSB равна
S=BD*SO/2= 3 =6
откуда ah=2 .
Площадь сечения DPQ равна
Ответ:
№4
Дана правильная треугольная пирамида SABC с вершиной S. Через середину ребра AC и точки пересечения медиан граней ASB и CSB проведена плоскость. Найдите площадь сечения пирамиды этой плоскостью, если AB=21,AS=12 .
Решение:
пусть LK∩SO=H. Тогда по теореме о трех перпендикулярах HK⊥AC как наклонная (HO⊥(ABC),OK⊥AC как проекция). Следовательно, и LK⊥AC.
Следовательно, и LK⊥AC.
Тогда SALC=AC⋅LK/2 Рассмотрим △SKB: BK=AB⋅ /2=21 /2⇒cosB=7 /12 .
Тогда по теореме косинусов для △KLB: KL2=729/4⇒KL=27/2
Значит, SALC=567/4=141,75
Ответ : 141,75
№5
Дана правильная четырехугольная призма ABCDA1B1C1D1. На ребре AA1 отмечена точка K так, что AK : KA1 = 1 : 2. Плоскость α проходит через точки B и K параллельно прямой AC. Эта плоскость пересекает ребро DD1 в точке M, АВ=4, АА1=6. Найдите площадь сечения.
Решение:
По теореме о трех перпендикулярах прямые BM и AC перпендикулярны, а значит, прямые BM и KL перпендикулярны. Площадь четырехугольника, диагонали которого взаимно перпендикулярны, равна половине произведения диагоналей. Найдем их: KL=AC=4 как диагональ квадрата, лежащего в основании призмы, тогда
по теореме Пифагора.
Тогда
Ответ: 8
Построить сечение пирамиды плоскостью p. Пирамида
Для построения натуральной величины фигуры сечения (рис. 4) применен способ перемены плоскостей проекций. В качестве дополнительной плоскости принята плоскость H 1 , параллельная плоскостиР и перпендикулярная плоскостиV . Полученная проекция треугольника1 1 2 1 3 1 является натуральной величиной фигуры сечения.
Пирамида с вырезом
В качестве примера построения сечений многогранника несколькими плоскостями рассмотрим построение пирамиды с вырезом, который образован тремя плоскостями − P , R , иT (рис. 5).
Плоскость P , параллельная горизонтальной плоскости проекций, пересекает поверхность пирамиды по пятиугольнику 1-2-3-K-6 . На горизонтальной плоскости проекций стороны пятиугольника параллельны проекциям сторон основания пирамиды. Построив горизонтальную проекцию пятиугольника, отмечаем точки4 и5 .
Фронтально-проецирующая плоскостьR
пересекает пирамиду по пятиугольнику 1-2-7-8-9
. Чтобы найти горизонтальные проекции точек8
и9
,
проведем через них дополнительные образующиеSM
иSN
.
Вначале на фронтальной проекции−
s
′
m
′
иs
′
n
′,
а затем на горизонтальной−
sm
иsn
.
Чтобы найти горизонтальные проекции точек8
и9
,
проведем через них дополнительные образующиеSM
иSN
.
Вначале на фронтальной проекции−
s
′
m
′
иs
′
n
′,
а затем на горизонтальной−
sm
иsn
.
Фронтально-проецирующая плоскостьΤ пересекает пирамиду по пяти-
угольнику 5-4-8-9-10 .
Построив горизонтальную проекцию выреза, строим его профильную проекцию.
Построение проекций линии пересечения цилиндра плоскостью
При пересечении цилиндра вращения плоскостью, параллельной оси вращения, в сечении получается пара прямых (образующих, рис. 6). Если секущая плоскость перпендикулярна к оси вращения, в результате сечения получится окружность (рис. 7). В общем случае, когда секущая плоскость наклонена к оси вращения цилиндра, в сечении получается эллипс (рис. 8).
Рассмотрим пример | построения проекций линии сечения | цилиндра | ||||
фронтально- | ||||||
проецирующей | ||||||
стью Q . В сечении получа- | ||||||
ется эллипс (рис. 9). | ||||||
Фронтальная | ||||||
ция линии сечения в этом | ||||||
случае совпадает с фрон- | ||||||
тальным следом плоскости | ||||||
Qv , а горизонтальная− с | ||||||
горизонтальной проекцией | ||||||
поверхности | цилиндра | |||||
окружностью. | Профильная | |||||
проекция линии | строится | |||||
по двум имеющимся про- | ||||||
екциям − горизонтальной и фронтальной.
В общем случае построение линии пересечения поверхности плоскостью сводится к нахождению общих точек, принадлежащих одновременно секущей плоскости и поверхности.
Для нахождения этих точек применяют метод дополнительных секущих плоскостей:
1. Проводят дополнительную плоскость;
2. Строят линии пересечения дополнительной плоскости с поверхностью и дополнительной плоскости с заданной плоскостью;
3. Определяют точки пересечения полученных линий.
Дополнительные плоскости проводят таким образом, чтобы они пересекали поверхность по наиболее простым линиям.
Нахождение точек линии пересечения начинают с определения характерных (опорных) точек. К ним относятся:
1. Верхние и нижние точки;
2. Левая и правая точки;
3. Точки границы видимости;
4. Точки, характеризующие данную линию пересечения (для эллипса − точки большой и малой осей).
Для более точного построения линии пересечения необходимо построить еще и дополнительные (промежуточные) точки.
В рассматриваемом примере точки 1 и8 являются нижней и верхней точками. Для горизонтальной и фронтальной проекций точка1 будет левой точкой, точка8 − правой. Для профильной проекции точки4 и5 − точки границы видимости: точки, расположенные ниже точек4 и5 на профильной проекции будут видимыми, все остальные− нет.
Точки 2, 3 и6, 7 − дополнительные, которые определяются для большей точности построения. Профильная проекция фигуры сечения – эллипс, у которого малая ось− отрезок 1-8, большая− 4-5 .
Построение проекций линий пересечения конуса плоскостью
В зависимости от направления секущей плоскости в сечении конуса вращения могут получиться различные линии, называемые линиями конических сечений.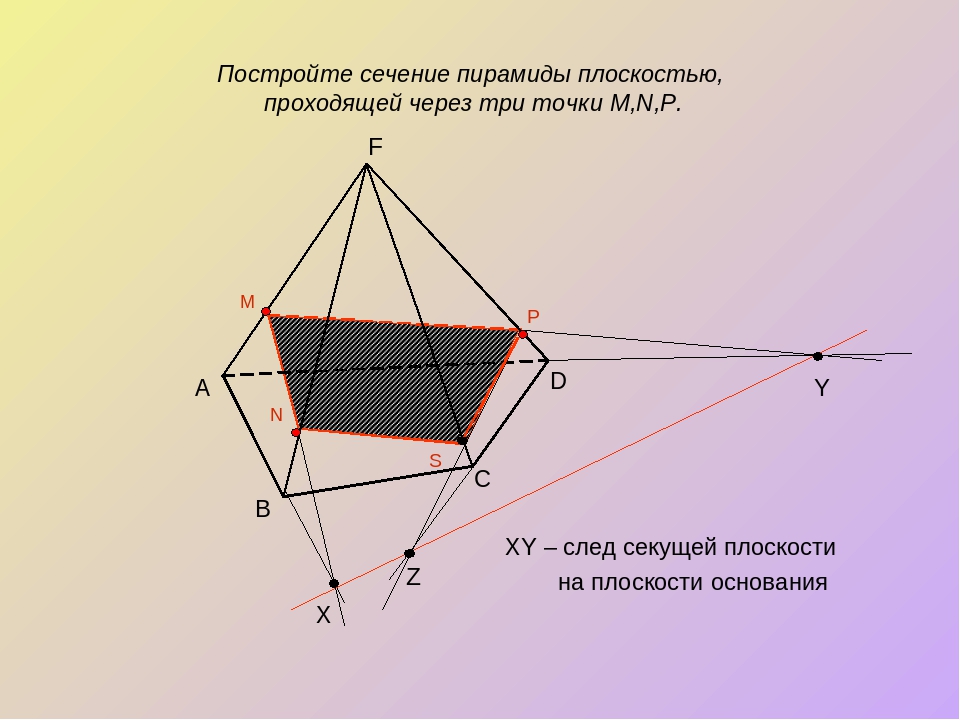
Если секущая плоскость проходит через вершину конуса, в его сечении получается пара прямых − образующих (треугольник) (рис. 10, а). В результате пересечения конуса плоскостью, перпендикулярной к оси конуса, получается окружность (рис. 10, б). Если секущая плоскость наклонена к оси вращения конуса и не проходит через его вершину, в сечении конуса могут получиться эллипс, парабола или гипербола (рис. 10, в, г, д) в зависимости от величины угла наклона секущей плоскости.
Эллипс получается в том случае, когда угол β наклона секущей плоскости меньше угла наклонаα образующих конуса к его основанию(β
Если углы α иβ равны, то есть секущая плоскость параллельна одной из образующих конуса, в сечении получается парабола (рис. 10, г).
Если секущая плоскость направлена под углом, который изменяется в пределах 90° β>α , то в сечении получается гипербола. В этом случае секу-
щая плоскость параллельна двум образующим конуса. Гипербола имеет две ветви, так как коническая поверхность двухполостная (рис. 10, д).
Известно, что точка принадлежит поверхно- | ||||
сти, если она принадлежит какой-нибудь линии | ||||
поверхности. Для конуса наиболее графически | ||||
простыми линиями являются прямые (образую- | ||||
щие) и окружности. Следовательно, если по усло- | ||||
вию задачи требуется найти горизонтальные про- | ||||
екции точек A иB , принадлежащих поверхности | ||||
конуса, то нужно через точки провести одну из | ||||
этих линий. | ||||
Горизонтальную проекцию точки A найдем | ||||
с помощью образующих. Для этого через точку A | ||||
и вершину конуса S проведем вспомогательную | ||||
фронтально-проецирующую плоскостьP(Pv). ЭтаB найдем, построив окружность, на которой она лежит. Для этого через точку проведем горизонтальную плоскостьT(Tv). Плоскость пересекает конус по окружности радиусаr . Строим горизонтальную проекцию этой окружности. Через точкуb ′ проведем линию связи до ее пересечения с окружностью. Задача также имеет два ответа− точ- ки b 1 иb 2 . Рассмотрим пример построения проекций линии пересечения конуса фронтально-проецирующей плоскостьюP(Pv), когда в сечении получается эллипс (рис. 12). Фронтальная проекция линии сечения совпадает с фронтальным следом плоскости Pv . Для удобства решения задачи обозначим крайние образующие конуса и определим характерные (опорные) точки. Нижняя точка 1 лежит на образующейAS, верхняя− 2 на образующейΒ S . Эти точки определяют положение большой оси эллипса. Малая ось эллипса перпендикулярна большой оси. Чтобы найти малую ось, разделим отрезок 1-2 пополам. Точки3 и4 определяют малую ось эллипса. Точки5 и6 , расположенные на образующихCS иDS, являются точками границы видимости для профильной плоскости проекций. Проекции точек1, 2, 5 и6 находятся на соответствующих проекциях образующих. Чтобы найти проекции точек3 и4, проводим дополнительную секущую плоскостьT(Tv), которая рассекает конус по окружности радиусаr . На этой окружности находятся проекции данных точек. На горизонтальную плоскость проекций окружность проеци- | ||||
Разберем, как построить сечение пирамиды, на конкретных примерах. Поскольку в пирамиде нет параллельных плоскостей, построение линии пересечения (следа) секущей плоскости с плоскостью грани чаще всего предполагает проведение прямой через две точки, лежащие в плоскости этой грани.
В простейших задачах требуется построить сечение пирамиды плоскостью, проходящей через данные точки, уже лежащие в одной грани.
Пример.
Построить сечение плоскостью (MNP)
Треугольник MNP — сечение пирамиды
Точки M и N лежат в одной плоскости ABS, следовательно, через них можем провести прямую. След этой прямой — отрезок MN. Он видимый, значит, соединяем M и N сплошной линией.
Точки M и P лежат в одной плоскости ACS, поэтому через них проведем прямую. След — отрезок MP. Мы его не видим, поэтому отрезок MP проводим штрихом. Аналогично строим след PN.
Треугольник MNP — искомое сечение.
Если точка, через которую требуется провести сечение, лежит не на ребре, а на грани, то она не будет концом следа-отрезка.
Пример. Построить сечение пирамиды плоскостью, проходящей через точки B, M и N, где точки M и N принадлежат, соответственно, граням ABS и BCS.
Здесь точки B и M лежат в одной грани ABS, поэтому можем через них провести прямую.
Аналогично проводим прямую через точки B и P. Получили, соответственно, следы BK и BL.
Точки K и L лежат в одной грани ACS, поэтому через них можем провести прямую. Ее след — отрезок KL.
Треугольник BKL — искомое сечение.
Однако не всегда через данные в условии точки удается провести прямую. В этом случае нужно найти точку, лежащую на прямой пересечения плоскостей, содержащих грани.
Пример. Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.
Точки M и N лежат в одной плоскость ABS, поэтому через них можно провести прямую. Получаем след MN. Аналогично — NP. Оба следа видимые, поэтому соединяем их сплошной линией.
Точки M и P лежат в разных плоскостях. Поэтому соединить их прямой не можем.
Продолжим прямую NP.
Она лежит в плоскости грани BCS. NP пересекается только с прямыми, лежащими в этой же плоскости. Таких прямых у нас три: BS, CS и BC. С прямыми BS и CS уже есть точки пересечения — это как раз N и P.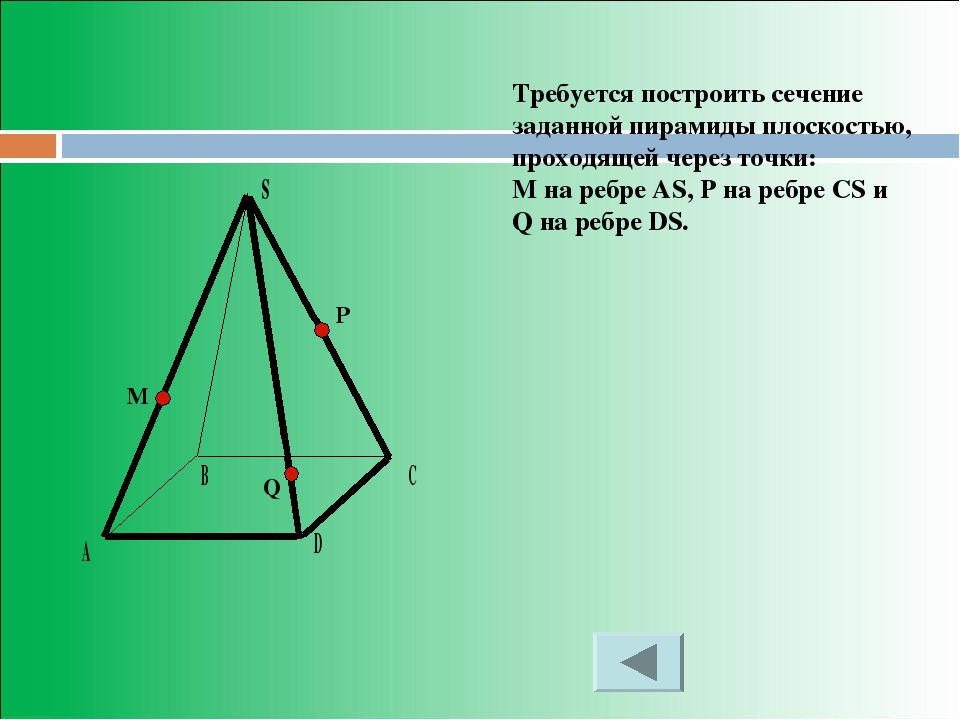 Значит, ищем пересечение NP с прямой BC.
Значит, ищем пересечение NP с прямой BC.
Точку пересечения (назовем ее H), получаем, продолжая прямые NP и BC до пересечения.
Эта точка H принадлежит как плоскости (BCS), поскольку лежит на прямой NP, так и плоскости (ABC), поскольку лежит на прямой BC.
Таким образом мы получили еще одну точку секущей плоскости, лежащей в плоскости (ABC).
Через H и точку M, лежащую в этой же плоскости, можем провести прямую.
Получим след MT.
T — точка пересечения прямых MH и AC.
Так как T принадлежит прямой AC, то через нее и точку P можем провести прямую, так как они обе лежат в одной плоскости (ACS).
4-угольник MNPT — искомое сечение пирамиды плоскостью, проходящей через данные точки M,N,P.
Мы работали с прямой NP, продлевая ее для отыскания точки пересечения секущей плоскости с плоскостью (ABC). Если работать с прямой MN, приходим к тому же результату.
Рассуждаем так: прямая MN лежит в плоскости (ABS), поэтому пересекаться может только с прямыми, лежащими в этой же плоскости. У нас таких прямых три: AB, BS и AS. Но с прямыми AB и BS уже есть точки пересечения: M и N.
Значит, продлевая MN, ищем точку пересечения ее с прямой AS. Назовем эту точку R.
Точка R лежит на прямой AS, значит, она лежит и в плоскости (ACS), которой принадлежит прямая AS.
Поскольку точка P лежит в плоскости (ACS), через R и P можем провести прямую. Получаем след PT.
Точка T лежит в плоскости (ABC), поэтому через нее и точку M можем провести прямую.
Таким образом, получили все то же сечение MNPT.
Рассмотрим еще один пример такого рода.
Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.
Через точки M и N, лежащие в одной плоскости (BCS), проводим прямую. Получаем след MN (видимый).
Через точки N и P, лежащие в одной плоскости (ACS), проводим прямую. Получаем след PN (невидимый).
Через точки M и P прямую провести не можем.
1) Прямая MN лежит в плоскости (BCS), где есть еще три прямые: BC, SC и SB. С прямыми SB и SC уже есть точки пересечения: M и N. Поэтому ищем точку пересечения MN с BC. Продолжив эти прямые, получаем точку L.
С прямыми SB и SC уже есть точки пересечения: M и N. Поэтому ищем точку пересечения MN с BC. Продолжив эти прямые, получаем точку L.
Точка L принадлежит прямой BC, а значит, она лежит в плоскости (ABC). Поэтому через L и P, которая также лежит в плоскости (ABC) можем провести прямую. Ее след — PF.
F лежит на прямой AB, а значит, и в плоскости (ABS). Поэтому через F и точку M, которая также лежит в плоскости (ABS), проводим прямую. Ее след — FM. Четырехугольник MNPF — искомое сечение.
2) Другой путь — продолжить прямую PN. Она лежит в плоскости (ACS) и пересекается с прямыми AC и CS, лежащими в этой плоскости, в точках P и N.
Значит, ищем точку пересечения PN с третьей прямой этой плоскости — с AS. Продолжаем AS и PN, на пересечении получаем точку E. Поскольку точка E лежит на прямой AS, принадлежащей плоскости (ABS), то через E и точку M, которая также лежит в (ABS), можем провести прямую. Ее след — FM. Точки P и F лежат водной плоскости (ABC), проводим через них прямую и получаем след PF (невидимый).
Правильная шестиугольная пирамида, пересеченная фронтально-проецирующей плоскостью Р, показана на рис. 180.
Как и в предыдущих примерах, фронтальная проекция сечения совпадает с фронтальным сле-
дом P v плоскости. Горизонтальную и профильную проекции фигуры сечения строят по точкам, которые являются точками пересечения плоскости Р с ребрами пирамиды.
Действительный вид фигуры сечения в этом примере определяется способом совмещения.
Развертка боковой поверхности усеченной пирамиды с фигурой сечения и фигурой основания приведена на рис. 180, б.
Сначала строят развертку неусеченной пирамиды, все грани которой, имеющие форму треугольника, одинаковы. На плоскости намечают точку s l (вершину пирамиды) и из нее, как из центра, проводят дугу окружности радиусом R, равным действительной длине бокового ребра пирамиды. Действительную длину ребра можно определить по профильной проекции пирамиды, например отрезки s»e» или s»b», так как эти ребра параллельны плоскости W и изображаются на ней действительной длиной.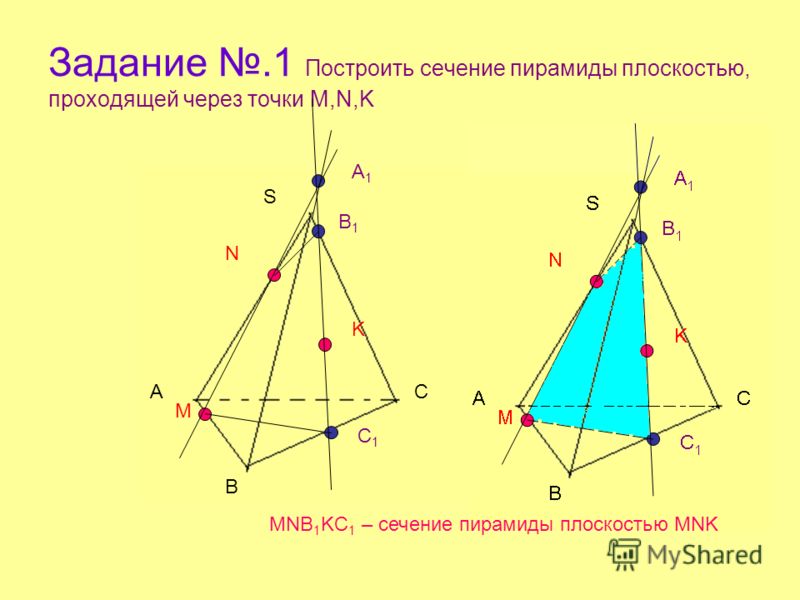 Далее по дуге окружности от любой точки, например а 1 , откладывают шесть одинаковых отрезков, равных действительной длине стороны шестиугольника – основания пирамиды. Действительную длину стороны основания пирамиды получаем на горизонтальной проекции (отрезок ab). Точки a 1 …f 1 соединяют прямыми с вершиной s 1 . Затем от вершины a 1 на этих прямых откладывают действительные длины отрезков ребер до секущей плоскости.
Далее по дуге окружности от любой точки, например а 1 , откладывают шесть одинаковых отрезков, равных действительной длине стороны шестиугольника – основания пирамиды. Действительную длину стороны основания пирамиды получаем на горизонтальной проекции (отрезок ab). Точки a 1 …f 1 соединяют прямыми с вершиной s 1 . Затем от вершины a 1 на этих прямых откладывают действительные длины отрезков ребер до секущей плоскости.
На профильной проекции усеченной пирамиды имеются действительные длины только двух от-
резкое – s»5 и s»2. Действительные длины остальных отрезков определяют способом вращения их вокруг оси, перпендикулярной к плоскости Н и проходящей через вершину s. Например, повернув отрезок s»6″ около оси до положения, параллельного плоскости W, получим на этой плоскости его действительную длину. Для этого достаточно через точку 6″ провести горизонтальную прямую до пересечения с действительной длиной ребра SE или SB. Отрезок s»6 0 ″ (см. рис. 180).
Полученные точки 1 1 2 1 , 3 1 , и т.д. соединяют прямыми и пристраивают фигуры основания и сечения, пользуясь методом триангуляции. Линии сгиба на развертке проводят штрихпунктирной линией с двумя точками.
Построение изометрической проекции усеченной пирамиды начинают с построения изометрической проекции основания пирамиды по размерам, взятым с горизонтальной проекции комплексного чертежа. Затем на плоскости основания по координатам точек 1…6 строят горизонтальную проекцию сечения (см. тонкие синие линии на рис. 180, а, в). Из вершин полученного шестиугольника проводят вертикальные прямые, на которых откладывают координаты, взятые с фронтальной или профильной проекций призмы, например, отрезки К { , К 2 , К 3 и т.д. Полученные точки 1…6 соединяем, получаем фигуру сечения. Соединив точки 1…6 с вершинами шестиугольника, основания пирамиды, получим изометрическую проекцию усеченной пирамиды. Невидимые ребра изображают штриховыми линиями.
Невидимые ребра изображают штриховыми линиями.
Пример сечения треугольной неправильной пирамиды фронтально-проецирующей плоскостью показан на рис. 181.
Все ребра на трех плоскостях проекций изображены с искажением. Горизонтальная проекция
основания представляет собой его действительный вид, так как основание пирамиды расположено на плоскости Н .
Действительный вид 1 0 , 2 0 , 3 0 фигуры сечения получен способом перемены плоскостей проекций. В данном примере горизонтальная плоскость проекций Н заменена новой плоскостью, которая параллельна плоскости Р; новая ось х 1 совмещена со следом Р V (рис. 181, а).
Развертку поверхности пирамиды строят следующим образом. Способом вращения находят действительную длину ребер пирамиды и их отрезков от основания до секущей плоскости Р.
Например, действительные длины ребра SC иего отрезка СЗ равны соответственно длине фронтальной проекции s»c» ребра и отрезка c 1 ′3 1 после поворота.
Затем строят развертку треугольной неправильной пирамиды (рис. 181, в). Для этого из произвольной точки S проводят прямую, на кот, откладывают действительную длину ребра SA. Из точки s делают засечку радиусом R 1 , равным действительной длине ребра SB, а из точки засечку радиусом R 2 , равным стороне основания пирамиды АВ, в результате чего получают точку b 1 и грань s 1 b 1 a 1 . Затем из точек s и b 1 как из центров, делают засечки радиусами, равными действительной длине ребра SC и стороне ВС получают грань s 1 b 1 с 1 пирамиды. Также строится грань s 1 с 1 a 1 .
От точек а 1 b 1 и с 1 откладывают действительные длины отрезков ребер, которые берут на фронтальной проекции (отрезки а 1 ′1 1 ′, b 1 ′2 1 ′,с 1 ′3 1 ′ ). Используя метод триангуляции, пристраивают основание и фигуру сечения.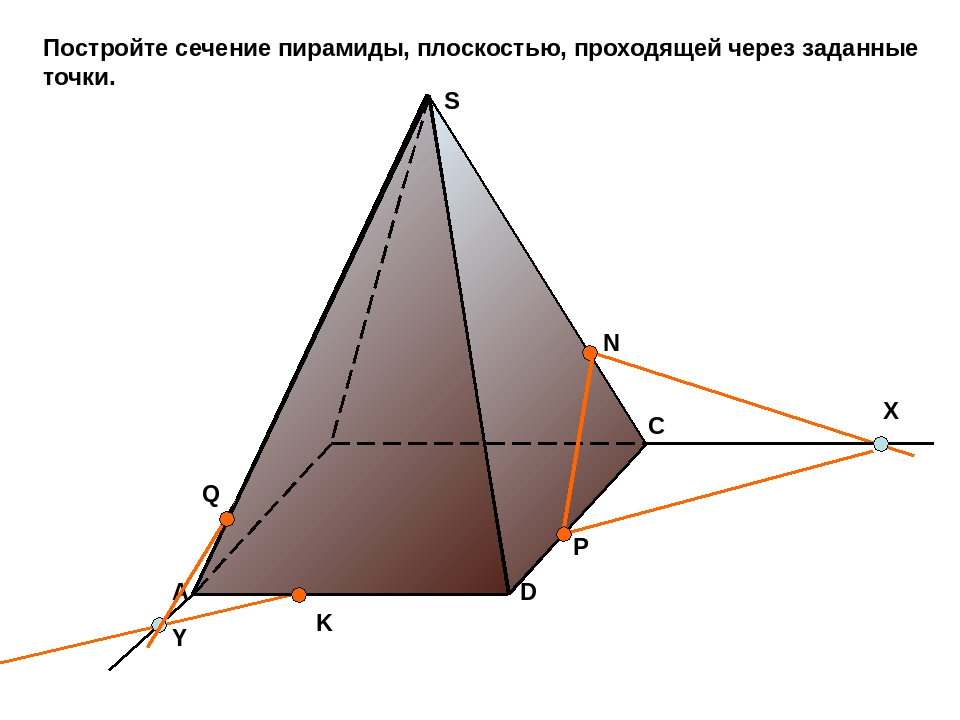
Для построения изометрической проекции усеченной пирамиды (рис. 181, б) проводят изометрическую ось х. По координатам т и п строят основание пирамиды ABC. Сторона основания АС параллельна оси х или совпадает с осью х. Как и в предыдущем примере, строят изометрическую проекцию горизонтальной проекции фигуры сечения 1 2 2 2 3 2 (используя точки I, III и IV). Из этих точек проводят вертикальные прямые, на которых откладывают отрезки, взятые с фронтальной или профильной проекции призмы К 1 , К 2 и К 3 . Полученные точки 1 , 2, 3 соединяют прямыми между собой и с вершинами основания.
Определение. Боковая грань — это треугольник, у которого один угол лежит в вершине пирамиды, а противоположная ему сторона совпадает со стороной основания (многоугольника).
Определение. Боковые ребра — это общие стороны боковых граней. У пирамиды столько ребер сколько углов у многоугольника.
Определение. Высота пирамиды — это перпендикуляр, опущенный из вершины на основание пирамиды.
Определение. Апофема — это перпендикуляр боковой грани пирамиды, опущенный из вершины пирамиды к стороне основания.
Определение. Диагональное сечение — это сечение пирамиды плоскостью, проходящей через вершину пирамиды и диагональ основания.
Определение. Правильная пирамида — это пирамида, в которой основой является правильный многоугольник, а высота опускается в центр основания.
Объём и площадь поверхности пирамиды
Формула. Объём пирамиды через площадь основы и высоту:
Свойства пирамиды
Если все боковые ребра равны, то вокруг основания пирамиды можно описать окружность, а центр основания совпадает с центром окружности. Также перпендикуляр, опущенный из вершины, проходит через центр основания (круга).
Если все боковые ребра равны, то они наклонены к плоскости основания под одинаковыми углами.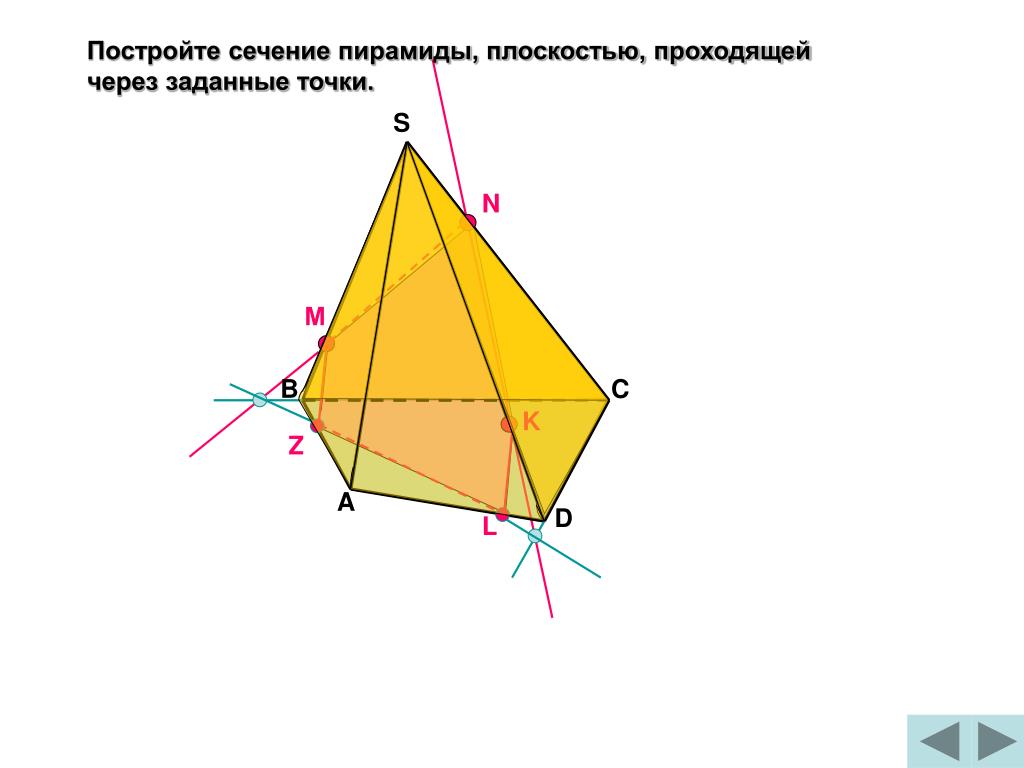
Боковые ребра равны тогда, когда они образуют с плоскостью основания равные углы или если вокруг основания пирамиды можно описать окружность.
Если боковые грани наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, а вершина пирамиды проектируется в ее центр.
Если боковые грани наклонены к плоскости основания под одним углом, то апофемы боковых граней равны.
Свойства правильной пирамиды
1. Вершина пирамиды равноудалена от всех углов основания.
2. Все боковые ребра равны.
3. Все боковые ребра наклонены под одинаковыми углами к основанию.
4. Апофемы всех боковых граней равны.
5. Площади всех боковых граней равны.
6. Все грани имеют одинаковые двугранные (плоские) углы.
7. Вокруг пирамиды можно описать сферу. Центром описанной сферы будет точка пересечения перпендикуляров, которые проходят через середину ребер.
8. В пирамиду можно вписать сферу. Центром вписанной сферы будет точка пересечения биссектрис, исходящие из угла между ребром и основанием.
9. Если центр вписанной сферы совпадает с центром описанной сферы, то сумма плоских углов при вершине равна π или наоборот, один угол равен π/n , где n — это количество углов в основании пирамиды.
Связь пирамиды со сферой
Вокруг пирамиды можно описать сферу тогда, когда в основании пирамиды лежит многогранник вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы будет точка пересечения плоскостей, проходящих перпендикулярно через середины боковых ребер пирамиды.
Вокруг любой треугольной или правильной пирамиды всегда можно описать сферу.
В пирамиду можно вписать сферу, если биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.
Связь пирамиды с конусом
Конус называется вписанным в пирамиду, если их вершины совпадают, а основание конуса вписано в основание пирамиды.
Конус можно вписать в пирамиду, если апофемы пирамиды равны между собой.
Конус называется описанным вокруг пирамиды, если их вершины совпадают, а основание конуса описана вокруг основания пирамиды.
Конус можно описать вокруг пирамиды если, все боковые ребра пирамиды равны между собой.
Связь пирамиды с цилиндром
Пирамида называется вписанной в цилиндр, если вершина пирамиды лежит на одной основе цилиндра, а основание пирамиды вписано в другую основу цилиндра.
Цилиндр можно описать вокруг пирамиды если вокруг основания пирамиды можно описать окружность.
Определение. Усеченная пирамида (пирамидальная призма) — это многогранник, который находится между основанием пирамиды и плоскостью сечения, параллельной основанию. Таким образом пирамида имеет большую основу и меньшую основу, которая подобна большей. Боковые грани представляют собой трапеции. Определение. Треугольная пирамида (четырехгранник) — это пирамида в которой три грани и основание являются произвольными треугольниками.В четырехгранник четыре грани и четыре вершины и шесть ребер, где любые два ребра не имеют общих вершин но не соприкасаются.
Каждая вершина состоит из трех граней и ребер, которые образуют трехгранный угол .
Отрезок, соединяющий вершину четырехгранника с центром противоположной грани называется медианой четырехгранника (GM).
Бимедианой называется отрезок, соединяющий середины противоположных ребер, которые не соприкасаются (KL).
Все бимедианы и медианы четырехгранника пересекаются в одной точке (S). При этом бимедианы делятся пополам, а медианы в отношении 3:1 начиная с вершины.
Определение. Наклонная пирамида — это пирамида в которой одно из ребер образует тупой угол (β) с основанием.Определение. Прямоугольная пирамида — это пирамида в которой одна из боковых граней перпендикулярна к основанию.Определение. Остроугольная пирамида — это пирамида в которой апофема больше половины длины стороны основания.
Определение. Тупоугольная пирамида — это пирамида в которой апофема меньше половины длины стороны основания.
Определение. Правильный тетраэдр — четырехгранник у которого все четыре грани — равносторонние треугольники. Он является одним из пяти правильных многоугольников. В правильного тетраэдра все двугранные углы (между гранями) и трехгранные углы (при вершине) равны.
Определение. Прямоугольный тетраэдр называется четырехгранник у которого прямой угол между тремя ребрами при вершине (ребра перпендикулярны). Три грани образуют прямоугольный трехгранный угол и грани являются прямоугольными треугольниками, а основа произвольным треугольником. Апофема любой грани равна половине стороны основы, на которую падает апофема.
Определение. Равногранный тетраэдр называется четырехгранник у которого боковые грани равны между собой, а основание — правильный треугольник. У такого тетраэдра грани это равнобедренные треугольники.
Определение. Ортоцентричный тетраэдр называется четырехгранник у которого все высоты (перпендикуляры), что опущены с вершины до противоположной грани, пересекаются в одной точке.
Определение. Звездная пирамида называется многогранник у которого основой является звезда.
Определение. Бипирамида — многогранник, состоящий из двух различных пирамид (также могут быть срезаны пирамиды), имеющих общую основу, а вершины лежат по разные стороны от плоскости основания.Построить сечение плоскостью проходящей через точки. Построение сечений многогранника на примере призмы
Преподаватель математики Щелковского филиала ГБПОУ МО «Красногорский колледж» Артемьев Василий Ильич.
Изучение темы «Решение задач на построение сечений» начинается в 10 классе или на первом курсе учреждений НПО. В случае, если кабинет математики оснащен средствами мультимедиа, то решение проблемы изучения облегчается с помощью различных программ. Одной из таких программ является программное обеспечение динамической математики GeoGebra 4.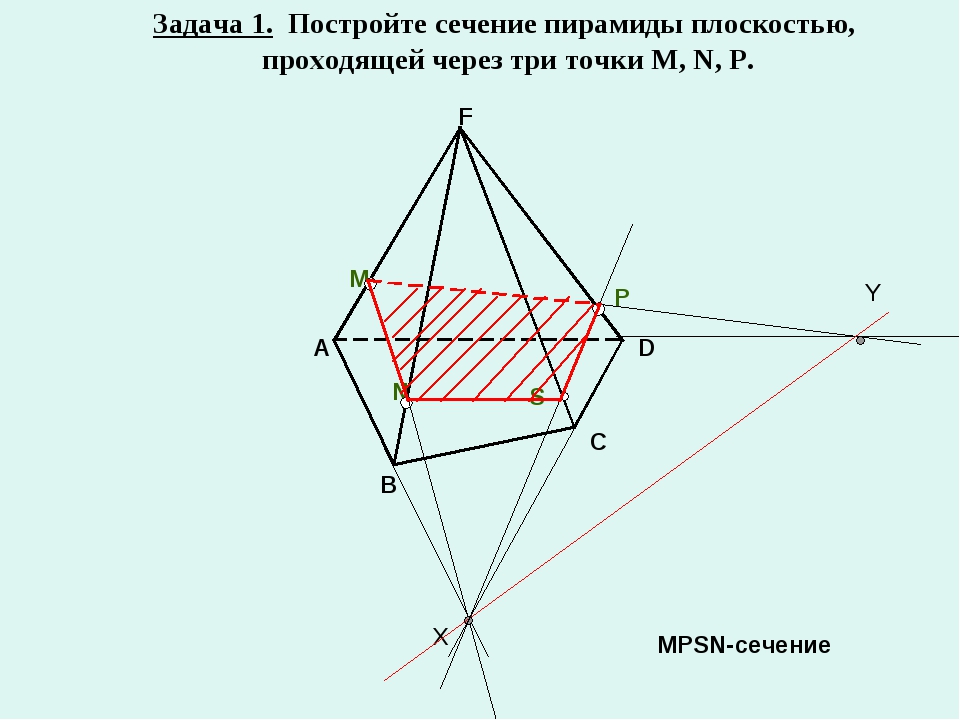 0.12. Она подходит для изучения и обучения на любом из этапов образования, облегчает создание математических построений и моделей обучающимися, которые позволяют проводить интерактивные исследования при перемещении объектов и изменение параметров.
0.12. Она подходит для изучения и обучения на любом из этапов образования, облегчает создание математических построений и моделей обучающимися, которые позволяют проводить интерактивные исследования при перемещении объектов и изменение параметров.
Рассмотрим применение этого программного продукта на конкретном примере.
Задача. Построить сечение пирамиды плоскостью PQR, если точка P лежит на прямой SA, точка Q лежит на прямой SB, точка R лежит на прямой SC.
Решение. Рассмотрим два случая. Случай 1. Пусть точка P принадлежит ребру SA.
1. Отметим с помощью инструмента «Точка» произвольные точки A, B, C, D. Щелкнем правой клавишей на точку D, выберем «Переименовать». Переименуем D на S и установим положение этой точки, как показано на рисунке 1.
2. С помощью инструмента «Отрезок по двум точкам» построим отрезки SA, SB, SC, AB, AC, BC.
3. Щелкнем правой клавишей мыши по отрезку AB и выбираем «Свойства» — «Стиль». Устанавливаем пунктирную линию.
4. Отметим на отрезках SA, SB, CS точки P, Q, R.
5. Инструментом «Прямая по двум точкам» построим прямую PQ.
6. Рассмотрим прямую PQ и точку R. Вопрос учащимся: Сколько плоскостей проходит через прямую PQ и точку R? Ответ обоснуйте. (Ответ. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна).
7. Строим прямые PR и QR.
8. Выбираем инструмент «Многоугольник» и по очереди щелкнем по точкам PQRP.
9. Инструментом « Перемещать» меняем положение точек и наблюдаем за изменениями сечения.
Рисунок 1.
10. Щелкнем по многоугольнику правой клавишей и выбираем «Свойства» — «Цвет». Заливаем многоугольник каким-нибудь нежным цветом.
11. На панели объектов щелкнем по маркерам и скроем прямые.
12. В качестве дополнительного задания можно измерить площадь сечения.
Для этого выберем инструмент «Площадь» и щелкнем левой клавишей мыши по многоугольнику.
Случай 2. Точка P лежит на прямой SA. Для рассмотрения решения задачи для этого случая можно пользоваться чертежом прежней задачи.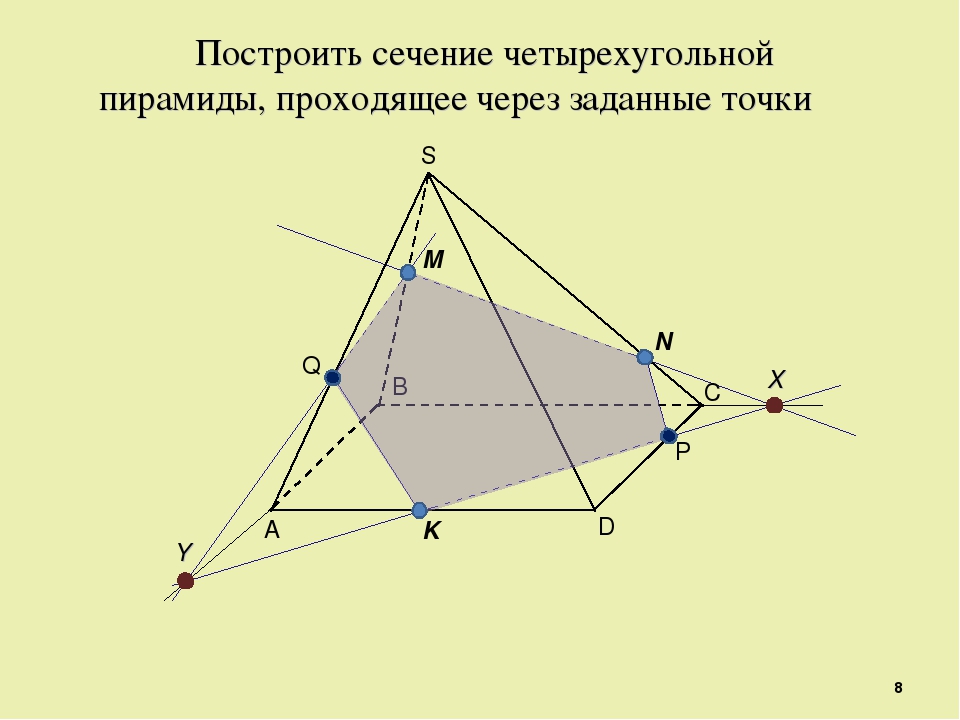 Скроем лишь многоугольник и точку Р.
Скроем лишь многоугольник и точку Р.
1. Инструментом «Прямая по двум точкам» построим прямую SA.
2. Отметим на прямой SA точку P1, как показано на рисунке 2.
3. Проведем прямую P1Q.
4. Выбираем инструмент «Пересечение двух объектов» , и щелкнем левой клавишей мыши по прямым АВ и P1Q. Найдем точку их пересечения К.
5. Проведем прямую P1R. Найдем точку пересечения М этой прямой с прямой АС.
Вопрос учащимся: сколько плоскостей можно провести через прямые P1Q и P1R? Ответ обоснуйте. (Ответ. Через две пересекающиеся прямые проходит плоскость, и притом только одна).
6. Проведем прямые КМ и QR. Вопрос учащимся. Каким плоскостям одновременно принадлежат точки К, М? Пересечением каких плоскостей является прямая КМ?
7. Построим многоугольник QRKMQ. Зальем нежным цветом и скроем вспомогательные прямые.
Рисунок 2.
С помощью инструмента «Перемещение» двигаем точку вдоль прямой AS.Рассматриваем различные положения плоскости сечения.
Задания для построения сечений:
1. Построить сечение, определяемое параллельными прямыми АА1 и СС1. Сколько плоскостей проходит через параллельные прямые?
2. Построить сечение проходящее через пересекающиеся прямые. Сколько плоскостей проходит через пересекающиеся прямые?
3. Построение сечений с использованием свойств параллельных плоскостей:
а) Построить сечение параллелепипеда плоскостью, проходящей через точку М и прямую АС.
б) Построить сечение призмы плоскостью, проходящей через ребро АВ и середину ребра В1С1.
в) Построить сечение пирамиды плоскостью, проходящей через точку К и параллельно плоскости основаниям пирамиды.
4. Построение сечений методом следов:
а) Дана пирамида SABCD. Построить сечение пирамиды плоскостью, проходящей через точки P, Q и R.
5) Проведем прямую QF и найдем точку Н пересечения с ребром SB.
6) Проведем прямые HR и PG.
7) Выделим инструментом «Многоугольник» полученное сечение и изменим цвет заливки.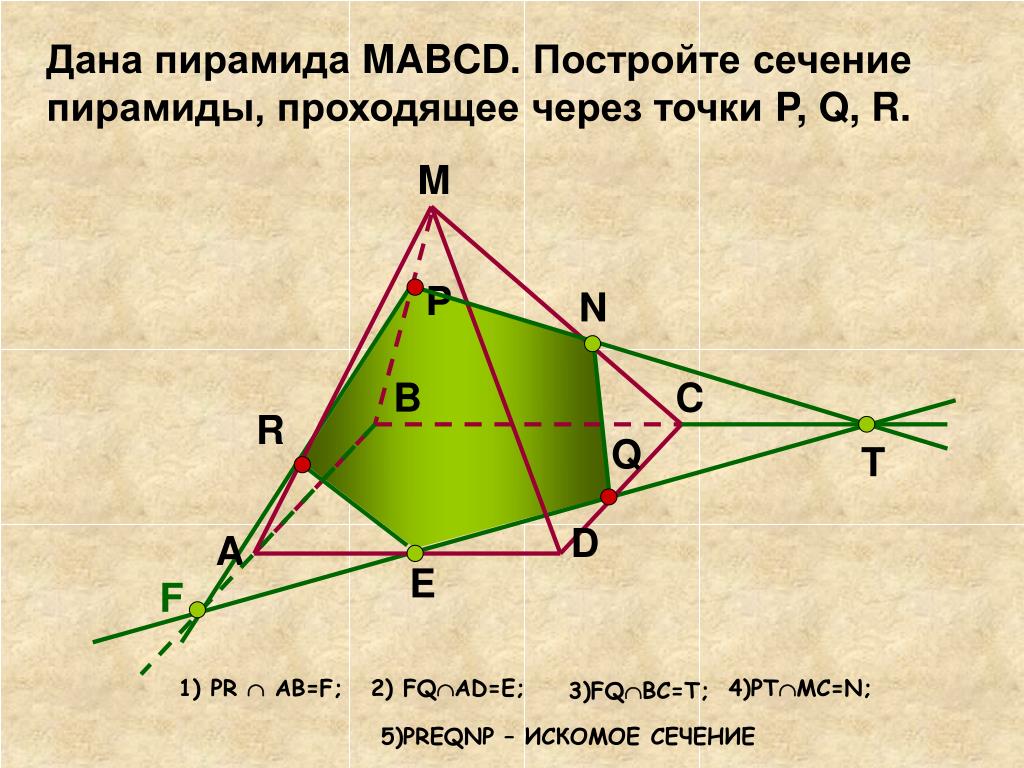
б) Самостоятельно постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через точки P, K и M. Список источников.
1. Электронный ресурс http://www.geogebra.com/indexcf.php
2. Электронный ресурс http://geogebra.ru/www/index.php (Сайт Сибирского института GeoGebra)
3. Электронный ресурс http://cdn.scipeople.com/materials/16093/projective_geometry_geogebra.PDF
4. Электронный ресурс. http://nesmel.jimdo.com/geogebra-rus/
5. Электронный ресурс http://forum.sosna24k.ru/viewforum.php?f=35&sid=(Форум GeoGebra для учителей и школьников).
6. Электронный ресурс www.geogebratube.org (Интерактивные материалы по работе с программой)
Практическое занятие: «Параллелепипед. Построение сечений параллелепипеда ».
1. Цель практической работы : . Закрепить знания теоретического материала о многогранниках, навыки решения задач на построение сечений, умения анализировать чертеж.
2.Дидактическое оснащение практической работы : АРМ, модели и развёртки многогранников, измерительные инструменты, ножницы, клей, плотная бумага.
Время:2 часа
Задания к работе:
Задание 1
Построить сечение параллелепипеда ABCDA 1 B 1 C 1 D 1 плоскостью, проходящей через точки M, N, P, лежащие, на прямых, соответственно, A 1 B 1, А D , DC
Образец и последовательность решения задачи:
1.Точки N и P лежат в плоскости сечения и в плоскости нижнего основания параллелепипеда. Построим прямую, проходящую через эти точки. Эта прямая является следом секущей плоскости на плоскость основания параллелепипеда.
2.Продолжим прямую, на которой лежит сторона AB параллелепипеда. Прямые AB и NP пересекутся в некоторой точке S. Эта точка принадлежит плоскости сечения.
3.Так как точка M также принадлежит плоскости сечения и пересекает прямую АА
1 в некоторой точке Х.
4.Точки X и N лежат в одной плоскости грани АА 1 D 1 D, соединим их и получим прямую XN.
5.Так как плоскости граней параллелепипеда параллельны, то через точку M можно провести прямую в грани A 1 B 1 C 1 D 1 , параллельную прямой NP. Эта прямая пересечет сторону В 1 С 1 в точке Y.
6.Аналогично проводим прямую YZ, параллельно прямой XN. Соединяем Z с P и получаем искомое сечение – MYZPNX.
Задание 2
Вариант1. Построить сечение параллелепипеда АВСDА1В1С1D1 плоскостью, заданной следующими точками M , N и P
1 Уровень: Все три точки лежит на рёбрах, выходящих из вершиныА
2 Уровень. M лежит в грани AA1D1D, N лежит в грани АА1В1В, P лежит в грани СС1D1D.
3 Уровень. M лежит на диагонали B1D, N лежит на диагонали АС1, P лежит на ребре С1D1.
Вариант2. Построить сечение параллелепипеда АВСDА1В1С1D1 плоскостью, проходящей через прямую DQ, где точка Q лежит на ребре СС1 и точку Р, заданную следующим образом
1 Уровень: Все три точки лежит на рёбрах, выходящих из вершиныС
2 Уровень: М лежит на продолжении ребра А1В1, причем точка А1 находится между точками В1 и Р.
3 Уровень: Р лежит на диагонали В1D
Порядок выполнения работы:
1.Изучите теоретический материал по темам:
Параллелепипед.
Прямой параллелепипед.
Наклонный параллелепипед.
Противолежащие грани параллелепипеда.
Свойства диагоналей параллелепипеда.
П онятие секущей плоскости и правила её построения.
Какие виды многоугольников получаются в сечении куба и параллелепипеда.
2. Постройте параллелепипед ABCDA 1 B 1 C 1 D 1
3.Разберите решение задачи № 1
4.Последовательно постройте сечение параллелепипеда ABCDA 1 B 1 C 1 D 1 плоскостью, проходящей через точки P, Q, R задачи № 1.
5.Постройте ещё три параллелепипеда и выделите на них сечения к задачам 1, 2, и 3 уровней
Критерии оценивания :
Литература: Атанасян Л. С. Геометрия: Учебник для 10-11 кл. общеобразоват. учреждений. Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кодомцев и др. — М.: Просвещение, 2010г Зив Б.Г. Задачи по геометрии: Пособие для учащихся 7-11 кл. общеобразоват. учреждений. / Б.Г. Зив, В.М. Мейлер, А.Г. Баханский. — М.: Просвещение, 2010. В. Н. ЛитвиненкоЗадачи на развитие пространственных представлений. Книга для учителя. — М.: Просвещение, 2010г
С. Геометрия: Учебник для 10-11 кл. общеобразоват. учреждений. Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кодомцев и др. — М.: Просвещение, 2010г Зив Б.Г. Задачи по геометрии: Пособие для учащихся 7-11 кл. общеобразоват. учреждений. / Б.Г. Зив, В.М. Мейлер, А.Г. Баханский. — М.: Просвещение, 2010. В. Н. ЛитвиненкоЗадачи на развитие пространственных представлений. Книга для учителя. — М.: Просвещение, 2010г
Дидактический материал к заданию практического занятия
К задаче № 1:
Некоторые возможные сечения:
Построить сечения параллелепипеда плоскостью, проходящей через данные точки
В предыдущих задачах для построения сечения нам
оказалось достаточно знаний теории.
Рассмотрим другую задачу.
Задача 1. Построить сечение тетраэдра, проходящее через
точку М, параллельно плоскости ABD.
M
Одна точка нам ничем не
поможет, но в задаче есть
дополнительное условие:
сечение должно быть
параллельно плоскости
ABD.
Что это нам дает?
1. Плоскости ADB и DBC пересекаются по прямой DB,
следовательно сечение, параллельное ADB, пересекает DBC по
(Если две параллельные
прямой, параллельной DB.
плоскости пересечены третьей,
то линии пересечения
параллельны)
M
Точка М принадлежит грани
DBC. Проведем через нее
N
прямую MK, параллельную DB.
2. Аналогично: (ADB) (ABC)=AB,
K
следовательно сечение будет
пересекать (ABC) по прямой,
параллельной AB.
K (ABC). Через точку K в плоскости ABC проведет прямую KN,
параллельную AB.
M
N
K
N (ADC), M (ADC),
следовательно MN (ADC) (и
плоскости сечения).
Проведем NM.
MKN – искомое сечение.
Итак:
M
N
1. Построение:
1. В плоскости (DBC) MK // DB,
MK BC = K.
2. В плоскости (ABC) KN // AB,
KN AC = N.
3. MN
Докажем, что MKN – искомое сечение
K
2. Доказательство.
1. Сечение проходит через точку М
2. N (ADC), M (ADC) => NM (ADC)
3. MK // DB, NK // AB по построению, следовательно
(NMK) // (ABD) по признаку.
Следовательно, MKN – искомое сечение
ч.т.д.
Задача 2. Постройте сечение параллелепипеда
ABCDA1B1C1D1, проходящее через середину ребра D1C1 и
точку D, параллельно прямой a.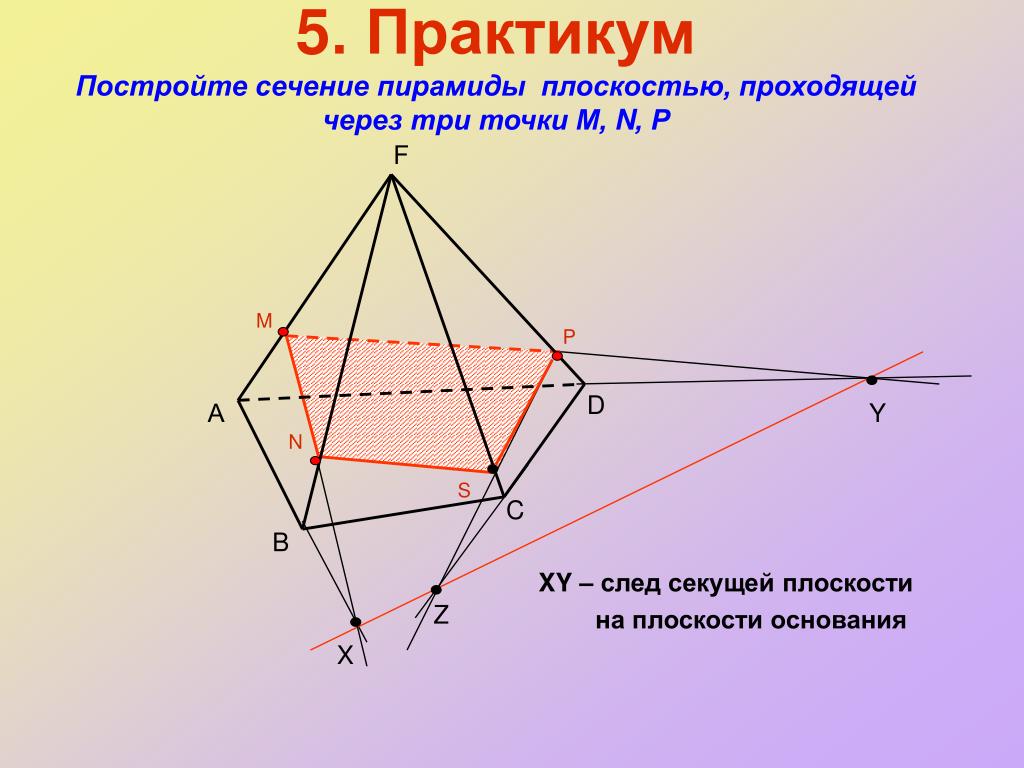 B1
C1
Рассуждения.
M
A1
D1
B
A
C
D
1. Отметим указанную в
условии точку (назовем ее
произвольным образом).
M – середина D1C1.
2. Точки M и D лежат
B1
C1
M
A1
A
значит их можно соединить.
D1
B
C
D
в одной плоскости DD1C1,
Больше соединять нечего.
3. Воспользуемся дополнительным условием: секущая
плоскость должна быть параллельна прямой a.
B1
C1
M
A1
B
C
S
A
Для этого она должна
содержать прямую,
параллельную прямой a.
Проще всего провести
такую прямую в плоскости
ABC, т.к. в ней лежат
прямая a и точка D,
принадлежащая сечению.
D
Проведем в плоскости ABC
через точку D прямую DS,
параллельную прямой a.
DS AB = S.
4. Т.к. (ABC) // (A1B1C1), проведем в плоскости
(A1B1C1), через точку M, прямую MP // SD.
MP B1C1 = P
5. Т.к. (DD1C1) // (AA1B1), то в
P
B
C
плоскости (AA1B1) можно
через точку S провести прямую
M
N
A
D
SN, параллельную DM.
SN BB1 = N
1
1
1
1
B
C
S
A
D
6. Точки N и P лежат в
плоскости (A1B1C1).
Соединим их.
SNPMD — искомое сечение.
Итак:
1. Построение.
1. MD
B1
A1
N
P
C1
S
A
M
3. В (A1B1C1), через точку
M, MP // DS, MP B1C1 = P
C
4. В плоскости (AA1B1),
через точку S, SN // DM,
SN BB1 = N
5. NP
D1
B
D
2. В (ABC), через точку D,
DS // a, DS AB = S
Докажем, что SNPMD искомое сечение.
2. Доказательство.
B1
A1
N
1. Сечение проходит через точку D и
середину ребра D1C1 — точку M по
построению.
P
C1
M
C
S
A
3. PM // SD, P B1C1 по
построению
D1
B
D
2. DS // a, (S AB) по построению,
следовательно (KNP) // a по
признаку.
4. SN // DM, N BB1 по
построению
5. P (BB1C1), N (BB1C1)
=> PN (BB1C1).
Следовательно, SNPMD искомое сечение ч.т.д.
Задача 3. Построить сечение параллелепипеда, параллельное
B1A и проходящее через точки M и N.
Рассуждения. 1. Соединим M и N (они лежат в плоскости (C1A1B1)).
B1
N
M
A1
D1
B
A
C1
C
D
Больше соединять нечего.
Воспользуемся дополнительным
условием: секущая плоскость должна
быть параллельна прямой B1A
2. Для того, чтобы секущая плоскость
оказалась параллельна AB1, нужно,
чтобы в ней лежала прямая,
параллельная AB1 (или DC1, т.к.
DC
// AB1 по свойству параллелепипеда).
B1
C1
Рассуждения.
M
A1
D1
B
A
C
D
1. Отметим указанную в
условии точку (назовем ее
произвольным образом).
M – середина D1C1.
2. Точки M и D лежат
B1
C1
M
A1
A
значит их можно соединить.
D1
B
C
D
в одной плоскости DD1C1,
Больше соединять нечего.
3. Воспользуемся дополнительным условием: секущая
плоскость должна быть параллельна прямой a.
B1
C1
M
A1
B
C
S
A
Для этого она должна
содержать прямую,
параллельную прямой a.
Проще всего провести
такую прямую в плоскости
ABC, т.к. в ней лежат
прямая a и точка D,
принадлежащая сечению.
D
Проведем в плоскости ABC
через точку D прямую DS,
параллельную прямой a.
DS AB = S.
4. Т.к. (ABC) // (A1B1C1), проведем в плоскости
(A1B1C1), через точку M, прямую MP // SD.
MP B1C1 = P
5. Т.к. (DD1C1) // (AA1B1), то в
P
B
C
плоскости (AA1B1) можно
через точку S провести прямую
M
N
A
D
SN, параллельную DM.
SN BB1 = N
1
1
1
1
B
C
S
A
D
6. Точки N и P лежат в
плоскости (A1B1C1).
Соединим их.
SNPMD — искомое сечение.
Итак:
1. Построение.
1. MD
B1
A1
N
P
C1
S
A
M
3. В (A1B1C1), через точку
M, MP // DS, MP B1C1 = P
C
4. В плоскости (AA1B1),
через точку S, SN // DM,
SN BB1 = N
5. NP
D1
B
D
2. В (ABC), через точку D,
DS // a, DS AB = S
Докажем, что SNPMD искомое сечение.
2. Доказательство.
B1
A1
N
1. Сечение проходит через точку D и
середину ребра D1C1 — точку M по
построению.
P
C1
M
C
S
A
3. PM // SD, P B1C1 по
построению
D1
B
D
2. DS // a, (S AB) по построению,
следовательно (KNP) // a по
признаку.
4. SN // DM, N BB1 по
построению
5. P (BB1C1), N (BB1C1)
=> PN (BB1C1).
Следовательно, SNPMD искомое сечение ч.т.д.
Задача 3. Построить сечение параллелепипеда, параллельное
B1A и проходящее через точки M и N.
Рассуждения. 1. Соединим M и N (они лежат в плоскости (C1A1B1)).
B1
N
M
A1
D1
B
A
C1
C
D
Больше соединять нечего.
Воспользуемся дополнительным
условием: секущая плоскость должна
быть параллельна прямой B1A
2. Для того, чтобы секущая плоскость
оказалась параллельна AB1, нужно,
чтобы в ней лежала прямая,
параллельная AB1 (или DC1, т.к.
DC
// AB1 по свойству параллелепипеда). Удобнее всего изображать такую прямую в грани DD1C1C, т.к.
(DD1C1) // (AA1B1), а AB1 (AA1B1).
Проведем в плоскости (DD1C1) прямую NK // AB1,
NK DD1 = K.
B1
N
M
A1
D1
B
3. Теперь в плоскости AA1D1
есть две точки, M и K,
принадлежащие сечению.
Соединим их.
C
K
A
C1
D
MNK – искомое сечение.
Итак:
1. Построение.
1. MN
2. В плоскости (DD1C1) NK // AB1,
NK DD1 = K. .
B1
N
A1
A
M
D1
C1
3. MK
Докажем, что MNK – искомое сечение
2. Доказательство.
B
C
1. Сечение проходит через точки M и N.
K
2. M (A1B1C1), N (A1B1C1) =>
D
MN (A1B1C1).
3. M (ADD1), K (ADD1) => MK (ADD1).
4. Т.к. NK // AB1 по построению, то (MNK) // AB1 по
признаку параллельности прямой и плоскости.
Следовательно, MNK — искомое сечение ч.т.д.
Задание 3.
1. В тетраэдре DABC постройте сечение плоскостью, проходящей
через середину ребра DC, вершину B и параллельной прямой AC.
2. Постройте сечение параллелепипеда плоскостью, проходящей
через середину ребра B1C1 и точку K, лежащую на ребре CD,
параллельной прямой BD, если DK: KC = 1: 3.
M
3. Построить сечение тетраэдра
плоскостью, проходящей через
точки M и C, параллельно
прямой a (рис. 1).
рис.1
4. В параллелепипеде ABCDA1B1C1D1 точка E принадлежит
ребру CD. Постройте сечение параллелепипеда плоскостью,
проходящей через эту точку и параллельной плоскости
BC1D.
5. Постройте сечение параллелепипеда плоскостью,
проходящей через AA1, параллельно MN, где M – середина
AB, N – середина BC.
6. Постройте сечение параллелепипеда плоскостью,
проходящей через середину ребра B1C1 параллельно
плоскости AA1C1.
Удобнее всего изображать такую прямую в грани DD1C1C, т.к.
(DD1C1) // (AA1B1), а AB1 (AA1B1).
Проведем в плоскости (DD1C1) прямую NK // AB1,
NK DD1 = K.
B1
N
M
A1
D1
B
3. Теперь в плоскости AA1D1
есть две точки, M и K,
принадлежащие сечению.
Соединим их.
C
K
A
C1
D
MNK – искомое сечение.
Итак:
1. Построение.
1. MN
2. В плоскости (DD1C1) NK // AB1,
NK DD1 = K. .
B1
N
A1
A
M
D1
C1
3. MK
Докажем, что MNK – искомое сечение
2. Доказательство.
B
C
1. Сечение проходит через точки M и N.
K
2. M (A1B1C1), N (A1B1C1) =>
D
MN (A1B1C1).
3. M (ADD1), K (ADD1) => MK (ADD1).
4. Т.к. NK // AB1 по построению, то (MNK) // AB1 по
признаку параллельности прямой и плоскости.
Следовательно, MNK — искомое сечение ч.т.д.
Задание 3.
1. В тетраэдре DABC постройте сечение плоскостью, проходящей
через середину ребра DC, вершину B и параллельной прямой AC.
2. Постройте сечение параллелепипеда плоскостью, проходящей
через середину ребра B1C1 и точку K, лежащую на ребре CD,
параллельной прямой BD, если DK: KC = 1: 3.
M
3. Построить сечение тетраэдра
плоскостью, проходящей через
точки M и C, параллельно
прямой a (рис. 1).
рис.1
4. В параллелепипеде ABCDA1B1C1D1 точка E принадлежит
ребру CD. Постройте сечение параллелепипеда плоскостью,
проходящей через эту точку и параллельной плоскости
BC1D.
5. Постройте сечение параллелепипеда плоскостью,
проходящей через AA1, параллельно MN, где M – середина
AB, N – середина BC.
6. Постройте сечение параллелепипеда плоскостью,
проходящей через середину ребра B1C1 параллельно
плоскости AA1C1.
Определение
Сечение — это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.
Замечание
Для построения сечений различных пространственных фигур необходимо помнить основные определения и теоремы о параллельности и перпендикулярности прямых и плоскостей, а также свойства пространственных фигур. Напомним основные факты.
Для более подробного изучения рекомендуется ознакомиться с темами “Введение в стереометрию. \circ\)
.
\circ\)
.
Важные аксиомы
1. Через три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
2. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
3. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
Важные теоремы
1. Если прямая \(a\) , не лежащая в плоскости \(\pi\) , параллельна некоторой прямой \(p\) , лежащей в плоскости \(\pi\) , то она параллельна данной плоскости.
2. Пусть прямая \(p\) параллельна плоскости \(\mu\) . Если плоскость \(\pi\) проходит через прямую \(p\) и пересекает плоскость \(\mu\) , то линия пересечения плоскостей \(\pi\) и \(\mu\) — прямая \(m\) — параллельна прямой \(p\) .
3. Если две пересекающиеся прямых из одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости будут параллельны.
4. Если две параллельные плоскости \(\alpha\) и \(\beta\) пересечены третьей плоскостью \(\gamma\) , то линии пересечения плоскостей также параллельны:
\[\alpha\parallel \beta, \ \alpha\cap \gamma=a, \ \beta\cap\gamma=b \Longrightarrow a\parallel b\]
5. Пусть прямая \(l\) лежит в плоскости \(\lambda\) . Если прямая \(s\) пересекает плоскость \(\lambda\) в точке \(S\) , не лежащей на прямой \(l\) , то прямые \(l\) и \(s\) скрещиваются.
6. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости, то она перпендикулярна этой плоскости.
7. Теорема о трех перпендикулярах.
Пусть \(AH\) – перпендикуляр к плоскости \(\beta\) . Пусть \(AB, BH\) – наклонная и ее проекция на плоскость \(\beta\) . Тогда прямая \(x\) в плоскости \(\beta\) будет перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции.
8. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то она перпендикулярна этой плоскости.
Замечание
Еще один важный факт, часто использующийся для построения сечений:
для того, чтобы найти точку пересечения прямой и плоскости, достаточно найти точку пересечения данной прямой и ее проекции на эту плоскость. \circ, \angle E\)
– общий), значит, \[\dfrac{PA}{KC}=\dfrac{EA}{EC}\]
\circ, \angle E\)
– общий), значит, \[\dfrac{PA}{KC}=\dfrac{EA}{EC}\]
Если обозначить ребро куба за \(a\) , то \(PA=\dfrac34a, \ KC=\dfrac15a, \ AC=a\sqrt2\) . Тогда:
\[\dfrac{\frac34a}{\frac15a}=\dfrac{a\sqrt2+EC}{EC} \Rightarrow EC=\dfrac{4\sqrt2}{11}a \Rightarrow AC:EC=4:11\]
Пример 2.
Дана правильная треугольная пирамида \(DABC\) с основанием \(ABC\) , высота которой равна стороне основания. Пусть точка \(M\) делит боковое ребро пирамиды в отношении \(1:4\) , считая от вершины пирамиды, а \(N\) – высоту пирамиды в отношении \(1:2\) , считая от вершины пирамиды. Найдите точку пересечения прямой \(MN\) с плоскостью \(ABC\) .
Решение
1) Пусть \(DM:MA=1:4, \ DN:NO=1:2\)
(см. рисунок). Т.к. пирамида правильная, то высота падает в точку \(O\)
пересечения медиан основания. Найдем проекцию прямой \(MN\)
на плоскость \(ABC\)
. Т.к. \(DO\perp (ABC)\)
, то и \(NO\perp (ABC)\)
. Значит, \(O\)
– точка, принадлежащая этой проекции. Найдем вторую точку. Опустим перпендикуляр \(MQ\)
из точки \(M\)
на плоскость \(ABC\)
. Точка \(Q\)
будет лежать на медиане \(AK\)
.
Действительно, т.к. \(MQ\)
и \(NO\)
перпендикулярны \((ABC)\)
, то они параллельны (значит, лежат в одной плоскости). Следовательно, т.к. точки \(M, N, O\)
лежат в одной плоскости \(ADK\)
, то и точка \(Q\)
будет лежать в этой плоскости. Но еще (по построению) точка \(Q\)
должна лежать в плоскости \(ABC\)
, следовательно, она лежит на линии пересечения этих плоскостей, а это – \(AK\)
.
Значит, прямая \(AK\) и есть проекция прямой \(MN\) на плоскость \(ABC\) . \(L\) – точка пересечения этих прямых.
2) Заметим, что для того, чтобы правильно нарисовать чертеж, необходимо найти точное положение точки \(L\) (например, на нашем чертеже точка \(L\) лежит вне отрезка \(OK\) , хотя она могла бы лежать и внутри него; а как правильно?).
Т.к. по условию сторона основания равна высоте пирамиды, то обозначим \(AB=DO=a\)
. \circ, \ \angle L\)
– общий). Значит,
\circ, \ \angle L\)
– общий). Значит,
\[\dfrac{MQ}{NO}=\dfrac{QL}{OL} \Rightarrow \dfrac{\frac45 a}{\frac 23a} =\dfrac{\frac{7}{10\sqrt3}a+x}{\frac1{2\sqrt3}a+x} \Rightarrow x=\dfrac a{2\sqrt3} \Rightarrow OL=\dfrac a{\sqrt3}\]
Следовательно, \(OL>OK\) , значит, точка \(L\) действительно лежит вне отрезка \(AK\) .
Замечание
Не стоит пугаться, если при решении подобной задачи у вас получится, что длина отрезка отрицательная. Если бы в условиях предыдущей задачи мы получили, что \(x\) – отрицательный, это как раз значило бы, что мы неверно выбрали положение точки \(L\) (то есть, что она находится внутри отрезка \(AK\) ).
Пример 3
Дана правильная четырехугольная пирамида \(SABCD\) . Найдите сечение пирамиды плоскостью \(\alpha\) , проходящей через точку \(C\) и середину ребра \(SA\) и параллельной прямой \(BD\) .
Решение
1) Обозначим середину ребра \(SA\) за \(M\) . Т.к. пирамида правильная, то высота \(SH\) пирамиды падает в точку пересечения диагоналей основания. Рассмотрим плоскость \(SAC\) . Отрезки \(CM\) и \(SH\) лежат в этой плоскости, пусть они пересекаются в точке \(O\) .
Для того, чтобы плоскость \(\alpha\) была параллельна прямой \(BD\) , она должна содержать некоторую прямую, параллельную \(BD\) . Точка \(O\) находится вместе с прямой \(BD\) в одной плоскости – в плоскости \(BSD\) . Проведем в этой плоскости через точку \(O\) прямую \(KP\parallel BD\) (\(K\in SB, P\in SD\) ). Тогда, соединив точки \(C, P, M, K\) , получим сечение пирамиды плоскостью \(\alpha\) .
2) Найдем отношение, в котором делят точки \(K\) и \(P\) ребра \(SB\) и \(SD\) . Таким образом мы полностью определим построенное сечение.
Заметим, что так как \(KP\parallel BD\) , то по теореме Фалеса \(\dfrac{SB}{SK}=\dfrac{SD}{SP}\) . Но \(SB=SD\) , значит и \(SK=SP\) . Таким образом, можно найти только \(SP:PD\) .
Рассмотрим \(\triangle ASC\)
. \(CM, SH\)
– медианы в этом треугольнике, следовательно, точкой пересечения делятся в отношении \(2:1\)
, считая от вершины, то есть \(SO:OH=2:1\)
. \circ\)
, то \(\triangle
ABD=\triangle CBD\)
, следовательно, \(AD=CD\)
, следовательно, \(\triangle DAC\)
– тоже равнобедренный и \(DK\perp AC\)
.
\circ\)
, то \(\triangle
ABD=\triangle CBD\)
, следовательно, \(AD=CD\)
, следовательно, \(\triangle DAC\)
– тоже равнобедренный и \(DK\perp AC\)
.
Применим теорему о трех перпендикулярах: \(BH\) – перпендикуляр на \(DAC\) ; наклонная \(BK\perp AC\) , значит и проекция \(HK\perp AC\) . Но мы уже определили, что \(DK\perp AC\) . Таким образом, точка \(H\) лежит на отрезке \(DK\) .
Соединив точки \(A\) и \(H\) , получим отрезок \(AN\) , по которому плоскость \(\alpha\) пересекается с гранью \(DAC\) . Тогда \(\triangle ABN\) – искомое сечение пирамиды плоскостью \(\alpha\) .
2) Определим точное положение точки \(N\) на ребре \(DC\) .
Обозначим \(AB=CB=DB=x\) . Тогда \(BK\) , как медиана, опущенная из вершины прямого угла в \(\triangle ABC\) , равна \(\frac12 AC\) , следовательно, \(BK=\frac12 \cdot \sqrt2 x\) .
Рассмотрим \(\triangle BKD\) . Найдем отношение \(DH:HK\) .
Заметим, что т.к. \(BH\perp (DAC)\) , то \(BH\) перпендикулярно любой прямой из этой плоскости, значит, \(BH\) – высота в \(\triangle DBK\) . Тогда \(\triangle DBH\sim \triangle DBK\) , следовательно
\[\dfrac{DH}{DB}=\dfrac{DB}{DK} \Rightarrow DH=\dfrac{\sqrt6}3x \Rightarrow HK=\dfrac{\sqrt6}6x \Rightarrow DH:HK=2:1\]
Рассмотрим теперь \(\triangle ADC\) . Медианы треугольника точной пересечения делятся в отношении \(2:1\) , считая от вершины. Значит, \(H\) – точка пересечения медиан в \(\triangle ADC\) (т.к. \(DK\) – медиана). То есть \(AN\) – тоже медиана, значит, \(DN=NC\) .
Задачи на построение сечений многогранников занимают значительное место как школьном курсе геометрии для старших классов, так и на экзаменах разного уровня. Решение этого вида задач способствует усвоению аксиом стереометрии, систематизации знаний и умений, развитию пространственного представления и конструктивных навыков. Общеизвестны трудности, возникающие при решении задач на построение сечений.
С самого раннего детства мы сталкиваемся с сечениями.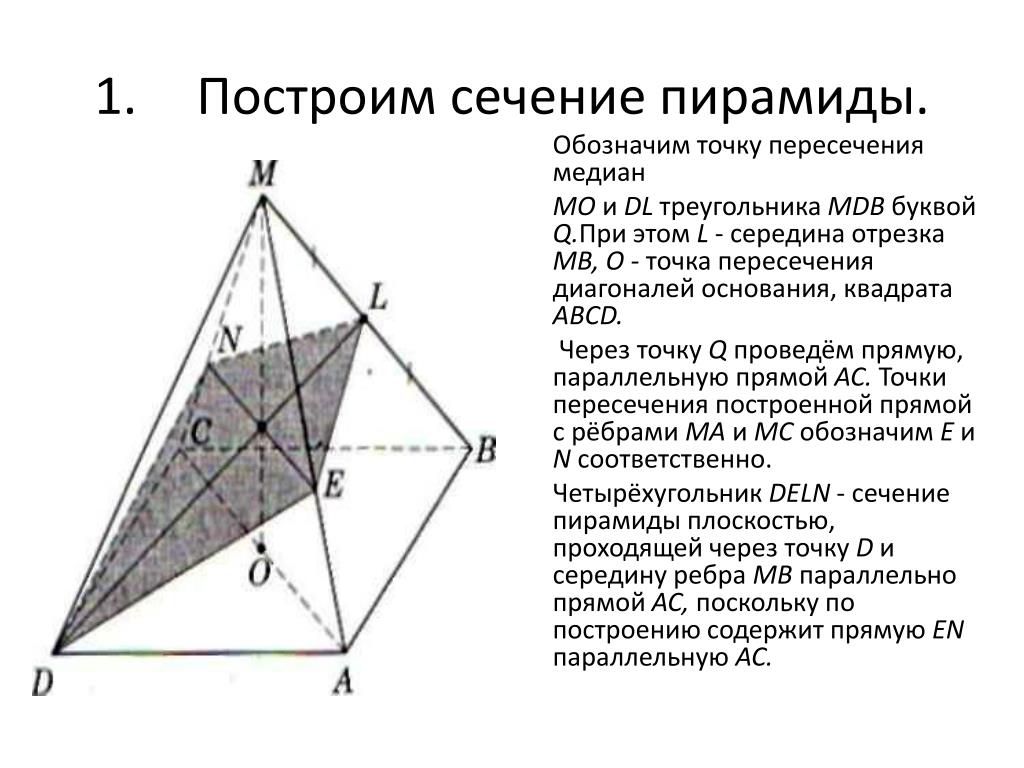 Режем хлеб, колбасу и другие продукты, обстругиваем палочку или карандаш ножом. Секущей плоскостью во всех этих случаях является плоскость ножа. Сечения (срезы кусочков) оказываются различными.
Режем хлеб, колбасу и другие продукты, обстругиваем палочку или карандаш ножом. Секущей плоскостью во всех этих случаях является плоскость ножа. Сечения (срезы кусочков) оказываются различными.
Сечение выпуклого многогранника есть выпуклый многоугольник, вершины которого в общем случае являются точками пересечения секущей плоскости с ребрами многоугольника, а стороны- линиями пересечения секущей плоскости с гранями.
Для построения прямой пересечения двух плоскостей достаточно найти две общие точки этих плоскостей и провести через них прямую. Это основано на следующих утверждениях:
1.если две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости;
2.если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
Как я уже сказал ппостроение сечений многогранников можно осуществлять на основании аксиом стереометрии и теорем о параллельности прямых и плоскостей. Вместе с тем, существуют определенные методы построения плоских сечений многогранников. Наиболее эффективными являются следующие три метода:
Метод следов
Метод внутреннего проектирования
Комбинированный метод.
В изучении геометрии и, в особенности, тех её разделов, где рассматриваются изображения геометрических фигур, изображения геометрических фигур помогают использования компьютерных презентаций. С помощью компьютера многие уроки геометрии становятся более наглядной и динамичной. Аксиомы, теоремы, доказательства, задачи на построения, задачи на построения сечений можно сопровождать последовательными построениями на экране монитора. Сделанные с помощью компьютера чертежи можно сохранять и вставлять их в другие документы.
Хочу показать несколько слайдов по теме: «Построения сечений в геометрических телах»
Для построения точки пересечения прямой и плоскости находят в плоскости прямую, пересекающую данную прямую. Тогда искомая точка является точкой пересечения найденной прямой с данной. Проследим это на следующих слайдах.
Проследим это на следующих слайдах.
Задача 1.
На ребрах тетраэдра DABC отмечены две точки М и N; М GAD, N б DC. Укажите точку пересечения прямой MN с плоскостью основания.
Решение: для того, чтобы найти точку пересечения прямой MN с плоскостью
основания мы продолжим АС и отрезок MN. Отметим точку пересечения этих прямых через X. Точка X принадлежит прямой MN и грани АС, а АС лежит в плоскости основания, значит точка X тоже лежит в плоскости основания. Следовательно, точка X есть точка пересечения прямой MN с плоскостью основания.
Рассмотрим вторую задачу. Немного усложним его.
Задача 2.
Дан тетраэдр DABC точки М и N, где М € DA, N С (DBC). Найти точку пересечения прямой MN с плоскостью ABC .
Решение: точка пересечения прямой MN с плоскостью ABC должна лежать в плоскости, которая содержит прямую MN и в плоскости основания. Продолжим отрезок DN до точки пересечения с ребром DC. Точку пересечения отметим через Е. Продолжим прямую АЕ и MN до точки их пересечения. Отметим X. Точка X принадлежит MN, значит она лежит на плоскости которая содержит прямую MN и X принадлежит АЕ, а АЕ лежит на плоскости ABC. Значит X тоже лежит в плоскости ABC. Следовательно X и есть точка пересечения прямой MN и плоскости ABC.
Усложним задачу. Рассмотрим сечение геометрических фигур плоскостями, проходящими через три данные точки.
Задача 3
На ребрах AC, AD и DB тетраэдра DABC отмечены точки М, N и Р. Построить сечение тетраэдра плоскостью MNP.
Решение: построим прямую, по которой плоскость MNP. Пересекается с плоскостью грани ABC. Точка М является общей точкой этих плоскостей. Для построения ещё одной общей точки продолжим отрезок АВ и NP. Точку пересечения отметим через X, которая и будет второй общей точкой плоскости MNP и ABC. Значит эти плоскости пересекаются по прямой MX . MX пересекает ребро ВС в некоторой точке Е. Так как Е лежит на MX, а MX прямая принадлежащей плоскости MNP, значит РЕ принадлежит MNP. Четырёхугольник MNPE искомое сечение.
Четырёхугольник MNPE искомое сечение.
Задача 4
Построим сечение прямой призмы АВСА1В1С1 плоскостью проходящей через точки P, Q ,R, где R принадлежит (AA 1C 1C ), Р принадлежит В 1С1,
Q принадлежит АВ
Решение: Все три точки P,Q,R лежат в разных гранях, поэтому построить линию пересечения секущей плоскости с какой- либо гранью призмы мы пока не можем. Найдем точку пересечения PR с ABC. Найдем проекции точек Р и R на плоскость основания PP1 перпендикулярно ВС и RR1 перпендикулярна АС. Прямая P1R1 пересекается с прямой PR в точке X. X точка пересечения прямой PR с плоскостью ABC. Она лежит в искомой плоскости К ив плоскости основания, как и точка Q. XQ- прямая пересекающая К с плоскостью основания. XQ пересекает АС в точке К. Следовательно, KQ отрезок пересечения плоскости Х с гранью ABC. К и R лежат в плоскости Х и в плоскости грани АА1С1С. Проведем прямую KR и точку пересечения с A1Q отметим Е. КЕ является линией пересечения плоскости Х с этой гранью. Найдем линию пересечения плоскости Х с плоскостью граней BB1A1A. КЕ пересекается с А1А в точке У. Прямая QY есть линия пересечения секущей плоскости с плоскостью AA1B1B. FPEKQ- искомое сечение.
Наклонное сечение пирамиды | СПЛАЙН
ЦЕЛЬ И ПОСТАНОВКА ЗАДАНИЯ. Чтобы научиться строить наклонное сечение пирамиды, внимательно изучите последовательность построения, а затем сделайте рисунок сечения пирамиды произвольной наклонной плоскостью.
РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ. Рассмотрите ортогональную проекцию наклонного сечения пирамиды на рис. 5.116. Прежде чем приступить к рисунку, постарайтесь представить пирамиду, секущую плоскость и то, как будет выглядеть сечение. Если это пока сложно для вас, попробуйте сначала представить сечение пирамиды горизонтальной плоскостью, а затем наклоните эту плоскость в соответствии с заданным положением. Проанализируйте, как в этом случае изменится квадрат горизонтального сечения.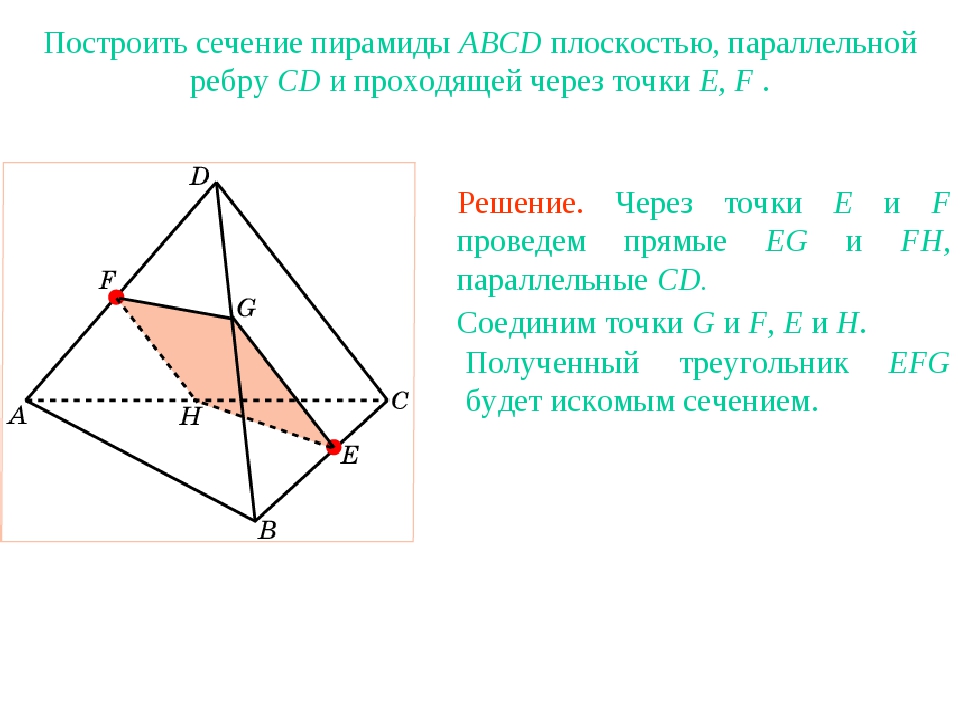 Две его стороны сохранят свое горизонтальное положение, но станут разными по длине. Та, что находится выше и ближе к вершине пирамиды – меньше той, что ближе к основанию. Две другие стороны примут наклонное положение, будут симметричны и равны по длине. Таким образом, в сечении пирамиды наклонной плоскостью получится трапеция. Попробуйте проанализировать, как будут меняться размеры и пропорции этой трапеции при перемещении секущей плоскости вверх и вниз по вертикали, а также при изменении угла ее наклона. Подобные упражнения, несомненно, помогут развить ваше пространственное воображение, а потому рекомендуем проделать их со всеми геометрическими телами.
Две его стороны сохранят свое горизонтальное положение, но станут разными по длине. Та, что находится выше и ближе к вершине пирамиды – меньше той, что ближе к основанию. Две другие стороны примут наклонное положение, будут симметричны и равны по длине. Таким образом, в сечении пирамиды наклонной плоскостью получится трапеция. Попробуйте проанализировать, как будут меняться размеры и пропорции этой трапеции при перемещении секущей плоскости вверх и вниз по вертикали, а также при изменении угла ее наклона. Подобные упражнения, несомненно, помогут развить ваше пространственное воображение, а потому рекомендуем проделать их со всеми геометрическими телами.
Построение наклонного сечения пирамиды выполняется в обычной последовательности, при помощи вспомогательных сечений. Чтобы построить сечение пирамиды наклонной плоскостью (рис. 5.117) достаточно одного вспомогательного сечения. Постройте вспомогательное сечение, перпендикулярное секущей плоскости и проходящее через вертикальную ось пирамиды (рис. 5.118). Проведите линию пересечения вспомогательного сечения с наклонной плоскостью – прямую а (рис. 5.119). Впоследствии эта прямая станет осью симметрии в трапеции сечения. Точки пересечения прямой а со сторонами треугольника вспомогательного сечения (А и В) определят положение горизонтальных сторон сечения. Проведите их через точки А и В, а затем достройте боковые стороны сечения (рис. 5.120).
Наклонное сечение пирамиды
Урок седьмого класса Введение в 3D-фигуры и сечения
Введение в 3D-фигуры и сечения Примечания : Этот урок является введением в 3D-фигуры и будет проводиться в основном учителем. Тем не менее, я буду использовать мнения студентов и предварительные знания при заполнении пустых разделов руководств. Учебная часть урока начнется с заметок о призмах — свойствах правильных призм и названии призм. После заполнения заметок я попрошу студентов назвать призмы, изображенные на заметках / смарт-доске.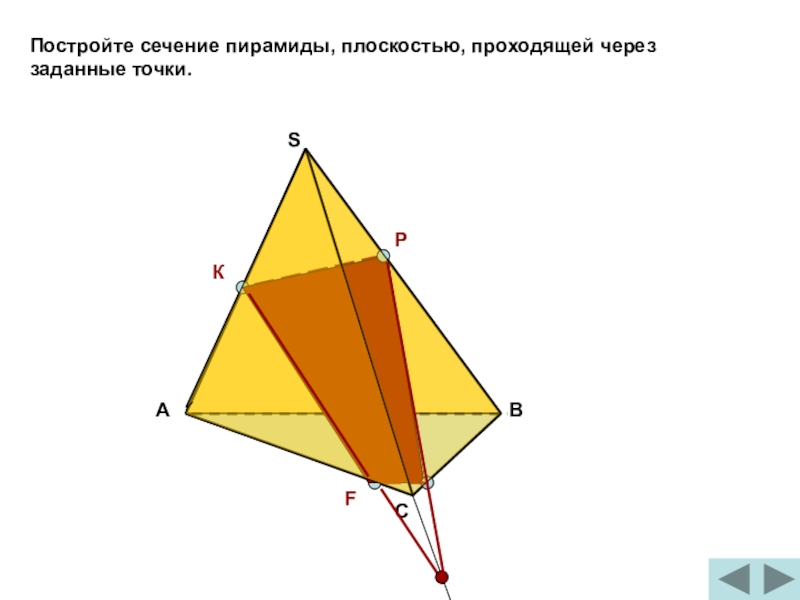 Далее проведу урок рисования! Обидно выполнить задачу со словом без изображения, особенно если вы не можете нарисовать картинку самостоятельно, поэтому я дам студентам урок мини-рисования по рисованию прямоугольных и треугольных призм — умение рисовать фигуры поможет им использовать их математические инструменты позже — искусство! (МП 5) . Далее мы перейдем к пирамидам и завершим примечания о свойствах пирамид и названии пирамид. Опять же, я попрошу учащихся поработать в своих группах таблиц, чтобы правильно назвать пирамиды, отображаемые на заметках / смарт-доске.Затем проведу еще один мини-урок по рисованию пирамид.
Далее проведу урок рисования! Обидно выполнить задачу со словом без изображения, особенно если вы не можете нарисовать картинку самостоятельно, поэтому я дам студентам урок мини-рисования по рисованию прямоугольных и треугольных призм — умение рисовать фигуры поможет им использовать их математические инструменты позже — искусство! (МП 5) . Далее мы перейдем к пирамидам и завершим примечания о свойствах пирамид и названии пирамид. Опять же, я попрошу учащихся поработать в своих группах таблиц, чтобы правильно назвать пирамиды, отображаемые на заметках / смарт-доске.Затем проведу еще один мини-урок по рисованию пирамид.
Задание за столом: Затем учащиеся будут соревноваться в быстром задании за столом, где их просят определить фигуру. Я поместил 6 фигурок на кубик и, используя генератор случайных чисел (на смарт-доске), буду вызывать группы, чтобы идентифицировать фигуру. Группы, ответившие правильно, будут вознаграждены.
Дополнительная инструкция: После испытания таблицы мы перейдем к обсуждению сечений.Поскольку студентам сложно представить себе эту концепцию, я собираюсь использовать сайт Interactivate: Cross Section Flyer, чтобы помочь в нашем обсуждении. Используя полосы прокрутки на веб-сайте, вы можете изменить количество боковых граней, поэтому я буду использовать эту функцию, чтобы настроить пирамиду и призмы, чтобы они имели прямоугольные основания, так как это поперечные сечения, на которых мы сосредоточимся. Используя вопросы в заметках, я скорректирую цифру в апплете и предоставлю столам время для обсуждения их ответов.Затем я попрошу столов ответить, что они видят / думают по поводу вопросов.
Треугольная пирамида — определение, формула и примеры
В этом уроке мы узнаем о типах пирамид, уделяя особое внимание треугольным пирамидам. площадь поверхности треугольной пирамиды, сеть треугольной пирамиды с помощью некоторых решенных примеров, а также несколько сложных и интерактивных вопросов для проверки вашего понимания.
Трехмерная фигура, у которой все грани — треугольники, известна как треугольная пирамида.
Знаете ли вы, что одна из самых старых пирамид, известных человеку, — это «Великая пирамида Гизы»? Он был построен примерно в 2550 году до нашей эры в Египте. Они входят в число семи чудес света.
Это пирамиды, хорошо, но это тоже треугольные пирамиды?
Давайте узнаем!
План урокаЧто такое треугольная пирамида? Краткое описание
Треугольная пирамида — это пирамида с треугольным основанием, ограниченная четырьмя треугольными гранями, где 3 грани пересекаются в одной вершине.
В правильной треугольной пирамиде все грани представляют собой равносторонние треугольники и известны как тетраэдры.
В правой треугольной пирамиде основание представляет собой равносторонний треугольник, а другие грани — равнобедренные треугольники.
В неправильной треугольной пирамиде равнобедренный или равнобедренный треугольник образует основание.
Сетки треугольной пирамидыДавайте займемся небольшим занятием.
Возьмите лист бумаги.
Вы можете увидеть две различные сети треугольной пирамиды, показанной ниже.
Скопируйте это на лист бумаги.
Обрежьте его по краю и сложите, как показано на рисунке ниже.
Сложенная бумага образует треугольную пирамиду.
Моделирование ниже иллюстрирует треугольную пирамиду в 3D.
Щелкните край треугольной пирамиды и перетащите ее.
Вы сможете увидеть все четыре грани по мере его вращения.
Кроме того, вы сможете просматривать сети треугольных пирамид, перемещая ползунок.\ circ \), поскольку они треугольные.
Если треугольная пирамида специально не упомянута как неправильная, все треугольные пирамиды считаются правильными треугольными пирамидами.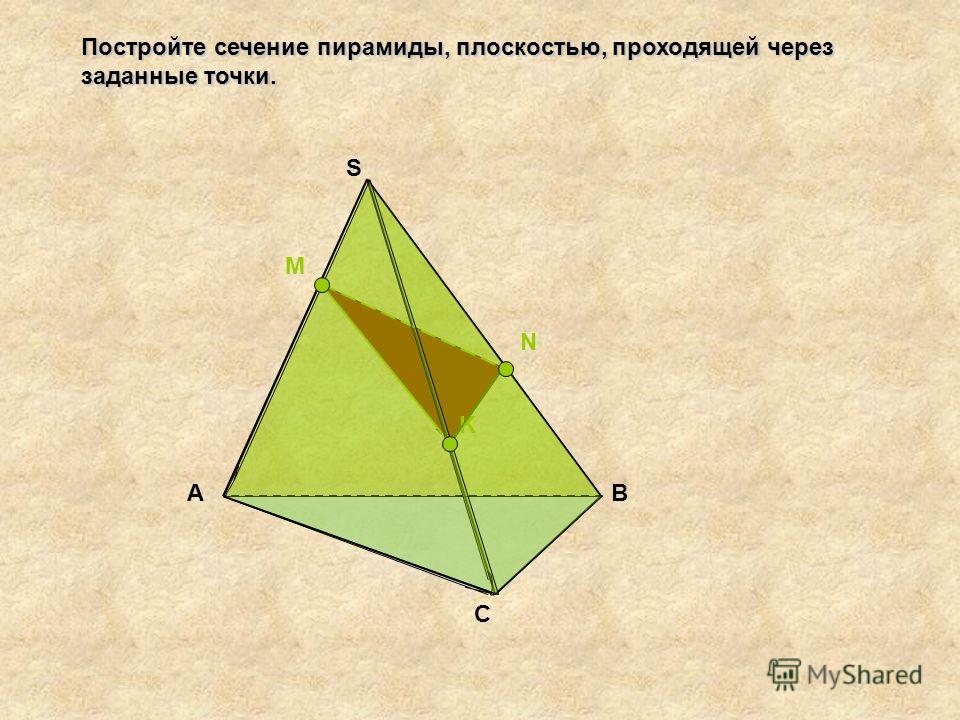
Какие части треугольной пирамиды?
- У него 4 грани, 6 кромок и 4 угла.
- В каждой вершине пересекаются по 3 ребра.
- У треугольной пирамиды нет параллельных граней.
- Правильная треугольная пирамида имеет равносторонние треугольники на всех гранях. Имеет 6 плоскостей симметрии.
- Треугольные пирамиды бывают правильными, неправильными и прямоугольными.
Каковы формулы треугольной пирамиды?
Треугольная пирамида Объем:
| \ (\ begin {align} \ frac {1} {3} \ text {Base Area} \ times \ text {Height} \ end {align} \) |
Площадь поверхности треугольной пирамиды (общая):
| \ (\ begin {align} \ text {Base Area} + \! \ Frac {1} {2} \ text {(Perimeter} \! \ Times \! \ Text {Slant Height}) \ end {align} \) |
Теперь рассмотрим правильную треугольную пирамиду , составленную из равносторонних треугольников со стороной \ (a \) .2 \) Калькулятор треугольной пирамиды Изучите калькулятор треугольной пирамиды ниже, чтобы найти площадь поверхности и объем правильной треугольной пирамиды: Сид узнал, что две треугольные пирамиды совпадают.Он начал наблюдать за их соответствием. В то время как он поместил основания обоих треугольников в положение, чтобы увидеть, перекрываются ли они, две конгруэнтные треугольные пирамиды слиплись вдоль его основания и образовали треугольную бипирамиду. Решая вопросы о треугольной пирамиде, Шрея застрял. Давайте поможем ей прийти к окончательному ответу. Вот вопрос: «Сумма длины ребер правильной треугольной пирамиды составляет 60 единиц. Найдите площадь поверхности одной из ее граней». Решение Мы знаем, что треугольная пирамида имеет 6 граней.2 \ Вы уже знакомы с формулами треугольной пирамиды для определения объема, а также общей площади поверхности. Возможно, вы заметили, что для определения общей площади поверхности и объема необходимо знать край.2} & = 6 \ times \ sqrt {3} \ times \ sqrt {2} \\  2 \\
2 \\
& = \ Sqrt {3} \ times 6 \ times 6 \\
& = 62.35
\ end {align} \] \ (\ следовательно \) Общая площадь поверхности = 62,35 единиц 2
& = \ frac {\ sqrt {3}} {4} \ times 10 \ times 10 \\
& = 25 \ sqrt {3} \\
& = 43,30
\ end {align} \] \ (\ следовательно \) Площадь одной из его граней = 43,30 единиц 2
a & = 6 \ sqrt {6}
\ end {align} \] \ (\ следовательно \) Длина ребра треугольной пирамиды равна \ (6 \ sqrt6 \)
Интерактивные вопросы о треугольной пирамиде
Вот несколько занятий для вас.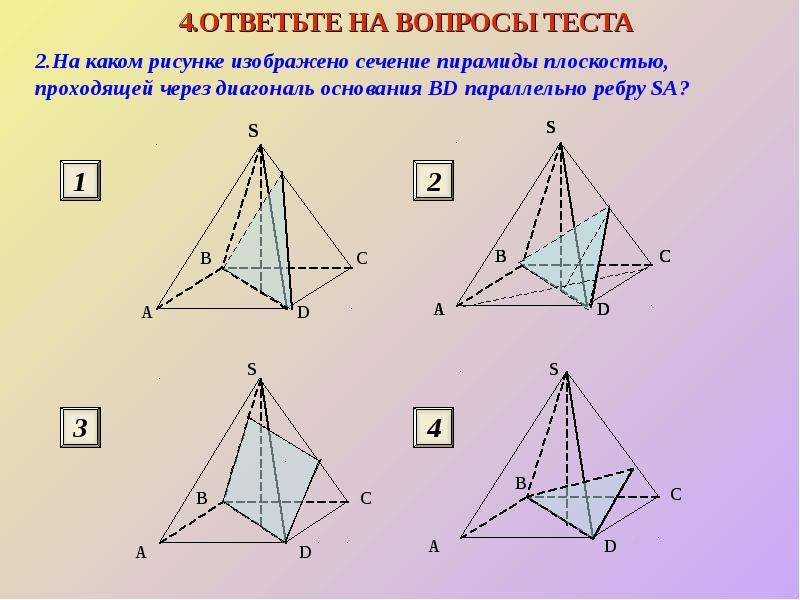
Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Подведем итоги
Мини-урок был посвящен увлекательной концепции Треугольной пирамиды.Математическое путешествие вокруг Треугольной пирамиды начинается с того, что ученик уже знает, и продолжается творческой выработкой новой концепции в молодых умах. Сделано таким образом, чтобы оно не только было понятным и понятным, но и навсегда осталось с ними. В этом заключается магия Куэмат.
О компании CuemathВ Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу «обучение-обучение-обучение» учителя исследуют тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, мы в Cuemath верим в логическое мышление и интеллектуальный подход к обучению.
Часто задаваемые вопросы (FAQ)
1. Сколько треугольников образуют треугольную пирамиду?
Четыре треугольника образуют треугольную пирамиду.
2. Является ли пирамида треугольной призмой?
Призма — это многогранник с параллельными верхним и нижним основаниями и прямоугольными боковыми гранями.Пирамида имеет одно основание и треугольные боковые грани, которые пересекаются в центральной вершине. Треугольная пирамида — это геометрическое тело с треугольным основанием, и все остальные грани также являются треугольниками с общей вершиной.
3. Почему пирамида представляет собой треугольник?
Каждая сторона пирамиды (каждое основание и вершина) образует треугольник . Треугольник на основе пирамида имеет четыре треугольные стороны. Это означает, что три стороны пирамиды имеют одинаковый размер, и пирамида выглядит так же, если вы ее повернете.Форма пирамиды позволяет равномерно распределять вес по всей конструкции.
Это означает, что три стороны пирамиды имеют одинаковый размер, и пирамида выглядит так же, если вы ее повернете.Форма пирамиды позволяет равномерно распределять вес по всей конструкции.
4. Составлена ли пирамида из равносторонних треугольников?
Когда основание представляет собой треугольник, пирамида представляет собой треугольную пирамиду. У него четыре грани, включая основание. Когда грани представляют собой равносторонние треугольники, это правильная треугольная пирамида.
Объем пирамиды
| ||||||||||||||||||||||
| Определение
Этот калькулятор площади поверхности поможет вам найти площадь наиболее распространенных трехмерных тел. Если вы когда-нибудь задумывались, как найти площадь поверхности или площадь боковой поверхности, этот калькулятор здесь, чтобы вам помочь.В этой статье вы можете найти формулы для площади поверхности сферы, куба, цилиндра, конуса, пирамиды и прямоугольной / треугольной призмы. Мы также объясним, как вычислить площадь поверхности сферы в качестве примера.
Что такое площадь поверхности? Определение площади поверхности
Площадь поверхности — общая площадь, которую занимает поверхность объекта . Другими словами, это общая площадь поверхности 3D-объекта.
Иногда площадь поверхности может быть разделена на сумму базовых площадей и площади боковой поверхности .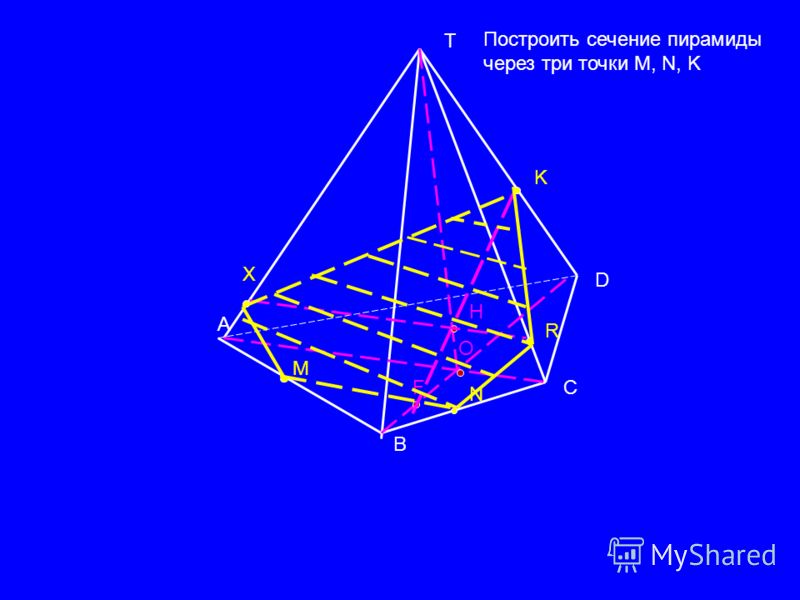 Боковая поверхность — это площадь всех сторон объекта, за исключением его основания и вершины. Это разделение используется для форм, где существует очевидное различие между основанием и другой частью — например, для цилиндра, конуса, пирамиды или треугольной призмы. Он редко применяется к твердым телам, для которых мы не уверены, какие грани следует рассматривать как основы (например, в кубе или коробке), и мы не используем его для гладких поверхностей, таких как сфера.
Боковая поверхность — это площадь всех сторон объекта, за исключением его основания и вершины. Это разделение используется для форм, где существует очевидное различие между основанием и другой частью — например, для цилиндра, конуса, пирамиды или треугольной призмы. Он редко применяется к твердым телам, для которых мы не уверены, какие грани следует рассматривать как основы (например, в кубе или коробке), и мы не используем его для гладких поверхностей, таких как сфера.
Формула для площади поверхности …
Наш калькулятор площади поверхности может найти площадь поверхности семи различных твердых тел.Формула зависит от типа твердого тела.
- Площадь поверхности сферы:
A = 4πr², где r — радиус сферы. - Площадь поверхности куба:
A = 6a², где a — длина стороны. - Площадь поверхности цилиндра:
A = 2πr² + 2πrh, где r — радиус, а h — высота цилиндра. - Площадь поверхности конуса:
A = πr² + πr√ (r² + h²), где r — радиус, а h — высота конуса. - Площадь поверхности прямоугольной призмы (прямоугольник):
A = 2 (ab + bc + ac), где a , b и c — длины трех сторон кубоида. - Площадь поверхности треугольной призмы:
A = 0,5 * √ ((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c)) + h * (a + b + c), где a , b и c — это длины трех сторон основания треугольной призмы, а h — высота (длина) призмы. - Площадь поверхности пирамиды:
A = l * √ (l² + 4 * h²) + l², где l — длина стороны квадратного основания, а h — высота пирамиды.
Но откуда берутся эти формулы? Как найти площадь поверхности основных трехмерных фигур? Продолжайте читать, и вы узнаете!
Площадь поверхности сферы
Чтобы рассчитать площадь поверхности сферы, все, что вам нужно знать, — это радиус сферы или ее диаметр.
-
A = 4 * π * r², гдеr— радиус.
Поскольку мы знаем, что диаметр сферы равен двум радиусам d = 2r , мы можем преобразовать уравнение в другую форму:
-
A = 4 * π * (d / 2) ² = π * d², гдеd— диаметр сферы.
Для вывода этой формулы площади поверхности требуется интегрирование. Если вам интересно, посмотрите это доказательство.
Площадь цилиндра
Чтобы узнать площадь поверхности цилиндра, у вас должно быть два значения: радиус (или диаметр) основания и высота цилиндра.Общее уравнение обычное — площадь основания умножить на высоту . В нашем случае круг — это основа.
Откуда взялась эта формула? Вы можете записать уравнение для площади поверхности цилиндра как:
-
A = A (сбоку) + 2 * A (основание)
Найти площадь основания несложно — запомним известную формулу площади круга: A (основание) = π * r² . Но какова форма боковой поверхности? Попробуйте представить, что мы его «разворачиваем».Вы узнаете это? Это прямоугольник ! Длина одной стороны равна высоте цилиндра, а вторая — окружности развернутого круга.
-
A (база) = π * r² -
A (боковой) = h * (2 * π * r)
Площадь конуса
Мы можем разделить поверхность конуса на две части:
-
A = A (боковой) + A (основание), так как у нас только одно основание, в отличие от цилиндра.
Основание — это снова площадь круга A (основание) = π * r² , но происхождение площади боковой поверхности может быть не так очевидно:
-
A (боковой) = π * r * √ (r² + h²)
Давайте посмотрим на этот вывод по шагам:
- Раскатайте боковую поверхность.
 Это круговой сектор, который является частью окружности с радиусом s ( s — наклонная высота конуса).
Это круговой сектор, который является частью окружности с радиусом s ( s — наклонная высота конуса). - Для окружности с радиусом s, длина окружности равна
2 * π * s. Длина дуги сектора равна2 * π * r. - Площадь сектора , который является нашей боковой поверхностью конуса, определяется по формуле:
-
A (сбоку) = (s * (длина дуги)) / 2 = (s * 2 * π * r) / 2 = π * r * s
Формула может быть получена из пропорции: отношение площадей фигур такое же, как отношение длины дуги к окружности:
(площадь сектора) / (площадь большого круга) = (длина дуги) / (окружность большого круга) так:
(площадь сектора) / (π * s²) = (2 * π * r) / (2 * π * s)
(площадь сектора) = (π * s²) * (2 * π * r) / (2 * π * s)
- Обычно у нас указывается не
s, аh, что составляет высоты конуса. Но это совсем не проблема! Мы можем легко преобразовать формулу, используя теорему Пифагора:
Таким образом, формула площади боковой поверхности выглядит следующим образом:
-
A (боковой) = π * r * √ (r² + h²)
- Наконец, сложите площади основания и боковой части, чтобы найти окончательную формулу для площади поверхности конуса :
-
A = A (сбоку) + A (основание) = π * r * s + π * r²дляrиsили -
A = π * r * √ (r² + h²) + π * r²дляrиh.
Площадь куба
Площадь поверхности куба — это самое простое, что вы можете себе представить: каждая из сторон представляет собой квадрат! Поскольку каждый куб имеет шесть одинаковых квадратных граней, площадь поверхности равна:
.
Поскольку площадь квадрата является произведением длины его сторон, окончательная формула для определения площади поверхности куба будет:
-
A = 6 * l², гдеl— сторона квадрата
Площадь пирамиды
Пирамида — это трехмерное тело с многоугольным основанием и треугольными боковыми гранями.Когда вы слышите пирамида , обычно предполагается, что это правильная квадратная пирамида . Правильный означает, что он имеет правильное основание многоугольника и представляет собой правую пирамиду (вершина прямо над центром тяжести его основания) и квадрат — что он имеет эту форму в качестве основания. Это вариант, который мы использовали в качестве пирамиды в этом калькуляторе площади поверхности.
Формула площади поверхности пирамиды:
-
A = l * √ (l² + 4 * h²) + l², гдеl— сторона основания, аh— высота пирамиды
Опять же, мы можем разделить уравнение на:
-
A = A (основание) + A (сбоку) = A (основание) + 4 * A (боковая поверхность)
Основание имеет форму квадрата, поэтому A (основание) = l² .Чтобы рассчитать площадь боковой поверхности, начнем с площади одной треугольной грани:
- Чтобы найти высоту треугольника, нам снова понадобится формула гипотенузы:
- Вычислите гипотенузу треугольника ABC (которая одновременно является высотой треугольной грани):
-
c = √ (h² + (l / 2) ²) = √ (h² + l² / 4)
- Площадь треугольника (в нашем случае это равнобедренный треугольник) можно рассчитать как:
-
A = высота * основание / 2так -
A (боковая сторона) = √ (h² + l² / 4) * l / 2
- Итоговая формула площади поверхности пирамиды:
-
A = l² + 4 * √ (h² + l² / 4) * l / 2 = l² + 2 * l * √ (h² + l² / 4) -
A = l² + l * √ (4 * h² + l²)
Площадь прямоугольной призмы
Чтобы вычислить площадь поверхности прямоугольной призмы, все, что вам нужно сделать, это вычислить площади сторон прямоугольника:
где:
-
A1 = длина * ширина -
A2 = ш * в -
A3 = длина * высота
Таким образом, окончательная формула:
-
A = 2 * (д * ш + ш * в + д * в)
Площадь поверхности треугольной призмы
Чтобы понять, откуда взялась формула для площади поверхности треугольной призмы, давайте взглянем на этот вывод:
- В этом случае легко вычислить площадь боковой поверхности.
 Как видно из рисунка, он состоит из трех прямоугольников с общей длиной одной стороны:
Как видно из рисунка, он состоит из трех прямоугольников с общей длиной одной стороны:
-
A (сбоку) = a * h + b * h + c * h = h * (a + b + c)
, который мы также можем записать сокращенно:
-
A (боковой) = h * P, гдеP— периметр базового треугольника
- Затем найдите площадь треугольного основания. Вы можете сделать это разными способами, в зависимости от того, что вам дают. В нашем калькуляторе мы реализовали расчет на основе формулы Герона — она используется, когда у вас есть три стороны треугольника (SSS).
A (основание) = 0,25 * √ ((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c)))
- Окончательная формула площади поверхности треугольной призмы:
-
A = A (сбоку) + 2 * A (основание) -
A = h * (a + b + c) + 0,5 * √ ((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c ))
Площадь поверхности тела
Вы можете рассчитать поверхность любого твердого тела, например, вашего тела — это не обязательно должна быть простая геометрическая форма! Если вам интересно, какова площадь внешней поверхности человеческого тела, воспользуйтесь этим калькулятором площади поверхности тела.
Как рассчитать площадь поверхности шара?
Если вы хотите найти площадь поверхности сферы, вам необходимо выполнить следующие шаги:
- Определите радиус сферы. Можно принять радиус 10 см.
- Введите это значение в формулу
A = 4πr². - Рассчитайте результат:
A = 4π * 10² = 1256 см². - Вы также можете использовать этот калькулятор площади поверхности, чтобы найти радиус сферы, если вы знаете ее площадь.
Прочие соображения
Единицами площади поверхности всегда являются квадратные единицы длины. Например, вы можете выразить это в см², дюймах, фут², м², а также в акрах и гектарах.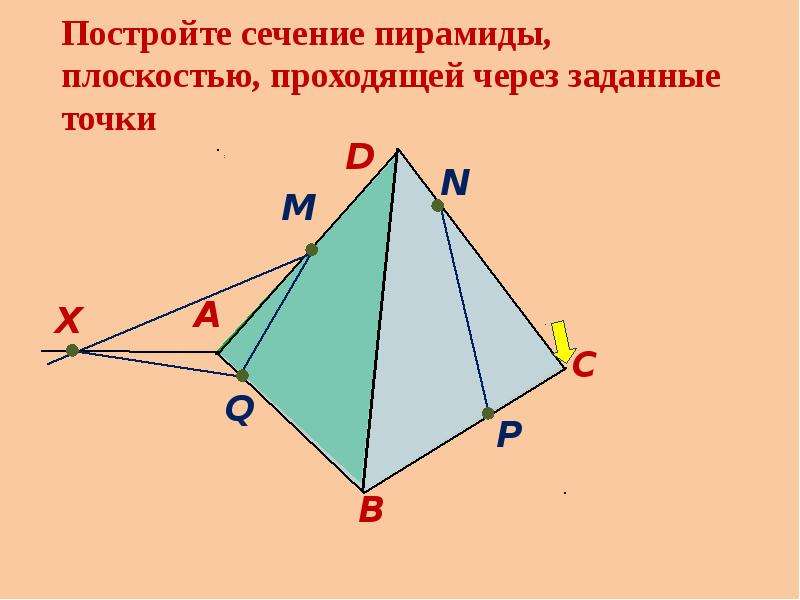
Если вы хотите определить объем любого из этих твердых веществ, воспользуйтесь нашим калькулятором объема.
Как разделить куб на 3 одинаковые пирамиды
Текст
Построим из графического картона ножницами и приклеим пирамиду, образующую куб.
Основание пирамиды будет нижней стороной куба, а вершина пирамиды будет одним из верхних углов куба.
Мы увидим, что объем этой пирамиды составляет ровно 1/3 объема куба. Кроме того, мы реконструируем куб из трех одинаковых пирамид, подобных этой.
Чтобы построить пирамиду, мы начинаем с модели (подробности смотрите в видео).
| Нажмите на изображение для увеличения |
Режем лист по модели.
И складываем и приклеиваем, чтобы получилась пирамида.
Строим 3 пирамиды по одной модели. И мы видим, что они точно помещаются в куб.
Три пирамиды полностью заполняют куб? Или внутри может быть пустота? Рассуждая об углах различных плоскостей, он видит, что внутри не может быть пустоты. Куб полностью заполнен.
Следовательно, объем исходной пирамиды составляет треть объема куба.Следовательно, это произведение площади его основания на высоту, деленное на 3.
Мы можем записать: V = S xhx 1/3
(где V — объем пирамиды, S — площадь ее основания, то есть одна из сторон куба, а h — высота, т.е. край куба).
Мы будем использовать этот результат, чтобы распространить его на любую пирамиду и даже на любой конус.
Этот результат является обобщением до трех измерений следующего хорошо известного факта на плоскости, касающегося площади поверхности треугольников: площадь поверхности треугольника — это произведение длины любой стороны на противоположную высоту , деленное на 2 .
В 3D мы имеем «тот же» факт, но с коэффициентом 1/3 вместо 1/2, то есть: объем любой пирамиды равен произведению площади ее основания на противоположную высоту , деленную на 3 .
Лирическое отступление : Вот еще один элементарный расчет объема пирамиды. (Под «элементарным» мы подразумеваем «без использования интегрального исчисления».) Мы только набросаем его. Думайте о пирамиде, как о большом количестве маленьких кубиков, расположенных этажами с уменьшающимся квадратным размером.Нижний этаж будет состоять из n 2 маленьких кубиков, следующий этаж из (n-1) 2 кубиков, следующий из (n-2) 2 и т. Д. До верхнего этажа только один маленький кубик. Такая пирамида содержит 1 + 4 + 9 + 16 + … + n 2 маленьких кубиков. Расчеты показывают, что 1 + 4 + 9 + 16 + … + n 2 = n (n + 1) (2n + 1) / 6. (Если мы назовем это число V (n), легко проверить, что V (n) — V (n-1) = n 2 .) Таким образом, отношение объема пирамиды ко всему большому кубу равно п (п + 1) (2 п + 1) / (6 п 3 ).Когда n становится все больше и больше, а пирамида из маленьких кубиков становится все более гладкой и гладкой, это соотношение стремится к 1/3.
А теперь немного повеселимся. , чтобы закончить урок: давайте поместим себя в четырехмерное пространство. Рассмотрим трехмерный куб в этом пространстве и точку P за пределами трехмерного пространства, в котором находится куб (хорошо, это немного сложно визуализировать :-). Проведем линии от P ко всем точкам трехмерного куба. Получаем 4-х мерную фигуру. Измерение четырехмерного объема этой четырехмерной фигуры является произведением трехмерного объема трехмерного куба на противоположную высоту , деленную на 4 .И четыре таких одинаковых гиперпирамиды можно собрать в гиперкуб.
Вот некоторая помощь в визуализации и работе в 4-х измерениях.
В конце средней школы, когда мы изучаем интегральное исчисление, тот факт, что гиперпирамида имеет (гипер-) объем 1/4 гиперкуба, станет легким результатом, поскольку интеграл от 0 до z of x 3 равно z 4 /4.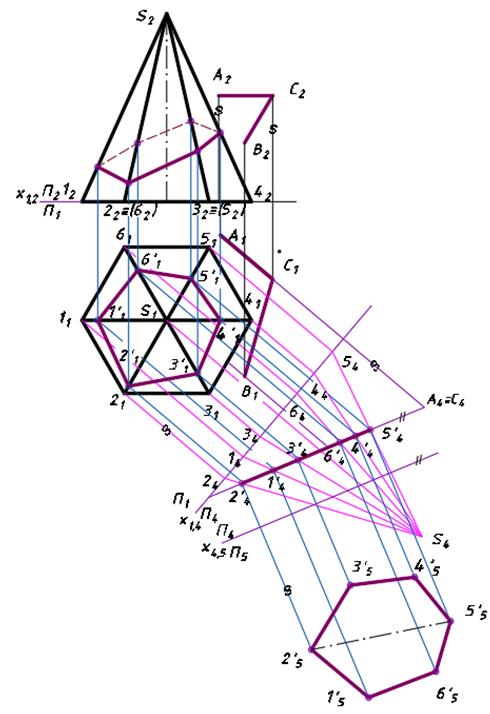
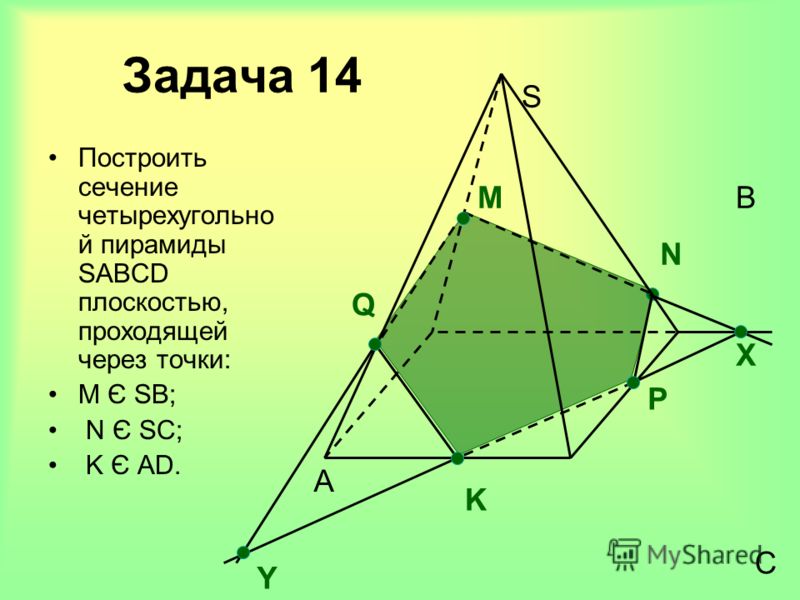
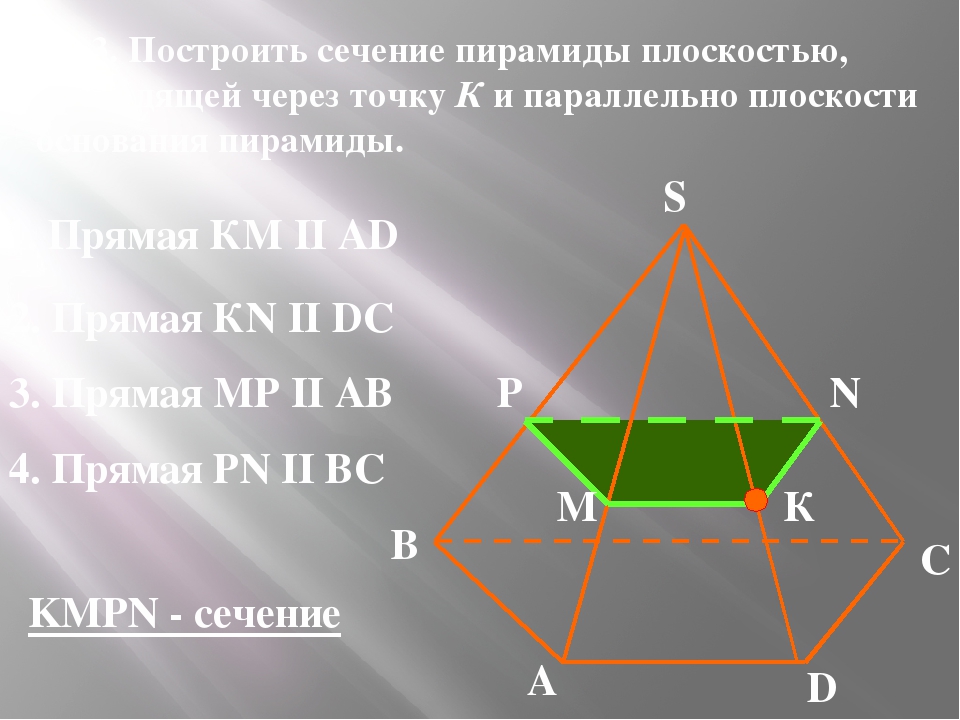
 см и высота 5 см.
см и высота 5 см.
 Это круговой сектор, который является частью окружности с радиусом s ( s — наклонная высота конуса).
Это круговой сектор, который является частью окружности с радиусом s ( s — наклонная высота конуса). Как видно из рисунка, он состоит из трех прямоугольников с общей длиной одной стороны:
Как видно из рисунка, он состоит из трех прямоугольников с общей длиной одной стороны: