Логарифмическое дифференцирование функций
Метод логарифмического дифференцирования становится пригодным при дифференцировании произведения нескольких функций или их частки. Его удобно применять при дифференцировании выражений, содержащих корни из дробей (функций), а также когда показатель функции также представляет собой функцию
В таких случаях целесообразно обе части выражения сначала прологарифмировать по основанию , а затем приступить к дифференцировке. Этот способ получил название логарифмического дифференцирования. Производную логарифма функции называют логарифмической производной. Суть метода с помощью формул можно описать следующим образом:
имеем сложную функцию вида
к обеим сторонам применяем логарифмирования
находим производные правой и левой части равенства
Приравниваем производные и выражаем
В этом суть метода, дальше все зависит от функции .
Если она представляет собой произведение функций
то по свойствам логарифма он будет равен сумме логарифмов
Если имеем дробь от функций
то применяя логарифмирования получим
Если имеем функцию в степени другой
то по свойствам логарифма получим
В случае корней дифференцировки значительно упрощается
Дальнейшее вычисление производных зависит от сложности самих функций. Рассмотрим конкретные примеры, чтобы данный материал стал для Вас более понятным и наглядным.
Задача.
Используя логарифмирования найти производную (Дубовик В.П., Юрик И.И. «Высшая математика. Сборник задач»)
1) (5.2.178)
2) (5.2.191)
3) (5.2.195)
4) (5.2.199)
Решение.
Примеры выбрано сложные для того, чтобы раскрыть всю силу метода логарифмического дифференцирования и рассмотреть типичные распространенные примеры.
1) Проведем логарифмирования левой и правой частей
Найдем производную правой части
Производная левой части показана при изложении теоретического материала. Записываем обе части
Далее переносим функцию из знаменателя в правую часть и не забываем поменять ее значение
Несмотря на сложный вид данный пример полностью решено.
2) Используем свойства логарифма к данному примеру
Проводим дифференцирования обеих частей равенства
Сведем к общему знаменателю правую сторону. В результате математических операций получим
Подставим в исходную равенство, перенеся функцию в правую часть
В результате ряда несложных математических манипуляций получили достаточно компактный конечный результат производной. При исчислении данного примера направления подобный результат пришлось бы искать очень долго.
3) Несмотря на сложный вид данное выражение, на основе свойств степеней, можно переписать в следующем виде
Применим к нему логарифмирования
Производная от правой части будет равна следующему выражению
Здесь для упрощения дальнейших выкладок введено обозначение .
Учитывая производную , окончательно получим
Можно оставлять в таком виде, поскольку суть данного урока научиться применять метод логарифмического дифференцирования. Но если Вы захотите для упрощения свести все к общему знаменателю, то получите следующее выражение
Поверьте это займет у Вас много времени.
4) Проводим логарифмирования функции
Логарифмическое дифференцирование, формулы и примеры решения задач
Задание. Найти производную функции
Решение. Если находить производную данной функции, используя таблицу производных и правила дифференцирования, то процесс будет очень трудоемким. Производную будем находить с помощью логарифмического дифференцирования. Прологарифмируем левую и правую части заданной функции:
Используя свойства логарифмов, преобразуем правую часть полученного равенства к следующему виду:
Таким образом, получаем, что логарифм заданной функции равен:
Дифференцируем левую и правую часть последнего равенства, не забывая, что является функцией переменной :
Итак,
Отсюда
Подставляя вместо функции ее выражение, окончательно будем иметь, что
Ответ.
Логарифмическая производная — примеры вычисления
Метод решения
Пусть
(1)
есть дифференцируемая функция от переменной x. В начале мы рассмотрим ее на множестве значений x, для которых y принимает положительные значения: . В дальнейшем мы покажем, что все полученные результаты применимы и для отрицательных значений .
В некоторых случаях, чтобы найти производную функции (1), ее удобно предварительно прологарифмировать
,
а затем вычислить производную. Тогда по правилу дифференцирования сложной функции,
.
Отсюда
(2) .
Производная от логарифма функции называется логарифмической производной:
.
- Логарифмическая производная функции y = f(x)
- – это производная натурального логарифма этой функции: (ln f(x) )′.
Случай отрицательных значений y
Теперь рассмотрим случай, когда переменная может принимать как положительные, так и отрицательные значения. В этом случае возьмем логарифм от модуля и найдем его производную:
.
Отсюда
(3) .
То есть, в общем случае, нужно найти производную от логарифма модуля функции .
Сравнивая (2) и (3) мы имеем:
.
То есть формальный результат вычисления логарифмической производной не зависит от того, взяли мы по модулю или нет. Поэтому, при вычислении логарифмической производной, мы можем не беспокоится о том, какой знак имеет функция .
Прояснить такую ситуацию можно с помощью комплексных чисел. Пусть, при некоторых значениях x, отрицательна: . Если мы рассматриваем только действительные числа, то функция не определена. Однако, если ввести в рассмотрение комплексные числа, то получим следующее:
.
То есть функции и отличаются на комплексную постоянную :
.
Поскольку производная от постоянной равна нулю, то
.
Свойство логарифмической производной
Из подобного рассмотрения следует, что логарифмическая производная не изменится, если умножить функцию на произвольную постоянную :
.
Действительно, применяя свойства логарифма, формулы производной суммы и производной постоянной, имеем:
.
Применение логарифмической производной
Применять логарифмическую производную удобно в тех случаях, когда исходная функция состоит из произведения степенных или показательных функций. В этом случае операция логарифмирования превращает произведение функций в их сумму. Это упрощает вычисление производной.
Далее мы приводим примеры вычисления производных для следующих функций:
; ; .
Пример 1
Найти производную функции:
.
Решение
Логарифмируем исходную функцию:
.
Дифференцируем по переменной x.
В таблице производных находим:
.
Применяем правило дифференцирования сложной функции.
;
;
;
;
(П1.1) .
Умножим на :
.
Итак, мы нашли логарифмическую производную:
.
Отсюда находим производную исходной функции:
.
Примечание
Если мы хотим использовать только действительные числа, то следует брать логарифм от модуля исходной функции:
.
Тогда
;
.
И мы получили формулу (П1.1). Поэтому результат не изменился.
Ответ
Пример 2
С помощью логарифмической производной, найдите производную функции
.
Решение
Логарифмируем:
(П2.1) .
Дифференцируем по переменной x:
;
;
;
;
;
.
Умножим на :
.
Отсюда мы получаем логарифмическую производную:
.
Производная исходной функции:
.
Примечание
Здесь исходная функция неотрицательная: . Она определена при . Если не предполагать, что логарифм может быть определен для отрицательных значений аргумента, то формулу (П2.1) следует записать так:
.
Поскольку
и
,
то это не повлияет на окончательный результат.
Ответ
.
Пример 3
Найдите производную
.
Решение
Дифференцирование выполняем с помощью логарифмической производной. Логарифмируем, учитывая что :
(П3.1) .
Дифференцируя, получаем логарифмическую производную.
;
;
;
(П3.2) .
Поскольку , то
.
Примечание
Проделаем вычисления без предположения, что логарифм может быть определен для отрицательных значений аргумента. Для этого возьмем логарифм от модуля исходной функции:
.
Тогда вместо (П3.1) имеем:
;
.
Сравнивая с (П3.2) мы видим, что результат не изменился.
Ответ
.
Автор: Олег Одинцов. Опубликовано: Изменено:
Производные логарифмов и логарифмическое дифференцирование
Что можно сказать о производной логарифмической функции y = lnx на основании таблицы производных? Можно сказать, что она существует и выражается формулой
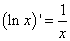 (1)
(1)
Однако в большинстве задач математического анализа, с которыми придётся столкнуться в дальнейшем, присутствует сложная логарифмическая функция. Она вычисляется несколько иначе.
В случае сложной логарифмической функции y = lnu, где u – дифференцируемая функция аргумента x, формула (1) примет вид
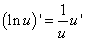 (2)
(2)
Пользуясь формулой (2), найдём производную логарифмической функции с произвольным положительным основанием a. Пусть
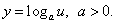
В результате применения свойств логарифмов:
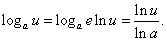
Так как
 — постоянный множитель, то
— постоянный множитель, то
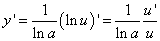
или
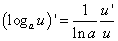 (3)
(3)
Если функция дана в виде
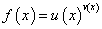 ,
,
то перед тем, как находить её производную, часто бывает выгодно прологарифмировать эту функцию.
Это прежде всего случаи, когда требуется найти производную произведения или частного функций, а также степенной функции, когда основание и степень — функции.
На основании свойств сложных функций доказано, что производная функции, вид которой приведён выше, может быть найдена по формуле
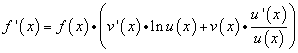 .
.
Пример 3. Найти производную функции
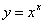 .
.
Решение. Логарифмируем обе части равенства и находим:
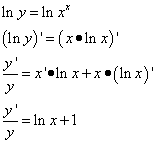
Решение. Окончательно находим производную данной функции:
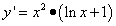
Пример 4.
Найти производную функции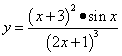 .
.
Решение. Логарифмируем обе части равенства:
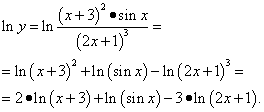
Дифференцируем:
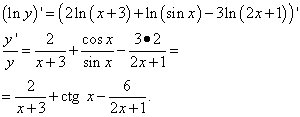
Выражаем и находим производную данной функции:
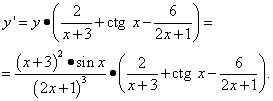

Поделиться с друзьями
Весь блок «Производная»
Логарифмическая производная — Википедия
Материал из Википедии — свободной энциклопедии
Логарифмическая произво́дная — производная от натурального логарифма функции.
(lnf)′=f′f{\displaystyle (\ln f)’={\frac {f’}{f}}}
Часто применяется для упрощения нахождения производной некоторых функций, например сложно-показательных.
Производная степенно-показательной функции[править | править код]
Пусть f(x)=u(x)g(x){\displaystyle f(x)=u(x)^{g(x)}} (для краткости f=ug{\displaystyle f=u^{g}}, где u и g — функции).
Тогда lnf=lnug=glnu{\displaystyle \ln f=\ln u^{g}=g\ln u}, (lnf)′=(glnu)′=g′⋅lnu+g⋅u′u{\displaystyle (\ln f)’=(g\ln u)’=g’\cdot \ln u+g\cdot {\frac {u’}{u}}}. С другой стороны, (lnf)′=f′f{\displaystyle (\ln f)’={\frac {f’}{f}}}, т.е. f′=f⋅(lnf)′{\displaystyle f’=f\cdot (\ln f)’}.
Окончательно имеем (ug)′=ug(g′⋅lnu+g⋅u′u){\displaystyle (u^{g})’=u^{g}(g’\cdot \ln u+g\cdot {\frac {u’}{u}})}
Производная произведения функций[править | править код]
Пусть задана функция f(x)=∏i=1ngi(x){\displaystyle f(x)=\prod _{i=1}^{n}g_{i}(x)} (для краткости f=∏i=1ngi{\displaystyle f=\prod _{i=1}^{n}g_{i}}).
Так как f′=f⋅(lnf)′=∏i=1ngi(ln∏j=1ngj)′=∏i=1ngi(∑j=1nlngj)′=∏i=1ngi∑j=1n(lngj)′=∏i=1ngi∑j=1ngj′gj{\displaystyle f’=f\cdot (\ln f)’=\prod _{i=1}^{n}g_{i}(\ln \prod _{j=1}^{n}g_{j})’=\prod _{i=1}^{n}g_{i}(\sum _{j=1}^{n}\ln g_{j})’=\prod _{i=1}^{n}g_{i}\sum _{j=1}^{n}(\ln g_{j})’=\prod _{i=1}^{n}g_{i}\sum _{j=1}^{n}{\frac {g_{j}’}{g_{j}}}}.
Окончательно получаем: f′=(∏i=1ngi)′=∏i=1ngi∑j=1ngj′gj=f⋅∑j=1ngj′gj{\displaystyle f’=(\prod _{i=1}^{n}g_{i})’=\prod _{i=1}^{n}g_{i}\sum _{j=1}^{n}{\frac {g_{j}’}{g_{j}}}=f\cdot \sum _{j=1}^{n}{\frac {g_{j}’}{g_{j}}}}.
Можно расписать формулу и прийти к другой форме:
- Если f=g1⋅g2⋅…⋅gn{\displaystyle f=g_{1}\cdot g_{2}\cdot \ldots \cdot g_{n}}, то f′=g1⋅g2⋅…⋅gn⋅(g1′g1+g2′g2+…+gn′gn){\displaystyle f’=g_{1}\cdot g_{2}\cdot \ldots \cdot g_{n}\cdot \left({\frac {g_{1}’}{g_{1}}}+{\frac {g_{2}’}{g_{2}}}+\ldots +{\frac {g_{n}’}{g_{n}}}\right)}
- Раскрыв скобки, получим: f′=g1′⋅g2⋅…⋅gn+g1⋅g2′⋅…⋅gn+…+g1⋅g2⋅…⋅gn′{\displaystyle f’=g_{1}’\cdot g_{2}\cdot \ldots \cdot g_{n}+g_{1}\cdot g_{2}’\cdot \ldots \cdot g_{n}+\ldots +g_{1}\cdot g_{2}\cdot \ldots \cdot g_{n}’}
В частности, если f=u1α1⋅u2α2⋅…⋅umαmv1β1⋅v2β2⋅…⋅vnβn{\displaystyle f={\frac {u_{1}^{\alpha _{1}}\cdot u_{2}^{\alpha _{2}}\cdot \ldots \cdot u_{m}^{\alpha _{m}}}{v_{1}^{\beta _{1}}\cdot v_{2}^{\beta _{2}}\cdot \ldots \cdot v_{n}^{\beta _{n}}}}}, то f′=u1α1⋅u2α2⋅…⋅umαmv1β1⋅v2β2⋅…⋅vnβn⋅(α1⋅u1′u1+α2⋅u2′u2+…+αm⋅um′um−β1⋅v1′v1−β2⋅v2′v2−…−βn⋅vn′vn){\displaystyle f’={\frac {u_{1}^{\alpha _{1}}\cdot u_{2}^{\alpha _{2}}\cdot \ldots \cdot u_{m}^{\alpha _{m}}}{v_{1}^{\beta _{1}}\cdot v_{2}^{\beta _{2}}\cdot \ldots \cdot v_{n}^{\beta _{n}}}}\cdot \left(\alpha _{1}\cdot {\frac {u_{1}’}{u_{1}}}+\alpha _{2}\cdot {\frac {u_{2}’}{u_{2}}}+\ldots +\alpha _{m}\cdot {\frac {u_{m}’}{u_{m}}}-\beta _{1}\cdot {\frac {v_{1}’}{v_{1}}}-\beta _{2}\cdot {\frac {v_{2}’}{v_{2}}}-\ldots -\beta _{n}\cdot {\frac {v_{n}’}{v_{n}}}\right)}
Найдем производную, dfdx{\displaystyle {\frac {df}{dx}}} от функции f(x)=xx{\displaystyle f(x)=x^{x}}:
- dfdx=f(lnf)′=xx(xlnx)′=xx(lnx+1){\displaystyle {\frac {df}{dx}}=f(\ln f)’=x^{x}(x\ln x)’=x^{x}(\ln x+1)}
| 1. |
Производная показательных функций
Сложность: лёгкое |
2 |
| 2. |
Касательная к графику логарифмической функции
Сложность: лёгкое |
2 |
| 3. |
Определение свойств функции по графику
Сложность: среднее |
2 |
| 4. |
Интервалы монотонности логарифмической функции
Сложность: среднее |
3 |
| 5. |
Производная сложной показательной функции
Сложность: среднее |
3 |
| 6. |
Производная сложной логарифмической функции
Сложность: среднее |
2 |
| 7. |
Производная сложных логарифмических функций
Сложность: среднее |
4 |
| 8. |
Производная произведения функций (логарифмирование)
Сложность: сложное |
1 |
| 9. |
Производная частного функций (логарифмирование)
Сложность: сложное |
1 |
| 10. |
Вычисление производной логарифмированием
Сложность: сложное |
3,5 |
|
Экстремумы показательной функции по основанию е
Сложность: сложное |
4 |
Логарифмическое дифференцирование
При вычислении производной от логарифма произведения, частного, степени или корня, для упрощения нахождения производной проводят предварительное преобразование (см. Пример 10(и)).
В ряде случаев для нахождения производной целесообразно заданную функцию сначала прологарифмировать (по умолчанию имеется в виду натуральный логарифм). Затем найти производную от этого логарифма и по ней отыскать производную от заданной функции. Такой прием называется логарифмическим дифференцированием.Метод логарифмического дифференцирования позволяет легко найти производную показательно-степенной функции вида
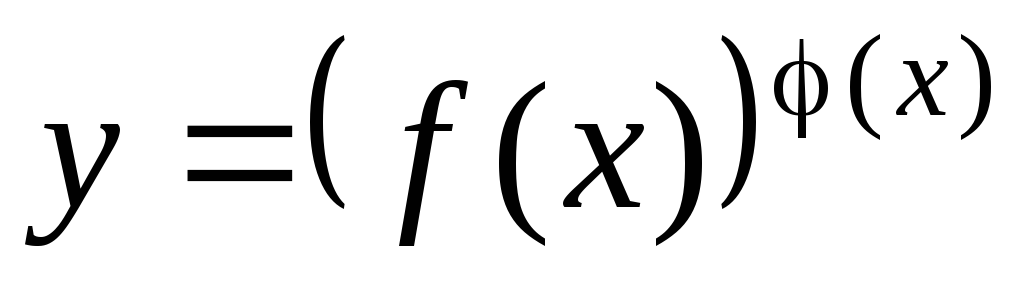 ,
,
где 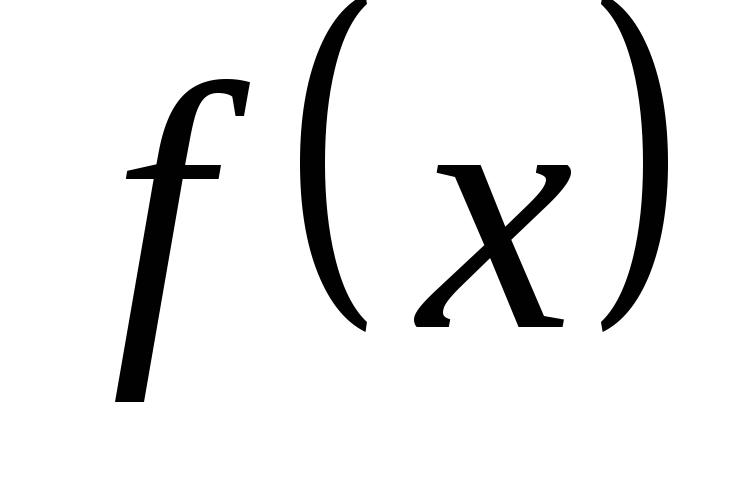 и
и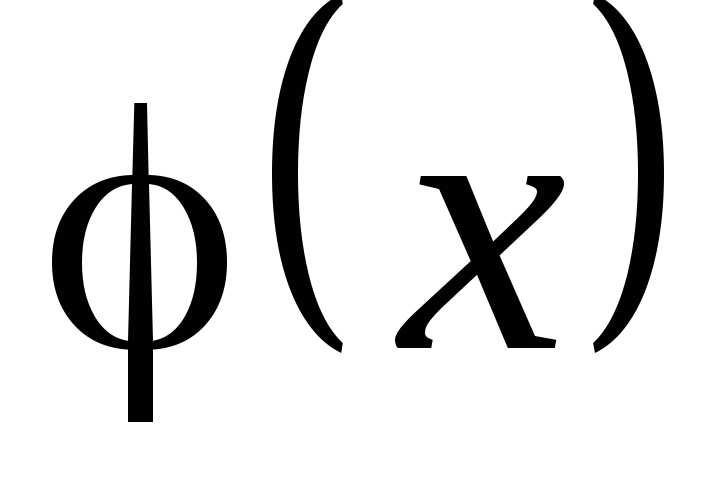 – дифференцируемые функции аргумента
– дифференцируемые функции аргумента 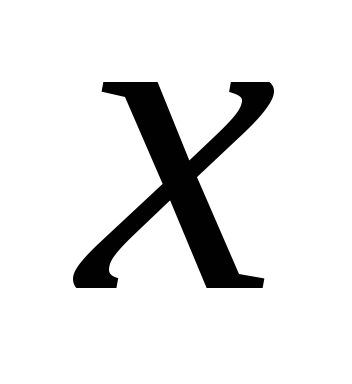 .
.
Пример 14.
Найти
производную функции 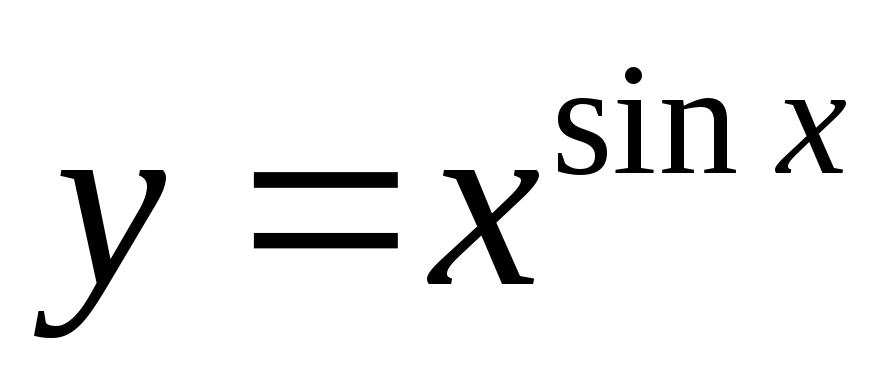
Решение.
Прологарифмируем обе части функции и преобразуем выражение:
 .
.
Теперь дифференцируем уравнение, как неявно заданную функцию:
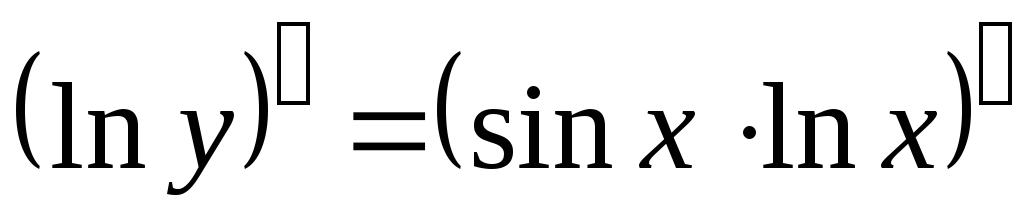 ;
;
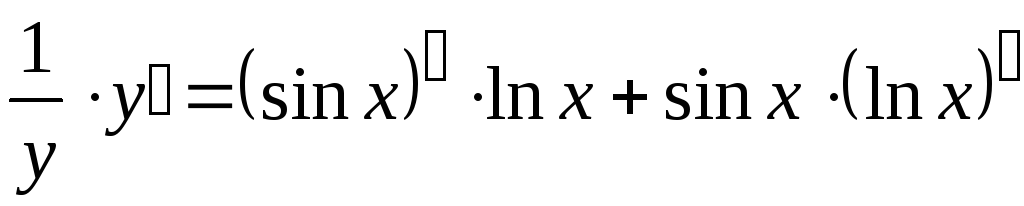 ;
;
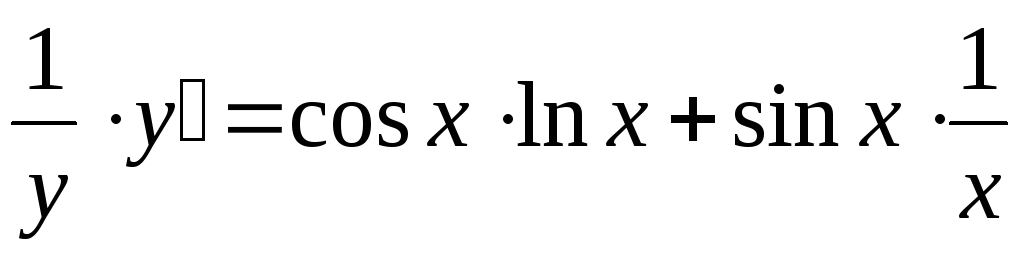 ;
;
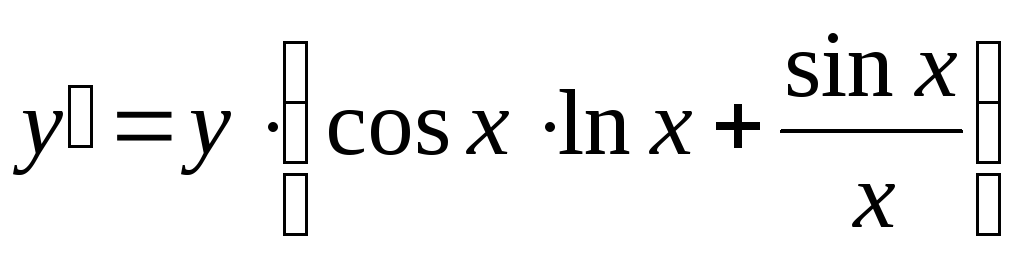 ;
;
Так
как 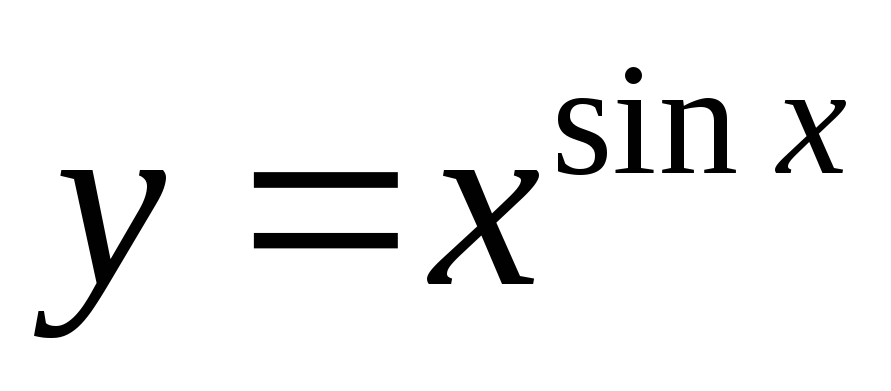
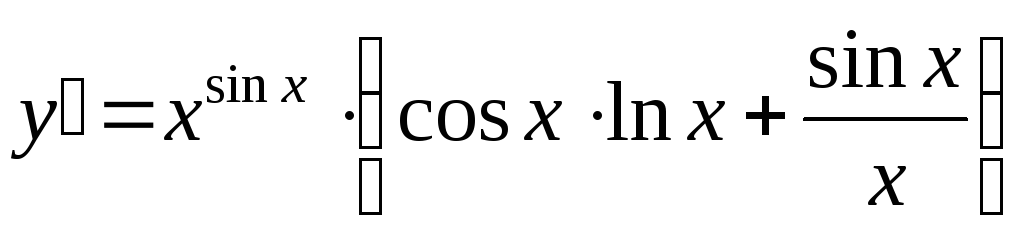 .
.
Производные высших порядков
Производной
2-го порядка от функции  называется производная от её первой
производной, т.е.
называется производная от её первой
производной, т.е.
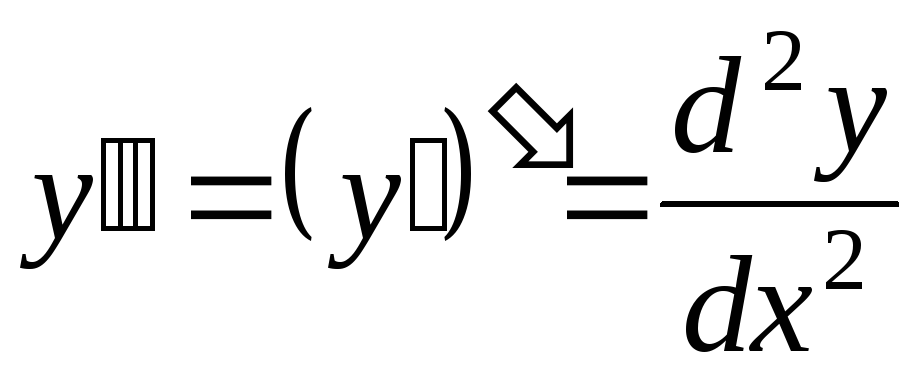 .
.
Аналогично,
производной 3-го порядка от функции 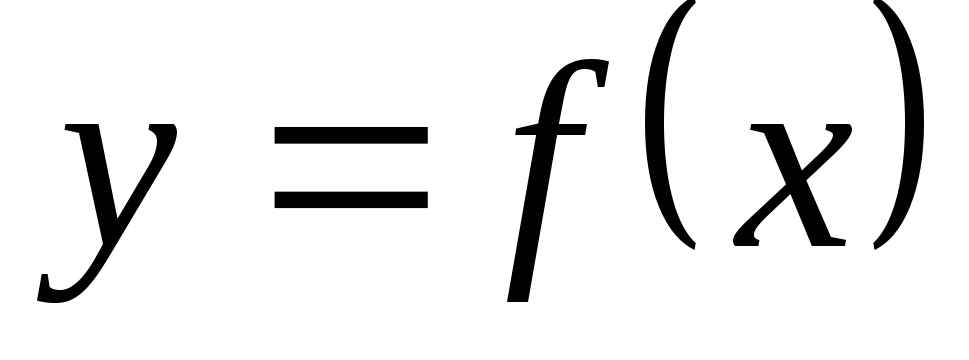 называется
производная от её второй производной,
т.е.
называется
производная от её второй производной,
т.е.
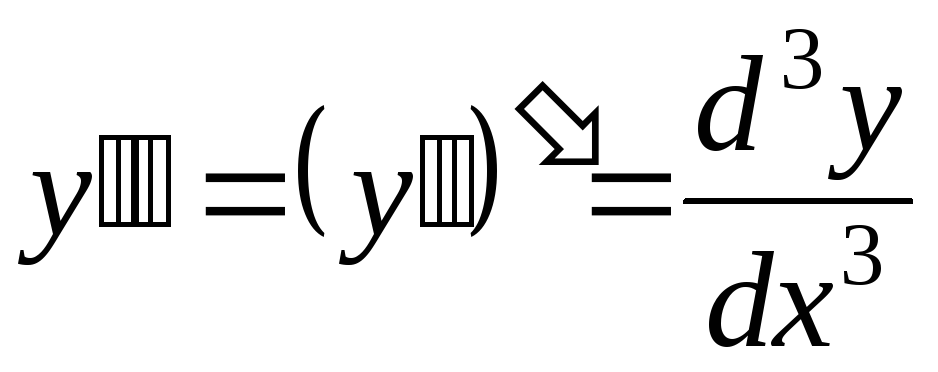 .
.
Таким
образом, производной 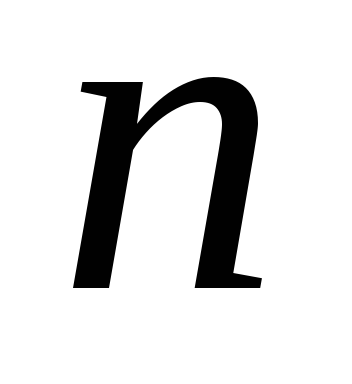 -го
порядка от функции
-го
порядка от функции 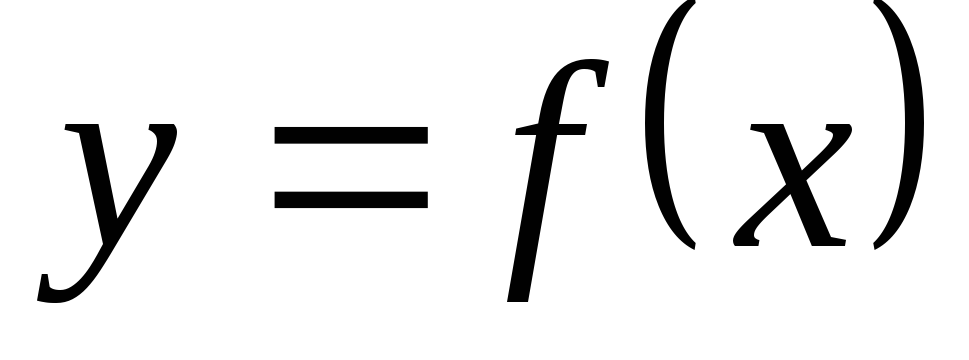
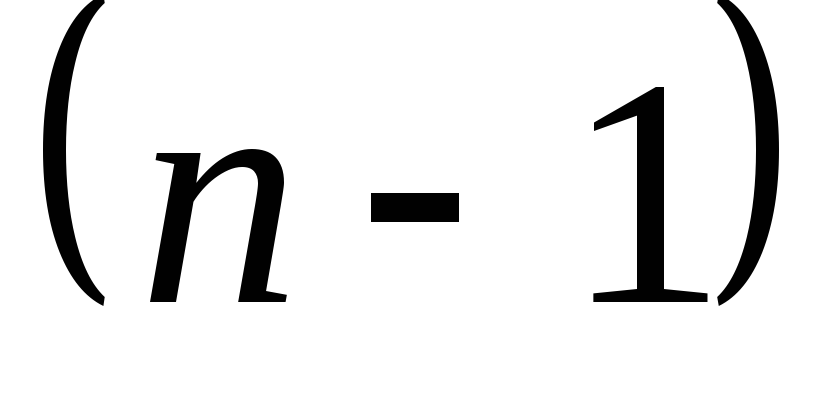 -го
порядка, т.е.
-го
порядка, т.е. 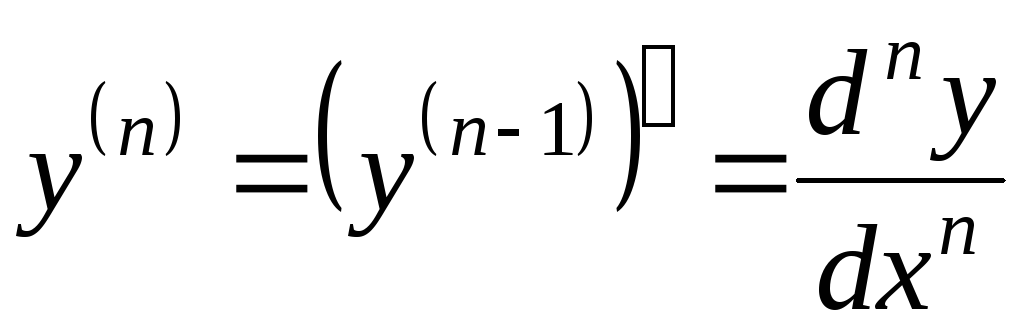 .
.
Следовательно,
для нахождения производной  -го
порядка необходимо последовательно
найти производную первого, затем второго,
затем третьего и т.д. до
-го
порядка необходимо последовательно
найти производную первого, затем второго,
затем третьего и т.д. до -го
порядка.
-го
порядка.
Пример 15.
Найти
третью производную  функции
функции 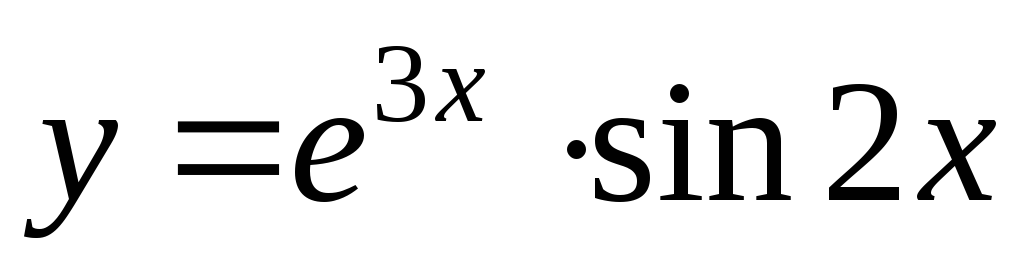 .
.
Решение.
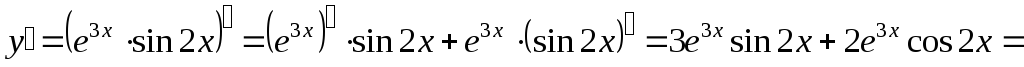
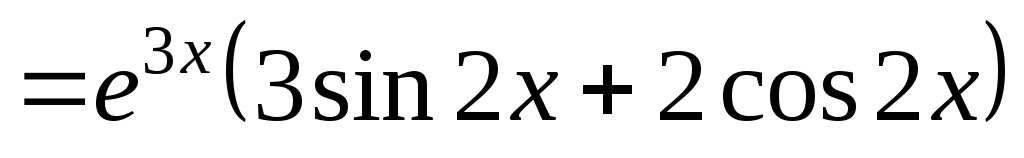 ;
;
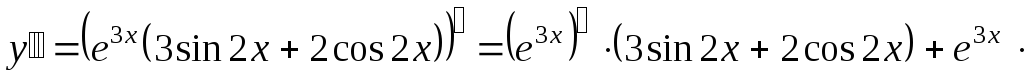
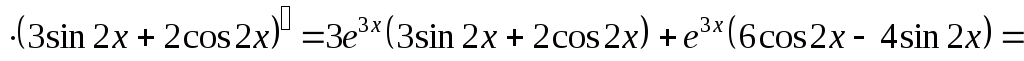
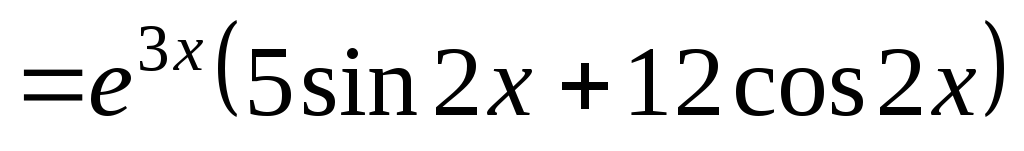 ;
;
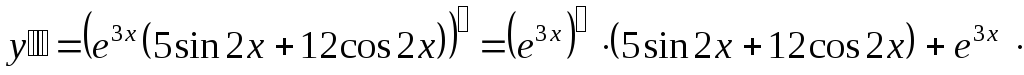
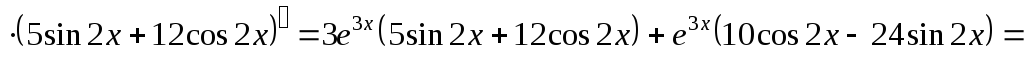
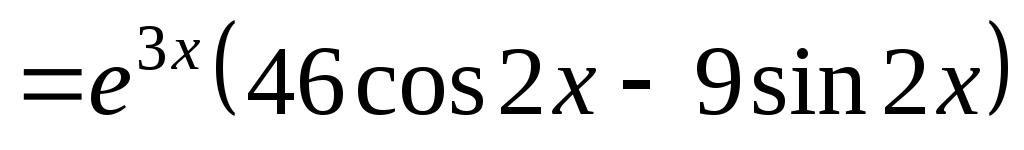 .
.
2.3. Дифференциал функции
Из определения производной и свойств пределов следует, что если
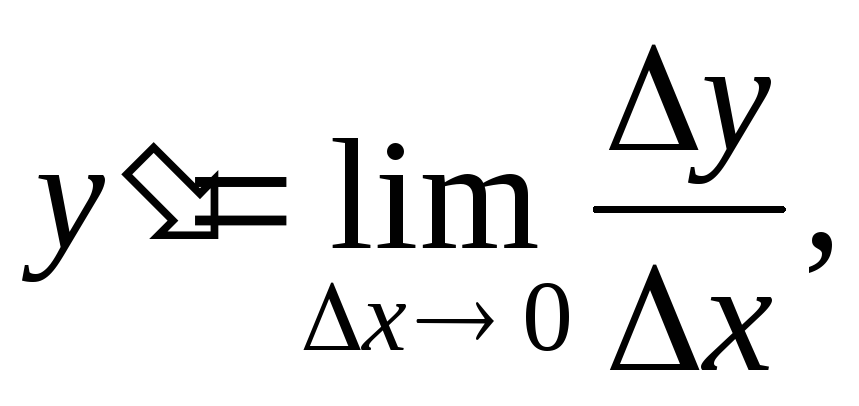 то
то 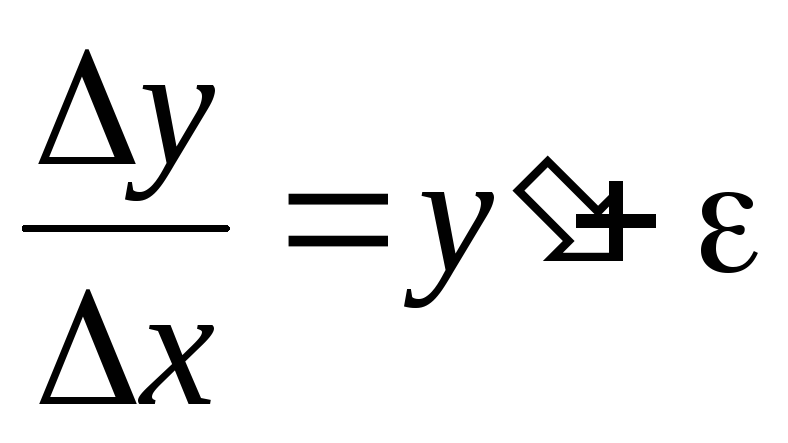 ,
,
где
–
бесконечно малая величина (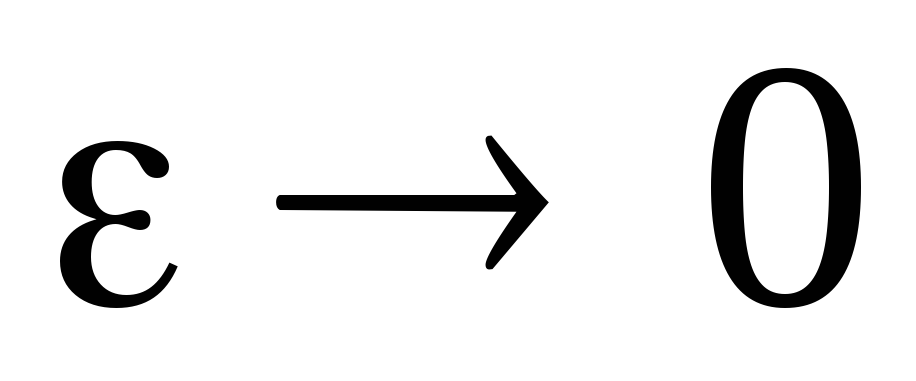 ).
).
Выражаем  и получаем, что:
и получаем, что: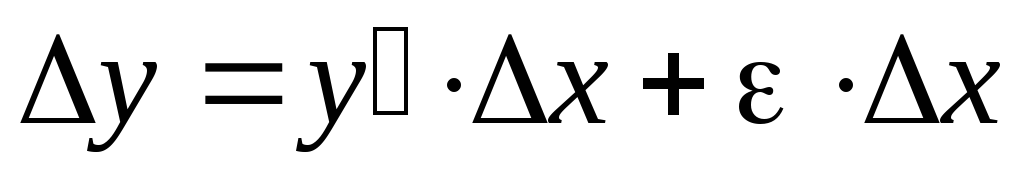 .
Так как
.
Так как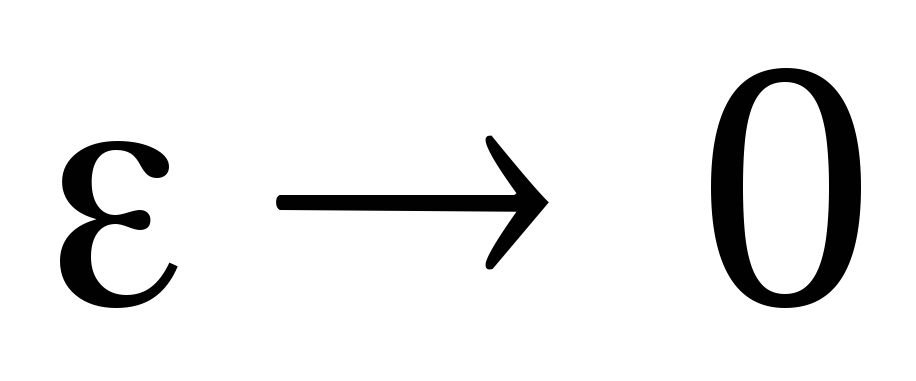 ,
то в дальнейшем ее можно не учитывать
и мы получим:
,
то в дальнейшем ее можно не учитывать
и мы получим: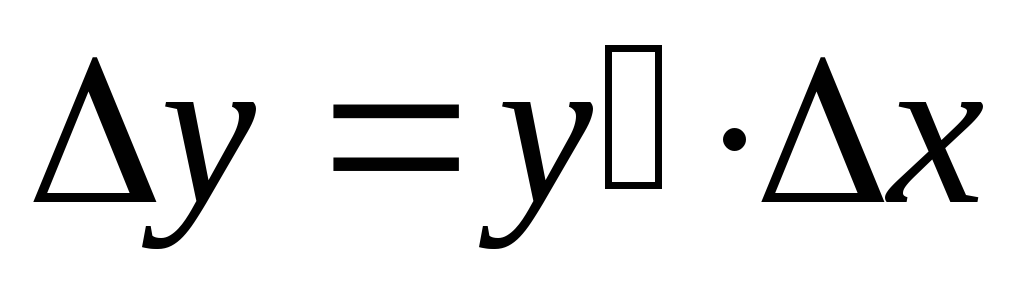
Главная
часть приращения функции, линейная
относительно приращения независимой
переменной 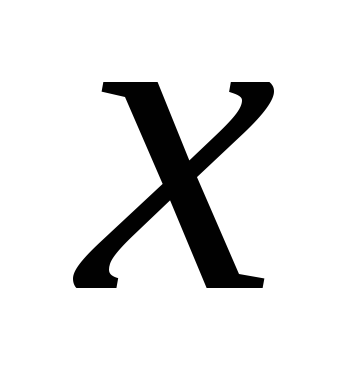 ,
называется дифференциалом функции
,
называется дифференциалом функции  и обозначается
и обозначается или
или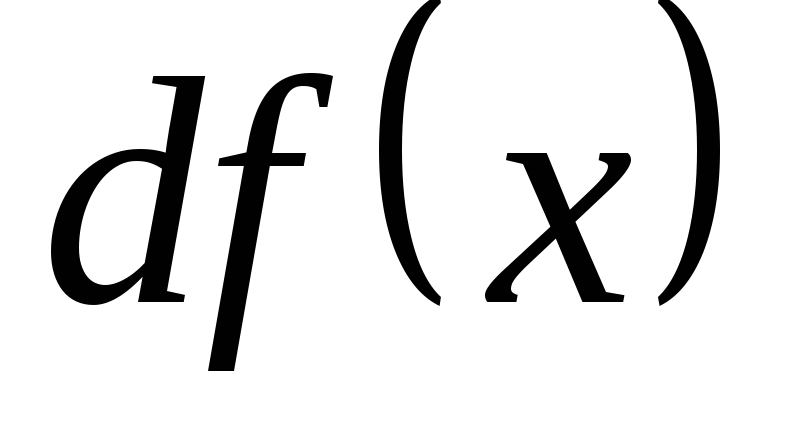 :
:
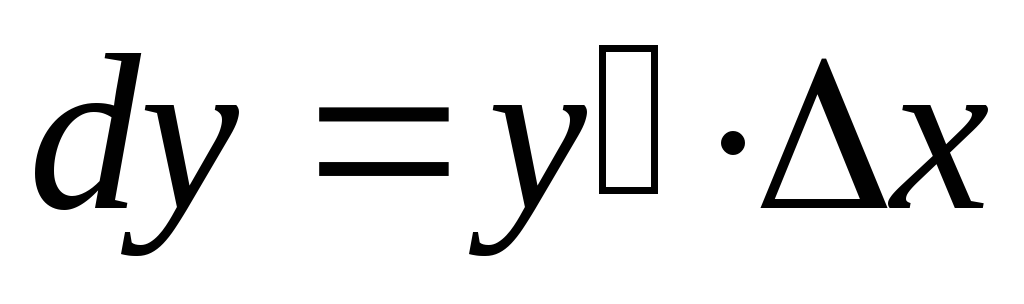 .
.
Т.
к. дифференциал 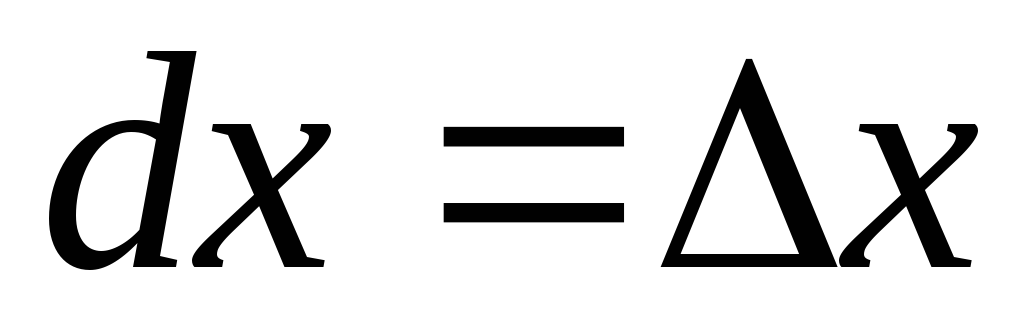 ,
то дифференциал
функции равен произведению производной
функции на дифференциал аргумента:
,
то дифференциал
функции равен произведению производной
функции на дифференциал аргумента:
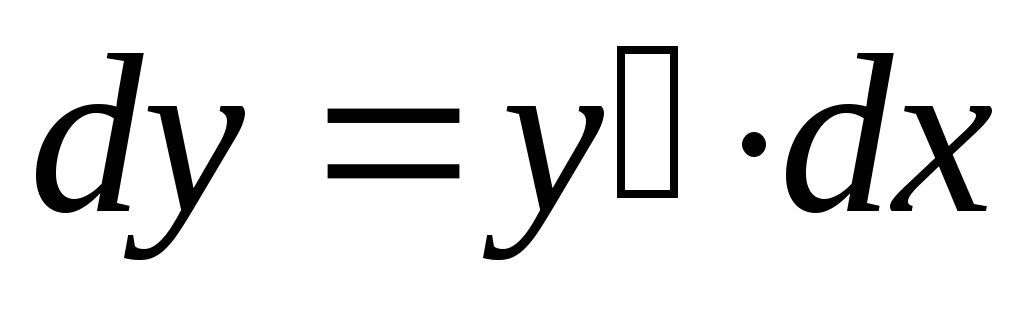 .
.
Таким
образом, для нахождения дифференциала
функции, необходимо найти производную  и умножить её
на дифференциал независимой переменной
и умножить её
на дифференциал независимой переменной 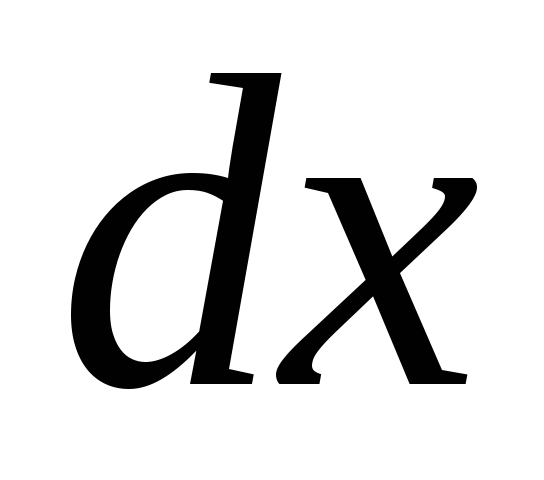 .
.
Пример 16.
Найти
дифференциал функции 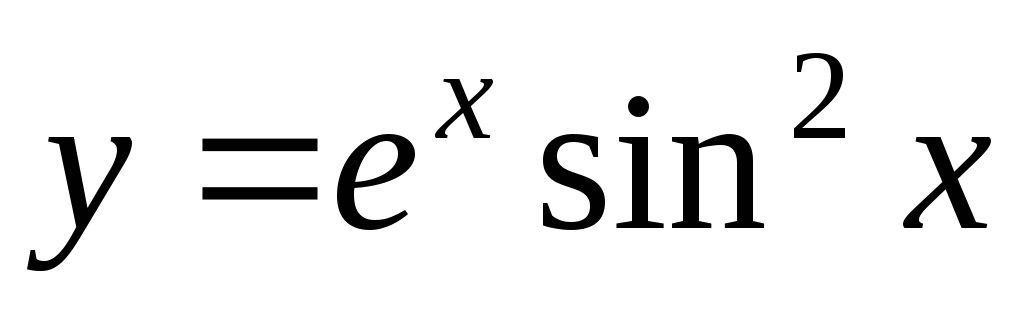 .
.
Решение.
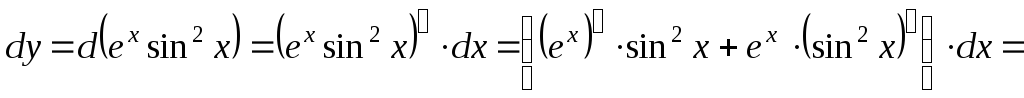
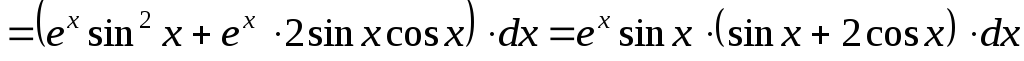 .
.
2.4. Применение дифференциального исчисления функции одной переменной
2.4.1. Применение производной при вычислении пределов.
Правило Лопиталя
При
вычислении предела функции подстановка
предельного значения аргумента часто
приводит к неопределенностям вида 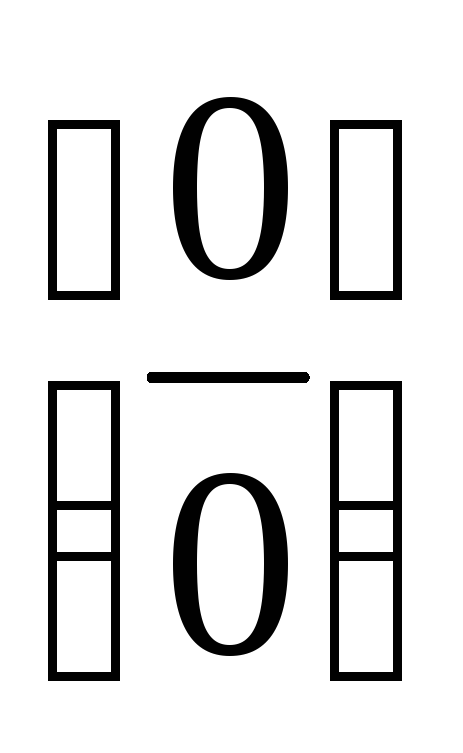 ,
,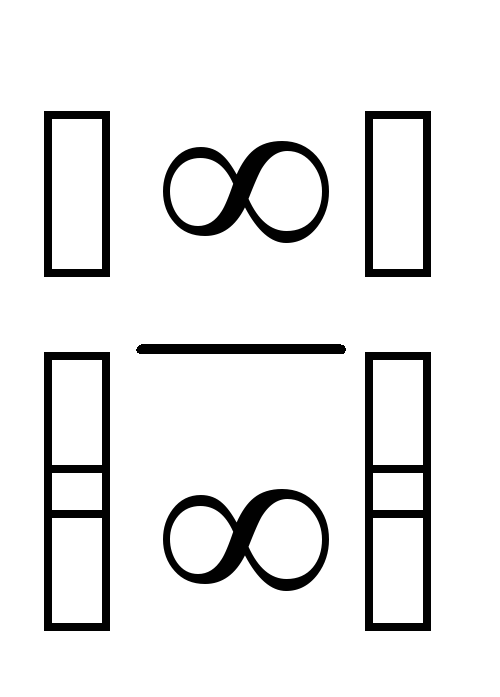 ,
от которых невозможно избавиться при
помощи ранее изученных приемов. Теорема,
известная под названиемправило
Лопиталя,
является одним из основных инструментов
для раскрытия таких неопределенностей.
,
от которых невозможно избавиться при
помощи ранее изученных приемов. Теорема,
известная под названиемправило
Лопиталя,
является одним из основных инструментов
для раскрытия таких неопределенностей.
Правило
Лопиталя: Пусть в некоторой окрестности точки 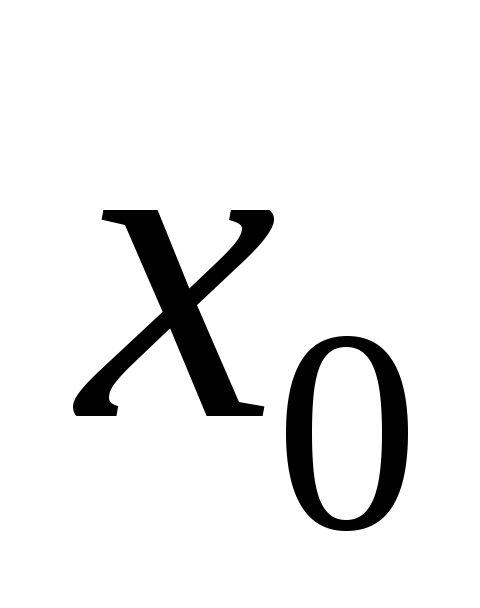 функции
функции и
и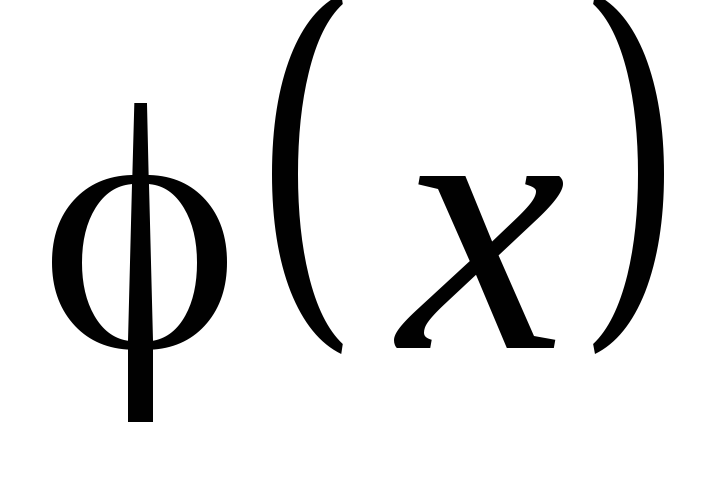 дифференцируемы и
дифференцируемы и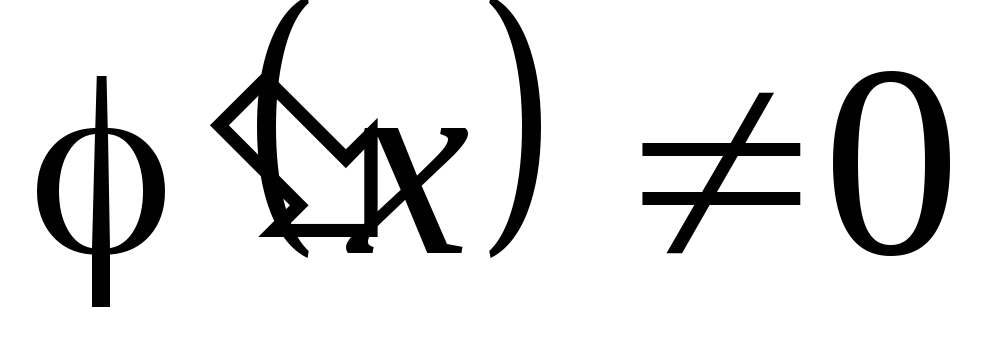 .
Если
.
Если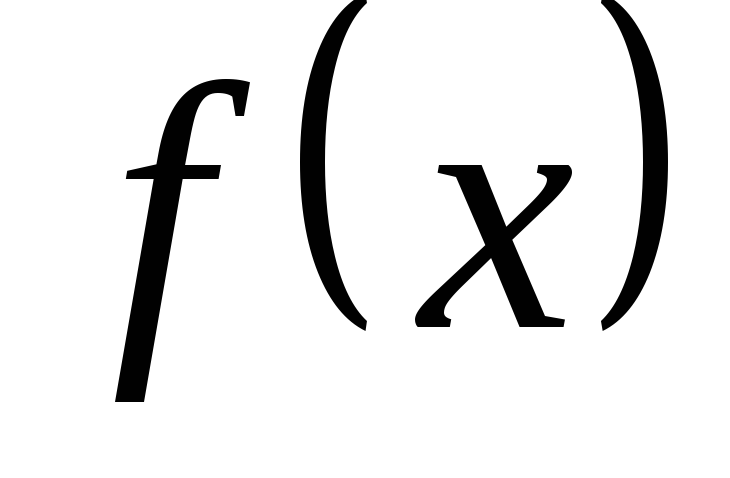 и
и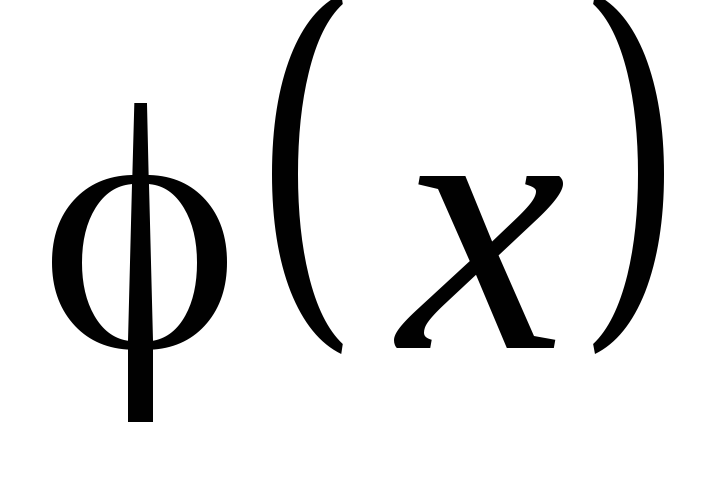 одновременно являются бесконечно малыми
или бесконечно большими функциями при
одновременно являются бесконечно малыми
или бесконечно большими функциями при  ,
то
,
то
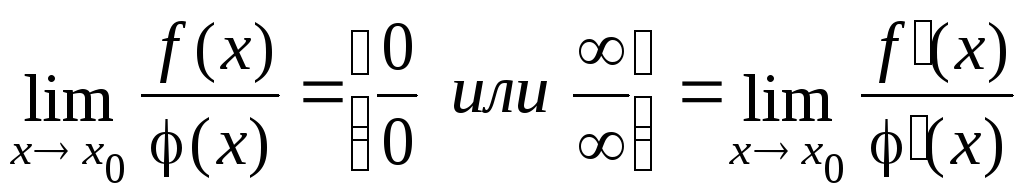 ,
,
при условии, что предел отношения производных существует.
Эта
теорема справедлива также и для
односторонних пределов, и в случае,
когда  .
.
В некоторых случаях раскрытие неопределенностей вида может потребовать неоднократного применения правила Лопиталя.
Неопределенности 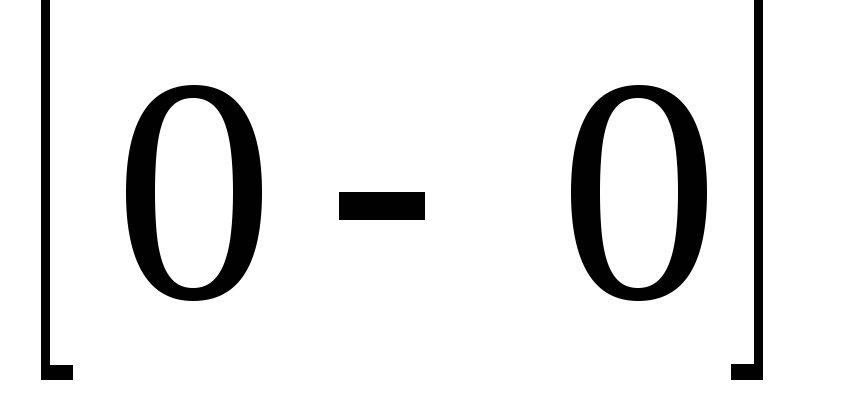 ,
,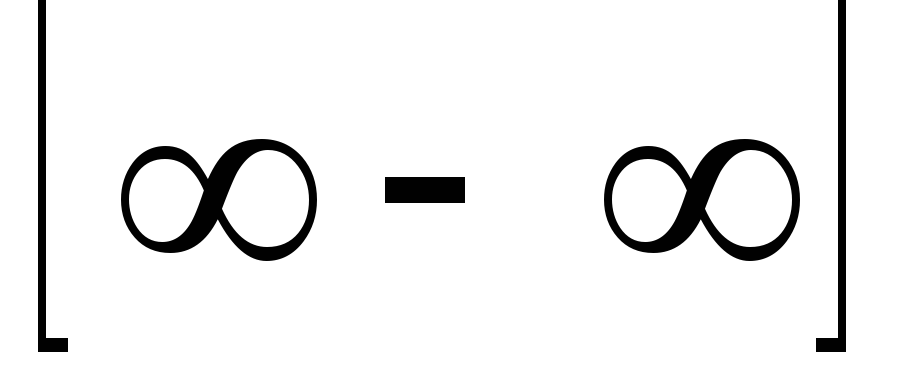 ,
,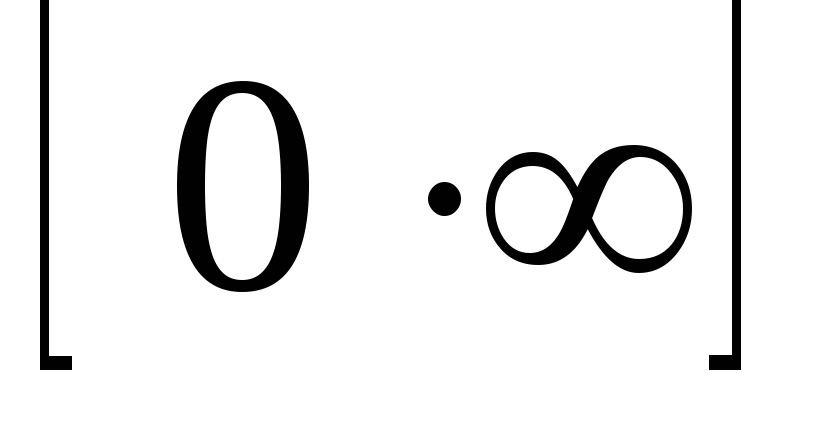 ,
,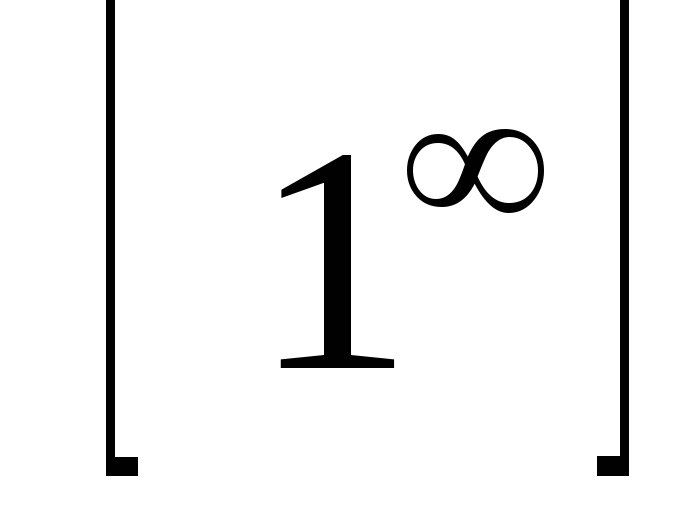 ,
,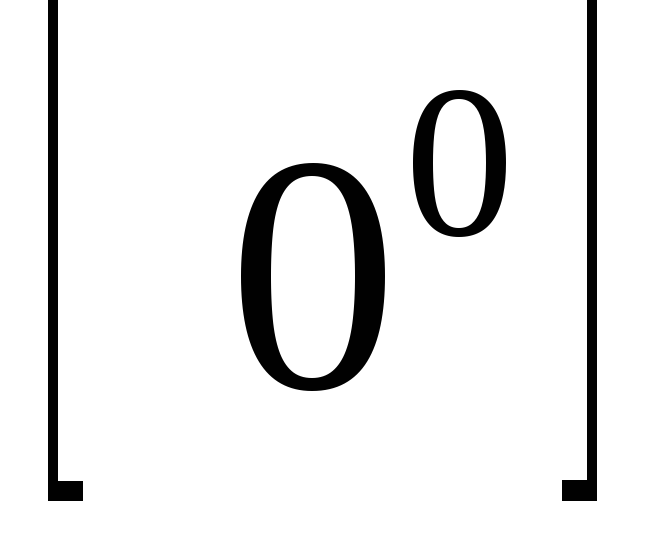 ,
, 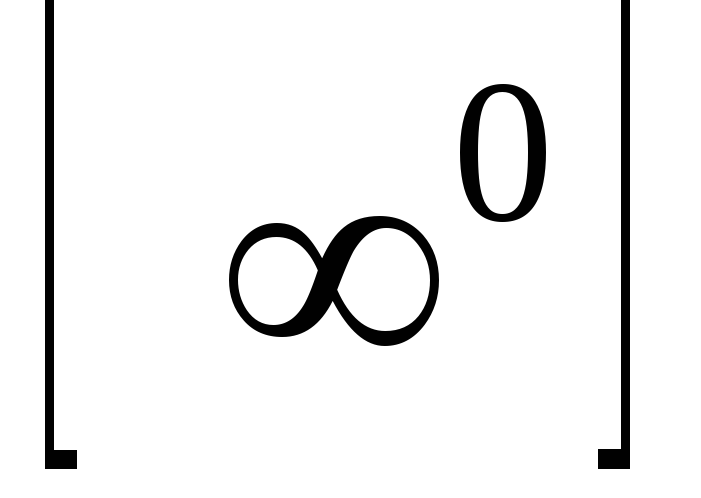 сводятся к
неопределенностям вида
сводятся к
неопределенностям вида 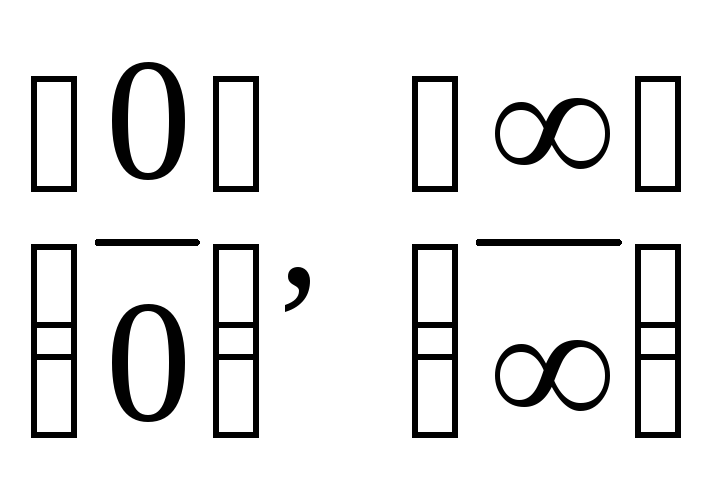 путем алгебраических преобразований.
путем алгебраических преобразований.
Пример 17.
Вычислить с помощью правила Лопиталя пределы:
а)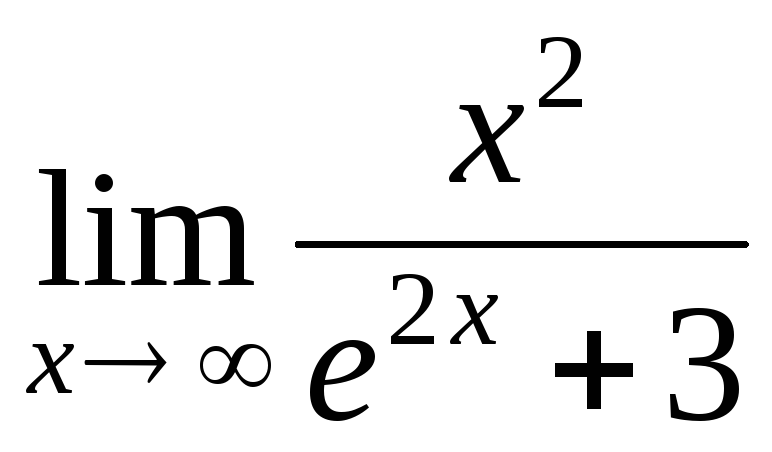 ; б)
; б)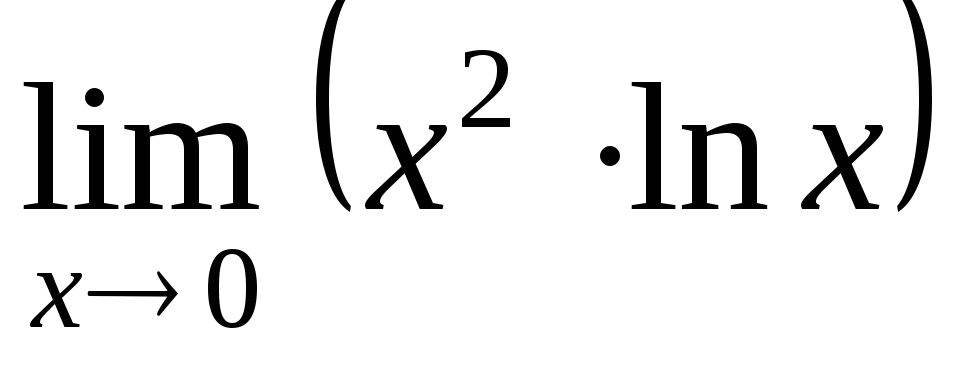 ; в)
; в)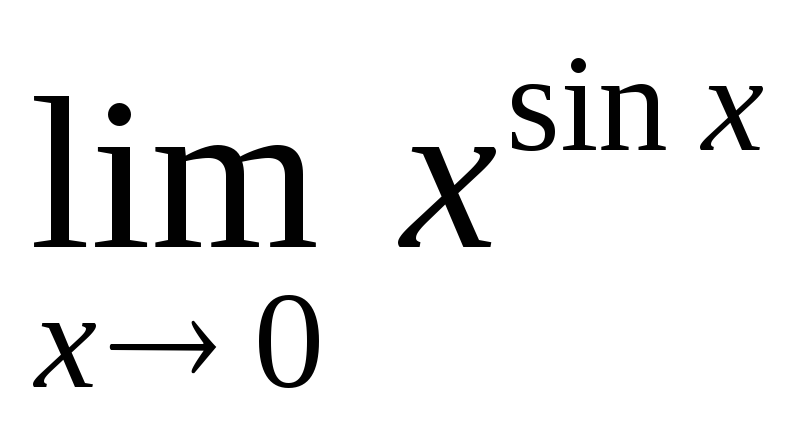 .
.
Решение.
а)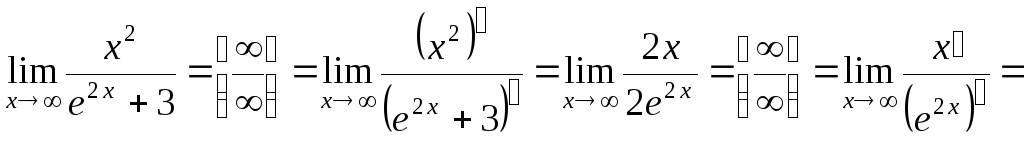
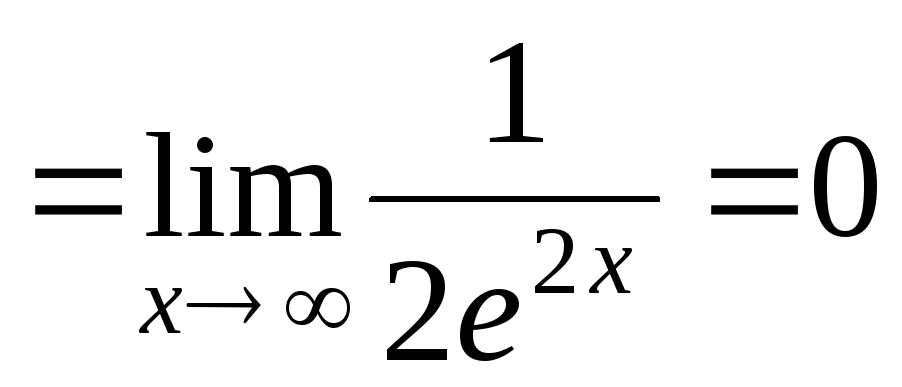 .
.
б)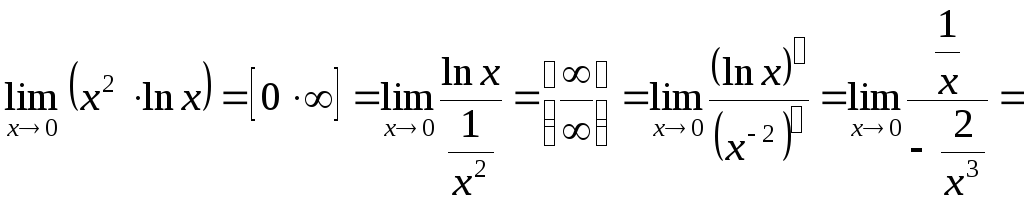
 .
.
в) 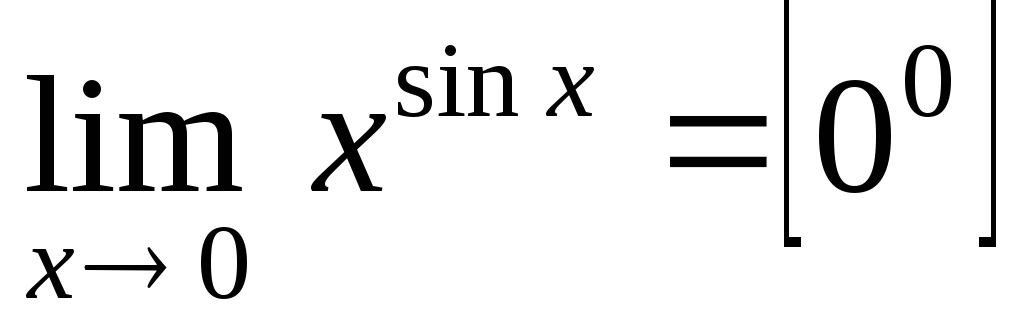 .
.
Обозначим
искомый предел через  и прологарифмируем выражение:
и прологарифмируем выражение:
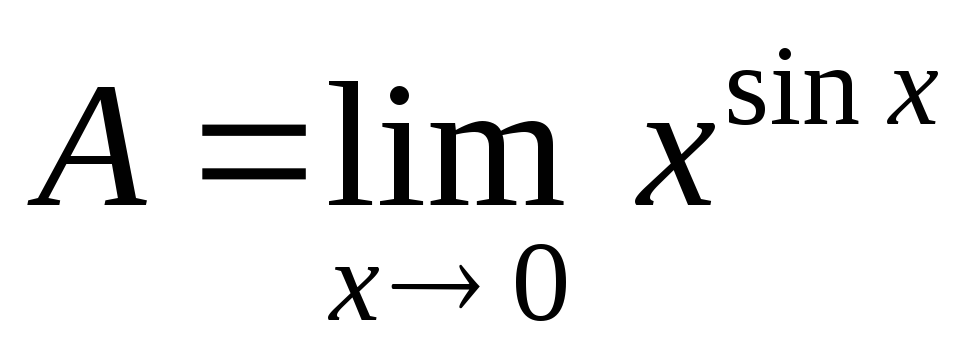 ;
;
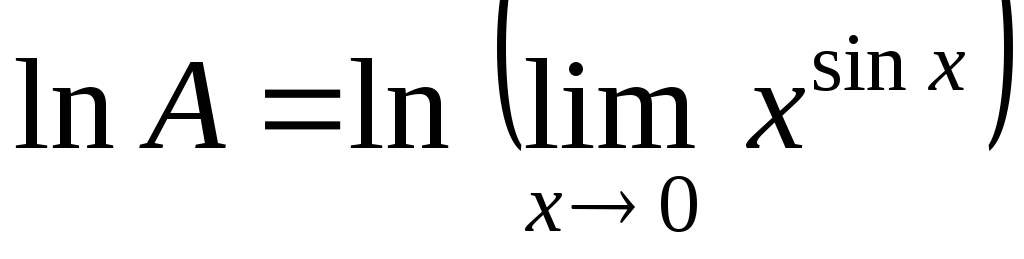 или
или 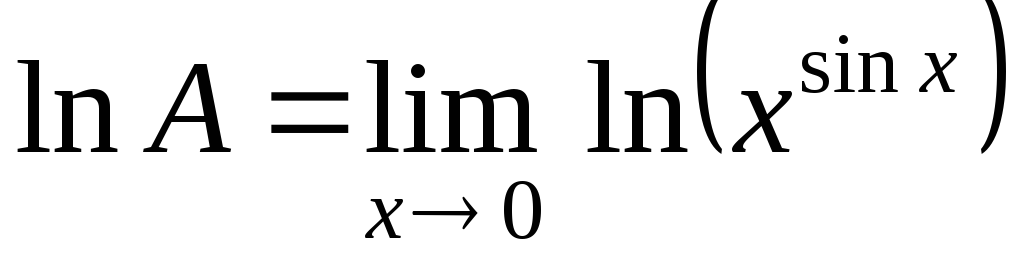 .
.
Тогда:
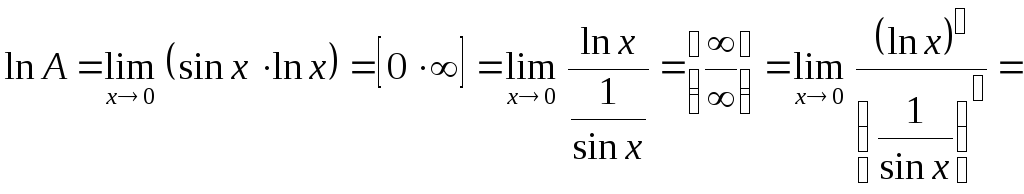
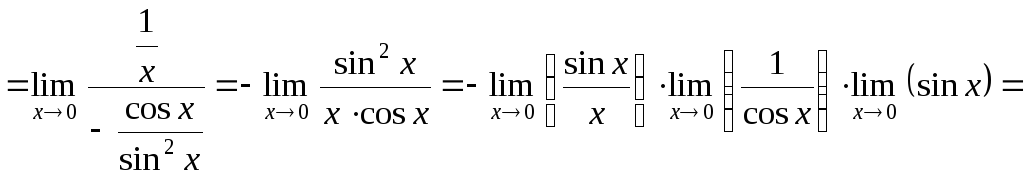
 .
.
Так
как 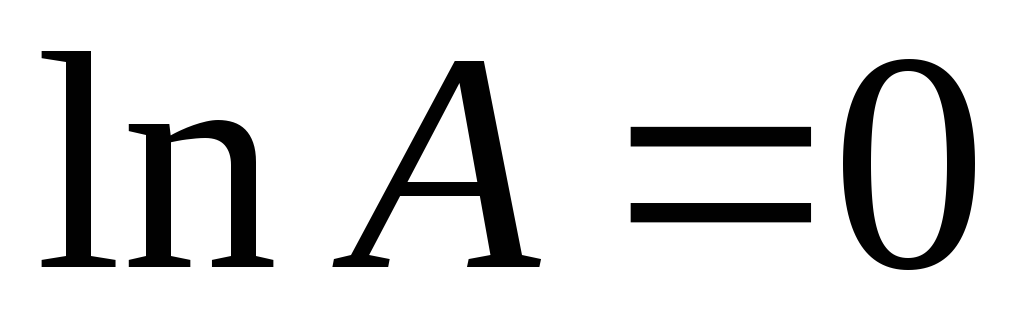 ,
то искомый предел
,
то искомый предел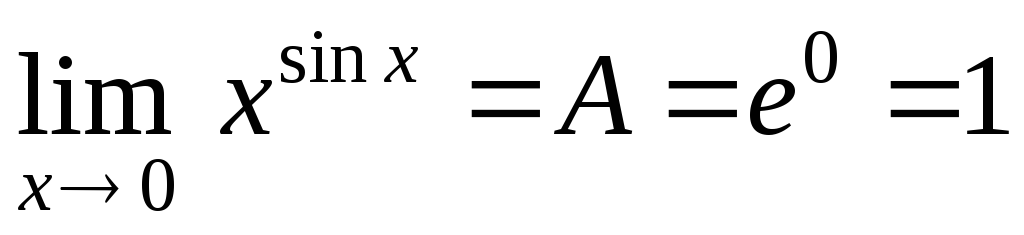 .
.