Логарифм. Примеры
Логарифмом числа b по основанию a обозначают выражение . Вычислить логарифм значит найти такой степень x (),при котором выполняется равенство
Основные свойства логарифма
Приведенные свойства необходимо знать, поскольку, на их основе решаются практически все задачи и примеры связаны с логарифмами. Остальные экзотических свойств можно вывести путем математических манипуляций с данными формулами
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
При вычислениях формулы суммы и разности логарифмов (3,4 ) встречаются довольно часто. Остальные несколько сложные, но в ряде задач являются незаменимыми для упрощения сложных выражений и вычисления их значений.
Распространены случаи логарифмов
Одними из распространенных логарифмов такие в которых основание ровное десять, экспоненте или двойке.
Логарифм по основанию десять принято называть десятичным логарифмом и упрощенно обозначать lg(x).
Из записи видно, что основы в записи не пишут. Для примера
Натуральный логарифм – это логарифм у которого за основу экспонента ( обозначают ln(x)).
Экспонента равна 2,718281828…. Чтобы запомнить экспоненту можете изучить правило: экспонента равна 2,7 и два раза год рождения Льва Николаевича Толстого. Зная это правило будете знать и точное значение экспоненты, и дату рождения Льва Толстого.
И еще один важный логарифм по основанию два обозначают
Производная от логарифм функции равна единице разделенной на переменную
Интеграл или первообразная логарифма определяется зависимостью
Приведенного материала Вам достаточно, чтобы решать широкий класс задач связанных с логарифмами и логарифмирования. Для усвоения материала приведу лишь несколько распространенных примеров из школьной программы и ВУЗов.
Примеры на логарифмы
Прологарифмировать выражения
Пример 1.
а). х=10ас^2 (а>0,с>0).
По свойствам 3,5 вычисляем
2.
По свойству разницы логарифмов имеем
3.
Используя свойства 3,5 находим
4. где .
На вид сложное выражение с использованием ряда правил упрощается к виду
——————————————
Нахождение значений логарифмов
Пример 2. Найти х, если
Решение. Для вычисления применим до последнего слагаемого 5 и 13 свойства
Подставляем в запись и скорбим
Поскольку основания равные, то приравниваем выражения
——————————————
Пример 3. Пусть задано значение логарифмов
yukhym.com
Выруби AdBlock ! ! !
ШВЕЦОВ К.И., БЕВЗ Г.П.
СПРАВОЧНИК ПО ЭЛЕМЕНТАРНОЙ МАТЕМАТИКЕ
АРИФМЕТИКА, АЛГЕБРА, 1965

СОДЕРЖАНИЕ ДАННОЙ СТАТЬИ
Очень часто в логарифмических преобразованиях пользуются также следующими формулами:

Пример 1. Что больше, log4 3 или log16 9?
Решение. Используя формулу  , получаем
, получаем

Пример 2. Вычислить  , зная, что log₂ 3 = а.
, зная, что log₂ 3 = а.
Решение.

35. Логарифмирование и потенцирование
1. Логарифмирование. Логарифмировать алгебраическое выражение — значит выразить логарифм его через логарифмы отдельных чисел, входящих в это выражение. Это можно сделать, используя теоремы о логарифме произведения, частного, степени и корня.
Логарифм произведения равен сумме логарифмов сомножителей:
log (ab) = log а + log b.
Логарифм частного (дроби) равен разности логарифмов делимого и делителя:

Логарифм степени равен произведению показателя степени на логарифм ее основания:
log а m = m log a.
Логарифм корня равен частному от деления логарифма подкоренного числа на показатель корня:

Примечание. При логарифмировании алгебраических выражений надо иметь в виду, что логарифм суммы не равен сумме логарифмов, т.е. нельзя вместо log(a + b) писать log а + log b. Нельзя также вместо log (а — b
) писать log а — log b.Логарифмирование алгебраических выражений проиллюстрируем на примерах.
Примеры. Прологарифмировать следующие выражения:
а) х = 3 bc ; log х = log 3 + log b + log c.
б) 
в) 
г) 
д) 
е) 
ж) 
2. Потенцирование. Если по данному результату логарифмирования находят выражение, от которого получен этот результат, то такую операцию называют потенцированием.
Примеры. Пропотенцировать следующие выражения:
а) 
б) 
в) 
мобильная версия страницы Смотрите также на этом сайте:
Пользуйтесь поиском вверху страницы! Все, что будет найдено со значком Ł — относится к данному сайту
cartalana.org
Логарифмическое дифференцирование
При вычислении производной от логарифма произведения, частного, степени или корня, для упрощения нахождения производной проводят предварительное преобразование (см. Пример 10(и)).
В ряде случаев для нахождения производной целесообразно заданную функцию сначала прологарифмировать (по умолчанию имеется в виду натуральный логарифм). Затем найти производную от этого логарифма и по ней отыскать производную от заданной функции. Такой прием называется
Метод логарифмического дифференцирования позволяет легко найти производную показательно-степенной функции вида
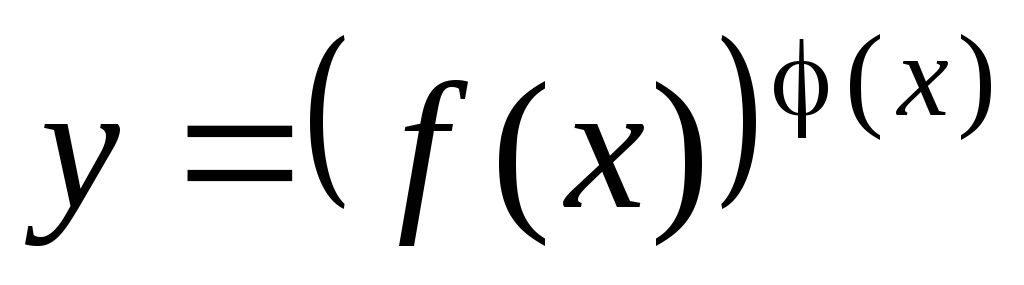 ,
,
где 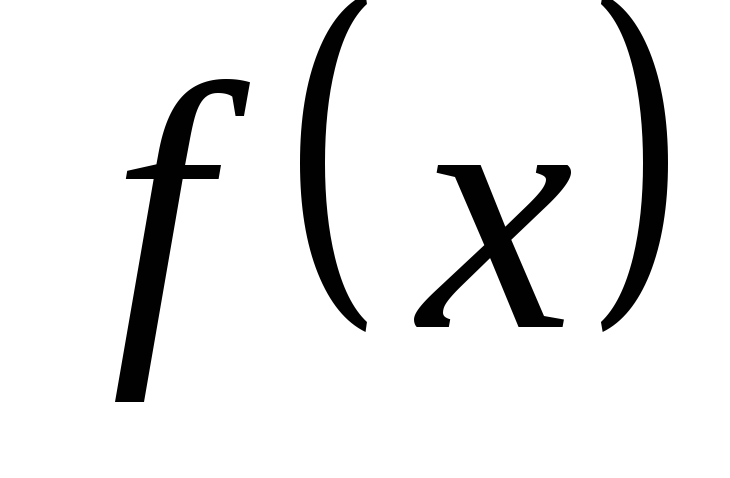 и
и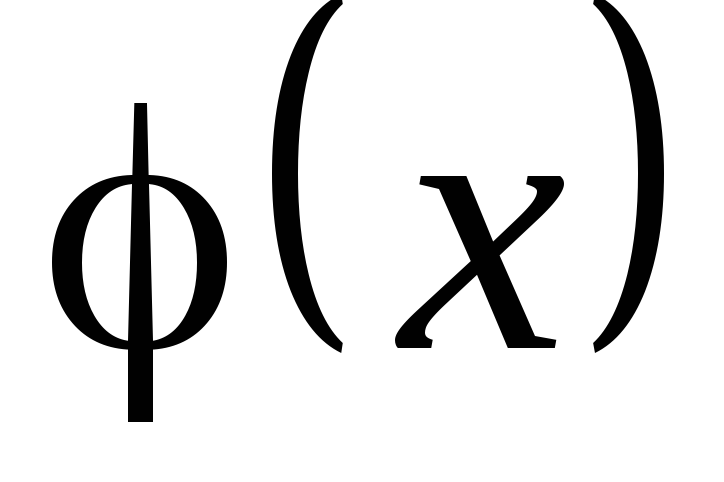 – дифференцируемые функции аргумента
– дифференцируемые функции аргумента 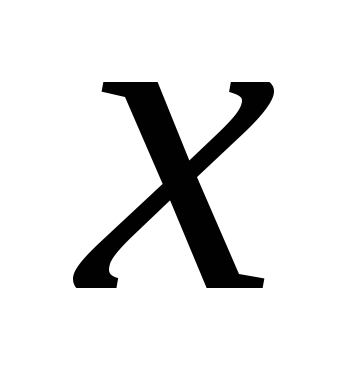 .
.
Пример 14.
Найти
производную функции 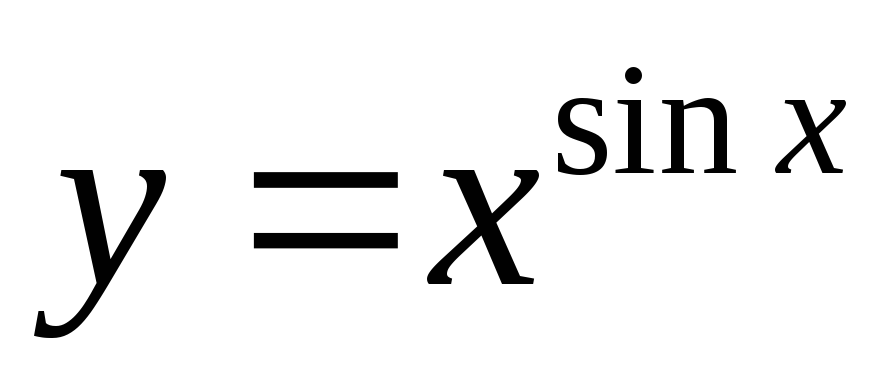 .
.
Решение.
Прологарифмируем обе части функции и преобразуем выражение:
 .
.
Теперь дифференцируем уравнение, как неявно заданную функцию:
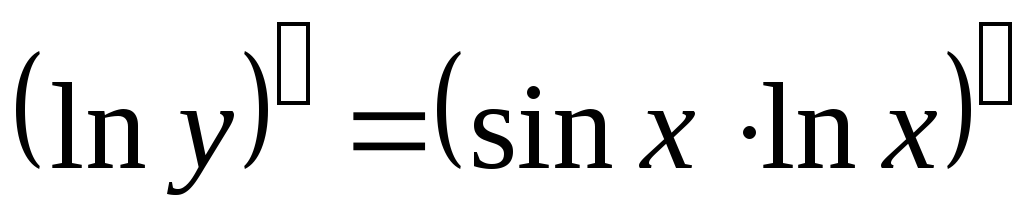 ;
;
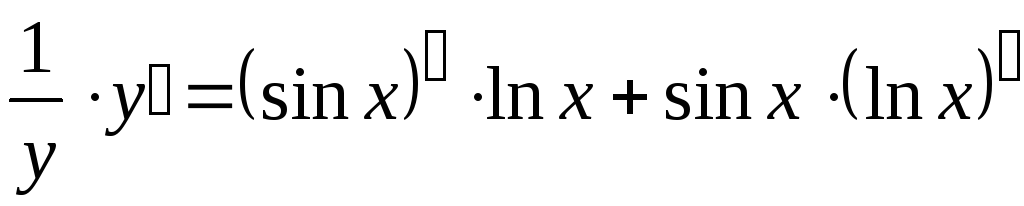 ;
;
 ;
;
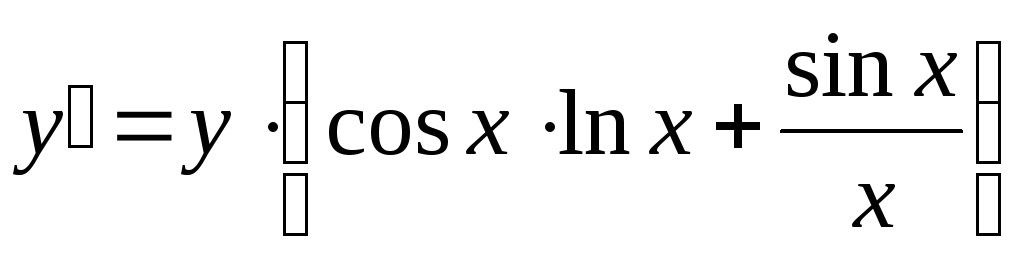 ;
;
Так
как 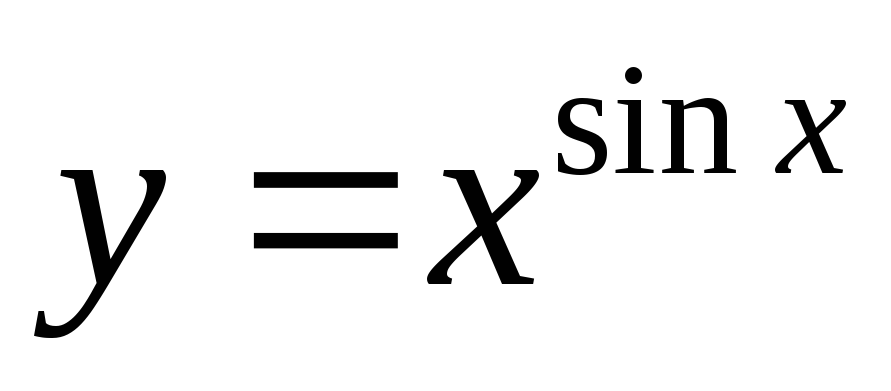 ,
то окончательно получаем:
,
то окончательно получаем:
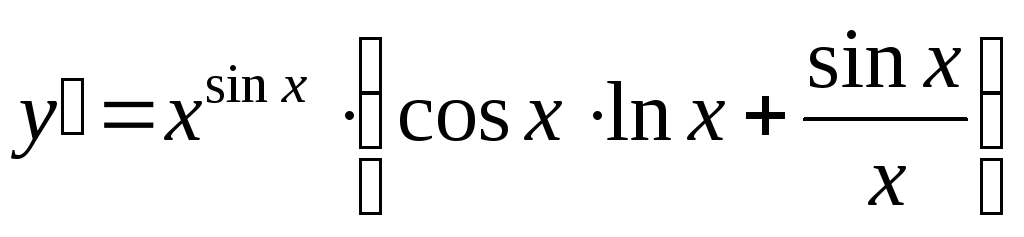
Производные высших порядков
Производной
2-го порядка от функции 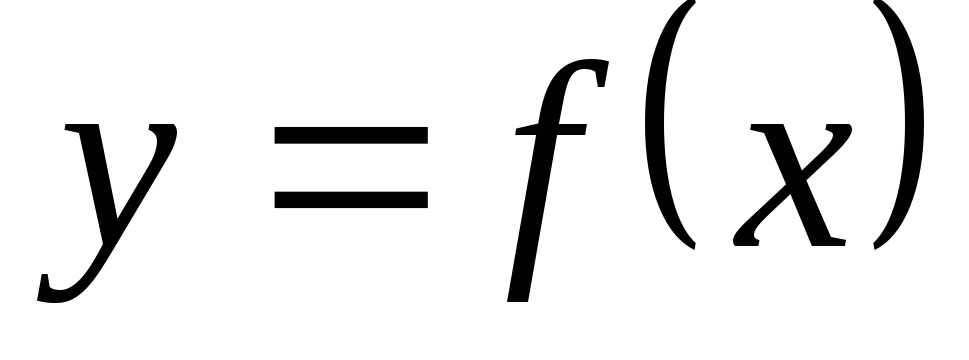 называется производная от её первой
производной, т.е.
называется производная от её первой
производной, т.е.
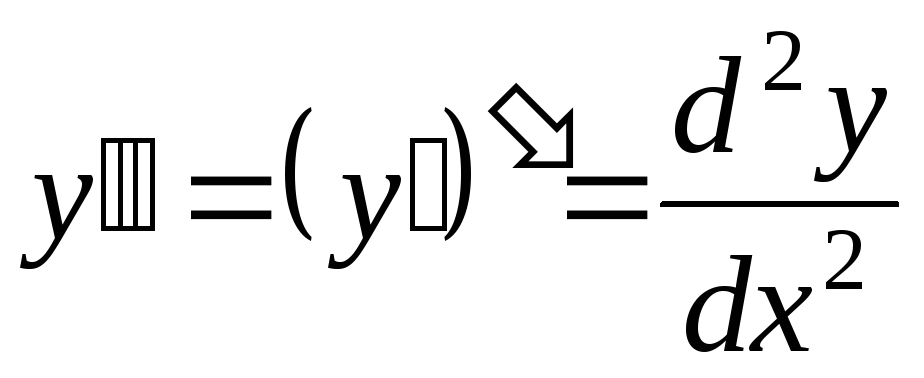 .
.
Аналогично,
производной 3-го порядка от функции  называется
производная от её второй производной,
т.е.
называется
производная от её второй производной,
т.е.
 .
.
Таким
образом, производной 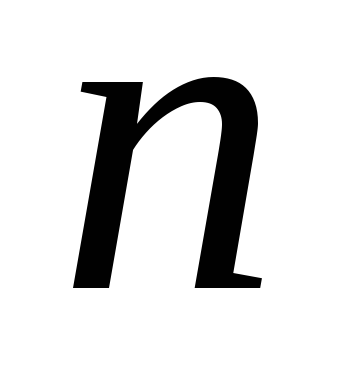 -го
порядка от функции
-го
порядка от функции 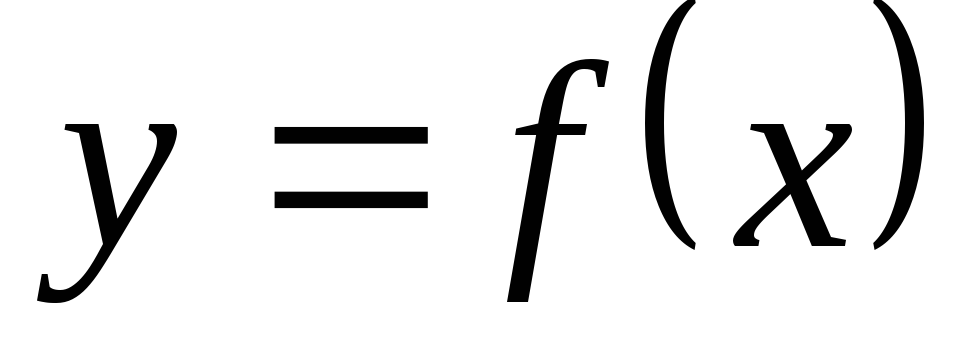 называется производная от производной
называется производная от производной 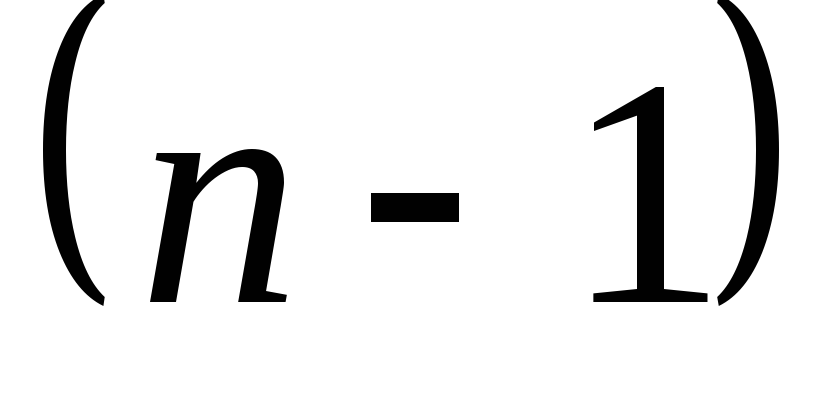
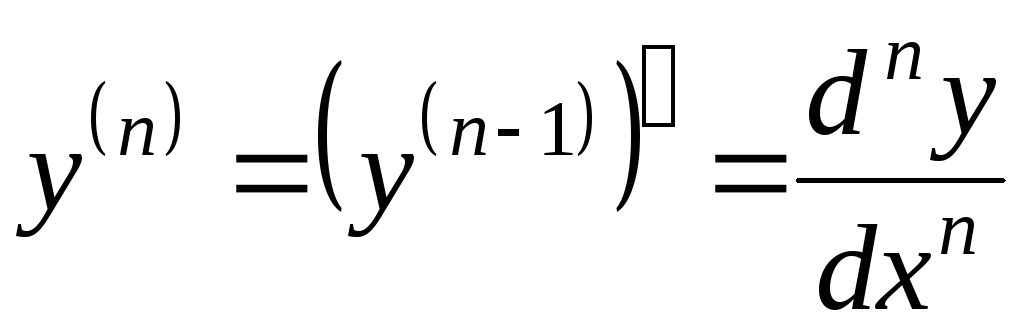 .
.
Следовательно,
для нахождения производной 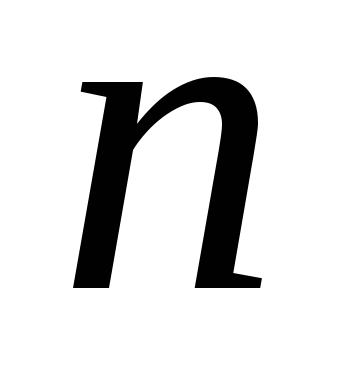 -го
порядка необходимо последовательно
найти производную первого, затем второго,
затем третьего и т.д. до
-го
порядка необходимо последовательно
найти производную первого, затем второго,
затем третьего и т.д. до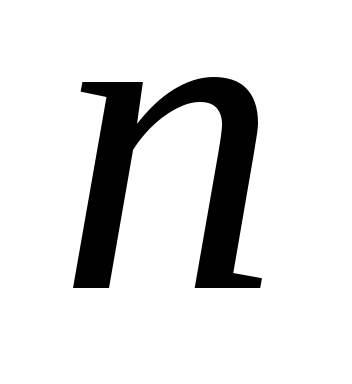 -го
порядка.
-го
порядка.
Пример 15.
Найти
третью производную  функции
функции  .
.
Решение.
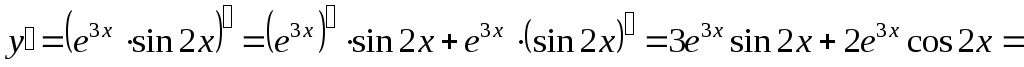
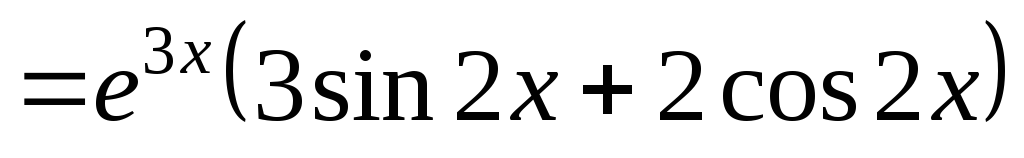 ;
;
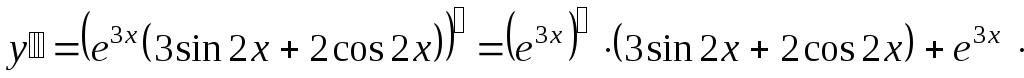
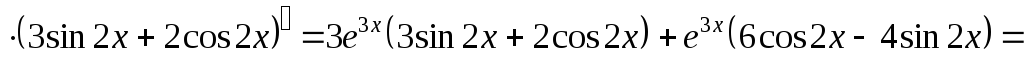
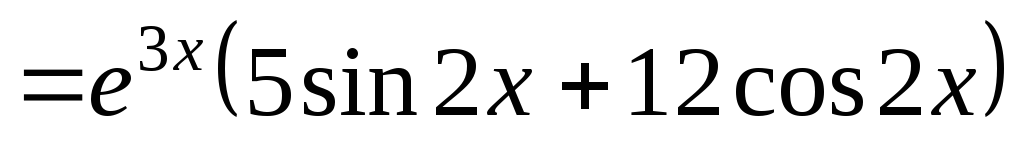 ;
;
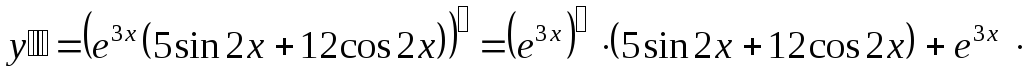
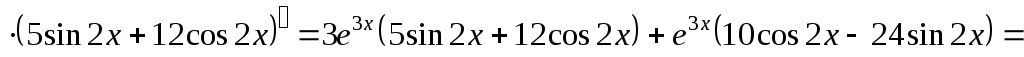
 .
.
2.3. Дифференциал функции
Из определения производной и свойств пределов следует, что если
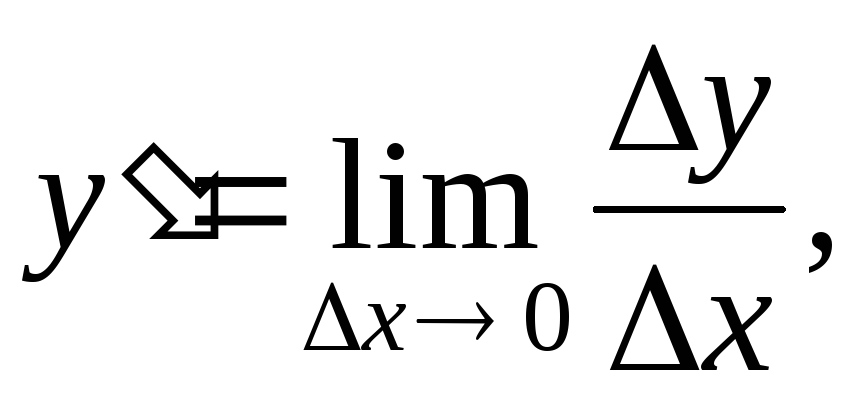
 ,
, где  –
бесконечно малая величина (
–
бесконечно малая величина (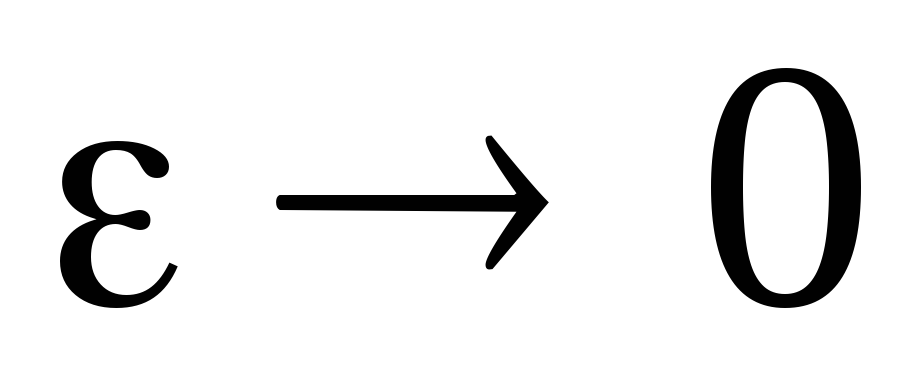 ).
).
Выражаем  и получаем, что:
и получаем, что: .
Так как
.
Так как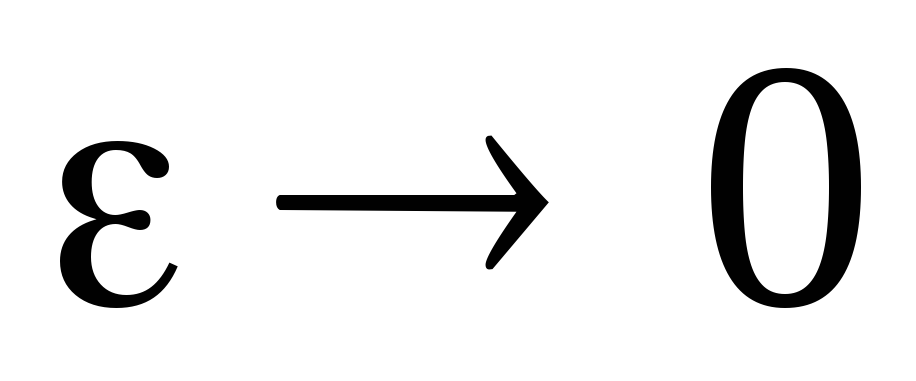 ,
то в дальнейшем ее можно не учитывать
и мы получим:
,
то в дальнейшем ее можно не учитывать
и мы получим: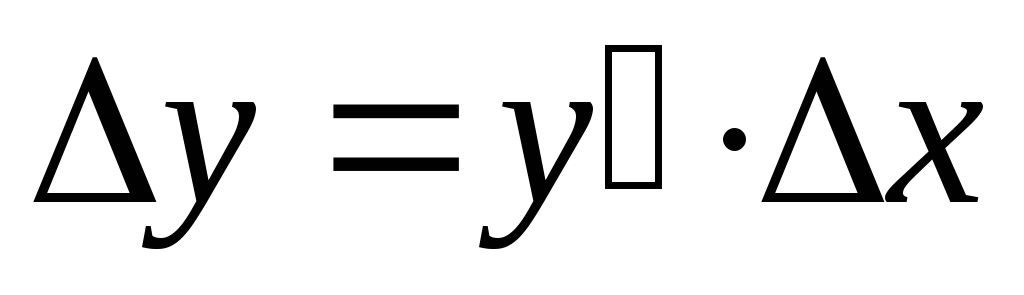
Главная
часть приращения функции, линейная
относительно приращения независимой
переменной 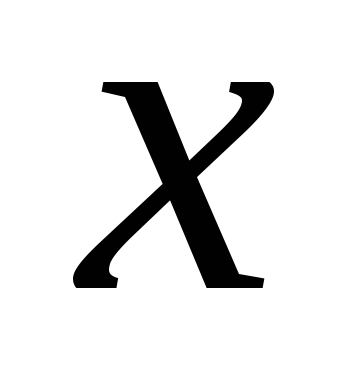
 и обозначается
и обозначается или
или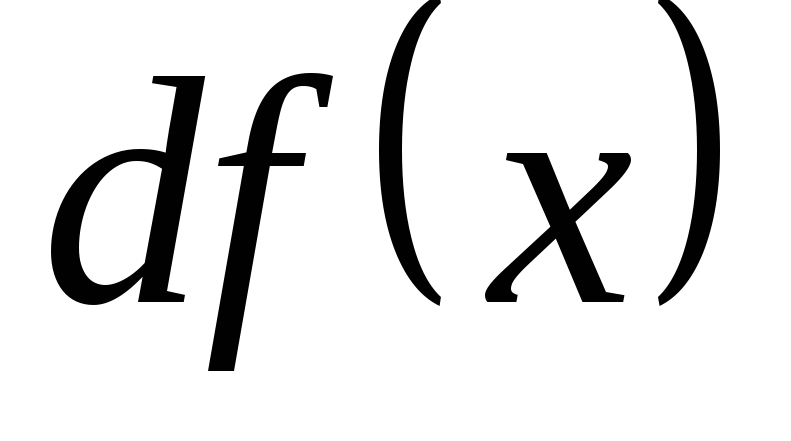 :
: 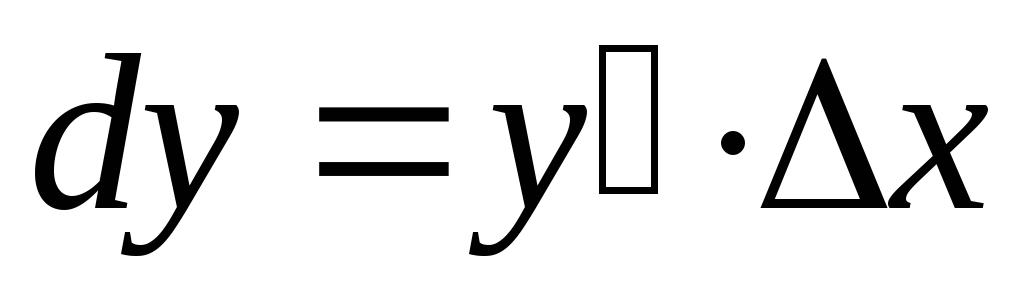 .
.
Т.
к. дифференциал 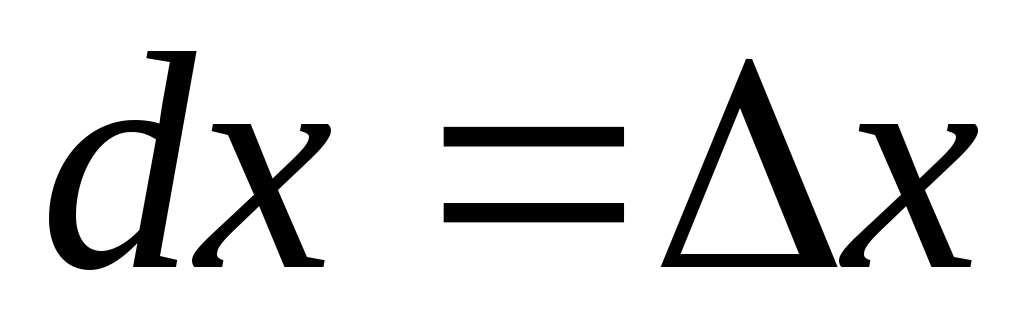 ,
то дифференциал
функции равен произведению производной
функции на дифференциал аргумента:
,
то дифференциал
функции равен произведению производной
функции на дифференциал аргумента:
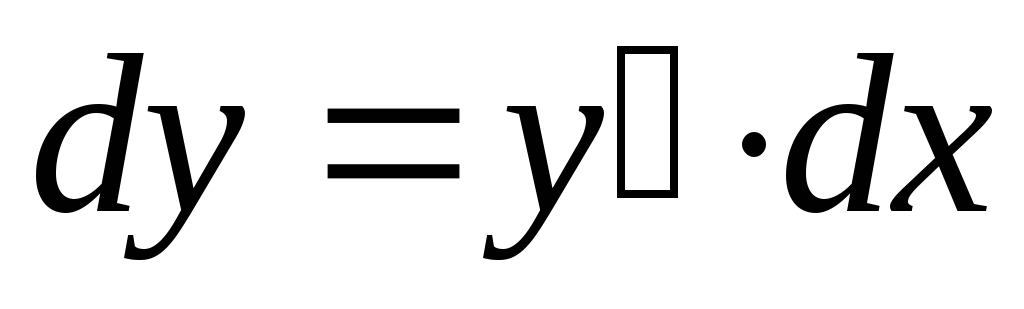 .
.
Таким
образом, для нахождения дифференциала
функции, необходимо найти производную  и умножить её
на дифференциал независимой переменной
и умножить её
на дифференциал независимой переменной  .
.
Пример 16.
Найти
дифференциал функции 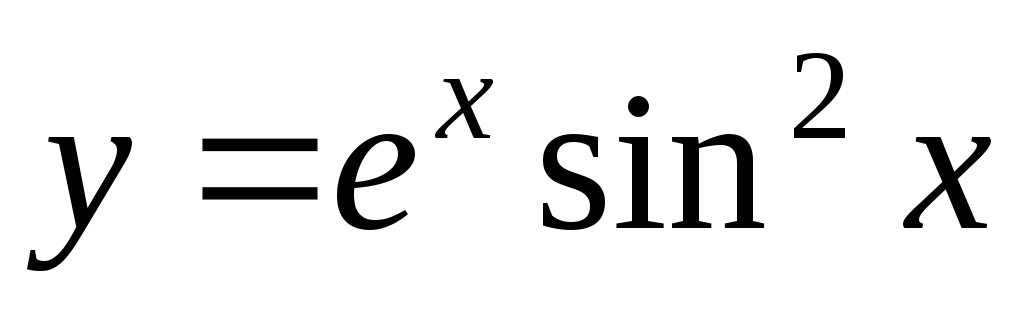 .
.
Решение.
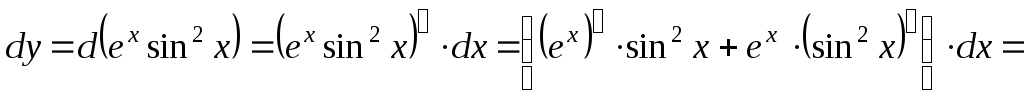
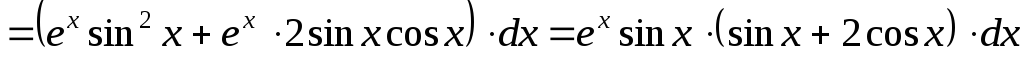 .
.
2.4. Применение дифференциального исчисления функции одной переменной
2.4.1. Применение производной при вычислении пределов.
Правило Лопиталя
При
вычислении предела функции подстановка
предельного значения аргумента часто
приводит к неопределенностям вида  ,
,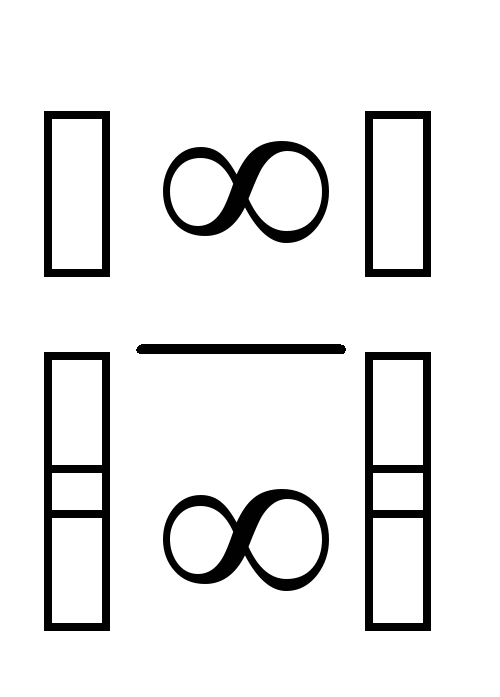 ,
от которых невозможно избавиться при
помощи ранее изученных приемов. Теорема,
известная под названиемправило
Лопиталя,
является одним из основных инструментов
для раскрытия таких неопределенностей.
,
от которых невозможно избавиться при
помощи ранее изученных приемов. Теорема,
известная под названиемправило
Лопиталя,
является одним из основных инструментов
для раскрытия таких неопределенностей.
Правило
Лопиталя: Пусть в некоторой окрестности точки 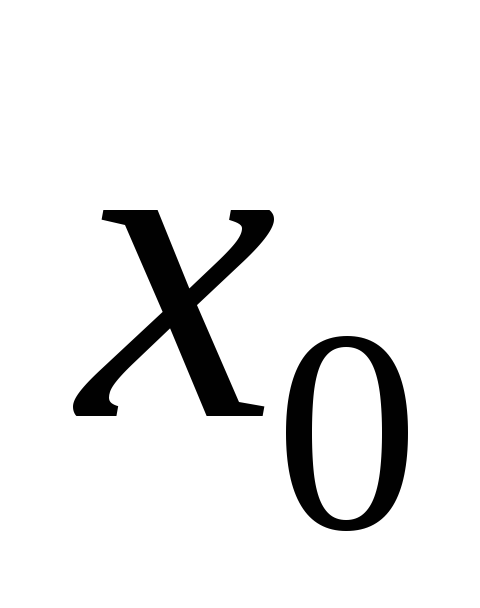 функции
функции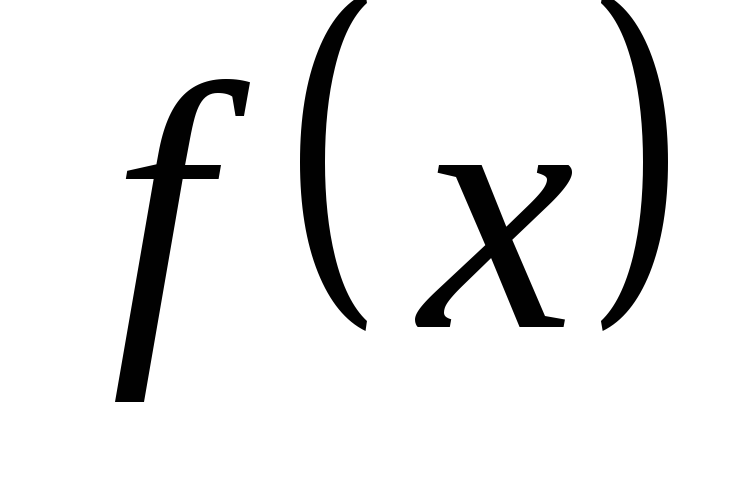 и
и дифференцируемы и
дифференцируемы и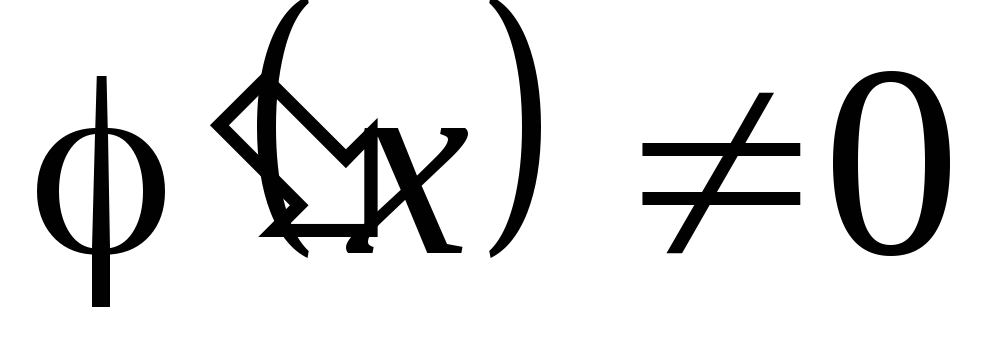 .
Если
.
Если и
и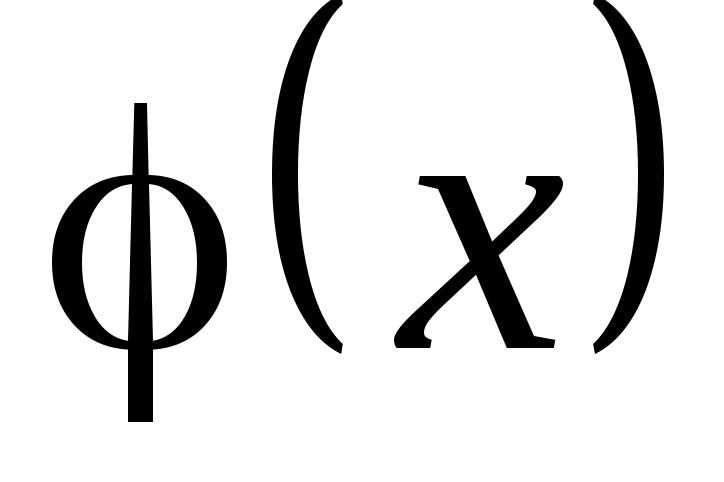 одновременно являются бесконечно малыми
или бесконечно большими функциями при
одновременно являются бесконечно малыми
или бесконечно большими функциями при  ,
то
,
то
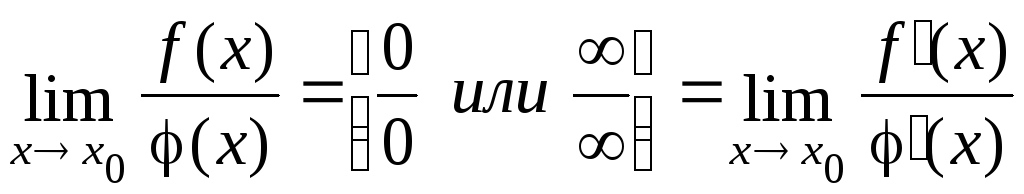 ,
,
при условии, что предел отношения производных существует.
Эта
теорема справедлива также и для
односторонних пределов, и в случае,
когда  .
.
В
некоторых случаях раскрытие
неопределенностей вида 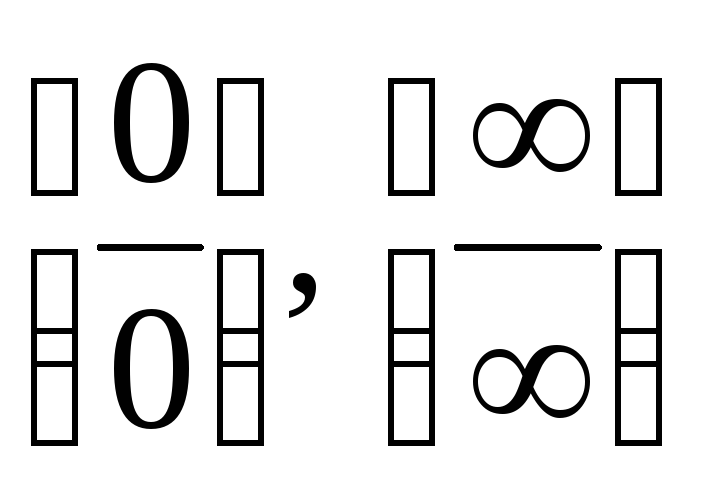 может потребовать неоднократного
применения правила Лопиталя.
может потребовать неоднократного
применения правила Лопиталя.
Неопределенности 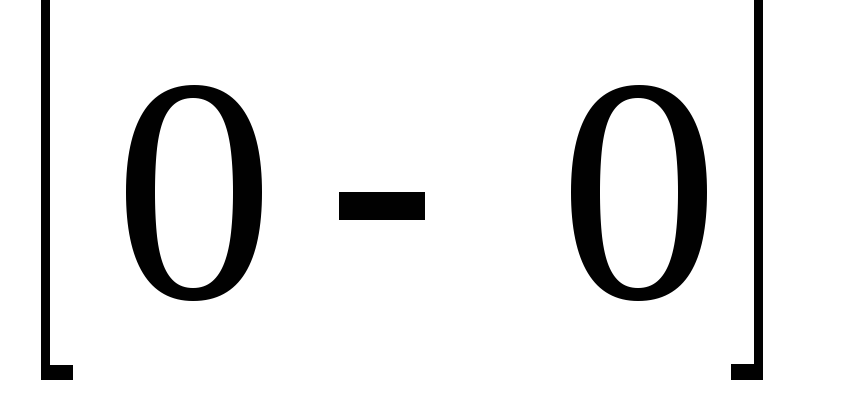 ,
,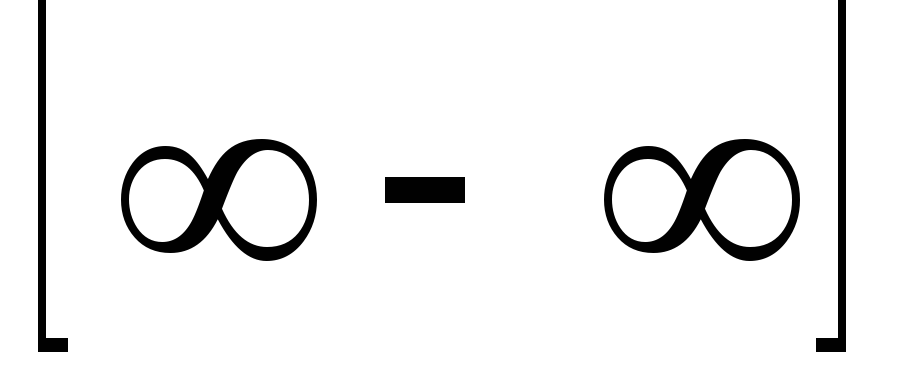 ,
, ,
,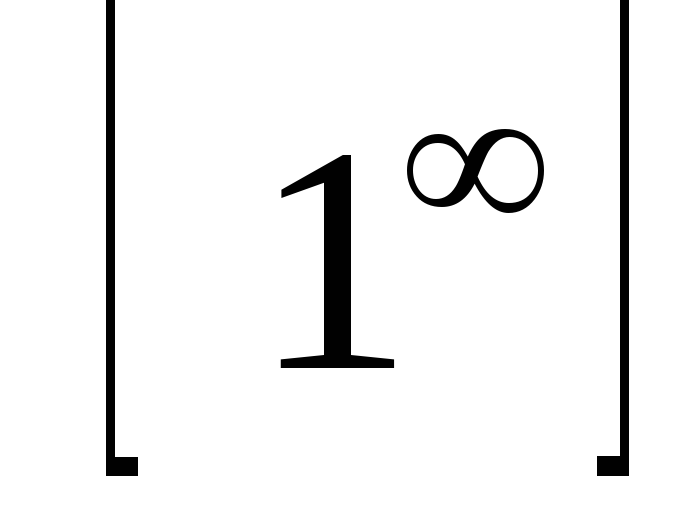 ,
, ,
, 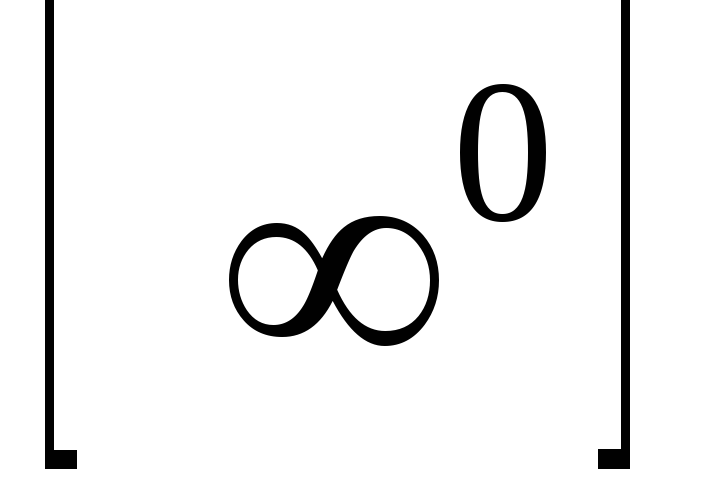 сводятся к
неопределенностям вида
сводятся к
неопределенностям вида 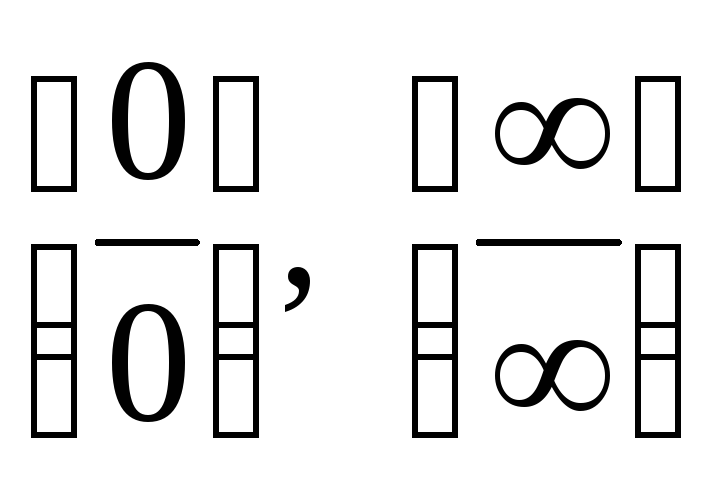 путем алгебраических преобразований.
путем алгебраических преобразований.
Пример 17.
Вычислить с помощью правила Лопиталя пределы:
а)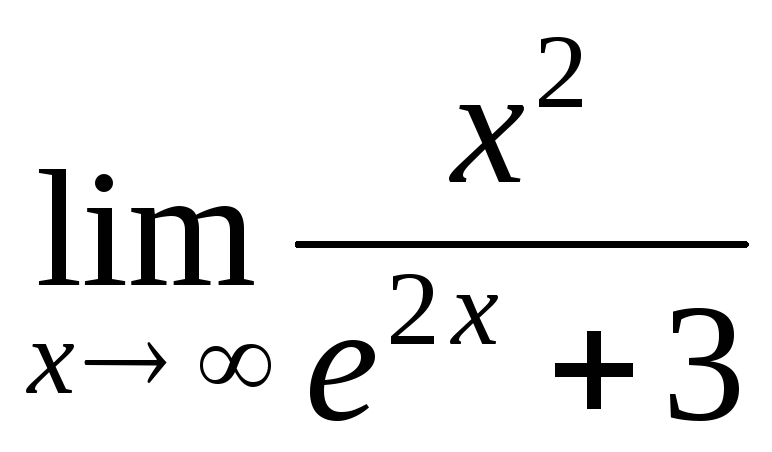 ; б); в)
; б); в)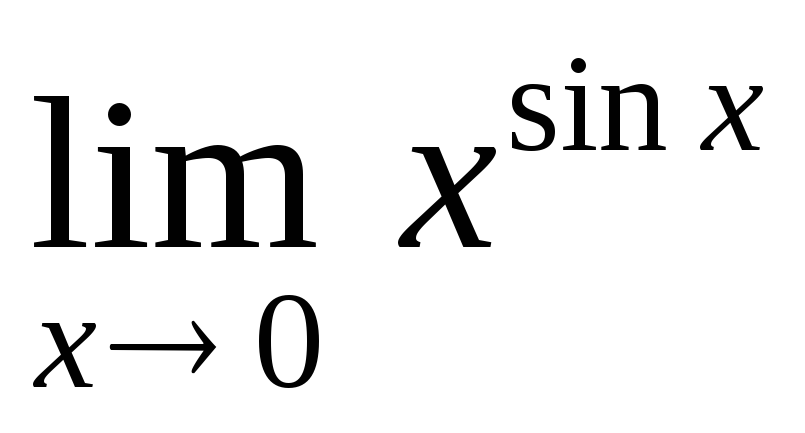 .
.
Решение.
а)
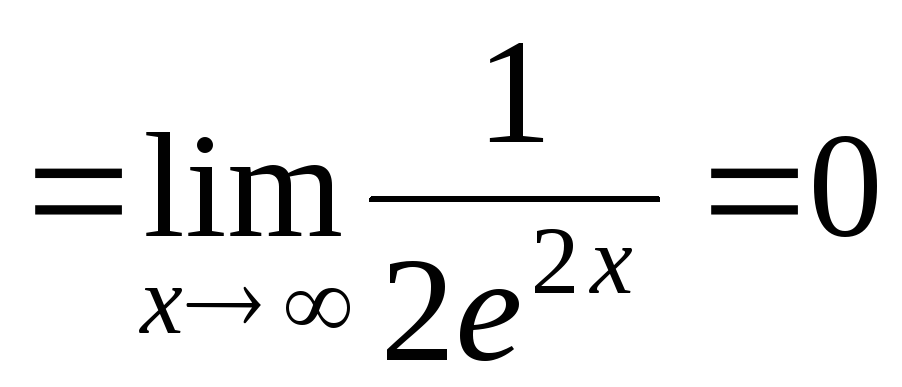 .
.
б)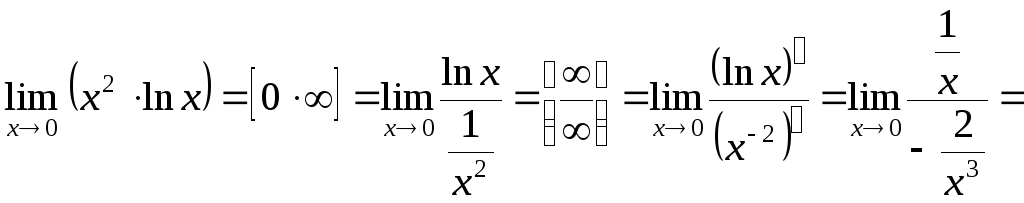
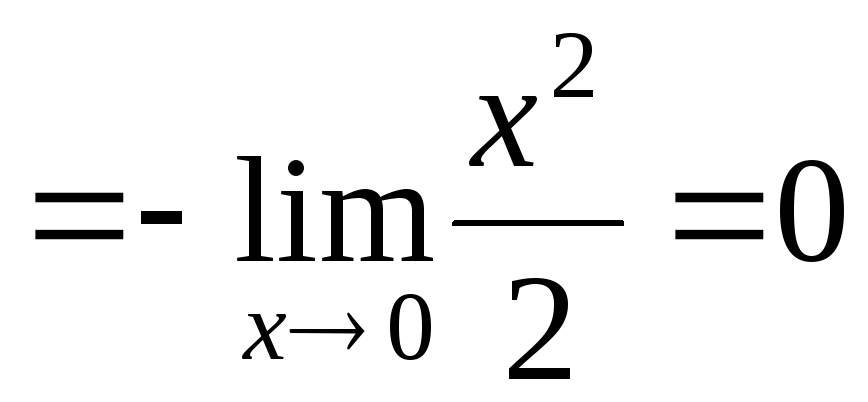 .
.
в) 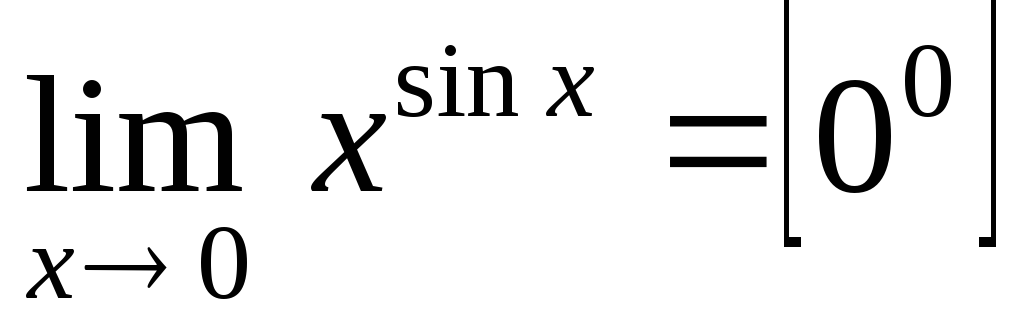 .
.
Обозначим
искомый предел через  и прологарифмируем выражение:
и прологарифмируем выражение:
 ;
;
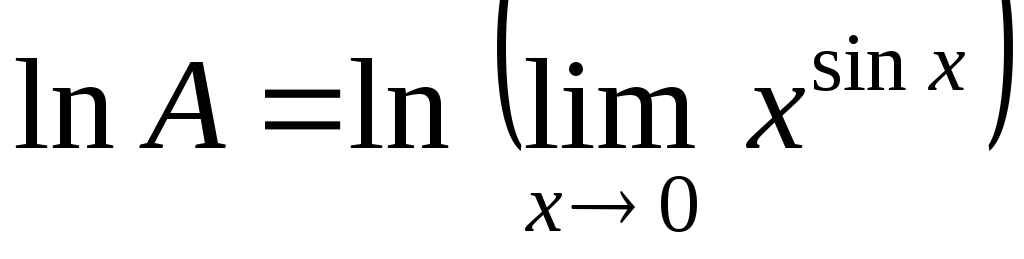 или
или 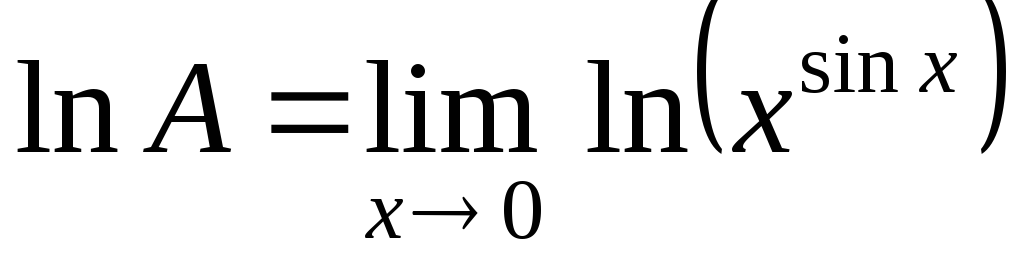 .
.
Тогда:


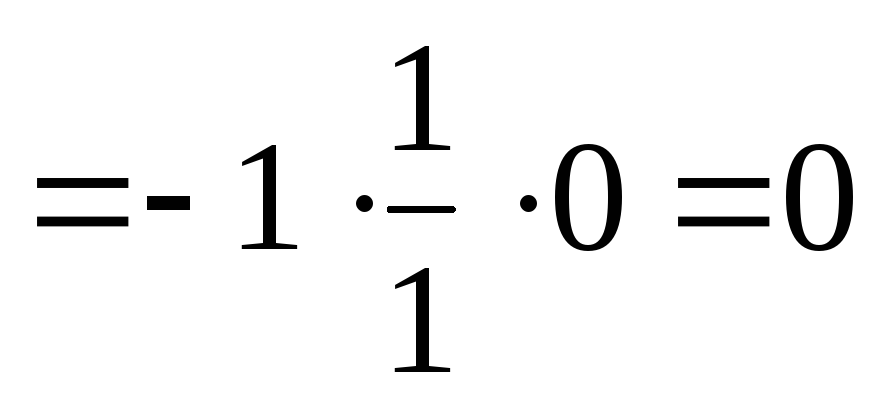 .
.
Так
как 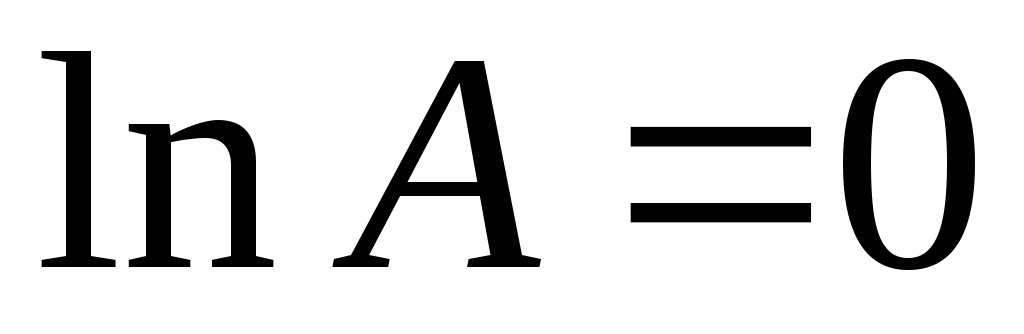 ,
то искомый предел
,
то искомый предел .
.
studfile.net
Логарифмическое дифференцирование функций
Если задана функция то прологарифмировав обе ее части, получим:
Тогда после дифференцирования
То есть имеем:
Выражая из последнего равенства искомую производную, окончательно получим, что
Нахождения производной показательно-степенной функции
Для нахождения производной этой функции используют логарифмическое дифференцирование.
Прологарифмировав левую и правую часть аналитического выражения функции, получим:
Дифференцируем и будем иметь:
В правой части применяем правило дифференцировании произведения:
Выражая искомую производную окончательно получим:
Последнюю формулу запишем в виде:
С этой формулы можно сделать вывод, что производная показательно-степенной функции равна сумме производных как показательной и степенной функций.
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com