Факторизация целых чисел — Википедия

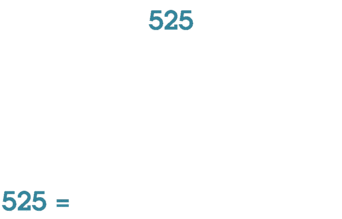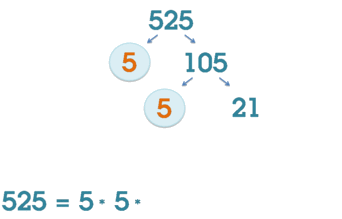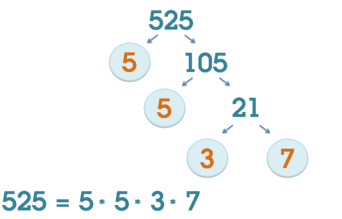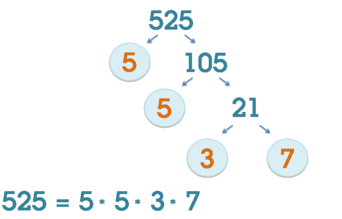Схематическая иллюстрация факторизации числа 525.

Факториза́цией натурального числа называется его разложение в произведение простых множителей. Существование и единственность (с точностью до порядка следования множителей) такого разложения следует из основной теоремы арифметики.

В отличие от задачи распознавания простоты числа, факторизация предположительно является вычислительно сложной задачей. В настоящее время неизвестно, существует ли эффективный не квантовый алгоритм факторизации целых чисел. Однако доказательства того, что не существует решения этой задачи за полиномиальное время, также нет.

Предположение о том, что для больших чисел задача факторизации является вычислительно сложной, лежит в основе широко используемых алгоритмов (например, RSA). Множество областей математики и информатики находят применение в решении этой задачи. Среди них: эллиптические кривые, алгебраическая теория чисел и квантовые вычисления.

Задача поиска эффективных способов разложения целых чисел на множители интересовала математиков с давних времён, особенно специалистов в области теории чисел. Существуют предположения о том, что Ферма был одним из первых, кто предложил метод разложения, заключающийся в том, чтобы представить число в виде разности квадратов n=x2−y2{\displaystyle n=x^{2}-y^{2}}, а затем, вычисляя gcd(n,x−y){\displaystyle \gcd(n,x-y)}, попытаться найти нетривиальный делитель n{\displaystyle n}. Данный способ позволяет находить два мало отличающихся по величине делителя числа быстрее, чем простой перебор делителей^[1].

Создание алгоритма RSA стимулировало бурные исследования в области факторизации целых чисел.

Далее Лежандр обнаружил, что при таком подходе достаточно получить сравнение x2≡y2modn{\displaystyle x^{2}\equiv y^{2}\mod n}, и использовал для этого цепные дроби. Также Эйлером и Гауссом были предложены некоторые способы нахождения чисел, связанных этим сравнением^[1].

Одним из ключевых моментов в развитии факторизации целых чисел было создание алгоритма RSA, что возобновило интерес учёных в данном направлении, так как имело практическое применение в области шифрования. Этот алгоритм был предложен в 1977 году тремя учёными Рональдом Ривестом, Ади Шамиром и Леонардом Адлеманом из Массачусетского Технологического Института и назван по первым буквам фамилий авторов методом RSA. Он основан на идее криптографии с открытым ключом и для взлома системы необходимо выполнить разложение числа на простые сомножители. На момент публикации алгоритма RSA были известны методы, которые позволяли факторизовать числа, состоящие не более чем из 25—30 цифр, а наиболее известным и применяемым все ещё оставался метод Ферма. Метод RSA позволяет факторизовывать числа из 100 и более десятичных знаков. Создатели, в свою очередь, пообещали за факторизацию числа из 129 десятичных знаков символические сто долларов США^[2].

На популярность задачи факторизации также повлияла публикация в 1977 году в журнале Scientific American Мартина Гарднера «Новый алгоритм шифрования, для взлома которого потребуются миллионы лет».^[3] Столь громкое название было воспринято в качестве вызова всему математическому сообществу. В результате этой гонки было предложено несколько новых и нестандартных идей факторизации^[2].

Эпопея с разложением 129-значного числа завершилась в 1994 году, когда коллектив под руководством А. Ленстры, используя 1600 компьютеров, подготовил за 220 дней систему линейных уравнений, содержавшую более полумиллиона неизвестных. Решение этой системы суперкомпьютером заняло два дня. Несмотря на то, что в то время уже были известны методы решета числового поля, данный результат был получен с помощью алгоритма квадратичного решета^[2].

Как правило, на вход таких алгоритмов подаётся число n∈N{\displaystyle n\in \mathbb {N} }, которое необходимо факторизовать, состоящее из N=[log2⁡n]+1{\displaystyle N=[\log _{2}n]+1} символов (если n{\displaystyle n} представлено в двоичном виде)^[4]. При этом алгоритм ищет первый простой делитель, после чего, при необходимости, можно запустить алгоритм заново для дальнейшей факторизации. Также, прежде чем начинать факторизацию большого числа, следует убедиться в том, что оно не простое. Для этого достаточно пройти тест числа на простоту. Эта задача детерминированно разрешима за полиномиальное время^[5].

В зависимости от сложности алгоритмы факторизации можно разбить на две группы. Первая группа — экспоненциальные алгоритмы, сложность которых экспоненциально зависит от длины входящих параметров (то есть от длины N{\displaystyle N} самого числа в бинарном представлении). Вторая группа — субэкспоненциальные алгоритмы.

Вопрос о существовании алгоритма факторизации с полиномиальной сложностью на классическом компьютере является одной из важных открытых проблем современной теории чисел. В то же время факторизация с полиномиальной сложностью возможна на квантовом компьютере с помощью алгоритма Шора (класс BQP)

[6].

Экспоненциальные алгоритмы[править | править код]

Перебор возможных делителей[править | править код]

Сложность O(nlog2⁡n){\displaystyle O({\sqrt {n}}\log ^{2}n)} или O(nlog⁡n){\displaystyle O({\sqrt {n}}\log n)}.

Один из самых простых и очевидных алгоритмов факторизации, заключающийся в том, чтобы последовательно делить факторизуемое число n{\displaystyle n} на натуральные числа от 1{\displaystyle 1} до ⌊n⌋{\displaystyle \lfloor {\sqrt {n}}\rfloor }. Формально достаточно делить только на простые числа в этом интервале, однако, для этого необходимо знать их множество. На практике составляется таблица простых чисел и производится проверка небольших чисел (например, до 216{\displaystyle 2^{16}}). Для очень больших чисел алгоритм не используется в силу низкой скорости работы^[7].

Пример алгоритма^[8]

Шаг 1. Начальная установка. Присвоить t=0,k=0,n=N{\displaystyle t=0,k=0,n=N}(В ходе выполнения алгоритма переменные t,k,n{\displaystyle t,k,n} подчинены следующим условиям: n=N/p1…pt{\displaystyle n=N/p_{1}…p_{t}} и n{\displaystyle n} не имеет простых множителей, меньших dk{\displaystyle d_{k}})

Шаг 2. n=1?{\displaystyle n=1?} Если n=1{\displaystyle n=1}, алгоритм заканчивается.

Шаг 3. Разделить. Присвоить q=⌊n/dk⌋,r=nmoddk.{\displaystyle q=\lfloor n/d_{k}\rfloor ,r=n\mod d_{k}.} (Здесь q{\displaystyle q} и r{\displaystyle r} соответственно частное и остаток от деления числа n{\displaystyle n} на dk{\displaystyle d_{k}}.)

Шаг 4. Остаток равен нулю? Если r≠0{\displaystyle r\neq 0}, то перейти к шагу 6.

Шаг 5. Множитель найден. Увеличить t{\displaystyle t} на 1{\displaystyle 1} и присвоить pt=dk,n=q{\displaystyle p_{t}=d_{k},n=q}. Возвратиться к шагу 2.

Шаг 6. Частное мало? Если q>dk{\displaystyle q>d_{k}}, увеличить k{\displaystyle k} на 1 и возвратиться к шагу 3.

Шаг 7. n — простое число. Увеличить t{\displaystyle t} на 1{\displaystyle 1}, присвоить pt=n{\displaystyle p_{t}=n} и завершить выполнение алгоритма.

Метод факторизации Ферма[править | править код]

Сложность O(n){\displaystyle O(n)} или O(exp(N)){\displaystyle O(exp(N))}.

Идея алгоритма заключается в поиске таких чисел A{\displaystyle A} и B{\displaystyle B}, что факторизуемое число n представимо в виде: n=A2−B2=(A−B)(A+B){\displaystyle n=A^{2}-B^{2}=(A-B)(A+B)}. Как и метод пробного деления, обычно не применяется на практике для факторизации больших чисел, так как имеет экспоненциальную сложность. Метод примечателен тем, что реализуем без операции деления, а только лишь с операциями сложения и вычитания^[9]. Следует так же отметить, что если n=pq{\displaystyle n=pq}, при условии того, что p{\displaystyle p} и q{\displaystyle q} — простые числа не сильно отличающиеся по величине, то метод Ферма факторизует n достаточно быстро^[10].

Пример модификации алгоритма^[11]

Шаг 1. Начальная установка. Присвоить x=2⌊N⌋+1,y=1,r=⌊N⌋2−N.{\displaystyle x=2\lfloor {\sqrt {N}}\rfloor +1,y=1,r=\lfloor {\sqrt {N}}\rfloor ^{2}-N.} (Во время выполнения этого алгоритма величины x, y, r отвечают соответственно величинам 2x+1,2y+1,x2−y2−N{\displaystyle 2x+1,2y+1,x^{2}-y^{2}-N} в уравнении N=uv=x2−y2(x=u+v2,y=u−v2){\displaystyle N=uv=x^{2}-y^{2}(x={\dfrac {u+v}{2}},y={\dfrac {u-v}{2}})}. Должно соблюдаться условие |r|<x,y<x{\displaystyle |r|<x,y<x}.)

Шаг 2. Выполнено? Если r=0{\displaystyle r=0}, то выполнение алгоритма завершается. Имеем

N=x−y2⋅x+y−22{\displaystyle N={\frac {x-y}{2}}\cdot {\frac {x+y-2}{2}}}

Шаг 3. Шаг по x. Присвоить r=r+x{\displaystyle r=r+x} и x=x+2{\displaystyle x=x+2}.

Шаг 4. Шаг по y. Присвоить r=r−y{\displaystyle r=r-y} и y=y+2{\displaystyle y=y+2}.

Шаг 5. Проверить r. Если r>0{\displaystyle r>0}, то возвратиться к шагу 4, иначе возвратиться к шагу 2.

ρ-алгоритм Полларда[править | править код]

Сложность O(n1/4){\displaystyle O(n^{1/4})}.

Алгоритм Полларда является вероятностным алгоритмом, позволяющим находить делитель составного числа n{\displaystyle n}, работающим со сложностью, зависящей лишь от величины делителя, но не величины факторизуемого числа n{\displaystyle n}. Это обуславливает удобство применимости данного алгоритма в тех случаях, когда другие алгоритмы, сложность которых зависит от n{\displaystyle n}, становятся неэффективны^[12]. Примечателен так же тем, что существует вариант реализации такого алгоритма, при котором достаточно в памяти хранить всего 3 целых числа^[13].

Пример алгоритма^[14]

Шаг 1. Выбираем небольшое число x0{\displaystyle x_{0}} и строим последовательность чисел xk,k=0,1,2,…,{\displaystyle {x_{k}},k=0,1,2,…,} определяя каждое следующее xk+1{\displaystyle x_{k+1}} по формуле: xk+1=xk2−1modn{\displaystyle x_{k+1}=x_{k}^{2}-1\mod n}

Шаг 2. Одновременно на каждом шаге i{\displaystyle i} вычисляем Н.О.Д d{\displaystyle d} числа n{\displaystyle n} и всевозможных разностей |xi−xj|{\displaystyle |x_{i}-x_{j}|}, где j<i{\displaystyle j<i}.

Шаг 3. Когда будет найден d=gcd(n,|xi−xj|){\displaystyle d=\gcd(n,|x_{i}-x_{j}|)}, отличный от 1{\displaystyle 1}, вычисление заканчивается. Найденное d{\displaystyle d} является делителем n{\displaystyle n}. Если n/d{\displaystyle n/d} не является простым числом, то процедуру можно продолжить, взяв вместо n{\displaystyle n} число n/d{\displaystyle n/d}.

Алгоритм Ленстры[править | править код]

Сложность O(n1/3log2⁡n){\displaystyle O(n^{1/3}\log ^{2}n)}.

Следует отметить, что несмотря на относительно неплохую эффективность среди экспоненциальных алгоритмов, в алгоритме Ленстры есть необходимость неоднократно вычислять квадратный корень в одном из шагов алгоритма, что, безусловно, является более трудоёмким, чем сложение или вычитание^[15].

Пример модификации алгоритма^[16]

Пусть r,s,n{\displaystyle r,s,n} — натуральные числа, удовлетворяющие условиям 1≤r<s<n;n1/3<s;gcd(r,s)=1{\displaystyle 1\leq r<s<n;\;n^{1/3}<s;\;\gcd(r,s)=1}

Шаг 1. С помощью обобщённого алгоритма Евклида найти r∗∈N,rr∗≡1mods{\displaystyle r^{*}\in \mathbb {N} ,rr^{*}\equiv 1\mod s}. Найти r′{\displaystyle r’} такое, что r′≡r∗nmods,0≤r′<s{\displaystyle r’\equiv r^{*}n\mod s,0\leq r'<s}.

Шаг 2. Для очередного значения i=0,1,2,…{\displaystyle i=0,1,2,…} найти числа ai,bi,ci{\displaystyle a_{i},b_{i},c_{i}} по следующим правилам:

a0=s,b0=0,c0=0{\displaystyle a_{0}=s,\;b_{0}=0,\;c_{0}=0} a1=rr′mods,0<a1≤s,b1=1,c1≡n−rr′sr∗(mods){\displaystyle a_{1}=rr’\mod s,0<a_{1}\leq s,\;b_{1}=1,\;c_{1}\equiv {\frac {n-rr’}{s}}r^{*}(\mod s)}

при i≥2{\displaystyle i\geq 2}:

ai=ai−2−qiai−1,bi=bi−2−qibi−1,ci=ci−2−qici−1(mods){\displaystyle a_{i}=a_{i-2}-q_{i}a_{i-1},\;\;b_{i}=b_{i-2}-q_{i}b_{i-1},\;\;c_{i}=c_{i-2}-q_{i}c_{i-1}(\mod s)}

qi{\displaystyle q_{i}} — частное от деления ai−2{\displaystyle a_{i-2}} на ai−1{\displaystyle a_{i-1}}, за исключением случая, когда i{\displaystyle i} нечётно и остаток от деления равен нулю.

Шаг 3. Для очередного выбора ai,bi,ci{\displaystyle a_{i},b_{i},c_{i}} найти все целые числа c{\displaystyle c}, удовлетворяющие условиям

c=cimods{\displaystyle c=c_{i}\mod s},

|c|<s,{\displaystyle |c|<s,\;\;\;\;\;\;} если i{\displaystyle i} четное,

2aibi≤c≤ns2+aibi,{\displaystyle 2a_{i}b_{i}\leq c\leq {\frac {n}{s^{2}}}+a_{i}b_{i},\;\;} если i{\displaystyle i} нечетное.

Шаг 4. Для каждого c из шага 3 решить в целых числах систему уравнений

{xai+ybi=c(xs+r)(ys+r′)=n{\displaystyle \left\{{\begin{array}{rcl}xa_{i}+yb_{i}\;\;\;\;\;\;&=&c\\(xs+r)(ys+r’)&=&n\\\end{array}}\right.}

Если x{\displaystyle x} и y{\displaystyle y} окажутся неотрицательными целыми числами, то добавить xs+r{\displaystyle xs+r}

Шаг 5. Если ai=0{\displaystyle a_{i}=0}, то алгоритм заканчивает работу. Иначе, возвращаемся на шаг 2 к следующему значению i{\displaystyle i}.

Алгоритм Полларда — Штрассена[править | править код]

Сложность O(n1/4log4⁡n){\displaystyle O(n^{1/4}\log ^{4}n)}.

Данный алгоритм имеет оценку сложности схожую с методом квадратичных форм Шенкса (что является наилучшей среди детерминированных алгоритмов факторизации), однако требует выделение O(n1/4log⁡n){\displaystyle O(n^{1/4}\log n)} памяти. Он может использоваться непосредственно для факторизации не очень больших целых чисел, а также в качестве вспомогательного алгоритма в субэкспоненциальном методе Диксона^[17] и для ускорения вычислений второго этапа метода факторизации с помощью эллиптических кривых.^[18]

Краткое описание алгоритма^[15]

Теорема. Пусть z∈N,y=z2{\displaystyle z\in \mathbb {N} ,y=z^{2}}. Тогда для любого натурального числа t{\displaystyle t} наименьший простой делитель числа gcd(n,y!){\displaystyle \gcd(n,y!)} может быть найден за O(zlog2⁡zlog2⁡t){\displaystyle O(z\log ^{2}z\log ^{2}t)} арифметических операций.

Алгоритм. Положим z=[n1/4]+1,y=z2>n1/2,t=n{\displaystyle z=[n^{1/4}]+1,y=z^{2}>n^{1/2},t=n}. Далее с помощью алгоритма теоремы найдём наименьший простой делитель числа gcd(n,y!){\displaystyle \gcd(n,y!)}. Поскольку y!{\displaystyle y!} делится на наименьший простой делитель p{\displaystyle p} числа n(p≤n1/2<y){\displaystyle n(p\leq n^{1/2}<y)}, то алгоритм выдаст именно это число p{\displaystyle p}.

Метод квадратичных форм Шенкса[править | править код]

Гарантированная сложность O(n1/4+ε)

ru.wikipedia.org

РАЗЛОЖИТЬ — это… Что такое РАЗЛОЖИТЬ?

разложить — 1. см. постлать. 2. см. развратить Словарь синонимов русского языка. Практический справочник. М.: Русский язык. З. Е. Александрова. 2011. разложить …   Словарь синонимов

РАЗЛОЖИТЬ 1 — РАЗЛОЖИТЬ 1, ожу, ожишь; оженный; сов., что. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 …   Толковый словарь Ожегова

РАЗЛОЖИТЬ 2 — РАЗЛОЖИТЬ 2, ожу, ожишь; оженный; сов. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 …   Толковый словарь Ожегова

разложить — РАЗЛОЖИТЬ, ожу, ожишь; оженный; совер., что. 1. Положить по разным местам, в определённом порядке. Р. вещи. Р. карты. 2. Положить или поместить, распластав, раздвинув. Р. ковёр. Р. складной стул. 3. Распределить между кем чем н. (какую н. сумму) …   Толковый словарь Ожегова

разложить — разделить — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия Синонимы разделить EN decompose …   Справочник технического переводчика

разложить — растянуть (разложить) (иноск.) отодрать розгами (намек на растягивание рук и ног при разложении на скамью) Ср. Берегитесь… я горяч как огонь, вскричал Павлуша старшим братьям. А ты знаешь, какая разница между тобою и огнем? возразил Павлуше… …   Большой толково-фразеологический словарь Михельсона

разложить — ложу/, ло/жишь; разло/женный; жен, а, о; св. см. тж. раскладывать, раскладываться, разложение, разлагать, разлагаться …   Словарь многих выражений

разложить — (разложу, разложишь) дэриури, дарин дарин, лаӈ лаӈ нэ̄ктэури; разложить книги по полкам дансава тахика̄нду дарин дарин нэ̄ктэури …   Русско-нанайский словарь

Разложить — I сов. перех. 1. Положить что либо в разные места, разместить отдельно одно от другого. 2. Положить в определённом порядке карты (гадая или раскладывая пасьянс). II сов. перех. 1. Положить что либо, расправив или растянув. 2. Раздвинуть какой… …   Современный толковый словарь русского языка Ефремовой

Разложить — I сов. перех. 1. Положить что либо в разные места, разместить отдельно одно от другого. 2. Положить в определённом порядке карты (гадая или раскладывая пасьянс). II сов. перех. 1. Положить что либо, расправив или растянув. 2. Раздвинуть какой… …   Современный толковый словарь русского языка Ефремовой

dic.academic.ru

Как 90 разложить на два взаимно простых множителя

Инструкция

В первую очередь определите, какие вообще есть множители у числа 90, то есть на какие числа его можно разделить без остатка. Начните с единицы и далее проверяйте все числа: вы получите 1, 2, 3, 5, 9, 10, 18, 30, 45. Попробуйте найти все множители числа 90 другим способом: разложите его на простые множители. Самое малое простое число (после 1) – это 2. Число 90 делится без остатка на него, поэтому оно будет первым среди простых множителей. Далее разделите 90 на 2, вы получите 45. Это число на 2 не делится.

Следующее простое число 3. Разделите 45 на 3 – вы получите 15. Теперь подберите третий множитель. Самое меньшее простое число, на которое можно разделить 15 без остатка, это 3. Значит, это третий множитель. Разделив 15 на 3, вы получите число 5. Оно делится только на само себя, значит, это ваш последний простой множитель. Таким образом, 90 можно разделить на следующие простые множители: 2, 3, 3, 5. Проверьте: перемножьте их между собой, у вас снова получится 90.

Теперь, зная простые множители, найдите все остальные, просто перемножив их между собой в разных сочетаниях. Например, один из составных множителей числа 90 будет число 2х3=6, другой 2х5=10, третий 3х5=15, четвертый 2х3х3=18, пятый 2х3х5=30, шестой 3х3х5=45.

Определите, какие из полученных множителей взаимно простые, то есть не имеют общих делителей (кроме единицы), причем их произведение должно быть равно 90. Так как число 90 может быть получено перемножением четырех чисел 2, 3, 3, 5, то взаимно простыми будут такие числа: 2 и 3х3х5, а также 2х3х3 и 5. Если в обоих множителях появится число 3, то они будут ему кратны, то есть не будут являться взаимно простыми. Таким образом, вы получили две пары взаимно простых множителей для числа 90, это 2 и 45, а также 18 и 5.

Проверьте себя: умножьте 2 на 45, вы получите 90. В то же время, разложив 45 на простые множители (5*3*3), вы поймете, что на 2 это число без остатка не делится. Точно также проверьте вторую пару взаимно простых множителей.

www.kakprosto.ru