Решение кубических уравнений методом разложения на множители
Пример 2. Решить уравнение -2x3 + 3x2 — 4x — 9 = 0.Решение.
Делителями свободного члена являются числа: ±1, ±3, ±9. Делителями старшего коэффициента являются числа: ±1, ±2.
Значит, корни исходного уравнения могут быть среди чисел: ±1, ±3, ±9,
.Снова простой подстановкой убеждаемся, что -1 является корнем уравнения. С помощью схемы Горнера делим левую часть исходного уравнения на x + 1.
Таким образом, -2x3 + 3x2 — 4x — 9 = (x + 1)(-2x2 + 5x — 9). Следовательно, исходное уравнение эквивалентно (x + 1) (-2x2 + 5x — 9)=0. Решая квадратное уравнение -2x2 + 5x — 9 = 0, получаем, что его дискриминант
Ответ: -1.
Пример 3. Решить уравнение 2x3 — x2 — 8x + 4 = 0.
Решение.
Делителями свободного члена являются числа: ±1, ±2, ±4. Делителями старшего коэффициента являются числа: ±1, ±2.
Значит, корни исходного уравнения могут быть среди чисел: ±1, ±2, ±4.
Простой подстановкой убеждаемся, что 2 является корнем уравнения. С помощью схемы Горнера делим левую часть исходного уравнения на x — 2.
Таким образом, 2x3 — x2 — 8x + 4 = (x — 2)(2x2 + 3x — 2). Следовательно, исходное уравнение эквивалентно (x — 2) (2x2 + 3x — 2) = 0. Решая квадратное уравнение 2x2 + 3x — 2 = 0, получаем,
Ответ: -2,
, 2.Еще один способ разложения на множители многочлена третьей степени — метод неопределенных коэффициентов. Он довольно громоздкий, но иногда бывает очень полезным при решении разного рода задач, а не только в случае разложения на множители. Разложение на множители любого многочлена третьей степени можно представить следующим образом a(x) = (x-x0)*(a3x2 + bx + c).
Раскрывая скобки, получим a(x) = a3x3 + x2(b — a3x0
) + x*(c — bx0) — cx0.Приравнивая теперь коэффициенты при одинаковых степенях x и свободные члены в исходном многочлене и в многочлене a(x), получим систему из четырех уравнений и четырех неизвестных a3,b,c и x0. Рассмотрим применение метода неопределенных коэффициентов на примерах.
Пример 4. Решить уравнение x3 + 2x2 — 5x — 6 = 0.
Решение.
Так как любой многочлен 3 степени можно представить в виде a3x3 + x2(b — a3x0) + x*(c — bx0) — cx0, то приравнивая коэффициенты при одинаковых степенях x, получаем следующую систему уравнений:
Выразим из первого уравнения x0 = b — 2 и подставим в два оставшихся. Получим
Теперь выразим переменную c из первого уравнения и подставим во второе.
Раскрывая скобки во втором уравнении и решая его, находим b:
Если b=4, то c=3, x
Если b = 1, то c = -6, x0 = -1. Следовательно, x3 + 2x2 — 5x — 6 = (x + 1)(x2 + x — 6)=(x + 1)(x + 3)(x — 2).
Если b = -1, то c = -2, x0 = -3. Следовательно, x3 + 2x2 — 5x — 6=(x + 3)(x2 — x — 2) = (x + 3)(x — 2)(x + 1).
Таким образом, исходное уравнение эквивалентно уравнению (x + 3)(x — 2)(x + 1) = 0.
Приравнивая к нулю каждый из множителей, получаем корни уравнения x = -3, x = 2, x = -1.
Ответ: -3, -1, 2.
Пример 5. Решить уравнение 2x3 + x2 — 5x + 2 = 0.
Решение.
Приравнивая соответствующие коэффициенты при одинаковых степенях x, получаем следующую систему уравнений:
Выразим из первого уравнения x0 =
и подставим в два оставшихся. ПолучимТеперь из первого уравнения выразим переменную c и подставим во второе.
Умножая левую и правую части второго уравнения на 4 и раскрывая скобки, находим b:
Если b=2, то c=-4, x0 =
. Следовательно, 2x3 + x2 — 5x + 2 = (x — )(2x2 + 2x — 4) = 2(x — )(x — 1)(x + 2).Если b = 3, то c = -2, x0 = 1. Следовательно, 2x3 + x2 — 5x + 2 = (x — 1)(2x2 + 3x — 2)=2(x — 1)(x —
)(x + 2).Если b = -3, то c = 1, x0 = -2. Следовательно, 2x3 + x2 — 5x + 2 = (x + 2)(2x2 — 3x + 1) = 2(x + 2)(x —
)(x — 1).Следовательно, исходное уравнение эквивалентно уравнению 2(x + 2)(x —
)(x — 1) = 0.Приравнивая к нулю каждый из множителей, получаем корни уравнения x = -2, x =
, x = 1.Ответ: -2,
, 1.Разложение на множители многочлена третьей степени
Пример 1. Разложить на множители многочлен x3 — 3x2 — 4x + 6.Решение.
Делители свободного члена: ±1, ±2, ±3, ±6. Значит, корни многочлена нужно искать среди них. Простой подстановкой убеждаемся, что корнем многочлена является число 1. Значит, исходный многочлен надо разделить на x — 1.
Воспользуемся схемой Горнера.
Таким образом, x3 — 3x2 — 4x + 6 = (x — 1)(x2 — 2x — 6). Чтобы найти оставшиеся 2 корня многочлена, решаем квадратное уравнение x2 — 2x — 6 = 0.
Но обычно в разложении на множители нас не интересуют иррациональные корни (то есть, такое разложение квадратичного многочлена на множители
Ответ: x3 — 3x2 — 4x + 6 = (x — 1)(x2 — 2x — 6).
Пример 2. Разложить на множители многочлен -2x3 + 3x2 — 4x — 9.
Решение.
Делители свободного члена: ±1, ±3, ±9. Делители старшего коэффициента: ±1, ±2.
Снова простой подстановкой убеждаемся, что -1 является корнем многочлена. С помощью схемы Горнера делим исходный многочлен на x + 1.
Таким образом, -2x3 + 3x2 — 4x — 9 = (x + 1)(-2x2 + 5x — 9). Решая квадратное уравнение -2x2 + 5x — 9 = 0, получаем, что его дискриминант
Ответ: -2x3 + 3x2 — 4x — 9 = (x + 1)(-2x2 + 5x — 9).
Пример 3. Разложить на множители многочлен 2x3 — x2 — 8x + 4.
Решение.
Простой подстановкой убеждаемся, что 2 является корнем многочлена. С помощью схемы Горнера делим исходный многочлен на x — 2.
Таким образом, 2x3 — x2 — 8x + 4 = (x — 2)(2x2 + 3x — 2).
Решая квадратное уравнение 2x2 + 3x — 2 = 0, получаем,
Следовательно, 2x2 + 3x — 2 = 2(x —
)(x + 2).Ответ: 2x3 — x2 — 8x + 4 = 2(x — 2)(x —
)(x + 2) = (2x — 1)(x — 2)(x + 2).Разложение на множители многочлена третьей степени методом неопределенных коэффициентов
Еще один способ разложения на множители многочлена третьей степени — метод неопределенных коэффициентов. Он достаточно трудоемкий, но иногда бывает очень полезным, причем для разного рода задач, а не только в случае разложения на множители. Разложение на множители любого многочлена третьей степени можно представить следующим образом a(x) = (x-x0)*(a3x2 + bx + c).
Раскрывая скобки, получим a(x) = a3x3 + x2(b — a3x0) + x*(c — bx0) — cx0.
Приравнивая теперь коэффициенты при одинаковых степенях x и свободные члены в исходном многочлене и в многочлене a(x), получим систему из четырех уравнений и четырех неизвестных a3,b,c и x0. Рассмотрим применение метода неопределенных коэффициентов на примерах.
Пример 4. Разложить на множители многочлен x3 + 2x2 — 5x — 6.
Решение.
Приравнивая соответствующие коэффициенты, получаем следующую систему уравнений
Выразим из первого уравнения x0 = b — 2 и подставим в два оставшихся. Получим
Теперь из первого уравнения выразим переменную c и подставим во второе.
Раскрывая скобки во втором уравнении и решая его, находим b:
Если b=4, то c=3, x0 = 2. Следовательно, x3 + 2x2 — 5x — 6 = (x — 2)(x2 — 4x + 3)=(x — 2)(x + 1)(x + 3).
Если b = 1, то c = -6, x0 = -1. Следовательно, x3 + 2x2 — 5x — 6 = (x + 1)(x2 + x — 6)=(x + 1)(x + 3)(x — 2).
Если b = -1, то c = -2, x0 = -3. Следовательно, x3 + 2x2 — 5x — 6=(x + 3)(x2 — x — 2) = (x + 3)(x — 2)(x + 1).
ru.intemodino.com
Решение кубических уравнений методом Горнера
Если не удается решить кубическое уравнение группировкой, то можно попробовать разложить многочлен на множители по схеме Горнера. Разберем на примере:
Дано уравнение
x3 + 6x2 — 25x + 18 = 0
Для начала нужно методом подбора найти один корень. Обычно он является делителем свободного члена. В данном случае делителями числа 18 являются ±1, ±2, ±3, ±6, ±9, ±18.
Подставим число 1: 1 + 6 — 25 + 18 = 0. Мы выяснили, что число 1 является корнем уравнения. Если бы делитель 1 не подошел, то мы бы проверяли все делители, пока не нашли тот, который бы являлся корнем.
Мы нашли 1 из корней многочлена. Корнем многочлена является 1, а значит исходный многочлен должен делиться на x — 1. Для того, чтобы выполнить деление многочленов, воспользуемся схемой Горнера:
В верхней строке выставляются коэффициенты исходного многочлена. В первой ячейке второй строки ставится найденный нами корень 1. Во второй строке пишутся коэффициенты многочлена, который получится в результате деления. Они считаются так:
| Во вторую ячейку второй строки запишем число 1, просто перенеся его из соответствующей ячейки первой строки. | |
| 1 ∙ 1 + 6 = 7 | |
| 1 ∙ 7 — 25 = -18 | |
| 1 ∙ (-18) + 18 = 0 |
Последнее число — это остаток от деления. Если он равен 0, значит мы все верно посчитали.
Таким образом мы исходный многочлен разложили на множители:
x3 + 6x2 — 25x + 18 = (x — 1)(x2 + 7x — 18)
И теперь, всего лишь, осталось найти корни квадратного уравнения
x2 + 7x — 18 = 0
D = b2 — 4ac = 72 — 4 ∙ 1 ∙ (-18) = 121
D > 0 ⇒ уравнение имеет 2 корня
| x1,2 = | -b ± √ D | = | -7 ± 11 | = -9; 2 |
| 2a | 2∙1 |
Мы нашли все корни уравнения:
x = 1; 2; -9
tutata.ru
Способы разложения на множители многочлена степени выше второй.
В общем случае эта задача предполагает творческий подход, так как не существует универсального метода ее решения. Но все же попробуем дать несколько наводок.
В
подавляющем числе случаев, разложение
многочлена на множители основано на
следствии из теоремы Безу, то есть
находится или подбирается корень  и
понижается степень многочлена на единицу
делением на
и
понижается степень многочлена на единицу
делением на 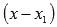 .
У полученного многочлена ищется
корень
.
У полученного многочлена ищется
корень 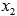
Если же корень найти не удается, то используются специфические способы разложения: от группировки, до ввода дополнительных взаимоисключающих слагаемых.
Дальнейшее изложение базируется на навыках решения уравнений высших степеней с целыми коэффициентами.
Вынесение за скобки общего множителя.
Начнем
с простейшего случая, когда свободный
член равен нулю, то есть многочлен имеет
вид 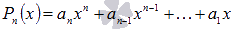 .
.
Очевидно,
что корнем такого многочлена является  ,
то есть многочлен представим в виде
,
то есть многочлен представим в виде 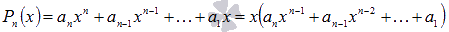 .
.
Этот способ есть ни что иное как вынесение общего множителя за скобки.
Пример.
Разложить
многочлен третьей степени 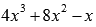
Решение.
Очевидно,
что 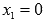 является
корнем многочлена, то есть х можно
вынести за скобки:
является
корнем многочлена, то есть х можно
вынести за скобки: 
Найдем
корни квадратного трехчлена 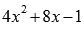
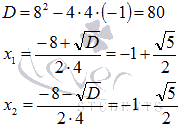
Таким
образом, 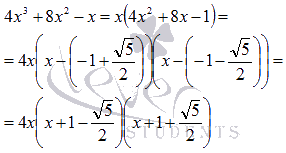
К началу страницы
Разложение на множители многочлена с рациональными корнями.
Сначала
рассмотрим способ разложения многочлена
с целыми коэффициентами вида 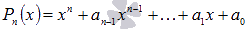 ,
коэффициент при старшей степени равен
единице.
,
коэффициент при старшей степени равен
единице.
В этом случае, если многочлен имеет целые корни, то они являются делителями свободного члена.
Пример.
Разложить
на множители выражение 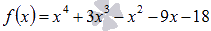 .
.
Решение.
Проверим,
имеются ли целые корни. Для этого
выписываем делители числа -18: 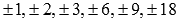 .
То есть, если многочлен имеет целые
корни, то они находятся среди выписанных
чисел. Последовательно проверим эти
числа по схеме
Горнера. Ее удобство еще и в том, что
в итоге получим и коэффициенты разложения
многочлена:
.
То есть, если многочлен имеет целые
корни, то они находятся среди выписанных
чисел. Последовательно проверим эти
числа по схеме
Горнера. Ее удобство еще и в том, что
в итоге получим и коэффициенты разложения
многочлена: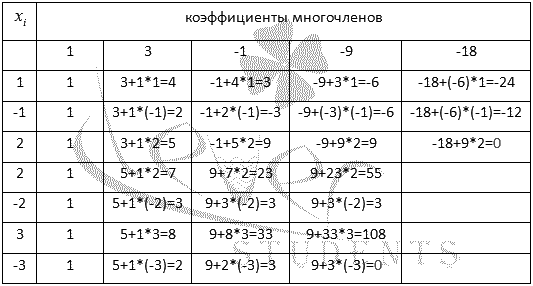
То
есть, х=2 и х=-3 являются
корнями исходного многочлена и он
представим в виде произведения: 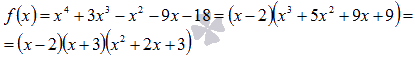
Осталось
разложить квадратный трехчлен  .
.
Дискриминант этого трехчлена отрицательный, следовательно, он не имеет действительных корней.
Ответ:
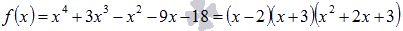 .
.
Замечание:
вместо схемы Горнера можно было воспользоваться подбором корня и последующим делением многочлена на многочлен.
Теперь
рассмотрим разложение многочлена с
целыми коэффициентами вида 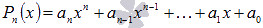 ,
причем коэффициент при старшей степени
не равен единице.
,
причем коэффициент при старшей степени
не равен единице.
В этом случае многочлен может иметь дробно рациональные корни.
Пример.
Разложить
на множители выражение 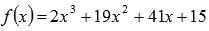 .
.
Решение.
Выполнив
замену переменной y=2x,
перейдем к многочлену с коэффициентом
равным единице при старшей степени. Для
этого сначала домножим выражение на 4. 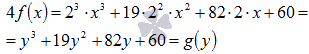
Если
полученная функция 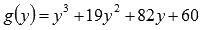 имеет
целые корни, то они находятся среди
делителей свободного члена. Запишем
их:
имеет
целые корни, то они находятся среди
делителей свободного члена. Запишем
их: 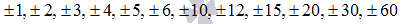
Вычислим
последовательно значения функции g(y) в
этих точках до получения нуля. 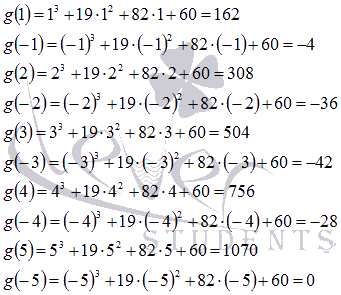
То
есть, y=-5 является
корнем 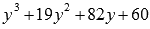 ,
следовательно,
,
следовательно, 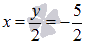 является
корнем исходной функции. Проведем
деление столбиком (уголком) многочлена
является
корнем исходной функции. Проведем
деление столбиком (уголком) многочлена 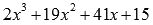 на
двучлен
на
двучлен  .
. 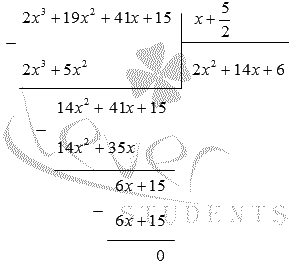
Таким
образом, 
Проверку
оставшихся делителей продолжать
нецелесообразно, так как проще разложить
на множители полученный квадратный
трехчлен 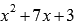
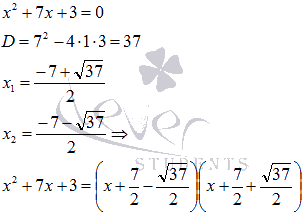
Следовательно, 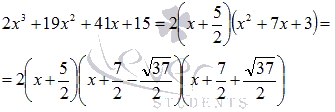
Незведені многочлени. Теорема про розклад многочлена у добуток незведених. Канонічний розклад многочлена.
studfile.net
Решение кубических уравнений ℹ️ как разложить на множители, формулы Кардано и Виета для нахождения корней, онлайн калькулятор

История и формулировки
Кубические уравнения составлялись ещё в Древней Греции и Египте. Археологами были найдены клинописные таблицы XVI века до нашей эры, содержащие описание возможного их решения. Вычислением кубов занимался Гиппократ, пытавшийся свести задачу к нахождению отрезков с помощью чертёжных инструментов. Архимед использовал для поиска ответа пересечение двух конусов.

Впервые методы решения такого рода уравнений были описаны в китайском учебнике «Математика в девяти книгах», составленном во втором столетии до нашей эры. В седьмом веке Омар Хайям на основании своих работ приходит к выводу, что решение уравнений третьей степени может иметь более одного ответа.
Математик Шараф ад-Дин публикует тракт об уравнениях, в котором описывает восемь различных типов кубических выражений, имеющих положительное решение. В своих вычислениях он использует численную аппроксимацию. Учёный не только разработал подход для решения с использованием производной функции и экстремумов, но и понял важность дискриминанта многочлена при нахождении кубов.
В 1530 году итальянский математик Никколо Тарталья разрабатывает методику решения, которой он после поделился с Джероламо Кардано. Согласно этому способу нужно было извлекать квадратный корень из отрицательного числа. Параллельно с этими исследованиями, основоположник символической алгебры Франсуа Виет, предлагает свой способ решения кубического равенства с тремя корнями. Позднее его работу описал и обосновал Рене Декарт.
Уравнением третьей степени называют выражение вида: a*y 3 + d*y 2 + c*y + n = 0. В математике оно называется кососимметрическим. Число y, значение которого необходимо найти, при подстановке превращает формулу в тождество. Называется оно корнем уравнения или просто решением. Кроме этого, y ещё является и корнем многочлена куба.
Таким образом, в кубических уравнениях стоит только одна переменная в третьей степени. Они всегда имеют три корня. При этом ответы могут быть равны друг другу и даже быть комплексными (но не более двух).
Формула квадратного уравнения

Используется при решении простейшего равенства методом разложения кубического уравнения на множители. Когда последний член равен нулю, решить такую задачу можно по методу квадратных уравнений. При n = 0, уравнение примет вид :
a*y 3 + d*y 2 + c*y + n = 0.
В полученном выражении каждый член представлен произведением на неизвестное, поэтому переменную y можно вынести за скобки: y*(d*y 2 + c) = 0. Уравнение в скобках является классическим квадратным, которое можно решать несколькими способами:
- разложением на множители;
- с использованием формулы корней квадратного уравнения;
- методом дополнения.
При выборе первого варианта разложение выполняют следующим образом. Например, необходимо решить равенство вида: *y 2 — 11*y — 16 = 0. Квадратный член можно записать в виде двух множителей: 3*y и y. Поэтому их можно записать сразу как произведение в скобках: (3 * + n) * (y + n) = 0. Так как определённый член можно записать в виде произведения 2*2 или 1*4, то формулу можно представить как (3 *y +1) * (y — 16).
Если раскрыть скобки, то получится равенство 3*y 2 — 12 *y + y + 16. Решением (-12*y + y) будет (-11*y). Как раз тот член, который нужен. Используя же произведение 2*2 — искомый член найти не получится.
Равенство раскладывают на два множителя: (3*y +1) (х — 16) = 0. Согласно аксиоме произведение двух членов равно нулю только тогда, когда хотя бы один из них равен нулю. Приравняв каждое выражение в скобках к нулю, можно записать два равенства: 3*y + 1 = 0 и y — 16 = 0. При решении каждого из них получится два ответа: y = 1/3 и y = 16.

Для проверки результата необходимо оба возможных решения подставить в формулу. Так как для квадратного уравнения существует только два решения, а для кубического три, то в этом случае третьим ответом будет ноль. Поэтому решением уравнения будет три корня: 0, 1/3, 16.
Но проще и нагляднее всего использовать второй вариант. Формула корней кубического уравнения имеет вид: y = ((-d + (d 2 — 4*a*c) ½ ) / 2*a и y = ((-d — (d 2 — 4*a*c) ½ ) / 2*a. Корни квадратного уравнения и будут ответом для кубического. Например, 5*y 2 — 7*y — 14 = 0. Приняв, что a = 5, d = -7, c = — 14 и подставив числовые значения, будет верным запись: y = 1 4 / 5 и y = -1. Дробное решение и отрицательное будет являться корнями кубического равенства.
Разложение на множители
Если определённый член не равен нулю, то посчитать игрек при помощи квадратных уравнений невозможно. В этом случае используется метод разложения на свободные множители. Например, 2 * y 3 + 9 * y 2 +13 * y + 6 = 0. Чтобы разложить кубическое уравнение на множители и определить неизвестное, придерживаются следующего порядка:
- Вычисляют множитель кубического коэффициента и свободного члена. Это те числа, которые при умножении друг на друга дают исходное число. Например, цифру шесть можно представить перемножением 6*1 и 2*3, то есть множителями шести являются: 1, 2, 3, 6. Коэффициентом кубического члена является двойка, соответственно её множители — цифры один и два.
- Выполняют деление множителей кубического члена на цифры разложения свободного. В результате действия получится набор, состоящий из дробных частей и целых чисел, при этом они могут быть и отрицательными. Для уравнения 2 * y 3 + 9 * y 2 +13 * y + 6 = 0 такой набор будет состоять из 1, -1, ½, -½, 1/3, -1/3, 1/6, -1/6, 2, -2, 2/3, -2/3 .
- Определяют ряды чисел, в которых существуют рациональные решения кубического выражения. Для рассматриваемого примера они будут следующие: -1*2 = -2; 9 + (-2) = 7; (-1) * 7 = -7; 13 +(-7) = 6; (-1)*6 = -6; 6+(-6) = 0 .
Вычисление рационального числа операция долгая и требующая внимания. Поэтому для быстрого нахождения ответа используется деление по схеме Горнера. По этой схеме выполняют деление целых цифр на коэффициенты всех членов равенства. Если в ответе получается только целая часть, то эти числа считаются вариантами решения. Таким методом можно находить и иррациональные выражения.

Чтобы освоить способ Горнера, необходимо тщательно в нём разобраться. Способ заключается в делении коэффициентов многочлена без учёта степенных показателей. Вычитание заменяется сложением как при делении в столбик. То есть уравнение, впрочем, как и неравенство, вида y 3 + 2*y 2 — 4 *y + 8, записывается как 1 2 -4 8 с необходимым делимым. В результате должен получиться многочлен с остатком. Если он будет нулевым, то одним из ответов уравнения и будет делимое .
Использование дискриминанта
Дискриминант степенного выражения представляет произведение квадратов разностей корней в различных сочетаниях. Другими словами, берут пару, состоящую из любых корней уравнения, вычитают друг из друга и возводят в квадрат. Это и будет один множитель. Затем берут другую пару и повторяют действия. Таким образом, перебирают все варианты.

При решении кубических равенств используют значения коэффициентов. Например, для уравнения y 3 — 3* y 2 + 3* y — 1, они будут равны: a = 1, d = -3, c = 3, n = -1. Затем вычисляют дельта нулевое. Это ключевая величина, которая после подставляется в формулу. В примере, Δ0 = d 2 — 3 * a * c, определяют как (-3) 2 — 3 * (1) * (3) = 9 − 3 * 3 = 0 .
Затем находят дельта один. Δ1 = 2 * d 3 — 9 * a * d * c + 27 * a 2 * n. Подставив значения в формулу, вычисляют Δ1:
2 (-3) 3 — 9 (1)(-3)*(3) + 27 (1) 2 * (-1) = 2 (-27) — 9 (-9) + 27 (-1) = -54 + 81 — 27 = 81 − 81 = 0 = Δ 1.
Используя найденное, по аналогии с квадратичным равенством находят дискриминант: d 2 — 4 * a * c. Применительно к кубическому виду применяется правило, что показатель отрицательный, когда уравнение может иметь только одно решение. Если же его значение равно нулю — одно или два. Уравнение кубического вида всегда должно иметь хотя бы одно решение, так как его график должен проходить через ось икс.
Так как в примере дельта-ноль и один равны нулю, то можно использовать следующее выражение:
- Δ1 2 — 4 * Δ0 3 / — 27 *a 2;
- (0) 2 — 4 * (0) 3 / — 27 * (1) 2;
- (0−0) / 27;
- Δ = 0.
Исходя из этого, уравнение имеет два решения. Вычислив С, можно определить возможные решения уравнения. Заменив по мере необходимости дельты, решается равенство:
C = ((Δ 1 2 — 4 Δ 0 3 ) +Δ) / 2) ½ = (((0 — 0) + 0)/2) ½ = 0.
Корни куба определяются по формуле: u n C + Δ0/(u n C)) / 3*a, где u = (-1 + √(-3))/2, а n равно одному, двум или трём. Если подставить эти значения в равенство, и оно будет верным, то эта цифра и является возможным решением уравнения. Этот способ показательный, но довольно сложный. Но если его понять, то проблем с решением уравнений любой сложности возникнуть не должно.
Теорема Виета и двучлен
Выражение вида: a*y 3 + d = 0 называется двухчленным или неполным уравнением. Для его решения нужно равенство привести к виду: y 3 + d/a = 0. Затем используя формулу сокращённого умножения для суммы кубов можно записать:
(y + 3 √ d/a) * (y 2 − ( 3 √ d/a)* y + 3 √ (d/a) 2 ) = 0.

Из первого множителя и находят значение игрека. Оно будет равно 3 √ d/a, ведь второй множитель — это квадратный трёхчлен с корнями комплексного вида.
Для проверки рациональных равенств удобно применять теорему Виета. Согласно ей корни уравнения связаны с коэффициентами выражениями:
- y1 + y2 + y3 = — d/a;
- y1 * y2 + y2 * y3 + y1 * y3 = c/a;
- y1 * y2 * y3 = — n/a.
Используя теорему, некоторые уравнения можно решить даже устно. Например, y3 + 2y — 24 = 0. Решение выполняется в следующей последовательности:
- записывают теорему применительно к равенству;
- определяют знаки корней;
- раскладывают определённый член.
Частным случаем применения теоремы являются тригонометрические формулы для кубического равенства:
S = Q 3 — R 2 , где Q = (a2 — 3d)/9, а R = (2 а 3 — 9ad + 27c) / 54.
В зависимости от знака S применяется одна из следующих формул : φ = (arcos (R/Q 3/2 ))/3 и φ = (arcos (ЇRЇ/Q 3/2 ))/3. Первое выражение справедливо при S > 0 и имеет три корня: y 1 = -2 (Q) ½ * cos (φ) — a/3; y 2 = — (Q) ½ cos (φ + 2p /3) — a/3; y 3 = -2 (Q) ½ * cos (φ — 2p/3) — a/3. А второе при S < 0 и имеет только одно решение: y = -2sgn®*[q] ½ * ch (φ) — a/3. В случае же когда S=0,то уравнение имеет следующие корни: y 1= -2*R1 /3 — a/3; y 2= y 3 =R1/3 — a/3.

Теорему Виета можно использовать и для наивысшей, четвёртой степени, при которой ещё существует аналитическое решение.
Подробный онлайн-калькулятор
Вычисление корней требует внимательности и усердия. Чтобы быстро находить решение, нужно не только знание теории, но и практические занятия. Конечно же, знать формулы и уметь решать уравнения нужно самому.

Но при самостоятельном вычислении существует вероятность допущения ошибки. Поэтому на помощь приходят своего рода решебники-онлайн. Они умеют не только точно и быстро определять корни равенства, но и показывать подробное вычисление. Благодаря этому можно не просто получить правильный ответ, но и разобраться в решении, понять различные нюансы, проверить свои знания.
Из наиболее популярных интернет-порталов, позволяющих найти корни кубического уравнения онлайн, можно выделить: mathforyou. net, allcalc.ru, wedmath.ru, kontrolnaya-radota.ru. Воспользоваться такими сайтами-решателями сможет любой пользователь, даже не имеющий представление о методах решения уравнений.
Для этого нужно просто заполнить предлагаемые на странице поля и нажать кнопку «Рассчитать» или «Решить». Калькулятор сам на основании запрограммированных формул, чаще всего по методу Вието — Кардано, выполнит расчёт и выведет на экран ответ. Кроме этого, будет предложено подробное решение с описанием. На этих сайтах также можно посмотреть и примеры решений, формулы, теоремы.
nauka.club
как кубическое уравнение разложить на множители
Вы искали как кубическое уравнение разложить на множители? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и как найти корни многочлена 3 степени, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «как кубическое уравнение разложить на множители».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как как кубическое уравнение разложить на множители,как найти корни многочлена 3 степени,как разложить кубический многочлен на множители,как разложить кубическое уравнение на множители,как разложить многочлен 4 степени на множители,как разложить на множители кубический многочлен,как разложить на множители кубическое уравнение,как разложить на множители многочлен 4 степени,кубический многочлен разложить на множители,кубическое уравнение разложить на множители,многочлен разложить,разложение кубического многочлена на множители,разложение кубического трехчлена на множители,разложение кубического уравнения на множители,разложение многочлена кубического на множители,разложение многочленов,разложение на многочлен множители,разложение на многочлены,разложение на множители двучлена,разложение на множители кубического многочлена,разложение на множители кубического трехчлена,разложение на множители кубического уравнения,разложение степени,разложите многочлен на линейные множители,разложите на линейные множители многочлен,разложить кубический многочлен на множители,разложить кубическое уравнение на множители,разложить многочлен на множители,разложить многочлены на,разложить на многочлены как,разложить на множители кубический многочлен,разложить на множители кубическое уравнение,решение алгебраических уравнений разложением на множители 10 класс,решение кубических уравнений методом горнера. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и как кубическое уравнение разложить на множители. Просто введите задачу в окошко и нажмите «решить» здесь (например, как разложить кубический многочлен на множители).
Где можно решить любую задачу по математике, а так же как кубическое уравнение разложить на множители Онлайн?
Решить задачу как кубическое уравнение разложить на множители вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
www.pocketteacher.ru
Способы разложения на множители многочлена степени выше второй.
В общем случае эта задача предполагает творческий подход, так как не существует универсального метода ее решения. Но все же попробуем дать несколько наводок.
В
подавляющем числе случаев, разложение
многочлена на множители основано на
следствии из теоремы Безу, то есть
находится или подбирается корень 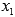 и
понижается степень многочлена на единицу
делением на
и
понижается степень многочлена на единицу
делением на 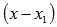 .
У полученного многочлена ищется
корень
.
У полученного многочлена ищется
корень 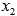 и
процесс повторяется до полного разложения.
и
процесс повторяется до полного разложения.
Если же корень найти не удается, то используются специфические способы разложения: от группировки, до ввода дополнительных взаимоисключающих слагаемых.
Дальнейшее изложение базируется на навыках решения уравнений высших степеней с целыми коэффициентами.
Вынесение за скобки общего множителя.
Начнем
с простейшего случая, когда свободный
член равен нулю, то есть многочлен имеет
вид 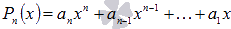 .
.
Очевидно,
что корнем такого многочлена является 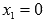 ,
то есть многочлен представим в виде
,
то есть многочлен представим в виде 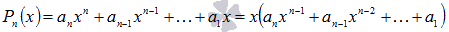 .
.
Этот способ есть ни что иное как вынесение общего множителя за скобки.
Пример.
Разложить
многочлен третьей степени  на
множители.
на
множители.
Решение.
Очевидно,
что 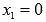 является
корнем многочлена, то есть х можно
вынести за скобки:
является
корнем многочлена, то есть х можно
вынести за скобки: 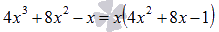
Найдем
корни квадратного трехчлена 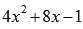

Таким
образом, 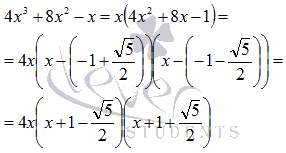
К началу страницы
Разложение на множители многочлена с рациональными корнями.
Сначала
рассмотрим способ разложения многочлена
с целыми коэффициентами вида 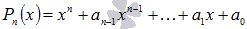 ,
коэффициент при старшей степени равен
единице.
,
коэффициент при старшей степени равен
единице.
В этом случае, если многочлен имеет целые корни, то они являются делителями свободного члена.
Пример.
Разложить
на множители выражение 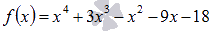 .
.
Решение.
Проверим,
имеются ли целые корни. Для этого
выписываем делители числа -18: 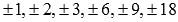 .
То есть, если многочлен имеет целые
корни, то они находятся среди выписанных
чисел. Последовательно проверим эти
числа по схеме
Горнера. Ее удобство еще и в том, что
в итоге получим и коэффициенты разложения
многочлена:
.
То есть, если многочлен имеет целые
корни, то они находятся среди выписанных
чисел. Последовательно проверим эти
числа по схеме
Горнера. Ее удобство еще и в том, что
в итоге получим и коэффициенты разложения
многочлена: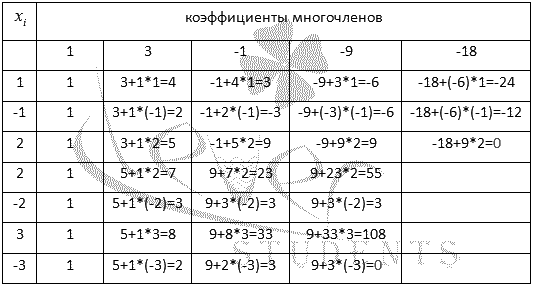
То
есть, х=2 и х=-3 являются
корнями исходного многочлена и он
представим в виде произведения: 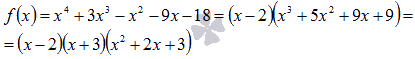
Осталось
разложить квадратный трехчлен  .
.
Дискриминант этого трехчлена отрицательный, следовательно, он не имеет действительных корней.
Ответ:
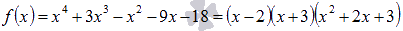 .
.
Замечание:
вместо схемы Горнера можно было воспользоваться подбором корня и последующим делением многочлена на многочлен.
Теперь
рассмотрим разложение многочлена с
целыми коэффициентами вида 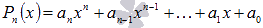 ,
причем коэффициент при старшей степени
не равен единице.
,
причем коэффициент при старшей степени
не равен единице.
В этом случае многочлен может иметь дробно рациональные корни.
Пример.
Разложить
на множители выражение 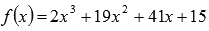 .
.
Решение.
Выполнив
замену переменной y=2x,
перейдем к многочлену с коэффициентом
равным единице при старшей степени. Для
этого сначала домножим выражение на 4. 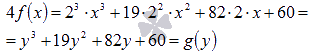
Если
полученная функция 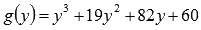 имеет
целые корни, то они находятся среди
делителей свободного члена. Запишем
их:
имеет
целые корни, то они находятся среди
делителей свободного члена. Запишем
их: 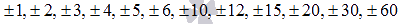
Вычислим
последовательно значения функции g(y) в
этих точках до получения нуля. 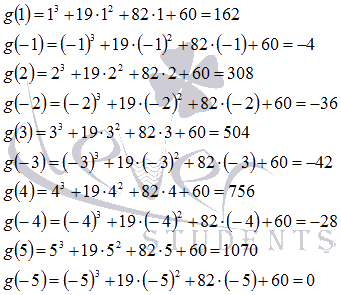
То
есть, y=-5 является
корнем 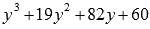 ,
следовательно,
,
следовательно, 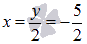 является
корнем исходной функции. Проведем
деление столбиком (уголком) многочлена
является
корнем исходной функции. Проведем
деление столбиком (уголком) многочлена 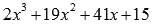 на
двучлен
на
двучлен 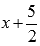 .
. 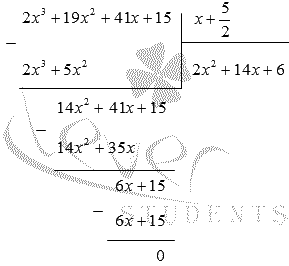
Таким
образом, 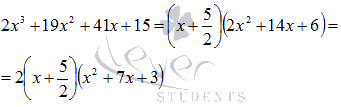
Проверку
оставшихся делителей продолжать
нецелесообразно, так как проще разложить
на множители полученный квадратный
трехчлен 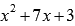
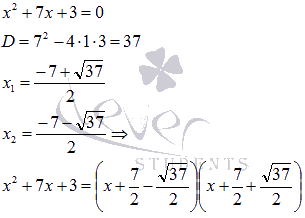
Следовательно, 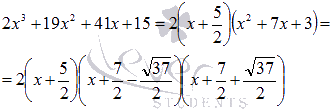
Незведені многочлени. Теорема про розклад многочлена у добуток незведених. Канонічний розклад многочлена.
studfile.net