Практика. Функции. Часть 4. Кусочно-заданные функции. Видеоурок. Алгебра 8 Класс

Рассмотрим пример построения графика функции с модулем.

Задание 5. Построить график функции:

Решение

В функции присутствует модуль, поэтому, прежде чем построить график, нам нужно его раскрыть.

Вспомним, что:

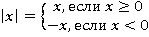
С учетом этого получим: если 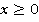, то . Упростив, получим функцию:

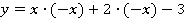Если , то . Упростив, получим:

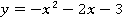
Сокращенно это можно записать так:

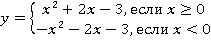
Функции, заданные таким образом, называются кусочно-заданными. Обратите внимание: при одних значениях аргумента у нас одна функция, при других – другая. Кусочно-заданные функции нередко встречаются при моделировании различных ситуаций в физике, экономике и пр.

Например, при малых удлинениях механическое напряжение в твердом теле линейно зависит от относительного удлинения. Но при бо̀льших удлинениях вид зависимости меняется (см. рис. 13). Соответственно, описать такую зависимость мы сможем только кусочно-заданной функцией.

Рис. 13. Иллюстрация к заданию 5

Вернемся к решению задачи. Мы получили различные функции на разных промежутках аргумента. Теперь осталось построить графики этих функций на этих промежутках, и мы получим график исходной функции.

Строить графики квадратичных функций мы уже умеем. Это можно делать несколькими способами: преобразовав график  или найдя вершину параболы и направление веток. Разберем оба способа.

Начнем с построения графика

 с помощью преобразований. Выделим полный квадрат:

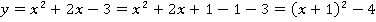
Функция примет вид:

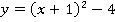
Строим график этой функции путем преобразования графика  (см. рис. 14).

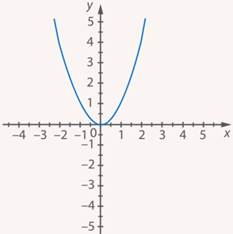
Рис. 14. Иллюстрация к заданию 5

К аргументу прибавляется  – график сместится на

 влево (см. рис. 15).

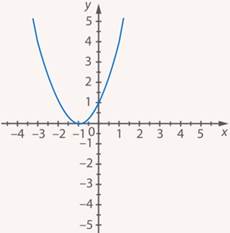
Рис. 15. Иллюстрация к заданию 5

Из значения функции вычитается  – график сместится на  вниз (см. рис. 16).

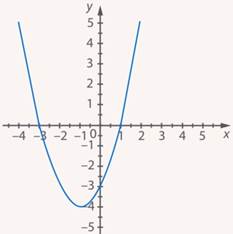
Рис. 16. Иллюстрация к заданию 5

Эта функция задана при условии 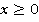, поэтому оставляем только часть графика (см. рис. 17).

Рис. 17. Иллюстрация к заданию 5

Теперь построим график 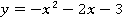. Применим другой способ. Найдем координаты вершины параболы:

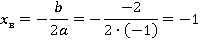
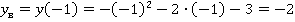
Коэффициент 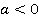, поэтому ветви параболы направлены вниз. Для более точного построения найдем значения функции в точках, ближайших к вершине:

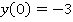
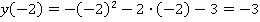
Получаем график функции 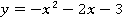 (см. рис. 18).

Рис. 18. Иллюстрация к заданию 5

Не забываем, что эта функция задана при условии , поэтому оставляем только часть графика (см. рис. 19).

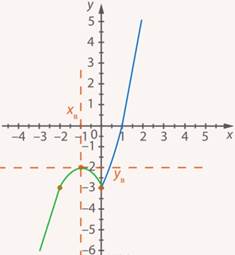
Рис. 19. Иллюстрация к заданию 5

Итак, мы получили график исходной функции (см. рис. 20).

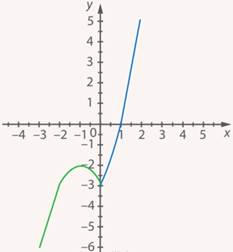
Рис. 20. Иллюстрация к заданию 5

С построением еще одного графика функции с модулем вы можете ознакомиться ниже.

---

 

Построение графика функции с двумя модулями

Задание. Построить график функции:

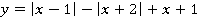
Решение

Здесь у нас два разных подмодульных выражения. Каждый модуль нужно раскрывать по отдельности:

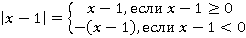
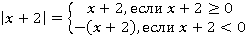
Чтобы сделать это более рационально, обратимся к предыдущему примеру. Там было одно значение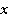

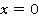, при котором модуль обращался в ноль:  – и прямая  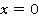разбивала плоскость на две части, в каждой из которых был свой график функции (см. рис. 21).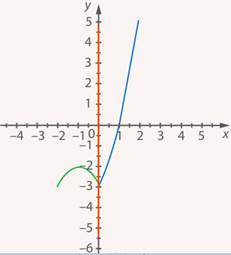

Рис. 21. Иллюстрация к заданию

Здесь у нас два выражения с модулями, и два таких значения:  и

. Соответственно, прямые  и  разобьют плоскости уже на 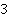 области, в каждой из которых нужно будет построить свой график (см. рис. 22).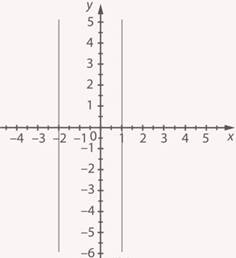

Рис. 22. Иллюстрация к заданию

1. Первая область:

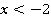
При таком условии оба подмодульных выражения будут отрицательны и модули раскроются со знаком «минус»:

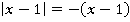
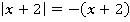
Получим функцию:

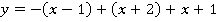
После упрощения:

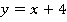
Это прямая, построим ее по 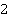 точкам (см. рис. 23):

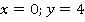
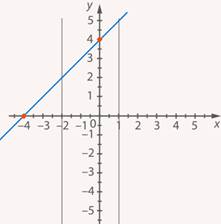
Рис. 23. Иллюстрация к заданию

Оставим только ту часть прямой, которая лежит в первой области (см. рис. 24).

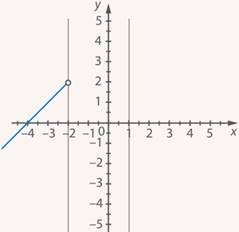
Рис. 24. Иллюстрация к заданию

2. Вторая область:

В этом случае:

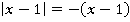
Получим функцию:

После упрощения:

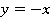
Это прямая, строим по 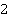 точкам (см. рис. 25):

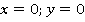
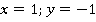
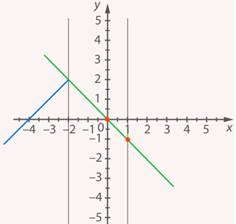
Рис. 25. Иллюстрация к заданию

Оставляем только часть прямой, которая лежит во второй области (см. рис. 26).

Рис. 26. Иллюстрация к заданию

3. Третья область:

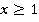
В этом случае:

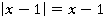
Получим функцию:

После упрощения:

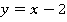
Это снова прямая, строим по двум точкам (см. рис. 27):

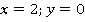
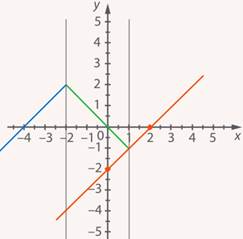
Рис. 27. Иллюстрация к заданию

Оставляем только часть прямой, которая лежит в третьей области (см. рис. 28). В итоге мы получили график исходной функции.

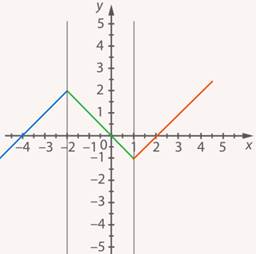
Рис. 28. Иллюстрация к заданию

---

Задания по теме «Кусочно-непрерывные функции»

Кусочно-непрерывные функции

1. Задание

Постройте график функции 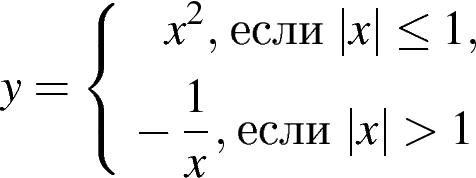  и определите, при каких значениях параметра  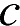прямая  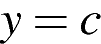имеет с графиком ровно одну общую точку.

2. Задание

Постройте график функции 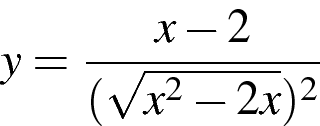 и найдите все значение 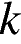, при которых прямая  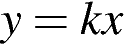имеет с графиком данной функции ровно одну общую точку.

3. Задание

Постройте график функции 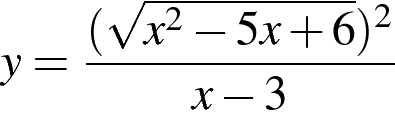 и найдите все значения 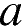, при которых прямая  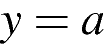не имеет с графиком данной функции общих точек.

4. Задание

Постройте график функции 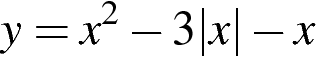   и определите, при каких значениях  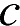  прямая  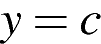  имеет с графиком три общие точки.

5. Задание

Постройте график функции 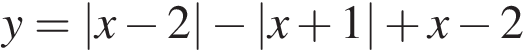 и найдите значения , при которых прямая  имеет с ним ровно две общие точки.

6. Задание

Постройте график функции

 

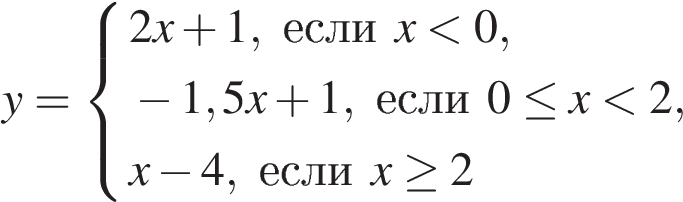
и определите, при каких значениях прямая 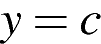 имеет с графиком ровно две общие точки.

7. Задание

Постройте график функции 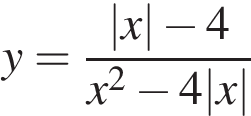 и определите, при каких значениях  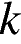прямая 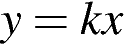не будет иметь с построенным графиком ни одной общей точки.

8. Задание

Постройте график функции 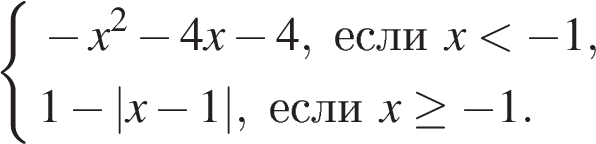 и определите, при каких значениях параметра a он имеет ровно две общие точки с прямой y = a.

9. Задание

Постройте график функции

 

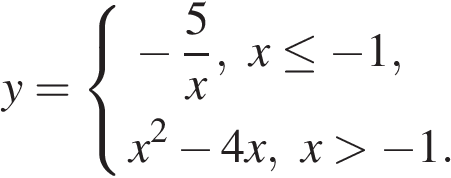
и определите, при каких значениях 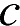 прямая  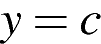будет пересекать построенный график в трёх точках.

10. Задание

Постройте график функции 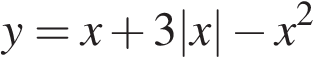 и определите, при каких значениях  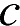прямая  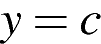имеет с графиком ровно три общие точки.

11. Задание

Постройте график функции

 

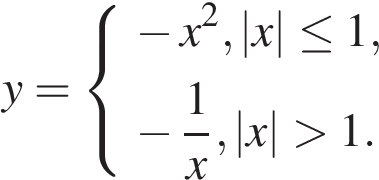
и определите, при каких значениях 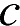 прямая  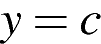будет иметь с графиком единственную общую точку.

12. Задание

Постройте график функции

 

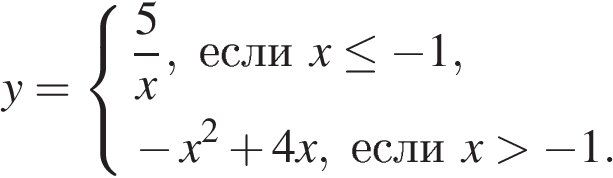
и определите, при каких значениях 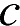 прямая  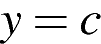будет пересекать построенный график в трёх точках.

13. Задание

Постройте график функции 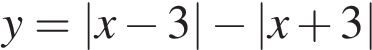 и найдите все значения  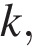при которых прямая  имеет с графиком данной функции ровно одну общую точку.

14. Задание

Постройте график функции 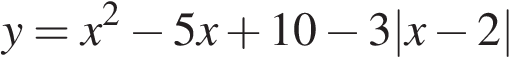 и найдите все значения  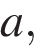при которых он имеет ровно три общие точки с прямой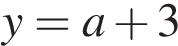 

15. Задание

Постройте график функции

 

 

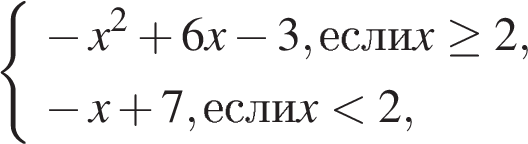
и определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.

16. Задание

Постройте график функции 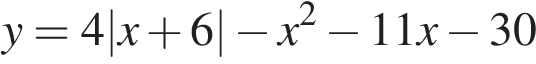 и определите, при каких значениях  прямая  имеет с графиком ровно три общие точки.

17. Задание

Постройте график функции 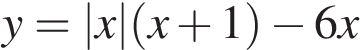 и определите, при каких значениях  прямая  имеет с графиком ровно две общие точки.

18. Задание

Постройте график функции 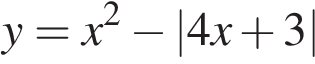 и определите, при каких значениях  прямая  имеет с графиком ровно три общие точки.

19. Задание

Постройте график функции 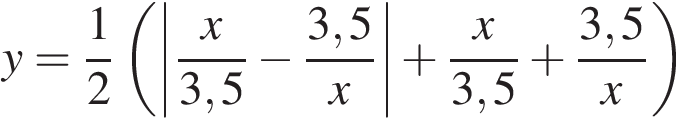 и определите, при каких значениях  прямая  имеет с графиком ровно одну общую точку.

20. Задание

Постройте график функции 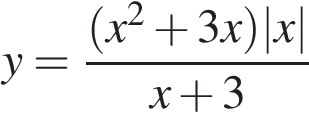 и определите, при каких значениях  прямая  не имеет с графиком ни одной общей точки.

21. Задание

Постройте график функции

 

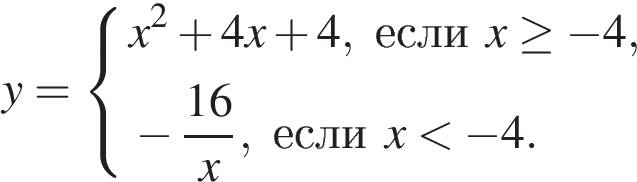
и определите, при каких значениях  прямая  имеет с графиком одну или две общие точки.

22. Задание

Постройте график функции

 

 

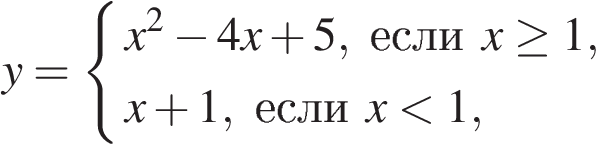
и определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.

23. Задание

Постройте график функции

 

 

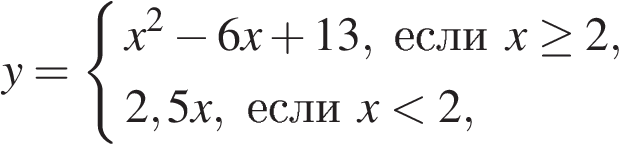
и определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.

24. Задание

Постройте график функции

 

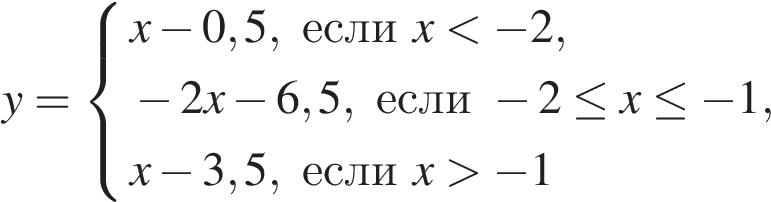
и определите, при каких значениях  прямая  имеет с графиком ровно две общие точки.

25. Задание

Постройте график функции 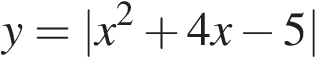. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?

26. Задание

Постройте график функции

 

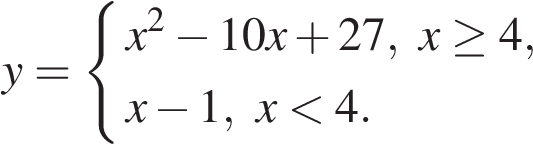
и определите, при каких значениях  прямая  имеет с графиком ровно две общие точки.

27. Задание

Постройте график функции 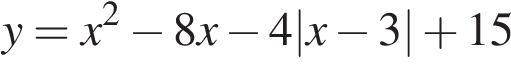 и найдите значения , при которых прямая  имеет с ним ровно три общие точки.

28. Задание

Найдите 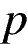 и постройте график функции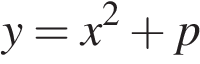, если известно, что прямая  имеет с графиком ровно одну общую точку.

Как решать кусочно заданные функции. Кусочные функции

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №13

«Кусочные функции»

Сапогова Валентина и

Донская Александра

Руководитель-консультант:

г. Бердск

1. Определение основных целей и задач.

2. Анкетирование.

2.1. Определение актуальности работы

2.2. Практическая значимость.

3. История функций.

4. Общая характеристика.

5. Способы задания функций.

6. Алгоритм построения.

8. Используемая литература.

1. Определение основных целей и задач.

Цель:

Выяснить способ решения кусочных функций и, исходя из этого, составить алгоритм их построения.

Задачи:

— Познакомиться с общим понятием о кусочных функциях;

— Узнать историю термина «функция»;

— Провести анкетирование;

— Выявить способы задания кусочных функций;

— Составить алгоритм их построения;

2. Анкетирование.

Среди старшеклассников было проведено анкетирование на умение строить кусочные функции. Общее количество опрошенных составило 54 человека. Среди них 6% — работу выполнили полностью. 28% работу смогли выполнить, но с определёнными ошибками. 62% — работу не смогли выполнить, хоть и предпринимали какие-либо попытки, а оставшиеся 4% вообще не приступали к работе.

Из этого анкетирования можно сделать вывод, что ученики нашей школы, которые проходят программу имеют не достаточную базу знаний, ведь этот автор не уделяет особого внимания на задания подобного рода. Именно из этого вытекает актуальность и практическая значимость нашей работы.

2.1. Определение актуальности работы.

Актуальность:

Кусочные функции встречаются, как в ГИА, так и в ЕГЭ, задания, которые содержат функции подобного рода, оцениваются в 2 и более баллов. И, следовательно, от их решения может зависеть ваша оценка.

2.2. Практическая значимость.

Результатом нашей работы будет являться алгоритм решения кусочных функций, который поможет разобраться в их построении. И добавит шансы на получения желаемой вами оценки на экзамене.

3. История функций.

— «Алгебра 9 класс» и др.;

Реальные процессы, происходящие в природе, можно описать с помощью функций. Так, можно выделить два основных типа течения процессов, противоположных друг другу – это постепенное или непрерывное и скачкообразное (примером может служить падение мяча и его отскок). Но если есть разрывные процессы, то существуют и специальные средства для их описания. С этой целью вводятся в обращение функции, имеющие разрывы, скачки, то есть на различных участках числовой прямой функция ведет себя по разным законам и, соответственно, задается разными формулами. Вводятся понятия точек разрыва, устранимого разрыва.

Наверняка вам уже встречались функции, заданные несколькими формулами, в зависимости от значений аргумента, например:

y = {x – 3, при x > -3;
{-(x – 3), при x

Такие функции называются кусочными или кусочно-заданными . Участки числовой прямой с различными формулами задания, назовем составляющими область определения. Объединение всех составляющих является областью определения кусочной функции. Те точки, которые делят область определения функции на составляющие, называются граничными точками . Формулы, определяющие кусочную функцию на каждой составляющей области определения, называются входящими функциями . Графики кусочно-заданных функций получаются в результате объединения частей графиков, построенных на каждом из промежутков разбиения.

Упражнения.

Построить графики кусочных функций:

1) {-3, при -4 ≤ x f(x) = {0, при x = 0,
{1, при 0

График первой функции – прямая, проходящая через точку y = -3. Она берет свое начало в точке с координатами (-4; -3), идет параллельно оси абсцисс до точки с координатами (0; -3). График второй функции – точка с координатами (0; 0). Третий график аналогичен первому – это прямая, проходящая через точку y = 1, но уже на участке от 0 до 5 по оси Ох.

Ответ: рисунок 1.

2) {3, если x ≤ -4,
f(x) = {|x 2 – 4|x| + 3|, если -4 {3 – (x – 4) 2 , если x > 4.

Рассмотрим отдельно каждую функцию и построим ее график.

Так, f(x) = 3 – прямая, параллельная оси Ох, но изображать ее нужно только на участке, где x ≤ -4.

График функции f(x) = |x 2 – 4|x| + 3| может быть получен из параболы y = x 2 – 4x + 3. Построив ее график, часть рисунка, которая лежит над осью Ox, необходимо оставить без изменений, а часть, которая лежит под осью абсцисс, симметрично отобразить относительно оси Ox. Затем симметрично отобразить часть графика, где
x ≥ 0 относительно оси Oy для отрицательных x. Полученный в результате всех преобразований график оставляем только на участке от -4 до 4 по оси абсцисс.

Презентация к уроку по алгебре (9 класс) по теме: Презентация по алгебре «Свойства функций. Кусочно-заданные функции» 9 класс

По теме: методические разработки, презентации и конспекты

Презентация по алгебре «Вычисление значений функции по формуле», 7 класс

Презентация для проведения урока в 7 классе по теме «Вычисление значений функции по формуле»….

презентация по теме «Функции и свойства функций» 9 класс

Презентация к уроку по теме «Функции и их свойства» , 9 класс. Может быть использована при повторении при подготовке к ГИА….

«Графики кусочно-заданных функций» (тетрадь на печатной основе, авторская работа)

Данная работа поможет учителям не только научит детей построению графиков кусочно-заданных функций, но и сэкономить драгоценное время на уроке. Тетрадь предназначена для учащихся 8 класса, может быть …

Построение кусочно-заданных функций с помощью программы Advanced Grapher

Построение кусочно-заданных функций…

Презентация на тему «Функция. График функции.»

Презентация содержит исторические сведения, нестандартные задания….

Методическое пособие «Построение кусочно заданных функций»

Понятие о кусочных функциях, построение графика кусочной функции….

Презентация «Влияние коэффициентов на расположение графика линейной функции» адресована учащимся 9 классов для самостоятельного повторения материала и подготовки к ОГЭ по математике, а также учителям, работающим в 7 классе.

В презентации представлено обобщение материала по теме «Линейная функция, ее свойства и график», рассмотрены все случаи расположения графика линейной функции при различных значениях коэффици…

Кусочно-непрерывная функция — это… Что такое Кусочно-непрерывная функция?



Кусочно-непрерывная функция

Кусочно-непрерывная функ­ция [sectionally, piecwise conti­nuous function] — функция, непрерывная во всех точках отрезка, на котором она определена, за исключением конечного числа точек (называемых точками разрыва 1-го рода).

Экономико-математический словарь: Словарь современной экономической науки. — М.: Дело. Л. И. Лопатников. 2003.

• Кусочно-линейные приближения
• Кэптивные фонды

Смотреть что такое «Кусочно-непрерывная функция» в других словарях:

• кусочно-непрерывная функция — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] кусочно непрерывная функция Функция, непрерывная во всех точках отрезка, на котором она определена, за исключением конечного числа точек (называемых… …   Справочник технического переводчика

• Кусочно-заданная функция — Кусочно заданная функция  функция, определённая на множестве вещественных чисел, заданная на каждом из интервалов, составляющих область определения, отдельной формулой. Формальное определение и задание Пусть заданы   точки смены формул …   Википедия

• Кусочно-линейная функция — Кусочно линейная функция  функция, определённая на множестве вещественных чисел, линейная на каждом из интервалов, составляющих область определения. Содержание 1 Формальное определение и задание 2 …   Википедия

• Кусочно-гладкая функция — Кусочно гладкая функция  функция, определённая на множестве вещественных чисел, дифференцируемая на каждом из интервалов, составляющих область определения. Формальное определение Пусть заданы   точки смены формул. Как и все кусочно… …   Википедия

• кусочно-линейная функция — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] кусочно линейная функция Нелинейная функция f(x) = f(x1, x2, …, xn), которая (при ее геометрическом представлении) состоит из переходящих друг… …   Справочник технического переводчика

• Кусочно-линейная функция — [piecewise linear function] нелинейная функция f(x) = f(x1, x2, …, xn), которая (при ее геометрическом представлении) состоит из переходящих друг в друга линейных участков. Любая функция, непрерывная в замкнутом интервале, может быть с… …   Экономико-математический словарь

• Функция ограниченной вариации — В математическом анализе вариацией функции называется числовая характеристика функции одного действительного переменного, связанная с её дифференциальными свойствами. Для функции из отрезка на вещественной прямой в является обобщением понятия… …   Википедия

• Обобщённая функция — или распределение математическое понятие, обобщающее классическое понятие функции. Потребность в таком обобщении возникает во многих физических и математических задачах. Понятие обобщённой функции даёт возможность выразить в математически… …   Википедия

• Обобщенная функция — Обобщённая функция или распределение  математическое понятие, обобщающее классическое понятие функции. Потребность в таком обобщении возникает во многих физических и математических задачах. Понятие обобщённой функции даёт возможность выразить в… …   Википедия

• Основная функция — Обобщённая функция или распределение  математическое понятие, обобщающее классическое понятие функции. Потребность в таком обобщении возникает во многих физических и математических задачах. Понятие обобщённой функции даёт возможность выразить в… …   Википедия