Дробные рациональные уравнения

Определение:

Дробным рациональным уравнением называется уравнение, обе части которого являются рациональными выражениями, причём хотя бы одно из них - дробным выражением.

Алгоритм решения:

·        найти общий знаменатель дробей, входящих в уравнение;

·        умножить обе части уравнения на общий знаменатель;

·        решить получившееся целое уравнение;

·        исключить из корней те, которые обращают общий знаменатель в ноль.

Пример.

Решить уравнение:

Знаменатель дроби, стоящей в правой части уравнения, можно разложить на множители, тогда найдем общий знаменатель:

Умножим на него обе части уравнения, получим уравнение:

Проверим, x=5 обращает общий знаменатель в ноль, а x=-2 знаменатель не обращает в ноль, значит x=-2 является корнем данного дробного рационального уравнения.

Получили корень x=-2.  

Пример.

Решить уравнение:

Найдём область допустимых значений переменной:

Приведём к общему знаменателю дроби:

Получим целое уравнение:

Преобразовав его, получаем квадратное уравнение:

Так как корни не входят в область допустимых значений, значит оба числа являются корнями исходного дробного рационального уравнения.

Пример.

Решить уравнение:

Введем замену:

Решаем по алгоритму:

Осуществим обратную подстановку и решим полученные квадратные уравнения:

Проверим найденные корни:

Ни при каком из полученных значений знаменатель не обращается в ноль. Значит, данное дробное рациональное уравнение имеет 4 корня.

Больших вычислений требует проверка. Каждый корень нужно подставлять в уравнение.

Пример.

От автобусной остановки отъехал автобус до аэропорта, находящегося на расстоянии 120 км. Один из пассажиров автобуса опоздал к отправлению на 10 минут, и решил поехать на такси. Автобус и такси приехали в аэропорт одновременно. Нужно найти скорость автобуса, если известно, что скорость такси на 10 км/ч больше.

Пусть х — скорость автобуса, тогда (х + 10) — скорость такси. Выразим время движения обоих транспортных средств и составим уравнение:

Решим полученное дробное рациональное уравнение:

Получаем скорость автобуса

videouroki.net

«Решение дробно-рациональных уравнений» 9 класс

«Решение дробно-рациональных уравнений»

Урок: алгебра 9 класс

Тема: Решение дробных рациональных уравнений

Цель: познакомить с новым видом уравнений — дробными рациональными уравнениями, дать представление об алгоритме решения дробных рациональных уравнений.

Задачи:

Образовательные

1. Формирование умения и навыков решения дробных рациональных уравнений.

2. Применение ЗУН упрощения рациональных выражений.

3. Контроль уровня усвоения знаний и умений решения уравнений, приведения подобных слагаемых, приведения к общему знаменателю, вычислительных навыков.

Развивающие

1. Развитие умений выделять главное, существенное в изученном материале.

2. Формирование умений сравнивать, классифицировать, обобщать факты и понятия.

3. Формировать умение пользоваться алгоритмом.

4. Развитие у учащихся самостоятельности в мышлении и в учебной деятельности.

5. Развитие у учащихся познавательного интереса, внимания, математической зоркости.

Воспитательные

1. Содействовать формированию мировоззренческих понятий.

2. Воспитывать чувство коллективизма, сопереживания за группу, товарища.

Оборудование: 1) Карточки с домашним заданием

2) Карточки с заданиями

3) Карточки «проверь себя».

4) Карточки помощницы.

5) Тексты разноуровневой самостоятельной работы.

6) Карточки с дополнительными заданиями.

7)Оценочные карточки.

8)Рефлексия

Структура урока:

1. Актуализация опорных знаний

2. Постановка темы и целей урока

3. Изучение нового материала

4. Закрепление пройденного материала

5. Итог урока

Силу уму придают упражнения а не покой, А. Поп(анг.поэт)

1.Организационный момент (2 мин)

Сегодня на уроке мне хотелось бы вас пригласить поглубже заглянуть в замечательный мир математики – в мир уравнений, в мир поиска, в мир исследований.

Но для начала давайте вспомним, а что такое уравнение? (Равенство, содержащее неизвестное).

— А что значит решить уравнение? (Значит найти все его корни или доказать, что их нет).

— А что является корнем уравнения? (Значение переменной, при котором уравнение обращается в верное равенство).

— Какие виды уравнений, вы знаете и умеете решать? (Линейные, квадратные, дробно-рациональные).

Все способы решений, известных вам уравнений, можно образно представить в виде “ключей”. Символ урока – связка ключей — “Линейные уравнения”, “Квадратные уравнения”, “Дробно-рациональные уравнения”, “

2. Проверка домашнего задания(3мин),взимопроверка)

НОМЕР ЗАДАНИЯ

Ответы

1. 0,5 х ² +0,7 =0

нет корней.

2. (х-5) (х+3)= 9

х₁ = — 4 , х₂ = 6.

3. (х-5) (х +3)=1 — 2х

х ₁= 4, х ₂ = — 4.

4. (х-5) (х +3) = 3 (х-5)

х=0, х=5.

5. 2 (х-1) – 1 = 3 — (1-2х)

нет корней

6.1 – 2х + 4х ² = х ² -2х + 1

х = 0.

7. 3 (1 – х) + 2 = 5 – 3х

х — любое число.

8. 2х ² + 3х +4 =0

нет корней

9. х ² +6х +4 = 0

х ₁ = — 3 ± √ 5.

10. 25х ² – 30х + 9 = 0

х _1,2 = 0,6

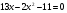3.: Определите вид каждого уравнения (3 мин)

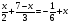
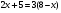
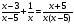
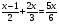
4,Целепологание индивидуально. Тема урока

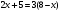
5. Решить уравнения: (2 мин)

6.Алгоритм решения уравнений линейных уравнений:

.а)Раскрыть скобки.

б). Перенести слагаемые с переменной в одну сторону, а числа в другую.

В).Найти корень уравнения. предварительно приведя слагаемые.

7.Историческая справка

Первым, кто описал решение линейных уравнений, был Мухаммед аль-Хорезми, написавший трактат «Ал-джебра (перенос слагаемых) и ал-мукабала (приведение подобных слагаемых)»

Для чего нужно уметь решать различные уравнения?

Уравнения оказывают помощь и в других науках, химии, (линейное уравнение)-по основному свойству пропорции.

3.Работа над квадратным уравнением( 5 МИНУТ)

1.х²-7х+12=0

2. 5х²-11х=6-0

3. 2х²-7х=0

Алгоритм решения квадратного уравнения

Физ-пауза 1 МИН

Звучит музыка (саксофон) – 1минута.

А знаете ли вы, что английский математик Д.Сильвестр называл музыку математикой чувств, а математику – музыкой раЗУМА 4.Работа над дробно-рациональным уравнением.

Ход урока

Вводная беседа учителя (2 мин.)

Один начинающий волшебник, герой шуточной песенки, неумело обращался с заклинаниями, в результате вместо грозы у него получилась коза, а вместо утюга – слон. Чтобы решать уравнения, нужно совершать ряд преобразований, и делать это следует очень осмотрительно.

Например, решая уравнения, мы могли бы рассуждать так: 5 МИНУТ

Пример 1

Пример 2

х(х+3) =2х,

х+3 = 2,

х = — 1.

Ответ: х= -1

х ² +х-1 = 4х-3 ,

х-1 х-1

х ² +х-1=4х-3,

х ² -3х+2=0,

х=1 или х=-2.

Ответ: х=1, х= — 2

На самом деле, стараясь избавиться от всего лишнего, мы допустили бы ошибки. Какие?

— В результате неравносильных преобразований в уравнении 1 потерян корень х = 0, а в примере 2 появился «посторонний» корень х = 1.

— Как же не попасть в подобную ловушку?

Прежде всего, надо четко знать, какие действия нужно выполнить в ходе решения

1. Алгоритм решения дробных рациональных уравнений: 2 МИНУТЫ

1 способ.

2 способ.

1. Найти общий знаменатель дробей, входящих в уравнение.

1. Найти допустимые значения дробей, входящих в уравнение.

2. Умножить обе части уравнения на общий знаменатель.

2. Найти общий знаменатель дробей,

входящих в уравнение.

3. Решить получившееся уравнение.

3.Умножить обе части уравнения

на общий знаменатель.

4. Исключить проверкой из корней уравнений те, которые обращают в нуль общий знаменатель.

4. Решить получившееся уравнение.

5. Исключить корни, не входящие в допустимые значения дробей уравнения.

Найди ошибку

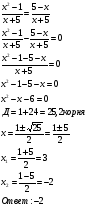
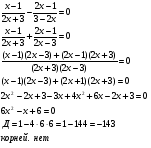
Решение уравнений. 3 МИН

1. Взаимопроверка – 4 варианта. Работа выполняется на листочках. Ответы записаны на обратной стороне доски. В ходе выполнения работы учащиеся определяют для себя алгоритм решения дробных рациональных уравнений. На каждой парте – таблица – напоминание «Алгоритм решения дробных рациональных уравнений». Приложение 1. 5 МИНУТ

Решить самостоятельно

В а р и а н т 1.

В а р и а н т 2.

В а р и а н т 3.

В а р и а н т 4.

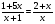
О т в е т ы: на доску с обратной стороны

I вариант: , (; ).

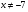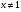II вариант: (; )

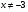III вариант: ()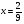

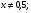
IV вариант: , (; ).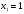

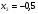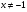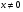5. План исследования уравнения: 2 МИН

1. Провести анализ уравнения.

2. Составить план решения.

3. Реализовать план решения.

4. Составить анализ метода решения и систематизировать опыт.

6.Подведение итогов

VI. Итог урока. (2 мин)

— Чем занимались сегодня на уроке?

— А зачем нужно уметь решать уравнения?

С помощью уравнений можно найти любое неизвестной, решать задачи. Этим мы и будем заниматься на следующих уроках

— А теперь вернемся на начало урока. Каждый из вас для себя поставил цель.

Достигли ли вы этих целей?

Домашнее задание

VII. Выставление оценок. (1 мин)

VIII. Рефлексия. (1 мин) Раздать учащимся карточки

Рефлексивный алгоритм

• Доволен ли ты тем, как прошел урок?

• Было ли тебе интересно?

• Сумел ли ты получить новые знания?

• Ты был активен на уроке?

• Ты с удовольствием будешь выполнять домашнее задание?

• Учитель был внимателен к тебе?

• Ты сумел показать свои знания?

Оценочный лист учащегося

Фамилия _________________

Имя ______________________

Вид задания

«5»

«4»

«3»

«2»

Домашнее задание

9-10

7-8

5-6

1-4

Этапы

Задания

Количество баллов

1

Домашнее задание

2

Линейное уравнение

3

Квадратное уравнение

4

Дробно-рациональное уравнение

5

Найди ошибку

6

Самостоятельная работа

Итоговое количество баллов

Оценка

ПОДУМАТЬ!!!!!

Задача на совместную работу

1. Двое рабочих выполнили работу за 12 дней. За сколько дней может выполнить работу каждый рабочий, если одному из них для выполнения всей работы потребуется на 10 дней больше, чем другому? Ученик у доски комментирует.

В этой задаче описывается процесс работы двух рабочих отдельно и вместе, который характеризуется величинами: производительность, сроки, работа. Составлю таблицу и заполню ее по тексту задачи.

Производительность (раб/день)

Сроки (дни)

Работа

1 рабочий

Х

1 (А)

2 рабочий

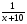
Х + 10

1 (А)

Вместе

+ =

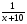12

1 (А)

Обычно, когда не определен конкретно объем выполняемой работы, то его без ограничения общности, принимают за 1. Решу уравнение:

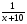+ = Умножу обе части на 12х(х+10). ОДЗ: х≠0; х≠-10

12(х+10) + 12х = Х (х+10)

х² — 14х – 120 = 0

по теоремам Виета

х₁ = -6 не удовлетворяет смыслу задачи

х₂ = 20 удовлетворяет ОДЗ

Соотнесу полученный результат с вопросом задачи.

Ответ: первому понадобится 20, а второму 30 дней чтобы выполнить эту работу самостоятельно.

infourok.ru

Презентация к уроку по алгебре (9 класс) по теме: 9 класс. Дробные рациональные уравнения.

Слайд 1

Дробные рациональные уравнения Подготовила: учитель математики МОУ сош №30 имени А.И.Колдунова Кутоманова Е.М. 2010-2011 учебный год

Слайд 2

Условие равенства дроби нулю При каком значении переменной дробь равна нулю? Дробь равна нулю, если числитель равен нулю, а знаменатель при этом нулю не равен. х³-25х=0, х(х²-25)=0, х=0, х=±5. Если х=0, то х²-6х+5≠0, если х=-5, то х²-6х+5≠0, если х=5,то х²-6х+5=0. Ответ: при х=0, х=-5. Выполним №288(а,б)

Слайд 3

Решим уравнение х³-25х=0, х(х²-25)=0, х=0, х=±5. Если х=0, то х²+6х+5≠0, если х=-5, то х²+6х+5=0, если х=5,то х²+6х+5 ≠ 0. Ответ: 0;5. Выполним №289(а)

Слайд 4

Определение Дробным рациональным уравнением называют уравнение, обе части которого являются рациональными выражениями, причём хотя бы одно из них – дробным выражением. Например:

Слайд 5

Алгоритм решения дробных рациональных уравнений 1.Находим общий знаменатель дробей, входящих в уравнение. 2.Умножаем обе части уравнения на этот знаменатель. 3.Решаем получившееся целое уравнение. 4.Исключаем из его корней те, которые обращают в нуль общий знаменатель дробей. 5.Записываем ответ.

Слайд 6

Решим уравнение: х-1 – общий знаменатель. Умножим обе части уравнения на х-1, получим 2(х-1)-(х+1)=0; 2х-2-х-1=0, х-3=0, х=3. Если х=3, то х-1=3-1=2 ≠0. Ответ:3

Слайд 7

Решим уравнение: Решение. (х+2)(х-3) – общий знаменатель. Умножим обе части уравнения на (х+2)(х-3), получим (х-1)(х-3)=(х-4)(х+2)- (х+2)(х-3), х²-х-3х+3=х²-4х+2х-8-х²-2х+3х+6, х²-3х+5=0, D =9-20

Слайд 8

Решим уравнение Общий знаменатель х-3. Умножим обе части уравнения на х-3, получим (х-2)(х-3)-(х-3)=0, х²-2х-3х+6-х+3=0, х²-6х+9=0, (х-3)²=0, х=3. Если х=3, знаменатель обращается в нуль, значит, х=3-посторонний корень. Ответ: корней нет

Слайд 9

Решим уравнение Решение. Умножим обе части уравнения на х-2, получим 2х²-(3х+2)=х(х-2), 2х²-3х-2=х²-2х, 2х²-3х-2-х²+2х=0, х²-х-2=0, D =1+8=9, х=(1±3):2, х₁=-1, х₂=2. Если х=-1, х-2=-1-2=-3≠0; если х=2, то х-2=2-2=0 . Ответ: -1.

Слайд 10

Решим уравнение Общий знаменатель: 4х(х+1)(х+2). Умножим обе части уравнения на 4х(х+1)(х+2), получим 4(х+2)+ 4х=х(х+1)(х+2), 4х+8+4х=х(х²+3х+2), 8х+8=х³+3х²+2х, х³+3х²-6х-8=0, (х³-8)+3х(х-2)=0, (х-2)(х²+2х+4)+3х(х-2)=0, (х-2)(х²+5х+4)=0, х-2=0 или х²+5х+4=0 х=2, D =25-16=9, х=(-5±3):2, х₁=-1, х₂=-4. Если х=2, то 4х(х+1)(х+2)≠0, если х=-1, то 4х(х+1)(х+2)=0, если х=-4, то 4х(х+1)(х+2)≠0. Ответ:2,-4.

nsportal.ru

Конспект урока по алгебре «Дробные рациональные уравнения. Основные понятия».(9 класс) + презентация

Тема урока: ДРОБНЫЕ РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ. ОСНОВНЫЕ ПОНЯТИЯ.

Дата проведения: 16 ноября 2017

Цели урока:

Обучающая:

• формирование понятия дробно- рационального уравнения;

• рассмотреть различные способы решения дробных рациональных уравнений;

• рассмотреть алгоритм решения дробных рациональных уравнений.

• обучить решению дробных рациональных уравнений по алгоритму;

• проверка уровня усвоения темы путем решения примеров.

Развивающая:

• развитие умения правильно оперировать полученными знаниями, логически мыслить;

• развитие интеллектуальных умений и мыслительных операций — анализ, синтез, сравнение и обобщение;

• развитие инициативы, умения принимать решения, не останавливаться на достигнутом;

Воспитывающая:

• воспитание познавательного интереса к предмету;

• воспитание самостоятельности при решении учебных задач;

• воспитание воли и упорства для достижения конечных результатов.

Тип урока: урок – объяснение нового материала.

Ход урока

1. Организационный момент.

Здравствуйте, ребята! Давайте повторим с вами основные понятия, необходимые при изучении данной темы:

• Какое выражение называется дробью? (отношение двух величин)

• Какие выражения называются рациональными? (Алгебраическое выражение, в котором указаны только действия сложения, вычитания, умножения и возведения в степень с натуральным показателем, называют целым рациональным выражением.) (Если кроме указанных действий входит действие деления, то выражение называют дробно-рациональным).

• Что такое уравнение? (Равенство с переменной или переменными.)

• Какие свойства используются при решении уравнений? (1. Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному. 2. Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.)

Данная тема объединяет ранее изученные темы такие как дроби и действия с дробями, уравнения различных видов и алгоритмы их решения следовательно вам необходимо применить свои знания и умения полученные ранее.

Итак, открываем тетради и записываем тему урока «Дробные рациональные уравнения. Основные понятия».

3. Объяснение нового материала.

Итак вспомнив понятия дадим основное определение дробно-рациональных уравнений.(слайд 2)

ОПРЕДЕЛЕНИЕ: уравнение вида — , где — и — целые выражения,

называется дробно — рациональным.

Уравнения данного вида можно решать несколькими способами, а именно: (слайд 3)

• Дробно — рациональные уравнения решают либо с использованием равносильного перехода и условия равенства дроби нулю;

• либо с использованием неравносильного перехода к уравнению — следствию и обязательной проверкой корней.

Ребята давайте вспомним способы решения дробно — рациональных уравнений: (слайд 4)

1. Приведение дробей к общему знаменателю;

2. Графический;

3. Введение новой переменной;

4. Выделение из дробей целой части;

5. Умножение дробей на общий знаменатель всех дробей.

Рассмотрим первый способ решения данных уравнений (слайд 5)

1 способ: сначала все слагаемые переносят в одну часть,

приводят дроби к общему знаменателю и представляют уравнение в стандартном виде,

после чего отдельно решают первое уравнение и второе неравенство.

Иногда вместо решения второго неравенства выполняют проверку корней первого уравнения, подставляя их во второе неравенство.

Применим этот способ для решение примера (слайд 6,7,8):

Решение:

Рассмотрим второй способ решения уравнений: ( слайд 9)

— уравнение умножают на общий знаменатель всех дробей,

— решают полученное целое уравнение и

— выполняют проверку корней –

— не обращают ли найденные корни знаменатель в нуль.

Рассмотрим пример (слайд 10):

5. Подведение итогов урока.

Итак, сегодня на уроке мы с вами познакомились с дробными рациональными уравнениями, научились решать эти уравнения различными способами. Какой метод решения дробных рациональных уравнений, по Вашему мнению, является более легким, доступным, рациональным? Но, независимо от метода решения дробных рациональных уравнений, о чем необходимо не забывать? В чем «коварство» дробных рациональных уравнений? На следующем уроке мы продолжим с вами работу по данной теме.

6. Домашнего задания. Открыли дневники и записываем домашнее задание.

Выучить определения и алгоритмы решения дробно-рациональных уравнений.

Тема урока: «Дробные рациональные уравнения»

Дата проведения: __ ноября 2017 года

Цели: продолжить формирование умения решать дробно-рациональные уравнения, используя при этом различные приемы и методы.

Развивать логическое мышление, вычислительные навыки, умение пользоваться ранее изученным материалом.

Воспитывать аккуратность, взаимоуважение, дисциплинированность.

Ход урока

I. Организационный момент. Сегодня мы продолжим рассматривать способы решения дробно — рациональных уравнений.

II. Устный опрос:

— Какое уравнение называется дробно-рациональным?

— Какие способы решения данных уравнений вы знаете?

— Какие уравнения называются равносильными?

— Какие свойства используются при решении уравнений?

III. Объяснение нового материала.

Рассмотрим дробно — рациональное уравнение и решим его способом выделения из дробей целой части (слайд 11 -12):

Продолжаем рассматривать различные способы решения дробно — рациональных уравнений, и следующий способ введение новой переменной (слайд 13,14,15):

Рассмотрим пример 4 (слайд 16-17).

Ребята у нас остался ещё один способ решения — графический (слайд 18-19)

Решить графически означает построить графики функций на одной координатной плоскости и найти точку пересечения или несколько точек, координаты которых и будут являться решением.

Решим дробно — рациональное уравнение графическим способом. .

IV. Формирование умений и навыков.

Упражнения:

1. № 293 (а), № 294 (а).

2. № 297 (а ), № 298 (б).

3. № 299 (а).

VI. Итоги урока.

Вопросы учащимся:

– Какими приемами и методами можно решать дробно-рациональные уравнения?

– Опишите решение дробно-рационального уравнения по алгоритму.

– В каких случаях при решении дробно-рациональных уравнений целесообразно использовать метод введения новой переменной?

Домашнее задание: № 296 (б), № 294 (б), № 297 (в), № 298 (б).

infourok.ru

Урок по «Дробные рациональные уравнения» (9 класс)

Класс 9.

Математика (алгебра)

Тема урока: «Дробные рациональные уравнения»

Тип урока: комбинированный.

Цели:

1. Образовательные: дать определение «дробно-рациональные уравнения», показать способы решения таких уравнений.

2. Развивающие: развитие умений и навыков решать примеры с данным типом уравнений, находить корни дробно-рациональных уравнений.

3. Воспитывающие: воспитывать внимание, внимательность, активность, аккуратность.

Задачи: заинтересовать учеников предметом, показать важность умения решать разные уравнения и задачи.

Материально- техническое оснащение:

Мультимедиа проектор, экран, презентация к уроку «Дробные рациональные уравнения»

Время: 45 минут

План урока.

Демонстрирует слайды, сопровождает рассказом.

Слушает, задает целенаправленные вопросы в роли рядового участника

Обсуждают предмет с учителем и получают при необходимости информацию, устанавливают цели, планируют траекторию работы.

Вырабатывают план действий, формируют задачи.

Выполняют поиск информации, сбор данных и фактов истории, первично исследуют полученную информацию, решают промежуточные задачи.

V. Физкультминутка. (1 мин.)

Выполняет физкультминутку

Выполняют физкультминутку

VI.Самостоятельная работа. (7 мин.)

Решение задач, предлагает вопросы на закрепление.

Решают уравнения в тетрадях, с последующей самопроверкой.

VII. Закрепление материала. (8 мин.)

Решение задач, предлагает вопросы на закрепление.

Решают задачи в тетрадях, у доски, задают вопросы учителю.

VIII. Подведение итогов урока.(3 мин)

Оценивает работу учащихся.

Говорят о том, чему научились на уроке. Убирают рабочие места.

ХОД УРОКА

I. Рефлексия начала урока.

Проверка готовности к уроку.

II. Сообщение новой темы, цели и задачи:

Учитель: Здравствуйте! Посмотрите, пожалуйста, друг на друга и от всей души улыбнитесь.

III. Повторение пройденной темы.

1. Проверка домашнего задания 

№279(а,б,в), №277(в)

Ответы №279(а,б,в): а) -3; 3; -4; 4; б) корней нет; в) —; .

Ответы №277(в): в) -4; 3.

2. Работа по карточкам ( по образцу):

Образец:

3х³ – 18х = 0

3х (х² -6) = 0

3х = 0 х² — 6 = 0

х = 0 х² = 6

х = — и

Ответ: —, 0, .

Реши уравнения:

1) х³ – 16х = 0; 2) 9х³ – 81х = 0.

3. Работа у доски:

Решите биквадратное уравнение: № 278(г). Ответ: — ;; -1; 1.

4. Устно повторяем 

1) Повторим:

1. 

— Как называется данное уравнение? Сколько корней имеет данное уравнение?

2. Скажите, какой степени это уравнение? Сколько корней может иметь данное уравнение? 

3. Скажите, какой степени это уравнение? Сколько корней может иметь данное уравнение? 

4. Как называется данное уравнение?

2) Повторим.

Продолжи фразу!!!

1. Линейное уравнение имеет …… корень

2. Квадратное уравнение имеет 2 корня, если……

3. Квадратное уравнение имеет 1 корень, если……

4. Квадратное уравнение не имеет корней, если……

3) Найдите, при каких переменных выражения имеют смысл

а) 2(1-х²) +3х -4;

б) х – 3 + х² — х +1;

4 2

в) х² — х — 7 ;

х

г) 2х – 4 ;

х² -1

д) 3х + 1;

х -1

IV. Изучение нового материала.

Учитель: Дробным рациональным уравнением, называется уравнение, обе части которого являются рациональными выражениями, причём хотя бы одно из них — дробным выражением

Для решения рационального уравнения его необходимо преобразовать в линейное или квадратное уравнение, решить это уравнение и отбросить те корни, которые не входят в ОДЗ (область допустимых значений) исходного рационального уравнения.

Откройте учебник на стр.78 и прочитаем правило.

Алгоритм решения дробных рациональных уравнений:

1. Найти допустимые значения дробей, входящих в уравнение.

2. Найти общий знаменатель дробей, входящих в уравнение.

3. Умножить обе части уравнения на общий знаменатель.

4. Решить получившееся уравнение.

5. Исключить корни, не входящие в допустимые значения дробей уравнения 

Учитель: А теперь вместе со мной давайте решим дробно-рациональное уравнение по алгоритму 

1). Ответ: -2.

2) Ответ: корней нет.

V. Физкультминутка 

• А теперь, ребята, встали.

• Быстро руки вверх подняли,

• В стороны, вперед, назад. Повернулись вправо, влево,

• Тихо сели, вновь за дело.

VI. Самостоятельная работа 

Займёмся подготовкой к аттестации.

Самостоятельная работа. Самоконтроль – 4 варианта. Проверка вашей честности. Работа выполняется в тетрадях. В ходе выполнения работы учащиеся определяют для себя алгоритм решения дробных рациональных уравнений. В учебнике, на стр.78 «Алгоритм решения дробных рациональных уравнений». Пользуясь алгоритмом, реши уравнение

В а р и а н т 1.

В а р и а н т 2.

В а р и а н т 3.

В а р и а н т 4.

О т в е т ы:

I вариант: ,  (; ).

II вариант:  (; )

III вариант:  ( )

IV вариант: ,  (; ).

VII. Закрепление и повторение материала. 

№290(а). Ответ: 10.

VIII. Подведение итогов урока.

1. Что нового вы узнали на уроке?

2. Чему вы научились на уроке?

3. Алгоритм решения дробных рациональных уравнений:

Учитель оценивает работу учащихся и выставляет оценки.

Домашнее задание: п. 13 (выучить определение и алгоритм решения),

1 уровень № 288, №302(повторение)

2 уровень №289(а), №290(б), №302(повторение)

Работа по карточкам:

Образец:

3х³ – 18х = 0

3х (х² -6) = 0

3х = 0 х² — 6 = 0

х = 0 х² = 6

х = — и

Ответ: —, 0, .

Реши уравнения:

1) х³ – 16х = 0; 2) 9х³ – 81х = 0.

Работа по карточкам:

Образец:

3х³ – 18х = 0

3х (х² -6) = 0

3х = 0 х² — 6 = 0

х = 0 х² = 6

х = — и

Ответ: —, 0, .

Реши уравнения:

1) х³ – 16х = 0; 2) 9х³ – 81х = 0.

Работа по карточкам:

Образец:

3х³ – 18х = 0

3х (х² -6) = 0

3х = 0 х² — 6 = 0

х = 0 х² = 6

х = — и

Ответ: —, 0, .

Реши уравнения:

1) х³ – 16х = 0; 2) 9х³ – 81х = 0.

Работа по карточкам:

Образец:

3х³ – 18х = 0

3х (х² -6) = 0

3х = 0 х² — 6 = 0

х = 0 х² = 6

х = — и

Ответ: —, 0, .

Реши уравнения:

1) х³ – 16х = 0; 2) 9х³ – 81х = 0.

infourok.ru

Урок алгебры в 9 классе «Дробные рациональные уравнения»

Дробные рациональные уравнения (9 класс)

Учитель математики Климочкина Г.Н.

Цель: продолжить формирование умения решать дробно-рациональные уравнения, используя алгоритм, известный учащимся из курса 8 класса.

Ход урока

I. Организационный момент

Проверка готовности учащихся к уроку, проверка присутствующих, общий настрой на урок.

— Сегодня на уроке мне хотелось бы пригласить поглубже заглянуть в замечательный мир математики – в мир уравнений, в мир поиска, в мир исследований.

Девиз урока: Силу уму придают упражнения, а не покой. (Александр Поуп)

Запишите: число, классная работа, тему урока «Дробные рациональные уравнения».

II. Объяснение нового материала.

Объяснение материала проводится в несколько э т а п о в.

1. И з у ч е н и е п о н я т и я дробно-рационального уравнения. Усвоение данного понятия проверяется при решении упражнения на распознавание этого вида уравнений.

З а д а н и е.

1). Какие из следующих уравнений являются дробно-рациональными? Ответ объясните.

а) ; г) ;

б) ; д) ;

в) ; е) .

2). Верно ли, что выражение обращается в нуль:

а) при х = 2; б) при х = –5; в) при х = 1.

2. У с л о в и е р а в е н с т в а д р о б и н у л ю.

При каком значении переменной дробь равна нулю?

Дробь равна нулю, если числитель равен нулю, а знаменатель при этом нулю не равен.

х³ — 25х = 0,

х(х² — 25) = 0,

х = 0, х = ±5.

Если х = 0, то х² — 6х + 5 ≠ 0,

если х = -5, то х² — 6х + 5 ≠ 0,

если х = 5, то х² — 6х + 5 = 0.

Ответ: при х = 0, х = -5.

3. Вывод алгоритма решения дробно-рациональных уравнений. Алгоритм приведен на с. 78 учебника. (Желательно, чтобы учащиеся занесли его в тетрадь.)

3. Рассмотрение примеров решения дробно-рациональных уравнений по изученному алгоритму (пример 1 и пример 3 из учебника).

III. Формирование умений и навыков.

Упражнения:

1. Устно (работа со слайдами):

1)

2)

3)

4)

5)

2. Письменно:

1. № 288 (а), № 289 (а).

2. № 290 (а), № 292 (а).

3. № 291 (в).

4. № 296 (а).

IV. Итоги урока.

Вопросы учащимся:

– Какие уравнения называются дробно-рациональными?

– Являются ли следующие уравнения дробно-рациональными:

?

– Опишите алгоритм решения дробно-рациональных уравнений.

Домашнее задание: № 289 (б), № 290 (б), № 291 (б), № 296 (б).

infourok.ru

Урок 17. дробные рациональные уравнения — Алгебра — 9 класс

Конспект

Когда обе части выражения представляют из себя рациональные выражения, и хотя бы одно является дробным, то такие уравнения называют дробными рациональными.

На простом примере вспомним алгоритм решения дробных рациональных уравнений.

В первую очередь необходимо привести все дроби уравнения к общему знаменателю, в нашем случае общий знаменатель равен 6x.

Первую дробь домножаем на 2, а вторую на x.

Стоит обратить внимание, что переменная x не может принимать значение ноль, так как в противном случае знаменатель первой дроби будет равен нулю.

Далее записываем обе дроби под одну дробную черту и приводим подобные в числителе.

После этого необходимо вспомнить, что дробь равна нулю только в ситуации, когда числитель равен нулю, а знаменатель не равен.

x² + 4x – 5 = 0; 6x ≠ 0.

Решив получившееся квадратное уравнение, мы получаем корни 1 и –5, удовлетворяющие условию x ≠ 0.

Записываем ответ.

Рассмотрим более сложные примеры дробных рациональных уравнений.

Начнём с того, что перенесём все члены уравнения в левую часть.

Далее вынесем знак минус из знаменателя второй дроби.

Теперь необходимо домножить x на знаменатель (x – 2) и записать всю левую часть уравнения под одну дробную черту.

Стоит обратить внимание на то, что x ≠ 2, иначе знаменатель дроби обратиться в нуль.

Как мы уже вспоминали, знаменатель не должен быть равен нулю, а числитель, наоборот равен нулю, так как сама дробь равна нулю.

Из этого мы получаем целое уравнение: 2x² – 3x – 2 – x(x – 2) = 0. Раскрыв скобки и приведя подобные, уравнение принимает стандартный вид квадратного уравнения.

x² – x – 2 = 0

Решив данное уравнение, получаем два корня: x₁ = 2 и x₂ = –1.

Осталось проверить, удовлетворяют ли они ограничениям переменной x.

Корень x₁ = 2 не удовлетворяет данному условию, а значит, не является корнем уравнения.

Значит, уравнение имеет один корень x = –1, его и запишем в ответе.

resh.edu.ru