Асимптоты графика функций: их виды, примеры решений
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Если предварительно построить асимптоты кривой, то многих случаях построение графика функции облегчается.
Судьба асимптоты полна трагизма. Представьте себе, каково это: всю жизнь двигаться
по прямой к заветной цели, подойти к ней максимально близко, но так и не достигнуть её. Например, стремиться
соединить свой жизненный путь с путём желанного человека, в какой-то момент приблизиться к нему почти
вплотную, но даже не коснуться его. Или стремиться заработать миллиард, но до достижения этой цели
и записи в книгу рекордов Гиннеса для своего случая не достаёт сотых долей цента. И тому подобное. Так
и с асимптотой: она постоянно стремится достигнуть кривой графика функции, приближается к нему на минимальное
возможное расстояние, но так и не касается его.
Определение 1. Асимптотами называются такие прямые, к которым сколь угодно близко приближается график функции, когда переменная стремится к плюс бесконечности или к минус бесконечности.
Определение 2. Прямая называется асимптотой графика функции, если расстояние от переменной точки М графика функции до этой прямой стремится к нулю при неограниченном удалении точки М от начала координат по какой-либо ветви графика функции.
Различают три вида асимптот: вертикальные, горизонтальные и наклонные.
Первое, что нужно узнать о вертикальных асимптотах: они параллельны оси Oy.
Определение. Прямая x = a
является вертикальной асимптотой графика функции , если точка x = a
является точкой разрыва второго рода для этой функции.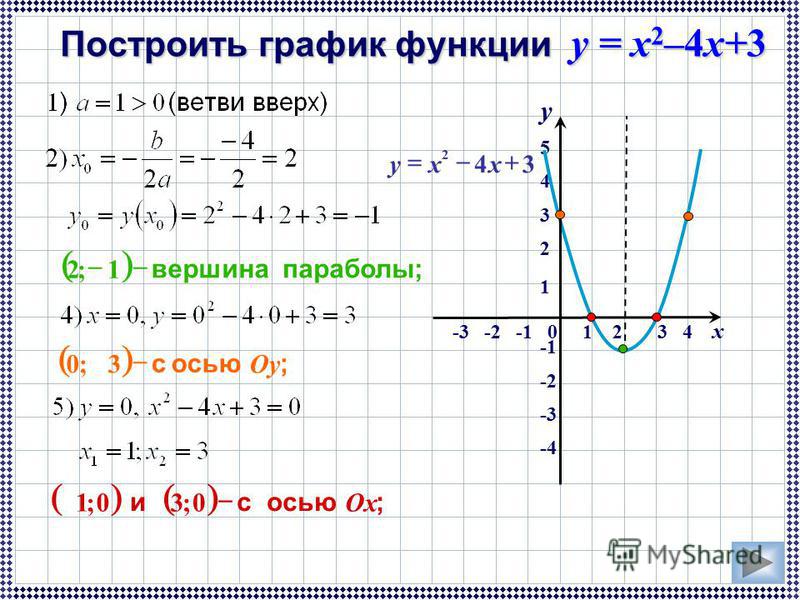
Из определения следует, что прямая x = a является вертикальной асимптотой графика функции f(x), если выполняется хотя бы одно из условий:
- (предел функции при значении аргумента, стремящимся к некоторому значению a слева, равен плюс или минус бесконечности)
- (предел функции при значении аргумента, стремящимся к некоторому значению a справа, равен плюс или минус бесконечности).
При этом функция f(x) может быть вообще не определена соответственно при x ≥ a и x ≤ a.
Замечание:
- символом
обозначается стремление
- символом
обозначается стремление x к a слева, причём x остаётся меньше a.

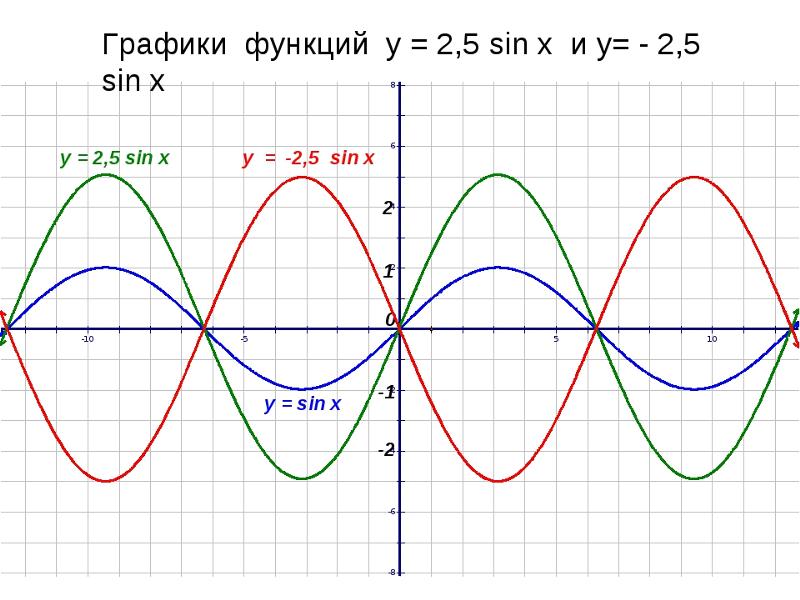
Пример 1. График функции y=lnx имеет вертикальную асимптоту x = 0 (т.е. совпадающую с осью Oy) на границе области определения, так как предел функции при стремлении икса к нулю справа равен минус бесконечности:
(рис. сверху).
Найти асимптоты графика функции самостоятельно, а затем посмотреть решения
Пример 2. Найти асимптоты графика функции .
Пример 3. Найти асимптоты графика функции
Первое, что нужно узнать о горизонтальных асимптотах: они параллельны оси Ox.
Если
(предел функции при стремлении аргумента к плюс или минус бесконечности равен некоторому значению b),
то y = b – горизонтальная асимптота кривой y = f(x)
(правая при иксе, стремящимся к плюс бесконечности, левая при иксе, стремящимся к минус бесконечности,
и двусторонняя, если пределы при стремлении икса к плюс или минус бесконечности равны).
Пример 5. График функции
при a > 1 имеет левую горизонтальную асимпототу y = 0 (т.е. совпадающую с осью Ox), так как предел функции при стремлении «икса» к минус бесконечности равен нулю:
Вертикальные и горизонтальные асимптоты, которые мы рассмотрели выше, параллельны
осям координат, поэтому для их построения нам требовалось лишь определённое число — точка на оси
абсцисс или ординат, через которую проходит асимптота. Для наклонной асимптоты необходимо больше —
угловой коэффициент k, который показывает угол наклона прямой, и свободный член b, который показывает,
насколько прямая находится выше или ниже начала координат. Не успевшие забыть аналитическую геометрию,
а из неё — уравнения прямой, заметят, что для наклонной асимптоты находят уравнение
прямой с угловым коэффициентом. Существование наклонной асимптоты определяется следующей теоремой,
на основании которой и находят названные только что коэффициенты.
Не успевшие забыть аналитическую геометрию,
а из неё — уравнения прямой, заметят, что для наклонной асимптоты находят уравнение
прямой с угловым коэффициентом. Существование наклонной асимптоты определяется следующей теоремой,
на основании которой и находят названные только что коэффициенты.
Теорема. Для того, чтобы кривая y = f(x) имела асимптоту y = kx + b, необходимо и достаточно, чтобы существовали конечные пределы k и b рассматриваемой функции при стремлении переменной x к плюс бесконечности и минус бесконечности:
(1)
и
(2)
Найденные таким образом числа k и b и являются коэффициентами наклонной асимптоты.
В первом случае (при стремлении икса к плюс бесконечности) получается правая
наклонная асимптота, во втором (при стремлении икса к минус бесконечности) – левая.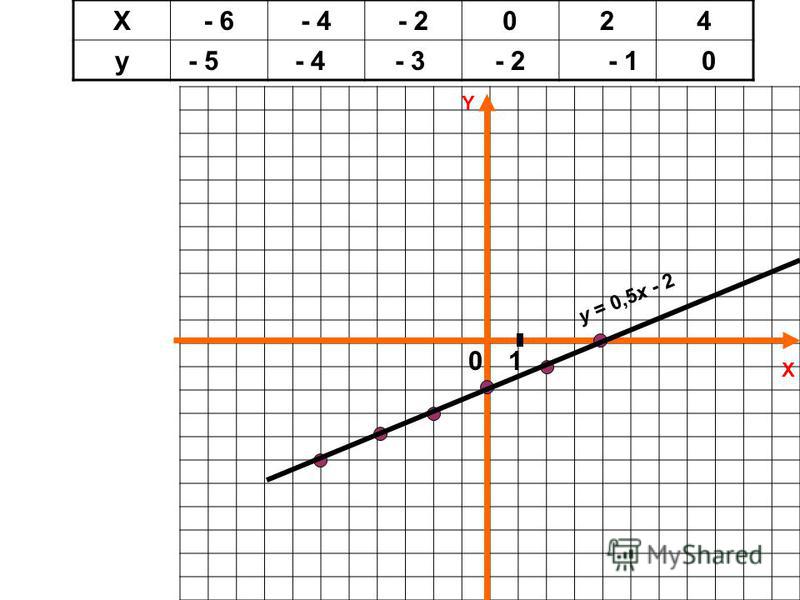 Правая наклонная асимптота изображена на рис. снизу.
Правая наклонная асимптота изображена на рис. снизу.
При нахождении уравнения наклонной асимптоты необходимо учитывать стремление икса и к плюс бесконечности, и к минус бесконечности. У некоторых функций, например, у дробно-рациональных, эти пределы совпадают, однако у многих функций эти пределы различны а также может существовать только один из них.
При совпадении пределов при иксе, стремящемся к плюс бесконечности и к минус бесконечности прямая y = kx + b является двусторонней асимптотой кривой.
Если хотя бы один из пределов, определяющих асимптоту y = kx + b, не существует, то график функции не имеет наклонной асимптоты (но может иметь вертикальную).
Нетрудно видеть, что горизонтальная асимптота y = b
является частным случаем наклонной y = kx + b
при k = 0.
Поэтому если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.
Пример 6. Найти асимптоты графика функции
Решение. Функция определена на всей числовой прямой, кроме x = 0, т.е.
Поэтому в точке разрыва x = 0 кривая может иметь вертикальную асимптоту. Действительно, предел функции при стремлении икса к нулю слева равен плюс бесконечности:
Следовательно, x = 0 – вертикальная асимптота графика данной функции.
Горизонтальной асимптоты график данной функции не имеет, так как предел функции при стремлении икса к плюс бесконечности равен плюс бесконечности:
Выясним наличие наклонной асимптоты:
Получили конечные пределы k = 2 и
b = 0. Прямая y = 2x является двусторонней
наклонной асимптотой графика данной функции (рис. внутри примера).
Прямая y = 2x является двусторонней
наклонной асимптотой графика данной функции (рис. внутри примера).
Пример 7. Найти асимптоты графика функции
Решение. Функция имеет одну точку разрыва x = −1. Вычислим односторонние пределы и определим вид разрыва:
,
.
Заключение: x = −1 — точка разрыва второго рода, поэтому прямая x = −1 является вертикальной асимптотой графика данной функции.
Ищем наклонные асимптоты. Так как данная функция — дробно-рациональная, пределы при и при будут совпадать. Таким образом, находим коэффициенты для подстановки в уравнение прямой — наклонной асимптоты:
Подставляя найденные коэффициенты в уравнение прямой с угловым коэффициентом, получаем уравнение наклонной асимптоты:
y = −3x + 5.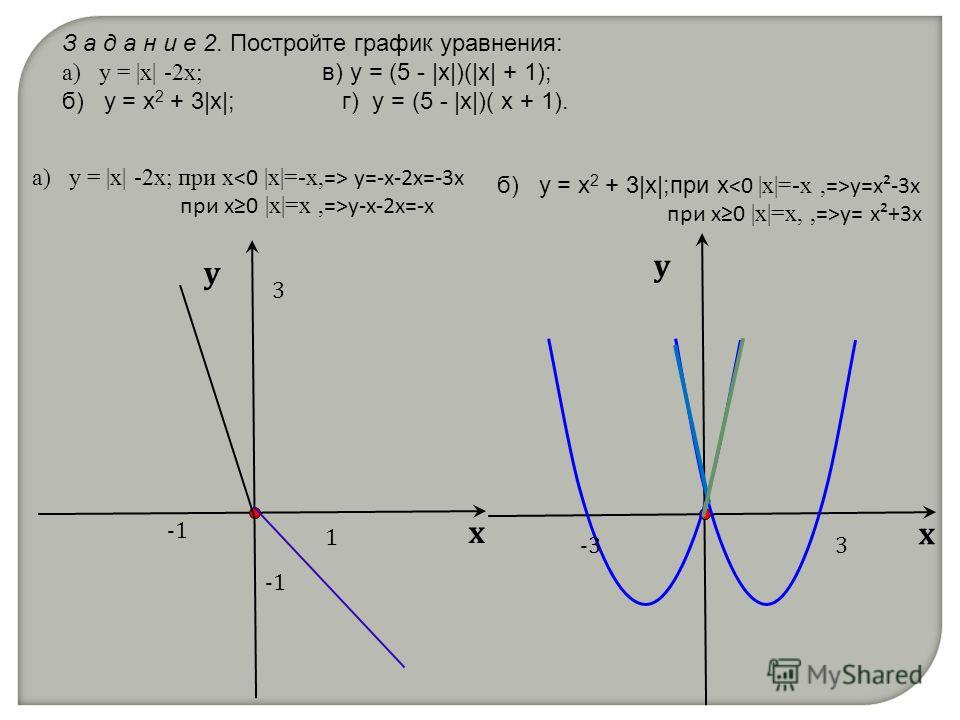
На рисунке график функции обозначен бордовым цветом, а асимптоты — чёрным.
Пример 8. Найти асимптоты графика функции
.
Решение. Так как данная функция непрерывна, её график не имеет вертикальных асимптот. Ищем наклонные асимптоты:
.
Таким образом, график данной функции имеет асимптоту y = 0 при и не имеет асиптоты при .
Пример 10. Найти асимптоты графика функции
Решение. Функция имеет область определения . Так как вертикальная асимптота графика этой функции может быть только на границе области определения, найдём односторонние пределы функции при :
,
.
Оба предела нашли, используя первый замечательный предел. Заключение: x = 0 — точка
устранимого разрыва, поэтому у графика функции нет вертикальных асимптот.
Ищем наклонные асимптоты:
Таким образом, при наклонной асимптотой графика данной функции является прямая y = x. Но при найденные пределы не изменяются. Поэтому при наклонной асимптотой графика данной функции также является y = x.
Пример 11. Найти асимптоты графика функции
.
Решение. Сначала найдём вертикальные асимптоты. Для этого найдём точки разрыва функции и их виды. Знаменатель не может быть равным нулю, поэтому должно соблюдаться условие . Функция имеет две точки разрыва: , . Чтобы установить вид разрыва, найдём односторонние пределы:
Так как все пределы равны бесконечности, обе точки разрыва — второго рода. Поэтому
график данной функции имеет две вертикальные асимптоты: x = 2 и
x = −2.
Ищем наклонные асимптоты. Так как данная функция является дробно-рациональной, пределы при и при совпадают. Поэтому, определяя коэффициенты прямой, ищем просто пределы:
Подставляем найденные коэффициенты в уравнение прямой с угловым коэффициентом, получаем уравнение наклонной асимптоты y = 2x. Таким образом, график данной функции имеет три асимптоты: x = 2, x = −2 и y = 2x.
Найти асимптоты графика функции самостоятельно, а затем посмотреть решения
Поделиться с друзьями
Весь блок «Производная»
стоимость на сегодня, график курса акций ZVEZ на БКС Экспресс
Baidu (BIDU) — разработчик крупнейшего интернет-поисковика в Китае. В списке ключевых приложений компании:— Поисковой бизнес Baidu Core
— Haokan для коротких видео
— Quanmin для создания флеш-видео
— Baidu Maps с голосовым помощником для путешествий
— iQIYI предлагает услуги онлайн-развлечений, включая оригинальный и лицензионный видеоконтент.
Среди новых перспективных направлений — электромобили и беспилотные роботакси. Компания основана в 2000 г. Капитализация — $79 млрд.
Факторы в пользу покупки
• За 2020 г. компания увеличила продажи на 6,3% г/г, с $15,4 до $16,4 млрд. В 2021 г. ожидается рост выручки на 17%, в 2022 г. — на 13%.
• Прибыль на акцию по итогам 2020 г. выросла выше ожидаемых $9,4 и составила $9,9 (+33%). Согласно консенсус-прогнозу, ожидается рост EPS на 4% к концу 2021 г., в 2022 г. — на 19%.
• Оценка и маржинальность. Чистая рентабельность бизнеса Net Margin=21 находится выше среднего по отрасли Internet Content & Information, близко к показателю Google. В то же время компания оценена дешевле по показателю цены к выручке (P/S). Форвардный P/E=17,4 меньше медианного по отрасли.
• Долги. Показатель соотношения debt/equity =0,4 на уровне отрасли. У большинства технологических компаний с высокой маржинальностью низкая долговая нагрузка.
• Свободный денежный поток вырос в 2020 г. на 117% и составил $2,88 млрд. За последние 8 лет он не опускался ниже $1,3 млрд. За счет этого есть возможности для дальнейшего развития новых направлений, в том числе искусственного интеллекта и роботакси, без увеличения долговой нагрузки.
на 117% и составил $2,88 млрд. За последние 8 лет он не опускался ниже $1,3 млрд. За счет этого есть возможности для дальнейшего развития новых направлений, в том числе искусственного интеллекта и роботакси, без увеличения долговой нагрузки.
Перспективы Baidu на рынке Китая
— Baidu позиционирует себя как ведущая компания в области искусственного интеллекта в КНР. В исследования и разработки в сфере ИИ компания инвестирует 21% полученной выручки. Для сравнения, конкуренты — Alibaba и Tencent — тратят 8,5% и 8,1% соответственно. Ожидается, что рынок программного обеспечения в Китае вырастет к 2025 г. в 7 раз.
— Дополнительно компания развивает направление облачных технологий, в 2020 г. его выручка выросла на 44%. К 2025 г. в Китае ожидается рост бизнеса облачных услуг на 37%.
— Baidu третий год подряд занимает первое место в отчете об испытаниях беспилотных автомобилей в Пекине. Baidu производит беспилотные Robotaxi Apollo в сотрудничестве с Пекином, Чаншей и Цанчжоу.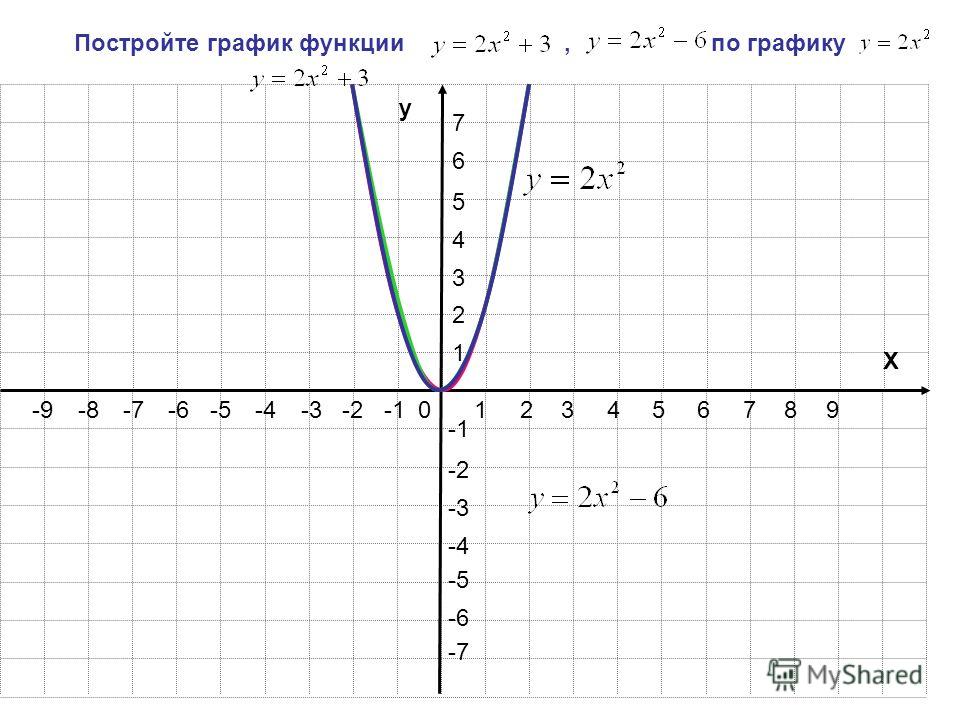 Apollo является лидером на китайском рынке с 4,3 млн накопленных тестовых миль. Baidu потратила 11,8 млрд юаней на разработку Apollo в 2020 г. Для сравнения, конкуренты в отрасли электрокаров NIO и Li Auto, потратили всего 1,7 млрд и 0,7 млрд соответственно. Baidu поставила цель стать первой мультимодальной автономной системой вождения. Рынок электромобилей Китая утроится за период 2021–2025 гг.
Apollo является лидером на китайском рынке с 4,3 млн накопленных тестовых миль. Baidu потратила 11,8 млрд юаней на разработку Apollo в 2020 г. Для сравнения, конкуренты в отрасли электрокаров NIO и Li Auto, потратили всего 1,7 млрд и 0,7 млрд соответственно. Baidu поставила цель стать первой мультимодальной автономной системой вождения. Рынок электромобилей Китая утроится за период 2021–2025 гг.
Техническая картина
С марта 2020 г. акции выросли на 332%, на пике в феврале стоили $355. Затем бумаги снизилась на 50% и дошли до месячного уровня поддержки $174, после этого на высоких объемах участники рынка выкупили акции. По сетке Фибоначчи коррекция составила 0,618 и остановилась над 200-дневной скользящей средней. После падения на дневном графике сформировался первый импульс роста, пробивший уровень $208,5, затем цена откатилась к нему и осталась над ним. Сформированное движение указывает на продолжение роста к целям: $258–266 — первый значимый рубеж сопротивления.
Нужно учитывать, что у Baidu высокая волатильность. Можно выделить под бумаги малую часть в портфеле акций роста, согласно своей инвестиционной стратегии.
Можно выделить под бумаги малую часть в портфеле акций роста, согласно своей инвестиционной стратегии.
Торговый план
Акции Baidu торгуются на СПБ бирже, могут быть интересны в области $208—220. Среднесрочный ориентир $258–266 (+18%). Горизонт: III квартал 2021 г.
О смене сентимента в худшую сторону укажет пробой дневного уровня $208 сверху вниз. Обращаем внимание, что амплитуда движения цены крайне высокая.
Риски
— Общерыночная коррекция вследствие ускорения роста ставок.
— В США принят закон об отчетности компаний. Китайские игроки, не соблюдающие стандарты аудита США в течение трех лет подряд, пройдут делистинг на американских фондовых биржах. Информации, подтверждающей несоблюдение требований аудита китайскими компаниями, пока не было.
Читайте также: Сделать сложный мир проще. История Baidu
БКС Мир инвестиций
Квест комната в Чернигове ⚡ Цены на квест комнаты для детей и взрослых ⭐️ XRoom
Ищете нестандартное развлечение? Поход в кино или посиделки в кафе порядком надоели? Душа требует движения, а эмоции – выхода? Тогда квест в Чернигове – то, что вам нужно. Квест в реальности заставит мозг работать активнее, сердце – учащенно биться, а творческий потенциал раскроется в полной мере: вам откроются возможности, о которых вы даже не подозревали. А потребуется для этого всего лишь 60 минут.
Квест в реальности заставит мозг работать активнее, сердце – учащенно биться, а творческий потенциал раскроется в полной мере: вам откроются возможности, о которых вы даже не подозревали. А потребуется для этого всего лишь 60 минут.
Квест комната XRoom в Чернигове – место настоящего драйва и неожиданных сценариев. Желаете стать главным героем экшена, организовать веселый досуг на большую компанию или день рождения для подростков? Тогда спешите забронировать свое развлечение уже сейчас – и станьте соучастником настоящего приключения.
Квест комнаты – что это?
Игра, похожая на реальность, в специальных помещениях с заданиями, тайниками, головоломками и секретами – вот что такое квест комната. Ваша задача – решить последовательно все задания, собрать ключи и выйти победителем за 60 минут. Непросто, зато как интересно! Квест в реальности превратит вас из мирных обывателей в заключенных, грабителей, героев мистических экшенов и мудрых ученых.
С первых мгновений вас ожидает неизведанное и загадочное:
- Неизвестное помещение, наполненное загадками и не всегда приятными неожиданностями.
 Вас там закроют, вы в курсе?
Вас там закроют, вы в курсе? - В закрытом помещении обостряются слух, зрение и желание найти выход, а инстинкт самосохранения притупляется. Вы готовы обнажить свои эмоции?
- Попытка решить сложные задачи активизирует мозг и интуицию. Вы готовы узнать, на что способен ваш интеллект?
- Работа в команде раскроет новые грани ваших друзей. Командная работа и взаимная поддержка – вот что пригодится вам на самом деле.
Взрослым, как и детям, нужны эмоции, острые ощущения, интрига и игра. Квест рум – хорошее место, чтобы отвлечься от бытовых проблем и рутинных мыслей. Quest room – место, где легенда становится реальностью, а вы – настоящим героем.
Забронировать квест в реальности в Чернигове можно прямо сейчас в XRoom – наша команда профессионалов-организаторов работает каждый день, чтобы ваша квест команда наслаждалась отдыхом. Просто прочтите отзывы наших клиентов – и скорее становитесь одними из них.
Зачем вам квест комната
Если вам нужна перезарядка, перезагрузка и выплеск адреналина, значит, вам нужна квест комната в Чернигове. Правильная организация отдыха подарит эмоции и взрослым, и детям. Для подростков, для двоих, на большую компанию – квесты в реальности каждому дают именно ту разрядку, которая нужна:
Правильная организация отдыха подарит эмоции и взрослым, и детям. Для подростков, для двоих, на большую компанию – квесты в реальности каждому дают именно ту разрядку, которая нужна:
- Квест для двоих кажется романтикой, но вам придется здорово потрудиться, чтобы выбраться из загадочной комнаты? Готовы превратить вторую половинку в надежного боевого товарища?
- Комната квест на большую компанию – это возможность одновременно пройти разные задания, а потом поменяться местами. И дружно делиться отзывами и впечатлениями после.
- Для подростков квест рум – возможность получить новый опыт и стать взрослее.
Каждый, кто приходит в Questroom в Чернигове, получает заряд эмоций, открывает в себе скрытые таланты и учится мыслить нестандартно.
Квест комнаты – какие есть в XRoom?
Квеструм в XRoom – это самые интересные направления, востребованные сюжеты и неожиданные декорации из всех что есть в Украине. Наши квест комнаты – это:
- Захватывающие приключенческие сюжеты – идеальный досуг для взрослых и детей.
 Такой квест нравится всем без исключения и всегда собирает сотни отзывов.
Такой квест нравится всем без исключения и всегда собирает сотни отзывов. - Логические задачи и поиски. Требуют повышенной концентрации и интеллектуально работы. Динамики в таком квесте меньше, но зато как развивает сообразительность!
- Детективы. Необычный для Украины жанр квест комнаты, но набирающий популярность. Желаете почувствовать себя известным сыщиком и распутать преступление века? Квест-комната в Чернигове ждет вас!
Забронировать квест-комнату в Чернигове: кому понравится
Квесты в реальности XRoom – подходят тем, кого утомили будни и однообразие, кому нужно отдохнуть, отвлечься и вдохнуть полной грудью. Quest room – место, где приветливый персонал соседствует с отточенными сюжетами, а цена, безупречные декорации квеста и инвентарь не пугают, а заставляют вновь и вновь возвращаться в Икс рум.
К нам в квест комнаты в Чернигове приходят:
Для веселого семейного отдыха Квест-комната – место, где и детям, и взрослым одинаково увлекательно, где объединяются интересы поколений и каждый находит поддержку среди самых близких людей. Нужно отпраздновать вместе день рождения или хотите необычно провести выходной? Мы предложим квест комнату для взрослых и детей – и даже самые маленькие игроки смогут проявить себя наравне с родителями. Приходите к Икс Рум – и ваш досуг обязательно останется в памяти каждого игрока.
Нужно отпраздновать вместе день рождения или хотите необычно провести выходной? Мы предложим квест комнату для взрослых и детей – и даже самые маленькие игроки смогут проявить себя наравне с родителями. Приходите к Икс Рум – и ваш досуг обязательно останется в памяти каждого игрока.
У вас намечается корпоратив и другие коллективные праздники: Квест комнаты в Чернигове – место веселья, командообразования и коллективного сплочения. Непринужденность соседствует с соревнованием – и это создает атмосферу интереса и азарта для всех сотрудников.
Хотите быстро сплотить коллектив нового предприятия? Закажите квеструм! В обстановке, где нужно сплотиться, незнакомые люди быстрее раскроются и станут ближе друг другу. А это – то что нужно для продуктивной работы.
Хотите сделать сюрприз для друзей: Наши цены на квесты позволят организовать неожиданный подарок для каждого. Это недорого – и очень весело.
Желаете провести время вдвоем, но в нестандартной обстановке? Желаете проверить своего партнера и увидеть его в неожиданном ракурсе? Хотите поработать для общих целей и научиться действовать сообща? В квест рум Икс Рум для этого созданы все условиях.
Квест комната для двоих – это еще и место романтических событий. Планируете сделать романтическое предложение неожиданно и интересно? Наша квест рум – место, где воплотятся самые дерзкие задумки и реализуются любые планы.
Хотите отдохнут душой и телом активно и с интересом? Комната квест в Чернигове ждет вас.
Квесты в реальности: правила поведения:
Чтобы отдых был комфортным, интересным и веселым, а главное – безопасным, помните о простых правилах для визита в квест комнаты:
- Мы не допускаем участников в состоянии алкогольного или наркотического опьянения. В таком случае, администратор может отказать в игре в одностороннем порядке.
- Внутри комнаты фото и видео съемка запрещена. Не нарушайте это простой правило.
- Чтобы весело провести время, специальные знания и навыки не нужны. Достаточно смекалки и находчивости.
- Для прохождения задания квеста вам не нужно прилагать больших физических усилий.
- В случае порчи инвентаря – придется возместить его стоимость.
 Развлекайтесь, но соблюдайте осторожность.
Развлекайтесь, но соблюдайте осторожность. - Хотите заказать квест-комнату через сайт? Проверьте правильность написания номера телефона. Тогда наш менеджер без проблем свяжется с вами для уточнения деталей. Если мы не подтвердили игру в течение суток – мы вправе ее отменить без предупреждения.
- Приходите на игру заранее, но не слишком. 10-15 минут будет достаточно, чтобы узнать правила игры и поведения выяснить задачи и настроиться на квест. Не опаздывайте – за вами уже записана команда, которая прибудет на локацию к своему времени, и мы не можем ее задерживать. При опоздании более чем на 15 минут ваша игра аннулируется.
- Не нужно приносить с собой закуски и напитки. Если вы забронировали несколько игр, то в перерывах вы можете посидеть в холле за чашкой кофе и чая местного приготовления.
Возрастные ограничения: квест комната х рум в Чернигове с заботой о каждом
Мы знаем, что взрослым и детям одинаково нужны развлечения и досуг.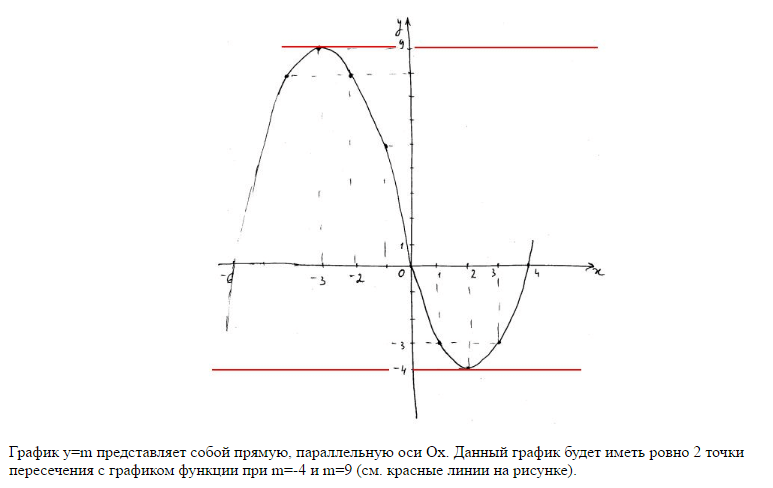 Чтобы ваш отдых был максимально безопасным и комфортным, обязательно учтите правила участия в квестах детей разных возрастов:
Чтобы ваш отдых был максимально безопасным и комфортным, обязательно учтите правила участия в квестах детей разных возрастов:
- Дети с 10 лет могут быть равноправными самостоятельными участниками в команде из 2-4 человек.
- Участники младше 10 лет в команде 2-6 человек могут играть только в присутствии взрослого старше 18 лет или нашего администратора.
Мы заботимся о безопасности каждого игрока, и просим вас соблюдать эти требования, чтобы избежать непредвиденных ситуаций.
Где отдохнуть в Чернигове? Квест комната Икс рум ждет вас
Хотите отдохнуть креативно, интересно и нестандартно? Думаете, вы уже везде были и видели все?
Тогда загляните в квест комнату XRoom в Чернигове. Здесь вы перенесетесь из привычных будней в эпицентр событий, а из мирного гражданина превратитесь в героя боевика или приключенческой саги. Здесь вас ждут эмоции, волнение, переживания – и обязательное желание повторить это снова.
Готовы? Тогда ознакомьтесь с нашими скидками:
- 10% в честь Дня Рождения.
 Воспользоваться можно в день рождения и в 6 дня после него, при наличии паспорта, свидетельства о рождении или водительского удостоверения.
Воспользоваться можно в день рождения и в 6 дня после него, при наличии паспорта, свидетельства о рождении или водительского удостоверения. - 15% при следующем посещении не позже 7 дней с предыдущей игры. Хотите получить бонус? Наш администратор раскроет секрет и пригласит вас на новое событие.
Хотите получить порцию адреналина и проверить свою изобретательность и сообразительность? Квест-комната в Чернигове ждет вас – звоните или пишите на сайте!
Графік лінійних рівнянь: 5 кроків 2021
Перш ніж почати, потрібно визначити деякі терміни:
- Рівняння рядка: рівняння рядка зазвичай записується як y = mx + b (це називається форма схилу-перехоплення де m — нахил і b — перехоплення y). Інші форми включають стандартну форму (ax + by = c, де a — натуральне число, а b і c — цілі числа) і форма точки-схилу (y-y1 = m (x-x1), де m — нахил і (x1, y1) — точка на лінії). Якщо ви хочете отримати більше інформації про це, ви можете переглянути моє відео тут.

- Схил: нахил показує, наскільки крута лінія. Вона визначається як зміна у над зміною в x, або підвищення над пробігом. Чим крутіша лінія, тим більше значення нахилу. Позитивний нахил піднімається зліва направо, а негативний нахил опускається зліва направо. Щоб дізнатися більше про схил, перегляньте моє відео тут.
- Перехоплення: Х-перехоплення — це місце, де лінія перетинає вісь x, а перехресний y — місце, де лінія перетинає вісь y. Щоб дізнатися більше про перехоплення, перегляньте моє відео тут.
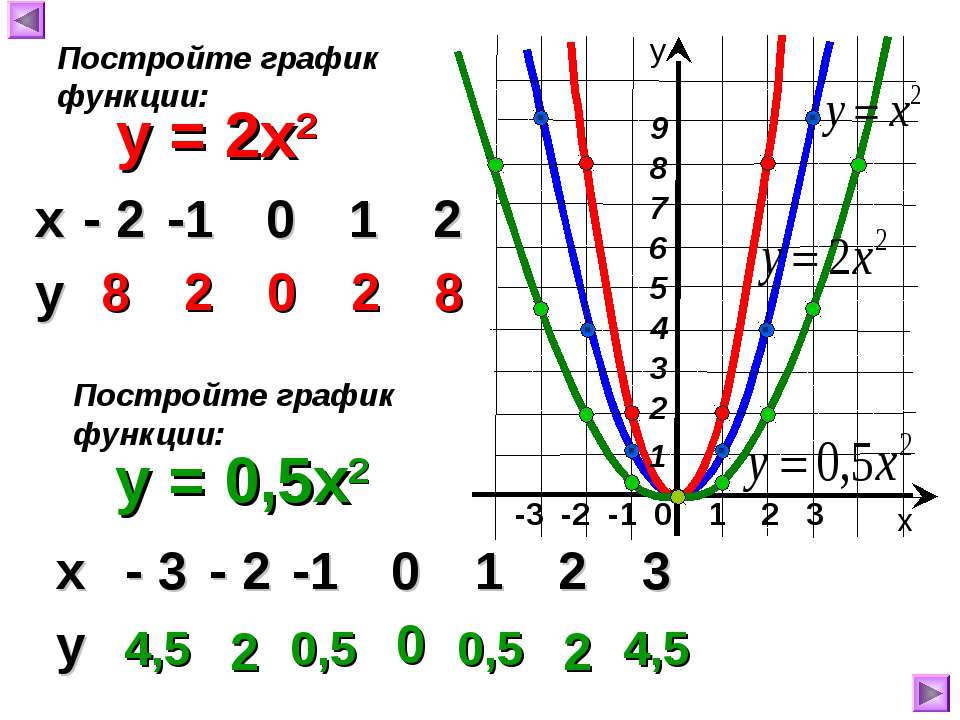
Крок 2: Метод таблиці
Для методу таблиці необхідно створити таблицю x / y, знайти точки на графіку, побудувати точки і підключити точки. Цей метод працює для будь-якого типу рівняння (не тільки рядків), але це найбільш трудомісткий процес.
- Намалюйте таблицю x / y.
- Далі ми повинні знайти кілька точок на лінії. Для цього спочатку виберіть кілька цифр і напишіть їх у стовпці x.
 Як правило, ви не хочете вибирати числа абсолютно випадковим чином — ви хочете вибрати кілька цільових точок — для параболи, наприклад, ви хочете вибрати цифри біля вершини параболи. Але оскільки це лінія, будь-яка точка зробить. Але зверніть увагу, що вибір невеликих номерів полегшить розрахунки. Крім того, ви хочете вибрати цифри в межах кордону площині, яку ви вказали. Для цієї задачі я вибрав -1, 0, 1, 2 і 3.
Як правило, ви не хочете вибирати числа абсолютно випадковим чином — ви хочете вибрати кілька цільових точок — для параболи, наприклад, ви хочете вибрати цифри біля вершини параболи. Але оскільки це лінія, будь-яка точка зробить. Але зверніть увагу, що вибір невеликих номерів полегшить розрахунки. Крім того, ви хочете вибрати цифри в межах кордону площині, яку ви вказали. Для цієї задачі я вибрав -1, 0, 1, 2 і 3. - Підключіть кожне значення x до рівняння і запишіть значення y у стовпці y. Моє рівняння було y = x-2, а значення y, які я отримав, були -3, -2, -1, 0, і 1. Наприклад, для x = -1 ми підключаємо -1 до рівняння. y = -1-2 = -3. Тому ми пишемо -3 поряд з -1.
- Складіть точки на графіку. Координати точок (x значення, y значення). Таким чином, точки, нанесені на графік, були (-1, -3), (0, -2), (1, -1), (2, 0) і (3, 1).
- Підключіть точки на графіку, щоб створити лінію.
Крок 3: Метод перехоплення
Для методу перехоплення потрібно лише знайти 2 точки — перехоплення x і y-перехоплення. Цей метод найкраще працює, коли перехоплює цілі числа. Незважаючи на те, що цей метод не може дати дуже точну лінію (коли перехоплення є дробами, ви повинні оцінити точне розташування точок), це дуже швидко і ефективно.
Цей метод найкраще працює, коли перехоплює цілі числа. Незважаючи на те, що цей метод не може дати дуже точну лінію (коли перехоплення є дробами, ви повинні оцінити точне розташування точок), це дуже швидко і ефективно.
- Знайдіть перехiд x. Для того, щоб знайти х-перехоплення, вставте y = 0 в рівняння і обчислити, щоб знайти x. Ви повинні підключити y = 0, тому що x-перехоплення, де лінія перетинає вісь x, а значення y завжди дорівнює нулю на осі x. Тоді координати x-перехоплення будуть (x-значення, 0).
- Для проблеми вище, ми підключаємо y = 0 і отримуємо 0 = x-2. Переставляємо, щоб отримати x = 2. Отже, х-перехоплення (2,0).
- Знайдіть y перехоплення. На цей раз підключіть x = 0 до рівняння і обчислити, щоб знайти y. Ми повинні підключити x = 0, оскільки x = 0 в будь-якій точці осі y. Координат перехоплення y (0, y значення).
- Підключіть x = 0 до задачі практики і отримаємо y = 0 — 2 = -2. У-перехоплення дорівнює (0, -2).

- Підключіть x = 0 до задачі практики і отримаємо y = 0 — 2 = -2. У-перехоплення дорівнює (0, -2).
- Ділянка двох точок.
- Підключіть точки.
Крок 4: Метод формули нахилу — перехоплення
Для методу перекриття нахилу необхідно спочатку змінити рівняння на вигляд y = mx + b. Потім можна побудувати b, y-перехоплення і знайти інші точки, використовуючи m, нахил. На мою думку, цей метод є найбільш ефективним, особливо якщо рівняння вже написано у формі схилу-перехоплення.
- Перегрупувати рівняння у форму перехрестя, y = mx + b. У вищезазначеній задачі, y = x-2 вже був у формі перекриття нахилу, так що нам не потрібно нічого робити для цього кроку.
- Знайдіть b, y-перехоплення і побудуйте точку на графіку. У цьому випадку y-перехоплення дорівнює -2, тому необхідно побудувати точку (0, -2).
- Знайти m, або схил. Оскільки нахил — це зміна y над зміною x (або підйом над пробігом), можна побудувати наступну точку, використовуючи нахил. У прикладі завдання нахил дорівнює 1, що дорівнює 1/1.
 Отже, зміна у над зміною x дорівнює 1 над 1. Це означає, що з перехрестя y (0, -2) необхідно перемістити одну одиницю вгору і одну одиницю вправо, щоб знайти іншу точку на графіку. Це підводить нас до (1, -1). Ми продовжуємо повторювати, пересуваючи одну одиницю вгору і одну одиницю вправо. Як тільки ми маємо достатньо точок, ми можемо з’єднати точки і створити лінію.
Отже, зміна у над зміною x дорівнює 1 над 1. Це означає, що з перехрестя y (0, -2) необхідно перемістити одну одиницю вгору і одну одиницю вправо, щоб знайти іншу точку на графіку. Це підводить нас до (1, -1). Ми продовжуємо повторювати, пересуваючи одну одиницю вгору і одну одиницю вправо. Як тільки ми маємо достатньо точок, ми можемо з’єднати точки і створити лінію. - Примітка: Переміщення 1 одиниці вгору, 1 одиниця вправо не є єдиним варіантом. У практичній задачі, нахил дорівнює 1, що також дорівнює -1 / -1, 2/2, 3/3 і т.д. Таким чином, ми можемо використовувати будь-яку з цих дробів для графіка лінії. Наприклад, якщо ми виберемо -1 / -1, ми можемо перемістити одну одиницю вниз і одну одиницю вліво від y-перехоплення. У будь-якому випадку, ми все одно отримаємо таку саму лінію.
Крок 5: більше практики!
Спробуйте виконати такі графіки:
- y = (1/5) x — 4
- x + y = -3
- 6x — 3y = 1
Якщо ви хочете перевірити свої відповіді, графік рівнянь на калькуляторі і порівняти результат з вашої відповіді, або дивитися моє відео з рішеннями тут. Проблеми починаються о 5:24.
Проблеми починаються о 5:24.
Дякуємо за читання, і якщо у вас є якісь питання, не соромтеся коментувати!
Как построить график y = (x-1) / (x + 5), используя асимптоты, точки пересечения, конечное поведение?
# y = (x-1) / (x + 5) #
Вертикальная асимптота (VA) определяется установкой знаменателя равным нулю.
# х + 5 = 0 #
# x = -5 # — это VA
Горизонтальная асимптота (HA) находится путем сравнения степени числителя со степенью знаменателя.
Если степень знаменателя больше степени числителя, HA будет # y = 0 #.
Если степень знаменателя равна степени числителя, HA — это старший коэффициент числителя, деленный на старший коэффициент знаменателя.цвет (красный) 1 +5) #
HA: # y = цвет (синий) 1 / цвет (синий) 1 = 1 #
Если степень знаменателя на единицу меньше степени числителя, имеется наклонная асимптота (OA). У этой функции нет открытого доступа.
Чтобы найти точку пересечения # y #, установите # x = 0 #.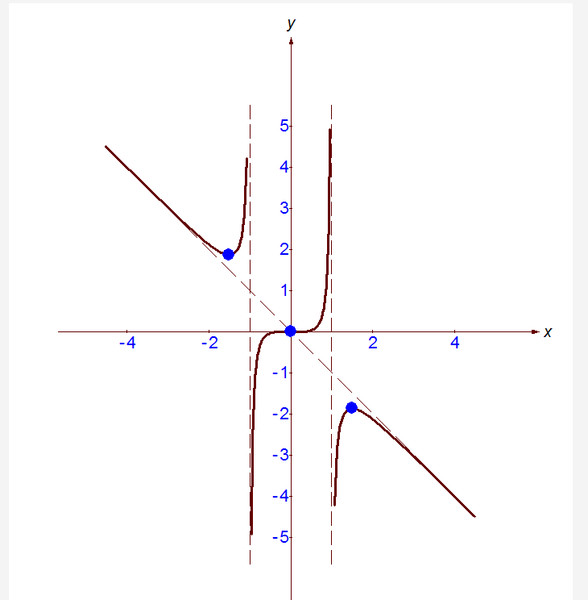
# у = (0-1) / (0 + 5) = -1 / 5 #
Перехват # y # — # (0, -1/5) #
Чтобы найти точку пересечения # x #, найдите значение, которое делает # y = 0 #. Это значение определяется установкой числителя равным нулю.
# х-1 = 0 #
# х = 1 #
Перехват # x # — # (1,0) #
Суммируем:
VA: # x = -5 #
HA: # y = 1 #
X-точка пересечения: # (1,0) #
Y-точка пересечения: # (0, -1/5) #
Чтобы найти конечное поведение:
Первый график перехватов. Обратите внимание, что точка пересечения # y # является «более отрицательной» и находится слева от точки пересечения # x #. Это означает, что по мере приближения к VA справа # y # приближается к отрицательной бесконечности.
Поскольку VA имеет «нечетную степень» # цвет (красный) 1 #, т.е.цвет (красный) 1 #, конечное поведение вокруг VA «нечетное». «Нечетное» поведение конца указывает, что поведение конца «противоположно» вокруг VA. Итак, когда вы приближаетесь к VA слева, # y # приближается к положительной бесконечности.
Проблема 5
Проблема 55. Ничья график y = f ( x ) = x 2 + 2 x — 8.
- a) Что такое перехват y ?
- б) Какие корни?
- в) Какие координаты вершины?
- г) Запишите уравнение в стандарте или вершине форма.
- e) Решите для x
x 2 + 2 x -8 > 0
Прежде чем рисовать график, нужно ответить на вопросы а), б), и в).
а) Что такое перехват и ?
Пересечение y — это точка на графике, координата которой x равна 0. Итак, пусть x = 0 в уравнении, и мы получим
. y = (0) 2 + 2 (0) — 8 = 0 + 0-8 = -8.Это показывает, что пересечение y всегда является постоянным членом в полиноме.
верх
б) Какие корни?
Корни — это еще одно название перехватов x . Они
точек на графике, координаты которых y равны 0. Итак, пусть y = 0 в
уравнение и получаем
Они
точек на графике, координаты которых y равны 0. Итак, пусть y = 0 в
уравнение и получаем
Это дает нам квадратное уравнение в x .& mbsp; Нам повезло чтобы на одной стороне уже был 0, так что мы готовы к факторизации.
0 = ( x — 2) ( x + 4)Установите коэффициенты = 0.
x — 2 = 0 или x + 4 = 0Решить для x
x = 2 или x = -4верх
в) Какие координаты вершины?
Если мы воспользуемся формулой для координаты x вершины, то
получаем
или
х = -1Теперь, когда у нас есть координата вершины x- , мы запускаем это число через функцию, чтобы найти координату y-
y = f (-1) = (-1) 2 + 2 (-1) — 8 = 1-2-8 = -9Итак, вершина находится в (-1, -9)
верх
Перед построением графика рекомендуется получить всю эту информацию. указывает, чтобы нарисовать график.Когда мы наносим точки, поскольку теперь мы знаем, что
координата x вершины равна -1, мы хотим, чтобы -1 находился в
середина x , которую мы рисуем. Нам также понадобятся корни, x = -4
и 2, чтобы быть в интервале, содержащем x , которые мы строим, и в
хотя бы одна точка по другую сторону корней от вершины.
указывает, чтобы нарисовать график.Когда мы наносим точки, поскольку теперь мы знаем, что
координата x вершины равна -1, мы хотим, чтобы -1 находился в
середина x , которую мы рисуем. Нам также понадобятся корни, x = -4
и 2, чтобы быть в интервале, содержащем x , которые мы строим, и в
хотя бы одна точка по другую сторону корней от вершины.
Когда мы строим эти точки, получаем
верх
г) Запишите уравнение в виде вершины.
Уравнение равно
y = x 2 + 2 x — 8Половина линейного коэффициента равна 1, а квадрат 1 равен 1, поэтому складываем и вычитаем 1
y = x 2 + 2 x + 1 — 1 — 8Это упрощается до
y = ( x + 1) 2 — 9, и мы видим координаты вершины в уравнении.
верх
e) Решите для x
x 2 + 2 x — 8 ≥ 0 В процессе построения графика мы обнаружили
что корни были в -4 и 2. Когда мы делим вещественное число на прямую
в промежутки между корнями, и проверьте x в каждом
интервал.
Когда мы делим вещественное число на прямую
в промежутки между корнями, и проверьте x в каждом
интервал.
Поскольку равенство разрешено, конечные точки интервалов, корни, являющиеся x , которые дадут ответы, равные 0 при подстановке в формулу будут решениями.Итак, рисуем квадратные скобки вокруг конечных точек.
Набор решений — это набор x , удовлетворяющий
x ≤ -4 или x ≥ 2
В интервальной записи получается
.(-∞, -4] ∪ [2, ∞)
верх
Вернуться к тесту
Определение функций с помощью графиков | Колледж алгебры
Результаты обучения
- Проверить работу с помощью теста вертикальной линии
- Проверьте однозначное соответствие с помощью теста горизонтальной линии
- Определить графики функций инструментария
Как мы видели в примерах выше, мы можем представить функцию с помощью графика. Графики отображают множество пар ввода-вывода на небольшом пространстве. Предоставляемая ими визуальная информация часто упрощает понимание взаимоотношений. Обычно мы строим графики с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси.
Графики отображают множество пар ввода-вывода на небольшом пространстве. Предоставляемая ими визуальная информация часто упрощает понимание взаимоотношений. Обычно мы строим графики с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси.
Наиболее распространенные графики называют входное значение [latex] x [/ latex] и выходное значение [latex] y [/ latex], и мы говорим, что [latex] y [/ latex] является функцией [latex] x [ / latex] или [latex] y = f \ left (x \ right) [/ latex], если функция называется [latex] f [/ latex].График функции — это набор всех точек [латекс] \ left (x, y \ right) [/ latex] в плоскости, которая удовлетворяет уравнению [латекс] y = f \ left (x \ right) [/ latex ]. Если функция определена только для нескольких входных значений, то график функции представляет собой только несколько точек, где координата x каждой точки является входным значением, а координата y каждой точки является соответствующее выходное значение. Например, черные точки на графике на графике ниже говорят нам, что [латекс] f \ left (0 \ right) = 2 [/ latex] и [latex] f \ left (6 \ right) = 1 [/ latex ].Однако набор всех точек [latex] \ left (x, y \ right) [/ latex], удовлетворяющих [latex] y = f \ left (x \ right) [/ latex], является кривой. Показанная кривая включает [латекс] \ left (0,2 \ right) [/ latex] и [latex] \ left (6,1 \ right) [/ latex], потому что кривая проходит через эти точки.
Например, черные точки на графике на графике ниже говорят нам, что [латекс] f \ left (0 \ right) = 2 [/ latex] и [latex] f \ left (6 \ right) = 1 [/ latex ].Однако набор всех точек [latex] \ left (x, y \ right) [/ latex], удовлетворяющих [latex] y = f \ left (x \ right) [/ latex], является кривой. Показанная кривая включает [латекс] \ left (0,2 \ right) [/ latex] и [latex] \ left (6,1 \ right) [/ latex], потому что кривая проходит через эти точки.
Тест вертикальной линии может использоваться для определения того, представляет ли график функцию. Вертикальная линия включает все точки с определенным значением [latex] x [/ latex]. Значение [latex] y [/ latex] точки, где вертикальная линия пересекает график, представляет собой выход для этого входного значения [latex] x [/ latex].Если мы можем нарисовать любую вертикальную линию , которая пересекает график более одного раза, тогда график , а не определяет функцию, потому что это значение [latex] x [/ latex] имеет более одного вывода. Функция имеет только одно выходное значение для каждого входного значения.
Функция имеет только одно выходное значение для каждого входного значения.
Практическое руководство. Имея график, используйте тест вертикальной линии, чтобы определить, представляет ли график функцию.
- Проверьте график, чтобы убедиться, что какая-либо вертикальная линия пересекает кривую более одного раза.
- Если такая линия есть, график не представляет функцию.
- Если ни одна вертикальная линия не может пересекать кривую более одного раза, график действительно представляет функцию.
Пример: применение теста вертикальной линии
Какой из графиков представляет функцию [латекс] y = f \ left (x \ right)? [/ Latex]
Показать решение Если какая-либо вертикальная линия пересекает график более одного раза, отношение, представленное на графике, не является функцией. Обратите внимание, что любая вертикальная линия будет проходить только через одну точку двух графиков, показанных в частях (a) и (b) графика выше. Из этого можно сделать вывод, что эти два графика представляют функции. Третий график не представляет функцию, потому что при максимальном значении x вертикальная линия пересекает график более чем в одной точке.
Из этого можно сделать вывод, что эти два графика представляют функции. Третий график не представляет функцию, потому что при максимальном значении x вертикальная линия пересекает график более чем в одной точке.
Попробуй
Представляет ли приведенный ниже график функцию?
Тест горизонтальной линии
После того, как мы определили, что график определяет функцию, простой способ определить, является ли она взаимно однозначной функцией, — это использовать тест горизонтальной линии .Проведите через график горизонтальные линии. Горизонтальная линия включает все точки с определенным значением [latex] y [/ latex]. Значение [latex] x [/ latex] точки, где вертикальная линия пересекает функцию, представляет вход для этого выходного значения [latex] y [/ latex].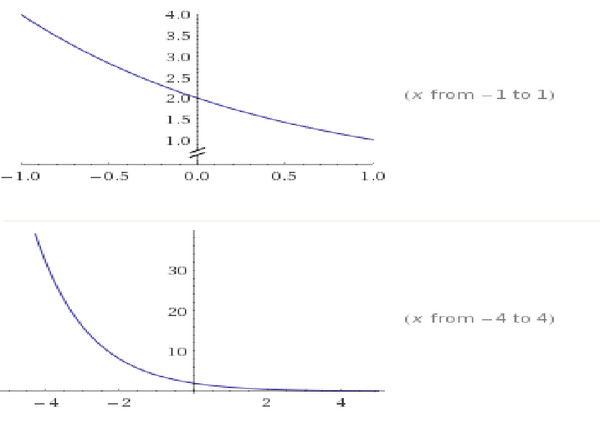 Если мы можем нарисовать любую горизонтальную линию , которая пересекает график более одного раза, тогда график , а не представляет функцию, потому что это значение [latex] y [/ latex] имеет более одного входа.
Если мы можем нарисовать любую горизонтальную линию , которая пересекает график более одного раза, тогда график , а не представляет функцию, потому что это значение [latex] y [/ latex] имеет более одного входа.
Практическое руководство. Имея график функции, используйте тест горизонтальной линии, чтобы определить, представляет ли график функцию взаимно однозначного соответствия.
- Проверьте график, чтобы увидеть, пересекает ли нарисованная горизонтальная линия кривую более одного раза.
- Если такая линия есть, функция не взаимно однозначная.
- Если ни одна горизонтальная линия не может пересекать кривую более одного раза, функция взаимно однозначна.
Пример: применение теста горизонтальной линии
Рассмотрим функции (a) и (b), показанные на графиках ниже.
Являются ли какие-либо функции взаимно однозначными?
Показать решение Функция в (а) не является взаимно однозначной.Горизонтальная линия, показанная ниже, пересекает график функции в двух точках (и мы даже можем найти горизонтальные линии, которые пересекают его в трех точках).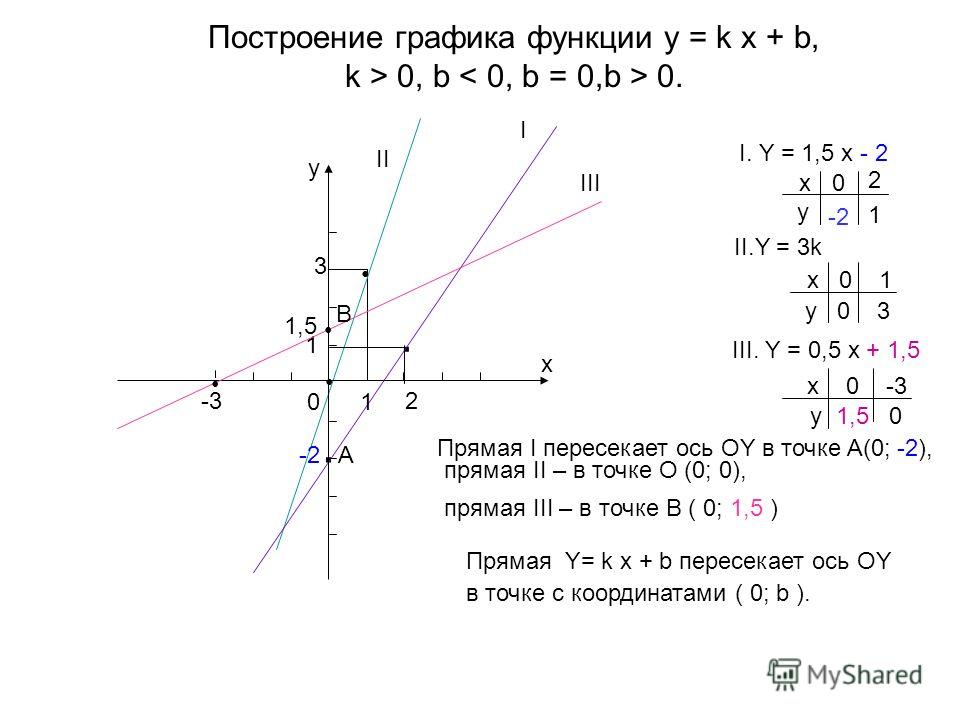
Функция в (b) взаимно однозначна. Любая горизонтальная линия будет пересекать диагональную не более одного раза.
Определение основных функций набора инструментов
В этом тексте мы исследуем функции — формы их графиков, их уникальные характеристики, их алгебраические формулы и способы решения с ними проблем.Учимся читать, начинаем с алфавита. Когда мы учимся арифметике, мы начинаем с чисел. При работе с функциями также полезно иметь базовый набор стандартных элементов. Мы называем их «функциями набора инструментов», которые образуют набор основных именованных функций, для которых нам известны график, формула и специальные свойства. Некоторые из этих функций запрограммированы на отдельные кнопки на многих калькуляторах. Для этих определений мы будем использовать [latex] x [/ latex] в качестве входной переменной и [latex] y = f \ left (x \ right) [/ latex] в качестве выходной переменной.
Мы будем часто видеть эти функции набора инструментов, комбинации функций набора инструментов, их графики и их преобразования на протяжении всей этой книги. Будет очень полезно, если мы сможем быстро распознать эти функции набора инструментов и их возможности по имени, формуле, графику и основным свойствам таблицы. Графики и примерные значения таблицы включены в каждую функцию, показанную ниже.
Попробуй
В этом упражнении вы построите график функций инструментария с помощью онлайн-инструмента построения графиков.
- Изобразите каждую функцию набора инструментов, используя обозначение функций.
- Составьте таблицу значений, которая ссылается на функцию и включает как минимум интервал [-5,5].
Внесите свой вклад!
У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.
Улучшить эту страницуПодробнее
Решите Свойства прямой yx = 5 Tiger Algebra Solver
Переставьте:
Измените уравнение, вычтя то, что находится справа от знака равенства из обеих частей уравнения:
yx- (5) = 0
Шаг 1:
Уравнение прямой
1. 1 Решите y-x-5 = 0
1 Решите y-x-5 = 0
Тигр понимает, что здесь есть уравнение прямой. Такое уравнение обычно записывается y = mx + b («y = mx + c» в Великобритании).
«y = mx + b» — это формула прямой линии, проведенной в декартовой системе координат, в которой «y» — вертикальная ось, а «x» — горизонтальная ось.
В этой формуле:
y сообщает нам, как далеко идет линия.
x сообщает нам, как далеко вдоль
м находится наклон или градиент, т.е. насколько крутой является линия.
b является пересечением по оси Y i.е. где линия пересекает ось Y
Пересечения X и Y и наклон называются свойствами линии. Теперь мы построим график линии yx-5 = 0 и вычислим ее свойства
График прямой линии:
Вычислите точку пересечения Y:
Обратите внимание, что когда x = 0, значение y равно 5/1, поэтому эта линия «разрезает» ось y в точке y = 5,00000
y-intercept = 5/1 = 5,00000
Вычислите точку пересечения X:
Когда y = 0, значение x равно 5 / -1 Следовательно, наша линия » обрезает «ось x при x = -5.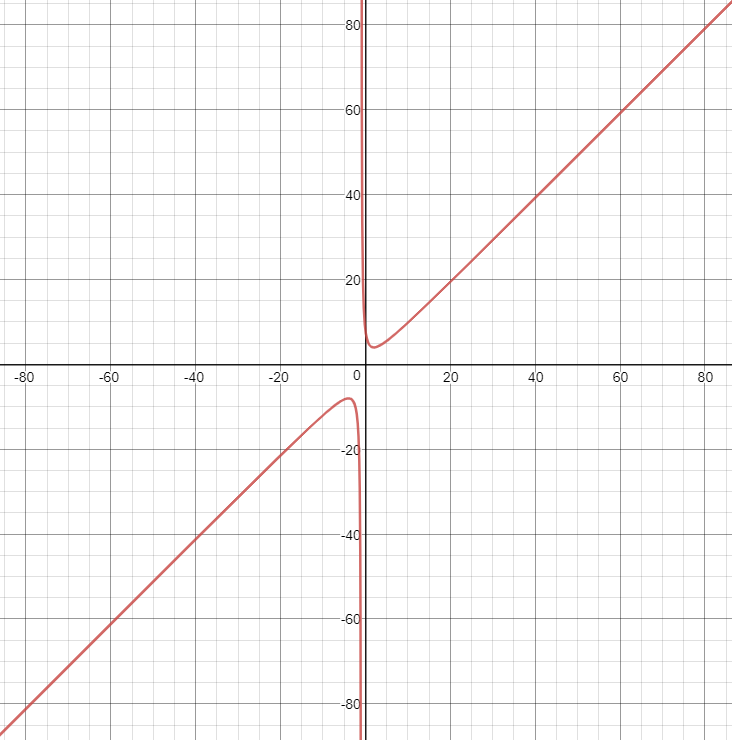 00000
00000
x-intercept = 5 / -1 = -5.00000
Расчет наклона:
Наклон определяется как изменение y, деленное на изменение x. Отметим, что для x = 0 значение y равно 5.000, а для x = 2.000 значение y равно 7.000. Таким образом, при изменении x на 2.000 (изменение x иногда называют «RUN») мы получаем изменение на 7.000 — 5.000 = 2.000 по y. (Изменение y иногда называют «ПОДЪЕМ», а наклон равен m = RISE / RUN)
Наклон = 2.000 / 2.000 = 1.000
Геометрическая фигура: прямая линия
- Наклон = 2.000 / 2.000 = 1.000
- пересечение по оси x = 5 / -1 = -5,00000
- пересечение по оси y = 5/1 = 5,00000
Общественный колледж МесаКонцепции алгебры колледжа — MAT 150 онлайн Задача: Найдите точку на графике кривой y = x 2 + 1, ближайшую к фиксированной точке (4,1). Предпосылки: Эта проблема относится к классу задач, обычно называемых проблемами минимизации, минимальными / максимальными проблемами или проблемами экстремумов.
В каждой задаче мы пытаемся найти наименьшее или наибольшее значение. Хотя исчисление можно использовать для нахождения точных решений этих проблем, мы будем использовать алгебру и наши графические калькуляторы для аппроксимации решения. Переформулировка задачи: Найдите точку (x, y) на графике кривой y = x 2 + 1, ближайшую к фиксированной точке (4,1). Сначала нарисуем график, чтобы получить более четкое представление о том, что происходит. Мы пытаемся найти точку A (x, y) на графике параболы, y = x 2 + 1, которая является ближайшей к Повторение задачи: Найдите точку A (x, y) на графике параболы, y = x 2 + 1, что минимизирует расстояние d между кривой и точка B (4,1). Задача делится на три части:1. Поскольку мы хотим минимизировать d, нам нужна функция, которая описывает расстояние между (x, y) и (4,1)
Часть 2:Используя графический калькулятор, мы зарисовываем график d и ищем точку, в которой встречается минимальное значение d. Используя функцию трассировки, мы можем увидеть, что минимальное значение d происходит (приблизительно) в точке (x, d ) = (1,12817, 3,4123 ) То есть d — это минимум , когда x приблизительно равен 1,12817.
Часть 3:Помните, что мы предполагаем, что найдет точку (x, y) на графике параболы, y = x 2 + 1, что минимизирует d . Пока мы знаем x и знаем d, но мы еще не нашли y. Итак, чтобы ответить на исходный вопрос, ближайшая точка параболы y = x 2 + 1 к точке (4,1) приблизительно равна (1.12817, 2.27277). © 1999 Джо Стейг |
Графики смещения, отражения и растяжения
1.5 — Графики смещения, отражения и растяженияОпределения
- Абсцисса
- Координата x
- Ордината
- Координата Y
- Сдвиг
- Перевод, в котором размер и форма графика функции не изменены, но
расположение графика.

- Масштаб
- Перевод, в котором изменен размер и форма графика функции.
- Отражение
- Перевод, в котором график функции отражается относительно оси.
Общие функции
Отчасти красота математики в том, что почти все основано на чем-то другом, и если вы можете понять основы, а затем применить новые элементы к старым. Это способность что делает возможным понимание математики.Если бы вы запомнили каждый кусок математики, представленной вам без связи с другими частями, вы 1) станете разочарованы в математике и 2) не очень разбираются в математике.
Есть несколько основных графиков, которые мы видели раньше. Применяя переводы к этим основным
графов, мы можем получить новые графы, которые по-прежнему обладают всеми свойствами старых. От
понимая основные графики и то, как к ним применяются переводы, мы узнаем каждый
новый график как небольшая вариация старого, а не как совершенно другой график, как у нас
никогда раньше не видел.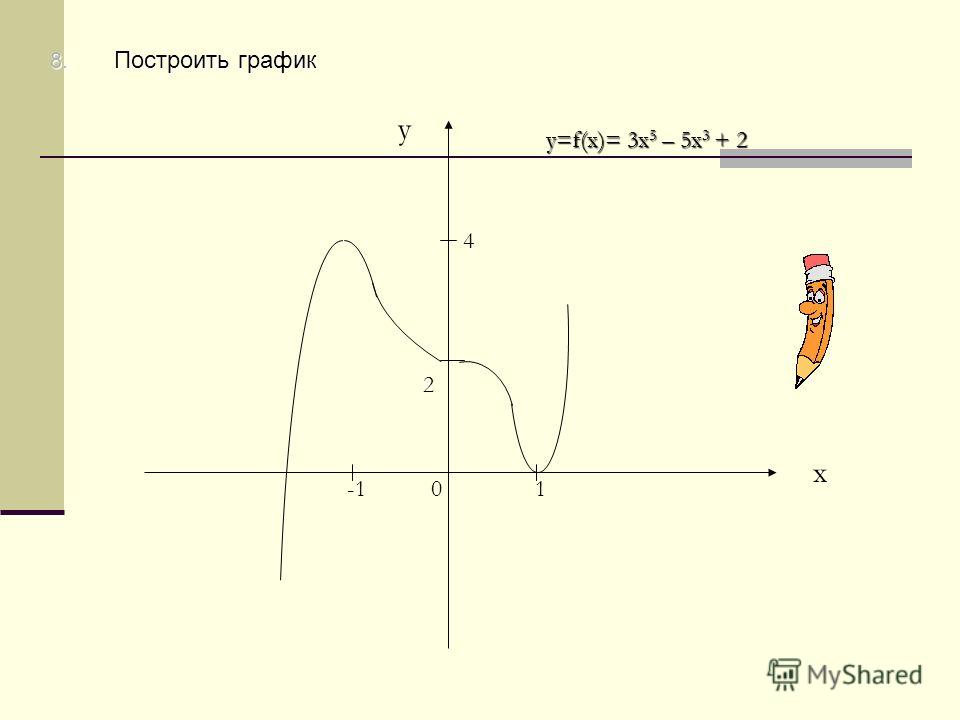 Понимание этих переводов позволит нам быстро распознать и
нарисуйте новую функцию, не прибегая к построению точек.
Понимание этих переводов позволит нам быстро распознать и
нарисуйте новую функцию, не прибегая к построению точек.
Это общие функции, графики которых вы должны знать сейчас:
- Постоянная функция: y = c
- Линейная функция: y = x
- Квадратичная функция: y = x 2
- Кубическая функция: y = x 3
- Функция абсолютного значения: y = | x |
- Функция квадратного корня: y = sqrt (x)
- Наибольшая целочисленная функция: y = int (x) говорилось в предыдущем разделе.
Постоянная функция | Линейная функция | Квадратичная функция |
Кубическая функция | Функция абсолютного значения | Функция квадратного корня |
В вашем тексте линейная функция называется функцией тождества, а квадратичная функция — возведением в квадрат. функция.
функция.
Переводы
Есть два типа переводов, которые мы можем сделать с графиком функции. Они меняются и масштабирование. Если считать отражения, их три, но отражения — это всего лишь частный случай второй перевод.
Смены
Сдвиг — это жесткий перевод, поскольку он не меняет форму или размер графика функция. Все, что будет делать сдвиг, — это изменить положение графика. Вертикальный сдвиг добавляет / вычитает константу к / из каждой координаты y, оставляя координату x неизменной.Горизонтальный сдвиг добавляет / вычитает константу к / из каждой координаты x, оставляя координату y неизменной. Вертикальные и горизонтальные сдвиги можно объединить в одно выражение.
Сдвиги добавляются / вычитаются из компонентов x или f (x). Если константа сгруппирована с x, тогда это горизонтальный сдвиг, иначе это вертикальный сдвиг.
Весы (растяжение / сжатие)
Масштаб — это нежесткий перевод, поскольку он изменяет форму и размер графика
функция.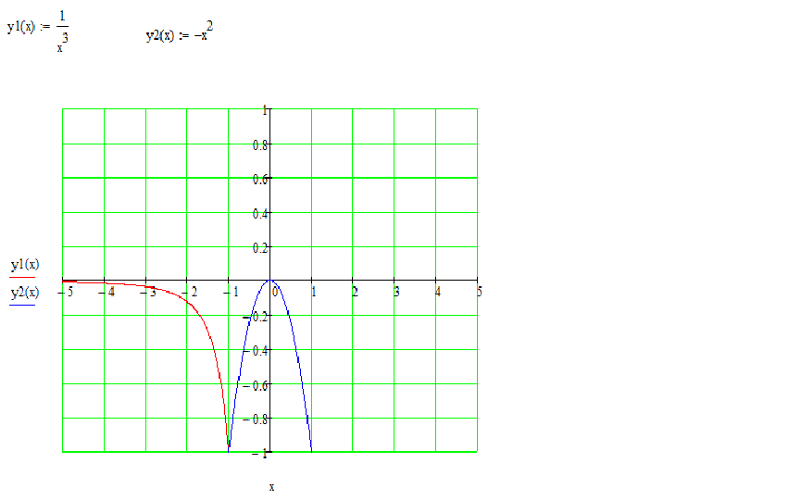 Масштаб будет умножать / делить координаты, и это изменит внешний вид, а также
Местоположение. Вертикальное масштабирование умножает / делит каждую координату y на константу, оставляя
координата x не изменилась. Горизонтальное масштабирование умножает / делит каждую координату x на
константа, оставляя координату y неизменной. Вертикальные и горизонтальные масштабы могут быть
объединены в одно выражение.
Масштаб будет умножать / делить координаты, и это изменит внешний вид, а также
Местоположение. Вертикальное масштабирование умножает / делит каждую координату y на константу, оставляя
координата x не изменилась. Горизонтальное масштабирование умножает / делит каждую координату x на
константа, оставляя координату y неизменной. Вертикальные и горизонтальные масштабы могут быть
объединены в одно выражение.
Коэффициенты масштабирования умножаются / делятся на компоненты x или f (x). Если константа сгруппирована с x, тогда это горизонтальное масштабирование, в противном случае это вертикальное масштабирование.
Отражения
Функция может быть отражена вокруг оси умножением на отрицательную единицу. Чтобы отразить ось Y, умножьте каждый x на -1, чтобы получить -x. Чтобы отразить ось x, умножьте f (x) на -1, чтобы получить -f (x).
Собираем все вместе
Рассмотрим основной график функции: y = f (x)
Все переводы могут быть выражены в форме:
y = a * f [b (x-c)] + d
| Вертикальный | Горизонтальный | |
|---|---|---|
| Масштаб | a | b |
| Сдвиг | d | c |
| действует нормально | действует наоборот |
Отступление
Понимание представленных здесь концепций является фундаментальным для понимания полиномиального и рационального
функции (ch 3) и особенно конические секции (ch 8). Это также будет играть очень большую роль в
Тригонометрия (Математика 117) и Исчисление (Математика 121, 122, 221 или 190).
Это также будет играть очень большую роль в
Тригонометрия (Математика 117) и Исчисление (Математика 121, 122, 221 или 190).
Ранее в тексте (раздел 1.2, задачи 61-64) была серия задач, в которых уравнение линии как:
х / а + у / б = 1
Где a — точка пересечения по оси X, а b — точка пересечения по оси Y линии. «А» может действительно быть подумал о том, как далеко нужно пройти по оси x (масштабирование по оси x), и буква «b» могла бы думать как далеко идти в направлении «y» (масштабирование по оси y).Итак, «а» и «б» есть собственно множители (даже если они появляются внизу). Что они умножение это 1 который находится с правой стороны. x + y = 1 будет иметь точки пересечения с координатами x и y 1.
Хорошо. Рассмотрим уравнение: y = f (x)
Это самый простой график функции. Но преобразования могут применимо и к нему. Его можно записать в формате, показанном ниже.
В этом формате «a» — вертикальный множитель, а «b» — горизонтальный. множитель.Мы знаем, что «a» влияет на y, потому что он сгруппирован с
y, а буква «b» влияет на
x, потому что он сгруппирован с x.
множитель.Мы знаем, что «a» влияет на y, потому что он сгруппирован с
y, а буква «b» влияет на
x, потому что он сгруппирован с x.
Буквы «d» и «c» — вертикальные и горизонтальные. сдвигов соответственно. Мы знаем, что это сдвиги, потому что они вычитаются из переменной скорее чем быть разделенными на переменные, что сделало бы их масштабными.
В этом формате все изменения кажутся противоположными ожидаемым. Если у вас есть выражение (y-2) / 3, это вертикальный сдвиг на 2 вправо (хотя в нем указано y минус 2), и это вертикальное растяжение на 3 (хотя там указано, что y делится на 3).Важно понимать, что в этом формат, когда константы сгруппированы с переменной, на которую они влияют, перевод является противоположное (обратное) тому, что думает большинство людей.
Однако этот формат не способствует созданию эскизов с помощью технологий,
потому что нам нравится писать функции как y =, а не (y-c) / d =.
Итак, если вы возьмете обозначение выше и решите его относительно y, вы получите обозначение ниже, которое
похоже, но не совсем в нашем базовом состоянии формы, приведенном выше.
y = a * f ((x-c) / b) + d
Обратите внимание, что для определения y вам нужно было инвертировать константы «a» и «d».Вместо деления на «а» вы теперь умножаете на «а». Ну, раньше будь то ты в любом случае пришлось применить обратную константу. Когда было сказано «разделить на», ты знал это Это означало «умножать каждый y на «. Когда говорилось» вычесть d «, вы знали, что вам действительно нужно» добавить d «. У вас есть обратное уже было применено, так что больше не делайте этого! С константами, влияющими на y, поскольку они были перемещены на другую сторону, принимайте их за чистую монету. Если там сказано «умножить на 2», делайте это, не разделить на 2.
Однако константы, влияющие на x, не изменились. Они по-прежнему противоположны
какими, по вашему мнению, они должны быть. И, что еще хуже, «x разделенное b», что на самом деле означает
умножение каждой координаты x на «b» было перевернуто и записано как «b умножить на x», так что это действительно
означает разделить каждый x на «b». «X минус c» на самом деле означает прибавление c к каждой координате x.
«X минус c» на самом деле означает прибавление c к каждой координате x.
Итак, окончательная форма (для технологии) такая же, как указано выше:
y = a * f [b (x-c)] + d
Хорошо, конец отступления.
Нормальное и обратное поведение
Вы заметите, что на диаграмме указано, что вертикальный перевод нормальный, а горизонтальный — нормальный. переводы инвертированы. Объяснение причин читайте в отступлении выше. Концепции в действительно важны для понимания многих графиков.
Примеры
- y = f (x)
- Нет перевода
- у = е (х + 2)
- +2 сгруппировано с x, поэтому это горизонтальный перевод.Поскольку он добавлен
к x, а не умноженному на x, это сдвиг, а не масштаб. Поскольку там написано плюс и горизонтальные изменения инвертированы, фактический перевод заключается в перемещении всего
график слева на две единицы или «вычтите два из каждой координаты x», оставив
только координаты y.

- у = е (х) +2
- +2 не сгруппирован с x, поэтому это вертикальный перевод. Поскольку он добавлен, это не умножение, а сдвиг, а не масштаб.Поскольку там написано плюс и вертикальный изменения действуют так, как выглядят, фактический перевод заключается в перемещении всего графа на два единиц вверх или «прибавьте два к каждой координате y», не трогая координаты x.
- y = f (x-3) +5
- На этот раз имеется сдвиг по горизонтали на три вправо и сдвиг по вертикали на пять вверх. Так перевод будет заключаться в перемещении всего графика вправо на три и пять вверх или «добавить три для каждой координаты x и пять для каждой координаты y «
- у = 3f (х)
- 3 умножается, поэтому это масштабирование, а не сдвиг.3 не сгруппированы с
x, так что это вертикальное масштабирование. Вертикальные изменения происходят так, как вы думаете.
должно быть, поэтому в результате мы «умножим каждую координату y на три», оставив только координаты x.

- у = -f (х)
- Y нужно умножить на -1. Это заставляет перенос «отражаться относительно оси x», оставляя только координаты x.
- y = f (2x)
- 2 умножается, а не складывается, поэтому это масштабирование, а не сдвиг.2 — это сгруппированы с x, поэтому это горизонтальное масштабирование. Горизонтальные изменения противоположны чем они кажутся, вместо того, чтобы умножать каждую координату x на два, перевод заключается в «делении каждой координаты x на два», оставляя координаты y без изменений.
- y = f (-x)
- Х нужно умножить на -1. Это заставляет перемещение «отражаться относительно оси y», оставляя только координаты y.
- y = 1/2 f (x / 3)
- Перевод здесь был бы таков: «умножить каждую координату y на 1/2 и умножить каждую координату x на 3 дюйма.
- у = 2f (х) +5
- Здесь может быть некоторая двусмысленность. Вы добавляете пять к каждой координате Y, а затем
умножьте на два «или вы» умножаете каждую координату y на два, а затем прибавляете пять «?
Вот тут-то и приходит мой предыдущий комментарий о математике, основанной на самой себе.
 играть. Существует порядок операций, который гласит, что умножение и деление
выполняется перед сложением и вычитанием. Если вы это помните, то решение
легкий. Правильное преобразование — «умножить каждую координату y на два, а затем
добавьте пять дюймов, не трогая координаты x.
играть. Существует порядок операций, который гласит, что умножение и деление
выполняется перед сложением и вычитанием. Если вы это помните, то решение
легкий. Правильное преобразование — «умножить каждую координату y на два, а затем
добавьте пять дюймов, не трогая координаты x. - y = f (2x-3)
- Теперь, когда порядок операций четко определен, двусмысленность здесь нужно сделать сначала снимается. Ответ не в том, чтобы «делить каждую координату x на два. и добавьте три «, как и следовало ожидать. Причина в том, что проблема , а не , записанная в стандартная форма. Стандартная форма — y = f [b (x-c)]. При написании в стандартной форме это проблема становится y = f [2 (x-3/2)]. Это означает, что правильный перевод — «разделить каждую координату x на два и добавить три половины», оставляя координаты y неизменными.
- у = 3f (х-2)
- Перевод здесь означает «умножить каждую координату y на три и добавить два к каждой координате x». В качестве альтернативы вы можете изменить порядок.
 Изменения x или y
можно сделать независимо друг от друга, но при наличии масштабов и сдвигов на одинаковые
переменной, важно сначала выполнить масштабирование, а затем — сдвиг.
Изменения x или y
можно сделать независимо друг от друга, но при наличии масштабов и сдвигов на одинаковые
переменной, важно сначала выполнить масштабирование, а затем — сдвиг.
Переводы и влияние на домен и диапазон
Любой горизонтальный перевод повлияет на домен и оставит диапазон неизменным.Любая вертикаль перевод повлияет на диапазон и оставит домен без изменений.
Примените тот же перевод к домену или диапазону, который вы применяете к x-координатам или y-координатам. Это работает, потому что область может быть записана в обозначении интервала как интервал между двумя координатами x. То же самое для диапазона как интервал между двумя координатами y.
Помните, что в следующей таблице домен и диапазон даны в виде интервалов. Если ты Если вы не знакомы с обозначением интервалов, обратитесь к главе о предварительных требованиях.Первая строка — это формулировка определения и должна использоваться для определения остальных ответов.
| График | Перевод | Домен | Диапазон |
|---|---|---|---|
| y = f (x) | нет | (-2,5) | [4,8] |
| y = f (x-2) | правый 2 | (0,7) | [4,8] |
| y = f (x) -2 | вниз 2 | (-2,5) | [2,6] |
| y = 3f (x) | умножить каждый y на 3 | (-2,5) | [12,24] |
| y = f (3x) | делим каждый x на 3 | (-2 / 3,5 / 3) | [4,8] |
| y = 2f (x-3) -5 | умножьте каждый y на 2 и вычтите 5; прибавьте 3 к каждому x | (1,8) | [3,11] |
| y = -f (x) | отразить относительно оси x | (-2,5) | [-8, -4] |
| y = 1 / f (x) | — величина, обратная каждому y | (-2,5) | [1 / 8,1 / 4] |
Обратите внимание на последние два, что порядок в диапазоне изменился. Это потому, что в интервале
обозначение, меньшее число всегда идет первым.
Это потому, что в интервале
обозначение, меньшее число всегда идет первым.
Действительно хорошие вещи
Понимание переводов также может помочь при поиске домена и диапазона функции. Допустим, ваша проблема — найти домен и диапазон функции y = 2-sqrt (x-3).
Начните с того, что вы знаете. Вы знаете, что основная функция — это sqrt (x), и вы знаете домен и диапазон sqrt (x) равны [0, + бесконечность). Вы знаете это, потому что знаете эти шесть общие функции на лицевой обложке вашего текста, которые будут использоваться в качестве строительных блоков для других функций.
| Функция | Перевод | Домен | Диапазон | |
|---|---|---|---|---|
| Начать с чего ты знаешь | y = sqrt (x) | Нет | [0, + бесконечность) | [0, + бесконечность) |
| Примените переводы | y = -sqrt (x) | Отражение относительно оси x | [0, + бесконечность) | (-infinity, 0] |
| y = 2-sqrt (x) | Добавьте 2 к каждой ординате | [0, + бесконечность) | (-бесконечность, 2] | |
| y = 2-sqrt (x-3) | Добавьте 3 к каждой абсциссе | [3, + бесконечность) | (-бесконечность, 2] |
Итак, для функции y = 2-sqrt (x-3) домен равен x≥3, а диапазон — y≤2.
И лучшая часть это то, что вы это поняли! Вы не только поняли это, но вы были в состоянии сделать это без построения графика на калькуляторе.
Нет ничего плохого в том, чтобы построить график, чтобы увидеть, что происходит, но вы должны уметь понять, что происходит без графика, потому что мы узнали, что график калькулятор не всегда точно показывает, что происходит. Это инструмент, который поможет вам понять и понимание, а не инструмент для его замены.
Я хочу, чтобы все вы «поняли» именно эту связность математики. Все подходит вместе так красиво.
Как построить график X через Y на калькуляторе TI-84
Обновлено 15 декабря 2020 г.
Джек Джерард
Калькулятор TI-84 предлагает ряд встроенных функций для решения и построения графиков уравнений. К сожалению, его основные возможности построения графиков ограничены функциями и уравнениями, которые характеризуют Y с точки зрения X .Реже вам понадобится построить график X с точки зрения Y , но если вы это сделаете, существующие параметры не совсем помогут. К счастью, TI-84 позволяет импортировать внешние приложения и использовать их почти так же, как и приложения, поставляемые с калькулятором. Репозиторий TI Calc, поддерживаемый сообществом, содержит ряд этих внешних приложений, в том числе приложение под названием XGraph от Джоэла Смита, которое позволяет построить график X с точки зрения Y .
К счастью, TI-84 позволяет импортировать внешние приложения и использовать их почти так же, как и приложения, поставляемые с калькулятором. Репозиторий TI Calc, поддерживаемый сообществом, содержит ряд этих внешних приложений, в том числе приложение под названием XGraph от Джоэла Смита, которое позволяет построить график X с точки зрения Y .
Что означает X в терминах Y?
Для большинства уравнений вы строите график Y в терминах X .Это означает, что ваше уравнение основано на значении Y и интерпретируется через значение X ; пример: y = x + 1. Значение Y зависит от значения X , поэтому для каждого X соответствующее значение Y равно этому значению X плюс 1. Построение графика X через Y меняет ситуацию. Вместо y = x + 1 вы должны создать график из x = y + 1. В этом случае ваше значение X зависит от значения Y , и для вычисления каждого X вы берете соответствующее ему значение Y и добавляете 1. К сожалению, это не так. На калькуляторе TI-84 легко построить график, если вы не рассчитываете и не наносите отдельные точки вручную, поскольку TI-84 не имеет опции «X =» в его функциях построения графиков.
В этом случае ваше значение X зависит от значения Y , и для вычисления каждого X вы берете соответствующее ему значение Y и добавляете 1. К сожалению, это не так. На калькуляторе TI-84 легко построить график, если вы не рассчитываете и не наносите отдельные точки вручную, поскольку TI-84 не имеет опции «X =» в его функциях построения графиков.
Установка XGraph
Одна вещь, которая есть у TI-84, — это средство расширения его функций с помощью закодированных приложений и программ.Приложение XGraph позаботится об этом, позволяя вводить уравнения в форме X через Y и строить их график. Файл загружается в виде файла .zip, который содержит XGRAPH.8XP и файл readme; извлеките файл XGRAPH.8XP в легкодоступное место. Подключите калькулятор TI-84 к компьютеру с помощью соединительного кабеля USB, поставляемого с калькулятором, а затем запустите программное обеспечение TI Connect от Texas Instruments (которое можно бесплатно загрузить с веб-сайта Texas Instruments, если оно еще не установлено. ).Выберите XGRAPH.8XP и подтвердите, что хотите отправить его на свой калькулятор, и подождите, пока TI Connect отправит и установит приложение. По завершении вы можете закрыть TI Connect и отключить калькулятор.
).Выберите XGRAPH.8XP и подтвердите, что хотите отправить его на свой калькулятор, и подождите, пока TI Connect отправит и установит приложение. По завершении вы можете закрыть TI Connect и отключить калькулятор.
Использование приложения
Нажмите кнопку PRGM на калькуляторе TI-84 и найдите запись «XGRAPH» в списке программ. Нажмите клавишу ENTER, на вашем экране появится «prgmXGRAPH»; снова нажмите ENTER, чтобы запустить приложение. При появлении запроса введите уравнение, но используйте букву X вместо Y .Если бы вы надеялись построить график такого уравнения, как x = 2 y + 1, ваш ввод XGraph будет «X =? 2X + 1». Нажмите клавишу ENTER и подождите, пока программа построит график; несмотря на то, что вы вводите X , график будет нарисован как X с точки зрения Y (что для приведенного выше примера будет графиком x = 2 y + 1.) По завершении нажмите кнопку «ON», чтобы прервать программу, и выберите «1: Quit» для выхода.

 Вас там закроют, вы в курсе?
Вас там закроют, вы в курсе? Такой квест нравится всем без исключения и всегда собирает сотни отзывов.
Такой квест нравится всем без исключения и всегда собирает сотни отзывов. Развлекайтесь, но соблюдайте осторожность.
Развлекайтесь, но соблюдайте осторожность. Воспользоваться можно в день рождения и в 6 дня после него, при наличии паспорта, свидетельства о рождении или водительского удостоверения.
Воспользоваться можно в день рождения и в 6 дня после него, при наличии паспорта, свидетельства о рождении или водительского удостоверения.
 Як правило, ви не хочете вибирати числа абсолютно випадковим чином — ви хочете вибрати кілька цільових точок — для параболи, наприклад, ви хочете вибрати цифри біля вершини параболи. Але оскільки це лінія, будь-яка точка зробить. Але зверніть увагу, що вибір невеликих номерів полегшить розрахунки. Крім того, ви хочете вибрати цифри в межах кордону площині, яку ви вказали. Для цієї задачі я вибрав -1, 0, 1, 2 і 3.
Як правило, ви не хочете вибирати числа абсолютно випадковим чином — ви хочете вибрати кілька цільових точок — для параболи, наприклад, ви хочете вибрати цифри біля вершини параболи. Але оскільки це лінія, будь-яка точка зробить. Але зверніть увагу, що вибір невеликих номерів полегшить розрахунки. Крім того, ви хочете вибрати цифри в межах кордону площині, яку ви вказали. Для цієї задачі я вибрав -1, 0, 1, 2 і 3.
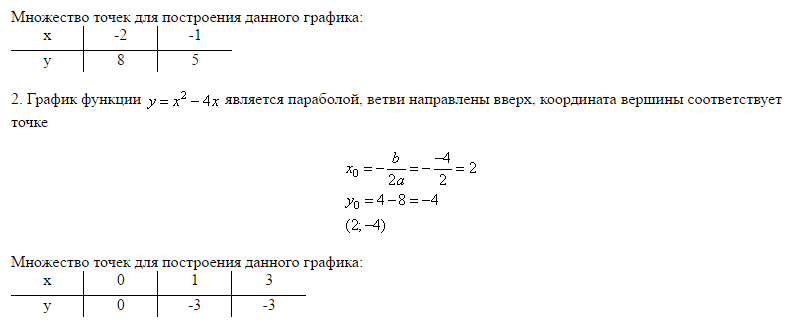 Отже, зміна у над зміною x дорівнює 1 над 1. Це означає, що з перехрестя y (0, -2) необхідно перемістити одну одиницю вгору і одну одиницю вправо, щоб знайти іншу точку на графіку. Це підводить нас до (1, -1). Ми продовжуємо повторювати, пересуваючи одну одиницю вгору і одну одиницю вправо. Як тільки ми маємо достатньо точок, ми можемо з’єднати точки і створити лінію.
Отже, зміна у над зміною x дорівнює 1 над 1. Це означає, що з перехрестя y (0, -2) необхідно перемістити одну одиницю вгору і одну одиницю вправо, щоб знайти іншу точку на графіку. Це підводить нас до (1, -1). Ми продовжуємо повторювати, пересуваючи одну одиницю вгору і одну одиницю вправо. Як тільки ми маємо достатньо точок, ми можемо з’єднати точки і створити лінію. Курсы математического анализа традиционно решают этот тип проблем, задав любой из следующих вопросов:
Курсы математического анализа традиционно решают этот тип проблем, задав любой из следующих вопросов: Часть нашего решения, относящаяся к алгебре, на самом деле такая же, как если бы мы использовали исчисление.
Часть нашего решения, относящаяся к алгебре, на самом деле такая же, как если бы мы использовали исчисление.



 играть. Существует порядок операций, который гласит, что умножение и деление
выполняется перед сложением и вычитанием. Если вы это помните, то решение
легкий. Правильное преобразование — «умножить каждую координату y на два, а затем
добавьте пять дюймов, не трогая координаты x.
играть. Существует порядок операций, который гласит, что умножение и деление
выполняется перед сложением и вычитанием. Если вы это помните, то решение
легкий. Правильное преобразование — «умножить каждую координату y на два, а затем
добавьте пять дюймов, не трогая координаты x. Изменения x или y
можно сделать независимо друг от друга, но при наличии масштабов и сдвигов на одинаковые
переменной, важно сначала выполнить масштабирование, а затем — сдвиг.
Изменения x или y
можно сделать независимо друг от друга, но при наличии масштабов и сдвигов на одинаковые
переменной, важно сначала выполнить масштабирование, а затем — сдвиг.