Квадратные уравнения и квадратичные неравенства с параметрами

Дорогой друг! Если ты никогда не решал задач с параметрами – прочитай статьи «Что такое параметр» и «Графический способ решения задач с параметрами». Квадратные уравнения, а тем более неравенства с параметрами только на первый взгляд кажутся простыми. Чтобы уверенно решать их, надо знать определенные приемы. О некоторых мы расскажем.

И заодно – стоит повторить темы «Квадратные уравнения» и «Квадратичные неравенства».

Разберем сначала подготовительные задачи. А в конце – реальную задачу ЕГЭ.

1. Найдите все значения a, при которых уравнение не имеет действительных корней.

Всегда ли это уравнение является квадратным относительно переменной х? – Нет, не всегда. В случае, когда коэффициент при равен нулю, оно станет линейным.

Рассмотрим два случая – когда это уравнение квадратное и когда оно линейное.

1)

Тогда уравнение примет вид 2 = 0. Такое уравнение не имеет действительных корней, что удовлетворяет условию задачи.

2)

Уравнение будет квадратным. Квадратное уравнение не имеет действительных корней тогда и только тогда, когда его дискриминант отрицательный.

Найдем дискриминант :

< 0.

< 0

< 0

Решив неравенство, получим

С учетом пункта 1, получим ответ: .

2. Найдите все значения a, при каждом из которых сумма квадратов действительных корней уравнения

минимальна.

Мы привыкли находить корни квадратного уравнения по известной формуле, с помощью дискриминанта. Однако для задач с параметрами такой способ подходит не всегда. А вот теорема Виета нам поможет.

В условии сказано: «Сумма квадратов действительных корней…» Это значит, во-первых, что корни есть, а во-вторых, их должно быть два. А это будет в случае, когда дискриминант положителен ( > 0).

Если и – корни квадратного уравнения
, то по теореме Виета:

В нашем случае:

Решим первое неравенство системы

Квадратный трехчлен в левой части не имеет корней, так как дискриминант равен -32, то есть отрицателен. Поэтому неравенство будет выполняться для всех действительных значений .

Возведем второе уравнение системы в квадрат:

Из этих двух уравнений выразим сумму квадратов и .

Значит, сумму квадратов корней уравнения можно выразить через параметр

График функции — парабола, ее ветви направлены вверх, минимум будет достигаться в ее вершине. Найдем вершину параболы:

Ответ: 1

3) Найдите все значения , при каждом из которых все решения уравнения

положительны.

Как и в первой задаче, уравнение является квадратным, кроме случая, когда . Рассмотрим этот случай отдельно

1) . Получим линейное уравнение

У него единственный корень, причем положительный. Это удовлетворяет условию задачи.

2) При уравнение будет квадратным. Нам надо, чтобы решения существовали, причем были положительными. Раз решения есть, то .

Покажем один из приемов решения квадратичных уравнений и неравенств с параметрами. Он основан на следующих простых утверждениях:

— Оба корня квадратного уравнения и положительны тогда и только тогда, когда их сумма положительна и произведение положительно.

Очевидно, что сумма и произведение двух положительных чисел также положительны. И наоборот – если сумма и произведение двух чисел положительны, то и сами числа положительны.

— Оба корня квадратного уравнения и отрицательны тогда и только тогда, когда их сумма отрицательна, а произведение положительно.

Корни квадратного уравнения и имеют разные знаки тогда и только тогда, когда их произведение отрицательно.

Сумма и произведение корней входят в формулировку теоремы Виета, которой мы и воспользуемся. Получим

Второе и третье неравенства имеют одинаковое решение . Решение первого неравенства:
.

Решение системы: .

С учетом пункта 1 получим ответ

Ответ:

4. При каких значениях параметра a уравнение

имеет единственное решение?

Уравнение является показательным, причем однородным. Мы умеем решать такие уравнения! Разделим обе части на .

Получим:

Сделаем замену 

Для того, чтобы исходное уравнение имело единственное решение, нужно, чтобы уравнение относительно t имело ровно один положительный корень.

1) В случае уравнение будет линейным

Значит, подходит. В этом случае уравнение имеет единственный положительный корень.

2) Если , уравнение будет квадратным.

Его дискриминант

Дискриминант является полным квадратом и поэтому всегда неотрицателен. Уравнение имеет либо один, либо два корня. В этом случае несложно найти корни в явном виде.

Один корень получился не зависящим от параметра, причем положительным. Это упрощает задачу.

Для того, чтобы уравнение имело единственный положительный корень, нужно, чтобы либо второй был отрицательным, либо равным нулю, либо чтобы корни совпадали. Рассмотрим все случаи.

а)

Тогда

б)

Объединив все случаи, получим ответ.

Ответ:

И наконец – реальная задача ЕГЭ.

5. При каких значениях a система имеет единственное решение?

Решением квадратного неравенства может быть:

1) отрезок

2) 2 луча

3) точка

4) ∅

В каких случаях система двух квадратных неравенств имеет единственное решение:

1) единственная общая точка двух лучей-решений ( или интервалов-решений)

2) одно из неравенств имеет решение – точку, которая является решением второго неравенства

Рассмотрим первый случай.

Решим систему

Если является решением 1 и 2 уравнений, то является решением уравнения (вытекает из второго первое) ⇒ или

Если , при этом система примет вид:

Второй корень первого уравнения:

Второй корень второго первого:

Единственное решение

Если , при этом система примет вид:

– бесконечно много решений, не подходит.

Рассмотрим второй случай.

– решением является точка, если – является решением второго неравенства.

– решением является точка, если – не является решением первого неравенства.

Ответ:

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России)                        +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

«Квадратные уравнения с параметрами»

Введение.

В заданиях ЕГЭ и ОГЭ по математике широкое распространение получили задачи, содержащие параметры. Решение задач с параметрами носит учебно-исследовательский характер, они играют важную роль в формировании логического мышления.

Как известно, решению задач с параметрами в школе уделяется очень мало времени. Поэтому решение задач с параметрами всегда вызывает большие трудности . Трудно рассчитывать на то, что учащиеся, подготовка которых не содержала «параметрическою терапию», смогут в жесткой атмосфере конкурсного экзамена успешно справиться с подобными задачами, следовательно, учащиеся должны специально готовиться к «встрече с параметрами».

В следующем году мы будем сдавать ОГЭ, а через два года ЕГЭ. Подготовку к этому ответственному экзамену мы начали в этом году, когда изучили методы решения линейных и квадратных уравнений .

Гипотеза исследования: если освоить методы решения квадратных уравнений с параметрами, то это позволит в дальнейшем овладеть приемами и способами решения более сложных задач с параметрами, тем самым обеспечит качественную подготовку к ЕГЭ.

Актуальность работы: усвоение методов решения квадратных уравнений с параметрами будет хорошим подспорьем при сдаче ОГЭ и ЕГЭ.

Цель работы: научиться решать квадратные уравнения с параметрами.

Задачи:

1. Изучить методы решения квадратных уравнений с параметрами;

2. Познакомить одноклассников с методами решения квадратных уравнений с параметрами на факультативе при подготовке к ОГЭ.

Объект исследования: уравнения с параметрами.

Предмет исследования: квадратные уравнения с параметрами.

1. Алгебраические методы решения уравнений второй степени с параметром.

1. 1. Что такое параметр?

Как это ни покажется странным, задачи с параметрами мы решаем чуть ли не ежедневно, при этом в большинстве своем не зная, что такое параметр. Например, придя в магазин покупать какой-либо товар, мы смотрим на его цену. Если цена будет очень высокой, мы не купим его. Если цена будет вполне приемлемой, мы принимаем решение купить товар. Но если цена товара резко уменьшилась (например, в результате распродажи), мы можем купить несколько единиц этого товара. Таким образом, если рассматривать цену товара как параметр, то от значений этого параметра будет зависеть, купим или не купим мы этот товар, а если и купим, то сколько единиц.

Та же самая картина имеет место и в математике при решении уравнений. При одних значениях коэффициентов уравнение может вообще не иметь решений, при других — одно решение, при третьих – бесконечно многих решений. Например, в школьном курсе алгебры мы часто встречались с ситуацией, когда квадратное уравнение в зависимости от значений коэффициентов имело два решения, одно решение или не имело решений вовсе.

ПАРАМЕТР (от греч. parametron — отмеривающий) в математике, величина, числовые значения которой позволяют выделить определенный элемент из множества элементов того же рода. (Большой Энциклопедический словарь (БЭС)).

Определение 1. Параметром называется независимая переменная величина, входящая в условие задачи или появляющаяся в процессе ее решения, «управляющая» решением задачи.¹

Определение 2. Задача, условие которой содержит или в ходе решения которой появляется хотя бы одна независимая переменная, удовлетворяющая определению понятия «параметр», называется задачей с параметром.¹

Если в уравнении (неравенстве) коэффициенты при некоторых величинах зависят от некоторой переменной или нескольких переменных, то эта переменная или переменные называются параметрами, а уравнения или неравенство параметрическим.

Решить уравнение или неравенство с параметрами означает:

1. Определить, при каких значениях параметров существуют решения;

2. Для каждой допустимой системы значений параметров найти соответствующее множество решений.

1.2. Квадратные уравнения. Теория.

Уравнение вида ах²+bх+с=0, а0, где a,b,c – некоторые действительные числа или выражения, зависящие от параметров, называется

квадратным. Левая его часть является квадратным трехчленом, то есть многочленом второй степени. Корни квадратного уравнения ах²+bх+с=0, а0 находятся по формуле

Выражение D = называется дискриминантом квадратного уравнения ах²+bх+с=0, а0.

Если D > 0, то уравнение имеет два различных действительных корня;

Если D = 0, то уравнение имеет два совпадающих действительных корня;

Если D < 0, то уравнение не имеет действительных корней.

В случае, когда второй коэффициент квадратного уравнения четен, то есть

b = 2k, корни удобно находить по формуле

Неполные квадратные уравнения, то есть такие, в которых b = 0 или

c = 0, удобно решать методом разложения на множители левой части уравнения.

Если уравнение имеет два различных корня х₁ и х₂, то его левая часть раскладывается на множители следующим образом:

ах²+bх+с = а(х — х₁)(х — х₂).

Если уравнение имеет единственный корень х₀, то его левая часть является полным квадратом:

ах²+bх+с = а(х – х₀)².

Уравнение вида ах²+bх+с=0 при а = 0 приводится к уравнению степени не выше первой. То есть случай а = 0 при необходимости следует рассматривать отдельно.

2.Примеры решения уравнений с параметром.

Пример№1

Найти все значения параметра а, при которых уравнение

ах² -(2а+6)х + 3а+3=0 имеет единственный корень.

Решение:

1. а=о, х= . х= 0,5

2. а≠0

Д= (2а+6)² -4а(3а+3)= -4(2а² -3а-9)=0

2а

2 -3а-9=0

а₁₌ 3 , а₂= -1,5

Ответ: 0; 3; -1,5

Пример №2

Найти значения параметра а, при котором уравнение

(а-2)х² +(3а+1)х + 2а -7 =0 имеет один корень х>1.

Рассмотрим квадратичную функцию у= ах²+ вх+с

α — число

Д<0

Д= 0

Д>0

α

α

f(α)

α

1. х_в<α

2. х_в = _α

3. х_{в > α}

1. х_в<α

2. х_в = _α

3) х_{в > α}

3. х_в<α

4. х_в = _α

3) х_{в > α}

х_в<α

+

?

—

х_{в > α}

+

Решение:

Если Д<0, то корней нет.

Если Д=0, то не более одного корня.

Если Д>0 ,то не более двух корней.

1. а=2 , 7х-3 =0 , х= 3/7 , 3/7<1 не подходит по условию.

2. а≠2

1

1

Х_в > 1

Д= а² +50а- 55= 0

а= -25 ± не подходит по условию, т.к.

х_в = >1 , <0, 3/5<х<2

(а-2)f(1)<0

(а-2)(а-2+3а+1+2а-7)<0

(а-2)(6а-8)<0 + 4/3 — 2 +

4/3<а<2

Рассмотрим частный случай, когда парабола проходит через единицу

1

f(1)=0 , а= 4/3 , -2х² +15х -13=0, х₁ =1, х₂ = 6,5

Ответ : 4/3≤ а<2

Пример №3 ?

Рассмотрим функцию f(х)= ах²

+вх+с , а≠0 , α< х<β

α β

α β

1. х_в<α

2. α<х_в<β

3. Х_в>β

4

1 2 3 5

6

α β

Особо рассмотреть случаи f(α)=0 и f(β)=0

3.Заключение.

Задачи с параметрами очень разнообразны и охватывают практически весь школьный курс. Нам очень многое еще придется изучить, но эта работа была очень полезной для нас. Я получила практические навыки решения квадратных уравнений с параметрами. Я поднялась на одну ступеньку выше в своем понимании методов решения математических задач.

Решение задач с параметрами развивает логическое мышление, учит думать нестандартно, анализировать, сравнивать, обобщать.

В моих планах изучение задач связанных с расположением корней квадратного трехчлена, решение квадратных неравенств с параметрами.

Я надеюсь, что навыки решений задач с параметрами помогут мне в подготовке к ЕГЭ по математики.

Онлайн урок квадратные уравнения с параметром

Давай повторим определения, которые ты уже знаешь и которые мы будем использовать на нашем уроке.

 

 

 

 

 

 

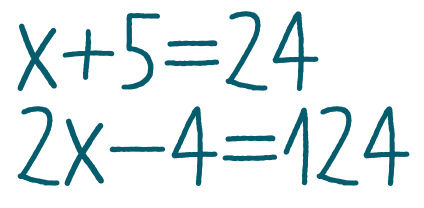
Уравнение — это равенство, содержащее одну или несколько переменных, значение которых нужно найти.

 

 

 

 

 

 

Значение переменной, которое обращает уравнение в истинное равенство, называется корнем уравнения.

 

 

 

 

 

 

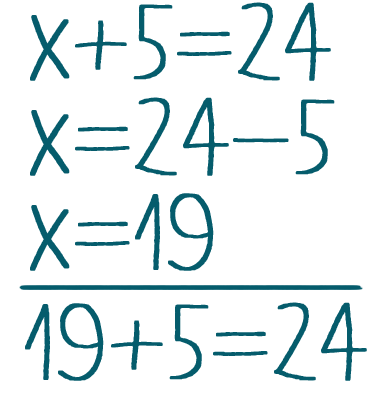
Решить уравнение — это значит найти все его корни либо доказать, что их нет.

 

 

 

 

Теперь установи соответствие между картинками и определениями, которые мы только что повторили.

 

 

 

 

 

x² ≠ ±2x ≠ ± √2x ≠ √2x ≠ — √2

 

 

 

 

 

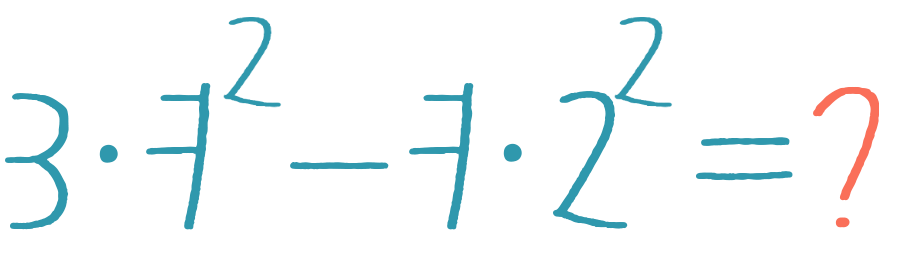
= 7(21 — 14) = 7 · 7 = 49= 7(3 — 2) = 7 · 1 = 7= 7²(3 — 4) = -49= 7(21 — 4) = 7 · 17 = 119

 

 

 

 

 

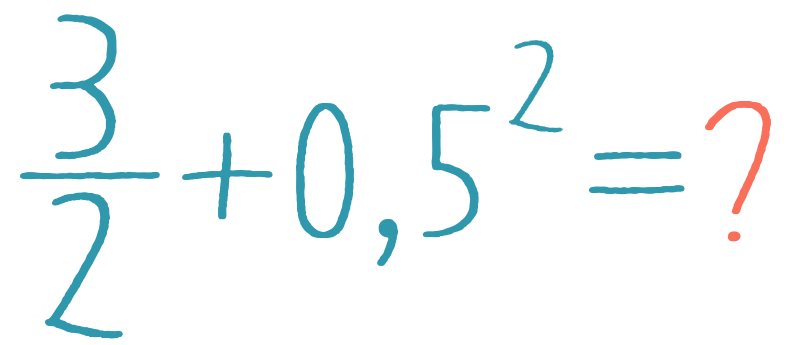
1,5 + 0,25 = 1,751,5 + 2,5 = 40,5 + 2,5 = 30,15 + 0,25 = 0,4

 

 

 

 

Сегодня на уроке ты:

 

 

1. Повторишь, как решать квадратные уравнения.

2. Повторишь теорему Виета.

3. Решишь 5 базовых  задач.

4. Решишь 4 сложные задачи с параметрами.

Квадратные уравнения с параметрами(занятие№2). 8класс.

Квадратные уравнения с параметрами (занятие№2). 8 класс.

Методические рекомендации.

Солодовникова Галина Николаевна, учитель математики

МБОУ Школа №16 г. Саров, Нижегородская область.

«Задачи с параметрами незаменимое средство для тренировки логического мышления».

Данный материал можно использовать на уроках алгебры в 8-ом классе общеобразовательной школы, на дополнительных занятиях по математике, а так же для самостоятельного ознакомления с данной темой учениками 8-ого класса.

Уравнение вида m+pх+g=0, где х-неизвестное, m,p,g-выражения, зависящие только от параметров, и m≠0, называется квадратным уравнением относительно х.

Занятие №2.

На первом занятии были рассмотрены и решены уравнения:

1) = а. Ответ. При а > 0 х = ± ; при а=0 х=0; при а < 0 корней нет.

2) 4- а = 0. Ответ. При а > 0 х= ±; при а= 0 х=0; если а <0 корней нет.

3)+а∙х=0. Ответ. х=0; х= — а.

4)+а∙х-2=0. Ответ. х= .

5)+ 3∙х — а=0. Ответ. При а > — х=; при а= х= — ;

при а < — корней нет.

6) + a∙x + 9 = 0. Ответ. При а < — 6 , а>6 х= ; при а= ± 6 х = ;

при – 6 < а < 6 корней нет.

На 2-ом занятии рассмотрим уравнения, содержащие параметр в коэффициенте перед .

1.Найдите корни уравнения в зависимости от параметра m:

m+3m∙x-(m+2) =0 (1).

Решение.

Уравнение имеет смысл при любых действительных значениях параметра m, но является квадратным только при m≠0.Найдем корни уравнения в зависимости от параметра m.

1. При m=0 уравнение примет вид: 0∙+3∙0∙x-2 =0, 0∙х=2 ,корней нет.

2.При m≠0 уравнение является квадратным.

Наличие корней и сами корни зависят от значения дискриминанта.

Найдем дискриминант данного уравнения.

D=- 4∙m∙ (- (m+2)) =9 +4 + 8m =13 + 8m.

1)найдем значения m, при которых D=0, решив уравнение 13+ 8m =0,

m ∙(13m +8) =0,

m=0 или m= — .

Итак:

при m=0 корней нет; при m= — уравнение имеет один корень (или два одинаковых)

х= = — .

2)найдем значения m, при которых Dнеравенство 13+8m > 0,

m ∙(13m +8) >0,

(*) или (**)

Решение системы(*) m>0,

Решение системы(**) m< -.

(Если ученики умеют решать неравенства методом интервалов, то предпочтение нужно отдать именно этому методу).

Итак: при m< — или m> 0 D >0,а значит уравнение (1) имеет два различных корня

х= .

3) найдем значения m, при которых Dнеравенство 13+8m < 0,

m ∙(13m +8) <0

(*) или (**)

Системы (*) решений не имеет,

Решение системы(**) — < m <0.

Итак: при — < m < 0 D< 0 , уравнение (1) корней не имеет.

Ответ. При — < m ≤0 корней нет;

при m=- х= — ;

при m>0, m < х= .

2.Решите уравнение в зависимости от параметра к.

(к+5)∙ — 2∙(к+1)x + 2к-4 =0 (2).

Решение.

Уравнение имеет смысл при любых действительных значениях параметра к, но является квадратным только при к+5≠0. Найдем корни уравнения в зависимости от параметра к.

1. При к+5=0, т.е. к= — 5 уравнение примет вид: 0∙-2∙(- 5 + 1)∙x+2∙(-5)-4 =0,

8х- 14 =0 ,

получили линейное уравнение, корнем которого является число .

2.При к≠ – 5 уравнение(2) является квадратным.

Наличие корней и сами корни зависят от значения дискриминанта.

Найдем дискриминант данного уравнения.

D=- 4∙ (к+5) ∙ (2к-4) =4+8к+4-4∙ (2-4к+10к-20) =4+8к+4-4∙ (2+6к-20) =

=4+8к+4-8-24к+80=-4-16к+84.

1)найдем значения к, при которых D=0, решив уравнение -4-16к+84=0.

Разделив обе части уравнения на (- 4), получим уравнение +4к-21=0, его корни к= — 7, к=3.

Итак:

при к=-7, к=3 уравнение(2) имеет один корень (или два одинаковых)

х= = .

2)найдем значения к, при которых Dнеравенство -4-16 к+84> 0.

Разделив обе части неравенства на (-4),получим неравенство +4к-21<0.

Разложив на множители левую часть, получим неравенство (к+7)∙(к-3)<0.

Решив это неравенство либо с помощью совокупности двух систем, либо методом интервалов, найдем, что при -7< к <3 D>0 и уравнение (2) имеет два различных корня

Х=

Вынесем за знак корня множитель 2 и сократим дробь.

Получим х = .

3)при к<-7, при к>3 D<0, уравнение (2) не имеет корней.

Ответ. При к=-5 х= ;

при к<-7; к>3 корней нет;

при к=-7 , к=3 х= ;

при -7< к <3 ,к≠-5, х=.

Задания для самостоятельной работы.

1)Решите уравнение отностительно х.

(к-5)∙ +3к∙x –(к-5) =0 . Ответ. При к=5 х=0; при к≠5 х=

2) найдите все значения а, при которых уравнение (2а -1)∙+2х-1=0

имеет два действительных различных корня. Ответ. При 0 <а < ; а> .

3) найдите все значения а, при которых уравнение (3а-5)∙-(6а-2)х+3а-2=0

Не имеет действительных корней. Ответ. При а< 0.6.

На третьем занятии можно рассмотреть решение уравнений, содержащих параметр в знаменателе дроби и сводящихся к квадратным.

Использована литература:

1)Задачи с параметрами. Г.А.Ястребинецкий. Москва «Просвещение» 1986.

2)Сборник задач по алгебре 8-9.М.Л.Галицкий, А.М.Гольдман, Л.И.Звавич. Москва «Просвещение» 1994.

Задачи с параметром в школьном курсе математики 8-го гласса

Задачи с параметрами играют важную роль в формировании логического мышления и математической культуры учащихся. Они имеют принципиально исследовательский характер, и с этим связаны как методическое значение таких задач, так и трудности выработки навыков их решения.

Важность понятия параметра связана с тем, что, как правило, именно в терминах параметров происходит описание свойств математических объектов: функций, уравнений, неравенств. Под параметрами мы понимаем входящие в алгебраические выражения величины, численные значения которых явно не заданы, однако считаются принадлежащими определенным числовым множествам. Учащимся 8 класса известны линейная функция и ее частный случай – прямая пропорциональность:

(параметры и определяют расположение графика функции на плоскости и точки пересечения с осями), а также линейное и квадратное уравнение и соответствующие неравенства:

(параметры , и определяют, вообще говоря, не только существование и количество корней, но и степень уравнения).

Решение задач с параметрами требует исследования, даже если это слово не упомянуто в формулировке задачи. Недостаточно механического применения формул, необходимо понимание закономерностей, навыки анализа конкретного случая на основе известных общих свойств объекта, системность и последовательность в решении, умение объединить рассматриваемые частные случаи в единый результат. Этим обусловлены трудности, возникающие у учащихся при решении таких задач, и этим же объясняется справедливое включение задач с параметрами в экзаменационные работы в школе и на вступительных экзаменах в вузы.

Таким образом, очевидна необходимость отработки приемов решения различных задач с параметрами. Ниже приводится система упражнений по решению и исследованию квадратных уравнений и неравенств с одним параметром в курсе 8 класса.

 Квадратные уравнения с параметром

1. При каких значениях уравнение имеет единственное решение?

Решение.

Ошибочно считать данное уравнение квадратным. На самом деле это уравнение степени не выше второй. Исходя из этого соображения, рассмотрим следующие случаи:

а) . При этом уравнение принимает вид , откуда , т.е. решение единственно.

б) , тогда – квадратное уравнение, дискриминант . Для того, чтобы уравнение имело единственное решение, нужно, чтобы , откуда .

Ответ: или .

2. При каких значениях уравнение имеет единственное решение?

Решение.

1) При исходное уравнение не имеет решения.

2) , тогда данное уравнение является квадратным и принимает вид . Искомые значения параметра – это корни дискриминанта, который обращается в нуль при .

Ответ: .

3. При каких значениях уравнение имеет более одного корня?

Решение.

1) При уравнение имеет единственный корень .

2) При исходное уравнение, будучи квадратным, имеет два корня, если его дискриминант положителен, т.е. . Решая неравенство, получаем . Из этого промежутка следует исключить число нуль.

Ответ: или .

4. При каких значениях уравнения и равносильны?

Решение.

1) При : имеет два различных корня, имеет один корень. Равносильности нет.

2) При решения уравнений совпадают.

3) При ни первое, ни второе уравнения решений не имеют. Как известно, такие уравнения считаются равносильными.

Ответ: .

5. При каких значениях уравнения и равносильны?

6. При каких значениях параметра уравнение имеет одно решение?

7. При каких значениях ровно один из корней уравнения равен нулю?

8. При каких значениях корни уравнения равны по модулю, но противоположны по знаку:

9. При каких значениях оба корня уравнения равны нулю?

а) ; б)

10. Решите уравнения:

I.

II.

III.

IV.

V.

11. При каких значениях произведение корней квадратного уравнения равно нулю?

12. При каких значениях сумма корней квадратного уравнения равна нулю?

13. В уравнении сумма квадратов корней равна 16. Найти .

14. В уравнении квадрат разности корней равен 16. Найти .

15. При каких значениях сумма корней уравнения равна сумме квадратов корней?

16. При каком значении параметра сумма квадратов корней уравнения наименьшая?

17. При каком значении параметра сумма квадратов корней уравнения наибольшая?

18. При каких значениях параметра один из корней квадратного уравнения в два раза больше другого?

19. Известно, что корни уравнения на 1 меньше корней уравнения . Найдите и корни каждого из уравнений.

20. Найдите наименьшее целое значение , при котором уравнение имеет два различных действительных корня.

21. При каких значениях уравнение имеет более двух корней?

22. При каких значениях уравнение имеет хотя бы один общий корень с уравнением ?

23. При каком соотношении между , , уравнение имеет один корень? Может ли данное уравнение иметь два действительных различных корня?

24. При каком значении параметра уравнение имеет три корня?

 Неравенства с параметром

1. Решите неравенство, где – параметр:

2. Найдите все значения , при которых квадратное уравнение имеет два действительных различных корня:

3. Найдите все значения , при которых квадратное уравнение не имеет действительных корней:

4. При каких значениях уравнение имеет положительное решение?

5. При каких значениях уравнение имеет отрицательное решение?

6. При каких значениях уравнение имеет одно положительное решение?

7. При каких значениях уравнение имеет решения, удовлетворяющее условию ?

8. При каких значениях система неравенств имеет хотя бы одно решение:

9. При каких значениях система неравенств не имеет решений:

10. При каких значениях система неравенств имеет хотя бы одно решение?

11. При каких значениях уравнение имеет корни разных знаков?

12. При каких значениях уравнение имеет корни и такие, что ?

13. Найдите все значения , при которых корни уравнения меньше, чем 1.

14. Найдите все значения , при которых один из корней уравнения меньше 1, а другой больше 1.

15. При каких значениях система уравнений

имеет решение ?

16. При каких значениях система уравнений

имеет решение ?

17. Для каждого решите неравенство:

I.

II.

III.

IV.

Методическая разработка по алгебре (9 класс): Урок «Решение квадратных уравнений с параметрами»

Класс:9 

Тема урока:  Решение квадратных уравнений с параметрами.

Тип урока:  Урок комплексного использования знаний

Цель урока:  выработка умений самостоятельного применения знаний в новых условиях.

 Задачи урока:

• Систематизация знаний по решению квадратных уравнений и развитие умений применить их при решении уравнений с параметрами.
• Развитие логического мышления, умения самостоятельно работать, навыков самоконтроля,  интереса учащихся к предмету,  навыков индивидуальной, групповой и коллективной работы.
• Воспитание отзывчивости, трудолюбия, аккуратности.

Форма работы:  групповая, фронтальная

Ход урока:

I. Организационный момент (3 мин)

Дидактическая задача этапа	Содержание деятельности учителя	Условия получения положительного результата
Организация начала урока. Подготовка учащихся к работе на уроке	Приветствие, выявление отсутствующих; проверка готовности учащихся к уроку; готовность наглядных пособий. Раскрытие общей цели урока	Кратковременность оргмомента; быстрое включение всех учащихся в деловой ритм; полная готовность класса и оборудования к уроку

II. Актуализация ЗУН (10 мин)

Дидактическая задача этапа	Содержание деятельности учителя	Условия получения положительного результата
Подготовка к активной УПД на основном этапе урока. Подготовка учащихся к тому виду учебно-познавательной деятельности, который будет доминировать на основном этапе урока. Актуализация опорных знаний и умений, формирование познавательных мотивов	Постановка триединой дидактической цели урока; организация действий учащихся по ее принятию	Умение определять и ставить триединые дидактические задачи урока, направленные на решение поставленной цели; владение приемами организации учащихся на деятельность по принятию задач урока.

В древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: “Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи”. Задачи часто обрекали в стихотворную форму. Попробуйте и вы решить древнеиндийскую задачу:

Обезьянок резвых стая,
Всласть поевши, развлекалась.
Их в квадрате часть восьмая
На поляне забавлялась,
А двенадцать по лианам
Стали прыгать, повисая…
Сколько ж было обезьянок,
Ты скажи мне в этой стае?

Решение:

(x/8)2+12=x

x2-64х=-768

x1=16, x2=48

При решении этой задачи вы составили и решили квадратное уравнение.

Ответьте, пожалуйста,  на следующие вопросы:

— Как называется выражение

— Как называются числа ?

— Какие уравнения называются квадратными уравнениями?

-Что называют корнем уравнения? Что значит решить уравнение?

-Полными квадратными уравнениями? Неполными?

— Приведенными  квадратными уравнениями? Неприведенными?

“Главная” функция в школьном курсе алгебры – это квадратный трехчлен, он постоянно всплывает в разных разделах программы. Постараемся поэтому познакомиться с ним поближе и подружиться.

Функция  называется квадратичной функцией. Как вы знаете, график этой функции – парабола.

Координаты вершины параболы  , где ,                    

Рассмотрим расположение графика функции в зависимости от старшего коэффициента  и знака дискриминанта

IV. Изучение нового материала.(15 мин)

Дидактическая задача этапа	Содержание деятельности учителя	Условия получения положительного результата
Усвоение новых знаний. Сформировать у учащихся конкретные представления об изучаемых фактах, явлениях, процессах, их сущности, связи; выделить главное, провести систематизацию  вместе с учащимися; на основе знаний выработать общую схему решения уравнений с параметрами	Самостоятельная работа учащихся; восприятие учащимися нового материала, его осмысление, обобщение, осознание, систематизация, конкретизация	Опора на жизненный опыт учащихся; индивидуальный подход по дозе помощи; организация учащихся на оперирование успеваемым содержанием
Первичная проверка понимания учащимися нового учебного материала. Установить осознанность усвоения учащимися нового материала; усвоение связей и отношений между фактами, явлениями, процессами	Проверка учителем того, поняли ли школьники, что является основным содержанием урока, которое нужно усвоить; проверка полноты и осознанного усвоения новых знаний	Использование системы заданий, требующих мыслительной и практической активности учащихся; выявление пробелов в знаниях и успехов учащихся в ходе проверки

Мы повторили и систематизировали знания о решении квадратных уравнений,  о квадратичной функции. А сейчас мы изучим новый тип квадратного уравнения- квадратное уравнение с параметрами. Что же это такое? Начнем  с того, что дадим определение параметра.

Параметр в уравнении или неравенстве — некоторая плавающая величина, т.е. число, принимающая различные значения.

Уравнение  с параметрами — математическое уравнение внешний вид и решение которого зависит от значений одного или нескольких параметров.

Решить уравнение с параметром означает, что нужно найти все системы значений параметров, при которых выполняется то или иное требование.

Мы только начинаем изучать квадратные уравнения с параметрами. Типов этих уравнений великое множество. Сегодня мы рассмотрим один из типов таких уравнений и научимся их решать.

При каких условиях корни уравнения         меньше числа М?

Работа по презентации

V. Работа в группах. (10 минут)

Дидактическая задача этапа	Содержание деятельности учителя	Условия получения положительного результата
Контроль и самоконтроль знаний Глубокая всесторонняя проверка знаний, умений и навыков учащихся; стимулирование учащихся на самообразование.	Проверка полноты, осознанности, действительности и прочности знаний, умений и навыков; проверка сформированности общих учебных умений, установление положительных и отрицательных сторон в знаниях; рекомендации учащимся по ликвидации пробелов путем самостоятельной работы или с помощью товарищей	Подготовка дополнительных вопросов для проверки осознанности и действительности знаний; использование нестандартных ситуаций в применении проверяемых знаний (Использование авторской программы).

1. Используя методику “мозговой штурм” учащиеся в малых группах с помощью учителя решают уравнения

 1 группа:  2 группа:  3 группа 

VI. Подведение итогов.(2 мин)

Дидактическая задача этапа	Содержание деятельности учителя	Условия получения положительного результата
Подведение итогов урока. Анализ успешности овладения знаниями и способами деятельности; показать типичные недостатки в знаниях, умениях, навыках	Дать общую характеристику класса, показать успешность овладения содержанием урока; вскрыть недостатки, показать пути их преодоления	Умение быстро схватывать типичное в успешности усвоения и недостатков, умение учесть реальные учебные возможности

 Учитель: “Все знания, полученные на нашем уроке, вам будут необходимы в дальнейшем. Я надеюсь, что вы не утратили интереса, а напротив будете стремиться к знаниям более глубоким и не только на уроках математики, но и на других уроках, чтобы войти во взрослую жизнь грамотными и активными”

2. Объявление оценок за работу на уроке

VII. Домашнее задание:  

Найти при каких условиях корни квадратного уравнения больше некоторого числа М.

Разработка урока по теме «Решение квадратных уравнений с параметрами»

Тема: Решение квадратных уравнений с параметрами.

Цели урока:

образовательные:

• систематизировать знания учащихся по решению квадратных уравнений;
• углубить знания учащихся по данной теме, рассмотреть решение квадратных уравнений с параметрами;

развивающие:

• развивать умения учащихся анализировать, сопоставлять, исследовать искомые решения

Тип урока: изучение нового материала.

Ход урока.

1. Орг. момент.

2. Актуализация опорных знаний учащихся.

– Решить уравнения:

а) а х = 5

Ответ: 1) если а = 0, то решений нет;

2) если а 0, то

б) х² = а

Ответ: 1) если а = 0, то х = 0;

2) если а > 0, то ;

3) если а < 0, то решений нет.

в) При каких значениях параметра p заданное уравнение является неполным квадратным уравнением?

Ответ: 1) р – 3 = 0; р = 3; ;

2) р = 0; .

г) При каких значениях параметра р уравнение является приведенным квадратным уравнением?

Ответ: 2 р – 5 = 1; р = 3; .

3. Новый материал

– При каких значениях параметра р уравнение имеет корень, равный 6? (р = -4)

– При каких значениях параметра р уравнение имеет один корень?

– От чего зависит количество решений квадратного уравнения?

– № 820 (б)

Решение: D =0

D =

– № 839 (а) Решить уравнение с параметром р

.

Решение: D = .

; ;

.

Ответ: .

– № 840 (а, б) Решить уравнение с параметром р

а) .

Решение: D = .

; ;

.

Ответ: .

б)

Решение: – Если р = 0, то .

– Если р 0, то D =

1) D > 0 – 2 корня

2) D = 0 – 1 корень

р = 4

;

3) D < 0 – корней нет

Ответ: при р = 4 ,

при – корней нет,

при

Вывод:

Решить уравнение с параметрами, это значит:

• исследовать, при каких значениях параметров уравнение имеет корни и сколько их при различных значениях параметров;
• найти все выражения для корней и указать для каждого из них те значения параметров, при которых это выражение действительно определяет корень уравнения.

4. Работа в парах

– № 840 (б)

Решение: 1) р = 0

х = .

2) р 0

а) если D > 0 – 2корня

; ;

б) если D < 0 – корней нет.

р > 4 корней нет

в) D = 0 – 1 корень

р = 4

Ответ: при р = 0 х = ;

при р = 4 ;

при р > 4 корней нет

при

5. Домашнее задание

– № 840 (в), № 841 (а)

6. Итог урока

Оценивание работы учащихся за урок

Литература:

1. А.Г. Мордкович “Алгебра 8”. Москва, Мнемозина, 2006
2. Н.Я. Виленкин, Г.С. Сурвилло и др. “Алгебра-8” – учеб. пособ. для школ и классов с углубленным изучением матем. Новосибирск, ВО “Наука”-1992
3. “Изучение сложных тем курса алгебры в средней школе” под ред. Фальке Л.Я. Москва, Илекса, Ставрополь, Сервис школа, 2002
4. В.П. Моденов “Задачи с параметрами” (координатно-параметрический метод). Москва, “Экзамен”, 2006